Anomaly-Aware Graph-Based Semi-Supervised Deep Support Vector Data Description for Anomaly Detection

Abstract

Anomaly detection in safety-critical systems often operates under severe label constraints, where only a small subset of normal and anomalous samples can be reliably annotated, while large unlabeled data streams are contaminated and high-dimensional. Deep one-class methods, such as deep support vector data description (DeepSVDD) and deep semi-supervised anomaly detection (DeepSAD), address this setting. However, they treat samples largely in isolation and do not explicitly leverage the manifold structure of unlabeled data, which can limit robustness and interpretability. This paper proposes Anomaly-Aware Graph-based Semi-Supervised Deep Support Vector Data Description (AAG-DSVDD), a boundary-focused deep one-class approach that couples a DeepSAD-style hypersphere with a label-aware latent k-nearest neighbor (k-NN) graph. The method combines a soft-boundary enclosure for labeled normals, a margin-based push-out for labeled anomalies, an unlabeled center-pull, and a k-NN graph regularizer on the squared distances to the center. The resulting graph term propagates information from scarce labels along the latent manifold, aligns anomaly scores of neighboring samples, and supports sample-level interpretability through graph neighborhoods, while test-time scoring remains a single distance-to-center computation. On a controlled two-dimensional synthetic dataset, AAG-DSVDD achieves a mean F1-score of $0.88\pm 0.02$ across ten random splits, improving on the strongest baseline by about $0.12$ absolute F1. On three public benchmark datasets (Thyroid, Arrhythmia, and Heart), AAG-DSVDD attains the highest F1 on all datasets with F1-scores of $0.719$, $0.675$, and $0.8$, respectively, compared to all baselines. In a multi-sensor fire monitoring case study, AAG-DSVDD reduces the average absolute error in fire starting time to approximately 473 s (about 30% improvement over DeepSAD) while keeping the average pre-fire false-alarm rate below $1\%$ and avoiding persistent pre-fire alarms. These results indicate that graph-regularized deep one-class boundaries offer an effective and interpretable framework for semi-supervised anomaly detection under realistic label budgets.

1. Introduction

Anomaly detection is a core problem in machine learning with applications in industrial fault detection, ECG monitoring, intrusion detection, and early fire detection in complex non-fire environments [1,2,3,4,5]. Its goal is to learn a compact description of normal operating behavior and flag deviations as anomalies under severe class imbalance, where anomalies are rare and structurally diverse. Unlike standard supervised classification, anomaly detection is typically constrained by scarce and costly labels [6,7]. Confirming normal behavior may require expert review, additional quality-control tests, or prolonged observation, while obtaining labeled anomalies often entails controlled stress tests or hazardous experiments [8,9,10]. These limitations are especially pronounced in safety-critical fire monitoring, where realistic multi-sensor fire scenarios must be run in specialized facilities, yielding only a modest number of labeled fire and non-fire sequences compared to the continuous stream of unlabeled sensor data from routine operation [5].

Classical work on one-class classification framed anomaly detection as the problem of estimating the support of normal data. Support vector data description (SVDD) represents the normal class by enclosing the mapped training examples within a minimum-radius hypersphere in feature space, classifying points that fall outside this sphere as anomalies [11]. In contrast, the one-class support vector machine (OC-SVM) learns a maximum-margin hyperplane that separates the mapped data from the origin, thereby implicitly characterizing the region of normal behavior [12]. Both approaches yield compact decision regions with a clear geometric interpretation, but they are usually trained on labeled normal samples and do not leverage the often abundant pool of unlabeled observations present in many practical applications. When expert-validated normal labels are limited and expensive to obtain, such supervised one-class methods can suffer from poor sample efficiency and instability.

The emergence of deep learning has driven substantial progress in anomaly detection. Deep one-class classification (DeepSVDD) builds on the SVDD framework by integrating a deep encoder that projects the data into a latent space, which is then bounded by a hypersphere [13]. Expanding on this concept, several deep SVDD extensions have been developed, including autoencoder-based approaches, such as DASVDD [14], structure-preserving mappings that better retain neighborhood relationships [15], variational extensions leveraging VAE encoders [16], and contrastive learning objectives that enhance latent space representation and sharpen the decision boundary [17]. Deep semi-supervised anomaly detection (DeepSAD) extends this approach by leveraging a limited number of labeled anomalous samples to guide the deep one-class decision boundary when large amounts of unlabeled data are available [8]. In parallel, autoencoders and their extensions have been extensively employed to learn compact latent embeddings and reconstruction-based anomaly scores in industrial and temporal data scenarios [18,19], whereas self-supervised anomaly detection utilizes contrastive learning and related pretext objectives to improve representations when labeled data are scarce [20,21]. Nevertheless, a large proportion of deep anomaly detection approaches still rely on surrogate training objectives—such as reconstruction losses or generic self-supervised losses—that are only indirectly aligned with the final decision boundary, and typically incorporate unlabeled data through proxy tasks instead of imposing task-specific constraints directly on the boundary learner [22,23,24]. In addition, the resulting decision mechanisms are often difficult to interpret or connect to the underlying domain structure, which is a crucial limitation in safety-critical settings [25,26,27].

In safety-critical fire-monitoring applications, there has been a growing reliance on machine learning methods applied to multi-sensor data streams obtained from temperature, smoke, gas, and particulate sensors. Gas-sensor array platforms employing multivariate calibration in combination with pattern-recognition algorithms have shown the capability to identify early-stage fires while compensating for sensor drift [28]. In indoor settings, researchers have investigated deep multi-sensor fusion by employing lightweight convolutional neural networks applied to fused temperature, smoke, and carbon monoxide (CO) signals [29]. Concurrently, transfer-learning frameworks have been introduced to adjust models originally trained in small-scale environments for application in larger rooms equipped with distributed multi-sensor nodes, thereby enhancing early detection capabilities across diverse deployment scenarios [30]. Complementary approaches based on signal processing and one-class modeling include a wavelet-based multi-modeling framework that learns separate detectors tailored to specific fire scenarios in multi-sensor settings [5]. In related work, a multi-class SVDD equipped with a dynamic time warping kernel has been proposed to distinguish between several fire and non-fire classes in sensor networks [4]. However, these sensor-driven frameworks are typically trained in a fully supervised regime at the window level, under the assumption that every time window is labeled as fire or non-fire. In practical deployments, obtaining such labels requires expensive and hazardous staged experiments in dedicated facilities that yield only a limited set of observations. Meanwhile, deployed multi-sensor systems continuously generate large volumes of unlabeled time-series data during normal operation.

Graph-based semi-supervised learning exploits unlabeled data by building a similarity graph and enforcing smoothness of labels or scores through Laplacian penalties on neighboring nodes [31,32]. In anomaly detection, such graph-based methods have been applied at node, edge, and graph levels across diverse domains [33,34]. Within SVDD, graph-based semi-supervised SVDD augments the objective with a k-NN graph Laplacian to leverage the structure of unlabeled data [35], while manifold-regularized SVDD further enforces similar scores for neighboring samples to improve robustness to noisy labels [36]. Related CNN–SVDD architectures combine convolutional feature learning with SVDD and graph regularization for industrial condition monitoring, such as wind-turbine health assessment [37].

Despite these advancements, boundary-focused deep anomaly detection for high-dimensional, multi-channel time series remains limited under realistic labeling constraints. DeepSAD introduces deep representations and, in principle, can use a small labeled set [8]. In its standard form, the method incorporates unlabeled data only through point-wise losses on individual samples. It does not include interaction terms that capture relationships among unlabeled instances in latent space. As a result, the manifold structure of unlabeled data is not directly reflected in the boundary-focused objective. This limitation restricts how effectively information from scarce labels can propagate along the geometry of the unlabeled data. DeepSAD-based methods have also been rarely studied in safety-critical multi-sensor monitoring, where labels are costly and hazardous to obtain, unlabeled streams are abundant, and both missed detections and false alarms carry substantial operational and safety risks [4,5,28,29,30]. These settings demand extensions of DeepSAD with several properties [25]. These gaps motivate extensions of DeepSAD that (i) preserve a boundary-focused one-class formulation while explicitly modeling manifold interactions among unlabeled samples, (ii) directly link anomaly scores of neighboring instances via the latent-space geometry, (iii) are tailored to semi-supervised label-budget constraints in multi-channel sensor monitoring, and (iv) provide sample-level interpretability by associating unlabeled samples with nearby labeled normal and anomalous patterns [25].

Motivated by these challenges, this paper introduces Anomaly-Aware Graph-based Semi-Supervised Deep SVDD (AAG-DSVDD), a boundary-focused deep one-class method for high-dimensional and multi-channel time series under realistic label budgets. Specifically:

1.

We introduce AAG-DSVDD, a semi-supervised, center-based objective that maintains the DeepSVDD-style hypersphere formulation while explicitly modeling manifold relationships through a label-aware k-NN graph on latent representations. Unlabeled samples preferentially connect to reliable labeled neighbors, and a graph regularizer on their squared distances to the center couples their anomaly scores. This design propagates information from the limited labeled set along the manifold structure of the unlabeled data. The resulting graph-regularized latent representation also supports sample-level interpretability, since anomaly scores for unlabeled samples can be inspected, together with their nearest labeled neighbors in latent space, and the graph regularizer encourages nearby points with strong graph connections to attain similar anomaly scores.

2.

We evaluate AAG-DSVDD on a controlled synthetic dataset and on three public benchmark datasets (Thyroid, Heart, and Arrhythmia) under semi-supervised label-budget constraints. On these benchmarks, we compare against four representative one-class baselines: OC-SVM, SVDD with an RBF kernel (SVDD-RBF), DeepSVDD, and DeepSAD. AAG-DSVDD consistently achieves higher F1-scores than these baselines, indicating more accurate separation between normal and anomalous samples.

3.

We further assess AAG-DSVDD on a real multi-sensor fire-monitoring case study under comparable semi-supervised label-budget constraints, using the same set of baselines. In this application, the experimental results demonstrate faster fire-event detection and competitive pre-fire false-alarm rates compared to these baselines.

4.

To the best of our knowledge, this constitutes the first AAG-DSVDD application to semi-supervised multi-sensor fire detection.

The remainder of this paper is organized as follows: Section 2 introduces the problem setting and DeepSAD. Section 3 presents the proposed AAG-DSVDD approach. Section 4 describes the experimental setup and results on a controlled synthetic dataset and three public benchmark datasets and presents an ablation study of AAG-DSVDD. Section 5 reports the multi-sensor fire-monitoring case study under semi-supervised label-budget constraints. Finally, Section 6 concludes the paper and outlines directions for future work.

2. Background and Problem Formulation

In this section, we formalize the semi-supervised anomaly detection setting considered in this work, introduce the notation used throughout the paper, and present the DeepSAD objective that serves as our baseline. We then discuss the limitations of DeepSAD in leveraging the geometry of unlabeled data and motivate the need for graph-based regularization.

2.1. Semi-Supervised Anomaly Detection Setting and Notation

Let $\mathcal{X}={\mathbb{R}}^m$ denote the input space and $\mathcal{Z}={\mathbb{R}}^p$ the latent space induced by a parametric encoder

$$\varphi (·;W):\mathcal{X}\to \mathcal{Z},$$

where $W=\{W_1,\dots ,W_L\}$ collects the weight matrices of all layers in the encoder network. For an input vector ${\mathbf{x}}_i\in \mathcal{X}$, we write

$${\mathbf{z}}_i=\varphi ({\mathbf{x}}_i;W)\in \mathcal{Z}$$

for its latent representation.

We consider a semi-supervised one-class anomaly detection setting, in which only a small subset of samples is labeled, while the remaining majority is unlabeled and may contain both normal and anomalous instances. Formally, the training data consist of three subsets: a set of labeled normal samples:

$${\mathcal{D}}_{\ell }^{+}=\{({\mathbf{x}}_i,y_i):y_i=+1\};$$

a set of labeled anomalous samples:

$${\mathcal{D}}_{\ell }^{-}=\{({\mathbf{x}}_i,y_i):y_i=-1\};$$

and a set of unlabeled samples:

$${\mathcal{D}}_u=\{{\mathbf{x}}_i:y_i=0\}.$$

We use the convention $y_i=+1$ for labeled normal samples, $y_i=-1$ for labeled anomalous samples, and $y_i=0$ for unlabeled samples. We denote the numbers of observations by $n_{+}$, $n_{-}$, and $n_u$ for ${\mathcal{D}}_{\ell }^{+}$, ${\mathcal{D}}_{\ell }^{-}$, and ${\mathcal{D}}_u$, respectively, and write $n=n_{+}+n_{-}+n_u$ for the total number of training observations.

The objective of one-class anomaly detection is to learn a decision function $f:\mathcal{X}\to \mathbb{R}$ that assigns an anomaly score $s_i=f\left({\mathbf{x}}_i\right)$ to each sample, where larger scores indicate stronger evidence of anomalous behavior. A threshold on $s_i$ then yields binary anomaly decisions. In center-based one-class models, the decision function is defined through distances to a learned center $\mathbf{c}\in \mathcal{Z}$. Specifically, for each sample ${\mathbf{x}}_i$, we define its latent representation ${\mathbf{z}}_i=\varphi ({\mathbf{x}}_i;W)$ and its squared Euclidean distance to the center

$$d_i^2={\parallel {\mathbf{z}}_i-\mathbf{c}\parallel }_2^2.$$

The scalar $d_i^2$ serves as the core anomaly score, optionally combined with a learned radius $R\ge 0$ to form a decision rule, such as “normal if $d_i^2\le R^2$” and “anomalous otherwise”.

In the semi-supervised setting considered here, the goal is to learn the encoder parameters W and the center vector $\mathbf{c}$ (and, if used, the radius R) from the labeled and unlabeled training data, such that labeled normals are mapped close to the center, labeled anomalies are mapped far from the center, and unlabeled points are taken into account in a way that is robust to possible contamination and that exploits their geometric structure in latent space.

2.2. Overview of DeepSAD

DeepSAD extends DeepSVDD to the semi-supervised setting by adding a label-dependent term for a small set of labeled examples while maintaining the same center-based hypersphere structure in latent space [8].

Using the notation from Section 2.1, we define the set of all labeled observations as ${\mathcal{D}}_{\ell }={\mathcal{D}}_{\ell }^{+}\cup {\mathcal{D}}_{\ell }^{-}$ and note that it contains $n_{+}+n_{-}$ samples, while ${\mathcal{D}}_u$ contains $n_u$ unlabeled samples, with $n=n_{+}+n_{-}+n_u$ in total. The DeepSAD loss can then be written in our notation as the following optimization problem over W:

$$\underset{W}{min}{\displaystyle \frac{1}{n}}\sum _{{\mathbf{x}}_i\in {\mathcal{D}}_u}\parallel \varphi ({\mathbf{x}}_i;W)-\mathbf{c}{\parallel }_2^2+{\displaystyle \frac{\eta }{n}}\sum _{({\mathbf{x}}_i,y_i)\in {\mathcal{D}}_{\ell }}{\left(\parallel \varphi ({\mathbf{x}}_i;W){-\mathbf{c}\parallel }_2^2\right)}^{y_i}+{\displaystyle \frac{\lambda }{2}}\sum _{\ell =1}^L\parallel W_{\ell }{\parallel }_F^2.$$

(1)

The first term in (1) is exactly the DeepSVDD loss applied to the unlabeled data, encouraging all unlabeled samples ${\mathbf{x}}_i\in {\mathcal{D}}_u$ to lie close to the center $\mathbf{c}$ in latent space. The second term is the semi-supervised extension: for labeled normals in ${\mathcal{D}}_{\ell }^{+}$ with $y_i=+1$, the exponent $y_i=1$ yields

$${\left(\parallel \varphi ({\mathbf{x}}_i;W){-\mathbf{c}\parallel }_2^2\right)}^{y_i}={\parallel \varphi ({\mathbf{x}}_i;W)-\mathbf{c}\parallel }_2^2,$$

which reduces to a standard squared-distance penalty and encourages these samples to be mapped close to the center $\mathbf{c}$. For labeled anomalies in ${\mathcal{D}}_{\ell }^{-}$ with $y_i=-1$, the exponent $y_i=-1$ yields

$${\left(\parallel \varphi ({\mathbf{x}}_i;W){-\mathbf{c}\parallel }_2^2\right)}^{y_i}={\parallel \varphi ({\mathbf{x}}_i;W)-\mathbf{c}\parallel }_2^{-2},$$

an inverse squared-distance penalty that is minimized by pushing these samples far away from the center. The scalar $\eta >0$ controls the relative weight of the labeled term relative to the unlabeled term, while $\lambda >0$ is the strength of the ${\ell }_2$ weight decay applied to the weight matrices $W_{\ell }$ via the Frobenius norms $\parallel W_{\ell }{\parallel }_F^2$.

The anomaly score for any sample $\mathbf{x}$ is defined as the Euclidean distance of its latent representation to the center:

$$s\left(\mathbf{x}\right)=\parallel \varphi (\mathbf{x};W)-\mathbf{c}{\parallel }_2.$$

(2)

A threshold on $s\left(\mathbf{x}\right)$ is then used to distinguish normal and anomalous samples. DeepSAD therefore preserves the center-based one-class decision mechanism while incorporating label information through the exponentiated term $\parallel \varphi ({\mathbf{x}}_i;W){-\mathbf{c}\parallel }_2^{2y_i}$ for $({\mathbf{x}}_i,y_i)\in {\mathcal{D}}_{\ell }$ and the weighting parameter $\eta$, in combination with the unlabeled DeepSVDD term.

2.3. Limitations of DeepSAD and Need for Graph-Based Regularization

Although DeepSAD is a flexible and effective framework for semi-supervised anomaly detection, its objective in (1) remains fundamentally point-wise: each sample contributes to the loss only through its own distance $\parallel \varphi ({\mathbf{x}}_i;W){-\mathbf{c}\parallel }_2$ and, for labeled samples, its own label $y_i$. The unlabeled term aggregates individual squared distances for ${\mathbf{x}}_i\in {\mathcal{D}}_u$, and the labeled term aggregates squared distances raised to the label exponent $(\parallel \varphi ({\mathbf{x}}_i;W)-\mathbf{c}{{\parallel }_2^2)}^{y_i}$ for $({\mathbf{x}}_i,y_i)\in {\mathcal{D}}_{\ell }$, but there are no interaction terms coupling different samples or encoding a neighborhood graph, local density, or manifold structure in latent space. Consequently, unlabeled data influence the model only indirectly through penalties on individual points, rather than through constraints that explicitly relate nearby samples.

This strictly point-wise approach also restricts how information from the small labeled subset can spread into the unlabeled pool. In realistic semi-supervised settings, both labeled normal and anomalous examples are scarce, whereas unlabeled data densely occupy the regions in which a robust decision boundary must be learned. Ideally, unlabeled instances lying in areas dominated by labeled normals should naturally acquire lower anomaly scores, while those residing close to labeled anomalies should be driven toward higher scores. In DeepSAD, such behavior can only arise indirectly through the shared encoder parameters W; there is no explicit mechanism that couples the anomaly scores of nearby points or enforces consistency along the underlying data manifold.

Moreover, the absence of an explicit structure over samples constrains interpretability. DeepSAD provides a scalar anomaly score for each sample through its distance to the center, but it does not reveal how a given unlabeled sample is positioned relative to nearby labeled normals and anomalies in latent space. For many safety-critical applications, it is desirable not only to identify an observation as anomalous, but also to relate this decision to representative neighboring patterns that support or contextualize the score.

Taken together, these limitations motivate the incorporation of an explicit neighborhood structure into the DeepSAD framework, so that label information can propagate along the data manifold and anomaly scores are encouraged to be locally consistent and more interpretable. In the next section, we introduce a DeepSAD variant that realizes this idea.

3. Anomaly-Aware Graph-Based Semi-Supervised Deep SVDD

In this section, we introduce AAG-DSVDD, a DeepSAD-style extension that preserves the center-based hypersphere geometry in latent space while explicitly exploiting the geometry of labeled and unlabeled data. The method combines (i) a soft-boundary enclosure on labeled normals, (ii) a margin-based push-out on labeled anomalies, (iii) a center-pull on unlabeled samples, and (iv) a graph regularizer on the squared-distance field over a label-aware, locally scaled latent k-NN graph.

We retain the notation of Section 2.1: ${\mathbf{x}}_i\in \mathcal{X}={\mathbb{R}}^m$ denotes an input vector, ${\mathbf{z}}_i=\varphi ({\mathbf{x}}_i;W)\in \mathcal{Z}={\mathbb{R}}^p$ its latent embedding, $\mathbf{c}\in \mathcal{Z}$ a latent center, and $y_i\in \{+1,0,-1\}$ the label indicating a labeled normal, unlabeled, or labeled anomalous sample, respectively. We write

$$d_i^2={\parallel {\mathbf{z}}_i-\mathbf{c}\parallel }_2^2$$

for the squared distance of ${\mathbf{x}}_i$ to the center, and we use the notation ${\left[u\right]}_{+}:=max\{0,u\}$ for the positive part of u.

3.1. Latent Encoder, Center, and Radius

The AAG-DSVDD model uses a deep encoder:

$$\varphi (·;W):\mathcal{X}\to \mathcal{Z},$$

implemented either as a multilayer perceptron (MLP) or as a long short-term memory (LSTM)-based sequence encoder [38] for multi-channel time series. For each input ${\mathbf{x}}_i\in \mathcal{X}$, we write

$${\mathbf{z}}_i=\varphi ({\mathbf{x}}_i;W)\in \mathcal{Z}$$

for its latent representation.

In the latent space, we maintain a center vector $\mathbf{c}\in \mathcal{Z}$ and a non-negative radius $R\ge 0$. The squared distance of ${\mathbf{x}}_i$ to the center is

$$d_i^2=\parallel {\mathbf{z}}_i-\mathbf{c}{\parallel }_2^2.$$

(3)

These distances $d_i^2$ form the basis of both the training objective and the anomaly score at test time, with the sign of $d_i^2-R^2$ indicating whether an observation lies inside or outside the learned hypersphere. The practical initialization and updating of $\mathbf{c}$ and R follow standard soft-boundary Deep SVDD practice and are detailed in Section 3.4.

3.2. Label-Aware Latent k-NN Graph with Local Scales

To exploit the geometry of the joint labeled–unlabeled sample, we construct a label-aware k-NN graph over latent embeddings with node-adaptive Gaussian weights. Let

$$\mathbf{Z}={[{\mathbf{z}}_1,\dots ,{\mathbf{z}}_n]}^{\top }\in {\mathbb{R}}^{n\times p}$$

denote the matrix of embeddings for all n training samples. For each node $i\in \{1,\dots ,n\}$, we find its k-nearest neighbors in latent space and denote their indices by ${\mathcal{N}}_K\left(i\right)$, using Euclidean distance in $\mathcal{Z}$ and recording the corresponding distances ${\left\{{\delta }_{ij}\right\}}_{j\in {\mathcal{N}}_K\left(i\right)}$.

We assign each node a local scale ${\sigma }_i>0$ from the empirical distribution of its neighbor distances. Concretely, we compute the median of the nonzero distances in $\{{\delta }_{ij}:j\in {\mathcal{N}}_K\left(i\right),j\ne i\}$ and use it as a robust estimate of the local density scale. This yields a self-tuning, node-adaptive Gaussian affinity:

$$w_{ij}=exp\left(-{\displaystyle \frac{\parallel {\mathbf{z}}_i-{\mathbf{z}}_j{\parallel }_2^2}{{\sigma }_i{\sigma }_j}}\right),j\in {\mathcal{N}}_K\left(i\right)\setminus \left\{i\right\},$$

(4)

in the spirit of locally scaled kernels for spectral clustering [39]. Using ${\sigma }_i{\sigma }_j$ in the denominator adapts the effective kernel width to the local density around both endpoints.

We then apply a label-aware edge policy. For nodes with $y_i=0$ (unlabeled), we retain all k-nearest neighbors in ${\mathcal{N}}_K\left(i\right)\setminus \left\{i\right\}$, irrespective of their labels. In contrast, when $y_i\in \{+1,-1\}$ (labeled), we scan the neighbors of i in order of increasing distance and retain only those nodes j with $y_j=0$ (unlabeled), until k neighbors are selected or the candidate list is exhausted. This construction ensures that most outgoing edges from labeled points terminate in unlabeled nodes, allowing for label information to propagate into the unlabeled pool while reducing the risk of overfitting to the sparse labeled set.

Let $W=\left(w_{ij}\right)\in {\mathbb{R}}^{n\times n}$ denote the resulting sparse affinity matrix, with $w_{ij}=0$ for pairs that do not form edges. To keep the overall scale comparable across nodes of different degrees, we row-normalize W to obtain

$$\tilde{W}=D_{\mathrm{row}}^{-1}W,D_{\mathrm{row}}=diag\left(\sum _j{w}_{ij}\right),$$

and then construct a symmetrized affinity matrix:

$$M={\displaystyle \frac{1}{2}}\left(\tilde{W}+{\tilde{W}}^{\top }\right).$$

Finally, we define

$$L=I-M\in {\mathbb{R}}^{n\times n},$$

(5)

a symmetric matrix that encodes the latent k-NN graph and will later be used through the quadratic form ${\left({\mathbf{d}}^2\right)}^{\top }L{\mathbf{d}}^2$ on the vector of squared distances ${\mathbf{d}}^2={(d_1^2,\dots ,d_n^2)}^{\top }$.

This formulation is motivated by earlier research on graph-based semi-supervised learning and manifold regularization, in which the smoothness of a function defined on a weighted graph captures the geometry of labeled and unlabeled data [31,32,35].

3.3. Loss Components and Overall Objective

Let ${\mathcal{D}}_{\ell }^{+}$, ${\mathcal{D}}_{\ell }^{-}$, and ${\mathcal{D}}_u$ denote the sets of labeled normals, labeled anomalies, and unlabeled samples, with cardinalities $n_{+}$, $n_{-}$, and $n_u$, respectively. For each training sample ${\mathbf{x}}_i$, we write ${\mathbf{z}}_i=\varphi ({\mathbf{x}}_i;W)$ for its latent embedding and

$$d_i^2={\parallel {\mathbf{z}}_i-\mathbf{c}\parallel }_2^2$$

for its squared distance to the center. We collect these distances into the following vector:

$${\mathbf{d}}^2={\left[\begin{array}{ccc}{d}_1^2& \dots & d_n^2\end{array}\right]}^{\top }\in {\mathbb{R}}^n.$$

Throughout this subsection, we use the notation ${\left[u\right]}_{+}=max\{0,u\}$ for the hinge operator, and we write hinge-type penalties with an exponent $r\ge 1$.

AAG-DSVDD combines four primary components: a graph-based regularizer on the squared-distance field, a soft-boundary enclosure on labeled normals, a margin-based push-out on labeled anomalies, and an unlabeled center-pull, together with a soft-boundary radius term and standard weight decay.

3.3.1. Graph Regularizer on Squared Distances

Using the symmetric matrix L defined in (5), which encodes the latent k-NN graph, we define a smoothness penalty on the squared distances as follows:

$${\mathcal{L}}_{\mathrm{graph}}\left(W\right)={\mathbf{d}}^{2\top }L{\mathbf{d}}^2,$$

(6)

where ${\mathbf{d}}^2={(d_1^2,\dots ,d_n^2)}^{\top }$ collects the squared distances $d_i^2={\parallel {\mathbf{z}}_i-\mathbf{c}\parallel }_2^2$. Since $L=I-M$ with M the normalized, symmetrized affinity matrix from Section 3.2, we can rewrite

$${\mathcal{L}}_{\mathrm{graph}}\left(W\right)={\parallel {\mathbf{d}}^2\parallel }_2^2-{\mathbf{d}}^{2\top }M{\mathbf{d}}^2.$$

For a given overall scale $\parallel {\mathbf{d}}^2{\parallel }_2^2$, minimizing ${\mathcal{L}}_{\mathrm{graph}}$ is equivalent to maximizing ${\mathbf{d}}^{2\top }M{\mathbf{d}}^2$. Because $M_{ij}\ge 0$ and is larger on pairs of nodes that are strongly connected in the latent k-NN graph, the term ${\mathbf{d}}^{2\top }M{\mathbf{d}}^2$ becomes large when neighboring nodes with high affinity carry similar squared distances. Thus, configurations in which $d_i^2$ varies smoothly over high-affinity regions of the graph are favored, whereas sharp changes in $d_i^2$ across strongly connected nodes tend to increase ${\mathcal{L}}_{\mathrm{graph}}$.

In effect, ${\mathcal{L}}_{\mathrm{graph}}$ encourages neighboring samples in latent space to have compatible anomaly scores $d_i^2$, allowing for information from the limited labeled normals and anomalies to diffuse into the unlabeled pool.

3.3.2. Labeled-Normal Soft-Boundary Enclosure

For labeled normals $({\mathbf{x}}_i,y_i)\in {\mathcal{D}}_{\ell }^{+}$, the model should treat the hypersphere of radius R as a soft boundary: most normal embeddings are expected to lie inside, while a small fraction of violations is tolerated. Using the squared distances $d_i^2={\parallel {\mathbf{z}}_i-\mathbf{c}\parallel }_2^2$, we penalize such violations through a hinge-type term:

$${\mathcal{L}}_{\mathrm{norm}}(W,R)={\displaystyle \frac{1}{\nu n_{+}}}\sum _{({\mathbf{x}}_i,y_i)\in {\mathcal{D}}_{\ell }^{+}}{\left({[d_i^2-R^2]}_{+}\right)}^r,$$

(7)

where ${\left[u\right]}_{+}=max\{0,u\}$ denotes the hinge operator, $\nu \in (0,1]$ is a soft-boundary parameter, and $r\ge 1$ controls the curvature of the penalty. Only labeled normals with $d_i^2>R^2$ contribute to ${\mathcal{L}}_{\mathrm{norm}}$. When a normal sample lies inside the hypersphere ($d_i^2\le R^2$), its contribution is zero, whereas normals outside the boundary incur a positive loss that grows as ${(d_i^2-R^2)}^r$. Normalizing by $\nu n_{+}$ ensures that the penalty scales with the proportion of violating normals rather than their absolute count, so that the effective tightness of the hypersphere is controlled by $\nu$, as in soft-boundary Deep SVDD [13], and not by the number of labeled normal samples. In particular, smaller values of $\nu$ correspond to a tighter enclosure (fewer tolerated violations), while larger values allow for a greater fraction of labeled normals to lie near or beyond the boundary.

3.3.3. Labeled-Anomaly Margin Push-Out

For labeled anomalies $({\mathbf{x}}_i,y_i)\in {\mathcal{D}}_{\ell }^{-}$, we enforce a clearance margin $m\ge 0$ beyond the hypersphere:

$${\mathcal{L}}_{\mathrm{anom}}(W,R)={\displaystyle \frac{\mathrm{\Omega }}{n_{-}}}\sum _{({\mathbf{x}}_i,y_i)\in {\mathcal{D}}_{\ell }^{-}}{\left({[m+R^2-d_i^2]}_{+}\right)}^r,$$

(8)

where $\mathrm{\Omega }>0$ is an anomaly weight coefficient. This term is active only when an anomaly lies inside the hypersphere or within the margin region $R^2\le d_i^2<R^2+m$. Under such conditions, ${[m+R^2-d_i^2]}_{+}^r$ pushes its embedding farther from the center, either by increasing $d_i^2$ or, through the joint optimization, discouraging increases in $R^2$ that would otherwise encapsulate it.

3.3.4. Unlabeled Center-Pull

Unlabeled samples ${\mathbf{x}}_i\in {\mathcal{D}}_u$ provide dense coverage of the data manifold but may contain contamination. To stabilize the global scale of the squared-distance field and keep the center anchored when $n_{+}$ is small, we apply a label-free pull-in on unlabeled distances:

$${\mathcal{L}}_{\mathrm{unl}}\left(W\right)={\displaystyle \frac{1}{n_u}}\sum _{{\mathbf{x}}_i\in {\mathcal{D}}_u}{d}_i^2.$$

(9)

This term reduces the mean of $d_i^2$ over the unlabeled pool toward $\mathbf{c}$, complementing the local smoothness imposed by ${\mathcal{L}}_{\mathrm{graph}}$. Its influence is controlled by a coefficient ${\eta }_{\mathrm{unl}}\ge 0$.

3.3.5. Overall Objective

Combining all components, the full AAG-DSVDD loss is

$$\begin{array}{cc}\hfill \mathcal{L}(W,R)=& R^2+{\mathcal{L}}_{\mathrm{norm}}(W,R)+{\mathcal{L}}_{\mathrm{anom}}(W,R)+{\eta }_{\mathrm{unl}}{\mathcal{L}}_{\mathrm{unl}}\left(W\right)+{\lambda }_u{\mathcal{L}}_{\mathrm{graph}}\left(W\right)\hfill \\ \hfill & +{\displaystyle \frac{\lambda }{2}}\sum _{\ell =1}^L\parallel W_{\ell }{\parallel }_F^2,\hfill \end{array}$$

(10)

where ${\lambda }_u\ge 0$ scales the graph regularizer, ${\eta }_{\mathrm{unl}}\ge 0$ controls the unlabeled center-pull, and $\lambda \ge 0$ is a weight-decay coefficient on the encoder parameters $W_{\ell }$. The explicit $R^2$ term discourages unnecessarily large hyperspheres; together with ${\mathcal{L}}_{\mathrm{norm}}$ and the soft-boundary radius update based on labeled normals, it yields behavior analogous to soft-boundary Deep SVDD, now coupled with anomaly margins, unlabeled pull-in, and graph-based smoothing. When ${\lambda }_u=0$ and ${\eta }_{\mathrm{unl}}=0$, the objective reduces to a soft-boundary Deep SVDD-like loss acting on labeled normals and labeled anomalies. Further setting $\mathrm{\Omega }=0$ recovers the standard soft-boundary Deep SVDD formulation on labeled normals alone.

The exponent $r\ge 1$ shapes the hinge-type penalties in ${\mathcal{L}}_{\mathrm{norm}}$ and ${\mathcal{L}}_{\mathrm{anom}}$. For $r=1$, violations are penalized linearly, yielding piecewise-constant gradients whenever ${[·]}_{+}>0$. For $r=2$, the penalty is quadratic in the violation, and the gradients scale linearly with its magnitude. In our experiments, we use $r=2$, which empirically produces smoother, magnitude-aware updates and improves training stability, particularly in the presence of scarce labels and the additional graph regularizer.

The different components of (10) interact to shape the decision boundary in a neighborhood-aware manner. The labeled-normal term ${\mathcal{L}}_{\mathrm{norm}}$ and the radius R establish a soft hypersphere around $\mathbf{c}$ that encloses most labeled normals and treats their squared distances $d_i^2$ as a reference scale for normal behavior. The anomaly margin term ${\mathcal{L}}_{\mathrm{anom}}$ pushes labeled anomalies beyond $R^2$ by at least m, so that regions of latent space associated with anomalous patterns are encouraged to have larger $d_i^2$ and lie outside the hypersphere. The unlabeled center-pull ${\mathcal{L}}_{\mathrm{unl}}$ stabilizes the global level of the squared-distance field when labeled normals are few, preventing uncontrolled drift of $d_i^2$ for unlabeled samples. Finally, the graph regularizer ${\mathcal{L}}_{\mathrm{graph}}$ couples these effects along the latent k-NN graph by favoring configurations in which strongly connected neighbors have compatible squared distances. As a result, unlabeled samples that are well embedded in normal-dominated neighborhoods tend to inherit small $d_i^2$ and be enclosed by the decision boundary, whereas unlabeled samples whose neighborhoods are influenced by anomalies are pushed toward larger $d_i^2$ and are more likely to lie outside the hypersphere, receiving higher anomaly scores $s\left(\mathbf{x}\right)=d^2\left(\mathbf{x}\right)-R^2$.

Taken together, this objective provides several practical advantages for semi-supervised anomaly detection under limited labels. First, it strictly generalizes soft-boundary Deep SVDD and DeepSAD. By suitable choices of $(\mathrm{\Omega },{\eta }_{\mathrm{unl}},{\lambda }_u)$, the practitioner can interpolate between purely one-class training on labeled normals, supervised separation of labeled anomalies, and graph-regularized semi-supervision on unlabeled data. Second, the label-aware graph term lets scarce anomaly labels influence whole latent neighborhoods rather than single points, which improves robustness in high-dimensional and partially labeled settings such as fire monitoring. Third, the additional structure appears only in the training loss. At test time, AAG-DSVDD keeps the simple distance-to-center scoring rule $s\left(\mathbf{x}\right)=d^2\left(\mathbf{x}\right)-R^2$, so inference remains lightweight and easy to interpret.

Finally, AAG-DSVDD also offers practitioners a practical way to obtain sample-level interpretation, which is important when most observations are unlabeled. Because the latent space has been shaped by the label-aware k-NN graph and its regularizer, nearby points with strong graph connections tend to share similar anomaly scores. A k-NN search in this space can therefore identify labeled neighbors for any unlabeled sample, whose labels and contextual descriptions provide an example-based interpretation of its anomaly score. In practice, this neighborhood inspection allows operators to see whether a high anomaly score is associated primarily with labeled anomalous patterns or with benign operating conditions, yielding a transparent, example-based explanation for each unlabeled sample.

3.4. Optimization and Anomaly Scoring

The encoder parameters W and the soft-boundary radius R are optimized by stochastic gradient methods with mini-batch training, combined with periodic closed-form updates of $R^2$ and periodic reconstruction of the latent k-NN graph. This procedure follows standard Deep SVDD practice while incorporating the additional semi-supervised and graph-based terms in (10). In our implementation, training runs for $T_{\mathrm{epochs}}$ epochs with mini-batches of size B.

We first perform a short warm-up phase on labeled normals in ${\mathcal{D}}_{\ell }^{+}$. During warm-up, the encoder is trained for a few epochs to minimize the average squared norm of the embeddings:

$${\displaystyle \frac{1}{n_{+}}}\sum _{({\mathbf{x}}_i,y_i)\in {\mathcal{D}}_{\ell }^{+}}\parallel \varphi ({\mathbf{x}}_i;W){\parallel }_2^2,$$

which stabilizes the latent representation around the origin. After the warm-up phase, we determine the center $\mathbf{c}$ as the empirical average of the embeddings corresponding to the labeled normal samples:

$$\mathbf{c}={\displaystyle \frac{1}{n_{+}}}\sum _{({\mathbf{x}}_i,y_i)\in {\mathcal{D}}_{\ell }^{+}}\varphi ({\mathbf{x}}_i;W),$$

and then keep $\mathbf{c}$ fixed. We employ a block-coordinate strategy for the soft-boundary radius. Following the standard training procedure of the soft-boundary Deep SVDD [3,13], we do not backpropagate through R. Instead, we treat $R^2$ as a scalar quantity that is updated independently of the gradient-based optimization. Using the current distances of the labeled normal samples, we set

$$R^2\leftarrow Q_{1-\nu }\left(\{d_i^2:({\mathbf{x}}_i,y_i)\in {\mathcal{D}}_{\ell }^{+}\}\right),$$

where $Q_{1-\nu }$ denotes the empirical $(1-\nu )$-quantile, and $\nu \in (0,1]$ controls the tolerated fraction of normal violations. During training, $R^2$ is held fixed within each epoch, while W is updated, and after selected epochs, we refresh $R^2$ by reapplying the same quantile rule to the current squared distances of labeled normals. In practice, this refresh is performed every $T_R$ epochs starting from a user-specified epoch $t_{\mathrm{start}}$. This yields a soft-boundary behavior, in which roughly a fraction $\nu$ of normals may lie on or outside the hypersphere, matching the interpretation of $\nu$ in the original soft-boundary Deep SVDD formulation [13].

Within each epoch, we sample mini-batches of size B from the combined training set ${\mathcal{D}}_{\ell }^{+}\cup {\mathcal{D}}_{\ell }^{-}\cup {\mathcal{D}}_u$. For each mini-batch, we compute embeddings ${\mathbf{z}}_i=\varphi ({\mathbf{x}}_i;W)$, squared distances $d_i^2={\parallel {\mathbf{z}}_i-\mathbf{c}\parallel }_2^2$, and the batch contributions of the labeled-normal, labeled-anomaly, and unlabeled terms ${\mathcal{L}}_{\mathrm{norm}}(W,R)$, ${\mathcal{L}}_{\mathrm{anom}}(W,R)$, and ${\mathcal{L}}_{\mathrm{unl}}\left(W\right)$. The graph term ${\mathcal{L}}_{\mathrm{graph}}\left(W\right)$ is not evaluated at the mini-batch level. Gradients of the resulting mini-batch loss are backpropagated through the encoder parameters W, while $R^2$ and the graph matrix are treated as constants. We use the Adam optimizer [40] with weight decay to minimize (10) with respect to W for fixed $R^2$.

To integrate the graph regularizer, we periodically reconstruct the label-aware latent k-NN graph using the current embeddings. At the start of each graph-refresh interval (every $T_{\mathrm{graph}}$ epochs), we first compute $\mathbf{Z}$ for all training samples, then rebuild the label-aware k-NN graph with local scaling, and finally construct the symmetric matrix L, as defined in Section 3.2. This matrix L is kept fixed until the next refresh. During this interval, if ${\lambda }_u>0$, we perform a separate full-batch gradient update on the graph term ${\lambda }_u{\mathcal{L}}_{\mathrm{graph}}\left(W\right)$ based on the current embeddings, thereby updating W while keeping L unchanged. We do not backpropagate gradients through the graph construction process or the quantile updates of $R^2$. Consequently, the optimization procedure alternates between mini-batch updates on the labeled and unlabeled objectives and occasional full-batch updates that smooth the squared-distance field over the latent k-NN graph.

Let $(W^{*},R^{*},\mathbf{c})$ denote the trained encoder parameters, radius, and center. For any test sample ${\mathbf{x}}_{\mathrm{test}}\in \mathcal{X}$, we compute its anomaly score as the signed squared radial distance:

$$s\left({\mathbf{x}}_{\mathrm{test}}\right)=\parallel \varphi ({\mathbf{x}}_{\mathrm{test}};W^{*})-\mathbf{c}{\parallel }_2^2-{R^{*}}^2.$$

(11)

By this convention, points outside the hypersphere have $s\left(\mathbf{x}\right)>0$ and are treated as anomalies, inliers satisfy $s\left(\mathbf{x}\right)<0$, and boundary points satisfy $s\left(\mathbf{x}\right)\approx 0$. A decision threshold $\tau$ on $s\left(\mathbf{x}\right)$ is chosen on a held-out validation set, for example, by targeting a desired false-alarm rate on validation normals or by maximizing a suitable detection metric. At test time, the graph is not required and AAG-DSVDD behaves as a standard center-based one-class model. Each input is processed by a single forward pass through $\varphi (·;W^{*})$ to obtain its embedding, and the anomaly score is computed from the squared distance:

$$s\left(\mathbf{x}\right)=\parallel \varphi (\mathbf{x};W^{*})-\mathbf{c}{\parallel }_2^2-{R^{*}}^2.$$

The AAG-DSVDD algorithm is summarized in Algorithm 1. The scoring and decision rule are summarized in Algorithm 2.

Computational Complexity

From a computational standpoint, AAG-DSVDD shares the same per-epoch feed-forward and backpropagation cost as DeepSVDD and DeepSAD, since all three methods use the same encoder architecture and mini-batch training scheme. For n training samples and mini-batch size B, this per-epoch cost is proportional to $(n/B)$ forward–backward passes through the encoder. The additional overhead in AAG-DSVDD comes from the graph regularization. The computational cost of the graph regularization is minimized by the locally connected structure of the label-aware latent k-NN graph. Although the graph matrix L has dimensions $n\times n$, it is mathematically sparse, as each node is connected to at most k neighbors, and edges originating from labeled samples are further restricted to connect only to unlabeled neighbors. Consequently, the number of non-zero entries in L scales linearly with n rather than quadratically. This allows for the graph regularization term ${\mathbf{d}}^{2\top }L{\mathbf{d}}^2$ to be evaluated in $O\left(nk\right)$ operations. Furthermore, the neighbor search—typically $O(nlogn)$ with spatial indexing—is amortized by performing the graph update only at intervals $T_{\mathrm{graph}}$, independent of the encoder’s gradient iterations. Finally, the graph is used solely for regularization during training. At inference, the model requires only a single forward pass through the encoder to compute the distance to the center, thereby maintaining the same fast inference speed as standard DeepSVDD and DeepSAD.

Regarding memory usage, the main additional cost compared to DeepSVDD and DeepSAD comes from storing the latent embedding matrix $\mathbf{Z}\in {\mathbb{R}}^{n\times p}$ and the sparse graph matrix L, which has $O\left(nk\right)$ non-zero entries. For the datasets examined in this paper, these requirements are easily accommodated on a single GPU or CPU. For larger-scale or streaming deployments, two mitigation strategies are particularly effective: (i) constructing the graph using only a subset of unlabeled samples or using mini-batch centroids, thereby reducing the effective n that determines the graph size; and (ii) lowering the graph refresh frequency $T_{\mathrm{graph}}$ or turning off the graph term after a fixed number of epochs once the latent representation has stabilized. These strategies enable users to balance graph accuracy against training overhead, while preserving the lightweight inference-time characteristics necessary for real-time fire monitoring.

Algorithm 1 AAG-DSVDD (training)

Inputs: ${\mathcal{D}}_{\ell }^{+}$, ${\mathcal{D}}_{\ell }^{-}$, ${\mathcal{D}}_u$, encoder $\varphi (·;W)$, hyperparameters $\nu , \mathrm{\Omega }, m, {\eta }_{\mathrm{unl}}, {\lambda }_u, r, K$, training schedule $T_{\mathrm{epochs}}, B, T_{\mathrm{graph}}, T_R, t_{\mathrm{start}}$, Adam optimizer with weight decay $\lambda$. Outputs: $W^{*}$, $\mathbf{c}$, $R^{*}$.   Initialization:  1.   Form $\mathcal{D}={\mathcal{D}}_{\ell }^{+}\cup {\mathcal{D}}_{\ell }^{-}\cup {\mathcal{D}}_u$ with labels $y_i\in \{+1,0,-1\}$.  2.   Warm-up on ${\mathcal{D}}_{\ell }^{+}$ for a few epochs, minimizing ${\displaystyle \frac{1}{|{\mathcal{D}}_{\ell }^{+}|}}{\sum }_{({\mathbf{x}}_i,y_i)\in {\mathcal{D}}_{\ell }^{+}}{\parallel \varphi ({\mathbf{x}}_i;W)\parallel }_2^2$.  3.   Set ${\displaystyle \mathbf{c}\leftarrow \frac{1}{|{\mathcal{D}}_{\ell }^{+}|}\sum _{({\mathbf{x}}_i,y_i)\in {\mathcal{D}}_{\ell }^{+}}\varphi ({\mathbf{x}}_i;W)}$ and keep $\mathbf{c}$ fixed.  4.   Compute $d_i^2={\parallel \varphi ({\mathbf{x}}_i;W)-\mathbf{c}\parallel }_2^2$ for $({\mathbf{x}}_i,y_i)\in {\mathcal{D}}_{\ell }^{+}$ and set ${\displaystyle R^2\leftarrow Q_{1-\nu }\left(\{d_i^2:({\mathbf{x}}_i,y_i)\in {\mathcal{D}}_{\ell }^{+}\}\right)}$.  5.   Compute embeddings for all ${\mathbf{x}}_i\in \mathcal{D}$ and build the label-aware latent k-NN graph with local scales, obtaining M and the associated symmetric matrix L as in Section 3.2. Epoch loop: For $t=1,\dots ,T_{\mathrm{epochs}}$:  1.   Mini-batch step (labeled and unlabeled terms). For each mini-batch $\mathcal{B}\subset \mathcal{D}$ of size B: Split $\mathcal{B}$ into ${\mathcal{B}}_{+}$, ${\mathcal{B}}_{-}$, and ${\mathcal{B}}_u$ according to $y\in \{+1,-1,0\}$. For all $\mathbf{x}\in \mathcal{B}$, compute $\mathbf{z}=\varphi (\mathbf{x};W)$ and $d^2\left(\mathbf{x}\right)={\parallel \mathbf{z}-\mathbf{c}\parallel }_2^2$. Compute ${\mathcal{L}}_{\mathrm{norm}}$, ${\mathcal{L}}_{\mathrm{anom}}$, and ${\mathcal{L}}_{\mathrm{unl}}$ for the batch using (7)–(9). Form $${\mathcal{L}}_{\mathrm{batch}}=R^2+{\mathcal{L}}_{\mathrm{norm}}+{\mathcal{L}}_{\mathrm{anom}}+{\eta }_{\mathrm{unl}}{\mathcal{L}}_{\mathrm{unl}}+{\displaystyle \frac{\lambda }{2}}\sum _{\ell }{\parallel W_{\ell }\parallel }_F^2.$$ Update W with one Adam step on ${\mathcal{L}}_{\mathrm{batch}}$ (with fixed $R^2$ and L).  2.   Radius refresh. If $t\ge t_{\mathrm{start}}$ and $tmod{T}_R=0$, recompute $d_i^2$ for $({\mathbf{x}}_i,y_i)\in {\mathcal{D}}_{\ell }^{+}$ and update $$R^2\leftarrow Q_{1-\nu }\left(\{d_i^2:({\mathbf{x}}_i,y_i)\in {\mathcal{D}}_{\ell }^{+}\}\right).$$  3.   Graph refresh and smoothness step. If $(t-1)mod{T}_{\mathrm{graph}}=0$, recompute embeddings for all ${\mathbf{x}}_i\in \mathcal{D}$ and rebuild the label-aware latent k-NN graph with local scales, obtaining an updated symmetric graph matrix L as in Section 3.2. If ${\lambda }_u>0$, compute $d_i^2={\parallel \varphi ({\mathbf{x}}_i;W)-\mathbf{c}\parallel }_2^2$ for all ${\mathbf{x}}_i\in \mathcal{D}$, stack ${\mathbf{d}}^2={[d_1^2,\dots ,d_n^2]}^{\top }$, evaluate ${\mathcal{L}}_{\mathrm{graph}}={\mathbf{d}}^{2\top }L{\mathbf{d}}^2$ as in (6), and take a gradient step on ${\lambda }_u{\mathcal{L}}_{\mathrm{graph}}$ with respect to W while keeping L fixed. Return: $(W^{*},R^{*},\mathbf{c})$.

Algorithm 2 AAG-DSVDD scoring and optional threshold selection

Require:  Trained $(W^{*},R^{*},\mathbf{c})$; input $\mathbf{x}$ (or a validation/test set).   1: Compute embedding $\mathbf{z}=\varphi (\mathbf{x};W^{*})$.   2: Compute score $s\left(\mathbf{x}\right)={\parallel \mathbf{z}-\mathbf{c}\parallel }_2^2-{\left(R^{*}\right)}^2$.   3: (Optional, validation) choose a threshold $\tau$ on a held-out validation set (e.g., to achieve a target false-alarm rate on validation normals or maximize a chosen detection metric).   4: Predict anomaly if $s\left(\mathbf{x}\right)>\tau$ and normal otherwise.

3.5. Calibration of AAG-DSVDD Hyperparameters

The hyperparameters of AAG-DSVDD fall into three groups: (i) encoder capacity, (ii) graph construction, and (iii) loss weights. Encoder capacity is controlled by the latent dimension, hidden-layer sizes, network depth, and the choice of encoder type (MLP or LSTM); together, these determine how flexible the representation $\varphi (·;W)$ is. The latent k-NN graph is governed by the neighborhood size k and the locally scaled Gaussian kernel used to build the affinity matrix. The learning objective includes the soft-boundary parameter $\nu$, the anomaly weight $\mathrm{\Omega }$ and margin m for labeled anomalies, the unlabeled center-pull weight ${\eta }_{\mathrm{unl}}$, the graph smoothness weight ${\lambda }_u$, the hinge exponent r, and the ${\ell }_2$ weight decay $\lambda$.

All hyperparameters are selected using a held-out validation set. In practice, we use a simple protocol. First, we fix a small number of encoder architectures (latent dimensions and depths) to avoid overfitting the network structure. Second, for each encoder candidate, we perform grid search over the scalar coefficients and structural graph parameters. Scalar regularization weights, such as $\nu$, $\mathrm{\Omega }$, m, ${\eta }_{\mathrm{unl}}$, ${\lambda }_u$, and $\lambda$, are tuned on logarithmic or linear grids. Structural parameters, such as k, the latent dimension, and the depth, are chosen from discrete sets of candidate values. The final configuration is selected based on validation performance.

Within this validation-based tuning protocol, encoder choices determine the expressive capacity of $\varphi (·;W)$, while the remaining hyperparameters control how this representation is converted into a decision boundary. The loss coefficients $\nu , \mathrm{\Omega }, m, {\eta }_{\mathrm{unl}}, {\lambda }_u$ directly shape the decision boundary. The soft-boundary parameter $\nu$ has the same role as in soft-boundary Deep SVDD. Smaller values enforce a tighter hypersphere around labeled normals. The anomaly weight $\mathrm{\Omega }$ and the margin m determine the strength and extent to which labeled anomalies are pushed away from the center. Larger values emphasize separation, but they can overreact to a small number of anomaly labels. The unlabeled weight ${\eta }_{\mathrm{unl}}$ determines how much the unlabeled pool pulls the center and the radius. High ${\eta }_{\mathrm{unl}}$ lets the boundary track the overall unlabeled distribution, which is useful when contamination is low. Low ${\eta }_{\mathrm{unl}}$ keeps the model closer to a purely labeled one-class setting. The graph weight ${\lambda }_u$ scales the smoothness penalty on squared distances over the latent k-NN graph. Larger ${\lambda }_u$ propagates supervision more strongly along the manifold but may oversmooth the boundary, often shrinking the effective decision region when the graph is dominated by normal and unlabeled samples. Smaller ${\lambda }_u$ limits geometric coupling and allows for more locally adaptive decision boundaries. The neighborhood size k controls graph density and the scale of smoothing. A larger k yields broader and more global regularization. A smaller k produces more localized and fine-grained boundaries.

4. Experiments on Synthetic and Public Datasets

We first study AAG-DSVDD in a controlled two-dimensional setting, where the geometry of normals, anomalies, and the learned decision boundary can be visualized. We compare AAG-DSVDD against DeepSVDD [13], DeepSAD [8], OC-SVM with a radial basis function (RBF) kernel (OC-SVM) [12], and classical SVDD with an RBF kernel (SVDD-RBF) [11]. Then, performance comparison is carried out on popular anomaly detection public datasets from the UCI repository. All methods operate in the same semi-supervised setting, where only a small fraction of the training normals and anomalies are labeled and the remaining training points form a contaminated unlabeled pool.

4.1. Synthetic Dataset Experiments

4.1.1. Synthetic Dataset Description

We generate a two-dimensional dataset with a curved normal manifold and off-manifold anomalies. Normal samples are obtained by first drawing a Gaussian vector $\tilde{\mathbf{x}}=({\tilde{x}}_1,{\tilde{x}}_2)$ with diagonal covariance and then applying a quadratic bending transform:

$$x_1={\tilde{x}}_1,x_2=b({\tilde{x}}_1^2-s_1^2)+{\tilde{x}}_2,$$

followed by global scaling and the addition of small Gaussian noise. The parameters are set to $s_1=2.0$, $s_2=1.5$, bend $b=0.25$, and noise level ${\sigma }_{\mathrm{noise}}=0.06$. This procedure produces a nonlinearly curved, banana-shaped normal region.

Anomalies are drawn from a mixture of two Gaussian distributions located above and below the banana. Concretely, half of the anomalous points are sampled from

$$\mathcal{N}({\mathit{\mu }}_{a1},{\mathrm{\Sigma }}_{a1}),{\mathit{\mu }}_{a1}={(0,3.5)}^{\top },{\mathrm{\Sigma }}_{a1}=\mathrm{diag}(0.5,0.75),$$

and the remaining half from

$$\mathcal{N}({\mathit{\mu }}_{a2},{\mathrm{\Sigma }}_{a2}),{\mathit{\mu }}_{a2}={(0,-4)}^{\top },{\mathrm{\Sigma }}_{a2}=\mathrm{diag}(0.5,0.75),$$

with small Gaussian noise added. In all experiments, we generate 1200 normal points and 800 anomalies, for a total of 2000 observations in ${\mathbb{R}}^2$.

The synthetic datasets are randomly partitioned at the observation level into training, validation, and test sets. We first reserve $30\%$ of the data as a test set. From the remaining $70\%$, we select $20\%$ as a validation set using stratified sampling, so that the proportions of normal and anomalous points are preserved in each split. This yields approximately $56\%$ of the data for training, $14\%$ for validation, and $30\%$ for testing. Within the training set, we construct a semi-supervised labeling scheme by retaining $10\%$ of the training normals as labeled normals with $y=+1$ and $10\%$ of the training anomalies as labeled anomalies with $y=-1$. All remaining training points are treated as unlabeled with $y=0$. This results in a setting where only a small subset of both classes is labeled, while the unlabeled pool contains a mixture of normals and anomalies, replicating realistic contamination in semi-supervised anomaly detection.

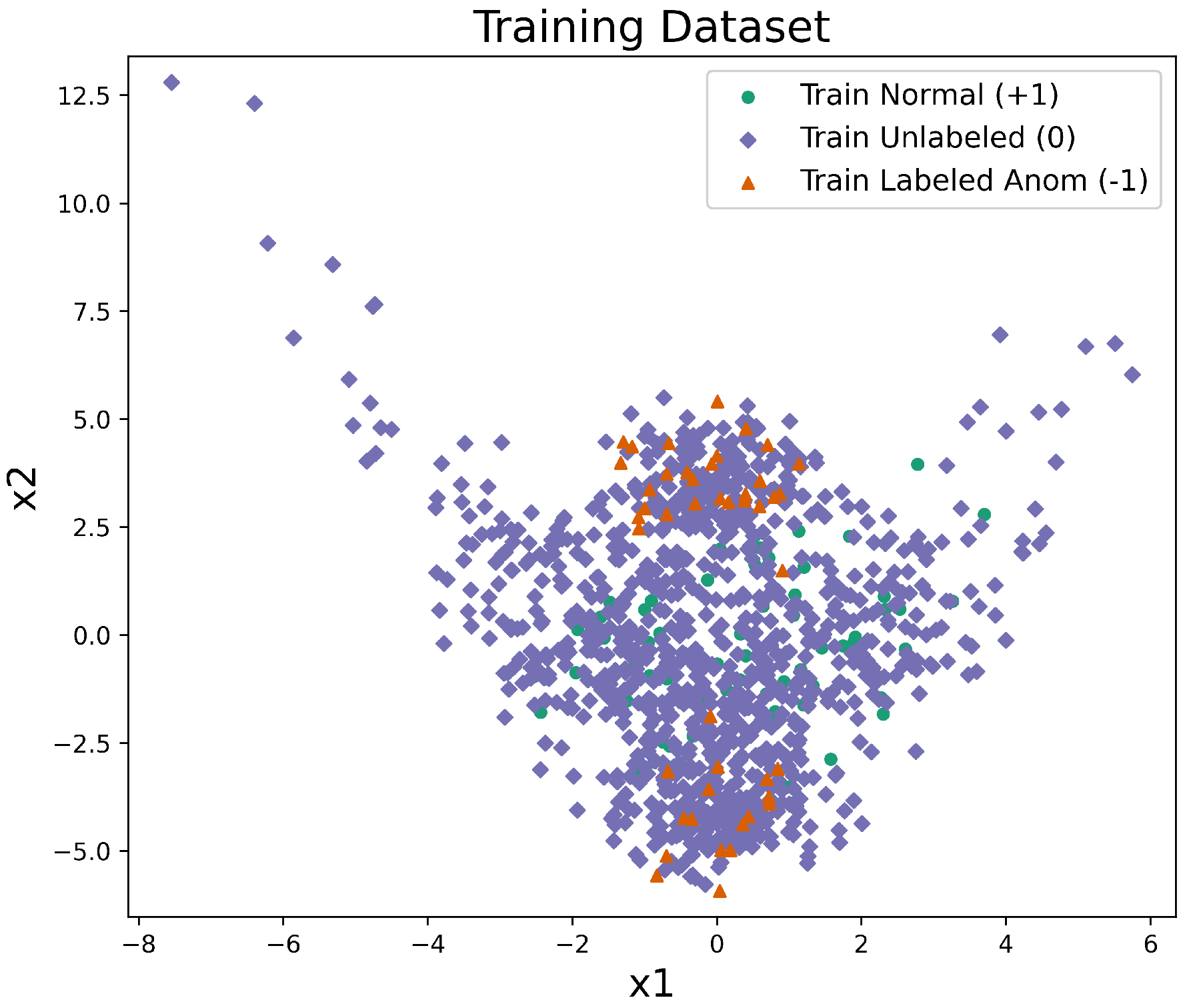
The same observation-level train/validation/test partitions and label budgets are used for all methods to ensure a fair comparison. For the deep methods, AAG-DSVDD and DeepSAD are trained on the full training set, using labeled normals ($y=+1$) and labeled anomalies ($y=-1$) together with the unlabeled points ($y=0$). In contrast, DeepSVDD is trained only on the labeled normal samples ($y=+1$), representing a supervised deep one-class baseline. The classical OC-SVM and SVDD-RBF baselines are trained on the training normals only ($y=+1$), ignoring unlabeled and anomaly samples during training. The validation set is used exclusively for hyperparameter selection, while the test set is held out for final evaluation. A sample training dataset from an experiment is shown in Figure 1.

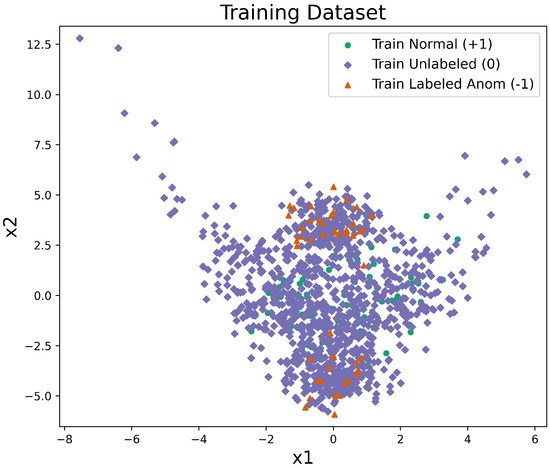
Figure 1. Example training split for the synthetic banana dataset under the semi-supervised labeling scheme. Labeled normals ($y=+1$) are shown as green circles, labeled anomalies ($y=$ −1) as orange triangles, and unlabeled points ($y=0$) as purple diamonds whose true class is hidden during training.

All experiments on the synthetic and public datasets were implemented on a Windows workstation equipped with a 13th Gen Intel Core i9-13900K (3.00 GHz), 64 GB of RAM, and an NVIDIA RTX 4090 GPU.

4.1.2. Evaluation Metrics for Synthetic Dataset Experiments

All methods output an anomaly score $s\left(\mathbf{x}\right)$, with larger values indicating more anomalous points. For AAG-DSVDD, we use the signed squared radial distance:

$$s\left(\mathbf{x}\right)={\parallel \varphi (\mathbf{x};W^{*})-\mathbf{c}\parallel }_2^2-{\left(R^{*}\right)}^2.$$

DeepSVDD and DeepSAD use their standard distance-based scores in latent space, which have the same form up to the learned center and radius. For OC-SVM and SVDD-RBF, we use their native decision functions, with signs adjusted where necessary, so that higher values correspond to a higher degree of abnormality.

For each method and each random seed, we select a decision threshold $\tau$ on the validation set by scanning candidate thresholds and choosing the one that maximizes the F1-score on the validation split. On the held-out test set, an observation $\mathbf{x}$ is then classified as anomalous if $s\left(\mathbf{x}\right)>\tau$ and normal otherwise. The anomaly class is treated as the positive class in all evaluations.

Given the resulting binary predictions, we compute the confusion counts $\mathrm{TP}$ (true positives), $\mathrm{FP}$ (false positives), $\mathrm{TN}$ (true negatives), and $\mathrm{FN}$ (false negatives) on the test set. From these we report precision, recall, F1-score, and accuracy:

$$\mathrm{Recall}={\displaystyle \frac{\mathrm{TP}}{\mathrm{TP}+\mathrm{FN}}},\mathrm{Precision}={\displaystyle \frac{\mathrm{TP}}{\mathrm{TP}+\mathrm{FP}}},$$

$$\mathrm{F}1={\displaystyle \frac{2·\mathrm{Precision}·\mathrm{Recall}}{\mathrm{Precision}+\mathrm{Recall}}},\mathrm{Accuracy}={\displaystyle \frac{\mathrm{TP}+\mathrm{TN}}{\mathrm{TP}+\mathrm{TN}+\mathrm{FP}+\mathrm{FN}}}.$$

To assess robustness to random initialization and sampling, we repeat the entire procedure over ten random seeds $0, 1, \dots , 9$. For each method, we summarize performance by reporting the mean and standard deviation of the test F1-score across these seeds.

4.1.3. Hyperparameters Selection and Training Procedure

For the synthetic banana experiment, the hyperparameter settings for AAG-DSVDD, DeepSVDD, DeepSAD, OC-SVM, and SVDD-RBF were obtained through validation-based tuning and then kept fixed for all reported runs. Concretely, we first fixed the encoder architecture and then tuned the AAG-DSVDD hyperparameters on the validation split by a small grid search. Scalar coefficients in the objective ($\{{\eta }_{\mathrm{unl}}, {\lambda }_u, \mathrm{\Omega }, m\}$) were selected from logarithmic or short linear grids. The neighborhood size of the latent k-NN graph was chosen from a discrete set of candidates. The final configuration corresponds to the setting that maximizes the validation F1-score subject to stable training behavior. The deep baselines were tuned in the same manner where DeepSVDD reuses the selected encoder and soft-boundary setting, and the labeled-term weight in DeepSAD is chosen from a short grid on the validation set. For OC-SVM and SVDD-RBF, we performed a small grid search over the one-class parameter and RBF kernel width around the scale heuristic and selected the configuration that maximizes validation F1. The one-class parameter $\nu$ was fixed at $0.05$ for all methods.

All deep methods use the same MLP encoder $\varphi (·;W)$ for fairness. The encoder maps ${\mathbb{R}}^2$ to a 16-dimensional latent space through two hidden layers of sizes 256 and 128 with ReLU activations. AAG-DSVDD and DeepSAD are trained with the Adam optimizer. DeepSVDD is trained with the AdamW optimizer, which showed better performance on the validation split. All models are trained for 50 epochs, with mini-batches of size 128 and a learning rate of ${10}^{-3}$. The ${\ell }_2$ weight decay (decoupled weight decay in the case of AdamW) is set to ${10}^{-4}$ for AAG-DSVDD and ${10}^{-6}$ for DeepSVDD and DeepSAD. The anomaly class is treated as the positive class in all evaluations.

For AAG-DSVDD we use the soft-boundary formulation of Section 3 with squared hinges ($r=2$), soft-boundary parameter $\nu =0.05$, anomaly weight $\mathrm{\Omega }=2$, and margin $m=1.0$. The unlabeled center-pull weight is set to ${\eta }_{\mathrm{unl}}=1.0$, and the graph smoothness weight to ${\lambda }_u=0.1$, which provides a moderate level of graph-based regularization. The latent k-NN graph uses $k=15$ neighbors with the locally scaled Gaussian affinities of Section 3.2. The radius update schedule and graph-refresh schedule follow Section 3.4, with quantile-based updates of $R^2$ at level $\nu =0.05$ and reconstruction of the latent k-NN graph every two epochs.

DeepSVDD uses the same encoder architecture and soft-boundary parameter $\nu =0.05$ but is trained on labeled normals only, following the standard one-class setup. It omits anomaly margins, unlabeled pull-in, and graph regularization. DeepSAD is instantiated with the same encoder and optimizes the semi-supervised DeepSAD objective on the same labeled and unlabeled splits, with labeled-term weight $\eta =0.05$. Unlabeled points contribute through the DeepSAD loss. Both AAG-DSVDD and DeepSAD exploit labeled anomalies, whereas DeepSVDD does not.

OC-SVM and SVDD-RBF are trained on the same training normals (ignoring anomaly labels) with an RBF kernel and $\nu =0.05$. OC-SVM uses the scale heuristic for the kernel width $\gamma$ (included in the scikit-learn OC-SVM library), while SVDD-RBF uses a fixed kernel width parameter ${\gamma }_{\mathrm{RBF}}=1$. These methods serve as classical non-deep one-class baselines with fixed kernels in the input space, in contrast to the learned latent geometry of the deep methods.

4.1.4. Results and Analysis

The performance comparison of the methods on the synthetic banana dataset is given in Table 1 and Table 2. Table 1 presents the performance of the methods in an experiment conducted on the synthetic banana dataset. AAG-DSVDD achieves the best performance on three metrics. It reaches an F1 score of 0.89 and an accuracy of 0.91. Its recall is 0.90, which is slightly lower than DeepSAD at 0.98, but AAG-DSVDD maintains a much higher precision of 0.87 compared to 0.49 for DeepSAD. DeepSVDD, OC-SVM, and SVDD-RBF also show imbalanced tradeoffs between recall and precision. DeepSAD and DeepSVDD favor recall and allow for many false alarms on normal samples, reducing their F1 scores and accuracies. OC-SVM and SVDD-RBF improve precision relative to deep one-class baselines but still fall short of AAG-DSVDD in F1, recall, and accuracy.

Table 1. Per-method test performance on the synthetic banana dataset under the semi-supervised setting. For each model F1, recall, precision, and accuracy are reported. Bold entries indicate the best value for each metric across all methods.

Model	F1	Recall	Precision	Accuracy
OC-SVM	0.6625	0.6667	0.6584	0.7283
SVDD-RBF	0.7259	0.8167	0.6533	0.7533
DeepSVDD	0.6055	0.6875	0.5410	0.6417
DeepSAD	0.6510	0.9792	0.4876	0.5800
AAG-DSVDD	0.8852	0.9000	0.8710	0.9067

Table 2. F1 performance on the synthetic banana dataset over 10 random seeds. The row “Mean ± Std” reports the average and standard deviation over seeds. The last two rows give one-sided paired t-test and Wilcoxon signed-rank p-values for the null hypothesis that each baseline has F1 at least as large as AAG-DSVDD. Bold values indicate the best performance for each seed and the best average performance.

Seed	OC-SVM	SVDD-RBF	DeepSVDD	DeepSAD	AAG-DSVDD
0	0.66	0.73	0.61	0.65	0.89
1	0.83	0.83	0.66	0.68	0.88
2	0.65	0.75	0.51	0.63	0.90
3	0.79	0.70	0.66	0.64	0.89
4	0.62	0.78	0.57	0.65	0.88
5	0.75	0.74	0.68	0.64	0.86
6	0.78	0.82	0.67	0.65	0.88
7	0.74	0.76	0.72	0.64	0.88
8	0.63	0.79	0.58	0.68	0.88
9	0.68	0.76	0.58	0.63	0.84
Mean ± Std	$0.71\pm 0.08$	$0.76\pm 0.04$	$0.62\pm 0.06$	$0.65\pm 0.02$	$0.88\pm 0.02$
$p_{t\text{-}\mathrm{test}}$	$4.0\times {10}^{-5}$	$1.1\times {10}^{-5}$	$4.7\times {10}^{-7}$	$8.7\times {10}^{-11}$	–
$p_{\mathrm{Wilcoxon}}$	$9.8\times {10}^{-4}$	$9.8\times {10}^{-4}$	$9.8\times {10}^{-4}$	$9.8\times {10}^{-4}$	–

Table 2 examines robustness in ten independent runs with different random seeds. AAG-DSVDD consistently achieves the highest F1 score, with a mean of 0.88 and a standard deviation of 0.02. The strongest baseline is SVDD-RBF, with a mean F1 of 0.76 and a standard deviation of 0.04. OC-SVM, DeepSVDD, and DeepSAD achieve mean F1 scores of 0.71, 0.62, and 0.65, respectively, with moderately greater variability. The paired t-tests and the Wilcoxon signed-rank tests in the bottom rows of Table 2 compare each baseline with AAG-DSVDD under the one-sided alternative that AAG-DSVDD has a higher F1. All t-test p-values are below $4.0\times {10}^{-5}$ and all Wilcoxon p-values equal $9.8\times {10}^{-4}$. These results show that the improvements of AAG-DSVDD over each baseline are not only large in magnitude but also statistically significant across different random realizations of the dataset and the semi-supervised labels.

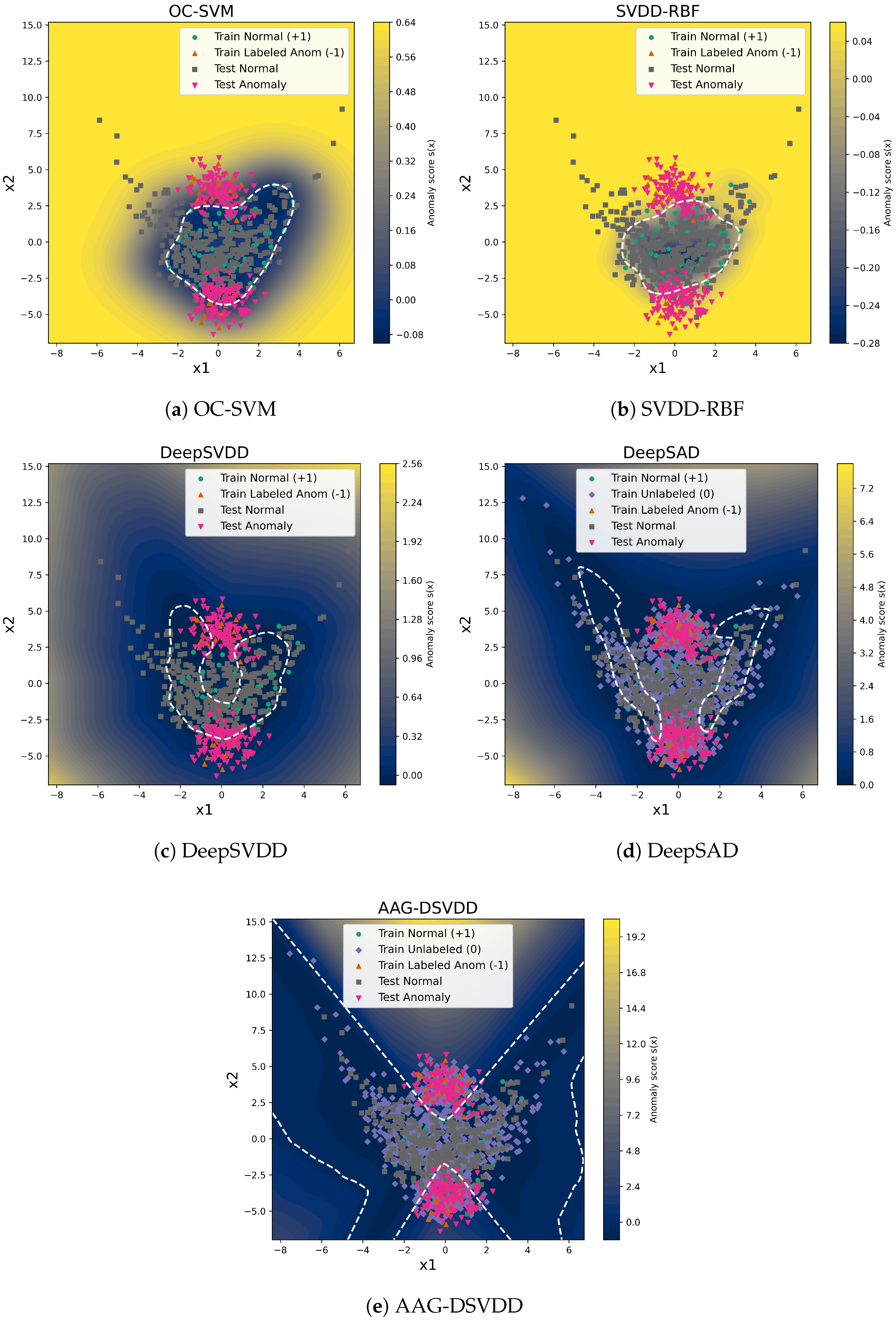
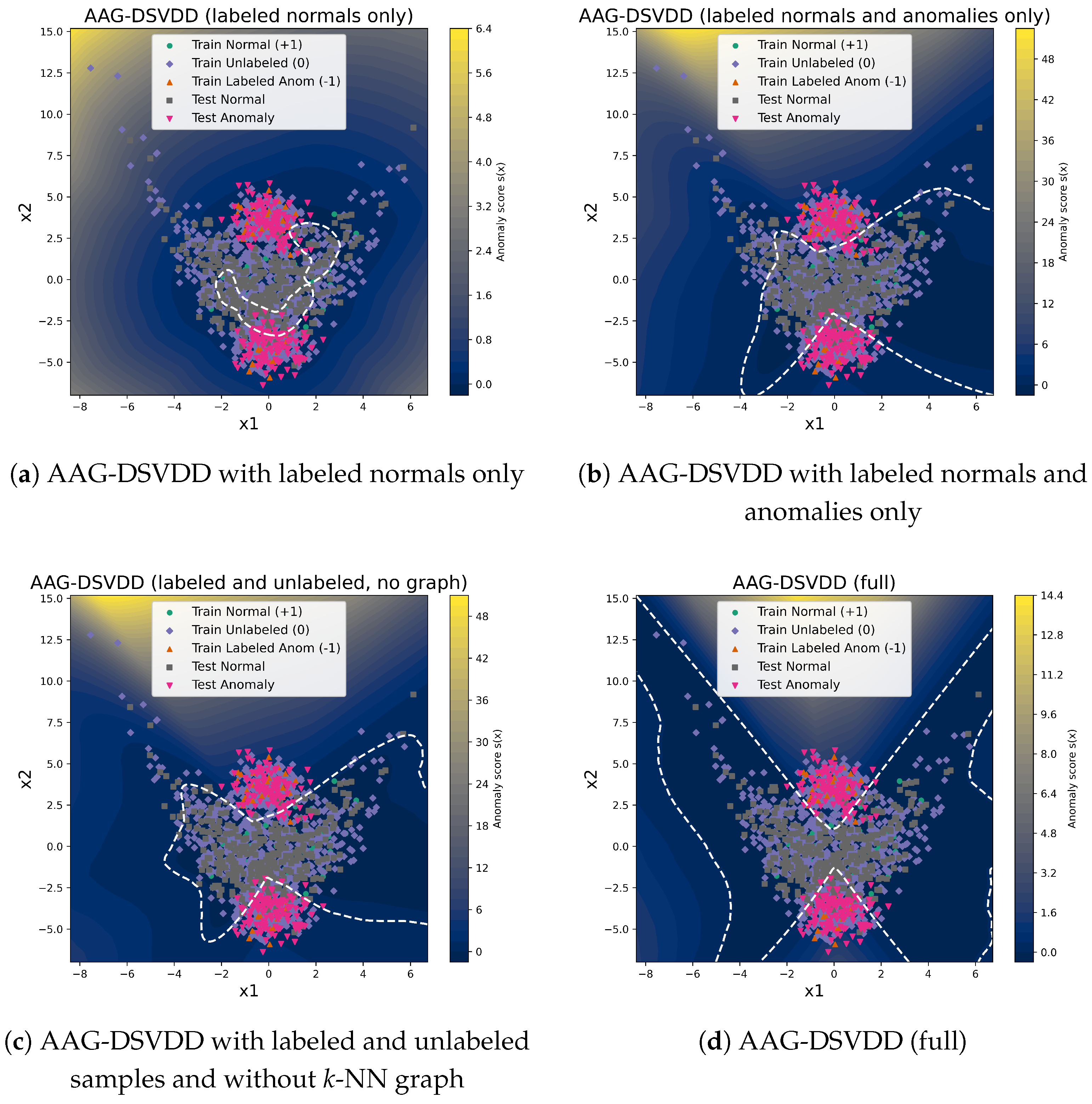
The decision boundaries obtained over an experiment are shown in Figure 2 for all the methods. These trends are consistent with how the different objectives use labels and geometry. DeepSVDD is trained only on labeled normals and fits a soft-boundary hypersphere in latent space. With few labeled normals, the learned region stays concentrated around the densest part of the data, so many legitimate normals in sparser areas are rejected as anomalies, which drives up false positives and reduces precision, accuracy, and F1. DeepSAD introduces labeled anomalies and an unlabeled term, but still relies on distances to a single center. In this setting, it tends to enlarge the decision region to recover anomalous points, which explains its very high recall but also its low precision.

Figure 2. Anomaly-score surfaces and decision boundaries on the synthetic banana dataset under the semi-supervised setting (10% labeled normals and 10% labeled anomalies). The background heat map shows the anomaly score $s\left(\mathbf{x}\right)$ (brighter regions indicate higher scores), and the white dashed contour marks the decision boundary corresponding to the F1-maximizing threshold on the validation set for each method.

OC-SVM and SVDD-RBF learn directly in the input space with fixed RBF kernels without representation learning or graph structure. They form smooth one-class boundaries around the global data cloud and achieve better precision than DeepSVDD and DeepSAD, yet they cannot adapt the feature space or exploit the unlabeled manifold structure, so they remain clearly dominated by AAG-DSVDD in F1 and accuracy. In contrast, AAG-DSVDD combines a DeepSVDD-style enclosure with a latent k-NN graph and anomaly-aware regularization. The graph term couples scores along the latent manifold so that unlabeled samples help stabilize the center and radius, while anomaly-weighted edges and push-out penalties move the boundary away from regions associated with anomalies. This produces a decision region that covers most normals and excludes anomaly clusters, consistent with the higher and more stable F1 scores observed for AAG-DSVDD in Table 1 and Table 2.

Note that all deep models in this comparison (DeepSVDD, DeepSAD, and AAG-DSVDD) produce one-class decision regions defined by a single hypersphere in latent space, with the radius set by the learned quantile on labeled normals. When these distance-based boundaries are visualized in the original input space (in Figure 2) after the nonlinear mapping of the encoder, the corresponding curves can appear highly curved or even disconnected, despite arising from a single hypersphere in the learned latent representation.

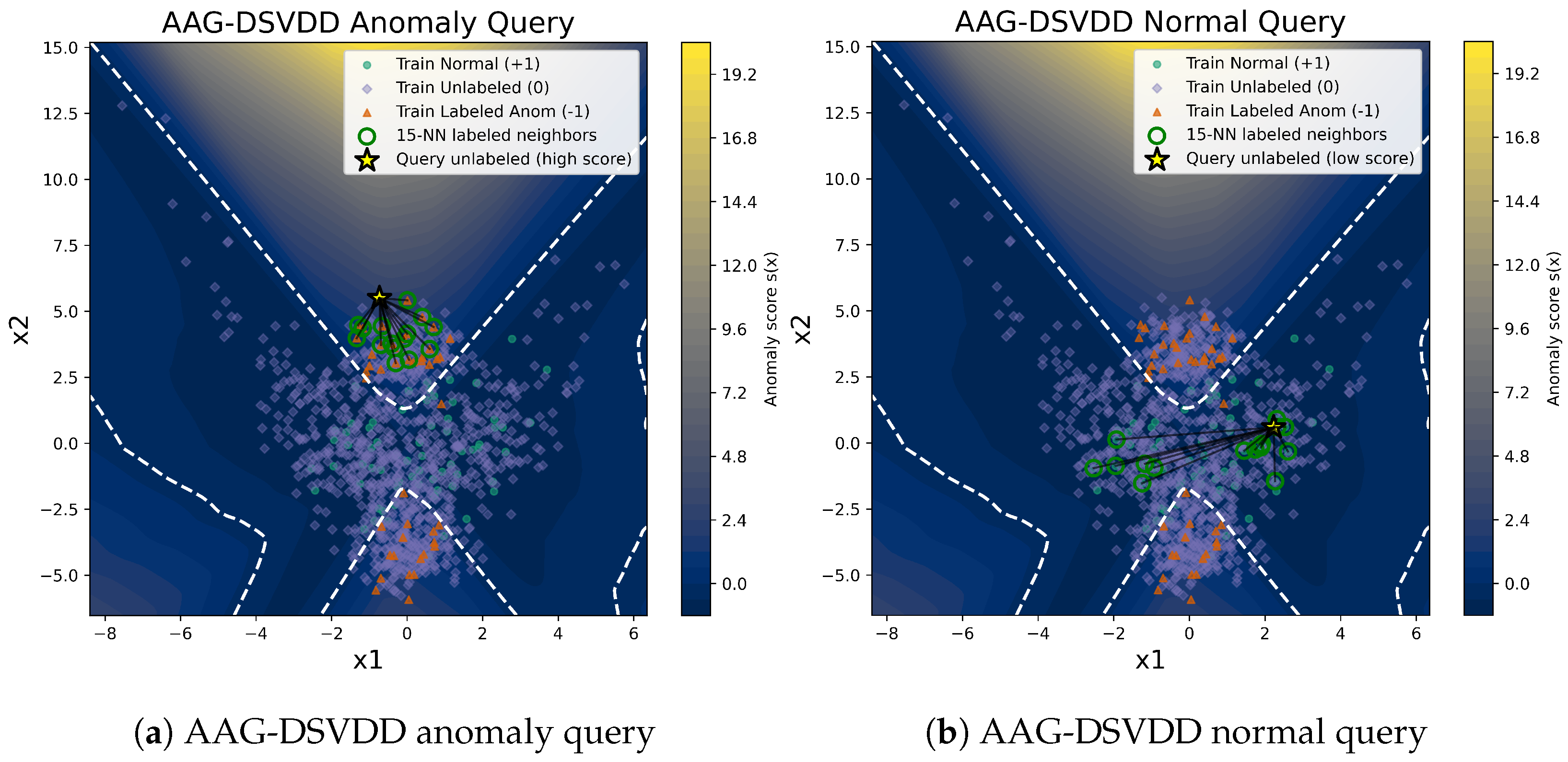
AAG-DSVDD also provides intuitive, example-based interpretation on this synthetic task. Figure 3 illustrates two representative unlabeled query points. One has a low anomaly score inside the learned normal region, and the other has a high anomaly score in the upper anomalous cluster. For each query, we perform a k-NN search in the latent space over the labeled training samples and overlay the resulting labeled neighbors in the input space together with the decision boundary. In the high-score query, the nearest neighbors are predominantly labeled anomalies concentrated in the upper anomalous region. This supports an anomalous interpretation and clarifies which abnormal pattern the model is matching. In the low-score query, the neighbors are labeled normals well inside the interior of the decision region. This indicates that the small score arises from similarity to benign operating conditions. These example-level views show that the graph-regularized latent representation and latent k-NN structure allow practitioners to inspect which labeled scenarios justify the anomaly score of an unlabeled sample instead of relying only on a scalar value.

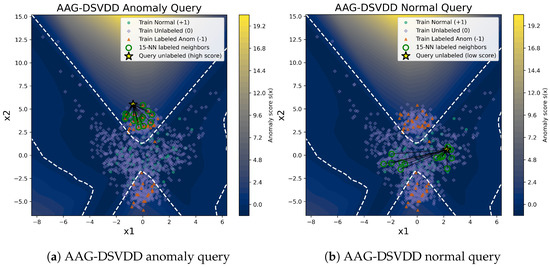
Figure 3. Sample-level interpretation for AAG-DSVDD on the synthetic dataset. The background shows the anomaly score $s\left(\mathbf{x}\right)$, and the white dashed curve is the decision boundary. (a) Anomaly query: a high-scoring anomalous test point (yellow star) and its labeled neighbors (green circles), which are dominated by labeled anomalies in the upper cluster. (b) Normal query: a low-scoring normal test point and its labeled neighbors, which lie well inside the decision region and are dominated by labeled normals.

In the normal query of Figure 3, several labeled normal neighbors appear relatively far from the query in the two-dimensional input plane but remain nearest neighbors in latent space. This visually illustrates that the learned, graph-regularized latent representation reorganizes the data. Points that are distant in input space can become close in latent space; thus, the neighbors used for interpretation reflect the learned manifold structure rather than the raw Euclidean geometry of the original features.

4.2. Public Datasets Experiments

4.2.1. Public Datasets Description

We evaluate the proposed method on three real-valued benchmark data sets from the UCI Machine Learning Repository: Annthyroid, Arrhythmia, and Cleveland Heart Disease. A summary of their characteristics is given in Table 3.

Table 3. Description of UCI public datasets used in the experiments.

Dataset	Sample Size (Normal/Anomaly)	Total Samples	Total Features
Thyroid	$6666/534$	7200	6
Arrhythmia	$245/207$	452	279
Heart	$164/139$	303	13

In the Annthyroid dataset, the target variable distinguishes between three clinical classes: normal thyroid function, hypothyroidism, and hyperthyroidism. We regard the normal-function class as the normal class and treat both hypo- and hyperthyroid samples as anomalies. The Arrhythmia data set contains sixteen rhythm categories: one “no arrhythmia” group and fifteen arrhythmia types. We consider the “no arrhythmia” class as normal and aggregate all fifteen arrhythmia classes into a single anomaly class. In the Cleveland Heart Disease dataset, the diagnosis variable takes five discrete values indicating absence or graded presence of coronary artery disease. We treat patients with diagnosis value 0 (no disease) as normal and samples with diagnosis $>$0 (presence of disease) as anomalous.

4.2.2. Public Datasets Experiment Setup

The benchmark datasets are handled analogously to the synthetic data. For each dataset, we first construct binary labels $y\in \{0,1\}$ according to the class definitions described above, where $y=0$ denotes a normal observation and $y=1$ denotes an anomaly. We then partition the observations into training, validation, and test sets using stratified sampling with respect to these binary labels. We first reserve $30\%$ of the data as a test set. From the remaining $70\%$, we select $20\%$ as a validation set and use the rest for training, which yields approximately $56\%$ of the data for training, $14\%$ for validation, and $30\%$ for testing.

Within the training set, we design a semi-supervised labeling scheme by retaining $10\%$ of the normal training samples as labeled normals with $y=+1$ and $10\%$ of the anomalous training samples as labeled anomalies with $y=-1$. All remaining training samples are considered unlabeled and assigned $y=0$. The validation set is used for threshold selection and hyperparameter tuning. The test set is used performance evaluation. Both validation and testing sets preserve their binary ground-truth labels $y\in \{0,1\}$. The resulting samples in each set are summarized in Table 4.

Table 4. Split statistics and semi-supervised labels for UCI data sets.

Dataset	Split	Sample Size	Normal	Anomaly	Labeled Normal $(+1)$	Labeled Anomaly $(-1)$	Unlabeled $\left(0\right)$
Thyroid	Train	4032	3733	299	373	30	3629
	Validation	1008	933	75	–	–	–
	Test	2160	2000	160	–	–	–
Arrhythmia	Train	252	136	116	14	12	226
	Validation	64	35	29	–	–	–
	Test	136	74	62	–	–	–
Heart	Train	169	92	77	9	8	152
	Validation	43	23	20	–	–	–
	Test	91	49	42	–	–	–

4.2.3. Hyperparameter Selection on Public Datasets

For the public datasets, we follow the same validation-based hyperparameter selection strategy as in the synthetic banana experiment and enforce a common architecture and optimization setup across all deep methods. All deep models (AAG-DSVDD, DeepSVDD, and DeepSAD) use an MLP encoder $\varphi (·;W)$ that maps ${\mathbb{R}}^D$ to a 16-dimensional latent space through two hidden layers of sizes 256 and 128 with ReLU activations. All deep models are trained with the Adam optimizer (DeepSVDD with AdamW) for 50 epochs, mini-batches of size 128, and learning rate ${10}^{-3}$. The ${\ell }_2$ weight decay is set to ${10}^{-4}$ for AAG-DSVDD and ${10}^{-6}$ for DeepSVDD and DeepSAD. The soft-boundary parameter in AAG-DSVDD and DeepSVDD is fixed at $\nu =0.05$ for all datasets. For the one-class baselines, OC-SVM and SVDD-RBF also use $\nu =0.05$; OC-SVM employs the scale heuristic for the RBF kernel width $\gamma$, while SVDD-RBF uses a dataset-specific RBF width ${\gamma }_{\mathrm{RBF}}$.

Within this shared setup, we tune the remaining scalar hyperparameters of all methods by grid searches on the validation split. For AAG-DSVDD, we select the unlabeled pull-in weight ${\eta }_{\mathrm{unl}}$, graph weight ${\lambda }_u$, anomaly weight $\mathrm{\Omega }$, margin m, and latent neighborhood size k, choosing the configuration that maximizes the validation F1-score under stable training. DeepSVDD and DeepSAD reuse the common encoder and optimization settings and are tuned as in the synthetic experiment, with the DeepSAD labeled-term weight selected on the validation set. For OC-SVM and SVDD-RBF, we perform short grids over the one-class and kernel parameters and retain $\nu =0.05$ and the dataset-specific RBF widths ${\gamma }_{\mathrm{RBF}}$ reported in Table 5. The final dataset-specific values are summarized in Table 5.

Table 5. Dataset-specific scalar hyperparameters for the public dataset experiments.

Dataset	AAG-DSVDD Scalars $({\mathit{\lambda }}_{\mathit{u}},\mathit{k},{\mathit{\eta }}_{\mathbf{unl}},\mathbf{\Omega },\mathit{m})$	SVDD-RBF ${\mathit{\gamma }}_{\mathbf{RBF}}$
Thyroid	$(0.01,7,0.01,2.0,1.0)$	15
Arrhythmia	$(0.001,5,30,2.0,1.0)$	$0.02$
Heart	$(0.01,5,0.01,2.0,0.775)$	$0.1$

4.2.4. Results and Analysis on Public Datasets

Table 6 reports the test performance of all methods on the three public datasets, using the metrics defined in Section 4.1.2. Across all datasets, AAG-DSVDD attains the highest F1-score and therefore offers the best overall balance between missed detections and false alarms. On Thyroid and Heart, it also achieves the highest accuracy and the strongest precision while maintaining high recall. On Arrhythmia, AAG-DSVDD still yields the best F1-score (0.675) with very high recall (0.919) and moderate precision. In this setting, SVDD-RBF attains slightly higher accuracy and precision but at the cost of a clear drop in recall.

Table 6. Test-set performance of all methods on the public datasets under the semi-supervised label-budget setting. For each dataset, we report F1, recall, precision, and accuracy.

Dataset	Method	F1	Recall	Precision	Accuracy
Thyroid	AAG-DSVDD	0.719	0.750	0.690	0.956
	DeepSVDD	0.171	0.125	0.270	0.910
	DeepSAD	0.668	0.831	0.559	0.939
	OC-SVM	0.230	0.175	0.337	0.913
	SVDD-RBF	0.270	0.244	0.302	0.902
Arrhythmia	AAG-DSVDD	0.675	0.919	0.533	0.596
	DeepSVDD	0.590	0.581	0.600	0.632
	DeepSAD	0.658	0.823	0.548	0.610
	OC-SVM	0.667	0.935	0.518	0.574
	SVDD-RBF	0.656	0.694	0.623	0.669
Heart	AAG-DSVDD	0.800	0.857	0.750	0.802
	DeepSVDD	0.642	0.810	0.531	0.582
	DeepSAD	0.714	0.952	0.571	0.648
	OC-SVM	0.702	0.786	0.635	0.692
	SVDD-RBF	0.727	0.857	0.632	0.703

Bold values indicate the best performance for each dataset and metric.

The baselines show clear trade-offs. DeepSVDD is trained only on labeled normals and tends to fit a compact region around the densest normal patterns. Its recall and F1-score are very low on Thyroid and Heart because many less typical normals are incorrectly flagged as anomalies. DeepSAD introduces labeled anomalies and an unlabeled term, which strongly improves recall. At the same time, it often enlarges the decision region too much, which lowers precision and reduces F1 and accuracy, especially on Thyroid and Heart.

OC-SVM and SVDD-RBF operate directly in the input space with fixed RBF kernels and no learned representation or graph structure. They often achieve better precision than DeepSVDD and DeepSAD, especially on Arrhythmia and Heart. However, they do not reach the F1 or accuracy of AAG-DSVDD on Thyroid and Heart and still struggle to balance precision and recall on Arrhythmia. Their fixed kernel geometry limits adaptation to complex data manifolds in the semi-supervised setting.

AAG-DSVDD combines a DeepSVDD-style enclosure with anomaly-aware graph regularization on the latent k-NN graph. The graph term couples scores of neighboring points, so unlabeled samples help refine the center and radius. Anomaly-weighted edges and margin-based push-out penalties move the boundary away from regions associated with anomalous behavior. On Thyroid and Heart, this produces a decision region that captures most normals and separates anomalies more cleanly, which leads to higher precision, F1, and accuracy than all baselines. On Arrhythmia, AAG-DSVDD remains competitive in precision and preserves very high recall, and this combination yields the best F1-score among all methods.

4.3. Effect of Graph Regularization Weight

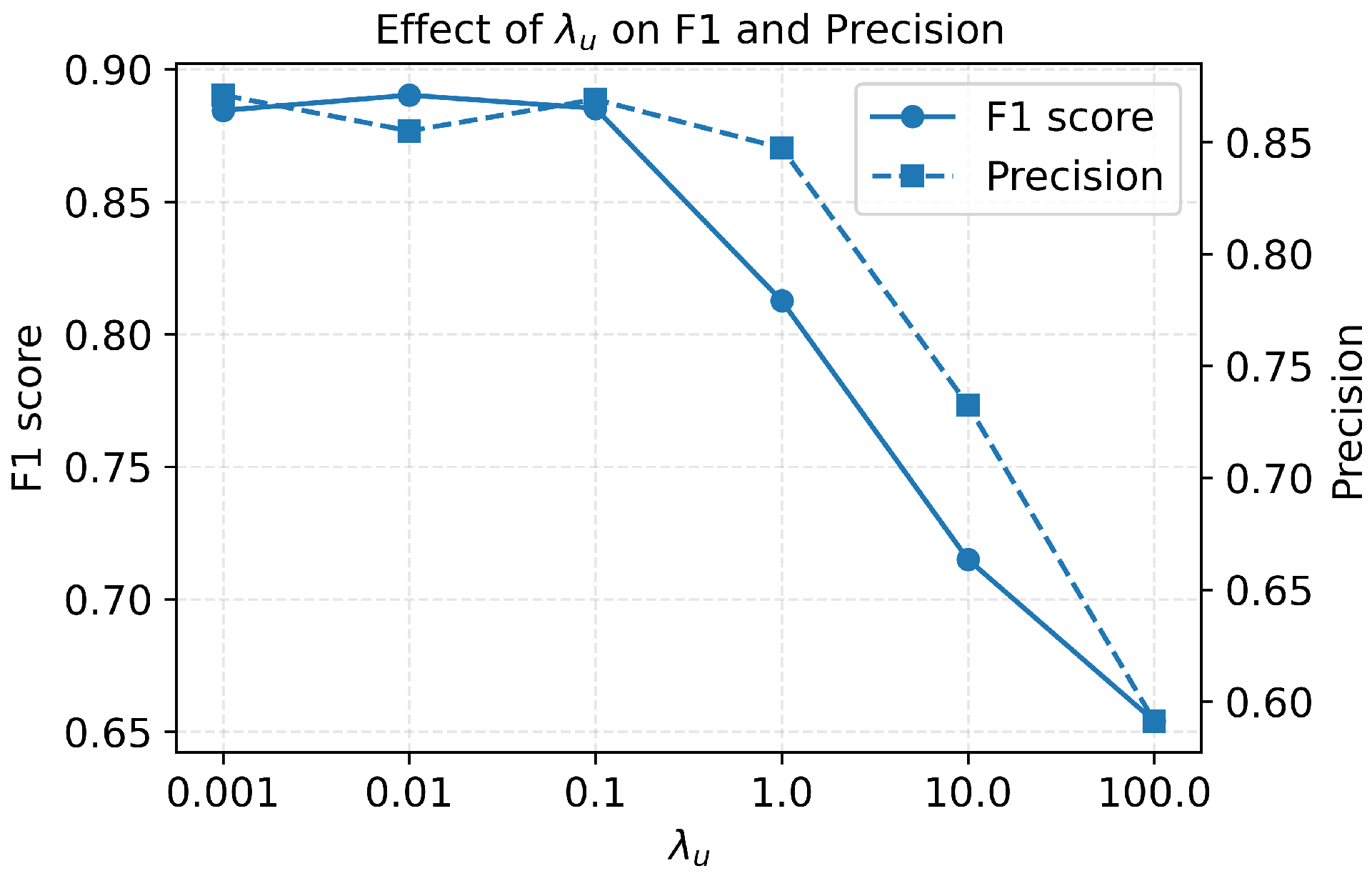
To assess the impact of the graph regularizer, we varied ${\lambda }_u\in \{{10}^{-3},{10}^{-2},{10}^{-1},1,10,100\}$ on the synthetic banana dataset while keeping all other hyperparameters fixed. Figure 4 reports the resulting F1-score and precision. For small to moderate values (${10}^{-3}$–${10}^{-1}$), performance is stable as F1 remains around $0.88$–$0.89$ and precision around $0.85$–$0.87$, indicating that the method benefits from graph-based smoothing but is not overly sensitive to the exact choice of ${\lambda }_u$ in this range.

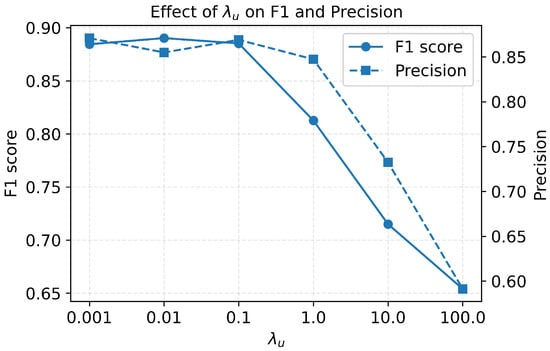
Figure 4. Effect of the graph regularization weight ${\lambda }_u$ on AAG-DSVDD performance on the synthetic banana dataset. The x-axis shows the values of ${\lambda }_u$, the left y-axis shows the F1-score, and the right y-axis shows the precision. The solid line plots the F1-score, whereas the dashed line plots precision. Performance is stable for small to moderate ${\lambda }_u$ values and degrades once ${\lambda }_u$ values become much larger.

As ${\lambda }_u$ increases beyond 1, both F1 and precision degrade monotonically. At ${\lambda }_u=1$, the F1-score drops to about $0.81$, and for very large regularization (${\lambda }_u=100$), it falls below $0.66$, with a corresponding precision below $0.60$. This pattern is consistent with an over-smoothing effect. Excessively strong graph regularization pushes squared distances toward locally uniform values, obscuring the boundary between normal and anomalous regions. Based on these results, we use ${\lambda }_u=0.1$ in the main synthetic experiments, a robust trade-off between leveraging the latent graph and avoiding over-regularization.

4.4. Ablation Study of AAG-DSVDD

We perform an ablation study on the synthetic banana dataset. The semi-supervised setting uses 10% labeled normals and 10% labeled anomalies in the training split. For this qualitative ablation on the banana data, we slightly adjust the AAG-DSVDD hyperparameters relative to Section 4.1.3 in order to obtain a clearer soft-boundary solution in the labeled-normal-only regime. We fix these settings for all four variants so that differences are due only to the loss terms. Table 7 summarizes the quantitative results.

Table 7. Ablation of AAG-DSVDD on the synthetic banana dataset. F1, recall (Rec.), precision (Prec.), accuracy (Acc.), TP, FP, TN, and FN metrics are reported over the testing set.

Variant	F1	Rec.	Prec.	Acc.	TP	FP	TN	FN
AAG-DSVDD (labeled normals only)	0.606	0.904	0.456	0.530	217	259	101	23
AAG-DSVDD (labeled normals and anomalies only)	0.834	0.900	0.777	0.857	216	62	298	24
AAG-DSVDD (labeled and unlabeled, without k-NN graph)	0.861	0.912	0.814	0.882	219	50	310	21
AAG-DSVDD (full)	0.876	0.917	0.840	0.897	220	42	318	20

In this ablation study, we use the soft-boundary formulation with squared hinges ($p=2$) and $\nu =0.15$. The anomaly hinge weight is $\mathrm{\Omega }=1.0$, and the margin is $m=1.0$. The graph smoothness weight is ${\lambda }_u=0.1$, and the unlabeled pull-in weight is ${\eta }_{\mathrm{unl}}=0.01$. The latent k-NN graph uses $k=16$ neighbors. The encoder has two hidden layers of sizes 256 and 128 and a 16-dimensional latent layer. We train with Adam, learning rate ${10}^{-3}$, weight decay ${10}^{-4}$, batch size 128, 50 epochs, and 2 warmup epochs.

We study four variants: (i) AAG-DSVDD (with labeled normals only) keeps only the soft-boundary hinge on labeled normals and the radius term $R^2$ and removes the anomaly hinge, the unlabeled pull, and the graph term. (ii) AAG-DSVDD (with labeled normals and anomalies only) activates the anomaly hinge on labeled anomalies and still disables the unlabeled pull and the graph term. (iii) AAG-DSVDD (with labeled and unlabeled observations, without k-NN graph) uses the full loss except for the k-NN graph loss term and sets ${\lambda }_u=0$. (iv) AAG-DSVDD (full) uses all loss components.

The labeled-normals-only variant behaves like a DeepSVDD-style soft-boundary model that sees only labeled normals. The anomaly hinge is inactive in this configuration. The objective therefore reduces to a hypersphere on labeled normals and corresponds to a zero-anomaly-label regime for AAG-DSVDD. On banana, it achieves $\mathrm{F}1=0.606$, recall $0.904$, precision $0.456$, and accuracy $0.530$, with TP $=217$, FP $=259$, TN $=101$, and FN $=23$. In Figure 5a, the dashed contour forms a compact region around the dense central part of the banana-shaped normal distribution. It truncates the low-density outer regions and misses many normal points in the periphery.

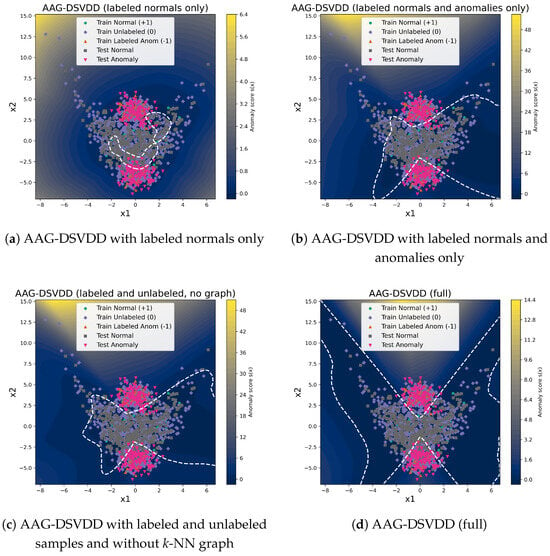
Figure 5. Decision boundaries of the AAG-DSVDD ablation variants on the synthetic banana dataset. The background shows the anomaly score surface $s\left(\mathbf{x}\right)$, and the white dashed line marks the level set at the F1-maximizing threshold on the validation set. (a) Labeled normals only. (b) Labeled normals and anomalies only. (c) Labeled normals, anomalies, and unlabeled center pull. (d) Full AAG-DSVDD with labeled normals, labeled anomalies, unlabeled pull, and graph regularization.

AAG-DSVDD (with labeled normals and anomalies only) adds the anomaly hinge. Labeled anomalies are pushed outside the hypersphere and labeled normals are kept inside. On the banana dataset, this variant reaches $\mathrm{F}1=0.834$, recall $0.900$, precision $0.777$, and accuracy $0.857$, with TP $=216$, FP $=62$, TN $=298$, and FN $=24$. The boundary in Figure 5b bends along the banana-shaped normal region and separates the two anomaly clusters more clearly than the labeled-normals-only model. Some false alarms remain near the far ends of the banana-shaped normal region where the density of normals is low.

AAG-DSVDD (with labeled and unlabeled, without k-NN graph) also turns on the unlabeled center-pull term while keeping ${\lambda }_u=0$. The unlabeled set is large and contains both normals and anomalies. The anomaly hinge prevents contaminated unlabeled anomalies from collapsing into the center. The center-pull still helps to align scores of unlabeled normals with the labeled core. On the banana dataset, this variant attains $\mathrm{F}1=0.861$, recall $0.912$, precision $0.814$, and accuracy $0.882$ with TP $=219$, FP $=50$, TN $=310$, and FN $=21$. In Figure 5c, the dashed contour tracks the banana-shaped manifold more closely and removes many of the remaining false alarms between the normal region and the anomaly clusters.

The full AAG-DSVDD model adds the graph regularizer on squared distances $d^2\left(x\right)$ over the latent k-NN graph. The graph term spreads label information along the manifold and smooths the score field. On the banana dataset, the full model achieves $\mathrm{F}1=0.876$, recall $0.917$, precision $0.840$, and accuracy $0.897$, with TP $=220$, FP $=42$, TN $=318$, and FN $=20$. The contour in Figure 5d is smoother along the banana-shaped normal manifold and around the anomaly clusters than in the no-graph variant. The main effect of the graph is a consistent reduction in false positives while keeping recall high.

In summary, the overall ablation study highlights three effects. First, in the zero-anomaly-label regime AAG-DSVDD reduces to a DeepSVDD-style boundary with limited coverage of low-density normal regions. Second, adding the anomaly hinge and unlabeled pull substantially improves the boundary and already yields high F1 and recall under contamination. Third, the graph regularizer gives a smaller yet consistent gain by smoothing scores along the latent manifold and removing additional false alarms.

5. Case Study: Anomaly-Aware Graph-Based Semi-Supervised Deep SVDD for Fire Monitoring

In this section, we present a case study that applies the proposed AAG-DSVDD framework to real multi-sensor fire monitoring data. The goal is to detect the onset of hazardous fire conditions as early as possible while maintaining a low false-alarm rate. We first describe the fire-monitoring dataset and its preprocessing. We then detail the semi-supervised training protocol, baselines, and evaluation metrics used to assess detection performance in this realistic setting.

5.1. Fire-Monitoring Dataset Description

We evaluate the proposed method on a multi-sensor residential fire detection dataset derived from the National Institute of Standards and Technology (NIST) “Performance of Home Smoke Alarms” experiments [41]. In these experiments, a full-scale residential structure was instrumented and subjected to a variety of controlled fire and non-fire conditions. Sensor responses were recorded over time in systematically designed scenarios.

In our setting, each scenario is represented as a five-channel multivariate time series sampled at 1 Hz. At each time step t in scenario s, the observation vector ${\mathbf{x}}_t^{\left(s\right)}\in {\mathbb{R}}^5$ contains measurements from five sensors in the following order: The first channel is a temperature sensor. The second channel measures CO concentration. The third channel records the output of an ionization smoke detector. The fourth channel records the output of a photoelectric smoke detector. The fifth channel measures smoke obscuration. Accordingly, each scenario s is stored as a matrix:

$${\mathbf{X}}^{\left(s\right)}\in {\mathbb{R}}^{T_s\times 5},$$

where $T_s$ denotes the duration of that scenario in seconds.

The dataset comprises multiple classes of fire scenarios. These include smoldering fires, such as the smoldering of upholstery or mattress experiments. They also include cooking-related heating and cooking fires and flaming fires. For each fire scenario, a true fire starting time (TFST) is annotated. This TFST indicates the earliest time at which the fire is deemed to have started based on the original NIST records and the observed sensor responses. Table 8 shows the description of the fire scenarios.

Table 8. Fire scenarios used for training and testing in the AAG-DSVDD fire monitoring case study.

Scenario ID	Split	Fire Type	Scenario Length (s)	TFST (s)
1	Train	Smoldering	9104	1000
2	Train	Heating	2382	854
3	Train	Flaming	1024	652
4	Train	Flaming	948	730
5	Test	Smoldering	4455	968
6	Test	Heating	2642	1001
7	Test	Flaming	1210	1001
8	Test	Flaming	1186	1001
9	Test	Flaming	1192	1001
10	Test	Flaming	975	739

Scenario Length is the duration of the scenario in seconds. TFST is the true fire starting time in seconds.

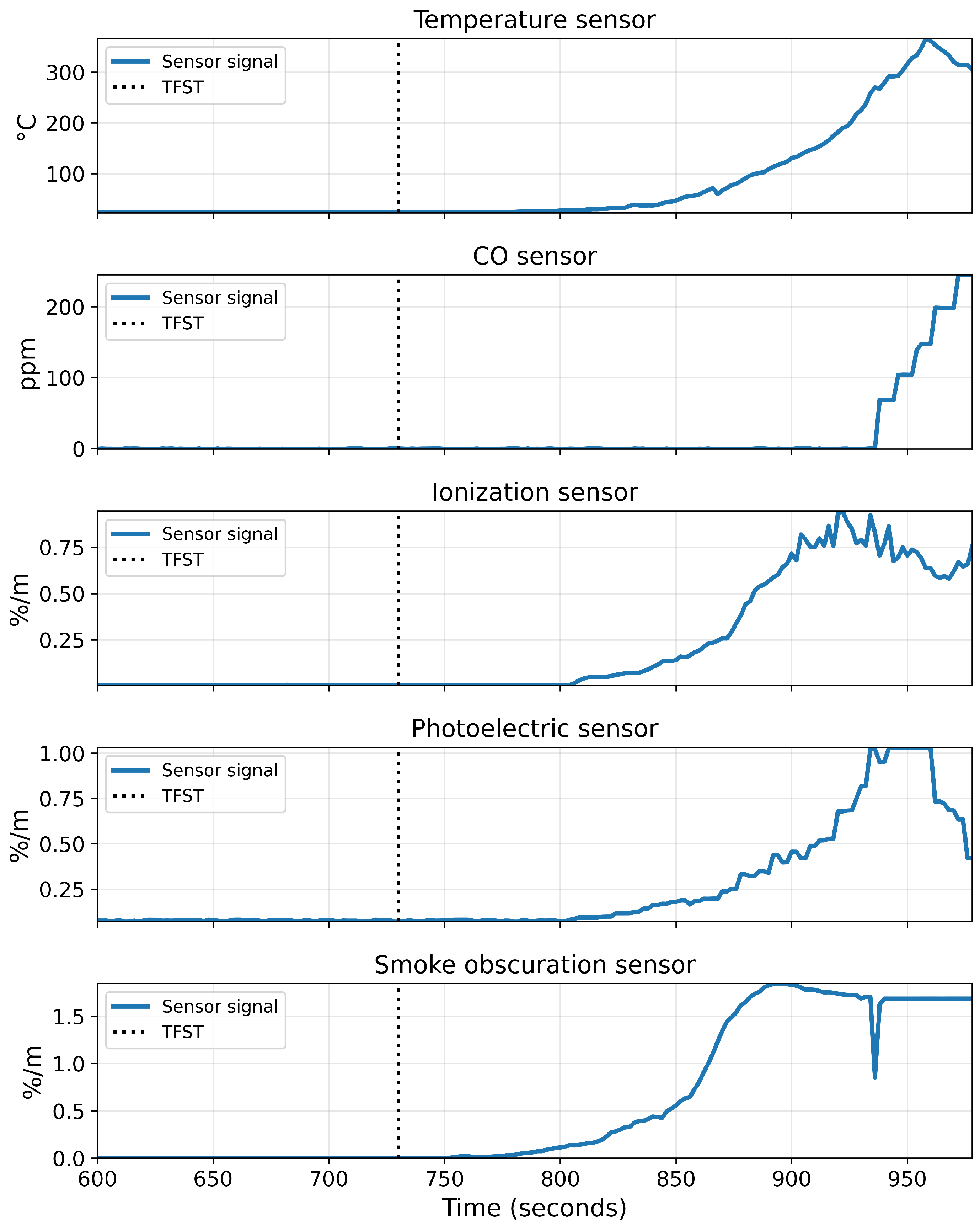
To build intuition about the multi-sensor fire dynamics, Figure 6 shows an excerpt from one fire scenario (Scenario 4 in Table 8). The plots show the five sensor channels sampled at 1 Hz: temperature (top), CO concentration, ionization smoke, photoelectric smoke, and smoke obscuration (bottom). The vertical dotted line marks the annotated ${\mathrm{TFST}}_s=730$ s.

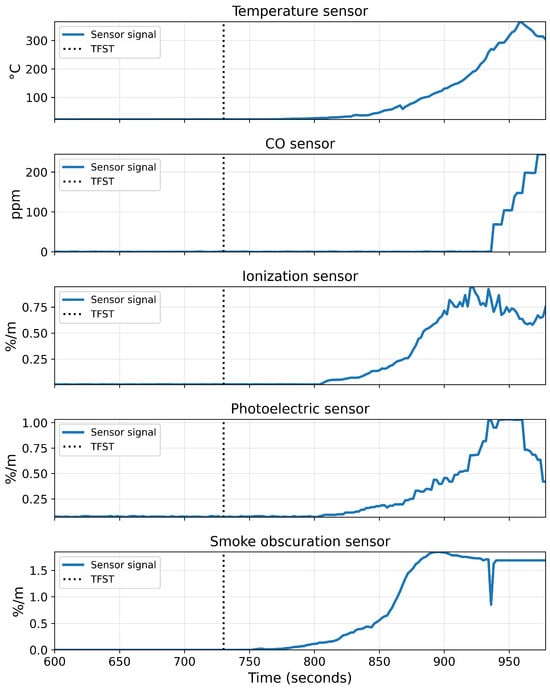
Figure 6. Example of multi-sensor signals from a flaming-fire scenario. Each panel shows one sensor channel sampled at 1 Hz: temperature (top), CO concentration, ionization smoke, photoelectric smoke, and smoke obscuration (bottom). The vertical dotted line marks the annotated TFST.

Before TFST, all channels remain close to their baseline levels, with only small fluctuations attributable to noise. Shortly after TFST, the smoke obscuration begins to rise, followed by increases in the photoelectric and ionization detector outputs, and then a delayed but pronounced growth in CO concentration and temperature. This sequence reflects the physical development of the fire and highlights the temporal coupling between channels. It also motivates the use of windowed multi-channel inputs and a boundary-focused model that leverages the joint evolution of these signals rather than relying on any single sensor in isolation.

5.2. Window Construction and Experiment Setup

5.2.1. Sliding-Window Observations

We adopt a sliding-window observation structure similar to that used in previous real-time fire detection studies on this dataset. For each fire scenario s, let ${\mathbf{x}}_t^{\left(s\right)}\in {\mathbb{R}}^5$ denote the five-dimensional sensor vector at second t, ordered as temperature, CO concentration, ionization detector output, photoelectric detector output, and smoke obscuration. We form an observation window of length w at time t as follows:

$${\mathbf{w}}_t^{\left(s\right)}=\left[{\mathbf{x}}_{t-w+1}^{\left(s\right)},{\mathbf{x}}_{t-w+2}^{\left(s\right)},\dots ,{\mathbf{x}}_t^{\left(s\right)}\right]\in {\mathbb{R}}^{w\times 5},$$

where w is the window length in seconds. Each scenario s thus produces a sequence of windows ${\left\{{\mathbf{w}}_t^{\left(s\right)}\right\}}_{t=1}^{T_s-w+1}$.

For each fire scenario s, an annotated ${\mathrm{TFST}}_s$ is given in seconds. We assign a binary label to each window based on the time of its last sample relative to this TFST. If the last time index of the window satisfies $t\ge {\mathrm{TFST}}_s$, the window is labeled as fire, and we set $y_t^{\left(s\right)}=1$. If the window ends strictly before the fire starts, that is, $t<{\mathrm{TFST}}_s$, the window is labeled as normal, and we set $y_t^{\left(s\right)}=0$. These end-of-window labels $y_t^{\left(s\right)}\in \{0,1\}$ form the base labels on which we build the semi-supervised setting in the next subsection.

For notational consistency with Section 2.1, we subsequently denote each window by ${\mathbf{x}}_i$ and its binary label by $y_i\in \{0,1\}$. When we use an LSTM encoder, ${\mathbf{x}}_i$ is treated as an ordered length multivariate time series w in ${\mathbb{R}}^{w\times 5}$. For methods that require fixed-length vector inputs, such as OC-SVM and kernel SVDD, we additionally define a flattened version ${\tilde{\mathbf{x}}}_i\in {\mathbb{R}}^m$ with $m=5w$ by stacking the entries of ${\mathbf{w}}_t^{\left(s\right)}$ along the time and channel dimensions into a single vector.

5.2.2. Experiment Setup

We construct an LSTM-ready dataset of five-channel windows with separate training, validation, and test splits. The training set is derived from four fire scenarios (1, 2, 3, and 4). From each of these scenarios, we sample fixed-length windows of size $w=32$ s using the sliding-window construction described in Section 5.2.1. In each training scenario, we draw approximately 250 windows, with about 40% taken from the pre-TFST region and labeled as normal and about 60% taken from the post-TFST region and labeled as fire. This yields roughly 100 normal and 150 fire windows per training scenario, for a total of 1000 training windows across all four scenarios. In all cases, the binary label of a window is determined by the label at its last time step. For a semi-supervised setting, we randomly retain 10% of normal and fire windows as labeled samples, while the rest are considered unlabeled.

For evaluation, we generate dense sliding windows of length $w=32$ s with unit stride over complete scenarios. The validation windows are drawn from the same four scenarios (1, 2, 3, and 4), using all overlapping windows rather than the subsampled training set. The test windows are drawn from six additional fire scenarios (5, 6, 7, 8, 9, and 10) that do not appear in the training set. In all splits, a window is labeled as normal if its last time step occurs before the annotated ${\mathrm{TFST}}_s$ for that scenario and as fire otherwise.

During the evaluation, each window is passed through the encoder and the AAG-DSVDD model to obtain an anomaly score $s\left(\mathbf{x}\right)=d^2\left(\mathbf{x}\right)-R^2$. A window is classified as fire when its score exceeds a global threshold $\tau$, which is selected using held-out validation windows from training scenarios. A scenario-level fire alarm is raised once $q=5$ consecutive windows are classified as fire. The estimated fire starting time (EFST) is defined as the time at which the model predicted a fire for q consecutive windows.

The same window-level train/validation/test partitions and semi-supervised label budgets are used for all methods to ensure a fair comparison. For the deep methods, AAG-DSVDD and DeepSAD are trained on the full training window set, using labeled normal windows ($y=+1$) and labeled fire windows ($y=-1$) together with the remaining unlabeled windows ($y=0$). In contrast, DeepSVDD is trained only on the labeled normal windows ($y=+1$), representing a supervised deep one-class baseline. The classical OC-SVM and SVDD-RBF baselines are trained on the normal training windows only ($y=+1$), ignoring unlabeled and fire windows during training. Validation windows from the training scenarios are used exclusively for hyperparameter selection and for choosing the global decision threshold, while test windows from held-out scenarios are used only for final evaluation.

The fire monitoring experiments were carried out on a Windows workstation equipped with a 13th Gen Intel Core i9-13900K (3.00 GHz), 64 GB of RAM, and an NVIDIA RTX 4090 GPU.

5.2.3. Evaluation Metrics for Fire Monitoring Experiments

For each fire scenario s, we obtain a sequence of ground-truth window labels:

$$y_t^{\left(s\right)}\in \{0,1\},t=1,\dots ,T_s,$$

and the corresponding predicted labels:

$${\widehat{y}}_t^{\left(s\right)}\in \{0,1\},t=1,\dots ,T_s,$$

where $T_s$ is the number of windows in that scenario, and ${\widehat{y}}_t^{\left(s\right)}=1$ denotes a predicted fire window.

For each scenario s, the ${\mathrm{TFST}}_s$ is provided by the dataset annotation and expressed in window indices. Equivalently, it can be written as the first time point at which the ground-truth label becomes fire:

$${\mathrm{TFST}}_s=min\left\{t\in \{1,\dots ,T_s\}:y_t^{\left(s\right)}=1\right\}.$$

(12)

Given the predicted labels ${\widehat{y}}_t^{\left(s\right)}$, we declare that a scenario-level fire alarm has been raised once q consecutive windows are classified as fire. In our experiments, we use $q=10$. The ${\mathrm{EFST}}_s$ is defined as the last index of the first run of q consecutive fire predictions, that is

$${\mathrm{EFST}}_s=\left\{\begin{array}{ll}min\left\{t\in \{q,\dots ,T_s\}:{\widehat{y}}_{t-q+1}^{\left(s\right)}=\dots ={\widehat{y}}_t^{\left(s\right)}=1\right\},\hfill & \mathrm{if}\mathrm{such}t\mathrm{exists},\hfill \\ T_s,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

(13)

This matches the implementation in which the alarm time is the index of the last window in the first run of q consecutive predicted fires.

The Fire Starting Time Accuracy (FSTA) for scenario s measures the temporal deviation of the estimated start time from the true start time. It is defined as the absolute difference between the estimated and true fire starting times:

$${\mathrm{FSTA}}_s=|{\mathrm{EFST}}_s-{\mathrm{TFST}}_s|.$$

(14)

By this definition, ${\mathrm{FSTA}}_s$ quantifies the magnitude of the error in seconds, treating early false alarms (${\mathrm{EFST}}_s<{\mathrm{TFST}}_s$) and late detections (${\mathrm{EFST}}_s>{\mathrm{TFST}}_s$) symmetrically. Lower values indicate better performance.

To quantify false alarms in the pre-fire region, we compute the false alarm rate (FAR) for each scenario with an annotated ${\mathrm{TFST}}_s>1$. Let

$${\mathcal{T}}_{\mathrm{pre}}^{\left(s\right)}=\{t:1\le t<{\mathrm{TFST}}_s\}$$

denote the set of pre-fire window indices. The per-scenario false alarm rate is

$${\mathrm{FAR}}_s={\displaystyle \frac{1}{\left|{\mathcal{T}}_{\mathrm{pre}}^{\left(s\right)}\right|}}\sum _{t\in {\mathcal{T}}_{\mathrm{pre}}^{\left(s\right)}}{\widehat{y}}_t^{\left(s\right)},$$

(15)

that is, the fraction of pre-TFST windows that are incorrectly classified as fire. In the reported tables, we express ${\mathrm{FAR}}_s$ as a percentage.

5.2.4. Model Architectures and Hyperparameters

For the fire-monitoring case study, the hyperparameter settings for AAG-DSVDD, DeepSVDD, DeepSAD, OC-SVM, and SVDD-RBF were obtained through validation-based tuning on the dense validation windows constructed from training scenarios (1–4) and then kept fixed for all reported runs. We first fixed the LSTM encoder architecture and window length based on preliminary experiments that balanced detection performance and computational cost. The scalar coefficients in the AAG-DSVDD objective, denoted by $\{{\eta }_{\mathrm{unl}},{\lambda }_u,\mathrm{\Omega },m\}$, were then tuned by a small grid search on the validation windows, using logarithmic or short linear grids. The neighborhood size k of the latent k-NN graph and the warm-up length for center initialization were chosen from discrete sets of candidates. The final configuration corresponds to the setting that achieves the best average EFST across the validation scenarios, subject to a reasonable trade-off between early detection (low EFST) and a low pre-TFST FAR. The deep baselines were tuned in a similar manner: DeepSVDD and DeepSAD use the same selected encoder architecture, and the labeled-term weight $\eta$ in DeepSAD is chosen from a logarithmic grid on the same validation windows. For OC-SVM and SVDD-RBF, we performed a small grid search over the RBF kernel width $\gamma$ around the scale heuristic on flattened windows and selected the configuration according to the same EFST/FAR selection criterion. The one-class parameter $\nu$ was fixed at $0.05$ for all methods.

All deep methods share the same LSTM-based encoder $\varphi (·;W)$ for fairness. Each input window is a sequence in ${\mathbb{R}}^{w\times 5}$ with $w=32$ and five sensor channels. We use an LSTM encoder with input size 5, hidden size 128, two layers, no bi-directionality, and dropout set to zero. Its last hidden state is projected to a 64-dimensional representation. Deep models are trained with Adam (DeepSVDD with AdamW) for 50 epochs, batch size 256, and learning rate ${10}^{-3}$. The ${\ell }_2$ weight decay is ${10}^{-4}$ for AAG-DSVDD and ${10}^{-6}$ for DeepSVDD and DeepSAD. Fire windows are treated as positive classes in all evaluations. Alarm logic uses $q=5$ consecutive fire windows to declare a fire at the scenario level.

For AAG-DSVDD, we use the soft-boundary formulation of Section 3 with squared hinges ($r=2$), soft-boundary parameter $\nu =0.05$, anomaly weight $\mathrm{\Omega }=0.5$, and margin $m=0$. The unlabeled center-pull weight is ${\eta }_{\mathrm{unl}}=11$, and the graph smoothness weight is ${\lambda }_u=100$, which imposes strong graph regularization. The latent k-NN graph uses $k=9$ neighbors with the locally scaled Gaussian affinities of Section 3.2. The radius update and graph-refresh schedules follow Section 3.4, with quantile-based updates of $R^2$ at level $\nu =0.05$ and reconstruction of the latent k-NN graph every two epochs. The warm-up phase for center initialization runs for two epochs.

DeepSVDD uses the same encoder and the same soft-boundary parameter $\nu =0.05$. It is trained only on labeled normal windows and does not use anomaly margins, unlabeled pull-in, or graph regularization. DeepSAD also uses the same architecture and optimizes the standard semi-supervised DeepSAD objective on the same labeled and unlabeled splits, with labeled-term weight $\eta =5$. In both AAG-DSVDD and DeepSAD, $10\%$ of normal windows are labeled normals, and $10\%$ of fire windows are labeled anomalies. DeepSVDD uses only the labeled normal subset.

OC-SVM and SVDD-RBF are trained on flattened windows. Each $32\times 5$ window is reshaped into a 160-dimensional vector, and only labeled-normal windows are used for training. Both methods use an RBF kernel with $\nu =0.05$. For OC-SVM, we set the kernel width parameter to $\gamma =0.2$, while for SVDD-RBF, we use $\gamma =0.1$. These classical one-class baselines operate directly in the input space and provide a non-deep comparison to the LSTM-based models.

5.3. Fire-Monitoring Results and Analysis

The per-scenario fire detection results for all methods are summarized in Table 9. For each test scenario we report ${\mathrm{TFST}}_s$, ${\mathrm{EFST}}_s$, ${\mathrm{FSTA}}_s$ (in seconds), and ${\mathrm{FAR}}_s$. By construction of the EFST metric, if ${\mathrm{EFST}}_s<{\mathrm{TFST}}_s$, then the method has raised a false alarm. In contrast, if ${\mathrm{EFST}}_s$ is equal to the duration of the scenario $T_s$, the method never produces q consecutive fire predictions before the scenario ends and therefore fails to raise any stable fire alarm. In this single-fire, per-scenario setting, the reported precision and recall values often degenerate to $0\%$ or $100\%$ and are therefore not very informative; accordingly, our discussion below focuses on the timing metrics (${\mathrm{TFST}}_s$, ${\mathrm{EFST}}_s$, ${\mathrm{FSTA}}_s$) and ${\mathrm{FAR}}_s$, which better capture the practical trade-off between early detection and false alarms.

Table 9. Per-scenario testing performance for the fire-detection case study. For each scenario (Scen.), we report TFST, EFST, FSTA, FAR, precision (Prec.), and recall (Rec.).

Scenario #	Scenario Length	TFST	OC-SVM					SVDD-RBF
			EFST	FSTA	FAR	Prec.	Rec.	EFST	FSTA	FAR	Prec.	Rec.
5	4455	968	308	660	13.9	0.0	—	4455	3487	0.0	—	0.0
6	2642	1001	753	248	6.2	0.0	—	2642	1641	0.0	—	0.0
7	1210	1001	1110	109	0.0	100.0	3.5	1210	209	0.0	—	0.0
8	1186	1001	1082	81	0.0	100.0	4.4	1186	185	0.0	—	0.0
9	1192	1001	1085	84	0.0	100.0	4.3	1192	191	0.0	—	0.0
10	975	739	849	110	0.0	100.0	3.5	975	236	0.0	—	0.0
Average			864.5	215.3	3.4	66.7	3.9	1943.3	991.5	0.0	—	0.0
Scenario #	Scenario Length	TFST	DeepSVDD					DeepSAD
			EFST	FSTA	FAR	Prec.	Rec.	EFST	FSTA	FAR	Prec.	Rec.
5	4455	968	5	963	37.0	0.0	—	4287	3319	0.0	100.0	0.1
6	2642	1001	5	996	96.1	0.0	—	738	263	1.7	0.0	—
7	1210	1001	1046	45	0.0	100.0	6.5	1171	170	0.0	100.0	2.5
8	1186	1001	699	302	2.0	0.0	—	1120	119	0.0	100.0	4.0
9	1192	1001	1056	55	0.2	71.4	5.7	1161	160	0.0	100.0	6.3
10	975	739	777	38	0.0	100.0	7.1	839	100	0.0	100.0	3.8
Average			598.0	399.8	22.6	45.2	6.4	1552.7	688.5	0.3	83.3	3.3
Scenario #	Scenario Length	TFST	AAG-DSVDD
			EFST	FSTA	FAR	Prec.	Rec.
5	4455	968	2067	1099	0.0	100.0	1.1
6	2642	1001	2288	1287	0.0	100.0	1.2
7	1210	1001	1164	163	0.0	100.0	2.6
8	1186	1001	1125	124	2.5	16.7	3.2
9	1192	1001	1129	128	1.6	44.4	7.5
10	975	739	776	37	0.0	100.0	7.2
Average			1424.8	473.0	0.7	76.9	3.8

Averages are computed over the six test scenarios. FSTA is reported in seconds and equals the absolute difference $|{\mathrm{EFST}}_s-{\mathrm{TFST}}_s|$ at 1 Hz sampling. FAR, precision, and recall are reported as percentages. Precision and recall are computed over windows from the start of the scenario up to EFST. The average precision/recall values in the bottom row are taken over scenarios in which the corresponding metric is defined, i.e., where there is at least one fire window before EFST (for recall) and at least one predicted fire window before EFST (for precision). Missing entries “—” therefore correspond to degenerate cases with no pre-EFST fires or no pre-EFST alarms and are excluded from these averages. Scenario-level precision and recall alone are not reliable indicators of early, low–false-alarm detection; they should be interpreted jointly with EFST, FSTA, and FAR.

SVDD-RBF is extremely conservative. In all six test scenarios, its ${\mathrm{EFST}}_s$ is exactly equal to the duration of the scenario. This means that it never detects a fire event at the level of a stable alarm. Therefore, the high FSTA values (from 209 s to 3487 s) reflect missed detections rather than late but successful alarms, which is in line with the average FAR for the SVDD-RBF being $0\%$. OC-SVM moves in the opposite direction. On average, it reduces FSTA to about 215 s, but this comes at the cost of non-negligible pre-fire activity. The mean FAR is $3.4\%$, and in the longest scenarios, it is as high as $13.9\%$ (scenario 5) and $6.2\%$ (scenario 6). In these two scenarios, ${\mathrm{EFST}}_s$ is smaller than ${\mathrm{TFST}}_s$. This indicates that OC-SVM raises false alarms well before the true fire onset. DeepSVDD achieves the second-smallest average FSTA (about 400 s) and detects the shorter flaming scenarios relatively quickly. However, it does so by triggering almost continuously in the pre-fire region. The average FAR is $22.6\%$, and scenarios 5 and 6 both exhibit ${\mathrm{EFST}}_s\ll {\mathrm{TFST}}_s$ (an alarm essentially at the beginning of the scenario). Thus, the one-class baselines either miss fires altogether (SVDD-RBF) or raise persistently early alarms that would be unacceptable in a deployed monitoring system (OC-SVM and especially DeepSVDD).

The semi-supervised deep methods, DeepSAD and AAG-DSVDD, achieve a more favorable balance between timeliness and reliability. DeepSAD maintains a very low average FAR of $0.3\%$, with at most $1.7\%$ in any scenario, but its timing behavior is mixed. In several scenarios (7, 8, 9, and 10), it produces moderate delays with FSTA between 100 and 170 s, while in scenario 5, it reacts extremely late (FSTA $=3319$ s). Moreover, in scenario 6, DeepSAD exhibits ${\mathrm{EFST}}_6<{\mathrm{TFST}}_6$, which indicates that its first stable alarm is actually a false alarm in the pre-fire region, despite the low FAR reported there. In general, the mean FSTA for DeepSAD in all scenarios is about 689 s.

AAG-DSVDD yields the best overall trade-off. Across the six test scenarios, it reduces the mean FSTA to approximately 473 s, representing a substantial improvement over SVDD-RBF and a reduction of roughly $30\%$ relative to DeepSAD, while keeping the average FAR below $1\%$ ($0.7\%$). Importantly, for AAG-DSVDD, we always have ${\mathrm{EFST}}_s\ge {\mathrm{TFST}}_s$, so the first stable alarm in all scenarios occurs at or after the true onset of the fire. The gains are most pronounced in scenarios 5 and 9, where AAG-DSVDD triggers earlier than all baselines with negligible FAR, and in scenario 10, where it achieves the smallest FSTA of all methods (37 s) with zero pre-fire false alarms.

A critical observation from these results is the robustness of AAG-DSVDD against early false alarms, particularly when compared to the noisy behavior of DeepSVDD. DeepSVDD triggers almost continuously in the pre-fire regions of scenarios 5 and 6, suggesting that its decision boundary is overly sensitive to local fluctuations in the sensor noise floor. In contrast, the graph regularization in AAG-DSVDD explicitly enforces smoothness on the anomaly scores of neighboring latent representations. By coupling the scores of unlabeled pre-fire windows (which lie on the normal manifold) with those of the labeled normal set, the graph term effectively dampens high-frequency noise in the anomaly score trajectory. This smoothing effect prevents transient sensor spikes from crossing the decision threshold, resulting in a stable monitoring signal that only rises when the collective evidence from the multi-sensor array indicates a genuine departure from the normal manifold.

These results are consistent with the design of AAG-DSVDD. The baseline one-class models construct their decision regions using only sparsely labeled normals (and, for DeepSAD, a small number of labeled fires) and do not explicitly exploit the geometry of the unlabeled windows. Consequently, they tend either to tighten the normal region so aggressively that many pre-TFST windows are classified as anomalous, leading to ${\mathrm{EFST}}_s<{\mathrm{TFST}}_s$, or to expand it so conservatively that no stable alarm is raised before the scenario ends, yielding ${\mathrm{EFST}}_s=T_s$.

In contrast, AAG-DSVDD regularizes the squared-distance field over a label-aware latent k-NN graph and couples labeled and unlabeled windows through its k-NN latent graph and unlabeled center-pull terms. This allows the model to propagate limited label information along the data manifold and to position the hypersphere boundary close to the true transition from normal to fire, resulting in earlier yet stable fire alarms with very few false activations on the NIST fire sensing dataset.

In particular, in scenario 5, which represents a smoldering scenario exhibiting a slow combustion process, both DeepSAD and AAG-DSVDD achieve $\mathrm{FAR}=0$ and $100\%$ precision, yet their detection times differ substantially. DeepSAD triggers the alarm very late (EFST $=4287$ s, FSTA $=3319$ s), whereas AAG-DSVDD raises the alarm earlier at EFST $=2067$ s (FSTA $=1099$ s). DeepSAD relies on a point-wise distance loss with an unlabeled pull-in term. As a result, many weak or slowly developing fire windows are drawn toward the center and remain in the normal region under the tight FAR constraint, so the alarm is delayed. AAG-DSVDD adds a label-aware graph regularizer on squared distances together with the anomaly push-out hinge. In this smoldering scenario, the scarce labeled fire windows act as anchors in the latent k-NN graph, drawing structurally similar unlabeled windows away from the center. As a result, their anomaly scores rise earlier, without increasing the FAR. This improvement is therefore mainly attributable to the label-aware graph regularization module, which propagates the limited anomaly labels to structurally similar unlabeled windows in this scenario.

Moreover, AAG-DSVDD supports sample-level interpretation through neighbor queries in its graph-regularized latent space. For any window, we compute its embedding and perform a k-NN search among the labeled training embeddings. The labels and scenarios of these neighbors provide a local, example-based view of the window’s anomaly score. To illustrate, we consider a late-stage smoldering-test window from scenario 5, taken around the EFST predicted by AAG-DSVDD (at 2067 s), which is correctly detected as fire. Table 10 lists its $k=9$ nearest labeled training windows in latent space. Eight of the nine neighbors come from a smoldering training scenario (scenario 1), and the remaining neighbor is a flaming training scenario (scenario 4) from an early fire stage. All neighbors lie at very small latent distances from the query. This neighborhood structure shows that the embedding of the queried smoldering window is tightly clustered with labeled smoldering fire windows from the training set and close to one early-stage flaming window, providing a concrete, example-based justification for its high anomaly score. In an operational setting, such neighbor-based views also help clarify the likely fire type, which is important for selecting appropriate evacuation and response procedures.

Table 10. Nearest labeled training windows in latent space for a smoldering-test window from scenario 3 (at 2067 s).

#	Scenario	Fire Type	${\mathit{d}}_{\mathbf{latent}}^2$
1	9	Flaming	0.0040
2	2	Smoldering	0.0041
3	2	Smoldering	0.0043
4	2	Smoldering	0.0047
5	2	Smoldering	0.0052
6	2	Smoldering	0.0052
7	2	Smoldering	0.0052
8	2	Smoldering	0.0052
9	2	Smoldering	0.0059

In our experiments on the NIST fire-monitoring dataset, AAG-DSVDD had training times of the same order as the DeepSVDD and DeepSAD baselines. All three deep methods completed training within a few tens of seconds, whereas the classical OC-SVM and SVDD-RBF baselines completed almost instantaneously. At inference, AAG-DSVDD processed test windows in roughly $1.71\times {10}^{-5}\pm 0.84\times {10}^{-6}$ s per window, compared to $1.19\times {10}^{-4}\pm 4.82\times {10}^{-6}$ s for DeepSVDD and $1.19\times {10}^{-4}\pm 5.17\times {10}^{-6}$ s for DeepSAD. The OC-SVM and SVDD-RBF baselines achieved $2.36\times {10}^{-6}\pm 1.98\times {10}^{-7}$ s and $1.48\times {10}^{-6}\pm 4.06\times {10}^{-7}$ s per window, respectively. In all cases, this per-window cost is negligible relative to the 1 Hz sampling rate, as such, the graph regularization in AAG-DSVDD does not compromise real-time deployability.

6. Conclusions and Future Work

This paper studied semi-supervised anomaly detection in high-dimensional and multi-channel time series under realistic label budgets and applied it to safety-critical fire monitoring. We proposed AAG-DSVDD, which preserves the center-based hypersphere structure of DeepSVDD/DeepSAD and augments it with a label-aware latent k-NN graph. By regularizing the squared-distance field over this graph and combining a soft-boundary term for labeled normals, a margin push-out for labeled anomalies, and an unlabeled center-pull, AAG-DSVDD propagates information from scarce labels along the latent manifold while retaining a simple distance-based decision rule at test time.

On the synthetic banana dataset, AAG-DSVDD consistently outperformed DeepSVDD, DeepSAD, OC-SVM, and SVDD-RBF. On the representative experiment, it achieved F1 $=0.8852$ and accuracy $=0.9067$, compared with F1 $=0.7259$ and accuracy $=0.7533$ for the strongest classical baseline (SVDD-RBF) and F1 $=0.6510$ and accuracy $=0.5800$ for DeepSAD. Over ten seeds, AAG-DSVDD reached a mean F1 of $0.88\pm 0.02$ versus $0.76\pm 0.04$ for SVDD-RBF and $0.71\pm 0.08$ for OC-SVM, with all gains statistically significant under paired tests. An ablation study on the same dataset confirms that each component of the objective contributes to performance. Starting from F1 $=0.606$ with labeled normals only, adding labeled anomalies raises F1 to $0.834$, incorporating the unlabeled center-pull term yields F1 $=0.861$, and the full model with graph regularization reaches F1 $=0.876$ with the highest precision and accuracy among all variants.

On three public benchmarks (Thyroid, Arrhythmia, and Heart), AAG-DSVDD achieved F1-scores of 0.719, 0.675, and 0.800, respectively, compared with best baseline F1-scores of 0.668 (DeepSAD) on Thyroid, 0.667 (OC-SVM) on Arrhythmia, and 0.727 (SVDD-RBF) on Heart. On Thyroid and Heart it also obtained the highest accuracies (0.956 and 0.802, versus at most 0.939 and 0.703 for the baselines), while maintaining competitive precision and recall (precision $0.690/0.533/0.750$ and recall $0.750/0.919/0.857$ on Thyroid/Arrhythmia/Heart). These results indicate that the proposed graph-regularized, center-based formulation can generalize beyond controlled synthetic data to heterogeneous real-world problems under the same semi-supervised label-budget setting.

In the fire-monitoring case study using the NIST dataset, AAG-DSVDD reduced the mean fire starting time accuracy to about 473 s (about a 30% improvement over DeepSAD) while keeping the average pre-fire false-alarm rate below $1\%$ and ensuring that the first stable alarm in every scenario occurred at or after the true fire onset. Qualitatively, the decision boundaries learned by AAG-DSVDD track the true normal manifold more closely than the baselines, covering valid normal regions while cleanly and effectively detecting anomaly clusters. In the fire-monitoring case study, its alarms align more closely with the physical development of the fire, avoiding the persistent false alarms of DeepSVDD and OC-SVM and the overly conservative behavior of SVDD-RBF while still supporting sample-level interpretability through its latent graph structure.

Beyond these quantitative gains, the latent graph provides a natural handle for interpretability, as anomaly scores of unlabeled samples can be related to nearby labeled normals and anomalies through their graph neighborhoods, while the final deployed model still operates via a single distance-to-center computation.

Despite its gains over the baselines, AAG-DSVDD has several limitations. First, it relies on a single center and radius in latent space and is therefore best suited to approximately unimodal or smoothly connected normal classes. On problems with strongly multimodal or clustered normals, a single hypersphere must either contract and cut into some normal modes (increasing false alarms) or expand and admit more anomalies. Moreover, the current formulation treats all anomalies as a single homogeneous class and does not model different anomaly types or varying severity. In applications where some anomalies are safety-critical while others are benign, it would be desirable to weight anomaly types differently or to enforce larger margins for high-severity anomalies; the present objective does not yet incorporate such severity-aware costs. For instance, in the Heart dataset, it could be more beneficial to increase the detection weight for more severe heart diseases. Extending the approach to multi-center or mixture-of-spheres variants, and to severity-aware anomaly weights, is an important direction for future work.