A Double Decomposition Method for Solving Systems of Two-Point Boundary-Value Problems

Abstract

The current manuscript introduces an efficient modification scheme, based on the Adomian decomposition method, for the numerical solution of systems of two-point boundary-value problems. Indeed, this introduced method is characterized by high computational flexibility in accurately solving both the systems of linear and nonlinear differential equations with two-point boundary conditions. Moreover, to assess the robustness of these schemes, several test numerical examples, including a well-known model in fluid dynamics, have been sought and treated. Comparatively, the results from the proposed method have been compared with those of the available exact solutions and those of deployed existing numerical methods in the literature. Lastly, in the presence of the methods used for comparison, the assessment of this method turned out to be positive, with rapid convergence and high precision speedily attained.

1. Introduction

Systems of second-order ordinary differential equations arise in modeling several physical phenomena in many fields, including engineering applications, financial applications, biological sciences, and mathematical physics, to mention just a few [1,2,3]. Nevertheless, most of the renowned computational algorithms for treating these equations, especially when nonlinear terms are present, with initial conditions, cannot be utilized when boundary conditions are considered; the so-called boundary-value problems (BVPs). Thus, different researchers delved into a search for optimal computational methods for this class of equations, considering the nature of prescribed conditions on the governing boundary, not initial conditions, and, on the other hand, the presence of nonlinearity, which poses additional threats to existing approaches. Indeed, the well-known finite difference method that has been proven to solve the class of second-order linear differential equations efficiently finds it hard to tackle the counterpart class of nonlinear equations effectively, let alone the class of coupled systems of nonlinear second-order differential equations with boundary conditions. In short, the literature on reliable computational methods for solving BVPs for coupled systems of nonlinear second-order differential equations is sparse, which thus prompts a great need for more effective methods for this class of equations, considering their frequent discovery while modeling various scenarios in the aforementioned fields. In this regard, we make mention of various considerations in [4,5,6,7,8], which lay several theoretical results for the existence of valid solutions for the coupled system of second-order differential equations; one may equally read the work of Valanarasu and Ramanujam [9], which devised an effective approach specifically of the class of coupled systems of second-order singular linear differential equations. In addition, an efficient numerical approach based on the Adomian Chebyshev decomposition method for two-point boundary value problems was deployed in [10] to solve the class of BVPs for systems of linear and nonlinear second-order differential equations. Furthermore, Öztürk [11] introduced numerical solutions of systems of differential equations using the operational matrix method with Chebyshev polynomials, while Biazar et al. [12] deployed the famous Adomian decomposition method (ADM) on certain systems of differential equations. Additionally, some of the salient characteristics of ADM in effectively solving the class of coupled second-order systems of differential equations, in particular, were unraveled by Sekar and Nalini [13] by solving dissimilar types of equations, including stiff systems, singular systems, and some sort of stable and unstable systems of equations. What is more, Sekar and Nalini [13] further made use of the Runge–Kutta method (RKM) to reaffirm the exactness of the devised ADM for the considered class of equations, in addition to comparing the results with those of the exact solution; the high accuracy of ADM has thus been reported. In addition, ADM has remained an effective and powerful semi-analytical method, which equally doubles as a numerical, or rather computational method for solving wide classes of functional equations. The convergence of ADM has been considered in [14,15,16,17]. Cherruault [14] gave the first proof of the convergence of the Adomian decomposition method using fixed-point theorems for abstract functional equations. A new formula that easily calculates Adomian’s polynomials used in the decomposition methods has been given in [15]. Gabet in [16] generalized the convergence results obtained by Cherruaulet in Banach space, while Babolian and Biazar [17] used Cherruaulet’s definition and considered the order of convergence of the method.

However, based on the aforementioned importance for the class of BVPs, featuring nonlinear coupled systems differential equations, the scarcity of reliable computational methods for solving the latter class of equations, as well as the effectiveness of ADM in handling wide classes of functional equations, the current study thus aims to make use of one of the promising modifications of ADM, the double decomposition method (DDM) [18] to computationally examine the class of nonlinear coupled systems of differential equations with the prescription of two-point boundary conditions. Moreover, DDM was initially introduced in 1993 by Adomian and Rach [18] to primarily augment the rapidity of the classical ADM. Certainly, the modification method for ADM has been proven to solve various types of coupled differential equations, including nonlinear models with different boundary conditions, with faster convergence and higher accuracy. Moreover, several scientists deployed DDM to different mathematical models and positively reported the virtues of the method over many other approaches; see the works of Aminataei and Hosseini [19] and AL-Zaid et al. [20] that examined various BVPs for nonlinear ordinary differential equations. In this study, we extend the work in [20] to apply DDM for solving BVPs of coupled systems of linear and nonlinear differential equations. Therefore, through the full utilization of DDM, the resultant computational recursive scheme of the governing BVP will be constructed and further simulated numerically for various test problems. In this regard, DDM will be deployed to assess the computational efficiency of the method. Moreover, the study is further set to report its findings in tables and graphical illustrations. Finally, the study is arranged as follows: Section 2 outlines the steps for DDM; Section 3 presents some numerical examples, while Section 4 gives some concluding remarks.

2. Double Decomposition Method for Systems of Boundary Value Problems

Consider the general form of the nonlinear coupled system of higher-order nonhomogeneous ordinary differential equations as follows:

$$u^{\left(n\right)}+F_1\left(x,u,v,u^{\prime },v^{\prime },\dots ,u^{n-1},v^{n-1}\right)=g_1\left(x\right),a\le x\le b,$$

$$v^{\left(m\right)}+F_2\left(x,u,v,u^{\prime },v^{\prime },\dots ,u^{m-1},v^{m-1}\right)=g_2\left(x\right),a\le x\le b,$$

(1)

or simply, in an operator notation form as follows:

$$L_{1}u+F_1\left(x,u,v,u^{\prime },v^{\prime },\dots ,u^{n-1},v^{n-1}\right)=g_1\left(x\right),a\le x\le b,$$

$$L_{2}v+F_2\left(x,u,v,u^{\prime },v^{\prime },\dots ,u^{m-1},v^{m-1}\right)=g_2\left(x\right),a\le x\le b,$$

(2)

where $L_1$ is a n-th order differential operator in the first equation and $L_2$ is m-th order differential operator in the second equation, that is, $L_1={\displaystyle \frac{d^n}{d{x}^n}}$, $L_2={\displaystyle \frac{d^m}{d{x}^m}}$, while $F_1$ and $F_2$ are nonlinear functions and $g_1,g_2$ are source terms.

Further, the inverse operators of $L_1$ and $L_2$ are defined as indefinite integration as follows:

$${L^{-1}}_1=\underset{nintegrals}{\underbrace{\int \int \dots \int \left(.\right)dxdx\dots dx,}}$$

$${L^{-1}}_2=\underset{mintegrals}{\underbrace{\int \int \dots \int \left(.\right)dxdx\dots dx.}}$$

Moreover, upon applying these inversion operators, ${L^{-1}}_1$ to both sides of the first equation and ${L^{-1}}_2$ to both sides of the second equation, one obtains:

$$u\left(x\right)=\mathsf{\Phi }\left(x\right)+{L^{-1}}_1{g}_1\left(x\right)-{L^{-1}}_1{F}_1,$$

$$v\left(x\right)=\mathsf{\Psi }\left(x\right)+{L^{-1}}_2{g}_2\left(x\right)-{L^{-1}}_2{F}_2,$$

(3)

where $\mathsf{\Phi }\left(x\right)$ and $\mathsf{\Psi }\left(x\right)$ are new functions, which arise from the application of ${L^{-1}}_1$ and ${L^{-1}}_2$, respectively. In addition, the standard ADM procedure [21] proceeds to decompose the unknown functions $u\left(x\right),$ and $v\left(x\right)$ into sums of infinite series of components as follows:

$$u={\sum }_{k=0}^{\infty }{u}_k,v={\sum }_{k=0}^{\infty }{v}_k,$$

while the nonlinear terms $F_1,$ and $F_2$ are equally decomposed into sums of infinite series of Adomian polynomials $A_k$ and $B_k,$ respectively, as follows [21,22]:

$$F_1={\sum }_{k=0}^{\infty }{A}_k,F_2={\sum }_{k=0}^{\infty }{B}_k.$$

Further, the deployed DDM [18,19,20] equally suggests that new functions $\mathsf{\Phi }\left(x\right)$ and $\mathsf{\Psi }\left(x\right)$ in Equation (3), the expression should evenly be decomposed into the following sums of infinite series of components:

$$\mathsf{\Phi }={\sum }_{k=0}^{\infty }{\mathsf{\Phi }}_k,\mathsf{\Psi }={\sum }_{k=0}^{\infty }{\mathsf{\Psi }}_k.$$

Thus, Equation (3), when expressed using the above decomposed components, yields:

$${\sum }_{k=0}^{\infty }{u}_k={\sum }_{k=0}^{\infty }{\mathsf{\Phi }}_k+{L^{-1}}_1{g}_1\left(x\right)-{L^{-1}}_1{\sum }_{k=0}^{\infty }{A}_k,$$

$${\sum }_{k=0}^{\infty }{v}_k={\sum }_{k=0}^{\infty }{\mathsf{\Psi }}_k+{L^{-1}}_2{g}_2\left(x\right)-{L^{-1}}_2{\sum }_{k=0}^{\infty }{B}_k.$$

(4)

Moreover, the inverse differential operators ${L^{-1}}_1$ and ${L^{-1}}_2$ in DDM, it is considered to be the nth and mth-fold indefinite integration, respectively; thus, one achieves

$$\begin{gathered} {\mathsf{\Phi }}_k=c_{0,k}+c_{1,k}x+{\displaystyle \frac{c_{2,k}}{2!}}{x}^2+{\displaystyle \frac{c_{3,k}}{3!}}{x}^3+\cdots +{\displaystyle \frac{c_{n-1,k}}{(n-1)!}}{x}^{n-1}, \\ {\mathsf{\Psi }}_k=d_{0,k}+d_{1,k}x+{\displaystyle \frac{d_{2,k}}{2!}}{x}^2+{\displaystyle \frac{d_{3,k}}{3!}}{x}^3+\cdots +{\displaystyle \frac{d_{m-1,k}}{\left(m-1\right)!}}{x}^{m-1}, \end{gathered}$$

where $c_{i,k},$ and $d_{j,k},i=0,1,\dots ,n-1,j=0,1,\dots ,m-1,$ are constants to be determined from the prescribed boundary conditions.

Furthermore, the DDM reveals the resulting solution from Equation (4) as follows:

$$\begin{gathered} u_0=c_{0,0}+c_{1,0}x+{\displaystyle \frac{c_{2,0}}{2!}}{x}^2+{\displaystyle \frac{c_{3,0}}{3!}}{x}^3+\cdots +{\displaystyle \frac{c_{n-1,0}}{(n-1)!}}{x}^{n-1}+{L^{-1}}_1{g}_1\left(x\right), \\ {v}_0=d_{0,0}+d_{1,0}x++{\displaystyle \frac{d_{2,0}}{2!}}{x}^2+{\displaystyle \frac{d_{3,0}}{3!}}{x}^3+\cdots +{\displaystyle \frac{d_{m-1,0}}{\left(m-1\right)!}}{x}^{m-1}+{L^{-1}}_2{g}_2\left(x\right), \\ {u}_k={\mathsf{\Phi }}_k-{L^{-1}}_1\left(A_{k-1}\right),k\ge 1, \\ {v}_k={\mathsf{\Psi }}_k-{L^{-1}}_2\left(B_{k-1}\right),k\ge 1. \end{gathered}$$

In addition, the approximate solution is thus obtained as follows:

$$\begin{gathered} {\phi }_1=u_0, \\ {\psi }_1=v_0, \\ {\phi }_2={\phi }_1+u_1=u_0+u_1, \\ {\psi }_2={\psi }_1+v_1=v_0+v_1, \\ ⋮ \end{gathered}$$

the constants $c_{i,k},$ and $d_{j,k},i=0,1,\dots ,n-1,j=0,1,\dots ,m-1,$ can be explicitly obtained by equalizing each partial sum ${\phi }_k\left(x\right)$ and ${\psi }_k\left(x\right)$ to the boundary value conditions and solving the obtained systems of linear equations.

${\phi }_1=u_0$ and ${\psi }_1=v_0$ is determined completely by matching ${\phi }_1$ and ${\psi }_1$ to the boundary conditions and solving the obtained systems of linear equations. So, we now go to the next approximation ${\phi }_2$ and ${\psi }_2$ by first determining

$$u_1={\mathsf{\Phi }}_1-{L^{-1}}_1\left(A_0\right),$$

$$v_1={\mathsf{\Psi }}_1-{L^{-1}}_2\left(B_0\right),$$

to achieve

$$\begin{gathered} {\phi }_2={\phi }_1+u_1=u_0+u_1, \\ {\psi }_2={\psi }_1+v_1=v_0+v_1. \end{gathered}$$

Matching ${\phi }_2$ and ${\psi }_2$ to the boundary conditions to evaluate the constants, ${\phi }_2$ and ${\psi }_2$ is determined completely. Continuing in this manner, we determine $u_2,u_3,\dots$ and $v_2,v_3,\dots$ until we arrive at a satisfactory ${\phi }_k$ and ${\psi }_k.$

3. Numerical Examples

The current section verifies the efficacy of the proposed DDM for the coupled systems of both the linear and nonlinear BVPs by portraying its applications on several test BVPs with boundary conditions, including a real physical model for the flow of blood in the human system. In addition, the section seeks to compare the proposed method with some existing computational methods in the literature. In addition, the section concludes by reporting the absolute error differences $E_{\mathrm{D}\mathrm{D}\mathrm{M}}$, between the proposed method, and that of the exact and comparing solutions in Table 1, Table 2, Table 3, Table 4, Table 5 and Table 6, while Figure 1, Figure 2, Figure 3 and Figure 4 display the graphical illustrations of the development.

Example 1. 

Consider the coupled system of linear second-order nonhomogeneous BVP as follows [23,24]:

$$\left\{\begin{array}{l}{u}^{″}\left(x\right)+(2x{-1)u}^{\prime }\left(x\right)+\cos \left(\pi x\right)v^{\prime }\left(x\right)=g_1\left(x\right),u\left(0\right)=u\left(1\right)=0,0\le x\le 1,\\ v^{″}\left(x\right)+xu\left(x\right)=g_2\left(x\right),v\left(0\right)=v\left(1\right)=0,0\le x\le 1,\end{array}\right.$$

where $g_1\left(x\right)$  and $g_2\left(x\right)$ are given by

$$g_1\left(x\right)=-{\pi }^{2}sin\left(\pi x\right)+\left(2x-1\right)\pi \cos \left(\pi x\right)+\left(2x-1\right)\cos \left(\pi x\right),$$

and

$$g_2\left(x\right)=2+xsin\left(\pi x\right)$$

In addition, the following exact analytical solution is satisfied by the system:

$$\begin{gathered} u\left(x\right)=\sin \left(\pi x\right), \\ v\left(x\right)=x^2-x. \end{gathered}$$

Accordingly, applying the inverse operator $L^{-1}\left(.\right)=\int \int \left(.\right)dxdx$ to both sides of the above system with DDM, we obtain the following recursive scheme:

$$\left\{\begin{array}{l}{u}_0\left(x\right)={\mathsf{\Phi }}_0+L^{-1}{g}_1\left(x\right),\\ v_0\left(x\right)={\mathsf{\Psi }}_0+L^{-1}{g}_2\left(x\right),\\ u_k\left(x\right)={\mathsf{\Phi }}_k-L^{-1}\left(\left(2x-1\right)u_{k-1}^{\prime }\right)-L^{-1}\left(\mathit{cos}\left(\pi x\right)v_{k-1}^{\prime }\right),k\ge 1,\\ v_k\left(x\right)={\mathsf{\Psi }}_k-L^{-1}\left(x{u}_{k-1}\right),k\ge 1,\end{array}\right.$$

where ${\mathsf{\Phi }}_k=c_{0,k}+c_{1,k}x$ and ${\mathsf{\Psi }}_k=d_{0,k}+d_{1,k}x$. Then,

$${\phi }_1=u_0,{\psi }_1=v_0.$$

In addition, the unknown constants are consequently obtained from the imposed boundary conditions.

Hence, matching ${\phi }_1=u_0$ and ${\psi }_1=v_0$ to the boundary conditions, we obtain the following systems of linear equations:

$$\begin{array}{l}{u}_0\left(0\right)=c_{0,0}+{\left.L^{-1}{g}_1\left(x\right)\right|}_{x=0}=0,\\ u_0\left(1\right)=c_{0,0}+c_{1,0}+{\left.L^{-1}{g}_1\left(x\right)\right|}_{x=1}=0,\end{array}$$

and

$$\begin{array}{l}{v}_0\left(0\right)=d_{0,0}+{\left.L^{-1}{g}_2\left(x\right)\right|}_{x=0}=0,\\ v_0\left(1\right)=d_{0,0}+d_{1,0}+{\left.L^{-1}{g}_2\left(x\right)\right|}_{x=1}=0.\end{array}$$

From the solution of the above systems of linear equations, we obtain the constants $c_{0,0},c_{1,0}$, $d_{0,0}$, and $d_{1,0}$ as:

$$c_{0,0}=-0.419631,c_{1,0}=-2\times {10}^{-30},d_{0,0}=0.064503,d_{1,0}=-1.129006.$$

So, ${\phi }_1$ and ${\psi }_1$ are obtained as follows:

$${\phi }_1=-0.419631-2\times {10}^{-30}x+1.534290\sin \left(\pi x\right)+0.419631\cos \left(\pi x\right)-0.839262xcos\left(\pi x\right),$$

$${\psi }_1=0.064503-1.129006x+x^2-0.064503\cos \left(\pi x\right)-0.101321xsin\left(\pi x\right),$$

so that ${\phi }_1=u_0$ and ${\psi }_1=v_0$ is determined completely.

Next, we proceed to determine ${\phi }_2$ and ${\psi }_2$ as follows:

$$\begin{gathered} {\phi }_2={\phi }_1+u_1, \\ {\psi }_2={\psi }_1+v_1, \\ {u}_1=c_{0,1}+c_{1,1}x-L^{-1}\left(\left(2x-1\right)u_0^{\prime }\right)-L^{-1}\left(\mathit{cos}\left(\pi x\right)v_0^{\prime }\right), \\ {v}_1=d_{0,1}+d_{1,1}x-L^{-1}\left(x{u}_0\right). \end{gathered}$$

More so, on using the boundary conditions in the above relation and solving the obtained systems of linear equations, we obtain the constants as follows:

$$c_{0,1}=0.857877,c_{1,1}=-0.052667,d_{0,1}=-0.150661,d_{1,1}=0.188867,$$

where the explicit expression of ${\phi }_2$ and ${\psi }_2$ follows as:

$$\begin{array}{l}{\phi }_2=-0.008062xcos{\left(\pi x\right)}^2+\left(0.850350x-0.438246+0.005132sin\left(\pi x\right)\right)cos\left(\pi x\right)\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+\left(0.700492+0.534290x^2-0.534290x\right)sin\left(\pi x\right)+0.438246-0.0446050x\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-{1.10}^{-30}{x}^2+0.026525x^3,\end{array}$$

$$\begin{gathered} {\psi }_2=-0.085035\left(x+0.787165\right)\left(x-1.287165\right)cos\left(\pi x\right)+\left(0.162404x-0.027067\right)sin\left(\pi x\right) \\ -0.086158-0.940139x+x^2+0.069938x^3+{1.666666}^{-30}{x}^4. \end{gathered}$$

Continuing in the same manner, we obtain ${\phi }_3$ and ${\psi }_3$, and so on.

Therefore, on comparing the first ten iterations ${\phi }_{10}$ and ${\psi }_{10}$ with the exact solution, Table 1 gives the absolute error between the exact and DDM solutions for $u\left(x\right)$ and $v\left(x\right)$ when $N=10$, while Figure 1 depicts the curves of ${\phi }_{10}$, ${\psi }_{10}$ and the exact analytical solution expression in the approximate region $0\le x\le 1.$

Table 1. Absolute error between the exact and DDM solutions when $N=10$ in Example 1.

$\mathit{x}$	$\left|\mathit{u}-{\mathit{\phi }}_{10}\right|$	$\left|{\mathit{v}-\mathit{\psi }}_{10}\right|$
0.0	$3.30267169\times {10}^{-28}$	$6.39594118\times {10}^{-28}$
0.1	$3.16761319\times {10}^{-10}$	$6.40221981\times {10}^{-11}$
0.2	$4.37656889\times {10}^{-10}$	$1.25182455\times {10}^{-10}$
0.3	$4.77997870\times {10}^{-10}$	$1.78863600\times {10}^{-10}$
0.4	$4.85749117\times {10}^{-10}$	$2.20320191\times {10}^{-10}$
0.5	$4.83478505\times {10}^{-10}$	$2.45187202\times {10}^{-10}$
0.6	$4.80267230\times {10}^{-10}$	$2.49388679\times {10}^{-10}$
0.7	$4.73129116\times {10}^{-10}$	$2.28968541\times {10}^{-10}$
0.8	$4.41536116\times {10}^{-10}$	$1.80364868\times {10}^{-10}$
0.9	$3.30257494\times {10}^{-10}$	$1.02079177\times {10}^{-10}$
1.0	$1.21103911\times {10}^{-26}$	$1.42978962\times {10}^{-27}$

Table 1. Absolute error between the exact and DDM solutions when $N=10$ in Example 1.

$\mathit{x}$	$\left|\mathit{u}-{\mathit{\phi }}_{10}\right|$	$\left|{\mathit{v}-\mathit{\psi }}_{10}\right|$
0.0	$3.30267169\times {10}^{-28}$	$6.39594118\times {10}^{-28}$
0.1	$3.16761319\times {10}^{-10}$	$6.40221981\times {10}^{-11}$
0.2	$4.37656889\times {10}^{-10}$	$1.25182455\times {10}^{-10}$
0.3	$4.77997870\times {10}^{-10}$	$1.78863600\times {10}^{-10}$
0.4	$4.85749117\times {10}^{-10}$	$2.20320191\times {10}^{-10}$
0.5	$4.83478505\times {10}^{-10}$	$2.45187202\times {10}^{-10}$
0.6	$4.80267230\times {10}^{-10}$	$2.49388679\times {10}^{-10}$
0.7	$4.73129116\times {10}^{-10}$	$2.28968541\times {10}^{-10}$
0.8	$4.41536116\times {10}^{-10}$	$1.80364868\times {10}^{-10}$
0.9	$3.30257494\times {10}^{-10}$	$1.02079177\times {10}^{-10}$
1.0	$1.21103911\times {10}^{-26}$	$1.42978962\times {10}^{-27}$

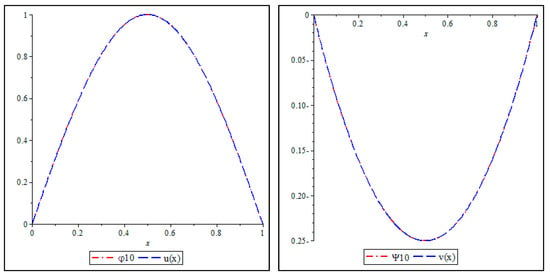
Figure 1. Comparison between the exact and DDM solutions for ${\phi }_{10}$ and ${\psi }_{10}$ in Example 1.

Table 2. Comparison between different methods when $N=21$ in Example 1.

Numerical Methods	LMQDQ [23]	B-Spline [24]	DDM
Maximum error for $u\left(x\right)$.	$1.7761\times {10}^{-4}$	$1.89578799\times {10}^{-3}$	$2.08977066\times {10}^{-17}$
Maximum error for $v\left(x\right)$	$2.8249\times {10}^{-5}$	$9.605012467\times {10}^{-5}$	$6.6\times {10}^{-18}$

Table 2. Comparison between different methods when $N=21$ in Example 1.

Numerical Methods	LMQDQ [23]	B-Spline [24]	DDM
Maximum error for $u\left(x\right)$.	$1.7761\times {10}^{-4}$	$1.89578799\times {10}^{-3}$	$2.08977066\times {10}^{-17}$
Maximum error for $v\left(x\right)$	$2.8249\times {10}^{-5}$	$9.605012467\times {10}^{-5}$	$6.6\times {10}^{-18}$

Notably, Table 2 compares the effectiveness of the proposed DDM on the examination of coupled system with the help of the LMQDQ [23] and B-spline [24] methods when $N=21$. Certainly, the proposed method has been noted to be the most truthful computational method among the three contending approaches, looking at the minimal error portrayed by the presented approach and indeed its closeness to the exact analytical solution.

Example 2. 

Consider the coupled system of nonlinear second-order nonhomogeneous BVP as follows [25]:

$$\left\{\begin{array}{l}{u}^{″}\left(x\right)-x{v}^{\prime }\left(x\right)+u\left(x\right)=g_1\left(x\right),u\left(0\right)=u\left(1\right)=0,0\le x\le 1,\\ v^{″}\left(x\right)+x{u}^{\prime }\left(x\right)+u\left(x\right)v\left(x\right)=g_2\left(x\right),v\left(0\right)=v\left(1\right)=0,0\le x\le 1,\end{array}\right.$$

where $g_1\left(x\right)$  and $g_2\left(x\right)$  are given as follows:

$$g_1\left(x\right)=x^3-2x^2+6x,$$

and

$$g_2\left(x\right)=x^5-x^4+2x^3+x^2-x+2$$

In addition, the following exact analytical solution set is satisfied by the system:

$$u\left(x\right)=x^3-x,v\left(x\right)=x^2-x$$

Consequently, applying the inverse operator $L^{-1}\left(.\right)=\int \int \left(.\right)dxdx$ to both sides of the above system with DDM, we obtain the following recursive scheme

$$\left\{\begin{array}{l}{u}_0\left(x\right)={\mathsf{\Phi }}_0+L^{-1}{g}_1\left(x\right),\\ v_0\left(x\right)={\mathsf{\Psi }}_0+L^{-1}{g}_2\left(x\right),\\ u_k\left(x\right)={\mathsf{\Phi }}_k+L^{-1}\left(x{v}_{k-1}^{\prime }\right)-L^{-1}\left(u_{k-1}\right),k\ge 1,\\ v_k\left(x\right)={\mathsf{\Psi }}_k-L^{-1}\left(x{u}_{k-1}^{\prime }\right)-L^{-1}\left(A_{k-1}\right),k\ge 1,\end{array}\right.$$

where ${\mathsf{\Phi }}_k=c_{0,k}+c_{1,k}x,{\mathsf{\Psi }}_k=d_{0,k}+d_{1,k}x,$ and $A_k$ are the Adomian polynomials for the nonlinear term $u\left(x\right)v\left(x\right)$, which are to be recursively determined using the inventive Adomian algorithm [21,22] as:

$$\begin{gathered} A_0={u_{0}v}_0 \\ {A}_1={u_{1}v}_0+{u_{0}v}_1, \\ {A}_2=u_2{v}_0+u_1{v}_1+u_0{v}_2, \\ ⋮ \end{gathered}$$

Furthermore, the first iteration takes the following form:

$${\phi }_1=u_0,{\psi }_1=v_0.$$

Next, the related unknown constants, $c_{0,0},c_{1,0},d_{0,0}$ and $d_{1,0}$ in the latter iteration are obtained from the already declared boundary conditions as follows:

$$c_{0,0}=0,c_{1,0}=-0.883333,d_{0,0}=0,d_{1,0}=-1.007142.$$

In addition, based on the acquired recursive formula for the system, one achieves the subsequent iteration, the expressions for ${\phi }_1$ and ${\psi }_1$ as follows:

$${\phi }_1=-0.883333x+x^3-{\displaystyle \frac{1}{6}}{x}^4+{\displaystyle \frac{1}{20}}{x}^5,$$

$${\psi }_1=-1.007142x+x^2-{\displaystyle \frac{1}{6}}{x}^3+{\displaystyle \frac{1}{12}}{x}^4+{\displaystyle \frac{1}{10}}{x}^5-{\displaystyle \frac{1}{30}}{x}^6+{\displaystyle \frac{1}{42}}{x}^7,$$

Continuing to use the above process, we obtain ${\phi }_2$, ${\psi }_2$ and so on.

In the same fashion, the sum of the first ten iterations, that is, ${\phi }_{10}$ and ${\psi }_{10}$ for the solution pair $u\left(x\right)$ and $v\left(x\right),$ is compared with the exact solution in Table 3 for the computational results (absolute error difference) when $N=10$, and in Figure 2 for the graphical depiction over the approximate region $0\le x\le 1.$

Table 3. Absolute error between the exact and DDM solutions when $N=10$ in Example 2.

$\mathit{x}$	$\left|\mathit{u}-{\mathit{\phi }}_{10}\right|$	$\left|{\mathit{v}-\mathit{\psi }}_{10}\right|$
0.0	0	0
0.1	$1.21349914\times {10}^{-10}$	$2.80111251\times {10}^{-11}$
0.2	$2.34858643\times {10}^{-10}$	$4.80132253\times {10}^{-11}$
0.3	$3.31564846\times {10}^{-10}$	$5.41878217\times {10}^{-11}$
0.4	$4.00955982\times {10}^{-10}$	$4.22369297\times {10}^{-11}$
0.5	$4.31368734\times {10}^{-10}$	$9.68286617\times {10}^{-12}$
0.6	$4.11918573\times {10}^{-10}$	$4.06617531\times {10}^{-11}$
0.7	$3.37640504\times {10}^{-10}$	$9.44684239\times {10}^{-11}$
0.8	$2.18713718\times {10}^{-10}$	$1.22803463\times {10}^{-10}$
0.9	$8.90017743\times {10}^{-11}$	$9.33944084\times {10}^{-11}$
1.0	0	$1\times {10}^{-29}$

Table 3. Absolute error between the exact and DDM solutions when $N=10$ in Example 2.

$\mathit{x}$	$\left|\mathit{u}-{\mathit{\phi }}_{10}\right|$	$\left|{\mathit{v}-\mathit{\psi }}_{10}\right|$
0.0	0	0
0.1	$1.21349914\times {10}^{-10}$	$2.80111251\times {10}^{-11}$
0.2	$2.34858643\times {10}^{-10}$	$4.80132253\times {10}^{-11}$
0.3	$3.31564846\times {10}^{-10}$	$5.41878217\times {10}^{-11}$
0.4	$4.00955982\times {10}^{-10}$	$4.22369297\times {10}^{-11}$
0.5	$4.31368734\times {10}^{-10}$	$9.68286617\times {10}^{-12}$
0.6	$4.11918573\times {10}^{-10}$	$4.06617531\times {10}^{-11}$
0.7	$3.37640504\times {10}^{-10}$	$9.44684239\times {10}^{-11}$
0.8	$2.18713718\times {10}^{-10}$	$1.22803463\times {10}^{-10}$
0.9	$8.90017743\times {10}^{-11}$	$9.33944084\times {10}^{-11}$
1.0	0	$1\times {10}^{-29}$

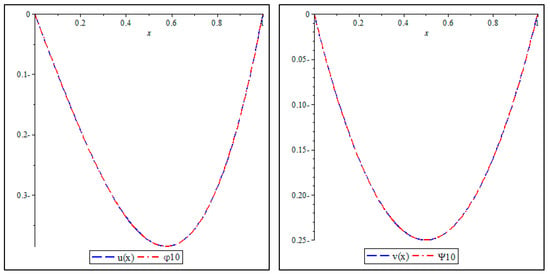
Figure 2. Comparison between the exact and DDM solutions $u\left(x\right)$ and $v\left(x\right)$ in Example 2.

Table 4. Comparison between HPM and DDM when $N=9$ in Example 2.

Numerical Methods	HPM [25]	DDM
Maximum error for $u\left(x\right)$.	$3.4\times {10}^{-5}$	$3.29\times {10}^{-9}$
Maximum error for $v\left(x\right)$	$2.9\times {10}^{-4}$	$9.88\times {10}^{-10}$

Table 4. Comparison between HPM and DDM when $N=9$ in Example 2.

Numerical Methods	HPM [25]	DDM
Maximum error for $u\left(x\right)$.	$3.4\times {10}^{-5}$	$3.29\times {10}^{-9}$
Maximum error for $v\left(x\right)$	$2.9\times {10}^{-4}$	$9.88\times {10}^{-10}$

Remarkably, while trying to assess the efficacy of the proposed method, the study refers to the good work of Saadatmandi et al. [25], where the notable homotopy perturbation method (HPM) was used to examine the governing coupled nonlinear system. Therefore, Table 4 shows the error difference comparison between the proposed DDM and HPM [25] when $N=9$, where one can easily note the truthfulness of the proposed approach over HPM, looking at the minimal error portrayed.

Example 3. 

Consider the coupled system of nonlinear BVP for the flow of magnetized blood in a blood vessel as follows [26]:

$$\left\{\begin{array}{l}{U}^{″}=H{a}^{2}U+Re\left({UV}^{\prime }-V{U}^{\prime }\right),U\left(0\right)=1,U\left(1\right)=0,\\ V^{\left(iv\right)}=H{a}^2{V}^{″}+Re\left(V^{\prime }{V}^{″}-V{V}^{‴}\right),V\left(0\right)=0,V^{\prime }\left(0\right)=0,V\left(1\right)=1,V^{\prime }\left(1\right)=0.\end{array}\right.$$

In fact, such a fluid dynamical model, presided over by the above coupled “equations models a laminar magnetohydrodynamic flow of a non-Newtonian viscous fluid in a semi-porous channel under the influence of an axial uniform static magnetic field. $U$ and $V$ are the mean axial and normal velocity components, respectively, $Ha$ is the Hartmann number, and $Re$ is the Reynolds number”; read [26] for more details about the physics of the model.

Further, applying the inverse operator $L^{-1}\left(.\right)=\int \int \left(.\right)dxdx$ to both sides of the first equation with DDM, we obtain the following recursive scheme:

$$\left\{\begin{array}{l}{U}_0={\mathsf{\Phi }}_0,\\ U_k={\mathsf{\Phi }}_k+L^{-1}\left(H{a}^2{U}_{k-1}\right)+Re{L}^{-1}\left(A_{k-1}-B_{k-1}\right),k\ge 1,\end{array}\right.$$

while applying the inverse operator $L^{-1}\left(.\right)=\int \int \int \int \left(.\right)dxdxdxdx$ to both sides of the second equation with DDM, we obtain the following recursive scheme

$$\left\{\begin{array}{l}{V}_0={\mathsf{\Psi }}_0,\\ V_k={\mathsf{\Psi }}_k+L^{-1}\left(H{a}^2{V}_{k-1}^{″}\right)+Re{L}^{-1}\left(C_{k-1}-D_{k-1}\right),k\ge 1,\end{array}\right.$$

where ${\mathsf{\Phi }}_k=c_{0,k}+c_{1,k}x,{\mathsf{\Psi }}_k=d_{0,k}+d_{1,k}x+{\displaystyle \frac{d_{2,k}}{2!}}{x}^2+{\displaystyle \frac{d_{3,k}}{3!}}{x}^3,$ and $A_k,B_k,C_k$ and $D_k$ arising the derived recursive schemes represent the Adomian polynomials for the nonlinear terms ${UV}^{\prime },V{U}^{\prime },V^{\prime }{V}^{″}$ and $V{V}^{‴}$; their computation is equally performed using the Adomian prescription [21,22]. Accordingly, the first iteration takes the following form:

$${\phi }_1=U_0,{\psi }_1=V_0,$$

where the corresponding unknown constants are computationally found to be:

$$c_{0,0}=1,c_{1,0}=-1,d_{0,0}=0,d_{1,0}=0,d_{2,0}=6,d_{3,0}=-12.$$

Next, the subsequent iteration, ${\phi }_1$ and ${\psi }_1$ are obtained as follows:

$${\phi }_1=1-x,{\psi }_1=3x^2-2x^3.$$

In the same fashion, we determine ${\phi }_2$, ${\psi }_2$ and so on.

Moreover, the computational simulation of the acquired approximate numerical results, via DDM, is given here, governing the flow of magnetized blood in the blood vessels of the human system. More specifically, two cases for fixed $Ha$ and $Re$ values are considered, and further sought the help of the Polynomial Least Squares Method (PLSM) [26] for computational validation. Thus, in Table 5 and Table 6, we estimated the error in $U$ using $ERR=\left|{\phi }_{10}-{\phi }_9\right|$, and in $V$ using $ERR=\left|{\psi }_{10}-{\psi }_9\right|$; as the governing model has no known exact analytical solution, and is further validated with the PLSM [26] solution. Additionally, Figure 3 and Figure 4 graphically portray this development. Eventually, in both solution pairs, the adopted DDM remarkably gave the most precise approximation, more especially, after looking at the error posed by the comparing PLSM [26].

Table 5. Comparison of the errors of the approximate solutions for $U$ and $V$ in Example 3.

$\mathit{x}$	Case 1 $\mathit{R}\mathit{e}=1,\hspace{1em}\hspace{1em}\mathit{H}\mathit{a}=0$		Case 2 $\mathit{R}\mathit{e}=1,\hspace{1em}\hspace{1em}\mathit{H}\mathit{a}=1$
	$\left|{\mathit{\phi }}_{10}-{\mathit{\phi }}_9\right|$	$\left|{\mathit{\psi }}_{10}-{\mathit{\psi }}_9\right|$	$\left|{\mathit{\phi }}_{10}-{\mathit{\phi }}_9\right|$	$\left|{\mathit{\psi }}_{10}-{\mathit{\psi }}_9\right|$
0	$1.00000000\times {10}^{-29}$	0	$1.00000000\times {10}^{-29}$	0
0.1	$1.25262381\times {10}^{-8}$	$8.12958379\times {10}^{-14}$	$1.76519854\times {10}^{-6}$	$1.44540468\times {10}^{-13}$
0.2	$2.49060498\times {10}^{-8}$	$7.24223852\times {10}^{-14}$	$3.45261734\times {10}^{-6}$	$6.96407098\times {10}^{-13}$
0.3	$3.67629968\times {10}^{-8}$	$3.29020106\times {10}^{-13}$	$4.96553553\times {10}^{-6}$	$1.81196373\times {10}^{-12}$
0.4	$4.74627020\times {10}^{-8}$	$1.23194797\times {10}^{-12}$	$6.19059193\times {10}^{-6}$	$3.54967865\times {10}^{-12}$
0.5	$5.60923969\times {10}^{-8}$	$2.45142377\times {10}^{-12}$	$7.00275071\times {10}^{-6}$	$5.70330687\times {10}^{-12}$
0.6	$6.14116314\times {10}^{-8}$	$3.47599168\times {10}^{-12}$	$7.26999253\times {10}^{-6}$	$7.64968715\times {10}^{-12}$
0.7	$6.17362715\times {10}^{-8}$	$3.61538097\times {10}^{-12}$	$6.85621712\times {10}^{-6}$	$8.33770806\times {10}^{-12}$
0.8	$5.46602019\times {10}^{-8}$	$2.49849342\times {10}^{-12}$	$5.61969091\times {10}^{-6}$	$6.67353352\times {10}^{-12}$
0.9	$3.63779071\times {10}^{-8}$	$7.87782932\times {10}^{-13}$	$3.40219347\times {10}^{-6}$	$2.77166523\times {10}^{-12}$
1.0	$5.77958582\times {10}^{-31}$	$5.80000000\times {10}^{-29}$	$1.40141742\times {10}^{-29}$	$1.80000000\times {10}^{-29}$

Table 5. Comparison of the errors of the approximate solutions for $U$ and $V$ in Example 3.

$\mathit{x}$	Case 1 $\mathit{R}\mathit{e}=1,\hspace{1em}\hspace{1em}\mathit{H}\mathit{a}=0$		Case 2 $\mathit{R}\mathit{e}=1,\hspace{1em}\hspace{1em}\mathit{H}\mathit{a}=1$
	$\left|{\mathit{\phi }}_{10}-{\mathit{\phi }}_9\right|$	$\left|{\mathit{\psi }}_{10}-{\mathit{\psi }}_9\right|$	$\left|{\mathit{\phi }}_{10}-{\mathit{\phi }}_9\right|$	$\left|{\mathit{\psi }}_{10}-{\mathit{\psi }}_9\right|$
0	$1.00000000\times {10}^{-29}$	0	$1.00000000\times {10}^{-29}$	0
0.1	$1.25262381\times {10}^{-8}$	$8.12958379\times {10}^{-14}$	$1.76519854\times {10}^{-6}$	$1.44540468\times {10}^{-13}$
0.2	$2.49060498\times {10}^{-8}$	$7.24223852\times {10}^{-14}$	$3.45261734\times {10}^{-6}$	$6.96407098\times {10}^{-13}$
0.3	$3.67629968\times {10}^{-8}$	$3.29020106\times {10}^{-13}$	$4.96553553\times {10}^{-6}$	$1.81196373\times {10}^{-12}$
0.4	$4.74627020\times {10}^{-8}$	$1.23194797\times {10}^{-12}$	$6.19059193\times {10}^{-6}$	$3.54967865\times {10}^{-12}$
0.5	$5.60923969\times {10}^{-8}$	$2.45142377\times {10}^{-12}$	$7.00275071\times {10}^{-6}$	$5.70330687\times {10}^{-12}$
0.6	$6.14116314\times {10}^{-8}$	$3.47599168\times {10}^{-12}$	$7.26999253\times {10}^{-6}$	$7.64968715\times {10}^{-12}$
0.7	$6.17362715\times {10}^{-8}$	$3.61538097\times {10}^{-12}$	$6.85621712\times {10}^{-6}$	$8.33770806\times {10}^{-12}$
0.8	$5.46602019\times {10}^{-8}$	$2.49849342\times {10}^{-12}$	$5.61969091\times {10}^{-6}$	$6.67353352\times {10}^{-12}$
0.9	$3.63779071\times {10}^{-8}$	$7.87782932\times {10}^{-13}$	$3.40219347\times {10}^{-6}$	$2.77166523\times {10}^{-12}$
1.0	$5.77958582\times {10}^{-31}$	$5.80000000\times {10}^{-29}$	$1.40141742\times {10}^{-29}$	$1.80000000\times {10}^{-29}$

Table 6. Comparison between PLSM and DDM in Example 3.

Numerical Methods	Case 1 $\mathit{R}\mathit{e}=1, \mathit{H}\mathit{a}=0$		Case 2 $\mathit{R}\mathit{e}=1, \mathit{H}\mathit{a}=1$
	PLSM [26]	DDM	PLSM [26]	DDM
Maximum error for $u\left(x\right)$	$9.50\times {10}^{-5}$	$6.17\times {10}^{-8}$	$1.48\times {10}^{-4}$	$7.27\times {10}^{-6}$
Maximum error for $v\left(x\right)$	$1.34\times {10}^{-6}$	$3.62\times {10}^{-12}$	$1.37\times {10}^{-7}$	$8.34\times {10}^{-12}$

Table 6. Comparison between PLSM and DDM in Example 3.

Numerical Methods	Case 1 $\mathit{R}\mathit{e}=1, \mathit{H}\mathit{a}=0$		Case 2 $\mathit{R}\mathit{e}=1, \mathit{H}\mathit{a}=1$
	PLSM [26]	DDM	PLSM [26]	DDM
Maximum error for $u\left(x\right)$	$9.50\times {10}^{-5}$	$6.17\times {10}^{-8}$	$1.48\times {10}^{-4}$	$7.27\times {10}^{-6}$
Maximum error for $v\left(x\right)$	$1.34\times {10}^{-6}$	$3.62\times {10}^{-12}$	$1.37\times {10}^{-7}$	$8.34\times {10}^{-12}$

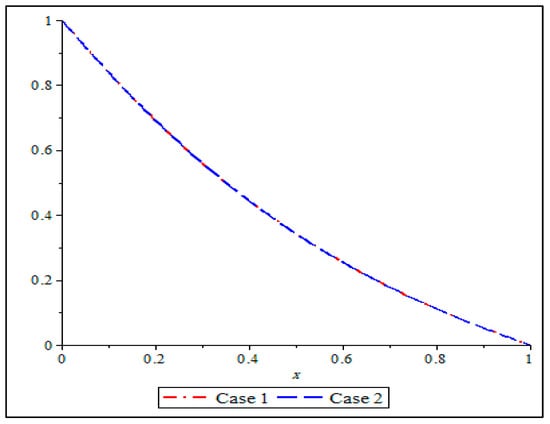
Figure 3. Comparison of approximate solutions of DDM for the two cases for $U$ in Example 3.

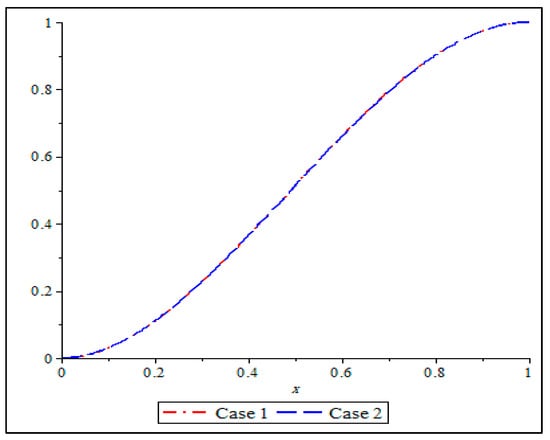
Figure 4. Comparison of approximate solutions of DDM for the two cases for $V$ in Example 3.

4. Conclusions

The present study numerically examines a class of BVPs, characterized by coupled systems of both linear and nonlinear differential equations via the application of the DDM. The DDM is an enhanced approach based on the classical ADM that attains convergence more rapidly. Moreover, several test models, including a real model for the flow of blood in the human system, were examined in the study, comprising both the homogenous and nonhomogeneous cases, where the proposed DDM was found to significantly outperform the other numerical methods considered. In addition, the effectiveness of DDM was reported in several Table 1, Table 2, Table 3, Table 4, Table 5 and Table 6 through the errors difference as an estimator, and Figure 1, Figure 2, Figure 3 and Figure 4, graphically portraying the relationship between the exact and approximate solutions. Now, based on the results reported in the aforementioned Tables and Figures, one may conclude that the deployed DDM has better convergence, considering the revealed minimal error. Moreover, the devised method is proven to be a robust numerical method with regard to high levels of accuracy. Lastly, the methodology used is highly recommended to examine various linear and nonlinear higher-order differential equations arising in the general science and real-life applications.