Energy-Preserving Algorithms for the Ginzburg–Landau Equation: Integrating Scientific Research with Talent Cultivation

Abstract

This study proposes a novel structure-preserving algorithm for the Ginzburg–Landau equation (GLE) by combining the Fourier pseudospectral method with the Exponential Average Vector Field (EAVF) scheme. The proposed numerical framework strictly preserves the energy dissipation property of GLE systems, as validated through theoretical analysis and numerical experiments on solitary wave dynamics. Compared to conventional methods such as the average vector field approach, the EAVF-based scheme demonstrates superior computational efficiency, including faster convergence and enhanced stability under larger time steps, enabling accurate long-term simulation of strongly nonlinear GLE systems. Furthermore, this research incorporates a pedagogical innovation through its implementation within an undergraduate innovation project. By adopting a “problem decomposition–code verification–modular development” training model, students engage in the full cycle of algorithm design, implementation, and validation. This practice-oriented approach significantly enhances students’ competencies in scientific programming, complex problem-solving, and research-oriented thinking, providing an effective paradigm for synergizing advanced computational research with talent cultivation in STEM education.

1. Introduction

Partial differential equations occupy a core position in science and engineering, with practical problems in natural sciences and engineering technology as their backdrop. Their theories and methods permeate physics, engineering, computer science, and other disciplines, serving as a bridge between mathematical theory and practical applications. However, in the teaching of partial differential equations, the traditional model usually emphasizes theoretical derivation but neglects practical programming, making it difficult to balance students’ understanding of practical problems and the cultivation of their innovative abilities. As a result, students often find the subject abstract and complex. In fact, while these models have solid practical applications and theoretical foundations, and many of their experimental results have been validated in the laboratory, numerical methods continue to play a vital role by bridging the gap between theory and experimentation, facilitating the development of analytical results, and proposing experimental pathways through computer simulations, while enhancing students’ sensory cognition.

Among the numerous partial differential equation models, the Ginzburg–Landau equation (GLE) is a core model for describing complex physical systems such as superconductive electrodynamics and fluid mechanics. Its numerical solution is of great significance for understanding physical phenomena and promoting engineering applications. However, the strong nonlinearity of this equation leads to instability issues during long-time simulation processes. Although traditional numerical methods such as the finite element method and Runge–Kutta methods can yield numerical solutions, they struggle to simultaneously guarantee energy conservation/dissipation characteristics and computational efficiency, limiting their applicability to long-term evolution simulations of physical systems. In recent years, many scholars have carried out in-depth research on this problem, proposing methods such as the finite element method, the finite difference method, etc. Gunzburger et al. [1] solved a series of problems of the GL superconducting model, proposed the finite element approximation of the optimal system, and deduced the error estimate. Kong et al. [2] applied the implicit method of higher-order tight-format coupling alternating directions to solve the two-dimensional GLE, and proposed five numerical formats with second-order temporal accuracy and fourth-order spatial accuracy. In addition, there are many efficient numerical methods for solving GLE [3,4]. There are also many studies on complex GLE [5,6], fractional GLE [7,8], and stochastic GLE [9,10], but most of these methods only solve numerically in terms of satisfying accuracy, without considering the geometry or physical structure of the system itself. This has become a key technical bottleneck in the long-term simulation of the GLE.

The innovation and entrepreneurship program for college students is an important pathway to cultivating innovative talents. In recent years, the trend of combining scientific research with undergraduate talent training has become more and more significant, and many colleges and universities have devoted themselves to the exploration and reform of this educational practice. The rapidly growing societal demand for innovative talents has exposed the limitations of the traditional undergraduate education model. This gap has prompted colleges and universities, which bear the dual mission of scientific research and talent training, to actively explore new educational pathways. Consequently, synergizing research exploration with undergraduate education has become an inevitable trend. From a strategic and policy perspective, studies have systematically explored the pathways for cultivating high-level innovative talents through the integration of science and education [11]. They have analyzed in-depth why it is necessary to foster innovative talents through the integration of scientific research and education, and pointed out that the current integration faces new challenges, such as the historical issue of the dual-track development of scientific research and education systems, the institutional issue of the separation between research and education systems, the resource issue of the lack of complementarity between scientific research and educational resources, and the positioning issue of insufficient coordination between scientific research and educational inputs. Many scientific researchers are actively engaged in the exploration of the combination of scientific research and teaching. For example, the authors address the challenge of ineffective integration between theory and practice in undergraduate electronic engineering in Chinese universities. This study leverages the framework of engineering education certification to explore a project-based teaching model that integrates scientific research achievements into the electronic comprehensive design course [12]. Coccorese et al. [13] investigate the research-teaching relationship within a medium-sized department of an Italian university. Their results point to a positive association between research productivity and teaching quality.

In view of this, this study relies on the college student innovation and entrepreneurship project titled “Research on Efficient Structure-Preserving Algorithms for Partial Differential Equations”, and deeply integrates the scientific research on the energy-preserving algorithm for GLE with talent cultivation. On one hand, aiming at the technical bottlenecks in the numerical solution of GLE, the Fourier pseudospectral method and the Exponential Average Vector Field (EAVF) algorithm are introduced to construct a numerical scheme that preserves energy dissipation. On the other hand, through the project model of “problem decomposition—code verification—modular development”, with the theoretical derivation and programming implementation of the GLE algorithm as the practical carrier, students’ abilities to decompose complex problems and their scientific research thinking are cultivated. This study not only provides a new method for the numerical solution of GLE, but also offers a replicable educational paradigm for the “scientific research feeding back teaching” in science and engineering disciplines.

The primary novelty of our work is twofold: (1) the development of a numerical scheme that simultaneously preserves the energy property and the oscillatory dynamics of the GLE system, addressing the limitations of existing approaches; (2) the deep integration of this algorithmic research within an undergraduate innovation project, creating a replicable ‘research-driven teaching’ paradigm. The research contributions of this article are in the following aspects:

(1)

This study constructs a numerical scheme that preserves energy conservation or dissipation properties for the GLE by combining the Fourier pseudo-spectral method with the EAVF algorithm.

(2)

It verifies through numerical experiments that the EAVF algorithm outperforms the AVF method in convergence speed and computational efficiency, especially with larger step sizes.

(3)

The research integrates scientific exploration of energy-preserving algorithms with college students’ innovation and entrepreneurship projects, forming a “research-driven” talent cultivation model that effectively enhances students’ comprehensive abilities.

The overall structure of this article is as follows: In Section 2, we elaborate on the physical background of GLE, present the one-dimensional GLE traffic flow model studied along with its initial and boundary conditions, review existing numerical methods for solving GLE, and introduce the concept of structure-preserving algorithms. In Section 3, we first describe the spatial discretization of GLE using the Fourier pseudospectral method and prove that the semi-discrete format maintains energy dissipation; then, we introduce the EAVF scheme, and propose and prove a theorem on its energy-preserving properties; finally, we present numerical experiments to verify the effectiveness and advantages of the EAVF algorithm compared with the AVF method. Section 4 focuses on discussing the implementation path of this algorithm research within the undergraduate innovation and entrepreneurship project and its talent cultivation outcomes, thereby forming a logical closed-loop from theoretical methods to educational practice. In the Conclusion, we summarize the research content and results, emphasize the role of research project-driven teaching practice in enhancing students’ abilities, and look forward to expanding this model to other scientific problems.

2. Background of the Research

The Ginzburg–Landau equation was first proposed by Ginzburg and Landau in 1950, with a rich physical background. It is mainly used to simulate the electrodynamic, quantum mechanical, and thermodynamic properties of superconductors. Benard convection, Taylor–Couette flow, planar Poiseuille flow, chemical turbulence, and superconductors can all be modeled using GLE. This project considers a one-dimensional GLE traffic flow model [14]:

$${\displaystyle \frac{\partial u}{\partial t}}=J\left({\displaystyle \frac{\delta H\left(u\right)}{\delta u}}\right),J=({\partial }_x+\epsilon {\partial }_{xx}),(x,t)\in [a,b]\times [0,T],$$

(1)

with the following initial and periodic boundary conditions

$$\left\{\begin{array}{cc}u(x,0)=u_0\left(x\right),\hfill & x\in [a,b],\hfill \\ u(a,t)=u(b,t),\hfill & t\in [0,T],\hfill \end{array}\right.$$

where $H\left(u\right)$ is the energy function with respect to the function $u,$ ${\displaystyle \frac{\delta H\left(u\right)}{\delta u}}$ is the variational derivative of H with respect to u, and $u_0\left(x\right)$ is a known function. The real-valued function $u(x,t)$ represents the wave displacement at position x and time $t.$ The operator $J=({\partial }_x+\epsilon {\partial }_{xx})$ encapsulates both the convective and dissipative mechanisms within the flow. The dissipative term $\epsilon {\partial }_{xx}$ models diffusion effects, and the evolution of $u(x,t)$ captures key phenomena such as solitary wave propagation, which can be analogous to the formation and dynamics of traffic jams. Under periodic boundary conditions, the GLE Equation (1) satisfies the following energy dissipation law

$${\displaystyle \frac{dH}{dt}}=⟨{\displaystyle \frac{\delta H\left(u\right)}{\delta u}},u_t⟩=⟨{\displaystyle \frac{\delta H\left(u\right)}{\delta u}},J{\displaystyle \frac{\delta H\left(u\right)}{\delta u}}⟩=-\epsilon {∥{\partial }_x{\displaystyle \frac{\delta H\left(u\right)}{\delta u}}∥}^2\le 0.$$

The $L^2$ inner product and norm are, respectively, defined as

$$⟨f,g⟩:={\int }_a^{b}f·gdx,\forall f,g\in L^2[a,b],\parallel f\parallel =\sqrt{⟨f,f⟩}.$$

The energy functional $H\left(u\right)$ in this model acts as a Lyapunov function for the system, and its specific form is determined by the physical context. For example, in superconductivity theory, $H\left(u\right)$ typically includes the Ginzburg–Landau free energy terms:

$$H\left(u\right)={\int }_{\Omega }\left({\alpha \left|u\right|}^2+{\beta \left|u\right|}^4+\kappa {|\nabla u|}^2\right)dx,$$

where $\alpha ,\beta ,\kappa$ are physical parameters.

For given initial conditions and appropriate boundary conditions (such as the periodic boundary conditions considered in this work), a unique weak or classical solution to Equation (1) exists on a finite time interval, provided the nonlinear terms satisfy certain growth and continuity conditions. Particularly, in one spatial dimension with polynomial nonlinearities in the energy functional, solution uniqueness can typically be established using classical PDE theory tools such as energy estimates and Gronwall’s inequality. Nevertheless, challenges to the existence and uniqueness of solutions can emerge in high-dimensional scenarios or strongly nonlinearly coupled systems, where phenomena like solution bifurcation or uncertainties in long-term dynamics may occur. The incorporation of appropriate assumptions is thus essential. For detailed theoretical foundations, we refer the reader to Reference [15].

Based on the idea that numerical methods should maintain the exact solution of the original system as much as possible, Feng Kang proposed the symplectic algorithm for Hamiltonian systems, which has evolved into a crucial research field in computational mathematics named the structure-preserving algorithms. In view of the above-mentioned energy dissipation property of the GLE system, traditional numerical methods always destroy this property, which leads to the distortion of the physical meaning of the solution. Therefore, the goal of this study is to construct an algorithm that can strictly maintain the conservation or dissipation of energy. Celledoni et al. [14] proved that the AVF method can maintain its energy characteristics, and Chen et al. [16] combined the invariant energy quadratization (IEQ) method with the Runge–Kutta method to convert the nonlinear part into a semi-implicit format by introducing a Lagrangian multiplier, and composed of two coupled equations for each time-step calculation to form a new linear system, constructing a fourth-order format that maintains the energy dissipation of the GLE. Yao et al. [17] constructed a high-order implicit-explicit finite element method with energy stability to solve the GLE under periodic boundary conditions. The fully-discrete scheme consists of the BDF-k in the temporal direction and the finite element method in the spatial direction, respectively. Furthermore, as an oscillatory differential equation, the solution of the system has oscillatory characteristics. However, the aforementioned numerical schemes fail to adequately account for this inherent oscillatory nature, leading to phase error accumulation and a loss of physical fidelity during long-term simulations. This limitation motivates the development of a numerical method capable of simultaneously preserving both the oscillatory structure and the energy dynamics of the system.

3. A New Type of Structure-Preserving Algorithm

In this section, we will systematically construct an energy-preserving numerical scheme for the GLE. Firstly, the Fourier pseudospectral method is employed for spatial discretization, and high-precision interpolation approximation is utilized to ensure that the semi-discrete system inherits the energy dissipation property of the original equation. Furthermore, the EAVF algorithm is introduced for temporal integration, which maintains the oscillatory structure of the system while improving computational efficiency.

3.1. Spatial Discretization via the Fourier Pseudospectral Method

First, the Fourier pseudospectral method is employed for spatial discretization of the GLE, and it is proven that the semi-discrete form of the GLE preserves the system’s energy dissipation property.

Divide the spatial domain $\Omega =[a,b]$ into N equal parts, where N is an even number. Define the spatial step $h={\displaystyle \frac{b-a}{N}},x_j=a+jh(j=0,1,2,\dots ,N-1)$ as the grid points. The Fourier pseudo-spectral method uses Fourier interpolation polynomials and their values at the interpolation points to construct the discrete form of the equation, and then obtains the discrete format of the solution. It has the characteristics of high precision and fast convergence. Therefore, this method is widely used for the structure-preserving spatial discretization of partial differential equations with periodic boundary conditions [18,19].

Define the interpolation space as $S_N=\mathrm{span}\{g_j\left(x\right),j=0,1,\dots ,N-1\},$ and the interpolation basis functions are

$$g_j\left(x\right)={\displaystyle \frac{1}{N}}\sum _{k=-N/2}^{N/2}{\displaystyle \frac{1}{c_k}}{e}^{ik\mu (x-x_j)},$$

with

$$c_k=\left\{\begin{array}{cc}1,\hfill & \left|k\right|\ne N/2,\hfill \\ 2,\hfill & \left|k\right|=N/2,\hfill \end{array}\right.$$

and $\mu ={\displaystyle \frac{2\pi }{b-a}}.$ Assume $I_N$ is the interpolation operator on the spatial domain $\Omega .$ For any function $u(x,t)\in C_0(\Omega ),$ we have

$${\left.I_{N}u(x,t)\right|}_{x=x_j}=u(x_j,t),j=0,1,\dots ,N-1.$$

Therefore,

$$I_{N}u(x,t)=\sum _{j=0}^{N-1}{u}_j\left(t\right)g_j\left(x\right)={\displaystyle \frac{1}{N}}\sum _{j=0}^{N-1}\sum _{k=-N/2}^{N/2}{\displaystyle \frac{1}{c_k}}{u}_j{e}^{ik\mu (x-x_j)}=\sum _{k=-N/2}^{N/2}{e}^{ik\mu x}{\displaystyle \frac{1}{N{c}_k}}\sum _{j=0}^{N-1}{u}_j{e}^{-ik\mu x_j}.$$

Based on the orthogonality of the basis functions, we have

$${\displaystyle \frac{1}{N}}\sum _{j=0}^{N-1}{e}^{-ik\mu x_j}=\left\{\begin{array}{cc}1,\hfill & k=nN,\hfill \\ 0,\hfill & k\ne nN.\hfill \end{array}\right.$$

The derivative values of the original function at the collocation points can be approximated by computing the derivative of the interpolation polynomial at $x=x_l;$ that is,

$${\left.{\displaystyle \frac{{\partial }^k}{\partial x^k}}{I}_{N}u(x,t)\right|}_{x=x_l}=\sum _{j=0}^{N-1}{u}_j{\left.{\displaystyle \frac{d^k{g}_j\left(x\right)}{d{x}^k}}\right|}_{x=x_l}={\left(D_k\mathbf{u}\right)}_l,$$

where $u={[u_0,u_1,...,u_{N-1}]}^T.$ The matrix $D_1$ is the following skew-symmetric matrix

$${\left(D_1\right)}_{j,l}=\left\{\begin{array}{cc}{\displaystyle \frac{1}{2}{(-1)}^{j+l}\mu cot\left(\mu \frac{x_j-x_l}{2}\right),}\hfill & j\ne l,\hfill \\ 0,\hfill & j=l.\hfill \end{array}\right.$$

The k-th order partial differential operator ${\partial }_x^k$ can be approximated by the Fourier differentiation matrix $D_k.$ Applying the Fourier pseudo-spectral method to the generalized GLE (1), we obtain the following semi-discrete system

$${\displaystyle \frac{d\mathbf{u}}{dt}}=\tilde{J}\nabla \tilde{H}\left(\mathbf{u}\right),\tilde{J}=\left(D_1+\epsilon D_2\right),$$

(2)

where $\tilde{H}$ is an approximate discretization of the Lyapunov function $H, \mathbf{u}=[u_0,u_1,\dots ,u_{N-1}]$ and $\nabla \tilde{H}\left(\mathbf{u}\right)$ is the gradient of the spatially discretized energy functional $\tilde{H}\left(\mathbf{u}\right)$ with respect to the solution vector $\mathbf{u}$. Furthermore, it is obvious that $\tilde{J}$ is a semi-negative definite matrix, and

$${\displaystyle \frac{d\tilde{H}}{dt}}={\left(\nabla \tilde{H}\right)}^T\tilde{J}\nabla \tilde{H}=-\epsilon {∥D_1\nabla \tilde{H}∥}^2\le 0.$$

Therefore, the semi-discrete system of GLE satisfies the energy dissipation law. The primary task next is to solve the system of ordinary differential Equation (2) using an efficient numerical scheme.

3.2. Oscillation-Preserving Exponential Average Vector Field Algorithm

Reference [20] proposed the EAVF algorithm based on the AVF method. This approach integrates concepts of gradient discretization and exponential integration, improving computational efficiency while preserving the system’s oscillatory characteristics and energy properties. For the following system

$$\left\{\begin{array}{c}{\displaystyle \frac{dy}{dt}=Q(My+\nabla U\left(y\right)),}\hfill \\ y\left(t_0\right)=y_0,\hfill \end{array}\right.$$

(3)

with M, a real symmetric matrix that embodies the oscillatory characteristics of the system, and U, a differentiable function. Then, $My+\nabla U\left(y\right)$ corresponds to the gradient of the function $L\left(y\right)={\displaystyle \frac{1}{2}}{y}^{T}My+U\left(y\right).$ Here, Q is a constant matrix whose properties determine whether the system is energy-conservative or dissipative. If Q is skew-symmetric, then (3) is a conservative system; if Q is semi-negative definite, then (3) is a dissipative system with the Lyapunov function $L\left(y\right)$.

Exponential integration is a highly efficient algorithm for solving differential equations with high oscillatory properties. Compared to non-exponential integration methods, it maintains high solution accuracy even with large time steps. Numerous exponential integration algorithms have been proposed for solving systems of first-order and second-order ordinary differential equations [20].

The constant variation formula for system (3) takes the following form:

$$y(t_0+\tau )=\exp \left(\tau QM\right)y\left(t_0\right)+\tau {\int }_0^1\exp \left((1-\xi )\tau QM\right)Q\nabla U\left(y(t_0+\xi \tau )\right)d\xi .$$

By replacing $\nabla U\left(y(t_0+\xi \tau )\right)$ in the above formula with the AVF, we obtain the EAVF as follows:

$$y^1=\exp \left(V\right)y^0+\tau \phi \left(V\right)Q{\int }_0^1\nabla U\left((1-\eta )y^0+\eta y^1\right)d\eta ,$$

(4)

where $V=\tau QM,y^1\approx y(t_0+\tau ),\phi \left(z\right)={\displaystyle \frac{\exp \left(z\right)-1}{z}}.$

Theorem 1. 

The EAVF scheme (4) can preserve the energy conservation or dissipation property of the original system (3); that is,

$$L\left(y^1\right)-L\left(y^0\right)=\left\{\begin{array}{cc}=0,\hfill & Q\mathit{is}a\mathit{skew-symmetric}\mathit{matrix},\hfill \\ \le 0,\hfill & Q\mathit{is}a\mathit{semi-negative}\mathit{definite}\mathit{matrix}.\hfill \end{array}\right.$$

Proof. 

First, assume that matrix M is an invertible matrix. Let $\overline{\nabla }U(y^1,y^0)={\int }_0^1\nabla U\left((1-\eta )y^0+\eta y^1\right)d\eta$, and denote $M^{-1}\nabla U=\overline{\nabla }U$. Then, we have

$$L\left(y^1\right)-L\left(y^0\right)={\displaystyle \frac{1}{2}}{y}^{1^T}M{y}^1+U\left(y^1\right)-{\displaystyle \frac{1}{2}}{y}^{0^T}M{y}^0-U\left(y^0\right),$$

where

$$\begin{array}{cc}\hfill {\displaystyle \frac{1}{2}}{y}^{1^T}M{y}^1& ={\displaystyle \frac{1}{2}}\left(y^{0^T}\exp {\left(V\right)}^T+\tau \overline{\nabla }{U}^T{Q}^T\phi {\left(V\right)}^T\right)M\left(\exp \left(V\right)y^0+\tau \phi \left(V\right)Q\overline{\nabla }U\right)\hfill \\ & ={\displaystyle \frac{1}{2}}{y}^{0^T}\exp {\left(V\right)}^{T}M\exp \left(V\right)y^0+\tau y^{0^T}\exp {\left(V\right)}^{T}M\phi \left(V\right)Q\overline{\nabla }U\hfill \\ & +{\displaystyle \frac{{\tau }^2}{2}}\overline{\nabla }{U}^T{Q}^T\phi {\left(V\right)}^{T}M\phi \left(V\right)Q\overline{\nabla }U.\hfill \end{array}$$

Since $V=\tau QM$ and $\phi \left(V\right)V=\left(\exp \right(V)-I)$, we have

$$\begin{array}{cc}\hfill {\displaystyle \frac{1}{2}}{y}^{1^T}M{y}^1& ={\displaystyle \frac{1}{2}}{y}^{0^T}\exp {\left(V\right)}^{T}M\exp \left(V\right)y^0+y^{0^T}\exp {\left(V\right)}^{T}M\phi \left(V\right)V\overline{\overline{\nabla }}U\hfill \\ \hfill & +{\displaystyle \frac{1}{2}}\overline{\overline{\nabla }}{U}^T{V}^T\phi {\left(V\right)}^{T}M\phi \left(V\right)V\overline{\overline{\nabla }}U\hfill \\ \hfill & ={\displaystyle \frac{1}{2}}{y}^{0^T}\exp {\left(V\right)}^{T}M\exp \left(V\right)y^0+y^{0^T}\exp {\left(V\right)}^{T}M(\exp \left(V\right)-I)\overline{\overline{\nabla }}U\hfill \\ \hfill & +{\displaystyle \frac{1}{2}}\overline{\overline{\nabla }}{U}^T(\exp {\left(V\right)}^T-I)M(\exp \left(V\right)-I)\overline{\overline{\nabla }}U\hfill \\ \hfill & ={\displaystyle \frac{1}{2}}{y}^{0^T}\exp {\left(V\right)}^{T}M\exp \left(V\right)y^0+y^{0^T}\left(\exp {\left(V\right)}^{T}M\exp \left(V\right)-\exp {\left(V\right)}^{T}M\right)\overline{\overline{\nabla }}U\hfill \\ \hfill & +{\displaystyle \frac{1}{2}}\overline{\overline{\nabla }}{U}^T\left(\exp {\left(V\right)}^{T}M\exp \left(V\right)-\exp {\left(V\right)}^{T}M-M\exp \left(V\right)+M\right)\overline{\overline{\nabla }}U.\hfill \end{array}$$

On the other hand,

$$\begin{array}{cc}\hfill U\left(y^1\right)-U\left(y^0\right)& =(y^{1^T}-y^{0^T})\overline{\nabla }U(y^1,y^0)\hfill \\ \hfill & =y^{0^T}\left(\exp {\left(V\right)}^T-I\right)\overline{\nabla }U+\tau \overline{\nabla }{U}^T{Q}^T\phi {\left(V\right)}^T\overline{\nabla }U\hfill \\ \hfill & =y^{0^T}\left(\exp {\left(V\right)}^{T}M-M\right)\overline{\overline{\nabla }}U+\overline{\overline{\nabla }}{U}^T{V}^T\phi {\left(V\right)}^{T}M\overline{\overline{\nabla }}U\hfill \\ \hfill & =y^{0^T}\left(\exp {\left(V\right)}^{T}M-M\right)\overline{\overline{\nabla }}U+\overline{\overline{\nabla }}{U}^T\left(\exp {\left(V\right)}^{T}M-M\right)\overline{\overline{\nabla }}U.\hfill \end{array}$$

Thus,

$$\begin{array}{cc}\hfill L\left(y^1\right)-L\left(y^0\right)& ={\displaystyle \frac{1}{2}}{y}^{1^T}M{y}^1-{\displaystyle \frac{1}{2}}{y}^{0^T}M{y}^0+U\left(y^1\right)-U\left(y^0\right)\hfill \\ \hfill & ={\displaystyle \frac{1}{2}}{y}^{0^T}\left(\exp {\left(V\right)}^{T}M\exp \left(V\right)-M\right)y^0+y^{0^T}\left(\exp {\left(V\right)}^{T}M\exp \left(V\right)-M\right)\overline{\overline{\nabla }}U\hfill \\ \hfill & +{\displaystyle \frac{1}{2}}\overline{\overline{\nabla }}{U}^T\left(\exp {\left(V\right)}^{T}M\exp \left(V\right)-M\right)\overline{\overline{\nabla }}U+{\displaystyle \frac{1}{2}}\overline{\overline{\nabla }}{U}^T\left(\exp {\left(V\right)}^{T}M-M\exp \left(V\right)\right)\overline{\overline{\nabla }}U\hfill \\ \hfill & ={\displaystyle \frac{1}{2}}{\left(y^0+\overline{\overline{\nabla }}U\right)}^T{N}_1\left(y^0+\overline{\overline{\nabla }}U\right)+{\displaystyle \frac{1}{2}}\overline{\overline{\nabla }}{U}^T{N}_2\overline{\overline{\nabla }}U,\hfill \end{array}$$

where $N_1=\exp {\left(V\right)}^{T}M\exp \left(V\right)-M$ and $N_2=\exp {\left(V\right)}^{T}M-M\exp \left(V\right)$. According to Lemma 2.2 in reference [20], it holds that

$$N_1,N_2=\left\{\begin{array}{cc}=0,\hfill & Q\mathrm{is}\mathrm{a}\mathrm{skew-symmetric}\mathrm{matrix},\hfill \\ \le 0,\hfill & Q\mathrm{is}\mathrm{a}\mathrm{semi-negative}\mathrm{definite}\mathrm{matrix}.\hfill \end{array}\right.$$

Thus, when matrix M is invertible, the conclusion of Theorem 1 holds. Secondly, if M is a non-invertible matrix, construct a series of symmetric invertible matrices $\left\{M_{\epsilon }\right\}$ ($\epsilon \to 0$) that converge to $M.$ Using the above-proved process, it can be known that the system corresponding to each $M_{\epsilon }$ satisfies Theorem 1. Thus, when $\epsilon \to 0$, the conclusion of the system corresponding to matrix M also holds. Similar detailed proofs can be found in Reference [20]. □

Applying the EAVF scheme to solve the system (2) after the spatial semi-discretization of the GLE traffic flow model can preserve the energy conservation or dissipation property of the original system. The effectiveness and superiority of the algorithm will be verified by numerical experiments.

The key distinction of our EAVF formulation lies in its dual preservation of both the Lyapunov stability (energy dissipation) and the oscillatory characteristics of the GLE system, addressing a gap in conventional AVF-based PDE solvers that primarily focus on energy properties. The method can also be extended to high-dimensional problems with appropriate spatial discretization. Additionally, while the current Fourier pseudospectral-based approach is specifically suited for periodic boundary conditions, alternative discretization schemes such as finite element methods would be required for non-periodic boundary scenarios.

3.3. Numerical Experiment

Take the following energy function (see, e.g., [16]):

$$H\left(u\right)={\int }_{\Omega }\left(3u^2-{\displaystyle \frac{1}{2}}{u}_x^2-{\displaystyle \frac{1}{4}}{u}^4\right)dx,$$

i.e.,

$${\displaystyle \frac{\delta H\left(u\right)}{\delta u}}=6u+{\partial }_x^{2}u-u^3.$$

In this case, the GLE takes the following form:

$${\displaystyle \frac{\partial u}{\partial t}}=({\partial }_x+\epsilon {\partial }_{xx})\left(6u+{\partial }_x^{2}u-u^3\right).$$

After discretizing the system space using the Fourier spectral method, a system of ordinary differential equations is obtained:

$${\displaystyle \frac{d\mathbf{u}}{dt}}=(D_1+\epsilon D_2)\left(6\mathbf{u}+D_2\mathbf{u}-{\mathbf{u}}^3\right).$$

It is rewritten into the form of system (3), that is,

$${\displaystyle \frac{d\mathbf{u}}{dt}}=QM\mathbf{u}+Q\nabla U\left(\mathbf{u}\right)=(D_1+\epsilon D_2)(6E+D_2)\mathbf{u}-(D_1+\epsilon D_2){\mathbf{u}}^3,$$

where

$$Q=D_1+\epsilon D_2=\tilde{J},M=6E+D_2.$$

Applying the EAVF method (4) to this equation, the EAVF scheme for the GLE model is obtained in the following form

$$\begin{array}{cc}\hfill {\displaystyle \frac{{\mathbf{u}}^{n+1}-\exp \left(V\right){\mathbf{u}}^n}{\tau }}& =\phi \left(V\right)\tilde{J}{\int }_0^1\nabla U\left((1-\eta ){\mathbf{u}}^n+\eta {\mathbf{u}}^{n+1}\right)d\eta \hfill \\ \hfill & =-{\displaystyle \frac{1}{4}}\phi \left(V\right)\tilde{J}\left({\left({\mathbf{u}}^n\right)}^3+{\left({\mathbf{u}}^{n+1}\right)}^3+{\mathbf{u}}^n{\left({\mathbf{u}}^{n+1}\right)}^2+\left({\mathbf{u}}^{n+1}\right){\left({\mathbf{u}}^n\right)}^2\right)\hfill \end{array}$$

Choose the initial condition of a single solitary wave:

$$u(x_0,0)=e^{-\lambda {\left(x-{\displaystyle \frac{1}{2}}\right)}^2},x\in [-10,10].$$

Since all the integrators in the experiment are implicit, the fixed-point iteration is used to solve the system of algebraic equations in each step with the error tolerance ${10}^{-16}$ and the maximum iteration number 1000, respectively.

To study the influence of parameter $\epsilon$ on energy dissipation, the control variable method is used for the experiment. First, take $\lambda =0.3$, the number of spatial grid points $N=200$; the time step sizes are taken as $\tau =0.001,0.01$, respectively. For $\epsilon =0,0.005,0.01,0.015,0.02$, the energy variation in the EAVF scheme is shown in Figure 1. It can be seen from Figure 1 that when $\epsilon =0$, the EAVF scheme can maintain the conservation of discrete energy. When $\epsilon >0$, the discrete energy dissipates, and the energy dissipation rate accelerates as $\epsilon$ increases. Figure 2 shows the waveform diagram when $\epsilon =0.01$.

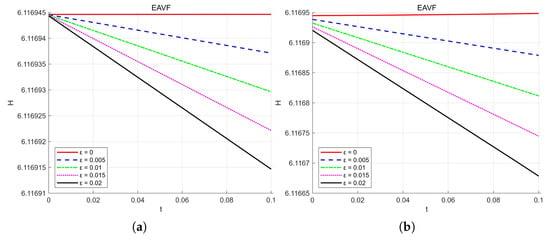
Figure 1. Energy variations solved by the EAVF method under different $\epsilon$ values. (a) $\tau =0.001$. (b) $\tau =0.01$. Experimental setup: spatial grid points $N=200$, nonlinearity parameter $\lambda =0.3.$ Key observations: When $\epsilon =0$, the discrete energy remains conserved; when $\epsilon >0$, the energy dissipates, and the dissipation rate accelerates as $\epsilon$ increases.

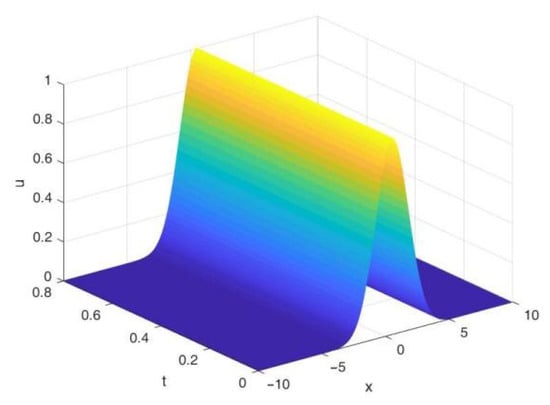
Figure 2. Waveform diagram solved by the EAVF method. Parameter values: $\epsilon =0.01, \lambda =0.3, \tau =0.01, N=200.$ Key observations: the scheme accurately captures the evolution of the initial Gaussian wave packet, demonstrating its capability to simulate solitary wave dynamics under dissipative effects. The preserved waveform structure highlights the method’s numerical stability.

The waveform evolution illustrated in Figure 2 provides critical insights into the behavior of solitary waves governed by the Ginzburg–Landau equation, with direct implications for modeling key physical phenomena. These numerical solutions accurately capture the dynamics of localized coherent structures, serving as robust analogs for flux vortex dynamics in superconductivity and optical soliton propagation in nonlinear waveguides. The observed stability in waveform evolution under energy dissipation conditions validates our scheme’s capability for simulating long-term behavior of such structures, while the preserved topological properties align with physical requirements for maintaining quantum coherence in superconducting systems and signal integrity in photonic applications. This dual demonstration of numerical robustness and physical fidelity highlights the method’s potential for simulating realistic scenarios across condensed matter physics and optical engineering domains.

Next, select the AVF energy-preserving scheme in the following form [18] for comparison.

$${\displaystyle \frac{{\mathbf{u}}^{n+1}-{\mathbf{u}}^n}{\tau }}=\left(3\tilde{J}+{\displaystyle \frac{\tilde{J}}{2}}{D}_2\right)({\mathbf{u}}^{n+1}+{\mathbf{u}}^n)-{\displaystyle \frac{\tilde{J}}{4}}\left({\left({\mathbf{u}}^n\right)}^3+{\left({\mathbf{u}}^{n+1}\right)}^3+{\mathbf{u}}^n{\left({\mathbf{u}}^{n+1}\right)}^2+\left({\mathbf{u}}^{n+1}\right){\left({\mathbf{u}}^n\right)}^2\right)$$

Obviously, both schemes are implicit methods and need an iterative solution. Take $\epsilon =0.02$, and for $\lambda =0.3,3,30$. Table 1 shows the comparison of the computation time consumption between EAVF and AVF in solving this problem. The results show that the EAVF method converges much faster than the AVF method, and this gap widens as $\lambda$ increases. At the same time, we find that the restriction of the AVF method on the step size is higher than that of the EAVF method, which means the EAVF scheme not only maintains strict energy dissipation but also achieves superior accuracy in capturing oscillatory solutions under larger time steps. Therefore, in actual computation, the EAVF method has the advantages of a large step size and high efficiency.

Table 1. Comparison of computational efficiency between EAVF and AVF method.

$\mathit{\lambda }=0.3$			$\mathit{\lambda }=3$			$\mathit{\lambda }=30$
$\mathbf{\tau }$	Method	CPU/s	$\mathbf{\tau }$	Method	CPU/s	$\mathbf{\tau }$	Method	CPU/s
$0.01$	EAVF	$0.0635$	$0.01$	EAVF	$0.0667$	$0.001$	EAVF	$0.3222$
	AVF	–		AVF	–		AVF	$0.8271$
$0.001$	EAVF	$0.2866$	$0.001$	EAVF	$0.3066$	$0.0001$	EAVF	$2.5198$
	AVF	$0.5386$		AVF	$0.6379$		AVF	$4.1943$
$0.0001$	EAVF	$1.8755$	$0.0001$	EAVF	$2.1663$	$0.00001$	EAVF	$18.7849$
	AVF	$3.2517$		AVF	$3.4640$		AVF	$31.6928$

To verify the order of the method, let $u_j^n$ be the numerical solution at time $t_n$ and $u(x_j,t_n)$ be the reference solution. The error 2-norm in time is defined as $e(\tau ,h)=\left|\right|u_j^n-u(x_j,t_n){\left|\right|}_2$. The temporal convergence order is calculated as

$$order\approx {log}_2(e(\tau ,h)/e(\tau /2,h)).$$

The temporal accuracy is examined by setting $\lambda =0.3$ and $\epsilon =0.02$. We list the convergence rates of the EAVF method in Table 2. We select the numerical solution with $\tau =0.0001$ as the reference solution. Based on Table 2, the EAVF method converges with second-order accuracy.

Table 2. Time accuracy test for EAVF method at t = 0.1.

$\mathit{\tau }$	Error	Order
$0.002$	4.491923 × 10−6	−
$0.001$	1.114537 × 10−6	$2.0109$
$0.0005$	2.701909 × 10−7	$2.0444$
$0.00025$	5.910426 × 10−8	$2.1926$

All computations in this study were conducted within the MATLAB R2024a environment, and the results demonstrate strong hardware independence under standard computational conditions.

4. Educational Practice Integration: Analyzing Project Organization, Implementation, and Talent Development Outcomes

4.1. Project Organization Framework and Implementation Pathway

In the implementation of the college student innovation and entrepreneurship project, the approach of “problem decomposition-code verification-modular development” is adopted. The specific schedule and the goals for cultivating students’ abilities in each link of the project are shown in Table 3.

Table 3. Core modules and training objectives.

Module	Duration	Key Tasks	Training Objectives
Theoretical Foundation	9 weeks	Master Fourier pseudospectral/EAVF theory	Enhance theoretical analysis and literature skills
Algorithmic Practice	10 weeks	Modular coding and example verification	Improve problem decomposition and programming ability
Achievement Optimization	14 weeks	Experiment design and result summarization	Strengthen data analysis and academic expression

4.2. Students’ Competency Enhancement Outcomes

By guiding students through the complete implementation of a structure-preserving algorithm for the GLE equation, this model has systematically enhanced their core competencies, with specific outcomes manifested at three levels:

(1) Engineering Practical Ability: By decomposing GLE into “Fourier discretization-EAVF integration-nonlinear iteration” modules, students’ accuracy in reproducing the literature examples rose from 40% to 90%, enabling independent completion of algorithm coding.

(2) Scientific Research Thinking: Students independently designed single/double solitary wave experiments, analyzed the influence of parameter $\epsilon$ on energy dissipation, and produced three high-quality reports, leading the project to be recommended for provincial-level funding.

(3) Comprehensive Academic Literacy: Two academic papers were drafted, reflecting significant progress in complex problem-solving and academic expression.

The successful practice of this model demonstrates that systematic training based on cutting-edge research projects is an effective pathway for cultivating innovative talents within the context of “Emerging Engineering Education.”

5. Conclusions

This study achieves innovative contributions through a dual-path approach. At the theoretical and methodological level, this study combines the Fourier pseudospectral method with the EAVF algorithm for temporal integration to construct a numerical scheme that strictly preserves the system’s energy conservation/dissipation characteristics. Both theoretical analysis and numerical experiments demonstrate the outstanding performance of this scheme in maintaining the oscillatory structure of the system. Particularly important, through controlled numerical comparative validation, the newly proposed EAVF scheme significantly outperforms the classical AVF method in balancing structure preservation with computational efficiency, providing a more effective tool for long-term simulation of strongly nonlinear systems. At the educational practice level, the study deeply integrates cutting-edge algorithmic research with undergraduate innovation and entrepreneurship education, adopting a model of “research problem-driven—theoretical method learning—algorithmic practice verification.” This model effectively enhances students’ abilities to analyze and solve complex problems, their algorithmic implementation skills, and their scientific research thinking capabilities.

Practice shows that teaching practices driven by scientific research projects can closely integrate theoretical knowledge with practical applications, stimulate students’ enthusiasm for innovation and scientific research, significantly enhance their innovative abilities and practical skills, and provide a new paradigm of “research feeding back into teaching” for cultivation of science and engineering talents. In the future, the application of this model to other scientific problems can be further expanded to deepen the integration of scientific research and teaching. Furthermore, this educational model exhibits favorable adaptability to different academic and cultural scenarios: this research offers a versatile framework adaptable across multiple dimensions. Academically, the methodological scope can be expanded by applying the structure-preserving algorithm to other types of partial differential equations (e.g., the Schrödinger equation), exploring discrete methods for more general boundary conditions (e.g., Dirichlet boundaries), and developing higher-order or adaptive time integration schemes, while retaining the effective modular process of “theoretical learning–practical verification” to extend the model’s applicability to various science and engineering disciplines. Culturally, the implementation can be tailored to local educational environments; for instance, in settings that emphasize collective learning, the “individual task division” can be adapted into “team collaboration modules.” By systematically implementing and evaluating this “research-driven teaching” model across a broader range of courses, the framework promises to deepen the integration of research and teaching, laying a solid foundation for cultivating high-quality talents with innovative spirit and practical abilities in diverse academic and cultural contexts.