Comparing Weighted RMSD, Weighted MD, Infit, and Outfit Item Fit Statistics Under Uniform Differential Item Functioning

Abstract

In educational large-scale assessment studies, uniform differential item functioning (DIF) across countries often challenges the application of a common item response model, such as the two-parameter logistic (2PL) model, to all participating countries. DIF occurs when certain items provide systematic advantages or disadvantages to specific groups, potentially biasing ability estimates and secondary analyses. Identifying misfitting items caused by DIF is therefore essential, and several item fit statistics have been proposed in the literature for this purpose. This article investigates the performance of four commonly used item fit statistics under uniform DIF: the weighted root mean square deviation (RMSD), the weighted mean deviation (MD), the infit, and the outfit statistics. Analytical approximations were derived to relate the uniform DIF effect size to these item fit statistics, and the theoretical findings were confirmed through a comprehensive simulation study. The results indicate that distribution-weighted RMSD and MD statistics are less sensitive to DIF in very easy or very difficult items, whereas difficulty-weighted RMSD and MD exhibit consistent detection performance across all item difficulty levels. However, the sampling variance of the difficulty-weighted statistics is notably higher for items with extreme difficulty. Infit and outfit statistics were largely ineffective in detecting DIF in items of moderate difficulty, with sensitivity limited to very easy or very difficult items. To illustrate the practical application of these statistics, they were computed for the PISA 2006 reading study, and the distribution of the statistics across participating countries was descriptively examined. The findings guide selecting appropriate item fit statistics in large-scale assessments and highlight the strengths and limitations of different approaches under uniform DIF conditions.

1. Introduction

Item response theory (IRT) models [1,2,3,4,5,6] are multivariate statistical models designed to analyze a vector of discrete random variables. IRT models are widely applied in the social sciences, particularly in educational large-scale assessment (LSA; [7,8]) studies, where cognitive tasks are administered. The use of IRT is advantageous because it accommodates complex test designs [9] and addresses measurement error in estimated abilities for secondary analyses [10].

This article focuses on dichotomous (i.e., binary) random variables. Let $\mathit{X}=(X_1,\dots ,X_I)$ denote a vector of I random variables $X_i\in \{0,1\}$, commonly referred to as items or scored item responses. A unidimensional IRT model [11] defines a parametric model for the probability distribution $\mathsf{P}(\mathit{X}=\mathit{x})$ for $\mathit{x}=(x_1,\dots ,x_I)\in {\{0,1\}}^I$ as

$${\displaystyle \mathsf{P}(\mathit{X}=\mathit{x};\mathit{\delta },\mathit{\gamma })=\int \prod _{i=1}^I\left[{P_i(\theta ;{\mathit{\gamma }}_i)}^{x_i}{\left(1-P_i(\theta ;{\mathit{\gamma }}_i)\right)}^{1-x_i}\right]\varphi (\theta ;\mu ,\sigma )\mathrm{d}\theta ,}$$

(1)

where $\varphi$ denotes the density of the normal distribution parameterized by the mean $\mu$ and standard deviation (SD) $\sigma$. The distribution parameters $\mu$ and $\sigma$ of the latent variable $\theta$, often referred to as a trait or ability variable, are collected in the vector $\mathit{\delta }=(\mu ,\sigma )$. The vector $\mathit{\gamma }=({\mathit{\gamma }}_1,\dots ,{\mathit{\gamma }}_I)$ comprises the item parameters for the item response functions (IRFs) $P_i(\theta ;{\mathit{\gamma }}_i)=\mathsf{P}(X_i=1|\theta )$ for $i=1,\dots ,I$. The IRF of the two-parameter logistic (2PL) model [12] is given by

$$P_i(\theta ;{\mathit{\gamma }}_i)=\Psi \left(a_i(\theta -b_i)\right),$$

(2)

where $a_i$ and $b_i$ denote the item discrimination and item difficulty parameters, respectively, and $\Psi \left(x\right)={(1+exp(-x))}^{-1}$ is the logistic distribution function. In this formulation, the item parameter vector is ${\mathit{\gamma }}_i=(a_i,b_i)$.

The Rasch model [13,14] represents a special case of the 2PL model in which all item discrimination parameters $a_i$ are fixed to 1.

For a sample of N individuals with independently and identically distributed observations (also referred to as cases, subjects, students, or persons) based on the realizations ${\mathit{x}}_1,\dots ,{\mathit{x}}_N$ from the distribution of the random variable $\mathit{X}$, the model parameters of the IRT model in (1) can be consistently estimated using marginal maximum likelihood estimation (MML; [15,16]), typically implemented with the expectation–maximization algorithm [17,18].

In LSA applications such as programme for international student assessment (PISA; [19]), a parametric model for the IRFs in (1) is typically specified. These studies involve a large number of countries, and it is generally assumed that the item parameters are identical across countries, implying parameter invariance. However, this assumption may be violated in practice because certain items can provide systematic advantages or disadvantages to specific countries. This phenomenon is known as differential item functioning (DIF; [20,21]), although alternative terms such as measurement bias or item bias are also used [22].

As a result, the assumed IRF represents a (slight) misspecification of the true IRT model (1) for a given country (or group, henceforth). The multivariate random vector $\mathit{X}$ is represented as

$$\mathsf{P}(\mathit{X}=\mathit{x};\mathit{\delta },\mathit{\gamma })\simeq \int \prod _{i=1}^I\left[P_i^{*}{(\theta ;{\mathit{\gamma }}_i)}^{x_i}{\left(1-P_i^{*}(\theta ;{\mathit{\gamma }}_i)\right)}^{1-x_i}\right]\varphi (\theta ;\mu ,\sigma )\mathrm{d}\theta ,$$

(3)

where $P_i^{*}$ denotes the assumed IRF and $P_i$ represents the IRF in the data-generating model for the group. In practical applications, it is typically expected that the approximation of $P_i$ by $P_i^{*}$ introduces only minimal distortion in estimating the distribution parameters $\mu$ and $\sigma$.

The assessment of the adequacy of parametric IRFs (i.e., item fit; [23,24,25]) is a central topic in psychometrics. The discrepancy between the true IRF $P_i$ and the assumed parametric IRF $P_i^{*}$ should be quantified using an appropriate effect size measure. Ideally, statistical inference for this effect size should also be available. Of primary interest is the identification of misfitting items i for which the assumed IRFs $P_i^{*}$ deviate substantially from $P_i$.

A wide range of item fit statistics has been proposed in the literature [25]. The present study focuses on the root mean square deviation (RMSD; [26,27,28,29,30,31,32,33,34,35,36,37,38]) and the related mean deviation (MD) statistic, as well as the infit and outfit statistics [39,40]. The motivation for examining these statistics arises from their operational use in current PISA studies. Item fit statistics are routinely analyzed in both the PISA field and main studies [41]. The field study generally involves relatively small sample sizes per item at the country level. In this context, the fit statistics are computed for each country and reported to participating PISA countries to identify potential issues with items, such as translation errors or country-specific test administration problems at the item level. The investigation of item fit statistics under small sample sizes is therefore particularly relevant, as the field study reports are expected to provide reliable information—that is, item fit statistics with sufficiently small sampling error. In the PISA main study, RMSD and MD item fit statistics are employed to identify items whose parameters deviate substantially from the assumed international item parameters defined across countries. Items flagged for DIF are then assigned country-specific parameters in the operational scaling procedure of the PISA main study [42]. Consequently, reliable DIF detection based on these item fit statistics is essential, as it influences decisions concerning the scaling model applied in official PISA reporting.

The performance of these item fit statistics is investigated under uniform DIF, that is, when the assumed item difficulties $b_i$ in the IRF $P_i^{*}$ of the 2PL model differ from the true item difficulties in the IRF $P_i$. The behavior of these statistics under uniform DIF is examined through analytical derivations and a simulation study. To the best of current knowledge, this study is the first to provide analytical approximations of these item fit statistics under DIF conditions.

The remainder of the article is structured as follows. Section 2 presents analytical results for various weighted RMSD and MD statistics under DIF. Section 3 provides analytical findings for the infit and outfit statistics under DIF. Results from a simulation study examining the performance of these item fit statistics under uniform DIF are reported in Section 4. An empirical example using PISA 2006 data is presented in Section 5. Finally, Section 6 concludes with a discussion.

2. Weighted RMSD and Weighted MD Under DIF

In this section, the definitions of weighted RMSD and weighted MD statistics, as proposed by Joo et al. [43], are reviewed. These item fit statistics are examined under uniform DIF in the 2PL model.

Assume that $P_i^{*}\left(\theta \right)=\Psi \left(a_i(\theta -b_i)\right)$ denotes the assumed IRF, while the IRF in the data-generating model is given by $P_i\left(\theta \right)=\Psi \left(a_i(\theta -b_i-{\delta }_i)\right)$. Here, ${\delta }_i$ represents the uniform DIF effect, also interpreted as a DIF effect size on the logit metric within the 2PL model. The RMSD and MD statistics assign weights to deviations $P_i\left(\theta \right)-P_i^{*}\left(\theta \right)$ to provide a summarized measure of model–data discrepancy.

2.1. Weighted RMSD and Weighted MD

In the definitions of the weighted RMSD and weighted MD statistics, a weighting function $w_i$ for item i is specified such that it integrates to 1; that is, $\int w_i\left(\theta \right)\mathrm{d}\theta =1$ (see [43]). The weighting function $w_i$ may be item-specific or common across items.

The weighted MD statistic is defined as

$${\mathsf{MD}}_{w,i}=\int \left[P_i\left(\theta \right)-P_i^{*}\left(\theta \right)\right]w_i\left(\theta \right)\mathrm{d}\theta$$

(4)

and represents the weighted average of the IRF differences $P_i-P_i^{*}$. The MD statistic is signed and operates on the probability difference metric. Since $P_i\left(\theta \right)$ and $P_i^{*}\left(\theta \right)$ take values in $[0,1]$, the MD statistic is bounded between $-1$ and 1, although substantial deviations from 0 are unlikely in practice. This statistic focuses on average differences implied by a misfitting IRF.

The RMSD statistic summarizes squared IRF differences by computing

$${\mathsf{RMSD}}_{w,i}=\sqrt{\int {\left[P_i\left(\theta \right)-P_i^{*}\left(\theta \right)\right]}^2{w}_i\left(\theta \right)\mathrm{d}\theta }.$$

(5)

Unlike the MD statistic, differences between $P_i$ and $P_i^{*}$ that cancel out on average do not vanish under RMSD. Consequently, RMSD can reveal discrepancies that remain hidden in MD. In particular, the presence of nonuniform DIF [21] (i.e., DIF in item discriminations $a_i$) may be detected by RMSD but remain undetected by MD.

The MD and RMSD statistics are mathematically related. Jensen’s inequality [44] implies ${\left[E\left(X\right)\right]}^2\le E\left(X^2\right)$ for any square-integrable random variable X, leading to

$$\left|E\left(X\right)\right|\le \sqrt{E\left(X^2\right)}.$$

(6)

Applying this result to $X=P_i\left(\theta \right)-P_i^{*}\left(\theta \right)$, where the expectation is taken with respect to the probability density $w_i\left(\theta \right)$, yields

$$|{\mathsf{MD}}_{w,i}|\le {\mathsf{RMSD}}_{w,i},$$

(7)

demonstrating that the absolute value of the MD statistic is bounded by the RMSD statistic.

2.2. Distribution-Weighted RMSD and MD Statistics

The RMSD and MD statistics were originally defined using a weighting function given by the normal density $w\left(\theta \right)=\varphi (\theta ;\mu ,\sigma )$ (see [28,32,36]), where $\mu$ and $\sigma$ denote the mean and SD of the $\theta$ distribution in the group. This approach is referred to as distribution-weighted (dist) item fit statistics for RMSD and MD. In this case, the weighting function is identical across items and depends solely on the location and shape of the $\theta$ distribution within the group.

To evaluate the integrals appearing in the RMSD and MD statistics, products of logit IRFs and normal densities must be computed. These integrals become easier to handle when the logit IRF is approximated by a probit IRF, resulting in expressions involving normal distribution functions and densities. In some cases, no closed-form solution exists, or the available closed form is too complex to interpret. In such situations, linear and quadratic Taylor expansions with respect to the uniform DIF effect ${\delta }_i$ are applied, enabling the examination of the behavior of the item fit statistics for ${\delta }_i$ values close to zero.

The difference $P_i-P_i^{*}$ between the IRFs $P_i$ and $P_i^{*}$ can be approximated as

$$P_i\left(\theta \right)-P_i^{*}\left(\theta \right)\simeq \Phi \left(D^{-1}{a}_i(\theta -b_i-{\delta }_i)\right)-\Phi \left(D^{-1}{a}_i(\theta -b_i)\right)\simeq -{\delta }_i{a}_i{D}^{-1}\varphi \left(D^{-1}{a}_i(\theta -b_i)\right),$$

(8)

where $\varphi$ denotes the standard normal density function. The first approximation in (8) replaces the logit IRFs with probit IRFs, expressed through the standard normal distribution function $\Phi$, using the constant $D=1.701$ (see [45,46,47]). The absolute difference between the logit IRF and its probit approximation does not exceed 0.0095. The second approximation in (8) applies a first-order Taylor expansion to the difference of probit IRFs.

The distribution-weighted MD statistic can be approximately expressed as (see also [48])

$${\mathsf{MD}}_{dist,i}\simeq -{\delta }_i{\displaystyle \frac{a_i}{\sqrt{2\pi \left(a_i^2{\sigma }^2+D^2\right)}}}exp\left[-{\displaystyle \frac{a_i^2{(\mu -b_i)}^2}{2\left(a_i^2{\sigma }^2+D^2\right)}}\right],$$

(9)

where the approximations in (8) and (A1) from Appendix A were applied. Setting $a_i=1$ and $\sigma =1$ simplifies (9) to

$${\mathsf{MD}}_{dist,i}=-0.202{\delta }_{i}exp\left(-0.128{(\mu -b_i)}^2\right).$$

(10)

Hence, it holds that

$${\mathsf{MD}}_{dist,i}\simeq -0.202{\delta }_i\mathrm{for}|\mu -b_i|=0.$$

(11)

Furthermore, we have ${\mathsf{MD}}_{dist,i}\simeq -0.178{\delta }_i$ for $|\mu - b_i|=1$, and ${\mathsf{MD}}_{dist,i}\simeq -0.128{\delta }_i$ for $|\mu - b_i|=2$. This indicates that the absolute value of the MD statistic decreases as the assumed item difficulties deviate further from the group mean $\mu$.

The distribution-weighted RMSD can be approximated as

$${\mathsf{RMSD}}_{dist,i}\simeq \left|{\delta }_i\right|{\displaystyle \frac{D{a}_i}{\sqrt{2\pi }{(2a_i^2{\sigma }^2/D^2+1)}^{1/4}}}exp\left[-{\displaystyle \frac{a_i^2{(\mu -b_i)}^2}{2(2a_i^2{\sigma }^2+D^2)}}\right],$$

(12)

based on the approximations in (8) and (A3). With $a_i=1$ and $\sigma =1$, (12) reduces to

$$\left|{\mathsf{RMSD}}_{dist,i}\right|\simeq 0.206\left|{\delta }_i\right|exp\left(-0.102{(\mu -b_i)}^2\right).$$

(13)

The coefficient $0.206$ in (13) is only slightly larger than the coefficient $0.202$ in (11) for the MD. This indicates that the MD and RMSD are nearly equivalent when uniform DIF is the source of item misfit, at least at the population level. The Simulation Study in Section 4 further demonstrates that, in small to moderately sized samples, sample-based RMSD estimates are considerably larger than the corresponding MD estimates. Similar to the MD statistic, the RMSD decreases as the absolute difference between item difficulty $b_i$ and group mean $\mu$ increases.

The computation of the RMSD statistic in (12) relies on two key approximations. First, the logit IRF is approximated by a probit IRF. Second, the difference between the group-specific probit IRF and the assumed probit IRF is approximated using a linear Taylor expansion with respect to the uniform DIF effect ${\delta }_i$. An upper bound for the resulting approximation error in the computed RMSD statistic is provided in Appendix B.

2.3. Difficulty-Weighted RMSD and MD

Section 2.2 shows that both MD and RMSD depend on the magnitude of $|\mu - b_i|$. This dependence can be critical when the group mean is much smaller than the item difficulties for most items, which poses challenges for detecting item misfit in low-performing countries in LSA studies [37]. Furthermore, distribution-weighted RMSD and MD are known to perform poorly in detecting uniform DIF for very easy or very difficult items, that is, when $|\mu - b_i|$ is large. To address these limitations, difficulty-weighted RMSD and MD statistics have been proposed in [43].

Difficulty-weighted (denoted by diff) MD and RMSD statistics (i.e., ${\mathsf{MD}}_{diff,i}$ and ${\mathsf{RMSD}}_{diff,i}$) use the normal density $\varphi (\theta ;b_i,1)$ with mean $b_i$ and SD 1 as the weighting function. In this way, item misfit receives maximal weight at the assumed item difficulty $b_i$. By definition, the difficulty-weighted RMSD and MD statistics can be obtained as special cases of the distribution-weighted counterparts by setting $\mu =b_i$ and $\sigma =1$ in Equations (9) and (12), yielding

$${\mathsf{MD}}_{diff,i}\simeq -{\delta }_i{\displaystyle \frac{a_i}{\sqrt{2\pi \left(a_i^2+D^2\right)}}},$$

(14)

$${\mathsf{RMSD}}_{diff,i}\simeq \left|{\delta }_i\right|{\displaystyle \frac{D{a}_i}{\sqrt{2\pi }{(2a_i^2/D^2+1)}^{1/4}}}.$$

(15)

The item difficulty $b_i$ no longer appears in the expressions (14) and (15). Consequently, for $a_i=1$, the approximate identities ${\mathsf{MD}}_{diff,i}\simeq -0.202{\delta }_i$ and ${\mathsf{RMSD}}_{diff,i}\simeq 0.206\left|{\delta }_i\right|$ hold, regardless of $\sigma$, $\mu$, and $b_i$.

2.4. Information-Weighted RMSD and MD

As an alternative weighting function, Joo et al. [43] proposed using the item information function corresponding to $P_i^{*}$ to weight differences between the IRFs $P_i$ and $P_i^{*}$. The item information function $I_i\left(\theta \right)$ for item i is defined as

$$I_i\left(\theta \right)=a_i{P}_i^{*}\left(\theta \right)\left(1-P_i^{*}\left(\theta \right)\right).$$

(16)

The factor $a_i$ cancels in the weighting function $w_i$, as this function must integrate to 1. Moreover, the product of logit functions in (16) can be reasonably well approximated by a normal density function $\varphi$ as

$$\Psi \left(x\right)\left(1-\Psi \left(x\right)\right)\simeq \varphi (x;0,S),$$

(17)

where the constant $S=1.595$ is obtained by matching the values of the functions on both sides of the approximation at $x=0$. The difference between $\Psi (1-\Psi )$ and its normal density approximation does not exceed 0.0115. Applying the approximation (17), the weighting function $w_i$ for item i is given by

$$\varphi (a_i(\theta -b_i);0,S)={\displaystyle \frac{\varphi (\theta ;b_i,S/a_i)}{a_i}}\propto \varphi (\theta ;b_i,S/a_i)\equiv w_i.$$

(18)

Information-weighted (denoted by info) RMSD and MD statistics are obtained as special cases of distribution-weighted RMSD and MD statistics with $\mu =b_i$ and $\sigma =S/a_i$. Using (9) and (12), the information-weighted MD and RMSD statistics are approximately

$${\mathsf{MD}}_{info,i}\simeq -{\delta }_i{\displaystyle \frac{a_i}{\sqrt{2\pi \left(S^2+D^2\right)}}}\mathrm{and}$$

(19)

$${\mathsf{RMSD}}_{info,i}\simeq \left|{\delta }_i\right|{\displaystyle \frac{D{a}_i}{\sqrt{2\pi }{(2S^2/D^2+1)}^{1/4}}}.$$

(20)

Information-weighted RMSD and MD statistics share with difficulty-weighted statistics the property of providing an assessment of item misfit due to uniform DIF independent of $\sigma$, $\mu$, and $b_i$. However, they remain dependent on item discrimination $a_i$. For items with $a_i=1$, the difficulty-weighted statistics typically appear larger in absolute value than the corresponding information-weighted MD and RMSD statistics.

2.5. Uniformly Weighted RMSD and MD

Finally, Joo et al. [43] proposed a uniform density on a chosen interval $[L,U]$ with $\Delta \equiv U-L>0$ as a weighting function. The lower and upper bounds of the interval can, for instance, be set to the 1st and 99th quantiles of the group-specific $\theta$ distribution. For a standard normal distribution, this corresponds to $[-2.33,2.33]$. The weighting function $w_i$ is defined as

$$w_i\left(\theta \right)={\Delta }^{-1}\mathbf{1}(L\le \theta \le U),$$

(21)

where $\mathbf{1}$ denotes the indicator function, taking the value 0 outside $[L,U]$. As the IRF difference $P_i-P_i^{*}$ is typically small outside $[L,U]$, $w_i$ can be approximated by the improper constant weighting function ${\tilde{w}}_i\left(\theta \right)\equiv {\Delta }^{-1}$, which does not integrate to 1.

RMSD and MD statistics using $w_i$ are referred to as uniformly weighted (denoted by unif) RMSD and MD statistics. For an improper weighting function, Raju [49] provided the explicit expression

$$\int [P_i\left(\theta \right)-P_i^{*}\left(\theta \right)]\mathrm{d}\theta =-{\delta }_i,$$

(22)

which is termed the signed area statistic. Using this result, the uniformly weighted MD is approximately

$${\mathsf{MD}}_{unif,i}\simeq -{\delta }_i{\displaystyle \frac{1}{\Delta }}.$$

(23)

It is evident that ${\mathsf{MD}}_{unif,i}$ approaches zero as the interval length $\Delta$ increases. Therefore, using the improper uniform weighting function equal to 1 for MD assessment is theoretically more appropriate, yielding a value of $-{\delta }_i$. This approach also allows direct estimation of the DIF effect size ${\delta }_i$, improving statistical efficiency when the signed area measure is computed. Raju [49] further derived

$$\int \left|P_i\left(\theta \right)-P_i^{*}\left(\theta \right)\right|\mathrm{d}\theta =\left|{\delta }_i\right|,$$

(24)

which is referred to as the unsigned area statistic.

For the uniformly weighted RMSD statistic, the difference in IRFs is approximated using (8). Applying a linear Taylor approximation to the resulting integral yields

$${\mathsf{RMSD}}_{unif,i}\simeq \left|{\delta }_i\right|\sqrt{{\displaystyle \frac{a_i}{2D\Delta \sqrt{\pi }}}}.$$

(25)

For $a_i=1$, this simplifies to ${\mathsf{RMSD}}_{unif,i}\simeq 0.407\left|{\delta }_i\right|/\sqrt{\Delta }$.

2.6. Estimation of Weighted RMSD and Weighted MD

Until this point, the variants of the RMSD and MD statistics have been described only at the population level, assuming that the group-specific IRF $P_i$ is known, as is the assumed IRF $P_i^{*}$. The observed IRF ${\widehat{P}}_i$, a sample-based estimate of $P_i$, is defined for a theta point ${\theta }_t$ ($t=1,\dots ,T$) as

$${\widehat{P}}_i\left({\theta }_t\right)={\displaystyle \frac{{\displaystyle \sum _{n=1}^N{h}_{nt}{x}_{ni}}}{{\displaystyle \sum _{n=1}^N{h}_{nt}}}},$$

(26)

where $h_{nt}$ is the posterior distribution of person n at grid point ${\theta }_t$. The posterior distribution is typically obtained by fitting the IRT model via MML [15], so the quantities in (26) can be directly computed from software output. A discrete evaluation of the weighting function $w_i$ is defined as

$$w_{it}={\displaystyle \frac{w_i\left({\theta }_t\right)}{{\displaystyle \sum _{u=1}^T{w}_i\left({\theta }_u\right)}}}\mathrm{for}t=1,\dots ,T.$$

(27)

The sample-based MD statistic is then defined as

$${\widehat{\mathsf{MD}}}_{w,i}=\sum _{t=1}^T\left[{\widehat{P}}_i\left({\theta }_t\right)-P_i^{*}\left({\theta }_t\right)\right]w_{it},.$$

(28)

Following the derivations in [35], it holds that

$$\mathsf{E}\left[{\widehat{\mathsf{MD}}}_{w,i}\right]={\mathsf{MD}}_{w,i}+\sum _{t=1}^T\mathsf{E}\left[{\widehat{P}}_i\left({\theta }_t\right)-P_i\left({\theta }_t\right)\right]w_{it}={\mathsf{MD}}_{w,i},$$

(29)

because $\mathsf{E}\left[{\widehat{P}}_i\left({\theta }_t\right)\right]=P_i\left({\theta }_t\right)$ (at least, asymptotically). Thus, on average, the MD statistic is largely unaffected by sampling errors in the estimate of $P_i$.

The sample-based RMSD is defined as

$${\widehat{\mathsf{RMSD}}}_{w,i}=\sqrt{\sum _{t=1}^T{\left[{\widehat{P}}_i\left({\theta }_t\right)-P_i^{*}\left({\theta }_t\right)\right]}^2{w}_{it}}.$$

(30)

Along the lines of [35] (see also [48]), it follows that

$$\mathsf{E}{\left({\widehat{\mathsf{RMSD}}}_{w,i}\right)}^2={\left({\mathsf{RMSD}}_{w,i}\right)}^2+\sum _{t=1}^T\mathsf{E}{\left[{\widehat{P}}_i\left({\theta }_t\right)-P_i\left({\theta }_t\right)\right]}^2{w}_{it}.$$

(31)

Equation (31) shows that the sampling variance of ${\widehat{P}}_i\left({\theta }_t\right)$ contributes explicitly to the expected value of the sample RMSD. As a result, the sample-based RMSD typically exceeds the population-based RMSD. The quantity $\mathsf{E}{[{\widehat{P}}_i\left({\theta }_t\right)-P_i\left({\theta }_t\right)]}^2$ is larger for extreme ${\theta }_t$ points, reflecting higher variability of the observed IRF at the tails. This variance contribution can be minimized by choosing $w_{it}$ as precision weights, that is, the inverse variances associated with ${\widehat{P}}_i\left({\theta }_t\right)$.

3. Infit and Outfit Under DIF

In this section, the expected values of the item fit statistics infit and outfit under uniform DIF are examined. These statistics are primarily applied for model fit assessment in the Rasch model [14,39,40,50,51,52].

First, the statistics are formally introduced. Let n denote a case and $x_{ni}$ the item response of case n on a dichotomous item i. Define the standardized residual [14,53,54] as

$$z_{ni}={\displaystyle \frac{x_{ni}-E_{ni}^{*}}{\sqrt{V_{ni}^{*}}}},$$

(32)

where $E_{ni}^{*}$ and $V_{ni}^{*}$ denote the expected value and variance of $x_{ni}$ under the assumption that $P_i^{*}$ is the true IRF.

Early studies used individual ability estimates ${\widehat{\theta }}_n$ to compute $E_{ni}^{*}$ and $V_{ni}^{*}$, which are given by

$$E_{ni}^{*}=P_i^{*}\left({\widehat{\theta }}_n\right)\mathrm{and}{V}_{ni}^{*}=P_i^{*}\left({\widehat{\theta }}_n\right)\left[1-P_i^{*}\left({\widehat{\theta }}_n\right)\right].$$

(33)

However, using ${\widehat{\theta }}_n$ instead of the true ability ${\theta }_n$ may bias the distribution of $z_{ni}$ even if the model holds. To address this, Wu and Adams [53,55] proposed computing infit and outfit statistics based on individual posterior distributions $h_n$ rather than ${\widehat{\theta }}_n$ [53,54]. Accordingly, the expected value and variance are computed as

$$E_{ni}^{*}=\int P_i^{*}\left(\theta \right)h_n\left(\theta \right)\mathrm{d}\theta \mathrm{and}{V}_{ni}^{*}=\int P_i^{*}\left(\theta \right)\left[1-P_i^{*}\left(\theta \right)\right]h_n\left(\theta \right)\mathrm{d}\theta .$$

(34)

In practice, $\theta$ is evaluated on a finite grid ${\theta }_t$ ($t=1,\dots ,T$) and the posterior distribution is represented by probabilities $h_{nt}$. The quantities in (34) are then approximated by

$$E_{ni}^{*}=\sum _{t=1}^T{P}_i^{*}\left({\theta }_t\right)h_{nt}\mathrm{and}{V}_{ni}^{*}=\sum _{t=1}^T{P}_i^{*}\left({\theta }_t\right)\left[1-P_i^{*}\left({\theta }_t\right)\right]h_{nt}.$$

(35)

The outfit statistic is defined as

$${\mathsf{Outfit}}_i={\displaystyle \frac{1}{N}}\sum _{n=1}^N{z}_{ni}^2,$$

(36)

If the IRT model holds (i.e., no item misfit such as uniform DIF), the residuals $z_{ni}$ are approximately normally distributed, and $z_{ni}^2$ follows a chi-square distribution with one degree of freedom. The expected value of $z_{ni}^2$ is therefore 1. Consequently, deviations of the outfit statistic from 1, such as values below 0.7 or above 1.3, indicate potential item misfit [51,56,57].

The infit statistic weights the squared standardized residuals $z_{ni}^2$ according to their variances:

$${\mathsf{Infit}}_i={\displaystyle \frac{{\displaystyle \sum _{n=1}^N{V}_{ni}^{*}{z}_{ni}^2}}{{\displaystyle \sum _{n=1}^N{V}_{ni}^{*}}}}.$$

(37)

Equivalently, it can be expressed as

$${\mathsf{Infit}}_i={\displaystyle \frac{{\displaystyle \frac{1}{N}\sum _{n=1}^N{\left(x_{ni}-E_{ni}^{*}\right)}^2}}{{\displaystyle \frac{1}{N}\sum _{n=1}^N{V}_{ni}^{*}}}}.$$

(38)

As a weighted average of chi-square distributed variables $z_{ni}^2$, the infit statistic also has an expected value of 1 under the model, and cutoffs of 0.7 and 1.3 are frequently used to detect item misfit.

Statistical inference for infit and outfit should be applied when stringent model fit assessment is required [50,54,58].

The following sections present the expected values of the outfit and infit statistics in the presence of uniform DIF.

3.1. Expected Value of Outfit Statistic

In this section, the expected value of the outfit statistic under uniform DIF is computed. The approach consists of evaluating the expected values of the squared residuals $z_{ni}^2$ in the outfit statistic while letting N tend to infinity.

First, note that

$$\mathsf{E}{\left[x_{ni}-P_i^{*}\left({\theta }_n\right)\right]}^2=\mathsf{Var}\left(x_{ni}\right)+{\left[P_i\left({\theta }_n\right)-P_i^{*}\left({\theta }_n\right)\right]}^2.$$

(39)

For a large number of items (i.e., estimated ability values ${\widehat{\theta }}_n$ converge to true ability values ${\theta }_n$) and a large number of cases ($N\to \infty$), the outfit statistic ${\displaystyle \frac{1}{N}}{\sum }_{n=1}^N{z}_{ni}^2$ converges to

$$\int {\displaystyle \frac{P_i\left(\theta \right)\left[1-P_i\left(\theta \right)\right]}{P_i^{*}\left(\theta \right)\left[1-P_i^{*}\left(\theta \right)\right]}}\varphi (\theta ;\mu ,\sigma )\mathrm{d}\theta +\int {\displaystyle \frac{{\left[P_i\left(\theta \right)-P_i^{*}\left(\theta \right)\right]}^2}{P_i^{*}\left(\theta \right)\left[1-P_i^{*}\left(\theta \right)\right]}}\varphi (\theta ;\mu ,\sigma )\mathrm{d}\theta =O_1+O_2,$$

(40)

where $O_1$ and $O_2$ denote the two summands in (40). Using the normal density approximation (17) for the item information function, the first summand in the outfit statistic in (40) can be expressed as

$$O_1\simeq \int {\displaystyle \frac{\varphi \left(a_i(\theta -b_i-{\delta }_i);0,S\right)}{\varphi \left(a_i(\theta -b_i);0,S\right)}}\varphi (\theta ;\mu ,\sigma )\mathrm{d}\theta .$$

(41)

The integral on the right side of (41) has a closed form using the identity (A2) from Appendix A. A quadratic Taylor approximation of the obtained closed form around ${\delta }_i=0$ yields

$$O_1\simeq 1+{\delta }_i{\displaystyle \frac{a_i^2}{S^2}}(\mu -b_i)+{\delta }_i^2\left[{\displaystyle \frac{a_i^4}{2S^4}}\left({\sigma }^2+{(\mu -b_i)}^2\right)-{\displaystyle \frac{a_i^2}{2S^2}}\right].$$

(42)

Next, the computation of $O_2$ is considered. Using the probit IRF approximation of the logit IRF difference $P_i-P_i^{*}$ and its linear Taylor expansion with respect to ${\delta }_i$ (see (8)) in (40), together with the normal density approximation (17) of the information function $P_i^{*}(1-P_i^{*})$, the integral $O_2$ can be expressed in closed form by applying the identity (A4) from Appendix A. A quadratic Taylor expansion of this result yields

$$O_2\simeq {\delta }_i^{2}K,\mathrm{where}K={\displaystyle \frac{a_i^{2}S}{2D^2\sigma \sqrt{\pi \left(C+\frac{1}{2{\sigma }^2}\right)}}}exp\left(-{\displaystyle \frac{C{(\mu -b_i)}^2}{2{\sigma }^2\left(C+\frac{1}{2{\sigma }^2}\right)}}\right)\mathrm{and}C=a_i^2\left({\displaystyle \frac{1}{D^2}}-{\displaystyle \frac{1}{2S^2}}\right).$$

(43)

Overall, the expected value of the outfit statistic can be approximated as

$$\mathsf{E}\left[{\mathsf{Outfit}}_i\right]=O_1+O_2\simeq 1+{\delta }_i{\displaystyle \frac{a_i^2}{S^2}}(\mu -b_i)+{\delta }_i^2{f}_2(\mu -b_i),$$

(44)

where $f_2$ is a function of the squared difference ${(\mu -b_i)}^2$, which can be derived from (42) and (43). For $a_i=1$ and $\sigma =1$, this reduces to

$$\mathsf{E}\left[{\mathsf{Outfit}}_i\right]\simeq 1+0.393{\delta }_i(\mu -b_i)+{\delta }_i^2\left[-0.119+0.078{(\mu -b_i)}^2+0.193exp\left(-0.115{(\mu -b_i)}^2\right)\right].$$

(45)

Since the outfit statistic cannot be negative, the approximation (45) is valid only for sufficiently small ${\delta }_i$. The linear term shows that the outfit decreases below 1 for positive DIF effects (${\delta }_i>0$) when $\mu -b_i<0$, i.e., for difficult items, and increases when $\mu -b_i>0$. Interestingly, for items with $b_i\approx \mu$, (45) simplifies to $1+0.074{\delta }_i^2$. This implies that very large DIF effects are required to detect item misfit in the outfit statistic for items of moderate difficulty. In this respect, the outfit statistic behaves in the opposite way of distribution-weighted RMSD and MD statistics, which are more sensitive to uniform DIF when $b_i\approx \mu$.

3.2. Expected Value of Infit Statistic

Next, the expected value of the infit statistic is computed. First, consider the numerator in the infit statistic (38) and decompose it as

$$\int P_i\left(\theta \right)\left[1-P_i\left(\theta \right)\right]\varphi (\theta ;\mu ,\sigma )\mathrm{d}\theta +\int {\left[P_i\left(\theta \right)-P_i^{*}\left(\theta \right)\right]}^2\varphi (\theta ;\mu ,\sigma )\mathrm{d}\theta =I_1+I_2.$$

(46)

The denominator in (38) converges to

$$\int P_i^{*}\left(\theta \right)\left[1-P_i^{*}\left(\theta \right)\right]\varphi (\theta ;\mu ,\sigma )\mathrm{d}\theta =I_3.$$

(47)

Using the approximation in (17), it follows that

$$I_1\simeq {\displaystyle \frac{1}{\sqrt{2\pi V_1}}}exp\left(-{\displaystyle \frac{{(\mu -b_i-{\delta }_i)}^2}{2V_1}}\right),\mathrm{where}{V}_1={\sigma }^2+{\displaystyle \frac{S^2}{a_i^2}}.$$

(48)

Similarly,

$$I_3\simeq {\displaystyle \frac{1}{\sqrt{2\pi V_1}}}exp\left(-{\displaystyle \frac{{(\mu -b_i)}^2}{2V_1}}\right).$$

(49)

Moreover,

$$I_2\simeq {\delta }_i^2{\displaystyle \frac{a_i^2}{2D^2\sqrt{2}\pi \sigma \sqrt{A}}}exp\left(-{\displaystyle \frac{a_i^2}{2{\sigma }^2{D}^{2}A}}{(\mu -b_i)}^2\right),\mathrm{where}A={\displaystyle \frac{a_i^2}{D^2}}+{\displaystyle \frac{1}{2{\sigma }^2}}.$$

(50)

Taking the expected value of the fraction in the infit statistic and applying a Taylor approximation around ${\delta }_i=0$ yields

$$\mathsf{E}\left[{\mathsf{Infit}}_i\right]\simeq {\displaystyle \frac{I_1}{I_3}}+{\displaystyle \frac{I_2}{I_3}}\simeq 1+{\delta }_i{\displaystyle \frac{\mu -b_i}{V_1}}+{\delta }_i^2\left({\displaystyle \frac{{(\mu -b_i)}^2}{2V_1^2}}-{\displaystyle \frac{1}{2V_1}}\right)+{\delta }_i^2{\displaystyle \frac{a_i^2\sqrt{V_1}}{2D^2\sqrt{\pi }\sigma \sqrt{A}}}exp\left(-{\displaystyle \frac{{(\mu -b_i)}^2}{2}}\left[{\displaystyle \frac{a_i^2}{D^2{\sigma }^{2}A}}-{\displaystyle \frac{1}{V_1}}\right]\right).$$

(51)

Setting $a_i=1$ and $\sigma =1$ simplifies the expression (51) to

$$\mathsf{E}\left[{\mathsf{Infit}}_i\right]=1+0.282{\delta }_i(\mu -b_i)+{\delta }_i^2\left(-0.141+0.040{(\mu -b_i)}^2+0.200exp\left(-0.063{(\mu -b_i)}^2\right)\right).$$

(52)

Comparing the linear term of the outfit statistic (0.393, see (45)) with the corresponding linear term in the infit statistic (0.282, see (52)) shows that uniform DIF is expected to induce larger deviations from 1 in the outfit than in the infit statistic. Hence, the power to detect model misfit caused by uniform DIF may be higher for the outfit than for the infit statistic.

As with the outfit, positive uniform DIF effects yield infit statistics smaller than 1 when $b_i>\mu$ and larger than 1 when $b_i<\mu$. For $b_i\approx \mu$, values slightly above 1 are expected, as indicated by the approximation $1+0.059{\delta }_i^2$ (see (52)).

4. Simulation Study

4.1. Method

The 2PL model was used for both data generation and analysis. The mean and SD of the normally distributed factor variable $\theta$ were set to 0 and 1, respectively. Non-normal distributions of $\theta$ were not simulated, as substantially different results were not expected in such conditions.

The simulation study included $I=50$ items to examine the behavior of the fit statistics under more typical conditions of longer tests, where ability estimates are relatively precise. Ten base items with known item discriminations $a_i$ and item difficulties $b_i$ were defined in the simulation and duplicated five times to create a test of 50 items. All item discriminations $a_i$ were fixed at 1, resulting in a test with average discrimination. The item difficulties $b_i$ were set to −2.00, −1.56, −1.11, −0.67, −0.22, 0.22, 0.67, 1.11, 1.56, and 2.00, producing a test with item difficulties uniformly distributed across a broad range of ability values. Exactly two out of the 50 items were simulated to exhibit uniform DIF, corresponding to 4% of the total items. A relatively small proportion of DIF items was selected to minimize the influence of DIF item misfit on the non-DIF items (i.e., items without DIF). Items j and $10-j+1$ for $j=1,\dots ,5$ were specified to have uniform DIF in difficulties $b_i$ with values $\delta$ and $-\delta$, respectively. For instance, for $j=1$, the first and tenth items were affected by DIF and assigned difficulties $-2.00+\delta$ and $2.00-\delta$. The DIF effect size $\delta$ was set to $-0.6$ and $0.6$, representing large DIF magnitudes [21,59].

Sample sizes N were set to 250, 500, 1000, 2000, and 4000, reflecting typical applications of item fit statistics in large-scale assessments using the 2PL model [8].

In each of the 5 (sample size N) × 5 (type of selected DIF items) × 2 (DIF effect size $\delta$) $=50$ simulation conditions, 750 replications were conducted. Item parameters were fixed at the parameters of the base items. Hence, the presence of DIF was ignored in the scaling step in order to allow detecting DIF by the item fit statistics ${\mathsf{RMSD}}_{dist}$, ${\mathsf{MD}}_{dist}$, ${\mathsf{RMSD}}_{diff}$, ${\mathsf{MD}}_{diff}$, $\mathsf{Infit}$ and $\mathsf{Outfit}$. In this scaling step, only the mean $\mu$ and the SD $\sigma$ were estimated.

The uniformly weighted RMSD and MD fit statistics were not computed in this Simulation Study, as the appropriate bounds for the uniform distribution domain are not clearly defined. The information-weighted RMSD and MD fit statistics were also not evaluated in this simulation, as they are expected to behave similarly to the difficulty-weighted fit statistics, with additional scaling by item discriminations.

Means, SDs, and percentiles (5th, 25th, 50th, 75th, and 95th) were computed for all item fit statistics.

Analyses were conducted in R (Version 4.4.1; [60]) using the TAM package (Version 4.3-25; [61]) for 2PL model fitting. Custom R functions were written for RMSD and MD statistics, while infit and outfit statistics were computed with TAM::msq.itemfit(), which uses numerical integration rather than the stochastic integration in TAM::tam.fit(). Replication materials are available at https://zenodo.org/records/17241167 (accessed on 4 October 2025). Figures were created using the R package ggplot2 (Version 4.0.0; [62,63]).

4.2. Results

Table 1 reports the mean and SD of the item fit statistics for DIF items as a function of item difficulty $b_i$, DIF effect size $\delta$, and sample size N. For items with difficulties close to the mean $\mu =0$ (e.g., $b_i=-0.22$), the distribution-weighted RMSD (${\mathsf{RMSD}}_{dist}$) exhibited mean and SD values very similar to the difficulty-weighted RMSD (${\mathsf{RMSD}}_{diff}$). The empirical RMSD closely matched the approximate expected value of $0.2·0.6=0.12$ derived in Section 2. MD values reflected the sign of the uniform DIF ${\delta }_i$. Consistent with Section 3, infit and outfit statistics did not indicate uniform DIF for items with $b_i$ near the mean, remaining close to 1 (e.g., for $b_i=-0.22$).

Table 1. Simulation Study: Mean and standard deviation (SD) of item fit statistics for items with differential item functioning (DIF) as a function of item difficulty $b_i$, DIF effect size ${\delta }_i$ and sample size N.

			Mean						SD
			Dist		Diff		Infit	Outfit	Dist		Diff		Infit	Outfit
${\mathit{b}}_{\mathit{i}}$	${\mathit{\delta }}_{\mathit{i}}$	$\mathit{N}$	RMSD	MD	RMSD	MD			RMSD	MD	RMSD	MD
−0.22	−0.6	250	0.129	0.117	0.133	0.120	0.982	0.975	0.027	0.027	0.028	0.028	0.047	0.066
		500	0.126	0.118	$\phantom{-}$0.129	$\phantom{-}$0.121	$\phantom{-}$0.983	$\phantom{-}$0.977	$\phantom{-}$0.020	$\phantom{-}$0.019	$\phantom{-}$0.021	$\phantom{-}$0.020	$\phantom{-}$0.033	$\phantom{-}$0.046
		1000	$\phantom{-}$0.125	$\phantom{-}$0.119	$\phantom{-}$0.128	$\phantom{-}$0.122	$\phantom{-}$0.981	$\phantom{-}$0.973	$\phantom{-}$0.014	$\phantom{-}$0.014	$\phantom{-}$0.015	$\phantom{-}$0.014	$\phantom{-}$0.023	$\phantom{-}$0.032
		2000	$\phantom{-}$0.123	$\phantom{-}$0.118	$\phantom{-}$0.126	$\phantom{-}$0.121	$\phantom{-}$0.982	$\phantom{-}$0.974	$\phantom{-}$0.010	$\phantom{-}$0.010	$\phantom{-}$0.011	$\phantom{-}$0.010	$\phantom{-}$0.016	$\phantom{-}$0.022
		4000	$\phantom{-}$0.123	$\phantom{-}$0.118	$\phantom{-}$0.125	$\phantom{-}$0.121	$\phantom{-}$0.982	$\phantom{-}$0.974	$\phantom{-}$0.007	$\phantom{-}$0.007	$\phantom{-}$0.008	$\phantom{-}$0.007	$\phantom{-}$0.012	$\phantom{-}$0.016
	$\phantom{-}$0.6	250	$\phantom{-}$0.134	−0.123	$\phantom{-}$0.133	−0.122	$\phantom{-}$1.064	$\phantom{-}$1.088	$\phantom{-}$0.028	$\phantom{-}$0.028	$\phantom{-}$0.027	$\phantom{-}$0.028	$\phantom{-}$0.051	$\phantom{-}$0.076
		500	$\phantom{-}$0.131	−0.123	$\phantom{-}$0.129	−0.122	$\phantom{-}$1.063	$\phantom{-}$1.086	$\phantom{-}$0.020	$\phantom{-}$0.020	$\phantom{-}$0.020	$\phantom{-}$0.020	$\phantom{-}$0.036	$\phantom{-}$0.053
		1000	$\phantom{-}$0.129	−0.124	$\phantom{-}$0.128	−0.123	$\phantom{-}$1.064	$\phantom{-}$1.087	$\phantom{-}$0.014	$\phantom{-}$0.014	$\phantom{-}$0.014	$\phantom{-}$0.014	$\phantom{-}$0.026	$\phantom{-}$0.038
		2000	$\phantom{-}$0.127	−0.123	$\phantom{-}$0.126	−0.122	$\phantom{-}$1.063	$\phantom{-}$1.085	$\phantom{-}$0.011	$\phantom{-}$0.010	$\phantom{-}$0.010	$\phantom{-}$0.010	$\phantom{-}$0.017	$\phantom{-}$0.025
		4000	$\phantom{-}$0.127	−0.123	$\phantom{-}$0.126	−0.122	$\phantom{-}$1.064	$\phantom{-}$1.086	$\phantom{-}$0.007	$\phantom{-}$0.007	$\phantom{-}$0.007	$\phantom{-}$0.007	$\phantom{-}$0.013	$\phantom{-}$0.019
−1.11	−0.6	250	$\phantom{-}$0.108	$\phantom{-}$0.092	$\phantom{-}$0.152	$\phantom{-}$0.125	$\phantom{-}$0.839	$\phantom{-}$0.791	$\phantom{-}$0.025	$\phantom{-}$0.023	$\phantom{-}$0.052	$\phantom{-}$0.048	$\phantom{-}$0.056	$\phantom{-}$0.085
		500	$\phantom{-}$0.104	$\phantom{-}$0.092	$\phantom{-}$0.139	$\phantom{-}$0.123	$\phantom{-}$0.841	$\phantom{-}$0.793	$\phantom{-}$0.018	$\phantom{-}$0.016	$\phantom{-}$0.037	$\phantom{-}$0.035	$\phantom{-}$0.041	$\phantom{-}$0.062
		1000	$\phantom{-}$0.102	$\phantom{-}$0.092	$\phantom{-}$0.130	$\phantom{-}$0.120	$\phantom{-}$0.836	$\phantom{-}$0.786	$\phantom{-}$0.013	$\phantom{-}$0.011	$\phantom{-}$0.025	$\phantom{-}$0.024	$\phantom{-}$0.027	$\phantom{-}$0.041
		2000	$\phantom{-}$0.100	$\phantom{-}$0.091	$\phantom{-}$0.125	$\phantom{-}$0.118	$\phantom{-}$0.839	$\phantom{-}$0.790	$\phantom{-}$0.009	$\phantom{-}$0.008	$\phantom{-}$0.018	$\phantom{-}$0.017	$\phantom{-}$0.021	$\phantom{-}$0.032
		4000	$\phantom{-}$0.100	$\phantom{-}$0.092	$\phantom{-}$0.125	$\phantom{-}$0.120	$\phantom{-}$0.839	$\phantom{-}$0.791	$\phantom{-}$0.006	$\phantom{-}$0.006	$\phantom{-}$0.012	$\phantom{-}$0.012	$\phantom{-}$0.014	$\phantom{-}$0.022
	$\phantom{-}$0.6	250	$\phantom{-}$0.126	−0.112	$\phantom{-}$0.142	−0.120	$\phantom{-}$1.237	$\phantom{-}$1.323	$\phantom{-}$0.029	$\phantom{-}$0.029	$\phantom{-}$0.035	$\phantom{-}$0.042	$\phantom{-}$0.080	$\phantom{-}$0.136
		500	$\phantom{-}$0.121	−0.112	$\phantom{-}$0.132	−0.119	$\phantom{-}$1.237	$\phantom{-}$1.322	$\phantom{-}$0.019	$\phantom{-}$0.019	$\phantom{-}$0.025	$\phantom{-}$0.028	$\phantom{-}$0.057	$\phantom{-}$0.099
		1000	$\phantom{-}$0.119	−0.111	$\phantom{-}$0.128	−0.120	$\phantom{-}$1.235	$\phantom{-}$1.322	$\phantom{-}$0.014	$\phantom{-}$0.013	$\phantom{-}$0.017	$\phantom{-}$0.019	$\phantom{-}$0.040	$\phantom{-}$0.070
		2000	$\phantom{-}$0.118	−0.112	$\phantom{-}$0.126	−0.120	$\phantom{-}$1.237	$\phantom{-}$1.324	$\phantom{-}$0.010	$\phantom{-}$0.010	$\phantom{-}$0.013	$\phantom{-}$0.014	$\phantom{-}$0.028	$\phantom{-}$0.048
		4000	$\phantom{-}$0.117	−0.111	$\phantom{-}$0.124	−0.120	$\phantom{-}$1.236	$\phantom{-}$1.322	$\phantom{-}$0.007	$\phantom{-}$0.007	$\phantom{-}$0.010	$\phantom{-}$0.010	$\phantom{-}$0.021	$\phantom{-}$0.036
−2.00	−0.6	250	$\phantom{-}$0.077	$\phantom{-}$0.057	$\phantom{-}$0.215	$\phantom{-}$0.145	$\phantom{-}$0.731	$\phantom{-}$0.670	$\phantom{-}$0.021	$\phantom{-}$0.019	$\phantom{-}$0.118	$\phantom{-}$0.118	$\phantom{-}$0.096	$\phantom{-}$0.154
		500	$\phantom{-}$0.072	$\phantom{-}$0.057	$\phantom{-}$0.174	$\phantom{-}$0.126	$\phantom{-}$0.729	$\phantom{-}$0.671	$\phantom{-}$0.015	$\phantom{-}$0.013	$\phantom{-}$0.087	$\phantom{-}$0.085	$\phantom{-}$0.063	$\phantom{-}$0.102
		1000	$\phantom{-}$0.070	$\phantom{-}$0.058	$\phantom{-}$0.154	$\phantom{-}$0.124	$\phantom{-}$0.727	$\phantom{-}$0.668	$\phantom{-}$0.011	$\phantom{-}$0.009	$\phantom{-}$0.067	$\phantom{-}$0.062	$\phantom{-}$0.046	$\phantom{-}$0.073
		2000	$\phantom{-}$0.069	$\phantom{-}$0.057	$\phantom{-}$0.140	$\phantom{-}$0.121	$\phantom{-}$0.730	$\phantom{-}$0.671	$\phantom{-}$0.008	$\phantom{-}$0.006	$\phantom{-}$0.048	$\phantom{-}$0.044	$\phantom{-}$0.032	$\phantom{-}$0.052
		4000	$\phantom{-}$0.069	$\phantom{-}$0.058	$\phantom{-}$0.132	$\phantom{-}$0.120	$\phantom{-}$0.729	$\phantom{-}$0.671	$\phantom{-}$0.006	$\phantom{-}$0.004	$\phantom{-}$0.031	$\phantom{-}$0.028	$\phantom{-}$0.022	$\phantom{-}$0.037
	$\phantom{-}$0.6	250	$\phantom{-}$0.101	−0.083	$\phantom{-}$0.177	−0.107	$\phantom{-}$1.416	$\phantom{-}$1.537	$\phantom{-}$0.027	$\phantom{-}$0.026	$\phantom{-}$0.067	$\phantom{-}$0.097	$\phantom{-}$0.143	$\phantom{-}$0.260
		500	$\phantom{-}$0.094	−0.080	$\phantom{-}$0.150	−0.111	$\phantom{-}$1.400	$\phantom{-}$1.522	$\phantom{-}$0.019	$\phantom{-}$0.018	$\phantom{-}$0.046	$\phantom{-}$0.062	$\phantom{-}$0.102	$\phantom{-}$0.182
		1000	$\phantom{-}$0.091	−0.080	$\phantom{-}$0.137	−0.113	$\phantom{-}$1.401	$\phantom{-}$1.525	$\phantom{-}$0.014	$\phantom{-}$0.012	$\phantom{-}$0.035	$\phantom{-}$0.044	$\phantom{-}$0.068	$\phantom{-}$0.125
		2000	$\phantom{-}$0.091	−0.081	$\phantom{-}$0.129	−0.116	$\phantom{-}$1.404	$\phantom{-}$1.527	$\phantom{-}$0.009	$\phantom{-}$0.009	$\phantom{-}$0.024	$\phantom{-}$0.029	$\phantom{-}$0.049	$\phantom{-}$0.092
		4000	$\phantom{-}$0.090	−0.080	$\phantom{-}$0.124	−0.115	$\phantom{-}$1.404	$\phantom{-}$1.528	$\phantom{-}$0.007	$\phantom{-}$0.006	$\phantom{-}$0.018	$\phantom{-}$0.022	$\phantom{-}$0.035	$\phantom{-}$0.063

Note. RMSD = root mean square deviation; MD = mean deviation; dist = RMSD and MD weighted by groupspecific distribution; diff = RMSD and MD weighted by a normal density located at item difficulty $b_i$.

For easier items (i.e., lower $b_i$), RMSD and absolute MD values weighted by the distribution were smaller than the difficulty-weighted counterparts. Notably, difficulty-weighted RMSD and MD exhibited similar means across large samples regardless of $b_i$, whereas ${\mathsf{RMSD}}_{dist}$ and ${\mathsf{MD}}_{dist}$ approached 0 for items with extreme difficulties. However, difficulty-weighted RMSD and MD exhibited substantially larger SDs, indicating that sampling error strongly affected these statistics for extreme items. The SD of these fit statistics decreased as the sample size increased. Bias due to sampling error in small to moderate samples was also more pronounced for difficulty-weighted RMSD.

As expected from the analytical results in Section 3, infit and outfit statistics detected uniform DIF for items with difficulties far from the mean. Deviations from 1 were asymmetric for items with negative versus positive DIF. For instance, for $b_i=-2.00$ and $N=4000$, infit was 0.729 for ${\delta }_i=-0.6$ and 1.404 for ${\delta }_i=0.6$, highlighting potential limitations of symmetric cutoffs such as 0.8 and 1.2 in misfit detection. The SD of outfit was substantially larger than that of infit, particularly for items with extreme difficulties.

Figure 1 presents percentile plots (5th, 25th, 50th, 75th, and 95th) of distribution-weighted and difficulty-weighted RMSD statistics for DIF items as a function of item difficulty, with a DIF effect of ${\delta }_i=-0.6$. Variability in item fit statistics was markedly higher for small sample sizes (e.g., $N=250$). In particular, the sampling distribution of the difficulty-weighted RMSD (${\mathsf{RMSD}}_{diff}$) for the item with $b_i=-2.00$ remained wide even for a large sample size of $N=2000$. This limitation may restrict the operational applicability of this statistic. Positive bias due to sampling error for ${\mathsf{RMSD}}_{diff}$ at $b_i=-2.00$ was also evident in small to moderate samples.

Figure 1. Simulation Study: Percentile plot of RMSD item fit statistics for items with differential item functioning (DIF) showing the 5th–95th percentile range (black rectangle), the 25th–75th percentile range (gray-shaded rectangle) and the median (thick black line).

Table 2 reports the mean and SD for items without DIF under simulation conditions with $\delta =-0.6$, where the fourth and seventh items exhibited DIF. While MD statistics were centered around the expected value of 0, RMSD statistics showed positive values that deviated substantially from 0 in small to moderate sample sizes. Asymptotically, RMSD values are expected to approach 0; however, sampling error induced notable bias, particularly for items with extreme difficulty ($b_i=-2.00$). For instance, the mean of the difficulty-weighted RMSD for this item was 0.158 at $N=250$. In contrast, infit and outfit statistics closely matched their expected value of 1.

Table 2. Simulation Study: Mean and standard deviation (SD) of item fit statistics for items without differential item functioning (DIF) as a function of item difficulty $b_i$ and sample size N.

		Mean						SD
		Dist		Diff		Infit	Outfit	Dist		Diff		Infit	Outfit
${\mathit{b}}_{\mathit{i}}$	$\mathit{N}$	RMSD	MD	RMSD	MD			RMSD	MD	RMSD	MD
−0.22	250	$\phantom{-}$0.051	$\phantom{-}$0.000	$\phantom{-}$0.053	$\phantom{-}$0.000	$\phantom{-}$0.997	$\phantom{-}$0.997	$\phantom{-}$0.016	$\phantom{-}$0.028	$\phantom{-}$0.017	$\phantom{-}$0.029	$\phantom{-}$0.047	$\phantom{-}$0.066
	500	$\phantom{-}$0.036	$\phantom{-}$0.000	$\phantom{-}$0.037	$\phantom{-}$0.000	$\phantom{-}$0.997	$\phantom{-}$0.997	$\phantom{-}$0.011	$\phantom{-}$0.020	$\phantom{-}$0.012	$\phantom{-}$0.020	$\phantom{-}$0.033	$\phantom{-}$0.046
	1000	$\phantom{-}$0.025	$\phantom{-}$0.000	$\phantom{-}$0.026	−0.001	$\phantom{-}$0.997	$\phantom{-}$0.996	$\phantom{-}$0.008	$\phantom{-}$0.014	$\phantom{-}$0.008	$\phantom{-}$0.014	$\phantom{-}$0.023	$\phantom{-}$0.032
	2000	$\phantom{-}$0.018	$\phantom{-}$0.000	$\phantom{-}$0.019	$\phantom{-}$0.000	$\phantom{-}$0.997	$\phantom{-}$0.996	$\phantom{-}$0.006	$\phantom{-}$0.010	$\phantom{-}$0.006	$\phantom{-}$0.010	$\phantom{-}$0.016	$\phantom{-}$0.023
	4000	$\phantom{-}$0.013	$\phantom{-}$0.000	$\phantom{-}$0.013	$\phantom{-}$0.000	$\phantom{-}$0.997	$\phantom{-}$0.996	$\phantom{-}$0.004	$\phantom{-}$0.007	$\phantom{-}$0.004	$\phantom{-}$0.007	$\phantom{-}$0.011	$\phantom{-}$0.016
−1.11	250	$\phantom{-}$0.048	$\phantom{-}$0.000	$\phantom{-}$0.079	$\phantom{-}$0.001	$\phantom{-}$0.998	$\phantom{-}$0.995	$\phantom{-}$0.015	$\phantom{-}$0.025	$\phantom{-}$0.039	$\phantom{-}$0.044	$\phantom{-}$0.068	$\phantom{-}$0.109
	500	$\phantom{-}$0.035	−0.001	$\phantom{-}$0.055	−0.003	$\phantom{-}$0.998	$\phantom{-}$0.997	$\phantom{-}$0.011	$\phantom{-}$0.018	$\phantom{-}$0.027	$\phantom{-}$0.033	$\phantom{-}$0.048	$\phantom{-}$0.079
	1000	$\phantom{-}$0.025	−0.001	$\phantom{-}$0.040	−0.002	$\phantom{-}$0.998	$\phantom{-}$0.998	$\phantom{-}$0.007	$\phantom{-}$0.013	$\phantom{-}$0.017	$\phantom{-}$0.022	$\phantom{-}$0.034	$\phantom{-}$0.055
	2000	$\phantom{-}$0.017	−0.001	$\phantom{-}$0.028	−0.002	$\phantom{-}$0.999	$\phantom{-}$0.997	$\phantom{-}$0.005	$\phantom{-}$0.009	$\phantom{-}$0.012	$\phantom{-}$0.016	$\phantom{-}$0.023	$\phantom{-}$0.036
	4000	$\phantom{-}$0.012	−0.001	$\phantom{-}$0.020	−0.002	$\phantom{-}$0.998	$\phantom{-}$0.997	$\phantom{-}$0.004	$\phantom{-}$0.006	$\phantom{-}$0.008	$\phantom{-}$0.011	$\phantom{-}$0.017	$\phantom{-}$0.028
−2.00	250	$\phantom{-}$0.045	$\phantom{-}$0.000	$\phantom{-}$0.158	$\phantom{-}$0.023	$\phantom{-}$1.003	$\phantom{-}$1.005	$\phantom{-}$0.014	$\phantom{-}$0.021	$\phantom{-}$0.098	$\phantom{-}$0.114	$\phantom{-}$0.112	$\phantom{-}$0.191
	500	$\phantom{-}$0.033	−0.001	$\phantom{-}$0.116	$\phantom{-}$0.008	$\phantom{-}$1.003	$\phantom{-}$0.999	$\phantom{-}$0.010	$\phantom{-}$0.015	$\phantom{-}$0.073	$\phantom{-}$0.081	$\phantom{-}$0.081	$\phantom{-}$0.133
	1000	$\phantom{-}$0.022	$\phantom{-}$0.000	$\phantom{-}$0.082	$\phantom{-}$0.005	$\phantom{-}$1.000	$\phantom{-}$0.997	$\phantom{-}$0.007	$\phantom{-}$0.011	$\phantom{-}$0.052	$\phantom{-}$0.055	$\phantom{-}$0.056	$\phantom{-}$0.092
	2000	$\phantom{-}$0.016	$\phantom{-}$0.000	$\phantom{-}$0.060	$\phantom{-}$0.001	$\phantom{-}$0.999	$\phantom{-}$0.993	$\phantom{-}$0.005	$\phantom{-}$0.008	$\phantom{-}$0.034	$\phantom{-}$0.038	$\phantom{-}$0.042	$\phantom{-}$0.067
	4000	$\phantom{-}$0.011	−0.001	$\phantom{-}$0.042	−0.002	$\phantom{-}$1.002	$\phantom{-}$1.000	$\phantom{-}$0.004	$\phantom{-}$0.005	$\phantom{-}$0.023	$\phantom{-}$0.026	$\phantom{-}$0.028	$\phantom{-}$0.046

Note. RMSD = root mean square deviation; MD = mean deviation; dist = RMSD and MD weighted by groupspecific distribution; diff = RMSD and MD weighted by a normal density located at item difficulty $b_i$.

Figure 2 presents percentile plots of RMSD statistics for items without DIF. Similar to items with DIF, the sampling distribution of the difficulty-weighted RMSD (${\mathsf{RMSD}}_{diff}$) was wide, with sampling bias particularly pronounced for items with extreme difficulty. In contrast, the distribution-weighted RMSD (${\mathsf{RMSD}}_{dist}$) exhibited comparable variability across items with different difficulties.

Figure 2. Simulation Study: Percentile plot of RMSD item fit statistics for items without differential item functioning (DIF) showing the 5th–95th percentile range (black rectangle), the 25th–75th percentile range (gray-shaded rectangle) and the median (thick black line).

5. Empirical Example

5.1. Method

This section employs the PISA 2006 dataset [64] for the reading domain. The dataset comprises participants from 26 selected countries that participated in PISA 2006. The complete PISA 2006 dataset is publicly available at https://www.oecd.org/en/data/datasets/pisa-2006-database.html (accessed on 4 October 2025) and can be accessed as the data.pisa2006Read dataset from the R package sirt (Version 4.2-133; [65]).

In PISA 2006, reading items were administered to a subset of students. The present analysis included only students who responded to at least one item from the reading domain. In total, 110,236 students were included, with country-specific sample sizes ranging from 2010 to 12,142 (mean = 4239.8, SD = 3046.7).

Student (sampling) weights were applied throughout the analysis. Within each country, weights were normalized to sum to 5000, ensuring equal contribution across countries. These normalized weights are also referred to as house weights.

Among the 28 reading items, some were originally scored polytomously but were recoded dichotomously for this empirical example, with only the highest category coded as correct. The remaining items were treated as dichotomous, consistent with the original PISA analysis.

In the first step, international item parameters were estimated using the 2PL model applied to the weighted pooled dataset across all countries. The resulting item discriminations $a_i$ and item difficulties $b_i$ are reported in Table 3. In the subsequent country-wise scaling step, only the country mean $\mu$ and country SD $\sigma$ were estimated, while item parameters were fixed at their international values from the pooled analysis. Item fit statistics were then computed at the country level based on these fixed parameters, which corresponds to the assumption of full invariance.

Table 3. Empirical Example, PISA 2006 Reading, Netherlands: International item parameters, DIF effect size ${\delta }_i$ and item fit statistics (with standard errors in parentheses).

Item	${\mathit{a}}_{\mathit{i}}$	${\mathit{b}}_{\mathit{i}}$	${\mathit{\delta }}_{\mathit{i}}$	Dist		Diff		Infit	Outfit
				RMSD	MD	RMSD	MD
R055Q01	1.394	−1.487	0.655 (0.054)	0.122 (0.012)	−0.118 (0.011)	0.133 (0.014)	−0.128 (0.013)	1.666 (0.008)	2.645 (0.030)
R055Q02	1.378	0.043	0.288 (0.048)	0.073 (0.012)	−0.070 (0.011)	0.072 (0.012)	−0.070 (0.011)	1.057 (0.005)	1.113 (0.011)
R055Q03	1.619	−0.334	0.176 (0.043)	0.048 (0.010)	−0.042 (0.011)	0.055 (0.010)	−0.049 (0.011)	0.989 (0.004)	1.030 (0.009)
R055Q05	2.116	−0.779	−0.055 (0.043)	0.037 (0.008)	0.018 (0.008)	0.042 (0.008)	0.003 (0.011)	0.850 (0.002)	0.719 (0.003)
R067Q01	1.226	−2.073	0.523 (0.064)	0.077 (0.013)	−0.064 (0.010)	0.108 (0.033)	−0.093 (0.048)	1.572 (0.009)	1.724 (0.011)
R067Q04	0.832	0.723	0.723 (0.093)	0.123 (0.013)	−0.118 (0.013)	0.132 (0.015)	−0.130 (0.015)	0.934 (0.003)	0.919 (0.003)
R067Q05	1.087	−0.307	0.304 (0.060)	0.072 (0.013)	−0.069 (0.013)	0.076 (0.014)	−0.072 (0.014)	1.051 (0.003)	1.087 (0.007)
R102Q04A	1.460	0.669	−0.371 (0.047)	0.094 (0.012)	0.090 (0.011)	0.094 (0.013)	0.088 (0.012)	1.103 (0.004)	1.215 (0.009)
R102Q05	1.330	0.244	−0.611 (0.048)	0.151 (0.012)	0.145 (0.011)	0.150 (0.012)	0.144 (0.011)	1.046 (0.004)	1.086 (0.008)
R102Q07	1.417	−1.494	0.823 (0.047)	0.177 (0.011)	−0.153 (0.010)	0.179 (0.016)	−0.153 (0.021)	2.000 (0.010)	2.415 (0.019)
R104Q01	1.626	−1.322	0.087 (0.072)	0.017 (0.014)	−0.012 (0.012)	0.021 (0.021)	−0.018 (0.028)	1.044 (0.004)	0.959 (0.006)
R104Q02	0.584	1.334	0.157 (0.112)	0.025 (0.010)	−0.017 (0.013)	0.018 (0.011)	0.000 (0.021)	0.969 (0.001)	0.960 (0.001)
R104Q05	1.133	3.129	0.622 (0.147)	0.034 (0.008)	−0.024 (0.004)	0.175 (0.087)	−0.166 (0.078)	0.639 (0.004)	0.594 (0.003)
R111Q01	1.365	−0.604	0.470 (0.039)	0.113 (0.009)	−0.108 (0.009)	0.112 (0.011)	−0.101 (0.014)	1.228 (0.004)	1.408 (0.012)
R111Q02B	1.047	1.912	−0.324 (0.065)	0.048 (0.010)	0.046 (0.010)	0.038 (0.016)	0.035 (0.019)	1.228 (0.004)	1.341 (0.006)
R111Q06B	1.588	0.542	0.162 (0.044)	0.042 (0.011)	−0.039 (0.010)	0.046 (0.012)	−0.044 (0.011)	0.990 (0.004)	0.973 (0.007)
R219Q01E	1.633	−0.250	−0.236 (0.054)	0.074 (0.014)	0.058 (0.013)	0.081 (0.015)	0.067 (0.014)	1.021 (0.006)	1.008 (0.010)
R219Q01T	1.860	−0.664	−0.246 (0.062)	0.077 (0.017)	0.054 (0.013)	0.099 (0.023)	0.081 (0.020)	1.023 (0.006)	1.049 (0.013)
R219Q02	1.533	−1.179	−0.120 (0.055)	0.031 (0.011)	0.020 (0.009)	0.038 (0.016)	0.026 (0.016)	0.921 (0.002)	1.048 (0.013)
R220Q01	1.761	0.305	0.170 (0.033)	0.058 (0.008)	−0.053 (0.008)	0.058 (0.009)	−0.054 (0.008)	0.981 (0.005)	0.986 (0.009)
R220Q02B	1.520	−0.376	0.102 (0.047)	0.050 (0.010)	−0.029 (0.012)	0.058 (0.012)	−0.032 (0.016)	1.006 (0.004)	1.060 (0.010)
R220Q04	1.301	−0.312	−0.260 (0.055)	0.062 (0.011)	0.054 (0.012)	0.060 (0.012)	0.051 (0.014)	0.888 (0.003)	0.854 (0.004)
R220Q05	1.976	−1.145	−0.007 (0.050)	0.023 (0.011)	−0.002 (0.009)	0.029 (0.017)	−0.013 (0.019)	0.920 (0.004)	0.701 (0.004)
R220Q06	1.166	−0.675	−0.110 (0.061)	0.032 (0.008)	0.018 (0.012)	0.038 (0.014)	0.015 (0.018)	0.917 (0.003)	0.882 (0.004)
R227Q01	0.778	−0.151	−0.778 (0.066)	0.131 (0.010)	0.129 (0.010)	0.131 (0.011)	0.129 (0.011)	0.942 (0.002)	0.937 (0.003)
R227Q02T	0.993	0.793	−0.907 (0.066)	0.194 (0.013)	0.184 (0.013)	0.193 (0.013)	0.183 (0.013)	1.230 (0.004)	1.289 (0.006)
R227Q03	1.664	−0.183	−0.159 (0.043)	0.057 (0.012)	0.046 (0.011)	0.063 (0.013)	0.054 (0.012)	1.042 (0.005)	1.094 (0.011)
R227Q06	1.765	−0.777	−0.286 (0.053)	0.082 (0.012)	0.064 (0.009)	0.100 (0.017)	0.088 (0.015)	0.903 (0.004)	0.876 (0.007)

Note. $a_i$ = item discrimination (international item parameter); $b_i$ = item difficulty (international item parameter); RMSD = root mean square deviation; MD = mean deviation; dist = RMSD and MD weighted by group-specific distribution; diff = RMSD and MD weighted by a normal density located at item difficulty $b_i$. The following entries are printed in bold font: absolute ${\delta }_i$ values larger than 0.4, RMSD values larger than 0.08, and infit statistics smaller than 0.7 and larger than 1.3.

In the next step, the distribution parameters $\mu$ and $\sigma$ were fixed, and country-specific DIF effects ${\delta }_i$ were estimated by allowing item difficulties to vary freely while fixing item discriminations to the base-item values (i.e., set to 1). The estimated ${\delta }_i$ can be interpreted as a DIF effect size on the logit scale of the 2PL model, whereas the additional item fit statistics represent alternative DIF quantifications.

The entire procedure was repeated 80 times using balanced repeated replicate weights [64], which allow estimation of standard errors (SE) for approximately normally distributed statistics [66,67]. Replicate weights were used to obtain standard errors for RMSD, MD, infit, outfit, and ${\delta }_i$ statistics.

Items were flagged (i.e., indicated as misfitting) if certain cutoffs of the fit statistics were exceeded: absolute ${\delta }_i$ values larger than 0.4, RMSD values larger than 0.08, and infit statistics smaller than 0.7 and larger than 1.3.

5.2. Results

Item fit statistics for PISA 2006 reading results in the Netherlands (NLD) are first reported as an example. A total of 2666 students participated in this country, and results for the 28 reading items are presented. The estimated country mean for NLD was 0.093 (SE = 0.032), and the estimated SD was 1.019 (SE = 0.030). The SD of the estimated DIF effects ${\delta }_i$ was 0.432, commonly referred to as the DIF SD [68].

Table 3 reports the item fit statistics for NLD along with their estimated SEs. For instance, 9 of the 28 items exceeded the cutoff value of 0.08 for the RMSD statistic weighted by the distribution (${\mathsf{RMSD}}_{dist}$). For 4 additional items (e.g., Item R067Q01), the difficulty-weighted RMSD (${\mathsf{RMSD}}_{diff}$) exceeded the threshold, while ${\mathsf{RMSD}}_{dist}$ did not. These items had difficulties that deviated substantially from 0. In most cases, items flagged by RMSD were also flagged by the corresponding MD statistic. For NLD, no further items were identified by infit or outfit beyond those already detected as misfitting by $|{\delta }_i|$, RMSD, or MD statistics.

This study did not attempt to provide substantive interpretations for why DIF occurred in some items for NLD. Although potential explanations such as translation issues or differences in opportunities-to-learn may be conjectured, clear substantive interpretations of DIF are generally the exception rather than the rule [69]. It is also relevant that current operational PISA practice removes items with country-specific DIF effects from group comparisons by assigning them unique item parameters in the scaling model [19,70]. As a result, PISA does not aim to explain DIF but instead treats it as construct-irrelevant [71], a stance that has been subject to criticism [72,73].

In the second part of this section, the distribution of item fit statistics across all countries is examined. The analysis is based on 724 cases (i.e., items crossed with countries, with some items excluded in certain countries for technical reasons in the official PISA dataset).

Figure 3 displays histograms of the distribution-weighted RMSD (${\mathsf{RMSD}}_{dist}$) and the difficulty-weighted RMSD (${\mathsf{RMSD}}_{diff}$). On average, the distribution-weighted RMSD produced smaller values ($M=0.060$) than the difficulty-weighted RMSD counterpart ($M=0.072$). Both distributions were notably skewed (skewness for ${\mathsf{RMSD}}_{dist}$: 1.843; for ${\mathsf{RMSD}}_{diff}$: 1.712).

Figure 3. Empirical Example, PISA 2006 Reading: Histogram of distribution-weighted RMSD (${\mathsf{RMSD}}_{dist}$; left panel) and difficulty-weighted RMSD (${\mathsf{RMSD}}_{diff}$; right panel) statistics.

Figure 4 presents a correlation plot of the computed item fit statistics. Corresponding $\mathsf{RMSD}$ and $\left|\mathsf{MD}\right|$ were highly correlated ($r=0.99$), whereas ${\mathsf{RMSD}}_{dist}$ and ${\mathsf{RMSD}}_{diff}$ showed a lower correlation of 0.82, indicating substantial differences between these measures. The DIF effect size $|{\delta }_i|$ and the RMSD and MD statistics were largely uncorrelated with infit or outfit. Notably, $|{\delta }_i|$ correlated slightly more with ${\mathsf{MD}}_{diff}$ than with ${\mathsf{MD}}_{dist}$.

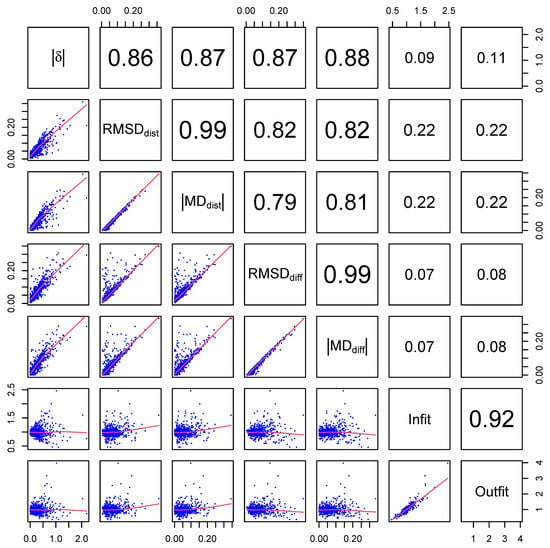
Figure 4. Empirical Example, PISA 2006 Reading: Correlation plot of item fit statistics.

Finally, Table 4 presents the patterns of item flagging based on $|{\delta }_i|$, ${\mathsf{RMSD}}_{dist}$, ${\mathsf{RMSD}}_{diff}$, and infit. Overall, 65.1% of items were not flagged, indicating that 34.9% were identified by at least one fit statistic. Specifically, 20.7% of items were flagged by $|{\delta }_i|$, indicating uniform DIF as the source of misfit. Additionally, 24.0% of items were flagged by ${\mathsf{RMSD}}_{dist}$, 32.7% by ${\mathsf{RMSD}}_{diff}$, and 6.4% by infit.

Table 4. Empirical Example, PISA 2006 Reading: Relative frequencies for patterns of flagged items based on the DIF effect size ${\delta }_i$, distribution-weighted and difficulty-weighted RMSD (${\mathsf{RMSD}}_{dist}$ and ${\mathsf{RMSD}}_{diff}$, respectively) and infit statistic.

Flagged Items
$\mathbf{\left|}\mathit{\delta }\mathbf{\right|}$	${\mathsf{RMSD}}_{\mathit{dist}}$	${\mathsf{RMSD}}_{\mathit{diff}}$	$\mathsf{Infit}$	%
0	0	0	0	65.1
0	0	0	1	0.8
0	0	1	0	5.5
0	0	1	1	0.4
0	1	1	0	7.3
0	1	1	1	0.1
1	0	0	0	1.1
1	0	0	1	0.3
1	0	1	0	1.1
1	0	1	1	1.7
1	1	1	0	13.5
1	1	1	1	3.0

Note. Flagged items are indicated by an entry of 1. Items were flagged according to the following rules: absolute ${\delta }_i$ values larger than 0.4, RMSD values larger than 0.08, and infit statistics smaller than 0.7 and larger than 1.3.

Only 3.0% of items were flagged by all four statistics. Moreover, 2.8% of items were flagged by ${\mathsf{RMSD}}_{diff}$ but not by ${\mathsf{RMSD}}_{dist}$. Notably, 14.2% of items were flagged when $|{\delta }_i|<0.4$, suggesting that the misfit could be due to nonuniform DIF or misspecification of the IRF functional form. Of these, 12.8% were additionally detected by ${\mathsf{RMSD}}_{diff}$, indicating limited incremental value of the infit statistic.

Table 5 displays the percentages of flagged items at the country level for the 26 countries included in this study. The results indicate considerable variation in the proportion of detected DIF items across countries. For instance, the average percentage was 24.1% for the distribution-weighted RMSD statistic (${\mathsf{RMSD}}_{dist}$), with an SD of $6.53\%$, ranging from 7.1% to 37.0%. For the difficulty-weighted RMSD statistic (${\mathsf{RMSD}}_{diff}$), the average percentage increased to 32.74% with an SD of 9.94%, ranging from 17.9% to 51.9%. These findings suggest that DIF may be viewed as a country-specific characteristic, with items in some countries exhibiting greater susceptibility to DIF than in others.

Table 5. Empirical Example, PISA 2006 Reading: Percentages of flagged items based on the DIF effect size ${\delta }_i$, distribution-weighted and difficulty-weighted RMSD (${\mathsf{RMSD}}_{dist}$ and ${\mathsf{RMSD}}_{diff}$, respectively) and infit statistic at the country level.

		Flagged Items
cnt	$\mathit{I}$	$\mathbf{\left|}\mathit{\delta }\mathbf{\right|}$	${\mathsf{RMSD}}_{\mathit{dist}}$	${\mathsf{RMSD}}_{\mathit{diff}}$	$\mathsf{Infit}$
AUS	28	7.1	21.4	25.0	0.0
AUT	27	11.1	11.1	18.5	0.0
BEL	28	14.3	7.1	17.9	10.7
CAN	28	17.9	21.4	32.1	3.6
CHE	28	25.0	17.9	28.6	7.1
CZE	28	25.0	25.0	28.6	3.6
DEU	28	21.4	21.4	28.6	7.1
DNK	27	29.6	37.0	44.4	3.7
ESP	28	17.9	32.1	39.3	7.1
EST	28	17.9	35.7	42.9	10.7
FIN	28	10.7	10.7	17.9	3.6
FRA	28	14.3	25.0	39.3	3.6
GBR	28	25.0	35.7	42.9	7.1
GRC	28	25.0	28.6	35.7	3.6
HUN	28	21.4	17.9	32.1	3.6
IRL	28	17.9	21.4	28.6	3.6
ISL	28	21.4	17.9	21.4	10.7
ITA	28	25.0	21.4	25.0	7.1
JPN	28	25.0	35.7	42.9	17.9
KOR	27	25.9	33.3	51.9	11.1
LUX	27	14.8	11.1	18.5	7.4
NLD	28	32.1	32.1	46.4	14.3
NOR	28	25.0	32.1	42.9	3.6
POL	28	21.4	25.0	39.3	3.6
PRT	28	32.1	32.1	35.7	3.6
SWE	28	14.3	14.3	25.0	7.1

Note. cnt = country label (see Appendix C; I = number of items; Items were flagged according to the following rules: absolute ${\delta }_i$ values larger than 0.4, RMSD values larger than 0.08, and infit statistics smaller than 0.7 and larger than 1.3.

6. Discussion

This article aimed to provide analytical and simulation evidence on how the uniform DIF effect ${\delta }_i$ is reflected in the item fit statistics RMSD, MD, infit, and outfit.

Closed-form approximations were derived for the item fit statistics. The distribution-weighted RMSD and MD statistics, as originally proposed and now applied in operational practice [42], attain the largest absolute values when item difficulties align with the mean of the ability distribution. In this case, RMSD and the absolute MD statistics are approximately $0.20|{\delta }_i|$, whereas they decrease to around $0.13|{\delta }_i|$ when $|\mu - b_i|=2$. The dependency of the item fit statistic on item difficulty is removed by using the difficulty-weighted RMSD and MD statistics. However, the difficulty-weighted statistics have the disadvantage of exhibiting substantially larger variances than their distribution-weighted counterparts.

Moreover, analytical approximations of the expected values of the outfit and infit statistics showed that they exhibit only slight deviations from 1 under uniform DIF when item difficulty $b_i$ is close to the group mean $\mu$. For positive DIF effects, the expected values of the infit and outfit statistics fall below 1 for difficult items (i.e., $b_i>\mu$), while they exceed 1 for easy items.

The simulation study indicated that distribution-weighted RMSD and MD statistics consistently detected uniform DIF, but only for items with difficulty levels near the mean. In contrast, difficulty-weighted RMSD and MD were sensitive to uniform DIF even for items with difficulties far from 0. These statistics were also more affected by sampling variability, exhibiting elevated SDs and positive bias for items with extreme difficulties, particularly in small-to-moderate samples. Notably, distribution-weighted RMSD produced substantially lower values for items with extreme difficulties compared to difficulty-weighted RMSD, complicating DIF detection for items with identical DIF effect sizes ${\delta }_i$ in the item difficulty parameter. Difficulty-weighted RMSD and MD statistics suffer from substantial sampling variability in small samples, particularly for items with extreme difficulties. Researchers might therefore consider using these difficulty-weighted versions; however, their effectiveness in detecting uniform DIF for such items is limited. Consequently, sufficiently large sample sizes are required if uniform DIF for items with extreme difficulties is to be detected using the difficulty-weighted RMSD and MD statistics.

The results of the simulation study and analytical derivations further indicate that item infit and outfit statistics are not suitable for detecting uniform DIF, except in the case of items with extreme difficulties. However, in such cases, difficulty-weighted RMSD and MD fit statistics provide viable alternatives.

An anonymous reviewer noted that in countries with extremely low or high performance, distribution-weighted RMSD and MD statistics may behave differently even under the same extent of DIF [37]. In such cases, difficulty-weighted or information-weighted RMSD and MD statistics may be preferable. However, these statistics would also exhibit greater variability when the items difficulty substantially deviates from the group mean.

A substantial body of literature addresses methods for DIF detection [74,75]. These methods often assess DIF directly through deviations in item parameters, such as differences in item difficulties or discriminations in the 2PL model [76]. In contrast, the RMSD, MD, infit, and outfit statistics provide aggregated measures that summarize DIF across IRT model parameters into a single discrepancy metric. The choice of metric for DIF detection ultimately depends on the researcher’s objectives. This study also demonstrated that uniform DIF is challenging to detect for items with extreme difficulty when using distribution-weighted RMSD or MD statistics. However, it may be argued that DIF in items with extreme difficulties is of lesser practical importance than DIF in items with moderate difficulties, as the latter receive greater weights in likelihood-based estimation of group differences, whereas the former contribute less. Consequently, for researchers primarily concerned with the practical impact of DIF in likelihood-based estimation, distribution-weighted RMSD or MD statistics may be more appropriate than their difficulty-weighted counterparts.

The empirical application using PISA data demonstrated that item fit statistics deviated substantially from perfect correlations with one another. This highlights the importance of selecting which aspects of misfit are of interest. The assessment of standard errors should also be incorporated in operational practice, as item fit statistics can exhibit considerable variability, particularly in smaller samples, such as those in PISA field test studies.

This article focused exclusively on weighted RMSD item fit statistics as originally defined. RMSD has been shown to exhibit positive bias for small to moderate sample sizes. Future research could explore bias-corrected RMSD estimates to reduce such bias in finite samples (see [35]).

An additional limitation is the exclusive focus on uniform DIF, that is, DIF in item difficulties. Nonuniform DIF, defined as DIF in item discriminations, may also be relevant in empirical applications and represents a promising direction for future research, although evidence indicates that uniform DIF occurs more frequently in practice than nonuniform DIF [77,78,79]. The MD statistic is expected to be less effective for nonuniform DIF than the RMSD fit statistic. Item infit and outfit statistics are expected to show greater sensitivity to misspecified item discriminations [54], and therefore, they may be more suitable for detecting nonuniform DIF than uniform DIF.

An anonymous reviewer raised the question of what would happen if anchoring were not perfect and no fixed item parameters were used. In the simulation study, only two of the 50 items were assumed to exhibit uniform DIF, which is likely a lower proportion of misfitting items than would typically be found in practice. This choice was made to examine the behavior of the fit statistics under ideal conditions, in which the anchor item set shows no DIF and has minimal influence on the item under investigation. The behavior of the item fit statistics can be expected to deteriorate as the proportion of DIF items increases. More specifically, for the RMSD item fit statistic, the average RMSD for non-DIF items would increase notably above zero, whereas the average RMSD for DIF items would decrease as the proportion of DIF items increases [35]. Consequently, as the quality of the anchor item set decreases in terms of DIF absence, detecting DIF in truly affected items becomes more difficult. Moreover, average values of the item fit statistics are not expected to change substantially if item parameters are estimated rather than fixed, although the variability of the item fit statistics would increase when item parameters are estimated.

Finally, this study focused solely on the 2PL model. It has been argued that a potentially misfitting 2PL model (or even the Rasch model) may still be the preferred operational scaling model, even when a more complex IRT model holds [73,80]. Notably, misspecification in the IRF is also reflected in the RMSD statistic in addition to DIF. This property may help explain why RMSD is preferred over MD in applications such as the PISA study, as MD only partially offsets the effect of IRF misfit. If the group-specific item parameters of the 2PL model are interpreted as the best approximation that minimizes the Kullback–Leibler distance, it may be advantageous to compute an RMSD statistic directly on group-specific 2PL item parameters rather than relying on nonparametric estimation of group-specific IRFs.