Abstract
This paper presents the Variable Landscape Search (VLS), a novel metaheuristic designed for global optimization of complex problems by dynamically altering the objective function landscape. Unlike traditional methods that operate within a static search space, VLS introduces an additional level of flexibility and diversity to the global optimization process. It does this by continuously and iteratively varying the objective function landscape through slight modifications to the problem formulation, the input data, or both. The innovation of the VLS metaheuristic stems from its unique capability to seamlessly fuse dynamic adaptations in problem formulation with modifications in input data. This dual-modality approach enables continuous exploration of interconnected and evolving search spaces, significantly enhancing the potential for discovering optimal solutions in complex, multi-faceted optimization scenarios, thereby making it adaptable across various domains. In this paper, one of the theoretical results is obtained as a generalization of three alternative metaheuristics, which have been reduced to special cases of VLS: Variable Formulation Search (VFS), Formulation Space Search (FSS), and Variable Search Space (VSS). As a practical application, the paper demonstrates the superior efficiency of a recent big data clustering algorithm through its conceptualization using the VLS paradigm.
Keywords:
variable landscape; variable landscape search (VLS); variable formulation search (VFS); formulation space search (FSS); variable search space (VSS); landscape meta-space; metaheuristic; global optimization; local search; search space variation; dynamic search spaces; big data clustering MSC:
90C59; 90C26
1. Introduction
Metaheuristic methods are higher-level heuristics designed to select and modify simpler heuristics, with the goal of efficiently exploring a solution space and finding near-optimal or optimal solutions []. They incorporate strategies to balance local search (exploitation of the current area in the solution space) and global search (exploration of the entire solution space), in order to escape from local optima and reach the global optimum []. Incorporating a mechanism to adaptively change the search space, the proposed Variable Landscape Search (VLS) approach can be classified as a metaheuristic method, given that it embodies these core elements of metaheuristic optimization strategies.
Let be an objective function defined over a feasible solution space . The objective function landscape (or simply, landscape) associated with f is defined as
Each element represents a feasible solution x and its corresponding objective value. The landscape therefore characterizes the geometric and topological structure of the optimization problem, encoding all feasible solutions, their objective values, and the relationships between them (e.g., gradients, basins of attraction, and local/global optima).
Given an objective function landscape , the associated search space is the subset of feasible solutions that correspond to locally optimal points on the landscape:
Hence, the search space represents all potential candidates for the global optimum. Because any global optimum is necessarily a local optimum, the search space is a reduced yet representative subset of S []. Furthermore, any feasible solution can be mapped to its nearest locally optimal solution in through an appropriate local search procedure [].
A local search provides only a greedy steepest descent to the nearest local optimum from an initial solution. Unless a way to globalize and continue the local search beyond suboptimal local extrema is found, the search will inevitably get stuck in poor solutions []. Metaheuristic approaches tackle this core challenge by developing innovative rules and meta-strategies that effectively and efficiently navigate the solution space, ensuring a thorough exploration []. However, most known metaheuristics operate within a static solution landscape, overlooking the potential to leverage information from related neighboring objective function landscapes. Thoroughly perturbing the original search space and combining the resulting configurations can effectively steer the global search towards more globally optimal solutions.
In the context of an optimization problem, there are two primary ways to influence the search space: altering the problem formulation, modifying the input data, or doing both simultaneously.
Let us consider these possibilities in more detail:
- Altering the problem formulation: This involves altering the formulation or structure of the problem to another that is either very similar or equivalent to it []. The formulation of a problem includes its objectives, constraints, and the relationships between different variables. Tweaking any of these aspects can lead to a different set of solutions that are considered viable. For instance, choosing the number of centroids in the minimum sum-of-squares clustering (MSSC) problem can be considered as changing the problem formulation, thereby altering the search space of the MSSC problem. Similarly, switching between the Monge and Kantorovich formulations of the optimal transport problem can become the source of new interrelated search spaces since the solutions of these two formulations generally may not coincide [].
- Modifying the input data: The input data are the raw details, observations, or parameters on which the problem is based. Altering these inputs can change the landscape of the objective function and, therefore, the distribution of optimal solutions as well []. For example, in a resource allocation problem, changing the quantity of available resources would directly impact the resulting optimal solutions []. The input data points for the minimum sum-of-squares clustering (MSSC) problem heavily influence the resulting centroids []. The choice of input marginal probability distributions or a cost function in the optimal transport problem clearly changes the landscape of optimal transportation plans [].
The input data of an optimization problem can be considered as a subset of a larger, overarching data space, which may include all possible data points that could be considered for problems of this type []. One way to modify the input data is by taking a new random sample of data points from this vast pool at each subsequent iteration. Although the resulting subsample is randomly composed, it still retains certain common properties with the original data pool, thereby approximating its spatial properties with a smaller number of objects. Additionally, it is worthwhile to explore other methods for altering input data. For instance, introducing random noise by adding new random data points or implementing small random shifts in the positions of the original data points are viable techniques. There exist numerous other potential methods, underscoring the versatility of the proposed approach. Conceptually, systematic minor changes to the input data can reshape the landscape of the objective function and alter the distribution of locally optimal solutions within it, thereby influencing the search process [].
Similarly, the subsequent problem reformulation is chosen from a set of all possible ways to frame or define the problem in an equivalent or slightly different manner. This set includes every conceivable method to state the objectives, constraints, and relationships for problems of a similar nature. A systematic slight modification of the problem formulation within a problem formulation space can be organized to yield solution spaces with a preserved degree of commonality, enabling iterative deformation and intentional reshaping of the solution space in a controlled manner to escape local minima [,]. The following methods can be used to change one formulation to another: coordinate system change, linearization, convexification methods, continuous/discrete reformulations, and others [].
In the paradigm of Variable Landscape Search (VLS), the search space can be understood as the set of all locally optimal solutions that satisfy the constraints and objectives as defined by the slightly varied problem formulation and the slightly varied input data. This space is critical in optimization, as it contains every solution that could potentially be the “best” or “optimal” solution, depending on the problem’s objectives []. In the context of VLS, a significant emphasis is placed on the utilization of a diverse array of problem reformulations and varied input data. Despite the apparent heterogeneity of these elements, it is crucial to recognize that the resultant search spaces share more similarities than differences. This commonality, predominantly in the form of similarity among the search spaces, underpins the feasibility of conducting a global search across these spaces. The phenomenon of similar resultant search spaces is essential for enabling the global search process in VLS. If these spaces did not maintain a fundamental similarity, the global search process would be untenable.
Thus, the input data and problem formulation together shape the objective function landscape. This gives rise to an adaptive process that can, in a systematic manner, dynamically combine varied input data and problem formulations or alter them separately, yielding a sequence of search spaces, each containing distinct yet interconnected locally optimal solutions. Using a suitable local search to explore these dynamic search spaces is expected to find a better solution than searching a static space or only changing the problem formulation.
The systematic processes of problem reformulation and input data alteration can be defined by a structure that provides an order relation among various reformulations and data variations. The concept of neighborhood structures is central to VLS, defining how potential solutions are explored in relation to the current solution. By iteratively and systematically exploring these neighborhoods, VLS increases the effectiveness of the search and promotes comprehensive exploration of the solution space.
Let us define and examine some essential concepts that will be extensively used throughout the article.
A neighborhood solution is a solution lying within the defined “neighborhood” of a given current solution in the solution space. The concept of a “neighborhood” typically relates to a defined proximity or closeness to a given solution []. The determination of what constitutes a “neighborhood solution” depends on the structure of the problem and the optimization algorithm being used. The process of iteratively exploring these “neighborhood solutions” and moving towards better solutions forms the core of local search algorithms and many metaheuristic methods []. The aim is to gradually improve upon the current solution by exploring its immediate vicinity in the solution space.
A neighborhood structure refers to a method or function that can form a set of promising solutions that are adjacent or “near” to a given solution in the solution space. The concept of “nearness” or adjacency is defined based on the problem at hand and the specific algorithm being used []. For instance, in a combinatorial optimization problem, two solutions might be considered neighbors if one can be reached from the other by a single elementary operation, such as swapping two elements in a permutation. This is an example of a trivial neighborhood structure. A more advanced neighborhood structure could involve generating new neighborhood solutions by integrating the current solution with those from its history, i.e., from the sequence of previous incumbent solutions. This method leverages the accumulated knowledge of previous solutions to explore more sophisticated solution spaces.
To solve a specific optimization problem, it is necessary to identify the most relevant neighborhood structure of potential solutions. This structure should facilitate an effective search for the optimal solution. Achieving this requires a deep understanding of the problem, consideration of its specific features, and a priori knowledge that enables efficient transitions from one potential solution to another.
The neighborhood structure is a fundamental concept in many local search and metaheuristic algorithms, such as Variable Neighborhood Search (VNS) [], simulated annealing [], tabu search [], and genetic algorithms []. These methods rely on iteratively exploring the neighborhood of the current solution to try to find a better solution. The definition of the neighborhood structure directly impacts the effectiveness of the search process, the diversity of solutions explored, and the ability of the algorithm to escape local optima. For example, in VNS, the order and rules for altering neighborhoods throughout the search process are significant factors in building an efficient heuristic [].
Assume that for some variation of input data and problem formulation, the optimization task becomes to minimize the objective function f over the feasible solution space (feasible region) S. Then, the corresponding fixed objective function landscape is the fixed set
of all feasible solutions paired with the corresponding objective function values that remain constant throughout the optimization process. This set coincides with the graph of the objective function when the function’s domain is restricted to the feasible region.
From now on, the terms “landscape” or “objective landscape” will simply refer to a fixed objective function landscape. Also, we will use the simplified notation L to refer to an arbitrary landscape when its underlying objective function and feasible space are not important in the given context.
For a given landscape , its search space is defined to be the subset
of all the local optima of the objective function contained in the feasible space. This static search space is characterized by its unchanging nature, where every possible locally optimal solution is defined at the outset of the optimization procedure. All solutions in this space are accessible to be tested, evaluated, or used at any point during the problem-solving process, and no new solutions are introduced nor existing ones excluded once the optimization process has commenced.
In the context of optimization algorithms, a variable objective function landscape refers to a landscape in which both the distribution of objective function values over the feasible region and the feasible region itself can vary throughout the optimization process due to slight variations in problem formulation and input data. As a result, the landscape’s search space changes as well. Unlike a fixed landscape, where all locally optimal solutions are predefined and static, a variable landscape allows for a degree of modification in the set of potential solutions. Additionally, it can enable the introduction of new potential solutions or the exclusion of existing ones based on certain conditions or criteria during the optimization iterations.
The manipulation of a landscape can be based on a variety of the strategies listed above. The primary goal of this controllable dynamism is to enhance the search process, promote diversity, prevent premature convergence to local optima, and increase the likelihood of achieving the global optimum. The concept of a variable objective function landscape is at the core of the Variable Landscape Search (VLS) metaheuristic, where the algorithm systematically modulates the landscape by utilizing a special approach (neighborhood structure) at each iteration, aiming to bypass local minima and aspire towards the global optimum.
Figure 1 provides an illustrative example of how manipulating a landscape according to the VLS paradigm can potentially advance the global search process. The figure demonstrates the results of three consecutive iterations, each consisting of a minor perturbation of the objective function landscape, followed by a search for the local minimum applied to an abstract problem. Each arrow signifies an iteration in which a new perturbed landscape is employed, and the algorithm moves from one solution to a better one for the current landscape. This creates a trajectory, allowing the visualization of how the algorithm is navigating the varying landscape and how it is making progress towards the global optimum. After each iteration, the landscape of the objective function is moderately modified (to a necessary and sufficient extent), which simultaneously extracts the current solution from the current local minimum trap and preserves sufficient commonality among the spatial forms of the resulting landscapes. Through systematic alteration of the objective function landscapes according to the VLS paradigm, an additional “degree of freedom” emerges in the optimization process. This allows the search to explore “additional dimensions” of the objective function. These dimensions are supplementary but maintain the integrity and commonality of the objective function properties, with the variability/commonality ratio being one of the key parameters.
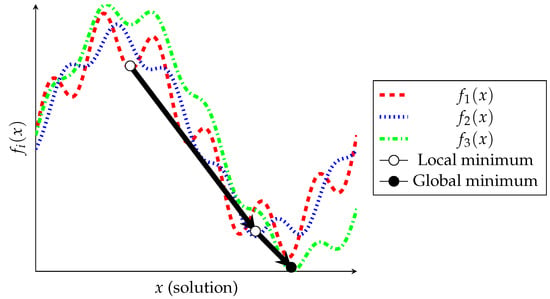
Figure 1.
Illustration of the process of landscape variation to overcome local minima.
This paper introduces the Variable Landscape Search (VLS) paradigm, a new metaheuristic framework that extends optimization beyond a fixed objective landscape. By systematically varying both problem formulations and input data, VLS constructs a series of interrelated landscapes that preserve structural commonality while introducing controlled variability. This mechanism enables exploration across multiple correlated search spaces, providing a novel pathway to escape local optima and discover globally superior solutions. The paper further formalizes the underlying concepts of variable landscapes, neighborhood structures, and landscape similarity; establishes the theoretical rationale for global exploration across related landscapes; and demonstrates how VLS unifies and generalizes existing landscape-based search strategies within a coherent metaheuristic framework.
2. Related Works
The concept of manipulating the landscape itself is less common in metaheuristics, but some methods can be interpreted as doing so, either directly or indirectly.
- Hyper-heuristics []: These are heuristics to choose heuristics, which can be seen as a form of manipulating the search space of the landscape. Instead of operating on the solutions directly, they operate on a space of heuristics that generate or improve solutions. The choice of a heuristic can significantly change the set of potential solutions (local optima) that are explored.
- Constructive metaheuristics, such as Ant Colony Optimization (ACO) [] and Greedy Randomized Adaptive Search Procedure (GRASP) [], can be interpreted as manipulating the search space of the landscape. They construct solutions step by step, and the choices made in the early steps change the part of the search space that is explored in later steps.
- Cooperative Co-evolutionary Algorithms (CCEAs) []: In these methods, the solution space is divided into several subspaces, and different search processes or different populations evolve in these distinct subspaces. The results are then combined, which can be seen as manipulating the search space.
- Variable Neighborhood Search (VNS) []: In VNS, the neighborhood structure itself (i.e., the definition of which solutions are “neighbors” and can be reached from a given solution) is varied during the search. This can be interpreted as a manipulation of the search space.
- Genetic Algorithms (GA) with adaptive representation []: Some versions of GAs use adaptive representation, where the encoding of the solutions (i.e., how solutions are represented as chromosomes) is changed during the search based on certain criteria. This can be seen as a manipulation of the search space.
- Variable Formulation Search (VFS) [] is a dynamic, adaptive representation of problem formulations rather than a static, predefined one. It refers to the flexibility in the formulation of an optimization problem, where the structure of the mathematical representation itself can be altered over the course of the problem-solving process. Unlike a static formulation space, where the mathematical model, decision variables, constraints, and objective function are fixed from the start, a variable formulation space allows for adaptive changes in the problem formulation. This can involve the introduction of new decision variables, the removal or modification of constraints, or even changes in the objective function based on certain criteria, algorithmic processes, or evolving insights into the problem during the course of the optimization iterations.
- Formulation Space Search (FSS) [] involves a broader strategy where the entire set of possible formulations is considered and structured with a metric or quasi-metric relationship. FSS does not merely adapt a single formulation but explores a structured space of multiple formulations, potentially switching between them based on their relational metrics. This approach extends the search space beyond traditional variable adjustments to include a comparative analysis of different formulations, thus offering a structured and ordered way to navigate through formulation changes.
Data consist of factual elements, observations, and raw information collected through various means, all of which require processing to address specific problems. In the context of optimization, problem formulation generally involves the mathematical representation of a problem, including decision variables, constraints, and objective function(s). These formulations are created independently of any specific data but require data to function effectively. Often, problem formulations are centered around the concepts of functionality, structure, and purpose. For instance, in clustering, the formulation might detail the use of a specific distance metric, the number of clusters to be formed, and any constraints on these clusters []. However, the specific data points to be clustered are inputs to the problem defined by this formulation, not components of the formulation itself.
Problem formulations play a crucial role in algorithm development by providing a clear framework that specifies the desired outcomes, operational constraints, and conditions relevant to the task. The manner in which a problem is defined and structured profoundly shapes the strategy for designing algorithms, influencing their complexity and the efficacy of the solutions they provide.
The distinction between problem formulation and data is evident, as each serves a unique and separate role. This underscores the importance of addressing them individually when developing novel heuristics. Treating these as separate yet interconnected concepts enhances the clarity and effectiveness of heuristic development, opening new possibilities and dimensions for optimization. This approach allows each conceptual component to be optimized based on its unique requirements and characteristics.
Among all the metaheuristics considered, the ones most similar to our proposed approach are Variable Formulation Search (VFS) [] and Formulation Space Search (FSS) []. Variable Landscape Search represents a broader strategy in optimization, extending the scope beyond what is offered by FSS and VFS. While the latter focus on exploring different objective landscapes by varying the problem formulation, Variable Landscape Search extends this concept by not only considering changes in problem formulation but also incorporating modifications in the input data. This dual approach allows for a more comprehensive exploration of potential solutions, making Variable Landscape Search a generalization of VFS and FSS. This approach acknowledges that altering the input data is as crucial as changing the formulation for discovering diverse objective landscapes and their corresponding search spaces. We will explore the details of how Variable Landscape Search generalizes Variable Formulation Search and Formulation Space Search in Section 9. This section will provide concrete examples of applying Variable Landscape Search to construct optimization heuristics.
The literature thus reveals a gradual evolution toward metaheuristics that expand or redefine the search domain, whether through adaptive representations, neighborhood variation, or flexible formulations. However, all existing approaches remain confined to manipulating a single dimension of the optimization process, typically the formulation or neighborhood structure, while treating the underlying data as static. This limitation restricts their ability to capture the full variability of real-world problems, where both model and data co-evolve. The motivation for the proposed Variable Landscape Search (VLS) arises precisely from this gap: by enabling simultaneous or alternating variation in both the formulation and data modalities, VLS generalizes previous paradigms such as VFS and FSS into a unified metaheuristic framework. This broader view allows exploration across multiple interconnected landscapes, thereby uncovering hidden solution regions that remain inaccessible to traditional single-landscape search methods.
3. Landscape Meta-Space
Let denote the overarching data space, representing all admissible datasets or input configurations for a given optimization problem, and let denote the formulation space, representing all admissible problem formulations, including possible objective functions, constraint sets, and parameterizations. For each pair , let the corresponding objective landscape be denoted by
where is the feasible region determined by the formulation F and input data X.
Then, the landscape meta-space is defined as the collection of all such landscapes:
Each element represents a distinct optimization landscape characterized by its own feasible region, objective topology, and corresponding search space of locally optimal solutions.
Conceptually, the landscape meta-space constitutes a higher-order search domain that aggregates all possible objective function landscapes arising from combinations of admissible formulations and input data. Unlike traditional metaheuristics that operate within a single static landscape, navigation in enables meta-level exploration—the controlled transition between landscapes themselves.
The landscape meta-space therefore serves as the foundational framework for the Variable Landscape Search (VLS) paradigm, wherein search operators are designed to traverse via strategically defined neighborhood structures and transition mappings between adjacent landscapes. By exploring not only the solutions within each landscape but also the inter-landscape relationships, this approach substantially broadens the scope of global optimization, allowing the discovery of superior or previously inaccessible optima across dynamically evolving problem contexts.
4. Landscape Neighborhood
Let denote the landscape meta-space as defined previously, where each element corresponds to a distinct objective function landscape . A landscape neighborhood of a given landscape is a subset of
defined as
where is a landscape distance (or similarity) metric, and is a proximity or similarity threshold.
The distance measure quantifies the degree of dissimilarity between two landscapes and may be defined in terms of:
- the divergence between their objective functions and ,
- the structural or topological difference between their feasible regions and ,
- or the statistical/semantic differences between their underlying datasets or formulations.
A landscape neighborhood thus defines a local region within the meta-space , consisting of landscapes that share a bounded degree of similarity, correlation, or structural alignment with the current landscape. This local region provides a manageable search horizon for transitioning between related problem formulations or datasets while maintaining computational tractability.
Formally, neighborhood exploration in the landscape meta-space can be modeled through a transition operator
where maps a current landscape to a neighboring landscape according to a defined neighborhood structure or transformation rule (e.g., modification of dataset, constraints, or representation).
The dynamism of the landscape neighborhood is a key advantage: by iteratively redefining through adaptive updates to or , the search process can expand or contract its exploration radius in response to search progress. This capability enables Variable Landscape Search (VLS) to systematically traverse the meta-space, evolving from local to broader neighborhoods to uncover superior or more diverse solution regions across multiple landscapes.
5. Variable Landscape Search (VLS) Metaheuristic
For a given optimization problem P, there exists the corresponding space of all its formulations , which is called the formulation space. Each formulation consists of a mathematically defined objective function f, which is to be minimized, as well as a mathematically defined set of constraints C. Alternatively, each set of constraints C can be included into the corresponding objective function f as penalizing terms.
Also, we assume that there exists overarching data space , which serves as the source of input data for an algorithm solving given problem formulations. Data space can be either finite or infinite, representing a data stream in the latter case.
We can influence the objective function landscape L in only two primary ways:
- By changing the input data ;
- By changing the problem formulation (or model) , i.e., by reformulating the problem.
Thus, we have the landscape evaluation map
where is an input dataset, is a formulation for the given problem P, and S is the feasible region resulting from evaluating constraints C on input data X.
In the most comprehensive implementation of the proposed approach, the search can be conducted through simultaneous variation of the two available modalities F and X. Alternatively, each modality can be fixed, allowing searches to be carried out using only one of the available modalities. For example, as a special case, the formulation space can be limited to a single fixed formulation F. Similarly, the overarching data space can be restricted to one fixed dataset X, which is then fully utilized at each iteration of the proposed approach.
The general form of optimization problem that we are looking at may be given as follows:
where , S, x and f denote, respectively, the landscape meta-space (the space of landscapes), a feasible solution space, a feasible solution, and a real-valued objective function. We restrict the landscape meta-space to the image of the landscape evaluation map :
Because distinct combinations of input data and formulations may, in principle, yield identical or equivalent landscapes, we ensure injectivity of the landscape evaluation map
by treating each landscape as implicitly annotated with its originating pair . That is, two landscapes are considered identical only if both their originating input data and formulations coincide:
Under this convention, is injective, and each landscape admits a unique pre-image , enabling unambiguous mapping between landscapes and their generating problem contexts.
5.1. VLS Ingredients
The following three steps are executed sequentially in each iteration of a VLS-based heuristic until a stopping condition is met, such as a limit on execution time or number of iterations:
- (1)
- Landscape shaking procedure by altering the problem formulation, input data, or both;
- (2)
- Improvement procedure (local search);
- (3)
- Neighborhood change procedure.
An initial objective landscape and a feasible solution are required to start the process, and these starting points are typically selected at random from the corresponding supersets.
Let us outline the steps listed above within the Basic Variable Landscape Search (BVLS) framework, drawing an analogy with the approach defined in []. We refer to this proposed framework as ’basic’ because, although many other variations of the VLS implementation can be introduced, the following represents the simplest and most straightforward approach.
5.2. Shaking Procedure
In this work, we distinguish between different types of a neighborhood structure: on the landscape meta-space, which is the product of neighborhood structures on the data and formulation spaces, and on a feasible solution space.
For an abstract space E, let be a set of operators such that each operator , , maps a given choice of element to a predefined neighborhood structure on E:
where is some distance function defined on E, and are some positive numbers (integer for combinatorial optimization problems).
Note that the order of operators in also defines the order of examining the various neighborhood structures of a given choice of element e, as specified in (2). Furthermore, the neighborhoods are purposely arranged in increasing distance from the incumbent element e; that is,
Alternatively, each operator may be constant with respect to element e, yielding a neighborhood structure that is independent of the choice of e. Also, the neighborhood structures may well be defined using more than one distance function or without any distance functions at all (e.g., by assigning fixed neighborhoods or according to some other rules).
Now, let us assume that a set of operators is defined on the data space , while another set of operators is defined on the formulation space . Their parameters can be conveniently accessed from the following matrix:
Then, the neighborhood structure on the landscape meta-space can be defined as the Cartesian product:
A simple shaking procedure consists in selecting a random element either from or depending on the current shaking phase i (see Algorithm 1). This shaking procedure is presented as an illustrative example; however, other variations or similar procedures could be utilized as alternatives, depending on specific requirements or preferences.
| Algorithm 1: Shaking procedure |
 |
5.3. Improvement Step
For each feasible solution space (S) associated with a given landscape , we assume the existence of a predefined neighborhood structure . Neighborhood structures are functions that define how to effectively select a subset of promising solutions from the neighborhood of a given solution. Specifically, for any point , denotes the subset of promising candidate solutions within the neighborhood of . This structure remains fixed for the given landscape and is used to guide the local search process.
Within an objective function landscape, an improvement step typically examines solutions that are near the current solution in order to find better objective values. In other words, the search relies on local information extracted from the neighborhood , which contains promising candidate solutions surrounding in the feasible region S.
This is precisely the role of the improvement step in BVLS. A local search can follow either the best improvement or the first improvement strategy. In the best improvement strategy, the entire neighborhood is explored, and the current solution is replaced by the best neighbor if it yields an improvement in the objective value. In contrast, the first improvement strategy explores the neighborhood sequentially and updates as soon as the first improving neighbor is found. The local search terminates when no solution in offers a better objective value than the current solution , indicating that a local optimum has been reached with respect to the given neighborhood structure.
Algorithm 2 presents the pseudocode for the best improvement local search procedure performed on a given landscape . Here, and denote the current and previous solutions at iteration t, respectively. Each landscape is associated with a specific objective function f, a feasible set S, and a neighborhood structure , all of which are accessed and used during the search.
| Algorithm 2: Best improvement local search on landscape |
 |
5.4. Neighborhood Change Step
An iteration of VLS starts with the shake operation, which moves the incumbent landscape L to a perturbed landscape . Then, the improvement step moves x to a local minimum ; that is,
At this point, the neighborhood change step takes over to decide how the search will continue in the next iteration of VLS. The routine commonly used is known as the sequential neighborhood change step. If (the new solution is better than the incumbent with respect to the objective function of the perturbed landscape ), then (the new solution with its landscape becomes the incumbent), and (the shake parameter is reset to its initial value); otherwise holds, (increment to the next larger neighborhood or return to the initial neighborhood, if k exceeds ). The pseudocode for the sequential neighborhood change step is shown in Algorithm 3. Other forms of the neighborhood change step can be also used. These include cyclic, pipe, random and skewed forms [].
| Algorithm 3: Sequential neighborhood change step |
 |
6. Basic Variable Landscape Search
The basic VLS scheme requires some stopping criterion for the main loop. Usually, this can be either a time limit or a maximum total iteration count .
Basic VLS operates by alternating between two distinct phases: one focused on shaking within the data dimension (), and the other on shaking within the dimension of problem formulation (). Each phase sets its own limit on the maximum number of iterations within the phase: and , respectively. For convenience, these two integer numbers are combined into a single vector .
Also, the minimum and maximum values of the shake parameter k are unique for each phase. The values stored in the matrix are used to define the admissible ranges of shaking power k in the data and formulation phases, respectively.
Before local search can be applied in the perturbed landscape , the incumbent solution x should be translated onto the feasible solution space of using the operator . Formally, each such operator is defined as a mapping
where and denote the feasible regions associated with landscapes L and , respectively. The operators are problem-dependent transformation rules that allow the algorithm to map a feasible solution from one landscape (problem representation, encoding, or formulation) to another, while preserving feasibility and meaning. Because feasibility constraints, variable domains, or representations may differ between landscapes, these operators must be explicitly known before the algorithm begins; otherwise, the search might produce invalid solutions when landscapes are changed dynamically. Consequently, the set of operators governing these transitions should be defined beforehand by the algorithm designer, as part of the initialization phase of the VLS framework. These operators specify how a feasible solution in one landscape is transformed into a feasible solution in another , depending on the structural relationship between landscapes. In simple cases, may represent an identity or projection operator, while in more complex formulations it may involve encoding, dimensionality adjustment, or constraint repair to ensure that feasibility and interpretability are preserved across landscape transitions.
The pseudocode for Basic Variable Landscape Search (BVLS) is given in Algorithm 4. For initialization, the following starting values can be used:
- Select a current landscape from (optionally at random);
- Select an initial current feasible solution from the feasible region S of landscape L (optionally at random).
| Algorithm 4: Basic Variable Landscape Search (BVLS) |
 |
7. Variations and Enhancements in VLS
It is worth noting that the basic VLS framework (referenced in Algorithm 4) may employ an alternative strategy to switch between phases: thoroughly exploiting one phase before moving to the next, or alternatively, using only one of the phases. This can be achieved by changing the condition of the inner loop at line 8 of Algorithm 4 to check whether the maximum number of non-improving iterations has been exceeded within the current phase instead of the total number of iterations. However, the current version of VLS presented in Algorithm 4 aims to strike a balance between phase switching and exploitation by choosing the appropriate bounds on the iteration counter for each phase i. This approach can be viewed as a kind of natural shaking arising from phase changes.
Another way to speed up the metaheuristic, increase its effectiveness, and achieve a natural balance in exploiting different phases is to distribute VLS jobs among multiple parallel workers in some proportion. Then, either a competitive, collective, or hybrid scheme can be used for communication between the parallel workers []. Determining the effectiveness and efficiency of these kinds of parallel settings constitutes a promising future research direction.
8. Analysis of the Proposed Approach
Incorporating a mechanism to adaptively change the objective landscape, VLS can be classified as a metaheuristic method, given that it embodies all the core elements of metaheuristic optimization strategies. VLS harmonizes local search (intensive search around the current area in the solution space) and global search (extensive search across the entire solution spaces of various landscapes) in order to escape from local optima and reach the global optimum.
Within the domain of optimization, the Variable Formulation Search (VFS) method shares several characteristics with the proposed Variable Landscape Search (VLS) approach. However, it is crucial to underscore that VFS is, in fact, a special case nested within the more encompassing and versatile VLS method proposed in this article.
VFS accomplishes variability in the solution space by facilitating a broadened exploration of potential solutions across diverse problem formulations. This method focuses on exploring different problem representations, objective functions, and constraint sets to create a dynamic landscape of diverse solutions.
Nonetheless, the VLS framework takes this concept a step further. In addition to variable problem formulations, the VLS approach incorporates the modification of the task’s input data (datasets) themselves. This extra dimension of flexibility allows for dynamic alteration of the landscape’s search space, thereby introducing a higher degree of variability and resilience into the solution search process.
Consequently, it is accurate to posit that the VLS approach is a generalization of the VFS methodology. VLS encapsulates the benefits of variable problem formulation inherent in VFS and extends them to include variations in the input data. The resultant enhanced navigability through a larger, more diversified solution landscape heightens the potential for identifying superior solutions and delivering robust optimization results. Hence, the proposed VLS methodology offers a substantial leap forward in the science of optimization, exhibiting higher adaptability and versatility compared to its predecessors.
The Variable Landscape Search (VLS) metaheuristic stands out among other optimization techniques due to its unique approach of directly and adaptively manipulating the search space itself during the search process. This is a distinctive aspect, as most traditional metaheuristics operate within a fixed search space and focus on manipulating the search process, such as modifying the trajectory, introducing randomness, or adaptively tuning parameters.
Here are some aspects that make VLS unique:
- Dynamic/Variable Solution Space: In most metaheuristics, the search space is predefined and remains static throughout the search process. In contrast, VLS changes the search space iteratively, which introduces a higher degree of dynamism and adaptability.
- Balance between Exploration and Exploitation: The VLS algorithm’s systematic manipulation of the objective function landscape helps to strike a better balance between exploration (searching new areas of the solution space) and exploitation (refining current promising solutions). This is achieved by altering the search space itself, which helps avoid entrapment in local minima and promotes exploration of previously inaccessible regions of the solution space.
- Robustness: The VLS approach can enhance the robustness of the search process, as the changing search space can provide different perspectives and opportunities to escape from suboptimal regions. This can potentially lead to more consistent and reliable optimization results.
- Adaptability: VLS is not tied to a specific problem domain. The concept of varying the objective landscape can be applied to a broad range of optimization problems, making VLS a flexible and adaptable metaheuristic.
- Complexity Management: By actively managing the search space, VLS provides a novel approach to deal with high-dimensional and complex optimization problems where traditional methods struggle.
- Opportunity for Hybridization: VLS provides an opportunity for hybridization with other metaheuristics, potentially leading to more powerful and efficient algorithms.
In summary, the VLS approach provides a fresh perspective on optimization, offering potential benefits in terms of robustness, adaptability, and the ability to manage complex problem domains. This novel approach to directly and adaptively manipulate the solution space could open new avenues in the design and application of metaheuristics.
9. Examples of Practical and Theoretical Applications
9.1. Big Data Clustering Using Variable Landscape Search
In this section, we will consider a practical example of how we have used the principles underlying the Variable Landscape Search metaheuristic to build an efficient and effective big data clustering algorithm, namely the Big-means algorithm [].
In the original article [], where the Big-means algorithm was proposed, only its description and a comparative experimental analysis were provided. However, this algorithm was not conceptualized within any existing metaheuristic framework. In fact, attempts to theoretically explain the remarkable efficiency of the Big-means algorithm using existing approaches were unsuccessful. This led us to recognize the uniqueness of the approach used and the possibility of its conceptualization and generalization within a new metaheuristic framework, which is the result presented in this article.
The Big-means algorithm is a heuristic approach designed to tackle the large-scale MSSC problem in big data environments. By working with a subset of the data in each iteration rather than the entire dataset, Big-means balances computational efficiency and solution quality. The algorithm’s pseudocode is presented in Algorithm 5, with a corresponding flowchart in Figure 2.
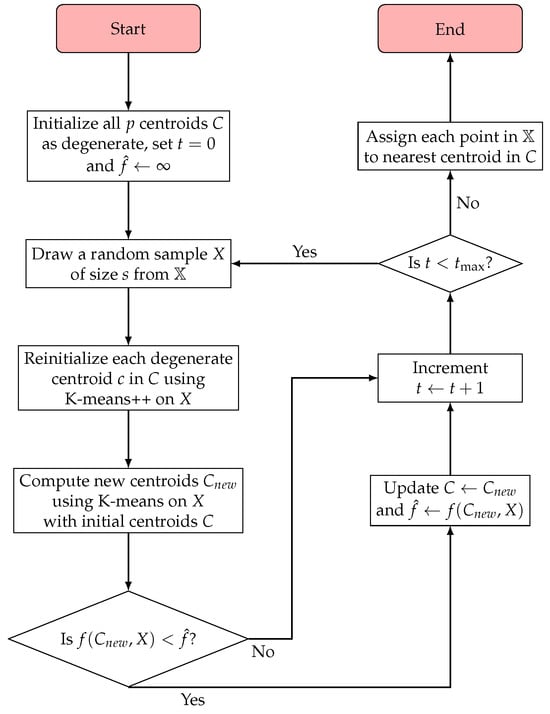
Figure 2.
Flowchart of the Big-means algorithm.
The algorithm commences by randomly sampling a subset X of size s from the dataset , where s is significantly smaller than the total number of feature vectors m. The initial centroid configuration C is determined using K-means++ for the first sample. As the algorithm iterates, it updates the centroids based on the clustering solution of each new sample, prioritizing the best solution found so far through a “keep the best” principle.
Big-means addresses degenerate (empty) clusters by reinitializing empty clusters using K-means++, introducing new potential cluster centers and enhancing the overall clustering solution. This approach minimizes the objective function by providing more opportunities for optimization.
| Algorithm 5: Big-Means Algorithm for Big Data Clustering |
 |
The Minimum Sum-of-Squares Clustering (MSSC) formulation seeks to partition the large-scale data into p clusters, minimizing the sum of squared Euclidean distances between data points and their associated centers . Mathematically, this is expressed as
where p is the number of clusters and denotes the Euclidean norm.
If we restrict ourselves only to the MSSC formulation (5), the space of all objective landscapes takes the following form:
The main idea of the Big-means algorithm and its variations is to follow the stochastic approach, according to which the true can be reasonably replaced by its stochastic version:
where denotes the distribution of s-sized samples drawn uniformly at random from . Thus, the search space of each landscape consists of all locally optimal feasible solutions C for the following MSSC optimization problem defined on sample :
The Big-means paradigm [] further restricts the space for an appropriate fixed range of the sample size s. The hope is that the resulting objective landscapes would have search spaces reasonably approximating the search space of the original landscape :
Specifically, the assumption is that by properly and swiftly combining promising local optima of objective landscapes in , one can obtain a close approximation to the global optima of the original objective landscape .
Then, the following neighborhood structure can defined on the corresponding data space:
The used absolute value distance metric in (7) clearly satisfies the required monotonicity property (3), producing a sequence of embedded neighborhoods due to the property that uniform samples of larger sizes subsume uniform samples of smaller sizes.
Moreover, the original Big-means algorithm [] posits that it might be enough to assume for some appropriate fixed choice of the sample size with :
In the context of the Big-means algorithm, each landscape corresponds to an MSSC problem defined on a particular random sample . When the algorithm transitions to a new landscape , the operator must translate the current centroid configuration C obtained on into a feasible initialization for the new sample . The transformation proceeds in two steps: (1) projection, where the current centroids C are carried over as-is, since they remain valid points in the feature space ; and (2) repair, where any degenerate (empty) centroids are reinitialized using the K-means++ strategy on the new sample . Formally, this mapping can be expressed as
Here, denotes the operation that reinitializes degenerate centroids using K-means++ on , effectively combining the projection and repair steps. This operator preserves the semantic meaning of centroids across stochastic landscapes and ensures that the resulting configuration remains a feasible and informative starting point for local search on .
Since algorithms based on the Big-means paradigm consider only one problem formulation (MSSC), they do not employ any neighborhood structure on the formulation space.
Various Big-means-based algorithms fall under the following cases of the general VLS framework (Algorithm 4):
- Big-means [] uses the K-means local search procedure and the sequential neighborhood change (Algorithm 3) with the following choice of parameters:
- BigOptimaS3 [] maintains several parallel workers, each of which follows the basic VLS scheme, using the K-means local search procedure and the sequential neighborhood change (Algorithm 3) with the following choice of parameters:Also, BigOptimaS3 adds a special procedure to end the search process. It picks the landscape sample size that is most likely to yield improvement in the objective function value based on the collected history of improving samples sizes across iterations. Then, BigOptimaS3 realizes the optimal landscape using and selects the centroids of the parallel worker giving the best result in the optimal landscape;
- BiModalClust [] represents a further evolution of Big-means-type algorithms within the VLS framework. Unlike standard VNS-based clustering approaches, BiModalClust introduces a bimodal optimization paradigm that simultaneously varies both the input data and the neighborhood structure of the solution landscape. In each iteration, both the shaking phase and the local search procedure operate on a sampled subset , rather than on the entire dataset, allowing scalable operation on large data streams. The neighborhood structure is defined through a shaking power parameter p, which controls the number of centroids to be reinitialized using a K-means++-inspired probability distribution conditioned on the remaining centroids. A K-means local search is then applied to S to refine the candidate solution before evaluating it on the global objective. BiModalClust conforms formally to the Variable Landscape Search (VLS) metaheuristic, under which it is categorized: its dual-modality design enables exploration across dynamically evolving landscapes, each defined by a distinct sample S and neighborhood configuration, thereby ensuring both scalability and enhanced robustness in big data clustering.
In all these algorithms, the local search within the initial feasible solution space S in Algorithm 4 is performed by starting from the distribution of points defined by K-means++ on S, while the incumbent solution x (C in the context of MSSC) is used to initialize the local search procedure in all subsequent iterations.
The conceptualization and execution of the Big-means algorithm are steeped in fundamental optimization principles. The approach encapsulates and harnesses the power of iterative exploration and manipulation of the search space, overcoming the traditional challenges associated with local minima and relentlessly pursuing the global optimum.
The perturbation introduced into the clustering results through the ’shaking’ procedure is a pivotal aspect of the Big-means algorithm. Each iteration yields a new sample, creating variability and diversity in the centroid configurations. Each sample serves as a sparse approximation of the full data cloud in the n-dimensional feature space. This stochastic sampling offers a pragmatic balance between exhaustive search (which is often computationally infeasible) and deterministic search (which risks entrapment in local minima). By including a diverse set of sparse approximations, the solution space exploration becomes more robust, adaptive, and capable of reaching the global optimum.
The Big-means algorithm is inherently an adaptive search strategy. Instead of maintaining a fixed search space, it allows the search space to evolve dynamically by sampling different parts of the data cloud in each iteration. This leads to an “adaptive landscape,” a powerful metaphor where the distribution of locally optimal solutions (the search space) can evolve over the course of optimization, much like species evolving in a changing environment.
This dynamism is beneficial on two fronts: it assists in avoiding entrapment in local optima and promotes a robust exploration of the solution space. If the algorithm is stuck in a local optimum with a given sample, a new random sample might change the landscape such that the local optimum becomes a hill and better solutions appear as valleys.
The visual representation in Figure 1 can be easily interpreted as Big-means iterations, where x is the incumbent set of centroids C, and each new landscape is the MSSC objective function restricted to a new sample . This figure is a testament to the Big-means algorithm’s underlying principle of systematically exploring and manipulating the search space according to the VLS approach. The interplay of randomness (through sampling) and determinism (through local optimization) in the algorithm provides a potent strategy to tackle the notorious problem of local minima in clustering algorithms.
The source code for the Big-means algorithm, which includes implementations of various parallelization strategies, is available at https://github.com/R-Mussabayev/bigmeans/, accessed on 11 November 2025.
9.2. Generalization of Alternative Metaheuristics
The idea of Variable Formulation Search (VFS) proposed in [] retains the same steps as the basic VNS metaheuristic [], except for using the special Accept(x, x’, r) procedure in all of them, where x is an incumbent solution, is a candidate solution, and r defines a range of considered formulations and their corresponding objective functions . The Accept procedure is listed in Algorithm 6. This procedure checks if the candidate solution leads to improvements in the objective functions by iteratively proceeding to the next formulation in case of a tie in the current one and rejecting as long as it causes a decrease in any of them. This approach is effective in tackling the issue of a flat landscape. This implies that, when a single formulation of an optimization problem is employed, a large number of solutions that are close to a given solution tend to have identical values in terms of their objective function. This scenario makes it challenging to identify which nearby solution is the better option for further exploration in the search process. However, our VLS metaheuristic subsumes this VFS idea by simply including the Accept procedure in the local search and neighborhood change steps.
The concept of Formulation Space Search (FSS), as discussed in Mladenovic’s study [], can be considered a specific instance within the broader framework of the Variable Landscape Search (VLS) metaheuristic. This interpretation becomes apparent when you observe that FSS represents what happens when VLS is confined to the single “formulation” phase. Essentially, FSS is a special case of VLS where the process is limited to just the formulation aspect.
The idea of Variable Search Space (VSS) proposed in [] also falls under the VLS metaheuristic. One can check that by restricting to the “formulation” phase, modifying the neighborhood change step to the cyclic one, and defining the neighborhood structure on the formulation space as
where is the shake parameter, and is a finite set of r available formulations for the underlying optimization problem.
| Algorithm 6: Accept procedure |
 |
Table 1 formalizes these relationships, clarifying how VFS, FSS, and VSS emerge as special cases of the VLS paradigm.

Table 1.
Mapping of Alternative Metaheuristics to the Core Components of the Variable Landscape Search (VLS) Framework.
10. Computational Complexity and Scalability Analysis
VLS executes three sequential stages per global iteration: (i) landscape shaking, (ii) local improvement, and (iii) neighborhood change. Let be the maximum number of iterations. Denote by , , and the per-iteration costs of these stages. The overall serial runtime is
1. Landscape Shaking Complexity.
If shaking modifies the data by sampling s points from , the cost is for index sampling, or if sampled vectors in are materialized. For formulation-based shaking with adjustable components, . In typical settings with and modest , is dominated by the local search.
2. Local Search Complexity.
If the local search evaluates candidate moves per local-search iteration and takes such iterations, then
where is the cost of evaluating f (and any feasibility repairs). For K-means as the local search on a sample of size s with p clusters in n dimensions,
3. Neighborhood Change Complexity.
If neighborhood change updates a few scalars, then . When applying an accept/reject rule across r alternative formulations, this can rise to .
4. Overall Scalability.
Per iteration, the dominant cost is typically ; with K-means it is . Thus the overall serial runtime is
VLS parallelizes naturally by assigning distinct landscapes to workers. With P workers, the wall-clock time satisfies
yielding linear or near-linear speedups when and workers exchange incumbents asynchronously. Here, denotes the total serial runtime of the algorithm, and represents the communication or synchronization overhead incurred during parallel execution.
11. Meta-Parameters and Sensitivity Analysis
The performance of the Variable Landscape Search (VLS) metaheuristic is influenced by several meta-parameters that govern the scope and dynamics of landscape exploration. Key parameters include the shaking intensity bounds , the phase iteration limits , the similarity threshold defining the landscape neighborhood, and the maximum iteration count . Each parameter regulates a specific trade-off between exploration and exploitation.
Empirical observations [,,,] indicate that a moderate shaking intensity promotes efficient escape from local optima while preserving structural continuity between landscapes. Excessive shaking, in contrast, can lead to overly stochastic transitions that slow convergence. Similarly, the phase iteration limits determine the relative emphasis on data versus formulation variation; balancing these phases yields more stable convergence patterns. The similarity threshold affects the breadth of landscape transitions—smaller values favor local refinement, while larger ones encourage global exploration. Lastly, termination criteria such as or non-improvement thresholds directly influence computational cost and result stability.
VLS exhibits robust behavior across a wide range of parameter settings, provided that the landscape variation maintains an appropriate ratio of variability to commonality. Sensitivity analysis suggests that adaptive parameter control—where shaking strength or neighborhood radius evolves based on search progress—can further enhance both convergence speed and solution quality, forming a promising direction for future research.
12. Discussion
The introduction of Variable Landscape Search (VLS) highlights the potential of adaptive landscape variation as a new perspective in global optimization. By systematically reshaping the objective landscape through variations in both problem formulations and input data, VLS adds an additional degree of freedom to the search process. This expanded view is consistent with the working hypothesis that adaptive manipulation of landscapes broadens the range of feasible exploration pathways beyond what conventional metaheuristics typically allow.
Placed in the context of prior research, VLS extends a line of work that has sought to overcome local minima through structural modifications of the search process. Approaches such as Variable Neighborhood Search and Variable Formulation Search have demonstrated the benefits of altering neighborhood structures or reformulations, yet they were largely bound to static data assumptions. VLS moves beyond this limitation by combining formulation-level variation with input data perturbations, thereby injecting stochastic diversity into the optimization trajectory. This mechanism resonates with ideas from stochastic sampling and resampling in large-scale clustering and learning but integrates them into a broader metaheuristic framework.
A key implication of this perspective is that optimization may benefit not only from better-designed local or global moves but also from carefully orchestrated variation of the landscapes themselves. This suggests new methodological directions, including metrics for assessing the “variability–commonality ratio” of successive landscapes to balance novelty with structural continuity. Another avenue lies in parallel and distributed implementations, where multiple landscapes could be explored simultaneously and their solutions cross-fertilized. Such directions emphasize that VLS is less a single algorithm than a flexible design principle, adaptable across domains where dynamic or high-dimensional optimization challenges arise.
To further substantiate the discussion on the superiority of the proposed VLS metaheuristic, we clarify that our claims are grounded in both theoretical generalization and empirical observations from previously published work. Specifically, several variations of the Big-means algorithm [,,,], which are here formally conceptualized within the VLS framework, have been extensively evaluated on large-scale clustering benchmarks, demonstrating significant improvements in convergence speed and clustering quality compared to conventional K-means and mini-batch K-means algorithms. These experimental results provide empirical evidence that the adaptive variation of landscapes in VLS effectively enhances exploration capabilities and accelerates convergence toward global optima. Moreover, the theoretical unification of Variable Formulation Search (VFS), Formulation Space Search (FSS), and Variable Search Space (VSS) within the VLS paradigm serves as an analytical validation of its generality and robustness. Thus, the superiority of VLS is supported not by abstract claims but by a combination of theoretical inclusiveness and demonstrated empirical efficiency in real-world optimization contexts.
VLS shifts attention from navigating within a fixed search space to actively reshaping that space. This broader interpretive lens opens conceptual opportunities for rethinking how metaheuristics are constructed, particularly in the context of data-intensive, evolving, and complex optimization problems.
13. Conclusions
This paper introduced Variable Landscape Search (VLS), a novel metaheuristic framework that operates by systematically varying both problem formulations and input data to reshape the objective landscape during optimization.
The main contributions of this work are twofold. On the practical side, the VLS perspective provides a theoretical foundation for the Big-means clustering algorithm, clarifying the source of its efficiency in large-scale settings and situating it within a broader optimization framework. On the theoretical side, we established that three existing approaches, including Variable Formulation Search (VFS) [], Formulation Space Search (FSS) [], and Variable Search Space (VSS) [], can be viewed as special cases of VLS. This positions VLS as a unifying and generalizable paradigm within the family of metaheuristics.
These contributions underscore the versatility of VLS as both a conceptual and practical tool. Future research will primarily focus on extending the Variable Landscape Search (VLS) framework to develop new VLS-based heuristics tailored to other classes of NP-hard optimization problems beyond clustering. The generality of the VLS paradigm allows it to be adapted to a wide range of combinatorial and continuous domains, including scheduling, routing, facility location, and feature selection. Each of these problem types can benefit from customized landscape representations and shaking mechanisms that exploit problem-specific structures while preserving the core principles of variable landscape exploration. Furthermore, adaptive control strategies for dynamically tuning VLS meta-parameters—such as shaking intensity, neighborhood size, and phase durations—could be explored using reinforcement learning or feedback-driven mechanisms. These would allow the algorithm to autonomously balance exploration and exploitation during runtime. Distributed and parallel implementations of VLS, particularly in cloud or GPU-based environments, offer opportunities for scaling to ultra-large datasets or real-time streaming scenarios. Communication-efficient strategies for coordinating searches across multiple evolving landscapes could substantially enhance scalability and robustness. The present study lays the groundwork for its role as a broadly applicable framework for global optimization.
Author Contributions
Conceptualization, R.M. (Rustam Mussabayev) and R.M. (Ravil Mussabayev); methodology, R.M. (Rustam Mussabayev); software, R.M. (Rustam Mussabayev); validation, R.M. (Rustam Mussabayev) and R.M. (Ravil Mussabayev); formal analysis, R.M. (Rustam Mussabayev); investigation, R.M. (Rustam Mussabayev); resources, R.M. (Rustam Mussabayev) and R.M. (Ravil Mussabayev;); data curation, R.M. (Ravil Mussabayev); writing—original draft preparation, R.M. (Rustam Mussabayev); writing—review and editing, R.M. (Rustam Mussabayev) and R.M. (Ravil Mussabayev); visualization, R.M. (Rustam Mussabayev); supervision, R.M. (Rustam Mussabayev); project administration, R.M. (Rustam Mussabayev); funding acquisition, R.M. (Rustam Mussabayev). All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Science Committee of the Ministry of Science and Higher Education of the Republic of Kazakhstan (grant no. BR21882268).
Data Availability Statement
No new data were created or analyzed in this study.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| VLS | Variable Landscape Search |
| BVLS | Basic Variable Landscape Search |
| VFS | Variable Formulation Search |
| FSS | Formulation Space Search |
| VNS | Variable Neighborhood Search |
| VSS | Variable Search Space |
| MSSC | Minimum Sum-of-Squares Clustering |
| ACO | Ant Colony Optimization |
| GRASP | Greedy Randomized Adaptive Search Procedure |
| CCEA | Cooperative Co-evolutionary Algorithm |
| GA | Genetic Algorithm |
| GPU | Graphics Processing Unit |
| NP-hard | Non-deterministic Polynomial-time hard |
References
- Sörensen, K.; Sevaux, M.; Glover, F. A History of Metaheuristics; Springer: Berlin/Heidelberg, Germany, 2018; Volume 2-2, pp. 791–808. [Google Scholar] [CrossRef]
- Cuevas, E.; Diaz, P.; Camarena, O. Experimental analysis between exploration and exploitation. Intell. Syst. Ref. Libr. 2021, 195, 249–269. [Google Scholar] [CrossRef]
- Locatelli, M.; Schoen, F. Global optimization based on local searches. Ann. Oper. Res. 2016, 240, 251–270. [Google Scholar] [CrossRef]
- Vanneschi, L.; Silva, S. Optimization Problems and Local Search. In Natural Computing Series; Springer: Berlin/Heidelberg, Germany, 2023; pp. 13–44. [Google Scholar] [CrossRef]
- Boyan, J.A.; Moore, A.W. Learning Evaluation Functions to Improve Optimization by Local Search. J. Mach. Learn. Res. 2000, 1, 77–112. [Google Scholar]
- Hussain, K.; Salleh, M.N.M.; Cheng, S.; Shi, Y. Metaheuristic research: A comprehensive survey. Artif. Intell. Rev. 2019, 52, 2191–2233. [Google Scholar] [CrossRef]
- Mladenović, N.; Brimberg, J.; Urošević, D. Formulation Space Search Metaheuristic; Springer: Berlin/Heidelberg, Germany, 2022; pp. 405–445. [Google Scholar] [CrossRef]
- Peyre, G.; Cuturi, M. Computational Optimal Transport. Found. Trends Mach. Learn. 2019, 11, 355–607. [Google Scholar] [CrossRef]
- Audet, C.; Hare, W. Biobjective Optimization; Springer Series in Operations Research and Financial Engineering; Springer: Berlin/Heidelberg, Germany, 2017; pp. 247–262. [Google Scholar] [CrossRef]
- Dehnokhalaji, A.; Ghiyasi, M.; Korhonen, P. Resource allocation based on cost efficiency. J. Oper. Res. Soc. 2017, 68, 1279–1289. [Google Scholar] [CrossRef]
- Gribel, D.; Vidal, T. HG-means: A scalable hybrid genetic algorithm for minimum sum-of-squares clustering. Pattern Recognit. 2019, 88, 569–583. [Google Scholar] [CrossRef]
- Mussabayev, R.; Mussabayev, R. High-Performance Hybrid Algorithm for Minimum Sum-of-Squares Clustering of Infinitely Tall Data. Mathematics 2024, 12, 1930. [Google Scholar] [CrossRef]
- Mussabayev, R.; Mladenovic, N.; Jarboui, B.; Mussabayev, R. How to Use K-means for Big Data Clustering? Pattern Recognit. 2023, 137, 109269. [Google Scholar] [CrossRef]
- Pardo, E.G.; Mladenović, N.; Pantrigo, J.J.; Duarte, A. Variable Formulation Search for the Cutwidth Minimization Problem. Appl. Soft Comput. 2013, 13, 2242–2252. [Google Scholar] [CrossRef]
- Brimberg, J.; Salhi, S.; Todosijević, R.; Urošević, D. Variable Neighborhood Search: The power of change and simplicity. Comput. Oper. Res. 2023, 155, 106221. [Google Scholar] [CrossRef]
- Hertz, A.; Plumettaz, M.; Zufferey, N. Variable space search for graph coloring. Discret. Appl. Math. 2008, 156, 2551–2560, In Proceedings of the 5th International Conference on Graphs and Optimization, Leukerbad, Switzerland, 20–24 August 2006. [Google Scholar] [CrossRef]
- Altner, D.S.; Ahuja, R.K.; Ergun, O.; Orlin, J.B. Very Large-Scale Neighborhood Search; Springer: Berlin/Heidelberg, Germany, 2014; pp. 339–368. [Google Scholar] [CrossRef]
- Lourenço, H.R.; Martin, O.C.; Stützle, T. Iterated local search: Framework and applications. Int. Ser. Oper. Res. Manag. Sci. 2019, 272, 129–168. [Google Scholar] [CrossRef]
- Hansen, P.; Mladenović, N.; Todosijević, R.; Hanafi, S. Variable neighborhood search: Basics and variants. EURO J. Comput. Optim. 2017, 5, 423–454. [Google Scholar] [CrossRef]
- Siddique, N.; Adeli, H. Simulated Annealing, Its Variants and Engineering Applications. Int. J. Artif. Intell. Tools 2016, 25. [Google Scholar] [CrossRef]
- Gendreau, M.; Potvin, J.Y. Tabu Search. Int. Ser. Oper. Res. Manag. Sci. 2019, 272, 37–55. [Google Scholar] [CrossRef]
- Kramer, O. Genetic Algorithm Essentials, 1st ed.; Studies in Computational Intelligence; Springer: Cham, Switzerland, 2017; p. IX, 92. [Google Scholar] [CrossRef]
- Duarte, A.; Mladenović, N.; Sánchez-Oro, J.; Todosijević, R. Variable Neighborhood Descent; Springer: Berlin/Heidelberg, Germany, 2018; Volume 1-2, pp. 341–367. [Google Scholar] [CrossRef]
- Drake, J.H.; Kheiri, A.; Özcan, E.; Burke, E.K. Recent advances in selection hyper-heuristics. Eur. J. Oper. Res. 2020, 285, 405–428. [Google Scholar] [CrossRef]
- Dorigo, M.; Stützle, T. Ant colony optimization: Overview and recent advances. Int. Ser. Oper. Res. Manag. Sci. 2019, 272, 311–351. [Google Scholar] [CrossRef]
- Resende, M.G.C.; Ribeiro, C.C. Greedy randomized adaptive search procedures: Advances and extensions. Int. Ser. Oper. Res. Manag. Sci. 2019, 272, 169–220. [Google Scholar] [CrossRef]
- Ma, X.; Li, X.; Zhang, Q.; Tang, K.; Liang, Z.; Xie, W.; Zhu, Z. A Survey on Cooperative Co-Evolutionary Algorithms. IEEE Trans. Evol. Comput. 2019, 23, 421–441. [Google Scholar] [CrossRef]
- Patnaik, L.M.; Mandavilli, S. Adaptation in genetic algorithms. In Genetic Algorithms for Pattern Recognition; CRC Press: Boca Raton, FL, USA, 2017; pp. 45–64. [Google Scholar] [CrossRef]
- Correa-Morris, J. An indication of unification for different clustering approaches. Pattern Recognit. 2013, 46, 2548–2561. [Google Scholar] [CrossRef]
- Mussabayev, R.; Mussabayev, R. Superior Parallel Big Data Clustering Through Competitive Stochastic Sample Size Optimization in Big-Means. In Proceedings of the Intelligent Information and Database Systems, Ras Al Khaimah, United Arab Emirates, 15–18 April 2024; Nguyen, N.T., Chbeir, R., Manolopoulos, Y., Fujita, H., Hong, T.P., Nguyen, L.M., Wojtkiewicz, K., Eds.; Springer: Singapore, 2024; pp. 224–236. [Google Scholar]
- Mussabayev, R.; Mussabayev, R. BiModalClust: Fused Data and Neighborhood Variation for Advanced K-Means Big Data Clustering. Appl. Sci. 2025, 15, 1032. [Google Scholar] [CrossRef]
- Mladenović, N.; Plastria, F.; Urošević, D. Formulation Space Search for Circle Packing Problems. In Proceedings of the Engineering Stochastic Local Search Algorithms. Designing, Implementing and Analyzing Effective Heuristicsz, Brussels, Belgium, 6–8 September 2007; Stützle, T., Birattari, M., Hoos, H.H., Eds.; Springer: Berlin/Heidelberg, Germany, 2007; pp. 212–216. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).