A Maximal Covering Location Problem Under Uncertainty Through Possibility Theory

Abstract

This study presents a practical framework for the maximal covering location problem (MCLP) under uncertainty. The approach combines possibility theory with chance-constrained programming to represent both imprecision and randomness in demand. Demand is modeled as fuzzy random variables. Using the Zadeh extension principle, both the fuzzy and fuzzy random formulations are transformed into equivalent deterministic mixed-integer programs. Clear linearization steps are provided for the objective function and constraints. Two specifications are examined to reflect different attitudes toward risk. The first specification uses possibility measures, reflecting an optimistic stance, while the second uses necessity measures and represents a conservative approach. Computational experiments conducted in an urban facility context show that increasing the possibility or probability level results in more conservative solutions and a smaller amount of covered demand. In contrast, lower thresholds lead to more exhaustive coverage with greater exposure to uncertainty. In the deterministic scenario, full coverage becomes attainable as the number of facilities increases. Under uncertainty, the models balance coverage with robustness based on the chosen risk tolerance levels. The proposed framework serves as a flexible decision support tool, enabling planners to align facility location choices with their risk tolerance while maintaining tractability with standard optimization solvers.

1. Introduction

In private facility locations, firms pursue measurable performance goals, most notably reducing total costs and increasing access to target markets. Because these objectives can be quantified, mathematical programming provides a sound and transparent basis for selecting locations that advance strategic aims. Public facility location presents a different challenge. Objectives such as equity, adequate service, and social welfare do not lend themselves easily to direct measurement, leading to the use of surrogate measures as a practical alternative to facilitate analysis. Two surrogates are most common. The first is the total weighted travel distance or time between demand points and facility locations. The second is the maximum distance or time required for any user to be served, generally known as the maximal service distance; this represents the system’s worst performance and is well documented in the regional planning literature for emergency services such as fire and ambulance coverage [1]. When resources are limited and cannot meet all demand points within the target distance, the decision becomes whether to prioritize universal coverage or strategically place a certain number of facilities to serve the largest possible share of demand. This consideration introduces a crucial point of interest for policymakers: the population served within an acceptable distance. Formulated in this way, the problem is to select facility locations that maximize the population within a defined service distance, subject to a facility budget constraint. This is the maximal covering location problem, whose aim is to provide service to the greatest feasible proportion of the population within the specified travel limit, as initially formulated in [1].

In situations where public agencies or private companies provide services to more than one community, the maximal covering location problem (MCLP) is used to determine the placement of a defined number of facilities such that as much demand as possible is served. Because its structure closely correlates with actual decisions in emergency response, public service provision, and network design, MCLP has motivated significant research on methods for solving its computational problems. In a covering model, a facility is considered to serve a customer if the travel distance or time between the customer and the facility is not greater than some prescribed threshold value, usually known as the coverage radius or coverage distance [2]. This threshold determines the effective range of a facility and enables the model to identify which demand points can be allocated to a facility. The challenge, therefore, is to choose facility locations within a fixed facility budget that maximize the number of demand points served within a specified radius.

This paper presents a new solution framework for the maximal covering location problem under uncertainty by combining possibility theory with fuzzy random chance-constrained programming. The central idea is to convert the original fuzzy random optimization model into an equivalent deterministic linear program. We achieve this by applying Zadeh’s extension principle [3] to propagate imprecision and by using possibility- and necessity-based chance constraints to reflect the decision-makers’ risk attitudes, yielding formulations suited to both optimistic and conservative preferences [4].

The remainder of the paper is structured as follows. Section 2 reviews key studies on the maximal covering location problem. Section 3 summarizes essential ideas from fuzzy set theory and fuzzy random theory. Section 4 formulates the maximal covering location problems (MCLPs) under uncertainty and presents the solution approaches. We then convert these formulations into deterministic models using possibility theory and fuzzy random chance-constrained programming. Section 5 reports computational results and includes an illustrative example to clarify the procedure. Section 6 concludes and outlines directions for future research.

2. Literature Review

In recent decades, the MCLP has become a central topic in operations research, tackling facility location optimization challenges. Originating in the mid-20th century, the problem became popular as a solution to the growing need for efficient resource allocation in many industries. Today, MCLP is studied due to its ongoing relevance in addressing real-world problems, advancements in optimization methodologies, and its potential to inform decision-making processes in various industries [5].

In recent years, researchers have advanced solution strategies for the maximal covering location problem across diverse settings. A genetic algorithm enhanced with local refinement improved solution quality [6]. A genetic algorithm with local search was designed to address a bilevel MCLP heuristically, which is formulated as a bilevel mathematical program [6]. Two evolutionary procedures, one based on a genetic algorithm and the other on discrete differential evolution, were proposed for the weighted anti-covering location problem, a closely related formulation [7]. Seeking tighter optimality gaps than typical genetic algorithms, the MCLP was recast as a Markov decision process, and a deep reinforcement learning method, Deep MCLP, was introduced [8]. For contexts with imprecise data, a fuzzy capacitated MCLP with fuzzy coverage degrees and fuzzy customer distances was solved using a hybrid population-based algorithm [9]. The modeling scope was broadened with a general framework for multi-type MCLP [6,7,8,9,10]. Finally, a multi-period facility–location model was introduced that maximizes coverage while enforcing a coverage–reliability constraint [11].

Decision-making in practice often relies on incomplete or noisy information; thus, location models must handle uncertainty. Two mature approaches are stochastic programming and fuzzy programming. Recent studies show how these ideas extend the maximal covering location problem. All inputs were treated as imprecise, and the problem was framed in a fuzzy setting, yielding a set of non-dominated fuzzy solutions [12]. Both the facility coverage radius and customer-to-facility distances were modeled as fuzzy, and finite capacity was imposed at each site, leading to a capacitated model with a fuzzy coverage area [13]. An uncertain maximal covering model was developed to locate smart recycling facilities, with service cost modeled as an uncertain parameter [14]. Reflecting operational realities, ambulance siting was analyzed to improve coverage for rare and random road crashes [15]. Extending to network reliability, reliability computation was studied for a probabilistic location set covering problem in wireless networks with equal-reliability servers covering moving cells in the service region [16].

Some researchers have generalized the maximal covering location problem to more realistic requirements. A robust stochastic model was proposed to site artesian wells in order to alleviate drought under uncertainty [17]. The minimum covering location problem was generalized by incorporating gradual coverage with distance-dependent decay, yielding a gradual minimum covering location problem with explicit distance constraints [18]. Their formulation captures the practical decline of service quality with distance rather than a hard cutoff. A hybrid covering location model that combines set covering and maximal covering was also introduced, enabling planners to guarantee a minimum service level while expanding coverage when resources permit [19]. Taken together, these contributions illustrate how the traditional framework can be adapted to uncertainty, distance-sensitive service, and mixed policy objectives.

Past efforts to solve the maximal covering location problem have often overlooked demand uncertainty. To address this gap, we consider fuzzy programming and stochastic programming simultaneously for uncertain demand. This paper develops new solution methods for the MCLP in which the parameters are modeled as fuzzy random variables, while the decision variables remain real. The approach integrates possibility theory [3], Zadeh’s extension principle [4], and fuzzy random chance-constrained programming (FRCCP) [20]. Koç and Sarıkaya [21] use the maximal covering method in determining distribution centers in disaster logistics. Recently, a bi-objective mathematical model for a maximal covering hub location problem was presented to minimize time and environmental risks [22]. Furthermore, the Maximum Coverage Model and Recommendation System for UAV Vertiports Location Planning is introduced by Chunliang et al. [23].

Our objective is to bridge the divide between deterministic and uncertainty-aware decision-making. We first provide a brief overview of fuzzy numbers, then formulate the problem in deterministic, fuzzy, and fuzzy random forms. A case study is conducted to demonstrate the effectiveness of the proposed methods using both deterministic and uncertain demand data, followed by a thorough analysis of the results.

3. Basic Concepts

In this section, key concepts related to fuzzy numbers are summarized, drawing on [24,25]. A fuzzy set on the real line is regarded as a fuzzy number when it is normal, convex, upper semicontinuous, and has compact support. These structural conditions clarify the behavior of fuzzy numbers and support their use in fuzzy logic and other mathematical applications. The LR fuzzy number, introduced by Dubois and Prade, is a widely used special case [26,27]. The following membership function defines the LR fuzzy number A:

$$\tilde{A}\left(x\right)=\left\{\begin{array}{c}L\left({\displaystyle \frac{A^0-x}{A^{-}}}\right)\hspace{1em}\hspace{1em}\hspace{1em}\mathrm{if} A^0-A^{-}\le x\le A^0\\ 1\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} \mathrm{if} A^0<x\le A^1\\ R\left({\displaystyle \frac{x-A^1}{A^{+}}}\right)\hspace{1em}\hspace{1em}\hspace{1em}\mathrm{if} A^1<x\le A^1+A^{+}\end{array}.\right.$$

(1)

where $\left[A^0\mathrm{‚}{A}^1\right]$ denotes the peak of the fuzzy number, with $A^0$ and $A^1$ representing the lower and upper bounds of this interval. $A^{-}\mathrm{‚}{A}^{+}$ represent the left and right spreads, respectively. The functions L and R are defined as L, R: $\left[0\mathrm{‚}1\right]\to \left[0\mathrm{‚}1\right]$ with the properties $L\left(0\right)=R\left(0\right)=1$ and $L\left(1\right)=R\left(1\right)=0$, ensuring they are strictly decreasing, continuous functions. A possible representation of an LR fuzzy number is $\tilde{A}={\left(A^0\mathrm{‚}{A}^1\mathrm{‚}{A}^{-}\mathrm{‚}{A}^{+}\right)}_{LR}$.

The concept of a fuzzy random variable (FRV), as defined by Puri and Ralescu, refers to a random variable whose realizations are fuzzy numbers. Specifically, an FRV is a Borel-measurable mapping from a probability space to the space of fuzzy numbers [24]. In essence, an FRV integrates randomness and fuzziness into a single mathematical construct, providing a flexible framework for modeling and analyzing uncertainty in diverse applications, including decision-making, control systems, and optimization, where considering both probabilistic and fuzzy aspects is essential.

4. Problem Definition

The maximal covering location problem (MCLP), introduced by Church and ReVelle [1], is an optimization framework used in facility location analysis. Its primary objective is to maximize the demand within a specified service distance S while considering a limited number of new facility sites. The MCLP is particularly useful when resources are constrained and full coverage of all demand points is unattainable. It supports decision-makers in selecting facility locations that maximize overall service coverage within the available resources.

In practice, most decisions are made under uncertainty. To address this, researchers have developed methods such as stochastic programming and fuzzy programming over the past two decades. Recent advances show that both fuzzy linear programming and fuzzy random linear programming (FRLP) can be reformulated as deterministic linear programs by using chance-constrained techniques [28]. In these approaches, an extended form of chance constrained programming (CCP) employs possibility and necessity measures to represent fuzzy stochastic constraints in FRLP models. This reformulation enables a solution with standard linear optimization tools while preserving the original uncertainty through adjustable confidence levels, allowing analysts to adopt more conservative or more optimistic decision stances as needed.

4.1. Model Formulation

4.1.1. Deterministic Model

To formulate this problem, we use the following notation, as shown in Table 1:

Table 1. Nomenclature.

Index
$i$ $j$	Demand nodes, $i\in N$ Candidate node for a facility to be located, j $\in N$
Parameter
$h_i$ $S$ $a_{ij}$ $P$	The number of demands at node i The time (or distance) standard within which a server is desired to be found 1 if the distance from i to j is not greater than S, and 0 otherwise The total required servers to be located
Decision Variable
$x_j$ $z_i$	Binary variable: 1 if a facility is located at j, and 0 otherwise Binary variable: 1 if i is covered, and 0 otherwise

Table 1 provides an overview of the nomenclature used in this research, including indices, parameters, and decision variables. The table below offers clear guidance on the mathematical formulation of the MCLP

Thus, MCLP can be formulated as follows:

$$\mathrm{M}\mathrm{a}\mathrm{x} z=\sum _i{h}_i{z}_i$$

(2)

$$\begin{gathered} s.t. \\ {z}_i\le \sum _j{a}_{ij}{x}_{j } ,\forall i, \end{gathered}$$

(3)

$$\sum _j{x}_j\le P,$$

(4)

$$z_i\in \left\{0‚ 1\right\},\forall i,$$

(5)

$$x_j\in \left\{0‚ 1\right\},\forall j.$$

(6)

The objective function (2) aims to maximize the number of covered demand nodes. Constraint (3) defines the relationship between the coverage and location variables, indicating that node i is covered if at least one facility is located at a potential site capable of covering node i. Constraint (4) limits the number of facilities located to P. Constraints (5) and (6) serve as internality constraints.

4.1.2. Fuzzy Maximal Covering Location Problem (FMCLP)

We intend to add fuzziness to the MCLP model. For this, the demand coefficients of the objective function will be considered as fuzzy numbers:

$$\mathrm{M}\mathrm{a}\mathrm{x} \tilde{Z}=\sum _i{\tilde{h}}_i{z}_i$$

(7)

$$\begin{gathered} s.t. \\ {z}_i\le \sum _j{a}_{ij}{x}_{j } ,\forall i, \end{gathered}$$

(8)

$$\sum _j{x}_j\le P,$$

(9)

$$z_i\in \left\{0‚ 1\right\},\forall i,$$

(10)

$$x_j\in \left\{0‚ 1\right\},\forall j.$$

(11)

where ${\tilde{h}}_j={\left(h_j^0\mathrm{‚}{h}_j^1\mathrm{‚}{\beta }_j\mathrm{‚}{\gamma }_j\right)}_{LR}$ represents an LR fuzzy variable involved in the objective function.

4.1.3. Possibility and Necessity-Based Model

In this section, fuzzy chance-constrained programming is used to transform the fuzzy linear program into an equivalent deterministic linear program. The reformulation relies on possibility and necessity measures and yields an equivalent deterministic model, as shown in [24].

Since the original formulation is not fully specified and imprecise, a lower objective value conservative bound is added. The optimization then maximizes this lower bound. In the case of constraints where coefficient values are fuzzy numbers, the level of satisfaction is realized by their degrees of possibility or necessity. The levels manage the conservatism of the solution and provide a practical linear program that expresses the structure of uncertainty in a transparent manner.

Each coefficient ${\tilde{c}}_j$ is a fuzzy number. Therefore, by Zadeh’s extension principle, the objective function $\tilde{Z}=\sum _{i=1}^n{\tilde{h}}_i{z}_i$ is also a fuzzy number, whose membership function is defined as follows:

$${\mu }_{\tilde{Z}}\left(t\right)=\left\{\begin{array}{c}\begin{array}{c}\hspace{1em}L\left({\displaystyle \frac{Z^0-t}{\beta }}\right) if\hspace{1em} t\le Z^0\\ \hspace{1em}1\hspace{1em}\hspace{1em} if{ Z}^0<t\le Z^1\end{array}\\ R\left({\displaystyle \frac{t-Z^1}{\gamma }}\right)\hspace{1em}\hspace{1em}\hspace{1em}\mathrm{Otherwise},\end{array}\right..$$

(12)

where

$$\tilde{Z}={\left(Z^0\mathrm{‚}{Z}^1\mathrm{‚}\beta \mathrm{‚}\gamma \right)}_{LR}, Z^0={\sum }_{i=1}^n{h}_i^0{z}_i, Z^1={\sum }_{i=1}^n{h}_i^1{z}_i, \beta ={\sum }_{i=1}^n{\beta }_i{z}_i, \mathrm{and} \gamma ={\sum }_{i=1}^n{\gamma }_j{z}_i.$$

By using the extension principle of Zadeh, the degree of possibility $Pos\left(\tilde{Z}\ge f\right)$ for the fuzzy constraint $\tilde{Z}\ge f$ based on the possibility distribution ${\mathsf{\mu }}_{\tilde{\mathrm{Z}}}\left(\mathrm{t}\right)$ is defined as follows:

$$Pos\left(\tilde{Z}\ge f\right)=\underset{y_1\mathrm{‚}{y}_2}{\sup }\left\{\mathrm{m}\mathrm{i}\mathrm{n}\left\{{\mu }_{\tilde{Z}}\left(y_1\right)\mathrm{‚}{\mu }_f\left(y_2\right)\right\}|y_1\ge y_2\right\}$$

Let $\eta$ be the permissible possibility level. We maximize lower bound variable $\mathrm{f}$ and apply the possibility measure $Pos\left(\tilde{Z}\ge f\right)$ to handle fuzzy numbers in the objective function of fuzzy programming by the following model:

$$\mathrm{Max}\hspace{1em}f$$

(13)

$$\begin{gathered} \mathrm{s}.\mathrm{t}. \\ Pos\left(\tilde{Z}\ge f\right)\ge \eta , \end{gathered}$$

(14)

$${ z}_i\le \sum _j{a}_{ij}{x}_{j } ,\forall i,$$

(15)

$$\sum _j{x}_j\le P,$$

(16)

$$z_i\in \left\{0‚ 1\right\},\forall i,$$

(17)

$$x_j\in \left\{0‚ 1\right\},\forall j.$$

(18)

4.1.4. Possibility-Based Model

The optimal solution of this possibility-based model is called the P-Optimal solution of FMCLP. We should reformulate $Pos\left(\tilde{Z}\ge f\right)\ge \eta$ to transform the above model into a deterministic model. In order to transform the above model into a deterministic one, we obtain the following theorem. This linearization proceeds along the CCP-based approach documented for fuzzy LPs [24]:

Theorem 1. 

Let $x$ be a non-negative decision vector, then

$$Pos\left(\tilde{Z}\ge f\right)\ge \eta ⟺\sum _{i=1}^n{h}_i^1{z}_i+R^{\mathrm{*}}(\eta )\sum _{i=1}^n{\gamma }_i{z}_i\ge f,$$

where $R^{*}$ pseudo-inverse functions are defined as $R^{\mathrm{*}}\left(\lambda \right)=\sup \left\{t\right|R(t)\ge \lambda \}$.

For more study about this theorem and for its proof, the reader can be referred to the recent study [24] about the fuzzy random programming method.

The optimal solution of the fuzzy model is equivalently obtained by the following problem:

$$\mathrm{M}\mathrm{a}\mathrm{x}\sum _{i=1}^n{h}_i^1{z}_i+R^{\mathrm{*}}(\eta )\sum _{i=1}^n{\gamma }_i{z}_i$$

(19)

$$\begin{gathered} s.t. \\ {z}_i\le \sum _j{a}_{ij}{x}_{j } ,\forall i, \end{gathered}$$

(20)

$$\sum _j{x}_j\le P,$$

(21)

$$z_i\in \left\{0‚ 1\right\},\forall i,$$

(22)

$$x_j\in \left\{0‚ 1\right\},\forall j.$$

(23)

By employing this deterministic reformulation with real-valued parameters, we derive P optimal (possibility-based) solutions for the original fuzzy maximal covering location problem. The resulting linear program is then solved with standard linear programming software.

4.1.5. Necessity-Based Model

The possibility-based model often generates optimistic solutions, which may not be suitable for decision-makers who are risk-averse and prefer more conservative options. In these situations, a necessity-based model is more appropriate, as it focuses on ensuring constraints and minimizing the risk of adverse outcomes.

By using the extension principle of Zadeh, the degree of necessity $Nec(\tilde{Z}\ge f)$ for the fuzzy constraint $\tilde{Z}\ge f$ based on the possibility distribution ${\mu }_{\tilde{Z}}(t)$ is determined as follows:

$$Nec\left(\tilde{Z}\ge f\right)={inf}_{y_1\mathrm{‚}{y}_2}\left\{max\right\{1-{\mu }_{\tilde{Z}}\left(y_1\right)\mathrm{‚}1-{\mu }_f\left(y_2\right)\left\}\right|y_1\ge y_2\}$$

Like the possibility case, the lower bound variable $f$ is maximized, and the necessity measure $Nec(\tilde{Z}\ge f)$ is applied to handle fuzzy numbers in the objective function of problem 1 by the following model:

$$\mathrm{Max}\hspace{1em}f$$

(24)

$$\begin{gathered} \mathrm{s}.\mathrm{t}. \\ Nec\left(\tilde{Z}\ge f\right)\ge \eta , \end{gathered}$$

(25)

$${ z}_i\le \sum _j{a}_{ij}{x}_{j } ,\forall i,$$

(26)

$$\sum _j{x}_j\le P,$$

(27)

$$z_i\in \left\{0‚ 1\right\},\forall i,$$

(28)

$$x_j\in \left\{0‚ 1\right\},\forall j.$$

(29)

The optimal solution of this model is referred to as the N-optimal solution of the FMCLP. To convert this model into a linear constraint, we obtain the following Theorem 2:

Theorem 2. 

Let x be a non-negative decision vector, then

$$Nec\left(\tilde{Z}\ge f\right)\ge \eta ⟺\sum _{i=1}^n{h}_i^0{z}_i+L^{\mathrm{*}}\left(1-\eta \right)\sum _{i=1}^n{\beta }_i{z}_i\ge f,$$

where $L^{*}$ is the pseudo-inverse function of L defined as $L^{\mathrm{*}}\left(\lambda \right)=\sup \left\{t \right| L(t)\ge \lambda \}$.

The optimal solution of the necessity-based fuzzy model is equal to the optimal solution of the following problem:

$$\mathrm{Max}\sum _{i=1}^n{h}_i^0{z}_i+L^{\mathrm{*}}\left(1-\eta \right)\sum _{i=1}^n{\beta }_i{z}_i$$

(30)

$$\begin{gathered} s.t. \\ {z}_i\le \sum _j{a}_{ij}{x}_{j } ,\forall i, \end{gathered}$$

(31)

$$\sum _j{x}_j\le P,$$

(32)

$$z_i\in \left\{0‚ 1\right\},\forall i,$$

(33)

$$x_j\in \left\{0‚ 1\right\},\forall j.$$

(34)

The model described above is an example of a deterministic LP problem [24].

4.2. Fuzzy Random Maximal Covering Location Problem (FRMCLP)

In practical optimization, many parameters are uncertain. Two well-established approaches address this challenge: stochastic programming, which treats unknowns as random variables with specified distributions, and fuzzy programming, which represents imprecision through membership functions and possibility measures. When both randomness and vagueness are present, a combined framework is required. Fuzzy stochastic programming integrates probability and possibility to capture these two facets of uncertainty at the same time. A key variant is FRVs, which uses FRVs to model cases where the realized values of random parameters are themselves fuzzy numbers. In such models, uncertainty is described with both probabilistic and possibilistic information, and outcomes are represented as fuzzy sets. In summary, fuzzy programming handles imprecision, stochastic programming handles randomness, and the combined methods offer a unified way to manage both.

Maximal covering location problem with FRVs:

The MCLP with FRV coefficients is formulated as follows:

$$\mathrm{M}\mathrm{a}\mathrm{x}\overline{\tilde{Z}}=\sum _{i=1}^n\overline{{\tilde{h}}_i}{z}_i$$

(35)

$$\begin{gathered} s.t. \\ {z}_i\le \sum _j{a}_{ij}{x}_{j } ,\forall i, \end{gathered}$$

(36)

$$\sum _j{x}_j\le P,$$

(37)

$$z_i\in \left\{0‚ 1\right\},\forall i,$$

(38)

$$x_j\in \left\{0‚ 1\right\},\forall j.$$

(39)

where $\overline{{\tilde{h}}_i}={({\overline{h}}_i^0\mathrm{‚}{\overline{h}}_i^1\mathrm{‚}{\beta }_i\mathrm{‚}{\gamma }_i)}_{LR}$ represents FRV, whose observed value for each $\omega \in \mathit{\Omega }$ is a fuzzy number ${\tilde{h}}_i\left(\omega \right)={(h_i^0\left(\omega \right)\mathrm{‚}{h}_i^1\left(\omega \right)\mathrm{‚}{\beta }_i\mathrm{‚}{\gamma }_i)}_{LR}$, respectively. Furthermore ${\overline{h}}_i^0$ and ${\overline{h}}_i^1$ are random variables defined as ${\overline{h}}_i^0=h_i^{\left(0\right)}+\overline{t}{h}_i^{\left(2\right)}\mathrm{‚}{\overline{h}}_i^1=h_i^{\left(1\right)}+\overline{t}{h}_i^{\left(2\right)}$ in which $\overline{\mathrm{t}}$ is a random variable with expected value $\mathrm{M}$ and the cumulative distribution function $T$, respectively. Reference [25] presented this definition of random variables.

In this section, the FRMCLP model is transformed into a deterministic model using fuzzy random CCP, which is based on possibility, necessity measures, along with Zadeh’s extension principle. Our reformulation of the FRMCLP adopts the same CCP-based deterministic transformation that is adapted to fuzzy random coefficients [24]. To effectively manage FRVs in the FRMCLP P model, we define the following programming model by applying fuzzy random CCP based on possibility measures:

$$\mathrm{Max}\hspace{1em}f$$

(40)

$$\begin{gathered} \mathrm{s}.\mathrm{t}. \\ \mathrm{P}\mathrm{r}\left\{\omega |\mathit{Pos}\left(\left(\tilde{z}\left(\omega \right)\ge f\right)\ge \eta \right)\right\}\ge \theta , \end{gathered}$$

(41)

$${ z}_i\le \sum _j{a}_{ij}{x}_{j } ,\forall i,$$

(42)

$$\sum _j{x}_j\le P,$$

(43)

$$z_i\in \left\{0‚ 1\right\},\forall i,$$

(44)

$$x_j\in \left\{0‚ 1\right\},\forall j.$$

(45)

where $\theta$ is the permissible probability level and $\eta$ is the permissible possibility level.

We need to reformulate the relationship between the constraint and possibility measures into proper forms. By applying Theorem 1, Theorem 3 is obtained to convert the final model into a deterministic problem.

Theorem 3. 

Let $\mathrm{x}$ be a non-negative decision vector, then

$$\mathrm{P}\mathrm{r}\left\{\omega \right|Pos((\tilde{z}(\omega )\ge f)\ge \eta )\}\ge \theta ⟺{\sum }_{i=1}^n\left(h_i^{\left(1\right)}+T^{*}\left(1-\theta \right)h_i^{\left(2\right)}\right)z_i+R^{*}(\eta ){\sum }_{i=1}^n{\gamma }_i{z}_i\ge f$$

where $T^{*}$ is a pseudo-inverse function defined as $T^{\mathrm{*}}\left(\lambda \right)=\mathit{inf}\left\{t| T\left(t\right)\ge \lambda \right\}.$

Using Theorem 3 of basic concepts, the problem is equivalently reformulated as follows:

$$Max {\sum }_{i=1}^n\left(h_i^{\left(1\right)}+T^{*}\left(1-\theta \right)h_i^{\left(2\right)}\right)z_i+R^{*}(\eta ){\sum }_{i=1}^n{\gamma }_i{z}_i$$

(46)

$$\begin{gathered} s.t. \\ {z}_i\le \sum _j{a}_{ij}{x}_{j } ,\forall i, \end{gathered}$$

(47)

$$\sum _j{x}_j\le P,$$

(48)

$$z_i\in \left\{0‚ 1\right\},\forall i,$$

(49)

$$x_j\in \left\{0‚ 1\right\},\forall j.$$

(50)

When we use necessity measures for pessimistic decision-makers, the following programming model is defined as the MCLP with $\mathrm{F}\mathrm{R}\mathrm{V}\mathrm{s}$:

$$\mathrm{Max}\hspace{1em}f$$

(51)

$$\begin{gathered} \mathrm{s}.\mathrm{t}. \\ \mathit{Pr}\left\{\omega |Nec\left(\tilde{z}\left(\omega \right)\ge f\right)\ge \eta \right\}\ge \theta , \end{gathered}$$

(52)

$${ z}_i\le \sum _j{a}_{ij}{x}_{j } ,\forall i,$$

(53)

$$\sum _j{x}_j\le P,$$

(54)

$$z_i\in \left\{0‚ 1\right\},\forall i,$$

(55)

$$x_j\in \left\{0‚ 1\right\},\forall j.$$

(56)

Now, we utilize Theorem 2 to reformulate relationships between constraints with necessity measures. This approach leads to the following Theorem 4.

Theorem 4. 

Let $\mathrm{x}$ be a non-negative decision vector, then

$$\mathrm{Pr}\left\{\omega |Nec\left(\tilde{z}\left(\omega \right)\ge f\right)\ge \eta \right\}\ge \theta ⟺{\sum }_{i=1}^n\left(h_i^{\left(0\right)}+T^{*}\left(1-\theta \right)h_i^{\left(2\right)}-L^{*}(1-\eta ){\beta }_i\right)z_i\ge f$$

Finally, the programming model of FRMCLP for pessimistic decision-makers is equivalently transformed into the following deterministic problem:

$$Max {\sum }_{i=1}^n\left(h_i^{\left(0\right)}+T^{*}\left(1-\theta \right)h_i^{\left(2\right)}- L^{*}(1-\eta ){\beta }_i\right)z_i$$

(57)

$$\begin{gathered} s.t. \\ {z}_i\le \sum _j{a}_{ij}{x}_{j } ,\forall i, \end{gathered}$$

(58)

$$\sum _j{x}_j\le P,$$

(59)

$$z_i\in \left\{0‚ 1\right\},\forall i,$$

(60)

$$x_j\in \left\{0‚ 1\right\},\forall j.$$

(61)

5. Case Study

We have utilized MCLP to plan a limited number of shopping centers in a context where we lack sufficient funds and facilities. This constraint prevents us from building enough shopping centers to meet all the demands. As a result, we intend to cover as many demands as possible within the designated area. To achieve this goal, we have divided a relatively large area of the city into specific demand regions. By establishing the origin of coordinates, we have assigned coordinates for each of the demand regions. In each of the regions, we collected data on demand and calculated the average. This data accounts for both certainty and uncertainty. To determine the optimal locations for our facilities, we will solve MCLP, fuzzy MCLP, and fuzzy random MCLP to address the problem.

All computations were performed on a Dell computer with a 2.5 GHz CPU Core 2 Duo and 3 GB RAM. The software used for coding and calculations is GAMS Ver.24.1.2. Furthermore, we have assumed the maximal covering distance of 1.5 km.

5.1. The Case Study Data in Certainty

The coordinates of 20 areas in the city of Tabriz with a demand for shopping centers have been identified and are listed in Table 2. The corresponding demand values are presented in Table 3, while the potential locations for establishing shopping centers have also been determined. Potential locations for establishing shopping centers, along with their coordinates, are presented in Table 4. These locations aim to meet the shopping center demands of the 20 identified areas.

Table 2. Coordinates of demand nodes in specific areas in Tabriz.

	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
x	3.2	2.9	2.7	3.2	2.4	3	2.9	3.3	3.4	2.5	2.1	1.9	2.2	2.5	2.9	1.7	1.9	1	3.4	1.9
y	3.1	3.2	3.6	2.9	3.3	3.5	2.7	2.8	3	6	2.8	4.7	4	1.4	1.2	4.2	2.1	3.2	5.6	3.8

Table 3. Demand value of each node.

i	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
$h_i$	710	620	560	350	200	190	170	160	140	120	120	100	90	90	90	80	80	70	60	60

Table 4. Coordinates of potential locations of facilities.

	1	2	3	4	5	6	7	8	9
x	2.9	2.6	2.9	1.7	3	1.7	2.4	1.2	2.7
y	2.9	2.5	2.1	5.3	5.1	3.3	4.8	4.7	4.1

Table 2 presents the locations of 20 demand nodes in specific areas of Tabriz that indicate a demand for shopping centers. These locations highlight the importance of strategically placing facilities to effectively serve as many people as possible. Additionally, the provided data is useful in optimizing the model.

Table 3 shows the demand values for each node, highlighting the importance of prioritizing facility placement by focusing on nodes with higher demand to improve coverage.

Table 4 presents nine potential locations for establishing shopping centers. These spots have been selected based on feasibility factors and their ability to fulfill customers’ needs. The distribution of these potential locations spans a wide geographical area, providing a wide coverage and assisting in choosing the best locations for constructing the centers.

5.2. Computational Results with Deterministic Parameters

Our goal is to identify the minimum number of facilities required to cover all demands. To accomplish this, we apply the basic MCLP model, based on the provided data. We will analyze various numbers of facilities to determine how many are necessary to cover all demands. The findings are summarized in Table 5, which shows the coverage of demand nodes by a single facility.

Table 5. Demand nodes covered by one facility.

i	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
$z_i$	1	1	1	1	1	1	1	1	1	0	1	1	1	0	0	1	0	0	0	1
total covered demands											3550

Regarding the coordinates of the facility located at (x = 2.7, y = 4.1), as indicated in Table 5, constructing a single facility will partially meet the demand while leaving other nodes uncovered. Figure 1 illustrates the facility’s location, distinguishing between covered and uncovered demand nodes. It highlights the established facility and identifies potential locations for additional centers.

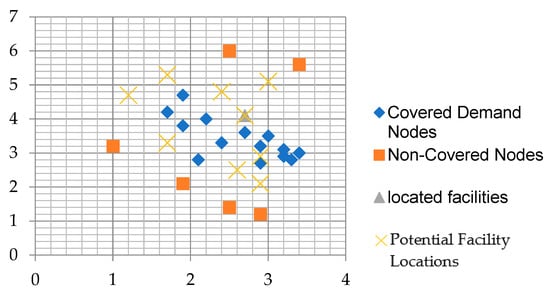
Figure 1. The location of covered and non-covered demand nodes and one located facility.

Table 6 and Figure 2 present the results of constructing two facilities that cover the demand nodes, illustrating how the selected locations collectively fulfill the service requirements and optimize coverage throughout the network.

Table 6. Demand nodes covered by constructing two facilities.

i	1	2	3	4	5		6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
$z_i$	1	1	1	1	1		1	1	1	1	1	1	1	1	1	1	1	1	0	1	1
	total covered demands											3990

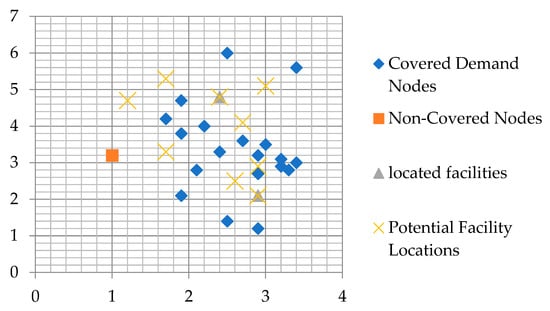
Figure 2. The location of covered and non-covered demand nodes and two facilities.

Table 6 displays the results of allocating two facilities at the coordinates (x = 2.9, y = 2.1) and (x = 2.4, y = 4.8), demonstrating an increase in the covered area. Figure 2 illustrates the location of these two facilities, showing both the nodes that are covered and those that remain uncovered. Notably, the number of uncovered areas has decreased due to this expansion; however, some regions still lack coverage.

The results of establishing three facilities to cover the demand nodes efficiently are comprehensively presented in Table 7 and Figure 3, illustrating their impact on overall service coverage and resource allocation.

Table 7. Demand nodes covered by constructing three facilities.

i	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
$z_i$	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1
total covered demands											4060

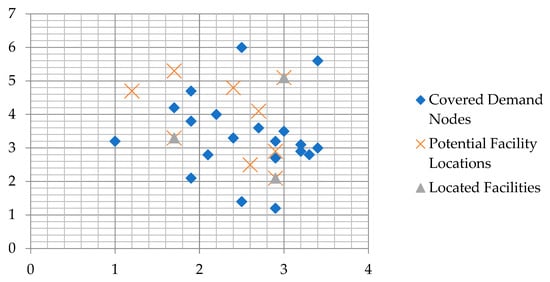
Figure 3. The location of covered demand nodes and three facilities.

Table 7 shows the results of the deterministic model when three facilities are allocated at (x = 2.9, y = 2.1), (x = 3, y = 5.1), and (x = 1.7, y = 3.3). This setup achieves comprehensive coverage of all 20 demand nodes, satisfying a total need of 4060. Hence, Figure 3 graphically illustrates the locations of the three facilities and their corresponding coverage, showing how allocating these three facilities effectively eliminates gaps and ensures coverage of all nodes.

5.3. Computational Results with Fuzzy and Fuzzy Stochastic Programming

First, fuzzy programming optimization is used for the problem under a fuzzy framework. Next, fuzzy stochastic programming is applied to address the problem under both fuzziness and randomness.

The uncertainty parameters in real-world decision-making require us to incorporate both fuzziness and randomness, which we refer to as fuzzy stochastic programming optimization.

5.3.1. Computational Results with Fuzzy Demand Parameter

In this section, the demand values are represented as fuzzy numbers, as illustrated in Table 8. The fuzzy data has been developed based on the original data, supplemented by input from experts and feedback collected through questionnaires, as summarized in Table 8. Additionally, possibility levels of 0.1, 0.3, 0.5, 0.7, and 0.9 have been considered.

Table 8. Fuzzy parameters of the case study.

	1	2	3	4	5	6	7	8	9	10
$h_i^0$	660	575	520	310	165	160	140	135	120	95
$h_i^1$	760	665	600	390	235	220	200	185	160	145
${\beta }_i$	50	40	40	35	30	35	25	30	25	30
${\gamma }_i$	40	40	50	40	25	30	30	25	25	30
	11	12	13	14	15	16	17	18	19	20
$h_i^0$	100	70	65	65	70	65	70	55	50	55
$h_i^1$	140	130	115	115	110	95	90	85	70	65
${\beta }_i$	20	20	25	35	15	15	10	15	5	5
${\gamma }_i$	25	30	20	30	20	20	15	10	10	5

The computation results of fuzzy programming for different possibility levels in both a possibility-based model and a necessity-based model for establishing three facilities to cover the demand nodes are listed in Table 9.

Table 9. Numerical results of the case study with fuzzy parameters for establishing three facilities to cover the demand nodes.

Covered Demands
Possibility Levels (η)	Possibility-Based Model (P-Optimal Solution)	Necessity-Based Model (N-Optimal Solution)
0.1	4324.5	3100.5
0.2	4284	3061
0.3	4243.5	3021.5
0.4	4203	2982
0.5	4162.5	2942.5
0.6	4122	2903
0.7	4081.5	2863.5
0.8	4041	2824
0.9	4000.5	2784.5

Table 9 presents the computation results of fuzzy programming for different possibility levels in both the possibility-based and necessity-based models, which aim to establish three facilities to cover the demand nodes.

The results, particularly illustrated in Figure 4 and Table 9, indicate that as the possibility level increases, the number of covered demands decreases in both the possibility and necessity models. This trend indicates that at higher possibility levels, the optimization of the objective function is affected, resulting in a reduction in covered demands. Furthermore, the covered demand in the possibility-based model is greater than that in the necessity-based model.

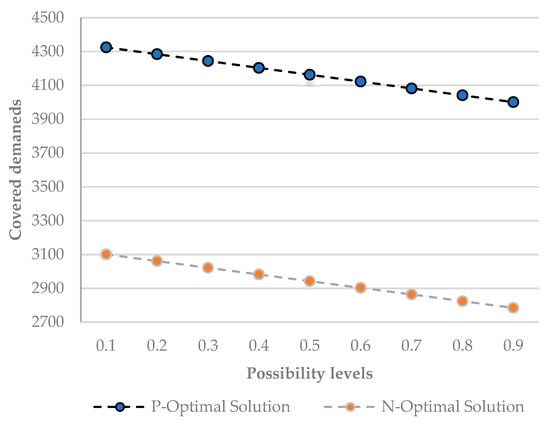
Figure 4. Coverage of the demands of the case study through fuzzy programming in establishing three facilities.

5.3.2. Computational Results with Fuzzy Random Demand Parameters

In real-world applications, uncertain parameters often exhibit both fuzzy and stochastic characteristics, leading to their modeling as fuzzy random variables. These variables are derived from the original data through expert consultations and questionnaire analyses. They are summarized in Table 10 as FRVs and represented as ordered quadruples $\left({\overline{h}}_i^0,{\overline{h}}_i^1{,\beta }_i,{\gamma }_i\right),$ where $\overline{t}$ is a normal random variable with $E\left(\overline{t}\right)=0$ and $Var\left(\overline{t}\right)=1$. The FRV parameters related to the demand coefficient in the objective function for 20 nodes are provided in Table 10, considering uncertainty, which includes base demand values, spreads, and stochastic elements.

Table 10. Fuzzy random parameters in the case study.

	1	2	3	4	5	6	7	8	9	10
${\overline{h}}_i^0$	660 + 15$\overline{t}$	575 + 14$\overline{t}$	520 + 13$\overline{t}$	310 + 12$\overline{t}$	165 + 11$\overline{t}$	160 + 11$\overline{t}$	140 + 10$\overline{t}$	135 + 10$\overline{t}$	120 + 9$\overline{t}$	95 + 8$\overline{t}$
${\overline{h}}_i^1$	760 + 15$\overline{t}$	665 + 14$\overline{t}$	600 + 13$\overline{t}$	390 + 12$\overline{t}$	235 + 11$\overline{t}$	220 + 11$\overline{t}$	200 + 10$\overline{t}$	185 + 10$\overline{t}$	160 + 9$\overline{t}$	145 + 8$\overline{t}$
${\beta }_i$	50	40	40	35	30	35	25	30	25	30
${\gamma }_i$	40	40	50	40	25	30	30	25	25	30
	11	12	13	14	15	16	17	18	19	20
${\overline{h}}_i^0$	100 + 8$\overline{t}$	70 + 7$\overline{t}$	65 + 7$\overline{t}$	65 + 6$\overline{t}$	70 + 6$\overline{t}$	65 + 5$\overline{t}$	70 + 4$\overline{t}$	55 + 3$\overline{t}$	50 + 2$\overline{t}$	55 + $\overline{t}$
${\overline{h}}_i^1$	140 + 8$\overline{t}$	130 + 7$\overline{t}$	115 + 7$\overline{t}$	115 + 6$\overline{t}$	110 + 6$\overline{t}$	95 + 5$\overline{t}$	90 + 4$\overline{t}$	85 + 3$\overline{t}$	70 + 2$\overline{t}$	65 + $\overline{t}$
${\beta }_i$	20	20	25	35	15	15	10	15	5	5
${\gamma }_i$	25	30	20	30	20	20	15	10	10	5

Table 11 and Table 12 present the results of the fuzzy stochastic programming computations for different possibility and probability levels in the possibility-based and necessity-based models, respectively. The aim of these results is to establish three facilities to cover the demand at the specified nodes.

Table 11. Numerical results of the case study through fuzzy stochastic programming, possibility-based model.

Possibility-Based Solution		Probability Level (θ)
		0.1	0.3	0.5	0.7	0.9
Possibility Level (η)	0.1	4494.962	4394.247	4324.5	4254.753	4154.038
	0.3	4413.962	4313.247	4243.5	4173.753	4073.038
	0.5	4332.962	4232.247	4162.5	4092.753	3992.038
	0.7	4251.962	4151.247	4081.5	4011.753	3911.038
	0.9	4170.962	4070.247	4000.5	3930.753	3830.038

Table 12. Numerical results of the case study through fuzzy stochastic programming, necessity-based model.

Necessity-Based Solution		Probability Level (θ)
		0.1	0.3	0.5	0.7	0.9
Possibility Level (η)	0.1	3270.962	3170.247	3100.5	3030.753	2930.038
	0.3	3191.962	3091.247	3021.5	2951.753	2851.038
	0.5	3112.962	3012.247	2942.5	2872.753	2772.038
	0.7	3033.962	2933.247	2863.5	2793.753	2693.038
	0.9	2954.962	2854.247	2784.5	2714.753	2614.038

The findings in Table 11 demonstrate the impact of possibility (η) and probability (θ) levels on the extent of coverage. Increasing either θ or η results in reduced overall demand coverage.

Table 12 presents the results of the necessity-based model under fuzzy random conditions. Like the possibility-based model, as the levels of θ and η increase, the covered demand decreases. The results from the necessity-based model are generally lower than those from the possibility-based model, highlighting the cautious approach that characterizes necessity-based decision-making.

Figure 5 and Figure 6 provide an alternative viewpoint to Table 11 and Table 12, illustrating the optimistic and pessimistic scenarios, respectively. Figure 5 and Figure 6 and Table 11 and Table 12 show the optimal solutions of the problem at different levels of probability and possibility, but the DM can choose a proper level based on his/her circumstances or any other constraints. In both instances, the results clearly indicate that when the probability level remains constant, an increase in the possibility level leads to a decrease in total covered demand. Likewise, when the possibility level remains steady, raising the probability level also results in a reduction in total covered demand.

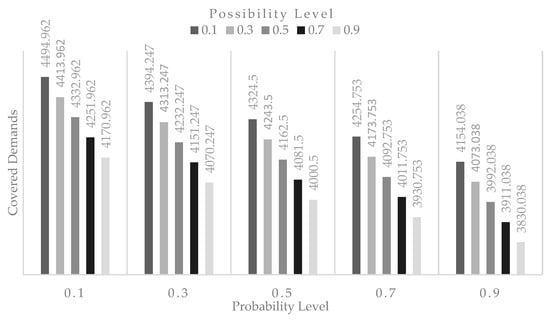
Figure 5. The optimal covered demands of the case study through fuzzy stochastic programming with a possibility-based model.

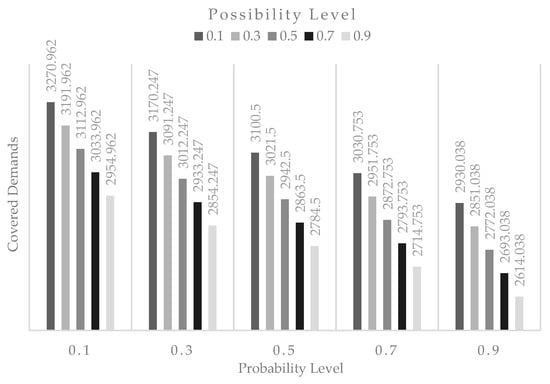
Figure 6. The optimal covered demands of the case study through fuzzy stochastic programming with a necessity-based model.

In the optimistic possibility-based model, the total covered demand is higher compared to the pessimistic necessity-based model. However, in both optimistic and pessimistic scenarios, total covered demand has an inverse relationship with both possibility and probability levels.

6. Conclusions

By analyzing our computational results alongside the number of facilities we can construct, we can identify the most suitable locations to meet maximum demand. This information simplifies the decision-making process for stakeholders when choosing the best locations from a range of potential sites. Furthermore, due to the uncertainty inherent in real-world decision-making, we employed various approaches, including fuzzy programming, fuzzy stochastic programming, possibility-based models, and necessity-based models. This variety allowed us to evaluate the differences in covered demands across these models. Additionally, our findings revealed that as we increase the levels of possibility and probability, the number of demands covered tends to decrease. Based on these conditions, by selecting an appropriate solution model, P-optimal for optimistic decision-makers and N-optimal for pessimistic decision-makers, and choosing suitable values for the possibility and probability levels, we can approximate the number of demands covered by the current location of facilities.