Dynamic, Bifurcation, and Lyapunov Analysis of Fractional Rössler Chaos Using Two Numerical Methods

Abstract

In this paper, we first used a Modified Numerical Approximation Method (NAM) and then a fractional Laplace Decomposition Method (LDM) to find the solution to the symmetric Rössler attractor. The newly proposed NAM is obtained through a nuanced discretization of the Caputo derivative, rendering it exceptionally effective in emulating the inherent sensitivity and memory-dependent characteristics of fractional-order systems. Second, a comprehensive analysis is conducted to examine how variations in the fractional parameters ${\rho }_1$, ${\rho }_2$, and ${\rho }_3$ influence the dynamic response of the system. Third, the simulation results, which include time series, bifurcation diagrams, and Lyapunov exponent spectra, show that the proposed method works well to find changes in system behavior that integer-order or lower-accuracy schemes cannot find. The fractional Laplace Decomposition Method (LDM) is straightforward to implement, computationally efficient, and exhibits outstanding accuracy. Other widely used approximation approaches achieve comparable results. The comparisons between NAM and LDM reveal that these two methodologies are not only highly consistent but also mutually reinforcing. Their straightforward application and robust consistency of numerical solutions indicate that these methods can be effectively utilized in the majority of fractional-order systems, resulting in more accurate and practical answers.

1. Introduction

Fractional calculus is rapidly on its way to becoming a mandatory area of applied mathematics, physics, and an interdisciplinary engineering science, whose help is drawn from abundant substantial research advancements. Fractional calculus presents its application in varied environments encompassing chaotic systems [1,2], sound encryption [3,4], and dynamic feature analysis with the help of fractional-order approaches.

Fractional-order derivative (FD) studies cross multiple disciplines, such as robotic systems control and modeling in the fractional-order context [5], numerical differentials of chaotic fractional models [6,7], and chaotic dynamics research in fractional predator–prey models [8]. Fractional-order approaches have also found applications in epidemiology, robotics, numerical analysis, and ecology studies [9]. Central activities in this discipline also include theoretical formulation and real-world applications, i.e., continuum mechanics [10] as well as integral and fractional derivatives research [11].

Working on hidden attractors [12], entropy-driven analysis in chaotic systems gives evidence for a variety of applications of fractional calculus in science and technology [13]. The modern development of computational approaches has advanced the solutions of FDEs and thus the possibility of their applications in physics and engineering, as well as in other interdisciplinary fields of biology, economics, and management [14].

The modeling of chaotic systems has been a highly researched area because of its wide applications in natural and technical sciences [15,16]. Chaotic systems have complex modeling, phase diagrams, algorithms, Lyapunov analysis, and monitoring of chaotic behavior while managing model parameters to integrate them into electrical circuits [17].

This research shows the possibility of solving complex problems using a fractional differential system due to the presence of noninteger-order derivatives. Based on the properties of fractional-order chaotic systems, this provides more detailed and precise solutions for modeling nonlinear dynamic phenomena [18]. The analysis of fractional-order chaotic systems focuses on some unique characteristics of traditional integer-order models that have not been grasped so far, such as memory effects, long-term dependencies, and the ability to adapt. This is directed towards creating new horizons for application in a wide range of areas in physics, engineering, biology, economics, and control systems in which fractional-order modeling is more adequate and descriptive [19,20,21,22,23,24,25,26].

The study of amplitude control in symmetric systems [27,28] further extends the realm, discovers new areas of applications of fractional calculus, gives deeper insights into chaotic systems, and opens wider perspectives in almost all fields of science. Further studies on other formulations of derivatives [29] and their relations with chaotic dynamics could lead to even more important developments in the future.

We numerically simulate and examine the dynamic characteristics of the fractional-order chaotic system proposed in [28].

$$\left\{\begin{array}{cc}\hfill {\mathcal{D}}_t^{{\rho }_1}{x}_1\left(t\right)& =-x_2-x_3,\hfill \\ \hfill {\mathcal{D}}_t^{{\rho }_2}{x}_2\left(t\right)& =x_1+a_1{x}_2,\hfill \\ \hfill {\mathcal{D}}_t^{{\rho }_3}{x}_3\left(t\right)& =a_2{x}_1+x_1\left|x_3\right|-a_3{x}_3,\hfill \end{array}\right.$$

(1)

where $D_t^{{\rho }_i}(·)$ denotes the fractional derivative of order ${\rho }_i$. with $x_1\left(0\right)=1$, $x_2\left(0\right)=0$, $x_3\left(0\right)=0$, and $a_1=0.5$, $a_2=0.2$, and $a_3=5.7$.

All parameter values were selected on the basis of theoretical considerations unique to the fractional-order system being studied. To guarantee system stability and investigate the pertinent dynamical regimes, such as periodic and chaotic behaviors, initial conditions were chosen. The simulations are based solely on the computed fractional-order differential equations and their numerical approximations, without the use of external or experimental datasets. Our paper’s contributions and novelties are as follows:

• For fractional-order chaotic systems, a more precise numerical approximation method (NAM) and a fractional Laplace decomposition method (LDM) are developed for more accurate and stable solutions. Both methods are tailored to fractional dynamics’ memory and sensitivity, making them more stable than typical methods.
• By integrating variable fractional parameters ${\rho }_1$, ${\rho }_2$, and ${\rho }_3$, we investigate the fundamental fractional chaotic system and uncover unexpected and previously unpublished complicated dynamics. This research improves our knowledge of the system’s nonlinear dynamics and shows that fractional orders really drive chaos.
• Recent advances in fractional discretization schemes have increased convergence and reduced numerical dispersion, making the new NAM an effective tool for simulating high-dimensional fractional systems.
• We validate the accuracy, efficiency, and wide applicability of NAM and LDM by applying them to several fractional chaotic systems and comparing the findings to the popular Adams–Bashforth–Moulton (ABM) technique.
• Numerical simulations—time series, bifurcation diagrams, and Lyapunov exponent spectra—show that the suggested approaches can describe delicate system dynamics transitions. These results show that the upgraded NAM and LDM outperform existing numerical methods and lay the groundwork for studying complex fractional-order chaotic processes.

2. Background

This section offers some initial definitions and concepts which formed the core of the theory of fractional calculus and its uses. To start with, we give the main definition of fractional derivatives.

Definition 1

([30,31]). A function $H\left(t\right)$ on $(t_0,t)$ has a Riemann–Liouville fractional derivative of order ρ, defined as follows:

$${}_{t_0}{}^{RL}D_t^{\rho }H\left(t\right)=\left\{\begin{array}{cc}{\displaystyle \frac{1}{\Gamma (m-\rho )}}{\displaystyle \frac{d^m}{d{t}^m}}{\int }_{t_0}^t{\displaystyle \frac{H\left(\tau \right)}{{(t-\tau )}^{\rho -m+1}}}d\tau ,\hfill & if0\le m-1<\rho <m,\hfill \\ {\displaystyle \frac{d^{m}H\left(t\right)}{d{t}^m}},\hfill & if\rho =mandm\in \mathbb{N}.\hfill \end{array}\right.$$

(2)

Definition 2

([30]). A function $H\left(t\right)\in C^m[t_0,t]$ defined on the interval $(t_0,t)$ possesses a Caputo fractional derivative of order ρ, expressed as follows:

$${}_{t_0}{}^{C}D_t^{\rho }H\left(t\right)=\left\{\begin{array}{cc}{\displaystyle \frac{1}{\Gamma (m-\rho )}}{\int }_{t_0}^t{\displaystyle \frac{H^{\left(m\right)}\left(\tau \right)}{{(t-\tau )}^{\rho -m+1}}}d\tau ,\hfill & 0\le m-1<\rho <m,\hfill \\ {\displaystyle \frac{d^{m}H\left(t\right)}{d{t}^m}},\hfill & \rho =m\in \mathbb{N}.\hfill \end{array}\right.$$

(3)

Definition 3

([32]). The Laplace transform for the Caputo’s fractional derivative is given by the following form:

$$L\left\{D_t^{\rho }H\left(t\right)\right\}=s^{\rho }{\mathbb{H}}_{\rho }\left(s\right)-{\Sigma }_{k=0}^{m-1}{s}^{\rho -k-1}{H}^k\left(0\right),m-1<\rho <m.$$

Corollary 1

([33]). A function $H\left(t\right)$ defined on the interval $(t_0,t)$ has a Grünwald–Letnikov (G–L) fractional derivative of order ρ, given by

$${}_{t_0}{}^{GL}D_t^{\rho }H\left(t\right)=\underset{h\to 0}{lim}{\displaystyle \frac{1}{h^{\rho }}}\sum _{j=0}^{⌊{\displaystyle \frac{t-t_0}{h}}⌋}{(-1)}^j\left({\displaystyle \genfrac{}{}{0pt}{}{\rho }{j}}\right)H(t-jh).$$

(4)

Proof. 

The coefficient

$${(-1)}^j\left({\displaystyle \genfrac{}{}{0pt}{}{\rho }{j}}\right)={\displaystyle \frac{{(-1)}^j\Gamma (\rho +1)}{\Gamma (j+1)\Gamma (\rho -j+1)}}$$

is defined as

$${\omega }_j^{\left(\rho \right)}={(-1)}^j\left({\displaystyle \genfrac{}{}{0pt}{}{\rho }{j}}\right)={\displaystyle \frac{{(-1)}^j\Gamma (\rho +1)}{\Gamma (j+1)\Gamma (\rho -j+1)}},j=0,1,\dots ,m.$$

(5)

Hence, the Grünwald–Letnikov fractional derivative of order $\rho$ can be equivalently expressed as

$${}_{t_0}{}^{GL}D_t^{\rho }H\left(t\right)=\underset{h\to 0}{lim}{\displaystyle \frac{1}{h^{\rho }}}\sum _{j=0}^{⌊{\displaystyle \frac{t-t_0}{h}}⌋}{\omega }_j^{\left(\rho \right)}H(t-jh).$$

(6)

By applying Newton’s binomial theorem, we can expand the expression and get the following formulation, which is able to write the fractional derivative in a more tractable form.

$${(1-t)}^m=\sum _{j=0}^m{(-1)}^j\left({\displaystyle \genfrac{}{}{0pt}{}{m}{j}}\right)t^j=\sum _{j=0}^m{\omega }_j^{\left(m\right)}{t}^j.$$

(7)

This results in the following conclusion:

$$\sum _{j=0}^{\infty }{\omega }_j^{\left(\rho \right)}{t}^j={(1-t)}^{\rho }.$$

(8)

As a final result, we derive the following:

$${}_{t_0}{}^{GL}D_t^{\rho }H\left(t\right)={\displaystyle \frac{1}{h^{\rho }}}\sum _{j=0}^{⌊{\displaystyle \frac{t-t_0}{h}}⌋}{\omega }_{j}H(t-jh)+o\left(h\right).$$

(9)

□

Theorem 1

([34]). If H is continuous and differentiable up to order $m-1$ on $(t_0,t)$, with $H^{\left(m\right)}\left(t\right)$ is integrable, then

$${}_{t_0}{}^{GL}D_t^{\rho }H\left(t\right)=\sum _{j=0}^{m-1}{\displaystyle \frac{H^{\left(j\right)}\left(t_0\right)}{\Gamma (1+j-\rho )}}{(t-t_0)}^{j-\rho }+{\displaystyle \frac{1}{\Gamma (m-\rho )}}{\int }_{t_0}^t{\displaystyle \frac{H^{\left(m\right)}\left(\tau \right)}{{(t-\tau )}^{\rho -m+1}}}d\tau ,$$

(10)

where $0\le m-1<\rho <m$.

Then:

$${}_{t_0}{}^{GL}D_t^{\rho }H\left(t\right)={}_{t_0}{}^{RL}D_t^{\rho }H\left(t\right),$$

and

$${}_{t_0}{}^{C}D_t^{\rho }H\left(t\right)={}_{t_0}{}^{RL}D_t^{\rho }H\left(t\right)-\sum _{j=0}^{m-1}{\displaystyle \frac{H^{\left(j\right)}\left(t_0\right)}{\Gamma (1+j-\rho )}}{(t-t_0)}^{j-\rho }.$$

(11)

If $H^{\left(j\right)}\left(t_0\right)=0$ for $j=0,1,\dots ,m-1$, then

$${}_{t_0}{}^{GL}D_t^{\rho }H\left(t\right)={}_{t_0}{}^{RL}D_t^{\rho }H\left(t\right)={}_{t_0}{}^{C}D_t^{\rho }H\left(t\right).$$

Proof. 

For a comprehensive proof, see [32]. □

From Theorem 1, if $H^{\left(j\right)}\left(t_0\right)=0$; $j=0,1,\dots ,m-1$, then

$${}_{t_0}{}^{GL}D_t^{\alpha }H\left(t\right)={}_{t_0}{}^{RL}D_t^{\alpha }H\left(t\right)={}_{t_0}{}^{C}D_t^{\alpha }H\left(t\right).$$

Applying the Taylor series expansion:

$$\overline{H}\left(t\right)=H\left(t\right)-\sum _{j=0}^{m-1}{\displaystyle \frac{H^{\left(j\right)}\left(t_0\right)}{\Gamma (1+j-\rho )}}{(t-t_0)}^{j-\rho },$$

then we obtain the following:

$${}_{t_0}{}^{GL}D_t^{\rho }H\left(t\right)={}_{t_0}{}^{RL}D_t^{\rho }H\left(t\right)={}_{t_0}{}^{C}D_t^{\rho }\overline{H}\left(t\right).$$

For simplicity, we define

$${}_{t_0}{}^{GL}D_t^{\rho }H\left(t\right)={}_{t_0}{}^{RL}D_t^{\rho }H\left(t\right)={}_{t_0}{}^{C}D_t^{\rho }H\left(t\right)=D_t^{\rho }H\left(t\right).$$

3. Proposed Algorithms (NAM)

In references [35,36,37], the authors introduced a recursive method utilizing generating functions to approximate fractional derivatives and integrals. In addition, they developed a flexible function construction strategy designed to enhance precision and is applicable to arbitrary values of p.

Definition 4

([37]). The n-order polynomial function is defined as

$$P_n\left(x\right)=\sum _{l=1}^n{\displaystyle \frac{1}{l}}{(1-x)}^l.$$

(12)

Theorem 2.

If $P_n\left(x\right)$ is a n-order polynomial, which can be written as

$$P_n\left(x\right)=\sum _{l=0}^n{P}_l{x}^l,$$

(13)

where $P_l$ solves the system:

$$\left(\begin{array}{ccccc}1& 1& 1& \dots & 1\\ 1& 2& 3& \dots & (p+1)\\ 1& 2^2& 3^2& \dots & {(p+1)}^2\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ 1& 2^n& 3^n& \dots & {(n+1)}^n\end{array}\right)\left(\begin{array}{c}{P}_0\\ P_1\\ P_2\\ ⋮\\ P_n\end{array}\right)=-\left(\begin{array}{c}0\\ 1\\ 2\\ ⋮\\ p\end{array}\right).$$

(14)

Proof. 

Ref. [34] By using Equations (12) and (13), we obtain the desired result:

$$\sum _{l=0}^n{P}_l{x}^l=\sum _{l=1}^n{\displaystyle \frac{1}{l}}{(1-x)}^l.$$

(15)

If $x=1$, then

$$\sum _{l=0}^n{P}_l=0.$$

(16)

Multiplying Equation (15) by x and differentiating gives

$$\sum _{l=0}^n(l+1)P_l{x}^l=\sum _{l=1}^n{\displaystyle \frac{1}{l}}{(1-x)}^l-x\sum _{l=1}^n{(1-x)}^{l-1}.$$

(17)

Setting $x=1$ in Equation (17) gives

$$\sum _{l=0}^n(l+1)P_l=-1.$$

Multiplying both sides of Equation (17) by x and differentiating gives

$$\sum _{l=0}^n{(l+1)}^2{P}_l{x}^l=\sum _{l=1}^n{\displaystyle \frac{1}{l}}{(1-x)}^l-3x\sum _{l=1}^n{(1-x)}^{l-1}+x^2\sum _{l=2}^n{\displaystyle \frac{1}{l-1}}{(1-x)}^{l-2}.$$

(18)

By substituting $x=1$, then

$$\sum _{l=0}^n{(l+1)}^2{P}_l=-2.$$

Repeating this process, we obtain

$$\begin{array}{cc}& P_0+P_1+P_2+\cdots +P_n=0,\hfill \\ & P_0+2P_1+3P_2+\cdots +(p+1)P_n=-1,\hfill \\ & P_0+2^2{P}_1+3^2{P}_2+\cdots +{(p+1)}^2{P}_n=-2,\hfill \\ & ⋮\hfill \\ & P_0+2^n{P}_1+3^n{P}_2+\cdots +{(p+1)}^n{P}_n=-p.\hfill \end{array}$$

Let $P_n\left(x\right)={\sum }_{l=0}^n{P}_l{x}^l$ be a real polynomial of degree at most n. We want to determine the coefficients $P_0,P_1,\dots ,P_n$ such that the following identities hold:

$$\sum _{l=0}^n{(k+1)}^l{P}_l=-k,\mathrm{for}k=0,1,2,\dots ,n.$$

These equations are obtained by evaluating the polynomial $P_n\left(x\right)$ at $x=k+1$ and requiring

$$P_n(k+1)=-k.$$

So, for each $k=0,1,\dots ,n$, we impose

$$\sum _{l=0}^n{P}_l{(k+1)}^l=-k.$$

This leads to the linear system:

$$\left(\begin{array}{ccccc}1& 1& 1& \cdots & 1\\ 1& 2& 2^2& \cdots & 2^n\\ 1& 3& 3^2& \cdots & 3^n\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ 1& (p+1)& {(p+1)}^2& \cdots & {(p+1)}^n\end{array}\right)\left(\begin{array}{c}{P}_0\\ P_1\\ P_2\\ ⋮\\ P_n\end{array}\right)=-\left(\begin{array}{c}0\\ 1\\ 2\\ ⋮\\ p\end{array}\right).$$

This proves that the coefficients $P_l$ are the unique solution to the above system. No generating function, asymptotic identity, or unjustified assumption was used. The result is purely derived from evaluating the polynomial at selected points and constructing a solvable linear system. □

Definition 5.

The generating function $P_n^{\left(\rho \right)}\left(x\right)$ for the Grünwald-Letnikov derivative of order ρ is follows:

$$P_n^{\left(\rho \right)}\left(x\right)={(P_0+P_{1}x+\cdots +P_Q{x}^Q)}^{\rho }.$$

(19)

Theorem 3

([38]). If the generating function $P_n^{\left(\rho \right)}\left(x\right)$ is stated as follows:

$$P_n^{\left(\rho \right)}\left(x\right)=\sum _{l=0}^{\infty }{R}_l^{(\rho ,Q)}{x}^l.$$

(20)

The coefficients $R_l^{(\rho ,Q)}$ are computed recursively, as detailed below [38]:

$$\begin{array}{cc}\hfill R_0^{(\rho ,Q)}& =P_0^{\rho },l=0,\hfill \\ \hfill R_l^{(\rho ,Q)}& =-{\displaystyle \frac{1}{P_0}}\sum _{j=1}^Q{P}_j\left(1-{\displaystyle \frac{1+\rho }{l}}\right)R_{l-j}^{(\rho ,Q)},l=1,2,\dots ,\hfill \\ \hfill R_l^{(\rho ,Q)}& =0,l<0.\hfill \end{array}$$

(21)

Proof. 

For the proof, see [38].

By using Theorem 3, if

$$P_Q^{\left(\rho \right)}\left(x\right)=\sum _{l=0}^{\infty }{R}_l^{(\rho ,Q)}{x}^l.$$

(22)

where

$$\begin{array}{cc}\hfill R_l^{(\rho ,Q)}& =P_0,l=0,\hfill \\ \hfill R_l^{(\rho ,Q)}& =-{\displaystyle \frac{1}{P_0}}\sum _{i=0}^{l-1}\left(1-i{\displaystyle \frac{1+\rho }{l}}\right)P_i{R}_{l-i}^{(\rho ,Q)},l=1,2,\dots ,Q-1,\hfill \\ \hfill R_l^{(\rho ,Q)}& =-{\displaystyle \frac{1}{P_0}}\sum _{i=0}^Q\left(1-i{\displaystyle \frac{1+\rho }{l}}\right)P_i{R}_{l-i}^{(\rho ,Q)},l=Q,Q+1,Q+2,\dots ,\hfill \\ \hfill R_l^{(\rho ,Q)}& =0,l<0.\hfill \end{array}$$

(23)

□

With a $\rho$-order, and $P_Q^{\left(\rho \right)}\left(x\right)$, the $\rho$-order G-FD is as follows:

$${}_{t_0}{}^{GL}D_t^{\rho }H\left(t\right)=\underset{h\to 0}{lim}{\displaystyle \frac{1}{h^{\rho }}}\sum _{i=0}^{⌊{\displaystyle \frac{t-t_0}{h}}⌋}{R}_i^{(\rho ,Q)}H(t-ih).$$

(24)

Then,

$$D_t^{\rho }H\left(t\right)\approx {\displaystyle \frac{1}{h^{\rho }}}\sum _{j=0}^m{R}_j^{(\rho ,Q)}H(t-jh)={\displaystyle \frac{1}{h^{\rho }}}H\left(t_k\right)-{\displaystyle \frac{1}{h^{\alpha }}}\sum _{i=1}^m{R}_j^{(\rho ,Q)}H\left(t_{k-j}\right),$$

(25)

and ${lim}_{m\to \infty }{H}_m=D_t^{\rho }H\left(t\right)$.

Thus, system (1) is solved using an accurate numerical technique as follows:

$$\left\{\begin{array}{cc}\hfill x_1\left(t_k\right)& =h^{{\rho }_1}[-x_2\left(t_{k-1}\right)-x_3\left(t_{k-1}\right)]+x_1\left(0\right)-\sum _{j=1}^m{R}_j^{({\rho }_1,Q)}\left(x_1\left(t_{k-j}\right)-x_1\left(0\right)\right),\hfill \\ \hfill x_2\left(t_k\right)& =h^{{\rho }_2}[x_1\left(t_k\right)+a_1{x}_2\left(t_{k-1}\right)]+x_2\left(0\right)-\sum _{j=1}^m{R}_j^{({\rho }_1,Q)}\left(x_2\left(t_{k-j}\right)-x_2\left(0\right)\right),\hfill \\ \hfill x_3\left(t_k\right)& =h^{{\rho }_3}[a_2{x}_1\left(t_k\right)+x_1\left(t_k\right)|x_3\left(t_{k-1}\right)|-a_3{x}_3\left(t_{k-1}\right)]+x_3\left(0\right)-\sum _{j=1}^m{R}_j^{({\rho }_3,Q)}(x_3\left(t_{k-j}\right)-x_3\left(0\right)).\hfill \end{array}\right.$$

(26)

4. Dynamical Systems

This section considers the time-dependent dynamics of the system through an investigation of its dynamic characteristics. We apply bifurcation analysis and Lyapunov exponents to analyze the stability and chaotic regions of the system.

4.1. Bifurcations

Bifurcation from Figure 1 illustrates how a dynamical system is constructed from stable to chaotic as $\rho$ is raised towards 1. At higher values of $\rho$, over which there are main period-doubling bifurcations, the resulting chaos filling phase space out to the five-tuple probability distribution with these or equivalent unitary CSS appears as a dense and fractal-patterned region.

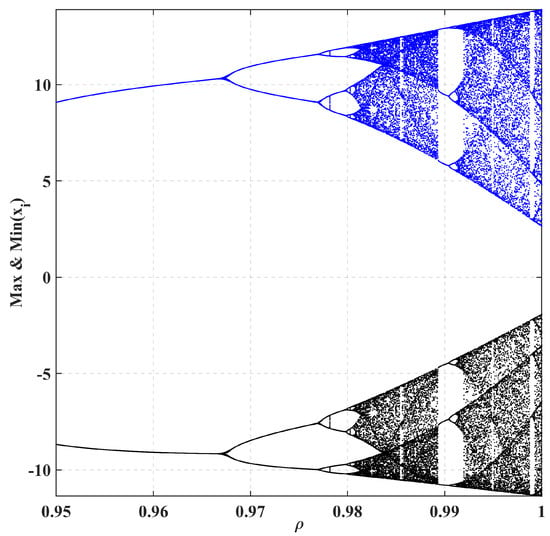
Figure 1. Bifurcation of system (1) using different values of $\rho$.

The fractal and intricate patterns produced when $\rho =1$ show the sensitivity of chaotic systems to infinitesimal changes in parameters and initial conditions. The diagram is used to illustrate how nonlinear mappings lead to chaos and how important parameter control is when trying to predict how a system will behave as time continues to evolve.

4.2. Lyapunov Exponents

The Lyapunov exponent (LE) is one of the key quantitative measures to determine the stability and chaotic dynamics of dynamical systems. It characterizes the average exponential rate of divergence or convergence of neighboring trajectories in the system’s phase space over time. A positive Lyapunov exponent is a signature of sensitive dependence on initial conditions and the existence of chaos, while a negative value signifies convergence to a stable attractor, and a zero value is characteristic of neutral or quasi-periodic dynamics. For an (n)-dimensional system, there are (n) exponents that form a Lyapunov spectrum, from which important properties such as system stability, dissipation, and the Kaplan–Yorke (fractal) dimension can be derived. The Lyapunov exponent is an effective tool to study complex, memory-dependent dynamical patterns.

Figure 2 and Figure 3 show the Lyapunov exponents (LEs) for three modes (LE1, LE2, and LE3) at varying values of $\rho =0.95$, $0.96$, and $0.97$ over time. When $\rho$ goes down, the LE2 and LE3 values tend to become negative, which means that these modes are moving from chaos to stability. On the other hand, LE1 stays positive or close to zero, which means that the behavior is still chaotic or only slightly stable. The results show how small changes in $\rho$ affect stability and chaotic behavior.

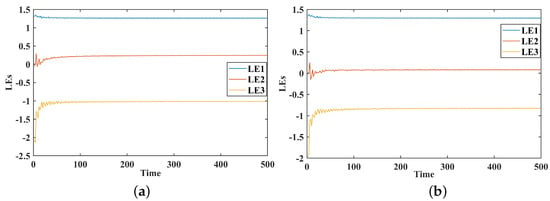
Figure 2. Lyapunov exponents in a dynamical system with Fractional Order (a) $\rho =0.95$, (b) $\rho =0.96$.

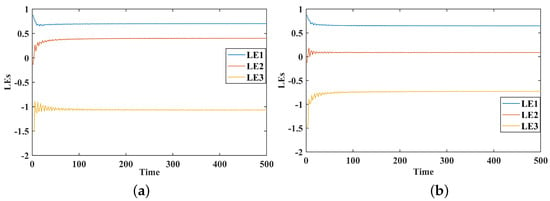
Figure 3. Lyapunov exponents in a dynamical system with Fractional Order (a) $\rho =0.97$, (b) $\rho =0.95$.

5. Numerical Simulations

In this section, we investigate the dynamic behavior of a system with parameters $[a_1,a_2,a_3]=[0.2,1.5,5.7]$ and p. Figure 4 gives periodic oscillations; the (b) panel corresponds to $p=[2.12,1.8,1]$ and reflects stable limit cycles, while the (a) panel corresponds to $p=[1,1,1]$ and presents the sensitivity according to amplitude and frequency changes. Figure 5 illustrates that the (b) panel equilibrates faster, while the (a) panel exhibits slower damping. The system is simulated with $[a_1,a_2,a_3]=[1.2,0.5,2.7]$; the (b) panel corresponds to $\rho =[0.12,0.98,1]$, while the (a) panel uses $\rho =[2,1,2]$. Figure 6 compares different parameter settings, the (b) panel ($p=[1.2,0.98,0.95]$) exhibits higher frequency and amplitude oscillations, whereas the (a) panel ($p=[0.91,0.87,1.1]$) shows lower amplitude oscillations with a simpler pattern.

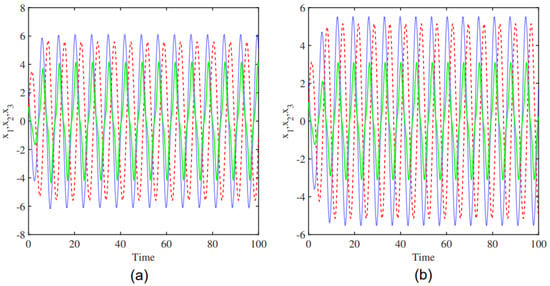
Figure 4. Time series with [$a_1$, $a_2$, $a_3$] = $[0.2,1.5,5.7]$: (a) $\rho =[1,1,1]$, (b) $\rho =[2.12,1.8,1]$.

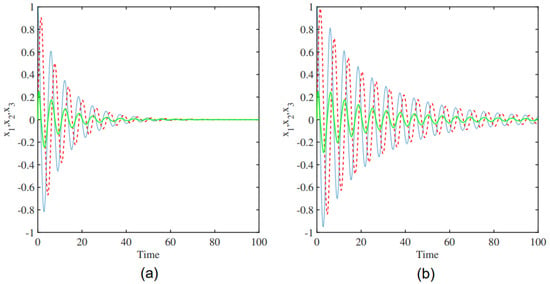
Figure 5. Time series with [$a_1$, $a_2$, $a_3$] = $[1.2,0.5,2.7]$: (a) $\rho =[2,1,2]$, (b) $\rho =[0.12,0.98,1]$.

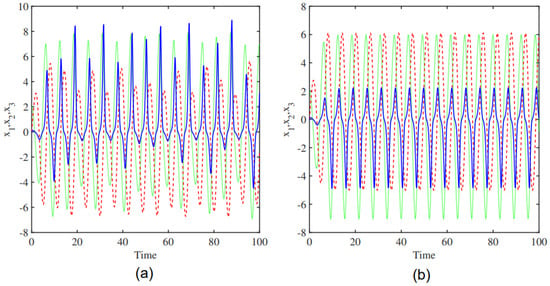
Figure 6. Time series with [$a_1$, $a_2$, $a_3$] = $[2.2,1.9,3.7]$: (a) $\rho =[0.91,0.87,1.1]$, (b) $\rho =[1.2,0.98,0.95]$.

Numerical simulations for different parameters $[a_1,a_2,a_3]$ and $\rho$ show several dynamic behaviors as obtained in the following Figure 7, Figure 8, Figure 9, Figure 10, Figure 11 and Figure 12.

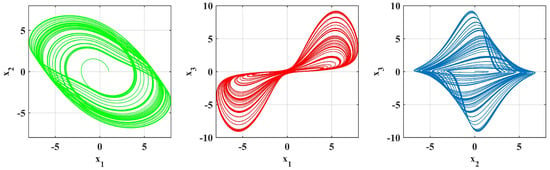
Figure 7. Simulation is performed with parameters [$a_1$, $a_2$, $a_3$] = $[0.2,1.5,5.7]$, $\rho =[0.99,0.93,0.91]$.

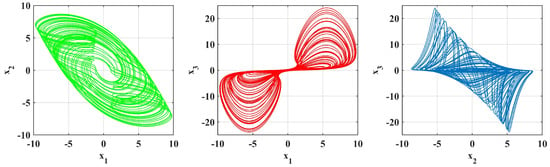
Figure 8. Simulation is performed with parameters [$a_1$, $a_2$, $a_3$] = $[0.3,1.5,5.7]$, $\rho =[0.95,1.03,0.98]$.

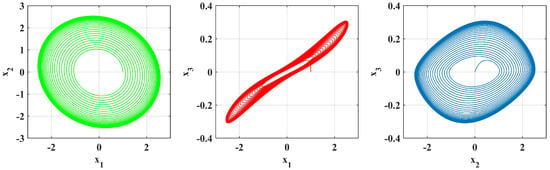
Figure 9. Simulation is performed with parameters [$a_1$, $a_2$, $a_3$] = $[0.7,0.5,5.1]$, $\rho =[1.95,1.93,1.98]$.

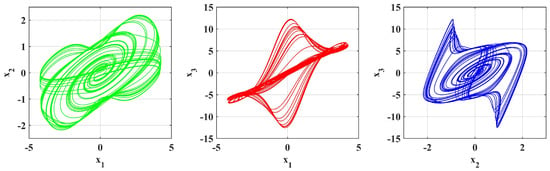
Figure 10. Simulation is performed with parameters [$a_1$, $a_2$, $a_3$] = $[0.5,0.5,3.7]$, $\rho =[2.5,2.3,2.8]$.

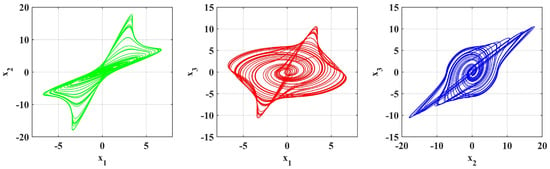
Figure 11. Simulation is performed with parameters [$a_1$, $a_2$, $a_3$] = $[0.4,1.4,4.7]$, $\rho =[0.99,1.03,1.08]$.

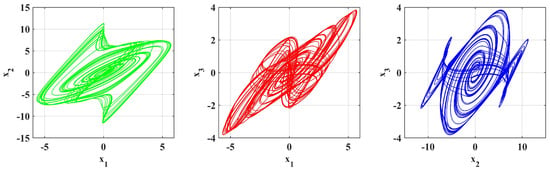
Figure 12. Simulation is performed with parameters [$a_1$, $a_2$, $a_3$] = $[1.3,1.5,5.4]$, $\rho =[1.95,1.89,0.97]$.

These extra simulations show that the system depends on parameters in different ways. As the parameters change, the system can have periodic orbits, chaotic attractors, and other 3D structures.

Figure 13 shows the new and complicated chaotic attractors of the chaos system given system (1). Simulations have been performed for the parameters $[a_1,a_2,a_3]=[1.3,1.5,5.4],$ $\rho =[2.97,2.99,2.99].$ Plots of projections of the chaotic attractor are shown on the $(x_1,x_2)$ plane (top-left), the $(x_1,x_3)$ plane, and the $(x_2,x_3)$ plane. The goal was to explore the sensitivity and memory effects created due to fractional derivatives and to demonstrate that the proposed methodology can capture these phenomena effectively. This procedure ensures that the parameters selected are typical representatives of the dynamic complexity of the system and the robustness of our numerical method.

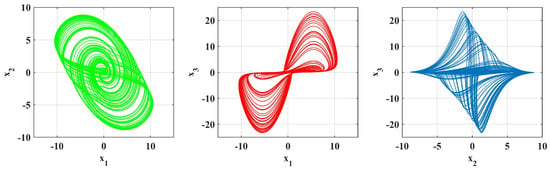
Figure 13. Simulation is performed with parameters [$a_1$, $a_2$, $a_3$] = $[1.3,1.5,5.4]$, $\rho =[2.97,2.99,2.99]$.

Fractional-Order Choas System

The simulation outcomes presented in Figure 14, Figure 15 and Figure 16 indicate the novelty of the developed system because they illustrate a richness of chaotic attractors obtained by various sets of parameters $a_1,a_2,a_3$ and $\rho$. The results shown in Figure 17, Figure 18 and Figure 19 demonstrate new and interesting dynamic phenomena that are caused by the (a) fractional parameters and system coefficients. These results also show the unusual effect of fractional-order derivatives on chaotic growth. For particular preset sets of parameters $a_1,a_2,a_3$ and orders $\rho =[{\rho }_1,{\rho }_2,{\rho }_3]$, the system shows complex attractors, biased trajectories, and regime changes between regular and chaotic motion, which are not seen in standard integer-order systems.

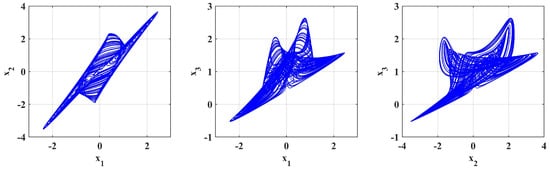
Figure 14. Simulation is performed with parameters [$a_1$, $a_2$, $a_3$] = $[5,12,10]$, $\rho =[0.9,1.02,1.27]$.

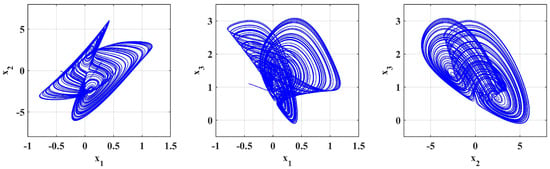
Figure 15. Simulation is performed with parameters [$a_1$, $a_2$, $a_3$] = $[3,1,5.1]$, $\rho =[0.9,1.18,1.38]$.

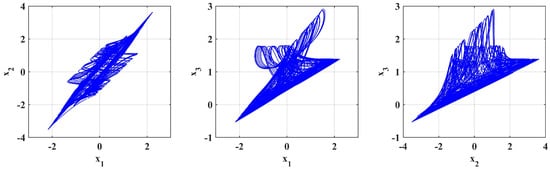
Figure 16. Simulation is performed with parameters [$a_1$, $a_2$, $a_3$] = $[1,5,1.5]$, $\rho =[1,1.17,1.28]$.

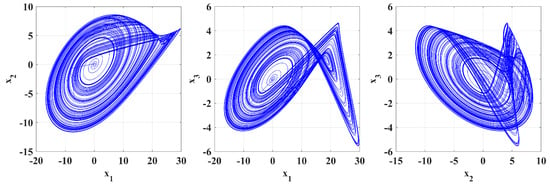
Figure 17. Simulation is performed with parameters [$a_1$, $a_2$, $a_3$] = $[1.93,1.8,1.01]$, $\rho =[0.91,0.97,1.28]$.

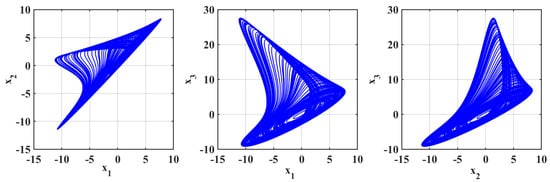
Figure 18. Simulation is performed with parameters [$a_1$, $a_2$, $a_3$] = $[0.3,5.2,1.5]$, $\rho =[0.9,1.97,1.98]$.

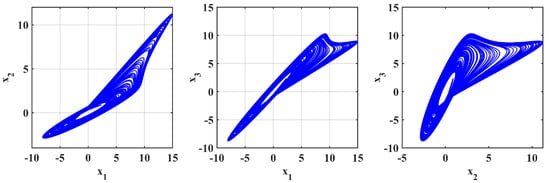
Figure 19. Simulation is performed with parameters [$a_1$, $a_2$, $a_3$] = $[1,2.1,0.5]$, $\rho =[1.2,1.99,0.96]$.

6. Application of Laplace Decomposition Method (LDM)

In this section, we present the following LDM algorithm given in [39] for the fractional-order chaotic system given by (1) within the Caputo fractional derivative.

Let $X_i\left(s\right)=L\left[x_i\left(t\right)\right],fori=1,2,3$. Applying the Laplace decomposition method to system (1), we obtain the following.

$$\left\{\begin{array}{cc}\hfill X_1\left(s\right)& ={\displaystyle \frac{x_1\left(0\right)}{s}}-s^{-{\rho }_1}L[x_2\left(t\right)+x_3\left(t\right)],\hfill \\ \hfill X_2\left(s\right)& ={\displaystyle \frac{x_2\left(0\right)}{s}}+s^{-{\rho }_2}L[x_1\left(t\right)+a_1{x}_2\left(t\right)],\hfill \\ \hfill X_3\left(s\right)& ={\displaystyle \frac{x_3\left(0\right)}{s}}+s^{-{\rho }_3}L[a_2{x}_1\left(t\right)+x_1\left(t\right)|x_3\left(t\right)|-a_3{x}_3\left(t\right)].\hfill \end{array}\right.$$

(27)

Using the given initial condition and operating the inverse Laplace transform of system (27), we obtained the following:

$$\left\{\begin{array}{cc}\hfill x_1\left(t\right)& =1-L^{-1}\left[s^{-{\rho }_1}L[x_2\left(t\right)+x_3\left(t\right)]\right],\hfill \\ \hfill x_2\left(t\right)& =L^{-1}\left[s^{-{\rho }_2}L[x_1\left(t\right)+a_1{x}_2\left(t\right)]\right],\hfill \\ \hfill x_3\left(t\right)& =L^{-1}[s^{-{\rho }_3}L[a_2{x}_1\left(t\right)+x_1\left(t\right)|x_3\left(t\right)|-a_3{x}_3\left(t\right)\left]\right].\hfill \end{array}\right.$$

(28)

Now, the LDM then represents a solution as an infinite series,

$$x_i\left(t\right)=\sum _{n=0}^{\infty }{x}_{in}\left(t\right),fori=1,2,3,$$

(29)

and the nonlinear terms are decomposed as

$$x_1\left(t\right)\left|x_3\left(t\right)\right|=\sum _{n=0}^{\infty }{N}_n\left(t\right),$$

(30)

where $N_n$ is the Adomain polynomial; for more details see [39].

Substituting Equations (29) and (30) into system (28) yields

$$\left\{\begin{array}{cc}\hfill \sum _{n=0}^{\infty }{x}_{1n}\left(t\right)& =1-L^{-1}[s^{-{\rho }_1}L[\sum _{n=0}^{\infty }{x}_{2n}\left(t\right)+\sum _{n=0}^{\infty }{x}_{3n}\left(t\right)]],\hfill \\ \hfill \sum _{n=0}^{\infty }{x}_{2n}\left(t\right)& =L^{-1}[s^{-{\rho }_2}L[\sum _{n=0}^{\infty }{x}_{1n}\left(t\right)+a_1\sum _{n=0}^{\infty }{x}_{2n}\left(t\right)]],\hfill \\ \hfill \sum _{n=0}^{\infty }{x}_{3n}\left(t\right)& =L^{-1}[s^{-{\rho }_3}L[a_2\sum _{n=0}^{\infty }{x}_{1n}\left(t\right)+\sum _{n=0}^{\infty }{N}_n\left(t\right)-a_3\sum _{n=0}^{\infty }{x}_{3n}\left(t\right)]].\hfill \end{array}\right.$$

(31)

With the following recursive formula given in [39], we obtain

$$x_{10}\left(t\right)=1,$$

$$x_{1n+1}\left(t\right)=-L^{-1}\left[s^{-{\rho }_1}L[x_{2n}\left(t\right)+x_{3n}\left(t\right)]\right],n\ge 0,$$

and

$$x_{20}\left(t\right)=0,$$

$$x_{2n+1}\left(t\right)=L^{-1}\left[s^{-{\rho }_2}L[x_{1n}\left(t\right)+a_1{x}_{2n}\left(t\right)]\right],n\ge 0,$$

and

$$x_{30}\left(t\right)=0,$$

$$x_{3n+1}\left(t\right)=L^{-1}\left[s^{-{\rho }_3}L[a_2{x}_{1n}\left(t\right)+N_n\left(t\right)-a_3{x}_{3n}\left(t\right)]\right],n\ge 0.$$

This gave the following:

$$x_{10}\left(t\right)=1,$$

$$x_{11}\left(t\right)=0,$$

$$x_{12}\left(t\right)=-{\displaystyle \frac{t^{{\rho }_1+{\rho }_2}}{\Gamma ({\rho }_1+{\rho }_2+1)}}-0.2{\displaystyle \frac{t^{{\rho }_1+{\rho }_3}}{\Gamma ({\rho }_1+{\rho }_3+1)}},$$

$$x_{13}\left(t\right)=-0.5{\displaystyle \frac{t^{{\rho }_1+2{\rho }_2}}{\Gamma ({\rho }_1+2{\rho }_2+1)}}-0.94{\displaystyle \frac{t^{{\rho }_1+2{\rho }_3}}{\Gamma ({\rho }_1+2{\rho }_3+1)}},$$

and

$$x_{20}\left(t\right)=0,$$

$$x_{21}\left(t\right)={\displaystyle \frac{t^{{\rho }_2}}{\Gamma ({\rho }_2+1)}},$$

$$x_{22}\left(t\right)=0.5{\displaystyle \frac{2t^{{\rho }_2}}{\Gamma (2{\rho }_2+1)}},$$

$$x_{23}\left(t\right)=-{\displaystyle \frac{t^{{\rho }_1+2{\rho }_2}}{\Gamma ({\rho }_1+2{\rho }_2+1)}}-0.2{\displaystyle \frac{t^{{\rho }_1+{\rho }_2+{\rho }_3}}{\Gamma ({\rho }_1+{\rho }_2+{\rho }_3+1)}}+0.25{\displaystyle \frac{t^{3{\rho }_2}}{\Gamma (3{\rho }_2+1)}},$$

and

$$x_{30}\left(t\right)=0,$$

$$x_{31}\left(t\right)=0.2{\displaystyle \frac{t^{{\rho }_3}}{\Gamma ({\rho }_3+1)}},$$

$$x_{32}\left(t\right)=-1.14{\displaystyle \frac{t^{2{\rho }_3}}{\Gamma (2{\rho }_3+1)}},$$

$$x_{33}\left(t\right)=-0.04{\displaystyle \frac{t^{{\rho }_1+2{\rho }_3}}{\Gamma ({\rho }_1+2{\rho }_3+1)}}-0.2{\displaystyle \frac{t^{{\rho }_1+{\rho }_2+{\rho }_3}}{\Gamma ({\rho }_1+{\rho }_2+{\rho }_3+1)}}+4.418{\displaystyle \frac{t^{3{\rho }_3}}{\Gamma (3{\rho }_3+1)}}.$$

Ultimately, this series solution can be expressed as

$$x_i\left(t\right)=\sum _{n=0}^{\infty }{x}_{in}\left(t\right),fori=1,2,3.$$

(32)

Table 1 displays the LDM solutions of system (1), when $[{\rho }_1,{\rho }_2,{\rho }_3]$ = $[1,1,1]$ and different values of t.

Table 1. Numerical findings for solving system (1) using LDM when parameters $[{\rho }_1,{\rho }_2,{\rho }_3]$ = $[1,1,1]$.

t	${\mathit{x}}_1\left(\mathit{t}\right)$	${\mathit{x}}_2\left(\mathit{t}\right)$	${\mathit{x}}_3\left(\mathit{t}\right)$
0	1	0	0
0.2	$0.976$	$0.19873$	$0.00957$
0.4	$0.904$	$0.38987$	$0.06057$
0.6	$0.784$	$0.5658$	$0.18641$
0.8	$0.616$	$0.71893$	$0.42053$
1	$0.4$	$0.84167$	$0.79633$

7. Numerical Solutions

By applying the numerical approximation method (NAM), which is the proposed method introduced in this article, and the Adams–Bashforth–Moulton (ABM), commonly used to solve ordinary differential equations, we present the solutions of system (1) for some parameter values and step sizes. Table 2 gives the solutions for $[{\rho }_1,{\rho }_2,{\rho }_3]=[1,1,1]$ at $t=1$, which shows that as the step size h becomes smaller, the numerical solution approaches the ABM benchmark. Similarly, Table 3 consolidates the solutions of $[{\rho }_1,{\rho }_2,{\rho }_3]=[0.98,0.99,1]$, depicting the same increasing trend toward closer approximation as the step decreases. Such findings highlight the effects of parameter adjustments and steps on the accuracy of the solution.

Table 2. Numerical findings for solving system (1) with parameters $[{\rho }_1,{\rho }_2,{\rho }_3]$ = $[1,1,1]$ for $t=1$.

h	${\mathit{x}}_1$	${\mathit{x}}_2$	${\mathit{x}}_3$
0.01	$-2.354122800700076$	$1.104844604472140$	$-0.165875871657015$
0.02	$-2.352658689648760$	$1.103443096816452$	$-0.165753906062924$
0.03	$-2.352170502803561$	$1.102976376005426$	$-0.165713217594248$
0.04	$-2.351926381113852$	$1.102743100343676$	$-0.165692867118208$
0.05	$-2.351779899330055$	$1.102603161502927$	$-0.165680654856076$
ABM	$-2.351776559284130$	$1.102609240290940$	$-0.165689240715236$

Table 3. Numerical findings for solving system (1) with parameters $[{\rho }_1,{\rho }_2,{\rho }_3]$ = $[0.98,0.99,1]$ for $t=1$.

h	${\mathit{x}}_1$	${\mathit{x}}_2$	${\mathit{x}}_3$
0.01	$-2.323690253009916$	$1.076151227278312$	$-0.161710454133959$
0.02	$-2.322206848722903$	$1.074786858047788$	$-0.161584733511023$
0.03	$-2.321712266139383$	$1.074332532825430$	$-0.161542798633966$
0.04	$-2.321464953623048$	$1.074105457428661$	$-0.161521825977763$
0.05	$-2.321423737882080$	$1.074970163704730$	$-0.161525551337436$

8. Validation of the Numerical Method

In this part, we make a comparison between the accuracy of NAM and ABM, and assess the impact of changing the step sizes in NAM. The error values in Table 4 demonstrate the numerical behavior of the methods. The first portion of the table shows the differences in errors between NAM and ABM. The results show that the changes in $\Delta x_1$, $\Delta y_1$, and $\Delta z_1$ are not very big for each time step. This means that NAM is just as accurate as ABM; thus, it may be used to solve differential equations quickly. As expected, the error values keep going up over time since numerical errors build up over time in iterative procedures.

Table 4. Comprehensive error comparison for different methods with $\alpha =1$.

	$\mathbf{\Delta }=|\mathbf{NAM}-\mathbf{ABM}$			$\mathbf{\Delta }=|{\mathbf{NAM}}_{0.01}-{\mathbf{NAM}}_{0.001}|$
$\mathit{t}$	$\mathbf{\Delta }{\mathit{x}}_{\mathbf{1}}$	$\mathbf{\Delta }{\mathit{y}}_{\mathbf{1}}$	$\mathbf{\Delta }{\mathit{z}}_{\mathbf{1}}$	$\mathbf{\Delta }{\mathit{x}}_{\mathbf{1}}$	$\mathbf{\Delta }{\mathit{y}}_{\mathbf{1}}$	$\mathbf{\Delta }{\mathit{z}}_{\mathbf{1}}$
0.10	5.59 $\times {10}^{-6}$	7.91 $\times {10}^{-7}$	2.27 $\times {10}^{-5}$	5.02 $\times {10}^{-5}$	7.03 $\times {10}^{-6}$	2.94 $\times {10}^{-4}$
0.15	3.22 $\times {10}^{-5}$	8.14 $\times {10}^{-6}$	2.46 $\times {10}^{-5}$	3.70 $\times {10}^{-5}$	9.40 $\times {10}^{-6}$	2.21 $\times {10}^{-4}$
0.20	2.01 $\times {10}^{-5}$	1.35 $\times {10}^{-6}$	1.91 $\times {10}^{-5}$	2.69 $\times {10}^{-5}$	1.12 $\times {10}^{-5}$	1.66 $\times {10}^{-4}$
0.25	2.23 $\times {10}^{-5}$	1.53 $\times {10}^{-6}$	1.21 $\times {10}^{-5}$	1.91 $\times {10}^{-5}$	1.27 $\times {10}^{-5}$	1.25 $\times {10}^{-4}$
0.30	1.14 $\times {10}^{-5}$	1.12 $\times {10}^{-6}$	1.33 $\times {10}^{-5}$	1.30 $\times {10}^{-5}$	1.38 $\times {10}^{-5}$	1.03 $\times {10}^{-3}$

The second part of the table gives the impact of step-size refinement in NAM, where errors are computed as discrepancies between solutions obtained using step sizes of $0.01$ and $0.001$. Halving the step size greatly lowers the error numbers, which shows that finer discretization makes things more accurate. Keep in mind that the values of $\Delta x_1$, $\Delta y_1$, and $\Delta z_1$ are very similar to the error trends in the comparison NAM–ABM, which shows that the approach is stable.

9. Discussion

In this work, the figures were drawn with the help of the package of MATLAB software (R2024a). We used two complementary methods to analyze the symmetric Rössler attractor in the context of fractional-order dynamics: the fractional Laplace decomposition method (LDM) and a modified numerical approximation method (NAM). It has been demonstrated that the long-memory and hereditary effects inherent in fractional-order systems are well captured by the NAM, which is based on a refined discretization of the Caputo derivative. Because of this, the approach is especially well suited to examining the transitions between periodic, quasi-periodic, and chaotic behaviors—transitions that are frequently understated when using coarse discretizations or integer-order models.

The applied relevance of LDM is also accentuated by the fact that it can give the same solutions at lower computational cost, particularly for researchers who want to develop the application of the technique to more complex systems. Time-series simulations, bifurcation diagrams, and Lyapunov exponent calculations are some of the numerical experiments used to measure how well the two methods capture the fine details of the system behavior.

The NAM and LDM comparative analysis demonstrates that both approaches support each other and increase trust in the results. LDM provides a more convenient way to approximate solutions that are consistent with other reliable methods, although NAM is especially useful for high-accuracy simulations of memory-driven phenomena. This dual validation increases the applicability of the suggested methods to a broad class of nonlinear fractional-order systems and highlights their dependability.

However, the innovation in the current study can be reinforced even more. Future research should focus on expanding the framework to recently developed fractional-order models [40,41,42,43] and comparing the effectiveness of NAM and LDM to more sophisticated numerical solvers and hybrid approaches [44,45,46], even though the analysis offers valuable information on the behavior of the symmetric Rössler attractor. In addition to increasing the precision and effectiveness of the methods, these studies will increase their applicability in biological systems, engineering, and physics.

In summary, the current work shows that NAM and LDM are useful, flexible, and complementary approaches for studying chaotic systems of fractional order. They offer a strong basis for future studies of intricate dynamical systems controlled by fractional derivatives by combining precision, ease of use, and computational viability.

10. Conclusions

In the current paper, it again confirms that both the fractional Laplace decomposition method (LDM) and the modified numerical approximation method (NAM) are efficient and reliable methods for the study of fractional-order chaotic systems. Their consistent and reliable nature in the representation of intricate memory-dependent dynamics of the symmetric Rössler attractor also increases their applicability to other areas. The established reliability, stability, and computational efficiency of these two alternative methods show that they can serve as sound frameworks for further studies of complex fractional-order models in most fields of science and engineering [40,41,42,43,44,46].