Supervised Focused Feature Network for Steel Strip Surface Defect Detection

Abstract

Accurate detection of strip steel surface defects is a critical step to ensure product quality and prevent potential safety hazards. In practical inspection scenarios, defects on strip steel surfaces typically exhibit sparse distributions, diverse morphologies, and irregular shapes, while background regions dominate the images, exhibiting highly similar texture characteristics. These characteristics pose challenges for detection algorithms to efficiently and accurately localize and extract defect features. To address these challenges, this study proposes a Supervised Focused Feature Network for steel strip surface defect detection. Firstly, the network constructs a supervised range based on annotation information and introduces supervised convolution operations in the backbone network, limiting feature extraction within the supervised range to improve feature learning effectiveness. Secondly, a supervised deformable convolution layer is designed to achieve adaptive feature extraction within the supervised range, enhancing the detection capability for irregularly shaped defects. Finally, a supervised region proposal strategy is proposed to optimize the sample allocation process using the supervised range, improving the quality of candidate regions. Experimental results demonstrate that the proposed method achieves a mean Average Precision (mAP) of 81.2% on the NEU-DET dataset and 72.5% mAP on the GC10-DET dataset. Ablation studies confirm the contribution of each proposed module to feature extraction efficiency and detection accuracy. Results indicate that the proposed network effectively enhances the efficiency of sparse defect feature extraction and improves detection accuracy.

1. Introduction

Strip steel occupies a pivotal position in industrial production and is widely used across global manufacturing sectors, including construction, automotive, machinery, and shipbuilding. However, various surface defects inevitably occur during the manufacturing and processing stages [1]. These defects not only affect the appearance of the product but also weaken its material properties, potentially leading to fatigue fractures and accelerated corrosion [2]. Therefore, achieving accurate detection of strip steel surface defects is essential to ensuring product quality, improving production efficiency, and implementing effective production management. Initially, surface defect detection relied on manual visual inspection, which was heavily influenced by subjective factors and exhibited low efficiency [3].

Early defect detection methods primarily relied on traditional image processing and machine learning techniques. A significant branch of this research treats defect detection as a texture analysis problem. Methods such as those utilizing Gabor filters [4] or wavelet transforms [5] focus on extracting handcrafted features that describe the defect’s texture. After feature extraction, supervised algorithms like Support Vector Machines (SVM) [6] are commonly employed for classification. This approach, consisting of texture analysis and a supervised classifier, offers the advantage of lower computational cost and can be effective for specific, well-defined defect types. However, the performance of such methods heavily depends on predefined feature extraction rules [7], which limits their robustness and adaptability in handling complex textures or variable lighting conditions.

In another approach, researchers combined image processing with fuzzy logic [8]. These techniques typically first use image processing to extract a set of quantitative features from a potential defect, such as area or contrast. These quantitative features are then subjected to fuzzification, where continuous input variables are mapped into fuzzy sets. Finally, classification is performed using a fuzzy inference system, which applies fuzzy logic rules—often derived from expert knowledge—to handle the uncertainty and ambiguity in defect classification. While this approach can effectively model the ambiguity in defect classification, its success is critically dependent on the manual definition of fuzzy sets and rules. This dependence makes it challenging to adapt to new defect types or changes in production conditions.

In recent years, deep learning has demonstrated significant advantages in tasks such as industrial image analysis, defect feature extraction, and recognition. Single-stage detection frameworks, represented by You Only Look Once (YOLO) series models [9], exhibit remarkable speed advantages. Two-stage detection architectures, such as Faster Region-based Convolutional Neural Networks (Faster R-CNN) [10], achieve higher detection accuracy in complex scenarios through Region Proposal Networks (RPN). Transformer-based detection models [11] leverage global modeling capabilities to capture long-range dependencies, demonstrating stronger robustness and multi-scale adaptability in complex scenarios.

However, strip steel surface defect detection presents unique challenges to deep learning methods. First, defect images are characterized by sparse defect distributions with high background proportions. As shown in Figure 1, background regions typically occupy the majority of strip steel images. Analysis of the NEU-DET dataset reveals that, in approximately 60% of images, defect regions account for no more than 40% of the total pixels. This high background proportion poses a major challenge: detection algorithms must accurately extract sparse target features amidst abundant background information while avoiding interference from background noise. Second, defect features are diverse and complex. Strip steel surface defects not only vary significantly in shape and size but also exhibit randomness in spatial distribution and frequency, often appearing as irregular patterns in local regions. This imposes higher requirements for precise localization and feature extraction capabilities.

To address these challenges, researchers have proposed various deep learning solutions, which can be broadly categorized by their primary strategies. One category focuses on enhancing feature representation and fusion to distinguish defects from the background. For example, EFD-YOLOv4 [12] and CABF-FCOS [13] utilize attention mechanisms and bidirectional feature fusion to suppress background noise. A second category aims to improve model accuracy by refining geometric properties or data characteristics, such as STD2 [14], which uses Deformable Pooling to adapt to defect shape variations, and FDFNet [15], which enhances defect-background contrast. A third category prioritizes efficiency through lightweight network design, as seen in LAACNet [16].

However, a fundamental limitation underlies all these approaches: whether they enhance features, refine geometry, or lighten the network, they still perform convolution operations indiscriminately across the entire image. This means substantial computational resources are wasted on processing vast, featureless background regions, which not only leads to inefficiency but also risks introducing redundant background noise that can interfere with the learning of sparse defect features.

In contrast to these strategies, this study approaches the problem of strip steel surface defect detection from a new perspective. Instead of indirectly mitigating the effects of background regions through post hoc feature fusion or attention, we introduce supervision signals directly into the core operational logic of the model. By integrating these signals into the feature extraction, region proposal, and deformable convolution processes, our method proactively forces the model to focus its computational resources only on regions of interest. This paradigm shift directly tackles the root cause of inefficiency and feature interference posed by high background-to-defect ratios. This design not only avoids wasteful computation on redundant backgrounds but also enhances the model’s ability to learn the sparse features of defects, thereby simultaneously improving both computational efficiency and detection accuracy. Based on the above analysis, this paper proposes a supervised focus feature network (SFF-NET) based on the Faster R-CNN framework. The main contributions of this paper are as follows:

(1) Design of the Supervised Convolutional Network (SCN): To address the issues of sparse defect regions and redundant background regions in strip steel images, SCN leverages constructed supervision signals to achieve selective feature extraction. This method focuses the feature learning process on target regions and their contextual signals, ensuring effective extraction of critical region features while optimizing computational efficiency. By skipping redundant computations in background regions, SCN effectively reallocates computational resources to defect-related areas. This not only improves efficiency but also enhances the model’s ability to learn from sparse, defect-critical regions.

(2) Design of the Supervised Region Proposal Strategy (SRPS): Considering the variability in the location, shape, and scale of strip steel surface defects, SRPS utilizes constructed supervision signals to optimize sample allocation during the feature learning process. This strategy ensures that each annotated box corresponds to at least one high-quality candidate region. By intelligently optimizing the candidate region assignment, SRPS reduces redundant computations during training while ensuring high-quality coverage of defect regions. This approach increases the diversity of positive samples, minimizes the introduction of redundant negative samples, and improves both the quality and efficiency of region proposals.

(3) Design and Implementation of the Supervised Deformable Convolutional Layer (SDCN): To handle the irregular shape characteristics of strip steel surface defects, SDCN integrates the supervision mechanism with deformable convolution. This approach maintains adaptability to irregular defect shapes while optimizing the computational range. By dynamically adjusting the sampling regions based on supervision signals, SDCN enhances the model’s ability to represent complex and irregular defect features. Additionally, it reduces computational costs by focusing operations on defect-relevant regions rather than the entire feature map and improves the model’s detection performance for irregular defects.

The remainder of this paper is organized as follows. Section 2 reviews and discusses the related work. Section 3 provides a detailed explanation of the architecture and functionality of the supervised focused feature model. Section 4 presents and evaluates the experimental results. Section 5 concludes the paper and outlines future research directions.

2. Related Work

In the field of steel strip surface defect detection, traditional methods [17,18,19,20] showed limited generalization capability in complex industrial scenarios. Deep learning, with its powerful automated feature extraction capabilities, has pushed detection technology into a new phase. This section systematically analyzes research progress from two aspects: feature extraction and computational efficiency optimization, and object localization and detection strategies.

2.1. Feature Extraction and Computational Efficiency Optimization

In steel strip surface defect detection, efficient and accurate feature extraction coupled with optimized utilization of computational resources is key to improving model performance. Current mainstream models primarily include CNN-based architectures such as Faster R-CNN, the YOLO series [21,22], and Single Shot MultiBox Detector (SSD) [23], as well as Transformer-based end-to-end detection models like DETR [24]. To address the limitations of these classical models in industrial scenarios, researchers have proposed various optimization methods.

To address the challenge of sparse defect distribution in steel strip images dominated by background regions, researchers have proposed various methods to enhance defect feature extraction capabilities. For instance, DSTEELNet [25] introduced dilated convolution and spatial pyramid pooling modules to expand the receptive field and enhance contextual information integration, effectively improving small object detection accuracy. TAFENet [26] further enhanced robustness against complex defects through a two-stage feature enhancement structure combined with residual spatial channel attention modules. Building upon YOLOv5, RDD-YOLO [27] incorporated Res2Net modules and dual feature pyramid networks to enhance feature reuse and semantic expression capabilities, while optimizing classification and regression tasks through decoupled head design.

To address the complexity and diversity in defect scales and shapes, researchers have focused on multi-scale feature extraction and fusion. YOLOv7-BA [28] combined sparse sampling with adaptive spatial feature fusion modules to enhance detection capabilities for fine-grained features and irregularly shaped defects. SA-FPN [29] reduced semantic gaps in multi-scale feature fusion through scale-aware attention guidance mechanisms and feature refinement modules. DsP-YOLO [30] achieved more efficient detection performance by enhancing local details and position information in Path Aggregation network feature paths. RT-DETR [31] proposed a hybrid encoder structure based on the Transformer architecture, significantly improving small object detection accuracy by decoupling cross-scale feature fusion and within-scale feature interaction.

To address the demands for real-time detection in industrial applications, researchers have explored comprehensive lightweight design solutions. A lightweight detector [32] design was achieved through channel pruning methods, reducing redundant channels and improving inference speed. YOLOv8n improvements [33] further reduced model parameters and computational complexity by introducing lightweight cross-scale feature fusion modules and inverse residual modules. While these lightweight solutions improved model efficiency, they often required trade-offs in detection accuracy.

The above research has achieved significant results in multi-scale feature extraction, attention mechanisms, and lightweight design for steel strip surface defect detection. Considering the characteristic of large uniform background areas in steel strip surface images, there remains room for further exploration in optimizing computational resource allocation for these low-information background regions while maintaining detection accuracy. This motivates us to explore new optimization solutions from the perspective of computational resource allocation.

2.2. Object Localization and Detection Strategies

Object localization and detection strategies are core components in steel strip surface defect detection, directly affecting detection accuracy and robustness. Existing methods primarily fall into two categories: Anchor-based and Anchor-free approaches, with recent research also exploring Transformer-based methods. Anchor-based methods, represented by Faster R-CNN, generate candidate regions through preset anchor boxes, combining IoU for positive and negative sample division in classification and regression tasks. To optimize boundary box quality, Cascade R-CNN [34] gradually increased IoU thresholds through multi-stage cascade structures, effectively improving detection accuracy for complex-shaped defects. GIoU [35] further improved boundary box regression accuracy by introducing minimum enclosing rectangles. Although these improvements enhanced detection performance to some extent, IoU-based allocation strategies often lead to sample imbalance issues when handling diverse steel strip surface defects.

In contrast, Anchor-free methods eliminate complex anchor box design, directly localizing targets through key points or center points, simplifying framework design. For example, an efficient anchor-free defect detector [36] proposed dynamic receptive field allocation and task decoupling mechanisms, improving localization and classification accuracy through feature reorganization and task alignment, showing excellent performance particularly in complex-shaped defect detection. However, Anchor-free methods still show limitations in small object localization accuracy without scale prior information. Transformer-based FC-DETR [37] optimized sample allocation quality and improved detection accuracy through foreground supervision modules and cascade hybrid matching strategies. However, the high computational complexity and training instability of Transformer models still pose significant challenges for their application in industrial scenarios.

The above research demonstrates that different object localization and detection strategies have their unique characteristics. Considering the diversity in steel strip surface defect shapes and scales, as well as the redundant computation issues in areas with limited information, there remains room for further exploration in developing more reasonable sample allocation mechanisms that better adapt to various defect features.

3. Supervised Focused Feature Network

Our proposed SFF-Net model is based on the Faster R-CNN architecture. As shown in Figure 2, SFF-Net consists of three key components: a backbone based on Residual Network (ResNet50) [38] and Feature Pyramid Network (FPN) [39], an RPN, and a head. During the training phase, the backbone incorporates Supervised Convolution (SCN), enabling the model to naturally focus on local features within supervised ranges, reducing computational cost on redundant background areas and improving training efficiency. Additionally, Supervised Deformable Convolution (SDCN) is introduced to ResNet50. By implementing dynamic sampling within supervised ranges, SDCN enhances the model’s global feature extraction capability for complex defect shapes. In the RPN, our proposed Supervised Region Proposal Strategy (SRPS) utilizes supervised ranges to directly guide sample allocation for candidate regions, improving both the quality and efficiency of region proposals. These supervised operations are implemented based on constructed supervision regions, achieving precise focus in feature extraction and region proposal, enhancing the model’s training efficiency and detection performance.

3.1. Supervised Range Acquisition

Supervised range acquisition serves as a fundamental component of SFF-NET, directly impacting the effectiveness of subsequent supervised convolution operations and sample allocation by precisely defining focus areas for feature extraction and sample assignment. To balance contextual information with computational efficiency while avoiding potential feature information loss during training, we design a method for obtaining supervised ranges based on the characteristics of strip steel defect images. This method includes the acquisition of key supervised range and RPN-compatible supervised ranges, aimed at reducing redundant computations and improving feature extraction quality in critical areas.

The key supervised region aims to expand the annotated box area and introduce a suitable amount of contextual information, ensuring the integrity of target features. Specifically, for each bounding box $\mathrm{s}\in \mathrm{S}$ in the dataset S, the smallest base anchor box $\mathrm{b}\in B_a$ in the base anchor box set $B_a$, with dimensions $\left(w^{*},h^{*}\right)$ that exceed both the width and height of the target s, is selected. Using the center point $\left(C_x,C_y\right)$ of the bounding box as a reference, the expanded region $U\left(s\right)$ is generated. The final key supervised region ${Sup}_{key}$ is defined as follows:

$${Sup}_{key}=\left\{U\left(s\right) | \mathrm{s}\in \mathrm{S}\right\}$$

(1)

$$\left(w^{\mathrm{*}},h^{\mathrm{*}}\right)={}_{(\mathrm{b}\in B_a)}{}^{argmin}\left\{\left(\mathrm{w}\left(b\right),\mathrm{h}\left(b\right)\right) | ,\mathrm{w}(\mathrm{b})>\mathrm{w}(\mathrm{s})\wedge \mathrm{h}(\mathrm{b})>\mathrm{h}(\mathrm{s}),\forall \mathrm{s}\in \mathrm{S}\right\}$$

(2)

$$U\left(s\right)=\left(C_x-w^{*}/2,C_y-h^{*}/2,C_x+w^{*}/2,C_y+h^{*}/2\right)$$

(3)

where n denotes the number of bounding boxes, $w\left(·\right)$ and $h\left(·\right)$ represent width and height functions, respectively, $U\left(s\right)$ signifies the function used to update dimensions, and $w^{\mathrm{*}}$ and $h^{\mathrm{*}}$ represent the dimensions of the smallest anchor satisfying the conditions. To clearly illustrate the calculation process of ${Sup}_{key}$, Algorithm 1 presents its pseudocode.

Algorithm 1. Key supervised region acquisition
Input:	S: bounding boxes {s1, s2, …}; $B_a$: Predefined base anchor boxes {b1, b2, …}
Output:	${Sup}_{key}$(corresponding to Equation (1))
1	${Sup}_{key}$← ∅ ⟵ Initialize the result set
2	for each bounding box s in S do:
3	FoundAnchorDims ← null
4	for each anchor box b in $B_a$ do:
5	if width(b) > width(s) and height(b) > height(s) then:
6	FoundAnchorDims ← (width(b), height(b)) ⟵ Record the dimensions of b
7	break
8	end if
9	end for
10	(w*, h*) ← FoundAnchorDims ⟵ End of Equation (2)
11	if (w*, h*) is not null then:
12	$(C_x$$, C_y$) ← GetCenter(s) ⟵ Obtain the center point of current bounding box
13	$\mathrm{U} \leftarrow (C_x$$- \mathrm{w}*/2, C_y$$- \mathrm{h}*/2, C_x$$+ \mathrm{w}*/2, C_y$+ h*/2)
14	${Sup}_{key}$$\leftarrow {Sup}_{key}$∪ {U}
15	end if
16	end for
17	$\mathrm{return} {Sup}_{key}$

Since the RPN stage relies on anchors at fixed positions to generate candidate regions, and these anchors do not completely overlap with the bounding boxes, using only the key supervised region might lead to missing supervision signals. To ensure the proper functioning of supervised operations within the RPN module, the RPN-compatible supervised region ${Sup}_A$ is further determined.

$${Sup}_A=a_{max}\cup \mathrm{a}$$

(4)

$$a_{max}=\left\{{argmax}_{IoU(a, s)} | a \in A, s \in S \right\}$$

(5)

$$\mathrm{a}=\left\{\begin{array}{c}{a}_{sup}, \mathrm{IoU}(a,s)>T_{sup},a \in A, s \in S \\ \\ a_{bg}, \mathrm{IoU}(a,s)<T_{bg}, a \in A, s \in S\end{array}\right.$$

(6)

where $a_{max}$ indicates the anchor box that obtains the maximum IoU with ground truth box s, and a contains anchor box $a_{sup}$ meeting the positive sample threshold $T_{sup}$ and $a_{bg}$ meeting the negative sample threshold $T_{bg}$. Following the design of Faster R-CNN, we set $T_{sup}=0.7$ and $T_{bg}=0.3$, and the number of negative samples is set to three times the number of target boxes, with negative samples being randomly selected to maintain the diversity and balance between positive and negative samples during training. To clearly illustrate the calculation process of ${Sup}_a$, Algorithm 2 presents its pseudocode.

Algorithm 2. RPN-compatible supervised range acquisition
Input:	S: bounding boxes {s1, s2, …}; A: All predefined base anchor boxes {a1, a2, …}
Output:	${Sup}_a$ (corresponding to Equation (4))
1	${Sup}_A$← ∅ ⟵ Initialize RPN-compatible supervised region.
2	For each bounding box s in S do:
3	$a_{max}$← FindAnchorWithMaxIoU(s, A) ⟵ Select anchor with the maximum IoU for s.
4	${Sup}_A$$\leftarrow {Sup}_A$∪$\{a_{max}$} ⟵$\mathrm{Add}{a}_{max}$ as a positive sample to the supervised region.
5	For each anchor a in A do:
6	If a ≠ $a_{max}$ then:
7	$\mathrm{If} \mathrm{IoU}(\mathrm{a}, \mathrm{s}) > T_{sup}$ then AddToPositiveSamples(${Sup}_A$, a)
8	$\mathrm{If} \mathrm{IoU}(\mathrm{a}, \mathrm{s}) < T_{bg}$ then AddToNegativeSamples(${Sup}_A$, a)
9	End if
10	End for
11	End for
12	Return ${Sup}_A$⟵ Output the final RPN-compatible supervised range.

Finally, the supervised ranges are merged to obtain the comprehensive supervised range ${Sup}_{all}$.

$${Sup}_{all}={Sup}_{key}\cup {Sup}_A$$

(7)

This comprehensive supervised range ${Sup}_{all}$, encoded as sparse matrices throughout the model training process, provides explicit operational guidance for SCN, SDCN, and SRPS. This method strikes a balance between preserving key information and controlling computational complexity, thereby enhancing the efficiency and accuracy of subsequent processing. In the experimental section, the effectiveness of this method will be further analyzed and verified through ablation experiments.

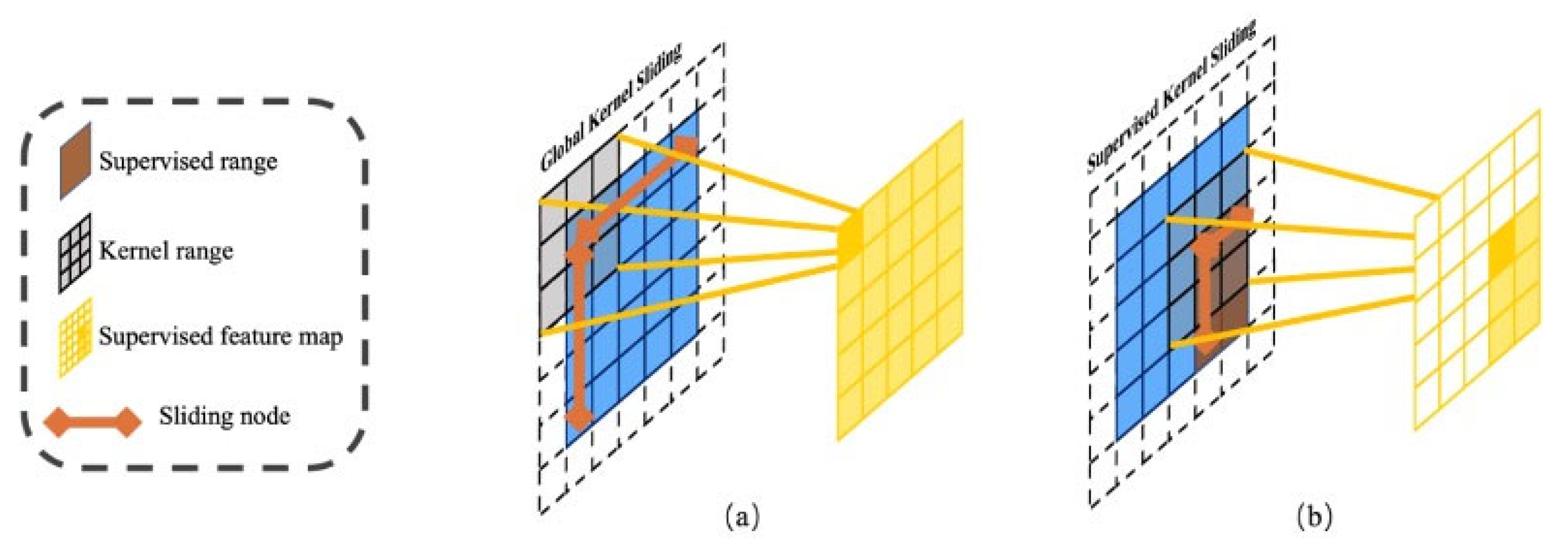
3.2. Supervised Convolutional Backbone Network Combined with Deformable Convolutions

Traditional convolution operations suffer from low computational efficiency when processing strip steel defect images, where background regions are extensive and highly similar. To address this characteristic, we introduce a supervision mechanism based on traditional convolution and propose SCN. SCN constrains convolution operations within the comprehensive supervised ranges ${Sup}_{all}$, avoiding redundant calculations on extensive similar background areas while concentrating computational resources on critical regions (defects and their surroundings) to optimize the model’s feature extraction capability and efficiency. A comparison between traditional convolution and supervised convolution is shown in Figure 3.

Traditional convolution operations utilize a fixed convolutional kernel to traverse all pixels of the input image in a left-to-right and top-to-bottom sequence. The definition of traditional convolution is as follows:

$$y\left(p_0\right)={\sum }_{p_n\in R} w\left(p_n\right)\cdot x\left(p_0+p_n\right)$$

(8)

where $p_0$ and $p_n$ represent the current point and its neighboring points, respectively, and $w\left(p_n\right)$ is the weight at $p_n$. R is the convolution kernel, i.e., the receptive field of x.

The definition of SCN is as follows:

$$y\left(p_0\right)=\left\{\begin{array}{cc}\sum _{{\mathrm{p}}_n\in \mathcal{R}} w\left({\mathrm{p}}_n\right)\cdot x(p_0+p_n)\hfill & \mathrm{i}\mathrm{f} {\mathrm{p}}_0\in {Sup}_{all}\hfill \\ 0\hfill & \mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}\hfill \end{array}\right.$$

(9)

where $p_0$ is the current convolution center position. If $p_0$ falls within the supervised range ${Sup}_{all}$, then convolution is performed. Otherwise, this position is skipped, and the process continues to evaluate the next position. The core concept of supervised convolution lies in restricting convolution operations within the supervised range ${Sup}_{all}$, skipping redundant computations in background regions to optimize computational efficiency and feature extraction capability. Compared to traditional convolution that traverses the entire feature map point by point, SCN more efficiently focuses on target region features by incorporating task-specific supervised range designs. For a clearer illustration of the SCN’s operational mechanism, the computational process defined in Equation (9) is detailed as pseudocode in Algorithm 3.

Algorithm 3. Supervised Convolution Process
Input	X(Input feature map), W(Convolution kernel weights), ${Sup}_{all}$
Output	Y(Output feature map)
1	Y ← InitializeZeroFeatureMap(ExpectedOutputDimensions)
2	for each position $p_0$ in the output map Y do:
3	if the center position $p_0$∈${Sup}_{all}$ then:
4	InputPatch ← GetReceptiveFieldRegion(X, center = $p_0$, size = KernelSize(W))
5	$\mathrm{Y}[p_0$$] \leftarrow \mathrm{E}\mathrm{l}\mathrm{e}\mathrm{m}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{W}\mathrm{i}\mathrm{s}\mathrm{e}\mathrm{M}\mathrm{u}\mathrm{l}\mathrm{t}\mathrm{i}\mathrm{p}\mathrm{l}\mathrm{y}\mathrm{A}\mathrm{n}\mathrm{d}\mathrm{S}\mathrm{u}\mathrm{m}(\mathrm{I}\mathrm{n}\mathrm{p}\mathrm{u}\mathrm{t}\mathrm{P}\mathrm{a}\mathrm{t}\mathrm{c}\mathrm{h},\mathrm{W})$← Perform standard convolution
6	end if
7	end for
8	return Y

When dealing with irregular defects, traditional convolution may lead to insufficient extraction of target features when dealing with irregular defects due to its fixed-shaped kernel. Deformable convolution transforms the fixed-shape convolution process into a variable convolution process that can adapt to the shape of the object, making it suitable for irregular defect detection [40]. The deformable convolution can be described as follows:

$$y\left(p_0\right)={\sum }_{p_n\in R} w\left(p_n\right)\cdot x\left(p_0+p_n+\mathsf{\Delta }{p}_n\right)$$

(10)

where $\mathsf{\Delta }{p}_n$ represents the predicted offset, obtained through a dedicated convolution layer.

To simultaneously achieve adaptive feature extraction and computational efficiency optimization, we combine the supervision mechanism with deformable convolution, proposing SDCN. The supervision mechanism ensures that deformation operations occur only in critical regions. The definition is as follows:

$$y\left(p_0\right)=\left\{\begin{array}{cc}\sum _{p_n\in R} w\left(p_n\right)\cdot x\left(p_0+p_n+\mathsf{\Delta }{p}_n\right), \hfill & \mathrm{i}\mathrm{f} p_0\in Su{p}_{\mathrm{all} }\hfill \\ 0,\hfill & \mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}\hfill \end{array}\right.$$

(11)

However, SDCN ensures that all deformation operations occur strictly within the supervised region $Su{p}_{\mathrm{all} }$. Specifically, after the model predicts the offset $\mathsf{\Delta }{p}_n$, the final sampling point $p_0+p_n+\mathsf{\Delta }{p}_n$ is checked to ensure it lies within $Su{p}_{\mathrm{all} }$. If the sampling point $p_0+p_n+\mathsf{\Delta }{p}_n$ falls outside the supervised region $Su{p}_{\mathrm{all} }$, it is clipped back to the nearest boundary of $Su{p}_{\mathrm{all} }$. This ensures that deformation operations remain focused on critical regions, while avoiding unnecessary sampling outside the supervised area.

SDCN is incorporated at the end of Stage 3, Stage 4, and Stage 5 modules in the backbone network. All parameters in the normal convolution layer are obtained from the training process of the whole detector. This multi-scale feature extraction strategy enables the model to simultaneously acquire target feature information at different resolutions, effectively enhancing the detection capability for defects of different scales.

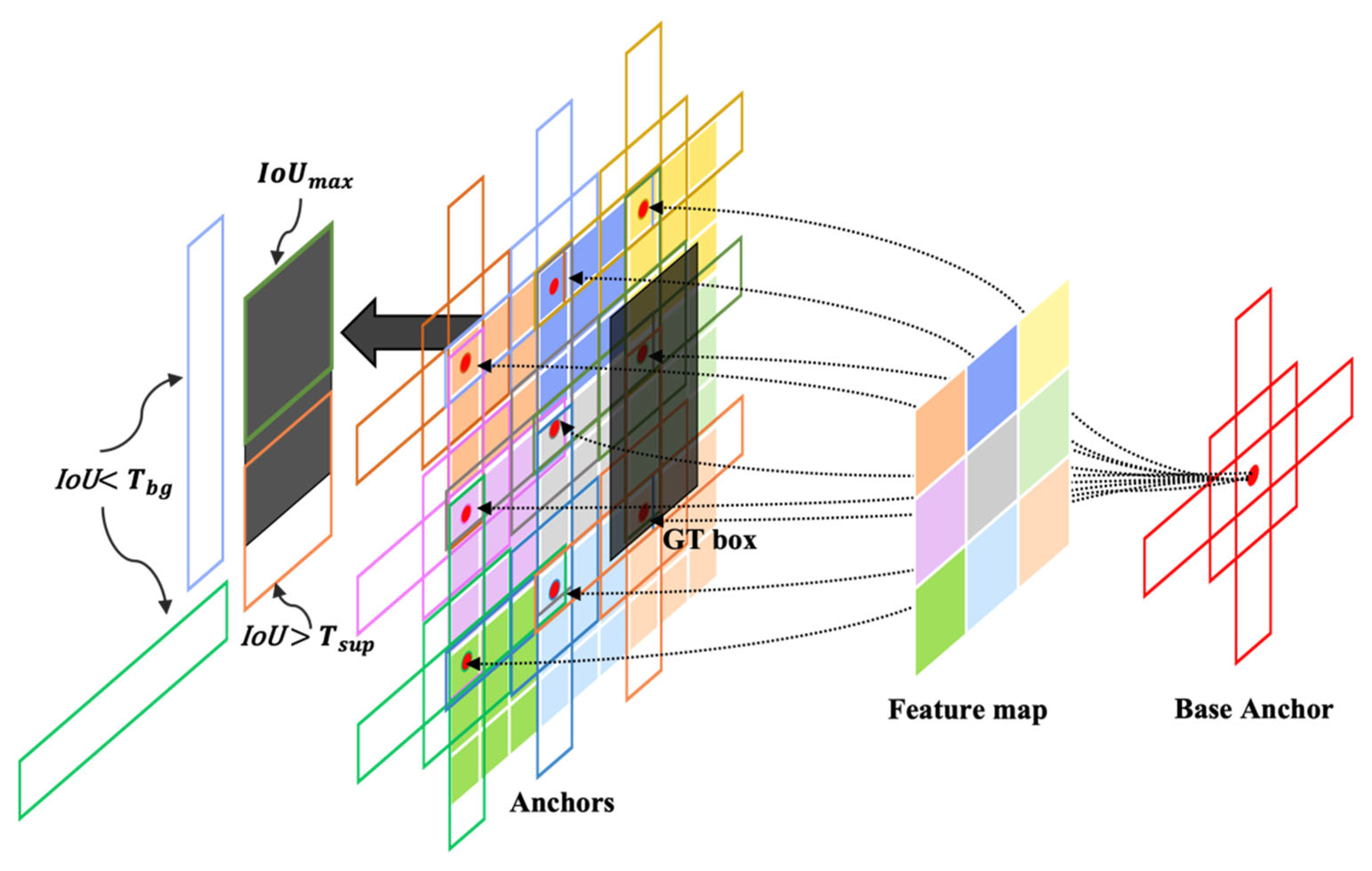
3.3. Supervised Region Proposal Strategy

In object detection tasks, high-quality region proposals are crucial for robust detection performance. RPNs primarily rely on the IoU between candidate regions and bounding boxes to allocate positive and negative samples. However, this method faces two major issues in strip defect detection scenarios. First, a significant amount of computational resources is wasted due to the repeated computation of IoU for anchor boxes in background regions during each training iteration. Second, limited by the IoU threshold, some small targets or special shaped targets may not be correctly allocated as positive samples, thus affecting the detection effect. To address these challenges, as shown in Figure 4, we propose an SRPS that specifically optimizes the RPN sample allocation process, effectively saving computational resources and improving allocation efficiency.

In conventional RPN, complete sample allocation is performed during each training iteration.

$$A_c=\left\{\begin{array}{cc}1\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} \hfill & \mathrm{i}\mathrm{f} \mathrm{IoU}(a,s)>T_{\mathrm{pos}}\hfill \\ 0\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em} \hfill & \mathrm{i}\mathrm{f} \mathrm{IoU}(a,s)<T_{\mathrm{neg}}\hfill \\ \mathrm{i}\mathrm{g}\mathrm{n}\mathrm{o}\mathrm{r}\mathrm{e}\mathrm{d}\hfill & \mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e} \hfill \end{array}\right.$$

(12)

where $T_{pos}$ and $T_{neg}$ denote the IoU thresholds for positive and negative samples, respectively. This approach not only incurs high computational costs but may also overlook some valuable potential samples.

By contrast, SRPS optimizes the RPN sample allocation strategy by utilizing the supervision range ${Sup}_A$ obtained in Section 3.1, which is compatible with the RPN stage, for sample allocation. ${Sup}_A$ includes the anchor box $a_{max}$ with the highest IoU for each ground truth box, anchor boxes $a_{sup}$ meeting the positive sample criteria, and proportionally selected negative sample anchor boxes $a_{bg}$. This pre-computed sample allocation process can be represented as:

$$A_c=\left\{a\mid a\in {Sup}_A\right\}$$

(13)

where $A_c$ denotes the set of samples involved in training, and a denotes the anchor boxes that meet the conditions.

Through this optimization of RPN sample allocation strategy, SRPS effectively eliminates the need for repetitive IoU computation during each training iteration, reducing computational overhead in the RPN stage. Meanwhile, this pre-computed deterministic allocation mechanism ensures that each ground truth box has at least one anchor box with maximum IoU as a positive sample, and enhances sample diversity through reasonable sampling strategies.

By integrating the above supervisory operations, the model achieves efficient feature learning. Algorithm 4 provides a step-by-step overview of the complete training process for the proposed model, illustrating how the supervision mechanisms are integrated and interact across different stages.

Algorithm 4. SFF-Net Overall Training Process
Input	TrainingDataset, Anchors
Output	TrainedModel
1.	Model ← Initialize()
2.	SupervisionRrangesCache ← DataPreprocessing (TrainingDataset, Anchors) ← Apply Section 3.1 to acquire supervised ranges
3.	for each training epoch do:
4.	for each (image, ${image}_{id}$$, {GT}_{boxes}$) in (TrainingDataset) do:
5.	${Sup}_{all}$$, {Sup}_A$$\leftarrow \mathrm{SupervisionRrangesCache} [{image}_{id}$] ← Retrieve the supervised ranges for the current image
6.	Featuremaps ← Model.Backbone(image, ${Sup}_{all}$)  ← Apply Section 3.2 to extract features using SCN and SDCN.
7.	$\mathrm{proposals}, {RPN}_{Loss}$$\leftarrow \mathrm{Model}.\mathrm{RPN}(\mathrm{Featuremaps}, {Sup}_A$$, {GT}_{boxes}$)  ← Apply Section 3.3 to perform sample assignment and calculate the RPN loss.
8.	${Head}_{Loss}$← Model.Head(Featuremaps, proposals, ${GT}_{boxes}$)  ← Calculate the detection head loss
9.	${Total}_{Loss}$$\leftarrow {RPN}_{Loss}$+ ${Head}_{Loss}$
10.	$\mathrm{UpdateParameters}(\mathrm{Model}, {Total}_{Loss}$)
11.	end for
12.	end for
13.	TrainedModel ← Model
14.	return TrainedModel

4. Experiments

4.1. Dataset

NEU-DET dataset was collected from an actual hot-rolled strip steel production line [41]. As shown in Figure 5, this dataset includes six types of typical defects: Crazing (Cr), Inclusion (In), Patches (Pa), Pitted Surface (Ps), Rolled-in Scale (Rs), and Scratches (Sc). Each defect category contains 300 grayscale images with a resolution of 200 × 200 pixels, resulting in a total of 1800 images. The dataset preserves challenging factors from industrial production environments, such as lighting condition variations, ambient light interference, and high-speed motion blur effects. These characteristics effectively reflect real-world challenges in industrial inspection and can validate algorithm adaptability in complex scenarios.

GC10-DET dataset was also collected from actual industrial production lines [42]. The dataset comprises 2294 grayscale images with a resolution of 2048 × 1000 pixels, covering ten types of typical defects. As shown in Figure 6, these defects include Punching (pu), Welding Line (wl), Crescent Gap (cg), Water Spot (ws), Oil Spot (os), Silk Spot (ss), Inclusion (in), Roll Pit (rp), Crease (cr), and Waist Fold (wf). The dataset also preserves uncertainty factors from real production environments, such as uneven illumination, material surface reflectivity variations, motion blur, and operational condition differences. These characteristics make the GC10-DET dataset a true reflection of industrial production complexity, suitable for evaluating algorithm robustness and generalization capability in practical scenarios.

4.2. Implementation Details

The experimental framework for this study is implemented using PyTorch, with Python 3.8 as the programming language and PyTorch 1.7.1 as the deep learning framework version. The experiments are conducted on the open-source platform PyCharm 2021.3, running on an Ubuntu 18.04 operating system environment. The hardware configuration includes an Nvidia GeForce RTX 3090 GPU with 24 GB of VRAM. Five-fold cross-validation was employed to tune model hyperparameters and select the optimal model, with initial training parameters shown in

Table 1. Experimental environment and training strategies.

Training Parameters	Values
Optimizer	SGD
Batch size	16
Learning rate	0.001
Epochs	250
Momentum	0.9
Weight decay	1 × 10−4
Dataset split ratio	8:2 (train:test)

. The reported results represent the average performance over 5-fold cross-validation, ensuring the robustness of the evaluation.

Considering uncertainty factors in actual industrial environments such as lighting variations and motion blur, although both NEU-DET and GC10-DET datasets preserve complex characteristics from real industrial environments, a series of data augmentation strategies were still employed during training to further enhance model adaptability and robustness. These operations include horizontal flipping with 50% probability, random rotation within ±10°, random translation within ±10%, random brightness adjustment to simulate lighting variations, random noise addition, and random sharpening.

4.3. Evaluation Metrics

To comprehensively evaluate the model’s detection performance, multiple evaluation metrics were employed, with IoU = 0.5 set as the criterion for detection box validity. Specifically, a prediction is considered valid when the Intersection over Union (IoU) between the predicted box and the ground truth box exceeds 0.5. Based on this criterion, the following evaluation metrics were introduced:

$$\mathrm{Precision}(\mathrm{P}) ={\displaystyle \frac{TP}{TP+FP}}$$

(14)

$$\mathrm{R}\mathrm{e}\mathrm{c}\mathrm{a}\mathrm{l}\mathrm{l}(\mathrm{R}) ={\displaystyle \frac{TP}{TP+FN}}$$

(15)

where True Positive (TP) represents correctly predicted positive cases with IoU above the threshold, False Positive (FP) denotes negative cases with IoU above the threshold but incorrectly predicted, and False Negative (FN) indicates positive cases with IoU below the threshold that the model failed to predict correctly. To measure the overall detection accuracy across multiple categories, Mean Average Precision (mAP), the most commonly used comprehensive performance metric in object detection, was selected. It is defined as the mean of Average Precision (AP) across all categories:

$$mAP={\displaystyle \frac{\sum _{i=0}^n {{\int }_0^1 \mathrm{P}\left( \mathrm{Recall} \right) d\left( \mathrm{Recall} \right)}_i}{n}}$$

(16)

where $\mathrm{P}\left(\mathrm{Recall}\right)$ represents Precision as a function of Recall, and n denotes the total number of prediction categories. Additionally, F1-score was introduced as a supplementary metric to balance the relationship between Precision and Recall, defined as:

$$\mathrm{F}1\text{-}\mathrm{score}=2·{\displaystyle \frac{Precision·Recall}{\mathrm{P}\mathrm{r}\mathrm{e}\mathrm{c}\mathrm{i}\mathrm{s}\mathrm{i}\mathrm{o}\mathrm{n}+Recall}}$$

(17)

To comprehensively evaluate the model’s computational efficiency, additional efficiency metrics were introduced. Params represents the total number of model parameters, measuring the model’s scale. Floating Point Operations (FLOPs) measure computational complexity, indicating the number of floating-point operations required for one forward inference. Frames Per Second (FPS) and Inference Time assess the model’s real-time performance, where FPS indicates the number of images the model can process per second, and Inference Time represents the time required to process a single image. Finally, Training Time Per Component was recorded to quantify the optimization effect of each module on model efficiency.

4.4. Ablation Experiment

4.4.1. Impact of SRPS, SCN, and SDCN Modules

To comprehensively evaluate the contributions of each module in SFF-Net, we conducted a series of ablation experiments to quantify their individual and combined impacts on both detection performance and computational efficiency. These experiments were performed on the NEU-DET dataset, utilizing a Faster R-CNN framework with a ResNet50-FPN backbone as the baseline model.

Table 2. Performance of SPRN, SCN and SDCN.

Baseline	SRPS	SCN	SDCN	mAP	F1	P	R
√	-	-	-	75.3	81.4	77.4	85.9
√	√	-	-	75.9	82.3	77.9	87.2
√	√	-	√	77.4	83.7	79.6	88.3
√	√	√	-	79.5	85.0	80.8	89.6
√	√	√	√	81.2	86.1	82.1	90.5

presents the detection performance of SFF-Net with various module configurations, illustrating the individual and combined contributions of SRPS, SCN, and SDCN. The results highlight the improvements achieved by integrating these modules into the baseline model.

SRPS enhancing sample assignment. SRPS addresses the limitations of the standard RPN by ensuring that each ground truth box is assigned at least one anchor box with the maximum IoU. This mechanism effectively mitigates the issue of insufficient positive samples and imbalanced assignments, particularly in scenarios with sparse defects and high background-to-defect ratios. Compared to the baseline, SRPS improved mAP from 75.3% to 75.9% and F1-score from 81.4% to 82.3%, with Recall increasing from 85.9% to 87.2%. These improvements demonstrate the enhanced target capture capability provided by SRPS, ensuring more balanced and effective sample assignments.

SRPS + SDCN adapting to irregular defects. The integration of SRPS and SDCN further refines the model’s ability to localize irregular and complex defect morphologies. SDCN dynamically adjusts sampling locations within supervised regions, enhancing feature extraction for defects with variable shapes and sizes. Adding SDCN to SRPS increased mAP from 75.9% to 77.4% and F1-score from 82.3% to 83.7%, with Recall improving from 87.2% to 88.3%. These results validate SDCN’s role in complementing SRPS by providing adaptive sampling capabilities, particularly for challenging defect geometries.

SRPS + SCN enhancing feature discrimination. The Supervised Convolutional Network (SCN) leverages supervised regions to focus convolution operations on defect-relevant areas, effectively suppressing background noise. However, SCN inherently depends on SRPS to define these supervised regions, as its operations are confined to regions pre-selected by SRPS. Adding SCN to the baseline and SRPS configuration boosted mAP to 79.5% and F1-score to 85.0%, with Precision increasing from 77.9% to 80.8% and Recall from 87.2% to 89.6%. These results demonstrate SCN’s strength in improving feature discrimination and detection accuracy by concentrating on defect-relevant features.

Full integration of SRPS, SCN, and SDCN. When all three modules were integrated, the model achieved its highest performance with mAP reaching 81.2%, F1-score increasing to 86.1%, and Recall improving to 90.5%. These results highlight the complementary nature of SRPS, SCN, and SDCN: SRPS ensures effective sample assignment, SCN enhances feature discrimination, and SDCN adapts to irregular defects.

Table 3. Efficiency of SPRN, SCN and SDCN.

Baseline	SRPS	SCN	SDCN	Params (M)	FLOPs (G)	Inference Time (ms)	Training Time (min)
√	-	-	-	41.5	91.4	22.2	106
√	√	-	-	41.5	91.3	22.2	105
√	√	-	√	44.7	92.1	22.3	107
√	√	√	-	41.5	72.8	17.0	78
√	√	√	√	44.7	73.6	17.2	81

illustrates the computational efficiency of SFF-Net with different module configurations, highlighting the performance and computational costs improvements achieved by each module.

SRPS maintaining efficiency while optimizing sample assignment. The introduction of SRPS maintained the parameter count at 41.5 M and slightly reduced FLOPs to 91.3 G, while cutting training time by 1 min. This improvement reflects SRPS’s ability to optimize sample assignment mechanisms by focusing on supervised regions. By reducing redundant computations in the RPN stage, SRPS achieved these efficiency gains without compromising assignment accuracy or increasing computational overhead.

SRPS + SCN significant efficiency gains. The addition of SCN to the SRPS configuration brought notable computational benefits. SCN leverages supervised regions to skip redundant background calculations, making it particularly effective for strip steel defect detection tasks dominated by large, homogeneous backgrounds. SCN reduced FLOPs by 20%, shortened inference time by 24%, and decreased training time by 26% compared to the SRPS-only configuration. These improvements demonstrate SCN’s ability to reallocate computational resources to defect-relevant regions, significantly reducing redundancy and improving overall efficiency.

SRPS + SDCN balancing complexity and efficiency. The integration of SDCN with SRPS introduced a modest increase in computational cost, with parameters rising by 3.2 M and FLOPs by 0.8 G. Despite this, the inference time remained nearly unchanged at 22.3 ms, and training time increased marginally to 107 min. The additional complexity of deformable convolution operations was effectively managed by confining them to supervised regions. This limited the computational burden while enabling adaptive sampling for irregular defects. The performance improvements achieved by SDCN clearly outweighed its minor computational overhead, demonstrating its capability to balance accuracy and efficiency.

Full integration of SRPS, SCN, and SDCN. When all three modules were integrated, SFF-Net achieved the optimal trade-off between detection performance and computational efficiency. The parameter count increased to 44.7 M, and FLOPs reached 73.6 G, representing only a slight increase compared to the SCN-only configuration. The inference time remained low at 17.2 ms, and the training time increased slightly to 81 min, reflecting an effective balance between computational cost and accuracy. These results confirm that the combined impact of SRPS, SCN, and SDCN enables SFF-Net to deliver superior detection performance while maintaining computational efficiency. Compared to the baseline, SFF-Net achieved 19.5% reduction in FLOPs, 22.5% improvement in inference time, and 23.5% decrease in training time.

In conclusion, SFF-NET achieves both detection performance improvement and computational efficiency optimization through the synergistic effect of three key modules. SRPS optimizes sample assignment strategy to enhance target capture capability. SCN enables efficient computational resource utilization and improves feature representation accuracy. SDCN enhances modeling capability for irregular defects. Notably, these performance improvements were achieved while reducing computational overhead, fully demonstrating the effectiveness of supervision mechanisms in strip steel defect detection.

4.4.2. Role of Supervised Range

To comprehensively evaluate the impact of supervised range, this section compares three different size configurations: annotation size, supervised size, and larger size. The results are presented in

Table 4. Influence of supervised range size.

Range Size	Performance Metrics				Efficiency Metrics
	mAP	F1	P	R	FLOPs(G)	Inference Time (ms)	Training Time (min)
annotation size	79.5	84.5	80.9	88.4	72.9	16.4	79
supervised size	81.2	86.1	82.1	90.5	73.6	17.2	81
lager size	80.3	84.9	81.0	89.1	75.3	18.5	84

, examining the comprehensive effects of supervised range on model performance and computational efficiency through quantitative and qualitative analysis.

In terms of performance metrics, the choice of supervised range significantly impacts detection effectiveness. Compared to annotation size, using supervised size improved the model’s mAP from 79.5% to 81.2% and F1-score to 86.1%. Precision increased from 80.9% to 82.1%, and Recall from 88.4% to 90.5%, indicating that appropriate expansion of supervised range not only enhanced the model’s defect discrimination accuracy but also improved target capture capability. To verify the rationality of supervised range selection, we further experimented with larger size configuration. Results showed that excessive expansion of supervised range led to performance degradation, with mAP dropping to 80.3% and F1-score to 84.9%. Although still showing improvement over annotation size, it was notably inferior to the designed supervised range, confirming that supervised range requires precise control rather than simply being larger.

From a computational efficiency perspective, adjustments to supervised range produced varying impacts on computational resource consumption. Under annotation size, the model’s FLOPs were 72.9 G, with 16.4 ms inference time and 79 min training time. After adopting the designed supervised range, despite appropriately expanding the feature extraction range, FLOPs only increased by 0.7 G, inference time by 0.8 ms, and training time by 2 min, demonstrating this range expansion’s computational economy. However, with larger range, FLOPs increased to 75.3 G, inference time extended to 18.5 ms, and training time rose to 84 min, further confirming that excessive supervised range leads to unnecessary computational burden.

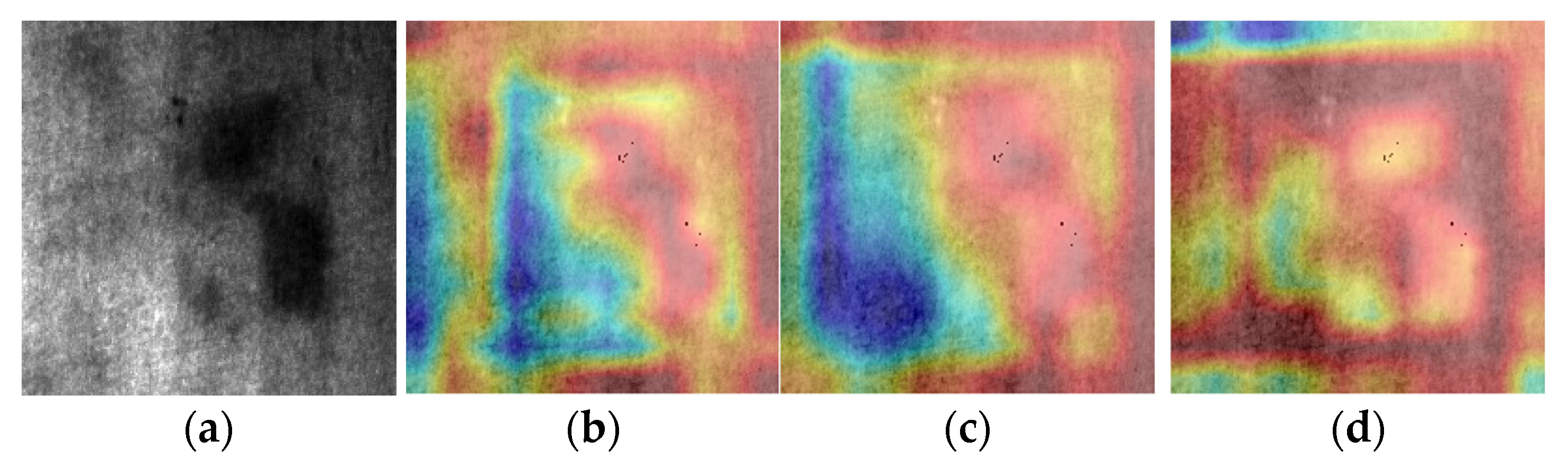
To intuitively understand the impact mechanism of different supervised ranges, Figure 7 displays the corresponding feature response heatmaps. Under annotation size configuration, heatmaps mainly concentrated on the defect area itself, lacking response to surrounding information. This limitation explains its lower detection performance. With the designed supervised range, heatmaps maintained strong responses to defect areas while including moderate contextual information, reflected in comprehensive performance improvement. Under larger range configuration, heatmaps showed overly dispersed features, validating that performance degradation might stem from redundant information interference.

In conclusion, supervised range design requires balance between feature extraction sufficiency and computational efficiency. Too small a range limits the model’s understanding of target context, while excessive range introduces irrelevant information and increases computational burden. Experimental results demonstrate that our proposed supervised range design method maintains computational efficiency while improving detection performance.

4.5. Comparison with Other Methods

To comprehensively evaluate the performance of SFF-Net, we compared it with a variety of classic one-stage and two-stage models, as well as advanced models incorporating attention mechanisms or Transformer structures, on the NEU-DET and GC10-DET steel surface defect datasets. These models include SSD, Cascade R-CNN, Deformable DETR, CABF-FCOS, RDD-YOLO, YOLOv7, YOLOv8n, DGYOLOv8, RT-DETR-R18, DsP-YOLO, and STD2. The comparison experiments focus on detection accuracy (performance on different defect categories), computational efficiency (FPS), and model complexity (parameters and FLOPs), with an emphasis on analyzing the adaptability and performance differences between SFF-Net and other models.

Performance comparison on NEU-DET dataset. As shown in

Table 5. Comparison of various detection algorithms on NEU-DET.

Method	AP%						mAP%	Params (M)	FLOPs (G)	FPS
	Cr	In	Pa	Ps	Rs	Sc
SSD	37.4	77.3	89.7	75.9	60.4	84.3	70.8	25.1	88.2	37.7
cascade R-CNN	41.3	78.6	93.9	92.4	63.9	91.9	77.0	71.1	271.8	59.0
Deformable DETR	26.4	66.0	73.7	67.1	39.1	78.1	58.4	39.8	204.9	34.5
CABF-FCOS	55.4	93.5	75.0	88.9	62.9	84.4	76.7	56.3	95.3	18.0
RDD-YOLO	52.9	85.9	94.4	86.2	70.7	96.6	81.1	57.0	145.6	57.8
YOLOv7	50.8	81.0	94.4	94.5	62.1	92.5	79.2	36.5	103.2	98.0
YOLOv8n	46.7	81.4	94.3	91.5	66.6	93.0	78.9	3.0	8.1	209.0
DGYOLOv8	85.0	90.0	94.1	99.5	84.1	94.4	91.2	5.0	11.7	40.7
RT-DETR-R18	47.9	78.7	96.0	91.4	67.6	94.2	79.3	19.9	55.4	163.0
DsP-YOLO	54.5	84.0	95.0	82.1	72.7	94.1	80.4	11.1	28.5	86.9
STD2	51.7	87.1	93.3	91.6	66.6	95.9	81.0	272.4	939.0	7.7
SFF-Net (Ours)	46.7	88.2	96.5	89.9	69.4	96.3	81.2 *	44.7	73.6	58.1

The asterisk (*) indicates that the improvement of our model over the Baseline is statistically significant (p < 0.05) via a Wilcoxon signed-rank test.

, SFF-Net achieved 81.2% mAP, outperforming most comparison models overall, particularly in handling large-scale defect categories with prominent features (e.g., Pa and Sc). Specifically, SFF-Net achieved 96.5% and 96.3% AP for the Pa and Sc categories, respectively, outperforming RDD-YOLO and DsP-YOLO, which incorporate advanced attention mechanisms. This performance improvement can be attributed to the SCN module’s ability to effectively focus on target regions and extract more discriminative features. By leveraging supervised mechanisms to optimize feature extraction, the SCN module significantly enhances detection precision. For defect categories with significant features (e.g., In and Ps), SFF-Net achieved APs of 88.2% and 89.9%, respectively, which, although slightly lower than CABF-FCOS’s performance on the In category, still maintains a high level overall. This indicates that SFF-Net has good generalization capability for medium-contrast defects with relatively prominent features.

However, for low-contrast defects or those with ambiguous textures (e.g., Cr and Rs), SFF-Net showed relatively weaker performance, achieving APs of 46.7% and 69.4%, which are lower than DsP-YOLO and DGYOLOv8. This gap highlights the limitations of SFF-Net in handling defects with low contrast or complex features. This may be due to the model’s supervised mechanisms lacking sufficient adaptability to complex backgrounds. For example, DsP-YOLO enhances attention to low-contrast regions via the CBAM module, while DGYOLOv8 incorporates a gated attention module (GAM) to improve feature selection for target regions. In comparison, SFF-Net lacks such specific optimizations in these scenarios, leading to relatively lower performance.

In terms of computational efficiency, SFF-Net achieved an inference speed of 58.1 FPS, significantly outperforming traditional two-stage models like Cascade R-CNN and high-complexity models like STD2. This demonstrates that SFF-Net effectively reduces unnecessary computational redundancy through the SCN module while maintaining high detection accuracy. Although SFF-Net’s speed is lower than that of lightweight models such as YOLOv8n, it achieved a 2.3% mAP improvement in overall detection performance, with particularly notable advantages in detecting complex defects. Additionally, SFF-Net’s parameter count is 44.7 M, and its FLOPs are 73.6 G, which are significantly lower than Cascade R-CNN and STD2. This demonstrates that SFF-Net achieves a better balance between performance and computational cost.

Performance comparison on GC10-DET dataset. As shown in

Table 6. Comparison of various detection algorithms on GC10-DET.

Method	AP%										mAP%	FPS
	Pu	wl	cg	ws	os	ss	in	rp	cr	wf
SSD	70.4	69.5	74.5	51.4	48.9	58.9	38.6	28.9	48.9	72.9	56.3	37.5
cascade R-CNN	99.0	91.2	95.2	77.6	64.2	63.9	35.2	27.7	26.9	86.2	66.7	51.0
Deformable DETR	91.7	94.3	94.2	82.5	64.5	57.8	20.5	26.4	45.5	72.5	65.0	34.4
CABF-FCOS	90.3	94.6	81.9	64.0	45.6	39.3	39.1	29.9	70.0	66.1	62.1	17.2
RDD-YOLO	96.8	95.8	98.6	87.2	69.2	70.1	35.9	49.5	58.9	89.4	75.1	57.5
YOLOv7	98.7	79.2	93.1	88.2	63.4	56.8	50.1	38.2	51.7	91.7	71.1	92.6
YOLOv8n	99.1	94.5	93.6	91.5	56.6	58.5	34.4	25.2	42.5	91.5	68.7	208.3
RT-DETR-R18	99.6	96.4	97.2	92.2	59.6	53.9	48.1	39.5	35.2	94.2	71.6	137.0
DsP-YOLO	96.7	92.5	98.7	70.8	66.5	58.5	23.0	79.9	94.5	81.6	76.3	85.4
STD2	99.5	51.7	99.0	80.5	65.4	65.8	45.6	41.1	75.2	100.0	72.4	8.4
SFF-Net (Ours)	91.9	84.9	99.1	69.2	70.1	65.3	30.5	42.4	79.9	91.6	72.5	56.0

, SFF-Net achieved 72.5% mAP, slightly lower than RDD-YOLO (75.1%) and DsP-YOLO (76.3%), but still superior to YOLOv8n (68.7%) and Cascade R-CNN (66.7%). Specifically, SFF-Net performed exceptionally well on categories with prominent features (e.g., cg and wf), achieving APs of 99.1% and 91.6%, respectively, validating its effectiveness in detecting defects with clear features. This strong performance can be attributed to the SDCN module’s adaptive feature extraction capability, which optimizes feature representation during detection and significantly enhances detection accuracy.

For defect categories with complex structures (e.g., os and cr), SFF-Net achieved APs of 70.1% and 79.9%, significantly outperforming RT-DETR-R18 (59.6% and 35.2%) and YOLOv8n (56.6% and 42.5%). This demonstrates SFF-Net’s strong adaptability in handling defect detection tasks with complex backgrounds and diverse morphologies. However, for extremely small or low-contrast defects (e.g., in and rp), SFF-Net achieved APs of 30.5% and 42.4%, which shows mixed results, while outperforming Cascade R-CNN and YOLOv8n on the rp category, it lags behind the specialized DsP-YOLO in the same category (42.4% vs. 79.9%). This limitation suggests that SFF-Net’s supervised mechanism still requires further optimization to improve its ability to capture fine details in extreme scenarios. In terms of computational efficiency, SFF-Net achieved an inference speed of 56.0 FPS, which, although slower than YOLOv8n (208.3 FPS), still maintains a good balance between accuracy and efficiency. Compared to RDD-YOLO and DsP-YOLO, SFF-Net demonstrates greater advantages in detecting complex defect categories, while also achieving competitive inference speed.

Visualization analysis. Figure 8 and Figure 9 show detection result comparisons between SFF-Net and other algorithms on NEU-DET and GC10-DET datasets. Results demonstrate SFF-Net’s stable detection capability on both datasets. For defects with prominent features, the model accurately localizes and classifies them, reliably detecting even low-contrast targets. For defects with complex backgrounds, while there’s room for improvement in localization precision, basic detection requirements are met. This performance characteristic mainly benefits from the synergistic effect of SCN and SRPN, enabling the model to focus on complete defect regions while effectively reducing interference from redundant background regions and extracting more accurate target features. The introduction of SDCN enhanced model adaptability to various defect morphologies. These results validate that supervised network design is suitable for strip steel defect detection scenarios with relatively uniform backgrounds but diverse defect features, ensuring effective feature extraction while improving detection accuracy.

4.6. Analysis of Failure Cases

Although SFF-Net significantly improves detection performance for most defect categories, its performance on small defects and low-contrast defects (e.g., Cr and Rs in the NEU-DET dataset, and in and rp in the GC10-DET dataset) is relatively weaker. Based on specific failure cases illustrated in Figure 10, the pink bounding boxes in the figure indicate the annotated bounding boxes. The limitations of SFF-Net are discussed in the following paragraphs.

First, for small-sized defects, consecutive downsampling operations excessively weaken their features on deeper feature maps, ultimately resulting in missed detections. For instance, As shown in Figure 10a, the isolated defects located far from the defect clusters are difficult for the model to distinguish from the background due to their small size and blurred boundaries, resulting in missed detections. Observing the sizes of defects in the failure cases, their long axis is often less than 10 pixels, a characteristic that is easily overlooked by detection networks. Second, for low-contrast defects, their boundary features are inherently weak and are further diluted during the convolution and downsampling processes, making it challenging for the model to extract sufficient discriminative features, which results in localization errors or missed detections. As shown in Figure 10b, these defects are difficult for the model to accurately identify due to their extremely low contrast with the background.

Furthermore, while the SCN and SDCN modules in SFF-Net restrict convolution operations to supervised regions, enabling the model to focus more on feature extraction in target areas, this supervision mechanism does not actively enhance the weak signals of small or low-contrast defects. Consequently, the model’s perception capability for these types of defects remains insufficient.

5. Conclusions

This paper proposes a detection network, SFF-Net, based on supervised feature extraction to address challenges in strip steel surface defect detection, such as sparse target distribution, large uniform background regions leading to redundant computations, and low learning efficiency. The network incorporates the Supervised Convolutional Network (SCN), which confines convolution operations to supervised regions, reducing computational redundancy and improving the model’s learning efficiency. This design also enables the model to focus on defect-related areas. The Supervised Deformable Convolutional Layer (SDCN) is designed to better handle irregularly shaped defects by adaptively adjusting sampling positions within supervised regions, enhancing the model’s ability to capture complex and diverse defect features while maintaining computational efficiency. Finally, the Supervised Region Proposal Strategy (SRPS) optimizes the sample allocation process to ensure high-quality candidate regions.

Experiments conducted on the NEU-DET dataset demonstrate that SFF-Net achieves competitive performance in defect detection while effectively reducing computational overhead. Compared to the baseline, SFF-Net improves the mAP by 5.9% and reduces FLOPs by 19.5%, highlighting its improvements in learning efficiency and accuracy. To evaluate the generalization capability of SFF-Net in strip steel surface defect detection, additional experiments are conducted on the GC10-DET dataset, where SFF-Net exhibits consistent performance, particularly for defects with prominent features. Therefore, SFF-Net provides an effective solution for strip steel surface defect detection.

Despite its advantages, SFF-Net shows weaker performance on small and low-contrast defects, as observed in the Cr and Rs categories of the NEU-DET dataset and the in and rp categories of the GC10-DET dataset. This limitation arises from the dilution of small-scale and low-contrast features in deep feature maps and the inability of the SCN module to actively enhance weak signals. To address these limitations, future research will explore the integration of attention mechanisms or feature enhancement techniques that incorporate contextual information. These methods aim to help the model distinguish low-contrast defects and amplify weak signals, thereby improving the accuracy of detecting small and low-contrast defects.