Abstract
Computer viruses continue to threaten the security of digital networks, and their complex propagation dynamics require refined modelling tools. Most existing models rely on integer-order dynamics or assume uniform memory effects, which limit their ability to capture heterogeneous behaviours observed in practice. To address this gap, we propose a discrete incommensurate fractional-order virus model based on Caputo-like delta differences, where each compartment is assigned a distinct fractional order to represent mismatched time scales. The model’s dynamics are analysed in terms of stability, bifurcation, and chaos. Numerical results reveal the emergence of rich chaotic attractors, emphasizing the impact of fractional memory on system evolution. To quantify complexity, we employ Approximate Entropy and Spectral Entropy and relate these indicators to the maximum Lyapunov exponent, confirming the system’s sensitivity and unpredictability. All numerical simulations and visualizations were performed using MATLAB (R2015a). The findings highlight the importance of heterogeneous memory in computer-virus modeling and offer new insights for developing theoretical foundations of robust cybersecurity strategies.
MSC:
34A08; 34D20; 34C28; 37N25; 68M12; 37D45
1. Introduction
In the modern digital age, computer viruses continue to represent a significant challenge for both individuals and large-scale network infrastructures. These malicious programs can replicate, spread autonomously, and cause data loss, system failures, and severe security breaches [1,2]. The increasing reliance on interconnected systems such as cloud computing, IoT (Internet of Things) devices, and wireless networks further amplifies their impact, making the understanding and control of such threats a matter of critical importance [3].
Mathematical modelling has proven to be a valuable approach in the analysis of the propagation dynamics of computer viruses. By formulating the interactions between susceptible, infected, and immunized nodes within a network as systems of differential or difference equations, researchers can simulate, predict, and devise control strategies against digital epidemics [4,5]. Traditional models, however, typically employ integer-order derivatives, which may fail to capture essential characteristics of virus propagation, including memory effects, persistence, and long-range dependence [6].
To address these shortcomings, fractional-order models have gained prominence due to their ability to incorporate memory and hereditary properties, making them more suitable for describing processes in real-world complex networks [7,8,9]. In contrast to classical models, fractional calculus allows for non-local interactions and more flexible dynamics [10,11,12,13], thereby providing a refined interpretation of the temporal behaviour of malware spread. Particularly, discrete-time fractional models are crucial for practical implementation in computer-based simulations and digital systems where time is inherently discrete. Indeed, in various applied sciences, it has been consistently demonstrated that fractionalization of classical models often yields results that better match experimental data when compared with their integer-order counterparts. This reinforces the view that fractional operators provide a more faithful mathematical representation of processes with memory and complexity, which justifies their adoption in the study of computer virus propagation.
Mishra and Saini (2007) presented foundational integer-order virus models in Applied Mathematics and Computation [14]. Later, fractional approaches appeared: Pinto and Machado (2014) introduced a Caputo fractional dynamics model for virus spread [15], and Al-Sayed et al. (2016) considered memory and human-intervention effects in a fractional setting [16]. More recently, Akgül (2021) developed a fractal fractional virus model [17], and Liu et al. (2025) proposed a fractional virus model emphasizing memory dependence [18]. Moreover, the potential for chaotic behaviour in such models has been largely underexplored, despite its relevance in understanding unpredictable and complex behaviours in virus diffusion [19,20,21,22,23,24,25]. Beyond virus modelling, chaotic systems and their fractional-order extensions have been extensively investigated for their ability to capture irregular, highly sensitive, and unpredictable dynamics. Fractional-order chaotic systems, in particular, have shown diverse behaviours including bifurcation, hyperchaos, and multistability, with wide-ranging applications in secure communications and information protection. Recent studies illustrate this breadth: memristive activation has been shown to influence chaotic dynamics in discrete neural networks [26], novel two-dimensional discrete hyperchaotic maps exhibit diverse oscillatory patterns [27], and fractional-order Hopfield neural networks have been integrated with advanced encryption schemes for medical data security [28]. Other works have introduced fractional Lorenz systems [29] and logistic modular maps [30] for efficient multi-image encryption. These developments underline both the theoretical richness and the practical significance of fractional-order chaotic systems, which motivate further exploration in the context of computer virus propagation.
This work puts forward a discrete incommensurate fractional-order model aimed at characterizing the spread of computer viruses that unveils previously unobserved chaotic dynamics. The proposed model introduces different fractional orders for each state variable using Caputo-like delta fractional differences [31], a novel structure not addressed in existing virus modelling literature. This configuration enables the model to reflect both memory dependence and mismatched time scales in the spread of digital infection phenomena that are often observed in real-world networks but not captured by classical or commensurate models. A key novelty of this work is the detection and analysis of chaos in the system. We apply Approximate Entropy to quantify the unpredictability and complexity of infection dynamics and Spectral Entropy to analyse the frequency domain characteristics of the time series. The combination of these tools allows for a deep understanding of how the virus model behaves under various parameter conditions, including the emergence of complex oscillations, bifurcations, and coexisting attractors. Our findings demonstrate that the proposed model exhibits rich chaotic dynamics depending on the initial conditions and the choice of fractional orders. These chaotic features may correspond to erratic and persistent infections in real systems, highlighting the importance of accounting for fractional-order and incommensurate effects in modelling and designing cybersecurity strategies. In contrast to earlier fractional virus models, which mainly adopt commensurate frameworks with identical fractional orders, our approach develops an incommensurate discrete-time formulation where each compartment is governed by a distinct fractional index. This heterogeneity captures diverse memory effects across different populations, reflecting more realistic propagation behaviours in networks. Furthermore, the joint use of Lyapunov exponents with Approximate and Spectral Entropy provides new insights into how incommensurability enhances sensitivity and unpredictability in virus diffusion, which has not been systematically addressed in the existing literature.
The main contributions and significance of this work can be summarized as follows:
- We propose a novel discrete incommensurate fractional-order computer virus model, where each state variable is governed by a distinct fractional index, enabling the capture of heterogeneous memory effects and mismatched time scales.
- We provide a detailed dynamical analysis that reveals the emergence of complex behaviours, including bifurcations, coexisting attractors, and chaotic dynamics, which have not been reported in earlier fractional virus models.
- To quantify complexity, we employ Approximate Entropy and Spectral Entropy jointly with Lyapunov exponents, offering complementary perspectives on unpredictability and frequency-domain characteristics of the system.
- The proposed framework highlights how incommensurability enriches the dynamic behaviour of virus diffusion, providing new insights for the design of cybersecurity strategies in digital networks.
After this Introduction, the paper continues as follows: Section 2 lays the groundwork by defining key concepts and theorems from discrete fractional calculus. Section 3 details the mathematical modelling of the discrete incommensurate computer virus model and discusses its equilibrium points. In Section 4 we explore the system’s chaotic behaviour using bifurcation diagrams, Lyapunov exponents, phase portraits, and Approximate Entropy and Spectral Entropy for complexity with numerical simulations that illustrate complex dynamic patterns under different parameter settings. Lastly, Section 6 summarizes the findings and indicates prospects for further research.
2. Essentials of Discrete Fractional Calculus
This section lays the groundwork by defining key concepts and theorems from discrete fractional calculus. These tools, including the Caputo-like fractional difference operator that extends the original Caputo derivative [31] to discrete time, will be essential for understanding and analysing the discrete fractional system for computer viruses, which we will explore later.
Definition 1
([32]). The fractional sum of order κ for a function takes the form
where and .
Definition 2
([33]). The operator known as the Caputo-like fractional difference of order κ for a function takes the form
with , and . stands for the m-th order difference operator, and is the falling factorial. Their definitions are given by
and
Remark 1.
For the special case , the Caputo-like operator simplifies to
Theorem 1
([34]). The sole solution to the initial value problem
is given by
where
3. The Incommensurate Model and Its Stability
In this section, we transform the standard computer virus model [35] into an incommensurate fractional-order system; this approach captures memory effects and the complex dynamics of virus spread. Intuitively, the Caputo-like delta difference operator introduces memory into the discrete-time system: the state at each time step depends not only on the current state but also on a weighted sum of past states. This allows the model to capture lingering effects of previous infections or interactions, which standard integer-order discrete-time models cannot account for. A commensurate version of this model, focusing on chaotic behaviour, was studied in our previous work [24]. The expression below employs the Caputo-like operator , with , for .
Based on this model’s structure,
- is the speed at which external computers access the internet.
- indicates the rate of computer network connections.
- represents the cure rate of latent computers.
- represents the cure rate of breaking out computers.
- specifies the rate at which latent computers progress to the breaking-out state.
The adoption of incommensurate fractional orders is motivated by the heterogeneous behaviours of different compartments in real-world networks. Specifically, susceptible computers typically react quickly to updates or antivirus patches, corresponding to shorter memory effects. Latent infections, by contrast, can remain dormant for long periods, reflecting prolonged memory of past exposures. Breaking-out computers actively spreading the virus exhibit intermediate memory dependence, since their infection activity depends on both current vulnerabilities and accumulated past interactions. Assigning distinct fractional orders to each compartment allows the model to reflect these mismatched time scales and heterogeneous memory effects, which are not captured by commensurate formulations.
We then analyse the model’s stability by investigating the equilibrium points and deriving stability conditions, offering insights into the system’s long-term dynamics. The determination of the fixed points for system (9) is generally accomplished through the following procedure:
Under the assumptions and , the system exhibits an infection-free fixed point at . In the case where and , we arrive to the viral fixed point , such that
To ensure a rigorous analysis of stability in discrete fractional systems with incommensurate derivatives, the following theorem is employed.
Theorem 2
([36]). Consider a system of fractional difference equations:
with and . M is the least common multiple of the denominators of , where , and for . Put .
where is the Jacobian matrix corresponding to (11). If all eigenvalues of (12) are located in , it follows that the trivial solution of (11) is locally asymptotically stable, so that
Numerical simulations were conducted to extensively investigate the chaotic regime of the system governed by the dynamics of fractional derivatives. Appropriate parameter values were carefully selected to create scenarios that manifest complex and irregular behaviour. These simulations are specifically designed to highlight the system’s characteristics when operating in a chaotic state.
Example 1.
Consider system (9) with parameters ; it follows that
Let ; it follows that ,
equivalent to
We applied the stability criterion from Theorem 2 for . Numerical root-finding shows that all eigenvalues lie outside ; therefore, the trivial solution is locally asymptotically stable.
Example 2.
Consider system (9) with parameters ; it follows that
Let ; it follows that ,
equivalent to
Solving this equation with the chosen parameters yields 150 solutions, . Using MATLAB, we verified that , satisfying , and . Theorem 2 confirms that the equilibrium point lacks stability.
Figure 1 presents the two illustrative examples of the incommensurate model (9). In Figure 1a, the system is locally asymptotically stable, while Figure 1b illustrates the chaotic dynamics of the system, marked by irregular and unpredictable fluctuations in its states. Such behaviour is characteristic of systems with sensitive parameters and fractional-order effects, where even small variations can produce markedly different outcomes.
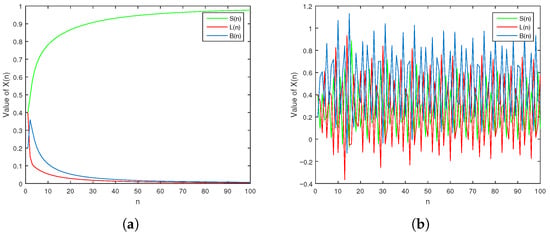
Figure 1.
Stateevolution of the incommensurate system (9): (a) Example 1, (b) Example 2.
4. Uncovering Complex Dynamics
The principal aim of this section is to explore the dynamics of the incommensurate discrete computer virus model. Unless otherwise stated, the parameters used in the simulations are chosen purely to demonstrate the emergence of bifurcations and chaos rather than being drawn from empirical data. The numerical representation of Equation (9), as established by Theorem 1, is presented subsequently
For the purpose of investigating chaotic behaviour in the fractional system (9), we apply the Jacobian matrix algorithm proposed by Wu and Baleanu [37] to compute the maximum Lyapunov exponent (). In this approach, J denotes the Jacobian matrix of the system.
where
with
Then,
such that are the eigenvalues of J.
The numerical analysis is structured into three cases with different parameter regimes. For each case, bifurcation diagrams, maximum Lyapunov exponents (MLEs), and phase portraits are presented to trace transitions to chaos. The following section complements these results with a complexity analysis based on Approximate Entropy (ApEn) and Spectral Entropy (SE) under varying fractional orders. To explore how the system’s dynamic behaviour evolves under varying fractional-order values, the parameters in Equation (9) are assigned as follows: and . The fractional orders are chosen within the interval and ; the initial conditions are fixed at . Based on these parameters and order settings, both the bifurcation diagram and the Lyapunov spectrum are generated. It appears that as the fractional-order parameters differ from one another, the incommensurate system displays a richer and more diverse range of dynamic behaviours. This is mainly because varying fractional orders impose different memory effects and dynamic responses, which enhance the system’s complexity and lead to a broader spectrum of dynamical phenomena. The disparity in fractional orders disrupts the temporal and dynamic harmony of the system’s internal connections, leading to more complex and varied chaotic and bifurcation patterns under identical parameter conditions. Moreover, it was noted that the distinct fractional orders assigned to each equation in (9) significantly affect the global dynamical properties of the incommensurate system. These varying orders have a significant impact on how the system evolves, affecting its stability and complexity. We consider three illustrative scenarios as depicted in Figure 2, Figure 3 and Figure 4. These figures provide a comparative visualization of the bifurcation diagrams and corresponding Lyapunov exponent under different incommensurate fractional-order combinations.
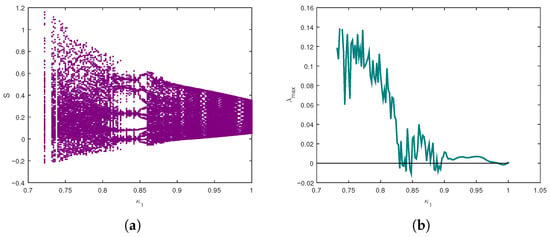
Figure 2.
Bifurcation diagram and maximum Lyapunov exponent (MLE) of (9) as varies for and : (a) Bifurcation diagram; (b) Corresponding maximum Lyapunov exponent.
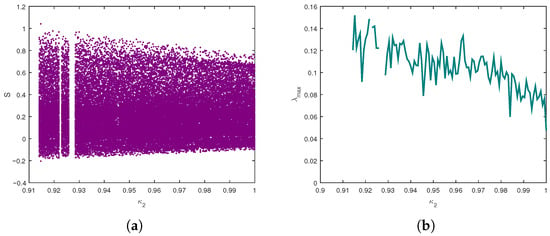
Figure 3.
Bifurcation diagram and maximum Lyapunov exponent (MLE) of (9) as varies for and : (a) Bifurcation diagram of the system; (b) Corresponding maximum Lyapunov exponent.
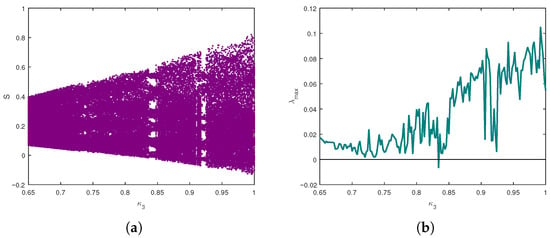
Figure 4.
Bifurcation diagram and maximum Lyapunov exponent (MLE) of (9) as varies for and : (a) Bifurcation diagram of the system; (b) Corresponding maximum Lyapunov exponent.
Figure 2 presents the case where and . The bifurcation diagram reveals a gradual contraction of the attractor branches, indicating a shift from chaotic to more stable behaviour as the parameter varies. In particular, the bifurcation diagram shows that multiple period-doublings and chaotic windows are most visible in the range –. The corresponding Lyapunov exponent plot confirms this observation: the MLE remains positive up to about , indicating chaotic dynamics, and then gradually declines toward zero and slightly negative values around –, which matches the collapse of chaotic branches in the bifurcation diagram and signals the transition toward more stable dynamics. In contrast, Figure 3 explores the dynamics when and . Here, the bifurcation diagram exhibits a more irregular and dispersed pattern, indicative of persistent or even enhanced chaotic dynamics. The LE spectrum supports this, with fluctuations around zero and occasional positive peaks that signal chaotic regimes. Figure 4 examines the case , . The bifurcation diagram reveals small period-doubling windows near , followed by dense chaotic regions in – and –1. The Lyapunov exponent stays low for , then rises around , in agreement with the onset of chaos observed in the diagram. Compared to Figure 2, this case exhibits stronger and more persistent chaos, showing that lower with higher amplifies system instability.
The transition from a sparse attractor to a dense one may be interpreted as the shift from sporadic infection bursts to persistent and widespread propagation, thereby indicating that chaotic regimes enhance both the intensity and unpredictability of virus spread in the network. These three cases collectively emphasize the susceptibility of the incommensurate system to fractional-order selection. Small changes in any of the fractional-order parameters can lead to qualitatively different dynamic responses. This reinforces the notion that the individual memory indices represented by the fractional orders act as critical modulators of nonlinear dynamics, shaping not only the route to chaos but also the intensity and structure of the chaotic attractors themselves.
The bifurcation diagram and (MLE) plot in Figure 5 depict the dynamical transitions of the incommensurate computer virus model as the parameter varies, with fixed fractional orders . For smaller values of , the system exhibits stable fixed points or periodic oscillations, reflecting predictable virus propagation dynamics, as confirmed by the negative MLE. As increases, a cascade of period-doubling bifurcations emerges, culminating in chaotic behaviour characterized by dense, irregular branching in the bifurcation diagram and a positive MLE. This chaotic regime signifies heightened sensitivity to initial conditions and unpredictable virus spread, peaking around intermediate values. Beyond a critical threshold of , the system stabilizes into periodic or quasi-periodic states, likely due to network saturation effects, as evidenced by the MLE returning to negative values. The incommensurate fractional orders introduce memory-dependent dynamics, amplifying the system’s sensitivity to . Practically, maintaining in the stable regime is crucial for containment, while chaotic regimes necessitate adaptive strategies to mitigate uncontrolled propagation.
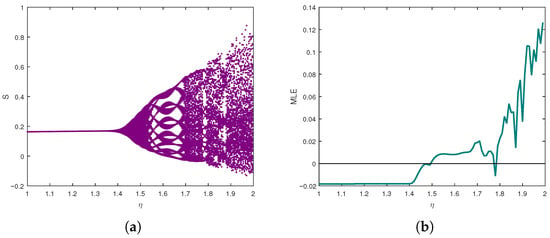
Figure 5.
Bifurcation diagram and maximum Lyapunov exponent (MLE) of (9) versus for , , and : (a) Bifurcation diagram of the system; (b) Corresponding maximum Lyapunov exponent.
Figure 6 depicts the phase portraits of the incommensurate computer virus model at multiple fractional-order values , , and . Subfigures (a), (b), and (c) correspond to different values of while keeping and . As increases from 0.75 to 0.87, the system transitions from scattered behaviour to more organized chaotic attractors, indicating a strong influence of memory on the system dynamics. Subfigures (d), (e), and (f) illustrate the effect of slight variations in around critical values, with and . Subfigures (g), (h), and (i) show attractors as increases from 0.82 to 0.99, for and . Throughout the figure, we observe that fluctuations in the fractional orders significantly impact the shape and stability of the phase space trajectories, underlining the pivotal role of memory effects in the dynamical evolution of the system.
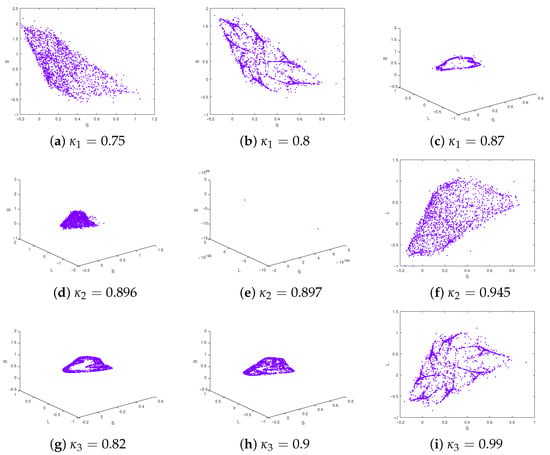
Figure 6.
Phase attractor of (9) for different fractional orders: (a–c) ; (d–f) ; (g–i) .
In the second case, we consider the system with parameters . Figure 7 illustrates the system’s complex dynamical behaviour under this configuration. Figure 7a presents the bifurcation diagram in relation to the fractional-order parameter , revealing a clear transition from periodic to chaotic dynamics as increases. This transition is further confirmed by the corresponding MLE plotted in Figure 7b, where the exponent becomes positive for , indicating the onset of chaos. Figure 8 depicts both the 2D and 3D phase portraits for different values of , with and . The 2D projections onto the S–L, S–B, and L–B planes provide a clearer view of the attractor structures. We observe that as the fractional order increases, the attractors become more complex and denser, indicating stronger chaotic dynamics. These trajectories illustrate rich dynamical behaviour and highlight the system’s sensitivity to variations in the fractional order. This characteristic is a distinctive feature of discrete fractional-order models, emphasizing their ability to capture irregular and unpredictable propagation patterns in computer virus dynamics.
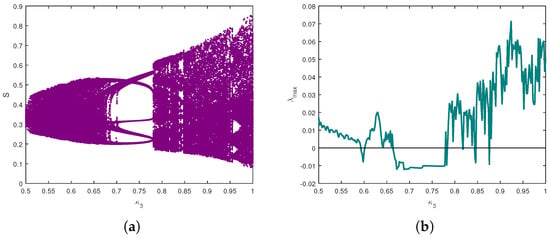
Figure 7.
Bifurcation diagram and maximum Lyapunov exponent (MLE) of (9) as varies for and : (a) Bifurcation diagram of the system; (b) Corresponding maximum Lyapunov exponent.
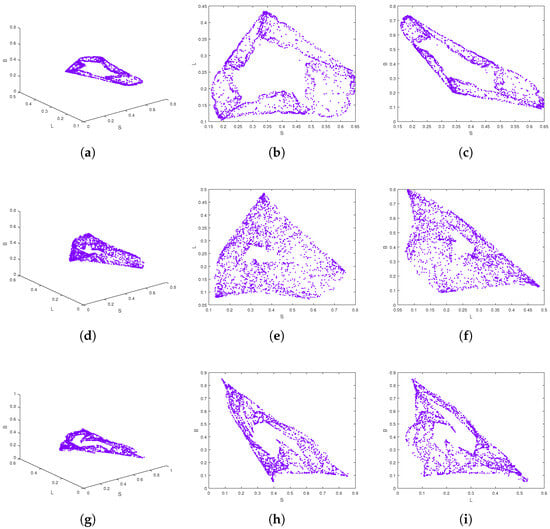
Figure 8.
Phase attractor of (9) for and and (a–c) , (d–f) , (g–i) .
Figure 9 presents a combined analysis showing how the system evolves in the long term depending on for . Figure 9a illustrates a bifurcation diagram, likely depicting the state variable S as is varied from to 1. This diagram reveals a transition from periodic behaviour to complex chaotic dynamics as increases. Figure 9b displays the corresponding (MLE) values against . Positive values of MLE serve as strong indicators of chaotic regions observed in the bifurcation diagram. Conversely, negative or near-zero MLE values align with the periodic windows seen, providing quantitative validation of the qualitative changes in system dynamics. The presence of both periodic windows (where MLE is negative) and wide chaotic regions (where MLE is positive) indicates rich and complex dynamics. The sharp transitions between these states stress the marked dependence of the system on fractional-order variations. This analysis is crucial for understanding the parameter range where chaotic behaviour occurs. Figure 10 presents 3D phase portraits for different values of , with and , together with their 2D projections onto the S–L, S–B, and L–B planes. These visualizations illustrate the system’s attractors and complement the bifurcation diagrams and MLE plots by revealing the geometric structure of the dynamics.
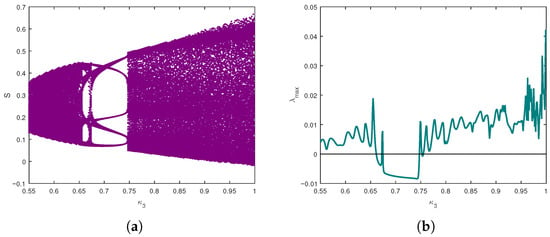
Figure 9.
Bifurcation diagram and maximum Lyapunov exponent (MLE) of (9) as varies for and : (a) Bifurcation diagram of the system; (b) Corresponding maximum Lyapunov exponent.
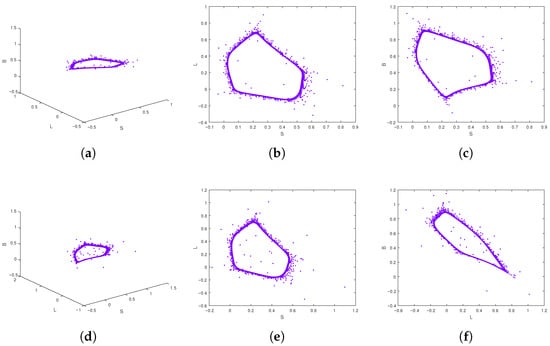
Figure 10.
Phase attractor of (9) for and and (a–c) , (d–f) .
5. Entropy and Complexity
To gauge the complexity and irregularity of dynamical systems, entropy analysis is a potent tool. This section explores Approximate Entropy (ApEn) and Spectral Entropy (SE) to assess the fractional-order system’s predictability. ApEn measures pattern regularity, while SE complexity efficiently analyses overall dynamic complexity, offering deeper insights into system dynamics.
5.1. Approximate Entropy
For a quantitative assessment of time series data complexity, we employ the Approximate Entropy (ApEn) algorithm, where higher ApEn values correlate with increased system complexity [38]. The computation of ApEn necessitates the specification of the embedding dimension (m) and the similarity threshold (r). The parameters are chosen as and , with denoting the standard deviation of the time series. These settings are widely adopted in nonlinear dynamics analysis, since provides a balance between sensitivity and computational efficiency, while ensures robustness to noise and comparability across different datasets. The theoretical basis for ApEn’s calculation is presented as follows:
where
Figure 11 displays the ApEn as a function of the fractional orders , , and of the incommensurate computer virus model (9) for . Each subfigure, (a), (b), and (c), illustrates how the complexity, quantified by ApEn, changes as one specific fractional order varies. Overall, these plots demonstrate that the complexity of the model (9) is highly sensitive to the specific values of its fractional orders. The varying patterns across , , and confirm that precise selection of these parameters is crucial for achieving or predicting different levels of structural complexity in the model.
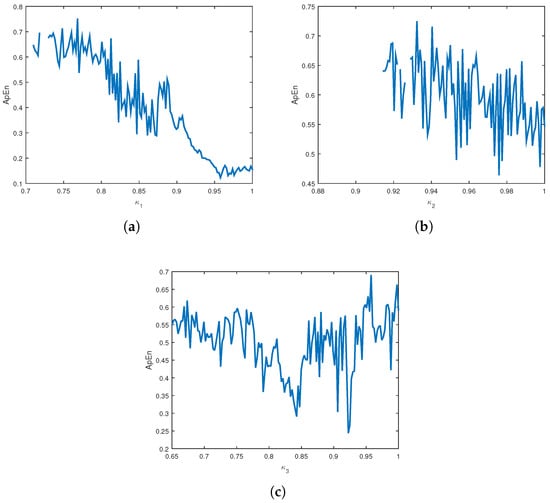
Figure 11.
ApEn of (9): (a) with respect to when ; (b) with respect to with ; (c) with respect to with .
5.2. SE Complexity
Here, we utilize the Spectral Entropy (SE) algorithm to quantitatively assess the complexity of the fractional computer virus system (9). A concise description of the SE computation steps is given below, following the approach in [39]
Step 1: Compute the mean-adjusted signal. Let denote the discrete time series of length N. The mean value is calculated as
Step 2: Perform the discrete Fourier transform (DFT) on the mean-subtracted signal:
where and j is the unit imaginary number.
Step 3: Compute the normalized power spectral density:
Step 4: Define the Spectral Entropy (SE) using the Shannon entropy formulation:
where denotes the entropy corresponding to a signal exhibiting maximum randomness.
Figure 12 illustrates the complexity of the model, as quantified by the Spectral Entropy, plotted against varying fractional orders , , and for . Each panel highlights how the system’s complexity varies with individual fractional orders. For , SE decreases until about before slightly rising, while for and strong fluctuations persist, with SE generally remaining high. These non-monotonic patterns confirm that system complexity is highly sensitive to fractional orders, underscoring their decisive role in shaping virus dynamics.
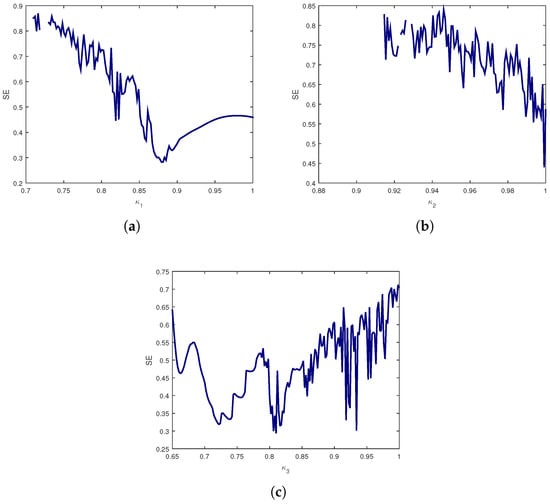
Figure 12.
SE complexity of (9): (a) with respect to when ; (b) with respect to with ; (c) with respect to with .
Entropy-based indicators (ApEn and SE) show strong agreement with MLE results: positive MLEs align with higher entropy values, indicating chaotic and unpredictable behaviour, whereas near-zero or negative MLEs correspond to lower entropy and more regular dynamics. This cross-validation confirms the robustness of entropy measures as complementary tools when Lyapunov exponents are costly or less stable.
The chaotic dynamics also carry direct cybersecurity implications. Sensitivity to initial conditions means that even minor delays in patching or variations in infection rates can drastically alter outcomes, while higher fractional memory leads to more irregular and less predictable spread. These insights point to the need for adaptive patching, resilient recovery mechanisms, and randomized update strategies. Although our study is theoretical, it lays a foundation for future work combining real datasets, heterogeneous network topologies, and control mechanisms to bridge abstract dynamics with practical cybersecurity applications.
6. Conclusions and Future Scope
In this work, we introduced a discrete incommensurate system using Caputo-like delta operators to capture the dynamics of computer virus propagation in digital environments. The study addresses a key limitation of existing integer-order and commensurate fractional-order models, which fail to reflect the heterogeneous memory effects observed in practice. By assigning distinct fractional orders to each compartment, our framework incorporates mismatched time scales, offering a more realistic description of virus spread.
The main contributions of this work are threefold. First, we demonstrated that the proposed system exhibits rich dynamical behaviours, including stability transitions, bifurcations, and chaos. Second, we quantified the system’s complexity using the maximum Lyapunov exponent, Approximate Entropy, and Spectral Entropy, confirming its sensitivity to parameters and initial conditions. Third, we highlighted the theoretical implications of incommensurate memory for cybersecurity, showing how fractional-order dynamics can replicate irregular and unpredictable propagation patterns that are otherwise overlooked.
Our findings stress the importance of fractional-order modelling in understanding digital epidemics. The coexistence of regular and chaotic behaviours implies that even small perturbations in parameters or initial states may drastically alter outcomes. This unpredictability underscores the need for cybersecurity strategies that are resilient to nonlinear and memory-dependent effects. In particular, our analysis suggests three promising directions for theoretical cybersecurity strategies:
- Adaptive patching or traffic throttling, to reduce effective infection rates and limit malware diffusion.
- Enhanced recovery mechanisms, analogous to cure rates, to stabilize the system by suppressing persistent outbreaks.
- Desynchronization strategies, such as randomized update schedules across nodes, to mitigate coordinated malicious activity.
Despite these contributions, the present work is limited to numerical simulations and does not incorporate real-world network traffic or empirical datasets. Moreover, the model is analysed in a homogeneous environment, whereas practical digital networks often exhibit heterogeneous connectivity and dynamic topologies. Future research may therefore focus on three main directions: integrating real-world datasets to validate the model against practical malware outbreaks, designing optimal control and synchronization schemes tailored to fractional-order dynamics, and extending the framework to networked or multi-agent environments where topology plays a critical role in virus propagation. Such efforts would bridge the gap between theoretical modelling and practical cybersecurity applications.
Author Contributions
Conceptualization, O.K.; Methodology, I.Z.; Software, I.Z.; Validation, O.K.; and A.O.; Formal analysis, L.E.A.; and M.A.; Investigation, I.Z.; Resources, L.E.A.; and M.A.; Data curation, I.Z.; and A.O.; Writing—original draft, I.Z.; Writing—review and editing, I.Z.; and O.K.; Visualization, I.Z.; Supervision, A.O.; Project administration, I.Z.; and A.O.; Funding acquisition, O.K. All authors have read and agreed to the published version of the manuscript.
Funding
Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2025R831), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia. The authors extend their appreciation to the Deanship of Scientific Research at Northern Border University, Arar, KSA for funding this research work through the project number “NBU-FPEJ-2025-2443-01”.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding authors.
Acknowledgments
Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2025R831), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia. The authors extend their appreciation to the Deanship of Scientific Research at Northern Border University, Arar, KSA for funding this research work through the project number “NBU-FPEJ-2025-2443-01”.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Chernikova, A.; Gozzi, N.; Perra, N.; Boboila, S.; Eliassi-Rad, T.; Oprea, A. Modeling self-propagating malware with epidemiological models. Appl. Netw. Sci. 2023, 8, 52. [Google Scholar] [CrossRef]
- Malik, M.S. IoT Malware: A Comprehensive Survey of Threats, Vulnerabilities, and Mitigation Strategies. Int. J. Electron. Crime Investig. 2024, 8, 1187. [Google Scholar] [CrossRef]
- Ferdous, J.; Islam, R.; Mahboubi, A.; Islam, M.Z. A Survey on ML Techniques for Multi-Platform Malware Detection: Securing PC, Mobile Devices, IoT, and Cloud Environments. Sensors 2025, 25, 1153. [Google Scholar] [CrossRef] [PubMed]
- Ahmad, I.; Bakar, A.A.; Jan, R.; Yussof, S. Dynamic behaviors of a modified computer virus model: Insights into parameters and network attributes. Alex. Eng. J. 2024, 103, 266–277. [Google Scholar] [CrossRef]
- Lazarov, A.D. Mathematical Modelling of Malware Intrusion in Computer Networks. Cybern. Inf. Technol. 2022, 22, 29–47. [Google Scholar] [CrossRef]
- Wang, J.; Chang, X.; Zhong, L. A SEIQRS Computer Virus Propagation Model and Impulse Control With Two Delays. Math. Methods Appl. Sci. 2025, 48, 6851–6865. [Google Scholar] [CrossRef]
- Wang, H.; Xin, Z.; He, S.; Sun, K. Design of a discrete memristive chaotic map: Fractional-order memory, dynamics, and application. Phys. Scr. 2024, 99, 095218. [Google Scholar] [CrossRef]
- Diallo, B.; Okelo, J.A.; Osman, S.; Karanja, S.; Aguegboh, N.S. Fractional-Order Model for Evolution of Bovine Tuberculosis with Vaccination and Contaminated Environment. J. Appl. Math. 2024, 2024, 6934895. [Google Scholar] [CrossRef]
- El-Shahed, M.; Moustafa, M. Dynamics of a Fractional-Order Eco-Epidemiological Model with Two Disease Strains in a Predator Population Incorporating Harvesting. Axioms 2025, 14, 53. [Google Scholar] [CrossRef]
- Zeng, J.; Chen, X.; Wei, L.; Li, D. Bifurcation analysis of a fractional-order eco-epidemiological system with two delays. Nonlinear Dyn. 2024, 112, 22505–22527. [Google Scholar] [CrossRef]
- Karaoğlu, E. On the stability analysis of a fractional order epidemic model including the general forms of nonlinear incidence and treatment function. Commun. Fac. Sci. Univ. Ankara Ser. A1 Math. Stat. 2024, 73, 285–305. [Google Scholar] [CrossRef]
- Narwal, Y.; Rathee, S. Fractional order mathematical modeling of lumpy skin disease. Commun. Fac. Sci. Univ. Ankara Ser. A1 Math. Stat. 2024, 73, 192–210. [Google Scholar] [CrossRef]
- Matouk, A.E.; Ameen, I.G.; Gaber, Y.A. Analyzing the dynamics of the fractional spatio-temporal SEIR epidemic model. AIMS Math. 2024, 9, 41489. [Google Scholar] [CrossRef]
- Mishra, B.K.; Saini, D.K. Mathematical models of computer viruses. Appl. Math. Comput. 2007, 187, 929–936. [Google Scholar] [CrossRef]
- Pinto, C.M.A.; Machado, J.A.T. Fractional dynamics of computer virus propagation. Math. Probl. Eng. 2014, 2014, 476502. [Google Scholar] [CrossRef]
- El-Sayed, A.M.A.; Arafa, A.A.M.; Khalil, M.; Hassan, A. A mathematical model with memory for the propagation of a computer virus under human intervention. Prog. Fract. Differ. Appl. 2016, 2, 105–113. [Google Scholar] [CrossRef]
- Akgül, A. A fractal fractional model for computer virus dynamics. Chaos Solitons Fractals 2021, 147, 110947. [Google Scholar] [CrossRef]
- Liu, Z.; Yang, X.; Yang, L. A Fractional Computer Virus Propagation Model with Saturation Effect. Fractal Fract. 2025, 9, 587. [Google Scholar] [CrossRef]
- Kahouli, O.; Zouak, I.; Abu Hammad, M.; Ouannas, A.; Ayari, M. On an incommensurate chaotic fractional discrete model of a computer virus: Stabilization and synchronization. AIMS Math. 2025, 10, 19940–19957. [Google Scholar] [CrossRef]
- Abu Hammad, M.; Zouak, I.; Ouannas, A.; Grassi, G. Fractional Discrete Computer Virus System: Chaos and Complexity Algorithms. Algorithms 2025, 18, 444. [Google Scholar] [CrossRef]
- Oudetallah, J.; Zouak, I.; Audeh, W.; Ouannas, A.; Khennaoui, A.-A.; Batiha, I.M.; Momani, S. Control of Chaos in the Fractional Computer Virus Model. In Proceedings of the 2025 1st International Conference on Computational Intelligence Approaches and Applications (ICCIAA), Amman, Jordan, 28–30 April 2025. [Google Scholar]
- Kahouli, O.; Zouak, I.; Ouannas, A.; Abidi, I.; Bahou, Y.; Elgharbi, S.; Chaabane, M. Control and Synchronization of Chaos in Some Fractional Computer Virus Models. Asian J. Control 2025, 1–9. [Google Scholar] [CrossRef]
- Oudetallah, J.; Zouak, I.; Audeh, W.; Ouannas, A.; Khennaoui, A.-A.; Batiha, I.M.; Momani, S. Synchronization of Computer Virus System Using Fractional Calculus. In Proceedings of the 2025 1st International Conference on Computational Intelligence Approaches and Applications (ICCIAA), Amman, Jordan, 28–30 April 2025. [Google Scholar]
- Kahouli, O.; Zouak, I.; Hammad, M.A.; Ouannas, A. Chaos, control, and synchronization in a discrete-time computer virus system with fractional orders. AIMS Math. 2025, 10, 13594–13621. [Google Scholar] [CrossRef]
- Jebril, I.H.; Dibi, K.; Zouak, I.; Ouannas, A.; Khennaoui, A.-A.; Batiha, I.M. Incommensurate Fractional Computer Virus System: Control and Simulation. In Proceedings of the 2025 12th International Conference on Information Technology (ICIT), Amman, Jordan, 27–30 May 2025; pp. 109–113. [Google Scholar]
- Yu, F.; He, T.; He, S.; Tan, B.; Shi, C. Influence of memristive activated gradient on chaotic dynamics in discrete neural networks. Int. J. Bifurc. Chaos 2025, 35, 2550146. [Google Scholar] [CrossRef]
- Lai, Q.; Yang, L.; Chen, G. Two-dimensional discrete memristive oscillatory hyperchaotic maps with diverse dynamics. IEEE Trans. Ind. Electron. 2024, 72, 969–979. [Google Scholar] [CrossRef]
- Feng, W.; Zhang, K.; Zhang, J.; Zhao, X.; Chen, Y.; Cai, B.; Zhu, Z.; Wen, H.; Ye, C. Integrating a fractional-order Hopfield neural network with differentiated encryption: Achieving high-performance privacy protection for medical images. Fractal Fract. 2025, 9, 426. [Google Scholar] [CrossRef]
- Feng, W.; Wang, Q.; Liu, H.; Ren, Y.; Zhang, J.; Zhang, S.; Qian, K.; Wen, H. Exploiting newly designed fractional-order 3D Lorenz chaotic system and 2D discrete polynomial hyper-chaotic map for high-performance multi-image encryption. Fractal Fract. 2023, 7, 887. [Google Scholar] [CrossRef]
- Li, H.; Yu, S.; Feng, W.; Chen, Y.; Zhang, J.; Qin, Z.; Zhu, Z.; Wozniak, M. Exploiting dynamic vector-level operations and a 2D-enhanced logistic modular map for efficient chaotic image encryption. Entropy 2023, 25, 1147. [Google Scholar] [CrossRef]
- Caputo, M. Linear models of dissipation whose Q is almost frequency independent—II. Geophys. J. Int. 1967, 13, 529–539. [Google Scholar] [CrossRef]
- Atici, F.M.; Eloe, P. Discrete Fractional Calculus with the Nabla Operator. Electron. J. Qual. Theory Differ. Equ. 2009, 62, 12. [Google Scholar] [CrossRef]
- Abdeljawad, T. On Riemann and Caputo Fractional Differences. Comput. Math. Appl. 2011, 62, 1602–1611. [Google Scholar] [CrossRef]
- Anastassiou, G.A. Principles of Delta Fractional Calculus on Time Scales and Inequalities. Math. Comput. Model. 2010, 52, 556–566. [Google Scholar] [CrossRef]
- Yang, L.X.; Yang, X.; Zhu, Q.; Wen, L. A Computer Virus Model with Graded Cure Rates. Nonlinear Anal. Real World Appl. 2013, 14, 414–422. [Google Scholar] [CrossRef]
- Shatnawi, M.T.; Djenina, N.; Ouannas, A.; Batiha, I.M.; Grassi, G. Novel Convenient Conditions for the Stability of Nonlinear Incommensurate Fractional-Order Difference Systems. Alex. Eng. J. 2022, 61, 1655–1663. [Google Scholar] [CrossRef]
- Wu, G.C.; Baleanu, D. Jacobian Matrix Algorithm for Lyapunov Exponents of the Discrete Fractional Maps. Commun. Nonlinear Sci. Numer. Simul. 2015, 22, 95–100. [Google Scholar] [CrossRef]
- Richman, J.S.; Moorman, J.R. Physiological Time-Series Analysis Using Approximate Entropy and Sample Entropy. Am. J. Physiol. Heart Circ. Physiol. 2000, 278, H2039–H2049. [Google Scholar] [CrossRef] [PubMed]
- He, S.; Sun, K.; Wang, H. Complexity Analysis and DSP Implementation of the Fractional-Order Lorenz Hyperchaotic System. Entropy 2015, 17, 8299–8311. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).