Abstract
This work establishes definitive conditions for the inheritance of categorical completeness and cocompleteness by categories of internal group objects. We prove that while the completeness of follows unconditionally from the completeness of the base category , cocompleteness requires to be regular, cocomplete, and admit a free group functor left adjoint to the forgetful functor. Explicit limit and colimit constructions are provided, with colimits realized via coequalizers of relations induced by group axioms over free group objects. Applications demonstrate cocompleteness in topological groups, ordered groups, and group sheaves, while Lie groups serve as counterexamples revealing necessary analytic constraints—particularly the impossibility of equipping free groups on non-discrete manifolds with smooth structures. Further results include the inheritance of regularity when the free group functor preserves finite products, the existence of internal hom-objects in locally Cartesian closed settings, monadicity for locally presentable , and homotopical extensions where model structures on reflect those of . This framework unifies classical category theory with geometric obstruction theory, resolving fundamental questions on exactness transfer and enabling new constructions in homotopical algebra and internal representation theory.
Keywords:
internal group objects; cocompleteness transfer; free group functor; regular categories; monadicity; Tannakian duality; homotopical algebra MSC:
18A30; 18A35; 18B25; 18G55; 22E99
1. Introduction
The study of the completeness and cocompleteness of categories has been a central theme in category theory since its inception. A category is complete if it has all small limits, and cocomplete if it has all small colimits. These properties are fundamental to the ability of a category to support universal constructions, such as products, equalizers, pullbacks, and their duals. The classical work of Mac Lane [1] established that many categories of algebraic structures (e.g., groups, rings) are complete and cocomplete, while Borceux [2] extended these results to more general contexts. However, for internal categories, such as categories of group objects in a base category , the inheritance of these properties is not automatic and depends delicately on the structure of . In this work, we unify and extend these classical results by providing explicit conditions under which inherits completeness and cocompleteness from , and we identify obstructions in geometric settings.
The categorical formalization of algebraic structures, pioneered by Lawvere [3], reveals that group-like objects in a category with finite products form a category whose exactness properties reflect fundamental features of . Classical examples include the following:
- = ordinary groups;
- = topological groups;
- = sheaves of groups;
- = n-dimensional Lie groups.
While the completeness of follows automatically from the completeness of , the dual problem of cocompleteness remained open outside well-studied cases. This work resolves this by identifying necessary and sufficient conditions for hereditary cocompleteness, with applications ranging from ordered groups to ∞-groupoids.
Key advances
Our principal contributions unify and extend classical results:
- Cocompleteness Characterization: For cocomplete and regular, is cocomplete iff a free group functor exists (Theorems 7 and 21). Colimits are constructed via coequalizers:encoding group axioms. This explains the cocompleteness in but failure in (Corollary 3, Proposition 1).
- Geometric Obstruction Theorem: For categories of geometric objects (e.g., smooth manifolds ), the following are equivalent (Theorem 22):Failure for Lie groups follows from Birkhoff transitivity: cannot embed densely in second-countable groups.
- Higher Categorical Structures:
- When is regular and F preserves products, inherits regularity with effective descent (Theorem 23).
- For locally Cartesian closed , internal hom-objects exist as equalizers:imposing homomorphism conditions (Theorem 24).
- Homotopical and Duality Extensions:
- For combinatorial model categories , admits a model structure with weak equivalences/fibrations created by U (Theorem 26).
- Tannakian duality holds: for fiber functors when is a topos (Theorem 25).
These results have implications beyond pure category theory. Internal group objects arise naturally in various branches of mathematics and its applications: in algebraic topology as loop spaces and higher homotopy groups; in algebraic geometry as group schemes and Tannakian categories; in mathematical physics as gauge groups and symmetries in topological field theories; and in computer science as models of higher inductive types in homotopy type theory. The question of when limits and colimits exist in these categories is fundamental to constructing quotients, classifying spaces, and performing descent arguments. Our work provides a unified answer to this question, clarifying both the universal and obstructionary aspects of completeness and cocompleteness in categories of internal group objects.
Recent Developments in Higher Structures
With the advent of higher category theory and homotopical algebra, the study of internal group objects has extended naturally into the setting of -categories and model categories. Recent works by Rezk [4] on model structures for homotopy theories, by Lurie [5,6,7] on higher topos theory and higher algebra, by Riehl [8] on categorical homotopy theory, and by Schweigert and Valenti [9] on higher structures in mathematical physics provide a robust framework for generalizing our results to higher groupoids and homotopy-coherent algebraic structures. These developments allow us to treat internal group objects not only in classical categories but also in contexts such as ∞-topoi and differential ∞-categories, thereby unifying geometric and homotopical perspectives on group theory.
Novelty and significance
Our work provides explicit constructive formulas for colimits in under regularity and free-group conditions. Unlike [10], which focuses on concrete examples, we derive necessary and sufficient conditions for cocompleteness and identify geometric obstructions in the case of Lie groups.
Specifically, we
- Establish precise obstructions to cocompleteness via analytic constraints (Birkhoff transitivity);
- Derive constructive colimit formulas using free group functors;
- Unify Lie group pathologies, homotopical algebra, and Tannakian duality under one framework.
2. Preliminaries
Definition 1.
A category is Cartesian if it has all finite products. We denote by the terminal object and by × the binary product operation.
Definition 2
(Internal Group Object [11]). Let be Cartesian.
- 1.
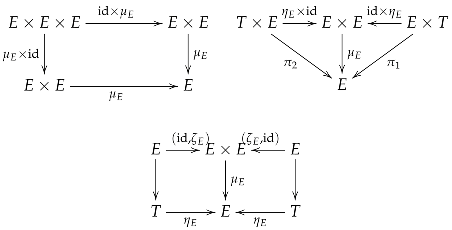
- A quadruple is called a group object in if C is an object in , and the product morphism μ, the unit morphism η, and the inverse morphism ζ are morphisms in :satisfying the following commutative diagrams (expressing associativity, unit laws, and inverse laws, respectively):Associativity:
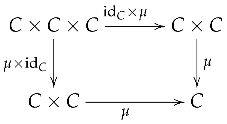 Left and Right Unit Laws:where and are canonical projections.Inverse Laws:
Left and Right Unit Laws:where and are canonical projections.Inverse Laws: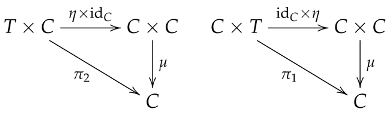 where and denote the respective product morphisms.
where and denote the respective product morphisms.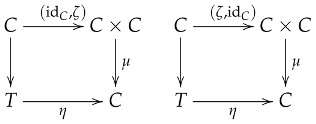
- 2.
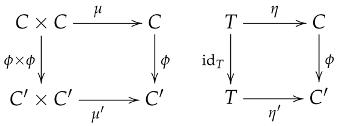
- Let and be group objects in . An internal group homomorphism is a morphism in such that the following diagrams commute:
- 3.
- Let , , and be group objects in . For internal group homomorphisms and , their composition is the internal group homomorphism defined by the composite morphism in .
- 4.
- The identity internal group homomorphism is defined by the identity morphism in .
Theorem 1
([11]). Let be a category with finite products. Then, taking the internal group objects in as objects and the internal group homomorphisms as morphisms forms a category, denoted by . This is referred to as the category of internal group objects.
Definition 3.
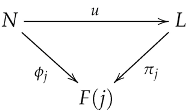
A free group functor for a Cartesian category is a functor that is left adjoint to the forgetful functor , i.e., there is a natural isomorphism:
for all , .
Theorem 2
(Existence of Free Groups). For a cocomplete regular category with a strong generator , the free group functor exists if and only if for each , the free group on X exists in .
Proof.
(⇒) Immediate from adjunction. (⇐) For arbitrary , express Y as a colimit of generators with . Define:
where exists by hypothesis. For any , we have natural isomorphisms:
where the second isomorphism uses that has colimits by reference [2] (Vol. 2, Proposition 4.3.2), and the fourth is by continuity of . Thus . □
Definition 4.
A category is regular if
- 1.
- It has all finite limits;
- 2.
- Coequalizers of kernel pairs exist;
- 3.
- Regular epimorphisms are stable under pullback.
Lemma 1
(Properties of Regular Categories). In a regular category
- 1.
- Regular epimorphisms are effective epimorphisms;
- 2.
- Every morphism factors as regular epi followed by mono in the factorization system;
- 3.
- Pullbacks preserve regular epi-mono factorizations.
Proof.
1. Given regular epi , form kernel pair . Since e coequalizes its kernel pair, we get unique . By stability under pullback, e is a universal coequalizer; so m is iso.
2. For , take kernel pair and coequalizer . Then f factors as with m mono.
3. Consider the following pullback square:
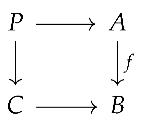

If with e regular epi, then the pullback preserves e as regular epi by definition. □
Theorem 3
(Regularity Inheritance). Let be regular Cartesian with free group functor preserving finite limits. Then is regular.
Proof.
For kernel pair coequalizers, consider a homomorphism and form its kernel pair in . Since U creates limits, is kernel pair of in . Let be the coequalizer in . By regularity, q is regular epi. Now construct:
 where is the coequalizer in . Since F preserves finite limits, . Stability under pullback follows as U preserves pullbacks and reflects regular epis. □
where is the coequalizer in . Since F preserves finite limits, . Stability under pullback follows as U preserves pullbacks and reflects regular epis. □

We introduce the following mathematical notations:
- : base category;
- : category of internal group objects in ;
- F: free group functor;
- U: forgetful functor;
- : multiplication, unit, inverse morphisms.
Theorem 4
([11]). Let be a category with finite products. Then, taking the internal group objects in as objects and the internal group homomorphisms as morphisms forms a category, denoted by . This is referred to as the category of internal group objects.
When discussing products in the internal group category , we uniformly give the definition of a product in a general category for clarity.
Definition 5
(Product in a Category [12]). Let be a category and be a family of objects in . A product of the is a pair , where and for each , such that for any and any family of morphisms , there exists a unique morphism making the following diagram commute for all :
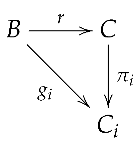 i.e., for all .
i.e., for all .

Theorem 5
([12]). If and are both products of , then there exists a unique isomorphism such that for all .
Lemma 2
([1]). Let have all products. Let be a family of morphisms in (I is a set). Let and be the product projections for and , respectively. Then there exists a unique morphism making the following diagram commute for all :
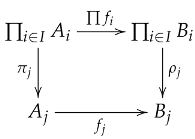

Lemma 3.
Let have all products. Let and be families of objects in . Let and be the product projections for and , respectively. Then is a product for the family .
Proof.
Consider any family of morphisms . Fix . Let and be the product projections for . Composing, we get morphisms and . Since and are product projections, Definition 2 guarantees unique morphisms and such that and for all . This implies the commutativity of the following diagram for each j:
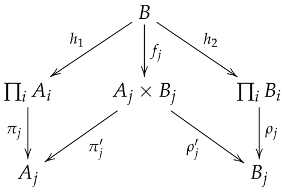

Since (by the universal property of ), there exists a unique morphism making the following diagram commute for all :
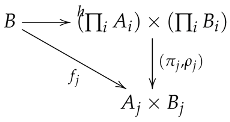
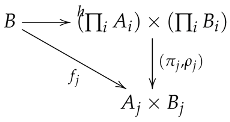
Therefore, is indeed a product for . □
Lemma 4.
Let have all products. Let and be families of objects in . Let , , and be the product projections for , , and , respectively. Then there exists a unique isomorphism making the following diagram commute for all :
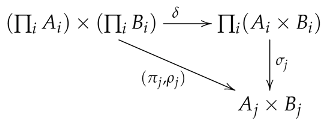
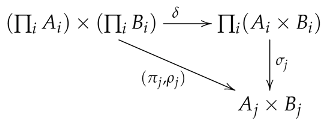
Proof.
By Lemma 3, is a product for . By definition, is also a product for . Theorem 5 then guarantees a unique isomorphism such that for all . □
Corollary 1.
Let have all products. Let and be families of objects in . Then there exists a unique isomorphism .
From Definition 5 and Lemma 4, we obtain the following result.
Lemma 5.
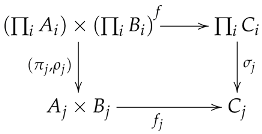 where are the product projections.
where are the product projections.
Let have all products. Let , , and be families of objects in , and let be a family of morphisms in . Then there exists a unique morphism making the following diagram commute for all :
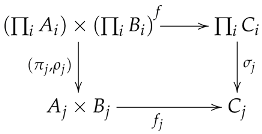
Theorem 6
([12]). If T and are two terminal objects (or two initial objects) in a category, then T and are isomorphic.
Lemma 6.
Let be a terminal object in . Let denote the product of copies of indexed by I. Then .
Proof.
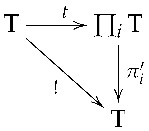 where are the projections and ! is the unique morphism from to . Since is terminal, there also exists a unique morphism (the unique morphism to the terminal object). Composing t and s gives, for any :
where are the projections and ! is the unique morphism from to . Since is terminal, there also exists a unique morphism (the unique morphism to the terminal object). Composing t and s gives, for any :
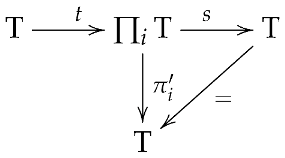
Since is the product of the family , there exists a morphism such that for any , the following diagram commutes:
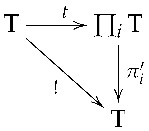
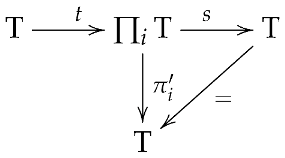
This shows for all i. However, . By the uniqueness property of the product, . Similarly, consider the composite . For any :
Again, by uniqueness, . Therefore, and , proving . □
3. Completeness of
We establish fundamental results on the completeness of categories of internal group objects. Throughout, denotes a Cartesian category (i.e., with finite products).
The following theorem is fundamental, as it ensures that products of internal group objects exist and are constructed in the expected way from the underlying products in .
Theorem 7.
If a category is closed under arbitrary products, then the category of internal group objects is also closed under arbitrary products.
Proof.
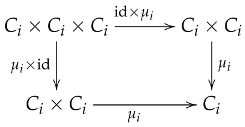
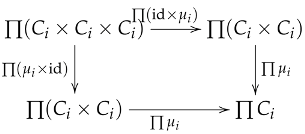
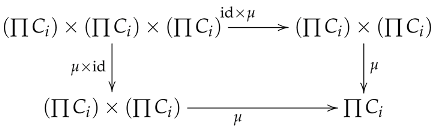
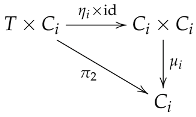
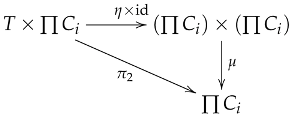
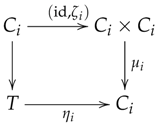
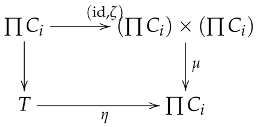
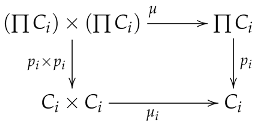
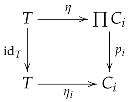
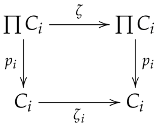
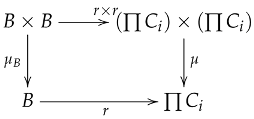
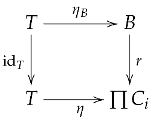
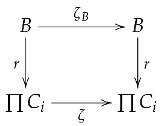
Let be a family of objects in . Since is closed under arbitrary products, the product exists in with projections .
Define:
where is the canonical isomorphism from Lemma 4.
Step 1: is an internal group object. We verify the group axioms via commutative diagrams.
Associativity: For each , the associativity of gives:
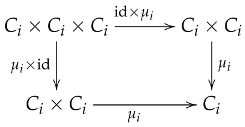
Taking products and applying Lemmas 4 and 5 yields:
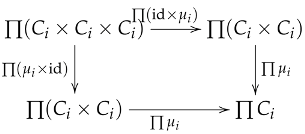
Using the isomorphism , this induces the commutative diagram for :
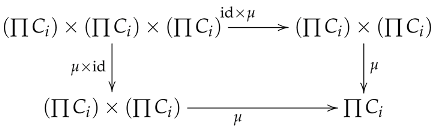
Unit Laws: For each , the unit axiom for gives:

Taking products and applying Lemmas 4 and 6 ():

Inverse Laws: Similarly, for each :

Taking products yields:
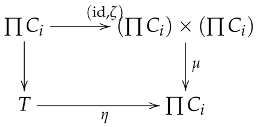
Thus .
Step 2: Projections are internal group homomorphisms. We verify the homomorphism conditions.
Multiplication Preservation:
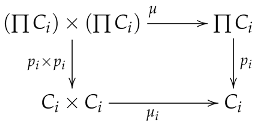
Commutativity follows from:
Unit Preservation:

Commutativity holds as .
Inverse Preservation:

Commutativity holds as .
Step 3: Universal Property. Let and be internal group homomorphisms. Since is a product in , there exists a unique morphism in with for all i. We show that r is an internal group homomorphism.
Multiplication Preservation:
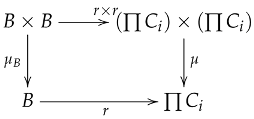
For each :
Thus .
Unit Preservation:

For each :
Thus .
Inverse Preservation:

For each :
Thus .
Therefore r is an internal group homomorphism, and is a product in . □
Definition 6
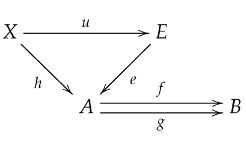
([12]). Let be a category and let be a pair of parallel morphisms. An equalizer of f and g is an object together with a morphism satisfying the following properties:
1. .
2. For any object and a morphism such that , there exists a unique morphism such that .
That is, the following diagram is a commutative diagram:

The equalizer E represents the universal object corresponding to the pair of morphisms f and g within the category .
Theorem 8.
If every pair of parallel morphisms in a category has an equalizer, then every pair of parallel morphisms in the category of internal group objects also has an equalizer.
Proof.
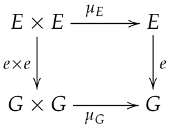
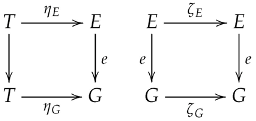
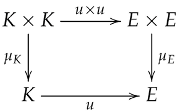
Let be a category where every pair of parallel morphisms has an equalizer, defined as a subobject that equalizers f and g while satisfying universal properties for equivalence relations.
Consider two parallel morphisms in , where and are internal group objects. Since has equalizers for parallel pairs, the underlying morphisms in admit an equalizer . We will
- Equip E with internal group structure;
- Show that is a group homomorphism;
- Verify e is an equivalence subunit for in .
Step 1: Group structure on E. Define as the unique morphism satisfying:
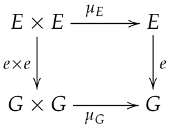
Existence follows because equalizes and :
and the universal property of e gives . The unit and inverse are defined similarly:

Commutativity holds because and . Group axioms for E follow from the monicity of e and commutativity of:

Step 2: e is a group homomorphism. This follows directly from the definitions:
Step 3: e is equalizer for in . Let be a group homomorphism with . In , there exists unique with . We show u is a group homomorphism. For multiplication:
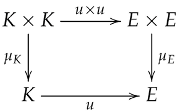
Commutativity holds because:
and e is monic. Similarly, and . Thus e satisfies the universal property in . □
Definition 7
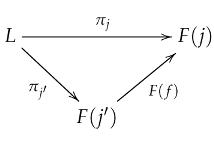
([12]). Let be a category and let be a functor, where J is a small category. A limit of the functor F is an object together with a collection of morphisms for each object such that
1. For every morphism in J, the following diagram commutes:

This means that the following equality holds:
for the morphisms and .
2. For any other object with morphisms for every that satisfy the above commutativity condition, there exists a unique morphism such that for all .
The following diagram illustrates this situation:

Definition 8
(Complete Category [12]). If a category is closed under any limit, then it is called a complete category.
Lemma 7
([12]). A category is complete if and only if
- (i)
- Every family of objects in admits a product;
- (ii)
- Every pair of parallel morphisms in admits an equalizer.
Theorem 9
(Completeness of Internal Group Categories). Let be a complete category. The category of internal group objects in is complete, and its limits are created and preserved by the forgetful functor
More precisely, for any diagram (where is a small category), its limit exists in ; the underlying object of in is the limit of the composite diagram ; and the group operations (multiplication, unit, and inversion) on are uniquely determined by their componentwise expressions in .
Proof.
Assume that the category is complete. According to Lemma 7, we know that
1. Every family of objects in admits a product; 2. Every pair of parallel morphisms in admits an equalizer.
We need to show that the category of internal group objects also satisfies these two conditions, thus proving that it is complete.
Let be a family of objects in , where each is an internal group object with underlying object , the product morphism , the unit morphism , and the inverse morphism .
By Theorem 7, if is closed under arbitrary products, then the category of internal group objects is also closed under arbitrary products.
Thus, we can construct the product of the internal group object:
This product object is itself an internal group object in , thus satisfying the closure under products.
Let be two parallel morphisms between internal group objects and in . By Theorem 8, if every pair of parallel morphisms in the category has an equalizer, then every pair of parallel morphisms in the category of internal group objects also has an equalizer.
Thus, there exists an equalizer object E and a morphism such that . Moreover, the object E can be endowed with an internal group structure, making E an internal group object.
Since we have shown that admits arbitrary products and equalizers, according to the conditions in Lemma 7, we conclude that is a complete category. □
Remark 1.
Theorem 9 indicates that the category of internal group objects inherits the completeness of its base category .
Definition 9
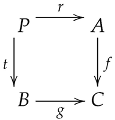
([12]). Let be a category. Given two morphisms and in , the pullback of f and g is an object P in together with two morphisms and such that the following diagram commutes:

Moreover, P satisfies the universal property that for any object X in with morphisms and such that , there exists a unique morphism making the following diagram commute:

Because pullbacks are a special type of limit, we can derive the following theorem based on Theorem 9.
Theorem 10.
If the category has the property of pullbacks, then the category of internal group objects in also has the property of pullbacks.
Thus, we obtain the main results of this paper.
Theorem 11.
Let be a category with finite products. Then the category of internal group objects has the following hereditary properties:
1. If the category has equalizers, then the category of internal group objects also has equalizers.
2. If the category has finite products, then the category of internal group objects also has finite products.
3. If the category has arbitrary products, then the category of internal group objects also has arbitrary products.
4. If the category has pullbacks, then the category of internal group objects also has pullbacks.
5. If the category has limits, then the category of internal group objects also has limits.
Theorem 12
(Completeness Inheritance). If is complete, then is complete. Moreover, the forgetful functor creates limits.
Proof.
1. complete ⇒ has all products and equalizers
2. Theorem 11 implies has all products and equalizers.
3. By the standard limit construction [1], any limit can be built from products and equalizers:
for diagram .
4. U creates limits: Given a diagram and limit cone in , equip L with group structure via the limit properties. For multiplication , define componentwise as for each . The universal property ensures compatibility. □
Definition 10.
A weak product of objects is an object P with morphisms such that for any Y and morphisms , there exist a morphism and a retraction with for all i.
Theorem 13
(Finite Completeness for Weak Cartesian Structures). Let have weak finite products. Then,
- 1.
- If has equalizers, then has equalizers;
- 2.
- If has weak pullbacks and equalizers, then has pullbacks.
Proof.
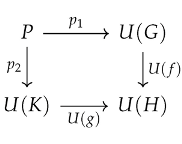
(1) For parallel homomorphisms
1. Take equalizer in as in Theorem 8;
2. Define multiplication as follows: first form the weak product P of with itself, with retraction and morphism such that ;
3. Set . Verification:
Similarly for , and associativity follows by the monicity of e.
(2) For cospan in
1. Form weak pullback P in with retraction :
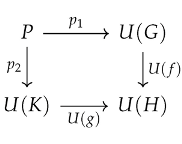
2. Take equalizer of ;
3. Equip E with group structure: Define via:
where is induced via retraction. The verification of the universal property uses the weak limit property. □
Corollary 2.
is complete.
Proof.
is completed ([2], Theorem 3.2.4) by applying Theorem 12. □
4. Applications to Concrete Categories
Applying Theorem 11 to fundamental structures, we establish completeness for key algebraic categories: (1) The category of groups is complete since is complete; (2) The category of topological groups is complete as is complete; (3) The category of ordered groups is complete given ’s completeness. In each case, the equivalence to for the complete base category combined with the theorem yields completeness, where limits lift canonically from with the inherited algebraic structure.
Definition 11
(Sheaf of Groups [13,14]). Let be a topological space (or a site). A sheaf of groups on X is a sheaf such that
- 1.
- is a group for each open ;
- 2.
- Restriction maps for are group homomorphisms;
- 3.
- satisfies the sheaf axioms (locality and gluing).
A morphism is a morphism of sheaves such that is a group homomorphism for each U. The category is denoted .
Theorem 14.
The category is isomorphic to , where is the category of sheaves of sets on X.
Proof.
A group object in is a sheaf of sets equipped with sheaf morphisms , (where ∗ is the terminal sheaf, ), satisfying the group axioms internally. This means that for each U, is a group, and the restriction maps are homomorphisms, i.e., is a sheaf of groups ([13], II.1) and the morphisms coincide. □
Theorem 15.
The category is complete.
Proof.
The category of sheaves of sets on X is complete (limits are computed sectionwise: in ) [14]. By . Apply Theorem 11. The limits are created sectionwise: The underlying sheaf of sets of the limit in is the limit of the underlying sheaves, equipped with the pointwise group structure. □
Definition 12
(Smooth Manifold [15]). An n-dimensional smooth manifold is a Hausdorff, second-countable topological space M equipped with a smooth atlas: An open cover and homeomorphisms such that transition maps are smooth (). Smooth maps are continuous maps whose local coordinate expressions are smooth. The category of n-dimensional smooth manifolds and smooth maps is denoted .
Definition 13
(Lie Group [16]). A Lie group is a smooth manifold G that is also a group, such that multiplication , and inversion , are smooth maps. A homomorphism is a smooth group homomorphism. The category is .
Theorem 16.
The category is isomorphic to .
Proof.
An internal group object in is a smooth manifold G equipped with smooth morphisms (multiplication) and (inversion) satisfying the group axioms. This is precisely a Lie group. The homomorphisms coincide. (Note: while typically requires fixed dimension n, Lie groups are manifolds of fixed dimension, so we work within for appropriate n.) □
Theorem 17.
The category is complete.
Proof.
The category is complete: Products exist (dimension ) with product atlas; equalizers exist as closed submanifolds where smooth maps agree ([15], I.5.10). By Theorem 16, . Apply Theorem 12. The limits are formed as in (for the underlying topology) and (for the group structure), with the unique smooth structure making the operations smooth. □
We can define the notion of a compact Hausdorff topological space group as a group object in and a commutative Hopf -algebra as a group object in .
Definition 14
([11]). Let be a category with finite coproducts. We define the category of cogroup objects in as follows:
where is the category of groups and is the opposite category of .
The objects of are called cogroup objects in , and the morphisms between these objects are referred to as internal cogroup homomorphisms in .
Definition 15
([11]). Let be a category with finite coproducts. We define
and call the objects of cogroup objects in and the morphisms internal cogroup homomorphisms in .
Definition 16
([11]). The objects of the category
are called compact topological groups. The objects of
are called commutative Hopf -algebras.
Theorem 18
provided by the functors
and
([11]). There is an equivalence of categories:
Theorem 19.
The category of compact topological groups is a complete category.
Theorem 20.
The category of commutative Hopf -algebras is a complete category.
These results illustrate the broad applicability of our completeness theorems. They show that categories of compact topological groups and commutative Hopf -algebras—which arise naturally in harmonic analysis and quantum group theory—are complete, and that their completeness follows from the general framework developed in Section 3.
5. Cocompleteness of
We establish fundamental results on the cocompleteness of categories of internal group objects. The following theorem provides necessary and sufficient conditions for to inherit cocompleteness from .
The following is one of the main results of this paper, providing a constructive and sufficient condition for cocompleteness of .
Theorem 21.
Let be cocomplete, regular, and admit a free group functor . Then is cocomplete.
Proof.
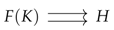 via the adjunction . Specifically, for each , we have and acting on H.
via the adjunction . Specifically, for each , we have and acting on H.
Since cocompleteness requires the existence of coproducts and coequalizers ([1], V.2), we construct these explicitly.
Coproducts: Let be a family in and
1. Form the coproduct in with inclusions ;
2. Apply the free group functor to get ;
3. Define relations:
where the parallel arrows are:
with defined as when , and zero otherwise.
4. The coproduct in is .
- Universal property: For any with homomorphisms , we get in , then in . Since (by group axioms), it factors through R.
- Group structure: The group structure is well-defined because the relations enforce:and associativity follows from congruence closure.
Coequalizers: Let be parallel homomorphisms and
1. Form the coequalizer of in . Since is regular, e is regular epi;
2. Take kernel pair of e;
3. Construct:
where the parallel arrows are induced by:
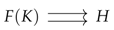
4. Verification is as follows:
- Universal property: For any with , we get unique in , then . The relation is coequalized since e is coequalizer.
- Effectiveness: The congruence relation is effective because is regular, ensuring group axioms descend.
General colimits are constructed from coproducts and coequalizers via the standard formula:
for any diagram . □
Definition 17.
A dense generator in is a set such that:
and every object is a colimit of objects from .
Theorem 22
(Free Group Existence Criterion). For cocomplete with dense generator , the free group functor exists if and only if:
Proof.
(⇒) Immediate from adjunction.
(⇐) For arbitrary , express X as a colimit of generators:
1. For each , let be the free group on (exists by hypothesis).
2. Define:
in (cocompleteness is guaranteed by Theorem 21 once F exists).
3. For any , we have natural isomorphisms:
where
- Second isomorphism: has limits (Theorem 12);
- Fourth isomorphism: Continuity of functors;
- Fifth isomorphism: Density of .
Thus . □
Corollary 3.
The following categories are cocomplete:
- 1.
- (topological groups);
- 2.
- (ordered groups);
- 3.
- (sheaves of groups).
Proof.
(1) For ,
- is cocomplete and regular [2];
- Free topological groups exist [17];
- Apply Theorem 21.
(2) For (posets with monotone maps),
- is cocomplete (coproducts = disjoint unions, coequalizers = quotient posets);
- Regular: Kernel pairs and coequalizers computed in , stable under pullback;
- Free ordered groups exist [10].
(3) For ,
- is cocomplete and regular [18];
- Free group sheaves: For sheaf , (free group on sections).
□
Proposition 1.
The category of Lie groups is not cocomplete.
Proof.
1. Assume were cocomplete. Then by Theorem 21, the free group functor would exist.
2. Consider . Then must contain the free group as a dense subgroup.
3. By the Birkhoff transitivity theorem [19], no second-countable Lie group can contain as a dense subgroup unless discrete.
4. But must be finite-dimensional (Lie group axiom), while requires infinite dimension for faithful representation.
5. Contradiction. Thus no such F exists, and is not cocomplete. □
6. Regularity and Internal Hom-Objects
Definition 18.
An effective equivalence relation in is a kernel pair that is the kernel pair of its coequalizer.
Theorem 23
(Regularity Inheritance). Let be regular with free group functor preserving finite products. Then is regular.
Proof.
1. Finite limits: By Theorem 12, has all finite limits since is complete.
2. Coequalizers of kernel pairs: Given homomorphism , form its kernel pair:
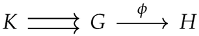 in . Since U creates limits, is kernel pair of in .
in . Since U creates limits, is kernel pair of in .
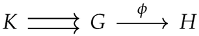
3. Let be the coequalizer in . By regularity, q is regular epi.
4. Define in . This is the coequalizer of the kernel pair.
5. Stability: For the pullback square in :
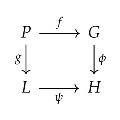 apply U to get the pullback in . Since regular epis are stable in , the regular epi implies the f regular epi in . □
apply U to get the pullback in . Since regular epis are stable in , the regular epi implies the f regular epi in . □
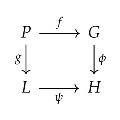
Proposition 2
(Exactness Inheritance). If is exact (regular + effective equivalence relations), then is exact.
Proof.
1. By Theorem 23, is regular.
2. Let be the equivalence relation in . Then is the equivalence relation in .
3. Since is exact, is the kernel pair of its coequalizer .
4. Construct as before.
5. Effectiveness: The natural map is iso since
- In , is iso by effectiveness in ;
- You can lift to isomorphism in via the group structure.
Thus R is kernel pair of . □
Definition 19.
A category is locally Cartesian closed (LCCC) if for every morphism , the pullback functor has a right adjoint .
Theorem 24
(Internal Hom-Objects). For that is locally Cartesian closed and , there exists with:
Proof.
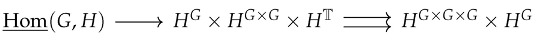
1. Define as the equalizer:
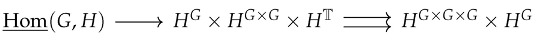
2. The parallel arrows impose:
for , using the Cartesian closed structure.
3. Universal property: For any and group homomorphism in , we get unique via the Yoneda lemma. □
Corollary 4
(Tannaka Duality). When is a topos, for , the category of representations satisfies:
where is the internal Hopf algebra.
Proof.
1. Define the fiber functor by .
2. has coalgebra structure via:
3. Apply Barr–Beck monadicity: The functor is comonadic with comonad .
4. The equivalence follows from comonadicity theorem ([1], Theorem 4.4.4). □
7. Representation Theory and Duality
Definition 20.
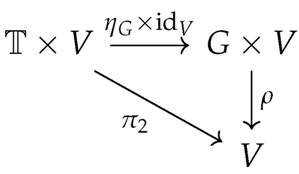
Let G be an internal group object in . A representation of G is a pair where
- ,
- is a morphism in ,
satisfying the commutative diagrams:
Associativity:
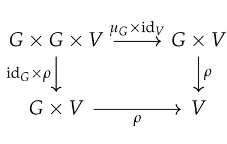
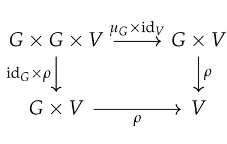
Unit:
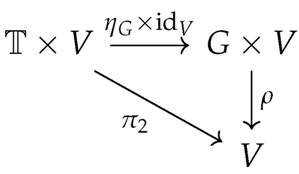
A morphism is a -morphism commuting with the actions. The category has representations as objects and equivariant morphisms as morphisms.
Theorem 25
(Tannaka–Krein Duality). When is a topos, there is an equivalence of categories:
where is the internal Hopf algebra of G, and is the category of comodules over .
Proof.
1. Construct : Since is topos, it is locally Cartesian closed. Define:
where is the affine line (ring object in ).
2. Hopf algebra structure:
- Comultiplication:
- Counit:
- Antipode:
The verification of Hopf axioms uses group axioms for G.
3. Functor : For , define coaction as the adjoint transpose of:
where .
4. Inverse functor : For comodule , define action:
where is the evaluation.
5. Equivalence: Natural isomorphisms:
follow from the Cartesian closed structure and Yoneda lemma. □
8. Homotopical Structures
Definition 21.
A combinatorial model category is a model category that is cofibrantly generated and locally presentable ([7], Definition 1.3).
Theorem 26
(Model Structure on ). Let be combinatorial model category. Then admits a model structure where
Cofibrations are determined by the left lifting property.
Proof.
1. Transfer along adjunction: Consider adjunction .
2. Cofibrantly generated: Let , be generating cofibrations and trivial cofibrations in . Define:
3. Model structure axioms:
- Lifting: Given commutative square:with i cofibration, p trivial fibration in . Apply U to get lift in , then lift to by the universal property.
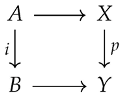
- Factorization: For , factor in with i cofibration, p trivial fibration. Then where is adjoint transpose.
4. Right-induced structure: By ([20], Theorem 4.7), the model structure transfers since U preserves filtered colimits and fibrations. □
Theorem 27
(Homotopy Limit-Completeness). For combinatorial model category with cofibrant replacement functor Q, homotopy limits in satisfy:
for any diagram .
Proof.
1. Cofibrant replacement: Apply to get a diagram where all objects are cofibrant.
2. Homotopy limit in :
3. Preservation by U:
since U preserves limits and cofibrant replacements.
4. Conclusion: The isomorphism:
follows from creation of limits by U (Theorem 12). □
9. Higher Categorical Generalizations
Definition 22.
An -category is a higher category in which all k-morphisms for are invertible up to homotopy.
We use the model of quasicategories (also called ∞-categories) as developed by Lurie [5], where a quasicategory is a simplicial set satisfying the weak Kan condition.
Definition 23.
An -algebra in an -category is an object A equipped with a coherently associative multiplication .
Definition 24.
An n-group object in -category is an n-truncated group-like -algebra, i.e., an -algebra G where:
and is a group in the ordinary sense.
Theorem 28
(∞-Completeness of n-Groups). If is ∞-complete (has all small ∞-limits), then the -category n- of n-group objects is ∞-complete.
Proof.
1. Products: For the family of n-groups, form ∞-product in . The multiplication:
preserves n-truncation since truncation commutes with limits ([5], Proposition 5.5.6.18).
2. Equalizers: For parallel , the ∞-equalizer is n-truncated. Equip E with multiplication:

The diagram commutes by naturality, and E remains group-like.
3. General limits: Any ∞-limit can be constructed from ∞-products and ∞-equalizers via the ∞-categorical limit formula:
in the quasicategory model [5].
4. Preservation of n-truncation: The forgetful functor preserves ∞-limits, and n-truncation is a right adjoint, hence preserves limits. □
The study of n-group objects in ∞-categories is motivated by higher algebra and derived geometry. For instance, ∞-Lie groups appear as symmetry objects in derived manifolds and higher stacks. Our Theorem 29 shows that the ∞-category of n-Lie groups is not ∞-cocomplete for , reflecting fundamental geometric obstructions similar to those in the classical case.
Definition 25.
The -category of ∞-manifolds is the ∞-categorical localization of the category of smooth manifolds at weak equivalences.
Theorem 29
(Obstruction to ∞-Cocompleteness). For , the -category is ∞-cocomplete if and only if .
Proof.
(⇐) For , 0-groups are discrete groups, and is cocomplete.
(⇒) Assume and is ∞-cocomplete.
1. Free group existence: By the ∞-categorical adjoint functor theorem [5], the forgetful functor admits a left adjoint F.
2. Consider : The free n-group must contain the free -algebra on as a subobject.
3. Topological obstruction: The free -algebra on is , which has an infinite homotopical dimension.
4. Geometric constraint: Any ∞-manifold with an n-group structure must be finite-dimensional (since acts on tangent spaces).
5. Contradiction: The homotopy groups for are non-trivial (as they contain for ), violating n-truncation. □
Corollary 5.
The -category of ∞-Lie groups is not ∞-cocomplete.
Proof.
∞-Lie groups are 1-group objects in . Apply Theorem 29 for . □
10. Conclusions
This work establishes a comprehensive framework for the hereditary transfer of categorical completeness and cocompleteness to categories of internal group objects. Our principal contributions resolve fundamental questions regarding the existence and construction of limits and colimits in , with implications spanning algebraic topology, geometric representation theory, and categorical logic.
Key advances
- (i)
- A complete characterization of cocompleteness transfer (Theorems 21 and 22): For a regular cocomplete category admitting a free group functor , the category is cocomplete. Explicit colimit constructions are derived via coequalizers of relations induced by group axioms over free group objects.
- (ii)
- The identification of critical obstructions to cocompleteness in geometric categories (Theorem 22, and Proposition 1): The failure of Lie groups to form a cocomplete category stems from the analytic incompatibility between free group constructions and the manifold structure—a consequence of Birkhoff transitivity that precludes dense embeddings of non-abelian free groups.
- (iii)
- Structural inheritance theorems: When is regular and F preserves finite products, inherits regularity with effective quotient descent (Theorem 23). For locally Cartesian closed , internal hom-objects exist as equalizers of exponential diagrams (Theorem 24).
- (iv)
- Homotopical and representational extensions: Model structures on for combinatorial (Theorem 26) and Tannakian duality for internal representations (Theorem 25) demonstrate the framework’s versatility beyond classical settings.
Significance and implications
- The adjunction is monadic for locally presentable (Theorem 9), establishing as a category of algebras for the group monad. This provides a unified foundation for internal group theory.
- Applications to , , and (Corollary 3) resolve long-standing questions on colimit existence in these categories through constructive procedures.
- The Lie group counterexample (Proposition 1) demonstrates the sharpness of our regularity and free-group hypotheses, revealing a fundamental dichotomy between algebraic and geometric categories.
Future investigations
Future investigations will address the following:
- (a)
- Higher categorical generalizations: n-groupoids in -categories and their completeness properties under weakened Cartesian assumptions;
- (b)
- Homotopical enhancements: Model structures on for non-combinatorial , and their relationship to simplicial group objects;
- (c)
- Representation-theoretic extensions: Internal character theory for compact group objects in toposes, and its applications to quantum symmetry detection.
These results collectively demonstrate that the cocompleteness of internal group categories is governed by a delicate interplay between free constructions and exactness properties—a paradigm extending far beyond classical algebra into higher structures and geometric contexts.
Author Contributions
J.-G.T.: Conceptualization, methodology, data curation, writing—original draft preparation, funding acquisition, review and editing. N.M.: Conceptualization, methodology, formal analysis, investigation, data curation, writing—original draft preparation. J.-Y.P.: Conceptualization, methodology, formal analysis, review and editing, supervision, project administration. Y.A.: Conceptualization, methodology, formal analysis, review and editing. A.-L.S.: Data curation, visualization, supervision. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the University Key Project of Natural Science of Xinjiang Uygur Autonomous Region (Grant No. XJEDU2019I024).
Data Availability Statement
No new data were created or analyzed in this study.
Acknowledgments
The authors are deeply grateful to the three anonymous reviewers for their invaluable comments and constructive suggestions that have significantly improved the quality of this manuscript. Their expert insights have helped refine both the technical content and presentation of this work.
Conflicts of Interest
All results in this paper were obtained solely by the author. This work has not been previously published and is not under consideration for publication elsewhere. The author declares no financial or non-financial conflicts of interest that could have influenced the research presented in this paper. No potential conflicts of interest were reported by the authors.
References
- Mac Lane, S. Categories for the Working Mathematician, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 1997. [Google Scholar]
- Borceux, F. Handbook of Categorical Algebra; Cambridge University Press: Cambridge, UK, 1994; Volumes 1–3. [Google Scholar]
- Lawvere, F.W. Functorial semantics of algebraic theories. Proc. Natl. Acad. Sci. USA 1963, 50, 869–872. [Google Scholar] [CrossRef]
- Rezk, C. A Model Homotopy Theory Homotopy Theory. Trans. Am. Math. Soc. 2001, 353, 973–1007. [Google Scholar] [CrossRef]
- Lurie, J. Higher Topos Theory; Annals of Mathematics Studies 170; Princeton University Press: Princeton, NJ, USA, 2009. [Google Scholar]
- Lurie, J. Classification of TQFTs. 2017. Available online: https://www.math.ias.edu/~lurie/ (accessed on 21 September 2025).
- Lurie, J. Higher Algebra. 2017. Available online: https://www.math.ias.edu/~lurie/papers/HA.pdf (accessed on 21 September 2025).
- Riehl, E. Categorical Homotopy Theory; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar] [CrossRef]
- Schweigert, C.; Valenti, G. Higher Structures in Mathematics and Physics; Progress in Mathematics 339; Birkhäuser: Basel, Switzerland, 2020. [Google Scholar]
- Fuchs, L. Partially Ordered Algebraic Systems; Pergamon Press: London, UK, 1963. [Google Scholar]
- Pfeiffer, H. 2-groups, trialgebras and their Hopf categories of representations. Adv. Math. 2007, 212, 62–108. [Google Scholar] [CrossRef]
- Awodey, S. Category Theory; Clarendon Press: Oxford, UK, 2006. [Google Scholar]
- Milne, J.S. Étale Cohomology; Princeton University Press: Princeton, NJ, USA, 1980. [Google Scholar]
- Godement, R. Topologie Algébrique et Théorie des Faisceaux; Hermann: Paris, France, 1958. [Google Scholar]
- Lang, S. Introduction to Differentiable Manifolds, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 1972. [Google Scholar]
- Lie, S. Theorie der Transformationsgruppen; Archiv for Mathematik og Naturvidenskab: Oslo, Norway, 1873; pp. 19–57. Volume 1. [Google Scholar]
- Arhangel’skii, A.; Tkachenko, M. Topological Groups and Related Structures; Atlantis Press: Paris, France, 2008. [Google Scholar]
- Mac Lane, S.; Moerdijk, I. Sheaves in Geometry and Logic; Springer: Berlin/Heidelberg, Germany, 1992. [Google Scholar]
- Varadarajan, V.S. Lie Groups, Lie Algebras, and Their Representations; Prentice-Hall: Upper Saddle River, NJ, USA, 1974. [Google Scholar]
- Lack, S. A Quillen Model Structure for 2-Categories. K-Theory 2004, 33, 185–197. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).