Maximum General Sum-Connectivity Index of Trees and Unicyclic Graphs with Given Order and Number of Pendant Vertices
Abstract
1. Introduction
- Tomescu and Kanwal [5] proved that the tree has the minimum for .
- Yao [6] determined the trees having the minimum for , where .
- Albalahi and Ali [7] determined the trees with the minimum for , where .
- Cui and Zhong [8] presented the trees having the maximum for , where .
- Tache and Tomescu [9] determined the trees with the maximum for .
- Tomescu and Arshad [10] showed that the unicyclic graph has the minimum for .
- Tache and Tomescu [9] determined the unicyclic graphs with the maximum for .
2. Preliminary Results
3. Main Results
4. Conclusions
- If and , then and is the only tree having the largest , so .
- If and , then and is the only tree having the largest , so .
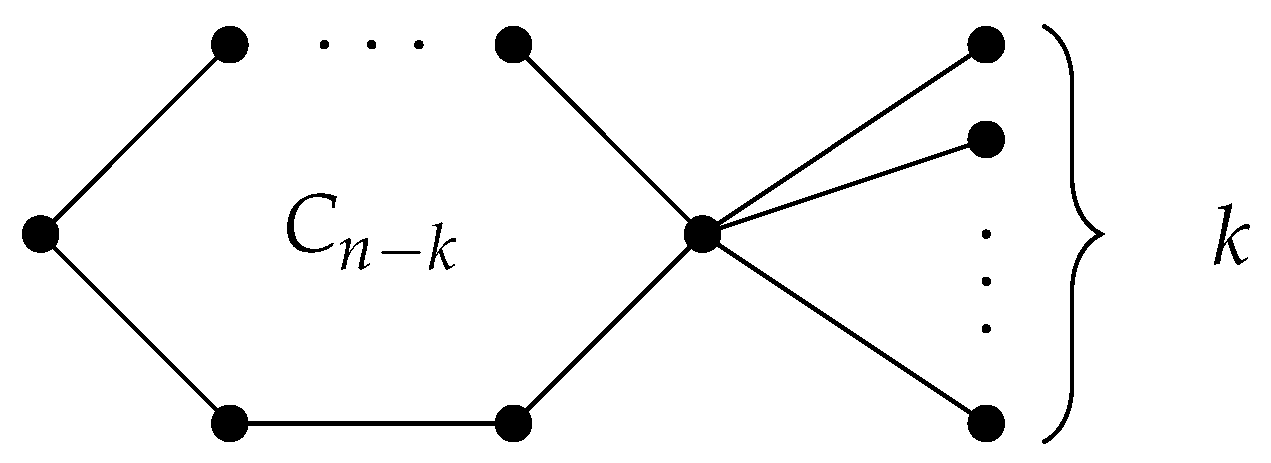
- If and , then and is the only unicyclic graph having the largest , so .
- If and , then and is the only unicyclic graph having the largest , so .
- If and , then and is the only unicyclic graph having the largest , so .
- Find trees with the minimum and maximum for .
- Find unicyclic graphs with the minimum for and .
- Find unicyclic graphs with the maximum for .
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhou, B.; Trinajstić, N. On general sum-connectivity index. J. Math. Chem. 2010, 47, 210–218. [Google Scholar] [CrossRef]
- Ali, A.; Zhong, L.; Gutman, I. Harmonic index and its generalizations: Extremal results and bounds. MATCH Commun. Math. Comput. Chem. 2019, 81, 249–311. [Google Scholar]
- Hanif, M.; Bhatti, A.A.; Saber, H.; Attiya, A.A.; Ali, A. On general sum-connectivity index and number of segments of fixed-order chemical trees. J. Math. 2025, 2025, 5042484. [Google Scholar] [CrossRef]
- Swartz, E.; Vetrík, T. General sum-connectivity index of unicyclic graphs with given maximum degree. Discrete Appl. Math. 2025, 366, 238–249. [Google Scholar] [CrossRef]
- Tomescu, I.; Kanwal, S. Ordering trees having small general sum-connectivity index. MATCH Commun. Math. Comput. Chem. 2013, 69, 535–548. [Google Scholar]
- Yao, Y. The smallest sum-connectivity index on trees with n vertices and k pendant vertices. Open J. Discrete Appl. Math. 2019, 2, 23–30. [Google Scholar] [CrossRef]
- Albalahi, A.; Ali, A. On the minimum general sum-connectivity of trees of fixed order and pendent vertices. J. Math. 2022, 2022, 1–4. [Google Scholar] [CrossRef]
- Cui, Q.; Zhong, L. On the general sum-connectivity index of trees with given number of pendent vertices. Discrete Appl. Math. 2017, 222, 213–221. [Google Scholar] [CrossRef]
- Tache, R.-M.; Tomescu, I. General sum-connectivity index with a ≥ 1 for trees and unicyclic graphs with k pendants. In Proceedings of the 17th International Symposium on Symbolic and Numeric Algorithms for Scientific Computing (SYNASC), Timisoara, Romania, 21–24 September 2015; pp. 307–311. [Google Scholar]
- Tomescu, I.; Arshad, M. On the general sum-connectivity index of connected unicyclic graphs with k pendant vertices. Discrete Appl. Math. 2015, 181, 306–309. [Google Scholar] [CrossRef]
- Vetrík, T.; Masre, M. General eccentric connectivity index of trees and unicyclic graphs. Discrete Appl. Math. 2020, 284, 301–315. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Swartz, E.; Vetrík, T. Maximum General Sum-Connectivity Index of Trees and Unicyclic Graphs with Given Order and Number of Pendant Vertices. Mathematics 2025, 13, 3061. https://doi.org/10.3390/math13193061
Swartz E, Vetrík T. Maximum General Sum-Connectivity Index of Trees and Unicyclic Graphs with Given Order and Number of Pendant Vertices. Mathematics. 2025; 13(19):3061. https://doi.org/10.3390/math13193061
Chicago/Turabian StyleSwartz, Elize, and Tomáš Vetrík. 2025. "Maximum General Sum-Connectivity Index of Trees and Unicyclic Graphs with Given Order and Number of Pendant Vertices" Mathematics 13, no. 19: 3061. https://doi.org/10.3390/math13193061
APA StyleSwartz, E., & Vetrík, T. (2025). Maximum General Sum-Connectivity Index of Trees and Unicyclic Graphs with Given Order and Number of Pendant Vertices. Mathematics, 13(19), 3061. https://doi.org/10.3390/math13193061





