Abstract
In cooperative coevolution (CC) frameworks, it is essential to identify the subproblems that can significantly contribute to finding the optimal solutions of the objective function. In traditional CC frameworks, subproblems are selected either sequentially or based on the degree of improvement in the fitness of the optimal solution. However, these classical methods have limitations in balancing between exploration and exploitation when selecting the subproblems. To overcome these weaknesses, we propose upper confidence bound (UCB)-based new subproblem selection methods for the CC frameworks. Our proposed methods utilize UCB algorithms to strike a balance between exploration and exploitation in subproblem selection, while also incorporating a non-stationary mechanism to account for the convergence of evolutionary algorithms. These strategies possess novel characteristics that distinguish our methods from existing approaches. In comprehensive experiments, the CC frameworks using our proposed subproblem selectors achieved remarkable optimization results when solving most benchmark functions comprised of 1000 interdependent variables. Thus, we found that our UCB-based subproblem selectors can significantly contribute to searching for optimal solutions in CC frameworks by elaborately balancing exploration and exploitation when selecting subproblems.
Keywords:
cooperative coevolution (CC); multi-armed bandit (MAB); upper confidence bound (UCB); evolutionary algorithms; differential evolution; global optimization; non-linear optimization MSC:
68T20; 68W50; 90C26; 90C59
1. Introduction
Since the development of evolutionary algorithms, many studies have been conducted to address the challenge of complex large-scale global optimization (LSGO) problems by utilizing evolutionary algorithms [1,2,3,4,5]. In particular, cooperative coevolutionary (CC) frameworks [6] have achieved notable performance in addressing many LSGO problems. Consequently, numerous studies have aimed to enhance the optimization abilities of CC frameworks to effectively addressing complex LSGO problems, particularly large-dimensional black-box functions [7,8,9,10,11].
The CC framework employs the divide-and-conquer strategy to effectively address LSGO problems [6,7]. In detail, the CC framework first divides the solution space, which is the domain space of the given objective function, into one or more subspaces, i.e., subproblems, with smaller dimensions than the original one. The CC framework then selects one subproblem to be explored in the subsequent evolutionary step. Thereafter, the evolutionary algorithms, such as genetic algorithms (GA) [12,13], differential evolution (DE) [14,15], and particle swarm optimization (PSO) [16,17], search for the optimal solutions locally within the subspace related to the selected subproblem by utilizing one or more individuals. In this process, the individuals are evolved through evolutionary operations such as crossover, mutation, and selection. Finally, the CC framework evaluates the fitness values of the evolved individuals and updates an optimal solution, i.e., an individual with the best fitness. These processes are repeated until either the optimal solution converges or the maximum number of fitness evaluations is exhausted.
One of the essential issues within the CC framework is the selection of the subproblem to be searched in the next step, which is referred to as the subproblem selection task [7]. The CC framework designates the subspace to be explored by the evolutionary algorithm in every evolutionary step. Because the decision variables contribute differently to fitness computation, their corresponding subproblems also play distinct roles in searching for optimal solutions. In this case, many CC frameworks attempt to intensively select and evolve the subproblems that make the most significant contribution to improving the fitness of the best individuals, thereby facilitating a rapid search for the optimal solution. Nevertheless, such fast solution searches often cause premature convergence, seriously impairing the efficacy and accuracy of solution searches [18,19].
To effectively prevent this phenomenon, CC frameworks should sometimes choose subproblems with relatively low contributions and search the subspaces they span. That is, the subproblem selection task in CC frameworks is inherently related to the exploration-and-exploitation trade-off problem [20,21,22]. In exploration-based subproblem selection, a broad search of various solutions in the solution space is performed to identify a diverse range of potential solutions. On the other hand, the exploitation-based mechanism focuses on selecting subproblems that have yielded the best solution search results to intensively search for candidate optimal solutions near the current optimal solution, thereby enabling faster convergence. If exploration-based subproblem selection is excessively performed, individuals will slowly converge, eventually failing to find the best solution within limited computational resources. Conversely, excessive exploitation-based subproblem selection can result in premature convergence by missing the opportunity to discover diverse candidate solutions. Thus, CC frameworks aim to balance the exploration- and exploitation-based subproblem selection mechanisms to effectively find the optimal solution.
In order to achieve this goal successfully, the multi-armed bandit (MAB) algorithms [23], such as -greedy algorithm [24], the -first and decreasing algorithms [25,26], and upper confidence bound (UCB) algorithms [27,28], have been widely utilized. Among them, the UCB algorithms have shown remarkable abilities in numerous applications requiring sophisticated control of exploration and exploitation. Therefore, it is reasonable to utilize the MAB algorithms as fundamental techniques to address the subproblem selection task in the CC framework.
Accordingly, in this paper, we propose MAB algorithms, specifically UCB algorithm-based new subproblem selection methods for the CC frameworks, to effectively control the balance between exploration and exploitation when selecting the subproblem to be explored in the next step. Our proposed subproblem selectors utilize the UCB algorithms as the base algorithm to identify the promising subproblems that can significantly contribute to improving the optimization results in each evolutionary step. Moreover, our subproblem selectors employ non-stationary mechanisms [29,30,31] to effectively address the characteristics of evolutionary algorithms in which the convergence status of individuals dynamically changes. In the empirical experiments with 1000-dimensional benchmark functions [32,33], we found that the CC frameworks with our proposed subproblem selectors could search for optimal solutions more effectively than traditional CC frameworks. In particular, when solving the benchmark functions with numerous non-separable variables, the CC frameworks with our subproblem selectors achieved better optimization results than those of the classical CC ones. These experimental results indicate that our proposed UCB-based subproblem selection methods are effective in addressing the LSGO functions with complex interdependencies.
This paper comprises five sections. In Section 2, we explain the background knowledge about evolutionary algorithms required to understand our study. In Section 3, we provide several preliminaries that are needed to study the subproblem selection methods used in the CC frameworks. In Section 4, we propose four new UCB-based subproblem selection methods and show their detailed implementations. In Section 5, we present the experiments conducted to evaluate the performance of the proposed subproblem selectors in practical CC frameworks, along with their results. Finally, we summarize our study results and explain future study plans in Section 6.
2. Related Works
An optimization problem aims to find the minimum (or maximum) solution to an objective function. If the domain of the function consists of large-scale dimensions, we primarily refer to such problem as an LSGO problem. In general, the objective functions addressed in the LSGO have a complicated surface in the solution space. Particularly, if there exist strong interdependencies among the variables of the objective function, they span relatively further complex solution spaces, having many local minima, saddle points, and multimodal peaks, which make the search for optimal solutions extremely challenging. In this case, traditional analytic or numerical methods are inadequate to address these complicated objective functions because they require excessive computational costs to find their optimal solutions.
Accordingly, various methods to solve LSGO problems effectively using evolutionary algorithms have been widely studied [1,2,3,4,5]. Evolutionary algorithms aim to find approximately optimal solutions for complex optimization problems by leveraging evolutionary processes such as natural selection, survival of the fittest, and reproduction [4]. Evolutionary algorithms commonly involve three core elements, i.e., individuals, fitness, and solution search mechanisms. Firstly, an individual represents a possible candidate solution of the objective function addressed by the evolutionary algorithm. To address the objective function with an n-dimensional domain, an individual is composed of n elements which are mapped to the variables spanning the solution space one by one. Secondly, an individual has a unique fitness, a numerical value evaluated by the objective function, to present its quality. Thirdly, the solution search mechanism defines detailed methods for finding an optimal solution to the objective function, i.e., an individual with the best fitness in the solution space. In the evolutionary algorithm, all individuals evolve iteratively through operations such as mutation, crossover, and selection in every evolutionary step until they no longer show significant evolution. Through these repeated processes, the evolutionary algorithm searches for the approximately optimal solution of the objective function in the solution space.
Evolutionary algorithms have shown a notable ability to solve various LSGO problems. For example, X. Huang et al. proposed a surrogate-assisted gray prediction evolutionary algorithm to efficiently solve large-dimensional optimization problems [5]. They demonstrated that the surrogate model and inferior offspring learning strategies can further enhance the solution search ability of the gray prediction evolutionary algorithm. M. Song et al. developed a learning-driven algorithm with dual evolution patterns to effectively tackle large-scale multi-objective optimization problems [2]. To this end, they proposed a method that learns dual evolution patterns in the evolutionary process to efficiently generate promising solutions. Moreover, Z.-J. Wang et al. studied effective methods using the distributed particle swarm optimization algorithm to efficiently address large-dimensional optimization problems [34]. They demonstrated that a dynamic group learning strategy and an adaptive renumbering strategy can significantly contribute to solving large-dimensional cloud workflow scheduling problems using the distributed PSO algorithms.
Nevertheless, evolutionary algorithms still face many challenges in effectively addressing the problems with complex interdependencies among their variables. In particular, the prohibitive computational cost required to solve LSGO problems makes searching for their optimal solutions extremely challenging. To overcome this difficulty, a divide-and-conquer-based evolutionary algorithm framework, known as the CC framework, has been widely utilized [6,7], which is demonstrated in the next section.
3. Preliminaries
3.1. CC Frameworks to Solve LSGO Problems
The CC framework is one of the most effective evolutionary algorithms for solving a LSGO problem. It is formulated as
where is an n-dimensional scalar function such that and is an n-dimensional decision vector in the domain of the function f. Before explaining the CC framework in detail, we first define a concept of subproblem as follows.
Definition 1.
For an objective function , a problem is a set of the decision variables spanning an n-dimensional domain space of f. That is,
In the CC framework, a problem for the given objective function f, i.e., is decomposed into K subsets by the problem decomposers such as DG [8], FII [35], RDG [36], EVIID [37], and ERDG [38]. To this end, the modern problem decomposers identify interdependencies among all the variables and group them into K disjoint subsets based on their interdependencies. The variable interdependency is defined as follows [8].
Definition 2.
For an objective function , if any two variables and in satisfy
they are interdependent. Otherwise, they are independent.
In Definition 2, and are constants used for perturbations of and , respectively. If two variables and are interdependent, it is notated as “”. Otherwise, two variables are independent and it is notated as “”.
According to the variable interdependency identification rule shown in Equation (2), all the variables in are clustered into one or more disjoint subsets by grouping the interdependent variables into one set. Accordingly, the problem is decomposed into K disjoint subsets, called subproblems, as follows.
Definition 3.
For an objective function , a subproblem is a disjoint subset of and the variables in the set are interdependent. If is the ith subproblem of f, i.e., , it satisfies that and .
That is, the subproblems of are generated by grouping all the variables in based on their interdependencies. The variables in the same subproblem are interdependent. Based on Definitions 1 and 2, the CC framework efficiently searches for a global optimal solution of the objective function with large-dimensional domain space in a divide and conquer manner.
Algorithm 1 shows a pseudocode of the traditional CC framework [6]. Algorithm 1 takes two inputs f and m where f is an objective function and m is the number of individuals used in the evolutionary algorithm. The parameter is the maximum number of allowable fitness evaluations. In the initial phase, the CC framework divides the objective function into K disjoint subproblems depending on the interdependencies among the variables that constitute the domain of the objective function. To this end, problem decomposers, such as DG [8], FII [35], RDG [36], EVIID [37], and ERDG [38], are utilized. Then, in the evolutionary phase, the CC framework chooses one of the K subproblems using the subproblem selector to determine the subproblem that will be evolved in the next step. Afterward, the CC framework evolves the individuals in the subpopulation related to the selected subproblem by using evolutionary algorithms, such as DE and PSO. Subsequently, the evolved individuals in the subpopulation are evaluated by the objective function, and the individual with the best fitness is identified as the optimal individual in the current step (to evaluate the fitness values of the individuals, a function “Feval” is utilized in the CC frameworks. This function is described in Appendix A). The evolutionary phase is repeated until the number of fitness evaluations (i.e., FEs) exceeds the maximum number of fitness evaluations (i.e., maxFEs) [7]. Finally, the CC framework returns the individual with the best fitness in the evolved population as the optimal solution for the objective function.
| Algorithm 1 Traditional algorithm: BasicCC |
|
3.2. Subproblem Selection Task in CC Frameworks
One of the essential tasks in the CC framework is choosing the subproblem that will be evolved by the evolutionary algorithm in the next step [7]. A subproblem is composed of one or more variables that comprise the domain of the objective function. Then, selecting a subproblem restricts the solution search range to the specific area corresponding to the selected subproblem in the solution space. Because the variables involved in the subproblems have distinct influences on the function in the CC framework, the selection of subproblems significantly affects the search for an optimal solution.
Figure 1 describes how the subproblem selection affects the ability to search for an optimal solution for the objective function . This objective function is decomposed into two subproblems and by the problem decomposers. At the current optimal solution, the gradient of is relatively sharper than that of . If the first subproblem is selected based on the exploitation mechanism, the solution search will be intensively conducted on , accelerating its convergence. However, this rapid process may lead to premature convergence into local minima or saddle points, thereby degrading the quality of the final solution. On the other hand, if the second subproblem is chosen instead of based on the exploration, its convergence becomes relatively slower because the axis of has a gentler slope than . However, the solution search on a smooth slope, like , can lead to discovering more optimal solutions by bypassing the local minima and saddle points on the solution surface.
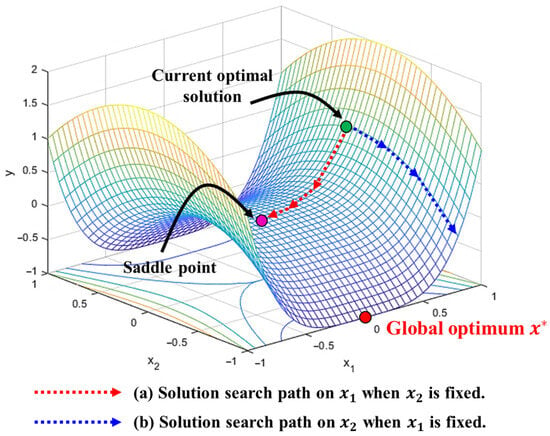
Figure 1.
An example illustrating how subproblem selection affects the solution search. At the current optimal solution, if the subproblem is chosen, the optimal solution converges to the saddle point. On the other hand, if the subproblem is selected, the saddle point can be avoided as the optimal solution is searched.
The example in Figure 1 illustrates that CC frameworks should search for candidate solutions across various scopes in the solution space, maintaining a balance between exploration and exploitation to discover the optimal solution successfully. Through such a solution search, we can avoid local minima or saddle points within the large-dimensional solution space. To perform these effective solution searches, the subproblem selectors in the CC frameworks must effectively address the exploration–exploitation trade-off when selecting the subproblem to be evolved in the next step. Accordingly, in the following section, we present novel subproblem selection methods to effectively identify the most promising subproblem that can most effectively balance exploration and exploitation during solution search.
4. Proposed Methods
In this section, we propose four new UCB-based subproblem selectors for generic CC frameworks. Figure 2 illustrates the overall architecture of our novel subproblem selectors. Our proposed subproblem selectors consist of three fundamental components: a reward evaluation function (REF), a contribution score computation function (CSF), and a subproblem selection function (SSF).
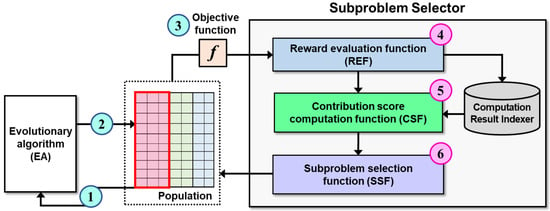
Figure 2.
The overall architecture of the proposed subproblem selector. Our proposed subproblem selector is composed of three fundamental functions, i.e., the REF, CSF, and SSF. The proposed subproblem selector can be applied in general CC frameworks. The numbers marked in the circle indicate the step in which each task is executed in the CC framework.
The proposed subproblem selector is utilized in the CC framework as follows: first, the CC framework extracts the subpopulation corresponding to the selected subproblem from the original population and evolves it using the evolutionary algorithm (Step 1). The evolved subpopulation is then re-merged into the original population (Step 2), and all individuals in the updated population are evaluated by the objective function (Step 3). Next, the REF in the subproblem selector computes a reward score for the evolved subproblem by referencing the individuals’ fitness values and indexes its computation results for incremental computation (Step 4). The CSF then calculates the contribution scores of all the subproblems by aggregating various information about them and their individuals, such as the reward scores, the number of evolutions of each subproblem, and the total number of steps (Step 5). After the CSF updates the contribution scores of the subproblems, the SSF selects a subproblem to be evolved in the next step based on the contribution scores (Step 6).
4.1. Component 1: Reward Evaluation Function (REF)
After the evolved subpopulation is merged into the population, the objective function evaluates all the individuals in the updated population to identify the new best individual. In this process, it is necessary to evaluate the degree of improvement in the best fitness after the subpopulation has evolved in order to measure how much the subproblem contributed to finding the best individual, i.e., the optimal solution. Let and be the non-negative fitness values of the best individuals observed before and after the ith subproblem evolves, respectively. We can then formulate the REF to evaluate the degree of improvement in the best fitness obtained after evolving the ith subproblem as
where is a positive smoothing factor to prevent that the denominator becomes zero (i.e., ). Accordingly, the reward score for each subproblem is always adjusted to a value between zero and one, regardless of when the subproblem has evolved and the individuals’ convergence status. Thus, the REF computes the reward score for the evolved subproblem using Equation (3) and passes its result to the CSF in the subproblem selector.
4.2. Component 2: Contribution Score Computation Function (CSF)
After the REF calculates the reward score of the evolved subproblem, the CSF computes the contribution scores of all the subproblems to evaluate how much each subproblem contributed to improving the fitness of the best individual. The simplest method to measure the contribution of the subproblem is to average all of its reward scores. However, this method causes several subproblems with relatively higher reward scores to be repeatedly selected. In this case, the specific scopes spanned by the selected subproblems are biasedly explored, thereby disturbing the exploration of various candidate solutions. Thus, subproblems with relatively small reward scores should sometimes be selected to explore various scopes in the solution space. It is a typical exploration–exploitation trade-off issue addressed by MAB algorithms.
Accordingly, the CSF utilizes various arm selection policies of the UCB algorithms to compute the contribution scores for the subproblems. The CSF computes the contribution score of the ith subproblem using
where is an average function and is a padding function, which are computed from the reward scores obtained after evolving the ith subproblem. n is the total number of evolutionary steps and is the number of times the ith subproblem is selected and evolved. In Equation (4), computes the empirical average of the reward scores and controls the trade-off between exploration and exploitation when selecting the subproblems. By varying these components, we can derive four new UCB-based contribution score computation methods. The detailed methods to calculate the contribution scores are explained in the following sections.
4.2.1. UCB1-Based Contribution Score Computation Method
Our first method utilizes the arm selection strategy of the UCB1 algorithm. In this method, the contribution score of the ith subproblem is determined by averaging all its reward scores and calculating the padding function. That is, the contribution score for the ith subproblem is computed by
where is the jth reward score obtained after evolving the ith subproblem. In Equation (5), the total number of evolutionary steps (i.e., n) follows a logarithmic scale, and the number of selections of the ith subproblem (i.e., ) follows a linear scale. Accordingly, in the initial evolutionary steps, subproblems with relatively low reward scores can often be selected by the padding function. It is the typical exploration mechanism that enables exploring various scopes in the solution space. Meanwhile, as the evolutionary process progresses, the subproblems with higher reward scores are selected more often than others based on the empirical average of the reward scores, which is the typical exploitation mechanism. Thus, we can more carefully control the balance between exploration and exploitation when selecting the subproblems in the CC framework.
4.2.2. UCB1-Tuned-Based Contribution Score Computation Method
The second method for computing the contribution scores in the CSF involves improving the padding function shown in Equation (5) by utilizing the UCB1-tuned mechanism. Because the padding function involved in Equation (5) does not consider the variance in the reward scores, the contribution scores computed by Equation (5) may be sensitive to the distribution of the reward scores, i.e., their variance. To overcome this weakness, it is necessary to consider the variance of all reward scores when computing the contribution scores. That is, we can modify the padding function by introducing the variance in the reward scores. Then, the contribution score for the ith subproblem is computed by
where indicates the minimum variance used to prevent the result of the padding function from becoming zero, and is the variance of reward scores obtained after evolving the ith subproblem, which is computed by
The variance in the reward scores can significantly contribute to enhancing the variety in the solution search by improving the possibility that the subproblems with relatively lower reward scores are selected for evolution. In detail, the padding function returns a larger value as the reward scores have a greater variance. As a result, the diversity of the solution search can be further enhanced by selecting various subproblems. On the other hand, as the evolutionary process progresses, the variance in the reward scores decreases because they converge toward their empirical average. Accordingly, the influence of their average is more strengthened than the padding function, and thus, the possibility of selecting subproblems with higher reward scores becomes further improved. Simultaneously, the contribution score computed by Equation (6) is relatively less sensitive to the distribution of the reward scores compared to the UCB1-based contribution score evaluated by Equation (5). These merits can help the CC framework perform a more stable solution search, even though the individuals’ convergence status is drastically changed.
4.2.3. Non-Stationary UCB1 and UCB1-Tuned-Based Contribution Score Computation Methods
The third and fourth methods apply the non-stationary mechanism to compute the contribution scores of the subproblems. In the CC framework with evolutionary algorithms, the distribution of reward scores is dynamically changed as the individuals in the subpopulation corresponding to the selected subproblem converge to the optimal solution. Accordingly, the average and variance of the reward scores also vary dynamically over time as the evolutionary process progresses. Thus, it is reasonable to consider the dynamic characteristics of the reward score distributions when computing the contribution scores of the subproblems.
To this end, we apply the non-stationary mechanism when computing the average and variance of the reward scores used to measure the contribution scores for the subproblems. Because the average and variance of the reward scores converge rapidly over time, these values are more strongly influenced by recent reward scores than by previous ones. In other words, as the evolutionary process progresses, the weights of past reward scores should be reduced to strengthen the influence of recent reward scores when calculating their average and variance. This mechanism can be implemented by introducing a decay factor, which is exponentially reduced over time, into the formulae to compute the average and variance of the reward scores. Accordingly, an exponentially weighted average of reward scores for the ith subproblem is formulated as
where is a decay factor to control the ratio of decreasing the past reward scores and is the sum of the weights, which is calculated by
In other words, the average of the previous reward scores decreases exponentially over time each time a new reward score is calculated. Accordingly, the reward scores that have been recently evaluated carry more significance than those from the past. Simultaneously, the influence of the past reward scores exponentially diminishes as the evolutionary process progresses. Thus, the empirical average of the reward scores is strongly affected by more recent reward scores rather than past ones.
Similar to Equation (8), an exponentially weighted variance of the reward scores for the ith subproblem is computed by applying the non-stationary mechanism as
Thus, we can derive the non-stationary UCB1-based contribution score computation method for the ith subproblem by applying Equations (8) and (9) into Equation (5) as
When compared to the UCB1-based contribution score presented in Equation (5), Equation (11) utilizes the weighted sum function, i.e., , instead of in calculating the average reward scores. Accordingly, the padding function is also computed non-stationary as the empirical average. Furthermore, we can also derive the non-stationary UCB1-tuned-based contribution score computation method by applying Equations (8)–(10) to Equation (6) as
where is the minimum variance used in the padding function, which is calculated by
When compared to the UCB1 and UCB1-tuned-based contribution scores, this computation method can more carefully adjust the trade-off between exploration and exploitation when selecting the subproblem to be evolved in the CC framework by considering their variance calculated based on the non-stationary mechanism. Accordingly, the non-stationary-based contribution score computation methods shown in Equations (11) and (12) can effectively evaluate the degree of contribution for each subproblem, even though the distributions of the reward scores vary dynamically over time. Therefore, the non-stationary-based contribution score computation methods can significantly contribute to searching for optimal solutions in the large-dimensional solution space when compared to existing UCB algorithm-based subproblem selection methods.
4.2.4. The CSF Algorithm
The CSF can be implemented by combining the four contribution score computation methods into one. Algorithm 2 describes the detailed pseudocode for the CSF. To calculate the contribution scores for the subproblems, the CSF takes four inputs: , , n, and K. represents the list of all the reward scores for the K subproblems where is a set of all reward scores recorded after evolving the ith subproblem (i.e., ). denotes the times each subproblem is selected and evolves. n is the total number of steps, i.e., the sum of times that all subproblems are selected and evolved. K is the number of subproblems. Meanwhile, and sp_name indicate the parameters of the CSF. is a decay factor used in the non-stationary UCB1 and UCB1-tuned-based contribution score computation methods shown in Equations (11) and (12). sp_name determines the base UCB algorithm for calculating the contribution scores.
| Algorithm 2 Sub-algorithm: CSF | |
| Require: [], [], n, K; , sp_name | |
| 1: conts = make_vector(K, 0) | |
| 2: for ; ; do | |
| 3: if sp_name == UCB then | ▹ Equation (5) |
| 4: | |
| 5: | |
| 6: else if sp_name == UCBT then | ▹ Equation (6) |
| 7: | |
| 8: | |
| 9: | |
| 10: else if sp_name == NSU then | ▹ Equation (11) |
| 11: | |
| 12: | |
| 13: | |
| 14: else if sp_name == NSUT then | ▹ Equation (12) |
| 15: | |
| 16: | |
| 17: | |
| 18: | |
| 19: else | |
| 20: error(“Incorrect subproblem selector name”) | |
| 21: return null | |
| 22: end if | |
| 23: conts | |
| 24: end for | |
| return conts | |
In Algorithm 2, the contribution scores for all subproblems are computed by one of the four UCB-based contribution score computation methods. After calculating the contribution scores, the CSF returns the list of evaluated contribution scores. The returned contribution scores are used to determine a subproblem to be evolved in the following step in the subproblem selection function (SSF).
4.3. Component 3: Subproblem Selection Function (SSF)
The SSF chooses a subproblem to be explored in the next step based on the contribution scores computed by the CSF. Similar to the policies that the MAB algorithms select an arm to be pulled in the following step, the SSF also preferentially selects the subproblem with the highest contribution score as
where K is the number of subproblems and is the contribution score of jth subproblem. Algorithm 3 describes the SSF algorithm. In Algorithm 3, is_init is a boolean variable that indicates the current evolutionary phase is initial or not. prev_idx is an index of the previously chosen subproblem. conts[] is a list variable containing the contribution scores of all the subproblems. Finally, K is the number of subproblems. In the initial evolutionary phase (i.e., is_init == true), each subproblem is chosen sequentially from the first to the last in a round-robin manner. This process is performed because each subproblem should be evolved at least once to obtain one or more reward scores for each of them. After the initial evolutionary phase is completed (i.e., is_init == false), the SSF determines the subproblem that will be evolved in the next step based on the contribution scores for the subproblems. In other words, the subproblem with the highest contribution score is preferentially chosen among all the subproblems, as shown in Equation (14). Finally, the SSF returns an index of the selected subproblem to the subproblem selector.
| Algorithm 3 Sub-algorithm: SSF | |
| Require: is_init, prev_idx, conts[], K | |
| 1: if is_init == true then | ▹ round-robin-based selection |
| 2: new_idx = prev_idx + 1 | |
| 3: else | ▹ contribution-based selection |
| 4: new_idx = (conts[1], ..., conts[K]) | |
| 5: end if | |
| return new_idx | |
4.4. Implementation of the UCB-Based Subproblem Selector and Utilization in the CC Frameworks
By combining the three core functions, we can implement an integrated UCB-based subproblem selector. Table 1 describes the names and abbreviations of the proposed UCB-based subproblem selectors. The first and second columns present the complete names and abbreviations of the four subproblem selectors. The third column lists the names of the CC frameworks that utilize our subproblem selector. Finally, the final column shows the values of the parameter sp_name, used to determine the base subproblem selector in Algorithm 2.

Table 1.
Names and abbreviations of the four proposed UCB-based subproblem selectors. The “CC frameworks” column indicates the names of CC frameworks that use the proposed subproblem selector. The “sp_name” column lists the valid values of the parameter “sp_name” used in Algorithm 2.
Meanwhile, Algorithm 4 describes a main algorithm of our proposed UCB-based subproblem selector. Our subproblem selector has six inputs as follows: is_init is a boolean variable to indicate whether the current evolutionary phase is initial or not; and are the fitness values of the previous and current best optimal solutions, respectively; prev_idx and idx are indices of the previously and currently selected subproblems, respectively; and K is the number of subproblems. In addition, it takes three parameters: , , and sp_name. is the decay factor used for the non-stationary UCB1 and UCB1-tuned-based contribution score computations; is the smoothing factor used in the REF; and finally, sp_name indicates the name of the base UCB algorithm.
| Algorithm 4 Main algorithm: subproblemSelector |
|
Meanwhile, Algorithm 5 illustrates how our proposed subproblem selector is utilized in the CC framework. Algorithm 5 takes two inputs and four parameters. Regarding its inputs, is n-dimensional objective function and m is a population size, i.e., the number of individuals used to make the population. Meanwhile, and are the parameters used in the CSF and REF, respectively. sp_name indicates the names of base UCB algorithm used in CSF. In Algorithm 5, the CC framework calls the proposed subproblem selector shown in Algorithm 4 to choose the subproblem to be searched in the next step. Simultaneously, the CC framework delivers the indices of the previously and currently selected subproblems (i.e., prev_i and i), as well as the past and latest best fitness values (i.e., and ), to the subproblem selector.
In the subproblem selector of Algorithm 4, the REF evaluates the reward score of the evolved subproblem as shown in Equation (3). Then, the CSF computes the contribution scores of all the subproblems based on their reward scores. After all the contribution scores have been updated, the SSF chooses a subproblem to be evolved in the next step by selecting the subproblems with the highest contribution scores among the K ones. After the subproblem selection is completed, the CC framework in Algorithm 5 evolves the selected subproblem using the evolutionary algorithm and evaluates the fitness values of the evolved individuals using the “Feval” function presented in Appendix A. Then, the new optimal solution with the best fitness is found from the evolved population. These processes are repeated until the number of fitness evaluations (FEs) exceeds the maximum number of FEs (maxFEs). After all the evolutionary processes are completed, the CC framework returns the individual with the best fitness as its final optimal solution.
As demonstrated in Algorithms 1 and 5, the CC frameworks generally restrict the number of FEs performed to evolve the population to maxFEs. In this case, it is important to minimize unnecessary evolutions for unpromising subproblems that contribute little to finding the optimal solution. The subproblem selector described in Algorithm 4 can not only prevent the unnecessary evolution of subproblems with low contribution to improving optimization performance but also maintain various solution searches by sophisticatedly controlling the trade-off between control exploration and exploitation. Accordingly, the CC framework, combined with our subproblem selector, can significantly improve optimization performance.
| Algorithm 5 Example algorithm: CC with UCB-based subproblem selector |
|
4.5. Theoretical Analysis
4.5.1. Computational Complexity Analysis
Among Algorithms 1–4, the main function called to choose a subproblem in the CC framework is the subproblem selector function shown in Algorithm 4. Accordingly, we analyze a time complexity required to perform Algorithm 4 in the CC framework as follows.
Theorem 1.
When an objective function is given, its domain space is decomposed to K disjoint subproblems, the time complexity needed to perform our proposed subproblem selectors in the CC framework is .
Proof of Theorem 1.
When Algorithm 4 is first executed, the variables used for incremental computations for each of the K subproblems are initialized in lines 2–6, which requires an time complexity. This work is performed only once at the first execution. After the initialization work is completed, lines 7–10 are executed within constant time, i.e., .
Afterward, the CSF is called to compute the contribution scores of all the subproblems at line 11. In the CSF, the average function and the padding function are calculated for each of the K subproblems to measure their contribution scores. These can be efficiently computed by using the incremental computation method. In detail, when calculating the contribution scores based on the UCB or UCB-tuned algorithm (i.e., sp_name == “UCB” or “UCBT”), the CSF can incrementally compute two terms and by maintaining the previous computation results for each subproblem to avoid unnecessary repeating of the calculations. Similarly, when the non-stationary UCB and UCB-tuned algorithms were used (i.e., sp_name == “NSU” or “NSUT”), three exponentially decayed terms, i.e., , , and , can also be incrementally computed while preserving their computation results for K subproblems. In this case, only complexity is needed to update each summation term. Because the contribution scores for K subproblems are updated whenever the CSF is executed, the total time complexity to execute the CSF once is .
After the CSF computes the contribution scores, the SSF selects a subproblem to be evolved among K subproblems. When “is_init == true”, all the subproblems are sequentially chosen by the SSF one by one in a round-robin manner. On the other hand, when “is_init == false”, the SSF chooses the subproblem with the best contribution score. Thus, the time complexity required to conduct the SSF once is .
Therefore, when the number of subproblems is K, the total time complexity needed to perform the subproblem selector of Algorithm 4 is derived as
where if Algorithm 4 is firstly performed, and 0 otherwise. □
In other words, our proposed subproblem selector has a linear time complexity that is proportional to the number of subproblems. Meanwhile, we can derive the space complexity needed to conduct our subproblem selector as follows.
Theorem 2.
When the number of subproblems is K, the space complexity required to perform our subproblem selector of Algorithm 4 is .
Proof of Theorem 2.
As explained in the proof of Theorem 1, the summation terms , , , , and should be retained for each of K subproblems to calculate them incrementally. To do this, K variables are needed to index them. Thus, space complexity is required to perform the subproblem selector shown in Algorithm 4. □
4.5.2. Theoretical Analysis of the Effects of the Decay Factor
In both NSUSP and NSUTSP algorithms, the decay factor controls how many previous reward scores are used to compute the contribution score of the ith subproblem. The following theorem demonstrates the exploration and exploitation effects in selecting the subproblems in our proposed methods according to the variations of .
Theorem 3.
As α becomes close to one, the exploitation effect is further enhanced in the subproblem selection task. On the contrary, the influence of the exploration is further strengthened in the subproblem selection as α decreases toward zero.
Proof of Theorem 3.
To analyze the effect of in the NSUSP and NSUTSP algorithms, we first represent of Equation (9) as a sum of geometric sequence as
Assume the number of times the ith subproblem is selected converges to infinite (i.e., ). Then, by taking the limit with respect to in Equation (16), we can derive
Equation (17) indicates that converges to if the ith subproblem is extremely often selected (i.e., ). Thus, we can analyze the influence of when calculating the contribution score of the ith subproblem by examining the padding function as . For convenient analysis, the padding functions used in NSUSP and NSUTSP, as shown in Equations (11) and (12), are denoted as
where q is a constant and is a function that returns 1 if is used in the NSUSP, of Equation (13), otherwise. Then, we can take the limit of Equation (18) as
where and are approximated results of and when .
In Equation (19), the padding function becomes close to zero as approaches one. That is, the influence of the padding function is reduced and thus the exploitation-based subproblem selection is further enhanced. On the other hand, as approaches zero, the padding function increases progressively. Consequently, the exploration-based subproblem selection is further enhanced. □
Theorem 3 indicates that the parameter plays a role in manually controlling the degree of exploration and exploitation in the subproblem selection task. Moreover, from the proof of Theorem 3, we also find that the effective range of for stable convergence is because Equation (16) diverges if is greater than one.
4.5.3. Theoretical Analysis of the Effects of the Smoothing Factor
The smoothing factor in Equation (3) is used to prevent the denominator from becoming zero. To analyze the effect of when computing the contribution scores of the subproblems, we denote as the reward score observed after evolving the ith subproblem at time t. Then, is expressed as
where is a fitness of the previous optimal solution and is a fitness of the optimal solution found after evolving the ith subproblem at time t. Accordingly, we can analyze the effect of in terms of the magnitude of the reward scores computed by the REF as follows.
Theorem 4.
As γ increases, the magnitude of the reward scores calculated by the REF decreases.
Proof of Theorem 4.
To analyze the effects of in the REF, we take the partial derivative of with respect to as
where the nominator and denominator on the right-hand side are clearly positive. In other words, Equation (21) is always less than or equal to zero. Thus, the increasing continuously decreases the magnitude of the reward scores computed by the REF. □
Meanwhile, can influence the average and variance of the reward scores. Accordingly, it can affect the exploration and exploitation effects in selecting the subproblems in our proposed methods. The following theorems describe how the variations of influence the average and variance of the reward scores.
Theorem 5.
As γ increases, the average of the reward scores computed by the REF decreases.
Proof of Theorem 5.
In general, the average of the reward scores for the ith subproblem is calculated by
where is the decay factor of at time t and is the sum of the decay factors shown in Equation (9). If Equation (22) is used in the UCBSP or UCBTSP algorithms, all the decay factors are set to one. In contrast, it is utilized in the NSUSP or NSUTSPCC algorithms, the decay factors can be set to any positive values less than one. Then, we can derive the partial derivative of Equation (22) with respect to as
where , , , and are non-negative for all time t. Thus, is less than zero. Therefore, increasing lowers the average . □
Theorem 6.
As γ increases, an upper bound of the variance of the reward scores decreases.
Proof of Theorem 6.
The reward score for the ith subproblem at time t, i.e., satisfies the following inequality
because . Then, the reward score always lies within an interval , i.e.,
Meanwhile, if a random variable X is defined on an interval , its variance has an upper bound (i.e., ). Accordingly, we can derive the upper bound of the variance of the reward scores for the ith subproblem as
Equation (26) indicates that as increases, the upper bound of the variance becomes lower quadratically. That is, the upper bound of the variance of the reward scores for the ith subproblem decreases as increases. □
Theorems 4–6 describe how variations in can affect the exploration and exploitation effects in selecting the subproblem in our proposed methods. In the UCBSP and NSUSP algorithms, their padding functions do not account for the variance of the reward scores, as shown in Equations (5) and (11). In this case, the variation of only affects their average functions. Accordingly, as approaches one, the average of the reward scores decreases, and thus the exploration effects can be further enhanced in the subproblem selection task.
Meanwhile, the padding functions in the UCBTSP and NSUTSP algorithms use the variance of the reward scores, as described in Equations (6) and (12). In this case, the variation of influences their average and padding functions simultaneously. That is, as becomes large, both the average and padding functions become small. Accordingly, the exploration and exploitation effects can be reduced when performing the subproblem selection task in the UCBTSP and NSUTSP.
5. Experiments
It is essential to evaluate how significantly our proposed subproblem selectors contributed to finding optimal solutions in practical CC frameworks. Accordingly, in this section, we present the detailed results of experiments conducted to evaluate the solution search abilities of CC frameworks that utilize practical subproblem selectors, including our proposed ones.
5.1. Configurations for Experiments
First, we used the high-dimensional global optimization functions involved in the CEC’2010 [32] and CEC’2013 [33] benchmark suites to evaluate the optimization performance of the CC frameworks with the subproblem selectors. The CEC’2010 and CEC’2013 benchmark suites are official benchmark problems that have been widely used to evaluate the optimization capabilities of various CC frameworks. The benchmark functions are 1000-dimensional scalar functions in which 1000 decision variables are wholly or partially interdependent. Because the functions involve intricately interdependent variables, these solution spaces are also considerably complicated. Therefore, the CEC’2010 and CEC’2013 benchmark functions are suitable for evaluating how much the subproblem selectors could contribute to improving the optimization performance in the CC frameworks.
Second, we adopted the SaNSDE [39] algorithm as a base optimizer used in the CC frameworks. The SaNSDE, one of the advanced DE algorithms, employs self-adaptive control mechanisms to enhance the searchability of individuals in the population. As a result, the SaNSDE has shown better results than traditional DE algorithms for various optimization problems in diverse LSGO studies [39]. Moreover, we adopted ERDG [38] as the base problem decomposer. ERDG is a state-of-the-art problem decomposer that splits a given LSGO function into diverse subproblems based on the interdependencies among the variables that constitute the function. As shown in Table 2, we decomposed 20 benchmark functions included in the CEC’2010 suite using the ERDG and found that , , and were decomposed into single subproblems. Similarly, among 15 CEC’2013 benchmark functions, ERDG decomposed , , , and into single subproblems. Accordingly, we used the remaining functions as benchmark problems, excluding these seven functions.

Table 2.
The number of variable groups generated after the ERDG decomposes each of the benchmark functions. Each variable group is addressed as an independent subproblem in the CC frameworks.
Third, we adopted five CC frameworks that utilize classical subproblem selectors: BasicCC, RandomCC, CBCC1, CBCC2, and BBCC, as models for comparison. BasicCC [6], the earliest CC framework shown in Algorithm 1, selects the subproblems in a round-robin manner. RandomCC, which is a variation of BasicCC [6], chooses the subproblem randomly at each evolutionary step according to the uniform distribution. CBCC1 [9] and CBCC2 [9] are typical contribution-based CC frameworks. Unlike BasicCC and RandomCC, CBCC1 and CBCC2 select a subproblem to be evolved based on the contribution scores of all the subproblems, i.e., the degree of fitness improvement of the best individual. Meanwhile, BBCC [10] utilizes the -greedy algorithm [25] to identify the subproblem to be evolved in the next step. Table 3 lists the parameter configurations of all the subproblem selectors evaluated in our experiments.

Table 3.
The detailed configurations of the parameters used in our experiments. The omitted parameters were set equivalent to the values shown in their research papers.
Fourth, we implemented nine CC frameworks, each incorporating one of nine subproblem selectors, to evaluate the optimization performance of the CC frameworks with the subproblem selectors including our proposed methods. We then search for the optimal solution of each benchmark function by utilizing each of the nine CC frameworks 25 times independently, based on the guidelines of CEC’2010 and CEC’2013. Afterward, we calculated the average fitness of the 25 optimal solutions the CC framework found for each benchmark function.
Fifth, we performed Wilcoxon rank-sum one-way ANOVA tests [41] to pairwise compare the fitness values achieved by the CC frameworks that utilize our proposed subproblem selectors and existing ones for each benchmark function. In the ANOVA tests, we analyzed whether the average fitness values found by the CC frameworks with our subproblem selectors were better, worse than, or equivalent to the results of the CC frameworks with the traditional subproblem selectors for each benchmark function. We then counted the number of benchmark functions for which the CC frameworks using our subproblem selectors achieved “win,” “lose,” and “tie” when compared to the CC frameworks using traditional subproblem selection methods. To this end, we used a significance level of p = 0.05 and conducted Holm’s p-correction method [41] for more accurate comparisons.
Finally, our experiments were conducted using MATLAB R2023b in a system environment with the following specifications: Intel CoreTM i7-14700K 3.40GHz CPU, 128GB RAM, and Windows 11 Professional operating system. The statistical ANOVA tests were performed using R 4.2.1.
5.2. Ablation Studies
5.2.1. Ablation Studies for the Decay Factor
As explained in Section 4.2, NSUSP and NSUTSP commonly use the decay factor to adjust the weights of the past reward scores in computing the average reward score. In other words, the decay factor can significantly impact the optimization performance of CC frameworks that utilize NSUSP and NSUTSP as subproblem selectors.
To evaluate the influence of the decay factor in NSUSP and NSUTSP, it is reasonable to measure the improvement in optimization results when the non-stationary mechanism is applied to UCBSP and UCBTSP. Accordingly, for each benchmark function, we compared the average fitness values of the final optimal solutions achieved by NSUSPCC and NSUTSPCC with those of UCBSPCC and UCBTSPCC in a pairwise manner using the Wilcoxon rank-sum ANOVA tests. To this end, we implemented 10 NSUSPCC and NSUTSPCC models by setting their decay factors to the five values: 0.1, 0.3, 0.5, 0.7, and 0.9. Afterward, we counted the benchmark functions for which NSUSPCC and NSUTSPCC models achieved better, worse, or equivalent results compared to UCBSPCC and UCBTSPCC, respectively, when the decay factor was set from .
Table 4 presents the comparison results between the optimization results obtained by NSUTSPCC with each of the five decay factor values and those of UCBTSPCC for the CEC’2010 and 2013 benchmark functions. In Table 4, the row labeled “Improved benchmark functions” indicates the number of benchmark functions for which NSUTSPCC achieved better optimization results than those of UCBTSPCC. On the other hand, the row labeled “Worse benchmark functions” describes the number of benchmark functions for which NSUTSPCC made worse results than those of UCBTSPCC. If NSUTSPCC and UCBTSPCC show statistically equivalent results, the number of its benchmark functions is written in the row labeled “Equivalent benchmark functions.”

Table 4.
The comparison results for the optimization results performed by NSUTSPCC with and UCBTSPCC. All detailed experimental results are shown in Tables S1 and S2 in the Supplementary File.
As shown in Table 4, we found that NSUTSPCC achieved the best optimization results compared to those of UCBSPCC when = 0.3. In detail, NSUTSPCC with = 0.3 yielded better optimization results for 10 CEC’2010 benchmark functions out of a total of 17. Similar to the results of NSUTSPCC with = 0.3, NSUTSPCC with = 0.1 also showed better results than those of UCBTSPCC for 10 CEC’2010 benchmark functions. However, the number of benchmark functions for which NSUTSPCC with = 0.3 showed worse results was less than that of NSUTSPCC with = 0.1. In the comparison tests with the CEC’2013 benchmark functions, NSUTSPCC showed the best optimization results when = 0.5. In detail, NSUTSPCC achieved better results for eight benchmark functions, and equivalent ones for one function when compared to the results of UCBTSPCC. NSUTSPCC with = 0.3 yielded better results than those of UCBTSPCC for seven benchmark functions. The number of benchmark functions for which NSUTSPCC showed equivalent results to those of UCBSPCC was two. When = 0.1, the results were equivalent to those when = 0.3.
Meanwhile, the comparison results between UCBSPCC and NSUSPCC with five decay factor values are described in Table 5. Unlike the results presented in Table 4, NSUSPCC yielded the best optimization results when = 0.5 for the CEC’2010 and 2013 benchmark functions. In detail, NSUSPCC with = 0.5 achieved better optimization results than those of UCBSPCC for 10 CEC’2010 benchmark functions. Similarly, when = 0.5, NSUSPCC outperformed UCBSPCC in seven out of the 13 CEC’2013 benchmark functions. Meanwhile, NSUSPCC with = 0.1 showed the second-best results for both the CEC’2010 and 2013 benchmark functions.

Table 5.
The comparison results for the optimization results performed by NSUSPCC with and UCBSPCC. All detailed experimental results are presented in Tables S3 and S4 in the Supplementary File.
Finally, Figure 3 summarizes the comprehensive results of Table 4 and Table 5. In detail, Figure 3a describes that NSUTSPCC achieved better results than those of UCBTSPCC for 17 benchmark functions when was set to 0.1, 0.3, or 0.5, respectively. Among these results, we found that NSUTSPCC with = 0.3 produced equivalent results to those of UCBTSPCC for five benchmark functions. Figure 3b shows that NSUSPCC achieved better results than UCBSPCC for 17 benchmark functions when was set to 0.1 and 0.5. However, NSUSPCC with = 0.5 yielded equivalent results to those of UCBSPCC for five benchmark functions, which were superior to those of NSUSPCC with = 0.1. Meanwhile, both NSUTSPCC and NSUSPCC showed significantly lower performance improvements compared to those of UCBTSPCC and UCBSPCC when was set to 0.7 or 0.9, respectively. These results are evident because the weights of the reward scores approach one, which is equivalent to the traditional average reward shown in Equations (5) and (6). Thus, as the decay factor converges to one, the results of NSUTSPCC and NSUSPCC become close to those of UCBTSPCC and UCBSPCC, respectively.
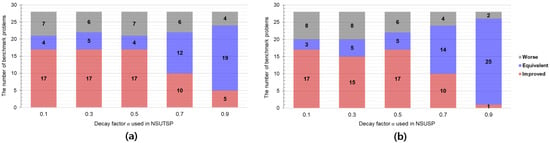
Figure 3.
The total number of benchmark functions improved/equivalent/worsen by NSUTSPCCs and NSUSPCCs with the five decay factor values (i.e., ) when compared to the results of UCBTSPCC and UCBSPCC, respectively. (a) shows the experimental results of NSUTSPCCs. (b) presents the experimental results of NSUSPCCs.
According to the results of these ablation studies, we determined the optimal values of the decay factor in NSUTSP and NSUSP as 0.3 and 0.5, respectively.
5.2.2. Ablation Studies for the Population Size m and Smoothing Factor
To analyze the influence of other parameters used in the base optimizer and reward evaluation function (REF), we conducted several additional parameter sensitivity tests using the NSUTSPCC. To this end, we adopted two significant control parameters, m and . The parameter m represents the number of individuals used in the base optimizer, i.e., the SaNSDE algorithm. That is, m determines the size of the population utilized to search for an optimal solution of the given objective function. The parameter is a smoothing factor used to prevent the denominator from becoming zero in Equation (3). To maintain a consistent experimental environment, we typically set the decay factor of the NSUTSPCC to 0.3 in both tests for m and .
Table 6 presents the means and medians of the average fitness values achieved by the NSUTSPCC for each of the CEC’2010 and 2013 benchmark functions, with m set to 50, 75, 100, 125, and 150, respectively. As shown in Table 6, the NSUTSPCC yielded the best results on average, in terms of both the mean and median, when m was set to 50. Similarly, when m was set to 75, the NSUTSPCC still showed relatively better results compared to larger population sizes, such as 125 and 150. These experimental results demonstrate that the population size, i.e., the number of individuals, affects the search ability of the base optimizer in the CC framework to find optimal solutions.

Table 6.
The mean and median of the fitness values achieved by NSUTSPCC after solving the CEC’2010 and CEC’2013 benchmark functions according to the settings of the population size m. The detailed results are provided in Tables S5 and S6 of the Supplementary File.
In fact, the number of optimal individuals can be differentiated considerably depending on the characteristics of the base optimizers and the objective functions being tackled. If the number of individuals is too large, the search performance may actually deteriorate due to severe mutual interference while the base optimizer searches for optimal solutions. On the other hand, if the number of individuals is too small, there is a risk that the diversity of the optimal search may decrease, potentially leading to a decline in search performance. Thus, it is required to carefully determine the population size by fully considering the features of the base optimizer algorithm and the LSGO problems within CC frameworks.
Meanwhile, Table 7 presents the mean and median of the average fitness values evaluated by the NSUTSPCC for the CEC’2010 and 2013 benchmark functions when the smoothing factor was set to five distinct values: , , , , and . As explained previously, plays a role in preventing the denominator of Equation (3) from becoming zero. Accordingly, it scales the reward scores within a range of zero to one.

Table 7.
The mean and median of the fitness values achieved by NSUTSPCC after solving the CEC’2010 and CEC’2013 benchmark functions according to the settings of the smoothing factor . The detailed results are provided in Tables S7 and S8 of the Supplementary File.
From the ablation study results shown in Table 7, we found that the overall optimization results were similarly evaluated in the five experiments. In particular, the median values were almost identical across the five distinct settings of for both the CEC’2010 and 2013 benchmark sets. These results indicate that if the smoothing factor in Equation (3) is set to sufficiently small values close to zero, it does not significantly affect the evaluation of the reward scores of the subproblems in the REF. Nevertheless, as discussed in Section 4.5.2, the smoothing factor can influence the evaluation of the reward scores of the subproblems if it is set to large values. Therefore, gamma must be set to minimal values close to zero to prevent unexpected effects caused by when computing the reward scores in the REF.
5.3. Optimization Test Results with Wilcoxon Rank-Sum ANOVA Tests
5.3.1. Optimization Test Results for the CEC’2010 Benchmark Functions
To evaluate how much our proposed subproblem selectors can contribute to improving the optimization performance in practical CC frameworks, we performed the optimization tests for the CC frameworks with nine subproblem selectors for the CEC’2010 and CEC’2013 benchmark functions. Table 8 describes the optimization test results of the CC frameworks when solving the CEC’2010 benchmark functions. Moreover, we compared the average fitness values evaluated by NSUTSPCC and other CC frameworks in a pairwise manner by conducting Wilcoxon rank-sum one-way ANOVA tests. These comparison results are shown in Table 8 as “W/T/L.” If the p-value is less than 0.05, the average fitness values evaluated by NSUTSPCC and the other CC framework are significantly different. In this case, if the average fitness value achieved by NSUTSPCC is better than the other, we determine its result as “W (win)”; conversely, if its value is worse than the other, we determine the result as “L (lose).” Meanwhile, if the p-value is greater than or equal to 0.05, we determine that the two results are statistically equivalent, i.e., “T (tie),” because they do not have significant differences. By performing these pairwise comparisons for all the benchmark functions, we evaluated the number of benchmark functions for which NSUTSPCC achieved better results than other CC frameworks.

Table 8.
The Wilcoxon rank-sum one-way ANOVA test results performed to compare the optimization results performed by NSUTSPCC and the CC frameworks with other subproblem selectors to solve the CEC’2010 benchmark functions.
From the experimental results in Table 8, we found that NSUTSPCC attained the “win” and “tie” results for eight and five benchmark functions, respectively, compared to those of NSUSPCC. Moreover, NSUTSPCC also achieved remarkable optimization results compared to UCBSPCC and UCBTSPCC. In detail, NSUTSPCC showed better results than UCBSPCC and UCBTSPCC by achieving the “win” for 12 and 10 benchmark functions, respectively. These experimental results indicate that our proposed NSUTSP contributes most to finding optimal solutions of objective functions with complicated interdependencies in practical CC frameworks among the four proposed UCB-based subproblem selectors.
In comparisons to the traditional CC frameworks, our NSUTSPCC also showed the most outperformed optimization results, i.e., achieved the “win” for most benchmark functions. On the other hand, the CC frameworks with traditional subproblem selectors exhibited relatively worse optimization results than those of NSUTSPCC. In detail, when compared to the results of BasicCC and RandomCC, NSUTSPCC showed superior results, i.e., the “win” for most benchmark functions, i.e., 12 and 17 benchmark functions, respectively. These results indicate that the subproblem selection task in the CC framework considerably influences the optimization performance when solving practical LSGO problems. Meanwhile, BBCC, which uses the -greedy strategy for the subproblem selection, presented better optimization results for only three benchmark functions. Similarly, CBCC1 and CBCC2 only achieved better results than NSUTSPCC for two and three benchmark functions, respectively. These comparison results show that our UCB-based subproblem selection strategies significantly help the CC frameworks solve the large-dimensional optimization problem by carefully identifying promising subproblems that have the most significant influence on searching for optimal solutions in the large-dimensional solution space.
5.3.2. Optimization Test Results for the CEC’2013 Benchmark Functions
Table 9 lists the average fitness values achieved by the CC frameworks with nine subproblem selectors when solving the CEC’2013 benchmark functions and their comparison results. As described in Table 9, NSUTSPCC still showed the best optimization results among the nine CC frameworks, even though the base benchmark functions were changed from the CEC’2010 to the CEC’2013 ones. In detail, NSUTSPCC achieved the “win” for seven benchmark functions compared to the results of both UCBSPCC and UCBTSPCC. Moreover, NSUTSPCC attained better or equivalent results for nine benchmark functions compared to those of NSUSPCC. These results indicate that our non-stationary mechanisms are more effective in identifying a promising subproblem that can contribute to further enhancing optimization performance in the CC frameworks, regardless of the base optimizers.

Table 9.
The Wilcoxon rank-sum one-way ANOVA test results performed to compare the optimization results performed by NSUTSPCC and the CC frameworks with other subproblem selectors to solve the CEC’2013 benchmark functions.
Moreover, NSUTSPCC also showed the best optimization results for most benchmark functions when compared to the traditional CC frameworks. In detail, NSUTSPCC showed better results, i.e., the “win” for an average of 7.8 benchmark functions when compared to five traditional CC methods. On the other hand, the average number of benchmark functions for which the traditional CC frameworks achieved better results than NSUTSPCC was only 1.6. Exceptionally, BBCC, utilizing -greedy, showed better optimization results than other traditional CC frameworks. Nevertheless, its results still were lower than those of our NSUTSPCC.
These results indicate that our subproblem selectors can significantly contribute to solving any complicated LSGO problems, such as the CEC’2013 benchmark functions, in the CC frameworks. Thus, we found that the UCB, particularly the non-stationary UCB mechanisms, could significantly contribute to identifying a promising subproblem in practical CC frameworks, as demonstrated by the experimental results.
5.3.3. Total Result Analysis and Discussion
Finally, Table 10 and Table 11 present the total and average numbers of benchmark functions for which the CC frameworks with our four subproblem selectors outperformed, tied, and underperformed compared to the existing CC frameworks for the CEC’2010 and the CEC’2013 benchmark suites, respectively. (The detailed ANOVA test results of NSUSPCC, UCBTSPCC, and UCBSPCC are presented in Tables S9–S14 in the Supplementary File.). These tables list the summarized comparison results between the CC frameworks equipped with the proposed four UCB-based subproblem selectors and the existing five CC frameworks when the CEC’2010 and CEC’2013 benchmark functions were used as the target problems, respectively.

Table 10.
The total comparison results between the CC frameworks using the proposed four UCB-based subproblem selectors and the CC frameworks with traditional subproblem selection mechanisms when solving the CEC’2010 benchmark functions.

Table 11.
The total comparison results between the CC frameworks using the proposed four UCB-based subproblem selectors and the CC frameworks with traditional subproblem selection mechanisms when solving the CEC’2013 benchmark functions.
As described in Table 10 and Table 11, all the CC frameworks utilizing our proposed subproblem selectors outperformed the traditional ones, achieving the “win” for most benchmark functions. In detail, NSUTSPCC attained the “win” for 13.2 and 7.8 functions on average for the CEC’2010 and CEC’2013 benchmark suites, respectively. Similarly, the average number of functions for which NSUSPCC achieved the “win” was 13.2 for the CEC’2010 benchmark suite, and 6.8 for the CEC’2013 ones. Meanwhile, UCBTSPCC also achieved remarkable optimization results that were almost equivalent to those of NSUTSPCC and NSUSPCC when compared to traditional CC frameworks. The average numbers of functions for which UCBTSPCC attained the “win” were 10.8 and 6.2 for the CEC’2010 and CEC’2013 benchmark suites, respectively. UCBSPCC also demonstrated significant optimization results compared to traditional CC frameworks; on average, UCBSPCC outperformed traditional CC methods for 10.8 and 5.2 functions when the CEC’2010 and CEC’2013 benchmark suites were used, respectively.
Based on the experimental results in Table 10 and Table 11, we found that our CC frameworks, particularly NSUTSPCC and NSUSPCC, achieved the best optimization results among all the compared CC frameworks. Simultaneously, UCBSP and UCBTSP also could remarkably help the CC frameworks search for optimal solutions for large-dimensional black-box objective functions. Therefore, we can conclude that our proposed UCB-based subproblem selectors, especially non-stationary UCB-based methods, can significantly improve the optimization performance in practical CC frameworks.
5.4. Convergence Curve Analysis
Figure 4 and Figure 5 illustrate the convergence curves of nine CC frameworks for 12 selected CEC’2010 benchmark functions. We found that most of the CC frameworks with our subproblem selectors achieved more stable and faster convergence than others that use classical subproblem selection mechanisms. In detail, UCBSPCC and UCBTSPCC also achieved faster or nearly equivalent convergence than the other CC frameworks for , , and . Meanwhile, NSUTSPCC and NSUSPCC demonstrated more stable and rapid convergence than the CC frameworks with traditional subproblem selection methods when solving –, which comprised more than half of the variables. For example, for –, which involve 500 separable and 500 non-separable variables, the four CC frameworks with our subproblem selectors resulted in more stable and faster convergence than those of the other CC frameworks. Likewise, the CC frameworks utilizing our UCB-based subproblem selectors showed the best convergence abilities for –, which comprise all non-separable variables and are decomposed into 20 subproblems. Meanwhile, the CC frameworks with classical subproblem selection mechanisms exhibited slower or worse convergence performance compared to our proposed ones. These results indicate that our four subproblem selectors have notable abilities as base subproblem selectors, contributing to improved optimization performance in practical CC frameworks.
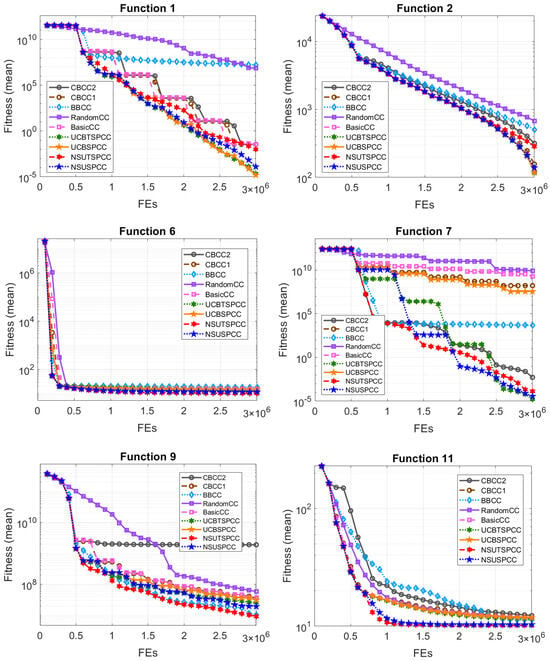
Figure 4.
Convergence curve plots for 12 selected CEC’2010 benchmark functions (1/2).
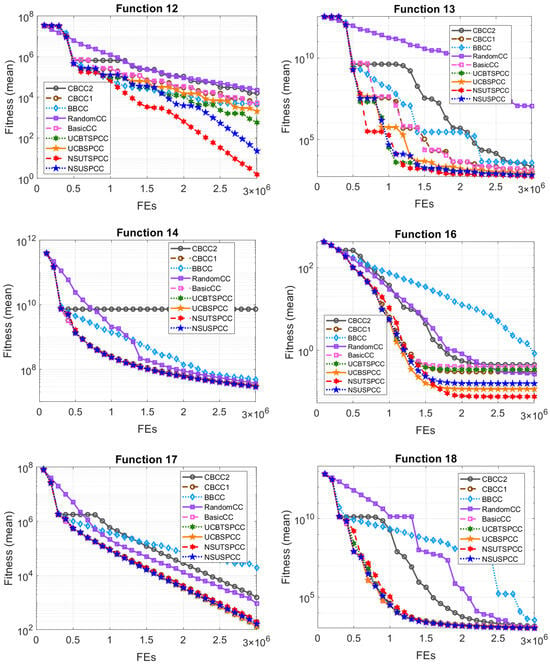
Figure 5.
Convergence curve plots for 12 selected CEC’2010 benchmark functions (2/2).
Figure 6 describes the convergence curve plots of the CC frameworks with nine subproblem selectors for the six chosen CEC’2013 benchmark functions. Unlike the CEC’2010 functions, the CEC’2013 ones are decomposed into several imbalance-sized subproblems, making it hard to find their optimal solutions. Nevertheless, we found that the CC frameworks using our proposed subproblem selectors generated more stable and faster convergence curves than those of other CC frameworks for many benchmark functions. In detail, UCBTSPCC and UCBSPCC showed better or almost similar convergence results when compared to those of NSUTSPCC and NSUSPCC for the benchmark functions that were composed of 1000 separable variables, such as and . Meanwhile, for the benchmark functions that constitute more than half of the variables, NSUTSPCC and NSUSPCC made better convergence curves than those of UCBSPCC and UCBTSPCC. For example, NSUTSPCC and NSUSPCC showed relatively better convergence performance than the others for , , , and . Notably, NSUTSPCC achieved superior fast convergence for and , which were composed of 700 separable and 300 non-separable variables. For , which involves 1000 non-separable variables decomposed into 20 subproblems, BBCC demonstrated notable convergence results. Nevertheless, our NSUTSPCC presented the better convergence curve than BBCC. Finally, for , which is composed of 905 non-separable variables and decomposed into two subproblems by ERDG, our NSUTSPCC and NSUSPCC achieved the best convergence results.
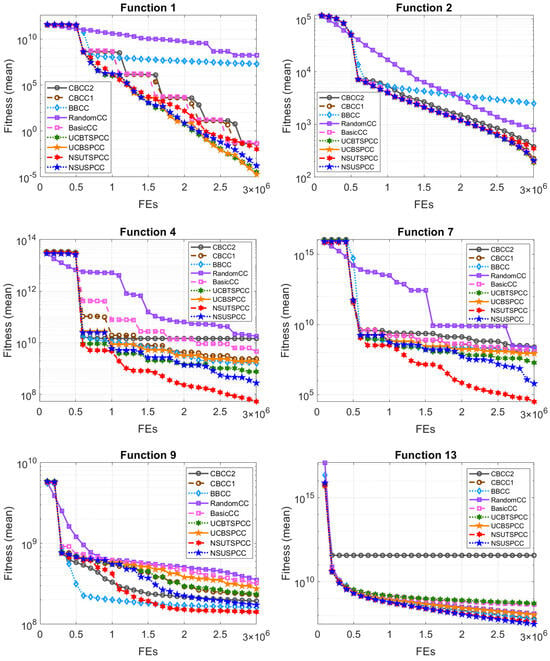
Figure 6.
Convergence curve plots for six selected CEC’2013 benchmark functions.
From the analysis of the convergence curves, we discovered that our CC frameworks have significantly greater convergence abilities for most benchmark functions, especially for the functions with many non-separable variables, when compared to other existing CC frameworks. These experimental results indicate that our proposed UCB-based subproblem selectors can contribute significantly to improving the optimization performance when solving objective functions with complicated variable interdependencies. In other words, our strategies using the UCB and its variation algorithms to identify promising subproblems can significantly help the CC frameworks improve convergence performance by carefully controlling exploration and exploitation in the solution search process.
5.5. Discussions
5.5.1. Discussion About the Experimental Results
In the experiments, the CC frameworks with our proposed subproblem selectors showed overall better optimization results across most benchmark functions. In particular, they achieved outperformed results for the benchmark functions in which more than half of the variables are non-separable, i.e., – (CEC’2010) and – (CEC’2013). These experimental results can be explained in terms of the characteristics of the benchmark functions and our UCB-based subproblem selectors. In general, non-separable variables are strongly coupled based on their interdependencies. Accordingly, the non-separable variable groups have a significant influence on finding the optimal solutions of the objective function. On the other hand, the separable variable groups have relatively weaker influences than the non-separable ones because there are no interdependencies among the variables in the separable variable group. As explained, the CC frameworks with our subproblem selectors achieved further outperformed results for – (CEC’2010) and – (CEC’2013). Because these benchmark functions are composed of more than half non-separable variable groups, each of them has a strong effect on searching for the optimal solution. In this case, it is essential to carefully control the trade-off between exploration and exploitation to choose subproblems. Thus, the CC frameworks with our subproblem selectors, which utilize the UCB algorithms—especially the non-stationary UCB and UCB-tuned algorithms—can exhibit better solution search ability for these benchmark functions than other CC frameworks with traditional subproblem selection methods.
Meanwhile, the NSUTSPCC and NSUSPCC showed relatively less overwhelming optimization performance on benchmark functions composed of many separable variables, i.e., – (CEC’2010) and – (CEC’2013), compared to their performance on functions composed of many non-separable variables. As presented in Table 2, they consist of a few non-separable variable groups and many separable variable groups. In this case, by intensively selecting the subproblems with the non-separable variable group, its ability to search for optimal solutions can be further enhanced because the non-separable variable group has more decisive influence on finding the optimal solution of the function than the separable variable groups. That is, the existing subproblem selection strategies that use a fixed ratio of exploration and exploitation-based selections, such as BBCC or CBCC, can achieve slightly better results than the CC frameworks with other subproblem selectors. On the other hand, our subproblem selectors, which adaptively control the ratio of exploration and exploitation-based subproblem selections, can yield relatively less satisfactory solution search results for several functions that require intensive exploitation-based subproblem selection. Nevertheless, when considering it is more difficult to address the LSGO function with many complicated non-separable variables, our proposed methods that exhibit further strong solution search ability for such complicated functions.
In summary, these experimental results are attributed to the features of our UCB-based subproblem selectors, which aim to prevent excessive exploitation in subproblem selection and maintain the exploration-exploitation trade-off. Therefore, our proposed subproblem selectors, especially NSUTSP and NSUSP, have strengths that are even more specialized in solving any complicated functions with many non-separable variables.
5.5.2. Utilization Method of the CC Framework with Proposed Subproblem Selectors to Address Actual Engineering Problems
In general, the CC framework addresses high-dimensional, complex functions composed of many dependent and independent variables with numerous non-separable variable groups. Then, many real-world problems, which consist of numerous separable or dependent elements, can be effectively solved using the CC framework. For example, elements with strong interactions in any system can be modeled as mutually dependent decision variables and grouped. To implement these strong interdependencies between variables, a rotation operation using matrix multiplication can be applied. Accordingly, highly interdependent variables can be formulated as a non-separable group of variables. Conversely, elements with weak interactions can be modeled as independently separable variables. This can be easily implemented by summing their values. Finally, the objective function is implemented by integrating these into a single function, which can be utilized as an optimization model for designing systems with numerous complex interdependencies. That is, we can find the optimal values for the elements (or factors) constituting the system by searching for optimal solutions that minimize the fitness of the function using the CC framework.
Figure 7 illustrates an example method for modeling various factors used in a battery manufacturing system as an objective function. In this example, we assume that there are 1000 factors that can cause negative effects in the battery manufacturing process, and they are mutually dependent or independent. Among the factors, 500 ones—including temperature, pressure, process time, and gas flow rate—should be simultaneously maintained within 10 independent modules. That is, since these factors have strong interdependencies, they can be modeled as 10 non-separable variable groups, with each group involving 50 interdependent variables. To made the interdependencies of the variables involved in a group, 50 variables related to each factor are combined by multiplying a rotation matrix M with the variables, as shown in Figure 7b. Through this method, we can model 10 non-separable groups, where one group contains 50 interdependent variables. On the other hand, the remaining 500 factors for sensor bias and fine calibration shown in Figure 7a have relatively weak interdependencies. These factors are modeled as separable variables by taking their weighted sum with shift operations, as shown in Figure 7c. Accordingly, we can design a complete objective function for this system by combining the separable variable term (a) and the non-separable variable group terms (b) into one function . Consequently, we can efficiently find the optimal values for 1000 factors affecting this system by searching for the global optimum of this objective function using the CC frameworks with our proposed subproblem selectors.
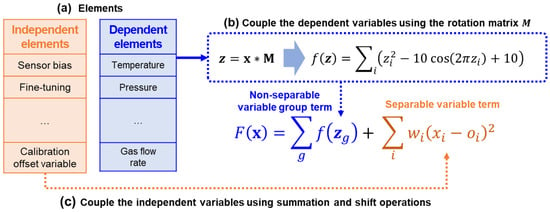
Figure 7.
An example process for designing an objective function to minimize various negative factors occurring in a battery manufacturing system. We assume that this system is composed of 500 dependent factors and 500 independent ones.
The example illustrated in Figure 7 shows that various real-world engineering and scientific problems can be modeled as objective functions and solved using the CC frameworks with our proposed methods. At this point, we can apply our subproblem selector to the CC framework to effectively explore the global optimum of LSGO, which involves numerous variables with complex interdependencies. This enables us to effectively explore the global optimum of the given objective function while maintaining a sophisticated balance between exploration and exploitation.
6. Conclusions
In this paper, we propose four new UCB-based subproblem selectors for the CC frameworks—UCBSP, UCBTSP, NSUSP, and NSUTSP—to accurately identify subproblems that significantly contribute to finding optimal solutions of the objective function while maintaining a trade-off between exploration and exploitation. Our proposed subproblem selectors utilize the UCB algorithms and non-stationary mechanisms to measure the contribution of each subproblem in the CC frameworks, while simultaneously considering the dynamic characteristics of the evolutionary algorithms. In the experiments, the CC frameworks with our proposed subproblem selectors yielded better optimization results than those with classical subproblem selection methods when solving most benchmark functions. These experimental results indicate that utilizing our proposed strategies to select the subproblems in the CC frameworks can significantly contribute to finding optimal solutions to any LSGO problems with complex interdependencies.
Nevertheless, our study still has several limitations. We conducted the performance evaluations using the limited evolutionary algorithm and problem decomposer, such as the SaNSDE optimizer and ERDG algorithm, respectively. Accordingly, in future studies, we will conduct more in-depth experiments using various base evolutionary algorithms, such as the DE and PSO algorithms, as well as other problem decomposers, for example, DG2 [11] and EVIID [37]. Furthermore, we plan to investigate various performance evaluation methods [42] to enhance the practicality of this study and conduct diverse experiments based on these findings.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/math13183052/s1.
Funding
This research was supported by Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (No. 2022R1I1A3065378).
Data Availability Statement
The original contributions presented in this study are included in the article/Supplementary Materials. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The author declares no conflicts of interest.
Appendix A. Fitness Evaluation Function (Feval)
As shown in Algorithms 1 and 5, the CC frameworks utilize the fitness evalution function (Feval) to evaluate fitness values of d-dimensional individuals by using an objective function f with n-dimensional domain space, i.e., (). Algorithm A1 describes the pseudocode of the Feval function.
In Algorithm A1, f is an objective function and P is a population (or subpopulation) matrix. Moreover, S is a variable subset of f, which is generated by the problem decomposer, and “cv” is an n-dimensional context vector used to evaluate a fitness of d-dimensional vector (). The first and second inputs are necessary and the others are optional. Before the objective function evaluates the fitness values of m individuals in an m by n subpopulation, all its individuals are instantiated into an m by n temporary matrix where its row vectors are n-dimensional context vectors. Simultaneously, all the entries, except for the instantiated ones, are fixed as constants. Afterward, the objective function evaluates the fitness values of the instantiated individuals. Accordingly, the CC framework can easily evaluate the fitness values of the individuals even if it is not an n-dimensional individual.
| Algorithm A1 Feval | |
| Require: , P, S, cv | |
| 1: m = the number of rows in P | |
| 2: fit_list = make_vector(m) | |
| 3: if S == null AND cv == null then | |
| 4: for ; ; do | |
| 5: fit_list = f(P) | |
| 6: end for | |
| 7: else | |
| 8: n = the dimension of cv | |
| 9: temp_P = make_matrix() | |
| 10: for ; ; do | |
| 11: temp_P = cv | |
| 12: end for | |
| 13: temp_P = P | ▹ Instantiation of P into temp_P |
| 14: for ; ; do | |
| 15: fit_list = f(temp_P) | |
| 16: end for | |
| 17: end if | |
| return fit_list | |
Appendix B. Supplementary Materials
The detailed ablation study results and additional ANOVA test results related to Section 5.2 and Section 5.3 are shown in the Supplementary File.
Funding
This research was supported by Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (No. 2022R1I1A3065378).
References
- Liu, J.; Sarker, R.; Elsayed, S.; Essam, D.; Siswanto, N. Large-scale evolutionary optimization: A review and comparative study. Swarm Evol. Comput. 2024, 85, 101466. [Google Scholar] [CrossRef]
- Song, M.; Song, W.; Wee Lai, K. Learning-Driven Algorithm with Dual Evolution Patterns for Solving Large-Scale Multiobjective Optimization Problems. IEEE Access 2025, 13, 30976–30992. [Google Scholar] [CrossRef]
- Lin, Y.; Lin, F.; Cai, G.; Chen, H.; Zou, L.; Liu, Y.; Wu, P. Evolutionary Reinforcement Learning: A Systematic Review and Future Directions. Mathematics 2025, 13, 833. [Google Scholar] [CrossRef]
- Hussain, K.; Mohd Salleh, M.N.; Cheng, S.; Shi, Y. Metaheuristic research: A comprehensive survey. Artif. Intell. Rev. 2019, 52, 2191–2233. [Google Scholar] [CrossRef]
- Huang, X.; Liu, H.; Zhou, Q.; Su, Q. A Surrogate-Assisted Gray Prediction Evolution Algorithm for High-Dimensional Expensive Optimization Problems. Mathematics 2025, 13, 1007. [Google Scholar] [CrossRef]
- Potter, M.A.; De Jong, K.A. A cooperative coevolutionary approach to function optimization. In Proceedings of the Parallel Problem Solving from Nature—PPSN III, Jerusalem, Israel, 9–14 October 1994; Davidor, Y., Schwefel, H.P., Männer, R., Eds.; Springer: Berlin/Heidelberg, Germany, 1994; pp. 249–257. [Google Scholar] [CrossRef]
- Ma, X.; Li, X.; Zhang, Q.; Tang, K.; Liang, Z.; Xie, W.; Zhu, Z. A Survey on Cooperative Co-Evolutionary Algorithms. IEEE Trans. Evol. Comput. 2019, 23, 421–441. [Google Scholar] [CrossRef]
- Omidvar, M.N.; Li, X.; Mei, Y.; Yao, X. Cooperative Co-Evolution With Differential Grouping for Large Scale Optimization. IEEE Trans. Evol. Comput. 2014, 18, 378–393. [Google Scholar] [CrossRef]
- Omidvar, M.N.; Li, X.; Yao, X. Smart use of computational resources based on contribution for cooperative co-evolutionary algorithms. In Proceedings of the 13th Annual Conference on Genetic and Evolutionary Computation, GECCO ’11, New York, NY, USA, 5–8 June 2011; pp. 1115–1122. [Google Scholar] [CrossRef]
- Kazimipour, B.; Omidvar, M.N.; Qin, A.; Li, X.; Yao, X. Bandit-based cooperative coevolution for tackling contribution imbalance in large-scale optimization problems. Appl. Soft Comput. 2019, 76, 265–281. [Google Scholar] [CrossRef]
- Omidvar, M.N.; Yang, M.; Mei, Y.; Li, X.; Yao, X. DG2: A faster and more accurate differential grouping for large-scale black-box optimization. IEEE Trans. Evol. Comput. 2017, 21, 929–942. [Google Scholar] [CrossRef]
- Katoch, S.; Chauhan, S.S.; Kumar, V. A review on genetic algorithm: Past, present, and future. Multimed. Tools Appl. 2021, 80, 8091–8126. [Google Scholar] [CrossRef]
- Alhijawi, B.; Awajan, A. Genetic algorithms: Theory, genetic operators, solutions, and applications. Evol. Intell. 2024, 17, 1245–1256. [Google Scholar] [CrossRef]
- Opara, K.R.; Arabas, J. Differential Evolution: A survey of theoretical analyses. Swarm Evol. Comput. 2019, 44, 546–558. [Google Scholar] [CrossRef]
- Das, S.; Suganthan, P.N. Differential evolution: A survey of the state-of-the-art. IEEE Trans. Evol. Comput. 2010, 15, 4–31. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, S.; Ji, G. A Comprehensive Survey on Particle Swarm Optimization Algorithm and Its Applications. Math. Probl. Eng. 2015, 2015, 931256. [Google Scholar] [CrossRef]
- Wang, D.; Tan, D.; Liu, L. Particle swarm optimization algorithm: An overview. Soft Comput. 2018, 22, 387–408. [Google Scholar] [CrossRef]
- Shakir Hameed, A.; Alrikabi, H.M.B.; Abdul–Razaq, A.A.; Ahmed, Z.H.; Nasser, H.K.; Mutar, M.L. Appling the Roulette Wheel Selection Approach to Address the Issues of Premature Convergence and Stagnation in the Discrete Differential Evolution Algorithm. Appl. Comput. Intell. Soft Comput. 2023, 2023, 8892689. [Google Scholar] [CrossRef]
- Rivera, M.M.; Guerrero-Mendez, C.; Lopez-Betancur, D.; Saucedo-Anaya, T. Dynamical Sphere Regrouping Particle Swarm Optimization: A Proposed Algorithm for Dealing with PSO Premature Convergence in Large-Scale Global Optimization. Mathematics 2023, 11, 4339. [Google Scholar] [CrossRef]
- Ma, Z.; Chen, J.; Guo, H.; Ma, Y.; Gong, Y.J. Auto-configuring Exploration-Exploitation Tradeoff in Evolutionary Computation via Deep Reinforcement Learning. In Proceedings of the Genetic and Evolutionary Computation Conference, GECCO ’24, New York, NY, USA, 14–18 July 2024; pp. 1497–1505. [Google Scholar] [CrossRef]
- Zangirolami, V.; Borrotti, M. Dealing with uncertainty: Balancing exploration and exploitation in deep recurrent reinforcement learning. Knowl.-Based Syst. 2024, 293, 111663. [Google Scholar] [CrossRef]
- Abdul Halim, A.H.; Das, S.; Ismail, I. Fundamental Tradeoffs Between Exploration and Exploitation Search Mechanisms. In Into a Deeper Understanding of Evolutionary Computing: Exploration, Exploitation, and Parameter Control: Volume 1; Springer Nature: Cham, Switzerland, 2024; pp. 101–199. [Google Scholar] [CrossRef]
- Gittins, J.; Glazebrook, K.; Weber, R. Multi-Armed Bandit Allocation Indices; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar] [CrossRef]
- Watkins, C. Learning from Delayed Rewards. Ph.D. Thesis, University of Cambridge, Cambridge, UK, 1989. [Google Scholar]
- Burtini, G.; Loeppky, J.; Lawrence, R. A Survey of Online Experiment Design with the Stochastic Multi-Armed Bandit. arXiv 2015. [Google Scholar] [CrossRef]
- Vermorel, J.; Mohri, M. Multi-armed Bandit Algorithms and Empirical Evaluation. In Proceedings of the Machine Learning: ECML 2005, Porto, Portugal, 3–7 October 2005; Gama, J., Camacho, R., Brazdil, P.B., Jorge, A.M., Torgo, L., Eds.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 437–448. [Google Scholar] [CrossRef]
- Agrawal, R. Sample mean based index policies by O(log n) regret for the multi-armed bandit problem. Adv. Appl. Probab. 1995, 27, 1054–1078. [Google Scholar] [CrossRef]
- Auer, P.; Cesa-Bianchi, N.; Fischer, P. Finite-time analysis of the multiarmed bandit problem. Mach. Learn. 2002, 47, 235–256. [Google Scholar] [CrossRef]
- Garivier, A.; Moulines, E. On Upper-Confidence Bound Policies for Non-Stationary Bandit Problems. arXiv 2008, arXiv:0805.3415. [Google Scholar] [CrossRef]
- Kocsis, L.; Szepesvári, C. Bandit Based Monte-Carlo Planning. In Proceedings of the Machine Learning: ECML 2006, Berlin, Germany, 18–22 September 2006; Fürnkranz, J., Scheffer, T., Spiliopoulou, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2006; pp. 282–293. [Google Scholar] [CrossRef]
- Wei, L.; Srivastava, V. Nonstationary Stochastic Bandits: UCB Policies and Minimax Regret. IEEE Open J. Control Syst. 2024, 3, 128–142. [Google Scholar] [CrossRef]
- Tang, K.; Li, X.; Suganthan, P.N.; Yang, Z.; Weise, T. Benchmark Functions for the CEC’2010 Special Session and Competition on Large-Scale Global Optimization; Technical Report; Nature Inspired Computation and Applications Laboratory, USTC: Hefei, China, 2010. [Google Scholar]
- Li, X.; Tang, K.; Omidvar, M.N.; Yang, Z.; Qin, K.; China, H. Benchmark Functions for the CEC 2013 Special Session and Competition on Large-Scale Global Optimization; Technical Report 33; Nature Inspired Computation and Applications Laboratory, USTC: Hefei, China, 2013. [Google Scholar]
- Wang, Z.J.; Zhan, Z.H.; Yu, W.J.; Lin, Y.; Zhang, J.; Gu, T.L.; Zhang, J. Dynamic Group Learning Distributed Particle Swarm Optimization for Large-Scale Optimization and Its Application in Cloud Workflow Scheduling. IEEE Trans. Cybern. 2020, 50, 2715–2729. [Google Scholar] [CrossRef]
- Hu, X.M.; He, F.L.; Chen, W.N.; Zhang, J. Cooperation coevolution with fast interdependency identification for large scale optimization. Inf. Sci. 2017, 381, 142–160. [Google Scholar] [CrossRef]
- Sun, Y.; Kirley, M.; Halgamuge, S.K. A recursive decomposition method for large scale continuous optimization. IEEE Trans. Evol. Comput. 2017, 22, 647–661. [Google Scholar] [CrossRef]
- Kim, K.S.; Choi, Y.S. An efficient variable interdependency-identification and decomposition by minimizing redundant computations for large-scale global optimization. Inf. Sci. 2020, 513, 289–323. [Google Scholar] [CrossRef]
- Yang, M.; Zhou, A.; Li, C.; Yao, X. An Efficient Recursive Differential Grouping for Large-Scale Continuous Problems. IEEE Trans. Evol. Comput. 2021, 25, 159–171. [Google Scholar] [CrossRef]
- Yang, Z.; Tang, K.; Yao, X. Self-adaptive differential evolution with neighborhood search. In Proceedings of the 2008 IEEE Congress on Evolutionary Computation (IEEE World Congress on Computational Intelligence), Hong Kong, China, 1–6 June 2008; pp. 1110–1116. [Google Scholar] [CrossRef]
- Mei, Y.; Omidvar, M.N.; Li, X.; Yao, X. A Competitive Divide-and-Conquer Algorithm for Unconstrained Large-Scale Black-Box Optimization. ACM Trans. Math. Softw. 2016, 42, 1–24. [Google Scholar] [CrossRef]
- Sheskin, D.J. Handbook of Parametric and Nonparametric Statistical Procedures; John Wiley & Sons: New York, NY, USA, 2003. [Google Scholar] [CrossRef]
- Zhou, Z.; Abawajy, J. Reinforcement Learning-Based Edge Server Placement in the Intelligent Internet of Vehicles Environment. IEEE Trans. Intell. Transp. Syst. 2025, 1–11. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).