Abstract
Given a discrete spatial structure X, we define continuous-time branching processes that model a population breeding and dying on X. These processes are usually called branching random walks, and denotes the number of individuals alive at site x at time t. They are characterised by breeding rates (governing the rate at which individuals at x send offspring to y) and by a multiplicative speed parameter . These processes also serve as models for epidemic spreading, where represents the infection rate from x to y. In this context, represents the number of infected individuals at x at time t, and the removal of an individual is due to either death or recovery. Two critical parameters of interest are the global critical parameter , related to global survival, and the local critical parameter , related to survival within finite sets (with ). In disease or pest control, the primary goal is to lower so that the process dies out, at least locally. Nevertheless, a process that survives globally can still pose a threat, especially if sudden changes cause global survival to transition into local survival. In fact, local modifications to the rates can affect the values of both critical parameters, making it important to understand when and how they can be increased. Using results on the comparison of the extinction probabilities for a single branching random walk across different sets, we extend the analysis to the extinction probabilities and critical parameters of pairs of branching random walks whose rates coincide outside a fixed set . We say that two branching random walks are equivalent if their rates coincide everywhere except on a finite subset of X. Given an equivalence class of branching random walks, we prove that if one process has , then is the maximal possible value of this parameter within the class. We describe the possible configurations for the critical parameters within these equivalence classes.
Keywords:
branching random walk; branching process; critical parameters; local survival; global survival; pure global survival phase MSC:
60J05; 60J80
1. Introduction
A branching process, or the Galton–Watson process (see [1]), is a process where a particle dies and gives birth to a random number of offspring, according to a given offspring law ( being the probability of having exactly n children). Different particles breed independently, according to . The process can either go extinct (i.e., no particles are alive from a certain time on) almost surely or survive (i.e., at least one particle in any generation) with positive probability. The probability of extinction can be computed as a function of .
A branching random walk (BRW hereafter) is a process where particles are described by their location , where X is an at most countable set (X is usually interpreted as a spatial variable but can also be seen as a “type”; see, for instance, [2]). The particles at site are replaced by a random number of children, which are placed at various locations on X. The breeding law depends on the site where the parent lives, and all particles breed independently. This class of processes (in continuous and discrete time) has been studied by many authors: see [3,4,5] for older results. Besides the classical environment , the process has been studied in other settings, such as finite sets [6] or trees [7,8,9,10,11,12]. Note that in the case of the branching random walk, there is no upper bound for the number of particles per site. When such an upper bound is fixed, say at most m particles per site, we see an m-type contact process. The branching random walk can be obtained as the limiting process as m goes to infinity [11,13].
BRWs can be considered in discrete time, where each particle is alive for one generation and its offspring all live in the next generation, or in continuous time, where generations overlap since particles may breed at different times during their whole lifetime. In particular, one can consider a family of parametrised processes where we fix the breeding rates between locations, and the parameter represents the reproductive speed (the larger , the shorter the time intervals between subsequent breedings; see Section 2 for details).
Since the BRW lives on a spatial structure, its behaviour is in general more complex than that of a branching process: indeed, survival and extinction can be studied globally (on the whole space X) but also locally (at a single site or in a finite set A). Starting the process with one particle at a given site x and fixing a set , only one of the following holds for the BRW: (1) it almost surely goes extinct, (2) it survives globally but not locally, (3) it survives globally and locally but with different probabilities (non-strong local survival), or (4) it survives globally and locally with equal probability (strong local survival). We stress that no strong local survival means that there is either non-strong local survival or almost sure local extinction.
When considering BRWs in continuous time, a fixed family may exhibit different behaviours for different values of the speed parameter , and the threshold that separates global extinction from global survival is called the global critical parameter . Analogously, the threshold between local extinction and local survival is called the local critical parameter . We note that the subscripts w and s stand for “weak” and “strong”, which are sometimes used as synonyms for “global” and “local”, respectively.
Many authors have addressed natural questions, such as how to identify the critical parameters [11,14] or establish criteria for survival and extinction [10,12,15,16,17,18]. Once survival with positive probability is established, one can address the problem of identifying and computing extinction probabilities; see [19]. In ecological or epidemiological contexts, the goal may be either to promote survival (e.g., of an endangered species) or to achieve extinction (e.g., for disease or pest control). In the case of continuous-time branching random walks, two key factors are involved: the speed parameter and the family of rates . If the goal is to drive an epidemic to extinction, one strategy is to lower (for example, wearing a mask to reduce respiratory infections such as COVID-19 serves this purpose). When , we know that the infection will eventually disappear from any site. However, if , it may still persist in the system. Another strategy is to reduce the infection rates , as doing so may increase the values of the critical parameters and thereby change the behaviour of the process for a fixed . More precisely, suppose that is fixed and that , are the critical parameters associated with the rates . After some modifications, the rates become , possibly leading to different critical parameters and . If , then the modified process dies out in all locations, even though the original process did not. Altering the infection rates corresponds to changing the interactions between sites, for example, by implementing social distancing or closing schools. However, in practice, such changes are typically feasible only on finite subsets of X (i.e., they are local changes). It is therefore of utmost importance to understand how local changes affect the critical parameters, as our goal is to actively influence the course of an epidemic through these interventions. Another important consideration arises when the process is in a purely global survival phase (): the epidemic appears to be "mild" since it disappears from all locations. However, local modifications can alter this balance, and if they reduce the local critical parameter (i.e., if ), the disease could reappear at all sites. Our results show that it is impossible to increase when the process is in a pure global survival phase. However, in other cases, it is possible to do so. For instance, isolating superspreaders may be effective, as illustrated in Example 1. In that example, there is a single superspreader location, the origin of the tree, denoted by o. When is large and , the process exhibits local survival. However, if is sufficiently small (i.e., the superspreader is isolated), the process becomes extinct both locally and globally.
The present paper is devoted to the question of what can be said when a BRW is modified locally, that is, when the breeding laws are changed only within a fixed set . For instance, one may ask how the modified BRW behaves if the original BRW does not exhibit strong local survival. Theorem 3 shows that there is global survival and no strong local survival in A for the original BRW if and only if the same holds for the modified BRW, regardless of the specific modifications made in A. As a corollary, we obtain that if the original BRW dies out locally in A and the modified BRW survives globally, then almost sure global extinction of the original BRW is equivalent to strong local survival in A for the modified one (see Corollary 3 and Figure 1). Moreover, for a fixed irreducible BRW, if there is global survival and no strong local survival in some set , then this property holds for every finite set .

Figure 1.
A phase diagram of and its modification , observed on a finite set . The process has a pure global survival phase (i.e., ), while has a lower global critical parameter and no pure global survival phase: . When , the modified process exhibits strong local survival. For , it exhibits non-strong local survival. For , the two processes behave identically: one exhibits strong local survival if and only if the other does.
Building on these results in discrete time, we show that in continuous time, local modification of the BRW in a finite subset A, which lowers the global critical parameter (typically achieved by adding a sufficiently fast reproduction rate at some site), implies that the global and local critical parameters of the modified BRW coincide (see Corollary 2). This leads to a general method for constructing examples such as Example 1, where the modified BRW exhibits strong local survival for some values of the parameter below a certain threshold and above another and non-strong local survival for intermediate values (see Figure 1 and Figure 2). This example was originally presented in [20], but it is included here with a simpler proof and within a more general framework. Furthermore, we prove that in general, a continuous-time BRW obtained via a local modification that lowers the global critical parameter dies out globally at its critical value, a property that does not always hold (see [21] (Example 3)).
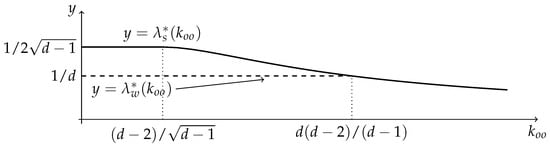
Figure 2.
The critical parameters and for the process on the tree . The rates are defined as for all , and . The functions (dashed) and (solid) coincide for . Moreover, for , and for .
Here is an outline of the paper. In Section 2, we recall the definitions of discrete-time and continuous-time BRWs, the extinction probability vectors, and their asymptotic behaviour, specifically whether extinction occurs as time tends to infinity. We also define global, local, and strong local survival, along with the critical parameters associated with continuous-time BRWs. Theorem 1 and Corollary 1 present known results about approximating a BRW using a sequence of BRWs, stated in a form that will be useful later. Proposition 1 provides a sufficient condition for the equality . In Section 3, we first compare the extinction probabilities of a single BRW restricted to different sets (Theorem 2) and then compare the extinction probabilities of two different BRWs (Theorem 3). Next, we study how the critical parameters of a continuous-time BRW are affected by local modifications of its rates (see Corollaries 2–4). Section 4 begins with the observation that if a BRW has a pure global survival phase (, meaning a range of values of the speed parameter exists where the process survives globally but eventually leaves all finite sets), then no local modification of the rates can increase the global critical parameter (see Proposition 2). This implies that the global critical parameter of a BRW with a pure global survival phase is maximal among those of all BRWs obtained through local modifications. Finally, in Section 4, we analyse the behaviour of the BRW on a homogeneous tree with one added reproductive loop at the origin (Example 1) and address several general questions about the critical parameters when the rates are modified in a subset A.
2. Basic Definitions and Preliminaries
2.1. Discrete-Time Branching Random Walks and Their Survival/Extinction
Given an at most countable set X, we define a discrete-time BRW as a process , where is the number of particles alive at at time n. The dynamics is described as follows: let , and let be a family of probability measures on the (countable) measurable space . A particle of generation n at site lives one unit of time; after that, a function is chosen at random according to the law . This function describes the number of children and their positions, that is, the original particle is replaced by particles at y, for all . The choice of f is independent for all breeding particles. The BRW is denoted by .
Some results rely on the first moment matrix , where each entry represents the expected number of children that a particle living at x sends to y (briefly, the expected number of particles from x to y). For the sake of simplicity, we require that .
To a generic discrete-time BRW, we associate a graph , where if and only if . In contrast, given a graph , we say that a BRW is adapted to the graph if if and only if . We say that there is a path of lenght n from x to y, and we write , if it is possible to find a finite sequence (where ) such that , , and for all (observe that there is always a path of length 0 from x to itself). If for some , then we write ; whenever and , we write . The equivalence relation ⇌ induces a partition of X: the class of x is called the irreducible class of x. If the graph is connected (that is, there is only one irreducible class), then we say that the BRW is irreducible. Irreducibility implies that the progeny of any particle can spread to any site of the graph with positive probability.
We consider initial configurations with only one particle placed at a fixed site x, and we denote by the law of the corresponding process. Evolution of processes with more than one initial particle can be obtained through superimposition.
In the following, wpp is shorthand for “with positive probability” (although when talking about survival, “wpp” will usually be tacitly understood). In order to avoid trivial situations where particles have one offspring almost surely, we henceforth assume the following.
Assumption 1.
For all , there is a vertex such that , that is, in every equivalence class (with respect to ⇌), there is at least one vertex where a particle can have, inside the class, a number of children different from 1 wpp.
We now introduce some definitions. The notation of the main quantities is summarised in Table 1. For a more formal statement, see Definition 1 and Equation (1).

Table 1.
Main notations. The BRW starts with one individual in .
Definition 1.
Given a BRW , , and , the probability of extinction in A, starting from a particle at x, is defined as
We denote by the extinction probability vector, whose x-entry is .
If , we write instead of . Note that depends on . When we need to stress this dependence, we write . Extinction probabilities have been the object of intense study in recent decades. We refer the reader, for instance, to [13,22,23].
Definition 2.
Let be a BRW starting from one particle at and let . We say that
- 1.
- The process survives locally wpp in A if ;
- 2.
- The process survives globally wpp if ;
- 3.
- There is strong local survival wpp in A if and non-strong local survival wpp in A if ;
- 4.
- There is no strong local survival in A if either or ;
- 5.
- The process is in a pure global survival phase if .
When there is no survival wpp, we say that there is extinction, and the fact that extinction occurs almost surely will be tacitly understood. When there is strong local survival, this means that for almost all realisations, the process either survives locally (hence globally) or it goes globally extinct. More precisely, there is strong survival at y starting from x if and only if the probability of local survival at y starting from x conditioned on global survival starting from x is 1.
We want to stress that for a BRW starting from , if and only if global survival is equivalent to strong local survival at A. On the other hand, if and only if there is global survival and no strong local survival at A.
In general, Definition 2 depends on the starting vertex. However, if the process is irreducible, then the process survives locally or globally starting from x if and only if the same holds when starting from y, for all . Strong local survival may still depend on the starting vertex, even in the irreducible case. If at all sites we have a positive probability of no children, then one can prove that strong local survival does not depend on the starting vertex (see [20] (Section 3)).
Moreover, if a BRW is irreducible, are nonempty, finite subsets, and is nonempty, then for all . The first equality holds since local survival does not depend on the target vertex and survival in a finite (nonempty) set is equivalent to local survival to a vertex in the set; more precisely, in the irreducible case, if a vertex y is visited infinitely often, then the conditional probability of visiting all other vertices infinitely many times is 1 (according to the Borel–Cantelli Lemma). The second inequality follows from the fact that any nonempty set contains a finite nonempty set.
Henceforth, we make use of the natural partial order between vectors, defined as follows: if and only if for all . Therefore, if and only if for all and for some ; moreover, if and only if for some .
2.2. Continuous-Time Branching Random Walks
Given an at most countable X and a nonnegative matrix , one can define a family of continuous-time branching random walks , where represents the number of particles alive at time t at site x, for any . The family is indexed by the reproductive speed parameter .
Each particle has an exponentially distributed lifetime with parameter 1. During its lifetime, each particle alive at x breeds into y according to the arrival times of its own Poisson process with the parameter (representing the reproduction rate). We denote this family of continuous-time BRWs (depending on ) using . It is not difficult to see that the introduction of a nonconstant death rate does not represent a significant generalisation. In fact, one can study a new BRW with a death rate = 1 and reproduction rates ; the two processes have the same behaviours in terms of survival and extinction (see [20] (Remark 2.1)).
With each continuous-time BRW, we associate a discrete-time counterpart, namely , where we simply take into account the number and the positions of all offspring born before the death of the parent. Clearly, from the knowledge of the discrete-time counterpart of , we cannot retrieve how many particles are alive at time t (and where), but the information about survival and extinction is intact. The extinction probabilities of a continuous-time BRW coincide with those of its discrete-time counterpart and depend on , although the dependence on will usually be omitted. In particular, we extend every definition from the discrete-time case to the continuous-time case in a natural way by using the discrete-time counterpart of a continuous-time process. More precisely, when we say that a continuous-time process has a certain property, we mean that its discrete-time counterpart has it; for instance, a continuous-time process is irreducible (by definition) if and only if its discrete-time counterpart is. We note that in the discrete-time counterpart of a continuous-time BRW, at every vertex, there is a positive probability of dying without breeding; hence, in the continuous-time irreducible case, either strong local survival is a common property of all starting vertices, or it holds nowhere. Moreover, it is easy to show that the expected number of children from x to y, for the discrete-time counterpart of the process, is .
Given , two critical parameters are associated with the continuous-time BRW: the global survival critical parameter and the local survival critical parameter (or, briefly, the global and local critical parameters, respectively) defined as
These values depend only on the irreducible class of x. In particular, they are constant if the BRW is irreducible, in which case we simply write and . Indeed, suppose that ; since there is a positive probability that a descendant of a particle in x is placed in y, if there is a positive probability of survival in a set A starting from y, then the same holds starting from x. Therefore, taking , and if , then . Moreover, if x is visited an infinite number of times, then according to Borel–Cantelli’s Lemma, an infinite number of descendants is placed at y: more precisely, the probability of visiting y infinitely often conditioned on visiting x infinitely often is 1. Thus, if , then . This last equality can also be proven using Equation (2); this simple exercise is left to the reader.
Note that while in the discrete-time case there is only one process that can be in a pure global survival phase or not, in continuous time, we have a family of processes, indexed by . Hence, we may have processes, in the same family, in pure global survival and others which are not in pure global survival. We say that a pure global survival phase exists starting from x if the interval is nonempty. No reasonable definition of a strong local survival critical parameter is possible (see [20]).
It is possible to identify in terms of the matrix K. Indeed, consider the nth power matrix with entries : it is possible to prove that
(see [21] (Theorems 4.1 and 4.7) or [11] (Lemma 3.1)). One can also write the local critical parameter in terms of a generating function. Let
The coefficients in the BRW theory play the same role played by the taboo probabilities in random walk theory: when , these are called first-return probabilities (see [24] (Section 1.C)). Roughly speaking, is the expected number of particles alive at y at time n, when the initial state is just one particle at x and the process behaves like a BRW except that every particle reaching y at any time is immediately killed (before breeding). The following characterisation holds (see [21]):
where the last equality is due to the fact that is a continuous, strictly increasing power series from to , where r is the radius of convergence (it is also left continuous in r even if is infinite). The characterisation of is less explicit: if we denote the usual subset of nonnegative, bounded functions on X using , we can characterise by the existence of solutions of certain inequalities (see [21] (Theorem 4.2))
where ( are the entries of the matrix , the nth power of the matrix N). Alternatively, there is global survival for a fixed starting from x if and only if exists such that and for all (see [21] (Theorem 4.2)).
Remark 1.
Even though we do not assume that the set X is infinite, the finite case is straightforward. Indeed, if X is finite and the BRW is irreducible, then coincides with the spectral radius of the nonnegative, irreducible matrix K (according to the Gelfand formula). It is easy to construct a solution to Equation (4) for any λ larger than the spectral radius of K: one can simply take a positive eigenvector corresponding to the Perron–Frobenius eigenvalue. Thus, in the finite case, the critical values are given by the inverse of the Perron–Frobenius eigenvalue of K. From a probabilistic point of view, the equality follows from the fact that survival in a finite set is equivalent to visiting at least one site infinitely often; by irreducibility, this implies survival at every site.
More formally, the equality when X is finite follows from [21] (Remark 4.1, Theorems 4.1 and 4.3) (since in the finite irreducible case; see that paper for the necessary definitions) and from [20] (Theorem 3.2, Corollary 3.1, and the subsequent discussion).
2.3. Spatial Approximation
Given a sequence of BRWs such that , we define , where , and the corresponding sequence of first moment matrices . Clearly, for all , is eventually well defined as . Indeed, , implies that given as finite, for every sufficiently large n. We wonder when a BRW can be approximated using a sequence of BRWs: more precisely, we are focusing on the local behaviour. Note that in the following results, we are not assuming that the BRW is irreducible.
Theorem 1
([13] (Theorem 5.2)). Let us fix a vertex . Suppose that and for all and all . Assume that for all , as .
- 1.
- If dies out locally (resp. globally) a.s. starting from , then dies out locally (resp. globally) a.s starting from for all ;
- 2.
- If survives locally starting from , then survives locally starting from eventually as .
Theorem 1 yields an analogous result for BRWs in continuous time.
Corollary 1
([23] (Corollary 5.3)). Let be a continuous-time BRW and consider a sequence of continuous-time BRWs such that . Suppose that for all , and as for all . Then, for every and . Moreover, given , we have , eventually as and as .
Among all possible choices of the sequence , there is one which is induced by on the subsets ; more precisely, one can take for all and . Roughly speaking, this choice means that all reproductions outside are suppressed. In this case, it is simply for all .
3. Strong Local Survival and Local Modifications
In this section, we examine how modifications on finite sets may influence the behaviour of a BRW. Since survival on a fixed set for a continuous-time BRW is equivalent to survival on the same set for its discrete-time counterpart, it is natural to use results from the discrete-time case to infer corresponding results for continuous-time BRWs.
We recall here [22] (Theorem 4.1), which is a fundamental tool for comparing extinction probability vectors. In the case of global survival (choose ), it gives equivalent conditions for strong local survival in terms of the extinction probabilities. We denote by the probability that the process, which starts with one particle at x, has no progeny ever in the set A. Theorem 2 compares the extinction probabilities of two sets. Specifically, it asserts that a BRW has a positive probability of surviving in a set B while becoming extinct in a set A if and only if it has a positive probability of surviving in B without ever visiting A. The “if” direction of this equivalence is straightforward, whereas the converse is not. This is a very powerful result, which has many applications.
Theorem 2
([22] (Theorem 4.1)). For any BRW and , the following statements are equivalent:
- 1.
- exists such that ;
- 2.
- exists such that ;
- 3.
- exists such that ;
- 4.
- exists such that starting from x, there is a positive chance of survival in B without ever visiting A;
- 5.
- exists such that starting from x, there is a positive chance of survival in B and extinction in A;
- 6.
From Theorem 2, which is stated for a single BRW, we derive Theorem 3 and Corollary 2, which give us information about the behaviour of a BRW after some modifications. To this aim, consider two BRWs and and denote by and their respective extinction probability vectors. If for all , for some set , we derive properties of from analogous properties of . Theorem 3 extends [25] (Theorem 4.2), which addresses the special case .
Theorem 3.
Let and be two BRWs. Suppose that is a nonempty set such that for all . Then, we have for all , and for all ,
If, in addition, for all , then
It is natural to compare the extinction probabilities of a set A with those of another generic set B for both processes. According to the previous theorem, one BRW has a positive probability of surviving in B and going extinct in A if and only if the same holds for the other. In particular, if the differences between the two BRWs are confined to , then the extinction probabilities of A and B coincide for one process if and only if they coincide for the other. We emphasise that this does not imply that all four extinction probabilities are identical; for example, it may happen that (almost sure extinction in A and B), while (the same positive probability of survival in both A and B).
Proof of Theorem 3.
We note that and have the same behaviour until they first hit A; hence, for all . If , then clearly, .
- Suppose now that ; this is equivalent to for some . Hence, according to Theorem 2, exists such that there is a positive probability of survival in B starting from x without ever visiting A. Since the two processes have the same behaviour until they first hit A, the same holds for , and this implies that ; thus, . The reverse implication follows by exchanging the role of and .The final double implication, follows from the previous one by exchanging the role of A and B. □
In particular, note that if , then the partial order of the sets () is preserved by the (well-defined) map .
Theorem 3, applied to continuous-time BRWs, leads to Corollary 2, which describes how local modifications of the BRW affect the critical parameters. This corollary is a slight extension of the first part of [25] (Corollary 4.4); specifically, we added the final line to the statement.
Corollary 2
([25] (Corollary 4.4)). Let and be two irreducible continuous-time BRWs such that for all where A is a finite nonempty set. Then the following are equivalent:
- 1.
- ;
- 2.
- ;
- 3.
- .
In particular, if (for instance, if ), then .
This corollary leads to the following significant conclusion: either the weak critical parameter of a BRW attains its maximum value (under finite modifications) or the BRW does not exhibit a pure global survival phase.
Proof of Corollary 2.
Observe that the discrete-time counterparts of these continuous-time BRWs satisfy the hypotheses of Theorem 3, namely their offspring distribution is the same outside A.
Clearly and We just need to prove that ; more precisely, we prove that . Take ; the - BRW survives globally by definition, and hence, (we denote by the extinction probabilities of ). On the other hand, since , the - BRW dies out a.s. in every set starting from every point, whence . According to Theorem 3, since , then , which implies . If the - BRW survives locally in the finite set A, this means that it survives locally at a vertex (⟺ at every vertex since the process is irreducible). This implies . We just proved that for every , we have a BRW that survives globally and thus , whence . □
According to Corollary 2, when and are two irreducible continuous-time BRWs such that for all where A is a finite nonempty set, then the only alternatives are
- 1.
- ;
- 2.
- ;
- 3.
- .
We are thus able to describe the behaviour of the modified BRW, when the original BRW has a pure global survival phase and the modified has no weak phase. The phase diagram can be seen in Figure 1. Note that while in general a BRW may survive or die out globally at its global critical parameter, here, we know the behaviour at (the process dies out globally). Moreover, for , there is local survival which is strong or non-strong depending on the behaviour of . These results are summarised in Corollary 3.
Corollary 3
([25] (Corollary 4.4)). Let and be two irreducible continuous-time BRWs such that for all where A is a finite nonempty set. Suppose that , and let be nonempty. Then, for the BRW ,
- 1.
- If , there is a.s. extinction in B.
- 2.
- If , there is strong survival in B.
- 3.
- If and dies out globally, then there is strong survival in B; conversely, if survives globally and B is finite; there is non-strong survival in B.
- 4.
- If and B is finite, then there is non-strong survival in B.
- 5.
- If and B is finite, then the survival is strong (resp., non-strong) in B if and only if the same holds for .
According to this corollary, if a BRW exhibits a pure global survival phase, then any local modification without such a phase necessarily displays a non-strong survival phase. The critical behaviour at for a general BRW is well understood: almost sure local extinction occurs (see [21] (Theorem 4.7)). In contrast, at the global critical point , the process may either survive (see [21] (Example 3)) or become extinct almost surely (see, for instance, [21] (Theorem 4.8)). However, if a BRW is obtained as a finite modification of another BRW, then at the global critical value , extinction occurs almost surely, as stated in the first point of the previous corollary.
Proof of Corollary 3.
We consider the following disjoint intervals for .
- 1.
- Suppose that : by definition, there is global extinction and hence also local extinction. From Corollary 3, we know that . If , according to [21] (Theorem 4.7), for any finite set C, the - BRW dies out locally at C. This means that . We also know that for all ) since . Note that and apply Theorem 3 to deducingThus, we have .
- 2.
- . By definition, since , there is global and local survival for the - BRW. This implies that for every (finite or infinite) set B. On the other hand, there is global and local extinction for the - BRW, which implies that . Again, according to Theorem 3, for every set B.
- 3.
- Clearly, since , we have for all finite subsets B. Hence,that is, according to Theorem 3, if and only if . This, again, implies for every nonempty finite subset B. If, on the other hand, dies out globally, then and for every nonempty subset B.
- 4.
- (we suppose that the interval is nonempty; otherwise, there is nothing to prove). Here, we have for every finite subset B. Theorem 3 yields , and by irreducibility, for every finite nonempty subset B.
- 5.
- . Now, and for every nonempty . Again, according to Theorem 3, we haveIf B is finite, then Theorem 3 yields the conclusion. □
In particular, if we know that exhibits non-strong local survival in a set A, for a fixed value of , we can deduce the behaviour of a BRW, which coincides with outside A.
Corollary 4.
Let and be two irreducible continuous-time BRWs such that for all where A is a nonempty (not necessarily finite) set. If exists such that survives non-strong locally in A, then
- 1.
- survives globally when ;
- 2.
- If A is finite and , then there is pure global survival for , if .
Proof.
If , , then according to Theorem 3, ; this implies (1) that (there is global survival) and (2) if and A is finite, then , where x is a generic point (there is a pure global survival phase). □
A simple class of irreducible BRWs where is described by the following result. Here, we consider the Alexandroff one-point compactification of X endowed by the discrete topology: the neighbourhoods of ∞ are . is defined accordingly.
Proposition 1.
Let be an irreducible BRW such that ; then, .
Proof.
By hypothesis, exists such that (1) and (2) for every , a finite exists such that . Suppose, by contradiction, that and let ; for every , since there is a.s. extinction in every finite set, according to Theorem 2, there is a positive probability of global survival starting from some without visiting . Since the total number of particles generated outside is dominated by a branching process with a reproduction rate , we have . Since this is true for every , we have proven that implies . We have two cases:
- 1.
- If , then , and therefore the set is empty, that is, .
- 2.
- If , then and imply which, in turn, implies ; thus, .
□
4. The Maximality of the Pure Global Survival Phase
Let us consider the set of irreducible continuous-time BRWs on X, namely . Define the relation on by if and only if a finite exists such that for all and all . An equivalent definition is if and only if the set is finite.
Clearly, , whence is reflexive; moreover, , and therefore is symmetric. Finally, for all , we have which implies that is transitive. The relation is an equivalence relation. To avoid a cumbersome notation, we denote by the equivalence class of and by the quotient set. Henceforth, given an irreducible BRW , we denote by and its global and local critical values, respectively.
Proposition 2.
Let such that . Then, for all , we have . Moreover, for all such that , we have .
Proof.
By contradiction, if , then, according to Corollary 2, we have , which contradicts the hypothesis. From the previous part, it easily follows that if and , then . □
We note that when X is finite, there is only one equivalence class: in this case, no BRW admits a pure global survival phase (see Remark 1), and the supremum of is clearly infinite. Hence, the case of real interest arises when X is infinite.
As an application of Proposition 2, we discuss the behaviour of the critical parameters of the BRW on the d-dimensional regular tree , when we add the possibility of reproduction from the origin of the tree to itself.
Example 1.
Consider the BRW on , where for all neighbouring couples . For this BRW, and , and the process exhibits a pure global survival phase. We modify this BRW by adding a loop at the origin o and choosing . We denote by and the global and local critical parameters, respectively, of this modified process. It is well known that for small values of , , while for that is sufficiently large, the critical parameters coincide (see, for instance, [20] (Example 4.2)). We are now able to prove that for , the two parameters coincide with the parameters of the original process (); for , we have , while and is monotonically decreasing. When , the two parameters coincide and tend to 0 as goes to infinity. The plot of the two functions and can be seen in Figure 2 (note that the axes do not share the same scale).
In order to compute the function , recall that the local critical parameter equals (see Section 2 or [21]), where
The computation of the generating function Φ in this case is simple: there is only one path from o to o of length 1 (the loop) whence ; on the other hand, the loop is not involved in any first-return path of length , and therefore the coefficient for is the same as in the homogeneous tree (that is, when ). Hence, Φ is the sum of and the analogous generating function of the homogeneous tree. It is an exercise to obtain for ,
Note that this provides an example in which there are several (more precisely, infinitely many) local modifications of a BRW, all with , and according to Proposition 2, they all share the same global critical parameter. Moreover, one of these modifications (the one with ) has no pure global survival phase but still the same global critical parameter.
Example 1 was first presented in [20] (Example 4.2), where the authors proved that if the loop rate is sufficiently large, then . The proof in [20] relies on a detailed analysis of the behaviour of a BRW along the branches of a homogeneous tree. In our case, we can instead employ results such as Corollary 2 and Proposition 2, which apply in more general settings than those considered in [20] (Example 4.2). This not only simplifies the proof compared to [20] (Example 4.2) but also enables us to completely characterise the critical parameters of as functions of .
In the following sections, we address several natural questions concerning these equivalence classes. We briefly summarise the main results (see also Table 2). A given class may or may not contain BRWs with a pure global survival phase (see Section 4.1); however, every class necessarily contains uncountably many BRWs without a pure global survival phase (see Section 4.2). If a class admits at least one BRW with a pure global survival phase, then there are uncountably many BRWs with a pure global survival phase, and the supremum of is finite and attained by all such BRWs (see Section 4.8 and Proposition 2). In this case, the same class may also contain BRWs without a pure global survival phase but with the same maximal value of (see Section 4.7). If a class contains only BRWs without a pure global survival phase, then the supremum of may be infinite (see Section 4.5) or finite; in the latter case, the supremum may or may not be attained (see Section 4.3 and Section 4.4, respectively). Finally, we show that classes exist in which is constant across all members (see Section 4.6).

Table 2.
A summary of Section 4. We analyse the behaviour of the critical parameters and of as varies in and compare them to the critical parameters and of .
4.1. Does Every Equivalence Class Have a BRW with a Pure Global Survival Phase?
The answer is negative. Let us start with a heuristic reasoning before moving on to a more formal proof. Take where if and 0 otherwise. Consider a modification restricted to an interval I. Conditioned to global survival, either an infinite number of particles visits I or an infinite number of particles visits , but in this case, according to Borel–Cantelli’s argument, the progeny of an infinite number of particles visits I. So, there is no pure global survival phase.
This can be proven rigorously in general as follows. We recall that is quasi-transitive if a finite exists such that for any , there is a bijective map satisfying and for all . For example, if the rates are translation-invariant, then is quasi-transitive (actually, it is transitive).
Lemma 1.
Let be a quasi-transitive, irreducible BRW on an infinite set X. Suppose that for all , the set is finite. If has no pure global survival phase, then every BRW in the same class has no pure global survival phase.
Proof.
Therefore, . □
Here are the main steps of the proofs. Given a subset , we denote by and the critical parameters of the BRW where is the restriction of K to (this is the BRW restricted to A). Clearly, and . M Moreover, according to Theorem 1, if and , then . Due to the quasi-transitivity of the BRW, there is such that is infinite; clearly, for every automorphism , we have , . Let us choose as finite for every n; observe that for every fixed finite , since X is infinite and the BRW is quasi-transitive, an automorphism exists such that . Indeed, let where (which is not, in general, a distance because it might not be symmetric, but it satisfies the triangular inequality). Let the automorphism be such that , whose existence is guaranteed by the fact that X is infinite and the set is finite for all . Thus, .
- Let be such that the matrices are the same outside I. Clearly, if or , then according to Corollary 2. Let us suppose that . Clearly, since and . Thus,
4.2. Does Every Equivalence Class Have a BRW with No Pure Global Survival Phase?
The answer is affirmative. Consider a BRW and denote by its global critical parameter. Let be fixed and define by
Roughly speaking, we modify the rate from o to itself by adding to . Clearly, , and therefore by taking , we have , and thus, according to Corollary 2, .
4.3. Is There a Class Without BRWs with a Pure Global Survival Phase Where the Supremum of Is Attained?
The answer to this question is affirmative: it is possible to construct a BRW with no pure global survival phase, such that all BRWs in its equivalence class have no pure global survival phase, and where the supremum of is attained. Consider the class of the BRW , where if and 0 otherwise. It is straightforward to show that : the first equality is immediate, while the second follows, for instance, from [26] (Theorem 4.3). Observe that if we restrict the same BRW to , the equalities still hold; this follows from [26] (Theorem 4.3), Theorem 1, and the fact that the critical parameters of a restricted BRW cannot be smaller than those of the original BRW. According to Lemma 1, there are no BRWs with a pure global survival phase in this class.
We now prove that the supremum of in the equivalence class of is 1. Let , and suppose that the modification is contained in . Then, through a coupling argument, we obtain since dominates its restriction to , which is equivalent to the restriction of to . Finally, to show that is not constant within the class, note that by adding a loop at 0 with a sufficiently large rate , one can construct a BRW in this class whose critical values satisfy .
4.4. If a Class Has No BRWs with a Pure Global Survival Phase and the Supremum of Is Finite, Is It Always Attained?
The answer is negative. Consider the class of where if and as . In this case, the supremum of equals , and indeed, take as where ; since is a generic positive constant, we have (since the restriction of a BRW to a subset gives a BRW with larger critical parameters). Then, the supremum is at least . The reversed inequality will be proven in the specific example we are going to construct. The sequence will consist of long stretches of finite consecutive constant rates . More specifically, according to Theorem 1, for any , such that the BRW on with rates if and 0 otherwise (where ), restricted to a set , has a local critical parameter close to , say . This does not depend on i. Define recursively as , where , and for all . Consider ; clearly, exists such that for all , and therefore . This shows that the supremum of in class is and is never attained.
4.5. Is The Supremum of Necessarily Finite in a Class?
The answer is negative: clearly, here, we are dealing with classes with no BRWs with a pure global survival phase. Take where if and 0 otherwise. This BRW satisfies the hypotheses of Proposition 1, where lim sup equals 0. Consider the following modification in , for all and . This process is dominated by a branching process with an expected number of children equal to , and therefore, . Thus, the supremum of in this class is infinite.
4.6. Can Be Constant in a Class?
The answer is affirmative. Clearly, according to Section 4.2 and Corollary 2, the class has no BRWs with a pure global survival phase. Take where if and as . According to spatial approximation (see [26] (Theorem 4.3)), Theorem 1, and domination, . Since according to spatial approximation for any modification, then, according to Corollary 2, (since ).
4.7. If There Is a BRW with a Pure Global Survival Phase in a Class, Can a BRW with No Pure Global Survival Phase Have the Same (Maximum) ?
The answer is affirmative. We rely on Example 1. It suffices to note that the BRW on where if x and y are neighbours and otherwise has a pure global survival phase, while the modified BRW which adds a loop at the origin o, of rate , has the same global critical parameter but no global survival phase.
4.8. Is There a Class Containing a Positive, Finite Number of BRWs with a Pure Global Survival Phase?
The answer is negative. We already know that classes without BRWs exhibiting a pure global survival phase exist. Suppose that has a pure global survival phase. Select a vertex , and set the rate . Then, according to the same arguments used in Example 1, we have According to Equation (3), if and only if some exists such that . Hence, for every sufficiently small , we have . All of these uncountably many BRWs with a pure global survival phase share the same global critical parameter , according to Proposition 2.
5. Conclusions
In this paper, we investigate the effect of modifying the rates of a continuous-time BRW in a finite subset of the underlying space. We say that two BRWs are equivalent if one can be obtained from the other through local modification.
Consider a BRW that exhibits a pure global survival phase; that is, . We prove that all other BRWs in its equivalence class that also have a pure global survival phase satisfy : the local critical parameter may change, but the global one does not. Moreover, is the maximal global survival critical parameter among all BRWs in the equivalence class. Indeed, let be a local modification of , and let denote its global survival critical parameter. Then, . If , then does not exhibit a pure global survival phase. In this case, becomes the threshold for between strong local survival in finite sets and non-strong local survival.
We analyse the existence of a pure global survival phase. Given any BRW, its equivalence class always contains uncountably many processes that do not exhibit a pure global survival phase. However, the converse does not hold: equivalence classes that contain no BRWs with a pure global survival phase exist.
We provide several examples illustrating the possible behaviour of within an equivalence class. The global survival critical parameter may remain constant across the class, or it may be unbounded. Even when it is bounded, its supremum may not be attained.
In this paper, we consider only modifications within finite sets. Allowing modifications on infinite sets would, in principle, lead to a situation where all processes become equivalent. To avoid this triviality, one could restrict attention to modifications of connected infinite sets whose complement is also infinite. However, studying such cases would require the development of new tools.
Among the possible generalisations of this work, a natural direction is to study the equivalence classes of general BRWs without assuming irreducibility. Caution is needed in the general case, as some equivalence classes may contain both irreducible and reducible processes. Recall that in general, the critical values may depend on the starting vertex. A key step toward this goal is to remove the irreducibility assumption from Corollaries 2 and 3. We believe this is feasible since these corollaries rely on Theorems 2 and 3, which do not require irreducibility.
Addressing other natural questions will likely require different techniques. It is already known that isolating a superspreader can increase the critical parameters and lead an epidemic to extinction. In general, understanding which locations have the greatest influence on the process can be far from obvious. In the context of global survival, some works study how generations move toward infinity by identifying the so-called ends of the process and analysing its limiting behaviour at the boundary (see [27,28,29]). We conjecture that the ends most likely to be reached are those whose neighbourhoods are the most influential.
Another active area of research is the study of BRWs in random environment (see [10,16,30,31]), where the rates are not deterministic but are instead chosen independently according to a fixed distribution. In this setting, a local modification can be interpreted as a perturbation of the stochastic homogeneity of the rates: for instance, one may fix the rates within a finite set A while allowing them to remain i.i.d. outside A. This corresponds to exerting control over the rates in A while preserving randomness elsewhere. If the random model is such that the critical parameters do not depend on the specific realisation of the environment, it is natural to ask whether this invariance persists after the modification and how the critical parameters behave in the modified system.
Author Contributions
D.B. and F.Z. contributed equally to this work. Conceptualization, D.B. and F.Z.; methodology, D.B. and F.Z.; formal analysis, D.B. and F.Z.; investigation, D.B. and F.Z.; writing—original draft preparation, D.B. and F.Z.; writing—review and editing, D.B. and F.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Acknowledgments
The authors thank the three anonymous referees for their useful comments on the previous version of the paper.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Galton, F.; Watson, H.W. On the probability of the extinction of families. J. Anthropol. Inst. Great Br. Irel. 1875, 4, 138–144. [Google Scholar]
- Kurtz, T.; Lyons, R.; Pemantle, R.; Peres, Y. A conceptual proof of the Kesten-Stigum theorem for multi-type branching processes. IMA Vol. Math. Appl. 1997, 84, 181–185. [Google Scholar]
- Athreya, K.B.; Ney, P.E. Branching Processes; Die Grundlehren der mathematischen Wissenschaften, 196; Springer: Berlin/Heidelberg, Germany, 1972. [Google Scholar]
- Biggins, J.D. Martingale convergence in the branching random walk. J. Appl. Probab. 1977, 14, 25–37. [Google Scholar] [CrossRef]
- Harris, T.E. The Theory of Branching Processes; Springer: Berlin/Heidelberg, Germany, 1963. [Google Scholar]
- Mountford, T.; Schinazi, R. A note on branching random walks on finite sets. J. Appl. Probab. 2005, 42, 287–294. [Google Scholar] [CrossRef][Green Version]
- Attia, N.; Amami, R.; Amami, R. Note on the Generalized Branching Random Walk on the Galton–Watson Tree. Fractal Fract. 2023, 7, 399. [Google Scholar] [CrossRef]
- Liggett, T.M. Branching random walks and contact processes on homogeneous trees. Probab. Theory Relat. Fields 1996, 106, 495–519. [Google Scholar] [CrossRef]
- Madras, N.; Schinazi, R. Branching random walks on trees. Stoch. Proc. Appl. 1992, 42, 255–267. [Google Scholar] [CrossRef]
- Müller, S. A criterion for transience of multidimensional branching random walk in random environment. Electron. J. Probab. 2008, 13, 1189–1202. [Google Scholar] [CrossRef]
- Pemantle, R.; Stacey, A.M. The branching random walk and contact process on Galton–Watson and nonhomogeneous trees. Ann. Probab. 2001, 29, 1563–1590. [Google Scholar] [CrossRef]
- Su, W. Branching random walks and contact processes on Galton-Watson trees. Electron. J. Probab. 2014, 19, 12. [Google Scholar] [CrossRef]
- Zucca, F. Survival, extinction and approximation of discrete-time branching random walks. J. Stat. Phys. 2011, 142, 726–753. [Google Scholar] [CrossRef]
- Stacey, A.M. Branching random walks on quasi-transitive graphs. Combin. Probab. Comput. 2003, 12, 345–358. [Google Scholar] [CrossRef]
- Bartsch, C.; Gantert, N.; Kochler, M. Survival and growth of a branching random walk in random environment. Markov Process. Related Fields 2009, 15, 525–548. [Google Scholar]
- Gantert, N.; Müller, S.; Popov, S.; Vachkovskaia, M. Survival of branching random walks in random environment. J. Theoret. Probab. 2010, 23, 1002–1014. [Google Scholar] [CrossRef]
- Machado, F.P.; Menshikov, M.V.; Popov, S. Recurrence and transience of multitype branching random walks. Stoch. Proc. Appl. 2001, 91, 21–37. [Google Scholar] [CrossRef]
- Müller, S. Recurrence for branching Markov chains. Electron. Commun. Probab. 2008, 13, 576–605. [Google Scholar] [CrossRef]
- Hautphenne, S.; Latouche, G.; Nguyen, G. Extinction probabilities of branching processes with countably infinitely many types. Adv. Appl. Probab. 2013, 45, 1068–1082. [Google Scholar] [CrossRef][Green Version]
- Bertacchi, D.; Zucca, F. Strong local survival of branching random walks is not monotone. Adv. Appl. Probab. 2014, 46, 400–421. [Google Scholar] [CrossRef][Green Version]
- Bertacchi, D.; Zucca, F. Characterization of the critical values of branching random walks on weighted graphs through infinite-type branching processes. J. Stat. Phys. 2009, 134, 53–65. [Google Scholar] [CrossRef][Green Version]
- Bertacchi, D.; Braunsteins, P.; Hautphenne, S.; Zucca, F. Extinction probabilities in branching processes with countably many types: A general framework. ALEA 2022, 19, 311–338. [Google Scholar] [CrossRef]
- Bertacchi, D.; Zucca, F. Recent results on branching random walks. In Statistical Mechanics and Random Walks: Principles, Processes and Applications; Nova Science Publishers: Hauppauge, NY, USA, 2012; pp. 289–340. [Google Scholar]
- Woess, W. Denumerable Markov Chains, Generating Functions, Boundary Theory, Random Walks on Trees; EMS Textbooks in Mathematics, European Mathematical Society (EMS): Zürich, Switserland, 2009. [Google Scholar]
- Bertacchi, D.; Zucca, F. A generating function approach to branching random walks. Braz. J. Probab. Stat. 2017, 31, 229–253. [Google Scholar] [CrossRef][Green Version]
- Bertacchi, D.; Coletti, C.F.; Zucca, F. Global survival of branching random walks and tree-like branching random walks. Ala. Law Enforc. Agency 2017, 14, 381–402. [Google Scholar] [CrossRef]
- Candellero, E.; Hutchcroft, T. On the boundary at infinity for branching random walk. Electron. Commun. Probab. 2023, 28, 12. [Google Scholar] [CrossRef]
- Candellero, E.; Roberts, M. The number of ends of critical branching random walks. ALEA Lat. Am. J. Probab. Math. Stat. 2015, 12, 55–67. [Google Scholar]
- Kaimanovich, V.; Woess, W. Limit distributions of branching Markov chains. Ann. Inst. Henri Poincaré Probab. Stat. 2023, 59, 1951–1983. [Google Scholar] [CrossRef]
- Machado, F.P.; Popov, S. One-dimensional branching random walk in a Markovian random environment. J. Appl. Probab. 2000, 37, 1157–1163. [Google Scholar] [CrossRef]
- Machado, F.P.; Popov, S. Branching random walk in random environment on trees. Stoch. Proc. Appl. 2003, 106, 95–106. [Google Scholar] [CrossRef][Green Version]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).