Abstract
Bugs, especially those in concurrent systems, are often hard to reproduce because they manifest only under rare conditions. Testers frequently encounter failures that occur only under specific inputs, often at low probability. We propose an approach to systematically amplify the occurrence of such elusive bugs. We treat the system under test as a black-box system and use repeated trial executions to train a predictive model that estimates the probability of a given input configuration triggering a bug. We evaluate this approach on a dataset of 17 representative concurrency bugs spanning diverse categories. Several model-based search techniques are compared against a brute-force random sampling baseline. Our results show that an ensemble stacking classifier can significantly increase bug occurrence rates across nearly all scenarios, often achieving an order-of-magnitude improvement over random sampling. The contributions of this work include the following: (i) a novel formulation of bug amplification as a rare-event classification problem; (ii) an empirical evaluation of multiple techniques for amplifying bug occurrence, demonstrating the effectiveness of model-guided search; and (iii) a practical, non-invasive testing framework that helps practitioners to expose hidden concurrency faults without altering the internal system architecture.
Keywords:
concurrency bugs; bug reproduction; rare-event detection; model-based testing; search-based software testing; black-box testing; ensemble methods; noise-tolerant learning; probabilistic bug amplification MSC:
68N19; 62P25
1. Introduction
Bugs that manifest nondeterministically, sometimes referred to as Heisenbugs [1] or intermittent bugs [2], pose a significant challenge for debugging and validation in complex software systems. This difficulty is particularly pronounced for concurrency bugs, which typically arise only under rare thread interleavings or delicate timing conditions. In practice, developers rely on techniques such as manual code inspection and brute-force stress testing to uncover such failures. Although stress testing may occasionally expose these elusive faults, it offers no guarantees of detecting and often fails to detect bugs that appear only under constrained conditions. As a consequence, critical concurrency issues can remain unresolved for extended periods, undermining confidence in the system’s reliability.
In this paper, we maximize the empirical failure probability observed during testing, under a fixed execution budget. We refer to this goal as bug amplification. In contrast to approaches such as rare-event simulation [3] and statistical model checking [4], which typically rely on internal instrumentation, white-box knowledge, or formal specifications, our method operates in a fully black-box manner. We assume no access to source code or internal system behavior. Instead, we systematically vary input parameters, such as workload configurations and timing-related settings, to increase the likelihood that a latent bug will manifest during execution.
Despite progress in the field, reliably exposing concurrency bugs in real-world systems remains an open challenge [5]. Systematic concurrency testing tools attempt to exhaustively explore possible thread schedules and can enable deterministic replay of bugs once discovered. However, their scalability is limited by the combinatorial explosion of scheduling interleavings. Alternatively, randomized scheduling introduces noise to execution timing and has shown improved coverage compared to naive stress tests [6,7], yet remains fundamentally probabilistic and may still miss deeply hidden bugs. Record-and-replay tools log nondeterministic events during execution for later reproduction, but their performance overhead and requirement for tightly controlled environments make them impractical in many settings. Collectively, these approaches fall short of providing a general, scalable solution for reliably triggering elusive concurrency failures.
To address this gap, we introduce a novel approach that frames bug amplification as a black-box optimization problem over the system’s input space. Rather than modifying internal code or instrumenting it, we run the system repeatedly under different input configurations and observe whether a failure occurs. These outcomes are used to train a predictive model estimating the probability of failure as a function of the input parameters. The model then guides the generation of future test inputs, focusing resources on regions of the input space more likely to expose the bug.
Casting this task as a classification problem presents unique difficulties. The target is a binary failure indicator with extreme class imbalance. Even for failure-prone configurations, the bug may only appear with low probability due to nondeterministic execution. To cope with this challenge, we perform multiple trials for each input and use the average failure rate as a noisy estimate of its true failure probability. This allows us to apply probability-calibrated classifiers despite the underlying stochasticity and imbalance, though it necessitates robust modeling techniques capable of tolerating label noise and extreme skew.
To evaluate the proposed strategy, we curated a benchmark of 17 concurrency bugs spanning a comprehensive taxonomy of bug symptoms and their underlying causes. These bugs, drawn from real-world and synthetic sources, cover a variety of symptoms (e.g., deadlocks, crashes, data races) and underlying causes (e.g., incorrect synchronization, ordering violations). For each problem, we identified key input parameters that influence bug manifestation and tuned the system so that failures would occur with low probability under default settings. This controlled setup enabled the rigorous assessment of amplification techniques under realistic yet challenging conditions.
We applied several model-based search techniques to the benchmark, including linear regression, decision trees, and nonlinear ensemble methods, and compared them against a baseline of brute-force random sampling. Under identical budget constraints, a stacked ensemble of classifiers consistently achieved the best overall performance, substantially increasing bug manifestation rates across the majority of scenarios.
This work makes the following contributions:
- Benchmark and Problem Formulation: We introduce a curated dataset of 17 concurrency bugs and frame the failure-triggering task as a problem with sparse positives and stochastic labels—posing distinct challenges for conventional learners.
- Evaluation of Amplification Techniques: We systematically compare several model-guided search strategies and show that ensemble-based learning significantly improves bug-triggering probability within practical testing budgets.
- Practical, Black-box Testing Framework: Our approach treats the system under test as a black-box, requiring no code changes or instrumentation, making it readily applicable in real-world testing workflows.
The remainder of this paper is organized as follows. Section 2 reviews the state of the art in bug reproduction, presenting leading techniques and key challenges in the field. Section 3 provides a detailed classification of concurrency bug types relevant to our study. Section 4 summarizes the benchmark problems used in our evaluation, outlining the criteria for selection. Section 5 describes the core research methods, focusing on the modeling of interleaving in multithreaded code. Section 6 introduces the four bug amplification methods that we developed and applied, and provides implementation and configuration specifics. Section 7 presents the experimental results and discusses their implications. Finally, the paper concludes with a summary of findings, a detailed list of the limitations of our approach, and directions for future research.
Research flow (at a glance): We proceed in six steps: (1) define a two-dimensional taxonomy and select a balanced benchmark (Section 3 and Section 4); (2) build a yield-driven simulation framework with controllable noise (Section 5); (3) define the fixed-budget, repeated-trial evaluation protocol with checkpoints and top-k analysis (Section 5.1); (4) instantiate four amplification methods (BF, SA, GA, Ens) under that unified protocol (Section 6); (5) present the Results and Discussion with aggregate and per-problem analyses (Section 7); and (6) report threats to validity and provide the public artifact for reproducibility (Section 5.2; Data Availability Statement).
2. The State of the Art in Bug Reproduction
Context. This section positions our study with respect to prior work; the Methods follow in Section 3, Section 4, Section 5 and Section 6, with the Results and Discussion in Section 7.
Reproducing nondeterministic concurrency failures remains a central challenge in software testing. These bugs typically occur only under rare thread interleavings or specific combinations of environmental and input parameters, making them elusive and difficult to diagnose [8].
Traditional techniques such as stress testing, heuristic scheduling perturbations, and detailed logging have been widely used in practice, but they offer no guarantees and are often insufficient for reliably exposing such rare failures [9]. CARDSHARK [10], for example, demonstrates how even kernel-level bugs may remain unstable without explicit noise control or scheduling alignment.
Industry Practice: When developers encounter rare failures in production, a common response is to attempt reproduction via repeated testing under varied conditions, manipulating input sizes, concurrency levels, or hardware settings [11]. Logging may provide diagnostic clues, but even lightweight instrumentation, such as coverage or profiling hooks, can perturb timing behavior enough to mask or induce concurrency bug manifestation [12]. Kernel-level concurrency testing frameworks such as the eBPF-based technique by Xu et al. [13] offer promising lightweight instrumentation for observing concurrency bugs in real-world deployments.
Systematic Exploration: Research tools such as CHESS [14], Nekara [15], and Fray [5] aim to improve bug reproducibility by exhaustively exploring thread schedules in bounded spaces. CHESS is a pioneering systematic testing tool for multithreaded Windows applications that explores all interleavings under a given bound. Nekara is an open-source, cross-platform library (2021) that enables developers to define semantics for concurrency primitives and systematically explore schedules in a controlled, repeatable manner. Fray, introduced in 2025, offers efficient black-box schedule control and instrumentation for JVM-based systems. These tools can replay discovered interleavings deterministically, a key advantage for debugging, but they require either source or binary instrumentation and do not scale well with large programs or vast input spaces.
Probabilistic Scheduling and Sampling: Techniques like Probabilistic Concurrency Testing (PCT) [16], iterative schedule fuzzing [17], and directional scheduling of synchronization primitives in Go programs [18] attempt to bias execution toward schedules more likely to reveal bugs. While these methods can improve exposure rates, they remain largely unguided by feedback from prior executions.
Learning-Based Approaches: Recent advances have begun exploring machine learning for bug localization and input generation [19,20], but most treat the system as a white box or focus on symbolic execution, mutation, or coverage estimation [21]. By contrast, our method treats the system as a black-box system and explicitly aims to maximize the empirical failure probability via predictive models over the input domain.
Building on these advances, our work treats bug reproduction as a noisy optimization problem over inputs, training predictive classifiers to guide searching. Instead of exploring schedules, we vary inputs and use learned models to amplify bug occurrence rates within constrained testing budgets, improving reproducibility and efficiency.
Beyond concurrency-focused studies, several recent surveys map adjacent areas of software security and testing. Firmware-oriented vulnerability detection for IoT devices synthesizes analysis pipelines and challenges [22]; surveys at the intersection of software security and large language models (LLMs) review LLM-enabled testing and analysis tasks [23]; and comprehensive fuzzing surveys systematize input-generation strategies and coverage heuristics [24]. Our contribution is complementary: we study failure amplification for concurrency bugs under a fixed evaluation budget. Nevertheless, the techniques surveyed, particularly fuzzing strategies and LLM-guided heuristics, can plug into our artifact as alternative generators or ranking signals (see Data Availability Statement).
We target scenarios where white- or gray-box signals are unavailable or impractical; hence, we deliberately adopt a black-box protocol.
3. Types of Concurrency Bugs
Methodological scope: Section 3, Section 4, Section 5 and Section 6 constitute the Methods: the taxonomy and benchmark (Section 3 and Section 4); the simulation framework (Section 5) together with the evaluation protocol (Section 5.1); and the amplification methods BF/SA/GA/Ens (Section 6).
Following prior work such as [25], we introduce a taxonomy to support the evaluation of our bug amplification techniques. This taxonomy classifies concurrency bugs along two orthogonal dimensions: observable effect and root cause.
In detail, the observable effect axis captures how a concurrency bug manifests at runtime, i.e., the observable effect or symptom from the system’s perspective. The root-cause axis reflects the underlying cause of the failure, identifying the specific logic error or design flaw in the program’s synchronization or concurrency control.
These root causes and effects are well-established foci in both academic research and industrial practice, as evidenced by large empirical studies and widely deployed detection/avoidance tools.
We classify observable effects into the following categories.
- Deadlock: A system state in which two or more threads are indefinitely blocked, each waiting for a resource that will never become available, e.g., because it is held by another. The system halts and cannot make further progress [26,27].
- Unexpected Data: Shared variables take on incorrect or inconsistent values due to unsynchronized access, race conditions, or improper interleaving of reads and writes [28,29].
- Concurrent Access: Multiple threads enter a critical section simultaneously, violating mutual exclusion and potentially corrupting the shared state or breaking invariants [30,31].
Meanwhile, the classification of the root cause of the concurrent bug is carried out using the following categories.
- Missing or Weak Guarding: Inadequate protection of critical sections, often due to absent atomicity checks, incorrect condition synchronization, or overreliance on scheduling assumptions [29,32].
- Non-Atomic Operations on Shared State: Access to shared data is implemented via sequences of non-atomic operations, allowing interleaving by other threads to interfere with correctness [33].
- Incorrect Command Ordering: Synchronization operations are issued in the wrong order, violating required temporal constraints. For example, a thread signals a condition before another begins waiting for it [34].
- Misuse of Concurrency Primitives: Synchronization constructs such as locks, semaphores, and condition variables are used incorrectly, e.g., in unintended contexts, or in ways that violate their semantics [35,36].
The cross-product of these two axes yields twelve distinct categories of concurrency bugs, each representing a unique pairing of effect and cause. Table 1 summarizes the distribution of our benchmark problems across this taxonomy, with each problem assigned to the cell corresponding to its observed effect and inferred root cause. As a root cause may have more than a single effect, a problem index may appear twice in the same column, but not in the same row.

Table 1.
Classification of concurrency problems by Effect (rows) and Root Cause (columns), showing the problem number and name. Note that some problems may produce multiple effects (e.g., Problems 12 and 4).
By including at least one benchmark problem in each cell, the analysis spans all combinations of effects and causes, ensuring broad coverage of concurrency failure modes.
4. Summary of Benchmark Problems
To evaluate our ability to amplify and detect failure cases in multithreaded systems, we assembled a benchmark that spans the primary classes of concurrency faults. Each problem instance illustrates a distinct error pattern, and the accompanying description clarifies the type of defect it represents. The benchmark is available in a GitHub repository: https://github.com/geraw/bug_amp (accessed on 6 September 2025).
The benchmark is based on the canonical puzzles from The Deadlock Empire https://deadlockempire.github.io/#menu (accessed on 6 September 2025), an interactive collection of multithreading challenges that can be executed step by step. To achieve the broader coverage outlined in the previous section, we extended this initial set with additional cases gathered from the literature and custom-crafted variants, until all combinations of Effect (Deadlock, Unexpected Data, Concurrent Access) and Root Cause (Missing or Weak Guarding, Non-Atomic Operations, Incorrect Command Ordering, Misuse of Concurrency Primitives) were represented.
To make the dataset’s scope and balance explicit, Table 2 summarizes the distribution of our 17 problems across the effect × root-cause taxonomy. These counts document breadth across categories and are intended for methodological coverage rather than prevalence.

Table 2.
Distribution across Effect × Root-Cause. Each cell shows a color (as a heatmap) swatch (1 = blue, 2 = yellow, 3 = red) and the count.
Section 9 provides a full description of each of the 17 concurrency problems enumerated below. For every problem, we explicitly document (i) the scenario, (ii) its observable effect, (iii) the underlying root cause according to our taxonomy, (iv) the mechanism, a mandatory one-sentence explanation that specifies the minimal interleaving/ordering that leads from cause to effect, and (v) a concise insight that summarizes the key lesson. Pseudocode snippets accompany each problem as minimal, language-agnostic reproductions annotated at the precise fault location; longer listings are deferred to the artifact. This curated collection provides a balanced testbed for assessing failure-amplification techniques across the full spectrum of concurrency bugs.
- Atomicity Bypass: A thread releases a lock before completing a read-modify-write, leading to data corruption, despite apparent locking. See Section 9.1.
- Broken Barrier: Improper barrier reuse or reset causes some threads to wait forever, expecting others to arrive. See Section 9.2.
- Broken Peterson: Incorrect implementation of Peterson’s algorithm allows both threads to enter the critical section. See Section 9.3.
- Delayed Write: Operations are reordered due to compiler or logic flaws, leading to stale reads or broken invariants. See Section 9.4.
- Flagged Deadlock: Threads use flags and spin loops incorrectly, creating interleaving paths that deadlock. See Section 9.5.
- If-Not-While: A thread waits using an if condition instead of a while loop, leading to missed signals and unsafe access. See Section 9.6.
- Lock Order Inversion: Classic deadlock: threads acquire two locks in opposite order, causing circular wait. See Section 9.7.
- Lost Signal: A thread sends a signal before another begins waiting on a condition variable; the signal is lost, causing a deadlock. See Section 9.8.
- Partial Lock: Only part of the critical section is protected by a lock; race conditions still occur. See Section 9.9.
- Phantom Permit: A semaphore is released without a corresponding Wait, allowing more threads than expected to enter the critical section. See Section 9.10.
- Race-To-Wait: Threads race to increment a shared counter and both wait on a condition that never becomes true due to non-atomic updates. See Section 9.11.
- Shared Flag: A single boolean flag is used for synchronization without proper mutual exclusion, allowing concurrent access. See Section 9.15.
- Signal-Then-Wait: A thread signals with notify_all() before the other enters the wait; the notification is missed despite a guarded while loop. See Section 9.16.
- Sleeping Guard: A thread goes to sleep on a condition variable without checking the actual shared state, causing missed wakeups and deadlock. See Section 9.17.
5. Interleaving Multithreaded Code
In this section, we describe our method for simulating multithreaded programs in a controlled and repeatable manner using Python generators (version 3.11.9). To enable systematic exploration and direct comparison across a variety of concurrency scenarios, we adopt a uniform representation strategy that brings clarity, modularity, and flexibility to our simulation framework.
Each problem is encoded as a collection of Python generator functions. Each generator models a single thread that operates on the System Under Test (SUT) and uses yield statements to explicitly mark points where execution may pause and control may be transferred to another thread. Modeling representation allows us to canonize a wide range of concurrency scenarios into a common format, facilitating repeatable experiments and meaningful comparisons under different timing conditions. Our framework further incorporates parameter-dependent delays, which can include both structured variation (e.g., based on thread-specific parameters or environment emulation) and random noise. This enables modeling of both deterministic scheduling and nondeterministic, real-world variability.
Together, these design choices provide a robust and extensible foundation for simulating complex concurrency behaviors and analyzing how timing-related parameters influence system correctness. The types of problems we address typically involve multiple threads, shared variables, and bugs that are triggered only under specific interleavings, often governed by subtle timing conditions. To simulate such behavior, we employ the simulate() function shown in Listing 1, which orchestrates the execution of multiple threads according to a parameter-driven timing model.
The simulate() function manages a set of thread generators. Each thread yields a value representing how long it wishes to “sleep” (i.e., delay its next execution step), and the simulation engine schedules the threads based on their wakeup times. The thread with the shortest delay is resumed first, simulating a time-based interleaving of execution steps. Importantly, the simulation does not involve real-time waiting or system-level delays. Instead, it operates in virtual time, advancing the logical clock and reordering thread execution based on the declared delays, thereby allowing efficient exploration of possible interleavings without wasting actual runtime.
Each thread is implemented as a generator function that performs a sequence of atomic operations, with yield statements marking the boundaries between them. These yield points indicate simulated delays during which other threads may execute. An illustrative example is provided in Listing 2.
| Listing 1. The core simulation loop controlling the execution of multiple threads. Each thread yields a delay, and the scheduler selects the next thread to execute based on wakeup times. |
 |
| Listing 2. A thread modeled as a generator. Yields represent delays between atomic steps. The delays depend on a system-wide coefficient C and problem-specific parameters , with optional noise added. |
 |
This example models a typical concurrency issue: the thread sets a shared variable x to a fixed value, but due to interleaved execution, another thread might overwrite it before the current one verifies its value. The timing between steps is simulated by yielding expressions that define how long each thread “sleeps” before proceeding. Each delay expression consists of three components. The first is a global coefficient C, which reflects the overall processing speed or workload of the simulated system. The second is a parameter , representing the nominal delay associated with a specific operation. The third component is a call to distortion(), which introduces random variation to simulate environmental unpredictability such as jitter or fluctuating system load.
This parametrization enables the simulation to model a wide range of execution environments and conditions. By adjusting the coefficient C, we can emulate machines with varying processing speeds or scheduling overhead. Changing the values allows us to control the logical duration of specific computation segments. The addition of noise via distortion() allows us to explore nondeterministic interleavings, helping to uncover rare or timing-sensitive bugs that would otherwise be difficult to reproduce.
Simulating Rare Failures: Many concurrency bugs, especially those related to race conditions and ordering violations, are notoriously difficult to reproduce in real systems because they manifest only under rare timing conditions. Our simulation framework addresses this challenge by treating delay parameters as inputs. Specifically, each test-case accepts a tuple of values representing delays (e.g., , , ), and runs the simulation multiple times using different random seeds for distortion(). Each simulation run returns a result indicating whether a failure (e.g., assertion violation) occurred. By aggregating the outcomes across many runs, we can estimate the probability that a particular configuration of delays leads to a bug. This approach is especially useful for identifying critical thresholds or delay combinations that increase the likelihood of failure.
Invariant Checking: Optionally, a predicate expected_invariant can be passed to the simulate() function. This predicate is evaluated after each execution step to ensure that the system remains in a valid state. Violations of this invariant are treated as test failures and help to pinpoint scenarios of the manifestation of concurrency bugs.
5.1. Evaluation Protocol
To enable a fair, consistent, and statistically robust evaluation of the bug amplification methods under study, we define a controlled experimental framework that governs how test-cases are generated, evaluated, and compared. This framework incorporates a fixed execution budget, multiple randomized trials, and an analysis of the top-performing test-cases across different metrics. Together, these components ensure that our assessment is not only reproducible, but also reflective of real-world usage scenarios such as iterative debugging and automated fault localization pipelines. Throughout all the experiments, the optimizer interacts with the system as a black-box system: only inputs and observed outcomes are available; internal signals (e.g., coverage, branch distances, lock-contention counters, and schedule traces) are neither collected nor used.
Budget Consumption: Each bug amplification method is constrained to a fixed execution budget of B runs of the SUT. The budget is progressively consumed in increasing blocks of test-case numbers, , allowing each method to iteratively improve its selection while avoiding early resource exhaustion. At each checkpoint, the accumulated executions are analyzed to update the observed probability of bug exposure. This staged consumption strategy supports convergence analysis and ensures that all methods operate under identical cost constraints while striving to maximize effectiveness. The specific mechanisms by which each method adheres to this budget constraint are detailed in their respective descriptions, and an overview of the budget split across iterations is provided in Table 3.

Table 3.
Budget allocation per method. Brute-Force () spends the first runs, where k is the minimum repeat size, on estimation of a random candidate and immediately reports that score; there is no exploitation phase. Simulated Annealing (SA) divides the budget into steps s and neighborhood size k, enabling explicit control of SUT invocations. The Genetic Algorithm (GA) uses a population of and evolves for generations. The Ensemble classifier (Ens) devotes the entire budget to model-guided search: at every step, it samples 100 random inputs (exploration) and 100 model-ranked inputs (exploitation), retrains, and repeats.
Nonetheless, while strict budget adherence is maintained throughout each method’s execution, the final evaluation phase in this study deliberately exceeds these constraints. This extended phase is not part of the methods themselves, but is introduced solely for the purpose of research evaluation. Specifically, to rigorously assess the quality of the selected test-cases, typically those with the highest observed failure likelihood, we subject each case to massive re-execution with the SUT, far beyond the original budget. This allows us to derive a precise and statistically robust estimate of its true failure-inducing potential.
Repeated trials: To obtain statistically meaningful estimates, each pair was executed 50 independent times. Each run exploited the full budget schedule above, producing a single best-scoring test-case, i.e., the input with the highest observed failure probability. Aggregating the best scores over 50 runs yields the sample mean and standard deviation that appear in all result plots.
Top- Analysis: In practice, automated debugging pipelines require three disjoint pools: development (debugging), model training (testing), and final assessment (validation). Reporting only the single best case risks overfitting, whereas presenting the entire budget is often impractical. Hence, we also study the 5th and 10th best inputs, providing a small yet diverse set that effectively supports such a pipeline.
5.2. Threats to Validity
Internal validity: Our evaluation followed a fixed-budget, repeated-trial protocol (Section 5.1), which helped to separate methodological effects from stochastic variation. All methods were executed under identical budgets and environments; where applicable, they drew from the same candidate pools and used the same randomization policy. Because each fitness evaluation was stochastic, we stabilized estimates by repeated sampling per candidate (the parameter k in Section 5.1) and aggregated results over multiple runs. We also checked that conclusions were stable under alternative random seeds and minor hyperparameter perturbations of the learning-guided method (Section 6.4).
Configuration sensitivity: Concurrency outcomes can depend on configuration (e.g., timeouts, thread counts, scheduling jitter). To assess robustness, we re-ran a representative subset under perturbed configurations and observed that relative method rankings remained stable within the fixed-budget regime. The scripts to reproduce these checks are packaged with the artifact (Data Availability Statement).
Construct validity: Our primary outcome is the empirical failure probability estimated from repeated executions under a fixed budget (Section 5.1). This metric directly matches the paper’s objective, amplifying failure occurrence, and is defined consistently across problems and methods. When a problem admits multiple effects (e.g., deadlock and unexpected data), a shared detection oracle is used and results are reported per effect class.
External validity: The benchmark targets methodological breadth rather than prevalence estimation. Problems were selected to cover a two-dimensional taxonomy of effect × root cause (Table 1); Table 2 summarizes the per-cell distribution. The set mixes real-world and synthetic cases to balance control and relevance. Generalization to other systems depends on how strongly a bug’s trigger correlates with observable inputs; when this signal is weak, guided search appropriately reverts toward exploration. Per-problem details appear in Section 9.
Reproducibility: The artifact (Data Availability Statement) packages code, data, configuration files, and pinned versions so that all experiments can be re-run and extended (e.g., different budgets, additional baselines such as adaptive random testing or other SBST variants) under the same fixed-budget protocol.
6. Bug Amplification Methods
See Figure 1 for the end-to-end study pipeline; Section 6.4 details the ensemble method’s explore–exploit inner loop.

Figure 1.
End-to-end research flow used in this study.
This section presents the search techniques used to amplify failure probability under identical, fixed-budget, stochastic evaluations. We compare a budget-controlled baseline (BF), a noise-aware local optimizer (SA), a global evolutionary search (GA), and a learning-guided ranker (ensemble classifier), all instantiated in a black-box mode that consumes only candidate inputs and binary failure outcomes. Our goal is to test whether advanced heuristics outperform naïve exploration in this setting.
- Method Selection rationale
We focus on four methods—, , , and an ensemble () classifier—because together they provide a budget-controlled baseline, a noise-aware local optimizer, a global evolutionary search, and a learning-guided ranker that operate consistently under our fixed, stochastic evaluation protocol (see Section 5.1 and “Repeated trials”). In this section, we also explain why off-the-shelf variants and several regression models were ineffective under these constraints, and why our preliminary attempt with genetic programming did not converge.
6.1. Baseline: Random Search
Random search serves as the baseline method in this study, providing a critical comparison point for evaluating the effectiveness of more sophisticated search techniques. This method operates without incorporating any domain-specific heuristics or optimization strategies, offering conceptual simplicity and ease of implementation. Its role is to help determine whether complex methods are truly necessary, or whether random exploration is sufficient for discovering high-probability failure-inducing test-cases. We adopt this brute-force baseline because it (i) is assumption-free and domain-agnostic, enabling fair comparison across heterogeneous benchmarks; (ii) is hyperparameter-light and robust to stochastic noise, which supports a fixed-budget, repeated-trial protocol and clear effect-size statistics; (iii) establishes a reproducible lower bound that any guided method should surpass; and (iv) is computationally inexpensive, ensuring observed gains are not artifacts of additional tuning or budget.
The process begins by randomly generating candidate test-cases. Each candidate is evaluated by executing it multiple times against the system under test, in order to estimate its likelihood of triggering a bug. Every execution yields a binary outcome—failure (bug-triggered) or success. A scenario’s estimated score is calculated as the frequency of failures across its executions, with the number of repetitions serving as a configurable parameter that trades evaluation accuracy for computational cost.
We used a fixed sampling parameter for each test-case. This value was chosen based on the statistical justification provided by the Law of Large Numbers (LLN) and the Central Limit Theorem (CLT), which suggest that 30 independent samples are generally sufficient to obtain a stable estimate of the mean and variance. This ensures that the bug exposure probability computed from the k test-cases is both statistically meaningful and computationally efficient.
Like all tested methods, random search operates within a fixed execution budget B as described earlier. Once the budget is consumed, candidates are ranked by their estimated failure probability, and the top-ranked scenarios are selected as the method’s output. Throughout the remainder of the paper, we refer to this approach as the brute-force () method.
In the Section 7 (Results), we examine scenarios where advanced search methods offer clear benefits and compare them with cases where the method performs adequately.
6.2. Simulated Annealing
Finding a concurrency bug in a continuous search space can be viewed as climbing an unknown, locally smooth probability landscape whose height at a point represents the likelihood that the corresponding test input triggers the fault. Our simulated annealing (SA) variant explores this landscape by iteratively sampling a small neighborhood of the current point and then moving in the direction where failures are more concentrated.
Why this variant? We experimented with off-the-shelf SA and regression methods and ultimately chose to develop this SA variant for three reasons. (i) Budget control: By fixing k candidates per step ( as described in Section 6.1) and s () optimization steps, we guarantee an exact run budget B. Most generic SA frameworks expose only the iteration count and can silently overshoot the allowed SUT executions. (ii) Noise awareness: Each fitness evaluation is stochastic, so the algorithm must cope with noisy measurements, a feature rarely found in off-the-shelf SA libraries. (iii) Geometric clarity: The center-of-mass update rule (see Figure 2) offers an intuitive, easily inspectable implementation that has proven effective in practice.
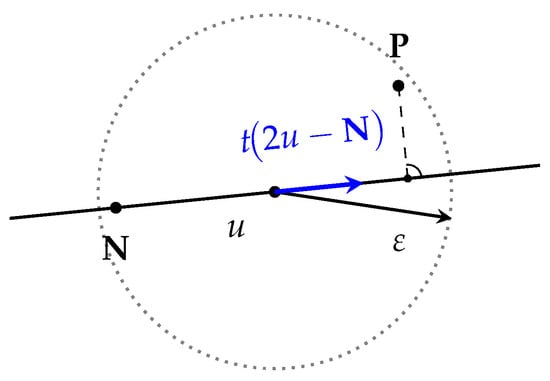
Figure 2.
Geometric intuition in 2D of the update step. The k candidates are sampled inside the dotted ball centered at u. We move from u to (blue arrow) and, if positives exist, bias the step toward the positive center . The dashed segment from is perpendicular to the search line. The radius of the sampling ball is marked by .
Neighborhood sampling: Let be the current input vector. We draw k random candidates from the ball . After executing each candidate, we label it positive () if it triggers the bug and negative () otherwise .
Center of mass estimate: We summarize the neighborhood by the averages
which act as coarse estimates of where the bug is less () or more () likely to occur.
Update rule: Intuitively, we wish to move away from the negatives and, if positives exist, steer toward their center of mass. We therefore (i) take a step from u opposite to and (ii) if positives are present, average that tentative step with ’s position. The construction is illustrated in Figure 2, and a Python sketch appears in Listing 3.
| Listing 3. An implementation of neighborhood sampling. |
 |
Edge cases: If no positive points or no negative points are found, we choose as a random point within . As gradually decreases (the usual annealing schedule), the search converges on increasingly precise regions of high failure probability while still escaping unpromising basins.
6.3. Genetic Algorithm-Based Search
To explore failure-inducing test-cases, we employed a genetic algorithm (GA) using the EC-KitY evolutionary computation framework [37]. The goal of the algorithm is to evolve test inputs that are likely to trigger failures in a concurrent system, guided by a fitness function that reflects the probability of failure.
We configured the GA with a population size of individuals per generation. The total number of generations is determined by dividing the available test-case budget by the population size, ensuring that each individual is evaluated once per generation. Fitness is computed using a user-defined BugHuntingEvaluator, which estimates the likelihood of a bug manifesting during execution. Since this is a maximization task, higher fitness indicates more failure-prone test-cases. Each individual is represented as a real-valued vector constrained within predefined bounds (depending on each problem).
We tuned the genetic algorithm’s hyperparameters to balance convergence speed and search diversity while staying within our evaluation budget. To this end, we selected a population size of , following classical guidelines by Goldberg [38] and more recent studies [39] that recommend sizes in the range of 30–100 to ensure sufficient diversity without excessive cost. We used a two-point crossover with a 0.5 probability to promote recombination of substructures, and uniform mutation applied to 10 randomly selected components with a 0.15 probability to inject controlled variation. Tournament selection with a size of four was chosen to provide moderate selective pressure while preserving population diversity. These values were selected based on standard practice and empirical effectiveness in evolutionary search.
The GA employs the following operators:
- Crossover: A two-point crossover (VectorKPointsCrossover) with a probability of 0.5 exchanges two genome segments between parent individuals. This promotes the recombination of useful substructures and accelerates convergence.
- Mutation: Uniform N-point mutation (FloatVectorUniformNPointMutation) is applied to 10 randomly selected vector components with a probability of 0.15. This introduces variation and helps the population explore new regions in the search space.
- Selection: We use tournament selection with a size of four, where the fittest individual among four randomly sampled candidates is chosen as a parent. This balances selective pressure and population diversity.
We applied elitism by retaining the single best individual in each generation, and terminated the run if no improvement was observed in the best fitness over 100 consecutive generations.
EC-KitY is a modular and extensible evolutionary computation toolkit for Python, designed to support a wide range of evolutionary techniques, including genetic algorithms, genetic programming, coevolution, and multi-objective optimization. It also provides seamless integration with machine learning pipelines, particularly via scikit-learn.
As part of our investigation into effective methods for test-case generation, we explored using Genetic Programming, based on the hypothesis that dependencies exist among the input parameters of failure-inducing scenarios. Specifically, we considered the possibility of defining a domain-specific language capable of capturing structural patterns and relations between parameters that frequently lead to failures. This hypothesis was inspired by prior work suggesting that, in most cases, only a small subset of input parameters is responsible for triggering bugs [40].
However, despite initial efforts, the genetic programming process failed to converge toward meaningful patterns, and the approach was ultimately abandoned. As a result, we redirected our efforts toward a more conventional search method, utilizing a generic Genetic Algorithm (GA) instead.
6.4. Classification-Based Method: Ensemble Stacking Classifier
In this study, we adopt an ensemble stacking classifier to combine complementary biases of linear, tree-based, and neural learners, yielding more stable failure-probability estimates under class imbalance than any single model. We evaluated multiple base classifiers (e.g., logistic regression, decision tree, random forest, multilayer perceptron) and found no single model to be consistently superior across benchmarks; regression models did not provide reliable prioritization of failure-prone test-cases. Accordingly, we use stacking with a simple linear meta-learner trained on out-of-fold predictions to rank candidates by estimated failure probability within our fixed-budget protocol, see Listing 4. Training labels come from the explore–exploit loop (repeated executions per input), and features are the input parameters used uniformly across methods, requiring no domain-specific engineering.
Architecture, Training Data, Features, and Hyperparameters
Training labels are obtained online from the explore–exploit loop (Section 5.1); class imbalance is handled via SMOTE and class-weighted losses; and features are the raw input parameters shared by all methods with only minimal normalization/encoding. The stacked ensemble comprises base classifiers (logistic regression, decision tree, random forest, multilayer perceptron) whose 5-fold out-of-fold probability predictions feed a logistic regression meta-learner; we set passthrough=True so the meta-learner also sees raw features. Hyperparameters follow standard library defaults with light tuning (e.g., tree depth/estimators, MLP iterations); the meta-learner uses class_weight=balanced with L2 regularization and fixed seeds. At inference time, the ensemble ranks candidates by estimated failure probability under the same fixed-budget protocol as the other methods; the artifact (Data Availability Statement) contains the exact instantiation.
| Listing 4. The Ensemble Stacking Classifier. After experimentation, we found that stacking the four most common classifiers and combining their predictions using logistic regression gives the best results. We configured passthrough = True to allow raw features to reach the meta-learner and cv = 5 for robust out-of-fold training. We also adjusted the number of iterations to cope with model complexity and used class_weight = ‘balanced’ due to skewed data, as bugs are rarely triggered. A two-layer neural network with an adaptive learning rate further enhances abstraction and generalization. |
 |
As illustrated in Figure 3, our ensemble-guided search alternates exploration and exploitation in fixed 100 + 100 (100 is a hyperparameter) batches, retraining the model each iteration and using the model from the previous iteration to guide the ranked selection.
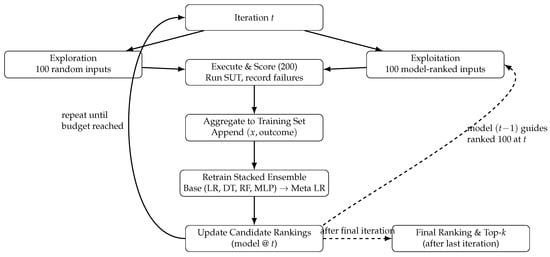
Figure 3.
Ensemble-guided search loop. In each iteration t, we add 200 new inputs via a parallel split: 100 random (exploration) and 100 model-ranked (exploitation, guided by the model learned at ). Both sets are executed and scored, results are aggregated, the stacked ensemble is retrained (base learners → meta-learner), and candidate rankings are updated. The loop repeats until the budget is exhausted; after the final iteration, we export the model’s Final Ranking and Top-k.
7. Results and Discussion
Results scope: We report aggregate and per-problem outcomes under the fixed-budget protocol, then discuss practical implications and limitations.
This section presents the empirical results obtained from evaluating our test generation framework on a suite of 17 benchmark concurrency problems, each containing a known, seeded bug. To assess effectiveness, we applied four black-box test generation methods: Brute-Force (), Ensemble Classifier (Ens), Genetic Algorithm (GA), and Simulated Annealing (SA). Each method was executed in 50 independent trials per problem to mitigate the influence of stochastic variability and enable robust statistical analysis. During each execution, the method generated a unique test suite, and we recorded whether any test-case within it successfully triggered the target bug. For every method–problem pair, we computed the empirical probability of failure discovery, alongside standard deviation and 95% confidence intervals.
The structure of this section follows the types of visualizations used to interpret the results: the overall bug detection rates per problem, convergence behavior as a function of the test budget, top-ranked test-case performance comparisons, and statistical significance analyses between methods. Each type of graph is introduced with an explanation of what it conveys, how the data is structured, and what insights emerge from the results.
7.1. Overall Success Rates per Problem
This subsection presents the average probability of successfully triggering each bug using the four tested methods. Each bar represents the mean probability computed across 50 independent runs for a fixed number of test-cases.
The graph in Figure 4 allows direct comparison of method effectiveness across the 17 problems. As observed for 500, 1100, 2100, and 3900 test-cases, the Ens method consistently outperforms the other methods in most cases, often achieving significantly higher success rates with lower variance. The method generally lags behind, especially on more complex bugs.
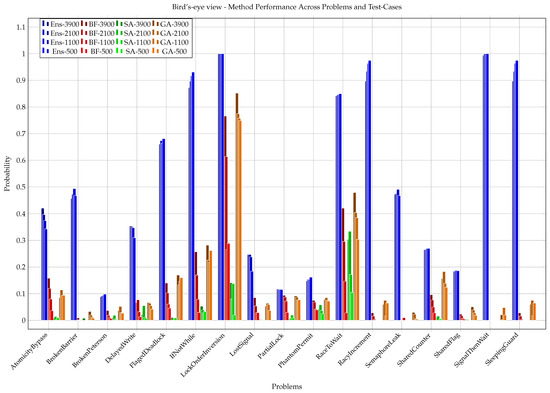
Figure 4.
Bird’s-eye view for all problems; the probability of triggering a bug after 500, 1100, 2100, and 3900 test-cases. Each bar is one experiment and based on 50 independent runs. The x-axis is all 17 problems, and for each problem, 4 methods and 4 (out of 20) test-cases are shown. The y-axis is the maximum probability for the best test-case.
Across all 17 benchmarks, the ensemble (Ens) already achieves a mean success probability of after the first 500 tests, compared to for GA, for , and only for SA; by the full 3900 test budget, these averages rise to 0.87, 0.46, 0.39, and 0.11 respectively. While the ensemble-based method consistently outperforms the other approaches in most configurations, its advantage over GA in this instance is less pronounced. Specifically, the comparison yields a one-sided Wilcoxon p-value of 0.048, with a 95% confidence interval of [0.03, 0.41]. These results indicate only marginal evidence of superiority, rather than a substantial widening of performance [41].
This type of visualization provides a macroscopic view of method performance per problem and confirms the robustness of the classifier-based approach.
Figure 5 provides a crucial “bird’s-eye view” of the comparative performance of the four search/optimization methods. This high-level summary allows one to quickly grasp the overall landscape of method effectiveness without delving into the intricacies of individual experimental variations. This visualization is generated by processing and aggregating data from all problems’ results. The x-axis represents the number of test-cases, while the y-axis indicates the average probability. From these aggregated curves, key insights can be gleaned, such as the convergence behavior of each method as the number of test-cases increases, their relative performance ceilings, and the efficiency with which they approach optimal solutions.
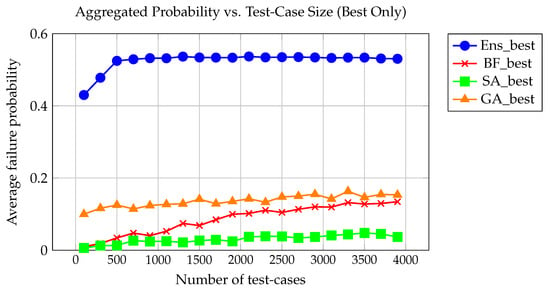
Figure 5.
Aggregated performance comparison of four methods across all 17 benchmark concurrency problems. The x-axis shows the number of test-cases used in each evaluation, and the y-axis shows the average fault-triggering probability. For each method, the curve represents the mean of the mean of the best test-case’s fault-triggering probability across all problems.
7.2. Per-Problem Bug-Detection Rates
To gain a deeper understanding of method behavior across varying bug difficulties, we divided the 17 benchmark problems into three groups based on their maximum observed bug detection probabilities: problems with low detectability (maximum probability below 0.2), medium detectability (between 0.2 and 0.6), and high detectability (above 0.6). This classification reflects the intrinsic challenge of each problem and enables structured comparison across problem types.
For illustrative purposes, we present in this section one representative problem from each group. These examples serve to demonstrate trends that consistently appear across the full suite of benchmarks. In all selected cases, the ensemble method (Ens) clearly outperforms the alternatives, both in terms of detection probability and convergence rate. The full set of graphs for all 17 problems is included in the Data Availability Statement.
Figure 6 shows representative cases from a low group (Shared Flag), a moderate group (Atomicity Bypass), and a high group (Race-To-Wait). Here, Ens rapidly increases its bug detection success rate, reaching a median of 50% after only 1000 tests. In contrast, the baseline method () lags behind at approximately 15%, while GA reaches around 20%. The SA method is the least effective, remaining near zero throughout. This pattern, where Ens dominates, GA and perform moderately, and SA struggles, recurs in nearly all problems, regardless of their detectability group.
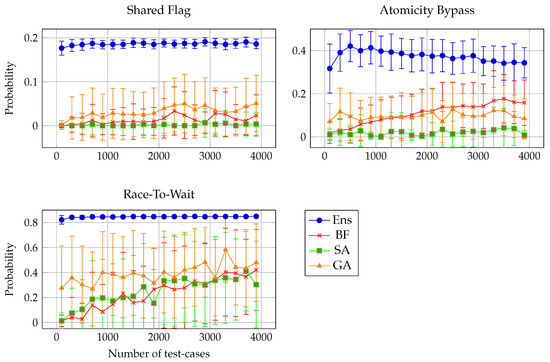
Figure 6.
Bug detection rates across three benchmark problems with different detectability levels. Based on 50 runs; error bars = SD.
Quantitatively, Ens exceeds the 0.20 success threshold on 9/9 “low-detectability” problems, while the next-best method (GA) manages it on only 3; in the medium tier (max ∈ [0.2, 0.6]), Ens surpasses 0.60 on 5/6 problems vs. 0 for and 1 for GA; and for high-detectability bugs, Ens reaches ≥ 0.90 on 4/5 problems within 1100 tests, a level that attains on just one problem.
These results reinforce findings from prior work [42,43], showing that learning-guided techniques not only improve final detection rates, but also significantly reduce the number of test-cases required to reveal faults, particularly in scenarios where failures are elusive or require precise triggering conditions.
7.3. Top-k Case Effectiveness
This section compares the performance of Ens compared to the method when selecting the top 5 and top 10 best test-cases from a larger candidate set. As previously explained, it is often necessary to generate multiple test scenarios for different phases of the process (development, debugging, testing, and validation). Therefore, we demonstrate the ability to generate either the 5th or the 10th test-case according to the two main methods: Ens and . These results, shown in Figure 7 for 5th-best and 10th-best for low detectability (Shared Flag), for medium detectability (Atomicity Bypass), and for high detectability (Race-To-Wait), demonstrate how prioritizing test-cases by a classifier model yields a higher likelihood of bug exposure.
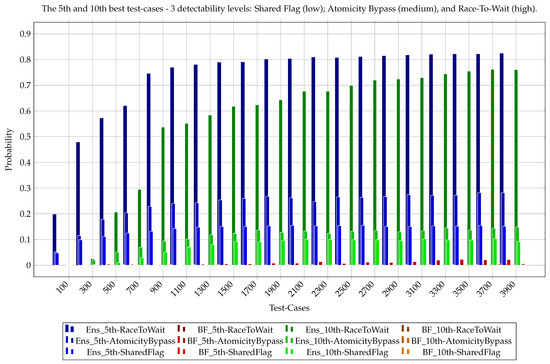
Figure 7.
The 5th and 10th best test-cases’ probability over three detectability levels of problems that cover three ranges of probability: Shared Flag (low), Atomicity Bypass (medium), and Race-To-Wait (high). Each bar is one experiment and based on 50 independent runs. The x-axis is all 20 test-cases, and for each problem, 2 chosen methods () and 3 (out of 17) problems are shown. The y-axis is the maximum probability for the best test-case.
We note that for most problems, especially those in the medium-to-high difficulty range (true probability of failure between 0.2 and 0.6), the classifier-based method (Ens) consistently outperforms all baselines. On average, the probability of detecting a fault in the top-1 test-case rises from 22% with to 45% with Ens, a relative improvement of more than 100%. In the top-10 ranking, the average success rate jumps from 40% () to 72% (Ens), with 9 out of 10 problem instances showing a statistically significant advantage (Wilcoxon one-sided test, ).
These graphs support the hypothesis that even partial ranking from learned models can significantly improve fault detection.
Averaging over the entire benchmark, the 5th best test-case chosen by Ens triggers the bug 31% of the time, vs. 11% for ; for the 10th best candidate, the rates are 24% vs. 6% (both differences significant at ).
7.4. Pairwise Statistical Significance Analysis
This section presents a detailed pairwise statistical comparison between the evaluated methods using one-sided Wilcoxon signed-rank tests, in accordance with contemporary best practices for nonparametric analysis [44]. Table 4 displays the results across all 17 benchmark problems, using the best-case test input identified for each method. Each row corresponds to a benchmark problem, and each column reports the outcome of a directional hypothesis comparing a pair of methods among Ens, , SA, and GA, where each cell shows the p-value for the hypothesis that the method in the row significantly outperforms the method in the column.

Table 4.
Wilcoxon one-sided signed-rank test results for best scores. Each cell shows the p-value for the hypothesis that the left method performs better than the right (e.g., Ens→BF). Green cells indicate significant results (), gray cells indicate no significance (), and red cells indicate evidence in the opposite direction.
Green cells indicate statistically significant superiority (), gray cells indicate non-significant differences (), and red cells represent reversed directions. In total, the table comprises 68 directional pairwise comparisons (17 problems × 4 method pairs). The Ens method shows a particularly strong trend: it significantly outperforms in 15 out of 17 cases, SA in all 17 cases, and GA in 16 cases. This consistency reflects both strong absolute performance and low variability. In contrast, significantly outperforms SA in 15 problems, but offers a limited advantage over GA, outperforming it significantly in only two problems. GA and SA, on the other hand, do not significantly outperform any other method in any problem, indicating weaker and less consistent behavior.
Only 14 of the 102 comparisons are statistically inconclusive (gray cells), highlighting that the majority of results are directional and meaningful. This overall structure reveals a clear hierarchy: Ens consistently outperforms all others; BF is reliably better than SA; and SA and GA rarely, if ever, show statistical superiority. Taken together, these patterns indicate robust performance for Ens across diverse bug types and failure modes, providing strong evidence for its practical adoption in test amplification.
7.5. Convergence Analysis Across Methods
In this analysis, we study convergence patterns by plotting the probability of success as a function of the number of test-cases, aggregated over all 17 benchmark problems. Figure 4 provides a bird’s-eye view that captures performance trends at four representative budget levels: 500, 1100, 2100, and 3900 test-cases. For each method, Ens, , SA, and GA, we plot the best failure-inducing probability obtained per problem, averaged over 50 independent runs.
The ensemble classifier-based method (Ens) exhibits remarkably fast and stable convergence. At just 500 test-cases, Ens already achieves a mean success probability of 51.8% across all problems. This value rises to 56.4% at 1100, 58.7% at 2100, and 59.8% at 3900. These gains are not only large in absolute terms, but also consistently achieved across a diverse range of problem types. This demonstrates the model’s ability to generalize its learned prioritization across different failure patterns.
In contrast, the Brute-Force approach () converges slowly. It begins with a mean success rate of just 3.1% at 500 test-cases, improving modestly to 6.2% at 1100, 10.0% at 2100, and only 13.6% at 3900 test-cases. This linear and limited improvement confirms the inefficiency of uninformed random exploration.
Simulated Annealing (SA) and Genetic Algorithm (GA) fall between these extremes. SA improves from 1.5% (at 500 test-cases) to 3.9% (at 3900), with substantial stagnation between checkpoints, reflecting a limited capacity to escape local minima. GA achieves a higher starting performance at 500 test-cases (mean 8.1%) and improves more rapidly than SA, reaching 17.3% at 3900, but still falls far short of Ens.
Overall, these convergence patterns reinforce the strength of learning-guided strategies. Ens not only achieves the highest final probabilities, but also reaches them faster, demonstrating both sample efficiency and consistent generalization. This advantage is particularly valuable in real-world testing scenarios where test execution budgets are constrained and high-probability failure discovery is critical.
7.6. Summary of Key Findings
Our evaluation of four amplification methods, Brute-Force (), Simulated Annealing (SA), Genetic Algorithm (GA), and Ensemble Classification (Ens), across 17 benchmark concurrency problems, led to several key findings that integrate both method-specific behavior and cross-cutting insights:
- Learning-based amplification significantly outperforms uninformed approaches: The ensemble classifier (Ens) consistently achieved the highest bug-triggering probabilities across nearly all test-case budgets and problems. With just 500 test-cases, Ens reached average success probabilities exceeding 0.53, whereas those of , SA, and GA remained below 0.13. At the full budget of 3900 test-cases, Ens achieved near-perfect detection (over 0.9 probability) in more than half of the problems, including LockOrderInversion, SignalThenWait, and IfNotWhile.
- Ensconverges faster and with fewer test-cases: While , SA, and GA showed gradual or erratic improvements, Ens rapidly identified failure-inducing cases. For example, in RacyIncrement, Ens surpassed 0.9 success probability with fewer than 1100 test-cases, while GA plateaued at 0.07 and at 0.03, even after 3900 cases. This sample efficiency makes Ens especially valuable for real-world systems with costly or time-limited testing resources.
- Traditional search methods offer limited scalability: showed minimal improvement over increasing test budgets, with average performance rarely exceeding 0.15 across problems. SA’s performance improved modestly, but remained inconsistent, failing to trigger bugs in several hard problems like SharedFlag and SemaphoreLeak. GA was more effective than and SA in moderately complex problems, but still lagged behind Ens in both speed and final success rates.
- Problem hardness varies significantly and affects method effectiveness: Some problems were consistently easy (e.g., SignalThenWait and LockOrderInversion) and triggered by all methods to varying degrees. Others, such as SharedFlag, SemaphoreLeak, and BrokenBarrier, remained elusive, with only Ens achieving meaningful success (e.g., 0.49 in SemaphoreLeak vs. <0.03 for others). This suggests that learning-based methods are better suited for navigating complex or deceptive search spaces.
- Ensrobustness is evident across all tested budgets: The bird’s-eye view (Figure 4) shows that across all 17 problems and at every tested budget (500, 1100, 2100, and 3900), Ens consistently led with or tied for the highest success rate. Notably, in 13 out of 17 problems, Ens reached probabilities above 0.85 with 3900 test-cases, while GA exceeded 0.5 in only 7, SA in 2, and in 1.
- Integration of feedback powersEnsperformance: Unlike the other methods, which rely on sampling or mutation heuristics, Ens uses supervised learning to predict and prioritize high-risk inputs. This allows it to generalize from early failures, focusing search efforts efficiently. The result is not only higher probabilities of detecting bugs, but also significantly fewer wasted executions.
- Ablation Study: We conducted ablation studies by removing components from the ensemble classifier and modifying its sampling heuristics. Specifically, we evaluated simplified variants of our pipeline, such as omitting SMOTE or disabling passthrough to the meta-learner. These reduced versions consistently underperformed relative to the full classifier configuration we present in the paper. In several cases, the simplified ensemble-based methods even performed worse than the Brute-Force baseline, highlighting the importance of each pipeline component in achieving effective bug amplification.
7.7. Discussion and Implications
Practically, the gains translate to fewer runs to reach actionable failure probabilities, accelerating triage and reproduction. Benefits concentrate on medium-detectability problems; easy cases saturate quickly, while hard cases show smaller but persistent lift across repetitions. Variance bands and p-values indicate stable improvements; where deltas are modest, effect sizes remain meaningful for budget allocation. Top-k scenario lists (e.g., 5th/10th) retain nontrivial failure rates, making them directly usable for debugging and regression. The protocol is black-box and budgeted, and artifacts/scripts enable reproduction and extension under identical conditions. Threats are discussed in Section 5.2, and data/code are linked in the Data Availability Statement.
8. Related Work
8.1. Concurrency Bug Debugging Methods
Over the past ten years, concurrent system bug hunting has evolved significantly, driven by the growing complexity of multithreaded software and the critical need to detect concurrency bugs, such as data races, deadlocks, and atomicity violations.
A survey of academic papers from sources like IEEE Xplore, ACM Digital Library, and SpringerLink reveals three dominant methodological categories: static analysis, dynamic analysis, and model checking, each encompassing diverse techniques with unique trade-offs, industrial applications, and ongoing refinements.
Static analysis: Techniques that scrutinize code without execution include abstract interpretation, data-flow analysis, type systems, symbolic execution, and machine learning-based bug prediction. Abstract interpretation [45] models program semantics to detect bugs across all paths, offering early detection but often producing false-positives due to over-approximation. Data-flow analysis [46] tracks dependencies and works well in structured parallelism (e.g., OpenMP), though its generalization to unstructured concurrency remains limited. Type systems, such as Rust’s ownership model [47], prevent bugs at compile-time with minimal runtime cost, though they require full language adoption. Symbolic execution [48] can uncover deep concurrency bugs through path exploration, but suffers from path explosion. Machine learning approaches [49] learn patterns from code to predict concurrency bugs, but depend heavily on the availability of labeled data. Tools like Coverity leverage static analysis in the industry, though concurrency-specific precision remains a challenge.
Dynamic analysis: This category executes programs to observe runtime behavior and includes methods like thread-aware fuzzing, runtime monitoring, and record-and-replay. Thread-aware fuzzing [50] explores interleavings to expose real bugs, but may suffer from incomplete coverage. Runtime monitoring [51] provides precise race detection at the cost of performance overhead. Record-and-replay [52] facilitates debugging by reproducing execution paths, albeit with recording overhead. Tools like ThreadSanitizer are widely used due to their balance of effectiveness and performance.
Model checking: This technique provides formal verification by exhaustively exploring program state-spaces. Explicit-state model checking [53] can prove correctness but is vulnerable to state explosion. Bounded model checking [54] uses SAT/SMT solvers to explore execution within depth bounds, trading completeness for scalability. Abstraction-based techniques [55] simplify systems but risk imprecision. Compositional approaches [56] decompose systems for modular checking, though assumptions can break down. Statistical model checking [57] approximates correctness via sampling and is used in domains like embedded systems and aerospace, where formal guarantees are difficult to obtain.
Hybrid approaches have emerged to balance strengths and weaknesses, e.g., KRACE [58] employs thread-scheduling perturbation and fuzzing to detect data races in kernel file systems. Benchmarks such as the Linux kernel and SPEC CPU continue to reveal challenges: static methods must reduce false-positives, dynamic tools need improved coverage, and model checking must scale better. Future directions involve tighter integration of these methods and greater automation to support concurrency bug detection at scale.
8.2. Concurrency Bug Datasets
The study of concurrency bugs has led to the development of a wide range of datasets, each designed to capture specific aspects of concurrent programming behavior. These datasets can be grouped into four broad categories: general-purpose concurrency bug datasets, language-specific datasets, smart contract datasets, and fuzzing-based datasets. Below, we summarize key datasets from each category, highlighting their structure, scope, and contributions to academic research.
General-Purpose Concurrency Bug Datasets: Early work in concurrency bug research focused on real-world software systems. Ref. [29] compiled 105 concurrency bugs from widely used applications such as MySQL and Apache. The dataset revealed common bug patterns and has influenced numerous studies in static and dynamic analysis. CHESS [14], developed by Microsoft Research, explores all thread interleaving to find concurrency bugs. RACEBENCH [59] is a benchmark suite containing 29 multithreaded programs with known races, offering a standardized environment for testing race detectors. DETECT [34] uses dynamic analysis and communication graphs to identify concurrency bugs.
Language-Specific Datasets: With the growing demand for language-aware tools, several datasets have been created targeting Java and Go. For Java, JaConTeBe [60] includes 47 confirmed bugs from eight Java projects. Defects4J [61] is a curated repository of real-world Java bugs, used extensively in software testing and repair. Bears [62] collects bugs from CI pipelines to support automated program repair. ManySStuBs4J [63] offers over 500 k single-statement bugs, indirectly supporting concurrency research. For Go, the Go Concurrency Bug Collection [35] contains 171 bugs from six Go applications https://github.com/system-pclub/go-concurrency-bugs (accessed on 6 September 2025). GoBench [64] expands this effort with 82 real bugs and 103 bug kernels.
Smart Contract Datasets: With the rise of blockchain applications, concurrency issues in smart contracts have gained prominence. ConFuzzius [65] combines evolutionary fuzzing and symbolic execution to detect concurrency-related bugs in Ethereum smart contracts, building a dataset of known vulnerabilities.
Fuzzing-Based Datasets: Gray-box fuzzing has proven valuable for stress-testing concurrent applications. MUZZ [50] presents a thread-aware fuzzing method for multithreaded programs, featuring a dataset of real-world apps annotated with concurrency bugs.
These datasets continue to support advances in concurrency research, enabling reproducibility, benchmarking, and tool evaluation across diverse programming environments.
9. Detailed Description of the Benchmark Problems
This section presents the benchmark problems used in our study. For each problem we report four concise fields designed for fast reading and reproducibility: Effect (the observable symptom, stated as the expected vs. observed outcome), Root Cause (a one-line diagnosis mapped to our taxonomy and naming the relevant primitive), Mechanism (a one-sentence explanation that makes the causal chain explicit by specifying the minimal interleaving/ordering and state conditions that lead from the root cause to the effect, so that the failure can be reproduced and validated), and Insight (an action-oriented fix or guard together with a test that would catch regressions). Pseudocode snippets are language-agnostic and annotated at the precise fault location; longer listings are deferred to the Data Availability Statement. Wording is harmonized across entries, with cross-references to the corresponding taxonomy categories for clarity and consistency.
9.1. Atomicity Bypass: Unexpected Data from Lock Misuse
- Description: Two threads increment a shared counter, assuming the critical section is protected. Each acquires the mutex and reads the counter, but erroneously releases the mutex before writing the updated value. Both then write the same value, so one increment is lost.
- Effect: Final counter equals 1 (expected 2)—unexpected data (lost update).
- Root Cause: Misuse of the mutex mechanism released before completing the read–modify–write, breaking atomicity and causing a lost update.
- Mechanism: Both threads read 0 under the lock; after unlocking, they race on the write, and one overwrite hides the other increment.
- Insight: Hold the lock across the entire increment (read–modify–write) or use an atomic fetch–add; add contention tests that assert that N concurrent increments yield N.
- Pseudocode (Algorithms 1 and 2):
| Algorithm 1 Thread 0 |
|
| Algorithm 2 Thread 1 |
|
9.2. Broken Barrier: Deadlock from Barrier Misuse with Incorrect Participant Count
- Description: Three threads participate in a barrier phase, but the barrier is configured for two participants. Additionally, one thread calls SignalAndWait() twice within the same phase before a reset, violating the intended usage.
- Effect: No forward progress for the duration of the timeout; threads block at SignalAndWait()—deadlock.
- Root Cause: Barrier misconfiguration (participants = 2 while three threads participate) combined with a double SignalAndWait() in the same phase, violating single-arrival semantics so the release condition is never satisfied.
- Mechanism: Two threads arrive and wait, while the third either does not arrive or is double-counted in the wrong phase; the phase cannot trip, leaving all waiters blocked indefinitely.
- Insight: Match the barrier’s participant count to the actual number of threads per phase and enforce exactly one SignalAndWait() per thread per phase; add timeouts/assertions to detect mismatched participants and double arrivals.
- Pseudocode (Algorithms 3–5):
| Algorithm 3 Thread 0 |
|
| Algorithm 4 Thread 1 |
|
| Algorithm 5 Thread 2 |
|
9.3. Broken Peterson: Mutual Exclusion Violation in Generalized Peterson’s Algorithm
- Description: A four-process generalization of Peterson’s algorithm maintains level[4] and last_to_enter[3]. The doorway step omits the update last_to_enter[level] = i, breaking the intended tie-breaking at each level.
- Effect: Two or more processes reach the critical section simultaneously—concurrent access.
- Root Cause: A missing update to last_to_enter[level] in the entry protocol, weakening the guard that enforces level-wise tie-breaking.
- Mechanism: When and advance to the same level, the stale last_to_enter[level] lets both predicates evaluate true, so they progress past the doorway and can enter the critical section together.
- Insight: Restore the doorway assignment last_to_enter[level] = i and assert the invariant “ process in CS”; add stress tests that co-schedule peers at equal levels to detect mutual-exclusion violations.
- Pseudocode (Algorithm 6):
| Algorithm 6 General Peterson Algorithm (Process i) |
|
9.4. Delayed Write: Assertion Failure from Non-Atomic Test-and-Set Simulation
- Description: A simulated test-and-set updates a shared variable x to target and later asserts x == target. The operation is not atomic: another thread can interleave and modify x between steps.
- Effect: Assertion fails with x! = target after the set (expected x == target)—unexpected data; concurrent access.
- Root Cause: Incorrect order in read–then–write on shared x without synchronization (no CAS/lock), allowing an interleaving that breaks happens-before.
- Mechanism: sets x: = target and yields; overwrites x; when checks x == target, the predicate is false.
- Insight: Replace the simulation with an atomic compare_and_swap/test_and_set or guard with a mutex; add preemption-injection tests that try to flip x between the set and the assertion.
- Pseudocode (Algorithms 7 and 8):
| Algorithm 7 Thread 0 |
|
| Algorithm 8 Thread 1 |
|
9.5. Flagged Deadlock: Deadlock from Misuse of Lock Primitives
- Description: Two threads acquire multiple locks along flag-dependent branches that mix recursive locks, try-locks, and conditional paths. Different branches may acquire the same lock set in different ways, and some paths fail to release on try-lock failure.
- Effect: No forward progress for the duration of the timeout; both threads block at SignalAndWait() or lock acquisition—deadlock (Table 1: Effect = Deadlock).
- Root Cause: Misuse of flag-dependent try-lock/recursive-lock usage and missing releases on failed attempts leads to inconsistent lock ownership and circular wait.
- Mechanism: holds and, due to flag f, attempts ; holds and attempts . Because one path used a try-lock without proper release/rollback, each thread waits for a lock the other holds, so the phase cannot complete.
- Insight: Prefer a single blocking primitive with a canonical acquisition order across all branches; on try-lock failure, release any held locks and retry in the canonical order. Add deadlock tests with timeouts and lock-order assertions; remove spin-waiting in favor of bounded backoff or blocking synchronization.
- Pseudocode (Algorithms 9 and 10):
| Algorithm 9 Thread 0 |
|
| Algorithm 10 Thread 1 |
|
9.6. If-Not-While: Deadlock and Missed Signals from Condition Variable Misuse
- Description: Two consumers wait on an empty queue using Monitor.Wait(mutex); a producer enqueues data and calls Monitor.PulseAll(mutex). The consumers guard the wait with if instead of while, so the predicate is not re-checked upon wakeup.
- Effect: Either deadlock, no forward progress with consumers blocked at Wait due to a missed signal, or unexpected data, when a consumer proceeds without the queue being populated (data loss/underflow).
- Root Cause: Guarding the condition variable with if rather than while weakens the guard, so wakeups do not revalidate the predicate under the lock and consumers can wait indefinitely.
- Mechanism: A consumer tests “empty” and calls Wait; the producer’s PulseAll occurs outside the consumer’s effective wait window. With an if guard, the thread may sleep indefinitely without re-checking the predicate.
- Insight: Use a while loop to re-check the predicate under the mutex after every wakeup; ensure the producer updates the predicate before Pulse/PulseAll. Add tests that inject spurious wakeups and varied timing to expose missed signals and stalled consumers.
- Pseudocode (Algorithms 11–13):
| Algorithm 11 Thread 0 |
|
| Algorithm 12 Thread 1 |
|
| Algorithm 13 Thread 2 |
|
9.7. Lock Order Inversion: Deadlock from Inconsistent Lock Acquisition Order
- Description: Two threads acquire the same pair of mutexes in opposite orders: locks then requests , while locks then requests .
- Effect: No forward progress for the duration of the timeout; each thread blocks while holding one mutex and waiting for the other—deadlock (Table 1: Effect = Deadlock).
- Root Cause: Acquiring the mutexes in inconsistent orders across threads constitutes incorrect ordering and creates a circular wait.
- Mechanism: holds and waits for ; holds and waits for ; neither can proceed, so the wait condition for both remains permanently false.
- Insight: Enforce a global lock-order policy (e.g., always acquire ) across all code paths; on violation, release and retry in canonical order. Add deadlock tests with timeouts and lock-order assertions; prefer multi-lock primitives or wrappers that impose a consistent acquisition order.
- Pseudocode (Algorithms 14 and 15):
| Algorithm 14 Thread 0 |
|
| Algorithm 15 Thread 1 |
|
9.8. Lost Signal: Deadlock from Missed Signal in Condition Variable Coordination
- Description: Two threads coordinate via a condition variable. checks a flag with if and then calls wait(), while sets the flag and calls notify_all(). If the notification occurs before begins waiting, the signal is lost and may block indefinitely.
- Effect: No forward progress; remains blocked on wait() after an early notify_all() —deadlock.
- Root Cause: Guarding the condition variable with if instead of while weakens the guard: an early notification is not revalidated under the lock, so the consumer can sleep indefinitely—missing/weak guard.
- Mechanism: sets the flag and issues notify_all() before enters wait(); with an if-guard, subsequently sleeps without re-checking the predicate and never observes the signal.
- Insight: Use a while loop to re-check the predicate under the mutex after every wakeup; update the predicate before notify_all(), and add tests that inject early notifications/spurious wakeups to detect stalled consumers.
- Pseudocode (Algorithms 16 and 17):
| Algorithm 16 Thread 0 (Waiter - Weak Guard) |
|
| Algorithm 17 Thread 1 (Signaler) |
|
9.9. Partial Lock: Race Condition from Insufficient Lock Coverage
- Description: Two threads update a shared variable i: increments by 2 and then checks i == 5, while decrements by 1. A lock is used but does not cover all relevant reads/writes or the check, allowing unsafe interleavings.
- Effect: Intermittent assertion failure on i == 5 (expected true, observed false)— unexpected data.
- Root Cause: Holding the lock for only parts of the read–modify–check sequence weakens the guard, so some accesses occur outside the critical section and interleave unsafely—missing/weak guard.
- Mechanism: sets i from 3 to 5 under lock and releases; then decrements to 4 under a separate/unguarded step; when checks i == 5 outside the lock, the predicate fails.
- Insight: Extend lock coverage to include the entire read–modify–check sequence (or use an atomic fetch–add plus an in-lock check); add contention tests that repeatedly exercise the increment/decrement pattern and assert the invariant.
- Pseudocode (Algorithms 18 and 19):
| Algorithm 18 Thread 0 |
|
| Algorithm 19 Thread 1 |
|
9.10. Phantom Permit: Mutual Exclusion Violation from Semaphore Misuse
- Description: Two threads share a binary semaphore guarding a critical section. uses the canonical Wait→ CS →Release sequence. calls Wait(timeout) and, on timeout, still invokes Release, injecting an extra permit (“phantom” permit).
- Effect: Two threads can be in the critical section simultaneously (expected at most one)—concurrent access.
- Root Cause: Invoking Release without a preceding successful Wait breaks the one-to-one pairing and inflates the semaphore count—misuse of primitives.
- Mechanism: times out in Wait and calls Release, increasing the semaphore from 0 to 1 while is inside CS; both and can then enter/remain in CS concurrently.
- Insight: Only call Release after a successful Wait; track ownership (e.g., a success flag/guard) or use RAII-style wrappers. Add tests that force timeouts and assert that the semaphore count never exceeds 1 and that CS concurrency is impossible.
- Pseudocode (Algorithms 20 and 21):
| Algorithm 20 Thread 0 (Acquirer) |
|
| Algorithm 21 Thread 1 (Timed Failer) |
|
9.11. Race-To-Wait: Deadlock from Non-Atomic Coordination
- Description: Two threads coordinate via a shared counter waiters. Each thread increments waiters and then waits until waiters == 2. The increment and the check are performed separately and without synchronization.
- Effect: No forward progress; both threads wait for waiters == 2 after observing 1—deadlock.
- Root Cause: Making the increment–then–check on waiters non-atomic (no lock/CAS) lets each thread decide based on a stale value, producing a liveness cycle.
- Mechanism: increments to 1 and checks waiters == 2 while does the same; interleaving allows both to observe 1 and enter the wait path, with no further increments to satisfy the predicate.
- Insight: Combine the increment and predicate check in a single atomic step (e.g., lock or fetch_add/CAS loop) or replace the ad hoc protocol with a barrier/condition variable; add tests that force preemption between the increment and check and assert that waits eventually complete.
- Pseudocode (Algorithms 22 and 23):
| Algorithm 22 Thread 0 |
|
| Algorithm 23 Thread 1 |
|
9.12. Racy Increment: Race Condition from Non-Atomic Compound Operations
- Description: Two threads execute a = a + 1; if (a == 1) enter critical section, intending that only the first incrementer enters. The increment is not atomic (read–modify–write), so interleavings allow both threads to observe a == 0 and proceed.
- Effect: Both threads enter the critical section simultaneously (expected at most one)—concurrent access; shared updates occur under false exclusivity, yielding an incorrect state—unexpected data.
- Root Cause: Treating the increment-and-check as atomic permits non-atomic interleavings on the shared variable; both threads can satisfy a == 1 concurrently—non-atomic operations on a shared state.
- Mechanism: reads a = 0 and computes 1; before it writes, also reads 0 and computes 1; both write 1 and each observes a == 1, entering the critical section together.
- Insight: Use an atomic fetch_add and test the previous value (enter only if it was 0), or guard with a mutex/CAS loop; add contention tests that assert the critical section’s exclusivity under heavy interleavings.
- Pseudocode (Algorithms 24 and 25):
| Algorithm 24 Thread 0 |
|
| Algorithm 25 Thread 1 (Expanded Assignment) |
|
9.13. Semaphore Leak: Mutual Exclusion Violation from Semaphore Misuse
- Description: Two threads use a semaphore to guard a critical section. follows Wait→ CS →Release. performs a time-limited Wait and calls Release even if the wait times out or fails.
- Effect: Multiple threads can enter the critical section simultaneously (expected at most one)—concurrent access.
- Root Cause: Calling Release without a preceding successful Wait inflates the semaphore count and breaks one-to-one pairing—misuse of primitives.
- Mechanism: times out in Wait yet executes Release, incrementing the permit count; while holds the CS, the extra permit admits as well, violating mutual exclusion.
- Insight: Only issue Release after a confirmed successful Wait; track acquisition with a success flag/guard or RAII wrapper. Add tests that force timeouts and assert that the semaphore count never exceeds one and that CS concurrency is impossible.
- Pseudocode (Algorithms 26 and 27):
| Algorithm 26 Thread 0 |
|
| Algorithm 27 Thread 1 |
|
9.14. Shared Counter: Mutual Exclusion Violation from Unsynchronized Counter
- Description: Two threads increment a shared counter and enter a critical section based on different thresholds (e.g., one at 5, the other at 3). The counter is updated and tested without synchronization, so reads/writes interleave unpredictably.
- Effect: Both threads may enter the critical section simultaneously (expected at most one)—concurrent access; threshold checks occur on stale values, yielding incorrect entry decisions—unexpected data.
- Root Cause: Performing the increment and threshold check on the shared counter without atomicity or ordering guarantees that each thread can decide on a stale/interleaved value—non-atomic operations on a shared state.
- Mechanism: and both read ; each increments to 3 and, due to racing writes/reads, both observe the threshold satisfied and enter, or one observes an outdated c and enters too early/late.
- Insight: Make the increment-and-gate decision atomic (e.g., fetch_add and test the previous value) or guard with a mutex; centralize threshold crossing (single arbiter) and add contention tests asserting exclusivity and correct entry counts under heavy interleavings.
- Pseudocode (Algorithms 28 and 29):
| Algorithm 28 Five-Headed Dragon |
|
| Algorithm 29 Three-Headed Dragon |
|
9.15. Shared Flag: Mutual Exclusion Violation from Weak Boolean Flag Guard
- Description: Two threads use a shared Boolean flag to guard a critical section: each spins while the flag is true, then sets it to true and enters. The check (flag == false) and the set (flag = true) are separate, non-atomic steps.
- Effect: Both threads can enter the critical section simultaneously (expected at most one)—concurrent access.
- Root Cause: Guarding the critical section with a non-atomic check-then-set turns the flag into a weak guard, so both threads can pass the gate concurrently—missing/weak guard.
- Mechanism: reads flag = false and is preempted; also reads false, sets true, and enters; when resumes it sets true and enters as well, violating exclusivity.
- Insight: Replace the flag with an atomic test-and-set (exchange/CAS) or a mutex; if a flag is retained, use a single atomic operation that both tests and sets with proper memory ordering. Add contention tests that assert the critical section’s exclusivity under heavy interleavings.
- Pseudocode (Algorithms 30 and 31):
| Algorithm 30 First Army |
|
| Algorithm 31 Second Army |
|
9.16. Signal-Then-Wait: Deadlock from Premature Signaling in Condition Synchronization
- Description: Two threads coordinate with a shared flag and condition variable. The signaling thread sets the flag and calls notify_all() before the waiting thread has armed its wait. Although the waiter uses a while guard, the notification is issued too early to be observed by a thread that has not yet begun waiting.
- Effect: No forward progress; the waiting thread blocks indefinitely despite the flag having been set—deadlock.
- Root Cause: Emitting notify_all() before the waiter has entered wait() (and without synchronizing the predicate update and signal under the mutex) violates the required sequencing between predicate update, wait, and notification—incorrect ordering.
- Mechanism: The producer sets the flag and signals; only afterward does the consumer check the predicate and call wait(). Because the signal occurred before the wait was armed and carries no state, the consumer sleeps with no subsequent notification to wake it.
- Insight: Update the predicate and issue notify_all() while holding the mutex; on the consumer side, test the predicate under the same mutex and call wait() only when it is false, re-checking in a while loop. Add tests that inject early notifications to ensure the waiter never blocks indefinitely when the predicate is already satisfied.
- Pseudocode (Algorithms 32 and 33):
| Algorithm 32 Thread 0 (Waiter) |
|
| Algorithm 33 Thread 1 (Signaler) |
|
9.17. Sleeping Guard: Deadlock from Missing or Weak Guard
- Description: A consumer checks a queue and, if empty, sets a waiting flag and calls wait(); a producer consults the flag and enqueues data. If the producer enqueues before the consumer sets the flag (or before the wait is armed), the consumer misses the notification and can block indefinitely.
- Effect: No forward progress; the consumer remains blocked on wait() even though the queue becomes non-empty—deadlock.
- Root Cause: Using a flag as the guard instead of the true predicate (queue non-empty) weakens the guard; without re-checking under the lock after wakeups, early enqueues/notifications are not observed—missing/weak guard.
- Mechanism: The producer enqueues an item and (optionally) signals before the consumer sets waiting and enters wait(); because the guard is the flag (not the queue state) and is not revalidated, the consumer sleeps indefinitely, despite there being available data.
- Insight: Guard the real predicate (e.g., !queue.empty()) under the mutex and re-check it in a while loop after every wake; update the predicate and signal while holding the mutex. Add tests that inject early enqueues/notifications and spurious wakeups to ensure the consumer never blocks when data is available.
- Pseudocode (Algorithms 34 and 35):
| Algorithm 34 Consumer |
|
| Algorithm 35 Producer |
|
10. Limitations of the Proposed Approach
While our approach to bug amplification demonstrates strong empirical performance across a diverse set of concurrency problems, it is important to acknowledge its current limitations and boundaries of applicability.
Dependence on Parameter Sensitivity: Our method assumes that the probability of bug manifestation is meaningfully influenced by the input parameters exposed to the test generation engine. For systems where concurrency faults are insensitive to external parameters (e.g., bugs that manifest only due to internal scheduler decisions or deep state interactions), our black-box approach may offer limited leverage.
Curse of Dimensionality: As the dimensionality of the input space increases, learning an accurate regression model under a fixed testing budget becomes increasingly difficult. While our ensemble classifier demonstrated strong generalization in the studied benchmarks, its performance may degrade in higher-dimensional or sparsely populated input spaces, particularly when failure-inducing regions are extremely narrow.
Noise Sensitivity and Stochastic Feedback: Although we mitigate stochasticity through repeated executions, our framework is still subject to noise in failure observations. In scenarios where bug-triggering is both rare and erratic, the resulting label noise can impair the quality of the learned models. This sensitivity places limits on how well regression-based methods can capture the underlying failure structure, especially early in the learning process.
Model Retraining Overhead: The iterative nature of our learning-based method requires frequent retraining of the classifier during test generation. While not a bottleneck in our Python-based implementation, this could become a concern for large-scale systems or industrial deployments with tight performance constraints, especially when test executions are costly.
No Schedule Control: Unlike techniques such as systematic concurrency testing or randomized schedulers, our approach does not manipulate the thread scheduler or execution order. As a result, bugs that require specific interleavings to manifest may remain elusive unless those conditions can be indirectly induced through parameter variation.
Despite these limitations, our method provides a practical, non-invasive tool for increasing the likelihood of bug detection in concurrent systems. It complements existing techniques by offering a black-box, input-driven strategy that is easy to integrate and effective across a wide range of problem types.
11. Summary and Conclusions
This paper addresses a fundamental challenge in software testing: reliably detecting concurrency bugs that manifest under rare interleavings and elusive execution schedules. These failures, though often critical, are notoriously hard to reproduce. To tackle this, we propose a probabilistic reformulation of the test generation task, treating bug detection as a problem of searching for inputs with maximized failure probability. This shift enables both a principled evaluation of search heuristics and the design of more effective testing strategies.
To evaluate our approach, we introduced a carefully curated benchmark of 17 multithreaded programs, each exhibiting a different concurrency failure. These programs span diverse root causes and error types, and the benchmark was built to ensure broad coverage and realism. For each problem, we examined the effectiveness of four black-box test generation methods: Brute-Force (), Genetic Algorithm (GA), Simulated Annealing (SA), and an Ensemble Classifier (Ens). Each method was executed in 50 independent trials per problem, producing a robust dataset for statistical comparison.
The central contribution of the paper lies in the design and implementation of the ensemble-guided test generation strategy. By treating bug-finding as a classification problem over test inputs, our method learns from past failures and adaptively focuses the search on high-potential areas of the input space. This method is fully black-box and does not require access to program internals. Our results demonstrate that this learning-based strategy consistently outperforms traditional heuristics across nearly all benchmark problems. Notably, Ens achieves higher detection rates using fewer test executions and converges more quickly to effective test inputs.
We further introduced a set of four graph-based analysis techniques that offer a detailed view of the methods’ behavior: per-problem success curves, comparisons of top-ranked test-cases, convergence dynamics, and statistical significance heatmaps. These visual tools enabled us to examine method effectiveness from multiple perspectives and to identify patterns in both algorithmic performance and problem hardness. The analysis reveals that Ens not only provides early bug discovery, but also maintains its advantage as the test budget increases, exhibiting both statistical robustness and practical scalability.
Finally, we propose a novel simulation-based search heuristic for continuous input spaces, inspired by simulated annealing and guided by probabilistic failure gradients. This formulation opens avenues for guided bug amplification over high-dimensional input domains. As part of future work, we will evaluate the approach on additional real-world and open-source systems and benchmark it against additional search methods and baselines, e.g., Adaptive Random Testing (ART), Search-Based Software Testing (SBST), and Statistical Debugging, under the same fixed-budget, stochastic evaluation protocol.
In conclusion, this paper contributes a new methodological framework for adaptive bug amplification, introduces a reusable benchmark of concurrency problems, and provides compelling empirical evidence that ensemble-guided testing can substantially improve the reliability and efficiency of concurrency bug detection. We believe these findings advance the state-of-the-art in automated software testing and lay a foundation for broader adoption of machine-learning methods in fault localization and test generation.
Author Contributions
Conceptualization, all (Y.W., G.W., O.M., E.F., G.A. and A.E.); methodology, all; software, Y.W.; validation, Y.W.; formal analysis, all; investigation, Y.W.; resources, all; data curation, Y.W.; writing—original draft preparation, Y.W.; writing—review and editing, all; visualization, Y.W.; supervision, G.W.; project administration, all; funding acquisition, all. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partially funded by the Lynne and William Frankel Center for Computer Science and the Israeli Science Foundation grant No. 2714/19.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
We implemented a modular Python-based framework for conducting the amplification experiments The original data presented in the study are openly available at https://github.com/geraw/bug_amp (accessed on 06 September 2025). The framework supports multiple amplification strategies, including Brute-Force (), Simulated Annealing (SA), Genetic Algorithm (GA), and an Ensemble Classifier-based method (Ens). It is designed to be easily extensible, encouraging researchers and practitioners to contribute and experiment with their own search techniques. By following the provided templates and interface guidelines, users can seamlessly integrate new amplification strategies into the framework. We warmly invite the community to build upon our work and adapt the system to their specific needs. All experiments were conducted on the high-performance computing (HPC) infrastructure at Ben-Gurion University of the Negev (BGU), which is managed using an internal SLURM workload manager. SLURM allowed us to schedule thousands of concurrent and independent test executions efficiently across a cluster of multi-core servers. The use of this environment significantly accelerated the experimentation process and allowed us to evaluate all methods consistently across all problem instances. Although the experiments were originally executed in a SLURM-based cluster environment, the entire codebase is portable. It can be executed on any standard Linux or Windows machine or cloud platform using Python 3 and common scientific libraries, without the need for SLURM. The repository includes detailed instructions for reproducing the experiments, ensuring transparency and repeatability across different platforms.
Acknowledgments
During the preparation of this study, we used ChatGPT 5 and Gemini 2.5 Flash for the purposes of searching for related work, coding, and writing. The authors have reviewed and edited the output and take full responsibility for the content of this publication. We also thank the anonymous reviewers for their constructive feedback, which improved the clarity and rigor of this work. Any remaining errors are our own.
Conflicts of Interest
Eitan Farchi and Gal Amram are both researchers at IBM Research Haifa. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ART | Adaptive Random Testing |
| BF | Brute-Force |
| BGU | Ben-Gurion University of the Negev |
| CAS | Compare And Swap |
| CI | Continuous Integration |
| CLT | Central Limit Theorem |
| Ens | Ensemble |
| GA | Genetic Algorithm |
| GP | Genetic Programming |
| LLN | Law of Large Numbers |
| HPC | High-Performance Computing |
| MLP | Multilayer Perceptron |
| PCT | Probabilistic Concurrency Testing |
| SA | Simulated Annealing |
| SBST | Search-Based Software Testing |
| SD | Standard Deviation |
| SLURM | Simple Linux Utility for Resource Management |
| SMOTE | Minority Over-sampling Technique |
| SUT | System Under Test |
References
- Gray, J. Why Do Computers Stop and What Can Be Done About It? Technical Report 85.7; Tandem Computers: Palo Alto, CA, USA, 1985. [Google Scholar]
- Bakhshi, R.; Kunche, S.; Pecht, M. Intermittent Failures in Hardware and Software. J. Electron. Packag. 2014, 136, 011014. [Google Scholar] [CrossRef]
- Heidelberger, P. Fast simulation of rare events in queueing and reliability models. ACM Trans. Model. Comput. Simul. 1995, 5, 43–85. [Google Scholar] [CrossRef]
- Younes, H.L.; Simmons, R.G. Statistical probabilistic model checking with a focus on time-bounded properties. Inf. Comput. 2006, 204, 1368–1409. [Google Scholar] [CrossRef]
- Kumar, R.; Lee, J.; Padhye, R. Fray: An Efficient General-Purpose Concurrency Testing Platform for JVM. arXiv 2025, arXiv:2501.12618. [Google Scholar] [CrossRef]
- Burckhardt, S.; Kothari, P.; Musuvathi, M.; Nagarakatte, S. A Randomized Scheduler with Probabilistic Guarantees of Finding Bugs. In Proceedings of the 15th International Conference on Architectural Support for Programming Languages and Operating Systems (ASPLOS ’10), Pittsburgh, PA, USA, 13–17 March 2010; pp. 167–178. [Google Scholar] [CrossRef]
- Zhao, H.; Wolff, D.; Mathur, U.; Roychoudhury, A. Selectively Uniform Concurrency Testing. ACM Program. Lang. (ASPLOS) 2025, 5, 1003–1019. [Google Scholar] [CrossRef]
- Ramesh, A.; Huang, T.; Riar, J.; Titzer, B.L.; Rowe, A. Unveiling Heisenbugs with Diversified Execution. ACM Program. Lang. 2025, 9, 393–420. [Google Scholar] [CrossRef]
- Fonseca, P. Effective Testing for Concurrency Bugs. Doctoral Thesis; MPI–SWS Technical Report No. MPI–SWS–2015–004; Max Planck Institute for Software Systems (MPI–SWS): Saarbrücken and Kaiserslautern, Germany, 2015. Available online: https://www.mpi-sws.org/tr/2015-004.pdf (accessed on 16 July 2025).
- Han, T.; Gong, X.; Liu, J. CARDSHARK: Understanding and Stabilizing Linux Kernel Concurrency Bugs Against the Odds. In Proceedings of the 33rd USENIX Security Symposium (USENIX Security 24), Philadelphia, PA, USA, 14–16 August 2024; pp. 1867–1884. [Google Scholar]
- Bianchi, F.A.; Pezzè, M.; Terragni, V. A Search-Based Approach to Reproduce Crashes in Concurrent Programs. In Proceedings of the 11th Joint Meeting on Foundations of Software Engineering (ESEC/FSE), Paderborn, Germany, 4–8 September 2017; pp. 221–232. [Google Scholar] [CrossRef]
- Rasheed, S.; Dietrich, J.; Tahir, A. On the Effect of Instrumentation on Test Flakiness. In Proceedings of the 2023 IEEE/ACM International Conference on Automation of Software Test (AST), San Francisco, CA, USA, 15–16 May 2023; pp. 329–341. [Google Scholar] [CrossRef]
- Xu, J.; Wolff, D.; Han, X.; Li, J.; Roychoudhury, A. Concurrency Testing in the Linux Kernel via eBPF. arXiv 2025, arXiv:2504.21394. [Google Scholar] [CrossRef]
- Musuvathi, M.; Qadeer, S.; Ball, T.; Basler, G.; Nainar, P.A.; Neamtiu, I. Finding and Reproducing Heisenbugs in Concurrent Programs. In Proceedings of the 8th USENIX Symposium on Operating Systems Design and Implementation (OSDI 2008), San Diego, CA, USA, 8–10 December 2008; pp. 267–280. [Google Scholar]
- Shashank, S.S.; Sachdeva, J.; Mukherjee, S.; Deligiannis, P. Nekara: A Generalized Concurrency Testing Library. In Proceedings of the 36th IEEE/ACM International Conference on Automated Software Engineering (ASE), Melbourne, Australia, 15–19 November 2021; pp. 634–646. [Google Scholar] [CrossRef]
- Lee, S.; Zhang, H.; Viswanathan, M. Probabilistic Concurrency Testing for Weak Memory Programs. In Proceedings of the 28th ACM SIGPLAN Symposium on Principles and Practice of Parallel Programming (PPoPP), Montreal, QC, Canada, 25 February–1 March 2023; pp. 133–147. [Google Scholar] [CrossRef]
- Elmas, T.; Burnim, J.; Necula, G.C.; Sen, K. CONCURRIT: A Domain Specific Language for Reproducing Concurrency Bugs. In Proceedings of the 34th ACM SIGPLAN Conference on Programming Language Design and Implementation (PLDI ’13), Seattle, WA, USA, 16–19 June 2013; pp. 441–452. [Google Scholar] [CrossRef]
- Chen, Y.; Liu, S.; Gan, Q. Effective Concurrency Testing for Go via Directional Primitive Scheduling. In Proceedings of the 38th IEEE/ACM International Conference on Automated Software Engineering (ASE), Luxembourg, 11–15 November 2023; pp. 138–149. [Google Scholar] [CrossRef]
- Li, X.; Li, W.; Zhang, Y.; Zhang, L. DeepFL: Integrating Multiple Fault Diagnosis Dimensions for Deep Fault Localization. In Proceedings of the 28th ACM SIGSOFT International Symposium on Software Testing and Analysis (ISSTA ’19), Beijing, China, 15–19 July 2019; ACM: New York, NY, USA, 2019; pp. 169–180. [Google Scholar] [CrossRef]
- Böttinger, K.; Godefroid, P.; Singh, R. Learn&Fuzz: Machine Learning for Input Fuzzing. arXiv 2018, arXiv:1701.07232. [Google Scholar] [CrossRef]
- Amalfitano, D.; Faralli, S.; Hauck, J.C.R.; Matalonga, S.; Distante, D. Artificial Intelligence Applied to Software Testing: A Tertiary Study. ACM Comput. Surv. 2023, 56, 58. [Google Scholar] [CrossRef]
- Feng, X.; Zhu, X.; Han, Q.L.; Zhou, W.; Wen, S.; Xiang, Y. Detecting Vulnerability on IoT Device Firmware: A Survey. IEEE/CAA J. Autom. Sin. 2023, 10, 25–41. [Google Scholar] [CrossRef]
- Zhu, X.; Zhou, W.; Han, Q.L.; Ma, W.; Wen, S.; Xiang, Y. When Software Security Meets Large Language Models: A Survey. IEEE/CAA J. Autom. Sin. 2025, 12, 317–334. [Google Scholar] [CrossRef]
- Zhu, X.; Wen, S.; Camtepe, S.; Xiang, Y. Fuzzing: A Survey for Roadmap. ACM Comput. Surv. 2022, 54, 230. [Google Scholar] [CrossRef]
- Leesatapornwongsa, T.; Lukman, J.F.; Lu, S.; Gunawi, H.S. TaxDC: A Taxonomy of Non-Deterministic Concurrency Bugs in Datacenter Distributed Systems. In Proceedings of the 51st ACM SIGPLAN Conference on Programming Language Design and Implementation (PLDI ’16), Santa Barbara, CA, USA, 13–17 June 2016; Volume 51, pp. 517–530. [Google Scholar] [CrossRef]
- Engler, D.R.; Ashcraft, K. RacerX: Effective, Static Detection of Race Conditions and Deadlocks. In Proceedings of the 19th ACM Symposium on Operating Systems Principles (SOSP ’03), Bolton Landing, NY, USA, 19–22 October 2003; pp. 237–252. [Google Scholar] [CrossRef]
- Wang, Y.; Kelly, T.; Kudlur, M.; Lafortune, S.; Mahlke, S. Gadara: Dynamic Deadlock Avoidance for Multithreaded Programs. In Proceedings of the 8th USENIX Symposium on Operating Systems Design and Implementation (OSDI ’08), San Diego, CA, USA, 8–10 December 2008. [Google Scholar]
- Xu, M.; Bodík, R.; Hill, M.D. A Serializability Violation Detector for Shared-Memory Server Programs. In Proceedings of the 2005 ACM SIGPLAN Conference on Programming Language Design and Implementation (PLDI ’05), Chicago, IL, USA, 12–15 June 2005; pp. 1–14. [Google Scholar] [CrossRef]
- Lu, S.; Park, S.; Seo, E.; Zhou, Y. Learning from Mistakes: A Comprehensive Study on Real World Concurrency Bug Characteristics. In Proceedings of the 13th International Conference on Architectural Support for Programming Languages and Operating Systems (ASPLOS ’08), Seattle, WA, USA, 1–5 March 2008; pp. 329–339. [Google Scholar] [CrossRef]
- Savage, S.; Burrows, M.; Nelson, G.; Sobalvarro, P.; Anderson, T. Eraser: A Dynamic Data Race Detector for Multithreaded Programs. ACM Trans. Comput. Syst. 1997, 15, 391–411. [Google Scholar] [CrossRef]
- Serebryany, K.; Potapenko, A.; Iskhodzhanov, T.; Vyukov, D. Dynamic Race Detection with LLVM Compiler: Compile-Time Instrumentation for ThreadSanitizer. In Runtime Verification (RV 2011); Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2012; Volume 7186, pp. 110–114. [Google Scholar] [CrossRef]
- Dudnik, P.; Swift, M.M. Condition Variables and Transactional Memory: Problem or Opportunity? In Proceedings of the 4th ACM SIGPLAN Workshop on Transactional Computing (TRANSACT ’09), Raleigh, NC, USA, 15 February 2009. [Google Scholar]
- Lu, S.; Tucek, J.; Qin, F.; Zhou, Y. AVIO: Detecting Atomicity Violations via Access-Interleaving Invariants. In Proceedings of the 12th International Conference on Architectural Support for Programming Languages and Operating Systems (ASPLOS ’06), San Jose, CA, USA, 21–25 October 2006; pp. 37–48. [Google Scholar] [CrossRef]
- Zhang, W.; Yao, C.; Lu, S.; Huang, J.; Tan, T.; Liu, X. ConSeq: Detecting Concurrency Bugs Through Sequential Errors. In Proceedings of the 16th International Conference on Architectural Support for Programming Languages and Operating Systems (ASPLOS ’11), Newport Beach, CA, USA, 5–11 March 2011; ACM: New York, NY, USA, 2011; pp. 251–264. [Google Scholar] [CrossRef]
- Tu, T.; Liu, X.; Song, L.; Zhang, Y. Understanding Real-World Concurrency Bugs in Go. In Proceedings of the 24th International Conference on Architectural Support for Programming Languages and Operating Systems (ASPLOS ’19), Providence, RI, USA, 13–19 April 2019; pp. 865–878. [Google Scholar] [CrossRef]
- Liu, Z.; Zhu, S.; Qin, B.; Chen, H.; Song, L. Automatically Detecting and Fixing Concurrency Bugs in Go Software Systems. In Proceedings of the 26th International Conference on Architectural Support for Programming Languages and Operating Systems (ASPLOS ’21), Virtual Event, 12–23 April 2021; pp. 616–629. [Google Scholar] [CrossRef]
- Sipper, M.; Green, B.; Ronen, Y.; Gat, T.; Hoffman, S.; Zohar, N. EC-KitY: Evolutionary computation tool kit in Python with seamless machine learning integration. SoftwareX 2023, 23, 101381. [Google Scholar] [CrossRef]
- Goldberg, D.E. Genetic Algorithms in Search, Optimization and Machine Learning; Addison-Wesley: Reading, MA, USA, 1989. [Google Scholar]
- Karafotias, G.; Hoogendoorn, M.; Eiben, A.E. Parameter Control in Evolutionary Algorithms: Trends and Challenges. IEEE Trans. Evol. Comput. 2015, 19, 167–187. [Google Scholar] [CrossRef]
- Elyasaf, A.; Farchi, E.; Margalit, O.; Weiss, G.; Weiss, Y. Generalized Coverage Criteria for Combinatorial Sequence Testing. IEEE Trans. Softw. Eng. 2023, 49, 4023–4034. [Google Scholar] [CrossRef]
- Wasserstein, R.L.; Lazar, N.A. The ASA’s Statement on p-Values: Context, Process, and Purpose. Am. Stat. 2016, 70, 129–133. [Google Scholar] [CrossRef]
- Liu, K.; Chen, Z.; Liu, Y.; Zhang, J.M.; Harman, M.; Han, Y.; Ma, Y.; Dong, Y.; Li, G.; Huang, G. LLM-Powered Test Case Generation for Detecting Bugs in Plausible Programs. arXiv 2024, arXiv:2404.10304. [Google Scholar] [CrossRef]
- Ouédraogo, W.C.; Plein, L.; Kaboré, K.; Habib, A.; Klein, J.; Lo, D.; Bissyandé, T.F. Enriching Automatic Test Case Generation by Extracting Relevant Test Inputs from Bug Reports. Empir. Softw. Eng. 2025, 30, 85. [Google Scholar] [CrossRef]
- Benavoli, A.; Corani, G.; Mangili, F. Should we really use post-hoc tests based on mean-ranks? arXiv 2015, arXiv:1505.02288. [Google Scholar] [CrossRef]
- Might, M.; Horn, D.V. A Family of Abstract Interpretations for Static Analysis of Concurrent Higher-Order Programs. In Static Analysis (SAS 2011); Lecture Notes in Computer Science; Yahav, E., Ed.; Springer: Berlin/Heidelberg, Germany, 2011; Volume 6887, pp. 180–197. [Google Scholar] [CrossRef]
- Bora, U.; Vaishay, S.; Joshi, S.; Upadrasta, R. OpenMP Aware MHP Analysis for Improved Static Data-Race Detection. In Proceedings of the 7th IEEE/ACM Workshop on the LLVM Compiler Infrastructure in HPC (LLVM-HPC ’21), St. Louis, Missouri, USA, 14 November 2021; IEEE/ACM: Piscataway, NJ, USA, 2021; pp. 1–11. [Google Scholar] [CrossRef]
- Matsakis, N.D.; Klock, F.S., II. The Rust Language. Ada Lett. 2014, 34, 103–104. [Google Scholar] [CrossRef]
- Godefroid, P.; Klarlund, N.; Sen, K. DART: Directed Automated Random Testing. In Proceedings of the 2005 ACM SIGPLAN Conference on Programming Language Design and Implementation (PLDI), Association for Computing Machinery, Chicago, IL, USA, 12–15 June 2005; pp. 213–223. [Google Scholar] [CrossRef]
- Tehrani, A.; Khaleel, M.; Akbari, R.; Jannesari, A. DeepRace: Finding Data Race Bugs via Deep Learning. arXiv 2019, arXiv:1907.07110. [Google Scholar] [CrossRef]
- Chen, H.; Guo, S.; Xue, Y.; Sui, Y.; Zhang, C.; Li, Y.; Wang, H.; Liu, Y. MUZZ: Thread-aware Grey-box Fuzzing for Effective Bug Hunting in Multithreaded Programs. In Proceedings of the 29th USENIX Security Symposium (USENIX Security ’20), Boston, MA, USA, 12–14 August 2020; pp. 2325–2342. [Google Scholar]
- Roemer, J.; Genç, K.; Bond, M.D. SmartTrack: Efficient Predictive Race Detection. In Proceedings of the 41st ACM SIGPLAN Conference on Programming Language Design and Implementation (PLDI ’20), London, UK, 15–20 June 2020; ACM: New York, NY, USA, 2020; pp. 747–762. [Google Scholar] [CrossRef]
- O’Callahan, R.; Jones, C.; Froyd, N.; Huey, K.; Noll, A.; Partush, N. Engineering Record And Replay For Deployability. In Proceedings of the 2017 USENIX Annual Technical Conference (USENIX ATC ’17), Santa Clara, CA, USA, 12–14 July 2017; USENIX Association: Berkeley, CA, USA, 2017; pp. 377–390. [Google Scholar]
- Holzmann, G.J. The Model Checker SPIN. IEEE Trans. Softw. Eng. 1997, 23, 279–295. [Google Scholar] [CrossRef]
- Clarke, E.M.; Biere, A.; Raimi, R.; Zhu, Y. Bounded Model Checking Using Satisfiability Solving. Form. Methods Syst. Des. 2001, 19, 7–34. [Google Scholar] [CrossRef]
- Clarke, E.M.; Grumberg, O.; Jha, S.; Lu, Y.; Veith, H. Counterexample-Guided Abstraction Refinement. In Proceedings of the 12th International Conference on Computer Aided Verification (CAV), Chicago, IL, USA, 15–19 July 2000; Lecture Notes in Computer Science. Springer: Berlin/Heidelberg, Germany, 2000; Volume 1855, pp. 154–169. [Google Scholar] [CrossRef]
- Namjoshi, K.S.; Trefler, R.J. Parameterized Compositional Model Checking. In Proceedings of the Tools and Algorithms for the Construction and Analysis of Systems (TACAS 2016), Eindhoven, The Netherlands, 4–7 April 2016; Lecture Notes in Computer Science. Volume 9636, pp. 589–606. [Google Scholar] [CrossRef]
- Legay, A.; Lukina, A.; Traonouez, L.; Yang, J.; Smolka, S.A.; Grosu, R. Statistical Model Checking. In Computing and Software Science; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2019; Volume 11506, pp. 478–504. [Google Scholar] [CrossRef]
- Xu, M.; Kashyap, S.; Zhao, H.; Kim, T. KRACE: Data Race Fuzzing for Kernel File Systems. In Proceedings of the 2020 IEEE Symposium on Security and Privacy (SP), Virtual, 18–20 May 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1643–1660. [Google Scholar] [CrossRef]
- Tian, Y.; Yu, Y.; Wang, P.; Zhou, R.; Jin, H.; Xie, T. RACEBENCH: A Benchmark Suite for Data Race Detection Tools. In Proceedings of the 19th ACM SIGSOFT Symposium and the 13th European Conference on Foundations of Software Engineering (ESEC/FSE ’11), Szeged, Hungary, 5–9 September 2011; ACM: New York, NY, USA, 2011; pp. 142–151. [Google Scholar] [CrossRef]
- Lin, Z.; Marinov, D.; Zhong, H.; Chen, Y.; Zhao, J. JaConTeBe: A Benchmark Suite of Real-World Java Concurrency Bugs. In Proceedings of the 30th IEEE/ACM International Conference on Automated Software Engineering (ASE ’15), Lincoln, NE, USA, 9–13 November 2015; IEEE/ACM: Piscataway, NJ, USA, 2015; pp. 178–189. [Google Scholar] [CrossRef]
- Just, R.; Jalali, D.; Ernst, M.D. Defects4J: A Database of Existing Faults to Enable Controlled Testing Studies for Java Programs. In Proceedings of the 2014 International Symposium on Software Testing and Analysis (ISSTA ’14), San Jose, CA, USA, 21–25 July 2014; pp. 437–440. [Google Scholar] [CrossRef]
- Madeiral, F.; Urli, S.; de Almeida Maia, M.; Monperrus, M. BEARS: An Extensible Java Bug Benchmark for Automatic Program Repair Studies. In Proceedings of the 26th IEEE International Conference on Software Analysis, Evolution and Reengineering (SANER ’19), Hangzhou, China, 24–27 February 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 468–478. [Google Scholar] [CrossRef]
- Karampatsis, R.; Sutton, C. How Often Do Single-Statement Bugs Occur?: The ManySStuBs4J Dataset. In Proceedings of the 17th International Conference on Mining Software Repositories (MSR ’20), Online Event, 29–30 June 2020; ACM: New York, NY, USA, 2020; pp. 573–577. [Google Scholar] [CrossRef]
- Yuan, T.; Li, G.; Lu, J.; Liu, C.; Li, L.; Xue, J. GoBench: A Benchmark Suite of Real-World Go Concurrency Bugs. In Proceedings of the 18th Annual IEEE/ACM International Symposium on Code Generation and Optimization (CGO ’21), Virtual Conference, 27 February–3 March 2021; IEEE/ACM: New York, NY, USA, 2021; pp. 187–199. [Google Scholar] [CrossRef]
- Torres, C.F.; Iannillo, A.K.; Gervais, A.; State, R. ConFuzzius: A Data Dependency-Aware Hybrid Fuzzer for Smart Contracts. In Proceedings of the 2021 IEEE European Symposium on Security and Privacy (EuroS&P ’21), Virtual Conference, 6–10 September 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 213–228. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).