Abstract
Mathematical modeling is indispensable in oncology for unraveling the interplay between tumor growth, vascular remodeling, and therapeutic resistance. We present a hybrid modeling framework (continuum-discrete) and present its hybrid mathematical formulation as a coupled partial differential equation–agent-based (PDE-ABM) system. It couples reaction–diffusion fields for oxygen, drug, and tumor angiogenic factor (TAF) with discrete vessel agents and stochastic phenotype transitions in tumor cells. Stochastic phenotype switching is handled with an exact Gillespie algorithm (a Monte Carlo method that simulates random phenotype flips and their timing), while moment-closure methods (techniques that approximate higher-order statistical moments to obtain a closed, tractable PDE description) are used to derive mean-field PDE limits that connect microscale randomness to macroscopic dynamics. We provide existence/uniqueness results for the coupled PDE-ABM system, perform numerical analysis of discretization schemes, and derive analytically tractable continuum limits. By linking stochastic microdynamics and deterministic macrodynamics, this hybrid mathematical formulation—i.e., the coupled PDE-ABM system—captures bidirectional feedback between hypoxia-driven angiogenesis and resistance evolution and provides a rigorous foundation for predictive, multiscale oncology models.
Keywords:
mathematical oncology; tumor microenvironment; tumor resistance; angiogenesis; hypoxia; multiscale modeling; hybrid modeling; reaction–diffusion equations; mean-field limit; stochastic phenotypic switching MSC:
35K51; 35K57; 60J25; 65M06; 65M12; 92B05; 92C17
1. Introduction
Cancer remains a leading cause of global mortality, accounting for 16.8% of all deaths and 22.8% of deaths related to non-communicable diseases [1]. Despite advances in targeted therapy, immunotherapy, and radiation therapy, therapeutic resistance persists as the main barrier to achieving durable cures, often resulting in relapse or refractory disease [2]. Here, we focus on how resistance mechanisms, particularly those driven by tumor angiogenesis, undermine current treatments and perpetuate a poor prognosis. Resistance arises from both intrinsic tumor heterogeneity (e.g., spatial and temporal genetic diversity [3]) and adaptive responses to therapy, with the tumor microenvironment (TME) playing a central role. Among these factors, dysregulated angiogenesis emerges as a critical facilitator of resistance. Tumors hijack pro-angiogenic pathways (e.g., vascular endothelial growth factor/vascular endothelial growth factor receptor (VEGF/VEGFR), hypoxia-inducible factor-1 (HIF-1)) to maintain growth, while suppressing antiangiogenic signals (e.g., thrombospondin-1 (TSP-1)) [4]. This “angiogenic switch” not only fuels tumor progression, but also establishes a resilient vascular niche that evades therapy. Although antiangiogenic agents (e.g., bevacizumab) initially improve progression-free survival by blocking VEGF, their long-term efficacy is limited by rapid resistance [5,6]. Specifically, tumors activate compensatory pathways (e.g., fibroblast growth factor 2 (FGF-2), interleukin-8 (IL-8), and angiopoietin-2 (ANGPT-2)) to restore angiogenesis [7], while stromal components (e.g., tumor-associated macrophages (TAMs), myeloid-derived suppressor cells (MDSCs)) further sustain vascular remodeling via cytokine secretion [8]. These findings reveal a paradox: inhibition of angiogenesis can inadvertently select more aggressive adaptive phenotypes. To overcome this challenge, we argue that disrupting the dynamic crosstalk between tumor cells and angiogenic TME is essential. Recent studies suggest that combinatorial targeting of both VEGF and compensatory pathways (e.g., FGF-2/IL-8) may delay resistance [9]. However, a systematic framework for predicting adaptive responses of tumors and optimizing combination regimens is still lacking. In this study, we propose a computational hybrid modeling framework (continuum-discrete) to identify vulnerabilities in angiogenic networks and investigate the bidirectional coupling between angiogenesis and tumor resistance evolution. To address this need, we first contextualize the existing modeling paradigms that inform such integrative frameworks.
Continuum models efficiently capture bulk tumor growth and transient dynamics. The Keller–Segel framework describes cell migration via partial differential equations (PDEs), where endothelial cells follow chemical gradients [10]. Such models assume continuous cell densities, overlooking individual cell heterogeneity. The Fisher-KPP equation [11,12] links proliferation and motility to model tumor spread as reaction–diffusion waves, but cannot resolve rare stochastic events such as resistance mutations. Discrete models track individual cell behavior and microenvironment heterogeneity. Anderson et al. [13] pioneered agent-based models (ABMs) to simulate capillary sprouting through stochastic tip-cell migration rules, but lack coupling to continuum metabolite fields (e.g., oxygen gradients) and microenvironmental feedback (e.g., hypoxia-driven angiogenesis). Despite these advances, both approaches face inherent limitations: Continuum models lack single-cell resolution for stochastic events (e.g., mutations, phenotype switching) and spatiotemporal heterogeneity, while discrete models are computationally prohibitive for large-scale dynamics (e.g., diffusion, fluid flow). This dichotomy motivates hybrid frameworks that transcend scale constraints.
Hybrid modeling framework (continuum-discrete) integrates agent-based rules with reaction–diffusion equations to reflect cancer’s multiscale nature [14,15,16]. Some hybrid modeling frameworks (continuum-discrete) address drug resistance evolution. Gevertz et al. [17] coupled continuous drug and oxygen fields with agent-based tumor dynamics to study preexisting and acquired resistance, but assumed stationary vessels, uniform resistance acquisition capacity, and continuous drug administration. Picco et al. [18] modeled environmentally mediated drug resistance (EMDR) using drug and signaling fields, generating EMDR by increasing vascular density but neglecting vascular remodeling. Other hybrid modeling frameworks (continuum-discrete) coupled tumor growth with angiogenesis [19,20]. Macklin et al. [21] developed a multiscale modeling framework (molecular→cell→tissue) integrating extracellular matrix, angiogenesis, and tumor progression. Despite these innovations, a critical gap persists: Most models simulate vascular remodeling or resistance in isolation, omitting spatiotemporal feedback where vessel adaptation alters resistance trajectories. One exception is Wang et al. [22], who proposed a hybrid modeling framework (continuum-discrete) that couples hypoxia-induced angiogenesis with resistance selection, but left unresolved three limitations: (i) inadequate mathematical analysis of the hybrid system, insufficient numerical scheme analysis, and absence of derived mean-field limits for agent dynamics. Our work directly addresses these gaps while extending their framework.
On the other hand, from a methodological perspective, hybrid models raise two interlinked challenges that motivate this work. First, coupling discrete stochastic dynamics to continuum fields requires careful analysis of well-posedness and the derivation of mean-field limits that quantify when and where PDE surrogates are valid. Second, hybrid numerical schemes must control combined discretization and sampling errors while preserving important qualitative properties (nonnegativity, mass conservation) across scales. Prior hybrid and multiscale works have made important progress on computational approaches and applications [13,23,24], but formal mathematical guarantees (existence/uniqueness, rigorous mean-field convergence) and a systematic numerical error analysis for angiogenesis–resistance couplings remain limited. In this paper, we address these gaps by providing well-posedness results for the coupled PDE-ABM system, a mean-field derivation that links the Gillespie-driven stochastic rules to deterministic PDE limits, and a numerical analysis that quantifies discretization vs. sampling errors for the hybrid solver.
We advance the hybrid modeling framework (continuum-discrete) in [22] through three innovations: First, we introduce a spatially resolved model that unifies stochastic phenotypic switching via a Gillespie algorithm to capture drug-induced resistance transitions. Second, we incorporate metabolite-regulated angiogenesis in which vessel agents respond to dynamic hypoxia (o) and tumor angiogenic factor (TAF) (c) gradients. Third, we establish bidirectional coupling that allows for emergent feedback between hypoxia, angiogenesis, and resistance evolution. Consequently, this framework yields three contributions: rigorous mathematical analysis of the coupled PDE-ABM system and numerical analysis of PDE discretization schemes; integration of exact stochastic resistance (Gillespie ABM) with physics-driven angiogenesis (PDE-coupled ABM); and derivation of analytically tractable continuum mean-field limits from discrete rules. The mean-field limit integrates the hybrid mathematical formulation (PDE-ABM) into one PDE system, linking stochastic microdynamics with deterministic macrodynamics. It motivates innovative hybrid numerical schemes that selectively retain the full ABM structure in critical regions while replacing it with efficient PDE surrogates elsewhere. By unifying PDE analysis, stochastic analysis, and numerical analysis, our hybrid modeling framework (continuum-discrete) moves beyond descriptive modeling to establish rigorous mathematical foundations for hybrid PDE-ABM systems.
This paper is structured as follows: Section 2 details the hybrid mathematical formulation (PDE-ABM). Section 3 links our model to classical mathematical biology frameworks and outlines contributions. Section 4 provides a mathematical analysis of the coupled system. Section 5 presents numerical analysis, including consistency, stability, convergence, and conservation properties. Section 6 concludes.
2. Hybrid Mathematical Formulation (PDE-ABM)
We use a hybrid mathematical framework that integrates continuum models (reaction–diffusion equations) with ABMs. This approach couples the dynamics of reaction–diffusion fields (TAF, drug, oxygen) with discrete tumor and vessel agents, allowing for the simulation of tumor growth and vascular remodeling at multiple spatial and temporal scales. For clarity, we distinguish between the hybrid modeling framework (methodological approach) and the hybrid mathematical formulation (mathematical coupling), as detailed in the Appendix A. Our framework is hybrid in method (continuum-discrete) and multiscale in scope (molecular→cell→tissue), as shown in Figure A1.
Building on the biological foundations presented in the Introduction, we formalize the hybrid mathematical formulation (PDE-ABM) that couples continuum and agent-based components. The system governs the dynamics of TAF (c), drug (d), and oxygen (o) via reaction–diffusion equations, while endothelial cell migration is modeled by a chemotaxis equation:
where n represents the endothelial cell density, and the chemotactic flux is modulated by TAF concentration gradients. The agent-based components simulate tumor and vessel cells, each characterized by local oxygen levels, accumulated drug, DNA damage, and other key factors. The tumor population is divided into normoxic () and hypoxic () subpopulations, and discrete tumor and vessel agents interact with the TME through stochastic, rule-based ABM dynamics. The model incorporates bidirectional feedback, where hypoxia induces angiogenesis, which alters drug delivery and selects for resistance.
The nondimensionalized system for the fields is derived from the dimensional system as described in Appendix B:
Here, , , , are diffusion coefficients; is the chemotactic sensitivity; is the saturation parameter; , , are decay rates; , are cellular uptake rates; , are supply rates from blood vessels; and , are production/uptake rates of TAF. The characteristic functions and describe the spatial extent of tumor cells and vessels, respectively, as given by
Here, denotes the center of position of a and v. We choose a closed domain with boundary and impose homogeneous Neumann conditions:
where is the outward unit normal at .
Tumor and vessel agents evolve on a lattice discretizing the ABM domain into squares of side length . Tip cell motion uses the von Neumann neighborhood structure (four orthogonal neighbors), while agent-microenvironment interactions use the Moore structure (eight neighbors including diagonals).
We construct a PDE domain with boundary approximating . Appendix C details the mapping and the numerical derivation of the discrete lattice in the ABM. Briefly, define the open -neighborhood of with . Convolve its characteristic with a compactly supported mollifier , and set
for small ensuring . This yields a domain whose boundary is proximal to . We obtain the discrete approximation by sampling on the ABM lattice, thresholding at level , and identifying boundary agents as those with Moore neighbors outside . Algorithm A1 summarizes the construction.
Each tumor cell has the following state:
denoting position, local oxygen, accumulated drug, DNA damage, death threshold, age, and maturation time. Each tip cell b has the following state:
for position and age since the last branching. Agent states update via Markov processes under the time discretization of :
where is the Markov transition operator [22]. Algorithm A2 summarizes the transition operator for each mark x of tumor and endothelial tip cells. Local cell density includes tumor–vessel interactions in our current model:
We decouple phenotype switching from cell division. Unlike classical mutation models linking resistance acquisition to division events [25,26], stochastic transitions occur through continuous-time Markov processes independent of division cycles. Mutation elevates the death threshold, DNA repair rate, and oxygen consumption rate but reduces the proliferation rate. Phenotypic traits
take sensitive () and resistant () values:
Cells stochastically switch between these states according to the reaction channels
where baseline rates and , drug sensitivity coefficients and , sensitive-to-resistant mutation rate and resistant-to-sensitive mutation rate
govern phenotypic switching. Each tumor cell bears a phenotypic mark
updated independently of the cell cycle via the Gillespie algorithm, which preserves the exact timing of rare events. This method allows the model to simulate the emergence of drug resistance without relying on cell division cycles [27]. Waiting times follow an exponential distribution with mean (: total propensity):
Each switching event selects the reacting agent by propensities, flips its phenotype (), and updates time-dependent quantities. Algorithm 1 encapsulates phenotype switching procedures. This Gillespie framework permits resistance emergence independent of cell division, capturing stochastic gene expression fluctuations. It thus recovers resistance in rare subpopulations that deterministic ordinary differential equation (ODE)/PDE models average out, and naturally quantifies treatment schedule effects on resistance probability and timing. Table 1 and Table 2 provide a comprehensive list of all symbols, subscripts, and superscripts, along with their definitions and references to their first appearance in the text.

Table 1.
Nomenclature for the hybrid modeling framework (continuum-discrete). All symbols are defined at first occurrence in the manuscript. Nondimensional parameter values used for numerical validation, as detailed in Section 5, are provided for the reader’s convenience and can be found in [22]. The parameter values listed correspond to the symbols on the left, in the order they appear. For example, correspond to the values , respectively.

Table 2.
Nomenclature for the hybrid modeling framework (continuum-discrete). All symbols are defined at first occurrence in the manuscript. No nondimensional value parameters in Table 2 are used for numerical validation, so we omit the nondimensional value.
Our model uniquely captures bidirectional feedback: how hypoxia induces angiogenesis, which alters drug delivery and selects resistance. The theoretical framework justifies how small changes in local oxygen or vessel density can produce nonlinear shifts in resistance trajectories. These feedback mechanisms align with clinical observations where antiangiogenic therapies may paradoxically increase resistance risk. Thus, the model could be used to explore: (i) critical thresholds in vessel remodeling that shift tumor response from chemosensitive to chemoresistant, and (ii) timing effects, e.g., whether antiangiogenic pretreatment amplifies or delays resistant onset.
| Algorithm 1 Stochastic phenotype switching via the Gillespie Direct Method. |
|
Our agent-based model represents capillary sprouting through stochastic branching events of endothelial tip cells, which respond to local TAF concentrations as specified in Equation (6) and Algorithm A2. Each branching event initiates a new tip cell that subsequently migrates chemotactically, capturing the initiating mechanism of angiogenesis in simplified form. Although the current framework does not simulate the full vascular morphology, including lumenization, anastomosis, or perfusion, it provides the mathematical foundation for incorporating these angiogenic modules. The model components map to biological processes as follows. The chemotaxis flux term models directed endothelial migration along the TAF (c) gradients, with the saturation factor representing receptor saturation or desensitization at high concentrations, thus capturing tip cell guidance to hypoxic regions. Reaction–diffusion equations govern the metabolite fields (), where the diffusion terms model interstitial transport of oxygen, drug, and TAF; decay terms represent clearance or degradation; and the source/sink terms model secretion by hypoxic cells, vascular supply, and cellular consumption. These continuum fields efficiently represent tissue-scale gradients that establish selective microenvironmental pressures, such as hypoxia-induced drug resistance [28]. Characteristic functions formalize the representation of cells and vessels as localized sources/sinks within finite neighborhoods (radius disks , capturing pericellular secretion/uptake while maintaining a continuum description elsewhere. Discrete agent-based rules govern vessel tip dynamics, branching, and anastomosis, capturing discrete events poorly approximated by continuum densities when tip numbers are small or vascular topology matters, while tumor agents track state variables (local oxygen, accumulated drug, damage) that mediate cell-level decisions including division, death, and phenotype switching, with lattice neighborhoods (von Neumann for motion, Moore for interactions) reflecting spatial locality. Stochastic phenotype transitions implement continuous-time Markov events with drug-dependent propensities (), representing non-divisional transcriptional/epigenetic transitions and drug-induced resistance through Gillespie algorithms that preserve exact timing statistics of rare switching events and allow quantification of resistance emergence probabilities and timelines. For regions with large populations and weak correlations (e.g., dense tumor cores), first-moment closure techniques approximate the agent-based model via deterministic mean-field PDEs (Equation (15)) where stochastic fluctuations average out, while the full agent-based description remains essential in low cell number regimes (invasion fronts, metastatic niches) where extinction or rare events dominate. Finally, numerical stability constraints, particularly the chemotaxis CFL condition (Section 5.4), reflect biological timescales by requiring sufficiently small time steps to resolve rapid chemotactic drift, biologically corresponding to regimes of strong TAF guidance and rapid vascular remodeling.
3. Relation to Classical Cancer Modeling Frameworks and Contributions
Having formalized our hybrid (continuum-discrete) and multiscale modeling framework (molecular→cell→tissue), we contextualize its biological relevance through its mathematical lineage. This section demonstrates that limiting cases of our hybrid mathematical formulation (PDE-ABM) reduce rigorously to three foundational frameworks: Keller–Segel chemotaxis (predicts spatial aggregation and hotspots; clinically relevant because delivery is heterogeneous), Fisher-KPP invasion waves (connects to invasion/front speed and informs surveillance interval and timing of local therapies), and Galton–Watson branching processes (connects to probability of resistant clone extinction or establishment—a quantitative measure of relapse risk). These connections are mathematically exact. For a small chemokine concentration c such that , the endothelial cell equation simplifies to the classical Keller–Segel form:
Our model generalizes Keller–Segel by incorporating nonlinear chemotactic saturation and ABM coupling.
While endothelial migration follows chemotactic principles, tumor proliferation exhibits distinct spatiotemporal dynamics. This divergence aligns with the Fisher-KPP paradigm, governed by the equation:
where denotes density, D diffusion, growth rate, and K carrying capacity. Under normoxic conditions () and negligible drug (), tumor density equation (Equation (15)) reduces to
This predicts traveling wavefronts with minimal speed . Crucially, our full model extends this framework by incorporating microenvironmental heterogeneity (oxygen gradients, drug distribution), which distorts wavefronts into clinically observed asymmetric invasion patterns.
Complementing continuum-scale dynamics, cellular-scale proliferation exhibits stochastic foundations. Absent spatial coupling and microenvironmental feedback (e.g., well-mixed conditions), tumor lineage expansion follows a Galton–Watson branching process. A normoxic cell divides with probability or dies with probability in time interval , yielding the offspring distribution:
For two phenotypes (drug-sensitive S, drug-resistant R), this extends to a two-type Galton–Watson process with expected offspring matrix:
Crucially, classical branching models restrict phenotypic switching to division events. In contrast, our framework implements phenotype switching via a continuous-time Markov process simulated using the Gillespie algorithm (Algorithm 1), enabling asynchronous phenotype evolution independent of the cell cycle. Figure 1 illustrates interactions between branching proliferation and stochastic phenotype switching.
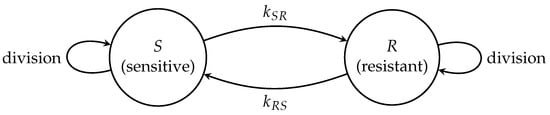
Figure 1.
ABM representation of tumor cell proliferation and phenotype switching. Drug-sensitive (S) and drug-resistant (R) cells undergo stochastic phenotype transitions () governed by mutation rates and . These transitions occur independently of cell division events and follow branching processes within each phenotypic state.
Our mathematically rigorous, biologically grounded hybrid modeling framework (continuum-discrete) extends classical theories through multiscale feedback, stochastic switching, and microenvironmental coupling. It advances hybrid modeling frameworks (continuum-discrete) by integrating agent-based stochastic phenotypic switching, continuum reaction–diffusion metabolite fields, and bidirectional vascular-resistance coupling. We provide analytical guarantees for model well-posedness, numerical robustness, and mean-field limits. Our contributions distinguish themselves from existing oncology hybrid models (e.g., [29,30,31]) in four key aspects:
- (i)
- Mean-Field Limits: Unlike direct continuum PDE-ABM coupling or variance reduction methods [29,30], we prove convergence from the stochastic agent-based description to a deterministic PDE limit using chemical master equations (CMEs) and moment closures. This yields a unified continuum system (16), linking stochastic microdynamics to deterministic macrodynamics. It motivates innovative hybrid numerical schemes retaining ABM structures in critical regions while employing efficient PDE surrogates elsewhere.
- (ii)
- Well-Posedness Analysis: While most stochastic-hybrid modeling frameworks (continuum-discrete) prioritize computation over analytical soundness [30,31], we establish complete well-posedness for our hybrid mathematical formulation (PDE-ABM). This includes the existence, uniqueness, and regularity of weak solutions (Theorems 1–3), plus analysis of numerical schemes: consistency (Section 5.3), conditional stability (Theorem 6), convergence (Theorem 7), nonnegativity (Theorem 8) and mass conservation (Theorem 9).
- (iii)
- Stochastic-Deterministic Feedback: Unlike [29], who model virus spread in lung tissue, our hybrid modeling framework (continuum-discrete) couples cell phenotype switching, angiogenic fields, and vascular remodeling. This reveals nonlinear resistance dynamics driven by environment-phenotype feedback, underpinned by rigorous mathematics and mean-field approximations.
- (iv)
- Clinical interpretability: While stochastic interacting particle fields (SIPFs) [31] or variance reduction techniques [30] emphasize algorithmic efficiency, our model explicitly links parameters (e.g., mutation rates, oxygen thresholds, drug uptake) to clinical outcomes (e.g., tumor front speed, resistance emergence). This offers a framework for optimizing treatment timing and dosage.
Thus, our work uniquely combines mathematical rigor (well-posedness, mean-field limits) with biologically interpretable hybrid modeling frameworks (continuum-discrete), delivering methodological novelty and translational potential beyond current stochastic-hybrid cancer models.
To make the clinical consequences of the analogies drawn above explicit, we summarize how each mathematical framework links model parameters to measurable clinical metrics.
The Keller–Segel analogy shows that chemotaxis drives vascular heterogeneity and uneven drug delivery. Chemotaxis-driven endothelial migration toward TAF generates aggregation or pattern-forming tendencies, clinically predicting vessel-density heterogeneity where localized high-vessel-density regions are adjacent to hypoxic niches [32]. Practically, this matters because heterogeneous drug delivery and oxygenation produce protected niches for resistant cell persistence [33,34], and lowering chemotactic sensitivity () reduces vascular “hotspots”, suggesting antiangiogenic normalization as a means of homogenizing drug delivery and perfusion [35]. A practical readout is the coefficient of variation (CV) [36] of vascular density or local perfusion versus ; a decreasing CV with reduction would quantify the improved uniformity of delivery.
Fisher-KPP dynamics link tumor invasion speed to therapy timing and surveillance. The diffusion-growth dynamics yield a minimal front speed , which can be interpreted as the tumor invasion rate [37]. Clinically, informs both the staging and the monitoring intervals in preclinical experiments; therapy that suppresses the net growth rate below the propagation threshold that sustains can stop front advance. Deviations from Fisher-KPP predictions highlight TME heterogeneity-driven invasion irregularities.
The Galton–Watson branch captures stochastic resistance emergence and the risk of relapse. Stochastic lineage branching links extinction probabilities to relapse risk driven either by de novo emergence of resistance clones or by rare preexisting resistant cells under different dosing regimens (see, e.g., [38] and references therein). Resistant clones are most likely to establish during pretreatment; therefore, early reduction in tumor burden reduces the probability of relapse [39]. A direct output of the model, the probability of resistance establishment (fraction of stochastic runs that produce persistent resistant clones) serves as a quantitative relapse risk metric.
Our framework translates mathematical parameters into clinically actionable metrics to guide decision-making. These analogies connect mathematical structure to actionable endpoints: vascular CV (delivery heterogeneity), (invasion speed), and clone establishment probability (relapse risk). This enables the prioritization of interventions (e.g., antiangiogenic + cytotoxic combinations), the tailoring of image frequency, and the quantitative assessment of resistance under dosing strategies.
4. Mathematical Analysis of the Coupled PDE-ABM Model
Biological motivation supports the hybrid modeling framework (continuum-discrete) design, but rigorous mathematical analysis remains essential to establish its validity and predictive reliability. This section systematically investigates the coupled PDE-ABM framework through three analytical pillars: (i) well-posedness of the PDE-ABM system (Section 4.1), guaranteeing solution existence, uniqueness, and regularity; (ii) master equation and mean-field analysis (Section 4.2), connecting discrete stochastic dynamics to deterministic continuum-scale approximations; and (iii) validity regimes for moment closure approximations, linking microscopic randomness with macroscopic behavior. This triad ensures mathematical robustness for therapeutic applications, including chemotherapy optimization and antiangiogenic interventions.
4.1. Well-Posedness
We establish the existence, uniqueness, and regularity of weak solutions for the coupled PDE-ABM system that governs the continuous fields . Without agent interactions, the PDEs reduce to a classical linear parabolic system with guaranteed well-posedness. We formalize this foundation using the Lions–Gelfand triple framework [40] (Theorem 10.9); see [41] for detailed proofs.
Lemma 1
(J.-L. Lions). Let be a Gelfand triple, with V and H Hilbert spaces and V densely and continuously embedded in H. The scalar product and the norm for H are and , and the norm for V is . Let . Suppose for almost every , is a time-dependent bilinear form satisfying:
- (i)
- For all , the function is measurable.
- (ii)
- for almost all and all .
- (iii)
- for almost all and all .
where , M, and C are constants. Then for and , there exists a unique function
satisfying the weak formulation:
with initial condition .
Figure 2 outlines the logical structure of J.-L. Lions lemma: Starting from the parabolic setup, it shows the Gelfand triple , conditions on the bilinear form (measurability, boundedness, coercivity), admissible inputs , , and the unique weak solution with . The final step establishes well-posedness, providing the functional analytic foundation for the coupled PDE model.
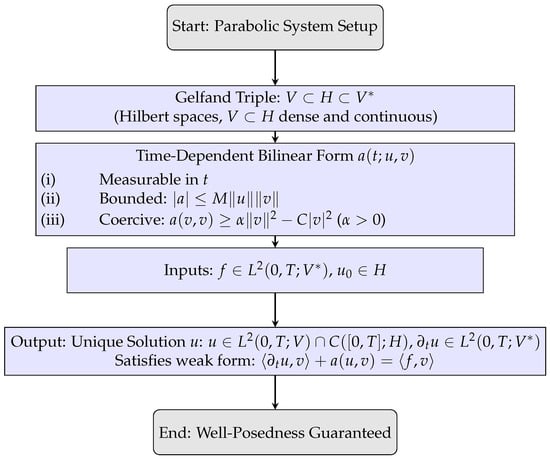
Figure 2.
Schematic flowchart illustrating the step-by-step conditions leading to weak solution well-posedness in J.-L. Lions’ lemma.
We now apply this result to the coupled reaction–diffusion equations on the finite time interval :
where and incorporates agent-dependent reaction terms:
We omit the analysis of the endothelial density equation:
Classical two-dimensional Keller–Segel systems exhibit chemotactic blow-up, that is, unbounded density in finite time [42,43], but admit global solutions under small-mass conditions. In particular, consider the following parabolic–elliptic Keller–Segel system:
where is the outward unit normal to and denotes the spatial average of n. Assume the initial mass satisfies:
Then, a global-in-time weak solution exists under the following conditions:
- (i)
- Bounded domain case: If U is a bounded, connected domain and ,
- (ii)
- Whole space case: If , with and .
This follows from [42,44] (Our endothelial PDE is parabolic–parabolic. Experimental observations of large chemoattractant diffusion coefficients justify the quasi-steady-state approximation , reducing the system to parabolic–elliptic Keller–Segel form. The small-mass global existence criteria then apply. We will rigorously derive analogous results for the full parabolic–parabolic case in future work).
Discrete agents represent the endothelial population in our hybrid mathematical formulation (PDE-ABM), replacing continuous density and further regularizing dynamics. Each tip occupies at most one lattice site. Vessel elongation occurs with a fixed period , and branching requires the tip cell age to exceed the threshold (). Anastomosis stabilizes the system: tip encounters cause emerging, reducing the tip count. These rules ensure a finite agent population and prevent uncontrolled mass concentration, consistent with lattice-based chemotaxis ABMs [13,25,26,45]. We thus focus our analysis on the subsystem. To manage PDE-ABM coupling, we introduce the following:
Assumption 1
(PDE-ABM Coupling).
- (i)
- The spatial domain is bounded with boundary .
- (ii)
- The initial data is nonnegative and belongs to .
- (iii)
- For all and lattice sites :
Assumption 1(iii) imposes a uniform local density bound, not global agent boundedness, as tumor proliferation may increase over time. This aligns with the biological crowding constraint in ABM rules: lattice sites accommodate finitely many agents within radius , and cell division halts at local density . Consequently, global agent growth does not compromise the local boundedness of PDE source terms, which is essential for coupled system well-posedness.
We define the weak formulation by seeking satisfying and for each , with:
and initial conditions . Here denotes the inner product, and is the duality pairing.
Theorem 1
(Existence and Uniqueness of Weak Solutions). Assumption 1 guarantees unique weak solutions for the coupled PDE-ABM system (11) with
Proof.
Apply Lemma 1 to each component via the Gelfand triple and coercive, bounded bilinear forms for . □
Theorem 1 establishes existence and uniqueness of weak solutions for each continuous field in the parabolic PDE system, using the Lions–Gelfand framework with the triple . Figure 3 summarizes the logical steps: construction of the functional setting, verification of bilinear form properties, admissible data, and the resulting weak solution. This result provides the analytic foundation for the full hybrid mathematical formulation (PDE-ABM).
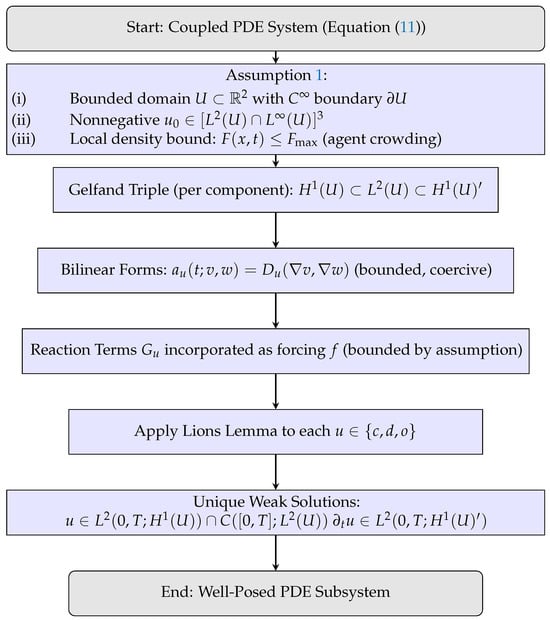
Figure 3.
Schematic flowchart illustrating the application of Lions lemma to the PDE subsystem under Assumption 1, yielding unique weak solutions.
Building on this, Theorem 2 extends well-posedness to the coupled PDE–ABM system by rigorously linking the deterministic PDE dynamics with the stochastic agent layer. The coupling is realized through a time discretization combined with an operator-splitting procedure, which ensures consistent integration of continuous and discrete dynamics within the same mathematical framework.
Theorem 2
(Well-posedness of the Coupled PDE-ABM System). Under Assumption 1 on with time steps :
- (i)
- The PDE subsystem admits a unique weak solution with Theorem 1 regularity.
- (ii)
- The ABM subsystem defines a càdlàg Markov process almost surely for agent marks
Proof.
Use mathematical induction over intervals . For , Theorem 1 establishes existence, uniqueness, and regularity on with initial data and fixed agent . Assume the result holds on . For :
- (i)
- Solve the parabolic subsystem on :which has unique weak solutions by Theorem 1.
- (ii)
- Evolve ABM marks on viawhere is the Markov transition operator. Agent trajectories are piecewise constant and exhibit right-continuity with left limits, thereby ensuring the càdlàg property of the corresponding Markov process.
Induction extends the result to . □
Theorem 2 establishes well-posedness of the hybrid PDE-ABM system by induction over the discretized mesh . Figure 4 summarizes the construction: PDE subsystems yield unique weak solutions (Theorem 1), after which the ABM is updated via the Markov operator , producing piecewise-constant càdlàg trajectories. Iterating across all intervals gives a uniquely defined coupled system on , highlighting the complementary roles of PDE regularity and ABM stochasticity.
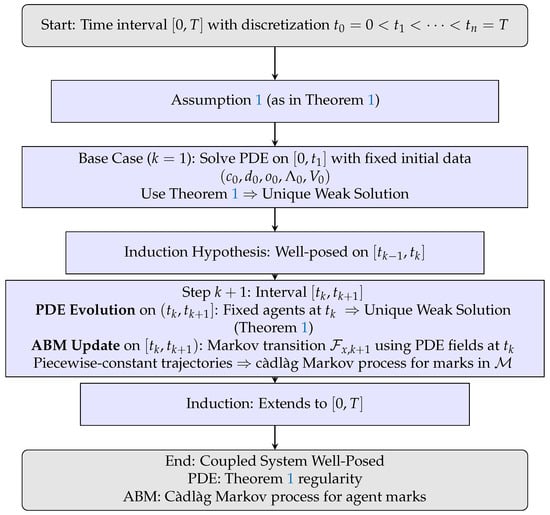
Figure 4.
Flowchart illustrating the inductive operator-splitting construction in Theorem 2. PDE updates ensure weak solutions (Theorem 1), while ABM updates define a càdlàg Markov process, yielding a well-posed coupled hybrid mathematical formulation (PDE-ABM). Remark 1 justifies the absence of splitting error.
Remark 1
(Justification of Stepwise Decoupling). Theorem 2 solves the PDE subsystem on each interval with fixed agent configuration . This approach directly implements the hybrid mathematical formulation’s operator–splitting scheme: PDE fields evolve continuously via (13) on , while agent updates occur discretely at . Consequently, PDE source terms are piecewise constant in time, preserving well-posedness as a linear parabolic problem on each subinterval. The ABM update (6) defines a Markov map at mesh points.
Since the alternating-update rule defines the hybrid modeling framework (continuum-discrete) itself, no splitting error accumulates. The piecewise-constant ABM forcing is an exact model component. The induction argument formalizes this sequential construction, guaranteeing existence and uniqueness on each and hence on .
We examine the decoupled system to highlight the ABM’s role. The resulting linear parabolic PDEs with Neumann boundary conditions admit a classical solution via spectral decomposition of the Neumann Laplacian (proof in [46]):
Theorem 3
(Well-Posedness of Sole PDE System). The system
admits a unique classical solution:
where the Neumann Laplacian eigenbasis satisfies
with eigenvalues . Coefficients are . Each is spatially smooth for and temporally analytic for .
The spectral result shows that without ABM interactions, the PDE subsystem decouples and remains fully regular. Figure 5 sketches the proof: expansion in the Neumann eigenbasis, projection by initial data, and reconstruction yield smooth, exponentially decaying solutions. On the other hand, even in the coupled case, agent density constraints ensure well-posedness despite agent-driven reaction terms, establishing our hybrid modeling framework (continuum-discrete) as both analytically sound and biologically interpretable.

Figure 5.
Flowchart for Theorem 3: spectral decomposition of the Neumann Laplacian yields explicit exponential-decay solutions, ensuring classical regularity.
Weak solution existence establishes a rigorous mathematical foundation for hybrid mathematical formulation (PDE-ABM) integrating microscopic interactions with macroscopic behaviors. The proof of well-posedness for the coupled PDE-ABM system guarantees that the model behaves predictably under biologically relevant conditions, e.g., bounded agent density due to cell crowding and realistic spatial constraints. This is critical for ensuring that simulated phenomena like angiogenesis, hypoxia-driven resistance, and spatial tumor heterogeneity reflect biological processes rather than numerical artifacts. From a clinical perspective, this mathematical well-posedness lays the foundation for future optimization of treatment regimens (e.g., dosing schedules) within a consistent modeling framework.
4.2. Master Equation Formulation and Mean-Field Limit
Having established deterministic well-posedness, we now analyze stochastic aspects of agent dynamics. Integrating stochastic agent-based dynamics within a continuum PDE framework requires principled linkages between microscopic randomness and macroscopic observables. The CME provides this foundation by capturing the probabilistic evolution of the agent state space. This section derives a lattice-based CME for the hybrid mathematical formulation (PDE-ABM), computes first-order moment equations, and establishes conditions justifying a deterministic mean-field approximation. By unifying the hybrid mathematical formulation (PDE-ABM) into a continuous description (16), our model connects microscale interactions with macroscale dynamics, replacing the computationally demanding ABM structure in dense tumor regions with an efficient PDE solver.
Related approaches have been developed in the literature on stochastic analysis. For example, mean-field equations under uncertainty have been studied using specialized numerical schemes such as the stochastic theta method for the G-Brownian motion [47], while extensions of backward stochastic differential equations to mean-field limits with time-delayed generators have established existence, uniqueness [48]. Beyond biological and stochastic contexts, dynamic mean-field game theory has been applied to socioeconomic transitions, including fiscal incentive strategies for green economy shifts where individual dynamics couple to collective outcomes [49].
We analyze a coarse-grained mesoscopic representation of the ABM component. Consider a regular lattice with spacing over the spatial domain. The local agent density function denotes the tumor agent count at site and time t.
Let represent the discrete ABM configuration at time t. A continuous-time Markov process on governs the stochastic evolution of , with state-dependent transition rates determined by agent rules, including proliferation, death, motility, and phenotypic switching.
Let denote the probability mass function over all ABM configurations. The CME governing the evolution of is:
where denotes the transition rate from configuration to . Each transition corresponds to elementary stochastic events with specific forms:
- (i)
- Brownian Movement: each cell jumps to neighboring site at ratewhere denotes the von Neumann neighborhood (four orthogonal neighbors) of . The coefficient originates from the Fokker–Planck equation for tumor agents undergoing Brownian motion: with independent standard Brownian motions.
- (ii)
- Regulated Proliferation: Using the Heaviside function H to identify normoxic states, only normoxic cells proliferate at rate
- (iii)
- Drug-Induced Death: Apoptosis occurs at constant rate : .
- (iv)
- Mutation: mutation preserves cell counts per voxel, and thus does not appear in the CME.
Define the expected local agent density:
The cádlág property yields
The CME governs the change rate due to proliferation, death, and movement:
This equation is unclosed because first-order moments depend on higher-order correlations through nonlinear functions. A tractable macroscopic approximation requires closure. The mean-field approximation assumes statistical independence between agent states, providing the first-moment closure:
Applying this closure yields:
Define the density gives , producing the CME for :
The deterministic approximation holds under the law of large numbers when local agent populations are large and suppress fluctuations. The continuum limit yields the macroscopic density equation:
where . In the continuum limit, the local cell count is
where and denote tumor and vessel agent spatial densities. The uniform bound implies the tumor cell density constraint:
where is the disk area. The maximum local cell count follows as
thus .
Therefore, applying first-order moment closure yields a deterministic approximation of the tumor density dynamics. This closure is valid under large-population and weak-correlation regimes.
Theorem 4
(Mean–Field Limit for the Tumor Cell Density). Let denote tumor cell agent counts evolving under the stochastic rules in Section 2 on a lattice with spacing . Assume:
- (i)
- Initial agent positions and states are i.i.d. with macroscopic density .
- (ii)
- The maximum local occupancy satisfieswhere is the maximal local cell–vessel occupancy value and the cell radius.
Then, as and , the tumor cell density satisfies:
Here is the macroscopic carrying capacity, H the Heaviside function, the positive part, and d the drug concentration. Diffusion arises from cellular Brownian motion; the reaction term models normoxic proliferation and drug-induced apoptosis.
Theorem 4 formalizes the deterministic continuum approximation of the tumor cell density. Figure 6 illustrates the derivation pathway from the discrete ABM to the macroscopic PDE through successive levels of approximation.
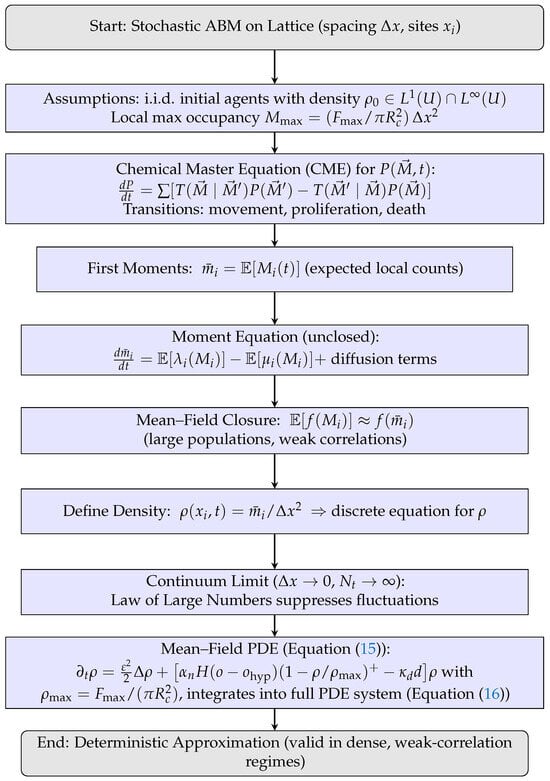
Figure 6.
Flowchart for Theorem 4: derivation of the mean–field PDE from the stochastic ABM via CME, moment equations, closure, and continuum limit.
We note that agent-based simulations are computationally intensive for tumor populations. The mean-field limit in Equation (15) unifies the hybrid mathematical formulation (PDE-ABM) into a computationally efficient continuum description:
The mean-field Equation (16) allows one to interpret complex, stochastic agent-based behavior through simpler, deterministic PDEs. This bridge from microscale (single-cell events like stochastic phenotype switching) to macroscale (tumor cell density evolution) enables: (i) analytical estimation of tumor front velocity, aiding prognosis (e.g., time to vascular invasion or metastatic risk), (ii) sensitivity to environmental factors (e.g., hypoxia, drug gradients) to be encoded directly in continuous equations, which may inform spatially-resolved treatment planning, and (iii) approximate solutions in real time, supporting integration into clinical decision-support tools, where full ABM simulations may be computationally prohibitive. On the other hand, mean-field approximations neglect fluctuations, so we clarify valid parameter regimes and biological relevance.
Remark 2
(Validity Regime of the Moment Closure). Equation (15) uses first–order moment closure , neglecting second-order moments and higher-order cumulants. This requires the following:
- (i)
- Large local populations: per site , making demographic noise under central limit scalings;
- (ii)
- Weak correlations: Negligible spatial correlations between neighboring voxels at scale , ensured by fast mixing (large ε) or weak interactions.
Fluctuations then contribute only corrections, so (15) captures population dynamics to leading order.
Biologically, these hold in dense tumor regions where local interactions average stochasticity. They fail in the following:
- (i)
- Early growth stages, invasion fronts, or metastatic niches with small and non-negligible extinction;
- (ii)
- Strongly heterogeneous microenvironments where correlations and clustering invalidate the weak–fluctuation assumption.
Solutions include second-order moment closure (e.g., pair approximations) or hybrid modeling frameworks (continuum-discrete) retaining ABM structures in critical regions while using PDE surrogates elsewhere. These are active multiscale modeling research areas.
4.3. Quantitative Assessment of the Mean-Field Approximation
The mean-field PDE Equation (15) arises from the ABM by averaging and closing higher moments via . Its accuracy depends on site populations and spatial correlations. Under central limit scaling, stochastic fluctuations scale as
implying for relative uncertainty . For instance, yields relative fluctuations, while yields . Thus, the PDE surrogate is accurate for large and weak correlations but fails in regimes of small populations or strong correlations (e.g., invasion fronts, niche seeding), where the ABM should be retained locally.
As an analytical benchmark, when tumor-cell dynamics reduce to Fisher-KPP form, the invasion speed is
which depends only on continuum parameters. With , , this yields (nondimensional), providing a mean-field reference before performing any ABM comparison.
Table 3 summarizes model-independent validity criteria with illustrative numerical estimates, offering practitioners explicit thresholds and scaling rules for when PDE surrogates suffice and when ABM detail must be retained.
5. Numerical Experiments and Simulation Results
We rigorously evaluate the numerical properties of the hybrid mathematical PDE-ABM formulation. This section describes the discretization framework for both the continuum (reaction–diffusion) and agent-based components, and provides a detailed analysis of consistency, stability, and convergence. We further validate these numerical methods through grid refinement tests and examine their biological relevance.
5.1. Hybrid Time-Stepping Framework
The hybrid PDE-ABM formulation is discretized on a square domain of area using a uniform Cartesian grid with spacing m, resulting in a mesh. The reaction–diffusion fields (TAF, drug, and oxygen) evolve via a semi-implicit alternating direction implicit (ADI) scheme, which provides unconditional stability for linear diffusion terms. We note also the development of nonlinear compact polynomial schemes for elliptic operators, which provide compact high-order stencils and efficient elliptic solves on smooth domains; see [50] for a recent implementation and analysis. Such compact polynomial elliptic solvers could be used as an alternative to the ADI/implicit elliptic substeps (or as an efficient Poisson/steady-TAF solver) to improve boundary accuracy and reduce the stencil width for high-order spatial discretization, particularly in production simulations that require high-order boundary treatment. In contrast, endothelial cell density is updated via an explicit forward Euler method for chemotaxis, subject to a CFL condition (Theorem 6) that ensures conditional stability.
To balance computational efficiency and stability, the ABM component is updated with a larger time step of , synchronized with the PDE updates at each interval. The hybrid time-stepping approach enables stable simulation of stiff PDE-ABM couplings. All simulations enforce homogeneous Neumann boundary conditions.
We select the endothelial cell PDE time step to ensure stability:
where denotes the chemotactic flux supremum norm for our parameters. Choosing ( s) with provides a conservative stability margin.
Table 4 summarizes the numerical parameters and scheme configurations.

Table 4.
Discretization parameters and numerical schemes for the hybrid mathematical formulation (PDE-ABM). Alternating direction implicit (ADI) handles reaction–diffusion fields while endothelial chemotaxis updates explicitly under the CFL constraint.
We detail the numerical scheme for endothelial cell chemotaxis. The discretization employs second-order central differences in space and forward Euler integration in time [22]. The chemotaxis–diffusion equation yields deterministic and probabilistic formulations. The deterministic update is
where F and G encode chemotactic drift computed at cell edges via linear interpolation.
For ABM compatibility, we express the update probabilistically:
with transition probabilities:
The implementation uses five intervals
We normalize such that (Assumption 2). Drawing , cells move according to the interval containing r. Sampling from with directional selection via (20) is equivalent to sampling from post-normalization.
Assumption 2
We implement the ADI method for TAF, drug, and oxygen Equation (2). For a general reaction–diffusion system , the ADI scheme is
where and , denote second-order central differences.
5.2. Mesh Selection and Justification
All numerical experiments use a uniform Cartesian grid on with spacing ( mesh), unless stated otherwise. This resolution balances the need to capture continuum length scales of the reaction–diffusion fields with the computational cost of ensemble ABM simulations. Manufactured-solution convergence tests (Section 5.3) confirm the expected truncation-error scaling (ADI: ; endothelial update: ) and show spatial orders near two for . Grid refinement across (Section 5.5) further validates numerical consistency and stability, establishing correctness of the discrete methods on this mesh.
The grid serves primarily for methodological demonstration and verification. Applications requiring cell-scale resolution or experimental comparison (e.g., when ) should employ finer meshes such as or higher and conduct grid refinement studies, as discussed in Section 5.3 and Section 6.
5.3. Consistency Verification
Section 5.1 established the discretization framework. We now examine approximation fidelity through a consistency analysis, quantifying local truncation errors. The endothelial chemotaxis scheme (17) and the ADI scheme yield
Appendix E details derivations. The endothelial scheme has truncation error, indicating first-order temporal and second-order spatial accuracy. The ADI scheme achieves , reflecting second-order convergence. These distinct characteristics motivate adaptive time-stepping for endothelial components while permitting larger ADI steps.
For grid discretization , define the discrete p-norm ():
We establish iterative norm control:
Theorem 5
(Discrete Energy Bound). Under one-sided homogeneous Neumann boundary approximation (31) on , the scheme satisfies
Proof.
For any ,
Cauchy–Schwarz inequality and yield
Given and (Assumption 2), Jensen’s inequality applied to Equation (18) gives
Thus,
Assuming bounded first-order partial derivatives of c, we have . Similarly, . The extra terms are thus bound by . □
We simulate truncation errors by excluding tumor and vessel agents (initialized to zero). This simplifies the TAF, drug, and oxygen PDEs to
Homogeneous Neumann conditions apply on . We use the ghost point method to handle Neumann conditions, e.g., at , we have for (However, mass conservation (see Section 5.5) requires one-sided approximations for Neumann conditions, e.g., at , we have , which introduces first-order error . In contrast, the ghost point method introduces second-order error but does not strictly preserve mass. Unless otherwise stated, we use one-sided approximation for our Neumann boundary conditions). This treatment introduces error, in alignment with truncation error of the ADI scheme. We use the following exact solutions as initial conditions:
We compute convergence order via:
where is the local truncation error for at resolution h. Figure 7 demonstrates convergence. Table 5 lists orders for with . Observed orders approach 2, confirming ADI’s second-order spatial accuracy.
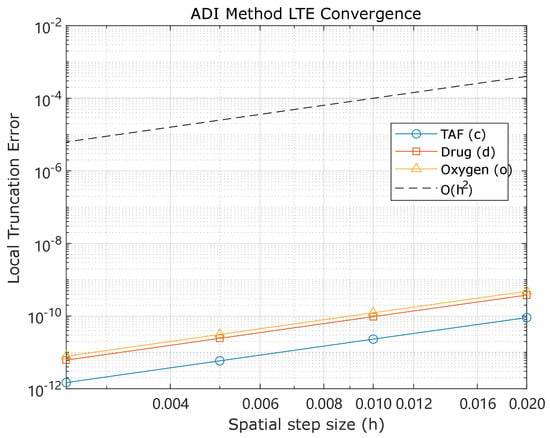
Figure 7.
Local truncation error convergence for c, d, and o using ADI across , validating second-order spatial accuracy. (Main production simulations in the manuscript used a 100 × 100 mesh; see Section 5.2 for discussion of mesh selection and recommendations for refinement).

Table 5.
Computed local truncation error orders for across spatial resolutions.
In summary, the endothelial discretization exhibits truncation error (first-order time, second-order space). The ADI scheme (second-order time and space). These results align with theory and substantiate the convergence results in subsequent sections.
The manufactured-solution convergence results in Figure 7 and Table 5 show spatial convergence orders near two for the ADI fields (), consistent with accuracy in the interior. Grid refinement tests across (Section 5.5) confirm numerical consistency and stability. These results justify the use of a mesh for algorithmic verification and illustrative simulations.
A limitation arises when the nondimensional cell diameter becomes comparable to , so that one cell occupies a single grid element, reducing geometric fidelity of voxelized source/sink terms. Applications requiring cell-scale precision should therefore employ finer meshes, such as or , combined with grid-convergence tests. The demonstrated truncation-error behavior implies that halving reduces spatial error by roughly a factor of four when discretization dominates.
5.4. Stability Enforcement
While consistency guarantees alignment between the discretization and governing equations, it does not ensure that bounded or biologically meaningful solutions exist over time. This subsection analyzes the numerical stability of the explicitly discretized endothelial cell scheme, which exhibits conditional stability. We invoke the Lax–Richtmyer equivalence theorem to confirm convergence.
Theorem 6
(Conditional Stability). The ADI scheme maintains unconditional stability for pure linear diffusion. The finite difference scheme for endothelial chemotaxis (Equation (17)) achieves conditional stability under the time step constraint:
Subject to the additional constraints:
all motility probabilities remain nonnegative.
Proof.
Define the auxiliary expressions:
It follows that
Equation (25) yields
The constraint becomes
Equation (26) bounds :
Under (27), this necessarily implies
This constitutes the chemotaxis CFL condition, where originates from diffusion-dominated constraints in two dimensions. With nonnegative and (Assumption 2), update (18) forms a convex combination. Thus,
Boundedness of the maximum norm over all time k establishes stability under the CFL and grid conditions. □
Figure 8 visualizes the stability criteria, showing the admissible region. This empirically validates Theorem 6’s CFL-type condition ensuring nonnegative . The theorem further guarantees that the update forms a convex combination, preserving endothelial density nonnegativity. This maintains biological realism and prevents unphysical numerical artifacts like negative concentrations.
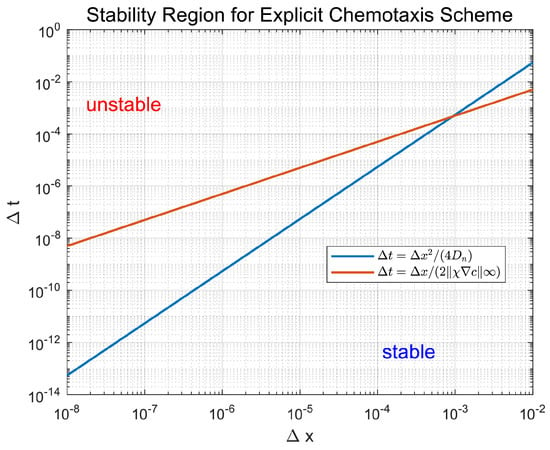
Figure 8.
Stability condition characterization. Admissible region consistent with Theorem 6’s CFL-type bound.
Consistency and conditional stability imply convergence via the Lax–Richtmyer equivalence theorem for linear initial value problems.
Theorem 7
(Convergence). Let be the exact endothelial chemotaxis solution and its numerical approximation. Under Theorem 6’s time step constraints and sufficient regularity of n and c, the scheme converges with
5.5. Biological Constraints Preservation
In addition to consistency, stability, and convergence, biological realism requires that the numerical scheme preserve the nonnegativity intrinsic to the modeled system. We now analyze whether the discretization maintains nonnegativity for endothelial cell densities. The explicit update scheme takes the form of a convex combination of neighboring cell densities:
where and (Assumption 2), provided the CFL condition holds. This structure guarantees:
Theorem 8
The second biological constraint is the conservation law, such as mass conservation or population invariance. Numerical schemes must respect this constraint, particularly in the absence of sources, sinks, or boundary fluxes. We therefore verify whether the total endothelial cell count remains constant under the proposed numerical scheme. Summing the probabilistic motility update (17) over all grid points , with , yield
We expand the second right-hand side term as
The telescoping summations simplify to
We impose homogeneous Neumann boundary conditions using one-sided approximations:
for . At , this yields
Analogous conditions hold at other boundaries: implies , implies , and implies . Combining (28)–(30) with these boundary conditions ensures exact mass conservation for pure diffusion or chemotaxis processes:
Theorem 9
The Neumann boundary conditions reflect biologically plausible zero-flux constraints at tissue boundaries. This mass conservation property ensures that endothelial cell mass remains invariant up to machine precision in the absence of external sources or sinks, maintaining physical and biological realism.
Having established the analytical and qualitative properties of the numerical scheme, we conduct a spatial grid refinement study to empirically validate the consistency and stability results derived in Section 5.3, Section 5.4 and Section 5.5. This test simulates the system in the absence of tumor and vessel agents.
We evaluate grid spacings with fixed time steps for PDE updates and for ABM decisions (disabled here). The simulation runs until , and convergence is measured using the step-change metric at each time step k:
where c and o represent TAF and oxygen concentrations, respectively. We choose
as initial conditions. No drug treatment or cellular dynamics are applied. Figure 9 shows that decays consistently across grid levels. Beyond , the decay becomes nearly linear on a logarithmic scale, with least-squares regression revealing closely matched slopes for all resolutions. This confirms the scheme’s temporal stability and spatial consistency. Table 6 reports numerical values at and estimated convergence slopes.
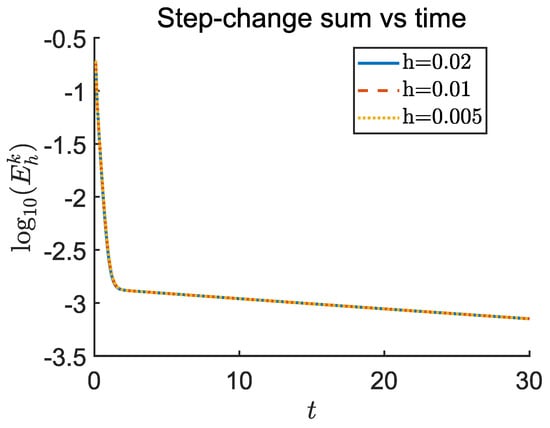
Figure 9.
The maximum norm for the oxygen and TAF fields is shown plotted against t, for grid spacings , , and . Fixed time steps and are used. The near-identical decay slopes beyond verify asymptotic stability and second-order spatial consistency of the PDE solver.

In summary, the hybrid numerical framework, combining explicit probabilistic updates for endothelial dynamics with ADI-based diffusion solvers, demonstrates mathematical consistency, conditional stability, and convergence. Rigorous verification of nonnegativity, mass conservation, and discrete energy control ensures biologically faithful and numerically reliable simulations of tumor growth and vascular remodeling.
5.6. Error Analysis and Biological Interpretation
We did not generate new experimental measurements. Biological and physical parameters appear only in Section 5 for numerical validation, all taken from established literature (e.g., [22]) with explicit citations for reproducibility. Because this work is methodological, model discrepancies with experiments arise from (i) truncation error due to discretization, (ii) stochastic sampling error from finite ABM ensembles, and (iii) structural error (e.g., from mean-field closure approximations).
For reaction–diffusion fields (TAF, drug, oxygen), the ADI scheme has local truncation error
second-order in space and time. The explicit endothelial chemotaxis update yields
first-order in time and second-order in space. Manufactured-solution tests (Figure 7, Table 5) confirm near-second-order spatial accuracy for . We impose Neumann conditions with one-sided differences, formally first-order at boundaries, yet conserving global mass.
The ABM implements the Gillespie algorithm, which samples the continuous-time Markov process. We denote the error introduced in the ABM component by . Quantification of this error remains for future work.
Structural discrepancies (e.g., first-moment closure) arise from the ABM-PDE framework and persist under mesh refinement; their magnitude depends on regimes such as small local populations or strong correlations. We state closure validity in Remark 2 and advocate hybrid ABM-PDE use in critical regions.
Table 7 summarizes leading-order errors: the ADI solver is nearly second-order, the endothelial update is spatially second-order and temporally first-order, and Neumann boundaries are first-order but conserve mass. The total predictive error for model output u satisfies
with for ADI and for endothelial updates, representing the first-order error introduced by one-sided Neumann boundary treatment, which can be lifted to second-order by ghost-point method, and denoting ABM stochastic error and structural error, respectively. Convergence tests confirm second-order spatial accuracy, and Section 5.4 analyzes stability. These results establish the numerical error baseline for all simulations reported here.

Table 7.
Summary of local truncation error orders and stochastic sampling error for the schemes employed. Formal leading-order estimates are compared with representative observed orders from manufactured-solution convergence tests.
We perform standard numerical diagnostics—truncation error analysis, discrete conservation checks, and CFL stability conditions—and explicitly link numerical accuracy and stability to the biological outcomes reported here. Numerical discretization alters formal error norms and changes the continuum fields (oxygen, TAF, drug) that drive discrete events in the agent-based model, including endothelial chemotaxis, branching, cell death, and stochastic phenotype switching. We therefore design validation tests to ensure that the paper’s biological conclusions remain robust to numerical choices.
Coarse spatial resolution smooths sharp TAF and drug gradients. Because chemotactic drift scales with spatial gradients of TAF, smoothed gradients reduce cue strength, suppress vessel aggregation and branching, and change local drug and oxygen delivery. Coarse grids thus tend to underestimate vascular heterogeneity and to underestimate resistance that arises from delivery-protected niches.
Violating stability constraints for advection, like chemotaxis or diffusion, produces nonphysical oscillations or artificial damping in the solver. For chemotaxis, these errors produce spurious tip motion and delay branching events. For drug and oxygen transport, they generate nonphysical local concentrations that alter cell death propensities in the ABM. Such numerical artifacts change quantitative outputs, such as invasion front speed and the timing of resistant emergence.
If the PDE time step exceeds the timescale of discrete events, coupling between continuum and discrete dynamics becomes temporally aliased; for example, a rapidly rising local drug pulse can be missed, and the measured probability of resistant establishment can change. To guard against these effects, we run grid and time step refinement studies, verify CFL compliance, and test coupling-frequency convergence for event timing and stochastic outcomes. These validation steps ensure that numerical error does not drive the biological conclusions.
6. Discussion
This study introduced a hybrid modeling framework (continuum-discrete) that rigorously couples stochastic cell-level dynamics with tissue-scale continuum processes. Our approach formalizes a hybrid methodology with precise mathematical guarantees for formulation, numerical discretization, and closed-form mean-field representation. We analyze the well-posedness of the hybrid mathematical formulation (PDE-ABM) and provide comprehensive numerical evidence for its consistency, stability, convergence, and conservation properties. The model integrates stochastic phenotypic switching, metabolite-regulated angiogenesis, and hypoxia-resistance feedback, thereby addressing key limitations in previous hybrid tumor models. Earlier studies often relied on heuristic simulations without mathematical and numerical analysis or treated angiogenesis and resistance in isolation [17,22]. Our framework extends the work by Wang et al. [22] by embedding an exact Gillespie-based mutation and phenotype switching algorithm with drug-modulated mutation rates, deriving a continuum mean-field limit that connects discrete rules to continuum equations, and establishing mathematical well-posedness and numerical robustness for the hybrid scheme. The mean-field limit integrates the hybrid mathematical formulation (PDE-ABM) into a unified PDE system (16), which motivates hybrid numerical schemes that retain full ABM structure in critical regions and replace it with efficient PDE surrogates elsewhere. These methodological advances enable rigorous and robust multiscale tumor modeling not achieved in previous descriptive or simulation-based studies.
Beyond its methodological contributions, the hybrid modeling framework (continuum-discrete) yields several biological and clinical insights. First, model-predicted resistance timelines can inform adaptive therapy protocols designed to suppress or delay resistance [51,52]. Second, simulations of oxygen gradients can guide hypoxia-targeted interventions and optimize the application of hypoxia-activated prodrugs, which may enhance the efficacy of subsequent chemotherapy or radiotherapy [53,54,55,56]. Third, our framework also motivates experimental validation and calibration, such as in vitro tracking of endothelial tip cell dynamics and resistance evolution. Designed for integration with experimental and clinical data, the model supports a translational modeling pipeline. For example, oxygen partial pressure measurement or PET imaging with 18F-FMISO can calibrate the simulated oxygen distribution , while microvessel density measurements from CD31-stained immunohistochemistry can validate the vascular network generated by ABM [53,57]. Time-resolved single-cell RNA-seq data under treatment provide drug-induced mutation rates by linking transcriptional states to phenotypic transitions. Longitudinal MRI during therapy offers radiomic profiles (e.g., tumor volume changes) for comparison with simulated resistance trajectories [58,59]. By supporting multiscale calibration and validation, the model enables in silico exploration of therapy optimization strategies.
In addition, by linking our mathematical analogies to measurable metrics—vascular heterogeneity, invasion speed, and resistant establishment probability—we enable translation into testable hypotheses. For example, reducing chemotactic sensitivity is predicted to (i) lower spatial hotspots of high-vessel-density regions and (ii) improve drug delivery homogenization to increase the efficacy of systemic therapy, supporting combined vascular-normalization and cytotoxic therapy when vascular CV is high. Large Fisher-KPP front speeds motivate closer imaging follow-up to detect early boundary advance. If resistance arises mainly in the pretreatment phase (per Galton–Watson-type models), early tumor burden reduction offers a robust strategy to lower relapse risk.
Several simplifying assumptions in the current framework merit consideration. First, simulations and analysis occur in a two-dimensional domain, which reduces the complexity of three-dimensional vascular geometry and cell–TME interactions compared with in vivo tumors. Extending the framework to three dimensions would capture the full complexity of tumor vasculature but requires greater computational resources. Second, while the mesh used in this study suffices for demonstrating numerical properties (consistency, stability, and convergence) and for qualitative behaviors in this hybrid modeling framework (continuum-discrete), it is borderline for high-precision, cell-scale resolution studies. For quantitative, production-level studies, we therefore recommend mesh refinement (e.g., or greater) combined with the grid refinement diagnostics. Such a refinement is straightforward (owing to the observed second-order spatial scaling of the ADI operator) but was outside the time and computational budget for the present methodological manuscript. Third, the model treats TAF and oxygen dynamics with simplified production, diffusion, and uptake mechanisms. Actual angiogenesis involves multiple signaling pathways such as VEGF and Dll4/Notch [60]), and diverse cell phenotypes including stalk cells [61] and pericytes [62]), which are not explicitly represented. Including these features may enhance biological fidelity. Third, the immune system remains unmodeled, even though immune infiltration, suppression, and therapy-induced immunogenicity are recognized as critical regulators of tumor evolution and resistance. This omission limits the model’s applicability to immunotherapy scenarios. Finally, the model does not account for pharmacokinetic/pharmacodynamic (PK/PD) effects, nor does it simulate treatment-induced vascular normalization or off-target toxicity.
While our hybrid mathematical formulation (PDE-ABM) captures hypoxia-driven angiogenesis and resistance evolution, neglecting immune activity and explicit PD relating local drug exposure to killing efficacy can shift predictions. Immune surveillance adds tumor-cell killing, raising extinction probability of resistant clones, lowering average tumor burden and invasion speed, and modulating angiogenic signaling via secreting cytokines [63]; its omission likely overestimates resistant establishment probability and invasion speed, especially in immunogenic or low-cell-number regimes. On the other hand, PD shape (e.g., -style killing with ) further alters drug efficacy: saturating PD (high with low ) dampens local drug heterogeneity, whereas shallow curves (high ) amplify spatial heterogeneity and increase protected niche sizes that select for resistance. Thus, neglecting PD may either over- or under-estimate treatment efficacy depending on where the true curve falls relative to simulated local concentrations. To quantify these influences, we recommend three metrics: (i) resistant establishment probability, sensitive to immune clearance at small clone sizes; (ii) invasion-front speed, reflecting altered tumor progression under immune and cytotoxicity pressure; and (iii) vascular heterogeneity, linking PD shape to delivery heterogeneity. Incorporating immune and PD refinements (Appendix F) enhances clinical relevance while preserving tractability for multiscale tumor dynamics.
Future work can extend this foundation in several directions. Extending to three-dimensional geometries will allow investigation of how vascular topology and spatial drug gradients influence resistance dynamics. Incorporating additional microenvironmental features, such as interstitial fluid flow and matrix density, can improve predictions of drug distribution and cell motility. Beyond single-agent therapy, simulating sequential and combination therapies, particularly integrating immunotherapy and antiangiogenic strategies, could identify schedules that exploit transient vessel normalization to suppress resistance. Linking model predictions with patient-specific imaging, such as DCE-MRI, would support personalized therapy strategies. In addition, the mean-field derivation also enables reduced ODE/PDE systems that approximate complex spatial-stochastic dynamics and facilitate analytical control strategies. Finally, while capillary sprouting is already represented at the tip-cell branching level in our current framework (Equation (6) and Algorithm A2), a full simulation of vascular network morphology (sprout lumenization, anastomosis, and perfusion) remains beyond the present scope and will be an important extension of the model.
In summary, the proposed hybrid modeling framework (continuum-discrete) establishes a rigorous and extensible framework for coupling discrete stochastic cell behavior with continuum tissue-scale dynamics. By uniting mathematical rigor, multiscale biological realism, and translational capacity, this work advances the field from descriptive hybrid models to predictive, clinically actionable in silico platforms for adaptive cancer therapy.
7. Conclusions
In this work, we developed a hybrid modeling framework (continuum-discrete) to investigate tumor angiogenesis and resistance evolution, with emphasis on a well-posed mathematical formulation and rigorous numerical analysis. Our key findings are as follows:
- (i)
- Mathematical Lineages: We established explicit connections between our hybrid mathematical formulation (PDE-ABM) and three foundational cancer modeling frameworks: Keller–Segel chemotaxis, Fisher-KPP invasion waves, and Galton–Watson branching processes. Our model extends these theories by incorporating multiscale feedback, stochastic phenotype switching, and microenvironmental coupling (Section 3). These links also enable the translation of model outputs to clinically relevant metrics, including vascular CV, invasion speed , and resistant establishment probability.
- (ii)
- Theoretical Foundations: We rigorously demonstrated the well-posedness of the coupled PDE-ABM system (Theorems 1–3). A mean-field limit (Theorem 4) further unified stochastic ABM dynamics and deterministic PDE limits, consolidating the hybrid mathematical formulation (PDE-ABM) into a continuum description (Equation (16)). The applicability of the moment closure was clarified (Remark 2), ensuring transparent validity conditions. To aid comprehension of these results, schematic flowcharts were added for key theorems (see Figure 3, Figure 4, Figure 5 and Figure 6).
- (iii)
- Local Truncation Error and Consistency: We conducted a systematic numerical analysis of the continuum-discrete scheme. Local truncation errors were derived for the explicit endothelial discretization and for the ADI scheme applied to TAF, drug, and oxygen fields (Section 5.3). Manufactured-solution tests confirmed the theoretical error orders, demonstrating second-order spatial convergence (Figure 7, Table 5). These analyses reinforce the numerical credibility of the hybrid modeling framework (continuum-discrete).
- (iv)
- Stability and Biological Fidelity: We established the CFL condition for the endothelial update (Theorem 6), ensuring stability and preventing unphysical artifacts. The scheme was further shown to preserve key biological constraints, including nonnegativity and mass conservation properties (Section 5.5). Grid refinement studies (Figure 9, Table 6) confirmed the consistency and stability across mesh refinements. Together, these results demonstrate that the proposed framework is both numerically robust and biologically faithful.
- (v)
- Future Applications: The hybrid approach has significant potential for simulating complex tumor dynamics, such as angiogenesis and resistance mechanisms, in biologically relevant settings. Future work will extend this framework to include more detailed biological processes, such as heterogeneous cell populations and feedback loops between tumor growth and angiogenesis.
In conclusion, our hybrid model provides an effective, numerically stable framework for simulating tumor-angiogenesis dynamics and resistance. The method’s ability to integrate discrete agent-based processes with continuum modeling opens up new opportunities for studying the role of cellular interactions, drug delivery, and resistance in cancer modeling.
Author Contributions
Conceptualization, L.S.W. and J.Y.; methodology, L.S.W., J.Y., and S.L.; software, L.S.W. and J.Y.; validation, L.S.W., J.Y., and Z.L.; formal analysis, L.S.W. and J.Y.; investigation, L.S.W., J.Y., and S.L.; resources, J.Y. and Z.L.; data curation, L.S.W. and J.Y.; writing—original draft preparation, L.S.W. and J.Y.; writing—review and editing, L.S.W., S.L., and Z.L.; visualization, L.S.W. and J.Y.; supervision, Z.L.; project administration, S.L. All authors have read and agreed to the published version of the manuscript.
Funding
The research of Louis Shuo Wang and Jiguang Yu is partially supported by the National Natural Science Foundation of China, Tianyuan Fund for Mathematics. (Project No. 12426516). This article was written while the above authors were visiting the Tianyuan Mathematical Center in Central China (Hubei); it is a pleasure for them to thank this institution for its kind hospitality. The research of Zonghao Liu is funded by the Major Scientific Research Program for Young and Middle-aged Health Professionals of Fujian Province, China (Grant No. 2021ZQNZD009).
Data Availability Statement
The original contributions presented in this study are included in the article. All parameter values are validated using experimental data sets from peer-reviewed publications (see Table 1 and Table 2). They are available under the CC-BY 4.0 license. Further inquiries can be directed to the corresponding authors.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ABM | Agent-based model |
| ADI | Alternating direction implicit |
| ANGPT-2 | Angiopoietin-2 |
| CME | Chemical master equation |
| CV | Coefficient of variation |
| EMDR | Environmentally mediated drug resistance |
| FGF-2 | Fibroblast growth factor 2 |
| HIF-1 | Hypoxia-inducible factor-1 |
| IL-8 | Interleukin-8 |
| MDSC | Myeloid-derived suppressor cell |
| ODE | Ordinary differential equation |
| PD | Pharmacodynamic |
| PDE | Partial differential equation |
| PK | pharmacokinetic |
| TAF | Tumor angiogenic factor |
| TAM | Tumor-associated macrophage |
| TME | Tumor microenvironment |
| TSP-1 | Thrombospondin-1 |
| VEGF | Vascular endothelial growth factor |
| VEGFR | Vascular endothelial growth factor receptor |
Appendix A. Terminological Clarification
We distinguish hybrid modeling framework and hybrid mathematical formulation. The former denotes the paradigm of coupling continuum PDEs (oxygen, drug, and TAF) with agent-based rules for cells and vessels; the latter specifies the concrete mathematical coupling of reaction–diffusion–chemotaxis PDEs with discrete stochastic updates (e.g., Gillespie-driven phenotype switching, vessel branching/anastomosis). Thus, hybrid modeling framework describes the methodological nature of the model, while hybrid mathematical formulation denotes its concrete mathematical coupling and implementation.
We also differentiate use hybrid (methodological: combining PDEs and ABM) from multiscale (biological: coupling molecular, cell, tissue). Our framework is hybrid in method and multiscale in scope. This distinction emphasizes that not all multiscale models are hybrid (e.g., purely PDE-based multiscale formalisms exist), and not all hybrid models are multiscale (e.g., combining ODEs and ABMs at a single scale). Figure A1 illustrates this relationship.
Figure A1.
Relationship between hybrid and multiscale modeling: overlapping but not synonymous.
Appendix B. Nondimensionalization
We begin with the dimensional system for tumor cell density (n), TAF (c), drug (d), and oxygen (o):
Here, , , , are diffusion rates; , , are decay rates; , are cellular uptake rates; , are supply rates from blood vessels; and , are production and uptake rates of TAF, respectively. The function represents the chemotactic sensitivity, where is the chemotactic saturation coefficient and corresponds to the half-maximal concentration.
To nondimensionalize the system, we introduce representative scales for the length (L), time (), and concentrations of all variables :
In this scaling, D is a representative diffusion rate, chosen to be comparable to the oxygen diffusion rate , and is the maximal oxygen concentration in the TME. We select L as the typical distance between the implanted tumor and vessels in experimental setups [64], which aligns the diffusion time with the cell cycle duration [65]. The resulting dimensionless parameter groups are as follows:
Dropping the tildes for notational simplicity yields the dimensionless system used in our study, as shown in Equation (2).
Appendix C. Implementation of Discrete ABM Lattice
This section details the mapping of the ABM domain, , to a PDE domain with boundary, and the construction of the ABM lattice . The ABM domain is , discretized into squares of side length . Our objective is to construct a small open neighborhood of with boundary, such that its corresponding discrete lattice is identical to the direct discretization of .
We fix a sufficiently small , specifically , and define the -neighborhood of the unit square as
Here, is the Euclidean distance from a point to a set . Let be a standard radial mollifier supported in the unit disk, such as
where the constant C normalizes the integral . For a given smoothing parameter , we define the scaled mollifier . We then convolve the characteristic function of , denoted , with this mollifier:
The resulting function is , with its values in the range . It is equal to 1 everywhere inside . We select a small such that . This allows us to define the PDE domain as
Since is smooth and is a regular value, the Regular Level Set Theorem [66] (Corollary 5.14) ensures that the boundary is a curve (i.e., every point of this curve has an open neighborhood that is the graph of a diffeomorphism). Our choice of guarantees that , making a close approximation of . We obtain the discrete approximation by sampling on the ABM lattice with spacing , applying a threshold at , and identifying boundary agents as those with Moore neighbors outside the defined domain. Algorithm A1 summarizes these steps.
| Algorithm A1 Construction of the discrete agent-based domain approximating the smooth PDE domain . |
|
Appendix D. Description of the Markov Transition Operator
At each discrete time step, every agent’s state x is updated via the Markov transition operator , which depends on the microenvironmental fields and the agent’s current state:
Algorithm A2 summarizes the state transitions for tumor and endothelial tip cells.
| Algorithm A2 Markov transition operator for tumor and vessel agents. |
|
Appendix E. Computation of Local Truncation Error
We compute the local truncation error for the explicit finite difference scheme and the semi-implicit ADI scheme.
First, apply Taylor expansions to the central difference scheme (17) in time and space gives
Combining the expansions yields
We approximate the chemotaxis fluxes using finite differences:
To approximate the midpoint fluxes, we use Taylor expansions of and c:
similar expansions hold for , , and . Combining the Taylor expansions above, we obtain the following update for the discrete fluxes:
where the second-order error coefficients are given by
Thus, the local truncation error is
Next, we analyze the ADI scheme for a generic reaction–diffusion equation . The two-step ADI scheme is
By substituting the exact solution into the scheme and expanding all terms using Taylor series around , we can analyze the error. For the first half step, expanding both sides gives
Thus, the local truncation error of the first half-step is
Similarly, for the second half-step:
This yields a local truncation error for the second half-step of
Summing both half-step errors, the total local truncation error becomes
Thus, the leading-order truncation error satisfies
Appendix F. Minimal Immune and Pharmacodynamic Extensions
For the minimal immune module (PDE + local killing), we introduce an immune-effector density :
where is immune diffusivity, chemotactic sensitivity towards tumor/TAF, recruitment rate, a half-saturation constant, immune decay. Immune-mediated tumor killing is implemented in the ABM as an additional death propensity for a tumor agent located at x:
with the pre-effector killing efficacy and the spatial average of I over the agent’s support.
To incorporate PD, we replace the simple linear drug-death coupling with an function:
with baseline death rate , maximal rate , and half-saturation . This form captures saturating killing and enables exploration of shallow vs steep PD curves.
For PK/local delivery modifications, we add vessel permeability in drug PDE:
where are localized source kernels for vessels and is a time-varying supply from each vessel (allowing e.g., bolus or continuous infusion).
References
- Bray, F.; Laversanne, M.; Sung, H.; Ferlay, J.; Siegel, R.L.; Soerjomataram, I.; Jemal, A. Global cancer statistics 2022: GLOBOCAN estimates of incidence and mortality worldwide for 36 cancers in 185 countries. CA Cancer J. Clin. 2024, 74, 229–263. [Google Scholar] [CrossRef]
- Vasan, N.; Baselga, J.; Hyman, D.M. A view on drug resistance in cancer. Nature 2019, 575, 299–309. [Google Scholar] [CrossRef]
- Australian Pancreatic Cancer Genome Initiative; ICGC Breast Cancer Consortium; ICGC MMML-Seq Consortium; ICGC PedBrain; Alexandrov, L.B.; Nik-Zainal, S.; Wedge, D.C.; Aparicio, S.A.J.R.; Behjati, S.; Biankin, A.V.; et al. Signatures of mutational processes in human cancer. Nature 2013, 500, 415–421. [Google Scholar] [CrossRef]
- Hanahan, D.; Folkman, J. Patterns and Emerging Mechanisms of the Angiogenic Switch during Tumorigenesis. Cell 1996, 86, 353–364. [Google Scholar] [CrossRef] [PubMed]
- Wang, N.; Jain, R.K.; Batchelor, T.T. New Directions in Anti-Angiogenic Therapy for Glioblastoma. Neurotherapeutics 2017, 14, 321–332. [Google Scholar] [CrossRef] [PubMed]
- Lugano, R.; Ramachandran, M.; Dimberg, A. Tumor angiogenesis: Causes, consequences, challenges and opportunities. Cell. Mol. Life Sci. 2020, 77, 1745–1770. [Google Scholar] [CrossRef] [PubMed]
- Incio, J.; Ligibel, J.A.; McManus, D.T.; Suboj, P.; Jung, K.; Kawaguchi, K.; Pinter, M.; Babykutty, S.; Chin, S.M.; Vardam, T.D.; et al. Obesity promotes resistance to anti-VEGF therapy in breast cancer by up-regulating IL-6 and potentially FGF-2. Sci. Transl. Med. 2018, 10, eaag0945. [Google Scholar] [CrossRef]
- Shojaei, F.; Wu, X.; Zhong, C.; Yu, L.; Liang, X.H.; Yao, J.; Blanchard, D.; Bais, C.; Peale, F.V.; Van Bruggen, N.; et al. Bv8 regulates myeloid-cell-dependent tumour angiogenesis. Nature 2007, 450, 825–831. [Google Scholar] [CrossRef]
- Bergers, G.; Hanahan, D. Modes of resistance to anti-angiogenic therapy. Nat. Rev. Cancer 2008, 8, 592–603. [Google Scholar] [CrossRef]
- Arumugam, G.; Tyagi, J. Keller-Segel Chemotaxis Models: A Review. Acta Appl. Math. 2021, 171, 6. [Google Scholar] [CrossRef]
- Wang, S.E.; Hinow, P.; Bryce, N.; Weaver, A.M.; Estrada, L.; Arteaga, C.L.; Webb, G.F. A Mathematical Model Quantifies Proliferation and Motility Effects of TGF-β on Cancer Cells. Comput. Math. Methods Med. 2009, 10, 71–83. [Google Scholar] [CrossRef] [PubMed]
- Simpson, M.J.; McCue, S.W. Fisher–KPP-type models of biological invasion: Open source computational tools, key concepts and analysis. Proc. R. Soc. A Math. Phys. Eng. Sci. 2024, 480, 20240186. [Google Scholar] [CrossRef]
- Anderson, A.; Chaplain, M. Continuous and Discrete Mathematical Models of Tumor-induced Angiogenesis. Bull. Math. Biol. 1998, 60, 857–899. [Google Scholar] [CrossRef] [PubMed]
- Zangooei, M.H.; Habibi, J. Hybrid multiscale modeling and prediction of cancer cell behavior. PLoS ONE 2017, 12, e0183810. [Google Scholar] [CrossRef]
- Wang, Z.; Butner, J.D.; Kerketta, R.; Cristini, V.; Deisboeck, T.S. Simulating cancer growth with multiscale agent-based modeling. Semin. Cancer Biol. 2015, 30, 70–78. [Google Scholar] [CrossRef]
- Zheng, X.; Wise, S.; Cristini, V. Nonlinear simulation of tumor necrosis, neo-vascularization and tissue invasion via an adaptive finite-element/level-set method. Bull. Math. Biol. 2005, 67, 211–259. [Google Scholar] [CrossRef]
- Gevertz, J.L.; Aminzare, Z.; Norton, K.A.; Perez-Velazquez, J.; Volkening, A.; Rejniak, K.A. Emergence of Anti-Cancer Drug Resistance: Exploring the Importance of the Microenvironmental Niche via a Spatial Model. arXiv 2014, arXiv:1412.0780. [Google Scholar] [CrossRef]
- Picco, N.; Milne, A.; Maini, P.; Anderson, A. The role of environmentally mediated drug resistance in facilitating the spatial distribution of residual disease. Nat. Portf. 2024; under review. [Google Scholar] [CrossRef]
- Wise, S.; Lowengrub, J.; Frieboes, H.; Cristini, V. Three-dimensional multispecies nonlinear tumor growth—I. J. Theor. Biol. 2008, 253, 524–543. [Google Scholar] [CrossRef]
- Frieboes, H.B.; Jin, F.; Chuang, Y.L.; Wise, S.M.; Lowengrub, J.S.; Cristini, V. Three-dimensional multispecies nonlinear tumor growth—II: Tumor invasion and angiogenesis. J. Theor. Biol. 2010, 264, 1254–1278. [Google Scholar] [CrossRef]
- Macklin, P.; McDougall, S.; Anderson, A.R.A.; Chaplain, M.A.J.; Cristini, V.; Lowengrub, J. Multiscale modelling and nonlinear simulation of vascular tumour growth. J. Math. Biol. 2009, 58, 765–798. [Google Scholar] [CrossRef]
- Wang, L.S.; Liu, Z.; Liang, Y.; Wang, J.; Yu, J. Multiscale Modeling of Tumor Angiogenesis and Resistance Evolution: A Hybrid PDE–ABM Framework for Cancer Prediction and Therapy Planning. Preprints 2025, 2025, 2025072175. [Google Scholar] [CrossRef]
- Rejniak, K.A.; Anderson, A.R.A. Hybrid models of tumor growth. WIREs Syst. Biol. Med. 2011, 3, 115–125. [Google Scholar] [CrossRef] [PubMed]
- Altrock, P.M.; Liu, L.L.; Michor, F. The mathematics of cancer: Integrating quantitative models. Nat. Rev. Cancer 2015, 15, 730–745. [Google Scholar] [CrossRef] [PubMed]
- Anderson, A.R.A. A hybrid mathematical model of solid tumour invasion: The importance of cell adhesion. Math. Med. Biol. A J. IMA 2005, 22, 163–186. [Google Scholar] [CrossRef]
- Anderson, A.R.A. A Hybrid Multiscale Model of Solid Tumour Growth and Invasion: Evolution and the Microenvironment. In Single-Cell-Based Models in Biology and Medicine; Anderson, A.R.A., Chaplain, M.A.J., Rejniak, K.A., Eds.; Birkhäuser Basel: Basel, Switzerland, 2007; pp. 3–28. [Google Scholar] [CrossRef]
- Gillespie, D.T. Exact stochastic simulation of coupled chemical reactions. J. Phys. Chem. 1977, 81, 2340–2361. [Google Scholar] [CrossRef]
- Lindsay, D.; Garvey, C.M.; Mumenthaler, S.M.; Foo, J. Leveraging Hypoxia-Activated Prodrugs to Prevent Drug Resistance in Solid Tumors. PLoS Comput. Biol. 2016, 12, e1005077. [Google Scholar] [CrossRef]
- Marzban, S.; Han, R.; Juhász, N.; Röst, G. A hybrid PDE–ABM model for viral dynamics with application to SARS-CoV-2 and influenza. R. Soc. Open Sci. 2021, 8, 210787. [Google Scholar] [CrossRef]
- Lejon, A.; Mortier, B.; Samaey, G. Variance-reduced simulation of stochastic agent-based models for tumor growth. arXiv 2015, arXiv:1509.06346. [Google Scholar] [CrossRef]
- Hu, B.; Wang, Z.; Xin, J.; Zhang, Z. A Stochastic Interacting Particle-Field Algorithm for a Haptotaxis Advection-Diffusion System Modeling Cancer Cell Invasion. arXiv 2024, arXiv:2407.05626. [Google Scholar] [CrossRef]
- Yuan, Y. Spatial Heterogeneity in the Tumor Microenvironment. Cold Spring Harb. Perspect. Med. 2016, 6, a026583. [Google Scholar] [CrossRef]
- Greulich, P.; Waclaw, B.; Allen, R.J. Mutational Pathway Determines Whether Drug Gradients Accelerate Evolution of Drug-Resistant Cells. Phys. Rev. Lett. 2012, 109, 088101. [Google Scholar] [CrossRef] [PubMed]
- Mumenthaler, S.M.; Foo, J.; Choi, N.C.; Heise, N.; Leder, K.; Agus, D.B.; Pao, W.; Michor, F.; Mallick, P. The Impact of Microenvironmental Heterogeneity on the Evolution of Drug Resistance in Cancer Cells. Cancer Inform. 2015, 14s4, CIN.S19338. [Google Scholar] [CrossRef] [PubMed]
- Mohammadi, M.; Sefidgar, M.; Aghanajafi, C.; Kohandel, M.; Soltani, M. Computational Multi-Scale Modeling of Drug Delivery into an Anti-Angiogenic Therapy-Treated Tumor. Cancers 2023, 15, 5464. [Google Scholar] [CrossRef] [PubMed]
- Everitt, B.; Skrondal, A. The Cambridge Dictionary of Statistics, 4th ed.; Finance Professional Collection; Cambridge University Press: Cambridge, NY, USA, 2010. [Google Scholar]
- El-Hachem, M.; McCue, S.W.; Simpson, M.J. Invading and Receding Sharp-Fronted Travelling Waves. Bull. Math. Biol. 2021, 83, 35. [Google Scholar] [CrossRef]
- Foo, J.; Michor, F. Evolution of Resistance to Targeted Anti-Cancer Therapies during Continuous and Pulsed Administration Strategies. PLoS Comput. Biol. 2009, 5, e1000557. [Google Scholar] [CrossRef]
- Komarova, N.L.; Wodarz, D. Drug resistance in cancer: Principles of emergence and prevention. Proc. Natl. Acad. Sci. USA 2005, 102, 9714–9719. [Google Scholar] [CrossRef]
- Brezis, H. Functional Analysis, Sobolev Spaces and Partial Differential Equations; Springer: New York, NY, USA, 2011. [Google Scholar] [CrossRef]
- Lions, J.L.; Kenneth, P.; Magenes, E. Non-Homogeneous Boundary Value Problems and Applications: Vol. 1; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Jäger, W.; Luckhaus, S. On explosions of solutions to a system of partial differential equations modelling chemotaxis. Trans. Am. Math. Soc. 1992, 329, 819–824. [Google Scholar] [CrossRef]
- Horstmann, D.; Winkler, M. Boundedness vs. blow-up in a chemotaxis system. J. Differ. Equ. 2005, 215, 52–107. [Google Scholar] [CrossRef]
- Calvez, V.; Carrillo, J.A. Volume effects in the Keller–Segel model: Energy estimates preventing blow-up. J. Math. Pures Appl. 2006, 86, 155–175. [Google Scholar] [CrossRef]
- Anderson, A.R.A.; Chaplain, M.A.J.; McDougall, S. A Hybrid Discrete-Continuum Model of Tumour Induced Angiogenesis. In Modeling Tumor Vasculature; Jackson, T.L.L., Ed.; Springer: New York, NY, USA, 2012; pp. 105–133. [Google Scholar] [CrossRef]
- Wang, L.S.; Yu, J. Nonlinear Coupling of Chemotactic Reaction-Diffusion and Social Opinion Clustering: A Cross-Disciplinary Framework. J. Nonlinear Sci. 2025; under review. [Google Scholar] [CrossRef]
- Zhao, P.; Yuan, H. The Modified Stochastic Theta Scheme for Mean-Field Stochastic Differential Equations Driven by G-Brownian Motion Under Local One-Sided Lipschitz Conditions. Mathematics 2025, 13, 1993. [Google Scholar] [CrossRef]
- Zhang, P.; Mohamed, N.A.; Ibrahim, A.I.N. Mean-Field and Anticipated BSDEs with Time-Delayed Generator. Mathematics 2023, 11, 888. [Google Scholar] [CrossRef]
- Grosset, L.; Sartori, E. Mean-Field Modeling of Green Technology Adoption: A Competition for Incentives. Mathematics 2025, 13, 691. [Google Scholar] [CrossRef]
- Kuzenov, V.V.; Ryzhkov, S.V.; Varaksin, A.Y. Development of a method for solving elliptic differential equations based on a nonlinear compact-polynomial scheme. J. Comput. Appl. Math. 2024, 451, 116098. [Google Scholar] [CrossRef]
- Balch, C.; Huang, T.H.M.; Brown, R.; Nephew, K.P. The epigenetics of ovarian cancer drug resistance and resensitization. Am. J. Obstet. Gynecol. 2004, 191, 1552–1572. [Google Scholar] [CrossRef] [PubMed]
- Markman, J.L.; Rekechenetskiy, A.; Holler, E.; Ljubimova, J.Y. Nanomedicine therapeutic approaches to overcome cancer drug resistance. Adv. Drug Deliv. Rev. 2013, 65, 1866–1879. [Google Scholar] [CrossRef] [PubMed]
- Harris, B.; Saleem, S.; Cook, N.; Searle, E. Targeting hypoxia in solid and haematological malignancies. J. Exp. Clin. Cancer Res. 2022, 41, 318. [Google Scholar] [CrossRef]
- Sun, X.; Xing, L.; Deng, X.; Hsiao, H.T.; Manami, A.; Koutcher, J.A.; Clifton Ling, C.; Li, G.C. Hypoxia targeted bifunctional suicide gene expression enhances radiotherapy in vitro and in vivo. Radiother. Oncol. 2012, 105, 57–63. [Google Scholar] [CrossRef]
- Sharma, A.; Arambula, J.F.; Koo, S.; Kumar, R.; Singh, H.; Sessler, J.L.; Kim, J.S. Hypoxia-targeted drug delivery. Chem. Soc. Rev. 2019, 48, 771–813. [Google Scholar] [CrossRef]
- Bottsford-Miller, J.N.; Coleman, R.L.; Sood, A.K. Resistance and Escape From Antiangiogenesis Therapy: Clinical Implications and Future Strategies. J. Clin. Oncol. 2012, 30, 4026–4034. [Google Scholar] [CrossRef]
- Wang, Y.; Dong, L.; Zhong, H.; Yang, L.; Li, Q.; Su, C.; Gu, W.; Qian, Y. Extracellular Vesicles (EVs) from Lung Adenocarcinoma Cells Promote Human Umbilical Vein Endothelial Cell (HUVEC) Angiogenesis through Yes Kinase-associated Protein (YAP) Transport. Int. J. Biol. Sci. 2019, 15, 2110–2118. [Google Scholar] [CrossRef]
- Cappellesso, F.; Orban, M.P.; Shirgaonkar, N.; Berardi, E.; Serneels, J.; Neveu, M.A.; Di Molfetta, D.; Piccapane, F.; Caroppo, R.; Debellis, L.; et al. Targeting the bicarbonate transporter SLC4A4 overcomes immunosuppression and immunotherapy resistance in pancreatic cancer. Nat. Cancer 2022, 3, 1464–1483. [Google Scholar] [CrossRef]
- Fuhr, V.; Vafadarnejad, E.; Dietrich, O.; Arampatzi, P.; Riedel, A.; Saliba, A.E.; Rosenwald, A.; Rauert-Wunderlich, H. Time-Resolved scRNA-Seq Tracks the Adaptation of a Sensitive MCL Cell Line to Ibrutinib Treatment. Int. J. Mol. Sci. 2021, 22, 2276. [Google Scholar] [CrossRef] [PubMed]
- Lobov, I.; Mikhailova, N. The Role of Dll4/Notch Signaling in Normal and Pathological Ocular Angiogenesis: Dll4 Controls Blood Vessel Sprouting and Vessel Remodeling in Normal and Pathological Conditions. J. Ophthalmol. 2018, 2018, 3565292. [Google Scholar] [CrossRef] [PubMed]
- Gerhardt, H. VEGF and endothelial guidance in angiogenic sprouting. Organogenesis 2008, 4, 241–246. [Google Scholar] [CrossRef] [PubMed]
- Stapor, P.C.; Sweat, R.S.; Dashti, D.C.; Betancourt, A.M.; Murfee, W.L. Pericyte Dynamics during Angiogenesis: New Insights from New Identities. J. Vasc. Res. 2014, 51, 163–174. [Google Scholar] [CrossRef]
- Naldini, A.; Carraro, F. Role of Inflammatory Mediators in Angiogenesis. Curr. Drug Target -Inflamm. Allergy 2005, 4, 3–8. [Google Scholar] [CrossRef]
- Balding, D.; McElwain, D. A mathematical model of tumour-induced capillary growth. J. Theor. Biol. 1985, 114, 53–73. [Google Scholar] [CrossRef]
- Chignola, R.; Foroni, R. Estimating the Growth Kinetics of Experimental Tumors From as Few as Two Determinations of Tumor Size: Implications for Clinical Oncology. IEEE Trans. Biomed. Eng. 2005, 52, 808–815. [Google Scholar] [CrossRef]
- Lee, J.M. Smooth Manifolds. In Introduction to Smooth Manifolds; Graduate Texts in Mathematics; Springer: New York, NY, USA, 2013; Volume 218, pp. 1–31. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).