Abstract
Partial differential equations are an integral part of modern scientific development. Hyperbolic partial differential equations are encountered in many fields and have many applications—both linear and nonlinear types, with some being semilinear and quasilinear. In this paper, a family of implicit numerical schemes for solving hyperbolic partial differential equations is derived, utilizing finite differences and tridiagonal sweep. Through the discrete Fourier transform, a necessary and sufficient condition for convergence is proven for the linear version of the family of difference schemes, expanding the known results on boundary conditions that ensure convergence. Numerical verification confirms the found condition. A series of experiments on different boundary conditions and semilinear hyperbolic PDEs show that the same condition seems to also hold in those cases. In view of the results, an optimal subset of the family is found. A comparison between the implicit schemes and an explicit analogue is conducted, demonstrating the gained efficiency of the implicit schemes.
Keywords:
hyperbolic partial differential equation; semilinear partial differential equation; finite differences; implicit scheme; convergence analysis MSC:
65M06; 65M12
1. Introduction
Differential equations are an indispensable tool not only in the field of mathematics but also in modeling processes in a plethora of fields. Hyperbolic partial differential equations (PDEs) have played an important role in describing such phenomena. The linear hyperbolic PDE is probably the most famous one of this kind—the wave equation. Semilinear variants are used to describe Josephson junctions [1], the planar vortex flows of an ideal fluid [2], classical dislocation theory [3], self-induced transparency [4], magnetic domain wall dynamics [5], and others [6,7,8]. Quasilinear hyperbolic PDEs can be used in shallow water wave theory, the description of the flow of one-dimensional gas, in the dynamics of a finite nonlinear string, and others [9].
Many such equations are difficult to solve analytically. This is true especially for nonlinear PDEs, despite the developed methods, some of which are the Inverse Scattering Transform [10,11], the Hirota method [12], and, more recently, the Simple Equations Method [13]. In order to deal with such difficulties, a variety of numerical methods have been developed for solving hyperbolic PDEs. Some of them are classical methods like the finite differences [14,15,16] and finite elements methods [17], whereas others are more recent—the generalized finite differences method [18], spectral/finite difference methods [19], the iterative finite difference method [20], the spatio-temporal cloud method [21], neural network-based methods [22], etc.
In the current paper, the focus is placed on a finite differences method. We will examine a family of difference schemes that has been used throughout the years [14,15,23,24], but its convergence with respect to the initial and boundary conditions has not been fully investigated. In [25], we proved a necessary condition for the convergence of the family of difference schemes. In this paper, we provide a more detailed and rigorous proof of the necessity, and we also provide the sufficiency. We further broaden the class of boundary conditions that ensures convergence.
This paper is structured in the following way: In Section 2, the problem of interest is presented, along with the required notation and theoretical background. The family of difference schemes is introduced, as well as the procedure used for computation with it and the convergence results, known in the literature. In Section 3, several auxiliary results are proven. In Section 4, the main result of this paper is formulated and proven. In Section 5, an outline of the algorithm used is presented, a numerical verification of the main result is conducted, numerical experiments concerning different boundary conditions and semilinear PDEs are carried out, conclusions are drawn, and an efficiency comparison with an explicit scheme is presented. In Section 6, the results of this paper are summarized, and future work is discussed.
2. Preliminaries
The focus of this research is the linear hyperbolic partial differential equation
defined in , where , in addition to the initial conditions
and either the Dirichlet boundary conditions
or the boundary conditions with one Dirichlet and one Neumann condition, which, without the loss of generality, we can express as
For brevity, we will use the general form of a linear PDE:
where is a linear differential operator, and F is the inhomogeneous term. Clearly, in the current case, . With , we will denote the analytical solution to (1).
Let us create a difference scheme by discretizing into a grid with steps , , , with h being the step for x and being the step for t. Let , , , , , , , , and , . We will further require the following sets: and
Analogously to (5), we will use the general form of a difference scheme:
which will be valid for both initial boundary value problems and initial value problems, i.e., .
In what follows, the notation will be introduced as the need arises. For notation that is not often recalled in the text, the reader can refer to Appendix A.
2.1. Theoretical Background
For the purposes of the analysis, we will make use of some well-known spaces. Let
where is the Euclidean norm in . Analogously, the Euclidean norm in will be denoted as . In , we will use the norms
and
in which case, we will refer to the space as . The space of Lebesgue square-integrable functions will be denoted as
with the norm
When using the norm of an operator, we will use the induced norm
where the norm is the appropriate one of the aforementioned three. When using the Euclidean norm, we can use an exact formula.
Proposition 1
([26]). If is an matrix, then
where is the spectral radius of , and is the Hermitian transpose of . If is Hermitian, then .
The following will be required for the auxiliary results:
Theorem 1
([27]). Let X and Y be normed spaces, and let be a bounded operator. If there exists such that , then
Theorem 2
([27]). For the spectral radius of the bounded operator , defined on the complex Banach space X, it is true that
Theorem 3
([27]). Let X be a complex Banach space, be a bounded linear operator, and Then,
In what follows, is the solution to the PDE, and the norms that are not explicitly pointed out could be or , which will be clear from the context.
Definition 1
Let us introduce the operator , for which . A general two-level difference scheme can be expressed as
where
are matrices, and Equation (8) can be expressed as an equation in :
where , and .
Definition 2
Definition 3
For the purposes of defining stability, we will utilize the homogeneous scheme
In our case, .
Definition 4
([26]). A difference scheme (10) is stable of order n with respect to the norm if there exist positive constants and non-negative constants , and β such that
for and .
Proposition 2
([26]). A difference scheme (10) is stable of order n with respect to if and only if there exist positive constants and non-negative constants , and β such that
for and .
Even though we define stability for a homogeneous scheme, the same definition also works for inhomogeneous schemes [26]. It is also worth pointing out that the linear growth of with respect to n is permissible due to the truncation error of the difference scheme being multiplied by . Then, in the proof of Proposition 2, due to , the leftover ensures the convergence of the method. For further details, please refer to [26].
Definition 5
([26]). Let . The discrete Fourier transform of is
for
It is easy to see that .
Proposition 3
([26]). If and is the discrete Fourier transform of , then
By taking the discrete Fourier transform of (10), we get the expression
which is equivalent to
Let us define the matrix
which is called the amplification matrix of the difference scheme. A simple consequence of Proposition 3 is
Theorem 4
([26]). Difference scheme (10) is stable of order n with respect to the norm if and only if there exist positive constants and non-negative constants , and β such that
for and every .
We will require a special case of Lax’s equivalence theorem.
Theorem 5
The next theorem will be paramount for the proof of the main result.
Theorem 6
([26]). Suppose that a three-level difference scheme is consistent of order with a partial differential order, which is second order in time and stable of order n. Then, if the initial conditions approximate in such a way that and , the difference scheme is convergent of order .
Finally, let us explain the connection between schemes for initial value problems and initial boundary value problems. By using the Fourier modes , and substituting them into the difference scheme, a necessary condition for the stability of the scheme is . This procedure is known as the discrete von Neumann stability criterion. For some problems, this criterion also leads to a sufficient condition.
Theorem 7
([26]). A scheme for solving an initial value problem with a periodic initial condition is stable with respect to the finite dimensional norm on one period if and only if it satisfies the discrete von Neumann stability criterion.
Let us point out that the finite dimensional norm is taken over one period of the function.
In [26], it is concluded that, if both boundary conditions are Dirichlet, with one being a zero condition or one being a zero Dirichlet condition and one being a zero Neumann condition, approximated via a second-order approximation, one can transform the problem into a problem with a periodic initial condition. This can be achieved by extending the initial condition evenly and/or oddly along the appropriate boundaries.
As a final note, the eigenvalues of the amplification matrix coincide with the values of , found via the discreet von Neumann procedure. Thus, the conclusions made via Theorem 7 can be applied to the approach used in this paper.
2.2. The Scheme
We will need the next proposition to create the difference scheme.
Proposition 4.
Let . Then,
for
The proof consists of a simple use of the Taylor expansion of and is therefore omitted. Using this proposition, instead of focusing on (1), we can examine
assuming that . Instead of using Proposition 4, a linear interpolation argument is given in [28]. By finding an approximate solution to (11), we will find an approximate solution to (1), with an additional error of .
Using the second-order approximations of and and dropping the truncation errors, we get the scheme
which is well-known [14,23,24]. In [14], convergence is established using only a necessary condition, whereas in [15], a more general version is presented, the stability of which is not discussed. This more general difference scheme uses Proposition 4 on instead of only on . We decided not to take this approach due to the nonlinear system that would need to be solved when modifying this scheme to be suitable for semilinear PDEs. In our case, we will get a linear system of equations even if . We will return to this point in Section 5.2.
Let . After some algebraic manipulation, (12) takes the form
for . Let the right-hand side of the equation be denoted as , . Then, we can express the equations more succinctly as
where, using the Dirichlet boundary conditions (3),
Since we need the values of for n and in order to find the values of the next layer, we will have to calculate the first layer in a different way. Since the scheme that calculates the first layer does not need to be stable [26], we will use an explicit scheme for the first layer, that is, . By supposing that the solution v exists in , using the second initial condition from (2) and dropping the truncation error term, we get that
By substituting in (13) and taking into account that , we are left with
from where we can find the values of , .
If we have the boundary conditions (4), then we can use the second-order approximation of in order to find that
where we assume that the solution v exists in and drop the truncation error term. This leads to an additional equation when in (13) of the form
In a similar manner to the Dirichlet case, we get the system
where
and the first layer can be found via the same equations as in the Dirichlet case with the addition of
In both cases, a tridiagonal linear system of equations has to be solved at each step. This can be efficiently carried out by a tridiagonal sweep, also known as the Thomas algorithm [26,29]. In order to ensure the stability of solving the system, we will use the following:
Proposition 5
([29]). If, for the system of equations,
it is true that , then the tridiagonal sweep is stable.
Some results concerning the scheme are presented.
Theorem 8
Theorem 9
3. Auxiliary Results
Let us first find a sufficient condition for the stability of the tridiagonal sweep.
Proposition 6.
Proof.
Since in (14), the unknowns are , we can apply Proposition 5. Because , , a sufficient condition for the stability of the tridiagonal sweep is
Due to , we will consider only the sign of . If , then the inequality is obviously fulfilled. If , then the inequality turns into
whose solution is .
In system (18), we have another equation for which we require that , which has already been checked. □
The remaining propositions and lemmas will aid us in proving the convergence of the scheme.
Proposition 7.
Let be a bounded linear operator. For the matrix that is the result of applying the discrete Fourier transform on , let it be true that for every and every h and τ, where is the eigenvalue of with the smallest modulus. Then,
Proof.
Let be an eigenvector of and its eigenvalue, respectively. Then,
Then, from Theorem 1, it follows that □
Proposition 8.
Let be a linear operator. Let be the matrix that is a result of applying the discrete Fourier transform on . If is bounded for every and every h and τ, then
Proof.
The following chain of inequalities proves the claim:
Proposition 9.
If a difference scheme (10) is stable of order n in the norm , then there exist positive constants , and C independent of , and ξ such that, for the spectral radius of the amplification matrix, it holds that
for and for every .
Proof.
By way of contradiction, let us assume that the inequality does not hold. Then, for every constant , there exists such that . Because the scheme is stable of order n, there exist , and so that from which is bounded for every and every fixed .
From Theorem 2, it follows that , while from Theorem 3, it follows that . Let us define a sequence such that when . Then, there exists a sequence for which it holds that By taking , there exists such that , Then, from the chain of inequalities
we reach a contradiction. □
Remark 1.
In order to examine the stability of the difference scheme, we will transform it into a scheme for solving a system of differential equations. Equivalent to scheme (13) is
where ,
Let us express this system as an equation in :
where
We apply the discrete Fourier transform to (23) by leaving out the nonhomogeneous term. If then we are left with
or, equivalently,
This algebraic manipulation is possible when . If it happens that for some , then , which holds only for the trivial solution , . From Theorem 3, . Not only is this case not of any practical interest, but it is also easy to see that the scheme is stable in this case. Consequently, we will assume that .
Lemma 1.
Let and . Then, for the operator , it holds that
Proof.
Let us consider the matrix that is a result of applying the discrete Fourier transform on . This is a Hermitian matrix with eigenvalues . Both eigenvalues are positive because
Thus, and
From Propositions 7 and 8, the claim of the lemma follows. □
Lemma 2.
Proof.
Taking into account (22) and substituting , it is easy to see that the truncation error is of the form . Thus, we can calculate the truncation error of in (13) for an estimate of . By using the Taylor expansion of around in (13), we are left with
The terms in the truncation error are made up of different fourth-order derivatives of . Since every fourth-order derivative of is in for every , then it is true that because either or can be absorbed into the big O notation. Because , we can apply Lemma 1. Then, for the difference scheme (23), it is true that
From Definition 3, it follows that the scheme is accurate of order to the PDE (1). □
Lemma 3.
Let , and every fourth derivative of be in for every , , and . Then, the initial conditions for (13) approximate in such a way so that and .
Proof.
Since , then . Let us consider the truncation error in the form of (23). Then, the equation for is
where
For , it is true that
where . Subtracting (24) from (25), we are left with where . Since and if then with which we can claim that . Like in the proof of Lemma 2, we will use the Taylor expansions of v and around and substitute in (16). For , we find that
where the terms in the truncation error consist of fourth-order derivatives of and Analogously to the proof of Lemma 2, we conclude that Using Lemma 1, we find that
Hence, . □
4. Main Result
Before moving on, let us point out that a similar argument for proving the necessity of the main result was first examined and published by some of the authors in [25]. Since the current approach slightly differs from the one used in [25], we will present it in its entirety.
Theorem 10.
Let , , and every fourth derivative of be in for every , , . Then, the difference scheme (13), used to solve an initial value problem, is convergent of order in if and only if
Proof.
Let the scheme be convergent and . Since the scheme is convergent and is used for a two-level scheme (that is, (22) for a linear PDE), by Theorem 5, it follows that the scheme is stable of order n. From Proposition 9, it is true that for every , where are the eigenvalues of . Let . Then, the eigenvalues are Assume that . If , then , whereas if , then . Therefore, , i.e., . Then, it is easy to calculate that .
If the denominator of A becomes negative for some , then, from the continuity of , there exists such that . From the continuity of A, when , it holds that from which we can conclude that there exists such that , which is a contradiction.
Let the denominator of A be positive for all . The inequality reduces to the inequalities
The first one is clearly true, whereas by analyzing the minimum and maximum value of on the interval , we see that the second inequality holds for . Since we assumed that , then the scheme is not stable of order n, hence reaching a contradiction and establishing the necessity of the claim.
In order to prove the sufficiency, we will use Theorem 6. By Lemmas 2 and 3, we have that the three-level difference scheme (13) approximates the PDE (1) of order and that the initial conditions approximate in such a way that and . What remains is to show the stability order n of the scheme.
To this end, we will use the Schur decomposition of . Let . Then, . The eigenvector of corresponding to is . Let . Then, using the Gram–Schmidt process with and , we find the unit vector , which is orthogonal to . Forming the unitary matrix , it is easy to calculate that
Noticing that and the fact that the spectral radius is unitarily invariant, we conclude that . By a simple induction argument, it can be shown that
Let . Then, and the eigenvalues of are
For , it holds that
Since the eigenvalue with + has a bigger modulus and is positive, we find that
from which we conclude that
By applying Theorem 4 with , , , and arbitrary , it follows that (13) is stable of order n. Therefore, by Theorem 6, the scheme is convergent of order .
Hence, we conclude that the scheme is convergent of order for an initial value problem if and only if . □
In order to formulate theorems for initial boundary value problems, we can use the arguments from the end of Section 2.1. First, we will present a way to weaken the assumptions.
Let us first look at the boundary conditions (3). Suppose that a solution to difference Equation (13) with exists for suitable initial and Dirichlet boundary conditions with the following property:
Without the loss of generality, let the former hold. In that case, by defining , we get a problem with a left zero Dirichlet condition, which allows us to use the previous result to conclude that the scheme would be stable. Finding solutions to (13) is no trivial task. Some boundary conditions that are suitable are , , , and for , with being the constants from the formulation of the problem (Section 2). As an example, if , then , where . Clearly, a linear combination of such conditions would also fulfill this property.
As far as the Neumann property goes, we have to tread more carefully. Assuming a left Neumann condition, is paramount for maintaining symmetry and allowing for an odd extension along the left boundary. That is why if we can assume that a solution to difference Equation (13) with exists for a suitable initial condition with the property
then, as in the Dirichlet case, by setting , we are left with a problem with zero Neumann and zero Dirichlet boundary conditions, thus being able to apply the reasoning from the end of Section 2.1. One such example of boundary conditions for which this holds is
where , whereas c and b are again the constants from the formulation of the problem. Another example is , where , and a is from the formulation of the problem.
We are ready to present theorems for initial boundary value problems.
Theorem 11.
Theorem 12.
Remark 2.
We can formulate a theorem analogous to 12 for a right Neumann boundary condition by replacing property (27), with there existing a solution of difference Equation (13) with an appropriate initial condition such that fulfills an equation analogous to (17) for a right Neumann boundary condition and , and the set with .
These results expand upon the previously known results in two ways. First, the condition is found to be both necessary and sufficient without any other restrictions on and , as in Theorems 8 and 9, respectively. The second is that, unlike in Theorem 8, the boundary conditions are more diverse than zero Dirichlet conditions.
5. Numerical Verification
In this section, we will conduct a numerical verification of the main result. The verification consists of repeatedly solving PDEs with varying values for . In the first example, , whereas due to the conclusions from the numerical verification, every other example has , where, in both cases, we go through the entire interval with a step of . In Example 1, we also present some results with negative . The measured errors are
where , . In Example 2, the errors also include the points along the left boundary, i.e., . All of the computations in this section are performed using a regular laptop (AMD A10 Pro-7350B CPU—2.10 GHz) and the programming language Julia (ver. 1.11.2.), and all calculations were performed using Float64. Pseudorandom components were not used. In order to avoid minute details in describing the procedure, a short pseudocode describing the algorithm is presented in Algorithm 1. The function tridiagonalsweep was implemented according to [26].
| Algorithm 1: Solving (1) with boundary conditions (3) using difference scheme (13). |
 |
Algorithm 1 can be adapted to a problem with a left Neumann condition by replacing the boundary condition in line 4 with (20) and in line 6 with , where is the vector from (19). An adaptation to a right Neumann boundary condition can be achieved in a similar manner. For completeness, we will mention that the already found values of were kept in a list for the convenient appending of new values and the reading of old values for calculating (16) and (15).
5.1. Linear Hyperbolic PDEs
Example 1.

Let us consider the equation along with the initial and boundary conditions
The exact solution is . The mesh is built with , which leads to . Clearly, , and . We also have two Dirichlet boundary conditions, for which there exists a solution with property (26) ( is constant). By Theorem 11, the difference scheme is convergent if and only if .
The results around are presented in Table 1. We see that the scheme has enormous errors when , but, from onward, the scheme’s errors become smaller in accordance with the expected order of the scheme (). This is due to the instability of the scheme for . Since the errors when and are qualitatively different, in Figure 1, only the errors when are presented.

Table 1.
Example 1 with , , , and .

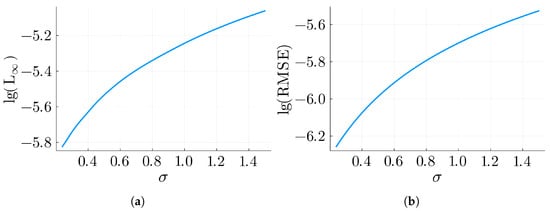
Figure 1.
Errors for Example 1 with , , , and . (a) L∞ for Example 1. (b) RMSE for Example 1.
As we can see, the errors seem to be growing with σ. This will be further discussed in Section 5.3. For now, we will continue with for the next examples.
Before we move on, we will solve this example with , thus leading to . Since and every other condition has not changed, then, according to Theorem 11, the scheme is convergent if and only if . In Table 1, we can observe that the condition holds.
Example 2.

Let us consider the equation along with the initial and boundary conditions
The exact solution is . The mesh is built with , which leads to . Since , , and for the boundary conditions, there exists a solution to difference scheme (13) with property (27) (boundary conditions (28) with , ), by Theorem 12, we conclude that the difference scheme is convergent if and only if .
Like in the previous example, the results around are presented in Table 2. They agree with the conclusions of Theorem 12. Analogous graphs are shown in Figure 2.

Table 2.
Example 2 with , , , and .

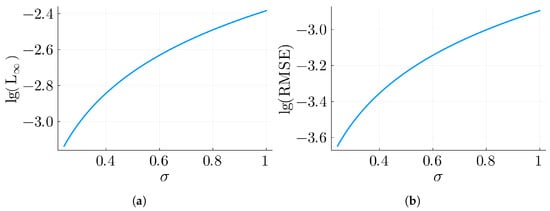
Figure 2.
Errors for Example 2 with , , , and . (a) L∞ for Example 2. (b) RMSE for Example 2.
Example 3.

Let us consider the equation along with the initial and boundary conditions
The exact solution is . The mesh is built with , which leads to . It can be checked that the obvious candidate for a solution of difference scheme (13) is not a solution. Further, even if we had the boundary condition , we would still not be able to apply Theorem 11 for similar reasons. If we were to ignore that requirement and assume that we could apply Theorem 12 (Theorem 11), we would conclude that the difference scheme is convergent if and only if .
In this example, we will observe the neighborhood of in Table 3. They agree with the conclusions of Theorems 11 and 12. Analogous graphs are shown in Figure 3.

Table 3.
Example 3 with , , , and .

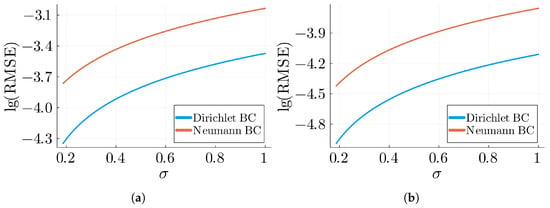
Figure 3.
Errors for Example 3 with , , , and . (a) L∞ for Example 3. (b) RMSE for Example 3.
5.2. Semilinear Hyperbolic PDEs
In this subsection, we will use the family of difference schemes to solve semilinear hyperbolic PDEs. Because of the form of the family of difference schemes, the simple modification of is enough to allow for the solving of semilinear PDEs. Since we already found the approximate value of when solving for the -st layer, we again have to only solve a tridiagonal system of linear equations at each time step. Let us point out that the results in this subsection are purely empirical because the proven theorems are valid only for linear hyperbolic PDEs.
Example 4.

Let us consider the sine-Gordon equation with the initial and boundary conditions
The exact solution is [3,28,30]. The mesh is built with which leads to . Even though we do not have a result for such an equation, if we were to apply the condition of Theorem 11, we would say that the difference scheme is convergent if and only if .
Let us examine the results around (Table 4). These calculations show that the conclusions of Theorem 11 match those of the numerical experiment. The errors can be seen in Figure 4.

Table 4.
Example 4 with , , , and .

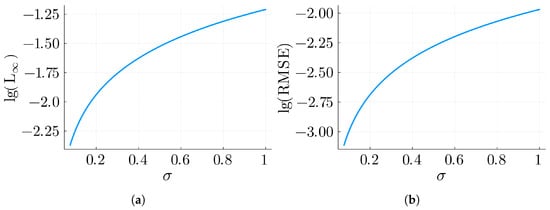
Figure 4.
Errors for Example 4 with , , , and . (a) L∞ for Example 4. (b) RMSE for Example 4.
Example 5.

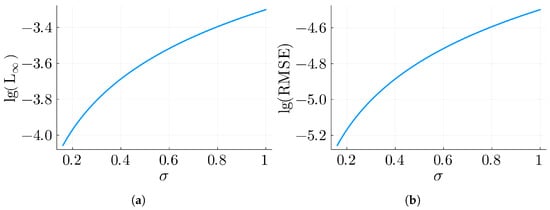
Let us consider the sinh-Gordon equation with the initial and boundary conditions
The exact solution is , found with the method described in [13]. The calculations were made with which leads to . Like in Example 4, if we assume that the conclusion of Theorem 11 holds, then the difference scheme would be convergent if and only if .
Table 5 and Figure 5 are analogous to the tables and figures of the previous examples. In Table 5, there are entries with NaN values. This is due to the blowing up of the solution, the way Julia handles floating point numbers, and the exponential growth of . For , , it is true that . As can be seen from L∞, we get values of an order of at least . Because Julia’s Float64 supports numbers with an exponent of up to 308 and , the huge discrepancy between and shows that values around 710 are easily reached, leading to Julia giving a value of Inf for anything bigger than about 710. Since the buildup of the solution is not in a single value, in the first layer where we see Inf, there would be more than one value of Inf. During subtraction in the tridiagonal sweep, the expression Inf - Inf is evaluated as NaN. From this point forward, every operation with NaN returns a NaN. Even though the values of do not have NaN (which is due to NaN returning false when compared with anything else other than NaN), we can also see irregularities in this column. Due to the limitations of Float64, we see more growth in than in . This could very well be because of the irregularities described in this paragraph rather than actually demonstrating a ramp-up in error closer to the σ condition.

Table 5.
Example 5 with , , , and .

Figure 5.
Errors for Example 5 with , , , and . (a) L∞ for Example 5. (b) RMSE for Example 5.
5.3. Conclusions and Speed
We can conclude that Examples 1 and 2 validate Theorems 11 and 12. It also seems that . This can easily be explained by Proposition 4. If one were to consider the Taylor expansion of , one would see that the truncation error has the form . Thus, the smaller the absolute value of , the smaller the truncation error. This is why we restricted the interval of values that can take to . For , the error would have increased, as can be seen in Figure 1. Since is restricted by the condition in Theorem 10, the optimal choice of for the smallest possible error is for . If , then clearly has the smallest absolute value out of all permissible ; i.e., an explicit scheme would be best suited for . This is the reason why negative values of are barely discussed.
Even though the theorems concern linear hyperbolic PDEs with specific boundary conditions, empirical evidence suggests that Theorems 11 and 12 may hold for more general problems. Example 3 shows the use of boundary conditions different from the required Dirichlet and Neumann boundary conditions, whereas Examples 4 and 5 solve a semilinear variant of (1). This shows that the theorems could be valid for a larger variety of boundary conditions and PDEs. In the corresponding figures, we can also see that the optimal choice of still remains for . It could also be the case that is the optimal choice for .
On some practical matters, we will discuss the choice of . Since for , the choice is obvious, we will assume that . Choosing according to the previous paragraph could be ill-advised in some cases. Let us look at Example 2. We observe that the boundary is irrational. In that case, it would be better to pick slightly bigger than the minimum bound in order to ensure stability. Additions as small as or even would prevent instability while adding an insignificant amount of truncation error to the numerical solution. Further, when using the scheme for problems that have not been described by Theorems 11 and 12, it would be best to conduct numerical experiments with a larger N, which would depend on the problem. This is because instability may be hard to detect near the boundary of the condition for stability if the scheme has not had enough steps to accumulate the buildup in error. This, in fact, was exploited in this paper when calculating the first layer with the explicit scheme. As a general recommendation, N can be taken in the hundreds, e.g., 500, 700, and 900. Needless to say, if the numerical solution starts exhibiting values that are beyond any reasonable expectations of the real solution, a likely explanation could be instability.
An important aspect of using an implicit difference scheme is whether the bigger step taken along t can speed up the process of solving the equation compared to an explicit scheme. Since we have to solve a system at every step, this aspect does not have an obvious answer. That is why we compared the implicit scheme with its explicit analogue (). In order to make the comparison, we fixed K to have the value stated in the examples and took the smallest so that . We solved the same equation 100 times in order to record the CPU time taken to run the schemes. The mean and median times of execution are presented in Table 6.

Table 6.
CPU times of execution for the explicit and the implicit scheme.
We can separate the results in two cases. The first one is the problems with smaller , that is, Examples 3 with both types of boundary conditions, 4 and 5. In these examples, lowering the steps in time does not compensate for the added computations required by solving a tridiagonal system. In Examples 1 and 2, we see a significant speedup of about two to three times when using the implicit scheme. In this case, is significantly larger, thus leading to requiring a much finer mesh in order to make the explicit scheme stable. Thus, if a big enough step in time is necessary to, e.g., investigate solutions with larger T, then the implicit scheme will be significantly faster than its explicit counterpart. How big should be in order for the implicit scheme to be more efficient is dependent on the type of problem and especially on the efficiency of the implementation. In our case, it appears that a value of 10 to 15 would be a good threshold.
6. Conclusions
In this paper, we examine the well-known scheme for solving hyperbolic partial differential equations. A necessary and sufficient condition for the convergence of the scheme is proven for linear PDEs with either two Dirichlet boundary conditions such that a solution to difference scheme (13) with property (26) exists, or a Dirichlet condition and a Neumann condition, approximated with a second-order approximation such that a solution to difference scheme (13) with property (26) exists. A numerical verification is conducted, during which the conclusions of Theorems 11 and 12 are confirmed. The optimal choice of is concluded to be when —the value of that turns the inequality in the condition of Theorems 11 and 12 into an equality. If , then using the explicit scheme, i.e., , would be optimal. Numerical experiments with different boundary conditions and semilinear hyperbolic PDEs show that the same conclusions hold for the examined cases. A comparison of the efficiency of the implicit scheme and an explicit scheme demonstrates that the speedup of using a bigger time step far outweighs the slowdown of having to additionally solve a tridiagonal system at every time step if is big enough. The threshold can vary with the problem being solved or the implementation of the scheme. The results of this paper suggest that a value between 10 and 15 would be optimal.
One limitation in this approach is the requirement that for . This condition is required for the proof of Lemma 1, upon which the proofs of Theorems 10–12 rely. If one were to use constant h and for computations, this requirement is merely a formality. However, if some sort of dynamic refinement regime is utilized, where h is not proportional to (e.g., , ), the conclusions of the theorems could not be used. Thus, a further study into the scheme could look into whether its stability would be preserved if such a regime were to be used.
Another limitation is the restrictive boundary conditions required by Theorems 11 and 12. While extending the conditions under which the discrete von Neumann condition also provides sufficiency may be possible, observing that the already given conditions are difficult to check, it appears advisable to consider a different approach if a future study is to be conducted. The empirical results of Example 3 suggest that the theorems could hold for a bigger class of boundary conditions. Such a result would be of great importance to the application of the scheme in practice.
Furthermore, the empirical results of the numerical experiment suggest that it is possible that the same condition for convergence also holds for some classes of semilinear hyperbolic PDEs. Considering that most phenomena describable by PDEs are nonlinear in nature [1,2,3,4,5,6,7,8,9], further research into the validity of this statement could be of particular interest. If convergence results for the scheme applied to semilinear or even quasilinear equations were to be developed, the ensured validity of the numerical results paired with the improved performance of using a bigger step in time could allow for a more in-depth numerical investigation of the solutions to numerous PDEs, along with the influence of the parameters found in the original equations.
Author Contributions
Conceptualization, P.A. and V.G.; methodology, P.A. and V.G.; software, S.C. and V.G.; investigation, P.A., S.C. and V.G.; writing—original draft preparation, P.A., S.C. and V.G.; writing—review and editing, P.A., S.C. and V.G.; visualization—S.C. and V.G. The listed authors contributed equally to the research and are listed in alphabetical order. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in the study are included in the article; further inquiries can be directed to the corresponding author.
Acknowledgments
The study of P. Atanasova is supported by the European Union–NextGenerationEU through the National Recovery and Resilience Plan of the Republic of Bulgaria, project DUECOS BG-RRP-2.004-0001-C01. The following have been reproduced/paraphrased from a previous publication of P. Atanasova and V. Gerogiev [25]: the descriptions of the general problem (in Section 2) for Dirichlet boundary conditions; the procedure for deriving and solving the difference scheme (in Section 2.2) for Dirichlet boundary conditions; the statement of Proposition 6 for Dirichlet boundary conditions; the derivation of the amplification matrix (in Section 3); the majority of the necessity of Theorem 10; and the conclusions about the optimal choice of in the first two paragraphs of Section 5.3 (first published in Slavova, A. (eds) New Trends in the Applications of Differential Equations in Sciences. NTADES 2024. Springer Proceedings in Mathematics & Statistics. Vol. 488, pp. 361–371, 2025, by Springer Nature) [25]. The authors appreciate the efforts of the anonymous reviewers to improve the quality and presentation of the article. All authors have read and agreed to the published version of the manuscript.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A. Notation
Here, we present a short reference list for some notation that is used throughout the paper but is not readily recalled upon usage.
References
- Geigenmüller, U.; Lobb, C.J.; Newrock, R.S.; Octavio, M. The two-dimensional physics of Josephson junction arrays. Solid State Phys. 2000, 54, 263–512. [Google Scholar] [CrossRef]
- Andreev, V.K.; Kaptsov, O.V.; Pukhnachov, V.V.; Rodinov, A.A. Applications of Group-Theoretical Methods in Hydrodynamics; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1998; pp. 191–209. [Google Scholar]
- Lamb, G.L. Elements of Soliton Theory; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1980; pp. 182–186. [Google Scholar]
- Lamb, G.L. Analytical Descriptions of Ultrashort Optical Pulse Propagation in a Resonant Medium. Rev. Mod. Phys. 1971, 43, 99–124. [Google Scholar] [CrossRef]
- Feldtkeller, E. Magnetic Domain Wall Dynamics. Phys. Status Solidi (B) 1968, 27, 161–170. [Google Scholar] [CrossRef]
- Perring, J.K.; Skyrme, T.H.R. A Model Unified Field Equation. Nucelear Phys. 1962, 31, 550–555. [Google Scholar] [CrossRef]
- Gojkovic, Z.; Ivancevic, T. Control of the extension–flexion cycle of human knees during bicycle riding by a synergy of solitary muscular excitations and contractions. Nonlinear Mech. 2016, 86, 2071–2080. [Google Scholar] [CrossRef][Green Version]
- Caputo, J.-G.; Dutykh, D. Wave dynamics on networks: Method and application to the sine-Gordon equation. Appl. Numer. Math. 2018, 131, 54–71. [Google Scholar] [CrossRef]
- Ames, W.F.; Lohner, R.J.; Adams, E. Group properties of utt = [F(u)ux]x. Int. J. -Non-Linear Mech. 1981, 16, 439–447. [Google Scholar] [CrossRef]
- Gardner, C.S.; Greene, J.M.; Kruskal, M.D.; Miura, R.M. Method for Solving the Korteweg-deVries Equation. Phys. Rev. Lett. 1967, 19, 1095–1097. [Google Scholar] [CrossRef]
- Gardner, C.S.; Greene, J.M.; Kruskal, M.D.; Miura, R.M. Korteweg-deVries Equation and Generalizations. VI. Methods for Exact Solution. Commun. Pure Appl. Math. 1974, 27, 97–133. [Google Scholar] [CrossRef]
- Hirota, R. Exact Solution of the Sine-Gordon Equation for Multiple Collisions of Solitons. J. Phys. Soc. Jpn. 1972, 33, 1459–1463. [Google Scholar] [CrossRef]
- Vitanov, N.K. Simple Equations Method (SEsM): An Effective Algorithm for Obtaining Exact Solutions of Nonlinear Differential Equations. Entropy 2022, 24, 1653. [Google Scholar] [CrossRef]
- O’Brien, G.G.; Hyman, M.A.; Kaplan, S. A Study of the Numerical Solution of Partial Differential Equations. J. Math. Phys. 1950, 29, 223–251. [Google Scholar] [CrossRef]
- Ramos, J.I. Numerical Methods for Nonlinear Second-Order Hyperbolic Partial Differential Equations. I. Time-Linearized Finite Difference Methods for 1-D Problems. Appl. Math. Comput. 2007, 190, 722–756. [Google Scholar] [CrossRef]
- Stampolidis, P.; Gousidou-Koutita, M.C. A Computational Study with Finite Difference Methods for Second Order Quasilinear Hyperbolic Partial Differential Equations in Two Independent Variables. Appl. Math. 2018, 9, 1193–1224. [Google Scholar] [CrossRef]
- Adjerid, S. A Posteriori Finite Element Error Estimation for Second-Order Hyperbolic Problems. Comput. Methods Appl. Mech. Eng. 2002, 191, 4699–4719. [Google Scholar] [CrossRef]
- Ureña, F.; Gavete, L.; García, A.; Benito, J.J.; Vargas, A.M. Solving Second Order Non-Linear Hyperbolic PDEs Using Generalized Finite Difference Method (GFDM). J. Comput. Appl. Math. 2020, 363, 1–21. [Google Scholar] [CrossRef]
- Luo, Z.; Jin, S. A Reduced-Order Extrapolation Spectral-Finite Difference Scheme Based on the POD Method for 2D Second-Order Hyperbolic Equations. Math. Model. Anal. 2017, 22, 569–586. [Google Scholar] [CrossRef]
- Ben-Romdhane, M.; Temimi, H. An Iterative Finite Difference Method for Solving Nonlinear Gordon-Type Problems. Mathematics 2025, 13, 2084. [Google Scholar] [CrossRef]
- Flores, J.; García, A.; Negreanu, M.; Salete, E.; Ureña, F.; Vargas, A.M. A Spatio-Temporal Fully Meshless Method for Hyperbolic PDEs. J. Comput. Appl. Math. 2023, 430, 115194. [Google Scholar] [CrossRef]
- Meuris, B.; Qadeer, S.; Stinis, P. Machine-learning-based spectral methods for partial differential equations. Sci. Rep. 2023, 13, 1739. [Google Scholar] [CrossRef]
- Krylov, V.I.; Bobkov, V.V. Nachala Teorii vychislitelnykh Metodov. Uravneniia v Chastnykh Proizvodykh; Nauka i Tekhnika: Tomsk, Russia, 1986; pp. 166–194. [Google Scholar]
- Zauderer, E. Partial Differetnial Equations of Applied Mathematics, 3rd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2006; p. 799. [Google Scholar]
- Atanasova, P.; Georgiev, V. Numerical Analysis of a Difference Scheme Family for Solving Semilinear Hyperbolic PDEs. In New Trends in the Applications of Differential Equations in Sciences. NTADES 2024. Springer Proceedings in Mathematics & Statistics; Slavova, A., Ed.; Springer: Cham, Switzerland, 2025; Volume 488, pp. 361–371. [Google Scholar] [CrossRef]
- Thomas, J.W. Numerical Partial Differential Equations: Finite Difference Methods (Texts in Applied Mathematics, 22); Springer: Greer, SC, USA, 1995; pp. 45, 52, 56–57, 79–81, 87, 99, 129–131, 264–266, 306–307, 315–316. [Google Scholar]
- Kreyszig, E. Introductory Functional Analysis with Applications; John Wiley & Sons: New York, NY, USA, 1978; pp. 101, 378, 381. [Google Scholar]
- Atanasova, P.; Georgiev, V. Numerical solving of the sine-Gordon equation. In Proceedings of the International Scientific Conference “Informatics, Mathematics, Education and Their Applications” IMEA’2023, Pamporovo, Bulgaria, 29 November–1 December 2023; pp. 23–30. Available online: https://imea2023.fmi-plovdiv.org/wp-content/uploads/2024/01/2_1_Atanasova_Georgiev_23_30.pdf (accessed on 29 August 2025).
- Morton, K.W.; Mayers, D.F. Numerical Solution of Partial Differential Equations: An Introduction; Cambridge University Press: Cambridge, MA, USA, 2005; pp. 24–25, 58–59. [Google Scholar]
- Georgiev, V.; Atanasova, P. On the Analytic Solutions of the Sine-Gordon Equation. Sci. Res. Union Sci. -Bulg.-Plovdiv. Ser. C. Tech. Technol. 2024, 21, 127–131. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).