1. Introduction
In the realm of financial mathematics, options have gained significant prominence due to their flexibility in both hedging strategies and speculative ventures. It is not uncommon for the volume of capital invested in options to surpass that allocated to the underlying assets themselves, as discussed in [
1,
2]. A rigorous theoretical framework exists to determine their fair value, thereby enabling options to be traded with greater confidence in financial markets [
3].
Options are typically traded over-the-counter (OTC), predominantly among large financial institutions. These contracts often exhibit non-standard features tailored to the specific requirements of the parties involved. An asset, broadly speaking, refers to any financial instrument—such as equities or commodities—whose present value is known but subject to future fluctuations [
4].
Among various derivatives, a European-style call option grants the holder the right (without obligation) to buy an underlying asset from the writer at a predetermined strike price on a specified expiration date. A cornerstone of classical option pricing theory is the partial differential equation (PDE) of the Black–Scholes type, which assumes a complete and frictionless market without transaction costs [
5]. The governing equation reads as follows:
where
shows the price of option,
X the underlying asset price,
r the risk-free interest rate,
q the dividend yield, and
the volatility of the asset return. The terminal conditions for put and call options are, respectively, furnished by the following:
wherein
K is the strike price and
T is the maturity date.
Despite its foundational role, the Black–Scholes model (
1) exhibits several limitations. Its underlying assumptions—such as geometric Brownian motion (GBM) for asset price dynamics and constant volatility—often fail to capture real market behavior. In practice, volatility is stochastic and market frictions such as transaction costs are non-negligible [
6]. Nevertheless, due to its analytic tractability and reasonable accuracy in certain scenarios, the model remains widely adopted by practitioners.
More realistic frameworks necessitate incorporating transaction costs, which fundamentally alter the dynamics of optimal portfolio rebalancing. Omitting such costs may result in an overestimation of returns and inefficient hedging strategies, as elaborated in [
7]. Transaction costs are generally classified into two broad categories: fixed costs, which are typically linear or piecewise linear functions of trade size (e.g., bank fees), and impact costs, which are nonlinear in nature and arise from the market influence of the trader’s own actions [
8].
This work is motivated by the need to model European option pricing in the presence of transaction costs, leading to nonlinear extensions of the Black–Scholes PDE, see the works [
9]. Specifically, the focus lies on pricing models governed by nonlinear parabolic equations, where volatility may depend on the Gamma of the option (that is to say, the second derivative
).
While Monte Carlo simulation techniques have historically been reserved for linear pricing problems, recent developments allow their application to nonlinear models as well [
10]. However, such methods face challenges due to the presence of time-dependent coefficients and the need to evaluate conditional expectations, which may be computationally intensive. Consequently, deterministic numerical techniques—including second-order finite difference (FD) methods and meshfree approaches via radial basis functions (RBFs)—have garnered considerable attention [
11,
12].
In recent years, meshfree methods—especially the RBF-produced FD (RBF-FD) method [
13]—have emerged as powerful numerical tools for resolving PDEs arising in mathematical finance. The primary motivation for using the RBF-FD approach lies in its ability to provide high-order accuracy while offering geometric flexibility and ease of implementation on scattered or non-uniform node distributions [
14]. These properties are particularly beneficial in option pricing problems, where steep gradients may develop near strike prices or boundaries, requiring localized refinement to maintain accuracy. Traditional FD methods often struggle to balance accuracy and computational efficiency in such cases, especially on non-uniform grids. The RBF-FD method circumvents these limitations by constructing differentiation weights through localized RBF interpolants, allowing robust treatment of irregular point distributions. Moreover, the adaptability of RBF-FD methods makes them well-suited for handling complex market models that include nonlinearities arising from transaction costs, stochastic volatility, or liquidity constraints. As a result, the RBF-FD framework offers a practical and efficient alternative to classical grid-based schemes, enhancing the precision of numerical pricing and hedging strategies in modern financial markets [
15,
16,
17].
An important theoretical development which is crucial in the study of nonlinear Black–Scholes equations having transaction costs is the transformation of the original pricing equation into the so-called Gamma equation, introduced in [
18]. This transformation involves expressing the option price
in terms of its second derivative in relation to the underlying asset price, denoted by
, referred to as the Gamma of the option. By reformulating the problem in terms of
H, one obtains a quasilinear parabolic PDE with more regular behavior, which is particularly beneficial in the analysis and numerical simulation of solutions under transaction cost [
19]-induced nonlinearities. Also, a regularized version of the volatility function by introducing its mean value modification is defined as
for a small parameter
. This modification ensures the Lipschitz continuity of the nonlinear operator, thereby facilitating convergence analysis and the application of comparison principles. While the current work directly tackles the nonlinear PDE in its original form using a discretization strategy, future studies may benefit from employing the Gamma transformation and mean value regularization as powerful tools for both analytical and numerical advancements in option pricing models with market frictions.
In this study, we explore specific RBF-FD approximations for evaluating the spatial derivatives in the nonlinear PDE. Both uniform and non-uniform node distributions are considered. The spatial semi-discretization yields a collection of nonlinear ordinary differential equations (ODEs), following a method-of-lines strategy [
20]. This is the first attempt to employ this type of modified multiquadric kernel for this nonlinear task, as our novelty. The significance of the paper is then to employ simpler differentiation weights arising from RBF-FD in the method-of-lines procedure and solve the nonlinear Black–Scholes PDE efficiently.
The rest of this research is organized as follows:
Section 2 outlines the necessary theoretical background. In
Section 3, we introduce a fully discretized meshfree RBF-FD method applied to the nonlinear Black–Scholes PDE with transaction costs, comparing its performance on both uniform and non-uniform stencils.
Section 4 describes the time integration strategy based on a classical explicit Runge–Kutta (RK) method.
Section 5 presents comprehensive computational aspects validating the robustness and effectiveness of the discussed scheme. Finally, concluding comments and perspectives are given in
Section 6.
2. Related Literature and Model Description
Over the past few years, numerous extensions of the classic Black–Scholes framework have been proposed to address market imperfections, particularly the presence of transaction costs and the inadequacy of constant volatility assumptions. One early and influential modification is due to [
21], who introduced a volatility correction motivated by a discrete binomial hedging framework. In their formulation, the modified volatility is defined as
where
with
representing the proportional transaction cost,
the discrete time interval between portfolio rebalancing steps, and
the baseline volatility.
Another notable contribution is the model by [
22], who proposed a nonlinear volatility term that depends on the Gamma of the option, incorporating market feedback effects. Their formulation is given by
where
and
,
are non-negative parameters quantifying the risk premium and transaction cost, respectively. For further elaboration on related nonlinear models and their numerical treatment, we refer the reader to [
10].
A different perspective was introduced by [
8], who developed a model based on utility maximization under exponential preferences, resulting in a nonlinear Black–Scholes equation with volatility furnished by
where the risk aversion-adjusted parameter
, with
denoting the risk aversion coefficient,
the quantity of options held short, and
a nonlinear auxiliary function encoding liquidity effects. The maturity is denoted by
T, and
r is the risk-free interest rate.
The function
satisfies the nonlinear first-order ODE:
whose implicit solution, as given in [
23], reads
In the classical derivation of the Black–Scholes formulation, the volatility term arises from the assumption of a continuously rebalanced hedging portfolio that perfectly replicates the option’s payoff. This idealized setting assumes frictionless markets, with no costs associated with trading. However, when transaction costs are introduced—whether proportional, fixed, or nonlinear—continuous rebalancing becomes impractical, because each infinitesimal trade incurs a cost. To mitigate this, traders must reduce the frequency of rebalancing, thereby introducing a discrepancy between the actual portfolio and the ideal replicating strategy. This discrepancy results in additional risk or variance in the hedged position. In turn, this increased uncertainty is captured in the pricing equation by modifying the volatility term [
24]. The resulting volatility becomes state-dependent and nonlinear, typically expressed as a function of the option’s Gamma (
), which quantifies the sensitivity of the hedge ratio to the underlying asset price. A higher Gamma implies more frequent trading and thus higher transaction costs. Consequently, the volatility term in the nonlinear Black–Scholes PDE reflects the combined effect of market uncertainty and the cost of maintaining a dynamic hedge in an imperfect market.
In this work, we adopt this model and utilize the closed-form expression (
10) for
wherever required. Notably,
is an increasing function on
. However, since the implicit relation must be inverted numerically for given values of
x, the associated nonlinear algebraic equations are solved using Newton’s method. In practice, we employ the built-in Mathematica function
FindRoot[] with the
Chop[] command to suppress numerical noise and round-off errors smaller than
.
Barles and Soner proved that the nonlinear model (
1)–(
8) admits a unique viscosity solution, ensuring the well-posedness of the PDE even under nonlinearity [
8].
To facilitate numerical treatment, we recast the time variable via the standard transformation
, defining
. Substituting into (
8) yields the following parabolic PDE [
25]:
where the payoff is given by either a call or a put option terminal condition.
The PDE (
11) is defined over a semi-infinite spatial domain [
26]:
which must be truncated in practice for numerical approximation. We thus restrict our attention to the computational area:
where
is chosen sufficiently large to minimize the truncation error while maintaining computational feasibility.
For European call options, the side conditions on the truncated domain are typically imposed as follows:
where
K is the strike price. These boundary conditions reflect the intrinsic behaviors of call options at extreme asset values.
The nonlinear character of (
11)—combined with its degenerate behavior near
and potential stiffness due to the term
—makes analytical treatment infeasible. Hence, the development of stable, accurate, and high-order numerical methods becomes essential, especially for realistic market models involving transaction costs and Gamma-dependent volatilities.
An additional theoretical consideration in the study of nonlinear Black–Scholes models arises from the control-theoretic interpretation of the PDE. In particular, many nonlinear pricing equations can be viewed as Hamilton–Jacobi–Bellman (HJB) equations derived from stochastic control problems involving optimal portfolio strategies under trading frictions [
27,
28,
29]. This viewpoint not only provides a justification for the nonlinearity but also connects the pricing model to a broader class of financial optimization problems. For instance, when transaction costs are modeled explicitly, the optimal hedging strategy becomes state-dependent, and the corresponding HJB equation introduces nonlinearity in the highest-order derivative. Understanding the nonlinear Black–Scholes PDE through this lens facilitates the application of viscosity solution theory and provides a deeper interpretation of the role of Gamma-dependent volatility in risk management. Such connections underscore the importance of designing robust numerical methods—like the RBF-FD scheme developed in this work—that can handle nonlinearity while preserving accuracy and stability.
A number of practically important extensions of the nonlinear Black–Scholes framework involve modeling early exercise features, payoff singularities, and liquidity-driven price impacts. For the American-style options, the pricing problem transforms into a free boundary problem, where the early exercise boundary must be determined as part of the solution. This introduces additional computational complexity and typically requires complementarity formulations or penalty methods. Moreover, the payoff functions for both European and American options often exhibit non-smooth behavior, particularly at the strike price. Such kinks or discontinuities in higher derivatives can significantly affect the convergence behavior of numerical schemes, especially for nonlinear PDEs where the volatility is a function of second-order derivatives. To address these challenges, numerical methods must be carefully designed to accommodate viscosity solutions and weak regularity. Furthermore, market liquidity considerations introduce another layer of nonlinearity, as trading activity may influence the asset price itself. In such models, nonlinearities emerge not only in the volatility but also in the drift term, reflecting slippage, spread effects, or order book depth.
3. RBF-FD Weights
The RBF-FD procedure derives the differentiation matrices (DMs) utilizing local interpolants formed from RBFs. Consider a collection of
N scattered and distinct nodes
in the domain, a function
is locally estimated by a linear combination of RBFs [
30,
31]:
whereas
shows the chosen RBF, and
are interpolation coefficients. The local stencil comprises the central knot
and its
closest neighbors with
.
To approximate derivatives, we form a localized system on each stencil and derive the differentiation weights
such that [
32]
This localized formulation ensures sparsity and efficiency in the resulting numerical scheme.
In this work, we introduce a revised version of the infinitely smooth multiquadric (MQ) function:
where
is the shape parameter and
l is the Euclidean distance between nodes. The exponent
is selected to enhance smoothness and flexibility. This formulation—unexplored in prior studies—enables the derivation of novel RBF-FD weights for first- and second-order derivatives.
To construct the differentiation weights analytically, we consider the first and second integrals [
33,
34] of the MQ function in one dimension:
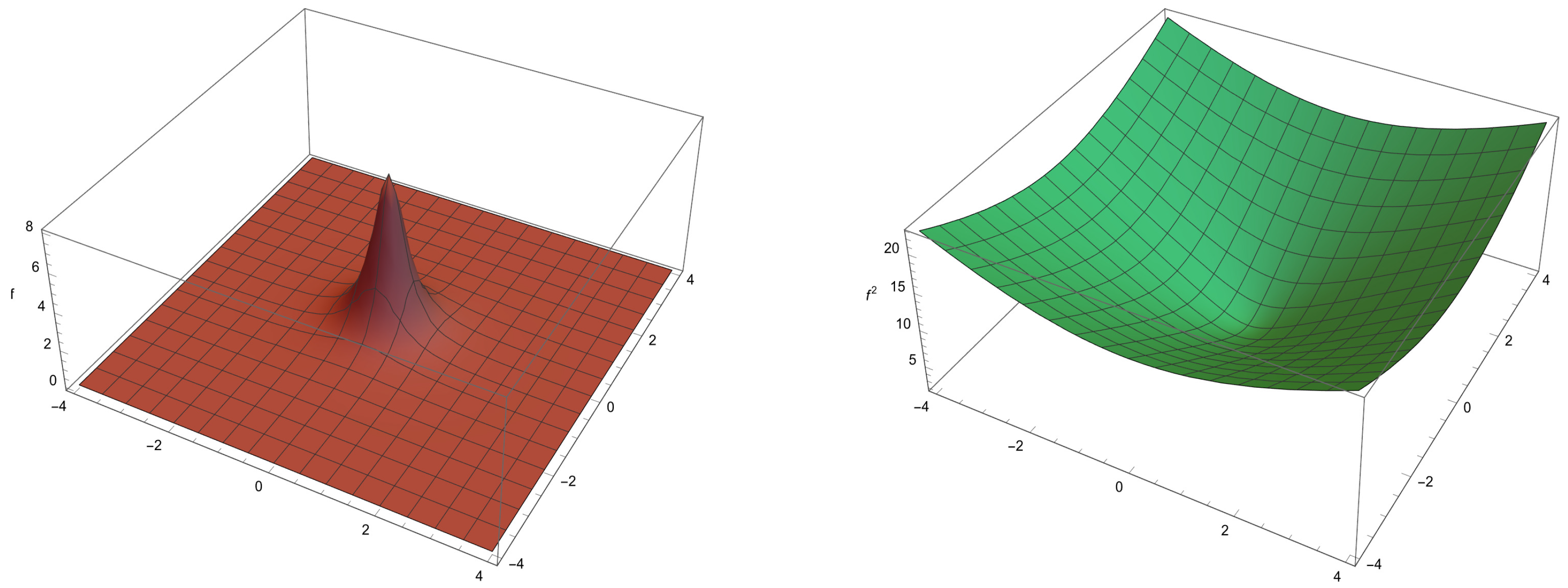
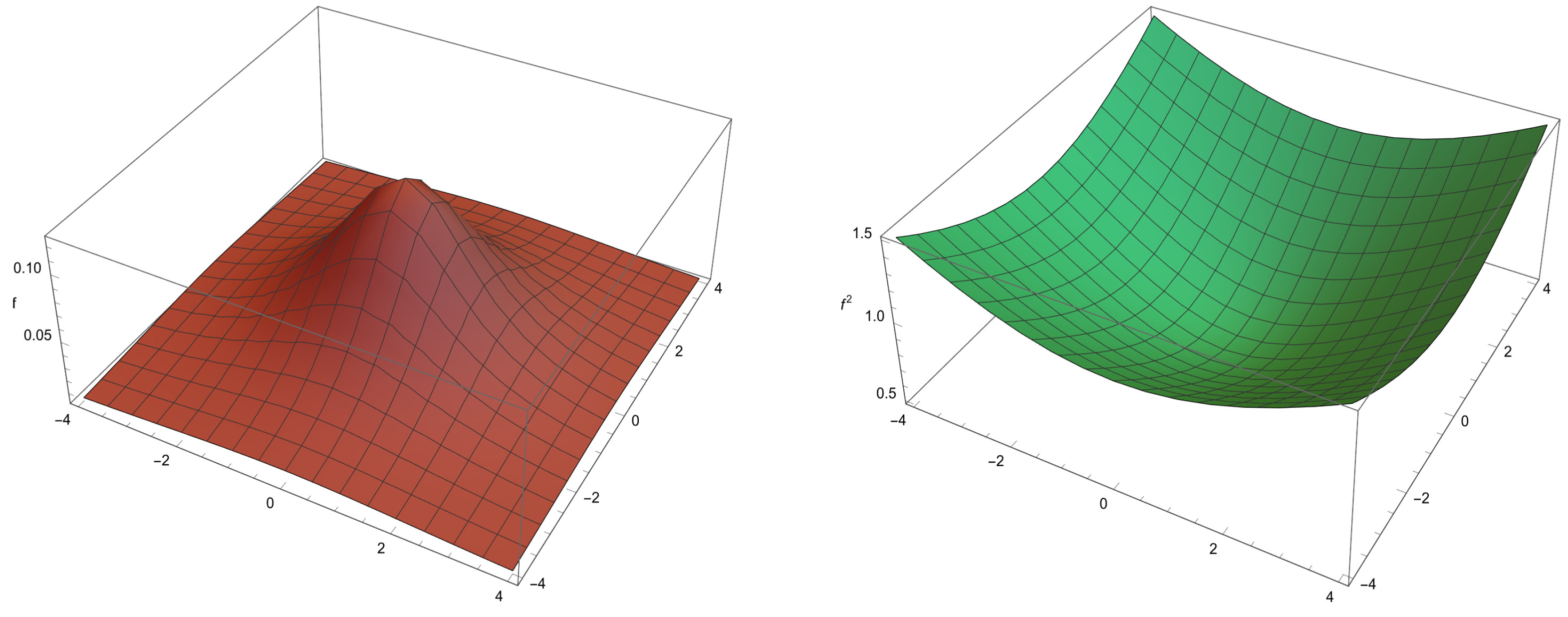
Plots of different kernels
f and
for various choices of
c are given in
Figure 1 and
Figure 2.
We now consider a local stencil of three unequally spaced nodes:
where
denotes the relative spacing between the forward node and the central node. For uniform spacing,
; for non-uniform stencils,
o varies with location.
For a three-point stencil (
), we express the first derivative approximation as follows:
To find the weights
, we apply the second integral of (19) and derive a system of algebraic equations based on Taylor expansions about
. Solving the obtaining set gives (see also the recent discussions in [
35]):
Theorem 1. Let be defined as in (19). Then, the RBF-FD formula for the first derivative given by (21) using the stencil (20) achieves second-order accuracy for any sufficiently smooth function . Proof. Substituting the weights (
22)–(24) into (
21) and expanding via Taylor series, we obtain the local truncation error:
The leading-order term confirms second-order convergence. □
To approximate the second derivative, we adopt the following form:
Solving the corresponding equations with Taylor series expansion gives the following explicit weights:
Theorem 2. The second derivative approximation defined by (26), using weights from Equations (27) to (29), achieves at least first-order convergence for any smooth function . Proof. Substituting the weights into (
26) and expanding the resulting expression yields the truncation error:
This ends the proof. □
The primary objective of this section is to construct analytically tractable and accurate weighting coefficients for first- and second-order derivatives using a modified MQ RBF within the RBF-FD framework. By selecting a novel form of the MQ kernel with exponent , we derive localized finite difference approximations on both uniform and non-uniform three-point stencils. The resulting differentiation formulas are expressed explicitly in terms of c, the local step size h, and the asymmetry parameter o, which governs non-uniform spacing. The analytical derivation of the weights through Taylor expansions ensures transparency, efficiency, and generalizability of the method. Furthermore, rigorous convergence analyses confirm that the proposed approximations achieve second-order and at least first-order accuracy for the first and second derivatives, respectively. These high-order, mesh-free, and flexible discretization formulas are essential for solving complex financial PDEs–especially those featuring nonlinearities and irregular domains–as they enable accurate and stable spatial discretization without requiring structured grids.
4. Construction of the Discrete System
Here, we construct the set of semi-discretized ODEs corresponding to the nonlinear Black–Scholes model (
11) using the newly developed RBF-FD weights. The construction is based on the application of differentiation matrices that encode the diffusion and convection terms. For further theoretical foundations, we refer the reader to [
36].
A differentiation matrix maps function values at discrete points to approximations of their derivatives at those same points. Specifically, for a vector
representing the values of a function sampled at node locations, the derivative is approximated as:
where
is the first-order differentiation matrix. Similarly, a second-order matrix can be constructed using the proposed approximations in Equations (
22)–(24) and (
27)–(29). These matrices are assembled by systematically applying the analytically derived RBF-FD stencil weights.
After incorporating boundary conditions, the resulting semi-discretized ODE system takes the compact form:
where
is a time-dependent matrix incorporating the nonlinear volatility effects, and
is the vector of numerical approximations to the solution at time
. The matrix
is considered to be continuous on a given interval in
.
To discretize the temporal component of the system, we utilize the classical explicit RK method of order four (RK4), which ensures a global error of and a local truncation error of .
Let the temporal domain be divided into k uniform steps with , and let for . Denoting the numerical approximation at time by , the update to is computed via the following four-stage process.
The classical explicit RK4 can be presented in a unified framework for explicit methods with
stages. In general, an
s-stage explicit RK method is written as
with each stage defined by
For RK4, the coefficients
are given by the classical Butcher tableau:
where
,
,
, and
.
This method achieves a local truncation error of and global accuracy of . To investigate time stability, we provide the following result.
The classic RK4 method holds significant practical importance in the numerical integration of time-dependent problems. Its widespread adoption is attributed to the following key features:
RK4 achieves global accuracy of order and local truncation error of order . It offers this level of precision while maintaining a relatively simple algorithmic structure, making it accessible for both implementation and analysis.
The RK4 scheme is widely used across various fields of science and engineering. It is particularly suitable for the time integration of systems of ODEs obtained from the spatial discretization of PDEs.
Although explicit in nature, the RK4 method allows for moderately large time steps in non-stiff systems while preserving numerical stability. This makes it a popular choice in simulations where implicit schemes would incur higher computational costs.
Unlike multi-step methods, RK4 does not require any prior values or historical data beyond the current time step, rendering it self-starting and thus advantageous for problems with variable time stepping or initial-value formulations.
Theorem 3. If the ODE system (32) is linear and satisfies a Lipschitz condition, then the RK4 time-stepping scheme (33) is conditionally stable. Proof. The Lipschitz condition guarantees the existence and uniqueness of solutions to the linear ODE system. A-stability, as introduced by Dahlquist, refers to the property that numerical solutions of the test equation with remain bounded for all step sizes.
Applying the RK4 method to System (
32), we can write the one-step update as follows:
The scheme is stable if the spectral radius of this matrix is bounded by one. Let
denote an eigenvalue of
B. Then, the corresponding eigenvalue of the update matrix is as follows:
Thus, the stability condition reads as follows:
This condition ensures conditional stability in time. This finishes the proof. □
Remark 1. Theorem 3 applies directly to the linearized version of (11). For the fully nonlinear case, Condition (36) is a necessary but not sufficient criterion for stability. Additional nonlinear stability analyses would be required, see [37] for more details. 5. Computational Aspects
Herein, we investigate the practicality and effectiveness of the furnished numerical procedure for solving the time-dependent PDE problem described in Equation (
11). The analysis focuses on the configurations of spatial discretization utilizing nonuniformly distributed nodes.
To construct the nonuniform grid for the spatial variable
X, we adopt a transformation technique inspired by the works in [
38]. This approach redistributes the nodes in a non-equidistant fashion, placing a higher concentration of points around the strike price
K, which is particularly advantageous in financial applications where accurate resolution near
K is critical. The transformation is given by
where
and the nodes
are equidistantly distributed in the interval
[
39]. In our simulations, we set
.
In all numerical experiments, the domain for the asset price is defined over the interval
, where we select
and
to ensure adequate coverage of the relevant financial range. All computations are carried out using Wolfram 14.0 [
40], which provides a robust environment for symbolic and numerical analysis.
RBF-FD schemes confirm that linking the shape parameter to nodal spacing is a standard and effective strategy to mitigate sensitivity issues, avoiding the need for repeated tuning. For this reason, the present analysis focused on the formulation and performance of the proposed method under this systematic choice. In the present study, the shape parameter has been chosen as
with
denoting the maximum spacing between neighboring discretization nodes. This selection is motivated by the fact that the conditioning of RBF-FD is strongly influenced by the balance between the nodal spacing and the scaling of the kernel. By linking
c directly to
, the method automatically adapts to both uniform and non-uniform point distributions. When the discretization is refined,
decreases accordingly, and the resulting reduction in
c preserves an appropriate scaling of the basis functions. This procedure avoids excessive sensitivity of the computed solutions to the choice of the shape parameter. The adopted scaling also provides robustness in the presence of irregular nodal sets. Since
reflects the coarsest local spacing, the kernel width adapts naturally to variations in the discretization, which is particularly important for financial PDE problems involving non-uniform point distributions. In the numerical tests reported in this work, this approach yielded stable convergence and accurate option prices without observable deterioration due to variations in
c.
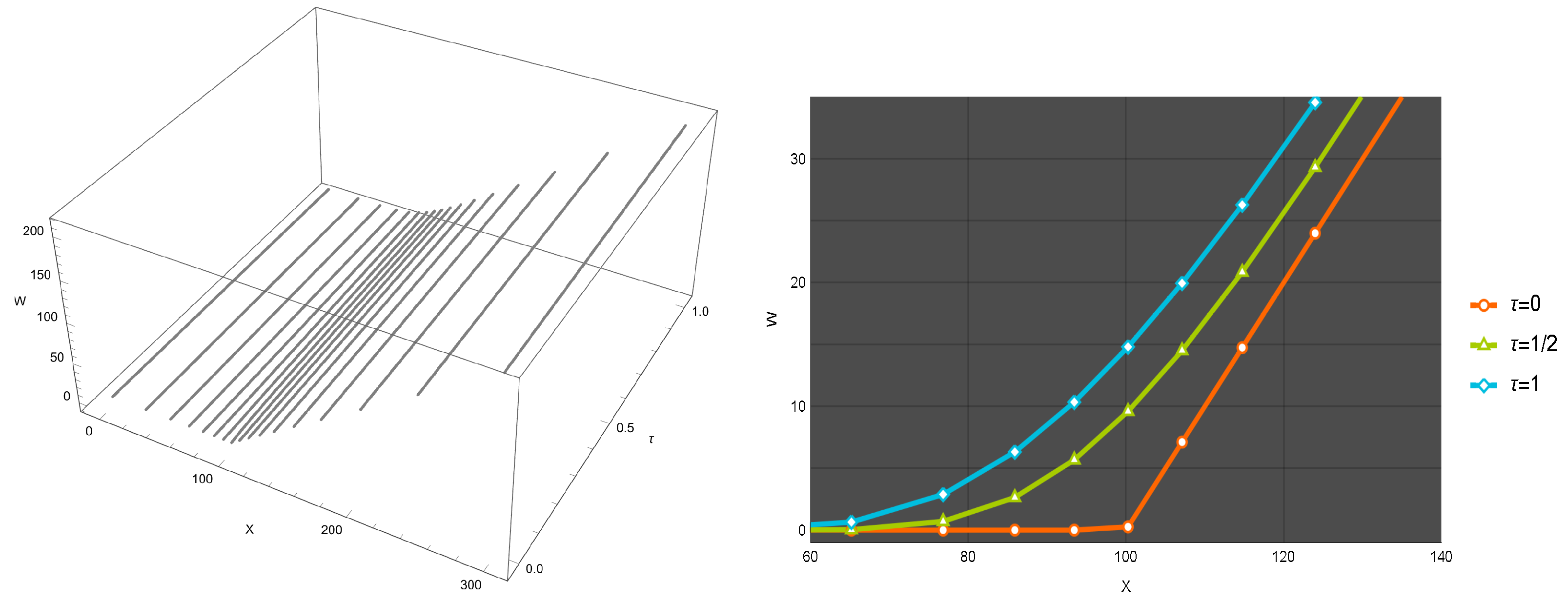
Example 1. In this numerical experiment, we adopt the set of parameters given below:This selection of a relatively small value for the parameter a reflects more realistic market conditions. The benchmark (reference) values for the solution at specific points are as follows [
26]:
,
, and
. Due to the inclusion of transaction costs in this model configuration, the computed numerical solution—obtained using the proposed method—is depicted in
Figure 3 and
Figure 4. This figure highlights the efficiency and accuracy of the proposed scheme, based on nonuniformly spaced discretization points (
37). This numerical evidence provides further insight into how the incorporation of transaction costs elevates the resulting approximations relative to the standard linear model.
The present framework is designed for practical applications in option pricing, where the use of highly non-uniform grids is not typically required. As illustrated in the reported experiments, moderate levels of non-uniformity already provide a clear advantage over standard uniform discretizations in terms of accuracy, particularly in capturing localized features of the option price near the strike. Within this regime, the use of compact three-point stencils remains efficient and does not compromise the stability of the scheme. In practice, reliable numerical solutions with accuracy of up to three or four decimal places are achieved before the degree of non-uniformity reaches a level that would adversely affect the conditioning of the differentiation matrices.
It is well understood in the literature on meshfree RBF-FD methods that extreme non-uniformity may introduce ill-conditioning. However, the current study avoids such situations, since the objective is to balance efficiency and accuracy in a practically relevant setting. The results confirm that, within the moderate non-uniform distributions considered, the three-point stencil design remains stable and accurate, making it a suitable choice for the nonlinear Black–Scholes framework investigated here.
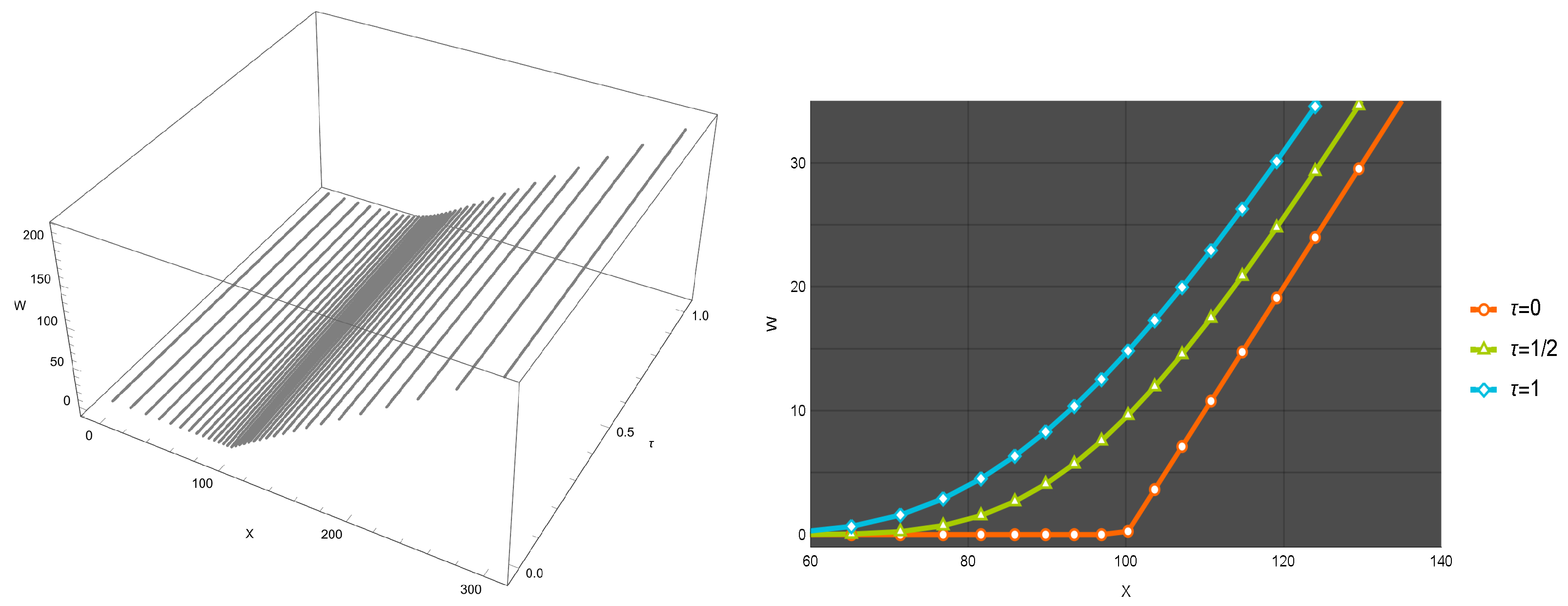
Before concluding this section, we examine how the proposed method performs on non-uniform stencils, whether its accuracy deteriorates under strong nonlinear effects, and how it behaves in terms of stability and positivity. To this end, two distinct nonlinear scenarios are considered, and the corresponding results are presented in
Figure 5. These results indicate that, under stronger nonlinear effects, stability and positivity can still be maintained by employing a finer time-step size.
6. Concluding Discussions
We have developed a novel high-order RBF-FD discretization scheme for resolving a nonlinear variant of the Black–Scholes equation that incorporates transaction costs via a Gamma-dependent volatility formulation. By introducing an analytically modified form of the multiquadric radial basis function with exponent , we have derived closed-form expressions for the finite difference weights on both uniform and non-uniform three-point stencils. These expressions have been rigorously validated through Taylor series expansion and local truncation error analysis, confirming second-order convergence for the first derivative and at least first-order convergence for the second derivative. The mathematical structure of the derived weights has offered flexibility and robustness for meshfree discretization of spatial operators in the pricing model.
To advance the solution in time, we have employed a classic fourth-rate explicit RK4 scheme, ensuring high-order temporal accuracy. The resulting semi-discretized system of nonlinear ODEs has been carefully constructed through differentiation matrices that encode the convection and diffusion components of the PDE. A theoretical stability analysis for the linearized system has been performed using eigenvalue-based criteria, confirming conditional time stability under an appropriate step size constraint.
The numerical framework presented in this work is highly adaptable and offers promising performance in capturing the nonlinear behavior of financial derivatives pricing models. The combination of analytical weight formulation, compact three-point stencils, and high-order time integration has resulted in a computational method that balances accuracy, efficiency, and generality. The flexibility of the proposed method in handling both uniform and non-uniform discretizations makes it particularly suited for problems with spatially varying features such as volatility clustering, sharp payoff transitions, and boundary singularities.
As part of future research, we plan to investigate the proposed solver for high-dimensional problems, including basket options and stochastic volatility models. Incorporating adaptive node refinement strategies and shape parameter optimization for the MQ function would further enhance the accuracy and efficiency of the method.