New Bounds of Hadamard’s and Simpson’s Inequalities Involving Green Functions

Abstract

This manuscript aims to assess some new refinements of right Hadamard’s and Simpson’s-like inequalities by bridging the concepts of Green function theory and convexity framework. It is a known fact that Green functions are convex and symmetric. By considering the identities based on Green functions for second-order differentiable functions and elementary results of inequalities, convexity and bounded variation of functions, we present various new upper estimates of trapezoidal and Simpson’s inequalities. Also, the accuracy of the results is determined by illustrative numerical examples and simulations. Lastly, we furnish some novel applications to linear combinations of means and composite error estimates.

1. Introduction and Preliminaries

The theory of convexity is a fascinating aspect of mathematical analysis due to significant contributions to various sub-domains of pure and applied analysis, including operational research, optimization, differential equations, functional analysis, and especially inequalities. Convexity of sets and functions has some distinctive attributes, like connected sets, being closed under Minkowski operation, being supported by hyperplanes at boundary points, and having level sets that are also convex; every local minima is a global minima; they have a nonempty sub-differential at interior points; they have the pointwise maximum property, the composition property, and the convex epigraph, respectively. These properties make them quite useful for the construction of new and refinement of existing results of inequalities. One can easily observe that various inequalities are proved directly or indirectly by leveraging the idea of convexity, which is fundamental in the literature. Let us recall the notion of convexity and elementary inequalities.

Definition 1  

([1]). Let I be an interval in $\mathbb{R}$. Then $\mathsf{\Psi }:I\to \mathbb{R}$ is said to be convex, if

$$\mathsf{\Psi }\left(\right(1-\mathsf{\ell })\varrho +\mathsf{\ell }y)\le (1-\mathsf{\ell })\mathsf{\Psi }\left(\varrho \right)+\mathsf{\ell }\mathsf{\Psi }\left(y\right),$$

for all $\varrho ,y$ belong to interval I and $\mathsf{\ell }\in [0,1]$.

Analogously, the definition for n distinct points is commonly known as Jensen’s inequality and stated as:

Theorem 1.  

Suppose that $\mathsf{\Psi }:[{\vartheta }_2,{\epsilon }_2]\to \mathbb{R}$ is a convex function, then

$$\mathsf{\Psi }\left(\sum _{i=1}^n{\mathsf{\ell }}_i{\varrho }_i\right)\le \sum _{i=1}^n{\mathsf{\ell }}_i\mathsf{\Psi }\left({\varrho }_i\right),\mathit{for}\mathit{all}{\mathsf{\ell }}_i\in [0,1],\mathit{and}{\varrho }_i\in [{\vartheta }_2,{\epsilon }_2]\mathit{such}\mathit{that}\sum _{i=1}^n{\mathsf{\ell }}_i=1.$$

Our next result provides the geometrical interpretations of convexity and also useful to check the concavity behaviour of functions.

Theorem 2  

(Hermite-Hadamard Inequality).  Suppose that $\mathsf{\Psi }:[{\vartheta }_2,{\epsilon }_2]\to \mathbb{R}$ is a convex function, then

$$({\epsilon }_2-{\vartheta }_2)\mathsf{\Psi }\left({\displaystyle \frac{{\vartheta }_2+{\epsilon }_2}{2}}\right)\le {\int }_{{\vartheta }_2}^{{\epsilon }_2}\mathsf{\Psi }\left(\varrho \right)\mathrm{d}\varrho \le ({\epsilon }_2-{\vartheta }_2){\displaystyle \frac{\mathsf{\Psi }\left({\vartheta }_2\right)+\mathsf{\Psi }\left({\epsilon }_2\right)}{2}}.$$

(1)

From the above double inequality, one can easily associate error inequalities of midpoint and trapezoidal quadrature rules to the left and right estimations of (1), respectively. In 1998, Dragomir and Agarwal [2] focused on the right estimation inequality (1) leveraging the convexity of differentiable functions, and presented the applications to the theory of integration and means. Following the idea of [2], Kirmaci [3] analyzed the left estimation of Hadamard’s inequality. Dragomir and Pearce [4] delivered the upper bounds of Hadamard’s type inequalities by using the quasi-convexity. Niculescu and Persson [5] published a comprehensive review on various Hermite-Hadamard inequalities along with applications in various directions. El Farissi [6] proposed a new ramification of Hadamard’s inequality. Gao [7] developed a more generalized Hermite-Hadamard inequality, which yielded several existing inequalities under certain constraints. For more details, consult [8,9,10,11,12].

To discuss further, we report the classical Simpson’s inequality for further proceedings.

Theorem 3  

([13]). If $\mathsf{\Psi }:[{\vartheta }_2,{\epsilon }_2]\to \mathbb{R}$ is four times continuously differentiable function on $({\vartheta }_2,{\epsilon }_2)$ and $\left|\right|{\mathsf{\Psi }}^{\left(4\right)}{\left|\right|}_{\infty }={sup}_{\sigma \in ({\vartheta }_2,{\epsilon }_2)}\left|{\mathsf{\Psi }}^{\left(4\right)}\left(\sigma \right)\right|<\infty$, then

$$\left|{\displaystyle \frac{1}{6}}\left[\mathsf{\Psi }\left({\vartheta }_2\right)+4\mathsf{\Psi }\left({\displaystyle \frac{{\vartheta }_2+{\epsilon }_2}{2}}\right)+\mathsf{\Psi }\left({\epsilon }_2\right)\right]-{\displaystyle \frac{1}{{\epsilon }_2-{\vartheta }_2}}{\int }_{{\vartheta }_2}^{{\epsilon }_2}\mathsf{\Psi }\left(\sigma \right)\mathrm{d}\sigma \right|\le {\displaystyle \frac{1}{2880}}\left|\right|{\mathsf{\Psi }}^{\left(4\right)}{\left|\right|}_{\infty }{({\epsilon }_2-{\vartheta }_2)}^4.$$

The above-mentioned studies paved a new way to explore the error analysis of quadrature and cubature rules of Newton-Cotes procedures. It is a fact that to approximate the remainder terms of midpoint, trapezoidal and Simpson’s procedures, we need second- and fourth-order bounded differentiable functions. If a function does not possess the second and fourth ordered differentiability, then there is no way to discuss the error analysis. To discuss the error terms of such functions, inequalities derived from first-order differentiable convex and bounded variation functions play a significant role. In the following perspective, Dragomir et al. [14] proved the Simpson’s error inequalities using the bounded variations of differentiable functions and furnished the applications to means and integration as well. Pecaric and Varosanec [15] also examined the Simpson’s inequalities through bounded variation functions of various orders of differentiability. Liu [16] presented the unified perturbed inequalities for diverse function classes. In [17], the authors extended the idea of Breckner convexity to higher-order strong convexity and computed the fractional bounds of Simpson’s type inequalities. Cortez et al. [18] worked on Simpson-Mercer-like inequalities with applications to iterative schemes along with dynamic analysis. In [19] Rangel-Oliveros and Nwaeze approximated the Simpson’s inequalities for exponential convexity along with applications. Ali et al. [20] established the fractional Simpson’s inequalities using convexity depending upon a pair of functions. For comprehensive exploration, see [21,22,23,24,25].

The Abel-Gontscharoff polynomial and two point right focal problem is discussed in [26]. The special case of Abel-Gontscharoff polynomial for two point focal for $n=2$ is described as

$$\mathsf{\Psi }\left(\varrho \right)=\mathsf{\Psi }\left({\vartheta }_2\right)+(\varrho -{\vartheta }_2){\int }_{{\vartheta }_2}^{{\epsilon }_2}{G}_{\wedge ,2}(\varrho ,v){\mathsf{\Psi }}^{″}\left(v\right)\mathrm{d}v,$$

(2)

where $G_{\wedge ,2}(\varrho ,v)$ is the Green function and is reported as:

$$G_1(\varrho ,v)=G_{\wedge ,2}(\varrho ,v)=\left\{\begin{array}{cc}{\vartheta }_2-v,\hfill & {\vartheta }_2\le v\le \varrho \hfill \\ {\vartheta }_2-\varrho ,\hfill & \varrho \le v\le {\epsilon }_2\hfill \end{array}\right.$$

Observing the identity (2) and related Green function, Mehmood et al. [27] defined three new Green’s type functions which are continuous, symmetric and convex. They are defined as:

Definition 2  

([27]). Let ${\vartheta }_2<{\epsilon }_2$ and then Green functions $G_k:[{\vartheta }_2,{\epsilon }_2]\times [{\vartheta }_2,{\epsilon }_2]\to \mathbb{R}$ are defined as:

$$G_1(\varrho ,v)=\left\{\begin{array}{cc}{\vartheta }_2-v,\hfill & {\vartheta }_2\le v\le \varrho ,\hfill \\ {\vartheta }_2-\varrho ,\hfill & \varrho \le v\le {\epsilon }_2,\hfill \end{array}\right.$$

$$G_2(\varrho ,v)=\left\{\begin{array}{cc}\varrho -{\epsilon }_2,\hfill & {\vartheta }_2\le v\le \varrho ,\hfill \\ v-{\epsilon }_2,\hfill & \varrho \le v\le {\epsilon }_2,\hfill \end{array}\right.$$

$$G_3(\varrho ,v)=\left\{\begin{array}{cc}\varrho -{\vartheta }_2,\hfill & {\vartheta }_2\le v\le \varrho ,\hfill \\ v-{\vartheta }_2,\hfill & \varrho \le v\le {\epsilon }_2,\hfill \end{array}\right.$$

$$G_4(\varrho ,v)=\left\{\begin{array}{cc}{\epsilon }_2-v,\hfill & {\vartheta }_2\le v\le \varrho ,\hfill \\ {\epsilon }_2-\varrho ,\hfill & \varrho \le v\le {\epsilon }_2.\hfill \end{array}\right.$$

Lemma 1  

([27]). Let $\mathsf{\Psi }:[{\vartheta }_2,{\epsilon }_2]\to \mathbb{R}$ be a twice differentiable function function and $G_k$$(k=1,2,3,4)$ be the above defined Green’s function. Then following identities hold:

$$\mathsf{\Psi }\left(\varrho \right)=\mathsf{\Psi }\left({\vartheta }_2\right)+(\varrho -{\vartheta }_2){\mathsf{\Psi }}^{\prime }\left({\epsilon }_2\right)+{\int }_{{\vartheta }_2}^{{\epsilon }_2}{G}_1(\varrho ,v){\mathsf{\Psi }}^{″}\left(v\right)dv,$$

(3)

$$\mathsf{\Psi }\left(\varrho \right)=\mathsf{\Psi }\left({\epsilon }_2\right)+(\varrho -{\epsilon }_2){\mathsf{\Psi }}^{\prime }\left({\vartheta }_2\right)+{\int }_{{\vartheta }_2}^{{\epsilon }_2}{G}_2(\varrho ,v){\mathsf{\Psi }}^{″}\left(v\right)dv,$$

(4)

$$\mathsf{\Psi }\left(\varrho \right)=\mathsf{\Psi }\left({\epsilon }_2\right)+({\epsilon }_2-{\vartheta }_2){\mathsf{\Psi }}^{\prime }\left({\epsilon }_2\right)+(\varrho -{\vartheta }_2){\mathsf{\Psi }}^{\prime }\left({\vartheta }_2\right)+{\int }_{{\vartheta }_2}^{{\epsilon }_2}{G}_3(\varrho ,v){\mathsf{\Psi }}^{″}\left(v\right)dv,$$

$$\mathsf{\Psi }\left(\varrho \right)=\mathsf{\Psi }\left({\vartheta }_2\right)+({\epsilon }_2-{\vartheta }_2){\mathsf{\Psi }}^{\prime }\left({\vartheta }_2\right)-({\epsilon }_2-\varrho ){\mathsf{\Psi }}^{\prime }\left({\epsilon }_2\right)+{\int }_{{\vartheta }_2}^{{\epsilon }_2}{G}_4(\varrho ,v){\mathsf{\Psi }}^{″}\left(v\right)dv.$$

In 1976 Vasic and Stankovic [28] explored the Popoviciu-like inequalities via identities involving Green functions. Butt et al. [29] examined the Popoviciu-like inequalities by considering Fink’s identity and Green’s functions. Siddique et al. [30] discussed the majorization inequalities by bridging the extended Montgomery identity and Green’s function approach. In [31] Iqbal et al. utilized fractional calculus, Green’s functions and convex functions to prove various Hermite-Hadamard-type inequalities.

Motivation and problem statement: The theory of inequalities addresses the problems related to the boundaries of several mathematical quantities, like definite integrals, which are difficult to evaluate analytically. Working on numerical quadrature and cubature rules, authors have tried to predict the bounds of definite integral and average mean value integral through diverse approaches. Our approach includes the development of error inequalities of two- and three-point closed Newton-Cotes schemes via identities governed by Green functions and using the convexity and bounded variation properties of functions. Moreover, we will discuss some of Hadamard’s left inequalities.

We structure our study in three different sections. First, we recover the facts and essential results; literature corresponds to under-considered inequalities, motivation and planning to achieve desired results. The next section is further categorized into subsections. The initial subsection contains the estimates of the right Hermite-Hadamard inequality, and the secondary part is devoted to the error analysis of Simpson’s rule. Finally, we offer some captivating applications to ensure the significance of the study. To the extent of our knowledge, this is the first study in which the error inequalities of midpoint, trapezoid and Simpson’s inequalities through Green function theory are addressed.

2. Results and Discussion

We now discuss main results of the paper.

2.1. Right-Hermite-Hadamard’s Inequalities

Theorem 4. 

Let $\mathsf{\Psi }:[{\vartheta }_2,{\epsilon }_2]\to \mathbb{R}$ be a twice differentiable function. If $|{\mathsf{\Psi }}^{″}|$ is a convex function on $[{\vartheta }_2,{\epsilon }_2]$, then the following inequality holds:

$$\left|{\displaystyle \frac{\mathsf{\Psi }\left({\vartheta }_2\right)+\mathsf{\Psi }\left({\epsilon }_2\right)}{2}}-{\displaystyle \frac{1}{{\epsilon }_2-{\vartheta }_2}}{\int }_{{\vartheta }_2}^{{\epsilon }_2}\mathsf{\Psi }\left(\varrho \right)d\varrho \right|\le {\displaystyle \frac{{\epsilon }_2-{\vartheta }_2}{4}}\left[|{\mathsf{\Psi }}^{\prime }\left({\vartheta }_2\right)|+|{\mathsf{\Psi }}^{\prime }\left({\epsilon }_2\right)|\right]+{\displaystyle \frac{{\left({\epsilon }_2-{\vartheta }_2\right)}^2}{6}}\left[|{\mathsf{\Psi }}^{″}\left({\vartheta }_2\right)|+|{\mathsf{\Psi }}^{″}\left({\epsilon }_2\right)|\right].$$

(5)

Proof. 

Integrating both (3) and (4) with respect to $\varrho$ from ${\vartheta }_2$ to ${\epsilon }_2$ and multiplying by ${\displaystyle \frac{1}{{\epsilon }_2-{\vartheta }_2}}$, we obtain

$${\displaystyle \frac{1}{{\epsilon }_2-{\vartheta }_2}}{\int }_{{\vartheta }_2}^{{\epsilon }_2}\mathsf{\Psi }\left(\varrho \right)d\varrho =\mathsf{\Psi }\left({\vartheta }_2\right)+\left({\displaystyle \frac{{\epsilon }_2-{\vartheta }_2}{2}}\right){\mathsf{\Psi }}^{\prime }\left({\epsilon }_2\right)+{\displaystyle \frac{1}{{\epsilon }_2-{\vartheta }_2}}{\int }_{{\vartheta }_2}^{{\epsilon }_2}{\int }_{{\vartheta }_2}^{{\epsilon }_2}{G}_1(\varrho ,v){\mathsf{\Psi }}^{″}\left(v\right)dvd\varrho$$

(6)

$${\displaystyle \frac{1}{{\epsilon }_2-{\vartheta }_2}}{\int }_{{\vartheta }_2}^{{\epsilon }_2}\mathsf{\Psi }\left(\varrho \right)d\varrho =\mathsf{\Psi }\left({\epsilon }_2\right)-\left({\displaystyle \frac{{\epsilon }_2-{\vartheta }_2}{2}}\right){\mathsf{\Psi }}^{\prime }\left({\vartheta }_2\right)+{\displaystyle \frac{1}{{\epsilon }_2-{\vartheta }_2}}{\int }_{{\vartheta }_2}^{{\epsilon }_2}{\int }_{{\vartheta }_2}^{{\epsilon }_2}{G}_2(\varrho ,v){\mathsf{\Psi }}^{″}\left(v\right)dvd\varrho .$$

(7)

Adding (6) and (7), we have

$$\begin{array}{cc}\hfill & {\displaystyle \frac{2}{{\epsilon }_2-{\vartheta }_2}}{\int }_{{\vartheta }_2}^{{\epsilon }_2}\mathsf{\Psi }\left(\varrho \right)d\varrho \hfill \\ \hfill & =\mathsf{\Psi }\left({\vartheta }_2\right)+\mathsf{\Psi }\left({\epsilon }_2\right)+{\displaystyle \frac{({\epsilon }_2-{\vartheta }_2)}{2}}[{\mathsf{\Psi }}^{\prime }\left({\epsilon }_2\right)-{\mathsf{\Psi }}^{\prime }\left({\vartheta }_2\right)]+{\displaystyle \frac{1}{{\epsilon }_2-{\vartheta }_2}}{\int }_{{\vartheta }_2}^{{\epsilon }_2}{\int }_{{\vartheta }_2}^{{\epsilon }_2}{G}_1(\varrho ,v){\mathsf{\Psi }}^{″}\left(v\right)dvd\varrho \hfill \\ \hfill & +{\displaystyle \frac{1}{{\epsilon }_2-{\vartheta }_2}}{\int }_{{\vartheta }_2}^{{\epsilon }_2}{\int }_{{\vartheta }_2}^{{\epsilon }_2}{G}_2(\varrho ,v){\mathsf{\Psi }}^{″}\left(v\right)dvd\varrho .\hfill \end{array}$$

(8)

We have

$$\begin{array}{cc}\hfill & {\displaystyle \frac{1}{{\epsilon }_2-{\vartheta }_2}}{\int }_{{\vartheta }_2}^{{\epsilon }_2}\mathsf{\Psi }\left(\varrho \right)d\varrho -{\displaystyle \frac{\mathsf{\Psi }\left({\vartheta }_2\right)+\mathsf{\Psi }\left({\epsilon }_2\right)}{2}}\hfill \\ \hfill & ={\displaystyle \frac{{\epsilon }_2-{\vartheta }_2}{4}}[{\mathsf{\Psi }}^{\prime }\left({\epsilon }_2\right)-{\mathsf{\Psi }}^{\prime }\left({\vartheta }_2\right)]+{\displaystyle \frac{1}{2({\epsilon }_2-{\vartheta }_2)}}{\int }_{{\vartheta }_2}^{{\epsilon }_2}{\int }_{{\vartheta }_2}^{{\epsilon }_2}{G}_1\left(\varrho ,v\right){\mathsf{\Psi }}^{″}\left(v\right)dvd\varrho +{\displaystyle \frac{1}{2({\epsilon }_2-{\vartheta }_2)}}{\int }_{{\vartheta }_2}^{{\epsilon }_2}{\int }_{{\vartheta }_2}^{{\epsilon }_2}{G}_2(\varrho ,v){\mathsf{\Psi }}^{″}\left(v\right)dvd\varrho .\hfill \end{array}$$

Now, from the definition of Green’s function, we obtain

$$\begin{array}{cc}\hfill & {\displaystyle \frac{1}{{\epsilon }_2-{\vartheta }_2}}{\int }_{{\vartheta }_2}^{{\epsilon }_2}\mathsf{\Psi }\left(\varrho \right)d\varrho -{\displaystyle \frac{\mathsf{\Psi }\left({\vartheta }_2\right)+\mathsf{\Psi }\left({\epsilon }_2\right)}{2}}\hfill \\ \hfill & ={\displaystyle \frac{{\epsilon }_2-{\vartheta }_2}{4}}[{\mathsf{\Psi }}^{\prime }\left({\epsilon }_2\right)-{\mathsf{\Psi }}^{\prime }\left({\vartheta }_2\right)]+{\displaystyle \frac{1}{2({\epsilon }_2-{\vartheta }_2)}}{\int }_{{\vartheta }_2}^{{\epsilon }_2}\left[{\int }_{{\vartheta }_2}^v({\vartheta }_2-\varrho )d\varrho +{\int }_v^{{\epsilon }_2}({\vartheta }_2-v)d\varrho \right]{\mathsf{\Psi }}^{″}\left(v\right)dv\hfill \\ \hfill & +{\displaystyle \frac{1}{2({\epsilon }_2-{\vartheta }_2)}}{\int }_{{\vartheta }_2}^{{\epsilon }_2}\left[{\int }_{{\vartheta }_2}^v(v-{\epsilon }_2)d\varrho +{\int }_v^{{\epsilon }_2}(\varrho -{\epsilon }_2)d\varrho \right]{\mathsf{\Psi }}^{″}\left(v\right)dv\hfill \\ \hfill & ={\displaystyle \frac{{\epsilon }_2-{\vartheta }_2}{4}}[{\mathsf{\Psi }}^{\prime }\left({\epsilon }_2\right)-{\mathsf{\Psi }}^{\prime }\left({\vartheta }_2\right)]+{\displaystyle \frac{1}{4({\epsilon }_2-{\vartheta }_2)}}{\int }_{{\vartheta }_2}^{{\epsilon }_2}\left[-4(v-{\vartheta }_2)({\epsilon }_2-v)-{({\epsilon }_2-v)}^2-{(v-{\vartheta }_2)}^2\right]{\mathsf{\Psi }}^{″}\left(v\right)dv.\hfill \end{array}$$

(9)

Let $v=\mathsf{\ell }{\vartheta }_2+(1-\mathsf{\ell }){\epsilon }_2$ and $dv=({\vartheta }_2-{\epsilon }_2)d\mathsf{\ell }$, then we have

$$\begin{array}{cc}\hfill & {\displaystyle \frac{1}{{\epsilon }_2-{\vartheta }_2}}{\int }_{{\vartheta }_2}^{{\epsilon }_2}\mathsf{\Psi }\left(\varrho \right)d\varrho -{\displaystyle \frac{\mathsf{\Psi }\left({\vartheta }_2\right)+\mathsf{\Psi }\left({\epsilon }_2\right)}{2}}\hfill \\ \hfill & ={\displaystyle \frac{{\epsilon }_2-{\vartheta }_2}{4}}[{\mathsf{\Psi }}^{\prime }\left({\epsilon }_2\right)-{\mathsf{\Psi }}^{\prime }\left({\vartheta }_2\right)]+{\displaystyle \frac{{({\epsilon }_2-{\vartheta }_2)}^2}{4}}{\int }_0^1\left(2{\mathsf{\ell }}^2-2\mathsf{\ell }-1\right){\mathsf{\Psi }}^{″}(\mathsf{\ell }{\vartheta }_2+(1-\mathsf{\ell }){\epsilon }_2)d\mathsf{\ell }.\hfill \end{array}$$

Using the properties of absolute value and triangle inequality, we have

$$\begin{array}{cc}\hfill & \left|{\displaystyle \frac{\mathsf{\Psi }\left({\vartheta }_2\right)+\mathsf{\Psi }\left({\epsilon }_2\right)}{2}}-{\displaystyle \frac{1}{{\epsilon }_2-{\vartheta }_2}}{\int }_{{\vartheta }_2}^{{\epsilon }_2}\mathsf{\Psi }\left(\varrho \right)d\varrho \right|\hfill \\ \hfill & \le {\displaystyle \frac{{\epsilon }_2-{\vartheta }_2}{4}}\left[\right|{\mathsf{\Psi }}^{\prime }\left({\vartheta }_2\right)|+|{\mathsf{\Psi }}^{\prime }\left({\epsilon }_2\right)\left|\right]+{\displaystyle \frac{1}{4({\epsilon }_2-{\vartheta }_2)}}{\int }_{{\vartheta }_2}^{{\epsilon }_2}\left|2{\mathsf{\ell }}^2-2\mathsf{\ell }-1\right|\left|{\mathsf{\Psi }}^{″}(\mathsf{\ell }{\vartheta }_2+(1-\mathsf{\ell }){\epsilon }_2)\right|d\mathsf{\ell }.\hfill \end{array}$$

(10)

Now, using the convexity of $|{\mathsf{\Psi }}^{″}|$, we have

$$\begin{array}{cc}\hfill & \left|{\displaystyle \frac{\mathsf{\Psi }\left({\vartheta }_2\right)+\mathsf{\Psi }\left({\epsilon }_2\right)}{2}}-{\displaystyle \frac{1}{{\epsilon }_2-{\vartheta }_2}}{\int }_{{\vartheta }_2}^{{\epsilon }_2}\mathsf{\Psi }\left(\varrho \right)d\varrho \right|\hfill \\ \hfill & \le {\displaystyle \frac{{\epsilon }_2-{\vartheta }_2}{4}}\left[\right|{\mathsf{\Psi }}^{\prime }\left({\vartheta }_2\right)|+|{\mathsf{\Psi }}^{\prime }\left({\epsilon }_2\right)\left|\right]+{\displaystyle \frac{{({\epsilon }_2-{\vartheta }_2)}^2}{4}}{\int }_0^1\left|2{\mathsf{\ell }}^2-2\mathsf{\ell }-1\right|\left[\mathsf{\ell }\right|{\mathsf{\Psi }}^{″}\left({\vartheta }_2\right)|+(1-\mathsf{\ell })|{\mathsf{\Psi }}^{″}\left({\epsilon }_2\right)\left|\right]d\mathsf{\ell }\hfill \\ \hfill & ={\displaystyle \frac{{\epsilon }_2-{\vartheta }_2}{4}}\left[|{\mathsf{\Psi }}^{\prime }\left({\vartheta }_2\right)|+|{\mathsf{\Psi }}^{\prime }\left({\epsilon }_2\right)|\right]+{\displaystyle \frac{{\left({\epsilon }_2-{\vartheta }_2\right)}^2}{6}}\left[|{\mathsf{\Psi }}^{″}\left({\vartheta }_2\right)|+|{\mathsf{\Psi }}^{″}\left({\epsilon }_2\right)|\right].\hfill \end{array}$$

This completes the proof. □

Example 1. 

Let $\mathsf{\Psi }:[0,{\epsilon }_2]\to \mathbb{R}$ be a convex function and defined as $\mathsf{\Psi }\left(\varrho \right)={\varrho }^4$. Additionally, ${\mathsf{\Psi }}^{″}\left(\varrho \right)$ is also a convex function and satisfying all the requirements of Theorem 4. Then we have the following graphical representations.

From Figure 1 and Table 1, it is clear that the right hand side exceeds the left hand side of inequality proved in Theorem 4.

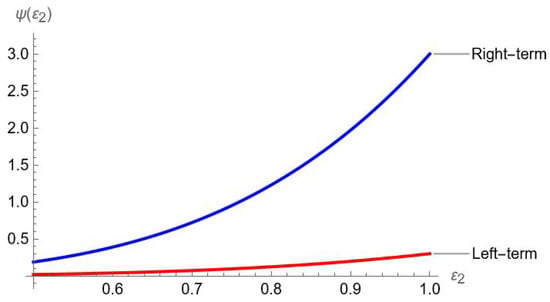
Figure 1. Visual analysis of Theorem 4.

Table 1. Comparison between left and right terms of Theorem 4.

${\mathit{\epsilon }}_2$	Left-Term	Right-Term
$0.5$	0.01875	0.18750
$0.6$	0.03888	0.38880
$0.8$	0.12288	1.22880
$0.9$	0.19683	1.96830
1	0.30000	3.000000

Theorem 5. 

Let $\mathsf{\Psi }:[{\vartheta }_2,{\epsilon }_2]\to \mathbb{R}$ be a twice differentiable function. If $|{\mathsf{\Psi }}^{″}{|}^q$ is a convex function, then

$$\begin{array}{cc}\hfill & \left|{\displaystyle \frac{\mathsf{\Psi }\left({\vartheta }_2\right)+\mathsf{\Psi }\left({\epsilon }_2\right)}{2}}-{\displaystyle \frac{1}{{\epsilon }_2-{\vartheta }_2}}{\int }_{{\vartheta }_2}^{{\epsilon }_2}\mathsf{\Psi }\left(\varrho \right)d\varrho \right|\hfill \\ \hfill & \le {\displaystyle \frac{{\epsilon }_2-{\vartheta }_2}{4}}\left[\right|{\mathsf{\Psi }}^{\prime }\left({\vartheta }_2\right)|+|{\mathsf{\Psi }}^{\prime }\left({\epsilon }_2\right)\left|\right]+{\displaystyle \frac{{\left({\epsilon }_2-{\vartheta }_2\right)}^2}{4}}\left[{\displaystyle \frac{1}{p}}B\left(p\right)+{\displaystyle \frac{1}{2q}}\left[\right|{\mathsf{\Psi }}^{″}\left({\vartheta }_2\right){|}^q+|{\mathsf{\Psi }}^{″}\left({\epsilon }_2\right){|}^q]\right],\hfill \end{array}$$

where

$$B\left(p\right)={\int }_0^1{\left|2{\mathsf{\ell }}^2-2\mathsf{\ell }-1\right|}^{p}d\mathsf{\ell },$$

and $p,q>1$ such that ${\displaystyle \frac{1}{p}}+{\displaystyle \frac{1}{q}}=1$.

Proof. 

From (10), we have

$$\begin{array}{cc}\hfill & \left|{\displaystyle \frac{\mathsf{\Psi }\left({\vartheta }_2\right)+\mathsf{\Psi }\left({\epsilon }_2\right)}{2}}-{\displaystyle \frac{1}{{\epsilon }_2-{\vartheta }_2}}{\int }_{{\vartheta }_2}^{{\epsilon }_2}\mathsf{\Psi }\left(\varrho \right)d\varrho \right|\hfill \\ \hfill & \le {\displaystyle \frac{{\epsilon }_2-{\vartheta }_2}{4}}[\left|{\mathsf{\Psi }}^{\prime }\left({\vartheta }_2\right)\right|+\left|{\mathsf{\Psi }}^{\prime }\left({\epsilon }_2\right)\right|]+{\displaystyle \frac{{({\epsilon }_2-{\vartheta }_2)}^2}{4}}{\int }_0^1\left|2{\mathsf{\ell }}^2-2\mathsf{\ell }-1\right|\left|{\mathsf{\Psi }}^{″}(\mathsf{\ell }{\vartheta }_2+(1-\mathsf{\ell }){\epsilon }_2)\right|d\mathsf{\ell }.\hfill \end{array}$$

Using Young’s inequality, we have

$$\begin{array}{cc}\hfill & \left|{\displaystyle \frac{\mathsf{\Psi }\left({\vartheta }_2\right)+\mathsf{\Psi }\left({\epsilon }_2\right)}{2}}-{\displaystyle \frac{1}{{\epsilon }_2-{\vartheta }_2}}{\int }_{{\vartheta }_2}^{{\epsilon }_2}\mathsf{\Psi }\left(\varrho \right)d\varrho \right|\hfill \\ \hfill & \le {\displaystyle \frac{{\epsilon }_2-{\vartheta }_2}{4}}\left[\right|{\mathsf{\Psi }}^{\prime }\left({\vartheta }_2\right)|+|{\mathsf{\Psi }}^{\prime }\left({\epsilon }_2\right)\left|\right]+{\displaystyle \frac{{({\epsilon }_2-{\vartheta }_2)}^2}{4}}\left[{\displaystyle \frac{1}{p}}{\int }_0^1{|2{\mathsf{\ell }}^2-2\mathsf{\ell }-1|}^{p}d\mathsf{\ell }+{\displaystyle \frac{1}{q}}{\int }_0^1{\left|{\mathsf{\Psi }}^{″}\left(\mathsf{\ell }{\vartheta }_2+(1-\mathsf{\ell }){\epsilon }_2\right)\right|}^{q}d\mathsf{\ell }\right].\hfill \end{array}$$

Using the convexity of $|{\mathsf{\Psi }}^{″}{|}^q$, we have

$$\begin{array}{cc}\hfill & \left|{\displaystyle \frac{\mathsf{\Psi }\left({\vartheta }_2\right)+\mathsf{\Psi }\left({\epsilon }_2\right)}{2}}-{\displaystyle \frac{1}{{\epsilon }_2-{\vartheta }_2}}{\int }_{{\vartheta }_2}^{{\epsilon }_2}\mathsf{\Psi }\left(\varrho \right)d\varrho \right|\hfill \\ \hfill & \le {\displaystyle \frac{{\epsilon }_2-{\vartheta }_2}{4}}\left[\right|{\mathsf{\Psi }}^{\prime }\left({\vartheta }_2\right)|+|{\mathsf{\Psi }}^{\prime }\left({\epsilon }_2\right)\left|\right]+{\displaystyle \frac{{({\epsilon }_2-{\vartheta }_2)}^2}{4}}\left[{\displaystyle \frac{1}{p}}{\int }_0^1{\left|2{\mathsf{\ell }}^2-2\mathsf{\ell }-1\right|}^{p}d\mathsf{\ell }\right.\hfill \\ \hfill & \left.+{\displaystyle \frac{1}{q}}{\int }_0^1\left[\mathsf{\ell }|{\mathsf{\Psi }}^{″}\left({\vartheta }_2\right){|}^q+(1-\mathsf{\ell }){\left|{\mathsf{\Psi }}^{″}\left({\epsilon }_2\right)\right|}^{q}d\mathsf{\ell }\right]\right]\hfill \\ \hfill & ={\displaystyle \frac{{\epsilon }_2-{\vartheta }_2}{4}}\left[\right|{\mathsf{\Psi }}^{\prime }\left({\vartheta }_2\right)|+|{\mathsf{\Psi }}^{\prime }\left({\epsilon }_2\right)\left|\right]+{\displaystyle \frac{{\left({\epsilon }_2-{\vartheta }_2\right)}^2}{4}}\left[{\displaystyle \frac{1}{p}}B\left(p\right)+{\displaystyle \frac{1}{2q}}\left[\right|{\mathsf{\Psi }}^{″}\left({\vartheta }_2\right){|}^q+|{\mathsf{\Psi }}^{″}\left({\epsilon }_2\right){|}^q]\right].\hfill \end{array}$$

This completes the proof. □

Example 2. 

Let $\mathsf{\Psi }:[0,{\epsilon }_2]\to \mathbb{R}$ be a convex function and defined as $\mathsf{\Psi }\left(\varrho \right)={\varrho }^4$. Additionally, ${\mathsf{\Psi }}^{″}\left(\varrho \right)$ is also convex function and satisfying all the requirements of Theorem 5. Then we have the following graphical representations.

Both Figure 2 and Table 2 provide the simulative and numerical verification of Theorem 5, respectively.

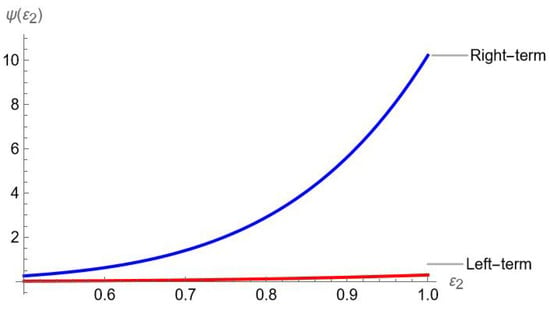
Figure 2. Visual analysis of Theorem 5.

Table 2. Comparison between left and right terms of Theorem 5.

${\mathit{\epsilon }}_2$	Left-Term	Right-Term
$0.5$	0.01875	0.25938
$0.6$	0.03888	0.63050
$0.8$	0.12288	2.91290
$0.9$	0.19683	5.62132

Theorem 6. 

Let $\mathsf{\Psi }:[{\vartheta }_2,{\epsilon }_2]\to \mathbb{R}$ be a twice differentiable function. If $|{\mathsf{\Psi }}^{″}{|}^q$ is a convex function, then

$$\begin{array}{cc}\hfill & \left|{\displaystyle \frac{\mathsf{\Psi }\left({\vartheta }_2\right)+\mathsf{\Psi }\left({\epsilon }_2\right)}{2}}-{\displaystyle \frac{1}{{\epsilon }_2-{\vartheta }_2}}{\int }_{{\vartheta }_2}^{{\epsilon }_2}\mathsf{\Psi }\left(\varrho \right)d\varrho \right|\hfill \\ \hfill & \le {\displaystyle \frac{{\epsilon }_2-{\vartheta }_2}{4}}\left[\right|{\mathsf{\Psi }}^{\prime }\left({\vartheta }_2\right)|+|{\mathsf{\Psi }}^{\prime }\left({\epsilon }_2\right)\left|\right]+{\displaystyle \frac{{\left({\epsilon }_2-{\vartheta }_2\right)}^2}{4}}\left[B^{{\displaystyle \frac{1}{p}}}\left(p\right){\left({\displaystyle \frac{|{\mathsf{\Psi }}^{″}\left({\vartheta }_2\right){|}^q+{\left|{\mathsf{\Psi }}^{″}\left({\epsilon }_2\right)\right|}^q}{2}}\right)}^{{\displaystyle \frac{1}{q}}}\right],\hfill \end{array}$$

$B\left(p\right)$ is defined in Theorem 5 and $p,q>1$ such that ${\displaystyle \frac{1}{p}}+{\displaystyle \frac{1}{q}}=1$.

Proof. 

From (10), we have

$$\begin{array}{cc}\hfill & \left|{\displaystyle \frac{\mathsf{\Psi }\left({\vartheta }_2\right)+\mathsf{\Psi }\left({\epsilon }_2\right)}{2}}-{\displaystyle \frac{1}{{\epsilon }_2-{\vartheta }_2}}{\int }_{{\vartheta }_2}^{{\epsilon }_2}\mathsf{\Psi }\left(\varrho \right)d\varrho \right|\hfill \\ \hfill & \le {\displaystyle \frac{{\epsilon }_2-{\vartheta }_2}{4}}\left[|{\mathsf{\Psi }}^{\prime }\left({\vartheta }_2\right)|+|{\mathsf{\Psi }}^{\prime }\left({\epsilon }_2\right)|\right]+{\displaystyle \frac{{({\epsilon }_2-{\vartheta }_2)}^2}{4}}{\int }_0^1\left|2{\mathsf{\ell }}^2-2\mathsf{\ell }-1\right|\left|{\mathsf{\Psi }}^{″}(\mathsf{\ell }{\vartheta }_2+(1-\mathsf{\ell }){\epsilon }_2)\right|d\mathsf{\ell }.\hfill \end{array}$$

Using Hölder’s inequality, we have

$$\begin{array}{cc}\hfill & \left|{\displaystyle \frac{\mathsf{\Psi }\left({\vartheta }_2\right)+\mathsf{\Psi }\left({\epsilon }_2\right)}{2}}-{\displaystyle \frac{1}{{\epsilon }_2-{\vartheta }_2}}{\int }_{{\vartheta }_2}^{{\epsilon }_2}\mathsf{\Psi }\left(\varrho \right)d\varrho \right|\hfill \\ \hfill & \le {\displaystyle \frac{{\epsilon }_2-{\vartheta }_2}{4}}\left[\right|{\mathsf{\Psi }}^{\prime }\left({\vartheta }_2\right)|+|{\mathsf{\Psi }}^{\prime }\left({\epsilon }_2\right)\left|\right]+{\displaystyle \frac{{({\epsilon }_2-{\vartheta }_2)}^2}{4}}\left[{\left({\int }_0^1{|2{\mathsf{\ell }}^2-2\mathsf{\ell }-1|}^{p}d\mathsf{\ell }\right)}^{{\displaystyle \frac{1}{p}}}{\left({\int }_0^1{\left|{\mathsf{\Psi }}^{″}\left(\mathsf{\ell }{\vartheta }_2+(1-\mathsf{\ell }){\epsilon }_2\right)\right|}^{q}d\mathsf{\ell }\right)}^{{\displaystyle \frac{1}{q}}}\right].\hfill \end{array}$$

Now using the convexity of $|{\mathsf{\Psi }}^{″}{|}^q$, we have

$$\begin{array}{cc}\hfill & \left|{\displaystyle \frac{\mathsf{\Psi }\left({\vartheta }_2\right)+\mathsf{\Psi }\left({\epsilon }_2\right)}{2}}-{\displaystyle \frac{1}{{\epsilon }_2-{\vartheta }_2}}{\int }_{{\vartheta }_2}^{{\epsilon }_2}\mathsf{\Psi }\left(\varrho \right)d\varrho \right|\hfill \\ \hfill & \le {\displaystyle \frac{{\epsilon }_2-{\vartheta }_2}{4}}\left[\right|{\mathsf{\Psi }}^{\prime }\left({\vartheta }_2\right)|+|{\mathsf{\Psi }}^{\prime }\left({\epsilon }_2\right)\left|\right]+{\displaystyle \frac{{({\epsilon }_2-{\vartheta }_2)}^2}{4}}\left[{\left({\int }_0^1{\left|2{\mathsf{\ell }}^2-2\mathsf{\ell }-1\right|}^{p}d\mathsf{\ell }\right)}^{{\displaystyle \frac{1}{p}}}\right.\hfill \\ \hfill & \left.{\left({\int }_0^1\left[\mathsf{\ell }|{\mathsf{\Psi }}^{″}\left({\vartheta }_2\right){|}^q+(1-\mathsf{\ell }){\left|{\mathsf{\Psi }}^{″}\left({\epsilon }_2\right)\right|}^{q}d\mathsf{\ell }\right]\right)}^{{\displaystyle \frac{1}{q}}}\right]\hfill \\ \hfill & ={\displaystyle \frac{{\epsilon }_2-{\vartheta }_2}{4}}\left[\right|{\mathsf{\Psi }}^{\prime }\left({\vartheta }_2\right)|+|{\mathsf{\Psi }}^{\prime }\left({\epsilon }_2\right)\left|\right]+{\displaystyle \frac{{\left({\epsilon }_2-{\vartheta }_2\right)}^2}{4}}\left[B^{{\displaystyle \frac{1}{p}}}\left(p\right){\left({\displaystyle \frac{|{\mathsf{\Psi }}^{″}\left({\vartheta }_2\right){|}^q+{\left|{\mathsf{\Psi }}^{″}\left({\epsilon }_2\right)\right|}^q}{2}}\right)}^{{\displaystyle \frac{1}{q}}}\right].\hfill \end{array}$$

This completes the proof. □

Example 3. 

Let $\mathsf{\Psi }:[0,{\epsilon }_2]\to \mathbb{R}$ be a convex function and defined as $\mathsf{\Psi }\left(\varrho \right)={\varrho }^4$. Additionally, ${\mathsf{\Psi }}^{″}\left(\varrho \right)$ is also convex function and satisfying all the requirements of Theorem 6. Now we have the following graphical representations.

Both Figure 3 and Table 3 are confirming the accuracy of Theorem 6.

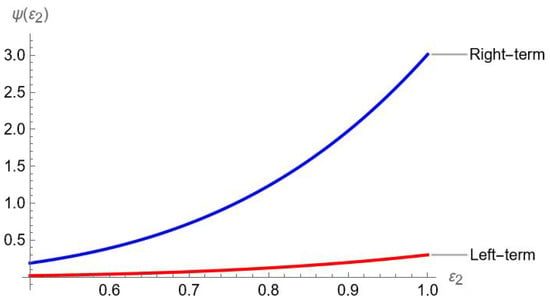
Figure 3. Visual analysis of Theorem 6.

Table 3. Comparison between left and right terms of Theorem 6.

${\mathit{\epsilon }}_2$	Left-Term	Right-Term
$0.5$	0.01875	0.18828
$0.6$	0.03888	0.39042
$0.8$	0.12288	1.23390
$0.9$	0.19683	1.97648
1	0.30000	3.01246

Theorem 7. 

Let $\mathsf{\Psi }:[{\vartheta }_2,{\epsilon }_2]\to \mathbb{R}$ be a twice differentiable function. If $|{\mathsf{\Psi }}^{″}{|}^q$ is a convex function, then

$$\begin{array}{cc}\hfill & \left|{\displaystyle \frac{\mathsf{\Psi }\left({\vartheta }_2\right)+\mathsf{\Psi }\left({\epsilon }_2\right)}{2}}-{\displaystyle \frac{1}{{\epsilon }_2-{\vartheta }_2}}{\int }_{{\vartheta }_2}^{{\epsilon }_2}\mathsf{\Psi }\left(\varrho \right)d\varrho \right|\hfill \\ \hfill & \le {\displaystyle \frac{{\epsilon }_2-{\vartheta }_2}{4}}\left[\right|{\mathsf{\Psi }}^{\prime }\left({\vartheta }_2\right)|+|{\mathsf{\Psi }}^{\prime }\left({\epsilon }_2\right)\left|\right]+{\displaystyle \frac{{\left({\epsilon }_2-{\vartheta }_2\right)}^2}{4}}{\left({\displaystyle \frac{4}{3}}\right)}^{1-{\displaystyle \frac{1}{q}}}{\left({\displaystyle \frac{2\left(|{\mathsf{\Psi }}^{″}\left({\vartheta }_2\right){|}^q+{\left|{\mathsf{\Psi }}^{″}\left({\epsilon }_2\right)\right|}^q\right)}{3}}\right)}^{{\displaystyle \frac{1}{q}}},\hfill \end{array}$$

where $q\ge 1$.

Proof. 

By using power mean inequality on (10), we have

$$\begin{array}{cc}\hfill & \left|{\displaystyle \frac{\mathsf{\Psi }\left({\vartheta }_2\right)+\mathsf{\Psi }\left({\epsilon }_2\right)}{2}}-{\displaystyle \frac{1}{{\epsilon }_2-{\vartheta }_2}}{\int }_{{\vartheta }_2}^{{\epsilon }_2}\mathsf{\Psi }\left(\varrho \right)d\varrho \right|\hfill \\ \hfill & \le {\displaystyle \frac{{\epsilon }_2-{\vartheta }_2}{4}}\left[\right|{\mathsf{\Psi }}^{\prime }\left({\vartheta }_2\right)|+|{\mathsf{\Psi }}^{\prime }\left({\epsilon }_2\right)\left|\right]+{\displaystyle \frac{{({\epsilon }_2-{\vartheta }_2)}^2}{4}}\left[{\left({\int }_0^1|2{\mathsf{\ell }}^2-2\mathsf{\ell }-1|d\mathsf{\ell }\right)}^{1-{\displaystyle \frac{1}{q}}}{\left({\int }_0^1|2{\mathsf{\ell }}^2-2\mathsf{\ell }-1|{\left|{\mathsf{\Psi }}^{″}\left(\mathsf{\ell }{\vartheta }_2+(1-\mathsf{\ell }){\epsilon }_2\right)\right|}^{q}d\mathsf{\ell }\right)}^{{\displaystyle \frac{1}{q}}}\right].\hfill \end{array}$$

Now using convexity of $|{\mathsf{\Psi }}^{″}{|}^q$, we have

$$\begin{array}{cc}\hfill & \left|{\displaystyle \frac{\mathsf{\Psi }\left({\vartheta }_2\right)+\mathsf{\Psi }\left({\epsilon }_2\right)}{2}}-{\displaystyle \frac{1}{{\epsilon }_2-{\vartheta }_2}}{\int }_{{\vartheta }_2}^{{\epsilon }_2}\mathsf{\Psi }\left(\varrho \right)d\varrho \right|\hfill \\ \hfill & \le {\displaystyle \frac{{\epsilon }_2-{\vartheta }_2}{4}}\left[\right|{\mathsf{\Psi }}^{\prime }\left({\vartheta }_2\right)|+|{\mathsf{\Psi }}^{\prime }\left({\epsilon }_2\right)\left|\right]+{\displaystyle \frac{{({\epsilon }_2-{\vartheta }_2)}^2}{4}}\left[{\left({\displaystyle \frac{4}{3}}\right)}^{1-{\displaystyle \frac{1}{q}}}\right.\hfill \\ \hfill & \left.{\left({\int }_0^1|2{\mathsf{\ell }}^2-2\mathsf{\ell }-1|\left[\mathsf{\ell }|{\mathsf{\Psi }}^{″}\left({\vartheta }_2\right){|}^q+(1-\mathsf{\ell }){\left|{\mathsf{\Psi }}^{″}\left({\epsilon }_2\right)\right|}^{q}d\mathsf{\ell }\right]\right)}^{{\displaystyle \frac{1}{q}}}\right]\hfill \\ \hfill & ={\displaystyle \frac{{\epsilon }_2-{\vartheta }_2}{4}}\left[\right|{\mathsf{\Psi }}^{\prime }\left({\vartheta }_2\right)|+|{\mathsf{\Psi }}^{\prime }\left({\epsilon }_2\right)\left|\right]+{\displaystyle \frac{{\left({\epsilon }_2-{\vartheta }_2\right)}^2}{4}}{\left({\displaystyle \frac{4}{3}}\right)}^{1-{\displaystyle \frac{1}{q}}}{\left({\displaystyle \frac{2\left(|{\mathsf{\Psi }}^{″}\left({\vartheta }_2\right){|}^q+{\left|{\mathsf{\Psi }}^{″}\left({\epsilon }_2\right)\right|}^q\right)}{3}}\right)}^{{\displaystyle \frac{1}{q}}}.\hfill \end{array}$$

This completes the proof. □

Example 4. 

Let $\mathsf{\Psi }:[0,{\epsilon }_2]\to \mathbb{R}$ be a convex function and defined as $\mathsf{\Psi }\left(\varrho \right)={\varrho }^4$. Additionally, ${\mathsf{\Psi }}^{″}\left(\varrho \right)$ is also convex function and satisfying all the requirements of Theorem 7. Now we have the following graphical representations.

Figure 4 and Table 4 illustrate the accuracy of Theorem 7, respectively.

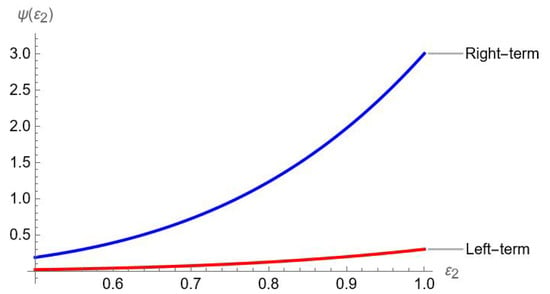
Figure 4. Visual analysis of Theorem 7.

Table 4. Comparison between left and right terms of Theorem 7.

${\mathit{\epsilon }}_2$	Left-Term	Right-Term
$0.5$	0.01875	0.18750
$0.6$	0.03888	0.38880
$0.8$	0.12288	1.22880
$0.9$	0.19683	1.96830
1	0.30000	3.00000

Theorem 8. 

Suppose that ${\mathsf{\Psi }}^{\prime }:[{\vartheta }_2,{\epsilon }_2]\to \mathbb{R}$ is a function of bounded variations on $[{\vartheta }_2,{\epsilon }_2]$. Then

$$\left|{\displaystyle \frac{\mathsf{\Psi }\left({\vartheta }_2\right)+\mathsf{\Psi }\left({\epsilon }_2\right)}{2}}-{\displaystyle \frac{1}{{\epsilon }_2-{\vartheta }_2}}{\int }_{{\vartheta }_2}^{{\epsilon }_2}\mathsf{\Psi }\left(\varrho \right)d\varrho \right|\le {\displaystyle \frac{({\epsilon }_2-{\vartheta }_2)}{2}}{V}_{{\vartheta }_2}^{{\epsilon }_2}\left({\mathsf{\Psi }}^{\prime }\right).$$

Here $V_{{\vartheta }_2}^{{\epsilon }_2}\left({\mathsf{\Psi }}^{\prime }\right)$ represents the total variation of ${\mathsf{\Psi }}^{\prime }$ on $[{\vartheta }_2,{\epsilon }_2]$.

Proof. 

From (9), we have

$$\begin{array}{cc}\hfill & \left|{\displaystyle \frac{\mathsf{\Psi }\left({\vartheta }_2\right)+\mathsf{\Psi }\left({\epsilon }_2\right)}{2}}-{\displaystyle \frac{1}{{\epsilon }_2-{\vartheta }_2}}{\int }_{{\vartheta }_2}^{{\epsilon }_2}\mathsf{\Psi }\left(\varrho \right)d\varrho \right|\hfill \\ \hfill & \le {\displaystyle \frac{b-a}{4}}{\int }_{{\vartheta }_2}^{{\epsilon }_2}\left|{\mathsf{\Psi }}^{″}\left(v\right)dv\right|\hfill \\ \hfill & +{\displaystyle \frac{1}{4({\epsilon }_2-{\vartheta }_2)}}{\int }_{{\vartheta }_2}^{{\epsilon }_2}\left|\left[-4(v-{\vartheta }_2)({\epsilon }_2-v)-{(v-{\vartheta }_2)}^2-{({\epsilon }_2-v)}^2\right]{\mathsf{\Psi }}^{″}\left(v\right)dv\right|.\hfill \end{array}$$

Now, we revisit the fact that if ${\mathsf{\Psi }}^{\prime }$ is the function of bounded variation and g is be a continuous function. Then ${\int }_{{\vartheta }_2}^{{\epsilon }_2}{\mathsf{\Psi }}^{\prime }g\left(\varrho \right)d\varrho$ exists and

$$\left|{\int }_{{\vartheta }_2}^{{\epsilon }_2}g\left(\varrho \right)d{\mathsf{\Psi }}^{\prime }\left(\varrho \right)\right|\le \underset{\varrho \in [{\vartheta }_2,{\epsilon }_2]}{max}\left|g\left(\varrho \right)\right|V_{{\vartheta }_2}^{{\epsilon }_2}\left({\mathsf{\Psi }}^{\prime }\right).$$

By using this definition, we have

$$\begin{array}{cc}\hfill & \left|{\displaystyle \frac{\mathsf{\Psi }\left({\vartheta }_2\right)+\mathsf{\Psi }\left({\epsilon }_2\right)}{2}}-{\displaystyle \frac{1}{{\epsilon }_2-{\vartheta }_2}}{\int }_{{\vartheta }_2}^{{\epsilon }_2}\mathsf{\Psi }\left(\varrho \right)d\varrho \right|\hfill \\ \hfill & \le {\displaystyle \frac{b-a}{4}}{\int }_{{\vartheta }_2}^{{\epsilon }_2}\left|d{\mathsf{\Psi }}^{\prime }\left(v\right)dv\right|\hfill \\ \hfill & +{\displaystyle \frac{1}{4({\epsilon }_2-{\vartheta }_2)}}{\int }_{{\vartheta }_2}^{{\epsilon }_2}\left|\left[4(v-{\vartheta }_2)({\epsilon }_2-v)+{(v-{\vartheta }_2)}^2+{({\epsilon }_2-v)}^2\right]d{\mathsf{\Psi }}^{\prime }\left(v\right)dv\right|\hfill \\ \hfill & \le {\displaystyle \frac{(b-a)}{4}}\left[\underset{\varrho \in [{\vartheta }_2,{\epsilon }_2]}{max}{V}_{{\vartheta }_2}^{{\epsilon }_2}\left({\mathsf{\Psi }}^{\prime }\right)\right.\hfill \\ \hfill & \left.+{\displaystyle \frac{1}{{\epsilon }_2-{\vartheta }_2}}\underset{\varrho \in [{\vartheta }_2,{\epsilon }_2]}{max}\left|\left[4(v-{\vartheta }_2)({\epsilon }_2-v)+{(v-{\vartheta }_2)}^2+{({\epsilon }_2-v)}^2\right]\right|V_{{\vartheta }_2}^{{\epsilon }_2}\left({\mathsf{\Psi }}^{\prime }\right)\right]\hfill \\ \hfill & \le {\displaystyle \frac{({\epsilon }_2-{\vartheta }_2)}{2}}{V}_{{\vartheta }_2}^{{\epsilon }_2}\left({\mathsf{\Psi }}^{\prime }\right).\hfill \end{array}$$

It finishes the proof. □

Example 5. 

Let $\mathsf{\Psi }:[0,{\epsilon }_2]\to \mathbb{R}$ be a convex function and defined as $\mathsf{\Psi }\left(\varrho \right)={\varrho }^4$. Additionally, ${\mathsf{\Psi }}^{″}\left(\varrho \right)$ is also convex function and satisfying all the requirements of Theorem 8. Now we have the following graphical representations.

Figure 5 and Table 5 provide the graphical and numerical analysis of Theorem 8, respectively.

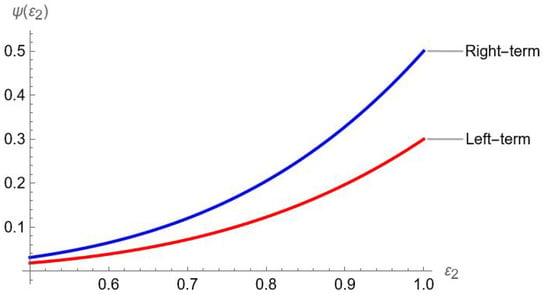
Figure 5. Visual analysis of Theorem 8.

Table 5. Comparison between left and right terms of Theorem 8.

${\mathit{\epsilon }}_2$	Left-Term	Right-Term
$0.5$	0.01875	0.03125
$0.6$	0.03888	0.06480
$0.8$	0.12288	0.20480
$0.9$	0.19683	0.32805
$1.0$	0.30000	0.50000

2.2. Simpson’s like Inequalities

Theorem 9. 

Let $\mathsf{\Psi }:[{\vartheta }_2,{\epsilon }_2]\to \mathbb{R}$ be a twice differentiable function. If $|{\mathsf{\Psi }}^{″}|$ is a convex function, then

$$\begin{array}{cc}\hfill & \left|{\displaystyle \frac{\mathsf{\Psi }\left({\vartheta }_2\right)+4\mathsf{\Psi }\left(\frac{{\vartheta }_2+{\epsilon }_2}{2}\right)+\mathsf{\Psi }\left({\epsilon }_2\right)}{6}}-{\displaystyle \frac{1}{{\epsilon }_2-{\vartheta }_2}}{\int }_{{\vartheta }_2}^{{\epsilon }_2}\mathsf{\Psi }\left(\varrho \right)d\varrho \right|\hfill \\ \hfill & \le {\displaystyle \frac{{\epsilon }_2-{\vartheta }_2}{12}}\left[\right|{\mathsf{\Psi }}^{\prime }\left({\vartheta }_2\right)|+|{\mathsf{\Psi }}^{\prime }\left({\epsilon }_2\right)\left|\right]+{\displaystyle \frac{{({\epsilon }_2-{\vartheta }_2)}^2}{72}}\left(17|{\mathsf{\Psi }}^{″}\left({\vartheta }_2\right)|+25|{\mathsf{\Psi }}^{″}\left({\epsilon }_2\right)|\right).\hfill \end{array}$$

(11)

Proof. 

Substituting $\varrho ={\epsilon }_2$, and $\varrho ={\displaystyle \frac{{\vartheta }_2+{\epsilon }_2}{2}}$ in (3) and $\varrho ={\vartheta }_2$, in (4), we have

$$\mathsf{\Psi }\left({\epsilon }_2\right)=\mathsf{\Psi }\left({\vartheta }_2\right)+({\epsilon }_2-{\vartheta }_2){\mathsf{\Psi }}^{\prime }\left({\epsilon }_2\right)+{\int }_{{\vartheta }_2}^{{\epsilon }_2}{G}_1({\epsilon }_2,v){\mathsf{\Psi }}^{″}\left(v\right)dv,$$

(12)

$$\mathsf{\Psi }\left({\vartheta }_2\right)=\mathsf{\Psi }\left({\epsilon }_2\right)-({\epsilon }_2-{\vartheta }_2){\mathsf{\Psi }}^{\prime }\left({\vartheta }_2\right)+{\int }_{{\vartheta }_2}^{{\epsilon }_2}{G}_2({\vartheta }_2,v){\mathsf{\Psi }}^{″}\left(v\right)dv,$$

(13)

$$4\mathsf{\Psi }\left({\displaystyle \frac{{\vartheta }_2+{\epsilon }_2}{2}}\right)=4\mathsf{\Psi }\left({\vartheta }_2\right)+2\left({\epsilon }_2-{\vartheta }_2\right){\mathsf{\Psi }}^{\prime }\left({\epsilon }_2\right)+4{\int }_{{\vartheta }_2}^{{\epsilon }_2}{G}_1\left({\displaystyle \frac{{\vartheta }_2+{\epsilon }_2}{2}},v\right){\mathsf{\Psi }}^{″}\left(v\right)dv.$$

(14)

Adding (12), (13) and (14), we have

$$\begin{array}{cc}\hfill & \mathsf{\Psi }\left({\vartheta }_2\right)+4\mathsf{\Psi }\left({\displaystyle \frac{{\vartheta }_2+{\epsilon }_2}{2}}\right)+\mathsf{\Psi }\left({\epsilon }_2\right)\hfill \\ \hfill & =5\mathsf{\Psi }\left({\vartheta }_2\right)+\mathsf{\Psi }\left({\epsilon }_2\right)+({\epsilon }_2-{\vartheta }_2)[3{\mathsf{\Psi }}^{\prime }\left({\epsilon }_2\right)-{\mathsf{\Psi }}^{\prime }\left({\vartheta }_2\right)]+{\int }_{{\vartheta }_2}^{{\epsilon }_2}{G}_1({\epsilon }_2,v){\mathsf{\Psi }}^{″}\left(v\right)dv\hfill \\ \hfill & +4{\int }_{{\vartheta }_2}^{{\epsilon }_2}{G}_1\left({\displaystyle \frac{{\vartheta }_2+{\epsilon }_2}{2}},v\right){\mathsf{\Psi }}^{″}\left(v\right)dv+{\int }_{{\vartheta }_2}^{{\epsilon }_2}{G}_2({\vartheta }_2,v){\mathsf{\Psi }}^{″}\left(v\right)dv\hfill \end{array}$$

(15)

Integrating (3) and (4) with respect to $\varrho$ from ${\vartheta }_2$ to ${\epsilon }_2$ and multiplying by ${\displaystyle \frac{5}{{\epsilon }_2-{\vartheta }_2}}$ and ${\displaystyle \frac{1}{{\epsilon }_2-{\vartheta }_2}}$, respectively, we obtain

$${\displaystyle \frac{5}{{\epsilon }_2-{\vartheta }_2}}{\int }_{{\vartheta }_2}^{{\epsilon }_2}\mathsf{\Psi }\left(\varrho \right)d\varrho =5\mathsf{\Psi }\left({\vartheta }_2\right)+{\displaystyle \frac{5({\epsilon }_2-{\vartheta }_2)}{2}}{\mathsf{\Psi }}^{\prime }\left({\epsilon }_2\right)+{\displaystyle \frac{5}{{\epsilon }_2-{\vartheta }_2}}{\int }_{{\vartheta }_2}^{{\epsilon }_2}{\int }_{{\vartheta }_2}^{{\epsilon }_2}{G}_1(\varrho ,v){\mathsf{\Psi }}^{″}\left(v\right)dvd\varrho$$

(16)

$${\displaystyle \frac{1}{{\epsilon }_2-{\vartheta }_2}}{\int }_{{\vartheta }_2}^{{\epsilon }_2}\mathsf{\Psi }\left(\varrho \right)d\varrho =\mathsf{\Psi }\left({\epsilon }_2\right)-{\displaystyle \frac{{\epsilon }_2-{\vartheta }_2}{2}}{\mathsf{\Psi }}^{\prime }\left({\vartheta }_2\right)+{\displaystyle \frac{1}{{\epsilon }_2-{\vartheta }_2}}{\int }_{{\vartheta }_2}^{{\epsilon }_2}{\int }_{{\vartheta }_2}^{{\epsilon }_2}{G}_2(\varrho ,v){\mathsf{\Psi }}^{″}\left(v\right)dvd\varrho .$$

(17)

Adding (16) and (17), we have

$$\begin{array}{cc}\hfill & {\displaystyle \frac{6}{{\epsilon }_2-{\vartheta }_2}}{\int }_{{\vartheta }_2}^{{\epsilon }_2}\mathsf{\Psi }\left(\varrho \right)d\varrho \hfill \\ \hfill & =5\mathsf{\Psi }\left({\vartheta }_2\right)+\mathsf{\Psi }\left({\epsilon }_2\right)+{\displaystyle \frac{{\epsilon }_2-{\vartheta }_2}{2}}[5{\mathsf{\Psi }}^{\prime }\left({\epsilon }_2\right)-{\mathsf{\Psi }}^{\prime }\left({\vartheta }_2\right)]+{\displaystyle \frac{5}{{\epsilon }_2-{\vartheta }_2}}{\int }_{{\vartheta }_2}^{{\epsilon }_2}{\int }_{{\vartheta }_2}^{{\epsilon }_2}{G}_1(\varrho ,v){\mathsf{\Psi }}^{″}\left(v\right)dvd\varrho \hfill \\ \hfill & +{\displaystyle \frac{5}{{\epsilon }_2-{\vartheta }_2}}{\int }_{{\vartheta }_2}^{{\epsilon }_2}{\int }_{{\vartheta }_2}^{{\epsilon }_2}{G}_2(\varrho ,v){\mathsf{\Psi }}^{″}\left(v\right)dvd\varrho .\hfill \end{array}$$

(18)

Subtracting (18) from (15), we have

$$\begin{array}{cc}\hfill & {\displaystyle \frac{\mathsf{\Psi }\left({\vartheta }_2\right)+4\mathsf{\Psi }\left(\frac{{\vartheta }_2+{\epsilon }_2}{2}\right)+\mathsf{\Psi }\left({\epsilon }_2\right)}{6}}-{\displaystyle \frac{1}{{\epsilon }_2-{\vartheta }_2}}{\int }_{{\vartheta }_2}^{{\epsilon }_2}\mathsf{\Psi }\left(\varrho \right)d\varrho \hfill \\ \hfill & ={\displaystyle \frac{{\epsilon }_2-{\vartheta }_2}{12}}[{\mathsf{\Psi }}^{\prime }\left({\epsilon }_2\right)-{\mathsf{\Psi }}^{\prime }\left({\vartheta }_2\right)]+{\displaystyle \frac{1}{6}}{\int }_{{\vartheta }_2}^{{\epsilon }_2}{G}_1\left({\epsilon }_2,v\right){\mathsf{\Psi }}^{″}\left(v\right)dv+{\displaystyle \frac{2}{3}}{\int }_{{\vartheta }_2}^{{\epsilon }_2}{G}_1\left({\displaystyle \frac{{\vartheta }_2+{\epsilon }_2}{2}},v\right){\mathsf{\Psi }}^{″}\left(v\right)dv\hfill \\ \hfill & -{\displaystyle \frac{5}{6({\epsilon }_2-{\vartheta }_2)}}{\int }_{{\vartheta }_2}^{{\epsilon }_2}{\int }_{{\vartheta }_2}^{{\epsilon }_2}{G}_1(\varrho ,v){\mathsf{\Psi }}^{″}\left(v\right)dvd\varrho +{\displaystyle \frac{1}{6}}{\int }_{{\vartheta }_2}^{{\epsilon }_2}{G}_2\left({\vartheta }_2,v\right){\mathsf{\Psi }}^{″}\left(v\right)dv-{\displaystyle \frac{1}{6({\epsilon }_2-{\vartheta }_2)}}{\int }_{{\vartheta }_2}^{{\epsilon }_2}{\int }_{{\vartheta }_2}^{{\epsilon }_2}{G}_2(\varrho ,v){\mathsf{\Psi }}^{″}\left(v\right)dvd\varrho .\hfill \end{array}$$

By using the definition of Green’s function, we have

$$\begin{array}{cc}\hfill & {\displaystyle \frac{\mathsf{\Psi }\left({\vartheta }_2\right)+4\mathsf{\Psi }\left(\frac{{\vartheta }_2+{\epsilon }_2}{2}\right)+\mathsf{\Psi }\left({\epsilon }_2\right)}{6}}-{\displaystyle \frac{1}{{\epsilon }_2-{\vartheta }_2}}{\int }_{{\vartheta }_2}^{{\epsilon }_2}\mathsf{\Psi }\left(\varrho \right)d\varrho \hfill \\ \hfill & ={\displaystyle \frac{{\epsilon }_2-{\vartheta }_2}{12}}[{\mathsf{\Psi }}^{\prime }\left({\vartheta }_2\right)-{\mathsf{\Psi }}^{\prime }\left({\epsilon }_2\right)]+{\displaystyle \frac{2}{3}}{\int }_{{\vartheta }_2}^{{\displaystyle \frac{{\vartheta }_2+{\epsilon }_2}{2}}}({\vartheta }_2-v){\mathsf{\Psi }}^{″}\left(v\right)dv+{\displaystyle \frac{2}{3}}{\int }_{{\displaystyle \frac{{\vartheta }_2+{\epsilon }_2}{2}}}^{{\epsilon }_2}\left({\displaystyle \frac{{\vartheta }_2-{\epsilon }_2}{2}}\right){\mathsf{\Psi }}^{″}\left(v\right)dv\hfill \\ \hfill & +{\displaystyle \frac{1}{6({\epsilon }_2-{\vartheta }_2)}}{\int }_{{\vartheta }_2}^{{\epsilon }_2}\left[6(v-{\vartheta }_2)({\epsilon }_2-v)+{\displaystyle \frac{5{(v-{\vartheta }_2)}^2}{2}}+{\displaystyle \frac{{({\epsilon }_2-v)}^2}{2}}\right]{\mathsf{\Psi }}^{″}\left(v\right)dv.\hfill \end{array}$$

(19)

Let $v=\mathsf{\ell }{\vartheta }_2+(1-\mathsf{\ell }){\epsilon }_2$ and $dv=({\vartheta }_2-{\epsilon }_2)d\mathsf{\ell }$, then

$$\begin{array}{cc}\hfill & {\displaystyle \frac{\mathsf{\Psi }\left({\vartheta }_2\right)+4\mathsf{\Psi }\left(\frac{{\vartheta }_2+{\epsilon }_2}{2}\right)+\mathsf{\Psi }\left({\epsilon }_2\right)}{6}}-{\displaystyle \frac{1}{{\epsilon }_2-{\vartheta }_2}}{\int }_{{\vartheta }_2}^{{\epsilon }_2}\mathsf{\Psi }\left(\varrho \right)d\varrho \hfill \\ \hfill & ={\displaystyle \frac{{\epsilon }_2-{\vartheta }_2}{12}}[{\mathsf{\Psi }}^{\prime }\left({\vartheta }_2\right)-{\mathsf{\Psi }}^{\prime }\left({\epsilon }_2\right)]-{\displaystyle \frac{{({\epsilon }_2-{\vartheta }_2)}^2}{3}}{\int }_0^{{\displaystyle \frac{1}{2}}}{\mathsf{\Psi }}^{″}(\mathsf{\ell }{\vartheta }_2+(1-\mathsf{\ell }){\epsilon }_2)d\mathsf{\ell }\hfill \\ \hfill & +{\displaystyle \frac{2{({\epsilon }_2-{\vartheta }_2)}^2}{3}}{\int }_{{\displaystyle \frac{1}{2}}}^1\left(\mathsf{\ell }-1\right){\mathsf{\Psi }}^{″}(\mathsf{\ell }{\vartheta }_2+(1-\mathsf{\ell }){\epsilon }_2)d\mathsf{\ell }\hfill \\ \hfill & +{\displaystyle \frac{{({\epsilon }_2-{\vartheta }_2)}^2}{12}}{\int }_0^1\left(5+2\mathsf{\ell }-6{\mathsf{\ell }}^2\right){\mathsf{\Psi }}^{″}(\mathsf{\ell }{\vartheta }_2+(1-\mathsf{\ell }){\epsilon }_2)d\mathsf{\ell }.\hfill \end{array}$$

Using the properties of absolute value and triangle inequality, we have

$$\begin{array}{cc}\hfill & \left|{\displaystyle \frac{\mathsf{\Psi }\left({\vartheta }_2\right)+4\mathsf{\Psi }\left(\frac{{\vartheta }_2+{\epsilon }_2}{2}\right)+\mathsf{\Psi }\left({\epsilon }_2\right)}{6}}-{\displaystyle \frac{1}{{\epsilon }_2-{\vartheta }_2}}{\int }_{{\vartheta }_2}^{{\epsilon }_2}\mathsf{\Psi }\left(\varrho \right)d\varrho \right|\hfill \\ \hfill & \le {\displaystyle \frac{{\epsilon }_2-{\vartheta }_2}{12}}\left[\right|{\mathsf{\Psi }}^{\prime }\left({\vartheta }_2\right)|+|{\mathsf{\Psi }}^{\prime }\left({\epsilon }_2\right)\left|\right]+{\displaystyle \frac{{({\epsilon }_2-{\vartheta }_2)}^2}{3}}{\int }_0^{{\displaystyle \frac{1}{2}}}\left|{\mathsf{\Psi }}^{″}(\mathsf{\ell }{\vartheta }_2+(1-\mathsf{\ell }){\epsilon }_2)\right|d\mathsf{\ell }\hfill \\ \hfill & +{\displaystyle \frac{2{({\epsilon }_2-{\vartheta }_2)}^2}{3}}{\int }_{{\displaystyle \frac{1}{2}}}^1\left|1-\mathsf{\ell }\right|\left|{\mathsf{\Psi }}^{″}(\mathsf{\ell }{\vartheta }_2+(1-\mathsf{\ell }){\epsilon }_2)\right|d\mathsf{\ell }\hfill \\ \hfill & +{\displaystyle \frac{{({\epsilon }_2-{\vartheta }_2)}^2}{12}}{\int }_0^1\left|6{\mathsf{\ell }}^2-2\mathsf{\ell }-5\right|\left|{\mathsf{\Psi }}^{″}(\mathsf{\ell }{\vartheta }_2+(1-\mathsf{\ell }){\epsilon }_2)\right|d\mathsf{\ell }.\hfill \end{array}$$

(20)

Using the convexity of $|{\mathsf{\Psi }}^{″}|$, we have

$$\begin{array}{cc}\hfill & \left|{\displaystyle \frac{\mathsf{\Psi }\left({\vartheta }_2\right)+4\mathsf{\Psi }\left(\frac{{\vartheta }_2+{\epsilon }_2}{2}\right)+\mathsf{\Psi }\left({\epsilon }_2\right)}{6}}-{\displaystyle \frac{1}{{\epsilon }_2-{\vartheta }_2}}{\int }_{{\vartheta }_2}^{{\epsilon }_2}\mathsf{\Psi }\left(\varrho \right)d\varrho \right|\hfill \\ \hfill & \le {\displaystyle \frac{{\epsilon }_2-{\vartheta }_2}{12}}\left[\right|{\mathsf{\Psi }}^{\prime }\left({\vartheta }_2\right)|+|{\mathsf{\Psi }}^{\prime }\left({\epsilon }_2\right)\left|\right]+{\displaystyle \frac{{({\epsilon }_2-{\vartheta }_2)}^2}{3}}{\int }_0^{{\displaystyle \frac{1}{2}}}\left(\mathsf{\ell }\right|{\mathsf{\Psi }}^{″}\left({\vartheta }_2\right)|+(1-\mathsf{\ell })|{\mathsf{\Psi }}^{″}\left({\epsilon }_2\right)\left|\right)d\mathsf{\ell }\hfill \\ \hfill & +{\displaystyle \frac{2{({\epsilon }_2-{\vartheta }_2)}^2}{3}}{\int }_{{\displaystyle \frac{1}{2}}}^1\left|1-\mathsf{\ell }\right|\left(\mathsf{\ell }\right|{\mathsf{\Psi }}^{″}\left({\vartheta }_2\right)|+(1-\mathsf{\ell })|{\mathsf{\Psi }}^{″}\left({\epsilon }_2\right)\left|\right)d\mathsf{\ell }\hfill \\ \hfill & +{\displaystyle \frac{{({\epsilon }_2-{\vartheta }_2)}^2}{12}}{\int }_0^1\left|6{\mathsf{\ell }}^2-2\mathsf{\ell }-5\right|\left(\mathsf{\ell }\right|{\mathsf{\Psi }}^{″}\left({\vartheta }_2\right)|+(1-\mathsf{\ell })|{\mathsf{\Psi }}^{″}\left({\epsilon }_2\right)\left|\right)d\mathsf{\ell }\hfill \\ \hfill & ={\displaystyle \frac{{\epsilon }_2-{\vartheta }_2}{12}}\left[\right|{\mathsf{\Psi }}^{\prime }\left({\vartheta }_2\right)|+|{\mathsf{\Psi }}^{\prime }\left({\epsilon }_2\right)\left|\right]+{\displaystyle \frac{{({\epsilon }_2-{\vartheta }_2)}^2}{72}}\left(17|{\mathsf{\Psi }}^{″}\left({\vartheta }_2\right)|+25|{\mathsf{\Psi }}^{″}\left({\epsilon }_2\right)|\right).\hfill \end{array}$$

It end the proof. □

Example 6. 

Let $\mathsf{\Psi }:[0,{\epsilon }_2]\to \mathbb{R}$ be a convex function and defined as $\mathsf{\Psi }\left(\varrho \right)={\varrho }^4$. Additionally, ${\mathsf{\Psi }}^{″}\left(\varrho \right)$ is a convex function and satisfying all the requirements of Theorem 9. Now we have the following graphical representations.

Both Figure 6 and Table 6 provide the both visual and numerical illustration of Theorem 9, respectively.

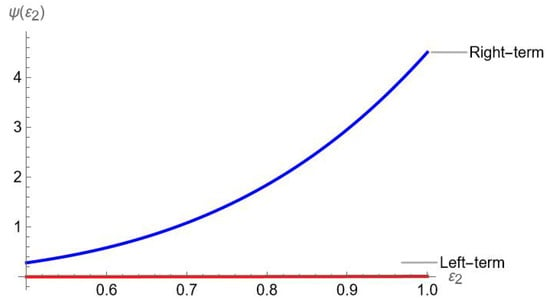
Figure 6. Visual analysis of Theorem 9.

Table 6. Comparison between left and right terms of Theorem 9.

${\mathit{\epsilon }}_2$	Left-Term	Right-Term
$0.5$	0.00052	0.28125
$0.6$	0.00108	0.58320
$0.8$	0.00341	1.84320
$0.9$	0.00547	2.95245
$1.0$	0.00833	4.50000

Corollary 1. 

By choosing $\mathsf{\Psi }\left({\vartheta }_2\right)=\mathsf{\Psi }\left({\epsilon }_2\right)=\mathsf{\Psi }\left({\displaystyle \frac{{\vartheta }_2+{\epsilon }_2}{2}}\right)$ in (11), we get the following bound for midpoint inequality

$$\begin{array}{cc}\hfill & \left|\mathsf{\Psi }\left({\displaystyle \frac{{\vartheta }_2+{\epsilon }_2}{2}}\right)-{\displaystyle \frac{1}{{\epsilon }_2-{\vartheta }_2}}{\int }_{{\vartheta }_2}^{{\epsilon }_2}\mathsf{\Psi }\left(\varrho \right)d\varrho \right|\hfill \\ \hfill & \le {\displaystyle \frac{{\epsilon }_2-{\vartheta }_2}{12}}\left[\right|{\mathsf{\Psi }}^{\prime }\left({\vartheta }_2\right)|+|{\mathsf{\Psi }}^{\prime }\left({\epsilon }_2\right)\left|\right]+{\displaystyle \frac{{({\epsilon }_2-{\vartheta }_2)}^2}{72}}\left(17{\mathsf{\Psi }}^{″}\left({\vartheta }_2\right)+25{\mathsf{\Psi }}^{″}\left({\epsilon }_2\right)\right).\hfill \end{array}$$

Theorem 10. 

Let $\mathsf{\Psi }:[{\vartheta }_2,{\epsilon }_2]\to \mathbb{R}$ be a twice differentiable function. If $|{\mathsf{\Psi }}^{″}{|}^q$ is a convex function, then

$$\begin{array}{cc}\hfill & \left|{\displaystyle \frac{\mathsf{\Psi }\left({\vartheta }_2\right)+4\mathsf{\Psi }\left(\frac{{\vartheta }_2+{\epsilon }_2}{2}\right)+\mathsf{\Psi }\left({\epsilon }_2\right)}{6}}-{\displaystyle \frac{1}{{\epsilon }_2-{\vartheta }_2}}{\int }_{{\vartheta }_2}^{{\epsilon }_2}\mathsf{\Psi }\left(\varrho \right)d\varrho \right|\hfill \\ \hfill & \le {\displaystyle \frac{{\epsilon }_2-{\vartheta }_2}{12}}\left[\right|{\mathsf{\Psi }}^{\prime }\left({\vartheta }_2\right)|+|{\mathsf{\Psi }}^{\prime }\left({\epsilon }_2\right)\left|\right]+{\displaystyle \frac{{({\epsilon }_2-{\vartheta }_2)}^2}{3p}}\left[{\displaystyle \frac{1}{2}}+{\displaystyle \frac{1}{2^p(p+1)}}+C\left(p\right)\right]+{\displaystyle \frac{{\left({\epsilon }_2-{\vartheta }_2\right)}^2}{12q}}\left[4\right|{\mathsf{\Psi }}^{″}\left({\vartheta }_2\right){|}^q+3|{\mathsf{\Psi }}^{″}\left({\epsilon }_2\right){|}^q],\hfill \end{array}$$

where

$$C\left(p\right)={\int }_0^1{\left|6{\mathsf{\ell }}^2-2\mathsf{\ell }-5\right|}^{p}dt,$$

and $p,q>1$ such that ${\displaystyle \frac{1}{p}}+{\displaystyle \frac{1}{q}}=1$.

Proof. 

By using Young’s inequality and (20), we have

$$\begin{array}{cc}\hfill & \left|{\displaystyle \frac{\mathsf{\Psi }\left({\vartheta }_2\right)+4\mathsf{\Psi }\left(\frac{{\vartheta }_2+{\epsilon }_2}{2}\right)+\mathsf{\Psi }\left({\epsilon }_2\right)}{6}}-{\displaystyle \frac{1}{{\epsilon }_2-{\vartheta }_2}}{\int }_{{\vartheta }_2}^{{\epsilon }_2}\mathsf{\Psi }\left(\varrho \right)d\varrho \right|\hfill \\ \hfill & \le {\displaystyle \frac{{\epsilon }_2-{\vartheta }_2}{12}}\left[\right|{\mathsf{\Psi }}^{\prime }\left({\vartheta }_2\right)|+|{\mathsf{\Psi }}^{\prime }\left({\epsilon }_2\right)\left|\right]+{\displaystyle \frac{{({\epsilon }_2-{\vartheta }_2)}^2}{3}}\left[{\displaystyle \frac{1}{p}}{\int }_0^{{\displaystyle \frac{1}{2}}}d\mathsf{\ell }+{\displaystyle \frac{1}{q}}{\int }_0^{{\displaystyle \frac{1}{2}}}|{\mathsf{\Psi }}^{″}(\mathsf{\ell }{\vartheta }_2+|1-\mathsf{\ell }|{\epsilon }_2{\left)\right|}^{q}d\mathsf{\ell }\right]\hfill \\ \hfill & +{\displaystyle \frac{2{({\epsilon }_2-{\vartheta }_2)}^2}{3}}\left[{\displaystyle \frac{1}{p}}{\int }_{{\displaystyle \frac{1}{2}}}^1{\left|1-\mathsf{\ell }\right|}^{p}d\mathsf{\ell }+{\displaystyle \frac{1}{q}}{\int }_{{\displaystyle \frac{1}{2}}}^1{\left|{\mathsf{\Psi }}^{″}(\mathsf{\ell }{\vartheta }_2+(1-\mathsf{\ell }){\epsilon }_2)\right|}^{q}d\mathsf{\ell }\right]\hfill \\ \hfill & +{\displaystyle \frac{{({\epsilon }_2-{\vartheta }_2)}^2}{12}}\left[{\displaystyle \frac{1}{p}}{\int }_0^1{\left|6{\mathsf{\ell }}^2-2\mathsf{\ell }-5\right|}^{p}d\mathsf{\ell }+{\displaystyle \frac{1}{q}}{\int }_0^1{\left|{\mathsf{\Psi }}^{″}(\mathsf{\ell }{\vartheta }_2+(1-\mathsf{\ell }){\epsilon }_2)\right|}^{q}d\mathsf{\ell }\right].\hfill \end{array}$$

Now using the convexity of $|{\mathsf{\Psi }}^{″}{|}^q$, we have

$$\begin{array}{cc}\hfill & \left|{\displaystyle \frac{\mathsf{\Psi }\left({\vartheta }_2\right)+4\mathsf{\Psi }\left(\frac{{\vartheta }_2+{\epsilon }_2}{2}\right)+\mathsf{\Psi }\left({\epsilon }_2\right)}{6}}-{\displaystyle \frac{1}{{\epsilon }_2-{\vartheta }_2}}{\int }_{{\vartheta }_2}^{{\epsilon }_2}\mathsf{\Psi }\left(\varrho \right)d\varrho \right|\hfill \\ \hfill & \le {\displaystyle \frac{{\epsilon }_2-{\vartheta }_2}{12}}\left[\right|{\mathsf{\Psi }}^{\prime }\left({\vartheta }_2\right)|+|{\mathsf{\Psi }}^{\prime }\left({\epsilon }_2\right)\left|\right]+{\displaystyle \frac{{({\epsilon }_2-{\vartheta }_2)}^2}{3}}\left[{\displaystyle \frac{1}{2p}}+{\displaystyle \frac{1}{q}}{\int }_0^{{\displaystyle \frac{1}{2}}}\left[\mathsf{\ell }|{\mathsf{\Psi }}^{″}\left({\vartheta }_2\right){|}^q+(1-\mathsf{\ell }){\left|{\mathsf{\Psi }}^{″}\left({\epsilon }_2\right)\right|}^q\right]d\mathsf{\ell }\right]\hfill \\ \hfill & +{\displaystyle \frac{2{({\epsilon }_2-{\vartheta }_2)}^2}{3}}\left[{\displaystyle \frac{{\left(\frac{1}{2}\right)}^{p+1}}{p(p+1)}}+{\displaystyle \frac{1}{q}}{\int }_{{\displaystyle \frac{1}{2}}}^1\left[\mathsf{\ell }|{\mathsf{\Psi }}^{″}\left({\vartheta }_2\right){|}^q+(1-\mathsf{\ell }){\left|{\mathsf{\Psi }}^{″}\left({\epsilon }_2\right)\right|}^q\right]d\mathsf{\ell }\right]\hfill \\ \hfill & +{\displaystyle \frac{{({\epsilon }_2-{\vartheta }_2)}^2}{12}}\left[{\displaystyle \frac{1}{p}}{\int }_0^1{\left|6{\mathsf{\ell }}^2-2\mathsf{\ell }-1\right|}^{p}d\mathsf{\ell }+{\displaystyle \frac{1}{q}}{\int }_0^1\left[\mathsf{\ell }|{\mathsf{\Psi }}^{″}\left({\vartheta }_2\right){|}^q+(1-\mathsf{\ell }){\left|{\mathsf{\Psi }}^{″}\left({\epsilon }_2\right)\right|}^q\right]d\mathsf{\ell }\right]\hfill \\ \hfill & ={\displaystyle \frac{{\epsilon }_2-{\vartheta }_2}{12}}\left[\right|{\mathsf{\Psi }}^{\prime }\left({\vartheta }_2\right)|+|{\mathsf{\Psi }}^{\prime }\left({\epsilon }_2\right)\left|\right]+{\displaystyle \frac{{({\epsilon }_2-{\vartheta }_2)}^2}{3p}}\left[{\displaystyle \frac{1}{2}}+{\displaystyle \frac{1}{2^p(p+1)}}+C\left(p\right)\right]+{\displaystyle \frac{{\left({\epsilon }_2-{\vartheta }_2\right)}^2}{12q}}\left[4\right|{\mathsf{\Psi }}^{″}\left({\vartheta }_2\right){|}^q+3|{\mathsf{\Psi }}^{″}\left({\epsilon }_2\right){|}^q].\hfill \end{array}$$

This completes the proof. □

Example 7. 

Let $\mathsf{\Psi }:[0,{\epsilon }_2]\to \mathbb{R}$ be a convex function and defined as $\mathsf{\Psi }\left(\varrho \right)={\varrho }^4$. Additionally, ${\mathsf{\Psi }}^{″}\left(\varrho \right)$ is a convex function and satisfying all the requirements of Theorem 10. Then we have the following graphical representation.

Figure 7 and Table 7 are the graphical and numerical justifications of Theorem 10, respectively.

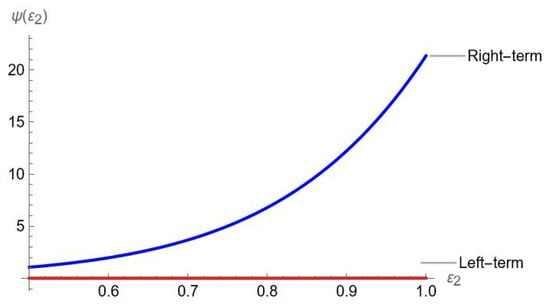
Figure 7. Visual analysis of Theorem 10.

Table 7. Comparison between left and right terms of Theorem 10.

${\mathit{\epsilon }}_2$	Left-Term	Right-Term
$0.5$	0.00052	1.05694
$0.6$	0.00108	1.97001
$0.8$	0.00341	6.78757
$0.9$	0.00547	12.23040

Theorem 11. 

Let $\mathsf{\Psi }:[{\vartheta }_2,{\epsilon }_2]\to \mathbb{R}$ be a twice differentiable function. If $|{\mathsf{\Psi }}^{″}{|}^q$ is a convex function, then

$$\begin{array}{cc}\hfill & \left|{\displaystyle \frac{\mathsf{\Psi }\left({\vartheta }_2\right)+4\mathsf{\Psi }\left(\frac{{\vartheta }_2+{\epsilon }_2}{2}\right)+\mathsf{\Psi }\left({\epsilon }_2\right)}{6}}-{\displaystyle \frac{1}{{\epsilon }_2-{\vartheta }_2}}{\int }_{{\vartheta }_2}^{{\epsilon }_2}\mathsf{\Psi }\left(\varrho \right)d\varrho \right|\hfill \\ \hfill & \le {\displaystyle \frac{{\epsilon }_2-{\vartheta }_2}{12}}\left[\right|{\mathsf{\Psi }}^{\prime }\left({\vartheta }_2\right)|+|{\mathsf{\Psi }}^{\prime }\left({\epsilon }_2\right)\left|\right]+{\displaystyle \frac{{({\epsilon }_2-{\vartheta }_2)}^2}{3}}\left[{\left({\displaystyle \frac{1}{2}}\right)}^{{\displaystyle \frac{1}{p}}}{\left({\displaystyle \frac{|{\mathsf{\Psi }}^{″}\left({\vartheta }_2\right){|}^q+3{\left|{\mathsf{\Psi }}^{″}\left({\epsilon }_2\right)\right|}^q}{8}}\right)}^{{\displaystyle \frac{1}{q}}}\right.\hfill \\ \hfill & +2{\left({\displaystyle \frac{1}{2^{p+1}(p+1)}}\right)}^{{\displaystyle \frac{1}{p}}}{\left({\displaystyle \frac{3|{\mathsf{\Psi }}^{″}\left({\vartheta }_2\right){|}^q+{\left|{\mathsf{\Psi }}^{″}\left({\epsilon }_2\right)\right|}^q}{8}}\right)}^{{\displaystyle \frac{1}{q}}}+\left.{\displaystyle \frac{C^{\frac{1}{p}}\left(p\right)}{4}}{\left({\displaystyle \frac{|{\mathsf{\Psi }}^{″}\left({\vartheta }_2\right){|}^q+{\left|{\mathsf{\Psi }}^{″}\left({\epsilon }_2\right)\right|}^q}{2}}\right)}^{{\displaystyle \frac{1}{q}}}\right],\hfill \end{array}$$

where $C\left(p\right)$ is defined in previous Theorem 10, and $p,q>1$ such that ${\displaystyle \frac{1}{p}}+{\displaystyle \frac{1}{q}}=1$.

Proof. 

Applying Hölder’s inequality on (20), we have

$$\begin{array}{cc}\hfill & \left|{\displaystyle \frac{\mathsf{\Psi }\left({\vartheta }_2\right)+4\mathsf{\Psi }\left(\frac{{\vartheta }_2+{\epsilon }_2}{2}\right)+\mathsf{\Psi }\left({\epsilon }_2\right)}{6}}-{\displaystyle \frac{1}{{\epsilon }_2-{\vartheta }_2}}{\int }_{{\vartheta }_2}^{{\epsilon }_2}\mathsf{\Psi }\left(\varrho \right)d\varrho \right|\hfill \\ \hfill & \le {\displaystyle \frac{{\epsilon }_2-{\vartheta }_2}{12}}\left[\right|{\mathsf{\Psi }}^{\prime }\left({\vartheta }_2\right)|+|{\mathsf{\Psi }}^{\prime }\left({\epsilon }_2\right)\left|\right]+{\displaystyle \frac{{({\epsilon }_2-{\vartheta }_2)}^2}{3}}\left[{\left({\int }_0^{{\displaystyle \frac{1}{2}}}{\left|1\right|}^{p}d\mathsf{\ell }\right)}^{{\displaystyle \frac{1}{p}}}{\left({\int }_0^1{\left|{\mathsf{\Psi }}^{″}(\mathsf{\ell }{\vartheta }_2+(1-\mathsf{\ell }){\epsilon }_2)\right|}^{q}d\mathsf{\ell }\right)}^{{\displaystyle \frac{1}{q}}}\right]\hfill \\ \hfill & +{\displaystyle \frac{2{({\epsilon }_2-{\vartheta }_2)}^2}{3}}\left[{\left({\int }_{{\displaystyle \frac{1}{2}}}^1{\left|1-\mathsf{\ell }\right|}^{p}d\mathsf{\ell }\right)}^{{\displaystyle \frac{1}{p}}}{\left({\int }_0^{{\displaystyle \frac{1}{2}}}{\left|{\mathsf{\Psi }}^{″}(\mathsf{\ell }{\vartheta }_2+(1-\mathsf{\ell }){\epsilon }_2)\right|}^{q}d\mathsf{\ell }\right)}^{{\displaystyle \frac{1}{q}}}\right]\hfill \\ \hfill & +{\displaystyle \frac{{({\epsilon }_2-{\vartheta }_2)}^2}{12}}\left[{\left({\int }_0^1{\left|6{\mathsf{\ell }}^2-2\mathsf{\ell }-5\right|}^{p}d\mathsf{\ell }\right)}^{{\displaystyle \frac{1}{p}}}{\left({\int }_0^1{\left|{\mathsf{\Psi }}^{″}(\mathsf{\ell }{\vartheta }_2+(1-\mathsf{\ell }){\epsilon }_2)\right|}^{q}d\mathsf{\ell }\right)}^{{\displaystyle \frac{1}{q}}}\right]\hfill \end{array}$$

Now using the convexity of $|{\mathsf{\Psi }}^{″}{|}^q$, we have

$$\begin{array}{cc}\hfill & \left|{\displaystyle \frac{\mathsf{\Psi }\left({\vartheta }_2\right)+4\mathsf{\Psi }\left(\frac{{\vartheta }_2+{\epsilon }_2}{2}\right)+\mathsf{\Psi }\left({\epsilon }_2\right)}{6}}-{\displaystyle \frac{1}{{\epsilon }_2-{\vartheta }_2}}{\int }_{{\vartheta }_2}^{{\epsilon }_2}\mathsf{\Psi }\left(\varrho \right)d\varrho \right|\hfill \\ \hfill & \le {\displaystyle \frac{{\epsilon }_2-{\vartheta }_2}{12}}\left[\right|{\mathsf{\Psi }}^{\prime }\left({\vartheta }_2\right)|+|{\mathsf{\Psi }}^{\prime }\left({\epsilon }_2\right)\left|\right]+{\displaystyle \frac{{({\epsilon }_2-{\vartheta }_2)}^2)}{3}}\left[{\left({\displaystyle \frac{1}{2}}\right)}^{{\displaystyle \frac{1}{p}}}{\left({\int }_0^{{\displaystyle \frac{1}{2}}}\left[\mathsf{\ell }|{\mathsf{\Psi }}^{″}\left({\vartheta }_2\right){|}^q+(1-\mathsf{\ell }){\left|{\mathsf{\Psi }}^{″}\left({\epsilon }_2\right)\right|}^q\right]d\mathsf{\ell }\right)}^{{\displaystyle \frac{1}{q}}}\right]\hfill \\ \hfill & +{\displaystyle \frac{2{({\epsilon }_2-{\vartheta }_2)}^2}{3}}\left[{\left({\displaystyle \frac{{\left(\frac{1}{2}\right)}^{p+1}}{p+1}}\right)}^{{\displaystyle \frac{1}{p}}}{\left({\int }_{{\displaystyle \frac{1}{2}}}^1\left[\mathsf{\ell }|{\mathsf{\Psi }}^{″}\left({\vartheta }_2\right){|}^q+(1-\mathsf{\ell }){\left|{\mathsf{\Psi }}^{″}\left({\epsilon }_2\right)\right|}^q\right]d\mathsf{\ell }\right)}^{{\displaystyle \frac{1}{q}}}\right]\hfill \\ \hfill & +{\displaystyle \frac{{({\epsilon }_2-{\vartheta }_2)}^2}{12}}\left[{\left({\int }_0^1{\left|6{\mathsf{\ell }}^2-2\mathsf{\ell }-5\right|}^{p}d\mathsf{\ell }\right)}^{{\displaystyle \frac{1}{p}}}{\left({\int }_0^1\left[\mathsf{\ell }|{\mathsf{\Psi }}^{″}\left({\vartheta }_2\right){|}^q+(1-\mathsf{\ell }){\left|{\mathsf{\Psi }}^{″}\left({\epsilon }_2\right)\right|}^q\right]d\mathsf{\ell }\right)}^{{\displaystyle \frac{1}{q}}}\right]\hfill \\ \hfill & ={\displaystyle \frac{{\epsilon }_2-{\vartheta }_2}{12}}\left[\right|{\mathsf{\Psi }}^{\prime }\left({\vartheta }_2\right)|+|{\mathsf{\Psi }}^{\prime }\left({\epsilon }_2\right)\left|\right]+{\displaystyle \frac{{({\epsilon }_2-{\vartheta }_2)}^2}{3}}\left[{\left({\displaystyle \frac{1}{2}}\right)}^{{\displaystyle \frac{1}{p}}}{\left({\displaystyle \frac{|{\mathsf{\Psi }}^{″}\left({\vartheta }_2\right){|}^q+3{\left|{\mathsf{\Psi }}^{″}\left({\epsilon }_2\right)\right|}^q}{8}}\right)}^{{\displaystyle \frac{1}{q}}}\right.\hfill \\ \hfill & +2{\left({\displaystyle \frac{1}{2^{p+1}(p+1)}}\right)}^{{\displaystyle \frac{1}{p}}}{\left({\displaystyle \frac{3|{\mathsf{\Psi }}^{″}\left({\vartheta }_2\right){|}^q+{\left|{\mathsf{\Psi }}^{″}\left({\epsilon }_2\right)\right|}^q}{8}}\right)}^{{\displaystyle \frac{1}{q}}}+\left.{\displaystyle \frac{C^{\frac{1}{p}}\left(p\right)}{4}}{\left({\displaystyle \frac{|{\mathsf{\Psi }}^{″}\left({\vartheta }_2\right){|}^q+{\left|{\mathsf{\Psi }}^{″}\left({\epsilon }_2\right)\right|}^q}{2}}\right)}^{{\displaystyle \frac{1}{q}}}\right].\hfill \end{array}$$

This completes the proof. □

Example 8. 

Let $\mathsf{\Psi }:[0,{\epsilon }_2]\to \mathbb{R}$ be a convex function and defined as $\mathsf{\Psi }\left(\varrho \right)={\varrho }^4$. Additionally, ${\mathsf{\Psi }}^{″}\left(\varrho \right)$ is also convex function and satisfying all the requirements of Theorem 11. Now we have the following graphical representation.

From Figure 8 and Table 8, it is clear that right hand side of Theorem 11 is greater than its left side.

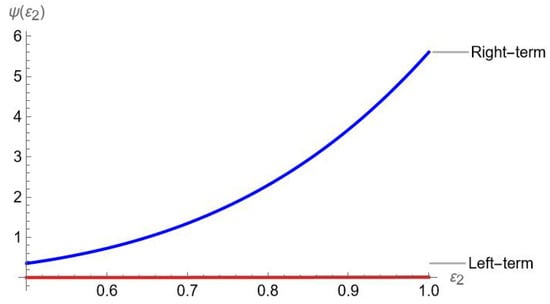
Figure 8. Visual analysis of Theorem 11.

Table 8. Comparison between left and right terms of Theorem 11.

${\mathit{\epsilon }}_2$	Left-Term	Right-Term
$0.5$	0.00052	0.35022
$0.6$	0.00108	0.72623
$0.8$	0.00341	2.29523
$0.9$	0.00547	3.67652
$1.0$	0.00833	5.60359

Theorem 12. 

Let $\mathsf{\Psi }:[{\vartheta }_2,{\epsilon }_2]\to \mathbb{R}$ be a twice differentiable function. If $|{\mathsf{\Psi }}^{″}{|}^q$ is a convex function, then

$$\begin{array}{cc}\hfill & \left|{\displaystyle \frac{\mathsf{\Psi }\left({\vartheta }_2\right)+4\mathsf{\Psi }\left(\frac{{\vartheta }_2+{\epsilon }_2}{2}\right)+\mathsf{\Psi }\left({\epsilon }_2\right)}{6}}-{\displaystyle \frac{1}{{\epsilon }_2-{\vartheta }_2}}{\int }_{{\vartheta }_2}^{{\epsilon }_2}\mathsf{\Psi }\left(\varrho \right)d\varrho \right|\hfill \\ \hfill & \le {\displaystyle \frac{{\epsilon }_2-{\vartheta }_2}{12}}\left[|{\mathsf{\Psi }}^{\prime }\left({\vartheta }_2\right)|+|{\mathsf{\Psi }}^{\prime }\left({\epsilon }_2\right)|\right]+{\displaystyle \frac{{({\epsilon }_2-{\vartheta }_2)}^2}{3}}\left[{\left({\displaystyle \frac{1}{2}}\right)}^{1-{\displaystyle \frac{1}{q}}}{\left({\displaystyle \frac{|{\mathsf{\Psi }}^{″}\left({\vartheta }_2\right){|}^q+3{\left|{\mathsf{\Psi }}^{″}\left({\epsilon }_2\right)\right|}^q}{8}}\right)}^{{\displaystyle \frac{1}{q}}}\right.\hfill \\ \hfill & \left.+2{\left({\displaystyle \frac{1}{8}}\right)}^{1-{\displaystyle \frac{1}{q}}}{\left({\displaystyle \frac{2|{\mathsf{\Psi }}^{″}\left({\vartheta }_2\right){|}^q+{\left|{\mathsf{\Psi }}^{″}\left({\epsilon }_2\right)\right|}^q}{24}}\right)}^{{\displaystyle \frac{1}{q}}}+{\displaystyle \frac{1}{{\left(4\right)}^{\frac{1}{q}}}}{\left({\displaystyle \frac{5|{\mathsf{\Psi }}^{″}\left({\vartheta }_2\right){|}^q+7{\left|{\mathsf{\Psi }}^{″}\left({\epsilon }_2\right)\right|}^q}{3}}\right)}^{{\displaystyle \frac{1}{q}}}\right],\hfill \end{array}$$

where $q\ge 1$.

Proof. 

Applying power mean inequality on (20), we have

$$\begin{array}{cc}\hfill & \left|{\displaystyle \frac{\mathsf{\Psi }\left({\vartheta }_2\right)+4\mathsf{\Psi }\left(\frac{{\vartheta }_2+{\epsilon }_2}{2}\right)+\mathsf{\Psi }\left({\epsilon }_2\right)}{6}}-{\displaystyle \frac{1}{{\epsilon }_2-{\vartheta }_2}}{\int }_{{\vartheta }_2}^{{\epsilon }_2}\mathsf{\Psi }\left(\varrho \right)d\varrho \right|\hfill \\ \hfill & \le {\displaystyle \frac{{\epsilon }_2-{\vartheta }_2}{12}}\left[\right|{\mathsf{\Psi }}^{\prime }\left({\vartheta }_2\right)|+|{\mathsf{\Psi }}^{\prime }\left({\epsilon }_2\right)\left|\right]+{\displaystyle \frac{{({\epsilon }_2-{\vartheta }_2)}^2}{3}}\left[{\left({\int }_0^{{\displaystyle \frac{1}{2}}}\left|1\right|d\mathsf{\ell }\right)}^{1-{\displaystyle \frac{1}{q}}}{\left({\int }_0^{{\displaystyle \frac{1}{2}}}{\left|{\mathsf{\Psi }}^{″}(\mathsf{\ell }{\vartheta }_2+(1-\mathsf{\ell }){\epsilon }_2)\right|}^{q}d\mathsf{\ell }\right)}^{{\displaystyle \frac{1}{q}}}\right]\hfill \\ \hfill & +{\displaystyle \frac{2{({\epsilon }_2-{\vartheta }_2)}^2}{3}}\left[{\left({\int }_{{\displaystyle \frac{1}{2}}}^1\left|1-\mathsf{\ell }\right|d\mathsf{\ell }\right)}^{1-{\displaystyle \frac{1}{q}}}{\left({\int }_{{\displaystyle \frac{1}{2}}}^1\left|1-\mathsf{\ell }\right|{\left|{\mathsf{\Psi }}^{″}(\mathsf{\ell }{\vartheta }_2+(1-\mathsf{\ell }){\epsilon }_2)\right|}^{q}d\mathsf{\ell }\right)}^{{\displaystyle \frac{1}{q}}}\right]\hfill \\ \hfill & +{\displaystyle \frac{{({\epsilon }_2-{\vartheta }_2)}^2}{12}}\left[{\left({\int }_{{\displaystyle \frac{1}{2}}}^1\left|6{\mathsf{\ell }}^2-2\mathsf{\ell }-5\right|d\mathsf{\ell }\right)}^{1-{\displaystyle \frac{1}{q}}}{\left({\int }_{{\displaystyle \frac{1}{2}}}^1\left|6{\mathsf{\ell }}^2-2\mathsf{\ell }-5\right|{\left|{\mathsf{\Psi }}^{″}(\mathsf{\ell }{\vartheta }_2+(1-\mathsf{\ell }){\epsilon }_2)\right|}^{q}d\mathsf{\ell }\right)}^{{\displaystyle \frac{1}{q}}}\right].\hfill \end{array}$$

Now using the convexity of $|{\mathsf{\Psi }}^{″}{|}^q$, we have

$$\begin{array}{cc}\hfill & \left|{\displaystyle \frac{\mathsf{\Psi }\left({\vartheta }_2\right)+4\mathsf{\Psi }\left(\frac{{\vartheta }_2+{\epsilon }_2}{2}\right)+\mathsf{\Psi }\left({\epsilon }_2\right)}{6}}-{\displaystyle \frac{1}{{\epsilon }_2-{\vartheta }_2}}{\int }_{{\vartheta }_2}^{{\epsilon }_2}\mathsf{\Psi }\left(\varrho \right)d\varrho \right|\hfill \\ \hfill & \le {\displaystyle \frac{{\epsilon }_2-{\vartheta }_2}{12}}\left[\right|{\mathsf{\Psi }}^{\prime }\left({\vartheta }_2\right)|+|{\mathsf{\Psi }}^{\prime }\left({\epsilon }_2\right)\left|\right]+{\displaystyle \frac{{({\epsilon }_2-{\vartheta }_2)}^2}{3}}\left[{\left({\displaystyle \frac{1}{2}}\right)}^{1-{\displaystyle \frac{1}{q}}}{\left({\int }_0^{{\displaystyle \frac{1}{2}}}\left[\mathsf{\ell }|{\mathsf{\Psi }}^{″}\left({\vartheta }_2\right){|}^q+(1-\mathsf{\ell }){\left|{\mathsf{\Psi }}^{″}\left({\epsilon }_2\right)\right|}^q\right]d\mathsf{\ell }\right)}^{{\displaystyle \frac{1}{q}}}\right]\hfill \\ \hfill & +{\displaystyle \frac{2{({\epsilon }_2-{\vartheta }_2)}^2}{3}}\left[{\left({\displaystyle \frac{1}{8}}\right)}^{1-{\displaystyle \frac{1}{q}}}{\left({\int }_{{\displaystyle \frac{1}{2}}}^1\left|1-\mathsf{\ell }\right|\left[\mathsf{\ell }|{\mathsf{\Psi }}^{″}\left({\vartheta }_2\right){|}^q+(1-\mathsf{\ell }){\left|{\mathsf{\Psi }}^{″}\left({\epsilon }_2\right)\right|}^q\right]d\mathsf{\ell }\right)}^{{\displaystyle \frac{1}{q}}}\right]\hfill \\ \hfill & +{\displaystyle \frac{{({\epsilon }_2-{\vartheta }_2)}^2}{12}}\left[{\left(4\right)}^{1-{\displaystyle \frac{1}{q}}}{\left({\int }_0^1\left|6{\mathsf{\ell }}^2-2\mathsf{\ell }-5\right|\left[\mathsf{\ell }|{\mathsf{\Psi }}^{″}\left({\vartheta }_2\right){|}^q+(1-\mathsf{\ell }){\left|{\mathsf{\Psi }}^{″}\left({\epsilon }_2\right)\right|}^q\right]d\mathsf{\ell }\right)}^{{\displaystyle \frac{1}{q}}}\right]\hfill \\ \hfill & ={\displaystyle \frac{{\epsilon }_2-{\vartheta }_2}{12}}\left[|{\mathsf{\Psi }}^{\prime }\left({\vartheta }_2\right)|+|{\mathsf{\Psi }}^{\prime }\left({\epsilon }_2\right)|\right]+{\displaystyle \frac{{({\epsilon }_2-{\vartheta }_2)}^2}{3}}\left[{\left({\displaystyle \frac{1}{2}}\right)}^{1-{\displaystyle \frac{1}{q}}}{\left({\displaystyle \frac{|{\mathsf{\Psi }}^{″}\left({\vartheta }_2\right){|}^q+3{\left|{\mathsf{\Psi }}^{″}\left({\epsilon }_2\right)\right|}^q}{8}}\right)}^{{\displaystyle \frac{1}{q}}}\right.\hfill \\ \hfill & \left.+2{\left({\displaystyle \frac{1}{8}}\right)}^{1-{\displaystyle \frac{1}{q}}}{\left({\displaystyle \frac{2|{\mathsf{\Psi }}^{″}\left({\vartheta }_2\right){|}^q+{\left|{\mathsf{\Psi }}^{″}\left({\epsilon }_2\right)\right|}^q}{24}}\right)}^{{\displaystyle \frac{1}{q}}}+{\displaystyle \frac{1}{{\left(4\right)}^{\frac{1}{q}}}}{\left({\displaystyle \frac{5|{\mathsf{\Psi }}^{″}\left({\vartheta }_2\right){|}^q+7{\left|{\mathsf{\Psi }}^{″}\left({\epsilon }_2\right)\right|}^q}{3}}\right)}^{{\displaystyle \frac{1}{q}}}\right].\hfill \end{array}$$

This completes the proof. □

Example 9. 

Let $\mathsf{\Psi }:[0,{\epsilon }_2]\to \mathbb{R}$ be a convex function and defined as $\mathsf{\Psi }\left(\varrho \right)={\varrho }^4$. Additionally, ${\mathsf{\Psi }}^{″}\left(\varrho \right)$ is a convex function and satisfying all the requirements of Theorem 12. Now we have the following graphical representations.

Both Figure 9 and Table 9 confirm the accuracy of Theorem 12.

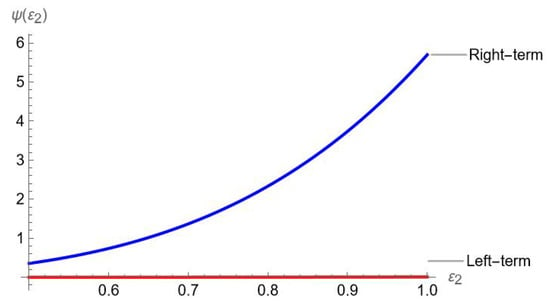
Figure 9. Visual analysis of Theorem 12.

Table 9. Comparison between left and right terms of Theorem 12.

${\mathit{\epsilon }}_2$	Left-Term	Right-Term
$0.5$	0.00052	0.35611
$0.6$	0.00108	0.73843
$0.8$	0.00341	2.33381
$0.9$	0.00547	3.73832
$1.0$	0.00833	5.69778

Theorem 13. 

Suppose that ${\mathsf{\Psi }}^{\prime }:[{\vartheta }_2,{\epsilon }_2]\to \mathbb{R}$ is a function of bounded variations on $[{\vartheta }_2,{\epsilon }_2]$. Then

$$\left|{\displaystyle \frac{\mathsf{\Psi }\left({\vartheta }_2\right)+4\mathsf{\Psi }\left(\frac{{\vartheta }_2+{\epsilon }_2}{2}\right)+\mathsf{\Psi }\left({\epsilon }_2\right)}{6}}-{\displaystyle \frac{1}{{\epsilon }_2-{\vartheta }_2}}{\int }_{{\vartheta }_2}^{{\epsilon }_2}\mathsf{\Psi }\left(\varrho \right)d\varrho \right|\le {\displaystyle \frac{7({\epsilon }_2-{\vartheta }_2)}{6}}{V}_{{\vartheta }_2}^{{\epsilon }_2}\left({\mathsf{\Psi }}^{\prime }\right).$$

Here $V_{{\vartheta }_2}^{{\epsilon }_2}\left({\mathsf{\Psi }}^{\prime }\right)$ represents the total variation of ${\mathsf{\Psi }}^{\prime }$ on $[{\vartheta }_2,{\epsilon }_2]$.

Proof. 

From (19), we have

$$\begin{array}{cc}\hfill & \left|{\displaystyle \frac{\mathsf{\Psi }\left({\vartheta }_2\right)+4\mathsf{\Psi }\left(\frac{{\vartheta }_2+{\epsilon }_2}{2}\right)+\mathsf{\Psi }\left({\epsilon }_2\right)}{6}}-{\displaystyle \frac{1}{{\epsilon }_2-{\vartheta }_2}}{\int }_{{\vartheta }_2}^{{\epsilon }_2}\mathsf{\Psi }\left(\varrho \right)d\varrho \right|\hfill \\ \hfill & \le {\displaystyle \frac{({\epsilon }_2-{\vartheta }_2)}{12}}{\int }_{{\vartheta }_2}^{{\epsilon }_2}\left|{\mathsf{\Psi }}^{″}\left(v\right)\right|dv+{\displaystyle \frac{2}{3}}{\int }_{{\vartheta }_2}^{{\displaystyle \frac{{\vartheta }_2+{\epsilon }_2}{2}}}\left|v-{\vartheta }_2\right|\left|{\mathsf{\Psi }}^{″}\left(v\right)\right|dv+{\displaystyle \frac{{\epsilon }_2-{\vartheta }_2}{3}}{\int }_{{\displaystyle \frac{{\vartheta }_2+{\epsilon }_2}{2}}}^{{\epsilon }_2}\left|{\mathsf{\Psi }}^{″}\left(v\right)\right|dv\hfill \\ \hfill & +{\displaystyle \frac{1}{6({\epsilon }_2-{\vartheta }_2)}}{\int }_{{\vartheta }_2}^{{\epsilon }_2}\left|6v-{\vartheta }_2({\epsilon }_2-v)+{\displaystyle \frac{5{(v-{\vartheta }_2)}^2}{2}}+{\displaystyle \frac{{({\epsilon }_2-v)}^2}{2}}\right|\left|{\mathsf{\Psi }}^{″}\left(v\right)\right|dv.\hfill \end{array}$$

Now, we revisit the fact that if and ${\mathsf{\Psi }}^{\prime }$ is the function of bounded variation and g is be a continuous function. Then ${\int }_{{\vartheta }_2}^{{\epsilon }_2}{\mathsf{\Psi }}^{\prime }g\left(\varrho \right)d\varrho$ exists and

$$\left|{\int }_{{\vartheta }_2}^{{\epsilon }_2}g\left(\varrho \right)d{\mathsf{\Psi }}^{\prime }\left(\varrho \right)\right|\le \underset{\varrho \in [{\vartheta }_2,{\epsilon }_2]}{max}\left|g\left(\varrho \right)\right|V_{{\vartheta }_2}^{{\epsilon }_2}\left({\mathsf{\Psi }}^{\prime }\right).$$

By using this definition, we have

$$\begin{array}{cc}\hfill & \left|{\displaystyle \frac{\mathsf{\Psi }\left({\vartheta }_2\right)+4\mathsf{\Psi }\left(\frac{{\vartheta }_2+{\epsilon }_2}{2}\right)+\mathsf{\Psi }\left({\epsilon }_2\right)}{6}}-{\displaystyle \frac{1}{{\epsilon }_2-{\vartheta }_2}}{\int }_{{\vartheta }_2}^{{\epsilon }_2}\mathsf{\Psi }\left(\varrho \right)d\varrho \right|\hfill \\ \hfill & \le {\displaystyle \frac{({\epsilon }_2-{\vartheta }_2)}{12}}{\int }_{{\vartheta }_2}^{{\epsilon }_2}\left|d{\mathsf{\Psi }}^{\prime }\left(v\right)\right|dv+{\displaystyle \frac{2}{3}}{\int }_{{\vartheta }_2}^{{\displaystyle \frac{{\vartheta }_2+{\epsilon }_2}{2}}}\left|v-{\vartheta }_2\right|\left|d{\mathsf{\Psi }}^{\prime }\left(v\right)\right|dv+{\displaystyle \frac{{\epsilon }_2-{\vartheta }_2}{3}}{\int }_{{\displaystyle \frac{{\vartheta }_2+{\epsilon }_2}{2}}}^{{\epsilon }_2}\left|d{\mathsf{\Psi }}^{\prime }\left(v\right)\right|dv\hfill \\ \hfill & +{\displaystyle \frac{1}{6({\epsilon }_2-{\vartheta }_2)}}{\int }_{{\vartheta }_2}^{{\epsilon }_2}\left|6v-{\vartheta }_2({\epsilon }_2-v)+{\displaystyle \frac{5{(v-{\vartheta }_2)}^2}{2}}+{\displaystyle \frac{{({\epsilon }_2-v)}^2}{2}}\right|\left|d{\mathsf{\Psi }}^{\prime }\left(v\right)\right|dv\hfill \\ \hfill & \le {\displaystyle \frac{{\epsilon }_2-{\vartheta }_2}{12}}\underset{v\in [{\vartheta }_2,{\epsilon }_2]}{max}{V}_{{\vartheta }_2}^{{\epsilon }_2}\left({\mathsf{\Psi }}^{\prime }\right)+{\displaystyle \frac{2}{3}}\underset{v\in [{\vartheta }_2,{\displaystyle \frac{{\vartheta }_2+{\epsilon }_2}{2}}]}{max}|v-{\vartheta }_2|V_{{\vartheta }_2}^{{\displaystyle \frac{{\vartheta }_2+{\epsilon }_2}{2}}}\left({\mathsf{\Psi }}^{\prime }\right)+{\displaystyle \frac{{\epsilon }_2-{\vartheta }_2}{3}}\underset{v\in [{\displaystyle \frac{{\vartheta }_2+{\epsilon }_2}{2}},{\epsilon }_2]}{max}{V}_{{\vartheta }_2}^{{\epsilon }_2}\left({\mathsf{\Psi }}^{\prime }\right)\hfill \\ \hfill & +{\displaystyle \frac{1}{6({\epsilon }_2-{\vartheta }_2)}}\underset{v\in \left[{\vartheta }_2,{\epsilon }_2\right]}{max}\left|6(v-{\vartheta }_2)({\epsilon }_2-v)+{\displaystyle \frac{5{(v-{\vartheta }_2)}^2}{2}}+{\displaystyle \frac{{({\epsilon }_2-v)}^2}{2}}\right|V_{{\vartheta }_2}^{{\epsilon }_2}\left({\mathsf{\Psi }}^{\prime }\right)\hfill \\ \hfill & ={\displaystyle \frac{7({\epsilon }_2-{\vartheta }_2)}{6}}{V}_{{\vartheta }_2}^{{\epsilon }_2}\left({\mathsf{\Psi }}^{\prime }\right).\hfill \end{array}$$

Hence, the intended inequality is proved. □

Example 10. 

Let $\mathsf{\Psi }:[0,{\epsilon }_2]\to \mathbb{R}$ be a convex function and defined as $\mathsf{\Psi }\left(\varrho \right)={\varrho }^4$. Additionally, ${\mathsf{\Psi }}^{″}\left(\varrho \right)$ is a convex function and satisfying all the requirements of Theorem 13. Then we have the following graphical representations.

Both Figure 10 and Table 10 justify the accuracy of inequality proved in Theorem 13.

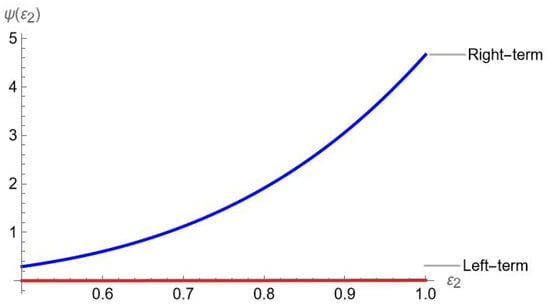
Figure 10. Visual analysis of Theorem 13.

Table 10. Comparison between left and right terms of Theorem 13.

${\mathit{\epsilon }}_2$	Left-Term	Right-Term
$0.5$	0.00052	0.29167
$0.6$	0.00108	0.60480
$0.8$	0.00341	1.91147
$0.9$	0.00547	3.06180
$1.0$	0.00833	4.66667

Corollary 2. 

For $\mathsf{\Psi }\left({\vartheta }_2\right)=\mathsf{\Psi }\left({\epsilon }_2\right)=\mathsf{\Psi }\left({\displaystyle \frac{{\vartheta }_2+{\epsilon }_2}{2}}\right)$, the Theorem 13 results the following estimate of left-Hadamard’s inequality,

$$\left|\mathsf{\Psi }\left({\displaystyle \frac{{\vartheta }_2+{\epsilon }_2}{2}}\right)-{\displaystyle \frac{1}{{\epsilon }_2-{\vartheta }_2}}{\int }_{{\vartheta }_2}^{{\epsilon }_2}\mathsf{\Psi }\left(\varrho \right)d\varrho \right|\le {\displaystyle \frac{7({\epsilon }_2-{\vartheta }_2)}{6}}{V}_{{\vartheta }_2}^{{\epsilon }_2}\left({\mathsf{\Psi }}^{\prime }\right).$$

3. Application to Means

Now, we develop some relations between means using the results proved in previous section.

For two positive numbers ${\vartheta }_2>0$ and ${\epsilon }_2>0$, define

$$A({\vartheta }_2,{\epsilon }_2)={\displaystyle \frac{{\vartheta }_2+{\epsilon }_2}{2}},G({\vartheta }_2,{\epsilon }_2)=\sqrt{ab},H({\vartheta }_2,{\epsilon }_2)={\displaystyle \frac{2ab}{{\vartheta }_2+{\epsilon }_2}},L({\vartheta }_2,{\epsilon }_2)={\displaystyle \frac{{\epsilon }_2-{\vartheta }_2}{ln\left({\epsilon }_2\right)-ln\left({\vartheta }_2\right)}}$$

$$L_s({\vartheta }_2,{\epsilon }_2)=\left\{\begin{array}{cc}{\left[{\displaystyle \frac{{{\epsilon }_2}^{s+1}-{{\vartheta }_2}^{s+1}}{(s+1)({\epsilon }_2-{\vartheta }_2)}}\right]}^{1/s},\hfill & {\vartheta }_2\ne {\epsilon }_2\hfill \\ {\vartheta }_2,\hfill & {\vartheta }_2={\epsilon }_2\hfill \end{array}\right.$$

$$I({\vartheta }_2,{\epsilon }_2)=\left\{\begin{array}{cc}{\displaystyle \frac{1}{e}}{\left({\displaystyle \frac{{{\epsilon }_2}^{{\epsilon }_2}}{{{\vartheta }_2}^{{\vartheta }_2}}}\right)}^{1/({\epsilon }_2-{\vartheta }_2)},\hfill & {\vartheta }_2\ne {\epsilon }_2\hfill \\ {\vartheta }_2,\hfill & {\vartheta }_2={\epsilon }_2.\hfill \end{array}\right.$$

These means are, respectively, called the arithmetic, geometric, harmonic, generalized logarithmic, and identric means of two positive number ${\vartheta }_2$ and ${\epsilon }_2$.

Proposition 1.  

Let $0<{\vartheta }_2<{\epsilon }_2$, then we have the following inequality

$$\left|H^{-1}({\vartheta }_2,{\epsilon }_2)-L^{-1}({\vartheta }_2,{\epsilon }_2)\right|\le {\displaystyle \frac{{\epsilon }_2-{\vartheta }_2}{2}}{H}^{-1}({{\vartheta }_2}^2,{{\epsilon }_2}^2)+{\displaystyle \frac{2{({\epsilon }_2-{\vartheta }_2)}^2}{3}}{H}^{-1}({{\vartheta }_2}^3,{{\epsilon }_2}^3).$$

Proof. 

The assertion follows directly from (5) for $\mathsf{\Psi }\left(\varrho \right)=1/\varrho$. □

Proposition 2.  

Let $0<{\vartheta }_2<{\epsilon }_2$, then we have the following inequality

$$\left|G^{-1}({\vartheta }_2,{\epsilon }_2)+ln\left(I({\vartheta }_2,{\epsilon }_2)\right)\right|\le {\displaystyle \frac{{\epsilon }_2-{\vartheta }_2}{2}}{H}^{-1}({\vartheta }_2,{\epsilon }_2)+{\displaystyle \frac{{({\epsilon }_2-{\vartheta }_2)}^2}{3}}{H}^{-1}({{\vartheta }_2}^2,{{\epsilon }_2}^2).$$

Proof. 

The assertion follows from (5) for $\mathsf{\Psi }\left(\varrho \right)=-ln\left(\varrho \right)$. □

Proposition 3.  

Let $0<{\vartheta }_2<{\epsilon }_2$, then we have the following inequality

$$\left|A({{\vartheta }_2}^n,{{\epsilon }_2}^n)-L_n^n({\vartheta }_2,{\epsilon }_2)\right|\le {\displaystyle \frac{n({\epsilon }_2-{\vartheta }_2)}{2}}A({{\vartheta }_2}^{n-1},{{\epsilon }_2}^{n-1})+{\displaystyle \frac{n(n-1){({\epsilon }_2-{\vartheta }_2)}^2}{3}}A({{\vartheta }_2}^{n-2},{{\epsilon }_2}^{n-2}).$$

Proof. 

The assertion follows from (5) for $\mathsf{\Psi }\left(\varrho \right)={\varrho }^n$. □

Proposition 4.  

Let $0<{\vartheta }_2<{\epsilon }_2$, then we have the following inequality

$$\left|{\displaystyle \frac{A({\vartheta }_2,{\epsilon }_2)}{3G^2({\vartheta }_2,{\epsilon }_2)}}+{\displaystyle \frac{2}{3}}{A}^{-1}({\vartheta }_2,{\epsilon }_2)-L^{-1}({\vartheta }_2,{\epsilon }_2)\right|\le {\displaystyle \frac{{\epsilon }_2-{\vartheta }_2}{6}}{H}^{-1}({{\vartheta }_2}^2,{{\epsilon }_2}^2)+{\displaystyle \frac{425{({\epsilon }_2-{\vartheta }_2)}^2}{18}}{H}^{-1}(25{{\vartheta }_2}^3,17{{\epsilon }_2}^3).$$

Proof. 

The assertion follows from (11) for $\mathsf{\Psi }\left(\varrho \right)=1/\varrho$. □

Proposition 5.  

Let $0<{\vartheta }_2<{\epsilon }_2$, then we have the following inequality

$$\begin{array}{c}\hfill \left|ln\left(G^{-{\displaystyle \frac{1}{3}}}({\vartheta }_2,{\epsilon }_2)A^{{\displaystyle \frac{-2}{3}}}({\vartheta }_2,{\epsilon }_2)\right)+ln\left(I({\vartheta }_2,{\epsilon }_2)\right)\right|\le {\displaystyle \frac{{\epsilon }_2-{\vartheta }_2}{6}}{H}^{-1}({\vartheta }_2,{\epsilon }_2)+{\displaystyle \frac{425{({\epsilon }_2-{\vartheta }_2)}^2}{36}}{H}^{-1}(25{{\vartheta }_2}^2,17{{\epsilon }_2}^2).\end{array}$$

Proof. 

The assertion follows from (11) for $\mathsf{\Psi }\left(\varrho \right)=-ln\left(\varrho \right)$. □

Proposition 6.  

Let $0<{\vartheta }_2<{\epsilon }_2$, then we have the following inequality

$$\left|{\displaystyle \frac{A({{\vartheta }_2}^n,{{\epsilon }_2}^n)+2A^n({\vartheta }_2,{\epsilon }_2)}{3}}-L_n^n({\vartheta }_2,{\epsilon }_2)\right|\le {\displaystyle \frac{n({\epsilon }_2-{\vartheta }_2)}{6}}A({{\vartheta }_2}^{n-1},{{\epsilon }_2}^{n-1})+{\displaystyle \frac{n(n-1){({\epsilon }_2-{\vartheta }_2)}^2}{36}}A(17{{\vartheta }_2}^{n-2},25{{\epsilon }_2}^{n-2}).$$

Proof. 

The assertion follows from (11), for $\mathsf{\Psi }:(0,\infty )\to \mathbb{R}$ and $\mathsf{\Psi }\left(\varrho \right)={\varrho }^n$. □

4. Composite Trapezoidal and Simpson’s Inequalities

Here, we generalize the estimates developed in the main section for composite trapezoidal’s rule. To conclude these bounds, consider the division of $[{\vartheta }_2,{\epsilon }_2]$ such that $P:{\vartheta }_2={\varrho }_0<{\varrho }_1<{\varrho }_2<\dots <{\varrho }_i<{\varrho }_{i+1}<\dots <{\varrho }_n={\epsilon }_2$, where $[{\varrho }_i,{\varrho }_{i+1}]$ be subinterval of $[{\vartheta }_2,{\epsilon }_2]$. Let $h={\varrho }_{i+1}-{\varrho }_i$ and $h={\displaystyle \frac{{\varrho }_{i+1}-{\varrho }_i}{2}}$ are the differences for trapezoidal and Simpson’s rules respectively.

$$\begin{array}{cc}\hfill & T(P,\mathsf{\Psi })=\sum _{i=0}^{n-1}\left[{\displaystyle \frac{h}{2}}\left[\mathsf{\Psi }\left({\varrho }_i\right)+\mathsf{\Psi }\left({\varrho }_{i+1}\right)\right]-{\int }_{{\varrho }_i}^{{\varrho }_{i+1}}\mathsf{\Psi }\left(\varrho \right)d\varrho \right]\hfill \\ \hfill & {\int }_{{\vartheta }_2}^{{\epsilon }_2}\mathsf{\Psi }\left(\varrho \right)d\varrho =T(P,\mathsf{\Psi })+R(P,\mathsf{\Psi }),\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill & S(P,\mathsf{\Psi })=\sum _{i=0}^{n-1}\left[{\displaystyle \frac{h}{3}}\left[\mathsf{\Psi }\left({\varrho }_i\right)+4\mathsf{\Psi }\left({\displaystyle \frac{{\varrho }_i+{\varrho }_{i+1}}{2}}\right)+\mathsf{\Psi }\left({\varrho }_i\right)\right]-{\int }_{{\varrho }_i}^{{\varrho }_{i+1}}\mathsf{\Psi }\left(\varrho \right)d\varrho \right]\hfill \\ \hfill & {\int }_{{\vartheta }_2}^{{\epsilon }_2}\mathsf{\Psi }\left(\varrho \right)d\varrho =S(P,\mathsf{\Psi })+\mathbb{V}(P,\mathsf{\Psi }),\hfill \end{array}$$

where $R(P,\mathsf{\Psi })$ and $\mathbb{V}(P,\mathsf{\Psi })$ are the remainder terms of trapezoidal and Simpson’s rules respectively.

Proposition 7.  

Considering Theorem 4, we have the following estimate

$$\left|R(P,\mathsf{\Psi })\right|\le \sum _{i=0}^{n-1}\left[{\displaystyle \frac{h^2}{4}}\left[|{\mathsf{\Psi }}^{\prime }\left({\varrho }_i\right)|+|{\mathsf{\Psi }}^{\prime }\left({\varrho }_{i+1}\right)|\right]+{\displaystyle \frac{h^3}{6}}\left[|{\mathsf{\Psi }}^{″}\left({\varrho }_i\right)|+|{\mathsf{\Psi }}^{″}\left({\varrho }_{i+1}\right)|\right]\right].$$

Proof. 

By applying Theorem 4 over $[{\varrho }_i,{\varrho }_{i+1}]$ and taking sum from $i=0$ to $i=n-1$ results the desired estimates. □

Proposition 8.  

Considering Theorem 8, we have the following estimate

$$\left|R(P,\mathsf{\Psi })\right|\le \sum _{i=0}^{n-1}\left[{\displaystyle \frac{h^2}{2}}{V}_{{\varrho }_i}^{{\varrho }_{i+1}}\left({\mathsf{\Psi }}^{\prime }\right)\right]$$

Proof. 

By applying Theorem 8 over $[{\varrho }_i,{\varrho }_{i+1}]$ and taking sum from $i=0$ to $i=n-1$ results the desired estimates. □

Proposition 9.  

Considering Theorem 9, we have the following estimate

$$\left|\mathbb{V}(P,\mathsf{\Psi })\right|\le \sum _{i=0}^{n-1}\left[{\displaystyle \frac{h^2}{3}}\left[|{\mathsf{\Psi }}^{\prime }\left({\varrho }_i\right)|+|{\mathsf{\Psi }}^{\prime }\left({\varrho }_{i+1}\right)|\right]+{\displaystyle \frac{h^3}{9}}\left[|{\mathsf{\Psi }}^{″}\left({\varrho }_i\right)|+|{\mathsf{\Psi }}^{″}\left({\varrho }_{i+1}\right)|\right]\right].$$

Proof. 

By applying Theorem 9 over $[{\varrho }_i,{\varrho }_{i+1}]$ and taking sum from $i=0$ to $i=n-1$ results the desired estimates. □

Proposition 10.  

Considering Theorem 13, we have the following estimate

$$\left|\mathbb{V}(P,\mathsf{\Psi })\right|\le \sum _{i=0}^{n-1}\left[{\displaystyle \frac{14h^2}{3}}{V}_{{\varrho }_i}^{{\varrho }_{i+1}}\left({\mathsf{\Psi }}^{\prime }\right)\right].$$

Proof. 

By applying Theorem 13 over $[{\varrho }_i,{\varrho }_{i+1}]$ and taking sum from $i=0$ to $i=n-1$ results the desired estimates. □

5. Concluding Remarks and Future Insights

Over the years, an immense number of strategies have been applied to conclude the sharp and upper estimates of various existing inequalities within different frameworks. In this investigation, we have concluded novel upper bounds of Simpson-like inequalities through convex and bounded variation function. From examples, we have noticed that results obtained leveraging the concept of bounded variation are sharp as compared to others. Moreover, the accuracy of proposed bounds is affirmed through simulations and examples of composite rules and relations between binary means. Following the idea and strategy in the paper, one can assess the error analysis of Newton’s, Boole’s, Maclaurin’s and Weddle’s quadrature procedures. In the future, we will focus on quantum and symmetric quantum analysis of Newton-Cotes schemes by taking into account the Green function approach. One of the potential research problems is to analyze the bounds of fractional integral and derivative operators.