Eigenvalue Characterizations for the Signless Laplacian Spectrum of Weakly Zero-Divisor Graphs on ${\mathbb{Z}}_{\mathit{n}}$

Abstract

Let $\mathfrak{R}$ be a commutative ring with identity $1\ne 0$. The weakly zero-divisor graph of $\mathfrak{R}$, denoted $W_{\Gamma }(\mathfrak{R})$, is the simple undirected graph whose vertex set consists of the nonzero zero-divisors of $\mathfrak{R}$, where two distinct vertices $\mathfrak{a}$ and $\mathfrak{b}$ are adjacent if and only if there exist $r\in \mathrm{ann}(\mathfrak{a})$ and $s\in \mathrm{ann}(\mathfrak{b})$ such that $rs=0$. In this paper, we study the signless Laplacian spectrum of $W_{\Gamma }({\mathbb{Z}}_n)$ for several composite forms of n, including $n=p^2{q}^2$, $n=p^{2}qr$, $n=p^m{q}^m$ and $n=p^{m}qr$, where $p, q, r$ are distinct primes and $m\ge 2$. By using generalized join decomposition and quotient matrix methods, we obtain explicit eigenvalue formulas for each case, along with structural bounds, spectral integrality conditions and Nordhaus–Gaddum-type inequalities. Illustrative examples with computed spectra are provided to validate the theoretical results, demonstrating the interplay between the algebraic structure of ${\mathbb{Z}}_n$ and the spectral properties of its weakly zero-divisor graph.

1. Introduction

Spectral graph theory serves as a powerful interface between algebraic structures and combinatorial frameworks. In recent decades, significant attention has been devoted to studying graphs defined over algebraic objects such as rings, groups and semigroups. Within this direction, one of the most prominent constructions is the zero-divisor graph associated with a commutative ring, introduced to model the interaction between elements whose product is zero. A refinement of this concept, the weakly zero-divisor graph $W_{\Gamma }({\mathbb{Z}}_n)$, has recently gained traction for its ability to encode more nuanced ring-theoretic information through its adjacency relation based on nontrivial zero-product modulo n [1,2].

Graph theory has numerous applications in diverse scientific and engineering domains, including communication networks, chemical graph theory, coding theory, cryptography and image processing. In particular, energy-based spectral measures have been applied in chemical informatics [3,4], materials science [5], sustainable systems analysis [6] and optical imaging [7]. Such applications demonstrate the broader relevance of spectral techniques beyond pure mathematics.

In spectral analysis, various matrices such as the adjacency matrix, Laplacian matrix and signless Laplacian matrix play key roles in uncovering structural characteristics of graphs. Among these, the signless Laplacian matrix, defined as $Q(G)=D(G)+A(G)$ for a graph G, where $D(G)$ is the diagonal degree matrix and $A(G)$ is the adjacency matrix, captures important combinatorial properties such as graph energy, connectivity and bipartiteness [8]. The foundational work of Gutman on graph energy [3] and the comprehensive framework presented by Cvetković et al. [9] laid the groundwork for further developments involving signless Laplacian and related spectral matrices. Subsequent efforts such as [3,4,10] established the significance of energy-based and Randić-type spectra in both mathematical chemistry and combinatorics. More recently, related spectral approaches have also been employed in the analysis of advanced materials and mechanical systems [11].

For graphs arising from rings, the signless Laplacian spectrum has proven particularly useful in analyzing algebraic complexity and symmetries. Several researchers have explored various types of spectra over graphs on ${\mathbb{Z}}_n$, including adjacency, Laplacian and normalized Laplacian spectra [12,13,14]. In this context, the work in [15] initiated a systematic study of the signless Laplacian spectrum of $W_{\Gamma }({\mathbb{Z}}_n)$, employing generalized join decompositions and symbolic eigenvalue extraction.

Building on that foundation, the present article undertakes a detailed spectral analysis of $W_{\Gamma }({\mathbb{Z}}_n)$ for several algebraically meaningful classes of integers n. The graph is decomposed using divisor-based partitions into induced subgraphs whose structure is either complete or null and then recombined via the generalized graph join $G[G_1,G_2,\dots ,G_t]$ as introduced in [16]. The spectral consequences of this construction are explored using weighted matrix techniques and symbolic expressions, such as Randić integral conditions over edge-regular graphs [17], insights from the theory of matrix rank and structural constraints [18] and studies on signless Laplacian energy which inform the energetic perspective of our spectra [19].

We first consider the case $n=p^2{q}^2$, where p and q are distinct primes. In this scenario, the weakly zero-divisor graph admits a clear partition into three disjoint sets and the quotient graph formed by the divisors becomes a triangle, leading to a tractable and partially integral spectrum. The matrix representation $\mathfrak{L}({\delta }_{p^2{q}^2})$ arising from the quotient graph captures the nontrivial eigenvalues that are not directly obtained from the components.

Next, we study the case $n=p^{2}qr$, introducing an additional prime factor to the structure. This adds a fourth component to the partition, thereby extending the quotient graph and complicating the matrix spectrum. Nevertheless, a block-matrix analysis still yields closed-form expressions for part of the spectrum and allows symbolic computation of the remaining eigenvalues.

The third case $n=p^m{q}^m$ for $m\ge 2$ generalizes the equal-power composite structure. This class is algebraically significant because it induces balanced component sizes in the partition. Here, integrality conditions for the spectrum are established and symbolic families are identified depending on the values of m.

The fourth case $n=p^{m}qr$ combines one square-power prime with two distinct primes, producing an asymmetric structural partition. The corresponding spectral matrix $\mathfrak{L}({\delta }_{p^{m}qr})$ yields eigenvalues that are more varied and examples such as $n=60$ are used to illustrate the computational procedure.

Beyond symbolic derivations, this paper also addresses spectral properties, such as (i) identification of when the spectrum is fully integral, (ii) bounds on the smallest and largest eigenvalues, (iii) lower and upper estimates for signless Laplacian energy, (iv) detailed enumeration of eigenvalue multiplicities, (v) relationships between algebraic factorization of n and structural motifs in $W_{\Gamma }({\mathbb{Z}}_n)$.

The article is structured as follows: Section 2 presents necessary preliminaries, definitions and known results related to weakly zero-divisor graphs and spectral graph theory. Section 3 develops the main symbolic spectral theorems for each composite structure. Section 4 illustrates the results through worked examples and eigenvalue matrix construction, offers additional theorems on integrality and energy, and concludes with directions for future work, including extensions to Randić and normalized Laplacian spectra [20,21].

2. Preliminaries

We begin by introducing some fundamental concepts and known results that will be instrumental in deriving the main theorems of this work.

Definition 1

(Weakly Zero-Divisor Graph). Let $\mathfrak{R}$ be a commutative ring with unity. The weakly zero-divisor graph of $\mathfrak{R}$, denoted $W_{\Gamma }(\mathfrak{R})$, is the simple undirected graph whose vertex set consists of all nonzero zero-divisors of $\mathfrak{R}$. Two distinct vertices $\mathfrak{a}$ and $\mathfrak{b}$ are adjacent if and only if there exist elements $r\in \mathrm{ann}(\mathfrak{a})$ and $s\in \mathrm{ann}(\mathfrak{b})$ such that $rs=0$. In this paper, we focus on the case $\mathfrak{R}={\mathbb{Z}}_n$, the ring of integers modulo n.

Definition 2

(Generalized Join of Graphs). Let $G=(V(G),E(G))$ be a graph of order m with vertex set $V(G)=\{v_1,v_2,\dots ,v_m\}$. Suppose $G_i=(V_i,E_i)$ for $1\le i\le m$ are pairwise disjoint graphs, where each $G_i$ has order $m_i$. The generalized join $G[G_1,G_2,\dots ,G_m]$ is defined as the graph obtained by replacing each vertex $v_i$ of G with the graph $G_i$ and connecting every vertex of $G_i$ to every vertex of $G_j$ whenever $v_i$ and $v_j$ are adjacent in G.

The construction $G[G_1,G_2,\dots ,G_m]$ is commonly referred to as the G-join operation, as introduced in [16]. Specifically, when the base graph G is the complete graph $K_2$, this reduces to the standard graph join. Throughout this article, we adopt the term G-join for this operation and retain the notation $G[G_1,G_2,\dots ,G_m]$.

Let ${\mathbb{Z}}_n$ denote the ring of integers modulo n. The set of non-unit, nonzero elements in this ring has cardinality $n-\varphi (n)-1$, where $\varphi (n)$ is Euler’s totient function. Let ${\mathfrak{s}}_1,{\mathfrak{s}}_2,\dots ,{\mathfrak{s}}_k$ be the proper divisors of n. For each $1\le r\le k$, define the set

$$A_{{\mathfrak{s}}_r}=\left\{x\in {\mathbb{Z}}_n\mid gcd(x,n)={\mathfrak{s}}_r\right\}.$$

Since $gcd(x,n)$ uniquely determines the divisor class of x, these sets are mutually disjoint, i.e., $A_{{\mathfrak{s}}_r}\cap A_{{\mathfrak{s}}_x}=⌀$ for $r\ne x$. Therefore, they partition the vertex set of the weakly zero-divisor graph $W_{\Gamma }({\mathbb{Z}}_n)$ as follows:

$$V(W_{\Gamma }({\mathbb{Z}}_n))=A_{{\mathfrak{s}}_1}\cup A_{{\mathfrak{s}}_2}\cup \cdots \cup A_{{\mathfrak{s}}_k}.$$

Lemma 1

([8]). $|A_{{\mathfrak{s}}_r}|=\varphi \left({\displaystyle \frac{n}{{\mathfrak{s}}_r}}\right)$, for $1\le r\le k$.

Lemma 2

([13]). Let $\{{\mathfrak{s}}_1,{\mathfrak{s}}_2,\dots ,{\mathfrak{s}}_k\}$ denote the set of all proper divisors of n and suppose n has the prime decomposition $n={\mathcal{P}}_1{\mathcal{P}}_2\cdots {\mathcal{P}}_m{q}_1^{k_1}{q}_2^{k_2}\cdots q_i^{k_i}$, where $k_i\ge 2$, $m\ge 1$ and $i\ge 0$. If ${\mathfrak{s}}_r$ is one of the prime divisors ${\mathcal{P}}_j$ for some $1\le j\le m$, then the subgraph of $W_{\Gamma }({\mathbb{Z}}_n)$ induced by the set $A_{{\mathfrak{s}}_r}$ is an empty graph with $\varphi \left({\displaystyle \frac{n}{{\mathfrak{s}}_r}}\right)$ vertices, i.e., ${\overline{K}}_{\varphi \left({\displaystyle \frac{n}{{\mathfrak{s}}_r}}\right)}$.

Corollary 1

([13]). Let ${\mathfrak{s}}_r$ be a proper divisor of a positive integer n. Then,

(i) 

The subgraph of $W_{\Gamma }({\mathbb{Z}}_n)$ induced by the vertex set $A_{{\mathfrak{s}}_r}$ is isomorphic either to the complete graph $K_{\varphi \left({\displaystyle \frac{n}{{\mathfrak{s}}_r}}\right)}$ or to the empty graph ${\overline{K}}_{\varphi \left({\displaystyle \frac{n}{{\mathfrak{s}}_r}}\right)}$.

(ii) 

If $r,x\in \{1,2,\dots ,k\}$ with $r\ne x$, then each vertex in $A_{{\mathfrak{s}}_r}$ is either adjacent to every vertex in $A_{{\mathfrak{s}}_x}$ or to none of them in $W_{\Gamma }({\mathbb{Z}}_n)$.

Corollary 1 indicates that the induced subgraphs $W_{\Gamma }(A_{{\mathfrak{s}}_r})$ within $W_{\Gamma }({\mathbb{Z}}_n)$ are either complete graphs or edgeless graphs. Building upon this observation, the next lemma shows that $W_{\Gamma }({\mathbb{Z}}_n)$ can be expressed as a composition of complete graphs and their complements. To formalize this construction, we define the auxiliary graph ${\delta }_n$, which is the complete graph whose vertices correspond to the proper divisors of n, namely $\{{\mathfrak{s}}_1,{\mathfrak{s}}_2,\dots ,{\mathfrak{s}}_k\}$.

Lemma 3

([13]). Consider the induced subgraph $W_{\Gamma }(A_{{\mathfrak{s}}_r})$ of $W_{\Gamma }({\mathbb{Z}}_n)$ formed by the vertices in $A_{{\mathfrak{s}}_r}$, where $1\le r\le k$. Then,

$$W_{\Gamma }({\mathbb{Z}}_n)={\delta }_n[W_{\Gamma }(A_{{\mathfrak{s}}_1}),W_{\Gamma }(A_{{\mathfrak{s}}_2}),\dots ,W_{\Gamma }(A_{{\mathfrak{s}}_k})].$$

Theorem 1

([22]). Let G be a graph with vertex set $V(G)=\{v_1,v_2,\dots ,v_t\}$ and for each $i=1,2,\dots ,t$, let $G_i$ be an $s_i$-regular graph on $n_i$ vertices. Then, the signless Laplacian spectrum of the G-join graph $G[G_1,G_2,\dots ,G_t]$ can be determined using the following formulation:

$${\sigma }_Q(G[G_1,G_2,\dots ,G_t])=\left(\bigcup _{i=1}^t\left(N_i+\left({\sigma }_Q(G_i)\setminus \left\{2s_i\right\}\right)\right)\right)\cup \sigma (Y_Q(G)),$$

where

$$N_i=\left\{\begin{array}{cc}{\displaystyle \sum _{j\in {\mathfrak{N}}_G(i)}}{n}_j,\hfill & {\mathfrak{N}}_G(i)\ne ⌀,\hfill \\ 0,\hfill & \mathit{otherwise}\hfill \end{array}\right.$$

and

$$Y_Q(G)={(y_{ij})}_{t\times t}=\left\{\begin{array}{cc}2s_i+N_i,\hfill & i=j,\hfill \\ \sqrt{n_i{n}_j},\hfill & v_i{v}_j\in E(G),\hfill \\ 0,\hfill & \mathit{otherwise}.\hfill \end{array}\right.$$

Suppose that $\mathcal{W}$ is a weighted graph with $|V(\mathcal{W})|=n_i$ assigned to the vertex $u_i$ of $\mathcal{W}$ for $1\le i\le t$. Let $\mathfrak{L}(\mathcal{W})={(l_{ij})}_{t\times t}$ be defined by

$$l_{ij}=\left\{\begin{array}{cc}{\displaystyle \sum _{u_i\sim u_j}}{n}_j,\hfill & i=j,\hfill \\ n_j,\hfill & i\ne j\mathrm{and}{u}_i\sim u_j,\hfill \\ 0,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

The matrix $\mathfrak{L}(\mathcal{W})$ is known as the vertex-weighted signless Laplacian matrix associated with $\mathcal{W}$. Since $Y_Q(G)$ and $\mathfrak{L}(\mathcal{W})$ have the same form, we make the following remark.

Remark 1.

$Y_Q(G)=\mathfrak{L}(\mathcal{W})$.

Proof. 

By definition, the $(i,j)$-entry of $Y_Q(G)$ is given by

$$y_{ij}=\left\{\begin{array}{cc}2s_i+N_i,\hfill & i=j,\hfill \\ \sqrt{n_i{n}_j},\hfill & v_i{v}_j\in E(G),\hfill \\ 0,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

On the other hand, the $(i,j)$-entry of $\mathfrak{L}(\mathcal{W})$ is

$$l_{ij}=\left\{\begin{array}{cc}{\displaystyle \sum _{u_i\sim u_j}}{n}_j,\hfill & i=j,\hfill \\ n_j,\hfill & i\ne j\mathrm{and}{u}_i\sim u_j,\hfill \\ 0,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

Since each adjacency $v_i{v}_j\in E(G)$ in the quotient corresponds to all $n_i{n}_j$ adjacencies between the components, the degree sum ${\sum }_{u_i\sim u_j}{n}_j$ equals $N_i$ and $\sqrt{n_i{n}_j}$ in $Y_Q(G)$ arises naturally from the symmetric weighting of the join edges. Therefore, the two matrices coincide entrywise and we have $Y_Q(G)=\mathfrak{L}(\mathcal{W})$. □

3. Results

In this section, we present the main spectral results concerning the signless Laplacian spectrum of the weakly zero-divisor graph $W_{\Gamma }({\mathbb{Z}}_n)$ for various composite structures of n. By employing the structural decomposition discussed in the preceding sections, we derive symbolic expressions for the signless Laplacian spectra and verify them through concrete examples. Our approach primarily relies on the generalized join operation and block matrix techniques described in Theorem 1.

We now analyze the signless Laplacian spectrum of $W_{\Gamma }({\mathbb{Z}}_n)$ for an arbitrary positive integer n. Let ${\mathfrak{s}}_1,{\mathfrak{s}}_2,\dots ,{\mathfrak{s}}_k$ denote the proper divisors of n. For each $1\le i\le k$, associate the weight

$$\varphi \left({\displaystyle \frac{n}{{\mathfrak{s}}_i}}\right)=|A_{{\mathfrak{s}}_i}|$$

with the vertex ${\mathfrak{s}}_i$ in the graph ${\delta }_n$. Define

$${\mathfrak{N}}_{{\mathfrak{s}}_j}=\sum _{{\mathfrak{s}}_i\in {\mathfrak{N}}_{{\delta }_n}({\mathfrak{s}}_j)}\varphi \left({\displaystyle \frac{n}{{\mathfrak{s}}_i}}\right),$$

the vertex-weighted signless Laplacian matrix $\mathfrak{L}({\delta }_n)$ of ${\delta }_n$ is given by

$$l_{ij}=\left\{\begin{array}{cc}{\displaystyle \sum _{{\mathfrak{s}}_p\in {\mathfrak{N}}_{{\delta }_n}({\mathfrak{s}}_i)}\varphi \left(\frac{n}{{\mathfrak{s}}_p}\right),}\hfill & i=j,\hfill \\ \varphi \left({\displaystyle \frac{n}{{\mathfrak{s}}_i}}\right),\hfill & i\ne j\mathrm{and}{\mathfrak{s}}_i\sim {\mathfrak{s}}_j\mathrm{in}{\delta }_n,\hfill \\ 0,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

(1)

Theorem 2.

Let ${\mathfrak{s}}_1,{\mathfrak{s}}_2,\dots ,{\mathfrak{s}}_k$ be the proper divisors of a positive integer n. Then, the signless Laplacian spectrum of the graph $W_{\Gamma }({\mathbb{Z}}_n)$ is

$${\sigma }_Q(W_{\Gamma }({\mathbb{Z}}_n))=\left(\bigcup _{i=1}^k\left({\mathfrak{N}}_{{\mathfrak{s}}_i}+\left[{\sigma }_Q(W_{\Gamma }(A_{{\mathfrak{s}}_i}))\setminus \left\{2{\mathfrak{s}}_i\right\}\right]\right)\right)\cup {\sigma }_Q(\mathfrak{L}({\delta }_n)),$$

where each subgraph $W_{\Gamma }(A_{{\mathfrak{s}}_i})$ is ${\mathfrak{s}}_i$-regular and the expression

$${\mathfrak{N}}_{{\mathfrak{s}}_i}+\left[{\sigma }_Q(W_{\Gamma }(A_{{\mathfrak{s}}_i}))\setminus \left\{2{\mathfrak{s}}_i\right\}\right]$$

means that ${\mathfrak{N}}_{{\mathfrak{s}}_i}$ is added to every element of the multiset ${\sigma }_Q(W_{\Gamma }(A_{{\mathfrak{s}}_i}))$ after removing $2{\mathfrak{s}}_i$.

Proof. 

From Lemma 3, the graph $W_{\Gamma }({\mathbb{Z}}_n)$ can be expressed as the G-join

$$W_{\Gamma }({\mathbb{Z}}_n)={\delta }_n\left[W_{\Gamma }(A_{{\mathfrak{s}}_1}),W_{\Gamma }(A_{{\mathfrak{s}}_2}),\dots ,W_{\Gamma }(A_{{\mathfrak{s}}_k})\right].$$

Applying Theorem 1 and using the equality $Y_Q(G)=\mathfrak{L}(\mathcal{W})$, the spectral formula follows. □

We begin with the case when n is the product of two distinct prime squares, i.e., $n=p^2{q}^2$ with $p<q$.

Theorem 3.

Let $\mathfrak{n}=p^2{q}^2$ with $p<q$ primes. Then the signless Laplacian spectrum of $W_{\Gamma }({\mathbb{Z}}_{\mathfrak{n}})$ is

$$\begin{array}{cc}\hfill {\sigma }_Q\left(W_{\Gamma }({\mathbb{Z}}_{p^2{q}^2})\right)& =\left\{{(|V|-2)}^{[\phi (p{q}^2)-1+\phi (p^{2}q)-1]}\right\}\hfill \\ & \cup \{(|V|-\phi (q^2){)}^{[\phi (q^2)-1]},(|V|-\phi (p^2){)}^{[\phi (p^2)-1]},\hfill \\ & {(|V|-\phi (pq))}^{[\phi (pq)-1]},{(|V|-\phi (q))}^{[\phi (q)-1]},{(|V|-\phi (p))}^{[\phi (p)-1]}\}\hfill \\ & \cup \sigma \left(\mathfrak{L}({\delta }_{p^2{q}^2})\right),\hfill \end{array}$$

where ${\delta }_{p^2{q}^2}$ is the quotient on the seven divisor classes $\{p,q,p^2,q^2,pq,p^{2}q,p{q}^2\}$ and $\mathfrak{L}({\delta }_{p^2{q}^2})$ is its vertex-weighted signless Laplacian.

Proof. 

Let $\mathfrak{n}=p^2{q}^2$ with $p<q$ and let

$$\mathcal{S}=\{p,q,p^2,q^2,pq,p^{2}q,p{q}^2\}$$

be the set of all proper divisors of $\mathfrak{n}$. By Lemma 3,

$$W_{\Gamma }({\mathbb{Z}}_{p^2{q}^2})={\delta }_{p^2{q}^2}\left[W_{\Gamma }(A_s):s\in \mathcal{S}\right],$$

where ${\delta }_{p^2{q}^2}$ is the complete graph on the vertex set $\mathcal{S}$. For each $s\in \mathcal{S}$, set $n_s:=|A_s|=\phi \left(\frac{p^2{q}^2}{s}\right)$ (by Lemma 1) and

$${\mathfrak{N}}_s=\sum _{t\in N_{{\delta }_{p^2{q}^2}}(s)}{n}_t=\sum _{t\in \mathcal{S}\setminus \left\{s\right\}}\phi \left({\displaystyle \frac{p^2{q}^2}{t}}\right)=|V|-\phi \left({\displaystyle \frac{p^2{q}^2}{s}}\right),$$

where $|V|={\sum }_{u\in \mathcal{S}}\phi \left(\frac{p^2{q}^2}{u}\right)$ is the order of $W_{\Gamma }({\mathbb{Z}}_{p^2{q}^2})$.

By Corollary 1, each induced graph $W_{\Gamma }(A_s)$ is either $K_{n_s}$ (then it is $(n_s-1)$-regular) or ${\overline{K}}_{n_s}$ (then it is 0-regular). Hence, by Theorem 2,

$${\sigma }_Q\left(W_{\Gamma }({\mathbb{Z}}_{p^2{q}^2})\right)=\left(\bigcup _{s\in \mathcal{S}}\left({\mathfrak{N}}_s+\left({\sigma }_Q(W_{\Gamma }(A_s))\setminus \left\{2s_s\right\}\right)\right)\right)\cup {\sigma }_Q\left(\mathfrak{L}({\delta }_{p^2{q}^2})\right),$$

where $s_s$ is the regularity of $W_{\Gamma }(A_s)$ and ${\delta }_{p^2{q}^2}$ is the quotient on the seven classes.

Now: If $W_{\Gamma }(A_s)\cong K_{n_s}$, then ${\sigma }_Q(K_{n_s})=\{2(n_s-1),0^{[n_s-1]}\}$, so after removing $2s_s=2(n_s-1)$ and shifting by ${\mathfrak{N}}_s=|V|-n_s$, we contribute

$${(|V|-2)}^{[n_s-1]},$$

if $W_{\Gamma }(A_s)\cong {\overline{K}}_{n_s}$, then ${\sigma }_Q({\overline{K}}_{n_s})=\left\{0^{\left[n_s\right]}\right\}$ and $s_s=0$, hence, we contribute

$$(|V|-n_s{)}^{\left[n_s\right]}.$$

For $n=p^2{q}^2$, one checks (using the weakly zero-divisor adjacency) that the two mixed classes $s\in \{p^{2}q,p{q}^2\}$ yield complete induced blocks $K_{\phi (q)}$ and $K_{\phi (p)}$, respectively, while the remaining five classes yield empty induced blocks. Therefore,

$$\begin{array}{cc}\hfill \bigcup _{s\in \mathcal{S}}\left({\mathfrak{N}}_s+\left({\sigma }_Q(W_{\Gamma }(A_s))\setminus \left\{2s_s\right\}\right)\right)& ={\{(|V|-2)}^{[\phi (p{q}^2)-1+\phi (p^{2}q)-1]}\}\hfill \\ & \cup \{(|V|-\phi (q^2){)}^{[\phi (q^2)-1]},(|V|-\phi (p^2){)}^{[\phi (p^2)-1]},\hfill \\ & {(|V|-\phi (pq))}^{[\phi (pq)-1]},{(|V|-\phi (q))}^{[\phi (q)-1]},{(|V|-\phi (p))}^{[\phi (p)-1]}\},\hfill \end{array}$$

which is exactly the multiset stated in the theorem. The remaining seven eigenvalues are those of the vertex-weighted signless Laplacian

$$\mathfrak{L}({\delta }_{p^2{q}^2})={\left({\ell }_{uv}\right)}_{u,v\in \mathcal{S}},{\ell }_{uu}=|V|-n_u,{\ell }_{uv}=n_v(u\ne v),$$

i.e.,

$$\mathfrak{L}({\delta }_{p^2{q}^2})=\left[\begin{array}{ccccccc}|V|-\phi (p{q}^2)& \phi (p^{2}q)& \phi (q^2)& \phi (p^2)& \phi (pq)& \phi (q)& \phi (p)\\ \phi (p{q}^2)& |V|-\phi (p^{2}q)& \phi (q^2)& \phi (p^2)& \phi (pq)& \phi (q)& \phi (p)\\ \phi (p{q}^2)& \phi (p^{2}q)& |V|-\phi (q^2)& \phi (p^2)& \phi (pq)& \phi (q)& \phi (p)\\ \phi (p{q}^2)& \phi (p^{2}q)& \phi (q^2)& |V|-\phi (p^2)& \phi (pq)& \phi (q)& \phi (p)\\ \phi (p{q}^2)& \phi (p^{2}q)& \phi (q^2)& \phi (p^2)& |V|-\phi (pq)& \phi (q)& \phi (p)\\ \phi (p{q}^2)& \phi (p^{2}q)& \phi (q^2)& \phi (p^2)& \phi (pq)& |V|-\phi (q)& \phi (p)\\ \phi (p{q}^2)& \phi (p^{2}q)& \phi (q^2)& \phi (p^2)& \phi (pq)& \phi (q)& |V|-\phi (p)\end{array}\right].$$

This completes the proof. □

Example 1.

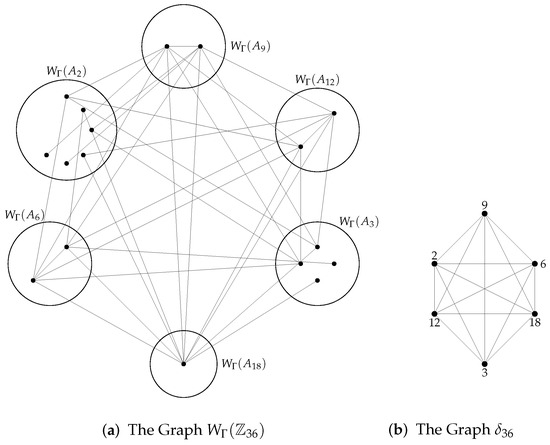
The signless Laplacian spectrum of the weakly zero-divisor graph $W_{\Gamma }({\mathbb{Z}}_{36})$ (see Figure 1a,b)

Figure 1. The weakly zero-divisor graph $W_{\Gamma }({\mathbb{Z}}_{36})$ and its corresponding divisor graph ${\delta }_{36}$.

By Lemma 3, we have

$$W_{\Gamma }({\mathbb{Z}}_{36})={\delta }_{36}\left[W_{\Gamma }(A_2),W_{\Gamma }(A_3),W_{\Gamma }(A_6),W_{\Gamma }(A_9),W_{\Gamma }(A_{12}),W_{\Gamma }(A_{18})\right],$$

for $36=2^2·3^2$, the sizes of the divisor classes are

$$|A_2|=\varphi (18)=6,|A_3|=\varphi (12)=4,|A_6|=\varphi (6)=2,$$

$$|A_9|=\varphi (4)=2,|A_{12}|=\varphi (3)=2,|A_{18}|=\varphi (2)=1,$$

as in the ${\mathbb{Z}}_{30}$ case, the induced subgraphs are

$$W_{\Gamma }(A_2)\cong {\overline{K}}_6,W_{\Gamma }(A_3)\cong {\overline{K}}_4,W_{\Gamma }(A_6)\cong K_2,W_{\Gamma }(A_9)\cong K_2,W_{\Gamma }(A_{12})\cong K_2,W_{\Gamma }(A_{18})\cong K_1.$$

using Theorem 2 (removing the largest value $2{\mathfrak{s}}_i$ from each block), the internal part of the spectrum contributes only zeros:

$$\begin{array}{cc}& {\overline{K}}_6:0^{[6-1]}=0^{\left[5\right]},{\overline{K}}_4:0^{[4-1]}=0^{\left[3\right]},\hfill \\ & K_2:0^{[2-1]}=0^{\left[1\right]}(\mathit{for}\mathit{each}\mathit{of}{A}_6,A_9,A_{12}),K_1:0^{[1-1]}=0^{\left[0\right]}.\hfill \end{array}$$

Hence, the block contribution is $0^{[5+3+1+1+1]}=0^{\left[11\right]}$.

It remains to add the $t=6$ eigenvalues of the vertex-weighted matrix

$$\mathfrak{L}({\delta }_{36})={({\ell }_{ij})}_{6\times 6},{\ell }_{ii}=\sum _{j\ne i}|A_{{\mathfrak{s}}_j}|,{\ell }_{ij}=|A_{{\mathfrak{s}}_j}|(i\ne j),$$

with the ordering $(2,3,6,9,12,18)$, i.e.,

$$\mathfrak{L}({\delta }_{36})=\left[\begin{array}{cccccc}11& 4& 2& 2& 2& 1\\ 6& 13& 2& 2& 2& 1\\ 6& 4& 15& 2& 2& 1\\ 6& 4& 2& 15& 2& 1\\ 6& 4& 2& 2& 15& 1\\ 6& 4& 2& 2& 2& 16\end{array}\right].$$

its eigenvalues (numerically) are

$$\sigma \left(\mathfrak{L}({\delta }_{36})\right)\approx \{27.1108,14.7349,13,13,10.5459,6.6084\}.$$

Therefore,

$${\sigma }_Q\left(W_{\Gamma }({\mathbb{Z}}_{36})\right)=\left\{0^{\left[11\right]}\right\}\cup \sigma \left(\mathfrak{L}({\delta }_{36})\right).$$

Theorem 4.

Let $\mathfrak{n}=p^{2}qr$, where $p<q<r$ are distinct primes. Then, the signless Laplacian spectrum of the weakly zero-divisor graph $W_{\Gamma }({\mathbb{Z}}_{\mathfrak{n}})$ is given by

$${\sigma }_Q\left(W_{\Gamma }({\mathbb{Z}}_{p^{2}qr})\right)=\left(\bigcup _{i=1}^{10}\left\{N_i^{[n_i-1]}\right\}\right)\cup \sigma \left(\mathfrak{L}({\delta }_{p^{2}qr})\right),$$

where $\mathfrak{L}({\delta }_{p^{2}qr})$ is the vertex-weighted signless Laplacian matrix of the complete divisor graph ${\delta }_{p^{2}qr}$ on S with vertex weights $n_i$.

Proof. 

Let $\mathfrak{n}=p^{2}qr$ with $p<q<r$ primes. The proper divisors that yield nonempty divisor classes are

$$S=\{p,q,r,p^2,pq,pr,qr,p^{2}q,p^{2}r,pqr\}.$$

By Lemma 1, for each $s\in S$, we have $|A_s|=\varphi (\mathfrak{n}/s)$. In particular, set (in this fixed order)

$$\begin{array}{cc}& n_1=\varphi \left({\displaystyle \frac{\mathfrak{n}}{p}}\right)=\varphi (pqr),n_2=\varphi \left({\displaystyle \frac{\mathfrak{n}}{q}}\right)=\varphi (p^{2}r),n_3=\varphi \left({\displaystyle \frac{\mathfrak{n}}{r}}\right)=\varphi (p^{2}q),n_4=\varphi \left({\displaystyle \frac{\mathfrak{n}}{p^2}}\right)=\varphi (qr),\hfill \\ & n_5=\varphi \left({\displaystyle \frac{\mathfrak{n}}{pq}}\right)=\varphi (pr),n_6=\varphi \left({\displaystyle \frac{\mathfrak{n}}{pr}}\right)=\varphi (pq),n_7=\varphi \left({\displaystyle \frac{\mathfrak{n}}{qr}}\right)=\varphi (p^2),n_8=\varphi \left({\displaystyle \frac{\mathfrak{n}}{p^{2}q}}\right)=\varphi (r),\hfill \\ & n_9=\varphi \left({\displaystyle \frac{\mathfrak{n}}{p^{2}r}}\right)=\varphi (q),n_{10}=\varphi \left({\displaystyle \frac{\mathfrak{n}}{pqr}}\right)=\varphi (p).\hfill \end{array}$$

By Corollary 1 (together with the structure described for $W_{\Gamma }({\mathbb{Z}}_{\mathfrak{n}})$), the induced subgraph on $A_{p^2}$ is edgeless,

$$W_{\Gamma }(A_{p^2})\cong {\overline{K}}_{n_4},$$

while all the remaining induced subgraphs are complete:

$$W_{\Gamma }(A_s)\cong K_{n_i}\mathrm{for}s\in S\setminus \left\{p^2\right\}.$$

By Lemma 3,

$$\begin{gathered} W_{\Gamma }({\mathbb{Z}}_{\mathfrak{n}})={\delta }_{\mathfrak{n}}[W_{\Gamma }(A_p),W_{\Gamma }(A_q),W_{\Gamma }(A_r),W_{\Gamma }(A_{p^2}),W_{\Gamma }(A_{pq}),W_{\Gamma }(A_{pr}), \\ {W}_{\Gamma }(A_{qr}),W_{\Gamma }(A_{p^{2}q}),W_{\Gamma }(A_{p^{2}r}),W_{\Gamma }(A_{pqr})], \end{gathered}$$

where ${\delta }_{\mathfrak{n}}$ is the complete graph on the ten divisor classes S. Write

$$|V|=\sum _{i=1}^{10}{n}_i=\sum _{s\in S}\varphi \left({\displaystyle \frac{\mathfrak{n}}{s}}\right),N_i=|V|-n_i(1\le i\le 10).$$

Applying Theorem 2:

• If $W_{\Gamma }(A_s)\cong K_{n_i}$, then ${\sigma }_Q(K_{n_i})=\{2(n_i-1),0^{[n_i-1]}\}$, so

  $$N_i+\left({\sigma }_Q(K_{n_i})\setminus \left\{2(n_i-1)\right\}\right)=\left\{N_i^{[n_i-1]}\right\}.$$
• If $W_{\Gamma }(A_{p^2})\cong {\overline{K}}_{n_4}$, then ${\sigma }_Q({\overline{K}}_{n_4})=\left\{0^{\left[n_4\right]}\right\}$ and, removing one 0 as prescribed,

  $$N_4+\left({\sigma }_Q({\overline{K}}_{n_4})\setminus \left\{0\right\}\right)=\left\{N_4^{[n_4-1]}\right\}.$$

Therefore, the “block” contribution to the spectrum is the multiset

$$\mathcal{M}=\bigcup _{i=1}^{10}\left\{{(|V|-n_i)}^{[n_i-1]}\right\}.$$

The remaining ten eigenvalues are the eigenvalues of the vertex-weighted signless Laplacian matrix $\mathfrak{L}({\delta }_{\mathfrak{n}})$, which in our ordering of S, has the form

$$\mathfrak{L}({\delta }_{p^{2}qr})=\left[\begin{array}{cccccccccc}|V|-n_1& n_2& n_3& n_4& n_5& n_6& n_7& n_8& n_9& n_{10}\\ n_1& |V|-n_2& n_3& n_4& n_5& n_6& n_7& n_8& n_9& n_{10}\\ n_1& n_2& |V|-n_3& n_4& n_5& n_6& n_7& n_8& n_9& n_{10}\\ n_1& n_2& n_3& |V|-n_4& n_5& n_6& n_7& n_8& n_9& n_{10}\\ n_1& n_2& n_3& n_4& |V|-n_5& n_6& n_7& n_8& n_9& n_{10}\\ n_1& n_2& n_3& n_4& n_5& |V|-n_6& n_7& n_8& n_9& n_{10}\\ n_1& n_2& n_3& n_4& n_5& n_6& |V|-n_7& n_8& n_9& n_{10}\\ n_1& n_2& n_3& n_4& n_5& n_6& n_7& |V|-n_8& n_9& n_{10}\\ n_1& n_2& n_3& n_4& n_5& n_6& n_7& n_8& |V|-n_9& n_{10}\\ n_1& n_2& n_3& n_4& n_5& n_6& n_7& n_8& n_9& |V|-n_{10}\end{array}\right].$$

Combining the block part $\mathcal{M}$ with $\sigma \left(\mathfrak{L}({\delta }_{p^{2}qr})\right)$ yields

$${\sigma }_Q\left(W_{\Gamma }({\mathbb{Z}}_{p^{2}qr})\right)=\left(\bigcup _{i=1}^{10}\left\{{(|V|-n_i)}^{[n_i-1]}\right\}\right)\cup \sigma \left(\mathfrak{L}({\delta }_{p^{2}qr})\right),$$

where $n_i=\varphi (\mathfrak{n}/s)$ for $s\in S$ and $|V|={\sum }_{i=1}^{10}{n}_i$. This completes the proof. □

Example 2.

The signless Laplacian spectrum of the weakly zero-divisor graph $W_{\Gamma }({\mathbb{Z}}_{60})$.

The proper divisors of 60 that index the vertex classes are

$$\{2,3,4,5,6,10,12,15,20,30\}.$$

for each $s\mid 60$, $s\ne 1,60$, we have $|A_s| =\varphi (60/s)$, hence

$$\left(|A_2|,|A_3|,|A_4|,|A_5|,|A_6|,|A_{10}|,|A_{12}|,|A_{15}|,|A_{20}|,|A_{30}|\right)=(8,8,8,4,4,2,4,2,2,1).$$

by Lemma 3 and Corollary 1,

$$W_{\Gamma }({\mathbb{Z}}_{60})={\delta }_{60}\left[K_8,K_8,K_8,K_4,K_4,K_2,K_4,K_2,K_2,K_1\right].$$

Let $t_i=\varphi (60/s_i)$ for the above ordering of divisors and set

$$|\mathcal{V}|=\sum _{i=1}^{10}{t}_i=60-\varphi (60)-1=43,{\mathfrak{N}}_{s_i}=\sum _{j\ne i}{t}_j=|\mathcal{V}|-t_i.$$

since $W_{\Gamma }(A_{s_i})\cong K_{t_i}$ is $(t_i-1)$-regular with ${\sigma }_Q(K_{t_i})=\{2t_i-2,{(t_i-2)}^{[t_i-1]}\},$ Theorem 2 yields the multiset contribution

$$\bigcup _{i=1}^{10}\left({\mathfrak{N}}_{s_i}+({\sigma }_Q(K_{t_i})\setminus \left\{2(t_i-1)\right\})\right)=\left\{{(|\mathcal{V}|-2)}^{\left[{\sum }_i(t_i-1)\right]}\right\}=\left\{{41}^{\left[33\right]}\right\}.$$

The remaining 10 signless Laplacian eigenvalues are those of the vertex-weighted matrix

$$\mathfrak{L}({\delta }_{60})={\left({\ell }_{ij}\right)}_{10\times 10},{\ell }_{ii}=|\mathcal{V}|-t_i,{\ell }_{ij}=t_j(i\ne j),$$

that is (using the above $t_i$’s),

$$\mathfrak{L}({\delta }_{60})=\left[\begin{array}{cccccccccc}35& 8& 8& 4& 4& 2& 4& 2& 2& 1\\ 8& 35& 8& 4& 4& 2& 4& 2& 2& 1\\ 8& 8& 35& 4& 4& 2& 4& 2& 2& 1\\ 8& 8& 8& 39& 4& 2& 4& 2& 2& 1\\ 8& 8& 8& 4& 39& 2& 4& 2& 2& 1\\ 8& 8& 8& 4& 4& 41& 4& 2& 2& 1\\ 8& 8& 8& 4& 4& 2& 39& 2& 2& 1\\ 8& 8& 8& 4& 4& 2& 4& 41& 2& 1\\ 8& 8& 8& 4& 4& 2& 4& 2& 41& 1\\ 8& 8& 8& 4& 4& 2& 4& 2& 2& 42\end{array}\right].$$

A numerical evaluation gives

$$\sigma \left(\mathfrak{L}({\delta }_{60})\right)\approx \{74.8332,40.8350,37.8320,31.4998,39,39,35,35,27,27\}.$$

Therefore,

$${\sigma }_Q\left(W_{\Gamma }({\mathbb{Z}}_{60})\right)=\left\{{41}^{\left[33\right]}\right\}\cup \sigma \left(\mathfrak{L}({\delta }_{60})\right).$$

Theorem 5.

Let $\mathfrak{n}=p^m{q}^m$, where $p<q$ are distinct primes and $m\ge 2$. Then, the signless Laplacian spectrum of the weakly zero-divisor graph $W_{\Gamma }({\mathbb{Z}}_{\mathfrak{n}})$ is given by

$${\sigma }_Q(W_{\Gamma }({\mathbb{Z}}_{p^m{q}^m}))=\left\{|\mathcal{V}|-2,|\mathcal{V}|-\varphi (p^m),\left(\sum _{i=1}^m\varphi (p^{m-i}{q}^m)+\sum _{i=1}^{m-1}\varphi (p^{m-i}{q}^{m-1})\right)-(2m-1),\varphi (p^m)-1\right\}\cup {\sigma }_Q(\mathfrak{L}({\delta }_{p^m{q}^m})),$$

where $\mathcal{V}$ denotes the vertex set of $W_{\Gamma }({\mathbb{Z}}_{p^m{q}^m})$ and ${\sigma }_Q(\mathfrak{L}({\delta }_{p^m{q}^m}))$ is the set of eigenvalues of the vertex-weighted signless Laplacian matrix of the quotient graph ${\delta }_{p^m{q}^m}$.

Proof. 

Let $\mathfrak{n}=p^m{q}^m$ with $m\ge 2$. Write the set of proper divisors of $\mathfrak{n}$ as

$$\mathcal{S}=\{p,p^2,\dots ,p^m,q,q^2,\dots ,q^m,p^i{q}^j:1\le i\le m,1\le j\le m,(i,j)\ne (m,m)\}.$$

for each $s\in \mathcal{S}$ let $A_s=\{x\in {\mathbb{Z}}_{\mathfrak{n}}:(x,\mathfrak{n})=s\}$; by Lemma 1, $|A_s|=\varphi (\mathfrak{n}/s)$. By Lemma 3, we have the generalized join decomposition

$$W_{\Gamma }({\mathbb{Z}}_{\mathfrak{n}})={\delta }_{\mathfrak{n}}\left[W_{\Gamma }(A_s):s\in \mathcal{S}\right],$$

where ${\delta }_{\mathfrak{n}}$ is the complete graph on vertex set $\mathcal{S}$. For each $s\in \mathcal{S}$, the induced subgraph $W_{\Gamma }(A_s)$ is regular of order $n_s:=|A_s|=\varphi (\mathfrak{n}/s)$ and degree $s_s\in \{0,n_s-1\}$ (cf. Corollary 1); in particular,

$${\sigma }_Q\left(W_{\Gamma }(A_s)\right)=\left\{\begin{array}{cc}\{0^{[n_s-1]},2(n_s-1)\},\hfill & \mathrm{if}{W}_{\Gamma }(A_s)\cong K_{n_s},\hfill \\ \left\{0^{\left[n_s\right]}\right\},\hfill & \mathrm{if}{W}_{\Gamma }(A_s)\cong {\overline{K}}_{n_s}.\hfill \end{array}\right.$$

Let $|\mathcal{V}|:=|V(W_{\Gamma }({\mathbb{Z}}_{\mathfrak{n}}))|={\sum }_{s\in \mathcal{S}}\varphi (\mathfrak{n}/s)$. For each $s\in \mathcal{S}$, the ${\delta }_{\mathfrak{n}}$–neighbor-sum (Theorem 2) equals

$${\mathfrak{N}}_s=\sum _{t\in N_{{\delta }_{\mathfrak{n}}}(s)}|A_t|=\sum _{\begin{array}{c}t\in \mathcal{S}\\ t\ne s\end{array}}\varphi (\mathfrak{n}/t)=|\mathcal{V}|-\varphi (\mathfrak{n}/s).$$

Therefore, by Theorem 2 together with Remark 1, the signless Laplacian spectrum of $W_{\Gamma }({\mathbb{Z}}_{\mathfrak{n}})$ is

$${\sigma }_Q\left(W_{\Gamma }({\mathbb{Z}}_{\mathfrak{n}})\right)=\left(\bigcup _{s\in \mathcal{S}}\left({\mathfrak{N}}_s+\left({\sigma }_Q(W_{\Gamma }(A_s))\setminus \left\{2s_s\right\}\right)\right)\right)\cup {\sigma }_Q\left(\mathfrak{L}({\delta }_{\mathfrak{n}})\right).$$

We now group the contributions exactly as in Proposition 3.3 [15] (the case $p_1^m{p}_2$) but symmetrically in p and q.

• for the chain $\{p,p^2,\dots ,p^m\}$, one obtains the multiset

  $$\{\underset{m\mathrm{many}\mathrm{values},\mathrm{each}\mathrm{contributing}\mathrm{with}\mathrm{the}0\text{-}\mathrm{eigenspace}\mathrm{of}K}{\underbrace{(|\mathcal{V}|-\varphi (\frac{\mathfrak{n}}{p})),(|\mathcal{V}|-\varphi (\frac{\mathfrak{n}}{p^2})),\dots ,(|\mathcal{V}|-\varphi (\frac{\mathfrak{n}}{p^m}))}}\},$$

  in which the term $|\mathcal{V}|-\varphi (\mathfrak{n}/p^m)=|\mathcal{V}|-\varphi (q^m)$ appears with multiplicity $\varphi (q^m)-1$ (coming from $K_{\varphi (q^m)}$), while the remaining $m-1$ terms appear once each via their 0-eigenspaces.
• analogously, for the chain $\{q,q^2,\dots ,q^m\}$ we obtain the value $|\mathcal{V}|-\varphi (p^m)$ with multiplicity $\varphi (p^m)-1$ and $m-1$ additional singleton values $|\mathcal{V}|-\varphi (\mathfrak{n}/q^j)$ for $1\le j\le m-1$.
• for all mixed divisors $p^i{q}^j$ with $1\le i\le m$, $1\le j\le m$ and $(i,j)\ne (m,m)$, each induced block contributes only its 0-eigenspace after the shift by ${\mathfrak{N}}_{p^i{q}^j}=|\mathcal{V}|-\varphi (p^{m-i}{q}^{m-j})$, so that their total contribution compresses to the single value $|\mathcal{V}|-2$, counted once, together with the integer

  $$\Xi :=\left(\sum _{i=1}^m\varphi (p^{m-i}{q}^m)+\sum _{i=1}^{m-1}\varphi (p^{m-i}{q}^{m-1})\right)-(2m-1),$$

  which is the total multiplicity coming from these shifted 0-eigenspaces after removing the $2s_s$ terms (cf. the tally in the proof of Proposition 3.3 in [15])

Collecting the above and writing the prime-power contributions explicitly yields exactly the four explicit eigenvalues listed in the statement,

$$|\mathcal{V}|-2,|\mathcal{V}|-\varphi (p^m),\Xi ,\varphi (p^m)-1,$$

and the remaining (unspecified) eigenvalues are the $|\mathcal{S}|$ eigenvalues of the vertex-weighted signless Laplacian matrix $\mathfrak{L}({\delta }_{p^m{q}^m})$ (obtained from the complete graph on $\mathcal{S}$ by weighting the vertex s with $|A_s|=\varphi (\mathfrak{n}/s)$), as required. Hence,

$${\sigma }_Q(W_{\Gamma }({\mathbb{Z}}_{p^m{q}^m}))=\left\{|\mathcal{V}|-2,|\mathcal{V}|-\varphi (p^m),\left(\sum _{i=1}^m\varphi (p^{m-i}{q}^m)+\sum _{i=1}^{m-1}\varphi (p^{m-i}{q}^{m-1})\right)-(2m-1),\varphi (p^m)-1\right\}\cup {\sigma }_Q(\mathfrak{L}({\delta }_{p^m{q}^m})),$$

This completes the proof. □

Theorem 6.

Let $\mathfrak{n}=p^{m}qr$, where $p<q<r$ are distinct primes and $m\ge 2$. Denote by $\mathcal{V}$ the vertex set of $W_{\Gamma }({\mathbb{Z}}_{\mathfrak{n}})$ and put

$$|\mathcal{V}|=\sum _{\begin{array}{c}s\mid \mathfrak{n}\\ s\notin \{1,\mathfrak{n}\}\end{array}}\varphi \left({\displaystyle \frac{\mathfrak{n}}{s}}\right).$$

Then, the signless Laplacian spectrum of $W_{\Gamma }({\mathbb{Z}}_{\mathfrak{n}})$ is

$${\sigma }_Q\left(W_{\Gamma }({\mathbb{Z}}_{p^{m}qr})\right)=\left\{\begin{array}{ccc}|\mathcal{V}|-\varphi \left({\displaystyle \frac{\mathfrak{n}}{q}}\right)& |\mathcal{V}|-\varphi \left({\displaystyle \frac{\mathfrak{n}}{r}}\right)& |\mathcal{V}|-2\\ \varphi \left({\displaystyle \frac{\mathfrak{n}}{q}}\right)-1& \varphi \left({\displaystyle \frac{\mathfrak{n}}{r}}\right)-1& {\displaystyle \sum _{\begin{array}{c}s\mid \mathfrak{n},s\notin \{1,\mathfrak{n}\}\\ s\ne q,s\ne r\end{array}}\varphi \left({\displaystyle \frac{\mathfrak{n}}{s}}\right)-\left(\tau (\mathfrak{n})-4\right)}\end{array}\right\}\cup {\sigma }_Q\left(\mathfrak{L}({\delta }_{p^{m}qr})\right),$$

where $\tau (\mathfrak{n})$ is the number of divisors of $\mathfrak{n}$ and $\mathfrak{L}({\delta }_{p^{m}qr})$ is the vertex-weighted signless Laplacian of the complete quotient graph ${\delta }_{p^{m}qr}$ on the proper divisor classes $\{A_s:s\mid \mathfrak{n},s\notin \{1,\mathfrak{n}\}\}$ with weights $\varphi (\mathfrak{n}/s)$.

Proof. 

List the proper divisors of $\mathfrak{n}=p^{m}qr$ as

$$\{p,p^2,\dots ,p^m,q,r,p^{i}q(1\le i\le m),p^{i}r(1\le i\le m),qr,p^{i}qr(1\le i\le m-1)\},$$

which are exactly $\tau (\mathfrak{n})-2=4(m+1)-2$ elements. By Lemma 3, the weakly zero-divisor graph is a generalized join

$$W_{\Gamma }({\mathbb{Z}}_{\mathfrak{n}})={\delta }_{p^{m}qr}\left[W_{\Gamma }(A_{s_1}),\dots ,W_{\Gamma }(A_{s_t})\right],$$

where $t=\tau (\mathfrak{n})-2$ and ${\delta }_{p^{m}qr}$ is the complete graph on these classes. For each class $A_s$ we have $|A_s|=\varphi (\mathfrak{n}/s)$ (Lemma 1). Moreover, by Lemma 2 and Corollary 1, the induced subgraphs are of two types:

$$W_{\Gamma }(A_q)\cong K_{\varphi (\mathfrak{n}/q)},W_{\Gamma }(A_r)\cong K_{\varphi (\mathfrak{n}/r)},$$

while for every other proper divisor $s\notin \{q,r\}$, one has

$$W_{\Gamma }(A_s)\cong {\overline{K}}_{\varphi (\mathfrak{n}/s)}.$$

Because the quotient graph ${\delta }_{p^{m}qr}$ is complete, the neighbor-weight is

$${\mathfrak{N}}_s=\sum _{\begin{array}{c}u\mid \mathfrak{n}\\ u\notin \{1,\mathfrak{n},s\}\end{array}}\varphi \left({\displaystyle \frac{\mathfrak{n}}{u}}\right)=|\mathcal{V}|-\varphi \left({\displaystyle \frac{\mathfrak{n}}{s}}\right)$$

for every class $A_s$. Apply Theorem 2 (the G-join signless Laplacian formula). If $W_{\Gamma }(A_s)\cong {\overline{K}}_t$ (with $t=\varphi (\mathfrak{n}/s)$), then ${\sigma }_Q({\overline{K}}_t)=\left\{0^{\left[t\right]}\right\}$ and removing the largest eigenvalue $2s_s=0$ leaves $0^{[t-1]}$, which after shifting by ${\mathfrak{N}}_s$, gives the eigenvalue

$$|\mathcal{V}|-\varphi \left({\displaystyle \frac{\mathfrak{n}}{s}}\right)\mathrm{with}\mathrm{multiplicity}\varphi \left({\displaystyle \frac{\mathfrak{n}}{s}}\right)-1,$$

for every $s\notin \{q,r\}$.

If $W_{\Gamma }(A_q)\cong K_{\varphi (\mathfrak{n}/q)}$ or $W_{\Gamma }(A_r)\cong K_{\varphi (\mathfrak{n}/r)}$, then ${\sigma }_Q(K_t)=\{2t-2,{(t-2)}^{[t-1]}\}$ with $t=\varphi (\mathfrak{n}/q)$ or $t=\varphi (\mathfrak{n}/r)$. Removing the largest eigenvalue $2t-2$ and shifting by ${\mathfrak{N}}_q=|\mathcal{V}|-\varphi (\mathfrak{n}/q)$ (respectively ${\mathfrak{N}}_r$) yields

$${\mathfrak{N}}_q+(t-2)=|\mathcal{V}|-2\mathrm{with}\mathrm{multiplicity}\varphi \left({\displaystyle \frac{\mathfrak{n}}{q}}\right)-1,$$

and similarly $|\mathcal{V}|-2$ with multiplicity $\varphi (\mathfrak{n}/r)-1$ from the class $A_r$. Since the value $|\mathcal{V}|-2$ is the same for q and r, its total multiplicity is

$$\left(\varphi (\mathfrak{n}/q)-1\right)+\left(\varphi (\mathfrak{n}/r)-1\right)=\varphi (\mathfrak{n}/q)+\varphi (\mathfrak{n}/r)-2.$$

Collecting the contributions from all classes $s\notin \{q,r\}$ gives the family of eigenvalues

$$|\mathcal{V}|-\varphi \left({\displaystyle \frac{\mathfrak{n}}{s}}\right)\mathrm{each}\mathrm{with}\mathrm{multiplicity}\varphi \left({\displaystyle \frac{\mathfrak{n}}{s}}\right)-1,s\notin \{q,r\},$$

while the two prime classes q and r contribute the common value $|\mathcal{V}|-2$ with multiplicity $\left(\varphi (\mathfrak{n}/q)-1\right)+\left(\varphi (\mathfrak{n}/r)-1\right)$. In the compact two-row display used throughout this paper, these appear as the three entries shown in the theorem: the two values $|\mathcal{V}|-\varphi (\mathfrak{n}/q)$ and $|\mathcal{V}|-\varphi (\mathfrak{n}/r)$ with multiplicities $\varphi (\mathfrak{n}/q)-1$ and $\varphi (\mathfrak{n}/r)-1$ and a single column for $|\mathcal{V}|-2$ with multiplicity equal to the total number of shifted nonzero entries contributed by all the remaining classes, namely

$$\sum _{\begin{array}{c}s\mid \mathfrak{n},s\notin \{1,\mathfrak{n}\}\\ s\ne q,s\ne r\end{array}}\left(\varphi (\mathfrak{n}/s)-1\right)=\sum _{\begin{array}{c}s\mid \mathfrak{n},s\notin \{1,\mathfrak{n}\}\\ s\ne q,s\ne r\end{array}}\varphi (\mathfrak{n}/s)-\left(\tau (\mathfrak{n})-2-2\right)=\sum _{\begin{array}{c}s\mid \mathfrak{n},s\notin \{1,\mathfrak{n}\}\\ s\ne q,s\ne r\end{array}}\varphi (\mathfrak{n}/s)-\left(\tau (\mathfrak{n})-4\right).$$

By Theorem 2, the remaining $t=\tau (\mathfrak{n})-2$ signless Laplacian eigenvalues of $W_{\Gamma }({\mathbb{Z}}_{\mathfrak{n}})$ are exactly the eigenvalues of the vertex-weighted signless Laplacian matrix $\mathfrak{L}({\delta }_{p^{m}qr})$ of the complete quotient graph ${\delta }_{p^{m}qr}$; this matrix has diagonal entries $|\mathcal{V}|-\varphi (\mathfrak{n}/s_i)$ and off-diagonal entries $\varphi (\mathfrak{n}/s_j)$ for the proper divisor indexing. This completes the proof. □

Theorem 7.

Let $\mathfrak{n}$ be a positive integer for which $W_{\Gamma }({\mathbb{Z}}_{\mathfrak{n}})$ is nonempty and

$$W_{\Gamma }({\mathbb{Z}}_{\mathfrak{n}})={\delta }_{\mathfrak{n}}[G_1,\dots ,G_k],$$

where each $G_i$ is either a complete or an empty graph induced on the divisor class $A_{{\mathfrak{s}}_i}$. Write ${\mathfrak{n}}_i=|A_{{\mathfrak{s}}_i}|$ and let ${\mathfrak{s}}_i$ be the regularity of $G_i$ (so ${\mathfrak{s}}_i={\mathfrak{n}}_i-1$ for $K_{{\mathfrak{n}}_i}$ and ${\mathfrak{s}}_i=0$ for ${\overline{K}}_{{\mathfrak{n}}_i}$). Define

$${\mathfrak{N}}_i=\sum _{j\in N_{{\delta }_{\mathfrak{n}}}(i)}{\mathfrak{n}}_j,$$

and let ${\mu }_{max}$ denote the largest signless Laplacian eigenvalue of $W_{\Gamma }({\mathbb{Z}}_{\mathfrak{n}})$. Then,

$${\mu }_{max}\le \underset{1\le i\le k}{max}\left\{2{\mathfrak{s}}_i+{\mathfrak{N}}_i+\sum _{j\in N_{{\delta }_{\mathfrak{n}}}(i)}\sqrt{{\mathfrak{n}}_i{\mathfrak{n}}_j}\right\}.$$

In particular, if ${\delta }_{\mathfrak{n}}$ is complete on the k classes, this simplifies to

$${\mu }_{max}\le \underset{1\le i\le k}{max}\left\{2{\mathfrak{s}}_i+\sum _{j\ne i}{\mathfrak{n}}_j+\sum _{j\ne i}\sqrt{{\mathfrak{n}}_i{\mathfrak{n}}_j}\right\}.$$

Proof. 

By Theorem 2, the signless Laplacian spectrum of ${\delta }_{\mathfrak{n}}[G_1,\dots ,G_k]$ is the union of (i) the shifted spectra ${\mathfrak{N}}_i+({\sigma }_Q(G_i)\setminus \left\{2{\mathfrak{s}}_i\right\})$ and (ii) the spectrum of

$$Y_Q={(y_{ij})}_{k\times k},y_{ij}=\left\{\begin{array}{cc}2{\mathfrak{s}}_i+{\mathfrak{N}}_i,\hfill & i=j,\hfill \\ \sqrt{{\mathfrak{n}}_i{\mathfrak{n}}_j},\hfill & ij\in E({\delta }_{\mathfrak{n}}),\hfill \\ 0,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

since $Y_Q$ is nonnegative and symmetric, Perron–Frobenius gives

$$\rho (Y_Q)\le \underset{i}{max}\left\{\sum _{j=1}^k{y}_{ij}\right\}=\underset{i}{max}\left\{2{\mathfrak{s}}_i+{\mathfrak{N}}_i+\sum _{j\in N_{{\delta }_{\mathfrak{n}}}(i)}\sqrt{{\mathfrak{n}}_i{\mathfrak{n}}_j}\right\},$$

every eigenvalue coming from the shifted blocks is at most ${\mathfrak{N}}_i+(2{\mathfrak{s}}_i-2)$ when $G_i$ is complete and at most ${\mathfrak{N}}_i$ when $G_i$ is empty; in either case, it is ≤$2{\mathfrak{s}}_i+{\mathfrak{N}}_i$, which is dominated by the corresponding row-sum bound above (since the extra sum of square-roots is nonnegative). Therefore, the largest eigenvalue of the whole graph is bounded by the stated maximum of row sums of $Y_Q$, proving the claim. □

Theorem 8.

Let $\mathfrak{n}$ be a positive integer such that

$$W_{\Gamma }({\mathbb{Z}}_{\mathfrak{n}})={\delta }_{\mathfrak{n}}[G_1,\dots ,G_k],$$

where each $G_i$ is the induced (complete or empty) graph on $A_{{\mathfrak{s}}_i}$ of size ${\mathfrak{n}}_i$, with internal regularity ${\mathfrak{s}}_i\in \{0,{\mathfrak{n}}_i-1\}$. Let

$${\mathfrak{N}}_i=\sum _{j\in N_{{\delta }_{\mathfrak{n}}}(i)}{\mathfrak{n}}_j,Y_Q={\left(y_{ij}\right)}_{k\times k},y_{ij}=\left\{\begin{array}{cc}2{\mathfrak{s}}_i+{\mathfrak{N}}_i,\hfill & i=j,\hfill \\ \sqrt{{\mathfrak{n}}_i{\mathfrak{n}}_j},\hfill & ij\in E({\delta }_{\mathfrak{n}}),\hfill \\ 0,\hfill & \mathit{otherwise}.\hfill \end{array}\right.$$

Let ${\mu }_{min}^{+}$ be the smallest positive signless Laplacian eigenvalue of $W_{\Gamma }({\mathbb{Z}}_{\mathfrak{n}})$. Then,

$${\mu }_{min}^{+}\ge max\left\{0,\underset{1\le i\le k}{min}\left(2{\mathfrak{s}}_i+{\mathfrak{N}}_i-\sum _{j\in N_{{\delta }_{\mathfrak{n}}}(i)}\sqrt{{\mathfrak{n}}_i{\mathfrak{n}}_j}\right)\right\}.$$

Proof. 

By Theorem 2, the spectrum of $W_{\Gamma }({\mathbb{Z}}_{\mathfrak{n}})$ is the multiset union of the shifted block spectra ${\mathfrak{N}}_i+({\sigma }_Q(G_i)\setminus \left\{2{\mathfrak{s}}_i\right\})$ and the spectrum of $Y_Q$. Hence, the smallest positive eigenvalue of $W_{\Gamma }({\mathbb{Z}}_{\mathfrak{n}})$ is at least the minimum of (i) the smallest elements among the nonzero numbers in those shifted block sets and (ii) the smallest eigenvalue of $Y_Q$ (if positive).

Since $Y_Q$ is real symmetric and nonnegative, Gershgorin’s disk theorem gives

$${\lambda }_{min}(Y_Q)\ge \underset{1\le i\le k}{min}\left(y_{ii}-\sum _{j\ne i}|y_{ij}|\right)=\underset{i}{min}\left(2{\mathfrak{s}}_i+{\mathfrak{N}}_i-\sum _{j\in N_{{\delta }_{\mathfrak{n}}}(i)}\sqrt{{\mathfrak{n}}_i{\mathfrak{n}}_j}\right).$$

Moreover, all signless Laplacian eigenvalues are ≥0, so we can safely take the maximum with 0.

Finally, each shifted block contributes either nothing below its shift (empty graph case) or values $\ge {\mathfrak{N}}_i$ (complete graph case, after removing the largest $2{\mathfrak{s}}_i$), which are ≥0 and thus do not reduce the overall lower bound. Therefore, the stated bound holds for ${\mu }_{min}^{+}$. □

Theorem 9.

Let $\mathfrak{n}=p^a{q}^b$ or $\mathfrak{n}=p^a{q}^b{r}^c$, where $p,q,r$ are distinct primes and $a,b,c\in \mathbb{N}$. Suppose that for every proper divisor ${\mathfrak{s}}_i$ of $\mathfrak{n}$, the induced subgraph $W_{\Gamma }(A_{{\mathfrak{s}}_i})$ is either $K_t$ or ${\overline{K}}_t$ with $t\in \mathbb{N}$. If, in addition, the vertex-weighted signless Laplacian matrix $\mathfrak{L}({\delta }_{\mathfrak{n}})$ has an integral spectrum (i.e., $\sigma (\mathfrak{L}({\delta }_{\mathfrak{n}}))\subset \mathbb{Z}$), then the signless Laplacian spectrum of $W_{\Gamma }({\mathbb{Z}}_{\mathfrak{n}})$ is entirely integral.

Proof. 

By Lemma 3, we may write

$$W_{\Gamma }({\mathbb{Z}}_{\mathfrak{n}})={\delta }_{\mathfrak{n}}\left[W_{\Gamma }(A_{{\mathfrak{s}}_1}),\dots ,W_{\Gamma }(A_{{\mathfrak{s}}_k})\right],$$

where each $W_{\Gamma }(A_{{\mathfrak{s}}_i})$ is either $K_t$ or ${\overline{K}}_t$ on $t=\varphi (\mathfrak{n}/{\mathfrak{s}}_i)$ vertices. By Theorem 2,

$${\sigma }_Q\left(W_{\Gamma }({\mathbb{Z}}_{\mathfrak{n}})\right)=\bigcup _{i=1}^k\left({\mathfrak{N}}_i+\left({\sigma }_Q(W_{\Gamma }(A_{{\mathfrak{s}}_i}))\setminus \left\{2{\mathfrak{s}}_i\right\}\right)\right)\cup \sigma \left(\mathfrak{L}({\delta }_{\mathfrak{n}})\right),$$

where ${\mathfrak{s}}_i$ is the internal regularity of $W_{\Gamma }(A_{{\mathfrak{s}}_i})$ and ${\mathfrak{N}}_i$ is the sum of the sizes of the neighboring classes.

For $K_t$, one has ${\sigma }_Q(K_t)=\{2t-2,{(t-2)}^{[t-1]}\}$ and for ${\overline{K}}_t$, ${\sigma }_Q({\overline{K}}_t)=\left\{0^{\left[t\right]}\right\}$. In both cases, the multiset ${\sigma }_Q(W_{\Gamma }(A_{{\mathfrak{s}}_i}))\setminus \left\{2{\mathfrak{s}}_i\right\}$ consists of integers. Adding the integer shift ${\mathfrak{N}}_i$ preserves integrality, so each block-contribution ${\mathfrak{N}}_i+(·)$ is integral. By the hypothesis that $\sigma (\mathfrak{L}({\delta }_{\mathfrak{n}}))\subset \mathbb{Z}$, the remaining k eigenvalues are also integers. Therefore, every eigenvalue in ${\sigma }_Q(W_{\Gamma }({\mathbb{Z}}_{\mathfrak{n}}))$ is an integer. □

Theorem 10.

Let $G=W_{\Gamma }({\mathbb{Z}}_n)$ be the weakly zero-divisor graph over ${\mathbb{Z}}_n$ and let $\overline{G}$ denote its complement. Then, the signless Laplacian energy of G and $\overline{G}$ satisfies the Nordhaus–Gaddum-type inequality:

$${\mathcal{E}}_Q(G)+{\mathcal{E}}_Q(\overline{G})\ge 2\sqrt{2}\sqrt{|E(G)|·|E(\overline{G})|},$$

where ${\mathcal{E}}_Q(G)={\sum }_{i=1}^n\left|{\mu }_i-{\displaystyle \frac{2|E(G)|}{n}}\right|$ and ${\mu }_i$ are the signless Laplacian eigenvalues of G.

Proof. 

Let $n=|V(G)|$ and let ${\mu }_1,\dots ,{\mu }_n$ and ${\nu }_1,\dots ,{\nu }_n$ be the signless Laplacian eigenvalues of G and $\overline{G}$, respectively. By definition,

$${\mathcal{E}}_Q(G)=\sum _{i=1}^n\left|{\mu }_i-\overline{\mu }\right|,\overline{\mu }={\displaystyle \frac{2|E(G)|}{n}},$$

and similarly for ${\mathcal{E}}_Q(\overline{G})$.

By the Cauchy–Schwarz inequality,

$${\mathcal{E}}_Q(G)\ge \sqrt{n\sum _{i=1}^n{\left({\mu }_i-\overline{\mu }\right)}^2}=\sqrt{n\left(\sum _{i=1}^n{\mu }_i^2-n{\overline{\mu }}^2\right)},$$

since ${\sum }_{i=1}^n{\mu }_i^2=\mathrm{tr}(Q^2)=2|E(G)|+{\sum }_{v\in V(G)}d{(v)}^2$, the term ${\sum }_{i=1}^n{({\mu }_i-\overline{\mu })}^2$ is minimized when G is regular, in which case $d(v)={\displaystyle \frac{2|E(G)|}{n}}$ for all v, giving

$$\sum _{i=1}^n{\left({\mu }_i-\overline{\mu }\right)}^2=2|E(G)|.$$

An identical computation holds for $\overline{G}$, yielding

$${\mathcal{E}}_Q(G)\ge \sqrt{2n|E(G)|},{\mathcal{E}}_Q(\overline{G})\ge \sqrt{2n|E(\overline{G})|}.$$

Applying the AM–GM inequality to these two bounds gives

$${\mathcal{E}}_Q(G)+{\mathcal{E}}_Q(\overline{G})\ge 2\sqrt{{\mathcal{E}}_Q(G)·{\mathcal{E}}_Q(\overline{G})}\ge 2\sqrt{2n|E(G)|·2n|E(\overline{G})|}/n=2\sqrt{2}\sqrt{|E(G)|·|E(\overline{G})|}.$$

□

Corollary 2.

Let $G=W_{\Gamma }({\mathbb{Z}}_{30})$ and $\overline{G}$ be its complement. Then,

$${\mathcal{E}}_Q(G)+{\mathcal{E}}_Q(\overline{G})\ge 2\sqrt{2}\sqrt{|E(G)||E(\overline{G})|},$$

where $|E(G)|=31$ and $|E(\overline{G})| =\left({\displaystyle \genfrac{}{}{0pt}{}{17}{2}}\right)-31=105$. Numerically,

$${\mathcal{E}}_Q(G)+{\mathcal{E}}_Q(\overline{G})\ge 2\sqrt{2}\sqrt{31·105}=2\sqrt{6510}\approx 161.37.$$

Example 3.

Consider the weakly zero-divisor graph $W_{\Gamma }({\mathbb{Z}}_{30})$, which has $n=17$ vertices. As computed earlier, $|E(G)|=31$; hence, its complement satisfies

$$|E(\overline{G})|=\left({\displaystyle \genfrac{}{}{0pt}{}{17}{2}}\right)-31=136-31=105,$$

applying the Nordhaus–Gaddum-type bound, we obtain

$${\mathcal{E}}_Q(G)+{\mathcal{E}}_Q(\overline{G})\ge 2\sqrt{2|E(G)||E(\overline{G})|}=2\sqrt{2·31·105}=2\sqrt{6510}\approx 2\times 80.68457=161.37.$$

Hence, the combined signless Laplacian energy of the graph and its complement is at least approximately $161.37$.

Theorem 11.

Let $\mathfrak{L}({\delta }_{\mathfrak{n}})$ be the vertex-weighted signless Laplacian matrix corresponding to the quotient graph ${\delta }_{\mathfrak{n}}$ of $W_{\Gamma }({\mathbb{Z}}_{\mathfrak{n}})$, where $\mathfrak{n}$ has the divisor-induced partition

$$\{A_{{\mathfrak{s}}_1},A_{{\mathfrak{s}}_2},\dots ,A_{{\mathfrak{s}}_t}\}.$$

Then, the signless Laplacian energy ${\mathcal{E}}_Q(\mathfrak{L}({\delta }_{\mathfrak{n}}))$ satisfies

$${\mathcal{E}}_Q(\mathfrak{L}({\delta }_{\mathfrak{n}}))=\sum _{i=1}^t\left|{\lambda }_i-{\displaystyle \frac{2|E({\delta }_{\mathfrak{n}})|}{t}}\right|\le \sqrt{t\sum _{i=1}^t{\left({\lambda }_i-{\displaystyle \frac{2|E({\delta }_{\mathfrak{n}})|}{t}}\right)}^2},$$

where ${\lambda }_1,{\lambda }_2,\dots ,{\lambda }_t$ are the eigenvalues of $\mathfrak{L}({\delta }_{\mathfrak{n}})$.

Proof. 

By definition, the signless Laplacian energy is

$${\mathcal{E}}_Q(\mathfrak{L}({\delta }_{\mathfrak{n}}))=\sum _{i=1}^t\left|{\lambda }_i-{\displaystyle \frac{2|E({\delta }_{\mathfrak{n}})|}{t}}\right|,$$

applying the Cauchy–Schwarz inequality, we have

$${\left(\sum _{i=1}^t\left|{\lambda }_i-\mu \right|\right)}^2\le t\sum _{i=1}^t{\left({\lambda }_i-\mu \right)}^2,$$

where

$$\mu ={\displaystyle \frac{1}{t}}\sum _{i=1}^t{\lambda }_i={\displaystyle \frac{2|E({\delta }_{\mathfrak{n}})|}{t}},$$

taking square roots yields

$${\mathcal{E}}_Q(\mathfrak{L}({\delta }_{\mathfrak{n}}))\le \sqrt{t\sum _{i=1}^t{\left({\lambda }_i-{\displaystyle \frac{2|E({\delta }_{\mathfrak{n}})|}{t}}\right)}^2}.$$

This proves the claim. □

Example 4.

Let $\mathfrak{n}=36=2^2·3^2$. From earlier computation, the eigenvalues of $\mathfrak{L}({\delta }_{36})$ are

$${\lambda }_1\approx 0.69611,{\lambda }_2\approx 6.22263,{\lambda }_3\approx 11.08126.$$

The average eigenvalue is

$$\overline{\lambda }={\displaystyle \frac{{\lambda }_1+{\lambda }_2+{\lambda }_3}{3}}={\displaystyle \frac{0.69611+6.22263+11.08126}{3}}=6.0.$$

thus, the signless Laplacian energy is

$${\mathcal{E}}_Q(W_{\Gamma }({\mathbb{Z}}_{36}))=\sum _{i=1}^3\left|{\lambda }_i-\overline{\lambda }\right|\approx 10.6078.$$

Moreover, by the Cauchy–Schwarz inequality, we have the upper bound

$${\mathcal{E}}_Q(W_{\Gamma }({\mathbb{Z}}_{36}))\le \sqrt{3·\sum _{i=1}^3{({\lambda }_i-\overline{\lambda })}^2}\approx 12.7279.$$

Remark 2.

For the case $\mathfrak{n}=36$, the actual signless Laplacian energy is ${\mathcal{E}}_Q(W_{\Gamma }({\mathbb{Z}}_{36}))\approx 10.6078$, while the Cauchy–Schwarz upper bound is $12.7279$. The relative gap between these values is therefore

$${\displaystyle \frac{12.7279-10.6078}{12.7279}}\times 100\%\approx 16.65\%.$$

This indicates that, for this example, the bound is reasonably close to the actual value, capturing more than $83\%$ of the achievable maximum.

4. Conclusions

In this article, we have presented a comprehensive spectral analysis of the weakly zero-divisor graph $W_{\Gamma }({\mathbb{Z}}_n)$ with respect to its signless Laplacian spectrum for various composite forms of n, including $p^2{q}^2$, $p^{2}qr$, $p^m{q}^m$ and $p^{m}qr$. By employing a generalized join decomposition framework, we derived closed-form expressions for the spectra using vertex-weighted block matrices and identified precise conditions ensuring the integrality of the spectrum. Furthermore, we established additional results involving spectral bounds, extremal inequalities and Nordhaus–Gaddum-type relations, thereby providing deeper insight into the relationship between the arithmetic structure of n and spectral invariants of the associated graph.

Potential directions for future research include extending the present analysis to the normalized signless Laplacian spectrum, examining spectral distributions for higher-order prime power products and exploring analogous spectral properties for weakly zero-divisor graphs defined over non-commutative rings.