Abstract
Reversible data hiding in encrypted point clouds presents unique challenges due to their unstructured geometry, absence of mesh connectivity, and high sensitivity to spatial perturbations. In this paper, we propose an efficient and secure reversible data hiding framework for encrypted point clouds, incorporating KD tree-based path planning, adaptive multi-MSB prediction, and a dual-model design. To establish a consistent spatial traversal order, a Hamiltonian path is constructed using a KD tree-accelerated nearest-neighbor algorithm. Guided by this path, a prediction-driven embedding strategy dynamically adjusts the number of most significant bits (MSBs) embedded per point, balancing capacity and reversibility while generating a label map that reflects local predictability. The label map is then compressed using Huffman coding to reduce the auxiliary overhead. For enhanced security and lossless recovery, the encrypted point cloud is divided into two complementary shares through a lightweight XOR-based (2, 2) secret sharing scheme. The Huffman tree and compressed label map are distributed across both encrypted shares, ensuring that neither share alone can reveal the original point cloud or the embedded message. Experimental evaluations on diverse 3D models demonstrate that the proposed method achieves near-optimal embedding rates, perfect reconstruction of the original model, and significant obfuscation of the geometric structure. These results confirm the practicality and robustness of the proposed framework for scenarios involving secure 3D point cloud transmission, storage, and sharing.
Keywords:
reversible data hiding; encrypted point clouds; KD tree; Hamiltonian path; Huffman coding; multi-MSB prediction MSC:
68U05; 68U01
1. Introduction
Cloud storage has become a ubiquitous and indispensable solution for managing vast volumes of digital information, ranging from personal files to critical enterprise data. Its inherent advantages—such as its scalability, accessibility, and cost efficiency—have established it as a cornerstone of modern data infrastructure. However, this growing reliance on cloud services has also introduced significant challenges related to data security and privacy. As data transmission and storage in cloud environments remain vulnerable to threats such as unauthorized access, data breaches, and cyberattacks, the need for robust protection mechanisms is more urgent than ever. Encryption acts as a fundamental defense by converting sensitive data into an unintelligible format that can only be deciphered using a valid decryption key. This process preserves both the confidentiality and integrity of the data, even in the presence of adversarial access, by preventing any meaningful interpretation of the stored content.
In addition to encryption, reversible data hiding (RDH) has gained prominence as a complementary technique that allows confidential information to be embedded into a host medium—such as images, audio, or 3D data—while preserving the host’s original state. A key advantage of RDH is its reversibility: after the embedded message is extracted, the host data can be perfectly restored to its original form without any loss. This property is particularly valuable in domains where data integrity and authenticity are critical, including medical imaging, legal evidence preservation, and military communications.
Various RDH techniques have been proposed, each offering different trade-offs among embedding capacity, fidelity, and complexity. Notable methods include histogram modification [1], difference expansion [2], and interpolation-based embedding [3]. Histogram modification reshapes the distribution of pixel values to create an embedding space. Difference expansion exploits the differences between neighboring pixels to embed bits while preserving perceptual quality. Interpolation-based methods embed data by increasing image resolution and adjusting pixel values based on neighboring pixels, achieving high embedding capacity with minimal visual distortion. More recently, dual-image-based reversible data hiding [4,5,6,7,8,9,10] has emerged as a powerful extension of traditional RDH methods. By leveraging two correlated images instead of one, this approach significantly enhances both embedding capacity and data security. The hidden message and auxiliary data are distributed across two separate media, ensuring that neither element by itself is sufficient to extract the secret message or reconstruct the original content. This dual-media dependency improves resistance to unauthorized access and introduces a new paradigm for secure information embedding and reversible recovery.
With the increasing deployment of 3D sensing technologies in critical infrastructure and embedded systems [11,12,13,14,15], point cloud data has become a vital component in safety-critical applications such as autonomous navigation, UAV-based mapping, industrial inspection, and structural health monitoring. In these scenarios, point clouds captured by LiDAR or depth cameras are continuously processed and transmitted by resource-constrained devices under strict requirements for real-time responsiveness, data confidentiality, and reliability. Any compromise or leakage of such 3D data can lead to privacy violations, operational failures, or security breaches. Therefore, ensuring the secure and reversible manipulation of point cloud data is of paramount importance. These practical demands drive the need for a robust and lightweight data hiding framework that can operate effectively in constrained environments while preserving geometric fidelity and resisting unauthorized access or analysis.
While dual-image-based RDH has shown promising results in 2D image domains, extending this concept to 3D point clouds presents significant challenges. Unlike images or meshes, point clouds lack explicit connectivity and a regular structure, making it difficult to define consistent embedding paths or apply traditional pixel-based embedding techniques. Furthermore, the increasing use of encrypted point clouds—especially in cloud-based 3D storage, virtual environments, and digital twins—calls for novel strategies that ensure both geometric confidentiality and reversible message embedding.
Although several RDH techniques have been adapted for encrypted point clouds, most existing schemes rely on a single encrypted model that offers limited resistance to partial exposure or unauthorized analysis. In scenarios where an attacker gains access to the host model, it may still be possible to retrieve embedded messages or infer sensitive geometric patterns. In contrast, a dual-model design introduces structural separation and interdependence, ensuring that access to only one model provides no meaningful information about the hidden data or the original geometry. While no method can fully prevent compromise when both models are exposed, this approach significantly enhances resilience against partial disclosure, strengthens data confidentiality, and raises the barrier for unauthorized recovery.
Beyond its algorithmic contributions, the proposed framework shows high applicability to safety-critical and mission-critical domains, where the secure and reversible manipulation of 3D data is essential. Internet-of-Things (IoT) environments, for example, handling encrypted point cloud transmission from embedded 3D sensors, require not only confidentiality but also reversible annotations for tasks like real-time diagnostics or autonomous navigation. The dual-model design adopted in our method—based on (2, 2) XOR secret sharing—ensures that no single share can reveal any sensitive geometry or embedded messages, making it highly resilient against partial data exposure. Moreover, its guaranteed reversibility supports temporary data overlays that can be cleanly removed, an important feature for secure decision-making in medical imaging, industrial inspection, and unmanned system operations. These features align well with the requirements of embedded systems and cybersecurity-aware infrastructures, where robustness, recoverability, and access control are jointly required. Compared to conventional point cloud security methods such as watermarking or encrypted geometry masking, which often sacrifice reversibility or lack support for embedded communication, the proposed framework offers a unified solution that enables both secure, reversible embedding and full geometry recovery. This makes it particularly suitable for scenarios requiring both confidentiality and usability, such as secure 3D data sharing in cloud environments and IoT-enabled sensing systems.
To address these challenges, we propose a novel reversible data hiding framework for encrypted point clouds that integrates KD tree-based path planning, prediction-driven embedding, and a dual-model security architecture. Our approach begins by constructing a spatially coherent Hamiltonian path [16], using nearest-neighbor traversal accelerated by a KD tree, establishing an efficient and locality-preserving embedding order. A multi-MSB prediction [17] strategy estimates the embedding capacity at each point along the path, generating a label map that is subsequently compressed using Huffman coding. The original point cloud is then partitioned into two dependent encrypted shares using an XOR-based (2, 2) secret sharing mechanism. Finally, the Huffman tree and the compressed label map are embedded across both models in a manner that enforces dual-model dependency, such that only their combination enables full recovery of the original geometry and embedded message. This integrated framework achieves secure, high-capacity, and fully reversible data hiding that is tailored to encrypted point clouds.
The remainder of this paper is organized as follows: Section 2 reviews related work and the research background, providing context and a survey of the relevant literature. Section 3 details the methodology of the proposed algorithm. Section 4 presents the experimental results and a performance analysis. Finally, Section 5 concludes the paper with a summary of the findings and directions for future research.
2. Related Work
RDH has evolved significantly over the past two decades, with extensive research aimed at improving embedding capacity, security, and reversibility across different media formats. In this section, we review two key research directions that form the foundation of the proposed approach: dual-media-based RDH, which introduces data redundancy and dependency across multiple carriers to enhance security and capacity, and RDH schemes for encrypted point clouds, which focus on embedding hidden information into geometric data under encryption constraints. By examining the development and limitations of these domains, we clarify the research gaps that our proposed framework aims to address.
2.1. Dual-Media-Based Reversible Data Hiding Algorithms
Dual-image-based RDH leverages two correlated digital images as cover media to enhance the embedding capacity, message privacy, and reconstruction reliability. By distributing both the embedded payload and auxiliary recovery data across two images, these methods improve resistance to attacks and reduce the risk of partial data compromise. In most cases, both images are required jointly for successful data extraction and complete image recovery, thereby increasing the overall system security.
Numerous studies have sought to improve various aspects of dual-image RDH, including embedding efficiency, robustness, and adaptability to other media types. For instance, Bhardwaj [18] proposes a novel reversible data hiding algorithm designed to secure and efficiently embed electronic patient information (EPI) in medical images. This algorithm addresses critical challenges such as the underflow problem in medical images and ensures the secure transmission of sensitive data without degrading image quality. Notably, it introduces an enhanced, separable reversible data hiding technique that operates in the encrypted domain, achieving a higher embedding rate than in previous approaches. Additionally, it incorporates a fragile watermark for authentication of the EPI at the receiver’s end, further strengthening the security and integrity of the transmitted data.
Kim et al. [19] introduced a novel technique that leverages matrix encoding to enhance the security and efficiency of data hiding in images. Halftone images, characterized by their binary nature, present unique challenges in terms of visual quality and data capacity. The proposed algorithm utilizes Hamming codes for error correction, ensuring minimal distortion and high data integrity. Their experimental results demonstrate the method’s effectiveness, achieving a balanced trade-off between embedding capacity and image quality. Yu et al. [20] proposed a dual-channel-based reversible data hiding algorithm to address the challenges of high-capacity and low-distortion embedding. Their approach first converts secret messages into novenary digits and embeds them into single-channel audio using a specially designed magic matrix. The two modified channels are then combined to form standard dual-channel audio. This method significantly improves steganographic quality, achieving an average 16% improvement in signal-to-noise ratio (SNR) compared to existing techniques. Huang et al. [21] presented the first dual high-dynamic-range (HDR) image-based reversible data hiding algorithm, employing homogeneity index modification. This method is notable for its high embedding capacity and enhanced message security. It embeds messages by modifying two intermediate pixels with even RGB values, using a multiple-base notational system to further strengthen security. Their experimental results confirm the algorithm’s feasibility, representing a significant advancement in HDR image processing and secure data embedding.
2.2. Reversible Data Hiding Algorithms in Encrypted Point Clouds
With the growing need for the secure and flexible manipulation of 3D content, reversible data hiding in encrypted 3D models has emerged as a critical research area. In this section, we review and compare four representative algorithms that demonstrate progressive advancements in embedding capacity, robustness, and reconstruction accuracy for encrypted point clouds.
Tsai [22] presented a novel method for embedding secret messages into encrypted 3D models while preserving the ability to perfectly recover both the embedded message and the original model. The proposed approach introduces a bounding volume-based coordinate normalization approach, followed by encryption using exclusive-or (XOR) operations. Spatial subdivision is then applied to control point distortion, and a space encoding scheme is used to determine the embedding location of secret bits. A key innovation of this approach is its support for separability, allowing message extraction and model recovery to be performed independently, depending on the keys available.
Reinders et al. [16] proposed a method for securely embedding hidden information within encrypted 3D models by leveraging a Hamiltonian path to impose a unique spatial order on the points of a 3D object, enabling accurate prediction during reconstruction. By substituting the MSBs of point coordinate mantissas, the method enables data embedding directly in the encrypted domain without requiring access to the original model or auxiliary files. To ensure reversibility and robust reconstruction, the algorithm identifies unpredictable points based on topological discontinuities and large Euclidean distances, embedding this auxiliary information within the encrypted data. The scheme is format-compliant, introduces no size expansion, and demonstrates high reconstruction accuracy across a large 3D object database, achieving near-perfect visual fidelity while maintaining a payload close to the theoretical maximum of 3 bits per point when embedding in 1 MSB per coordinate.
Hou et al. [23] introduced a separable and reversible data hiding scheme for encrypted 3D point clouds, focusing solely on spatial geometry and disregarding mesh topology. Their method employs octree-based spatial subdivision to group similar points and applies a multi-MSB prediction strategy for data embedding. Within each octree block, one reference point is selected to predict and embed data into the remaining points, thereby reducing auxiliary data and increasing embedding capacity. After model encryption, a label map containing the subdivision and prediction metadata is embedded using a Huffman-coded stream. A key-protected XOR scheme is then used to embed the secret message. The framework supports separable operations—message extraction, model recovery, or both—based on the availability of decryption and data hiding keys. Building upon the work of Hou et al. [23], Tsai et al. [24] proposed several enhancements to further improve embedding capacity and adaptability. They introduced an axis-specific coordinate normalization method to optimize the value range for embedding and developed a mechanism to estimate the minimum embedding capacity per point, enabling the dynamic control of octree subdivision based on user requirements. Instead of selecting arbitrary reference points, their method uses the geometric center of each block to improve prediction accuracy and ensure reliable reconstruction. These enhancements resulted in an embedding rate of 100% and an average capacity of 39.76 bits per point, representing an improvement of 13.28% over previous methods. The algorithm developed by Tsai et al. [24] achieves perfect data recovery and model reconstruction, marking a significant advancement in secure data hiding for encrypted point clouds.
2.3. Limitations of the Existing Algorithms for Encrypted Point Clouds
Despite its innovations, Tsai’s method [22] has several limitations. First, the scheme’s performance is highly sensitive to the selection of subdivision and embedding thresholds. Improper threshold settings can significantly increase message extraction errors, particularly when the point coordinate precision (i.e., the number of decimal places) is limited. Second, the scheme excludes boundary points from the embedding process to preserve accuracy, which slightly reduces the overall embedding capacity.
The Hamiltonian path algorithm proposed by Reinders et al. [16], while effective, relies on a greedy strategy that may yield suboptimal point orderings. At higher values of , this can result in an increased number of unpredictable points, thereby enlarging the size of the embedded auxiliary information and reducing the effective payload.
The method developed by Hou et al. [23] partitions the model into sub-blocks using an octree and randomly selects reference points within each block to predict embeddable points. However, if the selected reference is too far from other points in the block, prediction accuracy decreases, leading to reduced embedding efficiency. Additionally, sub-blocks containing too few points are excluded from embedding, which can limit the performance of sparsely populated models. In contrast, Tsai et al. [24] improved upon this design by selecting the geometric center of each subspace as the reference and applying coordinate normalization to enhance prediction consistency. Nevertheless, their method introduces a significant drawback: it requires storing the complete octree structure and a detailed label map as auxiliary information. When the octree subdivision threshold is set too high, this overhead increases rapidly, substantially degrading the pure embedding performance. Thus, while both methods advance prediction-based embedding, they each present practical limitations—whether in reference selection, embedding flexibility, or auxiliary data overhead—which must be managed carefully.
3. Proposed Algorithm
To address the dual challenges of secure 3D content protection and reversible data embedding, we propose a robust framework for reversible data hiding in encrypted point clouds. As illustrated in Figure 1, the overall process is divided into two main procedures: data embedding and data extraction.
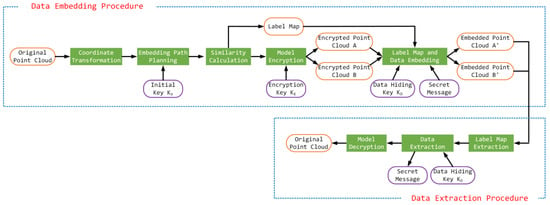
Figure 1.
The flowchart of the proposed dual-model-based reversible data hiding algorithm in encrypted point clouds.
In the embedding procedure, the original point cloud undergoes coordinate transformation and embedding path planning, guided by an initial key , to establish a unique traversal order. During label map generation, each embeddable point coordinate is assigned a label by evaluating its consistency with the preceding point along a predefined embedding path. The resulting label map is then efficiently compressed using Huffman encoding. The point cloud is subsequently encrypted using a symmetric key to generate a random point cloud, which is then XORed with the original point cloud to produce a second encrypted share. These two encrypted components form a (2, 2) XOR-based secret sharing pair and are stored independently. The compressed label map and a secret message, encrypted with a data hiding key , are then embedded across these two encrypted point clouds, resulting in a pair of embedded, encrypted models. In the extraction procedure, authorized users possessing the appropriate keys can selectively retrieve the hidden message, reconstruct the original 3D model, or perform both operations. The recovery process begins with the extraction of the label map, followed by message retrieval and model decryption, depending on the available credentials. This separable and reversible framework provides flexible access control, high embedding capacity, and accurate model reconstruction, making it well-suited for secure 3D data sharing, digital watermarking, and privacy-preserving computation.
3.1. Coordinate Transformation Process
The coordinate transformation process begins by converting point coordinate values into decimal form, followed by their representation in binary digits. This transformation is controlled by a user-defined compression threshold , which determines the level of detail to retain. We adopt our previously proposed algorithm [25] to perform this task. Let us assume that the input point cloud consists of points. The minimum boundary point , as defined in Equation (1), is computed by identifying the minimum coordinate value of each point along each axis. To normalize the coordinate values to a range between 0 and 1, Equation (2) is used to transform each point into a decimal value through a straightforward numerical calculation, where represents the maximum number of integer digits among all the adjusted coordinates. Next, a compression threshold , as described in Equation (3), is used to partially reverse the digits of each point coordinate and convert them into integer values . These integer values are then represented as binary digits using the procedure in Equation (4). The length required to encode each is determined using Equation (5). A higher threshold yields compressed values that more closely approximate the original coordinates, as defined in Equation (3).
3.2. The Embedding Path Planning Process
The embedding path planning process determines the traversal order of points, directly affecting the efficiency and accuracy of the subsequent prediction and embedding stages. Rather than relying on conventional neighborhood-based reference selection, this study employs a Hamiltonian path strategy [16] to construct a global, deterministic sequence of point pairs, thereby enhancing prediction consistency and overall embedding performance.
To accelerate the nearest-neighbor search during path planning, a KD tree (K-dimensional tree) is utilized. The KD tree is a widely used space-partitioning data structure for organizing points in a K-dimensional space and significantly reduces the time complexity of proximity queries. Instead of performing exhaustive searches over all unvisited points, the KD tree allows efficient retrieval of the nearest neighbor in logarithmic time, which greatly improves computational performance, especially for large-scale point clouds containing tens or hundreds of thousands of points.
The planning process begins by randomly selecting an initial reference point using a secret key . In the first iteration, the KD tree is queried to efficiently locate the nearest unvisited point to , which is then selected as the first embeddable point, forming the initial pair . In the second iteration, becomes the new reference point, and the KD tree is again used to identify the next-closest unvisited point , forming the next pair . This iterative process continues until all points have been visited, resulting in embeddable pairs for a point cloud containing points. For example, let us assume that point is randomly selected as the initial point, as shown in Figure 2a. The nearest unvisited point, , is selected to form the first pair , as illustrated in Figure 2b. In the next step, the closest point to , say, , is chosen to form the second pair , as shown in Figure 2c. This iterative process continues, ultimately producing a complete sequence of embeddable pairs, as visualized in Figure 2a–f, resulting in a total of 13 embeddable pairs.
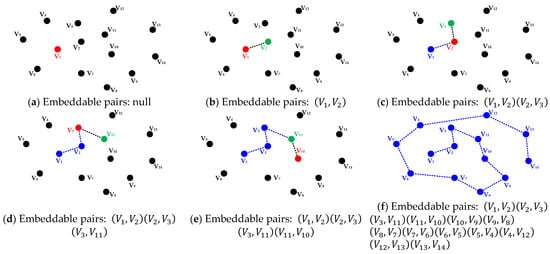
Figure 2.
Example of the process of reference point determination using the KD tree. The red point denotes the current reference point, the green point denotes the nearest unvisited point selected in the current iteration, and the blue points indicate previously visited points forming embeddable pairs.
This ordered sequence of embeddable pairs plays a pivotal role in the overall reversible data hiding framework, as it directly impacts similarity prediction, data embedding, data extraction, and model decryption processes. To ensure accurate reconstruction, the point sequence is recorded in the final output file according to the determined traversal order. For enhanced security, this sequence can optionally be shuffled using an additional secret key before output, increasing resistance to unauthorized analysis and reverse engineering.
3.3. Similarity Calculation Process
Following the construction of the Hamiltonian path, the multi-MSB similarity prediction process is applied to each embeddable pair along the path. The goal of this step is to determine how many of the MSBs in each coordinate in the embeddable point can be accurately predicted from its corresponding reference point. This prediction enables reversible data embedding by replacing only the predictable bits, ensuring both high embedding capacity and perfect recoverability.
For every embeddable pair , where is the reference point and is the embeddable point, prediction is performed independently for the three coordinate components—, , and —by comparing the binary sequences bit by bit, starting from the MSB. The embedding length for each coordinate is determined by the position of the first differing bit. If the first difference occurs at the -th bit (starting from 1), this implies that the first bits of the reference coordinate can be used to predict those of the embeddable coordinate. This value is recorded as the label for the corresponding coordinate. As a result, the bits of the embeddable coordinate can be replaced with auxiliary information and secret messages: the first predictable bits plus the -th bit, which can be recovered by inverting the predicted value during extraction. This approach ensures perfect restoration of the altered bits, thereby preserving reversibility. For example, as illustrated in Figure 3, if the first difference between a reference and embeddable coordinate appears at the 8th bit, the label is set to 7, indicating that 8 bits can be embedded, i.e., 7 predictable bits plus 1 inferred by flipping the 8th. This process is repeated for all three coordinates of each embeddable point, producing up to three individual labels per point. These labels are then compiled into a label map, representing the embedding potential along the Hamiltonian path. Due to the spatial similarity among neighboring points, many label values tend to repeat, allowing the label map to be effectively compressed using Huffman coding. This significantly reduces the size of the auxiliary information required for data extraction and model recovery.

Figure 3.
Example of multi-MSB prediction for each embeddable pair, with one reference point and one embeddable point. Green cells indicate matching bits between the reference and embeddable coordinates, while red cells indicate the first differing bit position used to determine the embedding length.
3.4. Model Encryption Process
To ensure secure protection of the original 3D point cloud prior to data embedding, this study adopts a (2, 2) XOR-based secret sharing scheme that splits the model into two independently stored encrypted components. This design guarantees that neither share reveals any meaningful geometric information on its own; both are required for an accurate reconstruction of the original model.
The encryption process begins by generating a random point cloud of the same size and format as the original model , using a secure random number generator initialized with a symmetric encryption key . Each coordinate in consists of independently generated random bit patterns that match the precision and range of the normalized coordinates in . A bitwise XOR operation is then performed between and , resulting in the second encrypted model, . This operation is applied coordinate-wise across all points, ensuring that the original geometric information is completely concealed. As a result, the encryption produces two output models: , the random share, and , the masked share. Since share is modified during the label map and data embedding process, it can no longer be regenerated solely from the encryption key . As a result, both encrypted models and must be explicitly stored to enable full reconstruction. This requirement preserves the integrity of the dual-model structure, ensuring that both components are indispensable for recovering the original point cloud and the embedded message. The use of XOR operations further enhances the scheme’s efficiency and reversibility, making it well-suited for large-scale 3D model encryption, with minimal computational overhead and full format compatibility.
3.5. Label Map and Data Embedding Process
Following the construction of the embedding path and the generation of the label map, the next step involves embedding both the auxiliary information and the encrypted secret message into the two encrypted point clouds. The auxiliary information consists of two essential components: the Huffman tree structure and the Huffman-encoded label map; both are critical for correctly interpreting the embedding length of each point during data extraction and model recovery.
In the proposed dual-model mechanism, the two encrypted models—produced via the XOR-based (2, 2) secret sharing scheme—are jointly utilized for data embedding. Rather than assigning each model a separate type of auxiliary information, the framework adopts an interleaved embedding strategy in which the Huffman tree and compressed label map are alternately embedded across the two models in point order. Specifically, auxiliary information is embedded into the first embeddable point of model , then into the first embeddable point of model , followed by the second embeddable point of model , the second of model , and so forth. This alternating pattern continues until all auxiliary information is embedded. This design achieves a more balanced distribution of embedded bits across both models and enhances robustness, as neither model contains all critical information independently. This interleaved approach not only preserves the reversibility and security of the data hiding process but also reinforces the core dual-model principle: both encrypted models are required for successful extraction and recovery.
Once the Huffman tree and label map are embedded, the algorithm proceeds to embed the encrypted secret message in the remaining embeddable space of the two models. The message is first encrypted using a data hiding key to ensure confidentiality and is then embedded according to the embedding length specified by the label map. Each embeddable point may carry a different number of bits (up to a maximum determined by the multi-MSB prediction), and embedding follows the same interleaving rule to preserve consistency. By structuring the embedding process in two phases—first embedding the label-related metadata, followed by the encrypted message—the framework ensures that both data extraction and model reconstruction can be performed accurately and reversibly. The combination of the dual-model design, interleaved embedding, and Huffman compression enables high embedding capacity, format compliance, and strong resistance to unauthorized access or analysis.
3.6. Label Map Extraction, Data Extraction, and Model Decryption Process
In the final stage of the reversible data hiding framework, the receiver obtains both embedded point clouds, and , which together contain the embedded auxiliary information and the secret message. The process begins with the extraction of the Huffman coding tree structure and the decoding of the compressed label map from the embedded content. This label map specifies the embedding capacity for each embeddable point coordinate, enabling accurate bitstream segmentation during message retrieval. Guided by the decoded label map, the embedded message is extracted bit by bit from the designated coordinates across both models. The recovered bitstream is then decrypted using the data hiding key , restoring the original secret message. After message extraction, the original 3D model is reconstructed through a two-step decryption process. Since the two encrypted models were generated using bitwise XOR secret sharing, the intermediate model can be perfectly recovered by computing . This operation is performed coordinate-wise across all points. Crucially, both and are required to perform this operation—neither share alone contains sufficient information—ensuring strong confidentiality.
Finally, to reverse any modifications made to the MSBs of the point coordinates during the embedding phase, the system reapplies the multi-MSB prediction based on the original reference-embeddable point pairs. Using the same prediction logic and the extracted embedded bits, the MSB segments of all embeddable points are restored to their original states, ensuring complete recovery of the coordinate values. This guarantees perfect reversibility, allowing both the hidden data and the original 3D model to be recovered without loss or distortion. By integrating dual-model decryption with precise auxiliary data parsing, the framework achieves a secure and fully reversible data hiding mechanism that is tailored to encrypted 3D point clouds.
3.7. Threat Model and Security Considerations
The proposed framework assumes a semi-honest adversary who may intercept one or both encrypted point cloud shares during transmission or storage, attempt to infer embedded content through geometric pattern analysis, or manipulate the point cloud geometry (e.g., coordinate tampering). To mitigate these threats, the system employs a dual-model (2, 2) XOR-based encryption scheme, ensuring that having access to only one encrypted share reveals no meaningful geometric structure or embedded message. Additionally, the embedded secret message is encrypted using a hiding key and is scattered across both models based on a compressed label map, further complicating unauthorized extraction. The use of multi-MSB prediction and interleaved embedding minimizes detectable patterns in the data distribution, reducing the risk of statistical or machine learning-based inference. Finally, since any geometric tampering would likely disrupt the bitwise consistency required for label decoding and message recovery, such attacks can be detected during extraction, due to decoding failure or message corruption. Overall, the proposed method provides resilience against passive and active adversaries under reasonable threat assumptions that are relevant to the field of secure 3D data transmission.
4. Experimental Results
We conducted extensive experiments to evaluate the feasibility and performance of the proposed algorithm. Figure 4 displays the visual representations of all the 3D polygonal models used in the experiments, while Table 1 provides the corresponding model details, including the number of points , number of polygons , and the model’s length, width, and height. The topological relationship between points was discarded during algorithm execution. The algorithm was implemented using MATLAB (Version Number: R2024b) and executed on a personal computer equipped with an AMD Ryzen™ 7 9800X3D 4.7 GHz CPU (Manufacturer Location: Advanced Micro Devices, Inc., Santa Clara, CA, USA) and 64 GB of memory. The secret message was randomly generated using MATLAB’s built-in random function. In this section, we present the experimental results of the proposed algorithm, including the embedding capacity, embedding rate, and execution time for each test model. In addition, we evaluate the algorithm’s reversibility, distortion, and security. The feasibility and performance of the proposed method are also compared with those of other state-of-the-art algorithms applied to different types of input multimedia.

Figure 4.
The test models used in our experiments.

Table 1.
Characteristics of different test models.
4.1. Algorithm Performance on Embedding Capacity, Embedding Rate, and Execution Time
Table 2 presents the experimental results, including the basic embedding length (BEL), average prediction embedding length (APrEL), average total embedding capacity (AToEC), average auxiliary information size (AAux), average pure embedding capacity (APuEC), and the number of points without embedded secret messages (NE) for each test model under a given compression threshold . All values represent the averages of 10 independent executions to ensure the stability and fairness of the results. BEL refers to the number of redundant bits available in the binary representation of each point coordinate. For example, a five-digit integer such as 99,999 can be represented using only 17 bits, leaving 15 leading zero bits in a standard 32-bit format. These unused bits can be repurposed for embedding. Accordingly, when , each point coordinate can accommodate up to 45 bits of embedded data, based on this redundancy. APrEL represents the average number of bits that can be predicted and embedded using multi-MSB prediction across all embeddable pairs. This value tends to be higher when the spatial distance between the reference and embeddable points is small, leading to greater prediction consistency. AToEC is calculated as the sum of BEL and APrEL, representing the total embedding capacity before accounting for the overhead. However, part of this capacity must be reserved for essential auxiliary information, such as the Huffman coding tree and the encoded label map, both of which are required for successful data extraction and model reconstruction. AAux indicates the size of this auxiliary information, which is typically embedded into the MSBs of selected point coordinates. The APuEC, or average pure embedding capacity, is calculated by subtracting the AAux from the combined embedding capacity of both models (AToEC) and then dividing the result by the total number of points across the two encrypted point clouds. On average, this overhead corresponds to approximately 51.09 bits per point.

Table 2.
Experimental results for each test model under the compression threshold .
.
Crucially, due to the proposed dual-model design, auxiliary information only needs to be embedded once across both encrypted models, rather than being duplicated in each. Since both models are jointly required for decoding, the auxiliary data can be distributed. This interdependent structure significantly reduces auxiliary overhead compared to conventional reversible data hiding schemes that operate on a single encrypted model, where metadata must be redundantly embedded. As a result, the proposed approach achieves a higher pure embedding capacity.
Some points, denoted as NE in Table 2, were excluded from secret message embedding because they served as the initial points in the traversal process. Although models such as Dragon and Elephant contain multiple disconnected subregions in their polygonal structures, the proposed method does not consider point connectivity or mesh topology. As a result, the entire model is treated as a unified set of points for path planning, and only a single initial point is required for constructing the Hamiltonian-like traversal. Consequently, the value of NE remains 1 for all models, regardless of the presence of multiple disjoint components in their geometric structure.
Table 2 also presents a comparison of execution times for Hamiltonian path construction with and without KD tree integration across various 3D models. The results clearly demonstrate that incorporating a KD tree significantly reduces the computation time, particularly for large-scale models. On average, the execution time decreases from 207.6005 s to just 3.2830 s, yielding an impressive 63× speedup. This performance improvement is especially pronounced in complex models such as HappyBuddha, Dragon, and DragonFusion, where the KD tree reduces computation time from over 700–1000 s to under 21 s. Even for smaller models like Cow and Bunny, the KD tree consistently enhances the path construction efficiency. These findings validate the effectiveness of KD tree-based nearest-neighbor searches in accelerating Hamiltonian path generation, making the proposed method practical for real-time applications and large-scale reversible data hiding in encrypted 3D point clouds.
4.2. Algorithm Performance on Reversibility, Distortion, and Security
To comprehensively evaluate the proposed method, we conducted three types of analysis: reversibility, distortion, and geometric security. Reversibility is assessed using two metrics: the coordinate value difference rate (CVDR) and the bit error rate (BER). CVDR measures the relative difference between the original point coordinates and the recovered coordinates , as defined in Equations (6) and (7), where a lower CVDR indicates higher fidelity in terms of point recovery. A CVDR of 0% indicates that the two compared models are identical in all coordinate values. BER, as defined in Equation (8), quantifies the accuracy of message recovery by comparing the original embedded message with the extracted message , where denotes the total length of the secret message. A BER of 0% confirms the perfect reversibility of the hidden data. For all tested models, both CVDR and BER are 0%, demonstrating that the proposed algorithm achieves the fully lossless reconstruction of both geometry and embedded data.
To assess geometric distortion, all models were normalized to the unit cube [0, 1], and two widely used metrics were employed: the normalized Hausdorff distance (NHD) and normalized root mean square error (NRMSE), as defined in Equations (9)–(11). These metrics evaluate both the worst-case and average geometric deviations between the original model and its encrypted and embedded versions. As shown in Table 3, NHD values average at around 0.6740, while NRMSE values range from 0.5243 to 0.5259 across 20 diverse models. These values indicate that both the encrypted and embedded models differ significantly from the original model in terms of geometric structure, highlighting the strong distortion effect introduced by the proposed encryption and embedding scheme.

Table 3.
The results of the geometric distortion evaluation.
To further illustrate the geometric obfuscation effect of the proposed encryption process, Figure 5 presents histograms of the normalized , , and coordinates for the original model (left column) and the two encrypted shares and (middle and right columns), using the Armadillo model as an example. The original model exhibits structured, non-uniform distributions across all three coordinate axes, reflecting its inherent geometric features and spatial correlations. In contrast, both encrypted models and display nearly uniform histograms, indicating that the original geometric patterns have been thoroughly randomized. This transformation demonstrates that the proposed encryption method effectively flattens the spatial distribution, thereby concealing the model’s original shape and structure. The uniformity observed in the encrypted shares confirms the success of the geometric obfuscation and enhances security in the encrypted domain, as no obvious statistical cues about the original geometry are revealed.
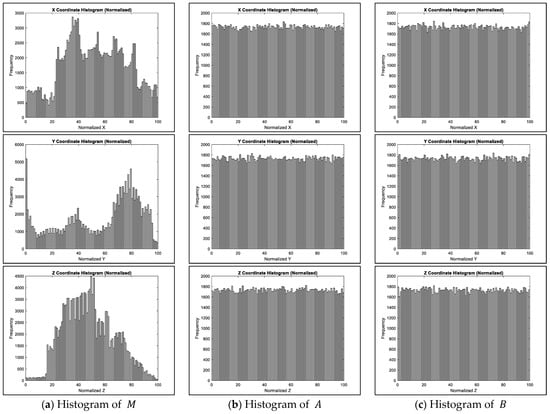
Figure 5.
Histogram of the original and two encrypted models of the Armadillo model.
While the current evaluation uses standard benchmark datasets to assess geometric distortion and recovery fidelity, we recognize that real-world industrial scenarios—such as sparse LIDAR scans or edge-degraded point clouds—present additional challenges. These include a lower point density, sensor noise, and irregular distribution, particularly in IoT and embedded-vision systems. Notably, the proposed method’s reliance on local prediction along a KD tree-constructed Hamiltonian path, rather than a global mesh structure, provides inherent adaptability to such degraded data. The dynamic label map further supports embedding in non-uniform regions. Future research will evaluate the algorithm’s robustness in such conditions, including automotive-grade LIDAR datasets and real-time streaming contexts that are relevant to ADAS and edge computing environments.
4.3. Computational Cost and Synchronization Considerations
The dual-model encryption design introduces a trade-off between enhanced security and added computational/storage complexity. In terms of time complexity, the KD tree-based path planning requires time for its initial construction and nearest-neighbor traversal. The multi-MSB prediction and label map generation processes operate in linear time , as does the Huffman encoding and decoding process.
During embedding and extraction, the interleaved embedding of the Huffman tree, label map, and secret message across two encrypted models requires synchronized traversal, based on a shared embedding path. This path, being deterministically generated using a key-driven KD tree sequence, allows consistent synchronization without the need for external signaling, provided that the keys are correctly preserved. Thus, the synchronization overhead is minimal in terms of software-based implementation but may require careful buffering in hardware-constrained systems.
The XOR-based (2, 2) secret sharing process adds negligible computational cost due to the bitwise XOR operations involved, which are hardware-efficient and parallelizable. However, the main storage overhead arises from the need to retain both encrypted models and , effectively doubling the storage requirements compared to single-model schemes. While this increases the system footprint, it also enables enhanced robustness against partial exposure and unauthorized access.
4.4. Performance Comparison with Current Algorithms
Table 4 presents a comparative analysis of the proposed algorithm against three existing reversible data hiding schemes for encrypted point clouds. The comparison focuses on four key aspects: embedding rate, embedding algorithm, embedding capacity, and reference determination strategy. All methods achieve an embedding rate close to 100%, indicating full utilization of the model for data hiding. However, the embedding algorithms vary: the method in Ref. [22] adopts spatial encoding, whereas the authors of [23,24] and the proposed approach employ bit substitution techniques.

Table 4.
Comparisons between the proposed and existing algorithms on encrypted point clouds.
In terms of pure embedding capacity, the proposed method significantly outperforms the others under consideration, achieving a maximum of 51.09 bits per point, compared to 35.10 [23] and 41.40 [24] under the same subdivision threshold . This improvement is primarily attributable to three key factors: the adaptive multi-bit embedding strategy, the KD tree-based reference selection that enhances prediction accuracy, and the dual-model design, which allows the auxiliary information to be interleaved across two encrypted shares. By distributing metadata such as the Huffman tree and label map across both models, the proposed framework reduces redundancy and minimizes overhead, thereby maximizing the pure usable capacity per point. Unlike prior works that rely on octree subdivision to determine the reference points, the proposed method leverages the spatial efficiency of KD tree structures to maintain geometric continuity while minimizing auxiliary data overhead. This not only improves prediction accuracy but also reduces the burden of storing structural metadata. Overall, this comparison underscores the advantages of the proposed framework in achieving high-capacity, reversible, and efficient data hiding within the encrypted domain.
Since the proposed algorithm is the first to extend the concept of dual-image-based reversible data hiding to encrypted point clouds, we provide a comprehensive overview of various embedding techniques and embedding capacities across different media formats in Table 5. This comparison also reflects how the choice of media and algorithms is often guided by specific application requirements. For image-based algorithms, each pixel in a grayscale image is typically represented by 8 bits, which inherently limits the embedding capacity. Nevertheless, the algorithm developed by Thi et al. [8], which integrates a pixel-value-average embedding strategy, achieves an impressive capacity of 3.45 bits per pixel. In contrast, the method proposed by Huang et al. [21], although distortion-free, exhibits a relatively low embedding capacity, making it more suitable for applications where visual fidelity is critical. Similar constraints are observed in reversible data hiding algorithms designed for encrypted images [18,19], where distortion is less of a concern. As such, integrating more advanced embedding strategies could further enhance capacity in the encrypted image domain. Reversible data hiding in audio applications [20] also presents an exciting direction, as the sampling rate and bit depth of audio signals allow for substantial embedding potential. The referenced method extends the dual-image-based concept by using a magic matrix and modulus operations. Future research could explore algorithmic innovations that address challenges related to audio compression, auditory masking, encryption, format variability, and real-time processing. In contrast, the proposed algorithm operates on encrypted 3D point clouds, where each coordinate value is represented using 32-bit precision, resulting in 96-bit binary representations per point (three coordinates per point). After accounting for auxiliary information—including the label map and Huffman coding tree—the pure embedding capacity reaches up to 51.09 bits per point. This highlights the advantages of working in the 3D domain, where high data redundancy and structured prediction strategies allow for significantly greater embedding capacity, particularly with the proposed dual-model design.

Table 5.
Comparison of reversible data hiding techniques across encrypted media types.
Although Table 5 presents a comparison of reversible data hiding techniques across different encrypted media formats—including images, audio, halftone images, and 3D models—the units of embedding capacity (e.g., bits per pixel, bits per sample, bits per block, or bits per point) differ across domains. As a result, a direct numerical comparison between these values is not meaningful. To address this limitation and enable a more balanced evaluation, we additionally report the theoretical maximum embedding capacity for each method, based on its media structure and data representation. The embedding efficiency—defined as the ratio of effective capacity to maximum capacity (EC/Max)—is also provided. This enables a normalized understanding of how well each technique utilizes the available embedding space, independent of its underlying unit. The proposed method, for instance, achieves approximately 53.22% of its theoretical maximum (51.09/96 bits per point), demonstrating high efficiency despite the additional constraints of encryption and reversibility.
5. Conclusions and Future Work
This study presents a pioneering exploration of RDH in encrypted point clouds through the explicit use of a dual-model approach. The proposed method significantly enhances embedding capacity while ensuring robust model privacy and message security. By incorporating encryption at the initial stage and generating two interdependent encrypted models, the algorithm is fortified against unauthorized access and data breaches. The experimental results validate the effectiveness of the proposed framework in securely embedding data within 3D models, maintaining an optimal balance between data integrity and embedding efficiency. Through the integration of techniques such as coordinate transformation, label map generation, and a novel interleaved embedding strategy, this work successfully extends the concept of dual-image-based RDH to the 3D domain, marking a substantial advancement in secure data embedding for complex spatial media. Moreover, the framework’s secure and reversible design makes it suitable for applications in safety-critical domains such as IoT sensing, autonomous systems, and embedded cybersecurity.
Several directions remain open for future research. First, applying the proposed algorithm to application domains such as healthcare, digital forensics, and virtual or augmented reality—where the confidentiality and integrity of 3D data are paramount—could demonstrate its practical value. Second, future work may investigate integrating our framework with lightweight cryptographic protocols and real-time embedded systems to support deployment in safety-critical applications such as IoT devices and autonomous platforms. Future research will also explore hardware-friendly designs and synchronization-aware embedding strategies to support efficient deployment of the dual-model framework on edge- and resource-constrained systems. Moreover, adapting the method for real-time operation in cyber-physical systems such as UAV mapping, live surveillance, and autonomous navigation will be an essential direction for future development, with a focus on streaming-based embedding and latency-aware optimization. Third, exploring cross-media reversible data hiding, which integrates audio, video, and 3D models, may unlock new possibilities in multimedia security. Additionally, evaluating this framework on real-world industrial datasets—such as sparse or degraded LIDAR point clouds, as used in automotive and IoT applications—will be an important future direction to validate its robustness and adaptability under deployment constraints. Future research will also include profiling the method’s performance under constrained computing environments, with a focus on memory usage, runtime latency, and embedded deployment feasibility for large-scale industrial scans. Moreover, we aim to investigate the secure provisioning of cryptographic keys in practical settings. Specifically, integrating physical-layer-assisted key generation schemes—such as MobileKey [26], which leverages wireless channel characteristics for real-time key agreement—may enable lightweight, context-aware key distribution without relying on pre-shared secrets. This integration will be studied in conjunction with our dual-model encryption and auxiliary embedding strategies to ensure usability and end-to-end security. Lastly, we plan to investigate potential side-channel inference risks [27]—such as those arising from timing, power, or cache-based leakage—which may compromise secure data hiding under practical implementations. Incorporating side-channel-resistant designs will be essential to strengthen the proposed framework against real-world deployment threats. In addition, we will explore practical countermeasures against physical and side-channel attacks, including randomized embedding sequences, hardware shielding, and secure execution environments. Future extensions will involve empirical evaluations of the framework’s resilience to such attacks, as well as examining interoperability with secure communication infrastructures and its scalability to distributed systems, such as IoT and edge networks.
Author Contributions
Conceptualization, Y.-Y.T., C.-Y.L. and C.-Y.H.; methodology, Y.-Y.T., C.-Y.L. and C.-Y.H.; funding acquisition, Y.-Y.T. and C.-Y.H.; software, Y.-Y.T., C.-Y.L. and C.-Y.H.; validation, C.-Y.L. and C.-Y.H.; data curation, C.-Y.L. and C.-Y.H.; writing—original draft preparation, Y.-Y.T. and C.-T.L.; writing—review and editing, Y.-Y.T. and C.-T.L.; supervision, Y.-Y.T. and C.-T.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded by the National Science and Technology Council of Taiwan under the grant numbers NSTC 114-2221-E-035-048 and NSTC 112-2813-C-468-020-E.
Data Availability Statement
The data presented in this study are available from the corresponding authors upon reasonable request, due to privacy considerations.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Ni, Z.; Shi, Y.Q.; Ansari, N.; Su, W. Reversible Data Hiding. IEEE Trans. Circuits Syst. Video Technol. 2006, 16, 354–362. [Google Scholar] [CrossRef] [PubMed]
- Tian, J. Reversible Data Embedding Using a Difference Expansion. IEEE Trans. Circuits Syst. Video Technol. 2003, 13, 890–896. [Google Scholar] [CrossRef]
- Luo, L.; Chen, Z.; Chen, M.; Zeng, X.; Xiong, Z. Reversible Image Watermarking Using Interpolation Technique. IEEE Trans. Inf. Forensics Secur. 2010, 5, 187–193. [Google Scholar] [CrossRef]
- Chang, C.-C.; Kieu, T.D.; Chou, Y.-C. Reversible Data Hiding Scheme Using Two Steganographic Images. In Proceedings of the IEEE Region 10 International Conference (TENCON), Taipei, Taiwan, 30 October–2 November 2007; pp. 1–4. [Google Scholar] [CrossRef]
- Chen, X.; Zhong, H.; Qiu, A. Reversible Data Hiding Scheme in Multiple Encrypted Images Based on Code Division Multiplexing. Multimed. Tools Appl. 2019, 78, 7499–7516. [Google Scholar] [CrossRef]
- Lu, T.-C.; Tseng, C.-Y.; Wu, J.-H. Dual Imaging-Based Reversible Hiding Technique Using LSB Matching. Signal Process. 2015, 108, 77–89. [Google Scholar] [CrossRef]
- Lu, T.-C.; Wu, J.-H.; Huang, C.-C. Dual-Image-Based Reversible Data Hiding Method Using Center Folding Strategy. Signal Process. 2015, 115, 195–213. [Google Scholar] [CrossRef]
- Thi, L.C.; Kim, S.N.; Van, A.P. Dual-Image Reversible Data Hiding Method Using Maximum Embedding Ability of Each Pixel. J. Inf. Secur. Appl. 2023, 74, 103470. [Google Scholar] [CrossRef]
- Xie, X.-Z.; Chang, C.-C.; Lin, C.-C. A Hybrid Reversible Data Hiding for Multiple Images with High Embedding Capacity. IEEE Access 2019, 8, 37–52. [Google Scholar] [CrossRef]
- Yao, H.; Mao, F.; Tang, Z.; Qin, C. High-Fidelity Dual-Image Reversible Data Hiding via Prediction-Error Shift. Signal Process. 2020, 170, 107447. [Google Scholar] [CrossRef]
- He, Z.; Fan, X.; Peng, Y.; Shen, Z.; Jiao, J.; Liu, M. EmPointMovSeg: Sparse Tensor-Based Moving-Object Segmentation in 3-D LiDAR Point Clouds for Autonomous Driving-Embedded System. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2023, 42, 41–53. [Google Scholar] [CrossRef]
- Hussain, T.; Khan, M.N.; Yang, B.; Attar, R.W.; Alhomoud, A. LiDAR Point Cloud Transmission: Adversarial Perspectives of Spoofing Attacks in Autonomous Driving. Comput. Secur. 2025, 157, 104544. [Google Scholar] [CrossRef]
- Su, Y.; Li, L.; Liu, Y.; Zhang, Y.; Ye, Y.; Jiang, X.; Chen, Z.; Xie, Y. A Novel Scheme to Encrypting Autonomous Driving Scene Point Clouds Based on Optical Chaos. J. Inf. Secur. Appl. 2025, 93, 104166. [Google Scholar] [CrossRef]
- Xiang, B.; Wielgosz, M.; Kontogianni, T.; Peters, T.; Puliti, S.; Astrup, R.; Schindler, K. Automated Forest Inventory: Analysis of High-Density Airborne LiDAR Point Clouds with 3D Deep Learning. Remote Sens. Environ. 2024, 305, 114078. [Google Scholar] [CrossRef]
- Yue, H.; Wang, Q.; Zhao, H.; Zeng, N.; Tan, Y. Deep Learning Applications for Point Clouds in the Construction Industry. Autom. Constr. 2024, 168, 105769. [Google Scholar] [CrossRef]
- Reinders, E.; van Rensburg, B.J.; Puteaux, P.; Puech, W. MSB-Based Reversible Data-Hiding in Encrypted 3D Object Using a Hamiltonian Path. In Proceedings of the IEEE 25th International Workshop on Multimedia Signal Processing, Poitiers, France, 27–29 September 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Yin, Z.; Xiang, Y.; Zhang, X. Reversible Data Hiding in Encrypted Images Based on Multi-MSB Prediction and Huffman Coding. IEEE Trans. Multimed. 2019, 22, 874–884. [Google Scholar] [CrossRef]
- Bhardwaj, R. Hiding Patient Information in Medical Images: An Enhanced Dual Image Separable Reversible Data Hiding Algorithm for E-Healthcare. J. Ambient Intell. Humaniz. Comput. 2023, 14, 321–337. [Google Scholar] [CrossRef]
- Kim, C.; Dao, N.-N.; Jung, K.-H.; Leng, L. Dual Reversible Data Hiding in Encrypted Halftone Images Using Matrix Encoding. Electronics 2023, 12, 3134. [Google Scholar] [CrossRef]
- Yu, H.; Wang, R.; Dong, L.; Yan, D.; Gong, Y.; Lin, Y. A High-Capacity Reversible Data Hiding Scheme Using Dual-Channel Audio. IEEE Access 2020, 8, 162271–162278. [Google Scholar] [CrossRef]
- Huang, Y.-H.; Kuo, P.-L.; Peng, C.-S.; Tsai, Y.-Y. Exploring Homogeneity Index Modification on Dual-HDR-Image-Based Reversible Data Hiding. Multimed. Tools Appl. 2025, 84, 12037–12059. [Google Scholar] [CrossRef]
- Tsai, Y.-Y. Separable Reversible Data Hiding for Encrypted Three-Dimensional Models Based on Spatial Subdivision and Space Encoding. IEEE Trans. Multimed. 2021, 23, 2286–2296. [Google Scholar] [CrossRef]
- Hou, G.; Ou, B.; Long, M.; Peng, F. Separable Reversible Data Hiding for Encrypted 3D Mesh Models Based on Octree Subdivision and Multi-MSB Prediction. IEEE Trans. Multimed. 2024, 26, 2395–2407. [Google Scholar] [CrossRef]
- Tsai, Y.-Y.; Jao, W.-T.; Lin, A.; Wang, S.-Y. Advanced Octree-Based Reversible Data Hiding in Encrypted Point Clouds. J. Inf. Secur. Appl. 2025, 89, 104006. [Google Scholar] [CrossRef]
- Tsai, Y.-Y.; Liu, H.-L. Integrating Coordinate Transformation and Random Sampling into High-Capacity Reversible Data Hiding in Encrypted Polygonal Models. IEEE Trans. Dependable Secur. Comput. 2023, 20, 3508–3519. [Google Scholar] [CrossRef]
- Song, K.; Zhu, Z.; Yang, H.; Ni, T.; Xu, W. Mobilekey: A Fast and Robust Key Generation System for Mobile Devices. In Proceedings of the 2022 ACM International Joint Conference on Pervasive and Ubiquitous Computing and the 2022 ACM International Symposium on Wearable Computers, Cambridge, UK, 11–15 September 2022; pp. 427–431. [Google Scholar] [CrossRef]
- Genkin, D.; Pachmanov, L.; Pipman, I.; Tromer, E.; Yarom, Y. ECDSA Key Extraction from Mobile Devices via Nonintrusive Physical Side Channels. In Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security, Vienna, Austria, 24–28 October 2016; pp. 1626–1638. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).