Weighted Prime Number Theorem on Arithmetic Progressions with Refinements

Abstract

We present an extension of the Dirichlet-type prime number theorem to weighted counting functions, the importance of which has recently been recognized for formulating Chebyshev’s bias. Moreover, we prove that their difference ${\pi }_w(x;q,a)-{\pi }_w(x;q,b)$ ($0\le w<1/2$) changes its sign infinitely many times as x grows for any coprime $a,b$$(a\ne b)$ with q, under the assumption that Dirichlet L-functions have no real nontrivial zeros. This result gives a justification of the theory of Aoki–Koyama that Chebyshev’s bias is formulated by the asymptotic behavior of ${\pi }_w(x;q,a)-{\pi }_w(x;q,b)$ at $w=1/2$.

1. Introduction

We define the weighted counting function of primes in arithmetic progressions as

$${\pi }_w(x;q,a)=\sum _{\genfrac{}{}{0.0pt}{}{p<x:\mathrm{prime}}{p\equiv a(modq)}}\frac{1}{p^w}(w\ge 0)$$

for $q\in \mathbb{Z}$. This is a generalization of the classical counting function $\pi (x;q,a)={\pi }_0(x;q,a)$. In 1837, Dirichlet proved that

$$\pi (x;q,a)\sim \pi (x;q,b)(x\to \infty )$$

for any a, b, which are coprime with q, where $f\left(x\right)\sim g\left(x\right)$ $(x\to \infty )$ means that $f\left(x\right)/g\left(x\right)\to 1$ as $x\to \infty$.

On the other hand, in 1853, Chebyshev [1] found the phenomenon that there tend to be more primes p satisfying $p\equiv 3(mod4)$ than those with $p\equiv 1(mod4)$. In fact, the inequality

$$\pi (x;4,3)\ge \pi (x;4,1)$$

(1)

holds for any x less than 26,861, which is the first prime number violating the inequality (1). However, both sides draw equal at the next prime 26,863, and $\pi (x;4,3)$ gets ahead again until 616,841. It is computed that more than 97% of $x<{10}^{11}$ satisfy the inequality (1). This phenomenon is called Chebyshev’s bias and is one of the major unsolved mysteries in number theory.

Later, Littlewood [2,3] proved that the difference $\pi (x;4,3)-\pi (x;4,1)$ changes its sign infinitely many times. In 2023, Aoki and Koyama [4] suggested that Littlewood’s phenomenon no longer holds if we put the weight $p^{-1/2}$. They actually obtained the asymptotic under the assumption of the Deep Riemann Hypothesis that

$${\pi }_{\frac{1}{2}}(x;4,3)-{\pi }_{\frac{1}{2}}(x;4,1)\sim \frac{1}{2}\log \log x(x\to \infty ).$$

(2)

The Deep Riemann Hypothesis (DRH) is a conjecture asserting the convergence of the Euler product of the corresponding L-function on the critical line. More precisely, in the case of Dirichlet L-functions, the DRH is stated as follows.

Conjecture 1

(Deep Riemann Hypothesis (DRH)). Let m be the order of the zero of a Dirichlet L-function $L(s,\chi )$ at $s=1/2$. Then, it holds that

$$\underset{x\to \infty }{lim}\left({\left(\log x\right)}^m\prod _{p\le x}{\left(1-\chi \left(p\right)p^{-\frac{1}{2}}\right)}^{-1}\right)={\displaystyle \frac{\sqrt{2}{L}^{\left(m\right)}(1/2,\chi )}{e^{m\gamma }m!}}.$$

Conjecture 1 was proposed by Kurokawa in his Japanese book [5] in 2012 and first appeared in English literature in [6] in 2014. It is known that the DRH implies the GRH.

When $q=4$, we find that $m=0$, and DRH asserts the convergence of the Euler product at $s=1/2$. Then, the asymptotic (2) follows from the Taylor expansion of the logarithm of the Euler product.

For more general q, Aoki–Koyama [4] defined the Chebyshev bias towards $p\equiv b(modq)$ (or against $p\equiv a(modq)$) as the asymptotic

$${\pi }_{\frac{1}{2}}(x;q,b)-{\pi }_{\frac{1}{2}}(x;q,a)\sim C\log \log x(x\to \infty )$$

(3)

with a constant $C>0$ depending on q. Under DRH, it is also proved for any $w>1/2$ that

$${\pi }_w(x;q,b)-{\pi }_w(x;q,a)=O\left(1\right)(x\to \infty ).$$

(4)

This was one of the reasons why Aoki–Koyama chose $w=1/2$ for formulating the bias.

The new formulation (3) concerns a different aspect from those dealt with by the definitions discovered by Rubinstein–Sarnak [7] and developed by Akbary–Ng–Shahabi [8], Devin [9], and so on. We find that (3) is an estimate of the size of the discrepancy caused by Chebyshev’s bias, which was ignored by the conventional definitions using the (logarithmic) length of the interval in terms of limiting distributions in the following sense.

For example, if, among the first 100 prime numbers, 50 of the first half are of the form $4k+3$ and those of the latter half are of the form $4k+1$, the inequality $\pi (x;4,3)\ge \pi (x;4,1)$ always holds in this interval even if their total number of elements are equal, and the maximum difference becomes 50. On the other hand, in the case that primes of the form $4k+3$ and $4k+1$ appear alternately, the maximum difference may be 1 even if the same inequality holds incessantly. The conventional definition cannot distinguish these two extreme cases because they have the same length of the interval where the inequality holds.

From this discussion, it is effective to apply the structure that “regards smaller primes as heavier elements”, reflecting the magnitudes of the primes, in order to elucidate Chebyshev’s bias. This is the reason why the weighted counting function is effective and why the formulation (2) is convincing. But there still remains an open problem concerning their choice of $w=1/2$. That is, the behavior of the left-hand side of (4) for $0<w<1/2$ was unknown.

In this paper, we will solve this problem by generalizing Littlewood’s theorem to $0\le w<1/2$. In what follows, we use the standard notation

$$Li\left(x\right)={\int }_2^x{\displaystyle \frac{dt}{\log t}}.$$

and $\phi \left(q\right)=\#{(\mathbb{Z}/q\mathbb{Z})}^{\times }$. Our first main theorem is as follows.

Theorem 1

(Weighted prime number theorem). Let $a\in \mathbb{Z}$ be coprime with $q\in \mathbb{Z}$. For $0\le w<1$, it holds that

$${\pi }_w(x;q,a)\sim {\displaystyle \frac{1}{\phi \left(q\right)}}Li\left(x^{1-w}\right)(x\to \infty ).$$

When $q=1$, the first author [10] proved the weighted prime number theorem:

$${\pi }_w(x;1,1)\sim Li\left(x^{1-w}\right)(x\to \infty )$$

for $0\le w<1$, and Theorem 1 is a generalization of it.

We write $f\left(x\right)=\Omega \left(g\right(x\left)\right)$$(x\to \infty )$ if the following holds: There exists a constant $C>0$ such that for any $x_0>0$, there exist $x_1,x_2>x_0$ such that $f\left(x_1\right)>Cg\left(x_1\right)$ and $f\left(x_2\right)<-Cg\left(x_2\right)$.

It is known by Stark [11] (Theorem 2) that for any coprime $a,b$$(a\ne b)$ with q

$$\pi (x;q,a)-\pi (x;q,b)=\Omega \left({\displaystyle \frac{x^{\frac{1}{2}}}{\log x}}\right)(x\to \infty )$$

(5)

under the assumption that the Dirichlet L-function $L(s,\chi )$ has no zeros in the interval $0<s<1$ for any Dirichlet character $\chi$ modulo q. Actually, Stark obtained the estimate (5) for more general cases $\phi \left(q\right)\pi (x;q,a)-\phi \left(q^{\prime }\right)\pi (x;q^{\prime },b)$, but for our purpose, the case $q=q^{\prime }$ is sufficient.

Our second main theorem is a generalization of it.

Theorem 2.

Suppose that $L(s,\chi )$ has no zeros in the interval $0<s<1$ for any Dirichlet character χ modulo q. For $0\le w<1/2$ and any coprime $a,b$$(a\ne b)$ with q, it holds that

$${\pi }_w(x;q,a)-{\pi }_w(x;q,b)=\Omega \left({\displaystyle \frac{x^{\frac{1}{2}-w}}{\log x}}\right)(x\to \infty ).$$

In particular, ${\pi }_w(x;q,a)-{\pi }_w(x;q,b)$$(0\le w<1/2)$ changes its sign infinitely many times.

This is a generalization of the theorem of the first author [10] for the case of $q=1$, where he proved that

$${\pi }_w(x;1,1)-\mathrm{Li}\left(x^{1-w}\right)(0\le w<1/2)$$

(6)

changes its sign infinitely many times.

Theorem 1 together with the estimate (4) justifies the choice of $w=1/2$ for the formulation of Chebyshev’s bias.

2. Weighted Prime Number Theorem

The following lemma was proved in the previous paper [10].

Lemma 1.

Assume $f\left(x\right)$ and $g\left(x\right)$ are positive valued functions on $x\ge 0$. If ${\displaystyle \underset{x\to \infty }{lim}{\int }_0^{x}f\left(t\right)dt=\infty }$ and $g\left(t\right)=o\left(1\right)$, it holds that

$${\int }_0^{x}f\left(t\right)g\left(t\right)dt=o\left({\int }_0^{x}f\left(t\right)dt\right)(x\to \infty ).$$

For q, $a\in \mathbb{Z}$ with $(a,q)=1$ and $0\le w<1$, we denote

$${\psi }_w(x;q,a)=\sum _{\begin{array}{c}p\equiv a(modq)\\ p^m\le x\end{array}}{\displaystyle \frac{\log p}{p^{mw}}},$$

where the sum is taken over pairs $(p,m)$, with m a positive integer and p a prime satisfying $p\equiv a(modq)$ and $p^m\le x$.

Lemma 2.

$${\psi }_w(x;q,a)\sim {\displaystyle \frac{x^{1-w}}{\phi \left(q\right)(1-w)}}(x\to \infty )$$

Proof. 

Putting $\psi (x;q,a)={\psi }_0(x;q,a)$, we have by partial summation that

$${\psi }_w(x;q,a)={\displaystyle \frac{\psi (x;q,a)}{x^w}}+w{\int }_2^x{\displaystyle \frac{\psi (t;q,a)}{t^{w+1}}}dt.$$

From the classical prime number theorem $\psi (x;q,a)=x/\phi \left(q\right)+o\left(x\right)$ $(x\to \infty )$, we compute

$${\psi }_w(x;q,a)={\displaystyle \frac{1}{\phi \left(q\right)}}\left(x^{1-w}+o\left(x^{1-w}\right)+w{\int }_2^x{\displaystyle \frac{1}{t^w}}dt+{\int }_2^{x}o\left({\displaystyle \frac{1}{t^w}}\right)dt\right).$$

Here, the last integral is estimated by Lemma 1 as

$${\int }_2^{x}o\left({\displaystyle \frac{1}{t^w}}\right)dt=o\left({\int }_2^x{\displaystyle \frac{1}{t^w}}dt\right).$$

Thus, we have

$$\begin{array}{cc}\hfill {\psi }_w(x;q,a)& ={\displaystyle \frac{1}{\phi \left(q\right)}}\left(x^{1-w}+o\left(x^{1-w}\right)+w{\int }_2^x{\displaystyle \frac{1}{t^w}}dt+o\left({\int }_2^x{\displaystyle \frac{1}{t^w}}dt\right)\right)\hfill \\ \hfill & ={\displaystyle \frac{1}{\phi \left(q\right)}}{\displaystyle \frac{x^{1-w}}{1-w}}+o\left(x^{1-w}\right).\hfill \end{array}$$

The proof is complete.   □

For $0\le w<1$, we put

$${\theta }_w(x;q,a)=\sum _{\begin{array}{c}p\equiv a(modq)\\ p\le x\end{array}}{\displaystyle \frac{\log p}{p^w}},$$

where the sum is taken over primes p satisfying $p\equiv a(modq)$ and $p\le x$.

Lemma 3.

It holds that

$${\psi }_w(x;q,a)-{\displaystyle \frac{\sqrt{x}\log x}{(1-2w)x^w}}\le {\theta }_w(x;q,a)\le {\psi }_w(x;q,a).$$

Proof. 

From the definitions, the right inequality is immediate. The left one is deduced as follows.

$$\begin{array}{cc}\hfill {\psi }_w(x;q,a)-{\theta }_w(x;q,a)& \le \log x\sum _{\begin{array}{c}p\equiv a(modq)\\ p\le \sqrt{x}\end{array}}{\displaystyle \frac{1}{p^{2w}}}\le \log x\sum _{2\le n\le \sqrt{x}}{\displaystyle \frac{1}{n^{2w}}}\hfill \\ \hfill & \le \log x{\int }_1^{\sqrt{x}}{\displaystyle \frac{dt}{t^{2w}}}\le {\displaystyle \frac{x^{\frac{1}{2}-w}\log x}{1-2w}}.\hfill \end{array}$$

The proof is complete.   □

Proof of Theorem 1.

From Lemmas 2 and 3, we have

$$\begin{array}{c}\hfill {\theta }_w(x;q,a)\sim {\psi }_w(x;q,a)\sim {\displaystyle \frac{x^{1-w}}{\phi \left(q\right)(1-w)}}(x\to \infty ).\end{array}$$

(7)

Now we will establish the relation between ${\theta }_w(x;q,a)$ and ${\pi }_w(x;q,a)$. Clearly, it holds that

$$\begin{array}{cc}\hfill {\theta }_w(x;q,a)& \le \sum _{\begin{array}{c}p\equiv a(modq)\\ p\le \sqrt{x}\end{array}}{\displaystyle \frac{\log x}{p^w}}=\left(\log x\right){\pi }_w(x;q,a).\hfill \end{array}$$

Hence,

$${\displaystyle \frac{{\theta }_w(x;q,a)}{\log x}}\le {\pi }_w(x;q,a).$$

On the other hand, for $0\le \epsilon <1$, we have $1<x^{1-\epsilon }\le x$ and

$$\begin{array}{cc}\hfill {\theta }_w(x;q,a)\ge \sum _{\begin{array}{c}p\equiv a(modq)\\ x^{1-\epsilon }\le p\le x\end{array}}{\displaystyle \frac{\log p}{p^w}}& \ge \sum _{\begin{array}{c}p\equiv a(modq)\\ x^{1-\epsilon }\le p\le x\end{array}}{\displaystyle \frac{\log x^{1-\epsilon }}{p^w}}\hfill \\ \hfill & =\log x^{1-\epsilon }\sum _{\begin{array}{c}p\equiv a(modq)\\ x^{1-\epsilon }\le p\le x\end{array}}{\displaystyle \frac{1}{p^w}}\hfill \\ \hfill & =\left(\log x^{1-\epsilon }\right)({\pi }_w(x;q,a)-{\pi }_w(x^{1-\epsilon };q,a)).\hfill \end{array}$$

Therefore,

$$\begin{array}{c}\hfill {\pi }_w(x;q,a)\le {\displaystyle \frac{1}{1-\epsilon }}·{\displaystyle \frac{{\theta }_w(x;q,a)}{\log x}}+{\pi }_w(x^{1-\epsilon };q,a).\end{array}$$

(8)

Since the last term is estimated as

$$\begin{array}{cc}\hfill {\pi }_w(x^{1-\epsilon };q,a)=\sum _{\begin{array}{c}p\equiv a(modq)\\ p\le x^{1-\epsilon }\end{array}}{\displaystyle \frac{1}{p^w}}& <\sum _{n\le x^{1-\epsilon }}{\displaystyle \frac{1}{n^w}}=O\left({\left(x^{1-w}\right)}^{1-\epsilon }\right),\hfill \end{array}$$

we conclude that

$$\begin{array}{c}\hfill {\displaystyle \frac{{\theta }_w(x;q,a)}{\log x}}\le {\pi }_w(x;q,a)\le {\displaystyle \frac{1}{1-\epsilon }}·{\displaystyle \frac{{\theta }_w(x;q,a)}{\log x}}+O\left({\left(x^{1-\epsilon }\right)}^{1-w}\right).\end{array}$$

(9)

Now, combining with (7), we reach

$${\pi }_w(x;q,a)\sim {\displaystyle \frac{{\theta }_w(x;q,a)}{\log x}}\sim {\displaystyle \frac{x^{1-w}}{\phi \left(q\right)(1-w)\log x}}\sim {\displaystyle \frac{\mathrm{Li}\left(x^{1-w}\right)}{\phi \left(q\right)}}.$$

The proof is complete.   □

3. Refinements

In this section, we prove Theorem 2. The following lemma plays the role for reducing the general weight w to the case of $w=0$.

Lemma 4.

$${\int }_0^{\infty }{\pi }_w(e^u;q,a)e^{-us}du={\displaystyle \frac{s+w}{s}}{\int }_0^{\infty }\pi (e^u;q,a)e^{-u(s+w)}du.$$

Proof. 

Denote by $p_n$ the n-th smallest element in the set of primes p such that $p\equiv a(modq)$. Putting $x=e^u$, we compute

$$\begin{array}{cc}\hfill {\int }_0^{\infty }{\pi }_w(e^u;q,a)e^{-us}du& ={\int }_1^{\infty }{\pi }_w(x;q,a)x^{-s-1}dx\hfill \\ \hfill & =\sum _{n=1}^{\infty }{\int }_{p_n}^{p_{n+1}}\sum _{\begin{array}{c}p\equiv a(modq)\\ p\le p_n\end{array}}{p}^{-w}{x}^{-s-1}dx\hfill \\ \hfill & =\sum _{n=1}^{\infty }\sum _{\begin{array}{c}p\equiv a(modq)\\ p\le p_n\end{array}}{p}^{-w}{\displaystyle \frac{p_n^{-s}-p_{n+1}^{-s}}{s}}\hfill \\ \hfill & ={\displaystyle \frac{1}{s}}\left(\sum _{n=1}^{\infty }\sum _{\begin{array}{c}p\equiv a(modq)\\ p\le p_n\end{array}}{p}^{-w}{p}_n^{-s}-\sum _{n=2}^{\infty }\sum _{\begin{array}{c}p\equiv a(modq)\\ p\le p_{n-1}\end{array}}{p}^{-w}{p}_n^{-s}\right)\hfill \\ \hfill & ={\displaystyle \frac{1}{s}}\left(p_1^{-s-w}+\sum _{n=2}^{\infty }{p}_n^{-s-w}\right)\hfill \\ \hfill & ={\displaystyle \frac{1}{s}}\sum _{n=1}^{\infty }{p}_n^{-s-w}.\hfill \end{array}$$

Hence, for $w=0$, we have

$${\int }_0^{\infty }\pi (e^u;q,a)e^{-us}du={\displaystyle \frac{1}{s}}\sum _{n=1}^{\infty }{p}_n^{-s}.$$

By substituting $s+w$ in the variable s, we obtain

$$\begin{array}{cc}\hfill {\int }_0^{\infty }\pi (e^u;q,a)e^{-u(s+w)}du& ={\displaystyle \frac{1}{s+w}}\sum _{n=1}^{\infty }{p}_n^{-s-w}\hfill \\ \hfill & ={\displaystyle \frac{s}{s+w}}{\int }_0^{\infty }{\pi }_w(e^u;q,a)e^{-us}du.\hfill \end{array}$$

The proof is complete.   □

We will apply the theory of Tauberian theorems, which was developed by Ingham in the following theorem.

Theorem 3

([12] (Theorem 1)). Let

$$F\left(s\right)={\int }_0^{\infty }A\left(u\right)e^{-su}du,$$

where $A\left(u\right)$ is real valued and absolutely integrable on every interval $0\le u\le U$, and the integral is absolutely convergent in some half plane $\sigma >{\sigma }_1\ge 0$.

Let $A^{*}\left(u\right)$ be a real trigonometrical polynomial

$$A^{*}\left(u\right)=\sum _{n=-N}^N{\alpha }_n{e}^{i{\gamma }_{n}u}({\gamma }_n\in \mathbb{R},{\gamma }_n={\gamma }_{-n},{\alpha }_n=\overline{{\alpha }_{-n}}),$$

and let

$$F^{*}\left(s\right)={\int }_0^{\infty }{A}^{*}\left(u\right)e^{-su}du=\sum _{n=-N}^N{\displaystyle \frac{{\alpha }_n}{s-i{\gamma }_n}}(\sigma >0).$$

Suppose that $F\left(s\right)-F^{*}\left(s\right)$ is regular in the region $\sigma \ge 0$, $-T\le t\le T$ for some $T>0$.

Then, it holds that

$$\underset{u\to \infty }{lim\; inf}A\left(u\right)\le \underset{u\to \infty }{lim}{A}_T^{*}\left(u\right)\le \underset{u\to \infty }{lim\; sup}A\left(u\right),$$

where

$$\begin{array}{cc}\hfill A_T^{*}\left(u\right)& =\sum _{|{\gamma }_n|\le T}\left(1-{\displaystyle \frac{|{\gamma }_n|}{T}}\right){\alpha }_n{e}^{i{\gamma }_{n}u}\hfill \\ \hfill & ={\alpha }_0+2\mathrm{Re}\left(\sum _{0<{\gamma }_n<T}\left(1-{\displaystyle \frac{{\gamma }_n}{T}}\right){\alpha }_n{e}^{i{\gamma }_{n}u}\right).\hfill \end{array}$$

This theorem was reformulated by Stark for the purpose of refining the estimate of $\pi (x;q,a)-\pi (x;q,b)$ as follows:

Theorem 4

([11] (p. 314)). Put $s=\sigma +it\in \mathbb{C}$. Let

$${\displaystyle \frac{F\left(s\right)}{s}}={\int }_0^{\infty }A\left(u\right)e^{-su}du,$$

where $A\left(u\right)$ is real valued and absolutely integrable on every interval $0\le u\le U$, and the integral is absolutely convergent for $\sigma >1$. For any real sequence ${\gamma }_n$$(n\in \mathbb{Z})$ with ${\gamma }_{-n}={\gamma }_n$ and coefficients ${\alpha }_n\in \mathbb{C}$ with ${\alpha }_{-n}=\overline{{\alpha }_n}$, set

$$F_1\left(s\right)=\sum _{n=-N}^N{\alpha }_n\log \left(s-{\displaystyle \frac{1}{2}}-i{\gamma }_n\right).$$

Suppose that for some $T>0$, $F^{\prime }\left(s\right)-F_1^{\prime }\left(s\right)$ is continuous in the region $\sigma \ge 1/2$, $-T\le t\le T$ and analytic in the interior of this region. Then, for any $u_0$,

$$\underset{u\to \infty }{lim\; sup}{\displaystyle \frac{uA\left(u\right)}{e^{u/2}}}\ge -\sum _{|{\gamma }_n|\le T}{\displaystyle \frac{{\alpha }_n}{\frac{1}{2}+i{\gamma }_n}}\left(1-{\displaystyle \frac{|{\gamma }_n|}{T}}\right)e^{i{\gamma }_n{u}_0}.$$

Theorem 4 follows from Theorem 3 applied to the derivative with respect to s of

$$\begin{array}{cc}\hfill {\displaystyle \frac{F\left(s\right)}{s}}& ={\int }_1^{\infty }\left(A\left(u\right)+{\displaystyle \frac{1}{u}}{\displaystyle \sum _{n=-N}^N}{\displaystyle \frac{{\alpha }_n}{\frac{1}{2}+i{\gamma }_n}}{e}^{({\displaystyle \frac{1}{2}}+i{\gamma }_n)u}\right)e^{-su}du.\hfill \\ \hfill & ={\displaystyle \sum _{n=-N}^N}{\displaystyle \frac{{\alpha }_n}{\frac{1}{2}+i{\gamma }_n}}\log \left(s-{\displaystyle \frac{1}{2}}-i{\gamma }_n\right)+\left(\mathrm{an}\mathrm{entire}\mathrm{function}\mathrm{in}s\right).\hfill \end{array}$$

(10)

The estimate (5) is an immediate consequence of Theorem 4 and the fact that the function

$${\int }_0^{\infty }\left(\pi (e^u;q,a)-\pi (e^u;q,b)\right)e^{-us}du$$

is analytic in $\mathrm{Re}\left(s\right)>1/2$ ([11] (Lemmas 1 and 2)).

Proof of Theorem 2.

From Lemma 4 and the above discussion, the function

$${\int }_0^{\infty }\left({\pi }_w(e^u;q,a)-{\pi }_w(e^u;q,b)\right)e^{-us}du$$

is analytic in $\mathrm{Re}\left(s\right)>{\displaystyle \frac{1}{2}}-w$. For $0<w<{\displaystyle \frac{1}{2}}$, we replace (10) with the following function:

$$\begin{array}{cc}\hfill {\displaystyle \frac{F_w\left(s\right)}{s+w}}& =\sum _{n=-N}^N{\displaystyle \frac{{\alpha }_n}{\frac{1}{2}+i{\gamma }_n}}\log \left(s+w-{\displaystyle \frac{1}{2}}-i{\gamma }_n\right)+\left(\mathrm{an}\mathrm{entire}\mathrm{function}\mathrm{in}s\right)\hfill \\ \hfill & ={\int }_1^{\infty }\left(A_w\left(u\right)+{\displaystyle \frac{1}{u}}\sum _{n=-N}^N{\displaystyle \frac{{\alpha }_n}{\frac{1}{2}+i{\gamma }_n}}{e}^{({\displaystyle \frac{1}{2}}-w+i{\gamma }_n)u}\right)e^{-su}du,\hfill \end{array}$$

where $A_w\left(u\right)={\pi }_w(e^u;q,a)-{\pi }_w(e^u;q,b)$. Then, for any $u_0$,

$$\underset{u\to \infty }{lim\; sup}{\displaystyle \frac{u{A}_w\left(u\right)}{e^{(\frac{1}{2}-w)u}}}\ge -\sum _{|{\gamma }_n|\le T}{\displaystyle \frac{{\alpha }_n}{\frac{1}{2}+i{\gamma }_n}}\left(1-{\displaystyle \frac{|{\gamma }_n|}{T}}\right)e^{i{\gamma }_n{u}_0}.$$

Consequently, it holds that

$$A_w\left(u\right)=\Omega \left({\displaystyle \frac{e^{(\frac{1}{2}-w)u}}{u}}\right),$$

which is the desired result.   □

4. Numerical Examples

Theorem 2 guarantees infinitely many sign changes of ${\pi }_w(x;q,a)-{\pi }_w(x;q,b)$, and one may want to know an example of x where the sign change occurs. But the history tells us that it is very hard to figure it out. Even in the simplest case when $q=1$ and $w=0$, the exact value giving a sign change of the difference (6) is not known. It was first proved by Skews in 1933 under the assumption of the Riemann Hypothesis that a sign change occurs at x less than ${10}^{{10}^{{10}^{34}}}$, and many works were done for improvements of the smallest x giving a sign change. The current record is obtained by Bays and Hudson [13] that a sign change occurs at x less than $1.3983\times {10}^{316}$. On the other hand, Kotnik [14] proved that there are no sign changes for $x<{10}^{14}$.

Therefore, it would also be difficult to give concrete examples of x where sign changes of ${\pi }_w(x;q,a)-{\pi }_w(x;q,b)$ occur for $0\le w<1/2$. However, the second author investigated the behavior of

$${\pi }_w(x;4,1)-{\pi }_w(x;4,3)=\sum _{p\le x}{\displaystyle \frac{\chi \left(p\right)}{p^w}}$$

(11)

with $\chi$ the nontrivial Dirichlet character modulo 4 for $w=0.4$ and $x\le {10}^{100}$, and introduced the results in his Japanese book [15]. Here, we quote the figures and calculations from it.

We denote by $\chi$ the nontrivial character modulo 4. Figure 1 shows the value of the series

$$r\left(x\right)=\sum _{p\le x}{\displaystyle \frac{\chi \left(p\right)}{p^w}}(x\le {10}^{100}),$$

for $w=0.5$ (upper in brown) and $w=0.4$ (lower in blue).

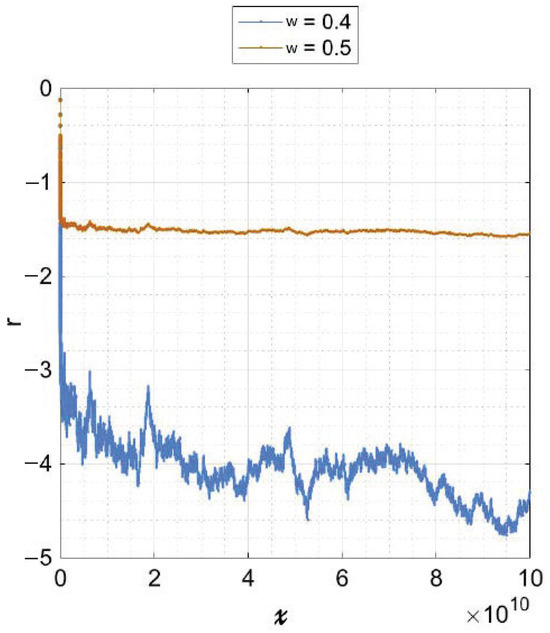
Figure 1. $r\left(x\right)$ with $w=0.4$ and $0.5$.

We see that the two behaviors of $r\left(x\right)$ are very different. Actually, for $w\ge 1/2$, as is implied by the DRH, the series $r\left(x\right)$ is very stable. On the other hand, the difference (11) drastically changes when we choose $w<1/2$.

5. Conclusions and Prospect

The main theorem obtained in this paper justifies our use of a weight $p^{1/2}$ in the formulation of the Chebyshev bias.

Aoki–Koyama’s paper [4] and subsequent research [16,17,18,19] have extended the Chebyshev bias to a wide range of cases. It is expected that similar theorems obtained in this paper will hold for all of them. The importance of weighted counting functions has only recently begun to be recognized for understanding the distribution of primes, and research extending classical results such as Littlewood’s work to weighted cases is likely to become increasingly important in the future.

Meanwhile, research is also being conducted to replace the Deep Riemann Hypothesis with other assumptions. Sheth [20] proved a weaker version of the Chebyshev bias by assuming only the Generalized Riemann Hypothesis instead of the Deep Riemann Hypothesis. His result yields an asymptotic formula similar to (3) as x runs through outside of an exceptional set with finite logarithmic measure. By relaxing the definition of the Chebyshev bias in this way, it may also be possible to demonstrate the Chebyshev bias assuming only the General Riemann Hypothesis.