Binary Secretary Bird Optimization Algorithm for the Set Covering Problem

Abstract

The Set Coverage Problem (SCP) is an important combinatorial optimization problem known to be NP-complete. The use of metaheuristics to solve the SCP includes different algorithms. In particular, binarization techniques have been explored to adapt metaheuristics designed for continuous optimization problems to the binary domain of the SCP. In this work, we present a new approach to solve the SCP based on the Secretary Bird Optimization Algorithm (SBOA). This algorithm is inspired by the natural behavior of the secretary bird, known for its ability to hunt prey and evade predators in its environment. Since the SBOA was originally designed for optimization problems in continuous space and the SCP is a binary problem, this paper proposes the implementation of several binarization techniques to adapt the algorithm to the discrete domain. These techniques include eight transfer functions and five different discretization methods. Taken together, these combinations create multiple SBOA adaptations that effectively balance exploration and exploitation, promoting an adequate distribution in the search space. Experimental results applied to the SCP together with its variant Unicost SCP and compared to Grey Wolf Optimizer and Particle Swarm Optimization suggest that the binary version of SBOA is a robust algorithm capable of producing high quality solutions with low computational cost. Given the promising results obtained, it is proposed as future work to focus on complex and large-scale problems as well as to optimize their performance in terms of time and accuracy.

1. Introduction

The use of optimization and, in particular, metaheuristics, is gaining more and more attention in modern industry as it allows to tackle problems that, until some time ago, were not possible to address. Today, it is possible to tackle complex and large-scale problems, with metaheuristics allowing us to obtain good quality solutions in a reasonable processing time [1]. Metaheuristics, in general, allow us to address different types of problems and can also adapt to changes in the environment, being able to work in different domains. All these characteristics make them attractive for solving current real-world problems in a variety of areas, such as logistics [2,3], manufacturing industry [4,5], transport [6,7], health [8,9], and mining [10,11], among others.

The Set Covering Problem (SCP) is a combinatorial optimization problem known to be NP-hard that is ever-present in various industries [12] and one of the 21 problems present in Karp [13]. It involves finding a subset of columns from a binary matrix A of size $m\times n$ that covers all rows at the lowest possible cost. This problem has significant applications in various fields, such as emergency service location [14], crew scheduling in mass transportation systems [15], and other related problems discussed in [16]. There is a special case of SCP where all sets have the same cost in this case the task is to minimize the selection of sets to cover the given universe. Practical applications in the industry are engineering design [17] and vehicle path planning [18], among others.

The use of metaheuristics to solve the SCP includes algorithms such as Genetic Algorithms [19], Particle Swarm Optimization [20], Ant Colony Optimization [21], Tabu Search [22], Electromagnetism metaheuristic [23], Artificial Bee Colony [24], and GRASP [25], among others. In particular, binarization techniques have been explored to adapt metaheuristics designed for continuous optimization problems to the binary domain of the SCP.

In this work, we present a new approach to solving the SCP based on the Secretary Bird Optimization Algorithm (SBOA) [26]. The SBOA was selected for this research for several compelling reasons, drawn directly from its original design and validated performance. First, it is a recent metaheuristic whose authors specifically engineered it to address common shortcomings of existing algorithms, aiming to improve convergence speed, enhance optimization accuracy, and effectively avoid local optima. These characteristics are highly desirable for tackling NP-hard problems like the SCP. Second, the SBOA achieves a robust balance between its exploration and exploitation phases by uniquely combining three different search strategies: differential evolution, Brownian motion, and Lévy flights. Finally, its effectiveness is not merely theoretical; the SBOA has demonstrated superior performance against numerous advanced algorithms on standard benchmark suites (CEC-2017 and CEC-2022) and has been successfully applied to solve twelve different constrained engineering problems.

Given these strengths, the SBOA emerges as a strong and novel candidate for adaptation to the binary domain to solve the SCP. The relevance of finding new and efficient solutions for this problem is underscored by its wide range of applications, which have become even more critical in modern industry. For example, in the post-pandemic era, supply chains and logistics face continuous challenges where the SCP is present [27], including the efficient allocation of resources and crews [28,29], balancing assembly lines, and optimizing the location of distribution centers to meet growing demand.

Since the SBOA was originally designed for optimization problems in continuous spaces and the SCP is a binary problem, this work proposes the implementation of several binarization techniques to adapt the algorithm to the discrete domain. These techniques include eight transfer functions with “S”-shaped and “V”-shaped variants and five different discretization methods. Together, these combinations create multiple adaptations of the SBOA that effectively balance exploration and exploitation, promoting an adequate distribution in the search space. The results suggest that the binary version of the SBOA (BSBOA) is a robust algorithm capable of producing high-quality solutions with low computational cost.

This article is organized as follows: We present a brief description of the Set Coverage Problem in Section 2, how to resolve SCP with continuos metaheuristics in Section 3, and an outline of the Secretary Bird Optimitation Algorithm in Section 4. We explain how and make the binary version of the SBOA in Section 5. Finally, we present our results, discussions, conclusions, and possible future lines of research in Section 6, Section 7 and Section 8.

2. Set Covering Problem

The Set Covering Problem (SCP) is a combinatorial optimization problem categorized as NP-hard. Its main objective is to find a minimal subset of elements that completely covers a universal set of requirements while minimizing the associated cost.

2.1. Formal Mathematical Formulation

Formally, let $U=\{u_1,u_2,\dots ,u_m\}$ be a universal set composed of m elements, and let $S=\{S_1,S_2,\dots ,S_n\}$ be a collection of n subsets, where each subset $S_j$ has an associated cost $c_j$. The problem consists of identifying an optimal subset $S^{\ast }\subseteq S$ that covers all elements in U at the minimum possible cost.

To model this problem and solve it computationally, the formal set-based definition is translated into a matrix formulation. A binary matrix represents the problem A with m rows and n columns. Each of the m rows corresponds to an element $u_i$ of the universal set U and each of the n columns represents an available subset $S_j$. The value in the matrix, $a_{i,j}$, is 1 if subset j covers element i (that is, $u_i\in S_j$), and 0 otherwise.

$$A=\left(\begin{array}{cccc}{a}_{1,1}& a_{1,2}& \dots & a_{1,n}\\ a_{2,1}& a_{2,2}& \dots & a_{2,n}\\ ⋮& ⋮& \ddots & ⋮\\ a_{m,1}& a_{m,2}& \dots & a_{m,n}\end{array}\right)$$

To decide which columns (subsets) are chosen, the binary decision variable $x_j$ is used, which takes the value of one if column j is selected for the solution, and zero if it is not.

Thus, the main objective is to minimize the total cost of the solution, summing the costs of only the selected columns, as indicated by Equation (1).

$$min\sum _{j=1}^n{c}_j{x}_j$$

(1)

The main constraint of this problem is the coverage constraint, which ensures that each element (row) is covered by at least one selected column. This is achieved with the following equation, which must hold for every row i:

$$\sum _{j=1}^n{a}_{i,j}{x}_j\ge 1$$

(2)

In addition, we must ensure that the decision variable is binary; therefore, $x_j\in \{0,1\}$.

2.2. SCP Practical Example

Let us assume a company needs to form an oversight committee for a new technology project. For the project to be successful, the committee must cover five areas of expertise: financial, legal, technical, marketing, and logistics. The company has identified six external consultants, each with a different set of skills and an associated cost (fee).

The goal is to apply the Set Covering Problem (SCP) to select the committee with the lowest total cost that guarantees coverage of all required areas of expertise.

2.2.1. Problem Definition

1.

Elements to be Covered: The five required areas of expertise.

• ${\mathrm{R}}_1$: Financial Expertise.
• ${\mathrm{R}}_2$: Legal Expertise.
• ${\mathrm{R}}_3$: Technical Expertise.
• ${\mathrm{R}}_4$: Marketing Expertise.
• ${\mathrm{R}}_5$: Logistics Expertise.

2.

Available Sets: The six candidates, each with their cost and skills.

• $C_1$: Anne (Cost: $4)—Skills: Financial, Legal.
• $C_2$: Ben (Cost: $3)—Skills: Technical, Marketing.
• $C_3$: Carla (Cost: $6)—Skills: Legal, Technical, Logistics.
• $C_4$: David (Cost: $4)—Skills: Marketing, Logistics.
• $C_5$: Elena (Cost: $5)—Skills: Financial, Technical.
• $C_6$: Frank (Cost: $4)—Skills: Legal, Marketing.

Thus, Table 1 shows the relationship between both previous lists in the so-called Incidence Matrix. This matrix reflects the coverage (columns) of each element (rows) and allows us to validate whether the requirements (problem constraints) are met.

Table 1. Incidence Matrix (A), where $a_{ij}=1$ if consultant j covers requirement i.

	C1 (Anne)	C2 (Ben)	C3 (Carla)	C4 (David)	C5 (Elena)	C6 (Frank)
R1 (Fin.)	1	0	0	0	1	0
R2 (Legal)	1	0	1	0	0	1
R3 (Tech.)	0	1	1	0	1	0
R4 (Mkt.)	0	1	0	1	0	1
R5 (Log.)	0	0	1	1	0	0

2.2.2. Mathematical Formulation

Let $x_j=1$ if consultant j is selected and 0 otherwise. The problem is formulated to minimize the total cost, subject to the constraint that each area of expertise is covered.

• Objective Function (minimize cost):

  $$min\left(Z\right)=4x_1+3x_2+6x_3+4x_4+5x_5+4x_6$$

  (3)
• Constraints (cover each expertise):

  $$\begin{array}{cccc}\hfill x_1+x_5& \ge 1\hfill & \hfill & \left(\mathrm{Financial}\right)\hfill \\ \hfill x_1+x_3+x_6& \ge 1\hfill & \hfill & \left(\mathrm{Legal}\right)\hfill \\ \hfill x_2+x_3+x_5& \ge 1\hfill & \hfill & \left(\mathrm{Technical}\right)\hfill \\ \hfill x_2+x_4+x_6& \ge 1\hfill & \hfill & \left(\mathrm{Marketing}\right)\hfill \\ \hfill x_3+x_4& \ge 1\hfill & \hfill & \left(\mathrm{Logistics}\right)\hfill \end{array}$$
• Decision Variables:

  $$x_j\in \{0,1\}\forall j\in \{1,\dots ,6\}$$

  (4)

2.2.3. Optimal Solution

The optimal solution for this problem is to select Anne ($C_1$), Ben ($C_2$), and David ($C_4$).

• Selected Consultants: {Anne, Ben, David}
• Coverage:

  -

  Anne covers the Financial and Legal areas.

  -

  Ben covers the Technical and Marketing areas.

  -

  David covers the Marketing and Logistics areas.

• Minimum Total Cost: $\$4\left(\mathrm{Anne}\right)+\$3\left(\mathrm{Ben}\right)+\$4\left(\mathrm{David}\right)=\$\mathbf{11}$.

This combination fulfills all expertise requirements at the lowest possible cost.

2.3. Unicost Set Covering Problem (Unicost SCP)

The unicost problem is a specific variant of the Set Covering Problem (SCP), in which all column costs are equal ($c_j=1$ for all $j\in J$). The primary objective in this case is to minimize the number of selected columns while ensuring that each row is covered by at least one of them. This variant simplifies the general SCP model by focusing exclusively on the minimum number of columns required to cover all rows, emphasizing structural optimization without considering cost variations.

Mathematically, the model can be formulated as follows:

$$\mathrm{Minimize}\sum _{j\in J}{x}_j$$

(5)

subject to

$$\sum _{j\in J}{a}_{ij}{x}_j\ge 1\mathrm{for}\mathrm{all}i\in I,$$

(6)

$$j\in \{0,1\}\mathrm{for}\mathrm{all}j\in J,$$

(7)

where $a_{ij}$ is a coefficient indicating whether column j covers row i, $x_j$ is a binary variable that takes the value 1 if column j is selected and 0 otherwise, I is the set of rows, and J is the set of columns.

The unicost problem, like the general SCP, is known to be NP-hard and has been applied in various fields, such as scheduling, logistics, and resource optimization.

3. Continuous Metaheuristics Solving Set Covering Problem

To apply the Secretary Bird Optimization Algorithm (SBOA) to the Set Covering Problem (SCP), it is necessary to adapt the original search approach, designed for a continuous space, to a binary environment. As discussed in Section 1, various metaheuristics have been successfully applied to solve the SCP, including Genetic Algorithms [30], Ant Colony Optimization [31], Particle Swarm Optimization [32], and others. All these metaheuristics have one characteristic in common: they are metaheuristics designed to solve continuous optimization problems that were modified to resolve binary problems like the SCP.

This adaptation is achieved through a Two-Step Technique that converts continuous solutions into binary solutions, ensuring compliance with the SCP requirements. This technique is fundamental for applying bioinspired algorithms to binary combinatorial optimization problems, such as the SCP.

Two-Step Technique

In the literature, there are different ways to binarize continuous metaheuristics [33], but the most widely used is the Two-Step Technique [34]. As its name suggests, the binarization process is performed in two stages:

• Application of a transfer function, which transforms the continuous value into a value within the range $[0,1]$.
• Application of a binarization rule, which determines the assignment of a 1 or a 0.

In the literature [33], a variety of transfer functions are proposed for this purpose. They are generally categorized into two main families based on their shape and behavior: S-shaped and V-shaped functions. These two families represent the most common and well-established approaches for mapping continuous search spaces to binary ones.

• S-Shaped Functions: These sigmoidal functions produce a value in the range $[0,1]$ that represents the probability of a solution’s component becoming ‘1’. An input value close to zero yields a probability near 0.5, while large positive or negative values push the probability towards 1 or 0, respectively. This behavior models a form of probabilistic switch.
• V-Shaped Functions: In contrast, these functions relate the probability of change to the magnitude of the continuous value, rather than its sign. A small step (a value close to zero) results in a low probability of changing the bit, while a large step increases this probability. This is conceptually linked to the notion of velocity or momentum in swarm algorithms, where a larger “move” is more likely to alter the solution’s state.

Table 2 and Figure 1 present the standard functions from both families that are commonly used in this research area. The notation $d_j^i$ observed in the table corresponds to the continuous value of the j-th dimension of the i-th individual, resulting from the perturbation performed by the continuous metaheuristic.

Table 2. S-shaped and V-shaped transfer functions.

S-Shaped		V-Shaped
Name	Equation	Name	Equation
S1	$T\left(d_j^i\right)={\displaystyle \frac{1}{1+e^{-2d_j^i}}}$	V1	$T\left(d_j^i\right)=\left|\mathrm{erf}\left(\sqrt{{\displaystyle \frac{\pi }{2}}{d}_j^i}\right)\right|$
S2	$T\left(d_j^i\right)={\displaystyle \frac{1}{1+e^{-d_j^i}}}$	V2	$T\left(d_j^i\right)=\left|tanh\left(d_j^i\right)\right|$
S3	$T\left(d_j^i\right)={\displaystyle \frac{1}{1+e^{-d_j^i/2}}}$	V3	$T\left(d_j^i\right)=\left|{\displaystyle \frac{d_j^i}{\sqrt{1+{\left(d_j^i\right)}^2}}}\right|$
S4	$T\left(d_j^i\right)={\displaystyle \frac{1}{1+e^{-d_j^i/3}}}$	V4	$T\left(d_j^i\right)=\left|{\displaystyle \frac{2}{\pi }}arctan\left({\displaystyle \frac{\pi }{2}}{d}_j^i\right)\right|$

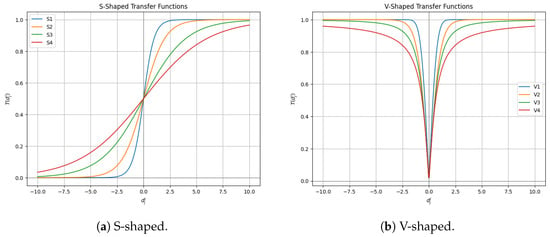
Figure 1. S-shaped and V-shaped transfer functions.

Additionally, in the literature [33], we can find five different binarization rules, of which we can highlight the following:

• Standard (STD): If the condition is satisfied, the standard binarization rule returns 1; otherwise, it returns 0. Mathematically, it is defined as follows:

  $$X_{\mathrm{new}}^j=\left\{\begin{array}{cc}1\hfill & \mathrm{if}\mathrm{rand}\le T\left(d_i^j\right),\hfill \\ 0\hfill & \mathrm{else}.\hfill \end{array}\right.$$

  (8)
• Elitist (ELIT): The best value is assigned if a random value is within the probability; otherwise, a zero value is assigned. Mathematically, it is defined as follows:

  $$X_{\mathrm{new}}^j=\left\{\begin{array}{cc}{X}_{\mathrm{Best}}^j\hfill & \mathrm{if}\mathrm{rand}<T\left(d_i^j\right),\hfill \\ 0\hfill & \mathrm{else}.\hfill \end{array}\right.$$

  (9)
• Complement (COM): If the condition is satisfied, the second step operator returns the complement of the actual value.

  $$\left\{\begin{array}{cc}{x}_{\mathrm{new}}^j=\mathrm{complement}\left(x_w^j\right)\hfill & \mathrm{if}\mathrm{rand}\le T\left(d_w^j\right),\hfill \\ 0\hfill & \mathrm{else}.\hfill \end{array}\right.$$

  (10)

4. Secretary Bird Optimization Algorithm

The Secretary Bird Optimization Algorithm (SBOA) is a metaheuristic inspired by the natural behavior of the secretary bird, particularly its unique strategies for hunting and evading predators. It was proposed in 2024 by Youfa Fu, Dan Liu, Jiadui Chen, and Ling He [26]. The algorithm was originally designed to solve continuous optimization problems, leveraging its exploration and exploitation phases to efficiently find optimal solutions.

The operation of the SBOA is divided into two main phases that mimic the bird’s survival instincts: exploration, which models its hunting strategy, and exploitation, which models its escape strategy.

4.1. Exploration Phase (Hunting Strategy)

This phase simulates how the secretary bird hunts its prey, like snakes, and corresponds to a global search in the solution space. The process is modeled in three stages that reflect the bird’s hunting tactics:

• Searching for Prey: The bird begins by exploring the terrain to locate hidden prey. The algorithm mimics this by creating a new solution based on the difference between two randomly selected solutions from the population. This enhances diversity and allows the algorithm to scan new, unexplored areas of the search space. This movement is modeled by Equation (11).

  $$x_{ij}^{\mathrm{new},\mathrm{P}1}=x_{ij}+(x_{{\mathrm{random}}_1}-x_{{\mathrm{random}}_2})·R_1,$$

  (11)
• Wearing Down the Prey: Once prey is found, the bird does not attack immediately but circles and provokes it to deplete its energy. The algorithm models this by moving towards the best solution found so far ($x_{\mathrm{best}}$), simulating how the bird focuses on its target, while introducing a random component to avoid premature convergence. This is shown in Equation (12).

  $$x_{ij}^{\mathrm{new},\mathrm{P}1}=x_{\mathrm{best}}+exp\left({\left({\displaystyle \frac{t}{T}}\right)}^4\right)·(RB-0.5)·(x_{\mathrm{best}}-x_{ij}),$$

  (12)
• Attacking the Prey: When the prey is exhausted, the bird executes a swift, lethal attack. To simulate this decisive action, the algorithm performs a “jump” toward the best solution using a Lévy flight (RL). This feature models the bird’s powerful strike, combining frequent small steps with occasional long jumps to accelerate convergence towards the global optimum. The movement is described in Equation (13).

  $$x_{ij}^{\mathrm{new},\mathrm{P}1}=x_{\mathrm{best}}+{\left(1-{\displaystyle \frac{t}{T}}\right)}^{\left(2\times {\displaystyle \frac{t}{T}}\right)}·x_{ij}·RL,$$

  (13)

4.2. Exploitation Phase (Escape Strategy)

This phase models how the secretary bird evades predators, which corresponds to a refined local search for a better solution. The bird chooses one of two strategies with equal probability:

• Camouflage ($C_1$): The bird may hide in its environment to avoid being detected. The algorithm simulates this by making small, subtle adjustments to its current position, moving locally around the best-known solution to refine it.
• Fleeing ($C_2$): If camouflage is not an option, the bird runs or flies to escape danger. The algorithm models this with a larger, more random movement that allows it to jump to other regions of the search space, effectively avoiding stagnation.

Both escape strategies are modeled using Equation (14).

$$x_{ij}^{\mathrm{new},\mathrm{evasion}}=\left\{\begin{array}{cc}{C}_1:x_{\mathrm{best}}+(2·RB-1)·{\left(1-{\displaystyle \frac{t}{T}}\right)}^2·x_{ij},\hfill & \mathrm{if}r<0.5,\hfill \\ C_2:x_{ij}+R_2·(x_{\mathrm{random}}-K·x_{ij}),\hfill & \mathrm{else}.\hfill \end{array}\right.$$

(14)

4.3. Solution Selection

A key aspect of the SBOA is how it determines if a new solution is superior to the current one. The algorithm employs a greedy selection mechanism for this purpose.

The quality of each solution is measured by an objective function (F), which, in the context of the Set Covering Problem, is the total cost to be minimized. After generating a new candidate position in either the exploration or exploitation phase, the algorithm compares the fitness of the new solution ($F_i^{\mathrm{new},\mathrm{P}1}$) with that of the current one ($F_i$).

The new solution is accepted only if it offers a better fitness value (i.e., a lower cost). Otherwise, the current solution is kept. This process, shown in Equation (15), ensures that the population’s quality either improves or remains the same in each iteration, guiding the search effectively towards the optimal solution.

$$X_i=\left\{\begin{array}{cc}{X}_i^{\mathrm{new},\mathrm{P}1}\hfill & \mathrm{if}{F}_i^{\mathrm{new},\mathrm{P}1}<F_i\hfill \\ X_i\hfill & \mathrm{else}\hfill \end{array}\right.$$

(15)

The pseudo-code of the SBOA is detailed in the pseudo-code of Algorithm 1.

Algorithm 1 Secretary Bird Optimization Algorithm.

Input: Problem Setting $(Dim,ub,lb,Pop\_size(N\left)\right)$, $Max\_Iter\left(T\right)$, $Curr\_Iter\left(t\right)$ Output: Best solution 1: Initialize the population randomly. 2: for  $t=1\to T$  do 3:     Update Secretary Bird $x_{\mathrm{best}}$. 4:     for $i=1\to N$ do 5:         Exploration Phase: 6:         if $t\le {\displaystyle \frac{1}{3}}T$ then 7:            Calculate new status using Searching Stage Equation (11). 8:            Update the i-th Secretary Bird using Update Equation (15). 9:         else if ${\displaystyle \frac{1}{3}}T<t<{\displaystyle \frac{2}{3}}T$ then 10:            Calculate new status using Consuming Stage Equation (12). 11:            Update the i-th Secretary Bird using Update Equation (15). 12:         else if ${\displaystyle \frac{1}{3}}T<t<{\displaystyle \frac{2}{3}}T$ then 13:            Calculate new status using Attacking Stage Equation (13). 14:            Update the i-th Secretary Bird using Update Equation (15). 15:         end if 16:         Exploitation Phase: 17:         if $r<0.5$ then 18:            Calculate new status using C1 in Exploitation Phase Equation (14). 19:         else 20:            Calculate new status using $C_2$ in Exploitation Phase Equation (14). 21:         end if 22:         Update the i-th Secretary Bird using Update Equation (15). 23:     end for 24:     Output the best solution obtained by SBOA for the given optimization problem. 25:     Save the best candidate solution so far. 26: end for 27: Output the best solution obtained by SBOA for the given optimization problem.

5. Binary Secretary Bird Optimization Algorithm

As explained in Section 4, the Algorithm Optimization based on the Behavior of the Secretary Bird (SBOA) is a metaheuristic designed to solve continuous optimization problems. To address problems such as feature selection, it is necessary to transform the solutions into the binary domain.

Furthermore, in Section 3, it was highlighted that the Two-Step Technique is one of the most widely used approaches for binarizing continuous metaheuristics. In [33,34], eight different transfer functions and five binarization rules are described, which can be applied in this context.

In this work, the binarization scheme was chosen based on established findings in the literature that analyze the relationship between different transfer functions, binarization rules, and the exploration–exploitation balance. For the experiments, we use the V3 transfer function and the Elitist discretization method, considering the work carried out by Lanza-Gutierrez et al. in [35], where they recommend the use of V3 to solve small and medium-sized problems and for a better exploration–exploitation relation recommend Elitist as a discretization technique.

Additionally, we selected a function from the V-shaped family because its behavior is particularly well-suited for swarm intelligence algorithms. Unlike S-shaped functions, V-shaped functions relate the probability of a bit changing to the magnitude (or “velocity”) of the agent’s move, not its direction. A larger step size corresponds to a higher probability of flipping a bit. Among these, the V3 transfer function, shown in Equation (16), was chosen due to recommendations in the literature for its robust performance on small and medium-sized problems.

$$T\left(d_j^i\right)=\left|{\displaystyle \frac{d_j^i}{\sqrt{1+{\left(d_j^i\right)}^2}}}\right|$$

(16)

To complement the transfer function, the elitist binarization rule was selected, as shown in Equation (17). This rule introduces a strong exploitation pressure by giving a chance to preserve bits from the best-found solution in the population ($X_{\mathrm{Best}}$). This element of elitism is intended to balance the highly explorative nature of the SBOA’s hunting phases, thereby creating a more focused and effective search process.

$$X_{\mathrm{new}}^k=\left\{\begin{array}{cc}{X}_{\mathrm{Best}}^k\hfill & \mathrm{if}\mathrm{rand}<T\left(d_i^k\right),\hfill \\ 0\hfill & \mathrm{else}.\hfill \end{array}\right.$$

(17)

In this way, the Binary Secretary Bird Optimization Algorithm (BSBOA) is constructed. The process begins with the initialization of the solutions in the binary domain. In each iteration, the binary solutions are modified using Equations (11)–(14), which represent the movement equations specific to the SBOA. Once the solutions are perturbed, they exit the binary domain, and a binarization process is applied using Equations (16) and (17). This cycle is repeated until the defined number of iterations is completed.

Algorithm 2 presents the binary version of the SBOA, where the key section is the binarization that occurs in line 23.

Algorithm 2 Binary Secretary Bird Optimization Algorithm.

Input: Problem Setting $(Dim,ub,lb,Pop\_size(N\left)\right)$, $Max\_Iter\left(T\right)$, $Curr\_Iter\left(t\right)$ Output: Best solution 1: Initialize the population randomly. 2: for  $t=1\to T$  do 3:     Update Secretary Bird $x_{\mathrm{best}}$. 4:     for $i=1\to N$ do 5:         Exploration Phase: 6:         if $t\le {\displaystyle \frac{1}{3}}T$ then 7:            Calculate new status using Searching Stage Equation (11). 8:            Update the i-th Secretary Bird using Update Equation (15). 9:         else if ${\displaystyle \frac{1}{3}}T<t<{\displaystyle \frac{2}{3}}T$ then 10:            Calculate new status using Consuming Stage Equation (12). 11:            Update the i-th Secretary Bird using Update Equation (15). 12:         else if ${\displaystyle \frac{1}{3}}T<t<{\displaystyle \frac{2}{3}}T$ then 13:            Calculate new status using Attacking Stage Equation (13). 14:            Update the i-th Secretary Bird using Update Equation (15). 15:         end if 16:         Exploitation Phase: 17:         if $r<0.5$ then 18:            Calculate new status using C1 in Exploitation Phase Equation (14). 19:         else 20:            Calculate new status using $C_2$ in Exploitation Phase Equation (14). 21:         end if 22:         Update the i-th Secretary Bird using Update Equation (15). 23:         Binarization of population X 24:     end for 25:     Save the best candidate solution so far. 26: end for 27: Output the best solution obtained by SBOA for the given optimization problem.

Algorithm Complexity Analysis

Each algorithm requires a certain amount of time to perform its optimization tasks, and these can vary for the same problem. Evaluating algorithmic complexity is an effective way to demonstrate performance in terms of runtime. Big O notation is one of the most widely used tools for complexity analysis [36], and we will use it in this paper to analyze the complexity of BSBOA. Let N be the population size, $Dim$ the number of decision variables, and T the maximum number of iterations. Thus, for the initialization process of random solutions, we have a complexity of $O\left(N\right)$. During the optimization process, the complexity is O(T × N) + 2 · O(T × N × Dim), which includes the search for the best positions per iteration (O(T × N)), the updating of the positions of all solutions per iteration (O(T × N × Dim)), and the binarization of all solutions per iteration (O(T × N × Dim)). Thus, the algorithmic complexity of our proposal is O(N × (T × Dim + 1)).

6. Experimental Result

To develop the validation of our proposal, we have used the instances offered in OR-library [37] for both the pesos version (SCP) [35] and for the Unicot version (USCP) [17]. Our proposal was compared to two continuous metaheuristics of great relevance, such as Binary Particle Swarm Optimization [38] and Binary Grey Wolf Optimizer [39].

6.1. Parameter Setting

Before performing experimentation, we perform internal tests for parameter configuration. Specifically, we have carried out experimentation with the population size and the number of iterations. For the population size, we tested from [10, 100] in increments of 10, and the population sizes we tested were [20, 50, 70, 100, 150, 200, 300, 400, 500, 600, 700, 800, 900, 1000].

Table 3 shows the subset of instances used for parameter configuration. We have used these instances because we consider that they are representative of the entire portfolio of existing instances of OR-library. The table contains the following details: The first column shows the name of the instance, the second column shows the sample to the type of problem that the instance (SCP or USCP) belongs, the third column refers to the amount of restrictions that the instance possesses, the fourth column refers to the amount of decision variables to optimize, the fifth column refers to the density of some that the matrix has in view of Section 3, and the last column refers to the optimal value of the instance. This experiment was conducted in a team using a Windows 10 operating system, an Intel Core i9-10900 K 3.70 GHz Processor, and 64 GB of RAM.

Table 3. Instances used for parameter configuration.

Instance	Type Problem	M	N	Density (%)	Optimum
41	SCP	200	1000	2.00	429
61	SCP	200	2000	5.00	138
b1	SCP	300	3000	5.00	69
d1	SCP	400	4000	5.00	60
clr10	USCP	511	210	12.30	25
clr11	USCP	1023	330	12.40	23
cyc06	USCP	240	192	2.10	60
cyc07	USCP	672	448	0.90	144

Table 4 shows the best configurations for each instance executed, considering computing time and the fitness reached. Thus, it is observed that the ideal population size for this experiment is 10. For the number of iterations, the value changes for each instance; therefore, we have determined that the average iterations will be used in experimentation. Thus, the number of iterations is 600.

Table 4. Parameter selection.

Pop	Iter	Instance	Best Fitness	Worst Fitness	Average	Time Seconds	Time Minutes
10	500	41	433	433	433	104.18	1.74
10	70	61	141	141	141	10.32	0.17
10	400	b1	69	69	69	233.97	3.9
10	600	clr10	25	27	25.43	51.69	0.86
10	900	clr11	23	26	24.57	185.9	3.1
10	600	cyc06	60	60	60	52.07	0.87
10	500	cyc07	144	154	149.71	240.98	4.02
10	1000	d1	60	61	60.43	1297.6	21.63

Thus, Table 5 shows the final configuration of the experimentation carried out in this work. The global configuration used by all the metaheuristics (All MH) and the parameters of each metaheuristic are highlighted.

Table 5. Configuration of parameters.

Parameter	Value
All MH	Population size	10
	Iterations	600
	Independent runs	31
	Transfer functions	V3
	Method of discretization	Elitist
PSO	$w_{min}$	0.1
	$w_{max}$	0.9
	$c_1$	2
	$c_2$	2
GWO	a	linearly decreases from 2 to 0
SBOA	CF	potentially decreases at 0

6.2. SCP and USCP Instances Resolved

Table 6 and Table 7 show the instances used to solve the SCP and USCP, respectively. Each table shows the instance name (column Instance), the number of constraints (column M), the number of decision variables (column N), the density of ones in the matrix mentioned in Section 2 (column Density %), and the instance’s optimum. It should be noted that the underlined and bold optima are not global optima but the best results reported in the literature. Thus, for the present work, we solved 22 instances for the SCP and 17 instances for the USCP.

Table 6. Instances used for the SCP.

Instance	M	N	Density (%)	Optimum
41	200	1000	2.00	429
42	200	1000	2.00	512
51	200	2000	2.00	253
52	200	2000	2.00	302
61	200	1000	5.00	138
62	200	1000	5.00	146
A1	300	3000	2.00	253
A2	300	3000	2.00	252
B1	300	3000	5.00	69
B2	300	3000	5.00	76
C1	400	4000	2.00	227
C2	400	4000	2.00	219
D1	400	4000	5.00	60
D2	400	4000	5.00	66
NRE1	500	5000	10.00	29
NRE2	500	5000	10.00	30
NRF1	500	5000	20.00	14
NRF2	500	5000	20.00	15
NRG1	1000	10,000	2.00	176
NRG2	1000	10,000	2.00	154
NRH1	1000	10,000	5.00	63
NRH2	1000	10,000	5.00	63

Table 7. Instances used for the USCP.

Instance	M	N	Density (%)	Optimum
U41	200	1000	2.00	38
U51	200	2000	2.00	34
U61	200	1000	5.00	21
UA1	300	3000	2.00	39
UB1	300	3000	5.00	22
UC1	400	4000	2.00	43
UD1	400	4000	5.00	24
UNRE1	500	5000	10.00	17
UNRF1	500	5000	20.00	10
UNRG1	1000	10,000	2.00	61
UNRH1	1000	10,000	5.00	34
CLR10	511	210	12.30	25
CLR11	1023	330	12.40	23
CLR12	2047	495	12.50	23
CYC06	240	192	2.10	60
CYC07	672	448	0.90	144
CYC08	1792	1024	0.40	344

6.3. Results of SCP

This subsection shows the results of running the SBOA with the previously established parameters and compared with the GWO and PSO algorithms. In Table 8 and Table 9, the results are shown when running the different instances of OR-library. For each algorithm and instance, the best known optimal value, the best value achieved, the worst value achieved, the average, and the standard deviation of the solutions obtained of the 30 executions are shown in the tables [40].

Table 8. Fitness results per SCP instance.

MH	Instance	Opt.	Best	Worst	Avg. Fitness	Std. Fitness
SBOA	41	429	433.0	433.0	433.0	0.0
GWO			433.0	438.0	433.419	1.29
PSO			433.0	437.0	433.258	0.983
SBOA	42	512	525.0	527.0	525.968	0.999
GWO			525.0	527.0	525.935	0.982
PSO			525.0	527.0	526.29	0.957
SBOA	51	253	267.0	269.0	267.29	0.52
GWO			267.0	268.0	267.194	0.395
PSO			267.0	269.0	267.323	0.59
SBOA	52	302	315.0	322.0	318.387	1.979
GWO			315.0	323.0	319.677	2.74
PSO			315.0	323.0	318.742	2.17
SBOA	61	138	141.0	145.0	141.935	1.605
GWO			141.0	145.0	142.968	1.926
PSO			141.0	145.0	141.839	1.568
SBOA	62	146	148.0	154.0	149.677	2.277
GWO			148.0	154.0	150.323	2.085
PSO			148.0	154.0	149.387	2.058
SBOA	A1	253	257.0	257.0	257.0	0.0
GWO			257.0	257.0	257.0	0.0
PSO			257.0	257.0	257.0	0.0
SBOA	A2	252	258.0	265.0	260.387	1.58
GWO			256.0	265.0	260.452	1.997
PSO			258.0	265.0	261.355	1.976
SBOA	B1	69	69.0	71.0	69.387	0.79
GWO			69.0	71.0	69.645	0.9
PSO			69.0	71.0	69.387	0.79
SBOA	B2	76	76.0	77.0	76.129	0.335
GWO			76.0	82.0	76.419	1.185
PSO			76.0	77.0	76.161	0.368
SBOA	C1	227	231.0	234.0	233.065	0.504
GWO			231.0	235.0	232.806	0.858
PSO			231.0	234.0	232.968	0.647
SBOA	C2	219	221.0	226.0	222.387	1.559
GWO			221.0	228.0	222.516	1.949
PSO			221.0	229.0	222.645	2.088
SBOA	D1	60	60.0	65.0	61.387	1.006
GWO			60.0	63.0	61.161	0.919
PSO			60.0	63.0	61.323	1.028
SBOA	D2	66	67.0	69.0	67.71	0.727
GWO			67.0	69.0	67.774	0.791
PSO			67.0	69.0	67.677	0.69
SBOA	NRE1	29	29.0	29.0	29.0	0.0
GWO			29.0	30.0	29.032	0.177
PSO			29.0	29.0	29.0	0.0
SBOA	NRE2	30	30.0	32.0	31.0	0.803
GWO			30.0	33.0	31.065	0.878
PSO			30.0	32.0	30.71	0.632
SBOA	NRF1	14	14.0	14.0	14.0	0.0
GWO			14.0	15.0	14.032	0.177
PSO			14.0	14.0	14.0	0.0
SBOA	NRF2	15	15.0	15.0	15.0	0.0
GWO			15.0	16.0	15.032	0.177
PSO			15.0	15.0	15.0	0.0

Table 9. Fitness results per SCP instance.

MH	Instance	Opt.	Best	Worst	Avg. Fitness	Std. Fitness
SBOA	NRG1	176	178.0	184.0	180.968	1.492
GWO			179.0	185.0	181.484	1.72
PSO			179.0	184.0	181.0	1.666
SBOA	NRG2	154	158.0	161.0	159.355	0.598
GWO			158.0	162.0	159.677	0.929
PSO			158.0	162.0	159.516	1.043
SBOA	NRH1	63	64.0	67.0	65.0	1.016
GWO			64.0	67.0	65.581	0.943
PSO			64.0	67.0	65.484	0.875
SBOA	NRH2	63	64.0	67.0	65.065	1.014
GWO			64.0	67.0	65.161	0.954
PSO			64.0	66.0	65.194	0.895

A convergence graph represents how the metaheuristic finds progressively better and better solutions as iterations increase. In order to find good solutions in a reasonable time to provide answers to real-world problems, it is expected that the number of iterations will not be excessive in order to avoid the excessive use of computational resources. As described in Crawford et al. [41] and Lemus-Romani et al. [42], graphs were used to document the optimization process while considering the fitness achieved as the iterations progressed. This is shown in Figure 2, Figure 3, Figure 4 and Figure 5, where the relationship between the number of iterations and the fitness achieved is shown, corresponding to the x and y axes, respectively, where it can be seen that there is good convergence without the algorithm being trapped in a local optimum [43].

Figure 2. Convergence analysis of the instances Scp 41, Scp 51 and Scp 61.

Figure 3. Convergence analysis of the instances Scp a1, Scp b1 and Scp c1.

Figure 4. Convergence analysis of the instances Scp d1, Scp nre1 and Scp nrf1.

Figure 5. Convergence analysis of the instances Scp nrg1 and Scp nrh1.

On the other hand, in Table 10 and Table 11, the execution of the different instances for the three Algorithms, the SBOA, GWO and PSO, are shown, considering their execution time.

Table 10. Time per SCP instance.

MH	Instance	Min. Time (s)	Max. Time (s)	Avg. Time (s)	Std. Time (s)
SBOA	41	157.704	213.129	183.116	16.07
GWO		153.028	187.257	173.556	9.494
PSO		154.711	170.525	165.33	4.352
SBOA	42	142.817	218.333	174.875	19.872
GWO		158.63	182.134	171.814	6.122
PSO		158.201	167.463	164.051	2.481
SBOA	51	253.613	374.187	313.787	30.033
GWO		236.581	282.194	267.529	14.559
PSO		237.17	271.079	259.171	8.931
SBOA	52	253.449	379.583	314.932	34.542
GWO		233.655	283.615	266.88	13.466
PSO		231.334	271.309	258.577	10.615
SBOA	61	98.435	157.754	122.681	13.947
GWO		110.113	123.04	116.26	3.258
PSO		102.526	116.973	109.84	2.943
SBOA	62	97.503	142.421	119.435	13.442
GWO		107.432	121.659	114.606	3.808
PSO		104.62	115.671	110.325	3.257
SBOA	A1	776.617	992.96	886.21	52.953
GWO		548.174	603.27	583.829	19.38
PSO		547.932	583.488	564.821	7.163
SBOA	A2	760.15	978.413	885.575	58.469
GWO		559.968	613.854	589.377	14.932
PSO		540.209	587.692	569.523	11.293
SBOA	B1	492.081	598.676	549.83	29.989
GWO		340.665	377.974	355.276	7.95
PSO		331.606	369.327	355.788	7.879
SBOA	B2	509.619	609.138	566.107	27.889
GWO		345.028	399.848	368.475	9.286
PSO		339.963	369.457	350.85	6.382
SBOA	C1	1624.884	2006.59	1800.822	104.886
GWO		1055.171	1174.378	1109.42	26.687
PSO		1057.741	1215.157	1083.767	32.262
SBOA	C2	1494.119	1967.28	1785.954	136.993
GWO		1019.127	1169.176	1117.342	30.362
PSO		1034.299	1112.982	1075.741	15.09
SBOA	D1	932.527	1160.315	1073.955	65.504
GWO		640.738	702.894	661.201	13.484
PSO		605.31	667.894	638.656	13.116
SBOA	D2	943.902	1147.318	1060.202	52.619
GWO		608.824	691.086	646.158	16.23
PSO		594.241	664.729	628.357	20.317

Table 11. Time per SCP instance.

MH	Instance	Min. Time (s)	Max. Time (s)	Avg. Time (s)	Std. Time (s)
SBOA	NRE1	1163.322	1343.931	1301.288	43.887
GWO		709.169	820.318	756.539	27.69
PSO		681.815	749.788	714.205	14.854
SBOA	NRE2	1111.717	1419.179	1314.766	74.668
GWO		683.767	845.554	754.179	40.734
PSO		669.604	855.131	758.741	49.429
SBOA	NRF1	1032.868	1327.712	1225.842	70.654
GWO		565.83	681.723	619.619	26.624
PSO		546.366	661.886	604.704	28.136
SBOA	NRF2	1099.421	1391.446	1272.068	76.519
GWO		573.592	701.44	633.946	30.842
PSO		588.031	713.309	635.212	26.661
SBOA	NRG1	17,984.637	54,355.97	26,594.345	12,842.352
GWO		30,569.108	62,689.422	53,273.186	11,121.198
PSO		32,644.973	61,491.48	55,582.678	6414.388
SBOA	NRG2	17,185.131	52,717.745	27,342.828	9971.869
GWO		25,719.309	61,376.891	53,300.762	10,461.981
PSO		31,367.547	59,373.087	54,333.041	5643.738
SBOA	NRH1	10,512.106	32,739.219	16,587.815	6416.691
GWO		15,165.461	34,183.717	30,025.251	4855.541
PSO		21,114.651	35,256.654	31,207.508	2997.95
SBOA	NRH2	10,276.136	29,402.972	15,774.859	5539.228
GWO		14,111.582	34,673.103	29,343.299	5608.793
PSO		19,751.687	34,721.174	30,023.669	3445.378

Figure 6, Figure 7, Figure 8 and Figure 9 show graphs with the performance of the three metaheuristics (SBOA, PSO and GWO), where it can be seen that although the times of the SBOA in relation to the iterations were not better than PSO and GWO, they were promising.

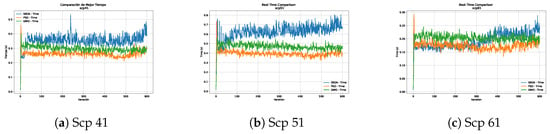
Figure 6. Time analysis of the instances Scp 41, Scp 51 and Scp 61.

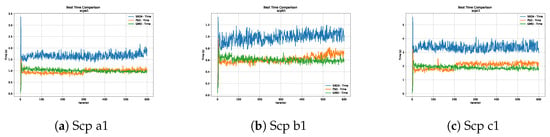
Figure 7. Time analysis of the instances Scp a1, Scp b1 and Scp c1.

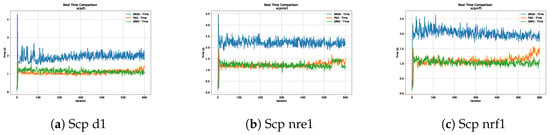
Figure 8. Time analysis of the instances Scp d1, Scp nre1 and Scp nrf1.

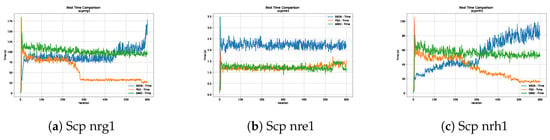
Figure 9. Time analysis of the instances Scp nrg1, Scp nre1 and Scp nrh1.

6.4. Results of USCP

Table 12 shows the results obtained when running the different instances of the USCP for the three metaheuristics investigated in this work (SBOA, GWO and PSO).

Table 12. Fitness results per USCP instance.

MH	Instance	Opt.	Best	Worst	Avg. Fitness	Std. Fitness
SBOA	U41	38	39.0	41.0	39.839	0.627
GWO			39.0	43.0	40.871	1.07
PSO			39.0	41.0	39.645	0.598
SBOA	U51	34	35.0	37.0	35.581	0.555
GWO			35.0	38.0	36.29	0.681
PSO			35.0	36.0	35.613	0.487
SBOA	U61	21	21.0	22.0	21.29	0.454
GWO			21.0	23.0	21.839	0.514
PSO			21.0	22.0	21.29	0.454
SBOA	UA1	39	39.0	41.0	40.323	0.642
GWO			40.0	43.0	41.387	0.656
PSO			40.0	41.0	40.452	0.498
SBOA	UB1	22	22.0	24.0	22.806	0.591
GWO			22.0	24.0	23.387	0.605
PSO			22.0	23.0	22.774	0.418
SBOA	UC1	43	43.0	45.0	44.323	0.532
GWO			44.0	48.0	46.387	0.79
PSO			44.0	46.0	44.774	0.551
SBOA	UD1	24	25.0	26.0	25.226	0.418
GWO			25.0	27.0	26.194	0.47
PSO			25.0	26.0	25.065	0.246
SBOA	UNRE1	17	17.0	18.0	17.516	0.5
GWO			17.0	18.0	17.774	0.418
PSO			17.0	17.0	17.0	0.0
SBOA	UNRF1	10	10.0	11.0	10.903	0.296
GWO			10.0	11.0	10.774	0.418
PSO			10.0	11.0	10.29	0.454
SBOA	UNRG1	61	62.0	63.0	62.484	0.5
GWO			63.0	68.0	66.194	0.895
PSO			62.0	64.0	63.29	0.579
SBOA	UNRH1	34	34.0	35.0	34.323	0.467
GWO			35.0	37.0	35.839	0.514
PSO			34.0	35.0	34.935	0.246
SBOA	CLR10	24	25.0	27.0	25.097	0.39
GWO			25.0	27.0	25.387	0.748
PSO			25.0	27.0	25.29	0.632
SBOA	CLR11	23	23.0	23.0	23.0	0.0
GWO			23.0	27.0	24.839	1.919
PSO			23.0	27.0	23.387	1.183
SBOA	CLR12	23	23.0	28.0	24.258	1.586
GWO			23.0	29.0	24.774	2.121
PSO			23.0	26.0	23.968	1.257
SBOA	CYC06	60	60.0	62.0	61.097	0.817
GWO			60.0	63.0	61.452	0.978
PSO			60.0	62.0	61.226	0.831
SBOA	CYC07	144	147.0	153.0	150.871	1.362
GWO			147.0	154.0	151.903	1.399
PSO			144.0	153.0	150.484	1.563
SBOA	CYC08	344	357.0	365.0	361.129	2.324
GWO			358.0	372.0	363.419	2.721
PSO			358.0	367.0	362.258	1.883

Figure 10, Figure 11, Figure 12, Figure 13, Figure 14 and Figure 15 show the convergence plots of the unicost instances, where it can be observed that, in general, the SBOA achieves good performance with few iterations without being trapped in a local optimum.

Figure 10. Convergence analysis of the instances UScp 41, UScp 51 and UScp 61.

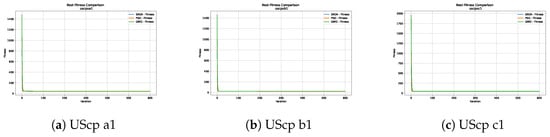
Figure 11. Convergence analysis of the instances UScp a1, UScp b1 and UScp c1.

Figure 12. Convergence analysis of the instances UScp d1, UScp unre1 and UScp unrg1.

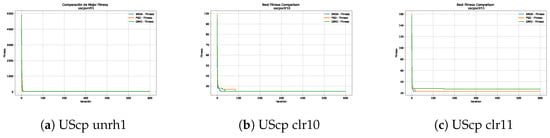
Figure 13. Convergence analysis of the instances UScp unrh1, UScp clr10 and UScp clr11.

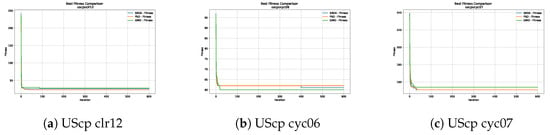
Figure 14. Convergence analysis of the instances UScp clr12, UScp cyc06 and UScp cyc07.

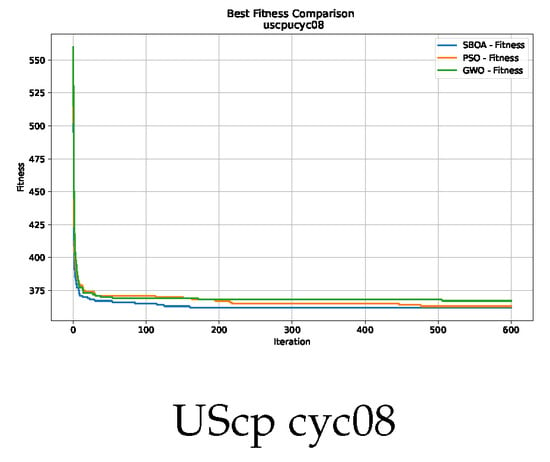
Figure 15. Convergence analysis of the instance UScp cyc08.

Table 13 and Table 14 show the times used for the different USCP instances for the three algorithms studied.

Table 13. Time per USCP instance.

MH	Instance	Min. Time (s)	Max. Time (s)	Avg. Time (s)	Std. Time (s)
SBOA	U41	127.133	165.55	144.041	9.186
GWO		122.253	138.701	128.183	3.852
PSO		117.762	144.135	128.764	5.967
SBOA	U51	240.841	298.561	261.01	14.843
GWO		212.336	229.391	219.389	4.053
PSO		219.169	248.563	233.324	8.576
SBOA	U61	87.424	119.14	98.912	7.76
GWO		68.666	86.004	77.182	4.104
PSO		62.444	78.625	73.111	3.677
SBOA	UA1	596.009	988.713	718.132	81.884
GWO		271.85	342.57	299.673	21.205
PSO		155.901	331.492	281.74	35.986
SBOA	UB1	261.626	572.229	354.131	96.36
GWO		163.543	178.737	169.919	3.133
PSO		163.947	189.483	177.069	6.403
SBOA	UC1	43.0	45.0	44.323	0.532
GWO		44.0	48.0	46.387	0.79
PSO		44.0	46.0	44.774	0.551
SBOA	UD1	466.161	1065.89	691.041	212.326
GWO		280.281	314.57	292.719	6.333
PSO		280.569	329.153	302.325	12.853
SBOA	UNRE1	863.663	1732.248	1337.399	330.758
GWO		410.564	705.947	434.391	50.715
PSO		423.553	497.961	460.517	18.005
SBOA	UNRF1	1070.355	1650.344	1551.32	130.705
GWO		424.606	683.387	589.47	95.124
PSO		449.775	535.65	485.254	25.765
SBOA	UNRG1	5414.287	14,309.31	7441.461	3000.263
GWO		8737.818	18,034.46	15,638.192	3071.343
PSO		13,479.719	21,729.841	18,346.111	2374.816
SBOA	UNRH1	4168.711	16,435.724	7474.938	3805.651
GWO		4775.536	11,231.733	9150.029	1921.657
PSO		6517.542	14,954.869	11,776.28	1780.385

Table 14. Time per USCP instance.

Metaheuristic	Instance	Min. Time (s)	Max. Time (s)	Avg. Time (s)	Std. Time (s)
SBOA	CLR10	58.212	86.825	75.066	6.622
GWO		23.831	29.506	26.374	1.434
PSO		29.711	36.123	32.689	1.824
SBOA	CLR11	126.482	196.981	141.176	11.534
GWO		53.558	69.384	61.066	4.716
PSO		66.438	85.256	71.301	4.728
SBOA	CLR12	604.751	1064.573	801.739	149.713
GWO		338.341	500.013	407.826	43.52
PSO		501.697	604.357	550.129	22.986
SBOA	CYC06	53.307	93.846	68.63	8.254
GWO		22.638	26.964	24.317	1.085
PSO		23.312	28.313	25.79	1.229
SBOA	CYC07	282.102	319.146	306.65	6.968
GWO		138.408	163.015	148.045	6.521
PSO		146.28	175.9	158.426	5.986
SBOA	CYC08		5163.509	4655.015	226.937
GWO		3080.423	3591.295	3391.635	126.319
PSO		3562.642	3902.347	3747.505	84.342

Figure 16, Figure 17, Figure 18, Figure 19, Figure 20 and Figure 21 show graphs with the performance of the three metaheuristics (SBOA, PSO and GWO), enabling us to compare it with the times achieved by the SBOA.

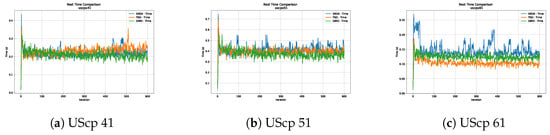
Figure 16. Time analysis of the instances UScp 41, UScp 51 and UScp 61.

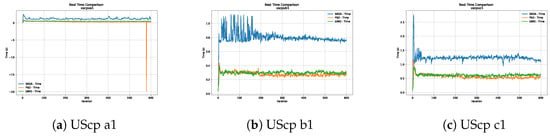
Figure 17. Time analysis of the instances UScp a1, UScp b1 and UScp c1.

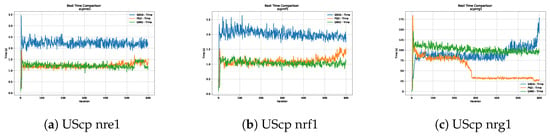
Figure 18. Time analysis of the instances UScp nre1, UScp nrf1 and UScp nrg1.

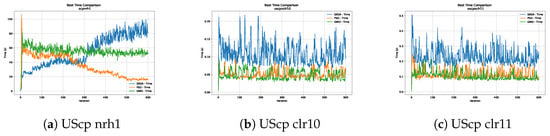
Figure 19. Time analysis of the instances UScp nrh1, UScp clr10 and UScp clr11.

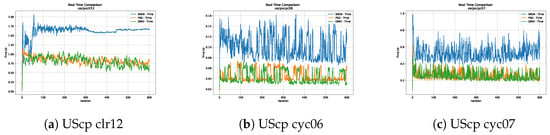
Figure 20. Time analysis of the instances UScp clr12, UScp cyc06 and UScp cyc07.

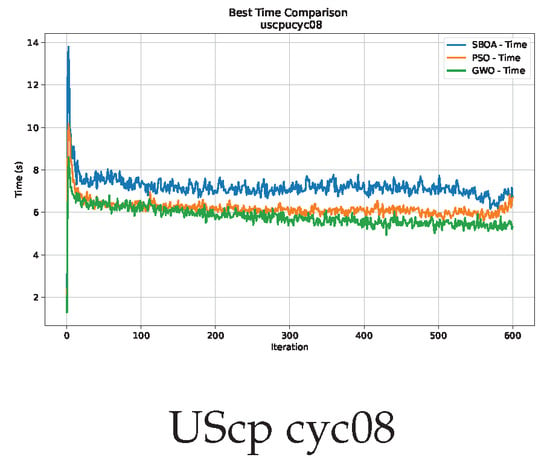
Figure 21. Time analysis of the instance cyc08.

Statistical Tests

To validate our work, Table 15, Table 16, Table 17 and Table 18 show the statistical significance tests for the algorithms worked on: SBP, PSO and GWO. This table shows the p-values that act as indicators of statistical significance. We use the nonparametric Wilcoxon–Mann–Whitney test to perform this validation [44] since we have two independent samples and we cannot assume normality for at least one of them. The hypotheses considered are the following:

$$H_0:{\mu }_A\ge {\mu }_B,$$

$$H_1:{\mu }_A<{\mu }_B$$

where ${\mu }_A$ and ${\mu }_B$ represent the average value delivered by algorithms A and B. We consider that if the p-value is less than 0.05, the hypothesis $H_0$ will be rejected, with hypothesis $H_1$ being accepted and these cases are highlighted in bold and underlined in the tables.

Table 15. Average p-value of the SBOA compared with PSO and GWO for SCP41, ScP42, SCP51, SCP52, SCP61 and SCP62.

	4.1			4.2			5.1			5.2			6.1			6.2
	SBO	PSO	GWO	SBO	PSO	GWO	SBO	PSO	GWO	SBO	PSO	GWO	SBO	PSO	GWO	SBO	PSO	GWO
SBO	-	≥0.05	≥0.05	-	≥0.05	≥0.05	-	≥0.05	≥0.05	-	≥0.05	≥0.05	-	≥0.05	0.03	-	≥0.05	≥0.05
PSO	≥0.05	-	≥0.05	≥0.05	-	≥0.05	≥0.05	-	≥0.05	≥0.05	-	≥0.05	≥0.05	-	0.02	≥0.05	-	≥0.05
GWO	≥0.05	≥0.05	-	≥0.05	≥0.05	-	≥0.05	≥0.05	-	≥0.05	≥0.05	-	0.03	0.02	-	≥0.05	≥0.05	-

Table 16. Average p-value of the SBOA compared with PSO and GWO for a1, a2, b1, b2, c1, c2, d1 and d2.

	a.1			a.2			b.1			b.2
	SBO	PSO	GWO	SBO	PSO	GWO	SBO	PSO	GWO	SBO	PSO	GWO
SBO	-	≥0.05	≥0.05	-	0.05	-	-	≥0.05	≥0.05	-	≥0.05	≥0.05
PSO	≥0.05	-	≥0.05	≥0.05	-	≥0.05	1.0	-	≥0.05	≥0.05	-	≥0.05
GWO	≥0.05	≥0.05	-	-	≥0.05	-	0.2	≥0.05	-	≥0.05	≥0.05	-
	c.1			c.2			d.1			d.2
	SBO	PSO	GWO	SBO	PSO	GWO	SBO	PSO	GWO	SBO	PSO	GWO
SBO	-	≥0.05	≥0.05	-	≥0.05	≥0.05	-	≥0.05	≥0.05	-	≥0.05	≥0.05
PSO	≥0.05	-	≥0.05	≥0.05	-	≥0.05	≥0.05	-	≥0.05	≥0.05	-	≥0.05
GWO	≥0.05	≥0.05	-	≥0.05	≥0.05	-	≥0.05	≥0.05	-	≥0.05	≥0.05	-

Table 17. Average p-value of the SBOA compared with PSO and GWO for nre1, nre2, nrf1, nrf2, nrg1, nrg2, nrh1 and nrh2.

	nre1			nre2			nrf1			nrf2
	SBO	PSO	GWO	SBO	PSO	GWO	SBO	PSO	GWO	SBO	PSO	GWO
SBO	-	≥0.05	≥0.05	-	≥0.05	≥0.05	-	≥0.05	≥0.05	-	≥0.05	≥0.05
PSO	≥0.05	-	≥0.05	≥0.05	-	≥0.05	≥0.05	-	≥0.05	≥0.05	-	≥0.05
GWO	≥0.05	≥0.05	-	≥0.05	≥0.05	-	≥0.05	≥0.05	-	0.33	≥0.05	-
	nrg1			nrg2			nrh1			nrh2
	SBO	PSO	GWO	SBO	PSO	GWO	SBO	PSO	GWO	SBO	PSO	GWO
SBO	-	≥0.05	≥0.05	-	≥0.05	≥0.05	-	0.003	0.02	-	≥0.05	≥0.05
PSO	≥0.05	-	≥0.05	≥0.05	-	≥0.05	0.03	-	≥0.05	≥0.05	-	≥0.05
GWO	≥0.05	≥0.05	-	≥0.05	≥0.05	-	0.02	≥0.05	-	≥0.05	≥0.05	-

Table 18. Average p-value of the SBOA compared with PSO and GWO for u41, u51, u61, ua1, ub1, uc1, uclr10, uclr12, ucyc06, ucyc07, ud1, unre1, unrf1, unre1 and unrh1.

	u41			u51			u61			ua1
	SBO	PSO	GWO	SBO	PSO	GWO	SBO	PSO	GWO	SBO	PSO	GWO
SBO	-	≥0.05	0.0	-	≥0.05	0.0	-	≥0.05	0.0	-	≥0.05	0.0
PSO	≥0.05	-	0.0	≥0.05	-	0.0	≥0.05	-	0.0	≥0.05	-	0.0
GWO	0.0	0.0	-	0.0	0.0	-	0.0	0.0	-	0.0	0.0	-
	ub1			uc1			uclr10			uclr12
	SBO	PSO	GWO	SBO	PSO	GWO	SBO	PSO	GWO	SBO	PSO	GWO
SBO	-	≥0.05	0.0	-	0.0	0.0	-	≥0.05	≥0.05	-	0.5	≥0.05
PSO	≥0.05	-	0.0	0.0	-	0.0	≥0.05	-	≥0.05	≥0.05	-	≥0.05
GWO	0.0	0.0	-	0.0	0.0	-	≥0.05	≥0.05	-	≥0.05	≥0.05	-
	ucyc06			ucyc07			ucyc07			ud1
	SBO	PSO	GWO	SBO	PSO	GWO	SBO	PSO	GWO	SBO	PSO	GWO
SBO	-	≥0.05	0.12	-	≥0.05	0.0	-	≥0.05	0.0	-	≥0.05	0.0
PSO	≥0.05	-	≥0.05	≥0.05	-	0.0	≥0.05	-	0.0	≥0.05	-	0.0
GWO	≥0.05	≥0.05	-	0.0	0.0	-	0.0	0.0	-	0.0	0.0	-
	unre1			unrf1			unre1			unrh1
	SBO	PSO	GWO	SBO	PSO	GWO	SBO	PSO	GWO	SBO	PSO	GWO
SBO	-	0.0	0.04	-	0.0	≥0.05	-	0.0	0.0	-	0.0	0.0
PSO	0.0	-	0.0	0.0	-	0.0	0.0	-	0.0	0.0	-	0.0
GWO	0.04	0.0	-	≥0.05	0.0	-	0.0	0.0	-	0.0	0.0	-

The BSBOA demonstrated remarkable ability in solving the Set Covering Problem (SCP) and its unicost variant (USCP) using the V3 transfer function and elitist rule. For the SCP, it stood out by generating high-quality solutions with lower costs compared to metaheuristics, like GWO and PSO; in the USCP, where costs are homogeneous, it maintained competitive performance with less pronounced differences. Additionally, the BSBOA achieved favorable execution times, establishing itself as an efficient and versatile option for combinatorial optimization problems.

7. Discussion

The experimental outcomes consistently show BSBOA’s ability to yield high-quality solutions, often surpassing GWO and PSO in solution value and robustness (lower standard deviations) for the SCP, while maintaining competitive performance for the USCP. The computational analysis confirms BSBOA’s operational efficiency with a generally low computational burden.

BSBOA’s effectiveness stems from SBOA’s core design, inspired by the secretary bird’s natural behaviors of hunting and evasion, fostering a well-balanced interplay between exploration and exploitation crucial for NP-hard problems. Its systematic adaptation from continuous to binary domains, involving a rigorous exploration of eight transfer functions and five discretization methods, was pivotal. The selection of the V3 transfer function and the Elitist rule, based on prior research for optimal exploration–exploitation balance in medium-sized problems, ensures this effective translation and harmonious interaction with the discrete solution space.

However, it is crucial to acknowledge certain trade-offs and constraints. The iterative nature of the binarization process, applying transfer functions and rules in each cycle, introduces a computational overhead that could be significant for extremely large-scale problems or real-time systems, despite current observed efficiencies. Moreover, while our systematic validation identified an optimal configuration (V3 and Elitist) for the tested instances, the generalizability of this specific setup across all possible SCP and USCP variations, particularly those with distinct structural properties or much higher dimensions, requires further extensive validation. The current reliance on standard benchmark instances, while a common practice, also represents a limitation in fully assessing its performance in the intricate, diverse conditions of real-world applications.

These considerations underscore the ongoing need for refinement and broader validation. Such endeavors are vital to fully realize BSBOA’s potential for industrial and engineering challenges.

8. Conclusions

In this work, a solution to the SCP was provided using the SBOA, which is inspired by the natural behavior of the secretary bird. On the one hand, the SBOA was originally designed to work on continuous space optimization problems; on the other hand, the SCP is a binary problem. Several binarization techniques were proposed to adapt the algorithm to the discrete domain. Combinations of eight transfer functions were used, along with five discretization methods. Subsequently, the binary version of the SBOA was compared with the GWO and PSO algorithms, providing a solution to the SCP and its USCP variant. The BSBOA is positioned as a robust and effective tool for resolving both the SCP and USCP, excelling in solution quality and execution efficiency compared to GWO and PSO. Its ability to handle different levels of complexity and balance exploration and exploitation makes it ideal for practical optimization applications. Future work is to extend its applicability to more complex and large-scale problems, as well as to optimize its performance in terms of time and accuracy.