Three-Step Iterative Methodology for the Solution of Extended Ordered XOR-Inclusion Problems Incorporating Generalized Cayley–Yosida Operators

Abstract

The system of extended ordered XOR-inclusion problems (in short, SEOXORIP) involving generalized Cayley and Yosida operators is introduced and studied in this paper. The solution is obtained in a real ordered Banach space using a fixed-point approach. First, we develop the fixed-point lemma for the solution of SEOXORIP. By using the fixed-point lemma, we develop a three-step iterative scheme for obtaining the approximate solution of SEOXORIP. Under the Lipschitz continuous assumptions of the cost mappings, the strong convergence of the scheme is demonstrated. Lastly, we provide a numerical example with a convergence graph generated using MATLAB 2018a to verify the convergence of the sequence generated by the proposed scheme.

1. Introduction

It is widely acknowledged that convex minimization problems, variational inequalities, equilibrium challenges, and feasibility dilemmas represent particular instances of variational inclusion problems. In the context of a single-valued mapping $A:X\to X$ and a multivalued (potentially nonlinear) operator $B:X\to 2^X$, the objective is to determine $x\in X$ such that

$$0\in (A+B)x.$$

(1)

which is designated as a variational inclusion problem, exhibiting applications in signal processing [1], image processing [2], machine learning [3], and applications to multiple sets split feasibility problems [4].

The inability of projection methods to effectively address variational inclusion problems necessitated the emergence of resolvent operator methods, which have proven to be efficient in solving these problems. In their seminal works, Fang and Huang [5,6] put forth the concepts of H-monotone operators and H-accretive mappings, and by establishing the resolvent operators that correspond to these concepts, they investigated a specific category of variational inclusions within the context of Hilbert and Banach spaces. Following this, Xia and Huang [7] proposed the notion of general H-monotone operators as an extension of J-proximal mapping [8] and articulated a proximal mapping that is associated with general H-monotone operators, which diverges from the resolvent operator linked with the H-accretive mapping [6].

In 1972, a multitude of solutions pertaining to nonlinear equations were presented and analyzed by Amann [9]. In the recent past, fixed-point theory alongside its applications has undergone rigorous examination within the context of real ordered Banach spaces. Consequently, it is of paramount significance and a natural progression for generalized nonlinear ordered variational inequalities (ordered equations) to be meticulously investigated and deliberated. In 2008, Li [10] delineated the framework of generalized nonlinear ordered variational inequalities and proposed a computational algorithm aimed at approximating solutions for a specific class of generalized nonlinear ordered variational inequalities (ordered equations) within real ordered Banach spaces. Over the past two to three years, various forms of ordered variational inequalities and ordered inclusion problems have been extensively scrutinized, as evidenced in works such as [11,12,13] and the associated references therein.

On the contrary, Glowinski, in the year 1989 [14], and Noor, between the years 2000 and 2001 [15,16], formulated a three-step iterative algorithm aimed at addressing various categories of variational inequalities through the application of the Lagrangian multiplier and auxiliary principle methodologies. Consequently, it can be inferred that three-step iterative algorithms occupy a pivotal and consequential role in solutions to diverse challenges encountered in both pure and applied scientific disciplines. Glowinski et al. [14] and Noor [17] demonstrated that the three-step schemes yielded superior numerical outcomes in comparison to the two-step and one-step approximation iterations. In the year 2018, Iqbal et al. [18] introduced a three-step iterative framework for generalized mixed ordered quasi-variational inclusion that incorporates the XOR operator, while more recently, Ali et al. [19] examined the convergence and stability of the three-step iterative algorithm applied to the Extended Cayley–Yosida Inclusion Problem within the context of 2-Uniformly Smooth Banach Spaces.

Remark 1.

It is imperative to acknowledge that the selection of the governing sequences can significantly influence the efficacy of iterative algorithms.

Motivated by the preceding research while adhering to Remark 1, this manuscript presents a framework for extended ordered XOR-inclusion problems that incorporate generalized Cayley and Yosida operators. The solution is attained within a real Banach space utilizing a fixed-point methodology. Initially, we established the fixed-point lemma pertinent to the solutions of the proposed system. By applying the fixed-point lemma, we formulated a three-step iterative scheme aimed at deriving an approximate solution for SEOXORIP. Under the assumptions of Lipschitz continuity pertaining to the cost mappings, we elucidate the strong convergence of the iterative scheme. Finally, we furnish a numerical example accompanied by a convergence graph generated through MATLAB 2018a to substantiate the convergence of the sequence produced by the proposed scheme.

2. Prerequisites and Formulation of SEOXORIP

Throughout this manuscript, we consider $\mathcal{X}$ to be a real ordered Banach space equipped with the norm ${\parallel .\parallel }_{\mathcal{X}}$ and the inner product ${⟨·,·⟩}_{\mathcal{X}\times \mathcal{X}}$, the metric $\mathrm{d}$ generated by the norm ${\parallel .\parallel }_{\mathcal{X}}$, $2^{\mathcal{X}}$ (correspondingly, $CB\left(\mathcal{X}\right)$) representing the nonempty collection of (closed and bounded) subsets of $\mathcal{X}$, and the Hausdorff metric $\mathbb{D}(.,.)$ on $CB\left(\mathcal{X}\right)$, which is defined as follows:

$$\mathbb{D}(A,B)=max\{\underset{\mathrm{s}\in A}{sup}\mathrm{d}(\mathrm{s},B),\underset{\mathrm{t}\in B}{sup}\mathrm{d}(A,\mathrm{t})\},\forall A,B\in CB\left(\mathcal{X}\right),$$

where $\mathrm{d}(\mathrm{s},B)={\displaystyle \underset{\mathrm{t}\in B}{inf}}\{\parallel \mathrm{s}-\mathrm{t}\parallel \}$ and $\mathrm{d}(A,\mathrm{t})={\displaystyle \underset{\mathrm{s}\in A}{inf}}\{\parallel \mathrm{s}-\mathrm{t}\parallel \}$.

A cone is a $\varphi \ne \mathrm{C}\subseteq \mathcal{X}$ convex and closed subset of $\mathcal{X}$ that satisfies, for any $x\in \mathrm{C}$ and scalar $\lambda >0$, $\lambda x\in \mathrm{C}$. $\mathrm{C}$ is called pointed cone if $\mathrm{C}\cap \{-\mathrm{C}\}=\varphi .$ For any $x,y\in \mathcal{X}$, we define an ordering ${\le }_{\mathrm{C}}$ such that $x{\le }_{\mathrm{C}}yifandonlyify-x\in \mathrm{C}$. If either $x{\le }_{\mathrm{C}}y$ or $y{\le }_{\mathrm{C}}x$, then x and y are called comparable elements, and this is denoted by $x\propto y$. The real Banach space $\mathcal{X}$ equipped with ordering ${\le }_{\mathrm{C}}$ is said to be an ordered Banach space.

Let $lub\{x,y\}$ and $glb\{x,y\}$ denote the least upper bound and greatest lower bound of the set $\{x,y\}$, respectively, for all $x,y\in \mathcal{X}.$ Suppose that $lub\{x,y\}$ and $glb\{x,y\}$ for the set $\{x,y\}$ exist; then, we define binary operations:

(i)

$x\vee y=lub\{x,y\},$

(ii)

$x\wedge y=glb\{x,y\},$

(iii)

$x\oplus y=(x-y)\vee (x-y),$

(iv)

$x\odot y=(x-y)\wedge (x-y).$

The operations $\vee ,\wedge ,$⊕, and ⊙ are called OR, AND, XOR, and XNOR operations, respectively. For more details, refer to [20].

Proposition 1

([11,13]). Let ⊕ be an XOR operation and ⊙ be an XNOR operation. Then, the following holds:

(i)

$x\odot x=0,$$x\odot y=y\odot x=-(x\oplus y)=-(y\oplus x);$

(ii)

If $x\propto 0,$ then $-x\oplus 0\le x\le x\oplus 0;$

(iii)

$\left(\lambda x\right)\oplus \left(\lambda y\right)=\left|\lambda \right|(x\oplus y);$

(iv)

If $x\propto y,$ then $x\oplus y=0$ if and only if $x=y;$

(v)

If $x,y$, and w are comparable to each other, then $(x\oplus y)\le (x\oplus w)+(w\oplus y);$

(ix)

If $x,y$, and w are comparable to each other, then $\left[\right(w\oplus x)\oplus (w\oplus y\left)\right]=(x\oplus y);$

(vi)

$\parallel x\oplus y\parallel \le \parallel x-y\parallel \le {\lambda }_P\parallel x\oplus y\parallel$;

(vii)

If $x\propto y,$ then $\parallel x\oplus y\parallel =\parallel x-y\parallel .$

Definition 1

([11,13]). A single-valued mapping $f:\mathcal{X}\to \mathcal{X}$ is called

(i)

A comparison mapping if, for every $x,y\in \mathcal{X}$ and $x\propto y$, then $f\left(x\right)\propto f\left(y\right),$ $x\propto f\left(x\right)$ and $y\propto f\left(y\right);$

(ii)

A strong comparison mapping if f is a comparison mapping and $f\left(x\right)\propto f\left(y\right)$ if and only if $x\propto y$ for any $x,y\in \mathcal{X};$

(iii)

A ${\wp }^f$-ordered compression mapping if f is a comparison mapping and

$$f\left(x\right)\oplus f\left(y\right)\le {\wp }^f(x\oplus y),for{\wp }^f\in (0,1)andx,y\in \mathcal{X}.$$

Definition 2.

Let $f,g:\mathcal{X}\to \mathcal{X}$ be strong comparison single-valued mappings. Then, the mapping $P:\mathcal{X}\times \mathcal{X}\to \mathcal{X}$ is called

(i)

A ${\wp }_P^f$-ordered compression mapping associated with f in the first component if there exists a constant ${\wp }_P^f>0$ such that

$$P(f\left(x\right),.)\oplus P(f\left(y\right),.)\le {\wp }_P^f(x\oplus y),$$

(ii)

A ${\wp }_P^{\mathfrak{g}}$-ordered compression mapping associated with g in the second component if there exists a constant ${\wp }_P^{\mathfrak{g}}>0$ such that

$$P(.,g\left(x\right))\oplus P(.,g\left(y\right))\le {\wp }_P^g(x\oplus y).$$

Definition 3

([21]). Let $(\mathcal{X},\mathrm{d})$ be a metric space and $\mathbb{D}$ be a Hausdorff metric on $CB\left(\mathcal{X}\right)$. Then, the multivalued map $\mathcal{S}:\mathcal{X}\times \mathcal{X}\to 2^{\mathcal{X}}$ is called a multivalued Lipschitz-type mapping with respect to $\mathcal{N}$ if there is a constant ${\lambda }_{{\mathcal{N}}_{\mathbb{D}}}>0$ such that

$$\mathbb{D}(\mathcal{S}(h,u_x),\mathcal{S}(h,u_y))\le {\lambda }_{{\mathcal{N}}_{\mathbb{D}}}\parallel x-y\parallel ,u_x\in \mathcal{N}\left(x\right)and{u}_y\in \mathcal{N}\left(y\right),\forall x,y\in \mathcal{X},$$

where $h:\mathcal{X}\to \mathcal{X}$ be single-valued mapping.

Definition 4

([22]). Let $h:\mathcal{X}\to \mathcal{X}$ be single-valued mapping, $\mathcal{N}:\mathcal{X}\to CB\left(\mathcal{X}\right)$ and $\mathcal{S}:\mathcal{X}\times \mathcal{X}\to 2^{\mathcal{X}}$ be a multivalued mappings. Then, $\mathcal{S}\left(h\right(·),z)$ is said to be α-strongly accretive with respect to h if there is a constant $\alpha >0$ such that

$$⟨u-v,x-y⟩\ge {\alpha \parallel x-y\parallel }^2,\forall x,y\in \mathcal{X},u\in \mathcal{S}(h\left(x\right),z),v\in \mathcal{S}(h\left(y\right),z).$$

Proposition 2

([22]). Let $h:\mathcal{X}\to \mathcal{X}$ be a single-valued mapping, $\mathcal{N}:\mathcal{X}\to CB\left(\mathcal{X}\right)$ be a multivalued mapping, and $\mathcal{S}:\mathcal{X}\times \mathcal{X}\to 2^{\mathcal{X}}$ be α-strongly accretive with respect to h. Then, the mapping ${[I+\lambda \mathcal{S}(h(·),z)]}^{-1}$ is single-valued for $\lambda \ge 0$ and $z\in \mathcal{N}\left(x\right).$

Definition 5

([22]). Let $h:\mathcal{X}\to \mathcal{X}$ be a single-valued mapping, $\mathcal{N}:\mathcal{X}\to CB\left(\mathcal{X}\right)$ be a multivalued mapping, and $\mathcal{S}:\mathcal{X}\times \mathcal{X}\to 2^{\mathcal{X}}$ be α-strongly accretive with respect to h. Then, $\mathcal{S}$ is said to be generalized α-maximal monotone with respect to h if

$$[I+\lambda \mathcal{S}(h,z\left)\right]\mathcal{X}=\mathcal{X},for\lambda >0andz\in \mathcal{N}\left(x\right).$$

Definition 6.

Let $h:\mathcal{X}\to \mathcal{X}$ be a single-valued mapping and $\mathcal{N}:\mathcal{X}\to CB\left(\mathcal{X}\right)$ be a multivalued mapping. Let $\mathcal{S}:\mathcal{X}\times \mathcal{X}\to 2^{\mathcal{X}}$ be generalized α-strongly accretive with respect to h. Then, the generalized proximal-point mapping ${\Re }_{I,\lambda }^{\mathcal{S}\left(h\right(·),z)}:\mathcal{X}\to \mathcal{X}$ associated with h and $\mathcal{N}$ is defined by

$${\Re }_{I,\lambda }^{\mathcal{S}\left(h\right(·),z)}\left(x\right)={[I+\lambda \mathcal{S}(h(·),z)]}^{-1}\left(x\right),\forall x\in \mathcal{X}.$$

(2)

Proposition 3

([11,22]). Let $h:\mathcal{X}\to \mathcal{X}$ be a single-valued mapping and $\mathcal{N}:\mathcal{X}\to CB\left(\mathcal{X}\right)$ be a multivalued mapping. Let $\mathcal{S}:\mathcal{X}\times \mathcal{X}\to 2^{\mathcal{X}}$ be generalized α-maximal monotone with respect to h. Then, the generalized proximal-point mapping ${\Re }_{I,\lambda }^{\mathcal{S}\left(h\right(·),z)}$ is ${\mathcal{L}}^{\Re }$-Lipschitz continuous. That is,

$$∥{\Re }_{I,\lambda }^{\mathcal{S}\left(h\right(·),z)}\left(x\right)-{\Re }_{I,\lambda }^{\mathcal{S}\left(h\right(·),z)}\left(y\right)∥\le {\mathcal{L}}^{\Re }\parallel x-y\parallel ,\forall x,y\in \mathcal{X},$$

where ${\mathcal{L}}^{\Re }=\left({\displaystyle \frac{1}{\alpha \lambda +1}}\right).$

Definition 7

([19]). The generalized Yosida approximation operator $Y_{I,\lambda }^{\mathcal{S}\left(h\right(·),z)}$ associated with the proximal-point mapping ${\Re }_{I,\lambda }^{\mathcal{S}\left(h\right(·),z)}$ is a single-valued mapping; that is, $Y_{I,\lambda }^{\mathcal{S}\left(h\right(·),z)}:\mathcal{X}\to \mathcal{X}$ is defined by

$$Y_{I,\lambda }^{\mathcal{S}\left(h\right(·),z)}\left(x\right)={\displaystyle \frac{1}{\lambda }}[I-{\Re }_{I,\lambda }^{\mathcal{S}\left(h\right(·),z)}]\left(x\right),\forall x\in \mathcal{X}.$$

(3)

Definition 8

([19]). The generalized Cayley operator $C_{I,\lambda }^{\mathcal{S}\left(h\right(·),z)}$ associated with the proximal-point mapping ${\Re }_{I,\lambda }^{\mathcal{S}\left(h\right(·),z)}$ is a single-valued mapping; that is, $C_{I,\lambda }^{\mathcal{S}\left(h\right(·),z)}:\mathcal{X}\to \mathcal{X}$ is defined by

$$C_{I,\lambda }^{\mathcal{S}\left(h\right(·),z)}\left(x\right)=[2{\Re }_{I,\lambda }^{\mathcal{S}\left(h\right(·),z)}-I]\left(x\right),\forall x\in \mathcal{X}.$$

(4)

Remark 2.

(i)

It is well known that the generalized Yosida approximation operator is Lipschitz-type continuous with constant ${\Theta }_Y={\displaystyle \frac{1}{\lambda }}\left(1+{\mathcal{L}}^{\Re }\right).$

(ii)

Similarly, the generalized Cayley operator is Lipschitz-type continuous with constant ${\Theta }_C=\left(2{\mathcal{L}}^{\Re }+1\right).$

SEOXORIP and the Existence of Its Solution

We assume that, for $k\in \mathbb{N}$, $i=1,2,\cdots ,k$. Let $f_i,g_i,h_i:\mathcal{X}\to \mathcal{X}$ and $P_i:\mathcal{X}\times \mathcal{X}\to \mathcal{X}$ be single-valued mappings. Suppose that ${\mathcal{S}}_i:\mathcal{X}\times \mathcal{X}\to 2^{\mathcal{X}}$ is a generalized ${\alpha }_i$-strongly accretive multivalued mapping with respect to $h_i$, and ${\mathcal{N}}_i:\mathcal{X}\to CB\left(\mathcal{X}\right)$ is a closed and bounded multivalued mapping. Then, our interest is in finding $(x_1,\cdots ,x_k)\in {\mathcal{X}}^k$ and $(v_1,\cdots ,v_k)\in \left\}\right\}{N}_1\left(x_1\right)\times \cdots \times \left\}\right\}{N}_k\left(x_k\right)$ such that

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{w}_1\in P_1(C_{I,{\lambda }_1}^{{\mathcal{S}}_1(h_1\left(x_1\right),v_2)}\left(x_1\right),Y_{I,{\lambda }_2}^{{\mathcal{S}}_2(h_2\left(x_2\right),v_3)}\left(x_2\right))+f_1\left(x_1\right)\oplus g_2\left(x_2\right)+{\mathcal{S}}_1(h_1\left(x_1\right),v_2),\hfill \\ w_2\in P_2(C_{I,{\lambda }_2}^{{\mathcal{S}}_2(h_2\left(x_2\right),v_3)}\left(x_2\right),Y_{I,{\lambda }_3}^{{\mathcal{S}}_3(h_3\left(x_3\right),v_4)}\left(x_3\right))+f_2\left(x_2\right)\oplus g_3\left(x_3\right)+{\mathcal{S}}_2(h_2\left(x_2\right),v_3),\hfill \\ ⋮\hfill \\ w_k\in P_k(C_{I,{\lambda }_k}^{{\mathcal{S}}_k(h_k\left(x_k\right),v_1)}\left(x_k\right),Y_{I,{\lambda }_1}^{{\mathcal{S}}_1(h_1\left(x_1\right),v_2)}\left(x_1\right))+f_k\left(x_k\right)\oplus g_1\left(x_1\right)+{\mathcal{S}}_k(h_k\left(x_k\right),v_1),\hfill \end{array}\right.\end{array}$$

(5)

holds, for some $\widehat{w}=(w_1,\cdots w_k)\in {\mathcal{X}}^k.$ This system is called an extended nonlinear system of ordered XOR-inclusion problems involving generalized Cayley–Yosida operators (in short, SEOXORIP).

Moreover, to highlight the level of generalization of our problem, we present several special cases below.

Special Cases:

• If we define $C_{I,{\lambda }_i}^{{\mathcal{S}}_i(h_i\left(x_i\right),v_{i+1})}\left(x_i\right)=f_i\left(x_i\right),$$Y_{I,{\lambda }_i}^{{\mathcal{S}}_i(h_i\left(x_i\right),v_{i+1})}\left(x_i\right)=x_i,\forall x_i$ and $f_i=g_{i+1}\forall i$, then SEOXORIP (5) becomes a system for finding $(x_1,x_2,\cdots ,x_k)\in {\mathcal{X}}^k$ such that

  $$\begin{array}{c}\hfill \left\{\begin{array}{c}{w}_1\in P_1(f_1\left(x_1\right),x_2)+{\mathcal{S}}_1(h_1\left(x_1\right),v_2),\hfill \\ w_2\in P_2(f_2\left(x_2\right),x_3)+{\mathcal{S}}_2(h_2\left(x_2\right),v_3),\hfill \\ ⋮\hfill \\ w_k\in P_k(f_k\left(x_k\right),x_1)+{\mathcal{S}}_k(h_k\left(x_k\right),v_1),\hfill \end{array}\right.\end{array}$$

  (6)

  for some $(w_1,w_2,\cdots ,w_k)\in {\mathcal{X}}^k$. System (6) was introduced and studied by [23].
• Let $i=1,2$. If we define $v_i=\left\{g_i\left(x_i\right)\right\}$ and $C_{I,{\lambda }_1}^{{\mathcal{S}}_i(h_i\left(x_i\right),v_{i+1})}\left(x_i\right)=Y_{I,{\lambda }_i}^{{\mathcal{S}}_i(h_i\left(x_i\right),v_{i+1})}\left(x_i\right)=x_i,\forall x_i$, then for ${\omega }_i=0,\forall i,$  system (5) reduces to the following System of Generalized Variational Inclusions (SGVI), that is, a problem where $(x,y)\in {\mathcal{X}}_1\times {\mathcal{X}}_2$ must be found, such that

  $$\begin{array}{c}\hfill \left\{\begin{array}{c}{\theta }_1\in P_1(x,y)+{\mathcal{S}}_1(h_1\left(x\right),g_2\left(y\right)),\hfill \\ {\theta }_2\in P_2(x,y)+{\mathcal{S}}_2(h_2\left(x\right),g_1\left(y\right)),\hfill \end{array}\right.\end{array}$$

  (7)

  hold, where ${\theta }_1=0$ and ${\theta }_2=0$ are the zeros of ${\mathcal{X}}_1$ and ${\mathcal{X}}_2$, respectively. System (7) was studied by Kazmi et al. [22].

By using the proximal-point mapping, we can characterize the solution of system (5) in terms of fixed-point equations.

Lemma 1.

SEOXORIP (5) has the solution $(x,v)$, i.e., $x=(x_1,\cdots ,x_k)\in {\mathcal{X}}^k$ and $v=(v_1,\cdots ,v_k)\in {\mathcal{N}}_1\left(x_1\right)\times \cdots \times {\mathcal{N}}_k\left(x_k\right),$ if and only if the following equations hold:

$$\begin{array}{cc}\hfill x_1& ={\Re }_{I,{\lambda }_1}^{{\mathcal{S}}_1(h_1(·),v_2)}\left[x_1-{\lambda }_1\{P_1(C_{I,{\lambda }_1}^{{\mathcal{S}}_1(h_1(·),v_2)}\left(x_1\right),Y_{I,{\lambda }_2}^{{\mathcal{S}}_2(h_2(·),v_3)}\left(x_2\right))+f_1\left(x_1\right)\oplus g_2\left(x_2\right)-w_1\}\right],\hfill \\ \hfill x_2& ={\Re }_{I,{\lambda }_2}^{{\mathcal{S}}_2(h_2(·),v_3)}\left[x_2-{\lambda }_2\{P_2(C_{I,{\lambda }_2}^{{\mathcal{S}}_2(h_2(·),v_3)}\left(x_2\right),Y_{I,{\lambda }_3}^{{\mathcal{S}}_3(h_3(·),v_4)}\left(x_3\right))+f_2\left(x_2\right)\oplus g_3\left(x_3\right)-w_2\}\right],\hfill \\ \hfill & ⋮\hfill \\ \hfill x_k& ={\Re }_{I,{\lambda }_k}^{{\mathcal{S}}_k(h_k(·),v_1)}\left[x_k-{\lambda }_k\{P_k(C_{I,{\lambda }_k}^{{\mathcal{S}}_k(h_k(·),v_1)}\left(x_k\right),Y_{I,{\lambda }_1}^{{\mathcal{S}}_1(h_1(·),v_2)}\left(x_1\right))+f_k\left(x_k\right)\oplus g_1\left(x_1\right)-w_k\}\right],\hfill \end{array}$$

(8)

where ${\lambda }_i^{\prime s}>0$ are non-negative real numbers.

Proof. 

The proof follows directly from Definition 6 of proximal-point mapping.

Now, we have the following theorem for the existence of the solution to system (5). □

Theorem 1.

Let $i=1,2,\cdots ,k$, $k\in \mathbb{N},and we setk+1=1$. Let $f_i,g_i,h_i:\mathcal{X}\to \mathcal{X}$ be ${\wp }^{f_i}$, ${\wp }^{g_i}$, and ${\wp }^{h_i}$ strongly ordered comparison mappings. Assume that $P_i:\mathcal{X}\times \mathcal{X}\to \mathcal{X}$ is a ${\wp }_{P_i}^{C_i}$-ordered compression mapping associated with $C_{I,{\lambda }_i}^{{\mathcal{S}}_i(h_i(·),z)}$ in the first component and ${\wp }_{P_i}^{Y_i}$-ordered compression mapping associated with $Y_{I,{\lambda }_i}^{{\mathcal{S}}_i(h_i(·),z)}$ in the second component. Let ${\mathcal{S}}_i:\mathcal{X}\times \mathcal{X}\to 2^{\mathcal{X}}$ be generalized ${\alpha }_i$-strongly accretive with respect to $h_i$ and ${\mathcal{N}}_i:\mathcal{X}\to CB\left(\mathcal{X}\right)$ be a closed and bounded multivalued mapping. Suppose ${\Re }_{I,{\lambda }_i}^{{\mathcal{S}}_i(h_i(·),z)}$, $Y_{I,{\lambda }_i}^{{\mathcal{S}}_i(h_i(·),z)}$, and $C_{I,{\lambda }_i}^{{\mathcal{S}}_i(h_i(·),z)}$ are Lipschitz continuous with constants ${\mathcal{L}}^{{\Re }_i}$, ${\Theta }_{Y_i}$, and ${\Theta }_{C_i}$, respectively.

Additionally,   let   $x_i\propto x_{i+1}$, $y_i\propto y_{i+1}$ $f_i\left(x_i\right)\propto f_i\left(y_i\right)$, $g_i\left(x_i\right)\propto g_i\left(y_i\right)$, and ${\Re }_{I,{\lambda }_i}^{{\mathcal{S}}_i(h_i(·),z)}\left(x_i\right)\propto {\Re }_{I,{\lambda }_i}^{{\mathcal{S}}_i(h_i(·),z)}\left(y_i\right)$, and for all constants ${\lambda }_1,{\lambda }_2,\cdots ,{\lambda }_k>0$, the following relations hold:

$$\begin{array}{cc}\hfill {\lambda }_1({\wp }_{P_1}^{C_1}{\Theta }_{C_1}+{\wp }^{f_1})+{\lambda }_k({\wp }_{P_k}^{Y_1}{\Theta }_{Y_1}+{\wp }^{g_1})& <\left({\displaystyle \frac{1}{{\mathcal{L}}^{{\Re }^1}}}-1\right),\hfill \\ \hfill {\lambda }_2({\wp }_{P_2}^{C_2}{\Theta }_{C_2}+{\wp }^{f_2})+{\lambda }_1({\wp }_{P_1}^{Y_2}{\Theta }_{Y_2}+{\wp }^{g_2})& <\left({\displaystyle \frac{1}{{\mathcal{L}}^{{\Re }^2}}}-1\right),\hfill \\ \hfill & ⋮\hfill \\ \hfill {\lambda }_k({\wp }_{P_k}^{C_k}{\Theta }_{C_k}+{\wp }^{f_k})+{\lambda }_{k-1}({\wp }_{P_{k-1}}^{Y_k}{\Theta }_{Y_k}+{\wp }^{g_k})& <\left({\displaystyle \frac{1}{{\mathcal{L}}^{{\Re }^k}}}-1\right),\hfill \end{array}$$

(9)

where

$${\mathcal{L}}^{{\Re }^i}=\left({\displaystyle \frac{1}{{\alpha }_i{\lambda }_i+1}}\right),{\Theta }_{Y_i}={\displaystyle \frac{1}{{\lambda }_i}}({\mathcal{L}}^{{\Re }^i}-1)and{\Theta }_{C_i}=2{\mathcal{L}}^{{\Re }^i}-1.$$

Then, SEOXORIP (5) admits a solution $(x_i,v_i).$

Proof. 

We define the mapping $\mathcal{Q}:{\mathcal{X}}^k⟶{\mathcal{X}}^k$ by

$$\begin{array}{c}\hfill \mathcal{Q}(x_1,\cdots ,x_k):=({\mathcal{Q}}_1(x_1,x_2),\cdots ,{\mathcal{Q}}_{\kappa }(x_k,x_1)),\forall (x_1,\cdots ,x_k)\in {\mathcal{X}}^k,\end{array}$$

where the mappings ${\mathcal{Q}}_i:\mathcal{X}\times \mathcal{X}\to \mathcal{X}$ are defined as

$$\begin{array}{ccc}\hfill {\mathcal{Q}}_1(x_1,x_2)& =& {\Re }_{I,{\lambda }_1}^{{\mathcal{S}}_1(h_1(·),v_2)}\left[x_1-{\lambda }_1\{P_1(C_{I,{\lambda }_1}^{{\mathcal{S}}_1(h_1(·),v_2)}\left(x_1\right),Y_{I,{\lambda }_2}^{{\mathcal{S}}_2(h_2(·),v_3)}\left(x_2\right))+f_1\left(x_1\right)\oplus g_2\left(x_2\right)-w_1\}\right],\hfill \\ \hfill {\mathcal{Q}}_2(x_2,x_3)& =& {\Re }_{I,{\lambda }_2}^{{\mathcal{S}}_2(h_2(·),v_3)}\left[x_2-{\lambda }_2\{P_2(C_{I,{\lambda }_2}^{{\mathcal{S}}_2(h_2(·),v_3)}\left(x_2\right),Y_{I,{\lambda }_3}^{{\mathcal{S}}_3(h_3(·),v_4)}\left(x_3\right))+f_2\left(x_2\right)\oplus g_3\left(x_3\right)-w_2\}\right],\hfill \\ & ⋮& \hfill \\ \hfill {\mathcal{Q}}_k(x_{\kappa },x_1)& =& {\Re }_{I,{\lambda }_k}^{{\mathcal{S}}_k(h_k(·),v_1)}\left[x_k-{\lambda }_k\{P_k(C_{I,{\lambda }_k}^{{\mathcal{S}}_k(h_k(·),v_1)}\left(x_k\right),Y_{I,{\lambda }_1}^{{\mathcal{S}}_1(h_1(·),v_2)}\left(x_1\right))+f_k\left(x_k\right)\oplus g_1\left(x_1\right)-w_k\}\right].\hfill \end{array}$$

Let $x_i,y_i\in \mathcal{X},v_i\in {\mathcal{N}}_i\left(x_i\right)$ such that $x_i\propto x_j,y_i\propto y_j,v_i\propto v_j$, and by applying Proposition 3, we have

$$\begin{array}{ccc}\hfill & & \parallel {\mathcal{Q}}_1(x_1,x_2)\oplus {\mathcal{Q}}_1(y_1,y_2)\parallel \hfill \\ & =& \parallel {\Re }_{I,{\lambda }_1}^{{\mathcal{S}}_1(h_1(·),v_2)}\left[x_1-{\lambda }_1\{P_1(C_{I,{\lambda }_1}^{{\mathcal{S}}_1(h_1(·),v_2)}\left(x_1\right),Y_{I,{\lambda }_2}^{{\mathcal{S}}_2(h_2(·),v_3)}\left(x_2\right))+f_1\left(x_1\right)\oplus g_2\left(x_2\right)-w_1\}\right]\hfill \\ & & \oplus {\Re }_{I,{\lambda }_1}^{{\mathcal{S}}_1(h_1(·),v_2)}\left[y_1-{\lambda }_1\{P_1(C_{I,{\lambda }_1}^{{\mathcal{S}}_1(h_1(·),v_2)}\left(y_1\right),Y_{I,{\lambda }_2}^{{\mathcal{S}}_2(h_2(·),v_3)}\left(y_2\right))+f_1\left(y_1\right)\oplus g_2\left(y_2\right)-w_1\}\right]\parallel \hfill \\ & \le & {\mathcal{L}}^{{\Re }_1}\{\parallel x_1\oplus y_1\parallel +{\lambda }_1\parallel P_1\left(C_{I,{\lambda }_1}^{{\mathcal{S}}_1(h_1(·),v_2)}\left(x_1\right),Y_{I,{\lambda }_2}^{{\mathcal{S}}_2(h_2(·),v_3)}\left(x_2\right)\right)\oplus P_1(C_{I,{\lambda }_1}^{{\mathcal{S}}_1(h_1(·),v_2)}\left(y_1\right),\hfill \\ & & Y_{I,{\lambda }_2}^{{\mathcal{S}}_2(h_2(·),v_3)}\left(y_2\right))\parallel +{\lambda }_1\parallel f_1\left(x_1\right)\oplus g_2\left(x_2\right)\oplus f_1\left(y_1\right)\oplus g_2\left(y_2\right)\parallel \}.\hfill \end{array}$$

(10)

By applying Proposition 1 and the ordered compressionness of $f_1$ and $g_2$, we have

$$\begin{array}{ccc}\hfill \parallel f_1\left(x_1\right)\oplus g_2\left(x_2\right)\oplus f_1\left(y_1\right)\oplus g_2\left(y_2\right)\parallel & =& \parallel f_1\left(x_1\right)\oplus f_1\left(y_1\right)\oplus g_2\left(x_2\right)\oplus g_2\left(y_2\right)\parallel \hfill \\ & \le & \parallel f_1\left(x_1\right)\oplus f_1\left(y_1\right)\parallel +\parallel g_2\left(x_2\right)\oplus g_2\left(y_2\right)\parallel \hfill \\ & \le & {\wp }^{f_1}\parallel x_1\oplus y_1\parallel +{\wp }^{g_2}\parallel x_2\oplus y_2\parallel .\hfill \end{array}$$

(11)

Since $P_1$ is a ${\wp }_{P_1}^{C_1}$-ordered compression mapping in the first component with respect to $C_{I,{\lambda }_1}^{{\mathcal{S}}_1(h_1(·),v_2)}$ and a ${\wp }_{P_1}^{Y_1}$-ordered compression mapping in the second component with respect to $Y_{I,{\lambda }_2}^{{\mathcal{S}}_2(h_2(·),v_3)}$, we have

$$\begin{array}{cc}\hfill & \parallel P_1\left(C_{I,{\lambda }_1}^{{\mathcal{S}}_1(h_1(·),v_2)}\left(x_1\right),Y_{I,{\lambda }_2}^{{\mathcal{S}}_2(h_2(·),v_3)}\left(x_2\right)\right)\oplus P_1\left(C_{I,{\lambda }_1}^{{\mathcal{S}}_1(h_1(·),v_2)}\left(y_1\right),Y_{I,{\lambda }_2}^{{\mathcal{S}}_2(h_2(·),v_3)}\left(y_2\right)\right)\parallel \hfill \\ \hfill & \le ∥P_1\left(C_{I,{\lambda }_1}^{{\mathcal{S}}_1(h_1(·),v_2)}\left(x_1\right),Y_{I,{\lambda }_2}^{{\mathcal{S}}_2(h_2(·),v_3)}\left(x_2\right)\right)\oplus P_1\left(C_{I,{\lambda }_1}^{{\mathcal{S}}_1(h_1(·),v_2)}\left(y_1\right),Y_{I,{\lambda }_2}^{{\mathcal{S}}_2(h_2(·),v_3)}\left(x_2\right)\right)∥\hfill \\ \hfill & +∥P_1\left(C_{I,{\lambda }_1}^{{\mathcal{S}}_1(h_1(·),v_2)}\left(y_1\right),Y_{I,{\lambda }_2}^{{\mathcal{S}}_2(h_2(·),v_3)}\left(x_2\right)\right)\oplus P_1\left(C_{I,{\lambda }_1}^{{\mathcal{S}}_1(h_1(·),v_2)}\left(y_1\right),Y_{I,{\lambda }_2}^{{\mathcal{S}}_2(h_2(·),v_3)}\left(y_2\right)\right)∥\hfill \\ \hfill & \le {\wp }_{P_1}^{C_1}∥C_{I,{\lambda }_1}^{{\mathcal{S}}_1(h_1(·),v_2)}\left(x_1\right)\oplus C_{I,{\lambda }_1}^{{\mathcal{S}}_1(h_1(·),v_2)}\left(y_1\right)∥+{\wp }_{P_1}^{Y_1}∥Y_{I,{\lambda }_2}^{{\mathcal{S}}_2(h_2(·),v_3)}\left(x_2\right)\oplus Y_{I,{\lambda }_2}^{{\mathcal{S}}_2(h_2(·),v_3)}\left(y_2\right)∥\hfill \\ \hfill & \le {\wp }_{P_1}^{C_1}{\Theta }_{C_1}\parallel x_1\oplus y_1\parallel +{\wp }_{P_1}^{Y_1}{\Theta }_{Y_1}\parallel x_2\oplus y_2\parallel \hfill \\ \hfill & \le {\wp }_{P_1}^{C_1}{\Theta }_{C_1}\parallel x_1-y_1\parallel +{\wp }_{P_1}^{Y_1}{\Theta }_{Y_1}\parallel x_2-y_2\parallel .\hfill \end{array}$$

(12)

Inserting (11) and (12) into (10) and applying Proposition 1, we get

$$\begin{array}{ccc}\hfill & & \parallel {\mathcal{Q}}_1(x_1,x_2)\oplus {\mathcal{Q}}_1(y_1,y_2)\parallel =\parallel {\mathcal{Q}}_1(x_1,x_2)-{\mathcal{Q}}_1(y_1,y_2)\parallel \hfill \\ & \le & {\mathcal{L}}^{{\Re }_1}\{\parallel x_1-y_1\parallel +{\lambda }_1({\wp }_{P_1}^{C_1}{\Theta }_{C_1}\parallel x_1-y_1\parallel +{\wp }_{P_1}^{Y_1}{\Theta }_{Y_1}\parallel x_2-y_2\parallel \hfill \\ & & +{\wp }^{f_1}\parallel x_1-y_1\parallel +{\wp }^{g_2}\parallel x_2-y_2\parallel \left)\right\}\hfill \\ & =& {\mathcal{L}}^{{\Re }_1}\left([1+{\lambda }_1({\wp }_{P_1}^{C_1}{\Theta }_{C_1}+{\wp }^{f_1})]\parallel x_1-y_1\parallel +{\lambda }_1({\wp }_{P_1}^{Y_1}{\Theta }_{Y_1}+{\wp }^{g_2})\parallel x_2-y_2\parallel \right).\hfill \end{array}$$

(13)

Continuing in similar fashion, let $x_i,y_i\in \mathcal{X},v_i\in {\mathcal{N}}_i\left(x_i\right)$ such that $x_i\propto x_j,y_i\propto y_j,$ and  $v_i\propto v_j$; applying Proposition 3, we have

$$\begin{array}{ccc}\hfill & & \parallel {\mathcal{Q}}_k(x_k,x_1)\oplus {\mathcal{Q}}_k(y_k,y_1)\parallel \hfill \\ & =& \parallel {\Re }_{I,{\lambda }_k}^{{\mathcal{S}}_k(h_k(·),v_1)}\left[x_k-{\lambda }_k\{P_k(C_{I,{\lambda }_k}^{{\mathcal{S}}_k(h_k(·),v_1)}\left(x_k\right),Y_{I,{\lambda }_1}^{{\mathcal{S}}_1(h_1(·),v_2)}\left(x_1\right))+f_k\left(x_k\right)\oplus g_1\left(x_1\right)-w_k\}\right]\hfill \\ & & -{\Re }_{I,{\lambda }_k}^{{\mathcal{S}}_k(h_k(·),v_1)}\left[y_k-{\lambda }_k\{P_k(C_{I,{\lambda }_k}^{{\mathcal{S}}_k(h_k(·),v_1)}\left(y_k\right),Y_{I,{\lambda }_1}^{{\mathcal{S}}_1(h_1(·),v_2)}\left(y_1\right))+f_k\left(y_k\right)\oplus g_1\left(y_1\right)-w_k\}\right]\parallel \hfill \\ & \le & {\mathcal{L}}^{{\Re }_k}\{\parallel x_k\oplus y_k\parallel +{\lambda }_k\parallel P_k\left(C_{I,{\lambda }_k}^{{\mathcal{S}}_k(h_k(·),v_1)}\left(x_k\right),Y_{I,{\lambda }_1}^{{\mathcal{S}}_1(h_1(·),v_2)}\left(x_1\right)\right)\oplus P_k(C_{I,{\lambda }_k}^{{\mathcal{S}}_k(h_k(·),v_1)}\left(y_k\right),\hfill \\ & & Y_{I,{\lambda }_1}^{{\mathcal{S}}_1(h_1(·),v_2)}\left(y_1\right))\parallel +{\lambda }_k\parallel f_k\left(x_k\right)\oplus g_1\left(x_1\right)\oplus f_k\left(y_k\right)\oplus g_1\left(y_1\right)\parallel \}.\hfill \end{array}$$

(14)

By applying Proposition 1 and the ordered compressionness of $f_k$ and $g_1$, we have

$$\begin{array}{ccc}\hfill \parallel f_k\left(x_k\right)\oplus g_1\left(x_1\right)\oplus f_k\left(y_k\right)\oplus g_1\left(y_1\right)\parallel & =& \parallel f_k\left(x_k\right)\oplus f_k\left(y_k\right)\oplus g_1\left(x_1\right)\oplus g_1\left(y_1\right)\parallel \hfill \\ & \le & \parallel f_k\left(x_k\right)\oplus f_k\left(y_k\right)\parallel +\parallel g_1\left(x_1\right)\oplus g_1\left(y_1\right)\parallel \hfill \\ & \le & {\wp }^{f_k}\parallel x_k-y_k\parallel +{\wp }^{g_1}\parallel x_1-y_1\parallel .\hfill \end{array}$$

(15)

Since $P_k$ is a ${\wp }_{P_k}^{C_k}$-ordered compression mapping associated with $C_{I,{\lambda }_k}^{{\mathcal{S}}_k(h_k(·),v_1)}$ in the first component and a ${\wp }_{P_k}^{Y_1}$-ordered compression mapping associated with $Y_{I,{\lambda }_1}^{{\mathcal{S}}_1(h_1(·),v_2)}$ in the second component, we have

$$\begin{array}{cc}\hfill & \parallel P_k\left(C_{I,{\lambda }_k}^{{\mathcal{S}}_k(h_k(·),v_1)}\left(x_k\right),Y_{I,{\lambda }_1}^{{\mathcal{S}}_1(h_1(·),v_2)}\left(x_1\right)\right)\oplus P_k\left(C_{I,{\lambda }_k}^{{\mathcal{S}}_k(h_k(·),v_1)}\left(y_k\right),Y_{I,{\lambda }_1}^{{\mathcal{S}}_1(h_1(·),v_2)}\left(y_1\right)\right)\parallel \hfill \\ \hfill & \le ∥P_k\left(C_{I,{\lambda }_k}^{{\mathcal{S}}_k(h_k(·),v_1)}\left(x_k\right),Y_{I,{\lambda }_k}^{{\mathcal{S}}_1(h_1(·),v_2)}\left(x_1\right)\right)\oplus P_k\left(C_{I,{\lambda }_k}^{{\mathcal{S}}_k(h_k(·),v_1)}\left(y_k\right),Y_{I,{\lambda }_1}^{{\mathcal{S}}_1(h_2(·),v_2)}\left(x_1\right)\right)∥\hfill \\ \hfill & +∥P_k\left(C_{I,{\lambda }_k}^{{\mathcal{S}}_k(h_k(·),v_1)}\left(y_k\right),Y_{I,{\lambda }_1}^{{\mathcal{S}}_1(h_1(·),v_2)}\left(x_1\right)\right)\oplus P_k\left(C_{I,{\lambda }_1}^{{\mathcal{S}}_k(h_k(·),v_1)}\left(y_1\right),Y_{I,{\lambda }_1}^{{\mathcal{S}}_1(h_1(·),v_2)}\left(y_1\right)\right)∥\hfill \\ \hfill & \le {\wp }_{P_k}^{C_k}∥C_{I,{\lambda }_k}^{{\mathcal{S}}_k(h_k(·),v_1)}\left(x_k\right)\oplus C_{I,{\lambda }_k}^{{\mathcal{S}}_k(h_k(·),v_1)}\left(y_k\right)∥+{\wp }_{P_k}^{Y_k}∥Y_{I,{\lambda }_1}^{{\mathcal{S}}_1(h_1(·),v_2)}\left(x_1\right)\oplus Y_{I,{\lambda }_1}^{{\mathcal{S}}_1(h_1(·),v_2)}\left(y_1\right)∥\hfill \\ \hfill & \le {\wp }_{P_k}^{C_k}{\Theta }_{C_k}\parallel x_k\oplus y_k\parallel +{\wp }_{P_k}^{Y_k}{\Theta }_{Y_k}\parallel x_1\oplus y_1\parallel \hfill \\ \hfill & \le {\wp }_{P_k}^{C_k}{\Theta }_{C_k}\parallel x_k-y_k\parallel +{\wp }_{P_k}^{Y_k}{\Theta }_{Y_k}\parallel x_1-y_1\parallel .\hfill \end{array}$$

(16)

Inserting (15) and (16) into (14) and applying Proposition 1, we get

$$\begin{array}{ccc}\hfill & & \parallel {\mathcal{Q}}_k(x_k,x_1)\oplus {\mathcal{Q}}_k(y_k,y_1)\parallel =\parallel {\mathcal{Q}}_k(x_k,x_1)-{\mathcal{Q}}_k(y_k,y_1)\parallel \hfill \\ & \le & {\mathcal{L}}^{{\Re }_k}\{\parallel x_k-y_k\parallel +{\lambda }_k({\wp }_{P_k}^{C_k}{\Theta }_{C_k}\parallel x_k-y_k\parallel +{\wp }_{P_k}^{Y_k}{\Theta }_{Y_1}\parallel x_1-y_1\parallel \hfill \\ & & +{\wp }^{f_k}\parallel x_k-y_k\parallel +{\wp }^{g_1}\parallel x_1-y_1\parallel \left)\right\}\hfill \\ & =& {\mathcal{L}}^{{\Re }_k}\left([1+{\lambda }_k({\wp }_{P_k}^{C_k}{\Theta }_{C_k}+{\wp }^{f_k})]\parallel x_k-y_k\parallel +{\lambda }_k({\wp }_{P_k}^{Y_1}{\Theta }_{Y_1}+{\wp }^{g_1})\parallel x_1-y_1\parallel \right).\hfill \end{array}$$

(17)

Based on (13) and (17), we have

$$\begin{array}{cc}\hfill \parallel {\mathcal{Q}}_1(x_1,x_2)-{\mathcal{Q}}_1(y_1,y_2)\parallel & +\cdots +\parallel {\mathcal{Q}}_k(x_k,x_1)-{\mathcal{Q}}_k(y_k,y_1)\parallel \hfill \\ \hfill & \le {\mathcal{L}}^{{\Re }_1}[1+{\lambda }_1({\wp }_{P_1}^{C_1}{\Theta }_{C_1}+{\wp }^{f_1})+{\lambda }_k({\wp }_{P_k}^{Y_1}{\Theta }_{Y_1}+{\wp }^{g_1})]\parallel x_1-y_1\parallel \hfill \\ \hfill & +{\mathcal{L}}^{{\Re }_2}[1+{\lambda }_2({\wp }_{P_2}^{C_2}{\Theta }_{C_2}+{\wp }^{f_2})+{\lambda }_1({\wp }_{P_1}^{Y_2}{\Theta }_{Y_2}+{\wp }^{g_2})]\parallel x_2-y_2\parallel \hfill \\ \hfill & +\cdots +\hfill \\ \hfill & +{\mathcal{L}}^{{\Re }_k}[1+{\lambda }_k({\wp }_{P_k}^{C_k}{\Theta }_{C_k}+{\wp }^{f_k})+{\lambda }_{k-}({\wp }_{P_{k-1}}^{Y_k}{\Theta }_{Y_k}+{\wp }^{g_k})]\parallel x_k-y_k\parallel ,\hfill \end{array}$$

that is,

$$\begin{array}{c}\hfill \sum _{i=1}^k\parallel {\mathcal{Q}}_i(x_i,x_{i+1})-{\mathcal{Q}}_i(y_i,y_{i+1})\parallel \le \sum _{i=1}^k{\Xi }_i^{k+i-1}{\mathcal{L}}^{{\Re }^i}\parallel x_i-y_i\parallel ,\end{array}$$

(18)

where

$$\begin{array}{cc}\hfill {\Xi }_1^k& ={\mathcal{L}}^{{\Re }_1}[1+{\lambda }_1({\wp }_{P_1}^{C_1}{\Theta }_{C_1}+{\wp }^{f_1})+{\lambda }_k({\wp }_{P_k}^{Y_1}{\Theta }_{Y_1}+{\wp }^{g_1})],\hfill \\ \hfill {\Xi }_2^1& ={\mathcal{L}}^{{\Re }_2}[1+{\lambda }_2({\wp }_{P_2}^{C_2}{\Theta }_{C_2}+{\wp }^{f_2})+{\lambda }_1({\wp }_{P_1}^{Y_2}{\Theta }_{Y_2}+{\wp }^{g_2})],\hfill \\ \hfill & ⋮\hfill \\ \hfill {\Xi }_k^{k-1}& ={\mathcal{L}}^{{\Re }_k}[1+{\lambda }_k({\wp }_{P_k}^{C_k}{\Theta }_{C_k}+{\wp }^{f_k})+{\lambda }_{k-}({\wp }_{P_{k-1}}^{Y_k}{\Theta }_{Y_k}+{\wp }^{g_k})].\hfill \end{array}$$

The norm $\parallel (x_1,\cdots ,x_k){\parallel }_{1}on{\mathcal{X}}^k$  is defined as

$$\begin{array}{c}\hfill \parallel (x_1,\cdots ,x_{\kappa }){\parallel }_1=\parallel x_1\parallel +\cdots +\parallel x_{\kappa }\parallel ,\forall (x_1,\cdots ,x_k)\in {\mathcal{X}}^k.\end{array}$$

(19)

Clearly, the structure $({\mathcal{X}}^k,\parallel .{\parallel }_1)$ forms a Banach space with respect to the norm (19). Thus, the definition of the mapping $\mathcal{Q}$, (18) and (19), implies that

$$\begin{array}{cc}\parallel \mathcal{Q}(x_1,\cdots ,x_{\kappa })-\mathcal{Q}(y_1,\cdots ,y_{\kappa }){\parallel }_1& =\parallel {\mathcal{Q}}_1(x_1,x_2)-{\mathcal{Q}}_1(y_1,y_2)\parallel +\cdots +\parallel {\mathcal{Q}}_k(x_k,x_1)-{\mathcal{Q}}_k(y_k,y_1)\parallel \hfill \\ \hfill & \le max\left\{{\Xi }_1^k,{\Xi }_2^1,\cdots ,{\Xi }_k^{k-1}\right\}(\parallel x_1-y_1\parallel +\parallel x_2-y_2\parallel \cdots +\parallel x_k-y_k\parallel ).\hfill \end{array}$$

(20)

From (9), we conclude that $max\left\{{\Xi }_1^k,{\Xi }_2^1,\cdots ,{\Xi }_k^{k-1}\right\}<1$. Therefore, there exists a unique fixed point $(x_1,\cdots ,x_k)\in {\mathcal{X}}^k$ of the mapping $\mathcal{Q}$. That is,

$$\begin{array}{c}\hfill \mathcal{Q}(x_1,\cdots ,x_k)=(x_1,\cdots ,x_k).\end{array}$$

This leads to

$$\begin{array}{cc}\hfill x_1& ={\Re }_{I,{\lambda }_1}^{{\mathcal{S}}_1(h_1(·),v_2)}\left[x_1-{\lambda }_1\{P_1(C_{I,{\lambda }_1}^{{\mathcal{S}}_1(h_1(·),v_2)}\left(x_1\right),Y_{I,{\lambda }_2}^{{\mathcal{S}}_2(h_2(·),v_3)}\left(x_2\right))+f_1\left(x_1\right)\oplus g_2\left(x_2\right)-w_1\}\right],\hfill \\ \hfill x_2& ={\Re }_{I,{\lambda }_2}^{{\mathcal{S}}_2(h_2(·),v_3)}\left[x_2-{\lambda }_2\{P_2(C_{I,{\lambda }_2}^{{\mathcal{S}}_2(h_2(·),v_3)}\left(x_2\right),Y_{I,{\lambda }_3}^{{\mathcal{S}}_3(h_3(·),v_4)}\left(x_3\right))+f_2\left(x_2\right)\oplus g_3\left(x_3\right)-w_2\}\right],\hfill \\ \hfill & ⋮\hfill \\ \hfill x_k& ={\Re }_{I,{\lambda }_k}^{{\mathcal{S}}_k(h_k(·),v_1)}\left[x_k-{\lambda }_k\{P_k(C_{I,{\lambda }_k}^{{\mathcal{S}}_k(h_k(·),v_1)}\left(x_k\right),Y_{I,{\lambda }_1}^{{\mathcal{S}}_1(h_1(·),v_2)}\left(x_1\right))+f_k\left(x_k\right)\oplus g_1\left(x_1\right)-w_k\}\right].\hfill \end{array}$$

(21)

Hence, Lemma (1) ensures that $(x,v)$ is a solution of system (5).    □

3. Three-Step Iterative Scheme and Its Convergence

In this section, leveraging Lemma 1, we formulate a three-step iterative algorithm aimed at determining the approximate solution for the newly established system of ordered XOR-inclusion problems involving Cayley and Yosida operators (Algorithm 1). The convergence properties of the sequence produced by the algorithm are demonstrated under certain appropriate assumptions.

Algorithm 1: Three-Step Iterative Algorithm for the Approximate Solution of SEOXORIP

Let $i=1,2,\cdots ,k$, $k\in \mathbb{N}and setk+1=1$; let $f_i,g_i,h_i:\mathcal{X}\to \mathcal{X}$ and $P_i:\mathcal{X}\times \mathcal{X}\to \mathcal{X}$ be single-valued mappings. Let ${\mathcal{N}}_i:\mathcal{X}\to CB\left(\mathcal{X}\right)$ be a $\mathbb{D}$-Lipschitz continuous mapping with constants ${\lambda }_{{\mathcal{N}}_{\mathbb{D}}}$ and let ${\mathcal{S}}_i:\mathcal{X}\times \mathcal{X}\to 2^{\mathcal{X}}$ be a generalized ${\alpha }_i$-strongly accretive mapping with respect to $h_i$. Then, Initially: Choose $(x_1^0,\cdots ,x_k^0)\in {\mathcal{X}}^k$ and $(v_1^0,\cdots ,v_k^0)\in {\mathcal{N}}_1\left(x_1^0\right)\times \cdots \times {\mathcal{N}}_k\left(x_k^0\right)$. Step I: Let $x_i^{(n+1)}\propto x_i^{\left(n\right)}$ and $v_i^{\left(n\right)}\propto v_j^{\left(n\right)}.$ We define $$\begin{array}{cc}\hfill x_1^{(n+1)}& ={\alpha }_1^n{\Re }_{I,{\lambda }_1}^{{\mathcal{S}}_1(h_1(·),v_2)}[y_1^n-{\lambda }_1\{P_1(C_{I,{\lambda }_1}^{{\mathcal{S}}_1(h_1(·),v_2)}\left(y_1^n\right),Y_{I,{\lambda }_2}^{{\mathcal{S}}_2(h_2(·),v_3)}\left(y_2^n\right))\hfill \\ \hfill & +f_1\left(y_1^n\right)\oplus g_2\left(y_2^n\right)-w_1\left\}\right]+(1-{\alpha }_1^n)x_1^n+{\alpha }_1^n{\delta }_1^n\hfill \\ \hfill y_1^{\left(n\right)}& ={\beta }_1^n{\Re }_{I,{\lambda }_1}^{{\mathcal{S}}_1(h_1(·),v_2)}[z_1^n-{\lambda }_1\{P_1(C_{I,{\lambda }_1}^{{\mathcal{S}}_1(h_1(·),v_2)}\left(z_1^n\right),Y_{I,{\lambda }_2}^{{\mathcal{S}}_2(h_2(·),v_3)}\left(z_2^n\right))\hfill \\ \hfill & +f_1\left(z_1^n\right)\oplus g_2\left(z_2^n\right)-w_1\left\}\right]+(1-{\beta }_1^n)x_1^{\left(n\right)}+{\beta }_1^n{\delta }_2^n\hfill \\ \hfill z_1^{\left(n\right)}& ={\gamma }_1^n{\Re }_{I,{\lambda }_1}^{{\mathcal{S}}_1(h_1(·),v_2)}[x_1^n-{\lambda }_1\{P_1(C_{I,{\lambda }_1}^{{\mathcal{S}}_1(h_1(·),v_2)}\left(x_1^n\right),Y_{I,{\lambda }_2}^{{\mathcal{S}}_2(h_2(·),v_3)}\left(x_2^n\right))\hfill \\ \hfill & +f_1\left(x_1^n\right)\oplus g_2\left(x_2^n\right)-w_1\left\}\right]+(1-{\gamma }_1^n)x_1^{\left(n\right)}+{\gamma }_1^n{\delta }_3^n\hfill \\ \hfill & ⋮\hfill \\ \hfill x_k^{(n+1)}& ={\alpha }_k^n{\Re }_{I,{\lambda }_1}^{{\mathcal{S}}_k(h_k(·),v_1)}[y_k^n-{\lambda }_k\{P_1(C_{I,{\lambda }_k}^{{\mathcal{S}}_k(h_k(·),v_1)}\left(y_k^n\right),Y_{I,{\lambda }_1}^{{\mathcal{S}}_1(h_1(·),v_2)}\left(y_1^n\right))\hfill \\ \hfill & +f_k\left(y_k^n\right)\oplus g_1\left(y_1^n\right)-w_k\left\}\right]+(1-{\alpha }_k^n)x_k^n+{\alpha }_k^n{\delta }_k^n\hfill \\ \hfill y_k^{\left(n\right)}& ={\beta }_k^n{\Re }_{I,{\lambda }_k}^{{\mathcal{S}}_k(h_k(·),v_1)}[z_k^n-{\lambda }_k\{P_k(C_{I,{\lambda }_k}^{{\mathcal{S}}_k(h_k(·),v_1)}\left(z_k^n\right),Y_{I,{\lambda }_1}^{{\mathcal{S}}_1(h_1(·),v_2)}\left(z_1^n\right))\hfill \\ \hfill & +f_k\left(z_k^n\right)\oplus g_1\left(z_1^n\right)-w_k\left\}\right]+(1-{\beta }_k^n)x_k^{\left(n\right)}+{\beta }_k^n{\delta }_{k+1}^n\hfill \\ \hfill z_k^{\left(n\right)}& ={\gamma }_k^n{\Re }_{I,{\lambda }_k}^{{\mathcal{S}}_k(h_k(·),v_1)}[x_k^n-{\lambda }_k\{P_k(C_{I,{\lambda }_k}^{{\mathcal{S}}_k(h_k(·),v_1)}\left(x_k^n\right),Y_{I,{\lambda }_1}^{{\mathcal{S}}_1(h_1(·),v_2)}\left(x_1^n\right))\hfill \\ \hfill & +f_k\left(x_k^n\right)\oplus g_1\left(x_1^n\right)-w_k\left\}\right]+(1-{\gamma }_k^n)x_k^{\left(n\right)}+{\gamma }_k^n{\delta }_{k+2}^n.\hfill \end{array}$$ (22) for $n=0,1,2,\cdots ,$ where ${\lambda }_i>0$ is a constant and ${\alpha }_i^n,{\beta }_i^n$, and ${\gamma }_i^n$ are real sequences in (0,1) such that $$\begin{array}{c}\hfill \sum _{n=1}^{\infty }{\alpha }_i^n=\infty ,\forall i.\end{array}$$ Step II:  Choose $v_i^{(n+1)}\in {\mathcal{N}}_i\left(x_i^{(n+1)}\right)$ such that $$\begin{array}{c}\hfill \parallel v_i^{(n+1)}\oplus v_i^{\left(n\right)}\parallel \le \left(1+{\displaystyle \frac{1}{n+1}}\right)\mathbb{D}({\mathcal{N}}_i\left(x_i^{(n+1)}\right),{\mathcal{N}}_i\left(x_i^{\left(n\right)}\right)),\end{array}$$ (23) where $\mathbb{D}(.,.)$ is the Hausdorff metric on $\mathcal{X}$. Step III:  If the accuracy is satisfactory and $x_i^{(n+1)}$ and $v_i^{\left(n\right)}$,  $\forall i$ satisfy step I, then stop; if not, set $n=n+1$ and return to step I.

Remark 3.

Algorithm 1 becomes a two-step iterative algorithm (Ishikawa-type) if ${\gamma }_i^n=0$ for all $n\ge 0$, and it reduces to a one-step iterative scheme (Mann-type) when choosing ${\beta }_i^n={\gamma }_i^n=0$ for all $n\ge 0.$ We also observe that if we define the appropriate operators for Algorithm 1, we can easily acquire many more methods that have been studied by several authors for addressing ordered variational inclusions, see, e.g., [24,25,26].

Lemma 2.

The sequence $v_n\to 0$ as $n\to \infty$ if $v_n$ and ${\eta }_n$ are sequences in $[0,\infty )$ such that

(i)

$0\le {\eta }_n<1,n=0,1,2,\cdots$ and $limsu{p}_n{\eta }_n<1$;

(ii)

$v_{n+1}\le {\eta }_n{v}_n,n=0,1,2,3,\cdots ,$ hold.

Theorem 2.

Let all the mappings and conditions be the same as in Theorem 1, except for condition (9). Additionally, if

$$\begin{array}{c}\hfill \parallel {\Re }_{I,{\lambda }_i}^{{\mathcal{S}}_i(h(·),u)}\left(x\right)\oplus {\Re }_{I,{\lambda }_i}^{{\mathcal{S}}_i(h(·),v)}\left(x\right)\parallel \le {\mathsf{\Lambda }}_i\parallel u\oplus v\parallel ,\end{array}$$

(24)

$$\begin{array}{cc}\hfill & \underset{n\ge 1}{sup}\{{\alpha }_i^n{\beta }_i^n{\nu }_i^2\{{\gamma }_i^n{\nu }_i+1\}+{\alpha }_i^n{\nu }_i+1\}<\underset{n\ge 1}{sup}\{{\alpha }_i^n{\beta }_i^n{\nu }_i^2{\gamma }_i^n{\nu }_i+{\alpha }_i^n{\nu }_i{\beta }_i^n+{\alpha }_i^n\},\hfill \\ \hfill & \underset{n\ge 1}{sup}\{{\alpha }_i^n{\beta }_i^n{\nu }_i({\nu }_i{\gamma }_i^n+1)({\delta }_{i+1}+{\mu }_{i+1})+{\alpha }_i^n{\beta }_i^n{\nu }_i{\delta }_{i+1}{\gamma }_{i+1}^n{\nu }_{i+1}\hfill \\ \hfill & +{\alpha }_i^n{\nu }_{i+1}{\beta }_{i+1}^n{\delta }_{i+1}{\nu }_{i+1}{\gamma }_{i+1}^n+{\alpha }_i^n{\delta }_{i+1}\},\hfill \\ \hfill & <\underset{n\ge 1}{sup}\{{\alpha }_i^n{\beta }_i^n{\nu }_i{\delta }_{i+1}{\gamma }_{i+1}^n+{\alpha }_i^n{\nu }_{i+1}{\beta }_{i+1}^n{\delta }_{i+1}{\gamma }_{i+1}^n+1+{\alpha }_i^n{\delta }_{i+1}{\beta }_{i+1}^n\},\hfill \\ \hfill & \underset{n\ge 1}{sup}\{{\alpha }_i^n{\gamma }_{i+1}^n{\delta }_{i+1}({\beta }_i^n{\nu }_i+{\beta }_{i+1}^n{\nu }_{i+1})({\delta }_{i+2}+{\mu }_{i+2})+{\alpha }_i^n{\beta }_{i+2}^n{\tau }_{i+2}{\nu }_{i+2}({\gamma }_{i+2}^n{\nu }_{i+2}+1)\hfill \\ \hfill & +{\alpha }_i^n{\beta }_i^n{\nu }_i{\tau }_{i+2}({\nu }_i{\gamma }_i^n+{\gamma }_{i+2}^n{\nu }_{i+2})+{\alpha }_i^n{\beta }_{i+1}^n{\delta }_{i+1}[{\gamma }_{i+1}^n{\delta }_{i+2}{\nu }_{i+2}+{\delta }_{i+2}+{\mu }_{i+2}]\}\hfill \\ \hfill & <\underset{n\ge 1}{sup}\left\{{\alpha }_i^n{\beta }_{i+2}^n{\tau }_{i+2}{\nu }_{i+2}{\gamma }_{i+2}^n+{\alpha }_i^n{\beta }_i^n{\nu }_i{\tau }_{i+2}{\gamma }_{i+2}^n+1+{\alpha }_i^n{\beta }_{i+1}^n{\delta }_{i+1}{\gamma }_{i+1}^n{\delta }_{i+2}+{\beta }_{i+1}^n\right\},\hfill \\ \hfill & \underset{n\ge 1}{sup}\{{\alpha }_i^n{\beta }_i^n{\nu }_i[{\gamma }_{i+1}^n{\delta }_{i+1}{\delta }_{i+3}+{\gamma }_{i+2}^n{\tau }_{i+2}({\delta }_{i+3}+{\mu }_{i+3})]+{\alpha }_i^n{\beta }_{i+1}^n{\delta }_{i+1}[{\gamma }_{i+1}^n{\nu }_{i+1}{\delta }_{i+3}\hfill \\ \hfill & +{\gamma }_{i+2}^n{\delta }_{i+2}{\delta }_{i+3}+{\gamma }_{i+2}^n{\delta }_{i+2}{\mu }_{i+3}+{\tau }_{i+3}+{\gamma }_{i+3}^n{\tau }_{i+3}{\nu }_{i+3}]\hfill \\ \hfill & +{\alpha }_i^n{\beta }_{i+2}^n{\tau }_{i+2}[{\gamma }_{i+2}^n{\nu }_{i+2}({\delta }_{i+3}+{\mu }_{i+3})+{\gamma }_{i+3}^n{\delta }_{i+3}{\nu }_{i+3}+{\delta }_{i+3}+{\tau }_{i+3}]\}\hfill \\ \hfill & <\underset{n\ge 1}{sup}\{1+{\gamma }_{i+3}^n{\tau }_{i+3}+{\alpha }_i^n{\beta }_{i+2}^n{\tau }_{i+2}{\gamma }_{i+3}^n{\delta }_{i+3}\},\hfill \\ \hfill & \underset{n\ge 1}{sup}\{{\alpha }_i^n{\beta }_i^n{\nu }_i{\tau }_{i+2}{\tau }_{i+4}{\gamma }_{i+2}^n+{\alpha }_i^n{\beta }_{i+1}^n{\delta }_{i+1}[{\delta }_{i+2}{\gamma }_{i+2}^n{\tau }_{i+4}+{\gamma }_{i+3}^n{\tau }_{i+3}({\delta }_{i+4}+{\mu }_{i+4})]\hfill \\ \hfill & +{\alpha }_i^n{\beta }_{i+2}^n[{\tau }_{i+2}{\tau }_{i+4}({\gamma }_{i+2}^n{\nu }_{i+2}+{\gamma }_{i+4}^n{\nu }_{i+4}+1)+{\gamma }_{i+3}^n{\delta }_{i+3}({\tau }_{i+3}{\delta }_{i+4}+{\tau }_{i+2}{\mu }_{i+4})]\}\hfill \\ \hfill & <\underset{n\ge 1}{sup}\{1+{\alpha }_i^n{\beta }_{i+2}^n{\tau }_{i+2}{\tau }_{i+4}{\gamma }_{i+4}^n\},\hfill \\ \hfill & \underset{n\ge 1}{sup}\{{\alpha }_i^n{\beta }_{i+1}^n{\gamma }_{i+3}^n{\delta }_{i+1}{\tau }_{i+3}{\tau }_{i+5}+{\alpha }_i^n{\beta }_{i+2}^n{\tau }_{i+2}[{\gamma }_{i+3}^n{\delta }_{i+3}{\tau }_{i+5}+{\gamma }_{i+4}^n{\tau }_{i+4}({\delta }_{i+5}+{\mu }_{i+5})]\}<1,\hfill \\ \hfill & \underset{n\ge 1}{sup}\left\{{\alpha }_i^n{\beta }_{i+2}^n{\gamma }_{i+4}^n{\tau }_{i+2}{\tau }_{i+4}{\tau }_{i+6}\right\}<1,\hfill \end{array}$$

(25)

and

$$\underset{n\to \infty }{lim}\parallel {\delta }_i^n\vee (-{\delta }_i^n)\parallel =0,\forall ,i=1,2,\cdots ,k.$$

hold, then the sequences $\left\{(x_i^{\left(n\right)},v_i^{\left(n\right)})\right\}$ generated by Algorithm 1 converge strongly to the solution $(x_i,v_i)$ of system (5).

Proof of Convergence.

Theorem 1 guarantees that System (5) admits the solution $(x_i,v_i)$. Let us assume that $x^{*}=(x_1^{*},x_2^{*},\cdots ,x_k^{*})$ is a unique solution of SEOXORIP (5). Then, we have

$$\begin{array}{cc}\hfill x_i^{*}& =\left[{\alpha }_i^n{\Re }_{I,{\lambda }_i}^{{\mathcal{S}}_i(h_i(·),v_{i+1})}\right(x_i^{*}-{\lambda }_i\{P_i\left(C_{I,{\lambda }_i}^{{\mathcal{S}}_i(h_i(·),v_{i+1})}\left(x_i^{*}\right),Y_{I,{\lambda }_{i+1}}^{{\mathcal{S}}_{i+1}(h_{i+1}(·),v_{i+2})}\left(x_{i+1}^{*}\right)\right)\hfill \\ \hfill & +f_i{\left(x_i\right)}^{*}\oplus g_{i+1}\left(x_{i+1}^{*}\right)-w_i\left\}\right)+(1-{\alpha }_i^n)x_i^{*}]\hfill \\ \hfill & =\left[{\beta }_i^n{\Re }_{I,{\lambda }_i}^{{\mathcal{S}}_i(h_i(·),v_{i+1})}\right[x_i^{*}-{\lambda }_i\{P_i\left(C_{I,{\lambda }_i}^{{\mathcal{S}}_i(h_i(·),v_{i+1})}\left(x_i^{*}\right),Y_{I,{\lambda }_{i+1}}^{{\mathcal{S}}_{i+1}(h_{i+1}(·),v_{i+2})}\left(x_{i+1}^{*}\right)\right)\hfill \\ \hfill & +f_i\left(x_i^{*}\right)\oplus g_{i+1}\left(x_{i+1}^{*}\right)-w_i\left\}\right]+(1-{\beta }_i^n)x_i^{*}]\hfill \\ \hfill & =\left[{\gamma }_i^n{\Re }_{I,{\lambda }_i}^{{\mathcal{S}}_i(h_i(·),v_{i+1})}\right[x_i^{*}-{\lambda }_i\{P_i\left(C_{I,{\lambda }_i}^{{\mathcal{S}}_i(h_i(·),v_{i+1})}\left(x_i^{*}\right),Y_{I,{\lambda }_{i+1}}^{{\mathcal{S}}_{i+1}(h_{i+1}(·),v_{i+2})}\left(x_{i+1}^{*}\right)\right)\hfill \\ \hfill & +f_i\left(x_i^{*}\right)\oplus g_{i+1}\left(x_{i+1}^{*}\right)-w_i\left\}\right]+(1-{\gamma }_i^n)x_i^{*}].\hfill \end{array}$$

(26)

From (22), (26), and Proposition 3, we obtain

$$\begin{array}{cc}\hfill & \parallel x_1^{(n+1)}\oplus x_1^{*}\parallel \hfill \\ \hfill & =\parallel \left[{\alpha }_1^n{\Re }_{I,{\lambda }_1}^{{\mathcal{S}}_1(h_1(·),v_2^n)}\right(y_1^n-{\lambda }_1\{P_1(C_{I,{\lambda }_1}^{{\mathcal{S}}_1(h_1(·),v_2^n)}\left(y_1^n\right),Y_{I,{\lambda }_2}^{{\mathcal{S}}_2(h_2(·),v_3^n)}\left(y_2^n\right))\hfill \\ \hfill & +f_1\left(y_1^n\right)\oplus g_2\left(y_2^n\right)-w_1\left\}\right)+(1-{\alpha }_1^n)x_1^n+{\alpha }_1^n{\delta }_1^n]\hfill \\ \hfill & \oplus \left[{\alpha }_1^n{\Re }_{I,{\lambda }_1}^{{\mathcal{S}}_1(h_1(·),v_2)}\right(x_1^{*}-{\lambda }_1\{P_1(C_{I,{\lambda }_1}^{{\mathcal{S}}_1(h_1(·),v_2)}\left(x_1^{*}\right),Y_{I,{\lambda }_2}^{{\mathcal{S}}_2(h_2(·),v_3)}\left(x_2^{*}\right))\hfill \\ \hfill & +f_1\left(x_1^{*}\right)\oplus g_2\left(x_2^{*}\right)-w_1\left\}\right)+(1-{\alpha }_1^n)x_1^{*}]\hfill \\ \hfill & \le {\alpha }_1^n\parallel {\Re }_{I,{\lambda }_1}^{{\mathcal{S}}_1(h_1(·),v_2^n)}(y_1^n-{\lambda }_1\{P_1(C_{I,{\lambda }_1}^{{\mathcal{S}}_1(h_1(·),v_2^n)}\left(y_1^n\right),Y_{I,{\lambda }_2}^{{\mathcal{S}}_2(h_2(·),v_3^n)}\left(y_2^n\right))\hfill \\ \hfill & +f_1\left(y_1^n\right)\oplus g_2\left(y_2^n\right)-w_1\left\}\right)\hfill \\ \hfill & \oplus {\Re }_{I,{\lambda }_1}^{{\mathcal{S}}_1(h_1(·),v_2)}(x_1^{*}-{\lambda }_1\{P_1(C_{I,{\lambda }_1}^{{\mathcal{S}}_1(h_1(·),v_2)}\left(x_1^{*}\right),Y_{I,{\lambda }_2}^{{\mathcal{S}}_2(h_2(·),v_3)}\left(x_2^{*}\right))\hfill \\ \hfill & +f_1\left(x_1^{*}\right)\oplus g_2\left(x_2^{*}\right)-w_1\left\}\right)\parallel +(1-{\alpha }_1^n)\parallel x_1^n\oplus x_1^{*}\parallel +\parallel {\alpha }_1^n{\delta }_1^n\parallel .\hfill \end{array}$$

In similar way to (10), using (24), we have

$$\begin{array}{ccc}\hfill & & \parallel x_1^{(n+1)}\oplus x_1^{*}\parallel \hfill \\ & \le & {\alpha }_1^n[{\mathsf{\Lambda }}_2\parallel v_2^n\oplus v_2\parallel +{\mathcal{L}}^{{\Re }_1}\{\parallel y_1^n\oplus x_1^{*}\parallel +{\lambda }_1\parallel P_1(C_{I,{\lambda }_1}^{{\mathcal{S}}_1(h_1(·),v_2^n)}\left(y_1^n\right),Y_{I,{\lambda }_2}^{{\mathcal{S}}_2(h_2(·),v_3)}\left(y_2^n\right))\hfill \\ & & \oplus P_1(C_{I,{\lambda }_1}^{{\mathcal{S}}_1(h_1(·),v_2^n)}\left(x_1^{*}\right),Y_{I,{\lambda }_2}^{{\mathcal{S}}_2(h_2(·),v_3)}\left(x_2^{*}\right))\parallel +{\lambda }_1\parallel f_1\left(y_1^n\right)\oplus g_2\left(y_2^n\right)\hfill \\ & & -f_1\left(x_1^{*}\right)\oplus g_2\left(x_2^{*}\right)\parallel \left\}\right]+(1-{\alpha }_1^n)\parallel x_1^n\oplus x_1^{*}\parallel +{\alpha }_1^n\parallel {\delta }_1^n\oplus 0\parallel .\hfill \end{array}$$

(27)

From Definitions 7 and 8 and (12), we have

$$\begin{array}{ccc}\hfill & & \parallel P_1\left(C_{I,{\lambda }_1}^{{\mathcal{S}}_1(h_1(·),v_2^n)}\left(y_1^n\right),Y_{I,{\lambda }_2}^{{\mathcal{S}}_2(h_2(·),v_3)}\left(y_2^n\right)\right)\oplus P_1\left(C_{I,{\lambda }_1}^{{\mathcal{S}}_1(h_1(·),v_2)}\left(x_1^{*}\right),Y_{I,{\lambda }_2}^{{\mathcal{S}}_2(h_2(·),v_3)}\left(x_2^{*}\right)\right)\parallel \hfill \\ & \le & {\wp }_{P_1}^{C_1}∥C_{I,{\lambda }_1}^{{\mathcal{S}}_1(h_1(·),v_2^n)}\left(y_1^n\right)\oplus C_{I,{\lambda }_1}^{{\mathcal{S}}_1(h_1(·),v_2)}\left(x_1^{*}\right)∥+{\wp }_{P_1}^{Y_1}∥Y_{I,{\lambda }_2}^{{\mathcal{S}}_2(h_2(·),v_3^n)}\left(y_2^n\right)\oplus Y_{I,{\lambda }_2}^{{\mathcal{S}}_2(h_2(·),v_3)}\left(x_2^{*}\right)∥\hfill \\ & \le & 3{\wp }_{P_1}^{C_1}\parallel y_1^n\oplus x_1^{*}\parallel +{\wp }_{P_1}^{C_1}{\mathsf{\Lambda }}_2\left(1+{\displaystyle \frac{1}{1+n}}\right){\lambda }_{{\mathbb{D}}_{{\mathcal{N}}_2}}\parallel y_2^n\oplus x_2^{*}\parallel +{\displaystyle \frac{{\wp }_{P_1}^{Y_1}}{{\lambda }_2}}(2\parallel y_2^n\oplus x_2^{*}\parallel \hfill \\ & & +{\mathsf{\Lambda }}_3\left(1+{\displaystyle \frac{1}{1+n}}\right){\lambda }_{{\mathbb{D}}_{{\mathcal{N}}_3}}\parallel y_3^n\oplus x_3^{*}\parallel ).\hfill \end{array}$$

(28)

Since $v_2^n\in {\mathcal{N}}_2\left(x_2^n\right)$, according to Nadler [27], ∃$v_2\in {\mathcal{N}}_2\left(x_2^{*}\right)$ such that

$$\begin{array}{ccc}\hfill \parallel v_2^n\oplus v_2\parallel & \le & \left(1+{\displaystyle \frac{1}{n+1}}\right)\mathbb{D}({\mathcal{N}}_2\left(x_2^n\right),{\mathcal{N}}_2\left(x_2^{*}\right)).\hfill \end{array}$$

(29)

Using the $\mathbb{D}$-Lipschitz continuity of ${\mathcal{N}}_2$, we obtain

$$\begin{array}{ccc}\hfill \parallel v_2^n\oplus v_2\parallel & \le & \left(1+{\displaystyle \frac{1}{n+1}}\right){\lambda }_{{\mathbb{D}}_{{\mathcal{N}}_2}}\parallel x_2^n\oplus x_2^{*}\parallel .\hfill \end{array}$$

(30)

Using (28), (30), and Proposition 3 in (27), we get

$$\begin{array}{ccc}\hfill & & \parallel x_1^{(n+1)}\oplus x_1^{*}\parallel \hfill \\ & \le & {\alpha }_1^n[{\mathsf{\Lambda }}_2\left(1+{\displaystyle \frac{1}{n+1}}\right){\lambda }_{{\mathbb{D}}_{{\mathcal{N}}_2}}\parallel x_2^n\oplus x_2^{*}\parallel +{\mathcal{L}}^{{\Re }_1}\{\parallel y_1^n\oplus x_1^{*}\parallel +{\lambda }_1(3{\wp }_{P_1}^{C_1}\parallel y_1^n\oplus x_1^{*}\parallel \hfill \\ & & +{\wp }_{P_1}^{C_1}{\mathsf{\Lambda }}_2\left(1+{\displaystyle \frac{1}{1+n}}\right){\lambda }_{{\mathbb{D}}_{{\mathcal{N}}_2}}\parallel y_2^n\oplus x_2^{*}\parallel +{\displaystyle \frac{{\wp }_{P_1}^{Y_1}}{{\lambda }_2}}(2\parallel y_2^n\oplus x_2^{*}\parallel \hfill \\ & & +{\mathsf{\Lambda }}_3\left(1+{\displaystyle \frac{1}{1+n}}\right){\lambda }_{{\mathbb{D}}_{{\mathcal{N}}_3}}\parallel y_3^n\oplus x_3^{*}\parallel )+{\lambda }_1\left({\wp }^{f_1}\parallel y_1^n\oplus x_1^{*}\parallel +{\wp }^{g_2}\parallel y_2^n\oplus x_2^{*}\parallel \right)\}]\hfill \\ & & +(1-{\alpha }_1^n)\parallel x_1^n\oplus x_1^{*}\parallel +{\alpha }_1^n\parallel {\delta }_1^n\oplus 0\parallel .\hfill \end{array}$$

(31)

By $\left(vii\right)$ of Proposition 1, we have

$$\begin{array}{ccc}\hfill \parallel x_1^{(n+1)}-x_1^{*}\parallel & =& \parallel x_1^{(n+1)}\oplus x_1^{*}\parallel \hfill \\ & =& {\alpha }_1^n{\mathcal{L}}^{{\Re }_1}\left(1+{\lambda }_1{\wp }^{f_1}\right)\parallel y_1^n-x_1^{*}\parallel +(1-{\alpha }_1^n)\parallel x_1^n\oplus x_1^{*}\parallel \hfill \\ & & +{\alpha }_1^n{\mathsf{\Lambda }}_2\left(1+{\displaystyle \frac{1}{1+n}}\right){\lambda }_{{\mathbb{D}}_{{\mathcal{N}}_2}}{\mathcal{L}}^{{\Re }_1}\left({\wp }_{P_1}^{C_1}+{\displaystyle \frac{2{\wp }_{P_1}^{Y_1}}{{\lambda }_2}}+{\lambda }_1{\wp }^{g_2}\right)\parallel y_2^n\oplus x_2^{*}\parallel \hfill \\ & & +{\alpha }_1^n{\mathsf{\Lambda }}_2\left(1+{\displaystyle \frac{1}{1+n}}\right){\lambda }_{{\mathbb{D}}_{{\mathcal{N}}_2}}\parallel x_2^n\oplus x_2^{*}\parallel \hfill \\ & & +{\alpha }_1^n{\displaystyle \frac{{\mathcal{L}}^{{\Re }_1}{\wp }_{P_1}^{Y_1}}{{\lambda }_2}}{\mathsf{\Lambda }}_3\left(1+{\displaystyle \frac{1}{1+n}}\right){\lambda }_{{\mathbb{D}}_{{\mathcal{N}}_3}}\parallel y_3^n\oplus x_3^{*}\parallel +{\alpha }_1^n\parallel {\delta }_1^n\oplus 0\parallel .\hfill \end{array}$$

(32)

Let

$${\nu }_1={\mathcal{L}}^{{\Re }_1}\left(1+{\lambda }_1{\wp }^{f_1}\right),{\delta }_2={\mathsf{\Lambda }}_2\left(1+{\displaystyle \frac{1}{1+n}}\right){\lambda }_{{\mathbb{D}}_{{\mathcal{N}}_2}}{\mathcal{L}}^{{\Re }_1}\left({\wp }_{P_1}^{C_1}+{\displaystyle \frac{2{\wp }_{P_1}^{Y_1}}{{\lambda }_2}}+{\lambda }_1{\wp }^{g_2}\right),$$

$${\mu }_2={\mathsf{\Lambda }}_2\left(1+{\displaystyle \frac{1}{1+n}}\right){\lambda }_{{\mathbb{D}}_{{\mathcal{N}}_2}}and{\tau }_3={\displaystyle \frac{{\mathcal{L}}^{{\Re }_1}{\wp }_{P_1}^{Y_1}}{{\lambda }_2}}{\mathsf{\Lambda }}_3\left(1+{\displaystyle \frac{1}{1+n}}\right){\lambda }_{{\mathbb{D}}_{{\mathcal{N}}_3}}.$$

$$\begin{array}{ccc}\hfill \parallel x_1^{(n+1)}\oplus x_1^{*}\parallel & =& {\alpha }_1^n{\nu }_1\parallel y_1^n\oplus x_1^{*}\parallel +{\alpha }_1^n{\delta }_2\parallel y_2^n\oplus x_2^{*}\parallel +{\alpha }_1^n{\mu }_2\parallel x_2^n\oplus x_2^{*}\parallel \hfill \\ & & +(1-{\alpha }_1^n)\parallel x_1^n\oplus x_1^{*}\parallel +{\alpha }_1^n{\tau }_3\parallel y_3^n\oplus x_3^{*}\parallel +{\alpha }_1^n\parallel {\delta }_1^n\oplus 0\parallel .\hfill \end{array}$$

(33)

Similarly, we calculate

$$\begin{array}{cc}\hfill & \parallel y_1^{\left(n\right)}\oplus x_1^{*}\parallel \hfill \\ & \le \parallel \left({\beta }_1^n{\Re }_{I,{\lambda }_1}^{{\mathcal{S}}_1(h_1(·),v_2)}\right[z_1^n-{\lambda }_1\{P_1(C_{I,{\lambda }_1}^{{\mathcal{S}}_1(h_1(·),v_2)}\left(z_1^n\right),Y_{I,{\lambda }_2}^{{\mathcal{S}}_2(h_2(·),v_3)}\left(z_2^n\right))\hfill \\ \hfill & +f_1\left(z_1^n\right)\oplus g_2\left(z_2^n\right)-w_1\left\}\right]+(1-{\beta }_1^n)x_1^{\left(n\right)}+{\beta }_1^n{\delta }_2^n)\oplus ({\beta }_1^n{\Re }_{I,{\lambda }_1}^{{\mathcal{S}}_1(h_1(·),v_2)}[x_1^{*}\hfill \\ \hfill & -{\lambda }_1\{P_1(C_{I,{\lambda }_1}^{{\mathcal{S}}_1(h_1(·),v_2)}\left(x_1^{*}\right),Y_{I,{\lambda }_2}^{{\mathcal{S}}_2(h_2(·),v_3)}\left(x_2^{*}\right))+f_1\left(x_1^{*}\right)\oplus g_2\left(x_2^{*}\right)-w_1\}]+(1-{\beta }_1^n)x_1^{*})\parallel .\hfill \end{array}$$

$$\begin{array}{cc}\hfill & \parallel y_1^{\left(n\right)}\oplus x_1^{*}\parallel \hfill \\ \hfill & \le {\beta }_1^n[{\mathsf{\Lambda }}_2\parallel v_2^n\oplus v_2\parallel +{\mathcal{L}}^{{\Re }_1}\{\parallel z_1^n\oplus x_1^{*}\parallel +{\lambda }_1\parallel P_1(C_{I,{\lambda }_1}^{{\mathcal{S}}_1(h_1(·),v_2^n)}\left(z_1^n\right),Y_{I,{\lambda }_2}^{{\mathcal{S}}_2(h_2(·),v_3)}\left(z_2^n\right))\hfill \\ \hfill & \oplus P_1(C_{I,{\lambda }_1}^{{\mathcal{S}}_1(h_1(·),v_2^n)}\left(x_1^{*}\right),Y_{I,{\lambda }_2}^{{\mathcal{S}}_2(h_2(·),v_3)}\left(x_2^{*}\right))\parallel +{\lambda }_1\parallel f_1\left(z_1^n\right)\oplus g_2\left(z_2^n\right)\oplus f_1\left(x_1^{*}\right)\oplus g_2\left(x_2^{*}\right)\parallel \left\}\right]\hfill \\ \hfill & +(1-{\beta }_1^n)\parallel x_1^n\oplus x_1^{*}\parallel +{\beta }_1^n\parallel {\delta }_2^n\oplus 0\parallel \hfill \\ \hfill & \le {\beta }_1^n[{\mathsf{\Lambda }}_2\left(1+{\displaystyle \frac{1}{n+1}}\right){\lambda }_{{\mathbb{D}}_{{\mathcal{N}}_2}}\parallel x_2^n\oplus x_2^{*}\parallel +{\mathcal{L}}^{{\Re }_1}\{\parallel z_1^n\oplus x_1^{*}\parallel +{\lambda }_1(3{\wp }_{P_1}^{C_1}\parallel z_1^n\oplus x_1^{*}\parallel \hfill \\ \hfill & +{\wp }_{P_1}^{C_1}{\mathsf{\Lambda }}_2\left(1+{\displaystyle \frac{1}{1+n}}\right){\lambda }_{{\mathbb{D}}_{{\mathcal{N}}_2}}\parallel z_2^n\oplus x_2^{*}\parallel +{\displaystyle \frac{{\wp }_{P_1}^{Y_1}}{{\lambda }_2}}(2\parallel z_2^n\oplus x_2^{*}\parallel \hfill \\ \hfill & +{\mathsf{\Lambda }}_3\left(1+{\displaystyle \frac{1}{1+n}}\right){\lambda }_{{\mathbb{D}}_{{\mathcal{N}}_3}}\parallel z_3^n\oplus x_3^{*}\parallel )+{\lambda }_1\left({\wp }^{f_1}\parallel z_1^n\oplus x_1^{*}\parallel +{\wp }^{g_2}\parallel y_2^n\oplus x_2^{*}\parallel \right)\}\left]\right]\hfill \\ \hfill & +(1-{\beta }_1^n)\parallel x_1^n\oplus x_1^{*}\parallel +{\beta }_1^n\parallel {\delta }_2^n\oplus 0\parallel \hfill \\ \hfill & ={\beta }_1^n{\mathcal{L}}^{{\Re }_1}\left(1+{\lambda }_1{\wp }^{f_1}\right)\parallel z_1^n\oplus x_1^{*}\parallel +(1-{\beta }_1^n)\parallel x_1^n\oplus x_1^{*}\parallel \hfill \\ \hfill & +{\beta }_1^n{\mathsf{\Lambda }}_2\left(1+{\displaystyle \frac{1}{1+n}}\right){\lambda }_{{\mathbb{D}}_{{\mathcal{N}}_2}}{\mathcal{L}}^{{\Re }_1}\left({\wp }_{P_1}^{C_1}+{\displaystyle \frac{2{\wp }_{P_1}^{Y_1}}{{\lambda }_2}}+{\lambda }_1{\wp }^{g_2}\right)\parallel z_2^n\oplus x_2^{*}\parallel \hfill \\ \hfill & +{\beta }_1^n{\mathsf{\Lambda }}_2\left(1+{\displaystyle \frac{1}{1+n}}\right){\lambda }_{{\mathbb{D}}_{{\mathcal{N}}_2}}\parallel x_2^n\oplus x_2^{*}\parallel \hfill \\ \hfill & +{\beta }_1^n{\displaystyle \frac{{\mathcal{L}}^{{\Re }_1}{\wp }_{P_1}^{Y_1}}{{\lambda }_2}}{\mathsf{\Lambda }}_3\left(1+{\displaystyle \frac{1}{1+n}}\right){\lambda }_{{\mathbb{D}}_{{\mathcal{N}}_3}}\parallel z_3^n\oplus x_3^{*}\parallel +{\beta }_1^n\parallel {\delta }_2^n\oplus 0\parallel \hfill \\ \hfill & ={\beta }_1^n{\nu }_1\parallel z_1^n\oplus x_1^{*}\parallel +{\beta }_1^n{\delta }_2\parallel z_2^n\oplus x_2^{*}\parallel +{\beta }_1^n{\mu }_2\parallel x_2^n\oplus x_2^{*}\parallel \hfill \\ \hfill & +(1-{\beta }_1^n)\parallel x_1^n\oplus x_1^{*}\parallel +{\beta }_1^n{\tau }_3\parallel z_3^n\oplus x_3^{*}\parallel +{\beta }_1^n\parallel {\delta }_2^n\oplus 0\parallel .\hfill \end{array}$$

(34)

In a similar way, by using the definition of $z_1^n$ in Algorithm 1, we obtain

$$\begin{array}{cc}\hfill & \parallel z_1^{\left(n\right)}\oplus x_1^{*}\parallel \hfill \\ & \le \parallel \left({\gamma }_1^n{\Re }_{I,{\lambda }_1}^{{\mathcal{S}}_1(h_1(·),v_2)}\right[x_1^n-{\lambda }_1\{P_1(C_{I,{\lambda }_1}^{{\mathcal{S}}_1(h_1(·),v_2)}\left(x_1^n\right),Y_{I,{\lambda }_2}^{{\mathcal{S}}_2(h_2(·),v_3)}\left(x_2^n\right))\hfill \\ \hfill & +f_1\left(x_1^n\right)\oplus g_2\left(x_2^n\right)-w_1\left\}\right]+(1-{\gamma }_1^n)x_1^{\left(n\right)}+{\gamma }_1^n{\delta }_2^n)\oplus ({\gamma }_1^n{\Re }_{I,{\lambda }_1}^{{\mathcal{S}}_1(h_1(·),v_2)}[x_1^{*}\hfill \\ \hfill & -{\lambda }_1\{P_1(C_{I,{\lambda }_1}^{{\mathcal{S}}_1(h_1(·),v_2)}\left(x_1^{*}\right),Y_{I,{\lambda }_2}^{{\mathcal{S}}_2(h_2(·),v_3)}\left(x_2^{*}\right))+f_1\left(x_1^{*}\right)\oplus g_2\left(x_2^{*}\right)-w_1\}]+(1-{\gamma }_1^n)x_1^{*})\parallel \hfill \\ \hfill & \le {\gamma }_1^n[{\mathsf{\Lambda }}_2\parallel v_2^n\oplus v_2\parallel +{\mathcal{L}}^{{\Re }_1}\{\parallel x_1^n\oplus x_1\parallel +{\lambda }_1\parallel P_1(C_{I,{\lambda }_1}^{{\mathcal{S}}_1(h_1(·),v_2^n)}\left(x_1^n\right),Y_{I,{\lambda }_2}^{{\mathcal{S}}_2(h_2(·),v_3)}\left(x_2^n\right))\hfill \\ \hfill & \oplus P_1(C_{I,{\lambda }_1}^{{\mathcal{S}}_1(h_1(·),v_2^n)}\left(x_1^{*}\right),Y_{I,{\lambda }_2}^{{\mathcal{S}}_2(h_2(·),v_3)}\left(x_2^{*}\right))\parallel +{\lambda }_1\parallel f_1\left(x_1^n\right)\oplus g_2\left(x_2^n\right)-f_1\left(x_1^{*}\right)\oplus g_2\left(x_2^{*}\right)\parallel \left\}\right]\hfill \\ \hfill & +(1-{\gamma }_1^n)\parallel x_1^n\oplus x_1^{*}\parallel +{\gamma }_1^n\parallel {\delta }_3^n\oplus 0\parallel \hfill \\ \hfill & \le {\gamma }_1^n[{\mathsf{\Lambda }}_2\left(1+{\displaystyle \frac{1}{n+1}}\right){\lambda }_{{\mathbb{D}}_{{\mathcal{N}}_2}}\parallel x_2^n\oplus x_2\parallel +{\mathcal{L}}^{{\Re }_1}\{\parallel x_1^n\oplus x_1^{*}\parallel +{\lambda }_1(3{\wp }_{P_1}^{C_1}\parallel x_1^n\oplus x_1^{*}\parallel \hfill \\ \hfill & +{\wp }_{P_1}^{C_1}{\mathsf{\Lambda }}_2\left(1+{\displaystyle \frac{1}{1+n}}\right){\lambda }_{{\mathbb{D}}_{{\mathcal{N}}_2}}\parallel x_2^n\oplus x_2^{*}\parallel +{\displaystyle \frac{{\wp }_{P_1}^{Y_1}}{{\lambda }_2}}(2\parallel x_2^n\oplus x_2^{*}\parallel \hfill \\ \hfill & +{\mathsf{\Lambda }}_3\left(1+{\displaystyle \frac{1}{1+n}}\right){\lambda }_{{\mathbb{D}}_{{\mathcal{N}}_3}}\parallel x_3^n\oplus x_3^{*}\parallel )+{\lambda }_1\left({\wp }^{f_1}\parallel x_1^n\oplus x_1^{*}\parallel +{\wp }^{g_2}\parallel x_2^n\oplus x_2^{*}\parallel \right)\}\left]\right]\hfill \\ \hfill & +(1-{\gamma }_1^n)\parallel x_1^n\oplus x_1^{*}\parallel +{\gamma }_1^n\parallel {\delta }_3^n\oplus 0\parallel .\hfill \end{array}$$

$$\begin{array}{cc}\hfill & \parallel z_1^{\left(n\right)}\oplus x_1^{*}\parallel \hfill \\ \hfill & ={\gamma }_1^n{\mathcal{L}}^{{\Re }_1}\left(1+{\lambda }_1{\wp }^{f_1}\right)\parallel x_1^n\oplus x_1^{*}\parallel +(1-{\gamma }_1^n)\parallel x_1^n\oplus x_1^{*}\parallel \hfill \\ \hfill & +{\gamma }_1^n{\mathsf{\Lambda }}_2\left(1+{\displaystyle \frac{1}{1+n}}\right){\lambda }_{{\mathbb{D}}_{{\mathcal{N}}_2}}{\mathcal{L}}^{{\Re }_1}\left({\wp }_{P_1}^{C_1}+{\displaystyle \frac{2{\wp }_{P_1}^{Y_1}}{{\lambda }_2}}+{\lambda }_1{\wp }^{g_2}\right)\parallel x_2^n\oplus x_2^{*}\parallel \hfill \\ \hfill & +{\gamma }_1^n{\mathsf{\Lambda }}_2\left(1+{\displaystyle \frac{1}{1+n}}\right){\lambda }_{{\mathbb{D}}_{{\mathcal{N}}_2}}\parallel x_2^n\oplus x_2^{*}\parallel \hfill \\ \hfill & +{\gamma }_1^n{\displaystyle \frac{{\mathcal{L}}^{{\Re }_1}{\wp }_{P_1}^{Y_1}}{{\lambda }_2}}{\mathsf{\Lambda }}_3\left(1+{\displaystyle \frac{1}{1+n}}\right){\lambda }_{{\mathbb{D}}_{{\mathcal{N}}_3}}\parallel x_3^n\oplus x_3^{*}\parallel +{\gamma }_1^n\parallel {\delta }_3^n\oplus 0\parallel \hfill \\ \hfill & =\left({\gamma }_1^n{\nu }_1+(1-{\gamma }_1^n)\right)\parallel x_1^n\oplus x_1^{*}\parallel +\left({\gamma }_1^n{\delta }_2+{\gamma }_1^n{\mu }_2\right)\parallel x_2^n\oplus x_2^{*}\parallel \hfill \\ \hfill & +{\gamma }_1^n{\tau }_3\parallel x_3^n\oplus x_3^{*}\parallel +{\gamma }_1^n\parallel {\delta }_3^n\oplus 0\parallel .\hfill \end{array}$$

(35)

Using (34) and (35) in (33), we have

$$\begin{array}{cc}\hfill & \parallel x_1^{n+1}\oplus x_1^{*}\parallel \hfill \\ \hfill & \le {\alpha }_1^n{\nu }_1\{{\beta }_1^n{\nu }_1\parallel z_1^n\oplus x_1^{*}\parallel +{\beta }_1^n{\delta }_2\parallel z_2^n\oplus x_2^{*}\parallel +{\beta }_1^n{\mu }_2\parallel x_2^n\oplus x_2^{*}\parallel \hfill \\ \hfill & +(1-{\beta }_1^n)\parallel x_1^n\oplus x_1^{*}\parallel +{\beta }_1^n{\tau }_3\parallel z_3^n\oplus x_3^{*}\parallel +{\beta }_1^n\parallel {\delta }_2^n\oplus 0\parallel \}\hfill \\ \hfill & +{\alpha }_1^n{\delta }_2\{{\beta }_2^n{\nu }_2\parallel z_2^n\oplus x_2^{*}\parallel +{\beta }_2^n{\delta }_3\parallel z_3^n\oplus x_3^{*}\parallel +{\beta }_2^n{\mu }_3\parallel x_3^n\oplus x_3^{*}\parallel \hfill \\ \hfill & +(1-{\beta }_2^n)\parallel x_2^n\oplus x_2^{*}\parallel +{\beta }_2^n{\tau }_4\parallel z_4^n\oplus x_4^{*}\parallel +{\beta }_2^n\parallel {\delta }_3^n\oplus 0\parallel \}\hfill \\ \hfill & +{\alpha }_1^n{\mu }_2\parallel x_2^n\oplus x_2^{*}\parallel +(1-{\alpha }_1^n)\parallel x_1^n\oplus x_1^{*}\parallel +{\alpha }_1^n\parallel {\delta }_1^n\oplus 0\parallel \hfill \\ \hfill & +{\alpha }_1^n{\tau }_3\{{\beta }_3^n{\nu }_3\parallel z_3^n\oplus x_3^{*}\parallel +{\beta }_3^n{\delta }_4\parallel z_4^n\oplus x_4^{*}\parallel +{\beta }_3^n{\mu }_4\parallel x_4^n\oplus x_4^{*}\parallel \hfill \\ \hfill & +(1-{\beta }_3^n)\parallel x_3^n\oplus x_3^{*}\parallel +{\beta }_3^n{\tau }_5\parallel z_5^n\oplus x_5^{*}\parallel +{\beta }_3^n\parallel {\delta }_4^n\oplus 0\parallel \}\hfill \\ \hfill & \le {\alpha }_1^n{\beta }_1^n{\nu }_1^2\parallel z_1^n\oplus x_1^{*}\parallel +\left({\alpha }_1^n{\beta }_1^n{\nu }_1{\delta }_2+{\alpha }_1^n{\nu }_2{\beta }_2^n{\delta }_2\right)\parallel z_2^n\oplus x_2^{*}\parallel \hfill \\ \hfill & +\left({\alpha }_1^n{\beta }_1^n{\nu }_1{\tau }_3+{\alpha }_1^n{\beta }_2^n{\delta }_2{\delta }_3+{\alpha }_1^n{\beta }_3^n{\tau }_3{\nu }_3\right)\parallel z_3^n\oplus z_3^{*}\parallel +\left({\alpha }_1^n{\beta }_2^n{\delta }_2{\tau }_4+{\alpha }_1^n{\beta }_3^n{\tau }_3{\delta }_4\right)\parallel z_4^n\oplus x_4^{*}\parallel \hfill \\ \hfill & +{\alpha }_1^n{\beta }_3^n{\tau }_3{\tau }_5\parallel z_5\oplus x_5^{*}\parallel +\left((1-{\alpha }_1^n)+{\alpha }_1^n{\nu }_1(1-{\beta }_1^n)\right)\parallel x_1^n\oplus x_1^{*}\parallel \hfill \\ \hfill & +\left({\alpha }_1^n{\beta }_1^n{\nu }_1{\mu }_2+{\alpha }_1^n(1-{\beta }_2^n){\delta }_2+{\alpha }_1^n{\mu }_2\right)\parallel x_2^{*}\oplus x_2\parallel +\left((1-{\beta }_3^n)+{\alpha }_1^n{\beta }_2^n{\delta }_2{\mu }_3\right)\parallel x_3\oplus x_3^{*}\parallel \hfill \\ \hfill & +{\alpha }_1^n{\beta }_3^n{\tau }_3{\tau }_4\parallel x_4^n\oplus x_4^{*}\parallel +{\alpha }_1^n{\nu }_1{\beta }_1^n\parallel {\delta }_2^n\oplus 0\parallel +{\alpha }_1^n{\delta }_2{\beta }_2^n\parallel {\delta }_3^n\oplus 0\parallel +{\alpha }_1^n{\tau }_3{\beta }_3^n\parallel {\delta }_4^n\oplus 0\parallel \hfill \\ \hfill & +{\alpha }_1^n\parallel {\delta }_1^n\oplus 0\parallel \hfill \\ \hfill & \le {\alpha }_1^n{\beta }_1^n{\nu }_1^2\{\left({\gamma }_1^n{\nu }_1+(1-{\gamma }_1^n)\right)\parallel x_1^n\oplus x_1^{*}\parallel +\left({\gamma }_1^n{\delta }_2+{\gamma }_1^n{\mu }_2\right)\parallel x_2^n\oplus x_2^{*}\parallel +{\gamma }_1^n{\tau }_3\parallel x_3^n\oplus x_3^{*}\parallel \hfill \\ \hfill & +{\gamma }_1^n\parallel {\delta }_3^n\oplus 0\parallel \}+\left({\alpha }_1^n{\beta }_1^n{\nu }_1{\delta }_2+{\alpha }_1^n{\nu }_2{\beta }_2^n{\delta }_2\right)\{\left({\gamma }_2^n{\nu }_2+(1-{\gamma }_2^n)\right)\parallel x_2^n\oplus x_2^{*}\parallel \hfill \\ \hfill & +\left({\gamma }_2^n{\delta }_3+{\gamma }_2^n{\mu }_3\right)\parallel x_3^n\oplus x_3^{*}\parallel +{\gamma }_2^n{\tau }_4\parallel x_4^n\oplus x_4^{*}\parallel +{\gamma }_2^n\parallel {\delta }_4^n\oplus 0\parallel \}+({\alpha }_1^n{\beta }_1^n{\nu }_1{\tau }_3+{\alpha }_1^n{\beta }_2^n{\delta }_2{\delta }_3\hfill \\ \hfill & +{\alpha }_1^n{\beta }_3^n{\tau }_3{\nu }_3\left)\right\{\left({\gamma }_3^n{\nu }_3+(1-{\gamma }_3^n)\right)\parallel x_3^n\oplus x_3^{*}\parallel +\left({\gamma }_3^n{\delta }_4+{\gamma }_3^n{\mu }_4\right)\parallel x_4^n\oplus x_4^{*}\parallel +{\gamma }_3^n{\tau }_5\parallel x_5^n\oplus x_5^{*}\parallel \hfill \\ \hfill & +{\gamma }_3^n\parallel {\delta }_4^n\oplus 0\parallel \}+\left({\alpha }_1^n{\beta }_2^n{\delta }_2{\tau }_4+{\alpha }_1^n{\beta }_3^n{\tau }_3{\delta }_4\right)\{\left({\gamma }_4^n{\nu }_4+(1-{\gamma }_4^n)\right)\parallel x_4^n\oplus x_4^{*}\parallel \hfill \\ \hfill & +\left({\gamma }_4^n{\delta }_5+{\gamma }_4^n{\mu }_5\right)\parallel x_5^n\oplus x_5^{*}\parallel +{\gamma }_4^n{\tau }_6\parallel x_6^n\oplus x_6^{*}\parallel +{\gamma }_4^n\parallel {\delta }_5^n\oplus 0\parallel \}+{\alpha }_1^n{\beta }_3^n{\tau }_3{\tau }_5\{({\gamma }_5^n{\nu }_5\hfill \\ \hfill & +(1-{\gamma }_5^n))\parallel x_5^n\oplus x_5^{*}\parallel +\left({\gamma }_5^n{\delta }_6+{\gamma }_5^n{\mu }_6\right)\parallel x_6^n\oplus x_6^{*}\parallel +{\gamma }_5^n{\tau }_7\parallel x_7^n\oplus x_7^{*}\parallel +{\gamma }_5^n\parallel {\delta }_7^n\oplus 0\parallel \}\hfill \\ \hfill & +\left((1-{\alpha }_1^n)+{\alpha }_1^n{\nu }_1(1-{\beta }_1^n)\right)\parallel x_1^n\oplus x_1^{*}\parallel +\left({\alpha }_1^n{\beta }_1^n{\nu }_1{\mu }_2+{\alpha }_1^n(1-{\beta }_2^n){\delta }_2+{\alpha }_1^n{\mu }_2\right)\parallel x_2^n\oplus x_2^{*}\parallel \hfill \\ \hfill & +\left((1-{\beta }_3^n)+{\alpha }_1^n{\beta }_2^n{\delta }_2{\mu }_3\right)\parallel x_3^n\oplus x_3^{*}\parallel +{\alpha }_1^n{\beta }_3^n{\tau }_3{\tau }_4\parallel x_4^n\oplus x_4\parallel +{\alpha }_1^n{\nu }_1{\beta }_1^n\parallel {\delta }_2^n\oplus 0\parallel \hfill \\ \hfill & +{\alpha }_1^n{\delta }_2{\beta }_2^n\parallel {\delta }_3^n\oplus 0\parallel +{\alpha }_1^n{\tau }_3{\beta }_3^n\parallel {\delta }_4^n\oplus 0\parallel +{\alpha }_1^n\parallel {\delta }_1^n\oplus 0\parallel .\hfill \end{array}$$

(36)

After simplification and by Proposition 1, we obtain

$$\begin{array}{cc}\hfill & \parallel x_1^{n+1}-x_1^{*}\parallel \hfill \\ \hfill & \le [{\alpha }_1^n{\beta }_1^n{\nu }_1^2\{{\gamma }_1^n({\nu }_1-1)+1\}+{\alpha }_1^n\{{\nu }_1(1-{\beta }_1^n)-1\}+1]\parallel x_1^n-x_1^{*}\parallel \hfill \\ \hfill & +[{\alpha }_1^n{\beta }_1^n{\nu }_1({\nu }_1{\gamma }_1^n+1)({\delta }_2+{\mu }_2)+{\alpha }_1^n{\beta }_1^n{\nu }_1{\delta }_2{\gamma }_2^n({\nu }_2-1)\hfill \\ \hfill & +{\alpha }_1^n{\nu }_2{\beta }_2^n{\delta }_2({\nu }_2{\gamma }_2^n-{\gamma }_2^n+1)+{\alpha }_1^n{\delta }_2(1-{\beta }_2^n)]\parallel x_2^n-x_2^{*}\parallel \hfill \\ \hfill & +[{\alpha }_1^n{\gamma }_2^n{\delta }_2({\beta }_1^n{\nu }_1+{\beta }_2^n{\nu }_2)({\delta }_3+{\mu }_3)+{\alpha }_1^n{\beta }_3^n{\tau }_3{\nu }_3({\gamma }_3^n{\nu }_3+1-{\gamma }_3^n)+{\alpha }_1^n{\beta }_1^n{\nu }_1{\tau }_3({\nu }_1{\gamma }_1^n\hfill \\ \hfill & +{\gamma }_3^n{\nu }_3-{\gamma }_3^n+1)+{\alpha }_1^n{\beta }_2^n{\delta }_2[{\gamma }_3^n{\delta }_3({\nu }_3-1)+{\delta }_3+{\mu }_3]-{\beta }_3^n+1]\parallel x_3^n-x_3^{*}\parallel \hfill \\ \hfill & +[{\alpha }_1^n{\beta }_1^n{\nu }_1[{\gamma }_2^n{\delta }_2{\delta }_4+{\gamma }_3^n{\tau }_3({\delta }_4+{\mu }_4)]+{\alpha }_1^n{\beta }_2^n{\delta }_2[{\gamma }_2^n{\nu }_2{\delta }_4+{\gamma }_3^n{\delta }_3{\delta }_4+{\gamma }_3^n{\delta }_3{\mu }_4\hfill \\ \hfill & +{\tau }_4+{\gamma }_4^n{\tau }_4({\nu }_4-1)]+{\alpha }_1^n{\beta }_3^n{\tau }_3[{\gamma }_3^n{\nu }_3({\delta }_4+{\mu }_4)+{\gamma }_4^n{\delta }_4({\nu }_4-1)+{\delta }_4+{\tau }_4]]\parallel x_4^n-x_4^{*}\parallel \hfill \\ \hfill & +[{\alpha }_1^n{\beta }_1^n{\nu }_1{\tau }_3{\tau }_5{\gamma }_3^n+{\alpha }_1^n{\beta }_2^n{\delta }_2[{\delta }_3{\gamma }_3^n{\tau }_5+{\gamma }_4^n{\tau }_4({\delta }_5+{\mu }_5)]+{\alpha }_1^n{\beta }_3^n[{\tau }_3{\tau }_5({\gamma }_3^n{\nu }_3+{\gamma }_5^n{\nu }_5-{\gamma }_5^n+1)\hfill \\ \hfill & +{\gamma }_4^n{\delta }_4({\tau }_4{\delta }_5+{\tau }_3{\mu }_5)\left]\right]\parallel x_5^n-x_5^{*}\parallel +[{\alpha }_1^n{\beta }_2^n{\gamma }_4^n{\delta }_2{\tau }_4{\tau }_6+{\alpha }_1^n{\beta }_3^n{\tau }_3[{\gamma }_4^n{\delta }_4{\tau }_6\hfill \\ \hfill & +{\gamma }_5^n{\tau }_5({\delta }_6+{\mu }_6)\left]\right]\parallel x_6^n-x_6^{*}\parallel +{\alpha }_1^n{\beta }_3^n{\gamma }_5^n{\tau }_3{\tau }_5{\tau }_7\parallel x_7^n-x_7^{*}\parallel +{\alpha }_1^n{\beta }_1^n{\nu }_1^2{\gamma }_1^n\parallel {\delta }_3^n\oplus 0\parallel \hfill \\ \hfill & +\left({\alpha }_1^n{\beta }_1^n{\nu }_1{\delta }_2+{\alpha }_1^n{\nu }_2{\beta }_2^n{\delta }_2\right){\gamma }_2^n\parallel {\delta }_4^n\oplus 0\parallel +\left({\alpha }_1^n{\beta }_1^n{\nu }_1{\tau }_3+{\alpha }_1^n{\beta }_2^n{\delta }_2{\delta }_3+{\alpha }_1^n{\beta }_3^n{\tau }_3{\nu }_3\right){\gamma }_3^n\parallel {\delta }_4^n\oplus 0\parallel \hfill \\ \hfill & +\left({\alpha }_1^n{\beta }_2^n{\delta }_2{\tau }_4+{\alpha }_1^n{\beta }_3^n{\tau }_3{\delta }_4\right){\gamma }_4^n\parallel {\delta }_5^n\oplus 0\parallel +{\alpha }_1^n{\beta }_3^n{\tau }_3{\tau }_5{\gamma }_5^n\parallel {\delta }_7^n\oplus 0\parallel +{\alpha }_1^n{\nu }_1{\beta }_1^n\parallel {\delta }_2^n\oplus 0\parallel \hfill \\ \hfill & +{\alpha }_1^n{\delta }_2{\beta }_2^n\parallel {\delta }_3^n\oplus 0\parallel +{\alpha }_1^n{\tau }_3{\beta }_3^n\parallel {\delta }_4^n\oplus 0\parallel +{\alpha }_1^n\parallel {\delta }_1^n\oplus 0\parallel .\hfill \end{array}$$

(37)

By applying the same logic as above, we have

$$\begin{array}{cc}\hfill & \parallel x_2^{n+1}-x_2^{*}\parallel \hfill \\ \hfill & \le [{\alpha }_2^n{\beta }_2^n{\nu }_2^2\{{\gamma }_2^n({\nu }_2-1)+1\}+{\alpha }_2^n\{{\nu }_2(1-{\beta }_2^n)-1\}+1]\parallel x_2^n-x_2^{*}\parallel \hfill \\ \hfill & +[{\alpha }_2^n{\beta }_2^n{\nu }_2({\nu }_2{\gamma }_2^n+1)({\delta }_3+{\mu }_3)+{\alpha }_2^n{\beta }_2^n{\nu }_2{\delta }_3{\gamma }_3^n({\nu }_3-1)+{\alpha }_2^n{\nu }_3{\beta }_3^n{\delta }_3({\nu }_3{\gamma }_3^n-{\gamma }_3^n+1)\hfill \\ \hfill & +{\alpha }_2^n{\delta }_3(1-{\beta }_3^n)]\parallel x_3^n-x_3^{*}\parallel +[{\alpha }_2^n{\gamma }_3^n{\delta }_3({\beta }_2^n{\nu }_2+{\beta }_3^n{\nu }_3)({\delta }_4+{\mu }_4)\hfill \\ \hfill & +{\alpha }_2^n{\beta }_4^n{\tau }_4{\nu }_4({\gamma }_4^n{\nu }_4+1-{\gamma }_4^n)+{\alpha }_2^n{\beta }_2^n{\nu }_2{\tau }_4({\nu }_2{\gamma }_2^n+{\gamma }_4^n{\nu }_4-{\gamma }_4^n+1)\hfill \\ \hfill & +{\alpha }_2^n{\beta }_3^n{\delta }_3[{\gamma }_4^n{\delta }_4({\nu }_4-1)+{\delta }_4+{\mu }_4]-{\beta }_4^n+1]\parallel x_4^n-x_4^{*}\parallel +\left[{\alpha }_2^n{\beta }_2^n{\nu }_2\right[{\gamma }_3^n{\delta }_3{\delta }_5\hfill \\ \hfill & +{\gamma }_4^n{\tau }_4({\delta }_5+{\mu }_5)]+{\alpha }_2^n{\beta }_3^n{\delta }_3[{\gamma }_3^n{\nu }_3{\delta }_5+{\gamma }_4^n{\delta }_4{\delta }_5+{\gamma }_4^n{\delta }_4{\mu }_5+{\tau }_5+{\gamma }_5^n{\tau }_5({\nu }_5-1)]\hfill \\ \hfill & +{\alpha }_2^n{\beta }_4^n{\tau }_4[{\gamma }_4^n{\nu }_4({\delta }_5+{\mu }_5)+{\gamma }_5^n{\delta }_5({\nu }_5-1)+{\delta }_5+{\tau }_5]]\parallel x_5^n-x_5^{*}\parallel +[{\alpha }_2^n{\beta }_2^n{\nu }_2{\tau }_4{\tau }_6{\gamma }_4^n\hfill \\ \hfill & +{\alpha }_2^n{\beta }_3^n{\delta }_3[{\delta }_4{\gamma }_4^n{\tau }_6+{\gamma }_5^n{\tau }_5({\delta }_6+{\mu }_6)]+{\alpha }_2^n{\beta }_4^n[{\tau }_4{\tau }_6({\gamma }_4^n{\nu }_4+{\gamma }_6^n{\nu }_6-{\gamma }_6^n+1)+{\gamma }_5^n{\delta }_5({\tau }_5{\delta }_6\hfill \\ \hfill & +{\tau }_4{\mu }_6\left)\right]]\parallel x_6^n-x_6^{*}\parallel +\left[{\alpha }_2^n{\beta }_3^n{\gamma }_5^n{\delta }_3{\tau }_5{\tau }_7+{\alpha }_2^n{\beta }_4^n{\tau }_4[{\gamma }_5^n{\delta }_5{\tau }_7+{\gamma }_6^n{\tau }_6({\delta }_7+{\mu }_7)]\right]\parallel x_7^n-x_7^{*}\parallel \hfill \\ \hfill & +{\alpha }_2^n{\beta }_4^n{\gamma }_6^n{\tau }_4{\tau }_6{\tau }_8\parallel x_8^n-x_8^{*}\parallel +{\alpha }_2^n{\beta }_2^n{\nu }_2^2{\gamma }_2^n\parallel {\delta }_4^n\oplus 0\parallel +\left({\alpha }_2^n{\beta }_2^n{\nu }_2{\delta }_3+{\alpha }_2^n{\nu }_3{\beta }_3^n{\delta }_3\right){\gamma }_3^n\parallel {\delta }_5^n\oplus 0\parallel \hfill \\ \hfill & +\left({\alpha }_2^n{\beta }_2^n{\nu }_2{\tau }_4+{\alpha }_2^n{\beta }_3^n{\delta }_3{\delta }_4+{\alpha }_2^n{\beta }_4^n{\tau }_4{\nu }_4\right){\gamma }_4^n\parallel {\delta }_5^n\oplus 0\parallel +\left({\alpha }_2^n{\beta }_3^n{\delta }_3{\tau }_5+{\alpha }_2^n{\beta }_4^n{\tau }_4{\delta }_5\right){\gamma }_5^n\parallel {\delta }_6^n\oplus 0\parallel \hfill \\ \hfill & +{\alpha }_2^n{\beta }_4^n{\tau }_4{\tau }_6{\gamma }_6^n\parallel {\delta }_8^n\oplus 0\parallel +{\alpha }_2^n{\nu }_2{\beta }_2^n\parallel {\delta }_3^n\oplus 0\parallel +{\alpha }_2^n{\delta }_3{\beta }_3^n\parallel {\delta }_4^n\oplus 0\parallel \hfill \\ \hfill & +{\alpha }_2^n{\tau }_4{\beta }_4^n\parallel {\delta }_5^n\oplus 0\parallel +{\alpha }_2^n\parallel {\delta }_2^n\oplus 0\parallel .\hfill \end{array}$$

(38)

Continuing in a similar way, we have

$$\begin{array}{cc}\hfill & \parallel x_k^{n+1}-x_k^{*}\parallel \hfill \\ \hfill & \le [{\alpha }_k^n{\beta }_k^n{\nu }_k^2\{{\gamma }_k^n({\nu }_k-1)+1\}+{\alpha }_k^n\{{\nu }_k(1-{\beta }_k^n)-1\}+1]\parallel x_k^n-x_k^{*}\parallel \hfill \\ \hfill & +[{\alpha }_k^n{\beta }_k^n{\nu }_k({\nu }_k{\gamma }_k^n+1)({\delta }_1+{\mu }_1)+{\alpha }_k^n{\beta }_k^n{\nu }_k{\delta }_1{\gamma }_1^n({\nu }_1-1)+{\alpha }_k^n{\nu }_1{\beta }_1^n{\delta }_1({\nu }_1{\gamma }_1^n-{\gamma }_1^n+1)\hfill \\ \hfill & +{\alpha }_k^n{\delta }_1(1-{\beta }_1^n)]\parallel x_1^n-x_1^{*}\parallel +[{\alpha }_k^n{\gamma }_1^n{\delta }_1({\beta }_k^n{\nu }_k+{\beta }_1^n{\nu }_1)({\delta }_2+{\mu }_2)\hfill \\ \hfill & +{\alpha }_k^n{\beta }_2^n{\tau }_2{\nu }_2({\gamma }_2^n{\nu }_2+1-{\gamma }_2^n)+{\alpha }_k^n{\beta }_k^n{\nu }_k{\tau }_2({\nu }_k{\gamma }_k^n+{\gamma }_2^n{\nu }_2-{\gamma }_2^n+1)\hfill \\ \hfill & +{\alpha }_k^n{\beta }_1^n{\delta }_1[{\gamma }_2^n{\delta }_2({\nu }_2-1)+{\delta }_2+{\mu }_2]-{\beta }_2^n+1]\parallel x_2^n-x_2^{*}\parallel \hfill \\ \hfill & +[{\alpha }_k^n{\beta }_k^n{\nu }_k[{\gamma }_1^n{\delta }_1{\delta }_3+{\gamma }_2^n{\tau }_2({\delta }_3+{\mu }_3)]+{\alpha }_k^n{\beta }_1^n{\delta }_1[{\gamma }_1^n{\nu }_1{\delta }_3+{\gamma }_2^n{\delta }_2{\delta }_3+{\gamma }_2^n{\delta }_2{\mu }_3\hfill \\ \hfill & +{\tau }_3+{\gamma }_3^n{\tau }_3({\nu }_3-1)]+{\alpha }_k^n{\beta }_2^n{\tau }_2[{\gamma }_2^n{\nu }_2({\delta }_3+{\mu }_3)+{\gamma }_3^n{\delta }_3({\nu }_3-1)+{\delta }_3+{\tau }_3]]\parallel x_3^n-x_3^{*}\parallel \hfill \\ \hfill & +[{\alpha }_k^n{\beta }_k^n{\nu }_k{\tau }_2{\tau }_4{\gamma }_2^n+{\alpha }_k^n{\beta }_1^n{\delta }_1[{\delta }_2{\gamma }_2^n{\tau }_4+{\gamma }_3^n{\tau }_3({\delta }_4+{\mu }_4)]\hfill \\ \hfill & +{\alpha }_k^n{\beta }_2^n[{\tau }_2{\tau }_4({\gamma }_2^n{\nu }_2+{\gamma }_4^n{\nu }_4-{\gamma }_4^n+1)+{\gamma }_3^n{\delta }_3({\tau }_3{\delta }_4+{\tau }_2{\mu }_4)]]\parallel x_4^n-x_4^{*}\parallel \hfill \\ \hfill & +\left[{\alpha }_k^n{\beta }_1^n{\gamma }_3^n{\delta }_1{\tau }_3{\tau }_5+{\alpha }_k^n{\beta }_2^n{\tau }_2[{\gamma }_3^n{\delta }_3{\tau }_5+{\gamma }_4^n{\tau }_4({\delta }_5+{\mu }_5)]\right]\parallel x_5^n-x_5^{*}\parallel \hfill \\ \hfill & +{\alpha }_k^n{\beta }_2^n{\gamma }_4^n{\tau }_2{\tau }_4{\tau }_6\parallel x_6^n-x_6^{*}\parallel +{\alpha }_k^n{\beta }_k^n{\nu }_k^2{\gamma }_k^n\parallel {\delta }_2^n\oplus 0\parallel +\left({\alpha }_k^n{\beta }_k^n{\nu }_k{\delta }_1+{\alpha }_k^n{\nu }_1{\beta }_1^n{\delta }_1\right){\gamma }_1^n\parallel {\delta }_3^n\oplus 0\parallel \hfill \\ \hfill & +\left({\alpha }_k^n{\beta }_k^n{\nu }_k{\tau }_2+{\alpha }_k^n{\beta }_1^n{\delta }_1{\delta }_2+{\alpha }_k^n{\beta }_2^n{\tau }_2{\nu }_2\right){\gamma }_2^n\parallel {\delta }_3^n\oplus 0\parallel +\left({\alpha }_k^n{\beta }_1^n{\delta }_1{\tau }_3+{\alpha }_k^n{\beta }_2^n{\tau }_2{\delta }_3\right){\gamma }_3^n\parallel {\delta }_4^n\oplus 0\parallel \hfill \\ \hfill & +{\alpha }_k^n{\beta }_2^n{\tau }_2{\tau }_4{\gamma }_4^n\parallel {\delta }_6^n\oplus 0\parallel +{\alpha }_k^n{\nu }_k{\beta }_k^n\parallel {\delta }_1^n\oplus 0\parallel +{\alpha }_k^n{\delta }_1{\beta }_1^n\parallel {\delta }_2^n\oplus 0\parallel \hfill \\ \hfill & +{\alpha }_k^n{\tau }_2{\beta }_2^n\parallel {\delta }_3^n\oplus 0\parallel +{\alpha }_k^n\parallel {\delta }_k^n\oplus 0\parallel .\hfill \end{array}$$

(39)

From (37)–(39), we have

$$\begin{array}{cc}\hfill & \parallel x_1^{(n+1)}-x_1\parallel +\parallel x_2^{(n+1)}-x_2\parallel +\cdots +\parallel x_{\kappa }^{(n+1)}-x_{\kappa }\parallel \hfill \\ \hfill & \le \sum _{i=1}^n\left({}_1\Omega _i^{\left(n\right)}{+}_2{\Omega }_i^{\left(n\right)}{+}_3{\Omega }_i^{\left(n\right)}{+}_4{\Omega }_i^{\left(n\right)}{+}_5{\Omega }_i^{\left(n\right)}{+}_6{\Omega }_i^{\left(n\right)}{+}_7{\Omega }_i^{\left(n\right)}\right)\parallel x_i^{\left(n\right)}-x_i\parallel \hfill \\ \hfill & +\sum _{i=1}^k{\alpha }_i^n{\beta }_i^n{\nu }_i^2{\gamma }_i^n\parallel {\delta }_{i+2}^n\vee (-{\delta }_{i+2}^n)\parallel +\sum _{i=1}^k\left({\alpha }_i^n{\beta }_i^n{\nu }_i{\delta }_{i+1}+{\alpha }_i^n{\nu }_{i+1}{\beta }_{i+1}^n{\delta }_{i+1}\right){\gamma }_{i+1}^n\parallel {\delta }_{i+3}^n\vee (-{\delta }_{i+3}^n)\parallel \hfill \\ \hfill & +\sum _{i=1}^k\left({\alpha }_i^n{\beta }_i^n{\nu }_i{\tau }_{i+2}+{\alpha }_i^n{\beta }_{i+1}^n{\delta }_{i+1}{\delta }_{i+2}+{\alpha }_i^n{\beta }_{i+2}^n{\tau }_{i+2}{\nu }_{i+2}\right){\gamma }_{i+2}^n\parallel {\delta }_{i+3}^n\vee (-{\delta }_{i+3}^n)\parallel \hfill \\ \hfill & +\sum _{i=1}^k\left({\alpha }_i^n{\beta }_{i+1}^n{\delta }_{i+1}{\tau }_{i+3}+{\alpha }_i^n{\beta }_{i+2}^n{\tau }_{i+2}{\delta }_{i+3}\right){\gamma }_{i+3}^n\parallel {\delta }_{i+4}^n\vee (-{\delta }_{i+4}^n)\parallel \hfill \\ \hfill & +\sum _{i=1}^k{\alpha }_i^n{\beta }_{i+2}^n{\tau }_{i+2}{\tau }_{i+4}{\gamma }_{i+4}^n\parallel {\delta }_{i+6}^n\vee (-{\delta }_{i+6}^n)\parallel +\sum _{i=1}^k{\alpha }_i^n{\nu }_i{\beta }_i^n\parallel {\delta }_{i+1}^n\vee (-{\delta }_{i+1}^n)\parallel \hfill \\ \hfill & +\sum _{i=1}^k{\alpha }_i^n{\delta }_{i+1}{\beta }_{i+1}^n\parallel {\delta }_{i+2}^n\vee (-{\delta }_{i+2}^n)\parallel +\sum _{i=1}^k{\alpha }_i^n{\tau }_{i+2}{\beta }_{i+2}^n\parallel {\delta }_{i+3}^n\vee (-{\delta }_{i+3}^n)\parallel \hfill \\ \hfill & +\sum _{i=1}^k{\alpha }_i^n\parallel {\delta }_i^n\vee (-{\delta }_i^n)\parallel .\hfill \end{array}$$

(40)

where

$$\begin{array}{cc}\hfill {}_1\Omega _i^{\left(n\right)}& =\left[{\alpha }_i^n{\beta }_i^n{\nu }_i^2\{{\gamma }_i^n({\nu }_i-1)+1\}+{\alpha }_i^n\{{\nu }_i(1-{\beta }_i^n)-1\}+1\right],\hfill \\ \hfill {}_2\Omega _i^{\left(n\right)}& =[{\alpha }_i^n{\beta }_i^n{\nu }_i({\nu }_i{\gamma }_i^n+1)({\delta }_{i+1}+{\mu }_{i+1})+{\alpha }_i^n{\beta }_i^n{\nu }_i{\delta }_{i+1}{\gamma }_{i+1}^n({\nu }_{i+1}-1)\hfill \\ \hfill & +{\alpha }_i^n{\nu }_{i+1}{\beta }_{i+1}^n{\delta }_{i+1}({\nu }_{i+1}{\gamma }_{i+1}^n-{\gamma }_{i+1}^n+1)+{\alpha }_i^n{\delta }_{i+1}(1-{\beta }_{i+1}^n)],\hfill \\ \hfill {}_3\Omega _i^{\left(n\right)}& =[{\alpha }_i^n{\gamma }_{i+1}^n{\delta }_{i+1}({\beta }_i^n{\nu }_i+{\beta }_{i+1}^n{\nu }_{i+1})({\delta }_{i+2}+{\mu }_{i+2})+{\alpha }_i^n{\beta }_{i+2}^n{\tau }_{i+2}{\nu }_{i+2}({\gamma }_{i+2}^n{\nu }_{i+2}\hfill \\ \hfill & +1-{\gamma }_{i+2}^n)+{\alpha }_i^n{\beta }_i^n{\nu }_i{\tau }_{i+2}({\nu }_i{\gamma }_i^n+{\gamma }_{i+2}^n{\nu }_{i+2}-{\gamma }_{i+2}^n+1)\hfill \\ \hfill & +{\alpha }_i^n{\beta }_{i+1}^n{\delta }_{i+1}[{\gamma }_{i+1}^n{\delta }_{i+2}({\nu }_{i+2}-1)+{\delta }_{i+2}+{\mu }_{i+2}]-{\beta }_{i+1}^n+1],\hfill \end{array}$$

$$\begin{array}{cc}\hfill {}_4\Omega _i^{\left(n\right)}& =[{\alpha }_i^n{\beta }_i^n{\nu }_i[{\gamma }_{i+1}^n{\delta }_{i+1}{\delta }_{i+3}+{\gamma }_{i+2}^n{\tau }_{i+2}({\delta }_{i+3}+{\mu }_{i+3})]+{\alpha }_i^n{\beta }_{i+1}^n{\delta }_{i+1}[{\gamma }_{i+1}^n{\nu }_{i+1}{\delta }_{i+3}\hfill \\ \hfill & +{\gamma }_{i+2}^n{\delta }_{i+2}{\delta }_{i+3}+{\gamma }_{i+2}^n{\delta }_{i+2}{\mu }_{i+3}+{\tau }_{i+3}+{\gamma }_{i+3}^n{\tau }_{i+3}({\nu }_{i+3}-1)]\hfill \\ \hfill & +{\alpha }_i^n{\beta }_{i+2}^n{\tau }_{i+2}[{\gamma }_{i+2}^n{\nu }_{i+2}({\delta }_{i+3}+{\mu }_{i+3})+{\gamma }_{i+3}^n{\delta }_{i+3}({\nu }_{i+3}-1)+{\delta }_{i+3}+{\tau }_{i+3}]],\hfill \\ \hfill {}_5\Omega _i^{\left(n\right)}& =[{\alpha }_i^n{\beta }_i^n{\nu }_i{\tau }_{i+2}{\tau }_{i+4}{\gamma }_{i+2}^n+{\alpha }_i^n{\beta }_{i+1}^n{\delta }_{i+1}[{\delta }_{i+2}{\gamma }_{i+2}^n{\tau }_{i+4}+{\gamma }_{i+3}^n{\tau }_{i+3}({\delta }_{i+4}+{\mu }_{i+4})]\hfill \\ \hfill & +{\alpha }_i^n{\beta }_{i+2}^n[{\tau }_{i+2}{\tau }_{i+4}({\gamma }_{i+2}^n{\nu }_{i+2}+{\gamma }_{i+4}^n{\nu }_{i+4}-{\gamma }_{i+4}^n+1)\hfill \\ \hfill & +{\gamma }_{i+3}^n{\delta }_{i+3}({\tau }_{i+3}{\delta }_{i+4}+{\tau }_{i+2}{\mu }_{i+4})\left]\right],\hfill \\ \hfill {}_6\Omega _i^{\left(n\right)}& =\left[{\alpha }_i^n{\beta }_{i+1}^n{\gamma }_{i+3}^n{\delta }_{i+1}{\tau }_{i+3}{\tau }_{i+5}+{\alpha }_i^n{\beta }_{i+2}^n{\tau }_{i+2}[{\gamma }_{i+3}^n{\delta }_{i+3}{\tau }_{i+5}+{\gamma }_{i+4}^n{\tau }_{i+4}({\delta }_{i+5}+{\mu }_{i+5})]\right],\hfill \\ \hfill {}_7\Omega _i^{\left(n\right)}& ={\alpha }_i^n{\beta }_{i+2}^n{\gamma }_{i+4}^n{\tau }_{i+2}{\tau }_{i+4}{\tau }_{i+6}.\hfill \end{array}$$

Let ${\Phi }^{\left(n\right)}=max\left({}_1\Omega _i^{\left(n\right)},{}_2\Omega _i^{\left(n\right)},{}_3\Omega _i^{\left(n\right)},{}_4\Omega _i^{\left(n\right)},{}_5\Omega _i^{\left(n\right)},{}_6\Omega _i^{\left(n\right)},{}_7\Omega _i^{\left(n\right)}\right)$. From (25) and by algebra of convergence of sequences ${}_k\Omega _i^{\left(n\right)}$ and $1\le k\le 7$, we may say that ${\Phi }^{\left(n\right)}\to \Phi$ as $n\to \infty$, where $\Phi =max\left({}_1\Omega _i,{}_2\Omega _i,{}_3\Omega _i,{}_4\Omega _i,{}_5\Omega _i,{}_6\Omega _i,{}_7\Omega _i\right)$. Condition (25) implies that $\Phi <1$, so ${\Phi }^{\left(n\right)}<1$ for sufficiently large n.

Let $v_{n+1}=\left(\parallel x_1^{(n+1)}-x_1\parallel +\parallel x_2^{(n+1)}-x_2\parallel +\cdots +\parallel x_k^{(n+1)}-x_k\parallel \right)$. Then, (40) can be written as

$$\begin{array}{ccc}\hfill v_{n+1}& \le & {\Phi }^{\left(n\right)}{v}_n,n=1,2,\cdots .\hfill \end{array}$$

Clearly, $lim{sup}_{n\ge 1}{\Phi }^{\left(n\right)}<1$ for ${\Phi }^{\left(n\right)}<1.$ With the help of Lemma 2, we may claim that $0\le {\Phi }_n<1.$ Hence, $\left\{(x_i^{\left(n\right)},v_i^{\left(n\right)})\right\}$ converge strongly to the solution $(x_i,v_i)$ of system (5). □

A numerical example is provided with a convergence graph.

4. Numerical Example

Let $k=2$, $\mathcal{X}=\mathbb{R}$, $x=(x_1,x_2)\in \mathbb{R}\times \mathbb{R}$ and $(v_1,v_2)\in {\mathcal{N}}_1\left(x_1\right)\times {\mathcal{N}}_2\left(x_2\right)$ such that

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{w}_1\in P_1(C_{I,{\lambda }_1}^{{\mathcal{S}}_1(h_1\left(x_1\right),v_2)}\left(x_1\right),Y_{I,{\lambda }_2}^{{\mathcal{S}}_2(h_2\left(x_2\right),v_1)}\left(x_2\right))+f_1\left(x_1\right)\oplus g_2\left(x_2\right)+{\mathcal{S}}_1(h_1\left(x_1\right),v_2),\hfill \\ w_2\in P_2(C_{I,{\lambda }_2}^{{\mathcal{S}}_2(h_2\left(x_2\right),v_1)}\left(x_2\right),Y_{I,{\lambda }_3}^{{\mathcal{S}}_2(h_2\left(x_2\right),v_1)}\left(x_1\right))+f_2\left(x_2\right)\oplus g_3\left(x_1\right)+{\mathcal{S}}_2(h_2\left(x_2\right),v_1),\hfill \end{array}\right.\end{array}$$

(41)

for some $\widehat{w}=(w_1,w_2)\in \mathbb{R}\times \mathbb{R}$.

Let the mappings $f_i,g_i,h_i:\mathbb{R}\to \mathbb{R}$, ${\mathcal{S}}_i:\mathbb{R}\times \mathbb{R}:\to 2^{\mathbb{R}}$, ${\mathcal{N}}_i:\mathbb{R}\times \mathbb{R}:\to CB\left(\mathbb{R}\right)$ be defined by

$$f_i\left(x_i\right)={\displaystyle \frac{2x_i}{7(i+1)}},g_i\left(x_i\right)={\displaystyle \frac{3x_i}{49i}},h_i\left(x_i\right)=2x_i,{\mathcal{S}}_i(h_i\left(x_i\right),v_{i+1})=\left\{{\displaystyle \frac{h_i\left(x_i\right)+3v_{i+1}}{2(i+1)}}\right\}$$

and ${\mathcal{N}}_i\left(x_i\right)=\left\{{\displaystyle \frac{5x_i}{16i}}\right\}.$

Suppose that the mapping $P_i:\mathbb{R}\times \mathbb{R}\to \mathbb{R}$ is defined as

$$P_i(x_i,x_{i+1})=\left({\displaystyle \frac{x_i+x_{i+1}}{7+i}}\right).$$

Now, we define the associated resolvent operator,

$$\begin{array}{c}\hfill {\Re }_{I,{\lambda }_i}^{{\mathcal{S}}_1(h_i,v_{i+1})}\left(x_i\right)=\left({\displaystyle \frac{2i(i+1)x_i-3v_{i+1}}{2(i^2+i+1)}}\right),\end{array}$$

(42)

the Yosida approximation operator,

$$\begin{array}{c}\hfill Y_{I,{\lambda }_i}^{{\mathcal{S}}_1(h_i,v_{i+1})}\left(x_i\right)=\left({\displaystyle \frac{(2x_i+3v_{i+1})i}{2(i^2+i+1)}}\right),\end{array}$$

(43)

and the Cayley operator,

$$\begin{array}{c}\hfill C_{I,{\lambda }_i}^{{\mathcal{S}}_1(h_i,v_{i+1})}\left(x_i\right)=\left({\displaystyle \frac{(i^2+i-1)x_i-3v_{i+1}}{i^2+i+1}}\right).\end{array}$$

(44)

Let us choose the controlling sequences $\left\{{\alpha }_i^n\right\}=\left\{{\displaystyle \frac{i}{6n}}\right\},\left\{{\beta }_i^n\right\}=\left\{{\displaystyle \frac{(7n-3)i}{12n}}\right\},\left\{{\gamma }_i^n\right\}=\left\{{\displaystyle \frac{(3n+1)i}{12n}}\right\}$, and $\left\{{\delta }_i^n\right\}=\left\{{\displaystyle \frac{i}{6n+3}}\right\}$. Clearly, $\left\{{\alpha }_i^n\right\}$, $\left\{{\beta }_i^n\right\}$, $\left\{{\gamma }_i^n\right\}$, and $\left\{{\delta }_i^n\right\}$ satisfy the conditions of Algorithm 1.

The sequences for the approximate solution of (41) are obtained by using Algorithm 1 in the following way:

$$\begin{array}{cc}\hfill x_i^{n+1}& ={\displaystyle \frac{i}{6n}}\left({\displaystyle \frac{160i^2(i+1)}{160i^2(i+1)+171}}\right)[y_i^n-{\displaystyle \frac{1}{2(7+i)(i^2+i+1)}}\{2(i^2+i-1)y_i^n\hfill \\ \hfill & +2i{y}_{i+1}^n(3i-6)v_{i+1}+w_i^n\left\}\right]+\left({\displaystyle \frac{6n-i}{6n}}\right)x_i^n+{\displaystyle \frac{i^2}{6n(6n+3)}},\hfill \end{array}$$

(45)

$$\begin{array}{cc}\hfill y_i^n& =\left({\displaystyle \frac{7n-3}{12n}}\right)\left({\displaystyle \frac{160i^3(i+1)}{160i^2(i+1)+171}}\right)[z_i^n-{\displaystyle \frac{1}{2(7+i)(i^2+i+1)}}\{2(i^2+i-1)z_i^n\hfill \\ \hfill & +2i{z}_{i+1}^n(3i-6)v_{i+1}+w_i^n\left\}\right]+\left(1-{\displaystyle \frac{(7n-3)i}{12n}}\right)x_i^n+{\displaystyle \frac{(7n-3)(i^2+i)}{12n(6n+3)}},\hfill \end{array}$$

(46)

and

$$\begin{array}{cc}\hfill z_i^n& =\left({\displaystyle \frac{3n+1}{12n}}\right)\left({\displaystyle \frac{160i^3(i+1)}{160i^2(i+1)+171}}\right)[x_i^n-{\displaystyle \frac{1}{2(7+i)(i^2+i+1)}}\{2(i^2+i-1)x_i^n\hfill \\ \hfill & +2i{x}_{i+1}^n(3i-6)v_{i+1}+w_i^n\left\}\right]+\left(1-{\displaystyle \frac{(3n+1)i}{12n}}\right)x_i^n+{\displaystyle \frac{(3n+1)(i^2+2i)}{12n(6n+3)}}.\hfill \end{array}$$

(47)

Also, it is verified that all conditions of Theorem 2 are satisfied. Clearly, for $\widehat{w}=(1,1),$ the sequence $x^n=(x_1^n,x_2^n)$ converges strongly to the solution $x=(-0.39,0.60)$ of system (41). In this regard the convergence graph (Figure 1) and computational table (Table 1) are shown below. Also, the convergence of each sequence individually involved in Algorithm 1 is shown in Figure 2.

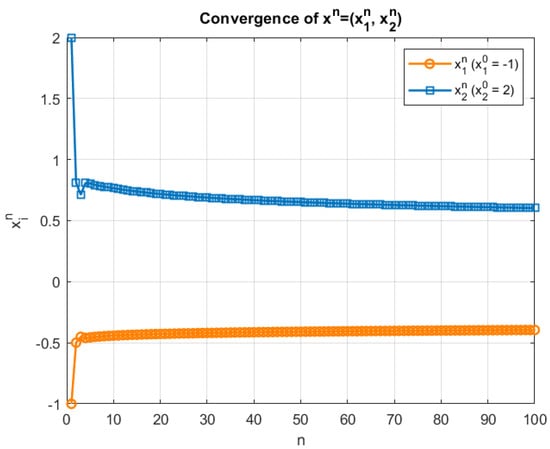
Figure 1. Convergence of $x^n=(x_1^n,x_2^n)$ with initial value $(-1,2)$.

Table 1. The computational table of $\left\{x^n\right\}$, $\left\{y^n\right\}$, and $\left\{z^n\right\}$ starting with $(x_1^0,x_2^0)=(-1,2)$ $(y_1^0,y_2^0)=(3,-2)$, and $(z_1^0,z_2^0)=(4,-1)$.

No. of	For ${\mathit{x}}^{\mathit{n}}=(-1,2)$	For ${\mathit{y}}^{\mathit{n}}=(3,-2)$	For ${\mathit{z}}^{\mathit{n}}=(4,-1)$
Iterations	${\mathit{x}}^{\mathit{n}}=({\mathit{x}}_{\mathbf{1}}^{\mathit{n}},{\mathit{x}}_{\mathbf{2}}^{\mathit{n}})$	${\mathit{y}}^{\mathit{n}}=({\mathit{y}}_{\mathbf{1}}^{\mathit{n}},{\mathit{y}}_{\mathbf{2}}^{\mathit{n}})$	${\mathit{z}}^{\mathit{n}}=({\mathit{z}}_{\mathbf{1}}^{\mathit{n}},{\mathit{z}}_{\mathbf{2}}^{\mathit{n}})$
n  = 1	(−1,2)	(3,−2)	(4,−1)
n = 2	(−0.49930, 0.81207)	(0.23862, 0.24273)	(−0.72659, 2.10466)
n = 3	(−0.45165, 0.71122)	(−0.44464,1.89461)	(−0.43555, 0.89865)
n = 4	(−0.46018, 0.80844 )	(−0.33075 , 0.90799)	(−0.43376, 0.89865)
n = 5	(−0.45581, 0.80425)	(−0.33841, 0.75610)	(−0.46637, 0.82427)
n = 10	(−0.44173, 0.76545)	(−0.36189, 0.69389)	(−0.4845, 0.74925)
n = 15	(−0.43366, 0.73856)	(−0.36339, 0.63498)	(−0.48451, 0.71074)
n = 20	(−0.42794, 0.71821)	(−0.36241, 0.60042)	(−0.48211, 0.68513)
n = 25	(−0.42341, 0.70210)	(−0.36087, 0.57680)	(−0.47936, 0.66615)
n = 30	(−0.41972, 0.68884)	(−0.35921, 0.55919)	(−0.47668, 0.65118)
n = 35	(−0.41659, 0.67762)	(−0.35758, 0.54531)	(−0.47417, 0.63887)
n = 40	(−0.41389, 0.66791)	(−0.35604, 0.53394)	(−0.47186, 0.62845)
n = 45	(−0.41149, 0.65938)	(−0.35458, 0.52436)	(−0.46972, 0.61943)
n = 55	(−0.40742, 0.64494)	(−0.35194, 0.50891)	(−0.46591 0.60444)
n = 70	(−0.40252, 0.62779)	(−0.34853, 0.49157)	(−0.46113, 0.58701)
n = 80	(−0.39981, 0.61841)	(−0.34656, 0.48248)	(−0.45835 0.57760)
n = 90	(−0.39742, 0.61020)	(−0.34479, 0.47473)	(−0.45588, 0.56946)
n = 100	(−0.39523, 0.60290)	(−0.34318, 0.46796)	(−0.45365, 0.56228)

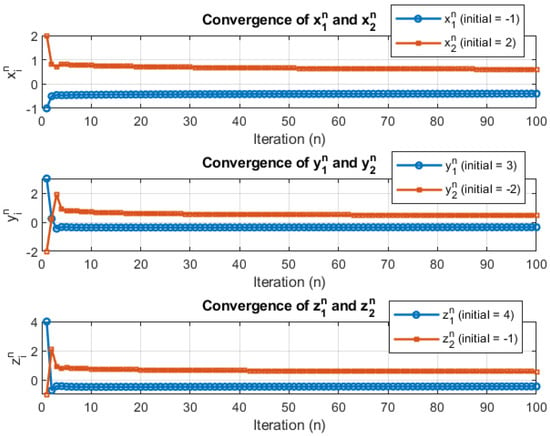
Figure 2. Convergence of $x^n=(x_1^n,x_2^n)$, $y^n=(y_1^n,y_2^n)$, and $z^n=(z_1^n,z_2^n)$ with initial values $(-1,2),(3,-2),and(4,-1)$, respectively.

Remark 4.

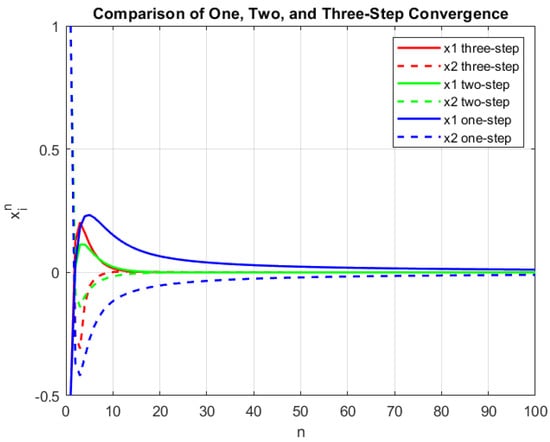
We select identical operators to those in the above numerical illustration and compare our innovative three-step iterative Algorithm 1 against the two-step iterative algorithm (Ishikawa-style) and the one-step iterative algorithm (Mann-style). By setting ${\gamma }_i^n=0$, we derive the sequences $\left\{x_i^n\right\}$ and $\left\{y_i^n\right\}$ as detailed below:

$$\begin{array}{cc}\hfill x_i^{n+1}& ={\displaystyle \frac{i}{6n}}\left({\displaystyle \frac{160i^2(i+1)}{160i^2(i+1)+171}}\right)[y_i^n-{\displaystyle \frac{1}{2(7+i)(i^2+i+1)}}\{2(i^2+i-1)y_i^n\hfill \\ \hfill & +2i{y}_{i+1}^n(3i-6)v_{i+1}+w_i^n\left\}\right]+\left({\displaystyle \frac{6n-i}{6n}}\right)x_i^n+{\displaystyle \frac{i^2}{6n(6n+3)}},\hfill \end{array}$$

(48)

$$\begin{array}{cc}\hfill y_i^n& =\left({\displaystyle \frac{7n-3}{12n}}\right)\left({\displaystyle \frac{160i^3(i+1)}{160i^2(i+1)+171}}\right)[z_i^n-{\displaystyle \frac{1}{2(7+i)(i^2+i+1)}}\{2(i^2+i-1)z_i^n\hfill \\ \hfill & +2i{z}_{i+1}^n(3i-6)v_{i+1}+w_i^n\left\}\right]+\left(1-{\displaystyle \frac{(7n-3)i}{12n}}\right)x_i^n+{\displaystyle \frac{(7n-3)(i^2+i)}{12n(6n+3)}}.\hfill \end{array}$$

(49)

Moreover, by taking ${\beta }_i^n={\gamma }_i^n=0,$ for all $n\ge 0$, we may approximate by using the Mann-style iterative scheme as follows:

$$\begin{array}{cc}\hfill x_i^{n+1}& ={\displaystyle \frac{i}{6n}}\left({\displaystyle \frac{160i^2(i+1)}{160i^2(i+1)+171}}\right)[y_i^n-{\displaystyle \frac{1}{2(7+i)(i^2+i+1)}}\{2(i^2+i-1)y_i^n\hfill \\ \hfill & +2i{y}_{i+1}^n(3i-6)v_{i+1}+w_i^n\left\}\right]+\left({\displaystyle \frac{6n-i}{6n}}\right)x_i^n+{\displaystyle \frac{i^2}{6n(6n+3)}}.\hfill \end{array}$$

(50)

The iterative methods that we are employing will stop their operations once the stopping criterion $\parallel x_i^{(n+1)}-x_i^n\parallel \le {10}^{-6}$ has been satisfactorily met. In the accompanying Table 2 and the illustrative Figure 3, we present a comprehensive comparison showcasing the performance of our innovative three-step Algorithm 1, alongside the well-established Ishikawa-type Equations (48) and (49), in conjunction with the Mann-type Algorithm (50), all of which are initiated with the chosen starting point of $(-0.5,1)$.

Table 2. The values of $x^n=(x_1^n,x_2^n)$ with the initial value $(-0.5,1)$.

No. ofIterations	Three-Step Iterative Algorithm ${\mathit{x}}^{\mathit{n}}=({\mathit{x}}_1^{\mathit{n}},{\mathit{x}}_2^{\mathit{n}})$	Two-Step Iterative Algorithm ${\mathit{x}}^{\mathit{n}}=({\mathit{x}}_1^{\mathit{n}},{\mathit{x}}_2^{\mathit{n}})$	One Step Iterative Algorithm ${\mathit{x}}^{\mathit{n}}=({\mathit{x}}_1^{\mathit{n}},{\mathit{x}}_2^{\mathit{n}})$
n  = 1	(−0.5,1)	(−0.5,1)	(−0.5,1)
n = 2	(0.12570, −0.25747)	(0.02153, −0.08605)	(0.03702, −0.37147)
n = 3	(0.20262, −0.30925)	(0.11337, −0.14096)	(0.18311, −0.41916)
n = 4	(0.16102, −0.13137)	(0.11288, −0.0982)	(0.22754, −0.34455)
n = 5	(0.11547, −0.05666)	(0.09339, −0.06932)	(0.2329, −0.27319)
n = 10	(0.01631, 0.00114)	(0.02223, −0.01653)	(0.15164, −0.11691)
n = 15	(0.00225, 0.00301)	(0.00459, −0.00439)	(0.09413, −0.07328)
n = 20	(0.00017, 0.00172)	(0.00071 −0.00100)	(0.06543, −0.05345)
n = 25	(0, 0.00093)	(0.00013, −0.0001)	(0.04982, −0.04209)
n = 30	(0, 0.00052)	(0, 0.00016)	(0.04026, −0.03471)
n = 35	(0, 0.00029)	(0, 0.00013)	(0.03382, −0.02954)
n = 40	(0, 0.00016)	(0, 0.00009)	(0.02918, −0.02571)
n = 45	(0, 0.00009)	(0, 0.00006)	(0.02566, −0.02276)
n = 55	(0, 0)	(0, 0.00003)	(0.02069, 0)
n = 70	(0, 0)	(0, 0)	(0.01604, 0)
n = 80	(0, 0)	(0, 0)	(0.01395, −0.01262)
n = 90	(0, 0)	(0, 0)	(0.01234, −0.0112)
n = 100	(0, 0)	(0, 0)	(0.01107, −0.01006)

Figure 3. Convergence of $x^n=(x_1^n,x_2^n)$ with initial value $(-0.5,1)$.

The numerical findings that are meticulously detailed in Table 2 and the graphical representation provided in Figure 3 strongly suggest that our newly proposed three-step Algorithm 1 demonstrates impressive performance and appears to possess a significant competitive edge over the other methods. Based on this analysis, we can confidently assert that our algorithm exhibits remarkable speed and efficiency, typically requiring an average of about 10 to 12 iterations to achieve convergence successfully.

5. Conclusions

In this manuscript, the framework of extended ordered XOR-inclusion problems incorporating Cayley and Yosida operators is presented and examined within the context of real ordered Banach spaces, which encompasses a broader scope than the problems addressed in [11,19,28]. We investigated the existence of solutions to SEOXORIP by utilizing proximal-point mappings under specific conditions deemed appropriate. A three-step iterative methodology is proposed for deriving approximate solutions to SEOXORIP, and an analysis of the convergence of the proposed methodology was conducted. Ultimately, we provided a numerical example accompanied by a convergence graph generated using MATLAB 2018a to substantiate the convergence of the sequence produced by the proposed methodology.