Abstract
Intuitionistic fuzzy sets (IFSs), proposed in 1983, are one of the most viable and widely explored extensions of Zadeh’s fuzzy sets. In the decade following their introduction, they were extended to interval-valued IFSs (IVIFSs), temporal IFSs, IFSs of the second type (incorrectly called “Pythagorean fuzzy sets” by some authors) IFSs of n-th type, and IFSs over different universes. For each of these extensions, at least one geometrical interpretation has been defined, and for IVIFSs, at least seven different interpretations are known. In the present paper, revisiting some existing results on IVIFSs, some necessary modifications, additions, and corrections to the planar and spatial geometrical interpretations are introduced here for the first time. A new, eighth, geometrical interpretation of IVIFSs is proposed. A basic logic operation and two modal operators are illustrated and a comparison is made between the planar and the new “two-rods” geometrical interpretations of identical IVIFS elements. Finally, a new operator over IVIFSs is proposed for the first time, some of its properties are proven, and its geometrical interpretations are described.
Keywords:
intuitionistic fuzzy sets; interval-valued intuitionistic fuzzy sets; geometrical interpretation; operator on interval-valued intuitionistic fuzzy sets MSC:
03E72; 51F99
1. Introduction
Interval-valued intuitionistic fuzzy sets (IVIFSs) emerged in 1988–1989 in [1], i.e., five years after the intuitionistic fuzzy sets (IFSs; see [2]). A complete exposition of their theory is given in [3].
Since the beginning of the present century, numerous attempts for extensions of the concept of IFSs have been introduced, but as it was proved in [4], a large number of them are representable by standard IFSs or by IVIFSs. Examples of these are, for instance, complex Atanassov’s IFSs [5,6], vague sets [7,8], generalized IFSs [9], generalized Atanassov’s IFSs [10], bipolar fuzzy sets [11], hesitant fuzzy sets [12,13], soft sets [14], variable fuzzy sets [15], bifuzzy sets [16], and others; and the remaining are representable by IVIFSs, e.g., inconsistent IFSs [17,18], picture fuzzy sets [19], neutrosophic sets [20], and others.
Over the years, a large volume of research has been dediated to the set-theoretical and logical foundations of IFSs and IVIFSs, as well as their practical applicability. A number of recent research papers utilize the concept of IVIFSs, specifically as a tool in multicriteria decision making under uncertainty, in alternative ranking [21], resource optimization, and in particular, the selection of suppliers, platforms [22], materials [23], employees [24], and others [25,26]. Apart from engineering and industrial applications, IVIFSs are often explored in the perspective of the theory of graphs (e.g., [27,28]) and algebra [29].
Much less explored is the theoretically motivated geometrical representations of IFSs and IVIFSs, and this aspect is chosen to focus on the efforts of our present investigation.
During the last 40 years, the IFSs were given a large number of different geometrical interpretations. An early seminal work in this direction is the 1989 preprint [30], which discusses through a wide range of cases the geometrical interpretation of IFSs in the Euclidian plane, along with several logical operations and functions, and nine operators over IFSs, including the interpretations of the nine operators over the IFSs of the second type (recently reinvented under the name “Pythagorean fuzzy sets”), and IFSs of n-th type have been lately “re-branded as” q-rung orthopair fuzzy sets [31,32]; but for all of them, there exists a bijective function mapping them to the standard IFS (see, e.g., refs. [4,33]).
Later, the IFS’s extension, IVIFS, was also developed in terms of its geometrical interpretation, mostly based on the analogy of IFSs by replacing a single point in the Euclidean plane with a rectangle, as in [34], or a single line depicting a degree of IFS membership or non-membership with a pair of lines corresponding to the boundaries of the intervals of IVIFS membership or non-membership degrees. For example, on the basis of the radar chart visualization of IFSs proposed in 2010 [35], the radar chart visualization of IVIFSs was constructed by analogy in 2021 [36].
This paper is structured as follows. All the necessary notions are recalled in Section 2.
While the book [3] systematizes seven different geometrical interpretations of the IVIFSs, two of them—which are more popular and labeled as the second and sixth geometrical interpretations—are specifically discussed here in Section 3, where their unique possible scenarios, which have not been previously detailed, are discussed in depth. While revisiting these results, we noted that in [3] (p. 13, Figure 2.7), the image depicting the sixth graphical interpretation was not accurately rendered, and for this reason, it is here corrected. In addition, it is worth noting that none of the remaining spatial visualizations comprising the IVIFSs’ sixth geometrical interpretation have ever been researched in detail or published.
Section 4 contains a novel geometrical interpretation of IVIFSs, which is rooted in an analogy with the existing IFS interpretation, proposed twenty years ago in [37] and the operation not explored thereafter. The unary operation “Negation” and the two basic modal operators “Necessity” and “Possibility” are presented in the new two-rods interpretation as compared to the planar geometrical interpretation.
Last but not least, reconsidering the existing results on operators defined over IVIFSs, in Section 5, we present the definition of a new operator. For comparison with the presently existing intuitionistic fuzzy topological operators over IVIFSs, which juxtapose to a given point from the interpretational triangle another point, the new operator defines the entire area in which all points corresponding to the given universe belong to. In a sense, this operator is an analogue of the convex hull, not for points but for the IVIFS elements (rectangles, or segments and points, in the degenerate cases). Two properties of the newly defined operator are discussed and proved, and a geometrical interpretation is provided.
Finally, Section 6 concludes the paper with a short summary of the results and ideas for future research.
2. Preliminaries
We will start by reminding the reader of the basic concepts in intuitionistic fuzzy sets (IFSs) and their extension interval-valued intuitionistic fuzzy sets (IVIFSs), as well as the ideas behind the geometrical interpretations of both concepts.
First, let E be a fixed universe. The set
where ; the functions and represent the degrees of membership and of non-membership of an element to A; and for each ,
is called an IFS.
Similarly, interval-valued intuitionistic fuzzy sets are defined in the following way: an IVIFS A over E is an object of the form
where
are intervals and for all ,
The intervals and contain the degrees of membership and of non-membership of the element to the fixed set .
Among the different possible geometric interpretations of intuitionistic fuzzy and interval-valued intuitionistic fuzzy sets, the triangular interpretation is the earliest one that has no analogue in the regular Zadeh’s fuzzy sets and it demonstrates to the fullest extent the specifics and richness of the concepts of IFSs and IVIFSs.
The triangular interpretation is set in the Cartesian coordinate system with the two coordinates representing the membership (abscissa) and the non-membership (ordinate), and the origin representing the complete “Uncertainty”. The two other vertices of the unitary triangle, namely the points and , respectively, represent the complete “Truth” and “Falsity” constants. As IFSs are a true extension of fuzzy sets, the representation of a fuzzy set into the triangular interpretation is a projection onto the hypotenuse. Accordingly, the further an element from the hypotenuse, the higher its degree of uncertainty (as complementary to 1 of the sum of degrees of membership and non-membership).
Here, we will give all versions of the two, while the other interpretations are unambiguous.
3. Planar and Spatial Geometrical Interpretations of IVIFSs: Regular and Degenerate Cases
The second-type geometrical interpretation of IVIFSs (planar, two-dimensional) and the sixth-type interpretation (spatial, three-dimensional) will be considered below. The idea for the planar interpretation of IFSs (and hence, IVIFSs) is rooted in the early work of Atanassov [30] from 1989, and was later elaborated in detail for the IVIFS case by Georgiev and Atanassov in [34]. Respectively, the geometrical interpretation of IFSs in the three-dimensional Euclidean space was first proposed by Tasseva, Szmidt, and Kacprzyk in 2005 [37], and apart from a mention in the book [3], an interpretation for IVIFSs was never elaborated in detail in the following years.
Figure 1 clearly shows IVIFSs as an extension of IFSs. A representative, regular, fully fledged IVIFS element is illustrated below with
Notably, in the case of the spatial interpretation, all the steps of the geometrical construction are outlined with dashed lines.
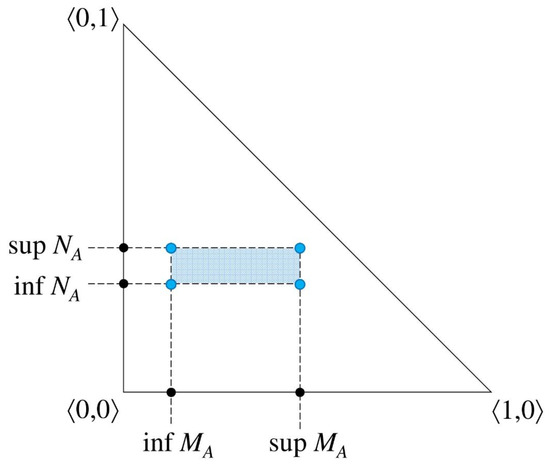
Figure 1.
An arbitrary regular element of an IVIFS with and —planar geometrical interpretation.
The sixth-type (spatial) geometrical interpretation is presented in Figure 2. This figure can be effectively considered a correction of Figure 2.7 from [3] (p. 13) (where the figure was mistakenly visualized as a rectangle instead of a parallelogram).
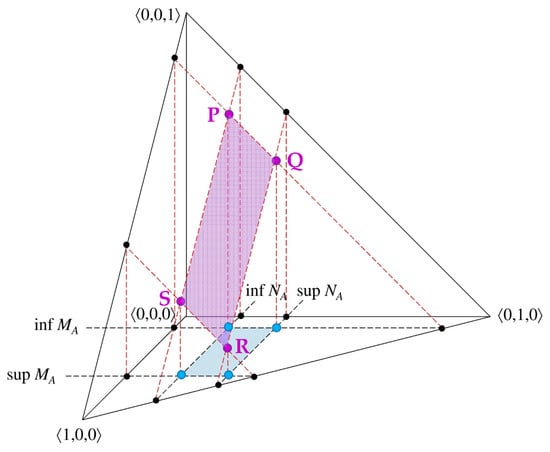
Figure 2.
An arbitrary regular element of an IVIFS with and —spatial geometrical interpretation.
Here, we label by the vertices of the projection of the planar IVIFS element onto the inclined plane formed by the points and . While not detailed in the existing literature, it is worth noting that the coordinates of each of the points are determined as follows:
- point P:
- point Q:
- point R:
- point S:
A very partial degenerate case of an element of an IVIFS with and is also demonstrated below in Figure 3 and Figure 4, and this degenerate case coincides with an authentic element of a (non-interval-valued) IFS.
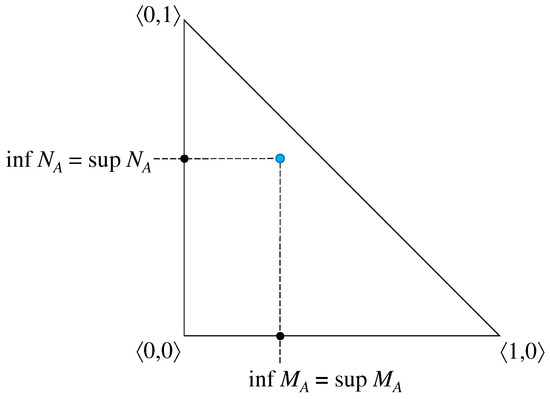
Figure 3.
A degenerate case of an element of an IVIFS with and —planar interpretation.
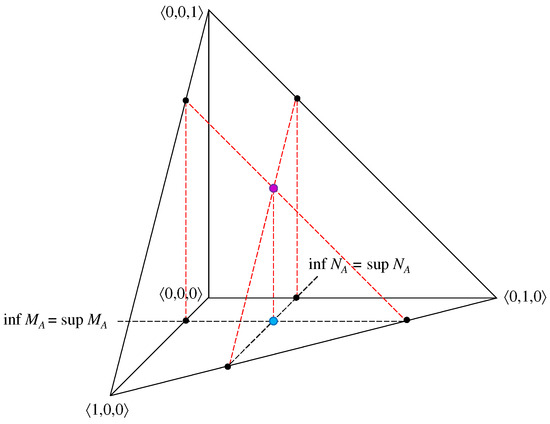
Figure 4.
A degenerate case of an element of an IVIFS with and —spatial interpretation.
Two other degenerate cases are when the rectangle that corresponds to an element of an IVIFS is projected onto a line segment either parallel to the abscissa or to the ordinate.
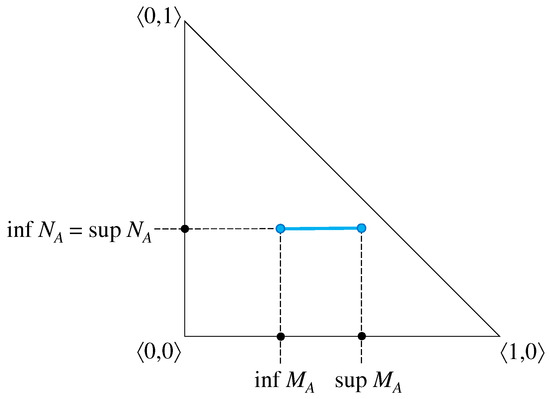
Figure 5.
A degenerate case of an element of an IVIFS with and —planar interpretation.
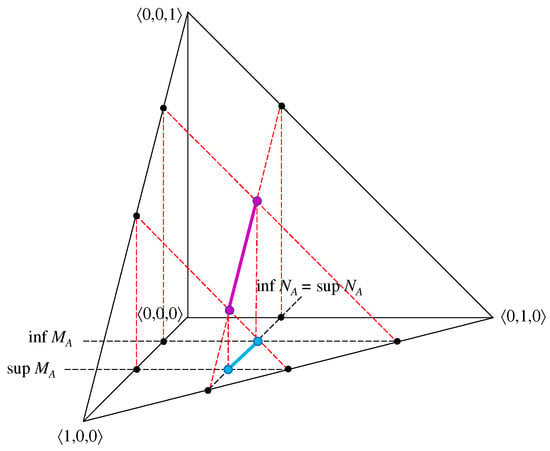
Figure 6.
A degenerate case of an element of an IVIFS with and —spatial interpretation.
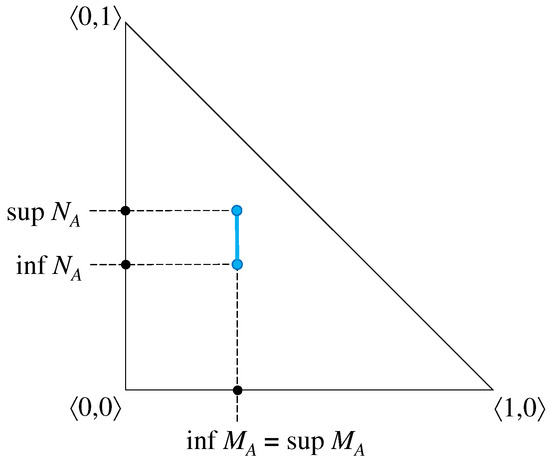
Figure 7.
A degenerate case of an element of an IVIFS with and — planar interpretation.
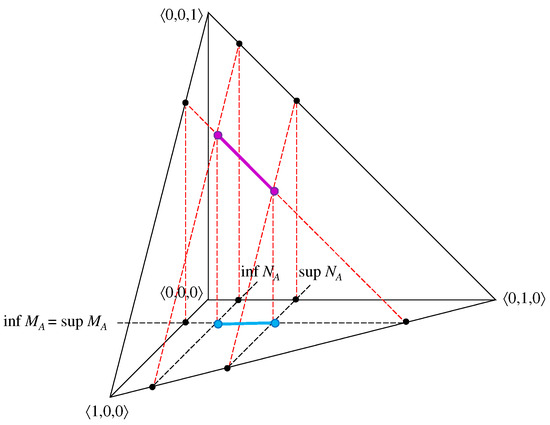
Figure 8.
A degenerate case of an element of an IVIFS with and —spatial interpretation.
4. A New Approach to IVIFS Geometrical Interpretation: Two-Rods Geometrical Interpretation
Here, for the first time, we give the geometrical interpretation of an IVIFS element, shown in Figure 9. The new approach is inspired and motivated by Atanassov’s 2016 paper [38], discussing the case of IFSs, which only now is being re-explored in light of IVIFSs. While the geometrical interpretation from [38] is not specifically termed, we call it here the “two-rods” geometrical interpretation. This new approach to the graphical interpretations of IVIFSs provides a yet unexplored alternative, complementing the existing approaches.
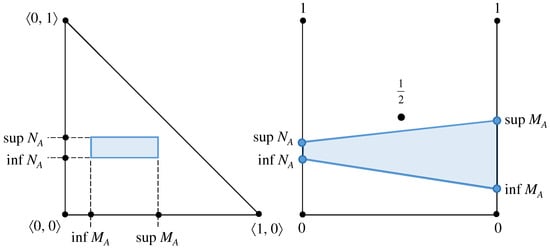
Figure 9.
Comparison between the planar and the two-rods geometrical interpretations of an arbitrary IVIFS element.
The two-rods geometrical interpretation provides a compact and insightful way to represent an IVIFS element using two parallel vertical axes, or “rods”, one for membership degree and the other one for non-membership degree. Similarly to [38], here, the left rod corresponds to the interval-valued intuitionistic fuzzy degree of non-membership, defined as the interval , while the right rod, respectively, corresponds to the IVIFS degree of membership . Notably, the distance between both rods can be arbitrary, while it is important that both rods are of the same unitary length.
The IVIFS element plotted in the following Figure 9 is identical to the one visualized in Figure 1 (planar, second-type interpretation) and in Figure 2 (spatial, sixth-type interpretation).
The point at height , marked as a central black dot, is important as it ensures that each of the plotted segments must be below it or—in a borderline case—the upper of both ends of the segment may pass through it. Each time a segment passes through the central dot, this corresponds to the case which, in the planar geometrical interpretation, corresponds to a point lying on the interpretational triangle’s hypotenuse, or, in other words, to an element of a fuzzy set.
4.1. IVIFS Degenerate Cases in the Two-Rods Graphical Interpretation
As we noted in Section 2, the vertices of the intuitionistic fuzzy interpretational triangle represent the three logical constants in IFSs and IVIFSs: “Uncertainty”, point ; “Falsity”, point ; and “Truth”, point . In the two-rods geometrical interpretation of the IVIFSs, they also hold special places, which not only explicates this new graphical approach, but also justifies its rationale and may suggest a future applicability of the approach. The next Figure 10 shows a comparison between the two-rods and the planar interpretation: exhibiting not only the logical constants but also some other special points that in the context of IVIFS represent some degenerate cases. Specifically, as IVIFS elements, these are
- Point U, logical constant “Uncertanty”: with
- Point F, logical constant “Falsity”: with
- Point T, logical constant “Truth”: with
- Point H – middle of the hypotenuse: with
- Point Z – an arbitrary point on the hypotenuse: with
- Point V – middle of the vertical axis: with
- Point W – the middle of the horizontal axis: with
- Point X – an arbitrary point within the triangle: with
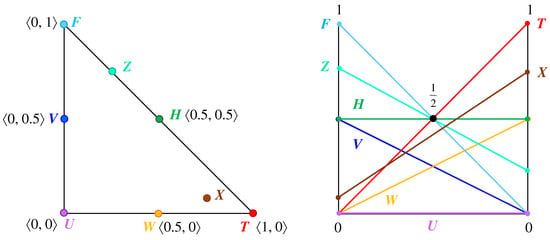
Figure 10.
Comparison between the planar and the two-rods geometrical interpretations: some degenerate cases of IVIFS that are special points on the IFS triangle.
The remaining degenerate cases of IVIFS elements having segmented forms, as illustrated in the planar geometrical interpretation in Figure 5 and Figure 7, are shown in the two-rods interpretation in Figure 11.
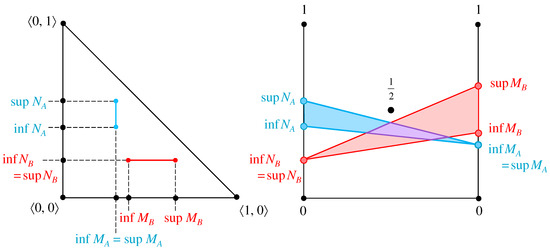
Figure 11.
Comparison between the planar and the two-rods geometrical interpretations: other degenerate cases of IVIFSs.
In general, the IFS elements, being degenerate cases of IVIFSs, are presented in the IFS triangle as points and in the two-rods interpretation as segments (Figure 10), while the degenerate IVIFS cases depicted in the IFS triangle as segments are represented in the newly proposed interpretation as triangles (Figure 11). Finally, the fully fledged IVIFS element which is depicted in the planar geometrical interpretation as a rectangle (respectively, square) is depicted as a trapezium (respectively, parallelogram) in the two-rods interpretation.
4.2. Operation “Negation” and Modal Operators “Necessity” and “Possibility” on IVIFSs in the Two-Rods Graphical Interpretation
All logical operations that are defined over binary (also, crisp), fuzzy, and intuitionistic fuzzy sets are respectively defined over IVIFSs. In the following figures, the unary operation “Negation” and the basic modal operators “Necessity” and “Possibility” over IVIFSs are demonstrated in the newly proposed geometrical interpretation, as compared to the planar (second-type) geometrical interpretation. We confine our discussion here only to these three most basic concepts, since the binary operations “Intersection” and “Union” exist for IVIFSs in multiple possibilities depending on the order in which the boundaries of the intervals of membership and non-membership for both IVIFS operands. This is a matter of an extensive future research and comparison.
Now, the operation “Negation” is formally defined over an IVIFS A as
(see [1,3] (p. 28)). Due to the simple form of this operation, it was not even graphically depicted in [3], but it will shown be here along with its new two-rods geometrical interpretation (see Figure 12).
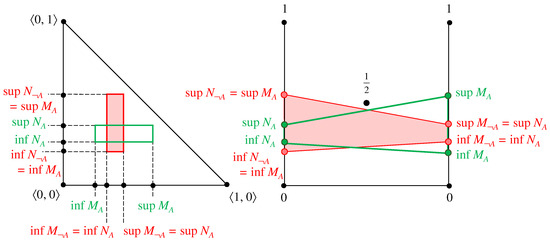
Figure 12.
Negation (red) of an arbitrary IVIFS element (green) in the planar and in the two-rods geometrical interpretation.
The modal operators “Necessity” and “Possibility” are defined in [1,3] (p. 53) and illustrated respectively in [3] (p. 54, Figures 4.1 and 4.2). The comparison between the planar and the two-rods geometrical interpretation is provided in the next Figure 13 and Figure 14 for both of these modal operators:
- “Necessity”: ;
- “Possibility”: .
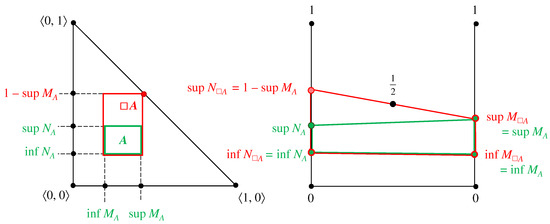
Figure 13.
Modal operator “Necessity” (red) applied to an arbitrary IVIFS element (green) in the planar and in the two-rods geometrical interpretation.
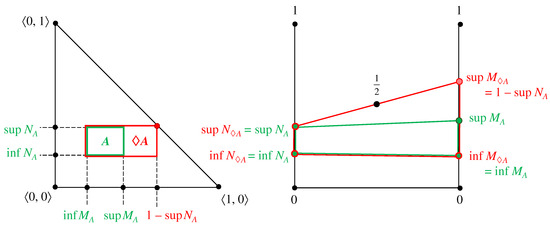
Figure 14.
Modal operator “Possibility” (red) applied to an arbitrary IVIFS element (green) in the planar and in the two-rods geometrical interpretation.
5. A New Operator Defined over IVIFSs and Its Geometrical Interpretation
In [3], two topological operators are defined over an IVIFS. Here, for the first time, we introduce the following operator that provides us with the ability to estimate the “spread” of the IVIFS elements within the intuitionistic fuzzy interpretational triangle. For this operator, the planar (second-type) geometrical interpretation is considered to be the most appropriate one. The result of the application of the new operator over the IVIFS A is as follows:
For the sake of brevity, let us denote by and the intervals to which the elements of the set belong with the respective degrees of intuitionistic fuzzy membership and non-membership:
Then, we can formulate the following theorem.
Theorem 1.
The definition of operator is correct with respect to the IVIFS definition.
Proof.
We must prove that
For (2), the validity is checked in the same way. For (3), we see immediately that the first inequality is obviously fulfilled, while the validity of the second one follows from
which proves the theorem. □
The planar geometrical interpretation of the operator is shown in Figure 15.
Theorem 2.
The operator is auto-dual, i.e., for each IVIFS
Proof.
Let A be an IVIFS. Then,
Therefore, the operator is auto-dual. □
All intuitionistic fuzzy topological operators, defined in [2], associate an element of the universe (depicted as a point in the interpretational triangle) with another element of the universe (i.e., another point). The new operator is interesting due to the fact that it determines the entire area to which all elements of the given IVIFS belong. In a sense, it plays the role of a convex hull, yet not for points but for whole IVIFS elements (that is, in the planar geometrical interpretation, rectangles, or—in the degenerate cases—segments and points).
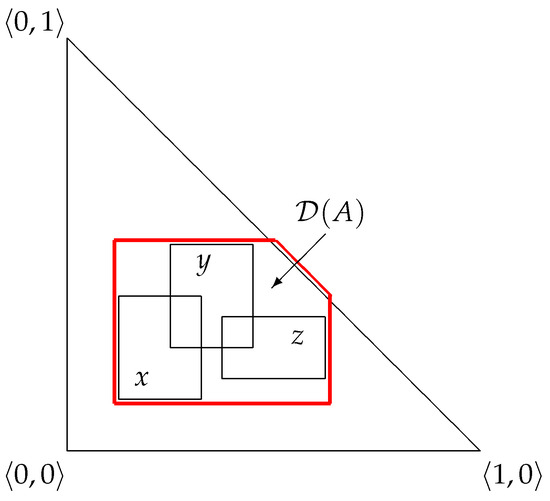
Figure 15.
Planar (second-type) geometrical interpretation of the IVIFS elements of the universe and the result of application of the operator (marked in red).
Obviously, if the points and happen to belong to the areas of some elements of the IVIFS, then the geometrical interpretation will coincide with the whole triangle. The same result will occur if the point happens to belong to the area of some element of the IVIFS.
For the reasons presented in the previous section regarding the interpretation of binary operations, this new topological operator is currently illustrated only by its planar (second-type) geometrical interpretation. Depending on the mutual position of the IVIFS elements over which the operator is applied, a range of subcases that require a separate detailed investigation regarding its interpretation in the new two-rods visualization would occur.
6. Conclusions
In the present paper, revisiting some existing results from the literature on interval-valued intuitionistic fuzzy sets, we systematized all possible planar (second-type) and spatial (sixth-type) geometrical interpretations of an IVIFS element in its regular and various degenerate cases. As such a thorough exposition so far has been missing, an important correction was made to the spatial geometrical interpretation of a regular IVIFS element, which in the book [3], was inaccurately rendered. Further, a new topological operator was proposed over IVIFSs, where two of its properties were studied and a planar geometrical interpretation for the result of its application was provided.
In addition, a new geometrical interpretation of IVIFSs was developed, as inspired from a decade-old idea [38] regarding the simpler case of IFSs, which was respectively compared to the existing planar geometrical interpretation. The new, two-rods geometrical interpretation has been explored for the cases of the modal operators “Necessity” and “Possibility”, as well as the unary operation “Negation”, while other basic binary operations like “Intersection” and “Union” are left to be studied in a future leg of the present research due to the numerous scenarios in which they appear with respect to the mutual position of the IVIFS elements.
Alongside filling in a void in the knowledge on the geometrical interpretations of interval-valued intuitionistic fuzzy sets, the new interpretation has the potential to provoke some new ideas and applications in future. Another direction of future research is the discussion and comparison of advantages and limitations of the present and other existing IVIFS visualization approaches. The authors’ hope with the present work is that it will not only improve the understanding of IVIFSs as an extension of IFSs and a standalone object of exploration, but will stimulate the interest in applying IVIFSs to various problems, contexts, and practical solutions due to the benefits of the improved visualization of this complex concept.
Author Contributions
Conceptualization, K.A., P.V. and V.A.; methodology, K.A. and P.V.; validation, P.V. and V.A.; formal analysis, P.V.; writing—original draft preparation, K.A.; writing—review and editing, V.A., P.V. and K.A.; visualization, V.A.; supervision, K.A.; project administration, P.V.; funding acquisition, K.A. and P.V. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Bulgarian Science Fund under grant number KP-06-N72/8.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author(s).
Acknowledgments
The authors are grateful to the anonymous reviewers for their insightful remarks that led to significant improvement of the paper.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Atanassov, K.; Gargov, G. Interval-valued intuitionistic fuzzy sets. Fuzzy Sets Syst. 1989, 31, 343–349. [Google Scholar] [CrossRef]
- Atanassov, K. On Intuitionistic Fuzzy Sets Theory; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Atanassov, K. Interval-Valued Intuitionistic Fuzzy Sets; Springer: Cham, Switzerland, 2020. [Google Scholar]
- Vassilev, P.; Atanassov, K. Extensions and Modifications of Intuitionistic Fuzzy Sets; “Prof. Marin Drinov” Academic Publishing House: Sofia, Bulgaria, 2019. [Google Scholar]
- Alkouri, A.U.M.; Salleh, A.R. Complex Intuitionistic Fuzzy Sets. In AIP Conference Proceedings; American Institutes of Physics: Kula Lampur, Malaysia, 2012; pp. 464–470. [Google Scholar]
- Alkouri, A.U.M.; Salleh, A.R. Some Operations on Complex Atanassov’s Intuitionistic Fuzzy Sets. AIP Conf. Proc. 2013, 1571, 987–993. [Google Scholar]
- Gau, W.-L.; Buehrer, D.J. Vague sets. IEEE Trans. Syst. Man, Cybern. 1993, 23, 610–614. [Google Scholar] [CrossRef]
- Bustince, H.; Burillo, P. Vague sets are intuitionistic fuzzy sets. Fuzzy Sets Syst. 1996, 79, 403–405. [Google Scholar] [CrossRef]
- Mondal, T.K.; Samanta, S. Generalized intuitionistic fuzzy sets. J. Fuzzy Math. 2002, 10, 839–862. [Google Scholar]
- Despi, I.; Opris, D.; Yalcin, E. Generalised Atanassov Intuitionistic Fuzzy Sets. In Proceedings of the Fifth International Conference on Information, Process, and Knowledge Management (eKNOW’2013), Nice, France, 24 February–1 March 2013; pp. 51–56. [Google Scholar]
- Lee, K.M. Bipolar-valued fuzzy sets and their operations. In Proceedings of the International Conference on Intelligent Technologies, Bangkok, Thailand, 12–14 December 2000; pp. 307–312. [Google Scholar]
- Torra, V. Hesitant fuzzy sets. Int. J. Intell. Syst. 2010, 25, 529–539. [Google Scholar] [CrossRef]
- Torra, V.; Narukawa, Y. On hesitant fuzzy sets and decision. In Proceedings of the 2009 IEEE International Conference on Fuzzy Systems, Jeju, Republic of Korea, 20–24 August 2009; pp. 1378–1382. [Google Scholar]
- Molodtsov, D. Soft set theory—first results. Comput. Math. Appl. 1999, 37, 19–31. [Google Scholar] [CrossRef]
- Zhao, R.; Wang, X.; Lu, Y.; Hao, Y. Water Environmental Evaluation Based on Variable Fuzzy Set Theory. J. Comput. Inf. Syst. 2011, 7, 377–384. [Google Scholar]
- Gerstenkorn, T.; Manko, J. Bifuzzy probabilistic sets. Fuzzy Sets Syst. 1995, 71, 207–214. [Google Scholar] [CrossRef]
- Hinde, C.; Patching, R. Inconsistent intuitionistic fuzzy sets. Dev. Fuzzy Sets Intuitionistic Fuzzy Sets Gen. Nets Relat. Top. 2008, 1, 133–153. [Google Scholar]
- Hinde, C.; Patching, R.; McCoy, S. Inconsistent intuitionistic fuzzy sets and mass assignment. Dev. Fuzzy Sets Intuitionistic Fuzzy Sets Gen. Nets Relat. Top. 2008, 1, 155–174. [Google Scholar]
- Cuong, B.C.; Kreinovich, V. Picture fuzzy sets-a new concept for computational intelligence problems. In Proceedings of the Third World Congress on Information and Communication Technologies WICT’2013, Hanoi, Vietnam, 15–18 December 2013; pp. 1–6. [Google Scholar]
- Smarandache, F. Neutrosophy. Neutrosophic Probability, Set, and Logic; American Research Press: Rehoboth, DE, USA, 1998. [Google Scholar]
- Selvaraj, J.; Majumdar, A. A New Ranking Method for Interval-Valued Intuitionistic Fuzzy Numbers and Its Application in Multi-Criteria Decision-Making. Mathematics 2021, 9, 2647. [Google Scholar] [CrossRef]
- Onar, S.C.; Kahraman, C.; Öztaysi, B. IoT Platform Selection Using Interval Valued Intuitionistic Fuzzy TOPSIS. In Proceedings of the 4th International Conference on Intelligent and Fuzzy Systems (INFUS), 24–26 August 2022; Lecture Notes in Networks and Systems; Springer: Cham, Switzerland, 2022; Volume 505, pp. 693–701. [Google Scholar]
- Saeed, M.; Sami Ul Haq, R.; Ahmed, S.; Siddiqui, F.; Mateen, N.; Ahmed, K.A.; Yi, J.B.; Pamučar, D. Sustainable selection of microwave absorbing materials: A green evaluation under interval-valued intuitionistic fuzzy environment. Clean. Mater. 2024, 11, 100236. [Google Scholar] [CrossRef]
- Traneva, V.; Tranev, S.; Mavrov, D. Interval-valued intuitionistic fuzzy decision-making method using index matrices and application in outsourcing. In Proceedings of the 16th Conference on Computer Science and Intelligence Systems (FedCSIS), Online, 2–5 September 2021; pp. 251–254. [Google Scholar]
- Alghazzawi, D.; Alolaiyan, H.; Ashfaq, H.; Shuaib, U.; Abd El-Wahed Khalifa, H.; Gomaa, H.B.; Xin, Q. Selecting an optimal approach to reduce energy crises under interval-valued intuitionistic fuzzy environment. Sci. Rep. 2024, 14, 8713. [Google Scholar] [CrossRef]
- Tiwari, A.; Danish Lohani, Q.M. Interval-valued intuitionistic fuzzy rough set system over a novel conflict distance measure with application to decision-making. MethodsX 2023, 10, 102012. [Google Scholar] [CrossRef]
- Guan, H.; Khan, W.A.; Saleem, S.; Arif, W.; Shafi, J.; Khan, A. Some Connectivity Parameters of Interval-Valued Intuitionistic Fuzzy Graphs with Applications. Axioms 2023, 12, 1120. [Google Scholar] [CrossRef]
- Mondal, U.; Pal, M.; Das, K. Interval-valued intuitionistic fuzzy soft graphs with application. TWMS J. Appl. Eng. Math. 2024, 14, 1–18. [Google Scholar]
- Palanivel, K.; Muralikrishna, P.; Hemavathi, P.; Chinram, R.; Singavananda, P. Interval valued intuitionistic fuzzy β-filters on β-algebras. Int. J. Anal. Appl. 2022, 20, 50. [Google Scholar] [CrossRef]
- Atanassov, K. Geometrical interpretation of the elements of the intuitionistic fuzzy objects. Math. Found. Artif. Intell. Semin. 1989. reprinted in Int. J. Bioautomation 2016, 20, S27–S42. [Google Scholar]
- Yager, R.R. Generalized Orthopair Fuzzy Sets. IEEE Trans. Fuzzy Syst. 2017, 25, 1222–1230. [Google Scholar]
- Tang, G.; Gu, X.; Chiclana, F.; Liu, P.; Yin, K. A multi-objective q-rung orthopair fuzzy programming approach to heterogeneous group decision making. Inf. Sci. 2023, 645, 119343. [Google Scholar]
- Atanassov, K.; Vassilev, P. On the intuitionistic fuzzy sets of n-th type. Stud. Comput. Intell. 2018, 738, 265–274. [Google Scholar]
- Georgiev, P.R.; Atanassov, K.T. Geometrical interpretations of the interval valued intuitionistic fuzzy sets. Notes Intuit. Fuzzy Sets 1996, 2, 1–10. [Google Scholar]
- Atanassova, V. Representation of fuzzy and intuitionistic fuzzy data by radar charts. Notes Intuit. Fuzzy Sets 2010, 16, 21–26. [Google Scholar]
- Atanassova, V.; Angelova, N. Representation of interval-valued intuitionistic fuzzy data by radar charts. In Uncertainty and Imprecision in Decision Making and Decision Support: New Challenges, Solutions and Perspectives; Atanassov, K., Atanassova, V., Kacprzyk, J., Kaluszko, A., Krawczak, M., Owsinski, J.W., Sotirov, S., Sotirova, E., Szmidt, E., Zadrozny, S., Eds.; IWIFSGN 2018; Advances in Intelligent Systems and Computing; Springer: Berlin/Heidelberg, Germany, 2021; Volume 1081, pp. 69–75. [Google Scholar]
- Tasseva, V.; Szmidt, E.; Kacprzyk, J. On one of the geometrical interpretations of the intuitionistic fuzzy sets. Notes Intuit. Fuzzy Sets 2005, 11, 21–27. [Google Scholar]
- Atanassov, K. A new geometrical interpretation of the intuitionistic fuzzy pairs. Notes Intuit. Fuzzy Sets 2016, 22, 12–18. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).