Abstract
The automotive industry is a key pillar of many national economies, and automotive body manufacturing is among the most complex production processes. In the automotive body manufacturing process, quality control and safety assurance are of paramount importance, directly influencing the overall safety performance, structural reliability, and comfort of vehicles. Therefore, it is crucial to analyze the primary factors that influence quality and safety during the car body manufacturing process. The study first focuses on four key processes of car body manufacturing—stamping, welding, painting, and assembly—using the man, machine, material, method, environment (4M1E) framework to analyze the factors affecting quality and safety. Subsequently, a quality and safety early-warning indicator system is established for the automotive body manufacturing process, followed by a comprehensive analysis of the constructed system. To address the issue of subjectivity in traditional technique for order of preference by similarity to an ideal solution (TOPSIS) evaluation methods, this paper employs the coefficient of variation method for objective analysis of criterion-level indicators, the trapezoidal fuzzy number method for subjective analysis of criterion-level indicators, and establishes a model for optimizing target weight that balances subjective and objective approaches. Furthermore, a relative entropy-based method is applied to comprehensively evaluate criterion-level indicators. This approach reduces the information loss associated with separate weighting schemes and overcomes a known limitation of traditional TOPSIS—its inability to distinguish alternatives that lie equidistant from ideal solutions. Finally, an evaluation model for quality and safety influencing factors in body manufacturing is developed and validated through a case study, demonstrating its feasibility. The results show that the proposed model can effectively identify the key quality and safety influencing factors in the automobile body manufacturing process, guarantee quality control and safety assurance in the body manufacturing process, and thus ensure that the automobile production process meets the quality and safety requirements.
Keywords:
automotive body quality; relative entropy method; influencing factors analysis; evaluation model MSC:
93A08
1. Introduction
As globalization accelerates and living standards rise, consumer demand for high-quality products has become ever more pronounced. In modern production processes, the quality of automotive products stands as a critical factor influencing the development and survival of enterprises. A company’s quality strategy directly determines its competitive strength and future returns [1]. Automotive manufacturing enterprises must take quality management as their foundation and core during operations, clarify their specific requirements at different stages of development, actively strengthen the optimal allocation and utilization of various management and construction resources, and aim to improve product quality and service quality. By proactively enhancing product quality and performance, they can achieve coordinated development between product quality and corporate growth. Currently, as competition in the automotive industry intensifies, vehicle production is no longer limited to incumbent automakers—many new entrants are joining the automotive manufacturing sector. Against the backdrop of declining market profits, vehicle recalls impose growing losses on enterprises. As the on-site production and manufacturing segment serves as a critical link responsible for automotive quality, strict and scientific control over quality must be enforced throughout the manufacturing process.
High product quality is the cornerstone of an automotive enterprise’s competitive success and ongoing development. Superior product quality arises from a fusion of unique corporate culture and rigorous quality management standards, thereby ensuring the enterprise’s overall competitiveness. Given the rapid changes in both internal and external aspects of automotive enterprise development, as the vehicle body constitutes one of the most critical links in the automotive production process, it is essential to identify the key influencing factors affecting automotive body product quality and propose targeted improvement strategies. By doing so, enterprises can enhance product competitiveness and elevate their quality management standards, thus continuously strengthening their position in the automotive industry.
In the formative years of quality management research (mid-20th century), scholars distilled key theories and methods from their management philosophies and practical experiences to improve product quality and organizational performance. For example, Dr. Joseph Juran’s “Quality Management Trilogy” and Dr. W. Edwards Deming’s “14 Points for Quality Management” laid the theoretical and practical foundations for modern quality management practices [2,3]. Recent studies on automotive body quality have focused on several key areas, including:
Li Zhuoshuai et al. conducted research on automotive body corrosion issues, implementing controls over stamping, welding, and painting processes to enhance the overall durability quality of vehicles [4]. Zhang Lijun et al. analyzed the material selection process for white bodies, using life cycle analysis (LCA) to comprehensively evaluate the energy consumption and carbon emissions of different materials in vehicles [5]. Zhou Wei et al. used an improved genetic algorithm to optimize the thickness of body panels, established an acoustic–solid coupling model for the white body, performed free modal analysis, and developed noise transfer functions to achieve thickness optimization of body panels [6]. Tang Qingming et al. employed the least squares method to build an intelligent analysis model for stamping processes in automotive manufacturing, using data mining technology to establish a mapping relationship between processes and quality. They ultimately identified 9 key factors to achieve quality prediction [7]. Yan Xin et al. extracted data such as online reviews of new energy vehicles, identified consumer experience and product defect data, established an evaluation model, analyzed the impact of reviews on product strategies, and further optimized product positioning, quality, and market strategies [8]. Wang Fei et al. used the analytic hierarchy process (AHP) for comprehensive performance evaluation of automotive body-integrated die-casting machines, constructing an evaluation index system for their usability. Through weight calculation, the study identified performance hierarchies in production and concluded that key component stiffness, repeated positioning accuracy, energy consumption, and critical part wear resistance significantly impact applicability [9].
Ali Hashemian et al. examined how flexible part tolerances affect the appearance quality of automotive bodies, with a focus on roof surface finish. Their assessment showed that manufacturing input tolerances have a significant impact on the surface quality of the final assembled vehicle [10]. Sun et al. developed a Bayesian state estimator for vehicle mass, modeling the mass as a constant state variable and motor torque as an observed output. By incorporating multiple parameters and a nonlinear particle filter, they achieved an intelligent real-time evaluation of electric vehicle mass [11]. Eva Harianja et al. integrated a multilayer perceptron neural network with multi-attribute decision-making techniques to mitigate the inconsistency issues of the analytic hierarchy process (AHP), thereby improving the consistency of pairwise comparison matrices in multi-criteria evaluations [12]. Geng Chen et al. proposed a parallel strategy, using machine learning to predict the quality of resistance welding electrodes for automotive body welding on data subsets with different distribution patterns. This approach enables accurate and effective estimation of resistance spot welding conditions in vehicle bodies, providing an online detection method for automotive body resistance spot welding quality [13]. Abdul Karim et al. analyzed the quality issues in the automotive body welding process and proposed using the minimum amount of heat input and appropriate filler metal alloying elements to improve welding quality, based on factors such as welding gun joints, production cost, and time [14]. Anbesh Jamwal et al. reviewed multi-criteria decision-making (MCDM) applications in sustainable manufacturing based on a comprehensive Scopus survey, noting most studies use fuzzy-based single models and emphasizing MCDM’s value in addressing social, economic, and environmental dimensions for manufacturing decisions [15].
In summary, numerous studies on automotive quality and safety have been conducted worldwide, but most focus on isolated stages of the production process rather than providing a comprehensive evaluation across the entire body manufacturing sequence. Additionally, existing literature on automotive body quality predominantly analyzes individual components, lacking integrated assessment methods to examine the full manufacturing chain. As a result, it fails to identify critical quality and safety influencing factors in the body manufacturing process.
Therefore, this paper focuses on the identification of key influencing factors for quality and safety in the automotive body manufacturing process. Guided by the five dimensions of the man, machine, material, method, and environment methodology (4M1E), the study systematically examines the stamping, welding, painting, and assembly stages. This analysis results in a scientific, structured framework of quality-influencing factors for the body manufacturing process. To ensure an objective and comprehensive determination of criterion-layer weights and to reduce the information loss associated with using solely subjective or objective weighting schemes, this study combines multiple methods. Specifically, the coefficient of variation method is adopted to derive objective weights, the trapezoidal fuzzy number method is employed to assess subjective weights, and a weight-balancing model is constructed to equitably integrate subjective and objective contributions. An improved technique for order of preference by similarity to an ideal solution (TOPSIS) method based on distances to ideal and anti-ideal solutions is adopted for the comprehensive evaluation of criterion-layer indicators, while the analytic hierarchy process is utilized to evaluate the indicator layer of the quality and safety system.
By integrating these methods, this research establishes a comprehensive indicator system for quality and safety factors in body manufacturing and formulates a quality and develops a quality and safety identification model. This comprehensive analysis method lays a solid foundation for improving bodywork quality and ensuring manufacturing safety.
2. Relevant Research
Research into quality and safety index systems for automobile body manufacturing involves complex, multi-factor interactions among numerous criteria. Common methods for establishing the index system include the analytic network process (ANP), principal component analysis (PCA), analytic hierarchy process (AHP), entropy weight method, fuzzy methods, and technique for order of preference by similarity to an ideal solution (TOPSIS) [16]. Since applying any single method has limitations, scholars have conducted extensive research by integrating these approaches. For example, Reference [17] uses a combination of subjective and objective weights to determine index weights, coupled with an improved TOPSIS model for groundwater quality evaluation. Reference [18] employs balanced weights and an enhanced TOPSIS method to assess the priority of aero-engine assembly tasks. Generally, the problem-solving framework across these studies follows a three-step process: determining evaluation indicators → solving index weights → conducting comprehensive evaluation based on weights and indicator values.
2.1. Methods for Determining Index Weights
In the context of multi-attribute decision-making, methods for determining index weights can be broadly categorized into three types: objective weighting methods, subjective weighting methods, and combined weighting methods.
- (1)
- Objective Weight Analysis Method
Commonly used objective analysis methods include the entropy weight method (EWM) [17] and the coefficient of variation method (CVM) [19]. The EWM focuses on analyzing indicator weights from the perspective of information theory: the greater the information content of an indicator, the larger its weight. However, this method requires that the data used are not overly concentrated. The CVM, by contrast, directly measures indicator importance based on the discrete degree of data, demonstrating lower sensitivity to data distribution patterns.
- (2)
- Subjective Weight Analysis Methods
The Analytic Hierarchy Process (AHP) is a systematic approach that resolves complex problems by constructing a hierarchical structure model, transforming intricate evaluation tasks into clear, understandable sub-problems [20]. Despite its strong systematicity, traditional AHP relies heavily on experts’ subjective judgments and experience, making it difficult to completely avoid subjective biases and thus having certain limitations.
Rough sets (RS) theory, proposed by Pawlak in 1982, excels in handling uncertain information without requiring prior data knowledge, and has been applied in fields such as machine learning, data mining, and fault diagnosis. However, RS theory involves substantial computational complexity and moderate feasibility. Reference [21] introduces the concepts of rough numbers and rough boundary intervals and proposes a rough AHP method for customer demand analysis, addressing some of the shortcomings of traditional AHP and RS theory.
- (3)
- Combined Weight Analysis Methods
Objective weight analysis, as a quantitative approach, relies on data information embedded in evaluation objects and specific mathematical models to calculate weight coefficients accurately. Theoretically, as the number of evaluation objects approaches infinity, objective weights tend to stabilize toward values following specific laws. In practical applications, however, evaluation sets are finite, so only approximate weight values can typically be obtained. Subjective weight analysis belongs to the category of qualitative analysis, where decision-makers determine weights through scoring based on personal experience, knowledge, and subjective judgments.
Consequently, these methods are highly influenced by decision-makers’ cognitive biases and preferences, leading to subjective and uncertain results. Given the limitations of single objective and subjective methods, scholars have proposed innovative combined weight approaches, including the experience factor method, weight multiplication method, and optimal mathematical model method [22,23,24].
2.2. Comprehensive Evaluation Methods
In multi-attribute decision-making, TOPSIS is a ranking method that approximates the ideal solution, characterized by simple computation, reasonable evaluation, and flexible application [18]. However, in specific scenarios, when a solution lies on the perpendicular bisector of the line segment connecting the positive ideal solution and the negative ideal solution, the indicator values involved in TOPSIS cannot effectively determine its superiority or inferiority, making it impossible to clearly distinguish the relative relationship between this solution and the positive and negative ideal solutions. Hernández-Torres et al. proposed an AHP-TOPSIS framework based on rating rubrics for industrial energy decision-making, featuring a robust methodological structure and systematic expert input processing [25]. Building upon these insights, this study employs a refined TOPSIS-AHP hybrid methodology to analyze quality and safety impact indicators in automotive body manufacturing processes. By integrating expert evaluations with quantitative modeling, this approach enhances the objectivity of indicator prioritization.
Reference [10] applied this improved TOPSIS to groundwater quality evaluation, demonstrating the feasibility of the method. Reference [16] proposed an improved TOPSIS method based on Kullback–Leibler divergence (KLD) and conducted case validation.
Based on the above research, we propose an integrated approach to an early-warning model for body manufacturing quality and safety, combining balanced weighting and an improved TOPSIS method. This approach involves four main steps:
- Construction of Index System: Drawing on the 4M1E framework (man, machine, material, method, and environment), the stamping, welding, painting, and final assembly stages in automotive body manufacturing are analyzed to identify quality and safety influencing factors. These factors are then structured into an early-warning indicator system.
- Balancing of Subjective and Objective Weights: The trapezoidal fuzzy scaling method and the coefficient of variation method are employed to perform subjective and objective weighting of the four criterion-level indicators (stamping, welding, painting, final assembly). A balancing model is then applied to integrate these weights, ensuring equal contribution from both perspectives in the final index system.
- Analysis of Process Influence Intensity: Based on the balanced quality-safety index weights, apply the TOPSIS method incorporating KLD to comprehensively evaluate the influence intensity of stamping, welding, painting, and final assembly processes on body manufacturing quality and safety.
- Identification of Key Factors: According to the influence intensity of each process, use the AHP method to analyze the indicator-level indices of each process, clarify the strength of influence on body manufacturing quality, identify key quality factors in the manufacturing process, and effectively enhance the overall manufacturing level.
Through this structured process, the key quality and safety influencing factors in automotive body manufacturing can be effectively identified and prioritized. This supports proactive quality control, enhances manufacturing precision, and ensures high-level reliability in body production.
3. Development of Influencing Factors Indicators for Quality and Safety in Automotive Body Manufacturing
The automotive body manufacturing process consists of four core stages: stamping (forming sheet metal into structural components), welding (joining parts into sub-assemblies or full body frames), painting (applying protective and decorative coatings), and final assembly (integrating elements such as doors, hoods, and interior systems). These stages collectively determine the vehicle’s structural integrity, durability, and surface quality, thereby exerting a direct impact on safety, reliability, and functional performance. This section employs the 4M1E method to analyze the automotive body manufacturing process, identify quality and safety factors affecting the process, and establish a quality and safety indicator system for the automotive body manufacturing process.
3.1. Quality and Safety Analysis Using the 4M1E Method
Total quality management (TQM) is a management system centered on product quality, where all employees participate to achieve effective quality control and improvement. TQM identifies five primary influences on quality often summarized as “man, machine, material, method, and environment” [26]. Therefore, from a macro perspective on body manufacturing quality, we incorporate these five 4M1E factors to analyze the four critical production stages (stamping, welding, painting, and final assembly). The specific analyses for each stage are as follows.
- (1)
- Quality and Safety Risk Analysis for the Automotive Body Stamping Stage
Automotive body stamping is the process of using specialized equipment and dies to plastically deform sheet steel into parts of specific shapes and dimensions. As the first stage of body manufacturing, stamping demands particular attention to die precision because it directly affects the quality characteristics of the final product at the very outset of production [27]. In the stamping stage, “human factors” refer to the skill level of personnel in design-stage operations and the adequacy of their training; “machine factors” encompass the stability of stamping equipment and die precision; “material factors” pertain to the steel’s thickness and surface cleanliness during forming; “method factors” involve the specific stamping techniques and operators’ procedures; and “environmental factors” cover the workers’ environment and the shock-absorption conditions present during stamping.
- (2)
- Quality and Safety Risk Analysis for the Automotive Body Welding Stage
Automotive body welding is the process of assembling stamped parts and joining them to form the vehicle’s body structure [28]. Analyzing this stage with the 4M1E framework reveals several risk factors: human factors include the welders’ proficiency; machine factors cover the welding torches’ pressure settings and positioning precision, which directly affect the consistency of weld joints; material factors focus on sheet metal thickness, since having an appropriate thickness is critical to weld integrity; method factors involve the choice of welding techniques and the rigor of quality inspection methods; and environmental factors consider workshop conditions such as humidity, as excessive moisture can impair weld quality and equipment performance.
- (3)
- Quality and Safety Risk Analysis for the Automotive Body Painting Stage
Automotive body painting applies protective coatings to prevent corrosion and wear while also enhancing the vehicle’s appearance [29]. Using the 4M1E framework to analyze this stage highlights several risk factors: human factors cover workers’ painting proficiency and workload (since prolonged, high-intensity tasks can lead to errors); machine factors include the stability of painting equipment and the precision of ovens or drying systems—both are crucial for uniform coatings and proper curing; material factors pertain to the properties of paints and electrophoretic solutions, as their chemical and physical characteristics dictate corrosion resistance and surface finish; method factors involve the specific painting processes and techniques, which must strictly follow standard procedures to avoid defects such as sagging or orange peel; and environmental factors include maintaining proper temperature and humidity and a dust-free paint booth, because contaminants or improper conditions can greatly diminish coating quality and durability.
- (4)
- Quality and Safety Risk Analysis for the Automotive Body Final Assembly Stage
After painting, the process moves to the final assembly, where all components are integrated to complete the vehicle body [30]. Analyzing final assembly with the 4M1E approach reveals these risk factors: human factors include assemblers’ technical skills and workload (poor skills or fatigue can cause installation errors or omissions); machine factors involve the reliability and precision of handling equipment and assembly tools, which affect how tightly and consistently parts are fitted; material factors concern the quality of incoming parts, since components that meet specifications in dimensions and properties are essential for structural integrity; method factors relate to adherence to standardized assembly procedures and processes, as strict compliance with technical specifications is required to prevent functional defects; and environmental factors cover the cleanliness and ergonomics of the assembly area as well as protection during component transport—dust, mishandling, or excessive vibration can damage parts and reduce final product quality.
To synthesize the above analysis, we constructed a fishbone diagram (Figure 1) that systematically illustrates how the five factors (“man, machine, material, method, environment”) relate to the four key processes (stamping, welding, painting, final assembly) in automotive body manufacturing, highlighting their interrelationships in contributing to quality and safety risks.
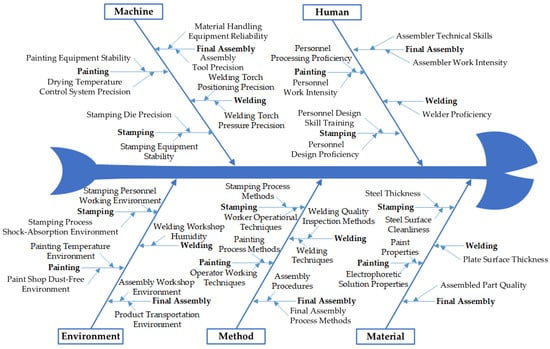
Figure 1.
Fishbone diagram of quality and safety risk influencing factors in automotive body manufacturing.
3.2. Development of Quality and Safety Indicator System for Automotive Body Manufacturing
Using the five factors of “man, machine, material, method, environment” to analyze the four processes of stamping, welding, painting, and final assembly in automotive body manufacturing, a total of 36 influencing factors affecting quality and safety in automotive body manufacturing were ultimately identified, as shown in Table 1.

Table 1.
Influencing factors for quality and safety in automotive body manufacturing.
4. Comprehensive Evaluation Process
4.1. Comprehensive Weight Evaluation Process
Since using a single subjective or objective evaluation method may lead to the loss of either subjective or objective information during the assessment, this paper employs a comprehensive evaluation approach. The article uses a combination of subjective and objective methods to weight the importance of influencing factors on the quality and safety of automobile body manufacturing. In the subjective weighting process, the trapezoidal fuzzy number method is used for evaluation to determine the subjective weight part in the balance model. In the objective weighting process, the coefficient of variation method is applied to determine the objective weight part in the balance model. The weight model, with the goal of balancing the contributions of subjective and objective weights, is used to balance the subjective and objective weights obtained from the trapezoidal fuzzy number method and the coefficient of variation method, thereby determining the evaluation index weights. Subsequently, by harmonizing weights through the subjective–objective weight balance model, the improved TOPSIS grounded in divergence theory conducts a quantitative assessment of the significance of four key processes—stamping, painting, welding, and final assembly—to determine their influence weights. Finally, the AHP method is applied to the indicators at the index layer of the four processes (stamping, painting, welding, and final assembly) to identify the key influencing factors affecting the quality and safety of automobile body manufacturing. The specific process is shown in Figure 2.
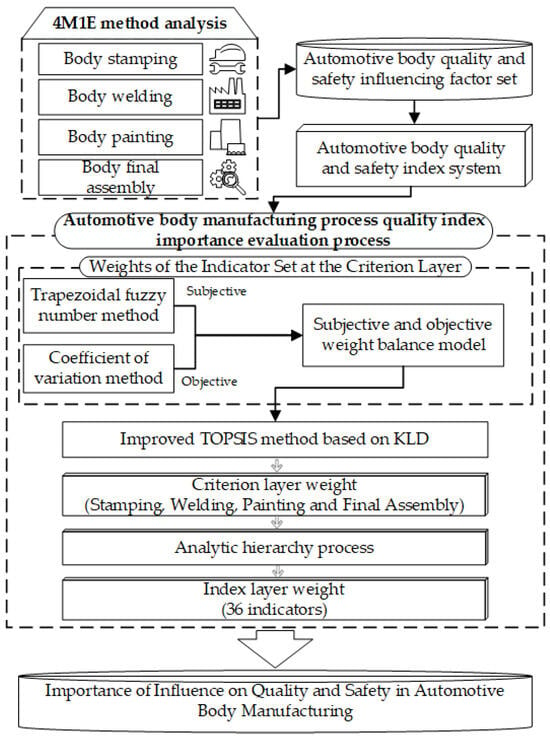
Figure 2.
Comprehensive analysis flowchart of quality and safety indicators for automotive body manufacturing.
4.2. Balancing Weight Calculation
4.2.1. Subjective Weight Assignment Using Trapezoidal Fuzzy Number Method
The shape of the membership function of trapezoidal fuzzy numbers is more complex than that of triangular fuzzy numbers [31]. The use of trapezoidal fuzzy numbers can more reasonably express the subjective evaluation opinions of decision-makers than the use of triangular fuzzy numbers [24]. Pérez-Fernández et al. optimized quality costs using AHP, ANP and lean tools, addressing transparency issues in expert input and intangible factors evaluation [32]. Thus, this paper employs their expert elicitation method to ensure rigorous criteria weighting and transparent assessment of non-quantifiable dimensions within the decision-making framework.
The membership function of trapezoidal fuzzy numbers can sequentially transform natural sequences 1, 2, …, i, …, n into the form of trapezoidal fuzzy numbers (1, 1, 3/2, 2), (1, 3/2, 5/2, 3), …, (i − 1, (i − 1)/2, (i + 1)/2, i + 1), …, (n − 1, (n − 1)/2, (n + 1)/2, n + 1). The commonly used descriptions for the 1–9 extreme comparison scale are “extremely inferior”, “strongly inferior”, “obviously inferior”, “slightly inferior”, “equal”, “slightly superior”, “obviously superior”, “strongly superior”, “extremely superior”, and they are represented by trapezoidal fuzzy numbers as follows1/9, 2/8, …, 9/1, They are represented by trapezoidal fuzzy numbers. According to the fuzzy operation rules, the trapezoidal fuzzy scale values are calculated one by one as follows (1/9, 1/9, 3/17, 1/4), (1/9, 3/17, 1/3, 3/7), …, (4, 17/3, 9, 9). The specific steps are as follows:
Step 1: Establishing the hierarchical structure of the quality and safety early-warning indicator system for automotive body manufacturing. The indicator system is structured into three hierarchical levels. Given the need to identify many-to-many relationships among influencing factors for automotive body manufacturing quality and safety during criterion-layer analysis and to ensure consistency in judgment, the number of indicators in the index layer is streamlined to fewer than ten for subjective analysis.
Establishing the hierarchical structure of the quality and safety early warning indicator system for automotive body manufacturing. The indicator system is structured into three hierarchical levels. Given the need to identify complex interaction relationships among influencing factors for automotive body manufacturing quality and safety during criterion-layer analysis and to ensure consistency in judgment, the number of indicators in the index layer is streamlined to fewer than ten for subjective analysis.
Step 2: Constructing the decision matrix A for influencing factors. Select j participants to evaluate each indicator within the streamlined set of influencing factors. The decision matrix A is formulated as follows:
where represents the relative relationship between the n automotive body manufacturing quality indicator and the m automotive body manufacturing quality indicator from the j participant.
Step 3: Conduct a consistency check. First, calculate the consistency index CI:
where CI is the consistency index; is the maximum eigenvalue of matrix A, n is the dimension of the matrix, and represents the i component of .
where CR is the consistency ratio and RI is the random index. When the calculated CR < 0.1, the decision-making matrix meets the consistency test and can be used. Otherwise, adjust the evaluation matrix until CR < 0.1.
Step 4: Construct the rough group decision matrix and calculate the rough numbers for quality and safety indicators in automotive body manufacturing by first integrating the S evaluation matrices for criterion level quality and safety indicators after they pass the consistency check, as required for processing with rough numbers:
where represents the relative relationship between indicator i and indicator j for automotive body manufacturing quality and safety from participant S, and the same applies to the rest.
Step 5: Conduct rough approximation set partitioning. Assume that U is a non-empty finite set, that is, the universe of discourse; Y is an arbitrary object in the index set U. Suppose the objects in U are partitioned into n parts, and a subset is defined in this set. Assume there are n partitions and there is an order relation . For any one of the partitions , its lower approximation set is the “lenient” range of the evaluation elements in the simplified indicator layer, which is defined as follows:
and the upper approximation set with respect to , that is, the “strict” range of the evaluation elements in the simplified indicator layer:
Step 6: Determine the upper and lower rough bounds and rough interval for automotive body manufacturing quality and safety indicators, which are composed of these indicators’ upper and lower rough bounds and expressed mathematically as shown in Equations (8) and (9):
where represents the lower rough bound of the rough set for the indicator i of automotive body manufacturing quality and safety, represents the upper rough bound of the rough set for indicator i, denotes the number of objects contained in the lower rough set of indicators i, and represents the number of objects contained in the upper rough set of indicator u of automotive body manufacturing quality and safety early-warning indicators.
Calculate the evaluation rough interval i for indicator of automotive body manufacturing quality and safety:
Step 7: Derive the rough pairwise comparison matrix for automotive body manufacturing quality and safety indicators. After obtaining the rough numbers and rough intervals for each automotive body manufacturing quality and safety indicator in the rough group decision matrix, construct the rough pairwise comparison matrix X:
where is a rough number for an automotive body manufacturing quality and safety indicator, and are its lower and upper bounds, respectively.
Step 8: Calculate the importance degree of each level of automotive body manufacturing quality and safety indicators. Decompose X into the lower rough boundary matrix and upper rough boundary matrix for automotive body manufacturing quality and safety indicators:
Calculate separately the eigenvectors and eigenvalues of automotive body manufacturing quality and safety indicators, and derive the importance degree of these indicators for their respective matrices:
where represents the eigenvalue matrix corresponding to the lower rough boundary matrix, represents the eigenvalue matrix corresponding to the upper rough boundary matrix, denotes the eigenvalue corresponding to the lower rough boundary of indicator i of automotive body manufacturing quality and safety, and represents the eigenvalue corresponding to the upper rough boundary of indicator i of automotive body manufacturing quality and safety.
Normalize the weights of automotive body manufacturing quality and safety indicators through Equations (16) and (17):
Determine the final weights for automotive body manufacturing quality and safety indicators through Equation (18):
Since relying solely on trapezoidal fuzzy numbers may overemphasize expert subjectivity and lack objective data-driven constraints, the index weights determined by the trapezoidal fuzzy number method are used as the subjective weight basis for the subjective–objective weight balancing model, ensuring the subjective–objective balance of index weights.
4.2.2. Objective Weighting by Coefficient of Variation Method
Since the entropy weight method may lead to the phenomenon of equalization of objective weights, making the primary–secondary relationship among various indicators not obvious, the coefficient of variation method is adopted for objective weight analysis. The specific steps are as follows:
Step 1: Collect raw data. Suppose there are m indicators in a set of automotive body manufacturing quality and safety indicators and n samples to be evaluated. That is, an evaluation matrix for automotive body manufacturing quality and safety indicators with n rows and m columns is formed, denoted as K:
where represents the relationship between sample i and indicator j in the automotive body manufacturing quality and safety evaluation.
Step 2: Normalize data for automotive body manufacturing quality and safety evaluation. Normalization of indicators means converting all indicators into positive indicators. In the evaluation system for automotive body manufacturing quality and safety indicators, positive indicators are those where a larger value is better, indicating that a higher calculated value has a greater impact on automotive body manufacturing quality. In contrast, negative indicators are those where a smaller value is better, meaning that a lower value under such indicators has a greater impact on automotive body manufacturing quality:
where represents the relative relationship after normalization between sample i and indicator j in the automotive body manufacturing quality and safety evaluation. Here, c is the influencing coefficient of automotive body manufacturing quality and safety, and represents indicator j.
Step 3: Calculation of the coefficient of variation for automotive body manufacturing quality and safety indicators. The mean value and standard deviation of these indicators are calculated through Equations (22) and (23):
Calculate the coefficient of variation of automotive body manufacturing quality and safety indicators using Equation (24):
Step 4: Calculate the weight of automotive body manufacturing quality and safety indicators:
Since the CVM, as a purely objective and data-driven approach, may lack sensitivity to expert judgment when applied in isolation, the index weights derived from CVM serve as the objective weight basis for the subjective and objective weight balance model. By capitalizing on the inherent insensitivity of CVM to data distribution patterns and supplementing it with subjective inputs, the integrated framework mitigates evaluation inaccuracies stemming from methodological biases, thus laying a robust foundation for the weight balance model.
4.2.3. Weight Balancing Model for Balanced Contributions of Subjective and Objective Weights
In multi-attribute decision-making, the use of a single subjective or objective evaluation method leads to the loss of weighting information during the evaluation process. This limitation stems from subjective methods relying excessively on decision-makers’ preferences—thereby introducing potential bias or inconsistency—while objective methods solely depend on mathematical calculations that overlook contextual or qualitative factors [33]. To mitigate such issues, this study proposes a weight-balancing model to integrate the two approaches, ensuring neither overemphasis on subjective judgment nor overreliance on objective data compromises the decision-making framework’s integrity. The specific establishment process is as follows:
The decision matrix for automotive body manufacturing quality indicators is revised by defining for benefit-type indicators and for cost-type indicators in automotive body manufacturing. Let represent benefit-type indicators, and , , , , , , , represent cost-type indicators for automotive body manufacturing, thereby obtaining the normalized decision matrix .
In multi-criteria comprehensive evaluation, the ranking results of evaluation objects depend on their weighted indicator values. Starting from the weighted indicator values and considering that the contributions of subjective and objective weights to the weighted indicator values trend toward equilibrium, let the balanced weight vector be:
where and are the subjective and objective weight balancing coefficients, respectively, with , > 0 and .
According to Equation (26), the subjective and objective weight contribution degrees of evaluation object i for indicator j are and , where denotes the subjective weight value of indicator j, and denotes the objective weight value of indicator j, and the degree of deviation of the weight contribution value for evaluation object i is denoted as . Since all evaluation objects of automotive body manufacturing indicators are equal, the total degree of deviation in weight contribution is the aggregation of .
A weight balancing model is established by taking the minimization of deviation between subjective and objective weights as the objective function and using subjective–objective balance coefficients as constraint conditions, thus constructing a model where subjective and objective weights tend to balance. The balance coefficients and are solved through the established balancing model, as shown in Equation (27):
Substituting with 1 − and setting the first-order derivative of the objective function to zero, we obtain:
According to the properties of the objective function, the minimum value of the objective function in Equation (27) is achieved at the value of in Equation (28). The value is calculated using .
4.3. Improved TOPSIS Comprehensive Evaluation Based on KLD
By formulating a weight-balancing model with the objective function of minimizing discrepancies between subjective and objective weights, the corresponding weights of the influencing factor set are derived. Considering that the sole application of TOPSIS may lead to discriminative failure of evaluation objects in the vicinity of the ideal point, this study conducts a systematic analysis of criterion-level indicators for automotive body manufacturing quality and safety based on divergence theory.
In information theory, the degree of difference C between the states and of two systems A and B can be calculated using the Kullback–Leibler Divergence:
Among them, C represents the relative entropy between system A and system B.
The smaller the value of C, the smaller the state difference between alternatives in the system. Although TOPSIS measures the geometric distance between alternatives, it cannot rank points on the perpendicular line relative to the ideal alternative. Introducing relative entropy, namely KLD, effectively resolves this limitation by quantifying the directional divergence of indicator distributions rather than merely relying on geometric proximity. In multi-attribute decision-making for automotive body manufacturing quality and safety, relative entropy measures how closely an evaluated alternative aligns with the ideal: lower C values signify greater similarity in indicator weight distributions, enabling differentiation of alternatives with identical geometric distance from the ideal (such as those on the perpendicular line) via their distributional dissimilarity. The approach works as follows: relative entropy assesses whether an alternative’s indicator weights diverge from the ideal (higher C, lower rank) or align closely (lower C, higher rank), thus complementing TOPSIS to ensure robust rankings even in geometrically ambiguous scenarios. The specific steps are as follows:
Step 1: Construct the standardized decision matrix for the evaluation indicators of the automotive body manufacturing criterion layer:
where represents the standardized indicator value of the j automotive body manufacturing quality index for the i evaluated indicator in the criterion layer of automotive body manufacturing quality.
Step 2: Construct the weighted-standardized decision matrix for automotive body manufacturing quality and safety index:
where represents the relative relationship after weighting between the i evaluated criterion-layer indicator for automotive body manufacturing quality and the j standardized indicator of automotive body manufacturing quality, and is the weight of the j automotive body manufacturing quality and safety indicator.
Step 3: Determine the ideal indicators and negative ideal indicators for automotive body manufacturing quality and safety. Let and denote, respectively, the subscript sets for benefit-type and cost-type indicators:
Step 4: Calculate the relative entropy of each evaluated criterion-layer indicator for automotive body manufacturing quality and safety with respect to the ideal indicators and negative ideal indicators:
where is the relative entropy between the automotive body manufacturing quality and safety indicator (i.e., the i column vector of matrix X) and the evaluated automotive body manufacturing indicator , and is the relative entropy between the automotive body manufacturing quality and safety indicator and the evaluated automotive body manufacturing indicator .
Step 5: Calculate the closeness (or ) of each evaluated automotive body manufacturing quality and safety indicator to the ideal solution:
Step 6: Rank the priority of automotive body manufacturing quality and safety indicators. Arrange the corresponding automotive body manufacturing quality and safety indicators in descending order of (or ), where those ranked earlier are superior to those later in the sequence.
Through the above calculations, it is possible to avoid excessive subjectivity or objectivity to a certain extent, incorporating both subjective and objective factors to better establish an early-warning index system for automotive body manufacturing quality and safety.
5. Example
Taking the automotive body manufacturing process for a compact sedan model in a medium-sized semi-automated facility that features 60% automated production equipment and has an annual output of 50,000 units as the research object, this study analyzes four core processes—stamping, welding, painting, and final assembly—to identify critical factors such as tool wear, welding precision, paint quality, and assembly tolerances impacting body quality, including dimensional accuracy, surface finish, structural integrity, and safety, such as crashworthiness and corrosion resistance. Specifically, it aims to identify the critical quality and safety influencing factors in the automotive body manufacturing process and quantify their weights through systematic process evaluation.
5.1. Criterion Layer Indicator Analysis
- (1)
- Objective Weight Analysis Using Coefficient of Variation Method
Given the one-to-many relationship (rather than many-to-many) between the criterion layer and the indicator layer, the analysis is conducted from five dimensions of “man, machine, material, method, and environment”: influencing factors under “man” include employee proficiency level and training duration; “machine” involves equipment precision requirements and failure rate standards; “material” covers material quality specifications and characteristic information; “method” includes process approaches for each manufacturing stage (stamping, welding, painting, final assembly) and implementation standard requirements; “environment” encompasses personnel working conditions and natural environmental specifications. Indicators are evaluated using sources such as the China Statistical Yearbook (2024), government reports, and expert assessments, with results summarized in Table 2.

Table 2.
Objective evaluation table.
Quantize the data in the table according to the rules specified in Table 3 of quantitative indicators.

Table 3.
Quantitative indicators table.
Through the coefficient of variation method using Equations (19)–(25), the objective weight calculation results are as follows (calculation process omitted):
- (2)
- Subjective Weight Analysis Using Trapezoidal Fuzzy Number Method
In the analysis, risks in automotive body manufacturing quality and safety are assessed across the five dimensions of “man, machine, material, method, and environment”. This layer is strongly dominated by the primary node “automotive body manufacturing quality” (no weak-dominated nodes). To address uncertainties in subjective expert judgments, 3 experts (with ≥10 years of experience in automotive engineering, quality management, or safety assessment) were surveyed via questionnaires to collect their evaluation results. They used triangular fuzzy numbers to represent linguistic terms like “high risk”, enabling the quantification of vague or imprecise information in risk evaluation. The results after processing are shown as follows:
After inspection, all met the consistency conditions and could be used for weight calculation. Construct the fuzzy rough group decision-making matrix for automotive body manufacturing quality and safety indicators, , where the constructed automotive body manufacturing quality and safety indicator matrix X is as follows:
Calculate the fuzzy-number rough boundary intervals for all agricultural product quality and safety indicators in X. Taking as an example, when partitioning according to the rough set: for the partition of , its upper rough set is , and the lower rough set is ; if partitioning according to the rough set , the upper rough set is , and the lower rough set is .
Calculate through Equations (8) and (9), it can be seen that for the partition with set , the upper rough-bound is 0.778 and the lower rough-bound is 1; for the partition with set , the upper rough-bound is 0.667 and the lower rough-bound is 0.778. Ultimately, its upper rough-bound is 0.889 and the lower rough-bound is 0.772.
Through Equation (10), the rough interval of is [0.722, 0.889]. Repeat the above steps to calculate all the evaluation sets in X, and finally, the rough intervals of all the values are:
Using Equations (12) and (13), construct the upper rough matrix and lower rough matrix for the automotive body manufacturing quality and safety indicators based on the evaluation matrix X:
Use MATLAB R2019b to calculate the eigenvectors and eigenvalues of automotive body manufacturing quality and safety indicators. The maximum eigenvalues corresponding to and are 5.603 and 4.681, respectively. The eigenvectors corresponding to the maximum eigenvalues are [−0.365, −0.429, −0.424, −0.510, −0.492]T and [0.351, 0.417, 0.418, 0.517, 0.511]T, respectively. The weight calculated by Equations (14) and (15) is [0.165, 0.193, 0.191, 0.230, 0.222]T, and the weight of is [0.158, 0.189, 0.189, 0.233, 0.231]T. Finally, the weight of “man, machine, material, method, environment” is [0.161, 0.191, 0.190, 0.232, 0.226]T.
An analysis is conducted on the five aspects of “man, machine, material, method, and environment”. The influencing factors for each aspect are as follows: the “man” aspect includes employee proficiency level and employee training duration; the “machine” aspect includes equipment precision requirements and equipment failure rate requirements; the “material” aspect includes material quality requirements and material quality characteristic information; the “method” aspect includes process methods for each stage (stamping process method, welding method, painting method, final assembly method) and standard execution requirements; the “environment” aspect includes personnel working environment and natural environment requirements. By repeating the above weight calculation process, the final subjective weights F are calculated as:
F = [0.0877, 0.0738, 0.1036, 0.0844, 0.0975, 0.0924, 0.1023, 0.1292, 0.1261, 0.1030]T
- (3)
- Comprehensive Weight Analysis Using KLD-Based TOPSIS Method
A weight-balancing model with the objective function of balancing the contributions of subjective and objective weights is used to calculate the subjective and objective weight components. The subjective and objective weight coefficients = 0.498 and = 0.502 are calculated through Equation (28), and then the balanced weight vector is obtained from Equation (26) as:
Balance processing, normalization processing, and weighted processing are performed on the above-calculated objective and subjective weights to obtain the weighted normalization processing table, as shown in Table 4:

Table 4.
Weighted normalization processing table.
For the above evaluation objects of automotive body manufacturing quality and safety indicators, calculate the positive and negative ideal points. Denote the positive ideal points of evaluation object as , and the negative ideal points as , . The KLD between the positive ideal point and negative ideal point of evaluation set object is calculated using Equations (33) and (34). Use Equation (33) to calculate the degree of proximity between evaluation object and the ideal point, and the calculation result is: = [0.4921, 0.3570, 0.4909, 0.5104]T. Finally, the we receive the calculated proportions: stamping accounts for 26.59%, welding accounts for 19.29%, painting accounts for 26.54%, and final assembly accounts for 27.58%.
5.2. Comprehensive Analysis of the Indicator Layer
After calculating the weights of each criterion layer process using the KLD-based TOPSIS method, the analytic hierarchy process (AHP) is employed to compute the weights of the indicator layer. The specific calculation steps are as follows:
For the indicator system of influencing factors on automotive body manufacturing quality and safety established in Section 3.2, an analysis of the indicator layer is conducted, and the indicator weights are solved using the analytic hierarchy process (AHP). The results are shown in Table 5 (calculation process omitted):

Table 5.
Comprehensive analysis table.
Through comprehensive analysis, it is evident that in the automotive body manufacturing process, factors such as stamping die precision in the stamping process, welding methods in the welding process, coating properties and electrophoretic solution properties in the painting process, and component quality in the final assembly process are more likely to impact automotive body manufacturing quality compared to other indicators. In particular, the quality of assembly components in the body assembly process has a significant impact on manufacturing quality, while the proficiency of personnel in the painting process has relatively lower importance compared to other indicators.
Through the above comprehensive analysis process, the problem of missing evaluation information caused by single subjective or objective evaluation methods is avoided to a certain extent, and the traditional TOPSIS method’s inability to distinguish the quality of alternatives in some cases is also addressed.
5.3. Comparison of Evaluation Methods
The weight analysis of quality indicators in the automobile body manufacturing process was conducted for the indicators in Table 5 using the entropy weight method (EWM) and analytic hierarchy process (AHP), respectively. The final calculated comparison results are shown in Figure 3.
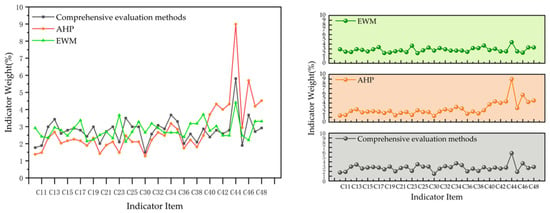
Figure 3.
Comparative results of different evaluation methods.
In Figure 3, the gray lines represent the index weights determined by the method proposed in this chapter, the orange lines denote the weights obtained by the AHP (analytic hierarchy process), and the green lines indicate the weights calculated by the EWM (entropy weight method). The horizontal axis denotes the indicator items in the evaluation process, while the vertical axis represents the indicator weights. The scatter points in the graphs correspond to the weight values of respective indicator items, with connecting lines illustrating the trend of weight variations among indicators.
As shown in Figure 3, a comparative evaluation was conducted on quality and safety indicators in automotive body manufacturing using the proposed hybrid analysis method, AHP, and EWM. AHP, anchored in subjective expert elicitation, tends to inflate the weights of specific indicators, diminishing the relative significance of other indicators and biasing results toward overweighted indicators. Conversely, EWM, deriving weights solely from data variability, struggles to discriminate critical factors under low-variability conditions, leading to minimal differentiation among indicators and failure to identify key manufacturing metrics. In contrast, the comprehensive evaluation method mitigates the susceptibility of AHP to subjective bias and the sensitivity of EWM to data sparsity, enhancing the robustness and accuracy of the multi-criteria evaluation paradigm.
In Figure 4, the horizontal axis denotes the weight values, while the vertical axis represents the distribution density of weights. The gray, orange, and green vertical lines beneath the normal distribution curve correspond to the positions of index weights derived from the proposed hybrid method, analytic hierarchy process (AHP), and entropy weight method (EWM), respectively. Given the non-negativity constraint of weight values, all vertical lines are positioned to the right of the horizontal axis zero point.
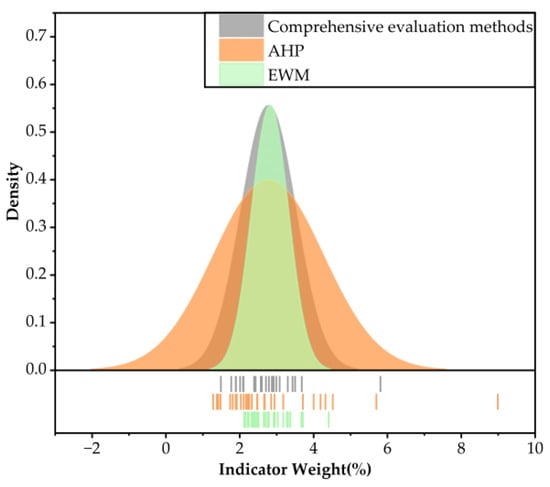
Figure 4.
Comparison chart of normal distribution for different analysis methods.
As illustrated in Figure 4, the normal distribution diagram reveals key insights. The analytic hierarchy process (AHP) shows an excessively dispersed indicator weight distribution. Individual indicators carry disproportionately high weights, which severely distorts the overall evaluation results. Conversely, the entropy weight method (EWM) exhibits overly concentrated weight allocation. This obscures differences among indicators and hinders the identification of critical quality determinants. In sharp contrast, the hybrid evaluation method proposed here integrates subjective and objective approaches. It reduces excessive discrepancies between indicators in AHP and overcomes EWM’s insensitivity to data variations. These improvements alleviate the limitations of single-method evaluations.
As shown by the comprehensive analysis of Figure 3 and Figure 4, when using the AHP method to analyze indicator weights, the weights of indicators C44 and C46 are excessively high. This weakens the weights of other indicators. In contrast, the EWM method analyzes indicator weights, with over 90% of indicator weights falling between 2% and 4%. This makes it impossible to identify key factors affecting quality and safety in automotive body manufacturing. However, the comprehensive analysis method proposed in this paper can accurately identify critical influencing factors in automotive body manufacturing. This lays a solid foundation for proactive quality control protocols, significantly reducing potential manufacturing defects and improving the reliability of the overall production process.
6. Conclusions
The quality of automotive body manufacturing represents a complex system engineering endeavor, necessitating collaborative efforts across multifaceted dimensions including manufacturing processes, quality management systems, personnel administration, and smart manufacturing frameworks. Through a comprehensive review of numerous domestic and international quality and safety standards for automotive body manufacturing, coupled with an analysis of relevant literature, and in conjunction with the “4M1E” quality analysis methodology, this study constructs a systematic set of influencing factors for quality and safety in automotive body manufacturing processes. Furthermore, by employing multiple weight evaluation approaches such as rough set theory, coefficient of variation theory, fuzzy number theory, and divergence theory, an indicator system for influencing factors and an evaluation framework for quality and safety in automotive body manufacturing are established. This integrative approach effectively mitigates the information loss inherent in traditional evaluations relying on single methods, whether subjective or objective, and addresses the critical limitation of the conventional TOPSIS method, which often fails to discriminate between alternatives in proximity to the perpendicular line of ideal points.
The results of this study demonstrate that the proposed comprehensive evaluation framework enables precise identification of key quality influencing factors, as evidenced by the balanced weight distributions and enhanced discriminative power observed in comparative analyses (Figure 3 and Figure 4). Such findings underscore the methodology’s efficacy in reconciling subjectivity–objectivity trade-offs and improving evaluation accuracy. Looking forward, future research will focus on three key directions:
- (1)
- Deepening the integration of advanced quality management methodologies with emerging technologies such as big data analytics and digital twin systems to facilitate real-time quality prediction;
- (2)
- Expanding the evaluation system to incorporate lifecycle considerations, including post-manufacturing quality feedback and recycling processes;
- (3)
- Developing adaptive weight adjustment mechanisms to address dynamic changes in manufacturing environments.
Notably, implementing these advancements faces challenges such as cross-disciplinary collaboration barriers, real-time data integration complexities, and the need for standardized evaluation protocols across diverse manufacturing scenarios. Overcoming these hurdles will be essential to realizing the full potential of proactive quality management, shifting the paradigm from reactive defect resolution to predictive risk mitigation in automotive body manufacturing. By anchoring technological innovation in systematic evaluation frameworks, this research provides a robust foundation for elevating quality and safety standards in automotive body manufacturing, thereby contributing to the advancement of intelligent manufacturing practices globally.
Author Contributions
Conceptualization, Y.X., L.G., S.J., S.Z., Z.G. and H.Q.; Methodology, Y.X., L.G., S.Z. and H.Q.; Resources, S.J. and Z.G.; Data curation, S.J.; Writing—original draft, L.G.; Writing—review & editing, Y.X., L.G. and H.Q.; Supervision, Y.X., S.Z. and Z.G.; Project administration, H.Q. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Gu, W.L. Research on Influencing Factors and Countermeasures of Product Quality Improvement in Y Enterprise. Master’s Thesis, Jiangsu University, Zhenjiang, China, 2021. [Google Scholar] [CrossRef]
- Zhao, T.J.; Liu, Q.S. Reflections on the Management of Enterprise Quality Costs. Financ. Account. 2019, 21, 44–47+60. [Google Scholar]
- Correia, D.; Lourenço Marques, J.; Teixeira, L. A framework to guide and support the design of a smart city based on the PDCA cycle approach. J. Syst. Inf. Technol. 2025, 27, 65–93. [Google Scholar] [CrossRef]
- Li, Z.S.; Nie, S.F.; Lin, H.Q.; Yu, K.K. Some Cases of Automobile Corrosion and Quality Control of Body Manufacturing Process. Electroplat. Finish. 2022, 41, 103–107. [Google Scholar] [CrossRef]
- Zhang, L.J.; Gao, Z.; Yu, H.Y. Selection of Body-in-White Material Based on Life Cycle Assessment. Automot. Eng. 2022, 44, 945–951. [Google Scholar] [CrossRef]
- Zhou, W.; Li, M.; Qiu, M.J.; Xilong, Z.; Liu, J.; Hongbo, Z. Vehicle Body Panel Thickness Optimization by a Genetic Algorithm. J. Tsinghua Univ. Sci. Technol. 2022, 62, 523–532. [Google Scholar] [CrossRef]
- Tang, M.Q.; Guo, G.; Chen, Q.H.; Qing, W. Business Intelligence of Automobile “Process-Quality” Stamping Production. Comput. Integr. Manuf. Syst. 2021, 27, 1120–1127. [Google Scholar] [CrossRef]
- Yan, X.; Shan, D.; Bian, Y.W. Product Strategy for New Energy Vehicles with Quality Defects: Based Online Review Analysis. Front. Eng. Manag. Sci. Technol. 2025, 44, 36–44. [Google Scholar]
- Wang, F.; Lin, M.; Liang, M.J. Applicability Evaluation Method and Its Application of Automobile Body Integrated Die-Casting Machines. Mach. Tool Hydraul. 2024, 52, 67–72. [Google Scholar] [CrossRef]
- Hashemian, A.; Imani, B.M. A new quality appearance evaluation technique for automotive bodies including effect of flexible parts tolerances. Mech. Based Des. Struct. Mach. 2018, 46, 157–167. [Google Scholar] [CrossRef]
- Sun, S.; Zhang, N.; Walker, P.; Lin, C. Intelligent estimation for electric vehicle mass with unknown uncertainties based on particle filter. IET Intell. Transp. Syst. 2020, 14, 463–467. [Google Scholar] [CrossRef]
- Harianja, E.; Lumbantoruan, G. Integrating MLP with Algorithm with AHP Modification for Car Evaluation. J. Phys. Conf. Ser. 2019, 1361, 012022. [Google Scholar] [CrossRef]
- Chen, G.; Sheng, B.; Luo, R.; Jia, P. A parallel strategy for predicting the quality of welded joints in automotive bodies based on machine learning. J. Manuf. Syst. 2022, 62, 636–649. [Google Scholar] [CrossRef]
- Abdul Karim, M.; Park, Y.-D. A Review on Welding of Dissimilar Metals in Car Body Manufacturing. J. Weld. Join. 2020, 38, 8–23. [Google Scholar] [CrossRef]
- Jamwal, A.; Agrawal, R.; Sharma, M.; Kumar, V. Review on multi-criteria decision analysis in sustainable manufacturing decision making. Int. J. Sustain. Eng. 2020, 14, 202–225. [Google Scholar] [CrossRef]
- Song, L.F.; Zhang, T.; Xue, Z.; Qiao, Y.; Zhou, J.; Xia, H.; Gao, L.; Chen, H. Research on Technology of Activated Rubber Powder Modified Asphalt Based on TOPSIS. J. Mater. Sci. Eng. 2020, 38, 226–231+314. [Google Scholar] [CrossRef]
- Zhang, D.B.; Liu, G.D.; Wang, L.; Zhong, R. Application of TOPSIS Model Based on Game Theory to Groundwater Quality Evaluation. J. Yangtze River Sci. Res. Inst. 2018, 35, 46–50+62. [Google Scholar]
- Li, L.H.; Mo, R.; Chang, Z.Y.; Zhang, H. Priority Evaluation Method for Aero-Engine Assembly Tasks Based on Balanced Weight and Improved TOPSIS. Comput. Integr. Manuf. Syst. 2015, 21, 1193–1201. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, C.; Lv, B. Comparative analysis of ecological sensitivity assessment using the coefficient of variation method and machine learning. Environ. Monit. Assess. 2024, 196, 1000. [Google Scholar] [CrossRef]
- Diao, X.; Jiang, J.; Mebarki, A.; Ni, L.; Duo, Y.; Chen, S.; Wang, Y.; Zhang, S. Risk analysis of domino effect of leakage accident of petrochemical pipeline based on analytic hierarchy process and fuzzy fault tree analysis. Saf. Sci. 2025, 187, 106852. [Google Scholar] [CrossRef]
- Khosravi, F.; Izbirak, G. A framework of index system for gauging the sustainability of iranian provinces by fusing analytical hierarchy process (AHP) and rough set theory (RST). Socio-Econ. Plan. Sci. 2024, 95, 101975. [Google Scholar] [CrossRef]
- Liu, G.; Xu, B.; Chen, L.L.; Liu, G.; Xu, B.; Chen, L.; Huang, X.; Chen, Z.; Zhang, W. Application of Improved Matter-Element Extension Model Based on AHP-CRITIC Comprehensive Weight in Groundwater Quality Evaluation. Environ. Monit. China 2024, 40, 125–133. [Google Scholar] [CrossRef]
- Zhai, Z.F.; Wang, L.Y.; Sun, M.Z.; Yan, C.; Liang, Y. Comprehensive Evaluation of Agricultural Water-Saving Technology Based on AHP and Rough Set Method. Acta Ecol. Sin. 2012, 32, 931–941. [Google Scholar] [CrossRef]
- Hou, F.B.; Tao, Y.H. Design of Optimal Planning Mathematical Model for Production Configurations of Auto Parts Enterprises. Mod. Electron. Tech. 2018, 41, 174–177+181. [Google Scholar] [CrossRef]
- Hernández-Torres, J.A.; Sánchez-Lozano, D.; Sánchez-Herrera, R.; Vera, D.; Torreglosa, J.P. Integrated multi-criteria decision-making approach for power generation technology selection in sustainable energy systems. Renew. Energy 2025, 243, 122481. [Google Scholar] [CrossRef]
- Xu, Z.; Dang, Y.; Munro, P. Knowledge-driven intelligent quality problem-solving system in the automotive industry. Adv. Eng. Inform. 2018, 38, 441–457. [Google Scholar] [CrossRef]
- Fujii, Y.; Urabe, M.; Yamasaki, Y.; Tamai, Y. Development of Press-Forming Technique for Bent Automotive Body Parts Using In-Plane Shear Deformation. Mater. Trans. 2022, 63, 622–628. [Google Scholar] [CrossRef]
- Liu, B.; Yang, J.; Li, J.; Liao, X.; Yang, Q.; Zhang, J.; Hu, T.; Jiang, S. Research on welding deformation control technology of battery electric vehicle framed aluminum body. Prog. Nat. Sci. Mater. Int. 2024, 34, 108–121. [Google Scholar] [CrossRef]
- Yang, Q.; Wang, X.; Wu, H. Study on lean production management of new energy vehicle body painting based on the dual perspectives of digital transformation and VSM. PLoS ONE 2025, 20, e0318253. [Google Scholar] [CrossRef]
- Nedzel’skii, F.A.; Anoprienko, A.K.; Romanova, Y.V. Improvement of the Assembly of Automobile Bodies by the Adhesive-Threaded Technology. J. Mach. Manuf. Reliab. 2024, 53, S211–S216. [Google Scholar] [CrossRef]
- Zhang, P. The Research on Multiple Attribute Decision Making Methods Based on Normal Wiggly Hesitant Fuzzy Set and Their Application to Decision Making. Master’s Thesis, Shandong University of Finance and Economics, Jinan, China, 2021. [Google Scholar] [CrossRef]
- Pérez-Fernández, L.; Sebastián, M.A.; González-Gaya, C. Methodology to Optimize Quality Costs in Manufacturing Based on Multi-Criteria Analysis and Lean Strategies. Appl. Sci. 2022, 12, 3295. [Google Scholar] [CrossRef]
- Pagone, E.; Salonitis, K.; Jolly, M. Automatically weighted high-resolution mapping of multi-criteria decision analysis for sustainable manufacturing systems. J. Clean. Prod. 2020, 257, 120272. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).