Decrease in Computational Load and Increase in Accuracy for Filtering of Random Signals
Abstract
1. Introduction
Preliminaries
2. Statement of the Problem
Motivation—Relation to Known Techniques
3. Contribution and Novelty
4. Solution of the Problem
4.1. Solution of Problem in (4)
4.1.1. Generic Basis for the Solution of Problem (7): Case in (9). Second-Degree Filter
4.1.2. Decrease in Computational Load
4.1.3. Error Associated with the Second-Degree Filter Determined by (23)
4.1.4. Solution of Equation (9) for
4.1.5. Error Associated with the Third-Degree Filter Determined by (47)–(49)
4.1.6. Solution of Equation (9) for Arbitrary p
4.1.7. Solution of Equation (9)
| Algorithm 1: Solution of Equation (9) |
 |
- In line 5, matrix is calculated as in (79).
4.1.8. The Error Associated with the Filter Represented by (79)–(82)
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Listing 1. MATLAB code for solving Equation (9) by Algorithm 1. |
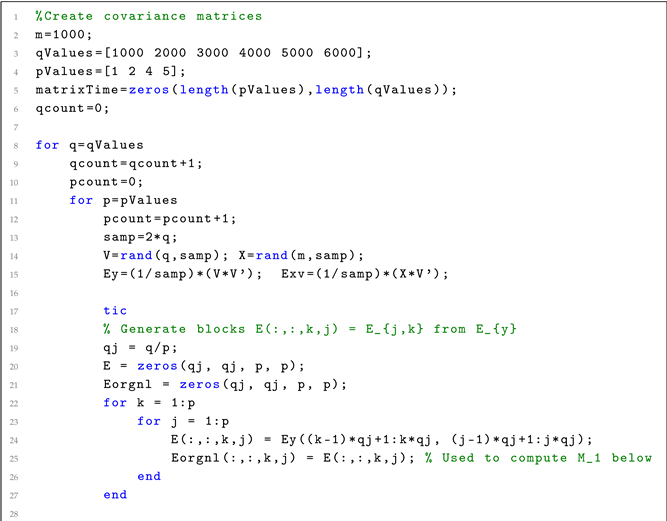  |
References
- Fomin, V.N.; Ruzhansky, M.V. Abstract Optimal Linear Filtering. SIAM J. Control. Optim. 2000, 38, 1334–1352. [Google Scholar] [CrossRef]
- Hua, Y.; Nikpour, M.; Stoica, P. Optimal reduced-rank estimation and filtering. IEEE Trans. Signal Process. 2001, 49, 457–469. [Google Scholar]
- Brillinger, D.R. Time Series: Data Analysis and Theory; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2001. [Google Scholar]
- Torokhti, A.; Howlett, P. An Optimal Filter of the Second Order. IEEE Trans. Signal Process. 2001, 49, 1044–1048. [Google Scholar] [CrossRef]
- Scharf, L. The SVD and reduced rank signal processing. Signal Process. 1991, 25, 113–133. [Google Scholar] [CrossRef]
- Stoica, P.; Jansson, M. MIMO system identification: State-space and subspace approximation versus transfer function and instrumental variables. IEEE Trans. Signal Process. 2000, 48, 3087–3099. [Google Scholar] [CrossRef]
- Billings, S.A. Nonlinear System Identification—Narmax Methods in the Time, Frequency, and Spatio-Temporal Domains; John Wiley and Sons, Ltd.: New York, NY, USA, 2013. [Google Scholar]
- Schoukens, M.; Tiels, K. Identification of Block-oriented Nonlinear Systems Starting from Linear Approximations: A Survey. Automatica 2017, 85, 272–292. [Google Scholar] [CrossRef]
- Li, D.; Wong, K.D.; Hu, Y.H.; Sayeed, A.M. Detection, classification, and tracking of targets. IEEE Signal Process. Mag. 2002, 19, 17–29. [Google Scholar]
- Mathews, V.J.; Sicuranza, G.L. Polynomial Signal Processing; John Willey & Sons, Inc: New York, NY, USA, 2001. [Google Scholar]
- Marelli, D.E.; Fu, M. Distributed weighted least-squares estimation with fast convergence for large-scale systems. Automatica 2015, 51, 27–39. [Google Scholar] [CrossRef] [PubMed]
- Perlovsky, L.; Marzetta, T. Estimating a covariance matrix from incomplete realizations of a random vector. IEEE Trans. Signal Process. 1992, 40, 2097–2100. [Google Scholar] [CrossRef]
- Ledoit, O.; Wolf, M. A well-conditioned estimator for large-dimensional covariance matrices. J. Multivar. Anal. 2004, 88, 365–411. [Google Scholar] [CrossRef]
- Ledoit, O.; Wolf, M. Nonlinear shrinkage estimation of large-dimensional covariance matrices. Ann. Stat. 2012, 40, 1024–1060. [Google Scholar] [CrossRef]
- Vershynin, R. How Close is the Sample Covariance Matrix to the Actual Covariance Matrix? J. Theor. Probab. 2012, 25, 655–686. [Google Scholar] [CrossRef]
- Won, J.H.; Lim, J.; Kim, S.J.; Rajaratnam, B. Condition-number-regularized covariance estimation. J. R. Stat. Soc. Ser. 2013, 75, 427–450. [Google Scholar] [CrossRef]
- Schneider, M.K.; Willsky, A.S. A Krylov Subspace Method for Covariance Approximation and Simulation of Random Processes and Fields. Multidimens. Syst. Signal Process. 2003, 14, 295–318. [Google Scholar] [CrossRef]
- Leclercq, M.; Vittrant, B.; Martin-Magniette, M.L.; Boyer, M.P.S.; Perin, O.; Bergeron, A.; Fradet, Y.; Droit, A. Large-Scale Automatic Feature Selection for Biomarker Discovery in High-Dimensional OMICs Data. Front. Genet. 2019, 10, 452. [Google Scholar] [CrossRef] [PubMed]
- Artoni, F.; Delorme, A.; Makeig, S. Applying dimension reduction to EEG data by Principal Component Analysis reduces the quality of its subsequent Independent Component decomposition. Neuroimage 2018, 175, 176–187. [Google Scholar] [CrossRef] [PubMed]
- Bellman, R.E. Dynamic Programming, 2nd ed.; Courier Corporation: North Chelmsford, MA, USA, 2003. [Google Scholar]
- Janakiraman, P.; Renganathan, S. Recursive computation of pseudo-inverse of matrices. Automatica 1982, 18, 631–633. [Google Scholar] [CrossRef]
- Olivari, M.; Nieuwenhuizen, F.M.; Bülthoff, H.H.; Pollini, L. Identifying time-varying neuromuscular response: A recursive least-squares algorithm with pseudoinverse. In Proceedings of the 2015 IEEE International Conference on Systems, Man, and Cybernetics, Hong Kong, China, 9–12 October 2015; IEEE: Hoboken, NJ, USA, 2015; pp. 3079–3085. [Google Scholar]
- Chen, Z.; Ding, S.X.; Luo, H.; Zhang, K. An alternative data-driven fault detection scheme for dynamic processes with deterministic disturbances. J. Frankl. Inst. 2017, 354, 556–570. [Google Scholar] [CrossRef]
- Feng, X.; Yu, W.; Li, Y. Faster matrix completion using randomized SVD. In Proceedings of the 2018 IEEE 30th International Conference on Tools with Artificial Intelligence (ICTAI), Volos, Greece, 5–7 November 2018; IEEE: Hoboken, NJ, USA, 2018; pp. 608–615. [Google Scholar]
- Zhang, J.; Erway, J.; Hu, X.; Zhang, Q.; Plemmons, R. Randomized SVD methods in hyperspectral imaging. J. Electr. Comput. Eng. 2012, 2012, 409357. [Google Scholar] [CrossRef]
- Drineas, P.; Mahoney, M.W. A randomized algorithm for a tensor-based generalization of the singular value decomposition. Linear Algebra Its Appl. 2007, 420, 553–571. [Google Scholar] [CrossRef]
- Neyshabur, B.; Panigrahy, R. Sparse matrix factorization. arXiv 2013, arXiv:1311.3315. [Google Scholar]
- Qiu, J.; Dong, Y.; Ma, H.; Li, J.; Wang, C.; Wang, K.; Tang, J. NetSMF: Large-scale network embedding as sparse matrix factorization. In Proceedings of the World Wide Web Conference, San Francisco, CA, USA, 13–17 May 2019; pp. 1509–1520. [Google Scholar]
- Wu, K.; Guo, Y.; Zhang, C. Compressing deep neural networks with sparse matrix factorization. IEEE Trans. Neural Netw. Learn. Syst. 2019, 31, 3828–3838. [Google Scholar] [CrossRef] [PubMed]
- Golub, G.; Van Loan, C. Matrix Computations, 4th ed.; Johns Hopkins Studies in the Mathematical Sciences; Johns Hopkins University Press: Baltimore, MD, USA, 2013. [Google Scholar]
- Friedland, S.; Torokhti, A. Generalized Rank-Constrained Matrix Approximations. SIAM J. Matrix Anal. Appl. 2007, 29, 656–659. [Google Scholar] [CrossRef][Green Version]
- Torokhti, A.; Soto-Quiros, P. Improvement in accuracy for dimensionality reduction and reconstruction of noisy signals. Part II: The case of signal samples. Signal Process. 2019, 154, 272–279. [Google Scholar] [CrossRef]
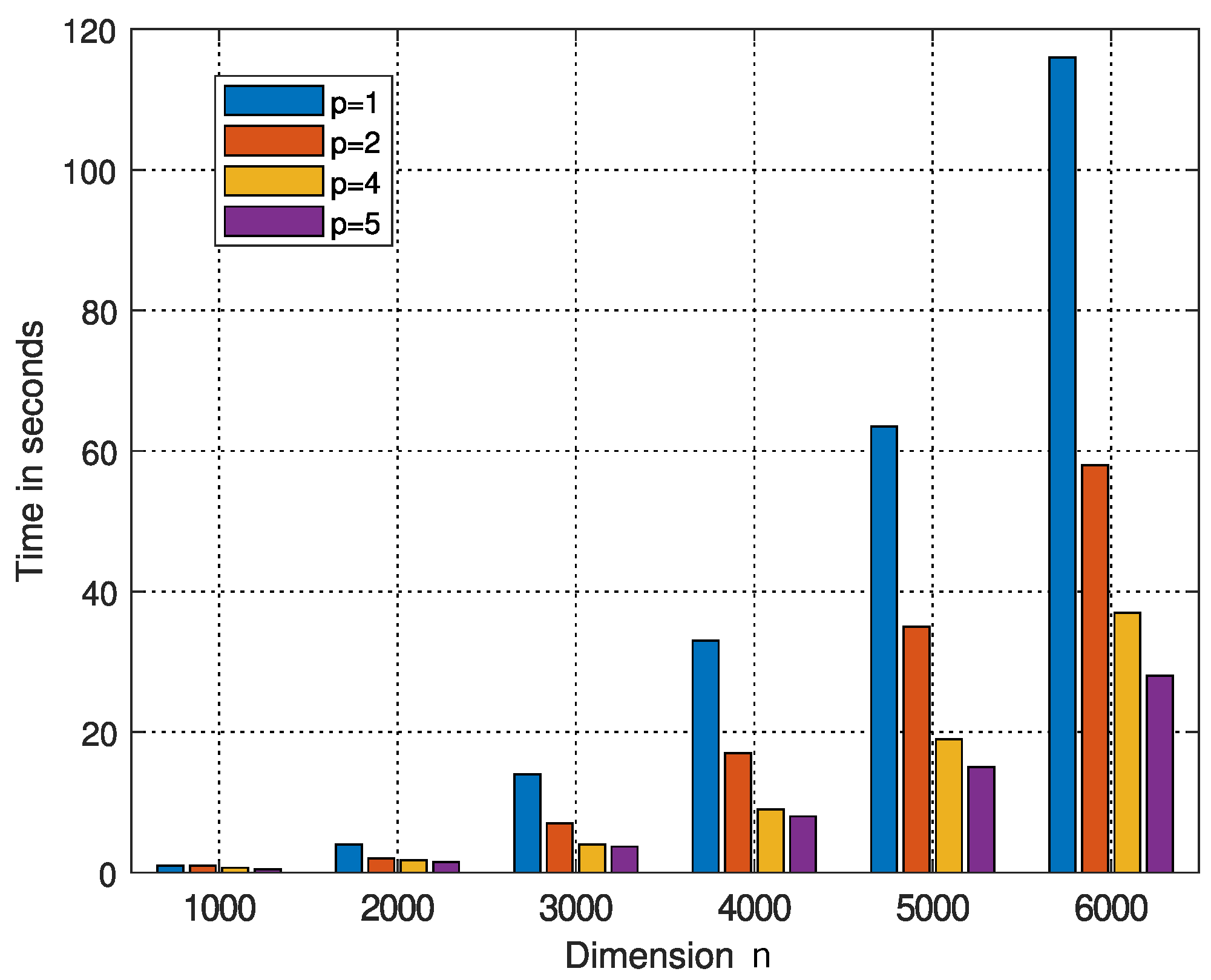

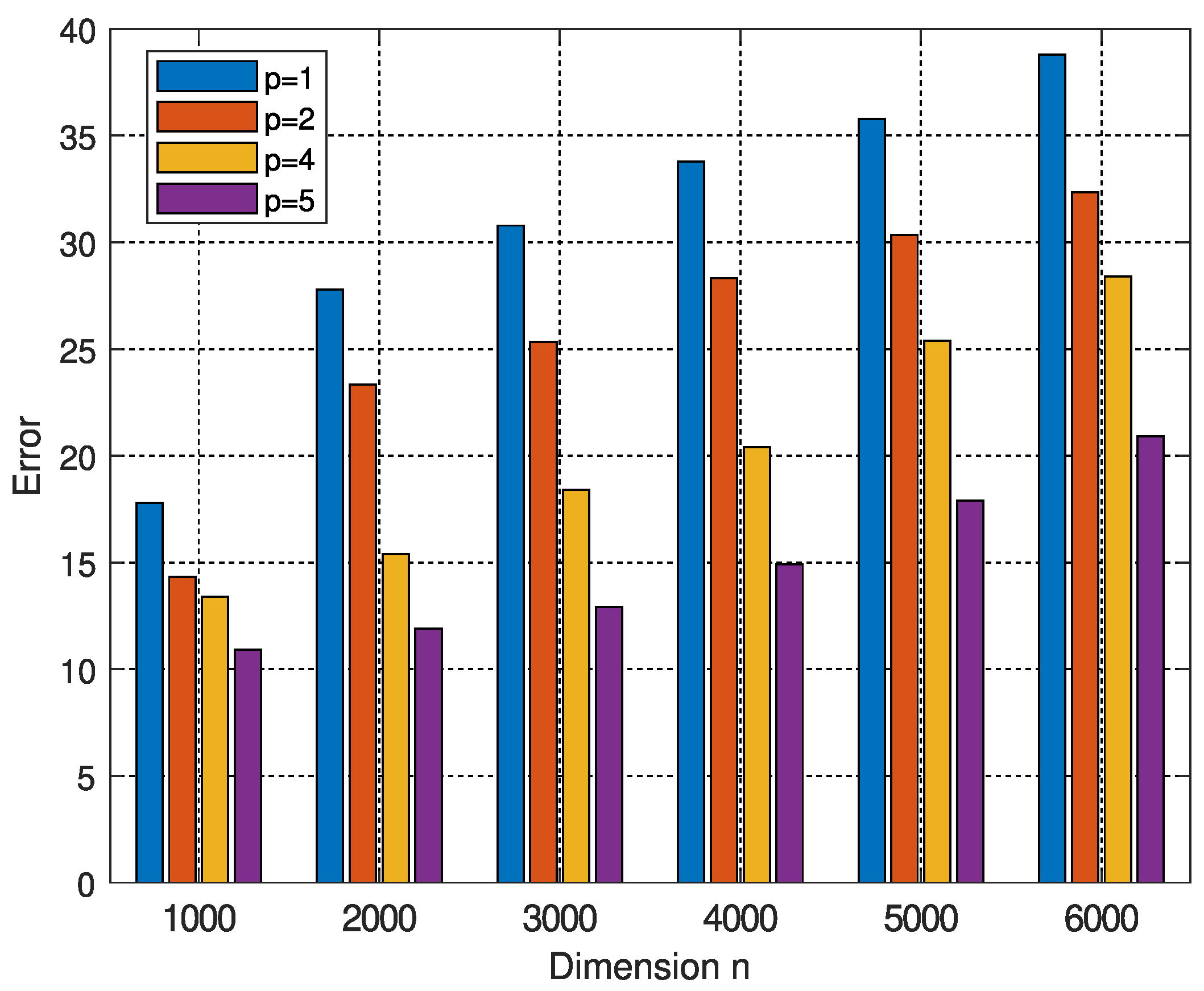
| q | 500 | 1000 | 2000 | 3000 | 4000 | 5000 | 6000 |
| Time |
| q | 500 | 1000 | 2000 | 3000 | 4000 | 5000 | 6000 |
| Time |
| Dimension n | ||||||
|---|---|---|---|---|---|---|
| 1000 | 2000 | 3000 | 4000 | 5000 | 6000 | |
| Time in seconds | ||||||
| Dimension n | ||||||
|---|---|---|---|---|---|---|
| 1000 | 2000 | 3000 | 4000 | 5000 | 6000 | |
| Time in seconds | ||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Howlett, P.; Torokhti, A.; Soto-Quiros, P. Decrease in Computational Load and Increase in Accuracy for Filtering of Random Signals. Mathematics 2025, 13, 1945. https://doi.org/10.3390/math13121945
Howlett P, Torokhti A, Soto-Quiros P. Decrease in Computational Load and Increase in Accuracy for Filtering of Random Signals. Mathematics. 2025; 13(12):1945. https://doi.org/10.3390/math13121945
Chicago/Turabian StyleHowlett, Phil, Anatoli Torokhti, and Pablo Soto-Quiros. 2025. "Decrease in Computational Load and Increase in Accuracy for Filtering of Random Signals" Mathematics 13, no. 12: 1945. https://doi.org/10.3390/math13121945
APA StyleHowlett, P., Torokhti, A., & Soto-Quiros, P. (2025). Decrease in Computational Load and Increase in Accuracy for Filtering of Random Signals. Mathematics, 13(12), 1945. https://doi.org/10.3390/math13121945





