Abstract
One of the reasons for the lack of commercial staircase service robots is the risk and severe impact of them falling down the stairs. Thus, the development of robust fall damage mitigation mechanisms is important for the commercial adoption of staircase robots, which in turn requires a robust fall detection model. A machine-learning-based approach was chosen due to its compatibility with the given scenario and potential for further development, with optical flow chosen as the means of sensing. Due to the costs, complexity, and potential system damage of compiling training datasets physically, simulation was used to generate said dataset, and the approach was verified by evaluating the models produced using data from experiments with a physical setup. This approach, producing fall detection models trained purely with physics-based simulation-generated data, is able to create models that can classify real-life fall data with an average of 79.89% categorical accuracy and detect the occurrence of falls with 99.99% accuracy without any further modifications, making it easy and thus attractive for commercial adoption. A study was also performed to study the effects of moving objects on optical flow fall detection, and it showed that moving objects have minimal to no impact on sparse optical flow in an environment with otherwise sufficient features. An active fall damage mitigation measure is proposed based on the models developed with this method.
MSC:
37M05
1. Introduction
1.1. Problem Statement
Field robots operating in urban environments are expected to traverse uneven terrain and varied environments. Terrain with discontinuous elevation changes specifically poses a challenge for robots to overcome. For urban environments, examples of terrain with severe and discontinuous elevation changes include stairs, steps, and curbs. Stairs are the focus of this work, as they are commonplace in urban areas. For example, Singapore, a largely urban nation, has a majority of its buildings being high-rises [1], which translates to a large number of stairs between levels. Robots that can traverse and operate in these places will thus have more paths of access and operation spaces opened to them, which expands their potential use cases [2].
However, at the point of writing, robots made for autonomous operations on stairs are not commercially available. One possible reason is the liability of robots falling down stairs during operation to the companies operating, distributing, and producing said robots. As the robot falls down the stairs, it builds up momentum, and this built-up momentum results in severe injuries to people or property on impact. Stairs have been noted to be a challenging terrain for robots, and robots operating on them face a constant risk of falling due to their geometry and other factors [3,4]. This constant risk of falling and its severe consequences are the largest factors against the commercial adoption of stair-accessing service robots.
Research has been conducted on fall prevention measures as a method to reduce this risk. One notable example is the work of Ramalingam et al., where a stair-accessing robot uses computer vision to identify potential slipping and collision hazards. The robot will then plan its path around these hazards to avoid them [5]. However, real-world conditions are chaotic and unpredictable, and fall prevention measures cannot help if dynamic environmental elements cause the robots to fall. For example, fall prevention measures cannot help in a scenario where a moving person or object collides with the robot. Thus, these measures alone may not be sufficient to assuage the fears of companies or clients. Fall damage mitigation measures are to be devised as a final safety net for staircase robots and thus encourage their development and adoption for commercial use.
1.2. Fall Damage Mitigation
Fall damage mitigation measures can be classified as either active or passive. Passive fall damage mitigation utilizes mechanical means of absorbing energy from the impact of the fall, such as with padding or elastic internal structures, demonstrated by the works of Chen et al. [6], Billeschou et al. [7], and Wang et al. [8]. These measures do not require active control measures for their operation, making them simpler to integrate into designs. However, the amount of energy these measures can absorb is proportional to the volume of the shock absorption material, leading to a trade-off between compactness, which in turn affects the robot’s maneuverability, and efficacy. Moreover, these measures generally do not prevent the robot from continuing to slide or tumble down the stairs and colliding with people or objects, which is the most significant hazard to arise from a staircase robot falling, as discussed earlier. Thus, active fall damage mitigation will be considered for the work reported in this paper.
Active fall damage mitigation measures initiate actuated or powered mechanisms in response to a fall or potential fall to arrest the robot’s fall before impact. This approach can be seen in the works of Yun et al. [9], Anne et al. [10], and Tam et al. [11], where robots extend out their limbs to brace against the environment to halt their falls. This type of result is desired for staircase robots, making it the preferred choice for staircase robots over passive measures.
However, active fall damage mitigation requires reliable fall detection methods to identify when and how the robot is falling in order to properly react and activate relevant measures. Thus, this work focuses on fall detection for stair-accessing robots to serve as a foundation for future works on active fall damage mitigation.
1.3. Fall Detection
Fall detection models processing the sensor data are either physics-based first principle models, such as an inverted pendulum model, or empirically-based models, such as a machine learning model. Inverted pendulum models, a physics-based model, are commonly used for predicting falls, with developments made over many years to enhance said capability in different scenarios [11,12]. For legged robots specifically, N-step capturability is used for fall detection, which is defined by whether a robot can resume its planned trajectory within N steps of its movement. One example is the work by Sun et al., which uses an N-step capturability model for fall detection as part of its locomotion controller and achieved a 95% fall detection success rate in simulations [13]. These models are rather well-researched, reliable, and accurate for their purposes. However, they generally assume the robot will fall from tipping over, while staircase robots may fall without tilting initially or at all due to being knocked off the steps, slipping, or other perturbations not represented in the models. Such cases will be further elaborated upon in Section 3.4. Thus, physics-based models are not suitable for this work.
Machine learning (ML) models are trained using datasets of body state data in order to determine the body state of the robot. In the context of fall detection, body states consist of when the robot is operating as per expectations and the different manners in which it is falling. One example is the work of Mungai et al., which managed to achieve a 100% accurate classification on 81 real-world data samples obtained via experimentation for a bipedal robot being pushed along its x-axis [14]. Other examples of ML-based fall detection include the works of Igual et al. and Zhang et al., where they managed to develop ML-based models for fall detection with 95% and 91.77% accuracy, respectively [15,16]. In this case, machine learning models can be trained to recognize falls triggered by being knocked off steps without being tilted, which inverted pendulum models cannot detect or represent. This makes ML models suitable for fall detection in the context of staircase robots.
Unlike the aforementioned works, the fall detectors produced by the approach developed in this work do not just aim to detect the occurrence of falls; they also seek to identify the manner in which the robot is falling. The trained fall detection models are able to first identify the presence and manner of a fall before engaging the corresponding fall damage mitigation control policy. Having an ML model first identify the presence of certain conditions before triggering a policy to act in response is commonly performed in robotics. One example was by Wang et al. for lychee picking, where a color-based filter is first used to identify the presence and location of ripe lychees before engaging a customized version of the Fully Convolutional Anchor-Free 3D Object Detection (Fcaf3d) neural network model to identify the point to cut the branches for harvesting [17]. Thus, this work focuses on properly identifying the manner in which the robot is falling, as compared with most works in existing literature, which seek to merely identify the occurrence of falls itself.
ML models require a large amount of data to train the models. For this work, simulations are used to generate the data required for training the models instead of collecting data using physical sensors and extensive experimentation. This is a common approach for creating training datasets when it is infeasible to create a sufficiently large one via real-world experimentation and data collection. One example is by Fernando et al., where a simulated forest environment in Unreal Engine is used to generate pictures of forest fires under different environmental conditions. A few ensemble deep-learning models were trained with the resulting dataset, and they achieved accuracies between 88.33% and 93.21% [18]. Zhu et al. use renders of 3D models of industrial parts to train neural network models to identify either the part or its assembly status. Depending on the tasks, the models achieved 42.1% to 93.5% accuracy [19]. Wu et al. generated nighttime photos of pineapples using photos taken during the day to facilitate nighttime pineapple harvesting using robots [20].
For fall detection, Collado-Villaverde et al. use Unity, a game engine with physics simulation capabilities, to generate fall data for human falls due to the difficulty and risks of gathering data from humans [21]. A similar issue arises for creating datasets for robot falls in this work for ML model training due to the high risk of damaging expensive and delicate sensors over repeated impacts and shocks from a physical data collection device falling down the stairs, as well as the manpower and time needed for the experiments. Thus, this work opts to use Gazebo, a software commonly used for simulating robot behavior and interactions, to generate the training dataset. The approach used for generating training datasets using Gazebo simulations will be elaborated upon in Section 4.3 and Section 5.1.
This approach, known as sim-to-real, has also been used in training classification models. The most common issue with this approach is known as the sim-to-real gap, where differences between the simulation and the actual environment cause inaccuracies to occur when the classification models, trained on datasets generated from simulations, are to classify data from the real world. This was the primary challenge faced in this work, as with other works on sim-to-real classification model training.
The ultimate goal of this study beyond this work is to deliver a fall damage mitigation system for stair-accessing commercial service robots. Thus, the fall detection models generated by the approach in this work will need to be shown to contribute towards this goal. A fall damage mitigation mechanism will thus be proposed, designed to work with the fall detection models generated. Such a mechanism is expected to halt the fall of the robot with minimal infrastructure requirements for its implementation.
1.4. Optical-Flow-Based Approach for Fall Detection
Fall detection requires sensor data, which for fall detection has traditionally been inertial measurement unit (IMU) data on the motion and orientation of the robot. This can be seen in Endo et al.’s [22] and Kurtz et al.’s [23] work. Instead of IMU data, this work instead opts to use optical flow data based on camera data. Robots generally already possess cameras, especially those used for reconnaissance, surveillance, and patrol, one example being the Falcon robot from Semwal et al. [24]. This allows for optical flow to be used in conjunction with, or instead of, IMUs for orientation and acceleration data. In some cases, the robots’ motions make IMUs impractical for tracking their motion and orientation, hence requiring an alternative sensor. Extremely small robots, such as microdrones, may not be able to accommodate a suitable IMU within their tight weight and volume budget and will thus opt to use optical flow instead if they already use a camera [25]. For some robots, their motions may have long flight times with large impulses during motion, such as legged robots with hopping gaits that subject themselves to large impulses when landing and jumping off the ground, and most of their gaits have them be in the air. That, in turn, results in unconstrained error growth, which affects orientation and motion tracking [26]. While IMUs are the most common sensors used for orientation and movement tracking, they may not be viable for all situations, which is why this work opts to explore the use of optical flow data for fall detection.
Optical flow has been shown to be reliable in determining the heading of robots in motion [25,27], which involves tracking the angular and linear velocity and acceleration. From these, the relative orientation can be calculated, thereby allowing cameras to fulfill a similar purpose to IMUs while avoiding the aforementioned downsides. In some situations, typical cameras face issues with exposure and motion blur. For these scenarios, using specialized visual sensors has been shown to overcome these issues [28,29].
One potential concern for using cameras over IMUs is in surroundings with moving visual elements. These may result in noise should they enter the camera’s field of view. Given that this system is meant for commercial service robots that operate in urban environments, such elements are expected in the form of pedestrians, vehicles, and other moving objects in the robot’s operating environment. Its impact on optical flow fall detection will thus need to be studied.
Most current literature on robot fall detection uses IMUs and/or sensor data on actuator/motor status, such as its position and current draw. While the use of optical flow data based on a camera installed on the robot is performed for heading detection [25,27], pose estimation [26], and vibration detection [30], it has not been performed for robot fall detection. As all these tasks are commonly performed with IMUs and the former three have been demonstrated to work with an optical-flow-based system, it stands to reason that optical-flow-based systems are viable for fall detection as well. Thus, this work seeks to utilize optical flow data for robot fall detection purposes.
1.5. Key Contributions and Introduction of Subsequent Parts
With this introduction and understanding of the field of robotics for fall detection and mitigation, this work aims to devise and verify an approach for generating a fall detection model via machine learning, trained with datasets generated using a simulation. The approach will be assessed through its performance in classifying data obtained from physical sensors. An active fall damage mitigation measure will then be proposed based on the fall detection model developed and the defined scenarios.
Compared with what was performed in existing literature, the approach in this work is unique in three respects. Firstly, it is designed for commercial service platforms, which tend to have simpler morphologies, on staircases, while most literature on robot fall detection is on legged platforms on flat terrain. Secondly, it not only detects the occurrence of falls, which is the case for most fall detection models, but it also determines the manner in which the robot is falling. Thirdly, it uses optical flow data, while most existing works opt to use IMU data supplemented by joint sensor data. This work approached the topic of robot fall detection from a different angle in a new context that is unexplored in current literature.
Section 2 presents the research objectives of this work, while Section 3 provides background information on falling detection for staircase robots. Section 4 presents the methodology used to generate fall detection models, which will be assessed by generating a fall detection model based on a physical model and then having the model classify fall data obtained from said physical model. Section 5 studies the effects of the presence of moving objects within the field of view of the camera for optical-flow-based fall detection. Section 6 proposes an active fall damage mitigation mechanism to work with the fall detection model. Section 7 discusses the results of this work and addresses limitations in its methodology, and Section 8 concludes this paper.
2. Research Objectives
Section 1 explored the main issue regarding the deployment of commercial stair-accessing service robots, their background, motivation for research, and related prior studies. Through this exploration, three objectives are identified for the study presented in this work.
The first objective is to verify that physics-based simulation-generated data is sufficient to train a robot for real-life fall detection applications. Given that this system is intended to be used for commercial platforms, the system has to be easy to use with minimal adjustments needed, as that translates to lower deployment costs for commercial entities. The trained model will be assessed on its ability to classify data from physical sensors with no adjustments or modifications.
The second objective is to assess the impact of moving visual elements in the camera’s field of view on fall detection via optical flow. As the system is meant for commercial service robots that operate in the field, it needs to be robust against expected sources of noise to be practical. Thus, the system’s performance in the presence of visual noise will be tested.
The last objective is to propose a suitable active fall mitigation measure that complements the fall detection system chosen. It is to demonstrate how the fall detection models developed by the approach in this work can contribute towards active fall damage mitigation for stair-accessing commercial service robots.
3. Background
3.1. Comparison Between Optical Flow and IMU Data for Fall Detection
For fall detection in robotics, as well as any other task that requires information on the robot’s movement in space relative to the world, an inertial measurement unit (IMU) is the most common sensor used. IMUs provide information on the robot’s current orientation, angular velocity, and linear acceleration. In the case of service robots, which have an extremely simple morphology, as discussed previously, that is all the information needed for fall detection.
Compared with using IMU data, optical flow data has two key shortcomings. Firstly, optical flow data may be influenced by noise arising from moving visual elements within the camera’s view, which is the subject of investigation for Section 5. Secondly, using optical flow data has greater computational requirements than using IMU data. In a previous work by the authors, machine learning methods have been employed for fall detection using IMU data [31]. The LSTM models used in that paper are built in the same manner, demonstrating that these models are generally sensor-agnostic. Thus, given the same model hyperparameters, detection duration, and sensor sampling rate, the models should be similar and thus have similar computational requirements. However, optical flow data has to be extracted from the camera data, which leads to additional computational costs compared with using IMU data, which can be used directly from the sensor without any preprocessing. Monitoring the computational load when running the optical flow data extraction program and running the classifier shows that the optical flow data extraction process imposes at least 9.12 to 10.13 times the classifier’s computational load. The need to preprocess raw sensor data to use an optical flow-based fall detection system will thus cause it to have a higher computational requirement than an IMU-based system, which does not need to do so.
However, an optical flow-based system addresses the downsides of an IMU-based system. As brought up in Section 1.3, IMUs have problems with sensor drift, as noted by Singh et al. [26]. This results in a mismatch between what the sensor detected and the actual movement of the robot that accumulates over time. Optical-flow-based methods do not have this issue, as they work by referencing movement in the environment relative to the robot. This makes optical flow-based systems a more viable alternative than IMU-based systems in scenarios where the effects of sensor drift are unacceptable. Moreover, as raised by Expert et al., certain classes of robots, such as microdrones, prefer to use optical flow over IMUs due to design constraints [25].
An optical-flow-based system can also be used to enhance the accuracy of an IMU-based system through sensor fusion. A similar approach was used by Hu et al., where a 3D LiDAR and a depth camera were used for assessing the depths of cracks on building surfaces by combining the data obtained from both sensors, achieving better results than solely using the depth camera [32]. Optical flow data and IMU data may be used in such a manner to produce a more accurate fall detection system as well.
Despite its shortcomings, an optical-flow-based fall detection system is a viable and sometimes preferable alternative to an IMU-based system. It can also be used in conjunction with the latter to improve its accuracy. Thus, optical-flow-based fall detection systems have significant research and practical value for study.
3.2. Framework of Study
The following framework is used for this study. The general framework can also be adapted for the study of other failure states for robots.
- Task space: the design specifications for the robot, namely the tasks it must perform, the terrain it has to traverse, and other relevant details about its operation. This work is primarily concerned with service robots made to traverse and operate on staircases.
- Design space: the design of the robot based on specifications in the task space. The focus of this work will be on the mechanical and control design of the robot.
- Incident space: the failure state for the robot. This work focuses on the robot falling on staircases.
- Sensor space: sensor data from the robot. This work uses optical flow data from a camera.
- Detection space: the processing of sensor data to determine (a) if it is in the incident space and (b) the manner in which it is in said space. In this work, it means if and how it is falling.
- Action space: the action of the robot as a response to entering the incident space, which in this case refers to the active fall damage mitigation measures triggered.
This work’s primary focus is on the detection space, given its objective of verifying the chosen approach of fall detection. The task space is constrained to commercial service robots. This constraint on the task space leads to a corresponding tightening of the design space.
3.3. Current Commercial Service Robots
Most ground-based, commercial mobile service robots consist of a single unit with either wheels or tracks for locomotion and no articulated limbs or segments. This is observed from the catalogs of commercial service robot companies with the largest market shares, as identified by market reports [33,34,35,36,37]. For the major companies producing commercial mobile ground service robots, the majority of them, such as Orionstar [38], Keenon Robotics [39], Gausium [40], Starship Technologies [41], Yujin Robot [42], and others [43,44,45,46,47,48], only produce service robots that are of the previously mentioned morphology.
For other commercial mobile ground service robot companies, Softbank Robotics [49] and ABB [50] mainly produce robot platforms of that morphology, with a minority of the platforms with articulated arms and a forklift end effector, respectively. GeckoSystems’s platform is a wheel-based platform with articulated arms for interaction [51]. Pudu Robotics, which has been established to have the largest number of commercial service robots deployed [37], has the majority of its platforms being of the aforementioned morphology, with some that have articulated arms and/or legs [52]. Boston Dynamics has two commercial ground-based platforms, Spot and Stretch, the former being a robot with four articulated legs and the latter being a wheeled platform with an articulated arm [53]. Based on these findings, it can be concluded that the majority of commercial mobile ground service robots’ morphologies are a single rigid body with wheels or tracks for locomotion.
Of the commercial mobile service robots observed, only two platforms, Boston Dynamics’s Spot and Pudu Robotics’s D9, are mechanically capable of climbing stairs. Both are legged platforms meant to operate in a multitude of rough and/or uneven terrain and are not specifically built for staircase environments. Being legged robots with articulated and actuated limbs, they also deviate from the aforementioned design trend for commercial service robots. It can thus be concluded that stair-accessing robots are rare in the commercial service robot landscape.
What are normally marketed as purpose-built staircase service robots, at the point of writing, are semi-autonomous or manually controlled powered logistics platforms for moving heavy loads on stairs. Some examples are platforms from Zonzini [54] and AATA International [55]. No purpose-built autonomous stair-accessing commercial service robots are found at present. Thus, the utilization of these platforms requires constant human control and supervision during their operation, representing a potential manpower cost reduction by automating these platforms. The lack of automation could be a result of liability issues, as stated in Section 1.1.
The aforementioned stair-accessing logistics platforms have the ability to lift and tilt their payloads to assist in loading and unloading and to keep their cargo level on stairs, as well as lift their front through a jointed bar below the platform to allow them to ascend stairs. However, during active operation on stairs, they generally behave like a single rigid body, as these articulated parts are locked during operation to ensure platform stability when moving. It is reasonable to assume that an autonomous version of these platforms will be mechanically identical in its operation.
3.4. Robot Fall Modeling
As established in Section 3.3, stair-accessing service robots can be treated as a single rigid body when operating on stairs. Thus, they can be treated as a single rigid body for fall modeling purposes. The forces acting upon such a body—contact forces, gravity, and other forces exerted on it—can be assembled into a wrench. A wrench is the summation of all forces and torques acting on a rigid body into a screw, which in turn is made up of a three-dimensional force vector and a three-dimensional torque vector about a point acting on said body [56].
This wrench can be broken down into six (6) components: the linear force components along the x, y, and z-axes and the torque components about these axes, the directions represented by , , and , respectively, as shown in Figure 1a. Movements along and are generally the focus of conventional fall detection using first principle models, as they can shift the robot’s center of mass (CoM) past its base, thus unbalancing the robot. The linear force components and torque along do not normally result in such a change in the robot’s CoM’s position relative to its base and are not accounted for in inverted pendulum fall detection models.
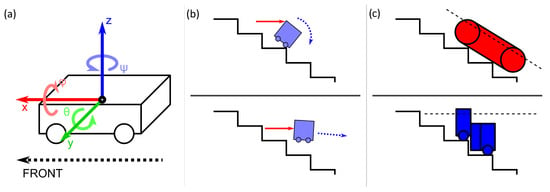
Figure 1.
(a) Axes of reference on a robot for discussions in this work. Forces along the x-axis are represented in red and torque about the x-axis is represented in pink, forces along the y-axis are represented in green and torque about the y-axis is represented in light green, and forces along the z-axis are represented in blue and torque about the z-axis is represented in light blue. (b) The two extreme possible ways for a robot to fall off stairs, in real-world scenarios, falls tend to be in between these two extremes. (c) Two general types of stair-climbing robots: those that align with the gradient of the steps and those that remain parallel to the ground when climbing.
However, for staircase robots, these components can still lead to falls without the and components, as it can lead to the robots being knocked off the steps they are on. Depending on the way the robot is knocked off the step, no significant movements along and may be present until the first impact occurs or later, and fall damage mitigation measures need to be triggered and fully deployed before impact. Figure 1b shows two scenarios in which a staircase robot can fall, where the second scenario is what inverted pendulum models cannot detect in time.
Most staircase steps’ depths are within a narrow range due to anthropometrical factors. Thus, it is possible to account for any movements that can force a robot off a step and expand the inverted pendulum model for the use of staircase robots. This work, however, chooses to use machine learning trained with simulation data to generate its fall detection model instead.
Using machine learning over first principles models allows for two potential pathways for further development. Firstly, the use of unsupervised learning can allow for better coverage of edge cases and rare scenarios. Secondly, reinforcement learning can be used to directly create a fall mitigation control model, with the robot having its active fall damage mitigation measure modeled in the simulation. The unsupervised learning approach has a greater capacity to address environments that are not standard stairs, such as spiral or curved staircases, while the reinforcement learning approach eliminates the need to separately develop a fall mitigation control model to work with the fall detection model, making the ML-based approach more preferable to a first-principles-based approach.
Meanwhile, using simulations to generate training data is easier and cheaper than doing so with a physical data collection setup, as there is no need to build a custom data collection environment at a location with a data collection device that may contain expensive and delicate sensors. It also allows for easier expansions for different scenarios, as there is no need to physically build a new setup for each scenario. Thus, this work opts to use simulation data for training ML models.
However, simulation data, while easier to produce, has an issue with the reality gap [57,58]. A significant reduction in performance as a result of this will negatively impact the viability of the developed models in real-world applications. Thus, a supervised ML-based fall detection model is first built to assess the viability of the approach. Both of the aforementioned approaches to further development can be taken using the foundation built by this work instead of starting from scratch. As such, the chosen approach has good potential for further development.
3.5. Ethical Considerations
Filippo Santoni de Sio presented the results of the Ethics of Connected and Automated Vehicles: recommendations on road safety, privacy, fairness, explainability and responsibility by the Horizon 2020 European Commission Expert Group, which gives a set of recommendations to ensure that autonomous vehicles minimize harm to people around them during their operation [59]. The recommendation to reduce physical harm to persons is the chief goal of this work, and recommendations on having the autonomous systems be auditable and accountable are relevant to this work.
Explainable artificial intelligence (XAI) aims to create machine learning systems where the factors that lead to their decisions are explained by the models. One example is the work by Lin et al., where the Shapley Additive ExPlanations (SHAP) technique is used to allow users of a machine learning model for tunnel-induced damage forecasts to comprehend the reasons leading to a particular forecast [60]. In the context of this work, such a technique can be used to detail the decision process behind a fall detection system’s forecast of potential falls and the manner of the fall, thus allowing for the model to be auditable and accountable. While an XAI system was not attempted in this work as it is outside its scope, it is a future priority for the system to fully fulfill its purpose in an accountable manner.
One other ethical concern for this fall detection system is that it is a machine-learning-based system. As noted by Perez-Cerrolaza et al., the accuracy of current state-of-the-art RL-based systems is orders of magnitude lower than industry standard [61]. Thus, presenting an ML-based safety system in an industrial or commercial context may lead to mismatched expectations. For ethical reasons, the true risk and rate of failure of such systems must be properly conveyed to all relevant stakeholders, and the system is to be supplemented by other means, mechanical, software-based, or otherwise, to better bridge the gap between the accuracy of ML-based systems and the expected industry standard.
4. Fall Detection for Robots on Staircases
4.1. Problem Definition
A brief study was conducted to assess the potential ways a stair-accessing commercial service robot could fall on the stairs. The platform for reference is the sTetro platform, a stair-assessing platform made for stair cleaning developed in the authors’ lab [5], which the authors are familiar with and have immediate access to.
The platform consists of three modules, one in front of the other, and the modules can move vertically relative to each other. To climb upstairs, the modules are moved up the next step one at a time until the whole robot is up on top of the next step, and the reverse is performed for descending. During operation, the robot is always oriented such that its front face is parallel to the rise of the steps, and the inter-modular movement mechanism is self-locking [5].
Thus, for fall modeling purposes, the platform can be taken as a single rigid cuboid body aligned with the stairs. For this work, the scenario is defined as the robot being stationary at a landing at the top of a flight of stairs, having just ended its task and being on standby. This scenario was chosen for this work as the robot on standby is quiter and less noticeable and is thus more likely to be accidentally bumped into by passers-by, leading to its fall.
For the scenario used, the robot will most likely be knocked into by people or other objects from its front and sides. It is much less likely to be hit from down the stairs of the robot due to it being more visible from there, as illustrated in Figure 2a. Given how the forces will generally be applied on the robot as a result, which is on its front and sides, five (5) classes of falls were identified to be possible: Backwards Fall (BF), Leftwards Fall (LF), Rightwards Fall (RF), Counterclockwise Pivot Fall (CCW), and Clockwise Pivot Fall (CW), forming the fall classes the model should identify. An additional No Fall (NF) condition is added as a control case.
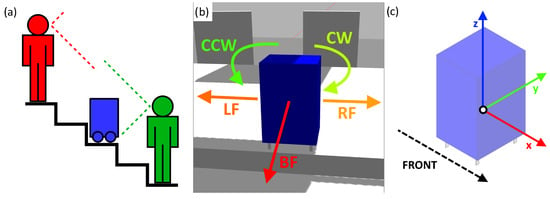
Figure 2.
(a) Field of view of people on staircases with the robot. (b) The possible fall types identified. (c) Axes of reference of the virtual model and prototype. The origin is at the geometrical center of the main body of the model (blue).
4.2. Setup for Physical Data Collection
To verify the model’s performance in classifying sensor data from real-world scenarios, a physical data collection setup is made for creating the test dataset based on the scenario outlined in Section 4.1. The setup for physical data collection is shown in Figure 3a. A physical prototype is constructed using a wooden frame, with a board at its base and four free-rolling caster wheels attached below to approximate the sTetro platform. The camera is attached to the front of the prototype near its top.

Figure 3.
(a) Setup for the physical data collection. (b) Camera view from cameras mounted at different angles.
A physical prototype is used here instead of the actual sTetro robot. Based on the scenario outlined in the previous subsection, robot autonomy and locomotion are not needed. Thus, a prototype capable of withstanding the impacts of repeated falls is used. The simpler prototype also minimizes the time and resources needed to repair it when something breaks as a result of the falls, which had happened once during data collection and was resolved with minimal issues.
For the physical test, the physical prototype started off two steps above the floor instead of being on top of a whole flight of stairs, and padding was added to both the corners of the prototype and the floor area it was to land on. These deviations from the established scenario are performed to further reduce the chances of damaging the prototype and the camera. While this does cause the prototype’s fall behavior to deviate from what would have happened in the scenario from the moment of first impact onwards, since the system needs to be able to react before the collision happens, it is only concerned with sensor data immediately after the moment of force application, prior to the first impact. Thus, this deviation is deemed acceptable.
The cameras are angled at 45 degrees upwards based on observations from a camera test, as seen in Figure 3b. When the camera was angled forward, parallel to the ground, or downward, the only thing within view of the camera was the stairs. Angling the camera upwards allows the camera to see more of its surroundings and be exposed to more visual features. Thus, the camera was angled upwards to maximize the number of visible viable features for optical flow.
Five different environments were used for data collection, as shown in Figure 4a. A total of 20 samples per class were collected for each environment, resulting in an evaluation dataset with a total of 600 data samples, with 100 samples per class evenly distributed across the five environments. The method to produce each fall type is presented in Table 1. The camera is triggered manually at the start and end of collecting each data sample.

Table 1.
Method of force application for each class of fall.
4.3. Simulation Setup
A simulated environment is set up as per Figure 5a–c, with the stationary virtual prototype positioned on the top landing of the stairs facing away from the steps. This environment is based on the scenario defined in Section 4.1, with the virtual prototype mirroring the design of the physical prototype shown in Section 4.2. Square tiles are arranged in a spherical pattern around the setup to provide visual features for optical flow. The virtual model is made to have the same general dimensions as the physical prototype used in Section 4.2 (Figure 5d).
The Gazebo environment has a gravitational constant of 9.8m/s2. The virtual prototype has the same dimensions as the physical prototype, with the free-rolling castor wheels represented by four cuboids to reduce simulation complexity. A frictional coefficient of 0.3 is used for the body of the virtual prototype. The simulation is illuminated with the default Gazebo settings, which is a white point light illuminating the environment from above, with shadows enabled.

Figure 4.
(a) The five environments used for data collection (b) A frame for one of the data samples illustrating the optical flow data extraction process. The optical flow vectors are represented with the red arrows in the same manner as in Figure 6.
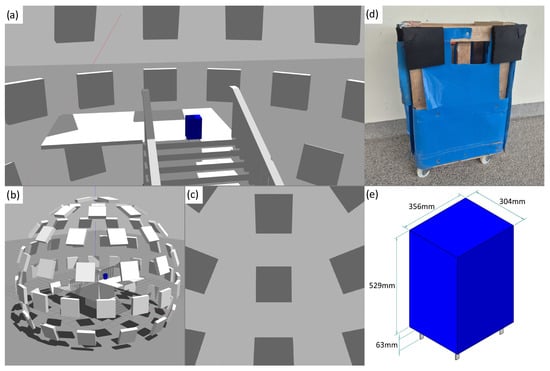
Figure 5.
(a) Simulated environment around the virtual model. (b) Simulated environment as seen from outside. (c) View from the camera. (a–c) are during the initial state of the simulation. (d) Physical prototype used for data collection in Section 4.2. (e) Virtual model made based on the prototype, with dimensions.

Figure 6.
Visualization of optical flow for each fall class. The arrows represent the movement of each feature from the previous frame, scaled by 10× about its location in the current frame for better visual clarity.
A Python script, running on Python 3.8.18, will apply a force to knock over the robot and record and compile the resulting camera data. Six ranges of force magnitude, direction, and points of application are identified to result in a fall corresponding to each case. The ranges are shown in Table 2, with the origin and axes shown in Figure 2c. The camera will capture images at 60 FPS, which will be used for optical flow data extraction. The pseudocode for this is presented in Algorithm 1. 2000 data samples were collected for each class.
| Algorithm 1 Pseudocode for optical flow dataset generation. |
| for number of classes do |
| for number of samples per class do |
| Generate values for the force to be applied, based on Table 2 |
| Applies force on robot in Gazebo via ROS commands |
| Start simulation and data collection |
| Run optical flow data collection as per the pseudocode in Algorithm 2 |
| Pause and reset simulation for next run (Simulation world is paused on startup by default) |
| end for |
| end for |

Table 2.
Magnitude and position of the force applied on the virtual model for each class along the x-, y- and z-axes. The resulting force will be a force with randomized magnitude, angle, and position within a defined range on the surface of the model. The minimum magnitudes are determined by the least amount of force needed to cause a fall at the point of the least leverage, i.e., the lowest point where a force is applied, with the maximum being set as twice the minimum force. For forces that do not contribute to the fall of its class, a range of −3.0 N to 3.0 N is defined to provide some variance between the samples. The range of locations for force application is determined by places the robot is likely to get hit, namely the top half of its front and side faces.
4.4. Detection of Falls Through Optical Flow
There are two types of optical flow: sparse and dense. Sparse optical flow picks up a specified number of features to track each frame, while dense optical flow does so for every pixel in a frame. Sparse optical flow is chosen as it uses fewer features, which means fewer calculations, and thus, less computational power is needed to utilize the resulting fall detection system. This is important, as the fall detection system is to be used for fall detection in real time; thus, the required computation must be kept to a minimum. The pseudocode shown in Algorithm 2 shows how the dataset is generated from the sensor data from the simulation.
| Algorithm 2 Pseudocode for sparse optical flow dataset extraction algorithm. |
| for number of frames specified, starting at second frame do |
| store grayscale of current frame and previous frame |
| generate list of best features to track from previous image with Shi-Tomasi Corner Detector |
| if list is empty then |
| pass |
| else |
| look for corresponding features and calculate magnitude of differences along X- and Y-axes for each pair of features in the current frame with the Lucas–Kanade method |
| generate 1D array of X- and Y-axes differences |
| if 1D array is not at full length (<10 valid features are found) then |
| fill in blank spaces with 0 |
| end if |
| write 1D array into CSV file |
| end if |
| end for |
The features used for sparse optical flow detection are then selected using the Shi-Tomasi Corner Detector, which searches for corners in each frame to serve as visual features. This approach uses the scoring function
and is better suited for tracking image features through affine transformation. In their work on their corner detector, Shi et al. found that an affine motion field is the most viable way of approximating feature movements, striking a good balance between simplicity and flexibility [62].
The Lucas–Kanade method is then used to calculate the change in feature movements. It takes a area around the feature and finds the change in position in the next frame. Assuming that the motions are small, the movement of each pixel can be approximated by what is known as the optical flow equation, which is
where
and
Given that there are two unknowns, u and v, the equation for the movement for a single pixel is underdefined.
The Lucas–Kanade method takes a area around the feature, as mentioned earlier, and as the movements of these pixels are assumed to be identical, there are now nine equations for two unknowns, and the problem is over-defined. The least squares fit method is used to find u and v, and the solution is given as
The simulation setup in Section 4.3 generates data samples as sequences of frames, which the sparse optical flow data extraction algorithm shown in Algorithm 2 uses as-is to generate a labeled dataset, which is henceforth referred to as the training dataset. The physical setup shown in Section 4.2, however, produces data samples as video clips. Thus, the algorithm for sparse optical flow data extraction is modified to first extract the individual frames from the video. The resulting dataset is henceforth referred to as the real-world dataset.
The training dataset is used to train 50 long short-term memory (LSTM) models. LSTM was chosen due to its capabilities in processing time-series data. The data to be analyzed and classified are a series of sensor data collected over time, making them time-series data. Recurrent neural networks (RNN) are designed for sequential data, which includes time series data, and among them, LSTM has been shown to be more adept at analyzing such data as compared with other RNN networks, given how it is more resistant against the vanishing gradient problem. Fifty models were made for evaluation to determine the average performance and consistency of the LSTM models produced by this approach.
The LSTM models used have an LSTM sigmoid layer, followed by a dropout layer of 0.5 to prevent overfitting, a dense ReLU layer, and lastly, a six-cell softmax layer. A total of 80% of the samples in each class from the training dataset are used for training, and 20% are used for testing.
4.5. Determining Optimal Hyperparameters for LSTM Models
There is a need to determine the best possible set of hyperparameters for the greatest possible accuracy. Four hyperparameters are identified for optimization, namely the following:
- Number of frames used: the duration of sensor data used for detection. In this context, it is the number of frames used for detection.
- Number of features: amount of visual features used for sparse optical flow-based fall detection.
- Number of epochs: number of epochs for training the LSTM classifier.
- Number of cells: the amount of cells per layer for the LSTM model.
Three different values per hyperparameter were assessed to find the most optimal combination. All four hyperparameters affect the LSTM models trained, while only the former two hyperparameters affect the optical flow dataset.
For the duration of detection, frame-by-frame analysis of 20 data samples per class from the dataset collected in Section 4.2 was performed. The results are presented in Table 3, with the shortest time from force application to first impact being 0.4 s. The duration is measured by counting the number of frames from when the movement started to when the first impact against the environment is observed. As the falls and the start of each video capture were triggered manually and thus have varying amounts of time between them, frame-by-frame analysis is the most reliable way to determine the initial moment of force application and the moment of impact. Thus, an active fall damage mitigation system is expected to be fully deployed within 0.4 s for it to be effective in this case. The duration of detection also has to account for the time needed for fall mitigation measures to activate and deploy. The three durations assessed are 0.1 s, 0.15 s, and 0.2 s from force application, which translates to 6, 9, and 12 frames, respectively.

Table 3.
Time taken from force application to fall, in seconds. The shortest time to fall (0.4 s for LF) is bolded.
For the number of visual features used, the quantities chosen for analysis are 10, 15, and 20 features. The numbers of epochs and cells for the LSTM models to be assessed are 60, 80, and 100 and 100, 150, and 200, respectively. For this test, 10 models for each combination of hyperparameters were tested, resulting in a total of 810 LSTM models generated. Nine test datasets were generated using physical data obtained from Section 4.2. The test datasets for this test contain 20 samples per class out of the full 100 samples per class due to time constraints.
Table 4 shows the average accuracy for each hyperparameter value tested, and Table 5 shows the average accuracy for each hyperparameter value combination. The standard deviation of the models’ accuracies for each combination of hyperparameter values ranges between 0.412 and 1.612. For the epoch and cell count used, overfitting was not observed based on the loss curve of the models.

Table 4.
Average accuracy for each hyperparameter value. The highest average accuracy for each hyperparameter is bolded and bracketed.

Table 5.
The average accuracy of the LSTM models for each hyperparameter combination, with a color gradient applied to better visualize the results (green—high, red—low). The average accuracy of the chosen hyperparameter combination is bolded and bracketed. The highest average accuracy is underlined and italicized.
Based on Table 4, the best combination of hyperparameter values is nine frames and 10 visual features used, with 80 epochs and 200 cells for training the LSTM model, hereby referred to as Combination A. While it is not the best-performing combination according to Table 5, it is still relatively high-performing compared with other combinations, being at the 85th percentile. The best-performing hyperparameter value combination hereby referred to as Combination B, is identical to Combination A except for using 15 visual features instead of 10.
A high degree of variation is observed between the accuracies of each model for any given combination, and Combination A and Combination B only differ in one hyperparameter value. Moreover, Combination A neighbors Combination B. Thus, the hyperparameter value combination used is chosen based on the best-performing individual hyperparameter value for each hyperparameter instead of the best-performing combination. Combination A will be used for all the following experiments in this work.
4.6. Results
Figure 7 shows the results of the 50 LSTM models categorizing the real-world dataset obtained from Section 4.2. The models have a mean accuracy of 77.32% with a standard deviation of 0.0053.
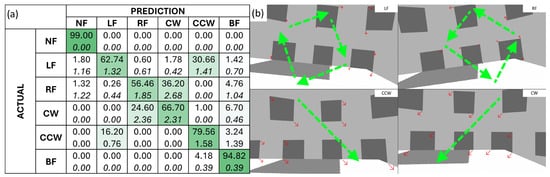
Figure 7.
(a) Confusion matrix depicting the prediction outcomes of 50 LSTM models on the real-world dataset. The mean prediction is given at the top of each cell, and the standard deviation of the outcomes is given in italics below. The cells are shaded based on the mean prediction, with a darker green for a higher mean. (b) Frames from the simulation with the optical flow vectors represented by red arrows visualized for the LF, RF, CCW, and CW classes. An illustration of the general optical vector flow for each fall class is given in green dashed arrows, while the actual optical flow vectors for each frame are shown in red arrows.
The major sources of miscategorization are between LF and CCW and between RF and CW. As shown in Figure 7a, the models are more likely to mistake LF for CCW and RF for CW than the reverse. Both NF and BF are detected with high accuracy, with a 0.63% false positive rate, a 0.00% false negative rate for NF, a 3.26% false positive rate, and a 4.41% false negative rate for BF.
The high rate of miscategorization between LF and CCW and between RF and CW may be due to the general optical flow vector pattern for the fall types. As seen in Figure 7b, the optical flow vectors for LF and RF go in a clockwise and anticlockwise direction, respectively, with the center of rotation depending on the exact fall motion of the robot and the position of the camera. Hence, depending on the position of the center of rotation and the distribution of the sparse optical flow features in the frame, the resulting sparse optical flow vectors may be similar to those for CCW and CW. Comparing Figure 7b and Figure 4b, the sparse optical flow features are relatively evenly distributed in the frame for the simulation, which is not the case observed in Figure 4b, where the sparse optical flow features are more clustered together.
Another difference observed between the video data obtained from the simulation and the real-life experiments for optical flow data extraction is motion blur. Motion blur is absent in the former and present in the latter. The amount of motion blur is dependent on the shutter speed, which, for the camera used in this work, is automatically adjusted depending on ambient light levels. With the current simulation and experiment setup, it is unfortunately impossible to gauge the effect of motion blur on optical flow feature extraction.
In terms of fall detection, which is the detection of the occurrence of falls, the LSTM models developed by this approach have an average score of 0.9968, with a 0.63% false negative rate and a 0.00% false positive rate. In this context, it will not detect a fall when the robot is operating normally, which ensures smooth operation for the robot without being mistakenly interrupted by the fall detection system activating the fall damage mitigation system. On the other hand, the fall detection system will miss 0.63% of fall instances and not activate the fall damage mitigation system. Given that the models are meant to be used in safety systems, false negatives are far more important than false positives. Thus, the current false negative rate, while low, is not ideal.
5. Optical Flow Fall Detection in Dynamic Environments
Commercial service robots are expected to operate in public environments, often in the vicinity of human activity. As such, robots utilizing optical flow will capture moving features as a result of moving objects within the camera’s field of view, especially if they obscure static features in the background that the optical flow algorithm can otherwise use. These features will create noise in the data, which will result in false detection.
As such, the fall classification system is to be assessed in two respects. Firstly, how is the model’s ability affected in scenarios where moving objects are present in the camera’s field of view? Secondly, for such a scenario, does generating the training dataset with a simulated environment that has moving visual features improve the model’s performance? The simulation setup, physical data collection and generation setup, and testing procedures will be based on the procedures established in Section 4, with some modifications.
5.1. Data Collection and Model Generation
The simulation setup for generating data in a dynamic environment is identical to the setup shown in Section 4.3 with one addition. Four checkerboard panels are positioned within the field of view of the camera, as shown in Figure 8a,b. At the start of the simulation, the panels will be subjected to a force that causes each panel to fly off in a random direction, creating random, moving features and obscuring static features in the background. The panels have collisions disabled to prevent them from affecting the fall of the robot should it collide with the latter. The movements of the panels are made to be completely random. This minimizes potential biases that may otherwise arise from their movement.
Figure 8.
(a) Simulated dynamic environment used for data generation. (b) View from the camera.
The hyperparameters used and the procedure for generating LSTM models are otherwise identical to Section 4. 2000 samples per class are generated to train 50 LSTM models. The resulting models, trained with the dataset generated from the aforementioned modified simulation setup, will henceforth be referred to as the test models. The models generated in Section 4 are used as a control and will be referred to as the control models for this section.
For physical data collection, the setup is shown in Figure 9e. The physical mockup is positioned on the edge of a raised platform. The platform is 160 mm above the ground, which is approximately the same height as a step on a flight of stairs. A screen is positioned before the platform and the robot such that it fills the camera’s field of view at the start of each round. As with the testing procedure in Section 4.2, padding was used to minimize potential damage to the mockup from testing.

Figure 9.
(a) Screenshot from the control video. (b) Camera view when testing with the control video. (c) Screenshot from video with moving features; the grey crosses move across the screen randomly during testing. (d) Camera view when testing the video with moving features. (e) Picture of the data collection setup.
Two test datasets were created with this setup. The first dataset was made with the screen displaying a static grid, as shown in Figure 9a and Figure 9b, respectively. The second dataset was made with the screen displaying the same grid but with moving grey crosses serving as dynamic visual features in the foreground, as shown in Figure 9c and Figure 9d, respectively. The procedure for data collection and dataset generation is otherwise identical to Section 4.2 and Section 4.4. The first dataset and second dataset are henceforth referred to as the control dataset and test dataset, respectively.
5.2. Results
Figure 10 shows the results of the control models categorizing both the control dataset and the test dataset. The trend of LW and CCW and RF and CW confusion observed in Section 4.6 holds true for both scenarios present. The control models achieved an average accuracy of 89.23% for the control dataset with a standard deviation of 0.0052 and an average accuracy of 92.96% for the test dataset with a standard deviation of 0.0064.
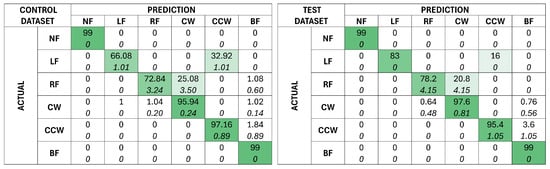
Figure 10.
Confusionmatrices depicting the prediction outcomes of 50 control models on the control (left) and test (right) dataset. The mean prediction is given at the top of each cell, and the standard deviation of the outcomes is given in italics below. The cells are shaded based on the mean prediction, with a darker green for a higher mean.
Figure 11 shows the results of the test models categorizing both the control dataset and the test dataset. As with the control models, the trend of LW and CCW, and RF and CW confusion holds true for both scenarios present, although they are less obvious due to their higher accuracy. The test models achieved an average accuracy of 94.65% for the control dataset with a standard deviation of 0.0075, and an average accuracy of 98.60% for the test dataset with a standard deviation of 0.0053.
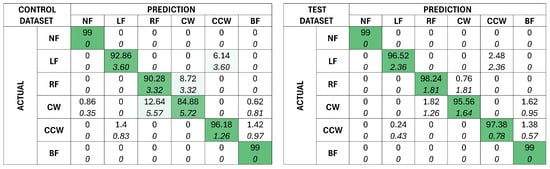
Figure 11.
Confusion matrices depicting the prediction outcomes of 50 test models on the control (left) and test (right) dataset. The mean prediction is given at the top of each cell, and the standard deviation of the outcomes are given in italics below. The cells are shaded based on the mean prediction, with a darker green for a higher mean.
The test models outperformed the control models reliably with similar levels of consistency overall. However, the standard deviation for individual outcomes is significantly higher for the test models than it was for the control models. To further evaluate the performance of the test models, the real-world dataset from Section 4.2 is used to assess them.
Figure 12a shows the results of using the test models to categorize the real-world dataset. As with the differences observed between the control and the test models categorizing the control and test datasets, the test models achieved a better overall accuracy than the control models, achieving an accuracy of 79.79% with a standard deviation of 0.0062. In terms of fall detection, it has an score of 99.99%, with a false positive rate of 0.00% and a false negative rate of 0.016%. Given the outcome of this experiment, the addition of noise in the form of dynamic visual features results in a more accurate detection model in environments with or without dynamic visual features present. The reason for this improved performance is unclear.

Figure 12.
(a) Confusion matrix depicting the prediction outcomes of 50 test models on the real-world dataset. The mean prediction is given at the top of each cell, and the standard deviation of the outcomes is given in italics below. The cells are shaded based on the mean prediction, with a darker green for a higher mean. (b) A frame from a test with dynamic visual features with the optical flow vectors visualized, the start of the arrows indicating the initial location of the features, the direction being the movement of the visual features, and the length being the magnitude of the movement, magnified 10x for better visual clarity.
The presence of dynamic visual features in the test dataset did not lead to a decrease in accuracy in either the control or test models, which may be a result of motion blur. Moving features will need to move faster than static features relative to the camera’s view in order to produce an optical flow that deviates significantly from the latter. However, due to the higher movement speed, moving features will end up blurrier to the camera. As sparse optical flow selects the best n number of features, features from static objects are more likely to be chosen over those from moving objects. This can be observed from Figure 12b, where the features selected were not from the dynamic moving features. The results from the test dataset being better than the control dataset, however, may simply be due to differences in motion while collecting the physical dataset. Since the falls of the physical prototypes were performed manually, they will result in differences in the falling motion caused, which in turn affects the results.
6. Proposal for Fall Prevention System
As stated in Section 1.2 and Section 1.3, the ultimate goal of this work is to develop an approach to generating fall detection models that can be used for active fall damage mitigation. Thus, a potential active fall damage mitigation system is proposed in this section to suggest how the models developed can be used for this purpose. The actual implementation and assessment of the proposed solution is, however, beyond the scope of this work.
6.1. Scenario
A robot is tasked with monitoring and inspecting an active construction site. It is to move between levels of the building under construction, and only stairs are available for traversal.
The robot in question is a reconfigurable stair-climbing platform based on the sTetro [5]. The robot consists of three segments that can move vertically relative to each other, and it uses said mechanism to climb upstairs step-by-step. The locations where an active fall damage mitigation mechanism can be mounted are indicated in Figure 13b, at the back and the top of the robot. No mechanism is to be mounted on the side to keep the robot narrow, allowing it to move better in narrow areas. The same is performed for the front of the robot, as most of the robot’s sensors are mounted at the front of the robot.
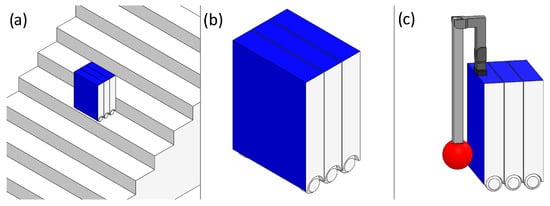
Figure 13.
(a) Model of proposed environment with service robot mockup. (b) Service robot close-up with available mounting area (c) Proposed fall damage mitigation system (3DoF arm).
6.2. System Proposal
A 3DoF arm is proposed for the fall damage mitigation mechanism, as shown in Figure 13c. In the event of a fall, the arm will stretch out based on the manner of the fall detected and brace against the steps behind it, as illustrated in Figure 14d–f. There are practically no infrastructural requirements for the use of this mechanism due to the design of the arm and the method of its usage, as it is bracing against the stairs itself.
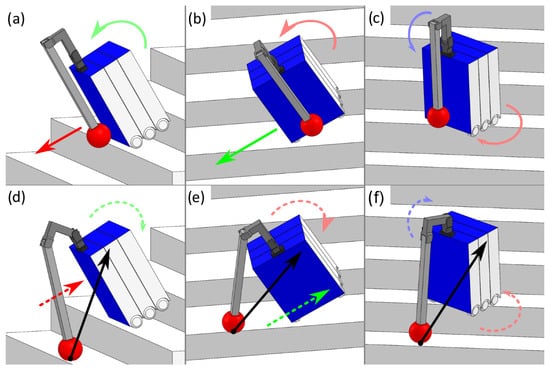
Figure 14.
Falls and the theoretical effects of the mitigation measures. With reference to the robot, linear movement along the x-axis are represented in red and rotational movement about the x-axis is represented in pink, linear movement along the y-axis are represented in green and rotational movement about the y-axis is represented in light green, and linear movement along the z-axis are represented in blue and rotational movement about the z-axis is represented in light blue. The black arrow illustrates the force acting on the robot as a result of the arm’s end effector making contact with the stairs. (a) Wrench for the BF fall scenario. (b) Wrench for the LF fall scenario. (c) Wrench for the CW fall scenario. (d) Arm movement and resulting wrench for the BF fall scenario. (e) Arm movement and resulting wrench for the LF fall scenario. (f) Arm movement and resulting wrench for the CW fall scenario.
As established in Section 3.4, the forces of the robot can be assembled into a wrench. Thus, as long as the forces produced by the arm pushing against the stairs can be assembled into a wrench of equal magnitude but in the opposite direction, it can halt the momentum of the robot falling. Aside from that, given that it forms another contact point for the robot with the stairs, it increases the chances of the robot settling into a stable three-point contact afterward.
Each of the five fall types corresponds to a combination of major force components along the x, y, and z-axes and/or major torque components about , , and , as shown in Figure 14a–c. While minor components can be present, the major components are what lead to the specific falls. Figure 14d–f showed how the arm can produce a counter-wrench to halt the fall of the robot, showing its potential effectiveness. Note that RF and CCW are not shown, as they are merely mirrored versions of LF and CW; hence, the arm will just need to mirror its motions along the same plane to halt falls from those categories. Thus, with the fall-type information obtained from the fall detection model, the controller can trigger a corresponding response to halt the robot’s fall.
The optical flow data is stored within a circular buffer, a special memory storage structure that stores the n most recent instances of data only. Its size is the amount of frames used for fall detection. This data structure is chosen as the model will only need the most recent few frames of data for fall detection. The buffer is updated every frame, and the data from the buffer is passed through the fall detection model.
The joints are powered by motors with worm gear gearboxes, as they are not backdrivable. This allows the arm to hold its position even without power, and the high gear ratio gives the arm enough strength to bear the weight of the robot and the load while it is partially borne by the robot. The arm has a textured soft rubber end effector, as shown in Figure 13c, providing grip regardless of the angle of contact while being mechanically simple. When the robot is in storage, the arm can be folded up, minimizing the space it occupies.
7. Discussion
The models trained in Section 4 have demonstrated that the approach presented in this work is viable for producing neural network models for fall detection on robots. By extension, this approach is also viable for training a neural network model to react and deploy countermeasures to catch the robot should it fall. The physics-based simulation-based approach in this work is demonstrably viable for training neural network models for fall detection on stair-accessing commercial service robots.
Being able to use a model that is solely trained with physical-simulation-generated datasets with no further adjustments needed allows for the neural network models to be trained for a relatively low cost. There is no need for a physical setup that has the required sensors for data collection, which could risk being damaged after sustaining repeated impacts from data collection. There is also no need for further refinement of the models after training, which translates to reduced manpower requirements and costs for using this system. This makes the system more attractive to corporate entities.
The presence of moving objects within the camera’s field of view is unavoidable for service robots, especially those meant to operate among people. Section 5.2 shows that the negative impacts from this are minimal for a sparse optical flow-based system, as moving objects form worse features than static objects and are thus not used over the latter. Assuming that the environment has sufficient features from static objects that are not obscured by the moving objects, those moving objects will not affect optical flow fall detection.
In terms of detecting the occurrence of falls, this approach produces models with similar performances to other robot fall detection models using conventional approaches. An accuracy of 99.99% with a 0.016% false negative rate is comparable with Sun et al.’s 95% fall detection rate [13], Mungai et al.’s 100% fall detection rate [14], Igual et al.’s 95% fall detection rate [15], and Zhang et al.’s 91.77% fall detection rate [16]. In this aspect, the fall detection accuracy of the models produced by this approach, which was verified with a real-world dataset obtained using a physical data collection setup, is on par with state-of-the-art models in the literature using conventional techniques.
As the models in the aforementioned works only look for the occurrence of falls, the categorical accuracy of the models from this approach is evaluated against other ML-based models using the sim-to-real training method. Wu et al.’s pineapple harvesting model achieved 86.6% accuracy [20], Fernando et al.’s SWIFT has an accuracy between 88.33% and 93.21% [18], and Zhu et al.’s models achieved accuracies ranging from 42.1% to 93.5%, depending on the task the models are supposed to fulfill [19]. The models produced by this work have a categorical accuracy ranging between 79% and 81%. Compared with the models mentioned earlier, the approach in this work has room for further refinement to produce models with comparable results.
This work produced an approach for developing fall detection models that not only detect the occurrence of falls but also the manner in which the fall occurs. It also uses sparse optical flow data for fall detection. These are the most novel aspects of this work compared with existing literature and represent a new way to approach robot fall detection.
Limitations
Motion blur from cameras having a potential negative impact on classification accuracy has been noted in Section 4.6, as it leads to visual features being obscured. There are two potential ways to mitigate issues stemming from this: firstly, using specialized cameras, as discussed in Section 1, and secondly, simulating motion blur in the simulation by replicating the relevant physical aspects of the camera, such as the shutter speed. Both approaches have their merits and drawbacks. However, a study comparing the performance improvements between the two is outside the scope of this work.
The data collection in this work is performed with a simple frame with a mounted sensor. This work assumes that the robot is stationary when the fall occurs and does not account for scenarios where the robot is moving as per its normal operations. Testing that scenario, however, will require some autonomy, control, and locomotion, which in turn may require fragile components. This increases the chances of damage from the repeated falls needed for dataset creation and the cost of the resulting damage. As such, that is left outside the scope of this work, as the focus is more on the viability of sim-to-real transfer for fall detection and classification.
This work used a supervised learning approach for training and thus required a labeled training dataset. Six classes of falls were identified based on a given scenario, and the simulation generated falls that fit within these classes for creating the training datasets. As the data generation process from the simulation is automated, the falls for each fall class, while varied, do not cover any potential edge cases to ensure that all data samples collected are correctly labeled. Thus, edge cases are underrepresented within the training data, which makes the resulting model prone to misclassifying these cases, as seen in Section 4.6 and Section 5.2.
As brought up in Section 4.6 and Section 5.2, the simulation environment allows for a fairly uniform distribution of optical flow features across the entire frame. This may not be available in real-world environments, as discussed in Section 4.6. Thus, this represents another source of bias in the training dataset, which is to be addressed in future works.
8. Conclusions
An approach to developing a neural network model for robot fall detection using optical flow data is devised and verified with experimentally obtained real-world sensor data. The approach utilizes a physics-based simulation to generate a training dataset for the neural network model, which is a more cost-effective method of generating said dataset as opposed to using a physical experimental setup.
The results presented in this paper demonstrate the accuracy of simulation-generated data-trained models for real-world fall detection. Thus, the chosen approach is valid for its application. Said approach, which is to use a simulation to generate a training dataset for creating a fall detection model, is more financially viable to implement compared with conventional methods utilizing data collection with physical sensors and setups. Creating a training dataset with a physical setup requires large amounts of resources, man-hours, and manpower, while the simulation-based approach depicted in this work can create an equally large and in-depth training dataset at a fraction of what the former approach needed. The viability of this approach demonstrated in this work shows that implementing a fall detection model can be financially and thus commercially viable for robot developers, making it suitable for adoption by industry.
This approach also has research potential if further developed and explored. The terrain and environment can be generated with a set of hyperparameters for more varied training scenarios, which in turn leads to more robust models. Alternatively, the approach can be adapted and expanded to work for non-regular terrain with changes in elevation, such as hill slopes and uneven ground. This approach to robot fall modeling has a lot of room for further research and development.
Author Contributions
Conceptualization, M.R.E.; Methodology, J.H.O. and A.A.H.; Software, J.H.O.; Validation, J.H.O.; Formal analysis, J.H.O.; Investigation, J.H.O.; Resources, J.H.O.; Data curation, J.H.O.; Writing—original draft, J.H.O.; Writing—review & editing, J.H.O., A.A.H. and K.L.W.; Visualization, J.H.O.; Supervision, A.A.H., M.R.E. and K.L.W.; Project administration, A.A.H. and M.R.E.; Funding acquisition, M.R.E. All authors have read and agreed to the published version of the manuscript.
Funding
This research is supported by the National Robotics Programme under its National Robotics Programme (NRP) BAU, Ermine III: Deployable Reconfigurable Robots, Award No. M22NBK0054, and PANTHERA 2.0: Deployable Autonomous Pavement Sweeping Robot through Public Trials, Award No. M23NBK0065, and also supported by A*STAR under its RIE2025 IAF-PP program, Modular Reconfigurable Mobile Robots (MR)2, Grant No. M24N2a0039.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Yuen, B. Romancing the high-rise in Singapore. Cities 2005, 22, 3–13. [Google Scholar] [CrossRef]
- Seo, T.; Ryu, S.; Won, J.H.; Kim, Y.; Kim, H.S. Stair-Climbing Robots: A Review on Mechanism, Sensing, and Performance Evaluation. IEEE Access 2023, 11, 60539–60561. [Google Scholar] [CrossRef]
- Pico, N.; Park, S.H.; Yi, J.S.; Moon, H. Six-Wheel Robot Design Methodology and Emergency Control to Prevent the Robot from Falling down the Stairs. Appl. Sci. 2022, 12, 4403. [Google Scholar] [CrossRef]
- Zhang, G.; Liu, H.; Qin, Z.; Moiseev, G.V.; Huo, J. Research on Self-Recovery Control Algorithm of Quadruped Robot Fall Based on Reinforcement Learning. Actuators 2023, 12, 110. [Google Scholar] [CrossRef]
- Ramalingam, B.; Elara Mohan, R.; Balakrishnan, S.; Elangovan, K.; Félix Gómez, B.; Pathmakumar, T.; Devarassu, M.; Mohan Rayaguru, M.; Baskar, C. sTetro-Deep Learning Powered Staircase Cleaning and Maintenance Reconfigurable Robot. Sensors 2021, 21, 6279. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Ding, W.; Yu, Z.; Meng, L.; Ceccarelli, M.; Huang, Q. Combination of hardware and control to reduce humanoids fall damage. Int. J. Humanoid Robot. 2020, 17, 2050002. [Google Scholar] [CrossRef]
- Billeschou, P.; Do, C.D.; Larsen, J.C.; Manoonpong, P. A compliant leg structure for terrestrial and aquatic walking robots. Robot. Sustain. Future 2021, 324, 69–80. [Google Scholar] [CrossRef]
- Wang, W.; Wu, S.; Zhu, P.; Li, X. Design and experimental study of a new thrown robot based on flexible structure. Ind. Robot. Int. J. 2015, 42, 441–449. [Google Scholar] [CrossRef]
- Yun, S.K.; Goswami, A. Tripod fall: Concept and experiments of a novel approach to humanoid robot fall damage reduction. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014; pp. 2799–2805. [Google Scholar] [CrossRef]
- Anne, T.; Dalin, E.; Bergonzani, I.; Ivaldi, S.; Mouret, J.B. First Do Not Fall: Learning to Exploit a Wall with a Damaged Humanoid Robot. IEEE Robot. Autom. Lett. 2022, 7, 9028–9035. [Google Scholar] [CrossRef]
- Tam, B.; Kottege, N. Fall Avoidance and Recovery for Bipedal Robots using Walking Sticks. In Proceedings of the Australasian conference on Robotics and Automation (ACRA), Brisbane, Australia, 5–7 December 2016. [Google Scholar]
- Li, Z.; Zhou, C.; Castano, J.; Wang, X.; Negrello, F.; Tsagarakis, N.G.; Caldwell, D.G. Fall Prediction of legged robots based on energy state and its implication of balance augmentation: A study on the humanoid. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 5094–5100. [Google Scholar] [CrossRef]
- Sun, H.; Yang, J.; Jia, Y.; Zhang, C.; Yu, X.; Wang, C. Fall prediction, control, and recovery of quadruped robots. ISA Trans. 2024, 151, 86–102. [Google Scholar] [CrossRef]
- Mungai, M.E.; Prabhakaran, G.; Grizzle, J.W. Fall Prediction for Bipedal Robots: The Standing Phase. In Proceedings of the 2024 IEEE International Conference on Robotics and Automation (ICRA), Yokohama, Japan, 13–17 May 2024; pp. 13135–13141. [Google Scholar]
- Igual, J.; Parik-Americano, P.; Becman, E.C.; Forner-Cordero, A. Time Series Classification for Predicting Biped Robot Step Viability. Sensors 2024, 24, 7107. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Gao, J.; Chen, Z.; Zhong, S.; Qiao, H. Fall analysis and prediction for humanoids. Robot. Auton. Syst. 2025, 190, 104995. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, G.; Cao, H.; Hu, K.; Wang, Q.; Deng, Y.; Gao, J.; Tang, Y. Geometry-Aware 3D Point Cloud Learning for Precise Cutting-Point Detection in Unstructured Field Environments. J. Field Robot. 2025. [Google Scholar] [CrossRef]
- Fernando, L.; Ghali, R.; Akhloufi, M.A. SWIFT: Simulated Wildfire Images for Fast Training Dataset. Remote Sens. 2024, 16, 1627. [Google Scholar] [CrossRef]
- Zhu, X.; Bilal, T.; Mårtensson, P.; Hanson, L.; Björkman, M.; Maki, A. Towards Sim-to-Real Industrial Parts Classification with Synthetic Dataset. In Proceedings of the 2023 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Vancouver, BC, Canada, 17–24 June 2023; pp. 4454–4463. [Google Scholar] [CrossRef]
- Wu, F.; Zhu, R.; Meng, F.; Qiu, J.; Yang, X.; Li, J.; Zou, X. An Enhanced Cycle Generative Adversarial Network Approach for Nighttime Pineapple Detection of Automated Harvesting Robots. Agronomy 2024, 14, 3002. [Google Scholar] [CrossRef]
- Collado-Villaverde, A.; Cobos, M.; Muñoz, P.; Barrero, D.F. A simulator to support machine learning-based wearable fall detection systems. Electronics 2020, 9, 1831. [Google Scholar] [CrossRef]
- Endo, D.; Watanabe, A.; Nagatani, K. Stair climbing control for 4-DOF tracked vehicle based on internal sensors. J. Robot. 2017, 2017, 3624589. [Google Scholar] [CrossRef]
- Kurtz, V.; Li, H.; Wensing, P.M.; Lin, H. Mini Cheetah, the falling cat: A case study in machine learning and trajectory optimization for robot acrobatics. In Proceedings of the 2022 International Conference on Robotics and Automation (ICRA), Philadelphia, PA, USA, 23–27 May 2022. [Google Scholar] [CrossRef]
- Semwal, A.; Mohan, R.E.; Melvin, L.M.; Palanisamy, P.; Baskar, C.; Yi, L.; Pookkuttath, S.; Ramalingam, B. False ceiling deterioration detection and mapping using a deep learning framework and the teleoperated reconfigurable ‘Falcon’ robot. Sensors 2021, 22, 262. [Google Scholar] [CrossRef]
- Expert, F.; Ruffier, F. Flying over uneven moving terrain based on optic-flow cues without any need for reference frames or accelerometers. Bioinspir. Biomimetics 2015, 10, 026003. [Google Scholar] [CrossRef]
- N. Singh, S.P.; Csonka, P.J.; Waldron, K.J. Optical Flow Aided Motion Estimation for Legged Locomotion. In Proceedings of the 2006 IEEE/RSJ International Conference on Intelligent Robots and Systems, Beijing, China, 9–15 October 2006; pp. 1738–1743. [Google Scholar] [CrossRef]
- Kröse, B.; Dev, A.; Groen, F. Heading direction of a mobile robot from the optical flow. Image Vis. Comput. 2000, 18, 415–424. [Google Scholar] [CrossRef]
- Liu, M.; Delbrück, T. ABMOF: A Novel Optical Flow Algorithm for Dynamic Vision Sensors. arXiv 2018, arXiv:abs/1805.03988. [Google Scholar]
- Mafrica, S.; Servel, A.; Ruffier, F. Minimalistic optic flow sensors applied to indoor and outdoor visual guidance and odometry on a car-like robot. Bioinspir. Biomimetics 2016, 11, 066007. [Google Scholar] [CrossRef] [PubMed]
- Pookkuttath, S.; Gomez, B.F.; Elara, M.R.; Thejus, P. An optical flow-based method for condition-based maintenance and operational safety in autonomous cleaning robots. Expert Syst. Appl. 2023, 222, 119802. [Google Scholar] [CrossRef]
- Ong, J.H.; Hayat, A.A.; Gomez, B.F.; Elara, M.R.; Wood, K.L. Deep Learning Based Fall Recognition and Forecasting for Reconfigurable Stair-Accessing Service Robots. Mathematics 2024, 12, 1312. [Google Scholar] [CrossRef]
- Hu, K.; Chen, Z.; Kang, H.; Tang, Y. 3D vision technologies for a self-developed structural external crack damage recognition robot. Autom. Constr. 2024, 159, 105262. [Google Scholar] [CrossRef]
- Fortune Business Insights. Service Robotics Market Size, Share, Trends|Global Report [2030]. 2025. Available online: https://www.fortunebusinessinsights.com/industry-reports/service-robotics-market-101805 (accessed on 25 January 2025).
- Maximize Market Research. Service Robotics Market—Global Industry Analysis and Forecast-2029. 2023. Available online: https://www.maximizemarketresearch.com/market-report/global-service-robotics-marke/32986/ (accessed on 25 January 2025).
- Allied Market Research. Service Robotics Market Size, Trends, Industry Revenue 2032. 2023. Available online: https://www.alliedmarketresearch.com/service-robotics-market (accessed on 25 January 2025).
- Stellar Market Research. Service Robotics Market: Industry Overview (2024–2030) by Component, Environment, Application and, Region. 2023. Available online: https://www.stellarmr.com/report/Service-Robotics-Market/431 (accessed on 25 January 2025).
- Pudu Robotics. Pudu Robotics Takes Lead in Global Commercial Service Robotics Market. 2024. Available online: https://www.pudurobotics.com/news/910 (accessed on 25 January 2025).
- OrionStar Robotics. OrionStar Robotics—Born for Truly Useful Robots. 2024. Available online: https://en.orionstar.com/ (accessed on 25 January 2025).
- Keenon Robotics. Keenon Robotics—Smart Service Robots & Solutions. 2024. Available online: https://www.keenon.com/en/contactus/index.html (accessed on 25 January 2025).
- Gausium. Products. 2025. Available online: https://gausium.com/products/ (accessed on 25 January 2025).
- Starship Technologies. Our Robots. Available online: https://www.starship.xyz/our-robots/ (accessed on 25 January 2025).
- Yujin Robot. GoCart AMR Robot based 3D Lidar|Yujin Robot. Available online: https://yujinrobot.com/en/products/standard-amr (accessed on 25 January 2025).
- Excelland Robotics. Excelland Robotics—Global Commercial Delivery Robot Company. 2024. Available online: https://www.uditech.com.cn/en/product.html (accessed on 25 January 2025).
- Aethon. Hospital Robots|Solutions for Healthcare. 2023. Available online: https://aethon.com/our-robots/ (accessed on 25 January 2025).
- Blue Ocean Robotics. Advanced UV Disinfection Solutions: Discover UVD Robots. Available online: https://uvd.blue-ocean-robotics.com/ (accessed on 25 January 2025).
- Lely Industries, N.V. Automated Farm Systems|Enhance Farm Efficiency | Lely. 2025. Available online: https://www.lely.com/solutions/ (accessed on 25 January 2025).
- Zebra technologies. Autonomous Mobile Robots|AMRs|Zebra. 2025. Available online: https://www.zebra.com/us/en/products/autonomous-mobile-robots.html (accessed on 25 January 2025).
- XAG. xa.com/en/xauv. 2025. Available online: https://www.xa.com/en/xauv (accessed on 25 January 2025).
- Softbank Robotics Group Corp. Solution|Softbank Robotics Group Corp. Available online: https://www.softbankrobotics.com/solution/ (accessed on 25 January 2025).
- ABB Robotics. Browse All ABB Robots|Robotics. 2025. Available online: https://new.abb.com/products/robotics/robots (accessed on 25 January 2025).
- GeckoSystems. GeckoSystems: Mobile Robot Solutions for Safety, Security and Service. 2025. Available online: https://www.geckosystems.com/ (accessed on 25 January 2025).
- Pudu Robotics. Products—PUDU. 2023. Available online: https://www.pudurobotics.com/products (accessed on 25 January 2025).
- Boston Dynamics. Product|Boston Dynamics. 2024. Available online: https://bostondynamics.com/products/ (accessed on 25 January 2025).
- Zonzini. Electric Stair Climbing Trolleys. Available online: https://www.zonzini.us/electric-stair-climbers-for-goods/ (accessed on 15 April 2025).
- AATA International. Stair Robot® Range of Stairclimbers. Available online: https://www.stair-robot.co.uk/stair-robot.html (accessed on 15 April 2025).
- Park, F.C.; Lynch, K.M. Modern Robotics: Mechanics, Planning, and Control; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
- Blumenkamp, J.; Baude, A.; Laue, T. Closing the Reality Gap with Unsupervised Sim-to-Real Image Translation for Semantic Segmentation in Robot Soccer. arXiv 2019, arXiv:1911.01529v2. [Google Scholar]
- Jonnarth, A.; Johansson, O.; Felsberg, M. Sim-to-real Transfer of Deep Reinforcement Learning Agents for Online Coverage Path Planning. arXiv 2024, arXiv:cs.RO/2406.04920. [Google Scholar]
- Santoni de Sio, F. The European Commission report on ethics of connected and automated vehicles and the future of ethics of transportation. Ethics Inf. Technol. 2021, 23, 713–726. [Google Scholar] [CrossRef]
- Lin, P.; Zhang, L.; Tiong, R.L. Multi-objective robust optimization for enhanced safety in large-diameter tunnel construction with interactive and explainable AI. Reliab. Eng. Syst. Saf. 2023, 234, 109172. [Google Scholar] [CrossRef]
- Perez-Cerrolaza, J.; Abella, J.; Borg, M.; Donzella, C.; Cerquides, J.; Cazorla, F.J.; Englund, C.; Tauber, M.; Nikolakopoulos, G.; Flores, J.L. Artificial Intelligence for Safety-Critical Systems in Industrial and Transportation Domains: A Survey. ACM Comput. Surv. 2024, 56, 1–40. [Google Scholar] [CrossRef]
- Shi, J.; Tomasi. Good features to track. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 21–23 June 1994; pp. 593–600. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).