A Study of Certain Geometric Properties and Hardy Spaces of the Normalized Miller-Ross Function

Abstract

The main objective of this research is to investigate specific sufficiency criteria for the strongly starlikeness, strongly convexity, starlikeness, convexity and pre-starlikeness of the normalized Miller-Ross function. Furthermore, we establish sufficient conditions under which the normalized Miller-Ross function belongs to Hardy spaces and the class-bounded analytic functions. Some of the various results which are derived in this paper are presumably new and their significance is illustrated through several interesting examples.

1. Introduction

Special functions are extremely important due to their role in mathematical analysis, especially functional analysis, physics, and other scientific fields. Although there is no generalized version of these functions, there are several mathematical functions on the list that are recognized as special functions, such as elementary functions and, in particular, trigonometric functions. With the contributions of Klein, Gauss, Euler, Jacobi, Bessel, and a few more, the idea of special functions grew during the eighteenth and nineteenth centuries. While Bessel developed the Bessel function to solve differential equations arising in physics, Euler introduced the elliptic integral and the Gamma function. The contributions of mathematicians such as Legendre, Hermite, and Chebyshev in the 20th century contributed to the expansion of the theory of special functions.

Geometric Function Theory is a significant branch of complex analysis that focuses on the geometric behavior of analytic functions. It is based on the theory of univalent functions, which has given rise to many related fields. Special functions play a fundamental role in geometric function theory, with one of the most notable applications being their connection to the resolution of the famous Bieberbach conjecture by L. de Branges [1]. Recently, researchers have established several interesting results on the geometric properties of some classes of analytic functions. Moreover, it is worth mentioning that researchers in these fields are obtaining interesting results and achieving their application thanks to new methodologies and theoretical techniques. This line of research has been studied in various works, including the Mittag-Leffler functions [2,3,4], Wright functions [5], Fox–Wright functions [6], Dini functions [7,8], modified Bessel functions [9], Bessel functions [10,11,12], hypergeometric functions [13,14,15], and Miller-Ross function [16]. Moreover, motivated by the results of Eker and Ece [16], further results on the geometric behavior of the Miller-Ross function were obtained by Mehrez [17]. Our aim in this paper is to make a further contribution to the subject by showing some new geometric properties of the Miller-Ross function.

Now, we recall some basic definitions related to the context. Assume that the class of analytic functions in the open unit disk

$$\mathcal{D}=\{t\in \mathbb{C}:|t|<1\},$$

is denoted by $\mathcal{H}.$ We denote by $\mathcal{A}$ the class of analytic functions $h\left(t\right)\in \mathcal{H},$ satisfying the normalization conditions $h\left(0\right)=h^{\prime }\left(0\right)-1=0$ such that

$$h\left(t\right)=t+\sum _{\mathfrak{y}=2}^{\infty }{a}_{\mathfrak{y}}{t}^{\mathfrak{y}},t\in \mathcal{D}.$$

(1)

A function $h:E\subseteq \mathbb{C}⟶\mathbb{C}$ is said to be univalent in a domain E if it never takes the same value twice; that is, if $f\left(t_1\right)=f\left(t_2\right)$ for $t_1,t_2\in E$ implies that $t_1=t_2.$ We denote the class of univalent functions in $\mathcal{A}$ by $\mathcal{S}.$ A function $h\in \mathcal{A}$ is known as a starlike function (with respect to the origin) in $\mathcal{D}$ if h is univalent in $\mathcal{D}$ and the domain $h\left(\mathcal{D}\right)$ is starlike with respect to the origin in $\mathbb{C}.$ Let us denote by ${\mathcal{S}}^{\ast }$ the class of starlike functions in the unit disk $\mathcal{D}.$ It is important to note that the characterization of such starlike functions in $\mathcal{D}$ is as follows [18]:

$$\Re \left(\frac{t{h}^{\prime }\left(t\right)}{h\left(t\right)}\right)>0\mathrm{for}\mathrm{all}t\in \mathcal{D}.$$

For a given $\delta \in [0,1)$, a function $h\left(t\right)\in \mathcal{A}\left(\mathcal{D}\right)$ is said to be starlike of order $\delta ,$ denoted by ${\mathcal{S}}^{\ast }\left(\delta \right),$ if the inequality

$$\Re \left(\frac{t{h}^{\prime }\left(t\right)}{f\left(t\right)}\right)>\delta ,$$

holds true for all $t\in \mathcal{D},$ (for more details, see [19]).

A function $h\left(t\right)$ in $\mathcal{A}$ is said to be convex in $\mathcal{D}$ if $h\left(t\right)$ is a univalent function in $\mathcal{D}$ with $h\left(\mathcal{D}\right)$ as a convex domain in $\mathbb{C}.$ We denote the class of convex functions by $\mathcal{C},$ which can also be described as follows [18]:

$$h\in \mathcal{C}⟺\Re \left(1+\frac{t{h}^{″}\left(t\right)}{h^{\prime }\left(t\right)}\right)>0,\mathrm{for}\mathrm{all}t\in \mathcal{D}.$$

Moreover, if

$$\Re \left(1+\frac{t{h}^{″}\left(t\right)}{f^{\prime }\left(t\right)}\right)>\delta ,\mathrm{for}\mathrm{all}t\in \mathcal{D},$$

where $\delta \in [0,1)$, then h is called convex of order $\alpha .$ We denote the class of convex functions of order $\delta$ by $\mathcal{C}\left(\delta \right).$ We remark that for all $\eta \in [0,1)$, we have

$${\mathcal{S}}^{\ast }\left(\delta \right)\subseteq {\mathcal{S}}^{\ast }\left(0\right)={\mathcal{S}}^{\ast }\mathrm{and}\mathcal{C}\left(\delta \right)\subseteq \mathcal{C}\left(0\right)=\mathcal{C}.$$

Let ${\tilde{\mathcal{S}}}^{\ast }\left(\delta \right)$ and $\tilde{\mathcal{C}}\left(\delta \right)$ denote the classes of strongly starlike and strongly convex functions of order $\delta$, respectively. These classes are analytically defined as follows:

• A function $h\in {\tilde{\mathcal{S}}}^{\ast }\left(\delta \right),\delta \in (0,1],$ if and only if

  $$\left|arg\left(\frac{t{h}^{\prime }\left(t\right)}{h\left(t\right)}\right)\right|<\frac{\delta \pi }{2}.$$
• A function $h\in \tilde{\mathcal{C}}\left(\delta \right),\delta \in (0,1],$ if and only if

  $$\left|arg\left(1+\frac{t{h}^{″}\left(t\right)}{h^{\prime }\left(t\right)}\right)\right|<\frac{\delta \pi }{2}.$$

It is worth mentioning that

$${\tilde{\mathcal{S}}}^{\ast }\left(1\right)={\mathcal{S}}^{\ast }\mathrm{and}\tilde{\mathcal{C}}\left(1\right)=\mathcal{C}.$$

Additionally, for a given $0\le \delta <1,$ we introduce the following classes of analytic functions described as follows [18,20]:

$$\begin{array}{cc}\hfill \mathcal{P}\left(\delta \right)& :=\left\{p\in \mathcal{H}\left(\mathcal{D}\right),p\left(0\right)=1\mathrm{and}\Re \left(p\right(t\left)\right)>\delta \right\},\hfill \\ \hfill \mathcal{R}\left(\delta \right)& :=\left\{h\in \mathcal{A}\left(\mathcal{D}\right)\mathrm{and}\Re \left(h^{\prime }\left(t\right)\right)>\delta \right\}.\hfill \end{array}$$

Additionally, we have the classes $\mathcal{P}$ and $\mathcal{R}$ for $\delta =0$.

Assume that $f\left(t\right)$ and $g\left(t\right)$ are analytic in $\mathcal{D}.$ Then, $f\left(t\right)$ is subordinate to $g\left(t\right)$ in $\mathcal{D},$ denoted by $f\left(t\right)\prec g\left(t\right)$ (or $f\prec g$), if there exists a Schwarz function $w\left(t\right),$ which is analytic in $\mathcal{D}$ satisfying the conditions $w\left(0\right)=0$ and $\left|w\right(t\left)\right|<1$ for any $t\in \mathcal{D},$ such that

$$f\left(t\right)=g\left(w\right(t\left)\right),\mathrm{for}\mathrm{all}t\in \mathcal{D}.$$

The convolution $f\ast g,$ or the Hadamard product of two power series

$$f\left(t\right)=t+\sum _{k=1}^{\infty }{a}_k{t}^{k+1},$$

and

$$g\left(t\right)=t+\sum _{k=1}^{\infty }{b}_k{t}^{k+1},$$

is defined as the power series [18]

$$f\ast g\left(t\right)=t+\sum _{k=1}^{\infty }{a}_k{b}_j{t}^{k+1}.$$

In [21], Ruscheweyh introduced another class of analytic functions, denoted by ${\mathcal{L}}_{\rho }(0\le \rho <1)$, known as pre-starlike functions, defined as follows:

$${\mathcal{L}}_{\rho }:=\left\{g\in \mathcal{A}:h_{\rho }\ast g\in {\mathcal{S}}^{\ast }\left(\rho \right)\right\},$$

where the function $h_{\rho }\left(t\right)$ is defined by

$$h_{\rho }\left(t\right)=\frac{t}{{(1-t)}^{2(1-\rho )}},(t\in \mathcal{D}).$$

(2)

The class of pre-starlike functions was extended in [22] by generalizing the class ${\mathcal{L}}_{\rho }$ to $\mathcal{L}[\rho ,\delta ]$, defined as follows:

$$\mathcal{L}[\rho ,\delta ]:=\left\{g\in \mathcal{A}:h_{\rho }\ast g\in {\mathcal{S}}^{\ast }\left(\delta \right)\right\},$$

where $\rho ,\delta \in [0,1).$

Let ${\mathcal{H}}^{\infty }$ denote the space of all bounded functions in $\mathcal{D}$. We suppose that $h\in \mathcal{H}$ and set

$${\mathcal{M}}_q(r,h)=\left\{\begin{array}{cc}{\left(\frac{1}{2\pi }\underset{0}{\overset{2\pi }{\int }}{\left|h\left(r{e}^{i\varphi }\right)\right|}^{q}d\varphi \right)}^{\frac{1}{q}},\hfill & \left(0<q<\infty \right),\hfill \\ & \\ max\left\{\left|h\left(t\right)\right|:\left|t\right|\le r\right\},\hfill & (q=\infty ).\hfill \end{array}\right.$$

It is well-known from [23] that $h\in \mathcal{D}$ belongs to the Hardy space ${\mathcal{H}}^q,$ where $0<q\le \infty$, if the set $\left\{{\mathcal{M}}_{\kappa }(r;h)|r\in [0,1)\right\}$ is bounded. Moreover, we note that for $0<\nu \le \mu \le \infty$ we have

$${\mathcal{H}}^{\infty }\subset {\mathcal{H}}^{\mu }\subset {\mathcal{H}}^{\nu }.$$

Now, consider the Miller-Ross function, which is defined by [24]

$${\mathbb{E}}_{\mathfrak{s},\mathfrak{u}}\left(t\right)=t^{\mathfrak{s}}\sum _{\mathfrak{y}=0}^{\infty }\frac{{\left(\mathfrak{u}t\right)}^{\mathfrak{y}}}{\Gamma (\mathfrak{s}+\mathfrak{y}+1)},(\mathfrak{s}>-1,\mathfrak{u},t\in \mathbb{C}).$$

To investigate the geometric properties of the Miller-Ross function, we consider the following normalized form [16,17]:

$$\begin{array}{cc}\hfill {\mathcal{E}}_{\mathfrak{s},\mathfrak{u}}\left(t\right)& =t^{1-\mathfrak{s}}\Gamma (\mathfrak{s}+1){\mathbb{E}}_{\mathfrak{s},\mathfrak{u}}\left(t\right)\hfill \\ \hfill & =t+\sum _{\mathfrak{y}=2}^{\infty }\frac{\Gamma (\mathfrak{s}+1)}{\Gamma (\mathfrak{s}+\mathfrak{y})}{\mathfrak{u}}^{\mathfrak{y}-1}{t}^{\mathfrak{y}},(t\in \mathcal{D}).\hfill \end{array}$$

(3)

In this paper, we consider the normalized form of the Miller-Ross function defined by (3). We present some new geometric properties for this class for a specific range of parameters.

The upcoming sections of the present paper are organized as follows: in Section 2, we recall some known lemmas that will be useful for establishing the mains results. In Section 3, some specific ranges of parameters are derived so that the normalized form of the Miller-Ross function ${\mathcal{E}}_{\mathfrak{s},\mathfrak{u}}\left(t\right)$ possesses certain geometric properties such as strongly starlikeness and strongly convexity as well as starlikeness, convexity and pre-starlikeness in the unit disk. In Section 4, as an application, we determine sufficient conditions on the parameters for which this function belongs to the Hardy spaces ${\mathcal{H}}^r$ and ${\mathcal{H}}^{\infty }.$ Moreover, some sufficient conditions are established so that some classes of functions related to the Miller-Ross function belong to the spaces $\mathcal{P}\left(\delta \right)$ and $\mathcal{R}\left(\beta \right).$

2. Relevant Lemmas

In this section, we include several lemmas, each of which will be used to prove the main results.

Lemma 1 

([25]). Let $h,g\in \mathcal{H}$ such that $h\left(0\right)=g\left(0\right)=1$. Assume that h is univalent and convex in $\mathcal{D}$, and that $g\prec h$ in $\mathcal{D}$. Then

$$(\mathfrak{y}+1)t^{-1-\mathfrak{y}}\underset{0}{\overset{t}{\int }}{\nu }^{\mathfrak{y}}g\left(\nu \right)d\nu \prec (\mathfrak{y}+1)t^{-1-\mathfrak{y}}\underset{0}{\overset{t}{\int }}{\nu }^{\mathfrak{y}}h\left(\nu \right)d\nu ,\forall \mathfrak{y}\in \mathbb{N}\cup \left\{0\right\}.$$

Lemma 2 

([26]). Let $\delta \in [0,1).$ A sufficient condition for the function $h\left(t\right)$ defined by (1) to be in ${\mathcal{S}}^{\ast }\left(\delta \right)$ and $\mathcal{C}\left(\delta \right)$, respectively, is that

$$\begin{array}{cc}\hfill \sum _{\mathfrak{y}=2}^{\infty }\left(\mathfrak{y}-\delta \right)\left|a_{\mathfrak{y}}\right|& \le 1-\delta ,\hfill \\ \hfill \sum _{\mathfrak{y}=2}^{\infty }\mathfrak{y}\left(\mathfrak{y}-\delta \right)\left|a_{\mathfrak{y}}\right|& \le 1-\delta ,\hfill \end{array}$$

respectively.

Lemma 3 

([27]). The digamma function $\psi \left(u\right)=\frac{{\Gamma }^{\prime }\left(u\right)}{\Gamma \left(u\right)}$ satisfies the inequality

$$log\left(u\right)-\gamma \le \psi \left(u\right)\le log\left(u\right),u>1,$$

where γ is the Euler–Mascheroni constant.

Lemma 4 

([28]). Let $\eta ,\kappa \in [0,1).$ The following inclusion holds true:

$$\mathcal{P}\left(\eta \right)\ast \mathcal{P}\left(\kappa \right)\subset \mathcal{P}\left(\upsilon \right),$$

where $\upsilon =1-2(1-\eta )(1-\kappa )$. In addition, the value of υ is the best possible.

Lemma 5 

([29]). For $\eta ,\kappa \in [0,1)$ and $\upsilon =1-2(1-\eta )(1-\kappa ),$ then the following inclusion holds true:

$$\mathcal{R}\left(\eta \right)\ast \mathcal{R}\left(\kappa \right)\subset \mathcal{R}\left(\upsilon \right).$$

Lemma 6 

([29]). If a function $h\in \mathcal{C}\left(\delta \right)(0\le \delta <1)$ and is not of the form

$$\left\{\begin{array}{cc}{n}_1+\frac{n_{2}z}{{(1-z{e}^{i\omega })}^{1-2\nu }},\hfill & \nu \ne \frac{1}{2},\hfill \\ & \\ n_1+n_{2}log(1-z{e}^{i\omega }),\hfill & \nu =\frac{1}{2},\hfill \end{array}\right.$$

for $n_1,n_2\in \mathbb{C},$ and for $\omega \in \mathbb{R},$ then each of the following statements holds true:

(i).

If $\nu \ge \frac{1}{2}$, then $h\in {\mathcal{H}}^{\infty }.$

(ii).

If $\nu \in [0,\frac{1}{2})$, then there exist $\delta =\delta \left(h\right)>0$ such that $h\in {\mathcal{H}}^{\delta +\frac{1}{1-2\nu }}.$

3. Starlikeness and Convexity of the Normalized Form of the Miller-Ross Function

Our first main result in this section reads as follows.

Theorem 1.

Let $0<\mathfrak{u}<\mathfrak{s}.$ If

$$k:=\frac{2\mathfrak{u}}{\mathfrak{s}+1}+\frac{{\mathfrak{u}}^2(3\mathfrak{s}-2\mathfrak{u})}{\mathfrak{s}{(\mathfrak{s}-\mathfrak{u})}^2}\in (0,1],$$

then ${\mathcal{E}}_{\mathfrak{s},\mathfrak{u}}\left(t\right)\in \widetilde{{\mathcal{S}}^{\ast }}\left(\delta \right)$, where

$$\delta :=\frac{2}{\pi }{sin}^{-1}\left(k\sqrt{1-\frac{k^2}{4}}+\frac{k}{2}\sqrt{1-k^2}\right).$$

Proof. 

For $t\in \mathcal{D},$ we obtain

$$\begin{array}{cc}\hfill \left|{\mathcal{E}}_{\mathfrak{s},\mathfrak{u}}^{\prime }\left(t\right)-1\right|& =\left|\sum _{\mathfrak{y}=2}^{\infty }\frac{\Gamma (\mathfrak{s}+1){\mathfrak{u}}^{\mathfrak{y}-1}\mathfrak{y}{t}^{\mathfrak{y}-1}}{\Gamma (\mathfrak{s}+\mathfrak{y})}\right|\hfill \\ \hfill & <\sum _{\mathfrak{y}=2}^{\infty }\frac{\mathfrak{y}\Gamma (\mathfrak{s}+1){\mathfrak{u}}^{\mathfrak{y}-1}}{\Gamma (\mathfrak{s}+\mathfrak{y})}\hfill \\ \hfill & =\frac{2\mathfrak{u}}{\mathfrak{s}+1}+\sum _{\mathfrak{y}=3}^{\infty }\frac{\mathfrak{y}\Gamma (\mathfrak{s}+1){\mathfrak{u}}^{\mathfrak{y}-1}}{\Gamma (\mathfrak{s}+\mathfrak{y})}.\hfill \end{array}$$

(4)

Then, by combining (4) with the inequality ([30], Lemma 1.1)

$$\frac{\Gamma (a+1)}{\Gamma (a+n)}\le \frac{1}{{(a+\alpha )}^{n-1}},\left(n\ge 3,\alpha \in [0,\sqrt{2}]\right),$$

(5)

we establish that

$$\begin{array}{cc}\hfill \left|{\mathcal{E}}_{\mathfrak{s},\mathfrak{u}}^{\prime }\left(t\right)-1\right|& \le \frac{2\mathfrak{u}}{\mathfrak{s}+1}+\sum _{\mathfrak{y}=3}^{\infty }\frac{\mathfrak{y}{\mathfrak{u}}^{\mathfrak{y}-1}}{{(\mathfrak{s}+\alpha )}^{\mathfrak{y}-1}}.\hfill \end{array}$$

(6)

Moreover, by using the fact that

$${(\mathfrak{s}+\alpha )}^{\mathfrak{y}-1}>{\mathfrak{s}}^{\mathfrak{y}-1},\left(\mathfrak{y}\ge 3,\mathfrak{s},\alpha >0\right),$$

and since

$$\sum _{\mathfrak{y}=3}^{\infty }\mathfrak{y}{\ell }^{\mathfrak{y}-1}=\frac{{\ell }^2(3-2\ell )}{{(1-\ell )}^2},\left(0<\ell <1\right),$$

the inequality (6) implies

$$\begin{array}{cc}\hfill \left|{\mathcal{E}}_{\mathfrak{s},\mathfrak{u}}^{\prime }\left(t\right)-1\right|& \le \frac{2\mathfrak{u}}{\mathfrak{s}+1}+\sum _{\mathfrak{y}=3}^{\infty }\mathfrak{y}{\left(\frac{\mathfrak{u}}{\mathfrak{s}}\right)}^{\mathfrak{y}-1}\hfill \\ \hfill & =\frac{2\mathfrak{u}}{\mathfrak{s}+1}+\frac{{\mathfrak{u}}^2(3\mathfrak{s}-2\mathfrak{u})}{\mathfrak{s}{(\mathfrak{s}-\mathfrak{u})}^2}\hfill \\ \hfill & =k<1.\hfill \end{array}$$

Hence, by using the above inequality, we get

$${\mathcal{E}}_{\mathfrak{s},\mathfrak{u}}^{\prime }\left(t\right)\prec 1+kt,$$

and consequently, we infer

$$|arg({\mathcal{E}}_{\mathfrak{s},\mathfrak{u}}^{\prime }\left(t\right)\left)\right|<{sin}^{-1}\left(k\right).$$

(7)

Now, we apply Lemma 1 for $\mathfrak{y}=0$ with

$$g\left(t\right)={\mathcal{E}}_{\mathfrak{s},\mathfrak{u}}^{\prime }\left(t\right)\mathrm{and}\nu \left(t\right)=1+kt,$$

and we establish that

$$\frac{{\mathcal{E}}_{\mathfrak{s},\mathfrak{u}}\left(t\right)}{t}\prec 1+\frac{k}{2}t.$$

Hence, we get

$$\left|\arg \left(\frac{{\mathcal{E}}_{\mathfrak{s},\mathfrak{u}}\left(t\right)}{t}\right)\right|<{sin}^{-1}\left(\frac{k}{2}\right).$$

(8)

From (7) and (8), it follows that

$$\begin{array}{cc}\hfill \left|arg\left(\frac{t{\mathcal{E}}_{\mathfrak{s},\mathfrak{u}}^{\prime }\left(t\right)}{{\mathcal{E}}_{\mathfrak{s},\mathfrak{u}}\left(t\right)}\right)\right|& =\left|arg\left(\frac{t}{{\mathcal{E}}_{\mathfrak{s},\mathfrak{u}}\left(t\right)}\right)+arg\left({\mathcal{E}}_{\mathfrak{s},\mathfrak{u}}^{\prime }\left(t\right)\right)\right|\hfill \\ \hfill & \le \left|arg\left(\frac{t}{{\mathcal{E}}_{\mathfrak{s},\mathfrak{u}}\left(t\right)}\right)\right|+|arg({\mathcal{E}}_{\mathfrak{s},\mathfrak{u}}^{\prime }\left(t\right)\left)\right|\hfill \\ \hfill & <{sin}^{-1}\left(\frac{k}{2}\right)+{sin}^{-1}\left(k\right)\hfill \\ \hfill & ={sin}^{-1}\left(k\sqrt{1-\frac{k^2}{4}}+\frac{k}{2}\sqrt{1-k^2}\right)\hfill \\ \hfill & =\frac{\pi }{2}·\frac{2}{\pi }{sin}^{-1}\left(k\sqrt{1-\frac{k^2}{4}}+\frac{k}{2}\sqrt{1-k^2}\right).\hfill \end{array}$$

This completes the proof of Theorem 1. □

Example 1.

The function ${\mathcal{E}}_{1,\frac{1}{3}}\left(t\right)$ belongs to the class $\widetilde{{\mathcal{S}}^{\ast }}\left(\delta \right)$ in $\mathcal{D},$ where

$$\delta =\frac{2}{\pi }{sin}^{-1}\left(\frac{11\left[\sqrt{455}+\sqrt{23}\right]}{288}\right)\approx 0.9648.$$

Theorem 2.

Let $\mathfrak{s}>0$ and $\mathfrak{u}\in (0,1).$ If

$$k_1:=\frac{2\mathfrak{u}(2-\mathfrak{u})}{(\mathfrak{s}+1){(\mathfrak{u}-1)}^2}\in (0,1],$$

then ${\mathcal{E}}_{\mathfrak{s},\mathfrak{u}}\left(t\right)\in \tilde{\mathcal{C}}\left({\delta }_1\right)$, where

$${\delta }_1:=\frac{2}{\pi }{sin}^{-1}\left(k_1\sqrt{1-\frac{k^2}{4}}+\frac{k_1}{2}\sqrt{1-k_1^2}\right).$$

Proof. 

Let $t\in \mathcal{D}.$ A straightforward computation yields

$$\left|{\left(t{\mathcal{E}}_{\mathfrak{s},\mathfrak{u}}^{\prime }\left(t\right)\right)}^{\prime }-1\right|\le \sum _{\mathfrak{y}=2}^{\infty }\frac{{\mathfrak{y}}^2\Gamma (\mathfrak{s}+1){\mathfrak{u}}^{\mathfrak{y}-1}}{\Gamma (\mathfrak{s}+\mathfrak{y})}.$$

(9)

We define the sequence ${\left(u_{\mathfrak{y}}\right)}_{\mathfrak{y}\ge 2}$ by

$$u_{\mathfrak{y}}=\frac{\mathfrak{y}}{\Gamma (\mathfrak{s}+\mathfrak{y})},\mathrm{for}\mathrm{all}\mathfrak{y}\ge 2.$$

Therefore, for $\mathfrak{y}\ge 2$ and $\mathfrak{s}>0,$ we have

$$\begin{array}{cc}\hfill u_{\mathfrak{y}+1}-u_{\mathfrak{y}}& =\frac{1}{\Gamma (\mathfrak{s}+\mathfrak{y})}\left[\frac{\mathfrak{y}+1}{\mathfrak{y}+\mathfrak{s}}-\mathfrak{y}\right]\hfill \\ \hfill & \le \frac{1}{\Gamma (\mathfrak{s}+\mathfrak{y})}\left[\frac{\mathfrak{y}+1}{\mathfrak{y}}-\mathfrak{y}\right]\hfill \\ \hfill & =\frac{-({\mathfrak{y}}^2-\mathfrak{y}-1)}{\Gamma (\mathfrak{s}+\mathfrak{y})}<0.\hfill \end{array}$$

(10)

By this observation and with the help of (9), we obtain

$$\begin{array}{cc}\hfill \left|{\left(t{\mathcal{E}}_{\mathfrak{s},\mathfrak{u}}^{\prime }\left(t\right)\right)}^{\prime }-1\right|& <\sum _{\mathfrak{y}=2}^{\infty }\frac{2\mathfrak{y}{\mathfrak{u}}^{\mathfrak{y}-1}}{\mathfrak{s}+1}\hfill \\ \hfill & =\frac{2\mathfrak{u}(2-\mathfrak{u})}{(\mathfrak{s}+1){(\mathfrak{u}-1)}^2}\hfill \\ \hfill & =k_1<1.\hfill \end{array}$$

(11)

Since $k_1\in (0,1]$ under the given hypothesis and in view of the above inequality, we establish that

$${\left(t{\mathcal{E}}_{\mathfrak{s},\mathfrak{u}}^{\prime }\left(t\right)\right)}^{\prime }\prec 1+k_{1}t.$$

This in turn implies that

$$\left|arg{\left(t{\mathcal{E}}_{\mathfrak{s},\mathfrak{u}}^{\prime }\left(t\right)\right)}^{\prime }\right|<{sin}^{-1}\left(k_1\right).$$

(12)

Now, we set $\mathfrak{y}=0$ in Lemma 1 with

$$g\left(t\right)={\left(t{\mathcal{E}}_{\mathfrak{s},\mathfrak{u}}^{\prime }\left(t\right)\right)}^{\prime }\mathrm{and}\nu \left(t\right)=1+k_{1}t.$$

We obtain

$${\mathcal{E}}_{\mathfrak{s},\mathfrak{u}}^{\prime }\left(t\right)\prec 1+\frac{k_1}{2}t,$$

which implies that

$$\left|arg\left({\mathcal{E}}_{\mathfrak{s},\mathfrak{u}}^{\prime }\left(t\right)\right)\right|<{sin}^{-1}\left(\frac{k_1}{2}\right).$$

(13)

By virtue of relations (12) and (13), we infer

$$\begin{array}{cc}\hfill \left|arg\left(\frac{{\left(t{\mathcal{E}}_{\mathfrak{s},\mathfrak{u}}^{\prime }\left(t\right)\right)}^{\prime }}{{\mathcal{E}}_{\mathfrak{s},\mathfrak{u}}^{\prime }\left(t\right)}\right)\right|& =\left|arg\left({\left(t{\mathcal{E}}_{\mathfrak{s},\mathfrak{u}}^{\prime }\left(t\right)\right)}^{\prime }\right)-arg\left({\mathcal{E}}_{\mathfrak{s},\mathfrak{u}}^{\prime }\left(t\right)\right)\right|\hfill \\ \hfill & \le \left|arg\left({\left(t{\mathcal{E}}_{\mathfrak{s},\mathfrak{u}}^{\prime }\left(t\right)\right)}^{\prime }\right)\right|+\left|arg\left({\mathcal{E}}_{\mathfrak{s},\mathfrak{u}}^{\prime }\left(t\right)\right)\right|\hfill \\ \hfill & <{sin}^{-1}\left(k_1\right)+{sin}^{-1}\left(\frac{k_1}{2}\right)\hfill \\ \hfill & ={sin}^{-1}\left(k_1\sqrt{1-\frac{k_1^2}{4}}+\frac{k_1}{2}\sqrt{1-k_1^2}\right)\hfill \\ \hfill & =\frac{\pi }{2}·\frac{2}{\pi }{sin}^{-1}\left(k_1\sqrt{1-\frac{k^2}{4}}+\frac{k_1}{2}\sqrt{1-k_1^2}\right).\hfill \end{array}$$

Hence, the desired result would follow readily. □

Example 2.

The function ${\mathcal{E}}_{\frac{1}{2},\frac{1}{5}}\left(t\right)$ belongs to the class $\tilde{\mathcal{C}}\left({\delta }_1\right)$ in $\mathcal{D},$ where

$${\delta }_1=\frac{2}{\pi }{sin}^{-1}\left(\frac{3\left[\sqrt{55}+\sqrt{7}\right]}{32}\right)\approx 0.7921.$$

Theorem 3.

Let $\delta \in [0,1),\mathfrak{s}\ge 1$ such that $0<\mathfrak{u}<\mathfrak{s}+1$. If the inequality

$$\frac{\mathfrak{us}}{\mathfrak{s}-\mathfrak{u}+1}\le (1-\delta )\left(\frac{\mathfrak{s}-2\mathfrak{u}+1}{\mathfrak{s}-\mathfrak{u}+1}\right),$$

(14)

holds, then ${\mathcal{E}}_{\mathfrak{s},\mathfrak{u}}\in {\mathcal{S}}^{\ast }\left(\delta \right).$

Proof. 

According to Lemma 2, we need only to prove that

$$\mathcal{E}(\mathfrak{s},\mathfrak{u},\delta ):=\sum _{\mathfrak{y}=2}^{\infty }(\mathfrak{y}-\delta )\left|b_{\mathfrak{y}}\right|\le 1-\delta ,$$

where

$$b_{\mathfrak{y}}:=\frac{\mathfrak{y}{\mathfrak{u}}^{\mathfrak{y}-1}\Gamma (\mathfrak{s}+1)}{\Gamma (\mathfrak{s}+\mathfrak{y})},\mathfrak{y}\ge 2.$$

According to the estimate ([31], Lemma 7)

$$\frac{\mathfrak{y}\Gamma (\mathfrak{s}+1)}{\Gamma (\mathfrak{s}+\mathfrak{y})}\le \frac{1}{{(\mathfrak{s}+1)}^{\mathfrak{y}-2}},\left(\mathfrak{s}\ge 1,\mathfrak{y}\ge 2\right),$$

(15)

we get

$$\begin{array}{cc}\hfill \mathcal{E}(\mathfrak{s},\mathfrak{u},\delta )& =\sum _{\mathfrak{y}=2}^{\infty }\frac{(\mathfrak{y}-1){\mathfrak{u}}^{\mathfrak{y}-1}\Gamma (\mathfrak{s}+1)}{\Gamma (\mathfrak{s}+\mathfrak{y})}+(1-\delta )\sum _{\mathfrak{y}=2}^{\infty }\frac{{\mathfrak{u}}^{\mathfrak{y}-1}\Gamma (\mathfrak{s}+1)}{\Gamma (\mathfrak{s}+\mathfrak{y})}\hfill \\ \hfill & =\sum _{\mathfrak{y}=2}^{\infty }\frac{{\mathfrak{u}}^{\mathfrak{y}-1}\mathfrak{y}\Gamma (\mathfrak{s}+1)}{\Gamma (\mathfrak{s}+\mathfrak{y})}-\sum _{\mathfrak{y}=2}^{\infty }\frac{{\mathfrak{u}}^{\mathfrak{y}-1}\Gamma (\mathfrak{s}+1)}{\Gamma (\mathfrak{s}+\mathfrak{y})}\hfill \\ \hfill & +(1-\delta )\sum _{\mathfrak{y}=2}^{\infty }\frac{{\mathfrak{u}}^{\mathfrak{y}-1}\Gamma (\mathfrak{s}+1)}{\Gamma (\mathfrak{s}+\mathfrak{y})}\hfill \\ \hfill & \le \sum _{\mathfrak{y}=2}^{\infty }\frac{{\mathfrak{u}}^{\mathfrak{y}-1}}{{(\mathfrak{s}+1)}^{\mathfrak{y}-2}}-\sum _{\mathfrak{y}=2}^{\infty }\frac{{\mathfrak{u}}^{\mathfrak{y}-1}}{{(\mathfrak{s}+1)}^{\mathfrak{y}-1}}+(1-\delta )\sum _{\mathfrak{y}=2}^{\infty }\frac{{\mathfrak{u}}^{\mathfrak{y}-1}}{{(\mathfrak{s}+1)}^{\mathfrak{y}-1}}\hfill \\ \hfill & =\mathfrak{u}\sum _{\mathfrak{y}=2}^{\infty }{\left(\frac{\mathfrak{u}}{\mathfrak{s}+1}\right)}^{\mathfrak{y}-2}-\sum _{\mathfrak{y}=2}^{\infty }{\left(\frac{\mathfrak{u}}{\mathfrak{s}+1}\right)}^{\mathfrak{y}-1}+(1-\delta )\sum _{\mathfrak{y}=2}^{\infty }{\left(\frac{\mathfrak{u}}{\mathfrak{s}+1}\right)}^{\mathfrak{y}-1}\hfill \\ \hfill & =\frac{\mathfrak{us}}{\mathfrak{s}-\mathfrak{u}+1}+(1-\delta )\frac{\mathfrak{u}}{\mathfrak{s}-\mathfrak{u}+1}.\hfill \end{array}$$

This sum is bounded above by $1-\delta$ if and only if (14) holds. Thus, the proof is complete. □

Example 3.

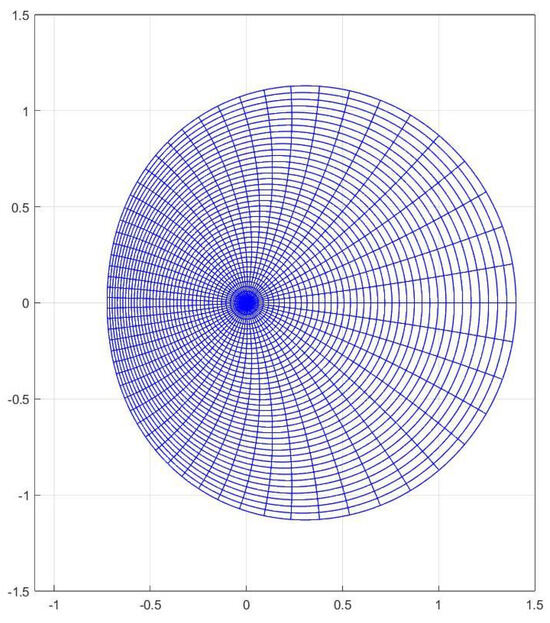
The function ${\mathcal{E}}_{1,2/3}\left(t\right)$ belongs to the class ${\mathcal{S}}^{\ast }.$ See Figure 1.

Figure 1. Image of the open unit disk under the function ${\mathcal{E}}_{1,2/3}\left(t\right)$.

Theorem 4.

Let $\delta \in [0,1),\mathfrak{s}\ge 1$ such that $0<\mathfrak{u}<\mathfrak{s}+1$. If the inequality

$$\frac{{\mathfrak{u}}^2(\mathfrak{s}+1)}{{(\mathfrak{s}-\mathfrak{u}+1)}^2}+\frac{\mathfrak{u}(\mathfrak{s}+1)}{\mathfrak{s}-\mathfrak{u}+1}\le (1-\delta )\left(\frac{\mathfrak{s}-2\mathfrak{u}-\mathfrak{u}\mathfrak{s}+1}{\mathfrak{s}-\mathfrak{u}+1}\right),$$

(16)

holds, then ${\mathcal{E}}_{\mathfrak{s},\mathfrak{u}}\in \mathcal{C}\left(\delta \right).$

Proof. 

In view of Lemma 2, we need only show that

$$\mathcal{F}(\mathfrak{s},\mathfrak{u},\delta ):=\sum _{\mathfrak{y}=2}^{\infty }\frac{\mathfrak{y}(\mathfrak{y}-\delta ){\mathfrak{u}}^{\mathfrak{y}-1}\Gamma (\mathfrak{s}+1)}{\Gamma (\mathfrak{s}+\mathfrak{y})}\le 1-\delta .$$

Again, by virtue of (15), we have

$$\begin{array}{cc}\hfill \mathcal{F}(\mathfrak{s},\mathfrak{u},\delta )& =\sum _{\mathfrak{y}=2}^{\infty }\frac{{\mathfrak{u}}^{\mathfrak{y}-1}{\mathfrak{y}}^2\Gamma (\mathfrak{s}+1)}{\Gamma (\mathfrak{s}+\mathfrak{y})}-\delta \sum _{\mathfrak{y}=2}^{\infty }\frac{{\mathfrak{u}}^{\mathfrak{y}-1}\mathfrak{y}\Gamma (\mathfrak{s}+1)}{\Gamma (\mathfrak{s}+\mathfrak{y})}\hfill \\ \hfill & \le \sum _{\mathfrak{y}=2}^{\infty }\frac{\mathfrak{y}{\mathfrak{u}}^{\mathfrak{y}-1}}{{(\mathfrak{s}+1)}^{\mathfrak{y}-2}}-\delta \sum _{\mathfrak{y}=2}^{\infty }\frac{{\mathfrak{u}}^{\mathfrak{y}-1}}{{(\mathfrak{s}+1)}^{\mathfrak{y}-2}}\hfill \\ \hfill & =\mathfrak{u}\sum _{\mathfrak{y}=2}^{\infty }\mathfrak{y}{\left(\frac{\mathfrak{u}}{\mathfrak{s}+1}\right)}^{\mathfrak{y}-2}-\mathfrak{u}\delta \sum _{\mathfrak{y}=2}^{\infty }{\left(\frac{\mathfrak{u}}{\mathfrak{s}+1}\right)}^{\mathfrak{y}-2}\hfill \\ \hfill & =\frac{{\mathfrak{u}}^2(\mathfrak{s}+1)}{{(\mathfrak{s}-\mathfrak{u}+1)}^2}+\frac{\mathfrak{u}(\mathfrak{s}+1)(2-\delta )}{\mathfrak{s}-\mathfrak{u}+1}.\hfill \end{array}$$

Then, the above inequality is bounded by $1-\delta$ if the inequality (16) holds. This completes the proof of Theorem 4. □

Example 4.

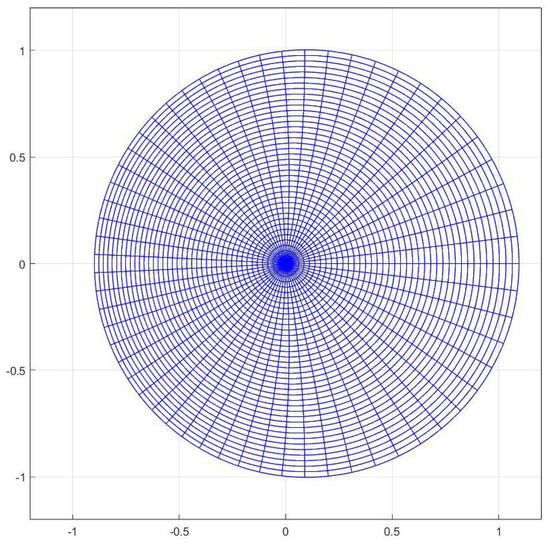
The function ${\mathcal{E}}_{1,\frac{1}{5}}\left(t\right)$ belongs to the class $\mathcal{C}$ in $\mathcal{D}.$ See Figure 2.

Figure 2. Image of the open unit disk under the function ${\mathcal{E}}_{1,\frac{1}{5}}\left(t\right)$.

At the end of this section, we present sufficient conditions imposed on the parameters for which the function ${\mathcal{E}}_{\mathfrak{s},\mathfrak{u}}\left(t\right)$ defined by (3) belongs to the class $\mathcal{L}[\rho ,\delta ].$

Theorem 5.

Assume that $\mathfrak{u}>0$, $\mathfrak{s}\ge 0$, $\rho \in [0,1/2)$ and $\delta \in [0,1)$. If the conditions

(i).

$e^{\frac{1+3\gamma }{3}}<\frac{3(\mathfrak{s}+2)}{3-2\rho }$,

(ii).

$3\mathfrak{u}\Gamma (\mathfrak{s}+1)\Gamma (3-2\rho )<(1-\delta )\left[\right(1-\mathfrak{u})\Gamma (\mathfrak{s}+2)\Gamma (2-2\rho )-u\Gamma (3-2\rho )\Gamma (\mathfrak{s}+1\left)\right]$ hold, then the function ${\mathcal{E}}_{\mathfrak{s},\mathfrak{u}}\left(t\right)$ belongs to the class $\mathcal{L}[\rho ,\delta ]$ in $\mathcal{D}.$

Proof. 

In order to establish the required result, it suffices to prove that

$$(h_{\rho }\ast {\mathcal{E}}_{\mathfrak{s},\mathfrak{u}})\left(t\right)=:g\left(t\right)\in {\mathcal{S}}^{\ast }\left(\delta \right),\mathrm{for}\mathrm{all}t\in \mathcal{D},$$

where the function $h_{\rho }\left(t\right)$ is defined by (2). By using the fact that

$$h_{\rho }\left(t\right)=t+\sum _{\mathfrak{y}=2}^{\infty }\frac{\Gamma (\mathfrak{y}+1-2\rho )}{\Gamma \left(\mathfrak{y}\right)\Gamma (2-2\rho )}{t}^{\mathfrak{y}},(t\in \mathcal{D}),$$

and (3), we establish that

$$\begin{array}{cc}\hfill g\left(t\right)& =(h_{\rho }\ast {\mathcal{E}}_{\mathfrak{s},\mathfrak{u}})\left(t\right)\hfill \\ \hfill & =t+\sum _{\mathfrak{y}=2}^{\infty }\frac{{\mathfrak{u}}^{\mathfrak{y}-1}\Gamma (\mathfrak{s}+1)\Gamma (\mathfrak{y}+1-2\rho )}{\Gamma \left(\mathfrak{y}\right)\Gamma (2-2\rho )\Gamma (\mathfrak{s}+\mathfrak{y})}{t}^{\mathfrak{y}}.\hfill \end{array}$$

(17)

Straightforward computations show that

$$\begin{array}{ccc}\hfill \left|g^{\prime }\left(t\right)-\frac{g\left(t\right)}{t}\right|& \le & \sum _{\mathfrak{y}=2}^{\infty }\frac{(\mathfrak{y}+1){\mathfrak{u}}^{\mathfrak{y}-1}\Gamma (\mathfrak{s}+1)\Gamma (\mathfrak{y}+1-2\rho )}{\Gamma \left(\mathfrak{y}\right)\Gamma (2-2\rho )\Gamma (\mathfrak{s}+\mathfrak{y})}\hfill \\ & =& \frac{\Gamma (\mathfrak{s}+1)}{\Gamma (2-2\rho )}\sum _{\mathfrak{y}=2}^{\infty }{\tau }_{\mathfrak{y}}(s,\rho ){\mathfrak{u}}^{\mathfrak{y}-1},\hfill \end{array}$$

(18)

where

$${\tau }_{\mathfrak{y}}={\tau }_{\mathfrak{y}}(s,\rho )=\frac{(\mathfrak{y}+1)\Gamma (\mathfrak{y}+1-2\rho )}{\Gamma (\mathfrak{s}+\mathfrak{y})\Gamma \left(\mathfrak{y}\right)},\mathfrak{y}\ge 2.$$

Now, we consider the function $T_1:[2,\infty )\to \mathbb{R}$ defined by

$$T_1\left(r\right)=\frac{(r+1)\Gamma (r+1-2\rho )}{\Gamma (\mathfrak{s}+r)\Gamma \left(r\right)},r\in [2,\infty ).$$

(19)

Logarithmic differentiation yields

$$T_1^{\prime }\left(r\right)=T_1\left(r\right)T_2\left(r\right),$$

(20)

where $T_2\left(r\right)$ is given by

$$T_2\left(r\right)=\frac{1}{r+1}+\psi (r+1-2\rho )-\psi (r+1)-\psi (\mathfrak{s}+r),r\in [2,\infty ).$$

(21)

From Lemma 3, we obtain

$$T_2\left(r\right)\le \frac{1}{r+1}+log(r+1-2\rho )-log(r+1)-log(\mathfrak{s}+r)+\gamma \left(1\right)=T_3\left(r\right),r\in [2,\infty ).$$

This leads to

$$T_3^{\prime }\left(r\right)=-\frac{1}{{(r+1)}^2}+\frac{1}{r+1-2\rho }-\frac{1}{r+1}-\frac{1}{\mathfrak{s}+r}<0,r\in [2,\infty ).$$

Since $T_3\left(r\right)<0$ and $T_1\left(r\right)$ is a decreasing function on $[2,\infty )$ under the given hypothesis (i), $T_1^{\prime }\left(r\right)<0$ for $r\in [2,\infty )$. This in turn implies that ${\left\{{\tau }_{\mathfrak{y}}\right\}}_{\mathfrak{y}\ge 2}$ is a decreasing sequence. From Equation (18), for $t\in \mathcal{D},$ it follows that

$$\begin{array}{cc}\hfill \left|g^{\prime }\left(t\right)-\frac{g\left(t\right)}{t}\right|& <\frac{\Gamma (\mathfrak{s}+1)}{\Gamma (2-2\rho )}\sum _{\mathfrak{y}=2}^{\infty }{\tau }_2(s,\rho ){\mathfrak{u}}^{\mathfrak{y}-1}\hfill \\ \hfill & =\frac{\Gamma (\mathfrak{s}+1)}{\Gamma (2-2\rho )}{\tau }_2(s,\rho )\sum _{\mathfrak{y}=2}^{\infty }{\mathfrak{u}}^{\mathfrak{y}-1}\hfill \\ \hfill & =\frac{\mathfrak{u}\Gamma (\mathfrak{s}+1){\tau }_2(s,\rho )}{(1-\mathfrak{u})\Gamma (2-2\rho )}.\hfill \end{array}$$

(22)

Moreover, for $t\in \mathcal{D}$, we obtain

$$\begin{array}{cc}\hfill \left|\frac{g\left(t\right)}{t}\right|& \ge 1-\left|\sum _{\mathfrak{y}=2}^{\infty }\frac{{\mathfrak{u}}^{\mathfrak{y}-1}\Gamma (\mathfrak{s}+1)\Gamma (\mathfrak{y}+1-2\rho )}{\Gamma \left(\mathfrak{y}\right)\Gamma (2-2\rho )\Gamma (\mathfrak{s}+\mathfrak{y})}{t}^{\mathfrak{y}-1}\right|\hfill \\ \hfill & =1-\sum _{\mathfrak{y}=2}^{\infty }\frac{{\mathfrak{u}}^{\mathfrak{y}-1}\Gamma (\mathfrak{s}+1)\Gamma (\mathfrak{y}+1-2\rho )}{\Gamma \left(\mathfrak{y}\right)\Gamma (2-2\rho )\Gamma (\mathfrak{s}+\mathfrak{y})}\hfill \\ \hfill & =1-\frac{\Gamma (\mathfrak{s}+1)}{\Gamma (2-2\rho )}\sum _{\mathfrak{y}=2}^{\infty }{q}_{\mathfrak{y}}(s,\rho ){\mathfrak{u}}^{\mathfrak{y}-1},\hfill \end{array}$$

(23)

where the sequence ${\left(q_{\mathfrak{y}}\right)}_{\mathfrak{y}\ge 2}$ is defined by

$$q_{\mathfrak{y}}=q_{\mathfrak{y}}(s,\rho )=\frac{\Gamma (\mathfrak{y}+1-2\rho )}{\Gamma (\mathfrak{s}+\mathfrak{y})\Gamma \left(\mathfrak{y}\right)}.$$

It is worth mentioning that

$$q_{\mathfrak{y}}=\frac{{\tau }_n}{\mathfrak{y}+1},\mathfrak{y}\ge 2.$$

The above relation implies that the sequence ${\left\{q_{\mathfrak{y}}\right\}}_{\mathfrak{y}\ge 2}$ is decreasing as the product of two positive, decreasing sequences. This fact, combining with (23), gives

$$\begin{array}{ccc}\hfill \left|\frac{g\left(t\right)}{t}\right|& \ge & 1-\frac{\Gamma (\mathfrak{s}+1)}{\Gamma (2-2\rho )}\sum _{\mathfrak{y}=2}^{\infty }{q}_2(s,\rho ){\mathfrak{u}}^{\mathfrak{y}-1}\hfill \\ & =& 1-\frac{\Gamma (\mathfrak{s}+1)q_2(s,\rho )\mathfrak{u}}{(1-\mathfrak{u})\Gamma (2-2\rho )}.\hfill \end{array}$$

(24)

Combining (22) and (24), we have

$$\begin{array}{cc}\hfill \left|\frac{t{g}^{\prime }\left(t\right)}{g\left(t\right)}-1\right|& <\frac{3\mathfrak{u}\Gamma (\mathfrak{s}+1)\Gamma (3-2\rho )}{(1-\mathfrak{u})\Gamma (\mathfrak{s}+2)\Gamma (2-2\rho )-\mathfrak{u}\Gamma (3-2\rho )\Gamma (\mathfrak{s}+1)}.\hfill \end{array}$$

Finally, the condition (ii) and the above inequality helps us to establish the desired result. □

4. Hardy Space of the Normalized Form of the Miller-Ross Function

In the first main result in this section, we present some immediate applications of convexity and univalence involving the normalized form of the Miller-Ross function associated with the Hardy space of analytic functions.

Theorem 6.

Under the assumptions of Theorem 4, the following assertions hold true:

(i).

If $\delta \in [0,\frac{1}{2})$, then

$${\mathcal{E}}_{\mathfrak{s},\mathfrak{u}}\in {\mathcal{H}}^{\frac{1}{1-2\delta }}.$$

(ii).

If $\delta \ge \frac{1}{2}$, then

$${\mathcal{E}}_{\mathfrak{s},\mathfrak{u}}\in {\mathcal{H}}^{\infty }.$$

Proof. 

By using the definition of the Gauss hypergeometric function as

$${}_{2}F_1(a,b,c;t)=\sum _{\mathfrak{y}=0}^{\infty }\frac{{\left(a\right)}_{\mathfrak{y}}{\left(b\right)}_{\mathfrak{y}}}{{\left(c\right)}_{\mathfrak{y}}}\frac{t^{\mathfrak{y}}}{\mathfrak{y}!},$$

where ${\left(a\right)}_k$ stands for the Pochhammer symbol, we deduce that

$$\begin{array}{cc}\hfill m+\frac{1}{{(1-t{e}^{i\theta })}^{1-2\delta }}& =m+l{t}_2{F}_1(1,1-2\delta ,1;t{e}^{i\theta })\hfill \\ \hfill & =m+l\frac{{(1-2\delta )}_{\mathfrak{y}}}{\mathfrak{y}!}{e}^{i\theta \mathfrak{y}}{t}^{\mathfrak{y}+1},\hfill \end{array}$$

(25)

where $\theta$ is any real number and $m,l\in \mathbb{C},\delta \ne \frac{1}{2}$. In addition, we have

$$\begin{array}{cc}\hfill m+llog(1-t{e}^{i\theta })& =m-l{t}_2{F}_1(1,1,t;t{e}^{i\theta })\hfill \\ \hfill & =m-l\sum _{\mathfrak{y}=0}^{\infty }\frac{1}{\mathfrak{y}+1}{e}^{i\theta \mathfrak{y}{t}^{\mathfrak{y}+1}}.\hfill \end{array}$$

(26)

Hence, we deduce that the function ${\mathcal{E}}_{\mathfrak{s},\mathfrak{u}}\left(t\right)$ cannot be expressed in the forms (25) for $\delta \ne \frac{1}{2}$ and (26) for $\delta =\frac{1}{2}$, respectively. But, the function ${\mathcal{E}}_{\mathfrak{s},\mathfrak{u}}\left(t\right)\in \mathcal{C}\left(\delta \right),$ by means of Theorem 4. Then, the proof is completed by applying Lemma 6. □

Theorem 7.

Assume that $\delta \in [0,1)$ and $0<\mathfrak{u}<\mathfrak{s}+1.$ Also, suppose that the inequality

$$\frac{\mathfrak{u}}{\mathfrak{s}-\mathfrak{u}+1}<1-\delta ,$$

holds, then $\frac{{\mathcal{E}}_{\mathfrak{s},\mathfrak{u}}\left(t\right)}{t}\in \mathcal{P}\left(\delta \right).$

Proof. 

It is sufficient to show that $\left|H\right(t)-1|<1$ for all $t\in \mathcal{D},$ where

$$H\left(t\right)=\frac{1}{1-\delta }\left[\frac{{\mathcal{E}}_{\mathfrak{s},\mathfrak{u}}\left(t\right)}{t}-\delta \right].$$

Straightforward calculations would yield

$$\begin{array}{cc}\hfill \left|h\left(t\right)-1\right|& =\frac{1}{1-\delta }\left|\sum _{\mathfrak{y}=2}^{\infty }\frac{{\mathfrak{u}}^{\mathfrak{y}-1}\Gamma (\mathfrak{s}+1)}{\Gamma (\mathfrak{s}+\mathfrak{y})}{t}^{\mathfrak{y}-1}\right|\hfill \\ \hfill & <\frac{1}{1-\delta }\sum _{\mathfrak{y}=2}^{\infty }\frac{{\mathfrak{u}}^{\mathfrak{y}-1}\Gamma (\mathfrak{s}+1)}{\Gamma (\mathfrak{s}+\mathfrak{y})}.\hfill \end{array}$$

(27)

Hence, by combining the above inequality with the relation

$$\frac{\Gamma (a+1)}{\Gamma (a+n)}\le \frac{1}{{(a+1)}^{n-1}},\left(n\in \mathbb{N}\setminus \left\{1\right\},a>0\right),$$

(28)

we establish that

$$\begin{array}{cc}\hfill \left|H\left(t\right)-1\right|& \le \frac{1}{1-\delta }\sum _{\mathfrak{y}=2}^{\infty }{\left(\frac{\mathfrak{u}}{\mathfrak{s}+1}\right)}^{\mathfrak{y}-1}\hfill \\ \hfill & =\frac{1}{1-\delta }\left(\frac{\mathfrak{u}}{\mathfrak{s}-\mathfrak{u}+1}\right)<1,\hfill \end{array}$$

under the given conditions. Therefore, the proof is complete. □

Theorem 8.

Let $0<\mathfrak{u}<\mathfrak{s}+1$. If $h\in \mathcal{R}$, then $({\mathcal{E}}_{\mathfrak{s},\mathfrak{u}}\ast h)\left(t\right)\in {\mathcal{H}}^{\infty }\cap \mathcal{R}.$

Proof. 

The assumption that $h^{\prime }\in \mathcal{P}$ follows from the fact that $h\in \mathcal{R}$. We set

$$g\left(t\right)={\mathcal{E}}_{\mathfrak{s},\mathfrak{u}}\left(t\right)\ast h\left(t\right).$$

Using the definition of convolution, we obtain

$$g^{\prime }\left(t\right)=\frac{{\mathcal{E}}_{\mathfrak{s},\mathfrak{u}}\left(t\right)}{t}\ast h^{\prime }\left(t\right).$$

From Theorem 7, it follows that

$$\frac{{\mathcal{E}}_{\mathfrak{s},\mathfrak{u}}\left(t\right)}{t}\in \mathcal{P}.$$

Thus, by applying Lemma 4, we get $h^{\prime }\in \mathcal{P}$. Moreover, since $Re\left\{h^{\prime }\left(t\right)\right\}>0$ in $\mathcal{D}$, this implies that

$$\left\{\begin{array}{c}{h}^{\prime }\in {\mathcal{H}}^q,q<1,\hfill \\ h\in {\mathcal{H}}^{\frac{q}{1-q}}for0<q<1.\hfill \end{array}\right.$$

Consequently, for $0<q<1$, we have $h\in {\mathcal{H}}^{\frac{q}{1-q}}$, and $h^{\prime }\in {\mathcal{H}}^q$ for $0<q<1$. Hence, $h\in {\mathcal{H}}^{\infty }$. In addition, we observe that

$$\left|g\left(t\right)\right|\le \left|t\right|+\sum _{\mathfrak{y}=2}^{\infty }\frac{{\mathfrak{u}}^{\mathfrak{y}-1}\Gamma (\mathfrak{s}+1)}{\Gamma (\mathfrak{s}+\mathfrak{y})}\left|a_{\mathfrak{y}}\right|\left|t^{\mathfrak{y}}\right|$$

$$\le 1+\sum _{\mathfrak{y}=2}^{\infty }\frac{{\mathfrak{u}}^{\mathfrak{y}-1}\Gamma (\mathfrak{s}+1)}{\Gamma (\mathfrak{s}+\mathfrak{y})}\left|a_{\mathfrak{y}}\right|.$$

Now, by using a result from MacGregor on the coefficients for the class $\mathcal{R},\left|a_{\mathfrak{y}}\right|\le \frac{2}{\mathfrak{y}},\mathfrak{y}\ge 2$, and the inequality (28), we obtain

$$\begin{array}{cc}\hfill \left|g\left(t\right)\right|& \le 1+\sum _{\mathfrak{y}=2}^{\infty }\frac{2{\mathfrak{u}}^{\mathfrak{y}-1}}{\mathfrak{y}{(\mathfrak{s}+1)}^{\mathfrak{y}-1}}\hfill \\ \hfill & =1+\sum _{\mathfrak{y}=1}^{\infty }\frac{2{\mathfrak{u}}^{\mathfrak{y}}}{(\mathfrak{y}+1){(\mathfrak{s}+1)}^{\mathfrak{y}}}<\infty .\hfill \end{array}$$

We observe that the series given above converges absolutely in $\left|t\right|=1$, under the given condition. On the other hand, by using the fact that [23], if $g^{\prime }\left(t\right)\in {\mathcal{H}}^q$, then the function $g\left(t\right)$ is continuous in $\overline{\mathcal{D}}$. Finally, since $\overline{\mathcal{D}}$ is a compact set, then the function $g\left(t\right)$ is bounded. This completes the proof of the theorem. □

Theorem 9.

Suppose that the hypothesis of the above theorem is satisfied. Suppose that the function $h\left(t\right)$ is of the form (1) and in the class $\mathcal{R}\left(\eta \right)$ for a fixed $\eta \in [0,1),$ then $({\mathcal{E}}_{\mathfrak{s},\mathfrak{u}}\ast h)\left(t\right)\in \mathcal{R}\left(\beta \right)$ where $\beta =1-2(1-\delta )(1-\eta ).$

Proof. 

Since $h\left(t\right)\in \mathcal{R}\left(\eta \right)$, this implies that $h^{\prime }\in \mathcal{P}\left(\eta \right)$. Now, we consider the function g defined by

$$g\left(t\right)=({\mathcal{E}}_{\mathfrak{s},\mathfrak{u}}\ast h)\left(t\right).$$

Therefore, we get

$$g^{\prime }\left(t\right)=\frac{{\mathcal{E}}_{\mathfrak{s},\mathfrak{u}}\left(t\right)}{t}\ast h^{\prime }\left(t\right).$$

From Theorem 7, it follows that $\frac{{\mathcal{E}}_{\mathfrak{s},\mathfrak{u}}}{t}\in \mathcal{P}\left(\delta \right)$. Moreover, by using Lemma 5, we deduce that $g^{\prime }\left(t\right)\in \mathcal{P}\left(\beta \right)$, where $\beta =1-2(1-\delta )(1-\eta )$. This in turn implies that $g\in \mathcal{R}\left(\beta \right)$. □

5. Conclusions

In the present paper, we have derived some new geometric properties for the normalized form of the Miller-Ross function, including strongly starlikeness, strongly convexity, starlikeness, convexity, and pre-starlikeness inside the unit disk. Moreover, as an application, we have established sufficient conditions so that this function belongs to the Hardy spaces ${\mathcal{H}}^p$ and ${\mathcal{H}}^{\infty }.$ Furthermore, we have determined some conditions for which the function $\frac{{\mathcal{E}}_{\mathfrak{s},\mathfrak{u}}\left(t\right)}{t}$ belongs to the class $\mathcal{P}\left(\delta \right)$. We have also successfully determined conditions on the parameters for which a function $h\in \mathcal{R}\left(\eta \right)$ with $0\le \eta <1$ implies that the convolution product ${\mathcal{E}}_{\mathfrak{s},\mathfrak{u}}\ast h$ belongs to the spaces ${\mathcal{H}}^{\infty }$ and $\mathcal{R}\left(\beta \right).$