A Subclass of Meromorphic Multivalent Functions Generated by a Symmetric q-Difference Operator

Abstract

This paper presents a novel symmetric q-analogue differential operator designed for meromorphic multivalent functions analytic in the punctured open unit disk. Employing this operator, a new family of meromorphic multivalent functions is proposed and examined in this work. A detailed investigation of this newly defined class of meromorphic multivalent functions is presented, highlighting key geometric characteristics, including sufficiency criteria, coefficient inequalities, distortion and growth behavior, as well as the radii of starlikeness and convexity.

1. Introduction and Definitions

Let ${\mathcal{M}}_{\mu }$ represent the class of all meromorphic functions f that are $\mu$-valent ($\mu \in {\mathbb{N}}^{*}=\left\{1,2,3,\dots \right\}$) and analytic in the open disk excluding the origin, denoted by $U^{*}$, defined as the set $\{u\in \mathbb{C}:0<|u|<1\}$ (see [1,2]). Each function in this class is assumed to satisfy a prescribed normalization condition:

$$T\left(u\right)={\displaystyle \frac{1}{u^{\mu }}}+\sum _{l=1}^{\infty }{t}_{l+\mu }{u}^{l+\mu }, u\in U^{*}.$$

(1)

Clearly, the class ${\mathcal{M}}_{\mu }$ coincides with the class $\mathcal{M}$ of functions that are univalent and meromorphic (see [2,3]) when $\mu =1$.

The function f $\in {\mathcal{M}}_{\mu }$ is said to belong to the class ${\mathcal{SM}}_{\mu }^{*}\left(\alpha \right)$, where $0\le \alpha <\mu$, consisting of meromorphic $\mu$-valent starlike functions of order $\alpha$ (see [4,5]), if it satisfies the following condition:

$$T\left(u\right)\in {\mathcal{SM}}_{\mu }^{*}\left(\alpha \right)\iff Re\left\{{\displaystyle \frac{u{f}^{\prime }\left(u\right)}{\mu T\left(u\right)}}\right\}<-\alpha , u\in U^{*}, 0\le \alpha <\mu .$$

(2)

It is evident that when $\alpha =0$, the class ${\mathcal{SM}}_{\mu }^{*}\left(0\right)$ coincides with ${\mathcal{SM}}_{\mu }^{*}$, the class of meromorphic $\mu$-valent starlike functions.

The class ${\mathcal{CM}}_{\mu }\left(\alpha \right)$, where $0\le \alpha <\mu$, consists of meromorphic $\mu$-valent convex functions of order $\alpha$ (see [3]). A function f $\in {\mathcal{M}}_{\mu }$ is said to belong to ${\mathcal{CM}}_{\mu }\left(\alpha \right)$ provided that for $u\in {\mathbb{U}}^{*}$, it satisfies the condition:

$$Re\left\{{\displaystyle \frac{{\left(u{f}^{\prime }\left(u\right)\right)}^{\prime }}{\mu f^{\prime }\left(u\right)}}\right\}<-\alpha , u\in U^{*}, 0\le \alpha <\mu .$$

(3)

In a similar manner, we refer to ${\mathcal{KM}}_{\mu }^{*}\left(\alpha \right)$ as the class of meromorphic $\mu$-valent close-to-convex functions of order $\alpha$ (see [5]), defined by the condition:

$$T\left(u\right)\in {\mathcal{KM}}_{\mu }^{*}\left(\alpha \right)\iff Re\left\{{\displaystyle \frac{u{f}^{\prime }\left(u\right)}{\mu e\left(u\right)}}\right\}<-\alpha , u\in U^{*}, 0\le \alpha <\mu ,$$

(4)

where $e\left(u\right)\in {\mathcal{SM}}_{\mu }^{*}$, for $u\in {\mathbb{U}}^{*}$.

Numerous subclasses of meromorphic functions have been introduced and extensively studied by various researchers in the past. For detailed discussions and foundational results on these subclasses, the reader is referred to the works presented in references [6,7,8,9,10,11,12,13].

The domain of symmetric q-calculus has attracted growing attention in recent years owing to its wide-ranging applicability across multiple areas of mathematics and mathematical physics, including fractional calculus, geometric function theory (GFT), and quantum mechanics [1]. A key aspect of its appeal lies in the fact that the derivative of a differentiable function f can be effectively approximated using the symmetric q-derivative. This operator is widely regarded as offering enhanced convergence behavior compared to the traditional q-derivative, though further rigorous investigation is needed to conclusively establish its superiority.

Rooted in the foundational principles of q-calculus—an area of study that emerged in the early 20th century—the symmetric q-calculus extends these ideas by introducing more nuanced operator characteristics. These refined operators are particularly well-suited for analyzing and characterizing function classes that exhibit intrinsic symmetry properties. As a result, symmetric q-calculus provides powerful tools for exploring both theoretical and applied problems where symmetry plays a pivotal role, deepening our understanding of mathematical structures and their physical interpretations.

The theory of q-calculus operators has found wide-ranging applications across several branches of mathematics and physics, including complex analysis, hypergeometric series, particle physics, and, most significantly, geometric function theory. A major milestone in this direction was the introduction of the concept of q-starlike functions by Ismail and his collaborators in 1990 [14], which marked the beginning of a new line of inquiry in geometric function theory. The groundwork for q-analogues of classical operators was laid by Jackson [15], who introduced the q-differential and q-integral operators and demonstrated their relevance to geometric function theory. Building on this, Arif et al. [16] applied convolution techniques to formulate the q-Noor integral operator, which was then utilized to define and examine new subclasses of analytic functions. In a related development, the work presented in [17] extended the theory by establishing a q-analogue of the differential operator, facilitating the identification and analysis of novel function classes within the analytic framework. For other contributions, the reader is referred to the following papers: [18,19,20,21,22,23,24,25,26,27,28,29].

The symmetric q-derivative operator was first introduced within the framework of geometric function theory by Kanas et al. [30], whose foundational contributions laid the groundwork for subsequent research in this area. Researchers have actively explored the theoretical implications and practical utility of the symmetric q-calculus in addressing complex challenges arising in both mathematical and physical contexts. Recent advances in this area have been explored in the works of [13,31,32,33,34,35,36,37,38,39]; see also the references cited therein for further reading.

To facilitate a clearer understanding of the present work, we first introduce several fundamental notations and concepts from symmetric q-difference calculus that are employed throughout this manuscript. The symmetric q-difference operator utilized in this study extends its impact far beyond the construction of a specific subclass of meromorphic multivalent functions. As highlighted in the introductory sections, this operator exhibits enhanced approximation properties near singularities and improved convergence as $q\to 1^{-}$, making it a powerful analytical tool for bridging discrete q-analysis with classical differential theory.

Its symmetric structure offers natural applicability in areas where duality, reversibility, or intrinsic symmetry play a fundamental role—such as in quantum mechanics, non-commutative geometry, and fractional q-calculus. The operator has also been suggested as a viable framework for studying stability, dynamic behavior, and mapping properties of generalized function classes under integral transforms.

Moreover, the paper identifies potential applications in q-deformed quantum harmonic oscillators, signal processing, and data analysis, thereby underscoring the versatility and theoretical depth of the operator in both mathematical physics and applied analysis. These connections reaffirm that the symmetric q-operator is not only structurally robust but also analytically expansive in its reach and relevance.

The quantity known as the symmetric q-number, represented by $\widetilde{{\left[\eta \right]}_q}$, is defined by the expression:

$$\widetilde{{\left[\eta \right]}_q}={\displaystyle \frac{q^{-\eta }-q^{\eta }}{q^{-1}-q}} , \mathrm{for} 0<q<1,\eta \in {\mathbb{N}}^{*} \mathrm{and} \widetilde{{\left[0\right]}_q}=0.$$

(5)

It should be emphasized that the symmetric q-number is distinct from the standard q-number and commonly features in the analysis of q-deformed quantum mechanical simple harmonic oscillators [40]. The definition of the symmetric q-shifted factorial is formulated as:

$$\widetilde{{\left[\eta \right]}_q}!=\left\{\begin{array}{c}\widetilde{{\left[\eta \right]}_q}·\widetilde{{\left[\eta -1\right]}_q}·\widetilde{{\left[\eta -2\right]}_q}·\dots ·1, \mathrm{for} \eta =1,2,\dots ;\\ 1, \mathrm{for} \eta =0.\end{array}\right.$$

(6)

Clearly, it turns out that $\widetilde{{\left[n\right]}_q}!\to n!$ as $q\to 1^{-}$.

The symmetric q-derivative operator $\widetilde{D_q}T\left(u\right)$ [41] acting on functions $T\left(u\right)\in {\mathcal{M}}_{\mu }$ is formulated as follows:

$$\widetilde{D_q}T\left(u\right)=\left\{\begin{array}{c}{\displaystyle \frac{T\left(qu\right)-T\left(q^{-1}u\right)}{u\left(q-q^{-1}\right)}}, 0<q<1,u\in U^{*};\\ f^{\prime }\left(0\right), \mathrm{for} u=0.\end{array}\right.$$

(7)

It is essential to point out that $\widetilde{D_q}T\left(u\right)\to$$f^{\prime }\left(u\right)$ as $q\to 1^{-}$.

Out of (1), we have $\widetilde{D_q}{u}^{\eta }=\widetilde{{\left[\eta \right]}_q}{u}^{\eta -1}$, and a power series of $\widetilde{D_q}f$, when $T\left(u\right)={\displaystyle \frac{1}{u^{\mu }}}+{\displaystyle \sum _{l=1}^{\infty }}{t}_{l+\mu }{u}^{l+\mu },$$u\in U^{*}$, is

$$u\widetilde{D_q}T\left(u\right)=-{\displaystyle \frac{\widetilde{{\left[\mu \right]}_q}}{u^{\mu }}}+\sum _{l=1}^{\infty }\widetilde{{\left[l+\mu \right]}_q}{t}_{l+\mu }{u}^{l+\mu }.$$

(8)

In this paper, inspired by the aforementioned articles and the work of Hu et al. [42], Shi et al. [43], and Ahmad et al. [44], we propose a novel symmetric q-differential operator for meromorphic $\mu$-valent functions. A new family of $\mu$-valent meromorphic functions is introduced based on Janowsky-type conditions by employing the new specific symmetric q-differential operator. We proceed to investigate various geometric properties of the functions in this class. In particular, we establish sufficient conditions for class membership, derive distortion bounds and coefficient estimates, and examine the radii of starlikeness and convexity. To validate the effectiveness of our results, we also consider several special cases of the involved parameters.

We proceed to define a new differential operator $\widetilde{{\mathcal{L}}_{\tau ,q}}:{\mathcal{M}}_{\mu }\to {\mathcal{M}}_{\mu }$ as follows:

$$\widetilde{{\mathcal{L}}_{\tau ,q}}T\left(u\right)=\left(1+\tau \widetilde{{\left[\mu \right]}_q}\right)T\left(u\right)+\tau u\widetilde{D_q}T\left(u\right),$$

(9)

where $0<q<1,\tau \ge 0,u\in U^{*}.$

Applying (1) and (8) in relation (9), we conclude that

$$\widetilde{{\mathcal{L}}_{\tau ,q}}T\left(u\right)={\displaystyle \frac{1}{u^{\mu }}}+\sum _{l=1}^{\infty }\left(1+\tau \widetilde{{\left[\mu \right]}_q}+\tau \widetilde{{\left[l+\mu \right]}_q}\right)t_{l+\mu }{u}^{l+\mu }.$$

(10)

We set:

$$\begin{array}{ccc}\hfill \widetilde{{\mathcal{L}}_{\tau ,q}^0}T\left(u\right)& =& T\left(u\right),\hfill \\ \hfill \widetilde{{\mathcal{L}}_{\tau ,q}^1}T\left(u\right)& =& \widetilde{{\mathcal{L}}_{\tau ,q}}T\left(u\right)\hfill \\ \hfill \widetilde{{\mathcal{L}}_{\tau ,q}^2}T\left(u\right)& =& \widetilde{{\mathcal{L}}_{\tau ,q}}\left(\widetilde{{\mathcal{L}}_{\tau ,q}}T\left(u\right)\right)={\displaystyle \frac{1}{u^{\mu }}}+\sum _{l=1}^{\infty }{\left(1+\tau \widetilde{{\left[\mu \right]}_q}+\tau \widetilde{{\left[l+\mu \right]}_q}\right)}^2{t}_{l+\mu }{u}^{l+\mu }.\hfill \end{array}$$

Analogously, we derive the following result:

$$\widetilde{{\mathcal{L}}_{\tau ,q}^{\varsigma }}T\left(u\right)={\displaystyle \frac{1}{u^{\mu }}}+\sum _{l=1}^{\infty }{\left(1+\tau \widetilde{{\left[\mu \right]}_q}+\tau \widetilde{{\left[l+\mu \right]}_q}\right)}^{\varsigma }{t}_{l+\mu }{u}^{l+\mu } , \varsigma \in \mathbb{N}.$$

(11)

Remark 1.

It is worth noting that the operator $\widetilde{{\mathcal{L}}_{\tau ,q}}$, as defined in (9) maintains a deep connection with classical differential operators widely used in the theory of harmonic and geometric function theory. In the limit as $q\to 1^{-}$, the symmetric q-derivative $\widetilde{D_q}$ converges to the ordinary derivative, and hence the operator $\widetilde{{\mathcal{L}}_{\tau ,q}}$, reduces to the classical linear form ${\mathcal{L}}_{\tau }T\left(u\right)=\left(1+\tau \mu \right)T\left(u\right)+\tau u{T}^{\prime }\left(u\right)$, which resembles known structures such as the Libera operator and certain weighted Salagean-type operators. These operators are fundamental tools in the analysis of starlike, convex, and close-to-convex functions, especially in establishing distortion bounds, growth estimates, and coefficient inequalities. Moreover, when combined with subordination conditions, the operator aligns with the framework of Janowski-type function classes—an established approach for generalizing classical geometric properties via the theory of differential subordinations. This connection reinforces the theoretical foundation of $\widetilde{{\mathcal{L}}_{\tau ,q}^{\varsigma }}$, positioning it as a natural q-deformation of classical analytic operators, while also enabling the extension of geometric function theory into the realm of symmetric q-calculus.

Remark 2.

As $q\to 1^{-}$, the symmetric q-differential operator defined in (9) reduces to the classical differential operator introduced in [45].

In what follows, all results are considered for $u\in U^{*}, 0<q<1, 0\le C<1,\tau \ge 0,0\le \alpha <\mu \mathrm{and} \varsigma \in \mathbb{N}$ unless specified otherwise.

A subclass ${\widetilde{\mathcal{KM}}}_{\tau ,q}\left(\mu ,\varsigma ,C\right)$ of ${\mathcal{M}}_{\mu }$ is now introduced, defined using the operator $\widetilde{{\mathcal{L}}_{\tau ,q}^{\varsigma }}$, as follows.

Definition 1.

Let f be a meromorphic function in ${\mathcal{M}}_{\mu }$. The function belongs to the subclass ${\widetilde{\mathcal{KM}}}_{\tau ,q}\left(\mu ,\varsigma ,C\right)$, if it satisfies the following condition:

$$-{\displaystyle \frac{u\widetilde{D_q}\left(\widetilde{{\mathcal{L}}_{\tau ,q}^{\varsigma }}T\left(u\right)\right)}{\widetilde{{\left[\mu \right]}_q}e\left(u\right)}}\prec {\displaystyle \frac{1+u\left[1-C\left(1+q\right)\right]}{1-qu}}$$

(12)

for which $e\left(u\right)\in {\mathcal{SM}}_{\mu }^{*}$. The symbol ≺ denotes the well-known concept of subordination (see [46]).

Remark 3.

We say that $f\in {\widetilde{\mathcal{KM}}}_{\tau ,q}\left(\mu ,\varsigma ,C\right)$ if and only if in the case that $-{\displaystyle \frac{u\widetilde{D_q}\left(\widetilde{{\mathcal{L}}_{\tau ,q}^{\varsigma }}T\left(u\right)\right)}{\widetilde{{\left[\mu \right]}_q}e\left(u\right)}}$, where $e\left(u\right)\in {\mathcal{SM}}_{\mu }^{*}$, takes all values in the circular domain centered at $\left(1-q-{\displaystyle \frac{Cq}{1+q}}\right)$ and radius ${\displaystyle \frac{C-1}{1-q^2}}$.

An equivalent condition for a function $f\in {\widetilde{\mathcal{KM}}}_{\tau ,q}\left(\mu ,\varsigma ,C\right)$ is given below and can be easily established.

$$\left|{\displaystyle \frac{\frac{u\widetilde{D_q}\left(\widetilde{{\mathcal{L}}_{\tau ,q}^{\varsigma }}T\left(u\right)\right)}{\widetilde{{\left[\mu \right]}_q}e\left(u\right)}+1}{1-C\left(1+q\right)-q\frac{u\widetilde{D_q}\left(\widetilde{{\mathcal{L}}_{\tau ,q}^{\varsigma }}T\left(u\right)\right)}{\widetilde{{\left[\mu \right]}_q}e\left(u\right)}}}\right|<1.$$

(13)

The following lemma due to Rogosinski plays a key role in establishing our main results.

Lemma 1

([47]). Let $\upsilon \left(u\right)$ be an analytic function with the series representation $\upsilon \left(u\right)=1+{\displaystyle \sum _{l=1}^{\infty }}{\upsilon }_l{u}^l$, and let $\omega \left(u\right)$ be an univalent and convex function in U represented by $\omega \left(u\right)=1+{\displaystyle \sum _{l=1}^{\infty }}\omega t_l{u}^l$. If $\upsilon \left(u\right)\prec \omega \left(u\right)$, then it follows that $\left|{\upsilon }_l\right|\le \left|\omega t_1\right|$, for all $l\in {\mathbb{N}}^{*}$.

2. Main Results

In this section, we first derive sufficient conditions that characterize membership in the newly introduced class, ${\widetilde{\mathcal{KM}}}_{\tau ,q}\left(\mu ,\varsigma ,C\right)$. Subsequently, we obtain sharp coefficient bounds for functions belonging to this class, thereby contributing to a deeper analytical understanding of their geometric and functional properties.

In what follows, we derive the core analytic conditions that characterize the newly defined subclass ${\widetilde{\mathcal{KM}}}_{\tau ,q}\left(\mu ,\varsigma ,C\right)$. These conditions are established using a combination of symmetric q-calculus techniques, subordination principles, and coefficient estimates. The primary goal is to provide a clear and tractable inequality that ensures class membership based on the behavior of the function’s coefficients. The first main result, presented below, offers such a condition and serves as the foundation for subsequent corollaries and sharpness results.

Theorem 1.

Let $f\in {\mathcal{M}}_{\mu }$ be a function with a series representation as given in (1). Then f belongs to the class ${\widetilde{\mathcal{KM}}}_{\tau ,q}\left(\mu ,\varsigma ,C\right)$ whenever the following inequality is fulfilled:

$$\sum _{l=1}^{\infty }\left({\left(1+\tau \widetilde{{\left[\mu \right]}_q}+\tau \widetilde{{\left[l+\mu \right]}_q}\right)}^{\varsigma }\left|t_{l+\mu }\right|+{\displaystyle \frac{4\mu \widetilde{{\left[\mu \right]}_q}}{\left(q+1\right)\left(l+\mu \right)}}-{\displaystyle \frac{2C\mu \widetilde{{\left[\mu \right]}_q}}{l+\mu }}\right)\le \left(1-C\right)\widetilde{{\left[\mu \right]}_q}.$$

(14)

This condition is sufficient for membership in the class ${\widetilde{\mathcal{KM}}}_{\tau ,q}\left(\mu ,\varsigma ,C\right)$.

Proof. 

To validate the sufficiency condition, we aim to verify that the subordination inequality (13) is indeed satisfied under the given assumptions.

$$\left|{\displaystyle \frac{\frac{u\widetilde{D_q}\left(\widetilde{{\mathcal{L}}_{\tau ,q}^{\varsigma }}T\left(u\right)\right)}{\widetilde{{\left[\mu \right]}_q}e\left(u\right)}+1}{1-C\left(1+q\right)-q\frac{u\widetilde{D_q}\left(\widetilde{{\mathcal{L}}_{\tau ,q}^{\varsigma }}T\left(u\right)\right)}{\widetilde{{\left[\mu \right]}_q}e\left(u\right)}}}\right|=\left|{\displaystyle \frac{u\widetilde{D_q}\left(\widetilde{{\mathcal{L}}_{\tau ,q}^{\varsigma }}T\left(u\right)\right)+\widetilde{{\left[\mu \right]}_q}e\left(u\right)}{\left[1-C\left(1+q\right)\right]\widetilde{{\left[\mu \right]}_q}e\left(u\right)-qu\widetilde{D_q}\left(\widetilde{{\mathcal{L}}_{\tau ,q}^{\varsigma }}T\left(u\right)\right)}}\right|.$$

Assume that $e\left(u\right)$ may be represented as the following power series:

$$e\left(u\right)={\displaystyle \frac{1}{u^{\mu }}}+\sum _{l=1}^{\infty }{e}_{l+\mu }{u}^{l+\mu }.$$

To simplify our computations, we define the following compact notation for the coefficient expression appearing repeatedly in the summation.

$${\Gamma }_{l,\tau ,\mu }^{\varsigma }={\left(1+\tau \widetilde{{\left[\mu \right]}_q}+\tau \widetilde{{\left[l+\mu \right]}_q}\right)}^{\varsigma }\widetilde{{\left[l+\mu \right]}_q}.$$

By first applying (9), and then making use of (7) and (10), we deduce—after appropriate simplifications—that the preceding expression is equivalent to:

$$\begin{array}{c}\hfill \left|{\displaystyle \frac{{\displaystyle \sum _{l=1}^{\infty }}{\Gamma }_{l,\tau ,\mu }^{\varsigma }{t}_{l+\mu }{u}^{l+2\mu }+{\displaystyle \sum _{l=1}^{\infty }}\widetilde{{\left[\mu \right]}_q}{e}_{l+\mu }{u}^{l+2\mu }}{\left(1-C\right)\left(1+q\right)\widetilde{{\left[\mu \right]}_q}+\left[1-C\left(1+q\right)\right]{\displaystyle \sum _{l=1}^{\infty }}\widetilde{{\left[\mu \right]}_q}{e}_{l+\mu }{u}^{l+2\mu }-q{\displaystyle \sum _{l=1}^{\infty }}{\Gamma }_{l,\tau ,\mu }^{\varsigma }\widetilde{{\left[l+\mu \right]}_q}{t}_{l+\mu }{u}^{l+2\mu }}}\right|\\ \hfill \le {\displaystyle \frac{{\displaystyle \sum _{l=1}^{\infty }}{\Gamma }_{l,\tau ,\mu }^{\varsigma }\left|t_{l+\mu }\right|+\widetilde{{\left[\mu \right]}_q}{\displaystyle \sum _{l=1}^{\infty }}\left|e_{l+\mu }\right|}{\left(1-C\right)\left(1+q\right)\widetilde{{\left[\mu \right]}_q}-\left[1-C\left(1+q\right)\right]\widetilde{{\left[\mu \right]}_q}{\displaystyle \sum _{l=1}^{\infty }}\left|e_{l+\mu }\right|-q{\displaystyle \sum _{l=1}^{\infty }}{\Gamma }_{l,\tau ,\mu }^{\varsigma }\left|t_{l+\mu }\right|}}.\end{array}$$

Given that $e\left(u\right)\in {\mathcal{SM}}_{\mu }^{*}$, it is known from [4] that its coefficients obey a specific inequality which we now apply to simplify the sum.

$$\left(l+\mu \right)\left|e_{l+\mu }\right|=2\mu .$$

(15)

Substituting this expression into our earlier inequality and invoking inequality (14), we obtain

$$\begin{array}{ccc}& & \left|{\displaystyle \frac{\frac{u\widetilde{D_q}\left(\widetilde{{\mathcal{L}}_{\tau ,q}^{\varsigma }}T\left(u\right)\right)}{\widetilde{{\left[\mu \right]}_q}e\left(u\right)}+1}{1-C\left(1+q\right)-q\frac{u\widetilde{D_q}\left(\widetilde{{\mathcal{L}}_{\tau ,q}^{\varsigma }}T\left(u\right)\right)}{\widetilde{{\left[\mu \right]}_q}e\left(u\right)}}}\right|\hfill \\ & \le & {\displaystyle \frac{{\displaystyle \sum _{l=1}^{\infty }}{\left(1+\tau \widetilde{{\left[\mu \right]}_q}+\tau \widetilde{{\left[l+\mu \right]}_q}\right)}^{\varsigma }\widetilde{{\left[l+\mu \right]}_q}\left|t_{l+\mu }\right|+2\mu \widetilde{{\left[\mu \right]}_q}{\displaystyle \sum _{l=1}^{\infty }}\frac{1}{l+\mu }}{\left(1-C\right)\left(1+q\right)\widetilde{{\left[\mu \right]}_q}-2\left[1-C\left(1+q\right)\right]\mu \widetilde{{\left[\mu \right]}_q}{\displaystyle \sum _{l=1}^{\infty }}\frac{1}{l+\mu }-q{\displaystyle \sum _{l=1}^{\infty }}{\Gamma }_{l,\tau ,\mu }^{\varsigma }\left|t_{l+\mu }\right|}}.\hfill \end{array}$$

Thus, since the transformed expression remains strictly less than 1, the inequality in (13) is satisfied, completing the proof of sufficiency.

In the reverse direction, suppose that $f\in {\widetilde{\mathcal{KM}}}_{\tau ,q}\left(\mu ,\varsigma ,C\right)$ is a function represented by the series expansion given in (1). Then, by applying (13), we deduce that the following relation holds for all $u\in U^{*}$:

$$\begin{array}{ccc}& & \left|{\displaystyle \frac{\frac{u\widetilde{D_q}\left(\widetilde{{\mathcal{L}}_{\tau ,q}^{\varsigma }}T\left(u\right)\right)}{\widetilde{{\left[\mu \right]}_q}e\left(u\right)}+1}{1-C\left(1+q\right)-q\frac{u\widetilde{D_q}\left(\widetilde{{\mathcal{L}}_{\tau ,q}^{\varsigma }}T\left(u\right)\right)}{\widetilde{{\left[\mu \right]}_q}e\left(u\right)}}}\right|\hfill \\ & =& \left|{\displaystyle \frac{{\displaystyle \sum _{l=1}^{\infty }}{\left(1+{\tau }_{l+\mu }\right)}^{\varsigma }\widetilde{{\left[l+\mu \right]}_q}{t}_{l+\mu }{u}^{l+2\mu }+{\displaystyle \sum _{l=1}^{\infty }}\widetilde{{\left[\mu \right]}_q}{e}_{l+\mu }{u}^{l+2\mu }}{\left(1-C\right)\left(1+q\right)\widetilde{{\left[\mu \right]}_q}+\left[1-C\left(1+q\right)\right]{\displaystyle \sum _{l=1}^{\infty }}\widetilde{{\left[\mu \right]}_q}{e}_{l+\mu }{u}^{l+2\mu }-q{\displaystyle \sum _{l=1}^{\infty }}{\Gamma }_{l,\tau ,\mu }^{\varsigma }{t}_{l+\mu }{u}^{l+2\mu }}}\right|.\hfill \end{array}$$

As $\left|Re\left(u\right)\right|\le \left|u\right|$, it follows that

$$Re\left\{{\displaystyle \frac{{\displaystyle \sum _{l=1}^{\infty }}{\left(1+\tau \widetilde{{\left[\mu \right]}_q}+\tau \widetilde{{\left[l+\mu \right]}_q}\right)}^{\varsigma }\widetilde{{\left[l+\mu \right]}_q}{t}_{l+\mu }{u}^{l+2\mu }+{\displaystyle \sum _{l=1}^{\infty }}\widetilde{{\left[\mu \right]}_q}{e}_{l+\mu }{u}^{l+2\mu }}{\left(1-C\right)\left(1+q\right)\widetilde{{\left[\mu \right]}_q}+\left[1-C\left(1+q\right)\right]{\displaystyle \sum _{l=1}^{\infty }}\widetilde{{\left[\mu \right]}_q}{e}_{l+\mu }{u}^{l+2\mu }-q{\displaystyle \sum _{l=1}^{\infty }}{\Gamma }_{l,\tau ,\mu }^{\varsigma }{t}_{l+\mu }{u}^{l+2\mu }}}\right\}<1.$$

(16)

Now, let us restrict u to real values such that the expression ${\displaystyle \frac{u\widetilde{D_q}\left(\widetilde{{\mathcal{L}}_{\tau ,q}^{\varsigma }}T\left(u\right)\right)}{\widetilde{{\left[\mu \right]}_q}e\left(u\right)}}$ remains real-valued. By clearing the denominator in (16) and considering the limiting behavior as $u\to 1^{-}$ on the real line yields (14), thereby establishing the desired condition. □

Remark 4.

The symmetric q-difference operator used in this study offers several advantages compared to classical q-derivatives and convolution-type operators. Unlike standard forward or backward q-derivatives, the symmetric form uses function values at both $qu$ and $q^{-1}u$, resulting in more stable and balanced behavior near singularities and ensuring better convergence as $q\to 1^{-}$. The operator exhibits improved rotational invariance, which is beneficial for function classes defined in circular domains such as the punctured unit disk. The operator is embedded within a parametric form $\widetilde{{\mathcal{L}}_{\tau ,q}^{\varsigma }}$, allowing tailored analysis through adjustment of τ and ς. This gives it broader applicability and adaptability than fixed-kernel convolution operators. As shown in Remark 1, the operator smoothly reduces to the classical derivative operator as $q\to 1^{-}$, ensuring compatibility with well-known results in classical function theory. The operator facilitates the derivation of precise subordination conditions and coefficient bounds, as demonstrated in Theorem 1. Such tractable inequalities are less accessible when using traditional convolution techniques. These advantages motivate the use of the symmetric q-difference operator in defining and analyzing the function class ${\widetilde{\mathcal{KM}}}_{\tau ,q}\left(\mu ,\varsigma ,C\right)$ and justify its theoretical and practical relevance.

Corollary 1.

Let $f\in \mathcal{M}$. Then f belongs to the class ${\widetilde{\mathcal{KM}}}_{\tau ,q}\left(1,\varsigma ,C\right)$ whenever the following inequality is fulfilled:

$$\sum _{l=1}^{\infty }\left({\left(1+\tau +\tau \widetilde{{\left[l+1\right]}_q}\right)}^{\varsigma }\widetilde{{\left[l+1\right]}_q}\left|t_{l+1}\right|+{\displaystyle \frac{4}{\left(q+1\right)\left(l+1\right)}}-{\displaystyle \frac{2C}{l+1}}\right)\le 1-C.$$

This condition is sufficient for membership in the class ${\widetilde{\mathcal{KM}}}_{\tau ,q}\left(1,\varsigma ,C\right)$.

Example 1.

For the function

$$T\left(u\right)={\displaystyle \frac{1}{u^{\mu }}}+{\displaystyle \frac{(1-C)\widetilde{{\left[\mu \right]}_q}-\frac{4\mu \widetilde{{\left[\mu \right]}_q}}{\left(q+1)\right)\left(\mu +l\right)}+\frac{C\mu \widetilde{{\left[\mu \right]}_q}}{\mu +l}}{{\left(1+\tau \widetilde{{\left[\mu \right]}_q}+\tau \widetilde{{\left[\mu +l\right]}_q}\right)}^{\varsigma }\widetilde{{\left[\mu +l\right]}_q}}}{u}^{\mu +1},$$

we obtain

$$\begin{array}{ccc}& & {\left(1+\tau \widetilde{{\left[\mu \right]}_q}+\tau \widetilde{{\left[\mu +l\right]}_q}\right)}^{\varsigma }\widetilde{{\left[\mu +l\right]}_q}{\displaystyle \frac{(1-C)\widetilde{{\left[\mu \right]}_q}-\frac{4\mu \widetilde{{\left[\mu \right]}_q}}{\left(q+1)\right)\left(\mu +l\right)}+\frac{2C\mu \widetilde{{\left[\mu \right]}_q}}{\mu +l}}{{\left(1+\tau \widetilde{{\left[\mu \right]}_q}+\tau \widetilde{{\left[\mu +l\right]}_q}\right)}^{\varsigma }\widetilde{{\left[\mu +l\right]}_q}}}+{\displaystyle \frac{4\mu \widetilde{{\left[\mu \right]}_q}}{\left(q+1)\right)\left(l+\mu \right)}}\hfill \\ & & -{\displaystyle \frac{2C\mu \widetilde{{\left[\mu \right]}_q}}{l+\mu }}=(1-C)\widetilde{{\left[\mu \right]}_q}.\hfill \end{array}$$

Hence, $f\in {\widetilde{\mathcal{KM}}}_{\tau ,q}\left(\mu ,\varsigma ,C\right)$, as well as the inequality (14) attains sharpness for this case.

To deepen the understanding of the analytic behavior of functions in the class ${\widetilde{\mathcal{KM}}}_{\tau ,q}\left(\mu ,\varsigma ,C\right)$, we now establish explicit coefficient estimates. These bounds offer direct insight into how the parameters of the symmetric q-operator influence the growth of the function’s series expansion. In particular, the next result provides a sharp upper bound for each coefficient $t_{l+\mu }$, derived using subordination techniques and classical inequalities. This theorem complements the general inequality in Theorem 14 by refining the functional structure of admissible elements within the class.

Theorem 2.

Assume that $f\in {\widetilde{\mathcal{KM}}}_{\tau ,q}\left(\mu ,\varsigma ,C\right)$ and has the series representation given by (1). Thus,

$$\left|t_{l+\mu }\right|\le {\displaystyle \frac{2\mu \widetilde{{\left[\mu \right]}_q}}{{\left(1+\tau \widetilde{{\left[\mu \right]}_q}+\tau \widetilde{{\left[l+\mu \right]}_q}\right)}^{\varsigma }\widetilde{{\left[l+\mu \right]}_q}}}\left({\displaystyle \frac{1}{l+\mu }}+\sum _{\nu =1}^{l-1}{\displaystyle \frac{\left(1+q\right)\left(1-C\right)}{\nu +\mu }}\right).$$

Proof. 

Assuming that $f\in {\mathcal{M}}_{\mu }$ and lies in the class ${\widetilde{\mathcal{KM}}}_{\tau ,q}\left(\mu ,\varsigma ,C\right)$. It must satisfy the conditions below:

$$-{\displaystyle \frac{u\widetilde{D_q}\left(\widetilde{{\mathcal{L}}_{\tau ,q}^{\varsigma }}T\left(u\right)\right)}{\widetilde{{\left[\mu \right]}_q}e\left(u\right)}}\prec {\displaystyle \frac{1+\left[1-C\left(1+q\right)\right]u}{1-qu}}.$$

Given that

$$\Phi \left(u\right)=-{\displaystyle \frac{u\widetilde{D_q}\left(\widetilde{{\mathcal{L}}_{\tau ,q}^{\varsigma }}T\left(u\right)\right)}{\widetilde{{\left[\mu \right]}_q}e\left(u\right)}},$$

(17)

as $Re\Phi \left(u\right)$$>0$, $\Phi \left(u\right)$ can be expressed as

$$\Phi \left(u\right)=1+\sum _{l=1}^{\infty }{\varphi }_l{u}^l.$$

Thus,

$$\Phi \left(u\right)\prec {\displaystyle \frac{1+\left[1-C\left(1+q\right)\right]u}{1-qu}}.$$

By performing basic calculations, we arrive at ${\displaystyle \frac{1+\left[1-C\left(1+q\right)\right]u}{1-qu}}=1+\left(1+q\right)\left(1-C\right)u+\dots$ and by means of Lemma 1, we deduce

$$\left|{\varphi }_l\right|\le \left(1+q\right)\left(1-C\right).$$

(18)

From (11) and (17), we obtain

$$1+{\displaystyle \sum _{l=1}^{\infty }}{\varphi }_l{u}^l={\displaystyle \frac{\frac{\widetilde{{\left[\mu \right]}_q}}{u^{\mu }}{\displaystyle \sum _{l=1}^{\infty }}{\left(1+\tau \widetilde{{\left[\mu \right]}_q}+\tau \widetilde{{\left[l+\mu \right]}_q}\right)}^{\varsigma }\widetilde{{\left[l+\mu \right]}_q}{t}_{l+\mu }{u}^{l+\mu }}{\widetilde{{\left[\mu \right]}_q}\left(\frac{1}{u^{\mu }}+{\displaystyle \sum _{l=1}^{\infty }}{e}_{l+\mu }{u}^{l+\mu }\right)}}.$$

After simplification, comparing the corresponding coefficients of $u^{l+\mu }$ yields

$$-{\left(1+\tau \widetilde{{\left[\mu \right]}_q}+\tau \widetilde{{\left[l+\mu \right]}_q}\right)}^{\varsigma }\widetilde{{\left[l+\mu \right]}_q}{t}_{l+\mu }=\widetilde{{\left[\mu \right]}_q}{e}_{l+\mu }+\widetilde{{\left[\mu \right]}_q}\sum _{\nu =1}^{l-1}{e}_{\nu +\mu }{\varphi }_{l-\nu }.$$

By considering the absolute value of both sides and invoking the triangle inequality along with (18), it follows that

$${\left(1+\tau \widetilde{{\left[\mu \right]}_q}+\tau \widetilde{{\left[l+\mu \right]}_q}\right)}^{\varsigma }\widetilde{{\left[l+\mu \right]}_q}\left|t_{l+\mu }\right|\le \widetilde{{\left[\mu \right]}_q}\left|e_{l+\mu }\right|+\left(1+q\right)\left(1-C\right)\widetilde{{\left[\mu \right]}_q}\sum _{\nu =1}^{l-1}\left|e_{\nu +\mu }\right|.$$

(19)

With the aid of (19) and (15), we arrive at

$${\left(1+\tau \widetilde{{\left[\mu \right]}_q}+\tau \widetilde{{\left[l+\mu \right]}_q}\right)}^{\varsigma }\widetilde{{\left[l+\mu \right]}_q}\left|t_{l+\mu }\right|\le \widetilde{{\left[\mu \right]}_q}2\mu {\left(l+\mu \right)}^{-1}+\left(1+q\right)\left(1-C\right)\widetilde{{\left[\mu \right]}_q}\sum _{\nu =1}^{l-1}2\mu {\left(\nu +\mu \right)}^{-1}.$$

So

$$\left|t_{l+\mu }\right|\le {\displaystyle \frac{2\mu \widetilde{{\left[\mu \right]}_q}}{{\left(1+\tau \widetilde{{\left[\mu \right]}_q}+\tau \widetilde{{\left[l+\mu \right]}_q}\right)}^{\varsigma }\widetilde{{\left[l+\mu \right]}_q}\left(l+\mu \right)}}+{\displaystyle \frac{2\left(1+q\right)\left(1-C\right)\mu \widetilde{{\left[\mu \right]}_q}}{{\left(1+\tau \widetilde{{\left[\mu \right]}_q}+\tau \widetilde{{\left[l+\mu \right]}_q}\right)}^{\varsigma }\widetilde{{\left[l+\mu \right]}_q}}}\sum _{\nu =1}^{l-1}{\left(\nu +\mu \right)}^{-1},$$

and the result follows as required. □

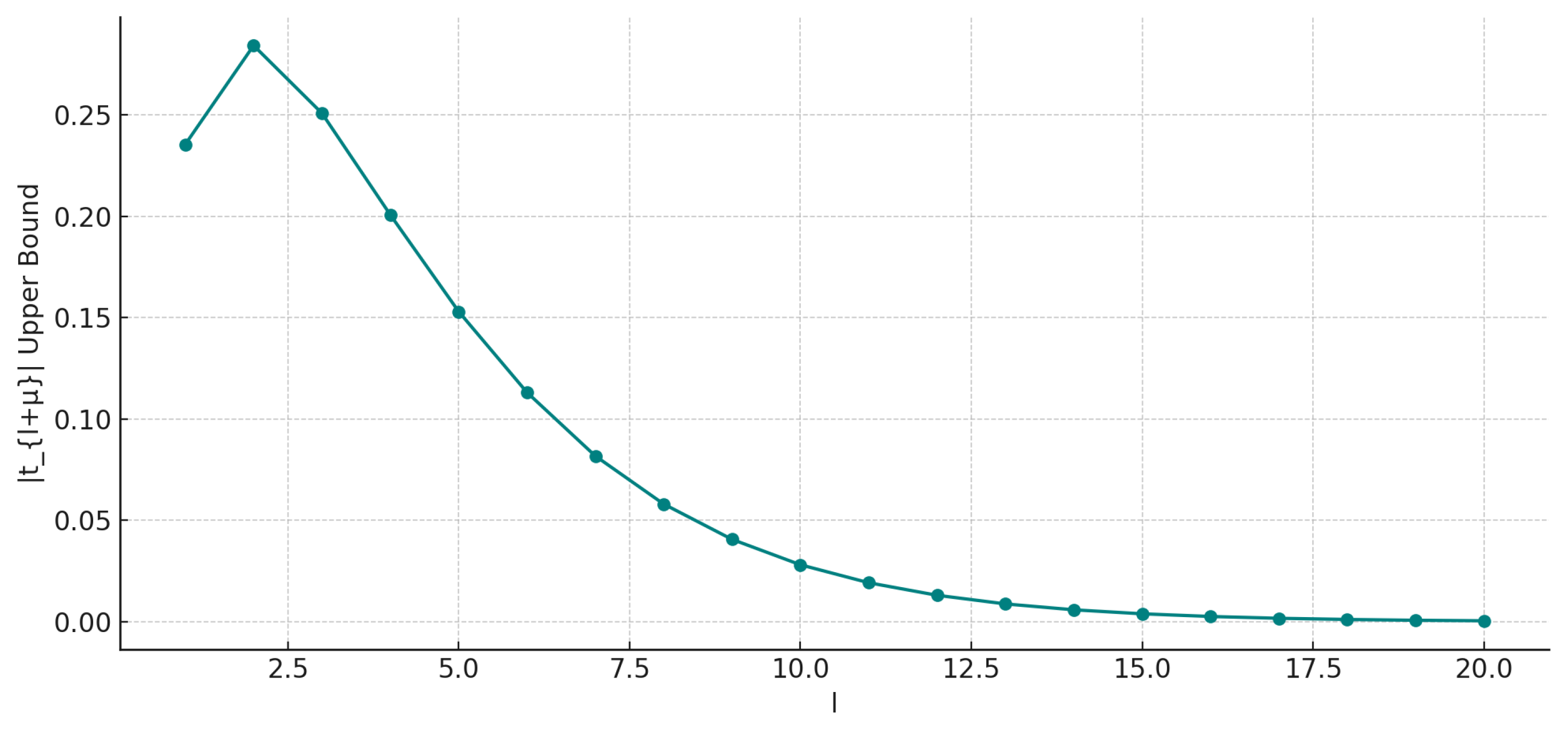
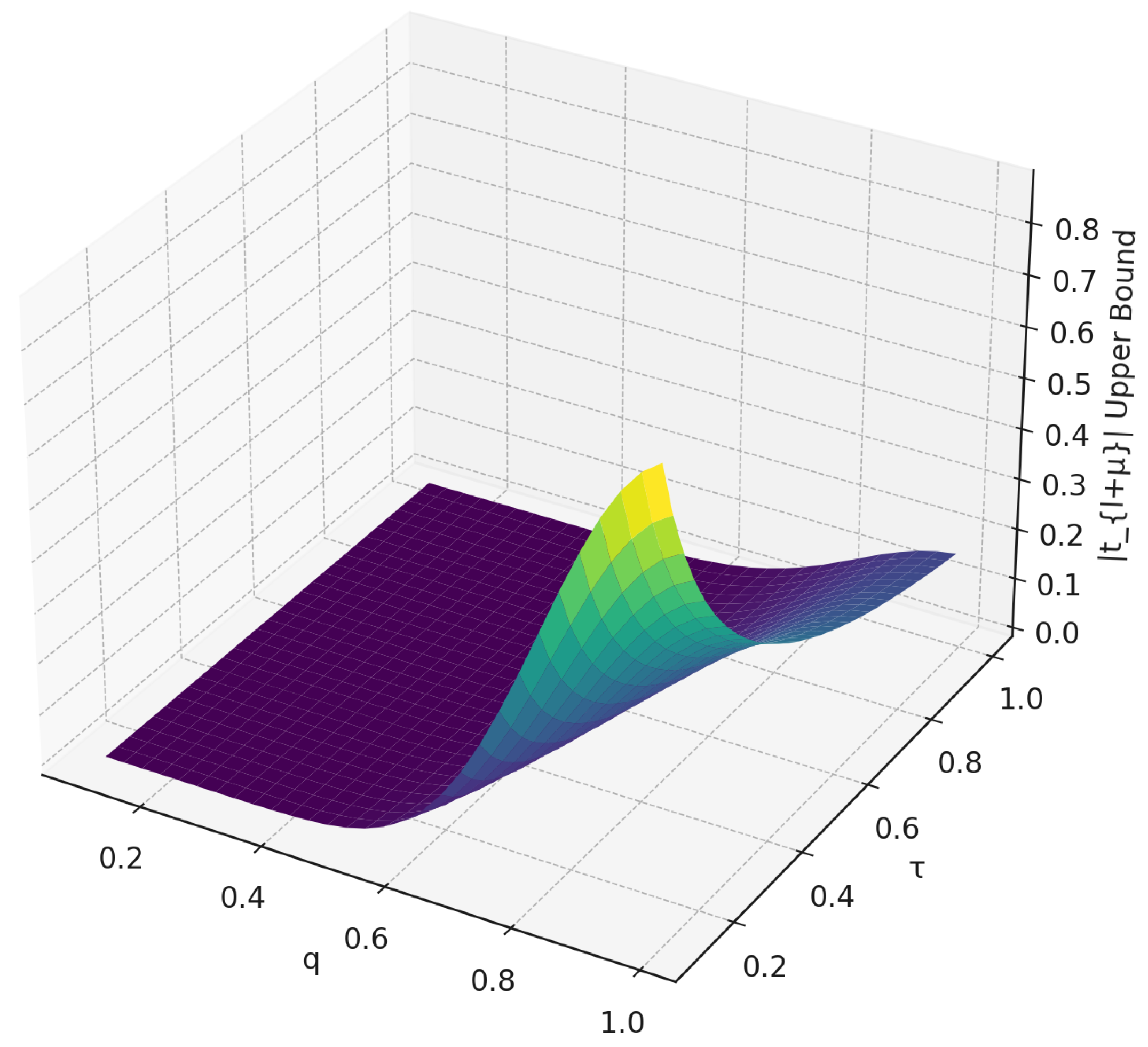
Figure 1 and Figure 2 offers a visual comparison between the numerical bounds for $|t_{l+\mu }|$ derived in Theorem 2. The 2D plot illustrates how the bounds vary with respect to the index l, providing insight into the decay behavior of the coefficients for fixed parameters. In contrast, the 3D plot shows the sensitivity of a specific coefficient bound (for $l=5$) to changes in the operator parameters q and $\tau$. Together, these plots enhance the interpretation of the theorem, highlighting both the local and parametric effects on the structure of the function class.

Corollary 2.

If $f\in {\widetilde{\mathcal{KM}}}_{\tau ,q}\left(1,\varsigma ,C\right)$ and has the series representation given in (1). Then

$$\left|t_{l+1}\right|\le {\displaystyle \frac{2}{{\left(1+\tau +\tau \widetilde{{\left[l+1\right]}_q}\right)}^{\varsigma }\widetilde{{\left[l+1\right]}_q}}}\left({\displaystyle \frac{1}{l+1}}+\sum _{\nu =1}^{l-1}{\displaystyle \frac{\left(1+q\right)\left(1-C\right)}{\nu +1}}\right).$$

As a natural continuation of the coefficient and distortion estimates, we now focus on bounding the magnitude of the symmetric q-derivative of the transformed function $\widetilde{{\mathcal{L}}_{\tau ,q}^{\varsigma }}T\left(u\right)$. This result is essential for understanding how the generalized derivative behaves across the punctured disk, particularly under the subordination framework. Theorem 3 provides sharp upper and lower bounds for the modulus of the operator in terms of the parameters $q,\tau ,\varsigma ,C$ and the radial distance $\rho$, thereby extending the analytic characterization of the proposed function class.

Theorem 3.

If $f\in {\widetilde{\mathcal{KM}}}_{\tau ,q}\left(\mu ,\varsigma ,C\right)$ and is given by (1), assuming $\left|u\right|=\rho$, we arrive at the following estimate:

$$\begin{array}{ccc}\hfill {\displaystyle \frac{\left[1-\left(1-C\left(1+q\right)\right)-\rho \right]{\left(1-\rho \right)}^{\mu +1}\widetilde{{\left[\mu \right]}_q}}{\left(1+q-\rho \right){\rho }^{\mu +1}}}& \le & \left|\widetilde{D_q}\left(\widetilde{{\mathcal{L}}_{\tau ,q}^{\varsigma }}T\left(u\right)\right)\right|\hfill \\ & \le & {\displaystyle \frac{\left[1+\left(1-C\left(1+q\right)\right)-\rho \right]{\left(1-\rho \right)}^{\mu +1}\widetilde{{\left[\mu \right]}_q}}{\left(1-q-\rho \right){\rho }^{\mu +1}}}.\hfill \end{array}$$

Proof. 

Let us assume that $f\in {\widetilde{\mathcal{KM}}}_{\tau ,q}\left(\mu ,\varsigma ,C\right)$. Therefore, we can express

$$-{\displaystyle \frac{u\widetilde{D_q}\left(\widetilde{{\mathcal{L}}_{\tau ,q}^{\varsigma }}T\left(u\right)\right)}{\widetilde{{\left[\mu \right]}_q}e\left(u\right)}}\prec {\displaystyle \frac{1+\left(1-C\left(1+q\right)\right)u}{1-qu}}.$$

Therefore, for $\left|u\right|=\rho$, we obtain

$$\left|-{\displaystyle \frac{u\widetilde{D_q}\left(\widetilde{{\mathcal{L}}_{\tau ,q}^{\varsigma }}T\left(u\right)\right)}{\widetilde{{\left[\mu \right]}_q}e\left(u\right)}}-{\displaystyle \frac{1+\left[1-C\left(1+q\right)\right]q{\rho }^2}{1+q^2{\rho }^2}}\right|\le {\displaystyle \frac{1+\left[1-C\left(1+q\right)\right]\rho }{1-q\rho }}.$$

(20)

By simplifying, we arrive at

$${\displaystyle \frac{1-\left[1-C\left(1+q\right)\right]\rho }{1+q\rho }}\le \left|-{\displaystyle \frac{u\widetilde{D_q}\left(\widetilde{{\mathcal{L}}_{\tau ,q}^{\varsigma }}T\left(u\right)\right)}{\widetilde{{\left[\mu \right]}_q}e\left(u\right)}}\right|\le {\displaystyle \frac{1+\left[1-C\left(1+q\right)\right]\rho }{1-q\rho }}.$$

(21)

Since $e\left(u\right)\in {\mathcal{SM}}_{\mu }^{*}$, it is well known [48] that

$${\displaystyle \frac{{\left(1-\rho \right)}^{\mu +1}}{{\rho }^{\mu }}}\le \left|e\left(u\right)\right|\le {\displaystyle \frac{{\left(1-\rho \right)}^{\mu +1}}{{\rho }^{\mu }}}, \left|u\right|=\rho \mathrm{and} 0\le \rho <1.$$

(22)

Making use of (21) and (22), the conclusion is established. □

To further explore the geometric behavior of functions in the class ${\widetilde{\mathcal{KM}}}_{\tau ,q}\left(\mu ,\varsigma ,C\right)$ we now derive sharp distortion bounds. These estimates describe how the modulus of a function in the class behaves on circles of fixed radius within the punctured unit disk. The following result establishes upper and lower bounds for ∣$T\left(u\right)$∣ in terms of the parameters of the symmetric q-operator, thereby providing insight into the radial growth and control of the function across the domain. Such estimates are fundamental in geometric function theory and confirm the analytical stability of the class under symmetric q-deformations.

Theorem 4.

Let $f\in {\widetilde{\mathcal{KM}}}_{\tau ,q}\left(\mu ,\varsigma ,C\right)$. For $\left|u\right|=\rho$, it holds that

$$\left|T\left(u\right)\right|\ge {\displaystyle \frac{1}{{\rho }^{\mu }}}-{\displaystyle \frac{\widetilde{{\left[\mu \right]}_q}\left(1-C\right)}{{\left(1+\tau \widetilde{{\left[\mu \right]}_q}+\tau \widetilde{{\left[\mu +1\right]}_q}\right)}^{\varsigma }\widetilde{{\left[\mu +1\right]}_q}}}{\rho }^{\mu },$$

and

$$\left|T\left(u\right)\right|\le {\displaystyle \frac{1}{{\rho }^{\mu }}}+{\displaystyle \frac{\widetilde{{\left[\mu \right]}_q}\left(1-C\right)}{{\left(1+\tau \widetilde{{\left[\mu \right]}_q}+\tau \widetilde{{\left[\mu +1\right]}_q}\right)}^{\varsigma }\widetilde{{\left[\mu +1\right]}_q}}}{\rho }^{\mu }.$$

Proof. 

Inasmuch that $\left|u\right|=\rho <1$, we have

$$\left|T\left(u\right)\right|=\left|{\displaystyle \frac{1}{u^{\mu }}}+\sum _{l=1}^{\infty }{t}_{l+\mu }{u}^{l+\mu }\right|\le {\displaystyle \frac{1}{\left|u^{\mu }\right|}}+\sum _{l=1}^{\infty }\left|t_{l+\mu }\right|{\left|u\right|}^{l+\mu }={\displaystyle \frac{1}{{\rho }^{\mu }}}+\sum _{l=1}^{\infty }\left|t_{l+\mu }\right|{\rho }^{l+\mu }.$$

We obtain ${\rho }^{\mu +l}<{\rho }^{\mu }$ and

$$\left|T\left(u\right)\right|\le {\displaystyle \frac{1}{{\rho }^{\mu }}}+{\rho }^{\mu }\sum _{l=1}^{\infty }\left|t_{l+\mu }\right|.$$

(23)

Analogously,

$$\left|T\left(u\right)\right|\ge {\displaystyle \frac{1}{{\rho }^{\mu }}}-{\rho }^{\mu }\sum _{l=1}^{\infty }\left|t_{l+\mu }\right|.$$

(24)

Since it has been demonstrated from (14) that

$$\sum _{l=1}^{\infty }\left({\left(1+\tau \widetilde{{\left[\mu \right]}_q}+\tau \widetilde{{\left[l+\mu \right]}_q}\right)}^{\varsigma }\widetilde{{\left[l+\mu \right]}_q}\left|t_{l+\mu }\right|+{\displaystyle \frac{4\mu \widetilde{{\left[\mu \right]}_q}}{\left(q+1\right)\left(l+\mu \right)}}-{\displaystyle \frac{2C\mu \widetilde{{\left[\mu \right]}_q}}{l+\mu }}\right)\le \left(1-C\right)\widetilde{{\left[\mu \right]}_q}.$$

However,

$$\begin{array}{ccc}& & {\left(1+\tau \widetilde{{\left[\mu \right]}_q}+\tau \widetilde{{\left[\mu +1\right]}_q}\right)}^{\varsigma }\widetilde{{\left[\mu +1\right]}_q}\sum _{l=1}^{\infty }\left|t_{l+\mu }\right|\hfill \\ & & \le \sum _{l=1}^{\infty }\left({\left(1+\tau \widetilde{{\left[\mu \right]}_q}+\tau \widetilde{{\left[l+\mu \right]}_q}\right)}^{\varsigma }\widetilde{{\left[l+\mu \right]}_q}\left|t_{l+\mu }\right|+{\displaystyle \frac{4\mu \widetilde{{\left[\mu \right]}_q}}{\left(q+1\right)\left(l+\mu \right)}}-{\displaystyle \frac{2C\mu \widetilde{{\left[\mu \right]}_q}}{l+\mu }}\right).\hfill \end{array}$$

Therefore,

$${\left(1+\tau \widetilde{{\left[\mu \right]}_q}+\tau \widetilde{{\left[\mu +1\right]}_q}\right)}^{\varsigma }\widetilde{{\left[\mu +1\right]}_q}\sum _{l=1}^{\infty }\left|t_{l+\mu }\right|\le \left(1-C\right)\widetilde{{\left[\mu \right]}_q},$$

and is equivalently written as

$$\sum _{l=1}^{\infty }\left|t_{l+\mu }\right|\le {\displaystyle \frac{\left(1-C\right)\widetilde{{\left[\mu \right]}_q}}{{\left(1+\tau \widetilde{{\left[\mu \right]}_q}+\tau \widetilde{{\left[\mu +1\right]}_q}\right)}^{\varsigma }\widetilde{{\left[\mu +1\right]}_q}}}.$$

(25)

Applying (23)–(25) at this point yields the required result. □

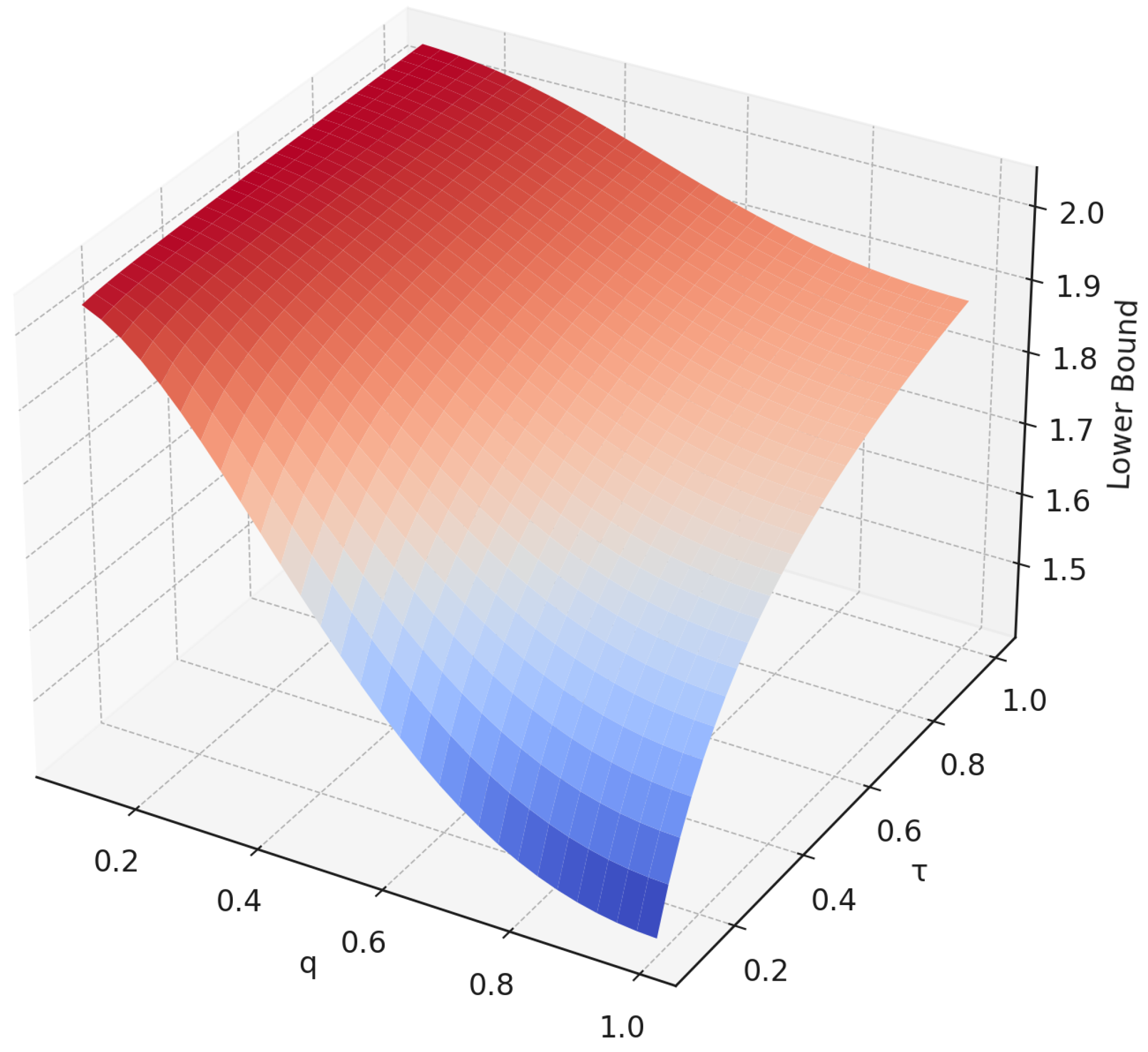
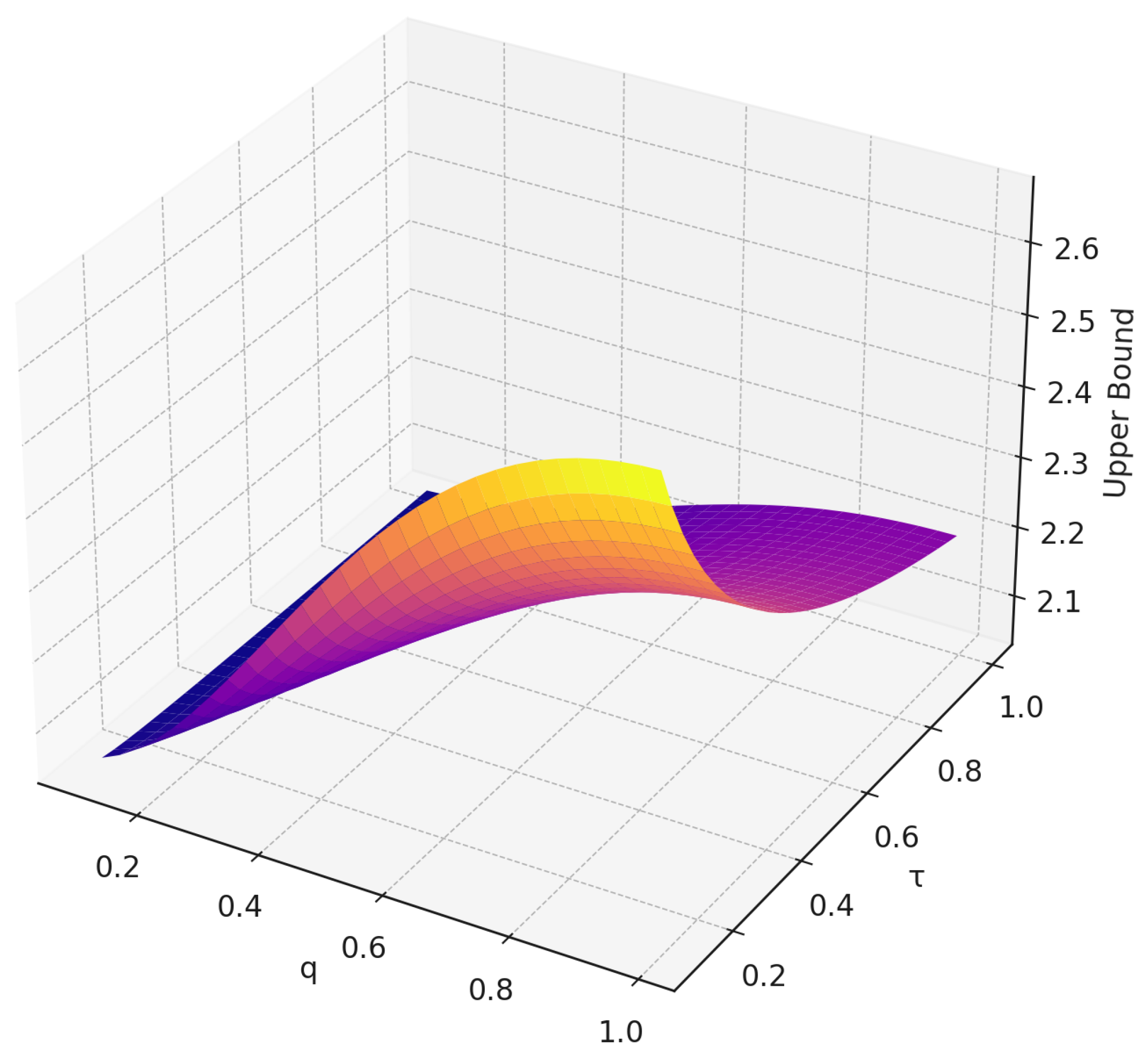
The graphical representations provided in Figure 3, Figure 4 and Figure 5 illustrate the behavior of the upper and lower distortion bounds for $\left|T\right(u\left)\right|$, as established in Theorem 4. These bounds are analyzed with respect to variations in the operator parameters q and $\tau$ while keeping the modulus $\rho$ fixed. The plots demonstrate how the symmetric q-difference operator influences the growth and contraction of the function within the punctured unit disk. This visual analysis enhances the theoretical results by revealing the sensitivity and stability of the distortion bounds under parameter shifts, offering deeper insight into the geometric properties of the defined function class.

Corollary 3.

Let $f\in {\widetilde{\mathcal{KM}}}_{\tau ,q}\left(1,\varsigma ,C\right)$. For $\left|u\right|=\rho$, it holds that

$${\displaystyle \frac{1}{\rho }}-{\displaystyle \frac{1-C}{{\left(1+\tau +\tau \widetilde{{\left[2\right]}_q}\right)}^{\varsigma }\widetilde{{\left[2\right]}_q}}}\rho \le \left|T\left(u\right)\right|\le {\displaystyle \frac{1}{\rho }}+{\displaystyle \frac{1-C}{{\left(1+\tau +\tau \widetilde{{\left[2\right]}_q}\right)}^{\varsigma }\widetilde{{\left[2\right]}_q}}}r.$$

To complete the analysis of the geometric and analytic behavior of the proposed function class, we now turn to the behavior of higher-order symmetric q-derivatives. This is particularly relevant for assessing the growth and smoothness of functions under multiple iterations of the q-difference operator. Theorem 5 provides sharp upper and lower bounds for the modulus of the $\varsigma$- th order symmetric q-derivative of $T\left(u\right)$, showing how the class remains analytically stable even under repeated operator application. These estimates generalize the earlier results and further demonstrate the robustness of the operator framework.

Theorem 5.

Assume that $f\in {\widetilde{\mathcal{KM}}}_{\tau ,q}\left(\mu ,\varsigma ,C\right)$ and takes the form described in (1). Thus, for every $\left|u\right|=\rho$, we obtain

$$\left|D_q^{\left(\varsigma \right)}T\left(u\right)\right|\le {\displaystyle \frac{\widetilde{{\left[\mu +\varsigma -1\right]}_q}!}{{\rho }^{\mu +\varsigma }\widetilde{{\left[\mu -1\right]}_q}!}}+{\rho }^{\mu }{\displaystyle \frac{\widetilde{{\left[\mu \right]}_q}\left(1-C\right)}{{\left(1+\tau \widetilde{{\left[\mu \right]}_q}+\tau \widetilde{{\left[\mu +1\right]}_q}\right)}^{\varsigma }}},$$

and

$$\left|D_q^{\left(\varsigma \right)}T\left(u\right)\right|\ge {\displaystyle \frac{\widetilde{{\left[\mu +\varsigma -1\right]}_q}!}{{\rho }^{\mu +\varsigma }\widetilde{{\left[\mu -1\right]}_q}!}}-{\rho }^{\mu }{\displaystyle \frac{\widetilde{{\left[\mu \right]}_q}\left(1-C\right)}{{\left(1+\tau \widetilde{{\left[\mu \right]}_q}+\tau \widetilde{{\left[\mu +1\right]}_q}\right)}^{\varsigma }}}.$$

Proof. 

To obtain the higher-order q-derivative $D_q^{\left(\varsigma \right)}T\left(u\right)$, we use the recursive application of the symmetric q-difference operator defined in Equation (7).

$$D_q^{\left(2\right)}T\left(u\right)=D_q\left(D_{q}T\left(u\right)\right)={\displaystyle \frac{\widetilde{{\left[\mu \right]}_q}\widetilde{{\left[\mu +1\right]}_q}}{u^{\mu +2}}}+\sum _{l=1}^{\infty }\widetilde{{\left[l+\mu \right]}_q}\widetilde{{\left[l+\mu -1\right]}_q}{t}_{l+\mu }{u}^{l+\mu -2}.$$

After observing the pattern from the second derivative $D_q^{\left(2\right)}T\left(u\right)$, we generalize to the $\varsigma$-th order, obtaining the following representation.

$$\begin{array}{ccc}\hfill D_q^{\left(\varsigma \right)}T\left(u\right)& =& D_q\left(D_q^{\left(\varsigma -1\right)}T\left(u\right)\right)\hfill \\ & =& {\left(-1\right)}^{\varsigma }{\displaystyle \frac{\widetilde{{\left[\mu \right]}_q}\widetilde{{\left[\mu +1\right]}_q}\dots \widetilde{{\left[\mu +\varsigma -1\right]}_q}}{u^{\mu +\varsigma }}}\hfill \\ & +& \sum _{l=1}^{\infty }\widetilde{{\left[l+\mu \right]}_q}\widetilde{{\left[l+\mu -1\right]}_q}\dots \widetilde{{\left[l+\mu -(\varsigma -1)\right]}_q}{t}_{l+\mu }{u}^{l+\mu -\varsigma }\hfill \\ & =& {\left(-1\right)}^{\varsigma }{\displaystyle \frac{\widetilde{{\left[\mu +\varsigma -1\right]}_q}!}{u^{\mu +\varsigma }\widetilde{{\left[\mu -1\right]}_q}!}}+\sum _{l=1}^{\infty }{\displaystyle \frac{\widetilde{{\left[l+\mu \right]}_q}!}{\widetilde{{\left[l+\mu -\varsigma \right]}_q}!}}{t}_{l+\mu }{u}^{l+\mu -\varsigma }.\hfill \end{array}$$

Given that the parameters satisfy $\varsigma \le l,l\ge \mu +1$ and $\left|u\right|=\rho <1$, one obtains ${\rho }^{l-\varsigma }\le {\rho }^{\mu }$. Thus, this leads to

$$\left|D_q^{\left(\varsigma \right)}T\left(u\right)\right|\le {\displaystyle \frac{\widetilde{{\left[\mu +\varsigma -1\right]}_q}!}{{\rho }^{\mu +\varsigma }\widetilde{{\left[\mu -1\right]}_q}!}}+{\rho }^{\mu }\sum _{l=1}^{\infty }{\displaystyle \frac{\widetilde{{\left[l+\mu \right]}_q}!}{\widetilde{{\left[l+\mu -\varsigma \right]}_q}!}}\left|t_{l+\mu }\right|.$$

(26)

Analogously,

$$\left|D_q^{\left(\varsigma \right)}T\left(u\right)\right|\ge {\displaystyle \frac{\widetilde{{\left[\mu +\varsigma -1\right]}_q}!}{{\rho }^{\mu +\varsigma }\widetilde{{\left[\mu -1\right]}_q}!}}-{\rho }^{\mu }\sum _{l=1}^{\infty }{\displaystyle \frac{\widetilde{{\left[l+\mu \right]}_q}!}{\widetilde{{\left[l+\mu -\varsigma \right]}_q}!}}\left|t_{l+\mu }\right|.$$

(27)

To bound the series involving $|t_{l+\mu }|$, we now apply the sufficient condition (14), which provides a convenient upper bound in terms of the parameters.

$$\left(1+\tau \widetilde{{\left[\mu \right]}_q}+\tau \widetilde{{\left[\mu +1\right]}_q}\right)\sum _{l=1}^{\infty }\widetilde{{\left[l+\mu \right]}_q}\left|t_{l+\mu }\right|\le \left(1-C\right)\widetilde{{\left[\mu \right]}_q}.$$

This leads to

$$\begin{array}{c}\hfill {\left(1+\tau \widetilde{{\left[\mu \right]}_q}+\tau \widetilde{{\left[\mu +1\right]}_q}\right)}^{\varsigma }\sum _{l=1}^{\infty }\widetilde{{\left[l+\mu \right]}_q}\left|t_{l+\mu }\right|\le \left(1-C\right)\widetilde{{\left[\mu \right]}_q}.\end{array}$$

Thus,

$$\sum _{l=1}^{\infty }\widetilde{{\left[l+\mu \right]}_q}\left|t_{l+\mu }\right|\le {\displaystyle \frac{\left(1-C\right)\widetilde{{\left[\mu \right]}_q}}{{\left(1+\tau \widetilde{{\left[\mu \right]}_q}+\tau \widetilde{{\left[\mu +1\right]}_q}\right)}^{\varsigma }}}.$$

Still, one can easily verify that

$$\sum _{l=1}^{\infty }{\displaystyle \frac{\widetilde{{\left[l+\mu \right]}_q}!}{\widetilde{{\left[l+\mu -\varsigma \right]}_q}!}}\left|t_{l+\mu }\right|\le \sum _{l=1}^{\infty }\widetilde{{\left[l+\mu \right]}_q}\left|t_{l+\mu }\right|,$$

giving

$$\sum _{l=1}^{\infty }{\displaystyle \frac{\widetilde{{\left[l+\mu \right]}_q}!}{\widetilde{{\left[l+\mu -\varsigma \right]}_q}!}}\left|t_{l+\mu }\right|\le {\displaystyle \frac{\left(1-C\right)\widetilde{{\left[\mu \right]}_q}}{{\left(1+\tau \widetilde{{\left[\mu \right]}_q}+\tau \widetilde{{\left[\mu +1\right]}_q}\right)}^{\varsigma }}}.$$

Substituting the upper bound into inequalities (26) and (27) completes the derivation of the desired estimates for the symmetric q-derivatives. □

The following two theorems establish the convexity and starlikeness radii for functions of the class ${\widetilde{\mathcal{KM}}}_{\tau ,q}\left(\mu ,\varsigma ,C\right)$.

Theorem 6.

Consider the case where $f\in {\widetilde{\mathcal{KM}}}_{\tau ,q}\left(\mu ,\varsigma ,C\right)$. Consequently $f\in {\mathcal{CM}}_{\mu }\left(\alpha \right)$, within the disk $\left|u\right|<{\mu }_1$, where

$${\rho }_1={\left({\displaystyle \frac{\mu \left(\mu -\alpha \right){\left(1+\tau \widetilde{{\left[\mu \right]}_q}+\tau \widetilde{{\left[l+\mu \right]}_q}\right)}^{\varsigma }\widetilde{{\left[l+\mu \right]}_q}}{\left(\mu +l\right)\left(\mu +l+\alpha \right)\widetilde{{\left[\mu \right]}_q}\left(1-C\right)}}\right)}^{{\displaystyle \frac{1}{l+2\mu }}}.$$

(28)

Proof. 

Assume that $f\in {\widetilde{\mathcal{KM}}}_{\tau ,q}\left(\mu ,\varsigma ,C\right)$. In order to establish that $f\in {\mathcal{CM}}_{\mu }\left(\alpha \right)$, demonstrating that the following condition holds is sufficient for the proof

$$\left|{\displaystyle \frac{u{f}^{″}\left(u\right)+\left(\mu +1\right)f^{\prime }\left(u\right)}{u{f}^{″}\left(u\right)+\left(1+2\alpha -\mu \right)f^{\prime }\left(u\right)}}\right|<1.$$

From (1) and elementary algebraic manipulation, it follows that

$$\sum _{l=1}^{\infty }{\displaystyle \frac{\left(\mu +l\right)\left(\mu +l+\alpha \right)}{\mu \left(\mu -\alpha \right)}}\left|t_{l+\mu }\right|{\left|u\right|}^{l+2\mu }<1.$$

(29)

By applying (14), we arrive at:

$$\sum _{l=1}^{\infty }{\left(1+\tau \widetilde{{\left[\mu \right]}_q}+\tau \widetilde{{\left[l+\mu \right]}_q}\right)}^{\varsigma }\widetilde{{\left[l+\mu \right]}_q}\left|t_{l+\mu }\right|\le \left(1-C\right)\widetilde{{\left[\mu \right]}_q}.$$

(30)

This leads to

$$\sum _{l=1}^{\infty }{\displaystyle \frac{{\left(1+\tau \widetilde{{\left[\mu \right]}_q}+\tau \widetilde{{\left[l+\mu \right]}_q}\right)}^{\varsigma }\widetilde{{\left[l+\mu \right]}_q}}{\widetilde{{\left[\mu \right]}_q}\left(1-C\right)}}\left|t_{l+\mu }\right|\le 1.$$

Inequality (29) holds provided that the following condition is satisfied:

$$\sum _{l=1}^{\infty }{\displaystyle \frac{\left(\mu +l\right)\left(\mu +l+\alpha \right)}{\mu \left(\mu -\alpha \right)}}\left|t_{l+\mu }\right|{\left|u\right|}^{l+2\mu }<\sum _{l=1}^{\infty }{\displaystyle \frac{{\left(1+\tau \widetilde{{\left[\mu \right]}_q}+\tau \widetilde{{\left[l+\mu \right]}_q}\right)}^{\varsigma }\widetilde{{\left[l+\mu \right]}_q}}{\left(1-C\right)\widetilde{{\left[\mu \right]}_q}}}\left|t_{l+\mu }\right|.$$

Hence,

$${\left|u\right|}^{l+2\mu }<{\displaystyle \frac{\mu \left(\mu -\alpha \right){\left(1+\tau \widetilde{{\left[\mu \right]}_q}+\tau \widetilde{{\left[l+\mu \right]}_q}\right)}^{\varsigma }\widetilde{{\left[l+\mu \right]}_q}}{\left(\mu +l\right)\left(\mu +l+\alpha \right)\widetilde{{\left[\mu \right]}_q}\left(1-C\right)}}.$$

It follows that

$$\left|u\right|<{\left({\displaystyle \frac{\mu \left(\mu -\alpha \right){\left(1+\tau \widetilde{{\left[\mu \right]}_q}+\tau \widetilde{{\left[l+\mu \right]}_q}\right)}^{\varsigma }\widetilde{{\left[l+\mu \right]}_q}}{\left(\mu +l\right)\left(\mu +l+\alpha \right)\widetilde{{\left[\mu \right]}_q}\left(1-C\right)}}\right)}^{{\displaystyle \frac{1}{l+2\mu }}}={\rho }_{1,}$$

and this yields the required result. □

Corollary 4.

Let $f\in {\widetilde{\mathcal{KM}}}_{\tau ,q}\left(1,\varsigma ,C\right)$. Hence $f\in \mathcal{CM}\left(\alpha \right)$, in the domain $\{u\in \mathbb{C}:|u|<{\rho }_1\}$ under the assumption that

$${\rho }_1={\left({\displaystyle \frac{\left(1-\alpha \right){\left(1+\tau +\tau \widetilde{{\left[l+1\right]}_q}\right)}^{\varsigma }\widetilde{{\left[l+\mu \right]}_q}}{\left(1+l\right)\left(1+l+\alpha \right)\left(1-C\right)}}\right)}^{{\displaystyle \frac{1}{l+2}}}.$$

Theorem 7.

Assume that $f\in {\widetilde{\mathcal{KM}}}_{\tau ,q}\left(\mu ,\varsigma ,C\right)$. Thus, the function f remains in the class ${\mathcal{SM}}_{\mu }^{*}\left(\alpha \right)$ throughout the subdisk $\left|u\right|<{\rho }_2$, where

$${\rho }_2={\left({\displaystyle \frac{\left(\mu -\alpha \right){\left(1+\tau \widetilde{{\left[\mu \right]}_q}+\tau \widetilde{{\left[l+\mu \right]}_q}\right)}^{\varsigma }\widetilde{{\left[l+\mu \right]}_q}}{\left(\mu +l+\alpha \right)\widetilde{{\left[\mu \right]}_q}\left(1-C\right)}}\right)}^{{\displaystyle \frac{1}{l+2\mu }}}.$$

Proof. 

It is known that the function f is a member of ${\mathcal{SM}}_{\mu }^{*}\left(\alpha \right)$ if next condition holds:

$$\left|{\displaystyle \frac{u{f}^{\prime }\left(u\right)+\mu T\left(u\right)}{u{f}^{\prime }\left(u\right)-\left(\mu -\alpha \right)T\left(u\right)}}\right|<1.$$

From (1), after a few simple steps, it can be deduced that

$$\sum _{l=1}^{\infty }{\displaystyle \frac{\mu +l+\alpha }{\mu -\alpha }}\left|t_{l+\mu }\right|{\left|u\right|}^{l+2\mu }<1.$$

(31)

Making use of (30), immediately yields

$$\sum _{l=1}^{\infty }{\displaystyle \frac{{\left(1+\tau \widetilde{{\left[\mu \right]}_q}+\tau \widetilde{{\left[l+\mu \right]}_q}\right)}^{\varsigma }\widetilde{{\left[l+\mu \right]}_q}}{\widetilde{{\left[\mu \right]}_q}\left(1-C\right)}}\left|t_{l+\mu }\right|\le 1.$$

For inequality (31) to hold, the condition reduced to

$$\sum _{l=1}^{\infty }{\displaystyle \frac{\mu +l+\alpha }{\mu -\alpha }}\left|t_{l+\mu }\right|{\left|u\right|}^{l+2\mu }<\sum _{l=1}^{\infty }{\displaystyle \frac{{\left(1+\tau \widetilde{{\left[\mu \right]}_q}+\tau \widetilde{{\left[l+\mu \right]}_q}\right)}^{\varsigma }\widetilde{{\left[l+\mu \right]}_q}}{\left(\mu +l+\alpha \right)\left(1-C\right)\widetilde{{\left[\mu \right]}_q}}}\left|t_{l+\mu }\right|.$$

(32)

This generated

$${\left|u\right|}^{l+2\mu }<{\displaystyle \frac{\left(\mu -\alpha \right){\left(1+\tau \widetilde{{\left[\mu \right]}_q}+\tau \widetilde{{\left[l+\mu \right]}_q}\right)}^{\varsigma }\widetilde{{\left[l+\mu \right]}_q}}{\left(\mu +l+\alpha \right)\left(1-C\right)\widetilde{{\left[\mu \right]}_q}}}.$$

So,

$$\left|u\right|<{\left({\displaystyle \frac{\left(\mu -\alpha \right){\left(1+\tau \widetilde{{\left[\mu \right]}_q}+\tau \widetilde{{\left[l+\mu \right]}_q}\right)}^{\varsigma }\widetilde{{\left[l+\mu \right]}_q}}{\left(\mu +l+\alpha \right)\left(1-C\right)\widetilde{{\left[\mu \right]}_q}}}\right)}^{{\displaystyle \frac{1}{l+2\mu }}}={\rho }_2.$$

Therefore we arrive at the desired conclusion. □

Corollary 5.

Assume that $f\in {\widetilde{\mathcal{KM}}}_{\tau ,q}\left(1,\varsigma ,C\right)$. Then f also lies in the class ${\mathcal{SM}}^{*}\left(\alpha \right)$ within the disk $\left|u\right|<{\rho }_2$, where

$${\rho }_2={\left({\displaystyle \frac{\left(1-\alpha \right){\left(1+\tau +\tau \widetilde{{\left[l+1\right]}_q}\right)}^{\varsigma }\widetilde{{\left[l+1\right]}_q}}{\left(1+l+\alpha \right)\left(1-C\right)\widetilde{{\left[\mu \right]}_q}}}\right)}^{{\displaystyle \frac{1}{l+2}}}.$$

(33)

3. Conclusions

Motivated by recent advances in quantum calculus, we have introduced a novel Janowski-type class of $\mu$-valent meromorphic functions defined via a symmetric q-differential operator. This innovative operator framework has allowed us to systematically explore and characterize the geometric properties of the proposed function class. In particular, we have established rigorous sufficiency conditions for class membership, derived sharp distortion bounds, provided precise coefficient estimates, and thoroughly examined the radii of starlikeness and convexity.

Our results have been shown to be valid and, in many cases, sharp for specific parameter selections, underscoring both the theoretical soundness and the practical relevance of the method. Importantly, the operator’s versatility enables the formulation of additional subclasses of meromorphic functions, suggesting a wide array of possibilities for extending this research. Such extensions have the potential to deepen the understanding of geometric function theory and foster new applications in areas such as fractional calculus, complex analysis, and quantum physics.

The newly introduced class of meromorphic multivalent functions defined via the symmetric q-differential operator holds significant potential for applications in both theoretical and applied mathematics. The symmetric q-calculus provides a more balanced approximation of classical derivatives, making it well-suited for modeling systems where time-reversal symmetry or duality principles are important. The operator structure can be extended to fractional operators, a growing area of research with applications in anomalous diffusion, viscoelastic materials, and control systems. By generalizing to non-integer orders, it is possible to model memory-dependent or nonlocal phenomena more effectively. The geometric properties established in this work may help ensure the stability or boundedness of such solutions. From the perspective of geometric function theory (GFT), the results on starlikeness, convexity, and coefficient estimates offer tools for constructing conformal or quasi-conformal mappings in the unit disk with prescribed symmetry or distortion properties.

Looking ahead, future research could focus on the construction of broader families of functions using generalized forms of the symmetric q-operator, the study of their mapping properties, or the investigation of connections with other areas of mathematical physics. These directions promise to further enrich the field and open up new avenues for exploration.

Moreover, the framework introduced in this study opens up several promising avenues for further exploration. One potential direction involves extending the symmetric q-differential operator to more generalized settings, such as weighted or fractional q-operators, to capture a broader class of function behaviors. Another compelling line of inquiry would be the investigation of the stability and dynamic properties of the newly defined function classes under various integral transforms, which could reveal deeper insights into their structural characteristics.

Additionally, an important next step could involve applying the proposed operator framework to complex systems modeled in quantum physics, where q-calculus plays a fundamental role in describing discrete symmetries and non-classical phenomena. Exploring connections with other areas of modern analysis—such as harmonic univalent functions, bi-univalent function theory, or applications in conformal mappings—could also substantially broaden the impact and relevance of the current results.

From a computational perspective, numerical simulations and graphical analyses of specific functions within the introduced classes could provide visual validation of the theoretical findings, as well as uncover unexpected geometric patterns worthy of deeper investigation. Finally, collaborative studies that integrate symmetric q-calculus with computational methods or machine learning models might lead to innovative applications in signal processing or data analysis, further underscoring the versatility of this mathematical framework.