Commutators of Pre-Lie n-Algebras and PL_∞-Algebras

Abstract

We show that a $P{L}_{\infty }$-algebra V can be described by a nilpotent coderivation of degree $-1$ on coalgebra $P^{*}V$. Based on this result, we can generalise the result of Lada to show that every $A_{\infty }$-algebra carries a $P{L}_{\infty }$-algebra structure and every $P{L}_{\infty }$-algebra carries an $L_{\infty }$-algebra structure. In particular, we obtain a pre-Lie n-algebra structure on an arbitrary partially associative n-algebra and deduce that pre-Lie n-algebras are n-Lie admissible.

1. Introduction

Left-symmetric algebras were introduced by Cayley [1] in 1896 as a kind of rooted tree algebras, becoming noticed after Vinberg [2] in 1960 and Koszul [3] in 1961 introduced them in the study of convex homogeneous cones and affine manifolds. Recall that a left-symmetric algebra is a space V endowed by a bilinear map $\mu :V\otimes V\to V$ satisfying

$$(x,y,z)=(y,x,z)$$

for all $x,y,z\in V$, where $(x,y,z):=\mu \left(\mu \right(x,y),z)-\mu (x,\mu (y,z\left)\right)$. The opposite of left-symmetric algebras are called right-symmetric algebras, and both are called pre-Lie algebras. It is easy to see that every associative algebra is a pre-Lie algebra. Any pre-Lie algebra $(V,\mu )$ is a Lie-admissible algebra, i.e., the commutator $[x,y]:=\mu (x,y)-\mu (y,x)$ defines a Lie bracket on V.

Many generalizations of pre-Lie algebras have been widely studied as well, For instance, homotopy pre-Lie algebras ($P{L}_{\infty }$-algebras) were developed in [4] in the operad context, while the concept of generalized pre-Lie algebras of order n was introduced in [5] without specific expression formulae for $n>3$. Similar generalizations of associative algebras and Lie algebras were introduced in [6,7,8,9]. The purpose of this paper is to analyse the relation of these n-ary and homotopy algebra structures of associative, pre-Lie, and Lie type. In [10], Lada introduced the commutators of an $A_{\infty }$-algebra and provided the structure of $L_{\infty }$-algebras on it. Inspired by this, we first show that a $P{L}_{\infty }$-algebra structure on V is equivalent to a nilpotent coderivation of degree $-1$ on coalgebra $P^{*}V$. Using coalgebra maps between corresponding coalgebras of $A_{\infty },P{L}_{\infty }$- and $L_{\infty }$-algebras, we can obtain a $P{L}_{\infty }$-algebra structure on an $L_{\infty }$-algebra and an $L_{\infty }$-algebra structure on a $P{L}_{\infty }$-algebra. As a special case, we can finally provide the commutators of n-ary algebras. The main results can be summarised as follows:

• Theorem 2, which states that the $P{L}_{\infty }$-algebra structure on V can be extended as a nilpotent coderivation of degree $-1$ on coalgebra $P^{*}V$.
• Theorem 3, which provides the relation of homotopy algebras, along with Corollary 2 providing the relation of n-ary algebras.

The rest of this paper is organised as follows. First, in Section 2, we provide some preliminaries and introduce a simple way to define the algebra expression formulae of pre-Lie type. There are two different definitions of associative-type homotopy algebras, namely, pre-Lie and Lie, which we refer to as the degree $-1$ and degree $n-2$ versions. We show that n-ary algebras in all three types can be identified with homotopy algebras of degree $n-2$ in the same type, while homotopy algebras of degree $-1$ are closely related to the coalgebras presented in Section 3. Also in Section 3, we illustrate that these two versions of homotopy algebras in the same type are equivalent and that homotopy algebras can be characterized by coderivations of corresponding coalgebras.

Using the three coalgebras in Section 3 and the coalgebra maps between them, in Section 4 we derive the relations among homotopy algebras based on their equivalent characterizations from Section 3. From Section 2, an n-ary algebra can be identified with a special homotopy algebra; thus, we obtain the corresponding relation among n-ary algebras.

2. Preliminaries

In this paper, we work over a field $\mathbb{K}$ of characteristic 0, and all vector spaces are over $\mathbb{K}$. The symmetric group of the set $\{1,2,\dots ,n\}$ is denoted by ${\mathbb{S}}_n$. Let $Sh(i_1,\dots ,i_m)$ denote the subset of ${\mathbb{S}}_n$ consisting of all $(i_1,\dots ,i_m)$-unshuffles of ${\mathbb{S}}_n$, where $i_1+\dots +i_m=n$. Recall that an $(i_1,\dots ,i_m)$-unshuffle is an element in ${\mathbb{S}}_n$ such that

$$\sigma (1+{\displaystyle \sum _{t=0}^{k-1}}{i}_t)<\dots <\sigma ({\displaystyle \sum _{t=0}^k}{i}_t),\mathrm{f}\mathrm{o}\mathrm{r} \mathrm{a}\mathrm{l}\mathrm{l} k=1,2,\dots ,m.$$

It is well-known that ${\displaystyle {\displaystyle \sum _{\sigma \in {\mathbb{S}}_n}}}\sigma$ is a nonzero integral in the Hopf algebra $\mathbb{K}{\mathbb{S}}_n$. We always use $w_n$ to denote the integral of $\mathbb{K}{\mathbb{S}}_n$ in the sequel.

For any vector spaces V and W over the field $\mathbb{K}$, we use $Hom(V,W)$ to denote the space of all $\mathbb{K}$-linear maps from V to W. The notation $V\otimes W$ means $V{\otimes }_{\mathbb{K}}W$, that is, the tensor product of V and W over the field $\mathbb{K}$. We use ${\otimes }^{n}V$ to denote the space ${\displaystyle \underset{n}{\underbrace{V\otimes V\otimes \dots \otimes V}}}$. It is well-known that ${\otimes }^{n}V$ is a right $\mathbb{K}{\mathbb{S}}_n$-module with the following action:

$${\rho }_{{\sigma }_1}(x_1\otimes \dots \otimes x_n)=sgn\left({\sigma }_1\right)(x_{{\sigma }_1\left(1\right)}\otimes \dots \otimes x_{{\sigma }_1\left(n\right)})$$

for ${\sigma }_1\in {\mathbb{S}}_n$ and $x_1\otimes x_2\otimes \dots \otimes x_n\in {\otimes }^{n}V$. The invariant subspace of ${\otimes }^{n}V$ under this action is denoted by ${\wedge }^{n}V$. The identity endomorphism of V is denoted by $i{d}_V$, while $i{d}_{{\otimes }^{n}V}$ is simply denoted by $I_n$.

Further, we assume that V is a $\mathbb{Z}$-graded vector space $V:={\oplus }_{n\in \mathbb{Z}}{V}^n$. We follow [11] for the terminology on the category of graded vector spaces. For any $x\in V^n$ for some $n\in \mathbb{Z}$, we say that x is homogeneous with degree n. The degree of a homogeneous element x is denoted by $\left|x\right|$. If $x_i\in V$ are homogeneous, then the degree of either $x_1\otimes \dots \otimes x_n\in {\otimes }^{n}V$ or $x_1\wedge \dots \wedge x_n\in {\wedge }^{n}V$ is defined as ${\displaystyle {\displaystyle \sum _{i=1}^n}}\left|x_i\right|$. Let $f:V\to W$ be a map of graded vector spaces; then, f is called a homogeneous linear map of cohomological degree n if $f\left(V^i\right)\subseteq W^{i+n}$ for any $n\in \mathbb{Z}$. The cohomological degree of a homogeneous linear map f is denoted by $\left|f\right|.$ Suppose that $f:V\to V^{\prime }$ and $g:W\to W^{\prime }$ are two homogeneous linear maps; then, the tensor product of f and g (denoted by $f\otimes g$) is a homogeneous linear map from $V\otimes W$ to $V^{\prime }\otimes W^{\prime }$ determined by

$$(f\otimes g)(x\otimes y):={(-1)}^{n\left|g\right|}f\left(x\right)\otimes g\left(y\right)$$

for any $x\in V^n,y\in W$.

For any transposition $(i,i+1)\in {\mathbb{S}}_n$ and $x_1\wedge x_2\wedge \dots \wedge x_n\in {\wedge }^{n}V$, we have

$$x_1\wedge x_2\wedge \dots \wedge x_n={(-1)}^{|x_i\left|\right|x_{i+1}|}{x}_1\wedge \dots \wedge x_{i+1}\wedge x_i\wedge \dots \wedge x_n.$$

Replacing the transposition by an arbitrary element $\sigma$ in ${\mathbb{S}}_n$ allows us to obtain the Koszul sign $ϵ\left(\sigma \right):=ϵ(\sigma ;x_1,\dots ,x_n)$ [12] recursively by transposition decomposition of $\sigma$; specifically,

$$x_1\wedge x_2\wedge \dots \wedge x_n=ϵ(\sigma ;x_1,\dots ,x_n)x_{\sigma \left(1\right)}\wedge x_{\sigma \left(2\right)}\wedge \dots \wedge x_{\sigma \left(n\right)}.$$

We have sometimes simplified $ϵ(\sigma ;x_1,\dots ,x_n)$ as $ϵ\left(\sigma \right)$.

Remark 1. 

By definition, $x_{\tau \left(1\right)}\wedge \dots \wedge x_{\tau \left(n\right)}=ϵ(\sigma ;x_{\tau \left(1\right)},\dots ,x_{\tau \left(n\right)})x_{\tau \sigma \left(1\right)}\wedge \dots \wedge x_{\tau \sigma \left(n\right)}$ for $\sigma ,\tau \in {\mathbb{S}}_n$. Converting both sides of the equation to multiples of $x_1\wedge \dots \wedge x_n$, we have

$$ϵ(\tau ;x_1,\dots ,x_n)=ϵ(\sigma ;x_{\tau \left(1\right)},\dots ,x_{\tau \left(n\right)})ϵ(\tau \sigma ;x_1,\dots ,x_n).$$

Because the value of ϵ is $\pm 1$, the above equation can be expressed as

$$ϵ(\sigma ;x_{\tau \left(1\right)},\dots ,x_{\tau \left(n\right)})=ϵ(\tau \sigma ;x_1,\dots ,x_n)ϵ(\tau ;x_1,\dots ,x_n):=ϵ\left(\tau \sigma \right)ϵ\left(\tau \right).$$

Similar to the case when V is non-graded, ${\otimes }^{n}V$ is a right $\mathbb{K}{\mathbb{S}}_n$-module with the action provided by

$${\rho }_{\sigma }^{\left(1\right)}(x_1\otimes \dots \otimes x_n):=ϵ\left(\sigma \right)(x_{\sigma \left(1\right)}\otimes \dots \otimes x_{\sigma \left(n\right)}).$$

With this action, we can prove that ${\wedge }^{n}V$ is the space of coinvariants ${\left({\otimes }^{n}V\right)}_{{\mathbb{S}}_n}:=\left({\otimes }^{n}V\right)/({\rho }_{\sigma }^{\left(1\right)}\left(\mathbf{x}\right)-\mathbf{x},\sigma \in {\mathbb{S}}_n,\mathbf{x}\in {\otimes }^{n}V)$ [13]. If a linear mapping ${\widehat{\mu }}_n$ from ${\otimes }^{n}V$ to V satisfies ${\widehat{\mu }}_n={\widehat{\mu }}_n\circ ({\rho }_{\sigma }^{\left(1\right)}\otimes I_1)$ for $\sigma \in {\mathbb{S}}_{n-1}$, then it can be regarded as a linear map from ${\wedge }^{n-1}V\otimes V$ to V. Similarly, any mapping $\widehat{\mu }$ from ${\otimes }^{n}V$ to V satisfying ${\widehat{\mu }}_n={\widehat{\mu }}_n\circ {\rho }_{\sigma }^{\left(1\right)}$ for any $\sigma \in {\mathbb{S}}_n$ can be viewed as a linear map from ${\wedge }^{n}V$ to V.

With the previous preparation, we can recall the following definitions of $A_{\infty }$-algebras in [9], $L_{\infty }$-algebras in [7], and $P{L}_{\infty }$-algebras in [4].

Definition 1. 

Let V be a graded vector space equipped with a collection $\{{\widehat{\mu }}_n:{\otimes }^{n}V\to V,n\ge 1\}$ of homogeneous linear maps of cohomological degree $-1$. Then, $(V,\left\{{\widehat{\mu }}_n\right\})$ is called:

• an $A_{\infty }$-algebra, if

  $${\displaystyle \sum _{i+j=n+1}}{\displaystyle \sum _{m=0}^{i-1}}{\widehat{\mu }}_i\circ (I_m\otimes {\widehat{\mu }}_j\otimes I_{i-m-1})=0,\forall n\ge 1.$$

  (1)
• a $P{L}_{\infty }$-algebra, if

  $$\left\{\begin{array}{c}{\widehat{\mu }}_n={\widehat{\mu }}_n\circ ({\rho }_{\sigma }^{\left(1\right)}\otimes I_1),for \sigma \in {\mathbb{S}}_{n-1},\hfill \\ {\displaystyle {\displaystyle \sum _{i+j=n+1}}}{\displaystyle {\displaystyle \sum _{m=0}^{i-1}}}{\displaystyle \frac{1}{(i-1)!(j-1)!}}{\widehat{\mu }}_i\circ (I_m\otimes {\widehat{\mu }}_j\otimes I_{i-m-1})\circ ({\rho }_{w_{i+j-2}}^{\left(1\right)}\otimes I_1)=0,\forall n\ge 1.\hfill \end{array}\right.$$

  (2)
• an $L_{\infty }$-algebra, if

  $$\left\{\begin{array}{c}{\widehat{\mu }}_n={\widehat{\mu }}_n\circ {\rho }_{\sigma }^{\left(1\right)},for\sigma \in {\mathbb{S}}_n,\hfill \\ {\displaystyle {\displaystyle \sum _{i+j=n+1}}}{\displaystyle {\displaystyle \sum _{m=0}^{i-1}}}{\displaystyle \frac{1}{(i-1)!j!}}{\widehat{\mu }}_i\circ (I_m\otimes {\widehat{\mu }}_j\otimes I_{i-m-1})\circ {\rho }_{w_{i+j-1}}^{\left(1\right)}=0,\forall n\ge 1.\hfill \end{array}\right.$$

  (3)

Remark 2. 

(1) Equation (2) can be replaced by

$$\begin{array}{c}{\displaystyle \sum _{i+j=n+1}}({\displaystyle \sum _{\sigma \in Sh(j-1,1,i-2)}}ϵ\left(\sigma \right){\widehat{\mu }}_i({\widehat{\mu }}_j(x_{\sigma \left(1\right)},\dots ,x_{\sigma \left(j\right)}),x_{\sigma (j+1)},\dots ,\hfill \\ x_{\sigma (i+j-2)},x_{i+j-1})={\displaystyle \sum _{\sigma \in Sh(i-1,j-1)}}{(-1)}^{1+({\displaystyle \sum _{r=1}^{i-1}}|x_{\sigma \left(r\right)}|)}ϵ\left(\sigma \right){\widehat{\mu }}_i(x_{\sigma \left(1\right)},\dots ,x_{\sigma (i-1)},\hfill \\ {\widehat{\mu }}_j(x_{\sigma \left(i\right)},\dots ,x_{\sigma (i+j-2)},\dots ,x_{i+j-1})\left)\right).\hfill \end{array}$$

(2) We can replace “${\rho }_{w_{i+j-2}}^{\left(1\right)}\otimes I_1$” by “$I_1\otimes {\rho }_{w_{i+j-2}}^{\left(1\right)}$” to obtain the notion of right-symmetric ∞-algebras, which is exactly that of $P{L}_{\infty }$-algebras in [4].

(3) It can be noticed that for $\left\{{\widehat{\mu }}_n\right\}$ satisfying Equation (2), the opposite operations $\left\{{\widehat{\mu }}_n^{op}\right\}$ defined by

$${\widehat{\mu }}_n^{op}(x_1,x_2,\dots ,x_n):={\widehat{\mu }}_n(x_n,x_{n-1},\dots ,x_1)$$

are not $P{L}_{\infty }$-algebras in [4] in general; in fact, the tensor rules of the maps contribute to this phenomenon. The procedure can be demonstrated by the following example:

$$\begin{array}{cc}\hfill & (g\circ (I_1\otimes f\otimes I_1))(x\otimes y_1\otimes y_2\otimes z)={(-1)}^{\left|f\right|\left|x\right|}g(x\otimes f(y_1\otimes y_2)\otimes z),\hfill \\ \hfill & (g^{op}\circ (I_1\otimes f^{op}\otimes I_1))(z\otimes y_2\otimes y_1\otimes x)={(-1)}^{\left|f\right|\left|z\right|}g(x\otimes f(y_1\otimes y_2)\otimes z).\hfill \end{array}$$

This is also the reason that $P{L}_{\infty }$-algebras in [4] have different signs from Equation (2). Although there is such an obstruction for graded vector spaces, we can obtain the corresponding notions of right-symmetric algebras simply by reversing left-symmetric operations in non-graded cases.

Another right $\mathbb{K}{\mathbb{S}}_n$-module action on ${\otimes }^{n}V$ is defined via

$${\rho }_{\sigma }^{\left(2\right)}(x_1\otimes \dots \otimes x_n):=sgn\left(\sigma \right)ϵ\left(\sigma \right)(x_{\sigma \left(1\right)}\otimes \dots \otimes x_{\sigma \left(n\right)}).$$

Replacing ${\rho }^{\left(1\right)}$ by ${\rho }^{\left(2\right)}$ and equipping the above structure equations with sign functions can provide the following equivalent definition of Definition 1.

Definition 2. 

Let V be a graded vector space equipped with a collection $\{{\mu }_n:{\otimes }^{n}V\to V,n\ge 1\}$ of homogeneous linear maps of cohomological degree $n-2$. Here, V is called:

• an $A_{\infty }$-algebra, if

  $${\displaystyle \sum _{i+j=n+1}}{\displaystyle \sum _{m=0}^{i-1}}{(-1)}^{j(i-m-1)+m}{\mu }_i\circ (I_m\otimes {\mu }_j\otimes I_{i-m-1})=0,\forall n\ge 1.$$

  (4)
• a $P{L}_{\infty }$-algebra, if

  $$\left\{\begin{array}{c}{\mu }_n={\mu }_n\circ ({\rho }_{\sigma }^{\left(2\right)}\otimes I_1),for\sigma \in {\mathbb{S}}_{n-1},\hfill \\ {\displaystyle \sum _{i+j=n+1}}{\displaystyle \sum _{m=0}^{i-1}}{\displaystyle \frac{{(-1)}^{j(i-m-1)+m}}{(i-1)!(j-1)!}}{\mu }_i\circ (I_m\otimes {\mu }_j\otimes I_{i-m-1})\circ ({\rho }_{w_{i+j-2}}^{\left(2\right)}\otimes I_1)=0,\forall n\ge 1.\hfill \end{array}\right.$$

  (5)
• an $L_{\infty }$-algebra, if

  $$\left\{\begin{array}{c}{\mu }_n={\mu }_n\circ {\rho }_{\sigma }^{\left(2\right)},for\sigma \in {\mathbb{S}}_n,\hfill \\ {\displaystyle \sum _{i+j=n+1}}{\displaystyle \sum _{m=0}^{i-1}}{\displaystyle \frac{{(-1)}^{j(i-m-1)+m}}{(i-1)!j!}}{\mu }_i\circ (I_m\otimes {\mu }_j\otimes I_{i-m-1})\circ {\rho }_{w_{i+j-1}}^{\left(2\right)}=0,\forall n\ge 1.\hfill \end{array}\right.$$

  (6)

These two different forms of homotopy algebras in the same type are equivalent. The detailed proof of this is presented in Section 3.2.

Remark 3. 

Explicitly, for $n\ge 1$ and $x_1,x_2,\dots ,x_{i+j-1}\in V$, Equation (5) means that:

$$\begin{array}{cc}\hfill & {\displaystyle \sum _{i+j=n+1}}({\displaystyle \sum _{\sigma \in Sh(j-1,1,i-2)}}{(-1)}^{j(i-1)}sgn\left(\sigma \right)ϵ\left(\sigma \right){\mu }_i({\mu }_j(x_{\sigma \left(1\right)},\dots ,x_{\sigma \left(j\right)}),x_{\sigma (j+1)},\dots ,x_{\sigma (i+j-2)}.\hfill \\ \hfill & x_{i+j-1})={\displaystyle \sum _{\sigma \in Sh(i-1,j-1)}}{(-1)}^{i+j({\displaystyle \sum _{r=1}^{i-1}}|x_{\sigma \left(r\right)}|)}sgn\left(\sigma \right)ϵ\left(\sigma \right){\mu }_i(x_{\sigma \left(1\right)},\dots ,x_{\sigma (i-1)},{\mu }_j(x_{\sigma \left(i\right)},\dots .\hfill \\ \hfill & x_{\sigma (i+j-2)},\dots ,x_{i+j-1}\left)\right)).\hfill \end{array}$$

In Definition 2, if (4) is replaced by

$${\displaystyle \sum _{i=0}^{n-1}}\mu \circ (I_i\otimes \mu \otimes I_{n-1-i})=0,$$

(7)

then V is called a partially associative n-algebra in [6]. Imitating the method for constructing $P{L}_{\infty }$-algebras and referring to the definition of partially associative n-algebras, we introduce the following definition of pre-Lie n-algebras.

Definition 3. 

Suppose that V is a vector space and $\mu \in Hom({\otimes }^{n}V,V)$; then, $(V,\mu )$ is a  pre-Lie n-algebra  if μ satisfies

$$\left\{\begin{array}{c}\mu =\mu \circ ({\rho }_{\sigma }\otimes I_1),for\sigma \in {\mathbb{S}}_{n-1},\hfill \\ {\displaystyle \sum _{i=0}^{n-1}}{\displaystyle \frac{{(-1)}^{i(n-1)}}{{((n-1)!)}^2}}\mu \circ (I_i\otimes \mu \otimes I_{n-1-i})\circ ({\rho }_{w_{2n-2}}\otimes I_1)=0.\hfill \end{array}\right.$$

(8)

Remark 4. 

(1) In [6], a Lie n-algebra is defined as a vector V with $\mu \in Hom({\otimes }^{n}V,V)$ such that

$$\left\{\begin{array}{c}\mu =\mu \circ {\rho }_{\sigma },for\sigma \in {\mathbb{S}}_n,\hfill \\ {\displaystyle \sum _{i=0}^{n-1}}{\displaystyle \frac{{(-1)}^{i(n-1)}}{(n-1)!n!}}\mu \circ (I_i\otimes \mu \otimes I_{n-1-i})\circ {\rho }_{w_{2n-1}}=0.\hfill \end{array}\right.$$

(9)

Thus, a Lie n-algebra in [6] can be regarded as a pre-Lie n-algebra.

(2) A pre-Lie algebra in [14] is nothing but a pre-Lie 2-algebra.

Next, we prove that a pre-Lie n-algebra is exactly the left-symmetric version of the generalized pre-Lie algebras of order n in [5]. To achieve this aim, let us recall a result in [15]. For any vector space V, let $C^n(V,V):=\{\mu \in Hom({\otimes }^{n+1}V,V)|\mu =\mu \circ ({\rho }_{\sigma }\otimes I_1),for\sigma \in {\mathbb{S}}_{n-1}\}$ and $C(V,V):={\oplus }_{n\in \mathbb{N}}{C}^n(V,V)$. Then, the following result holds.

Theorem 1 

([15]). $C(V,V)$ is a graded Lie algebra with a bracket provided by

$${[f,g]}^{\circ }:=f\circ g-{(-1)}^{mn}g\circ f,forf\in C^m(V,V),g\in C^n(V,V),$$

(10)

where $f\circ g\in C^{m+n}(V,V)$ is defined by

$$\begin{array}{cc}\hfill & (f\circ g)(x_1,\dots x_{m+n+1})\hfill \\ \hfill =& {\displaystyle \sum _{\sigma \in Sh(n,1,m-1)}}sgn\left(\sigma \right)f(g(x_{\sigma \left(1\right)},\dots ,x_{\sigma \left(n\right)},x_{\sigma (n+1)}),x_{\sigma (n+2)},\dots ,x_{\sigma (m+n)},x_{m+n+1})\hfill \\ \hfill & +{(-1)}^{mn}{\displaystyle \sum _{\sigma \in Sh(m,n)}}sgn\left(\sigma \right)f(x_{\sigma \left(1\right)},\dots ,x_{\sigma \left(m\right)},g(x_{\sigma (m+1)},\dots ,x_{\sigma (m+n)},x_{m+n+1})).\hfill \end{array}$$

(11)

Then, we obtain the following necessary and sufficient condition of a pre-Lie n-algebra.

Lemma 1. 

Suppose that $\mu \in C^{n-1}(V,V)$; then, $(V,\mu )$ is a pre-Lie n-algebra if and only if $\mu \circ \mu =0$.

Proof. 

Because

$$\begin{array}{cc}\hfill & {\displaystyle \sum _{i=0}^{n-1}}{\displaystyle \frac{{(-1)}^{i(n-1)}}{{((n-1)!)}^2}}\mu \circ (I_i\otimes \mu \otimes I_{n-1-i})\circ ({\rho }_{w_{2n-2}}\otimes I_1)(x_1,\dots ,x_{2n-1})\hfill \\ \hfill =& {\displaystyle \sum _{\sigma \in {\mathbb{S}}_{2n-2}}}sgn(\sigma )({\displaystyle \sum _{i=0}^{n-2}}{\displaystyle \frac{{(-1)}^{i(n-1)}}{{((n-1)!)}^2}}\mu (x_{\sigma (1)},\dots ,x_{\sigma (i)},\mu (x_{\sigma (i+1)},\dots ,x_{\sigma (i+n)}),x_{\sigma (i+n+1)},\dots ,\hfill \\ \hfill & x_{\sigma (2n-2)},x_{2n-1})+{\displaystyle \frac{{(-1)}^{n-1}}{{((n-1)!)}^2}}\mu (x_{\sigma (1)},\dots ,x_{\sigma (n-1)},\mu (x_{\sigma (n)},\dots ,x_{\sigma (2n-2)},x_{2n-1})))\hfill \\ \hfill =& {\displaystyle \sum _{\sigma \in {\mathbb{S}}_{2n-2}}}sgn(\sigma )({\displaystyle \sum _{i=0}^{n-2}}{\displaystyle \frac{{(-1)}^{in}}{{((n-1)!)}^2}}\mu (\mu (x_{\sigma (i+1)},\dots ,x_{\sigma (i+n)}),x_{\sigma (1)},\dots ,x_{\sigma (i)},x_{\sigma (i+n+1)},\dots ,\hfill \\ \hfill & x_{\sigma (2n-2)},x_{2n-1})+{\displaystyle \frac{{(-1)}^{n-1}}{{((n-1)!)}^2}}\mu (x_{\sigma (1)},\dots ,x_{\sigma (n-1)},\mu (x_{\sigma (n)},\dots ,x_{\sigma (2n-2)},x_{2n-1})))\hfill \\ \hfill =& {\displaystyle \frac{1}{n-1}}({\displaystyle \sum _{i=0}^{n-2}}{\displaystyle \sum _{\sigma \in Sh(n-1,1,n-2)}}sgn(\sigma )\mu (\mu (x_{\sigma (1)},\dots ,x_{\sigma (n)}),x_{\sigma (n+1)},\dots ,x_{\sigma (2n-2)},\hfill \\ \hfill & x_{2n-1}))+{(-1)}^{n-1}{\displaystyle \sum _{\sigma \in Sh(n-1,n-1)}}sgn(\sigma )\mu (x_{\sigma (1)},\dots ,x_{\sigma (n-1)},\mu (x_{\sigma (n)},\dots ,\hfill \\ \hfill & x_{\sigma (2n-2)},x_{2n-1}))\hfill \\ \hfill =& {\displaystyle \sum _{\sigma \in Sh(n-1,1,n-2)}}sgn(\sigma )\mu (\mu (x_{\sigma (1)},\dots ,x_{\sigma (n)}),x_{\sigma (n+1)},\dots ,x_{\sigma (2n-2)},x_{2n-1})+\hfill \\ \hfill & {(-1)}^{n-1}{\displaystyle \sum _{\sigma \in Sh(n-1,n-1)}}sgn(\sigma )\mu (x_{\sigma (1)},\dots ,x_{\sigma (n-1)},\mu (x_{\sigma (n)},\dots ,x_{\sigma (2n-2)},x_{2n-1}))\hfill \\ \hfill =& (\mu \circ \mu )(x_1,\dots ,x_{2n-1})\hfill \end{array}$$

for any $x_1,\dots ,x_{2n-1}\in V$, it is the case that $\mu \circ \mu =0$ if and only (8) holds. □

A short calculation reveals that if $(V,\mu )$ is a pre-Lie algebra in Definition 3, then $(V,{\mu }^{op})$ is a generalized pre-Lie algebra of order n in [5].

Remark 5. 

Note that Lie n-algebras and n-Lie algebras are two different n-generalizations of Lie algebras [16], while n-Lie algebras are special Lie n-algebras [6]. Correspondingly, our pre-Lie n-algebras (generalized pre-Lie algebras of order n in [5]) are different from the n-pre-Lie algebras in [5], while our n-pre-Lie algebras are special pre-Lie n-algebras.

In the remainder of this section, we show that an n-ary algebra (associative, Lie, or pre-Lie) is a special corresponding homotopy algebra in Definition 2.

Although an n-ary algebra’s structure equations are analogous to those of the homotopy algebras in Definition 1, there are differences in the signs of the structure equations when we take in elements. Because signs are determined by the parity of relevant numbers, Hanlon and Wachs get around this dilemma using superspaces, i.e., bi-graded vector space in [17]. However, this approach is not applicable to general spaces. It seems that we can solve this problem simply by regarding V as a graded vector space concentrated in cohomological degree 0. In fact, such a graded vector space can only be equipped with a non-zero bilinear map ${\mu }_2$, since $|{\mu }_n|=0$ if and only if $n=2$. Thus, we take another tack.

For any n-ary algebra $(V,\mu )$, we construct an associated homotopy algebra $(\overline{V}={\oplus }_n{\overline{V}}^i,\left\{{\mu }_i\right\})$, where

$$\begin{array}{ccc}\hfill {\overline{V}}^i=\left\{\begin{array}{cc}V,\hfill & \mathrm{i}\mathrm{f} i=0,n-2 \mathrm{or} 2n-4,\hfill \\ 0,\hfill & \mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e},\hfill \end{array}\right.& \mathrm{a}\mathrm{n}\mathrm{d}& {\mu }_i=0 \mathrm{u}\mathrm{n}\mathrm{l}\mathrm{e}\mathrm{s}\mathrm{s} i=n.\hfill \end{array}$$

(12)

Thus, for any non-zero homogeneous element $(x_1,\dots ,x_n)\in {\otimes }^n\overline{V}$, the corresponding degree $|x_1|+\dots +|x_n|=k(n-2)$ for some non-negative integer k. With the forgetful image $(x_1^{\prime },\dots ,x_n^{\prime })$ in ${\otimes }^{n}V$, we can provide the function of ${\mu }_n$ as follows:

$$\begin{array}{c}\hfill {\mu }_n(x_1,\dots ,x_n)=\left\{\begin{array}{cc}\mu (x_1^{\prime },\dots ,x_n^{\prime }),\hfill & \mathrm{i}\mathrm{f} |x_1\otimes \dots \otimes x_n|=0 \mathrm{or} n-2,\hfill \\ 0,\hfill & \mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}.\hfill \end{array}\right.\end{array}$$

(13)

Note that the equal sign in Equation (13) means that the values of two functions are equal and ${\mu }_n:{\otimes }^n\overline{V}\to \overline{V}$ is a homogeneous linear map of cohomological degree $n-2$. Now, we can identify an n-ary algebra with a homotopy algebra in Definition 2.

Proposition 1. 

• $(V,\mu )$ is a partially associative n-algebra if and only if $(\overline{V},\left\{{\mu }_i\right\})$ is an $A_{\infty }$-algebra.
• $(V,\mu )$ is a pre-Lie n-algebra if and only if $(\overline{V},\left\{{\mu }_i\right\})$ is a $P{L}_{\infty }$-algebra.
• $(V,\mu )$ is a Lie n-algebra if and only if $(\overline{V},\left\{{\mu }_i\right\})$ is an $L_{\infty }$-algebra.

3. Coalgebras, Coderivations, and Homotopy Algebras

In this section, we explain the equivalence of different forms of the same homotopy algebra in Section 2 and relate $P{L}_{\infty }$-algebras to coderivations of a coalgebra. Thus, V is always a graded vector space unless otherwise specified.

3.1. Coalgebras and Coalgebra Maps Between Them

Given a graded vector space V, there are three cofree objects on V of interest to us: the cofree coalgebra $T^{*}V$, the cofree commutative coalgebra ${\wedge }^{*}V$, and the cofree left Perm-coalgebra $P^{*}V$ in [4]. Below, we present their graded structures and coalgebra structures:

• $T^{*}V:={\oplus }_{n\ge 1}\left({\otimes }^{n}V\right)$ is a graded vector space equipped with a comultiplication map

  $$\begin{array}{c}\hfill \Delta (x_1\otimes \dots \otimes x_n)={\displaystyle \sum _{i=1}^{n-1}}(x_1\otimes \dots \otimes x_i)\otimes (x_{i+1}\otimes \dots \otimes x_n).\end{array}$$

  (14)
• The comultiplication of ${\wedge }^{*}V:={\oplus }_{n\ge 1}\left({\wedge }^{n}V\right)$ is provided by

  $$\begin{array}{c}\hfill \Delta (x_1\wedge \dots \wedge x_n)={\displaystyle \sum _{i=1}^{n-1}}{\displaystyle \sum _{\sigma \in Sh(i,n-i)}}ϵ\left(\sigma \right)(x_{\sigma \left(1\right)}\wedge \dots \wedge x_{\sigma \left(i\right)})\otimes (x_{\sigma (i+1)}\wedge \dots \wedge x_{\sigma \left(n\right)}).\end{array}$$

  (15)
• The n-part of $P^{*}V$ is denoted by $P^{n}V:=\left({\wedge }^{n-1}V\right)\otimes V$ and its comultiplication is defined by

  $$\begin{array}{cc}\hfill & \Delta (x_1\wedge \dots \wedge x_{n-1}\otimes x_n)\hfill \\ \hfill =& {\displaystyle \sum _{i=1}^{n-1}}{\displaystyle \sum _{\sigma \in Sh(i-1,1,n-i-1)}}ϵ\left(\sigma \right)(x_{\sigma \left(1\right)}\wedge \dots \wedge x_{\sigma (i-1)}\otimes x_{\sigma \left(i\right)})\otimes (x_{\sigma (i+1)}\wedge \dots \wedge x_{\sigma (n-1)}\otimes x_n).\hfill \end{array}$$

  (16)

Expanding the coalgebra map in [18], we obtain the following result.

Lemma 2. 

There is a commutative diagram of coalgebras

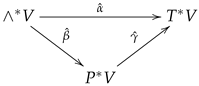in which

$$\widehat{\alpha }(x_1\wedge \dots \wedge x_n):={\displaystyle \sum _{\sigma \in {\mathbb{S}}_n}}ϵ\left(\sigma \right)x_{\sigma \left(1\right)}\otimes \dots \otimes x_{\sigma \left(n\right)},$$

$$\widehat{\beta }(x_1\wedge \dots \wedge x_n):={\displaystyle \sum _{\sigma \in Sh(n-1,1)}}ϵ\left(\sigma \right)x_{\sigma \left(1\right)}\wedge \dots \wedge x_{\sigma (n-1)}\otimes x_{\sigma \left(n\right)},$$

$$\widehat{\gamma }(x_1\wedge \dots \wedge x_{n-1}\otimes x_n):={\displaystyle \sum _{\sigma \in {\mathbb{S}}_{n-1}}}ϵ\left(\sigma \right)x_{\sigma \left(1\right)}\otimes \dots \otimes x_{\sigma (n-1)}\otimes x_n$$

are injective coalgebra maps.

Proof. 

Because $w_n$ is an integral of ${\mathbb{KS}}_n$, $\widehat{\alpha }={\displaystyle \sum _{n\ge 1}}{\rho }_{w_n}^{\left(1\right)}$ and $\widehat{\gamma }={\displaystyle \sum _{n\ge 1}}{\rho }_{w_{n-1}}^{\left(1\right)}\otimes I_1$, similarly, we can prove that $\widehat{\beta }={\displaystyle \sum _{n\ge 1,\sigma \in Sh(n-1,1)}}{\rho }_{\sigma }^{\left(1\right)}$. Then, we show that $\widehat{\gamma }\widehat{\beta }=\widehat{\alpha }$ according to the discussion in Remark 1. For any $x_1\wedge \dots \wedge x_n\in {\wedge }^{n}V$,

$$\begin{array}{cc}\hfill & \left(\widehat{\gamma }\widehat{\beta }\right)(x_1\wedge \dots \wedge x_n)\hfill \\ \hfill =& {\displaystyle \sum _{\sigma \in Sh(n-1,1)}}{\displaystyle \sum _{\tau \in {\mathbb{S}}_{n-1}}}ϵ\left(\sigma \right)ϵ(\tau ;x_{\sigma \left(1\right)},\dots ,x_{\sigma (n-1)})x_{\tau \sigma \left(1\right)}\otimes \dots \otimes x_{\tau \sigma (n-1)}\otimes x_{\sigma \left(n\right)}\hfill \\ \hfill =& {\displaystyle \sum _{\sigma \in Sh(n-1,1)}}{\displaystyle \sum _{\begin{array}{c}\tau \in {\mathbb{S}}_n\\ \tau \left(n\right)=n\end{array}}}ϵ\left(\sigma \right)ϵ(\tau ;x_{\sigma \left(1\right)},\dots ,x_{\sigma \left(n\right)})x_{\tau \sigma \left(1\right)}\otimes \dots \otimes x_{\tau \sigma \left(n\right)}\hfill \\ \hfill =& {\displaystyle \sum _{\sigma \in {\mathbb{S}}_n}}ϵ\left(\sigma \right)x_{\sigma \left(1\right)}\otimes \dots \otimes x_{\sigma \left(n\right)}\hfill \\ \hfill =& \widehat{\alpha }(x_1\wedge \dots \wedge x_n).\hfill \end{array}$$

Next, we show that $\widehat{\alpha },\widehat{\beta },\widehat{\gamma }$ are injective coalgebra maps. Taking $\widehat{\alpha }$ as an example, we need to verify that $(\widehat{\alpha }\otimes \widehat{\alpha })\Delta =\Delta \widehat{\alpha }$. Let $x_i\in V$ be homogeneous elements; then,

$$\begin{array}{cc}\hfill & ((\widehat{\alpha }\otimes \widehat{\alpha })\Delta )(x_1\wedge \dots \wedge x_n)\hfill \\ \hfill =& {\displaystyle \sum _{i=0}^n}{\displaystyle \sum _{\sigma \in Sh(i,n-i)}}ϵ\left(\sigma \right)\widehat{\alpha }(x_{\sigma \left(1\right)}\wedge \dots \wedge x_{\sigma \left(i\right)})\otimes \widehat{\alpha }(x_{\sigma (i+1)}\wedge \dots \wedge x_{\sigma \left(n\right)})\hfill \\ \hfill =& {\displaystyle \sum _{i=0}^n}{\displaystyle \sum _{\sigma \in {\mathbb{S}}_n}}ϵ\left(\sigma \right)(x_{\sigma \left(1\right)}\otimes \dots \otimes x_{\sigma \left(i\right)})\otimes (x_{\sigma (i+1)}\otimes \dots \otimes x_{\sigma \left(n\right)})\hfill \\ \hfill =& (\Delta \widehat{\alpha })(x_1\wedge \dots \wedge x_n).\hfill \end{array}$$

Denoting the canonical epimorphism ${\pi }_n:{\otimes }^{n}V\to {\wedge }^{n}V,x_1\otimes \dots \otimes x_n\mapsto x_1\wedge \dots \wedge x_n$ and $\pi :={\displaystyle \sum _{n\ge 1}}{\displaystyle \frac{1}{n!}}{\pi }_n$, a short calculation reveals that $\pi \widehat{\alpha }=I{d}_{{\wedge }^{*}V}$, which means that $\widehat{\alpha }$ is injective.

Similarly, we can prove that $\widehat{\beta },\widehat{\gamma }$ are injective coalgebra maps. □

3.2. Equivalent Definitions of Homotopy Algebras

From Section 2, we know that there are two differential definitions of $A_{\infty }$ and $L_{\infty }$ algebras in [9,19] and [7,18]. Next, we show that the above two different definitions of these two kinds of homotopy algebras are equivalent. These homotopy algebras are characterized through coderivations of some coalgebras. Similarly, we can obtain the same conclusion for $P{L}_{\infty }$-algebras. To avoid confusion, we use pure letters with a subscript (for instance, ${\mathfrak{a}}_n$) to mean a map of degree $n-2$, letters with a hat (for instance, ${\widehat{\mathfrak{b}}}_n$) to mean a map of degree $-1$, and letters with a tilde (for instance, ${\tilde{\mathfrak{c}}}_n$) to mean a coderivation. Furthermore, maps denoted by ${\mathfrak{a}}_n$ and ${\widehat{\mathfrak{a}}}_n$ are in one-to-one correspondence, as are those denoted by ${\widehat{\mathfrak{a}}}_n$ and $\tilde{\mathfrak{a}}$.

For a graded vector space V, its suspension is denoted by $sV$, i.e., ${\left(sV\right)}^i=V^{i-1}$. In [7], Lada and Stasheff presented a bijection between the families of maps ${\mu }_n:{\otimes }^{n}V\to V$ of degree $n-2$ and maps ${\widehat{\mu }}_n:{\otimes }^n\left(sV\right)\to sV$ of degree $-1$, as follows:

$$\begin{array}{c}\hfill {\widehat{\mu }}_n(s{x}_1,\dots ,s{x}_n)=\left\{\begin{array}{cc}{(-1)}^{{\displaystyle \sum _{i=1}^{n/2}}\left|x_{2i-1}\right|}s{\mu }_n(x_1,\dots ,x_n),\hfill & \mathrm{i}\mathrm{f} n \mathrm{i}\mathrm{s} \mathrm{e}\mathrm{v}\mathrm{e}\mathrm{n},\hfill \\ -{(-1)}^{{\displaystyle \sum _{i=1}^{(n-1)/2}}\left|x_{2i}\right|}s{\mu }_n(x_1,\dots ,x_n),\hfill & \mathrm{i}\mathrm{f} n \mathrm{i}\mathrm{s} \mathrm{o}\mathrm{d}\mathrm{d},.\hfill \end{array}\right.\end{array}$$

(17)

Recalling that a linear map $f:C\to C$ is a coderivation of a coalgebra C if

$${\Delta }_{C}f=(f\otimes I{d}_C+I{d}_C\otimes f){\Delta }_C,$$

where ${\Delta }_C$ is the comultiplication of the coalgebra C, then a collection of maps $\{{\widehat{\mu }}_n:{\otimes }^{n}V\to V\}$ of degree $-1$ can be uniquely extended as a coderivation $\tilde{\mu }:T^{*}V\to T^{*}V$, where the component $\tilde{\mu }:{\otimes }^{k}V\to {\otimes }^{l}V$ is defined as

$${\displaystyle \sum _{i=0}^{l-1}}{I}_i\otimes {\widehat{\mu }}_{k-l+1}\otimes I_{l-i-1}.$$

In this way, we can prove the equivalence of three descriptions of $A_{\infty }$-algebras.

Lemma 3 

([19]). For a graded vector space V, the following statements are equivalent:

• $(V,\left\{{\mathfrak{m}}_n\right\})$ satisfies Equation (4).
• $(sV,\left\{{\widehat{\mathfrak{m}}}_n\right\})$ satisfies Equation (1).
• $\tilde{\mathfrak{m}}$ is a coderivation of coalgebra $T^{*}\left(sV\right)$ of degree $-1$ such that ${\tilde{\mathfrak{m}}}^2=0$.

Let $(V,\left\{{\mathfrak{l}}_n\right\})$ be an $L_{\infty }$-algebra in the sense of Definition 2. Then, $(sV,\left\{{\widehat{\mathfrak{l}}}_n\right\})$ is proved to be an $L_{\infty }$-algebra in the sense of Definition 1 (see [7]). As discussed in Section 2, ${\widehat{\mathfrak{l}}}_n$ can be seen as a linear map from ${\wedge }^n\left(sV\right)$ to $sV$. Note that a collection of maps $\{{\widehat{\mu }}_n:{\wedge }^{n}V\to V\}$ of degree $-1$ is in one-to-one correspondence with a coderivation $\tilde{\mu }:{\wedge }^{*}V\to {\wedge }^{*}V$, where the component $\tilde{\mu }:{\wedge }^{k}V\to {\wedge }^{l}V$ is defined as

$${\displaystyle \sum _{i=0}^{l-1}}{\displaystyle \frac{1}{(l-1)!(k-l+1)!}}(I_i\wedge {\widehat{\mu }}_{k-l+1}\wedge I_{l-i-1})\circ {\rho }_{w_k}^{\left(1\right)}.$$

Then, we can restate the results in [7] in the following way.

Lemma 4. 

For a graded vector space V, the following statements are equivalent:

• $(V,\left\{{\mathfrak{l}}_n\right\})$ satisfies Equation (6).
• $(sV,\left\{{\widehat{\mathfrak{l}}}_n\right\})$ satisfies Equation (1).
• $\tilde{\mathfrak{l}}$ is a coderivation of coalgebra ${\wedge }^{*}\left(sV\right)$ of degree $-1$ such that ${\tilde{\mathfrak{l}}}^2=0$.

Because $P{L}_{\infty }$-algebras have equal status with $A_{\infty }$-algebras and $L_{\infty }$-algebras, we naturally consider similar equivalent characterizations of $P{L}_{\infty }$-algebras. For a $P{L}_{\infty }$-algebra $(V,\left\{{\mathfrak{p}}_n\right\})$ in Definition 2, we can obtain an induced coderivation of coalgebra $P^{*}\left(sV\right)$ of degree $-1$. As a preliminary, we present the following lemma.

Lemma 5. 

For any $\sigma \in {\mathbb{S}}_{n-1}$, we have the following:

$$\begin{array}{c}\hfill {(-1)}^{{\displaystyle \sum _{i=1}^{n/2}}\left|x_{\sigma (2i-1)}\right|}sgn\left(\sigma \right)ϵ(\sigma ;x_1,\dots ,x_{n-1})={(-1)}^{{\displaystyle \sum _{i=1}^{n/2}}\left|x_{2i-1}\right|}ϵ(\sigma ;s{x}_1,\dots ,s{x}_{n-1})\end{array}$$

(18)

if n is even and

$$\begin{array}{c}\hfill {(-1)}^{{\displaystyle \sum _{i=1}^{(n-1)/2}}\left|x_{\sigma \left(2i\right)}\right|}sgn\left(\sigma \right)ϵ(\sigma ;x_1,\dots ,x_{n-1})={(-1)}^{{\displaystyle \sum _{i=1}^{(n-1)/2}}\left|x_{2i}\right|}ϵ(\sigma ;s{x}_1,\dots ,s{x}_{n-1}),\end{array}$$

(19)

if n is odd.

Proof. 

In [7], Lada and Stasheff illustrate this lemma using the example of $\sigma =(j,j+1)$ for some integer j. For ease of reading, we present a complete proof here.

Assume that n is even; then, $\sigma$ can be uniquely decomposed by the following procedures into a product of different transpositions in the form of $(k,k+1)$.

Suppose that $\sigma$ is not the identity $\left(1\right)$ of ${\mathbb{S}}_{n-1}$, and let j be the largest integer such that $\sigma \left(j\right)\ne j$. Then, there is an integer i smaller than j such that $\sigma \left(i\right)=j$. Define ${\sigma }_1:=\sigma (i,i+1)(i+1,i+2)\dots (j-1,j)$. If ${\sigma }_1=\left(1\right)$, then we have $\sigma =(j-1,j)(j-2,j-1)\dots (i,i+1)$. If ${\sigma }_1\ne \left(1\right)$, then the largest integer $j_1$ such that ${\sigma }_1\left(j_1\right)\ne j_1$ is smaller than j. This process is repeated until we obtain the identity permutation.

We use $\left|\sigma \right|$ to refer to the number of transpositions in the above discomposition of $\sigma$ and $\left|\right(1\left)\right|:=0$. Thus, we can derive Equation (18) by induction on $\left|\sigma \right|$.

The conclusion is obvious when $\left|\sigma \right|=0$. Suppose that $\sigma$ is a non-identity permutation. If $\left|\sigma \right|=1$, then $\sigma =(i,i+1)$ for some i. At this point, we have

$$\begin{array}{cc}\hfill ϵ(\sigma ;x_1,\dots ,x_{n-1})& ={(-1)}^{|x_i\left|\right|x_{i+1}|},\hfill \\ \hfill sgn\left(\sigma \right)& =-1,\hfill \\ \hfill {(-1)}^{{\displaystyle \sum _{i=1}^{n/2}}\left|x_{\sigma (2i-1)}\right|}& ={(-1)}^{({\displaystyle \sum _{i=1}^{n/2}}|x_{2i-1}\left|\right)+|x_i|+|x_{i+1}|}.\hfill \end{array}$$

Placing this result into Equation (18) allows us to easily finish the proof for $\sigma =(i,i+1)$:

$$\begin{array}{cc}\hfill & {(-1)}^{{\displaystyle \sum _{i=1}^{n/2}}\left|x_{\sigma (2i-1)}\right|}sgn\left(\sigma \right)ϵ(\sigma ;x_1,\dots ,x_{n-1})\hfill \\ \hfill =& {(-1)}^{{\displaystyle \sum _{i=1}^{n/2}}\left|x_{2i-1}\right|}{(-1)}^{1+|x_i|+|x_{i+1}|+|x_i\left|\right|x_{i+1}|}\hfill \\ \hfill =& {(-1)}^{{\displaystyle \sum _{i=1}^{n/2}}\left|x_{2i-1}\right|}{(-1)}^{(1+|x_i\left|\right)(1+|x_{i+1}\left|\right)}\hfill \\ \hfill =& {(-1)}^{{\displaystyle \sum _{i=1}^{n/2}}\left|x_{2i-1}\right|}ϵ(\sigma ;s{x}_1,\dots ,s{x}_{n-1}).\hfill \end{array}$$

Now. we assume that the conclusion is true if $\left|\sigma \right|=k$ and consider the case with $\left|\sigma \right|=k+1$. From the decomposition of $\sigma$ we have $\sigma =\tau \delta$, where $\left|\tau \right|=k$ and $\delta =(i,i+1)$ for some i. Defining $x_{\tau \left(1\right)}\otimes \dots \otimes x_{\tau (n-1)}:=y_1\otimes \dots \otimes y_{n-1}$, we have $x_{\sigma \left(1\right)}\otimes \dots \otimes x_{\sigma (n-1)}:=y_{\delta \left(1\right)}\otimes \dots \otimes y_{\delta (n-1)}$. Based on the properties of the Koszul sign, we can verify Equation (18) as follows:

$$\begin{array}{cc}\hfill & {(-1)}^{{\displaystyle \sum _{i=1}^{n/2}}\left|x_{\sigma (2i-1)}\right|}sgn\left(\sigma \right)ϵ(\sigma ;x_1,\dots ,x_{n-1})\hfill \\ \hfill =& {(-1)}^{{\displaystyle \sum _{i=1}^{n/2}}\left|y_{\delta (2i-1)}\right|}sgn\left(\tau \right)sgn\left(\delta \right)ϵ(\delta ;y_1,\dots ,y_{n-1})ϵ(\tau ;x_1,\dots ,x_{n-1})\hfill \\ \hfill =& {(-1)}^{{\displaystyle \sum _{i=1}^{n/2}}\left|y_{2i-1}\right|}ϵ(\delta ;s{y}_1,\dots ,s{y}_{n-1})sgn\left(\tau \right)ϵ(\tau ;x_1,\dots ,x_{n-1})\hfill \\ \hfill =& ϵ(\delta ;s{x}_{\tau \left(1\right)},\dots ,s{x}_{\tau (n-1)}){(-1)}^{{\displaystyle \sum _{i=1}^{n/2}}\left|x_{\tau (2i-1)}\right|}sgn\left(\tau \right)ϵ(\tau ;x_1,\dots ,x_{n-1})\hfill \\ \hfill =& {(-1)}^{{\displaystyle \sum _{i=1}^{n/2}}\left|x_{2i-1}\right|}ϵ(\delta ;s{x}_{\tau \left(1\right)},\dots ,s{x}_{\tau (n-1)})ϵ(\tau ;s{x}_1,\dots ,s{x}_{n-1})\hfill \\ \hfill =& {(-1)}^{{\displaystyle \sum _{i=1}^{n/2}}\left|x_{2i-1}\right|}ϵ(\sigma ;s{x}_1,\dots ,s{x}_{n-1}).\hfill \end{array}$$

Hence, Equation (18) holds for any $\sigma \in {\mathbb{S}}_{n-1}$. Equation (19) can be calculated in an analogous way. □

Then, we construct the coderivation associated with given $P{L}_{\infty }$-algebra structure maps.

Proposition 2. 

(1) Let $\{{\mathfrak{p}}_n:{\otimes }^{n}V\to V\}$ be a collection of linear maps of degree $n-2$. Then, for $n\ge 1$, we have ${\mathfrak{p}}_n={\mathfrak{p}}_n\circ ({\rho }_{\sigma }^{\left(2\right)}\otimes I_1)$ for any $\sigma \in {\mathbb{S}}_{n-1}$ if and only if ${\widehat{\mathfrak{p}}}_n={\widehat{\mathfrak{p}}}_n\circ ({\rho }_{\sigma }^{\left(1\right)}\otimes I_1)$ for any $\sigma \in {\mathbb{S}}_{n-1}$.

(2) A collection of maps $\{{\widehat{\mathfrak{q}}}_n:P^{n}V\to V\}$ of degree $-1$ can be uniquely extended as a coderivation $\tilde{\mathfrak{q}}:P^{*}V\to P^{*}V$, where the component $\tilde{\mathfrak{q}}:P^{k}V\to P^{l}V$ is defined as

$${\displaystyle \frac{1}{(l-1)!(k-l)!}}({\displaystyle \sum _{i=0}^{l-2}}{I}_i\wedge {\widehat{\mathfrak{q}}}_{k-l+1}\wedge I_{l-i-2}\otimes I_1+I_{l-1}\wedge {\widehat{\mathfrak{q}}}_{k-l+1})\circ ({\rho }_{w_{k-1}}^{\left(1\right)}\otimes I_1).$$

Proof. 

(1) Suppose that n is even. For ${\mathfrak{p}}_n$ satisfying ${\mathfrak{p}}_n={\mathfrak{p}}_n\circ ({\rho }_{\sigma }^{\left(2\right)}\otimes I_1)$, we have

$$\begin{array}{cc}\hfill & {\widehat{\mathfrak{p}}}_n(s{x}_{\sigma \left(1\right)},\dots ,s{x}_{\sigma (n-1)},s{x}_n)\hfill \\ \hfill =& {(-1)}^{{\displaystyle \sum _{i=1}^{n/2}}\left|x_{\sigma (2i-1)}\right|}s{\mathfrak{p}}_n(x_{\sigma \left(1\right)},\dots ,x_{\sigma (n-1)},x_n)\hfill \\ \hfill =& {(-1)}^{{\displaystyle \sum _{i=1}^{n/2}}\left|x_{\sigma (2i-1)}\right|}sgn\left(\sigma \right)ϵ(\sigma ;x_1,\dots ,x_{n-1})s{\mathfrak{p}}_n(x_1,\dots ,x_n)\hfill \\ \hfill =& ϵ(\sigma ;s{x}_1,\dots ,s{x}_{n-1}){(-1)}^{{\displaystyle \sum _{i=1}^{n/2}}\left|x_{2i-1}\right|}s{\mathfrak{p}}_n(x_1,\dots ,x_n)\hfill \\ \hfill =& ϵ(\sigma ;s{x}_1,\dots ,s{x}_{n-1}){\widehat{\mathfrak{p}}}_n(s{x}_1,\dots ,s{x}_n).\hfill \end{array}$$

Conversely, for ${\widehat{\mathfrak{p}}}_n$ satisfying ${\widehat{\mathfrak{p}}}_n={\widehat{\mathfrak{p}}}_n\circ ({\rho }_{\sigma }^{\left(1\right)}\otimes I_1)$, we have

$$\begin{array}{cc}\hfill & {\mathfrak{p}}_n(x_{\sigma \left(1\right)},\dots ,x_{\sigma \left(n\right)})\hfill \\ \hfill =& {(-1)}^{{\displaystyle \sum _{i=1}^{n/2}}\left|x_{\sigma (2i-1)}\right|}{s}^{-1}{\widehat{\mathfrak{p}}}_n(s{x}_{\sigma \left(1\right)},\dots ,s{x}_{\sigma (n-1)},s{x}_n)\hfill \\ \hfill =& {(-1)}^{{\displaystyle \sum _{i=1}^{n/2}}\left|x_{\sigma (2i-1)}\right|}ϵ(\sigma ;s{x}_1,\dots ,s{x}_{n-1})s^{-1}{\widehat{\mathfrak{p}}}_n(s{x}_1,\dots ,s{x}_n)\hfill \\ \hfill =& {(-1)}^{{\displaystyle \sum _{i=1}^{n/2}}\left|x_{2i-1}\right|}sgn\left(\sigma \right)ϵ(\sigma ;x_1,\dots ,x_{n-1})s^{-1}{\widehat{\mathfrak{p}}}_n(s{x}_1,\dots ,s{x}_n)\hfill \\ \hfill =& sgn\left(\sigma \right)ϵ(\sigma ;x_1,\dots ,x_{n-1}){\mathfrak{p}}_n(x_1,\dots ,x_n).\hfill \end{array}$$

A similar discussion applies in the case where n is odd.

(2) Because the component $\tilde{\mathfrak{q}}:P^{n}V\to V$ is exactly ${\widehat{\mathfrak{q}}}_n$, the uniqueness is given. Thus, all we need to do is check $\tilde{\mathfrak{q}}$ that is a coderivation. In fact, we only need to show that the components from $P^{k}V$ to $P^{i}V\otimes P^{j}V$ are equal. Note that the component $\tilde{\mathfrak{q}}:P^{k}V\to P^{l}V$ is computed as follows:

$$\begin{array}{cc}\hfill & \tilde{\mathfrak{q}}(x_1\wedge \dots \wedge x_{k-1}\otimes x_k)\hfill \\ \hfill =& {\displaystyle \frac{1}{(l-1)!(k-l)!}}({\displaystyle \sum _{i=0}^{l-2}}{I}_i\wedge {\widehat{\mathfrak{q}}}_{k-l+1}\wedge I_{l-i-2}\otimes I_1+I_{l-1}\wedge {\widehat{\mathfrak{q}}}_{k-l+1})\circ ({\rho }_{w_{k-1}}^{(1)}\otimes I_1)(x_1\wedge \dots \wedge \hfill \\ \hfill & x_{k-1}\otimes x_k)\hfill \\ \hfill =& {\displaystyle \sum _{\sigma \in {\mathbb{S}}_{k-1}}}{\displaystyle \frac{ϵ(\sigma )}{(l-1)!(k-l)!}}({\displaystyle \sum _{i=0}^{l-2}}{(-1)}^{{\displaystyle \sum _{r=1}^i}\left|x_{\sigma (r)}\right|}{x}_{\sigma (1)}\wedge \dots \wedge x_{\sigma (i)}\wedge {\widehat{\mathfrak{q}}}_{k-l+1}(x_{\sigma (i+1)},\dots ,\hfill \\ \hfill & x_{\sigma (i+k-l+1)})\wedge x_{\sigma (i+k-l+2)}\wedge \dots \wedge x_{\sigma (k-1)}\otimes x_k\hfill \\ \hfill & +{(-1)}^{{\displaystyle \sum _{t=1}^{l-1}}\left|x_{\sigma (t)}\right|}{x}_{\sigma (1)}\wedge \dots \wedge x_{\sigma (l-1)}\wedge {\widehat{\mathfrak{q}}}_{k-l+1}(x_{\sigma (l)},\dots ,x_{\sigma (k-1)},x_k))\hfill \\ \hfill =& {\displaystyle \sum _{\sigma \in Sh(k-l,1,l-2)}}ϵ(\sigma ){\widehat{\mathfrak{q}}}_{k-l+1}(x_{\sigma (1)},\dots ,x_{\sigma (k-l+1)})\wedge x_{\sigma (k-l+2)}\wedge \dots \wedge x_{\sigma (k-1)}\otimes x_k\hfill \\ \hfill & +{\displaystyle \sum _{\sigma \in Sh(l-1,k-l)}}{(-1)}^{{\displaystyle \sum _{t=1}^{l-1}}\left|x_{\sigma (t)}\right|}ϵ(\sigma )x_{\sigma (1)}\wedge \dots \wedge x_{\sigma (l-1)}\otimes {\widehat{\mathfrak{q}}}_{k-l+1}(x_{\sigma (l)},\dots ,x_{\sigma (k-1)},x_k).\hfill \end{array}$$

Using this, we can obtain the component of $\Delta \tilde{\mathfrak{q}}:P^{k}V\to P^{i+j}V\to P^{i}V\otimes P^{j}V$:

$$\begin{array}{cc}\hfill & \Delta \tilde{\mathfrak{q}}(x_1\wedge \dots \wedge x_{k-1}\otimes x_k)\hfill \\ \hfill =& {\displaystyle \sum _{\sigma \in Sh(k-i-j,1,i+j-2)}}ϵ\left(\sigma \right)\Delta ({\widehat{\mathfrak{q}}}_{k-i-j+1}(x_{\sigma \left(1\right)},\dots ,x_{\sigma (k-i-j+1)})\wedge x_{\sigma (k-i-j+2)}\wedge \dots \wedge x_{\sigma (k-1)}\otimes x_k)\hfill \\ \hfill & +{\displaystyle \sum _{\sigma \in Sh(i+j-1,k-i-j)}}{(-1)}^{{\displaystyle \sum _{t=1}^{i+j-1}}\left|x_{\sigma \left(t\right)}\right|}ϵ\left(\sigma \right)\Delta (x_{\sigma \left(1\right)}\wedge \dots \wedge x_{\sigma (i+j-1)}\otimes {\widehat{\mathfrak{q}}}_{k-i-j+1}(x_{\sigma (i+j)},\dots ,\hfill \\ \hfill & x_{\sigma (k-1)},x_k\left)\right)\hfill \\ \hfill =& {\displaystyle \sum _{\sigma \in Sh(k-i-j,1,i-2,1,j-1)}}ϵ\left(\sigma \right)({\widehat{\mathfrak{q}}}_{k-i-j+1}(x_{\sigma \left(1\right)},\dots ,x_{\sigma (k-i-j+1)})\wedge x_{\sigma (k-i-j+2)}\wedge \dots \wedge x_{\sigma (k-j-1)}\hfill \\ \hfill & \otimes x_{\sigma (k-j)})\otimes (x_{\sigma (k-j+1)}\wedge \dots \wedge x_{\sigma (k-1)}\otimes x_k)\hfill \\ \hfill & +{\displaystyle \sum _{\sigma \in Sh(i-1,k-i-j,1,j-1)}}{(-1)}^{{\displaystyle \sum _{t=1}^{i-1}}\left|x_{\sigma \left(t\right)}\right|}ϵ\left(\sigma \right)(x_{\sigma \left(1\right)}\wedge \dots \wedge x_{\sigma (i-1)}\otimes {\widehat{\mathfrak{q}}}_{k-i-j+1}(x_{\sigma \left(i\right)},\dots ,x_{\sigma (k-j)}))\hfill \\ \hfill & \otimes (x_{\sigma (k-j+1)}\wedge \dots \wedge x_{\sigma (k-1)}\otimes x_k)\hfill \\ \hfill & +{\displaystyle \sum _{\sigma \in Sh(i-1,1,k-i-j,1,j-2)}}{(-1)}^{{\displaystyle \sum _{t=1}^i}\left|x_{\sigma \left(t\right)}\right|}ϵ\left(\sigma \right)(x_{\sigma \left(1\right)}\wedge \dots \wedge x_{\sigma (i-1)}\otimes x_{\sigma \left(i\right)})\otimes \left({\widehat{\mathfrak{q}}}_{k-i-j+1}\right(x_{\sigma (i+1)}\hfill \\ \hfill & ,\dots ,x_{\sigma (k-j+1)})\wedge x_{\sigma (k-j+2)}\wedge \dots \wedge x_{\sigma (k-1)}\otimes x_k)\hfill \\ \hfill & +{\displaystyle \sum _{\sigma \in Sh(i-1,1,j-1,k-i-j)}}{(-1)}^{{\displaystyle \sum _{t=1}^{i+j-1}}\left|x_{\sigma \left(t\right)}\right|}ϵ\left(\sigma \right)(x_{\sigma \left(1\right)}\wedge \dots \wedge x_{\sigma (i-1)}\otimes x_{\sigma \left(i\right)})\otimes (x_{\sigma (i+1)}\wedge \dots \wedge \hfill \\ \hfill & x_{\sigma (i+j-1)}\otimes {\widehat{\mathfrak{q}}}_{k-i-j+1}(x_{\sigma (i+j)},\dots ,x_{\sigma (k-1)},x_k)).\hfill \end{array}$$

(20)

On the other hand, we can consider the component $P^{k}V\to P^{k-j}V\otimes P^{j}V\to P^{i}V\otimes P^{j}V$ of $(\tilde{\mathfrak{q}}\otimes I{d}_{P^{*}V})\Delta$ and $P^{k}V\to P^{i}V\otimes P^{k-i}V\to P^{i}V\otimes P^{j}V$ of $(I{d}_{P^{*}V}\otimes \tilde{\mathfrak{q}})\Delta$:

$$\begin{array}{cc}\hfill & ((\tilde{\mathfrak{q}}\otimes I{d}_{P^{*}V})\Delta )(x_1\wedge \dots \wedge x_{k-1}\otimes x_k)\hfill \\ \hfill =& {\displaystyle \sum _{\sigma \in Sh(k-j-1,1,j-1)}}ϵ\left(\sigma \right)\tilde{\mathfrak{q}}(x_{\sigma \left(1\right)}\wedge \dots \wedge x_{\sigma (k-j-1)}\otimes x_{\sigma (k-j)})\otimes (x_{\sigma (k-j+1)}\wedge \dots \wedge x_{\sigma (k-1)}\otimes x_k)\hfill \\ \hfill =& {\displaystyle \sum _{\sigma \in Sh(k-i-j,1,i-2,1,j-1)}}ϵ\left(\sigma \right)({\widehat{\mathfrak{q}}}_{k-i-j+1}(x_{\sigma \left(1\right)},\dots ,x_{\sigma (k-i-j+1)})\wedge x_{\sigma (k-i-j+2)}\wedge \dots \wedge x_{\sigma (k-j-1)}\hfill \\ \hfill & \otimes x_{\sigma (k-j)})\otimes (x_{\sigma (k-j+1)}\wedge \dots \wedge x_{\sigma (k-1)}\otimes x_k)\hfill \\ \hfill & +{\displaystyle \sum _{\sigma \in Sh(i-1,k-i-j,1,j-1)}}{(-1)}^{{\displaystyle \sum _{t=1}^{i-1}}\left|x_{\sigma \left(t\right)}\right|}ϵ\left(\sigma \right)(x_{\sigma \left(1\right)}\wedge \dots \wedge x_{\sigma (i-1)}\otimes {\widehat{\mathfrak{q}}}_{k-i-j+1}(x_{\sigma \left(i\right)},\dots ,x_{\sigma (k-j)}))\hfill \\ \hfill & \otimes (x_{\sigma (k-j+1)}\wedge \dots \wedge x_{\sigma (k-1)}\otimes x_k)\hfill \end{array}$$

(21)

$$\begin{array}{cc}\hfill & ((I{d}_{P^{*}V}\otimes \tilde{\mathfrak{q}})\Delta )(x_1\wedge \dots \wedge x_{k-1}\otimes x_k)\hfill \\ \hfill =& {\displaystyle \sum _{\sigma \in Sh(i-1,1,k-i-1)}}{(-1)}^{{\displaystyle \sum _{t=1}^i}\left|x_{\sigma \left(t\right)}\right|}ϵ\left(\sigma \right)(x_{\sigma \left(1\right)}\wedge \dots \wedge x_{\sigma (i-1)}\otimes x_{\sigma \left(i\right)})\otimes \tilde{\mathfrak{q}}(x_{\sigma (i+1)}\wedge \dots \wedge x_{\sigma (k-1)}\hfill \\ \hfill & \otimes x_k)\hfill \\ \hfill =& {\displaystyle \sum _{\sigma \in Sh(i-1,1,k-i-j,1,j-2)}}{(-1)}^{{\displaystyle \sum _{t=1}^i}\left|x_{\sigma \left(t\right)}\right|}ϵ\left(\sigma \right)(x_{\sigma \left(1\right)}\wedge \dots \wedge x_{\sigma (i-1)}\otimes x_{\sigma \left(i\right)})\otimes \left({\widehat{\mathfrak{q}}}_{k-i-j+1}\right(x_{\sigma (i+1)}\hfill \\ \hfill & ,\dots ,x_{\sigma (k-j+1)})\wedge x_{\sigma (k-j+2)}\wedge \dots \wedge x_{\sigma (k-1)}\otimes x_k)\hfill \\ \hfill & +{\displaystyle \sum _{\sigma \in Sh(i-1,1,j-1,k-i-j)}}{(-1)}^{{\displaystyle \sum _{t=1}^{i+j-1}}\left|x_{\sigma \left(t\right)}\right|}ϵ\left(\sigma \right)(x_{\sigma \left(1\right)}\wedge \dots \wedge x_{\sigma (i-1)}\otimes x_{\sigma \left(i\right)})\otimes (x_{\sigma (i+1)}\wedge \dots \wedge \hfill \\ \hfill & x_{\sigma (i+j-1)}\otimes {\widehat{\mathfrak{q}}}_{k-i-j+1}(x_{\sigma (i+j)},\dots ,x_{\sigma (k-1)},x_k)).\hfill \end{array}$$

(22)

It can be easily seen that (20) = (21) + (22), which means that $\tilde{\mathfrak{q}}$ is a coderivation of $P^{*}V$. □

Based on the one-to-one correspondence $\left\{{\mathfrak{p}}_n\right\}\leftrightarrow \left\{{\widehat{\mathfrak{p}}}_n\right\}\leftrightarrow \tilde{\mathfrak{p}}$, we provide the following theorem.

Theorem 2. 

For a graded vector space V, the following statements are equivalent:

• $(V,\left\{{\mathfrak{p}}_n\right\})$ satisfies Equation (5).
• $(sV,\left\{{\widehat{\mathfrak{p}}}_n\right\})$ satisfies Equation (2).
• $\tilde{\mathfrak{p}}$ is a coderivation of coalgebra $P^{*}\left(sV\right)$ of degree $-1$ such that ${\tilde{\mathfrak{p}}}^2=0$.

3.3. Proof of Theorem 2

According to Proposition 2, the stability of ${\mathfrak{p}}_n$ under the action of ${\rho }^{\left(2\right)}$, stability of ${\widehat{\mathfrak{p}}}_n$ under the action of ${\rho }^{\left(1\right)}$, and condition that $\tilde{\mathfrak{p}}$ is a coderivation are all equivalent. Thus, the rest of our task is to show the equivalence of the reminders of Equations (2) and (5) as well as that of ${\tilde{\mathfrak{p}}}^2=0$. In fact, we only need to consider the relation of three corresponding composited maps. In this subsection, we show that there is a one-to-one correspondence between the composited maps in (1) and (2), then we explore the relation of the composited maps in (2) and ${\tilde{\mathfrak{p}}}^2$. Based on these facts and inspired by [7], we are then able to provide a proof of Theorem 2.

In order to discuss the relation of the composited maps in Equations (2) and (5), we require the following lemma.

Lemma 6. 

Using the same notation as Theorem 2, we have:

• $$\begin{array}{cc}\hfill & {\widehat{\mathfrak{p}}}_i({\widehat{\mathfrak{p}}}_j(s{x}_1,\dots ,s{x}_j),s{x}_{j+1},\dots ,s{x}_{i+j-1})\hfill \\ \hfill =& \left\{\begin{array}{cc}{(-1)}^{(j(i-1)+{\displaystyle \sum _{r=1}^{(i+j)/2-1}}|x_{2r}|)}s{\mathfrak{p}}_i({\mathfrak{p}}_j(x_1,\dots ,x_j),x_{j+1},\dots ,x_{i+j-1}),\hfill & i+j even,\hfill \\ -{(-1)}^{(j(i-1)+{\displaystyle \sum _{r=1}^{(i+j-1)/2}}|x_{2r-1}|)}s{\mathfrak{p}}_i({\mathfrak{p}}_j(x_1,\dots ,x_j),x_{j+1},\dots ,x_{i+j-1}),\hfill & i+j odd.\hfill \end{array}\right.\hfill \end{array}$$
• $$\begin{array}{cc}\hfill & {\widehat{\mathfrak{p}}}_i(s{x}_1,\dots ,s{x}_{i-1},{\widehat{\mathfrak{p}}}_j(s{x}_i,\dots ,s{x}_{i+j-1}))\hfill \\ \hfill =& \left\{\begin{array}{cc}{(-1)}^{({\displaystyle \sum _{r=1}^{(i+j)/2-1}}|x_{2r}|+(j-1)({\displaystyle \sum _{t=1}^{i-1}}|x_t|))}s{\mathfrak{p}}_i(x_1,\dots ,x_{i-1},{\mathfrak{p}}_j(x_i,\dots ,x_{i+j-1})),\hfill & i+j even,\hfill \\ -{(-1)}^{({\displaystyle \sum _{r=1}^{(i+j-1)/2}}|x_{2r-1}|+(j-1)({\displaystyle \sum _{t=1}^{i-1}}|x_t|))}s{\mathfrak{p}}_i(x_1,\dots ,x_{i-1},{\mathfrak{p}}_j(x_i,\dots ,x_{i+j-1})),\hfill & i+j odd.\hfill \end{array}\right.\hfill \end{array}$$

Proof. 

The proof is a simple calculation. Let $x_i\in V$ be homogeneous elements. Then,

$$\begin{array}{cc}\hfill & {\widehat{\mathfrak{p}}}_i({\widehat{\mathfrak{p}}}_j(s{x}_1,\dots ,s{x}_j),s{x}_{j+1},\dots ,s{x}_{i+j-1})\hfill \\ \hfill =& \left\{\begin{array}{cc}-{(-1)}^{{\displaystyle \sum _{r=1}^{(j-1)/2}}\left|x_{2r}\right|}{\widehat{\mathfrak{p}}}_i(s{\mathfrak{p}}_j(x_1,\dots ,x_j),s{x}_{j+1},\dots ,s{x}_{i+j-1}),\hfill & \mathrm{i}\mathrm{f} j \mathrm{i}\mathrm{s} \mathrm{o}\mathrm{d}\mathrm{d},\hfill \\ {(-1)}^{{\displaystyle \sum _{r=1}^{j/2}}\left|x_{2r-1}\right|}{\widehat{\mathfrak{p}}}_i(s{\mathfrak{p}}_j(x_1,\dots ,x_j),s{x}_{j+1},\dots ,s{x}_{i+j-1}),\hfill & \mathrm{i}\mathrm{f} j \mathrm{i}\mathrm{s} \mathrm{even},\hfill \end{array}\right.\hfill \\ \hfill =& \left\{\begin{array}{c}-{(-1)}^{{\displaystyle \sum _{r=1}^{(j-1)/2}}\left|x_{2r}\right|}{(-1)}^{1+{\displaystyle \sum _{t=1}^{(i-1)/2}}\left|x_{2r+j-1}\right|}\hfill \\ s{\mathfrak{p}}_i({\mathfrak{p}}_j(x_1,\dots ,x_j),x_{j+1},\dots ,x_{i+j-1}),\hfill & i \mathrm{odd},j\mathrm{odd},\hfill \\ -{(-1)}^{{\displaystyle \sum _{r=1}^{(j-1)/2}}\left|x_{2r}\right|}{(-1)}^{j-2+{\displaystyle \sum _{q=1}^j}|x_q|+{\displaystyle \sum _{t=2}^{i/2}}\left|x_{2t+j-2}\right|}\hfill \\ s{\mathfrak{p}}_i({\mathfrak{p}}_j(x_1,\dots ,x_j),x_{j+1},\dots ,x_{i+j-1}),\hfill & i \mathrm{even},j \mathrm{odd},\hfill \\ {(-1)}^{{\displaystyle \sum _{r=1}^{j/2}}\left|x_{2r-1}\right|}{(-1)}^{1+{\displaystyle \sum _{t=1}^{(i-1)/2}}\left|x_{2r+j-1}\right|}\hfill \\ s{\mathfrak{p}}_i({\mathfrak{p}}_j(x_1,\dots ,x_j),x_{j+1},\dots ,x_{i+j-1}),\hfill & i \mathrm{odd},j \mathrm{even},\hfill \\ {(-1)}^{{\displaystyle \sum _{r=1}^{j/2}}\left|x_{2r-1}\right|}{(-1)}^{j-2+{\displaystyle \sum _{q=1}^j}|x_q|+{\displaystyle \sum _{t=2}^{i/2}}\left|x_{2t+j-2}\right|}\hfill \\ s{\mathfrak{p}}_i({\mathfrak{p}}_j(x_1,\dots ,x_j),x_{j+1},\dots ,x_{i+j-1}),\hfill & i \mathrm{even},j \mathrm{even},\hfill \end{array}\right.\hfill \\ \hfill =& \left\{\begin{array}{cc}{(-1)}^{\left({\displaystyle \sum _{r=1}^{(i+j)/2-1}}\right|x_{2r}\left|\right)}s{\mathfrak{p}}_i({\mathfrak{p}}_j(x_1,\dots ,x_j),x_{j+1},\dots ,x_{i+j-1}),\hfill & i \mathrm{odd},j \mathrm{odd},\hfill \\ {(-1)}^{\left({\displaystyle \sum _{r=1}^{(i+j-1)/2}}\right|x_{2r-1}\left|\right)}s{\mathfrak{p}}_i({\mathfrak{p}}_j(x_1,\dots ,x_j),x_{j+1},\dots ,x_{i+j-1}),\hfill & i \mathrm{even},j \mathrm{odd},\hfill \\ {(-1)}^{(1+{\displaystyle \sum _{r=1}^{(i+j-1)/2}}|x_{2r-1}\left|\right)}s{\mathfrak{p}}_i({\mathfrak{p}}_j(x_1,\dots ,x_j),x_{j+1},\dots ,x_{i+j-1}),\hfill & i \mathrm{odd},j \mathrm{even},\hfill \\ {(-1)}^{\left({\displaystyle \sum _{r=1}^{(i+j)/2-1}}\right|x_{2r}\left|\right)}s{\mathfrak{p}}_i({\mathfrak{p}}_j(x_1,\dots ,x_j),x_{j+1},\dots ,x_{i+j-1}),\hfill & i \mathrm{even},j \mathrm{even},\hfill \end{array}\right.\hfill \\ \hfill =& \left\{\begin{array}{cc}{(-1)}^{(j(i-1)+{\displaystyle \sum _{r=1}^{(i+j)/2-1}}|x_{2r}\left|\right)}s{\mathfrak{p}}_i({\mathfrak{p}}_j(x_1,\dots ,x_j),x_{j+1},\dots ,x_{i+j-1}),\hfill & i+j \mathrm{even},\hfill \\ -{(-1)}^{(j(i-1)+{\displaystyle \sum _{r=1}^{(i+j-1)/2}}|x_{2r-1}\left|\right)}s{\mathfrak{p}}_i({\mathfrak{p}}_j(x_1,\dots ,x_j),x_{j+1},\dots ,x_{i+j-1}),\hfill & i+j \mathrm{odd}.\hfill \end{array}\right.\hfill \end{array}$$

By now, we have completed the proof of (1). Similarly, we can prove (2). □

We obtain the following proposition.

Proposition 3. 

Let $(V,\left\{{\mathfrak{p}}_n\right\})$ be a $P{L}_{\infty }$-algebra in the sense of Definition 2 and

$${\mathfrak{P}}_n:={\displaystyle \sum _{i+j=n+1}}{\displaystyle \sum _{m=0}^{i-1}}{\displaystyle \frac{{(-1)}^{j(i-m-1)+m}}{(i-1)!(j-1)!}}{\mathfrak{p}}_i\circ (I_m\otimes {\mathfrak{p}}_j\otimes I_{i-m-1})\circ ({\rho }_{w_{i+j-2}}^{\left(2\right)}\otimes I_1).$$

Then, ${\displaystyle \sum _{i+j=n+1}}{\displaystyle \sum _{m=0}^{i-1}}{\displaystyle \frac{1}{(i-1)!(j-1)!}}{\widehat{\mathfrak{p}}}_i\circ (I_m\otimes {\widehat{\mathfrak{p}}}_j\otimes I_{i-m-1})\circ ({\rho }_{w_{i+j-2}}^{\left(1\right)}\otimes I_1)=-{\widehat{\mathfrak{P}}}_n.$

Proof. 

Assume that $i+j=n+1$ is even. According to Lemma 18 and Lemma 6, we derive

$$\begin{array}{cc}\hfill & {\displaystyle \sum _{m=0}^{i-1}}{\displaystyle \frac{1}{(i-1)!(j-1)!}}{\widehat{\mathfrak{p}}}_i\circ (I_m\otimes {\widehat{\mathfrak{p}}}_j\otimes I_{i-m-1})\circ ({\rho }_{w_{i+j-2}}^{(1)}\otimes I_1)(s{x}_1,\dots ,s{x}_n)\hfill \\ \hfill =& {\displaystyle \sum _{\sigma \in Sh(j-1,1,i-2)}}ϵ(\sigma ;s{x}_1,\dots ,s{x}_n){\widehat{\mathfrak{p}}}_i({\widehat{\mathfrak{p}}}_j(s{x}_{\sigma (1)},\dots ,s{x}_{\sigma (j)}),s{x}_{\sigma (j+1)},\dots ,s{x}_{\sigma (i+j-2)},s{x}_{i+j-1})\hfill \\ \hfill & +{\displaystyle \sum _{\sigma \in Sh(i-1,j-1)}}{(-1)}^{({\displaystyle \sum _{r=1}^{i-1}}|s{x}_{\sigma (r)}|)}ϵ(\sigma ;s{x}_1,\dots ,s{x}_n){\widehat{\mathfrak{p}}}_i(s{x}_{\sigma (1)},\dots ,s{x}_{\sigma (i-1)},{\widehat{\mathfrak{p}}}_j(s{x}_{\sigma (i)},\dots ,\hfill \\ \hfill & s{x}_{\sigma (i+j-2)},\dots ,s{x}_{i+j-1}))\hfill \\ \hfill =& {\displaystyle \sum _{\sigma \in Sh(j-1,1,i-2)}}ϵ(\sigma ;s{x}_1,\dots ,s{x}_n){(-1)}^{(j(i-1)+{\displaystyle \sum _{r=1}^{(i+j)/2-1}}|x_{\sigma (2r)}|)}s{\mathfrak{p}}_i({\mathfrak{p}}_j(x_{\sigma (1)},\dots ,x_{\sigma (j)}),x_{\sigma (j+1)}\hfill \\ \hfill & ,\dots ,x_{\sigma (i+j-2)},x_{i+j-1})\hfill \\ \hfill & +{\displaystyle \sum _{\sigma \in Sh(i-1,j-1)}}{(-1)}^{({\displaystyle \sum _{r=1}^{i-1}}|s{x}_{\sigma (r)}|)}ϵ(\sigma ;s{x}_1,\dots ,s{x}_n){(-1)}^{({\displaystyle \sum _{r=1}^{(i+j)/2-1}}|x_{\sigma (2r)}|+(j-1)({\displaystyle \sum _{t=1}^{i-1}}|x_{\sigma (t)}|))}\hfill \\ \hfill & s{\mathfrak{p}}_i(x_{\sigma (1)},\dots ,x_{\sigma (i-1)},{\mathfrak{p}}_j(x_{\sigma (i)},\dots ,x_{\sigma (i+j-2)},x_{i+j-1}))\hfill \\ \hfill =& {(-1)}^{({\displaystyle \sum _{r=1}^{(i+j)/2-1}}|x_{2r}|)}{\displaystyle \sum _{\sigma \in Sh(j-1,1,i-2)}}sgn(\sigma )ϵ(\sigma ){(-1)}^{j(i-1)}s{\mathfrak{p}}_i({\mathfrak{p}}_j(x_{\sigma (1)},\dots ,x_{\sigma (j)}),x_{\sigma (j+1)},\dots ,\hfill \\ \hfill & x_{\sigma (i+j-2)},x_{i+j-1})\hfill \\ \hfill & +{(-1)}^{({\displaystyle \sum _{r=1}^{(i+j)/2-1}}|x_{2r}|)}{\displaystyle \sum _{\sigma \in Sh(i-1,j-1)}}sgn(\sigma )ϵ(\sigma ){(-1)}^{(i-1+j({\displaystyle \sum _{t=1}^{i-1}}|x_{\sigma (t)}|))}s{\mathfrak{p}}_i(x_{\sigma (1)},\dots ,x_{\sigma (i-1)},{\mathfrak{p}}_j\hfill \\ \hfill & (x_{\sigma (i)},\dots ,x_{\sigma (i+j-2)},x_{i+j-1}))\hfill \\ \hfill =& {(-1)}^{({\displaystyle \sum _{r=1}^{(i+j)/2-1}}|x_{2r}|)}s({\displaystyle \sum _{m=0}^{i-1}}{\displaystyle \frac{{(-1)}^{j(i-m-1)+m}}{(i-1)!(j-1)!}}{\mathfrak{p}}_i\circ (I_m\otimes {\mathfrak{p}}_j\otimes I_{i-m-1})\circ ({\rho }_{w_{i+j-2}}^{(2)}\otimes I_1)\hfill \\ \hfill & (x_1,\dots ,x_n)).\hfill \end{array}$$

Because ${(-1)}^{({\displaystyle \sum _{r=1}^{(i+j)/2-1}}|x_{2r}|)}={(-1)}^{({\displaystyle \sum _{r=1}^{(n+1)/2-1}}|x_{2r}|)}$, it can be exchanged with ${\displaystyle \sum _{i+j=n+1}}$. Thus, we finish our proof when n is odd. The other case follows from a similar calculation. □

We next consider the relation between the composited map of Equation (2) and the square of the associated coderivation.

Proposition 4. 

Let $(V,\left\{{\widehat{\mathfrak{q}}}_n\right\})$ be a $P{L}_{\infty }$-algebra in the sense of Definition 1. Then, the component $P^{k}V\to P^{k-n+1}V$ of ${\tilde{\mathfrak{q}}}^2$ is provided by

$$\begin{array}{cc}\hfill & {\displaystyle \sum _{\sigma \in Sh(n-1,1,k-n-1)}}ϵ\left(\sigma \right){\widehat{\mathfrak{Q}}}_n(x_{\sigma \left(1\right)},\dots ,x_{\sigma \left(n\right)})\wedge x_{\sigma (n+1)}\wedge \dots \wedge x_{\sigma (k-1)}\otimes x_k\hfill \\ \hfill & +{\displaystyle \sum _{\sigma \in Sh(k-n,n-1)}}ϵ\left(\sigma \right)x_{\sigma \left(1\right)}\wedge \dots \wedge x_{\sigma (k-n)}\otimes {\widehat{\mathfrak{Q}}}_n(x_{\sigma (k-n+1)},\dots ,x_{\sigma (k-1)},x_k),\hfill \end{array}$$

where

$${\widehat{\mathfrak{Q}}}_n:={\displaystyle \sum _{i+j=n+1}}{\displaystyle \sum _{m=0}^{i-1}}{\displaystyle \frac{1}{(i-1)!(j-1)!}}{\widehat{\mathfrak{q}}}_i\circ (I_m\otimes {\widehat{\mathfrak{q}}}_j\otimes I_{i-m-1})\circ ({\rho }_{w_{i+j-2}}^{\left(1\right)}\otimes I_1).$$

Proof. 

We first compute the component $P^{k}V\to P^{k-j+1}V\to P^{k-i-j+2}V$ of ${\tilde{\mathfrak{q}}}^2$:

$$\begin{array}{cc}\hfill & {\tilde{\mathfrak{q}}}^2(x_1\wedge \dots \wedge x_{k-1}\otimes x_k)\hfill \\ \hfill =& {\displaystyle \sum _{\sigma \in Sh(j-1,1,k-j-1)}}ϵ(\sigma )\tilde{\mathfrak{q}}({\widehat{\mathfrak{q}}}_j(x_{\sigma (1)},\dots ,x_{\sigma (j)})\wedge x_{\sigma (j+1)}\wedge \dots \wedge x_{\sigma (k-1)}\otimes x_k)\hfill \\ \hfill & +{\displaystyle \sum _{\sigma \in Sh(k-j,j-1)}}{(-1)}^{{\displaystyle \sum _{t=1}^{k-j}}|x_{\sigma (t)}|}ϵ(\sigma )\tilde{\mathfrak{q}}(x_{\sigma (1)}\wedge \dots \wedge x_{\sigma (k-j)}\otimes {\widehat{\mathfrak{q}}}_j(x_{\sigma (k-j+1)},\dots ,x_{\sigma (k-1)},x_k))\hfill \\ \hfill =& {\displaystyle \sum _{\sigma \in Sh(j-1,1,i-2,1,k-i-j)}}ϵ(\sigma ){\widehat{\mathfrak{q}}}_i({\widehat{\mathfrak{q}}}_j(x_{\sigma (1)},\dots ,x_{\sigma (j)}),x_{\sigma (j+1)},\dots ,x_{\sigma (i+j-1)})\wedge x_{\sigma (i+j)}\wedge \dots \wedge \hfill \\ \hfill & x_{\sigma (k-1)}\otimes x_k\hfill \\ \hfill & +{\displaystyle \sum _{\sigma \in Sh(i-1,j-1,1,k-i-j)}}{(-1)}^{{\displaystyle \sum _{r=1}^{i-1}}|x_{\sigma (r)}|}ϵ(\sigma ){\widehat{\mathfrak{q}}}_i(x_{\sigma (1)},\dots ,x_{\sigma (i-1)},{\widehat{\mathfrak{q}}}_j(x_{\sigma (i)},\dots ,x_{\sigma (i+j-1)}))\wedge \hfill \\ \hfill & x_{\sigma (i+j)}\wedge \dots \wedge x_{\sigma (k-1)}\otimes x_k\hfill \\ \hfill & +{\displaystyle \sum _{\sigma \in Sh(i-1,1,j-1,1,k-i-j-1)}}{(-1)}^{{\displaystyle \sum _{r=1}^i}|x_{\sigma (r)}|}ϵ(\sigma ){\widehat{\mathfrak{q}}}_i(x_{\sigma (1)},\dots ,x_{\sigma (i)})\wedge {\widehat{\mathfrak{q}}}_j(x_{\sigma (i+1)},\dots ,x_{\sigma (i+j)})\hfill \\ \hfill & \wedge \dots \wedge x_{\sigma (k-1)}\otimes x_k\hfill \\ \hfill & +{\displaystyle \sum _{\sigma \in Sh(i-1,1,k-i-j,j-1)}}{(-1)}^{{\displaystyle \sum _{t=1}^{k-j}}|x_{\sigma (t)}|}ϵ(\sigma ){\widehat{\mathfrak{q}}}_i(x_{\sigma (1)},\dots ,x_{\sigma (i)})\wedge x_{\sigma (i+1)}\wedge \dots \wedge x_{\sigma (k-j)}\otimes {\widehat{\mathfrak{q}}}_j\hfill \\ \hfill & (x_{\sigma (k-j+1)},\dots ,x_{\sigma (k-1)},x_k)\hfill \\ \hfill & +{\displaystyle \sum _{\sigma \in Sh(j-1,1,k-i-j,i-1)}}{(-1)}^{1+{\displaystyle \sum _{r=1}^{k-i}}|x_{\sigma (r)}|}ϵ(\sigma ){\widehat{\mathfrak{q}}}_j(x_{\sigma (1)},\dots ,x_{\sigma (j)})\wedge \dots \wedge x_{\sigma (k-i)}\otimes {\widehat{\mathfrak{q}}}_i(x_{\sigma (k-i+1)},\hfill \\ \hfill & \dots ,x_{\sigma (k-1)},x_k)\hfill \\ \hfill & +{\displaystyle \sum _{\sigma \in Sh(k-i-j+1,j-1,1,i-2)}}ϵ(\sigma )x_{\sigma (1)}\wedge \dots \wedge x_{\sigma (k-i-j+1)}\otimes {\widehat{\mathfrak{q}}}_i({\widehat{\mathfrak{q}}}_j(x_{\sigma (k-i-j+2)},\dots ,x_{\sigma (k-i+1)}),\hfill \\ \hfill & \dots ,x_{\sigma (k-1)},x_k)\hfill \\ \hfill & +{\displaystyle \sum _{\sigma \in Sh(k-i-j+1,i-1,j-1,1)}}{(-1)}^{{\displaystyle \sum _{t=k-i-j+2}^{k-j}}|x_{\sigma (t)}|}ϵ(\sigma )x_{\sigma (1)}\wedge \dots \wedge x_{\sigma (k-i-j+1)}\otimes {\widehat{\mathfrak{q}}}_i(x_{\sigma (k-i-j+2)},\hfill \\ \hfill & \dots ,x_{\sigma (k-j)},{\widehat{\mathfrak{q}}}_j(x_{\sigma (k-j+1)},\dots ,x_{\sigma (k-1)},x_k)).\hfill \end{array}$$

Note that component $P^{k}V\to P^{k-n+1}V$ of ${\tilde{\mathfrak{q}}}^2$ is the sum of components $P^{k}V\to P^{k-j+1}V\to P^{k-i-j+2}V$ satisfying $i+j=n+1$. Thus, we add ${\displaystyle \sum _{i+j=n+1}}$ to the above result, and the middle three items can be eliminated as follows:

$$\begin{array}{cc}\hfill & {\displaystyle \sum _{i+j=n+1}}{\displaystyle \sum _{\sigma \in Sh(i-1,1,j-1,1,k-i-j-1)}}{(-1)}^{{\displaystyle \sum _{r=1}^i}|x_{\sigma (r)}|}ϵ(\sigma ){\widehat{\mathfrak{q}}}_i(x_{\sigma (1)},\dots ,x_{\sigma (i)})\wedge {\widehat{\mathfrak{q}}}_j(x_{\sigma (i+1)},\dots ,x_{\sigma (i+j)})\hfill \\ \hfill & \wedge \dots \wedge x_{\sigma (k-1)}\otimes x_k\hfill \\ \hfill =& {\displaystyle \frac{1}{2}}({\displaystyle \sum _{i+j=n+1}}{\displaystyle \sum _{\sigma \in Sh(i-1,1,j-1,1,k-i-j-1)}}{(-1)}^{{\displaystyle \sum _{r=1}^i}|x_{\sigma (r)}|}ϵ(\sigma ){\widehat{\mathfrak{q}}}_i(x_{\sigma (1)},\dots ,x_{\sigma (i)})\wedge {\widehat{\mathfrak{q}}}_j(x_{\sigma (i+1)},\dots ,\hfill \\ \hfill & x_{\sigma (i+j)})\wedge \dots \wedge x_{\sigma (k-1)}\otimes x_k\hfill \\ \hfill & +{\displaystyle \sum _{i+j=n+1}}{\displaystyle \sum _{\sigma \in Sh(j-1,1,i-1,1,k-i-j-1)}}{(-1)}^{{\displaystyle \sum _{r=1}^j}|x_{\sigma (r)}|}ϵ(\sigma ){\widehat{\mathfrak{q}}}_j(x_{\sigma (1)},\dots ,x_{\sigma (j)})\wedge {\widehat{\mathfrak{q}}}_i(x_{\sigma (j+1)},\dots ,\hfill \\ \hfill & x_{\sigma (i+j)})\wedge \dots \wedge x_{\sigma (k-1)}\otimes x_k)\hfill \\ \hfill =& {\displaystyle \frac{1}{2}}({\displaystyle \sum _{i+j=n+1}}{\displaystyle \sum _{\sigma \in Sh(i-1,1,j-1,1,k-i-j-1)}}{(-1)}^{{\displaystyle \sum _{r=1}^i}|x_{\sigma (r)}|}ϵ(\sigma ){\widehat{\mathfrak{q}}}_i(x_{\sigma (1)},\dots ,x_{\sigma (i)})\wedge {\widehat{\mathfrak{q}}}_j(x_{\sigma (i+1)},\dots ,\hfill \\ \hfill & x_{\sigma (i+j)})\wedge \dots \wedge x_{\sigma (k-1)}\otimes x_k\hfill \\ \hfill & +{\displaystyle \sum _{i+j=n+1}}{\displaystyle \sum _{\sigma \in Sh(j-1,1,i-1,1,k-i-j-1)}}{(-1)}^{1+{\displaystyle \sum _{r=1}^i}|x_{\sigma (r)}|}ϵ(\sigma ){\widehat{\mathfrak{q}}}_i(x_{\sigma (1)},\dots ,x_{\sigma (i)})\wedge {\widehat{\mathfrak{q}}}_j(x_{\sigma (i+1)},\dots ,\hfill \\ \hfill & x_{\sigma (i+j)})\wedge \dots \wedge x_{\sigma (k-1)}\otimes x_k)\hfill \\ \hfill =& 0,\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill & {\displaystyle \sum _{i+j=n+1}}{\displaystyle \sum _{\sigma \in Sh(i-1,1,k-i-j,j-1)}}{(-1)}^{{\displaystyle \sum _{t=1}^{k-j}}|x_{\sigma (t)}|}ϵ(\sigma ){\widehat{\mathfrak{q}}}_i(x_{\sigma (1)},\dots ,x_{\sigma (i)})\wedge \dots \wedge x_{\sigma (k-j)}\otimes {\widehat{\mathfrak{q}}}_j\hfill \\ \hfill & (x_{\sigma (k-j+1)},\dots ,x_{\sigma (k-1)},x_k)\hfill \\ \hfill & +{\displaystyle \sum _{i+j=n+1}}{\displaystyle \sum _{\sigma \in Sh(j-1,1,k-i-j,i-1)}}{(-1)}^{1+{\displaystyle \sum _{r=1}^{k-i}}|x_{\sigma (r)}|}ϵ(\sigma ){\widehat{\mathfrak{q}}}_j(x_{\sigma (1)},\dots ,x_{\sigma (j)})\wedge \dots \wedge x_{\sigma (k-i)}\otimes {\widehat{\mathfrak{q}}}_i\hfill \\ \hfill & (x_{\sigma (k-i+1)},\dots ,x_{\sigma (k-1)},x_k)\hfill \\ \hfill =& {\displaystyle \sum _{i+j=n+1}}{\displaystyle \sum _{\sigma \in Sh(i-1,1,k-i-j,j-1)}}{(-1)}^{{\displaystyle \sum _{t=1}^{k-j}}|x_{\sigma (t)}|}ϵ(\sigma ){\widehat{\mathfrak{q}}}_i(x_{\sigma (1)},\dots ,x_{\sigma (i)})\wedge \dots \wedge x_{\sigma (k-j)}\otimes {\widehat{\mathfrak{q}}}_j\hfill \\ \hfill & (x_{\sigma (k-j+1)},\dots ,x_{\sigma (k-1)},x_k)\hfill \\ \hfill & +{\displaystyle \sum _{i+j=n+1}}{\displaystyle \sum _{\sigma \in Sh(i-1,1,k-i-j,j-1)}}{(-1)}^{1+{\displaystyle \sum _{t=1}^{k-j}}|x_{\sigma (t)}|}ϵ(\sigma ){\widehat{\mathfrak{q}}}_i(x_{\sigma (1)},\dots ,x_{\sigma (i)})\wedge x_{\sigma (i+1)}\wedge \dots \wedge x_{\sigma (k-j)}\hfill \\ \hfill & \otimes {\widehat{\mathfrak{q}}}_j(x_{\sigma (k-j+1)},\dots ,x_{\sigma (k-1)},x_k)\hfill \\ \hfill =& 0.\hfill \end{array}$$

The remaining four terms can be simplified by ${\widehat{\mathfrak{Q}}}_n$:

$$\begin{array}{cc}\hfill & {\tilde{\mathfrak{q}}}^2(x_1\wedge \dots \wedge x_{k-1}\otimes x_k)\hfill \\ \hfill =& {\displaystyle \sum _{\sigma \in Sh(j-1,1,i-2,1,k-i-j)}}ϵ(\sigma ){\widehat{\mathfrak{q}}}_i({\widehat{\mathfrak{q}}}_j(x_{\sigma (1)},\dots ,x_{\sigma (j)}),x_{\sigma (j+1)},\dots ,x_{\sigma (i+j-1)})\wedge x_{\sigma (i+j)}\wedge \dots \wedge \hfill \\ \hfill & x_{\sigma (k-1)}\otimes x_k\hfill \\ \hfill & +{\displaystyle \sum _{\sigma \in Sh(i-1,j-1,1,k-i-j)}}{(-1)}^{{\displaystyle \sum _{r=1}^{i-1}}|x_{\sigma (r)}|}ϵ(\sigma ){\widehat{\mathfrak{q}}}_i(x_{\sigma (1)},\dots ,x_{\sigma (i-1)},{\widehat{\mathfrak{q}}}_j(x_{\sigma (i)},\dots ,x_{\sigma (i+j-1)}))\wedge \hfill \\ \hfill & x_{\sigma (i+j)}\wedge \dots \wedge x_{\sigma (k-1)}\otimes x_k\hfill \\ \hfill & +{\displaystyle \sum _{\sigma \in Sh(k-i-j+1,j-1,1,i-2)}}ϵ(\sigma )x_{\sigma (1)}\wedge \dots \wedge x_{\sigma (k-i-j+1)}\otimes {\widehat{\mathfrak{q}}}_i({\widehat{\mathfrak{q}}}_j(x_{\sigma (k-i-j+2)},\dots ,x_{\sigma (k-i+1)}),\hfill \\ \hfill & \dots ,x_{\sigma (k-1)},x_k)\hfill \\ \hfill & +{\displaystyle \sum _{\sigma \in Sh(k-i-j+1,i-1,j-1,1)}}{(-1)}^{{\displaystyle \sum _{t=k-i-j+2}^{k-j}}|x_{\sigma (t)}|}ϵ(\sigma )x_{\sigma (1)}\wedge \dots \wedge x_{\sigma (k-i-j+1)}\otimes {\widehat{\mathfrak{q}}}_i(x_{\sigma (k-i-j+2)},\hfill \\ \hfill & \dots ,x_{\sigma (k-j)},{\widehat{\mathfrak{q}}}_j(x_{\sigma (k-j+1)}\wedge \dots \wedge x_{\sigma (k-1)}\otimes x_k))\hfill \\ \hfill =& {\displaystyle \sum _{\sigma \in Sh(n-1,1,k-n-1)}}ϵ(\sigma ){\widehat{\mathfrak{Q}}}_n(x_{\sigma (1)},\dots ,x_{\sigma (n)})\wedge x_{\sigma (n+1)}\wedge \dots \wedge x_{\sigma (k-1)}\otimes x_k\hfill \\ \hfill & +{\displaystyle \sum _{\sigma \in Sh(k-n,n-1)}}ϵ(\sigma )x_{\sigma (1)}\wedge \dots \wedge x_{\sigma (k-n)}\otimes {\widehat{\mathfrak{Q}}}_n(x_{\sigma (k-n+1)},\dots ,x_{\sigma (k-1)},x_k).\hfill \end{array}$$

Now, we have completed the proof of this proposition. □

Putting the above conclusions together, we can now prove Theorem 2.

Proof of Theorem 2 

For a graded vector space V equipped with a collection $\{{\mathfrak{p}}_n:{\otimes }^{n}V\to V,n\ge 1\}$ of homogeneous linear maps of cohomological degree $n-2$, let

$${\mathfrak{P}}_n:={\displaystyle \sum _{i+j=n+1}}{\displaystyle \sum _{m=0}^{i-1}}{\displaystyle \frac{{(-1)}^{j(i-m-1)+m}}{(i-1)!(j-1)!}}{\mathfrak{p}}_i\circ (I_m\otimes {\mathfrak{p}}_j\otimes I_{i-m-1})\circ ({\rho }_{w_{i+j-2}}^{\left(2\right)}\otimes I_1)$$

and

$${\widehat{\mathfrak{Q}}}_n:={\displaystyle \sum _{i+j=n+1}}{\displaystyle \sum _{m=0}^{i-1}}{\displaystyle \frac{1}{(i-1)!(j-1)!}}{\widehat{\mathfrak{p}}}_i\circ (I_m\otimes {\widehat{\mathfrak{p}}}_j\otimes I_{i-m-1})\circ ({\rho }_{w_{i+j-2}}^{\left(1\right)}\otimes I_1).$$

By Proposition 3, we have ${\widehat{\mathfrak{Q}}}_n=-{\widehat{\mathfrak{P}}}_n$. Then,

$$\begin{array}{cc}\hfill & (V,\left\{{\mathfrak{p}}_n\right\})\mathrm{satisfies}\mathrm{Equation}\left(5\right),\hfill \\ \hfill ⟺& {\mathfrak{P}}_n=0,\mathrm{for}\mathrm{all}n\ge 1,\hfill \\ \hfill ⟺& {\widehat{\mathfrak{Q}}}_n=0,\mathrm{for}\mathrm{all}n\ge 1,\hfill \\ \hfill ⟺& (sV,\left\{{\widehat{\mathfrak{p}}}_n\right\})\mathrm{satisfies}\mathrm{Equation}\left(2\right).\hfill \end{array}$$

Analogously, we can obtain the equivalence of (2) and (3) by Proposition 4:

$$\begin{array}{cc}\hfill & (sV,\left\{{\widehat{\mathfrak{p}}}_n\right\})\mathrm{satisfies}\mathrm{Equation}\left(2\right),\hfill \\ \hfill ⟺& {\widehat{\mathfrak{Q}}}_n=0,\mathrm{for}\mathrm{all}n\ge 1,\hfill \\ \hfill ⟺& {\tilde{\mathfrak{p}}}^2=0,\hfill \end{array}$$

where the implication that ${\tilde{\mathfrak{p}}}^2=0⟹{\widehat{\mathfrak{Q}}}_n=0,n\ge 1$ results from the fact that component $P^{n}V\to V$ of ${\tilde{\mathfrak{p}}}^2$ is exactly ${\widehat{\mathfrak{Q}}}_n$. □

4. Relation Among n-Ary Algebras and Homotopy Algebras

In this section, we derive the relation of homotopy algebras from the results in the previous section. In particular, we obtain the relation of n-ary algebras.

For simplicity, we use $(V,\left\{{\mu }_n\right\})$ to denote a homotopy algebra in the sense of Definition 2 and use $(V,\left\{{\widehat{\mu }}_n\right\})$ to denote a homotopy algebra in the sense of Definition 1. Maps between $(V,\left\{{\mu }_n\right\})$ are denoted by pure letters, while maps between $(V,\left\{{\widehat{\mu }}_n\right\})$ are denoted by letters with hats. Where no confusion occurs, we simply denote the component of a map f by f.

Applying the functor $Hom(-,V)$ to the commutative diagram in Lemma 2, we derive

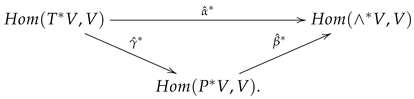This diagram provides commutators of $A_{\infty }$-algebras.

Lemma 7 

([10]). If $(V,\left\{{\widehat{\mathfrak{m}}}_n\right\})$ is an $A_{\infty }$-algebra, then $(V,\left\{\widehat{\alpha }\left({\widehat{\mathfrak{m}}}_n\right)\right\})$ is an $L_{\infty }$-algebra.

The previous lemma can be naturally generalized to $P{L}_{\infty }$-algebras.

Theorem 3. 

• Suppose that $(V,\left\{{\widehat{\mathfrak{m}}}_n\right\})$ is an $A_{\infty }$-algebra; then, $(V,\left\{\widehat{\gamma }\left({\widehat{\mathfrak{m}}}_n\right)\right\})$ is a $P{L}_{\infty }$-algebra.
• For a $P{L}_{\infty }$-algebra $(V,\left\{{\widehat{\mathfrak{p}}}_n\right\})$, the collection $\left\{\widehat{\beta }\left({\widehat{\mathfrak{p}}}_n\right)\right\}$ defines an $L_{\infty }$-algebra structure on V.

Proof. 

We denote the associated coderivation of $\left\{{\widehat{\mathfrak{m}}}_n\right\}$ (resp. $\left\{\widehat{\gamma }\left({\widehat{\mathfrak{m}}}_n\right)\right\}$) by $\tilde{\mathfrak{m}}$ (resp. $\tilde{\mathfrak{q}}$). We first show that the diagram below is commutative.

Because $\widehat{\gamma }=\widehat{\alpha }\otimes I_1$ and $\pi \widehat{\alpha }=I{d}_{{\wedge }^{*}V}$, where $\pi$ is defined in the proof of Lemma 2, the equation $\widehat{\gamma }\tilde{\mathfrak{q}}=\tilde{\mathfrak{m}}\widehat{\gamma }$ holds if and only if the equation $\tilde{\mathfrak{q}}=(\pi \otimes I_1)\tilde{\mathfrak{m}}\widehat{\gamma }$ holds. We can check their components $P^{k}V\to P^{l}V$ as follows. For any homogeneous elements $x_i\in V$, we have

$$\begin{array}{cc}\hfill & \tilde{\mathfrak{q}}(x_1\wedge \dots \wedge x_{k-1}\otimes x_k)\hfill \\ \hfill =& {\displaystyle \sum _{\sigma \in Sh(k-l,1,l-2)}}ϵ\left(\sigma \right)\widehat{\gamma }\left({\widehat{\mathfrak{m}}}_{k-l+1}\right)(x_{\sigma \left(1\right)},\dots ,x_{\sigma (k-l+1)})\wedge x_{\sigma (k-l+2)}\wedge \dots \wedge x_{\sigma (k-1)}\otimes x_k\hfill \\ \hfill & +{\displaystyle \sum _{\sigma \in Sh(l-1,k-l)}}{(-1)}^{{\displaystyle \sum _{t=1}^{l-1}}\left|x_{\sigma \left(t\right)}\right|}ϵ\left(\sigma \right)x_{\sigma \left(1\right)}\wedge \dots \wedge x_{\sigma (l-1)}\otimes \widehat{\gamma }\left({\widehat{\mathfrak{m}}}_{k-l+1}\right)(x_{\sigma \left(l\right)},\dots ,x_{\sigma (k-1)},x_k)\hfill \\ \hfill =& {\displaystyle \sum _{\sigma \in Sh(1,\dots ,1,l-2)}}ϵ\left(\sigma \right){\widehat{\mathfrak{m}}}_{k-l+1}(x_{\sigma \left(1\right)},\dots ,x_{\sigma (k-l+1)})\wedge x_{\sigma (k-l+2)}\wedge \dots \wedge x_{\sigma (k-1)}\otimes x_k\hfill \\ \hfill & +{\displaystyle \sum _{\sigma \in Sh(l-1,1,\dots ,1)}}{(-1)}^{{\displaystyle \sum _{t=1}^{l-1}}\left|x_{\sigma \left(t\right)}\right|}ϵ\left(\sigma \right)x_{\sigma \left(1\right)}\wedge \dots \wedge x_{\sigma (l-1)}\otimes {\widehat{\mathfrak{m}}}_{k-l+1}(x_{\sigma \left(l\right)},\dots ,x_{\sigma (k-1)},x_k).\hfill \end{array}$$

On the other hand, we obtain

$$\begin{array}{cc}\hfill & (\pi \otimes I_1)\tilde{\mathfrak{m}}\widehat{\gamma }(x_1\wedge \dots \wedge x_{k-1}\otimes x_k)\hfill \\ \hfill =& {\displaystyle \sum _{\sigma \in {\mathbb{S}}_{k-1}}}ϵ(\sigma )(\pi \otimes I_1)\tilde{\mathfrak{m}}(x_{\sigma (1)}\otimes \dots \otimes x_{\sigma (k-1)}\otimes x_k)\hfill \\ \hfill =& {\displaystyle \sum _{\sigma \in {\mathbb{S}}_{k-1}}}{\displaystyle \sum _{i=0}^{l-2}}{(-1)}^{{\displaystyle \sum _{r=1}^i}|x_{\sigma (r)}|}ϵ(\sigma )(\pi \otimes I_1)(x_{\sigma (1)}\otimes \dots \otimes x_{\sigma (i)}\otimes {\widehat{\mathfrak{m}}}_{k-l+1}(x_{\sigma (i+1)},\dots ,x_{\sigma (i+k-l+1)})\hfill \\ \hfill & \otimes \dots \otimes x_{\sigma (k-1)}\otimes x_k)\hfill \\ \hfill & +{\displaystyle \sum _{\sigma \in {\mathbb{S}}_{k-1}}}{(-1)}^{{\displaystyle \sum _{r=1}^{l-1}}|x_{\sigma (r)}|}ϵ(\sigma )(\pi \otimes I_1)(x_{\sigma (1)}\otimes \dots \otimes x_{\sigma (l-1)}\otimes {\widehat{\mathfrak{m}}}_{k-l+1}(x_{\sigma (l)},\dots ,x_{\sigma (k-1)},x_k))\hfill \\ \hfill =& {\displaystyle \sum _{\sigma \in {\mathbb{S}}_{k-1}}}{\displaystyle \sum _{i=0}^{l-2}}{\displaystyle \frac{{(-1)}^{{\displaystyle \sum _{r=1}^i}|x_{\sigma (r)}|}ϵ(\sigma )}{(l-1)!}}{x}_{\sigma (1)}\wedge \dots \wedge x_{\sigma (i)}\wedge {\widehat{\mathfrak{m}}}_{k-l+1}(x_{\sigma (i+1)},\dots ,x_{\sigma (i+k-l+1)})\wedge \dots \wedge \hfill \\ \hfill & x_{\sigma (k-1)}\otimes x_k\hfill \\ \hfill & +{\displaystyle \sum _{\sigma \in {\mathbb{S}}_{k-1}}}{\displaystyle \frac{{(-1)}^{{\displaystyle \sum _{r=1}^{l-1}}|x_{\sigma (r)}|}ϵ(\sigma )}{(l-1)!}}{x}_{\sigma (1)}\wedge \dots \wedge x_{\sigma (l-1)}\otimes {\widehat{\mathfrak{m}}}_{k-l+1}(x_{\sigma (l)},\dots ,x_{\sigma (k-1)},x_k)\hfill \\ \hfill =& {\displaystyle \sum _{\sigma \in Sh(1,\dots ,1,l-2)}}ϵ(\sigma ){\widehat{\mathfrak{m}}}_{k-l+1}(x_{\sigma (1)},\dots ,x_{\sigma (k-l+1)})\wedge x_{\sigma (k-l+2)}\wedge \dots \wedge x_{\sigma (k-1)}\otimes x_k\hfill \\ \hfill & +{\displaystyle \sum _{\sigma \in Sh(l-1,1,\dots ,1)}}{(-1)}^{{\displaystyle \sum _{r=1}^{l-1}}|x_{\sigma (r)}|}ϵ(\sigma )x_{\sigma (1)}\wedge \dots \wedge x_{\sigma (l-1)}\otimes {\widehat{\mathfrak{m}}}_{k-l+1}(x_{\sigma (l)},\dots ,x_{\sigma (k-1)},x_k).\hfill \end{array}$$

For an $A_{\infty }$-algebra $(V,\left\{{\widehat{\mathfrak{m}}}_n\right\})$, by Lemma 3 we have ${\tilde{\mathfrak{m}}}^2=0$. Then, $\widehat{\gamma }{\tilde{\mathfrak{q}}}^2={\tilde{\mathfrak{m}}}^2\widehat{\gamma }=0$. Because $\widehat{\gamma }$ is injective, by Lemma 2 we have ${\tilde{\mathfrak{q}}}^2=0$. Applying Theorem 2, we derive that $(V,\left\{\widehat{\gamma }\left({\widehat{\mathfrak{m}}}_n\right)\right\})$ is a $P{L}_{\infty }$-algebra.

The other term can be deduced in a similar way. □

Remark 6. 

The last result in Theorem 3 coincides with a result in [20] which is proved by constructing a graded Lie map.

As equivalent definitions, homotopy algebras in the form of $(V,\left\{{\mu }_n\right\})$ have analogous relations. Replacing ${\rho }^{\left(1\right)}$ by ${\rho }^{\left(2\right)}$, we obtain the commutators of $(V,\left\{{\mu }_n\right\})$.

Corollary 1. 

Define $\alpha :={\displaystyle \sum _{n\ge 1}}{\rho }_{w_n}^{\left(2\right)}$, $\beta :={\displaystyle \sum _{n\ge 1}}{\displaystyle \sum _{\sigma \in Sh(n-1,1)}}{\rho }_{\sigma }^{\left(2\right)}$ and $\gamma :={\displaystyle \sum _{n\ge 1}}{\rho }_{w_{n-1}}^{\left(2\right)}\otimes I_1$.

• Suppose that $(V,\left\{{\mathfrak{m}}_n\right\})$ is an $A_{\infty }$-algebra; then, $(V,\left\{\gamma \left({\mathfrak{m}}_n\right)\right\})$ is a $P{L}_{\infty }$-algebra.
• For a $P{L}_{\infty }$-algebra $(V,\left\{{\mathfrak{p}}_n\right\})$, the collection $\left\{\beta \left({\mathfrak{p}}_n\right)\right\}$ defines an $L_{\infty }$-algebra structure on V.

Proof. 

Likewise, it is enough to verify the first claim. For the following diagram,

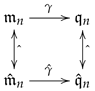its commutativity can be deduced from $\widehat{\gamma \left({\mathfrak{m}}_n\right)}=\widehat{\gamma }\left({\widehat{\mathfrak{m}}}_n\right)$. Without loss of generality, we assume that n is even:

$$\begin{array}{cc}\hfill & \widehat{\gamma \left({\mathfrak{m}}_n\right)}(s{x}_1,\dots ,s{x}_n)\hfill \\ \hfill =& {(-1)}^{{\displaystyle \sum _{i=1}^{n/2}}\left|x_{2i-1}\right|}s\gamma \left({\mathfrak{m}}_n\right)(x_1,\dots ,x_n)\hfill \\ \hfill =& {(-1)}^{{\displaystyle \sum _{i=1}^{n/2}}\left|x_{2i-1}\right|}{\displaystyle \sum _{\sigma \in {\mathbb{S}}_{n-1}}}sgn\left(\sigma \right)ϵ\left(\sigma \right)s{\mathfrak{m}}_n(x_{\sigma \left(1\right)},\dots ,x_{\sigma (n-1)},x_n).\hfill \end{array}$$

By Lemma 5, we can derive the composited map on the other side as follows:

$$\begin{array}{cc}\hfill & {(-1)}^{{\displaystyle \sum _{i=1}^{n/2}}\left|x_{2i-1}\right|}{\displaystyle \sum _{\sigma \in {\mathbb{S}}_{n-1}}}sgn\left(\sigma \right)ϵ\left(\sigma \right)s{\mathfrak{m}}_n(x_{\sigma \left(1\right)},\dots ,x_{\sigma (n-1)},x_n)\hfill \\ \hfill =& {\displaystyle \sum _{\sigma \in {\mathbb{S}}_{n-1}}}{(-1)}^{{\displaystyle \sum _{i=1}^{n/2}}\left|x_{\sigma (2i-1)}\right|}ϵ(\sigma ;s{x}_1,\dots ,s{x}_{n-1})s{\mathfrak{m}}_n(x_{\sigma \left(1\right)},\dots ,x_{\sigma (n-1)},x_n)\hfill \\ \hfill =& {\displaystyle \sum _{\sigma \in {\mathbb{S}}_{n-1}}}ϵ(\sigma ;s{x}_1,\dots ,s{x}_{n-1}){\widehat{\mathfrak{m}}}_n(s{x}_{\sigma \left(1\right)},\dots ,s{x}_{\sigma (n-1)},s{x}_n)\hfill \\ \hfill =& \widehat{\gamma }\left({\widehat{\mathfrak{m}}}_n\right)(s{x}_1,\dots ,s{x}_n).\hfill \end{array}$$

Hence $\widehat{\gamma \left({\mathfrak{m}}_n\right)}=\widehat{\gamma }\left({\widehat{\mathfrak{m}}}_n\right)$. If $(V,\left\{{\mathfrak{m}}_n\right\})$ is an $A_{\infty }$-algebra, then $(sV,\left\{{\widehat{\mathfrak{m}}}_n\right\})$ is an $A_{\infty }$-algebra by Lemma 3. Hence by Theorem 3, $(sV,\left\{\widehat{\gamma }\left({\widehat{\mathfrak{m}}}_n\right)\right\})$ is a $P{L}_{\infty }$-algebra. As a result of Theorem 2, $\left\{\gamma \left({\mathfrak{m}}_n\right)\right\}$ provides a $P{L}_{\infty }$-algebra structure on V. □

Using Proposition 1, we can immediately obtain the relation of n-ary algebras.

Corollary 2. 

Let V be a vector space.

• Every partially associative n-algebra $(V,\mathfrak{m})$ carries a pre-Lie n-algebra structure $\mathfrak{p}$ defined by

  $$\mathfrak{p}(x_1,\dots ,x_n):={\displaystyle \sum _{\sigma \in {\mathbb{S}}_{n-1}}}sgn\left(\sigma \right)\mathfrak{m}(x_{\sigma \left(1\right)},\dots ,x_{\sigma (n-1)},x_n).$$
• Every pre-Lie n-algebra $(V,\mathfrak{p})$ carries a Lie n-algebra structure $\mathfrak{l}$ defined by

  $$\mathfrak{l}(x_1,\dots ,x_n):={\displaystyle \sum _{\sigma \in Sh(n-1,1)}}sgn\left(\sigma \right)\mathfrak{p}(x_{\sigma \left(1\right)},\dots ,x_{\sigma \left(n\right)}).$$

In particular, we have the following corollary.

Corollary 3. 

A pre-Lie n-algebra $(V,\mathfrak{p})$ is n-Lie admissible, that is,

$$\mathfrak{l}(x_1,\dots ,x_n):={\displaystyle \sum _{\sigma \in {\mathbb{S}}_n}}sgn\left(\sigma \right)\mathfrak{p}(x_{\sigma \left(1\right)},\dots ,x_{\sigma \left(n\right)})$$

is a Lie n-algebra structure.

Proof. 

This is the case is because

$$\begin{array}{c}\hfill {\displaystyle \sum _{\sigma \in {\mathbb{S}}_n}}sgn\left(\sigma \right)\mathfrak{p}(x_{\sigma \left(1\right)},\dots ,x_{\sigma \left(n\right)})=(n-1)!{\displaystyle \sum _{\sigma \in Sh(n-1,1)}}sgn\left(\sigma \right)\mathfrak{p}(x_{\sigma \left(1\right)},\dots ,x_{\sigma \left(n\right)})\end{array}$$

for a pre-Lie n-algebra operation $\mathfrak{p}$. □

Example 1. 

Consider the ${\mathbb{Z}}_2$-graded vector space $V:=V^0\oplus V^1$ over $\mathbb{K}$, where $V^0$ is a two-dimensional even subspace with basis $\{a,b\}$ and where $V^1$ is a one-dimensional odd subspace with basis $\left\{c\right\}$. We can turn this into an $A_{\infty }$-algebra as follows. First, we put ${\mathfrak{m}}_n=0$ for any $n\notin \{2,3\}$. Second, we define the binary operation ${\mathfrak{m}}_2$ by

$${\mathfrak{m}}_2(a\otimes a)=a,{\mathfrak{m}}_2(b\otimes b)=b,{\mathfrak{m}}_2(a\otimes c)={\mathfrak{m}}_2(c\otimes b)=c,$$

with all other ${\mathfrak{m}}_2$ values on basis elements being zero. Third, we define ${\mathfrak{m}}_3$ by

$${\mathfrak{m}}_3(a\otimes b\otimes a)={\mathfrak{m}}_3(b\otimes a\otimes a)=-{\mathfrak{m}}_3(b\otimes a\otimes b)=-{\mathfrak{m}}_3(b\otimes b\otimes a)=c,$$

with all other ${\mathfrak{m}}_3$ values on basis elements being zero.

By applying Corollary 1, we obtain the following results:

• The associated $P{L}_{\infty }$-algebra structure on V is provided by ${\mathfrak{p}}_n=0$ for any $n\notin \{2,3\}$, ${\mathfrak{p}}_2={\mathfrak{m}}_2$, and ${\mathfrak{p}}_3$ is zero except

  $${\mathfrak{p}}_3(a\otimes b\otimes b)=-{\mathfrak{m}}_3(b\otimes a\otimes b)=c.$$
• The associated $L_{\infty }$-algebra structure on V is provided by ${\mathfrak{l}}_n=0$ for any $n\ne 2$ and ${\mathfrak{l}}_2$ is zero except

  $${\mathfrak{l}}_2(a\otimes c)={\mathfrak{l}}_2(c\otimes a)={\mathfrak{l}}_2(b\otimes c)={\mathfrak{l}}_2(c\otimes b)=c.$$