Abstract
This study establishes a fractional-order model (FOM) to describe the rumor spreading process. Members of society in this FOM are classified into three categories that change with time—the population that is ignorant of the rumors and does not know them, the population that is aware of the truth of the rumors but does not believe them, and the spreaders of rumors—taking into consideration awareness programs (APs) through media reports as a subcategory that changes over time where paying attention to these APs makes ignorant individuals avoid believing rumors and become better-informed individuals. We prove the positivity and boundedness of the FOM solutions. The feasible equilibrium points (EPs) and their local asymptotical stability (LAS) are analyzed based on the control reproduction number (CRN). Then, we examine the influence of model parameters that emerge with the CRN through a sensitivity analysis.A fractional optimal control problem (FOCP) is formulated by considering three time-dependent control measures in the suggested FOM to capture the spread of rumors; , , and represent the contact control between rumor spreaders and ignorant people, control media reports, and control rumor spreaders, respectively. We derive the necessary optimality conditions (NOCs) by applying Pontryagin’s maximum principle (PMP). Different optimal control strategies are proposed to reduce the negative effects of rumor spreading and achieve the maximum social benefit. Numerical simulation is implemented using a forward–backward sweep (FBS) approach based on the predictor–corrector method (PCM) to clarify the efficiency of the proposed strategies in order to decrease the number of rumor spreaders and increase the number of aware populations.
Keywords:
rumor model; stability analysis; optimal control problems; fractional derivative; numerical simulation MSC:
93C95; 26A33; 34D20; 34H05
1. Introduction
Rumors can influence public opinion and individual beliefs, leading to changes in attitudes toward economic, political, and social issues [1,2]. A rumor is an unsubstantiated truth that has a harmful impact on society; nevertheless, interventions can be implemented to minimize these negative effects [3]. As a result, understanding how rumors spread is critical to obtaining scientific information and developing the best strategies to mitigate their detrimental effects. Various mathematical models (MMs) have been constructed to investigate the dynamics of rumor spreading and identify the main aspects that may influence its dynamic behavior [4,5,6,7]. All of these studies have contributed substantially to understanding the propagation of rumors. Most MMs for rumor spreading are based on compartmentalized epidemic models, which classify the population into compartments, such as susceptible, infected, recovered, etc., according to the status of the epidemic models. In the deterministic rumor model, the total population is classified into three main classes [8]: ignorants (unaware individuals), spreaders (disseminate individuals), and stiflers (people who know the rumor but do not spread it). This is identical to the SIR model, with the exception of the transmission from the spreader (infected) to the stifler (recovered) compartment. Also, this rumor model can be expanded by splitting the stifler compartment into two groups: those who hear the rumor and decide whether or not to spread it (e.g., refs. [7,9,10]). Moreover, a rumor model has been developed that includes a forgetting rate component [11]. Other assumptions have been considered depending on the objective of the MM (see, e.g., refs. [3,5,12]). Rumor MMs can be classified into two categories: network and non-network models [13,14]. Briefly, a non-network model is developed without taking into account the influence of network features or topologies on the dynamics of rumor transmission. Research utilizing non-network models has two significant features: understanding rumor transmission dynamics, and the effects of the intervention on rumor spread dynamics. The first trend when it comes to this topic is to investigate the influence of factors such as forgetting mechanisms, emergencies, and human decisions on the propagation of rumors. On the other hand, some studies focus on influence interventions such as education, scientific knowledge, government action, and media coverage [15,16,17]. A network model is a networking concept designed to investigate the influence of network features such as cliques, clusters, and the strength of node connectivity on the dynamics of rumor spread. These mentioned features depict the actual structure of a community, making this network model more reasonable [18,19,20]. Fractional calculus (FC) has developed into a significant area of system dynamics [21]. When modeling real-world occurrences, fractional derivatives and fractional integrals yield better results than classical derivatives due to several important properties, including hereditary features, so that the state of the considered system depends on all historical states, and an extra degree of freedom included in the change in fractional order [22,23,24]. The Caputo fractional derivative (CFD) [25] is best for modeling scenarios involving fractional derivatives, where it is employed in different fields such as chaos theory, engineering, computer science, biology, and others (see [26,27,28,29,30]). Furthermore, FOMs provide innovative approaches to characterizing memory effects and identifying these effects on the behavior of solutions. In the same context, it was found that the dynamic behavior of rumors is affected by historical information. Singh [31] investigated the propagation of rumors in a social network under the Atangana–Baleanu operator, and a memory effect on the populations of different repositories was demonstrated. Ren et al. [32] studied a model of rumor transmission in a mobile social network utilizing a fractional-order derivative. They additionally developed their system using a physical stochastic process. Graef et al. [33] developed a fractional-order SIR rumor model to study users’ abandonment and adoption of online social networks. Memory effects on the information transmission process are investigated in [34,35], which show that numerous redundant contacts of the same rumor change people’s initial ideas of it and that cumulative features influence individuals’ behaviors in social networks. Briefly, memory effects in FC allow it to better represent the process of rumor propagation.
The optimization or minimization of a cost function subject to dynamic restrictions on both state and control variables is known as an optimal control problem (OCP). A system of differential equations that depicts the paths taken by the state and control variables to minimize the cost function is known as the state constraints. Functions involving state and control variables are a component of control problems and are called cost or objective functions. The PMP can be used to generate NOC and optimal control signals [36]. FOCPs arise when dynamic constraints are represented by FDEs or the cost function is represented by a fractional integral [37]. So, the FOCPs are an extension of the traditional OCPs. Both the old and new definitions of fractional derivatives make it easy to show FOCPs; nevertheless, Riemann–Liouville and Caputo’s definitions are the ones that are most frequently employed. FOCPs offer several features over their traditional integer-order counterparts such as flexibility, accuracy, robustness, increased system lifespan, etc. [38,39]. Hence, FOCPs have become the most substantial tool for solving many real-life problems in different fields. For example, in [40], authors have developed a FOM for the epidemic with the dread effect of infectious disease and treatment control measures, identifying potential functions for illness control parameters and fear level. In [41], the author examined a FOM with some control efforts to look into the best ways to address the dynamics of transmission of university students’ fear and hostility toward mathematics. In [42], the authors proposed FOCP to reduce the transmission dynamics of Zika virus infections with different control strategies. In [43], some control measures are used to reduce malaria disease between populations. Optimal control conditions for the 2I2SR rumor spreading model in the fractional context are examined in [44]. In [45], the authors provided a novel FOM for examining the spread of online game addiction and used real data in China to fit model parameters. In addition, they used isolation and treatment control measures to construct FOCP.
Our contribution to this research is to extend the findings of [46] by generalizing the model to a fractional context and introducing two additional control efforts alongside the existing one in the original model. Therefore, we introduce the modified MM for rumor spreading, containing three concrete control measures on the ground to compensate for the shortcomings in [46]. We provide some theoretical analyses to prove the suggested model’s validity and efficiency, including existence, uniqueness, positivity, and boundedness, using some mathematical theories. EPs are also found, and the stability criteria of the model are examined. Several simulations of this model are also presented after formulating it as FOCP and imposing a set of different strategies resulting from the intersection of the proposed controls, clarifying the effect of these strategies, and comparing them with each other to obtain the best strategy through which we can limit the spread of rumors in society.
This work is structured as follows. Section 2 provides the fundamental FC preliminary steps and some key theorems that allow us to obtain the main findings. Section 3 is divided into subsections where the description of the FOM for rumor dynamics is presented in Section 3.1, the proof of existence and uniqueness of the solution is given in Section 3.2, positivity and boundedness of the solution are demonstrated in Section 3.3. Section 4 is divided into various subsections. In Section 4.1 and Section 4.2, we investigate EPs and their stability theorems, respectively, as well as computing . In Section 4.3, we introduce the sensitivity index for the parameters of to identify the most important parameters that allow us to gauge how controls affect the behavior of the suggested solutions. Section 4.4 presents the methodology of the used method and the behavior of solutions for the proposed FOM without control measures. In Section 5, we formulate an objective function aimed at reducing rumor spreaders and increasing awareness of the population against the danger of rumor spreading in order to construct FOCP and derive NOCs. Section 6 explains the simulation results and illustrates how the behavior of the model variables changes when controls are present. Section 7 contains the work’s conclusion.
2. Preliminaries
Here, we offer the concepts required to carry out this study [25,47].
Definition 1.
The Riemann–Liouville fractional integral (R-LFI) is given as:
- (i)
- Left R-LFI
- (ii)
- Right R-LFI
Definition 2.
The Riemann–Liouville fractional derivative (R-LFD) of order is given by
- (i)
- Left R-LFD
- (ii)
- Right R-LFD
Definition 3.
The CFD of order is defined as
- (i)
- Left CFD
- (ii)
- Right CFD
Theorem 1
([48]). The relation between R-LFD and CFD is
where , and .
Lemma 1
([49]). Let and . Then, we have
Definition 4.
Let be of exponential order ( s.t. for ). If the Laplace transform (LT) of exists for , then the LT of is
Definition 5.
The Mittag–Leffler function of two parameters , is given by
Additionally, the LT of (see, e.g., ref. [48]) is
Lemma 2
([50]). The unique positive EPs of the system (5) are LAS if every eigenvalue of its Jacobian matrix (JM) satisfies the following condition:
3. Model Formulation
In this section, we present the components of the proposed FOM and also show the transmission dynamics between these components through some of the various parameters. Proving the existence, uniqueness, positivity and boundedness of the projected solution is discussed here in detail.
3.1. Description of FOM
The spread of rumors among the population is one of the most important problems that have a negative impact and often leads to economic and social problems (see, e.g., ref. [51]). In the following FOM, we consider the total population of to be divided into three compartments; and are the categories of people who do not know the rumor (ignorant individuals), who know the rumor but are reluctant to believe it (aware individuals) and who spread the rumor (spreaders), respectively. Since the spread of rumors varies over time, media reports will also be subject to changes over time, so we denote these changes by . The basic assumptions of the dynamics of rumor spreading in the proposed FOM are as follows:
- ■
- New rumor spreaders come from the connection between and . This occurs through the connection rate , where the rumor propagation complies with the mass action law.
- ■
- refers to the impact of , where the term represents the highest accessibility of media influence. Thus, becomes under the impact of the awareness program on the contact rate with the half-saturation constant h; denotes the rate of implementation of APs, which is proportional to the number of . Here, represents the proportionality constant that governs the deployment of APs. transfer to at the rate due to forgetting mechanisms or some social factors.
- ■
- In addition, we define as the recruitment rate and as the removal rate; demonstrates the depletion rate of APs due to their ineffectiveness.
- ■
- The suggested control measures are as follows. is used to control the contact of rumor spreaders with ignorant people by spreading the harm of rumors, enhancing people’s ability to recognize and disbelieve rumors, is used to control media reports to limit the negative effects of rumors, and is utilized to control the spreaders of rumors by taking some necessary actions such as designing a system to track rumors and imposing penalties on those who spread rumors; its effectiveness can be measured by d.
- ■
- It should be mentioned that these proposed control measures are assumed to be constant during the steady-state analysis and later treated as time-dependent functions in the formulation of the FOCP.
We assume that all the above parameters of the FOM are positive constants and our proposed model involves a homogeneous network. The dynamics of rumor spreading within CFD are determined using the propagation aspects in Figure 1.
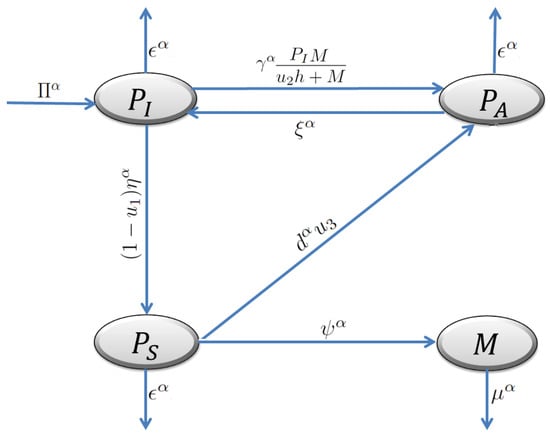
Figure 1.
Schematic description of the transmission dynamics between FOM (3) compartments.
In view of the above assumptions, the rumor dynamics within modifying the units of both sides (see, e.g., ref. [52]) are governed by the following system of FDEs:
with the ICs:
3.2. Existence and Uniqueness
Here, we employ the fixed-point principle to investigate the existence and uniqueness of the solution for FOM (3). Suppose that is a Banach space, where . To simplify the analysis of the system (3) and (4), we can rewrite it as follows:
where ; is a Banach space with . The function is a nonlinear continuous function and defined as such that
This is well-defined operator and it the norm, as
By transforming into a fixed-point problem, we now state the main theorem of existence and uniqueness of the projected solution where and the FOM parameters have non-negative values.
Proof.
We apply the steps of Schauder’s fixed-point theorem [53] in order to prove that there is at least one solution.
- Step 1 ( is continuous):-Suppose that is a positive sequence in Y such that as We want to show that .The functions given in Equation (6) and satisfy this as . Thus, for , we haveThen, we havewhere is a positive constant defined in Equation (9). In the same way, we can obtain the result for other components of g as:and are positive constants. Consequently, in at in Y. Generally, from Equations (10) and (11), we haveand from the above equation, we can writeUsing Lebesgue’s dominated convergence theorem, . Hence, is continuous operator.
- Step 2 ( is a bounded operator into bounded sets in Y):-Here, it suffices to show that , ∃ s.t. for each , where (compact and convex), one has .Let and we havethen, , this means is a bounded operator.
- Step 3 ( is a relatively compact operator):-Let where and be a bounded subset of Y (as in Step 2), then for every we obtainIf , then the right-hand side of Equation (12) tends to zero. From Step 1 into Step 3 with the Arzelà–Ascoli theorem, the operator is relativity compact. Thus, all conditions of Schauder’s fixed-point theorem are satisfied; this means that has a fixed point on I. The remaining part of this theorem (uniqueness of solution) can be proven as follows. Let be two solutions of the system (3) and (4), and from Equation (7), we have, the function satisfies the following Lipschitz condition:where is Lipschitz constant. From Equation (13), it is easy to deduce that
□
3.3. Positivity and Boundedness of the Solution
We now demonstrate the positivity and boundedness of the set solution , where . In order to prove non-negative solutions of FOM (3), we state the following lemma:
Lemma 3
([54]). Suppose that and belong to for and . Then, we have
where , .
Corollary 1
([55]). Let and belong to for . It follows from Lemma 3 that
- if ∀ , then is non-decreasing ∀ .
- if ∀ , then is non-increasing ∀ .
Theorem 3.
Suppose that is the set of initial positive values. Then, the set solution of FOM is positively invariant for all .
Proof.
Theorem 4.
For the FOM (3), the region of attraction can be given as the following set: .
4. Stability and Sensitivity Analysis
In this section, we study in detail how to obtain the EPs and their stability theorems, as well as the sensitivity analysis of the parameters in CRN. Finally, we present the solutions of FOM (3) in the absence of controls.
4.1. Existence of EPs and CRN
We evaluate all EPs of the following reduced system (where ):
Now, let us consider CFD of the state variables as equal to zero and solve the obtained system. Thus, we obtain the following two positive equilibriums:
- The rumor-free equilibrium (RFE) . In this case, the CRN represents “the expected number of newly infected population (rumor spreading) resulting from contact in the entire infection period in the whole susceptible population (ignorant individuals)” [56]. Using the next generation matrix (NGM) approach [57], we can compute CRN as is the spectral radius of , where and are defined as:Thus, the NGM becomesTherefore, the expression of CRN is
- For the existence of rumor-spreading equilibrium (RSE) , we define the next theorem.Theorem 5.The unique positive EP exists, whenever .
4.2. Stability of Equilibria
We now present the local stability of the EPs and as follows:
Theorem 6.
If , then the FOM (18) around RFE is LAS.
Proof.
The JM at RFE point is given by
Calculating the eigenvalues for the above matrix (where the eigen matrix is is the identity matrix) gives: if , , and . All eigenvalues have a negative real part, then the condition (2) will be , which means the RFE point is LAS. But if , then has a positive value, which means that the condition (2) is not fulfilled. Accordingly, the FOM around will be unstable, leading to checking the stability of RSE point . □
Proof.
The JM at can be written as
where and . All eigenvalues of are given by solving the following characteristic equation.
where
According to Routh–Hurwitz criteria [58], Equation (22) has four negative real parts , if and only if the condition satisfies such that , , and using Lemma 2, i.e., , then the FOM around RES is LAS, whenever . □
4.3. Sensitivity Analysis
This section explains the sensitivity analysis for the parameters of as stated in Equation (19). The sensitivity analysis would therefore demonstrate the important impacts of these parameters on and the spread of rumors. In light of this, the sensitivity index that follows is created as
where is the parameters in . Using the parameters , and the previously computed , we can obtain the following sensitivity index:
This means that if the parameters and increase, then also increases, provided that all other factors stay unchanged. As a result, the rumor spreads on a larger scale. This indicates that the propagation of the rumor will be aided if gullible people accept the claims and spread them on their own. Next, we looked at the parameters , and d, from which we can obtain the sensitivity index. Moreover, the values of the sensitivity index with these parameters are presented in Table 1.

Table 1.
Values of the sensitivity index for the parameters in at .
This indicates that decreases with an increase in the parameters and when other parameters remain unchanged, indicating a reduction in the scale of rumor propagation. It is evident that a disseminator’s disinterest in a rumor or decision to stop spreading a rumor for other reasons would slow this spreading and aid in managing the distribution scale of the rumor. Furthermore, fractional order plays a significant role in retarding the spread of rumors. As can be seen in Figure 2, decreasing the value of results in a corresponding decrease in the value of .
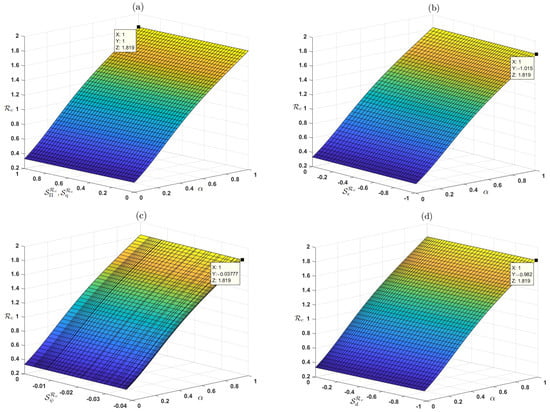
Figure 2.
Behavior of sensitivity indices ((a) , , (b) , (c) and (d) ) and with .
4.4. Numerical Simulation Without Control
Here, the behavior of the solutions for FOM (3) will be shown in the absence of the proposed controls. In this case, the value of is greater than one, and therefore, the spread of the rumor will persist over time among the population and its effect will remain effective. To illustrate this, we use PCM [59] to obtain the simulation of and M solutions through the application of the following general scheme on (5); the interval is replaced by a set of points , , , then the solution is approximated as such that .
where
and
where is the approximation after i corrector steps, is the predictor and is the last approximation after q corrector steps.
Simulations of the solutions for FOM (3) by implementing the previous method are depicted in sub-figures in Figure 3, where the values of parameters and ICS are as follows [12,46,60]: and . These sub-figures show that the number of ignorant, aware, spreaders and media reports declined to equilibrium after reaching a peak at the beginning of the period. In addition, the impact of fractional order is presented at . Therefore, in the next section, we look to reduce the climax period of rumor spreading through some effective control measures.
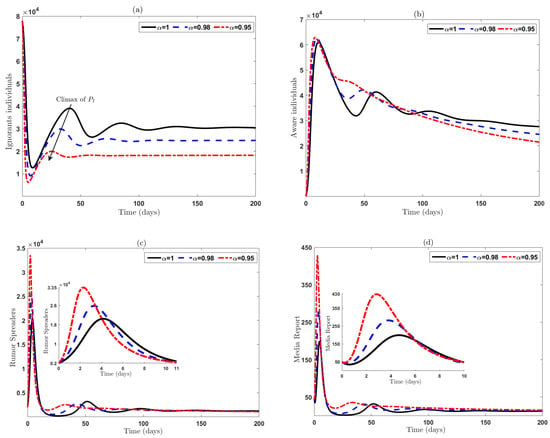
Figure 3.
Behavior of FOM solutions: (a) ignorant individuals, (b) aware individuals, (c) rumor spreaders and (d) media reports where .
5. Formulating of the FOCP
This section aims to reduce rumor spreaders and increase awareness of the population against the danger of rumor spreading by formulating FOCP while preserving the minimization of the cost of its control strategy. To this end, we construct the FOCP starting from the following objective function.
subject to the FOM (3) with ICs (4), where B is the weight balance for the spreading and are the weight balance for control measures.
The control set is given as:
In order to drive fractional NOCs for the proposed FOCP, we use the PMP [36,37]. So, we suppose that the Hamiltonian is given as
where are the adjoint variables. According to PMP, the adjoint equations are presented as
with transversality conditions
where are the optimal solutions for FOM (3) and are the optimal controls that minimize . Applying Theorem 1 and Lemma 1, the adjoint Equation (30) can be written as
where . Moreover, the optimality condition is
where , which minimize over the region , are given by
where
6. Simulation and Discussion
We now present the effectiveness of imposing control measures in the rumor FOM (3) by solving the FOCP (28) numerically adopting the previous theoretical analysis. We carried out different control strategies considering a combination of double control measures. We do not look for a single control measure because the population usually searches to take multiple actions in parallel to stop the growth of rumors. All numerical results are simulated by MATLAB (R2017a) using the FBS approach [23,24,27] based on the method explained in Section 4.4, as follows:
Step 0: Initialization of the IC values and parameters.
Step 1: Splitting the interval into N equal sub-intervals and the step-size is , and for This represents the beginning of the main for loop in our algorithm.
Step 2: Evaluating the values of and from the following equations.
where is given in Equation (34) and the initial values of controls are determined using the initial ICs and (31). The subsequent values of (for ) can be derived from the iterative solving of Equations (3) and (32) with the ICs and transversality conditions as in the steps below.
Step 3: Applying the PCM of FOM (3) to obtain new starting points:
The values and are given as follows:
where and are defined in Equations (26) and (27), respectively.
Step 4: Implementing the PCM to solve Equation (32), subject to the terminal conditions, the control values and state variables.
where
Step 5: Updating the values of and by entering the new values of state and co-state obtained from Step 3 and Step 4 into Step 2.
Step 6: Examining the convergence of our results by the variations between the variable values in the previous iteration and the present one. If these differences are negligible, then stop the iteration in our algorithm. Otherwise, go back to Step 3.
Now we discuss the optimality solution with different values of the fractional operator (where ) in the following strategies:
Strategy A: The effect of intervention control measures and .
Strategy B: The effect of intervention control measures and .
Strategy C: The effect of intervention control measures and .
Strategy D: The effect of all intervention control measures , and .
In Figure 4, we compare the effects of strategies A, B, C, and D, as well as the case without controls on the ignorant population with , and in Figure 4a, Figure 4b and Figure 4c, respectively. As can be seen from Figure 4a, all strategies have a significant impact in reducing the ignorant individuals in the first 10 days. However, the declining value of Strategy D is the largest and the declining value of Strategy A is the smallest compared with the uncontrolled case. In Figure 4b,c, we note that the fractional operator has a big effect on the behavior of the solution, where the value of the decrease is less than the integer case (i.e., ), and reaching stability is faster, as it is clear that the number of oscillations decreases as the value of decreases. We conclude that the absence of spreading the harmful effects of rumors and reducing the friction between rumor spreaders and those ignorant of it (i.e., ) gives an undesired result in reducing the number of individuals ignorant of rumors (i.e., Strategy A).
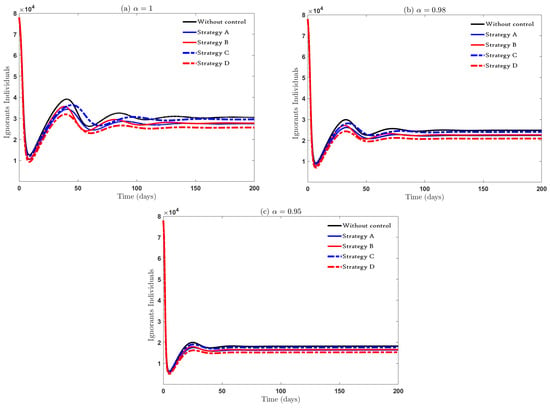
Figure 4.
The influence of suggested control strategies on .
The impact of the proposed strategies on aware individuals is depicted in Figure 5. We note that all strategies work to increase the number of aware individuals to reach the peak in the first 20 days of the control intervention period, but there is a difference in the speed of reaching that peak, as the fastest strategy is Strategy D and Strategy B is the slowest. It is also clear from the Figure 5b,c that the effect of fractional order increases the speed of reaching the peak and the state of stability. The observation is that the absence of publishing correct media broadcasts to limit the negative effects of rumors (i.e., ) gives an unsatisfactory result in increasing the number of individuals aware of rumors in society (i.e., Strategy B).
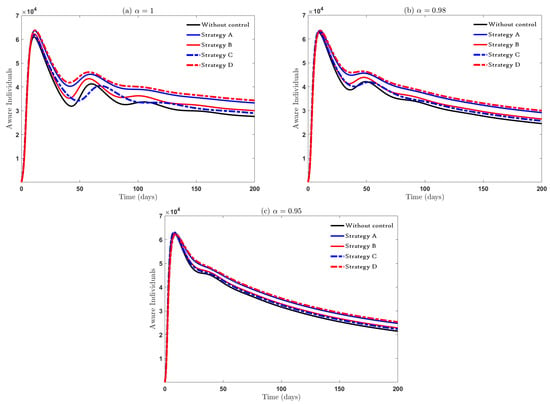
Figure 5.
The influence of suggested control strategies on .
The behavior and impact of the four strategies on rumor spreading among individuals are presented in Figure 6. We observe that at the beginning of the rumor propagation period, the number of spreaders reaches its climax, but after applying control measures, the situation begins to stabilize, and the number of spreaders decreases dramatically until stability is achieved. It is also clear from Figure 6a that Strategy D most noticeably reduces the peak number of spreaders, on the contrary, while Strategy A and Strategy C have a higher peak number of spreaders than the other strategies. The fractional order impact on rumor spreaders is displayed in Figure 6b,c. We conclude that not paying attention to the communication of rumor spreaders with ignorant people (i.e., ) and not controlling rumor spreaders (i.e., ) leads to an increase in rumors among individuals, as evident in Strategy A and Strategy C, respectively.
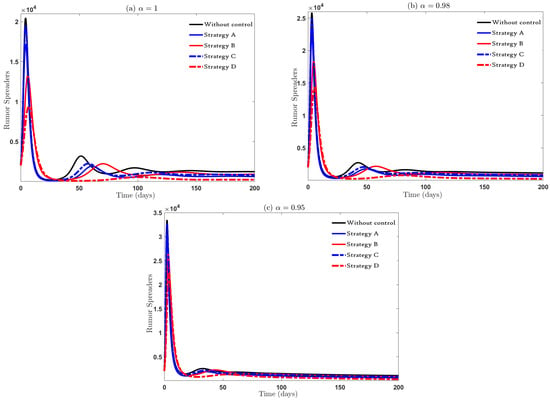
Figure 6.
The influence of suggested control strategies on .
Figure 7 illustrates the trend of media reports under suggested control strategies and the scenario without control. Clearly, the number of media broadcasts is lower in controlled cases compared to uncontrolled cases under any strategy. Thus, the proposed measures help expand media coverage. However, Strategy D is most effective in increasing media reports, whereas Strategy C has the least impact among the proposed strategies. The effect of the fractional operator on the trend of media reports is also evident in Figure 7b,c. We find from the previous results that all strategies effectively reduce the spread of rumors, but their effects on the variables differ. Despite this, they unanimously suggest that Strategy D performs best across all variables and is the most effective in curbing rumor spread in society. Moreover, formulating the problem in a fractional context helps all model variables reach stability more quickly than with integer order models.
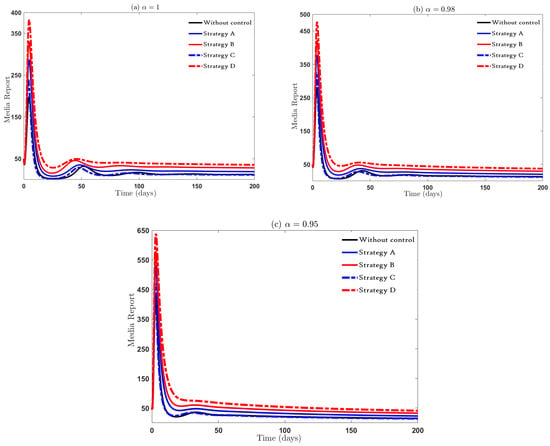
Figure 7.
The influence of suggested control strategies on .
7. Conclusions
This research addresses a novel FOM of rumor spreading and investigates the process under new communication modes, by considering the effect of media reporting. To do this, we construct a FOM containing three classes of the population to represent the ignorant, aware and spreaders of the rumors. Additionally, media reports are considered as a variable that varies over time to show the influence of both positive and negative media reports on the propagation of rumors. We demonstrated that the FOM solutions are bounded and positive. The EPs and stability criteria of the FOM are discussed, and the CRN is evaluated utilizing the NGM approach. Then, using the sensitivity analysis, we examined the impact of model parameters that appear in the CRN. To reduce the overall cost of preventing rumor diffusion, the FOCP is established by taking into account three time-dependent control measures in the proposed FOM. The optimal control solution is computed using PMP within the anticipated time frame. We proposed four different control strategies that aim to reduce the negative consequences of rumors with the help of awareness through media reports. Finally, using numerical simulation, the effects of various parameters on the rumor propagation process are visualized. We also explore the FOCP to regulate the scale of rumor spreading. This approach offers a fresh perspective on researching the best way to stop rumors from spreading. It is demonstrated by theoretical analysis and numerical simulation that while favorable media coverage and reports cannot stop rumors from spreading, they can accelerate their spread by impairing people’s capacity to recognize false information.
Thus, our research offers a new perspective on how to counter the spread of rumors, based on theoretical analysis and numerical simulations.
Author Contributions
Conceptualization, H.M.A. and I.G.A.; methodology, H.M.A. and I.G.A.; software, I.G.A. and H.M.A.; validation, H.M.A., S.O. and I.G.A.; formal analysis, I.G.A. and H.M.A.; investigation, H.M.A., S.O. and I.G.A.; resources, I.G.A. and H.M.A.; data curation, H.M.A., S.O. and I.G.A.; writing—original draft preparation, I.G.A. and H.M.A.; writing—review and editing, H.M.A., S.O. and I.G.A.; visualization, H.M.A., S.O. and I.G.A.; supervision, S.O.; project administration, I.G.A. and H.M.A.; funding acquisition, S.O. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The authors confirm that the data supporting the findings of this study are available within the cited article.
Acknowledgments
The authors are thankful to the Deanship of Graduate Studies and Scientific Research at the University of Bisha for supporting this work through the Fast-Track Research Support Program.
Conflicts of Interest
The authors declare no conflicts of interest regarding the publication of this paper.
References
- Kawachi, K. Deterministic models for rumor transmission. Nonlinear Anal. Real World Appl. 2008, 9, 1989–2028. [Google Scholar] [CrossRef]
- Misra, A.K. A simple mathematical model for the spread of two political parties. Nonlinear Anal. Model. Control. 2012, 13, 343–354. [Google Scholar] [CrossRef]
- Huo, L.A.; Huang, P.; Fang, X. An interplay model for authorities’ actions and rumor spreading in emergency event. Phys. A Stat. Mech. Appl. 2011, 390, 3267–3274. [Google Scholar] [CrossRef]
- Ma, J.; Li, D.; Tian, Z. Rumor spreading in online social networks by considering the bipolar social reinforcement. Phys. A Stat. Mech. Appl. 2016, 447, 108–115. [Google Scholar] [CrossRef]
- Huo, L.A.; Song, N. Dynamical interplay between the dissemination of scientific knowledge and rumor spreading in emergency. Phys. A Stat. Mech. Appl. 2016, 461, 73–84. [Google Scholar] [CrossRef]
- Tian, R.Y.; Zhang, X.F.; Liu, Y.-J. SSIC model: A multi-layer model for intervention of online rumors spreading. Phys. A Stat. Mech. Appl. 2015, 427, 181–191. [Google Scholar] [CrossRef]
- Wang, J.; Zhao, L.; Huang, R. SIRaRu rumor spreading model in complex networks. Phys. A Stat. Mech. Appl. 2014, 398, 43–55. [Google Scholar] [CrossRef]
- Thompson, K.; Estrada, R.; Daugherty, D.; Cintron-Arias, A. A Deterministic Approach to the Spread of Rumors; Technical Report BU-1642-M; Cornell University, Department of Biological Statistics and Computational Biolology: Ithaca, NY, USA, 2003. [Google Scholar]
- Ndii, M.Z.; Allingham, D.; Hickson, R.I.; Glass, K. The effect of Wolbachia on dengue dynamics in the presence of two serotypes of dengue: Symmetric and asymmetric epidemiological characteristics. Epidemiol. Infect. 2016, 144, 2874–2882. [Google Scholar] [CrossRef] [PubMed]
- Jin, F.; Dougherty, E.; Saraf, P.; Cao, Y.; Ramakrishnan, N. Epidemiological Modeling of News and Rumors on Twitter. In Proceedings of the 7th SNA-KDD Workshop, Chicago, IL, USA, 11 August 2013. [Google Scholar]
- Zhao, L.; Xie, W.; Gao, H.O.; Qiu, X.; Wang, X.; Zhang, S. A rumor spreading model with variable forgetting rate. Phys. A Stat. Mech. Appl. 2013, 392, 6146–6154. [Google Scholar] [CrossRef]
- Zhao, L.J.; Cui, H.; Qiu, X.; Wang, X.; Wang, J. SIR rumor spreading model in the new media age. Phys. A Stat. Mech. Appl. 2013, 392, 995–1003. [Google Scholar] [CrossRef]
- Ganesh, A.J. Rumour Spreading on Graphs. Technical Report in University of Bristol on 30 August 2015. Available online: https://people.maths.bris.ac.uk/~maajg/teaching/complexnets/rumours.pdf (accessed on 1 April 2025).
- Funk, S.; Jansen, V.A.A. The talk of the town: Modelling the spread of information and changes in behaviour. In Modeling the Interplay Between Human Behavior and the Spread of Infectious Diseases; Springer: New York, NY, USA, 2013; pp. 93–102. [Google Scholar]
- Aldila, D.; Paramartha, H.P.; Tasman, H. An analysis Of rumor spreading model with contra productive intervention. Int. J. Pure Appl. Math. 2017, 112, 519–530. [Google Scholar] [CrossRef]
- Afassinou, K. Analysis of the impact of education rate on the rumor spreading mechanism. Phys. A Stat. Mech. Appl. 2014, 414, 43–52. [Google Scholar] [CrossRef]
- Zhao, L.; Wang, Q.; Cheng, J.; Zhang, D.; Ma, T.; Chen, Y.; Wang, J. The impact of authorities’ media and rumor dissemination on the evolution of emergency. Phys. A Stat. Mech. Appl. 2012, 391, 3978–3987. [Google Scholar] [CrossRef]
- Zhuang, Y.; Arenas, A.; Yagan, O. Clustering determines the dynamics of complex contagions in multiplex networks. Phys. Rev. E 2017, 95, 012312. [Google Scholar] [CrossRef] [PubMed]
- Zhu, L.; Wang, Y. Rumor spreading model with noise interference in complex social networks. Phys. A Stat. Mech. Appl. 2017, 469, 750–760. [Google Scholar] [CrossRef]
- Camargo, D.; Popov, S. Total flooding time and rumor propagation on graphs. J. Stat. Phys. 2017, 166, 1558–1571. [Google Scholar] [CrossRef]
- Saeedian, M.; Khalighi, M.; Azimi-Tafreshi, N.; Jafari, G.R.; Ausloos, M. Memory effects on epidemic evolution: The susceptible-infected-recovered epidemic model. Phys. Rev. E 2017, 95, 022409. [Google Scholar] [CrossRef]
- Naik, P.A.; Yavuz, M.; Qureshi, S.; Naik, M.-u.-d.; Owolabi, K.M.; Soomro, A. Abdul Hamid GanieMemory impacts in hepatitis C: A global analysis of a fractional-order model with an effective treatment. Comput. Method Prog. Biomed. 2024, 254, 108306. [Google Scholar] [CrossRef]
- Ali, H.M.; Ameen, I. Stability and optimal control analysis for studying the transmission dynamics of a fractional-order MSV epidemic model. J. Comput. Appl. Math. 2023, 434, 115352. [Google Scholar] [CrossRef]
- Ameen, I.; Baleanu, D.; Ali, H.M. Different strategies to confront maize streak disease based on fractional optimal control formulation. Chaos Solitons Fractals 2022, 164, 112699. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations; Academic Press: New York, NY, USA, 1999. [Google Scholar]
- Alzahrani, F.; Razzaq, O.A.; Rehman, D.U.; Khan, N.A.; Alshomrani, A.S.; Ullah, M.Z. Repercussions of unreported populace on disease dynamics and its optimal control through system of fractional order delay differential equations. Chaos Solitons Fractals 2022, 158, 111997. [Google Scholar] [CrossRef]
- Kheiri, H.; Jafari, M. Stability analysis of a fractional order model for the HIV/AIDS epidemic in a patchy environment. J. Comput. Appl. Math. 2019, 346, 323–339. [Google Scholar] [CrossRef]
- Alqahtani, Z.; Almuneef, A.; DarAssi, M.H.; AbuHour, Y.; Al-arydah, M.T.; Safi, M.A.; Al-Hdaibat, B. Mathematical analysis of fractional Chlamydia pandemic model. Sci. Rep. 2024, 14, 31113. [Google Scholar] [CrossRef]
- Feng, Y.; Zhang, X.; Chen, Y.; Wei, L. A compact finite difference scheme for solving fractional Black-Scholes option pricing model. J. Inequal. Appl. 2025, 2025, 36. [Google Scholar] [CrossRef]
- Zhang, X.; Wei, L.; Liu, J. Application of the LDG method using generalized alternating numerical flux to the fourth-order time-fractional sub-diffusion model. Appl. Math. Lett. 2025, 168, 109580. [Google Scholar] [CrossRef]
- Singh, J. A new analysis for fractional rumor spreading dynamical model in a social network with Mittag-Leffler law. Chaos Interdiscip. J. Nonlinear Sci. 2019, 29, 013137. [Google Scholar] [CrossRef]
- Ren, G.; Yu, Y.; Lu, Z.; Chen, W. A Fractional Order Model for Rumor Spreading in Mobile Social Networks from A Stochastic Process. In Proceedings of the 2021 9th International Conference on Systems and Control (ICSC), Caen, France, 24–26 November 2021; pp. 312–318. [Google Scholar]
- Graef, J.; Kong, L.; Ledoan, A.; Wang, M. Stability analysis of a fractional online social network model. Math. Comput. Simul. 2020, 178, 625–645. [Google Scholar] [CrossRef]
- Wang, C.; Tan, Z.; Ye, Y.; Wang, L.; Cheong, L.H.; Xie, N. A rumor spreading model based on information entropy. Sci. Rep. 2017, 7, 9615. [Google Scholar] [CrossRef] [PubMed]
- Yang, R.; Han, D. Multi-message topic dissemination probabilistic model with memory attenuation based on Social-Messages Network. Int. J. Mod. Phys. C 2019, 30, 1940011. [Google Scholar] [CrossRef]
- Pontryagin, L.S.; Boltyanskii, V.; Gamkrelidze, R.V. The Mathematical Theory of Optimal Processes; Gordon and Breach Science Publishers: London, UK, 1986. [Google Scholar]
- Ali, H.M.; Pereira, F.L.; Gama, S.M.A. A new approach to the Pontryagin maximum principle for nonlinear fractional optimal control problems. Math. Meth. Appl. Sci. 2016, 39, 3640–3649. [Google Scholar] [CrossRef]
- Syam, S.M.; Siri, Z.; Altoum, S.H.; Kasmani, R.M. A new method for solving fractional optimal control problems. J. Vib. Control 2024, 2024, 10775463241264329. [Google Scholar] [CrossRef]
- Ali, H.M.; Ameen, I.G.; Gaber, Y.A. The effect of curative and preventive optimal control measures on a fractional order plant disease model. Math. Comput. Simul. 2024, 220, 496–515. [Google Scholar] [CrossRef]
- Mandal, M.; Jana, S.; Nandi, S.K.; Kar, T.K. Modelling and control of a fractional-order epidemic model with fear effect. Energy Ecol. Environ. 2020, 5, 421–432. [Google Scholar] [CrossRef]
- Teklu, S.W. Analysis of fractional order model on higher institution students anxiety towards mathematics with optimal control theory. Sci. Rep. 2023, 13, 6867. [Google Scholar] [CrossRef]
- Ali, H.M.; Ameen, I. Optimal control strategies of a fractional-order model for Zika virus infection involving various transmissions. Chaos Solitons Fractals 2021, 146, 110864. [Google Scholar] [CrossRef]
- Sun, D.; Li, Q.; Zhao, W. Stability and Optimal Control of a Fractional SEQIR Epidemic Model with Saturated Incidence Rate. Fractal Fract. 2023, 7, 533. [Google Scholar] [CrossRef]
- Ye, M.; Li, J.; Jiang, H. Dynamic analysis and optimal control of a novel fractional-order 2I2SR rumor spreading model. Nonlinear Anal. Model. Control 2023, 28, 1–24. [Google Scholar] [CrossRef]
- Guo, Y.; Li, T. Fractional-order modeling and optimal control of a new online game addiction model based on real data. Commun. Nonlinear Sci. 2023, 121, 107221. [Google Scholar] [CrossRef]
- Wang, L.; Zhao, X. Stability analysis and optimal control of a rumor spreading model with media report. Physica A 2019, 517, 551–562. [Google Scholar]
- Baleanu, D.; Diethelm, K.; Scalas, E.; Trujillo, J.J. Fractional Calculus: Models and Numerical Methods, Series on Complexity, Nonlinearity and Chaos; World Scientific Publishing Company: Singapore; Hackensack, NJ, USA; London, UK; Hong Kong, China, 2012; Volume 3. [Google Scholar]
- Diethelm, K. The Analysis of Fractional Differential Equations, an Application-Oriented Exposition Using Operators of Caputo Type; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Ameen, I.; Baleanu, D.; Ali, H.M. An efficient algorithm for solving the fractional optimal control of SIRV epidemic model with a combination of vaccination and treatment. Chaos Soliton Fractal 2020, 137, 109892. [Google Scholar] [CrossRef]
- Tavazoei, M.S.; Haeri, M. Chaotic attractors in incommensurate fractional order systems. Phys. D 2008, 237, 2628–2637. [Google Scholar] [CrossRef]
- Lu, B.; Sun, J.; Chen, B.; Wang, Q.; Tan, Q. A Study on the Effectiveness of Rumor Control via Social Media Networks to Alleviate Public Panic About COVID-19. Front. Public Health 2022, 10, 765581. [Google Scholar] [CrossRef] [PubMed]
- Islam, M.R.; Peace, A.; Medina, D.; Oraby, T. Integer versus fractional order SEIR deterministic and stochastic models of measles. Int. J. Environ. Res. Public Health 2020, 17, 2–19. [Google Scholar] [CrossRef] [PubMed]
- Granas, A.; Dugundji, J. Fixed Point Theory; Springer: New York, NY, USA, 2003. [Google Scholar]
- Odibat, Z.M.; Shawagfeh, N.T. Generalized Taylor’s formula. Appl. Math. Comput. 2007, 186, 286–293. [Google Scholar] [CrossRef]
- Li, Y.; Chen, Y.; Podlubny, I. Stability of fractional-order nonlinear dynamic systems: Lyapunov direct method and generalized Mittag Leffler stability. Comput. Math. Appl. 2010, 59, 1810–1821. [Google Scholar] [CrossRef]
- Heffernan, J.M.; Smith, R.J.; Wahl, L.M. Perspectives on the basic reproductive ratio. J. R. Soc. Interface 2005, 2, 281–293. [Google Scholar] [CrossRef]
- Driessche, P.V.; Watmough, J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 2002, 180, 29–48. [Google Scholar] [CrossRef]
- Ahmed, E.; El-Sayed, A.M.A.; El-Saka, H.A.A. On some Routh-Hurwitz conditions for fractional order differential equations and their applications in Lorenz, Rössler, Chua and Chen systems. Phys. Lett. A 2006, 358, 1–4. [Google Scholar] [CrossRef]
- Ameen, I.; Novati, P. The solution of fractional order epidemic model by implicit Adams methods. Appl. Math. Model. 2017, 43, 78–84. [Google Scholar] [CrossRef]
- Zhao, L.J.; Wang, Q.; Cheng, J.; Chen, Y.; Wang, J.; Huang, W. Rumor spreading model with consideration of forgetting mechanism: A case of online blogging Live Journal. Phys. A 2011, 390, 2619–2625. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).