Abstract
Predicting stock trends has garnered extensive attention from investors and researchers due to its potential to optimize stock investment returns. The fluctuation of stock prices is complex and influenced by multiple factors, presenting two major challenges: the first challenge lies in the the temporal dependence of individual stocks and the spatial correlation among multiple stocks. The second challenge emerges from having insufficient historical data availability for newly listed stocks. To address these challenges, this paper proposes a spatio-temporal hypergraph transformer (STHformer). The proposed model employs a temporal encoder with an aggregation module to capture temporal patterns, utilizes self-attention to dynamically generate hyperedges, and selects cross-attention to implement hypergraph-associated convolution. Furthermore, pretraining based on reconstruction of masked sequences is implemented. This framework enhances the model’s cold-start capability, making it more adaptable to newly listed stocks with insufficient training data. Experimental results show that the proposed model, after pretraining on data from over two thousand stocks, performed well on datasets from the stock markets of the United States and China.
Keywords:
stock trend prediction; self-supervised pretraining; hypergraph neural network; time series analysis MSC:
68T07; 91B84
1. Introduction
Stock price prediction, aimed at forecasting future trends in the stock market through the analysis of historical data, is a crucial technique for guiding profitable investment decisions. However, due to the complex interplay of macroeconomic factors, capital flows, significant events, and other variables, stock price series diverge from typical stationary sequences, exhibiting high volatility and chaos. Consequently, accurately predicting stock prices and utilizing the information to formulate intricate investment strategies remains an open question.
Researchers have made extensive efforts to enhance the accuracy of stock price predictions. Most traditional stock price prediction models utilize fundamental statistical methods and machine learning techniques to learn potential patterns from stock price data, such as support vector machines (SVMs) [1], random forests [2], and XGBoost [3]. However, these methods typically rely on analyzing static patterns in historical sequences and thus fail to capture the nonlinear characteristics of stock price series. With the advancement of deep learning, deep neural networks have been widely employed to extract temporal features from stock time series. Researchers have explored and proposed models like long short-term memory (LSTM) [4], graph neural networks (GNNs) [5,6], and Transformers [7,8,9] to better capture the complex patterns and dynamic changes in stock price series.
Existing models often focus primarily on utilizing historical information of a single stock to predict its future trends, overlooking the natural correlations among stocks resulting from industry chains and company attributes. The future price of a stock is intuitively and insightfully influenced by other stocks. If these useful pieces of information can be effectively extracted, predictions would become more accurate. A few studies have attempted to utilize graph networks to capture the information across different stocks. However, these approaches are often oversimplified or require extensive manual efforts. For example, the studies by Feng et al. [10] and Kim et al. [11] on stock correlations were based on predefined industry relationships. On the one hand, traditional graph networks can only model pairwise relationships between stocks, failing to model the real relationships of multiple stocks in the market, while hypergraph networks with hyperedge structures can capture the high-order relationships among stocks. On the other hand, predefined static architectures lack the capacity to learn dynamic inter-stock correlations. Therefore, how to effectively leverage the dynamic relationships among stocks to enhance prediction performance remains a challenge.
In financial markets, new stocks are constantly being listed, and index datasets are also regularly updated, such as the China securities index 300 (CSI300) and national association of securities dealers automated quotations 100 (NASDAQ100). Typically, models rely on existing historical data and market features for training and prediction. However, when dealing with newly listed stocks, these stocks often lack sufficient historical data, which limits the predictive power of the model. Effectively predicting the performance of these “new stocks” has become a pressing problem. Inspired by the recent significant progress in pretraining methods in the natural language processing (NLP) and computer vision (CV) domains [12], various pretrained time series analysis approaches have been proposed [13,14]. The adoption of pretraining paradigms enables deep models to learn prior knowledge from large-scale unlabeled data, further enhancing the performance of various downstream tasks. Currently, there has been limited work on applying pretraining methods to stock prediction. Some researchers have pretrained the encoder of their model by using contrastive learning based on stock price co-movement [15]. However, the behavior of different stocks may not always adhere to similar patterns, especially when dealing with newly listed stocks.
To sum up, research on stock price trend prediction using stock relationships faces two major challenges:
- Traditional methods rely on simple correlations between stock pairs, without considering the complex high-order relationships among multiple stocks. This leads to an inability to capture the complex dynamic relationships in the stock market and results in inefficient utilization of available data.
- Newly listed stocks usually lack historical data, which poses a cold-start problem for traditional models that heavily rely on historical sequence modeling. Pretraining methods, while promising in other fields, face challenges in stock prediction due to the heterogeneous behavior of different stocks. This highlights the need for more adaptive pretraining frameworks tailored to financial data.
To address the aforementioned challenges, inspired by self-attention mechanisms and hypergraph learning technology, we propose a spatio-temporal hypergraph transformer (STHformer). Firstly, a temporal encoder is utilized to capture the essential representation of the sequence, while the temporal aggregation module enhances the model’s overall representation of temporal characteristics. Secondly, we develop a hybrid attention hypergraph module to extract relationships among stocks. Specifically, it generates hyperedges among stocks through self-attention, and then performs hypergraph-related convolution through an improved cross-attention. We formulate and prove Theorem 1 to establish that our proposed architecture is equivalent to a novel hypergraph convolution framework. This framework uniquely enables the modeling of dynamic higher-order relationships among stocks Finally, we adopt a self-supervised masked sequence reconstruction task to pretrain the model, enabling it to adapt to evolving index datasets. Our contributions are summarized as follows:
- We propose a spatio-temporal hypergraph transformer for stock trend prediction. The network considers the temporal correlation of each stock through a temporal encoder, and the spatial correlation between stocks through a hybrid attention hypergraph module, which consists of self-attention and cross-attention mechanisms. The self-attention dynamically generates hyperedges, while the cross-attention performs convolution operations on the hypergraph associations to model complex and high-order stock relationships.
- We design an efficient pretraining and fine-tuning framework, employing a pretraining task that reconstructs masked time series to enhance the model’s generalization ability and reduce its dependency on historical data, thereby making it applicable to newly listed stocks with limited available samples.
- Experiments on the CSI300 and NASDAQ100 datasets demonstrated the effectiveness of STHformer, with superior predictive performance and long-term profitability compared to several state-of-the-art solutions.
2. Related Work
2.1. Spatial-Temporal Models
Time series prediction is a crucial task that has attracted significant attention in recent years, due to its extensive applications. To capture temporal dependencies, Xu et al. [16] devised a Tensorized LSTM with adaptive shared memory capabilities, specifically tailored to grasp long-term temporal dependencies. Meanwhile, Liu et al. [17] developed a prediction framework based on temporal convolutional networks (TCNs), to extract unique and valuable features from time series. Recently, Transformer-based approaches have emerged as a dominant paradigm, due to their ability to model long-range dependencies through self-attention mechanisms. Liu et al. [18] employed a transposed Transformer architecture to capture temporal multivariate correlations. For the problem of long-term time series forecasting, Transformer architectures have achieved significant results. Their effectiveness primarily originates from the self-attention mechanism’s ability to model distant temporal relationships. Zhou et al. [19] proposed the Informer model, which employs a sparse attention matrix to significantly reduce computational complexity, and adopts a generative decoder for prediction. Ren et al. [20] introduced the temporal diffusion Transformer (TDT), which leverages the physical principles of diffusion processes to model the intrinsic evolution of time series, improving prediction performance by incorporating multi-scale periodicity and energy-minimization constraints.
However, the aforementioned models consider each series in isolation, neglecting the complex relationships among them and failing to harness these connections to enhance prediction accuracy. In response to this problem, researchers have explored the use of graph convolutional networks (GCNs) to capture the mutual influence among series by treating time series as nodes in a graph and the relationships between series as edges. Relevant studies have already demonstrated the effectiveness of GCNs in time series forecasting. For instance, Wu et al. [21] improved the graph convolution module and incorporated a graph learning module to learn the relationships among variables from data. To achieve faster training speeds with fewer parameters, Yu et al. [22] proposed a method to grasp the essential temporal features and the most valuable spatial features through graph convolution and gated temporal convolution. Du et al. [23] utilized a LSTM Network with Attention Layer to extract temporal features and self-attention mechanisms to capture spatial relationships. Zhang et al. [24] constructed a spatio-temporal forecasting model leveraging a multi-head attention model, where scaled dot-product attention with positional encoding was used to capture temporal features, and a graph attention network with a multi-head attention mechanism was employed to capture spatial features.
However, graph networks can only capture the spatio-temporal dependencies between node pairs and are unable to handle high-order correlations among time series. To address the aforementioned issue, Wang et al. [25] employed the K-nearest neighbors method to dynamically generate hypergraph structures, which were then utilized in a spatio-temporal hypergraph network. Shang et al. [26] introduced the framework of multi-scale hypergraphs to explore the interactions between temporal patterns at different scales and thereby further improve prediction accuracy.
Numerous research endeavors have demonstrated that designing spatio-temporal deep neural networks that concurrently consider temporal dependencies and spatial relationships can enhance the performance of time series forecasting models. The model proposed in this paper is capable of extracting crucial temporal features, to reduce computation time, while also mining dynamic spatial relationships.
2.2. Self-Supervised Pretraining in Time Series Modeling
In recent years, pretrained models have witnessed significant advancements. The success of autoencoder-based approaches underscores the robust representational power of the masked reconstruction pretraining framework. Nie et al. [27] proposed a method for predicting masked subsequence-level patches, aiming to capture local semantic information, while minimizing memory usage. They employed masked modeling as an auxiliary task to enhance the prediction and classification performance of their Transformer-based methods. By bridging masked modeling with manifold learning, Dong et al. [14] simplified the reconstruction task by combining corrupted yet complementary temporal variations across multiple masked subsequences. Zhou et al. [13] evaluated their approach by freezing the self-attention and feedforward layers in a pretrained Transformer and fine-tuning it across all major types of tasks involving time series analysis. The results demonstrated that the model achieved comparable or state-of-the-art performance across all temporal analysis tasks. Furthermore, Xu et al. [15] introduced a self-supervised method based on contrastive learning, which pretrains a multi-scale encoder through the task of detecting co-movements in stock prices, ultimately utilizing a GRU for the final prediction.
2.3. Stock Price Forecasting
Researchers have investigated various methods using deep neural networks for stock prediction over recent years. Gupta et al. [28] and Hu et al. [29] employed recurrent neural networks to model individual stock price movements. Alternatively, Yao et al. [30] utilized convolutional neural networks to predict short-term trends. To improve the accuracy of stock prediction, various approaches have been explored. Qiu et al. [31] introduced a self-attention mechanism, Ma et al. [32] explored multitask learning approaches, while Li et al. [33] proposed market-gating techniques and Lin et al. [34] introduced a method based on deep reinforcement learning. Later studies achieved remarkable results by taking into account the relationships among stocks. For instance, Sawhney et al. [35] proposed a spatial-temporal hypergraph attention network for stock ranking (STHAN-SR) to rank stocks based on profit. It captures the complex relationships between stocks through hypergraph and temporal attention mechanisms. Huynh et al. [36] utilized a hypergraph to capture non-pairwise correlations with temporal generative filters tailored to individual patterns for each stock. Su et al. [37] employed adaptive hypergraph generation and adaptive spatial-temporal convolution to model the extrinsic and intrinsic relationships of stocks, and for the first time, took noise into account by utilizing noise-aware attention to enhance prediction accuracy.
However, existing stock prediction methods fail to provide accurate predictions for newly listed stocks. The model proposed in this paper is designed to address this issue.
3. Preliminary
Problem Formulation
- Stock Trend Forecasting: Assuming that there are N stocks in the stock market, a set of historical sequence data at day t is represented by , where T is the length of the sequence, and F is the dimension of the original feature, such as open, high, low, close and volume. Each stock i has historical sequence data at day t. If the closing price of stock is higher than the opening price of , the stock is labeled with “up” (), otherwise it is labeled with “down” (), where h is a specified horizon ahead of the current timestamp. The objective of stock trend forecasting is to establish a mapping relationship, which is defined as follows:where is the input stock sequence data and , is the predicted trend for all stocks at day t+h.
- Hypergraph: A hypergraph is constructed to model the interdependence among stocks, where the hyperedges encode higher-order relationships between them. The collection of vertices is denoted by V, while the set of hyperedges is represented by E. Each hyperedge is associated with a positive weight w, and these weights are collectively organized in a diagonal matrix .
4. Model
The overall architecture of our framework, illustrated in Figure 1, is referred to as a pretrained spatio-temporal hypergraph transformer. The essential vectors in the process of the computation are summarized in Table 1. This includes the following four key components:
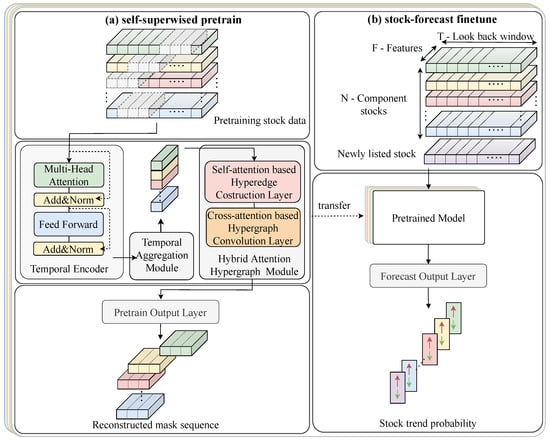
Figure 1.
The overall framework of the proposed method.

Table 1.
Nomenclature.
- Temporal Encoder: This module employs a Transformer encoder to extract the temporal correlations in each stock’s daily data.
- Temporal Aggregation Module: This module integrates information across various time points to produce a localized embedding. This embedding captures all significant signals along the temporal axis, while maintaining the intricate local details of the stock’s behavior over time
- Hybrid Attention Hypergraph Module: This module is designed to explore the spatial relationships between stocks. It comprises two attention layers: the self-attention-based hyperedge construction layer dynamically generates hyperedges, while the cross-attention-based hypergraph convolution layer performs hypergraph convolution on stock nodes based on the generated hyperedge matrix.
- Self-Supervised Pretraining Scheme: This strategy involves reconstructing the original time series from the masked time series, with the objective of learning the valuable low-level information from data in an unsupervised manner.
4.1. Temporal Encoder
In view of the demonstrated efficacy of attention mechanisms in processing time series data, we utilize a Transformer encoder to develop the temporal encoder. The historical sequence of stock i on the trading day t is denoted as . It is mapped to the embedding space of dimension U via a learnable linear projection , and sinusoidal position encoding is incorporated into the embedded input to represent the sequential information in the time series:
The data from the feature mapping layer are then fed to the Transformer encoder. The multi-head attention transform these data into a query matrix , key matrix , and value matrix :
where , , denote the parameter matrix; h denotes the h-th head. Subsequently, a scaled production is used for obtaining the attention output :
Finally, the outputs from multiple heads are concatenated and multiplied by a weight matrix to obtain the final output, and feed-forward layers, , are utilized to aggregate contexts with residual connections:
where is the final representation of the stock i.
4.2. Temporal Aggregation Module
Existing works typically generate one or more embedding representations for each stock after modeling stock correlations, resulting in increased computational costs. In contrast, our method queries all historical time embeddings for each stock using their final time embedding to produce a comprehensive stock embedding before correlation modeling. This strategy enhances computational efficiency, while preventing the loss of temporal information. To aggregate the obtained representation encoding, we employ a temporal attention mechanism along the time axis:
where the latest temporal embedding is used to query the overall temporal embeddings, and the attention score is calculated through the transformation matrix . The temporal embedding of each stock is updated to based on the normalized attention scores.
4.3. Hybrid Attention Hypergraph Module
The interconnections between stocks can be regarded as a type of spatial relationship. Traditional graph-based models are unable to capture high-order spatial relationships. Moreover, traditional hypergraph-based models have static hypergraph structures, making them unable to capture dynamic spatial relationships. This paper employs a hybrid attention hypergraph module to capture the time-varying spatial relationships among nodes, without any prior knowledge like industry information. This module consists of a dynamic hyperedge generation layer and a hypergraph convolutional layer, as shown in Figure 2. In the modeling of the spatial relationship, each node represents a stock, while the hyperedges capture higher-order relationships among multiple stocks, not just pairs. For example, if several stocks in the same industry react to news together, our model captures this group behavior. The incidence matrix is built using self-attention, which maps nodes to edges. Finally, the hypergraph convolutional layer is used to perform cross-attention with the incidence matrix and multiply the node features to look at how each stock relates to the group and updates the stock information based on the group’s behavior. The details of each layer will be described in the following subsections.
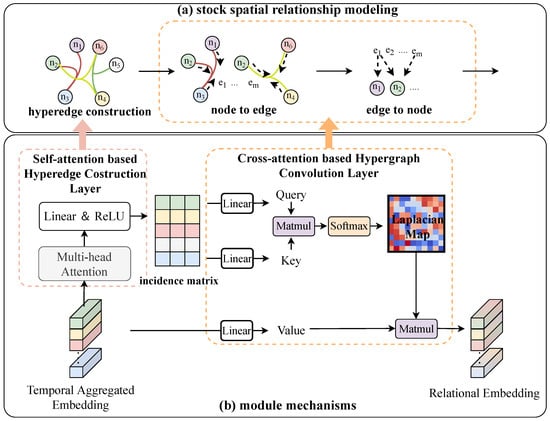
Figure 2.
The hybrid attention hypergraph module flow.
4.3.1. Self-Attention-Based Hyperedge Construction Layer
To accurately capture the time-varying hypergraph structures embedded in time series data, we introduce a dynamic hyperedge construction layer based on a self-attention mechanism.
Specifically, we first feed the aggregated temporal embedding into a multi-head attention layer, which can capture information from different representation subspaces of the input data by applying multiple attention mechanisms in parallel. This is denoted as . The process of extracting the embedding is as follows:
where , , denote the parameter matrix.
Subsequently, the embedding M is fed into a fully connected layer with a ReLU activation function to generate hyperedges and construct a dynamic incidence matrix:
where and are the learnable parameters, represents the dynamic incidence matrix embedded in stock data, N denotes the number of stocks, and U represents the number of hyperedges. This matrix captures the complex relationships among multiple stocks by representing how each stock is connected to various hyperedges. In this paper, we set the number of hyperedges as equal to the number of the hidden size U.
Specifically, the incidence matrix enables the modeling of higher-order associations among N stocks via each hyperedge. This approach goes beyond simple pairwise relationships and captures more intricate interactions within the stock market.
4.3.2. Cross-Attention-Based Hypergraph Convolution Layer
In this study, we use a cross-attention-based hypergraph convolution layer to extract the high-order relational embedding of stocks. Specifically, this layer employs a cross-attention-based architecture to aggregate and update node information based on the incidence matrix obtained above. We revise the cross-attention mechanism to compute the hypergraph convolution, which can be formulated as follows:
where are the query matrix and the key matrix generated from the incidence matrix, and V is the node feature obtained form the aggregated embedding. are the learnable parameters, is the aggregated stock features through self-queries of the incidence matrix, represents the node degree matrix, and represents the edge degree matrix, both of which are diagonal matrices.
Specifically, the incidence matrix captures complex interactions among multiple stocks via hyperedges, and these relationships are embedded into through the aggregation process. During the process of self-querying, and adaptively adjust the association weights among these stocks and balance the information flow. The calculation process for their diagonal elements is as follows:
where is the element of the incidence matrix H. represents the sum of node connections for each hyperedge, indicating how many stocks contribute to a hyperedge. indicates the sum of hyperedge connections for each stock, indicating how many hyperedges a stock is involved in.
The cross-attention convolutional layer aggregates node features through hyperedges, which inherently captures the shared characteristics among a group of stocks. For instance, if the fluctuation of a particular stock is correlated with other stocks within the same hyperedge, the model will incorporate this relationship, thereby better understanding the interdependencies among stocks. Although the hybrid attention mechanism differs in design from conventional hypergraph convolution operations, it can still be fundamentally regarded as a variant of hypergraph convolution. Compared to traditional hypergraph convolution, this approach not only preserves the capability to model high-order relationships but also improves the model’s flexibility and expressive power. This enhancement allows the model to capture complex relationships among stocks in evolving market conditions. The capability of the cross-attention convolutional layer to model high-order relationships can be formally explained by the following theorem.
Theorem 1.
Our cross-attention convolution layer in Equation (10) can be regarded as following special hypergraph convolution:
Proof of Theorem 1.
By bringing Equation (9) into Equation (10), the expression of cross-attention is obtained as follows:
Through the commutative law of matrix transposition and utilizing the distinctive properties of the identity matrix , the operational sequence can be exchanged to obtain
Consequently, we define , which yields the formulation presented in Equation (12). W is considered as the normalized edge weight matrix of the hypergraph. □
Based on Theorem 1, the cross-attention-based hypergraph convolution layer is equivalent to a special hypergraph convolution operation, and W is the learnable weight matrix, which dynamically adjusts the importance of hyperedges, ensuring that the module can flexibly adapt to different stock relationships. For example, during iterations, the model may enhance the associations of stocks with larger recent fluctuations. The cross-attention-based hypergraph convolution layer completes the information aggregation from stocks to stock groups, and the feature updating from stock groups to stocks, by multiplying the weight matrix, incidence matrix self-query, and the temporal embeddings of stocks. Meanwhile, the attention matrix is adaptively scaled using the node degree matrix and the hyperedge degree matrix , ensuring a balanced weight distribution among different stocks and stock groups. The function maps the weights to a probability distribution, highlighting important associations among stocks. Through these mechanisms, the cross-attention layer is capable of utilizing the hypergraph structure to model the complex high-order relationships among stocks.
4.4. Self-Supervised Pretraining Scheme
A masked time series modeling task was adopted for self-supervised pretraining of the model. Given as a mini-batch of a stock sample, we can generate a masked series for each variate by randomly masking a portion of the time steps along the time dimension, formalized as
where denotes the masked portion, and the values of the masked time points are replaced by zeros. These masked sequences are used as input to the model, after passing through the encoder and decoder, we can obtain the reconstructed original time series, namely .
Following the masked modeling paradigm, the model is supervised by a reconstruction loss:
The pretraining process of the proposed STHformer framework is shown in Algorithm 1.
| Algorithm 1 The pretraining algorithm of STHformer |
|
4.5. Fine-Tuning Scheme Tailored for Stock Price Classification
Finally, the comprehensive stock embedding is fed into a predictor to output the probabilities of future trends of each stock. The calculation process is as follows:
where the is the probability matrix of stock node, C is the number of classes, is the weight matrix, and is the bias vector.
The cross-entropy loss function is utilized to guide the model’s learning and optimization of parameters:
where and denote the ground truth and predicted trend of stock i on day .
The comprehensive fine-tuning process of the proposed STHformer framework is shown in Algorithm 2.
| Algorithm 2 The fine-tuning algorithm of STHformer |
|
5. Experiments and Analysis
5.1. Experimental Settings
5.1.1. Dataset
We used 2000 stocks from China Securities Index 2000 (CSI2000), covering the time period from 2012 to 2018, to pretrain our model. We evaluated the effectiveness of our approach using constituent stocks of two prominent indices: the CSI300 Index, and the NASDAQ100 Index. The historical stock price data we used for the Chinese market came from www.baostock.com (accessed on 4 June 2024) and the data for NASDAQ100 came from Yahoo https://finance.yahoo.com (accessed on 4 June 2024). We used six price attributes for each stock: opening price, closing price, highest price, lowest price, previous day’s closing price, and trading volume. The details of the processed datasets are shown in Table 2.

Table 2.
Sample division for fine-tuning.
5.1.2. Evaluation Metrics
To measure the classification performance in the experiments, we adopted accuracy (ACC), recall (REC), and F1-score (F1). Their specific definitions are outlined below:
- Accuracy:where TP stands for true positive, TN for true negative, FP for false positive, and FN for false negative.
- Recall:
- F1-score:
To fully assess the investment performance of the methods in the real-world stock market, we utilized three widely used profitability metrics, including the annualized rate of return (AR), Sharpe ratio (SR) and maximum drawdown (MDD):
- AR: The annualized return measures the geometric mean growth rate of an investment portfolio over a one-year period, reflecting its compounded profitability. In our experiment, we computed AR based on 252 trading days per year.where N denotes the total number of trading days in the evaluation period, and is the daily return on day n.
- SR: Sharpe ratio quantifies a portfolio’s risk-adjusted performance by comparing its excess return to its return volatility. Mathematically, it is defined aswhere is the sequence of portfolio returns. To ensure comparability across time horizons, we annualized the ratio as follows:
- MDD: Maximum drawdown measures the short-term loss in cumulative portfolio value.where and represent the cumulative return at moment i and moment j, respectively.
5.1.3. Compared Methods
- Transformer [8]: Transformer uses a self-attention mechanism along the time axis to present global information in the input data.
- GATs [6]: A graph-based baseline, which utilizes graph attention networks to model the relationships between different stocks.
- PatchTST [27]: A Transformer-based model which utilizes channel independence to handle multivariate time series and employs patch technology to extract local semantic information from the time series.
- StockMixer [38]: A MLP-based model, which consists of indicator mixing, time mixing, and stock mixing to capture the complex correlations in stock data.
- DTSMLA [23]: A multi-level attention prediction model, which considers the influence of the market on stock through a gating mechanism and uses a multi-task process to predict price changes.
- MASTER [33]: A Transformer-based model, which introduces a gating mechanism to integrate market information and mines the cross-time stock correlation with learning-based methods.
5.1.4. Backtesting Settings
To evaluate the profitability of our method in different markets, a backtest experiment was conducted using a trading strategy. The backtest experiment was based on two assumptions: (1) All buy and sell orders could be executed at the daily closing price. (2) Trading activity had no market impact. The details of backtest experiment are as follows:
- Cost: A trading cost distribution of 0.1% was applied to CSI300 and NASDAQ100.
- Trading Period: The backtesting period spanned from 1 April 2020 to 1 May 2024.
- Select Stocks: The strategy selected the top 10% stocks with the highest predicted probability of price appreciation for trading day t.
- Initial Funding and Position Distribution: We assumed an initial capital of 10 million units of the local currency. Portfolio weights were allocated equally among all selected stocks, maintaining uniform position sizing.
- Trading Strategy: The strategy established equal-weighted long positions in all selected stocks at the closing price of day t, maintaining these positions for a fixed 15-trading-day horizon before liquidating at the closing price on day . In the next trading period, the strategy was repeated. It is noteworthy that, due to the recent overall bear market of the CSI300 Index, we introduced a stop-loss mechanism in our trading. This mechanism terminated the current buy–sell transaction when the maximum drawdown within the period exceeded the threshold , which was set to 0.1 in our experiment.
5.2. Hyperparameter Settings
In this paper, the time window T was set as 60, and the batch size of baselines and our model was equal to the daily stock quantity. To select the optimal hyperparameters, we employed grid search to tune our approach as well as the other comparative methods, specifically evaluating their performance based on the validation set. This included tuning the learning rate in {} to identify optimal model configurations.
- Transformer [8]: We tuned the number of hidden layers within {32, 64, 128} for encoding layers and tested the number of parallel attention heads within {2, 4, 8}.
- GATS [6]: We tuned the number of hidden units within {32, 64, 128} and the number of layers within {1, 2, 3}, respectively.
- PatchTST [27]: We followed the original settings in the works, tuning the numbers of hidden layer width within {32, 64, 128} and tuning the patch length within {5, 10, 15}, respectively.
- StockMixer [38]: We followed the original settings in the works, tuning the number of market dimensions within {10, 20, 30} and tuning the multi-scale factor within {1, 2, 3, 4}, respectively.
- DTSMLA [23]: We followed the original settings in the work and tuned the number of attention heads within {2, 4, 8}.
- MASTER [33]: We maintained the original architecture of the model, tuning the number of attention heads in the intra-stock layer within {2, 4, 8} and tuning the number of attention heads in the inter-stock layer within {2, 4, 8}, respectively.
5.3. Performance Comparison
5.3.1. Predictive Performance
The experimental results presented in Table 3 demonstrate STHformer’s consistent superiority across all evaluation metrics on both benchmark datasets. The comprehensive comparisons reveal that our proposed method achieved statistically significant improvements over all baseline approaches.

Table 3.
Comparison of predictive performance and backtest performance on the CSI300 dataset and NASDAQ100 dataset. All methods were evaluated through 10 independent trials with randomized initializations. The classification metrics are presented in the form of means (standard deviation).
On the CSI300 dataset, PatchTST and GATs outperformed the Transformer. Some advanced methods like MASTER and DTSMLA showed a better performance to simpler models. STHformer demonstrated statistically improvements across all evaluation metrics. Specifically, STHformer achieved substantial gains over DTSMLA, including at least 5.5% improvements in F1, a 10.9% increase in REC, and 1.5% enhancement in ACC. On the NASDAQ100 Dataset, our model achieved substantial enhancements of at least 10.1%, 7.8%, and 9.9% in F1-score, compared to StockMixer, DTSMLA, and MASTER.
Additionally, we calculated the F1 score for all stocks on each day and conducted a Wilcoxon signed-rank test across the time dimension to further validate the performance improvements of our proposed model. We computed the paired differences in F1 scores between STHformer and the other models for each day, ranking these differences by their absolute values, while ignoring the zeros. The test statistic was then calculated based on the sum of the ranks of the positive and negative differences.The results of the Wilcoxon test show that the positive rank sum was much larger than the negative rank sum. We used the smaller negative rank sum as the test statistic to calculate the relative statistic and found that its absolute value was far greater than 3, indicating that the difference between the positive and negative rank sums was significant. The p-value derived from the test statistic indicated the probability of observing such differences by chance. Furthermore, the effect size was calculated from the standardized statistic and the square root of the sample size. For the CSI 300 dataset, all effect sizes were greater than 0.1, while for the NASDAQ100 dataset, all effect sizes were greater than 0.4. This suggests that the observed difference was not only statistically significant but also practically meaningful. Table 4 demonstrates STHformer’s statistically significant outperformance across the CSI300 and NASDAQ100 datasets at a significance level of = 0.05. The obtained p-values were much lower than 0.05 and provide strong evidence that the observed improvements reflect genuine model capabilities rather than random chance. This confirms that the advantages of our method are statistically significant.

Table 4.
Results of Wilcoxon signed-rank test on all datasets.
5.3.2. Backtesting Performance
Figure 3 presents the cumulative returns of all methods under identical trading conditions. STHformer demonstrated superior financial performance for both the Chinese and American markets, generating significantly higher terminal wealth. This outperformance across distinct markets confirms the model’s enhanced stock selection capability.
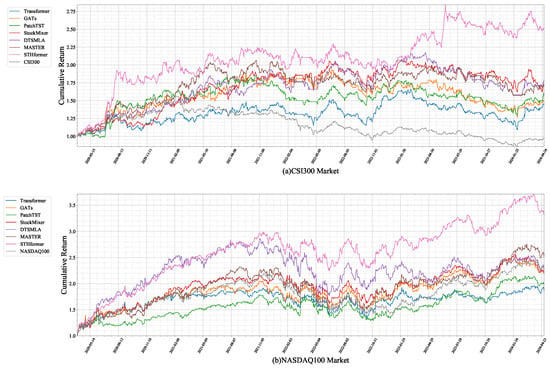
Figure 3.
Backtest performance illustration of all methods.
5.4. Model Stability Performance
To test the model’s stability under different conditions, we selected the backtest results during the Russia–Ukraine war period for analysis. Figure 4 presents the cumulative return for all models during the Russia–Ukraine war period. The event period, marked by fluctuating market conditions, presented a challenging environment for the models. The different models exhibited varying levels of adaptability to the market volatility induced by the war. STHformer showed a stronger cumulative return, while the others demonstrated more moderate responses. It is worth noting that, on the CSI300 dataset, most models executed a stop-loss strategy due to the decline reaching the stop-loss threshold, while STHformer had a smaller decline, staying below the threshold, and thus actually carry out trades.
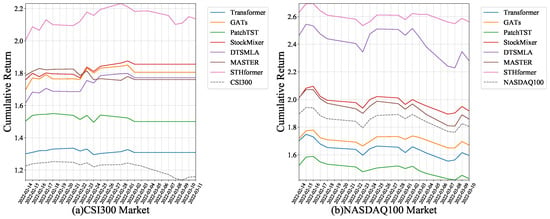
Figure 4.
Stability performance illustration of all methods during the Russia–Ukraine War event.
5.5. Ablation Study
We conducted systematic ablation experiments to evaluate the contribution of each key component in our framework. The following variant models were compared:
- STHformer w/o HA & Pre: The hybrid attention module and pretraining process in STHformer was removed and all other components were retained.
- STHformer w/o HA: The hybrid attention module in STHformer was removed and all other components were retained.
- STHformer w/o Pre: The pretraining process in STHformer was removed and all other components were retained.
The results of the ablation experiments in Table 5 demonstrate the individual contributions of STHformer’s components, which will be analyzed from the following perspectives:

Table 5.
Comparisons of ablation experiment results on CSI300 dataset and NASDAQ100 dataset.
5.5.1. Effectiveness of Hybrid Attention Module
The hybrid attention module played a crucial role in capturing the dynamic high-order relationships among stocks. By focusing on spatial interactions, this module enabled the model to better represent complex financial data. Compared to STHformer w/o HA, STHformer achieved notable improvements in F1 and AR, by 7.15% and 30.15%, on the CSI300 dataset. When applied to the NASDAQ100, STHformer showed a significant increase in F1 and AR, by 9.64% and 70.79%, respectively. This indicates that the hybrid attention module effectively captured dynamic high-order relationships among stocks, thereby enhancing the model’s ability to represent complex financial data. The performance degradation without this module suggests that it is essential for capturing the complex interactions that are critical for accurate predictions.
5.5.2. Effectiveness of Pretraining Strategy
Pretraining is a key component of enhancing the model’s representation learning and robustness, allowing it to better capture complex patterns in data. The pretrained model learned generalizable features from large datasets, which enhanced its ability to adapt to different datasets and tasks. It also enabled the model to obtain strong cold-start capabilities, so as to achieve better prediction performance on newly listed stocks with insufficient historical data. Compared to STHformer w/o Pre, STHformer demonstrated a notable increase in F1 and AR, by 5.55% and 15.80%, on the CSI300 dataset. When applied to the NASDAQ100 dataset, STHformer showed improvements in F1 and AR of 6.37% and 34.24%, respectively. This highlights the importance of pretraining for improving the model’s generalization ability on different datasets and for improving the model’s ability to cold-start.
5.6. Parameter Analysis
- Number of hidden sizes: Figure 5a shows the comparison of F1 scores for the STHformer model with different hidden layer sizes. The experimental results indicate that the model achieved the best predictive performance when the hidden layer size was set to . It is worth noting that as the hidden layer size was increased further, the predictive performance of STHformer tended to stabilize. Based on this analysis, this chapter adopted as the optimal hidden layer configuration for the model.
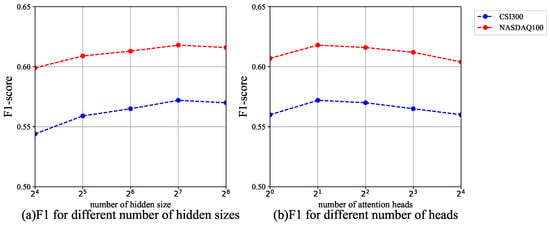 Figure 5. STHformer parameter analysis.
Figure 5. STHformer parameter analysis. - Number of heads: Figure 5b demonstrates the predictive performance comparison of the STHformer model with different numbers of attention heads in the hyperedge generation layer. The experimental results show that the STHformer model achieved the best predictive performance when the number of heads was set to , significantly outperforming configurations with more attention heads. Based on the results, this chapter adopted attention heads in the hyperedge generation layer as the optimal hyperparameter configuration for the model.
5.7. Complexity Analysis
In this paper, the time complexity of the model was represented by the time required to complete a single training epoch, while the space complexity was indicated by the number of model parameters. As shown in Table 6, although the training time of STHformer was slightly longer than DTSMLA and MASTER, its parameter scale was at a relatively low level. Considering the overall performance improvement, this increase in training time was reasonable and acceptable. It is worth noting that although the Transformer architecture shares some structural similarities with STHformer, there are significant differences in the specific design and parameterization. For instance, the Transformer employs multiple layers, leading to a substantial overall parameter count. In contrast, STHformer achieved better performance with a more optimized parameter set, thereby demonstrating a more efficient utilization of resources. The combination of low parameter counts and reasonable training time makes STHformer highly scalable for real-world applications. Although STHformer requires a longer training time during the pretraining stage, it is important to note that pretraining is usually performed only once. The main computational load in practical applications comes from the fine-tuning stage, which can be updated multiple times as new data became available. In this regard, STHformer (finetune) exhibited both low parameter counts and training time, making it highly scalable and suitable for real-world scenarios where frequent updates are necessary.

Table 6.
Complexity analysis of the models.
6. Conclusions
This paper proposes a spatio-temporal hypergraph transformer (STHformer) for multi-stock trend forecasting. Firstly, a temporal encoder is employed to learn the sequences’ internal representation. Secondly, the final time embedding is used to query all historical time embeddings for each stock, to produce a comprehensive stock embedding. Thirdly, treating different stocks as distinct positions, a hybrid attention hypergraph module captures the high-order spatial correlations, characterizing dynamic relationships. Finally, a pretraining strategy utilizing masked autoencoding enhances the overall adaptability. Extensive experiments conducted on the CSI300 and NASDAQ100 datasets demonstrated that STHformer achieved superior performance compared to representative stock prediction methods, with improvements of at least 5.53% in F1 score and at least 15.4% in Sharpe ratio. In our future work, we plan to incorporate multitask learning into the pretraining process, aiming to enhance the model’s understanding and predictive capabilities for time series data by jointly optimizing the loss functions across different tasks. Moreover, in this paper, our model focused on daily data and did not consider intraday data. Therefore, we plan to incorporate intraday data to enhance the performance. Finally, we will apply the model to other financial datasets, such as futures and exchange rates.
Author Contributions
Conceptualization, Y.W. and L.X.; methodology, Y.W.; software, Y.W.; validation, Y.W. and L.X.; formal analysis, H.W.; investigation, Y.W.; resources, L.X.; data curation, H.X.; writing—original draft preparation, Y.W.; writing—review and editing, L.X.; visualization, H.W.; supervision, L.X.; project administration, L.X.; funding acquisition, H.X. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Natural Science Foundation of Guangdong Province, China [grant number 2020A1515011208], Science and Technology Program of Guangzhou [grant number 202102080353], Characteristic Innovation Project of Guangdong Province [grat number 2019KTSCX117] and PCL-CMCC Foundation for Science and Innovation [grant number 2024ZY2B0050].
Data Availability Statement
This study utilizes three datasets: the CSI300 dataset and CSI2000 dataset sourced from Baostock (www.baostock.com), covering the time period from 1 April 2012, to 1 May 2024, and the NASDAQ100 dataset obtained from Yahoo Finance (https://finance.yahoo.com) for the same time period.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Wen, Q.; Yang, Z.; Song, Y.; Jia, P. Automatic stock decision support system based on box theory and SVM algorithm. Expert Syst. Appl. 2010, 37, 1015–1022. [Google Scholar] [CrossRef]
- Elagamy, M.N.; Stanier, C.; Sharp, B. Stock market random forest-text mining system mining critical indicators of stock market movements. In Proceedings of the 2018 2nd International Conference on Natural Language and Speech Processing (ICNLSP), Algiers, Algeria, 25–26 April 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–8. [Google Scholar]
- Dezhkam, A.; Manzuri, M.T. Forecasting stock market for an efficient portfolio by combining XGBoost and Hilbert–Huang transform. Eng. Appl. Artif. Intell. 2023, 118, 105626. [Google Scholar] [CrossRef]
- Teng, X.; Zhang, X.; Luo, Z. Multi-scale local cues and hierarchical attention-based LSTM for stock price trend prediction. Neurocomputing 2022, 505, 92–100. [Google Scholar] [CrossRef]
- Li, S.; Wu, J.; Jiang, X.; Xu, K. Chart GCN: Learning chart information with a graph convolutional network for stock movement prediction. Knowl.-Based Syst. 2022, 248, 108842. [Google Scholar] [CrossRef]
- Veličković, P.; Cucurull, G.; Casanova, A.; Romero, A.; Lio, P.; Bengio, Y. Graph attention networks. arXiv 2017, arXiv:1710.10903. [Google Scholar]
- Zhang, Q.; Qin, C.; Zhang, Y.; Bao, F.; Zhang, C.; Liu, P. Transformer-based attention network for stock movement prediction. Expert Syst. Appl. 2022, 202, 117239. [Google Scholar] [CrossRef]
- Ding, Q.; Wu, S.; Sun, H.; Guo, J.; Guo, J. Hierarchical Multi-Scale Gaussian Transformer for Stock Movement Prediction. In Proceedings of the IJCAI, Yokohama, Japan, 7–15 January 2021; pp. 4640–4646. [Google Scholar]
- Zhang, Q.; Zhang, Y.; Bao, F.; Liu, Y.; Zhang, C.; Liu, P. Incorporating stock prices and text for stock movement prediction based on information fusion. Eng. Appl. Artif. Intell. 2024, 127, 107377. [Google Scholar] [CrossRef]
- Feng, F.; He, X.; Wang, X.; Luo, C.; Liu, Y.; Chua, T.S. Temporal relational ranking for stock prediction. ACM Trans. Inf. Syst. (TOIS) 2019, 37, 1–30. [Google Scholar] [CrossRef]
- Kim, R.; So, C.H.; Jeong, M.; Lee, S.; Kim, J.; Kang, J. Hats: A hierarchical graph attention network for stock movement prediction. arXiv 2019, arXiv:1908.07999. [Google Scholar]
- Li, Y.; Pan, Y.; Yao, T.; Chen, J.; Mei, T. Scheduled sampling in vision-language pretraining with decoupled encoder-decoder network. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtually, 2–9 February 2021; Volume 35, pp. 8518–8526. [Google Scholar]
- Zhou, T.; Niu, P.; Wang, X.; Sun, L.; Jin, R. One fits all: Power general time series analysis by pretrained lm. Adv. Neural Inf. Process. Syst. 2023, 36, 43322–43355. [Google Scholar]
- Dong, J.; Wu, H.; Zhang, H.; Zhang, L.; Wang, J.; Long, M. SimMTM: A simple pre-training framework for masked time-series modeling. In Proceedings of the 37th International Conference on Neural Information Processing Systems, New Orleans, LA, USA, 10–16 December 2023; pp. 29996–30025. [Google Scholar]
- Xu, R.; Cheng, D.; Chen, C.; Luo, S.; Luo, Y.; Qian, W. Multi-scale time based stock appreciation ranking prediction via price co-movement discrimination. In Proceedings of the International Conference on Database Systems for Advanced Applications, Virtual, 11–14 April 2022; Springer: Berlin/Heidelberg, Germany; 2022, pp. 455–467. [Google Scholar]
- Xu, D.; Cheng, W.; Zong, B.; Song, D.; Ni, J.; Yu, W.; Liu, Y.; Chen, H.; Zhang, X. Tensorized LSTM with adaptive shared memory for learning trends in multivariate time series. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 9–11 February 2020; Volume 34, pp. 1395–1402. [Google Scholar]
- Liu, M.; Zeng, A.; Chen, M.; Xu, Z.; Lai, Q.; Ma, L.; Xu, Q. Scinet: Time series modeling and forecasting with sample convolution and interaction. Adv. Neural Inf. Process. Syst. 2022, 35, 5816–5828. [Google Scholar]
- Liu, Y.; Hu, T.; Zhang, H.; Wu, H.; Wang, S.; Ma, L.; Long, M. itransformer: Inverted transformers are effective for time series forecasting. arXiv 2023, arXiv:2310.06625. [Google Scholar]
- Zhou, H.; Zhang, S.; Peng, J.; Zhang, S.; Li, J.; Xiong, H.; Zhang, W. Informer: Beyond efficient transformer for long sequence time-series forecasting. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtually, 2–9 February 2021; Volume 35, pp. 11106–11115. [Google Scholar]
- Ren, Z.; Yu, J.; Huang, J.; Yang, X.; Leng, S.; Liu, Y.; Yan, S. Physically-guided temporal diffusion transformer for long-term time series forecasting. Knowl.-Based Syst. 2024, 304, 112508. [Google Scholar] [CrossRef]
- Wu, Z.; Pan, S.; Long, G.; Jiang, J.; Chang, X.; Zhang, C. Connecting the dots: Multivariate time series forecasting with graph neural networks. In Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Virtual Event, 6–10 July 2020; pp. 753–763. [Google Scholar]
- Yu, B.; Yin, H.; Zhu, Z. Spatio-temporal graph convolutional networks: A deep learning framework for traffic forecasting. In Proceedings of the 27th International Joint Conference on Artificial Intelligence, Stockholm, Sweden, 13–19 July 2018; pp. 3634–3640. [Google Scholar]
- Du, Y.; Xie, L.; Liao, S.; Chen, S.; Wu, Y.; Xu, H. DTSMLA: A dynamic task scheduling multi-level attention model for stock ranking. Expert Syst. Appl. 2024, 243, 122956. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, M.; Xu, W. Spatial-temporal multi-head attention networks for traffic flow forecasting. In Proceedings of the 5th International Conference on Computer Science and Application Engineering, Sanya, China, 19–21 October 2021; pp. 1–7. [Google Scholar]
- Wang, S.; Zhang, Y.; Lin, X.; Hu, Y.; Huang, Q.; Yin, B. Dynamic Hypergraph Structure Learning for Multivariate Time Series Forecasting. IEEE Trans. Big Data 2024, 10, 556–567. [Google Scholar] [CrossRef]
- Shang, Z.; Chen, L. Mshyper: Multi-scale hypergraph transformer for long-range time series forecasting. arXiv 2024, arXiv:2401.09261. [Google Scholar]
- Nie, Y.; Nguyen, N.H.; Sinthong, P.; Kalagnanam, J. A time series is worth 64 words: Long-term forecasting with transformers. arXiv 2022, arXiv:2211.14730. [Google Scholar]
- Gupta, U.; Bhattacharjee, V.; Bishnu, P.S. StockNet—GRU based stock index prediction. Expert Syst. Appl. 2022, 207, 117986. [Google Scholar] [CrossRef]
- Hu, J.; Chang, Q.; Yan, S. A GRU-based hybrid global stock price index forecasting model with group decision-making. Int. J. Comput. Sci. Eng. 2023, 26, 12–19. [Google Scholar] [CrossRef]
- Yao, Y.; Zhang, Z.y.; Zhao, Y. Stock index forecasting based on multivariate empirical mode decomposition and temporal convolutional networks. Appl. Soft Comput. 2023, 142, 110356. [Google Scholar] [CrossRef]
- Qiu, J.; Wang, B.; Zhou, C. Forecasting stock prices with long-short term memory neural network based on attention mechanism. PLoS ONE 2020, 15, e0227222. [Google Scholar] [CrossRef] [PubMed]
- Ma, T.; Tan, Y. Stock ranking with multi-task learning. Expert Syst. Appl. 2022, 199, 116886. [Google Scholar] [CrossRef]
- Li, T.; Liu, Z.; Shen, Y.; Wang, X.; Chen, H.; Huang, S. MASTER: Market-Guided Stock Transformer for Stock Price Forecasting. In Proceedings of the AAAI Conference on Artificial Intelligence, Vancouver, BC, Canada, 20–27 February 2024; Volume 38, pp. 162–170. [Google Scholar]
- Lin, W.; Xie, L.; Xu, H. Deep-Reinforcement-Learning-Based Dynamic Ensemble Model for Stock Prediction. Electronics 2023, 12, 4483. [Google Scholar] [CrossRef]
- Sawhney, R.; Agarwal, S.; Wadhwa, A.; Derr, T.; Shah, R.R. Stock selection via spatiotemporal hypergraph attention network: A learning to rank approach. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtually, 2–9 February 2021; Volume 35, pp. 497–504. [Google Scholar]
- Huynh, T.T.; Nguyen, M.H.; Nguyen, T.T.; Nguyen, P.L.; Weidlich, M.; Nguyen, Q.V.H.; Aberer, K. Efficient integration of multi-order dynamics and internal dynamics in stock movement prediction. In Proceedings of the Sixteenth ACM International Conference on Web Search and Data Mining, Singapore, 27 February–3 March 2023; pp. 850–858. [Google Scholar]
- Su, H.; Wang, X.; Qin, Y.; Chen, Q. Attention based adaptive spatial–temporal hypergraph convolutional networks for stock price trend prediction. Expert Syst. Appl. 2024, 238, 121899. [Google Scholar] [CrossRef]
- Fan, J.; Shen, Y. StockMixer: A Simple Yet Strong MLP-Based Architecture for Stock Price Forecasting. In Proceedings of the AAAI Conference on Artificial Intelligence, Vancouver, BC, Canada, 20–27 February 2024; Volume 38, pp. 8389–8397. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).