On Spirallikeness of Entire Functions

Abstract

In this article, we establish conditions under which certain entire functions represented as infinite products of their positive zeros are $\alpha$-spirallike of order $cos\left(\alpha \right)/2$. The discussion includes several examples featuring special functions such as Bessel, Struve, Lommel, and q-Bessel functions.

1. Introduction and Problem Formation

This study is a continuous development of the earlier work of the authors [1], where the radius of Spirallikeness discussed for functions belongs to the following classes:

$$\begin{array}{cc}\hfill {\mathbb{H}}_1& ≔\left\{f_{\nu }\in \mathcal{A} |f_{\nu }\left(z\right):=z\prod _{n=1}^{\infty }\left(1-{\displaystyle \frac{z}{a_n^2\left(\nu \right)}}\right), \nu \in \mathbb{R}\right\},\hfill \end{array}$$

(1)

$$\begin{array}{cc}\hfill {\mathbb{H}}_2& ≔\left\{{\mathtt{g}}_{\nu }\in \mathcal{A} |{\mathtt{g}}_{\nu }\left(z\right):=z\prod _{n=1}^{\infty }\left(1-{\displaystyle \frac{z^2}{b_n^2\left(\nu \right)}}\right),\nu \in \mathbb{R}\right\},\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill {\mathbb{H}}_3& ≔\left\{{\mathtt{h}}_{\nu }\in \mathcal{A} |{\mathtt{h}}_{\nu }\left(z\right):=z{\left(\prod _{n=1}^{\infty }\left(1-{\displaystyle \frac{z^2}{d_n^2\left(\nu \right)}}\right)\right)}^{\mu \left(\nu \right)}, \nu \in \mathbb{R}\setminus \left\{0\right\}\right\}.\hfill \end{array}$$

(3)

Here, $\mathcal{A}$ is the well-known class consisting of functions (f) that are analytic and univalent on the unit disc ($\mathbb{D}=\{z\in \mathbb{C}:|z|<1\}$) and normalized by $f\left(0\right)=f^{\prime }\left(0\right)-1$. Sequences $\left\{a_n\left(\nu \right)\right\}$, $\left\{b_n\left(\nu \right)\right\}$, and $\left\{d_n\left(\nu \right)\right\}$ represent the n-th zeros of the functions expressed as $f_{\nu }$, ${\mathtt{g}}_{\nu }$, and ${\mathtt{h}}_{\nu }$, respectively, and $\mu \left(\nu \right)$ is any positive real function of ($\nu$) for which the infinite product converges. The nature of these zeros varies with respect to $\nu$ so that each of the mentioned infinite products converges uniformly on every compact subset of $\mathbb{C}$. These subclasses were introduced and studied in [2] to determine the radius of k-parabolic Starlikeness. Several examples are provided in [1,2], which validate that classes ${\mathbb{H}}_1$, ${\mathbb{H}}_2$, and ${\mathbb{H}}_3$ are, indeed, nonempty. We remark that the univalency of $f_{\nu }$ (as well as that of $g_{\nu }$ and $h_{\nu }$) holds only when $a_n>1$ ($b_n>1$ and $d_n>1$) for all $n\ge 1$. Furthermore, we note that

$${\mathtt{h}}_{\nu }\left(z\right)=zexp\left(\mu \left(\nu \right)Log\left(\prod _{n=1}^{\infty }\left(1-{\displaystyle \frac{z^2}{d_n^2\left(\nu \right)}}\right)\right)\right).$$

First, let us recall some basic notions and preliminary results required to answer Problem 1. Class ${\mathtt{S}}^{*}\left(\alpha \right)$, well-known as star-like of order $\alpha$, consists of $f\in \mathcal{A}$ that satisfy the following characterization:

$$\begin{array}{c}\hfill Re\left(\frac{z{f}^{\prime }\left(z\right)}{f\left(z\right)}\right)>\alpha ,\hspace{1em}z\in \mathbb{D}\hspace{1em}0\le \alpha <1.\end{array}$$

(4)

In [3], Rønning defined class ${\mathtt{S}}_p^{*}$, which is related to a parabolic region and the function expressed as $f\in {\mathtt{S}}_p^{*}$ if it satisfies the following condition:

$$\begin{array}{c}\hfill \mathrm{Re}\left({\displaystyle \frac{z{f}^{\prime }\left(z\right)}{f\left(z\right)}}\right)>\left|{\displaystyle \frac{z{f}^{\prime }\left(z\right)}{f\left(z\right)}}-1\right|,\hspace{1em}z\in \mathbb{D}.\end{array}$$

(5)

In [4], class ${\mathtt{S}}_p^{*}$ is further generalized as ${\mathtt{S}}_p^{*}\left(\alpha \right)$, $\alpha <1$. A function is $f\in {\mathtt{S}}_p^{*}\left(\alpha \right)$ if

$$\begin{array}{c}\hfill Re\left(\frac{z{f}^{\prime }\left(z\right)}{f\left(z\right)}\right)>\left|\frac{z{f}^{\prime }\left(z\right)}{f\left(z\right)}-1\right|+\alpha , z\in \mathbb{D}.\end{array}$$

(6)

Equation (6) is defined as a parabola with its vertex at $w=(1+\alpha )/2$. As the value of $\alpha$ increases, the parabola becomes narrower, and it degenerates when $\alpha =1$. $\alpha =0$, corresponds to the previous class ${\mathtt{S}}_p^{*}$, and notably, ${\mathtt{S}}_p^{*}\left(\alpha \right)\subset {\mathtt{S}}^{*}\left(0\right)$ for $-1\le \alpha <1$. However, when $\alpha <-1$, the class includes non-univalent functions. Refer to [3,4,5,6,7,8] for more details and related properties of class ${\mathtt{S}}_p^{*}\left(\alpha \right)$ and further generalizations.

The concept of parabolic Starlikeness is extended in [9] to encompass Starlikeness in a conic region, and $\mathcal{ST}(k,\sigma )$ represents the concern class. The function is $f\in \mathcal{ST}(k,\sigma )$ if

$$\begin{array}{c}\hfill Re\left(\frac{z{f}^{\prime }\left(z\right)}{f\left(z\right)}\right)>k\left|\frac{z{f}^{\prime }\left(z\right)}{f\left(z\right)}-1\right|+\sigma ,\end{array}$$

(7)

for $k\ge 0$, $0\le \sigma <1$, and $z\in \mathbb{D}$. The class is also known as k-Starlikeness of order $\sigma$.

The concept of Spirallikeness is the main topic of this article. The function expressed as $f\in \mathcal{A}$ is called spirallike if

$$Re\left(e^{-i\alpha }{\displaystyle \frac{z{f}^{\prime }\left(z\right)}{f\left(z\right)}}\right)>0, z\in \mathbb{D},$$

for some $\alpha \in (-\pi /2,\pi /2)$. A function (f) is convex spirallike if $z{f}^{\prime }\left(z\right)$ is spirallike, combining the properties of convexity and spirallike behavior. The notion of $\alpha$-Spirallikeness of order $\delta$ was introduced by Libra in [10] through the following analytic characterization:

$$\begin{array}{c}\hfill Re\left(e^{-i\alpha }{\displaystyle \frac{z{f}^{\prime }\left(z\right)}{f\left(z\right)}}\right)>\delta cos\left(\alpha \right), z\in \mathbb{D}, 0\le \delta <1.\end{array}$$

(8)

In this study, we consider a subclass ($S{P}_p(\alpha ,\sigma )$) introduced by Selvaraj and Geetha [11]. A function ($f\in A$) belongs to subclass $S{P}_p(\alpha ,\sigma )$ of spirallike functions if the following condition is satisfied:

$$\begin{array}{c}\hfill Re\left\{e^{-i\alpha }{\displaystyle \frac{z{f}^{\prime }\left(z\right)}{f\left(z\right)}}\right\}>\left|{\displaystyle \frac{z{f}^{\prime }\left(z\right)}{f\left(z\right)}}-1\right|+\sigma ,\hspace{1em}z\in \mathbb{D}, \left|\alpha \right|<{\displaystyle \frac{\pi }{2}},\hspace{1em}0\le \sigma <1.\end{array}$$

(9)

Class $S{P}_p(\alpha ,\sigma )$ is the generalization of $S{P}_p(\alpha ,0)$ studied in [12]. It is stated that $f\in S{P}_p(\alpha ,0)$ if and only if

$$\begin{array}{c}\hfill Re\left(e^{-i\alpha }{\displaystyle \frac{z{f}^{\prime }\left(z\right)}{f\left(z\right)}}\right)>\left|{\displaystyle \frac{z{f}^{\prime }\left(z\right)}{f\left(z\right)}}-1\right|,\hspace{1em}z\in \mathbb{D},\hspace{1em}\left|\alpha \right|<{\displaystyle \frac{\pi }{2}}.\end{array}$$

(10)

Geometrically, inequality (10) implies that $z{f}^{\prime }\left(z\right)/f\left(z\right)$ lies in the parabolic region:

$$P_{\alpha }=\left\{\omega \in \mathbb{C}:Re\left(e^{-i\alpha }\omega \right)>\left|\omega -1\right|\right\}.$$

The parabolic region ($P_{\alpha }$) for different values ($\alpha$) is visualized in Figure 1. As explained in [12], if $\omega \in P_{\alpha }$, then $Re\left(e^{-i\alpha }\omega \right)>cos\left(\alpha \right)/2$. This fact can also be observed in Figure 1 (the dotted red vertical lines represent $cos\left(\alpha \right)/2$). From (8), we can conclude that this is geometrically equivalent to $\alpha$-Spirallikeness of order $1/2$. In addition, the introduction of the $\sigma$ parameter in the definition of $S{P}_p(\alpha ,\sigma )$ refines this classical notion by allowing finer control over functional behavior, particularly in its proximity to the boundary of the spirallike condition. In this way, class $S{P}_p(\alpha ,\sigma )$ captures a broader spectrum of functions that exhibit spirallike tendencies with varying degrees of strength.

Despite this enriched generalization, the inclusion and behavior of classical special functions within the framework of $S{P}_p(\alpha ,\sigma )$ remain largely unexplored. This observation presents a compelling direction for investigation: identifying and analyzing the conditions under which well-known special functions fall within this refined spirallike class, thereby contributing to both the theory of univalent functions and the deeper understanding of the analytic properties of special functions.

We aim to answer the following problem in a broader and more general context:

Problem 1.

How can sufficient conditions be established for which functions of the classes ${\mathbb{H}}_1,{\mathbb{H}}_2,$ and ${\mathbb{H}}_3$ belong to the class $S{P}_p(\alpha ,\sigma )$?

The following result proven in [13] is useful for this study.

Lemma 1

([13]). If $\left|z\right|\le r<a<b$, and $\lambda \in [0,1]$, then

$$\begin{array}{c}\hfill \left|{\displaystyle \frac{z}{b-z}}-\lambda {\displaystyle \frac{z}{a-z}}\right|\le {\displaystyle \frac{r}{b-r}}-\lambda {\displaystyle \frac{r}{a-r}}.\end{array}$$

(11)

As a consequence, it follows that

$$\begin{array}{c}\hfill Re\left({\displaystyle \frac{z}{b-z}}-\lambda {\displaystyle \frac{z}{a-z}}\right)\le {\displaystyle \frac{r}{b-r}}-\lambda {\displaystyle \frac{r}{a-r}}\end{array}$$

(12)

and

$$\begin{array}{c}\hfill Re\left({\displaystyle \frac{z}{b-z}}\right)\le \left|{\displaystyle \frac{z}{b-z}}\right|\le {\displaystyle \frac{r}{b-r}}.\end{array}$$

(13)

The rest of this paper is organized as follows: In Section 2, we state and prove our main results about the inclusion of the functions expressed as ${\mathtt{f}}_{\nu }\left(z\right)\in {\mathbb{H}}_1$, ${\mathtt{g}}_{\nu }\left(z\right)\in {\mathbb{H}}_2$, and ${\mathtt{h}}_{\nu }\left(z\right)\in {\mathbb{H}}_3$ in class $S{P}_p(\alpha ,\sigma )$. In Section 3, we present several examples of special functions that belong to classes ${\mathbb{H}}_1$, ${\mathbb{H}}_2$, and ${\mathbb{H}}_3$ and their relations to the class $S{P}_p(\alpha ,\sigma )$. Several other examples are given in Section 4.

2. Main Results

We begin by introducing the function expressed as ${\mathcal{T}}_1$, which plays a fundamental role in deriving sufficient conditions for the Spirallikeness of functions ($f_{\nu }\in {\mathbb{H}}_1$). We define

$$\begin{array}{c}\hfill {\mathcal{T}}_1:({\nu }_1,{\nu }_2)⟶\mathbb{R}, {\mathcal{T}}_1\left(\nu \right)={\displaystyle \frac{f_{\nu }^{\prime }\left(1\right)}{f_{\nu }\left(1\right)}}\end{array}$$

(14)

and assume that the function expressed as ${\mathcal{T}}_1$ is continuous in the interval of $({\nu }_1,{\nu }_2)$. Although the continuity of ${\mathcal{T}}_1$ may not be straightforward, it is intimately connected to the behavior of $a_n\left(\nu \right)$, the zeros of $f_{\nu }$ viewed as functions of the $\nu$ parameter. The following lemma describes the continuity and monotonicity of ${\mathcal{T}}_1$ and clarifies its connection to the zeros ($a_n\left(\nu \right)$).

Lemma 2.

The functions expressed as $\nu \mapsto {\mathcal{T}}_1\left(\nu \right)$ and $\nu \mapsto a_n\left(\nu \right)$ have the following connections:

(I)  

If $a_n\left(\nu \right)$ is a continuous function of ν in the interval of $({\nu }_1,{\nu }_2)$, then the function expressed as ${\mathcal{T}}_1$ is also continuous in the interval of $({\nu }_1,{\nu }_2)$ or on some sub-intervals of $({\nu }_1,{\nu }_2)$ where the function expressed as ${\mathcal{T}}_1$ is well-defined.

(II) 

If $a_n\left(\nu \right)$ is monotone (increasing or decreasing) in the interval of $({\nu }_1,{\nu }_2)$, then the function expressed as ${\mathcal{T}}_1$ has the same behavior in the interval of $({\nu }_1,{\nu }_2)$ or some sub-intervals of $({\nu }_1,{\nu }_2)$ where the function expressed as ${\mathcal{T}}_1$ is well-defined.

Proof. 

(I) 

As $f_{\nu }\in {\mathbb{H}}_1$, it can be represented as $f_{\nu }\left(z\right):=z{\prod }_{n=1}^{\infty }\left(1-{\displaystyle \frac{z}{a_n^2\left(\nu \right)}}\right)$, where $a_n\left(\nu \right)$ is the n-th zero of the functions ($f_{\nu }$). The logarithmic differentiation of $f_{\nu }$ yields

$$\begin{array}{c}\hfill {\displaystyle \frac{z{f}_{\nu }^{\prime }\left(z\right)}{f_{\nu }\left(z\right)}}=1-\sum _{n=1}^{\infty }{\displaystyle \frac{z}{a_n^2\left(\nu \right)-z}}\end{array}$$

(15)

Hence, for $\nu \in I\subseteq ({\nu }_1,{\nu }_2),$

$$\begin{array}{c}\hfill {\mathcal{T}}_1\left(\nu \right)={\displaystyle \frac{f_{\nu }^{\prime }\left(1\right)}{f_{\nu }\left(1\right)}}=1-\sum _{n=1}^{\infty }{\displaystyle \frac{1}{a_n^2\left(\nu \right)-1}},\end{array}$$

(16)

where I is the largest sub-interval of $({\nu }_1,{\nu }_2)$ such that ${\mathcal{T}}_1$ is well-defined. To prove that ${\mathcal{T}}_1$ is continuous, let ${\left({\nu }_k\right)}_{k=1}^{\infty }$ be a sequence in interval I such that

$$\begin{array}{c}\hfill \underset{k\to \infty }{lim}{\nu }_k={\nu }^{\prime }, \nu \in I\end{array}$$

(17)

For all $n\ge 1$, continuity of $a_n$ implies that

$$\begin{array}{c}\hfill \underset{k\to \infty }{lim}{a}_n\left({\nu }_k\right)=a_n\left({\nu }^{\prime }\right)\end{array}$$

(18)

Hence,

$$\begin{array}{cc}\hfill |{\mathcal{T}}_1\left({\nu }_k\right)-{\mathcal{T}}_1\left({\nu }^{\prime }\right)|& =\left|\left(1-\sum _{n=1}^{\infty }{\displaystyle \frac{1}{a_n^2\left({\nu }_k\right)-1}}\right)-\left(1-\sum _{n=1}^{\infty }{\displaystyle \frac{1}{a_n^2\left({\nu }^{\prime }\right)-1}}\right)\right|\hfill \\ & =\left|\sum _{n=1}^{\infty }{\displaystyle \frac{1}{a_n^2\left({\nu }^{\prime }\right)-1}}-\sum _{n=1}^{\infty }{\displaystyle \frac{1}{a_n^2\left({\nu }_k\right)-1}}\right|\hfill \\ & =\left|\sum _{n=1}^{\infty }{\displaystyle \frac{a_n^2\left({\nu }_k\right)-a_n^2\left({\nu }^{\prime }\right)}{(a_n^2\left({\nu }^{\prime }\right)-1)(a_n^2\left({\nu }_k\right)-1)}}\right|\hfill \\ & \le \sum _{n=1}^{\infty }{\displaystyle \frac{|a_n^2\left({\nu }_k\right)-a_n^2\left({\nu }^{\prime }\right)|}{(a_n^2\left({\nu }^{\prime }\right)-1)(a_n^2\left({\nu }_k\right)-1)}}\hfill \end{array}$$

(19)

Combining (18) and (19) yields

$$\begin{array}{c}\hfill \underset{k\to \infty }{lim}{\mathcal{T}}_1\left({\nu }_k\right)={\mathcal{T}}_1\left({\nu }^{\prime }\right)\end{array}$$

(20)

(II) 

Now, suppose that $a_n\left(\nu \right)$ is monotone in the interval of $({\nu }_1,{\nu }_2)$ and ${\nu }^{\prime }<{\nu }^{″}$ in the interval. Using (16), we obtain

$$\begin{array}{cc}\hfill {\mathcal{T}}_1\left({\nu }^{\prime }\right)-{\mathcal{T}}_1\left({\nu }^{″}\right)& =\left(1-\sum _{n=1}^{\infty }{\displaystyle \frac{1}{a_n^2\left({\nu }^{\prime }\right)-1}}\right)-\left(1-\sum _{n=1}^{\infty }{\displaystyle \frac{1}{a_n^2\left({\nu }^{\prime \prime }\right)-1}}\right)\hfill \\ \hfill & =\sum _{n=1}^{\infty }{\displaystyle \frac{1}{a_n^2\left({\nu }^{\prime \prime }\right)-1}}-\sum _{n=1}^{\infty }{\displaystyle \frac{1}{a_n^2\left({\nu }^{\prime }\right)-1}}\hfill \\ & =\sum _{n=0}^{\infty }{\displaystyle \frac{a_n^2\left({\nu }^{\prime }\right)-a_n^2\left({\nu }_2\right)}{(a_n^2\left({\nu }^{\prime \prime }\right)-1)(a_n^2\left({\nu }^{\prime }\right)-1)}}\hfill \end{array}$$

(21)

Since $a_n\left(\nu \right)>1$, it follows that if $a_n\left(\nu \right)$ is monotonic (increasing or decreasing), then ${\mathcal{T}}_1\left(\nu \right)$ exhibits the same monotonicity. □

In a similar manner, we define the functions expressed as ${\mathcal{T}}_2$ and ${\mathcal{T}}_3$, related to $g_{\nu }\in {\mathbb{H}}_2$ and ${\mathtt{h}}_{\nu }\in {\mathbb{H}}_3$, respectively, as follows.

$$\begin{array}{c}\hfill {\mathcal{T}}_2\left(\nu \right)≔{\displaystyle \frac{g_{\nu }^{\prime }\left(1\right)}{g_{\nu }\left(1\right)}}=1-2\sum _{n=1}^{\infty }{\displaystyle \frac{1}{b_n^2\left(\nu \right)-1}},\end{array}$$

(22)

$$\begin{array}{c}\hfill {\mathcal{T}}_3\left(\nu \right)≔{\displaystyle \frac{{\mathtt{h}}_{\nu }^{\prime }\left(1\right)}{{\mathtt{h}}_{\nu }\left(1\right)}}=1-2\mu \left(\nu \right)\sum _{n=1}^{\infty }{\displaystyle \frac{1}{d_n^2\left(\nu \right)-1}}.\end{array}$$

(23)

Moreover, ${\mathcal{T}}_2$ follows the the continuity and monotonicity behavior of $b_n\left(\nu \right)$. But for ${\mathcal{T}}_3$, the connection with $d_n\left(\nu \right)$ is slightly different due to the presence of $\mu \left(\nu \right)$. The following two lemmas present the conditions for both cases without proof.

Lemma 3.

If $b_n\left(\nu \right)$ is a continuous, monotone function of ν in the interval of $({\nu }_1,{\nu }_2)$, then the function expressed as ${\mathcal{T}}_2$ has the same behavior in $({\nu }_1,{\nu }_2)$ or some sub-intervals of $({\nu }_1,{\nu }_2)$ where the function expressed as ${\mathcal{T}}_2$ is well-defined.

Lemma 4.

Let ${\mathtt{h}}_{\nu }\in {\mathbb{H}}_3$ and $d_n\left(\nu \right)$ be the n-th zero of ${\mathtt{h}}_{\nu }$ and $\mu \left(\nu \right)$ be the positive function in the power of the product representation of ${\mathtt{h}}_{\nu }$. If the function expressed as $\nu \mapsto \mu \left(\nu \right)/(d_n{\left(\nu \right)}^2-1)$ is continuous or monotone in the interval of $({\nu }_1,{\nu }_2)$, then the function expressed as ${\mathcal{T}}_3$ has the same behavior in $({\nu }_1,{\nu }_2)$ or some sub-intervals of $({\nu }_1,{\nu }_2)$ where the function expressed as ${\mathcal{T}}_3$ is well-defined. In particular, if $\mu \left(\nu \right)$ is a constant function of ν and $d_n\left(\nu \right)$ is a continuous, monotone function of ν in the interval of $({\nu }_1,{\nu }_2)$, then ${\mathcal{T}}_3$ has the same behavior.

Next, we state the first main result.

Theorem 1.

Let $f_{\nu }\in {\mathbb{H}}_1$ and $\alpha ,\sigma \in \mathbb{R}$ such that $cos\left(\alpha \right)>\sigma$. Suppose that the function expressed as ${\displaystyle {\mathcal{T}}_1\left(\nu \right)}$ is continuous in an interval of $I=({\nu }_1,{\nu }_2)$. Then, the following results are true.

(I) 

Assume that ${\mathcal{T}}_1\left(\nu \right)$ is increasing in I. Function $f_{\nu }$ is in class $S{P}_p(\alpha ,\sigma )$ in the following cases.

(a) 

For ${\nu }_{f_{\nu }}<\nu <{\nu }_2$, where ${\nu }_{f_{\nu }}$ is the unique solution of the equation expressed as

$$2f_{\nu }^{\prime }\left(1\right)+(cos(\alpha )-2-\sigma )f_{\nu }\left(1\right)=0,$$

in $I=({\nu }_1,{\nu }_2)$, provided that

$$\begin{array}{c}\hfill \left.\begin{array}{cc}\mathit{\text{The right-hand limit:}}\hfill & {\displaystyle \underset{\nu \to {\nu }_1^{+}}{lim}\left(2{\mathcal{T}}_1\left(\nu \right)+(cos\left(\alpha \right)-2-\sigma )\right)<0}\hfill \\ \mathit{and}\hfill & \\ \mathit{\text{The right-hand limit:}}\hfill & {\displaystyle \underset{\nu \to {\nu }_2^{-}}{lim}\left(2{\mathcal{T}}_1\left(\nu \right)+(cos(\alpha )-2-\sigma )\right)>0}\hfill \end{array}\right\};\end{array}$$

(24)

(b) 

For ${\nu }_1<\nu <{\nu }_2$, provided that the right-hand limit is ${\displaystyle \underset{\nu \to {\nu }_1^{+}}{lim}\left(2{\mathcal{T}}_1\left(\nu \right)+(cos\left(\alpha \right)-2-\sigma )\right)>0}$.

(II) 

Assume that ${\mathcal{T}}_1\left(\nu \right)$ is decreasing in I. Function $f_{\nu }$ is in class $S{P}_p(\alpha ,\sigma )$ in the following cases:

(a) 

For ${\nu }_1<\nu <{\nu }_{f_{\nu }}$, where ${\nu }_{f_{\nu }}$ is the unique solution of the equation expressed as

$$2f_{\nu }^{\prime }\left(1\right)+(cos\left(\alpha \right)-2-\sigma )f_{\nu }\left(1\right)=0,$$

in $I=({\nu }_1,{\nu }_2)$, provided that

$$\begin{array}{c}\hfill \left.\begin{array}{cc}\mathit{\text{The right-hand limit:}}\hfill & {\displaystyle \underset{\nu \to {\nu }_1^{+}}{lim}\left(2{\mathcal{T}}_1\left(\nu \right)+(cos\left(\alpha \right)-2-\sigma )\right)>0}\hfill \\ \mathit{and} \hfill & \\ \mathit{\text{The right-hand limit:}}\hfill & {\displaystyle \underset{\nu \to {\nu }_2^{-}}{lim}\left(2{\mathcal{T}}_1\left(\nu \right)+(cos\left(\alpha \right)-2-\sigma )\right)<0}\hfill \end{array}\right\};\end{array}$$

(25)

(b) 

For ${\nu }_1<\nu <{\nu }_2$, provided that the left-hand limit is

$$\underset{\nu \to {\nu }_2^{-}}{lim}\left(2{\mathcal{T}}_1\left(\nu \right)+(cos\left(\alpha \right)-2-\sigma )\right)>0.$$

(III) 

The result applies in additional cases (that is, ${\mathcal{T}}_1$ is neither increasing nor decreasing or one or more of the conditions from the previous cases is not satisfied), given that

$$\begin{array}{c}\hfill \sum _{n=1}^{\infty }{\displaystyle \frac{1}{a_n^2\left(\nu \right)-1}}<{\displaystyle \frac{cos\left(\alpha \right)-\sigma }{2}}.\end{array}$$

(26)

Proof. 

(I) 

For $0<r<1$, we define the following function:

$$\begin{array}{c}\hfill {\varphi }_{f_{\nu }}\left(r\right)=2 r {\displaystyle \frac{f_{\nu }^{\prime }\left(r\right)}{f_{\nu }\left(r\right)}}+(cos\left(\alpha \right)-2-\sigma )\end{array}$$

According to (15), this function can be simplified as

$$\begin{array}{c}\hfill {\varphi }_{f_{\nu }}\left(r\right)=2-2\sum _{n=1}^{\infty }{\displaystyle \frac{r}{a_n^2\left(\nu \right)-r}}+(\cos \left(\alpha \right)-2-\sigma )\end{array}$$

which implies that

$$\begin{array}{c}\hfill {\varphi }_{f_{\nu }}^{\prime }\left(r\right)=-2\sum _{n=1}^{\infty }{\displaystyle \frac{a_n^2\left(\nu \right)}{{(a_n^2\left(\nu \right)-r)}^2}}<0.\end{array}$$

Thus, ${\varphi }_{f_{\nu }}\left(r\right)>{\varphi }_{f_{\nu }}\left(1\right)$, and ${\varphi }_{f_{\nu }}$ is strictly decreasing. On the other hand, combining (13) with (15) yields

$$\begin{array}{cc}\hfill Re\left(e^{-i\alpha }{\displaystyle \frac{z{f}_{\nu }^{\prime }\left(z\right)}{f_{\nu }\left(z\right)}}\right)-\left|z {\displaystyle \frac{f_{\nu }^{\prime }\left(z\right)}{f_{\nu }\left(z\right)}}-1\right|-\sigma & \ge cos\left(\alpha \right)+r {\displaystyle \frac{f_{\nu }^{\prime }\left(r\right)}{f_{\nu }\left(r\right)}}-1-1+r {\displaystyle \frac{f_{\nu }^{\prime }\left(r\right)}{f_{\nu }\left(r\right)}}-\sigma \hfill \\ & =2 r {\displaystyle \frac{f_{\nu }^{\prime }\left(r\right)}{f_{\nu }\left(r\right)}}+(cos\left(\alpha \right)-2-\sigma )\hfill \\ & ={\varphi }_{f_{\nu }}\left(r\right)\hfill \end{array}$$

Hence,

$$\begin{array}{cc}\hfill Re\left(e^{-i\alpha }{\displaystyle \frac{z{f}_{\nu }^{\prime }\left(z\right)}{f_{\nu }\left(z\right)}}\right)-\left|z {\displaystyle \frac{f_{\nu }^{\prime }\left(z\right)}{f_{\nu }\left(z\right)}}-1\right|-\sigma & \ge {\varphi }_{f_{\nu }}\left(r\right)\hfill \\ \hfill & >{\varphi }_{f_{\nu }}\left(1\right)\hfill \\ \hfill & =2{\displaystyle \frac{f_{\nu }^{\prime }\left(1\right)}{f_{\nu }\left(1\right)}}+(cos\alpha -2-\sigma )\hfill \\ & =2{\mathcal{T}}_1\left(\nu \right)+(cos\alpha -2-\sigma )\hfill \end{array}$$

(27)

As ${\mathcal{T}}_1$ is increasing in interval I and satisfies (24), there exists a unique root (${\nu }_{f_{\nu }}$) of the equation expressed as ${\displaystyle 2{\mathcal{T}}_1\left(\nu \right)+(cos\alpha -2-\sigma )=0\Rightarrow 2f_{\nu }^{\prime }\left(1\right)+(cos\alpha -2-\sigma )f_{\nu }\left(1\right)=0}$. Hence, if $\nu >{\nu }_{f_{\nu }}$, then $2{\mathcal{T}}_1\left(\nu \right)+(cos\left(\alpha \right)-2-\sigma )>0$. In the case in which ${\displaystyle \underset{\nu \to {\nu }_1^{+}}{lim}\left(2{\mathcal{T}}_1\left(\nu \right)+(cos\left(\alpha \right)-2-\sigma )\right)>0}$, the same result holds for all $\nu >{\nu }_1$ in interval I.

(II) 

Assume now that ${\mathcal{T}}_1$ is decreasing and satisfies (25). These conditions ensure the existence of a unique root (${\nu }_{f_{\nu }}$) of the equation expressed as ${\displaystyle 2{\mathcal{T}}_1\left(\nu \right)+(cos\alpha -2-\sigma )=0}$ in interval I. Hence, for all $\nu <{\nu }_{f_{\nu }}$ in the interval, ${\displaystyle 2{\mathcal{T}}_1\left(\nu \right)+(cos\alpha -2-\sigma )>0}$. Moreover, the same result holds when ${\displaystyle \underset{\nu \to {\nu }_2^{-}}{lim}\left(2{\mathcal{T}}_1\left(\nu \right)+(cos\left(\alpha \right)-2-\sigma )\right)>0}$. Therefore, in both cases, the function is $f_{\nu }\in S{P}_p(\alpha ,\sigma )$.

(III) 

Suppose that ${\mathcal{T}}_1$ is neither increasing nor decreasing or that one or more of the conditions from the previous cases is not satisfied. To show that $f_{\nu }\in S{P}_p(\alpha ,\sigma )$, we analyze the conditions on $\nu$ under which

$${\displaystyle Re\left(e^{-i\alpha }\frac{z{f}_{\nu }^{\prime }\left(z\right)}{f_{\nu }\left(z\right)}\right)-\left|z \frac{f_{\nu }^{\prime }\left(z\right)}{f_{\nu }\left(z\right)}-1\right|-\sigma >0.}$$

Now, according to (16) and (27), we obtain

$$\begin{array}{cc}\hfill {\displaystyle Re\left(e^{-i\alpha }\frac{z{f}_{\nu }^{\prime }\left(z\right)}{f_{\nu }\left(z\right)}\right)-\left|z \frac{f_{\nu }^{\prime }\left(z\right)}{f_{\nu }\left(z\right)}-1\right|-\sigma }& \ge 2-2\sum _{n=1}^{\infty }{\displaystyle \frac{1}{a_n^2\left(\nu \right)-1}}+(cos\alpha -2-\sigma )\hfill \\ & =cos\alpha -\sigma -2\sum _{n=1}^{\infty }{\displaystyle \frac{1}{a_n^2\left(\nu \right)-1}}.\hfill \end{array}$$

Therefore, if ${\displaystyle \sum _{n=1}^{\infty }\frac{1}{a_n^2\left(\nu \right)-1}<\frac{cos\left(\alpha \right)-\sigma }{2}}$, then the desired result is obtained. □

Analogously, the following two theorems, stated without proof, provide conditions on $\nu$ under which $g_{\nu },{\mathtt{h}}_{\nu }$ belong to class $S{P}_p(\alpha ,\sigma )$.

Theorem 2.

Let $g_{\nu }\in {\mathbb{H}}_2$ and $\alpha ,\sigma \in \mathbb{R}$ such that $cos\left(\alpha \right)>\sigma$. Suppose that function ${\displaystyle {\mathcal{T}}_2\left(\nu \right)}$ is continuous in an interval of $I=({\nu }_1,{\nu }_2)$. Then, the following results are true.

(I) 

Assume that ${\mathcal{T}}_2\left(\nu \right)$ is increasing in I. Function $g_{\nu }$ is in class $S{P}_p(\alpha ,\sigma )$ in the following cases.

(a) 

For ${\nu }_{g_{\nu }}<\nu <{\nu }_2$, where ${\nu }_{g_{\nu }}$ is the unique solution of the equation expressed as

$$2g_{\nu }^{\prime }\left(1\right)+(cos\left(\alpha \right)-2-\sigma )g_{\nu }\left(1\right)=0,$$

in $I=({\nu }_1,{\nu }_2)$, provided that

$$\begin{array}{c}\hfill \left.\begin{array}{cc}\mathit{\text{The right-hand limit:}}\hfill & {\displaystyle \underset{\nu \to {\nu }_1^{+}}{lim}\left(2{\mathcal{T}}_2\left(\nu \right)+(cos\left(\alpha \right)-2-\sigma )\right)<0}\hfill \\ \mathit{and}\hfill & \\ \mathit{\text{The right-hand limit:}}\hfill & {\displaystyle \underset{\nu \to {\nu }_2^{-}}{lim}\left(2{\mathcal{T}}_2\left(\nu \right)+(cos\left(\alpha \right)-2-\sigma )\right)>0}\hfill \end{array}\right\};\end{array}$$

(28)

(b) 

For ${\nu }_1<\nu <{\nu }_2$, provided that the right-hand limit is

$$\underset{\nu \to {\nu }_1^{+}}{lim}\left(2{\mathcal{T}}_2\left(\nu \right)+(cos\left(\alpha \right)-2-\sigma )\right)>0.$$

(II) 

Assume that ${\mathcal{T}}_2\left(\nu \right)$ is decreasing in I. Function $g_{\nu }$ is in class $S{P}_p(\alpha ,\sigma )$ in the following cases:

(a) 

For ${\nu }_1<\nu <{\nu }_{g_{\nu }}$, where ${\nu }_{g_{\nu }}$ is the unique solution of the equation expressed as

$$2g_{\nu }^{\prime }\left(1\right)+(cos\left(\alpha \right)-2-\sigma )g_{\nu }\left(1\right)=0,$$

in $I=({\nu }_1,{\nu }_2)$, provided that

$$\begin{array}{c}\hfill \left.\begin{array}{cc}\mathit{\text{The right-hand limit:}}\hfill & {\displaystyle \underset{\nu \to {\nu }_1^{+}}{lim}\left(2{\mathcal{T}}_2\left(\nu \right)+(cos\left(\alpha \right)-2-\sigma )\right)>0}\hfill \\ \mathit{and}\hfill & \\ \mathit{\text{The right-hand limit:}}\hfill & {\displaystyle \underset{\nu \to {\nu }_2^{-}}{lim}\left(2{\mathcal{T}}_2\left(\nu \right)+(cos\left(\alpha \right)-2-\sigma )\right)<0}\hfill \end{array}\right\};\end{array}$$

(29)

(b) 

For ${\nu }_1<\nu <{\nu }_2$, provided that the left-hand limit is

$$\underset{\nu \to {\nu }_2^{-}}{lim}\left(2{\mathcal{T}}_2\left(\nu \right)+(cos\left(\alpha \right)-2-\sigma )\right)>0.$$

(III) 

The result applies in additional cases, given that

$$\begin{array}{c}\hfill \sum _{n=1}^{\infty }{\displaystyle \frac{1}{b_n^2\left(\nu \right)-1}}<{\displaystyle \frac{cos\left(\alpha \right)-\sigma }{4}}.\end{array}$$

(30)

Theorem 3.

Let ${\mathtt{h}}_{\nu }\in {\mathbb{H}}_3$ and $\alpha ,\sigma \in \mathbb{R}$ such that $cos\left(\alpha \right)>\sigma$. Suppose that function ${\displaystyle {\mathcal{T}}_3\left(\nu \right)}$ is continuous in an interval of $I=({\nu }_1,{\nu }_2)$. Then, the following results are true.

(I) 

Assume that ${\mathcal{T}}_3\left(\nu \right)$ is increasing in I. Function ${\mathtt{h}}_{\nu }$ is in class $S{P}_p(\alpha ,\sigma )$ in the following cases.

(a) 

For ${\nu }_{{\mathtt{h}}_{\nu }}<\nu <{\nu }_2$, where ${\nu }_{{\mathtt{h}}_{\nu }}$ is the unique solution of the equation expressed as

$$2{\mathtt{h}}_{\nu }^{\prime }\left(1\right)+(cos\left(\alpha \right)-2-\sigma ){\mathtt{h}}_{\nu }\left(1\right)=0,$$

in $I=({\nu }_1,{\nu }_2)$, provided that

$$\begin{array}{c}\hfill \left.\begin{array}{cc}\mathit{\text{The right-hand limit:}}\hfill & {\displaystyle \underset{\nu \to {\nu }_1^{+}}{lim}\left(2{\mathcal{T}}_3\left(\nu \right)+(cos\left(\alpha \right)-2-\sigma )\right)<0}\hfill \\ \mathit{and} \hfill & \\ \mathit{\text{The right-hand limit:}}\hfill & {\displaystyle \underset{\nu \to {\nu }_2^{-}}{lim}\left(2{\mathcal{T}}_3\left(\nu \right)+(cos\left(\alpha \right)-2-\sigma )\right)>0}\hfill \end{array}\right\};\end{array}$$

(31)

(b) 

For ${\nu }_1<\nu <{\nu }_2$, provided that the right-hand limit is ${\displaystyle \underset{\nu \to {\nu }_1^{+}}{lim}\left(2{\mathcal{T}}_3\left(\nu \right)+(cos\left(\alpha \right)-2-\sigma )\right)>0}$.

(II) 

Assume that ${\mathcal{T}}_3\left(\nu \right)$ is decreasing in I. Function $g_{\nu }$ is in class $S{P}_p(\alpha ,\sigma )$ in the following cases:

(a) 

For ${\nu }_1<\nu <{\nu }_{{\mathtt{h}}_{\nu }}$, where ${\nu }_{{\mathtt{h}}_{\nu }}$ is the unique solution of the equation expressed as

$$2{\mathtt{h}}_{\nu }^{\prime }\left(1\right)+(cos\left(\alpha \right)-2-\sigma ){\mathtt{h}}_{\nu }\left(1\right)=0,$$

in $I=({\nu }_1,{\nu }_2)$, provided that

$$\begin{array}{c}\hfill \left.\begin{array}{cc}\mathit{\text{The right-hand limit:}}\hfill & {\displaystyle \underset{\nu \to {\nu }_1^{+}}{lim}\left(2{\mathcal{T}}_3\left(\nu \right)+(cos\left(\alpha \right)-2-\sigma )\right)>0}\hfill \\ \mathit{and}\hfill & \\ \mathit{\text{The right-hand limit}}\hfill & {\displaystyle \underset{\nu \to {\nu }_2^{-}}{lim}\left(2{\mathcal{T}}_3\left(\nu \right)+(cos\left(\alpha \right)-2-\sigma )\right)<0}\hfill \end{array}\right\};\end{array}$$

(32)

(b) 

For ${\nu }_1<\nu <{\nu }_2$, provided that the left-hand limit is

$$\underset{\nu \to {\nu }_2^{-}}{lim}\left(2{\mathcal{T}}_3\left(\nu \right)+(cos\left(\alpha \right)-2-\sigma )\right)>0.$$

(III) 

The result applies in additional cases, given that

$$\begin{array}{c}\hfill \mu \left(\nu \right)\sum _{n=1}^{\infty }{\displaystyle \frac{1}{d_n^2\left(\nu \right)-1}}<{\displaystyle \frac{cos\left(\alpha \right)-\sigma }{4}}.\end{array}$$

(33)

Remark 1.

Note that when $\sigma \ge cos\left(\alpha \right)$, function $f_{\nu }\left(z\right)$ no longer satisfies the Spirallikeness condition. To see this, observe that for $z=\left|z\right|=r<a_1\left(\nu \right)$,

$$\begin{array}{cc}\hfill Re\left(e^{-i\alpha }r {\displaystyle \frac{f_{\nu }^{\prime }\left(r\right)}{f_{\nu }\left(r\right)}}\right)-\left|r {\displaystyle \frac{f_{\nu }^{\prime }\left(r\right)}{f_{\nu }\left(r\right)}}-1\right|-\sigma & \le (\sigma +1)r {\displaystyle \frac{f_{\nu }^{\prime }\left(r\right)}{f_{\nu }\left(r\right)}}-(\sigma +1)\hfill \\ & =(\sigma +1)(r {\displaystyle \frac{f_{\nu }^{\prime }\left(r\right)}{f_{\nu }\left(r\right)}}-1)<0.\hfill \end{array}$$

The last inequality follows from the fact that

$$\begin{array}{c}\hfill 1-r {\displaystyle \frac{f_{\nu }^{\prime }\left(r\right)}{f_{\nu }\left(r\right)}}=\sum _{n=1}^{\infty }{\displaystyle \frac{r}{a_1^2\left(\nu \right)-r}}>0.\end{array}$$

Similarly, functions $g_{\nu }$ and ${\mathtt{h}}_{\nu }$ also fail to meet this condition under the same circumstances.

As observed from the relationship between ${\mathcal{T}}_1\left(\nu \right)$ and $a_n\left(\nu \right)$ in Equation (16), the conditions for Spirallikeness of the function expressed as $f_{\nu }\in {\mathbb{H}}_1$ can be reformulated in terms of the properties of its zeros. This reformulation provides a clearer understanding of the geometric behavior of $f_{\nu }$ and its connection to the distribution of the zeros as a function of $\nu$, which is the main idea of the next theorem.

Theorem 4.

Let $f_{\nu }\in {\mathbb{H}}_1$ and $\alpha ,\sigma \in \mathbb{R}$ such that $cos\left(\alpha \right)>\sigma$. Suppose that $a_n\left(\nu \right)$ is continuous as a function of ν and that the series expressed ${\displaystyle \sum _{n=1}^{\infty }\frac{1}{a_n^2\left(\nu \right)-1}}$ is well defined in an interval of $I=({\nu }_1,{\nu }_2)$. The following results are true.

(I) 

Assume that $a_n\left(\nu \right)$ is increasing in ν in I. Function $f_{\nu }$ is in class $S{P}_p(\alpha ,\sigma )$ in the following cases.

(a) 

For ${\nu }_{f_{\nu }}<\nu <{\nu }_2$, where ${\nu }_{f_{\nu }}$ is the unique solution of the equation expressed as

$$2f_{\nu }^{\prime }\left(1\right)+(cos(\alpha )-2-\sigma )f_{\nu }\left(1\right)=0,$$

in $I=({\nu }_1,{\nu }_2)$, provided that

$$\begin{array}{c}\hfill \left.\begin{array}{cc}\mathit{\text{The right-hand limit:}}\hfill & {\displaystyle \underset{\nu \to {\nu }_1^{+}}{lim}\left(\sum _{n=1}^{\infty }\frac{1}{a_n^2\left(\nu \right)-1}\right)>\frac{cos\left(\alpha \right)-\sigma }{2}}\hfill \\ \mathit{and}\hfill & \\ \mathit{\text{The right-hand limit:}}\hfill & {\displaystyle \underset{\nu \to {\nu }_2^{-}}{lim}\left(\sum _{n=1}^{\infty }\frac{1}{a_n^2\left(\nu \right)-1}\right)<\frac{cos\left(\alpha \right)-\sigma }{2}}\hfill \end{array}\right\};\end{array}$$

(34)

(b) 

For ${\nu }_1<\nu <{\nu }_2$, provided that the right-hand limit is

$$\underset{\nu \to {\nu }_1^{+}}{lim}\left(\sum _{n=1}^{\infty }{\displaystyle \frac{1}{a_n^2\left(\nu \right)-1}}\right)<{\displaystyle \frac{cos\left(\alpha \right)-\sigma }{2}}.$$

(II) 

Assume that $a_n\left(\nu \right)$ is decreasing in ν in I. Function $f_{\nu }$ is in class $S{P}_p(\alpha ,\sigma )$ in the following cases:

(a) 

For ${\nu }_1<\nu <{\nu }_{f_{\nu }}$, where ${\nu }_{f_{\nu }}$ is the unique solution of the equation expressed as

$$2f_{\nu }^{\prime }\left(1\right)+(cos\left(\alpha \right)-2-\sigma )f_{\nu }\left(1\right)=0,$$

in $I=({\nu }_1,{\nu }_2)$, provided that

$$\begin{array}{c}\hfill \left.\begin{array}{cc}\mathit{\text{The right-hand limit:}}\hfill & {\displaystyle \underset{\nu \to {\nu }_1^{+}}{lim}\left(\sum _{n=1}^{\infty }\frac{1}{a_n^2\left(\nu \right)-1}\right)<\frac{cos\left(\alpha \right)-\sigma }{2}}\hfill \\ \mathit{and}\hfill & \\ \mathit{\text{The right-hand limit:}}\hfill & {\displaystyle \underset{\nu \to {\nu }_2^{-}}{lim}\left(\sum _{n=1}^{\infty }\frac{1}{a_n^2\left(\nu \right)-1}\right)>\frac{cos\left(\alpha \right)-\sigma }{2}}\hfill \end{array}\right\};\end{array}$$

(35)

(b) 

For ${\nu }_1<\nu <{\nu }_2$, provided that the left-hand limit is

$$\underset{\nu \to {\nu }_2^{-}}{lim}\left(\sum _{n=1}^{\infty }{\displaystyle \frac{1}{a_n^2\left(\nu \right)-1}}\right)<{\displaystyle \frac{cos\left(\alpha \right)-\sigma }{2}}.$$

(III) 

The result applies in additional cases, given that

$$\begin{array}{c}\hfill \sum _{n=1}^{\infty }{\displaystyle \frac{1}{a_n^2\left(\nu \right)-1}}<{\displaystyle \frac{cos\left(\alpha \right)-\sigma }{2}}.\end{array}$$

(36)

Proof. 

Since $a_n\left(\nu \right)$ is continuous, part (I) of Lemma 2 implies that ${\mathcal{T}}_1$ is continuous in I. Moreover, the second part of the same lemma establishes that ${\mathcal{T}}_1$ inherits the monotonicity behavior of $a_n\left(\nu \right)$ in I. Moreover,

$$\begin{array}{cc}\hfill 2{\mathcal{T}}_1\left(\nu \right)+(cos\left(\alpha \right)-2-\sigma )& =2-2\sum _{n=1}^{\infty }{\displaystyle \frac{1}{a_n^2\left(\nu \right)-1}}+(cos\left(\alpha \right)-2-\sigma )\hfill \\ & =cos\left(\alpha \right)-\sigma -2\sum _{n=1}^{\infty }{\displaystyle \frac{1}{a_n^2\left(\nu \right)-1}}\hfill \end{array}$$

This implies that if $2{\mathcal{T}}_1\left(\nu \right)+(cos\left(\alpha \right)-2-\sigma )>0$, then ${\displaystyle \sum _{n=1}^{\infty }\frac{1}{a_n^2\left(\nu \right)-1}<\frac{cos\left(\alpha \right)-\sigma }{2}}$. Similarly, when $2{\mathcal{T}}_1\left(\nu \right)+(cos\left(\alpha \right)-2-\sigma )<0$, the relation expressed as ${\displaystyle \sum _{n=1}^{\infty }\frac{1}{a_n^2\left(\nu \right)-1}>\frac{cos\left(\alpha \right)-\sigma }{2}}$ is satisfied. Therefore, all cases are directly derived from Theorem 1. □

In a similar manner, the following two theorems, given without proof, establish conditions on $\nu$ ensuring that $g_{\nu }$ and $\mathtt{h}\nu$ belong to class $S{P}_p(\alpha ,\sigma ).$

Theorem 5.

Let $g_{\nu }\in {\mathbb{H}}_2$ and $\alpha ,\sigma \in \mathbb{R}$ such that $cos\left(\alpha \right)>\sigma$. Suppose that the series expressed as ${\displaystyle \sum _{n=1}^{\infty }\frac{1}{b_n^2\left(\nu \right)-1}}$ is well defined on an interval of $I=({\nu }_1,{\nu }_2)$. The following results are true.

(I) 

Assume that $b_n\left(\nu \right)$ is increasing in ν on I. Function $g_{\nu }$ is in class $S{P}_p(\alpha ,\sigma )$ in the following cases.

(a) 

For ${\nu }_{g_{\nu }}<\nu <{\nu }_2$, where ${\nu }_{g_{\nu }}$ is the unique solution of the equation expressed as

$$2g_{\nu }^{\prime }\left(1\right)+(cos(\alpha )-2-\sigma )g_{\nu }\left(1\right)=0,$$

in $I=({\nu }_1,{\nu }_2)$, provided that

$$\begin{array}{c}\hfill \left.\begin{array}{cc}\mathit{\text{The right-hand limit}}\hfill & {\displaystyle \underset{\nu \to {\nu }_1^{+}}{lim}\left(\sum _{n=1}^{\infty }\frac{1}{b_n^2\left(\nu \right)-1}\right)>\frac{cos\left(\alpha \right)-\sigma }{4}}\hfill \\ \mathit{and}\hfill & \\ \mathit{\text{The right-hand limit:}}\hfill & {\displaystyle \underset{\nu \to {\nu }_2^{-}}{lim}\left(\sum _{n=1}^{\infty }\frac{1}{b_n^2\left(\nu \right)-1}\right)<\frac{cos\left(\alpha \right)-\sigma }{4}}\hfill \end{array}\right\};\end{array}$$

(37)

(b) 

For ${\nu }_1<\nu <{\nu }_2$, provided that the right-hand limit is

$$\underset{\nu \to {\nu }_1^{+}}{lim}\left(\sum _{n=1}^{\infty }{\displaystyle \frac{1}{b_n^2\left(\nu \right)-1}}\right)<{\displaystyle \frac{cos\left(\alpha \right)-\sigma }{4}}.$$

(II) 

Assume that $b_n\left(\nu \right)$ is decreasing in ν in I. Function $g_{\nu }$ is in class $S{P}_p(\alpha ,\sigma )$ in the following cases:

(a) 

For ${\nu }_1<\nu <{\nu }_{g_{\nu }}$, where ${\nu }_{g_{\nu }}$ is the unique solution of the equation expressed as

$$2g_{\nu }^{\prime }\left(1\right)+(cos\left(\alpha \right)-2-\sigma )g_{\nu }\left(1\right)=0,$$

in $I=({\nu }_1,{\nu }_2)$, provided that

$$\begin{array}{c}\hfill \left.\begin{array}{cc}\mathit{\text{The right-hand limit:}}\hfill & {\displaystyle \underset{\nu \to {\nu }_1^{+}}{lim}\left(\sum _{n=1}^{\infty }\frac{1}{b_n^2\left(\nu \right)-1}\right)<\frac{cos\left(\alpha \right)-\sigma }{4}}\hfill \\ \mathit{and}\hfill & \\ \mathit{\text{The right-hand limit:}}\hfill & {\displaystyle \underset{\nu \to {\nu }_2^{-}}{lim}\left(\sum _{n=1}^{\infty }\frac{1}{b_n^2\left(\nu \right)-1}\right)>\frac{cos\left(\alpha \right)-\sigma }{4}}\hfill \end{array}\right\};\end{array}$$

(38)

(b) 

For ${\nu }_1<\nu <{\nu }_2$, provided that the left-hand limit is

$$\underset{\nu \to {\nu }_2^{-}}{lim}\left(\sum _{n=1}^{\infty }{\displaystyle \frac{1}{b_n^2\left(\nu \right)-1}}\right)<{\displaystyle \frac{cos\left(\alpha \right)-\sigma }{4}}.$$

(III) 

The result applies in additional cases, given that

$$\begin{array}{c}\hfill \sum _{n=1}^{\infty }{\displaystyle \frac{1}{b_n^2\left(\nu \right)-1}}<{\displaystyle \frac{cos\left(\alpha \right)-\sigma }{4}}.\end{array}$$

(39)

Theorem 6.

Let ${\mathtt{h}}_{\nu }\in {\mathbb{H}}_3$ and $\alpha ,\sigma \in \mathbb{R}$ such that $cos\left(\alpha \right)>\sigma$. Suppose that the series expressed as ${\displaystyle \sum _{n=1}^{\infty }\frac{1}{d_n^2\left(\nu \right)-1}}$ is well defined in an interval of $I=({\nu }_1,{\nu }_2)$. The following results are true.

(I) 

Assume that $d_n\left(\nu \right)$ is increasing in ν in I. Function ${\mathtt{h}}_{\nu }$ is in class $S{P}_p(\alpha ,\sigma )$ in the following cases.

(a) 

For ${\nu }_{{\mathtt{h}}_{\nu }}<\nu <{\nu }_2$, where ${\nu }_{{\mathtt{h}}_{\nu }}$ is the unique solution of the equation expressed as

$$2{\mathtt{h}}_{\nu }^{\prime }\left(1\right)+(cos(\alpha )-2-\sigma ){\mathtt{h}}_{\nu }\left(1\right)=0,$$

in $I=({\nu }_1,{\nu }_2)$, provided that

$$\begin{array}{c}\hfill \left.\begin{array}{cc}\mathit{\text{The right-hand limit:}}\hfill & {\displaystyle \underset{\nu \to {\nu }_1^{+}}{lim}\left(\mu \left(\nu \right)\sum _{n=1}^{\infty }\frac{1}{d_n^2\left(\nu \right)-1}\right)>\frac{cos\left(\alpha \right)-\sigma }{4}}\hfill \\ \mathit{and}\hfill & \\ \mathit{\text{The right-hand limit:}}\hfill & {\displaystyle \underset{\nu \to {\nu }_2^{-}}{lim}\left(\mu \left(\nu \right)\sum _{n=1}^{\infty }\frac{1}{d_n^2\left(\nu \right)-1}\right)<\frac{cos\left(\alpha \right)-\sigma }{4}}\hfill \end{array}\right\},\end{array}$$

(40)

(b) 

For ${\nu }_1<\nu <{\nu }_2$, provided that the right-hand limit is

$$\underset{\nu \to {\nu }_1^{+}}{lim}\left(\mu \left(\nu \right)\sum _{n=1}^{\infty }{\displaystyle \frac{1}{d_n^2\left(\nu \right)-1}}\right)<{\displaystyle \frac{cos\left(\alpha \right)-\sigma }{4}}.$$

(II) 

Assume that $d_n\left(\nu \right)$ is decreasing in ν in I. Function ${\mathtt{h}}_{\nu }$ is in class $S{P}_p(\alpha ,\sigma )$ in the following cases:

(a) 

For ${\nu }_1<\nu <{\nu }_{{\mathtt{h}}_{\nu }}$, where ${\nu }_{g_{\nu }}$ is the unique solution of the equation expressed as

$$2{\mathtt{h}}_{\nu }^{\prime }\left(1\right)+(cos\left(\alpha \right)-2-\sigma ){\mathtt{h}}_{\nu }\left(1\right)=0,$$

in $I=({\nu }_1,{\nu }_2)$, provided that

$$\begin{array}{c}\hfill \left.\begin{array}{cc}\text{The right-hand limit}:\hfill & {\displaystyle \underset{\nu \to {\nu }_1^{+}}{lim}\left(\mu \left(\nu \right)\sum _{n=1}^{\infty }\frac{1}{d_n^2\left(\nu \right)-1}\right)<\frac{cos\left(\alpha \right)-\sigma }{4}}\hfill \\ \mathrm{and} \hfill & \\ \text{The right-hand limit}:\hfill & {\displaystyle \underset{\nu \to {\nu }_2^{-}}{lim}\left(\mu \left(\nu \right)\sum _{n=1}^{\infty }\frac{1}{d_n^2\left(\nu \right)-1}\right)>\frac{cos\left(\alpha \right)-\sigma }{4}}\hfill \end{array}\right\};\end{array}$$

(41)

(b) 

For ${\nu }_1<\nu <{\nu }_2$, provided that the left-hand limit is

$$\underset{\nu \to {\nu }_2^{-}}{lim}\left(\mu \left(\nu \right)\sum _{n=1}^{\infty }{\displaystyle \frac{1}{d_n^2\left(\nu \right)-1}}\right)<{\displaystyle \frac{cos\left(\alpha \right)-\sigma }{4}}.$$

(III) 

The result applies in additional cases, given that

$$\begin{array}{c}\hfill \mu \left(\nu \right)\sum _{n=1}^{\infty }{\displaystyle \frac{1}{d_n^2\left(\nu \right)-1}}<{\displaystyle \frac{cos\left(\alpha \right)-\sigma }{4}}.\end{array}$$

(42)

3. Application to Special Functions

In this section, we explore various examples of special functions within the ${\mathbb{H}}_1$, ${\mathbb{H}}_2$, and ${\mathbb{H}}_3$ classes and examine the conditions that ensure their $\alpha$-spiral-likness of order $cos\left(\alpha \right)/2$ in light of the earlier sections.

3.1. Functions Involving sin Functions

For $\nu \ne 0$, consider the function expressed as

$$\begin{array}{c}\hfill {\mathcal{E}}_{\nu }\left(z\right)≔\prod _{n=1}^{\infty }\left(1-{\displaystyle \frac{z}{n^2{\pi }^2-{\nu }^2}}\right)={\displaystyle \frac{\nu csc\left(\nu \right)sin\left(\sqrt{{\nu }^2+z}\right)}{\sqrt{{\nu }^2+z}}}\end{array}$$

Example 1.

The normalized function $f_{\nu }\left(z\right)=z{\mathcal{E}}_{\nu }\left(z\right)\in {\mathbb{H}}_1$ with zeros $a_n\left(\nu \right)=\sqrt{n^2{\pi }^2-{\nu }^2}$, $n=1,2,3,\dots$, and $\nu \in (-\pi ,\pi )$.

To determine the values of $\nu$ for which function $f_{\nu }\left(z\right)$ belongs to class $S{P}_p(\alpha ,\sigma )$ under the condition that $cos\left(\alpha \right)>\sigma$, we first observe that $a_n\left(\nu \right)$ is continuous and

$$\begin{array}{c}\hfill {\displaystyle \frac{d}{d\nu }}{a}_n\left(\nu \right)={\displaystyle \frac{-\nu }{\sqrt{n^2{\pi }^2-{\nu }^2}}}.\end{array}$$

Thus, $a_n\left(\nu \right)$ is a decreasing function with respect to $\nu$ in $(0,\pi )$ and increasing in $(-\pi ,0)$. Furthermore, explicit computations yield

$$\begin{array}{c}\hfill S\left(\nu \right)≔\sum _{n=1}^{\infty }{\displaystyle \frac{1}{a_n^2\left(\nu \right)-1}}=\sum _{n=1}^{\infty }{\displaystyle \frac{1}{(n^2{\pi }^2-{\nu }^2)-1}}={\displaystyle \frac{1-\sqrt{1+{\nu }^2}cot\left(\sqrt{1+{\nu }^2}\right)}{2+2{\nu }^2}}.\end{array}$$

In the interval of $(-\pi ,\pi )$ the equation expressed as $sin\left(\sqrt{1+{\nu }^2}\right)=0$ holds only for $\nu =\pm 2.97819$. Consequently, the function $S\left(\nu \right)$ is well defined in $(-2.97819,2.97819)$. Furthermore, $S\left(\nu \right)$ is an even and positive function within this interval, attaining its minimum value at $\nu =0$, where $S\left(0\right)=0.178954$. Hence, the conditions (35) in Theorem 4 are satisfied in the interval of $(0,2.97819)$ if

$$\begin{array}{c}\hfill \underset{\nu \to 0^{+}}{lim}\sum _{n=1}^{\infty }{\displaystyle \frac{1}{a_n^2\left(\nu \right)-1}}=\underset{\nu \to 0^{+}}{lim}S\left(\nu \right)=S\left(0\right)<{\displaystyle \frac{cos\left(\alpha \right)-\sigma }{2}}\Rightarrow \sigma <cos\left(\alpha \right)-0.357908\end{array}$$

(43)

In this case, $f_{\nu }\in S{P}_p(\alpha ,\sigma )$ for all $\nu \in (0,{\nu }_{f_{\nu }})$, where ${\nu }_{f_{\nu }}$ is the unique root of the equation expressed as

$$\begin{array}{cc}\hfill & 2f_{\nu }^{\prime }\left(1\right)+(cos\left(\alpha \right)-2-\sigma )f_{\nu }\left(1\right)=0\hfill \\ \hfill \Rightarrow & cos\left(\alpha \right)-{\displaystyle \frac{1}{{\nu }^2+1}}+{\displaystyle \frac{cot\left(\sqrt{{\nu }^2+1}\right)}{\sqrt{{\nu }^2+1}}}-\sigma =0.\hfill \end{array}$$

(44)

Table 1. Values of ${\nu }_{f_{\nu }}$ and the  solution of (44) for selected values of $\alpha$ and $\sigma$.

$\alpha =0\Rightarrow \sigma <cos\left(\alpha \right)-0.357908=0.642092$
$\sigma$	0	$0.2$	$0.4$	$0.5$	$0.6$
${\nu }_{f_{\nu }}$	2.55498	2.41242	2.12362	1.82564	1.15206
$\alpha =\pi /6\Rightarrow \sigma <cos\left(\alpha \right)-0.357908=0.508117$
$\sigma$	0	$0.2$	$0.3$	$0.4$	$0.5$
${\nu }_{f_{\nu }}$	2.46906	2.24714	2.04187	1.66706	0.537909
$\alpha =\pi /4\Rightarrow \sigma <cos\left(\alpha \right)-0.357908=0.349199$
$\sigma$	0	0.1	0.2	0.25	0.3
${\nu }_{f_{\nu }}$	2.30731	2.13892	1.85381	1.61724	1.23068
$\alpha =\pi /3\Rightarrow \sigma <cos(\alpha )-0.357908=0.142092$
$\sigma$	0	0.1	0.11	0.12	0.14
${\nu }_{f_{\nu }}$	1.82564	1.15206	1.02352	0.864558	0.276299

presents the root computations (${\nu }_{f_{\nu }}$) for the selected values of $\alpha$, along with the corresponding values of $\sigma$, ensuring that conditions (35) are satisfied for the chosen values.

Since function $S\left(\nu \right)$ is even and positive in the interval of $(-2.97819,2.97819)$, it is increasing in $(-2.97819,0)$, and it satisfies conditions (34) in Theorem 4 under the same condition on $\alpha$ and $\sigma$. Furthermore, the root of Equation (44) is $-{\nu }_{f_{\nu }}$, whose computed values are presented in Table 1. Therefore, if $\nu \in (-{\nu }_{f_{\nu }},{\nu }_{f_{\nu }})$, where ${\nu }_{f_{\nu }}$ is the solution of Equation (44), then $f_{\nu }\in S{P}_p(\alpha ,\sigma )$.

For better illustration, Figure 2 shows an image of function $f_{\nu }\left(z\right)$ when $\nu =2.1$. According to Table 1, this function belongs to the $S{P}_p({\displaystyle \frac{\pi }{6}},0.3)$ class. Similarly, Figure 3 presents a graph of $f_{\nu }, \nu =-0.8$. Due to the symmetry described in the example, this function falls into the $S{P}_p({\displaystyle \frac{\pi }{3}},0.12)$ class. Finally, if condition (43) is not satisfied, Theorem 4 is not applicable. Next, we examine the Spirallikeness of $f_{\nu }$ in the interval of $(2.97819,\pi )$. In this range, $S\left(\nu \right)$ is negative, which implies that ${\displaystyle S\left(\nu \right)=\sum _{n=1}^{\infty }\frac{1}{a_n^2\left(\nu \right)-1}<\frac{cos\left(\alpha \right)-\sigma }{2}}$. As a result, $S\left(\nu \right)$ satisfies (36) in the third case of Theorem 4. Therefore, for any $\nu \in (2.97819,\pi )$, $f_{\nu }$ belongs to the $S{P}_p(\alpha ,\sigma )$ class. A similar argument applies to the symmetric interval of $(-\pi ,-2.97819)$.

3.2. Functions Involving Gamma Functions

Consider the function expressed as

$$\begin{array}{c}\hfill g_{\nu }\left(z\right)=z\prod _{n=1}^{\infty }\left(1-{\displaystyle \frac{z^2}{{(n+\nu )}^2}}\right)={\displaystyle \frac{z {\left(\mathsf{\Gamma }(1+\nu )\right)}^2}{\mathsf{\Gamma }(1-z+\nu )\mathsf{\Gamma }(1+z+\nu )}}, \nu >-1\end{array}$$

Example 2.

The function $g_{\nu }\in {\mathbb{H}}_2$ with zeros $b_n\left(\nu \right)=n+\nu$.

By computing the derivative of $g_{\nu }$ for $r>0$, we obtain

$$\begin{array}{c}\hfill g_{\nu }^{\prime }\left(r\right)={\displaystyle \frac{{\left(\mathsf{\Gamma }(1+\nu )\right)}^2(1+r \psi (1-r+\nu )-r \psi (1+r+\nu ))}{\mathsf{\Gamma }(1-r+\nu )\mathsf{\Gamma }(1+r+\nu )}}.\end{array}$$

Here, $\psi \left(z\right)$ is the digamma function, which is defined as the logarithmic derivative of the gamma function ($\mathsf{\Gamma }\left(z\right)$):

$$\psi \left(z\right)={\displaystyle \frac{d}{dz}}ln\left(\mathsf{\Gamma }\left(z\right)\right)={\displaystyle \frac{{\mathsf{\Gamma }}^{\prime }\left(z\right)}{\mathsf{\Gamma }\left(z\right)}}.$$

(45)

The digamma function ($\psi \left(z\right)$) can be represented as follows:

• Integral form:

  $$\psi \left(z\right)={\int }_0^{\infty }\left({\displaystyle \frac{e^{-t}}{t}}-{\displaystyle \frac{e^{-zt}}{1-e^{-t}}}\right)dt,\hspace{1em}Re\left(z\right)>0.$$

  (46)
• Series expansion (for $z>0$):

  $$\psi \left(z\right)=-\gamma +\sum _{n=1}^{\infty }\left({\displaystyle \frac{1}{n}}-{\displaystyle \frac{1}{n+z-1}}\right),$$

  (47)

  where $\gamma$ is the Euler–Mascheroni constant.

For positive integers (n), the digamma function is directly related to the harmonic number as follows:

$$\psi \left(n\right)=-\gamma +\sum _{k=1}^{n-1}{\displaystyle \frac{1}{k}}.$$

(48)

For a detailed overview of digamma functions, see [14].

Notably, function $g_{\nu }\left(z\right)$ covers various functions that involve sine or cosine. Specifically, when $\nu ={\displaystyle \frac{k+1}{2}}, k\in \mathbb{N}$, the resulting function ($g_{\nu }$) involves cosine, whereas for $\nu =k, k\in \mathbb{N}$, the $g_{\nu }$ function involves sine. We examine conditions on $\nu$ for which $g_{\nu }$ belongs to $S{P}_p(\alpha ,\sigma )$ when $\alpha \in \{0,{\displaystyle \frac{\pi }{6}},{\displaystyle \frac{\pi }{4}},{\displaystyle \frac{\pi }{3}},{\displaystyle \frac{\pi }{2.1}}\}$ in view of Theorem 2, provided that $cos\left(\alpha \right)>\sigma$. Function ${\mathcal{T}}_2$ is defined as follows in this example:

$$\begin{array}{c}\hfill {\mathcal{T}}_2\left(\nu \right)={\displaystyle \frac{g_{\nu }^{\prime }\left(1\right)}{g_{\nu }\left(1\right)}}=1+\psi \left(\nu \right)-\psi (2+\nu ),\end{array}$$

(49)

which is continuous on $(0,\infty )$. Moreover, it is increasing in this interval, since $b_n\left(\nu \right)=n+\nu$ is an increasing function of $\nu$ in the same interval. The relations (28) hold in an appropriate interval $({\nu }_1,{\nu }_2)$ when $\alpha \in \{0,{\displaystyle \frac{\pi }{6}},{\displaystyle \frac{\pi }{4}},{\displaystyle \frac{\pi }{3}},{\displaystyle \frac{\pi }{2.1}}$}. Thus, Theorem 2 (I) ensures that $g_{\nu }\in S{P}_p(\alpha ,\sigma )$ for all $\nu >v_{g_{\nu }}$, where ${\nu }_{g_{\nu }}$ is the unique root of the equation in the interval of $({\nu }_1,{\nu }_2)$.

$$\begin{array}{c}\hfill 2g_{\nu }^{\prime }\left(1\right)+(cos\left(\alpha \right)-2-\sigma )g_{\nu }\left(1\right)=0\Rightarrow 2\psi \left(\nu \right)-2\psi (2+\nu )+cos\left(\alpha \right)-\sigma =0.\end{array}$$

(50)

Table 2. Values of ${\nu }_{g_{\nu }}$ and the  solution of (50) for selected values of $\alpha$ and $\sigma$.

$\alpha =0\Rightarrow \sigma <cos\left(\alpha \right)=1$
$\sigma$	0	$1/4$	$1/2$	$3/4$	$0.9$
${\nu }_{g_{\nu }}$	3.56155	4.8798	7.53113	15.5156	39.5062
$\alpha =\pi /6\Rightarrow \sigma <cos\left(\alpha \right)=0.866025$
$\sigma$	0	$1/4$	$1/2$	$3/4$	$0.8$
${\nu }_{g_{\nu }}$	4.17231	6.03151	10.451	33.9825	60.0869
$\alpha =\pi /4\Rightarrow \sigma <cos\left(\alpha \right)=0.707107$
$\sigma$	0	$1/4$	$1/2$	$0.6$	$0.7$
${\nu }_{g_{\nu }}$	5.20071	8.27917	18.8266	36.8526	562.343
$\alpha =\pi /3\Rightarrow \sigma <cos(\alpha )=0.5$
$\sigma$	0	$0.1$	$0.2$	$0.3$	$0.49$
${\nu }_{g_{\nu }}$	7.53113	9.52494	12.8521	19.5125	399.501
$\alpha =\pi /2.1\Rightarrow \sigma <cos\left(\alpha \right)=0.0747301$
$\sigma$	0	$0.01$	$0.02$	$0.03$	$0.07$
${\nu }_{g_{\nu }}$	53.0306	61.2991	72.5894	88.928	845.15

presents the values of ${\nu }_{g_{\nu }}$ corresponding to the mentioned values of $\alpha$.

Figure 4 and Figure 5 illustrate the graph of $g_{\nu }$ when $\nu =8.3$ and $\nu =72.6$, respectively, as shown in Table 2, $g_{8.3}\in S{P}_p({\displaystyle \frac{\pi }{4}},{\displaystyle \frac{1}{4}})$, while $g_{72.6}\in S{P}_p({\displaystyle \frac{\pi }{2.1}},0.02)$.

Observe that in all cases, as $(cos\alpha -\sigma )⟶0$, the root (${\nu }_{g_{\nu }}$) becomes significantly larger compared to its values for other choices of $\sigma$.

For our next example involving a gamma function, consider the function expressed as

$$\begin{array}{c}\hfill {\mathtt{h}}_{\nu }\left(z\right)=z\prod _{n=1}^{\infty }{\left(1-{\displaystyle \frac{z^2}{{(n\pi +\nu )}^2}}\right)}^{{\displaystyle \frac{1}{\nu }}}=z {\left({\displaystyle \frac{ {\left(\mathsf{\Gamma }\left(\frac{\pi +\nu }{\pi }\right)\right)}^2}{\mathsf{\Gamma }\left(\frac{\pi -z+\nu }{\pi }\right)\mathsf{\Gamma }\left(\frac{\pi +z+\nu }{\pi }\right)}}\right)}^{{\displaystyle \frac{1}{\nu }}}, \nu >0.\end{array}$$

Example 3.

Function ${\mathtt{h}}_{\nu }$ in class ${\mathbb{H}}_3$ with positive zeros ($d_n\left(\nu \right)=n\pi +\nu$).

Based on Theorem 3, function ${\mathcal{T}}_3$ is defined as follows.

$$\begin{array}{c}\hfill {\mathcal{T}}_3\left(\nu \right)=1+{\displaystyle \frac{1}{\nu \pi }}\left[\psi \left({\displaystyle \frac{\pi +\nu -1}{\pi }}\right)-\psi \left({\displaystyle \frac{\pi +\nu +1}{\pi }}\right)\right]\end{array}$$

(51)

Note that ${\displaystyle \frac{d}{d\nu }}\left(d_n\left(\nu \right)\right)=1>0$ implies that $d_n\left(\nu \right)=n\pi +\nu$ is increasing in $\nu$. Hence, function ${\mathcal{T}}_3\left(\nu \right)$ is increasing in the interval of $(0,\infty )$. Moreover, the conditions (31) hold in an appropriate interval of $({\nu }_1,{\nu }_2)$ for each of $\alpha \in \{0,{\displaystyle \frac{\pi }{6}},{\displaystyle \frac{\pi }{4}},{\displaystyle \frac{\pi }{3}},{\displaystyle \frac{\pi }{2.1}}\}$. Hence, the equation expressed as

$$\begin{array}{cc}\hfill & 2{\mathtt{h}}_{\nu }^{\prime }\left(1\right)+(cos\left(\alpha \right)-2-\sigma ){\mathtt{h}}_{\nu }\left(1\right)=0\hfill \\ \hfill \Rightarrow & cos\left(\alpha \right)-\sigma +{\displaystyle \frac{2}{\pi \nu }}\left[\psi \left({\displaystyle \frac{\pi +\nu -1}{\pi }}\right)-\psi \left({\displaystyle \frac{\pi +\nu +1}{\pi }}\right)\right]=0\hfill \end{array}$$

(52)

has a unique root (${\nu }_{{\mathtt{h}}_{\nu }}$) in the chosen interval of $({\nu }_1,{\nu }_2)$ for each of the selected values of $\alpha$.

Table 3. Values of ${\nu }_{{\mathtt{h}}_{\nu }}$ and the  solution of (52) for selected values of $\alpha$ and $\sigma$.

$\alpha =0\Rightarrow \sigma <cos\left(\alpha \right)=1$
$\sigma$	0	$1/4$	$1/2$	$3/4$	$0.9$
${\nu }_{g_{\nu }}$	0.553903	0.697249	0.951185	1.56042	2.82896
$\alpha =\pi /6\Rightarrow \sigma <cos\left(\alpha \right)=0.866025$
$\sigma$	0	$1/4$	$1/2$	$3/4$	$0.8$
${\nu }_{g_{\nu }}$	0.622088	0.81231	1.19493	2.57871	3.63989
$\alpha =\pi /4\Rightarrow \sigma <cos\left(\alpha \right)=0.707107$
$\sigma$	0	$1/4$	$1/2$	$0.6$	$0.7$
${\nu }_{g_{\nu }}$	0.730152	1.01663	1.77215	2.71094	12.6066
$\alpha =\pi /3\Rightarrow \sigma <cos\left(\alpha \right)=0.5$
$\sigma$	0	$0.1$	$0.2$	$0.3$	$0.49$
${\nu }_{g_{\nu }}$	0.951185	1.12085	1.37563	1.81392	10.5072
$\alpha =\pi /2.1\Rightarrow \sigma <cos\left(\alpha \right)=0.0747301$
$\sigma$	0	$0.01$	$0.02$	$0.03$	$0.07$
${\nu }_{g_{\nu }}$	3.37947	3.68311	4.06739	4.57529	15.6266

below provides the computed values of ${\nu }_{{\mathtt{h}}_{\nu }}$ corresponding to the specified values of $\alpha$.

Figure 6 and Figure 7 illustrate representative cases from Table 3. Specifically, the graph of ${\mathtt{h}}_{0.9}$ serves as an example of a function in the $S{P}_p({\displaystyle \frac{\pi }{6}},{\displaystyle \frac{1}{4}})$ class, while ${\mathtt{h}}_{10.6}$ belongs to $S{P}_p({\displaystyle \frac{\pi }{3}},0.49)$.

3.3. Functions Associated the Normalized Bessel Functions

The positive zeros ($j_n\left(\nu \right)$) of the well-known classical Bessel function ($J_{\nu }$) follow an increasing order of $j_1\left(\nu \right)<j_2\left(\nu \right)<\dots$ for $\nu \ge 0$. The Bessel function can also be represented by

$$\begin{array}{c}\hfill J_{\nu }\left(z\right)={\displaystyle \frac{z^{\nu }}{2^{\nu }\mathsf{\Gamma }(\nu +1)}}\prod _{n=1}^{\infty }\left(1-{\displaystyle \frac{z^2}{j_n^2\left(\nu \right)}}\right).\end{array}$$

(53)

For a more in-depth understanding of the classical Bessel functions, we refer readers to [15].

A logarithmic differentiation of (53) yields

$$\begin{array}{c}\hfill {\displaystyle \frac{z{J}_{\nu }^{\prime }\left(z\right)}{J_{\nu }\left(z\right)}}=\nu -\sum _{n=1}^{\infty }{\displaystyle \frac{2z^2}{j_n^2\left(\nu \right)-z^2}}.\end{array}$$

(54)

The following three normalizations can be obtained from (53):

$$\begin{array}{cc}\hfill 2^{\nu }\mathsf{\Gamma }(\nu +1)z^{1-{\displaystyle \frac{\nu }{2}}}{J}_{\nu }\left(\sqrt{z}\right)& =z\prod _{n=1}^{\infty }\left(1-{\displaystyle \frac{z}{j_n^2\left(\nu \right)}}\right);\hfill \\ \hfill 2^{\nu }\mathsf{\Gamma }(\nu +1)z^{1-\nu }{J}_{\nu }\left(z\right)& =z\prod _{n=1}^{\infty }\left(1-{\displaystyle \frac{z^2}{j_n^2\left(\nu \right)}}\right);\hfill \\ \hfill {\left(2^{\nu }\mathsf{\Gamma }(\nu +1)J_{\nu }\left(z\right)\right)}^{{\displaystyle \frac{1}{\nu }}}& =z\prod _{n=1}^{\infty }{\left(1-{\displaystyle \frac{z^2}{j_n^2\left(\nu \right)}}\right)}^{{\displaystyle \frac{1}{\nu }}}.\hfill \end{array}$$

Below, we present examples for ${\mathbb{H}}_1$, ${\mathbb{H}}_2$, and ${\mathbb{H}}_3$.

Example 4

(The normalized Bessel function). $j_n\left(\nu \right)$ denotes the n-th zero of the Bessel functions ($J_{\nu }\left(z\right)$). Then,

(i) 

${\mathcal{B}}_1(\nu ,z)≔2^{\nu }\mathsf{\Gamma }(\nu +1)z^{1-{\displaystyle \frac{\nu }{2}}}{J}_{\nu }\left(\sqrt{z}\right)\in {\mathbb{H}}_1,$ with $a_n\left(\nu \right)=j_n\left(\nu \right)$;

(ii) 

${\mathcal{B}}_2(\nu ,z)=2^{\nu }\mathsf{\Gamma }(\nu +1)z^{1-\nu }{J}_{\nu }\left(z\right)\in {\mathbb{H}}_2$ with $b_n\left(\nu \right)=j_n\left(\nu \right)$;

(iii) 

${\mathcal{B}}_3(\nu ,z)={\left(2^{\nu }\mathsf{\Gamma }(\nu +1)J_{\nu }\left(z\right)\right)}^{{\displaystyle \frac{1}{\nu }}}=z{\prod }_{n=1}^{\infty }{\left(1-{\displaystyle \frac{z^2}{j_n^2\left(\nu \right)}}\right)}^{{\displaystyle \frac{1}{\nu }}}\in {\mathbb{H}}_3$ with $d_n\left(\nu \right)=j_n\left(\nu \right)$ and $\mu \left(\nu \right)≔1/\nu$.

Logarithmic differentiation of ${\mathcal{B}}_i(\nu ,z)$, $i=1,2,3$ yields

$$\begin{array}{cc}\hfill {\mathcal{T}}_1\left(\nu \right)={\displaystyle \frac{{\mathcal{B}}_1^{\prime }(\nu ,1)}{{\mathcal{B}}_1(\nu ,1)}}& =1-{\displaystyle \frac{\nu }{2}}+{\displaystyle \frac{ J_{\nu }^{\prime }\left(1\right)}{2 J_{\nu }\left(1\right)}}\hfill \end{array}$$

(55)

$$\begin{array}{cc}\hfill {\mathcal{T}}_2\left(\nu \right)={\displaystyle \frac{{\mathcal{B}}_2^{\prime }(\nu ,1)}{{\mathcal{B}}_2(\nu ,1)}}& =1-\nu +{\displaystyle \frac{J_{\nu }^{\prime }\left(1\right)}{J_{\nu }\left(1\right)}}\hfill \end{array}$$

(56)

$$\begin{array}{cc}\hfill {\mathcal{T}}_3\left(\nu \right)={\displaystyle \frac{{\mathcal{B}}_3^{\prime }(\nu ,1)}{{\mathcal{B}}_3(\nu ,1)}}& ={\displaystyle \frac{J_{\nu }^{\prime }\left(1\right)}{\nu J_{\nu }\left(1\right)}}\hfill \end{array}$$

(57)

The next theorem provides sufficient conditions that ensure these functions belong to the $S{P}_p(\alpha ,\sigma )$ class.

Theorem 7.

The normalized Bessel function (${\mathcal{B}}_i(\nu ,z)$, $i=1,2,3$) has the following properties:

1. 

If ${\displaystyle 0<cos\left(\alpha \right)-\sigma <-\frac{J_0^{\prime }\left(1\right)}{J_0\left(1\right)}}$, then ${\mathcal{B}}_1(\nu ,z)\in S{P}_p(\alpha ,\sigma )$ for all $\nu >{\nu }_1$, where ${\nu }_1$ is the unique root of the equation expressed as $J_{\nu -1}\left(1\right)+(-2\nu +cos\left(\alpha \right)-\sigma )J_{\nu }\left(1\right)=0$. Otherwise, when ${\displaystyle cos\left(\alpha \right)-\sigma >-\frac{J_0^{\prime }\left(1\right)}{J_0\left(1\right)}}$, ${\mathcal{B}}_1(\nu ,z)\in S{P}_p(\alpha ,\sigma )$ for all $\nu >0$.

2. 

The function expressed as ${\mathcal{B}}_2(\nu ,z)\in S{P}_p(\alpha ,\sigma )$ for all $\nu >{\nu }_2$, where ${\nu }_2$ is the unique root of the equation expressed as $2J_{\nu -1}\left(1\right)+(-4\nu +cos\left(\alpha \right)-\sigma )J_{\nu }\left(1\right)=0$.

3. 

The function expressed ${\mathcal{B}}_3(\nu ,z)\in S{P}_p(\alpha ,\sigma )$ for all $\nu >{\nu }_3$, where ${\nu }_3$ is the unique root of the equation expressed sa $2J_{\nu -1}\left(1\right)+(cos\left(\alpha \right)-4-\sigma )\nu J_{\nu }\left(1\right)=0$.

Proof. 

It is known ([15], p. 508, [16], p. 236) that the function expressed as $\nu \mapsto {\mathtt{j}}_{\nu ,n}$ is increasing in $(0,\infty )$ for each fixed $n\in \mathbb{N}$. Thus, functions ${\mathcal{T}}_i\left(\nu \right),i\in \{1,2,3\}$ have the same monotonic behavior.

• Moreover, from (55), we obtain

  $$\begin{array}{cc}\hfill 2{\mathcal{T}}_1\left(\nu \right)+cos\left(\alpha \right)-2-\sigma & =2-\nu +{\displaystyle \frac{J_{\nu }^{\prime }\left(1\right)}{J_{\nu }\left(1\right)}}+cos\left(\alpha \right)-2-\sigma \hfill \\ & ={\displaystyle \frac{J_{\nu }^{\prime }\left(1\right)}{J_{\nu }\left(1\right)}}+cos\left(\alpha \right)-\sigma -\nu .\hfill \end{array}$$

  (58)
  The well-known recurrence relation of the Bessel function ($x{J}_{\nu }^{\prime }\left(x\right)=-\nu J_{\nu }\left(x\right)+J_{\nu -1}\left(x\right)$), leads to further simplification:

  $$\begin{array}{c}\hfill {\displaystyle \frac{J_{\nu }^{\prime }\left(1\right)}{J_{\nu }\left(1\right)}}=-\nu +{\displaystyle \frac{J_{\nu -1}\left(1\right)}{J_{\nu }\left(1\right)}}.\end{array}$$
  Substituting the aboveinto (58) yields

  $$\begin{array}{c}\hfill 2{\mathcal{T}}_1\left(\nu \right)+cos\left(\alpha \right)-2-\sigma ={\displaystyle \frac{J_{\nu -1}\left(1\right)}{J_{\nu }\left(1\right)}}-2\nu +cos\left(\alpha \right)-\sigma \end{array}$$

  (59)
  Now, according to [17], for $x>0$, which is not a zero of $J_{\nu +1}$, we have

  $$\begin{array}{c}\hfill \underset{\nu \to \infty }{lim}x{\displaystyle \frac{J_{\nu }\left(x\right)}{J_{\nu +1}\left(x\right)}}-2\nu =2.\end{array}$$

  (60)
  Hence,

  $$\begin{array}{c}\hfill \underset{\nu \to \infty }{lim}{\displaystyle \frac{J_{\nu -1}\left(1\right)}{J_{\nu }\left(1\right)}}-2(\nu -1)=2\Rightarrow \underset{\nu ⟶\infty }{lim}{\displaystyle \frac{J_{\nu -1}\left(1\right)}{J_{\nu }\left(1\right)}}-2\nu =0\end{array}$$

  (61)
  By combining (61) and (59), we conclude

  $$\begin{array}{c}\hfill \underset{\nu \to \infty }{lim}(2{\mathcal{T}}_1\left(\nu \right)+cos\left(\alpha \right)-2-\sigma )=cos\left(\alpha \right)-\sigma >0.\end{array}$$

  (62)
  Consequently, the validity of either case (I-a or I-b) of Theorem 1 is determined by the limiting behavior of this expression as $\nu \to 0^{+}$.

  $$\begin{array}{c}\hfill \underset{\nu \to 0^{+}}{lim}(2{\mathcal{T}}_1\left(\nu \right)+cos\left(\alpha \right)-2-\sigma )={\displaystyle \frac{J_0^{\prime }\left(1\right)}{J_0\left(1\right)}}+cos\left(\alpha \right)-\sigma =cos\left(\alpha \right)-\sigma -0.575081.\end{array}$$
  Thus, if $(cos(\alpha )-\sigma )\in (0,0.575081)$, then the equation expressed as

  $$\begin{array}{c}\hfill 2{\mathcal{T}}_1\left(\nu \right)+cos\left(\alpha \right)-2-\sigma =0\Rightarrow J_{\nu -1}\left(1\right)+(cos\left(\alpha \right)-\sigma -2\nu )J_{\nu }\left(1\right)=0.\end{array}$$

  (63)

  has a unique root ${\nu }_1$ in the interval of $(0,\infty )$. According to Theorem 1, ${\mathcal{B}}_1(\nu ,z)\in S{P}_p(\alpha ,\sigma )$ for all $\nu >{\nu }_1$. In contrast, when $(cos(\alpha )-\sigma )\in (0.575081,1)$, it follows that ${\displaystyle \underset{\nu \to 0^{+}}{lim}(2{\mathcal{T}}_1\left(\nu \right)+cos\left(\alpha \right)-2-\sigma )>0}$, thereby satisfying condition (I-b) of Theorem 1.
• By following a similar approach as in Part 1, we derive

  $$\begin{array}{c}\hfill 2{\mathcal{T}}_2\left(\nu \right)+cos\left(\alpha \right)-2-\sigma =2{\displaystyle \frac{J_{\nu -1}\left(1\right)}{J_{\nu }\left(1\right)}}+cos\left(\alpha \right)-\sigma -4\nu .\end{array}$$

  (64)
  Furthermore, applying the limit in (60), we obtain

  $$\begin{array}{c}\hfill \underset{\nu \to \infty }{lim}(2{\mathcal{T}}_2\left(\nu \right)+cos\left(\alpha \right)-2-\sigma )=cos\left(\alpha \right)-\sigma >0.\end{array}$$

  (65)
  On the other hand,

  $$\begin{array}{c}\hfill \underset{\nu \to 0^{+}}{lim}\left(2{\mathcal{T}}_2\left(\nu \right)+cos\left(\alpha \right)-2-\sigma \right)=2{\displaystyle \frac{J_0^{\prime }\left(1\right)}{J_0\left(1\right)}}+cos\left(\alpha \right)-\sigma =cos\left(\alpha \right)-\sigma -1.15016.\end{array}$$

  (66)
  Since $0<cos\left(\alpha \right)-\sigma <1$, the limit in (66) is negative. Hence, (65) and (66) show that the equation expressed as

  $$\begin{array}{c}\hfill 2J_{\nu -1}\left(1\right)+J_{\nu }\left(1\right)(cos\left(\alpha \right)-\sigma -4\nu )=0.\end{array}$$

  (67)

  has a unique root in the interval of $(0,\infty )$.
• The third part of the theorem follows the same technique as the previous ones, leading to the following two limits:

  $$\begin{array}{cc}\hfill \underset{\nu \to \infty }{lim}(2{\mathcal{T}}_3\left(\nu \right)+cos\left(\alpha \right)-2-\sigma )& =\underset{\nu \to \infty }{lim}\left(2{\displaystyle \frac{J_{\nu -1}\left(1\right)}{\nu J_{\nu }\left(1\right)}}+cos\left(\alpha \right)-4-\sigma \right)\hfill \\ & =\underset{\nu \to \infty }{lim}\left({\displaystyle \frac{2}{\nu }}\left[{\displaystyle \frac{J_{\nu -1}\left(1\right)}{J_{\nu }\left(1\right)}}-2\nu \right]+cos\left(\alpha \right)-\sigma \right)\hfill \\ & =cos\left(\alpha \right)-\sigma >0,\hfill \end{array}$$

  (68)

  and

  $$\begin{array}{cc}\hfill \underset{\nu \to 0^{+}}{lim}(2{\mathcal{T}}_3\left(\nu \right)+cos\left(\alpha \right)-2-\sigma )& =\underset{\nu \to 0^{+}}{lim}\left(2{\displaystyle \frac{J_{\nu -1}\left(1\right)}{\nu J_{\nu }\left(1\right)}}+cos\left(\alpha \right)-4-\sigma \right)\hfill \\ & =\underset{\nu \to 0^{+}}{lim}\left({\displaystyle \frac{2}{\nu }}{\displaystyle \frac{J_{-1}\left(1\right)}{J_0\left(1\right)}}+cos\left(\alpha \right)-4-\sigma \right)=-\infty .\hfill \end{array}$$

  (69)
  Thus, the equation expressed as

  $$\begin{array}{c}\hfill 2J_{\nu -1}\left(1\right)+(cos\left(\alpha \right)-4-\sigma )\nu J_{\nu }\left(1\right)=0\end{array}$$

  (70)

  has a unique root in the interval of $(0,\infty )$. □

Table 4. Values of ${\nu }_1$ and the  solution of (59) when $0<cos\left(\alpha \right)-\sigma <0.575081$.

$\alpha =0\Rightarrow 0.424919<\sigma <1$
$\sigma$	0.43	0.5	0.75	0.8	0.9
${\nu }_1$	0.0072437	0.122499	1.08276	1.57111	4.04163
$\alpha =\pi /6\Rightarrow 0.290944<\sigma <0.866025$
$\sigma$	0.3	0.4	0.5	0.7	0.8
${\nu }_1$	0.0130035	0.191305	0.470319	2.07371	6.60199
$\alpha =\pi /4\Rightarrow 0.132025<\sigma <0.707107$
$\sigma$	0.15	0.2	0.4	0.5	0.7
${\nu }_1$	0.0262358	0.109304	0.72229	1.48708	69.3588
$\alpha =\pi /3\Rightarrow -0.075081<\sigma <0.5$
$\sigma$	0	$0.1$	$0.2$	$0.3$	$0.49$
${\nu }_1$	0.122499	0.359469	0.759532	1.57111	49.0049
$\alpha =\pi /2.1\Rightarrow -0.50035<\sigma <0.0747301$
$\sigma$	0	$0.01$	$0.02$	$0.03$	$0.07$
${\nu }_1$	5.72324	6.75303	8.1604	10.1987	104.708

,

Table 5. Values of ${\nu }_2$ and the  solution of (67).

$\alpha =0\Rightarrow \sigma <cos\left(\alpha \right)=1$
$\sigma$	0	0.25	0.5	0.75	0.9
${\nu }_2$	0.122499	0.439036	1.08276	3.04992	9.02272
$\alpha =\pi /6\Rightarrow \sigma <cos(\pi /6)=0.866025$
$\sigma$	0	0.25	0.5	0.75	0.8
${\nu }_2$	0.268808	0.717669	1.79878	7.64479	14.1612
$\alpha =\pi /4\Rightarrow \sigma <cos(\pi /4)=0.707107$
$\sigma$	0	0.25	0.5	0.6	0.7
${\nu }_2$	0.516494	1.26564	3.87127	8.36066	139.707
$\alpha =\pi /3\Rightarrow \sigma <cos(\pi /3)=0.5$
$\sigma$	0	$0.1$	$0.2$	$0.3$	$0.49$
${\nu }_2$	1.08276	1.57111	2.39088	4.04163	99.0025
$\alpha =\pi /2.1\Rightarrow \sigma <cos(\pi /(2.1\left)\right)=0.0747301$
$\sigma$	0	$0.01$	$0.02$	$0.03$	$0.07$
${\nu }_2$	12.3989	14.464	17.2845	21.367	123.985

and

Table 6. Values of ${\nu }_3$ and the  solution of (70).

$\alpha =0\Rightarrow \sigma <cos\left(\alpha \right)=1$
$\sigma$	0	0.25	0.5	0.75	0.9
${\nu }_3$	0.645715	0.78672	1.02863	1.58863	2.72421
$\alpha =\pi /6\Rightarrow \sigma <cos(\pi /6)=0.866025$
$\sigma$	0	0.25	0.5	0.75	0.8
${\nu }_3$	0.71331	0.897324	1.25506	2.50153	3.44398
$\alpha =\pi /4\Rightarrow \sigma <cos(\pi /4)=0.707107$
$\sigma$	0	0.25	0.5	0.6	0.7
${\nu }_3$	0.818548	1.08986	1.77987	2.61923	11.3816
$\alpha =\pi /3\Rightarrow \sigma <cos(\pi /3)=0.5$
$\sigma$	0	$0.1$	$0.2$	$0.3$	$0.49$
${\nu }_3$	1.02863	1.18668	1.42066	1.81747	9.52282
$\alpha =\pi /2.1\Rightarrow \sigma <cos(\pi /(2.1\left)\right)=0.0747301$
$\sigma$	0	$0.01$	$0.02$	$0.03$	$0.07$
${\nu }_3$	3.21306	3.4823	3.82281	4.27258	14.0561

present the values of the unique root corresponding to specific choices of $\alpha$ and $\sigma$, offering an illustrative example of Theorem 7.

3.4. Examples Involving Derivatives of Bessel Functions

For the next example, consider the function expressed as

$$\begin{array}{c}\hfill N_{\nu }(a,b,c,z)≔a{z}^2{J}_{\nu }^{\prime \prime }\left(z\right)+bz{J}_{\nu }^{\prime }\left(z\right)+c{J}_{\nu }\left(z\right),\hspace{1em}a,b,c\in \mathbb{R}\hspace{1em}\mathrm{and}\hspace{1em}\nu >0.\end{array}$$

In [18], the monotonic properties of the $n^{th}$ positive zeros of $N_{\nu }$ were established with the following condition ($\mathcal{P}$):

$$\begin{array}{c}\hfill Condition \mathcal{P}: \left(i\right) c=0 \mathrm{and} a \ne b; \mathrm{or} \left(ii\right) c>0 \mathrm{and} b>a.\end{array}$$

(71)

It is shown that under $Condition \mathcal{P}$, for a fixed $n\in \mathbb{N}$, the $n^{th}$ positive zeros of $N_{\nu }$ are an increasing function of $\nu$ in $(0,\infty )$. However, it is not clear under $Condition \mathcal{P}$ whether all the zeros of $N_{\nu }$ are real or imaginary. It is proven in [19] that, in addition to $Condition \mathcal{P}$, if $\nu \ge max\{0,Q_{{\nu }_0}\}$, then all the zeros of $N_{\nu }$ are real. Here, $Q_{{\nu }_0}$ is the largest real root of the function expressed as

$$\begin{array}{c}\hfill Q(a,b,c,\nu )≔a\nu (\nu -1)+b\nu +c.\end{array}$$

(72)

In this study, we depend on condition ${\mathcal{P}}_1$, as stated below:

$$\begin{array}{c}\hfill Condition {\mathcal{P}}_1: \nu \ge \overline{\nu }=max\{0,Q_{{\nu }_0}\} \mathrm{and} \mathrm{either} \left(i\right) c=0 \mathrm{and} a \ne b; \mathrm{or} \left(ii\right) c>0 \mathrm{and} b>a.\end{array}$$

(73)

Following the notion proposed in [20], we have the following representation of $N_{\nu }$:

$$\begin{array}{c}\hfill N_{\nu }(a,b,c,z)={\displaystyle \frac{Q(a,b,c,\nu )z^{\nu }}{2^{\nu }\mathsf{\Gamma }(\nu +1)}}\prod _{n=1}^{\infty }\left(1-{\displaystyle \frac{z^2}{{\lambda }_n^2\left(\nu \right)}}\right),\end{array}$$

(74)

where ${\lambda }_n\left(\nu \right)$ is the nth positive zero of $N_{\nu }$. In [20], $Condition {\mathcal{P}}_1$ played a central role in the study of the Starlikeness of $N_{\nu }(a,b,c,z)=2^{\nu }\mathsf{\Gamma }(\nu +1)Q^{-1}(a,b,c,\nu )z^{1-\nu /2}{N}_{\nu }\left(\sqrt{z}\right)$. Recently, the radiiof uniformly convex $\gamma$-Spirallikeness [21] and $S{P}_p(\alpha ,\sigma )$ [1] were studied for the following three normalized forms of $N_{\nu }$:

Example 5.

For $a,b,c$, and ν, as stated in $Condition {\mathcal{P}}_1$, we have

(i) 

${\mathcal{N}}_1(\nu ,z)={\displaystyle \frac{2^{\nu }\mathsf{\Gamma }(\nu +1)z^{1-\frac{\nu }{2}}}{Q(a,b,c,\nu )}}{N}_{\nu }(a,b,c,\sqrt{z})=z{\prod }_{n=1}^{\infty }\left(1-{\displaystyle \frac{z}{{\lambda }_n^2\left(\nu \right)}}\right)\in {\mathbb{H}}_1$ with $a_n\left(\nu \right)={\lambda }_n\left(\nu \right)$;

(ii) 

${\mathcal{N}}_2(\nu ,z)={\displaystyle \frac{2^{\nu }\mathsf{\Gamma }(\nu +1)z^{1-\nu }}{Q(a,b,c,\nu )}}{N}_{\nu }(a,b,c,z)=z{\prod }_{n=1}^{\infty }\left(1-{\displaystyle \frac{z^2}{{\lambda }_n^2\left(\nu \right)}}\right)\in {\mathbb{H}}_2$ with $b_n\left(\nu \right)={\lambda }_n\left(\nu \right)$;

(iii) 

${\mathcal{N}}_3(\nu ,z)={\left[{\displaystyle \frac{2^{\nu }\mathsf{\Gamma }(\nu +1)}{Q(a,b,c,\nu )}}{N}_{\nu }(a,b,c,z)\right]}^{{\displaystyle \frac{1}{\nu }}}=z{\prod }_{n=1}^{\infty }{\left(1-{\displaystyle \frac{z^2}{{\lambda }_n^2\left(\nu \right)}}\right)}^{{\displaystyle \frac{1}{\nu }}}\in {\mathbb{H}}_3$ with $d_n\left(\nu \right)={\lambda }_n\left(\nu \right)$.

By applying logarithmic differentiation, along with the established relationships between ${\mathcal{N}}_i$ and $N_{\nu }$ for $i=1,2,3$, we define

$$\begin{array}{cc}\hfill {\mathcal{T}}_1\left(\nu \right)& ={\displaystyle \frac{{\mathcal{N}}_1^{\prime }(\nu ,1)}{{\mathcal{N}}_1(\nu ,1)}}=1-{\displaystyle \frac{\nu }{2}}+{\displaystyle \frac{N_{\nu }^{\prime }(a,b,c,1)}{2N_{\nu }(a,b,c,1)}};\hfill \end{array}$$

(75)

$$\begin{array}{cc}\hfill {\mathcal{T}}_2\left(\nu \right)& ={\displaystyle \frac{{\mathcal{N}}_2^{\prime }(\nu ,1)}{{\mathcal{N}}_2(\nu ,1)}}=1-\nu +{\displaystyle \frac{N_{\nu }^{\prime }(a,b,c,1)}{N_{\nu }(a,b,c,1)}};\hfill \end{array}$$

(76)

$$\begin{array}{cc}\hfill {\mathcal{T}}_3\left(\nu \right)& ={\displaystyle \frac{{\mathcal{N}}_3^{\prime }(\nu ,1)}{{\mathcal{N}}_3(\nu ,1)}}={\displaystyle \frac{1}{\nu }}{\displaystyle \frac{N_{\nu }^{\prime }(a,b,c,1)}{N_{\nu }(a,b,c,1)}}.\hfill \end{array}$$

(77)

We note that, when $Condition {\mathcal{P}}_1$ is met, the real zeros (${\lambda }_n\left(\nu \right)$) of $N_{\nu }$ increase, and consequently, ${\mathcal{T}}_i,i=1,2,3$ are increasing functions of $\nu$. However, the interval of existence of ${\mathcal{T}}_i,i=1,2,3$ depends on the singularities of $N_{\nu }^{\prime }(a,b,c,1)/N_{\nu }(a,b,c,1)$—more specifically, on the zeros of $N_{\nu }(a,b,c,1)$ in the interval of $(\overline{\nu },\infty )$.

Since, ${\mathcal{T}}_1$ is increasing, we implement Theorem 1 (I) and investigate the right-hand side of

$$\begin{array}{c}\hfill 2{\mathcal{T}}_1\left(\nu \right)+cos\left(\alpha \right)-\sigma -2={\displaystyle \frac{N_{\nu }^{\prime }(a,b,c,1)}{N_{\nu }(a,b,c,1)}}+cos\left(\alpha \right)-\sigma -\nu .\end{array}$$

(78)

Clearly, the number of zeros of $N_{\nu }(a,b,c,1)=(-a+b)J_{\nu -1}\left(1\right)+(c-b\nu +a(-1+\nu +{\nu }^2))J_{\nu }\left(1\right)$ is the deciding factor for the interval in which ${\mathcal{T}}_1\left(\nu \right)$ is well defined. Finding the number of zeros of $N_{\nu }(a,b,c,1)=(-a+b)J_{\nu -1}\left(1\right)+(c-b\nu +a(-1+\nu +{\nu }^2))J_{\nu }\left(1\right)$ in $(\overline{\nu },\infty )$ depending on the triplet $(a,b,c)$ is a different problem altogether. Here, we discuss whether there are zeros (or not) of $N_{\nu }(a,b,c,1)$ in $(\overline{\nu },\infty )$ and, if $Condition {\mathcal{P}}_1$ met, what the situation of the Spirallikeness of ${\mathcal{N}}_1(\nu ,z)$ is. Thus, we consider two cases as follows.

I.

Suppose that $N_{\nu }(a,b,c,1)$ has no zeros in $(\overline{\nu },\infty )$. Then, we have three different situations:

• For $a,b,c$, and $\nu$, as stated in $Condition {\mathcal{P}}_1$,

  $$M_1(a,b,c,\nu )≔\frac{N_{\nu }^{\prime }(a,b,c,1)}{N_{\nu }(a,b,c,1)}+cos\left(\alpha \right)-\sigma -\nu >0.$$
  Then, ${\mathcal{N}}_1(\nu ,z)\in S{P}_p(\alpha ,\sigma )$ for all $\nu >\overline{\nu }$ with $\alpha$ and $\sigma$, as stated in Theorem 1.
• For $a,b,c$, and $\nu$, as stated in $Condition {\mathcal{P}}_1$,

  $$\underset{\nu \to {\overline{\nu }}^{+}}{lim}{M}_1(a,b,c,\nu )<0 \mathrm{and} \underset{\nu \to \infty }{lim}{M}_1(a,b,c,\nu )>0.$$
  Then, ${\mathcal{N}}_1(\nu ,z)\in S{P}_p(\alpha ,\sigma )$ for all $\nu >{\nu }_0$ with $\alpha$ and $\sigma$, as stated in Theorem 1. Here, ${\nu }_0$ is the unique root of $M_1(a,b,c,\nu )=0$ in $(\overline{\nu },\infty )$. Now, a calculation leads to

  $$\begin{array}{c}\hfill \frac{N_{\nu }^{\prime }(a,b,c,1)}{N_{\nu }(a,b,c,1)}=\frac{J_{\nu -1}\left(1\right)\left(a\left({\nu }^2-1\right)+c\right)-J_{\nu }\left(1\right)\left(a\left({\nu }^3+{\nu }^2-\nu +1\right)+b(1-\nu )(\nu +1)+c\nu \right)}{J_{\nu }\left(1\right)\left(a\left({\nu }^2+\nu -1\right)-b\nu +c\right)+(b-a)J_{\nu -1}\left(1\right)}.\end{array}$$

  (79)
  Thus, $M_1(a,b,c,\nu )=0$ is reduced to

  $$\begin{array}{c}\hfill \frac{J_{\nu }\left(1\right)\left(2a\nu \left({\nu }^2+\nu -1\right)+a+2\nu (c-b\nu )+b\right)-J_{\nu -1}\left(1\right)\left(a\left({\nu }^2+\nu -1\right)-b\nu +c\right)}{(a-b)J_{\nu -1}\left(1\right)-J_{\nu }\left(1\right)\left(a\left({\nu }^2+\nu -1\right)-b\nu +c\right)}+cos\left(\alpha \right)-\sigma =0.\end{array}$$
  Hence, ${\nu }_0$ is the unique root of the equation expressed as

  $$\begin{array}{cc}\hfill & J_{\nu }\left(1\right)\left(2a\nu \left({\nu }^2+\nu -1\right)+a+2\nu (c-b\nu )+b\right)-J_{\nu -1}\left(1\right)\left(a\left({\nu }^2+\nu -1\right)-b\nu +c\right)\hfill \\ \hfill & =(\sigma -cos\left(\alpha \right))\left((a-b)J_{\nu -1}\left(1\right)-J_{\nu }\left(1\right)\left(a\left({\nu }^2+\nu -1\right)-b\nu +c\right)\right).\hfill \end{array}$$

  (80)
• For $a,b,c$, and $\nu$, as stated in $Condition {\mathcal{P}}_1$, both

  $$\underset{\nu \to {\overline{\nu }}^{+}}{lim}{M}_1(a,b,c,\nu )<0 \mathrm{and} \underset{\nu \to \infty }{lim}{M}_1(a,b,c,\nu )<0.$$
  In this situation, Theorem 1 fails to provide any conclusion regarding the Spirallikeness of ${\mathcal{N}}_1(\nu ,z)$.

II.

For an arbitrary $m\in \mathbb{N}$, suppose that $N_{\nu }(a,b,c,1)$ has m zeros in $(\overline{\nu },\infty )$. These zeros are denoted and arranged as follows for further discussion:

$$\overline{\nu }<{\tilde{\nu }}_1<{\tilde{\nu }}_2<\dots <{\tilde{\nu }}_m.$$

Then, let us consider the following intervals:

$$\begin{array}{cc}\hfill I_0& =(\overline{\nu },{\tilde{\nu }}_1)\hfill \\ \hfill I_i& =({\tilde{\nu }}_i,{\tilde{\nu }}_{i+1}), i=1,2,\dots ,m-1\hfill \\ \hfill I_m& =({\tilde{\nu }}_m,\infty ).\hfill \end{array}$$

Now, similar to case (I), we have three different situations that need to be handled separately in each interval. If $M_1(a,b,c,\nu )>0$ in some or all intervals ($I_i$, $i=0,1,\dots ,m$), then ${\mathcal{N}}_1(\nu ,z)\in S{P}_p(\alpha ,\sigma )$ in those intervals. Furthermore, if $M_1(a,b,c,\nu )=0$ have a root (${\nu }_{0,i}$) in any $I_i$, $i=0,1,\dots ,m$, then ${\mathcal{N}}_1(\nu ,z)\in S{P}_p(\alpha ,\sigma )$ for $\nu \in ({\nu }_{0,i},{\nu }_{i+1})$ in the corresponding interval(s) ($I_i$). Finally, if $M_1(a,b,c,\nu )<0$ through in any interval ($I_i$), the Spirallikeness cannot be described by Theorem 1 in that particular interval ($I_i$).

Let us illustrate this case with some specific choices of a, b, and c, as well as $\alpha$ and $\sigma$, following $cos\left(\alpha \right)>\sigma$.

Consider the case of $c=0$, $a=-1$, and $b=2$. Then, (72) yields

$$\begin{array}{c}\hfill Q(-1,2,0,\nu )=-(\nu -3)\nu .\end{array}$$

This implies $\overline{\nu }=3$. Next,

$$\begin{array}{c}\hfill M_1(-1,2,0,\nu )={\displaystyle \frac{\left(2{\nu }^3+6{\nu }^2-2\nu -1\right)J_{\nu }\left(1\right)-\left({\nu }^2+3\nu -1\right)J_{\nu -1}\left(1\right)}{3J_{\nu -1}\left(1\right)-\left({\nu }^2+3\nu -1\right)J_{\nu }\left(1\right)}}+cos\left(\alpha \right)-\sigma \end{array}$$

We calculate the zeros of $N_{\nu }(-1,2,0,\nu )=3J_{\nu -1}\left(1\right)-\left({\nu }^2+3\nu -1\right)J_{\nu }\left(1\right)$ numerically using Mathematica https://www.wolfram.com/mathematica/online/, and for $\nu >0$, there are two zeros of $N_{\nu }(-1,2,0,\nu )$, namely at $\nu =0.157168<\overline{\nu }$ and $\nu =3.1996>\overline{\nu }$. This can also be observed in Figure 8.

Thus, we have two intervals for the discussion of the positivity of $M_1(-1,2,0,\nu )$, namely $I_0=(3,3.1996)$ and $I_1=(3.1996,\infty )$. Now,

$$\underset{\nu \in I_0}{min}{M}_1(-1,2,0,\nu )=M_1(-1,2,0,3)=1.85764+cos\left(\alpha \right)-\sigma >0$$

on $I_0$. This leads to the conclusion that ${\mathcal{N}}_1(\nu ,z)\in S{P}_p(\alpha ,\sigma )$ in $I_0$.

Next, ${\displaystyle \underset{\nu \to 3.{1996}^{+}}{lim}{M}_1(-1,2,0,\nu )<0}$. In this case, ${\mathcal{N}}_1(\nu ,z)\in S{P}_p(\alpha ,\sigma )$ if there exists ${\nu }_0\in I_1$ such that $M_1(-1,2,0,\nu )>0$ on $({\nu }_0,\infty )$, and the existence of ${\nu }_0$ is highly dependent on the value of $cos\left(\alpha \right)-\sigma$.

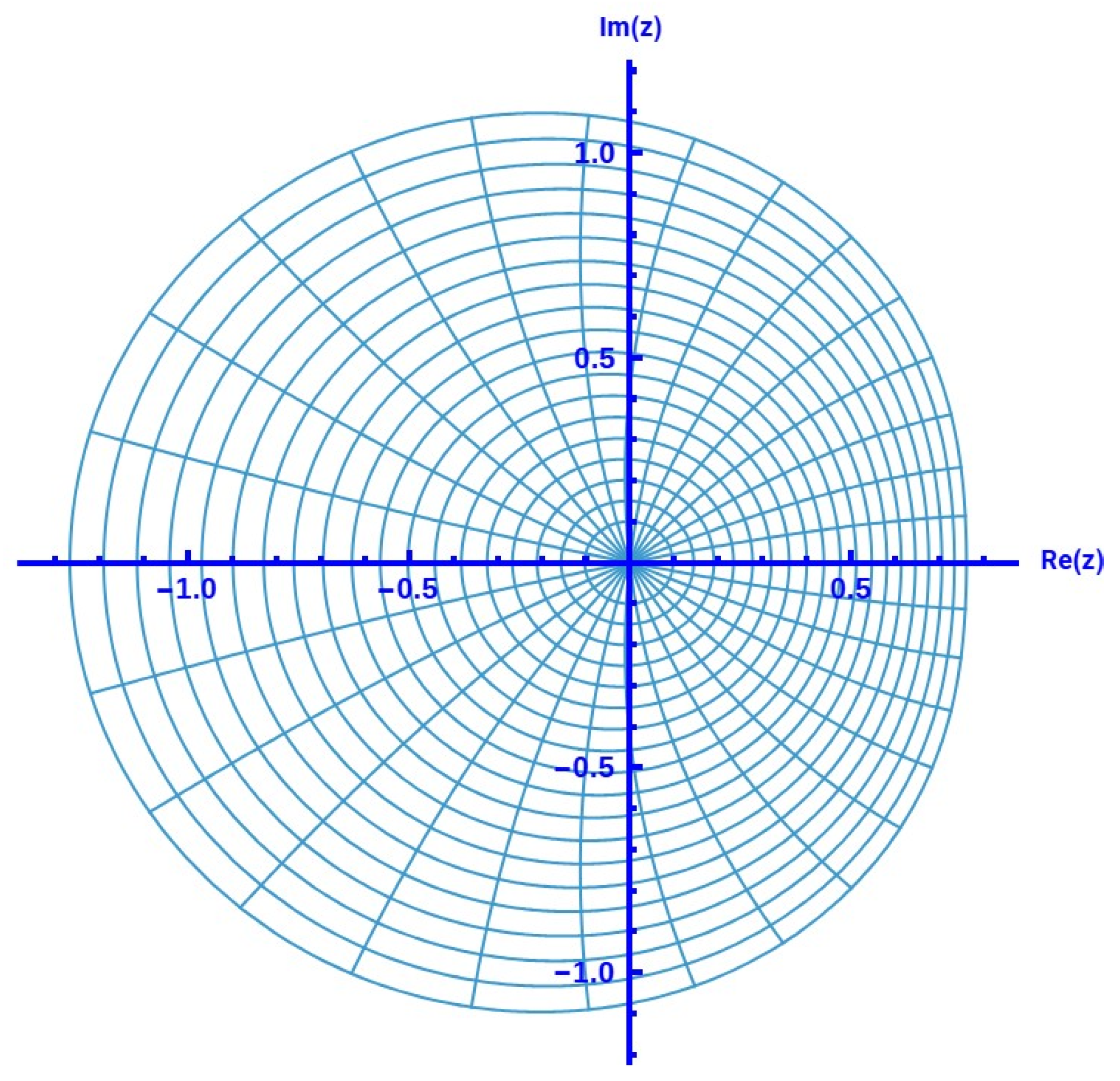
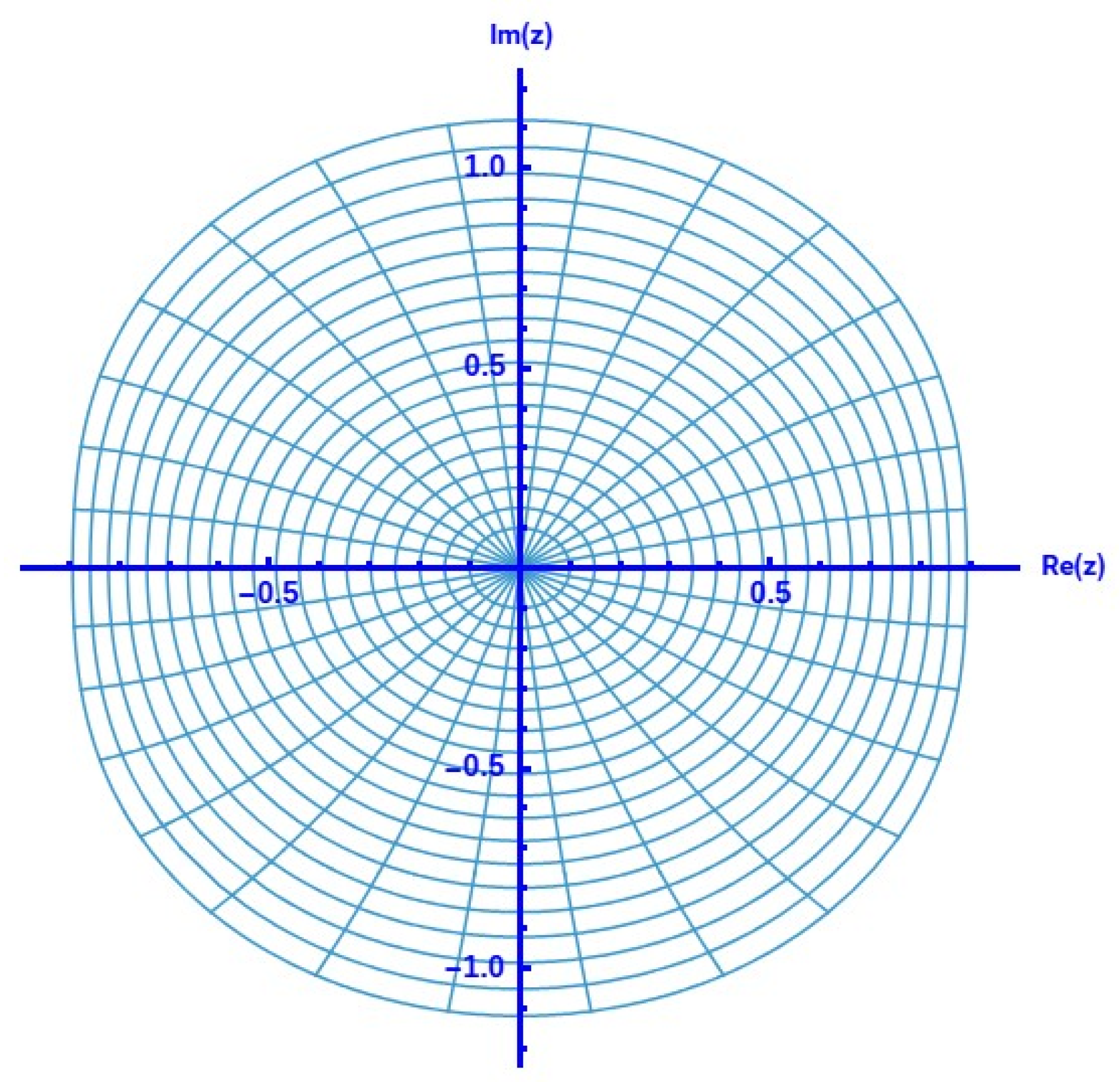
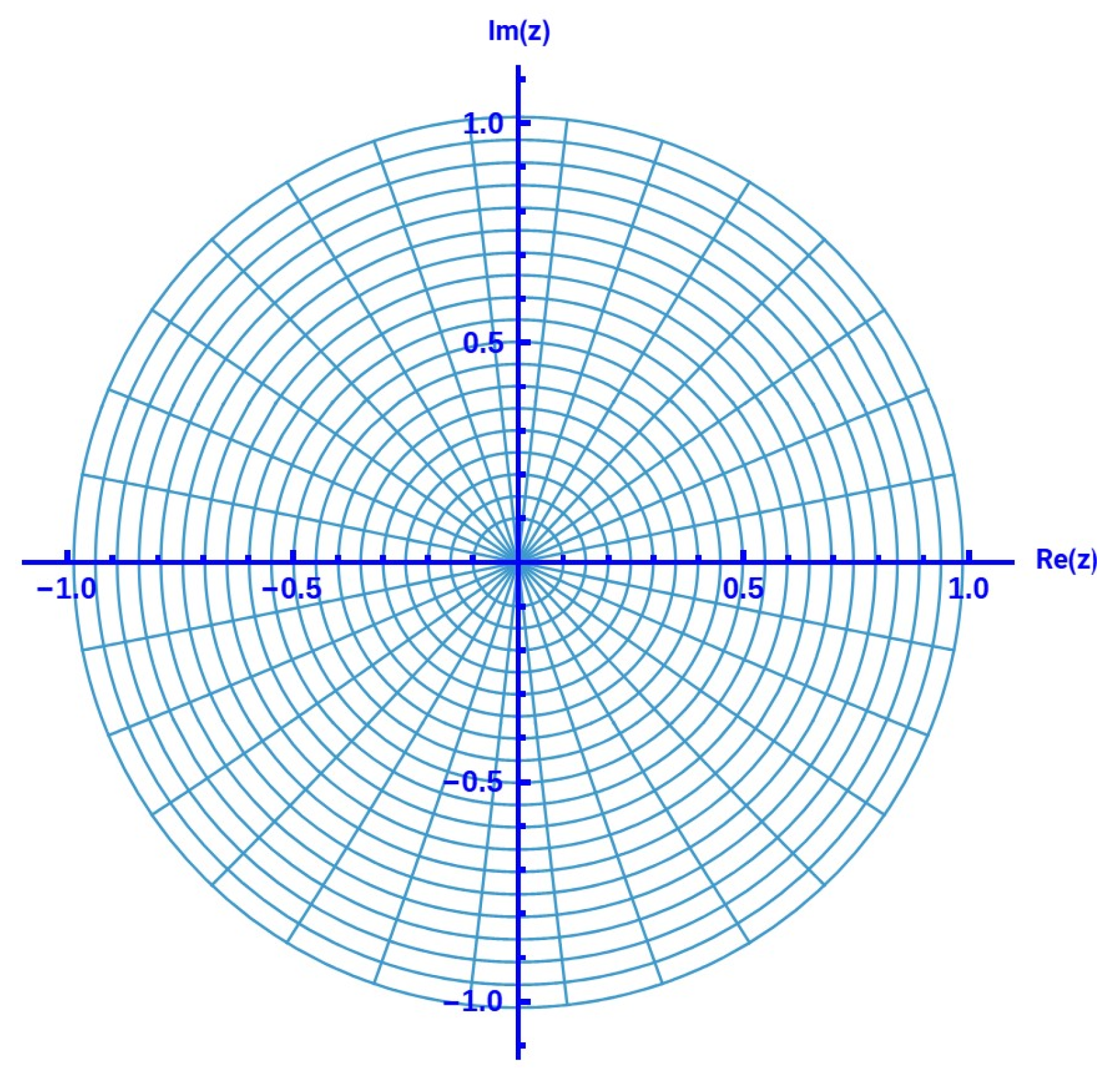
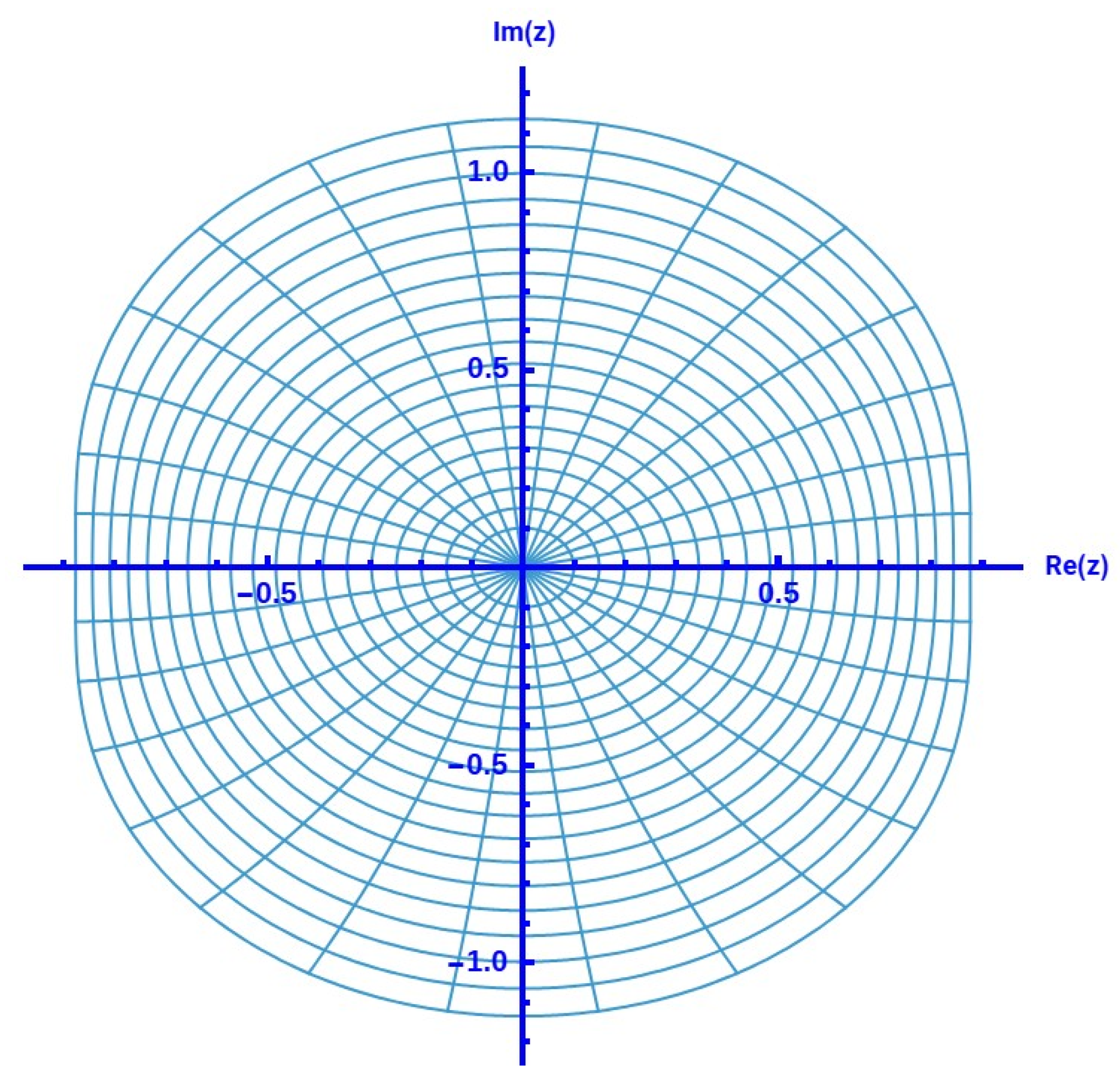
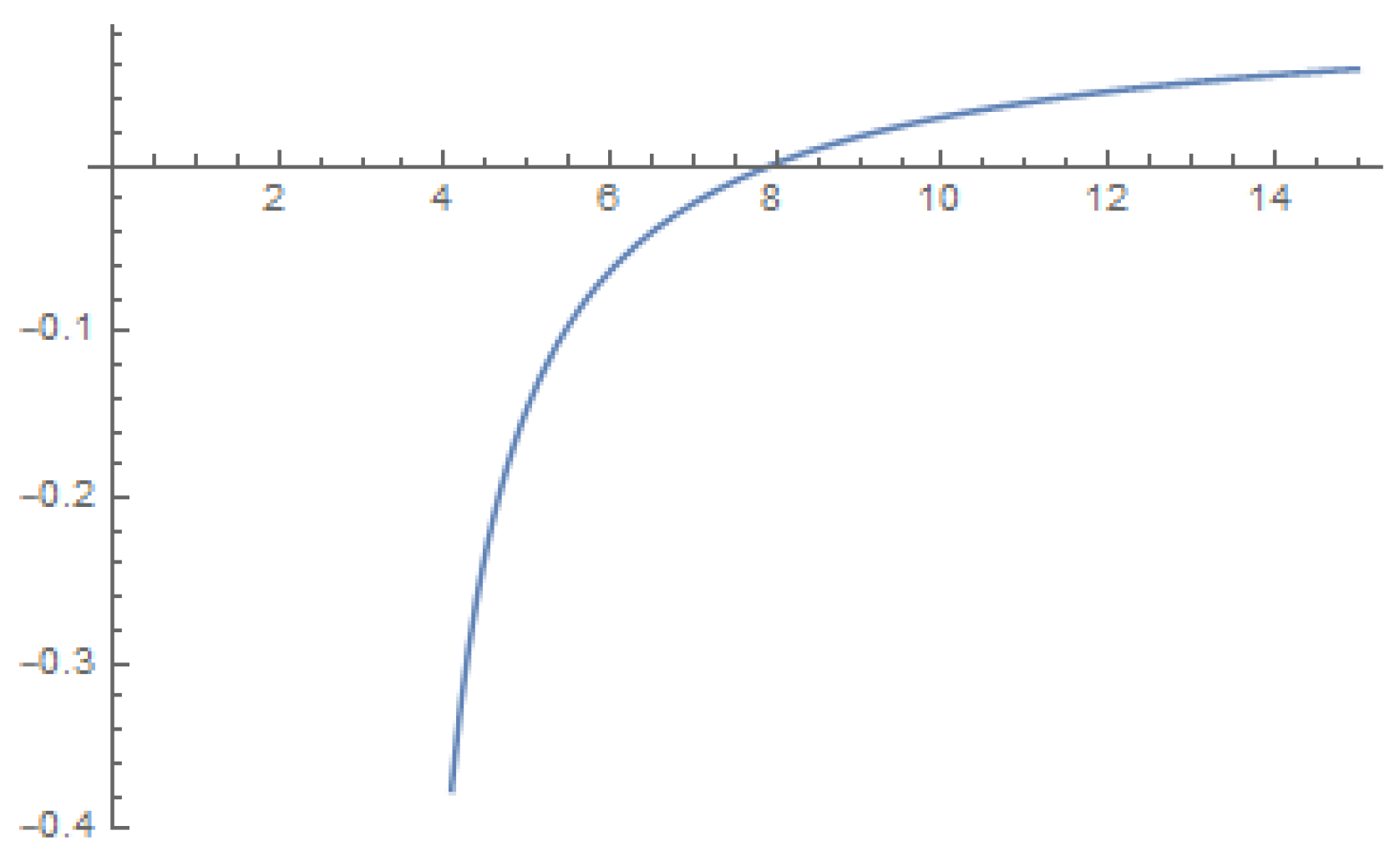
• Suppose that $cos\left(\alpha \right)-\sigma =0.1$; then, $M_1(-1,2,0,\nu )>0$ for ${\nu }_0\approx 7.90945$ (see Figure 9).
• $cos\left(\alpha \right)-\sigma =0.01$; then, $M_1(-1,2,0,\nu )>0$ for ${\nu }_0\approx 52.9703$ (see Figure 10).
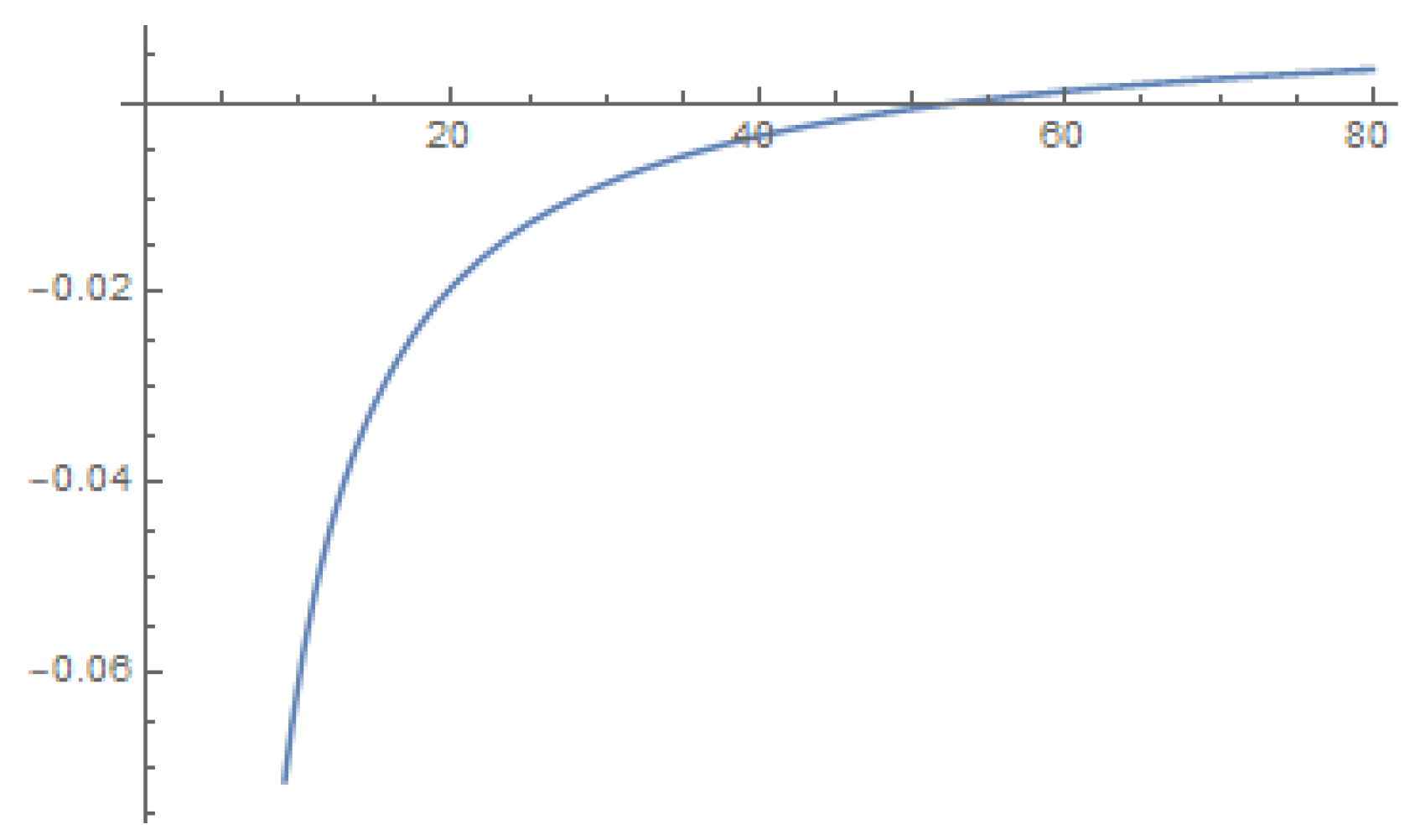
• Finally, we consider $cos\left(\alpha \right)-\sigma =0.001$. In this case, we are unable to find the exact numeric value of ${\nu }_0$ for which $M_1(-1,2,0,\nu )>0$. The graph in Figure 11 is asymptotic in nature. We note that Mathematica could not provide a clear graph for $\nu >154$ due to the very small value of the denominator. Therefore, we can not decide about a higher value of $\nu$, but it is ensured that, at least for $\nu \in (3.1996,154)$, Theorem 1 is inconclusive regarding the Spirallikeness of ${\mathcal{N}}_1(\nu ,z)$.

Considering all aspects of the above discussion and more numerical experiments, we state the following open problems:

Open Problem 1. 

Under $Condition {\mathcal{P}}_1$,

$$N_{\nu }(a,b,c,1)=(-a+b)J_{\nu -1}\left(1\right)+(c-b\nu +a(1+\nu +{\nu }^2))J_{\nu }\left(1\right)$$

have a unique root in $(\overline{\nu },\infty )$.

Open Problem 2. 

Suppose the $Condition {\mathcal{P}}_1$ holds and $cos\left(\alpha \right)-\sigma$ is very small. Then, ${lim}_{\nu \to \infty }{M}_1(a,b,c,\nu )<0$ is probable.

We conclude this section by noting that a similar argument can be made for ${\mathcal{N}}_2$ and ${\mathcal{N}}_3$.

4. Outline of Several Other Examples

In this section, we provide some more examples that can be included in the $S{P}_p(\alpha ,\sigma )$ class. Due to similarity in the types of calculation and verification, we just outline functions as infinite product representations.

• Struve functions: Let ${\mathtt{h}}_{\nu ,n}$ represent the nth positive zero of the Struve function, denoted by ${\mathtt{S}}_{\nu }$. Then, ${\mathtt{S}}_{\nu }$ can express (see [22]) in the following manner:

  $$\begin{array}{c}\hfill {\mathtt{S}}_{\nu }\left(z\right)={\displaystyle \frac{z^{\nu +1}}{2^{\nu }\sqrt{\pi }\mathsf{\Gamma }\left(\nu +\frac{3}{2}\right)}}\prod _{n=1}^{\infty }\left(1-{\displaystyle \frac{z^2}{{\mathtt{h}}_{\nu ,n}^2}}\right) \mathrm{for} \left|\nu \right|\le 1/2.\end{array}$$

  (81)
  For more details, we refer readers to [22,23]. Using (81), we can construct following example:

  Example 6.

  For $\left|\nu \right|\le 1/2$,

  (i) 

  ${\mathcal{S}}_1(\nu ,z)=\sqrt{\pi }{2}^{\nu }\mathsf{\Gamma }\left(\nu +{\displaystyle \frac{3}{2}}\right)z^{{\displaystyle \frac{1-\nu }{2}}}{\mathtt{S}}_{\nu }\left(\sqrt{z}\right)\in {\mathbb{H}}_1,$ with $a_n\left(\nu \right)={\mathtt{h}}_{\nu ,n}$;

  (ii) 

  ${\mathcal{S}}_2(\nu ,z)=\sqrt{\pi }{2}^{\nu }\mathsf{\Gamma }\left(\nu +{\displaystyle \frac{3}{2}}\right)z^{1-\nu }{\mathtt{S}}_{\nu }\left(z\right)\in {\mathbb{H}}_2$ with $b_n\left(\nu \right)={\mathtt{h}}_{\nu ,n}$;

  (iii) 

  ${\mathcal{S}}_3(\nu ,z)={\left(\sqrt{\pi }{2}^{\nu }\mathsf{\Gamma }\left(\nu +{\displaystyle \frac{3}{2}}\right){\mathtt{S}}_{\nu }\left(z\right)\right)}^{{\displaystyle \frac{1}{\nu +1}}}\in {\mathbb{H}}_3$ with $d_n\left(\nu \right)={\mathtt{h}}_{\nu ,n}$ and $\mu \left(\nu \right)≔1/(\nu +1)$.

  For $\nu =1/2$, it follows that

  $$\begin{array}{cc}\hfill {\mathcal{S}}_1(1/2,z)& =2\left(1-cos\left(\sqrt{z}\right)\right), {\mathcal{S}}_2(1/2,z)=2(1-cos\left(z\right)), \mathrm{and} \hfill \\ \hfill {\mathcal{S}}_3(1/2,z)& =2^{2/3}{\left({\displaystyle \frac{1-cos\left(z\right)}{\sqrt{z}}}\right)}^{2/3}.\hfill \end{array}$$
  Furthermore, for $\nu =-1/2$, we have

  $$\begin{array}{cc}\hfill {\mathcal{S}}_1(-1/2,z)& =\sqrt{z}sin\left(\sqrt{z}\right), {\mathcal{S}}_2(-1/2,z)=zsin\left(z\right), \mathrm{and} \hfill \\ \hfill {\mathcal{S}}_3(-1/2,z)& ={\displaystyle \frac{{sin}^2\left(z\right)}{z}}.\hfill \end{array}$$
  Thus, the inclusion properties of ${\mathcal{S}}_i(\nu ,z)$ ($i=1,2,3)$ in the $S{P}_p(\alpha ,\sigma )$ class can be obtained by using the respective main theorems presented in Section refsec-2. In special cases, the Spirallikeness of the trigonometric functions mentioned above can also be established.
• Wright Functions: The nth positive zero of ${\lambda }_{\rho ,\delta }\left(z\right)=\varphi (\rho ,\delta ,-z^2)$ is denoted by ${\lambda }_{\rho ,\delta ,n}$. Here, $\varphi (\rho ,\delta ,z)$ is the well-known Wright function [24]. For $\rho >0$ and $\delta >0$, it was proven in [25] that the function expressed as $z\mapsto {\lambda }_{\rho ,\delta }=\varphi (\rho ,\delta ,-z^2)$ possesses infinitely many real zeros, and its Weierstrass decomposition is expressed as follows:

  $$\mathsf{\Gamma }\left(\delta \right)\varphi (\rho ,\delta ,-z^2)=\prod _{n=1}^{\infty }\left(1-{\displaystyle \frac{z^2}{{\lambda }_{\rho ,\delta ,n}^2}}\right).$$
  The infinite product converges uniformly on a compact subset of the complex plane. We present the following example related to $\varphi (\rho ,\delta ,.)$.
  Example 7 (The normalized Wright function).

  For $\rho ,\delta >0$, ${\lambda }_{\rho ,\delta ,n}$ denotes the n-th zero of the function expressed as ${\lambda }_{\rho ,\delta }\left(z\right)$. Then,

  $$\begin{array}{cc}\hfill {\mathcal{W}}_1(\rho ,\delta ,z)& =z\mathsf{\Gamma }\left(\delta \right){\lambda }_{\rho ,\delta }\left(\sqrt{z}\right)=z\prod _{n=1}^{\infty }\left(1-{\displaystyle \frac{z}{{\lambda }_{\rho ,\delta ,n}^2}}\right)\in {\mathbb{H}}_1\hfill \end{array}$$

  (82)

  $$\begin{array}{cc}\hfill {\mathcal{W}}_2(\rho ,\delta ,z)& =z\mathsf{\Gamma }\left(\delta \right){\lambda }_{\rho ,\delta }\left(z\right)=z\prod _{n=1}^{\infty }\left(1-{\displaystyle \frac{z^2}{{\lambda }_{\rho ,\delta ,n}^2}}\right)\in {\mathbb{H}}_2\hfill \end{array}$$

  (83)

  $$\begin{array}{cc}\hfill {\mathcal{W}}_3(\rho ,\delta ,z)& ={\left(z^{\delta }\mathsf{\Gamma }\left(\delta \right){\lambda }_{\rho ,\delta }\left(z\right)\right)}^{{\displaystyle \frac{1}{\delta }}}=z\prod _{n=1}^{\infty }{\left(1-{\displaystyle \frac{z^2}{{\lambda }_{\rho ,\delta ,n}^2}}\right)}^{\frac{1}{\delta }}\in {\mathbb{H}}_3.\hfill \end{array}$$

  (84)
  The Wright function is related to the classical Bessel function of the first kind of $\nu$ by

  $${\lambda }_{1,1+\nu }\left(z\right)=\varphi (1,1+\nu ,-z^2)=z^{-\nu }{J}_{\nu }\left(2z\right).$$
  For various geometric properties of ${\lambda }_{\rho ,\delta }$, we refer readers to [1,25,26,27,28,29]. Now, the connection between the $S{P}_p(\alpha ,\sigma )$ class and ${\mathcal{W}}_i(\rho ,\delta ,z)$, $(i=1,2,3)$ can be established based on applicable main results reported in Section refsec-2.
• q-Bessel Functions: We consider Jackson and Hahn–Exton q-Bessel functions (${\mathtt{J}}_{\nu }^{\left(2\right)}(z;q)$ and ${\mathtt{J}}_{\nu }^{\left(3\right)}(z;q)$). For $z\in \mathbb{C}$, $\nu >-1$, and $q\in (0,1)$, both functions are defined by series expansions:

  $$\begin{array}{cc}\hfill {\mathtt{J}}_{\nu }^{\left(2\right)}(z;q)& ≔{\displaystyle \frac{{\left(q^{\nu +1};q\right)}_{\infty }}{{\left(q;q\right)}_{\infty }}}\sum _{n\ge 0}{\displaystyle \frac{{(-1)}^n{\left(\frac{z}{2}\right)}^{2n+\nu }}{{\left(q;q\right)}_{\infty }{\left(q^{\nu +1};q\right)}_n}}{q}^{n(n+\nu )},\hfill \end{array}$$

  (85)

  $$\begin{array}{cc}\hfill {\mathtt{J}}_{\nu }^{\left(3\right)}(z;q)& ≔{\displaystyle \frac{{\left(q^{\nu +1};q\right)}_{\infty }}{{\left(q;q\right)}_{\infty }}}\sum _{n\ge 0}{\displaystyle \frac{{(-1)}^n{z}^{2n+\nu }}{{\left(q;q\right)}_{\infty }{\left(q^{\nu +1};q\right)}_n}}{q}^{{\displaystyle \frac{n(n+1)}{2}}}.\hfill \end{array}$$

  (86)
  Here, ${\left(a;q\right)}_i$ is the well-known q-Pochhammer symbol defined as follows:

  $$\begin{array}{cc}\hfill {(a;q)}_0& =1,\hfill \\ \hfill {(a;q)}_n& =\prod _{k=1}^n\left(1-a{q}^{k-1}\right),\hfill \\ \hfill {(a;q)}_{\infty }& =\prod _{k\ge 1}\left(1-a{q}^{k-1}\right).\hfill \end{array}$$
  There is a wealth of literature [30,31,32,33,34,35] on the q-extension of Bessel functions, and we confine our discussion to the specific requirements of this study. The Hadamard factorization for the following normalized q-Bessel functions is given in Lemma 5:

  $$\begin{array}{cc}\hfill z\to {\mathcal{J}}_{\nu }^{\left(2\right)}(z;q)& =2^{\nu }{c}_{\nu }\left(q\right)z^{-\nu }{\mathtt{J}}_{\nu }^{\left(2\right)}(z;q) \mathrm{and}\hfill \\ \hfill z\to {\mathcal{J}}_{\nu }^{\left(3\right)}(z;q)& =c_{\nu }\left(q\right)z^{-\nu }{\mathtt{J}}_{\nu }^{\left(3\right)}(z;q),\hspace{1em}{c}_{\nu }\left(q\right)={\left(q;q\right)}_{\infty }/{\left(q^{\nu +1};q\right)}_{\infty }\hfill \end{array}$$
  Lemma 5

  ([34]). For $\nu >-1$, the functions expressed as $z\to {\mathcal{J}}_{\nu }^{\left(2\right)}(z;q)$ and $z\to {\mathcal{J}}_{\nu }^{\left(3\right)}(z;q)$ are entire functions of order zero and pose the Hadamard factorization for the following form:

  $$\begin{array}{c}\hfill {\mathcal{J}}_{\nu }^{\left(2\right)}(z;q)=\prod _{n\ge 1}\left(1-{\displaystyle \frac{z^2}{j_{\nu ,n}^2\left(q\right)}}\right), {\mathcal{J}}_{\nu }^{\left(3\right)}(z;q)=\prod _{n\ge 1}\left(1-{\displaystyle \frac{z^2}{l_{\nu ,n}^2\left(q\right)}}\right),\end{array}$$

  (87)

  where $j_{\nu ,n}\left(q\right)$ and $l_{\nu ,n}\left(q\right)$ are the $n^{th}$ positive zero of functions ${\mathcal{J}}_{\nu }^{\left(2\right)}(.;q)$ and ${\mathcal{J}}_{\nu }^{\left(3\right)}(.;q)$, respectively.
  The above-mentioned facts provide us with the following examples:

  Example 8.

  For $\nu >-1$ and $q\in (0,1)$, $j_{\nu ,n}\left(q\right)$ denotes the n-th zero of the q-Bessel functions (${\mathtt{J}}_{\nu }^{\left(2\right)}(z;q)$). Then,

  $$\begin{array}{cc}\hfill {}_{2}f_{\nu ,q}\left(z\right)& =z{\mathcal{J}}_{\nu }^{\left(2\right)}(\sqrt{z};q)=z\prod _{n\ge 1}\left(1-{\displaystyle \frac{z}{j_{\nu ,n}^2\left(q\right)}}\right)\in {\mathbb{H}}_1,\hfill \end{array}$$

  (88)

  $$\begin{array}{cc}\hfill {}_{2}g_{\nu ,q}\left(z\right)& =z{\mathcal{J}}_{\nu }^{\left(2\right)}(z;q)=z\prod _{n\ge 1}\left(1-{\displaystyle \frac{z^2}{j_{\nu ,n}^2\left(q\right)}}\right)\in {\mathbb{H}}_2,\hfill \end{array}$$

  (89)

  $$\begin{array}{cc}\hfill {}_{2}h_{\nu ,q}\left(z\right)& ={\left(z^{\nu }{\mathcal{J}}_{\nu }^{\left(2\right)}(z;q)\right)}^{\frac{1}{\nu }}=z\prod _{n\ge 1}{\left(1-{\displaystyle \frac{z^2}{j_{\nu ,n}^2\left(q\right)}}\right)}^{\frac{1}{\nu }}\in {\mathbb{H}}_3.\hfill \end{array}$$

  (90)
  Example 9.

  For $\nu >-1$ and $q\in (0,1)$, $l_{\nu ,n}\left(q\right)$ denotes the n-th zero of the q-Bessel functions (${\mathtt{J}}_{\nu }^{\left(3\right)}(z;q)$). Then,

  $$\begin{array}{cc}\hfill {}_{3}f_{\nu ,q}\left(z\right)& =zexp\left(\beta z\right){\mathcal{J}}_{\nu }^{\left(3\right)}(\sqrt{z};q)\in {\mathbb{H}}_1,\hfill \end{array}$$

  (91)

  $$\begin{array}{cc}\hfill {}_{3}g_{\nu ,q}\left(z\right)& =z{\mathcal{J}}_{\nu }^{\left(3\right)}(z;q)\in {\mathbb{H}}_2,\hfill \end{array}$$

  (92)

  $$\begin{array}{cc}\hfill {}_{3}h_{\nu ,q}\left(z\right)& ={\left(z^{\nu }{\mathcal{J}}_{\nu }^{\left(3\right)}(z;q)\right)}^{\frac{1}{\nu }}\in {\mathbb{H}}_3.\hfill \end{array}$$

  (93)

5. Conclusions

In this article, we have focused on the Spirallikeness of three classes of functions represented by convergent infinite products whose factors involve the positive zeros of the function. We showed that functions admitting a Hadamard factorization may belong to the classes ${\mathbb{H}}_i$, $i=1,2,3$, and we derived sufficient conditions for their inclusion in the $S{P}_p(\alpha ,\sigma )$ class. Moreover, since the positive zeros play a crucial role in the factorization of functions in the presented classes, our results provide sufficient conditions for studying the Spirallikeness of the function in light of certain properties of these zeros, particularly their monotonicity with respect to the $\nu$ parameter. The results were applied to a variety of examples involving well-known special functions such as the gamma function, normalized Bessel functions, and derivatives of the Bessel function. These normalized functions have also been previously studied in different contexts, including with respect to the radius of Starlikeness, convexity, and parabolic Starlikeness. Additionally, our framework encompasses other functions, such as the Lommel, Dini, and q-Struve–Bessel functions; the cross product of Bessel functions; Ramanujan-type entire functions; Mittag-Leffler functions; and products of Bessel and modified Bessel functions. However, since the nature of the analysis for these functions closely resembles that of the examples presented in Section 3 and Section 4, they were not explicitly discussed here.