Abstract
The Kuralay-II system (K-IIS) plays a pivotal role in modeling sophisticated nonlinear wave processes, particularly in the field of optics. This study introduces novel soliton solutions for the K-IIS, derived using the Riccati–Bernoulli sub-ODE method combined with Bäcklund transformation and conformable fractional derivatives. The obtained solutions are expressed in trigonometric, hyperbolic, and rational forms, highlighting the adaptability and efficacy of the proposed approach. To enhance the understanding of the results, the solutions are visualized using 2D representations for fractional-order variations and 3D plots for integer-type solutions, supported by detailed contour plots. The findings contribute to a deeper understanding of nonlinear wave–wave interactions and the underlying dynamics governed by fractional-order derivatives. This work underscores the significance of fractional calculus in analyzing complex wave phenomena and provides a robust framework for further exploration in nonlinear sciences and optical wave modeling.
Keywords:
Bäcklund transformation; Riccati–Bernoulli sub-ODE method; fractional Kuralay-II system (K-IIS); solitary wave solutions MSC:
32G34; 32W50; 34B15; 93C20
1. Introduction
This research work begins by reviewing the existing literature on the topic and introducing the Kuralay-II system. This section provides the reader with a brief overview of the work’s goals, a summary of previous work and a guide to the manuscript’s layout.
Nonlinear partial differential equations (NPDEs) have been used in many applied sciences over the past few decades, such as atomic, particle, optical, nuclear, and biological physics [1,2]. Such equations are necessary when describing various subtle effects, due to which different nonlinear models have been created. A variety of techniques have been developed to solve numerical, analytical, and some semi-analytical solutions, including the spline scheme [3], finite difference method [4], Adomian decomposition technique [5], variational iteration [6] and several expansion techniques, such as sine–cosine expansion and the modified simple equation method [7,8]. Recently, a considerable amount of attention has been paid to work on the interactions of nonlinear dynamic systems and solitons because of their widespread utility in optics and fluid mechanics, as well as in materials science [9,10]. Powerful analytical solutions for numerous differential equations have been extended through generalized systems and algebraic constraints, and the application of fractional and perturbation models reflect the physical phenomena of waves, fluids and electromagnetic vibrations [11]. This paper adds to the literature as a development of the mathematical proficiency and generality of solutions by using the Bäcklund transformation and fractional calculus. The hope is that, by combining these techniques with previously existing ones, an enhanced approach to analysis and decision-making in the context of uncertainty and complexity will be developed [12,13,14,15,16].
It is necessary to use fractional partial differential equations (FPDEs) to describe many natural processes in biology, applied physics, chemistry, economics, etc. Some of the real applications of these theories involve the study of material and wave behaviors in such domains, which require nonlinear PDEs such as the extended Zakharov–Kuznetsov equation [17], fifth-order Lax equation [18], Fokas equation [19], Clannish Random Walker Parabolic [20], Oskolkov equation [21], Schrödinger dynamical systems [22] and dispersive long-wave equations [23]. There are some new techniques, including Lie symmetry analysis [24], the Jacobi elliptic function method [25], the Khater method [26] and the (–)-expansion method [27]. These are employed to find analytical soliton solutions, such as exact solutions in the form of solitons for the fractional partial differential equations (FPDEs) [28,29,30,31,32]. Searching for various explicit solutions with the help of analytical methods is essential for the study of behavior in different scientific fields, such as fluid mechanics, wave propagation and engineering applications at the basis of nonlinear partial differential equations (NPDEs). The NPDE soliton solutions are useful as they are explicit solutions, and solitons preserve their shape and velocity through time-introducing stability and order into the nonlinear system [33,34,35]. Solitons play the role of stable information bearers, which makes them important in theoretical as well as practical studies. Thus, to obtain new soliton solutions, a range of strong techniques are applied. The general methods of solving the NPDEs include the Sin-Gordon [36] and exp-function [37] approaches, the Sardar sub-equation [38], the extended direct algebraic method (EDAM) [39] and the Hirota bilinear approach [40]. These methods, which are constantly being fine-tuned, help in the development of the toolkit that is used in the analysis of new solutions.
The objective of this paper is to discuss the influence of this new derivative on the solutions of the time–space fractional Kuralay-II system by employing the Riccati–Bernoulli sub-ODE method combined with the Bäcklund transformation, which have not been adopted in previous studies. The fractional derivative represents both integer and fractional-order behaviors. It improves classical calculus by including memory effects, which are important in many scientific processes. Many fractional models exist in parallel to experimental data so that their application across the fields of physics and engineering is feasible. In particular, the present work reveals that lower fractional orders correspond to greater-magnitude derivatives with convergence as the fractional orders rise, indicating the derivative ability to track unique soliton dynamics. Our study, based on trigonometric, hyperbolic and rational functions, reveals different solutions and relations between the considered fractional NPDEs and integer ones. These methods provide a basic but effective means to obtain different solutions to specific FNLPDEs more effectively than conventional approaches. The Kuralay-II system (K-IIS) plays a critical role in understanding and modeling nonlinear wave phenomena across various physical and engineering domains. Its applications are particularly prominent in the field of nonlinear optics, where it is utilized to describe wave interactions in optical fibers, waveguides and other photonic systems. The soliton solutions derived in this study offer valuable insights into the behavior of optical pulses, making them relevant for several advanced technologies. The K-IIS has been used to model the features of solitons in optical communication systems. In this regard, the soliton solutions determined from fractional derivatives encompass higher-order dispersion and nonlinearity that cannot be described by the standard integer-order models. This is particularly advantageous in the development of high-data-capacity, long-haul communication networks, where pulse spreading and distortion effects have to be kept at their lowest.
Other novel and developing uses of the K-IIS are in investigations of nonlinear waves in metamaterials. These manmade materials possess novel characteristics, including a negative refractive index; as such, to describe wave behaviors within them, highly sophisticated models are need. It is expected that the fractional-order solutions obtained in this work can be applied to analyze energy localization and transmission in nonlinear metamaterial layers for the purpose of designing new devices for efficient wave control, e.g., cloaking systems or energy concentrator equipment. This analytically exact work offers practical tools for the armory of researchers and engineers, enabling them to analytically study nonlinear phenomena in a wide array of disciplines, from photonics and materials science to nanotechnology and fluid dynamics.
This article considers the nonlinear fractional Kuralay-II system (K-IIS), which has been discussed in [41]:
For the study of the Kuralay-II system, while assigning the values to (f), we take as a complex function and as a real function and . The spatial dimension is outlined by variable (x), while the temporal dimension is represented by variable (t). This time–space fractional Kuralay-II equation is useful to model complex natural processes because it contains the integer and fractional orders of derivatives. The elements of Cauchy’s fraction in the given equation improve the modeling in a wide range of fields, such as applied mathematics, physics, nonlinear optical phenomena, fluid dynamics, communication systems, etc. [42]. This fractional approach enables researchers to better understand problems across these fields and offers analysis and calculation benefits. It is the fundamental correlation between gauge and geometrical equivalence that is paramount in soliton theory, particularly in the study of the fractional Kuralay-II equation. Some new soliton solutions have been obtained through sophisticated techniques and analyses in recent research. For instance, Sagidullayeva et al. [41] used the Hirota bilinear method to show that two nonlinear models are gauge-equivalent. Faridi et al. [42] and Mathananaranjan [43] used different expansions to derive soliton, solitary wave and modulation instability solutions to some of these equations. Zafar et al. [44] and Khan et al. [45] discussed exact solutions with the help of different techniques, such as -function and Jacobi elliptic function expansion, and found some applications in science and engineering. According to previous studies on the fractional Kuralay-II system equations, there is no work on periodic perturbation solitons (PPSs) utilizing our outlined Riccati–Bernoulli sub-ODE and Bäcklund transformation techniques. This illustrates the present research gap in the literature. To fill this gap, our study applies these methods to acquire and analyze PPSs in the fractional Kuralay-II system to gain a further understanding of soliton dynamics, periodicity and the real-world applications of this model to a wide range of nonlinear systems.
In our work, we employ conformable fractional derivatives (CFDs) [46], which are suitable tools for the modeling of fractional systems since they enrich the integer-order calculus in terms of the properties. The conformable fractional derivative is defined for a function as
Such properties enable us to obtain straightforward physical explanations and improve the effectiveness in projecting existing circumstances in various disciplines, including fluid mechanics and wave theory. In our study, the CFDs enable the continuous treatment of the periodic perturbation solitons in the fractional Kuralay-II model, which incorporates memory effects but is numerically manageable. This is essential in achieving improved accuracy for soliton solutions, as well as a deeper understanding of the model’s dynamical properties under fractional effects.
2. Methodology
Consider the nonlinear partial differential equation (PDE)
where U is some polynomial in and its partial derivatives, but, more specifically, the last derivatives and nonlinear terms thereof. Our method [47,48,49] proceeds by applying the wave transformation
with constants a and b, transforming Equation (4) into an ordinary differential equation (ODE):
where V is a polynomial in and its derivatives. We assume the formal solution form for Equation (6):
where the constants () are decided with or , where is derived from a Bäcklund transformation:
where and are constants with (), and where satisfies the Riccati equation:
From previous studies [50], it is known that the Riccati equation has solutions
In the case of finding the integer (m) for Equation (7), we use a compromise between the highest derivatives and the nonlinear terms in the transformed ODE. Defining the degree of as allows us to compute the degrees of related expressions, such as
Since the ODE is satisfied by both our assumptions and the Riccati solutions, we replace Equations (7) and (9) with Equation (4) to obtain an algebraic system, which is soluble, using Maple for the values of , , , and . This gives exact traveling wave solutions for the original PDE as it yields, in general, solutions for various well-known traveling wave equations. In case , this particular approach will be reduced to the modified extended tanh-function method.
3. Execution of the Problem
In this paper, we use the proposed Riccati–Bernoulli sub-ODE method to find the optical soliton solutions of Equation (1). The process begins with the introduction of a complex wave transformation formulated as follows:
Upon substituting Equation (13) into Equation (1) and separating the imaginary and real components, we obtain
Integrating the second part of Equation (14) with respect to y and assuming that the constant of integration is zero, we find
Substituting Equation (15) back into Equation (14) simplifies the real part of the system, reducing it to a single nonlinear ordinary differential equation (NODE):
where is the constraint condition of the imaginary part. With this reformulation, we are then able to use the Riccati–Bernoulli sub-ODE method in conjunction with the Bäcklund transformation to systematically break down and analyze the nonlinearity of the system, which is important in understanding the spatial–temporal behaviours of optical solitons in a fractional-order context. This methodology sheds light on the effects that fractional parameters have on soliton behavior for use in nonlinear optics and other systems where wave–wave interactions occur. If the balancing procedure is implemented between and (), then () is obtained. By substituting Equations (7) and (9) into Equation (16), and then equating the coefficients of various powers of to zero, a set of algebraic equations results. It helps to reach a conclusion regarding the most suitable unknown parameters for a given system, which provides the exact solutions for the same. The equations obtained in the course of this procedure form a system of algebraic equations, which can be easily solved by different programs for example Maple, Mathematica, MATLAB or analogous. This enables the identification of multiple distinct solution cases, outlined as follows:
- Case 1:
- Case 2:
In this regard, the two cases obtained using the algebraic system described above may be used to identify families of solutions with regard to . These solution families show different behaviors of the system in different cases. The emergent solution behaviors reveal the temporal dynamics of the system, as well as the physical manifestations and mechanisms under a variety of fractional-order controls and initial states. Moreover, these families of solutions include all the interconnections distinguished in the system, while revealing the impacts of different on soliton behavior and stability, and it has significance for fluid dynamics and nonlinear waves.
From here, we concentrate on solving Case 1 by inserting the obtained values of () and reveal a set of unique solutions for Equation (1). The solutions obtained here have periodic perturbations in solitons, which suggests that the soliton profile oscillates temporally within this setting. All such fluctuations indicate that the solitons undergo rhythmic disturbances that affect their amplitude as well as stability. This is important for the analysis of the time dependence of the behavior and possible resonances in the system under changes in conditions.
Solution set 1: ().
or
Solution set 2: ().
or
Solution set 3: ().
Here, we show the associated solutions for (Case 2) and ().
or
Solution set 4: ().
or
Solution set 5: ().
4. Results and Discussion
In this paper, a new approach to solving space–time fractional nonlinear PDEs in nuclear physics, particle physics and fluid dynamics is proposed, employing the Bäcklund transformation and the Riccati–Bernoulli sub-ODE method to develop a closed-form solution in terms of periodic perturbations. In this work, this approach has been utilized to perform a direct and simplified transformation from PDEs to ODEs with the aim of obtaining clear and exact hyperbolic, rational and trigonometric solitons and analyzing their periodic characteristics. This understanding of periodic disturbances in a space–time fractional scheme not only enriches soliton theory but also gives adequate grounds for stability and wave analysis, with potential areas of application including topological solitons and materials science. Table 1, comparison of the proposed method with the alternative approach, the extended exp-function method [51].

Table 1.
Comparison of the proposed method with the alternative approach, the extended exp-function method [51].
As shown in the study on the fractional Kuralay-II system—see Figure 1, Figure 2, Figure 3 and Figure 4—a periodic perturbation is displayed with the integer-order and the fractional-order parameter (), as shown in the plots of the real and imaginary components. Moreover, the contour representations in all figures confirm the presence of fractal patterns, which increases the richness of the analysis. The following is a detailed view of each figure.
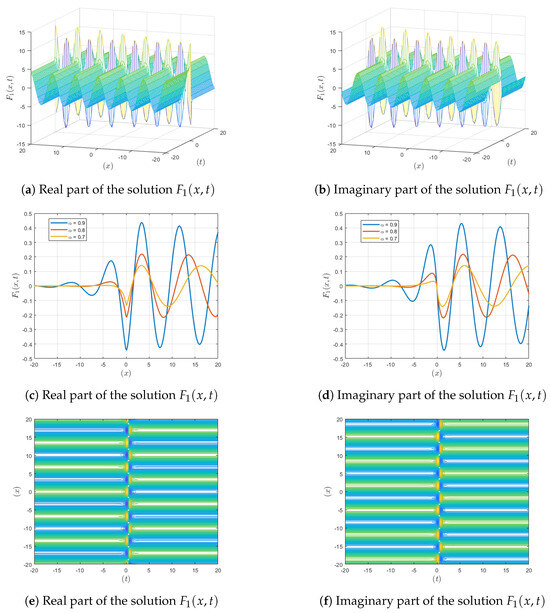
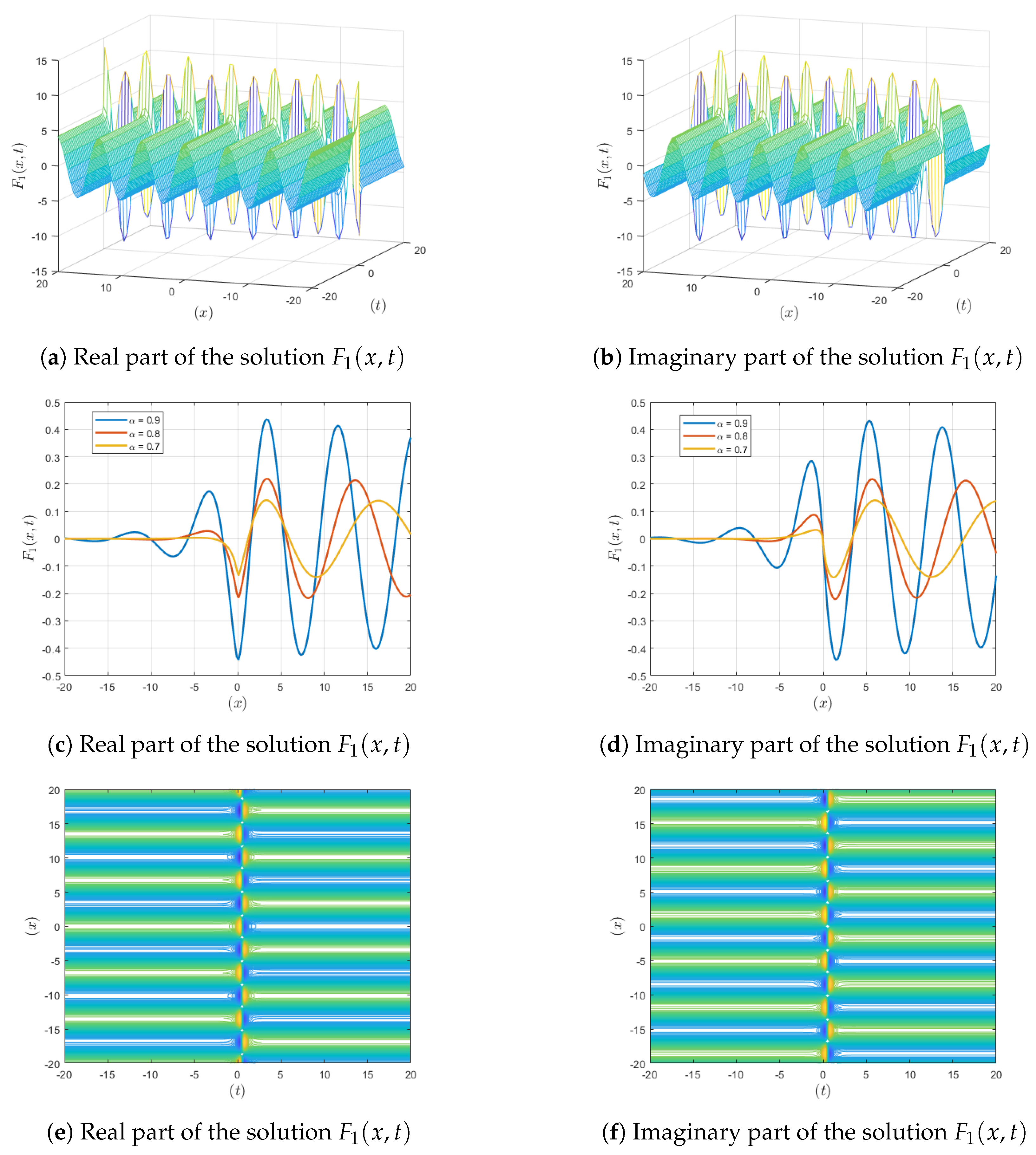
Figure 1.
Visualization of the solution , showing , contour and fractional-order variations.
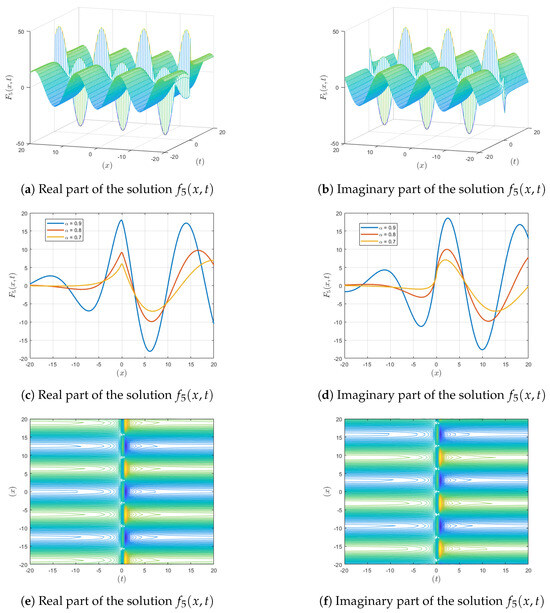
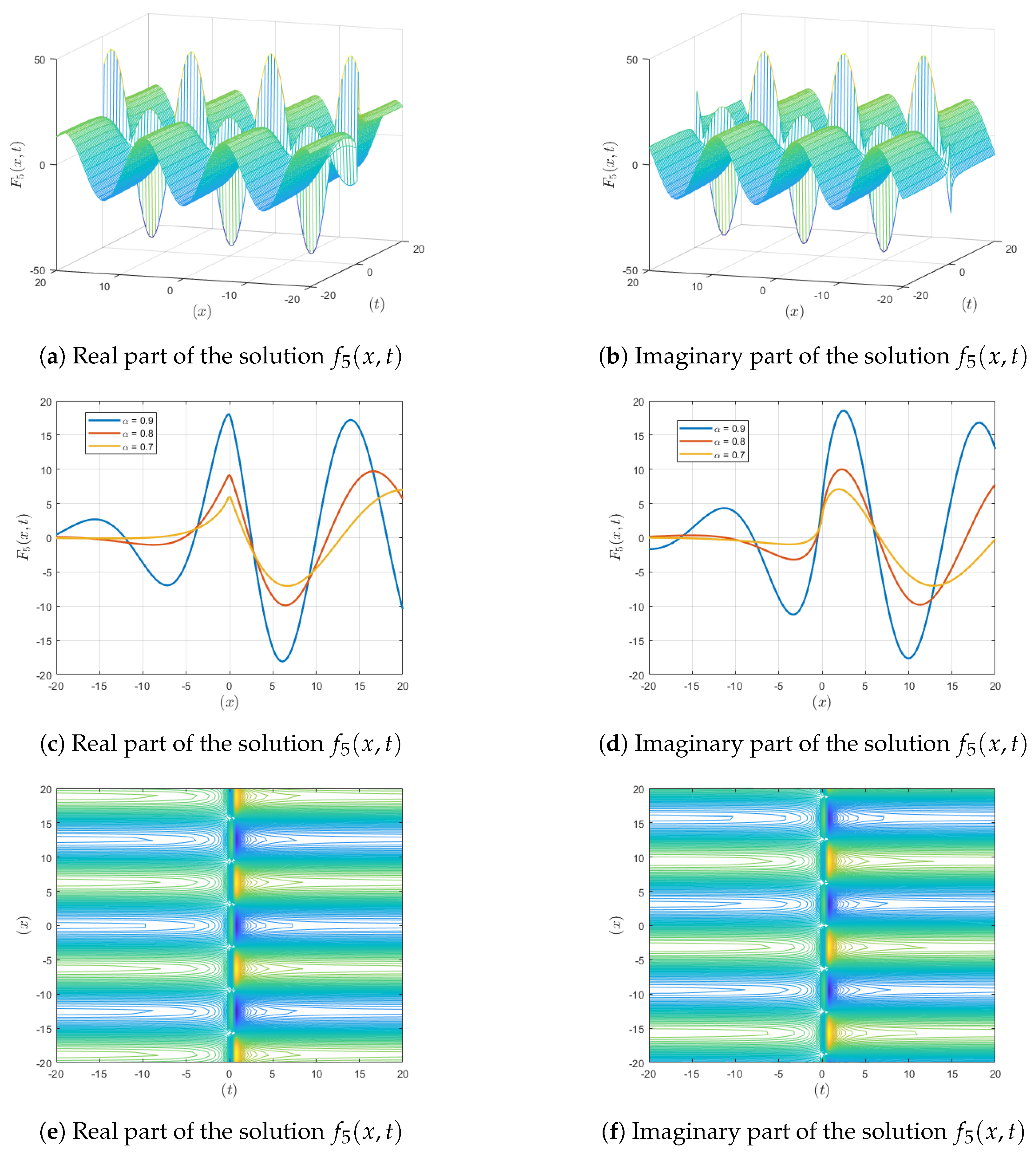
Figure 2.
Visualization of the solution , showing , contour and fractional-order variations.
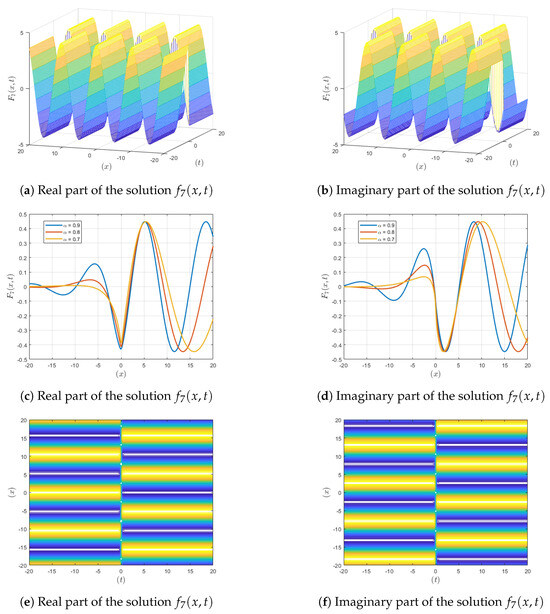
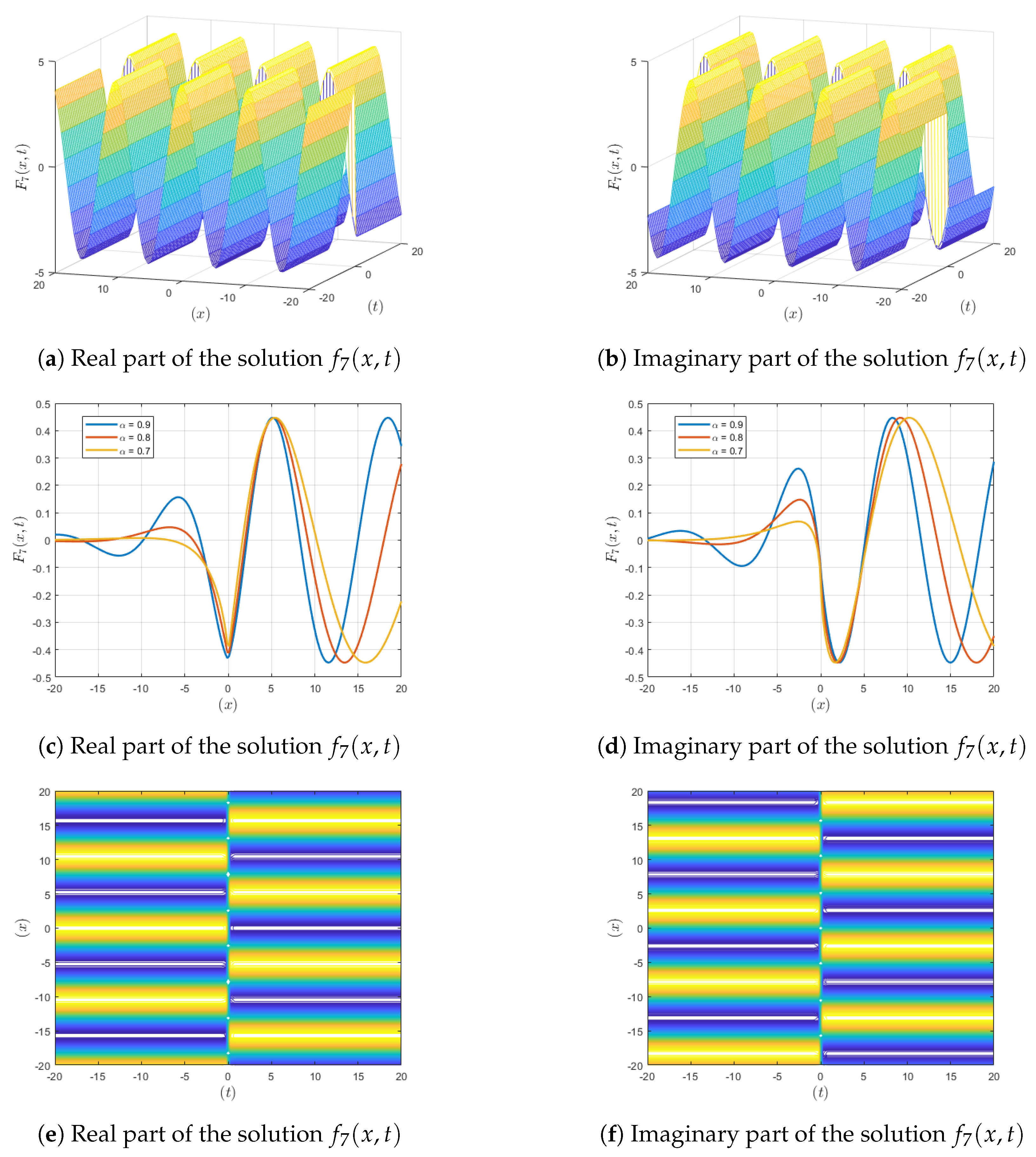
Figure 3.
Visualization of the solution , showing , contour and fractional-order variations.
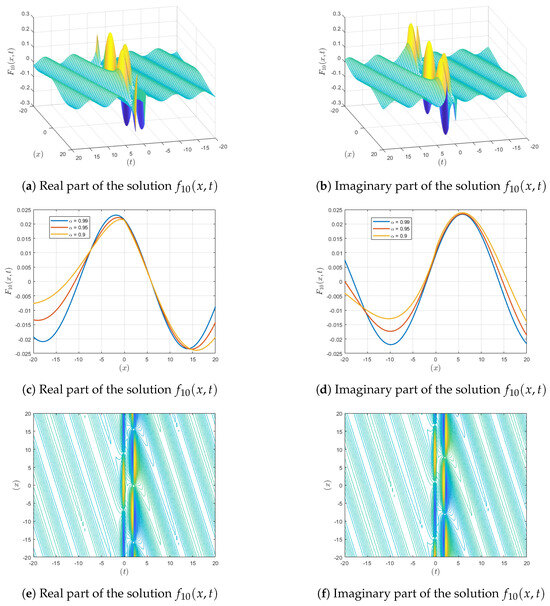
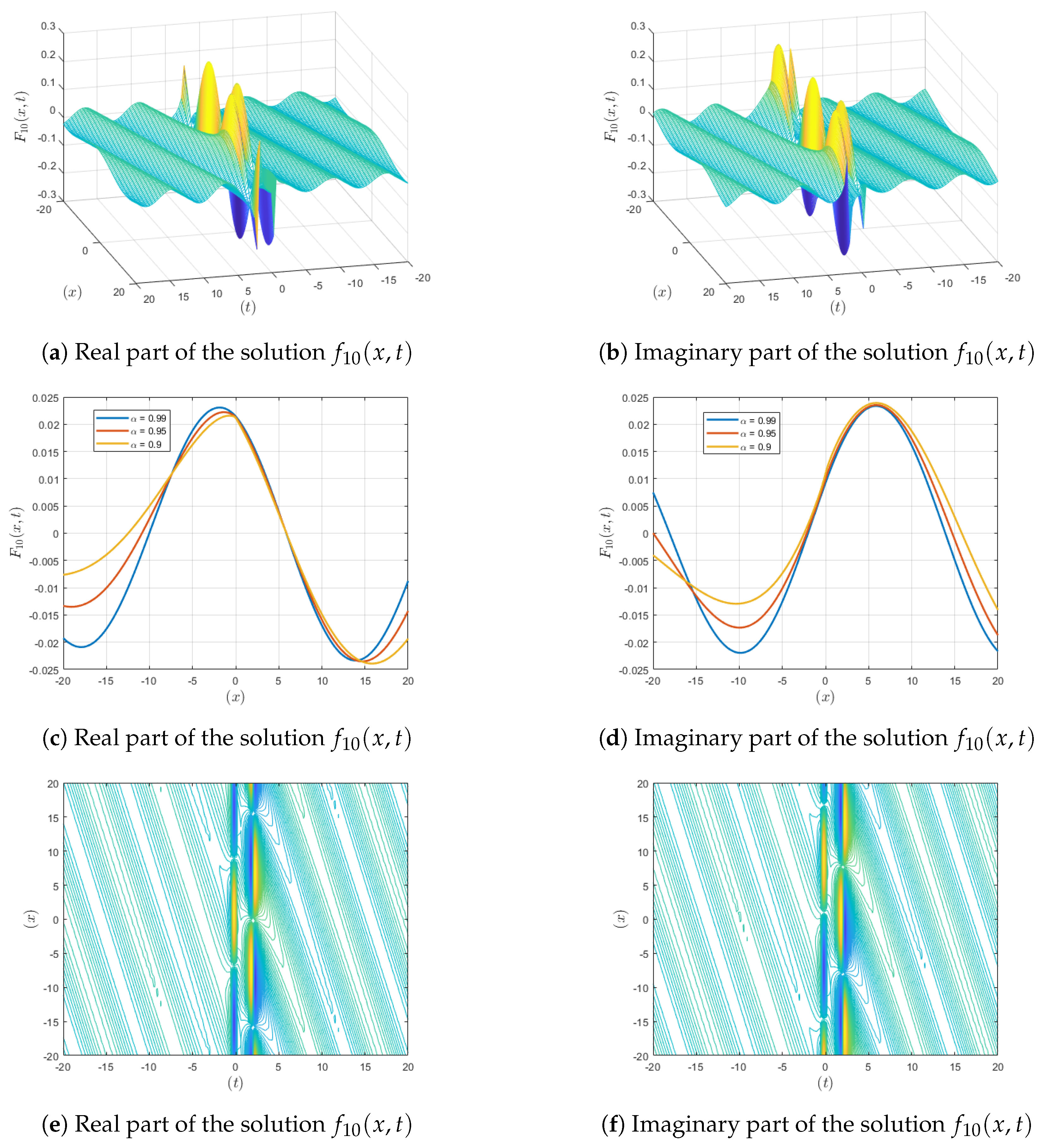
Figure 4.
Visualization of the solution , showing , contour and fractional-order variations.
Figure 1: For fractional values and , both the real and imaginary parts show a reduction in amplitude as the fractional parameter decreases, gradually moving toward convergence. The integer-order plot shows the full periodic perturbation in three dimensions, highlighting the system’s unaltered amplitude and wavelength properties. In the contour representation, fractal patterns emerge, illustrating the self-similarity within the periodic perturbations. This fractal aspect implies potential applications in fractal-based optical systems, where understanding these structures can lead to innovations in signal integrity.
Figure 2: As in the case of Figure 1, but with a longer wavelength. This larger wavelength shows how the fractional order affects the spatial spread over long extents, but the real and imaginary parts are slightly more convergent. The longer wavelength is more apparent in the integer-order plot because it provides a spatial reference for the fractional wavelength’s impact. The fractal contour patterns continue here with relatively more distant periodical peaks; these are useful in wave transmission systems in which wavelength modifications are vital.
Figure 3: In this depiction, the fractional-order solutions converge more quickly and stabilize the real and imaginary parts. This accelerated rate of convergence indicates that it may be possible to have controlled damping in engineered systems to achieve rapid stabilization. The integer-order three-dimensional representation is characterized by steady oscillations and fractal patterns pointing to a faster decrease in amplitude. The fractal structures used here describe the fast convergence behavior, which is useful in areas requiring fast stabilization, such as resonant damping in structural engineering.
Figure 4: Unlike the other figures, there is no superposition; the periodically interrupted oscillation is constant at any fractional values of the parameter. Both the real and imaginary components exhibit oscillation, with the constant amplitudes signifying the capability for energy storage in long-term periods. Moreover, the representation of the integer order exhibits persistent periodicity, which is useful in cases when regular oscillatory behavior is needed, such as in wave guides or optical lattices. The contour plots of the displays are self-similar throughout the periodic wave, which is useful in fields where stable fractal wave structures are employed for unbroken signal transmission, such as the fractal antennas used in telecommunications. Figure 5, Visualization of the intensity of of sub-figures (a), (b) and (c). Figure 6, Visualization of the intensity of . Figure 7, Visualization of the intensity of of sub-figures (a), (b) and (c).
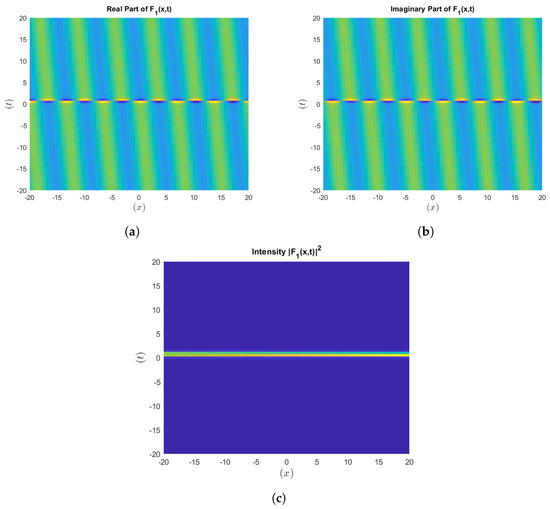
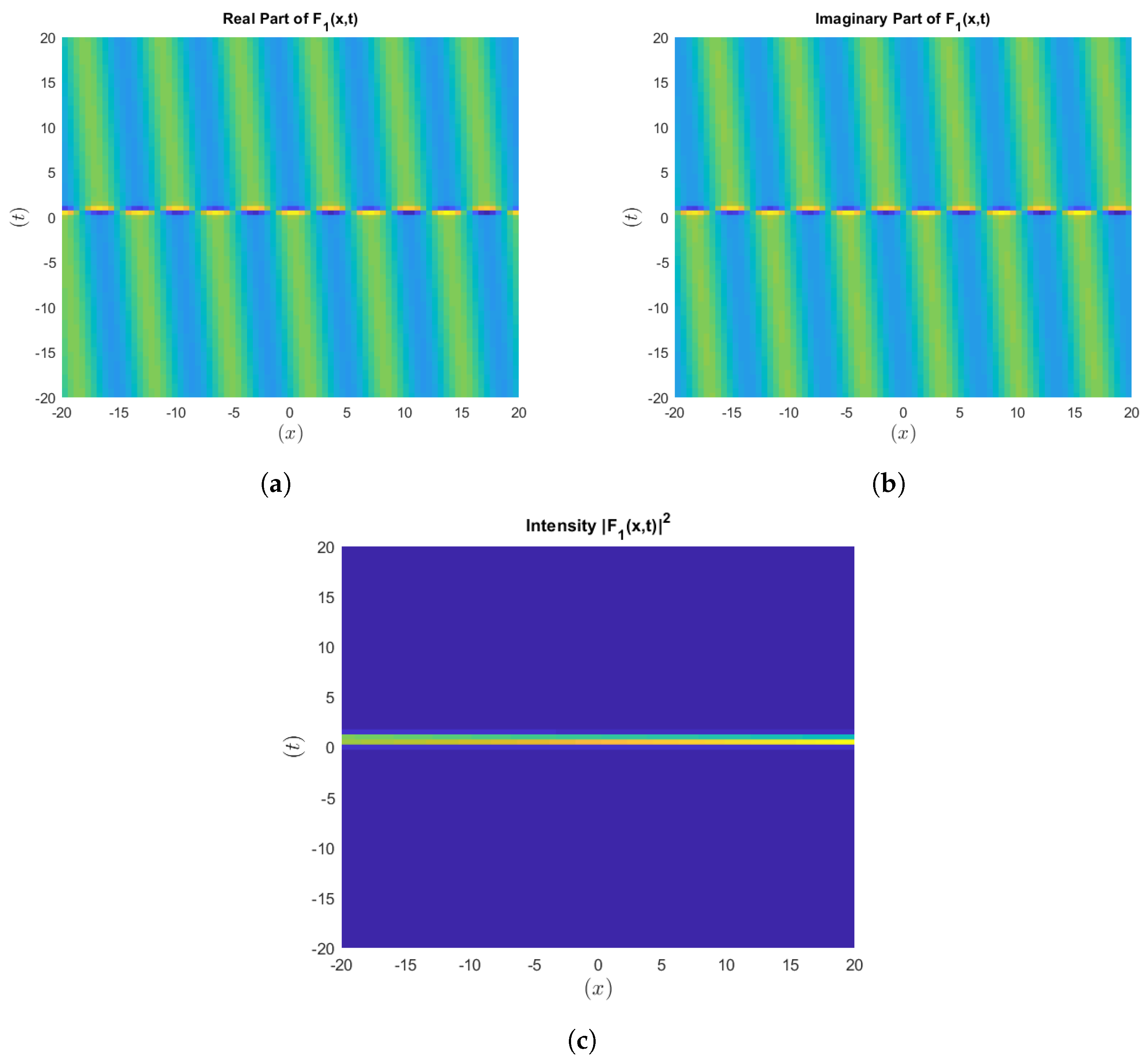
Figure 5.
Visualization of the intensity of .
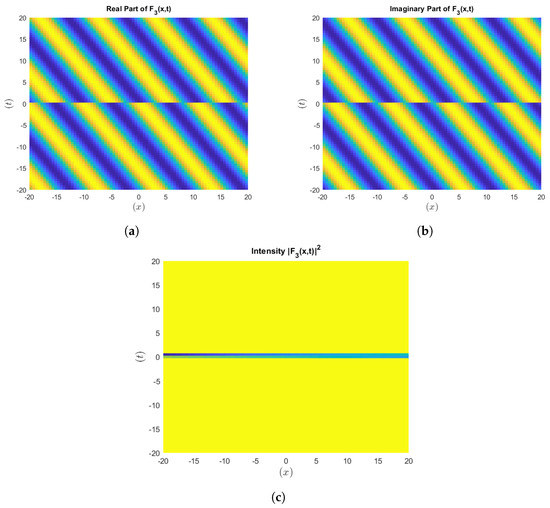
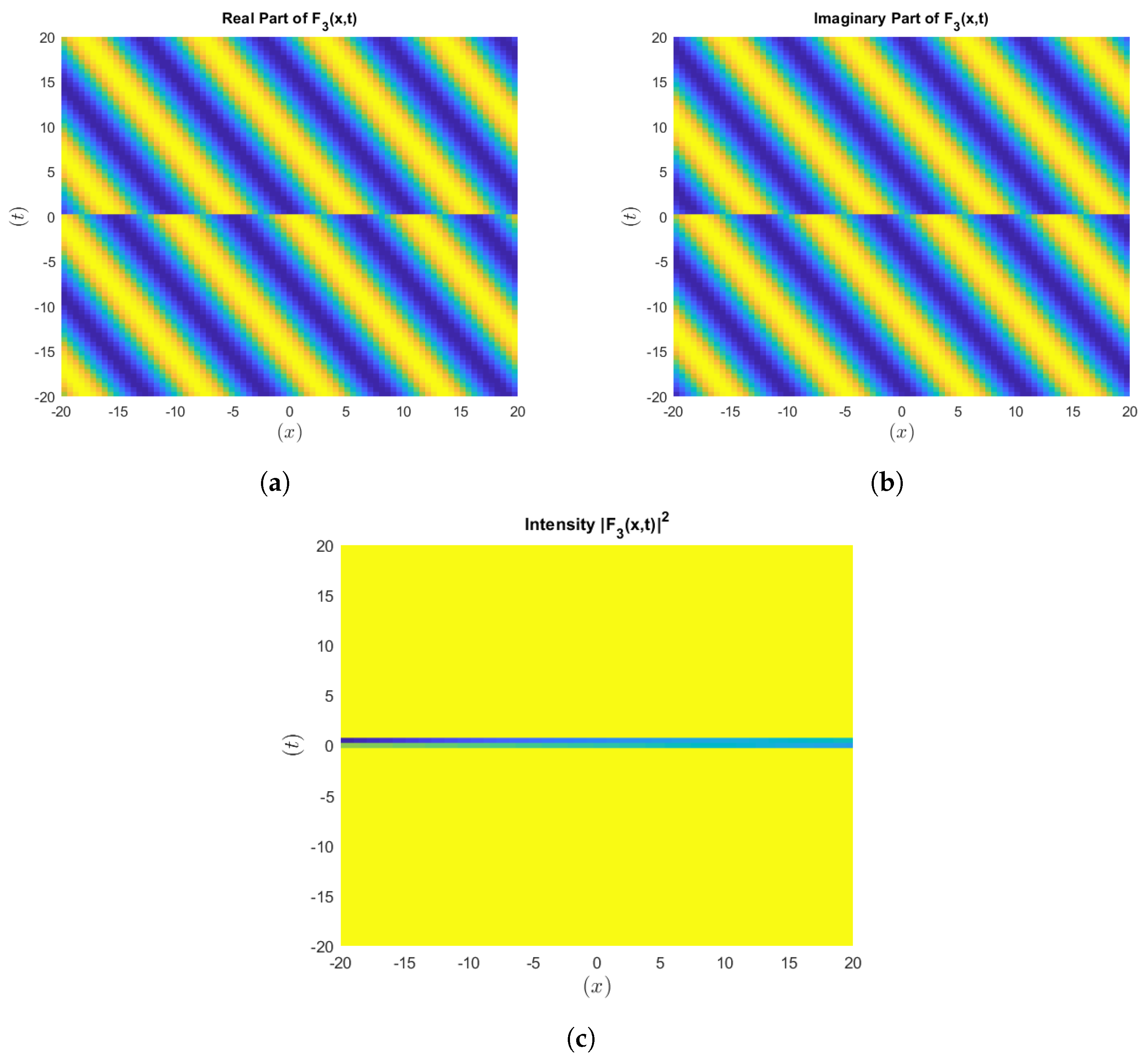
Figure 6.
Visualization of the intensity of .
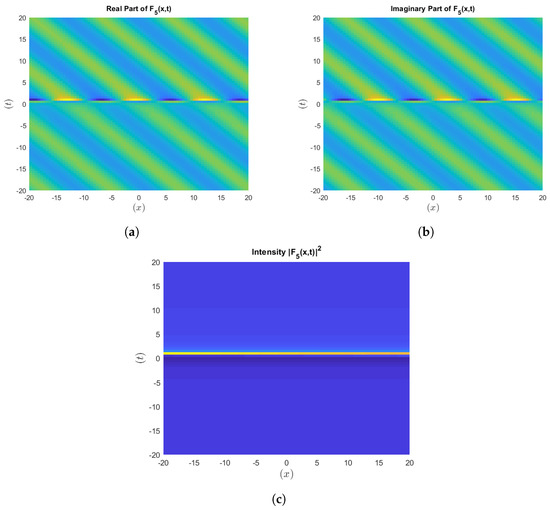
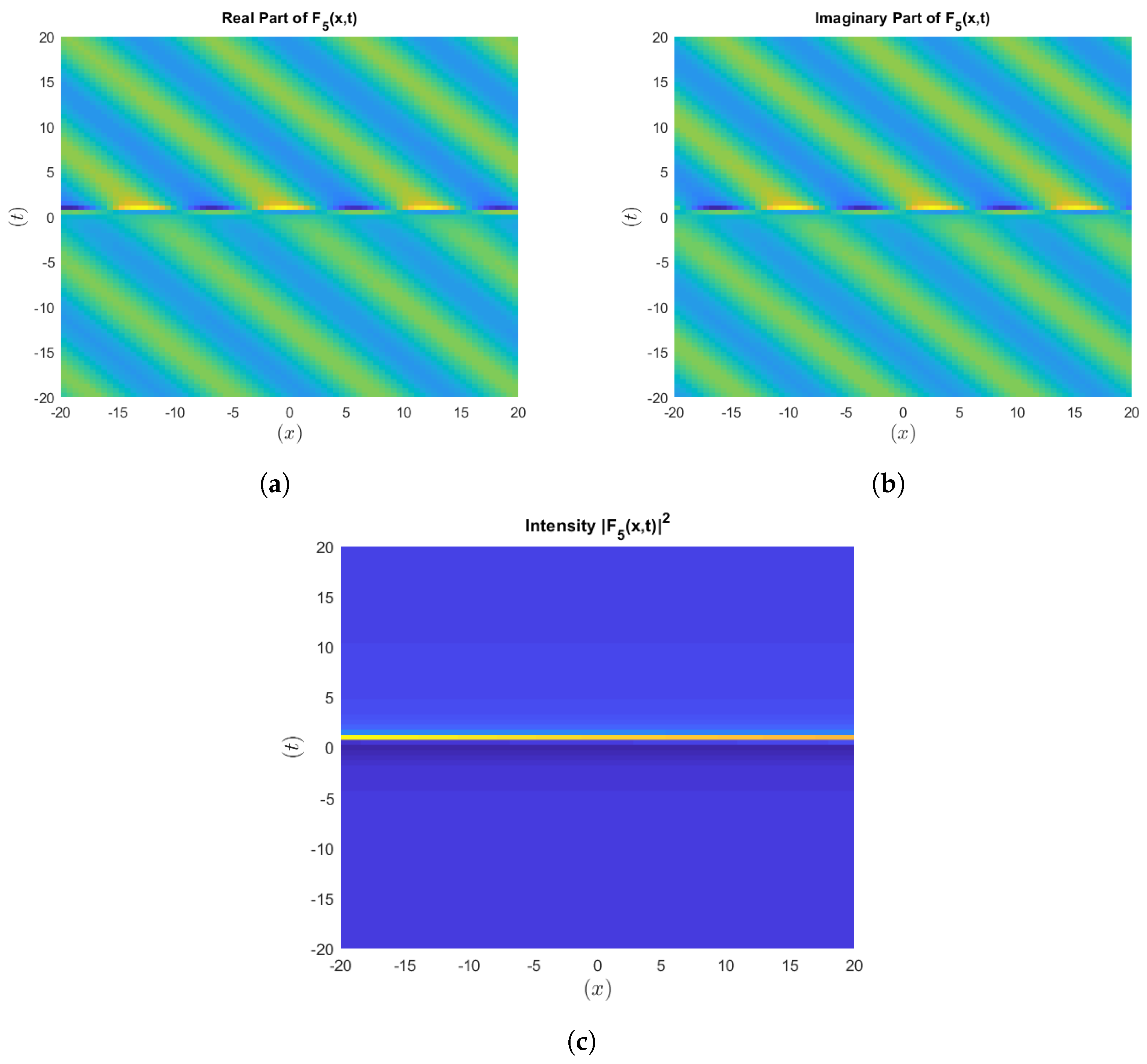
Figure 7.
Visualization of the intensity of .
To strengthen our results, we include figures that represent the intensity of the wave solutions in terms of the squared modulus of the analytic solution. These visualizations give some information concerning the localization of the energy, as well as the general behavior of the wave solutions, which is critically important in the analysis of the nonlinear optics. This addition provides better robustness, making our findings consistent with the norms employed in nonlinear optics and similar disciplines.
5. Conclusions
In this study, we have investigated the periodic perturbation feature of solutions of the Kuralay-II system with fractional derivatives using the Ricatti–Bernoulli sub-ODE method and Bäcklund transformation. Based on the and plots of the real and imaginary parts of integer and fractional-order values, our results show the different behaviors of the waves in terms of convergence, amplitude modulation and changes in wavelength. Significantly, the features that appear in the contour plots include fractals, which give more depth to the self-similar features present in periodic solutions. Thus, this work proves that the fractional Kuralay-II system can flexibly approximate various wave dynamics, which is valuable since the fractional-order approach is effective in simulating both the periods and convergence of waveforms. Altogether, the fractional Kuralay-II system offers a suitable context for the modeling and analysis of wave phenomena, as well as for related areas of optics, signal processing and engineering, where the control of wave behavior, stabilities and energy losses is essential. Further developments of this work may investigate the complex relationships between the fractional parameters and waveforms and the deeper utilization of this model in numerous scientific and engineering fields.
Author Contributions
Conceptualization, K.A.R. and M.Y.A.; methodology, H.A.; software, T.S.A.; validation, A.A.; formal analysis, K.A.R.; investigation, M.Y.A.; resources, H.A.; data curation, A.A.; writing—original draft preparation, K.A.R.; writing—review and editing, M.Y.A.; visualization, H.A.; supervision, A.A.; project administration, T.S.A.; funding acquisition, M.Y.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in the study are included in the article; further inquiries can be directed to the corresponding author.
Acknowledgments
The authors gratefully acknowledge the funding of the Deanship of Graduate Studies and Scientific Research, Jazan University, Saudi Arabia, through project number RG24-L02.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Gao, W.; Rezazadeh, H.; Pinar, Z.; Baskonus, H.M.; Sarwar, S.; Yel, G. Novel explicit solutions for the nonlinear Zoomeron equation by using newly extended direct algebraic technique. Opt. Quant. Electron. 2020, 52, 52. [Google Scholar] [CrossRef]
- Zhu, C.; Al-Dossari, M.; Rezapour, S.; Gunay, B. On the exact soliton solutions and different wave structures to the (2+1) dimensional Chaffee-Infante equation. Results Phys. 2024, 57, 107431. [Google Scholar] [CrossRef]
- Ghasemi, M. High order approximations using spline-based differential quadrature method: Implementation to the multi-dimensional PDEs. Appl. Math. Model. 2017, 46, 63–80. [Google Scholar] [CrossRef]
- Perrone, N.; Kao, R. A general finite difference method for arbitrary meshes. Comput. Struct. 1975, 5, 45–57. [Google Scholar] [CrossRef]
- Mahmood, S.; Shah, R.; Khan, H.; Arif, M. Laplace adomian decomposition method for multi dimensional time fractional model of Navier-Stokes equation. Symmetry 2019, 11, 149. [Google Scholar] [CrossRef]
- Abdou, M.A.; Soliman, A.A. New applications of variational iteration method. Phys. D 2005, 211, 1–8. [Google Scholar] [CrossRef]
- Yusufoglu, E.; Bekir, A. Solitons and periodic solutions of coupled nonlinear evolution equations by using the sine-cosine method. Int. J. Comput. Math. 2006, 83, 915–924. [Google Scholar] [CrossRef]
- Kaplan, M.; Bekir, A.; Akbulut, A.; Aksoy, E. The modified simple equation method for nonlinear fractional differential equations. Rom. J. Phys. 2015, 60, 1374–1383. [Google Scholar]
- Meng, S.; Meng, F.; Zhang, F.; Li, Q.; Zhang, Y.; Zemouche, A. Observer design method for nonlinear generalized systems with nonlinear algebraic constraints with applications. Automatica 2024, 162, 111512. [Google Scholar] [CrossRef]
- Lei, M.; Liao, H.; Wang, S.; Zhou, H.; Zhu, J.; Wan, H.; Payne, G.F.; Liu, C.; Qu, X. Electro-sorting create heterogeneity: Constructing a multifunctional Janus film with integrated compositional and microstructural gradients for guided bone regeneration. Adv. Sci. 2024, 11, 2307606. [Google Scholar] [CrossRef]
- Ali, R.; Alam, M.M.; Barak, S. Exploring chaotic behavior of optical solitons in complex structured conformable perturbed Radhakrishnan-Kundu-Lakshmanan model. Phys. Scr. 2024, 99, 095209. [Google Scholar] [CrossRef]
- Alshammari, S.; Al-Sawalha, M.M.; Shah, R. Approximate analytical methods for a fractional-order nonlinear system of Jaulent–Miodek equation with energy-dependent Schrödinger potential. Fractal Fract. 2023, 7, 140. [Google Scholar] [CrossRef]
- Qin, Y.; Khan, A.; Ali, I.; Al Qurashi, M.; Khan, H.; Baleanu, D. An efficient analytical approach for the solution of certain fractional-order dynamical systems. Energies 2020, 13, 2725. [Google Scholar] [CrossRef]
- Alderremy, A.A.; Iqbal, N.; Aly, S.; Nonlaopon, K. Fractional series solution construction for nonlinear fractional reaction-diffusion Brusselator model utilizing Laplace residual power series. Symmetry 2022, 14, 1944. [Google Scholar] [CrossRef]
- Al-Sawalha, M.M.; Khan, A.; Ababneh, O.Y.; Botmart, T. Fractional view analysis of Kersten-Krasil’shchik coupled KdV-mKdV systems with non-singular kernel derivatives. AIMS Math. 2022, 7, 18334–18359. [Google Scholar] [CrossRef]
- Yasmin, H.; Alshehry, A.S.; Ganie, A.H.; Mahnashi, A.M.; Shah, R. Perturbed Gerdjikov–Ivanov equation: Soliton solutions via Backlund transformation. Optik 2024, 298, 171576. [Google Scholar] [CrossRef]
- Ghanbari, B.; Osman, M.S.; Baleanu, D. Generalized exponential rational function method for extended Zakharov–Kuznetsov equation with conformable derivative. Mod. Phys. Lett. A 2019, 34, 1950155. [Google Scholar] [CrossRef]
- Akbulut, A.; Tascan, F.; Ozel, E. Trivial conservation laws and solitary wave solution of the fifth order Lax equation. Partial Differ. Equ. Appl. Math. 2021, 4, 100101. [Google Scholar] [CrossRef]
- Khatri, H.; Gautam, M.S.; Malik, A. Localized and complex soliton solutions to the integrable (4 + 1)-dimensional Fokas equation. SN Appl. Sci. 2019, 1, 1070. [Google Scholar] [CrossRef]
- Alam, M.N.; Ilhan, O.A.; Uddin, M.S.; Rahim, M.A. Results for the Fractional Clannish Random Walker’s Parabolic Equation and the Nonlinear Fractional Cahn-Allen Equation. Adv. Math. Phys. 2022, 5635514. [Google Scholar] [CrossRef]
- Alam, M.N.; Islam, S.; Ilhan, O.A.; Bulut, H. Some new results of nonlinear model arising in incompressible visco-elastic Kelvin–Voigt fluid. Math. Methods Appl. Sci. 2022, 45, 10347–10362. [Google Scholar] [CrossRef]
- Younas, U.; Seadawy, A.R.; Younis, M.; Rizvi, S.T.R. Optical solitons and closed form solutions to the (3 + 1)-dimensional resonant Schrödinger dynamical wave equation. Int. J. Mod. Phys. B 2020, 34, 2050291. [Google Scholar] [CrossRef]
- Arshad, M.; Seadawy, A.; Lu, D.; Wang, J. Travelling wave solutions of generalized coupled Zakharov–Kuznetsov and dispersive long wave equations. Results Phys. 2016, 6, 1136–1145. [Google Scholar] [CrossRef]
- Kumar, S.; Nisar, K.S.; Niwas, M. On the dynamics of exact solutions to a (3 + 1)-dimensional YTSF equation emerging in shallow sea waves: Lie symmetry analysis and generalized Kudryashov method. Results Phys. 2023, 48, 106432. [Google Scholar] [CrossRef]
- Irshad, A.; Ahmed, N.; Nazir, A.; Khan, U.; Mohyud-Din, S.T. Novel exact double periodic soliton solutions to strain wave equation in micro structured solids. Phys. Stat. Mech. Appl. 2020, 550, 124077. [Google Scholar] [CrossRef]
- Bibi, S.; Mohyud-Din, S.T.; Khan, U.; Ahmed, N. Khater method for nonlinear Sharma-Tasso-Olever (STO) equation of fractional order. Results Phys. 2017, 7, 4440–4450. [Google Scholar] [CrossRef]
- Alam, M.N. An analytical method for finding exact solutions of a nonlinear partial differential equation arising in electrical engineering. Open J. Math. Sci. 2023, 7, 10–18. [Google Scholar] [CrossRef]
- Elsayed, E.M.; Shah, R.; Nonlaopon, K. The Analysis of the Fractional-Order Navier-Stokes Equations by a Novel Approach. J. Funct. Spaces 2022, 2022, 8979447. [Google Scholar] [CrossRef]
- Naeem, M.; Rezazadeh, H.; Khammash, A.A.; Zaland, S. Analysis of the Fuzzy Fractional-Order Solitary Wave Solutions for the KdV Equation in the Sense of Caputo-Fabrizio Derivative. J. Math. 2022, 2022, 3688916. [Google Scholar] [CrossRef]
- Alqhtani, M.; Saad, K.M.; Shah, R.; Hamanah, W.M. Discovering novel soliton solutions for (3+1)-modified fractional Zakharov–Kuznetsov equation in electrical engineering through an analytical approach. Opt. Quantum Electron. 2023, 55, 1149. [Google Scholar] [CrossRef]
- Alqhtani, M.; Saad, K.M.; Weera, W.; Hamanah, W.M. Analysis of the fractional-order local Poisson equation in fractal porous media. Symmetry 2022, 14, 1323. [Google Scholar] [CrossRef]
- El-Tantawy, S.A.; Matoog, R.T.; Shah, R.; Alrowaily, A.W.; Ismaeel, S.M. On the shock wave approximation to fractional generalized Burger–Fisher equations using the residual power series transform method. Phys. Fluids 2024, 36, 023105. [Google Scholar] [CrossRef]
- Tian, H.; Zhao, M.; Liu, J.; Wang, Q.; Yu, X.; Wang, Z. Dynamic analysis and sliding mode synchronization control of chaotic systems with conditional symmetric fractional-order memristors. Fractal Fract. 2024, 8, 307. [Google Scholar] [CrossRef]
- Liu, L.; Zhang, S.; Zhang, L.; Pan, G.; Yu, J. Multi-UUV maneuvering counter-game for dynamic target scenario based on fractional-order recurrent neural network. IEEE Trans. Cybern. 2023, 53, 4015–4028. [Google Scholar] [CrossRef]
- Li, M.; Wang, T.; Chu, F.; Han, Q.; Qin, Z.; Zuo, M.J. Scaling-basis chirplet transform. IEEE Trans. Ind. Electron. 2021, 68, 8777–8788. [Google Scholar] [CrossRef]
- Iftikhar, A.; Ghafoor, A.; Zubair, T.; Firdous, S.; Mohyud-Din, S.T. Solutions of (2 + 1) dimensional generalized KdV, Sin Gordon and Landau-Ginzburg-Higgs equations. Sci. Res. Essays 2013, 8, 1349–1359. [Google Scholar]
- He, J.H.; Wu, X.H. Exp-function method for nonlinear wave equations. Chaos Soliton. Fract. 2006, 30, 700–708. [Google Scholar] [CrossRef]
- Cinar, M.; Secer, A.; Ozisik, M.; Bayram, M. Derivation of optical solitons of dimensionless Fokas-Lenells equation with perturbation term using Sardar sub-equation method. Opt. Quant. Electron. 2022, 54, 402. [Google Scholar] [CrossRef]
- Al-Sawalha, M.M.; Yasmin, H.; Shah, R.; Ganie, A.H.; Moaddy, K. Unraveling the dynamics of singular stochastic solitons in stochastic fractional Kuramoto-Sivashinsky equation. Fractal Fract. 2023, 7, 753. [Google Scholar] [CrossRef]
- Wang, K.J.; Shi, F. Multi-soliton solutions and soliton molecules of the (2 + 1)-dimensional Boiti-Leon-Manna-Pempinelli equation for the incompressible fluid. Europhys. Lett. 2024, 145, 42001. [Google Scholar] [CrossRef]
- Sagidullayeva, Z.; Nugmanova, G.; Myrzakulov, R.; Serikbayev, N. Integrable Kuralay equations: Geometry, solutions and generalizations. Symmetry 2022, 14, 1374. [Google Scholar] [CrossRef]
- Faridi, W.A.; Bakar, M.A.; Myrzakulova, Z.; Myrzakulov, R.; Akgül, A.; El Din, S.M. The formation of solitary wave solutions and their propagation for Kuralay equation. Results Phys. 2023, 52, 106774. [Google Scholar] [CrossRef]
- Mathanaranjan, T. Optical soliton, linear stability analysis and conservation laws via multipliers to the integrable Kuralay equation. Optik 2023, 290, 171266. [Google Scholar] [CrossRef]
- Zafar, A.; Raheel, M.; Ali, M.R.; Myrzakulova, Z.; Bekir, A.; Myrzakulov, R. Exact solutions of M-fractional Kuralay equation via three analytical schemes. Symmetry 2023, 15, 1862. [Google Scholar] [CrossRef]
- Khan, M.I.; Ma, W.X.; Farooq, A. Exploring Exact Solitary Wave Solutions of Kuralay-II Equation based on the Truncated M-fractional Derivative using the Jacobi Elliptic Function Expansion Method. Opt. Quant. Electron 2024, 56, 1105. [Google Scholar]
- Singh, B.K.; Agrawal, S. A new approximation of conformable time fractional partial differential equations with proportional delay. Appl. Numer. Math. 2020, 157, 419–433. [Google Scholar] [CrossRef]
- Abdelrahman, M.A.E.; Sohaly, M.A. Solitary waves for the modified Korteweg-de Vries equation in deterministic case and random case. J. Phys. Math. 2017, 8, 1000214. [Google Scholar]
- Yang, X.F.; Deng, Z.C.; Wei, Y. A Riccati-Bernoulli sub-ode method for nonlinear partial differential equations and its application. Adv. Differ. Equ. 2015, 1, 117–133. [Google Scholar] [CrossRef]
- Abdelrahman, M.A.E.; Sohaly, M.A. Solitary waves for the nonlinear Schrödinger problem with the probability distribution function in the stochastic input case. Eur. Phys. J. Plus 2017, 132, 339. [Google Scholar] [CrossRef]
- Lu, D.; Shi, Q. New Jacobi elliptic functions solutions for the combined KdV-mKdV equation. Int. J. Nonlinear Sci. 2010, 10, 320–325. [Google Scholar]
- Arafat, S.Y.; Islam, S.R. Bifurcation analysis and soliton structures of the truncated M-fractional Kuralay-II equation with two analytical techniques. Alex. Eng. J. 2024, 105, 70–87. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).