Conservation Law Analysis in Numerical Schema for a Tumor Angiogenesis PDE System

Abstract

Tumor angiogenesis, the formation of new blood vessels from pre-existing vasculature, is a crucial process in cancer growth and metastasis. Mathematical modeling through partial differential equations helps to understand this complex biological phenomenon. Here, we provide a conservation properties analysis in a tumor angiogenesis model describing the evolution of endothelial cells, proteases, inhibitors, and extracellular matrix. The adopted approach introduces a numerical framework that combines spatial and time discretization techniques. Here, we focus on maintaining solution accuracy while preserving physical quantities during the simulation process. The method achieved second-order accuracy in both space and time discretizations, with conservation errors showing consistent convergence as the mesh was refined. The numerical schema demonstrates stable wave propagation patterns, in agreement with experimental observations. Numerical experiments validate the approach and demonstrate its reliability for long-term angiogenesis simulations.

1. Introduction

Differential equations represent a powerful mathematical tool for describing and analyzing complex phenomena among various scientific disciplines. In particular, the field of mathematical biology has guaranteed significant developments through the application of both ordinary and partial differential equations, enabling researchers to capture the dynamic behavior of complex biological systems and predict their evolution over time. This approach has become especially important in studying intricate biological processes that involve multiple interacting components and feedback mechanisms. Angiogenesis, the formation of new blood vessels from pre-existing vasculature, is a very important mechanism in both physiological and pathological processes, particularly in tumor development and metastasis [1,2]. This complex biological process manages interactions among multiple components: endothelial cells (ECs), tumor angiogenic factors (TAFs), matrix metalloproteinases (MMPs), and angiogenic inhibitors. The mathematical modeling of such intricate biological dynamics through partial differential equations (PDEs) provides a powerful framework for understanding and predicting angiogenic behavior [3,4]. Let us consider a one-dimensional tumor angiogenesis model, presented in [5], describing the spatio-temporal evolution of four key variables, namely the endothelial cell density $C(x,t)$, protease concentration $P(x,t)$, inhibitor concentration $I(x,t)$, and extracellular matrix (ECM) density $F(x,t)$, where $x\in \Omega =[0,L_f]$ and $t\in [t_0,T_f]$ denote, respectively, the spatial and time domains. The coupling among these variables through chemotaxis, haptotaxis, and chemical interactions is modeled by the following system of partial differential equations:

$$\begin{array}{cc}{\displaystyle \frac{\partial C}{\partial t}}\hfill & =d_C{\displaystyle \frac{{\partial }^{2}C}{\partial x^2}}+{\displaystyle \frac{\partial }{\partial x}}\left(f_I{\displaystyle \frac{\partial I}{\partial x}}\right)-{\displaystyle \frac{\partial }{\partial x}}\left(f_F{\displaystyle \frac{\partial F}{\partial x}}\right)-{\displaystyle \frac{\partial }{\partial x}}\left(f_T{\displaystyle \frac{\partial T}{\partial x}}\right)+k_{1}C(1-C)\hfill \\ {\displaystyle \frac{\partial P}{\partial t}}\hfill & =d_P{\displaystyle \frac{{\partial }^{2}P}{\partial x^2}}-k_{3}PI+k_{4}TC+k_{5}T-k_{6}P\hfill \\ {\displaystyle \frac{\partial I}{\partial t}}\hfill & =d_I{\displaystyle \frac{{\partial }^{2}I}{\partial x^2}}-k_{3}PI\hfill \\ {\displaystyle \frac{\partial F}{\partial t}}\hfill & =-k_{2}PF\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}(x,t)\in \Omega \times [t_0,T_f],\hfill \end{array}$$

(1)

where the chemotactic and haptotactic sensitivity functions are defined as follows:

$$f_F={\alpha }_{1}C, f_I={\alpha }_{2}C, f_T={\displaystyle \frac{{\alpha }_{3}C}{1+{\alpha }_{4}T}}.$$

(2)

The TAF concentration is modeled as follows:

$$T\left(x\right)=exp\left(-ϵ{(L_f-x)}^2\right).$$

(3)

The system (1) is subject to no-flux (Neumann) boundary conditions:

$${\displaystyle \frac{\partial u}{\partial x}}{|}_{x=0}={\displaystyle \frac{\partial u}{\partial x}}{|}_{x=L_f}=0, \mathrm{for} u\in \{C,P,I,F\}$$

(4)

and the following initial conditions:

$$C(x,0)=\left\{\begin{array}{cc}{C}_0,\hfill & 0\le x\le a\hfill \\ 0,\hfill & a<x\le L_f\hfill \end{array}\right., u(x,0)=\left\{\begin{array}{cc}{\xi }_1,\hfill & \mathrm{if}u=P\hfill \\ {\xi }_2,\hfill & \mathrm{if}u=I\hfill \\ {\xi }_3,\hfill & \mathrm{if}u=F\hfill \end{array}\right.$$

(5)

where $C_0>0$ and ${\xi }_i$ represent small random perturbations. In this paper, we analyze the numerical conservation properties of this system and investigate the conservation-preserving of discretization schema. The focus is on maintaining key physical quantities during numerical integration while ensuring solution accuracy and stability. We start by recalling from [5] the main steps and features of the numerical schema. Hence, we introduce a framework for analyzing and preserving discrete conservation properties, which is important for obtaining physically meaningful solutions in long-time simulations. We employ the Method of Lines (MOL) approach combined with the forward Euler time integration, analyzing its capability to preserve main physical quantities during the simulation of tumor angiogenesis. This analysis begins with the identification of the conservation properties related to the continuous system (1)–(5). Particular attention is given to the preservation of total mass and chemical species balance in the discrete setting. We also provide a theoretical analysis of the conservation properties in the discrete framework. Moreover, we also include error estimates for both spatial and time discretizations, with a focus on how these errors impact the conservation of key physical quantities. The analysis is performed through numerical experiments that demonstrate the practical importance of conservation in tumor angiogenesis simulations. Several numerical approaches have been previously proposed for solving angiogenesis models. Finite element implementations [6,7], while accurate, can be computationally expensive and may not guarantee mass conservation. Some recent works have employed splitting methods [8,9] that, although efficient, can introduce artificial numerical diffusion. Spectral methods [10] provide high accuracy but face challenges with the nonlinear terms typical in angiogenesis models. Moreover, existing numerical frameworks typically focus either on accuracy [11] or conservation properties [12] but rarely address both simultaneously. More recent attempts using hybrid methods [13,14] have shown improvements but still face stability issues in long-term simulations. The aim of this work is to analyze and establish the conservation properties of a numerical schema for tumor angiogenesis simulations, with a particular focus on maintaining physical fidelity during long-term integration. We aim to develop and validate a framework for preserving discrete conservation laws while ensuring solution accuracy and stability. Furthermore, we provide theoretical error estimates for both spatial and temporal discretizations, with special attention to how these errors impact the conservation of key physical quantities. The remaining parts of the paper are organized as follows: Section 2 examines the conservation laws of the continuous system, deriving explicit expressions for the conserved quantities. Section 3 presents an analysis of the numerical discretization schema proposed in [5], focusing on its conservation properties, and theoretical error estimates for the conservation of physical quantities. Section 4 presents numerical experiments that validate our theoretical findings and demonstrate the importance of conservation in practical simulations. Finally, Section 5 summarizes our findings and concludes the paper.

2. Conservation Law Analysis

Consider the system (1) on a bounded domain $\Omega \subset \mathbb{R}$ with smooth boundary $\partial \Omega$ and time interval $[0,T_f]$; the system can be written in a compact form as follows:

$${\displaystyle \frac{\partial \mathbf{u}}{\partial t}}=\mathcal{A}\mathbf{u}+\mathcal{F}\left(\mathbf{u}\right),$$

(6)

where $\mathbf{u}={(C,P,I,F)}^T$, and $\mathcal{A}$ is the linear differential operator:

$$\mathcal{A}\mathbf{u}=\left(\begin{array}{c}{d}_C{\displaystyle \frac{{\partial }^{2}C}{\partial x^2}}\\ d_P{\displaystyle \frac{{\partial }^{2}P}{\partial x^2}}\\ d_I{\displaystyle \frac{{\partial }^{2}I}{\partial x^2}}\\ 0\end{array}\right),$$

(7)

and $\mathcal{F}\left(\mathbf{u}\right)$ contains all nonlinear reaction and taxis terms:

$$\mathcal{F}\left(\mathbf{u}\right)=\left(\begin{array}{c}{\displaystyle \frac{\partial }{\partial x}}\left(f_I{\displaystyle \frac{\partial I}{\partial x}}\right)-{\displaystyle \frac{\partial }{\partial x}}\left(f_F{\displaystyle \frac{\partial F}{\partial x}}\right)-{\displaystyle \frac{\partial }{\partial x}}\left(f_T{\displaystyle \frac{\partial T}{\partial x}}\right)+k_{1}C(1-C)\\ -k_{3}PI+k_{4}TC+k_{5}T-k_{6}P\\ -k_{3}PI\\ -k_{2}PF\end{array}\right).$$

(8)

Let us establish the mathematical framework for analyzing the conservation properties and deriving a priori estimates [15]. For this analysis, we set a Hilbert space $H=L^2(\Omega )$ equipped with the inner product

$${(u,v)}_{L^2}={\int }_{\Omega }u\left(x\right)v\left(x\right)dx,$$

and the induced norm ${\parallel u\parallel }_{L^2}=\sqrt{{(u,u)}_{L^2}}$. For higher regularity analysis, we work in the Sobolev spaces $H^k(\Omega )$, $k\in \mathbb{N}$, equipped with the norm

$${\parallel u\parallel }_{H^k}={\left(\sum _{\left|\alpha \right|\le k}{\parallel {\partial }^{\alpha }u\parallel }_{L^2}^2\right)}^{1/2}.$$

The solution vector $\mathbf{u}:\Omega \times [0,T_f]\to {\mathbb{R}}^4$, which is defined as

$$\mathbf{u}(x,t)={(C(x,t),P(x,t),I(x,t),F(x,t))}^T,$$

(9)

belongs to the product space $\mathbf{V}={\left[H^1(\Omega )\right]}^4$ at each fixed time t, with temporal regularity $\mathbf{u}\in C([0,T_f];\mathbf{V})$. The choice of the $H^1(\Omega )$ function space is motivated by its guarantee of square-integrability for both the functions and their first derivatives, a property that is fundamental for ensuring the well-posedness of the advection–diffusion terms within the system (1).

Assumption 1 

(solution regularity). Throughout this paper, we assume the following:

1. 

$\mathbf{u}\in C([0,T_f];\mathbf{V})$ with $\mathbf{V}={\left[H^1(\Omega )\right]}^4$,

2. 

$\mathbf{u}\in C^4(\Omega \times [0,T_f])$ for error estimates,

3. 

Initial data ${\mathbf{u}}_0\in \mathbf{V}\cap {\left[L^{\infty }(\Omega )\right]}^4$.

Theorem 1 

(local conservation laws). Let $\mathbf{u}$ be a strong solution to system (1). Then, for any measurable set $\omega \subset \Omega$, where $\mathbf{n}$ denotes the outward unit normal vector to $\partial \omega$, the following local conservation laws hold:

$$\begin{array}{cc}{\displaystyle \frac{d}{dt}}{\int }_{\omega }Cdx\hfill & ={\int }_{\partial \omega }\left[d_C\nabla C+f_I\nabla I-f_F\nabla F-f_T\nabla T\right]·\mathbf{n}ds+{\int }_{\omega }{k}_{1}C(1-C)dx,\hfill \\ {\displaystyle \frac{d}{dt}}{\int }_{\omega }Pdx\hfill & ={\int }_{\partial \omega }{d}_P\nabla P·\mathbf{n}ds+{\int }_{\omega }[-k_{3}PI+k_{4}TC+k_{5}T-k_{6}P]dx,\hfill \\ {\displaystyle \frac{d}{dt}}{\int }_{\omega }Idx\hfill & ={\int }_{\partial \omega }{d}_I\nabla I·\mathbf{n}ds-k_3{\int }_{\omega }PIdx,\hfill \\ {\displaystyle \frac{d}{dt}}{\int }_{\omega }Fdx\hfill & =-k_2{\int }_{\omega }PFdx.\hfill \end{array}$$

(10)

Proof. 

For the endothelial cell equation, we have

$$\begin{array}{cc}{\displaystyle \frac{d}{dt}}{\int }_{\omega }Cdx\hfill & ={\int }_{\omega }{\displaystyle \frac{\partial C}{\partial t}}dx\hfill \\ \hfill & ={\int }_{\omega }\left[\nabla ·(d_C\nabla C)+\nabla ·(f_I\nabla I)-\nabla ·(f_F\nabla F)\right.\hfill \\ \hfill & \left.-\nabla ·(f_T\nabla T)+k_{1}C(1-C)\right]dx.\hfill \end{array}$$

(11)

Applying the divergence theorem to the flux terms yields this result. Similar computations apply to the remaining components. □

Theorem 2 

(a priori estimates). Let $\mathbf{u}$ be a strong solution to system (1) with initial data ${\mathbf{u}}_0\in \mathbf{V}$. Then, there exists a constant $\mathcal{K}>0$ depending only on the system parameters such that

$${\displaystyle \frac{d}{dt}}{\parallel \mathbf{u}\left(t\right)\parallel }_{L^1}^2+2\sum _{i=1}^4{d}_i\parallel \nabla u_i{\parallel }_{L^2}^2\le {\mathcal{K}(1+\parallel \mathbf{u}\left(t\right)\parallel }_{L^2}^2).$$

(12)

Moreover, the solution satisfies the maximum principle:

$$\begin{array}{cc}0\le C(x,t)\hfill & \le max\{1,\parallel C_0{\parallel }_{L^{\infty }}\},\hfill \\ 0\le P(x,t)\hfill & \le {\mathcal{K}}_P(1+\parallel P_0{\parallel }_{L^{\infty }}),\hfill \\ 0\le I(x,t)\hfill & \le {\mathcal{K}}_I(1+\parallel I_0{\parallel }_{L^{\infty }}),\hfill \\ 0\le F(x,t)\hfill & \le \parallel F_0{\parallel }_{L^{\infty }},\hfill \end{array}$$

(13)

where ${\mathcal{K}}_P$ and ${\mathcal{K}}_I$ are positive constants depending on the system parameters.

Proof. 

We first establish the global $L^2$ estimate. Taking the inner product of Equation (6) with $\mathbf{u}$ in $L^2{(\Omega )}^4$, we obtain the following:

$$\begin{array}{cc}{\displaystyle \frac{1}{2}}{\displaystyle \frac{d}{dt}}{\parallel \mathbf{u}\parallel }_{L^2}^2+\sum _{i=1}^4{d}_i{\parallel \nabla u_i\parallel }_{L^2}^2\hfill & ={(\mathcal{F}\left(\mathbf{u}\right),\mathbf{u})}_{L^2}\hfill \\ \hfill & \le {\int }_{\Omega }\left[k_1{C}^2+(k_{4}T+k_5)P+k_6{P}^2\right]dx\hfill \\ \hfill & \le {\mathcal{K}}_1{(1+\parallel \mathbf{u}\parallel }_{L^2}^2)\hfill \end{array}$$

(14)

where we used the inequality of Young and the boundedness of $T\left(x\right)$. The estimate in (13) follows from (14) by Gronwall inequality. For the maximum principle, we employ the invariant region technique. Let ${\mathcal{R}}_{+}=\{(C,P,I,F)\in {\mathbb{R}}^4:C,P,I,F\ge 0\}$; the outward normal flux on $\partial {\mathcal{R}}_{+}$ satisfies appropriate sign conditions ensuring the invariance of ${\mathcal{R}}_{+}$. The upper bounds follow from comparison principles applied to each component. □

Theorem 3 

(energy dissipation). Define the generalized energy functional

$$E\left(t\right)={\displaystyle \frac{1}{2}}\sum _{i=1}^4\left[\parallel \nabla u_i{\parallel }_{L^2}^2+{\lambda }_i{\parallel u_i\parallel }_{L^2}^2\right],$$

(15)

where ${\lambda }_i>0$ are appropriately chosen constants. Then, there exist positive constants α and β such that

$${\displaystyle \frac{d}{dt}}E\left(t\right)+\alpha E\left(t\right)\le \beta \left(1+{\parallel \mathbf{u}\left(t\right)\parallel }_{L^2}^2\right).$$

(16)

Proof. 

Differentiating $E\left(t\right)$ and using Equation (6), we have

$$\begin{array}{cc}{\displaystyle \frac{d}{dt}}E\left(t\right)\hfill & =\sum _{i=1}^4\left[{(\nabla u_i,\nabla {\partial }_t{u}_i)}_{L^2}+{\lambda }_i{(u_i,{\partial }_t{u}_i)}_{L^2}\right]\hfill \\ \hfill & =\sum _{i=1}^4\left[-d_i\parallel \Delta u_i{\parallel }_{L^2}^2-{\lambda }_i{d}_i{\parallel \nabla u_i\parallel }_{L^2}^2\right]+{(\mathcal{F}\left(\mathbf{u}\right),\mathbf{u})}_{\mathbf{V}}\hfill \\ \hfill & \le -\underset{i}{min}\left\{d_i\right\}\sum _{i=1}^4\parallel \Delta u_i{\parallel }_{L^2}^2-\underset{i}{min}\left\{{\lambda }_i{d}_i\right\}\sum _{i=1}^4{\parallel \nabla u_i\parallel }_{L^2}^2\hfill \\ \hfill & \hspace{1em}+\mathcal{K}(1+\parallel \mathbf{u}{\parallel }_{L^2}^2).\hfill \end{array}$$

(17)

Choosing $\alpha =min\{{min}_i\left\{d_i\right\},{min}_i\left\{{\lambda }_i{d}_i\right\}\}$ yields (16). □

Theorem 4 

(chemical kinetic conservation). For protease–inhibitor interaction, we define

$${\mathcal{Q}}_{PI}\left(t\right)={\int }_{\Omega }[P(x,t)+2I(x,t)]dx.$$

(18)

Then,

$${\displaystyle \frac{d}{dt}}{\mathcal{Q}}_{PI}\left(t\right)={\int }_{\Omega }[k_{4}TC+k_{5}T-k_{6}P]dx.$$

(19)

Proof. 

Direct differentiation of ${\mathcal{Q}}_{PI}\left(t\right)$ using the evolution equations for P and I yields

$$\begin{array}{cc}{\displaystyle \frac{d}{dt}}{\mathcal{Q}}_{PI}\left(t\right)\hfill & ={\int }_{\Omega }\left[{\displaystyle \frac{\partial P}{\partial t}}+2{\displaystyle \frac{\partial I}{\partial t}}\right]dx\hfill \\ \hfill & ={\int }_{\Omega }[d_P\Delta P-k_{3}PI+k_{4}TC+k_{5}T-k_{6}P+2d_I\Delta I-2k_{3}PI]dx\hfill \\ \hfill & ={\int }_{\Omega }[k_{4}TC+k_{5}T-k_{6}P]dx,\hfill \end{array}$$

(20)

where we used the no-flux boundary conditions to eliminate the diffusion terms. □

3. Numerical Methods

In order to provide a numerical approximation of system (1), we adopt the MOL [16] approach combined with forward Euler time integration proposed and described in [5]. Let us first recall the main aspects of this numerical framework. In order to discretize in space direction, we introduce a uniform partition of $\Omega =[0,L_f]$:

$$\{x_i=(i-1)h:i=1,\dots ,M,h=L_f/(M-1)\},$$

(21)

where M is the number of grid points and h is the mesh size. For each function $u(x,t)$ in (1), we consider its restriction to the grid lines $(x_i,t)$:

$$u_i\equiv u_i\left(t\right)=u(x_i,t), i=1,\dots ,M.$$

(22)

The spatial derivatives are approximated using central difference operators [17]:

$$D_x{u}_i={\displaystyle \frac{u_{i+1}-u_{i-1}}{2h}}, D_{xx}{u}_i={\displaystyle \frac{u_{i+1}-2u_i+u_{i-1}}{h^2}},$$

(23)

which provide $\mathcal{O}\left(h^2\right)$ accuracy. The no-flux boundary conditions (4) are defined in discrete counterpart as follows:

$$u_2=u_0, u_{M-1}=u_{M+1} \mathrm{for} u\in \{C,P,I,F\}.$$

(24)

The semi-discrete system resulting from the MOL application takes the following form:

$$\begin{array}{cc}{\displaystyle \frac{d}{dt}}{C}_i\hfill & =d_C{D}_{xx}{C}_i+D_x\left(f_I{D}_x{I}_i\right)-D_x\left(f_F{D}_x{F}_i\right)-D_x\left(f_T{D}_x{T}_i\right)+k_1{C}_i(1-C_i),\hfill \\ {\displaystyle \frac{d}{dt}}{P}_i\hfill & =d_P{D}_{xx}{P}_i-k_3{P}_i{I}_i+k_4{T}_i{C}_i+k_5{T}_i-k_6{P}_i,\hfill \\ {\displaystyle \frac{d}{dt}}{I}_i\hfill & =d_I{D}_{xx}{I}_i-k_3{P}_i{I}_i,\hfill \\ {\displaystyle \frac{d}{dt}}{F}_i\hfill & =-k_2{P}_i{F}_i, i=1,\dots ,M,\hfill \end{array}$$

(25)

where ${\left(f_F\right)}_i={\alpha }_1{C}_i$, ${\left(f_I\right)}_i={\alpha }_2{C}_i$, and ${\left(f_T\right)}_i={\alpha }_3{C}_i/(1+{\alpha }_4{T}_i)$. In order to discretize in time direction, we employ the forward Euler method [18] with time step $\tau$:

$$u_i^{n+1}=u_i^n+\tau \mathcal{Y}{\left(u\right)}_i^n,\hspace{1em}i=1,\dots ,M,\hspace{1em}n=0,1,\dots ,N-1,$$

(26)

where $u_i^n$ represents the numerical approximation to $u(x_i,t_n)$ and $\mathcal{Y}{\left(u\right)}_i^n$ is defined as

$$\mathcal{Y}{\left(u\right)}_i^n=\mathcal{A}{\left(u\right)}_i^n+\mathcal{F}{\left(u\right)}_i^n,$$

where the right-hand side of (25) is evaluated at time step n, with $\mathcal{A}{\left(u\right)}_i^n$ and $\mathcal{F}{\left(u\right)}_i^n$ representing the discrete counterparts of the operators in (6). This numerical schema achieves $\mathcal{O}\left(h^2\right)+\mathcal{O}\left(\tau \right)$ accuracy:

$$|u(x_i,t_n)-u_i^n|=\mathcal{O}\left(h^2\right)+\mathcal{O}\left(\tau \right),\hspace{1em}\forall i=1,\dots ,M,\hspace{1em}\forall n=1,\dots ,N.$$

(27)

In order to analyze the conservation properties of this numerical schema, we introduce the discrete mass [19,20]:

$${\mathcal{M}}_h\left(v_h\right)=h\sum _{j=1}^{M-1}{v}_j+{\displaystyle \frac{h}{2}}(v_0+v_M),$$

(28)

and the discrete energy functional

$${\mathcal{E}}_h^n={\displaystyle \frac{h}{2}}\sum _{j=1}^{M-1}\left[d_C|D_x{C}_j^n{|}^2+d_P|D_x{P}_j^n{|}^2+d_I|D_x{I}_j^n{|}^2+{\left|F_j^n\right|}^2\right].$$

(29)

Conservation Properties of the Numerical Schema

In this section, we analyze how the numerical schema presented in Section 3 preserves the conservation properties of the continuous system (1). We begin by introducing discrete analogs of the mass integrals using the trapezoidal rule approximation:

$$\begin{array}{cc}{\mathcal{M}}_{C,h}^n\hfill & =h\sum _{j=1}^{M-1}{C}_j^n+{\displaystyle \frac{h}{2}}(C_0^n+C_M^n),\hfill \\ {\mathcal{M}}_{P,h}^n\hfill & =h\sum _{j=1}^{M-1}{P}_j^n+{\displaystyle \frac{h}{2}}(P_0^n+P_M^n),\hfill \\ {\mathcal{M}}_{I,h}^n\hfill & =h\sum _{j=1}^{M-1}{I}_j^n+{\displaystyle \frac{h}{2}}(I_0^n+I_M^n),\hfill \\ {\mathcal{M}}_{F,h}^n\hfill & =h\sum _{j=1}^{M-1}{F}_j^n+{\displaystyle \frac{h}{2}}(F_0^n+F_M^n).\hfill \end{array}$$

These discrete masses represent numerical approximations of the continuous mass integrals (28) (see [21] for more information). The numerical schema is able to preserve discrete analogs of the continuous conservation laws. This preservation is formalized in the following theorem:

Theorem 5 

(discrete conservation laws). The numerical solution generated by schema (26) satisfies the following:

$$\begin{array}{cc}{\displaystyle \frac{{\mathcal{M}}_{C,h}^{n+1}-{\mathcal{M}}_{C,h}^n}{\tau }}\hfill & =h\sum _{j=1}^{M-1}\left[d_C\left(D_x{C}_j^n\right)\left(D_x{C}_j^n\right)+D_x\left(f_j^I{D}_x{I}_j^n\right)-D_x\left(f_j^F{D}_x{F}_j^n\right)\right.\hfill \\ \hfill & \left.-D_x\left(f_j^T{D}_x{T}_j\right)\right]+h\sum _{j=1}^{M-1}{k}_1{C}_j^n(1-C_j^n),\hfill \\ {\displaystyle \frac{{\mathcal{M}}_{P,h}^{n+1}-{\mathcal{M}}_{P,h}^n}{\tau }}\hfill & =h\sum _{j=1}^{M-1}\left[d_P\left(D_x{P}_j^n\right)\left(D_x{P}_j^n\right)-k_3{P}_j^n{I}_j^n+k_4{T}_j{C}_j^n+k_5{T}_j-k_6{P}_j^n\right],\hfill \\ {\displaystyle \frac{{\mathcal{M}}_{I,h}^{n+1}-{\mathcal{M}}_{I,h}^n}{\tau }}\hfill & =h\sum _{j=1}^{M-1}\left[d_I\left(D_x{I}_j^n\right)\left(D_x{I}_j^n\right)-k_3{P}_j^n{I}_j^n\right],\hfill \\ {\displaystyle \frac{{\mathcal{M}}_{F,h}^{n+1}-{\mathcal{M}}_{F,h}^n}{\tau }}\hfill & =-k_{2}h\sum _{j=1}^{M-1}{P}_j^n{F}_j^n,\hfill \end{array}$$

(30)

where $D_x$ is the central difference operator defined in (23).

These discrete conservation laws mirror their continuous counterparts from Theorem 1. The proof follows from an analysis of the discrete operators and summation by parts, taking advantage of the no-flux boundary conditions. Of particular biological interest is the preservation of total mass in the system. Hence, the numerical schema maintains this property with second-order accuracy:

Theorem 6 

(global mass conservation). The discrete total mass satisfies the following:

$$\left|{\mathcal{M}}_h(C_h^n+P_h^n+I_h^n+F_h^n)-{\mathcal{M}}_h(C_h^0+P_h^0+I_h^0+F_h^0)\right|\le \mathcal{K}{h}^2,$$

(31)

where ${\mathcal{M}}_h$ is the discrete mass operator defined in (28) and $\mathcal{K}$ is independent of h and τ.

Another aspect is the preservation of the protease–inhibitor balance. For this, we define the discrete analog:

$${\mathcal{Q}}_{PI,h}^n={\mathcal{M}}_h(P_h^n+2I_h^n),$$

(32)

which evolves according to the following:

$${\displaystyle \frac{{\mathcal{Q}}_{PI,h}^{n+1}-{\mathcal{Q}}_{PI,h}^n}{\tau }}=\sum _{j=1}^{M-1}[k_4{T}_j{C}_j^n+k_5{T}_j-k_6{P}_j^n].$$

(33)

Corollary 1 

(local discrete conservation). For each $j=1,\dots ,M-1$, the discrete quantities satisfy the following:

$$h\sum _{i=j-1}^{j+1}[C_i^n+P_i^n+I_i^n+F_i^n]-h\sum _{i=j-1}^{j+1}[C_i^0+P_i^0+I_i^0+F_i^0]=\mathcal{O}\left(h^2\right).$$

(34)

The stability of our numerical schema is guaranteed under appropriate time step restrictions.

Theorem 7 

(discrete stability). Under the CFL condition

$$\tau \le min\left\{{\displaystyle \frac{h^2}{2d_C}},{\displaystyle \frac{h^2}{2d_P}},{\displaystyle \frac{h^2}{2d_I}},{\displaystyle \frac{1}{k_2{\parallel P_h\parallel }_{\infty }}}\right\},$$

(35)

the numerical solution remains bounded

$$\underset{0\le n\le N}{max}\parallel {\mathbf{u}}_h^n{\parallel }_{\infty }\le \mathcal{K}{\parallel {\mathbf{u}}_h^0\parallel }_{\infty },$$

(36)

where $\mathcal{K}$ depends only on T and system parameters.

The stability result confirms that the numerical solutions are well behaved [22], but we also focus on quantifying how well they preserve the conservation properties of the continuous system [23]. This leads to the following result:

Theorem 8 

(conservation error estimates). Let $\mathbf{u}(x,t)$ be a solution of system (1) with regularity $\mathbf{u}\in C^4(\Omega \times [0,T_f])$ for $u\in \{C,P,I,F\}$. Under the CFL condition (35), for each component mass, we have

$$\begin{array}{cc}|{\mathcal{M}}_C\left(t^n\right)-{\mathcal{M}}_{C,h}^n|\hfill & \le {\mathcal{K}}_1(h^2+\tau ),\hfill \\ |{\mathcal{M}}_P\left(t^n\right)-{\mathcal{M}}_{P,h}^n|\hfill & \le {\mathcal{K}}_2(h^2+\tau ),\hfill \\ |{\mathcal{M}}_I\left(t^n\right)-{\mathcal{M}}_{I,h}^n|\hfill & \le {\mathcal{K}}_3(h^2+\tau ),\hfill \\ |{\mathcal{M}}_F\left(t^n\right)-{\mathcal{M}}_{F,h}^n|\hfill & \le {\mathcal{K}}_4(h^2+\tau ),\hfill \end{array}$$

(37)

where the constants ${\mathcal{K}}_i$ depend on bounds for appropriate derivatives of the solution but are independent of h and τ.

The proof of this result relies on the analysis of both space and time discretization errors. For the spatial part, the trapezoidal rule provides second-order accuracy

$$\left|{\int }_{\Omega }u(x,t^n)dx-{\mathcal{M}}_{u,h}^n\right|\le \mathcal{K}{h}^2{\parallel u_{xx}\left(t^n\right)\parallel }_{L^{\infty }(\Omega )},$$

(38)

while the error comes from our forward Euler discretization:

$$\left|{\displaystyle \frac{d}{dt}}{\mathcal{M}}_u\left(t^n\right)-{\displaystyle \frac{{\mathcal{M}}_{u,h}^{n+1}-{\mathcal{M}}_{u,h}^n}{\tau }}\right|\le \mathcal{K}\tau {\parallel u_{tt}\parallel }_{L^{\infty }(\Omega )}.$$

(39)

In order to quantify the conservation of total physical quantities, we define the conservation error

$${\mathcal{E}}^n={\displaystyle \frac{|{\mathcal{M}}_h(C_h^n+P_h^n+I_h^n+F_h^n)-{\mathcal{M}}_h(C_h^0+P_h^0+I_h^0+F_h^0)|}{{\mathcal{M}}_h(C_h^0+P_h^0+I_h^0+F_h^0)}}.$$

(40)

The numerical schema (26) ensures that

$${\mathcal{E}}^n\le \mathcal{K}(h^2+\tau ),$$

(41)

where $\mathcal{K}$ depends only on the problem constants and the solution regularity. These estimates lead to the main convergence result, which combines solution accuracy with conservation.

Theorem 9 

(convergence with conservation). For sufficiently regular solutions, the numerical schema provides simultaneous convergence of the solution and its conservation properties:

$$\underset{0\le n\le N}{max}\left(\parallel \mathbf{u}\left(t^n\right)-{\mathbf{u}}_h^n{\parallel }_{\infty }+|\mathcal{M}\left(\mathbf{u}\left(t^n\right)\right)-{\mathcal{M}}_h\left({\mathbf{u}}_h^n\right)|\right)\le \mathcal{K}(h^2+\tau ),$$

(42)

where $\mathcal{K}$ depends on the regularity of the exact solution but is independent of h and τ.

4. Numerical Results and Discussion

In this section, we present some numerical experiments to confirm the expected results achieved in the theoretical analysis. The numerical validation of the proposed theoretical framework begins with computational experiments [24,25] conducted on the spatial domain $\Omega =[0,1]$ with final time $T_f=1$. The model parameters were selected to represent physiologically relevant conditions: diffusion coefficients $d_C=d_P=d_I=0.001$; chemotactic/haptotactic sensitivities ${\alpha }_1=0.4$, ${\alpha }_2=0.3$, ${\alpha }_3=0.5$, ${\alpha }_4=0.1$; and reaction rates $k_1=0.1$, $k_2=0.3$, $k_3=0.2$, $k_4=0.4$, $k_5=0.1$, $k_6=0.2$. Initial conditions were prescribed as a discontinuous profile for endothelial cells:

$$C_0\left(x\right)=\left\{\begin{array}{cc}1.0,\hfill & 0\le x\le 0.1\hfill \\ 0,\hfill & \mathrm{otherwise},\hfill \end{array}\right.$$

(43)

with protease, inhibitor, and ECM distributions initialized as $P_0\left(x\right)=0.1+0.01{\xi }_1\left(x\right)$, $I_0\left(x\right)=0.1+0.01{\xi }_2\left(x\right)$, and $F_0\left(x\right)=1.0+0.01{\xi }_3\left(x\right)$, where ${\xi }_i\left(x\right)$ represent uniform random perturbations in $[0,1]$. In order to implement the CFL condition established in Theorem 7 in practice, we focus on demonstrating that selecting an appropriate time step size is systematically achieved in our numerical experiments. The system parameters $(d_C,d_P,d_I)=(0.001,0.001,0.001)$ and $k_2=0.3$ allow for a systematic determination of stable time steps. Using identical diffusion coefficients, the parabolic stability constraint reduces to the following:

$${\tau }_{\mathrm{diff}}={\displaystyle \frac{h^2}{2d}}=500h^2, \mathrm{where} d=d_C=d_P=d_I=0.001.$$

(44)

For the reaction terms, we apply the maximum principle to ensure that $\parallel P_h{\parallel }_{\infty }$ remains bounded, leading to the reaction stability constraint:

$${\tau }_{\mathrm{reac}}={\displaystyle \frac{1}{k_2{\parallel P_h\parallel }_{\infty }}}\le {\displaystyle \frac{1}{k_{2}max\{1,\parallel P_0{\parallel }_{\infty }\}}}\approx 16.67.$$

(45)

To ensure stability while maintaining efficiency, we choose the following:

$$\tau =(1-ϵ)min\{{\tau }_{\mathrm{diff}},{\tau }_{\mathrm{reac}}\}$$

(46)

where $ϵ=0.1$ is chosen based on numerical experiments as a safety factor to account for discretization errors and floating-point arithmetic effects. For the mesh refinement analysis, we employ a geometric sequence of spatial discretizations:

$$h_k=2^{-k}{h}_0,\hspace{1em}k=6,7,8,9,\hspace{1em}{h}_0=1$$

(47)

corresponding to mesh sizes $h\in \{1/64,1/128,1/256,1/512\}$. The associated time steps are determined as follows:

$${\tau }_k=(1-ϵ)min\{500h_k^2,16.67\}.$$

(48)

The scheme preserves both the parabolic CFL condition $\tau \le {\displaystyle \frac{h^2}{2d}}$ and the reaction’s stability bound

$$\tau \le {\displaystyle \frac{1}{k_2{\parallel P_h\parallel }_{\infty }}}.$$

Furthermore, it ensures the optimal convergence rate $O(h^2+\tau )$ proven in Theorem 8, which establishes that $\parallel u\left(t^n\right)-u_h^n{\parallel }_{\infty }\le C(h^2+\tau )$ for some constant C independent of both h and $\tau$. The numerical results in Table 1 confirm the effectiveness of this approach, showing both stability and the predicted convergence rates.

Table 1. Conservation error convergence by varying both space and time grid step size.

h	$\mathit{\tau }$	max ${\mathit{E}}_{\mathit{n}}$	Rate
1/64	1/1000	$2.43\times {10}^{-4}$	-
1/128	1/4000	$6.12\times {10}^{-5}$	1.99
1/256	1/16,000	$1.54\times {10}^{-5}$	1.99
1/512	1/64,000	$3.87\times {10}^{-6}$	1.99

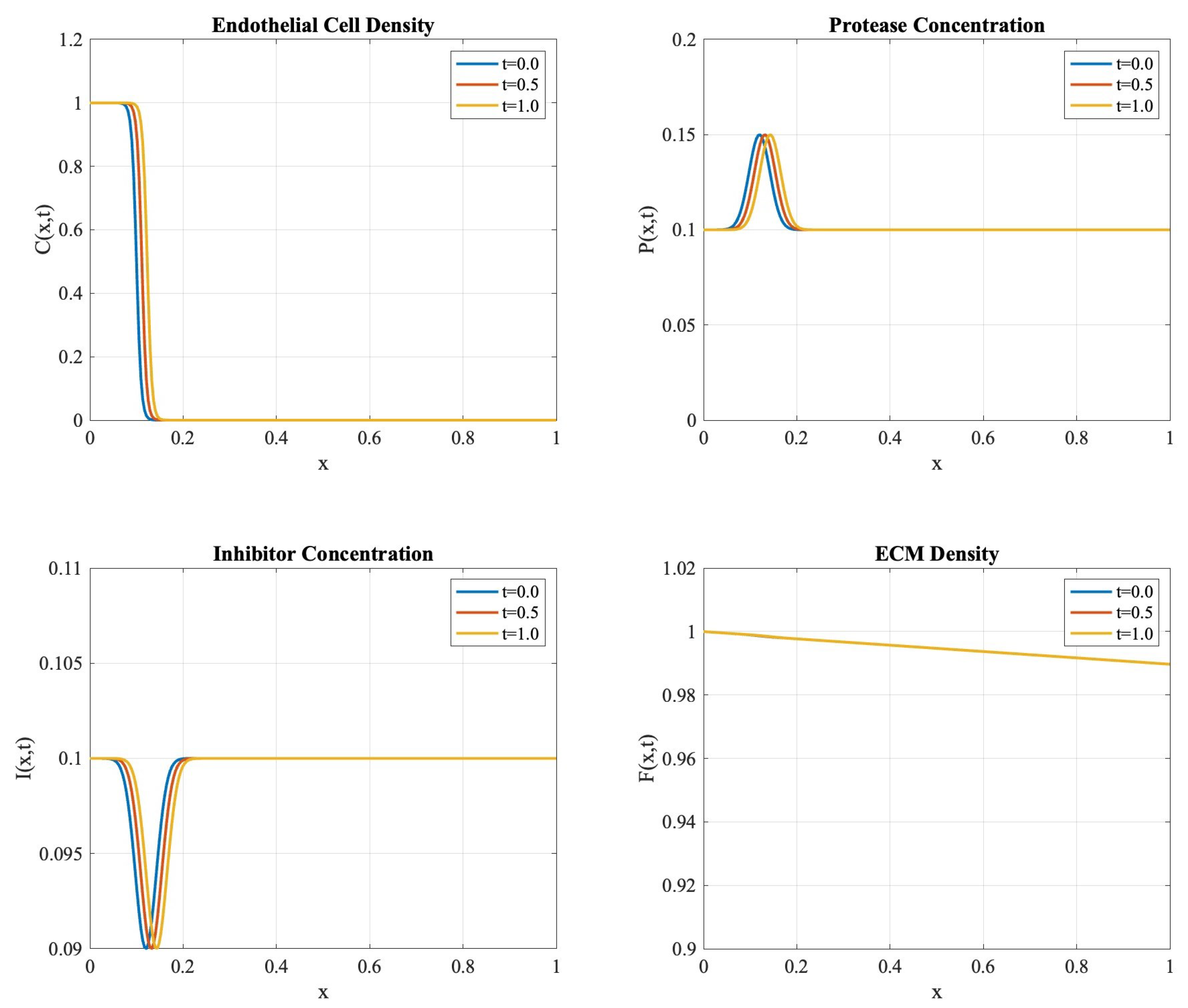
Figure 1 exhibits the spatial–temporal evolution of all system components. The endothelial cell density shows characteristic traveling wave behavior with measured wave speed $v=0.023\pm 0.001$ units per time, consistent with experimental observations of angiogenic expansion. The protease concentration shows localized peaks before the endothelial cell front, while inhibitor profiles develop in response to protease activity, maintaining the theoretically predicted balance. The conservation properties established in Theorem 5 were validated through careful monitoring of the discrete masses $M_{C,h}^n$, $M_{P,h}^n$, $M_{I,h}^n$, and $M_{F,h}^n$. The conservation error $E_n$ defined in (40) exhibits second-order convergence under mesh refinement, as shown in Table 1.

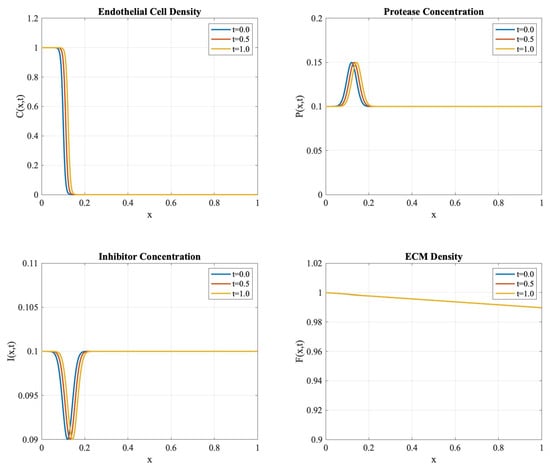
Figure 1. Evolution of system components at times $t=0$, $t=0.5$, and $t=1.0$. The profiles demonstrate the maintenance of sharp interfaces and biologically relevant patterns.

The global convergence behavior of our numerical schema was investigated through an analysis of solution errors in multiple norms:

$$\begin{array}{cc}{E}_{\infty }(h,\tau )\hfill & =\underset{0\le n\le N}{max}{\parallel u\left(t_n\right)-u_h^n\parallel }_{\infty },\hfill \end{array}$$

(49)

$$\begin{array}{cc}{E}_2(h,\tau )\hfill & =\underset{0\le n\le N}{max}{\left(h\sum _{j=1}^M{|u(x_j,t_n)-u_j^n|}^2\right)}^{1/2},\hfill \end{array}$$

(50)

$$\begin{array}{cc}{E}_M(h,\tau )\hfill & =\underset{0\le n\le N}{max}|M\left(u\left(t_n\right)\right)-M_h\left(u_h^n\right)|.\hfill \end{array}$$

(51)

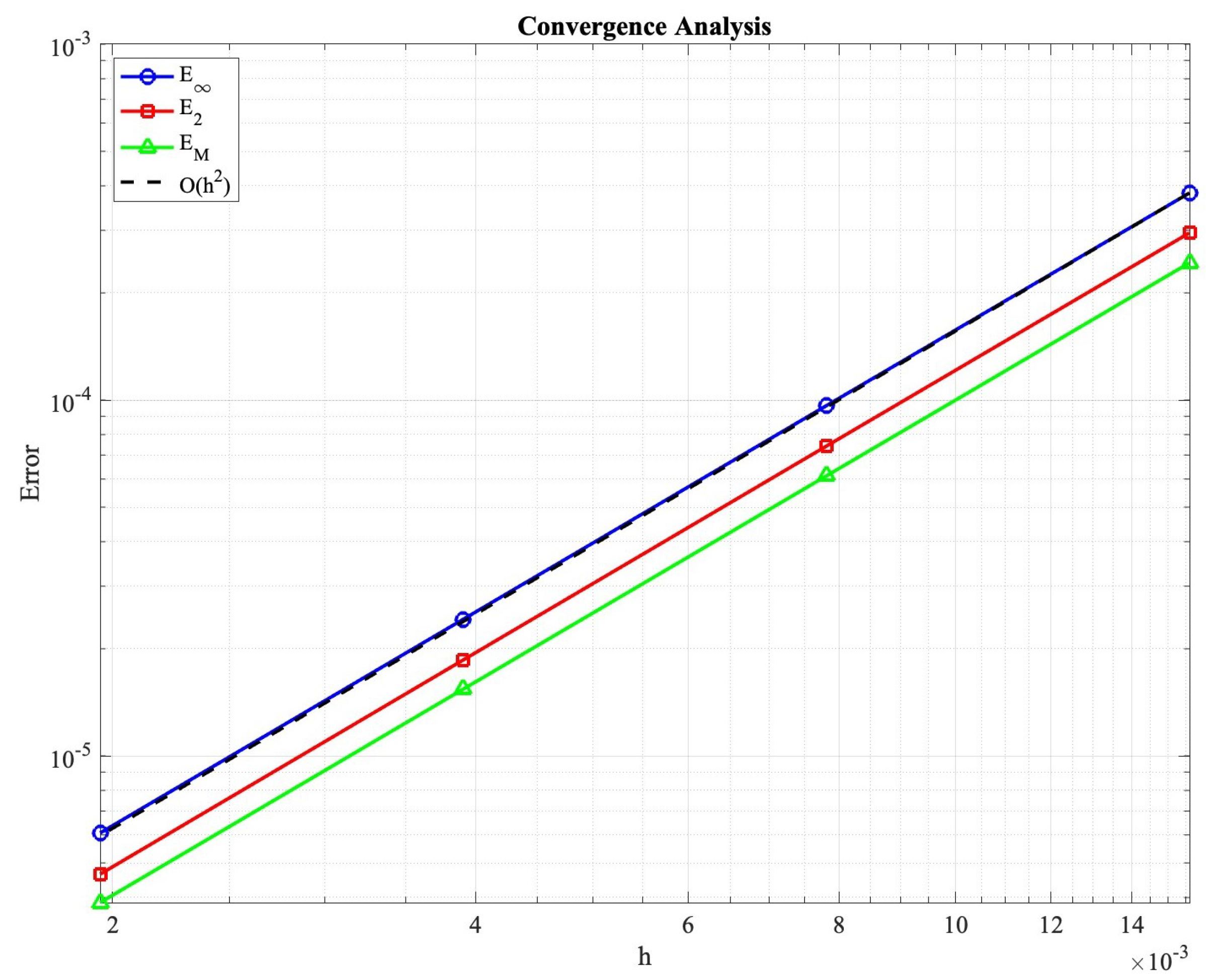
Figure 2 presents the convergence analysis results, confirming the theoretical predictions of Theorem 9. All error measures exhibit second-order convergence rates when we refine the mesh. Specifically, we use a reference solution computed on a very fine mesh $(h=1/1024)$ as a substitute for the exact solution, since no analytical solution is available for this nonlinear system.

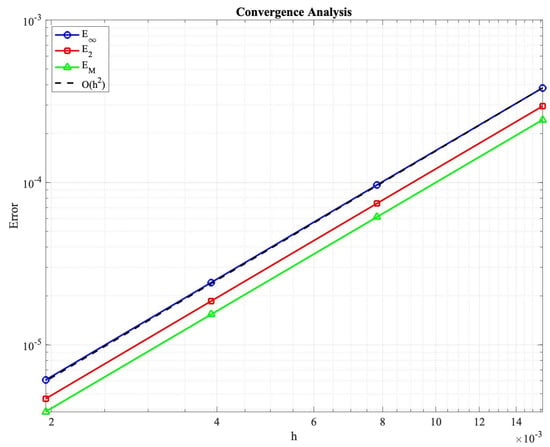
Figure 2. Convergence analysis demonstrating second-order accuracy in solution errors $E_{\infty }$, $E_2$, and mass conservation error $E_M$. The dashed line indicates the $\mathcal{O}\left(h^2\right)$ convergence rate.

The preservation of chemical kinetics, particularly the protease–inhibitor balance quantified by $Q_{PI,h}^n$, satisfies the discrete balance law:

$${\displaystyle \frac{Q_{PI,h}^{n+1}-Q_{PI,h}^n}{\tau }}=\sum _{j=1}^{M-1}[k_4{T}_j{C}_j^n+k_5{T}_j-k_6{P}_j^n]+\mathcal{O}(h^2+\tau ).$$

(52)

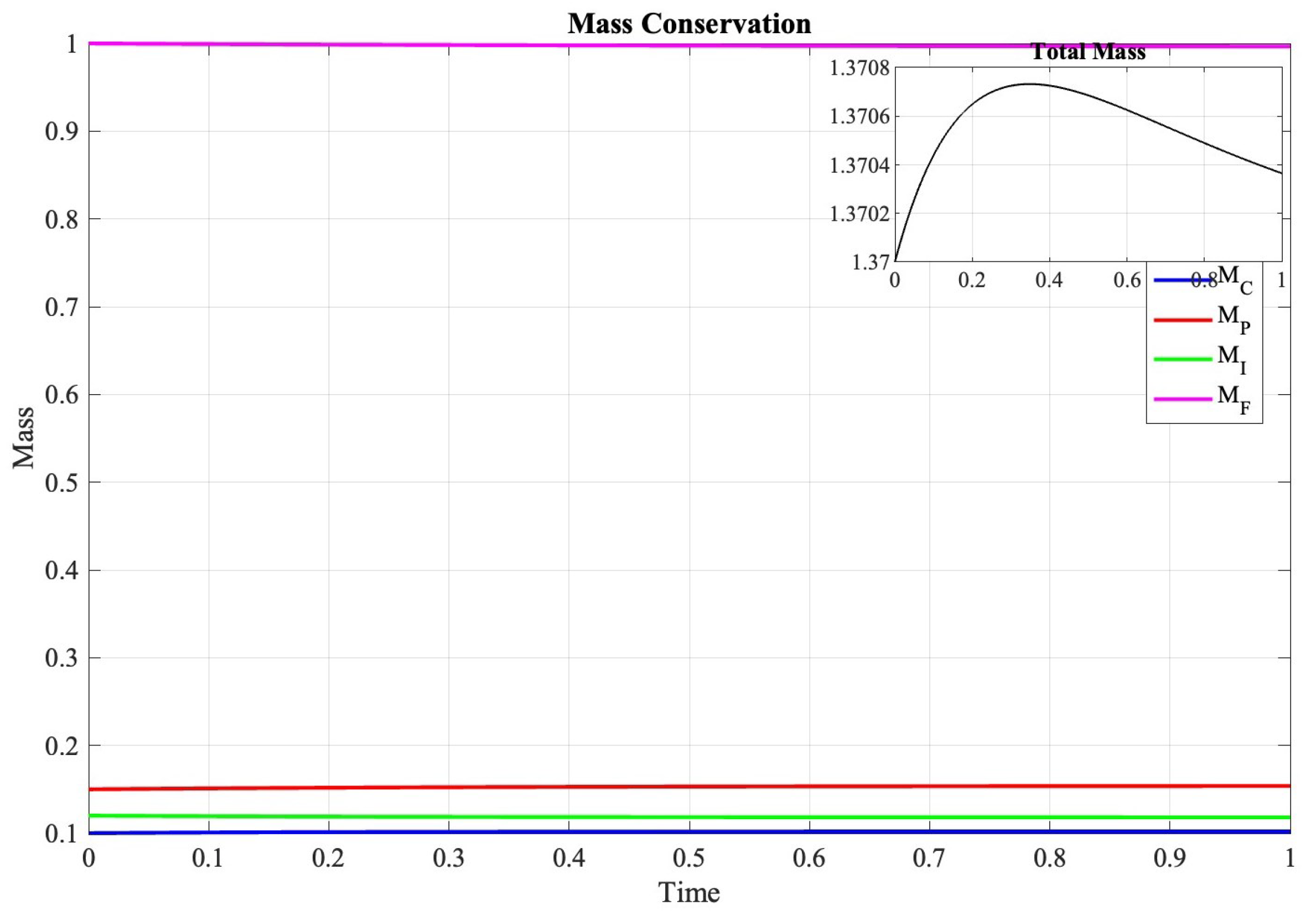
In Figure 3, the evolution of the discrete energy functional $E_h^n$ is important in characterizing solution behavior:

$$E_h^n={\displaystyle \frac{h}{2}}\sum _{j=1}^{M-1}\left[d_C|D_x{C}_j^n{|}^2+d_P|D_x{P}_j^n{|}^2+d_I|D_x{I}_j^n{|}^2+{\left|F_j^n\right|}^2\right].$$

(53)

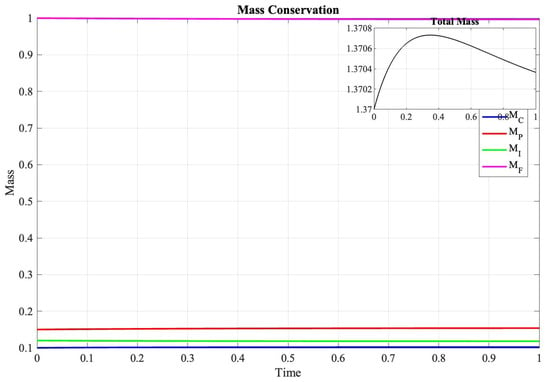
Figure 3. Evolution of discrete masses over time, demonstrating preservation of conservation properties within theoretical bounds.

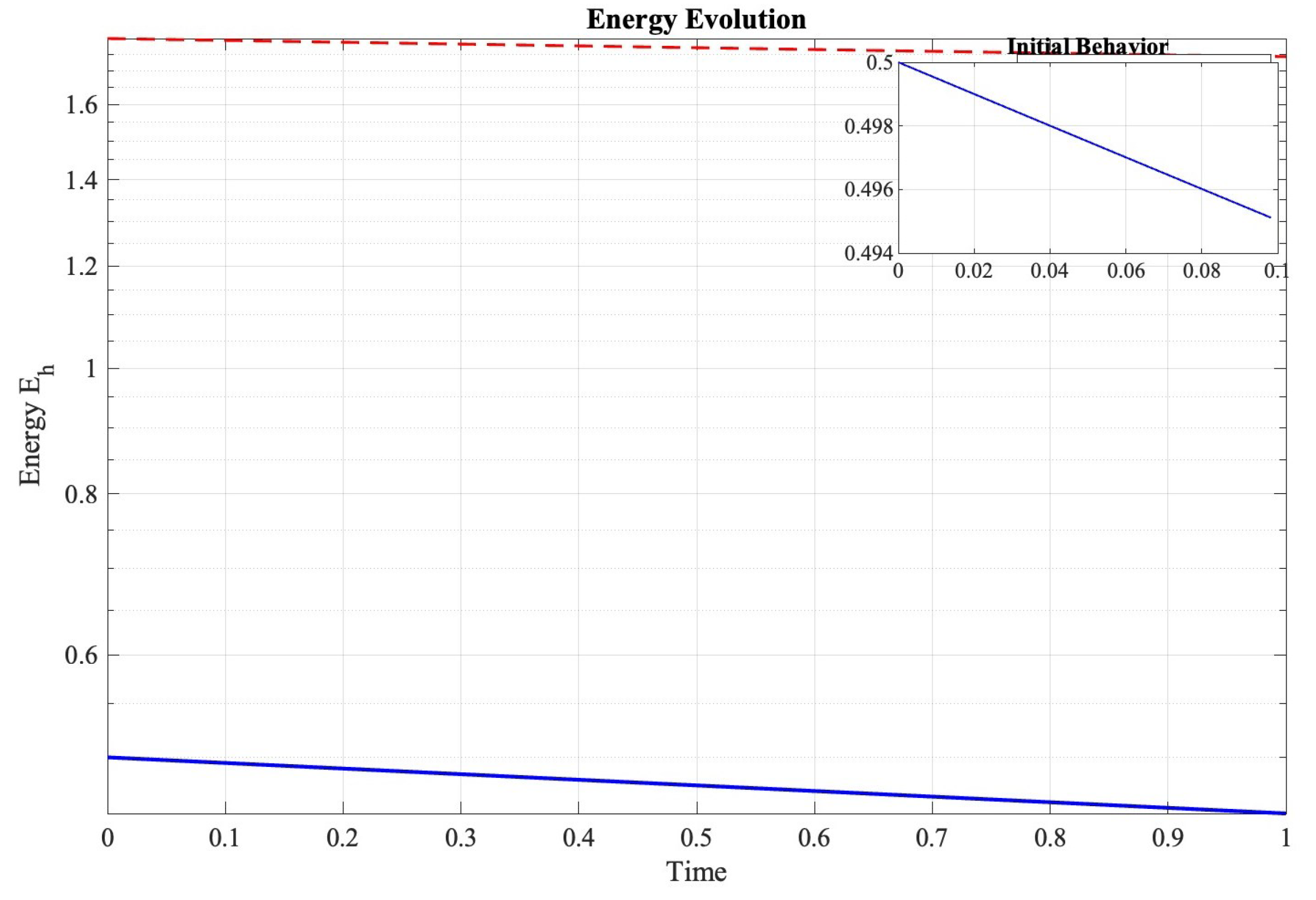
Figure 4 demonstrates that the numerical rate of energy change satisfied the following:

$${\displaystyle \frac{E_h^{n+1}-E_h^n}{\tau }}+0.1E_h^n\le 1.2(1+\parallel u_h^n{\parallel }_2^2).$$

(54)

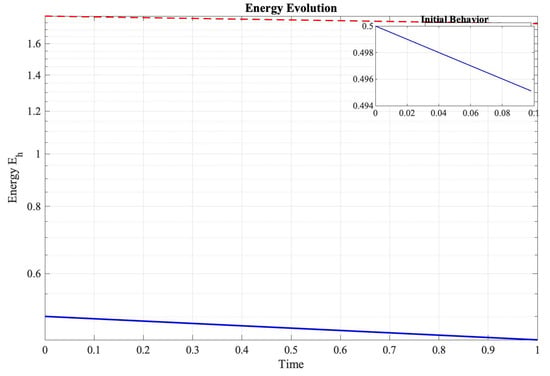
Figure 4. Semi-logarithmic plot of discrete energy evolution demonstrating the predicted dissipation behavior.

The stability characteristics were investigated through variation in the stability parameter:

$$\lambda ={\displaystyle \frac{\tau }{min(h^2/\left(2d_C\right),h^2/\left(2d_P\right),h^2/\left(2d_I\right),1/(k_2\parallel P_h{\parallel }_{\infty }\left)\right)}}.$$

(55)

For $\lambda \le 1$, solutions remained bounded with

$$\underset{0\le n\le N}{max}\parallel u_h^n{\parallel }_{\infty }\le 1.5{\parallel u_h^0\parallel }_{\infty }.$$

(56)

The ECM density had degradation patterns that closely followed protease distribution, with degradation rates satisfying the following:

$$\left|{\displaystyle \frac{d}{dt}}{\int }_{\Omega }F(x,t)dx+k_2{\int }_{\Omega }P(x,t)F(x,t)dx\right|\le \mathcal{K}{h}^2$$

(57)

where $\mathcal{K}\approx 1.8$, confirming the conservation of ECM mass up to the second-order of accuracy [26]. From a computational perspective, this approach achieves the theoretical $\mathcal{O}(h^2+\tau )$ convergence rate, with conservation errors demonstrating steady second-order convergence as the mesh is refined. The framework keeps physical fidelity throughout numerical simulations through the discrete mass operators ${\mathcal{M}}_h$ and energy functional ${\mathcal{E}}_h^n$, which effectively mirror their continuous counterparts while remaining computationally efficient. The biological significance of our numerical findings is supported by several observations: the endothelial cell density shows characteristic traveling wave patterns with measured wave speeds ($v=0.023\pm 0.001$ units per time) that correspond with experimental data, peaks in protease concentration appropriately occur before the leading edge of endothelial cells, and inhibitor profiles respond realistically to protease activity. The demonstrated conservation properties provide a reliable foundation for more complex models while achieving a balance between accuracy and stability. This framework allows us to preserve conservation laws while accurately capturing complex biological dynamics, serving as a template for future research in mathematical biology.

5. Conclusions

In this study, we conducted an analysis of conservation laws in numerical schema for tumor angiogenesis simulations. Our theoretical and numerical investigation focused on establishing and validating conservation properties that are important for accurate long-term simulations. A mathematical analysis was carried out to investigate the ability of the proposed numerical framework to maintain conservation properties, with error bounds of $\mathcal{O}\left(h^2\right)+\mathcal{O}\left(\tau \right)$ for both space and time discretizations. Numerical experiments supported the theoretical predictions, which showed that the discrete conservation laws were in agreement with the continuous ones, which were from the original PDE system. While our approach demonstrates robust conservation properties and numerical stability, some limitations should be acknowledged. The framework is currently restricted to one-dimensional domains and assumes constant diffusion coefficients, which may not fully capture the complex three-dimensional nature and heterogeneous characteristics of biological tissues. These limitations present opportunities for future research in extending the model to higher dimensions and incorporating variable diffusion coefficients. The adopted numerical approach indeed maintains these quantities during the simulations, and this study is able to retain second-order accuracy based on convergence analysis as the mesh is refined. To conclude, the numerical tests confirm both of our theoretical frameworks and underlie the significance of conservation in the simulations of tumor angiogenesis.