New Analytical Formulas for the Rank of Farey Fractions and Estimates of the Local Discrepancy

Abstract

New analytical formulas are derived for the rank and the local discrepancy of Farey fractions. The new rank formula is applicable to all Farey fractions and involves sums of a lower order compared to the searched one. This serves to establish a new unconditional estimate for the local discrepancy of Farey fractions that decrease with the order of the Farey sequence. This estimate improves the currently known estimates. A new recursive expression for the local discrepancy of Farey fractions is also given. A second new unconditional estimate of the local discrepancy of any Farey fraction is derived from a sum of the Mertens function, again, improving the currently known estimates.

1. Introduction and Statement of Main Results

The Farey sequence $F_n$ of order $n\in \mathbb{N}$ is an ascending sequence of irreducible fractions between 0 and 1 whose denominators do not exceed n. These fractions are referred to as Farey fractions. An introduction and thorough reviews of the theory of Farey sequences can be found in [1,2,3,4], along with a few applications in [5,6]. Throughout this paper, we exclude the fraction $0/1$ from $F_n$. For given $n\in \mathbb{N}$ and $x\in ]0,1]$, $I_n\left(x\right)$ is defined as the number of elements in $F_n$ within $]0,x]$. We define $F_n^x$ as a subsequence of $F_n$ given by

$$F_n^x=F_n\cap ]0,x],$$

and, therefore,

$$I_n\left(x\right)=\left|F_n^x\right|.$$

The local discrepancy ${\widehat{r}}_n(h/k)$ of the Farey fraction $h/k$ in $F_n$ is defined as [7,8]

$${\widehat{r}}_n(h/k)=\frac{h}{k}\left|F_n\right|-I_n(h/k).$$

We also introduce the discrepancy ${\widehat{r}}_q^{\phi }(h/k)$, at the level of the Euler Totient function $\phi \left(x\right)$, such that the number of Farey fractions in $F_q$ lower than $h/k$ and with denominators equal to q is given by

$$\frac{h}{k}\phi \left(q\right)-{\widehat{r}}_q^{\phi }\left(\frac{h}{k}\right),$$

and, therefore,

$${\widehat{r}}_n(h/k)=\sum _{q=1}^n{\widehat{r}}_q^{\phi }\left(\frac{h}{k}\right).$$

Note that $h/k$ is not necessarily an element of $F_n$. The absolute discrepancy of the Farey sequence $F_n$ is generally defined as

$$D_n=\underset{\alpha \in F_n}{sup}\frac{|{\widehat{r}}_n\left(\alpha \right)|}{|F_n|}.$$

It is important to recall an equivalent formulation of the Riemann Hypothesis (RH). The Franel–Landau formulation [9,10] is expressed as

$$\frac{1}{|F_n|}\sum _{h/k\in F_n}\left|{\widehat{r}}_n(h/k)\right|=O\left(n^{\frac{1}{2}+ϵ}\right)\forall ϵ>0\iff \mathrm{RH}.$$

This direct connection between local discrepancies and RH shows the importance of progressing in computing estimates of ${\widehat{r}}_n(h/k)$. The unconditional estimate of ${\widehat{r}}_n(h/k)$ is not generally addressed in the literature, while $D_n$ has been evaluated to be $O(1/n)$ in [7] and, therefore, using $|F_n|=O\left(n^2\right)$, we can write

$${\widehat{r}}_n(h/k)=O\left(n\right).$$

(1)

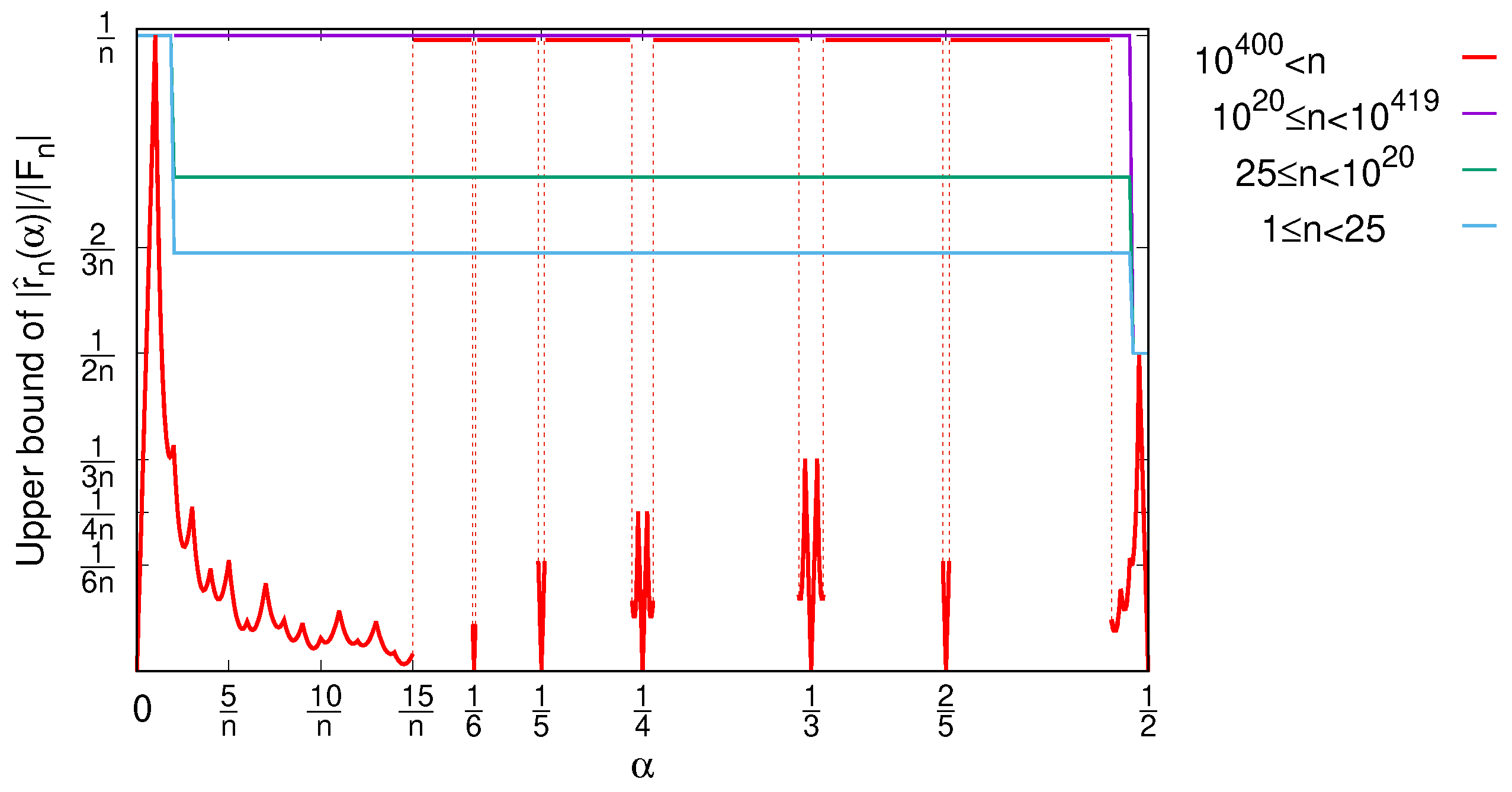
The absolute discrepancy of the Farey sequence was derived in [11] and found to be $D_n=1/n$ by finding an upper bound of an integral of the Mertens function. This result has been qualified as “most remarkable” in [12]. Figure 1 shows an illustration of the different bounds for the local discrepancies versus the corresponding Farey fraction $\alpha$ for different ranges of n, as derived in [11].

Figure 1. Illustration of the results in [11], showing the upper bounds of the local discrepancy of Farey fractions, $|{\widehat{r}}_n\left(\alpha \right)|/|F_n|$, versus the Farey fractions $\alpha$ in $[0,1/2]$ (without respecting the actual separation ratios in the horizontal axis). Note that the red curve for $\alpha \le 15/n$ has been plotted using expression (2), while in [11] (page 361) tabulated values are given.

The following approximations are derived in [11] (page 361) for $n>{10}^{400}$,

$$\begin{array}{ccc}\hfill I_n\left(\alpha \right)& {}^w=& n\sum _{j=1}^{\lfloor n\alpha \rfloor }\frac{\phi \left(j\right)}{j}-\frac{1}{\alpha }\Phi \left(\lfloor n\alpha \rfloor \right),\hfill \\ \hfill \left|{\widehat{r}}_n\left(\alpha \right)\right|& {}^w\le & \frac{|F_n|}{n}\left(n\alpha -\frac{{\pi }^2}{3}\sum _{j=1}^{\lfloor n\alpha \rfloor }\frac{\phi \left(j\right)}{j}+\frac{{\pi }^2}{3\alpha n}\Phi \left(\lfloor n\alpha \rfloor \right)\right),\hfill \end{array}$$

(2)

where $\Phi \left(x\right)$ is the Totient summatory function and “${}^w=$” and “${}^w\le$” are introduced in [11] to imply that the terms with relative influence below ${10}^{-100}$ are neglected. Neither the validity range of these approximations for $\alpha$ nor the estimates of the neglected terms are given in [11]. These approximations are only used for $\alpha \le 15/n$ in [11] and, indeed, above this value of $\alpha$, the quantity in parenthesis in (2) can take negative values. For example, for $\alpha =33.6/n$, we would have $\left|{\widehat{r}}_n(33.6/n)\right|{}^w\le -0.001\left|F_n\right|/n$, which does not hold.

Knowing the missing terms that complete the above approximations for any n and $\alpha$ could lead to new bounds or estimates for the local discrepancies of Farey fractions. Partial developments in this direction are found in [13,14] for unit fractions. In Theorem 1 and Corollary 1, we develop new general expressions for $I_n\left(\alpha \right)$ and ${\widehat{r}}_n\left(\alpha \right)$, obtaining, for ${\widehat{r}}_n\left(\alpha \right)$,

$$\begin{array}{ccc}\hfill {\widehat{r}}_n\left(\alpha \right)& =& |F_n|\alpha -n\sum _{j=1}^{\lfloor n\alpha \rfloor }\frac{\phi \left(j\right)}{j}+\frac{1}{\alpha }\Phi \left(\lfloor n\alpha \rfloor \right)\hfill \\ & & -{\widehat{r}}_{\lfloor n\alpha \rfloor }\left(\{1/\alpha \}\right)+\sum _{j=1}^{\lfloor n\alpha \rfloor }\sum _{d|j}\mu \left(d\right)\left\{\frac{n}{d}\right\},\hfill \end{array}$$

(3)

where $\mu \left(d\right)$ is the Möbius funtion and $\left\{x\right\}$ represents the fractional part of x. This identity unexpectedly connects the discrepancy of $\alpha$ in $F_n$ with the discrepancy of $\{1/\alpha \}$ in $F_{\lfloor n\alpha \rfloor }$. Furthermore, the new general identity (3) can be applied iteratively to ${\widehat{r}}_{\lfloor n\alpha \rfloor }\left(\{1/\alpha \}\right)$ for a finite number of steps, as $\{1/\alpha \}$ is always a Farey fraction of a lower order than $\alpha$. This identity is used in Theorem 2 to derive a new unconditional estimate of ${\widehat{r}}_n\left(\alpha \right)$ for any $\alpha \asymp O\left(n^{-ϵ}\right)$, with $ϵ\in ]0,1]$, given by

$${\widehat{r}}_n\left(\alpha \right)=O\left(n{\delta }_A\left(n^{1-ϵ}\right)\right),\mathrm{for}\alpha \asymp O\left(n^{-ϵ}\right),ϵ\in ]0,1],$$

where the function ${\delta }_A\left(x\right)$ is a monotonic decreasing function defined as

$$\begin{array}{ccc}\hfill {\delta }_A\left(x\right)& =& exp\left(-A\frac{{\log }^{0.6}x}{{\left(\log \log x\right)}^{0.2}}\right),\mathrm{with}A>0.\hfill \end{array}$$

This new unconditional estimate of ${\widehat{r}}_n\left(\alpha \right)$ improves the existing one, $O\left(n\right)$, from [7,11] for $\alpha$ values that decrease with n.

In this work, we derive another unconditional estimate of ${\widehat{r}}_n(h/k)$. For later convenience, we define the local discrepancy with an offset as

$$r_n(h/k)={\widehat{r}}_n(h/k)-\frac{k-1}{2k}.$$

In Theorem 3, we demonstrate that

$$\begin{array}{ccc}\hfill \sum _{d=1}^n{r}_{\lfloor n/d\rfloor }(h/k)& =& \sum _{i=1}^b{⟨\frac{ih}{k}⟩}_k,\hfill \end{array}$$

(4)

with $b=nmodk$ and ${⟨·⟩}_k$, the fractional part with an offset defined as

$${⟨x⟩}_k=\left\{x\right\}-\frac{k-1}{2k}.$$

Note that for $h/k$ being a Farey fraction and for any positive integers a and p, we have

$$\sum _{d=a}^{a+pk-1}{⟨\frac{dh}{k}⟩}_k=0.$$

(5)

Expression (4) can be used iteratively for an efficient calculation of $r_n(h/k)$ as done, e.g., in [15], to compute $I_n(h/k)$. Applying the Möbius inversion formula to (4) and making further developments, the following two identities are also demonstrated in Theorem 3,

$$\begin{array}{ccc}\hfill r_n(h/k)& =& \sum _{d=1}^n\mu \left(d\right)\sum _{i=1}^{\widehat{b}}{⟨\frac{ih}{k}⟩}_k\hfill \end{array}$$

(6)

$$\begin{array}{ccc}& =& \sum _{d=1}^{n}M\left(\frac{n}{d}\right){⟨\frac{dh}{k}⟩}_k,\hfill \end{array}$$

(7)

with $\widehat{b}=\lfloor n/d\rfloor modk$ and $M\left(n\right)$ representing the Mertens function defined as $M\left(n\right)={\sum }_{d=1}^n\mu \left(d\right)$. Expression (6) is new and can be used to demonstrate again that $r_n(h/k)=O\left(n\right)$ as the sum over i is bounded by $k/8$, as it is shown in Lemma 3 given below. Expression () is not new, as it already has been given in similar forms in [3,7,11], but here, it adopts a simpler form thanks to the introduction of ${⟨·⟩}_k$ and the local discrepancy with an offset.

Theorem 4 establishes a second new unconditional estimate of the local discrepancy for a Farey fraction, $h/k$, such that $k=O\left(n^{1-ϵ}\right)$, with $1>ϵ>0$, as

$$r_n(h/k)=O\left(n{\log }^{0.4}n{\log }^{0.2}\log n{\delta }_A\left(n^{ϵ}\right)\right),\mathrm{for}A>0.$$

It is important to note that this estimate includes the general case of $h/k$ being constant. Again, this unconditional estimate improves the existing one, $O\left(n\right)$, from [7,11] for Farey fractions with denominators that can grow sublinearly with the order of the Farey sequence and complements the estimate given in Theorem 2.

2. Results

Lemma 1.

The number ${\mathcal{N}}_n^{h/k}\left(q\right)$ of Farey fractions in $F_n^{h/k}$ with numerators equal to q for $k\le n$ is given by

$${\mathcal{N}}_n^{h/k}\left(q\right)=n\frac{\phi \left(q\right)}{q}-\frac{k}{h}\phi \left(q\right)+{\widehat{r}}_q^{\phi }\left(\{k/h\}\right)-\sum _{d|q}\mu \left(d\right)\left\{\frac{n}{d}\right\},$$

Proof. 

Using Corollary 5 in [14], we determine the number of Farey fractions with numerators equal to q in $F_n^{1/\lfloor k/h\rfloor }$ as

$${\mathcal{N}}_n^{1/\lfloor k/h\rfloor }\left(q\right)=n\frac{\phi \left(q\right)}{q}-\lfloor k/h\rfloor \phi \left(q\right)-\sum _{d|q}\mu \left(d\right)\left\{\frac{n}{d}\right\},\mathrm{if}\lfloor k/h\rfloor <n/q.$$

To determine ${\mathcal{N}}_n^{h/k}\left(q\right)$ from ${\mathcal{N}}_n^{1/\lfloor k/h\rfloor }\left(q\right)$, we need to compute the number of Farey fractions with numerators equal to q in $F_n\cap \left[\frac{h}{k},\frac{1}{\lfloor k/h\rfloor }\right]$. To this end, we define $F_n^{\prime }$ as

$$F_n^{\prime }=\left\{\frac{u}{l}\in F_n\cap \left[\frac{1}{\lfloor k/h\rfloor +1},\frac{1}{\lfloor k/h\rfloor }\right]:u\le q\right\},$$

and a bijective map $\tilde{M}$ between $F_n^{\prime }$ and $F_q$ as

$$\begin{array}{ccc}\hfill \tilde{M}& :& F_q\to F_n^{\prime },\frac{t}{q^{\prime }}\mapsto \frac{q^{\prime }}{q^{\prime }(\lfloor k/h\rfloor +1)-t},\hfill \\ \hfill {\tilde{M}}^{-1}& :& F_n^{\prime }\to F_q,\frac{h^{\prime }}{k^{\prime }}\mapsto \frac{h^{\prime }(\lfloor k/h\rfloor +1)-k^{\prime }}{h^{\prime }}.\hfill \end{array}$$

This implies that the number of Farey fractions with numerators equal to q in $F_n^{\prime }$ is the same as the number of Farey fractions with denominators equal to q in $F_q$, that is $\phi \left(q\right)$. Furthermore, the image of $h/k$ under ${\tilde{M}}^{-1}$ is given by

$$\frac{h(\lfloor k/h\rfloor +1)-k}{h}=1-\left\{\frac{k}{h}\right\}=1-\frac{kmodh}{h},$$

and the number of Farey fractions in $F_q$ with denominators equal to q and larger than $1-\{k/h\}$ is given by

$$\phi \left(q\right)\left\{\frac{k}{h}\right\}-{\widehat{r}}_q^{\phi }\left(\{k/h\}\right).$$

Therefore,

$${\mathcal{N}}_n^{h/k}\left(q\right)={\mathcal{N}}_n^{1/\lfloor k/h\rfloor }\left(q\right)-\phi \left(q\right)\left\{\frac{k}{h}\right\}+{\widehat{r}}_q^{\phi }\left(\{k/h\}\right).$$

□

Lemma 2.

The largest numerator among the Farey fractions in $F_n^{\alpha }$, with $\alpha \in [0,1]$, is equal to or below $\lfloor n\alpha \rfloor$.

Proof. 

This is immediate from the fact that the largest denominator in $F_n^{\alpha }$ is n and $\lfloor n\alpha \rfloor$ is the largest integer that fulfills $\lfloor n\alpha \rfloor /n\le \alpha$. □

Theorem 1.

The rank $I_n(h/k)$ of the Farey fraction $h/k$ in $F_n$ is given by

$$\begin{array}{ccc}\hfill I_n(h/k)& =& n\sum _{j=1}^{\lfloor nh/k\rfloor }\frac{\phi \left(j\right)}{j}-\frac{k}{h}\Phi \left(\lfloor nh/k\rfloor \right)\hfill \\ & & +{\widehat{r}}_{\lfloor nh/k\rfloor }\left(\{k/h\}\right)-\sum _{j=1}^{\lfloor nh/k\rfloor }\sum _{d|j}\mu \left(d\right)\left\{\frac{n}{d}\right\},\hfill \end{array}$$

Proof. 

Per Lemma 2, we obtain $I_n(h/k)$ by adding ${\mathcal{N}}_n^{h/k}\left(q\right)$ for all $q\le \lfloor nh/k\rfloor$,

$$I_n(h/k)=\sum _{q=1}^{\lfloor nh/k\rfloor }{\mathcal{N}}_n^{h/k}\left(q\right).$$

The desired result is achieved by using Lemma 1 in this relation. □

Corollary 1.

The local discrepancy of the Farey fraction $h/k$ in $F_n$ is given by

$$\begin{array}{ccc}\hfill {\widehat{r}}_n(h/k)& =& |F_n|\frac{h}{k}-n\sum _{j=1}^{\lfloor nh/k\rfloor }\frac{\phi \left(j\right)}{j}+\frac{k}{h}\Phi \left(\lfloor nh/k\rfloor \right)\hfill \\ & & -{\widehat{r}}_{\lfloor nh/k\rfloor }\left(\{k/h\}\right)+\sum _{j=1}^{\lfloor nh/k\rfloor }\sum _{d|j}\mu \left(d\right)\left\{\frac{n}{d}\right\}.\hfill \end{array}$$

Proof. 

This follows from the definition of the local discrepancy and Theorem 1. □

Theorem 2.

The unconditional estimate of the local discrepancy of the Farey fraction $h/k$ is given by

$${\widehat{r}}_n(h/k)=\frac{3}{{\pi }^2}\frac{k}{h}{\left\{\frac{hn}{k}\right\}}^2+O\left(n{\delta }_A\left(n\frac{h}{k}\right)\right)+O\left(n\frac{h}{k}\log \left(n\frac{h}{k}\right)\right).$$

For $h/k\asymp O\left(n^{-ϵ}\right)$, with $ϵ\in ]0,1]$, the estimate simplifies to the following expression,

$${\widehat{r}}_n(h/k)=O\left(n{\delta }_A\left(n^{1-ϵ}\right)\right),\mathrm{for}h/k\asymp O\left(n^{-ϵ}\right).$$

Proof. 

Recalling Theorem 1,

$$\begin{array}{ccc}\hfill {\widehat{r}}_n(h/k)& =& |F_n|\frac{h}{k}-n\sum _{j=1}^{\lfloor nh/k\rfloor }\frac{\phi \left(j\right)}{j}+\frac{k}{h}\Phi \left(\lfloor nh/k\rfloor \right)\hfill \\ & & -{\widehat{r}}_{\lfloor nh/k\rfloor }\left(\{k/h\}\right)+\sum _{j=1}^{\lfloor nh/k\rfloor }\sum _{d|j}\mu \left(d\right)\left\{\frac{n}{d}\right\},\hfill \end{array}$$

(8)

we proceed to provide estimates for the different terms in the right hand side of the above expression, assuming $h/k=O\left(n^{-ϵ}\right)$ with $ϵ\in [0,1[$ and using known estimates from, e.g., [11,16,17] as follows:

$$\begin{array}{ccc}\hfill |F_n|\frac{h}{k}& =& \frac{3}{{\pi }^2}{n}^2\frac{h}{k}+E\left(n\right)\frac{h}{k},\hfill \\ \hfill n\sum _{j=1}^{\lfloor nh/k\rfloor }\frac{\phi \left(j\right)}{j}& =& \frac{6}{{\pi }^2}{n}^2\frac{h}{k}-\frac{6}{{\pi }^2}n\left\{\frac{hn}{k}\right\}+nH(nh/k),\hfill \\ \hfill \frac{k}{h}\Phi \left(\lfloor nh/k\rfloor \right)& =& \frac{3}{{\pi }^2}{n}^2\frac{h}{k}-\frac{6}{{\pi }^2}n\left\{\frac{hn}{k}\right\}+\frac{3}{{\pi }^2}\frac{k}{h}{\left\{\frac{hn}{k}\right\}}^2+E(nh/k)\frac{k}{h},\hfill \\ \hfill E\left(x\right)& =& O\left(x{\log }^{2/3}x{\left(\log \log x\right)}^{4/3}\right),\hfill \\ \hfill E\left(x\right)& =& xH\left(x\right)+O\left(x{\delta }_A\left(x\right)\right),\hfill \\ \hfill {\widehat{r}}_{\lfloor nh/k\rfloor }\left(\{k/h\}\right)& =& O(nh/k),\hfill \end{array}$$

with $A>0$. Combining the above results we obtain the following relation,

$$\begin{array}{ccc}\hfill {\widehat{r}}_n(h/k)& =& \frac{3}{{\pi }^2}\frac{k}{h}{\left\{\frac{hn}{k}\right\}}^2+E\left(n\right)\frac{h}{k}\hfill \\ & & +O\left(n{\delta }_A\left(n\frac{h}{k}\right)\right)+O(nh/k)+\sum _{j=1}^{\lfloor nh/k\rfloor }\sum _{d|j}\mu \left(d\right)\left\{\frac{n}{d}\right\}.\hfill \end{array}$$

(9)

For the sum with the Möbius function we establish the following estimate,

$$\sum _{j=1}^{\lfloor nh/k\rfloor }\sum _{d|j}\mu \left(d\right)\left\{\frac{n}{d}\right\}=\sum _{j=1}^{\lfloor nh/k\rfloor }\mu \left(j\right)⌊\frac{nh}{kj}⌋\left\{\frac{n}{j}\right\}=O\left(n\frac{h}{k}\log \left(n\frac{h}{k}\right)\right).$$

Combining the above estimates the desired result is obtained. For the case $h/k=O\left(n^{-1}\right)$, we directly evaluate identity (8), obtaining

$${\widehat{r}}_n(h/k)=O\left(n\right),$$

which is compatible with the formulation of the theorem and with the main result in [11]. □

Lemma 3.

For $\widehat{b}$, h, and k integers fulfilling $0\le \widehat{b}\le k$, $\gcd (h,k)=1$ and $1\le h\le k-1$ we have

$$\begin{array}{c}\hfill \left|\sum _{i=1}^{\widehat{b}}{⟨\frac{ih}{k}⟩}_k\right|\equiv \left|\sum _{i=1}^{\widehat{b}}\left(\left\{\frac{ih}{k}\right\}-\frac{k-1}{2k}\right)\right|\le \frac{k}{8}.\end{array}$$

Proof. 

Since gcd$(h,k)=1$, the fractional part $\{ih/k\}$ takes different values for all $i\in \left[[1,\widehat{b}]\right]$ and, therefore, we can establish the following bounds

$$\begin{array}{c}\hfill \sum _{i=1}^{\widehat{b}}\frac{i}{k}\le \sum _{i=1}^{\widehat{b}}\left\{\frac{ih}{k}\right\}\le \sum _{i=1}^{\widehat{b}}\frac{k-i}{k},\end{array}$$

$$\begin{array}{c}\hfill \frac{\widehat{b}(\widehat{b}+1)}{2k}\le \sum _{i=1}^{\widehat{b}}\left\{\frac{ih}{k}\right\}\le \frac{\widehat{b}(2k-\widehat{b}-1)}{2k}.\end{array}$$

Subtracting $\widehat{b}(k-1)/\left(2k\right)$ we obtain

$$\begin{array}{c}\hfill -\frac{{(k-2)}^2}{8k}\le -\frac{\widehat{b}(k-\widehat{b}-2)}{2k}\le \sum _{i=1}^{\widehat{b}}{⟨\frac{ih}{k}⟩}_k\le \frac{\widehat{b}(k-\widehat{b})}{2k}\le \frac{k}{8}.\end{array}$$

□

Theorem 3.

For $n\in \mathbb{N}$, $h/k$ being a Farey fraction and b defined as $b\equiv nmodk$, we have

$$\begin{array}{ccc}\hfill \sum _{d=1}^n{r}_{\lfloor n/d\rfloor }(h/k)& =& \sum _{i=1}^b{⟨\frac{ih}{k}⟩}_k,\hfill \end{array}$$

(10)

and, by Möbius inversion, we also have

$$\begin{array}{ccc}\hfill r_n(h/k)& =& \sum _{d=1}^n\mu \left(d\right)\sum _{i=1}^{\widehat{b}}{⟨\frac{ih}{k}⟩}_k,\hfill \end{array}$$

(11)

with $\widehat{b}=\lfloor n/d\rfloor modk$. Furthermore,

$$\begin{array}{ccc}\hfill r_n(h/k)& =& \sum _{d=1}^{n}M\left(\frac{n}{d}\right){⟨\frac{dh}{k}⟩}_k\hfill \end{array}$$

(12)

where $M\left(x\right)$ is the Mertens function.

Proof. 

$I_{\lfloor n/d\rfloor }(h/k)$ represents the number of simple fractions of the form $p/q$ and $0\le p\le q\le n$ below or equal $h/k$ with gcd$(p,q)=d$. Therefore the sum over d,

$$\sum _{d=1}^n{I}_{\lfloor n/d\rfloor }(h/k)=\sum _{i=1}^n⌊\frac{ih}{k}⌋,$$

gives the total number of fractions below or equal $h/k$. This argument is commonly used, see, e.g., [15]. Developing the right hand side of the above of the Farey fractionn $b\equiv nmodk$, we obtain

$$\begin{array}{ccc}\hfill \sum _{i=1}^n⌊\frac{ih}{k}⌋& =& \sum _{i=1}^n\left(\frac{ih}{k}-\left\{\frac{ih}{k}\right\}\right)\hfill \\ & =& \frac{h}{2k}(n+1)n-\sum _{i=1}^n\left\{\frac{ih}{k}\right\}\hfill \\ & =& \frac{h}{2k}(n+1)n-⌊\frac{n}{k}⌋\sum _{i=1}^{k-1}\left\{\frac{ih}{k}\right\}-\sum _{i=1}^b\left\{\frac{ih}{k}\right\}\hfill \\ & =& \frac{h}{2k}(n+1)n-⌊\frac{n}{k}⌋\frac{k-1}{2}-\sum _{i=1}^b\left\{\frac{ih}{k}\right\}\hfill \\ & =& \frac{h}{2k}(n+1)n-(n-b)\frac{k-1}{2k}-\sum _{i=1}^b\left\{\frac{ih}{k}\right\}.\hfill \end{array}$$

Inserting the following quantity,

$$\sum _{d=1}^n\left|F_{\lfloor n/d\rfloor }\right|=\sum _{d=1}^n{I}_{\lfloor n/d\rfloor }(1/1)=\sum _{i=1}^n⌊\frac{i·1}{1}⌋=\frac{1}{2}(n+1)n,$$

in the above derivation gives

$$\sum _{d=1}^n{I}_{\lfloor n/d\rfloor }(h/k)=\frac{h}{k}\sum _{d=1}^n\left|F_{\lfloor n/d\rfloor }\right|-n\frac{k-1}{2k}+b\frac{k-1}{2k}-\sum _{i=1}^b\left\{\frac{ih}{k}\right\}.$$

Since $r_n(h/k)$ is defined as

$$r_n(h/k)=\frac{h}{k}\left|F_n\right|-I_n(h/k)-\frac{k-1}{2k},$$

we retrieve the desired result as follows:

$$\begin{array}{ccc}\hfill \sum _{d=1}^n{r}_{\lfloor n/d\rfloor }(h/k)& =& \sum _{i=1}^b{⟨\frac{ih}{k}⟩}_k.\hfill \end{array}$$

Identity (11) is directly obtained by Möbius inversion and (12) is derived as follows,

$$\begin{array}{ccc}\hfill r_n(h/k)& =& \sum _{d=1}^n\mu \left(d\right)\sum _{i=1}^{\widehat{b}}{⟨\frac{ih}{k}⟩}_k\hfill \\ & =& \sum _{d=1}^n\left(M\left(\frac{n}{d}\right)-M\left(\frac{n}{d+1}\right)\right)\sum _{i=1}^{d modk}{⟨\frac{ih}{k}⟩}_k\hfill \\ & =& M\left(n\right){⟨\frac{h}{k}⟩}_k+\sum _{d=2}^{n}M\left(\frac{n}{d}\right){⟨\frac{dh}{k}⟩}_k=\sum _{d=1}^{n}M\left(\frac{n}{d}\right){⟨\frac{dh}{k}⟩}_k\hfill \end{array}$$

with $\widehat{b}=\lfloor n/d\rfloor modk$. Identity (12) is very similar to Formula (1) of [11] and to its further derivations within the proof of Lemma 4 in [11]. □

Corollary 2.

For any constant $\alpha \in ]0,1]$, we have

$$\sum _{j=1}^{\lfloor n\alpha \rfloor }\sum _{d|j}\mu \left(d\right)\left\{\frac{n}{d}\right\}=O\left(n{\log }^{2/3}n{\left(\log \log n\right)}^{4/3}\right).$$

Proof. 

By inspecting estimate (9) for the case with constant $h/k=\alpha$, we realize that the largest growing term, the sum with the Möbius function, must have the same asymptotic behavior as the second largest term, $E\left(n\right)\alpha$, so that their sum can result in the known estimate, ${\widehat{r}}_n(h/k)=O\left(n\right)$, on the left hand side. □

Theorem 4.

The unconditional estimate of the local discrepancy of the Farey fraction $h/k$ is given by

$$r_n(h/k)=O\left(n{\log }^{0.4}n{\log }^{0.2}\log n{\delta }_A\left(n^{\widehat{ϵ}}\right)\right)+O\left(k{n}^{\widehat{ϵ}}\right),$$

for $1>\widehat{ϵ}>0$.

For the case $k=O\left(n^{1-{ϵ}^{\prime }}\right)$, with ${ϵ}^{\prime }>\widehat{ϵ}$, the second O term can be neglected and the estimate is given by

$$r_n(h/k)=O\left(n{\log }^{0.4}n{\log }^{0.2}\log n{\delta }_A\left(n^{\widehat{ϵ}}\right)\right).$$

Proof. 

Let us start from the expression (12) of the local discrepancy of the Farey fraction $h/k$ given in Theorem 3

$$r_n(h/k)=\sum _{d\le n}M\left(\frac{n}{d}\right){⟨\frac{dh}{k}⟩}_k.$$

(13)

Splitting the sum in (13) in two parts at $f\left(n\right)=\lfloor n^{1-\widehat{ϵ}}\rfloor$ for any $\widehat{ϵ}$ such that $1>\widehat{ϵ}>0$ gives

$$\begin{array}{ccc}\hfill \sum _{d\le n}M\left(\frac{n}{d}\right){⟨\frac{dh}{k}⟩}_k& =& \sum _{d=1}^{f\left(n\right)}M\left(\frac{n}{d}\right){⟨\frac{dh}{k}⟩}_k\hfill \\ & & +\sum _{d=f\left(n\right)+1}^{n}M\left(\frac{n}{d}\right){⟨\frac{dh}{k}⟩}_k.\hfill \end{array}$$

(14)

For any monotonically increasing function $g\left(x\right)$ in the range $[n/a,n]$, with $a\ge 1$, we have

$$\sum _{d=1}^{a}g(n/d)\le g\left(n\right)+{\int }_1^{a}g(n/x)\mathrm{d}x$$

for any $n>a$. Since $M\left(x\right)=O\left(x{\delta }_A\left(x\right)\right)$ for $A>0$, see [17], we establish the following estimate for the first sum in the right hand side of inequality (14) as

$$\sum _{d=1}^{f\left(n\right)}\left|M(n/d)\right|=O\left(n{\log }^{0.4}n{\log }^{0.2}\log n{\delta }_A\left(n^{\widehat{ϵ}}\right)\right),$$

where we have used that

$${\int }_1^{f\left(n\right)}\frac{n}{x}{\delta }_A(n/x)\mathrm{d}x={\int }_{\frac{n}{f\left(n\right)}}^n\frac{n}{u}{\delta }_A\left(u\right)\mathrm{d}u=O\left(n{\log }^{0.4}n{\log }^{0.2}\log n{\delta }_A\left(n^{\widehat{ϵ}}\right)\right)$$

as demonstrated in Lemma 4.

The second sum in the r.h.s of (14) can be bounded as

$$\begin{array}{ccc}\hfill \left|\sum _{d=f\left(n\right)+1}^{n}M\left(\frac{n}{d}\right){⟨\frac{dh}{k}⟩}_k\right|& \le & \sum _{d\in J}\left|\left(M\left(\frac{n}{d}\right)-M\left(\frac{n}{d+{\alpha }_d}\right)\right){⟨\frac{dh}{k}⟩}_k\right|\hfill \\ & & +\sum _{d=n-k+1}^n\left|M\left(\frac{n}{d}\right){⟨\frac{dh}{k}⟩}_k\right|\hfill \end{array}$$

(15)

where we have used the fact that for every $d<n-k+1$ there exists one ${\alpha }_d<k$ such that

$${⟨\frac{dh}{k}⟩}_k=-{⟨\frac{(d+{\alpha }_d)h}{k}⟩}_k.$$

The set J is a subset of $\left[\right[f\left(n\right)+1,n-k\left]\right]$ such that the map A

$$A:J\to \left[[f\left(n\right)+1,n-k]\right]-J,d\mapsto d+{\alpha }_d$$

is bijective. The second sum in the r.h.s of Expression (15) includes the elements that cannot be paired when $d+{\alpha }_d>n$ and accepts the following bound,

$$\sum _{d=n-k+1}^n\left|M\left(\frac{n}{d}\right){⟨\frac{dh}{k}⟩}_k\right|\le \frac{kn}{2(n-k+1)},$$

where we have used that $\left|M\right(x\left)\right|\le x$, for all x.

To derive a bound for the first sum in the r.h.s of Expression (15) we use the fact that

$$\left|M\left(\frac{n}{d}\right)-M\left(\frac{n}{d+{\alpha }_d}\right)\right|\le \frac{{\alpha }_{d}n}{d^2}\le \frac{kn}{d^2},$$

where we have used that $\left|M\right(x)-M(y\left)\right|\le |x-y|$. Furthermore,

$$\sum _{d\in J}\frac{kn}{d^2}\left|{⟨\frac{dh}{k}⟩}_k\right|\le \frac{1}{2}\sum _{d=f\left(n\right)+1}^{n-k+1}\frac{kn}{d^2}\le \frac{kn}{2\left(f\right(n)+1)}-\frac{kn}{2(n-k+1)}.$$

Combining the above bounds and recalling that $f\left(n\right)=\lfloor n^{1-\widehat{ϵ}}\rfloor$, we conclude that

$$\left|\sum _{d=f\left(n\right)+1}^{n}M\left(\frac{n}{d}\right){⟨\frac{dh}{k}⟩}_k\right|\le \frac{k{n}^{\widehat{ϵ}}}{2}=O(k{n}^{\widehat{ϵ}}).$$

Inserting the above estimates into inequality (14), we obtain the wanted result. □

Lemma 4.

For any $a>x$, we have

$${\int }_x^a\frac{{\delta }_A\left(u\right)}{u}\mathrm{d}u=O\left({\log }^{0.4}x{\log }^{0.2}\log x{\delta }_A\left(x\right)\right).$$

Proof. 

This is demonstrated using the following derivative,

$$\begin{array}{ccc}& & \frac{\mathrm{d}}{\mathrm{d}x}\left(\frac{5}{3A}\frac{{\log }^{0.4}x{\log }^{0.2}\log x}{\left(1-\frac{1}{3\log \log x}\right)}{\delta }_A\left(x\right)\right)=\hfill \\ \hfill & & \frac{{\delta }_A\left(x\right)}{x}\left(-1+\frac{{\log }^{0.2}\log x}{A{\log }^{0.6}x}\frac{(6{\log }^2\log x+\log \log x-6)}{{(3\log \log x-1)}^2}\right)=\hfill \\ \hfill & & \frac{{\delta }_A\left(x\right)}{x}\left(-1+O\left(\frac{{\log }^{0.2}\log x}{{\log }^{0.6}x}\right)\right),\hfill \end{array}$$

and therefore,

$${\int }_x^a\frac{{\delta }_A\left(u\right)}{u}\mathrm{d}u=O\left({\left.\frac{{\log }^{0.4}u{\log }^{0.2}\log u}{\left(1-\frac{1}{3\log \log u}\right)}{\delta }_A\left(u\right)\right|}_{u=a}^{u=x}\right).$$

The factor in the denominator inside the O term can be neglected for large x. □

3. Discussion

We have developed new exact formulas for the rank and discrepancy of Farey fractions using an interesting technique based on a bijection between Farey subsequences. These formulas complete an approximation presented in the classical paper [11]. It is remarkable that this formula, see Corollary 1, connects the local discrepancy of two different Farey fractions, namely $\alpha$ and $\{1/\alpha \}$. As a curiosity, the largest solution of the equation $\alpha =\{1/\alpha \}$ is the fractional part of the Golden ratio, $\left(\sqrt{5}-1\right)/2$, which is not a Farey fraction. These new formulas are used to compute a new estimate of the local discrepancy in Theorem 2 that improves the currently known estimates.

The new notation introduced in this work, namely the discrepancy with an offset $r_n(h/k)={\widehat{r}}_n(h/k)-(k-1)/\left(2k\right)$ and the fractional part with the same offset ${⟨·⟩}_k$, simplifies the known formula and has helped in the development of the new formulas for $r_n(h/k)$ in Theorem 3. These are the basis for the development of the second new estimate of $r_n(h/k)$ in Theorem 4. The new and previous estimates of $r_n(h/k)$, or equivalently ${\widehat{r}}_n(h/k)$, are put together in the following expression:

$${\widehat{r}}_n(h/k)=\left\{\begin{array}{cc}O\left(n{\delta }_A\left(n^{1-ϵ}\right)\right),\hfill & \mathrm{for}h/k\asymp O\left(n^{-ϵ}\right),\mathrm{Theorem} 2\hfill \\ O\left(n{\log }^{0.4}n{\log }^{0.2}\log n{\delta }_A\left(n^{\widehat{ϵ}}\right)\right),\hfill & \mathrm{for}k=O\left(n^{1-\widehat{ϵ}}\right),\mathrm{Theorem} 4\hfill \\ O\left(n\right),\hfill & \mathrm{otherwise},\hfill \end{array}\right.$$

with $ϵ\in ]0,1]$, $\widehat{ϵ}\in ]0,1[$, and $A>0$. The cases where $k\asymp O\left(n\right)$ or $h/k=O\left(n^{-1}\right)$ remain with the known estimate ${\widehat{r}}_n(h/k)=O\left(n\right)$ from [7]. For the cases $h/k\asymp O\left(n^{-ϵ}\right)$ or $k=O\left(n^{1-\widehat{ϵ}}\right)$, the new unconditional estimates of ${\widehat{r}}_n(h/k)$ are sublinear in n. Theorem 4 applies to $h/k$ being constant.

The Fanel–Landau formulation of the Riemann Hypothesis is expressed as

$$\frac{1}{|F_n|}\sum _{h/k\in F_n}\left|{\widehat{r}}_n(h/k)\right|=O\left(n^{\frac{1}{2}+ϵ}\right)\forall ϵ>0\iff \mathrm{RH}.$$

The known estimate ${\widehat{r}}_n(h/k)=O\left(n\right)$, for all $h/k$ in $F_n$, implies that

$$\frac{1}{|F_n|}\sum _{h/k\in F_n}\left|{\widehat{r}}_n(h/k)\right|=O\left(n\right),$$

which is far from $O\left(n^{\frac{1}{2}+ϵ}\right)$. For the RH to be true, ${\widehat{r}}_n(h/k)$ would need to be ${\widehat{r}}_n(h/k)=O\left(n^{\frac{1}{2}+ϵ}\right)$ for most of the Farey fractions in $F_n$. The new sublinear estimates of ${\widehat{r}}_n(h/k)$ in Theorems 2 and 4 go in the direction of the RH, but further developments would be needed for a significant improvement.