An Approximation Algorithm for the Combination of G-Variational Inequalities and Fixed Point Problems

Abstract

In this paper, we introduce a modified form of the G-variational inequality problem, called the combination of G-variational inequalities problem, within a Hilbert space structured by graphs. Furthermore, we develop an iterative scheme to find a common element between the set of fixed points of a G-nonexpansive mapping and the solution set of the proposed G-variational inequality problem. Under appropriate assumptions, we establish a strong convergence theorem within the framework of a Hilbert space endowed with graphs. Additionally, we present the concept of the G-minimization problem, which diverges from the conventional minimization problem. Applying our main results, we demonstrate a strong convergence theorem for the G-minimization problem. Finally, we provide illustrative examples to validate and support our theoretical findings.

1. Introduction

In this study, we explore the intersection of graph theory and functional analysis by considering a nonempty closed convex subset C within a real Hilbert space H, with the inner product $⟨·,·⟩$. Let $T:C\to C$ be a nonlinear mapping. A point $x\in C$ is called a fixed point of T if $Tx=x$. The set of fixed points of T is the set $F\left(T\right):=\{x\in C:Tx=x\}$. Throughout this paper, we define the inverse function $A^{-1}$ from H to C by $A^{-1}y=\{x\in H:y\in Ax\}$. We utilize a directed graph $G=\left(V\right(G),E(G\left)\right)$, where $V\left(G\right)$ represents the vertices and $E\left(G\right)$ the edges, under the assumption that G has no parallel edges. The inverse graph $G^{-1}$, obtained by reversing the direction of each edge, is defined formally as

$$E\left(G^{-1}\right)=\{(x,y):(y,x)\in E\left(G\right)\}.$$

For vertices x and y in G, a path from x to y of length $n\in \mathbb{N}\cup \left\{0\right\}$ is a sequence ${\left\{x_i\right\}}_{i=0}^n$ of $n+1$ vertices such that $x_0=x$, $x_n=y$, and $(x_{i-1},x_i)\in E\left(G\right)$ for $i=1,2,\cdots ,n$. A graph G is termed connected if a directed path exists between any two vertices.

A set $X\subset V\left(G\right)$ is defined as a dominating set if for every vertex $v\in V\left(G\right)-X$, there exists a vertex $x\in X$ such that $(x,v)\in E\left(G\right)$. In this context, we say that x dominates v, or equivalently, v is dominated by x.

Fixed point theorems, an essential component of nonlinear analysis, find extensive applications in mathematics and various applied sciences. Researchers often utilize these theorems to approximate solutions to fixed point problems associated with nonlinear mappings. Furthermore, these methods extend to other domains, such as variational inequality problems and equilibrium problems, which are well documented in the literature [1,2,3].

The classical variational inequality problem (VIP) is to find a point $u\in C$ such that

$$\begin{array}{c}\hfill ⟨Au,v-u⟩\ge 0,\forall v\in C,\end{array}$$

(1)

where A is a mapping from C to H. The set of the solutions of VIP, denoted by $VI(C,A)$, has been extensively studied due to its diverse applications in optimization, control problems, and economics. Many researchers have investigated this problem, resulting in significant theoretical advancements and the development of efficient numerical methods. See [4,5,6,7].

Jachymski pioneered the integration of graph structures into fixed point theory within metric spaces. He introduced the concept of G-contraction, providing a generalization of the Banach contraction principle for single-valued G-contractions, as articulated in Definition 1.

Definition 1

([8]). Let $(X,d)$ be a metric space and let $G=\left(V\left(G\right),E\left(G\right)\right)$ be a directed graph such that $V\left(G\right)=X$ and $E\left(G\right)$ contain loops, i.e., $\Delta =\left\{\right(x,x):x\in X\}\subset E\left(G\right)$. A mapping $f:X\to X$ is termed a G-contraction if it preserves edges of G, i.e.,

$$\begin{array}{c}\hfill \forall x,y\in X,(x,y)\in E\left(G\right)\Rightarrow \left(f\right(x),f(y\left)\right)\in E\left(G\right)\end{array}$$

and there exists $\alpha \in (0,1)$ such that for any $x, y\in X$,

$$\begin{array}{c}\hfill (x,y)\in E\left(G\right)\Rightarrow d\left(f\right(x), f(y\left)\right)\le \alpha d(x, y)\end{array}$$

In recent years, the concept of G-contraction has been refined and extended by numerous authors (see [8] and references cited therein). Consider C, a nonempty convex subset of a Banach space, and $G=\left(V\right(G),E(G\left)\right)$, a directed graph where $V\left(G\right)=C$. A mapping $T:C\to C$ is referred to as G-nonexpansive if the following conditions are satisfied. (1) T is edge-preserving, i.e., for any $x,y\in C$ such that $(x,y)\in E\left(G\right)$, then $(Tx,Ty)\in E\left(G\right)$; and (2) $\parallel Tx-Ty\parallel \le \parallel x-y\parallel$, whenever $(x,y)\in E\left(G\right)$ for all $x,y\in C$.

This concept was introduced by Tiammee et al. [9] in 2015. They also presented Property G (see more details in the Preliminaries) and proposed the following Halpern iteration process for approximating the fixed points of G-nonexpansive mappings in Hilbert spaces endowed with a directed graph structure. Suppose C satisfies Property G. Let $\left\{x_n\right\}$ be a sequence defined by the iteration:

$$\begin{array}{c}\hfill x_{n+1}={\beta }_{n}u+(1-{\beta }_n)T{x}_n,n\ge 0,\end{array}$$

(2)

where $\left\{{\beta }_n\right\}\subseteq [0,1]$ and $T:C\to C$ is a G-nonexpansive mapping. If the sequence $\left\{x_n\right\}$ is dominated by $P_{F\left(T\right)}{x}_0$ and in turn dominates $x_0$, then $\left\{x_n\right\}$ converges strongly to $P_{F\left(T\right)}{x}_0$ under appropriate control conditions.

In 2017, Kangtunyakarn [10] introduced the G-S-mapping and a Halpern iteration process for solving the fixed point problem of a finite family of G-nonexpansive mappings in Hilbert spaces with graphs. Let $\left\{x_n\right\}$ be generated by $x_0=u\in C$ and

$$\begin{array}{c}\hfill x_{n+1}={\beta }_{n}u+(1-{\beta }_n)S{x}_n,n\ge 0,\end{array}$$

(3)

where $\left\{{\beta }_n\right\}\subseteq [0,1]$ and S is a G-S-mapping. The sequence $\left\{x_n\right\}$ converges strongly to a point in $F\left(S\right)={\bigcap }_{i=1}^{N}F\left(T_i\right)$ under suitable conditions. During the last few years, there has been significant progress in developing iterative methods for solving the fixed point problem of G-nonexpansive mappings; for further details, see [11,12,13,14,15,16] and the references therein.

The variational inequality problem seeks a point $x^{*}\in C$ such that

$$\begin{array}{c}\hfill ⟨(aA+(1-a)B)x^{*},y-x^{*}⟩\ge 0,\forall y\in C,a\in (0,1)\end{array}$$

(4)

where $A,B:C\to H$ are mappings. This problem, introduced by Kangtunyakarn [17], reduces to the standard variational inequality problem (1) when $A=B$. This formulation has significant applications in economics, finance, engineering, optimization, and game theory [2,18,19,20].

Recently, Kangtunyakarn [21] introduced the concept of G-variational inequality problems, which differ from classical variational inequality problems in Hilbert spaces:

Definition 2

([21]). Let C be a nonempty closed convex subset of a real Hilbert H and let $G=\left(V\left(G\right), E\left(G\right)\right)$ be a directed graph with $C=V\left(G\right)$. The G-variational inequality problems is to find a point $x^{*}\in C$ such that

$$\begin{array}{c}\hfill ⟨y-x^{*}, A{x}^{*}⟩\ge 0,\end{array}$$

(5)

for all $y\in C$ with $(x^{*},y)\in E\left(G\right)$ and $A:C\to H$ is a mapping. The set of all the solutions of (5) is denoted by $G-VI(C,A)$.

Moreover, he introduced a Halpern iteration for solving G-variational inequality problems and the fixed point problem of a G-nonexpansive mapping in Hilbert spaces with graphs. Let $\left\{x_n\right\}$ be a sequence generated by $x_0=u\in C$ and defined by

$$\begin{array}{c}\hfill x_{n+1}={\alpha }_{n}u+{\beta }_n{P}_C(I-\lambda A)x_n+{\gamma }_{n}S{x}_n,n\ge 0,\end{array}$$

(6)

where $\left\{{\alpha }_n\right\}$, $\left\{{\beta }_n\right\}$, and $\left\{{\gamma }_n\right\}$ are sequences in $[0,1]$ such that ${\alpha }_n+{\beta }_n+{\gamma }_n=1$ and $\lambda$ lies within the interval $(0,2\alpha )$. The mapping $S:C\to C$ is a G-nonexpansive mapping, and $A:C\to H$ is a G-$\alpha$-inverse strongly monotone operator with $A^{-1}\left(0\right)\ne \varnothing$. Under appropriate conditions, the sequence $\left\{x_n\right\}$ converges strongly to a solution of the algorithm (5) in Hilbert spaces endowed with graphs.

Building on Definition 2 and the variational inequality problem, we introduce the combination of G-variational inequality problem, which seeks a point $x^{*}\in C$ such that

$$\begin{array}{c}\hfill ⟨(aA+(1-a)B)x^{*},y-x^{*}⟩\ge 0\end{array}$$

(7)

for all $y\in C$ with $(x^{*},y)\in E\left(G\right)$ and $A,B:C\to H$ are mappings. The set of all the solutions of (7) is denoted by $G-VI(C,aA+(1-a\left)B\right)$. If $a=1$, it reduces to the G-variational inequality problem.

We present the following example to illustrate that the combination of the G-variational inequality problem is distinct from the standard variational inequality problem:

Example 1.

Let $A,B:{\mathbb{R}}^3\to {\mathbb{R}}^3$ define by $A(x_1,x_2,x_3)=(x_1+1,x_2+2,x_3+3)$ for all $x_1,x_2,x_3\in \mathbb{R}$ and $B(x_1,x_2,x_3)=\left\{\begin{array}{cc}(0,0,x_3)\hfill & \mathit{if}{x}_1,x_2,x_3\in \mathbb{Z}\hfill \\ (2x_1,2x_2,2x_3)\hfill & \mathit{if}{x}_1,x_2,x_3\notin \mathbb{Z}\hfill \end{array}\right.$, respectively.

Let $G=({\mathbb{R}}^3,E\left(G\right))$ and $E\left(G\right)=\{(\mathbf{x},\mathbf{y}):x_i,y_i\in \mathbb{N}with{y}_i=x_i+2,\forall i=1,2,3\}$, where $\mathbf{x}=(x_1,x_2,x_3), \mathbf{y}=(y_1,y_2,y_3)\in {\mathbb{R}}^3$ and $a\in (0,1)$. Then, $(1,1,1)\in G-VI(C,aA+(1-a\left)B\right)$ but $(1,1,1)\notin VI(C,aA+(1-a\left)B\right)$.

In this paper, motivated by the Definition 2 in [17] and Kangtunyakarn [21], we introduce a new combination of the G-variational inequality problem (7). We also propose a modified method, inspired by Kangtunyakarn [21], for solving problem (7) and the fixed point problem of G-nonexpansive mappings. Furthermore, we establish a strong convergence theorem to solve the combination of the G-variational inequality problem and the fixed point problem for G-nonexpansive mappings in a Hilbert space endowed with a graph structure. Additionally, we apply our main theorem to address the G-minimization problem, which involves finding a point in the convex set C that minimizes a certain objective function while respecting the graph structure imposed by G. This application illustrates the utility of our results in optimization contexts where graph-based constraints are significant.

Moreover, we present examples demonstrating the effectiveness of our approach, particularly in differentiating between G-variational inequality problems and standard variational inequality problems. These examples highlight the necessity of considering the graph structure when dealing with complex systems, where the relationships between elements (as represented by the graph’s edges) critically influence the problem’s solution.

Our findings extend existing theories in nonlinear analysis and provide new tools for tackling variational inequality and fixed point problems in settings where the underlying structure can be naturally represented by a graph. This work not only broadens the scope of potential applications in mathematics and applied sciences but also opens up new avenues for future research in areas such as network theory, optimization, and computational mathematics.

2. Preliminaries

In this section, we present essential definitions and lemmas that will be utilized in the subsequent analysis. Additionally, we introduce new lemmas that serve as crucial tools for proving our main results.

For every point $x\in H$, there exists a unique point $x_0$ in C such that

$$∥x-x_0∥=d\left(x,C\right),$$

where $d\left(x,C\right)={min}_{y\in C}∥x-y∥$. The mapping $P_C:H\to C$ defined by $P_{C}x=x_0$ is called metric projection onto C.

The following lemma highlights a fundamental property of the metric projection $P_C$.

Lemma 1

([22]). Let $x\in H$ and $y\in C$. Then, $P_{C}x=y$ if and only if there holds the inequality

$$\begin{array}{c}\hfill ⟨x-y, y-z⟩\ge 0\forall z\in C.\end{array}$$

The next definitions and lemmas are vital for proving the strong convergence theorem in a Hilbert space endowed with a directed graph.

Definition 3

([9]). Let $G=\left(V\right(G),E(G\left)\right)$ be a directed graph. A graph G is called transitive if for any $x,y,z\in V\left(G\right)$ with $(x,y)$ and $(y,z)$ are in $E\left(G\right)$, then $(x,z)\in E\left(G\right)$.

The following property is crucial in proving the main result, as it facilitates the selection of an appropriate subsequence and ensures conditions related to the connectivity of the graph G. Consequently, it supports the convergence of the sequence in the proof.

Property G [9] Let C be a nonempty subset of a normed space X and let $G=\left(V\right(G),E(G\left)\right)$, where $V\left(G\right)=C$ be a directed graph then C is said to have Property G if every sequence $\left\{a_n\right\}$ in C converging weakly to $x\in C$, there exists a subsequence $\left\{a_{n_k}\right\}$ of $\left\{a_n\right\}$ such that $(a_{n_k},x)\in E\left(G\right)$ for all $k\in \mathbb{N}$.

Definition 4

([21]). Let C be a nonempty closed convex subset of a real Hilbert space H and let $G=\left(V\left(G\right),E\left(G\right)\right)$ be a directed graph with $C=V\left(G\right)$. The mapping $A:C\to H$ is said to be $G-\alpha$-inverse strongly monotone (shortly, α-GISM) if there exists $\alpha >0$ such that

$$⟨Ax-Ay, x-y⟩\ge \alpha {∥Ax-Ay∥}^2,$$

for all $x,y\in C$ with $\left(x,y\right)\in E\left(G\right)$.

Lemma 2

([21]). Let C be a nonempty closed convex subset of a Hilbert space H and let $G=\left(V\right(G),E(G\left)\right)$ be a directed graph with $V\left(G\right)=C$. Let $E\left(G\right)$ is convex and G is transitive with $E\left(G\right)=E\left(G^{-1}\right)$ and let $A:C\to H$ be α-GISM operator with $A^{-1}\left(0\right)\ne \varnothing$. Then, $G-VI(C,A)=A^{-1}\left(0\right)=F\left(P_C(I-\lambda A)\right)$, for all $\lambda >0$.

The following lemma is essential for proving the main result. In establishing this lemma, Kangtunyakarn [21] utilized Property G as a fundamental component of the proof.

Lemma 3

([21]). Let H be a Hilbert space and C be a nonempty closed convex subset of H with C having a property G. Let $G=\left(V\right(G),E(G\left)\right)$ be a directed graph where $V\left(G\right)=C$ and $E\left(G\right)$ is a convex set. Let $A:C\to H$ be α-GISM mapping with $F\left(P_C(I-\lambda A)\right)\times F\left(P_C(I-\lambda A)\right)\subset E\left(G\right)$ for all $\lambda \in (0,2\alpha )$. Then, $F\left(P_C(I-\lambda A)\right)$ is closed and convex.

Lemma 4

([9]). Let X be a normed space and C be a subset of X having Property G. Let $G=\left(V\right(G),E(G\left)\right)$ be a directed graph such that $V\left(G\right)=C$ and $E\left(G\right)$ is convex. Suppose $T:C\to C$ is a G-nonexpansive mapping and $F\left(T\right)\times F\left(T\right)\subset E\left(G\right).$ Then $F\left(T\right)$ is closed and convex.

The following lemma establishes a critical connection between the solution set of the combination of the G-variational inequalities problem, the zero mapping, and the fixed point problem in a Hilbert space endowed with a graph.

Lemma 5.

Let C be a nonempty closed convex subset of Hilbert space H and let $G=\left(V\right(G),E(G\left)\right)$ be a directed graph with $V\left(G\right)=C$. Let $E\left(G\right)$ is convex and G is transitive with $E\left(G\right)=E\left(G^{-1}\right)$ and let $A,B:C\to H$ be α-GISM and β-GISM mappings with $\eta =min\{\alpha ,\beta \}$, respectively. Let ${(aA+(1-a)B)}^{-1}\left(0\right)\ne \varnothing$. Then, $G-VI(C,aA+(1-a)B)={(aA+(1-a)B)}^{-1}\left(0\right)=F\left(P_C(I-\lambda (aA+(1-a)B))\right)$, for all $\lambda >0$.

Proof. 

Let $x_0\in {(aA+(1-a)B)}^{-1}\left(0\right)$ and $y\in C$ with $(x_0,y)\in E\left(G\right).$

Since $(aA+(1-a)B)x_0=0$, we have

$$\begin{array}{c}\hfill ⟨y-x_0,(aA+(1-a)B)x_0⟩=0,\end{array}$$

for all $y\in C$ with $(x_0,y)\in E\left(G\right).$

From the definition of $G-VI(C,aA+(1-a\left)B\right)$, we have $x_0\in G-VI(C,aA+(1-a)B)$. As a consequence, we have

$$\begin{array}{c}\hfill {(aA+(1-a)B)}^{-1}\left(0\right)\subseteq G-VI(C,aA+(1-a)B).\end{array}$$

(8)

Let $x_0\in G-VI(C,aA+(1-a)B)$ and $x^{*}\in {(aA+(1-a)B)}^{-1}\left(0\right)$.

From the definition of $G-VI(C,aA+(1-a\left)B\right)$, we have

$$\begin{array}{c}\hfill ⟨y-x_0,(aA+(1-a)B)x_0⟩\ge 0\end{array}$$

(9)

for all $y\in C$ with $(x_0,y)\in E\left(G\right).$

From (8) and $x^{*}\in {(aA+(1-a)B)}^{-1}\left(0\right)$, we have $x^{*}\in G-VI(C,aA+(1-a)B)$.

It follows that

$$\begin{array}{c}\hfill ⟨y-x^{*},(aA+(1-a)B)x^{*}⟩=0,\end{array}$$

for all $y\in C$ with $(x^{*},y)\in E\left(G\right).$

Since $E\left(G\right)=E\left(G^{-1}\right)$ and $(x^{*},y)\in E\left(G\right)$, we have $(y,x^{*})\in E\left(G\right)$.

Since $(x_0,y),(y,x^{*})\in E\left(G\right)$ and G is transitive, we have $(x_0,x^{*})\in E\left(G\right)$.

From $x^{*}\in {(aA+(1-a)B)}^{-1}\left(0\right)$, definitions of $A,B$ and (9), we have

$$\begin{array}{ccc}\hfill \eta \parallel (aA+(1-a)B)x_0{\parallel }^2& =& \eta \parallel (aA+(1-a)B)x_0-(aA+(1-a)B)x^{*}{\parallel }^2\hfill \\ & \le & \eta [a\parallel A{x}_0-A{x}^{*}{\parallel }^2+(1-a)\parallel B{x}_0-B{x}^{*}{\parallel }^2]\hfill \\ & \le & \alpha a\parallel A{x}_0-A{x}^{*}{\parallel }^2+\beta (1-a){\parallel B{x}_0-B{x}^{*}\parallel }^2\hfill \\ & \le & a⟨A{x}_0-A{x}^{*},x_0-x^{*}⟩+(1-a)⟨B{x}_0-B{x}^{*},x_0-x^{*}⟩\hfill \\ & =& ⟨(aA+(1-a)B)x_0-(aA+(1-a)B)x^{*},x_0-x^{*}⟩\hfill \\ & =& ⟨(aA+(1-a)B)x_0,x_0-x^{*}⟩\le 0.\hfill \end{array}$$

So, we have $(aA+(1-a)B)x_0=0.$ It follows that $x_0\in {(aA+(1-a)B)}^{-1}\left(0\right)$.

Therefore,

$$\begin{array}{c}\hfill G-VI(C,aA+(1-a)B)\subseteq {(aA+(1-a)B)}^{-1}\left(0\right).\end{array}$$

(10)

From (8) and (10), we have

$$\begin{array}{c}\hfill G-VI(C,aA+(1-a)B)={(aA+(1-a)B)}^{-1}\left(0\right).\end{array}$$

Let $x_0\in {(aA+(1-a)B)}^{-1}\left(0\right)$, we have $0=(aA+(1-a)B)x_0$.

From $x_0\in C$ and $P_C$ is a nonexpansive mapping, we have

$$\begin{array}{ccc}\hfill \parallel x_0-P_C(I-\lambda (aA+(1-a)B))x_0\parallel & \le & \parallel x_0-(I-\lambda (aA+(1-a)B))x_0\parallel \hfill \\ & =& \lambda \parallel (aA+(1-a)B)x_0\parallel =0.\hfill \end{array}$$

So, we have $x_0\in F\left(P_C(I-\lambda (aA+(1-a)B))\right)$.

Therefore, it concludes that

$$\begin{array}{c}\hfill {(aA+(1-a)B)}^{-1}\left(0\right)\subseteq F(P_C(I-\lambda (aA+(1-a)B)).\end{array}$$

(11)

Let $x_0\in F\left(P_C(I-\lambda (aA+(1-a)B))\right)$ and $y\in C$ with $(x_0,y)\in E\left(G\right).$

From Lemma 1, we have

$$\begin{array}{c}\hfill ⟨(I-\lambda (aA+(1-a)B))x_0-x_0,x_0-y⟩\ge 0.\end{array}$$

It implies that

$$\begin{array}{c}\hfill ⟨(aA+(1-a)B)x_0,y-x_0⟩\ge 0,\end{array}$$

for all $y\in C$ and $(x_0,y)\in E\left(G\right).$

From (7), we have $x_0\in G-VI(C,aA+(1-a)B)$.

Since $G-VI(C,aA+(1-a)B)={(aA+(1-a)B)}^{-1}\left(0\right)$, we have $x_0\in {(aA+(1-a)B)}^{-1}\left(0\right)$.

Therefore, it concludes that

$$\begin{array}{c}\hfill F\left(P_C(I-\lambda (aA+(1-a)B))\right)\subseteq {(aA+(1-a)B)}^{-1}\left(0\right).\end{array}$$

(12)

From (11) and (12), we have

$$\begin{array}{c}\hfill {(aA+(1-a)B)}^{-1}\left(0\right)=F\left(P_C(I-\lambda (aA+(1-a)B))\right).\end{array}$$

□

The following lemma illustrates that the solution set of the combination of the G-variational inequalities problem is the intersection of the solution sets of two G-variational inequalities problems in a Hilbert space endowed with a graph.

Lemma 6.

Let C be a nonempty closed convex subset of Hilbert space H and let $G=\left(V\right(G),E(G\left)\right)$ be a directed graph with $V\left(G\right)=C$. Let $A,B:C\to H$ be α-GISM and β-GISM mappings with $\eta =min\{\alpha ,\beta \}$, respectively. Let $G-VI(C,A)\cap G-VI(C,B)\ne \varnothing .$ Then, $G-VI(C,aA+(1-a\left)B\right)=G-VI(C,A)\cap G-VI(C,B)$, $\forall a\in (0,1)$.

Proof. 

Firstly, we show that $G-VI(C,A)\cap G-VI(C,B)\subseteq G-VI(C,aA+(1-a\left)B\right)$.

Let $x_0\in G-VI(C,A)\cap G-VI(C,B)$.

From definition of $G-VI(C,A)$ and $G-VI(C,B)$, we have

$$\begin{array}{c}\hfill ⟨y-x_0,A{x}_0⟩\ge 0\end{array}$$

(13)

and

$$\begin{array}{c}\hfill ⟨y-x_0,B{x}_0⟩\ge 0,\end{array}$$

(14)

for all $y\in C$ with $(x_0,y)\in E\left(G\right)$.

For every $a\in (0,1)$, (13) and (14), we have

$$\begin{array}{c}\hfill ⟨y-x_0,aA{x}_0⟩\ge 0\end{array}$$

(15)

and

$$\begin{array}{c}\hfill ⟨y-x_0,(1-a)B{x}_0⟩\ge 0.\end{array}$$

(16)

Summing up (15) and (16), we have

$$\begin{array}{c}\hfill ⟨y-x_0,aA{x}_0+(1-a)B{x}_0⟩\ge 0,\end{array}$$

for all $y\in C$ with $(y,x_0)\in E\left(G\right)$. So, we get $x_0\in G-VI(C,aA+(1-a)B)$

Therefore, it concludes that $G-VI(C,A)\cap G-VI(C,B)\subseteq G-VI(C,aA+(1-a\left)B\right)$.

Secondly, we show that $G-VI(C,aA+(1-a\left)B\right)\subseteq G-VI(C,A)\cap G-VI(C,B).$

Let $x_0\in G-VI(C,aA+(1-a)B)$. It follows that

$$\begin{array}{c}\hfill ⟨y-x_0,aA{x}_0+(1-a)B{x}_0⟩\ge 0,\end{array}$$

(17)

for all $y\in C$ with $(y,x_0)\in E\left(G\right)$.

Let $x^{*}\in G-VI(C,A)\cap G-VI(C,B).$ It follows that

$$\begin{array}{c}\hfill ⟨y-x^{*},A{x}^{*}⟩\ge 0\end{array}$$

(18)

and

$$\begin{array}{c}\hfill ⟨y-x^{*},B{x}^{*}⟩\ge 0,\end{array}$$

(19)

for all $y\in C$ with $(y,x^{*})\in E\left(G\right)$.

For each $a\in (0,1)$, we have

$$\begin{array}{c}\hfill ⟨y-x^{*},aA{x}^{*}⟩\ge 0\end{array}$$

and

$$\begin{array}{c}\hfill ⟨y-x^{*},(1-a)B{x}^{*}⟩\ge 0,\end{array}$$

for all $y\in C$ with $(y,x^{*})\in E\left(G\right)$.

Since $(y,x^{*})\in E\left(G\right)$ and $E\left(G\right)=E\left(G^{-1}\right)$, we have $(x^{*},y)\in E\left(G\right)$.

Since $(x^{*},y)$, $(y,x_0)\in E\left(G\right)$ and G is transitive, we have $(x^{*},x_0)\in E\left(G\right)$.

From $(x^{*},x_0)\in E\left(G\right)$, monotonicity of B, (17) and (19), we have

$$\begin{array}{ccc}\hfill ⟨x^{*}-x_0,aA{x}_0⟩& =& ⟨x^{*}-x_0,aA{x}_0+(1-a)B{x}_0⟩-⟨x^{*}-x_0,(1-a)B{x}_0⟩\hfill \\ & \ge & (1-a)⟨x_0-x^{*},B{x}_0⟩\hfill \\ & =& (1-a)[⟨x_0-x^{*},B{x}_0-B{x}^{*}⟩+⟨x_0-x^{*},B{x}^{*}⟩]\hfill \\ & \ge & 0.\hfill \end{array}$$

(20)

It implies that

$$\begin{array}{c}\hfill ⟨x^{*}-x_0,A{x}_0⟩\ge 0.\end{array}$$

(21)

From A is $\alpha$-GISM, $(x^{*},x_0)\in E\left(G\right)$, (18) and (21), we have

$$\begin{array}{ccc}\hfill 0& \le & ⟨x^{*}-x_0,A{x}_0⟩\hfill \\ & =& ⟨x^{*}-x_0,A{x}_0-A{x}^{*}⟩+⟨x^{*}-x_0,A{x}^{*}⟩\hfill \\ & \le & -\alpha \parallel A{x}^{*}-A{x}_0{\parallel }^2+⟨x^{*}-x_0,A{x}^{*}⟩\hfill \\ & \le & -\alpha \parallel A{x}^{*}-A{x}_0{\parallel }^2.\hfill \end{array}$$

(22)

It implies that

$$\begin{array}{c}\hfill A{x}^{*}=A{x}_0.\end{array}$$

(23)

Let $y\in C$ with $(y,x_0)\in E\left(G\right)$. From (18), (21), and (23), we have

$$\begin{array}{ccc}\hfill ⟨y-x_0,A{x}_0⟩& =& ⟨y-x^{*},A{x}_0⟩+⟨x^{*}-x_0,A{x}_0⟩\hfill \\ & \ge & ⟨y-x^{*},A{x}_0⟩\hfill \\ & =& ⟨y-x^{*},A{x}^{*}⟩\hfill \\ & \ge & 0.\hfill \end{array}$$

So, we can conclude that

$$\begin{array}{c}\hfill x_0\in G-VI(C,A).\end{array}$$

(24)

From $(x^{*},x_0)\in E\left(G\right)$ and (17), it implies that

$$\begin{array}{ccc}\hfill (1-a)⟨x^{*}-x_0,B{x}_0⟩& \ge & -a⟨x^{*}-x_0,A{x}_0⟩\hfill \\ & =& a⟨x_0-x^{*},A{x}_0⟩\hfill \end{array}$$

(25)

From (25), monotonicity of A, and (18), we have

$$\begin{array}{ccc}\hfill (1-a)⟨x^{*}-x_0,B{x}_0⟩& \ge & a⟨x_0-x^{*},A{x}_0⟩\hfill \\ & =& a[⟨x_0-x^{*},A{x}_0-A{x}^{*}⟩+⟨x_0-x^{*},A{x}^{*}⟩]\hfill \\ & \ge & 0,\hfill \end{array}$$

From $a\in (0,1)$, we have

$$\begin{array}{c}\hfill ⟨x^{*}-x_0,B{x}_0⟩\ge 0.\end{array}$$

(26)

From B is $\beta$-GISM, $(x^{*},x_0)\in E\left(G\right)$, (19), and (26), we have

$$\begin{array}{ccc}\hfill 0& \le & ⟨x^{*}-x_0,B{x}_0⟩\hfill \\ & =& ⟨x^{*}-x_0,B{x}_0-B{x}^{*}⟩+⟨x^{*}-x_0,B{x}^{*}⟩\hfill \\ & \le & -\beta \parallel B{x}_0-B{x}^{*}\parallel +⟨x^{*}-x_0,B{x}^{*}⟩\hfill \\ & \le & -\beta \parallel B{x}_0-B{x}^{*}\parallel .\hfill \end{array}$$

It implies that

$$\begin{array}{c}\hfill B{x}^{*}=B{x}_0.\end{array}$$

(27)

Let $y\in C$ with $(y,x_0)\in E\left(G\right)$. From (19), (26), and (27), we have

$$\begin{array}{ccc}\hfill ⟨y-x_0,B{x}_0⟩& =& ⟨y-x^{*},B{x}_0⟩+⟨x^{*}-x_0,B{x}_0⟩\hfill \\ & \ge & ⟨y-x^{*},B{x}_0⟩\hfill \\ & =& ⟨y-x^{*},B{x}^{*}⟩\hfill \\ & \ge & 0.\hfill \end{array}$$

So, we can conclude that

$$\begin{array}{c}\hfill x_0\in G-VI(C,B).\end{array}$$

(28)

From (24) and (28), we have $x_0\in G-VI(C,A)\cap G-VI(C,B)$.

Therefore,

$$\begin{array}{c}\hfill G-VI(C,aA+(1-a\left)B\right)\subseteq G-VI(C,A)\cap G-VI(C,B).\end{array}$$

Hence,

$$\begin{array}{c}\hfill G-VI(C,aA+(1-a\left)B\right)=G-VI(C,A)\cap G-VI(C,B).\end{array}$$

□

The following example demonstrates the potential application of Lemma 6.

Example 2.

Let $A,B:\mathbb{R}\to \mathbb{R}$ define by

$$\begin{array}{c}\hfill A\left(x\right)=\left\{\begin{array}{cc}0\hfill & \mathit{if}x=0\hfill \\ x-sin\pi x\hfill & \mathit{if}x\ne 0\hfill \end{array}\right.\end{array}$$

and

$$\begin{array}{c}\hfill B\left(x\right)=\left\{\begin{array}{cc}8x+1\hfill & \mathit{if}x\notin \mathbb{Z}\hfill \\ 2x-1\hfill & \mathit{if}x\in \mathbb{Z}\hfill \end{array}\right..\end{array}$$

Let $G=(\mathbb{R},E(G\left)\right)$ with $E\left(G\right)=\left\{\right(x,y)\in \mathbb{N}\times \mathbb{N}:y=x+2\}$ and $a\in (0,1)$. Then, $A,B$ are 1-GISM and ${\displaystyle \frac{1}{2}}$-GISM, respectively. It is obvious that $1\in G-VI(C,aA+(1-a\left)B\right)$, for all $a\in (0,1)$. From Lemma 6, we can conclude that $1\in G-VI(C,A)\cap G-VI(C,B).$

The following lemma is instrumental in demonstrating the convergence of the sequence $\left\{x_n\right\}$ in our main theorem.

Lemma 7

([23]). Let $\left\{s_n\right\}$ be a sequence of nonnegative real numbers satisfying

$$s_{n+1}\le (1-{\alpha }_n)s_n+{\delta }_n,\forall n\ge 0$$

where $\left\{{\alpha }_n\right\}$ is a sequence in $(0,1)$ and $\left\{{\delta }_n\right\}$ is a sequence such that

(1) 

${\displaystyle \sum _{n=1}^{\infty }}{\alpha }_n=\infty ,$

(2) 

$\underset{n\to \infty }{lim\; sup}{\displaystyle \frac{{\delta }_n}{{\alpha }_n}}\le 0or{\displaystyle \sum _{n=1}^{\infty }}\left|{\delta }_n\right|<\infty .$

Then, ${lim}_{n\to \infty }{s}_n=0.$

This lemma provides a critical tool for establishing the convergence of sequences in the context of our main results. It ensures that under the given conditions, the sequence $\left\{s_n\right\}$ converges to zero, which is fundamental in the analysis of iterative methods in variational inequality and fixed point problems.

Together, these preliminary results form the foundation for the more advanced theorems and proofs that follow, particularly in the context of G-variational inequality problems and G-nonexpansive mappings in Hilbert spaces. The combination of these elements facilitates a deeper understanding of the structure and solutions of such problems, especially when the underlying set is equipped with a graph structure, which adds a layer of complexity and richness to the analysis.

3. Main Result

We present the following theorem for solving the G-variational inequalities problem and the fixed point problem by utilizing a combination of G-variational inequality problem and Lemma 6.

Theorem 1.

Let C be a nonempty closed convex subset of Hilbert space H and let $G=\left(V\right(G),E(G\left)\right)$ be a directed graph with $V\left(G\right)=C$ has property G and $E\left(G\right)$ is convex and G is transitive with $E\left(G\right)=E\left(G^{-1}\right)$. Let $T:C\to C$ be G-nonexpansive mapping. Let $A,B:C\to H$ be α-GISM and β-GISM mappings with ${(aA+(1-a)B)}^{-1}\left(0\right)\ne \varnothing$, respectively. Let $f:C\to C$ be a G-contraction mapping with coefficient $\gamma \in (0,1).$ Assume that $\Gamma =F\left(T\right)\cap G-VI(C,A)\cap G-VI(C,B)\ne \varnothing$ with $F\left(T\right)\times F\left(T\right)\subset E\left(G\right)$ and $G-VI(C,A)\times G-VI(C,B)\subset E\left(G\right)$, and there exists $x_0\in C$ such that $(x_0,f\left(x_0\right)),(x_0,T{x}_0),(x_0,P_C(I-\lambda (aA+(1-a)B))x_0)\in E\left(G\right).$ Let the sequence $\left\{x_n\right\}$ be generated by $x_0\in C$ and

$$\begin{array}{c}\hfill x_{n+1}={\alpha }_{n}f\left(x_n\right)+{\beta }_n{P}_C(I-\lambda (aA+(1-a)B))x_n+{\gamma }_{n}T{x}_n\end{array}$$

(29)

where $\{\left\{{\alpha }_n\right\}$, $\left\{{\beta }_n\right\}$, $\left\{{\gamma }_n\right\}\}$$\subset [0,1]$, with ${\alpha }_n+{\beta }_n+{\gamma }_n=1$, $\lambda \in (0,2\eta )$ with $\eta =min\{\alpha ,\beta \}$ and $a\in (0,1)$.

Suppose the following conditions hold,

(i) 

${\displaystyle \sum _{n=0}^{\infty }}{\alpha }_n=\infty ,\underset{n\to \infty }{lim}{\alpha }_n=0,$

(ii) 

${\displaystyle \sum _{n=0}^{\infty }}|{\alpha }_{n+1}-{\alpha }_n|<\infty ,{\displaystyle \sum _{n=0}^{\infty }}|{\beta }_{n+1}-{\beta }_n|<\infty .$

Then, $\left\{x_n\right\}$ converges strongly to $P_{\Gamma }f\left(x_0\right)$, $P_{\Gamma }f\left(x_0\right)$ is dominated by $\left\{x_n\right\}$, $\left\{x_n\right\}$ dominates $x_0$, and $\left\{P_C(I-\lambda (aA+(1-a)B))x_n\right)\}$ is dominated by $x_0$.

Proof. 

We divide the proof into five steps:

Step 1. We show that the sequence $\left\{x_n\right\}$ is bounded.

From Lemmas 2, 3 and 6, we have $G-VI(C,aA+(1-a\left)B\right)$ which is closed and convex. From Lemma 4, we have $F\left(T\right)$ which is closed and convex. Then, $\Gamma$ is closed and convex. Put $z^{*}=P_{\Gamma }f\left(x_0\right)$. Since $z^{*}$ dominates by $\left\{x_n\right\}$, we have $(x_n,z^{*})\in E\left(G\right)$ for all $n\in \mathbb{N}$. From Lemmas 5 and 6, we have

$$\begin{array}{ccc}\hfill G-VI(C,A)\cap G-VI(C,B)& =& G-VI(C,aA+(1-a\left)B\right)\hfill \\ & =& {(aA+(1-a)B)}^{-1}\left(0\right)\hfill \\ & =& F\left(P_C(I-\lambda (aA+(1-a)B))\right).\hfill \end{array}$$

(30)

Since $z^{*}\in \Gamma$, we have $(aA+(1-a)B)z^{*}=0$ and $z^{*}=P_C(I-\lambda (aA+(1-a)B))z^{*}$.

It follows that

$$\begin{array}{ccc}\hfill \parallel P_C(I& -& \lambda (aA+(1-a)B))x_n-z^{*}{\parallel }^2\hfill \\ & \le & \parallel (I-\lambda (aA+(1-a)B))x_n-z^{*}{\parallel }^2\hfill \\ & =& \parallel x_n-z^{*}{\parallel }^2-2\lambda ⟨x_n-z^{*},(aA+(1-a)B))x_n⟩\hfill \\ & & +{\lambda }^2\parallel (aA+(1-a)B))x_n{\parallel }^2\hfill \\ & =& \parallel x_n-z^{*}{\parallel }^2-2\lambda a⟨x_n-z^{*},A{x}_n-A{z}^{*}⟩\hfill \\ & & -2\lambda (1-a)⟨x_n-z^{*},B{x}_n-B{z}^{*}⟩+{\lambda }^2\parallel (aA+(1-a)B){)x_n\parallel }^2\hfill \\ & \le & \parallel x_n-z^{*}{\parallel }^2-2\lambda a\alpha \parallel A{x}_n-A{z}^{*}{\parallel }^2-2\lambda (1-a)\beta {\parallel B{x}_n-B{z}^{*}\parallel }^2\hfill \\ & & +{\lambda }^2\parallel (aA+(1-a)B))x_n{\parallel }^2\hfill \\ & =& \parallel x_n-z^{*}{\parallel }^2-2\lambda a\alpha \parallel A{x}_n-A{z}^{*}{\parallel }^2-2\lambda (1-a)\beta {\parallel B{x}_n-B{z}^{*}\parallel }^2\hfill \\ & & +{\lambda }^2{\parallel a(A{x}_n-A{z}^{*})+(1-a)(B{x}_n-B{z}^{*})\parallel }^2\hfill \\ & \le & \parallel x_n-z^{*}{\parallel }^2-2\lambda a\alpha \parallel A{x}_n-A{z}^{*}{\parallel }^2-2\lambda (1-a)\beta {\parallel B{x}_n-B{z}^{*}\parallel }^2\hfill \\ & & +{\lambda }^{2}a\parallel A{x}_n-A{z}^{*}{\parallel }^2+{\lambda }^2(1-a){\parallel B{x}_n-B{z}^{*}\parallel }^2\hfill \\ & \le & \parallel x_n-z^{*}{\parallel }^2-2\lambda a\eta \parallel A{x}_n-A{z}^{*}{\parallel }^2-2\lambda (1-a)\eta {\parallel B{x}_n-B{z}^{*}\parallel }^2\hfill \\ & & +{\lambda }^{2}a\parallel A{x}_n-A{z}^{*}{\parallel }^2+{\lambda }^2(1-a){\parallel B{x}_n-B{z}^{*}\parallel }^2\hfill \\ & =& \parallel x_n-z^{*}{\parallel }^2-\lambda a(2\eta -\lambda ){\parallel A{x}_n-A{z}^{*}\parallel }^2\hfill \\ & & -\lambda (1-a)(2\eta -\lambda )\parallel B{x}_n-B{z}^{*}{\parallel }^2\hfill \\ & \le & \parallel x_n-z^{*}{\parallel }^2,\hfill \end{array}$$

(31)

where $(x_n,z^{*})\in E\left(G\right)$, for all $n\in \mathbb{N}$.

From the definition of $\left\{x_n\right\}$ and (31), we have

$$\begin{array}{ccc}\hfill \parallel x_{n+1}-z^{*}\parallel & \le & {\alpha }_n\parallel f\left(x_n\right)-z^{*}\parallel +{\beta }_n\parallel P_C(I-\lambda (aA+(1-a)B))x_n-z^{*}\parallel +{\gamma }_n\parallel T{x}_n-z^{*}\parallel \hfill \\ & \le & {\alpha }_n\parallel f\left(x_n\right)-z^{*}\parallel +{\beta }_n\parallel x_n-z^{*}\parallel +{\gamma }_n\parallel x_n-z^{*}\parallel \hfill \\ & \le & {\alpha }_n\parallel f\left(x_n\right)-f\left(z^{*}\right)\parallel +{\alpha }_n\parallel f\left(z^{*}\right)-z^{*}\parallel +{\beta }_n\parallel x_n-z^{*}\parallel +{\gamma }_n\parallel x_n-z^{*}\parallel \hfill \\ & \le & {\alpha }_n\gamma \parallel x_n-z^{*}\parallel +{\alpha }_n\parallel f\left(z^{*}\right)-z^{*}\parallel +{\beta }_n\parallel x_n-z^{*}\parallel +{\gamma }_n\parallel x_n-z^{*}\parallel \hfill \\ & =& {\alpha }_n\gamma \parallel x_n-z^{*}\parallel +{\alpha }_n\parallel f\left(z^{*}\right)-z^{*}\parallel +(1-{\alpha }_n)\parallel x_n-z^{*}\parallel \hfill \\ & =& (1-{\alpha }_n(1-\gamma ))\parallel x_n-z^{*}\parallel +{\alpha }_n\parallel f\left(z^{*}\right)-z^{*}\parallel ,\hfill \end{array}$$

where $(x_n,z^{*})\in E\left(G\right)$, for all $n\in \mathbb{N}$.

From mathematical induction, we can conclude that

$$\begin{array}{c}\hfill \parallel x_n-z^{*}\parallel \le max\{\parallel x_0-z^{*}\parallel ,{\displaystyle \frac{\parallel f\left(z^{*}\right)-z^{*}\parallel }{1-\gamma }}\}\forall n\in \mathbb{N}.\end{array}$$

Therefore, $\left\{x_n\right\}$ is bounded and so are $\left\{T{x}_n\right\}$ and $\left\{f\left(x_n\right)\right\}$.

Step 2. We show that $(x_n,x_{n+1})\in E\left(G\right)$.

Since $(x_0,f\left(x_0\right)),(x_0,P_C(I-\lambda (aA+(1-a)B))x_0),(x_0,T{x}_0)\in E\left(G\right)$ and $E\left(G\right)$ is convex, we have $(x_0,x_1)\in E\left(G\right)$.

From $\left\{P_C(I-\lambda (aA+(1-a)B))x_n\right\}$ dominates by $x_0$, we have $(x_0,P_C(I-\lambda (aA+(1-a)B))x_n)\in E\left(G\right)$ for all $n\in \mathbb{N}$.

From f is G-contraction mapping, T is G-nonexpansive mapping and $(x_0,x_1)\in E\left(G\right)$, we have $(f\left(x_0\right),f\left(x_1\right))$ and $(T{x}_0,T{x}_1)\in E\left(G\right)$.

From transitivity of G and $(x_0,f\left(x_0\right))$, $(f\left(x_0\right),f\left(x_1\right)),(x_0,T{x}_0)$, $(T{x}_0,T{x}_1)\in E\left(G\right)$, we have $(x_0,f\left(x_1\right))$ and $(x_0,T{x}_1)\in E\left(G\right)$.

Since $(x_0,f\left(x_1\right)),(x_0,P_C(I-\lambda (aA+(1-a)B))x_1),(x_0,T{x}_1)\in E\left(G\right)$ and $E\left(G\right)$ is convex, we have $(x_0,x_2)\in E\left(G\right)$.

From f is G-contraction mapping, T is G-nonexpansive mapping, we have $(f\left(x_0\right),$$f\left(x_2\right))$, and $(T{x}_0,T{x}_2)\in E\left(G\right)$.

From transitivity of G and $(x_0,f\left(x_0\right)),(f\left(x_0\right),f\left(x_2\right)),(x_0,T{x}_1)$, $(T{x}_1,T{x}_2)\in E\left(G\right)$, we have $(x_0,f\left(x_2\right))$ and $(x_0,T{x}_2)\in E\left(G\right)$.

Suppose that $(x_0,f\left(x_k\right))$, $(x_0,T{x}_k)\in E\left(G\right)$ for all $k\in \mathbb{N}$.

Since $(x_0,f\left(x_k\right)),(x_0,P_C(I-\lambda (aA+(1-a)B))x_k),(x_0,T{x}_k)\in E\left(G\right)$ and $E\left(G\right)$ is convex, we have $(x_0,x_{k+1})\in E\left(G\right)$.

From f is G-contraction mapping, T is G-nonexpansive mapping, we have $(f\left(x_0\right),$$f\left(x_{k+1}\right))$ and $(T{x}_0,T{x}_{k+1})\in E\left(G\right)$.

By transitivity of G and $(x_0,f\left(x_0\right)),(f\left(x_0\right),f\left(x_{k+1}\right)),(x_0,T{x}_0)$ and $(T{x}_0,T{x}_{k+1})\in E\left(G\right)$, we have $(x_0,f\left(x_{k+1}\right))$, $(x_0,T{x}_{k+1})\in E\left(G\right)$.

By induction, we have $(x_0,f\left(x_n\right))$ and $(x_0,T{x}_n)\in E\left(G\right)$ for all $n\in \mathbb{N}$.

Since $E\left(G\right)$ is convex and $(x_0,f\left(x_n\right)),(x_0,T{x}_n),(x_0,P_C(I-\lambda (aA+(1-a)B))x_n)\in E\left(G\right)$, we have $(x_0,x_{n+1})\in E\left(G\right)$, for all $n\in \mathbb{N}$.

Since $\left\{x_n\right\}$ dominates $x_0$, we have $(x_n,x_0)\in E\left(G\right)$ for all $n\in \mathbb{N}$.

From $(x_n,x_0),(x_0,x_{n+1})\in E\left(G\right)$, for all $n\in \mathbb{N}$, and G is transitive, we have $(x_n,x_{n+1})\in E\left(G\right)$ for all $n\in \mathbb{N}$.

Step 3. We show that ${lim}_{n\to \infty }\parallel T{x}_n-x_n\parallel =0$ and ${lim}_{n\to \infty }\parallel P_C(I-\lambda (aA+(1-a)B))x_n-x_n\parallel =0.$ Use a similar method to (31); it can conclude that

$$\begin{array}{ccc}\hfill \parallel P_C(I-\lambda (aA+(1-a)B))x_{n+1}& -& P_C(I-\lambda (aA+(1-a)B))x_n\parallel \hfill \\ & \le & \parallel x_{n+1}-x_n\parallel \hfill \end{array}$$

(32)

where $(x_n,x_{n+1})\in E\left(G\right)$, for all $n\in \mathbb{N}$.

We now show that ${lim}_{n\to \infty }\parallel x_{n+1}-x_n\parallel =0.$

From the definition of $x_n$,$(x_n,x_{n+1})\in E\left(G\right)$ and (32), we have

$$\begin{array}{ccc}\hfill \parallel x_{n+1}-x_n\parallel & \le & {\alpha }_n\parallel f\left(x_n\right)-f\left(x_{n-1}\right)\parallel +|{\alpha }_n-{\alpha }_{n-1}|\parallel f\left(x_{n-1}\right)\parallel \hfill \\ & & +{\beta }_n\parallel P_C(I-\lambda (aA+(1-a)B))x_n-P_C(I-\lambda (aA+(1-a)B))x_{n-1}\parallel \hfill \\ & & +|{\beta }_n-{\beta }_{n-1}|\parallel P_C(I-\lambda (aA+(1-a)B))x_{n-1}\parallel +{\gamma }_n\parallel T{x}_n-T{x}_{n-1}\parallel \hfill \\ & & +|{\gamma }_n-{\gamma }_{n-1}|\parallel T{x}_{n-1}\parallel \hfill \\ & \le & {\alpha }_n\parallel f\left(x_n\right)-f\left(x_{n-1}\right)\parallel +|{\alpha }_n-{\alpha }_{n-1}|\parallel f\left(x_{n-1}\right)\parallel \hfill \\ & & +{\beta }_n\parallel x_n-x_{n-1}\parallel +|{\beta }_n-{\beta }_{n-1}|\parallel P_C(I-\lambda (aA+(1-a)B))x_{n-1}\parallel \hfill \\ & & +{\gamma }_n\parallel x_n-x_{n-1}\parallel +|{\gamma }_n-{\gamma }_{n-1}|\parallel T{x}_{n-1}\parallel \hfill \\ & =& (1-{\alpha }_n(1-\gamma ))\parallel x_n-x_{n-1}\parallel +|{\alpha }_n-{\alpha }_{n-1}|\parallel f\left(x_{n-1}\right)\parallel \hfill \\ & & +|{\beta }_n-{\beta }_{n-1}|\parallel P_C(I-\lambda (aA+(1-a)B))x_{n-1}\parallel +|{\gamma }_n-{\gamma }_{n-1}|\parallel T{x}_{n-1}\parallel \hfill \\ & \le & (1-{\alpha }_n(1-\gamma ))\parallel x_n-x_{n-1}\parallel \hfill \\ & & +\left(\right|{\alpha }_n-{\alpha }_{n-1}|+|{\beta }_n-{\beta }_{n-1}\left|\right|{\gamma }_n-{\gamma }_{n-1}\left|\right)L,\hfill \end{array}$$

(33)

where $L={max}_{n\in \mathbb{N}}\{\parallel f\left(x_n\right)\parallel ,\parallel P_C(I-\lambda (aA+(1-a)B))x_n\parallel ,\parallel T{x}_n\parallel \}$.

Applying Lemma 7, conditions (i) and (ii), we have

$$\begin{array}{c}\hfill \underset{n\to \infty }{lim}\parallel x_{n+1}-x_n\parallel =0.\end{array}$$

(34)

From (31) and the definition of $x_n$, we have

$$\begin{array}{ccc}\hfill \parallel x_{n+1}-z^{*}{\parallel }^2& \le & {\alpha }_n\parallel f\left(x_n\right)-z^{*}{\parallel }^2+{\beta }_n\parallel P_C(I-\lambda (aA+(1-a)B))x_n-z^{*}{\parallel }^2+{\gamma }_n{\parallel T{x}_n-z^{*}\parallel }^2\hfill \\ & & -{\beta }_n{\gamma }_n{\parallel P_C(I-\lambda (aA+(1-a)B))x_n-T{x}_n\parallel }^2\hfill \\ & \le & {\alpha }_n\parallel f\left(x_n\right)-z^{*}{\parallel }^2+(1-{\alpha }_n){\parallel x_n-z^{*}\parallel }^2\hfill \\ & & -{\beta }_n{\gamma }_n{\parallel P_C(I-\lambda (aA+(1-a)B))x_n-T{x}_n\parallel }^2.\hfill \end{array}$$

It implies that

$$\begin{array}{ccc}\hfill {\beta }_n{\gamma }_n\parallel P_C(I& -& \lambda (aA+(1-a)B))x_n-T{x}_n{\parallel }^2\hfill \\ & \le & {\alpha }_n\parallel f\left(x_n\right)-z^{*}{\parallel }^2+\parallel x_n-z^{*}{\parallel }^2-{\parallel x_{n+1}-z^{*}\parallel }^2\hfill \\ & \le & {\alpha }_n\parallel f\left(x_n\right)-z^{*}{\parallel }^2+(\parallel x_n-z^{*}\parallel +\parallel x_{n+1}-z^{*}\parallel \left)\right(\parallel x_{n+1}-x_n\parallel ).\hfill \end{array}$$

From (34) and the condition (i), we have

$$\begin{array}{c}\hfill \underset{n\to \infty }{lim}\parallel P_C(I-\lambda (aA+(1-a)B))x_n-T{x}_n\parallel =0.\end{array}$$

(35)

From the definition of $x_n$, we have

$$\begin{array}{ccc}\hfill \parallel T{x}_n-x_n\parallel & \le & \parallel T{x}_n-x_{n+1}\parallel +\parallel x_{n+1}-x_n\parallel \hfill \\ & \le & {\alpha }_n\parallel T{x}_n-f\left(x_n\right)\parallel +\parallel P_C(I-\lambda (aA+(1-a)B))x_n-T{x}_n\parallel +\parallel x_{n+1}-x_n\parallel .\hfill \end{array}$$

From the above inequality, condition (i), (34) and (35), we obtain

$$\begin{array}{c}\hfill \underset{n\to \infty }{lim}\parallel T{x}_n-x_n\parallel =0.\end{array}$$

(36)

From

$$\begin{array}{ccc}\hfill \parallel P_C(I-\lambda (aA+(1-a)B))x_n-x_n\parallel & \le & \parallel P_C(I-\lambda (aA+(1-a)B))x_n-T{x}_n\parallel +\parallel T{x}_n-x_n\parallel ,\hfill \end{array}$$

Equations (35) and (36), we have

$$\begin{array}{c}\hfill \underset{n\to \infty }{lim}\parallel P_C(I-\lambda (aA+(1-a)B))x_n-x_n\parallel =0.\end{array}$$

(37)

Step 4. We will show that ${lim\; sup}_{n\to \infty }⟨x_n-z^{*},f\left(z^{*}\right)-z^{*}⟩\le 0$, where $z^{*}=P_{\Gamma }f\left(z^{*}\right)$.

Since the sequence $\left\{x_n\right\}$ is bounded and G has $\mathbf{Property}\mathbf{G}$, without loss of generality, we may assume that there is a sequence $\left\{x_{n_k}\right\}$ of $\left\{x_n\right\}$ such that $x_{n_k}\rightharpoonup w$ as $k\to \infty$ and $(x_{n_k},w)\in E\left(G\right)$.

Assume that $Tw\ne w$.

Since a Hilbert space H has an Opial’s property, T is a G-nonexpansive mapping and (36), we have

$$\begin{array}{ccc}\hfill \underset{k\to \infty }{lim\; inf}\parallel x_{n_k}-w\parallel & <& \underset{k\to \infty }{lim\; inf}\parallel x_{n_k}-Tw\parallel \hfill \\ & \le & \underset{k\to \infty }{lim\; inf}(\parallel x_{n_k}-T{x}_{n_k}\parallel +\parallel T{x}_{n_k}-Tw\parallel )\hfill \\ & \le & \underset{k\to \infty }{lim\; inf}\parallel x_{n_k}-w\parallel .\hfill \end{array}$$

This is a contradiction. Then $w=Tw$. Hence, $w\in F\left(T\right)$.

Assume that $P_C(I-\lambda (aA+(1-a)B))w\ne w$.

Use a similar method to (31); it can conclude that

$$\begin{array}{c}\hfill \parallel P_C(I-\lambda (aA+(1-a)B))x_{n_k}-P_C(I-\lambda (aA+(1-a)B))w\parallel \le \parallel x_{n_k}-w\parallel ,\end{array}$$

(38)

where $(x_{n_k},w)\in E\left(G\right)$.

Since a Hilbert space H has an Opial’s property and (38), we have

$$\begin{array}{ccc}\hfill \underset{k\to \infty }{lim\; inf}\parallel x_{n_k}-w\parallel & <& \underset{k\to \infty }{lim\; inf}\parallel x_{n_k}-P_C(I-\lambda (aA+(1-a)B))w\parallel \hfill \\ & \le & \underset{k\to \infty }{lim\; inf}(\parallel x_{n_k}-P_C(I-\lambda (aA+(1-a)B))x_{n_k}\parallel \hfill \\ & & +\parallel P_C(I-\lambda (aA+(1-a)B))x_{n_k}-P_C(I-\lambda (aA+(1-a)B))w\parallel )\hfill \\ & \le & \underset{k\to \infty }{lim\; inf}\parallel x_{n_k}-w\parallel .\hfill \end{array}$$

This is a contradiction. Then $P_C(I-\lambda (aA+(1-a)B))w=w$.

From (30), we have $w\in G-VI(C,A)\cap G-VI(C,B)$.

Therefore, $w\in \Gamma$.

From $w\in \Gamma$, we have

$$\begin{array}{ccc}\hfill \underset{n\to \infty }{lim\; sup}⟨x_n-z^{*},f\left(z^{*}\right)-z^{*}⟩& =& \underset{k\to \infty }{lim}⟨x_{n_k}-z^{*},f\left(z^{*}\right)-z^{*}⟩\hfill \\ & =& ⟨w-z^{*},f\left(z^{*}\right)-z^{*}⟩\le 0,\hfill \end{array}$$

(39)

where $z^{*}=P_{\Gamma }f\left(z^{*}\right)$.

Step 5. Finally, we show that ${lim}_{n\to \infty }{x}_n=z^{*}$, where $z^{*}=P_{\Gamma }f\left(z^{*}\right)$.

From the definition of $x_n$ and (31), we have

$$\begin{array}{ccc}\hfill \parallel x_{n+1}-z^{*}{\parallel }^2& =& \parallel {\alpha }_{n}f\left(x_n\right)+{\beta }_n{P}_C(I-\lambda (aA+(1-a)B))x_n+{\gamma }_{n}T{x}_n-z^{*}{\parallel }^2\hfill \\ & \le & \parallel {\beta }_n(P_C(I-\lambda (aA+(1-a)B))x_n-z^{*})+{\gamma }_n(T{x}_n-z^{*}){\parallel }^2\hfill \\ & & +2{\alpha }_n⟨x_{n+1}-z^{*},f\left(x_n\right)-z^{*}⟩\hfill \\ & \le & {\beta }_n\parallel P_C(I-\lambda (aA+(1-a)B))x_n-z^{*}{\parallel }^2+{\gamma }_n{\parallel T{x}_n-z^{*}\parallel }^2\hfill \\ & & +2{\alpha }_n⟨x_{n+1}-z^{*},f\left(x_n\right)-z^{*}⟩\hfill \\ & \le & (1-{\alpha }_n){\parallel x_n-z^{*}\parallel }^2+2{\alpha }_n⟨x_{n+1}-z^{*},f\left(x_n\right)-f\left(z^{*}\right)⟩\hfill \\ & & +2{\alpha }_n⟨x_{n+1}-z^{*},f\left(z^{*}\right)-z^{*}⟩\hfill \\ & \le & (1-{\alpha }_n)\parallel x_n-z^{*}{\parallel }^2+2{\alpha }_n\alpha \parallel x_{n+1}-z^{*}\parallel \parallel x_n-z^{*}\parallel \hfill \\ & & +2{\alpha }_n⟨x_{n+1}-z^{*},f\left(z^{*}\right)-z^{*}⟩\hfill \\ & \le & (1-{\alpha }_n)\parallel x_n-z^{*}{\parallel }^2+{\alpha }_n\alpha \parallel x_{n+1}-z^{*}{\parallel }^2+{\alpha }_n\alpha {\parallel x_n-z^{*}\parallel }^2\hfill \\ & & +2{\alpha }_n⟨x_{n+1}-z^{*},f\left(z^{*}\right)-z^{*}⟩\hfill \end{array}$$

It implies that

$$\begin{array}{ccc}\hfill \parallel x_{n+1}-z^{*}{\parallel }^2& \le & (1-{\displaystyle \frac{2{\alpha }_n(1-\alpha )}{1-{\alpha }_n\alpha }}){\parallel x_n-z^{*}\parallel }^2\hfill \\ & & +{\displaystyle \frac{{\alpha }_n}{1-{\alpha }_n\alpha }}(\parallel x_n-z^{*}{\parallel }^2+2⟨x_{n+1}-z^{*},f\left(z^{*}\right)-z^{*}⟩)\hfill \end{array}$$

Applying Lemma 7 with condition (i) and Equation (39), it can be summarized that sequence $\left\{x_n\right\}$ converges strongly to $z^{*}=P_{\Gamma }f\left(z^{*}\right)$. This completes the proof. □

The subsequence results can be established based on the main theorem. Hence, the proofs are not provide.

Corollary 1.

Let C be a nonempty closed convex subset of Hilbert space H and let $G=\left(V\right(G),E(G\left)\right)$ be a directed graph with $V\left(G\right)=C$ has property G and $E\left(G\right)$ is convex and G is transitive with $E\left(G\right)=E\left(G^{-1}\right)$. Let $T:C\to C$ be G-nonexpansive mapping, let $A:C\to H$ be α-GISM mapping with ${\left(A\right)}^{-1}\left(0\right)\ne \varnothing$. Let $f:C\to C$ be a G-contraction mapping with coefficient $\gamma \in (0,1).$ Assume that $\Gamma =F\left(T\right)\cap G-VI(C,A)\ne \varnothing$ with $F\left(T\right)\times F\left(T\right)\subset E\left(G\right)$ and $G-VI(C,A)\times G-VI(C,A)\subset E\left(G\right)$, and there exists $x_0\in C$ such that $x_0,f\left(x_0\right)),(x_0,T{x}_0),(x_0,P_C(I-\lambda A)x_0)\in E\left(G\right).$ Let the sequence $\left\{x_n\right\}$ be generated by $x_0\in C$ and

$$\begin{array}{c}\hfill x_{n+1}={\alpha }_{n}f\left(x_n\right)+{\beta }_n{P}_C(I-\lambda A)x_n+{\gamma }_{n}T{x}_n\end{array}$$

where $\{\left\{{\alpha }_n\right\}$, $\left\{{\beta }_n\right\}$, $\left\{{\gamma }_n\right\}\}$$\subset [0,1]$, with ${\alpha }_n+{\beta }_n+{\gamma }_n=1$, $\lambda \in (0,2\alpha )$ and $a\in (0,1)$.

Suppose the following conditions hold

(i) 

${\displaystyle \sum _{n=0}^{\infty }}{\alpha }_n=\infty ,\underset{n\to \infty }{lim}{\alpha }_n=0,$

(ii) 

${\displaystyle \sum _{n=0}^{\infty }}|{\alpha }_{n+1}-{\alpha }_n|<\infty ,{\displaystyle \sum _{n=0}^{\infty }}|{\beta }_{n+1}-{\beta }_n|<\infty .$

Then, $\left\{x_n\right\}$ converges strongly to $P_{\Gamma }f\left(x_0\right)$, $P_{\Gamma }f\left(x_0\right)$ is dominated by $\left\{x_n\right\}$, $\left\{x_n\right\}$ dominates $x_0$, and $\left\{P_C(I-\lambda A)x_n\right)\}$ is dominated by $x_0$.

Remark 1.

Our results of this paper improve and extend the work of Kangtunyakarn [21] and Tiammee et al. [9] in the following ways:

1. 

Under the conditions of Theorem 1, if we select the contraction mapping f as the constant function $f\left(x_n\right)=u$ and set $A=B$ in our algorithm (29), we derive

$$\begin{array}{c}\hfill x_{n+1}={\alpha }_{n}u+{\beta }_n{P}_C(I-\lambda A)x_n+{\gamma }_{n}T{x}_n.\end{array}$$

(40)

This is exactly the same as the Halpern iteration (6) described in [21]. Therefore, the result of Kangtunyakarn [21] is a specific case of Theorem 1.

2. 

By setting ${\beta }_n=0$ and $f\left(x_n\right)=u$ in our algorithm (29), under the conditions of Theorem 1, we have

$$\begin{array}{c}\hfill x_{n+1}={\alpha }_{n}u+(1-{\alpha }_n)T{x}_n.\end{array}$$

(41)

This implies that the above algorithm coincides with the Halpern iteration (2) presented in [9]. Consequently, the result of Tiammee et al. [9] is a special case of Theorem 1.

4. Application

We are the first to study the G-minimization problem and we have also applied our main theorem to solve such a problem.

Let $f:C\to (-\infty ,+\infty ]$ be a convex, lower semi-continuous function. The G-minimization problem is to find $x^{*}\in C$ such that

$$\begin{array}{c}\hfill f\left(x^{*}\right)\le f\left(y\right)\end{array}$$

(42)

for all $y\in C$ and $(x^{*},y)\in E\left(G\right)$. A point $x^{*}$ is G-minimizer of f. We denote the set of solution of (42) by $G-{min}_{y\in C}f\left(y\right)$. The minimizers of the objective convex functionals in spaces with nonlinearity play a crucial role in the branch of analysis and geometry. Numerous applications in computer vision, machine learning, electronic structure computation, system balancing, and robot manipulation can be considered as solving optimization problems (see [24,25,26,27]).

We provide an example to illustrate the difference between a G-minimizer and a minimizer of function f.

Example 3.

Let $f:{\mathbb{R}}^2\to \mathbb{R}$ be a function define by $f(x_1,x_2)=x_1^3+sin\pi x$ for all $(x_1,x_2)\in {\mathbb{R}}^2$ and let $G=\left(V\right(G),E(G\left)\right)$ be such that $V\left(G\right)={\mathbb{R}}^2$, $E\left(G\right)=\{((x_1,x_2),(y_1,y_2))\in {\mathbb{R}}^2:(x_1,x_2),(y_1,y_2)\in [0,10]\times [0,10]\}$. Then we can see that $(0,0)$ is a G-minimizer of f, but $(0,0)$ is not a minimizer of function f.

Let $f:C\to (-\infty ,+\infty ]$ be a proper convex function. The subdifferential $\partial f$ of f is defined by

$$\begin{array}{c}\hfill \partial f\left(x\right)=\{z\in C:f(y)\ge ⟨y-x,z⟩+f(x)\forall y\in C\}\end{array}$$

for all $x\in C$. Let f be a convex, lower semi-continuous function of C into $(-\infty ,+\infty ]$.

For each $r>0$, the resolvent operator $J_r$ of f is defined by $J_r\left(x\right)={(I+r\partial f)}^{-1}\left(x\right)$ for all $x\in C$.

Let $A\subset C\times C$ be a set-valued mapping. Then, A is called accretive if for any $(x_1,y_1),(x_2,y_2)\in A$, $⟨x_1-x_2,y_1-y_2⟩\ge 0.$ If there exist $r>0$ such that $R(I+rA)=C$, then A is called m-accretive.

Theorem 2

([22]). Let C be nonempty closed convex subset of Hilbert space H and let $f:C\to (-\infty ,+\infty ]$ be a convex, lower semi-continuous function. Then, the subdifferential $\partial f$ of f is m-accretive.

Lemma 8.

Let C be nonempty closed convex subset of Hilbert space H and let $f:C\to (-\infty ,+\infty ]$ be a convex, lower semi-continuous function. Let $G=\left(V\right(G),E(G\left)\right)$ be a directed graph with $V\left(G\right)=C$. Let $J_{\lambda }$ be the resolvent of $\partial f$ for $\lambda >0$, i.e., $J_{\lambda }={(I+\lambda \partial f)}^{-1}$. Then, for any $z\in C$,

$$\begin{array}{c}\hfill J_{\lambda }z=argmi{n}_{y\in C}\{f\left(y\right)+{\displaystyle \frac{1}{2\lambda }}{\parallel y-z\parallel }^2\}\end{array}$$

(43)

for all $y\in C$ with $(J_{\lambda }z,y)\in E\left(G\right)$. Moreover, we have $J_{\lambda }$ is a G-nonexpansive mapping.

Proof. 

For each $z\in C$, define a function $g:C\to (-\infty ,\infty ]$ by

$$\begin{array}{c}\hfill g\left(x\right)={\displaystyle \frac{1}{2\lambda }}{\parallel x-z\parallel }^2\end{array}$$

for all $x\in C$.

For each $z\in C$. Let $x^{*}=J_{\lambda }z$ and $(x^{*},y)\in E\left(G\right)$ for all $y\in C$.

$$\begin{array}{ccc}\hfill x^{*}=J_{\lambda }z& ⟺& z\in x^{*}+\lambda \partial f\left(x^{*}\right)\hfill \\ & ⟺& 0\in \lambda \partial f\left(x^{*}\right)+x^{*}-z\hfill \\ & ⟺& 0\in \partial f\left(x^{*}\right)+{\displaystyle \frac{1}{\lambda }}(x^{*}-z)\hfill \\ & ⟺& 0\in \partial f\left(x^{*}\right)+\partial g\left(x^{*}\right)\hfill \\ & ⟺& 0\in \partial (f+g)\left(x^{*}\right)\hfill \\ & ⟺& ⟨0,y-x^{*}⟩+(f+g)\left(x^{*}\right)\le (f+g)\left(y\right)\forall y\in C\hfill \\ & ⟺& (f+g)\left(x^{*}\right)\le (f+g)\left(y\right)\hfill \\ & ⟺& f\left(x^{*}\right)+{\displaystyle \frac{1}{2\lambda }}\parallel x^{*}{-z\parallel }^2\le f\left(y\right)+{\displaystyle \frac{1}{2\lambda }}{\parallel y-z\parallel }^2\forall y\in Cwith(x^{*},y)\in E\left(G\right)\hfill \\ & ⟺& x^{*}=G-\underset{y\in C}{min}\{f\left(y\right)+{\displaystyle \frac{1}{2\lambda }}{\parallel y-z\parallel }^2\}.\hfill \end{array}$$

Consequently, we can conclude that $J_{\lambda }z=argmi{n}_{y\in C}\{f\left(y\right)+{\displaystyle \frac{1}{2\lambda }}{\parallel y-z\parallel }^2\}$ for all $y\in C$ with $(J_{\lambda }z,y)\in E\left(G\right).$

Next, we show that $J_{\lambda }$ is a G-nonexpansive mapping.

Let $J_{\lambda }x$, $J_{\lambda }z\in C$. From (43), we have $J_{\lambda }x=argmi{n}_{y\in C}\{f\left(y\right)+{\displaystyle \frac{1}{2\lambda }}{\parallel y-x\parallel }^2\}$ with $(J_{\lambda }x,y)\in E\left(G\right)$ and $J_{\lambda }z=argmi{n}_{y\in C}\{f\left(y\right)+{\displaystyle \frac{1}{2\lambda }}{\parallel y-z\parallel }^2\}with(J_{\lambda }z,y)\in E\left(G\right).$ Since $E\left(G\right)=E\left(G^{-1}\right)$ and $(J_{\lambda }z,y)\in E\left(G\right)$, we have $(y,J_{\lambda }z)\in E\left(G\right)$.

Since $(J_{\lambda }x,y),(y,J_{\lambda }z)\in E\left(G\right)$ and G is transitive, we have $(J_{\lambda }x,J_{\lambda }z)\in E\left(G\right)$. Thus, $J_{\lambda }$ is edge-preserving. Since $x\in (I+\lambda \partial f)J_{\lambda }x$, we have ${\displaystyle \frac{1}{\lambda }}(I-J_{\lambda })x\in \partial f{J}_{\lambda }x$. So, we get $(J_{\lambda }x,{\displaystyle \frac{1}{\lambda }}(I-J_{\lambda })x)\in \partial f$.

Similarly, since $z\in (I+\lambda \partial f)J_{\lambda }z$, we have ${\displaystyle \frac{1}{\lambda }}(I-J_{\lambda })z\in \partial f{J}_{\lambda }z$. So, we get $(J_{\lambda }z,{\displaystyle \frac{1}{\lambda }}(I-J_{\lambda })z)\in \partial f$.

Since ${\displaystyle \frac{1}{\lambda }}(I-J_{\lambda })x\in \partial f{J}_{\lambda }x,{\displaystyle \frac{1}{\lambda }}(I-J_{\lambda })z\in \partial f{J}_{\lambda }z$ and $\partial f$ is m-accretive, we have

$$\begin{array}{ccc}\hfill \lambda \parallel {\displaystyle \frac{1}{\lambda }}(I-J_{\lambda })x-{\displaystyle \frac{1}{\lambda }}(I-J_{\lambda }){z\parallel }^2& =& ⟨x-z-(J_{\lambda }x-J_{\lambda }z),{\displaystyle \frac{1}{\lambda }}(I-J_{\lambda })x-{\displaystyle \frac{1}{\lambda }}(I-J_{\lambda })z⟩\hfill \\ & =& ⟨x-z,{\displaystyle \frac{1}{\lambda }}(I-J_{\lambda })x-{\displaystyle \frac{1}{\lambda }}(I-J_{\lambda })z⟩\hfill \\ & & -⟨J_{\lambda }x-J_{\lambda }z,{\displaystyle \frac{1}{\lambda }}(I-J_{\lambda })x-{\displaystyle \frac{1}{\lambda }}(I-J_{\lambda })z⟩\hfill \\ & \le & ⟨x-z,{\displaystyle \frac{1}{\lambda }}(I-J_{\lambda })x-{\displaystyle \frac{1}{\lambda }}(I-J_{\lambda })z⟩.\hfill \end{array}$$

(44)

Using (44), we obtian

$$\begin{array}{ccc}\hfill \parallel J_{\lambda }x-J_{\lambda }{z\parallel }^2& =& \parallel x-z-((I-J_{\lambda })x-(I-J_{\lambda })z){\parallel }^2\hfill \\ & =& {\parallel x-z\parallel }^2-2\lambda ⟨x-z,{\displaystyle \frac{1}{\lambda }}(I-J_{\lambda })x-{\displaystyle \frac{1}{\lambda }}(I-J_{\lambda })z⟩\hfill \\ & & +{\lambda }^2{\parallel {\displaystyle \frac{1}{\lambda }}(I-J_{\lambda })x-{\displaystyle \frac{1}{\lambda }}(I-J_{\lambda })z\parallel }^2\hfill \\ & \le & {\parallel x-z\parallel }^2-2{\lambda }^2{\parallel {\displaystyle \frac{1}{\lambda }}(I-J_{\lambda })x-{\displaystyle \frac{1}{\lambda }}(I-J_{\lambda })z\parallel }^2\hfill \\ & & +{\lambda }^2{\parallel {\displaystyle \frac{1}{\lambda }}(I-J_{\lambda })x-{\displaystyle \frac{1}{\lambda }}(I-J_{\lambda })z\parallel }^2\hfill \\ & \le & {\parallel x-z\parallel }^2.\hfill \end{array}$$

Hence $J_{\lambda }$ is a G-nonexpansive mapping. □

Lemma 9.

Let C be a nonempty closed convex subset of Hilbert space H and let $G=\left(V\right(G),E(G\left)\right)$ be a directed graph with $V\left(G\right)=C$. Let $E\left(G\right)$ is convex and G is transitive with $E\left(G\right)=E\left(G^{-1}\right)$ and let $f:C\to (-\infty ,+\infty ]$ be a convex, lower semi-continuous function. Let $J_{\lambda }$ be the resolvent mapping of f such that $F\left(J_{\lambda }\right)\ne \varnothing$. Then, for $\lambda >0$, we have $x^{*}\in F\left(J_{\lambda }\right)$ if and only if $x^{*}$ is a G-minimizer of f.

Proof. 

First, we show that if $x^{*}\in F\left(J_{\lambda }\right)$ then $x^{*}$ is a G-minimizer of f.

Let $x^{*}$$\in F\left(J_{\lambda }\right)$ and $(J_{\lambda }{x}^{*},z)\in E\left(G\right)$ for all $z\in C$.

From Lemma, we obtain that

$$\begin{array}{ccc}\hfill f\left(x^{*}\right)& =& f\left(x^{*}\right)+{\displaystyle \frac{1}{2\lambda }}\left|\right|x^{*}-x^{*}{\left|\right|}^2\hfill \\ & \le & f\left(z\right)+{\displaystyle \frac{1}{2\lambda }}\left|\right|z-x^{*}{\left|\right|}^2,\hfill \end{array}$$

(45)

for all $z\in C$ and $(x^{*},z)\in E\left(G\right)$.

Let $y\in C$ with $(x^{*},y)\in E\left(G\right)$ and let $\overline{z}=(1-t)y+t{x}^{*}$ for all $t\in [0,1)$. Since $(x^{*},x^{*}),(x^{*},y)\in E\left(G\right)$ and $E\left(G\right)$ is convex, we have $(x^{*},\overline{z})\in E\left(G\right)$.

From (45), $(x^{*},\overline{z})\in E\left(G\right)$ and the convexity of f, we obtain

$$\begin{array}{ccc}\hfill f\left(x^{*}\right)& \le & f\left(\overline{z}\right)+{\displaystyle \frac{1}{2\lambda }}\left|\right|\overline{z}-x^{*}{\left|\right|}^2\hfill \\ & \le & (1-t)f\left(y\right)+tf\left(x^{*}\right)+{\displaystyle \frac{1}{2\lambda }}{(1-t)}^2\left|\right|y-x^{*}{\left|\right|}^2.\hfill \end{array}$$

It implies that

$$\begin{array}{c}\hfill f\left(x^{*}\right)\le f\left(y\right)+{\displaystyle \frac{1}{2\lambda }}(1-t)\left|\right|y-x^{*}{\left|\right|}^2,\end{array}$$

for all $y\in C$ with $(x^{*},y)\in E\left(G\right)$.

Taking limit at $t\to 1$, we have

$$\begin{array}{c}\hfill f\left(x^{*}\right)\le f\left(y\right)\end{array}$$

for all $y\in C$ with $(x^{*},y)\in E\left(G\right)$.

Therefore, we conclude that $x^{*}$ is a G-minimizer of f.

Next, we show that if $x^{*}$ is a G-minimizer of f, then $x^{*}\in F\left(J_{\lambda }\right)$.

Let $x^{*}$ be a minimizer of f, we have

$$\begin{array}{c}\hfill f\left(x^{*}\right)\le f\left(y\right),\end{array}$$

for all $y\in C$ with $(x^{*},y)\in E\left(G\right)$.

From Lemma, we obtain that

$$\begin{array}{c}\hfill f\left(J_{\lambda }{x}^{*}\right)+{\displaystyle \frac{1}{2\lambda }}\left|\right|J_{\lambda }{x}^{*}-x^{*}{\left|\right|}^2\le f\left(y\right)+{\displaystyle \frac{1}{2\lambda }}\left|\right|y-x^{*}{\left|\right|}^2\end{array}$$

(46)

for all $y\in C$ with $(J_{\lambda }{x}^{*},y)\in E\left(G\right)$.

Let $z=(1-t)x^{*}+t{J}_{\lambda }{x}^{*}$ for all $t\in [0,1)$. Since $(x^{*},y)\in E\left(G\right)$ and $E\left(G\right)=E\left(G^{-1}\right)$, we have $(y,x^{*})\in E\left(G\right)$.

Since $(J_{\lambda }{x}^{*},y),(y,x^{*})\in E\left(G\right)$ and G is transitive, we have $(J_{\lambda }{x}^{*},x^{*})\in E\left(G\right)$.

Since $(J_{\lambda }{x}^{*},x^{*}),(J_{\lambda }{x}^{*},J_{\lambda }{x}^{*})\in E\left(G\right)$ and $E\left(G\right)$ is convex, we have $(J_{\lambda }{x}^{*},z)\in E\left(G\right)$.

From (46), $(J_{\lambda }{x}^{*},z)\in E\left(G\right)$ and the convexity of f, we obtain that

$$\begin{array}{ccc}\hfill {\displaystyle \frac{1}{2\lambda }}\left|\right|J_{\lambda }{x}^{*}-x^{*}{\left|\right|}^2& \le & f\left(z\right)+{\displaystyle \frac{1}{2\lambda }}\left|\right|z-x^{*}{\left|\right|}^2-f\left(J_{\lambda }{x}^{*}\right)\hfill \\ & \le & (1-t)f\left(x^{*}\right)+tf\left(J_{\lambda }{x}^{*}\right)+{\displaystyle \frac{1}{2\lambda }}\left|\right|z-x^{*}{\left|\right|}^2-f\left(J_{\lambda }{x}^{*}\right)\hfill \\ & \le & {\displaystyle \frac{1}{2\lambda }}{(1-t)}^2\left|\right|J_{\lambda }{x}^{*}-x^{*}{\left|\right|}^2,\hfill \end{array}$$

the last inequality is determined from $x^{*}$ is a G-minimizer of f, i.e., $f\left(x^{*}\right)\le f\left(J_{\lambda }\left(x^{*}\right)\right)$.

It implies that

$$\begin{array}{c}\hfill {\displaystyle \frac{1}{2\lambda }}(1-{(1-t)}^2)\left|\right|J_{\lambda }{x}^{*}-x^{*}{\left|\right|}^2\le 0.\end{array}$$

Hence $x^{*}\in F\left(J_{\lambda }\right)$. □

To apply our main result, we need the following lemma.

Lemma 10

([21]). Let C be a nonempty closed convex subset of Hilbert space H and let $G=\left(V\left(G\right),E\left(G\right)\right)$ be a directed graph with $V\left(G\right)=C$ dominates z for all $z\in C$. Let $E\left(G\right)$ be convex and G be a transitive with $E\left(G\right)=E\left(G^{-1}\right)$. Let $S:C\to C$ be a G-nonexpansive mapping with $F\left(S\right)\ne \varnothing$ and $F\left(S\right)\times F\left(S\right)\subseteq E\left(G\right)$. Then

(i) 

$I-S$ is ${\displaystyle \frac{1}{2}}$-GISM.

(ii) 

$G-VI\left(C,I-S\right)=F\left(S\right)$.

Theorem 3.

Let C be a nonempty closed convex subset of Hilbert space H and let $G=\left(V\right(G),E(G\left)\right)$ be a directed graph with $V\left(G\right)=C$ has property G and $E\left(G\right)$ is convex and G is transitive with $E\left(G\right)=E\left(G^{-1}\right)$. Let $T:C\to C$ be G-nonexpansive mapping, let $g:C\to (-\infty ,\infty ]$ be a proper convex lower semi-continuous function, let $J_{\lambda }$ be the resolvent of $\partial g$ for $\lambda >0$ and let $f:C\to C$ be a G-contraction mapping with coefficient $\gamma \in (0,1).$ Assume that $\Gamma =F\left(T\right)\cap F\left(J_{\lambda }\right)\ne \varnothing$ with $F\left(T\right)\times F\left(T\right)\subset E\left(G\right)$ and $F\left(J_{\lambda }\right)\times F\left(J_{\lambda }\right)\subset E\left(G\right)$, and there exists $x_0\in C$ such that $(x_0,f\left(x_0\right)),(x_0,T{x}_0),(x_0,P_C(I-\lambda (I-J_{\lambda }))x_0)\in E\left(G\right).$ Let the sequence $\left\{x_n\right\}$ be generated by $x_0\in C$ and

$$\begin{array}{c}\hfill x_{n+1}={\alpha }_{n}f\left(x_n\right)+{\beta }_n{P}_C(I-\lambda (I-J_{\lambda }))x_n+{\gamma }_{n}T{x}_n\end{array}$$

where $\{\left\{{\alpha }_n\right\}$, $\left\{{\beta }_n\right\}$, $\left\{{\gamma }_n\right\}\}$$\subset [0,1]$, with ${\alpha }_n+{\beta }_n+{\gamma }_n=1$ and $a\in (0,1)$.

Suppose the following conditions hold

(i) 

${\displaystyle \sum _{n=0}^{\infty }}{\alpha }_n=\infty ,\underset{n\to \infty }{lim}{\alpha }_n=0,$

(ii) 

${\displaystyle \sum _{n=0}^{\infty }}|{\alpha }_{n+1}-{\alpha }_n|<\infty ,{\displaystyle \sum _{n=0}^{\infty }}|{\beta }_{n+1}-{\beta }_n|<\infty .$

Then, $\left\{x_n\right\}$ converge strongly to $P_{\Gamma }f\left(x_0\right)$, $P_{\Gamma }f\left(x_0\right)$ is dominated by $\left\{x_n\right\}$, $\left\{x_n\right\}$ dominates $x_0$, and $\left\{P_C(I-\lambda (I-J_{\lambda }))x_n\right)\}$ is dominated by $x_0$.

Proof. 

From Lemma 10 and $J_{\lambda }$ is a G-nonexpansive, we have

$$G-VI(C,I-J_{\lambda })=F\left(J_{\lambda }\right).$$

(47)

From Corollary 1 and (47), we can conclude the desired results. □

Next, we give examples to support our main result.

Example 4.

Let $G=\left(\right[0,5],E(G\left)\right)$ be a directed graph, where $E\left(G\right)=\left\{\right(x,y):x,y\in [0,1]$ and $|x-y|\le 1\}$.

Let the mappings $A,B,f,S,T:[0,5]\to \mathbb{R}$ be defined by

$$\begin{array}{c}\hfill A\left(x\right)=x-{\displaystyle \frac{x^3}{4}}-{\displaystyle \frac{15}{32}}\end{array}$$

(48)

$$\begin{array}{c}\hfill B\left(x\right)={\displaystyle \frac{x^2}{12}}-{\displaystyle \frac{1}{48}}\end{array}$$

(49)

$$\begin{array}{c}\hfill f\left(x\right)={\displaystyle \frac{x}{5}}-{\displaystyle \frac{1}{5}}\end{array}$$

(50)

$$\begin{array}{c}\hfill S\left(x\right)={\displaystyle \frac{x^3}{4}}+{\displaystyle \frac{15}{32}}\end{array}$$

(51)

$$\begin{array}{c}\hfill T\left(x\right)={\displaystyle \frac{1}{5}}sin\left(\pi x\right)+{\displaystyle \frac{3}{10}},\end{array}$$

(52)

for all $x\in [0,5]$.

Suppose that the sequence $\left\{x_n\right\}$ is generated by $x_0=1$ and

$$\begin{array}{c}\hfill x_{n+1}={\displaystyle \frac{1}{12n+1}}f\left(x_n\right)+{\displaystyle \frac{5n+1}{12n+1}}{P}_{[0,5]}(I-\lambda ({\displaystyle \frac{1}{4}}A+{\displaystyle \frac{3}{4}}B))x_n+{\displaystyle \frac{7n-1}{12n+1}}T{x}_n\end{array}$$

(53)

for all $n\ge 0$. Then, the sequence $\left\{x_n\right\}$ converges strongly to $P_{F\left(T\right)\cap G-VI(C,A)\cap G-VI(C,B)}f\left(x_0\right)={\displaystyle \frac{1}{2}}$.

Solution:   It is obvious that ${\displaystyle \frac{1}{2}}\in {(aA+(1-a)B)}^{-1}\left(0\right)$ and $E\left(G\right)=E\left(G^{-1}\right)$.

First, we show that S is a G-nonexpansive mapping.

Let $x,y\in [0,5]$ with $(x,y)\in E\left(G\right)$. Then, it follows that $x,y\in [0,1]$ with $|x-y|\le 1$.

Since ${\displaystyle \frac{x^3}{4}}$, ${\displaystyle \frac{y^3}{4}}$, ${\displaystyle \frac{5}{8}}\in [0,1]$ and $[0,1]$ is a convex set, we have

$$\begin{array}{c}\hfill Sx={\displaystyle \frac{1}{4}}{x}^3+{\displaystyle \frac{3}{4}}\left({\displaystyle \frac{5}{8}}\right)\in [0,1]\end{array}$$

and

$$\begin{array}{c}\hfill Sy={\displaystyle \frac{1}{4}}{y}^3+{\displaystyle \frac{3}{4}}\left({\displaystyle \frac{5}{8}}\right)\in [0,1].\end{array}$$

From (51), we have

$$\begin{array}{ccc}\hfill |Sx-Sy|& =& |({\displaystyle \frac{x^3}{4}}+{\displaystyle \frac{15}{32}})-({\displaystyle \frac{y^3}{4}}+{\displaystyle \frac{15}{32}})|=|{\displaystyle \frac{x^3}{4}}-{\displaystyle \frac{y^3}{4}}|\hfill \\ & =& {\displaystyle \frac{1}{4}}|x^2+xy+y^2\left|\right|x-y|\le {\displaystyle \frac{1}{4}}\left(3\right)|x-y|\hfill \\ & \le & |x-y|\le 1.\hfill \end{array}$$

Then $(Sx,Sy)\in E\left(G\right)$. Therefore S is a G-nonexpansive mapping.

Similarly, we can conclude that T is a G-nonexpansive mapping.

Since $Ax=(I-S)x$, S is a G-nonexpansive mapping and Lemma 10, we have A is ${\displaystyle \frac{1}{2}}$-GISM. It is obvious that B is 4-GISM and f is a G-contraction with $F\left(T\right)\cap G-VI(C,A)\cap G-VI(C,B)=\left\{{\displaystyle \frac{1}{2}}\right\}$.

From convexity of $[0,1]$, we have

$$\begin{array}{ccc}\hfill (I-{\displaystyle \frac{1}{2}}({\displaystyle \frac{1}{4}}A+{\displaystyle \frac{3}{4}}B))z& =& {\displaystyle \frac{7}{8}}z+{\displaystyle \frac{1}{8}}({\displaystyle \frac{z^3}{4}}-{\displaystyle \frac{z^2}{4}}+{\displaystyle \frac{17}{32}})\in [0,1],\hfill \end{array}$$

for all $z\in [0,1]$.

It follows that

$$\begin{array}{c}\hfill P_{[0,5]}(I-{\displaystyle \frac{1}{2}}({\displaystyle \frac{1}{4}}A+{\displaystyle \frac{3}{4}}B))z\in [0,1],\end{array}$$

(54)

for all $z\in [0,1]$.

Since $x_0=1\in [0,1]$, definitions of f and T, we have

$$\begin{array}{c}\hfill |x_0-f{x}_0|=|x_0-({\displaystyle \frac{x_0}{5}}-{\displaystyle \frac{1}{5}})|=|{\displaystyle \frac{4x_0}{5}}+{\displaystyle \frac{1}{5}}|\le 1\end{array}$$

(55)

and

$$\begin{array}{c}\hfill |x_0-T{x}_0|=|x_0-({\displaystyle \frac{1}{5}}sin(\pi x_0)+{\displaystyle \frac{3}{10}})|\le 1.\end{array}$$

(56)

So, we get $(x_0,f{x}_0),(x_0,T{x}_0)\in E\left(G\right)$.

From (54), we obtain

$$\begin{array}{c}\hfill |x_0-P_{[0,5]}(I-{\displaystyle \frac{1}{2}}({\displaystyle \frac{1}{4}}A+{\displaystyle \frac{3}{4}}B))x_0|\le 1.\end{array}$$

(57)

From (54) and (57), we have $(x_0,P_{[0,5]}(I-{\displaystyle \frac{1}{2}}({\displaystyle \frac{1}{4}}A+{\displaystyle \frac{3}{4}}B))x_0)\in E(G)$.

Since $x_0\in [0,1]$, (54) and (53), we have

$$\begin{array}{c}\hfill x_1={\displaystyle \frac{1}{12(1)+1}}f(x_0)+{\displaystyle \frac{5(1)+1}{12(1)+1}}{P}_{[0,5]}(I-\lambda ({\displaystyle \frac{1}{4}}A+{\displaystyle \frac{3}{4}}B))x_0+{\displaystyle \frac{7(1)-1}{12(1)+1}}T{x}_0.\end{array}$$

(58)

From the convexity of $[0,1]$, we have $x_1\in [0,1]$. Continue the method of (86), we have $x_n\in [0,1]$ for all $n\in \mathbb{N}$.

From $F\left(T\right)\cap G-VI(C,A)\cap G-VI(C,B)=\left\{{\displaystyle \frac{1}{2}}\right\}$, we have $P_{F\left(T\right)\cap G-VI(C,A)\cap G-VI(C,B)}$$f\left(x_0\right)={\displaystyle \frac{1}{2}}$.

From $x_0,{\displaystyle \frac{1}{2}}$ and $x_n\in [0,1]$, we have

$$\begin{array}{c}\hfill |x_n-x_0|\le 1,\end{array}$$

and

$$\begin{array}{c}\hfill |x_n-{\displaystyle \frac{1}{2}}|\le 1,\end{array}$$

for all $n\in \mathbb{N}$.

It follows that $(x_n,x_0)$ and $(x_n,P_{F\left(T\right)\cap G-VI(C,A)\cap G-VI(C,B)}f\left(x_0\right))=(x_n,{\displaystyle \frac{1}{2}})\in E\left(G\right)$.

From (54) and $x_n\in [0,1]$, we have

$$\begin{array}{c}\hfill P_{[0,5]}(I-{\displaystyle \frac{1}{2}}({\displaystyle \frac{1}{4}}A+{\displaystyle \frac{3}{4}}B))x_n\in [0,1],\end{array}$$

(59)

for all $n\in \mathbb{N}$.

From $x_0,x_n\in [0,1]$ and (57), we have

$$\begin{array}{c}\hfill |x_0-P_{[0,5]}(I-{\displaystyle \frac{1}{2}}({\displaystyle \frac{1}{4}}A+{\displaystyle \frac{3}{4}}B))x_n|\le 1,\end{array}$$

for all $n\in \mathbb{N}$.

It follows that $(x_0,P_{[0,5]}(I-{\displaystyle \frac{1}{2}}({\displaystyle \frac{1}{4}}A+{\displaystyle \frac{3}{4}}B))x_n)\in E(G)$. Then we can conclude that $P_{F\left(T\right)\cap G-VI(C,A)\cap G-VI(C,B)}f\left(x_0\right)$ is dominated by $\left\{x_n\right\}$, $\left\{x_n\right\}$ dominates $x_0$, and $\left\{P_C(I-\lambda (aA+(1-a)B))x_n\right)\}$ is dominated by $x_0$.

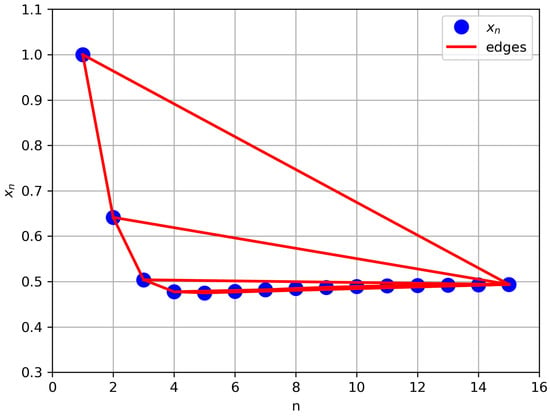
All conditions of Example 4 satisfies Theorem 1, so we can conclude that sequence $\left\{x_n\right\}$ converges strongly to $P_{F\left(T\right)\cap G-VI(C,A)\cap G-VI(C,B)}f\left(x_0\right)={\displaystyle \frac{1}{2}}.$ The numerical results for the sequences $\left\{x_n\right\}$ is shown in Figure 1.

Figure 1. The convergence behaviors of $\left\{x_n\right\}$ with $x_0=1$ and $N=15$.

Example 5.

Let $C=\{(x_1,x_2)\in {\mathbb{R}}^2:-3x_1+x_2\le 9\}$ be a convex set and let $G=(C,E(G\left)\right)$ be a directed graph, where $E\left(G\right)=\{((x_1,x_2),(y_1,y_2)):(x_1,x_2),(y_1,y_2)\in [0,1]\times [0,1]\}$. Let the mappings $A,B,f,S,T:C\to {\mathbb{R}}^2$ be defined by

$$\begin{array}{c}\hfill A(x_1,x_2)=({\displaystyle \frac{x_1^3}{4}}-{\displaystyle \frac{1}{32}},{\displaystyle \frac{x_2^3}{4}}-{\displaystyle \frac{1}{32}})\end{array}$$

(60)

$$\begin{array}{c}\hfill B(x_1,x_2)=({\displaystyle \frac{x_1}{2}}-{\displaystyle \frac{1}{4}},{\displaystyle \frac{2x_2}{3}}-{\displaystyle \frac{1}{3}})\end{array}$$

(61)

$$\begin{array}{c}\hfill f(x_1,x_2)=({\displaystyle \frac{x_1}{5}}+{\displaystyle \frac{1}{5}},{\displaystyle \frac{x_2}{5}}+{\displaystyle \frac{1}{5}})\end{array}$$

(62)

$$\begin{array}{c}\hfill T(x_1,x_2)=({\displaystyle \frac{x_1}{6}}+{\displaystyle \frac{5}{12}},{\displaystyle \frac{x_2^2}{2}}+{\displaystyle \frac{3}{8}}),\end{array}$$

(63)

for all $(x_1,x_2)\in C$.

Suppose that the sequence $\left\{x^n\right\}$ is generated by $x^0=(x_1^0,x_2^0)$, where $x_1^0=1$, $x_2^0=1$ and

$$\begin{array}{ccc}\hfill x^{n+1}& =& ({\displaystyle \frac{1}{{(12n+2)}^2}})f(x^n)+(1-{\displaystyle \frac{1}{12n+2}})P_C(I-\lambda ({\displaystyle \frac{1}{2}}A\hfill \\ & & +{\displaystyle \frac{1}{2}}B))x^n+({\displaystyle \frac{1}{12n+2}}-{\displaystyle \frac{1}{{(12n+2)}^2}})T{x}^n\hfill \end{array}$$

(64)

where $x^n=(x_1^n,x_2^n)$ for all $n\ge 0$. Then, the sequence $\left\{x^n\right\}$ converges strongly to $P_{F\left(T\right)\cap G-VI(C,A)\cap G-VI(C,B)}f\left(x^0\right)=({\displaystyle \frac{1}{2}},{\displaystyle \frac{1}{2}})$.

Solution:   It is obvious that $({\displaystyle \frac{1}{2}},{\displaystyle \frac{1}{2}})\in {(aA+(1-a)B)}^{-1}\left(0\right)$, and $E\left(G\right)=E\left(G^{-1}\right)$.

From (60)–(63) and the definition of $E\left(G\right)$, it is easy to see that T is G-nonexpansive mapping, $A,B$ are ${\displaystyle \frac{2}{3}}$-GISM, ${\displaystyle \frac{1}{2}}$-GISM, respectively, and f is G-contraction with $F\left(T\right)\cap G-VI(C,A)\cap G-VI(C,B)=\left\{({\displaystyle \frac{1}{2}},{\displaystyle \frac{1}{2}})\right\}$.

From convexity of $[0,1]$, we have

$$\begin{array}{ccc}\hfill (I-{\displaystyle \frac{1}{2}}({\displaystyle \frac{1}{2}}A+{\displaystyle \frac{1}{2}}B))z& =& ({\displaystyle \frac{7z_1}{8}}-{\displaystyle \frac{z_1^3}{16}}+{\displaystyle \frac{9}{128}},{\displaystyle \frac{5z_2}{6}}-{\displaystyle \frac{z_2^3}{16}}+{\displaystyle \frac{35}{384}})\in [0,1]\times [0,1],\hfill \end{array}$$

(65)

for all $z=(z_1,z_2)\in [0,1]\times [0,1]$.

Since C is half-space, we have

$$\begin{array}{c}\hfill P_C(x_1,x_2)=\left\{\begin{array}{cc}({\displaystyle \frac{x_1+3x_2-27}{10}},{\displaystyle \frac{3x_1+9x_2+9}{10}})\hfill & \mathit{if}-3x_1+x_2>9,\hfill \\ (x_1,x_2)\hfill & \mathit{if}-3x_1+x_2\le 9,\hfill \end{array}\right.\end{array}$$

(66)

for all $(x_1,x_2)\in {\mathbb{R}}^2$.

From (65) and (74), we have

$$\begin{array}{c}\hfill P_C(I-{\displaystyle \frac{1}{2}}({\displaystyle \frac{1}{2}}A+{\displaystyle \frac{1}{2}}B))z\in [0,1]\times [0,1],\end{array}$$

(67)

for all $z=(z_1,z_2)\in [0,1]\times [0,1]$.

Since $x^0,f{x}^0,T{x}^0\in [0,1]\times [0,1]$ and (67), we have $(x^0,f{x}^0),(x^0,T{x}^0)$ and $(x^0,P_C(I-{\displaystyle \frac{1}{2}}({\displaystyle \frac{1}{2}}A+{\displaystyle \frac{1}{2}}B))x^0)\in E(G)$.

Since $x^0=(x_1^0,x_2^0)=(1,1)\in [0,1]\times [0,1]$ and (64), we have

$$\begin{array}{ccc}\hfill x^1& =& (x_1^1,x_2^1)\hfill \\ & =& ({\displaystyle \frac{1}{{(12(0)+2)}^2}})f(x^0)+(1-{\displaystyle \frac{1}{12(0)+2}})P_C(I-\lambda ({\displaystyle \frac{1}{2}}A+{\displaystyle \frac{1}{2}}B))x^0\hfill \\ & & +({\displaystyle \frac{1}{12(0)+2}}-{\displaystyle \frac{1}{{(12(0)+2)}^2}})T{x}^0\hfill \\ & =& {\displaystyle \frac{1}{4}}f(x_1^0,x_2^0)+{\displaystyle \frac{1}{2}}{P}_C(I-\lambda ({\displaystyle \frac{1}{2}}A+{\displaystyle \frac{1}{2}}B))(x_1^0,x_2^0)+{\displaystyle \frac{1}{4}}T(x_1^0,x_2^0)\hfill \\ & =& {\displaystyle \frac{1}{4}}({\displaystyle \frac{x_1^0}{5}}+{\displaystyle \frac{1}{5}},{\displaystyle \frac{x_2^0}{5}}+{\displaystyle \frac{1}{5}})+{\displaystyle \frac{1}{2}}({\displaystyle \frac{7x_1^0}{8}}-{\displaystyle \frac{{(x_1^0)}^3}{16}}+{\displaystyle \frac{9}{128}},{\displaystyle \frac{5x_2^0}{6}}-{\displaystyle \frac{{(x_2^0)}^3}{16}}+{\displaystyle \frac{35}{384}})\hfill \\ & & +{\displaystyle \frac{1}{4}}({\displaystyle \frac{x_1^0}{6}}+{\displaystyle \frac{5}{12}},{\displaystyle \frac{{(x_2^0)}^2}{2}}+{\displaystyle \frac{3}{8}}).\hfill \end{array}$$

(68)

Since $[0,1]\times [0,1]$ is convex, then we have $x^1=(x_1^1,x_2^1)\in [0,1]\times [0,1]$. Continue the method of (68), we have $x^n=(x_1^n,x_2^n)\in [0,1]\times [0,1]$ for all $n\in \mathbb{N}$.

From (67), we have $P_C(I-{\displaystyle \frac{1}{2}}({\displaystyle \frac{1}{2}}A+{\displaystyle \frac{1}{2}}B))x^n\in [0,1]\times [0,1]$. Since $F(T)\cap G-VI(C,A)\cap G-VI(C,B)=\{({\displaystyle \frac{1}{2}},{\displaystyle \frac{1}{2}})\}$, we have $P_{F(T)\cap G-VI(C,A)\cap G-VI(C,B)}f(x^0)=P_{\{({\displaystyle \frac{1}{2}},{\displaystyle \frac{1}{2}})\}}f(x^0)=({\displaystyle \frac{1}{2}},{\displaystyle \frac{1}{2}})$.

Since $x^0,x^n,P_C(I-{\displaystyle \frac{1}{2}}({\displaystyle \frac{1}{2}}A+{\displaystyle \frac{1}{2}}B))x^n$, $P_{F(T)\cap G-VI(C,A)\cap G-VI(C,B)}f(x^0)\in [0,1]\times [0,1]$ and the definition of $E(G)$, we have

$$\begin{array}{c}\hfill (x^0,x^n),(x^0,P_C(I-{\displaystyle \frac{1}{2}}({\displaystyle \frac{1}{2}}A+{\displaystyle \frac{1}{2}}B))x^n)\end{array}$$

and

$$\begin{array}{c}\hfill (x^n,P_{F(T)\cap G-VI(C,A)\cap G-VI(C,B)}f(x^0))\in E(G).\end{array}$$

We can conclude that $P_{F\left(T\right)\cap G-VI(C,A)\cap G-VI(C,B)}f\left(x^0\right)$ is dominated by $\left\{x^n\right\}$, $\left\{x^n\right\}$ dominates $x^0$, and $\left\{P_C(I-\lambda (aA+(1-a)B))x^n\right)\}$ is dominated by $x^0$.

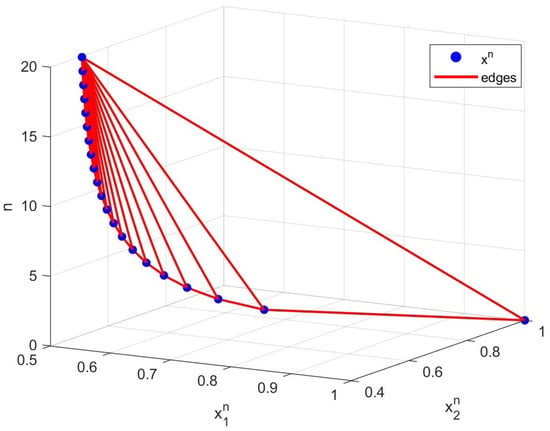
All conditions of Example 5 satisfies Theorem 1, so we can conclude that sequence $\left\{x^n\right\}$ converges strongly to $P_{F\left(T\right)\cap G-VI(C,A)\cap G-VI(C,B)}f\left(x^0\right)=({\displaystyle \frac{1}{2}},{\displaystyle \frac{1}{2}}).$ The numerical results for the sequences $\left\{x^n\right\}$ is shown in Figure 2.

Figure 2. The convergence behaviors of $\left\{x^n\right\}$ with $x^0=(1,1)$ and $N=20$.

Example 6.

Let $C=[0,1]$, and consider the directed graph $G=(C,E(G\left)\right)$, where the edge set is defined as $E\left(G\right)=\left\{\right(x,y):x,y\in [0,1],|x-y|\le 0.75\}$. Define the mappings $f,T,J_{\lambda },g:C\to \mathbb{R}$ by

$$\begin{array}{ccc}\hfill f\left(x\right)& =& {\displaystyle \frac{x}{2}}\hfill \end{array}$$

(69)

$$\begin{array}{ccc}\hfill T\left(x\right)& =& {\displaystyle \frac{x^2}{4}}\hfill \end{array}$$

(70)

$$\begin{array}{ccc}\hfill g\left(x\right)& =& {\displaystyle \frac{x^2}{2}}\hfill \end{array}$$

(71)

$$\begin{array}{ccc}\hfill J_{\lambda }\left(x\right)& =& {\displaystyle \frac{x}{2}},\hfill \end{array}$$

(72)

for all $x\in C$. Assume the sequence $\left\{x_n\right\}$ is generated by $x_0=0.5$ and

$$\begin{array}{ccc}\hfill x_{n+1}& =& {\displaystyle \frac{1}{n+1}}f\left(x_n\right)+0.5\left(1-{\displaystyle \frac{1}{n+1}}\right)P_{[0,1]}(I-\lambda (I-J_{\lambda }))x_n\hfill \\ & & +\left(1-{\displaystyle \frac{1}{n+1}}-0.5\left(1-{\displaystyle \frac{1}{n+1}}\right)\right)T{x}_n\hfill \end{array}$$

(73)

for all $n\ge 0$. We shall now demonstrate the computation $x_1$, $x_2$, and $x_3$.

Solution:   We first show that T is a G-nonexpansive mapping. Let $x,y\in [0,1]$ with $(x,y)\in E\left(G\right)$. Then, $x,y\in [0,1]$ with $|x-y|\le 0.75$. From definition of T, it follows that

$$\begin{array}{c}\hfill Tx={\displaystyle \frac{x^2}{4}}\in [0,1]\end{array}$$

and

$$\begin{array}{c}\hfill Ty={\displaystyle \frac{y^2}{4}}\in [0,1].\end{array}$$

From Equation (70), we obtain

$$\begin{array}{ccc}\hfill |Tx-Ty|& =& \left|{\displaystyle \frac{x^2}{4}}-{\displaystyle \frac{y^2}{4}}\right|\hfill \\ & =& {\displaystyle \frac{1}{4}}|x+y||x-y|\le {\displaystyle \frac{1}{4}}\left(2\right)|x-y|\hfill \\ & \le & |x-y|\le 0.75.\hfill \end{array}$$

Thus, $(Tx,Ty)\in E\left(G\right)$, proving that T is a G-nonexpansive mapping. It is easy to verify that f is a G-contraction.

Next, we choose $\lambda =1$. By the definition of $J_{\lambda }$, we have

$$\begin{array}{c}\hfill (I-\left(1\right)(I-J_{\lambda }))z={\displaystyle \frac{z}{2}}\in [0,1],\end{array}$$

for all $z\in [0,1]$. Consequently,

$$\begin{array}{c}\hfill P_{[0,1]}(I-\left(1\right)(I-J_{\lambda }))z\in [0,1],\end{array}$$

(74)

for all $z\in [0,1]$.

Given that $x_0={\displaystyle \frac{1}{2}}\in [0,1]$ and using the definitions of f and T, we have

$$\begin{array}{c}\hfill |x_0-f\left(x_0\right)|=\left|{\displaystyle \frac{1}{2}}-{\displaystyle \frac{1}{4}}\right|={\displaystyle \frac{1}{4}}\le 0.75\end{array}$$

(75)

and

$$\begin{array}{c}\hfill |x_0-T\left(x_0\right)|=\left|{\displaystyle \frac{1}{2}}-{\displaystyle \frac{1}{16}}\right|\le 0.75.\end{array}$$

(76)

Thus, $(x_0,f\left(x_0\right)),(x_0,T\left(x_0\right))\in E\left(G\right)$.

From Equation (74), we obtain

$$\begin{array}{c}\hfill |x_0-P_{[0,1]}(I-\left(1\right)(I-J_{\lambda }))x_0|\le 0.75.\end{array}$$

(77)

Combining Equations (74) and (77), we conclude $(x_0,P_{[0,1]}(I-\left(1\right)(I-J_{\lambda }))x_0)\in E\left(G\right)$.

Since $x_0\in [0,1]$, using Equation (73), we compute

$$\begin{array}{ccc}\hfill x_1& =& {\displaystyle \frac{1}{0+1}}f\left(x_0\right)+0.5\left(1-{\displaystyle \frac{1}{(0+1)}}\right)P_{[0,1]}(I-\left(1\right)(I-J_{\lambda }))x_0\hfill \\ & & +\left(1-{\displaystyle \frac{1}{0+1}}-0.5\left(1-{\displaystyle \frac{1}{(0+1)}}\right)\right)T\left(x_0\right)\hfill \\ & =& f\left({\displaystyle \frac{1}{2}}\right)+0.5(1-1)P_{[0,1]}(I-\left(1\right)(I-J_{\lambda })){\displaystyle \frac{1}{2}}+\left(1-1-0.5(1-1)\right)T\left({\displaystyle \frac{1}{2}}\right)\hfill \\ & =& {\displaystyle \frac{1}{4}}.\hfill \end{array}$$

(78)

Similarly, we compute $x_2$ and $x_3$ as follows: since $x_1={\displaystyle \frac{1}{4}}\in [0,1]$, definitions of f and T, we have

$$\begin{array}{c}\hfill |x_1-f{x}_1|=|x_1-{\displaystyle \frac{x_1}{2}}|=|{\displaystyle \frac{x_1}{2}}|={\displaystyle \frac{1}{8}}\le 0.75\end{array}$$

(79)

and

$$\begin{array}{c}\hfill |x_1-T{x}_1|=|x_1-{\displaystyle \frac{x_1^2}{4}}|={\displaystyle \frac{15}{64}}\le 0.75.\end{array}$$

(80)

So, we get $(x_1,f{x}_1),(x_1,T{x}_1)\in E\left(G\right)$.

From (74), we obtain

$$\begin{array}{c}\hfill |x_1-P_{[0,1]}(I-\left(1\right)(I-J_{\lambda }))x_1|=|x_1-{\displaystyle \frac{x_1}{2}}|\le 0.75.\end{array}$$

(81)

From (74) and (81), we have $(x_1,P_{[0,1]}(I-\left(1\right)(I-J_{\lambda }))x_1)\in E\left(G\right)$.

Since $x_1\in [0,1]$ and (73), we have

$$\begin{array}{ccc}\hfill x_2& =& {\displaystyle \frac{1}{1+1}}f(x_1)+0.5(1-{\displaystyle \frac{1}{(1+1)}})P_{[0,1]}(I-(1)(I-J_{\lambda }))x_1\hfill \\ & & +(1-{\displaystyle \frac{1}{1+1}}-0.5(1-{\displaystyle \frac{1}{(1+1)}}))T{x}_1\hfill \\ & =& {\displaystyle \frac{1}{2}}f({\displaystyle \frac{1}{4}})+0.5(1-{\displaystyle \frac{1}{2}})P_{[0,1]}(I-(1)(I-J_{\lambda }))({\displaystyle \frac{1}{4}})+(1-{\displaystyle \frac{1}{2}}-0.5(1-{\displaystyle \frac{1}{2}}))T({\displaystyle \frac{1}{4}})\hfill \\ & =& {\displaystyle \frac{25}{256}}.\hfill \end{array}$$

(82)

Finally, for $x_3$: since $x_2={\displaystyle \frac{25}{256}}\in [0,1]$, definitions of f and T, we have

$$\begin{array}{c}\hfill |x_2-f{x}_2|=|x_2-{\displaystyle \frac{x_2}{2}}|=|{\displaystyle \frac{x_2}{2}}|={\displaystyle \frac{25}{512}}\le 0.75\end{array}$$

(83)

and

$$\begin{array}{c}\hfill |x_2-T{x}_2|=|x_2-{\displaystyle \frac{x_2^2}{4}}|=0.0952721\le 0.75\end{array}$$

(84)

So, we get $(x_2,f{x}_2),(x_2,T{x}_2)\in E\left(G\right)$.

From (74), we obtain

$$\begin{array}{c}\hfill |x_2-P_{[0,1]}(I-\left(1\right)(I-J_{\lambda }))x_2|=|x_2-{\displaystyle \frac{x_2}{2}}|\le 0.75\end{array}$$

(85)

From (74) and (85), we have $(x_2,P_{[0,1]}(I-\left(1\right)(I-J_{\lambda }))x_2)\in E\left(G\right)$.

Since $x_2\in [0,1]$ and (73), we have

$$\begin{array}{ccc}\hfill x_3& =& {\displaystyle \frac{1}{2+1}}f(x_2)+0.5(1-{\displaystyle \frac{1}{(2+1)}})P_{[0,1]}(I-(1)(I-J_{\lambda }))x_2\hfill \\ & & +(1-{\displaystyle \frac{1}{2+1}}-0.5(1-{\displaystyle \frac{1}{(2+1)}}))T{x}_2\hfill \\ & =& {\displaystyle \frac{1}{3}}f({\displaystyle \frac{25}{256}})+0.5(1-{\displaystyle \frac{1}{3}})P_{[0,1]}(I-(1)(I-J_{\lambda }))({\displaystyle \frac{25}{256}})+(1-{\displaystyle \frac{1}{3}}-0.5(1-{\displaystyle \frac{1}{3}}))T({\displaystyle \frac{25}{256}})\hfill \\ & =& 0.0333468.\hfill \end{array}$$

(86)

We have presented a summary of the numerical calculations as shown in Table 1 and Table 2.

Table 1. Explanation of $x_1,x_2,x_3$.

Step	${\mathit{\alpha }}_{\mathit{n}}$	${\mathit{\beta }}_{\mathit{n}}$	${\mathit{\gamma }}_{\mathit{n}}$	Expression for ${\mathit{x}}_{\mathit{n}}$	Value of ${\mathit{x}}_{\mathit{n}}$
$x_1$	1	0	0	${\alpha }_{0}f\left(x_0\right)+{\beta }_0{P}_{[0,1]}(I-\left(1\right)(I-J_{\lambda }))x_0+{\gamma }_{0}T\left(x_0\right)$	0.25
$x_2$	0.5	0.25	0.25	${\alpha }_{1}f\left(x_1\right)+{\beta }_1{P}_{[0,1]}(I-\left(1\right)(I-J_{\lambda }))x_1+{\gamma }_{1}T\left(x_1\right)$	0.0976563
$x_3$	0.333	0.333	0.333	${\alpha }_{2}f\left(x_2\right)+{\beta }_2{P}_{[0,1]}(I-\left(1\right)(I-J_{\lambda }))x_2+{\gamma }_{2}T\left(x_2\right)$	0.0333468

Table 2. Explanation of Members in $E\left(G\right)$.

Condition	Members $(\mathit{x},\mathit{y})$	Source Equation	Condition Satisfied $\left(\right|\mathit{x}-\mathit{y}|\le 0.75)$
$(x_0,f\left(x_0\right))$	$(0.5,0.25)$	$f\left(x_0\right)={\displaystyle \frac{0.5}{2}}=0.25$	$|0.5-0.25|=0.25\le 0.75$
$(x_0,T\left(x_0\right))$	$(0.5,0.125)$	$T\left(x_0\right)={\displaystyle \frac{{\left(0.5\right)}^2}{4}}=0.0625$	$|0.5-0.0625|=0.4375\le 0.75$
$(x_0,P_C(I-\lambda (I-J_{\lambda }))x_0)$	$(0.5,0.25)$	$P_C(I-\lambda (I-J_{\lambda }))x_0=P_{[0,1]}\left({\displaystyle \frac{0.5}{2}}\right)=0.25$	$|0.5-0.25|=0.25\le 0.75$
$(x_1,f\left(x_1\right))$	$(0.25,0.125)$	$f\left(x_1\right)={\displaystyle \frac{0.25}{2}}=0.125$	$|0.25-0.125|=0.125\le 0.75$
$(x_1,T\left(x_1\right))$	$(0.25,0.015625)$	$T\left(x_1\right)={\displaystyle \frac{{\left(0.25\right)}^2}{4}}=0.015625$	$|0.25-0.015625|=0.234375\le 0.75$
$(x_1,P_C(I-\lambda (I-J_{\lambda }))x_1)$	$(0.25,0.125)$	$P_C(I-\lambda (I-J_{\lambda }))x_0=P_{[0,1]}\left({\displaystyle \frac{0.25}{2}}\right)=0.125$	$|0.25-0.125|=0.125\le 0.75$
$(x_2,f\left(x_2\right))$	$(0.0976563,0.04882815)$	$f\left(x_2\right)={\displaystyle \frac{0.0976563}{2}}=0.04882815$	$|0.0976563-0.04882815|=0.04882815\le 0.75$
$(x_2,T\left(x_2\right))$	$(0.0976563,0.002384188)$	$T\left(x_2\right)={\displaystyle \frac{{\left(0.0976563\right)}^2}{4}}=0.002384188$	$|0.0976563-0.002384188|=0.095272112\le 0.75$
$(x_2,P_C(I-\lambda (I-J_{\lambda }))x_2)$	$(0.0976563,0.04882815)$	$P_C(I-\lambda (I-J_{\lambda }))x_2=P_{[0,1]}\left({\displaystyle \frac{0.0976563}{2}}\right)=0.04882815$	$|0.0976563-0.04882815|=0.04882815\le 0.75$

5. Conclusions

This research explores the integration of G-variational inequality problems and fixed point theory within a Hilbert space endowed with a graph structure. The main contributions include the development of a new iterative method and a strong convergence theorem, which demonstrate the convergence of sequences to solutions that are part of the intersection of the solution sets for G-variational inequalities and fixed point problems. The study provides new lemmas that are essential for understanding G-nonexpansive mappings and G-inverse strongly monotone operators.

The research extends existing theories in nonlinear analysis and functional analysis, particularly those involving graph structures in metric spaces. By doing so, it broadens the scope of applications to optimization problems where constraints can be naturally represented by graphs, thus making the theory applicable to network theory, computational mathematics, and various applied sciences.

The paper also differentiates the combination of the G-variational inequality problems from the combination of the classical variational inequality problems, highlighting the necessity of incorporating graph structures when dealing with complex systems. The provided examples effectively demonstrate how G-variational inequality problems can be distinguished from standard variational inequality problems. Additionally, the assumptions of transitivity and convexity of $E\left(G\right)$ are crucial for ensuring the validity of the convergence results. Transitivity maintains consistent connections between points on the graph, supporting the effectiveness of the iterative methods, while convexity preserves the geometric properties of the solution sets, which is essential for proving the convergence theorems.

Overall, this work lays a solid foundation for future research and applications in areas that require advanced mathematical tools and frameworks, particularly those involving graph-based constraints.