Abstract
This study explores a new dimension of accelerated life testing by analyzing competing risk data through Tampered Random Variable (TRV) modeling, a method that has not been extensively studied. This method is applied to simple step-stress life testing (SSLT), and it considers multiple causes of failure. The lifetime of test units under changeable stress levels is modeled using Power Rayleigh distribution with distinct scale parameters and a constant shape parameter. The research introduces unique tampering coefficients for different failure causes in step-stress data modeling through TRV. Using SSLT data, we calculate maximum likelihood estimates for the parameters of our model along with the tampering coefficients and establish three types of confidence intervals under the Type-II censoring scheme. Additionally, we delve into Bayesian inference for these parameters, supported by suitable prior distributions. Our method’s validity is demonstrated through extensive simulations and real data application in the medical and electrical engineering fields. We also propose an optimal stress change time criterion and conduct a thorough sensitivity analysis.
Keywords:
tampered random variable; competing risk; step stress; censoring scheme; maximum likelihood estimation; Bayes estimation; bootstrap method; simulation analysis MSC:
62E10; 62F15; 62N05; 60E05; 62P30
1. Introduction
With ongoing improvements in the manufacturing sector, numerous industrial products, known for their high reliability and complex designs, are becoming increasingly usable in everyday life. Accelerated life testing (ALT) addresses the challenge of evaluating such products by exposing them to stress levels higher than their usual operating conditions, producing rapid failures in turn. These growing stress factors—such as temperature, voltage, and humidity—significantly influence the lifespan of electronic equipment, including electric bulbs, fans, computers, toasters, and more. By employing these high-stress factors in ALT experiments, valuable insights concerning product reliability can be rapidly acquired within a condensed experimental time frame. Analyzing reliability and making inferences from it have gained significant interest in the literature, as illustrated by references [1,2,3].
ALT experiments can be conducted in two ways: with a starting constant high-stress level or with a changeable stress factor that can be varied during different time intervals. In the realm of ALT, there exists a specific class known as step-stress life testing (SSLT). This method permits experimenters to incrementally increase the stress levels at predetermined time points during the experiment. A basic form of SSLT is exemplified in experiments involving only two stress levels, denoted as and , along with a single, pre-determined point in time, , at which the stress level shifts.
To understand how lifetime distributions vary under different stress levels, some basic modeling assumptions are typically discussed:
- Cumulative Exposure models (CE). In this method, specific restrictions are applied to ensure that the lifetime distributions at each progressive stress level align at their designated transition points, maintaining continuity. This approach is detailed in works by Sedyakin [4] and Nelson [5].
- Tampered Failure Rate (TFR) modeling. This technique involves adjusting the failure rates, increasing them at each subsequent stress level. Key references for TFR modeling include Bhattacharyya and Soejoeti [6], and Madi [7].
- The Tampered Random Variable (TRV) model. Here, the focus is on reducing the remaining lifetime for each new stress level. For more information on this approach, you can refer to Goel [8] and DeGroot and Goel [9].
- Step-stress partially accelerated life testing with a large amount of censored data. This approach addresses the gap in estimating non-homogeneous distribution and acceleration factor parameters under multiple censored data conditions. For more details, one can refer to Khan and Aslam [10].
Additionally, Sultana and Dewanji [11] explored the relationships between the TRV model and the two other models, TFR and CE, within a multi-step stress environment. They noted that TRV modeling aligns with CE and TFR when the fundamental lifetime distribution is exponential and the distributions at each stress level adhere to a scale-based parametric family. Thus, it is observed that the above three models converge when the fundamental distribution is exponential. TRV modeling stands out for its ability to be generalized to multiple-step-stress situations more effectively than the other two models. It also offers advantages in terms of modeling discrete and multivariate lifetimes, which are more complex tasks for the CE and TFR models.
Comparing factors that lead to risk model failures is essential for comprehending the contributing factors, detecting common changes, assessing model performance, and influencing decision making and risk management. It assists in identifying important issues that must be resolved to increase the precision and dependability of the model. The development of more reliable models can be made possible by recognizing similar patterns among various occurrences or outcomes that can be identified by understanding these components. Additionally, it offers useful information for model creators and validators, enabling them to improve model development processes, assumptions, and validation processes for more accurate and dependable models. The competing risks concept refers to the possibility of individual failure in a specific field owing to distinct factors. The cause-of-failure indication and the individual failure time are examples of observable data in this approach. When examining data on competing risks, the failure variables are typically unrelated to one another which means that the two risk factors are statistically independent. In the industrial and mechanical domains, fatigue and aging deterioration can lead to an assembly device failing due to electrical/optical signal (voltage, current, or light intensity) falling to an intolerable level. Numerous studies in the existing literature utilize CEM and TFR modeling within competing risk scenarios. However, to the best of our knowledge, research incorporating TRV modeling into the context of competing risk data is notably scarce. See for example Sultana et al. [12], Ramadan et al. [13] and Tolba et al. [14].
In this work, TRV is used with the SSLT model under two independent competing risk factors where the failure times follow the Power Rayleigh distribution. The sample is observed under the Type-II censored scheme. The censoring schemes have been introduced to solve the lack of information in lifetime experiments, saving time and costs. Type-I censoring has a predetermined time, while Type-II censoring has predetermined failure units.
The main goals of this study are summarized below:
- Performing an inferential analysis to obtain point and interval estimation of the unknown parameters of the distribution and the acceleration factor using both the maximum likelihood estimator and the Bayesian method.
- Applying numerical methods like Monte Carlo simulation to assess the performance of estimators obtained from Maximum Likelihood Estimation (MLE) and Bayesian methods, focusing on their bias, mean squared error, and the coverage probability (CP) for the confidence intervals.
- Evaluating real-world data sets from the medical field concerning AIDS infection, alongside another study from electrical engineering involving the causes of the failure of electronic components, serves to empirically assess the effectiveness of the newly proposed model.
The structure of the remainder of this document is as follows: Section 2 outlines the SSLT model under the TRV framework with the Power Rayleigh distribution. Section 3 details the methodologies used for point estimation, specifically using maximum likelihood and Bayesian methods. Section 4 is dedicated to interval estimation, exploring three distinct methods. Section 5 focuses on simulation analysis and presents the results in tabular form. The determination of the optimal time for stress change and an analysis of sensitivity are discussed in Section 6. An application using real-world data is examined in Section 7. The paper concludes with a summary of the findings in Section 8.
2. Model Description
In this study, we consider the SSLT model with random failure time variables denoted by and along with the stress levels and that are assumed to follow a Power Rayleigh distribution with a common shape parameter and distinct scale parameters and . The two risk factors are called cause I and cause II and both are performed using Type-II censored samples. At a prefixed time , the stress level moves from to . During the first stress level, the units will operate until a specific time , following which any remaining survivals that have not failed by time are moved to be tested under accelerated conditions with an acceleration factor . Consequently, the system will operate under the second stress level until we obtain the required failure times. The effect of stress transition from the first stress to the accelerated condition may be explained by multiplying the remaining lifetime by the acceleration factor . Hence the TRV for and is expressed as
and
where is the time at which the stress changes and the acceleration parameter is .
We consider Power Rayleigh distribution as a lifetime model. The Rayleigh distribution, a continuous distribution of significant practical relevance, has been the subject of extensive study by various authors who have explored its statistical properties, inference methods, and reliability analysis. Additionally, a variety of extended versions of the Rayleigh distribution have been introduced. For example, Rosaiah and Kantam [15] applied the inverse Rayleigh to failure times data. Merovci [16] introduced the transmuted Rayleigh and modeled the amount of nicotine in blood. Cordeiro et al. [17] studied the beta-generalized Rayleigh distribution and its application. More generalizations of Rayleigh distribution can be found in the literature and one may refer to [18,19,20,21,22,23,24].
The Power Rayleigh (PR) distribution was first introduced by Neveen et al. [25]. It is a versatile and flexible statistical model known for its ability to handle a wide range of data types. This distribution is particularly useful due to its capability to model data that exhibit a skewed pattern, which is common in many practical situations. The Power Rayleigh distribution is characterized by two parameters that allow it to adapt to various data shapes and sizes, making it more flexible than the standard Rayleigh distribution. Its applications are diverse, ranging from reliability engineering and survival analysis to modeling wind speed and signal processing. The flexibility in shape and scale provided by the Power Rayleigh distribution makes it a valuable tool for analyzing and interpreting real-world data in various scientific and engineering fields. We assume that the Power Rayleigh distribution has a shape parameter and scale parameter , where both have positive support, and then the cumulative distribution function (CDF) becomes
and the probability density function (PDF) is
Consider a set of n units subjected to a life test starting at stress level . Failures and their corresponding risks are documented over time. At a designated moment the stress level shifts from to , and the test runs until r (with ) failures are noted. If r equals n, a complete dataset is collected as in a simple SSLT without data truncation. We assume that each unit’s failure is attributable to one of two competing risks, each described by a Power Rayleigh distribution with a consistent shape parameter but distinct scale parameters for , aligned with the TRV model.
The CDF for the lifetime associated with risk j for is then expressed as follows:
and the corresponding PDF of is given by
Let us denote the overall failure time of a unit under test as U, which is obtained by . Then, the CDF and PDF are easily obtained as
and
respectively, where and . Furthermore, let C denote the indicator for the cause of failure. Then, under our assumptions, the joint PDF of is given by
for .
In competing risk models, the assumption of independence is often considered to be impractical. Identifiable issues may emerge if dependencies exist within the model or due to a lack of covariates in the data. To mitigate these issues, we postulate a latent failure time model and treat the risks and as independent. Let represent the number of units failing from risk j before time and after , with , ensuring . The sequence of observed failure times is . Let denote the observed value for , denote the observed value for , and let be the vector of these counts.
In the next section, classical and Bayesian estimation methods are constructed to estimate the unknown parameters for the Power Rayleigh and the accelerated constant under the two competing risk factors with the Type-II censoring scheme.
3. Point Estimation
In this study, two approaches to estimation are examined: the frequentist maximum likelihood estimation (MLE) and the Bayesian estimation method. Section 4 is dedicated to conducting a simulation analysis and applying numerical techniques to evaluate the efficacy of these estimation strategies.
3.1. Maximum Likelihood Estimation
In this section, the maximum likelihood estimation MLE method is employed to determine the unknown parameters of the Power Rayleigh distribution within the TRV framework. Numerical methods, including the renowned Newton–Raphson technique, are utilized to compute the necessary estimators. Subsequently, assuming the TRV model, we construct the likelihood function of based on Type-II censored data as
The log-likelihood function can be written as
The maximum likelihood estimations of the parameters are obtained by differentiating the log-likelihood function with respect to the parameters and setting the result to zero, so we have the following normal equations.
and
For known and , the MLEs of and are given by
and
3.2. Bayesian Inference
In this section, we apply the Bayesian estimation technique to determine the unknown parameters of the Power Rayleigh distribution. The fundamental principle of the Bayesian approach posits that the model’s parameters are random variables with a predefined distribution, referred to as the prior distribution. Given the availability of prior knowledge, selecting an appropriate prior is crucial. We opt for the gamma conjugate prior distribution for the parameters for many reasons, such as the flexibility in its nature with a non-informative domain and the calculations’ simplicity making analytical or computational updates to the posterior easier. Also, the positive of the domain makes it suitable for modeling parameters. We perform the Bayesian inference method for estimating the unknown parameters . We assume independent gamma priors for , and and a uniform prior for . That is, and have where ,, are non-negative hyperparameters, and follows uniform prior as follows:
The estimates have been developed under the square error loss function (SELF) and the linear exponential loss function (LLF). Hence, the joint prior density of the independent parameters is given by
The joint posterior density function for the parameters can be derived by incorporating the observed censored samples, and the prior distributions of these parameters are as follows:
Thus, the conditional posterior densities of the parameters , and can be obtained by simplifying Equation (15) as follows
and
Since the Equations (16)–(19) cannot be computed explicitly, numerical techniques are employed. One of the most powerful numerical techniques in Bayesian estimation is the Monte Carlo Markov Chain method (MCMC). In this scenario, we suggest employing the Metropolis–Hastings (M-H) sampling method within the Gibbs algorithm, utilizing a normal proposal distribution as recommended by Tierney [26]. The procedure for Gibbs sampling incorporating the (M-H) approach is outlined as follows:
- (1)
- Set initial values
- (2)
- Set
- (3)
- Using the following M-H algorithm, from , , and generate , and with the normal proposal distributionsand from the main diagonal in the inverse Fisher information matrix we obtained , and .
- (4)
- Generate a proposal for from , from , from , and from
- (i)
- The acceptance probabilities are
- (ii)
- From a Uniform distribution , and are generated.
- (iii)
- If , accept the proposal and set , otherwise set .
- (iv)
- If , accept the proposal and set , otherwise set .
- (v)
- If , accept the proposal and set , otherwise set .
- (vi)
- If , accept the proposal and set , otherwise set
- (5)
- Set
- (6)
- Steps (3)–(5), are repeated N times to obtain , and , j = 1, 2, …N.
To guarantee convergence and eliminate the impact of initial value selection, the first M simulated variants are eliminated. For a sufficiently high N, the chosen samples are then . The SEL function-based approximate BEs of are generated using
The approximate Bayes estimates for , under the Entropy loss function are given as
4. Interval Estimation
Confidence interval estimation is a fundamental statistical method used to indicate the reliability of an estimate. It provides a range of values, derived from sample data, that is likely to contain the true value of an unknown population parameter. The concept is central to inferential statistics and has numerous applications across various fields such as engineering, economics, medicine, and the social sciences. Among its key properties, the asymptotic interval is notable for its reliance on large sample sizes, where the distribution of the estimate approaches a normal distribution, making it increasingly accurate as the sample size grows. This property is particularly useful for electrical engineering projects where large data sets are analyzed for reliability and performance assessments.
Credible intervals, on the other hand, are used in Bayesian statistics and represent the range within which a parameter lies with a certain probability, given the observed data and a prior belief about the parameter’s distribution. This approach is valuable in research and development projects within electrical engineering, where prior knowledge or expert opinions can be quantitatively incorporated into the analysis, offering a more nuanced understanding of uncertainty.
Bootstrap intervals utilize resampling techniques to generate an empirical distribution of the estimator by drawing samples with replacements from the original dataset. This method does not assume a specific distribution, making it versatile and robust, especially in complex engineering studies where theoretical distributions are hard to justify. The bootstrap approach is particularly important for evaluating the uncertainty of estimates derived from small or non-standard datasets, providing a powerful tool for uncertainty quantification in both academic research and practical applications.
The application and importance of these intervals lie in their ability to quantify the uncertainty in estimates, guiding decision making and hypothesis testing. In electrical engineering, for example, they can be used to assess the reliability of system parameters, evaluate the performance of new designs, or validate models against empirical data. By understanding and applying these concepts, researchers, and practitioners can enhance the rigor and credibility of their findings, contributing to more reliable and effective solutions in their respective fields. The following subsections work out the previously mentioned interval estimations.
4.1. Asymptotic Confidence Interval
This subsection presents the observed Fisher information matrix, commonly employed for the construction of asymptotic confidence intervals (ACIs).
The MLEs are approximately normal with a mean of and a variance matrix . Here, is the observed Fisher information matrix, and it is defined as
where the second partial derivatives are as follows:
Consequently, the estimated asymptotic variance–covariance matrix for the MLEs can be obtained by taking the inverse of the observed information matrix which is given by
The two-sided confidence interval can be written as
where is the percentile of the standard normal distribution with right-tail probability .
4.2. Credible Interval
Using the Metropolis–Hastings algorithm within the Gibbs sampling framework, we determined the credible confidence interval (CCI). For clarity, we refer to Section 3.2, and the algorithm steps mentioned there. Proceeding after step (6), the CCIs of where with is given by
4.3. Bootstrap Interval
Bootstrap confidence intervals offer a versatile approach to estimating the uncertainty of an estimator when the underlying distribution is unknown or complex. There are two main types: the bootstrap-t and the bootstrap percentile (bootstrap-p) methods.
4.3.1. Parametric Boot-p
The bootstrap percentile (p) method involves generating a large number of bootstrap samples from the original data. For each sample, the statistic of interest is calculated, creating a distribution of these statistics. The confidence interval is then directly obtained by taking percentiles from this empirical distribution. The following steps describe the algorithm of this method:
- (1)
- Based on obtain , and by maximizing Equations (10)–(13).
- (2)
- Generate from the PR distribution with parameters , and based on Type-II censoring under TRV, by considering the algorithm presented in [27].
- (3)
- Obtain the bootstrap parameter estimation , with boots using the MLEs under the bootstrap sampling.
- (4)
- Repeat steps (2) and (3) boot times, and obtain
- (5)
- Obtain by arrange in ascending orders.
Define for a given z, where denotes the cumulative distribution function of The approximate bootstrap-p CI of is given by
4.3.2. Parametric Boot-t
The bootstrap-t method is an adaptation of the traditional t-interval, designed to handle situations where the sample size is small or the data do not meet the assumptions of normality. It involves resampling the original data with replacements to generate a large number of bootstrap samples. These are used to calculate a t-statistic, analogous to the one used in traditional t-tests but derived from the bootstrap distribution. This collection of t-statistics forms a distribution from which confidence intervals can be derived, the bootstrap-t algorithm is itemized as follows:
- (1)
- Repeat the initial three steps of the parametric Boot-p procedure.
- (2)
- Calculate the variance–covariance matrix utilizing the delta method.
- (3)
- Define the statistic as
- (4)
- Generate from repeating steps N Boot times
- (5)
- Sort the sequence by arranging in in ascending order.
Define , where is the cumulative distribution function of for a given z.
Then, the approximate bootstrap-t CI of is obtained by
5. Simulation Analysis
In this section, we present various simulation methods to demonstrate the theoretical results. Initially, we create accelerated PR datasets using the inverse transformation technique. To achieve this, we employ a quantile function derived from the equation where V represents a random sample from the uniform distribution. Consequently, we generate random samples of sizes 40, and 100 using Equation (27).
where . Moreover, within the Type-II censoring framework, we employed two distinct predetermined numbers of failures for each sample size. Thus, we selected m = 25 and m = 35 for n = 40, and r = 75 and r = 90 for n = 100, respectively. We examined two different sets of actual parameter values in this context. In the initial approach, we set = (1.5, 1.8, 1.2, 0.8), (1.5, 1.8, 1.2, 0.3), (0.6, 0.7, 2, 0.3), and (0.6, 0.7, 2, 0.8) with two distinct stress transition points: = 0.60 and = 0.90. In all scenarios, we determined the stress transition points based on the ranges of the generated samples, which varied depending on the chosen actual parameter values.
We employed the software developed by R Team et al. [28] for computational tasks. For MLE computations, we utilized the “L-BFGS-B” method within the “optim” function to optimize the profile log-likelihood function described in Equation (9) within the restricted area of . We set the significance level to for approximate confidence intervals. Subsequently, we conducted simulations repeatedly for 5000 iterations. Observing that the means of the gamma priors yield the real parameter values with the given hyper-parameters. The determination of hyper-parameters relies on informative priors, which are derived from the Maximum Likelihood Estimates (MLEs) of by aligning the mean and variance of with those of specified priors (Gamma priors). Here, , where k denotes the number of available samples from the PR distribution. By equating the moments of with those of the gamma priors, we derive the following set of equations:
By solving the aforementioned system of equations, the estimated hyper-parameters can be expressed as follows:
We executed the MCMC algorithm 12,000 times for each of the 5000 replications. We then discarded the initial 2000 values during the burn-in period. Given that Markov chains inherently produce samples with autocorrelation, we opted for a thinning strategy, selecting every third variate to achieve uncorrelated samples from the post-burn-in sample pool. As a result, we generated 1000 uncorrelated samples from Markov chains by repeating this thinning process 5000 times.
In the simulation scenario, we present bias values and mean squared errors (MSEs) for the point estimates, along with average lengths (ALs) and corresponding coverage probabilities (CPs) of the approximate confidence intervals. Table 1, Table 2, Table 3 and Table 4 display all results from these simulation schemes. The performance of the point and interval estimations can be itemized as follows:

Table 1.
Some simulation measures from MLE, bootstrap, Bayesian based on SELF, and ELF for parameters of PR distribution based on TRV: , .

Table 2.
Some simulation measures from MLE, bootstrap, Bayesian based on SELF, and ELF for parameters of PR distribution based on TRV: , , .

Table 3.
Some simulation measures from MLE, bootstrap, Bayesian based on SELF, and ELF for parameters of PR distribution based on TRV: , , .

Table 4.
Some simulation measures from MLE, bootstrap, Bayesian based on SELF, and ELF for parameters of PR distribution based on TRV: , , .
- Our observations consistently show reduced biases, MSEs, and ALs as sample sizes increase.
- The CPs mostly align closely with their anticipated 95% level.
- In general, the informative Bayes estimation method outperforms MLE, with the disparity between the two estimators decreasing as the sample size grows. This highlights the Bayesian methods’ advantage for smaller samples.
- In particular, confidence intervals based on the Highest Posterior Density (HPD) method tend to be smaller than those based on the Approximate Confidence Interval (ACI) method, while still providing similar CPs.
- Altering the pre-determined number of failures or stress change time yields comparable performances across all cases, demonstrating the consistent efficiency and productivity of the theoretical findings.
- Increasing the sample size generally leads to improvements in bias, MSE, and the precision of confidence intervals across all methods. This is expected because larger samples provide more information about the population. The number of bootstrap samples m also influences the Bootstrap method’s accuracy and precision, with a higher m usually leading to better estimates.
- changing the stress transition time point affects the estimation, especially for Bayesian estimation under ELF that adjusts based on the distribution’s tail properties. Different values can lead to variations in bias and MSE, suggesting the importance of choosing an appropriate value for accurate estimation.
6. The Optimal Stress Change Time and Sensitivity Analysis
In this section, we describe an optimal method based on asymptotic variances in maximum likelihood estimators. The inverse Fisher information matrix’s diagonals can be used to compute the parameters’ asymptotic variances. In this section, we used the sum of coefficients of variations (SVCs) as the optimal function instead of the sum of parameter variances, as recommended and implemented by Samanta et al. ([29,30]). Samanta et al. [29] proposed a method to calculate an optimal solution by minimizing the predicted value of the SVC. Since the sum of variances can be calculated using the variance of any specific parameter if the parameter values are on a different scale. That is why we employed the expected value of the SVC by maximizing , where
where is the element in the main diagonal of the inverse Fisher information matrix that was described by Equation (22). However, the closed forms of the parameters’ posterior variances may be imprecisely estimated. Samanta et al. [30] recommend adopting the Gibbs sampling technique for computation.
- Step 1: Obtain the samples , and using given , n, r and parameter values.
- Step 2: The objective function is calculated.
- Step 3: For N times, repeat Step 1 to Step 2, and obtain .
- Step 4: The median of the objective functions is obtained and applied to .
- Step 5: For all possible values of repeat Step 1 to Step 4.
- Step 6: The optimal for which is the minimum is obtained.
Optimal stress change time values, indicated by are determined for given , and for and are reported in Table 5.

Table 5.
Optimal stress change time for different sample sizes and parameter values by SVC .
From Table 5, it is evident that the optimal stress change times, denoted as , fall within the range of 0.6 to 0.9 for the first parameter set. As the range of the generated dataset is not extensive, there is not a significant deviation in the range of in this initial case. It is noticeable that the stress change times utilized in the simulations closely align with the optimal stress change times. Hence, the consistency and effectiveness of the simulation outcomes are contingent upon accurately determining the stress change time.
7. Real Data Examples
In this section, two real data sets are examined for the suitability of the PR model with tampered random variables under the Type-II censoring framework.
7.1. HIV Infection to AIDS
This example discusses the application of a real-life dataset focusing on male individuals and their progression from HIV infections to AIDS over nearly 15 years. According to the United States Center for Disease Control and Prevention, 54% of total diagnosed adult AIDS cases in the U.S. up to 1996 were due to intimate contact with a person who was HIV positive, also, an additional 40% of incident cases occurred in that same year. A subset of the 54% who also engaged in injection drug use accounted for an additional 7% of cumulative and 5% of incident cases in 1996. These data were collected during the era of antiretroviral combined therapy in 1996. For further background information, readers are directed to studies by Dukers et al. [31] and Xiridou et al. [32], while Putter et al. [33] and Geskus et al. [34] cite this dataset as an example for competing risk analysis. The dataset encompasses instances where some patients either remained uninfected or their outcomes were censored in the study.
We focused on a pre-determined number of failures, setting r as 150 from a complete dataset of . We also examined stress change times: . For clarity, we present the competing risk data as follows in Table 6, where the black color is and the gold color is .

Table 6.
Data from HIV Infection to AIDS dataset.
Table 7 showcases the MLE alongside various fit metrics for the HIV Infection to AIDS dataset, utilizing both the baseline model and SSLT as complete datasets. The analysis derived from Table 7 indicates an adequate fit of the model to the data, evidenced by a Kolmogorov–Smirnov P-value (KSPV) exceeding . Furthermore, the table provides a range of fit indices, including the Consistent Akaike Information Criterion (CAIC), Akaike Information Criterion (AIC), Bayesian Information Criterion (BIC), and Hannan–Quinn Information Criterion (HQIC), all of which serve as measures of goodness-of-fit.

Table 7.
MLE and different measures of HIV Infection to AIDS data.
Table 8 presents the maximum likelihood and Bayesian point estimation in addition to the interval estimates for the PR parameters derived from step-stress life testing using the Tampered Random Variable model. Table 8 presents a reliability analysis that evaluates the reliability function of various models through maximum likelihood and Bayesian methods for estimating parameters. The models analyzed include those with a risk factor from cause I, from cause II, and both under standard conditions, followed by an examination under an accelerated framework. Additionally, the reliability of the TRV model is analyzed in the context of two competing risk factors. The findings suggest that the TRV model exhibits the greatest reliability among the models assessed, underscoring the robustness of our proposed model. Figure 1 depicts the likelihood profile for the PR parameters based on SSLT under the TRV model which indicates the existence of the maximum value for the log-likelihood function. Figure 2 illustrates the trace plots and marginal posterior probability density functions of the parameters for the PR distribution, employing SSLT under the TRV model, as obtained via Bayesian estimation.

Table 8.
MLE and Bayesian estimation for the parameters of PR based on SSLT under TRV.
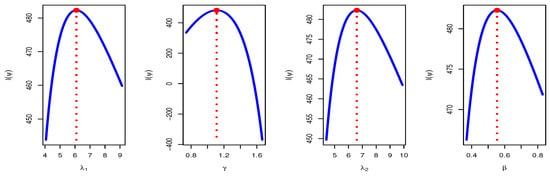
Figure 1.
Likelihood profile (blue line) for parameters of PR based on SSLT under TRV model with the maximum likelihood estimation (red dot): HIV infection to AIDS data.
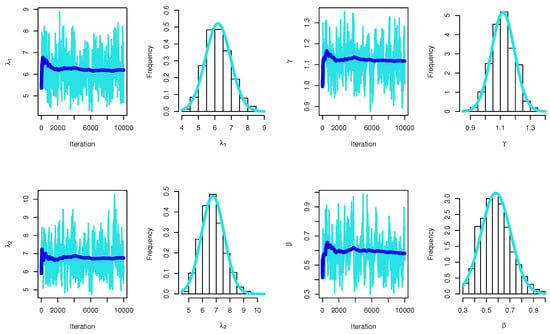
Figure 2.
MCMC plots for parameters of PR based on SSLT under TRV model for HIV Infection to AIDS data.(The blue color indicates the convergence line).
7.2. Electrical Appliances Data
The real-world dataset analyzed in reference [35] (p. 441) examines 36 small electronic components subjected to an automated life test, where failures are categorized into 18 types. However, out of the 33 identified failures, only seven modes were observed, with modes 6–9 recurring more than twice. Mode 9 failure is particularly significant. Consequently, the dataset is categorized into two failure causes, c = 0 (mode 9 failure) and c = 1 (all other modes). The provided data presents the failure times in sequence along with the respective cause of each failure, the stress change time is selected to be as detailed in Table 9.

Table 9.
Electrical appliances data.
Table 10 discusses MLE and different measures used for the electrical appliances data in baseline model and SSLT model as complete data. From the results in Table 10, we note that the data are fitting of this model where the KSPV is greater than 0.05. Also, some different measures have been obtained as CAIC, AIC, BIC goodness-of-ft measures, and HQIC.

Table 10.
MLE and different measures for electrical appliances data.
Table 11 presents the maximum likelihood and Bayesian point estimation in addition to the interval estimates for the PR parameters derived from step-stress life testing using the Tampered Random Variable model for the electrical appliances data. Similar to the discussion of reliability analysis in the first data set in Table 8, the reliability analysis presented in Table 11 indicates that the TRV model outperformed the other models. Figure 3 depicts the likelihood profile of PR parameters based on SSLT under the TRV model for electrical appliances data. From Figure 3, we can conclude that the parameters of PR distribution based on SSLT under TRV have maximum value for the log-likelihood function for electrical appliances data. Figure 4 shows the trace plots and marginal posterior probability density functions of the parameters for the PR distribution based on SSLT under the TRV model, derived through Bayesian estimation for the electrical appliances data.

Table 11.
MLE and Bayesian estimation for the parameters of PR based on SSLT under TRV: electrical appliances data.
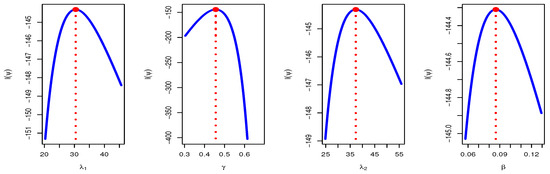
Figure 3.
Likelihood profile (blue line) for parameters of PR based on SSLT under TRV model with the maximum likelihood estimation (red dot): electrical appliances data.
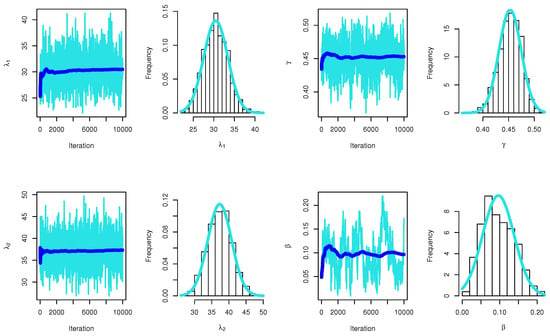
Figure 4.
MCMC plots for parameters of PR based on SSLT under TRV model: electrical appliances (The blue color indicates the convergence line).
8. Conclusions
In conclusion, this work has significantly contributed to the field of reliability engineering through the application of the Tampered Random Variable (TRV) model within the step-stress life testing (SSLT) framework, particularly focusing on the Power Rayleigh distribution in the context of competing risks. By integrating TRV with SSLT under such complex scenarios, the study has addressed critical gaps in current research, particularly the various applications of TRV modeling in competing risk analyses.
The methodological advancements presented in this paper, including the use of maximum likelihood estimation and the Bayesian methods for inferential analysis, as well as Monte Carlo simulations for estimator performance evaluation, represent a robust approach to understanding and improving product reliability under varied stress conditions. These techniques have been validated through empirical analysis of real-world datasets from the medical sector, regarding AIDS infection, and the electrical engineering domain, focusing on electronic component failures. The reliability evaluations underscore the model’s empirical suitability and the potential for broader application.
Furthermore, the study’s exploration of Type-II censoring schemes as a solution to information shortage in lifetime experiments highlights the practical value of the research, offering other options for more cost-effective and efficient testing methodologies. The comparison of TRV modeling with other established models (CEM and TFR) within a competing risks framework not only clarifies the conditions under which these models converge but also showcases the unique advantages of TRV in handling complex, multi-step-stress situations and discrete or multivariate lifetime data.
The comprehensive analysis and the resulting insights into model precision, reliability, and risk management presented in this study provide a solid foundation for future research in this area. It opens up new ways for the development of more accurate and dependable models, enhancing the decision making process and risk management strategies in the medical, industrial, and mechanical domains.
Author Contributions
Conceptualization, H.H.A.; Methodology, H.H.A. and D.A.R.; Software, E.M.A.; Validation, D.A.R.; Formal analysis, H.H.A., E.M.A. and D.A.R.; Investigation, H.H.A. and D.A.R.; Resources, E.M.A.; Data curation, E.M.A.; Writing—original draft, H.H.A. and D.A.R.; Writing—review and editing, D.A.R. and H.H.A.; Funding acquisition, H.H.A. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Deanship of Scientific Research, Vice Presidency for Graduate Studies and Scientific Research, King Faisal University, Saudi Arabia, Grant No. [GrantA071].
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Xu, A.; Wang, B.; Zhu, D.; Pang, J.; Lian, X. Bayesian reliability assessment of permanent magnet brake under small sample size. IEEE Trans. Reliab. 2024; early access. [Google Scholar] [CrossRef]
- Wang, W.; Cui, Z.; Chen, R.; Wang, Y.; Zhao, X. Regression analysis of clustered panel count data with additive mean models. Stat. Pap. 2023, 1–22. [Google Scholar] [CrossRef]
- Zhou, S.; Xu, A.; Tang, Y.; Shen, L. Fast Bayesian inference of reparameterized gamma process with random effects. IEEE Trans. Reliab. 2024, 73, 399–412. [Google Scholar] [CrossRef]
- Sedyakin, N. On one physical principle in reliability theory. Techn. Cybern. 1966, 3, 80–87. [Google Scholar]
- Nelson, W. Accelerated life testing-step-stress models and data analyses. IEEE Trans. Reliab. 1980, 29, 103–108. [Google Scholar] [CrossRef]
- Bhattacharyya, G.; Soejoeti, Z. A tampered failure rate model for step-stress accelerated life test. Commun. Stat.-Theory Methods 1989, 18, 1627–1643. [Google Scholar] [CrossRef]
- Madi, M.T. Multiple step-stress accelerated life test: The tampered failure rate model. Commun. Stat.-Theory Methods 1993, 22, 295–306. [Google Scholar] [CrossRef]
- Goel, P.K. Some Estimation Problems in the Study of Tampered Random Variables; Technical Report No. 50; Department of Statistics, Carnegie-Mellon University: Pittsburgh, PA, USA, 1971; p. 2436. [Google Scholar]
- DeGroot, M.H.; Goel, P.K. Bayesian estimation and optimal designs in partially accelerated life testing. Nav. Res. Logist. Q. 1979, 26, 223–235. [Google Scholar] [CrossRef]
- Khan, M.A.; Aslam, M. Statistical inferences under step stress partially accelerated life testing based on multiple censoring approaches using simulated and real-life engineering data. Sci. Rep. 2020, 10, 1–18. [Google Scholar] [CrossRef]
- Sultana, F.; Dewanji, A. Tampered random variable modeling for multiple step-stress life test. Commun. Stat.-Theory Methods 2021, 52, 5387–5406. [Google Scholar] [CrossRef]
- Sultana, F.; Çetinkaya, Ç.; Kundu, D. Step-stress Life-testing under Tampered Random Variable Modeling for Weibull Distribution in Presence of Competing Risk Data. Qual. Reliab. Eng. 2023; accepted paper. [Google Scholar] [CrossRef]
- Ramadan, D.A.; Almetwally, E.M.; Tolba, A.H. Statistical inference to the parameter of the Akshaya distribution under competing risks data with application HIV infection to aids. Ann. Data Sci. 2023, 10, 1499–1525. [Google Scholar] [CrossRef]
- Tolba, A.H.; Almetwally, E.M.; Sayed-Ahmed, N.; Jawa, T.M.; Yehia, N.; Ramadan, D.A. Bayesian and non-Bayesian estimation methods to independent competing risks models with type II half logistic weibull sub-distributions with application to an automatic life test. Therm. Sci. 2022, 26, 285–302. [Google Scholar] [CrossRef]
- Rosaiah, K.; Kantam, R.R.L. Acceptance sampling based on the inverse Rayleigh distribution. Econ. Qual. Control 2005, 20, 277–286. [Google Scholar] [CrossRef]
- Merovci, F. Transmuted Rayleigh distribution. Aust. J. Stat. 2013, 42, 21–31. [Google Scholar] [CrossRef]
- Cordeiro, G.M.; Cristino, C.T.; Hashimoto, E.M.; Ortega, E.M. The beta generalized Rayleigh distribution with applications to lifetime data. Stat. Pap. 2013, 54, 133–161. [Google Scholar] [CrossRef]
- Ahmad, A.; Ahmad, S.P.; Ahmed, A. Transmuted inverse Rayleigh distribution: A generalization of the inverse Rayleigh distribution. Math. Theory Model 2014, 4, 90–98. [Google Scholar]
- Gomes, A.E.; da-Silva, C.Q.; Cordeiro, G.M.; Ortega, E.M. A new lifetime model: The Kumaraswamy generalized Rayleigh distribution. J. Stat. Comput. Simul. 2014, 84, 290–309. [Google Scholar] [CrossRef]
- Nofal, Z.M.; Abd El Hadi, N.E. Exponentiated transmuted generalized Raleigh distribution: A new four-parameter Rayleigh distribution. Pak. J. Stat. Oper. Res. 2015, 11, 115–134. [Google Scholar]
- Iriarte, Y.A.; Vilca, F.; Varela, H.; Gomez, H.W. Slashed generalized Rayleigh distribution. Commun. Stat.-Theory Methods 2017, 46, 4686–4699. [Google Scholar] [CrossRef]
- El-Sherpieny, E.S.A.; Almetwally, E.M.; Muse, A.H.; Hussam, E. Data analysis for COVID-19 deaths using a novel statistical model: Simulation and fuzzy application. PLoS ONE 2023, 18, e0283618. [Google Scholar] [CrossRef]
- Haj Ahmad, H.; Bdair, O.M.; Naser, M.F.M.; Asgharzadeh, A. The rayleigh lindley distribution: A new generalization of rayleigh distribution with physical applications. Rev. Investig. Oper. 2023, 44, 205–222. [Google Scholar]
- Shen, Z.; Alrumayh, A.; Ahmad, Z.; Abu-Shanab, R.; Al-Mutairi, M.; Aldallal, R. A new generalized Rayleigh distribution with analysis to big data of an online community. Alex. Eng. J. 2022, 61, 11523–11535. [Google Scholar] [CrossRef]
- Mahmoud, M.; Kilany, N.; El-Refai, L. Inference of the lifetime performance index with power Rayleigh distribution based on progressive first-failure–censored data. Qual. Reliab. Eng. Int. 2020, 36, 1528–1536. [Google Scholar] [CrossRef]
- Tierney, L. Markov chains for exploring posterior distributions. Ann. Stat. 1994, 22, 1701–1728. [Google Scholar] [CrossRef]
- Balakrishnan, N.; Sandhu, R.A. Best linear unbiased and maximum likelihood estimation for exponential distributions under general progressive Type-ll censored samples. Indian J. Stat. Ser. B 1996, 58, 1–9. [Google Scholar]
- R Core Team, R. R: A Language and Environment for Statistical Computing; R Core Team, R: Vienna, Austria, 2021. [Google Scholar]
- Samanta, D.; Kundu, D.; Ganguly, A. Order restricted bayesian analysis of a simple step stress model. Sankhya B 2018, 80, 195–221. [Google Scholar] [CrossRef]
- Samanta, D.; Gupta, A.; Kundu, D. Analysis of weibull step-stress model in presence of competing risk. IEEE Trans. Reliab. 2019, 68, 420–438. [Google Scholar] [CrossRef]
- Dukers, N.H.; Renwick, N.; Prins, M.; Geskus, R.B.; Schulz, T.F.; Weverling, G.J.; Coutinho, R.A.; Goudsmit, J. Risk factors for human herpesvirus 8 seropositivity and seroconversion in a cohort of homosexula men. Am. J. Epidemiol. 2000, 151, 213–224. [Google Scholar] [CrossRef]
- Xiridou, M.; Geskus, R.; De Wit, J.; Coutinho, R.; Kretzschmar, M. The contribution of steady and casual partnerships to the incidence of HIV infection among homosexual men in Amsterdam. Aids 2003, 17, 1029–1038. [Google Scholar] [CrossRef]
- Putter, H.; Fiocco, M.; Geskus, R.B. Tutorial in biostatistics: Competing risks and multi-state models. Stat. Med. 2007, 26, 2389–2430. [Google Scholar] [CrossRef]
- Geskus, R.B.; González, C.; Torres, M.; Del Romero, J.; Viciana, P.; Masiá, M.; Blanco, J.R.; Iribarren, M.; De Sanjosé, S.; Hernández-Novoa, B.; et al. Incidence and clearance of anal high-risk human papillomavirus in HIV-positive men who have sex with men: Estimates and risk factors. Aids 2016, 30, 37. [Google Scholar] [CrossRef] [PubMed]
- Lawless, J.F. Statistical Models and Methods for Lifetime Data; John Wiley and Sons: New York, NY, USA, 2011. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).