Hyers–Ulam Stability of 2D-Convex Mappings and Some Related New Hermite–Hadamard, Pachpatte, and Fejér Type Integral Inequalities Using Novel Fractional Integral Operators via Totally Interval-Order Relations with Open Problem

Abstract

The aim of this paper is to introduce a new type of two-dimensional convexity by using total-order relations. In the first part of this paper, we examine the Hyers–Ulam stability of two-dimensional convex mappings by using the sandwich theorem. Our next step involves the development of Hermite–Hadamard inequality, including its weighted and product forms, by using a novel type of fractional operator having non-singular kernels. Moreover, we develop several nontrivial examples and remarks to demonstrate the validity of our main results. Finally, we examine approximate convex mappings and have left an open problem regarding the best optimal constants for two-dimensional approximate convexity.

1. Introduction

Fractional calculus is a branch of mathematical analysis that generalizes the concept of differentiation and integration to non-integer orders. This theory originated from a correspondence exchange between Leibniz and L’Hopital, where a question was posed about the interpretation of an order $\frac{1}{2}$ derivative. Many famous mathematicians dedicated themselves to the study of fractional calculus during this period, including Lagrange, Lacroix, Fourier, Laplace, Abel, Liouville, and Riemann. It was discovered at the end of the 20th century that fractional calculus was capable of expressing natural phenomena more precisely than ordinary calculus, making it useful for describing real-world systems. Several applications have been found in physics [1], chemistry [2], engineering [3], biology, [4] and economics [5,6].

Mathematical inequalities involving fractional integrals play a significant role in various fields of mathematics as well as their applications, including analysis, differential equations, and probability theory. These types of inequalities are important for understanding many mathematical models and systems. Integral inequalities in convex analysis typically refer to integrals of convex functions over certain intervals or domains. These inequalities relate the integral of a convex function to other values, and they commonly offer bounds or estimates that are useful in a number of mathematical applications.

The concept of convex mapping can be applied to many different mathematical structures, including topological spaces, function spaces, metric spaces, and many others. Generalized convexity adds certain modifications to conventional convex mappings, allowing them to support a wider range of sets and functions. Following are some recently introduced classes of generalized convex mappings: $\mathtt{p}$-convex, harmonic convex, exponentially convex, Godunova–Levin, preinvexity, $({\mathtt{h}}_{\mathtt{1}},{\mathtt{h}}_{\mathtt{2}})$-convex, coordinated convex, log-convex, and many more (see refs. [7,8,9]). The Hermite–Hadamard inequality has been interpreted in various ways by different authors by using these novel classes. The Inequality of Hermite and Hadamard was introduced by two French mathematicians, Charles Hermite (1822–1901) and Jacques Salomon Hadamard (1865–1963). C. Hermite and J. S. Hadamard contributed greatly to the field of mathematics in the areas of number theory, complex analysis, and much more. To learn more about their contributions, see [10,11]. The well known Hermite–Hadamard inequality for convex functions is formulated as follows. Let $\aleph :\mathsf{\Omega }\subseteq \mathsf{R}\to \mathsf{R}$ be a convex function defined on the interval $\mathsf{\Omega }$ with ${\mathsf{\nu }}_1,{\mathsf{\nu }}_2\in \mathsf{\Omega }.$ Then, the following inequality holds:

$$\aleph \left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2}\right)\le \frac{1}{{\mathsf{\nu }}_2-{\mathsf{\nu }}_1}{\int }_{{\mathsf{\nu }}_1}^{{\mathsf{\nu }}_2}\aleph \left(\mathsf{\theta }\right)\mathtt{d}\mathsf{\theta }\le \frac{\aleph \left({\mathsf{\nu }}_1\right)+\aleph \left({\mathsf{\nu }}_2\right)}{2}.$$

(1)

Thus, if a function is convex, its weighted average value at the endpoints will equal or exceed its value at the midpoint of any interval in a set of real numbers. A large number of different fields of mathematics and economics use the Hermite–Hadamard inequality, but convexity also plays an important role. In economics, for instance, the Hermite–Hadamard inequality is used to prove the existence and uniqueness of some economic models (such as general equilibrium models or firm behavior models). The Hermite–Hadamard inequality has many applications in information theory, such as the study of error-correcting codes. For more detailed applications of the Hermite–Hadamard inequality, see [12].

The main purpose of the bidimensional convex function is that every convex mapping is convex over its coordinates. Furthermore, there exists a bidimensional convex function that is not convex (see, for example, [13]). In [14], the following Hermite–Hadamard type inequality was proved for convex functions that are coordinated with the rectangle from the plane ${\mathsf{R}}^2$.

Suppose that a function $\aleph :[{\mathsf{\nu }}_1,{\mathsf{\nu }}_2]\times [{\mathsf{\nu }}_3,{\mathsf{\nu }}_4]\subseteq {\mathsf{R}}^2\to \mathsf{R}$ is convex on coordinates. Then, one has the following inequalities:

$$\begin{array}{c}\aleph \left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2},\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right)\le \frac{1}{2}\left[\frac{1}{{\mathsf{\nu }}_2-{\mathsf{\nu }}_1}{\int }_{{\mathsf{\nu }}_1}^{{\mathsf{\nu }}_2}\aleph \left(\mathtt{x},\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right)\mathtt{dx}+\frac{1}{{\mathsf{\nu }}_4-{\mathsf{\nu }}_3}{\int }_{{\mathsf{\nu }}_3}^{{\mathsf{\nu }}_4}\aleph \left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2},\mathtt{y}\right)\mathtt{dy}\right]\hfill \\ \le \frac{1}{({\mathsf{\nu }}_2-{\mathsf{\nu }}_1)({\mathsf{\nu }}_4-{\mathsf{\nu }}_3)}{\int }_{{\mathsf{\nu }}_1}^{{\mathsf{\nu }}_2}{\int }_{{\mathsf{\nu }}_3}^{{\mathsf{\nu }}_4}\aleph (\mathtt{x},\mathtt{y})\mathtt{dy}\mathtt{dx}\hfill \\ \le \frac{1}{4}\left[\frac{1}{{\mathsf{\nu }}_2-{\mathsf{\nu }}_1}{\int }_{{\mathsf{\nu }}_1}^{{\mathsf{\nu }}_2}\left[\aleph (\mathtt{x},{\mathsf{\nu }}_3)+\aleph (\mathtt{x},{\mathsf{\nu }}_4)\right]\mathtt{dx}+\frac{1}{{\mathsf{\nu }}_4-{\mathsf{\nu }}_3}{\int }_{{\mathsf{\nu }}_3}^{{\mathsf{\nu }}_4}\left[\aleph ({\mathsf{\nu }}_1,\mathtt{y})+\aleph ({\mathsf{\nu }}_2,\mathtt{y})\right]\mathtt{dy}\right]\hfill \\ \le \frac{\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)+\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)+\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)+\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)}{4}.\hfill \end{array}$$

(2)

The Hermite–Hadamard inequality provides a powerful tool for computations involving interval values as well as a means to rigorously estimate a function’s range over intervals. It is particularly useful in applications that require consideration of uncertainty or variability in input values. Taking advantage of its wide range of applications in different disciplines, authors have recently developed mathematical inequalities in the setup of interval-valued $(\mathtt{I}.\mathtt{V})$ mappings, which make use of different types of operators and order relations. Zhao et al. [15], inspired by interval-valued functions, recently demonstrated inequality (2) in the setting of partial-order relations utilizing the classical integral operator. In their study, Alomari and Darus [16] used s-convex monotonic nondecreasing functions in the first sense and s-convex functions of two variables on coordinates and developed a few new bounds on the Hermite–Hadamard inequality. Ozdemir et al. [17] employed m-convex and $(\alpha ,m)$-convex functions of two variables on the coordinates to produce various innovative bounds for the well-known double inequality. Alomari and Darus [18] employed log-convex functions on coordinates to build Hermite–Hadamard inequality and its several new forms. Lai et al. [19] defined $\mathtt{I}.\mathtt{V}$ preinvex mappings on the coordinates and developed the Hermite–Hadamard inequality and its different forms by using interval partial-order relations. Wannalookkhee et al. [20] employed quantum integrals and discovered the Hermite–Hadamard inequality on coordinates, with applications spanning numerous disciplines. As the result of applying quantum integrals, Kalsoom et al. [21] created a Hermite–Hadamard-type inequality associated with generalized pre- and quasi-invex mappings. Akurt et al. [22] introduced new Hermite–Hadamard inequalities by using fractional integral operators with singular kernels that produced two interesting identities for two-variable mappings. Shi et al. [23] employed two different forms of generalized convex mappings to build Hermite–Hadamard and its weighted variant utilizing interval-valued mappings. Afzal et al. [24] proposed the idea of Godunova–Levin functions in harmonic terms and derived some novel bounds of the Hermite–Hadamard inequality and its discrete Jensen version. In this paper, we mainly deal with the center-radius-order relations. Some recent advancements related to these concepts are presented in light of other generalized classes of convex mappings. In 2014, authors in [25] introduced the idea of total $\mathtt{CR}$-order utilizing the interval’s midpoint and radius, which is a complete order relation. In 2020, Rahman [26] explored the nonlinear constrained optimization issue using $\mathtt{CR}$-order and defined the $\mathtt{CR}$-convex mapping. Inspired by these results, Liu et al. [27,28] originally used two distinct types of convex mappings, namely log-convex and harmonic convex, to establish a connection with the Hermite–Hadamard inequality. As part of their recent work, Afzal et al. [29,30,31,32] used first-center and radius-order to extend $\mathtt{h}$-Godunova–Levin results to a more generalized class called $({\mathtt{h}}_{\mathtt{1}},{\mathtt{h}}_{\mathtt{2}})$-Godunova–Levin functions and harmonic $\mathtt{h}$-Godunova–Levin to harmonic $({\mathtt{h}}_{\mathtt{1}},{\mathtt{h}}_{\mathtt{2}})$-Godunova–Levin functions. Sahoo et al. [33,34] employed classical and Riemann–Liouville fractional integral operators and used center- and radius-order relations to provide new bounds for Hermite–Hadamard and its several extended forms. We refer to these works for more recent developments about similar conclusions using various other kinds of convex mappings and integral operators (see Refs. [35,36,37,38,39,40]). The Ulam stability problem, first posed by Ulam [41] in 1940, presents an open problem relating to approximate homomorphisms of groups. Consider two metric groups ${\mathtt{H}}_{\mathtt{1}}$ and ${\mathtt{H}}_{\mathtt{2}}$, and consider a non-negative mapping $\aleph :{\mathtt{H}}_{\mathtt{1}}\to {\mathtt{H}}_{\mathtt{2}}$ with metric $\mathtt{d}(·,·)$ such that

$$\mathtt{d}(\aleph \left({\mathsf{\nu }}_1{\mathsf{\nu }}_2\right),\aleph \left({\mathsf{\nu }}_1\right)\aleph \left({\mathsf{\nu }}_2\right))\le \mathsf{ϵ},{\mathsf{\nu }}_1,{\mathsf{\nu }}_2\in {\mathtt{H}}_{\mathtt{1}}.$$

Is there a group homomorphism $\mathtt{h}$ and ${\delta }_{\mathsf{ϵ}}>0$ such that $\mathtt{d}(\aleph \left({\mathsf{\nu }}_1\right),\mathtt{h}\left({\mathsf{\nu }}_1\right))\le {\delta }_{\mathsf{ϵ}},$${\mathsf{\nu }}_1\in {\mathtt{H}}_{\mathtt{1}}?$ A first assertion, essentially due to Hyers [42], is the following one, which answers Ulam’s question.

Theorem 1. 

Let $\mathtt{G}$ be a additive semigroup, $\mathtt{X}$ be a Banach function space, $\mathsf{ϵ}\ge 0$, and $\aleph :\mathtt{G}\to \mathtt{X}$ satisfy the following inequality:

$$\parallel \aleph ({\mathsf{\nu }}_1+{\mathsf{\nu }}_2)-\aleph \left({\mathsf{\nu }}_1\right)-\aleph \left({\mathsf{\nu }}_2\right)\parallel \le \mathsf{ϵ},forall{\mathsf{\nu }}_1,{\mathsf{\nu }}_2\in \mathtt{G};$$

then, there exists a unique function $\gimel :\mathtt{G}\to \mathtt{X}$ satisfying $\gimel ({\mathsf{\nu }}_1+{\mathsf{\nu }}_2)=\gimel \left({\mathsf{\nu }}_1\right)+\gimel \left({\mathsf{\nu }}_2\right)$ and for which

$$\parallel \aleph \left({\mathsf{\nu }}_1\right)-\gimel \left({\mathsf{\nu }}_1\right)\parallel \le \mathsf{ϵ},forall{\mathsf{\nu }}_1\in \mathtt{G}.$$

Stability problems have been studied for numerous functional equations, including differential equations, approximation convexity, dynamical systems, variational problems, etc. This topic was probably introduced by Hyers and Ulam [43] in 1952, who introduced and investigated $\mathsf{ϵ}$-convex functions. If is a convex subset of a real linear space $\mathtt{Y}$ and $\mathsf{ϵ}$ is a nonnegative number, then a mapping $\aleph :\mathsf{\Omega }\to \mathsf{R}$ is called $\mathsf{ϵ}$-convex if

$$\begin{array}{cc}\hfill \aleph \left({\mathtt{r}}_{\mathtt{1}}{\mathsf{\nu }}_1+(1-{\mathtt{r}}_{\mathtt{1}}){\mathsf{\nu }}_2\right)& \le {\mathtt{r}}_{\mathtt{1}}\aleph \left({\mathsf{\nu }}_1\right)+(1-{\mathtt{r}}_{\mathtt{1}})\aleph \left({\mathsf{\nu }}_2\right)+\mathsf{ϵ},({\mathsf{\nu }}_1,{\mathsf{\nu }}_2)\in \mathsf{\Omega },{\mathtt{r}}_{\mathtt{1}}\in [0,1].\hfill \end{array}$$

The topic of approximate convexity and its connection to other generalized convex mappings is rarely discussed, but a few recent advancements have been discussed by several authors. Using harmonically convex mappings, Bracamonte et al. [44] discussed the sandwich theorem and Hyers–Ulam stability results. Forti [45] discussed Hyers–Ulam stability of functional equations with applications spanning varied disciplines. Ernst and Théra [46] investigated the Ulam stability of a set of $\mathsf{ϵ}$-approximate proper lower semicontinuous mappings. In regard to the infinite version of the Hyers–Ulam stability theorem, Emanuele Casini and Pierluigi Papinia [47] provided an interesting counterexample. Bracamonte et al. [48] defined an approximate convexity result for reciprocally strongly convex functions; specifically, they proved a Hyers–Ulam stability result for this class of functions. Flavia Corina [49] used set-valued mappings to explore convexity and its associated sandwich theorem, among other fascinating properties. Dilworth et al. [50] discussed the best optimal constants in a Hyers and Ulam theorem using extremal approximate convex functions. To view further comparable findings about Hyers–Ulam stability and optimum constants, please see Refs. [51,52,53,54,55,56].

Novelty and Significance

The key concepts in adjusting inequalities within interval mappings are “order relations“ and “convex functions“. However, authors have recently used the classical Riemann integral operator and a partial-order relation “${\subseteq }_{\mathtt{p}}$“ that does not generalize the results for real-value function inequalities. In reference [57], the authors demonstrate with Example 3 that, when the interval mapping is warped, this order relation is not the famous settled Milne type inequality while setting up interval-valued functions. To address this issue, the authors introduce a new order relation called the total order relation, often known as the center-radius order “$\mathtt{CR}$,“ which enables us to easily compare intervals and may be considered an extension of the standard order “≤“. Furthermore, this is the first time we are exploring the stability of $\mathcal{2}\mathcal{D}$-convex mappings using the Hyers–Ulam technique with the aid of the sandwich theorem. Furthermore, this type of order relation is first coupled with two-dimensional convex mappings. Using these new conceptions, we established three well-known inequalities: Hermite–Hadamard, Pachpatte’s, and Fejér-type integral inequalities. To demonstrate the beauty of this order relation and novel fractional operators, we show with remarks that, after different setups, we obtain various previous results, and all of the previously developed results using different operators and order relations are special cases of this type of new operator and order relationship. Inspiration from strong relevant literature concerning produced results, in particular publications [15,44,58], urges us to construct new and better versions of three well-known inequalities with applications. This article is structured as follows. In Section 2, we revisit some interval and fractional calculus concepts that are essential for proceeding with this article. In Section 3, we discuss the Hyers–Ulam stability of two-dimensional convex mappings. In Section 4, we construct a novel version of the Hermite–Hadamard inequality together with its newly weighted and product forms of inequalities. In Section 5, we discuss the findings and draw conclusions. Lastly, in Section 6, we provide a new definition for two-dimensional approximation convexity and leave an open problem about the best optimal constants.

2. Preliminaries

This section reviews the fundamentals of interval analysis, including definitions, notations, properties, and findings. Additionally, we start this section by fixing a few notations that are used throughout the paper:

• ${{\mathsf{R}}_{\mathtt{i}}}^{+}$: a collection of positive intervals in $\mathsf{R}$;
• ${{\mathsf{R}}_{\mathtt{i}}}^{-}$: a collection of negative intervals in $\mathsf{R}$;
• ${\mathsf{R}}_{\mathtt{i}}$: a collection of both positive and negative intervals in $\mathsf{R}$;
• $\underline{\aleph }=\overline{\aleph }$: interval mapping degenerated;
• ⊆: partial-order relation;
• ≤: standard-order relation;
• ${⪯}_{\mathtt{CR}}$: total-order relation.

2.1. Interval Calculus

The pack of all compact subsets of $\mathsf{R}$ in one-dimensional Euclidean space is denoted by ${{\mathsf{R}}_{\mathtt{i}}}^{+}$.

$${\mathsf{R}}_{\mathtt{i}}=\{[{\mathsf{\nu }}_1,{\mathsf{\nu }}_2]:{\mathsf{\nu }}_1,{\mathsf{\nu }}_2\in \mathsf{R}and{\mathsf{\nu }}_1\le {\mathsf{\nu }}_2\}$$

The Hausdorff metric in ${\mathsf{R}}_{\mathtt{i}}$ is defined as follows:

$$\begin{array}{c}\hfill \mathtt{H}({\mathsf{\nu }}_1,{\mathsf{\nu }}_2)=sup\{\mathtt{d}({\mathsf{\nu }}_1,{\mathsf{\nu }}_2),\mathtt{d}({\mathsf{\nu }}_2,{\mathsf{\nu }}_1)\},\end{array}$$

(3)

where $\mathtt{d}({\mathsf{\nu }}_1,{\mathsf{\nu }}_2)={sup}_{\mathtt{a}\in {\mathsf{\nu }}_1}\mathtt{d}(\mathtt{a},{\mathsf{\nu }}_2)$, and $\mathtt{d}(\mathtt{a},{\mathsf{\nu }}_2)={min}_{\mathtt{b}\in {\mathsf{\nu }}_2}\mathtt{d}(\mathtt{a},\mathtt{b})={min}_{\mathtt{b}\in {\mathsf{\nu }}_2}|\mathtt{a}-\mathtt{b}|$.

Remark 1. 

According to (3), the Hausdorff metric has a parallel representation as follows:

$$\mathtt{H}([\underline{{\mathsf{\nu }}_1},\overline{{\mathsf{\nu }}_1}],[\underline{{\mathsf{\nu }}_2},\overline{{\mathsf{\nu }}_2}])=sup\left\{\right|\underline{{\mathsf{\nu }}_1}-\underline{{\mathsf{\nu }}_2}|,|\overline{{\mathsf{\nu }}_1}-\overline{{\mathsf{\nu }}_2}\left|\right\}.$$

This is referred to as the Moore metric in interval space.

It is generally known that the metric space $\left({\mathsf{R}}_{\mathtt{i}},\mathtt{H}\right)$ is complete. Next, we define the Minkowski sum and scalar multiplication on ${\mathsf{R}}_{\mathtt{i}}$ using

$$\mathtt{A}+\mathtt{B}=\{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2\mid {\mathsf{\nu }}_1\in \mathtt{A},{\mathsf{\nu }}_2\in \mathtt{B}\}\mathrm{and}\gamma \mathtt{A}=\{\gamma {\mathsf{\nu }}_1\mid {\mathsf{\nu }}_1\in \mathtt{A}\}.$$

For instance, if $\mathtt{A}=[\underline{{\mathsf{\nu }}_1},\overline{{\mathsf{\nu }}_1}]$ and $\mathtt{B}=[\underline{{\mathsf{\nu }}_2},\overline{{\mathsf{\nu }}_2}]$ are two bounded intervals, the difference is defined as follows:

$$\mathtt{A}-\mathtt{B}=[\underline{{\mathsf{\nu }}_1}-\overline{{\mathsf{\nu }}_2},\overline{{\mathsf{\nu }}_1}-\underline{{\mathsf{\nu }}_2}],$$

with the product

$$\mathtt{A}·\mathtt{B}=[min\{\underline{{\mathsf{\nu }}_1{\mathsf{\nu }}_2},\underline{{\mathsf{\nu }}_1}\overline{{\mathsf{\nu }}_2},\overline{{\mathsf{\nu }}_1}\underline{{\mathsf{\nu }}_2},\overline{{\mathsf{\nu }}_1}\overline{{\mathsf{\nu }}_2}\},sup\{\underline{{\mathsf{\nu }}_1{\mathsf{\nu }}_2},\underline{{\mathsf{\nu }}_1}\overline{{\mathsf{\nu }}_2},\overline{{\mathsf{\nu }}_1}\underline{{\mathsf{\nu }}_2},\overline{{\mathsf{\nu }}_1}\overline{{\mathsf{\nu }}_2}\}]$$

and the division

$$\frac{\mathtt{A}}{\mathtt{B}}=\left[min\left\{\frac{\underline{{\mathsf{\nu }}_1}}{\underline{{\mathsf{\nu }}_2}},\frac{{\mathsf{\nu }}_1}{\overline{{\mathsf{\nu }}_2}},\frac{\overline{{\mathsf{\nu }}_1}}{\underline{{\mathsf{\nu }}_2}},\frac{\overline{{\mathsf{\nu }}_1}}{\overline{{\mathsf{\nu }}_2}}\right\},sup\left\{\frac{\underline{{\mathsf{\nu }}_1}}{\overline{{\mathsf{\nu }}_2}},\frac{\underline{{\mathsf{\nu }}_1}}{\overline{{\mathsf{\nu }}_2}},\frac{\overline{{\mathsf{\nu }}_1}}{\underline{{\mathsf{\nu }}_2}},\frac{\overline{{\mathsf{\nu }}_1}}{\overline{{\mathsf{\nu }}_2}}\right\}\right],$$

where $0\notin \mathtt{B}$. The order relation that is employed in this note is defined by Bhunia and Samanta in their work [59], wherein they define the total order relation “$\mathtt{CR}$“.

Definition 1 

(see [29]). The center-radius total-order relation for closed and bounded intervals ${\mathsf{\nu }}_1=[\underline{\mathtt{d}},\overline{\mathtt{d}}]=⟨{\mathtt{d}}_{\mathtt{C}},{\mathtt{d}}_{\mathtt{R}}⟩=⟨\frac{\overline{\mathtt{d}}+\underline{\mathtt{d}}}{2},\frac{\overline{\mathtt{d}}-\underline{\mathtt{d}}}{2}⟩$, ${\mathsf{\nu }}_2=[\underline{\mathtt{e}},\overline{\mathtt{e}}]=⟨{\mathtt{e}}_{\mathtt{C}},{\mathtt{e}}_{\mathtt{R}}⟩=⟨\frac{\overline{\mathtt{e}}+\underline{\mathtt{e}}}{2},\frac{\overline{\mathtt{e}}-\underline{\mathtt{e}}}{2}⟩\in {\mathsf{R}}_{\mathtt{i}}$ are represented as:

$${\mathsf{\nu }}_1{⪯}_{\mathtt{CR}}{\mathsf{\nu }}_2⟺\left\{\begin{array}{cc}{\mathtt{d}}_{\mathtt{c}}<{\mathtt{e}}_{\mathtt{c}},\hfill & \mathit{if}{\mathtt{d}}_{\mathtt{c}}\ne {\mathtt{e}}_{\mathtt{c}};\hfill \\ {\mathtt{d}}_{\mathtt{r}}\le {\mathtt{e}}_{\mathtt{r}},\hfill & \mathit{if}{\mathtt{d}}_{\mathtt{c}}={\mathtt{e}}_{\mathtt{c}}.\hfill \end{array}\right.$$

Definition 2 

(see [30]). Let $\aleph :[{\mathsf{\nu }}_1,{\mathsf{\nu }}_2]\to {\mathsf{R}}_{\mathtt{i}}$ be an interval-valued mapping defined by $\aleph \left({\mathsf{\nu }}_2\right)=[\underline{\aleph }\left(\mathsf{\nu }\right),\overline{\aleph }\left(\mathsf{\nu }\right)].$$\aleph \in {\mathsf{IR}}_{\left([{\mathsf{\nu }}_1,{\mathsf{\nu }}_2]\right)}$ iff $\underline{\aleph }\left(\mathsf{\nu }\right),\overline{\aleph }\left(\mathsf{\nu }\right)\in {\mathsf{R}}_{\left([{\mathsf{\nu }}_1,{\mathsf{\nu }}_2]\right)}$ and

$$\left(\mathsf{IR}\right){\int }_{{\mathsf{\nu }}_1}^{{\mathsf{\nu }}_2}\aleph \left(\mathsf{\nu }\right)\mathsf{d}\mathsf{\nu }=\left[\left(\mathsf{R}\right){\int }_{{\mathsf{\nu }}_1}^{{\mathsf{\nu }}_2}\underline{\aleph }\left(\mathsf{\nu }\right)\mathsf{d}\mathsf{\nu },\left(\mathsf{R}\right){\int }_{{\mathsf{\nu }}_1}^{{\mathsf{\nu }}_2}\overline{\aleph }\left(\mathsf{\nu }\right)\mathsf{d}\mathsf{\nu }\right].$$

Theorem 2 

(see [29]). Let $\aleph ,\zeta :[{\mathsf{\nu }}_1,{\mathsf{\nu }}_2]\to {\mathsf{R}}_{\mathtt{i}}$ be an interval-valued mapping defined by $\zeta =[\underline{\zeta },\overline{\zeta }],\aleph =[\underline{\aleph },\overline{\aleph }].$ If $\aleph \left(\mathsf{\nu }\right){⪯}_{\mathtt{CR}}\zeta \left(\mathsf{\nu }\right)$ for all $\mathsf{\nu }\in [{\mathsf{\nu }}_1,{\mathsf{\nu }}_2]$; then

$${\int }_{{\mathsf{\nu }}_1}^{{\mathsf{\nu }}_2}\aleph \left(\mathsf{\nu }\right)\mathsf{d}\mathsf{\nu }{⪯}_{\mathtt{CR}}{\int }_{{\mathsf{\nu }}_1}^{{\mathsf{\nu }}_2}\zeta \left(\mathsf{\nu }\right)\mathsf{d}\mathsf{\nu }.$$

Interval-Valued Double Integral

A set of numbers ${\{{\mathtt{a}}_{\mathtt{i}-1},{\Im }_{\mathtt{i}},{\mathtt{a}}_{\mathtt{i}}\}}_{i=1}^m$ is called a tagged partition ${\mathtt{P}}^{\prime }$ of $[{\mathsf{\nu }}_1,{\mathsf{\nu }}_2]$ if ${\mathtt{P}}^{\prime }:{\mathsf{\nu }}_1={\eta }_0<{\eta }_1<\cdots <{\eta }_m={\mathsf{\nu }}_2$ with ${\mathtt{a}}_{\mathtt{i}-1}\le {\Im }_{\mathtt{i}}\le {\mathtt{a}}_{\mathtt{i}}$∀$\mathsf{i}=1,2,3,\dots ,\mathtt{m}$. Further, if we consider $\Delta {\mathtt{a}}_{\mathtt{i}}={\mathtt{a}}_{\mathtt{i}}-{\mathtt{a}}_{\mathtt{i}-1},$ then ${\mathtt{P}}^{\prime }$ is said to be $\mathsf{\delta }$-fine. Let $\mathtt{P}(\mathsf{\delta },[{\mathsf{\nu }}_1,{\mathsf{\nu }}_2])$ denote the set of all $\mathsf{\delta }$-fine partitions of $[{\mathsf{\nu }}_1,{\mathsf{\nu }}_2]$; if ${\{{\mathtt{a}}_{\mathtt{i}-1},{\Im }_{\mathtt{i}},{\mathtt{a}}_{\mathtt{i}}\}}_{\mathsf{i}=\mathsf{1}}^{\mathsf{m}}$ is a $\mathsf{\delta }$-fine ${\mathtt{P}}^{\prime }$ of $[{\mathsf{\nu }}_1,{\mathsf{\nu }}_2]$ and ${\{{\mathtt{b}}_{\mathtt{j}-1},{\eta }_{\mathtt{j}},{\mathtt{b}}_{\mathtt{j}}\}}_{\mathtt{j}=\mathtt{1}}^{\mathtt{n}}$ is a $\mathsf{\delta }$-fine ${\mathtt{P}}^{″}$ of $[{\mathsf{\nu }}_3,{\mathsf{\nu }}_4]$, then the rectangles’

$${\Delta }_{i,j}=[{\mathtt{a}}_{\mathtt{i}-1},{\mathtt{a}}_{\mathtt{i}}]\times [{\mathtt{b}}_{\mathtt{j}-1},{\mathtt{b}}_{\mathtt{j}}]$$

partition rectangles of $\Delta =[{\mathsf{\nu }}_1,{\mathsf{\nu }}_2]\times [{\mathsf{\nu }}_3,{\mathsf{\nu }}_4]$ with the points $({\Im }_{\mathtt{i}},{\eta }_{\mathtt{j}})$ are inside the rectangles $[{\mathtt{a}}_{\mathtt{i}-1},{\mathtt{a}}_{\mathtt{i}}]\times [{\mathtt{b}}_{\mathtt{j}-1},{\mathtt{b}}_{\mathtt{j}}].$ Moreover, if $\mathtt{P}(\mathsf{\delta },\Delta )$, we denote the pack of all $\mathsf{\delta }$-fine partitions of Δ with ${\mathtt{P}}^{\prime }\times {\mathtt{P}}^{″}$, where ${\mathtt{P}}^{\prime }\in \mathtt{P}(\mathsf{\delta },[{\mathsf{\nu }}_1,{\mathsf{\nu }}_2])$ and ${\mathtt{P}}^{″}\in \mathtt{P}(\mathsf{\delta },[{\mathsf{\nu }}_3,{\mathsf{\nu }}_4]).$ Let $\Delta {\mathtt{A}}_{\mathtt{i},\mathtt{j}}$ be the area of the ${\Delta }_{\mathtt{i},\mathtt{j}}.$ In each segment of area of ${\Delta }_{\mathtt{i},\mathtt{j}}$ where $1\le \mathsf{i}\le \mathsf{m}$, $1\le \mathsf{j}\le \mathsf{n}$, consider any arbitrary point $({\Im }_{\mathtt{i}},{\eta }_{\mathsf{j}})$, and we obtain

$$\mathtt{S}(\aleph ,\mathtt{P},\mathsf{\delta },\Delta )=\sum _{\mathtt{i}=1}^{\mathtt{m}}\sum _{\mathtt{j}=1}^{\mathtt{n}}\aleph ({\Im }_{\mathtt{i}},{\eta }_{\mathtt{j}})\Delta {\mathtt{A}}_{\mathtt{i},\mathtt{j}}.$$

We call $\mathtt{S}(\aleph ,\mathtt{P},\mathsf{\delta },\Delta )$ an integral sum of ℵ related to $\mathtt{P}\in \mathtt{P}(\mathsf{\delta },\Delta ).$ For further detail, we refer to [15].

Theorem 3. 

Let $\aleph :\Delta \to {\mathsf{R}}_{\mathtt{i}}.$ Then, ℵ is known as $\mathtt{ID}$-integrable on Δ with $\mathtt{ID}$-integral $\mathtt{U}=\left(\mathtt{ID}\right){\int \int }_{\Delta }\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_2)\mathtt{dA}$ if, for any $ϵ>0,$ there exists $\delta >0$ such that

$$\mathtt{d}\left(\mathtt{S}(\aleph ,\mathtt{P},\mathsf{\delta },\Delta ),\mathtt{U}\right)<ϵ$$

for each $\mathtt{P}\in \mathtt{P}(\mathsf{\delta },)$. The set of all $\mathtt{ID}$-integrable mappings on Δ will be represented by ${\mathtt{ID}}_{(\Delta )}.$

Theorem 4. 

Let $\Delta =[{\mathsf{\nu }}_1,{\mathsf{\nu }}_2]\times [{\mathsf{\nu }}_3,{\mathsf{\nu }}_4].$ If $\aleph :\Delta \to {\mathsf{R}}_{\mathtt{i}}$ is $\mathtt{ID}$-integrable on $\Delta ,$ then we have

$$\left(\mathtt{ID}\right){\int \int }_{\Delta }\aleph (\mathtt{x},\mathtt{y})\mathtt{dA}=\left(\mathsf{IR}\right){\int }_{{\mathsf{\nu }}_1}^{{\mathsf{\nu }}_2}\left(\mathsf{IR}\right){\int }_{{\mathsf{\nu }}_3}^{{\mathsf{\nu }}_4}\aleph (\mathtt{x},\mathtt{y})\mathtt{dx}\mathtt{dy}.$$

Example 1. 

Let $\aleph :\Delta =[0,1]\times [1,2]\to {{\mathsf{R}}_{\mathtt{i}}}^{+}$ be defined as

$$({\mathsf{\nu }}_1,{\mathsf{\nu }}_2)=[{\mathsf{\nu }}_1{\mathsf{\nu }}_2,{\mathsf{\nu }}_1+{\mathsf{\nu }}_2];$$

then, $\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_2)$ is integrable on Δ, and $\left(\mathtt{ID}\right){\int \int }_{\Delta }\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_2)\mathtt{dA}=[\frac{3}{4},2].$

Theorem 5 

(see [60]). Suppose that the two mappings $\aleph ,\gimel :[{\mathsf{\nu }}_1,{\mathsf{\nu }}_2]\to$${\mathsf{R}}_{\mathsf{I}}^{+}$ are both interval-valued convex such that $\aleph \left(\mathsf{\nu }\right)=[\underline{\aleph }\left(\mathsf{\nu }\right),\overline{\aleph }\left(\mathsf{\nu }\right)]$ as well as $\gimel \left(\mathsf{\nu }\right)=[\underline{\gimel }\left(\mathsf{\nu }\right),\overline{\gimel }\left(\mathsf{\nu }\right)]$. Then, one has the inclusion relation

$$\begin{array}{cc}\hfill \frac{\alpha }{{\mathsf{\nu }}_2-{\mathsf{\nu }}_1}\left[{\mathtt{J}}_{{{\mathsf{\nu }}_1}^{+}}^{\alpha }\aleph \left(\mathsf{\nu }\right)\gimel \left(\mathsf{\nu }\right)+{\mathtt{J}}_{{{\mathsf{\nu }}_2}^{-}}^{\alpha }\aleph \left(\mathsf{\nu }\right)\gimel \left(\mathsf{\nu }\right)\right]\supseteq & \mathtt{P}({\mathsf{\nu }}_1,{\mathsf{\nu }}_2)\frac{{\mathsf{\theta }}_1^2-2{\mathsf{\theta }}_1+4-\left({\mathsf{\theta }}_1^2+2{\mathsf{\theta }}_1+4\right)e^{-{\mathsf{\theta }}_1}}{{\mathsf{\theta }}_1^3}\hfill \\ \hfill & + \mathtt{Q}({\mathsf{\nu }}_1,{\mathsf{\nu }}_2)\frac{2{\mathsf{\theta }}_1-4+\left(2{\mathsf{\theta }}_1+4\right)e^{-{\mathsf{\theta }}_1}}{{\mathsf{\theta }}_1^3},\hfill \end{array}$$

where

$$\begin{array}{cc}& \mathtt{P}({\mathsf{\nu }}_1,{\mathsf{\nu }}_2)=\aleph \left({\mathsf{\nu }}_1\right)\gimel \left({\mathsf{\nu }}_1\right)+\aleph \left({\mathsf{\nu }}_2\right)\gimel \left({\mathsf{\nu }}_2\right),\hfill \\ & \mathtt{Q}({\mathsf{\nu }}_1,{\mathsf{\nu }}_2)=\aleph \left({\mathsf{\nu }}_1\right)\gimel \left({\mathsf{\nu }}_2\right)+\aleph \left({\mathsf{\nu }}_2\right)\gimel \left({\mathsf{\nu }}_1\right).\hfill \end{array}$$

Theorem 6 

(see [60]). Under the same hypotheses mentioned in Theorem 5, we have the successive inclusion relation:

$$\begin{array}{cc}\hfill 2\aleph \left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2}\right)\gimel \left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2}\right)\supseteq & \frac{1-\alpha }{2\left(1-e^{-{\mathsf{\theta }}_1}\right)}\left[{\mathtt{J}}_{{{\mathsf{\nu }}_1}^{+}}^{\alpha }\aleph \left({\mathsf{\nu }}_2\right)\gimel \left({\mathsf{\nu }}_2\right)+{\mathtt{J}}_{{{\mathsf{\nu }}_2}^{-}}^{\alpha }\aleph \left({\mathsf{\nu }}_1\right)\gimel \left({\mathsf{\nu }}_1\right)\right]\hfill \\ \hfill & +\mathtt{P}({\mathsf{\nu }}_1,{\mathsf{\nu }}_2)\frac{{\mathsf{\theta }}_1-2+\left({\mathsf{\theta }}_1+2\right)e^{-{\mathsf{\theta }}_1}}{{\mathsf{\theta }}_1^2\left(1-e^{-{\mathsf{\theta }}_1}\right)}+\mathtt{Q}({\mathsf{\nu }}_1,{\mathsf{\nu }}_2)\frac{{\mathsf{\theta }}_1^2-2{\mathsf{\theta }}_1+4-\left({\mathsf{\theta }}_1^2+2{\mathsf{\theta }}_1+4\right)e^{-{\mathsf{\theta }}_1}}{2{\mathsf{\theta }}_1^2\left(1-e^{-{\mathsf{\theta }}_1}\right)}.\hfill \end{array}$$

Inspired by the concept of classical integrals in the context of interval-valued mappings, here we propose the following fractional integrals with non-singular kernels.

Definition 3. 

Let $\aleph :[{\mathsf{\nu }}_1,{\mathsf{\nu }}_2]\times [{\mathsf{\nu }}_3,{\mathsf{\nu }}_4]\subset {\mathsf{R}}^2\to {\mathsf{R}}_{\mathtt{i}}$ be a bidimensional interval-valued mapping represented as $\aleph ({\eta }_1,{\eta }_2)=$$[\underline{\aleph }({\eta }_1,{\eta }_2),\overline{\aleph }({\eta }_1,{\eta }_2)]$. The fractional operators having non-singular kernels are represented as ${\mathtt{J}}_{{{\mathsf{\nu }}_1}^{+},{{\mathsf{\nu }}_4}^{+}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2},{\mathtt{J}}_{{{\mathsf{\nu }}_1}^{+},{{\mathsf{\nu }}_4}^{-}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2},{\mathtt{J}}_{{{\mathsf{\nu }}_2}^{-},{{\mathsf{\nu }}_4}^{+}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}$ and ${\mathtt{J}}_{{{\mathsf{\nu }}_2}^{-},{{\mathsf{\nu }}_4}^{-}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}$ of order ${\mathsf{\theta }}_1\in (0,1),{\mathsf{\theta }}_2\in (0,1)$ along with ${\mathsf{\nu }}_1,{\mathsf{\nu }}_4\ge 0$, which are defined as follows:

$$\begin{array}{cc}& {\mathtt{J}}_{{{\mathsf{\nu }}_1}^{+},{{\mathsf{\nu }}_4}^{+}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\aleph (\mathtt{x},\mathtt{y})=\frac{1}{{\mathsf{\theta }}_1{\mathsf{\theta }}_2}{\int }_{{\mathsf{\nu }}_1}^{\mathtt{x}}{\int }_{{\mathsf{\nu }}_4}^{\mathtt{y}}{e}^{-\frac{1-{\mathsf{\theta }}_1}{{\mathsf{\theta }}_1}\left(\mathtt{x}-\mathtt{t}\right)}{e}^{-\frac{1-{\mathsf{\theta }}_2}{{\mathsf{\theta }}_2}\left(\mathtt{y}-\mathtt{s}\right)}\aleph (\mathtt{t},\mathtt{s})\mathtt{ds}\mathtt{dt},\mathtt{x}>{\mathsf{\nu }}_1,\mathtt{y}>{\mathsf{\nu }}_4,\hfill \\ & {\mathtt{J}}_{{{\mathsf{\nu }}_1}^{+},{{\mathsf{\nu }}_4}^{-}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\aleph (\mathtt{x},\mathtt{y})=\frac{1}{{\mathsf{\theta }}_1{\mathsf{\theta }}_2}{\int }_{{\mathsf{\nu }}_1}^{\mathtt{x}}{\int }_{\mathtt{y}}^{{\mathsf{\nu }}_4}{e}^{-\frac{1-{\mathsf{\theta }}_1}{{\mathsf{\theta }}_1}\left(\mathtt{x}-\mathtt{t}\right)}{e}^{-\frac{1-{\mathsf{\theta }}_2}{{\mathsf{\theta }}_2}\left(\mathtt{s}-\mathtt{y}\right)}\aleph (\mathtt{t},\mathtt{s})\mathtt{ds}\mathtt{dt},\mathtt{x}>{\mathsf{\nu }}_1,\mathtt{y}<{\mathsf{\nu }}_4,\hfill \\ & {\mathtt{J}}_{{{\mathsf{\nu }}_2}^{-},{{\mathsf{\nu }}_4}^{+}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\aleph (\mathtt{x},\mathtt{y})=\frac{1}{{\mathsf{\theta }}_1{\mathsf{\theta }}_2}{\int }_{\mathtt{x}}^{{\mathsf{\nu }}_2}{\int }_{{\mathsf{\nu }}_4}^{\mathtt{y}}{e}^{-\frac{1-{\mathsf{\theta }}_1}{{\mathsf{\theta }}_1}(\mathtt{t}-\mathtt{x})}{e}^{-\frac{1-{\mathsf{\theta }}_2}{{\mathsf{\theta }}_2}\left(\mathtt{y}-\mathtt{s}\right)}\aleph (\mathtt{t},\mathtt{s})\mathtt{ds}\mathtt{dt},\mathtt{x}<{\mathsf{\nu }}_2,\mathtt{y}>{\mathsf{\nu }}_4,\hfill \end{array}$$

as well as

$${\mathtt{J}}_{{{\mathsf{\nu }}_2}^{-},{{\mathsf{\nu }}_4}^{-}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\aleph (\mathtt{x},\mathtt{y})=\frac{1}{{\mathsf{\theta }}_1{\mathsf{\theta }}_2}{\int }_{\mathtt{x}}^{{\mathsf{\nu }}_2}{\int }_{\mathtt{y}}^v{e}^{-\frac{1-{\mathsf{\theta }}_1}{{\mathsf{\theta }}_1}(\mathtt{t}-\mathtt{x})}{e}^{-\frac{1-{\mathsf{\theta }}_2}{{\mathsf{\theta }}_2}\left(\mathtt{s}-\mathtt{y}\right)}\aleph (\mathtt{t},\mathtt{s})\mathtt{ds}\mathtt{dt},\mathtt{x}<{\mathsf{\nu }}_2,\mathtt{y}<{\mathsf{\nu }}_4,$$

respectively. We observe that

$$\underset{\begin{array}{c}{\mathsf{\theta }}_1\to 1\\ {\mathsf{\theta }}_2\to 1\end{array}}{lim}{\mathtt{J}}_{{{\mathsf{\nu }}_1}^{+},{{\mathsf{\nu }}_4}^{+}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\aleph (\mathtt{x},\mathtt{y})=\frac{1}{{\mathsf{\theta }}_1{\mathsf{\theta }}_2}{\int }_{{\mathsf{\nu }}_1}^{\mathtt{x}}{\int }_{{\mathsf{\nu }}_4}^{\mathtt{y}}\aleph (\mathtt{t},\mathtt{s})\mathtt{ds}\mathtt{dt}.$$

It is straightforward to provide the consecutive $\mathtt{I}.\mathtt{V}$ fractional integrals in accordance with Definition 3 as follows:

$$\begin{array}{cc}& {\mathtt{J}}_{{{\mathsf{\nu }}_1}^{+}}^{{\mathsf{\theta }}_1}\aleph \left(\mathtt{x},\frac{{\mathsf{\nu }}_4+{\mathsf{\nu }}_3}{2}\right)=\frac{1}{{\mathsf{\theta }}_1}{\int }_{{\mathsf{\nu }}_1}^{\mathtt{x}}{e}^{-\frac{1-{\mathsf{\theta }}_1}{{\mathsf{\theta }}_1}(\mathtt{x}-\mathtt{t})}\aleph \left(\mathtt{t},\frac{{\mathsf{\nu }}_4+{\mathsf{\nu }}_3}{2}\right)\mathtt{dt},\mathtt{x}>{\mathsf{\nu }}_1,\hfill \\ & {\mathtt{J}}_{{{\mathsf{\nu }}_2}^{-}}^{{\mathsf{\theta }}_1}\aleph \left(\mathtt{x},\frac{{\mathsf{\nu }}_4+{\mathsf{\nu }}_3}{2}\right)=\frac{1}{{\mathsf{\theta }}_1}{\int }_{\mathtt{x}}^{{\mathsf{\nu }}_2}{e}^{-\frac{1-{\mathsf{\theta }}_1}{{\mathsf{\theta }}_1}(\mathtt{t}-\mathtt{x})}\aleph \left(\mathtt{t},\frac{{\mathsf{\nu }}_4+{\mathsf{\nu }}_3}{2}\right)\mathtt{dt},\mathtt{x}<{\mathsf{\nu }}_2,\hfill \\ & {\mathtt{J}}_{{{\mathsf{\nu }}_4}^{+}}^{{\mathsf{\theta }}_2}\aleph \left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2},\mathtt{y}\right)=\frac{1}{{\mathsf{\theta }}_2}{\int }_{{\mathsf{\nu }}_4}^{\mathtt{y}}{e}^{-\frac{1-{\mathsf{\theta }}_2}{{\mathsf{\theta }}_2}\left(\mathtt{y}-\mathtt{s}\right)}\aleph \left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2},\mathtt{s}\right)\mathtt{ds},\mathtt{y}>{\mathsf{\nu }}_4,\hfill \end{array}$$

along with

$${\mathtt{J}}_{{{\mathsf{\nu }}_4}^{-}}^{{\mathsf{\theta }}_2}\aleph \left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2},\mathtt{y}\right)=\frac{1}{{\mathsf{\theta }}_2}{\int }_{\mathtt{y}}^{{\mathsf{\nu }}_4}{e}^{-\frac{1-{\mathsf{\theta }}_2}{{\mathsf{\theta }}_2}\left(\mathtt{s}-\mathtt{y}\right)}\aleph \left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2},\mathtt{s}\right)\mathtt{ds},\mathtt{y}<{\mathsf{\nu }}_4.$$

After that, we go over the definition of the bidimensional convexity under partial- and standard-order relations as given by the authors of [14,15].

Definition 4 

(see [14]). Let $\aleph :\mathsf{\Omega }=[{\mathsf{\nu }}_1,{\mathsf{\nu }}_2]\times [{\mathsf{\nu }}_3,{\mathsf{\nu }}_4]\subseteq {\mathsf{R}}^2\to {{\mathsf{R}}_{\mathtt{i}}}^{+}$ be a bidimensional convex function under standard-order relation if

$$\begin{array}{cc}\hfill \aleph \left({\mathtt{r}}_{\mathtt{1}}{\mathsf{\nu }}_1+(1-{\mathtt{r}}_{\mathtt{1}}){\mathsf{\nu }}_2,{\mathtt{s}}_{\mathtt{1}}{\mathsf{\nu }}_3+(1-{\mathtt{s}}_{\mathtt{1}}){\mathsf{\nu }}_4\right)& \le {\mathsf{\nu }}_1{\mathsf{\nu }}_2\aleph ({\mathtt{r}}_{\mathtt{1}},{\mathsf{\nu }}_3)+{\mathsf{\nu }}_2(1-{\mathsf{\nu }}_1)\aleph ({\mathtt{r}}_{\mathtt{1}},{\mathsf{\nu }}_4)\hfill \\ \hfill & +{\mathsf{\nu }}_1(1-{\mathsf{\nu }}_2)\aleph ({\mathtt{s}}_{\mathtt{1}}.{\mathsf{\nu }}_3)+(1-{\mathsf{\nu }}_1)(1-{\mathsf{\nu }}_2)\aleph ({\mathtt{s}}_{\mathtt{1}},{\mathsf{\nu }}_4)\hfill \end{array}$$

holds true for every $({\mathsf{\nu }}_1,{\mathsf{\nu }}_2),({\mathsf{\nu }}_3,{\mathsf{\nu }}_4)\in \mathsf{\Omega }$ along with ${\mathtt{r}}_{\mathtt{1}},{\mathtt{s}}_{\mathtt{1}}\in [0,1]$.

Definition 5 

(see [15]). Let $\aleph :\mathsf{\Omega }=[{\mathsf{\nu }}_1,{\mathsf{\nu }}_2]\times [{\mathsf{\nu }}_3,{\mathsf{\nu }}_4]\subseteq {\mathsf{R}}^2\to {{\mathsf{R}}_{\mathtt{i}}}^{+}$ be a bidimensional interval-valued function defined as $\aleph =[\underline{\aleph }(\mathtt{a},\mathtt{b}),\overline{\aleph }(\mathtt{a},\mathtt{b})]$ with $0\le {\mathsf{\nu }}_1<{\mathsf{\nu }}_2,0\le {\mathsf{\nu }}_3<{\mathsf{\nu }}_4$. Then, ℵ is bidimensional interval-valued convex under partial-order if

$$\begin{array}{cc}\hfill \aleph \left({\mathtt{r}}_{\mathtt{1}}{\mathsf{\nu }}_1+(1-{\mathtt{r}}_{\mathtt{1}}){\mathsf{\nu }}_2,{\mathtt{s}}_{\mathtt{1}}{\mathsf{\nu }}_3+(1-{\mathtt{s}}_{\mathtt{1}}){\mathsf{\nu }}_4\right)& \supseteq {\mathsf{\nu }}_1{\mathsf{\nu }}_2\aleph ({\mathtt{r}}_{\mathtt{1}},{\mathsf{\nu }}_3)+{\mathsf{\nu }}_2(1-{\mathsf{\nu }}_1)\aleph ({\mathtt{r}}_{\mathtt{1}},{\mathsf{\nu }}_4)\hfill \\ \hfill & +{\mathsf{\nu }}_1(1-{\mathsf{\nu }}_2)\aleph ({\mathtt{s}}_{\mathtt{1}}.{\mathsf{\nu }}_3)+(1-{\mathsf{\nu }}_1)(1-{\mathsf{\nu }}_2)\aleph ({\mathtt{s}}_{\mathtt{1}},{\mathsf{\nu }}_4)\hfill \end{array}$$

holds true for every $({\mathsf{\nu }}_1,{\mathsf{\nu }}_2),({\mathsf{\nu }}_3,{\mathsf{\nu }}_4)\in \mathsf{\Omega }$ along with ${\mathtt{r}}_{\mathtt{1}},{\mathtt{s}}_{\mathtt{1}}\in [0,1]$.

As the order relation “⊇” is not a generalization of standard order relation “≤” and has some flaws regarding setting inequality, the authors of [58] have recently introduced a total order relation that works smoothly with all kinds of inequalities.

Definition 6 

(see [34]). Let $\aleph :\mathsf{\Omega }=[{\mathsf{\nu }}_1,{\mathsf{\nu }}_2]\to {{\mathsf{R}}_{\mathtt{i}}}^{+}$ be a interval-valued function defined as $\aleph =[\underline{\aleph }\left(\mathtt{a}\right),\overline{\aleph }\left(\mathtt{a}\right)]$ with $0\le {\mathsf{\nu }}_1<{\mathsf{\nu }}_2.$ Then, ℵ is $\mathtt{I}.\mathtt{V}$$\mathtt{CR}$-convex iff

$$\begin{array}{cc}\hfill \aleph \left({\mathtt{r}}_{\mathtt{1}}{\mathsf{\nu }}_1+(1-{\mathtt{r}}_{\mathtt{1}}){\mathsf{\nu }}_2\right)& {⪯}_{\mathtt{CR}}{\mathtt{r}}_{\mathtt{1}}\aleph \left({\mathsf{\nu }}_1\right)+(1-{\mathtt{r}}_{\mathtt{1}})\aleph \left({\mathsf{\nu }}_2\right)\hfill \end{array}$$

holds true for every $({\mathsf{\nu }}_1,{\mathsf{\nu }}_2)\in \mathsf{\Omega }$ along with ${\mathtt{r}}_{\mathtt{1}}\in [0,1]$.

Taking motivation from the above definitions, now we are in a good position to extend Definition 6 into two dimensions in the setup of a total-order relation.

Definition 7. 

Let $\aleph :\mathsf{\Omega }=[{\mathsf{\nu }}_1,{\mathsf{\nu }}_2]\times [{\mathsf{\nu }}_3,{\mathsf{\nu }}_4]\subseteq {\mathsf{R}}^2\to {{\mathsf{R}}_{\mathtt{i}}}^{+}$ be a bidimensional interval-valued function defined as $\aleph =[\underline{\aleph }(\mathtt{a},\mathtt{b}),\overline{\aleph }(\mathtt{a},\mathtt{b})]$ with $0\le {\mathsf{\nu }}_1<{\mathsf{\nu }}_2,0\le {\mathsf{\nu }}_3<{\mathsf{\nu }}_4$. Then, ℵ is bidimensional $\mathtt{I}.\mathtt{V}$$\mathtt{CR}$-convex iff

$$\begin{array}{cc}\hfill \aleph \left({\mathtt{r}}_{\mathtt{1}}{\mathsf{\nu }}_1+(1-{\mathtt{r}}_{\mathtt{1}}){\mathsf{\nu }}_2,{\mathtt{s}}_{\mathtt{1}}{\mathsf{\nu }}_3+(1-{\mathtt{s}}_{\mathtt{1}}){\mathsf{\nu }}_4\right)& {⪯}_{\mathtt{CR}}{\mathsf{\nu }}_1{\mathsf{\nu }}_2\aleph ({\mathtt{r}}_{\mathtt{1}},{\mathsf{\nu }}_3)+{\mathsf{\nu }}_2(1-{\mathsf{\nu }}_1)\aleph ({\mathtt{r}}_{\mathtt{1}},{\mathsf{\nu }}_4)\hfill \\ \hfill & +{\mathsf{\nu }}_1(1-{\mathsf{\nu }}_2)\aleph ({\mathtt{s}}_{\mathtt{1}}.{\mathsf{\nu }}_3)+(1-{\mathsf{\nu }}_1)(1-{\mathsf{\nu }}_2)\aleph ({\mathtt{s}}_{\mathtt{1}},{\mathsf{\nu }}_4)\hfill \end{array}$$

holds true for every $({\mathsf{\nu }}_1,{\mathsf{\nu }}_2),({\mathsf{\nu }}_3,{\mathsf{\nu }}_4)\in \mathsf{\Omega }$ along with ${\mathtt{r}}_{\mathtt{1}},{\mathtt{s}}_{\mathtt{1}}\in [0,1]$.

Remark 2. 

• Setting $\underline{\aleph }\ne \overline{\aleph }$, we obtain Definition 2 given by by Zhao et al. in [15].
• Setting $\underline{\aleph }=\overline{\aleph }$, we obtain Inequality (2.1) given by by Dragomir in [14].

Proposition 1. 

Let $\aleph :[{\mathsf{\nu }}_1,{\mathsf{\nu }}_2]\times [{\mathsf{\nu }}_3,{\mathsf{\nu }}_4]\subseteq {\mathsf{R}}^2\to {{\mathsf{R}}_{\mathtt{i}}}^{+}$ be a bidimensional interval-valued function defined as $\aleph =[\underline{\aleph }(\mathtt{a},\mathtt{b}),\overline{\aleph }(\mathtt{a},\mathtt{b})]$ with $0\le {\mathsf{\nu }}_1<{\mathsf{\nu }}_2,0\le {\mathsf{\nu }}_3<{\mathsf{\nu }}_4$. Then, ℵ is bidimensional interval-valued $\mathtt{CR}$-convex if and only if ${\aleph }_{\mathtt{C}}$ and ${\aleph }_{\mathtt{R}}$ are bidimensional convex functions.

Proof. 

Since ${\aleph }_c$ and ${\aleph }_r$ are bidimensional convex mappings, then for each $({\mathsf{\nu }}_1,{\mathsf{\nu }}_2),({\mathsf{\nu }}_3,{\mathsf{\nu }}_4)\in [0,1]\times [0,1],$ we have

$$\begin{array}{cc}\hfill {\aleph }_{\mathtt{C}}\left({\mathtt{r}}_{\mathtt{1}}{\mathsf{\nu }}_1+(1-{\mathtt{r}}_{\mathtt{1}}){\mathsf{\nu }}_2,{\mathtt{s}}_{\mathtt{1}}{\mathsf{\nu }}_3+(1-{\mathtt{s}}_{\mathtt{1}}){\mathsf{\nu }}_4\right)& \le {\mathsf{\nu }}_1{\mathsf{\nu }}_2{\aleph }_{\mathtt{C}}({\mathtt{r}}_{\mathtt{1}},{\mathsf{\nu }}_3)+{\mathsf{\nu }}_2(1-{\mathsf{\nu }}_1){\aleph }_{\mathtt{C}}({\mathtt{r}}_{\mathtt{1}},{\mathsf{\nu }}_4)\hfill \\ \hfill & +{\mathsf{\nu }}_1(1-{\mathsf{\nu }}_2){\aleph }_{\mathtt{C}}({\mathtt{s}}_{\mathtt{1}}.{\mathsf{\nu }}_3)+(1-{\mathsf{\nu }}_1)(1-{\mathsf{\nu }}_2){\aleph }_{\mathtt{C}}({\mathtt{s}}_{\mathtt{1}},{\mathsf{\nu }}_4)\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill {\aleph }_{\mathtt{R}}\left({\mathtt{r}}_{\mathtt{1}}{\mathsf{\nu }}_1+(1-{\mathtt{r}}_{\mathtt{1}}){\mathsf{\nu }}_2,{\mathtt{s}}_{\mathtt{1}}{\mathsf{\nu }}_3+(1-{\mathtt{s}}_{\mathtt{1}}){\mathsf{\nu }}_4\right)& \le {\mathsf{\nu }}_1{\mathsf{\nu }}_2{\aleph }_{\mathtt{R}}({\mathtt{r}}_{\mathtt{1}},{\mathsf{\nu }}_3)+{\mathsf{\nu }}_2(1-{\mathsf{\nu }}_1){\aleph }_{\mathtt{R}}({\mathtt{r}}_{\mathtt{1}},{\mathsf{\nu }}_4)\hfill \\ \hfill & +{\mathsf{\nu }}_1(1-{\mathsf{\nu }}_2){\aleph }_{\mathtt{R}}({\mathtt{s}}_{\mathtt{1}}.{\mathsf{\nu }}_3)+(1-{\mathsf{\nu }}_1)(1-{\mathsf{\nu }}_2){\aleph }_{\mathtt{R}}({\mathtt{s}}_{\mathtt{1}},{\mathsf{\nu }}_4).\hfill \end{array}$$

Now, if

$$\begin{array}{cc}\hfill {\aleph }_{\mathtt{C}}\left({\mathtt{r}}_{\mathtt{1}}{\mathsf{\nu }}_1+(1-{\mathtt{r}}_{\mathtt{1}}){\mathsf{\nu }}_2,{\mathtt{s}}_{\mathtt{1}}{\mathsf{\nu }}_3+(1-{\mathtt{s}}_{\mathtt{1}}){\mathsf{\nu }}_4\right)& \ne {\mathsf{\nu }}_1{\mathsf{\nu }}_2{\aleph }_{\mathtt{C}}({\mathtt{r}}_{\mathtt{1}},{\mathsf{\nu }}_3)+{\mathsf{\nu }}_2(1-{\mathsf{\nu }}_1){\aleph }_{\mathtt{C}}({\mathtt{r}}_{\mathtt{1}},{\mathsf{\nu }}_4)\hfill \\ \hfill & +{\mathsf{\nu }}_1(1-{\mathsf{\nu }}_2){\aleph }_{\mathtt{C}}({\mathtt{s}}_{\mathtt{1}}.{\mathsf{\nu }}_3)+(1-{\mathsf{\nu }}_1)(1-{\mathsf{\nu }}_2){\aleph }_{\mathtt{C}}({\mathtt{s}}_{\mathtt{1}},{\mathsf{\nu }}_4),\hfill \end{array}$$

this implies

$$\begin{array}{cc}\hfill {\aleph }_{\mathtt{C}}\left({\mathtt{r}}_{\mathtt{1}}{\mathsf{\nu }}_1+(1-{\mathtt{r}}_{\mathtt{1}}){\mathsf{\nu }}_2,{\mathtt{s}}_{\mathtt{1}}{\mathsf{\nu }}_3+(1-{\mathtt{s}}_{\mathtt{1}}){\mathsf{\nu }}_4\right)& {⪯}_{\mathtt{CR}}{\mathsf{\nu }}_1{\mathsf{\nu }}_2{\aleph }_{\mathtt{C}}({\mathtt{r}}_{\mathtt{1}},{\mathsf{\nu }}_3)+{\mathsf{\nu }}_2(1-{\mathsf{\nu }}_1){\aleph }_{\mathtt{C}}({\mathtt{r}}_{\mathtt{1}},{\mathsf{\nu }}_4)\hfill \\ \hfill & +{\mathsf{\nu }}_1(1-{\mathsf{\nu }}_2){\aleph }_{\mathtt{C}}({\mathtt{s}}_{\mathtt{1}}.{\mathsf{\nu }}_3)+(1-{\mathsf{\nu }}_1)(1-{\mathsf{\nu }}_2){\aleph }_{\mathtt{C}}({\mathtt{s}}_{\mathtt{1}},{\mathsf{\nu }}_4).\hfill \end{array}$$

Otherwise, one has

$$\begin{array}{cc}\hfill {\aleph }_{\mathtt{R}}\left({\mathtt{r}}_{\mathtt{1}}{\mathsf{\nu }}_1+(1-{\mathtt{r}}_{\mathtt{1}}){\mathsf{\nu }}_2,{\mathtt{s}}_{\mathtt{1}}{\mathsf{\nu }}_3+(1-{\mathtt{s}}_{\mathtt{1}}){\mathsf{\nu }}_4\right)& \le {\mathsf{\nu }}_1{\mathsf{\nu }}_2{\aleph }_{\mathtt{R}}({\mathtt{r}}_{\mathtt{1}},{\mathsf{\nu }}_3)+{\mathsf{\nu }}_2(1-{\mathsf{\nu }}_1){\aleph }_{\mathtt{R}}({\mathtt{r}}_{\mathtt{1}},{\mathsf{\nu }}_4)\hfill \\ \hfill & +{\mathsf{\nu }}_1(1-{\mathsf{\nu }}_2){\aleph }_{\mathtt{R}}({\mathtt{s}}_{\mathtt{1}}.{\mathsf{\nu }}_3)+(1-{\mathsf{\nu }}_1)(1-{\mathsf{\nu }}_2){\aleph }_{\mathtt{R}}({\mathtt{s}}_{\mathtt{1}},{\mathsf{\nu }}_4).\hfill \end{array}$$

This implies that

$$\begin{array}{cc}\hfill {\aleph }_{\mathtt{R}}\left({\mathtt{r}}_{\mathtt{1}}{\mathsf{\nu }}_1+(1-{\mathtt{r}}_{\mathtt{1}}){\mathsf{\nu }}_2,{\mathtt{s}}_{\mathtt{1}}{\mathsf{\nu }}_3+(1-{\mathtt{s}}_{\mathtt{1}}){\mathsf{\nu }}_4\right)& {⪯}_{\mathtt{CR}}{\mathsf{\nu }}_1{\mathsf{\nu }}_2{\aleph }_{\mathtt{R}}({\mathtt{r}}_{\mathtt{1}},{\mathsf{\nu }}_3)+{\mathsf{\nu }}_2(1-{\mathsf{\nu }}_1){\aleph }_{\mathtt{R}}({\mathtt{r}}_{\mathtt{1}},{\mathsf{\nu }}_4)\hfill \\ \hfill & +{\mathsf{\nu }}_1(1-{\mathsf{\nu }}_2){\aleph }_{\mathtt{R}}({\mathtt{s}}_{\mathtt{1}}.{\mathsf{\nu }}_3)+(1-{\mathsf{\nu }}_1)(1-{\mathsf{\nu }}_2){\aleph }_{\mathtt{R}}({\mathtt{s}}_{\mathtt{1}},{\mathsf{\nu }}_4),\hfill \end{array}$$

By virtue of the aforementioned results and Definition 7, this may be lead as follows:

$$\begin{array}{cc}\hfill \aleph \left({\mathtt{r}}_{\mathtt{1}}{\mathsf{\nu }}_1+(1-{\mathtt{r}}_{\mathtt{1}}){\mathsf{\nu }}_2,{\mathtt{s}}_{\mathtt{1}}{\mathsf{\nu }}_3+(1-{\mathtt{s}}_{\mathtt{1}}){\mathsf{\nu }}_4\right)& {⪯}_{\mathtt{CR}}{\mathsf{\nu }}_1{\mathsf{\nu }}_2\aleph ({\mathtt{r}}_{\mathtt{1}},{\mathsf{\nu }}_3)+{\mathsf{\nu }}_2(1-{\mathsf{\nu }}_1)\aleph ({\mathtt{r}}_{\mathtt{1}},{\mathsf{\nu }}_4)\hfill \\ \hfill & +{\mathsf{\nu }}_1(1-{\mathsf{\nu }}_2)\aleph ({\mathtt{s}}_{\mathtt{1}}.{\mathsf{\nu }}_3)+(1-{\mathsf{\nu }}_1)(1-{\mathsf{\nu }}_2)\aleph ({\mathtt{s}}_{\mathtt{1}},{\mathsf{\nu }}_4).\hfill \end{array}$$

This concludes the proof.

 □

Example 2. 

Let $\aleph :[{\mathsf{\nu }}_1,{\mathsf{\nu }}_2]\times [{\mathsf{\nu }}_3,{\mathsf{\nu }}_4]\subseteq {\mathsf{R}}^2\to {{\mathsf{R}}_{\mathtt{i}}}^{+}$ be a bidimensional interval-valued function defined as

$$\aleph =[-3e^{2\mathtt{x}+1}-2e^{\mathtt{y}+\mathtt{5}}+5,4e^{2\mathtt{x}+1}+3e^{\mathtt{y}+\mathtt{5}}+7],(\mathtt{x},\mathtt{y})\in [0,4]\times [0,4].$$

Then,

$${\aleph }_{\mathtt{C}}=\frac{e^{2\mathtt{x}+1}+e^{\mathtt{y}+5}+12}{2}\mathrm{and}{\aleph }_{\mathtt{R}}=\frac{7e^{2\mathtt{x}+1}+5e^{\mathtt{y}+5}+2}{2}.$$

Remark 3. 

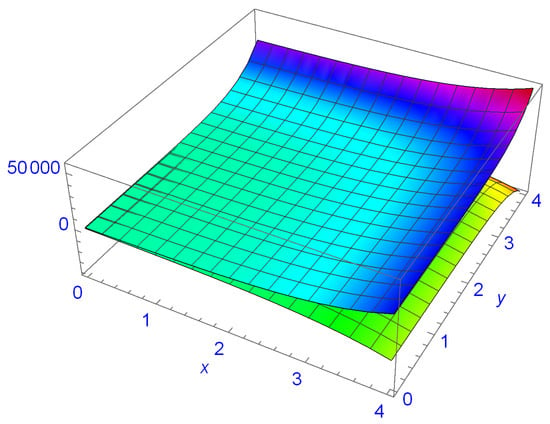
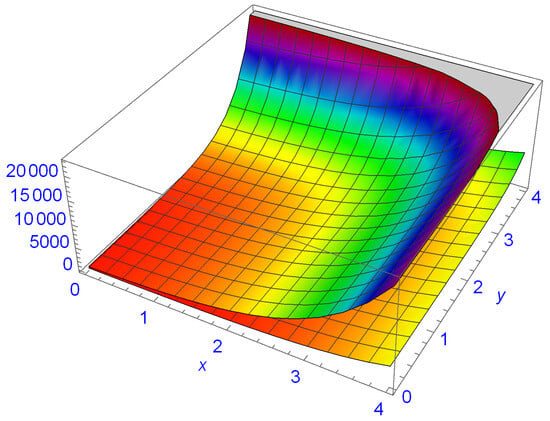
As shown below, Figure 1 contains interval-valued mappings with both concave and convex mappings at the left and right endpoints. However, when the center- and radius-order are applied, the newly developed mappings, as well as their views in Figure 2, clearly show that both mappings at the left and right endpoints are convex in nature.

Figure 1. Graphical behavior of the total $\mathtt{CR}$ interval-valued bidimensional mapping ℵ.

Figure 2. Graphical behavior of total $\mathtt{CR}$ interval-valued bidimensional convex mappings ${\aleph }_{\mathtt{C}}$ and ${\aleph }_{\mathtt{R}}$.

3. Hyers–Ulam Stability of Two-Dimensional Convex Functions

This section presents two main discoveries. The first outcome is a sandwich theorem for $\mathcal{2}\mathcal{D}$-convex functions, which is related to the separation by convex mappings theorem in [61]. In our second contribution, we demonstrate Hyers–Ulam stability for two-dimensional convex functions, providing an approximate convexity result. The corollary stated below is a direct consequence of Theorem 3 presented in article [44].

Corollary 1. 

Let $=[{\mathsf{\nu }}_1,{\mathsf{\nu }}_2]\times [{\mathsf{\nu }}_3,{\mathsf{\nu }}_4]\subseteq {\mathsf{R}}^2$ be an interval and let ℵ and ℷ both be two variables with real-valued mappings defined on Ω; then, the following results are equivalent:

• (i) there exists a two-variable convex mapping $\mathtt{h}:\mathsf{\omega }\to {\mathsf{R}}^2$ such that $\aleph \le \mathtt{h}\le \gimel$ on Ω;
• (ii) there exists a two-dimensional convex mapping ${\mathtt{h}}_{\mathtt{1}}:\to {\mathsf{R}}^2$ and a concave mapping ${\mathtt{h}}_{\mathtt{2}}:\to {\mathsf{R}}^2$ such that $\aleph \le {\mathtt{h}}_{\mathtt{1}}\le \gimel$ and $\aleph \le {\mathtt{h}}_{\mathtt{2}}\le \gimel$ on Ω;
• (iii) the following result holds true for every $({\mathsf{\nu }}_1,{\mathsf{\nu }}_2),({\mathsf{\nu }}_3,{\mathsf{\nu }}_4)\in \mathsf{\Omega }$ along with ${\mathtt{r}}_{\mathtt{1}},{\mathtt{s}}_{\mathtt{1}}\in [0,1]$.

  $$\begin{array}{cc}\hfill \aleph \left({\mathtt{r}}_{\mathtt{1}}{\mathsf{\nu }}_1+(1-{\mathtt{r}}_{\mathtt{1}}){\mathsf{\nu }}_2,{\mathtt{s}}_{\mathtt{1}}{\mathsf{\nu }}_3+(1-{\mathtt{s}}_{\mathtt{1}}){\mathsf{\nu }}_4\right)& \le {\mathsf{\nu }}_1{\mathsf{\nu }}_2\gimel ({\mathtt{r}}_{\mathtt{1}},{\mathsf{\nu }}_3)+{\mathsf{\nu }}_2(1-{\mathsf{\nu }}_1)\gimel ({\mathtt{r}}_{\mathtt{1}},{\mathsf{\nu }}_4)\hfill \\ \hfill & +{\mathsf{\nu }}_1(1-{\mathsf{\nu }}_2)\gimel ({\mathtt{s}}_{\mathtt{1}}.{\mathsf{\nu }}_3)+(1-{\mathsf{\nu }}_1)(1-{\mathsf{\nu }}_2)\gimel ({\mathtt{s}}_{\mathtt{1}},{\mathsf{\nu }}_4),\hfill \\ \hfill \gimel \left({\mathtt{r}}_{\mathtt{1}}{\mathsf{\nu }}_1+(1-{\mathtt{r}}_{\mathtt{1}}){\mathsf{\nu }}_2,{\mathtt{s}}_{\mathtt{1}}{\mathsf{\nu }}_3+(1-{\mathtt{s}}_{\mathtt{1}}){\mathsf{\nu }}_4\right)& \ge {\mathsf{\nu }}_1{\mathsf{\nu }}_2\aleph ({\mathtt{r}}_{\mathtt{1}},{\mathsf{\nu }}_3)+{\mathsf{\nu }}_2(1-{\mathsf{\nu }}_1)\aleph ({\mathtt{r}}_{\mathtt{1}},{\mathsf{\nu }}_4)\hfill \\ \hfill & +{\mathsf{\nu }}_1(1-{\mathsf{\nu }}_2)\aleph ({\mathtt{s}}_{\mathtt{1}}.{\mathsf{\nu }}_3)+(1-{\mathsf{\nu }}_1)(1-{\mathsf{\nu }}_2)\aleph ({\mathtt{s}}_{\mathtt{1}},{\mathsf{\nu }}_4)\hfill \end{array}$$

  (4)

Following Corollary 1, we obtain the following stability result for two-dimensional convex mappings of the Hyers–Ulam type.

Proposition 2. 

Let $\mathsf{\Omega }\subseteq {\mathsf{R}}^2$ be an interval and $\mathsf{ϵ}$ be a positive constant. A mapping $\aleph :\mathsf{\Omega }=[{\mathsf{\nu }}_1,{\mathsf{\nu }}_2]\times [{\mathsf{\nu }}_3,{\mathsf{\nu }}_4]\subseteq {\mathsf{R}}^2$ satisfies the following inequality:

$$\begin{array}{cc}\hfill & |\aleph \left({\mathtt{r}}_{\mathtt{1}}{\mathsf{\nu }}_1+(1-{\mathtt{r}}_{\mathtt{1}}){\mathsf{\nu }}_2,{\mathtt{s}}_{\mathtt{1}}{\mathsf{\nu }}_3+(1-{\mathtt{s}}_{\mathtt{1}}){\mathsf{\nu }}_4\right)-{\mathsf{\nu }}_1{\mathsf{\nu }}_2\aleph ({\mathtt{r}}_{\mathtt{1}},{\mathsf{\nu }}_3)+{\mathsf{\nu }}_2(1-{\mathsf{\nu }}_1)\aleph ({\mathtt{r}}_{\mathtt{1}},{\mathsf{\nu }}_4)\hfill \\ & -{\mathsf{\nu }}_1(1-{\mathsf{\nu }}_2)\aleph ({\mathtt{s}}_{\mathtt{1}}.{\mathsf{\nu }}_3)-(1-{\mathsf{\nu }}_1)(1-{\mathsf{\nu }}_2)\aleph ({\mathtt{s}}_{\mathtt{1}},{\mathsf{\nu }}_4)|\le \mathsf{ϵ}\hfill \end{array}$$

(5)

which holds true for every $({\mathsf{\nu }}_1,{\mathsf{\nu }}_2),({\mathsf{\nu }}_3,{\mathsf{\nu }}_4)\in \mathsf{\Omega }$ along with ${\mathtt{r}}_{\mathtt{1}},{\mathtt{s}}_{\mathtt{1}}\in [0,1]$, iff there exists another two-variable convex mapping $\mathsf{\phi }:\mathsf{\Omega }=[{\mathsf{\nu }}_1,{\mathsf{\nu }}_2]\times [{\mathsf{\nu }}_3,{\mathsf{\nu }}_4]\subseteq {\mathsf{R}}^2$ such that

$$\begin{array}{c}\hfill |\aleph (\mathtt{x},\mathtt{y})-\mathsf{\phi }(\mathtt{x},\mathtt{y})|\le \frac{\mathsf{ϵ}}{4},\mathtt{x},\mathtt{y}\in \mathsf{\Omega }.\end{array}$$

(6)

Proof. 

If ℵ satisfies (7), then (4) holds with $\gimel =\aleph +\mathsf{ϵ}$. Therefore, by virtue of Corollary 1, there exists a two-variable convex function $\mathtt{h}:\mathsf{\Omega }\to {\mathsf{R}}^2$ such that $\aleph \le \mathtt{h}\le \aleph +\mathsf{ϵ}$. Putting $\mathsf{\phi }(\mathtt{x},\mathtt{y}):=\mathtt{h}(\mathtt{x},\mathtt{y})-\frac{\mathsf{ϵ}}{4}$, $\mathtt{x},\mathtt{y}\in \mathsf{\Omega }$, we get a convex mapping $\mathsf{\phi }:\mathsf{\Omega }\to {\mathsf{R}}^2$ satisfying (6). Now suppose that (6) holds with a convex function $\mathsf{\phi }$. Then,

$$\begin{array}{cc}\hfill & |\aleph \left({\mathtt{r}}_{\mathtt{1}}{\mathsf{\nu }}_1+(1-{\mathtt{r}}_{\mathtt{1}}){\mathsf{\nu }}_2,{\mathtt{s}}_{\mathtt{1}}{\mathsf{\nu }}_3+(1-{\mathtt{s}}_{\mathtt{1}}){\mathsf{\nu }}_4\right)-{\mathsf{\nu }}_1{\mathsf{\nu }}_2\aleph ({\mathtt{r}}_{\mathtt{1}},{\mathsf{\nu }}_3)+{\mathsf{\nu }}_2(1-{\mathsf{\nu }}_1)\aleph ({\mathtt{r}}_{\mathtt{1}},{\mathsf{\nu }}_4)\hfill \\ & -{\mathsf{\nu }}_1(1-{\mathsf{\nu }}_2)\aleph ({\mathtt{s}}_{\mathtt{1}}.{\mathsf{\nu }}_3)-(1-{\mathsf{\nu }}_1)(1-{\mathsf{\nu }}_2)\aleph ({\mathtt{s}}_{\mathtt{1}},{\mathsf{\nu }}_4)|\hfill \\ & =|\aleph \left({\mathtt{r}}_{\mathtt{1}}{\mathsf{\nu }}_1+(1-{\mathtt{r}}_{\mathtt{1}}){\mathsf{\nu }}_2,{\mathtt{s}}_{\mathtt{1}}{\mathsf{\nu }}_3+(1-{\mathtt{s}}_{\mathtt{1}}){\mathsf{\nu }}_4\right)-\mathsf{\phi }\left({\mathtt{r}}_{\mathtt{1}}{\mathsf{\nu }}_1+(1-{\mathtt{r}}_{\mathtt{1}}){\mathsf{\nu }}_2,{\mathtt{s}}_{\mathtt{1}}{\mathsf{\nu }}_3+(1-{\mathtt{s}}_{\mathtt{1}}){\mathsf{\nu }}_4\right)\hfill \\ & - {\mathsf{\nu }}_1{\mathsf{\nu }}_2\aleph ({\mathtt{r}}_{\mathtt{1}},{\mathsf{\nu }}_3)+{\mathsf{\nu }}_2(1-{\mathsf{\nu }}_1)\aleph ({\mathtt{r}}_{\mathtt{1}},{\mathsf{\nu }}_4)\hfill \\ & - {\mathsf{\nu }}_1(1-{\mathsf{\nu }}_2)\aleph ({\mathtt{s}}_{\mathtt{1}}.{\mathsf{\nu }}_3)-(1-{\mathsf{\nu }}_1)(1-{\mathsf{\nu }}_2)\aleph ({\mathtt{s}}_{\mathtt{1}},{\mathsf{\nu }}_4)\hfill \\ & + {\mathsf{\nu }}_1{\mathsf{\nu }}_2\mathsf{\phi }({\mathtt{r}}_{\mathtt{1}},{\mathsf{\nu }}_3)+{\mathsf{\nu }}_2(1-{\mathsf{\nu }}_1)\mathsf{\phi }({\mathtt{r}}_{\mathtt{1}},{\mathsf{\nu }}_4)\hfill \\ & + {\mathsf{\nu }}_1(1-{\mathsf{\nu }}_2)\mathsf{\phi }({\mathtt{s}}_{\mathtt{1}}.{\mathsf{\nu }}_3)+(1-{\mathsf{\nu }}_1)(1-{\mathsf{\nu }}_2)\mathsf{\phi }({\mathtt{s}}_{\mathtt{1}},{\mathsf{\nu }}_4)|\hfill \\ & \le |\aleph \left({\mathtt{r}}_{\mathtt{1}}{\mathsf{\nu }}_1+(1-{\mathtt{r}}_{\mathtt{1}}){\mathsf{\nu }}_2,{\mathtt{s}}_{\mathtt{1}}{\mathsf{\nu }}_3+(1-{\mathtt{s}}_{\mathtt{1}}){\mathsf{\nu }}_4\right)-\mathsf{\phi }\left({\mathtt{r}}_{\mathtt{1}}{\mathsf{\nu }}_1+(1-{\mathtt{r}}_{\mathtt{1}}){\mathsf{\nu }}_2,{\mathtt{s}}_{\mathtt{1}}{\mathsf{\nu }}_3+(1-{\mathtt{s}}_{\mathtt{1}}){\mathsf{\nu }}_4\right)|\hfill \\ & + {\mathsf{\nu }}_1{\mathsf{\nu }}_2|\mathsf{\phi }({\mathtt{r}}_{\mathtt{1}},{\mathsf{\nu }}_3)-\aleph ({\mathtt{r}}_{\mathtt{1}},{\mathsf{\nu }}_3)|+{\mathsf{\nu }}_2(1-{\mathsf{\nu }}_1)|\mathsf{\phi }({\mathtt{r}}_{\mathtt{1}},{\mathsf{\nu }}_4)-\aleph ({\mathtt{r}}_{\mathtt{1}},{\mathsf{\nu }}_4)|\hfill \\ & + {\mathsf{\nu }}_1(1-{\mathsf{\nu }}_2)|\mathsf{\phi }({\mathtt{s}}_{\mathtt{1}}.{\mathsf{\nu }}_3)-\aleph ({\mathtt{s}}_{\mathtt{1}}.{\mathsf{\nu }}_3)|+(1-{\mathsf{\nu }}_1)(1-{\mathsf{\nu }}_2)|\mathsf{\phi }({\mathtt{s}}_{\mathtt{1}},{\mathsf{\nu }}_4)-\aleph ({\mathtt{s}}_{\mathtt{1}},{\mathsf{\nu }}_4)|\hfill \\ & \le \frac{\mathsf{ϵ}}{4}+\frac{\mathsf{ϵ}}{4}+\frac{\mathsf{ϵ}}{4}+\frac{\mathsf{ϵ}}{4}\le \mathsf{ϵ}.\hfill \end{array}$$

(7)

This finishes the proof. □

4. Novel Two-Dimensional Hermite–Hadamard-Type Inequalities via Fractional Integral Operators

The objective of this part is to use bidimensional convex mappings to build Hermite–Hadamard and its numerous novel variations under the center-radius-order relation.

Theorem 7. 

Let $\aleph :[{\mathsf{\nu }}_1,{\mathsf{\nu }}_2]\times [{\mathsf{\nu }}_3,{\mathsf{\nu }}_4]\subseteq {\mathsf{R}}^2\to {{\mathsf{R}}_{\mathtt{i}}}^{+}$ be a bidimensional interval-valued function defined as $\aleph =[\underline{{\aleph }_1}(\mathtt{a},\mathtt{b}),\overline{{\aleph }_2}(\mathtt{a},\mathtt{b})]$ with $0\le {\mathsf{\nu }}_1<{\mathsf{\nu }}_2,0\le {\mathsf{\nu }}_3<{\mathsf{\nu }}_4$. Then, one has the double $\mathtt{CR}$-order relation:

$$\begin{array}{cc}\hfill & \aleph \left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2},\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right)\hfill \\ & {⪯}_{\mathtt{CR}}\frac{(1-{\mathsf{\theta }}_1)(1-{\mathsf{\theta }}_2)}{4(1-{\mathtt{e}}^{-{ð}_1})(1-{\mathtt{e}}^{-{ð}_2})}\left[{\mathtt{J}}_{{{\mathsf{\nu }}_1}^{+},{{\mathsf{\nu }}_3}^{+}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)+{\mathtt{J}}_{{{\mathsf{\nu }}_1}^{+},{{\mathsf{\nu }}_4}^{-}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3\right.)\hfill \\ \hfill & +{\mathtt{J}}_{{{\mathsf{\nu }}_2}^{-},{{\mathsf{\nu }}_3}^{+}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)+{\mathtt{J}}_{{{\mathsf{\nu }}_2}^{-},{\mathsf{\nu }}_4-}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)]\hfill \\ \hfill & {⪯}_{\mathtt{CR}}\frac{\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)+\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)+\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)+\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)}{4},\hfill \end{array}$$

(8)

where ${ð}_1=\frac{1-{\mathsf{\theta }}_1}{{\mathsf{\theta }}_1}({\mathsf{\nu }}_2-{\mathsf{\nu }}_1)$ and ${ð}_2=\frac{1-{\mathsf{\theta }}_2}{{\mathsf{\theta }}_2}({\mathsf{\nu }}_4-{\mathsf{\nu }}_3)$.

Proof. 

Taking into account bidimensional interval-valued mapping ℵ, and if we take $\mathtt{x}={\mathtt{r}}_{\mathtt{1}}{\mathsf{\nu }}_1+\left(1-{\mathtt{r}}_{\mathtt{1}}\right){\mathsf{\nu }}_2,\mathtt{y}=\left(1-{\mathtt{r}}_{\mathtt{1}}\right){\mathsf{\nu }}_1+{\mathtt{r}}_{\mathtt{1}}{\mathsf{\nu }}_2,\mathtt{u}=$${\mathsf{s}}_{\mathsf{1}}{\mathsf{\nu }}_3+\left(1-{\mathsf{s}}_{\mathsf{1}}\right){\mathsf{\nu }}_4$, and $\mathtt{w}=\left(1-{\mathsf{s}}_{\mathsf{1}}\right){\mathsf{\nu }}_3+{\mathsf{s}}_{\mathsf{1}}{\mathsf{\nu }}_4$, then we have

$$\begin{array}{cc}\hfill & \aleph \left(\frac{\mathtt{x}+\mathtt{y}}{2},\frac{\mathtt{u}+\mathtt{w}}{2}\right)=\aleph \left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2},\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right)\hfill \\ \hfill {⪯}_{\mathtt{CR}}& \frac{1}{4}\left[\aleph \left({\mathtt{r}}_{\mathtt{1}}{\mathsf{\nu }}_1+\left(1-{\mathtt{r}}_{\mathtt{1}}\right){\mathsf{\nu }}_2,{\mathsf{s}}_{\mathsf{1}}{\mathsf{\nu }}_3+\left(1-{\mathsf{s}}_{\mathsf{1}}\right){\mathsf{\nu }}_4\right)+\aleph \left({\mathtt{r}}_{\mathtt{1}}{\mathsf{\nu }}_1+\left(1-{\mathtt{r}}_{\mathtt{1}}\right){\mathsf{\nu }}_2,\left(1-{\mathsf{s}}_{\mathsf{1}}\right){\mathsf{\nu }}_3+{\mathsf{s}}_{\mathsf{1}}{\mathsf{\nu }}_4\right)\right.\hfill \\ \hfill & \left.+\aleph \left(\left(1-{\mathtt{r}}_{\mathtt{1}}\right){\mathsf{\nu }}_1+{\mathtt{r}}_{\mathtt{1}}{\mathsf{\nu }}_2,{\mathsf{s}}_{\mathsf{1}}{\mathsf{\nu }}_3+\left(1-{\mathsf{s}}_{\mathsf{1}}\right){\mathsf{\nu }}_4\right)+\aleph \left(\left(1-{\mathtt{r}}_{\mathtt{1}}\right){\mathsf{\nu }}_1+{\mathtt{r}}_{\mathtt{1}}{\mathsf{\nu }}_2,\left(1-{\mathsf{s}}_{\mathsf{1}}\right){\mathsf{\nu }}_3+{\mathsf{s}}_{\mathsf{1}}{\mathsf{\nu }}_4\right)\right].\hfill \end{array}$$

(9)

Multiplying relation (9) by ${\mathtt{e}}^{-{ð}_1{\mathtt{r}}_{\mathtt{1}}}{\mathtt{e}}^{-{ð}_2{\mathsf{s}}_{\mathsf{1}}}$ and integrating the resultant output with reference to $\left({\mathtt{r}}_{\mathtt{1}},{\mathsf{s}}_{\mathsf{1}}\right)$ on $[0,1]\times [0,1]$ reveals that

$$\begin{array}{cc}\hfill & \aleph \left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2},\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right){\int }_0^1{\int }_0^1{\mathtt{e}}^{-{ð}_1{\mathtt{r}}_{\mathtt{1}}}{\mathtt{e}}^{-{ð}_2{\mathsf{s}}_{\mathsf{1}}}\mathrm{d}{\mathsf{s}}_{\mathsf{1}}\mathrm{d}{\mathtt{r}}_{\mathtt{1}}\hfill \\ \hfill & {⪯}_{\mathtt{CR}}\frac{1}{4}\{{\int }_0^1{\int }_0^1{\mathtt{e}}^{-{ð}_1{\mathtt{r}}_{\mathtt{1}}}{\mathtt{e}}^{-{ð}_2{\mathsf{s}}_{\mathsf{1}}}[\aleph ({\mathtt{r}}_{\mathtt{1}}{\mathsf{\nu }}_1+\left(1-{\mathtt{r}}_{\mathtt{1}}\right){\mathsf{\nu }}_2,{\mathsf{s}}_{\mathsf{1}}{\mathsf{\nu }}_3+\left(1-{\mathsf{s}}_{\mathsf{1}}\right){\mathsf{\nu }}_4)\hfill \\ \hfill & +\aleph ({\mathtt{r}}_{\mathtt{1}}{\mathsf{\nu }}_1+\left(1-{\mathtt{r}}_{\mathtt{1}}\right){\mathsf{\nu }}_2,\left(1-{\mathsf{s}}_{\mathsf{1}}\right){\mathsf{\nu }}_3+{\mathsf{s}}_{\mathsf{1}}{\mathsf{\nu }}_4)]\mathrm{d}{\mathsf{s}}_{\mathsf{1}}\mathrm{d}{\mathtt{r}}_{\mathtt{1}}\hfill \\ \hfill & +{\int }_0^1{\int }_0^1{\mathtt{e}}^{-{ð}_1{\mathtt{r}}_{\mathtt{1}}}{\mathtt{e}}^{-{ð}_2{\mathsf{s}}_{\mathsf{1}}}[\aleph (\left(1-{\mathtt{r}}_{\mathtt{1}}\right){\mathsf{\nu }}_1+{\mathtt{r}}_{\mathtt{1}}{\mathsf{\nu }}_2,{\mathsf{s}}_{\mathsf{1}}{\mathsf{\nu }}_3+\left(1-{\mathsf{s}}_{\mathsf{1}}\right){\mathsf{\nu }}_4)\hfill \\ \hfill & +\aleph \left((1-{\mathtt{r}}_{\mathtt{1}}\right){\mathsf{\nu }}_1+{\mathtt{r}}_{\mathtt{1}}{\mathsf{\nu }}_2,\left(1-{\mathsf{s}}_{\mathsf{1}}\right){\mathsf{\nu }}_3+{\mathsf{s}}_{\mathsf{1}}{\mathsf{\nu }}_4\left)\right]\mathrm{d}{\mathsf{s}}_{\mathsf{1}}\mathrm{d}{\mathtt{r}}_{\mathtt{1}}\}.\hfill \end{array}$$

Changing the variable and doing various computations may allow us to determine

$$\begin{array}{cc}& \frac{\left(1-{\mathtt{e}}^{-{ð}_1}\right)\left(1-{\mathtt{e}}^{-{ð}_2}\right)}{{ð}_1{ð}_2}\aleph \left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2},\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right)\hfill \\ & {⪯}_{\mathtt{CR}}\frac{1}{4({\mathsf{\nu }}_2-{\mathsf{\nu }}_1)({\mathsf{\nu }}_4-{\mathsf{\nu }}_3)}\left\{{\int }_{{\mathsf{\nu }}_1}^{{\mathsf{\nu }}_2}{\int }_{{\mathsf{\nu }}_3}^{{\mathsf{\nu }}_4}{\mathtt{e}}^{-\frac{1-{\mathsf{\theta }}_1}{{\mathsf{\theta }}_1}({\mathsf{\nu }}_2-\mathtt{x})}{\mathtt{e}}^{-\frac{1-{\mathsf{\theta }}_2}{{\mathsf{\theta }}_2}({\mathsf{\nu }}_4-\mathtt{y})}\aleph (\mathtt{x},\mathtt{y})\mathrm{d}\mathtt{y}\mathrm{d}\mathtt{x}\right.\hfill \\ & +{\int }_{{\mathsf{\nu }}_1}^{{\mathsf{\nu }}_2}{\int }_{{\mathsf{\nu }}_3}^{{\mathsf{\nu }}_4}{\mathtt{e}}^{-\frac{1-{\mathsf{\theta }}_1}{{\mathsf{\theta }}_1}({\mathsf{\nu }}_2-\mathtt{x})}{\mathtt{e}}^{-\frac{1-{\mathsf{\theta }}_2}{{\mathsf{\theta }}_2}(\mathtt{y}-{\mathsf{\nu }}_3)}\aleph (\mathtt{x},\mathtt{y})\mathrm{d}\mathtt{y}\mathrm{d}\mathtt{x}\hfill \\ & +{\int }_{{\mathsf{\nu }}_1}^{{\mathsf{\nu }}_2}{\int }_{{\mathsf{\nu }}_3}^{{\mathsf{\nu }}_4}{\mathtt{e}}^{-\frac{1-{\mathsf{\theta }}_1}{{\mathsf{\theta }}_1}(\mathtt{x}-{\mathsf{\nu }}_1)}{\mathtt{e}}^{-\frac{1-{\mathsf{\theta }}_2}{{\mathsf{\theta }}_2}({\mathsf{\nu }}_4-\mathtt{y})}\aleph (\mathtt{x},\mathtt{y})\mathrm{d}\mathtt{y}\mathrm{d}\mathtt{x}\hfill \\ & \left.+{\int }_{{\mathsf{\nu }}_1}^{{\mathsf{\nu }}_2}{\int }_{{\mathsf{\nu }}_3}^{{\mathsf{\nu }}_4}{\mathtt{e}}^{-\frac{1-{\mathsf{\theta }}_1}{{\mathsf{\theta }}_1}(\mathtt{x}-{\mathsf{\nu }}_1)}{\mathtt{e}}^{-\frac{1-{\mathsf{\theta }}_2}{{\mathsf{\theta }}_2}(\mathtt{y}-{\mathsf{\nu }}_3)}\aleph (\mathtt{x},\mathtt{y})\mathrm{d}\mathtt{y}\mathrm{d}\mathtt{x}\right\}\hfill \\ & =\frac{{\mathsf{\theta }}_1{\mathsf{\theta }}_2}{4({\mathsf{\nu }}_2-{\mathsf{\nu }}_1)({\mathsf{\nu }}_4-{\mathsf{\nu }}_3)}\left[{\mathtt{J}}_{{{\mathsf{\nu }}_1}^{+},{{\mathsf{\nu }}_3}^{+}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)+{\mathtt{J}}_{{{\mathsf{\nu }}_1}^{+},{{\mathsf{\nu }}_4}^{-}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)\right.\hfill \\ & \left.+{\mathtt{J}}_{{{\mathsf{\nu }}_2}^{-},{{\mathsf{\nu }}_3}^{+}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)+{\mathtt{J}}_{{{\mathsf{\nu }}_2}^{-},{{\mathsf{\nu }}_4}^{-}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)\right].\hfill \\ \end{array}$$

This proves the first $\mathtt{CR}$ relation. As for the second relation, given Definition 7, we have

$$\begin{array}{cc}\hfill \aleph \left({\mathtt{r}}_{\mathtt{1}}{\mathsf{\nu }}_1+\left(1-{\mathtt{r}}_{\mathtt{1}}\right){\mathsf{\nu }}_2,{\mathsf{s}}_{\mathsf{1}}{\mathsf{\nu }}_3+\left(1-{\mathsf{s}}_{\mathsf{1}}\right){\mathsf{\nu }}_4\right){⪯}_{\mathtt{CR}}& {\mathtt{r}}_{\mathtt{1}}{\mathsf{s}}_{\mathsf{1}}\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)+{\mathsf{s}}_{\mathsf{1}}\left(1-{\mathtt{r}}_{\mathtt{1}}\right)\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)\hfill \\ & +{\mathtt{r}}_{\mathtt{1}}\left(1-{\mathsf{s}}_{\mathsf{1}}\right)\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)+{\mathsf{s}}_{\mathsf{1}}\left(1-{\mathtt{r}}_{\mathtt{1}}\right)\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4),\hfill \\ \hfill \aleph \left({\mathtt{r}}_{\mathtt{1}}{\mathsf{\nu }}_1+\left(1-{\mathtt{r}}_{\mathtt{1}}\right){\mathsf{\nu }}_2,\left(1-{\mathsf{s}}_{\mathsf{1}}\right){\mathsf{\nu }}_3+{\mathsf{s}}_{\mathsf{1}}{\mathsf{\nu }}_4\right){⪯}_{\mathtt{CR}}& {\mathtt{r}}_{\mathtt{1}}\left(1-{\mathsf{s}}_{\mathsf{1}}\right)\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)+\left(1-{\mathsf{s}}_{\mathsf{1}}\right)\left(1-{\mathtt{r}}_{\mathtt{1}}\right)\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)\hfill \\ & +{\mathtt{r}}_{\mathtt{1}}{\mathsf{s}}_{\mathsf{1}}\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)+\left(1-{\mathtt{r}}_{\mathtt{1}}\right){\mathsf{s}}_{\mathsf{1}}\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4),\hfill \\ \hfill \aleph \left(\left(1-{\mathtt{r}}_{\mathtt{1}}\right){\mathsf{\nu }}_1+{\mathtt{r}}_{\mathtt{1}}{\mathsf{\nu }}_2,{\mathsf{s}}_{\mathsf{1}}{\mathsf{\nu }}_3+\left(1-{\mathsf{s}}_{\mathsf{1}}\right){\mathsf{\nu }}_4\right){⪯}_{\mathtt{CR}}& \left(1-{\mathtt{r}}_{\mathtt{1}}\right){\mathsf{s}}_{\mathsf{1}}\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)+{\mathtt{r}}_{\mathtt{1}}{\mathsf{s}}_{\mathsf{1}}\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)\hfill \\ & +\left(1-{\mathtt{r}}_{\mathtt{1}}\right)\left(1-{\mathsf{s}}_{\mathsf{1}}\right)\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)+{\mathtt{r}}_{\mathtt{1}}{\mathsf{s}}_{\mathsf{1}}\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4),\hfill \end{array}$$

as well as

$$\begin{array}{cc}\hfill \aleph \left(\left(1-{\mathtt{r}}_{\mathtt{1}}\right){\mathsf{\nu }}_1+{\mathtt{r}}_{\mathtt{1}}{\mathsf{\nu }}_2,\left(1-{\mathsf{s}}_{\mathsf{1}}\right){\mathsf{\nu }}_3+{\mathsf{s}}_{\mathsf{1}}{\mathsf{\nu }}_4\right){⪯}_{\mathtt{CR}}& \left(1-{\mathtt{r}}_{\mathtt{1}}\right)\left(1-{\mathsf{s}}_{\mathsf{1}}\right)\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)+{\mathtt{r}}_{\mathtt{1}}\left(1-{\mathsf{s}}_{\mathsf{1}}\right)\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)\hfill \\ & +{\mathsf{s}}_{\mathsf{1}}\left(1-{\mathtt{r}}_{\mathtt{1}}\right)\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)+{\mathtt{r}}_{\mathtt{1}}{\mathsf{s}}_{\mathsf{1}}\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4).\hfill \end{array}$$

Including the above-mentioned relations, it follows that

$$\begin{array}{cc}\hfill & \aleph \left({\mathtt{r}}_{\mathtt{1}}{\mathsf{\nu }}_1+\left(1-{\mathtt{r}}_{\mathtt{1}}\right){\mathsf{\nu }}_2,{\mathsf{s}}_{\mathsf{1}}{\mathsf{\nu }}_3+\left(1-{\mathsf{s}}_{\mathsf{1}}\right){\mathsf{\nu }}_4\right)+\aleph \left({\mathtt{r}}_{\mathtt{1}}{\mathsf{\nu }}_1+\left(1-{\mathtt{r}}_{\mathtt{1}}\right){\mathsf{\nu }}_2,\left(1-{\mathsf{s}}_{\mathsf{1}}\right){\mathsf{\nu }}_3+{\mathsf{s}}_{\mathsf{1}}{\mathsf{\nu }}_4\right)\hfill \\ \hfill & +\aleph \left(\left(1-{\mathtt{r}}_{\mathtt{1}}\right){\mathsf{\nu }}_1+{\mathtt{r}}_{\mathtt{1}}{\mathsf{\nu }}_2,{\mathsf{s}}_{\mathsf{1}}{\mathsf{\nu }}_3+\left(1-{\mathsf{s}}_{\mathsf{1}}\right){\mathsf{\nu }}_4\right)+\aleph \left(\left(1-{\mathtt{r}}_{\mathtt{1}}\right){\mathsf{\nu }}_1+{\mathtt{r}}_{\mathtt{1}}{\mathsf{\nu }}_2,\left(1-{\mathsf{s}}_{\mathsf{1}}\right){\mathsf{\nu }}_3+{\mathsf{s}}_{\mathsf{1}}{\mathsf{\nu }}_4\right)\hfill \\ \hfill & {⪯}_{\mathtt{CR}}\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)+\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)+\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)+\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4).\hfill \end{array}$$

(10)

Multiplying the $\mathtt{CR}$ relation above with ${\mathtt{e}}^{-{ð}_1{\mathtt{r}}_{\mathtt{1}}}{\mathtt{e}}^{-{ð}_2{\mathsf{s}}_{\mathsf{1}}}$, then integrating the resultant output about $\left({\mathtt{r}}_{\mathtt{1}},{\mathsf{s}}_{\mathsf{1}}\right)$, we obtain

$$\begin{array}{cc}& {\int }_0^1{\int }_0^1{\mathtt{e}}^{-{ð}_1{\mathtt{r}}_{\mathtt{1}}}{\mathtt{e}}^{-{ð}_2{\mathsf{s}}_{\mathsf{1}}}\left[\aleph \left({\mathtt{r}}_{\mathtt{1}}{\mathsf{\nu }}_1+\left(1-{\mathtt{r}}_{\mathtt{1}}\right){\mathsf{\nu }}_2,{\mathsf{s}}_{\mathsf{1}}{\mathsf{\nu }}_3+\left(1-{\mathsf{s}}_{\mathsf{1}}\right){\mathsf{\nu }}_4\right)\right.\hfill \\ & \left.+\aleph \left({\mathtt{r}}_{\mathtt{1}}{\mathsf{\nu }}_1+\left(1-{\mathtt{r}}_{\mathtt{1}}\right){\mathsf{\nu }}_2,\left(1-{\mathsf{s}}_{\mathsf{1}}\right){\mathsf{\nu }}_3+{\mathsf{s}}_{\mathsf{1}}{\mathsf{\nu }}_4\right)\right]\mathrm{d}{\mathsf{s}}_{\mathsf{1}}\mathrm{d}{\mathtt{r}}_{\mathtt{1}}\hfill \\ & +{\int }_0^1{\int }_0^1{\mathtt{e}}^{-{ð}_1{\mathtt{r}}_{\mathtt{1}}}{\mathtt{e}}^{-{ð}_2{\mathsf{s}}_{\mathsf{1}}}[\aleph (\left(1-{\mathtt{r}}_{\mathtt{1}}\right){\mathsf{\nu }}_1+{\mathtt{r}}_{\mathtt{1}}{\mathsf{\nu }}_2,{\mathsf{s}}_{\mathsf{1}}{\mathsf{\nu }}_3\hfill \\ & +\left(1-{\mathsf{s}}_{\mathsf{1}}\right){\mathsf{\nu }}_4)+\aleph \left((1-{\mathtt{r}}_{\mathtt{1}}\right){\mathsf{\nu }}_1+{\mathtt{r}}_{\mathtt{1}}{\mathsf{\nu }}_2,\left(1-{\mathsf{s}}_{\mathsf{1}}\right){\mathsf{\nu }}_3+{\mathsf{s}}_{\mathsf{1}}{\mathsf{\nu }}_4\left)\right]\mathrm{d}{\mathsf{s}}_{\mathsf{1}}\mathrm{d}{\mathtt{r}}_{\mathtt{1}}\hfill \\ & {⪯}_{\mathtt{CR}}{\int }_0^1{\int }_0^1{\mathtt{e}}^{-{ð}_1{\mathtt{r}}_{\mathtt{1}}}{\mathtt{e}}^{-{ð}_2{\mathsf{s}}_{\mathsf{1}}}[\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)+\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)+\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)+\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)]\mathrm{d}{\mathsf{s}}_{\mathsf{1}}\mathrm{d}{\mathtt{r}}_{\mathtt{1}}.\hfill \end{array}$$

Changing the variables results in the following:

$$\begin{array}{cc}& \frac{(1-{\mathsf{\theta }}_1)(1-{\mathsf{\theta }}_2)}{4\left(1-{\mathtt{e}}^{-{ð}_1}\right)\left(1-{\mathtt{e}}^{-{ð}_2}\right)}\left[{\mathtt{J}}_{{{\mathsf{\nu }}_1}^{+},{{\mathsf{\nu }}_3}^{+}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)+{\mathtt{J}}_{{{\mathsf{\nu }}_1}^{+},{{\mathsf{\nu }}_4}^{-}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)\right.\hfill \\ & \left.+{\mathtt{J}}_{{{\mathsf{\nu }}_2}^{-},{{\mathsf{\nu }}_3}^{+}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)+{\mathtt{J}}_{{{\mathsf{\nu }}_2}^{-},{{\mathsf{\nu }}_4}^{-}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)\right]\hfill \\ & {⪯}_{\mathtt{CR}}\frac{\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)+\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)+\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)+\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)}{4}.\hfill \end{array}$$

Consequently, Theorem 7 is proved. Following Theorem 7, we derive the following results that have been documented in the literature.

□

Remark 4. 

• If ${\mathsf{\theta }}_1\to 1,{\mathsf{\theta }}_2\to 1$ with $\underline{\aleph }\ne \overline{\aleph }$, we obtain the following result by Zhao et al. [15]:

  $$\begin{array}{cc}\hfill \aleph \left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2},\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right)\supseteq & \frac{1}{({\mathsf{\nu }}_2-{\mathsf{\nu }}_1)({\mathsf{\nu }}_4-{\mathsf{\nu }}_3)}{\int }_{{\mathsf{\nu }}_1}^{{\mathsf{\nu }}_2}{\int }_{{\mathsf{\nu }}_3}^{{\mathsf{\nu }}_4}\aleph (\mathtt{x},\mathtt{y})\mathrm{d}\mathtt{y}\mathrm{d}\mathtt{x}\hfill \\ & \supseteq \frac{\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)+\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)+\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)+\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)}{4}.\hfill \end{array}$$
• If ${\mathsf{\theta }}_1\to 1,{\mathsf{\theta }}_2\to 1$ with $\underline{\aleph }=\overline{\aleph }$, we obtain the following result by Dragomir [14]:

  $$\begin{array}{cc}\hfill \aleph \left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2},\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right)\le & \frac{1}{({\mathsf{\nu }}_2-{\mathsf{\nu }}_1)({\mathsf{\nu }}_4-{\mathsf{\nu }}_3)}{\int }_{{\mathsf{\nu }}_1}^{{\mathsf{\nu }}_2}{\int }_{{\mathsf{\nu }}_3}^{{\mathsf{\nu }}_4}\aleph (\mathtt{x},\mathtt{y})\mathrm{d}\mathtt{y}\mathrm{d}\mathtt{x}\hfill \\ & \le \frac{\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)+\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)+\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)+\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)}{4}.\hfill \end{array}$$
• If $\underline{\aleph }=\overline{\aleph }$, we obtain the following result, which is new as well:

  $$\begin{array}{cc}\hfill & \aleph \left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2},\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right)\hfill \\ & \le \frac{(1-{\mathsf{\theta }}_1)(1-{\mathsf{\theta }}_2)}{4(1-{\mathtt{e}}^{-{ð}_1})(1-{\mathtt{e}}^{-{ð}_2})}\left[{\mathtt{J}}_{{{\mathsf{\nu }}_1}^{+},{{\mathsf{\nu }}_3}^{+}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)+{\mathtt{J}}_{{{\mathsf{\nu }}_1}^{+},{{\mathsf{\nu }}_4}^{-}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)\right.\hfill \\ \hfill & \left.+{\mathtt{J}}_{{{\mathsf{\nu }}_2}^{-},{{\mathsf{\nu }}_3}^{+}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)+{\mathtt{J}}_{{{\mathsf{\nu }}_2}^{-},{\mathsf{\nu }}_4-}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)\right]\hfill \\ \hfill & \le \frac{\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)+\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)+\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)+\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)}{4}.\hfill \end{array}$$
• If ${\mathsf{\theta }}_1\to 1,{\mathsf{\theta }}_2\to 1$ with $\underline{\aleph }\ne \overline{\aleph }$, we obtain the following result by Khan et al. [62]:

  $$\begin{array}{cc}\hfill \aleph \left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2},\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right){\le }_p& \frac{1}{({\mathsf{\nu }}_2-{\mathsf{\nu }}_1)({\mathsf{\nu }}_4-{\mathsf{\nu }}_3)}{\int }_{{\mathsf{\nu }}_1}^{{\mathsf{\nu }}_2}{\int }_{{\mathsf{\nu }}_3}^{{\mathsf{\nu }}_4}\aleph (\mathtt{x},\mathtt{y})\mathrm{d}\mathtt{y}\mathrm{d}\mathtt{x}\hfill \\ & {\le }_p\frac{\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)+\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)+\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)+\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)}{4}.\hfill \end{array}$$

Example 3. 

If one has $\aleph (\mathtt{x},\mathtt{y})=\left[2e^{3\mathtt{x}}{e}^{3\mathtt{y}},\left(4+e^{\mathtt{x}}\right)\left(4+e^{\mathtt{y}}\right)\right],[{\mathsf{\nu }}_1,{\mathsf{\nu }}_2]=[0,1],[{\mathsf{\nu }}_3,{\mathsf{\nu }}_4]=[0,1],{\mathsf{\theta }}_1=1$, and ${\mathsf{\theta }}_2=1$, then all the postulates in Theorem 3.2 are satisfied. Now we consider

$$\begin{array}{cc}& \aleph \left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2},\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right)=\left[2e^3,{(4+e^{\frac{1}{2}})}^2\right]\approx [40.17107,31.90805],\hfill \\ & \frac{(1-{\mathsf{\theta }}_1)(1-{\mathsf{\theta }}_2)}{4\left(1-{\mathtt{e}}^{-{ð}_1}\right)\left(1-{\mathtt{e}}^{-{ð}_2}\right)}\left[{\mathtt{J}}_{{{\mathsf{\nu }}_1}^{+},{{\mathsf{\nu }}_3}^{+}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)+{\mathtt{J}}_{{{\mathsf{\nu }}_1}^{+},{{\mathsf{\nu }}_4}^{-}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)\right.\hfill \\ & \left.+{\mathtt{J}}_{{{\mathsf{\nu }}_2}^{-},{{\mathsf{\nu }}_3}^{+}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)+{\mathtt{J}}_{{{\mathsf{\nu }}_2}^{-},{{\mathsf{\nu }}_4}^{-}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)\right]\approx [114.04725,64.60196],\hfill \\ & \frac{\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)+\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)+\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)+\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)}{4}\approx [222.2993,93.8679].\hfill \\ \end{array}$$

Thus,

$$[40.17107,31.90805]{⪯}_{\mathtt{CR}}[114.04725,64.60196]{⪯}_{\mathtt{CR}}[222.2993,93.8679].$$

As a result, the conclusions described in Theorem 7 are true.

Weighted Hermite–Hadamard or Fejér-Type Inequality

By using the weight function of two variables, we can prove the following theorem relating to weighted Hermite–Hadamard or Fejér-type inequalities.

Theorem 8. 

Let $\aleph :[{\mathsf{\nu }}_1,{\mathsf{\nu }}_2]\times [{\mathsf{\nu }}_3,{\mathsf{\nu }}_4]\subseteq {\mathsf{R}}^2\to {{\mathsf{R}}_{\mathtt{i}}}^{+}$ be a bidimensional interval-valued function defined as $\aleph =[\underline{{\aleph }_1}(\mathtt{x},\mathtt{y}),\overline{{\aleph }_2}(\mathtt{x},\mathtt{y})]$ with $0\le {\mathsf{\nu }}_1<{\mathsf{\nu }}_2,0\le {\mathsf{\nu }}_3<{\mathsf{\nu }}_4]$. If the function $\mathsf{\phi }:[{\mathsf{\nu }}_1,{\mathsf{\nu }}_2]\times [{\mathsf{\nu }}_3,{\mathsf{\nu }}_4]\subset {\mathsf{R}}^2\to \mathsf{R}$ is symmetric with respect to two variable forms, i.e.

$$\mathsf{\phi }(\mathtt{x},\mathtt{y})=\left\{\begin{array}{c}\mathsf{\phi }({\mathsf{\nu }}_1+{\mathsf{\nu }}_2-\mathtt{x},\mathtt{y}),\hfill \\ \mathsf{\phi }(\mathtt{x},{\mathsf{\nu }}_3+{\mathsf{\nu }}_4-\mathtt{y}),\hfill \\ \mathsf{\phi }({\mathsf{\nu }}_1+{\mathsf{\nu }}_2-\mathtt{x},{\mathsf{\nu }}_3+{\mathsf{\nu }}_4-\mathtt{y}),\hfill \end{array}\right.$$

then we have

$$\begin{array}{cc}& \aleph \left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2},\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right)\left[{\mathtt{J}}_{{{\mathsf{\nu }}_1}^{+},{{\mathsf{\nu }}_3}^{+}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\mathsf{\phi }({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)+{\mathtt{J}}_{{{\mathsf{\nu }}_1}^{+},{{\mathsf{\nu }}_4}^{-}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\mathsf{\phi }({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)\right.\hfill \\ & \left.+{\mathtt{J}}_{{{\mathsf{\nu }}_2}^{-},{{\mathsf{\nu }}_3}^{+}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\mathsf{\phi }({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)+{\mathtt{J}}_{{{\mathsf{\nu }}_2}^{-},{{\mathsf{\nu }}_4}^{-}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\mathsf{\phi }({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)\right]\hfill \\ & {⪯}_{\mathtt{CR}}\left[{\mathtt{J}}_{{{\mathsf{\nu }}_1}^{+},{{\mathsf{\nu }}_3}^{+}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)\mathsf{\phi }({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)+{\mathtt{J}}_{{{\mathsf{\nu }}_1}^{+},{{\mathsf{\nu }}_4}^{-}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)\mathsf{\phi }({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)\right.\hfill \\ & \left.+{\mathtt{J}}_{{{\mathsf{\nu }}_2}^{-},{{\mathsf{\nu }}_3}^{+}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)\mathsf{\phi }({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)+{\mathtt{J}}_{{{\mathsf{\nu }}_2}^{-},{{\mathsf{\nu }}_4}^{-}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)\mathsf{\phi }({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)\right]\hfill \\ & {⪯}_{\mathtt{CR}}\frac{\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)+\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)+\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)+\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)}{4}\left[{\mathtt{J}}_{{{\mathsf{\nu }}_1}^{+},{{\mathsf{\nu }}_3}^{+}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\mathsf{\phi }({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)+{\mathtt{J}}_{{{\mathsf{\nu }}_1}^{+},{{\mathsf{\nu }}_4}^{-}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\mathsf{\phi }({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)\right.\hfill \\ & \left.+{\mathtt{J}}_{{{\mathsf{\nu }}_2}^{-},{{\mathsf{\nu }}_3}^{+}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\mathsf{\phi }({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)+{\mathtt{J}}_{{{\mathsf{\nu }}_2}^{-},{{\mathsf{\nu }}_4}^{-}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\mathsf{\phi }({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)\right].\hfill \end{array}$$

Proof. 

Taking into account relation (9) of Theorem 7, multiply both sides by $4{\mathtt{e}}^{-{ð}_1{\mathtt{r}}_{\mathtt{1}}}{\mathtt{e}}^{-{ð}_2{\mathsf{s}}_{\mathsf{1}}}\mathsf{\phi }\left({\mathtt{r}}_{\mathtt{1}}{\mathsf{\nu }}_1+\right.$$\left.\left(1-{\mathtt{r}}_{\mathtt{1}}\right){\mathsf{\nu }}_2,{\mathsf{s}}_{\mathsf{1}}{\mathsf{\nu }}_3+\left(1-{\mathsf{s}}_{\mathsf{1}}\right){\mathsf{\nu }}_4\right)$ and integrate the resultant output with reference to $\left({\mathtt{r}}_{\mathtt{1}},{\mathsf{s}}_{\mathsf{1}}\right)$ on $[0,1]\times [0,1]$, which reveals that

$$\begin{array}{cc}& 4\aleph \left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2}\right.\left.\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right){\int }_0^1{\int }_0^1{\mathtt{e}}^{-{ð}_1{\mathtt{r}}_{\mathtt{1}}}{\mathtt{e}}^{-{ð}_2{\mathsf{s}}_{\mathsf{1}}}\mathsf{\phi }\left({\mathtt{r}}_{\mathtt{1}}{\mathsf{\nu }}_1+\left(1-{\mathtt{r}}_{\mathtt{1}}\right){\mathsf{\nu }}_2,{\mathsf{s}}_{\mathsf{1}}{\mathsf{\nu }}_3+\left(1-{\mathsf{s}}_{\mathsf{1}}\right){\mathsf{\nu }}_4\right)\mathrm{d}{\mathsf{s}}_{\mathsf{1}}\mathrm{d}{\mathtt{r}}_{\mathtt{1}}\hfill \\ & {⪯}_{\mathtt{CR}}{\int }_0^1{\int }_0^1{\mathtt{e}}^{-{ð}_1{\mathtt{r}}_{\mathtt{1}}}{\mathtt{e}}^{-{ð}_2{\mathsf{s}}_{\mathsf{1}}}\mathsf{\phi }\left({\mathtt{r}}_{\mathtt{1}}{\mathsf{\nu }}_1+\left(1-{\mathtt{r}}_{\mathtt{1}}\right){\mathsf{\nu }}_2,{\mathsf{s}}_{\mathsf{1}}{\mathsf{\nu }}_3+\left(1-{\mathsf{s}}_{\mathsf{1}}\right){\mathsf{\nu }}_4\right)\hfill \\ & \times \left[\aleph \left({\mathtt{r}}_{\mathtt{1}}{\mathsf{\nu }}_1+\left(1-{\mathtt{r}}_{\mathtt{1}}\right){\mathsf{\nu }}_2,{\mathsf{s}}_{\mathsf{1}}{\mathsf{\nu }}_3+\left(1-{\mathsf{s}}_{\mathsf{1}}\right){\mathsf{\nu }}_4\right)+\aleph \left({\mathtt{r}}_{\mathtt{1}}{\mathsf{\nu }}_1+\left(1-{\mathtt{r}}_{\mathtt{1}}\right){\mathsf{\nu }}_2,\left(1-{\mathsf{s}}_{\mathsf{1}}\right){\mathsf{\nu }}_3+{\mathsf{s}}_{\mathsf{1}}{\mathsf{\nu }}_4\right)\right]\mathrm{d}{\mathsf{s}}_{\mathsf{1}}\mathrm{d}{\mathtt{r}}_{\mathtt{1}}\hfill \\ & +{\int }_0^1{\int }_0^1{\mathtt{e}}^{-{ð}_1{\mathtt{r}}_{\mathtt{1}}}{\mathtt{e}}^{-{ð}_2{\mathsf{s}}_{\mathsf{1}}}\mathsf{\phi }\left({\mathtt{r}}_{\mathtt{1}}{\mathsf{\nu }}_1+\left(1-{\mathtt{r}}_{\mathtt{1}}\right){\mathsf{\nu }}_2,{\mathsf{s}}_{\mathsf{1}}{\mathsf{\nu }}_3+\left(1-{\mathsf{s}}_{\mathsf{1}}\right){\mathsf{\nu }}_4\right)\hfill \\ & \times \left[\aleph \left(\left(1-{\mathtt{r}}_{\mathtt{1}}\right){\mathsf{\nu }}_1+{\mathtt{r}}_{\mathtt{1}}{\mathsf{\nu }}_2,{\mathsf{s}}_{\mathsf{1}}{\mathsf{\nu }}_3+\left(1-{\mathsf{s}}_{\mathsf{1}}\right){\mathsf{\nu }}_4\right)+\aleph \left(\left(1-{\mathtt{r}}_{\mathtt{1}}\right){\mathsf{\nu }}_1+{\mathtt{r}}_{\mathtt{1}}{\mathsf{\nu }}_2,\left(1-{\mathsf{s}}_{\mathsf{1}}\right){\mathsf{\nu }}_3+{\mathsf{s}}_{\mathsf{1}}{\mathsf{\nu }}_4\right)\right]\mathrm{d}{\mathsf{s}}_{\mathsf{1}}\mathrm{d}{\mathtt{r}}_{\mathtt{1}}.\hfill \end{array}$$

By altering the variable and performing different calculations, we may obtain

$$\begin{array}{cc}& \aleph \left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2},\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right)\frac{4}{({\mathsf{\nu }}_2-{\mathsf{\nu }}_1)({\mathsf{\nu }}_4-{\mathsf{\nu }}_3)}{\int }_{{\mathsf{\nu }}_1}^{{\mathsf{\nu }}_2}{\int }_{{\mathsf{\nu }}_3}^{{\mathsf{\nu }}_4}{\mathtt{e}}^{-\frac{1-{\mathsf{\theta }}_1}{{\mathsf{\theta }}_1}({\mathsf{\nu }}_2-\xi )}{\mathtt{e}}^{-\frac{1-{\mathsf{\theta }}_2}{{\mathsf{\theta }}_2}({\mathsf{\nu }}_4-\delta )}\aleph (\xi ,\delta )\mathsf{\phi }(\xi ,\delta )\mathrm{d}\delta \mathrm{d}\xi \hfill \\ & {⪯}_{\mathtt{CR}}\frac{1}{({\mathsf{\nu }}_2-{\mathsf{\nu }}_1)({\mathsf{\nu }}_4-{\mathsf{\nu }}_3)}\left\{{\int }_{{\mathsf{\nu }}_1}^{{\mathsf{\nu }}_2}{\int }_{{\mathsf{\nu }}_3}^{{\mathsf{\nu }}_4}{\mathtt{e}}^{-\frac{1-{\mathsf{\theta }}_1}{{\mathsf{\theta }}_1}({\mathsf{\nu }}_2-\xi )}{\mathtt{e}}^{-\frac{1-{\mathsf{\theta }}_2}{{\mathsf{\theta }}_2}({\mathsf{\nu }}_4-\delta )}\aleph (\xi ,\delta )\mathsf{\phi }(\xi ,\delta )\mathrm{d}\delta \mathrm{d}\xi \right.\hfill \\ & +{\int }_{{\mathsf{\nu }}_1}^{{\mathsf{\nu }}_2}{\int }_{{\mathsf{\nu }}_3}^{{\mathsf{\nu }}_4}{\mathtt{e}}^{-\frac{1-{\mathsf{\theta }}_1}{{\mathsf{\theta }}_1}({\mathsf{\nu }}_2-\xi )}{\mathtt{e}}^{-\frac{1-{\mathsf{\theta }}_2}{{\mathsf{\theta }}_2}(\delta -{\mathsf{\nu }}_3)}\aleph (\xi ,\delta )\mathsf{\phi }(\xi ,{\mathsf{\nu }}_3+{\mathsf{\nu }}_4-\delta )\mathrm{d}\delta \mathrm{d}\xi \hfill \\ & +{\int }_{{\mathsf{\nu }}_1}^{{\mathsf{\nu }}_2}{\int }_{{\mathsf{\nu }}_3}^{{\mathsf{\nu }}_4}{\mathtt{e}}^{-\frac{1-{\mathsf{\theta }}_1}{{\mathsf{\theta }}_1}(\xi -{\mathsf{\nu }}_1)}{\mathtt{e}}^{-\frac{1-{\mathsf{\theta }}_2}{{\mathsf{\theta }}_2}({\mathsf{\nu }}_4-\delta )}\aleph (\xi ,\delta )\mathsf{\phi }({\mathsf{\nu }}_1+{\mathsf{\nu }}_2-\xi ,\delta )\mathrm{d}\delta \mathrm{d}\xi \hfill \\ & \left.+{\int }_{{\mathsf{\nu }}_1}^{{\mathsf{\nu }}_2}{\int }_{{\mathsf{\nu }}_3}^{{\mathsf{\nu }}_4}{\mathtt{e}}^{-\frac{1-{\mathsf{\theta }}_1}{{\mathsf{\theta }}_1}(\xi -{\mathsf{\nu }}_1)}{\mathtt{e}}^{-\frac{1-{\mathsf{\theta }}_2}{{\mathsf{\theta }}_2}(\delta -{\mathsf{\nu }}_3)}\aleph (\xi ,\delta )\mathsf{\phi }({\mathsf{\nu }}_1+{\mathsf{\nu }}_2-\xi ,{\mathsf{\nu }}_3+{\mathsf{\nu }}_4-\delta )\mathrm{d}\delta \mathrm{d}\xi \right\}\hfill \\ & =\frac{{\mathsf{\theta }}_1{\mathsf{\theta }}_2}{({\mathsf{\nu }}_2-{\mathsf{\nu }}_1)({\mathsf{\nu }}_4-{\mathsf{\nu }}_3)}\left[{\mathtt{J}}_{{{\mathsf{\nu }}_1}^{+},{\mathsf{\nu }}_3}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)\mathsf{\phi }({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)+{\mathtt{J}}_{{{\mathsf{\nu }}_1}^{+},{{\mathsf{\nu }}_4}^{-}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)\mathsf{\phi }({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)\right.\hfill \\ & \left.+{\mathtt{J}}_{{{\mathsf{\nu }}_2}^{-},{{\mathsf{\nu }}_3}^{+}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)\mathsf{\phi }({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)+{\mathtt{J}}_{{{\mathsf{\nu }}_2}^{-},{{\mathsf{\nu }}_4}^{-}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)\mathsf{\phi }({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)\right].\hfill \end{array}$$

Since $\mathsf{\phi }(\mathtt{x},\mathtt{y})$ has symmetry, it leads to

$$\begin{array}{cc}& \aleph \left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2},\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right)\frac{4}{({\mathsf{\nu }}_2-{\mathsf{\nu }}_1)({\mathsf{\nu }}_4-{\mathsf{\nu }}_3)}{\int }_{{\mathsf{\nu }}_1}^{{\mathsf{\nu }}_2}{\int }_{{\mathsf{\nu }}_3}^{{\mathsf{\nu }}_4}{\mathtt{e}}^{-\frac{1-{\mathsf{\theta }}_1}{{\mathsf{\theta }}_1}({\mathsf{\nu }}_2-\xi )}{\mathtt{e}}^{-\frac{1-{\mathsf{\theta }}_2}{{\mathsf{\theta }}_2}({\mathsf{\nu }}_4-\delta )}\aleph (\xi ,\delta )\mathsf{\phi }(\xi ,\delta )\mathrm{d}\delta \mathrm{d}\xi \hfill \\ & =\frac{{\mathsf{\theta }}_1{\mathsf{\theta }}_2}{({\mathsf{\nu }}_2-{\mathsf{\nu }}_1)({\mathsf{\nu }}_4-{\mathsf{\nu }}_3)}\aleph \left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2},\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right)\left[{\mathtt{J}}_{{{\mathsf{\nu }}_1}^{+},{{\mathsf{\nu }}_3}^{+}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\mathsf{\phi }({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)+{\mathtt{J}}_{{{\mathsf{\nu }}_1}^{+},{{\mathsf{\nu }}_4}^{-}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\mathsf{\phi }({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)\right.\hfill \\ & \left.+{\mathtt{J}}_{{{\mathsf{\nu }}_2}^{-},{{\mathsf{\nu }}_3}^{+}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\mathsf{\phi }({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)+{\mathtt{J}}_{{{\mathsf{\nu }}_2}^{-},{{\mathsf{\nu }}_4}^{-}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\mathsf{\phi }({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)\right].\hfill \end{array}$$

This concludes the first $\mathtt{CR}$ relation. For the second relation, considering relation (10) of Theorem 7, and multiplying both sides by ${\mathtt{e}}^{-{ð}_1{\mathtt{r}}_{\mathtt{1}}}{\mathtt{e}}^{-{ð}_2{\mathsf{s}}_{\mathsf{1}}}\mathsf{\phi }\left({\mathtt{r}}_{\mathtt{1}}{\mathsf{\nu }}_1+\left(1-{\mathtt{r}}_{\mathtt{1}}\right){\mathsf{\nu }}_2,{\mathsf{s}}_{\mathsf{1}}{\mathsf{\nu }}_3+\left(1-{\mathsf{s}}_{\mathsf{1}}\right){\mathsf{\nu }}_4\right)$ and integrating, we have

$$\begin{array}{cc}& {\int }_0^1{\int }_0^1{\mathtt{e}}^{-{ð}_1{\mathtt{r}}_{\mathtt{1}}}{\mathtt{e}}^{-{ð}_2{\mathsf{s}}_{\mathsf{1}}}\mathsf{\phi }\left({\mathtt{r}}_{\mathtt{1}}{\mathsf{\nu }}_1+\left(1-{\mathtt{r}}_{\mathtt{1}}\right){\mathsf{\nu }}_2,{\mathsf{s}}_{\mathsf{1}}{\mathsf{\nu }}_3+\left(1-{\mathsf{s}}_{\mathsf{1}}\right){\mathsf{\nu }}_4\right)\hfill \\ & \times \left[\aleph \left({\mathtt{r}}_{\mathtt{1}}{\mathsf{\nu }}_1+\left(1-{\mathtt{r}}_{\mathtt{1}}\right){\mathsf{\nu }}_2,{\mathsf{s}}_{\mathsf{1}}{\mathsf{\nu }}_3+\left(1-{\mathsf{s}}_{\mathsf{1}}\right){\mathsf{\nu }}_4\right)+\aleph \left({\mathtt{r}}_{\mathtt{1}}{\mathsf{\nu }}_1+\left(1-{\mathtt{r}}_{\mathtt{1}}\right){\mathsf{\nu }}_2,\left(1-{\mathsf{s}}_{\mathsf{1}}\right){\mathsf{\nu }}_3+{\mathsf{s}}_{\mathsf{1}}{\mathsf{\nu }}_4\right)\right]\mathrm{d}{\mathsf{s}}_{\mathsf{1}}\mathrm{d}{\mathtt{r}}_{\mathtt{1}}\hfill \\ & +{\int }_0^1{\int }_0^1{\mathtt{e}}^{-{ð}_1{\mathtt{r}}_{\mathtt{1}}}{\mathtt{e}}^{-{ð}_2{\mathsf{s}}_{\mathsf{1}}}\mathsf{\phi }\left({\mathtt{r}}_{\mathtt{1}}{\mathsf{\nu }}_1+\left(1-{\mathtt{r}}_{\mathtt{1}}\right){\mathsf{\nu }}_2,{\mathsf{s}}_{\mathsf{1}}{\mathsf{\nu }}_3+\left(1-{\mathsf{s}}_{\mathsf{1}}\right){\mathsf{\nu }}_4\right)\hfill \\ & \times \left[\aleph \left(\left(1-{\mathtt{r}}_{\mathtt{1}}\right){\mathsf{\nu }}_1+{\mathtt{r}}_{\mathtt{1}}{\mathsf{\nu }}_2,{\mathsf{s}}_{\mathsf{1}}{\mathsf{\nu }}_3+\left(1-{\mathsf{s}}_{\mathsf{1}}\right){\mathsf{\nu }}_4\right)+\aleph \left(\left(1-{\mathtt{r}}_{\mathtt{1}}\right){\mathsf{\nu }}_1+{\mathtt{r}}_{\mathtt{1}}{\mathsf{\nu }}_2,\left(1-{\mathsf{s}}_{\mathsf{1}}\right){\mathsf{\nu }}_3+{\mathsf{s}}_{\mathsf{1}}{\mathsf{\nu }}_4\right)\right]\mathrm{d}{\mathsf{s}}_{\mathsf{1}}\mathrm{d}{\mathtt{r}}_{\mathtt{1}}\hfill \\ & {⪯}_{\mathtt{CR}}{\int }_0^1{\int }_0^1{\mathtt{e}}^{-{ð}_1{\mathtt{r}}_{\mathtt{1}}}{\mathtt{e}}^{-{ð}_2{\mathsf{s}}_{\mathsf{1}}}\mathsf{\phi }\left({\mathtt{r}}_{\mathtt{1}}{\mathsf{\nu }}_1+\left(1-{\mathtt{r}}_{\mathtt{1}}\right){\mathsf{\nu }}_2,{\mathsf{s}}_{\mathsf{1}}{\mathsf{\nu }}_3+\left(1-{\mathsf{s}}_{\mathsf{1}}\right){\mathsf{\nu }}_4\right)\hfill \\ & \times [\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)+\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)+\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)+\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)]{\mathrm{ds}}_1\mathrm{d}{\mathtt{r}}_{\mathtt{1}}.\hfill \end{array}$$

Changing the variables results in

$$\begin{array}{cc}& \frac{{\mathsf{\theta }}_1{\mathsf{\theta }}_2}{({\mathsf{\nu }}_2-{\mathsf{\nu }}_1)({\mathsf{\nu }}_4-{\mathsf{\nu }}_3)}\left[{\mathtt{J}}_{{{\mathsf{\nu }}_1}^{+},{{\mathsf{\nu }}_3}^{+}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)\mathsf{\phi }({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)+{\mathtt{J}}_{{{\mathsf{\nu }}_1}^{+},{{\mathsf{\nu }}_4}^{-}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)\mathsf{\phi }({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)\right.\hfill \\ & \left.+{\mathtt{J}}_{{{\mathsf{\nu }}_2}^{-},{{\mathsf{\nu }}_3}^{+}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)\mathsf{\phi }({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)+{\mathtt{J}}_{{{\mathsf{\nu }}_2}^{-},{{\mathsf{\nu }}_4}^{-}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)\mathsf{\phi }({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)\right]\hfill \\ & {⪯}_{\mathtt{CR}}\frac{\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)+\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)+\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)+\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)}{4}\hfill \\ & \times \frac{{\mathsf{\theta }}_1{\mathsf{\theta }}_2}{({\mathsf{\nu }}_2-{\mathsf{\nu }}_1)({\mathsf{\nu }}_4-{\mathsf{\nu }}_3)}\left[{\mathtt{J}}_{{{\mathsf{\nu }}_1}^{+},{{\mathsf{\nu }}_3}^{+}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\mathsf{\phi }({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)+{\mathtt{J}}_{{{\mathsf{\nu }}_1}^{+},{{\mathsf{\nu }}_4}^{-}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\mathsf{\phi }({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)\right.\hfill \\ & \left.+{\mathtt{J}}_{{{\mathsf{\nu }}_2}^{-},{{\mathsf{\nu }}_3}^{+}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\mathsf{\phi }({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)+{\mathtt{J}}_{{{\mathsf{\nu }}_2}^{-},{{\mathsf{\nu }}_4}^{-}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\mathsf{\phi }({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)\right].\hfill \end{array}$$

Consequently, Theorem 8 is proved. Following Theorem 8, we derive the following results that have been documented in the literature. □

Remark 5. 

• If we take $\mathsf{\phi }(\mathtt{x},\mathtt{y})=1$, then Theorem 8 becomes Theorem 7.
• If we set $\underline{\aleph }=\overline{\aleph }$, we obtain the following new result in the setting of standard-order relations, namely:

  $$\begin{array}{cc}& \aleph \left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2},\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right)[{\mathtt{J}}_{{{\mathsf{\nu }}_1}^{+},{{\mathsf{\nu }}_3}^{+}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\mathsf{\phi }({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)+{\mathtt{J}}_{{{\mathsf{\nu }}_1}^{+},{{\mathsf{\nu }}_4}^{-}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\mathsf{\phi }({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)\hfill \\ & +{\mathtt{J}}_{{{\mathsf{\nu }}_2}^{-},{{\mathsf{\nu }}_3}^{+}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\mathsf{\phi }({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)+{\mathtt{J}}_{{{\mathsf{\nu }}_2}^{-},{{\mathsf{\nu }}_4}^{-}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\mathsf{\phi }({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)]\hfill \\ & \le [{\mathtt{J}}_{{{\mathsf{\nu }}_1}^{+},{{\mathsf{\nu }}_3}^{+}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)\mathsf{\phi }({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)+{\mathtt{J}}_{{{\mathsf{\nu }}_1}^{+},{{\mathsf{\nu }}_4}^{-}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)\mathsf{\phi }({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)\hfill \\ & +{\mathtt{J}}_{{{\mathsf{\nu }}_2}^{-},{{\mathsf{\nu }}_3}^{+}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)\mathsf{\phi }({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)+{\mathtt{J}}_{{{\mathsf{\nu }}_2}^{-},{{\mathsf{\nu }}_4}^{-}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)\mathsf{\phi }({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)]\hfill \\ & \le \frac{\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)+\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)+\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)+\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)}{4}[{\mathtt{J}}_{{{\mathsf{\nu }}_1}^{+},{{\mathsf{\nu }}_3}^{+}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\mathsf{\phi }({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)+{\mathtt{J}}_{{{\mathsf{\nu }}_1}^{+},{{\mathsf{\nu }}_4}^{-}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\mathsf{\phi }({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)\hfill \\ & +{\mathtt{J}}_{{{\mathsf{\nu }}_2}^{-},{{\mathsf{\nu }}_3}^{+}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\mathsf{\phi }({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)+{\mathtt{J}}_{{{\mathsf{\nu }}_2}^{-},{{\mathsf{\nu }}_4}^{-}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\mathsf{\phi }({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)].\hfill \end{array}$$
• If we take $\mathsf{\phi }(\mathtt{x},\mathtt{y})=1$ with ${\theta }_1\to 1,{\theta }_2\to 1$ and $\underline{\aleph }=\overline{\aleph }$, we obtain Theorem 1 as reported in [14];
• If we take ${\theta }_1\to 1,{\theta }_2\to 1$, we obtain Theorem 9 as reported in [62];
• If we take ${\theta }_1\to 1,{\theta }_2\to 1$ with $\underline{\aleph }\ne \overline{\aleph }$, we obtain Theorem 7 as reported in [15].

Theorem 9. 

Using the same hypotheses as in Theorem 7, we obtain the following double $\mathtt{CR}$-order relations:

$$\begin{array}{cc}& \aleph \left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2},\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right){⪯}_{\mathtt{CR}}\frac{(1-{\mathsf{\theta }}_1)(1-{\mathsf{\theta }}_2)}{4\left(1-{\mathtt{e}}^{-\frac{{ð}_1}{2}}\right)\left(1-{\mathtt{e}}^{-\frac{p_2}{2}}\right)}\left[{\mathtt{J}}_{{\left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2}\right)}^{+},{\left(\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right)}^{+}}\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)\right.\hfill \\ & \left.+{\mathtt{J}}_{{\left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2}\right)}^{+},{\left(\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right)}^{-}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)+{\mathtt{J}}_{{\left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2}\right)}^{-},{\left(\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right)}^{+}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)+{\mathtt{J}}_{{\left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2}\right)}^{-},{\left(\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right)}^{-}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)\right]\hfill \\ & {⪯}_{\mathtt{CR}}\frac{\aleph {({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)}^2+\aleph \left({\mathsf{\nu }}_2,{{\mathsf{\nu }}_3}^2\right)+\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)+\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)}{4}.\hfill \\ \end{array}$$

Proof. 

Taking into account bidimensional interval-valued function ℵ, for instance, if we consider $\mathtt{x}=\frac{{\mathtt{r}}_{\mathtt{1}}}{2}{\mathsf{\nu }}_1+\frac{2-{\mathtt{r}}_{\mathtt{1}}}{2}{\mathsf{\nu }}_2,\mathtt{y}=\frac{2-{\mathtt{r}}_{\mathtt{1}}}{2}{\mathsf{\nu }}_1+\frac{{\mathtt{r}}_{\mathtt{1}}}{2}{\mathsf{\nu }}_2$, $\mathtt{u}=\frac{{\mathsf{s}}_{\mathsf{1}}}{2}{\mathsf{\nu }}_3+\frac{2-{\mathsf{s}}_{\mathsf{1}}}{2}{\mathsf{\nu }}_4,$ and $\mathtt{w}=\frac{2-{\mathsf{s}}_{\mathsf{1}}}{2}{\mathsf{\nu }}_3+\frac{{\mathsf{s}}_{\mathsf{1}}}{2}{\mathsf{\nu }}_4$, then we have

$$\begin{array}{cc}& \aleph \left(\frac{\mathtt{x}+\mathtt{y}}{2},\frac{\mathtt{u}+\mathtt{w}}{2}\right)=\aleph \left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2},\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right)\hfill \\ \hfill {⪯}_{\mathtt{CR}}& \frac{1}{4}\left[\aleph \left(\frac{{\mathtt{r}}_{\mathtt{1}}}{2}{\mathsf{\nu }}_1+\frac{2-{\mathtt{r}}_{\mathtt{1}}}{2}{\mathsf{\nu }}_2,\frac{{\mathsf{s}}_{\mathsf{1}}}{2}{\mathsf{\nu }}_3+\frac{2-{\mathsf{s}}_{\mathsf{1}}}{2}{\mathsf{\nu }}_4\right)+\aleph \left(\frac{{\mathtt{r}}_{\mathtt{1}}}{2}{\mathsf{\nu }}_1+\frac{2-{\mathtt{r}}_{\mathtt{1}}}{2}{\mathsf{\nu }}_2,\frac{2-{\mathsf{s}}_{\mathsf{1}}}{2}{\mathsf{\nu }}_3+\frac{{\mathsf{s}}_{\mathsf{1}}}{2}{\mathsf{\nu }}_4\right)\right.\hfill \\ & \left.+\aleph \left(\frac{2-{\mathtt{r}}_{\mathtt{1}}}{2}{\mathsf{\nu }}_1+\frac{{\mathtt{r}}_{\mathtt{1}}}{2}{\mathsf{\nu }}_2,\frac{{\mathsf{s}}_{\mathsf{1}}}{2}{\mathsf{\nu }}_3+\frac{2-{\mathsf{s}}_{\mathsf{1}}}{2}{\mathsf{\nu }}_4\right)+\aleph \left(\frac{2-{\mathtt{r}}_{\mathtt{1}}}{2}{\mathsf{\nu }}_1+\frac{{\mathtt{r}}_{\mathtt{1}}}{2}{\mathsf{\nu }}_2,\frac{2-{\mathsf{s}}_{\mathsf{1}}}{2}{\mathsf{\nu }}_3+\frac{{\mathsf{s}}_{\mathsf{1}}}{2}{\mathsf{\nu }}_4\right)\right].\hfill \end{array}$$

Multiplying the above $\mathtt{CR}$ relation with ${\mathtt{e}}^{-\frac{{ð}_1}{2}{\mathtt{r}}_{\mathtt{1}}}{\mathtt{e}}^{-\frac{{ð}_2}{2}{\mathsf{s}}_{\mathsf{1}}}$ and integrating, we have

$$\begin{array}{cc}& \aleph \left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2},\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right){\int }_0^1{\int }_0^1{\mathtt{e}}^{-\frac{{ð}_1}{2}{\mathtt{r}}_{\mathtt{1}}}{\mathtt{e}}^{-\frac{{ð}_2}{2}{\mathsf{s}}_{\mathsf{1}}}\mathrm{d}{\mathsf{s}}_{\mathsf{1}}\mathrm{d}{\mathtt{r}}_{\mathtt{1}}\hfill \\ & {⪯}_{\mathtt{CR}}\frac{1}{4}\left[{\int }_0^1{\int }_0^1{\mathtt{e}}^{-\frac{{ð}_1}{2}{\mathtt{r}}_{\mathtt{1}}}{\mathtt{e}}^{-\frac{{ð}_2}{2}{\mathsf{s}}_{\mathsf{1}}}\right[\aleph \left(\frac{{\mathtt{r}}_{\mathtt{1}}}{2}{\mathsf{\nu }}_1+\frac{2-{\mathtt{r}}_{\mathtt{1}}}{2}{\mathsf{\nu }}_2,\frac{{\mathsf{s}}_{\mathsf{1}}}{2}{\mathsf{\nu }}_3+\frac{2-{\mathsf{s}}_{\mathsf{1}}}{2}{\mathsf{\nu }}_4\right)\hfill \\ & +\aleph \left(\frac{{\mathtt{r}}_{\mathtt{1}}}{2}{\mathsf{\nu }}_1+\frac{2-{\mathtt{r}}_{\mathtt{1}}}{2}{\mathsf{\nu }}_2,\frac{2-{\mathsf{s}}_{\mathsf{1}}}{2}{\mathsf{\nu }}_3+\frac{{\mathsf{s}}_{\mathsf{1}}}{2}{\mathsf{\nu }}_4\right)]\mathrm{d}{\mathsf{s}}_{\mathsf{1}}\mathrm{d}{\mathtt{r}}_{\mathtt{1}}\hfill \\ & +{\int }_0^1{\int }_0^1{\mathtt{e}}^{-\frac{{ð}_1}{2}{\mathtt{r}}_{\mathtt{1}}}{\mathtt{e}}^{-\frac{{ð}_2}{2}{\mathsf{s}}_{\mathsf{1}}}[\aleph \left(\frac{2-{\mathtt{r}}_{\mathtt{1}}}{2}{\mathsf{\nu }}_1+\frac{{\mathtt{r}}_{\mathtt{1}}}{2}{\mathsf{\nu }}_2,\frac{{\mathsf{s}}_{\mathsf{1}}}{2}{\mathsf{\nu }}_3+\frac{2-{\mathsf{s}}_{\mathsf{1}}}{2}{\mathsf{\nu }}_4\right)\hfill \\ & +\aleph \left(\frac{2-{\mathtt{r}}_{\mathtt{1}}}{2}{\mathsf{\nu }}_1+\frac{{\mathtt{r}}_{\mathtt{1}}}{2}{\mathsf{\nu }}_2,\frac{2-{\mathsf{s}}_{\mathsf{1}}}{2}{\mathsf{\nu }}_3+\frac{{\mathsf{s}}_{\mathsf{1}}}{2}{\mathsf{\nu }}_4\right)\left]\mathrm{d}{\mathsf{s}}_{\mathsf{1}}\mathrm{d}{\mathtt{r}}_{\mathtt{1}}\right].\hfill \end{array}$$

By changing the variable and performing different computations, we may determine that

$$\begin{array}{cc}& \frac{4\left(1-{\mathtt{e}}^{-\frac{{ð}_1}{2}}\right)\left(1-{\mathtt{e}}^{-\frac{{ð}_2}{2}}\right)}{{ð}_1{ð}_2}\aleph \left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2},\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right)\hfill \\ & {⪯}_{\mathtt{CR}}\frac{1}{({\mathsf{\nu }}_2-{\mathsf{\nu }}_1)({\mathsf{\nu }}_4-{\mathsf{\nu }}_3)}\left\{{\int }_{\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2}}^{{\mathsf{\nu }}_2}{\int }_{\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}}^{{\mathsf{\nu }}_4}{\mathtt{e}}^{-\frac{1-{\mathsf{\theta }}_1}{{\mathsf{\theta }}_1}({\mathsf{\nu }}_2-\mathtt{x})}{\mathtt{e}}^{-\frac{1-{\mathsf{\theta }}_2}{{\mathsf{\theta }}_2}({\mathsf{\nu }}_4-\mathtt{y})}\aleph (\mathtt{x},\mathtt{y})\mathrm{d}\mathtt{y}\mathrm{d}\mathtt{x}\right.\hfill \\ & +{\int }_{\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2}}^{{\mathsf{\nu }}_2}{\int }_{{\mathsf{\nu }}_3}^{\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}}{\mathtt{e}}^{-\frac{1-{\mathsf{\theta }}_1}{{\mathsf{\theta }}_1}({\mathsf{\nu }}_2-\mathtt{x})}{\mathtt{e}}^{-\frac{1-{\mathsf{\theta }}_2}{{\mathsf{\theta }}_2}(\mathtt{y}-{\mathsf{\nu }}_3)}\aleph (\mathtt{x},\mathtt{y})\mathrm{d}\mathtt{y}\mathrm{d}\mathtt{x}\hfill \\ & +{\int }_{{\mathsf{\nu }}_1}^{\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2}}{\int }_{\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}}^{{\mathsf{\nu }}_4}{\mathtt{e}}^{-\frac{1-{\mathsf{\theta }}_1}{{\mathsf{\theta }}_1}(\mathtt{x}-{\mathsf{\nu }}_1)}{\mathtt{e}}^{-\frac{1-{\mathsf{\theta }}_2}{{\mathsf{\theta }}_2}({\mathsf{\nu }}_4-\mathtt{y})}\aleph (\mathtt{x},\mathtt{y})\mathrm{d}\mathtt{y}\mathrm{d}\mathtt{x}\hfill \\ & \left.+{\int }_{{\mathsf{\nu }}_1}^{\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2}}{\int }_{{\mathsf{\nu }}_3}^{\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}}{\mathtt{e}}^{-\frac{1-{\mathsf{\theta }}_1}{{\mathsf{\theta }}_1}(\mathtt{x}-{\mathsf{\nu }}_1)}{\mathtt{e}}^{-\frac{1-{\mathsf{\theta }}_2}{{\mathsf{\theta }}_2}(\mathtt{y}-{\mathsf{\nu }}_3)}\aleph (\mathtt{x},\mathtt{y})\mathrm{d}\mathtt{y}\mathrm{d}\mathtt{x}\right\}\hfill \\ & =\frac{{\mathsf{\theta }}_1{\mathsf{\theta }}_2}{({\mathsf{\nu }}_2-{\mathsf{\nu }}_1)({\mathsf{\nu }}_4-{\mathsf{\nu }}_3)}\left[{\mathtt{J}}_{{\left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2}\right)}^{+},{\left(\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right)}^{+}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)+{\mathtt{J}}_{{\left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2}\right)}^{+},{\left(\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right)}^{-}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)\right.\hfill \\ & \left.+{\mathtt{J}}_{{\left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2}\right)}^{-},{\left(\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right)}^{+}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)+{\mathtt{J}}_{{\left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2}\right)}^{-},{\left(\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right)}^{-}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)\right].\hfill \end{array}$$

This proves the first $\mathtt{CR}$ relation. Regarding the second relation, taking into account Definition 7, we have

$$\begin{array}{cc}\hfill \aleph \left(\frac{{\mathtt{r}}_{\mathtt{1}}}{2}{\mathsf{\nu }}_1+\frac{2-{\mathtt{r}}_{\mathtt{1}}}{2}{\mathsf{\nu }}_2,\frac{{\mathsf{s}}_{\mathsf{1}}}{2}{\mathsf{\nu }}_3+\frac{2-{\mathsf{s}}_{\mathsf{1}}}{2}{\mathsf{\nu }}_4\right){⪯}_{\mathtt{CR}}& \frac{1}{4}\left[{\mathtt{r}}_{\mathtt{1}}{\mathsf{s}}_{\mathsf{1}}\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)+{\mathsf{s}}_{\mathsf{1}}\left(2-{\mathtt{r}}_{\mathtt{1}}\right)\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)\right.\hfill \\ & \left.+{\mathtt{r}}_{\mathtt{1}}\left(2-{\mathsf{s}}_{\mathsf{1}}\right)\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)+\left(2-{\mathsf{s}}_{\mathsf{1}}\right)\right)\left(2-{\mathtt{r}}_{\mathtt{1}}\right)\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)]\hfill \\ \hfill \aleph \left(\frac{{\mathtt{r}}_{\mathtt{1}}}{2}{\mathsf{\nu }}_1+\frac{2-{\mathtt{r}}_{\mathtt{1}}}{2}{\mathsf{\nu }}_2,\frac{2-{\mathsf{s}}_{\mathsf{1}}}{2}{\mathsf{\nu }}_3+\frac{{\mathsf{s}}_{\mathsf{1}}}{2}{\mathsf{\nu }}_4\right){⪯}_{\mathtt{CR}}& \frac{1}{4}\left[{\mathtt{r}}_{\mathtt{1}}\left(2-{\mathsf{s}}_{\mathsf{1}}\right)\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)+\left(2-{\mathsf{s}}_{\mathsf{1}}\right)\left(2-{\mathtt{r}}_{\mathtt{1}}\right)\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)\right.\hfill \\ & \left.+{\mathtt{r}}_{\mathtt{1}}{\mathsf{s}}_{\mathsf{1}}\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)+\left(2-{\mathtt{r}}_{\mathtt{1}}\right){\mathsf{s}}_{\mathsf{1}}\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)\right]\hfill \\ \hfill \aleph \left(\frac{2-{\mathtt{r}}_{\mathtt{1}}}{2}{\mathsf{\nu }}_1+\frac{{\mathtt{r}}_{\mathtt{1}}}{2}{\mathsf{\nu }}_2,\frac{{\mathsf{s}}_{\mathsf{1}}}{2}{\mathsf{\nu }}_3+\frac{2-{\mathsf{s}}_{\mathsf{1}}}{2}{\mathsf{\nu }}_4\right){⪯}_{\mathtt{CR}}& \frac{1}{4}\left[\left(2-{\mathtt{r}}_{\mathtt{1}}\right){\mathsf{s}}_{\mathsf{1}}\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)+{\mathtt{r}}_{\mathtt{1}}{\mathsf{s}}_{\mathsf{1}}\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)\right.\hfill \\ & \left.+\left(2-{\mathtt{r}}_{\mathtt{1}}\right)\left(2-{\mathsf{s}}_{\mathsf{1}}\right)\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)+{\mathtt{r}}_{\mathtt{1}}\left(2-{\mathsf{s}}_{\mathsf{1}}\right)\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)\right]\hfill \\ \aleph \left(\frac{2-{\mathtt{r}}_{\mathtt{1}}}{2}{\mathsf{\nu }}_1+\frac{{\mathtt{r}}_{\mathtt{1}}}{2}{\mathsf{\nu }}_2,\frac{{\mathsf{s}}_{\mathsf{1}}}{2}{\mathsf{\nu }}_3+\frac{2-{\mathsf{s}}_{\mathsf{1}}}{2}{\mathsf{\nu }}_4\right)\hfill & {⪯}_{\mathtt{CR}}\frac{1}{4}\left[\left(2-{\mathtt{r}}_{\mathtt{1}}\right){\mathsf{s}}_{\mathsf{1}}\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)+{\mathtt{r}}_{\mathtt{1}}{\mathsf{s}}_{\mathsf{1}}\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)\right.\hfill \\ & \left.+\left(2-{\mathtt{r}}_{\mathtt{1}}\right)\left(2-{\mathsf{s}}_{\mathsf{1}}\right)\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)+{\mathtt{r}}_{\mathtt{1}}\left(2-{\mathsf{s}}_{\mathsf{1}}\right)\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)\right]\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill \aleph \left(\frac{2-{\mathtt{r}}_{\mathtt{1}}}{2}{\mathsf{\nu }}_1+\frac{{\mathtt{r}}_{\mathtt{1}}}{2}{\mathsf{\nu }}_2,\frac{2-{\mathsf{s}}_{\mathsf{1}}}{2}{\mathsf{\nu }}_3+\frac{{\mathsf{s}}_{\mathsf{1}}}{2}{\mathsf{\nu }}_4\right){⪯}_{\mathtt{CR}}& \frac{1}{4}\left[\left(2-{\mathtt{r}}_{\mathtt{1}}\right)\left(2-{\mathsf{s}}_{\mathsf{1}}\right)\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)+{\mathtt{r}}_{\mathtt{1}}\left(2-{\mathsf{s}}_{\mathsf{1}}\right)\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)\right.\hfill \\ & \left.+{\mathsf{s}}_{\mathsf{1}}\left(2-{\mathtt{r}}_{\mathtt{1}}\right)\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)+{\mathtt{r}}_{\mathtt{1}}{\mathsf{s}}_{\mathsf{1}}\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)\right].\hfill \end{array}$$

Adding the above relations, we obtain

$$\begin{array}{cc}& \aleph \left(\frac{{\mathtt{r}}_{\mathtt{1}}}{2}{\mathsf{\nu }}_1+\frac{2-{\mathtt{r}}_{\mathtt{1}}}{2}{\mathsf{\nu }}_2,\frac{{\mathsf{s}}_{\mathsf{1}}}{2}{\mathsf{\nu }}_3+\frac{2-{\mathsf{s}}_{\mathsf{1}}}{2}{\mathsf{\nu }}_4\right)+\aleph \left(\frac{{\mathtt{r}}_{\mathtt{1}}}{2}{\mathsf{\nu }}_1+\frac{2-{\mathtt{r}}_{\mathtt{1}}}{2}{\mathsf{\nu }}_2,\frac{2-{\mathsf{s}}_{\mathsf{1}}}{2}{\mathsf{\nu }}_3+\frac{{\mathsf{s}}_{\mathsf{1}}}{2}{\mathsf{\nu }}_4\right)\hfill \\ & +\aleph \left(\frac{2-{\mathtt{r}}_{\mathtt{1}}}{2}{\mathsf{\nu }}_1+\frac{{\mathtt{r}}_{\mathtt{1}}}{2}{\mathsf{\nu }}_2,\frac{{\mathsf{s}}_{\mathsf{1}}}{2}{\mathsf{\nu }}_3+\frac{2-{\mathsf{s}}_{\mathsf{1}}}{2}{\mathsf{\nu }}_4\right)+\aleph \left(\frac{2-{\mathtt{r}}_{\mathtt{1}}}{2}{\mathsf{\nu }}_1+\frac{{\mathtt{r}}_{\mathtt{1}}}{2}{\mathsf{\nu }}_2,\frac{2-{\mathsf{s}}_{\mathsf{1}}}{2}{\mathsf{\nu }}_3+\frac{{\mathsf{s}}_{\mathsf{1}}}{2}{\mathsf{\nu }}_4\right)\hfill \\ & {⪯}_{\mathtt{CR}}\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)+\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)+\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)+\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4).\hfill \end{array}$$

Multiplying the aforementioned $\mathtt{CR}$ relation by ${\mathtt{e}}^{-\frac{{ð}_1}{2}{\mathtt{r}}_{\mathtt{1}}}{\mathtt{e}}^{-\frac{{ð}_2}{2}{\mathsf{s}}_{\mathsf{1}}}$ and then integrating the resultant output about $\left({\mathtt{r}}_{\mathtt{1}},{\mathsf{s}}_{\mathsf{1}}\right)$, we obtain

$$\begin{array}{cc}& {\int }_0^1{\int }_0^1{\mathtt{e}}^{-\frac{{ð}_1}{2}{\mathtt{r}}_{\mathtt{1}}}{\mathtt{e}}^{-\frac{{ð}_2}{2}{\mathsf{s}}_{\mathsf{1}}}\left[\aleph \left(\frac{{\mathtt{r}}_{\mathtt{1}}}{2}{\mathsf{\nu }}_1+\frac{2-{\mathtt{r}}_{\mathtt{1}}}{2}{\mathsf{\nu }}_2,\frac{{\mathsf{s}}_{\mathsf{1}}}{2}{\mathsf{\nu }}_3+\frac{2-{\mathsf{s}}_{\mathsf{1}}}{2}{\mathsf{\nu }}_4\right)\right.\hfill \\ & \left.+\aleph \left(\frac{{\mathtt{r}}_{\mathtt{1}}}{2}{\mathsf{\nu }}_1+\frac{2-{\mathtt{r}}_{\mathtt{1}}}{2}{\mathsf{\nu }}_2,\frac{2-{\mathsf{s}}_{\mathsf{1}}}{2}{\mathsf{\nu }}_3+\frac{{\mathsf{s}}_{\mathsf{1}}}{2}{\mathsf{\nu }}_4\right)\right]{\mathrm{ds}}_1\mathrm{d}{\mathtt{r}}_{\mathtt{1}}\hfill \\ & +{\int }_0^1{\int }_0^1{\mathtt{e}}^{-\frac{{ð}_1}{2}{\mathtt{r}}_{\mathtt{1}}}{\mathtt{e}}^{-\frac{{ð}_2}{2}{\mathsf{s}}_{\mathsf{1}}}\left[\aleph \left(\frac{2-{\mathtt{r}}_{\mathtt{1}}}{2}{\mathsf{\nu }}_1+\frac{{\mathtt{r}}_{\mathtt{1}}}{2}{\mathsf{\nu }}_2,\frac{{\mathsf{s}}_{\mathsf{1}}}{2}{\mathsf{\nu }}_3+\frac{2-{\mathsf{s}}_{\mathsf{1}}}{2}{\mathsf{\nu }}_4\right)\right.\hfill \\ & \left.+\aleph \left(\frac{2-{\mathtt{r}}_{\mathtt{1}}}{2}{\mathsf{\nu }}_1+\frac{{\mathtt{r}}_{\mathtt{1}}}{2}{\mathsf{\nu }}_2,\frac{2-{\mathsf{s}}_{\mathsf{1}}}{2}{\mathsf{\nu }}_3+\frac{{\mathsf{s}}_{\mathsf{1}}}{2}{\mathsf{\nu }}_4\right)\right]\mathrm{d}{\mathsf{s}}_{\mathsf{1}}\mathrm{d}{\mathtt{r}}_{\mathtt{1}}\hfill \\ & {⪯}_{\mathtt{CR}}{\int }_0^1{\int }_0^1{\mathtt{e}}^{-\frac{{ð}_1}{2}{\mathtt{r}}_{\mathtt{1}}}{\mathtt{e}}^{-\frac{{ð}_2}{2}{\mathsf{s}}_{\mathsf{1}}}[\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)+\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)+\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)+\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)]\mathrm{d}{\mathsf{s}}_{\mathsf{1}}\mathrm{d}{\mathtt{r}}_{\mathtt{1}}.\hfill \\ \end{array}$$

Changing the variables results in

$$\begin{array}{cc}& \frac{{\mathsf{\theta }}_1{\mathsf{\theta }}_2}{4({\mathsf{\nu }}_2-{\mathsf{\nu }}_1)({\mathsf{\nu }}_4-{\mathsf{\nu }}_3)}\left[{\mathtt{J}}_{{\left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2}\right)}^{+},{\left(\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right)}^{+}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)+{\mathtt{J}}_{{\left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2}\right)}^{+},{\left(\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right)}^{-}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)\right.\hfill \\ & \left.+{\mathtt{J}}_{{\left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2}\right)}^{-},{\left(\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right)}^{+}}\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)+{\mathtt{J}}_{{\left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2}\right)}^{-},{\left(\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right)}^{-}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)\right]\hfill \\ & {⪯}_{\mathtt{CR}}\frac{\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)+\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)+\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)+\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)}{4}.\hfill \end{array}$$

Consequently, Theorem 9 is proved. Following Theorem 9, we derive the following results that have been documented in the literature. □

Remark 6. 

• If ${\mathsf{\theta }}_1\to 1,{\mathsf{\theta }}_2\to 1$, we obtain Theorem 7 as reported in [15].
• If we take ${\mathsf{\theta }}_1\to 1,{\mathsf{\theta }}_2\to 1$ with $\underline{\aleph }=\overline{\aleph }$, we obtain Theorem 1 as reported in [14].

Example 4. 

If $\aleph (\mathtt{x},\mathtt{y})=\left[(\mathtt{x}+1)(\mathtt{y}+1)2e^{4\mathtt{x}}{e}^{4\mathtt{y}},\left(8+2e^{\mathtt{x}}\right)\left(4+2e^{\mathtt{y}}\right)\right],[{\mathsf{\nu }}_1,{\mathsf{\nu }}_2]=[0,1],[{\mathsf{\nu }}_3,{\mathsf{\nu }}_4]=[0,1],{\mathsf{\theta }}_1=1$, and ${\mathsf{\theta }}_2=1$, then all the postulates in Theorem 9 are satisfied. Now, we consider

$$\begin{array}{cc}& \aleph \left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2},\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right)=\left[\frac{9e^4}{2},(8+2e^{\frac{1}{2}})(4+2e^{\frac{1}{2}})\right]\approx [245.69167,82.4457],\hfill \\ & \frac{(1-{\mathsf{\theta }}_1)(1-{\mathsf{\theta }}_2)}{4\left(1-e^{-\frac{{\mathsf{\theta }}_1}{2}}\right)\left(1-e^{-\frac{{\mathsf{\theta }}_2}{2}}\right)}\left[{\mathtt{J}}_{\left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2}\right)+,\left(\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right)+}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)+{\mathtt{J}}_{{\left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2}\right)}^{{\mathsf{\theta }}_1},\left(\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right)-}^{{\mathsf{\theta }}_1}\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)\right.\hfill \\ & \left.+{\mathtt{J}}_{{\left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2}\right)}^{-},{\left(\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right)}^{+}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)+{\mathtt{J}}_{{\left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2}\right)}^{-},{\left(\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right)}^{-}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)\right]\approx [290.5473,123.754],\hfill \\ & \frac{\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)+\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)+\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)+\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)}{4}\approx [322.776,161.954].\hfill \\ \end{array}$$

Thus,

$$[245.69167,82.4457]{⪯}_{\mathtt{CR}}[290.5473,123.754]{⪯}_{\mathtt{CR}}[322.776,161.954].$$

As a result, the conclusions described in Theorem 9 are true.

Theorem 10. 

Let $\aleph ,\gimel :[{\mathsf{\nu }}_1,{\mathsf{\nu }}_2]\times [{\mathsf{\nu }}_3,{\mathsf{\nu }}_4]\subseteq {\mathsf{R}}^2\to {{\mathsf{R}}_{\mathtt{i}}}^{+}$ be two bidimensional convex interval-valued functions defined as $\aleph =[\underline{\aleph }(\mathtt{x},\mathtt{y}),\overline{\aleph }(\mathtt{x},\mathtt{y})]$ and $\gimel =[\underline{\eta }(\mathtt{x},\mathtt{y}),\overline{\eta }(\mathtt{x},\mathtt{y})]$ with $0\le {\mathsf{\nu }}_1<{\mathsf{\nu }}_2,0\le {\mathsf{\nu }}_3<{\mathsf{\nu }}_4]$. Then, one has the double $\mathtt{CR}$-order relations:

$$\begin{array}{cc}& \frac{{\mathsf{\theta }}_1{\mathsf{\theta }}_2}{({\mathsf{\nu }}_2-{\mathsf{\nu }}_1)({\mathsf{\nu }}_4-{\mathsf{\nu }}_3)}\left[{\mathtt{J}}_{{{\mathsf{\nu }}_1}^{+},{{\mathsf{\nu }}_3}^{+}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)\gimel ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)+{\mathtt{J}}_{{{\mathsf{\nu }}_1}^{+},{{\mathsf{\nu }}_4}^{-}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)\gimel ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)\right.\hfill \\ & \left.+{\mathtt{J}}_{{{\mathsf{\nu }}_2}^{-},{{\mathsf{\nu }}_3}^{+}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)\gimel ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)+{\mathtt{J}}_{{{\mathsf{\nu }}_2}^{-},{{\mathsf{\nu }}_4}^{-}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)\gimel ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)\right]\hfill \\ & {⪯}_{\mathtt{CR}}{\mathtt{A}}_{\mathtt{1}}{\mathtt{A}}_{\mathtt{2}}\mathtt{C}({\mathsf{\nu }}_1,{\mathsf{\nu }}_2,{\mathsf{\nu }}_3,{\mathsf{\nu }}_4)+{\mathtt{A}}_{\mathtt{1}}{\mathtt{B}}_{\mathtt{2}}\mathtt{D}({\mathsf{\nu }}_1,{\mathsf{\nu }}_2,{\mathsf{\nu }}_3,{\mathsf{\nu }}_4)+{\mathtt{A}}_{\mathtt{2}}{\mathtt{B}}_{\mathtt{1}}\mathtt{E}({\mathsf{\nu }}_1,{\mathsf{\nu }}_2,{\mathsf{\nu }}_3,{\mathsf{\nu }}_4)+{\mathtt{B}}_{\mathtt{1}}{\mathtt{B}}_{\mathtt{2}}({\mathsf{\nu }}_1,{\mathsf{\nu }}_2,{\mathsf{\nu }}_3,{\mathsf{\nu }}_4),\hfill \end{array}$$

where

$${\mathtt{A}}_{\mathtt{i}}=\frac{{\mathsf{\theta }}_{\mathtt{i}}^2-2{\mathsf{\theta }}_{\mathtt{i}}+4-\left({\mathsf{\theta }}_{\mathtt{i}}^2+2{\mathsf{\theta }}_{\mathtt{i}}+4\right){\mathtt{e}}^{-{\mathsf{\theta }}_{\mathtt{i}}}}{{\mathsf{\theta }}_{\mathtt{i}}^3},{\mathtt{B}}_{\mathtt{i}}=\frac{2{\mathsf{\theta }}_{\mathtt{i}}-4+\left(2{\mathsf{\theta }}_{\mathtt{i}}+4\right){\mathtt{e}}^{-{\mathsf{\theta }}_{\mathtt{i}}}}{{\mathsf{\theta }}_{\mathtt{i}}^3},\mathtt{i}=1,2,$$

$$\begin{array}{cc}\hfill & \mathtt{C}({\mathsf{\nu }}_1,{\mathsf{\nu }}_2,{\mathsf{\nu }}_3,{\mathsf{\nu }}_4)=\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)\gimel ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)+\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)\gimel ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)\hfill \\ & +\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)\gimel ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)+\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)\gimel ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4),\hfill \\ \hfill & \mathtt{D}({\mathsf{\nu }}_1,{\mathsf{\nu }}_2,{\mathsf{\nu }}_3,{\mathsf{\nu }}_4)=\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)\gimel ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)+\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)\gimel ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)\hfill \\ & +\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)\gimel ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)+\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)\gimel ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3),\hfill \\ \hfill & \mathtt{E}({\mathsf{\nu }}_1,{\mathsf{\nu }}_2,{\mathsf{\nu }}_3,{\mathsf{\nu }}_4)=\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)\gimel ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)+\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)\gimel ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)\hfill \\ & +\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)\gimel ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)+\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)\gimel ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4),\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill & ({\mathsf{\nu }}_1,{\mathsf{\nu }}_2,{\mathsf{\nu }}_3,{\mathsf{\nu }}_4)=\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)\gimel ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)+\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)\gimel ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)\hfill \\ & +\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)\gimel ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)+\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)\gimel ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3).\hfill \end{array}$$

Proof. 

By virtue of bidimensional interval-valued functions $\aleph ,\gimel$, we have that

${\aleph }_{\mathtt{x}}\left(\mathtt{y}\right):[{\mathsf{\nu }}_3,{\mathsf{\nu }}_4]\to {{\mathsf{R}}_{\mathtt{i}}}^{+},{\aleph }_{\mathtt{x}}\left(\mathtt{y}\right)=\aleph (\mathtt{x},\mathtt{y}),{\gimel }_{\mathtt{x}}\left(\mathtt{y}\right):[{\mathsf{\nu }}_3,{\mathsf{\nu }}_4]\to {{\mathsf{R}}_{\mathtt{i}}}^{+},{\gimel }_{\mathtt{x}}\left(\mathtt{y}\right)=\gimel (\mathtt{x},\mathtt{y})$ and

${\aleph }_{\mathtt{y}}\left(\mathtt{x}\right):[{\mathsf{\nu }}_1,{\mathsf{\nu }}_2]\to {{\mathsf{R}}_{\mathtt{i}}}^{+},{\aleph }_{\mathtt{y}}\left(\mathtt{x}\right)=\aleph (\mathtt{x},\mathtt{y}),{\gimel }_{\mathtt{y}}\left(\mathtt{x}\right):[{\mathsf{\nu }}_1,{\mathsf{\nu }}_2]\to {{\mathsf{R}}_{\mathtt{i}}}^{+},{\gimel }_{\mathtt{y}}\left(\mathtt{x}\right)=\gimel (\mathtt{x},\mathtt{y})$ are both bidimensional interval-valued mappings, analogously, for each $\mathtt{x}\in [{\mathsf{\nu }}_1,{\mathsf{\nu }}_2]$ accompanying $\mathtt{y}\in [{\mathsf{\nu }}_3,{\mathsf{\nu }}_4]$. Now, by considering Theorem 2.4 within [60], we have

$$\begin{array}{c}\frac{1}{{\mathsf{\nu }}_4-{\mathsf{\nu }}_3}\left[{\int }_{{\mathsf{\nu }}_3}^{{\mathsf{\nu }}_4}{\aleph }_{\mathtt{x}}\left(\mathtt{y}\right){\gimel }_{\mathtt{x}}\left(\mathtt{y}\right){\mathtt{e}}^{-\frac{1-{\mathsf{\theta }}_2}{{\mathsf{\theta }}_2}({\mathsf{\nu }}_4-\mathtt{y})}\mathrm{d}\mathtt{y}+{\int }_{{\mathsf{\nu }}_3}^{{\mathsf{\nu }}_4}{\aleph }_{\mathtt{y}}\left(\mathtt{y}\right){\gimel }_{\mathtt{x}}\left(\mathtt{y}\right){\mathtt{e}}^{-\frac{1-{\mathsf{\theta }}_2}{{\mathsf{\theta }}_2}(\mathtt{y}-{\mathsf{\nu }}_3)}\mathrm{d}\mathtt{y}\right]\\ {⪯}_{\mathtt{CR}}\frac{{{ð}_2}^2-2{ð}_2+4-\left({{ð}_2}^2+2{ð}_2+4\right){\mathtt{e}}^{-{ð}_2}}{{{ð}_2}^3}\left[{\aleph }_{\mathtt{x}}\left({\mathsf{\nu }}_3\right){\gimel }_{\mathtt{x}}\left({\mathsf{\nu }}_3\right)+{\aleph }_{\mathtt{x}}\left({\mathsf{\nu }}_4\right){\gimel }_{\mathtt{x}}\left({\mathsf{\nu }}_4\right)\right]\\ +\frac{2{ð}_2-4+\left(2{ð}_2+4\right){\mathtt{e}}^{-{ð}_2}}{{{ð}_2}^3}\left[{\aleph }_{\mathtt{x}}\left({\mathsf{\nu }}_3\right){\gimel }_{\mathtt{x}}\left({\mathsf{\nu }}_4\right)+{\aleph }_{\mathtt{x}}\left({\mathsf{\nu }}_4\right){\gimel }_{\mathtt{x}}\left({\mathsf{\nu }}_3\right)\right].\end{array}$$

This can be written as

$$\begin{array}{c}\frac{1}{{\mathsf{\nu }}_4-{\mathsf{\nu }}_3}\left[{\int }_{{\mathsf{\nu }}_3}^{{\mathsf{\nu }}_4}{\mathtt{e}}^{-\frac{1-{\mathsf{\theta }}_2}{{\mathsf{\theta }}_2}({\mathsf{\nu }}_4-\mathtt{y})}\aleph (\mathtt{x},\mathtt{y})\gimel (\mathtt{x},\mathtt{y})\mathrm{d}\mathtt{y}+{\int }_{{\mathsf{\nu }}_3}^{{\mathsf{\nu }}_4}{\mathtt{e}}^{-\frac{1-{\mathsf{\theta }}_2}{{\mathsf{\theta }}_2}(\mathtt{y}-{\mathsf{\nu }}_3)}\aleph (\mathtt{x},\mathtt{y})\gimel (\mathtt{x},\mathtt{y})\mathrm{d}\mathtt{y}\right]\\ {⪯}_{\mathtt{CR}}\frac{{{ð}_2}^2-2{ð}_2+4-\left({{ð}_2}^2+2{ð}_2+4\right){\mathtt{e}}^{-{ð}_2}}{{{ð}_2}^3}[\aleph (\mathtt{x},{\mathsf{\nu }}_3)\gimel (\mathtt{x},{\mathsf{\nu }}_3)+\aleph (\mathtt{x},{\mathsf{\nu }}_4)\gimel (\mathtt{x},{\mathsf{\nu }}_4)]\\ +\frac{2{ð}_2-4+\left(2{ð}_2+4\right){\mathtt{e}}^{-{ð}_2}}{{{ð}_2}^3}[\aleph (\mathtt{x},{\mathsf{\nu }}_3)\gimel (\mathtt{x},{\mathsf{\nu }}_4)+\aleph (\mathtt{x},{\mathsf{\nu }}_4)\gimel (\mathtt{x},{\mathsf{\nu }}_3)].\end{array}$$

Multiplying the above $\mathtt{CR}$-order relation by $\frac{1}{{\mathsf{\nu }}_2-{\mathsf{\nu }}_1}{\mathtt{e}}^{-\frac{1-{\mathsf{\theta }}_1}{{\mathsf{\theta }}_1}({\mathsf{\nu }}_2-\mathtt{x})}$ and $\frac{1}{{\mathsf{\nu }}_2-{\mathsf{\nu }}_1}{\mathtt{e}}^{-\frac{1-{\mathsf{\theta }}_1}{{\mathsf{\theta }}_1}(\mathtt{x}-{\mathsf{\nu }}_1)}$, separately, and by integrating the outcome with respect to x across $[{\mathsf{\nu }}_1,{\mathsf{\nu }}_2]$, we determine that

$$\begin{array}{cc}\hfill & \frac{1}{({\mathsf{\nu }}_2-{\mathsf{\nu }}_1)({\mathsf{\nu }}_4-{\mathsf{\nu }}_3)}\left[{\int }_{{\mathsf{\nu }}_1}^{{\mathsf{\nu }}_2}{\int }_{{\mathsf{\nu }}_3}^{{\mathsf{\nu }}_4}{\mathtt{e}}^{\frac{{\mathsf{\theta }}_1-1}{{\mathsf{\theta }}_1}({\mathsf{\nu }}_2-\mathtt{y})}{\mathtt{e}}^{\frac{{\mathsf{\theta }}_2-1}{{\mathsf{\theta }}_2}({\mathsf{\nu }}_4-\mathtt{y})}\gimel (\mathtt{x},\mathtt{y})\aleph (\mathtt{x},\mathtt{y})\mathrm{d}\mathtt{y}\mathrm{d}\mathtt{x}\right.\hfill \\ \hfill & \left.+{\int }_{{\mathsf{\nu }}_1}^{{\mathsf{\nu }}_2}{\int }_{{\mathsf{\nu }}_3}^{{\mathsf{\nu }}_4}{\mathtt{e}}^{-\frac{1-{\mathsf{\theta }}_1}{{\mathsf{\theta }}_1}({\mathsf{\nu }}_2-\mathtt{x})}{\mathtt{e}}^{-\frac{1-{\mathsf{\theta }}_2}{{\mathsf{\theta }}_2}(\mathtt{y}-{\mathsf{\nu }}_3)}\aleph (\mathtt{x},\mathtt{y})\gimel (\mathtt{x},\mathtt{y})\mathrm{d}\mathtt{y}\mathrm{d}\mathtt{x}\right]\hfill \\ \hfill & {⪯}_{\mathtt{CR}}\frac{{{ð}_2}^2-2{ð}_2+4-\left({{ð}_2}^2+2{ð}_2+4\right){\mathtt{e}}^{-{ð}_2}}{{{ð}_2}^3({\mathsf{\nu }}_2-{\mathsf{\nu }}_1)}{\int }_{{\mathsf{\nu }}_1}^{{\mathsf{\nu }}_2}{\mathtt{e}}^{-\frac{1-{\mathsf{\theta }}_1}{{\mathsf{\theta }}_1}({\mathsf{\nu }}_2-\mathtt{x})}[\aleph (\mathtt{x},{\mathsf{\nu }}_3)\gimel (\mathtt{x},{\mathsf{\nu }}_3)+\aleph (\mathtt{x},{\mathsf{\nu }}_4)\gimel (\mathtt{x},{\mathsf{\nu }}_4)]\mathrm{d}\mathtt{x}\hfill \\ \hfill & +\frac{2{ð}_2-4+\left(2{ð}_2+4\right){\mathtt{e}}^{-{ð}_2}}{{{ð}_2}^3({\mathsf{\nu }}_2-{\mathsf{\nu }}_1)}{\int }_{{\mathsf{\nu }}_1}^{{\mathsf{\nu }}_2}{\mathtt{e}}^{-\frac{1-{\mathsf{\theta }}_1}{{\mathsf{\theta }}_1}({\mathsf{\nu }}_2-\mathtt{x})}[\aleph (\mathtt{x},{\mathsf{\nu }}_3)\gimel (\mathtt{x},{\mathsf{\nu }}_4)+\aleph (\mathtt{x},{\mathsf{\nu }}_4)\gimel (\mathtt{x},{\mathsf{\nu }}_3)]\mathrm{d}\mathtt{x},\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill & \frac{1}{({\mathsf{\nu }}_2-{\mathsf{\nu }}_1)({\mathsf{\nu }}_4-{\mathsf{\nu }}_3)}\left[{\int }_{{\mathsf{\nu }}_1}^{{\mathsf{\nu }}_2}{\int }_{{\mathsf{\nu }}_3}^{{\mathsf{\nu }}_4}{\mathtt{e}}^{-\frac{1-{\mathsf{\theta }}_1}{{\mathsf{\theta }}_1}(\mathtt{x}-{\mathsf{\nu }}_1)}{\mathtt{e}}^{-\frac{1-{\mathsf{\theta }}_2}{{\mathsf{\theta }}_2}({\mathsf{\nu }}_4-\mathtt{y})}\aleph (\mathtt{x},\mathtt{y})\gimel (\mathtt{x},\mathtt{y})\mathrm{d}\mathtt{y}\mathrm{d}\mathtt{x}\right.\hfill \\ \hfill & \left.+{\int }_{{\mathsf{\nu }}_1}^{{\mathsf{\nu }}_2}{\int }_{{\mathsf{\nu }}_3}^{{\mathsf{\nu }}_4}{\mathtt{e}}^{-\frac{1-{\mathsf{\theta }}_1}{{\mathsf{\theta }}_1}(\mathtt{x}-{\mathsf{\nu }}_1)}{\mathtt{e}}^{-\frac{1-{\mathsf{\theta }}_2}{{\mathsf{\theta }}_2}(\mathtt{y}-{\mathsf{\nu }}_3)}\aleph (\mathtt{x},\mathtt{y})\gimel (\mathtt{x},\mathtt{y})\mathrm{d}\mathtt{y}\mathrm{d}\mathtt{x}\right]\hfill \\ \hfill & {⪯}_{\mathtt{CR}}\frac{{{ð}_2}^2-2{ð}_2+4-\left({{ð}_2}^2+2{ð}_2+4\right){\mathtt{e}}^{-{ð}_2}}{{{ð}_2}^3({\mathsf{\nu }}_2-{\mathsf{\nu }}_1)}{\int }_{{\mathsf{\nu }}_1}^{{\mathsf{\nu }}_2}{\mathtt{e}}^{-\frac{1-{\mathsf{\theta }}_1}{{\mathsf{\theta }}_1}(\mathtt{x}-{\mathsf{\nu }}_1)}[\aleph (\mathtt{x},{\mathsf{\nu }}_3)\gimel (\mathtt{x},{\mathsf{\nu }}_3)+\aleph (\mathtt{x},{\mathsf{\nu }}_4)\gimel (\mathtt{x},{\mathsf{\nu }}_4)]\mathrm{d}\mathtt{x}\hfill \\ \hfill & +\frac{2{ð}_2-4+\left(2{ð}_2+4\right){\mathtt{e}}^{-{ð}_2}}{{{ð}_2}^3({\mathsf{\nu }}_2-{\mathsf{\nu }}_1)}{\int }_{{\mathsf{\nu }}_1}^{{\mathsf{\nu }}_2}{\mathtt{e}}^{-\frac{1-{\mathsf{\theta }}_1}{{\mathsf{\theta }}_1}(\mathtt{x}-{\mathsf{\nu }}_1)}[\aleph (\mathtt{x},{\mathsf{\nu }}_3)\gimel (\mathtt{x},{\mathsf{\nu }}_4)+\aleph (\mathtt{x},{\mathsf{\nu }}_4)\gimel (\mathtt{x},{\mathsf{\nu }}_3)]\mathrm{d}\mathtt{x}.\hfill \end{array}$$

Summing the above two relations consecutively, we conclude that

$$\begin{array}{cc}\hfill & \frac{{\mathsf{\theta }}_1{\mathsf{\theta }}_2}{({\mathsf{\nu }}_2-{\mathsf{\nu }}_1)({\mathsf{\nu }}_4-{\mathsf{\nu }}_3)}\left[{\mathtt{J}}_{{{\mathsf{\nu }}_1}^{+},{{\mathsf{\nu }}_3}^{+}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)\gimel ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)+{\mathtt{J}}_{{{\mathsf{\nu }}_1}^{+},{{\mathsf{\nu }}_4}^{-}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)\gimel ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)\right.\hfill \\ \hfill & \left.+{\mathtt{J}}_{{{\mathsf{\nu }}_2}^{-},{{\mathsf{\nu }}_3}^{+}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)\gimel ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)+{\mathtt{J}}_{{{\mathsf{\nu }}_2}^{-},{{\mathsf{\nu }}_4}^{-}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)\gimel ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)\right]\hfill \\ \hfill & {⪯}_{\mathtt{CR}}\frac{{{ð}_2}^2-2{ð}_2+4-\left({{ð}_2}^2+2{ð}_2+4\right){\mathtt{e}}^{-{ð}_2}}{{{ð}_2}^3({\mathsf{\nu }}_2-{\mathsf{\nu }}_1)}{\mathsf{\theta }}_1\left\{\left[{\mathtt{J}}_{{{\mathsf{\nu }}_1}^{+}}^{{\mathsf{\theta }}_1}\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)\gimel ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)\right.\right.\hfill \\ \hfill & \left.\left.+{\mathtt{J}}_{{{\mathsf{\nu }}_2}^{-}}^{{\mathsf{\theta }}_1}\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)\gimel ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)\right]+\left[{\mathtt{J}}_{{{\mathsf{\nu }}_1}^{+}}^{{\mathsf{\theta }}_1}\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)\gimel ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)+{\mathtt{J}}_{{{\mathsf{\nu }}_2}^{-}}^{{\mathsf{\theta }}_1}\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)\gimel ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)\right]\right\}\hfill \\ \hfill & +\frac{2{ð}_2-4+\left(2{ð}_2+4\right){\mathtt{e}}^{-{ð}_2}}{{{ð}_2}^3({\mathsf{\nu }}_2-{\mathsf{\nu }}_1)}{\mathsf{\theta }}_1\left\{\left[{\mathtt{J}}_{{{\mathsf{\nu }}_1}^{+}}^{{\mathsf{\theta }}_1}\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)\gimel ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)\right.\right.\hfill \\ \hfill & \left.\left.+{\mathtt{J}}_{{{\mathsf{\nu }}_2}^{-}}^{{\mathsf{\theta }}_1}\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)\gimel ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)\right]+\left[{\mathtt{J}}_{{{\mathsf{\nu }}_1}^{+}}^{{\mathsf{\theta }}_1}\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)\gimel ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)+{\mathtt{J}}_{{{\mathsf{\nu }}_2}^{-}}^{{\mathsf{\theta }}_1}\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)\gimel ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)\right]\right\}.\hfill \end{array}$$

(11)

This also indicates that

$$\begin{array}{cc}\hfill & \frac{{\mathsf{\theta }}_1}{{\mathsf{\nu }}_2-{\mathsf{\nu }}_1}\left[{\mathtt{J}}_{{{\mathsf{\nu }}_1}^{+}}^{{\mathsf{\theta }}_1}\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)\gimel ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)+{\mathtt{J}}_{{{\mathsf{\nu }}_2}^{-}}^{{\mathsf{\theta }}_1}\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)\gimel ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)\right]\hfill \\ \hfill & {⪯}_{\mathtt{CR}}\frac{{{ð}_1}^2-2{ð}_1+4-\left({{ð}_1}^2+2{ð}_1+4\right){\mathtt{e}}^{-{ð}_1}}{{{ð}_1}^3}[\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)\gimel ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)+\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)\gimel ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)]\hfill \\ \hfill & +\frac{2{ð}_1-4+\left(2{ð}_1+4\right){\mathtt{e}}^{-{ð}_1}}{{{ð}_1}^3}[\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)\gimel ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)+\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)\gimel ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)],\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill & \frac{{\mathsf{\theta }}_1}{{\mathsf{\nu }}_2-{\mathsf{\nu }}_1}\left[{\mathtt{J}}_{{{\mathsf{\nu }}_1}^{+}}^{{\mathsf{\theta }}_1}\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)\gimel ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)+{\mathtt{J}}_{{{\mathsf{\nu }}_2}^{-}}^{{\mathsf{\theta }}_1}\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)\gimel ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)\right]\hfill \\ \hfill & {⪯}_{\mathtt{CR}}\frac{{{ð}_1}^2-2{ð}_1+4-\left({{ð}_1}^2+2{ð}_1+4\right){\mathtt{e}}^{-{ð}_1}}{{{ð}_1}^3}[\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)\gimel ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)+\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)\gimel ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)]\hfill \\ \hfill & +\frac{2{ð}_1-4+\left(2{ð}_1+4\right){\mathtt{e}}^{-{ð}_1}}{{{ð}_1}^3}[\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)\gimel ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)+\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)\gimel ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)],\hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill & \frac{{\mathsf{\theta }}_1}{{\mathsf{\nu }}_2-{\mathsf{\nu }}_1}\left[{\mathtt{J}}_{{{\mathsf{\nu }}_1}^{+}}^{{\mathsf{\theta }}_1}\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)\gimel ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)+{\mathtt{J}}_{{{\mathsf{\nu }}_2}^{-}}^{{\mathsf{\theta }}_1}\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)\gimel ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)\right]\hfill \\ \hfill & {⪯}_{\mathtt{CR}}\frac{{{ð}_1}^2-2{ð}_1+4-\left({{ð}_1}^2+2{ð}_1+4\right){\mathtt{e}}^{-{ð}_1}}{{{ð}_1}^3}[\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)\gimel ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)+\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)\gimel ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)]\hfill \\ \hfill & +\frac{2{ð}_1-4+\left(2{ð}_1+4\right){\mathtt{e}}^{-{ð}_1}}{{{ð}_1}^3}[\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)\gimel ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)+\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)\gimel ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)],\hfill \\ \hfill \end{array}$$

(14)

and

$$\begin{array}{cc}\hfill \frac{{\mathsf{\theta }}_1}{{\mathsf{\nu }}_2-{\mathsf{\nu }}_1}& \left[{\mathtt{J}}_{{\mathsf{\nu }}_1+}^{{\mathsf{\theta }}_1}\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)\gimel ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)+{\mathtt{J}}_{{{\mathsf{\nu }}_2}^{-}}^{{\mathsf{\theta }}_1}\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)\gimel ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)\right]\hfill \\ \hfill {⪯}_{\mathtt{CR}}& \frac{{{ð}_1}^2-2{ð}_1+4-\left({{ð}_1}^2+2{ð}_1+4\right){\mathtt{e}}^{-{ð}_1}}{{{ð}_1}^3}[\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)\gimel ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)+\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)\gimel ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)]\hfill \\ \hfill & +\frac{2{ð}_1-4+\left(2{ð}_1+4\right){\mathtt{e}}^{-{ð}_1}}{{{ð}_1}^3}[\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)\gimel ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)+\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)\gimel ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)].\hfill \end{array}$$

(15)

Substituting the relations (12)–(15) into the relation (11), we obtain the desired result. Thus, Theorem 10 is finished. □

Remark 7. 

• If ${\mathsf{\theta }}_1\to 1,{\mathsf{\theta }}_2\to 1$ with $\underline{\aleph }\ne \overline{\aleph }$ and $\underline{\gimel }\ne \overline{\gimel }$, we obtain Theorem 8 as reported in [15]:

  $$\begin{array}{cc}& \frac{1}{({\mathsf{\nu }}_2-{\mathsf{\nu }}_1)({\mathsf{\nu }}_4-{\mathsf{\nu }}_3)}{\int }_{{\mathsf{\nu }}_1}^{{\mathsf{\nu }}_2}{\int }_{{\mathsf{\nu }}_3}^{{\mathsf{\nu }}_4}\aleph (\mathtt{x},\mathtt{y})\gimel (\mathtt{x},\mathtt{y})\mathrm{d}\mathtt{y}\mathrm{d}\mathtt{x}\hfill \\ & \supseteq \frac{1}{9}\mathtt{C}({\mathsf{\nu }}_1,{\mathsf{\nu }}_2,{\mathsf{\nu }}_3,{\mathsf{\nu }}_4)+\frac{1}{18}[\mathtt{D}({\mathsf{\nu }}_1,{\mathsf{\nu }}_2,{\mathsf{\nu }}_3,{\mathsf{\nu }}_4)+\mathtt{E}({\mathsf{\nu }}_1,{\mathsf{\nu }}_2,{\mathsf{\nu }}_3,{\mathsf{\nu }}_4)]+\frac{1}{36}\mathsf{\Psi }({\mathsf{\nu }}_1,{\mathsf{\nu }}_2,{\mathsf{\nu }}_3,{\mathsf{\nu }}_4).\hfill \end{array}$$
• If ${\mathsf{\theta }}_1\to 1,{\mathsf{\theta }}_2\to 1$ with $\underline{\aleph }=\overline{\aleph }$ and $\underline{\gimel }=\overline{\gimel }$, we obtain Theorem 4 as reported in [63]:

  $$\begin{array}{cc}& \frac{1}{({\mathsf{\nu }}_2-{\mathsf{\nu }}_1)({\mathsf{\nu }}_4-{\mathsf{\nu }}_3)}{\int }_{{\mathsf{\nu }}_1}^{{\mathsf{\nu }}_2}{\int }_{{\mathsf{\nu }}_3}^{{\mathsf{\nu }}_4}\aleph (\mathtt{x},\mathtt{y})\gimel (\mathtt{x},\mathtt{y})\mathrm{d}\mathtt{y}\mathrm{d}\mathtt{x}\hfill \\ & \le \frac{1}{9}\mathtt{C}({\mathsf{\nu }}_1,{\mathsf{\nu }}_2,{\mathsf{\nu }}_3,{\mathsf{\nu }}_4)+\frac{1}{18}[\mathtt{D}({\mathsf{\nu }}_1,{\mathsf{\nu }}_2,{\mathsf{\nu }}_3,{\mathsf{\nu }}_4)+\mathtt{E}({\mathsf{\nu }}_1,{\mathsf{\nu }}_2,{\mathsf{\nu }}_3,{\mathsf{\nu }}_4)]+\frac{1}{36}\mathsf{\Psi }({\mathsf{\nu }}_1,{\mathsf{\nu }}_2,{\mathsf{\nu }}_3,{\mathsf{\nu }}_4).\hfill \end{array}$$
• If ${\mathsf{\theta }}_1\to 1,{\mathsf{\theta }}_2\to 1$, we obtain Theorem 10 as reported in [62].

Theorem 11. 

Using the same hypotheses as in Theorem 10, we obtain the following double $\mathtt{CR}$-order relation:

$$\begin{array}{cc}& 4\aleph \left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2},\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right)\gimel \left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2},\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right)\hfill \\ & {⪯}_{\mathtt{CR}}\frac{(1-{\mathsf{\theta }}_2)(1-{\mathsf{\theta }}_1)}{4\left(1-{\mathtt{e}}^{-{ð}_1}\right)\left(1-{\mathtt{e}}^{-{ð}_2}\right)}\left[{\mathtt{J}}_{{{\mathsf{\nu }}_1}^{+},{{\mathsf{\nu }}_3}^{+}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)+{\mathtt{J}}_{{{\mathsf{\nu }}_1}^{+},{{\mathsf{\nu }}_4}^{-}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)\right.\hfill \\ & \left.+{\mathtt{J}}_{{{\mathsf{\nu }}_2}^{-},{{\mathsf{\nu }}_3}^{+}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)+{\mathtt{J}}_{{{\mathsf{\nu }}_2}^{-},{{\mathsf{\nu }}_4}^{-}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)\right]\hfill \\ & +\left[{\alpha }_1{\alpha }_2+{\alpha }_1{\beta }_2+{\alpha }_2{\beta }_1\right]\mathtt{C}({\mathsf{\nu }}_1,{\mathsf{\nu }}_2,{\mathsf{\nu }}_3,{\mathsf{\nu }}_4)+\left[{\alpha }_1{\alpha }_2+{\alpha }_1{\beta }_2+{\beta }_1{\beta }_2\right]\mathtt{D}({\mathsf{\nu }}_1,{\mathsf{\nu }}_2,{\mathsf{\nu }}_3,{\mathsf{\nu }}_4)\hfill \\ & +\left[{\alpha }_1{\alpha }_2+{\alpha }_2{\beta }_1+{\beta }_1{\beta }_2\right]\mathtt{E}({\mathsf{\nu }}_1,{\mathsf{\nu }}_2,{\mathsf{\nu }}_3,{\mathsf{\nu }}_4)+\left[{\alpha }_1{\beta }_2+{\alpha }_2{\beta }_1+{\beta }_1{\beta }_2\right]({\mathsf{\nu }}_1,{\mathsf{\nu }}_2,{\mathsf{\nu }}_3,{\mathsf{\nu }}_4),\hfill \end{array}$$

where

$${\alpha }_{\mathtt{i}}=\frac{{\mathsf{\theta }}_{\mathtt{i}}-2+\left({\mathsf{\theta }}_{\mathtt{i}}+2\right){\mathtt{e}}^{-{\mathsf{\theta }}_{\mathtt{i}}}}{{\mathsf{\theta }}_{\mathtt{i}}^2\left(1-{\mathtt{e}}^{-{\mathsf{\theta }}_{\mathtt{i}}}\right)},{\beta }_{\mathtt{i}}=\frac{{\mathsf{\theta }}_{\mathtt{i}}^2-2{\mathsf{\theta }}_{\mathtt{i}}+4-\left({\mathsf{\theta }}_{\mathtt{i}}^2+2{\mathsf{\theta }}_{\mathtt{i}}+4\right){\mathtt{e}}^{-{\mathsf{\theta }}_{\mathtt{i}}}}{2{\mathsf{\theta }}_{\mathtt{i}}^2\left(1-{\mathtt{e}}^{-{\mathsf{\theta }}_{\mathtt{i}}}\right)},(\mathtt{i}=1,2).$$

Proof. 

By virtue of bidimensional interval-valued functions ℵ, and ℷ and taking into account Theorem 2.5 within reference [60], we have

$$\begin{array}{cc}\hfill & 2\aleph \left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2},\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right)\gimel \left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2},\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right)\hfill \\ \hfill & {⪯}_{\mathtt{CR}}\frac{1-{\mathsf{\theta }}_1}{2\left(1-{\mathtt{e}}^{-{ð}_1}\right)}\left[{\mathtt{J}}_{{\mathsf{\nu }}_1}^{{\mathsf{\theta }}_1}\aleph \left({\mathsf{\nu }}_2,\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right)\gimel \left({\mathsf{\nu }}_2,\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right)+{\mathtt{J}}_{{\mathsf{\nu }}_2}^{{\mathsf{\theta }}_1}\aleph \left({\mathsf{\nu }}_1,\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right)\gimel \left({\mathsf{\nu }}_1,\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right)\right]\hfill \\ \hfill & +{\alpha }_1\left[\aleph \left({\mathsf{\nu }}_1,\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right)\gimel \left({\mathsf{\nu }}_1,\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right)+\aleph \left({\mathsf{\nu }}_2,\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right)\gimel \left({\mathsf{\nu }}_2,\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right)\right]\hfill \\ \hfill & +{\beta }_1\left[\aleph \left({\mathsf{\nu }}_2,\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right)\gimel \left({\mathsf{\nu }}_1,\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right)+\aleph \left({\mathsf{\nu }}_1,\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right)\gimel \left({\mathsf{\nu }}_2,\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right)\right]\hfill \end{array}$$

(16)

and

$$\begin{array}{cc}\hfill & 2\aleph \left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2},\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right)\gimel \left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2},\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right)\hfill \\ \hfill & {⪯}_{\mathtt{CR}}\frac{1-{\mathsf{\theta }}_2}{2\left(1-{\mathtt{e}}^{-{ð}_2}\right)}\left[{\mathtt{J}}_{{{\mathsf{\nu }}_3}^{+}}^{{\mathsf{\theta }}_2}\aleph \left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2},{\mathsf{\nu }}_4\right)\gimel \left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2},{\mathsf{\nu }}_4\right)+{\mathtt{J}}_{{{\mathsf{\nu }}_4}^{-}}^{{\mathsf{\theta }}_2}\aleph \left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2},{\mathsf{\nu }}_3\right)\gimel \left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2},{\mathsf{\nu }}_3\right)\right]\hfill \\ \hfill & +{\alpha }_2\left[\aleph \left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2},{\mathsf{\nu }}_3\right)\gimel \left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2},{\mathsf{\nu }}_3\right)+\aleph \left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2},{\mathsf{\nu }}_4\right)\gimel \left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2},{\mathsf{\nu }}_4\right)\right]\hfill \\ \hfill & +{\beta }_2\left[\aleph \left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2},{\mathsf{\nu }}_3\right)\gimel \left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2},{\mathsf{\nu }}_4\right)+\aleph \left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2},{\mathsf{\nu }}_4\right)\gimel \left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2},{\mathsf{\nu }}_3\right)\right].\hfill \end{array}$$

(17)

Summing relations (16) and (17), then multiplying the result by constant 2, we find that

$$\begin{array}{cc}\hfill & 8\aleph \left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2},\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right)\gimel \left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2},\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right)\hfill \\ \hfill & {⪯}_{\mathtt{CR}}\frac{1-{\mathsf{\theta }}_1}{2(1-{\mathtt{e}}^{-{ð}_1})}\left[2{\mathtt{J}}_{{{\mathsf{\nu }}_1}^{+}}^{{\mathsf{\theta }}_1}\aleph \left({\mathsf{\nu }}_2,\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right)\gimel \left({\mathsf{\nu }}_2,\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right)+2{\mathtt{J}}_{{{\mathsf{\nu }}_2}^{-}}^{{\mathsf{\theta }}_1}\aleph \left({\mathsf{\nu }}_1,\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right)\gimel \left({\mathsf{\nu }}_1,\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right)\right]\hfill \\ \hfill & +\frac{1-{\mathsf{\theta }}_2}{2(1-{\mathtt{e}}^{-{ð}_2})}\left[2{\mathtt{J}}_{{{\mathsf{\nu }}_3}^{+}}^{{\mathsf{\theta }}_2}\aleph \left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2},{\mathsf{\nu }}_4\right)\gimel \left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2},{\mathsf{\nu }}_4\right)+2{\mathtt{J}}_{{{\mathsf{\nu }}_4}^{-}}^{{\mathsf{\theta }}_2}\aleph \left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2},{\mathsf{\nu }}_3\right)\gimel \left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2},{\mathsf{\nu }}_3\right)\right]\hfill \\ \hfill & +{\alpha }_1\left[2\aleph \left({\mathsf{\nu }}_1,\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right)\gimel \left({\mathsf{\nu }}_1,\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right)+2\aleph \left({\mathsf{\nu }}_2,\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right)\gimel \left({\mathsf{\nu }}_2,\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right)\right]\hfill \\ \hfill & +{\alpha }_2\left[2\aleph \left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2},{\mathsf{\nu }}_3\right)\gimel \left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2},{\mathsf{\nu }}_3\right)+2\aleph \left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2},{\mathsf{\nu }}_4\right)\gimel \left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2},{\mathsf{\nu }}_4\right)\right]\hfill \\ \hfill & +{\beta }_1\left[2\aleph \left({\mathsf{\nu }}_1,\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right)\gimel \left({\mathsf{\nu }}_2,\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right)+2\aleph \left({\mathsf{\nu }}_2,\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right)\gimel \left({\mathsf{\nu }}_1,\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right)\right]\hfill \\ \hfill & +{\beta }_2\left[2\aleph \left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2},{\mathsf{\nu }}_3\right)\gimel \left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2},{\mathsf{\nu }}_4\right)+2\aleph \left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2},{\mathsf{\nu }}_4\right)\gimel \left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2},{\mathsf{\nu }}_3\right)\right].\hfill \end{array}$$

(18)

This further implies that

$$\begin{array}{cc}\hfill & 2\aleph \left({\mathsf{\nu }}_1,\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right)\gimel \left({\mathsf{\nu }}_1,\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right)\hfill \\ \hfill {⪯}_{\mathtt{CR}}& \frac{1-{\mathsf{\theta }}_2}{2\left(1-{\mathtt{e}}^{-{ð}_2}\right)}\left[{\mathtt{J}}_{{{\mathsf{\nu }}_3}^{+}}^{{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)\gimel ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)+{\mathtt{J}}_{{{\mathsf{\nu }}_4}^{-}}^{{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)\gimel ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)\right]\hfill \\ \hfill & +{\alpha }_2[\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)\gimel ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)+\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)\gimel ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)]\hfill \\ \hfill & +{\beta }_2[\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)\gimel ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)+\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)\gimel ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)]\hfill \end{array}$$

(19)

$$\begin{array}{cc}\hfill & 2\aleph \left({\mathsf{\nu }}_2,\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right)\gimel \left({\mathsf{\nu }}_2,\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right)\hfill \\ \hfill {⪯}_{\mathtt{CR}}& \frac{1-{\mathsf{\theta }}_2}{2\left(1-{\mathtt{e}}^{-{ð}_2}\right)}\left[{\mathtt{J}}_{{{\mathsf{\nu }}_3}^{+}}^{{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)\gimel ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)+{\mathtt{J}}_{{{\mathsf{\nu }}_4}^{-}}^{{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)\gimel ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)\right]\hfill \\ \hfill & +{\alpha }_2[\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)\gimel ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)+\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)\gimel ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)]\hfill \\ \hfill & +{\beta }_2[\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)\gimel ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)+\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)\gimel ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)]\hfill \end{array}$$

(20)

$$\begin{array}{cc}\hfill & 2\aleph \left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2},{\mathsf{\nu }}_3\right)\gimel \left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2},{\mathsf{\nu }}_3\right)\hfill \\ \hfill & {⪯}_{\mathtt{CR}}\frac{1-{\mathsf{\theta }}_1}{2(1-{\mathtt{e}}^{-{ð}_1})}\left[{\mathtt{J}}_{{\mathsf{\nu }}_1}^{{\mathsf{\theta }}_1}\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)\gimel ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)+{\mathtt{J}}_{{{\mathsf{\nu }}_2}^{-}}^{{\mathsf{\theta }}_1}\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)\gimel ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)\right]\hfill \\ \hfill & +{\alpha }_1[\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)\gimel ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)+\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)\gimel ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)]\hfill \\ \hfill & +{\beta }_1[\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)\gimel ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)+\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)\gimel ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)]\hfill \end{array}$$

(21)

$$\begin{array}{cc}\hfill & 2\aleph \left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2},{\mathsf{\nu }}_4\right)\gimel \left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2},{\mathsf{\nu }}_4\right)\hfill \\ \hfill & {⪯}_{\mathtt{CR}}\frac{1-{\mathsf{\theta }}_1}{2(1-{\mathtt{e}}^{-{ð}_1})}\left[{\mathtt{J}}_{{{\mathsf{\nu }}_1}^{+}}^{{\mathsf{\theta }}_1}\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)\gimel ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)+{\mathtt{J}}_{{\mathsf{\nu }}_2-1}^{{\mathsf{\theta }}_1}\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)\gimel ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)\right]\hfill \\ \hfill & +{\alpha }_1[\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)\gimel ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)+\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)\gimel ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)]\hfill \\ \hfill & +{\beta }_1[\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)\gimel ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)+\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)\gimel ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)]\hfill \end{array}$$

(22)

$$\begin{array}{cc}\hfill & 2\aleph \left({\mathsf{\nu }}_1,\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right)\gimel \left({\mathsf{\nu }}_2,\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right)\hfill \\ \hfill & {⪯}_{\mathtt{CR}}\frac{1-{\mathsf{\theta }}_2}{2(1-{\mathtt{e}}^{-{ð}_2})}\left[{\mathtt{J}}_{{{\mathsf{\nu }}_3}^{+}}^{{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)\gimel ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)+{\mathtt{J}}_{{{\mathsf{\nu }}_4}^{-}}^{{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)\gimel ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)\right]\hfill \\ \hfill & +{\alpha }_2[\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)\gimel ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)+\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)\gimel ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)]\hfill \\ \hfill & +{\beta }_2[\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)\gimel ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)+\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)\gimel ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)]\hfill \end{array}$$

(23)

$$\begin{array}{cc}\hfill & 2\aleph \left({\mathsf{\nu }}_2,\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right)\gimel \left({\mathsf{\nu }}_1,\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right)\hfill \\ \hfill & {⪯}_{\mathtt{CR}}\frac{1-{\mathsf{\theta }}_2}{2(1-{\mathtt{e}}^{-{ð}_2})}\left[{\mathtt{J}}_{{{\mathsf{\nu }}_3}^{+}}^{{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)\gimel ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)+{\mathtt{J}}_{{{\mathsf{\nu }}_4}^{-}}^{{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)\gimel ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)\right]\hfill \\ \hfill & +{\alpha }_2[\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)\gimel ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)+\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)\gimel ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)]\hfill \\ \hfill & +{\beta }_2[\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)\gimel ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)+\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)\gimel ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)]\hfill \end{array}$$

(24)

$$\begin{array}{cc}\hfill & 2\aleph \left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2},{\mathsf{\nu }}_3\right)\gimel \left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2},{\mathsf{\nu }}_4\right)\hfill \\ \hfill & {⪯}_{\mathtt{CR}}\frac{1-{\mathsf{\theta }}_1}{2(1-{\mathtt{e}}^{-{ð}_1})}\left[{\mathtt{J}}_{{{\mathsf{\nu }}_1}^{+}}^{{\mathsf{\theta }}_1}\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)\gimel ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)+{\mathtt{J}}_{{{\mathsf{\nu }}_2}^{-}}^{{\mathsf{\theta }}_1}\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)\gimel ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)\right]\hfill \\ \hfill & +{\alpha }_1[\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)\gimel ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)+\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)\gimel ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)]\hfill \\ \hfill & +{\beta }_1[\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)\gimel ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)+\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)\gimel ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)]\hfill \end{array}$$

(25)

$$\begin{array}{cc}\hfill & 2\aleph \left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2},{\mathsf{\nu }}_4\right)\gimel \left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2},{\mathsf{\nu }}_3\right)\hfill \\ & {⪯}_{\mathtt{CR}}\frac{1-{\mathsf{\theta }}_1}{2(1-{\mathtt{e}}^{-{ð}_1})}\left[{\mathtt{J}}_{{{\mathsf{\nu }}_1}^{+}}^{{\mathsf{\theta }}_1}\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)\gimel ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)+{\mathtt{J}}_{{{\mathsf{\nu }}_2}^{-}}^{{\mathsf{\theta }}_1}\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)\gimel ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)\right]\hfill \\ \hfill & +{\alpha }_1[\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)\gimel ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)+\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)\gimel ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)]\hfill \\ \hfill & +{\beta }_1[\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)\gimel ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)+\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)\gimel ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)].\hfill \end{array}$$

(26)

Substituting relations (19)–(26) into relation (18), it follows that

$$\begin{array}{cc}\hfill & 8\aleph \left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2},\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right)\gimel \left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2},\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right)\hfill \\ \hfill & {⪯}_{\mathtt{CR}}\frac{1-{\mathsf{\theta }}_1}{2(1-{\mathtt{e}}^{-{ð}_1})}\left[2{\mathtt{J}}_{{{\mathsf{\nu }}_1}^{+}}^{{\mathsf{\theta }}_1}\aleph \left({\mathsf{\nu }}_2,\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right)\gimel \left({\mathsf{\nu }}_2,\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right)+2{\mathtt{J}}_{{{\mathsf{\nu }}_2}^{-}}^{{\mathsf{\theta }}_1}\aleph \left({\mathsf{\nu }}_1,\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right)\gimel \left({\mathsf{\nu }}_1,\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right)\right]\hfill \\ \hfill & +\frac{1-{\mathsf{\theta }}_2}{2(1-{\mathtt{e}}^{-{ð}_2})}\left[2{\mathtt{J}}_{{{\mathsf{\nu }}_3}^{+}}^{{\mathsf{\theta }}_2}\aleph \left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2},{\mathsf{\nu }}_4\right)\gimel \left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2},{\mathsf{\nu }}_4\right)+2{\mathtt{J}}_{{{\mathsf{\nu }}_4}^{-}}^{{\mathsf{\theta }}_2}\aleph \left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2},{\mathsf{\nu }}_3\right)\gimel \left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2},{\mathsf{\nu }}_3\right)\right]\hfill \\ \hfill & +\frac{(1-{\mathsf{\theta }}_2){\alpha }_1}{2(1-{\mathtt{e}}^{-{ð}_2})}[{\mathtt{J}}_{{{\mathsf{\nu }}_3}^{+}}^{{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)\gimel ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)+{\mathtt{J}}_{{{\mathsf{\nu }}_4}^{-}}^{{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)\gimel ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)\hfill \\ \hfill & +{\mathtt{J}}_{{{\mathsf{\nu }}_3}^{+}}^{{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)\gimel ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)+{\mathtt{J}}_{{{\mathsf{\nu }}_4}^{-}}^{{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)\gimel ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)]\hfill \\ \hfill & +\frac{(1-{\mathsf{\theta }}_2){\beta }_1}{2(1-{\mathtt{e}}^{-{ð}_2})}[{\mathtt{J}}_{{{\mathsf{\nu }}_3}^{+}}^{{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)\gimel ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)+{\mathtt{J}}_{{{\mathsf{\nu }}_4}^{-}}^{{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)\gimel ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)\hfill \\ \hfill & +{\mathtt{J}}_{{{\mathsf{\nu }}_3}^{+}}^{{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)\gimel ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)+{\mathtt{J}}_{{{\mathsf{\nu }}_4}^{-}}^{{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)\gimel ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)]\hfill \\ \hfill & +\frac{(1-{\mathsf{\theta }}_1){\alpha }_2}{2(1-{\mathtt{e}}^{-{ð}_1})}[{\mathtt{J}}_{{{\mathsf{\nu }}_1}^{+}}^{{\mathsf{\theta }}_1}\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)\gimel ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)+{\mathtt{J}}_{{{\mathsf{\nu }}_2}^{-}}^{{\mathsf{\theta }}_1}\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)\gimel ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)\hfill \\ \hfill & +{\mathtt{J}}_{{{\mathsf{\nu }}_1}^{+}}^{{\mathsf{\theta }}_1}\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)\gimel ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)+{\mathtt{J}}_{{{\mathsf{\nu }}_2}^{-}}^{{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)\gimel ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)]\hfill \\ \hfill & +\frac{(1-{\mathsf{\theta }}_1){\beta }_2}{2(1-{\mathtt{e}}^{-{ð}_1})}[{\mathtt{J}}_{{{\mathsf{\nu }}_1}^{+}}^{{\mathsf{\theta }}_1}\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)\gimel ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)+{\mathtt{J}}_{{{\mathsf{\nu }}_2}^{-}}^{{\mathsf{\theta }}_1}\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)\gimel ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)\hfill \\ \hfill & +{\mathtt{J}}_{{{\mathsf{\nu }}_1}^{+}}^{{\mathsf{\theta }}_1}\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)\gimel ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)+{\mathtt{J}}_{{{\mathsf{\nu }}_2}^{-}}^{{\mathsf{\theta }}_1}\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)\gimel ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)]\hfill \\ \hfill & +2{\alpha }_1{\alpha }_{2}C({\mathsf{\nu }}_1,{\mathsf{\nu }}_2,{\mathsf{\nu }}_3,{\mathsf{\nu }}_4)+2{\alpha }_1{\beta }_{2}D({\mathsf{\nu }}_1,{\mathsf{\nu }}_2,{\mathsf{\nu }}_3,{\mathsf{\nu }}_4)+2{\alpha }_2{\beta }_{1}E({\mathsf{\nu }}_1,{\mathsf{\nu }}_2,{\mathsf{\nu }}_3,{\mathsf{\nu }}_4)+2{\beta }_1{\beta }_2({\mathsf{\nu }}_1,{\mathsf{\nu }}_2,{\mathsf{\nu }}_3,{\mathsf{\nu }}_4).\hfill \end{array}$$

(27)

It follows that

$$\begin{array}{cc}\hfill 2{\mathtt{J}}_{{{\mathsf{\nu }}_1}^{+}}^{{\mathsf{\theta }}_1}& \aleph \left({\mathsf{\nu }}_2,\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right)\gimel \left({\mathsf{\nu }}_2,\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right)\hfill \\ \hfill {⪯}_{\mathtt{CR}}& \frac{1-{\mathsf{\theta }}_2}{2\left(1-{\mathtt{e}}^{-{ð}_2}\right)}\left[{\mathtt{J}}_{{{\mathsf{\nu }}_1}^{+},{{\mathsf{\nu }}_3}^{+}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)+{\mathtt{J}}_{{{\mathsf{\nu }}_1}^{+},{{\mathsf{\nu }}_4}^{-}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)\right]\hfill \\ \hfill & +{\alpha }_2\left[{\mathtt{J}}_{{{\mathsf{\nu }}_1}^{+}}^{{\mathsf{\theta }}_1}\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)\gimel ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)+{\mathtt{J}}_{{{\mathsf{\nu }}_1}^{+}}^{{\mathsf{\theta }}_1}\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)\gimel ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)\right]\hfill \\ \hfill & +{\beta }_2\left[{\mathtt{J}}_{{{\mathsf{\nu }}_1}^{+}}^{{\mathsf{\theta }}_1}\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)\gimel ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)+{\mathtt{J}}_{{{\mathsf{\nu }}_1}^{+}}^{{\mathsf{\theta }}_1}\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)\gimel ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)\right]\hfill \end{array}$$

(28)

$$\begin{array}{cc}\hfill 2{\mathtt{J}}_{{{\mathsf{\nu }}_2}^{-}}^{{\mathsf{\theta }}_1}F& \left({\mathsf{\nu }}_1,\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right)\gimel \left({\mathsf{\nu }}_1,\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right)\hfill \\ \hfill {⪯}_{\mathtt{CR}}& \frac{1-{\mathsf{\theta }}_2}{2(1-{\mathtt{e}}^{-{ð}_2})}\left[{\mathtt{J}}_{{{\mathsf{\nu }}_2}^{-},{{\mathsf{\nu }}_3}^{+}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)+{\mathtt{J}}_{{{\mathsf{\nu }}_2}^{-},{{\mathsf{\nu }}_4}^{-}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)\right]\hfill \\ \hfill & +{\alpha }_2\left[{\mathtt{J}}_{{{\mathsf{\nu }}_2}^{-}}^{{\mathsf{\theta }}_1}\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)\gimel ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)+{\mathtt{J}}_{{{\mathsf{\nu }}_2}^{-}}^{{\mathsf{\theta }}_1}\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)\gimel ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)\right]\hfill \\ \hfill & +{\beta }_2\left[{\mathtt{J}}_{{{\mathsf{\nu }}_2}^{-}}^{{\mathsf{\theta }}_1}\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)\gimel ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)+{\mathtt{J}}_{{{\mathsf{\nu }}_2}^{-}}^{{\mathsf{\theta }}_1}\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)\gimel ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)\right]\hfill \end{array}$$

(29)

$$\begin{array}{cc}\hfill 2{\mathtt{J}}_{{{\mathsf{\nu }}_3}^{+}}^{{\mathsf{\theta }}_2}F& \left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2},{\mathsf{\nu }}_4\right)\gimel \left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2},{\mathsf{\nu }}_4\right)\hfill \\ \hfill {⪯}_{\mathtt{CR}}& \frac{1-{\mathsf{\theta }}_1}{2(1-{\mathtt{e}}^{-{ð}_1})}\left[{\mathtt{J}}_{{{\mathsf{\nu }}_1}^{+},{{\mathsf{\nu }}_3}^{+}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)+{\mathtt{J}}_{{{\mathsf{\nu }}_2}^{-},{{\mathsf{\nu }}_3}^{+}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)\right]\hfill \\ \hfill & +{\alpha }_1\left[{\mathtt{J}}_{{{\mathsf{\nu }}_3}^{+}}^{{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)\gimel ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)+{\mathtt{J}}_{{{\mathsf{\nu }}_3}^{+}}^{{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)\gimel ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)\right]\hfill \\ \hfill & +{\beta }_1\left[{\mathtt{J}}_{{{\mathsf{\nu }}_3}^{+}}^{{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)\gimel ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)+{\mathtt{J}}_{{{\mathsf{\nu }}_3}^{+}}^{{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)\gimel ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)\right]\hfill \end{array}$$

(30)

$$\begin{array}{cc}\hfill 2{\mathtt{J}}_{{{\mathsf{\nu }}_4}^{-}}^{{\mathsf{\theta }}_2}F& \left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2},{\mathsf{\nu }}_3\right)\gimel \left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2},{\mathsf{\nu }}_3\right)\hfill \\ \hfill {⪯}_{\mathtt{CR}}& \frac{1-{\mathsf{\theta }}_1}{2(1-{\mathtt{e}}^{-{ð}_1})}\left[{\mathtt{J}}_{{{\mathsf{\nu }}_1}^{+},{{\mathsf{\nu }}_4}^{-}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)+{\mathtt{J}}_{{{\mathsf{\nu }}_2}^{-},{{\mathsf{\nu }}_4}^{-}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)\right]\hfill \\ \hfill & +{\alpha }_1\left[{\mathtt{J}}_{{{\mathsf{\nu }}_4}^{-}}^{{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)\gimel ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)+{\mathtt{J}}_{{{\mathsf{\nu }}_4}^{-}}^{{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)\gimel ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)\right]\hfill \\ \hfill & +{\beta }_1\left[{\mathtt{J}}_{{{\mathsf{\nu }}_4}^{-}}^{{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)\gimel ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)+{\mathtt{J}}_{{{\mathsf{\nu }}_4}^{-}}^{{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)\gimel ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)\right].\hfill \end{array}$$

(31)

Substituting relations (28)–(31) into relation (27), it follows that

$$\begin{array}{cc}\hfill 8\aleph (\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2}& ,\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2})\gimel \left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2},\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right)\hfill \\ \hfill {⪯}_{\mathtt{CR}}& \frac{(1-{\mathsf{\theta }}_2)(1-{\mathsf{\theta }}_1)}{2(1-{\mathtt{e}}^{-{ð}_1})\left(1-{\mathtt{e}}^{-{ð}_2}\right)}[{\mathtt{J}}_{{{\mathsf{\nu }}_1}^{+},{{\mathsf{\nu }}_3}^{+}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)+{\mathtt{J}}_{{{\mathsf{\nu }}_1}^{+},{{\mathsf{\nu }}_4}^{-}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)\hfill \\ \hfill & +{\mathtt{J}}_{{{\mathsf{\nu }}_2}^{-},{{\mathsf{\nu }}_3}^{+}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)+{\mathtt{J}}_{{{\mathsf{\nu }}_2}^{-},{{\mathsf{\nu }}_4}^{-}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)]\hfill \\ \hfill & +\frac{(1-{\mathsf{\theta }}_2){\alpha }_1}{1-{\mathtt{e}}^{-{ð}_2}}[{\mathtt{J}}_{{{\mathsf{\nu }}_3}^{+}}^{{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)\gimel ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)+{\mathtt{J}}_{{{\mathsf{\nu }}_4}^{-}}^{{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)\gimel ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)\hfill \\ \hfill & +{\mathtt{J}}_{{{\mathsf{\nu }}_3}^{+}}^{{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)\gimel ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)+{\mathtt{J}}_{{{\mathsf{\nu }}_4}^{-}}^{{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)\gimel ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)]\hfill \\ \hfill & +\frac{(1-{\mathsf{\theta }}_2){\beta }_1}{1-{\mathtt{e}}^{-{ð}_2}}[{\mathtt{J}}_{{{\mathsf{\nu }}_3}^{+}}^{{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)\gimel ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)+{\mathtt{J}}_{{{\mathsf{\nu }}_4}^{-}}^{{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)\gimel ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)\hfill \\ \hfill & +{\mathtt{J}}_{{{\mathsf{\nu }}_3}^{+}}^{{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)\gimel ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)+{\mathtt{J}}_{{{\mathsf{\nu }}_4}^{-}}^{{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)\gimel ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)]\hfill \\ \hfill & +\frac{(1-{\mathsf{\theta }}_1){\alpha }_2}{1-{\mathtt{e}}^{-{ð}_1}}[{\mathtt{J}}_{{{\mathsf{\nu }}_1}^{+}}^{{\mathsf{\theta }}_1}\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)\gimel ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)+{\mathtt{J}}_{{{\mathsf{\nu }}_2}^{-}}^{{\mathsf{\theta }}_1}\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)\gimel ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)\hfill \\ \hfill & +{\mathtt{J}}_{{\mathsf{\nu }}_1+}^{{\mathsf{\theta }}_1}\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)\gimel ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)+{\mathtt{J}}_{{{\mathsf{\nu }}_2}^{-}}^{{\mathsf{\theta }}_1}\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)\gimel ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)]\hfill \\ \hfill & +\frac{(1-{\mathsf{\theta }}_1){\beta }_2}{1-{\mathtt{e}}^{-{ð}_1}}[{\mathtt{J}}_{{{\mathsf{\nu }}_1}^{+}}^{{\mathsf{\theta }}_1}\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)\gimel ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)+{\mathtt{J}}_{{{\mathsf{\nu }}_2}^{-}}^{{\mathsf{\theta }}_1}\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)\gimel ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)\hfill \\ \hfill & +{\mathtt{J}}_{{{\mathsf{\nu }}_1}^{+}}^{{\mathsf{\theta }}_1}\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)\gimel ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)+{\mathtt{J}}_{{{\mathsf{\nu }}_2}^{-}}^{{\mathsf{\theta }}_1}\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)\gimel ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)]\hfill \\ \hfill & +2{\alpha }_1{\alpha }_2\mathtt{C}({\mathsf{\nu }}_1,{\mathsf{\nu }}_2,{\mathsf{\nu }}_3)+2{\alpha }_1{\beta }_2\mathtt{D}({\mathsf{\nu }}_1,{\mathsf{\nu }}_2,{\mathsf{\nu }}_3,{\mathsf{\nu }}_4)\hfill \\ \hfill & +2{\alpha }_2{\beta }_1\mathtt{E}({\mathsf{\nu }}_1,{\mathsf{\nu }}_2,{\mathsf{\nu }}_3)+2{\beta }_1{\beta }_2\mathsf{\Psi }({\mathsf{\nu }}_1,{\mathsf{\nu }}_2,{\mathsf{\nu }}_3).\hfill \end{array}$$

(32)

□

We may obtain the necessary result by applying relation (27) to each integral in (32). This leads to the completion of Theorem 11.

Remark 8. 

• If ${\mathsf{\theta }}_1\to 1,{\mathsf{\theta }}_2\to 1$ with $\underline{\aleph }\ne \overline{\aleph }$ and $\underline{\gimel }\ne \overline{\gimel }$, we obtain Theorem 8 as reported in [15]:

  $$\begin{array}{cc}& \frac{1}{({\mathsf{\nu }}_2-{\mathsf{\nu }}_1)({\mathsf{\nu }}_4-{\mathsf{\nu }}_3)}{\int }_{{\mathsf{\nu }}_1}^{{\mathsf{\nu }}_2}{\int }_{{\mathsf{\nu }}_3}^{{\mathsf{\nu }}_4}\aleph (\mathtt{x},\mathtt{y})\gimel (\mathtt{x},\mathtt{y})\mathrm{d}\mathtt{y}\mathrm{d}\mathtt{x}\hfill \\ & \supseteq \frac{1}{9}\mathtt{C}({\mathsf{\nu }}_1,{\mathsf{\nu }}_2,{\mathsf{\nu }}_3,{\mathsf{\nu }}_4)+\frac{1}{18}[\mathtt{D}({\mathsf{\nu }}_1,{\mathsf{\nu }}_2,{\mathsf{\nu }}_3,{\mathsf{\nu }}_4)+E({\mathsf{\nu }}_1,{\mathsf{\nu }}_2,{\mathsf{\nu }}_3,{\mathsf{\nu }}_4)]+\frac{1}{36}\mathsf{\Psi }({\mathsf{\nu }}_1,{\mathsf{\nu }}_2,{\mathsf{\nu }}_3,{\mathsf{\nu }}_4).\hfill \end{array}$$
• If ${\mathsf{\theta }}_1\to 1,{\mathsf{\theta }}_2\to 1$ with $\underline{\aleph }=\overline{\aleph }$ and $\underline{\gimel }=\overline{\gimel }$, we obtain Theorem 4 as reported in [63]:

  $$\begin{array}{cc}& \frac{1}{({\mathsf{\nu }}_2-{\mathsf{\nu }}_1)({\mathsf{\nu }}_4-{\mathsf{\nu }}_3)}{\int }_{{\mathsf{\nu }}_1}^{{\mathsf{\nu }}_2}{\int }_{{\mathsf{\nu }}_3}^{{\mathsf{\nu }}_4}\aleph (\mathtt{x},\mathtt{y})\gimel (\mathtt{x},\mathtt{y})\mathrm{d}\mathtt{y}\mathrm{d}\mathtt{x}\hfill \\ & \le \frac{1}{9}\mathtt{C}({\mathsf{\nu }}_1,{\mathsf{\nu }}_2,{\mathsf{\nu }}_3,{\mathsf{\nu }}_4)+\frac{1}{18}[\mathtt{D}({\mathsf{\nu }}_1,{\mathsf{\nu }}_2,{\mathsf{\nu }}_3,{\mathsf{\nu }}_4)+E({\mathsf{\nu }}_1,{\mathsf{\nu }}_2,{\mathsf{\nu }}_3,{\mathsf{\nu }}_4)]+\frac{1}{36}\mathsf{\Psi }({\mathsf{\nu }}_1,{\mathsf{\nu }}_2,{\mathsf{\nu }}_3,{\mathsf{\nu }}_4).\hfill \end{array}$$
• If ${\mathsf{\theta }}_1\to 1,{\mathsf{\theta }}_2\to 1$, we obtain Theorem 10 as reported in [62].

Theorem 12. 

Using the same hypotheses as in Theorem 7, we obtain the following double $\mathtt{CR}$-order relation:

$$\begin{array}{cc}\hfill \aleph \left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2},\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right){⪯}_{\mathtt{CR}}& \frac{1-{\mathsf{\theta }}_1}{4(1-{\mathtt{e}}^{-{ð}_1})}\left[{\mathtt{J}}_{{{\mathsf{\nu }}_1}^{+}}^{{\mathsf{\theta }}_1}\aleph \left({\mathsf{\nu }}_2,\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right)+{\mathtt{J}}_{{{\mathsf{\nu }}_2}^{-}}^{{\mathsf{\theta }}_1}\aleph \left({\mathsf{\nu }}_1,\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right)\right]\hfill \\ & +\frac{1-{\mathsf{\theta }}_2}{4(1-{\mathtt{e}}^{-{ð}_1})}\left[{\mathtt{J}}_{{{\mathsf{\nu }}_3}^{+}}^{{\mathsf{\theta }}_2}\aleph \left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2},{\mathsf{\nu }}_4\right)+{\mathtt{J}}_{{{\mathsf{\nu }}_4}^{-}}^{{\mathsf{\theta }}_2}\aleph \left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2},{\mathsf{\nu }}_3\right)\right]\hfill \\ \hfill {⪯}_{\mathtt{CR}}& \frac{(1-{\mathsf{\theta }}_1)(1-{\mathsf{\theta }}_2)}{4(1-{\mathtt{e}}^{-{ð}_1})(1-{\mathtt{e}}^{-{ð}_2})}[{\mathtt{J}}_{{{\mathsf{\nu }}_1}^{+},{{\mathsf{\nu }}_3}^{+}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)+{\mathtt{J}}_{{{\mathsf{\nu }}_1}^{+},{{\mathsf{\nu }}_4}^{-}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)\hfill \\ & +{\mathtt{J}}_{{{\mathsf{\nu }}_2}^{-},{{\mathsf{\nu }}_3}^{+}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)+{\mathtt{J}}_{{{\mathsf{\nu }}_2}^{-},{{\mathsf{\nu }}_4}^{-}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)]\hfill \\ \hfill {⪯}_{\mathtt{CR}}& \frac{1-{\mathsf{\theta }}_1}{8(1-{\mathtt{e}}^{-{ð}_1})}\left[{\mathtt{J}}_{{{\mathsf{\nu }}_1}^{+}}^{{\mathsf{\theta }}_1}\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)+{\mathtt{J}}_{{{\mathsf{\nu }}_1}^{+}}^{{\mathsf{\theta }}_1}\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)\right.\hfill \\ & \left.+{\mathtt{J}}_{{{\mathsf{\nu }}_2}^{-}}^{{\mathsf{\theta }}_1}\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)+{\mathtt{J}}_{{{\mathsf{\nu }}_2}^{-}}^{{\mathsf{\theta }}_1}\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)\right]\hfill \\ & +\frac{1-{\mathsf{\theta }}_2}{8(1-{\mathtt{e}}^{-{ð}_2})}\left[{\mathtt{J}}_{{{\mathsf{\nu }}_3}^{+}}^{{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)+{\mathtt{J}}_{{{\mathsf{\nu }}_3}^{+}}^{{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)\right.\hfill \\ & \left.+{\mathtt{J}}_{{{\mathsf{\nu }}_4}^{-}}^{{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)+{\mathtt{J}}_{{{\mathsf{\nu }}_4}^{-}}^{{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)\right]\hfill \\ \hfill {⪯}_{\mathtt{CR}}& \frac{\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)+\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)+\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)+\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)}{4}.\hfill \end{array}$$

Proof. 

By virtue of bidimensional interval-valued function ℵ, it results in the mappings ${\aleph }_{\mathtt{x}}:[{\mathsf{\nu }}_3,{\mathsf{\nu }}_4]\to \mathsf{R},{\aleph }_{\mathtt{x}}\left(\mathtt{y}\right)=\aleph (\mathtt{x},\mathtt{y})$ being convex in nature and defined over $[{\mathsf{\nu }}_3,{\mathsf{\nu }}_4]$ for each $\mathtt{x}\in [{\mathsf{\nu }}_1,{\mathsf{\nu }}_2]$; we have

$$\begin{array}{c}\hfill {\aleph }_{\mathtt{x}}\left(\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right){⪯}_{\mathtt{CR}}\frac{1-{\mathsf{\theta }}_2}{2\left(1-{\mathtt{e}}^{-{ð}_2}\right)}\left[{\mathtt{J}}_{{\mathsf{\nu }}_3+}^{{\mathsf{\theta }}_2}{\aleph }_{\mathtt{x}}\left({\mathsf{\nu }}_2\right)+{\mathtt{J}}_{{\mathsf{\nu }}_4-}^{{\mathsf{\theta }}_2}{\aleph }_{\mathtt{x}}\left({\mathsf{\nu }}_3\right)\right]{⪯}_{\mathtt{CR}}\frac{{\aleph }_{\mathtt{x}}\left({\mathsf{\nu }}_3\right)+{\aleph }_{\mathtt{x}}\left({\mathsf{\nu }}_4\right)}{2},\mathtt{x}\in [{\mathsf{\nu }}_1,{\mathsf{\nu }}_2].\end{array}$$

This indicates that

$$\begin{array}{cc}\hfill \aleph \left(\mathtt{x},\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right)& {⪯}_{\mathtt{CR}}\frac{1-{\mathsf{\theta }}_2}{2\left(1-{\mathtt{e}}^{-{ð}_2}\right)}\left[\frac{1}{{\mathsf{\theta }}_2}{\int }_{{\mathsf{\nu }}_3}^{{\mathsf{\nu }}_4}{\mathtt{e}}^{-\frac{1-{\mathsf{\theta }}_2}{{\mathsf{\theta }}_2}({\mathsf{\nu }}_4-\mathtt{y})}\aleph (\mathtt{x},\mathtt{y})\mathrm{d}\mathtt{y}+\frac{1}{{\mathsf{\theta }}_2}{\int }_{{\mathsf{\nu }}_3}^{{\mathsf{\nu }}_4}{\mathtt{e}}^{-\frac{1-{\mathsf{\theta }}_2}{{\mathsf{\theta }}_2}(\mathtt{y}-{\mathsf{\nu }}_3)}\aleph (\mathtt{x},\mathtt{y})\mathrm{d}\mathtt{y}\right]\hfill \\ \hfill & {⪯}_{\mathtt{CR}}\frac{\aleph (\mathtt{x},{\mathsf{\nu }}_3)+\aleph (\mathtt{x},{\mathsf{\nu }}_4)}{2}.\hfill \end{array}$$

Multiplying the above $\mathtt{CR}$ relation by $\frac{1-{\mathsf{\theta }}_1}{2\left(1-{\mathtt{e}}^{-{ð}_1}\right)}\frac{1}{{\mathsf{\theta }}_1}{\mathtt{e}}^{-\frac{1-{\mathsf{\theta }}_1}{{\mathsf{\theta }}_1}({\mathsf{\nu }}_2-\mathtt{x})}$ and $\frac{1-{\mathsf{\theta }}_1}{2\left(1-{\mathtt{e}}^{-{ð}_1}\right)}\frac{1}{{\mathsf{\theta }}_1}{\mathtt{e}}^{-\frac{1-{\mathsf{\theta }}_1}{{\mathsf{\theta }}_1}(\mathtt{x}-{\mathsf{\nu }}_1)}$, separately, and by integrating the outcome with respect to $\mathtt{x}$ across $[{\mathsf{\nu }}_1,{\mathsf{\nu }}_2]$, we determine that

$$\begin{array}{cc}\hfill & \frac{1-{\mathsf{\theta }}_1}{2(1-{\mathtt{e}}^{-{ð}_1})}\frac{1}{{\mathsf{\theta }}_1}{\int }_{{\mathsf{\nu }}_1}^{{\mathsf{\nu }}_2}{\mathtt{e}}^{-\frac{1-{\mathsf{\theta }}_1}{{\mathsf{\theta }}_1}({\mathsf{\nu }}_2-\mathtt{x})}\aleph \left(\mathtt{x},\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right)\mathrm{d}\mathtt{x}\hfill \\ \hfill & {⪯}_{\mathtt{CR}}\frac{(1-{\mathsf{\theta }}_1)(1-{\mathsf{\theta }}_2)}{4(1-{\mathtt{e}}^{-{ð}_1})(1-{\mathtt{e}}^{-{ð}_2})}[\frac{2}{{\mathsf{\theta }}_1{\mathsf{\theta }}_2}{\int }_{{\mathsf{\nu }}_1}^{{\mathsf{\nu }}_2}{\int }_{{\mathsf{\nu }}_3}^{{\mathsf{\nu }}_4}{\mathtt{e}}^{-\frac{1-{\mathsf{\theta }}_1}{{\mathsf{\theta }}_1}({\mathsf{\nu }}_2-\mathtt{y})}{\mathtt{e}}^{-\frac{1-{\mathsf{\theta }}_2}{{\mathsf{\theta }}_2}({\mathsf{\nu }}_4-\mathtt{y})}\aleph (\mathtt{x},\mathtt{y})\mathrm{d}\mathtt{y}\mathrm{d}\mathtt{x}\hfill \\ \hfill & +\frac{1}{{\mathsf{\theta }}_1{\mathsf{\theta }}_2}{\int }_{{\mathsf{\nu }}_1}^{{\mathsf{\nu }}_2}{\int }_{{\mathsf{\nu }}_3}^{{\mathsf{\nu }}_4}{\mathtt{e}}^{-\frac{1-{\mathsf{\theta }}_1}{{\mathsf{\theta }}_1}({\mathsf{\nu }}_2-\mathtt{x})}{\mathtt{e}}^{-\frac{1-{\mathsf{\theta }}_2}{{\mathsf{\theta }}_2}(\mathtt{y}-{\mathsf{\nu }}_3)}\aleph (\mathtt{x},\mathtt{y})\mathrm{d}\mathtt{y}\mathrm{d}\mathtt{x}]\hfill \\ \hfill & {⪯}_{\mathtt{CR}}\frac{1-{\mathsf{\theta }}_1}{4(1-{\mathtt{e}}^{-{ð}_1})}\left[\frac{1}{{\mathsf{\theta }}_1}{\int }_{{\mathsf{\nu }}_1}^{{\mathsf{\nu }}_2}{\mathtt{e}}^{-\frac{1-{\mathsf{\theta }}_1}{{\mathsf{\theta }}_1}({\mathsf{\nu }}_2-\mathtt{x})}\aleph (\mathtt{x},{\mathsf{\nu }}_3)\mathrm{d}\mathtt{x}+\frac{1}{{\mathsf{\theta }}_1}{\int }_{{\mathsf{\nu }}_1}^{{\mathsf{\nu }}_2}{\mathtt{e}}^{-\frac{1-{\mathsf{\theta }}_1}{{\mathsf{\theta }}_1}({\mathsf{\nu }}_2-\mathtt{x})}\aleph (\mathtt{x},{\mathsf{\nu }}_4)\mathrm{d}\mathtt{x}\right]\hfill \end{array}$$

(33)

and

$$\begin{array}{cc}\hfill & \frac{1-{\mathsf{\theta }}_1}{2(1-{\mathtt{e}}^{-{ð}_1})}\frac{1}{{\mathsf{\theta }}_1}{\int }_{{\mathsf{\nu }}_1}^{{\mathsf{\nu }}_2}{\mathtt{e}}^{-\frac{1-{\mathsf{\theta }}_1}{{\mathsf{\theta }}_1}(\mathtt{x}-{\mathsf{\nu }}_1)}\aleph \left(\mathtt{x},\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right)\mathrm{d}\mathtt{x}\hfill \\ \hfill & {⪯}_{\mathtt{CR}}\frac{(1-{\mathsf{\theta }}_1)(1-{\mathsf{\theta }}_2)}{4(1-{\mathtt{e}}^{-{ð}_1})(1-{\mathtt{e}}^{-{ð}_2})}[\frac{1}{{\mathsf{\theta }}_1{\mathsf{\theta }}_2}{\int }_{{\mathsf{\nu }}_1}^{{\mathsf{\nu }}_2}{\int }_{{\mathsf{\nu }}_3}^{{\mathsf{\nu }}_4}{\mathtt{e}}^{-\frac{1-{\mathsf{\theta }}_1}{{\mathsf{\theta }}_1}(\mathtt{x}-{\mathsf{\nu }}_1)}{\mathtt{e}}^{-\frac{1-{\mathsf{\theta }}_2}{{\mathsf{\theta }}_2}({\mathsf{\nu }}_4-\mathtt{y})}\aleph (\mathtt{x},\mathtt{y})\mathrm{d}\mathtt{y}\mathrm{d}\mathtt{x}\hfill \\ \hfill & +\frac{1}{{\mathsf{\theta }}_1{\mathsf{\theta }}_2}{\int }_{{\mathsf{\nu }}_1}^{{\mathsf{\nu }}_2}{\int }_{{\mathsf{\nu }}_3}^{{\mathsf{\nu }}_4}{\mathtt{e}}^{-\frac{1-{\mathsf{\theta }}_1}{{\mathsf{\theta }}_1}(\mathtt{x}-{\mathsf{\nu }}_1)}{\mathtt{e}}^{-\frac{1-{\mathsf{\theta }}_2}{{\mathsf{\theta }}_2}(\mathtt{y}-{\mathsf{\nu }}_3)}\aleph (\mathtt{x},\mathtt{y})\mathrm{d}\mathtt{y}\mathrm{d}\mathtt{x}]\hfill \\ \hfill & {⪯}_{\mathtt{CR}}\frac{1-{\mathsf{\theta }}_1}{4(1-{\mathtt{e}}^{-{ð}_1})}\left[\frac{1}{{\mathsf{\theta }}_1}{\int }_{{\mathsf{\nu }}_1}^{{\mathsf{\nu }}_2}{\mathtt{e}}^{-\frac{1-{\mathsf{\theta }}_1}{{\mathsf{\theta }}_1}(\mathtt{x}-{\mathsf{\nu }}_1)}\aleph (\mathtt{x},{\mathsf{\nu }}_3)\mathrm{d}\mathtt{x}+\frac{1}{{\mathsf{\theta }}_1}{\int }_{{\mathsf{\nu }}_1}^{{\mathsf{\nu }}_2}{\mathtt{e}}^{-\frac{1-{\mathsf{\theta }}_1}{{\mathsf{\theta }}_1}(\mathtt{x}-{\mathsf{\nu }}_1)}\aleph (\mathtt{x},{\mathsf{\nu }}_4)\mathrm{d}\mathtt{x}\right].\hfill \end{array}$$

(34)

By using a similar logic to the mapping ${\aleph }_{\mathtt{y}}:[{\mathsf{\nu }}_1,{\mathsf{\nu }}_2]\to \mathsf{R},{\aleph }_{\mathtt{y}}=\aleph (\mathtt{x},\mathtt{y})$, one has

$$\begin{array}{cc}\hfill & \frac{1-{\mathsf{\theta }}_2}{2(1-{\mathtt{e}}^{-{ð}_2})}\frac{1}{{\mathsf{\theta }}_2}{\int }_{{\mathsf{\nu }}_3}^{{\mathsf{\nu }}_4}{\mathtt{e}}^{-\frac{1-{\mathsf{\theta }}_2}{{\mathsf{\theta }}_2}({\mathsf{\nu }}_4-\mathtt{y})}\aleph \left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2},y\right)\mathrm{d}\mathtt{y}\hfill \\ \hfill & {⪯}_{\mathtt{CR}}\frac{(1-{\mathsf{\theta }}_1)(1-{\mathsf{\theta }}_2)}{4\left(1-{\mathtt{e}}^{-{ð}_1}\right)\left(1-{\mathtt{e}}^{-{ð}_2}\right)}[\frac{1}{{\mathsf{\theta }}_1{\mathsf{\theta }}_2}{\int }_{{\mathsf{\nu }}_1}^{{\mathsf{\nu }}_2}{\int }_{{\mathsf{\nu }}_3}^{{\mathsf{\nu }}_4}{\mathtt{e}}^{-\frac{1-{\mathsf{\theta }}_1}{{\mathsf{\theta }}_1}({\mathsf{\nu }}_2-\mathtt{x})}{\mathtt{e}}^{-\frac{1-{\mathsf{\theta }}_2}{{\mathsf{\theta }}_2}({\mathsf{\nu }}_4-\mathtt{y})}\aleph (\mathtt{x},\mathtt{y})\mathrm{d}\mathtt{y}\mathrm{d}\mathtt{x}\hfill \\ \hfill & +\frac{1}{{\mathsf{\theta }}_1{\mathsf{\theta }}_2}{\int }_{{\mathsf{\nu }}_1}^{{\mathsf{\nu }}_2}{\int }_{{\mathsf{\nu }}_3}^{{\mathsf{\nu }}_4}{\mathtt{e}}^{-\frac{1-{\mathsf{\theta }}_1}{{\mathsf{\theta }}_1}(\mathtt{x}-{\mathsf{\nu }}_1)}{\mathtt{e}}^{-\frac{1-{\mathsf{\theta }}_2}{{\mathsf{\theta }}_2}({\mathsf{\nu }}_4-\mathtt{y})}\aleph (\mathtt{x},\mathtt{y})\mathrm{d}\mathtt{y}\mathrm{d}\mathtt{x}]\hfill \\ \hfill & {⪯}_{\mathtt{CR}}\frac{1-{\mathsf{\theta }}_2}{4(1-{\mathtt{e}}^{-{ð}_2})}\left[\frac{1}{{\mathsf{\theta }}_2}{\int }_{{\mathsf{\nu }}_3}^{{\mathsf{\nu }}_4}{\mathtt{e}}^{-\frac{1-{\mathsf{\theta }}_2}{{\mathsf{\theta }}_2}({\mathsf{\nu }}_4-\mathtt{y})}\aleph ({\mathsf{\nu }}_1,\mathtt{y})\mathrm{d}\mathtt{y}+\frac{1}{{\mathsf{\theta }}_2}{\int }_{{\mathsf{\nu }}_3}^{{\mathsf{\nu }}_4}{\mathtt{e}}^{-\frac{1-{\mathsf{\theta }}_2}{{\mathsf{\theta }}_2}({\mathsf{\nu }}_4-\mathtt{y})}\aleph ({\mathsf{\nu }}_2,\mathtt{y})\mathrm{d}\mathtt{y}\right]\hfill \end{array}$$

(35)

and

$$\begin{array}{cc}\hfill & \frac{1-{\mathsf{\theta }}_2}{2(1-{\mathtt{e}}^{-{ð}_2})}\frac{1}{{\mathsf{\theta }}_2}{\int }_{{\mathsf{\nu }}_3}^{{\mathsf{\nu }}_4}{\mathtt{e}}^{-\frac{1-{\mathsf{\theta }}_2}{{\mathsf{\theta }}_2}(\mathtt{y}-{\mathsf{\nu }}_3)}\aleph \left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2},y\right)\mathrm{d}\mathtt{y}\hfill \\ \hfill & {⪯}_{\mathtt{CR}}\frac{(1-{\mathsf{\theta }}_1)(1-{\mathsf{\theta }}_2)}{4(1-{\mathtt{e}}^{-{ð}_1})(1-{\mathtt{e}}^{-{ð}_2})}[\frac{1}{{\mathsf{\theta }}_1{\mathsf{\theta }}_2}{\int }_{{\mathsf{\nu }}_1}^{{\mathsf{\nu }}_2}{\int }_{{\mathsf{\nu }}_3}^{{\mathsf{\nu }}_4}{\mathtt{e}}^{-\frac{1-{\mathsf{\theta }}_1}{{\mathsf{\theta }}_1}({\mathsf{\nu }}_2-\mathtt{x})}{\mathtt{e}}^{-\frac{1-{\mathsf{\theta }}_2}{{\mathsf{\theta }}_2}(\mathtt{y}-{\mathsf{\nu }}_3)}\aleph (\mathtt{x},\mathtt{y})\mathrm{d}\mathtt{y}\mathrm{d}\mathtt{x}\hfill \\ \hfill & +\frac{1}{{\mathsf{\theta }}_1{\mathsf{\theta }}_2}{\int }_{{\mathsf{\nu }}_1}^{{\mathsf{\nu }}_2}{\int }_{{\mathsf{\nu }}_3}^{{\mathsf{\nu }}_4}{\mathtt{e}}^{-\frac{1-{\mathsf{\theta }}_1}{{\mathsf{\theta }}_1}(\mathtt{x}-{\mathsf{\nu }}_1)}{\mathtt{e}}^{-\frac{1-{\mathsf{\theta }}_2}{{\mathsf{\theta }}_2}(\mathtt{y}-{\mathsf{\nu }}_3)}\aleph (\mathtt{x},\mathtt{y})\mathrm{d}\mathtt{y}\mathrm{d}\mathtt{x}]\hfill \\ \hfill & {⪯}_{\mathtt{CR}}\frac{1-{\mathsf{\theta }}_2}{4(1-{\mathtt{e}}^{-{ð}_2})}\left[\frac{1}{{\mathsf{\theta }}_2}{\int }_{{\mathsf{\nu }}_3}^{{\mathsf{\nu }}_4}{\mathtt{e}}^{-\frac{1-{\mathsf{\theta }}_2}{{\mathsf{\theta }}_2}(\mathtt{y}-{\mathsf{\nu }}_3)}\aleph ({\mathsf{\nu }}_1,\mathtt{y})\mathrm{d}\mathtt{y}+\frac{1}{{\mathsf{\theta }}_2}{\int }_{{\mathsf{\nu }}_3}^{{\mathsf{\nu }}_4}{\mathtt{e}}^{-\frac{1-{\mathsf{\theta }}_2}{{\mathsf{\theta }}_2}(\mathtt{y}-{\mathsf{\nu }}_3)}\aleph ({\mathsf{\nu }}_2,\mathtt{y})\mathrm{d}\mathtt{y}\right].\hfill \end{array}$$

(36)

Adding relations (33)–(36), we obtain

$$\begin{array}{cc}& \frac{1-{\mathsf{\theta }}_1}{4(1-{\mathtt{e}}^{-{ð}_1})}\left[{\mathtt{J}}_{{{\mathsf{\nu }}_1}^{+}}^{{\mathsf{\theta }}_1}\aleph \left({\mathsf{\nu }}_2,\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right)+{\mathtt{J}}_{{{\mathsf{\nu }}_2}^{-}}^{{\mathsf{\theta }}_1}\aleph \left({\mathsf{\nu }}_1,\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right)\right]\hfill \\ & +\frac{1-{\mathsf{\theta }}_2}{4(1-{\mathtt{e}}^{-{ð}_2})}\left[{\mathtt{J}}_{{{\mathsf{\nu }}_3}^{+}}^{{\mathsf{\theta }}_2}\aleph \left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2},{\mathsf{\nu }}_4\right)+{\mathtt{J}}_{{{\mathsf{\nu }}_4}^{-}}^{{\mathsf{\theta }}_2}\aleph \left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2},{\mathsf{\nu }}_3\right)\right]\hfill \\ & {⪯}_{\mathtt{CR}}\frac{(1-{\mathsf{\theta }}_2)(1-{\mathsf{\theta }}_1)}{4(1-{\mathtt{e}}^{-{ð}_1})(1-{\mathtt{e}}^{-{ð}_2})}[{\mathtt{J}}_{{{\mathsf{\nu }}_1}^{+},{{\mathsf{\nu }}_3}^{+}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)+{\mathtt{J}}_{{{\mathsf{\nu }}_1}^{+},{{\mathsf{\nu }}_4}^{-}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)\hfill \\ & +{\mathtt{J}}_{{{\mathsf{\nu }}_2}^{-},{{\mathsf{\nu }}_3}^{+}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)+{\mathtt{J}}_{{{\mathsf{\nu }}_2}^{-},{{\mathsf{\nu }}_4}^{-}}^{{\mathsf{\theta }}_1,{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)]\hfill \\ & {⪯}_{\mathtt{CR}}\frac{1-{\mathsf{\theta }}_1}{8(1-{\mathtt{e}}^{-{ð}_1})}\left[{\mathtt{J}}_{{{\mathsf{\nu }}_1}^{+}}^{{\mathsf{\theta }}_1}\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)+{\mathtt{J}}_{{{\mathsf{\nu }}_1}^{+}}^{{\mathsf{\theta }}_1}\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)+{\mathtt{J}}_{{{\mathsf{\nu }}_2}^{-}}^{{\mathsf{\theta }}_1}\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)+{\mathtt{J}}_{{{\mathsf{\nu }}_2}^{-}}^{{\mathsf{\theta }}_1}\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)\right]\hfill \\ & +\frac{1-{\mathsf{\theta }}_2}{8(1-{\mathtt{e}}^{-{ð}_2})}\left[{\mathtt{J}}_{{{\mathsf{\nu }}_3}^{+}}^{{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)+{\mathtt{J}}_{{{\mathsf{\nu }}_3}^{+}}^{{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)+{\mathtt{J}}_{{{\mathsf{\nu }}_4}^{-}}^{{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)+{\mathtt{J}}_{{{\mathsf{\nu }}_4}^{-}}^{{\mathsf{\theta }}_2}\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)\right].\hfill \\ \end{array}$$

This yields the second and third relations in Theorem 12. Using the first relation from Theorem 9, we can determine that

$$\begin{array}{cc}\hfill \aleph \left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2},\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right){⪯}_{\mathtt{CR}}& \frac{1-{\mathsf{\theta }}_1}{2(1-{\mathtt{e}}^{-{ð}_1})}[\frac{1}{{\mathsf{\theta }}_1}{\int }_{{\mathsf{\nu }}_1}^{{\mathsf{\nu }}_2}{\mathtt{e}}^{-\frac{1-{\mathsf{\theta }}_1}{{\mathsf{\theta }}_1}({\mathsf{\nu }}_2-\mathtt{x})}\aleph \left(\mathtt{x},\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right)\mathrm{d}\mathtt{x}\hfill \\ & +\frac{1}{{\mathsf{\theta }}_1}{\int }_{{\mathsf{\nu }}_1}^{{\mathsf{\nu }}_2}{\mathtt{e}}^{-\frac{1-{\mathsf{\theta }}_1}{{\mathsf{\theta }}_1}(\mathtt{x}-{\mathsf{\nu }}_1)}\aleph \left(\mathtt{x},\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right)\mathrm{d}\mathtt{x}]\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill \aleph \left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2},\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right){⪯}_{\mathtt{CR}}& \frac{1-{\mathsf{\theta }}_2}{2\left(1-{\mathtt{e}}^{-{ð}_2}\right)}\left[\frac{1}{{\mathsf{\theta }}_2}{\int }_{{\mathsf{\nu }}_3}^{{\mathsf{\nu }}_4}{\mathtt{e}}^{-\frac{1-{\mathsf{\theta }}_2}{{\mathsf{\theta }}_2}({\mathsf{\nu }}_4-\mathtt{y})}\aleph \left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2},y\right)\mathrm{d}\mathtt{y}\right.\hfill \\ & \left.+\frac{1}{{\mathsf{\theta }}_2}{\int }_{{\mathsf{\nu }}_3}^{{\mathsf{\nu }}_4}{\mathtt{e}}^{-\frac{1-{\mathsf{\theta }}_2}{{\mathsf{\theta }}_2}(\mathtt{y}-{\mathsf{\nu }}_3)}\aleph \left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2},y\right)\mathrm{d}\mathtt{y}\right].\hfill \end{array}$$

By addition,

$$\begin{array}{cc}& \aleph \left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2},\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right){⪯}_{\mathtt{CR}}\frac{1-{\mathsf{\theta }}_1}{4(1-{\mathtt{e}}^{{ð}_1)}}\left[{\mathtt{J}}_{{{\mathsf{\nu }}_1}^{+}}^{{\mathsf{\theta }}_1}\aleph \left({\mathsf{\nu }}_2,\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right)+{\mathtt{J}}_{{{\mathsf{\nu }}_2}^{-}}^{{\mathsf{\theta }}_1}\aleph \left({\mathsf{\nu }}_1,\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right)\right]\hfill \\ & +\frac{1-{\mathsf{\theta }}_2}{4(1-{\mathtt{e}}^{{ð}_2})}\left[{\mathtt{J}}_{{{\mathsf{\nu }}_3}^{+}}^{{\mathsf{\theta }}_2}\aleph \left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2},{\mathsf{\nu }}_4\right)+{\mathtt{J}}_{{{\mathsf{\nu }}_4}^{-}}^{{\mathsf{\theta }}_2}\aleph \left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2},{\mathsf{\nu }}_3\right)\right].\hfill \\ \end{array}$$

This deduces the first relation in Theorem 12. Finally, again we have

$$\begin{array}{cc}& \frac{1-{\mathsf{\theta }}_1}{2(1-{\mathtt{e}}^{-{ð}_1)}}[\frac{1}{{\mathsf{\theta }}_1}{\int }_{{\mathsf{\nu }}_1}^{{\mathsf{\nu }}_2}{\mathtt{e}}^{-\frac{1-{\mathsf{\theta }}_1}{{\mathsf{\theta }}_1}({\mathsf{\nu }}_2-\mathtt{x})}\aleph (\mathtt{x},{\mathsf{\nu }}_3)\mathrm{d}\mathtt{x}\hfill \\ & +\frac{1}{{\mathsf{\theta }}_1}{\int }_{{\mathsf{\nu }}_1}^{{\mathsf{\nu }}_2}{\mathtt{e}}^{-\frac{1-{\mathsf{\theta }}_1}{{\mathsf{\theta }}_1}(\mathtt{x}-{\mathsf{\nu }}_1)}\aleph (\mathtt{x},{\mathsf{\nu }}_3)\mathrm{d}\mathtt{x}]{⪯}_{\mathtt{CR}}\frac{\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)+\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)}{2},\hfill \\ & \frac{1-{\mathsf{\theta }}_1}{2(1-{\mathtt{e}}^{-{ð}_1})}[\frac{1}{{\mathsf{\theta }}_1}{\int }_{{\mathsf{\nu }}_1}^{{\mathsf{\nu }}_2}{\mathtt{e}}^{-\frac{1-{\mathsf{\theta }}_1}{{\mathsf{\theta }}_1}({\mathsf{\nu }}_2-\mathtt{x})}\aleph (\mathtt{x},{\mathsf{\nu }}_4)\mathrm{d}\mathtt{x}\hfill \\ & +\frac{1}{{\mathsf{\theta }}_1}{\int }_{{\mathsf{\nu }}_1}^{{\mathsf{\nu }}_2}{\mathtt{e}}^{-\frac{1-{\mathsf{\theta }}_1}{{\mathsf{\theta }}_1}(\mathtt{x}-{\mathsf{\nu }}_1)}\aleph (\mathtt{x},{\mathsf{\nu }}_4)\mathrm{d}\mathtt{x}]{⪯}_{\mathtt{CR}}\frac{\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)+\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)}{2},\hfill \\ & \frac{1-{\mathsf{\theta }}_2}{2(1-{\mathtt{e}}^{-{ð}_2})}[\frac{1}{{\mathsf{\theta }}_2}{\int }_{{\mathsf{\nu }}_3}^{{\mathsf{\nu }}_4}{\mathtt{e}}^{-\frac{1-{\mathsf{\theta }}_2}{{\mathsf{\theta }}_2}({\mathsf{\nu }}_4-\mathtt{y})}\aleph ({\mathsf{\nu }}_1,\mathtt{y})\mathrm{d}\mathtt{y}\hfill \\ & +\frac{1}{{\mathsf{\theta }}_2}{\int }_{{\mathsf{\nu }}_3}^{{\mathsf{\nu }}_4}{\mathtt{e}}^{-\frac{1-{\mathsf{\theta }}_2}{{\mathsf{\theta }}_2}(\mathtt{y}-{\mathsf{\nu }}_3)}\aleph ({\mathsf{\nu }}_1,\mathtt{y})\mathrm{d}\mathtt{y}]{⪯}_{\mathtt{CR}}\frac{\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)+\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)}{2}\hfill \\ & \mathrm{and}\hfill \end{array}$$

$$\begin{array}{cc}& \frac{1-{\mathsf{\theta }}_2}{2\left(1-{\mathtt{e}}^{-{ð}_2}\right)}\left[\frac{1}{{\mathsf{\theta }}_2}{\int }_{{\mathsf{\nu }}_3}^{{\mathsf{\nu }}_4}{\mathtt{e}}^{-\frac{1-{\mathsf{\theta }}_2}{{\mathsf{\theta }}_2}({\mathsf{\nu }}_4-\mathtt{y})}\aleph ({\mathsf{\nu }}_2,\mathtt{y})\mathrm{d}\mathtt{y}\right.\hfill \\ & \left.+\frac{1}{{\mathsf{\theta }}_2}{\int }_{{\mathsf{\nu }}_3}^{{\mathsf{\nu }}_4}{\mathtt{e}}^{-\frac{1-{\mathsf{\theta }}_2}{{\mathsf{\theta }}_2}(\mathtt{y}-{\mathsf{\nu }}_3)}\aleph ({\mathsf{\nu }}_2,\mathtt{y})\mathrm{d}\mathtt{y}\right]{⪯}_{\mathtt{CR}}\frac{\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)+\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)}{2}.\hfill \end{array}$$

Summing the above four $\mathtt{CR}$-order relations yields the final relation in Theorem 12. Therefore, the proof of Theorem 12 is complete.

□

Remark 9. 

• If we take ${\mathsf{\theta }}_1\to 1,{\mathsf{\theta }}_2\to 1$, then we have

  $$\begin{array}{cc}& \underset{{\mathsf{\theta }}_1\to 1}{lim}\frac{1-{\mathsf{\theta }}_1}{4\left(1-{\mathtt{e}}^{-{ð}_1}\right)}=\frac{1}{4({\mathsf{\nu }}_2-{\mathsf{\nu }}_1)},\hfill \\ & \underset{{\mathsf{\theta }}_2\to 1}{lim}\frac{1-{\mathsf{\theta }}_2}{4\left(1-{\mathtt{e}}^{-{ð}_2}\right)}=\frac{1}{4({\mathsf{\nu }}_4-{\mathsf{\nu }}_3)},\hfill \\ & \mathit{and}\hfill \end{array}$$

  $$\underset{\begin{array}{c}{\mathsf{\theta }}_1\to 1\\ {\mathsf{\theta }}_2\to 1\end{array}}{lim}\frac{(1-{\mathsf{\theta }}_2)(1-{\mathsf{\theta }}_1)}{4\left(1-{\mathtt{e}}^{{ð}_1}\right)\left(1-{\mathtt{e}}^{{ð}_2}\right)}=\frac{1}{4({\mathsf{\nu }}_2-{\mathsf{\nu }}_1)({\mathsf{\nu }}_4-{\mathsf{\nu }}_3)},$$

  and we obtain Theorem 9 as reported in [15] in the setting of partial-order relations.
• If we take ${\mathsf{\theta }}_1\to 1,{\mathsf{\theta }}_2\to 1$ with $\underline{\aleph }=\overline{\aleph }$, we obtain the following result as reported in [14] in the setting of standard-order relations, which is

  $$\begin{array}{cc}\hfill \aleph \left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2},\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right)\le & \frac{1}{2}\left[\frac{1}{{\mathsf{\nu }}_2-{\mathsf{\nu }}_1}{\int }_{{\mathsf{\nu }}_1}^{{\mathsf{\nu }}_2}\aleph \left(\mathtt{x},\frac{{\mathsf{\nu }}_3+{\mathsf{\nu }}_4}{2}\right)\mathrm{d}\mathtt{x}+\frac{1}{{\mathsf{\nu }}_4-{\mathsf{\nu }}_3}{\int }_{{\mathsf{\nu }}_3}^{{\mathsf{\nu }}_4}\aleph \left(\frac{{\mathsf{\nu }}_1+{\mathsf{\nu }}_2}{2},y\right)\mathrm{d}\mathtt{y}\right]\hfill \\ \hfill \le & \frac{1}{({\mathsf{\nu }}_2-{\mathsf{\nu }}_1)({\mathsf{\nu }}_4-{\mathsf{\nu }}_3)}{\int }_{{\mathsf{\nu }}_1}^{{\mathsf{\nu }}_2}{\int }_{{\mathsf{\nu }}_3}^{{\mathsf{\nu }}_4}\aleph (\mathtt{x},\mathtt{y})\mathrm{d}\mathtt{y}\mathrm{d}\mathtt{x}\hfill \\ \hfill \le & \frac{1}{4}\left[\frac{1}{{\mathsf{\nu }}_2-{\mathsf{\nu }}_1}{\int }_{{\mathsf{\nu }}_1}^{{\mathsf{\nu }}_2}\aleph (\mathtt{x},{\mathsf{\nu }}_3)\mathrm{d}\mathtt{x}+\frac{1}{{\mathsf{\nu }}_2-{\mathsf{\nu }}_1}{\int }_{{\mathsf{\nu }}_1}^{{\mathsf{\nu }}_2}\aleph (\mathtt{x},{\mathsf{\nu }}_4)\mathrm{d}\mathtt{x}\right.\hfill \\ \hfill & \left.+\frac{1}{{\mathsf{\nu }}_4-{\mathsf{\nu }}_3}{\int }_{{\mathsf{\nu }}_3}^{{\mathsf{\nu }}_4}\aleph ({\mathsf{\nu }}_1,\mathtt{y})\mathrm{d}\mathtt{y}+\frac{1}{{\mathsf{\nu }}_4-{\mathsf{\nu }}_3}{\int }_{{\mathsf{\nu }}_3}^{{\mathsf{\nu }}_4}\aleph (v,\mathtt{y})\mathrm{d}\mathtt{y}\right]\hfill \\ \hfill \le & \frac{\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_3)+\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_3)+\aleph ({\mathsf{\nu }}_1,{\mathsf{\nu }}_4)+\aleph ({\mathsf{\nu }}_2,{\mathsf{\nu }}_4)}{4}.\hfill \end{array}$$

5. Discussion and Conclusions

Research on integral inequalities associated with fractional operators has served as a source of inspiration for many researchers. According to recent trends, researchers are increasingly incorporating fractional operators into the theory of inequalities. Mathematicians have used new methods to generalize well-known inequalities to offer new bounds and applications. In this paper, we use two-dimensional convexity to develop three important inequalities, including the famous Hermite–Hadamard inequality and its weighted and product forms along with various other interesting properties. Additionally, we investigate the Hyers–Ulam stability of two-dimensional convex mappings in the context of approximate convexity by using the sandwich theorem. We show that the recent results developed in [14,15,62,63] are generalized with different settings in our newly developed results. Furthermore, we show that the order relation we use covers the full spectrum of recent order relations under different configurations. Furthermore, this is the first time a total-order relation has been used with two-dimensional convex mappings. In the form of corollaries and remarks, some special cases of the presented results have been discussed. Moreover, we developed some interesting examples to demonstrate the validity of our findings. On the coordinates, this innovative concept can be used to represent various inequalities, including those of the Ostrowski, Jensen–Mercer, Bullen, and Simpson types. These inequalities can also be applied to interval-valued quantum calculus, fuzzy calculus, and stochastic calculus.

6. Open Problem and Future Recommendations

If Ω is a convex subset of a real linear space $\mathtt{Y}$ and $\mathsf{ϵ}$ is a nonnegative number, then a function $\aleph :\mathsf{\Omega }\to \mathsf{R}$ is called $\mathsf{ϵ}$-convex if

$$\begin{array}{cc}\hfill \aleph \left({\mathtt{r}}_{\mathtt{1}}{\mathsf{\nu }}_1+(1-{\mathtt{r}}_{\mathtt{1}}){\mathsf{\nu }}_2\right)& \le {\mathtt{r}}_{\mathtt{1}}\aleph \left({\mathsf{\nu }}_1\right)+(1-{\mathtt{r}}_{\mathtt{1}})\aleph \left({\mathsf{\nu }}_2\right)+\mathsf{ϵ},({\mathsf{\nu }}_1,{\mathsf{\nu }}_2)\in \mathsf{\Omega },{\mathtt{r}}_{\mathtt{1}}\in [0,1].\hfill \end{array}$$

It is likely that the study of approximate convexity began with the 1952 paper by Hyers and Ulam [43], who introduced and investigated $\mathsf{ϵ}$-convex. The authors asked whether there exists another function $\gimel :\mathsf{\Omega }\to \mathsf{R}$ that meets the following criteria $|\gimel (ß)-\aleph (ß\left)\right|\le \mathtt{K}\mathsf{ϵ}$$\forall ß\in \mathsf{\Omega }$, with constant $\mathtt{K}$ only depending upon linear space $\mathtt{Y}.$ Despite the setting of any norm, Hyers and Ulam have provided a very nice and positive answer for the case of linear space $\mathtt{Y}={\mathsf{R}}^{\mathsf{n}}$, and the best approximate they provided can be summarized as follows: ${\mathtt{K}}_{\mathtt{n}}=min({\mathtt{P}}_{\mathtt{n}},{\mathtt{Q}}_{\mathtt{n}})$ where ${\mathtt{P}}_{\mathtt{n}}=\frac{{\mathtt{n}}^{\mathtt{2}}+\mathtt{3}\mathtt{n}}{\mathtt{4}\mathtt{n}+\mathtt{4}}$ and ${\mathtt{Q}}_{\mathtt{n}}=\frac{\mathtt{m}}{2}$ for $2^{\mathtt{m}-\mathtt{1}}\le \mathtt{n}\le 2^{\mathtt{m}}$ (see [64] for further information on these constants and related problems). From the outlined definitions in the Preliminaries section and these results, it is now possible to provide a two-dimensional approximate convexity as follows:

$$\begin{array}{cc}\hfill \aleph \left({\mathtt{r}}_{\mathtt{1}}{\mathsf{\nu }}_1+(1-{\mathtt{r}}_{\mathtt{1}}){\mathsf{\nu }}_2,{\mathtt{s}}_{\mathtt{1}}{\mathsf{\nu }}_3+(1-{\mathtt{s}}_{\mathtt{1}}){\mathsf{\nu }}_4\right)& \le {\mathsf{\nu }}_1{\mathsf{\nu }}_2\aleph ({\mathtt{r}}_{\mathtt{1}},{\mathsf{\nu }}_3)+{\mathsf{\nu }}_2(1-{\mathsf{\nu }}_1)\aleph ({\mathtt{r}}_{\mathtt{1}},{\mathsf{\nu }}_4)\hfill \\ \hfill & +{\mathsf{\nu }}_1(1-{\mathsf{\nu }}_2)\aleph ({\mathtt{s}}_{\mathtt{1}}.{\mathsf{\nu }}_3)+(1-{\mathsf{\nu }}_1)(1-{\mathsf{\nu }}_2)\aleph ({\mathtt{s}}_{\mathtt{1}},{\mathsf{\nu }}_4)+\mathsf{ϵ}\hfill \end{array}$$

which holds true for every $({\mathsf{\nu }}_1,{\mathsf{\nu }}_2),({\mathsf{\nu }}_3,{\mathsf{\nu }}_4)\in \mathsf{\Omega }$, along with ${\mathtt{r}}_{\mathtt{1}},{\mathtt{s}}_{\mathtt{1}}\in [0,1]$. The question is, what are the best optimal constants ${\mathtt{P}}_{\mathtt{n}}$ and ${\mathtt{Q}}_{\mathtt{n}}$ for this two-dimensional approximate convexity? Additionally, we offer a novel approach to developing these results based on stochastic integration, as defined in [65].