The Stability of Solutions of the Variable-Order Fractional Optimal Control Model for the COVID-19 Epidemic in Discrete Time
Abstract
1. Introduction
Model Formulation
2. Preliminaries
- 1.
- For the condition for stability is .
- 2
- For the condition for stability either Routh–Hurwitz conditions [45] or , ,
3. Properties of Solution
3.1. Non-Negativity and Boundedness of the Solutions
3.2. Equilibrium Points and Basic Reproduction Number
3.3. Existence and Uniqueness (E&U) of the Solution
3.4. The Stability of Equilibrium Points
4. Optimal Control Problem
5. Numerical Simulation
5.1. Numerical Strategy without Control
5.2. Numerical Strategy with Control
5.3. Solution Algorithm of V-FOCP in Discrete Time
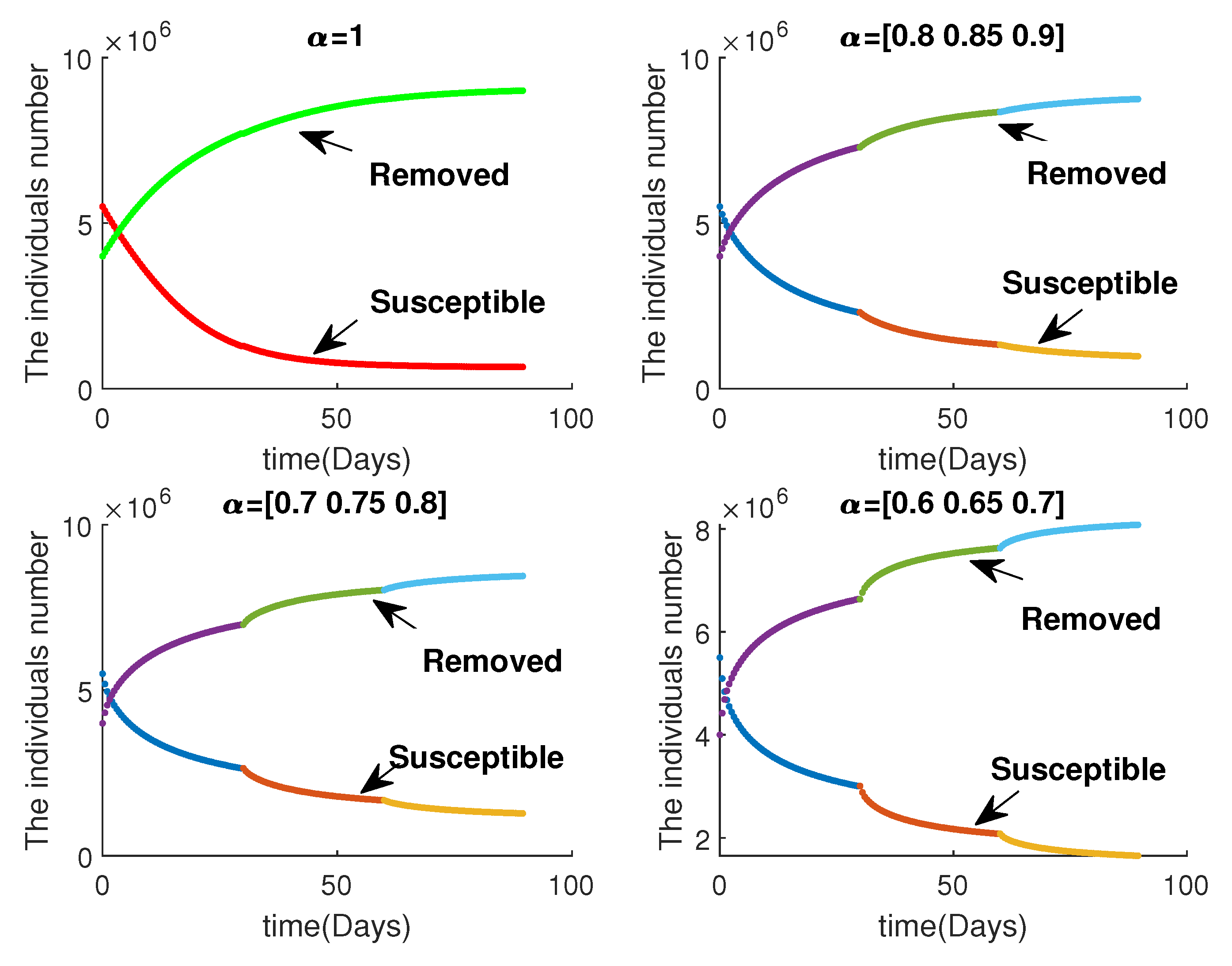
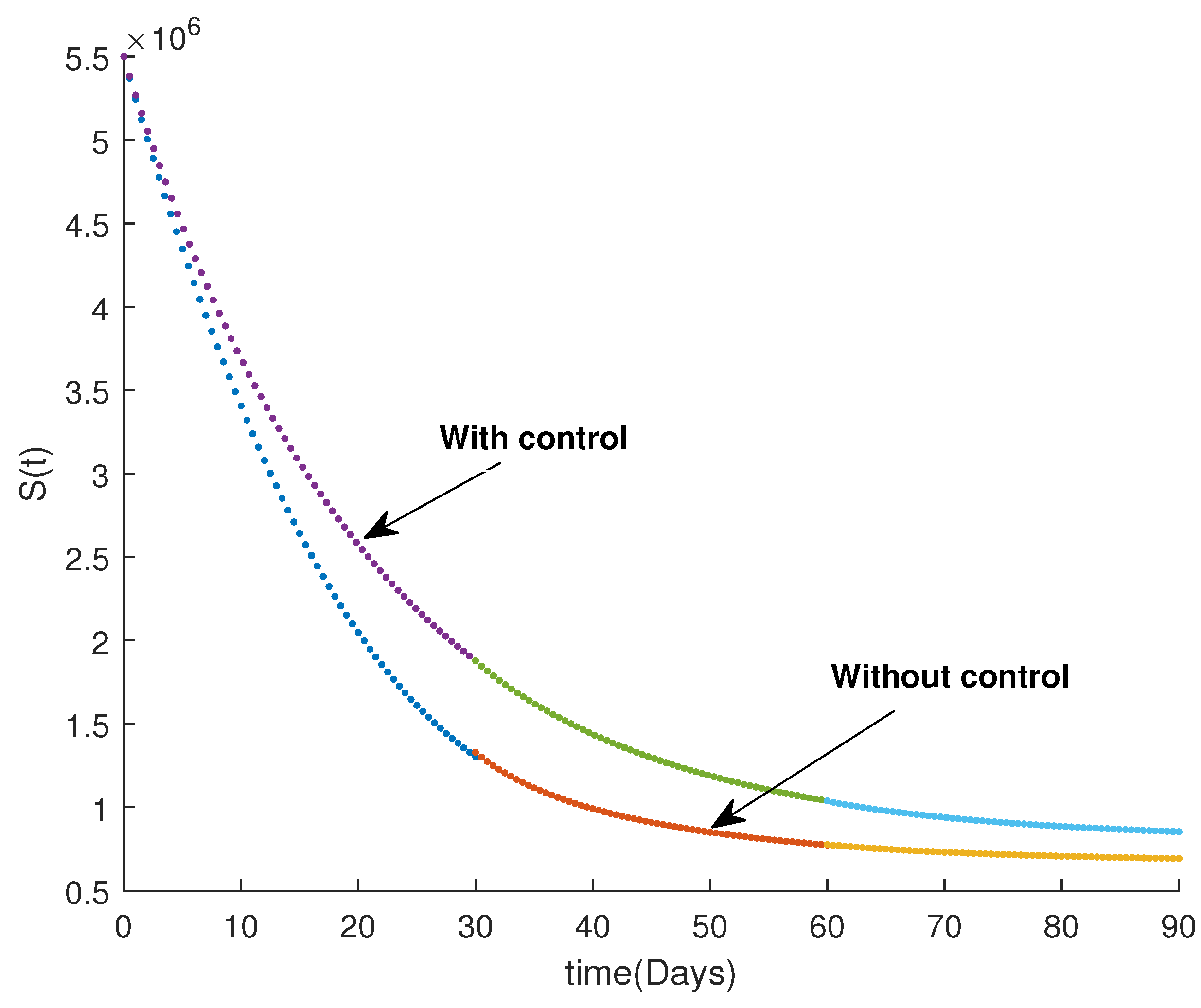
6. Numerical Results and Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Riyapan, P.; Shuaib, S.E.; Intarasit, A. A mathematical model of COVID-19 pandemic: A case study of Bangkok, Thailand. Comput. Math. Methods Med. 2021, 2021, 6664483. [Google Scholar] [CrossRef] [PubMed]
- Zarb, P.; Coignard, B.; Griskeviciene, J.; Muller, A.; Vankerckhoven, V.; Weist, K.; Goossens, M.M.; Vaerenberg, S.; Hopkins, S.; Catry, B.; et al. The European Centre for Disease Prevention and Control (ECDC) pilot point prevalence survey of healthcare-associated infections and antimicrobial use. Eurosurveillance 2012, 17, 20316. [Google Scholar] [CrossRef]
- Woo, P.C.Y.; Lau, S.K.P.; Huang, Y.; Yuen, K.Y. Coronavirus diversity, phylogeny and interspecies jumping. Exp. Biol. Med. 2009, 234, 1117–1127. [Google Scholar] [CrossRef]
- Woo, P.C.Y. Discovery of seven novel Mammalian and avian coronaviruses in the genus deltacoronavirus supports bat coronaviruses as the gene source of alphacoronavirus and betacoronavirus and avian coronaviruses as the gene source of gammacoronavirus and deltacoronavirus. J. Virol. 2012, 86, 3995–4008. [Google Scholar]
- Su, S.; Wong, G.; Shi, W.; Liu, J.; Lai, A.C.K.; Zhou, J.; Liu, W.; Bi, Y.; Gao, G.F. Epidemiology, genetic recombination, and pathogenesis of coronaviruses. Trends Microbiol. 2016, 24, 490–502. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Kalyar, F.; Chughtai, A.A.; MacIntyre, C.R. Use of a risk assessment tool to determine the origin of severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2). Risk Anal. 2024; early view. [Google Scholar]
- Singh, A.; Deolia, P. COVID-19 outbreak: A predictive mathematical study incorporating shedding effect. J. Appl. Math. Comput. 2023, 69, 1239–1268. [Google Scholar] [CrossRef] [PubMed]
- Brauer, F.; Driessche, P.D.; Wu, J. Lecture Notes in Mathematical Epidemiology; Springer: Berlin, Germany, 2008; Volume 75, pp. 3–22. [Google Scholar]
- Debbouche, A.; Nieto, J.J.; Torres, D.F.M. Focus point: Cancer and HIV/AIDS dynamics—From optimality to modelling. Eur. Phys. J. Plus 2021, 136, 165. [Google Scholar] [CrossRef]
- Dutta, P.; Samanta, G.; Nieto, J.J. Periodic transmission and vaccination effects in epidemic dynamics: A study using the SIVIS model. Nonlinear Dyn. 2024, 112, 2381–2409. [Google Scholar] [CrossRef]
- Manimaran, J.; Shangerganesh, L.; Debbouche, A.; Cortés, J.C. A time-fractional HIV infection model with nonlinear diffusion. Results Phys. 2021, 25, 104293. [Google Scholar] [CrossRef]
- Martcheva, M. An Introduction to Mathematical Epidemiology; Springer: New York, NY, USA, 2015. [Google Scholar]
- Zaman, G.; Jung, I.H.; Torres, D.F.M.; Zeb, A. Mathematical modeling and control of infectious diseases. Comput. Math. Methods Med. 2017, 2017, 7149154. [Google Scholar] [CrossRef]
- Tyagi, S.; Martha, S.C.; Abbas, S.; Debbouche, A. Mathematical modeling and analysis for controlling the spread of infectious diseases. Chaos Solitons Fractals 2021, 144, 110707. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Zeb, A.; Egbelowo, O.F.; Erturk, V.S. Dynamics of a fractional order mathematical model for COVID-19 epidemic. Adv. Differ. Equ. 2020, 2020, 1–16. [Google Scholar] [CrossRef] [PubMed]
- Çakan, S. Dynamic analysis of a mathematical model with health care capacity for COVID-19 pandemic. Chaos Solitons Fractals 2020, 139, 110033. [Google Scholar] [CrossRef] [PubMed]
- Higazy, M. Novel fractional order SIDARTHE mathematical model of COVID-19 pandemic. Chaos Solitons Fractals 2020, 138, 110007. [Google Scholar] [CrossRef] [PubMed]
- Kumar, S.; Cao, J.; Abdel-Aty, M. A novel mathematical approach of COVID-19 with non-singular fractional derivative. Chaos Solitons Fractals 2020, 139, 110048. [Google Scholar] [CrossRef]
- Ming, W.K.; Huang, J.; Zhang, C.J.P. Breaking down of healthcare system: Mathematical modelling for controlling the novel coronavirus (2019-nCoV) outbreak in Wuhan, China. BioRxiv 2020. [Google Scholar] [CrossRef]
- Zeb, A.; Alzahrani, E.; Erturk, V.S.; Zaman, G. Mathematical model for coronavirus disease 2019 (COVID-19) containing isolation class. BioMed Res. Int. 2020, 2020, 3452402. [Google Scholar] [CrossRef] [PubMed]
- Abbas, S.; Benchohra, M.; Lazreg, J.E.; Nieto, J.J.; Zhou, Y. Fractional Differential Equations and Inclusions. Classical and Advanced Topics; World Scientific: Singapore, 2023. [Google Scholar]
- Trisilowati; Darti, I.; Musafir, R.R.; Rayungsari, M.; Suryanto, A. Dynamics of a Fractional-Order COVID-19 Epidemic Model with Quarantine and Standard Incidence Rate. Axioms 2023, 12, 591. [Google Scholar] [CrossRef]
- Yousif, R.; Jeribi, A.; Al-Azzawi, S. Fractional-Order SEIRD Model for Global COVID-19 Outbreak. Mathematics 2023, 11, 1036. [Google Scholar] [CrossRef]
- Agarwal, P.; Nieto, J.J.; Torres, D.F.M. Mathematical Analysis of Infectious Diseases; Academic Press: Cambridge, MA, USA, 2022. [Google Scholar]
- Baba, B.A.; Bilgehan, B. Optimal control of a fractional order model for the COVID-19 pandemic. Chaos Solitons Fractals 2021, 144, 110678. [Google Scholar] [CrossRef]
- Baba, I.A.; Humphries, U.W.; Rihan, F.A.; Valdés, J.E.N. Fractional–Order Modeling and Control of COVID-19 with Shedding Effect. Axioms 2023, 12, 321. [Google Scholar] [CrossRef]
- Das, M.; Samanta, G.P. Optimal control of fractional order COVID-19 epidemic spreading in Japan and India 2020. Biophys. Rev. Lett. 2020, 15, 207–236. [Google Scholar] [CrossRef]
- Hanif, A.; Butt, A.I.K.; Ahmad, W. Numerical approach to solve Caputo-Fabrizio-fractional model of corona pandemic with optimal control design and analysis. Math. Methods Appl. Sci. 2023, 46, 9751–9782. [Google Scholar] [CrossRef]
- Rosa, S.; Torres, D.F.M. Fractional modelling and optimal control of COVID-19 transmission in Portugal. Axioms 2022, 11, 170. [Google Scholar] [CrossRef]
- Sweilam, N.; Al-Mekhlafi, S.; Shatta, S.; Baleanu, D. Numerical treatments for the optimal control of two types variable-order COVID-19 model. Results Phys. 2022, 42, 105964. [Google Scholar] [CrossRef] [PubMed]
- Baleanu, D.; Defterli, O.; Agrawal, O.P. A central difference numerical scheme for fractional optimal control problems. J. Vib. Control 2009, 15, 583–597. [Google Scholar] [CrossRef]
- Heydari, M.H.; Avazzadeh, Z. A new wavelet method for variable-order fractional optimal control problems. Asian J. Control 2018, 20, 1804–1817. [Google Scholar] [CrossRef]
- Sierociuk, D.; Malesza, W.; Macias, M. Numerical schemes for initialized constant and variable fractional-order derivatives: Matrix approach and its analog verification. J. Vib. Control 2016, 22, 2032–2044. [Google Scholar] [CrossRef]
- Chiranjeevi, T.; Biswas, R.K. Discrete-time fractional optimal control. Mathematics 2017, 5, 25. [Google Scholar] [CrossRef]
- El-Kihal, F.; Abouelkheir, I.; Rachik, M.; Elmouki, I. Optimal control and computational method for the resolution of isoperimetric problem in a discrete-time SIRS system. Math. Comput. Appl. 2018, 23, 52. [Google Scholar] [CrossRef]
- Talbi, I.; Ouannas, A.; Khennaoui, A.A.; Berkane, A.; Batiha, I.M.; Grassi, G.; Pham, V.T. Different dimensional fractional-order discrete chaotic systems based on the Caputo h-difference discrete operator: Dynamics, control, and synchronization. Adv. Differ. Equ. 2020, 2020, 1–15. [Google Scholar] [CrossRef]
- Darti, I.; Rayungsari, M.; Musafir, R.R.; Suryanto, A. A SEIQRD epidemic model to study the dynamics of COVID-19 disease. Commun. Math. Biol. Neurosci. 2023, 2023, 5. [Google Scholar]
- Xu, C.; Yu, Y.; Ren, G.; Sun, Y.; Si, X. Stability analysis and optimal control of a fractional-order generalized SEIR model for the COVID-19 pandemic. Appl. Math. Comput. 2023, 457, 128210. [Google Scholar] [CrossRef] [PubMed]
- Abdeljawad, T.; Mert, R.; Torres, D.F.M. Variable order Mittag–Leffler fractional operators on isolated time scales and application to the calculus of variations. In Fractional Derivatives with Mittag–Leffler Kernel: Trends and Applications in Science and Engineering; Springer International Publishing: New York, NY, USA, 2019; pp. 35–47. [Google Scholar]
- Huang, L.L.; Wu, G.C.; Baleanu, D.; Wang, H.Y. Discrete fractional calculus for interval–valued systems. Fuzzy Sets Syst. 2021, 404, 141–158. [Google Scholar] [CrossRef]
- Almatroud, O.A.; Hioual, A.; Ouannas, A.; Sawalha, M.M.; Alshammari, S.; Alshammari, M. On Variable-Order Fractional Discrete Neural Networks: Existence, Uniqueness and Stability. Fractal Fract. 2023, 7, 118. [Google Scholar] [CrossRef]
- Ghaziani, R.K.; Alidousti, J.; Eshkaftaki, A.B. Stability and dynamics of a fractional order Leslie–Gower prey–predator model. Appl. Math. Model. 2016, 40, 2075–2086. [Google Scholar] [CrossRef]
- Petráš, I. Fractional-Order Nonlinear Systems: MODELING, Analysis and Simulation; Springer Science & Business Media: Berlin, Germany, 2011. [Google Scholar]
- Ahmed, E.; El-Sayed, A.M.A.; El-Saka, H.A.A. Equilibrium points, stability and numerical solutions of fractional-order predator–prey and rabies models. J. Math. Anal. Appl. 2007, 325, 542–553. [Google Scholar] [CrossRef]
- Tsvetkov, D.P.; Angelova-Slavova, R. Positive periodic solutions for periodic predator-prey systems of Leslie-Gower or Holling-Tanner type. Nonlinear Stud. 2020, 27, 991–1002. [Google Scholar]
- Erawaty, N.; Amir, A.K. Stability analysis for routh-hurwitz conditions using partial pivot. J. Phys. Conf. Ser. 2019, 1341, 062017. [Google Scholar] [CrossRef]
- Li, H.L.; Zhang, L.; Hu, C.; Jiang, Y.L.; Teng, Z. Dynamical analysis of a fractional-order predator-prey model incorporating a prey refuge. J. Appl. Math. Comput. 2017, 54, 435–449. [Google Scholar] [CrossRef]
- Murray, J.D. Mathematical biology: I. An introduction. Interdisciplinary applied mathematics. In Mathematical Biology; Springer: Berlin/Heidelberg, Germany, 2002; Volume 17. [Google Scholar]
- Alkama, M.; Rachik, M.; Elmouki, I. A discrete isoperimetric optimal control approach for BCG immunotherapy in superficial bladder cancer: Discussions on results of different optimal doses. Int. J. Appl. Comput. Math. 2017, 3, 1–18. [Google Scholar] [CrossRef]
- Zakary, O.; Rachik, M.; Elmouki, I. A new epidemic modeling approach: Multi-regions discrete-time model with travel-blocking vicinity optimal control strategy. Infect. Dis. Model. 2017, 2, 304–322. [Google Scholar] [CrossRef] [PubMed]
- Zakary, O.; Rachik, M.; Elmouki, I.; Lazaiz, S. A multi-regions discrete-time epidemic model with a travel-blocking vicinity optimal control approach on patches. Adv. Differ. Equ. 2017, 2017, 1–25. [Google Scholar] [CrossRef]
- Özköse, F.; Yılmaz, S.; Yavuz, M.; Öztürk, İ.; Şenel, M.T.; Bağcı, B.; Doğan, M.; Önal, Ö. A fractional modeling of tumor–immune system interaction related to Lung cancer with real data. Eur. Phys. J. Plus 2022, 137, 40. [Google Scholar] [CrossRef]






| Parameters | Description | Value | Reference |
|---|---|---|---|
| Recruitment rate | assumed | – | |
| Saturation factor | assumed | – | |
| Contact rate | 9.0631 | [38] | |
| The transmission probabilities | 0.2761 | [38] | |
| Self protection rate | 0.0439 | [38] | |
| Transmission rate from temporarily removed to susceptible population | 0.0028 | [38] | |
| Rate of progression from exposed group to the infected group | 0.1736 | [38] | |
| Isolation rate | 0.516 | [38] | |
| Death rate in infected group caused by COVID-19 | 0.018 | [38] | |
| Death rate in isolated group caused by COVID-19 | [38] | ||
| Recovery rate | 0.0534 | [38] | |
| Self recovery rate | [38] | ||
| Natural death rate | [38] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Boukhobza, M.; Debbouche, A.; Shangerganesh, L.; Nieto, J.J. The Stability of Solutions of the Variable-Order Fractional Optimal Control Model for the COVID-19 Epidemic in Discrete Time. Mathematics 2024, 12, 1236. https://doi.org/10.3390/math12081236
Boukhobza M, Debbouche A, Shangerganesh L, Nieto JJ. The Stability of Solutions of the Variable-Order Fractional Optimal Control Model for the COVID-19 Epidemic in Discrete Time. Mathematics. 2024; 12(8):1236. https://doi.org/10.3390/math12081236
Chicago/Turabian StyleBoukhobza, Meriem, Amar Debbouche, Lingeshwaran Shangerganesh, and Juan J. Nieto. 2024. "The Stability of Solutions of the Variable-Order Fractional Optimal Control Model for the COVID-19 Epidemic in Discrete Time" Mathematics 12, no. 8: 1236. https://doi.org/10.3390/math12081236
APA StyleBoukhobza, M., Debbouche, A., Shangerganesh, L., & Nieto, J. J. (2024). The Stability of Solutions of the Variable-Order Fractional Optimal Control Model for the COVID-19 Epidemic in Discrete Time. Mathematics, 12(8), 1236. https://doi.org/10.3390/math12081236








