Abstract
This study is motivated by the need to develop generic neuro-fuzzy motion controllers for autonomous vehicles that may traverse rugged terrains. Three types of target problems are investigated. These problems differ in terms of the expected motion behavior, including cautious, intermediate, and courageous behaviors. The target problems are defined as evolutionary multi-objective problems aiming to evolve near optimal neuro-fuzzy controllers that can operate in a variety of scenarios. To enhance the evolution, sequential transfer optimization is considered, where each of the source problems is defined and solved as a bi-objective problem. The performed experimental study demonstrates the ability of the proposed search approach to find neuro-fuzzy controllers that produce the required motion behaviors when operating in various environments with different motion difficulties. Moreover, the results of this study substantiate the hypothesis that solutions with performances near the edges of the obtained approximated bi-objective Pareto fronts of the source problems provide better transferability as compared with those that are associated with performances near the center of the obtained fronts.
Keywords:
multi-objective optimization; Pareto-optimization; fuzzy-inference system; evolutionary transfer optimization; fuzzy control; non-specialized controllers MSC:
93C42; 68W50
1. Introduction
Increasing interest from the car industry in autonomous driving and the availability of new technologies have given rise to vast research efforts on the control of autonomous vehicles (e.g., [1,2]). However, such studies have hardly dealt with off-road autonomous driving. This study is motivated by the expected difficulties that a motion control system of an autonomous vehicle will face when traversing rugged terrains. For such off-road situations, it is envisioned that a range of motion behaviors might be of interest, spanning from a cautious behavior to a courageous one. As a first step towards the development of such control systems, this study considers an academic problem that applies a dynamic model of a cart that interacts with various environments. These environments differ by their motion difficulties, which are expressed by various friction functions and varying speed limitations. An attractive approach to address the development challenges of such controllers is to use a multi-objective evolutionary neuro-fuzzy optimization approach (e.g., [3,4]). The use of such an evolutionary approach, as compared with a traditional neuro-fuzzy approach, e.g., ANFIS [5], has three main advantages. First, it avoids the need to rely on an expert to determine the relevant fuzzy rules. Second, it avoids the need to create data sets for the tuning of the parameters of the membership functions. In addition, the use of an evolutionary search is most suited for solving multi-objective optimization problems, i.e., to find a set of Pareto-optimal solutions [6]. In this kind of optimization problem, no prior articulation of the objective preferences is provided. As described in the following, this study utilizes the above three advantages while focusing on the use of multi-objective optimization in conjunction with transfer optimization.
This study deals with a Sequential Transfer Optimization (STO) approach [7,8]. Namely, it assumes the existence of relevant knowledge from solving multi-objective source problems to the solution of multi-objective target problem(s). Moreover, this study involves an evolutionary STO in which a genetic transfer is employed. Namely, the knowledge is transferred via the use of individual solutions of the source problems to serve as an initial population for solving the target problems [9,10].
When defining the target optimization problem for the development of robot motion controllers, it is important to realize the difference between specialized and non-specialized controllers [11]. Specialized controllers are optimized for a particular environment, whereas non-specialized controllers are optimized for a set of environments. For the current motivation, it appears that the development of controllers for rugged terrains should focus on non-specialized controllers that may cope with a variety of terrains. According to [11], defining the problem as a meta-problem, which aims at performance optimization for a set of environments, produces both specialized and non-specialized neuro-controllers.
Following [11], this study considers the target problem as a meta-problem, i.e., the problem is a multi-objective optimization problem in which each objective is associated with a different environment. In this study, we define three types of behavior-based meta-problems. These problems differ by the desired behavior, including cautious, courageous, and intermediate behaviors. For example, we aim at non-specialized controllers that produce courageous behaviors in each one of the environments.
We seek to extract knowledge from a set of source problems to support solving the three types of target problems considered. The source problems are defined as optimization problems that differ by the source environment. Each of these problems is defined as a bi-objective Pareto-optimization problem in which one of the objectives corresponds to a cautious behavior and the other one corresponds to a courageous behavior. Each of these bi-objective source problems is solved using Pareto-optimization. Solving a set of source problems, which differ by the considered environment, results in a set of Pareto-optimal sets. The union of these sets is expected to hold relevant knowledge to support solving the target problems. Namely, it is expected to hold controllers of different behaviors that are relevant to different environments. While the diverse solutions of the union set are considered an advantage, they raise the following difficulty.
In general, a union set of Pareto-optimal sets of solutions from several source problems has a large cardinality. This cardinality is expected to be much beyond the size of the population that is needed to solve the target meta-problem. This study aims to answer a major question that results from the large cardinality of the union set. Namely, what subset of the individual solutions of the bi-objective source problems is more suited to serve as the initial populations for solving the target meta-problem? To provide an answer to this research question, two types of knowledge extraction techniques are suggested and investigated. The first type involves an initial population of edge controllers, i.e., controllers with performance vectors that are located close to the edges of the obtained fronts. The second type of knowledge extraction is based on an initial population of center controllers, i.e., controllers whose performance vectors are located close to the center of the obtained fronts. In addition, these types of knowledge extraction are compared with random initialization. We compare the three types of initial populations with respect to the three behavior-based target meta-problems considered here. We aim to substantiate the hypothesis that the use of edge controllers is a preferred approach regardless of the considered target problem.
Given the state-of-the-art, as presented in Section 2.3, the main contributions of this paper are:
- (a)
- It is the first study that defines target meta-problems that aim to find non-specialized Neuro-Fuzzy Controllers (NFCs) that produce various motion behaviors.
- (b)
- It is the first study that applies knowledge extraction from solving multi-objective source problems to support finding non-specialized NFCs that produce various motion behaviors for environments that are different due to their motion difficulties.
- (c)
- It is the first study that raises the hypothesis that the genetic transfer of edge solutions of multi-objective source problems is preferred over that of the center solutions. Furthermore, it is the first study to substantiate the hypothesis with respect to the considered type of evolutionary neuro-fuzzy control problem.
The rest of this paper is organized as follows. Section 2 describes the background for this study and locates this study with respect to the state-of-the-art. Section 3 introduces the problem formulation and the proposed solution approach. Next, in Section 4, details are provided on the experimental study. Finally, Section 5 summarizes and concludes this study.
2. Background
This section provides the background for this study and a state-of-the-art analysis related to the contributions of this study. First, Section 2.1 presents the basic principles of evolutionary multi-objective optimization. Then, Section 2.2 describes the use of such optimization in the design of NFCs. Finally, Section 2.3 provides the positioning of this research with respect to the state-of-the-art.
2.1. Multi-Objective Optimization
Engineering design commonly involves decisions under conflicting objectives. In such situations, improving performance in one objective may deteriorate the performance in the other objectives. To make decisions based on the understanding of the performance tradeoffs, more than two decades ago, engineers started to apply Pareto-based optimization [6]. This type of optimization results in a set of Pareto-optimal solutions and their associated Pareto-front in the objective space. This allows a posteriori solution selection based on assessable performance tradeoffs that are exposed by the obtained front. The following highlights the fundamentals of Pareto optimization.
Pareto-based multi-objective optimization is commonly described as a vector optimization problem with M objectives to be optimized. Without the loss of generality, the problem can be defined as a minimization problem as follows:
where is the set of feasible solutions and is the performance vector.
Let two solutions of (1), and , be associated with and , respectively. Then, is said to dominate , denoted by , if the following condition is satisfied:
Without loss of generality, for a given minimization problem, the Pareto-optimal-Set (PS) is the set of all Non-Dominated Solutions (NDS) of the feasible set . Namely, a solution is called Pareto-optimal if and only if there is no solution for which . The set of performance vectors corresponding to the aforementioned set is known as the Pareto-Front (PF). Solving (1) means finding the PS and the associated PF.
Usually, there is no analytical solution to real-life Multi-objective Optimization Problems (MOPs) [12]. Therefore, computational techniques are commonly employed to obtain at least good approximations of the PS and PF. Dedicated evolutionary algorithms for solving MOPs are termed Multi-Objective Evolutionary Algorithms (MOEAs). MOEAs, including NSGA-II [13], which is used in this study, follow the ideas of natural evolution, such as selection, recombination, and mutation, aiming to evolve a population of solutions towards the Pareto-optimal solutions. With over two decades of proven success, MOEAs are the leading algorithms for solving MOPs. This is evident from reviews such as in [12,14,15].
2.2. Neuro-Fuzzy Systems and Control
Fuzzy Inference Systems (FISs) are computational frameworks that implement fuzzy reasoning to make decisions. The mathematical basis, which was founded by L. Zadeh (1965), defines linguistic variables, fuzzy sets, and logical operators extending crisp set theory [16]. Fuzzy sets are defined using Membership Functions (MFs), while Fuzzy Rules (FRs) express relationships between such sets. The structure and parameters of FRs and MFs determine the mapping of given inputs to outputs. There are at least two main differences between mapping by an FIS as compared with mapping by a Neural Network (NN). First, an FIS can be formed based on expert knowledge, while an NN commonly requires data. Second, an FIS is interpretable, while an NN is considered to be a black box. The main advantage of using an NN is that the mapping can be learned and adapted. A Neuro-Fuzzy (NF) approach synergistically combines the main features of FISs and NNs. The advantages of the NF approach over the FIS approach have created new research and application opportunities [3,17,18,19]. As evident from the literature, over the years, both FISs and NF systems have been applied to control design [20,21,22]. The common approach to tuning NF controllers is supervised learning based on some data (e.g., [23,24]). However, the design of NFCs can be based on evolutionary techniques [25] to reach the desired optimum/optima without adhering to any data (e.g., [26]).
Using the concept of Pareto optimization for the design of controllers is not new (see review [27]). However, applying Pareto-based optimization/adaptation to the design of neuro-fuzzy systems is rare (e.g., [4,28,29]). Several studies tried to find Pareto-optimal fuzzy controllers with static structure, e.g., [30,31,32], whereas in [26], such studies were extended to also include the rule structure.
2.3. Positioning of This Research
The idea of defining and solving meta-problems for obtaining specialized and non-specialized controllers has been recently suggested in [11]. The current study is the first study to use this idea in the context of evolutionary neuro-fuzzy control.
Applying STO to solving neuro-fuzzy control problems is not new [33,34,35,36,37,38,39,40]. However, in this study, several uncommon/unique aspects concerning the use of STO for such problems should be noted. First, commonly in STO studies on solving neuro-fuzzy control problems, the knowledge that is transferred is data, which is used in the context of supervised learning (e.g., [33,34,35]). In contrast, the current study applies a different type of knowledge that is transferred, namely, a genetic type. Second, the majority of STO studies on solving neuro-fuzzy control problems are based on using just one source problem (e.g., [37]), while the current study is based on the use of multiple source problems. Moreover, in contrast to the current study, to the best of our knowledge, no study on NF systems concerns source problems that are defined as MOPs. To substantiate this claim, we conducted the following Scopus search:
(TITLE-ABS-KEY ((neuro-fuzzy OR “neuro fuzzy”))) AND (“source problem” OR “source task” OR sequential) AND (“transfer learning” OR “transfer optimization”). A manual check of all the resulting documents revealed no study that deals with source problems that are defined as MOPs.
While the above positioning is restricted to STO studies that are concerned with neuro-fuzzy problems, to the best of our knowledge, this study contains a major difference with respect to any STO study. We claim that this study is the first to raise and investigate the hypothesis that the use of edge solutions of multi-objective source problems for genetic transfer is preferred over the use of the center solutions. To substantiate this novelty assertion, we conducted the following Scopus search:
(TITLE-ABS-KEY ((Pareto OR multi-objective OR “multi objective”) AND transfer)) AND (“transfer learning” OR “transfer optimization”) AND (sequential OR “source problem” OR “source task”). A manual check of all the resulting documents revealed no study that concerns the suggested hypothesis.
For convenience, Table 1 summarizes the positioning results according to the main research attributes as well as the application focus of the related studies. In the table, X/V refers to non-existing/existing features, respectively.

Table 1.
Positioning Table with respect to STO Neuro-Fuzzy studies.
3. Problem Description and Solution Approach
This paper deals with using transfer optimization to solve a target problem, which is defined as a set of SOPs in Section 3.1. In addition to the target problem definition, this section describes the proposed research methodology. The main steps of the methodology are described in Figure 1. First, starting from the left side of the figure, several MOPs are generated, which serve as source problems. Next, each source MOP is solved separately using MOEA, as described in Section 3.2. Solving each of the source problems results in a set of non-dominated solutions. Then, the obtained solutions are used to form an initial population, which is to be used for solving the target problem. This step, which is the knowledge extraction step, is detailed in Section 3.3. In this study, we examine two alternatives for generating the initial population. Finally, each of the extracted populations is used as an initial population to solve the target problem. To evaluate the obtained results, the target problem is also solved using an initial random population. In this study, the well-known NSGA-II [13] is used to solve both source and target problems. However, it should be noted that many alternative MOEAs can be used. In case the considered MOPs would involve a large number of objectives, then it is recommended to use an algorithm that was designed to cope with more than three objectives (see [41]).
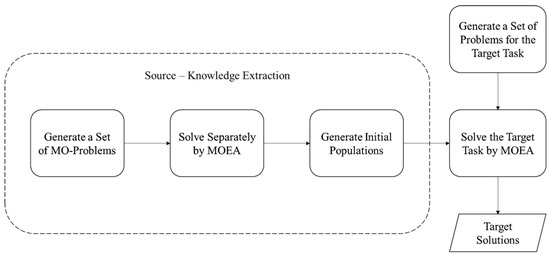
Figure 1.
Proposed transfer optimization methodology.
3.1. Target Meta-Problem
The considered target problem is a multi-objective fuzzy control meta-problem in which each objective is associated with finding an optimal controller for a specific task. This meta-problem is defined as follows. Let be a given set of fuzzy control problems. Then, the target meta-problem is formulated as follows:
where is the feasible set of fuzzy controllers for the target meta-problem, and is a scalar objective function that is used to evaluate the controllers’ performance. The main goal is to search for a set of non-specialized controllers, i.e., controllers that evolved to provide a successful behavior in all of the given set of control problems, following the approach in [11].
3.2. Source Problems and Their Solutions
In this study, each source problem is formulated as a MOP. Let be a given set of source fuzzy control problems. Each of these problems is formulated as follows:
where is the set of feasible fuzzy controllers of the source problem. Each fuzzy controller is evaluated using scalar objective functions, . Assuming no prior objective preferences, the solution of (4) results in a set of non-dominated solutions for each of the source problems.
3.3. Knowledge Extraction and Research Hypothesis
This study deals with the STO of NFCs. As mentioned in the introduction section, two types of knowledge extraction techniques are proposed and studied here. The first type involves an initial population of edge controllers, i.e., controllers whose performance vectors are located close to the edges of the obtained fronts. The second type of knowledge extraction is based on an initial population of center controllers, i.e., controllers whose performance vectors are located close to the line connecting the ideal and the nadir points. For a given front, the ideal point is a vector of the best objective values, whereas the nadir point is a vector of the worst objective values of the considered front.
This study deals with bi-objective source problems. Hence, the following presents a step-by-step procedure of the knowledge extraction approach as implemented in this study. Given a non-dominated set (NDS) of solutions and their performance vectors (PVs) of a source problem, then:
- Define the number of transferred edge-controllers (), such that
- For each edge:
- Find the edge PV and store the associated solutions in a set of extracted edge controllers (EEC).
- Select the controllers that their PVs are the closest to the edge PV and add them to EEC.
- Define the number of transferred center controllers (), such that .
- Find the line connecting the ideal and the nadir points.
- Select the controllers for which their PVs are the closest to the line found in 4 and store them in a set of extracted center controllers (ECC).
Repeat this process for all source problems and create the union of the EECs (UEECs) and the union of the ECCs (UECCs). Each of these unions contains extracted knowledge as needed to investigate the suggested hypotheses, as presented below.
Figure 2 illustrates these two types of controllers. In the figure, an example of normalized PVs is shown and marked as dots. Assuming that , the PVs of the EECs are marked by circles, whereas squares mark the PVs of ECCs.
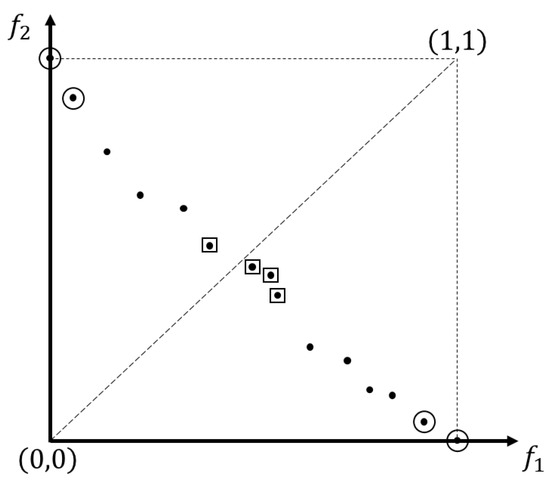
Figure 2.
Knowledge extraction illustration.
The main research question that this study aims to solve is which of the proposed two types of knowledge extraction techniques is preferred from a transferability viewpoint. It is hypothesized that the edge controllers are preferred over the center ones. This hypothesis is intuitively justified by the expected higher diversity of the edge controllers. In addition, a secondary hypothesis is examined, which suggests that each of the proposed types of knowledge extraction techniques is better than the case of using random initial population, i.e., the case of no knowledge transfer.
4. Numerical Study
This section is organized as follows. First, Section 4.1 provides a detailed description of the source and target problems. Section 4.2 describes the applied NFC. Then, the comparison methods are given in Section 4.3. Next, in Section 4.4, the experimental setup is described. Finally, the obtained results and their analysis are provided in Section 4.5.
4.1. Source and Target Problems
The considered numerical study is based on simulations of a theoretical cart and environment interaction model. The study involves a set of constrained motion source control problems of a point-mass cart, and an additional set of target scenarios, as presented in the following. In this study, the cart is assumed to travel horizontally along a linear path. The linear path is defined by start and goal points. Each path is characterized by a friction function and a speed limitation function. These functions could be viewed as representing various types of motion difficulties as expected in rugged terrains. The equation of motion of the considered cart model and the involved constraints are:
where is the position of the cart, is the mass of the cart, is a damping coefficient as a function of the position , is the control force, is the speed limit of the cart, and is the saturation value of the control force. In addition, the path imposes a speed constraint function . An interaction between the cart and a given path is termed here as a scenario.
Both the target and the source optimization problems, which are defined in Equations (6) and (7), use the following two cost functions. The first function reflects a desire to find NFCs that bring the cart from the initial position to the goal point as fast as possible, whereas the second one corresponds to the case of safe motion behavior. These are defined as follows:
where is the time it takes to reach the goal point, using the considered NFC, and is the time it would take to reach the goal if the entire motion involves the maximal speed limit. During the evolutionary process, a controller is considered numerically feasible if the following constraints are met, where is the simulation time limit.
Figure 3 presents the and functions that are used in the source problems scenarios, whereas Figure 4 and Figure 5 present them for the first and the second set of the target problems, respectively. In these figures, the solid and the dashed curves present and , respectively. It should be noted that the functions used in the source and target problems were randomly created. In particular, for each , a random number of Gaussian functions was selected, and their parameters were also randomly selected. Any Gaussian that exceeded the value of 0.8 was truncated. The functions were created as a function of the resulting functions.
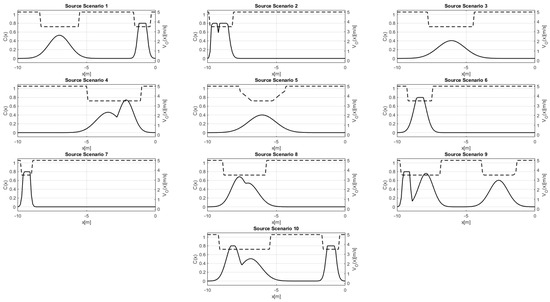
Figure 3.
Source control problems.
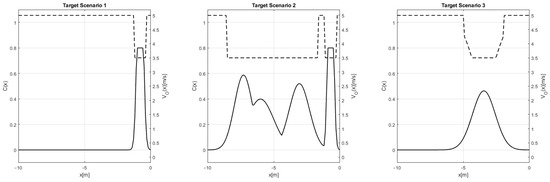
Figure 4.
Target set 1.
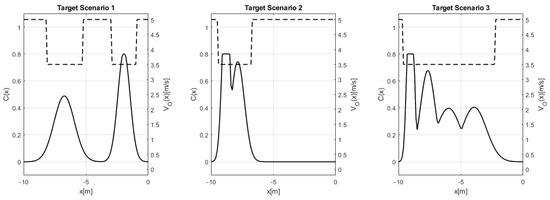
Figure 5.
Target set 2.
In this study, each of the target sets is composed of three different scenarios, as given in Figure 4 and Figure 5. For each target set, three alternative MOPs are examined. These are defined as follows:
The three alternative MOPs are defined in accordance with the knowledge extraction techniques (see Section 3.3). corresponds to the center controllers, whereas and correspond to the edge controllers, i.e., to the fast and safe controllers, respectively. In total, we examine six target problems, i.e., three alternative MOPs, each with two target sets. These three MOP definitions are expected to encourage three types of behaviors. Namely, and are expected to encourage courageous behavior and cautious behavior, respectively, whereas is expected to encourage intermediate behavior. In the context of this study, it should be noted that these terminologies correspond not only to the speed but also to the level of motion difficulty as presented in .
The bi-objective source problem is given by:
where is the feasible set of fuzzy controllers, as described in Equation (8).
4.2. Fuzzy Controllers
The cart is controlled by a neuro-fuzzy inference system. The controller receives three inputs, including the relative location of the goal point , the normalized velocity of the cart , and an effective damping coefficient . Each of these inputs is mapped into the range of [−1, 1], as given in Equations (11)–(13), respectively. The NFC maps these inputs into a force to be applied to the cart, as described in Equation (5).
where is a pre-defined number, which has been set as .
In the current implementation, the NFC is based on zero-order Takagi-Sugeno (TS) rules [42]. The main reason for choosing TS rules, in which the rules result in crisp outputs, is that it avoids the need for defuzzification. Selecting zero-order TS rules reduces the number of search parameters for the evolutionary search; hence, it results in a major reduction in the required computational resources. Each input belongs to one of three fuzzy sets. These fuzzy sets are based on the general Gaussian membership function. This results in 27 combinations of the TS rules, where each rule is considered as follows:
where are the indices of the inputs’ fuzzy sets , respectively. is the index of the output . The final crisp conclusion is calculated as the average of the rule conclusions.
The decision variables of the optimization problem include the parameters of , and . Given that each general Gaussian function has two parameters, and the total number of rules is 27, then the total number of decision variables results in 9 (input sets) 2 (parameters) + 27 (rules) = 45 variables.
4.3. Comparison Methods
In this study, the substantiations of the research hypotheses are achieved by comparing the results of solving the target meta-problems as obtained by each of the knowledge extraction techniques and by the random initialization technique (see Section 3). In particular, two indicators are used to evaluate the transfer capabilities of the compared techniques based on the Hyper-Volume (HV) metric [43]. The first indicator, which is inspired by the Asymptotic Performance (AP) measure [44], calculates the final value of the HV for each of the compared approaches. The second indicator, which is based on the Time-to-Threshold (ToT) measure [44], is calculated as the number of generations it took HV to reach a threshold. In addition, the obtained best performance in each scenario of the target meta-problem is also compared.
Given the stochastic nature of the applied MOEA, 31 runs were conducted for each approach to make statistical inferences. As commonly done when comparing MOEAs, the medians and Inter-Quartile Ranges (IQRs) are used rather than the means and the standard deviations. For the statistical comparisons, the Wilcoxon rank-sum test was applied for each pair of compared techniques.
4.4. Experimental Setup
Here, NSGA-II [13], which is a well-known MOEA, is applied to solving the optimization problems presented in Equations (9) and (10). The run parameters that were applied for solving each of the source MOPs and the target MOPs are summarized in Table 2. In this study, the applied stopping criterion of NSGA-II is the total number of generations. It should be noted that the run parameters for the source problems were selected to ensure convergence in all source problems. To deal with the constraint problem, a penalty approach is applied. Here, a non-feasible controller is penalized by adding a high penalty value, which practically serves as a death penalty. It should be noted that the population size for the target meta-problem is a result of the applied knowledge extraction technique (see Section 4.5.1).

Table 2.
Run parameters.
4.5. Experimental Results and Analyses
This section, in which the results are presented, is organized as follows. First, in Section 4.5.1, typical results obtained by solving one of the ten source control problems are presented, including the knowledge extraction from the presented results. Then, the results of the target meta-problems are presented and analyzed in Section 4.5.2.
4.5.1. Demonstration of Knowledge Extraction
In this section, typical results are presented based on solving a randomly selected source control problem. Figure 6 shows the approximated Pareto front as obtained by solving the problem in Equation (10).
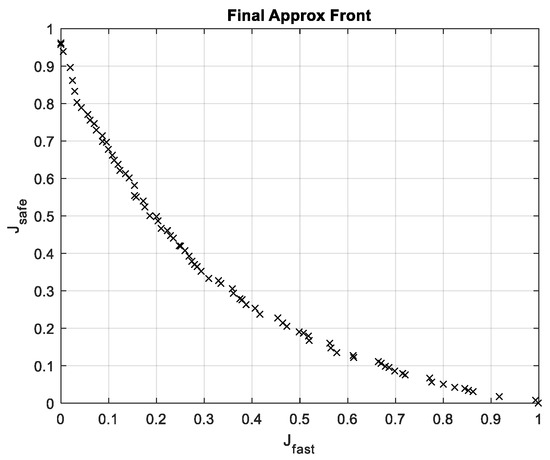
Figure 6.
Approximated front for the selected source problem.
In the figure, each point represents the performance vector of a non-dominated NFC. As expected, the tradeoff between the objectives is evident. This tradeoff is further shown in Figure 7. In Figure 7, the behaviors of the edge controllers are presented. The left solid curves show the position and the velocity versus time for the fastest NFC, and the right solid curves show these behaviors for the safest one. The dashed curves show the corresponding damping coefficient and speed limit. It is evident from Figure 7 that the velocity, as obtained by applying the fastest NFC, quickly reaches the vicinity of the speed limit. In this case, the goal point is reached in less than 2.5 s. In contrast, the application of the safest NFC results in a much lower velocity, and the goal-point is reached after about twenty seconds.
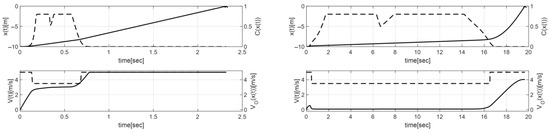
Figure 7.
Controller behavior: fastest controller (left), safest controller (right).
The convergence curve of the run of the presented case is shown in Figure 8. This figure shows the HV measure at each generation. It is suggested from the figure that convergence is reached.
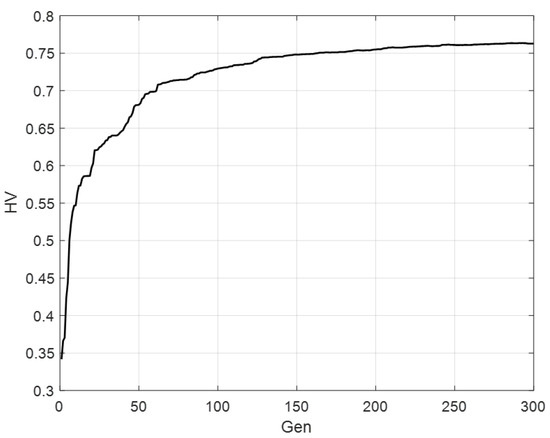
Figure 8.
Convergence curve for the presented source problem.
Following the method presented in Section 3.3, the knowledge extraction from the results of solving the presented source problem is presented in Figure 9. In the left plot, the extraction of center controllers, which are marked as squares, is presented. The circles in the right plot present the selected edge-controllers. It should be noted that for this demonstration, six controllers were selected from each source problem for each of the controller types.
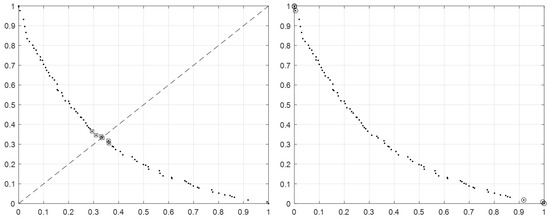
Figure 9.
Knowledge extraction: (left) center controllers, (right) edge controllers.
Given that ten source problems are used in this study, and that each of these problems provides six edge controllers and six center controllers, then the population size is sixty for solving each of the corresponding meta-problems.
4.5.2. Results and Analysis of the Target Meta-Problems
Table 3 and Table 4 summarize the results of the ToT, AP, and the best performances in each of the objectives for target sets 1 and 2, respectively. For each method, the tables outline the medians and IQRs of the indicators. In the tables, the superior values are marked in bold numbers. In general, better medians are obtained when using the edge controller for the initialization as compared to either using the center controllers or the random controllers. In addition, better results were obtained by the center-controllers than with the random ones.

Table 3.
Transfer capabilities comparison—target set 1.

Table 4.
Transfer capabilities comparison—target set 2.
The results of the rank-sum Wilcoxon test are presented in Table 5, which allows statistical inference. In the table, + is assigned for comparison in which the statement is statistically correct, − is assigned for cases where the opposite statement is statically correct, and ≈ is assigned for cases where the obtained p-values are larger than the significance level, i.e., the compared cases are statistically equivalent. For example, the entry 3/1/2 in the 1st row and column of the table means that the statement that using the edge controllers was better than using the center ones was found to be correct in three out of the six meta problems, etc. The last row of the table provides the accumulated numbers with respect to all the indicators.

Table 5.
Statistical comparisons.
As shown in the table, when comparing initialization using the edge controllers, as opposed to using the center controllers, there are 20 comparisons in which using the edge controllers was better than using the center controllers. The opposite statement was found to be correct in 4 comparisons and no statistical superiority was found in 6 of the 30 comparisons. These observations suggest that, in general, edge controllers are better than the center-controllers for the considered meta-problems in terms of the obtained values of most indicators. These findings substantiate the first hypothesis of this study.
When comparing initialization by the edge controllers with that of the random controllers, the accumulated results show that there was no comparison in which the latter controllers were superior. When comparing initialization by the center controllers with that of the random controllers, there was only one case out of the 30 in which the random ones were superior. These findings substantiate the second hypothesis of this study.
4.5.3. Detailed Demonstration of the Transferability Results
The following presents some details of the results and analysis for the case of with the first target set. The boxplots in Figure 10 show the statistical results of the HV metric, as obtained by each initialization. The left plot in the figure presents the results achieved by the edge controller initialization, the results of center controller initialization are presented in the center plot, and the right plot shows the result of the random initialization. The results of this demonstration suggest that the best results are achieved by the edge controller initialization. It can be observed that the edge results are better in terms of higher median values as well as lower variance and outliers. It is also evident that the center controller initialization is superior to those achieved when a random initialization is used.
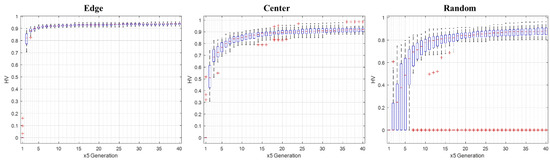
Figure 10.
Statistical results: HV versus generations. Initialization by the edge-, center- and random-controllers, in the (left), (center), and (right) panels, respectively.
To make statistical inferences, the rank-sum test, with a significance level of 0.05, is applied for each comparison. Table 6 outlines p-values as obtained by the test. Bold results represent comparisons where initialization by the edge controllers is statistically superior, whereas underlined results are for comparisons where initialization by the center controllers is superior.

Table 6.
Statistical tests (p-values).
The obtained results show that edge controllers are better than the center controllers for the considered meta-problem in terms of the obtained values of most indicators. In addition, the results indicate that both the center and edge controllers are better than the random ones for the considered problem. These findings substantiate the two hypotheses of this study (see Section 3.3).
4.5.4. Demonstration of the Obtained Behaviors
This section provides discussion and analysis regarding the obtained behaviors by solving each of the target meta-problems, as defined in Section 4.1. Figure 11 and Figure 12 present the behaviors of randomly selected NFCs as obtained by solving the three MOPs for target set 1 and target set 2, respectively. Each row of the figures provides the results for a specific scenario of the target sets as obtained by the three MOPs. The solid curve in each of the figures shows the velocity versus time, whereas the dashed curves show the corresponding speed limit.

Figure 11.
Motion Behavior—Target Set 1.

Figure 12.
Motion Behavior—Target set 2.
Considering the results of (in the middle panels), as compared with those of solving and , it is observed that the obtained NFCs provide higher velocities without any violation of the speed limits. As expected from the definition of , its solutions exhibit safe yet courageous behaviors. Furthermore, when comparing the results of solving and , it can be observed that the solutions of resulted in slower motions. As expected from the definitions of these two problems, exhibits the most cautious behaviors, while exhibits intermediate behaviors.
The following provides a statistical comparison between the NFCs of and those of , which aims to highlight the clear difference between cautious and courageous behaviors. In particular, the presented statistics are obtained for the case of using initialization by the edge NFCs, using 31 runs per each of the MOPs as applied per each scenario of each of the target sets. The statistics are provided with respect to an average-time to reach the goal point at each of the presented scenarios. Table 7 summarizes the medians and IQRs of the average times. Each of these averages is calculated as follows. For each of the runs, the average is taken over the entire set of the obtained approximated Pareto optimal NFCs (of each MOP and target set). To obtain this average time, first, each of these NFCs of the run is applied to the considered scenario to find its resulting time to reach the goal point. Next, these times are used to find the average time for the run of the considered scenario. In addition, the last row of Table 7 provides the accumulated results of the Wilcoxon rank-sum tests over the six scenarios. As expected, these results clearly show that the average times as obtained using the definition of are statistically shorter than those obtained by .

Table 7.
Behavior comparison of time to goal point.
In summary, the time-to-goal results in Table 7 further emphasize the differences between the outcomes of courageous and cautious behaviors. While not presented here, similar conclusions about the time to the goal point were obtained not just for the initialization by the edge controllers but also by the other two types, including initialization by center controllers and by random controllers. Namely, each of the initialization types resulted in the expected behavior as associated with the considered MOP.
5. Summary and Conclusions
This study concerns the evolutionary search for generic neuro-fuzzy motion controllers in conjunction with the use of sequential transfer optimization. The search aims to evolve near optimal neuro-fuzzy controllers that can operate in a variety of scenarios. Three types of target meta-problems are defined, which differ by the expected motion behavior, including cautious, intermediate, and courageous behaviors. Each of these meta-problems is defined as a multi-objective problem, where each objective is associated with optimizing the performance in a particular scenario.
A unique kind of sequential transfer optimization is proposed that involves multiple source problems, where each of the source problems is defined and solved as a bi-objective problem. The use of multiple source problems aims to diversify the source solutions with respect to scenarios, whereas the use of the two objectives aims to diversify the source solutions with respect to the obtained behaviors. This kind of multiple-source problem raises the dilemma of which of the source solutions should be transferred to solve the target problems. The main research hypothesis is that solutions with performances near the edges of the obtained approximated bi-objective Pareto fronts provide better transferability as compared with those that are associated with performances near the center of the obtained fronts.
Given the stochastic nature of the applied search technique, a statistical numerical study was conducted. First, ten source problems were defined and solved. Next, a total of six target meta-problems were defined. Each of these target problems was solved using three types of initializations including random initializations and two additional types in accordance with the aforementioned hypothesis.
The main contribution of this study is that it substantiates the hypothesis that edge controllers should be preferred over the center ones. This has a pragmatic impact on applying sequential transfer optimization to the development of neuro-fuzzy controllers for the considered motion control type of problems. This is because the proposed approach produces useful information out of the large and diverse knowledge that is created by solving many Pareto-based source problems. As shown in this study, and similar studies, using selected solutions from source problems to serve as an initial population to solve a target problem is much more efficient as compared with the traditional use of a random initial population. In addition, this study shows that the proposed approach is useful for finding neuro-fuzzy controllers that produce different motion behaviors when operating in various environments with different motion difficulties.
This study assumed that experts select the source problems based on their cognitive abilities to choose relevant problems to the considered target problems. It is suggested to investigate in the future the influence of restricting the transferred solutions based on similarity measures among tasks (e.g., [8]). It should be noted that the current study defines and substantiates the considered hypotheses for bi-objective source problems. Future work should also deal with extending the hypotheses to source problems with more than two objectives. In particular, the definition of edge controller should be revised and investigated.
Author Contributions
Conceptualization, A.M.; methodology, A.S. and A.M.; software, A.S.; validation, J.G. and A.M.; formal analysis, A.S.; investigation, A.S. and A.M.; writing—original draft preparation, J.G. and A.S.; writing—review and editing, A.M.; visualization, A.S.; supervision, A.M.; project administration, A.M.; funding acquisition, A.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Israeli Ministry of Innovation, Science and Technology, grant number: 3-17388.
Data Availability Statement
All code programs will be provided on request.
Acknowledgments
The authors would like to thank the Israeli Ministry of Innovation, Science, and Technology for supporting this research.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Kuutti, S.; Bowden, R.; Jin, Y.; Barber, P.; Fallah, S. A Survey of Deep Learning Applications to Autonomous Vehicle Control. IEEE Trans. Intell. Transp. Syst. 2020, 22, 712–733. [Google Scholar] [CrossRef]
- Yao, Q.; Tian, Y.; Wang, Q.; Wang, S. Control Strategies on Path Tracking for Autonomous Vehicle: State of the Art and Future Challenges. IEEE Access 2020, 8, 161211–161222. [Google Scholar] [CrossRef]
- De Campos Souza, P.V. Fuzzy Neural Networks and Neuro-Fuzzy Networks: A Review the Main Techniques and Applications Used in the Literature. Appl. Soft Comput. 2020, 92, 106275. [Google Scholar] [CrossRef]
- Fazzolari, M.; Alcala, R.; Nojima, Y.; Ishibuchi, H.; Herrera, F. A Review of the Application of Multiobjective Evolutionary Fuzzy Systems: Current Status and Further Directions. IEEE Trans. Fuzzy Syst. 2013, 21, 45–65. [Google Scholar] [CrossRef]
- Jang, J.-S.R. ANFIS: Adaptive-Network-Based Fuzzy Inference System. IEEE Trans. Syst. Man. Cybern. 1993, 23, 665–685. [Google Scholar] [CrossRef]
- Deb, K. Multi-Objective Optimisation Using Evolutionary Algorithms: An Introduction. In Multi-Objective Evolutionary Optimisation for Product Design and Manufacturing; Wang, L., Ng, A.H.C., Deb, K., Eds.; Springer: London, UK, 2011; pp. 3–34. ISBN 978-0-85729-652-8. [Google Scholar]
- Gupta, A.; Ong, Y.S.; Feng, L. Insights on Transfer Optimization: Because Experience Is the Best Teacher. IEEE Trans. Emerg. Top. Comput. Intell. 2018, 2, 51–64. [Google Scholar] [CrossRef]
- Tan, K.C.; Feng, L.; Jiang, M. Evolutionary Transfer Optimization—A New Frontier in Evolutionary Computation Research. IEEE Comput. Intell. Mag. 2021, 16, 22–33. [Google Scholar] [CrossRef]
- Koçer, B.; Arslan, A. Genetic Transfer Learning. Expert. Syst. Appl. 2010, 37, 6997–7002. [Google Scholar] [CrossRef]
- Moshaiov, A.; Tal, A. Family Bootstrapping: A Genetic Transfer Learning Approach for Onsetting the Evolution for a Set of Related Robotic Tasks. In Proceedings of the 2014 IEEE Congress on Evolutionary Computation, CEC, Beijing, China, 6–11 July 2014; pp. 2801–2808. [Google Scholar]
- Salih, A.; Moshaiov, A. Evolving Topology and Weights of Specialized and Non-Specialized Neuro-Controllers for Robot Motion in Various Environments. Neural Comput. Appl. 2022, 34, 17071–17086. [Google Scholar] [CrossRef]
- Pereira, J.L.J.; Oliver, G.A.; Francisco, M.B.; Cunha, S.S.; Gomes, G.F. A Review of Multi-Objective Optimization: Methods and Algorithms in Mechanical Engineering Problems. Arch. Comput. Methods Eng. 2022, 29, 2285–2308. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A Fast and Elitist Multiobjective Genetic Algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Li, K.; Wang, R.; Zhang, T.; Ishibuchi, H. Evolutionary Many-Objective Optimization: A Comparative Study of the State-of-the-Art. IEEE Access 2018, 6, 26194–26214. [Google Scholar] [CrossRef]
- Cho, J.-H.; Wang, Y.; Chen, R.; Chan, K.S.; Swami, A. A Survey on Modeling and Optimizing Multi-Objective Systems. IEEE Commun. Surv. Tutor. 2017, 19, 1867–1901. [Google Scholar] [CrossRef]
- Jang, J.-S.R.; Sun, C.-T.; Mizutani, E. Neuro-Fuzzy and Soft Computing; Prentice Hall: Upper Saddle River, NJ, USA, 1997; ISBN 0-13-261066-3. [Google Scholar]
- Vieira, J.; Mota, A.; Morgado Dias, F. Neuro-Fuzzy Systems: A Survey Artificial Neural Networks Fault Tolerance View Project Vision. 3D View Project Neuro-Fuzzy Systems: A Survey; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Shihabudheen, K.V.; Pillai, G.N. Recent Advances in Neuro-Fuzzy System: A Survey. Knowl. Based Syst. 2018, 152, 136–162. [Google Scholar] [CrossRef]
- Kar, S.; Das, S.; Ghosh, P.K. Applications of Neuro Fuzzy Systems: A Brief Review and Future Outline. Appl. Soft Comput. 2014, 15, 243–259. [Google Scholar] [CrossRef]
- Sugeno, M. An Introductory Survey of Fuzzy Control. Inf. Sci. 1985, 36, 59–83. [Google Scholar] [CrossRef]
- Feng, G. A Survey on Analysis and Design of Model-Based Fuzzy Control Systems. IEEE Trans. Fuzzy Syst. 2006, 14, 676–697. [Google Scholar] [CrossRef]
- Precup, R.-E.; Hellendoorn, H. A Survey on Industrial Applications of Fuzzy Control. Comput. Ind. 2011, 62, 213–226. [Google Scholar] [CrossRef]
- Masood, M.K.; Hew, W.P.; Rahim, N.A. Review of ANFIS-Based Control of Induction Motors. J. Intell. Fuzzy Syst. 2012, 23, 143–158. [Google Scholar] [CrossRef]
- Kabini, K. Review of ANFIS and Its Application in Control of Machining Processes. Sustain. Res. Innov. Proc. 2011, 3, 1–9. [Google Scholar]
- Lughofer, E. Evolving Fuzzy and Neuro-Fuzzy Systems: Fundamentals, Stability, Explainability, Useability, and Applications. In Handbook on Computer Learning and Intelligence: Volume 2: Deep Learning, Intelligent Control and Evolutionary Computation; World Scientific: Hackensack, NJ, USA, 2022; pp. 133–234. [Google Scholar]
- Moshaiov, A.; Salih, A. Multi-Objective Structure and Parameter Evolution of Neuro-Fuzzy Systems. In Proceedings of the 2021 IEEE Symposium Series on Computational Intelligence, SSCI 2021—Proceedings, Orlando, FL, USA, 5–7 December 2021; pp. 1–7. [Google Scholar]
- Fleming, P.J.; Purshouse, R.C. Evolutionary Algorithms in Control Systems Engineering: A Survey. Control Eng. Pract. 2002, 10, 1223–1241. [Google Scholar] [CrossRef]
- Bejarano, L.A.; Espitia, H.E.; Montenegro, C.E. Clustering Analysis for the Pareto Optimal Front in Multi-Objective Optimization. Computation 2022, 10, 37. [Google Scholar] [CrossRef]
- Li, W.; Li, D.; Feng, Y.; Zou, D. Fuzzy Weighted Pareto–Nash Equilibria of Multi-Objective Bi-Matrix Games with Fuzzy Payoffs and Their Applications. Mathematics 2023, 11, 4266. [Google Scholar] [CrossRef]
- Silva, F.L.; da Silva, S.F.; Mazzariol Santiciolli, F.; Eckert, J.J.; Silva, L.C.A.; Dedini, F.G. Multi-Objective Optimization of the Steering System and Fuzzy Logic Control Applied to a Car-Like Robot BT—Multibody Mechatronic Systems; Pucheta, M., Cardona, A., Preidikman, S., Hecker, R., Eds.; Springer: Cham, Switzerland, 2021; pp. 195–202. [Google Scholar]
- Kubota, N.; Nojima, Y.; Kojima, F.; Fukuda, T. Multi-Objective Behavior Coordinate for a Mobile Robot with Fuzzy Neural Networks. In Proceedings of the IEEE-INNS-ENNS International Joint Conference on Neural Networks. IJCNN 2000. Neural Computing: New Challenges and Perspectives for the New Millennium, Como, Italy, 27 July 2000; Volume 6, pp. 311–316. [Google Scholar]
- Van Nguyen, T.T.; Phung, M.D.; Tran, Q.V. Behavior-Based Navigation of Mobile Robot in Unknown Environments Using Fuzzy Logic and Multi-Objective Optimization. arXiv 2017, arXiv:1703.03161. [Google Scholar] [CrossRef]
- Aouf, A.; Boussaid, L.; Sakly, A. TLBO-Based Adaptive Neurofuzzy Controller for Mobile Robot Navigation in a Strange Environment. Comput. Intell. Neurosci. 2018, 2018, 4. [Google Scholar] [CrossRef] [PubMed]
- Juang, C.-F.; Bui, T.B. Reinforcement Neural Fuzzy Surrogate-Assisted Multiobjective Evolutionary Fuzzy Systems with Robot Learning Control Application. IEEE Trans. Fuzzy Syst. 2019, 28, 434–446. [Google Scholar] [CrossRef]
- Shell, J.; Coupland, S. Fuzzy Transfer Learning: Methodology and Application. Inf. Sci. 2015, 293, 59–79. [Google Scholar] [CrossRef]
- Fouladvand, S.; Salavati, S.; Masajedi, P.; Ghanbarzadeh, A. A Modified Neuro-Evolutionary Algorithm for Mobile Robot Navigation: Using Fuzzy Systems and Combination of Artificial Neural Networks. Int. J. Knowl.-Based Intell. Eng. Syst. 2015, 19, 125–133. [Google Scholar] [CrossRef]
- Chou, C.-Y.; Juang, C.-F. Navigation of an Autonomous Wheeled Robot in Unknown Environments Based on Evolutionary Fuzzy Control. Inventions 2018, 3, 3. [Google Scholar] [CrossRef]
- Ferdaus, M.M.; Pratama, M.; Anavatti, S.G.; Garratt, M.A.; Pan, Y. Generic Evolving Self-Organizing Neuro-Fuzzy Control of Bio-Inspired Unmanned Aerial Vehicles. IEEE Trans. Fuzzy Syst. 2019, 28, 1542–1556. [Google Scholar] [CrossRef]
- Ferdaus, M.M.; Hady, M.A.; Pratama, M.; Kandath, H.; Anavatti, S.G. Redpac: A Simple Evolving Neuro-Fuzzy-Based Intelligent Control Framework for Quadcopter. In Proceedings of the 2019 IEEE International Conference on Fuzzy Systems (FUZZ-IEEE), New Orleans, LA, USA, 23–26 June 2019; pp. 1–7. [Google Scholar]
- Ferdaus, M.M.; Pratama, M.; Anavatti, S.G.; Garratt, M. A Generic Self-Evolving Neuro-Fuzzy Controller Based High-Performance Hexacopter Altitude Control System. In Proceedings of the 2018 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Miyazaki, Japan, 7–10 October 2018; pp. 2784–2791. [Google Scholar]
- Li, B.; Li, J.; Tang, K.; Yao, X. Many-Objective Evolutionary Algorithms: A Survey. ACM Comput. Surv. (CSUR) 2015, 48, 13. [Google Scholar] [CrossRef]
- Takagi, T.; Sugeno, M. Fuzzy Identification of Systems and Its Applications to Modeling and Control. IEEE Trans. Syst. Man. Cybern. 1985, SMC-15, 116–132. [Google Scholar] [CrossRef]
- Zitzler, E.; Thiele, L. Multiobjective Evolutionary Algorithms: A Comparative Case Study and the Strength Pareto Approach. IEEE Trans. Evol. Comput. 1999, 3, 257–271. [Google Scholar] [CrossRef]
- Taylor, M.E.; Stone, P. Transfer Learning for Reinforcement Learning Domains: A Survey. J. Mach. Learn. Res. 2009, 10, 257–271. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).