On Fall-Colorable Graphs

Abstract

A fall k-coloring of a graph G is a proper k-coloring of G such that each vertex has at least one neighbor in each of the other color classes. A graph G which has a fall k-coloring is equivalent to having a partition of the vertex set $V\left(G\right)$ in k independent dominating sets. In this paper, we first prove that for any fall k-colorable graph G with order n, the number of edges of G is at least $\left(n\right(k-1)+r(k-r\left)\right)/2$, where $r\equiv n(modk)$ and $0\le r\le k-1$, and the bound is tight. Then, we obtain that if G is k-colorable ($k\ge 2$) and the minimum degree of G is at least $\frac{k-2}{k-1}n$, then G is fall k-colorable and this condition of minimum degree is the best possible. Moreover, we give a simple proof for an NP-hard result of determining whether a graph is fall k-colorable, where $k\ge 3$. Finally, we show that there exist an infinite family of fall k-colorable planar graphs for $k\in \{5,6\}$.

1. Introduction

In this paper, we only consider simple and undirected graphs. For a graph $G=\left(V\right(G),E(G\left)\right)$, we use $V\left(G\right)$ and $E\left(G\right)$ to represent the sets of vertices and edges of G, respectively. We use $d_G\left(v\right)$ to represent the degree of a vertex $v\in V\left(G\right)$, that is, the number of neighbors of v in G. If $d_G\left(v\right)=r$ for any $v\in V\left(G\right)$, then the graph G is called an r-regular graph. For a vertex $v\in V\left(G\right)$, let $N_G\left(v\right)=\{u:uv\in E\left(G\right)\}$ and $N_G\left[v\right]=N_G\left(v\right)\cup \left\{v\right\}$ denote the open neighborhood and the closed neighborhood of v, respectively. The maximum degree and minimum degree of G are denoted by $\Delta \left(G\right)$ and $\delta \left(G\right)$, respectively. When no confusion can arise, $N_G\left(v\right)$, $N_G\left[v\right]$, $\Delta \left(G\right)$, and $\delta \left(G\right)$ are simplified by $N\left(v\right)$, $N\left[v\right]$, $\Delta$, and $\delta$, respectively. A plane graph is a graph drawn in the plane such that its edges intersect only at their ends; a planar graph is a graph that can be drawn as a plane graph.

Let G be a graph. A (proper) k-coloring f of G is a mapping from $V\left(G\right)$ to $\{1,2,\dots ,k\}$ such that $f\left(u\right)\ne f\left(v\right)$ for any $uv\in E\left(G\right)$. Hence, a k-coloring can be regarded as a partition $\{V_1,V_2,\dots ,V_k\}$ of $V\left(G\right)$, where $V_i$ denotes the set of vertices assigned color i, and is called a color class of f, where $i=1,2,\dots ,k$. If a graph G admits a k-coloring, the G is called k-colorable. The minimum number k such that G is k-colorable is called the chromatic number of G and is denoted by $\chi \left(G\right)$.

Let f be a k-coloring of a graph G. If a vertex $v\in V\left(G\right)$ has all colors in its closed neighborhood under f, namely $\left|f\right(N\left[v\right]\left)\right|=k$, then the vertex v is called colorful with respect to f. Furthermore, the coloring f is called colorful whenever each of its color classes contains at least one colorful vertex. The maximum order of a colorful coloring of a graph G is called the b-chromatic number of G, and is denoted by $\phi \left(G\right)$. A fall k-coloring of a graph G is a k-coloring of G such that every vertex is colorful.

The problem of b-chromatic numbers was introduced by Irving and Manlove in 1999 [1] and studied extensively in the literature (see the survey in [2]), whereas fall coloring was introduced in [3] and studied in [4,5,6]. It follows from [6] that fall coloring strongly chordal graphs is doable in polynomial time, even with an unbounded number of colors.

A dominating set in a graph G is a subset $S\subseteq V\left(G\right)$ such that each vertex in $V\left(G\right)$ is either in S or has at least one neighbor in S. If S is a dominating set and independent, then S is an independent dominating set (IDS) of G. The independent domination number ${\gamma }_i\left(G\right)$ is the minimum cardinality of an IDS of G. A graph G has a fall k-coloring if and only if $V\left(G\right)$ can be partitioned into k independent dominating sets [7].

Note that a graph may have no fall coloring. For instance, the cycle $C_n$ has a fall coloring only when n is a multiple of three or is even [3]. Hence, determining which graphs are fall-colorable is an interesting problem. In fact, in 1976 Cockayne and Hedetniemi [7] first studied fall-colorable graphs but used another term, indominable graphs. They found several families of graphs which have fall colorings.

In this paper, we further discuss fall-colorable graphs. First, the size of a k-colorable graph is determined, including the boundaries. Then, a sufficient condition of a graph to be k-colorable ($k\ge 2$) is proposed and the tightness of this condition is discussed. Moreover, we give a simple proof for an NP-hard result of determining whether a graph is fall k-colorable, where $k\ge 3$. Finally, we show that there exist an infinite family of fall k-colorable planar graphs for $k\in \{5,6\}$ and find some sufficient conditions for a maximal planar graph to be fall-colorable.

For other notations and terminologies in graph theory, we refer to [8].

2. Some Properties of Fall-Colorable Graphs

In this section, we discuss some properties of fall k-colorable graphs. The following, Lemmas 1 and 2, can be obtained straight from previous studies, such as [3,7].

Lemma 1

([3]). Let G be a fall k-colorable graph and f a fall k-coloring. We have the following:

(i) $\delta \left(G\right)\ge k-1$;

(ii) The subgraph induced by the union of any r color classes under f is fall r-colorable, where $r\le k$.

Lemma 2

([7]). A graph G is fall k-colorable if and only if G has a k-coloring such that the subgraph induced by the union of any two color classes has no isolated vertices.

Theorem 1.

Let G be a fall k-colorable graph of order n. Then,

$$\left|E\left(G\right)\right|\ge \frac{n(k-1)+r(k-r)}{2},$$

where $r\equiv n(modk)$ and $0\le r\le k-1$.

Proof. 

Let $f=(V_1,V_2,\dots ,V_k)$ be a fall k-coloring of G and $|V_i|=n_i$, where $i=1,2,\dots ,k$. Then, $n=n_1+n_2+\cdots +n_k$. Without a loss of generality, we assume that $n_1\le n_2\le \cdots \le n_k$. For any two color classes $V_i$ and $V_j$ with $i<j$, by Theorem 2, we know that the subgraph $G_{i,j}$ induced by $V_i\cup V_j$ has no isolated vertices. Since $G_{i,j}$ is a bipartite graph, we have $|E\left(G_{i,j}\right)|\ge |V_j|=n_j$. Hence,

$$\begin{array}{cc}\hfill \left|E\right(G\left)\right|& =\sum _{1\le i<j\le k}\left|E\left(G_{i,j}\right)\right|\ge \sum _{1\le i<j\le k}{n}_j\hfill \\ \hfill & =n_2+2n_3+\cdots +(k-1)n_k\hfill \\ \hfill & =(\sum _{i=1}^{k}i·n_i)-n.\hfill \end{array}$$

(1)

Now, we prove that if ${\sum }_{i=1}^{k}i·n_i$ is the minimum then $(V_1,V_2,\dots ,V_k)$ is an equitable partition of $V\left(G\right)$, namely $|n_p-n_q|\le 1$, for any $p,q\in \{1,2,\dots ,k\}$.

Suppose, to the contrary, that $(V_1,V_2,\dots ,V_k)$ is not an equitable partition of $V\left(G\right)$. Then, there exists $a\in \{1,2,\dots ,k\}$ such that $n_{a+1}-n_a\ge 2$ or $b,c\in \{1,2,\dots ,k\}$ with $b<c$ such that $n_{b+1}-n_b=n_{c+1}-n_c=1$. If the former occurs, let $n_a^{\prime }=n_a+1$, $n_{a+1}^{\prime }=n_{a+1}-1$, and $n_i^{\prime }=n_i$ for any $i\in \{1,2,\dots ,k\}\setminus \{a,a+1\}$. Then,

$$\begin{array}{cc}\hfill \sum _{i=1}^{k}i·n_i-\sum _{i=1}^{k}i·n_i^{\prime }& =\sum _{i=1}^{k}i·(n_i-n_i^{\prime })\hfill \\ \hfill & =a(n_a-n_a^{\prime })+(a+1)(n_{a+1}-n_{a+1}^{\prime })\hfill \\ \hfill & =a(n_a-n_a-1)+(a+1)(n_{a+1}-n_{a+1}+1)\hfill \\ \hfill & =1>0.\hfill \end{array}$$

However, this contradicts the minimality of ${\sum }_{i=1}^{k}i·n_i$.

If the latter occurs, let $n_b^{\prime }=n_b+1$, $n_{c+1}^{\prime }=n_{c+1}-1$, and $n_i^{\prime }=n_i$ for any $i\in \{1,2,\dots ,k\}\setminus \{b,c+1\}$. Similar to the former case, we can obtain ${\sum }_{i=1}^{k}i·n_i-{\sum }_{i=1}^{k}i·n_i^{\prime }=c-b+1>0$, which is a contradiction. Therefore, if ${\sum }_{i=1}^{k}i·n_i$ is a minimum then $(V_1,V_2,\dots ,V_k)$ is an equitable partition of $V\left(G\right)$.

Let $n=kt+r$, where $r\equiv n(modk)$ and $0\le r\le k-1$. Now, we consider the case of ${\sum }_{i=1}^{k}i·n_i$ as the minimum. Note that $n_1\le n_2\le \cdots \le n_k$. It therefore follows that $n_1=\cdots =n_{k-r}=t$ and $n_{k-r+1}=\cdots =n_k=t+1$. Hence,

$$\begin{array}{cc}\hfill \sum _{i=1}^{k}i·n_i& =\sum _{i=1}^{k-r}i·t+\sum _{i=k-r+1}^{k}i·(t+1)\hfill \\ \hfill & =\sum _{i=1}^{k}i·t+\sum _{i=k-r+1}^{k}i\hfill \\ \hfill & =t·\frac{k(k+1)}{2}+\frac{r(2k-r+1)}{2}\hfill \\ \hfill & =\frac{n-r}{k}·\frac{k(k+1)}{2}+\frac{r(2k-r+1)}{2}\hfill \\ \hfill & =\frac{n(k+1)+r(k-r)}{2}.\hfill \end{array}$$

(2)

Together with Formulae (1) and (2), we have

$$\begin{array}{cc}\hfill \left|E\right(G\left)\right|& \ge (\sum _{i=1}^{k}i·n_i)-n\hfill \\ \hfill & \ge \frac{n(k+1)+r(k-r)}{2}-n\hfill \\ \hfill & =\frac{n(k-1)+r(k-r)}{2}.\hfill \end{array}$$

□

Theorem 2.

For any fall k-colorable graph G with order n, if G is $(k-1)$-regular, then $n\equiv 0(modk)$. Moveover, for any fall k-coloring f of G, each color class of f has exactly $\frac{n}{k}$ vertices.

Proof. 

Let $V_i$ be any color class of the fall k-coloring f of G. Then, for any two vertices u and v in $V_i$; we can obtain $N_G\left(u\right)\cap N_G\left(v\right)=\varnothing$. Otherwise, if there exists a vertex $x\in N_G\left(u\right)\cap N_G\left(v\right)$, since G is $(k-1)$-regular, we can deduce that x is adjacent to at most $k-2$ color classes, which implies that x is not a colorful vertex of f; this is a contradiction. Let $V_i=\{v_1,v_2,\dots ,v_t\}$. Then, $N_G\left[v_1\right],N_G\left[v_2\right],\dots ,N_G\left[v_t\right]$ is a t-partition of $V\left(G\right)$. Since $|N_G\left[v_j\right]|=k$ for each $j=1,2,\dots ,t$, we have $n=kt$ and so $n\equiv 0(modk)$. Note that $|V_i|=t=\frac{n}{k}$, we can discover that each color class of f has exactly $\frac{n}{k}$ vertices. □

3. A Sufficient Condition

In 2010, Balakrishnan and Kavaskar [9] showed that any graph G with $\delta \left(G\right)\ge \left|V\right(G\left)\right|-2$ admits a fall coloring. In this section, we improve this result by relaxing the condition $\delta \left(G\right)\ge \left|V\right(G\left)\right|-2$ to $\delta \left(G\right)>\frac{k-2}{k-1}\left|V\left(G\right)\right|$ for any $k\ge 2$ and prove that the condition of $\delta \left(G\right)$ is the best possible. First, we give a useful lemma obtained by Zarankiewicz [10]:

Lemma 3

([10]). Let G be a k-colorable graph with n vertices and $\delta \left(G\right)>\frac{k-2}{k-1}n$, where $k\ge 2$. We have $\chi \left(G\right)=k$.

Theorem 3.

Let G be a k-colorable graph with n vertices and $\delta \left(G\right)>\frac{k-2}{k-1}n$, where $k\ge 2$. Then, G is fall k-colorable.

Proof. 

If $k=2$, then $\delta \left(G\right)>\frac{k-2}{k-1}n=0$ and G has no isolated vertices. Hence, G is fall 2-colorable.

Now, assume that $k\ge 3$. Let v be an arbitrary vertex of G and $G_v$ be the subgraph of G induced by $N_G\left(v\right)$. Then, $|V\left(G_v\right)|=|N_G\left(v\right)|=d_G\left(v\right)>\frac{k-2}{k-1}n$. Hence, for any vertex x in $G_v$, we have

$$\begin{array}{cc}\hfill d_{G_v}\left(x\right)& >\frac{k-2}{k-1}n-(n-|V\left(G_v\right)\left|\right)\hfill \\ \hfill & =|V\left(G_v\right)|-\frac{1}{k-1}n\hfill \\ \hfill & >|V\left(G_v\right)|-\frac{1}{k-1}·\frac{k-1}{k-2}\left|V\left(G_v\right)\right|\hfill \\ \hfill & =\frac{(k-1)-2}{(k-1)-1}\left|V\left(G_v\right)\right|.\hfill \end{array}$$

Note that G is k-colorable, so $G_v$ is $(k-1)$-colorable. Hence, by Lemma 3, we can see that $\chi \left(G_v\right)=k-1$, which yields that $\left|f\right(N_G\left(v\right)\left)\right|=k-1$ for any k-coloring f of G. That is to say, v is a colorful vertex with respect to f. Since v is an arbitrary vertex of G, we can deduce that f is a fall k-coloring of G. Hence, the graph G is fall k-colorable. □

Now, we show that the condition $\delta \left(G\right)>\frac{k-2}{k-1}n$ in Theorem 3 is the best possible. We will construct a family of graphs that are not fall k-colorable, $G_{\ell }$, with $\delta \left(G_{\ell }\right)=\frac{k-2}{k-1}\left|V\left(G_{\ell }\right)\right|$.

We use $K_n$ to denote the complete graph of order n and use $T_{r,s}$ to denote the complete r-partite graph with s vertices in each class, where $r\ge 2$. The join of two graphs G and H, denoted as $G\vee H$, is the graph obtained from the disjointed union of G and H, and we add edges joining every vertex of G to every vertex of H.

For any $k\ge 3$ and $\ell \ge 1$, let $G_{\ell }^1=\overline{K_{\ell }}$, $G_{\ell }^2=T_{2,\ell }$, $G_{\ell }^3=T_{k-2,3\ell }$, and $G_{\ell }=(G_{\ell }^1\cup G_{\ell }^2)\vee G_{\ell }^3$. For example, when $k=4$ and $\ell =1$, the graph $G_{\ell }$ is shown in Figure 1.

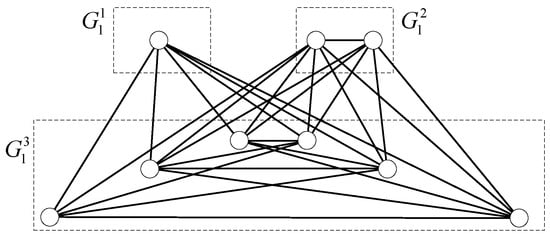
Figure 1. The graph $G_{\ell }$ when $k=4$ and $\ell =1$.

Then, $|V\left(G_{\ell }\right)|=|V\left(G_{\ell }^1\right)|+|V\left(G_{\ell }^2\right)|+|V\left(G_{\ell }^3\right)|=\ell +2\ell +3\ell (k-2)=3\ell (k-1).$

For any $v\in V\left(G_{\ell }^1\right)\cap V\left(G_{\ell }\right)$, $d_{G_{\ell }}\left(v\right)=3\ell (k-2)$; for any $v\in V\left(G_{\ell }^2\right)\cap V\left(G_{\ell }\right)$, $d_{G_{\ell }}\left(v\right)=3\ell (k-2)+\ell =(3k-5)\ell$; for any $v\in V\left(G_{\ell }^3\right)\cap V\left(G_{\ell }\right)$, $d_{G_{\ell }}\left(v\right)=3\ell (k-3)+\ell +2\ell =3\ell (k-2)$. Hence, $\delta \left(G_{\ell }\right)=3\ell (k-2)=\frac{k-2}{k-1}\left|V\left(G_{\ell }\right)\right|$.

Note that for any k-coloring of $G_{\ell }$, $\left|f\right(V\left(G_{\ell }^3\right)\left)\right|=k-2$. Hence, each vertex in $V\left(G_{\ell }^1\right)$ is not a colorful vertex with respect to f. So, $G_{\ell }$ is not fall k-colorable.

4. Complexity

The problem of determining whether a graph is fall k-colorable ($k\ge 3$) has been shown to be NP-complete [3,11,12,13]. In this section, we give a simple proof for the NP-complete result of the FALL k-COLORABLE problem, which is defined as follows:

FALL k-COLORABLE:

Instance: Given a graph $G=(V,E)$ and a positive integer k.

Question: Is G fall k-colorable?

k-COLORABLE:

Instance: Given a graph $G=(V,E)$ and a positive integer k.

Question: Is G k-colorable?

It is well known that the k-COLORABLE problem is NP-hard for any $k\ge 3$ [14]. We will prove that the fall k-colorable problem is NP-hard by using a reduction from the k-COLORABLE problem.

Theorem 4.

FALL k-COLORABLE is NP-complete for any $k\ge 3$.

Proof. 

We show that the FALL k-COLORABLE problem is NP-complete by a reduction from k-COLORABLE. For any graph G of order n with the vertex set $\{v_1,v_2,\cdots ,v_n\}$, we construct a graph $G^{\prime }$ as follows:

First, take n copies $K_k^1,K_k^2,\cdots ,K_k^n$ of the complete graph $K_k$. Then, add these n copies of $K_k$ to G and identify $v_i$ and a vertex of $K_k^i$ into a single vertex, where $i=1,2,\cdots ,n$.

We claim that G is k-colorable if and only if $G^{\prime }$ is fall k-colorable.

Let $G^{\prime }$ be fall k-colorable. Let $f^{\prime }$ be a fall k-coloring of $G^{\prime }$. By this definition, $f^{\prime }$ is a proper k-coloring of $G^{\prime }$. Then, the restriction of $f^{\prime }$ to $V\left(G\right)$ is a k-coloring of G. So, G is k-colorable. Conversely, assume that G has a k-coloring f. By the construction of $G^{\prime }$, f can be extended to a k-coloring $f^{\prime }$ of $G^{\prime }$. Since every vertex of $G^{\prime }$ belongs to a subgraph of $G^{\prime }$ which is isomorphic to $K_k$, we can see that $f^{\prime }$ is a fall k-coloring of $G^{\prime }$. So, $G^{\prime }$ is fall k-colorable. □

Furthermore, the k-COLORABLE problem remains NP-hard under several restrictions. Garey and Johnson [15] proved the following:

Lemma 4

([15]). Three-COLORABLE is NP-complete even when restricted to planar graphs with a maximum degree of four.

By Lemma 4 and using a similar approach to that in the proof of Theorem 4, we can obtain the following result.

Corollary 1.

FALL 3-COLORABLE is NP-complete even when restricted to planar graphs with a maximum degree of six.

5. Fall Colorings of Planar Graphs

In this section, we discuss the fall colorings of planar graphs. Since $\delta \left(G\right)\le 5$ for any planar graph G, it follows from Lemma 1 (i) that ${\psi }_f\left(G\right)\le 6$. In [7], Cockayne and Hedetniemi found that each uniquely k-colorable graph is fall k-colorable. Note that for any integer $k\le 4$, there exist an infinite family of planar graphs that are uniquely k-colorable [16,17,18,19,20,21], but uniquely five-colorable planar graphs do not exist [18]. Hence, there exist an infinite family of planar fall k-colorable graphs for any $k\le 4$. Now, we show that there also exist an infinite family of planar fall k-colorable graphs for $k\in \{5,6\}$.

We can see that the icosahedron $G_{12}$ in Figure 2, which is a planar graph, has a fall five-coloring (Figure 2a) and a fall six-coloring (Figure 2b).

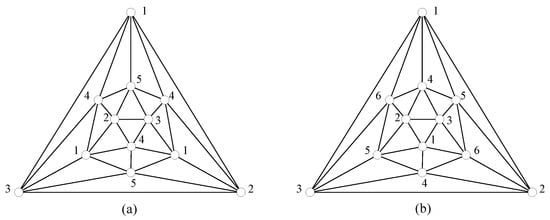
Figure 2. Two fall colorings of the icosahedron $G_{12}$; (a) a fall 5-coloring and (b) a fall 6-coloring.

Theorem 5.

There exist an infinite family of planar fall k-colorable graphs for $k\in \{5,6\}$.

Proof. 

From the icosahedron $G_{12}$, we can construct a family of graphs $\left\{H_i\right\}$ as follows:

(1) $H_1=G_{12}$;

(2) For integer $i\ge 2$, $H_i$ can be obtained by embedding a copy of $G_{12}$ in some interior face of $H_{i-1}$ and identifying the boundaries of this face and the exterior face of $G_{12}$.

It can be checked that $H_i$ is a planar graph of order $9i+3$. Note that every three-coloring of the exterior triangle of $G_{12}$ can be extended to a fall five-coloring by Figure 2a or a fall six-coloring by Figure 2b of $G_{12}$. We can recursively obtain a fall five-coloring and a fall six-coloring of $H_i$. Hence, for any integer i, $H_i$ is a planar fall k-colorable graph for $k\in \{5,6\}$. □

Now, we discuss the fall colorings of maximal planar graphs. A planar graph G is maximal if $G+uv$ is not planar for any two nonadjacent vertices u and v of G. For example, the icosahedron $G_{12}$ in Figure 2 is a maximal planar graph.

Theorem 6.

([12]). If a maximal planar graph G is three-colorable, then G is fall three-colorable.

Since a maximal planar graph G is three-colorable if and only if every vertex in G has an even degree [22,23], we can obtain the following result:

Corollary 2.

Let G be a maximal planar graph. If each vertex in G has an even degree, then G is fall three-colorable.

Theorem 7.

Let G be a maximal planar graph. If each vertex in G has an odd degree, then G is fall four-colorable.

Proof. 

It follows from the Four Color Theorem [24,25] that G is four-colorable. Let f be a four-coloring of G. Since G is a maximal planar graph, we know that the neighbors of each vertex v form a cycle $C_v$ of order $d_G\left(v\right)$. Note that v has an odd degree in G. Hence, $C_v$ contains three colors under the coloring f, that is, v is colorful with respect to f. So, f is a fall four-coloring of G. □

6. Conclusions and Open Problems

In this paper, we first show that $\left|E\right(G\left)\right|\ge \left(n\right(k-1)+r(k-r\left)\right)/2$ for any fall k-colorable graph G with order n, where $r\equiv n(modk)$ and $0\le r\le k-1$, and this bound is tight. Then, we obtain that if G is k-colorable ($k\ge 2$) and the minimum degree $\delta \left(G\right)\ge \frac{k-2}{k-1}n$, then G is fall k-colorable and this condition of the minimum degree is the best possible. Moreover, we give a simple proof for an NP-hard result of determining whether a graph is fall k-colorable, where $k\ge 3$.

For a maximal planar graph G, if G has a fall k-coloring, then by Theorems 1, 5, 6, and 7 we can obtain that $k\in \{3,4,5,6\}$. This prompts us to propose the following problem:

Problem 1.

For each $k\in \{3,4,5,6\}$, which maximal planar graphs G have fall k-colorings?

For any outerplane graph G, note that the minimum degree $\delta \left(G\right)\le 2$. If G has a fall k-coloring, then by Lemma 1 we have $k\le \delta \left(G\right)+1\le 3$.