WOA: Wombat Optimization Algorithm for Solving Supply Chain Optimization Problems

Abstract

Supply Chain (SC) Optimization is a key activity in today’s industry with the goal of increasing operational efficiency, reducing costs, and improving customer satisfaction. Traditional optimization methods often struggle to effectively use resources while handling complex and dynamic Supply chain networks. This paper introduces a novel biomimetic metaheuristic algorithm called the Wombat Optimization Algorithm (WOA) for supply chain optimization. This algorithm replicates the natural behaviors observed in wombats living in the wild, particularly focusing on their foraging tactics and evasive maneuvers towards predators. The theory of WOA is described and then mathematically modeled in two phases: (i) exploration based on the simulation of wombat movements during foraging and trying to find food and (ii) exploitation based on simulating wombat movements when diving towards nearby tunnels to defend against its predators. The effectiveness of WOA in addressing optimization challenges is assessed by handling the CEC 2017 test suite across various problem dimensions, including 10, 30, 50, and 100. The findings of the optimization indicate that WOA demonstrates a strong ability to effectively manage exploration and exploitation, and maintains a balance between them throughout the search phase to deliver optimal solutions for optimization problems. A total of twelve well-known metaheuristic algorithms are called upon to test their performance against WOA in the optimization process. The outcomes of the simulations reveal that WOA outperforms the other algorithms, achieving superior results across most benchmark functions and securing the top ranking as the most efficient optimizer. Using a Wilcoxon rank sum test statistical analysis, it has been proven that WOA outperforms other algorithms significantly. WOA is put to the test with twenty-two constrained optimization problems from the CEC 2011 test suite and four engineering design problems to showcase its ability to solve real-world optimization problems. The results of the simulations demonstrate that WOA excels in real-world applications by delivering superior solutions and outperforming its competitors.

1. Introduction

Supply Chain Management (SCM) plays a vital role in the success and competitiveness of modern businesses by ensuring the seamless flow of goods and services from suppliers to the final customer [1]. The complexity of supply chain networks, with multiple overlapping firms, dynamic demand patterns, and resource constraints, poses significant challenges for optimal performance [2]. Supply chain quality is essential for businesses to increase efficiency, reduce costs, and adapt to market demand that changes at every moment [3,4].

Various studies have been presented in the literature in the field of SCM. A novus multi-objective three-stage supply chain network is proposed, which aims to optimize sustainability, resiliency and responsive measures, simultaneously [5]. To uncover optimal strategic and planning choices, a multi-objective mixed integer programming framework is proposed to analyze Supply Chains from environmental, economic, and technological standpoints, while handling multiple periods, products, supply zones, and various feedstocks [6]. A behavioral three-way decision making model with a Fermatean fuzzy Mahalanobis distance is proposed to deal with SCM problems [7]. For supply chain management in hesitant situations, a new model based on an interval type-2 Pythagorean fuzzy set is proposed [8]. A multi-objective, multi-product, and multi-period two-stage sustainable opened- and closed-loop supply chain plan is proposed to maintain the supply among production centers and various hospitals during the COVID-19 pandemic situation [9].

One of the fundamental aspects of SCM is the integration of key processes and functions within and across organizations. Effective SCM requires collaboration not only among different departments within a company but also with external partners such as suppliers, manufacturers, distributors, and retailers. This collaborative approach enables organizations to streamline operations, reduce costs, improve quality, and respond quickly to changing market demands [10]. Furthermore, advancements in technology have revolutionized SCM practices, enabling a real-time visibility and control over supply chain activities. For instance, the use of data analytics, Artificial Intelligence, and the Internet of Things (IoT) has enabled companies to gather and analyze vast amounts of data, leading to better forecasting accuracy, inventory optimization, and decision-making. These technological innovations have transformed SCM into the “Triple-A Supply Chain”—agile, adaptable, and aligned with the overarching business strategy [11]. SCM plays a pivotal role in driving operational efficiency, enhancing customer satisfaction, and creating a competitive advantage. By embracing collaboration, leveraging technology, and addressing emerging challenges, organizations can build resilient, sustainable, and agile supply chains that are well-positioned to thrive in an increasingly complex and interconnected world.

Traditional optimization techniques such as linear programming and mathematical modeling have been widely used for supply chain optimization [12]. However, these methods often struggle to cope with the inherent complexity and uncertainty of real-world supply chains. Consequently, there is an increased interest in developing metaheuristic algorithms that take inspiration from nature to efficiently solve Supply Chain Optimization problems [13]. Among these bio-inspired optimization methods, swarm intelligence-based algorithms have shown promise due to their ability to mimic collective biological systems. One such algorithm inspired by the feeding behavior of the honeybee swarm is Bee Swarm Optimization (BSO). BSO mimics the spatially embedded cooperation and decision-making processes found in honey bee colonies, making it ideally suited for optimization projects characterized by large solution areas and dynamic environments [14].

Optimization problems involve multiple possible solutions, with the goal of finding the most optimal solution from all the options available [15]. These problems are typically represented mathematically through decision variables, constraints, and an objective function. The primary objective in optimization is to assign values to the decision variables in a way that maximizes or minimizes the objective function while satisfying the problem’s constraints [16]. Problem-solving methods for optimizing solutions can fall into deterministic and stochastic categories [17].

Although deterministic approaches excel in solving convex, differentiable, continuous, linear, and low-dimensional optimization problems, they struggle when faced with complex optimization problems, particularly in high dimensions where they may become trapped at local optima [18]. In real-world applications within mathematics, engineering, and other fields, many optimization problems are complex, non-convex, non-derivative, discontinuous, nonlinear, and high-dimensional. The limitations and challenges of deterministic approaches in handling such optimization problems have prompted researchers to develop stochastic approaches [19].

Metaheuristic algorithms are recognized as efficient stochastic methods capable of generating optimal solutions for optimization problems through random search within the problem-solving space. Employing random operators and trial-and-error processes, these algorithms initially create a set of candidate solutions as the algorithm population. Through iteration and algorithm update steps, the positions of population members are altered to enhance these candidates, ultimately leading to the identification of the most optimal solution encountered throughout the algorithm’s execution [20]. The randomness involved in the process of metaheuristic algorithms implies that reaching the global optimum is not guaranteed. However, the results achieved through these algorithms are deemed acceptable as they are situated near the global optimum. Hence, these outcomes are referred to as quasi-optimal solutions. Enhancing these quasi-optimal solutions to be closer to the global optimum stands as a significant goal in the realm of metaheuristic algorithms and optimization. Consequently, this pursuit serves as the primary driving force for researchers in their quest to create numerous innovative metaheuristic algorithms [21].

Effectively managing a random search at both global and local levels is essential for the success of metaheuristic algorithms in optimization processes. Global search involves a deep exploration of the problem-solving space to avoid being trapped in local optima and in order to pinpoint the main optima region. On the other hand, a local search focuses on exploitating the near solutions and potential areas within the problem-solving space to achieve improved outcomes closer to the global optimum. To handle the stochastic search effectively, a metaheuristic algorithm must strike a balance between exploration and exploitation throughout the problem-solving process [22].

The main research question is whether new metaheuristic algorithms are still necessary despite the variety that already exists. The No Free Lunch (NFL) theorem [23] addresses this concern by stating that there is no one universal metaheuristic algorithm that can outperform all others for every optimization problem. This means that the effectiveness of a metaheuristic algorithm for one set of optimization challenges does not guarantee a similar success for a different set. Therefore, the outcome of implementing a metaheuristic algorithm in an optimization scenario cannot be predicted as a definite success or failure. As per the NFL theorem, it is possible for an algorithm to achieve the best solution when dealing with one optimization problem, but it may get trapped in a local optimum when faced with another problem. The NFL theorem promotes ongoing research in metaheuristic algorithms, pushing researchers to develop innovative approaches to solving optimization problems effectively. This theorem has inspired the authors of this paper to introduce a novel metaheuristic algorithm for addressing optimization challenges.

Motivated by the NFL theorem, the aspects of innovation, novelty, and originality of this paper are in introducing a new metaheuristic algorithm called Wombat Optimization Algorithm (WOA) that imitates the behavior of wombats in their habitat.

What is evident from the best knowledge obtained from the literature review, so far, is that no metaheuristic algorithm has been designed based on the simulation of wombats’ natural behaviors. Meanwhile, the activity of foraging and the escaping strategy from predators are intelligent processes among wombats that have a special potential in the design of a new optimizer. In order to address this research gap in the studies of metaheuristic algorithms, in this paper, a new biomimetics metaheuristic algorithm is designed based on the mathematical modeling of wombats’ natural behaviors in the wild.

The key contributions of this paper are as listed:

• WOA is designed based on simulating wombat’s natural behaviors in the wild.
• The basic inspiration of WOA is taken from the foraging of the wombat and the strategy of this animal when escaping from its predators.
• The theory of WOA is expressed and mathematically modeled in two phases: (i) the exploration based on the simulation of wombat movements during foraging and (ii) the exploitation based on simulating wombat movements when it dives towards nearby tunnels to defend against its predators.
• The capability of WOA in optimization applications has been evaluated in the CEC 2017 test suite for problem dimensions equal to 10, 30, 50, and 100.
• WOA’s ability to tackle optimization tasks in real-world applications has been evaluated on twenty-two constrained optimization problems from the CEC 2011 test suite and four engineering design problems.
• Two well-known metaheuristic algorithms are employed to compare with the performance of WOA.

This paper is organized in the following manner: firstly, a literature review is outlined in Section 2. Next, the proposed Wombat Optimization Algorithm (WOA) is introduced and outlined in Section 3. Section 4 covers simulation studies and their results. The efficacy of WOA in addressing real-world applications is explored in Section 5. Lastly, conclusions and recommendations for future research are detailed in Section 6.

2. Literature Review

Metaheuristic algorithms have drawn on influences from various natural sources, including swarm behavior in the animal kingdom, principles of biology and genetics, concepts from the field of physics, studies of human behavior, and evolutionary occurrences. These algorithms can be categorized into five distinct groups based on the design inspiration they exhibit: swarm-based, evolutionary-based, physics-based, human-based, and game-based approaches.

Swarm-based metaheuristic algorithms are inspired by the natural swarming behaviors of various animals in their design, including insects, birds, aquatic creatures, reptiles, and other wildlife species. Among the most famous swarm-based metaheuristic algorithms are: Ant Colony Optimization (ACO) [24], Particle Swarm Optimization (PSO) [25], Firefly Algorithm (FA) [14,26], and Artificial Bee Colony (ABC) [27]. ACO used in its design the skill of ants in finding the optimal communication path between the colony and the food source. PSO is inspired in its design by the search process in the movement of fish and birds with the aim of finding food sources. FA is developed inspired by the optical communication and information exchange between fireflies. The butterfly optimization algorithm (BA) is an advanced metaheuristic for optimization created by Arora that draws inspiration from biology, which is centered on the behavior of butterflies when they are seeking food [28]. ABC is designed based on modeling the hierarchical cooperation and activities of colony bees to obtain food resources. Mantis Search Algorithm (MSA) is developed based on modeling the sexual cannibalism and hunting behavior of praying mantises [29]. Genghis Khan Shark Optimizer (GKSO) is inspired, in its design, by the Genghis Khan shark’s hunting and self-defense strategy in the wild [30]. Gazelle Optimization Algorithm (GOA) uses, in its design, gazelles’ survival ability in their predator-dominated environment [31]. Among natural behaviors in wildlife, foraging, hunting strategy, survival efforts, chasing processes, digging, and migration are very significant; they are employed as sources of inspiration in the design of algorithms such as: Whale Algorithm (WA) [32], Reptile Search Algorithm (RSA) [33], Orca Predation Algorithm (OPA) [34], Grey Wolf Optimizer (GWO) [35], Tunicate Swarm Algorithm (TSA) [36], African Vultures Optimization Algorithm (AVOA) [37], Marine Predator Algorithm (MPA) [38], and White Shark Optimizer (WSO) [39].

Evolutionary metaheuristic algorithms draw upon principles from biology and genetics, incorporating ideas such as natural selection, survival of the fittest, Darwin’s theory of evolution, and other related evolutionary principles in their design. Among the most popular evolutionary-based metaheuristic algorithms are Genetic Algorithm (GA) [40] and Differential Evolution (DE) [41]. GA and DE use, in their design, a simulation of the reproduction process, and apply genetic and biological concepts such as mutation, selection, and crossover. The basic inspiration in the design of Artificial Immune System (AIS) comes from the mechanism of the human body’s defense system against microbes and diseases [42]. Some other evolutionary-based metaheuristic algorithms are: Cultural Algorithm (CA) [43], Genetic programming (GP) [44], and Evolution Strategy (ES) [45].

Physics-based metaheuristic algorithms are use their design of phenomena, transformations, processes, forces, laws, and other concepts of physics. Simulated Annealing (SA) is one of the most widely used physics-based metaheuristic algorithms. The main idea in the design of SA comes from the physical transformations in the metal annealing process, where with the aim of achieving the ideal crystal, the metals are first melted under heat, then slowly cooled and frozen [46]. Gravitational Search Algorithm (GSA) [47] is inspired by modeling the gravitational attraction between objects at different distances. Fick’s Law Optimization (FLA) is designed based on the modeling of Fick’s first law of diffusion, which according to this law, molecules tend to diffuse from higher to lower concentration areas [48]. Rime (RIME) algorithm is designed with inspiration from the physical phenomenon of rime-ice [49]. Some other physics-based metaheuristic algorithms are: Thermal Exchange Optimization (TEO) [50], Water Cycle Algorithm (WCA) [51], Nuclear Reaction Optimization (NRO) [52], Henry Gas Optimization (HGO) [53], Lichtenberg Algorithm (LA) [54], Multi-Verse Optimizer (MVO) [55], Electro-Magnetism Optimization (EMO) [56], Black Hole Algorithm (BHA) [57], and Archimedes Optimization Algorithm (AOA) [58].

Human-based metaheuristic algorithms use, in their design, behaviors, choices, thoughts, decisions, teaching and learning processes, and other human activities in individual and social life. Teaching-Learning Based Optimization (TLBO) [59] can be mentioned among the most widely used human-based metaheuristic algorithms. TLBO uses the modeling of educational communication and knowledge exchange in the classroom environment between the teacher and students and students with each other. Mother Optimization Algorithm (MOA) is proposed with inspiration from Eshrat’s care of her children [60]. Mountaineering Team-Based Optimization (MTBO) is developed with the inspiration of social behavior and human cooperation needed to reach a mountaintop [61]. Deep Sleep Optimizer (DSO) is developed inspired by the sleeping patterns of humans and is based on modeling the fall and rise of homeostatic pressure during the human sleep process [62]. Some other human-based metaheuristic algorithms are: Gaining Sharing Knowledge based Algorithm (GSK) [63], Fireworks Algorithm (FA) [64], War Strategy Optimization (WSO) [65], Coronavirus Herd Immunity Optimizer (CHIO) [66], and Ali Baba and the Forty Thieves (AFT) [67].

Game-based metaheuristic algorithms use, in their design, the rules of individual and team games as well as the behavior of players, coaches, runners, and other influential people in these games. Volleyball Premier League (VPL) [68] and Running City Game Optimizer (RCGO) [69] are examples of game-based metaheuristic algorithms.

Supply chain management (SCM) has evolved from a simple logistical process to a critical strategic tool for businesses worldwide. It involves the coordination of various activities, including procurement, production, inventory management, and distribution, to ensure the smooth flow of goods and services from suppliers to end customers. This holistic approach to managing the flow of materials, information, and finances across the entire supply chain has become indispensable in today’s competitive business environment [70]. With the increasing complexity and dynamic nature of modern supply chains, traditional optimization techniques often fall short in providing optimal solutions within reasonable time frames. This has led to the emergence of metaheuristic algorithms as powerful optimization tools capable of addressing the challenges posed by real-world SCM problems [71]. Unlike traditional optimization methods, which may get stuck in local optima, metaheuristics offer robust and flexible approaches for finding high-quality solutions in a reasonable amount of time [72]. The application of metaheuristic algorithms in SCM is vast and encompasses various areas such as inventory management, facility location, vehicle routing, production scheduling, and supply chain network design. For example, metaheuristic algorithms can be used to optimize inventory replenishment policies, minimize transportation costs, balance production capacities, and design resilient supply chain networks [73].

An overview of the applications of metaheuristic algorithms in dealing with SCM is presented in Table 1.

Table 1. Applications of metaheuristic algorithms on SCM problem.

	Reference	Description	Year
1	[14]	This paper conducts a comprehensive comparison study of the Firefly algorithm’s performance using various test functions, emphasizing its application in the lot size optimization within supply chain management. Demonstrating a superior performance over deterministic methods, the Firefly algorithm efficiently addresses the complexities arising from cost minimization and service level maximization conflicts in the supply chain evolution.	2018
2	[74]	This paper introduces a closed-loop supply chain network configuration model addressing research gaps, and employs an innovative metaheuristic algorithm called improved PSO (IPSO) for location-allocation decisions and a gradient descent search method for pricing–inventory decisions. IPSO, integrating mutation and replicator dynamics, demonstrates a superior performance compared to traditional PSO, simulated annealing (SA), and genetic algorithm (GA) methods; this is confirmed through numerical evaluations across various problem scales.	2018
3	[75]	This paper addresses a distribution–allocation problem in a two-stage supply chain, formulating it as an integer–programming model to minimize total supply chain operation costs. Employing an Ant Colony Optimization (ACO), the study demonstrates computational efficiency in obtaining solutions within a reasonable time frame, with an average gap of approximately 10% from optimal solutions.	2018
4	[76]	This paper presents an enhanced artificial bee colony (ABC) optimization algorithm tailored for supply chain network (SCN) management, addressing the challenge of finding multi-objective Pareto optimal solutions (POS) efficiently. By extending the application field of SCN based on complex networks and integrating a naive Bayes classifier to accelerate the search speed, the proposed approach demonstrates its capability in optimizing a three-echelon SCN, achieving a global multi-objective POS while improving the solution-finding speed.	2019
5	[77]	This paper introduces a bi-level optimization model for rice supply chain management, aiming to minimize the total cost while considering the perspectives of two decision-makers. Utilizing meta-heuristic algorithms such as Genetic Algorithm (GA) and Particle Swarm Optimization (PSO), along with hybrid and modified versions, this study demonstrates the effectiveness of the proposed model in optimizing the rice supply chain, with the modified algorithm (GPA) showing promising results.	2019
6	[78]	This paper addresses the evolving role of inventory management in the context of supply chain management, emphasizing the need for new strategies to enhance the supply chain integration and agility. By leveraging the system theory and integration theory, this paper proposes an optimized inventory management model utilizing ant colony algorithm and fuzzy model that aim to improve the supply chain efficiency and market responsiveness.	2019
7	[79]	This paper presents a hybrid algorithm combining a genetic algorithm and particle swarm optimization to optimize supply chain scheduling in a mass customization mode, leveraging the genetic algorithm’s global search capability and the particle swarm optimization’s fast convergence speed.	2019
8	[80]	This paper introduces an enhanced African Buffalo Optimization (ABO) algorithm for petroleum supply chain distribution, leveraging swarm intelligence to optimize product scheduling and distribution costs. By applying standard ABO and its improved variants, such as chaotic ABO and chaotic-Levy ABO, it demonstrates a superior performance compared to existing exact algorithms, offering efficient solutions for complex real-world supply chain networks.	2020
9	[81]	This paper addresses the challenges of perishable product management in supply chains, proposing a holistic model integrated with the improved bacteria-forging algorithm (IBFA) to optimize production, inventory, and distribution processes. Through two case studies, the IBFA demonstrates effectiveness in optimizing perishable supply chain networks, offering valuable insights for decision-makers in managing time-sensitive products efficiently.	2020
10	[82]	This paper presents a risk-based optimization framework for supply chain management, addressing strategic, tactical, and operational decisions to mitigate internal and external risks. Utilizing a new genetic algorithm integrated with an artificial neural network, it effectively minimizes supply–demand mismatches and reduces inventory levels, enhancing the profitability compared to traditional techniques and regular genetic algorithms.	2020
11	[83]	This paper introduces a novel multi-level serial closed-loop supply chain model, incorporating batch deliveries, a quality-dependent return rate, a random defective rate, a rework process, and learning effects, particularly focusing on the impact of learning on inventory control. It employs metaheuristic algorithms such as a genetic algorithm, invasive weed optimization algorithm, and moth flame optimization algorithm to address the complexity of the proposed model, demonstrating the significant influence of the learning effect on the manufacturing/remanufacturing time and system costs in closed-loop supply chain problems.	2021
12	[84]	This paper introduces a novel approach for a dual-channel, multi-product, multi-period, multi-echelon closed-loop supply chain network design (SCND) under uncertainty, specifically tailored for the tire industry. It utilizes a fuzzy approach to handle uncertain parameters and proposes two hybrid meta-heuristic algorithms, integrating red deer and whale optimization algorithms with a genetic algorithm and simulated annealing, respectively; this demonstrates their effectiveness in delivering high-quality solutions within a reasonable computational time.	2021
13	[85]	This paper presents a location-inventory optimization model for supply chain configuration, addressing stochastic customer demand and replenishment lead time. It employs a two-phase approach integrating the queuing theory and stochastic optimization to determine optimal distribution center locations and inventory policies, with a hybrid genetic algorithm designed to handle the NP-hard complexity of the problem; this offers a computationally tractable solution for supply chain optimization.	2021
14	[86]	This paper aims to optimize economic and environmental dimensions in a sustainable supply chain network through a mixed-integer linear programming (MILP) model, integrating sustainable supplier selection and performance optimization. Utilizing multi-objective genetic and particle swarm algorithms, it achieves a balance between cost minimization, time efficiency, and sustainability indexes, offering robust solutions for supply chain managers seeking to enhance their sustainability performance.	2021
15	[87]	This paper introduces a sustainable Closed-Loop Supply Chain Network (CLSCN) design for the olive industry, integrating economic, environmental, and social factors through a multi-objective optimization framework. It proposes novel hybrid optimization algorithms, including the Virus Colony Search (VCS) algorithm with simulated annealing (SA) and Electromagnetism-like Algorithm (EMA) with Genetic Algorithm (GA), demonstrating a superior efficiency in addressing the complex challenges of large-scale networks, which offer valuable insights for supply chain managers in the olive industry.	2022
16	[88]	This paper explores the utilization of the Particle Swarm Optimization (PSO) algorithm for the supply chain network design, and aims to optimize network configurations and improve operational efficiency. By leveraging PSO, the study offers insights into enhancing supply chain network design processes through efficient optimization techniques.	2022
17	[89]	This paper introduces a hybrid MDE_Restart and modified differential evolution (MDE) tailored for designing closed-loop supply chain networks, considering quantity discounts and fixed-charge transportation. By incorporating these algorithms, the algorithms efficiently optimize supply chain network configurations, addressing cost-saving strategies and logistical complexities.	2022
18	[90]	This paper focuses on designing a novel supply chain network by considering transportation delays and employing meta-heuristic techniques. It explores the application of meta-heuristics to optimize the supply chain network design, taking into account transportation delays for enhanced efficiency and performance.	2022
19	[91]	This paper introduces a novel metaheuristic approach tailored for a multi-objective supply chain network design, hybridizing a simulated annealing, tabu search, and variable neighborhood algorithms, along with linear programming. By combining these techniques, the approach aims to leverage the strengths of each algorithm, enhancing the solution quality and efficiency in supply chain network optimization.	2023
20	[92]	This paper presents a hybrid metaheuristic approach combining a greedy randomized adaptive search procedure (GRASP) and genetic algorithm (GA) integrated with a learning component to address a real-world supply chain scheduling problem effectively. By combining metaheuristic techniques with learning mechanisms, it offers a robust solution framework tailored to enhance scheduling efficiency in complex supply chain environments.	2023
21	[93]	This paper applies an improved multi-objective particle swarm optimization algorithm to address disruptions in the two-stage vehicle routing problem with time windows. By leveraging enhanced optimization techniques, it effectively balances multiple objectives, ensuring efficient routing solutions despite disruptions, and thus enhances the overall supply chain performance.	2023
22	[94]	This paper proposes the integration of the Grey Wolf Optimizer and Whale Optimization Algorithm to address stochastic inventory management challenges in a two-level supply chain for reusable products. By combining both algorithms, it enhances inventory control strategies, optimizing stock levels and minimizing costs in dynamic supply chain environments.	2023
23	[95]	This paper introduces a multi-objective dragonfly algorithm tailored for optimizing sustainable supply chains, particularly under resource-sharing conditions. By employing the dragonfly algorithm, it efficiently balances multiple objectives, enhancing sustainability practices in supply chain management through an optimized resource allocation.	2024
24	[96]	This paper presents a hybrid meta-heuristic approach aimed at designing a bi-objective cosmetic tourism supply chain, demonstrating its applicability through a case study. By leveraging meta-heuristic methods, it offers an optimized framework to balance the cost-efficiency and service quality within the cosmetic tourism sector.	2024
25	[97]	This paper proposes a hybrid whale optimization algorithm tailored for optimizing limited capacity vehicle routing in supply chain management. By integrating whale optimization techniques, it enhances routing efficiency, and addresses constraints and complexities inherent in supply chain logistics.	2024

3. Wombat Optimization Algorithm

In this section, first, the basic inspiration employed in designing the proposed Wombat Optimization Algorithm (WOA) approach is described, then its implementation steps are mathematically modeled.

3.1. Inspiration of WOA

A wombat is a short-legged, muscular quadrupedal marsupials of the family Vombatidae, which is native to Australia [98]. This animal is adaptable and habitat tolerant, and lives in heathland, mountainous, and forested areas of eastern and southern Australia, as well as in an isolated patch in Epping Forest National Park in central Queensland [99]. The appearance characteristics of wombats are as follows: their fur color can vary from gray to black or from a sandy color to brown. Wombats are about 1 m long and weigh between 17 and 39 kg [99,100]. An image of the wombat is shown in Figure 1.

Figure 1. Wombat taken from: free media Wikimedia Commons.

The wombat is an herbivore animal whose main diet is grass and also feeds on roots, bark, herbs, and sedges. Wombats have adapted to survive in habitats with limited nutrition and low food availability. Using the burrows permits wombats to maximize their foraging range and creates a thermally stable environment that helps in the maintenance of a low metabolic rate. Their energy-efficient foraging strategies and low metabolic rates lead to very low energy requirements, allowing them to survive on low-quality food and inhabit areas of scarce food availability. Although wombats can subsist on low-quality diets, their survival still relies on the availability of a habitat that provides adequate nutrition, as nutritional stress increases the risk of illness and death for animals [101].

Wombats have great skill and ability in digging. They dig extensive burrow systems with their powerful claws and rodent-like front teeth. The backward-facing pouch is a special distinctive adaptation in wombats. This pouch has the advantage of the wombat not collecting soil on its young in the pouch while digging. In addition to the effect of an increased foraging range, these excavated tunnels are a suitable defensive position for wombats when they are attacked by their predators. Wombats are slow animals and move slowly; however, when attacked and threatened, they run away at a speed of 40 km/h. Tasmanian and Dingos are the main predators of wombats. When a wombat is attacked by a predator, it dives into one of the nearby tunnels and uses its rump to stop the pursuing predator. The main defense of wombats is their toughened rear hide, with most of the posterior made of cartilage. This feature, as well as not having a substantial tail, makes the stalking predator who enters the tunnel unable to bite the wombat and hunt it [99].

Among the wombat’s natural behaviors and lifestyles in the wild, two stand out the most: (i) their extensive foraging activity in the wild and (ii) their escape strategy from predators by diving into nearby tunnels. The mathematical modeling of these intelligent processes in the wombat lifestyle was employed in order to design a new metaheuristic algorithm called Wombat Optimization Algorithm (WOA), which is presented below.

3.2. Algorithm Initialization

The proposed WOA approach is a population-based metaheuristic algorithm, where wombats form the population members of the algorithm. In order to visualize and create a mentality, the habitat of wombats in the wild corresponds to the problem-solving space, and the position of each wombat in this habitat corresponds to the position of a candidate solution in the problem-solving space. Each wombat determines values for decision variables based on its position in the problem-solving space. Therefore, each wombat as a WOA member corresponds to a candidate solution to the problem that can be mathematically modeled using a vector. The community of wombats in the form of these vectors together makes the WOA population, which can be mathematically modeled using a matrix according to Equation (1). At the beginning of the implementation of the algorithm, the position of each wombat in the problem-solving space is randomly initialized using Equation (2).

$$X={\left[\begin{array}{c}{X}_1\\ ⋮\\ X_i\\ ⋮\\ X_N\end{array}\right]}_{N\times m}={\left[\begin{array}{ccccc}{x}_{\mathrm{1,1}}& \cdots & x_{1,d}& \cdots & x_{1,m}\\ ⋮& \ddots & ⋮& ⋰& ⋮\\ x_{i,1}& \cdots & x_{i,d}& \cdots & x_{i,m}\\ ⋮& ⋰& ⋮& \ddots & ⋮\\ x_{N,1}& \cdots & x_{N,d}& \cdots & x_{N,m}\end{array}\right]}_{N\times m}$$

(1)

$$x_{i,d}=l{b}_d+r·(u{b}_d-l{b}_d)$$

(2)

Here, $X$ is the WOA population matrix, $X_i$ is the $i$th wombat (i.e., candidate solution), $x_{i,d}$ is its $d$th dimension in the search space (i.e., decision variable), $N$ is the number of wombat population, $m$ is the number of decision variables, $r$ is a random number in interval $\left[0, 1\right]$, and ${lb}_d$ and ${ub}_d$ are the lower bound and upper bound of the $d$th decision variable, respectively.

As stated, the position of each wombat represents a candidate solution to the problem. Therefore, the objective function of the problem corresponding to each wombat can be evaluated. The set of evaluated values for the objective function of the problem can be represented using a vector using Equation (3).

$$F={\left[\begin{array}{c}{F}_1\\ ⋮\\ F_i\\ ⋮\\ F_N\end{array}\right]}_{N\times 1}={\left[\begin{array}{c}F\left(X_1\right)\\ ⋮\\ F\left(X_i\right)\\ ⋮\\ F\left(X_N\right)\end{array}\right]}_{N\times 1}$$

(3)

Here, $F$ is the vector of the evaluated objective function and $F_i$ is the evaluated objective function based on the $i$th wombat.

The evaluated values for the objective function are considered as a suitable criterion for measuring the quality of candidate solutions and population members. Thus, the best evaluated value for the objective function corresponds to the best WOA member, and the worst value obtained for the objective function corresponds to the worst WOA member. Since the position of the wombats in the problem-solving space is updated in each iteration, the best member of the population must also be updated in each iteration.

3.3. Mathematical Modelling of WOA

The proposed approach of WOA is able to provide suitable solutions for optimization problems in an iteration-based process based on the searching power of its members in the problem-solving space. The design of WOA was inspired by the natural behavior of wombats in nature. In the WOA design, the position of the wombats in the problem-solving space is updated in each iteration in two phases: (i) an exploration based on the simulation of the foraging process of the wombats and (ii) an exploitation based on the simulation of the strategy of the wombats escaping from their predators towards the tunnels. The full description and mathematical model of each of these phases of updating the position of wombats in the problem-solving space is presented below.

3.3.1. Phase 1: Foraging Process (Exploration Phase)

In the first phase of WOA, the position of wombats in the problem-solving space is updated based on the simulation of this animal’s foraging strategy. The wombat is a herbivorous animal that has a high searching power for finding forage in a wide range of its habitat. Modeling the position change of the wombat while moving towards forage leads to the creation of extensive changes in the position of WOA members in the problem-solving space and, as a result, increasing the exploration power of the algorithm in order to manage the global search. In the WOA design, for each wombat, the position of other population members that have a better value for the objective function is considered as the forage position. The set of forage positions for each wombat is identified using Equation (4).

$$C{FP}_i=\left\{X_k:F_k<F_i \mathrm{a}\mathrm{n}\mathrm{d} k\ne i\right\}, \mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e} i=\mathrm{1,2}, \dots , N \mathrm{a}\mathrm{n}\mathrm{d} k\in \left\{\mathrm{1,2}, \dots , N\right\}$$

(4)

Here, $C{FP}_i$ is the set of candidate forage positions for the $i$th wombat, $X_k$ is the population member with a better objective function value than the $i$th wombat, and $F_k$ is its objective function value.

In the design of WOA, it is assumed that the wombat chooses one of these fodder positions completely randomly and moves towards it. Based on the modeling of the wombat’s movement towards the selected forage in this foraging process, a new position for each WOA member is calculated using Equation (5). This new position, if it leads to the improvement of the objective function value, replaces the previous position of the corresponding member using Equation (6).

$$x_{i,j}^{P1}=x_{i,j}+r_{i,j} ·({SFP}_{i,j}-I_{i,j}·x_{i,j}),$$

(5)

$$X_i=\left\{\begin{array}{cc}\hfill X_i^{P1},& F_i^{P1}\le F_i,\hfill \\ \hfill X_i,& else,\hfill \end{array}\right.$$

(6)

Here, $S{FP}_i$ is the selected forage position for the $i$th wombat, $S{AFP}_{i,j}$ is its $j$th dimension, $X_i^{P1}$ is the new position calculated for the $i$th wombat based on the foraging phase of the proposed WOA, $x_{i,j}^{P1}$ is its $j$th dimension, $F_i^{P1}$ is its objective function value, $r_{i,j}$ are random numbers from the interval $\left[0, 1\right]$, and $I_{i,j}$ are numbers which are randomly selected as 1 or 2.

3.3.2. Phase 2: Escape Strategy (Exploitation Phase)

In the second phase of WOA, the position of wombats in the problem-solving space is updated based on the simulation of the escape strategy of this animal against the attacks of its predators. The wombat, with its high digging ability, makes many tunnels in its habitat. When the wombat is in danger and attacked by a predator, it escapes by diving towards one of the tunnels located near it and tries to save itself. Modeling the wombat’s position change while escaping from the predator towards the tunnel leads to small changes in the position of the WOA members in the problem-solving space, and, as a result, increases the exploitation power of the algorithm in order to manage the local search.

In the WOA design based on the modeling of the wombat’s position change and dive towards the nearby tunnel, a new position for each member of the WOA is calculated using Equation (7). This new position, if it leads to the improvement of the value of the objective function, replaces the previous position of the corresponding member using Equation (8).

$$x_{i,j}^{P2}=x_{i,j}+\left(1-2 r_{i,j}\right)· \frac{u{b}_j-l{b}_j}{t}$$

(7)

$$X_i=\left\{\begin{array}{cc}\hfill X_i^{P2},& F_i^{P2}\le F_i\hfill \\ \hfill X_i,& else\hfill \end{array}\right.$$

(8)

Here, $X_i^{P2}$ is the new position calculated for the $i$th wombat based on the escape phase of the proposed WOA, $x_{i,j}^{P2}$ is its $j$th dimension, $F_i^{P2}$ is its objective function value, $r_{i,j}$ are random numbers from the interval $\left[0, 1\right]$, and $t$ is the iteration counter.

3.4. Repetition Process, Pseudocode, and Flowchart of WOA

The first iteration of WOA is completed after updating the position of all wombats in the problem-solving space based on foraging and escape phases. After that, with the updated values, the algorithm enters the next iteration; the process of updating the position of wombats in the problem-solving space continues until the last iteration of the algorithm based on Equations (4)–(8). In each iteration, the position of the best wombat is identified and stored as the best candidate solution. After the full implementation of the algorithm, the best candidate solution obtained during the iterations of the algorithm is presented as the WOA solution for the given problem.

Different criteria can be considered as the stopping condition of the algorithm. Among these criteria, we can mention: (i) the maximum number of algorithm iterations—in this case, the algorithm stops after passing the specified number of iterations; (ii) the maximum number of objective function evaluations (FEs)—in this case, after the number of evaluations of the objective function reaches the maximum number of FEs (MFEs), which is specified at the beginning of the implementation, the algorithm stops; (iii) the error determined between the successive solutions obtained—in this case, when the difference between the solutions obtained during several iterations of the algorithm is very small, based on the comparison of this difference with a “specified value”, the algorithm stops.

The implementation steps of WOA are shown as a flowchart in Figure 2, and the WOA pseudocode is presented in Algorithm 1.

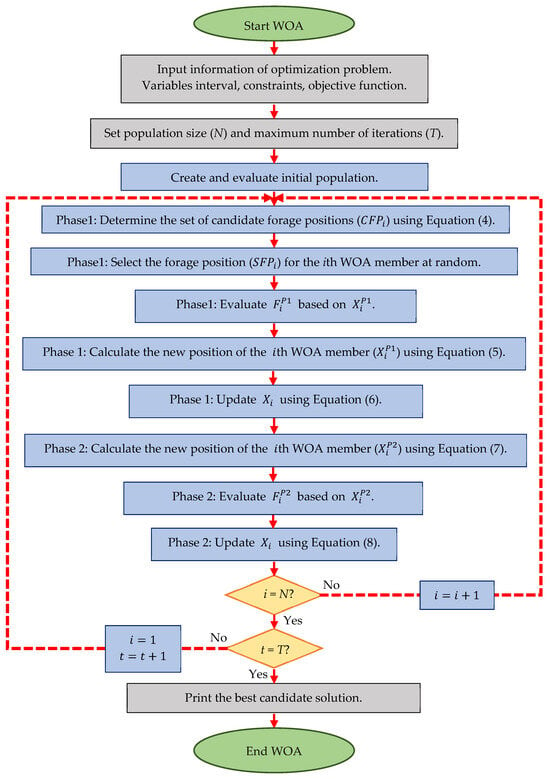
Figure 2. Flowchart of WOA.

Algorithm 1. Pseudocode of WOA
Start WOA.
1.	Input problem information: variables, objective function, and constraints.
2.	Set WOA population size (N) and iterations (T).
3.	Generate the initial population matrix at random using Equation (2). $x_{i,d}\leftarrow l{b}_d+r·(u{b}_d-l{b}_d)$
4.	Evaluate the objective function.
5.		For $t=1$ to T
6.			For $i=1$ to $N$
7.			Phase 1: foraging process (exploration phase)
8.				Determine the candidate foraging positions set for the ith wombat using Equation (4). $C{FP}_i\leftarrow \left\{X_{k_i}:F_{k_i}<F_i \mathrm{a}\mathrm{n}\mathrm{d} k_i\ne i\right\}$
9.				Select the target foraging position for the ith wombat at random.
10.				Calculate new position of ith wombat using Equation (5). $x_{i,d}^{P1}\leftarrow x_{i,d}+r·\left(S{FP}_{i,d}-I·x_{i,d}\right)$
11.				Update ith wombat using Equation (6). $X_i\leftarrow \left\{\begin{array}{cc}\hfill X_i^{P1},& F_i^{P1}<F_i\hfill \\ \hfill X_i,& else\hfill \end{array}\right.$
12.			Phase 2: escape strategy (exploitation phase)
13.				Calculate new position of ith wombat using Equation (7). $x_{i,d}^{P2}\leftarrow x_{i,d}+(1-2r)·\frac{\left(u{b}_d-l{b}_d\right)}{t}$
14.				Update ith wombat using Equation (8). $X_i\leftarrow \left\{\begin{array}{cc}\hfill X_i^{P2},& F_i^{P2}<F_i\hfill \\ \hfill X_i,& else\hfill \end{array}\right.$
15.			end
16.			Save the best candidate solution so far.
17.		end
18.	Output the best quasi-optimal solution obtained with the WOA.
End WOA.

3.5. Computational Complexity of WOA

In this subsection, the computational complexity of the proposed WOA approach is evaluated. The preparation and initialization steps of WOA have a computational complexity equal to O(Nm), where N is the number of wombats and m is the number of decision variables of the problem. In each iteration, the position of the wombats in the problem-solving space is updated in two phases: foraging and escape. Therefore, the process of updating the position of wombats has a computational complexity equal to O(2NmT), where T is the maximum number of iterations of the algorithm. According to this, the total computational complexity of the proposed WOA approach is equal to O(Nm(1 + 2T)).

4. Simulation Studies and Results

In this section, the ability of WOA to tackle optimization problems is evaluated on the CEC 2017 test suite.

4.1. Performance Comparison

Twelve well-known metaheuristic algorithms consisting of GA [40], PSO [25], GSA [47], TLBO [59], MVO [55], GWO [35], WA [32], MPA [38], TSA [36], RSA [33], AVOA [37], and WSO [39] are employed to compete with the performance of WOA. The simulation results are presented using six statistical indicators: mean, best, worst, standard deviation (std), median, and rank.

Considering that in order to optimize each of the benchmark functions, metaheuristic algorithms are used in several independent implementations, the statistical indicators are described as follows:

• Mean: represents the average values obtained for the objective function from independent executions.
• Best: indicates the best value obtained for the objective function among the values obtained from independent executions.
• Worst: represents the worst value obtained for the objective function among the values obtained from independent executions.
• std: represents the standard deviation between the values obtained for the objective function from independent runs.
• Median: represents the median index between the values obtained for the objective function from independent executions.
• Rank: indicates the rank of each metaheuristic algorithm in competition with other metaheuristic algorithms in dealing with the corresponding benchmark function. The evaluated values for the mean index have been applied as a ranking criterion for metaheuristic algorithms in handling each of the benchmark functions.

It should be mentioned that in order to provide a fair comparison, in the simulation studies, the original versions of competing algorithms published by their main researchers have been used. Also, regarding GA and PSO, the standard versions published by Professor Seyed Ali Mirjalili have been used. Also, the complete information and details about the experimental test suites and their optimal values are available in their respective references introduced in each subsection.

4.2. Evaluation CEC 2017 Test Suite

In this subsection, the ability of WOA and competitor algorithms to tackle the CEC 2017 test suite is challenged. The CEC 2017 test suite consists of thirty benchmark functions, as follows: (i) three unimodal functions of C17-F1 to C17-F3, (ii) seven multimodal functions of C17-F4 to C17-F10, (iii) ten hybrid functions of C17-F11 to C17-F20, and (iv) ten composition functions of C17-F21 to C17-F30. Among the functions of this test suite, C17-F2 is not considered in simulation studies due to its unstable behavior (as with all similar papers). Complete information, details, and descriptions of the CEC 2017 test suite are available at [102]. Based on the mentioned reference, the CEC 2017 test suite is designed to evaluate the performance of metaheuristic algorithms in handling optimization problems. Also, in order to provide a scalability analysis, it is recommended that this evaluation be conducted for the problem size equal to 10, 30, 50, and 100. The WOA approach along with competitor algorithms are employed in handling the CEC 2017 test suite in fifty-one independent runs, where each run consists of 10,000 m function evaluations (FEs), where m is the number of problem dimensions.

The implementation results of the WOA and competitor algorithms, in order to tackle the CEC 2017 test suite, are reported in Table 2, Table 3, Table 4 and Table 5. The boxplot diagrams obtained from the implementation of metaheuristic algorithms in the CEC 2017 test suite are plotted in Figure 3, Figure 4, Figure 5 and Figure 6. What is evident based on the analysis of simulation results and the performance of metaheuristic algorithms, in handling the CEC 2017 test suite for the problem dimension equal to 10 (m = 10), is that WOA has been the first best optimizer for the functions C17-F1, C17-F3 to C17-F21, C17-F23, C17-F24, and C17-F26 to C17-F30. For the problem dimension equal to 30 (m = 30), the proposed WOA approach is the first best optimizer for functions C17-F1, C17-F3 to C17-F22, C17-F24, C17-F25, and C17-F27 to C17-F30. For the problem dimension equal to 50 (m = 50), the proposed WOA approach is the first best optimizer for functions C17-F1, C17-F3 to C17-F25, and C17-F27 to C17-F30. For the problem dimension equal to 100 (m = 100), the proposed WOA approach is the first best optimizer for functions C17-F1 and C17-F3 to C17-F30.

Table 2. Optimization results of CEC 2017 test suite (dimension = 10).

		WOA	WSO	AVOA	RSA	MPA	TSA	WA	MVO	GWO	TLBO	GSA	PSO	GA
C17-F1	mean	524.961	3.68 × 109	11,334,927	6.88 × 109	35,084,157	1.18 × 109	15,674,087	11,337,403	70,711,270	1.1 × 108	11,332,842	11,334,457	19,310,478
	best	100.1337	3.12 × 109	5502.3	5.98 × 109	11,140.13	2.51 × 108	3,927,333	9510.768	22,309.98	44,355,673	3666.026	3831.382	7,525,902
	worst	1643.927	4.61 × 109	41,171,813	8.19 × 109	1.27 × 108	2.56 × 109	44,332,889	41,178,924	2.57 × 108	2.39 × 108	41,171,769	41,172,250	50,095,279
	std	815.4352	7.07 × 108	21,743,683	1.09 × 109	67,320,940	1.11 × 109	20,897,376	21,746,650	1.36 × 108	95,173,739	21,744,868	21,743,910	22,413,972
	median	177.8917	3.5 × 109	2,081,197	6.68 × 109	6,430,710	9.61 × 108	7,218,063	2,080,588	12,960,037	79,143,997	2,077,968	2,080,873	9,810,366
	rank	1	12	4	13	8	11	6	5	9	10	2	3	7
C17-F3	mean	300.0133	5557.276	656.894	6946.686	1400.974	7992.835	1617.886	655.6564	2519.006	942.4917	7357.19	655.6196	10,395.98
	best	300.0059	3581.433	457.7548	4316.696	788.3982	3686.656	697.5888	457.7633	1284.363	572.9928	4624.991	457.7548	3742.932
	worst	300.0269	7096.024	1020.343	8967.983	2521.695	10,914.74	2497.271	1017.701	4777.81	1370.432	9845.627	1017.617	16,177.44
	std	0.010542	1671.14	281.9285	2309.198	870.3135	3337.817	985.4242	281.1508	1754.111	380.3548	2325.601	281.1151	7133.237
	median	300.0103	5775.823	574.7391	7251.033	1146.902	8684.974	1638.342	573.5806	2006.926	913.2708	7479.071	573.5532	10,831.78
	rank	1	9	4	10	6	12	7	3	8	5	11	2	13
C17-F4	mean	400.0001	751.2581	405.3619	1042.661	406.6922	520.9873	419.1006	404.4076	410.0676	408.3385	405.2283	415.8432	412.0756
	best	400	586.876	401.9679	703.3198	402.434	453.5618	406.6237	402.2056	404.8878	407.2968	403.3221	400.8574	409.9993
	worst	400.0001	900.4412	407.4674	1375.483	411.3215	597.1338	450.3308	406.3686	422.7592	409.3592	407.1639	450.4723	415.491
	std	5.78 × 10−5	152.6885	2.677108	312.0505	4.771091	76.66537	22.76622	1.921951	9.280025	1.249711	2.269339	25.33462	2.583055
	median	400.0001	758.8575	406.0061	1045.92	406.5066	516.6267	409.7239	404.528	406.3117	408.349	405.2136	406.0215	411.406
	rank	1	12	4	13	5	11	10	2	7	6	3	9	8
C17-F5	mean	501.2465	546.0639	534.1456	553.7107	512.9544	547.9623	532.0536	520.3087	513.0506	527.3509	540.8192	523.167	523.243
	best	500.9952	534.7172	522.2683	542.2803	508.392	534.761	519.3133	512.3122	508.6237	522.2608	536.0831	510.4081	519.8081
	worst	501.9918	552.3599	548.102	565.0885	518.0915	568.2777	554.9786	528.5494	519.6668	531.4124	547.4567	540.5667	528.8225
	std	0.54073	8.790434	14.05316	13.95646	5.549972	16.79014	17.81217	7.228481	5.293944	4.521172	5.229482	15.44505	4.31056
	median	500.9995	548.5892	533.1059	553.737	512.6671	544.4053	526.9612	520.1866	511.9559	527.8652	539.8686	520.8466	522.1708
	rank	1	11	9	13	2	12	8	4	3	7	10	5	6
C17-F6	mean	600	622.427	612.2172	628.1889	601.2043	617.3465	616.2108	601.8572	601.1587	605.0758	612.1393	605.4632	607.3961
	best	600	619.185	611.5093	625.8807	600.7171	610.5267	605.3716	600.5972	600.6819	603.4816	602.2599	601.1933	604.9474
	worst	600	625.5096	613.8456	630.9364	602.4192	627.8731	631.1437	603.7271	601.5874	607.7086	624.9582	613.9345	610.6874
	std	1.07 × 10−5	2.916798	1.19743	2.547556	0.883737	8.071126	11.75541	1.530068	0.464716	2.088418	11.51153	6.314501	2.755938
	median	600	622.5067	611.7571	627.9693	600.8405	615.4931	614.164	601.5523	601.1827	604.5565	610.6696	603.3624	606.9748
	rank	1	12	9	13	3	11	10	4	2	5	8	6	7
C17-F7	mean	711.1269	773.8425	752.7079	779.2108	724.7594	795.6833	750.3349	729.0217	725.6989	743.4845	719.6236	730.2951	733.1163
	best	710.6728	763.7127	739.358	771.616	720.5128	769.7413	741.4602	719.2818	718.4864	741.0113	717.5532	725.009	725.6534
	worst	711.7996	781.9515	770.3003	788.1838	729.2209	824.3351	770.0493	743.626	739.1095	749.3562	722.4981	738.5156	737.3097
	std	0.557349	8.20286	15.95527	8.430984	3.992319	25.77542	14.4834	11.23972	10.09514	4.278801	2.643607	6.336684	5.80094
	median	711.0176	774.8529	750.5867	778.5216	724.6519	794.3284	744.915	726.5895	722.5999	741.7853	719.2215	728.8279	734.751
	rank	1	11	10	12	3	13	9	5	4	8	2	6	7
C17-F8	mean	801.493	836.5212	825.3888	840.8137	812.7774	837.1173	828.9696	812.2052	814.9513	829.8901	817.6965	819.6812	815.5957
	best	800.9951	832.909	816.7434	833.08	808.9252	825.9835	817.4319	809.8082	810.071	825.6459	812.9463	815.4581	813.4852
	worst	801.9913	839.8716	836.8082	844.1263	814.9398	849.0655	837.2411	814.2366	818.9738	834.1117	821.7669	824.7868	819.6825
	std	0.625643	4.106245	9.089877	5.640705	3.021479	11.21621	9.411005	1.981852	4.121949	5.248666	4.306634	5.348324	3.024761
	median	801.4927	836.6521	824.0018	843.0243	813.6223	836.7101	830.6028	812.3881	815.3803	829.9015	818.0364	819.24	814.6075
	rank	1	11	8	13	3	12	9	2	4	10	6	7	5
C17-F9	mean	900.0001	1258.633	1098.563	1289.325	905.2467	1230.161	1226.46	902.2423	909.8499	909.7766	901.6947	904.5936	905.1876
	best	900	1154.645	936.8189	1222.699	900.3306	1084.935	1020.774	900.1655	900.4985	906.7986	900.1068	900.7778	903.7061
	worst	900.0002	1353.104	1424.462	1385.924	913.4677	1425.538	1416.941	904.3529	926.9905	914.1982	904.3501	908.9463	906.639
	std	7.79 × 10−5	94.16625	245.839	75.6181	6.435353	160.7559	181.196	2.39487	13.43242	3.417026	2.078648	3.688939	1.633171
	median	900	1263.392	1016.485	1274.339	903.5942	1205.086	1234.063	902.2255	905.9554	909.0547	901.161	904.3251	905.2027
	rank	1	12	9	13	6	11	10	3	8	7	2	4	5
C17-F10	mean	1006.185	2048.638	1692.933	2234.895	1516.181	1865.468	1860.324	1694.942	1657.459	1959.836	2031.652	1806.718	1650.865
	best	1000.291	1839.737	1453.377	2112.631	1390.911	1703.387	1464.124	1437.155	1490.811	1654.871	1835.794	1505.414	1440.627
	worst	1012.673	2158.672	2116.927	2501.24	1591.233	2041.845	2239.508	2057.339	1862.253	2179.157	2126.146	2105.82	1942.696
	std	7.243172	154.8632	323.4461	195.0429	102.7074	193.9076	389.1079	310.5663	166.8985	244.947	145.7272	269.4419	230.3456
	median	1005.888	2098.073	1600.713	2162.856	1541.291	1858.321	1868.831	1642.636	1638.385	2002.658	2082.333	1807.82	1610.069
	rank	1	12	5	13	2	9	8	6	4	10	11	7	3
C17-F11	mean	1100	2683.382	1141.513	3058.505	1127.007	4055.888	1143.172	1127.319	1146.088	1143.141	1135.218	1138.149	1975.904
	best	1100	1839.028	1127.583	1349.535	1113.181	3951.528	1127.72	1110.857	1118.875	1132.683	1128.479	1126.371	1129.13
	worst	1100.001	3501.686	1173.067	4740.709	1158.696	4106.402	1156.527	1137.324	1205.743	1153.139	1150.954	1162.916	4405.576
	std	0.000283	815.3282	23.12782	1661.682	23.39048	76.74835	14.47537	12.74923	44.16577	10.87845	11.5536	18.17365	1763.102
	median	1100	2696.406	1132.701	3071.889	1118.075	4082.811	1144.22	1130.547	1129.868	1143.371	1130.72	1131.655	1184.456
	rank	1	11	6	12	2	13	8	3	9	7	4	5	10
C17-F12	mean	1359.825	2.4 × 108	929,553.9	4.78 × 108	568,255.9	888,267	1,779,172	881,104.4	1,142,893	3,608,347	875,189.1	189,031.5	593,640.7
	best	1327.313	53,915,999	484,966.2	1.06 × 108	19,884.71	371,868.6	313,281.2	202,852.7	37,219	1,113,386	565,303.2	13,728.52	362,439
	worst	1448.931	4.19 × 108	1,359,296	8.36 × 108	889,303.6	1,107,630	2,934,334	2,197,536	1,788,904	6,350,176	1,176,097	296,681.6	920,789.6
	std	64.77141	2.01 × 108	496,292.9	4.02 × 108	416,840.9	377,092.8	1,261,767	976,176	840,175.8	2,935,492	295,957.3	134,450.5	296,135.4
	median	1331.529	2.43 × 108	93,6976.9	4.85 × 108	681,917.6	1,036,785	1,934,537	562,014.4	1,372,724	3,484,914	879,677.9	222,858	545,667.2
	rank	1	12	8	13	3	7	10	6	9	11	5	2	4
C17-F13	mean	1305.374	11,655,637	14,180.79	23,302,984	5439.062	10,388.91	6892.523	6316.144	8736.138	13,092.15	8581.79	6243.416	38,661.03
	best	1303.143	972,780.5	3993.255	1,935,730	3723.541	7241.321	4322.375	2751.979	5612.16	11,906.26	4996.23	3423.765	7889.229
	worst	1308.551	38,684,347	22,836.04	77,357,428	6652.159	14,879.49	11,845.78	10,488.98	11,899	14,978.26	11,762.01	13,427.3	124,179.4
	std	2.47525	19,652,738	10,768.36	39,303,453	1520.15	3548.894	3725.073	4326.323	2821.555	1439.779	3025.513	5229.269	62,071.96
	median	1304.901	3,482,711	14,946.94	6,959,389	5690.273	9717.419	5700.966	6011.811	8716.695	12,742.04	8784.46	4061.298	11,287.73
	rank	1	12	10	13	2	8	5	4	7	9	6	3	11
C17-F14	mean	1400.753	3207.7	1996.796	4252.9	1941.351	2922.796	1655.636	1691.51	2217.031	1704.358	4401.207	2657.575	9419.632
	best	1400	2606.891	1642.946	3737.137	1435.115	1476.268	1476.898	1432.284	1460.546	1495.409	3613.673	1433.413	2990.105
	worst	1401.013	3876.434	2385.618	5141.442	2906.859	4249.915	1986.245	2289.494	4304.612	2036.772	6062.121	5278.611	17,992.18
	std	0.545908	565.9558	341.6936	704.1598	751.2384	1521.565	251.4321	442.8159	1516.819	263.5596	1232.247	1962.027	6855.379
	median	1400.999	3173.738	1979.311	4066.511	1711.715	2982.502	1579.7	1522.132	1551.482	1642.626	3964.516	1959.138	8348.119
	rank	1	10	6	11	5	9	2	3	7	4	12	8	13
C17-F15	mean	1500.361	8206.493	4878.424	10,697.31	3981.327	6034.93	5502.834	2329.873	5228.696	2443.426	17,486.45	7388.224	4370.894
	best	1500.042	3488.99	2446.287	3143.54	3227.091	2862.292	2592.865	2075.444	3462.448	2166.282	8842.964	3174.407	2648.946
	worst	1500.53	13,039.77	9793.3	21,824.41	4899.528	9552.295	10704.09	2624.681	6095.701	2655.137	25,606.14	11,618.1	6725.968
	std	0.250209	4560.742	3631.9	8934.354	755.0654	3082.463	3882.324	246.7207	1315.114	222.6099	8586.324	3809.992	2135.416
	median	1500.437	8148.604	3637.054	8910.65	3899.345	5862.567	4357.191	2309.684	5678.318	2476.142	17,748.34	7380.193	4054.331
	rank	1	11	6	12	4	9	8	2	7	3	13	10	5
C17-F16	mean	1600.761	1900.516	1769.426	1909.745	1684.399	1930.692	1865.015	1773.953	1714.428	1679.426	1948.241	1846.807	1764.529
	best	1600.357	1858.353	1665.83	1785.955	1641.831	1791.517	1738.35	1699.341	1624.246	1662.43	1848.973	1777.256	1717.698
	worst	1601.121	1979.798	1834.815	2094.593	1715.063	2054.979	1951.499	1825.699	1790.109	1726.151	2090.318	1959.936	1790.358
	std	0.343607	58.85268	79.01002	142.7659	34.28364	130.2233	108.7908	58.22458	74.35455	33.96555	117.4983	88.81498	35.40944
	median	1600.783	1881.956	1788.531	1879.216	1690.351	1938.136	1885.106	1785.385	1721.678	1664.561	1926.837	1825.019	1775.03
	rank	1	10	6	11	3	12	9	7	4	2	13	8	5
C17-F17	mean	1700.1	1794.496	1746.171	1791.903	1735.826	1780.923	1807.866	1808.464	1758.08	1751.196	1811.173	1747.11	1749.567
	best	1700.021	1778.527	1731.06	1789.161	1721.966	1766.755	1757.178	1760.989	1724.312	1739.839	1739.63	1738.738	1743.096
	worst	1700.332	1810.988	1771.569	1793.685	1775.099	1793.03	1852.752	1894.233	1840.709	1768.62	1909.589	1761.195	1763.32
	std	0.168756	14.47357	20.15118	2.196325	28.50737	11.88133	43.6283	68.30667	60.14773	14.19162	91.70801	10.91586	10.10979
	median	1700.023	1794.234	1741.026	1792.383	1723.12	1781.953	1810.766	1789.316	1733.649	1748.162	1797.736	1744.254	1745.926
	rank	1	10	3	9	2	8	11	12	7	6	13	4	5
C17-F18	mean	1805.472	1,937,812	11,592.43	3,859,328	11,046.44	11,729.46	19,340.8	17,743.35	17,038.9	23,534.35	10,141.58	18,372.21	12,240.5
	best	1800.031	104,413.2	8000.928	195,598.3	4158.101	9774.936	7238.468	8762.729	5623.329	17,578.48	7200.72	6277.813	7047.84
	worst	1820.536	5,610,349	15,888.78	11,198,386	16512.9	13,065.45	28,477.64	28,146.98	27,452.73	27,845.99	12,745.91	30,442.87	17,841.83
	std	10.9348	2,776,083	3713.951	5,548,994	6115.074	1540.453	10,707.21	9103.721	12,055.93	5135.676	3058.828	14,952.74	4993.52
	median	1800.659	1,018,243	11,240	2,021,664	11,757.38	12,038.73	20,823.55	17,031.85	17,539.77	24,356.47	10,309.85	18,384.07	12,036.17
	rank	1	12	4	13	3	5	10	8	7	11	2	9	6
C17-F19	mean	1900.489	264,028.9	6348.121	478,141.9	5596.938	86,747.54	25,361.63	3104.113	5451.765	4986.742	29,163.34	18,689.69	5992.339
	best	1900.044	18,200.91	2222.255	31,876.91	2317.711	2226.212	6057.374	2041.355	2139.168	2329.755	10,083.21	2650.034	4067.144
	worst	1901.65	553,293.8	11,531.75	1,024,005	9413.121	172,704.7	45,687.83	4337.454	11913.97	9200.897	40,551.08	55,068.56	9728.734
	std	0.843567	254,409.1	4310.376	486,854.9	3935.834	105,192.3	17,629.55	1270.007	4791.592	3211.506	15,355.66	26,810.95	2785.874
	median	1900.132	242,310.5	5819.24	428,342.7	5328.461	86,029.65	24,850.65	3018.822	3876.958	4208.157	33,009.53	8520.081	5086.739
	rank	1	12	7	13	5	11	9	2	4	3	10	8	6
C17-F20	mean	2000.313	2175.272	2145.223	2180.725	2092.282	2170.138	2169.607	2124.244	2144.786	2078.53	2201.482	2144.152	2063.786
	best	2000.313	2138.484	2060.859	2140.017	2072.717	2099.604	2106.196	2060.449	2112.075	2064.749	2153.605	2126.705	2052.918
	worst	2000.314	2214.292	2222.772	2228.079	2122.777	2240.64	2218.295	2190.924	2206.125	2090.257	2274.333	2159.383	2073.555
	std	0.000283	33.81929	80.32377	44.73422	23.34473	63.8206	60.64228	58.24183	45.69562	12.21004	63.21432	15.68442	9.418732
	median	2000.313	2174.157	2148.63	2177.402	2086.817	2170.154	2176.97	2122.802	2130.471	2079.557	2188.996	2145.261	2064.335
	rank	1	11	8	12	4	10	9	5	7	3	13	6	2
C17-F21	mean	2200.001	2280.477	2227.83	2263.934	2257.213	2303.242	2292.873	2254.468	2295.2	2285.987	2332.458	2298.927	2284.957
	best	2200.001	2249.031	2221.539	2234.916	2254.723	2232.628	2230.706	2217.681	2291.546	2221.212	2319.818	2292.665	2237.284
	worst	2200.001	2299.235	2245.112	2279.751	2259.75	2335.255	2321.995	2291.123	2299.385	2311.381	2343.962	2304.255	2307.614
	std	2.8 × 10−5	25.23157	12.54734	21.8615	2.315335	52.22696	45.57287	45.21834	3.510268	47.25579	10.93935	6.319345	34.98016
	median	2200.001	2286.822	2222.334	2270.535	2257.189	2322.543	2309.395	2254.534	2294.934	2305.677	2333.025	2299.395	2297.466
	rank	1	6	2	5	4	12	9	3	10	8	13	11	7
C17-F22	mean	2300.073	2571.208	2307.705	2718.942	2305.009	2582.069	2317.746	2291.98	2307.446	2314.881	2301.621	2310.61	2313.767
	best	2300	2490.179	2305.984	2576.992	2300.945	2401.37	2314.879	2252.49	2301.163	2310.086	2300.305	2300.737	2310.489
	worst	2300.29	2652.786	2309.022	2824.241	2309.371	2724.336	2321.613	2305.396	2318.213	2324.244	2303.027	2332.724	2316.405
	std	0.157881	78.2743	1.374266	113.2176	3.86487	156.7579	3.573589	28.65228	8.222771	7.222682	1.246748	16.19632	2.736905
	median	2300	2570.935	2307.908	2737.267	2304.861	2601.284	2317.246	2305.016	2305.204	2312.598	2301.577	2304.49	2314.087
	rank	2	11	6	13	4	12	10	1	5	9	3	7	8
C17-F23	mean	2600.92	2665.481	2633.228	2672.943	2614.362	2688.441	2637.739	2618.393	2613.966	2633.55	2734.861	2634.733	2642.783
	best	2600.003	2642.314	2624.602	2652.475	2611.916	2628.43	2626.288	2609.954	2609.142	2627.041	2691.153	2629.055	2630.113
	worst	2602.87	2679.861	2646.159	2701.372	2617.068	2718.074	2650.653	2627.122	2619.397	2639.076	2828.285	2642.301	2647.923
	std	1.436886	19.03012	10.69532	24.51551	2.657748	44.22326	14.33956	8.128652	5.671674	6.129323	70.40567	6.238909	9.268331
	median	2600.403	2669.875	2631.075	2668.961	2614.232	2703.63	2637.008	2618.248	2613.662	2634.042	2710.003	2633.788	2646.549
	rank	1	10	5	11	3	12	8	4	2	6	13	7	9
C17-F24	mean	2630.488	2736.642	2723.622	2779.479	2630.653	2656.202	2718.873	2666.403	2710.841	2715.63	2709.95	2722.235	2693.422
	best	2516.678	2703.685	2702.511	2761.6	2616.912	2561.42	2696.792	2538.642	2690.129	2703.164	2545.013	2715.962	2569.749
	worst	2732.318	2784.69	2737.033	2822.656	2637.477	2755.003	2741.205	2719.384	2722.25	2724.215	2813.878	2737.598	2754.381
	std	126.7869	40.6602	17.32047	31.51329	10.15127	114.4679	19.7997	93.14654	16.04728	10.58233	125.6036	11.18284	91.04191
	median	2636.477	2729.096	2727.472	2766.829	2634.112	2654.192	2718.748	2703.793	2715.493	2717.571	2740.456	2717.689	2724.778
	rank	1	12	11	13	2	3	9	4	7	8	6	10	5
C17-F25	mean	2932.639	3066.739	2914.879	3161.296	2917.869	3064.189	2910.844	2920.721	2931.977	2928.472	2920.837	2921.558	2941.165
	best	2898.048	3017.402	2904.637	3116.49	2913.655	2911.445	2812.602	2905.152	2918.794	2915.322	2906.249	2904.347	2931.162
	worst	2945.793	3173.63	2940.741	3212.379	2923.322	3419.166	2945.908	2937.131	2938.605	2941.319	2935.273	2938.318	2950.055
	std	25.12849	79.20248	18.8118	43.35503	4.454837	260.217	71.34755	18.78415	9.723656	15.99494	16.53881	19.6432	8.745852
	median	2943.359	3037.962	2907.07	3158.158	2917.25	2963.072	2942.433	2920.3	2935.254	2928.624	2920.912	2921.784	2941.722
	rank	9	12	2	13	3	11	1	4	8	7	5	6	10
C17-F26	mean	2900.001	3382.176	2990.346	3517.29	3011.931	3425.317	3128.223	2936.255	3184.076	3144.248	3588.783	2938.909	2934.265
	best	2900	3252.231	2846.112	3388.782	2892.096	3063.183	3005.502	2897.578	2944.427	2917.405	2846.112	2909.225	2766.749
	worst	2900.005	3502.992	3201.721	3719.105	3294.533	3840.003	3368.513	3027.513	3710.957	3689.633	4010.845	2971.58	3052.759
	std	0.002495	125.409	190.2343	170.3872	205.9921	381.348	178.6263	66.51778	385.449	397.2118	558.1185	36.64296	135.6199
	median	2900	3386.74	2956.775	3480.638	2930.547	3399.042	3069.438	2909.964	3040.459	2984.976	3749.087	2937.416	2958.777
	rank	1	10	5	12	6	11	7	3	9	8	13	4	2
C17-F27	mean	3089.518	3176.16	3115.12	3190.533	3104.729	3155.518	3165.966	3095.863	3112.479	3111.787	3187.075	3126.028	3142.268
	best	3089.518	3139.627	3096.185	3115.983	3092.25	3101.018	3163.933	3090.591	3093.739	3095.769	3175.598	3095.543	3110.642
	worst	3089.519	3229.181	3165.894	3318.713	3133.92	3186.781	3169.918	3103.99	3163.082	3146.687	3197.672	3167.57	3180.087
	std	0.000258	41.31607	36.87161	96.41772	21.33304	42.61764	2.941028	6.231611	36.776	26.11514	10.3653	33.26104	31.2902
	median	3089.518	3167.916	3099.202	3163.719	3096.373	3167.136	3165.006	3094.436	3096.547	3102.347	3187.515	3120.499	3139.172
	rank	1	11	6	13	3	9	10	2	5	4	12	7	8
C17-F28	mean	3100.001	3472.447	3230.597	3598.736	3218.691	3467.955	3264.961	3232.373	3304.368	3290.91	3376.088	3277.745	3237.54
	best	3100.001	3448.59	3140.143	3544.749	3167.015	3338.977	3180.891	3121.73	3185.832	3223.642	3362.853	3192.413	3152.068
	worst	3100.002	3495.874	3318.446	3645.846	3243.613	3611.565	3337.289	3336.943	3357.895	3337.106	3390.385	3327.361	3420.354
	std	0.000467	21.14141	86.66249	46.20507	38.58309	152.4255	81.7028	124.7467	86.67706	54.3051	12.33499	67.19946	134.348
	median	3100.002	3472.663	3231.9	3602.175	3232.067	3460.638	3270.832	3235.409	3336.873	3301.446	3375.557	3295.603	3188.87
	rank	1	12	3	13	2	11	6	4	9	8	10	7	5
C17-F29	mean	3132.242	3295.9	3258.581	3320.121	3203.311	3225.803	3302.263	3203.027	3245.45	3209.785	3300.22	3246.042	3226.48
	best	3130.077	3269.628	3196.236	3259.654	3166.071	3172.458	3229.774	3150.143	3186.591	3182.227	3223.206	3167.381	3187.635
	worst	3134.842	3320.122	3310.054	3371.149	3244.88	3261.33	3396.269	3264.241	3336.404	3238.622	3500.764	3296.54	3248.091
	std	2.701737	22.71632	64.10475	64.06077	37.75313	41.05607	75.19883	51.00489	78.42987	26.51012	145.7147	63.85654	31.07757
	median	3132.023	3296.925	3264.017	3324.841	3201.146	3234.712	3291.504	3198.863	3229.403	3209.146	3238.454	3260.124	3235.097
	rank	1	10	9	13	3	5	12	2	7	4	11	8	6
C17-F30	mean	3423.707	1,659,881	332,889.1	2,617,672	413,992.4	548,981.2	804,162.1	338,396.8	766,098.9	174,698.1	662,631.2	395,413.9	1,165,787
	best	3394.834	1,300,276	112,282.8	734,672.7	15,907.74	273,256.2	142,949	10,169.88	27,840.67	24,936.49	582,053.2	10,531.89	532,136.6
	worst	3449.444	2,183,767	675,809.4	3,928,496	611,011.8	883,172.6	2,706,390	955,766.7	1,099,071	228,475.1	733,085.5	715,543.4	2,356,340
	std	31.91655	413,046.5	262,887.1	1,473,594	294,132.7	283,788.3	1,380,451	458,510.5	550,547.6	108,731.4	68,368.52	385,165.3	931,541.8
	median	3425.275	1,577,740	271,732.1	2,903,759	514,525	519,748	183,654.5	193,825.3	968,742	222,690.3	667,693	427,790.1	887,336.2
	rank	1	12	3	13	6	7	10	4	9	2	8	5	11
Sum rank		38	319	178	351	107	287	240	117	188	191	240	184	199
Mean rank		1.310345	11	6.137931	12.10345	3.689655	9.896552	8.275862	4.034483	6.482759	6.586207	8.275862	6.344828	6.862069
Total rank		1	11	4	12	2	10	9	3	6	7	9	5	8

Table 3. Optimization results of CEC 2017 test suite (dimension = 30).

		WOA	WSO	AVOA	RSA	MPA	TSA	WA	MVO	GWO	TLBO	GSA	PSO	GA
C17-F1	mean	100.321	1.77 × 1010	10,685.55	2.76 × 1010	26,598.07	1.21 × 1010	1.14 × 109	370,179.6	1.12 × 109	4.15 × 109	7,073,087	9.45 × 108	1.2 × 108
	best	100.1471	1.52 × 1010	4334.555	2.47 × 1010	12,240.79	7.57 × 109	9.03 × 108	284,867.6	1.85 × 108	2.62 × 109	7494.322	6473.386	89,553,528
	worst	100.4886	2.21 × 1010	14,216.89	3.4 × 1010	40,439.21	1.64 × 1010	1.42 × 109	471,460.9	3.38 × 109	6.19 × 109	24,666,807	3.78 × 109	1.65 × 108
	std	0.179642	3.5 × 109	4844.679	4.69 × 109	14,830.93	4.5 × 109	2.89 × 108	100,748.3	1.65 × 109	1.62 × 109	12,897,361	2.05 × 109	35,735,136
	median	100.3241	1.67 × 1010	12,095.38	2.6 × 1010	26,856.13	1.21 × 1010	1.13 × 109	362,195.1	4.63 × 108	3.9 × 109	1,809,023	2,161,490	1.12 × 108
	rank	1	12	2	13	3	11	9	4	8	10	5	7	6
C17-F3	mean	300.0097	65,817.27	30,416.06	49,852.4	1097.134	32,095.35	156,312.3	1549.657	28,375	23,677.99	64,815.85	21,801.7	112,811.6
	best	300.0066	60,055.35	16,758.56	38,605.67	847.3858	30,389.58	129,345	1309.708	24,870.1	20,293.19	55,814.11	15,738.98	85,487.74
	worst	300.0127	72,311.27	39,191.48	54,205.29	1350.318	33,835.91	179,603.5	2032.346	31,610.35	25,577.04	71,261.16	27,862.37	156,686.7
	std	0.002977	6574.407	10,469.64	8190.228	245.7846	1825.463	22,754.38	358.527	3004.585	2601.686	7609.278	6045.363	36,800.58
	median	300.0096	65,451.23	32,857.1	53,299.32	1095.416	32,077.96	158,150.4	1428.288	28,509.77	24,420.87	66,094.06	21,802.72	104,535.9
	rank	1	11	7	9	2	8	13	3	6	5	10	4	12
C17-F4	mean	458.562	4497.82	507.4049	6769.478	492.9231	3218.49	737.6698	495.3664	545.8814	771.9046	561.2869	581.0463	707.4596
	best	458.5618	2595.808	489.4793	4395.695	482.5108	864.6459	692.8323	486.716	515.4298	631.5341	545.044	507.0297	669.8195
	worst	458.5622	6028.379	518.5563	9395.177	514.5439	5241.204	788.9501	511.4194	563.6119	1048.057	575.9539	705.3547	728.9632
	std	0.000194	1548.396	14.71553	2259.035	16.0097	2010.662	45.95634	11.93234	22.85959	203.8477	13.76958	97.14601	28.81583
	median	458.5619	4683.547	510.7919	6643.519	487.3189	3384.056	734.4484	491.665	552.242	704.0139	562.0749	555.9004	715.5279
	rank	1	12	4	13	2	11	9	3	5	10	6	7	8
C17-F5	mean	502.4884	759.2186	678.7108	785.6342	582.8792	724.9132	744.6379	607.2809	608.9598	709.0273	676.9627	616.1536	663.1888
	best	500.9962	743.9431	652.0313	766.2516	560.4361	703.8315	717.82	599.627	589.0987	686.5317	665.416	597.8302	637.5721
	worst	503.9807	768.9604	725.745	802.0721	605.8082	740.3558	761.3818	623.7057	629.428	734.2369	692.8394	647.6527	707.261
	std	1.397794	12.27923	35.68684	20.43924	20.69349	18.39896	20.39776	12.13838	21.08365	22.59552	12.54084	23.73591	33.09432
	median	502.4883	761.9856	668.5334	787.1066	582.6362	727.7327	749.6749	602.8954	608.6563	707.6703	674.7977	609.5657	653.961
	rank	1	12	8	13	2	10	11	3	4	9	7	5	6
C17-F6	mean	600	654.6673	632.4048	656.7921	603.2431	652.7484	652.2338	617.4266	609.0318	630.1329	638.9866	632.5584	621.3114
	best	600	653.9089	630.8969	652.8186	601.9816	642.2756	645.0398	609.885	604.0154	624.9456	638.0784	623.9718	616.4128
	worst	600.0001	656.0022	634.622	661.0946	604.636	658.9347	655.7002	625.5434	613.3883	637.7483	640.1017	639.599	624.5343
	std	1.52 × 10−5	0.998103	1.821507	4.163943	1.25521	8.359827	5.402937	8.205328	4.240661	5.980629	0.909554	7.604179	3.935982
	median	600	654.3791	632.0501	656.6276	603.1775	654.8916	654.0976	617.139	609.3618	628.919	638.8832	633.3314	622.1492
	rank	1	12	7	13	2	11	10	4	3	6	9	8	5
C17-F7	mean	733.4794	1149.718	1047.868	1177.137	846.3755	1099.994	1155.758	851.3168	872.5922	1000.192	930.0361	867.6688	927.5223
	best	732.8198	1112.149	987.1501	1159.234	819.4609	996.6506	1125.986	806.6683	819.8287	954.6034	902.5773	844.6827	892.1004
	worst	734.5219	1179.25	1148.194	1210.139	899.933	1197.918	1201.539	895.7276	898.4205	1048.75	972.079	880.6517	981.6722
	std	0.821002	34.04323	80.55568	24.77527	39.60517	99.38956	35.21412	43.22535	39.05309	55.27444	32.84374	17.78993	41.52581
	median	733.2879	1153.737	1028.063	1169.588	833.054	1102.703	1147.754	851.4358	886.0599	998.7069	922.744	872.6705	918.1583
	rank	1	11	9	13	2	10	12	3	5	8	7	4	6
C17-F8	mean	803.3309	1021.091	930.2196	1046.227	890.5574	1003.64	984.4257	892.4033	891.5049	979.1958	938.1944	912.7277	954.795
	best	801.2034	1011.594	912.4427	1032.472	883.8529	976.3113	944.1651	871.6459	886.7197	966.3352	924.3735	904.7129	941.7634
	worst	804.1585	1034.679	944.4631	1064.184	898.683	1073.681	1015.226	910.3595	896.6279	1004.115	954.112	923.136	968.5517
	std	1.546284	11.69464	16.26743	16.48438	6.663041	51.0861	32.80419	19.18577	4.439787	18.41799	14.71108	8.383976	13.55689
	median	803.9808	1019.045	931.9863	1044.126	889.8469	982.2843	989.1557	893.8039	891.336	973.1666	937.146	911.5309	954.4324
	rank	1	12	6	13	2	11	10	4	3	9	7	5	8
C17-F9	mean	900.0022	7729.349	3598.754	7501.126	1083.68	8081.899	7771.083	4022.987	1751.6	4236.939	3098.017	2740.35	1223.889
	best	900.0004	6605.951	2725.803	7351.551	929.6087	5012.326	5997.402	3226.378	1415.743	3109.149	2785.48	1804.64	1093.835
	worst	900.0041	8766.843	4100.425	7639.374	1235.592	10819.73	9225.736	5938.477	2231.569	6265.575	3681.672	3942.438	1392.341
	std	0.001864	984.4253	663.0424	128.2036	153.9209	2607.127	1782.945	1396.078	423.1381	1550.553	449.7933	994.7306	150.2506
	median	900.0022	7772.301	3784.395	7506.789	1084.761	8247.768	7930.596	3463.546	1679.544	3786.515	2962.458	2607.161	1204.69
	rank	1	11	7	10	2	13	12	8	4	9	6	5	3
C17-F10	mean	2293.287	6161.473	4970.392	6622.948	3984.589	5717.134	5674.292	4429.204	4522.973	6636.188	4562.963	4692.383	5436.048
	best	1851.787	5913.34	4392.466	6187.534	3628.026	4920.649	5125.305	4124.072	4226.684	6274.225	4281.89	4528.713	5127.049
	worst	2525.041	6425.839	5438.008	7098.43	4431.083	6171.876	6716.889	4608.699	4889.435	6841.112	4892.324	4922.59	5962.139
	std	326.89	228.4198	488.6168	410.0172	403.212	596.2858	796.7545	244.2174	302.233	282.4372	272.9881	194.1375	422.2879
	median	2398.16	6153.356	5025.548	6602.914	3939.624	5888.006	5427.487	4492.023	4487.887	6714.707	4538.82	4659.114	5327.501
	rank	1	11	7	12	2	10	9	3	4	13	5	6	8
C17-F11	mean	1102.987	5439.926	1229.088	6315.685	1169.603	3839.968	5650.465	1267.103	1860.916	1721.151	2335.093	1223.375	6563.117
	best	1100.996	4528.502	1194.603	5196.955	1122.164	2846.381	4178.43	1222.495	1316.98	1463.139	1877.74	1202.507	2653.878
	worst	1105.978	6181.07	1257.057	7071.274	1203.082	5608.655	8180.955	1305.658	3315.691	2216.072	2798.627	1247.863	11,992.73
	std	2.342682	788.3692	28.52432	933.6639	38.06213	1355.985	1902.04	46.13961	1056.634	366.1953	470.4549	20.28718	4354.439
	median	1102.488	5525.066	1232.346	6497.256	1176.583	3452.417	5121.237	1270.129	1405.496	1602.697	2332.003	1221.566	5802.928
	rank	1	10	4	12	2	9	11	5	7	6	8	3	13
C17-F12	mean	1744.793	4.74 × 109	14,077,924	7.36 × 109	21,567.55	3.42 × 109	1.67 × 108	7,582,675	35,462,664	2.04 × 108	1.34 × 108	1,736,496	5,192,897
	best	1722.03	3.92 × 109	1,986,436	6.56 × 109	15,405.16	1.76 × 109	42741714	3,524,230	3,450,345	1.3 × 108	25,975,685	194,511.4	3,598,379
	worst	1765.102	6.02 × 109	34,372,937	9.27 × 109	27,519.43	4.47 × 109	3.34 × 108	18,338,244	74,357,427	3.54 × 108	4.29 × 108	3,445,088	6,796,896
	std	21.92568	9.78 × 108	15,515,092	1.4 × 109	5617.799	1.28 × 109	1.46 × 108	7,815,448	33,643,265	1.1 × 108	2.14 × 108	1,525,452	1,578,420
	median	1746.021	4.51 × 109	9,976,162	6.81 × 109	21,672.81	3.72 × 109	1.46 × 108	4,234,113	32,021,441	1.66 × 108	41,173,549	1,653,192	5,188,156
	rank	1	12	6	13	2	11	9	5	7	10	8	3	4
C17-F13	mean	1315.798	3.85 × 109	101,532.1	7.12 × 109	1887.503	9.87 × 108	610,702.2	61,970.73	509,838.4	59,480,600	25,222.23	22,449.95	8,037,399
	best	1314.59	1.88 × 109	56,657.5	3.73 × 109	1613.809	13308283	288,394.3	25,154.7	62,267.1	41,306,521	20,486.39	9619.251	2,181,265
	worst	1318.65	5.4 × 109	160,172.5	8.74 × 109	2423.737	3.43 × 109	902,630.9	123,812.2	1,580,771	87,708,503	36,797.09	50,129.18	17,287,717
	std	2.105422	1.59 × 109	46,800.18	2.49 × 109	398.4184	1.78 × 109	348,460.4	50,365.05	787,069.2	21,850,050	8488.768	20,311.38	7,045,508
	median	1314.976	4.07 × 109	94,649.2	8 × 109	1756.233	2.54 × 108	625,891.7	49,457.99	198,157.7	54,453,689	21,802.71	15,025.68	6,340,306
	rank	1	12	6	13	2	11	8	5	7	10	4	3	9
C17-F14	mean	1423.017	1,277,259	183,187.8	1,480,089	1440.332	791,751.8	1,498,444	14,169.61	359,607.7	94,702.5	771,020	13,109.59	1,352,841
	best	1422.014	787,819.4	26,021.81	744,142.8	1436.987	566,674.5	24,657.71	3833.51	23,619.68	55,233.67	500,470.5	2607.809	224,311.9
	worst	1423.993	1,616,727	423,495.8	2,203,774	1445.092	1,118,344	4,576,709	23,795.94	770,200.4	108,892.3	1,163,897	23,553.04	2,280,465
	std	0.879535	422,235.6	190,861.1	764,154.8	4.048836	275,535.4	2,274,956	9358.04	412,483.5	28,647.14	339,781.1	9957.207	1,032,057
	median	1423.031	1,352,245	141,616.7	1,486,220	1439.623	740,994.6	696,204.1	14,524.49	322,305.3	107,342	709,856	13,138.76	1,453,294
	rank	1	10	6	12	2	9	13	4	7	5	8	3	11
C17-F15	mean	1503.13	2.05 × 108	25,743.45	4.02 × 108	1618.316	9,678,759	3,396,917	29,333.47	10,656,380	3,457,075	11,347.81	3746.102	643,946.8
	best	1502.463	1.77 × 108	7875.273	3.47 × 108	1580.989	3,813,143	156,980.8	17,207.13	66,683.28	785,367	8201.244	1804.924	118,632.2
	worst	1504.267	2.27 × 108	41,482.5	4.44 × 108	1635.05	22,514,054	11,028,248	48,172.5	39,897,745	6,507,175	15,205.02	6514.516	1,442,109
	std	0.93123	26,757,116	15,445.93	51,771,108	27.29623	9,394,647	5,612,367	14,605.73	21,226,082	2,553,297	3185.324	2268.093	659,103.4
	median	1502.895	2.08 × 108	26,808	4.09 × 108	1628.612	6,193,920	1,201,219	25,977.13	1,330,545	3,267,879	10,992.5	3332.485	507,522.8
	rank	1	12	5	13	2	10	8	6	11	9	4	3	7
C17-F16	mean	1663.474	3568.439	2681.411	4011.115	2025.858	2863.893	3518.566	2403.561	2373.8	2993.528	3129.43	2634.281	2647.031
	best	1614.728	3307.657	2463.193	3449.388	1732.302	2484.554	3053.124	2208.194	2178.559	2769.271	2909.499	2432.865	2320.343
	worst	1744.12	3799.785	3079.244	4528.846	2279.902	3082.457	4174.815	2533.493	2538.963	3234.539	3233.052	2868.664	2965.881
	std	67.44314	219.693	298.9312	563.965	268.2093	284.3054	518.5014	157.2443	187.9758	224.2454	162.5764	197.8732	334.0578
	median	1647.523	3583.156	2591.603	4033.113	2045.613	2944.28	3423.162	2436.28	2388.839	2985.152	3187.584	2617.798	2650.95
	rank	1	12	7	13	2	8	11	4	3	9	10	5	6
C17-F17	mean	1728.1	2906.339	2276.907	3111.512	1864.483	2815.605	2529.508	2011.992	1912.264	2088.643	2310.644	2183.728	2062.855
	best	1718.761	2505.616	2188.535	2859.858	1754.049	2111.488	2211.204	1942.285	1789.284	1944.841	2207.173	2033.956	2002.551
	worst	1733.661	3373.82	2323.812	3576.698	1926.041	4638.687	2713.882	2123.907	2032.748	2253.828	2422.94	2469.859	2120.463
	std	7.3012	400.4036	68.35209	363.2455	82.57814	1324.987	240.9524	85.26455	119.8597	140.5146	108.6653	214.9267	53.74566
	median	1729.989	2872.96	2297.64	3004.747	1888.92	2256.123	2596.472	1990.888	1913.512	2077.951	2306.232	2115.549	2064.203
	rank	1	12	8	13	2	11	10	4	3	6	9	7	5
C17-F18	mean	1825.697	19,134,446	1,784,006	22,000,517	1896.582	24,464,933	3,973,536	431,441.6	283,040.9	1,122,150	347,272.9	92,986.63	2,454,920
	best	1822.525	5,512,424	190,522.6	7,113,201	1873.99	897,701.2	1,339,457	109,027.9	53,417.9	521,268.4	194,965.1	66,344.71	1,916,677
	worst	1828.42	37,159,552	3,558,889	43,221,783	1909.634	46,361,733	8,200,701	1,166,914	726,273.5	1,410,592	675,556.9	110,216.2	3,598,176
	std	2.940364	15,225,802	1,718,031	16,663,827	17.43949	27,476,116	3,208,798	537,005.1	344,619.5	444,998.7	241,287.1	20,875.12	838,994.8
	median	1825.921	16,932,904	1,693,307	18,833,543	1901.352	25,300,149	3,176,993	224,912.2	176,236.1	1,278,369	259,284.8	97,692.8	2,152,413
	rank	1	11	8	12	2	13	10	6	4	7	5	3	9
C17-F19	mean	1910.989	3.91 × 108	46,201.22	6.59 × 108	1923.783	1.98 × 108	9,646,131	633,054.8	2,715,875	3,872,544	55,673.87	30,583.08	1,091,994
	best	1908.841	2.92 × 108	10,342.48	4.76 × 108	1921.202	2462344	1,255,746	16,582.08	48,298.05	2,010,392	30,482.7	6525.453	431,854.3
	worst	1913.095	5.09 × 108	102,145.5	9.99 × 108	1928.709	5.49 × 108	16,655,746	1,422,547	8,756,365	5,504,512	74,705.12	90,345.84	1,939,444
	std	2.102558	1.18 × 108	43,520.53	2.52 × 108	3.66218	2.75 × 108	7,642,858	744,628.8	4,412,469	1,870,463	20,035.8	43,510.04	691,979.8
	median	1911.01	3.81 × 108	36,158.43	5.81 × 108	1922.611	1.21 × 108	10,336,517	546,545.1	1,029,419	3,987,636	58,753.83	12,730.52	998,338
	rank	1	12	4	13	2	11	10	6	8	9	5	3	7
C17-F20	mean	2065.788	2666.708	2488.247	2703.24	2176.891	2633.528	2625.151	2467.592	2311.588	2598.428	2741.657	2428.342	2379.616
	best	2029.523	2605.081	2389.124	2582.79	2061.08	2544.675	2514.937	2273.525	2156.315	2559.647	2496.684	2366.306	2309.465
	worst	2161.127	2707.276	2610.711	2770.116	2265.33	2699.37	2756.968	2771.258	2427.864	2682.556	3094.92	2526.675	2429.376
	std	69.26648	47.36501	101.173	90.30704	93.03145	70.35704	109.9008	232.2741	123.5691	62.23832	275.3768	76.14184	55.62911
	median	2036.251	2677.238	2476.577	2730.026	2190.577	2645.033	2614.349	2412.791	2331.087	2575.755	2687.512	2410.193	2389.813
	rank	1	11	7	12	2	10	9	6	3	8	13	5	4
C17-F21	mean	2308.457	2540.531	2417.334	2579.458	2366.656	2481.146	2532.292	2393.024	2382.704	2454.294	2505.054	2412.967	2452.339
	best	2304.034	2473.562	2270.813	2523.092	2356.969	2323.993	2485.02	2366.912	2363.935	2442.938	2490.751	2398.042	2428.045
	worst	2312.988	2583.263	2523.659	2647.808	2382.758	2571.81	2574.088	2410.418	2392.152	2465.164	2529.138	2427.061	2491.924
	std	4.85283	57.52589	115.3898	58.98792	12.3411	120.1462	49.41104	20.0951	14.3016	11.45574	18.53136	13.92777	29.96371
	median	2308.402	2552.65	2437.431	2573.466	2363.449	2514.39	2535.03	2397.382	2387.364	2454.536	2500.163	2413.382	2444.694
	rank	1	12	6	13	2	9	11	4	3	8	10	5	7
C17-F22	mean	2300	6159.173	4657.782	5994.363	2302.935	6695.427	5766.815	3423.993	2575.187	4598.67	5034.764	4055.344	2573.944
	best	2300	5928.784	2302.786	5294.995	2301.914	6538.31	5117.091	2305.37	2487.172	2588.565	3455.537	2407.683	2523.642
	worst	2300	6518.352	5567.576	6696.946	2304.658	6769.164	6346.252	4812.837	2755.307	6827.122	5728.707	5649.372	2612.918
	std	1.62 × 10−5	274.163	1711.374	655.6563	1.339246	118.2848	555.9797	1425.549	133.29	2511.471	1153.281	1622.328	48.22624
	median	2300	6094.778	5380.383	5992.757	2302.583	6737.117	5801.959	3288.882	2529.133	4489.496	5477.406	4082.16	2579.608
	rank	1	12	8	11	2	13	10	5	4	7	9	6	3
C17-F23	mean	2655.08	3018.554	2837.832	3056.017	2645.995	3021.88	2919.91	2708.483	2717.86	2822.111	3411.74	2819.805	2870.907
	best	2653.742	2981.599	2706.483	3034.102	2470.219	2961.012	2820.609	2671.598	2656.103	2751.266	3359.518	2740.294	2794.193
	worst	2657.377	3094.294	2977.502	3079.451	2713.035	3176.547	3008.021	2732.925	2747.202	2876.312	3492.82	2876.436	2935.906
	std	1.799914	55.76503	121.7223	20.26983	127.8613	112.9976	85.5247	31.9586	46.1351	56.99409	67.68839	63.58293	63.44241
	median	2654.601	2999.163	2833.671	3055.257	2700.363	2974.98	2925.506	2714.705	2734.068	2830.434	3397.31	2831.244	2876.765
	rank	2	10	7	12	1	11	9	3	4	6	13	5	8
C17-F24	mean	2831.41	3179.108	3080.486	3247.481	2884.089	3155.71	3043.27	2899.284	2909.649	2992.612	3212.592	3053.298	3118.4
	best	2829.993	3148.056	2987.524	3181.273	2868.279	3081.824	3001.568	2868.587	2903.318	2971.289	3182.137	2996.218	3054.623
	worst	2832.367	3235.118	3181.558	3355.926	2891.028	3192.796	3062.056	2910.707	2916.474	3019.755	3239.389	3132.246	3167.446
	std	1.246615	41.75542	93.32452	86.33596	11.62732	56.14136	30.91586	22.30369	7.143926	21.84854	27.18451	62.55752	57.99264
	median	2831.64	3166.629	3076.431	3226.362	2888.524	3174.11	3054.728	2908.921	2909.401	2989.701	3214.421	3042.364	3125.765
	rank	1	11	8	13	2	10	6	3	4	5	12	7	9
C17-F25	mean	2886.699	3607.338	2903.209	4034.452	2891.322	3286.095	3021.418	2903.769	2960.975	3016.538	2962.433	2893.83	3039.035
	best	2886.691	3351.181	2891.293	3622.768	2884.514	3025.628	2994.287	2887.918	2932.78	2935.079	2952.332	2886.612	3026.66
	worst	2886.707	3797.754	2929.039	4582.416	2897.572	3553.351	3035.361	2945.401	3010.463	3108.206	2973.024	2907.626	3049.263
	std	0.008281	203.0261	18.91256	434.8985	6.422317	280.701	20.65282	30.30356	38.97607	91.19975	9.395447	10.248	10.24702
	median	2886.698	3640.208	2896.252	3966.311	2891.6	3282.7	3028.012	2890.879	2950.329	3011.433	2962.188	2890.541	3040.108
	rank	1	12	4	13	2	11	9	5	6	8	7	3	10
C17-F26	mean	3578.642	7191.58	5930.556	7592.481	2946.315	6888.12	6644.515	4198.092	4046.729	4972.932	6029.691	4239.941	3930.149
	best	3559.834	6900.181	5052.814	7020.282	2944.882	6436.43	6142.829	3961.442	3776.856	4029.515	5311.602	3351.804	3667.33
	worst	3607.678	7714.518	6446.821	8605.164	2948.392	7173.169	7227.66	4629.422	4464.713	5868.921	6403.494	5296.398	4251.832
	std	24.78747	413.0478	667.2934	809.7776	1.837083	343.8081	484.8852	337.687	319.4722	917.6972	554.0416	988.2099	266.8256
	median	3573.529	7075.81	6111.295	7372.239	2945.993	6971.44	6603.786	4100.752	3972.672	4996.647	6201.834	4155.781	3900.718
	rank	2	12	8	13	1	11	10	5	4	7	9	6	3
C17-F27	mean	3207.019	3485.171	3310.871	3591.283	3214.68	3391.644	3360.18	3226.155	3238.747	3285.286	4415.11	3258.442	3382.154
	best	3200.749	3440.015	3247.081	3395.86	3200.487	3306.869	3245.524	3214.623	3233.545	3239.157	4102.348	3228.323	3330.64
	worst	3210.656	3560.736	3366.02	3794.608	3235.278	3558.765	3442.945	3240.714	3244.368	3336.16	4646.306	3288.853	3408.592
	std	5.058023	58.64719	65.96591	186.4574	17.31647	124.2857	91.58785	12.91307	4.872405	43.73311	288.9247	27.10588	38.09436
	median	3208.335	3469.966	3315.191	3587.332	3211.478	3350.472	3376.125	3224.641	3238.538	3282.914	4455.893	3258.296	3394.692
	rank	1	11	7	12	2	10	8	3	4	6	13	5	9
C17-F28	mean	3100.001	4285.25	3250.432	4906.953	3214.97	3860.244	3368.505	3244.141	3476.948	3526.458	3425.149	3293.725	3467.208
	best	3100.001	4120.25	3223.868	4691.505	3198.214	3477.346	3325.773	3218.444	3339.576	3422.609	3375.396	3200.642	3426.086
	worst	3100.002	4470.17	3282.301	5138.813	3245.539	4244.468	3402.752	3263.228	3804.826	3756.546	3524.057	3444.734	3515.851
	std	0.000279	162.3279	26.25194	231.8527	23.01676	389.897	39.78086	22.17692	240.0732	169.8819	73.55874	123.6083	45.20616
	median	3100.001	4275.291	3247.779	4898.747	3208.065	3859.581	3372.747	3247.447	3381.696	3463.339	3400.573	3264.762	3463.448
	rank	1	12	4	13	2	11	6	3	9	10	7	5	8
C17-F29	mean	3353.754	4851.084	4121.031	5001.458	3660.494	4742.849	4637.501	3787.273	3751.439	4243.614	4621.073	4009.663	4090.916
	best	3325.389	4563.675	3862.67	4546.162	3505.413	4354.465	4402.309	3683.409	3644.544	4001.869	4383.912	3918.357	3812.083
	worst	3370.802	5223.509	4289.381	5578.57	3800.919	5394.339	4800.5	3857.366	3817.267	4596.087	4819.164	4198.991	4285.209
	std	21.42802	354.7397	214.9723	559.2864	141.8741	517.0823	184.0793	81.46193	81.81261	284.1425	223.7357	140.0438	243.4827
	median	3359.413	4808.575	4166.036	4940.55	3667.822	4611.296	4673.597	3804.159	3771.972	4188.251	4640.607	3960.652	4133.187
	rank	1	12	7	13	2	11	10	4	3	8	9	5	6
C17-F30	mean	5007.886	9.69 × 108	967,976.9	1.91 × 109	7685.968	26,018,831	26,550,655	2,096,592	4,320,872	25,632,186	1,534,343	186,989.6	477,732.2
	best	4955.467	7.14 × 108	342,528.9	1.37 × 109	6376.112	8,896,654	5,296,448	379,268.5	965,771.3	13,721,797	1,339,279	7199.128	133,974.4
	worst	5086.458	1.07 × 109	1,712,217	2.11 × 109	10243.41	60,792,294	42,544,236	3,000,293	11,663,420	53,762,742	1,846,430	700,983.7	912,455.9
	std	64.19995	1.86 × 108	623,282.9	3.91 × 108	1971.76	25,636,640	16,897,513	1,272,216	5,376,945	20,524,746	237,645.7	373,095	412,438
	median	4994.809	1.05 × 109	908,581.1	2.08 × 109	7062.174	17,193,188	29,180,967	2,503,403	2,327,149	17,522,103	1,475,832	19,887.82	432,249.3
	rank	1	12	5	13	2	10	11	7	8	9	6	3	4
Sum rank		31	334	182	361	57	305	284	128	151	232	231	139	204
Mean rank		1.068966	11.51724	6.275862	12.44828	1.965517	10.51724	9.793103	4.413793	5.206897	8	7.965517	4.793103	7.034483
Total rank		1	12	6	13	2	11	10	3	5	9	8	4	7

Table 4. Optimization results of CEC 2017 test suite (dimension = 50).

		WOA	WSO	AVOA	RSA	MPA	TSA	WA	MVO	GWO	TLBO	GSA	PSO	GA
C17-F1	mean	167.6264	4.01 × 1010	8,007,497	6.29 × 1010	5,583,217	2.56 × 1010	5.17 × 109	4,531,953	6.28 × 109	1.39 × 1010	1.15 × 1010	1.7 × 109	6.98 × 109
	best	126.0994	3.58 × 1010	1,491,085	5.5 × 1010	2,154,824	2.35 × 1010	3.05 × 109	2,705,326	4.53 × 109	9.46 × 109	9.18 × 109	6.98 × 108	6.65 × 109
	worst	271.4742	4.3 × 1010	17,609,984	6.87 × 1010	14,156,721	2.75 × 1010	7.74 × 109	7,406,938	8.6 × 109	1.88 × 1010	1.38 × 1010	2.27 × 109	7.52 × 109
	std	75.88761	3.42 × 109	7,567,671	6.52 × 109	6,265,152	1.79 × 109	2.41 × 109	2,191,601	1.85 × 109	4.92 × 109	2.04 × 109	7.51 × 108	4.46 × 108
	median	136.4659	4.09 × 1010	6,464,460	6.39 × 1010	3,010,662	2.56 × 1010	4.94 × 109	4,007,774	6 × 109	1.37 × 1010	1.15 × 1010	1.92 × 109	6.88 × 109
	rank	1	12	4	13	3	11	6	2	7	10	9	5	8
C17-F3	mean	300.2116	112,004.4	104,024.9	111,611	17,766.86	78,909.34	162,630.4	36,755.62	92,889.39	71,655.61	125,081.8	102,805.1	182,386.1
	best	300.1823	97,129.76	80,477.71	102,028.7	15,348.2	70,273.23	123,563.9	30,579.6	82,551.01	55,088.66	113,761.2	77,910.13	152,472.6
	worst	300.2503	128,985.2	124,821.2	120,366	20,968.46	84,785.32	246,104.1	45,348.9	104,599.5	80,168.88	139,795.6	131,722	208,965
	std	0.033257	14,597.57	21,674.61	8694.823	2745.606	7008.744	62,662.51	6803.146	9837.971	12,691.57	14,166.48	25,403.04	25,191.69
	median	300.2068	110,951.3	105,400.4	112,024.6	17,375.39	80,289.4	140,426.8	35,546.99	92,203.53	75,682.45	123,385.3	100,794.1	184,053.3
	rank	1	10	8	9	2	5	12	3	6	4	11	7	13
C17-F4	mean	470.3686	10,071.59	642.1439	16,104.43	530.5117	5747.804	1475.15	551.9914	1137.245	2048.337	2228.839	855.6596	1197.148
	best	428.5135	7865.26	623.1879	10,691.43	495.3216	4628.795	1013.992	517.5974	880.9504	1224.21	1880.598	623.2301	1048.451
	worst	525.7259	11,459.94	660.4907	19,217.95	582.6329	7377.38	1723.722	593.1173	1342.65	3386.974	2369.606	1380.74	1285.019
	std	53.94877	1745.048	17.65661	4230.075	44.44626	1262.625	345.3018	33.84099	230.0578	1034.815	253.8902	383.5973	112.1706
	median	463.6175	10,480.57	642.4484	17,254.17	522.0461	5492.52	1581.443	548.6255	1162.689	1791.083	2332.577	709.334	1227.56
	rank	1	12	4	13	2	11	8	3	6	9	10	5	7
C17-F5	mean	504.7288	976.9834	814.9919	996.5644	733.4819	1008.531	880.709	735.2051	726.2984	909.4273	780.3419	768.9047	837.7757
	best	503.9816	954.1396	768.5579	979.2845	652.789	912.1348	853.5763	659.9295	681.9306	855.3089	719.0789	706.3429	791.6068
	worst	505.9733	995.7666	863.1035	1004.302	796.7098	1078.585	912.485	831.2809	765.683	934.5178	821.5439	818.6237	870.407
	std	1.037272	18.69201	42.99374	12.66144	65.70971	82.6346	30.91893	80.31735	41.20787	39.72203	48.73799	51.09316	36.48948
	median	504.4802	979.0137	814.1531	1001.335	742.2144	1021.703	878.3874	724.8049	728.79	923.9413	790.3724	775.326	844.5445
	rank	1	11	7	12	3	13	9	4	2	10	6	5	8
C17-F6	mean	600.0001	667.1328	643.7797	668.516	611.1885	663.6183	668.9465	628.7456	618.8348	646.474	642.2786	639.3753	636.0119
	best	600.0001	665.0235	641.7376	666.1094	608.4438	650.1405	664.4751	621.5264	615.1583	637.5851	638.1159	637.3589	628.5636
	worst	600.0002	671.6192	647.0243	670.5864	614.8163	675.9291	674.55	644.8989	624.5364	653.4284	645.3967	641.8655	643.5578
	std	3.6 × 10−5	3.347275	2.720798	2.51233	2.970403	12.24043	4.534764	11.84805	4.380584	7.167769	3.362949	2.518508	6.936408
	median	600.0001	665.9441	643.1784	668.684	610.747	664.2017	668.3804	624.2785	617.8223	647.4412	642.8008	639.1384	635.9631
	rank	1	11	8	12	2	10	13	4	3	9	7	6	5
C17-F7	mean	756.7331	1535.785	1451.18	1602.464	1025.281	1462.324	1479.277	1042.06	1049.958	1325.932	1280.7	1139.351	1211.321
	best	754.7569	1526.437	1415.509	1559.985	969.1676	1372.439	1449.139	1007.534	1016.325	1231.712	1149.903	1044.527	1174.18
	worst	758.355	1543.363	1510.942	1683.606	1072.794	1544.286	1528.089	1077.788	1077.995	1363.107	1382.466	1276.858	1227.522
	std	1.690713	7.874028	45.66337	62.50891	54.65011	97.47111	37.76279	32.42597	32.00245	68.66304	108.7352	112.7872	27.14247
	median	756.9102	1536.669	1439.134	1583.132	1029.581	1466.286	1469.939	1041.458	1052.756	1354.456	1295.217	1118.009	1221.79
	rank	1	12	9	13	2	10	11	3	4	8	7	5	6
C17-F8	mean	805.7235	1281.736	1084.086	1300.207	1008.015	1293.369	1218.107	1015.645	1023.669	1216.397	1094.768	1038.767	1173.316
	best	802.987	1253.643	1043.275	1289.143	977.598	1217.081	1138.848	995.7582	990.7447	1170.67	1081.05	1000.462	1152.877
	worst	810.9472	1308.327	1124.019	1310.883	1039.324	1375.293	1299.282	1055.217	1059.548	1261.467	1112.127	1093.102	1189.707
	std	3.891779	30.44582	49.90051	10.54183	34.90235	72.49341	71.36606	30.29916	34.74648	40.4744	17.51668	43.41583	17.36832
	median	804.4798	1282.487	1084.526	1300.402	1007.569	1290.551	1217.148	1005.803	1022.192	1216.726	1092.947	1030.752	1175.341
	rank	1	11	6	13	2	12	10	3	4	9	7	5	8
C17-F9	mean	900.0289	25,201	9936.355	25,329.64	3290.004	26,383.12	23,106.2	14196.65	5658.015	17,118.01	8191.838	7937.962	9610.758
	best	900.014	24,168.61	9519.686	23,784.42	2056.94	24,003.81	21,578.85	8569.512	4660.123	13,030.35	7558.024	7190.92	8018.21
	worst	900.0468	27,900.64	10,437.08	27,003.04	4765.598	29,781.7	27,323.03	18431.63	6601.21	19,875.64	9237.851	8875.758	11349.46
	std	0.01475	1962.375	493.1408	1516.334	1217.749	2675.839	3063.247	5116.457	984.3236	3166.783	824.6416	760.402	1918.351
	median	900.0275	24,367.38	9894.327	25,265.56	3168.739	25,873.49	21,761.46	14892.73	5685.363	17,783.04	7985.74	7842.586	9537.68
	rank	1	11	7	12	2	13	10	8	3	9	5	4	6
C17-F10	mean	4347.184	10,843.9	7721.58	11,659.42	6524.229	10026.29	10,031.48	7276.712	7948.804	11,517.56	7904.065	7363.204	9978.914
	best	3555.175	10,423.1	7263.151	11,420.12	5635.227	9273.366	9378.091	6582.977	6280.484	11,226.63	7234.616	6969.158	9310.296
	worst	5099.82	11,538.38	8268.684	12,116.67	7132.467	10936.95	10,994.81	7717.154	11,328.31	11,809.74	8836.616	7622.011	10,364.5
	std	701.6805	524.6606	470.4982	351.1623	792.9569	745.8822	769.787	535.6862	2498.75	271.406	780.2277	302.3093	516.2341
	median	4366.87	10,707.05	7677.242	11,550.45	6664.611	9947.433	9876.513	7403.358	7093.211	11,516.95	7772.514	7430.824	10,120.43
	rank	1	11	5	13	2	9	10	3	7	12	6	4	8
C17-F11	mean	1128.436	10,727.34	1488.956	14,476.8	1254.002	9077.844	3827.922	1464.276	4520.409	3838.572	9927.132	1533.288	16,503.58
	best	1121.251	9914.495	1407.395	12,921.91	1206.11	7869.994	3428.789	1369.366	2877.275	3623.898	9320.694	1360.509	9815.447
	worst	1133.134	11,227.32	1576.143	15,662.22	1284.76	10,800.72	4697.146	1551.43	7556.229	4236.206	11,195.74	1736.516	21,977.06
	std	5.923824	635.5737	84.6736	1246.464	38.0633	1374.633	638.5052	89.62537	2355.628	310.4132	932.1324	176.9033	5475.211
	median	1129.68	10,883.77	1486.142	14,661.53	1262.57	8820.332	3592.877	1468.153	3824.066	3747.092	9596.049	1518.063	17,110.9
	rank	1	11	4	12	2	9	6	3	8	7	10	5	13
C17-F12	mean	3078.008	2.93 × 1010	53,871,294	4.78 × 1010	14,277,715	1.74 × 1010	8.91 × 108	57,787,339	6.47 × 108	3.4 × 109	1.46 × 109	1.08 × 109	1.42 × 108
	best	2706.091	2.46 × 1010	25,209,560	3.48 × 1010	13,449,352	7.33 × 109	7.37 × 108	33,148,852	1.05 × 108	1.92 × 109	4.84 × 108	13,290,816	47,805,759
	worst	3331.239	3.51 × 1010	80,624,222	6.55 × 1010	14,947,205	2.92 × 1010	1.21 × 109	89,443,451	1.2 × 109	6.68 × 109	2.62 × 109	3.12 × 109	1.94 × 108
	std	292.7712	5.17 × 109	32,291,028	1.54 × 1010	760,963.4	9.85 × 109	2.38 × 108	25,727,978	5.94 × 108	2.43 × 109	9.62 × 108	1.57 × 109	70,138,147
	median	3137.35	2.87 × 1010	54,825,697	4.54 × 1010	14,357,152	1.65 × 1010	8.08 × 108	54,278,526	6.43 × 108	2.5 × 109	1.37 × 109	5.98 × 108	1.63 × 108
	rank	1	12	3	13	2	11	7	4	6	10	9	8	5
C17-F13	mean	1340.28	1.65 × 1010	105,293.6	2.89 × 1010	16,204.5	6.77 × 109	63,729,289	167,199.9	2.4 × 108	3.93 × 108	12,446,144	3.2 × 108	27,879,335
	best	1333.996	9.52 × 109	29,172.41	1.46 × 1010	8578.998	3.6 × 109	47,914,168	107,057.6	1.09 × 108	3.2 × 108	26,968.58	40,209.71	18,175,689
	worst	1343.224	2.25 × 1010	223,251.6	4.16 × 1010	19,074.17	1.05 × 1010	72,366,520	255,509.5	6.03 × 108	5.37 × 108	41,938,948	8.09 × 108	37,257,697
	std	4.646652	6.21 × 109	90,174.33	1.23 × 1010	5538.318	3.2 × 109	11,767,927	68,584.33	2.64 × 108	1.06 × 108	21,765,316	4.29 × 108	9,274,410
	median	1341.95	1.7 × 1010	84,375.25	2.98 × 1010	18,582.42	6.47 × 109	67,318,233	153,116.2	1.24 × 108	3.57 × 108	3,909,329	2.36 × 108	28,041,976
	rank	1	12	3	13	2	11	7	4	8	10	5	9	6
C17-F14	mean	1429.46	17,441,082	822,120.1	32,517,129	1561.83	1,805,814	3,203,867	128,744.8	774,214.6	581,995.3	10,178,081	386,111.7	7,532,667
	best	1425.996	5,697,256	254,996.6	9,973,419	1548.751	477,397.5	2,836,637	81,748.39	60,752.32	479,983.5	2,308,023	139,031.1	3,706,936
	worst	1431.941	34,142,896	1,957,448	65,836,531	1586.155	2,863,875	3,807,204	249,421.1	1,493,528	671,406.1	16,711,153	618,100.9	12,964,035
	std	2.852912	13,064,360	842,196.9	25,860,705	18.65168	1,076,896	456,136.3	87,853.5	636,598.3	108,666.5	7,106,301	213,379	4,253,542
	median	1429.951	14,962,089	538,017.7	27,129,284	1556.208	1,940,992	3,085,814	91,904.86	771,289	588,295.8	10,846,575	393,657.3	6,729,849
	rank	1	12	7	13	2	8	9	3	6	5	11	4	10
C17-F15	mean	1530.669	1.75 × 109	26,266.61	2.81 × 109	2255.297	1.15 × 109	6,667,483	82,292.93	3,998,260	47,416,347	1.33 × 108	8029.767	5,763,300
	best	1526.369	1.24 × 109	16,530.74	2.2 × 109	2123.062	3.94 × 108	615,181.2	34,547.42	29,138.76	27,804,041	13,562.88	2648.243	1,958,974
	worst	1532.963	2.29 × 109	47,711.7	3.33 × 109	2401.548	2.49 × 109	12,448,843	122,345.1	10,529,706	61,720,972	5.15 × 108	15,030.42	12,507,241
	std	3.19211	5.4 × 108	15,739.97	5.48 × 108	160.4214	1.06 × 109	5,660,871	42,491.58	4,986,475	15,436,400	2.77 × 108	6009.479	5076,922
	median	1531.672	1.74 × 109	20,412	2.86 × 109	2248.29	8.48 × 108	6,802,954	86,139.62	2,717,098	50,070,187	8,024,911	7220.201	4,293,493
	rank	1	12	4	13	2	11	8	5	6	9	10	3	7
C17-F16	mean	2062.899	5121.056	3824.554	5995.639	2748.242	4017.813	4589.463	3134.537	3132.586	3952.043	3556.756	3143.54	3528.57
	best	1728.611	4523.679	3559.4	4722.823	2587.266	3595.314	4006.777	2986.486	2810.824	3683.669	3335.878	2810.153	3071.889
	worst	2242.667	6384.314	4114.639	8610.895	3016.507	4258.369	5046.269	3245.454	3535.893	4112.649	3777.515	3534.84	3830.919
	std	253.4768	943.9009	255.9887	1949.356	216.8432	320.5015	492.5712	121.2415	346.1602	207.5341	276.0826	381.2236	361.9129
	median	2140.159	4788.116	3812.089	5324.42	2694.598	4108.784	4652.403	3153.104	3091.813	4005.928	3556.816	3114.583	3605.736
	rank	1	12	8	13	2	10	11	4	3	9	7	5	6
C17-F17	mean	2021.158	5956.996	3226.767	8264.058	2554.858	3494.992	3882.346	2898.832	2830.145	3623.719	3402.804	3087.376	3244.424
	best	1900.437	4709.275	2905.357	6233.664	2485.465	2945.246	3544.347	2506.005	2730.899	3172.458	3095.79	2934.416	3086.565
	worst	2138.273	7115.822	3588.397	10488.47	2608.789	3820.341	4049.34	3231.852	3031.293	3886.678	3615.218	3328.279	3390.05
	std	146.0793	1080.149	346.3384	1906.807	56.72245	414.3017	254.7996	327.6241	149.4111	346.4202	241.5617	205.5091	154.8192
	median	2022.961	6001.443	3206.657	8167.048	2562.59	3607.189	3967.848	2928.736	2779.194	3717.871	3450.104	3043.404	3250.542
	rank	1	12	6	13	2	9	11	4	3	10	8	5	7
C17-F18	mean	1830.914	50,910,288	1,629,703	75,518,961	26,076.32	23,578,215	30,386,714	1,783,979	3,857,322	5,522,929	5,663,162	562,637.9	6,377,248
	best	1822.262	40,744,777	220,232.4	33,960,504	3729.858	2,119,833	8,228,326	1,047,278	746,437.6	3,793,764	2,674,842	237,427.6	2,291,774
	worst	1842.122	60,032,637	2,982,184	1.05 × 108	38,990.49	67,348,823	54,999,657	2,773,664	7,687,381	7,675,586	10,577,631	918,505.6	15,323,252
	std	9.036632	9,065,965	1,520,288	37,884,753	16,764.33	32,622,247	25,173,665	897,576.1	3,945,036	1,786,705	3,919,143	339,318.2	6,551,592
	median	1829.635	51,431,869	1,658,198	81,660,379	30,792.46	12,422,102	29,159,436	1,657,486	3,497,734	5,311,183	4,700,086	547,309.1	3,946,983
	rank	1	12	4	13	2	10	11	5	6	7	8	3	9
C17-F19	mean	1925.187	1.83 × 109	175,319.7	2.58 × 109	2080.868	1.8 × 109	4,601,206	3,446,693	782,677.2	34,089,610	304,610.5	265,357.5	667,542.3
	best	1924.439	8.73 × 108	61,984.29	1.74 × 109	2019.962	6,575,871	692,607	2,623,760	383,448.8	28,940,951	175,433.2	2610.44	522,323.7
	worst	1926.122	3.06 × 109	360,841.9	3.19 × 109	2110.964	5.25 × 109	10,843,830	4,274,312	1,203,045	43,289,205	666,715	661,774.8	904,038.4
	std	0.860715	1 × 109	141,150.6	7.02 × 108	45.24112	2.55 × 109	4,747,367	733,387.1	372,925.2	6,951,139	262,814.8	342,049.9	196,041
	median	1925.093	1.7 × 109	139,226.4	2.7 × 109	2096.272	9.66 × 108	3,434,194	3,444,350	772,107.7	32,064,142	188,146.8	198,522.3	621,903.5
	rank	1	12	3	13	2	11	9	8	7	10	5	4	6
C17-F20	mean	2160.178	3442.542	3063.524	3622.694	2655.984	3177.474	3389.766	3072.911	2631.922	3406.875	3585.842	3079.083	2997.597
	best	2104.428	3124.74	2684.261	3342.27	2374.521	2780.33	3097.53	2855.502	2404.817	3342.69	3415.061	2895.567	2861.424
	worst	2323.896	3557.618	3400.293	3766.414	2938.174	3343.03	3761.81	3479.89	2831.881	3439.221	3865.962	3175.281	3060.95
	std	118.7923	230.6985	320.1173	215.7375	258.4841	291.0508	300.2597	311.588	231.9714	48.05564	212.2806	141.0455	102.1433
	median	2106.193	3543.906	3084.771	3691.046	2655.62	3293.268	3349.863	2978.127	2645.496	3422.795	3531.172	3122.742	3034.007
	rank	1	11	5	13	3	8	9	6	2	10	12	7	4
C17-F21	mean	2314.897	2815.369	2655.367	2841.386	2448.553	2791.812	2785.666	2532.422	2497.099	2700.2	2713.84	2589.969	2651.518
	best	2309.047	2792.814	2567.11	2764.471	2428.126	2724.519	2702.324	2505.307	2454.213	2676.686	2670.536	2535.381	2629.592
	worst	2329.685	2840.618	2775.6	2907.834	2473.091	2900.378	2855.04	2562.591	2530.805	2738.246	2748.307	2655.528	2672.443
	std	10.75944	26.85998	96.14359	70.10397	24.92191	82.33755	69.45541	28.46343	36.99248	31.21705	35.87157	55.85716	19.30608
	median	2310.427	2814.023	2639.379	2846.618	2446.497	2771.175	2792.65	2530.896	2501.69	2692.934	2718.259	2584.483	2652.018
	rank	1	12	7	13	2	11	10	4	3	8	9	5	6
C17-F22	mean	3095.197	11,840.37	9249.944	12,696.53	5345.01	11,003.98	10,954.55	7801.322	7717.179	12,324.35	9446.36	8313.732	7690.125
	best	2300	10,975.8	7776.947	11,596.14	2320.141	10,078.43	10,143.6	5540.057	7020.447	11,020.41	8401.309	6787.63	3472.311
	worst	5480.642	12,857.63	11,440.49	13,850.78	8518.314	11,754.03	12,053.19	9542.076	8719.371	13,582.63	10510.72	9523.203	11754.54
	std	1730.723	1070.614	1718.974	1196.586	3672.687	947.0155	1013.265	1977.833	882.5331	1580.879	1106.249	1437.482	4065.796
	median	2300.072	11,764.03	8891.173	12,669.61	5270.792	11,091.74	10,810.71	8061.576	7564.448	12,347.19	9436.704	8472.049	7766.826
	rank	1	11	7	13	2	10	9	5	4	12	8	6	3
C17-F23	mean	2743.356	3522.458	3163.124	3574.045	2890.254	3470.182	3471.906	2957.6	2978.637	3156.257	4157.751	3221.163	3211.292
	best	2729.99	3468.745	3103.497	3536.953	2876.706	3327.088	3347.389	2928.115	2921.935	3102.22	4022.999	3175.524	3122.573
	worst	2752.658	3584.607	3224.911	3602.28	2910.242	3696.189	3536.369	3007.989	3069.34	3201.246	4270.164	3258.832	3312.274
	std	10.90086	54.02718	60.61126	30.90234	15.64305	189.7784	94.17823	39.29736	68.89713	44.52035	110.9169	45.81438	84.90131
	median	2745.389	3518.24	3162.044	3578.472	2887.034	3428.726	3501.933	2947.148	2961.636	3160.781	4168.92	3225.148	3205.16
	rank	1	11	6	12	2	9	10	3	4	5	13	8	7
C17-F24	mean	2919.045	3847.144	3371.663	4035.006	3066.455	3707.052	3587.628	3114.077	3157.447	3327.43	3964.13	3337.517	3474.692
	best	2909.048	3676.633	3286.074	3705.929	3036.433	3653.584	3501.846	3099.923	3102.28	3264.618	3930.479	3218.163	3437.316
	worst	2924.414	4249.168	3510.814	4862.616	3104.766	3796.277	3627.87	3128.441	3249.73	3380.066	4004.08	3438.186	3554.507
	std	7.426455	293.3714	105.578	605.7561	33.51764	71.98341	62.89371	17.60413	69.95648	54.41671	33.20185	105.599	58.59073
	median	2921.359	3731.388	3344.882	3785.739	3062.311	3689.174	3610.399	3113.971	3138.889	3332.518	3960.981	3346.859	3453.474
	rank	1	11	7	13	2	10	9	3	4	5	12	6	8
C17-F25	mean	2983.146	6829.727	3143.338	9097.362	3068.428	5065.94	3806.319	3059.523	3724.506	3955.333	3889.831	3104.751	3734.483
	best	2980.236	5803.049	3130.278	7503.99	3047.782	4307.608	3529.563	3042.159	3589.955	3618.063	3650.817	3075.541	3654.743
	worst	2991.832	7484.653	3168.235	10,080.95	3087.127	5794.215	4009.619	3074.003	3864.58	4364.674	4340.166	3144.476	3819.331
	std	6.301683	809.5386	18.46922	1315.955	17.70878	696.2403	222.5587	14.42115	158.7741	407.2211	351.8383	36.3899	73.3475
	median	2980.258	7015.603	3137.419	9402.253	3069.401	5080.969	3843.047	3060.966	3721.744	3919.297	3784.171	3099.493	3731.929
	rank	1	12	5	13	3	11	8	2	6	10	9	4	7
C17-F26	mean	3776.426	10,652.91	8534.427	11,323.3	3325.099	9657.961	10,469.34	5002.569	5496.103	7681.45	8923.373	6591.812	7180.913
	best	3748.802	10,443.43	8119.655	10,835.26	3121.405	8167.252	9930.223	4602.366	5163.312	7082.217	8703.873	6292.621	5924.898
	worst	3793.641	10,877.13	8836.358	11,924.37	3616.373	10,615.63	11,579.66	5158.965	5766.863	8289.045	9132.306	6928.002	8926.379
	std	21.16802	194.836	326.5236	505.9885	244.4607	1142.821	816.3939	291.0878	296.3572	540.8842	191.6014	306.9423	1552.268
	median	3781.631	10,645.54	8590.849	11,266.78	3281.309	9924.48	10,183.75	5124.472	5527.119	7677.269	8928.657	6573.312	6936.186
	rank	2	12	8	13	1	10	11	3	4	7	9	5	6
C17-F27	mean	3251.261	4348.03	3702.277	4476.939	3384.497	4286.968	4117.349	3369.912	3559.135	3688.956	6588.379	3562.867	4106.793
	best	3227.704	4129.783	3644.608	4219.639	3275.973	3765.898	3724.24	3341.168	3526.837	3590.577	6432.25	3381.815	4029.947
	worst	3313.632	4498.215	3779.963	4662.284	3486.386	4627.164	4543.237	3400.365	3626.446	3806.875	6832.622	3731.943	4239.398
	std	45.3921	187.0499	64.78135	216.8054	93.81539	414.8289	407.9824	29.25056	49.90718	114.969	204.9979	161.818	104.6721
	median	3231.855	4382.06	3692.267	4512.915	3387.814	4377.406	4100.96	3369.058	3541.628	3679.186	6544.321	3568.855	4078.914
	rank	1	11	7	12	3	10	9	2	4	6	13	5	8
C17-F28	mean	3258.85	7012.212	3517	8677.989	3352.894	6008.631	4353.142	3307.718	4068.218	4644.052	4515.449	3706.903	4502.021
	best	3258.849	6426.532	3448.857	7793.552	3315.88	5059.151	3926.172	3300.093	3871.664	4210.448	4463.991	3479.946	4336.583
	worst	3258.85	8489.764	3585.606	11,002.56	3398.346	6982.711	4526.662	3314.243	4314.975	5031.442	4585.251	4065.912	4619.871
	std	0.000533	1079.786	76.37052	1689.597	44.0203	1051.027	310.8789	6.66045	218.9069	366.2977	56.36689	273.6725	146.5477
	median	3258.85	6566.276	3516.769	7957.92	3348.674	5996.33	4479.867	3308.267	4043.116	4667.159	4506.277	3640.876	4525.815
	rank	1	12	4	13	3	11	7	2	6	10	9	5	8
C17-F29	mean	3263.048	10,588.92	5059.259	14583.27	4100.139	6011.158	7469.708	4606.515	4632.07	5762.626	6880.677	4608.764	5499.832
	best	3247.145	7486.596	5016.757	8384.624	3741.342	5762.752	5345.065	4358.302	4408.46	5030.464	5877.658	4335.869	5181.465
	worst	3278.796	13,936.26	5136.191	22186.49	4346.972	6349.622	9360.184	5095.699	4893.259	6417.663	8694.154	4747.897	5993.378
	std	18.99864	3226.438	57.3369	6681.957	297.9412	270.9063	1802.677	361.0841	219.7824	708.8003	1403.934	204.2896	398.6318
	median	3263.125	10,466.42	5042.044	13880.98	4156.121	5966.129	7586.791	4486.03	4613.28	5801.188	6475.448	4675.645	5412.243
	rank	1	12	6	13	2	9	11	3	5	8	10	4	7
C17-F30	mean	623,587.7	2.2 × 109	15,251,890	3.7 × 109	1,652,759	1.12 × 109	1.07 × 108	47,981,163	94,371,290	2.03 × 108	1.25 × 108	3,775,782	39,873,421
	best	582,420	1.7 × 109	9,443,607	2.27 × 109	1,250,370	1.37 × 108	72,559,067	43,747,505	45,867,478	1.41 × 108	96,019,075	2,769,992	32,144,348
	worst	655,644.6	2.99 × 109	20,575,454	5.8 × 109	2,692,256	2.26 × 109	1.48 × 108	55,029,646	1.4 × 108	2.57 × 108	1.63 × 108	4,958,921	55,632,636
	std	35,548.22	6.13 × 108	6,080,569	1.66 × 109	757,580.8	1.19 × 109	41,126,849	5,402,394	51,729,113	52,698,117	30,723,168	1,095,078	11,797,567
	median	628,143.1	2.06 × 109	15,494,250	3.36 × 109	1,334,205	1.03 × 109	1.04 × 108	46,573,751	95,686,827	2.06 × 108	1.2 × 108	3,687,107	35,858,349
	rank	1	12	4	13	2	11	8	6	7	10	9	3	5
Sum rank		30	335	166	367	63	294	269	112	144	248	254	150	207
Mean rank		1.034483	11.55172	5.724138	12.65517	2.172414	10.13793	9.275862	3.862069	4.965517	8.551724	8.758621	5.172414	7.137931
Total rank		1	12	6	13	2	11	10	3	4	8	9	5	7

Table 5. Optimization results of CEC 2017 test suite (dimension = 100).

		WOA	WSO	AVOA	RSA	MPA	TSA	WA	MVO	GWO	TLBO	GSA	PSO	GA
C17-F1	mean	1,516,167	1.53 × 1011	4.3 × 1010	1.97 × 1011	4.08 × 1010	1.25 × 1011	8.26 × 1010	4.05 × 1010	7.88 × 1010	1.02 × 1011	1.32 × 1011	5.39 × 1010	7.81 × 1010
	best	1,335,206	1.45 × 1011	3.93 × 1010	1.94 × 1011	3.6 × 1010	1.1 × 1011	7.62 × 1010	3.57 × 1010	7.1 × 1010	9.61 × 1010	1.24 × 1011	4.87 × 1010	7.22 × 1010
	worst	1,695,059	1.6 × 1011	4.78 × 1010	2.02 × 1011	4.56 × 1010	1.4 × 1011	8.68 × 1010	4.52 × 1010	8.87 × 1010	1.09 × 1011	1.43 × 1011	5.96 × 1010	8.78 × 1010
	std	162,257	6.82 × 109	4.1 × 109	4.61 × 109	4.31 × 109	1.34 × 1010	5.05 × 109	4.32 × 109	9.06 × 109	6.16 × 109	8.79 × 109	4.9 × 109	7.37 × 109
	median	1,517,202	1.53 × 1011	4.24 × 1010	1.96 × 1011	4.07 × 1010	1.25 × 1011	8.37 × 1010	4.05 × 1010	7.78 × 1010	1.01 × 1011	1.31 × 1011	5.37 × 1010	7.63 × 1010
	rank	1	12	4	13	3	10	8	2	7	9	11	5	6
C17-F3	mean	304.3666	404,220.1	335,856.2	333,279.5	222,594.4	360,796.8	646,706.9	429,658.5	363,907.9	315,501.5	347,236.8	479,900.6	504,380.7
	best	303.4984	355,538	311,476.3	314,638.8	174,570.9	289,123.5	557,408	383,428.5	320,724.9	303,915.9	320,413.9	368,656.4	465,316.6
	worst	304.9872	433,336	347,280.5	348,819.3	248,814.9	412,038.3	730,946	497,551.4	393,597	332,473.2	375,203.8	643,174.9	517,599.7
	std	0.685925	36,832.02	17,890.95	17,179.27	37,212.91	56,628.81	80,870.54	57,209.63	34,905.84	13,485.17	28,261.48	132,232.9	28,332.22
	median	304.4903	414,003.2	342,334	334,829.9	233,495.9	371,012.7	649,236.8	418,827	370,654.9	312,808.4	346,664.7	453,885.5	517,303.2
	rank	1	9	5	4	2	7	13	10	8	3	6	11	12
C17-F4	mean	602.3573	35,048.41	6177.611	55,574.52	5817.781	15,883.28	12,480.82	5644.298	8133.492	12,346.82	28,039.38	6794.114	11,315.35
	best	592.1863	32,231.84	4385.111	51,161.87	3994.814	10,394.76	10,939.38	3834.588	5963.792	10,235.7	25,037.75	5230.308	9715.221
	worst	612.5252	37,708.02	7700.378	61,112	7586.922	21,117.42	14,308.66	7325.128	11,333.46	14,624.21	30,780.79	7827.886	13,392.26
	std	12.74023	3097.53	1499.009	4592.548	1621.898	4820.493	1610.579	1567.93	2473.563	1952.352	2740.741	1201.699	1685.327
	median	602.3589	35,126.89	6312.477	55,012.11	5844.694	16,010.48	12,337.62	5708.738	7618.358	12,263.68	28,169.48	7059.131	11,076.96
	rank	1	12	4	13	3	10	9	2	6	8	11	5	7
C17-F5	mean	512.9536	1991.191	1543.592	1970.979	1484.777	2092.568	1889.655	1491.709	1456.78	1912.733	1558.131	1609.451	1720.727
	best	510.9635	1982.272	1530.613	1939.522	1409.772	2067.901	1834.609	1414.382	1414.156	1889.659	1536.821	1535.314	1618.619
	worst	514.9436	2001.98	1559.029	1997.362	1545.338	2121.256	1982.255	1530.253	1481.497	1941.475	1582.696	1733.143	1782.729
	std	1.976171	9.414798	13.4072	29.31266	71.1504	26.73081	70.35415	59.11108	34.69417	23.79624	22.94323	100.6244	78.18375
	median	512.9536	1990.256	1542.363	1973.516	1492	2090.558	1870.877	1511.101	1465.734	1909.9	1556.504	1584.673	1740.78
	rank	1	12	5	11	3	13	9	4	2	10	6	7	8
C17-F6	mean	600.0013	704.1609	675.0138	703.0254	658.9907	707.1478	702.5191	683.3602	660.866	687.6997	676.402	674.7254	675.7973
	best	600.0012	698.5307	670.7235	695.9336	652.6971	695.2064	696.7071	675.0774	660.2419	684.5793	675.1257	666.1367	669.5922
	worst	600.0014	708.4778	677.9762	706.6793	665.8922	715.3754	710.0099	689.9493	661.7202	689.887	678.0049	681.0534	681.9123
	std	0.000128	5.084045	3.413167	5.324081	5.877588	10.58996	6.60503	7.320229	0.762225	2.542322	1.535974	7.840827	5.815911
	median	600.0013	704.8175	675.6778	704.7443	658.6868	709.0048	701.6798	684.2071	660.7509	688.1661	676.2386	675.8557	675.8424
	rank	1	12	5	11	2	13	10	8	3	9	7	4	6
C17-F7	mean	811.4227	3457.223	3109.954	3533.302	2299.591	3343.039	3438.302	2407.454	2417.591	3120.778	3137.408	2714.359	2778.54
	best	810.0491	3375.576	2994.927	3449.146	2279.916	3169.02	3352.697	2244.344	2346.107	3001.314	3068.81	2482.492	2694.302
	worst	813.2053	3577.581	3225.432	3607.817	2314.143	3507.437	3607.208	2541.564	2485.314	3226.357	3223.866	2819.661	2976.299
	std	1.590756	100.0488	112.2285	71.29051	16.22815	166.2251	124.9158	134.7031	68.87138	113.7655	73.01565	169.7354	144.9954
	median	811.2181	3437.867	3109.729	3538.122	2302.152	3347.849	3396.651	2421.954	2419.471	3127.72	3128.478	2777.641	2721.78
	rank	1	12	7	13	2	10	11	3	4	8	9	5	6
C17-F8	mean	812.4555	2352.625	1907.109	2388.387	1707.37	2337.773	2285.496	1722.842	1762.975	2242.908	1964.73	1886.548	2098.938
	best	808.9723	2301.434	1852.513	2354.271	1606.764	2271.676	2165.488	1650.271	1675.758	2212.837	1909.207	1841.257	2070.596
	worst	816.9321	2419.687	1949.623	2420.097	1755.839	2422.639	2414.234	1821.131	1882.416	2271.299	2077.863	1927.735	2160.298
	std	3.696911	53.69952	44.50814	34.56564	73.91288	79.19452	133.3679	80.45573	95.27606	29.55326	84.03673	39.03489	45.18471
	median	811.9587	2344.689	1913.151	2389.59	1733.438	2328.389	2281.131	1709.984	1746.864	2243.749	1935.925	1888.6	2082.429
	rank	1	12	6	13	2	11	10	3	4	9	7	5	8
C17-F9	mean	901.3877	95,778.14	54,485.84	87,431.46	51,854.85	115,464.2	87,115.74	75,728.14	60,626.52	85,597.32	52,591.35	58,625.37	67,134.68
	best	901.1356	82,780.35	48,201.51	80,334.99	45,413.99	94,652.93	71,084.88	62,978.75	51,207.81	79,960.75	46,111.03	48,608.69	62,335.69
	worst	901.7337	114,084.9	60,830.25	98,027.24	61,351.93	144,028	109,314.3	90,235.55	64,552.32	95,693.13	60,758.1	70,280.44	76,296.1
	std	0.273174	14,462.67	5611.921	8168.747	7334.162	22,552.8	19,542.06	12,157.21	6923.12	7533.46	6596.97	9684.641	6812.769
	median	901.3407	93,123.66	54,455.81	85,681.81	50,326.74	111,588	84,031.88	74,849.13	63,372.98	83,367.71	51,748.13	57,806.17	64,953.45
	rank	1	12	4	11	2	13	10	8	6	9	3	5	7
C17-F10	mean	11,023.25	29,357.21	19,975.73	30,225.95	18,608.25	28,761.31	28,079.24	20,644.56	19,465.96	30,232.27	20,797.7	20,697.94	26,618.16
	best	9625.835	29,164.51	18,005.85	29,931.72	18,332.5	28,051.2	27,572.57	20,441.47	18,605.78	29,288.6	19,663.97	19,271.02	26,156.05
	worst	11,859	29,484.77	21,765.39	30,561.54	18,929.71	29,670.88	28,769.44	21,101.1	20,145.67	31,001.67	21,762.55	21426.35	26,880.79
	std	1054.006	159.5784	1781.614	295.033	298.1571	778.3132	544.9852	333.4346	731.7527	852.0359	957.8658	1068.043	346.429
	median	11,304.08	29,389.79	20,065.84	30,205.26	18,585.4	28,661.58	27,987.48	20,517.84	19,556.2	30,319.41	20,882.13	21,047.19	26,717.91
	rank	1	11	4	12	2	10	9	5	3	13	7	6	8
C17-F11	mean	1163.085	128,944	62,804.62	156,576	23,728.35	63,625.08	157,842.4	23,595.09	77,997.79	67,841.35	134,368.6	54,853.93	11,2319.2
	best	1140.345	106,463.3	51,483.53	126,405	12,360.39	29,004.28	100,990	12,495.8	66,001.38	49,256.24	117,182.2	37,943.29	79,398.03
	worst	1221.75	147,250	71,587.79	214,915.1	33,195.32	91,022.76	230,731.5	32,624.91	90,103.86	82,629.14	162,186.3	79,482.6	155,925.4
	std	42.68713	18,797.15	9668.458	43,108.25	9378.95	27,967.46	67,208.3	9039.573	12,793.34	15,346.66	21,236.22	19,717.07	35,141.57
	median	1145.123	131,031.3	64,073.59	142,492	24,678.85	67,236.65	149,824	24,629.84	77,942.96	69,740.02	129,053	50,994.92	106,976.7
	rank	1	10	5	12	3	6	13	2	8	7	11	4	9
C17-F12	mean	676,048.3	8.74 × 1010	1.83 × 1010	1.31 × 1011	1.8 × 1010	5.53 × 1010	2.66 × 1010	1.81 × 1010	2.54 × 1010	3.23 × 1010	6.19 × 1010	2.45 × 1010	2.6 × 1010
	best	349,148.1	5.86 × 1010	9.51 × 109	9.36 × 1010	9.36 × 109	2.84 × 1010	1.62 × 1010	9.31 × 109	1.7 × 1010	2.05 × 1010	5.21 × 1010	1.77 × 1010	1.66 × 1010
	worst	1,118,035	1.05 × 1011	3.01 × 1010	1.47 × 1011	2.98 × 1010	9.18 × 1010	3.96 × 1010	2.99 × 1010	3.86 × 1010	4.15 × 1010	8.14 × 1010	3.91 × 1010	3.75 × 1010
	std	349,383.1	2.17 × 1010	9.37 × 109	2.74 × 1010	9.31 × 109	2.88 × 1010	1.05 × 1010	9.33 × 109	1.01 × 1010	9.87 × 109	1.46 × 1010	1.07 × 1010	9.45 × 109
	median	618,505.2	9.31 × 1010	1.68 × 1010	1.41 × 1011	1.65 × 1010	5.06 × 1010	2.52 × 1010	1.66 × 1010	2.3 × 1010	3.36 × 1010	5.7 × 1010	2.07 × 1010	2.5 × 1010
	rank	1	12	4	13	2	10	8	3	6	9	11	5	7
C17-F13	mean	253,424	2.51 × 1010	6.72 × 109	3.49 × 1010	6.72 × 109	2.08 × 1010	7.07 × 109	6.72 × 109	7.34 × 109	8.58 × 109	1.25 × 1010	7.88 × 109	6.84 × 109
	best	180,323.1	2.16 × 1010	4.77 × 109	2.98 × 1010	4.77 × 109	1.48 × 1010	5.19 × 109	4.77 × 109	6.42 × 109	6.92 × 109	8.31 × 109	4.9 × 109	4.87 × 109
	worst	303,130.6	2.74 × 1010	8.05 × 109	3.88 × 1010	8.05 × 109	2.49 × 1010	8.29 × 109	8.05 × 109	8.71 × 109	1.03 × 1010	1.44 × 1010	9.91 × 109	8.14 × 109
	std	56,539.46	3.05 × 109	1.51 × 109	4.93 × 109	1.51 × 109	4.67 × 109	1.45 × 109	1.51 × 109	1.06 × 109	1.5 × 109	3.06 × 109	2.39 × 109	1.51 × 109
	median	265,121.2	2.57 × 1010	7.03 × 109	3.54 × 1010	7.03 × 109	2.18 × 1010	7.39 × 109	7.03 × 109	7.12 × 109	8.55 × 109	1.36 × 1010	8.36 × 109	7.17 × 109
	rank	1	12	3	13	2	11	6	4	7	9	10	8	5
C17-F14	mean	1572.614	32,796,858	7,211,091	55,421,181	2,863,311	8,678,759	12,413,197	4,807,125	9,155,851	11,989,909	10,397,492	3,341,629	9,740,522
	best	1516.484	27,175,468	4,650,636	49,263,581	1,303,261	3,942,082	6,805,263	3,723,206	7,553,150	9,080,631	7,617,039	1,529,156	7,487,023
	worst	1663.892	39,732,530	12,786,669	63,069,551	5,534,993	16,933,191	15,588,982	6,074,250	11,475,961	14,257,407	13,341,815	5,826,270	12,737,203
	std	69.91953	5,768,013	4,104,978	6,645,773	2,027,270	6,227,013	4,385,549	1,050,496	1,901,201	2,334,225	3,075,337	2,033,148	2,378,073
	median	1555.041	32,139,716	5,703,530	54,675,796	2,307,496	6,919,881	13,629,271	4,715,522	8,797,148	12,310,798	10,315,558	3,005,545	9,368,931
	rank	1	12	5	13	2	6	11	4	7	10	9	3	8
C17-F15	mean	144,150.8	1.4 × 1010	3.8 × 109	1.93 × 1010	3.8 × 109	1.18 × 1010	3.85 × 109	3.8 × 109	4.13 × 109	4.59 × 109	4.62 × 109	4.02 × 109	3.81 × 109
	best	4562.241	9.47 × 109	78967366	1.82 × 1010	78957867	2.44 × 108	1.12 × 108	79043502	1.07 × 109	7.77 × 108	1.08 × 109	9.49 × 108	85192625
	worst	268,664.2	1.72 × 1010	7.12 × 109	2.21 × 1010	7.12 × 109	2.2 × 1010	7.21 × 109	7.12 × 109	7.35 × 109	8.8 × 109	8.17 × 109	7.13 × 109	7.13 × 109
	std	124,679.9	3.53 × 109	3.32 × 109	2.04 × 109	3.32 × 109	1.03 × 1010	3.34 × 109	3.32 × 109	2.99 × 109	3.71 × 109	3.26 × 109	2.95 × 109	3.32 × 109
	median	151,688.4	1.46 × 1010	4 × 109	1.85 × 1010	4 × 109	1.24 × 1010	4.03 × 109	4 × 109	4.05 × 109	4.39 × 109	4.62 × 109	4.01 × 109	4.01 × 109
	rank	1	12	3	13	2	11	6	4	8	9	10	7	5
C17-F16	mean	2711.935	17,174.88	9375.173	19,623.56	8311.666	14,284.4	15,388.92	9020.2	8693.29	12,256.45	11,966.85	8946.221	11,627.33
	best	2171.807	16768	8840.315	17,307.92	7484.04	11,795.09	13,404.39	8181.357	8183.509	11,795.62	10,870.01	8301.795	11,189.96
	worst	3397.492	17,477.21	9750.725	21,005.77	9216.336	17,104.19	17,091.2	10,130.72	9887.515	13,130.6	13,242.33	9658.277	12,050.38
	std	554.7989	322.4398	417.7672	1803.457	771.0536	2373.199	1831.816	937.1179	870.3778	658.3726	1132.17	606.7179	422.8393
	median	2639.22	17,227.16	9454.826	20,090.28	8273.144	14,119.16	15,530.05	8884.361	8351.069	12,049.8	11,877.53	8912.406	11,634.49
	rank	1	12	6	13	2	10	11	5	3	9	8	4	7
C17-F17	mean	2719.119	2,859,157	72,922.96	5,557,980	72,131.87	213,674.1	80,324.18	72,343.81	72,698.6	74,840.53	99,748.34	73,090.37	73,790.17
	best	2281.869	820,982.1	7450.644	1,630,264	6251.242	10,021.8	14,217.56	6789.644	6205.114	8979.266	30,935.83	7128.748	7986.58
	worst	3430.818	6,394,172	187,120	12,676,416	186,320.4	567,637.8	191,528.7	186,543	186,583.2	189,235.9	208,491.4	187,594.3	188,157.9
	std	558.0556	2,812,131	85,474.06	5,676,889	85,545.59	265,068.4	83,954.93	85,493.88	85,479.75	85,675.52	83,607.67	85,762.04	85,643.93
	median	2581.895	2,110,737	48,560.6	3,962,620	47,977.92	138,518.4	57,775.23	48,021.31	49,003.05	50,573.48	79,783.06	48,819.23	49,508.09
	rank	1	12	5	13	2	11	9	3	4	8	10	6	7
C17-F18	mean	2080.041	43,320,838	6,564,402	72,852,157	4,855,312	14,556,523	12,639,015	7,947,771	11,949,564	15,417,798	12,476,212	8,958,554	8,694,657
	best	1960.054	22,408,897	3,451,247	31,364,844	1,868,141	5,452,327	10,816,785	4,455,339	10,497,296	10,421,393	6,109,246	5,153,947	5,726,531
	worst	2280.201	79,446,911	12,552,937	1.34 × 108	9,884,703	29,746,027	17,059,651	12,011,997	13,473,301	20,060,107	26,891,473	12,804,802	13,328,202
	std	161.2402	27,321,562	4,534,181	47,821,021	3,931,731	11,908,143	3,221,100	4,142,439	1,322,654	5,344,174	10,528,302	3,879,765	3,545,898
	median	2039.954	35,713,773	5,126,713	62,910,719	3,834,201	11,513,869	11,339,812	7,661,875	11,913,831	15,594,846	8,452,065	8,937,734	7,861,948
	rank	1	12	3	13	2	10	9	4	7	11	8	6	5
C17-F19	mean	61,748.67	1 × 1010	1.6 × 109	1.64 × 1010	1.59 × 109	4.93 × 109	1.68 × 109	1.61 × 109	1.83 × 109	2.04 × 109	2.64 × 109	1.77 × 109	1.6 × 109
	best	28,457.22	8.4 × 109	7.08 × 108	1.4 × 1010	7.06 × 108	2.19 × 109	8.55 × 108	7.2 × 108	9.25 × 108	8.98 × 108	1.28 × 109	7.36 × 108	7.15 × 108
	worst	120,720.4	1.1 × 1010	3.17 × 109	1.95 × 1010	3.17 × 109	9.8 × 109	3.28 × 109	3.18 × 109	3.88 × 109	4.18 × 109	3.55 × 109	3.55 × 109	3.17 × 109
	std	44,376.67	1.24 × 109	1.18 × 109	2.62 × 109	1.18 × 109	3.66 × 109	1.19 × 109	1.19 × 109	1.5 × 109	1.6 × 109	1.15 × 109	1.34 × 109	1.18 × 109
	median	48,908.51	1.03 × 1010	1.25 × 109	1.6 × 1010	1.25 × 109	3.88 × 109	1.3 × 109	1.26 × 109	1.26 × 109	1.53 × 109	2.87 × 109	1.4 × 109	1.26 × 109
	rank	1	12	3	13	2	11	6	5	8	9	10	7	4
C17-F20	mean	3192.086	7130.906	6393.398	7299.105	5276.316	6959.367	6967.721	6151.266	6325.791	7103.617	6489.606	5859.28	6457.287
	best	2806.809	6808.312	6109.925	7129.09	5045.377	6348.678	6695.818	5888.305	5531.282	6370.5	6421.941	5285.222	5855.375
	worst	3662.17	7490.974	6574.384	7590.303	5525.349	7714.511	7259.143	6429.487	7172.125	7522.64	6582.129	6676.82	6750.557
	std	477.9763	314.8365	222.1951	218.8722	215.1906	638.3543	254.492	284.0463	817.6685	548.4264	86.85834	679.1682	448.8849
	median	3149.682	7112.17	6444.642	7238.512	5267.269	6887.139	6957.962	6143.636	6299.877	7260.663	6477.178	5737.539	6611.607
	rank	1	12	6	13	2	9	10	4	5	11	8	3	7
C17-F21	mean	2342.176	4188.739	3779.132	4270.657	3227.956	4079.587	4147.674	3495.198	3322.433	3806.318	4471.37	3723.178	3614.558
	best	2338.709	4114.013	3669.137	4244.832	3181.924	3937.603	3931.265	3449.182	3221.864	3729.714	4055.845	3583.959	3544.929
	worst	2346.037	4266.859	3902.14	4295.032	3282.258	4175.805	4333.397	3536.524	3389.484	3912.206	4752.5	3990.996	3648.176
	std	3.665624	79.16902	103.8808	29.06097	53.37993	127.4037	205.1013	41.8701	80.45601	83.27279	323.4225	199.7949	51.13789
	median	2341.98	4187.042	3772.625	4271.381	3223.821	4102.471	4163.017	3497.543	3339.192	3791.675	4538.567	3658.878	3632.564
	rank	1	11	7	12	2	9	10	4	3	8	13	6	5
C17-F22	mean	11,739.23	30,994.01	23,384.21	32,095.1	22,352.12	30,326.85	29,242.02	21,417.37	25,422.62	32,013.72	23,983.29	24,489.45	29,017.48
	best	11,119.3	30,075.84	22,490.17	31,500.23	21,787.95	29,175.81	27,864.92	20,809.38	22,402.63	30,983.09	23,517.19	23,565.24	28,318.76
	worst	12,601.83	31,600.08	24,267.14	32,537.09	23,468.11	31,407.58	30,393.46	21,919.53	32,490.6	32,540.98	24,547.06	25,549.11	29,790.33
	std	710.0898	724.585	954.1855	471.0018	822.8792	993.6619	1177.489	614.6335	5203.31	767.0319	480.0112	892.852	846.0033
	median	11,617.89	31,150.06	23,389.75	32,171.53	22,076.2	30,362.01	29,354.86	21,470.28	23,398.62	32,265.4	23,934.46	24,421.73	28,980.41
	rank	1	11	4	13	3	10	9	2	7	12	5	6	8
C17-F23	mean	2877.727	5335.872	4519.972	5337.317	3977.314	5416.469	5211.363	4102.366	4191.726	4587.384	7041.698	5024.99	4622.327
	best	2872.132	4997.802	4221.97	5000.581	3728.194	4661.79	4908.279	3863.827	3978.938	4394.935	6710.592	4517.884	4333.783
	worst	2884.046	5864.65	4907.744	5687.42	4328.774	6439.532	5445.403	4512.721	4505.866	4913.43	7655.644	5482.702	4914.352
	std	5.680984	452.1518	317.9708	316.7113	291.3638	865.3568	256.43	329.4372	267.7258	268.7275	463.7404	476.1133	276.0704
	median	2877.366	5240.518	4475.086	5330.634	3926.144	5282.276	5245.886	4016.458	4141.051	4520.585	6900.278	5049.687	4620.587
	rank	1	10	5	11	2	12	9	3	4	6	13	8	7
C17-F24	mean	3327.447	7886.427	5769.584	9210.235	4658.192	6640.867	6445.247	4827.658	5046.403	5353.607	9421.163	6164.117	5771.57
	best	3295.552	6464.283	5637.382	6718.893	4473.416	6152.522	6265.655	4623.676	4901.073	5232.309	8823.528	5947.672	5725.84
	worst	3358.031	8782.206	5997.682	10,868.67	4778.794	6965.134	6914.643	5007.57	5208.561	5474.359	10,683.4	6591.619	5869.716
	std	32.22484	1216.41	174.9711	2158.227	148.0329	376.426	340.9264	171.9483	137.0123	107.5114	925.7061	316.4479	73.28173
	median	3328.102	8149.61	5721.635	9626.686	4690.279	6722.905	6300.346	4839.693	5037.989	5353.881	9088.86	6058.588	5745.361
	rank	1	11	6	12	2	10	9	3	4	5	13	8	7
C17-F25	mean	3185.319	13,621.26	6158.626	17,685.42	5854.182	10,407.81	8281.036	5668.024	7696.225	9357.009	10,782.02	6159.339	8673.186
	best	3137.451	13,175.62	5874.24	16,774.98	5525.795	9757.495	7967.185	5414.785	7568.199	8317.647	9996.874	5775.093	8297.837
	worst	3261.663	14,777.9	6306.101	19,985.54	6071.564	10,823.99	8445.885	5787.387	7759.344	10,598.91	11,914.95	6553.009	9020.787
	std	65.17418	841.0861	212.8684	1678.96	258.6572	528.3488	233.3135	190.7562	94.35572	1075.754	879.8981	391.0103	400.1571
	median	3171.081	13,265.76	6227.082	16,990.57	5909.685	10,524.88	8355.538	5734.962	7728.679	9255.739	10,608.12	6154.627	8687.061
	rank	1	12	4	13	3	10	7	2	6	9	11	5	8
C17-F26	mean	5757.952	37,193.55	27,227.65	41,177.42	18,510.85	33,041.44	33,462.01	18,650.87	22,019.9	26,712.68	33,396.34	24,595.13	26,133.1
	best	5646.247	36,733.23	25,412.47	39,715.86	18,068.12	31,789.29	31,148.83	17,807.37	20,853.1	23,898.52	32,052.6	23,399.85	25,081.9
	worst	5844.973	37,635.59	29,237.01	42,336.9	18,942.44	33,830.05	35,359.83	20,364.71	23,138.15	30,674.2	34,728.87	26,044.33	26,978.04
	std	91.28724	415.7299	1720.476	1453.452	397.9235	955.4753	2252.226	1276.208	1016.806	3118.981	1212.525	1190.45	862.7783
	median	5770.294	37,202.68	27,130.55	41,328.47	18,516.41	33,273.21	33,669.69	18,215.69	22,044.18	26,139.01	33,401.95	24,468.18	26,236.23
	rank	1	12	8	13	2	9	11	3	4	7	10	5	6
C17-F27	mean	3309.533	8413.641	4941.936	10,403.75	4518.881	6584.147	6182.604	4579.257	4887.567	5053.728	11,592.43	4882.433	5832.661
	best	3278.054	7319.58	4778.345	8225.096	4394.241	6282.218	5747.394	4470.018	4725.611	4830.724	11,482.1	4710.85	5678.883
	worst	3344.536	9440.875	5158.581	12,589.14	4644.012	6958.631	6611.83	4766.147	4990.301	5317.197	11,679.04	5142.374	6221.073
	std	30.85406	1273.237	196.9127	2577.408	112.8625	318.6922	497.2107	143.7892	127.6033	252.7201	102.8588	209.1422	282.3403
	median	3307.771	8447.055	4915.409	10400.39	4518.636	6547.869	6185.595	4540.431	4917.178	5033.496	11604.28	4838.254	5715.343
	rank	1	11	6	12	2	10	9	3	5	7	13	4	8
C17-F28	mean	3322.391	19,124.17	8228.098	24,056.9	7598.395	15,624.76	12,041.44	7388.135	11,298.65	12,578.59	17,710.22	10,204.86	12,789.79
	best	3318.875	17,065.35	7197.902	22,331.46	6570.65	12,257.6	11,111.72	6294.01	9252.347	9838.745	16,660.03	9234.102	11,046.66
	worst	3327.996	21,746.03	9068.445	27,362.32	8439.783	18,176.46	13,059.65	8155.359	13,490.62	14,852.93	18,903.68	11,933.8	14,382.35
	std	4.773791	2116.867	960.0067	2485.287	953.9716	3086.372	903.5436	974.9369	1931.088	2567.625	1034.585	1295.006	1824.745
	median	3321.347	18,842.64	8323.022	23,266.91	7691.572	16,032.5	11,997.19	7551.585	11,225.82	12,811.35	17,638.59	9825.769	12,865.07
	rank	1	12	4	13	3	10	7	2	6	8	11	5	9
C17-F29	mean	4450.864	129,137.8	12,401.25	240,458.7	10,561.93	18,327.61	17,050.81	11,770	11,516.29	14,283.47	22,687.26	11,745.72	13,885.43
	best	4169.308	77,696.06	11,141.29	133,351.7	9227.36	14,046.88	14,833.47	9752.072	10,037.44	12,895.33	19,928.78	9989.551	12,433.35
	worst	4829.632	172,665.1	13,122.9	330,129.5	12,124.78	23,225.48	20,262.89	13,789.26	13,308.87	16,034.41	27,552.97	12,884.31	15,331.96
	std	307.1237	44,029.41	949.0543	91,266.81	1480.877	4162.944	2513.505	1797.003	1495.106	1567.513	3635.824	1344.408	1358
	median	4402.258	133,095	12,670.4	249,176.9	10,447.79	18,019.05	16,553.44	11,769.34	11,359.43	14,102.08	21,633.65	12,054.51	13,888.2
	rank	1	12	6	13	2	10	9	5	3	8	11	4	7
C17-F30	mean	165,913.2	1.98 × 1010	4.3 × 109	2.95 × 1010	4.28 × 109	1.33 × 1010	5.29 × 109	4.35 × 109	5.51 × 109	6.82 × 109	9.2 × 109	4.69 × 109	4.73 × 109
	best	103,285.2	1.62 × 1010	2.64 × 109	2.62 × 1010	2.61 × 109	8.07 × 109	3.49 × 109	2.69 × 109	4.22 × 109	3.56 × 109	7.87 × 109	2.71 × 109	3.08 × 109
	worst	204,149.6	2.17 × 1010	5.31 × 109	3.22 × 1010	5.3 × 109	1.64 × 1010	6.66 × 109	5.38 × 109	6.64 × 109	9.56 × 109	1.06 × 1010	6.56 × 109	5.77 × 109
	std	48,066.28	2.7 × 109	1.27 × 109	2.69 × 109	1.29 × 109	3.98 × 109	1.44 × 109	1.28 × 109	1.1 × 109	3.1 × 109	1.33 × 109	1.72 × 109	1.28 × 109
	median	178,108.9	2.06 × 1010	4.62 × 109	2.99 × 1010	4.61 × 109	1.43 × 1010	5.49 × 109	4.66 × 109	5.6 × 109	7.07 × 109	9.17 × 109	4.74 × 109	5.02 × 109
	rank	1	12	3	13	2	11	7	4	8	9	10	5	6
Sum rank		29	336	140	355	65	293	265	114	156	249	272	162	203
Mean rank		1	11.58621	4.827586	12.24138	2.241379	10.10345	9.137931	3.931034	5.37931	8.586207	9.37931	5.586207	7
Total rank		1	12	4	13	2	11	9	3	5	8	10	6	7

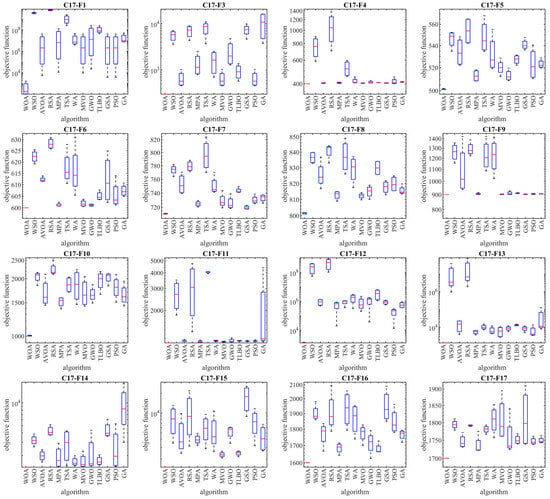
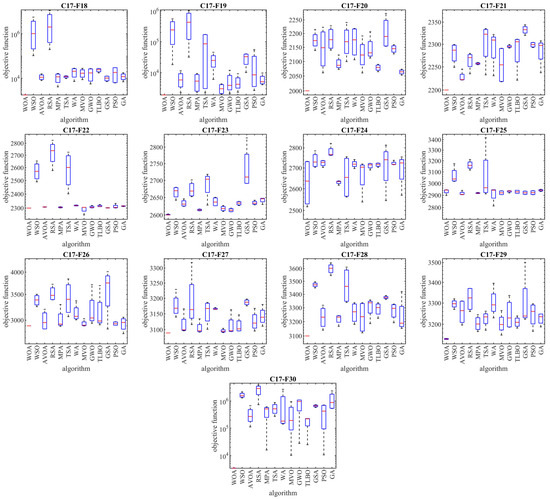
Figure 3. Boxplot diagrams of WOA and competitor algorithms’ performances on CEC 2017 test suite (dimension = 10).

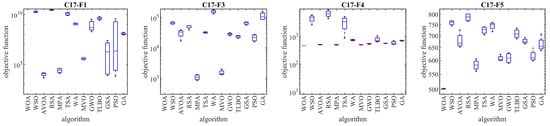
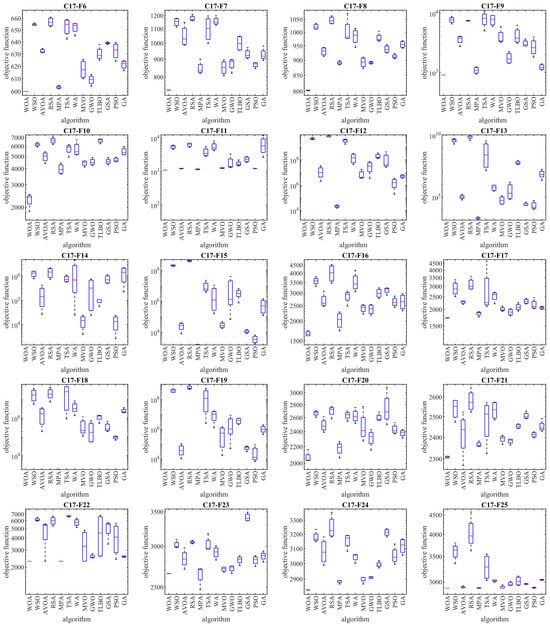
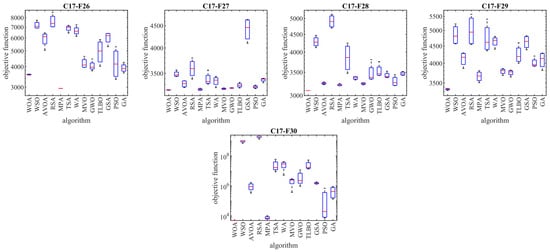
Figure 4. Boxplot diagrams of WOA and competitor algorithms’ performances on CEC 2017 test suite (dimension = 30).

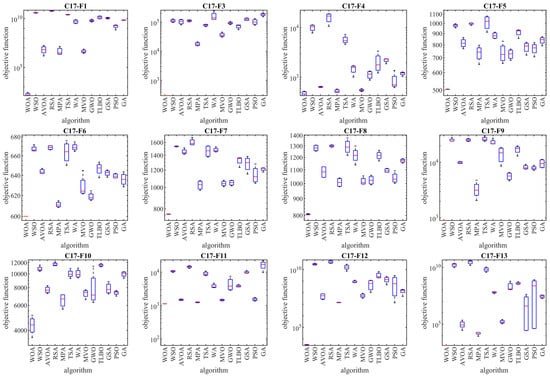
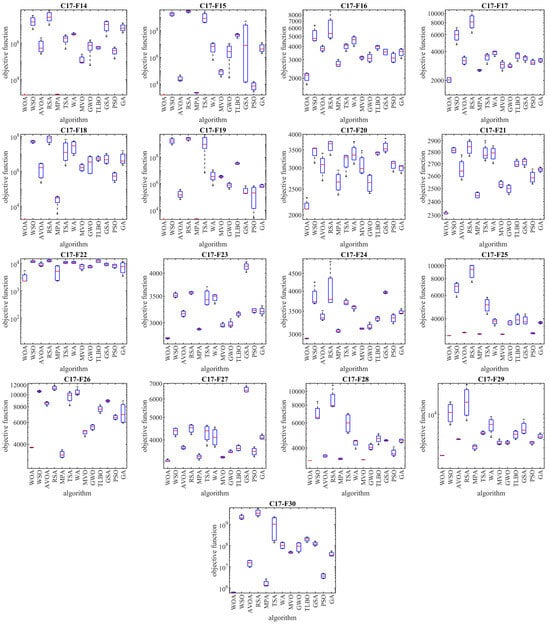
Figure 5. Boxplot diagrams of WOA and competitor algorithms’ performances on CEC 2017 test suite (dimension = 50).

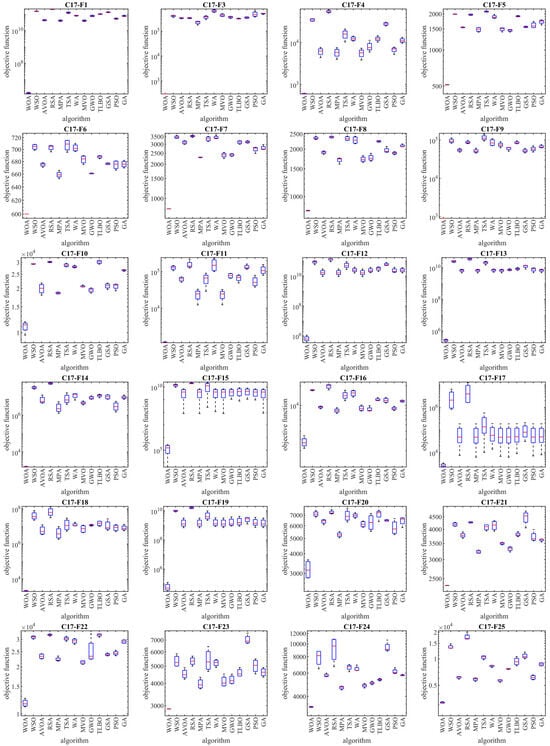
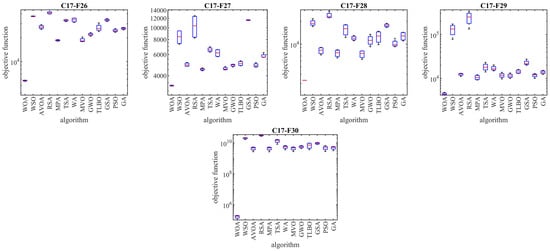
Figure 6. Boxplot diagrams of WOA and competitor algorithms performances on CEC 2017 test suite (dimension = 100).

As mentioned, the CEC 2017 test suite has functions of unimodal, multimodal, hybrid, and composition types. Each of these types of functions have been chosen with a special motivation to measure the quality of metaheuristic algorithms.

Unimodal functions C17-F1 and C17-F3 are types of functions that do not have local optima and only have one main optimal solution. These types of functions are suitable in order to evaluate the exploitation ability of metaheuristic algorithms in local search management with the aim of achieving solutions closer to the global optimum. The findings obtained from the optimization results of unimodal functions show that WOA has a high ability in the exploitation and local search by providing better results for these functions and obtaining the rank of the first best optimization.

Multimodal functions C17-F4 to C17-F10 are types of functions that have several local optimal solutions in addition to the main optimum. These types of functions challenge the exploration ability of metaheuristic algorithms in providing a global search and escaping from local optima. The findings obtained from the optimization of multimodal functions show that WOA, by achieving better results in most of the multimodal benchmark functions C17-F4 to C17-F10 and obtaining the rank of the first best optimizer, has a successful performance in its exploration to manage the global search in the problem-solving space.

Hybrid functions C17-F11 to C17-F20 and composition functions C17-F21 to C17-F30 are complex optimization problems for which it is very challenging to find a suitable solution. These types of optimization problems are very suitable for evaluating the ability of metaheuristic algorithms in balancing the exploration and exploitation during the search process. The analysis of the simulation results shows that WOA achieved better results in most of the benchmark functions C17-F11 to C17-F30 compared to the competing algorithms and was identified as the first best optimizer for these functions. The findings obtained from the optimization results of hybrid and composition functions show that WOA has a high ability to balance the exploration and exploitation during the search process in the problem-solving space in order to identify the main optimal area, escape from local optima, and converge towards the global optima.

The optimization findings are that WOA has achieved suitable solutions for the CEC 2017 test suite with its high capability in managing exploration and exploitation, and balancing them during the search process. The simulation findings are that WOA provided a superior performance by providing better results for most of the benchmark functions and obtained the rank of the first best optimizer in order to tackle the CEC 2017 test suite for problem dimensions equal to 10, 30, 50, and 100.

4.3. Statistical Analysis

Comparing the performance of metaheuristic algorithms using statistical indicators showed that WOA provided a superior performance against competitor algorithms in handling the CEC 2017 test suite. In this subsection, using statistical analysis, it has been checked whether this superiority of WOA is statistically significant or not. For this purpose, the Wilcoxon rank sum test [103] is employed, which is a non-parametric test effective in determining the significant difference between the means of two data samples. In this test, the presence or absence of a significant difference between the performance of two metaheuristic algorithms is determined using a criterion called the p-value.

The results of implementing the Wilcoxon rank sum test on the performance of WOA against the performance of each of the competitor algorithms are reported in Table 6. Based on the obtained results, in cases where the p-value is less than 0.05, WOA has a statistically significant superiority in its competition with the corresponding algorithm. The findings obtained from the statistical analysis are that WOA has a significant statistical superiority over all twelve competitor algorithms in order to tackle the CEC 2017 test suite for all four problem dimensions equal to 10, 30, 50, and 100.

Table 6. Wilcoxon rank sum test results.

Compared Algorithm	Objective Function Type
	CEC 2017
	D = 10	D = 30	D = 50	D = 100
WOA vs. WSO	2.34 × 10−23	2.34 × 10−23	2.34 × 10−23	2.34 × 10−23
WOA vs. AVOA	4.51 × 10−21	3.63 × 10−23	2.34 × 10−23	2.34 × 10−23
WOA vs. RSA	2.34 × 10−23	2.34 × 10−23	2.34 × 10−23	2.34 × 10−23
WOA vs. MPA	2.39 × 10−20	1.86 × 10−18	7.93 × 10−20	2.34 × 10−23
WOA vs. TSA	1.13 × 10−22	2.34 × 10−23	2.34 × 10−23	2.34 × 10−23
WOA vs. WA	1.13 × 10−22	2.34 × 10−23	2.34 × 10−23	2.34 × 10−23
WOA vs. MVO	1.08 × 10−20	2.54 × 10−23	2.34 × 10−23	2.34 × 10−23
WOA vs. GWO	6.23 × 10−23	2.34 × 10−23	2.34 × 10−23	2.34 × 10−23
WOA vs. TLBO	4.40 × 10−23	2.34 × 10−23	2.34 × 10−23	2.34 × 10−23
WOA vs. GSA	1.92 × 10−20	2.41 × 10−23	2.34 × 10−23	2.34 × 10−23
WOA vs. PSO	1.85 × 10−21	2.81 × 10−23	2.34 × 10−23	2.34 × 10−23
WOA vs. GA	3.21 × 10−21	2.34 × 10−23	2.34 × 10−23	2.34 × 10−23

5. WOA for Real-World Applications

One of the most special applications of metaheuristic algorithms is their efficiency in handling real world applications. In this section, the ability of WOA to tackle optimization tasks in real world applications is evaluated. With this aim, twenty-two constrained optimization problems from the CEC 2011 test suite and four engineering design problems have been selected.

5.1. Evaluation of CEC 2011 Test Suite

In this subsection, the capability of WOA and competitor algorithms to tackle the CEC 2011 test suite is challenged. The CEC 2011 test suite consists of twenty-two constrained optimization problems from real-world applications. The complete information, details, and description of the CEC 2011 test suite are available at [104]. The proposed WOA approach and each of the competitor algorithms are implemented in the CEC-2011 functions in twenty-five independent implementations, where each implementation contains 150,000 FEs.

The optimization results of the CEC 2011 test suite using WOA and competitor algorithms are reported in Table 7. The boxplot diagrams obtained from the implementation of metaheuristic algorithms on this test suite are plotted in Figure 7. The optimization results confirm that WOA has a high ability to manage exploration and exploitation, and establishing a balance between them has achieved suitable solutions for CEC 2011 test suite optimization problems. Simulation results show that WOA has provided a superior performance compared to competitor algorithms in order to tackle the CEC 2011 test suite, by achieving better results for all twenty-two optimization problems, from C11-F1 to C11-F22. In addition, the results obtained from the statistical analysis (reported in the last row of Table 7) confirm that WOA has a significant statistical superiority against all twelve competitor algorithms. The simulation findings are that WOA has an effective and promising performance for solving optimization tasks in real-world applications.

Table 7. Optimization results of CEC 2011 test suite.

		WOA	WSO	AVOA	RSA	MPA	TSA	WA	MVO	GWO	TLBO	GSA	PSO	GA
C11-F1	mean	5.920262	18.52663	15.16499	21.56805	11.33142	19.04654	15.37237	15.90785	13.67427	19.06925	21.36973	18.71864	22.57361
	best	0.000222	17.09155	12.21476	20.346	6.522873	18.14175	12.09345	14.46938	7.050046	17.57006	20.17668	13.35202	21.73935
	worst	12.30613	20.76811	18.18784	23.58074	14.46037	20.30098	18.50624	17.30895	18.27028	20.08999	22.71724	22.70728	23.63095
	std	7.47645	1.924815	3.321668	1.624078	4.151913	1.085949	3.129896	1.424224	5.170443	1.164633	1.161529	4.826403	0.856825
	median	5.687347	18.12343	15.12867	21.17272	12.17123	18.87171	15.4449	15.92653	14.68838	19.30847	21.29249	19.40762	22.46208
	rank	1	7	4	12	2	9	5	6	3	10	11	8	13
C11-F2	mean	−26.3177	−12.8865	−17.5678	−10.9051	−20.4131	−10.7076	−15.8648	−8.95953	−18.6879	−10.4312	−13.6981	−18.7223	−11.861
	best	−27.0674	−15.1073	−19.0665	−11.9228	−21.772	−14.6118	−19.5431	−9.68292	−21.4408	−10.9708	−16.5241	−20.3832	−14.776
	worst	−25.4327	−11.2966	−16.3181	−9.8404	−19.6827	−8.42276	−12.3284	−8.07994	−16.363	−9.76332	−11.0327	−16.3227	−9.94689
	std	0.767656	2.014547	1.251378	1.022455	1.012268	3.197516	3.892676	0.899112	2.3012	0.5459	3.318668	1.875111	2.256416
	median	−26.3854	−12.5709	−17.4432	−10.9286	−20.0989	−9.89801	−15.7938	−9.03763	−18.4739	−10.4953	−13.6178	−19.0916	−11.3606
	rank	1	8	5	10	2	11	6	13	4	12	7	3	9
C11-F4	mean	1.15 × 10−5	1.15 × 10−5	1.15 × 10−5	1.15 × 10−5	1.15 × 10−5	1.15 × 10−5	1.15 × 10−5	1.15 × 10−5	1.15 × 10−5	1.15 × 10−5	1.15 × 10−5	1.15 × 10−5	1.15 × 10−5
	best	1.15 × 10−5	1.15 × 10−5	1.15 × 10−5	1.15 × 10−5	1.15 × 10−5	1.15 × 10−5	1.15 × 10−5	1.15 × 10−5	1.15 × 10−5	1.15 × 10−5	1.15 × 10−5	1.15 × 10−5	1.15 × 10−5
	worst	1.15 × 10−5	1.15 × 10−5	1.15 × 10−5	1.15 × 10−5	1.15 × 10−5	1.15 × 10−5	1.15 × 10−5	1.15 × 10−5	1.15 × 10−5	1.15 × 10−5	1.15 × 10−5	1.15 × 10−5	1.15 × 10−5
	std	5.11 × 10−19	1.6 × 10−11	1.84 × 10−9	3.6 × 10−11	7.5 × 10−15	2.54 × 10−14	8.21 × 10−15	7.14 × 10−13	6.23 × 10−15	5.35 × 10−14	8.21 × 10−15	8.21 × 10−15	8.21 × 10−15
	median	1.15 × 10−5	1.15 × 10−5	1.15 × 10−5	1.15 × 10−5	1.15 × 10−5	1.15 × 10−5	1.15 × 10−5	1.15 × 10−5	1.15 × 10−5	1.15 × 10−5	1.15 × 10−5	1.15 × 10−5	1.15 × 10−5
	rank	1	11	13	12	6	8	4	10	7	9	3	2	5
C11-F4	mean	0	0	0	0	0	0	0	0	0	0	0	0	0
	best	0	0	0	0	0	0	0	0	0	0	0	0	0
	worst	0	0	0	0	0	0	0	0	0	0	0	0	0
	std	0	0	0	0	0	0	0	0	0	0	0	0	0
	median	0	0	0	0	0	0	0	0	0	0	0	0	0
	rank	1	1	1	1	1	1	1	1	1	1	1	1	1
C11-F5	mean	−34.1274	−25.3054	−27.6103	−21.9186	−31.2097	−26.9288	−27.277	−26.8311	−30.0246	−15.4951	−27.0801	−13.982	−14.5831
	best	−34.7492	−26.9675	−28.7894	−23.6021	−32.9597	−31.4995	−28.4862	−30.2509	−33.3254	−18.4743	−30.112	−16.5844	−15.7199
	worst	−33.3862	−23.1915	−26.5679	−20.3882	−29.8239	−21.4147	−25.5644	−25.0695	−27.3302	−12.563	−25.7886	−10.9928	−11.6236
	std	0.612897	1.83648	1.001872	1.468926	1.522608	4.536216	1.341271	2.59256	2.883084	2.646096	2.222197	2.725695	2.165669
	median	−34.187	−25.5314	−27.5421	−21.8421	−31.0276	−27.4004	−27.5287	−26.002	−29.7214	−15.4715	−26.2099	−14.1755	−15.4944
	rank	1	9	4	10	2	7	5	8	3	11	6	13	12
C11-F6	mean	−24.1117	−11.5689	−15.0589	−10.8741	−17.558	−7.04179	−15.7029	−8.41901	−15.4776	−3.38045	−17.0515	−3.98565	−4.61934
	best	−27.4295	−14.9999	−17.6727	−13.1917	−19.688	−16.3449	−16.76	−15.8571	−17.3553	−6.33468	−19.2839	−6.33468	−7.20694
	worst	−23.0057	−10.3548	−12.7552	−9.82115	−15.6047	−3.70338	−13.844	−2.2514	−13.272	−2.2514	−13.2814	−2.2514	−2.2514
	std	2.415411	2.499014	2.209968	1.701466	2.190167	6.782714	1.495767	7.622797	1.984471	2.162231	2.99605	2.254466	2.747428
	median	−23.0058	−10.4603	−14.9038	−10.2419	−17.4696	−4.05944	−16.1038	−7.78378	−15.6416	−2.46787	−17.8204	−3.67826	−4.5095
	rank	1	7	6	8	2	10	4	9	5	13	3	12	11
C11-F7	mean	0.860704	1.524206	1.300685	1.742041	1.05467	1.31307	1.61969	1.020956	1.150376	1.602382	1.158741	1.18923	1.617492
	best	0.582273	1.431499	1.164474	1.691573	0.884743	1.142584	1.502413	0.954741	0.944097	1.533211	0.972963	1.033932	1.295765
	worst	1.02503	1.63923	1.516461	1.840269	1.228983	1.683647	1.709441	1.094387	1.270791	1.67048	1.339876	1.320852	1.87706
	std	0.219736	0.106572	0.185293	0.072846	0.153806	0.272484	0.114798	0.064616	0.16602	0.062818	0.18654	0.15491	0.264865
	median	0.917757	1.513047	1.260902	1.718161	1.052477	1.213025	1.633453	1.017348	1.193308	1.602919	1.161063	1.201069	1.648571
	rank	1	9	7	13	3	8	12	2	4	10	5	6	11
C11-F8	mean	220.0005	277.6632	246.6622	305.8148	234.1027	258.3854	264.4916	235.2387	237.5108	235.2387	250.7556	406.231	234.1343
	best	220	251.6885	227.4027	269.7514	220	220	237.6085	220	220	220	220	244.4432	220
	worst	220.0017	334.1912	290.719	339.1266	268.1246	358.4392	328.9023	264.7165	274.9408	276.0768	315.8379	508.5788	264.7165
	std	0.000887	42.01262	32.4559	34.61493	25.133	73.2542	47.12799	22.05357	28.33688	29.83652	49.40421	126.0563	23.08083
	median	220.0001	262.3866	234.2635	307.1905	224.1431	227.5512	245.7277	228.1192	227.5512	222.4391	233.5923	435.9509	225.9103
	rank	1	11	7	12	2	9	10	5	6	4	8	13	3
C11-F9	mean	8790.002	410,333.3	285,603.8	762,286.5	35,854.99	67,949.88	283,047.3	114,772.9	51,768.13	306,726.2	595,870.4	776,555.6	1,376,387
	best	5458.199	283,319.9	248,962.7	507,159.8	27,825.15	48,803.45	164,739	80,402.87	32,993.23	263,471.3	514,867.4	625,999.7	1,316,025
	worst	14,043.01	471,682	304,142.5	884,417.5	40,457.49	86,352.61	470,358	164,409	68,076.97	389,185.7	638,175	948,077.3	1,461,666
	std	4040.653	95,135.33	28,249.6	188,460.6	6266.359	17,450.66	151,014.4	38,686.66	15,788.04	62,887.79	60,538.4	183,780.7	76,656.13
	median	7829.4	443,165.6	294,654.9	828,784.3	37,568.66	68,321.73	248,546.1	107,140	53,001.16	287,123.9	615,219.7	766,072.7	1,363,928
	rank	1	9	7	11	2	4	6	5	3	8	10	12	13
C11-F10	mean	−21.4888	−13.895	−15.95	−12.7165	−17.4163	−14.1871	−13.1306	−14.4043	−13.988	−12.0259	−13.3259	−12.0953	−11.8895
	best	−21.8298	−16.2174	−17.4476	−14.2163	−18.6948	−18.78	−14.5671	−18.3793	−14.6603	−13.4858	−14.2649	−13.5768	−13.3855
	worst	−20.7878	−12.7937	−15.2701	−11.9908	−16.8936	−11.7495	−12.25	−12.5215	−13.533	−11.2532	−12.8896	−11.2964	−11.1289
	std	0.51802	1.737931	1.099165	1.112377	0.934674	3.454422	1.213161	2.935488	0.529854	1.091506	0.693359	1.11322	1.117415
	median	−21.6689	−13.2844	−15.5412	−12.3295	−17.0384	−13.1095	−12.8527	−13.3582	−13.8794	−11.6822	−13.0746	−11.7541	−11.5218
	rank	1	7	3	10	2	5	9	4	6	12	8	11	13
C11-F11	mean	571,779.3	5,999,874	2,648,971	8,128,942	3,114,159	6,099,038	2,805,219	2,869,907	4,628,352	5,587,178	2,941,547	5,594,892	6,222,972
	best	260,907.2	5,483,070	2,284,468	7,837,324	2,705,685	5,076,329	2,399,476	2,560,562	4,165,084	5,253,401	2,510,786	5,253,401	5,944,075
	worst	828,623.2	6,665,190	3,120,138	8,574,787	3,570,106	7,373,167	3,210,022	3,533,015	4,998,465	6,004,643	3,473,410	6,020,072	6,613,747
	std	271,081	542,972.8	396,212.7	371,819.1	391,498.2	1,036,183	365,879.7	495,888.1	405,687.3	339,178.4	433,897.4	345,852.3	306,823
	median	598,793.4	5,925,619	2,595,638	8,051,828	3,090,424	5,973,327	2,805,688	2,693,025	4,674,930	5,545,334	2,890,996	5,553,048	6,167,032
	rank	1	10	2	13	6	11	3	4	7	8	5	9	12
C11-F12	mean	1,199,853	7,479,512	3,987,123	10,853,249	2,524,194	5,138,886	5,685,715	2,561,020	2,628,290	11,614,335	5,668,192	3,247,870	11,726,387
	best	1,155,987	7,286,677	3,943,464	10,245,989	2,488,397	4,860,267	5,392,176	2,453,329	2,562,613	10,937,396	5,464,611	3,038,451	11,638,161
	worst	1,249,397	7,602,988	4,032,975	11,339,100	2,546,660	5,287,471	5,879,621	2,705,870	2,667,686	12,117,293	5,861,509	3,437,648	11,815,640
	std	48,990.45	157,213.9	46,095.01	493,305.2	28,942.93	216,610.9	248,987.5	129,431.7	50,150.42	545,223.2	202,462	179,948.4	88,261.18
	median	1,197,013	7,514,192	3,986,026	10,913,953	2,530,859	5,203,902	5,735,532	2,542,441	2,641,430	11,701,325	5,673,323	3,257,691	11,725,874
	rank	1	10	6	11	2	7	9	3	4	12	8	5	13
C11-F13	mean	15,444.2	15,747.56	15,462.13	16,062.99	15,472.71	15,491.53	15,523.08	15,503.87	15,499.14	15,800.2	94,122.04	15,491.98	25,603.61
	best	15,444.19	15,615.02	15,458.99	15,775.05	15,467.8	15,481.32	15,489.71	15,486.85	15,491.02	15,583.92	69,341.16	15,476.68	15,472.85
	worst	15,444.21	16,057.77	15,465.63	16,780.46	15,476.73	15,504.51	15,566.16	15,532.73	15,504.56	16,196.76	127,726.1	15,514.5	55,761.14
	std	0.009492	228.4789	3.631027	526.9678	4.052593	12.51904	39.70056	21.89707	6.60613	302.8927	28,704.65	17.50225	21,955.18
	median	15,444.2	15,658.73	15,461.95	15,848.21	15,473.15	15,490.15	15,518.23	15,497.95	15,500.49	15,710.07	89,710.42	15,488.37	15,590.23
	rank	1	9	2	11	3	4	8	7	6	10	13	5	12
C11-F14	mean	18,295.37	84,347.02	18,862.44	165,621.7	18,924.06	19,567.68	19,354.71	19,489.67	19,359.55	222,569.2	19,262.01	19,284.7	19,275.81
	best	18,241.6	65,506.07	18,781.45	123,456.2	18,819.82	19,303.23	19,202.1	19,373.79	19,212.11	26,986.31	189,75.04	19,085	18,992.03
	worst	18,388.09	115,558.2	18,965.39	236,014.5	19,128.24	20,133.47	19,621.83	19,729.76	19,672.11	424,243.1	194,25.74	19,478.09	19,667.87
	std	74.3835	24,392	86.50791	55,001.51	157.737	416.1025	208.3449	178.9331	236.1096	208,242.4	218.2802	180.0378	308.9479
	median	18,275.89	78,161.91	18,851.47	151,508.1	18,874.1	19,417.01	19,297.46	19,427.57	19,276.99	219,523.7	193,23.63	19,287.86	19,221.67
	rank	1	11	2	12	3	10	7	9	8	13	4	6	5
C11-F15	mean	32,883.86	650,468.8	92,369.12	1,352,560	40,138.91	55,205.78	169,619.1	40,244.67	40,229.24	10,771,451	226,222	40,375.8	5,551,934
	best	32,782.17	271,127.2	40,110.6	568,557.3	32,995.64	33,050.45	33,115.17	33,080.06	33,083.28	2,263,411	195,120.8	33,226.12	2,529,334
	worst	32,956.46	1,602,488	151,796.6	3,495,893	61,511.95	121,372.5	256,751.7	61,641.05	61,576.55	16,075,634	241,709.5	61,741.75	9,524,069
	std	80.05006	697,002.6	65,178.35	1,563,707	15,559.87	48,170.45	104,809.1	15,576.87	15,541.15	6,852,966	230,23.66	15,554.75	3,500,886
	median	32,898.39	364,129.9	88,784.62	672,895.2	33,024.03	33,200.08	194,304.8	33,128.79	33,128.56	12,373,379	234,028.9	33,267.67	5,077,167
	rank	1	10	7	11	2	6	8	4	3	13	9	5	12
C11-F16	mean	133,550.1	703,415	138,536	1,403,686	140,265.6	145,473.8	143,407.7	143,159.8	145,994	6,2043,183	13,101,196	55,536,227	53,325,786
	best	131,374.3	246,334.3	136,637.1	375,226.2	137,977	142,750	139,921.5	137,747.4	143,833.8	60,461,255	6,676,681	45,947,447	43,107,759
	worst	136,310.9	1,601,011	139,646.6	3,422,312	142,394.4	147,531.3	146,681	148,454.6	149,411.7	63,828,826	23,666,403	66,355,130	68,195,957
	std	2485.302	665,515.2	1524.71	1,496,671	1996.452	2562.744	3320.921	5100.992	2655.197	1,541,259	8,022,477	9,605,670	11,637,972
	median	133,257.7	483,157.3	138,930.1	908,603.1	140,345.5	145,807	143,514.1	143,218.5	145,365.2	61,941,326	11,030,850	54,921,167	50,999,714
	rank	1	8	2	9	3	6	5	4	7	13	10	12	11
C11-F17	mean	1,942,580	6.68 × 109	2.04 × 109	1.12 × 1010	4.28 × 108	1.32 × 109	7.19 × 109	4.28 × 108	4.28 × 108	1.6 × 1010	8.25 × 109	1.5 × 1010	1.57 × 1010
	best	1,930,112	5.81 × 109	1.82 × 109	8.26 × 109	3.53 × 108	1.09 × 109	5.18 × 109	3.54 × 108	3.53 × 108	1.55 × 1010	7.37 × 109	1.33 × 1010	1.46 × 1010
	worst	1,960,928	7.28 × 109	2.25 × 109	1.36 × 1010	4.89 × 108	1.51 × 109	9.48 × 109	4.89 × 108	4.89 × 108	1.66 × 1010	8.67 × 109	1.71 × 1010	1.77 × 1010
	std	14,267.83	7.39 × 108	1.93 × 108	2.51 × 109	76,568,346	2.36 × 108	1.96 × 109	75,864,138	77,049,182	5.11 × 108	6.58 × 108	1.88 × 109	1.53 × 109
	median	1,939,641	6.81 × 109	2.05 × 109	1.16 × 1010	4.35 × 108	1.34 × 109	7.05 × 109	4.36 × 108	4.36 × 108	1.59 × 1010	8.48 × 109	1.47 × 1010	1.52 × 1010
	rank	1	7	6	10	2	5	8	4	3	13	9	11	12
C11-F18	mean	942,071.3	39,002,043	5,225,655	83,242,808	1,331,483	2,083,589	7,334,852	1,342,897	1,372,893	22,275,175	8,414,772	94,729,029	80,543,508
	best	938,434.3	27,142,508	3,317,244	57,796,090	1,231,127	1,818,711	3,642,196	1,252,325	1,242,609	17,905,004	6,490,541	79,547,500	77,656,371
	worst	944,717.9	44,319,634	8,421,550	95,032,965	1,430,320	2,436,791	12,309,055	1,464,872	1,446,163	23,968,676	10,370,522	1.05 × 108	83,404,566
	std	2879.013	8744,359	2,550,735	18,970,390	93,792.18	325,410.3	4,017,629	113,531.6	98,639.56	3,197,990	1,867,130	12,510,156	2,562,690
	median	942,566.6	42,273,015	4,581,913	90,071,089	1,332,242	2,039,427	6,694,080	1,327,197	1,401,400	23,613,511	8,399,013	97,085,841	80,556,548
	rank	1	10	6	12	2	5	7	3	4	9	8	13	11
C11-F19	mean	1,025,359	38,536,034	5,431,254	81,659,875	1,582,314	2,506,819	7,915,361	1,818,631	1,739,213	25,611,750	5,159,819	1.21 × 108	80,945,378
	best	967,951.9	32,919,084	4,979,236	70,562,763	1,454,990	2,261,152	2,374,900	1,690,635	1,569,596	18,093,559	2,405,906	1.1 × 108	78,871,078
	worst	1,167,157	48,758,390	6,389,283	1.02 × 108	1,697,732	2,966,563	13,675,125	2,132,012	1,866,203	31,728,882	6,505,243	1.4 × 108	83,257,847
	std	103,552.7	7,792,611	706,256.2	16,208,978	118,857.1	343,390.1	5,839,402	228,869.5	144,387.5	6,482,922	2,064,322	14,152,758	1,964,094
	median	983,163.1	36,233,332	5,178,249	76,830,811	1,588,268	2,399,782	7,805,710	1,725,938	1,760,526	26,312,280	5,864,064	1.17 × 108	80,826,295
	rank	1	10	7	12	2	5	8	4	3	9	6	13	11
C11-F20	mean	941,261.4	40,715,344	4,689,034	87,925,596	1,249,157	1,853,275	5,657,508	1,257,852	1,275,793	24,691,264	10,532,525	1.12 × 108	80,959,574
	best	936,155	35,993,358	4,221,624	77,097,157	1,188,138	1,663,778	5,304,682	1,189,654	1,212,396	24,264,091	7,209,401	1.02 × 108	77,136,100
	worst	946,881.4	48,046,992	5,149,736	1.04 × 108	1,348,472	2,168,143	5,988,199	1,356,101	1,362,726	25,203,932	15,925,303	1.21 × 108	83,877,964
	std	5210.106	5,623,721	440,855.7	12,696,862	83,228.39	261,499.9	307,056.5	83,129.73	78,198.29	426,162.3	4,144,658	11,649,640	3,136,568
	median	941,004.7	39,410,513	4,692,388	85,093,522	1,230,009	1,790,590	5,668,575	1,242,826	1,264,026	24,648,517	9,497,698	1.12 × 108	81,412,115
	rank	1	10	6	12	2	5	7	3	4	9	8	13	11
C11-F21	mean	12.71464	44.59437	24.63935	62.88515	20.65716	30.34746	36.60303	28.75179	25.15152	79.78782	37.93642	83.30049	81.11724
	best	9.974473	38.49198	23.1396	49.33457	18.68511	26.91123	34.40424	26.98306	22.80864	43.64733	34.63593	73.67434	50.9247
	worst	14.97518	51.845	26.01877	77.1268	22.35827	32.03725	40.06733	30.97292	26.89316	111.9269	40.35983	92.19885	97.53857
	std	2.506567	6.127726	1.334083	13.14267	1.894926	2.562575	2.657618	2.087682	1.899426	30.57257	2.612935	10.17235	23.27926
	median	12.95445	44.02025	24.69952	62.53961	20.79262	31.22069	35.97027	28.52559	25.45215	81.78852	38.37496	83.66439	88.00285
	rank	1	9	3	10	2	6	7	5	4	11	8	13	12
C11-F22	mean	16.12533	42.87057	29.35531	54.50291	23.51882	32.62949	42.53537	32.73843	27.64423	81.8037	42.78463	84.61793	74.80509
	best	11.50154	39.32057	24.46946	43.04177	20.29214	28.59364	36.92265	27.9468	26.83196	56.99264	37.41968	71.37893	72.92364
	worst	19.55305	46.75956	33.05165	61.22284	25.7834	35.15256	45.86543	36.30337	28.67607	95.76237	49.47311	93.13173	76.66462
	std	4.361195	3.817162	4.400959	8.773434	2.616952	3.112768	4.531827	3.833639	1.006521	18.78402	5.581022	10.67689	1.702093
	median	16.72337	42.70108	29.95006	56.87352	23.99987	33.38588	43.6767	33.35177	27.53445	87.22989	42.12286	86.98053	74.81605
	rank	1	9	4	10	2	5	7	6	3	12	8	13	11
Sum rank		22	192	110	232	55	147	146	119	98	222	158	199	224
Mean rank		1	8.727272727	5	10.54545455	2.5	6.681818182	6.636363636	5.409090909	4.454545455	10.09090909	7.181818182	9.045454545	10.18181818
Total rank		1	9	4	13	2	7	6	5	3	11	8	10	12
Wilcoxon: p-value			2.08 × 10−17	1.19 × 10−16	2.08 × 10−17	8.64 × 10−17	4.45 × 10−17	2.08 × 10−17	4.85 × 10−14	8.64 × 10−17	6.52 × 10−17	1.04 × 10−16	3.08 × 10−17	6.52 × 10−17

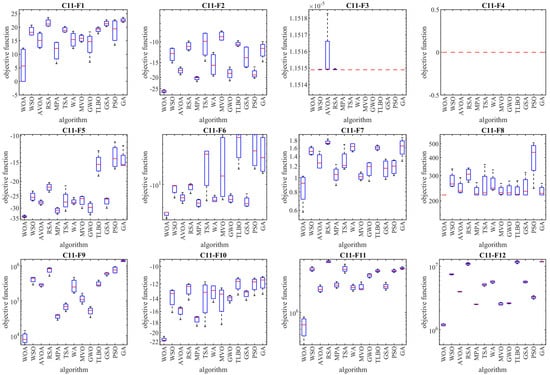
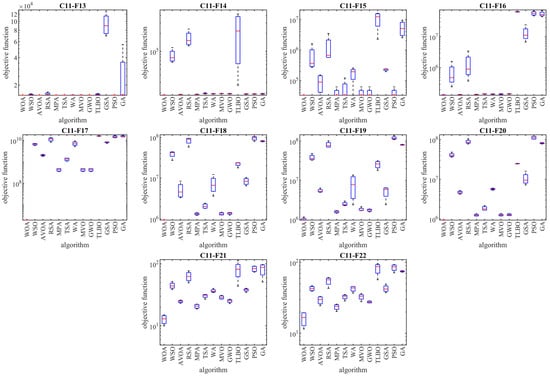
Figure 7. Boxplot diagrams of WOA and competitor algorithms’ performances on CEC 2011 test suite.

5.2. Pressure Vessel Design Problem

Pressure vessel design is a design challenge in engineering according to the schematic shown in Figure 8, whose main goal is to minimize the construction cost. The mathematical model of this design is as follows [105]:

$$\begin{array}{c}Consider: X=\left[x_1, x_2, x_3, x_4\right]=\left[T_s, T_h, R, L\right].\\ Minimize: f\left(x\right)=0.6224x_1{x}_3{x}_4+1.778x_2{x}_3^2+3.1661x_1^2{x}_4+19.84x_1^2{x}_3.\end{array}$$

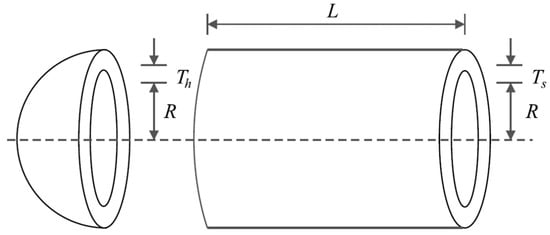
Figure 8. Schematic of pressure vessel design.

Subject to:

$$\begin{array}{c}{g}_1\left(x\right)=-x_1+0.0193x_3 \le 0, g_2\left(x\right)=-x_2+0.00954x_3\le 0,\\ g_3\left(x\right)=-\pi x_3^2{x}_4-\frac{4}{3}\pi x_3^3+\mathrm{1,296,000}\le 0, g_4\left(x\right)=x_4-240 \le 0.\end{array}$$

With

$$0\le x_1,x_2\le 100 {\mathrm{a}\mathrm{n}\mathrm{d} 10\le x}_3,x_4\le 200.$$

The results of tackling the pressure vessel design by employing WOA and competitor algorithms are presented in Table 8 and Table 9. The convergence curve of WOA, which shows the process of achieving a suitable solution for the pressure vessel design, is drawn in Figure 9. Based on the optimization results, WOA has provided the optimal design with the value of the objective function equal to (5882.8955) and the values of the design variables equal to (0.7780271, 0.3845792, and 40.312284, 200). From the simulation results, WOA has a superior performance compared to competitor algorithms for solving the pressure vessel design; this is because it provides better results for statistical indicators and design variables.

Table 8. Performance of optimization algorithms on pressure vessel design problem.

Algorithm	Optimum Variables				Optimum Cost
	Ts	Th	R	L
WOA	0.7780271	0.3845792	40.312284	200	5882.8955
WSO	0.7785743	0.3850406	40.33987	199.99921	5892.7241
AVOA	0.8077815	0.4000706	41.820565	181.53993	5958.3704
RSA	1.1657617	0.618108	59.030247	51.040811	7539.4546
MPA	0.7785731	0.385039	40.339812	200	5892.7186
TSA	0.7797175	0.3860026	40.39751	200	5913.295
WA	0.9184693	0.4581458	46.795024	127.0907	6278.6632
MVO	0.8925866	0.4435107	45.896035	135.96236	6168.4843
GWO	0.7799598	0.3865326	40.394098	199.25911	5900.0698
TLBO	1.5048208	0.5179771	52.061183	91.428726	10,045.366
GSA	1.0516581	0.9936889	43.266773	192.83972	10,649.957
PSO	1.4503006	0.6067838	61.672694	47.379388	9264.5722
GA	1.2669853	0.6949238	54.28441	102.03966	9807.9948

Table 9. Statistical results of optimization algorithms on pressure vessel design problem.

Algorithm	Mean	Best	Worst	Std	Median	Rank
WOA	5882.8955	5882.8955	5882.8955	1.89 × 10−12	5882.8955	1
WSO	6033.3406	5892.7241	6301.1769	129.69301	5979.5913	3
AVOA	6288.5195	5958.3704	7122.1164	337.49432	6268.861	5
RSA	11,099.696	7539.4546	17,037.653	2446.6213	10,488.489	9
MPA	6026.8703	5892.7186	6278.0162	1.25 × 102	5979.5828	2
TSA	6328.6201	5913.295	7106.1523	386.81073	6182.2211	6
WA	7671.313	6278.6632	11,658.477	1334.6086	7337.9574	8
MVO	6520.5761	6168.4843	7126.8347	276.2229	6507.5194	7
GWO	6127.4971	5900.0698	6566.7221	199.96154	6076.6533	4
TLBO	23,429.698	10,045.366	48262.31	10,853.982	20,946.159	12
GSA	17,499.525	10,649.957	26,357.093	5289.9309	16,741.248	10
PSO	24,528.908	9264.5722	40,820.506	10,185.804	26,943.18	13
GA	21,217.998	9807.9948	36,887.804	8512.6048	19,018.661	11

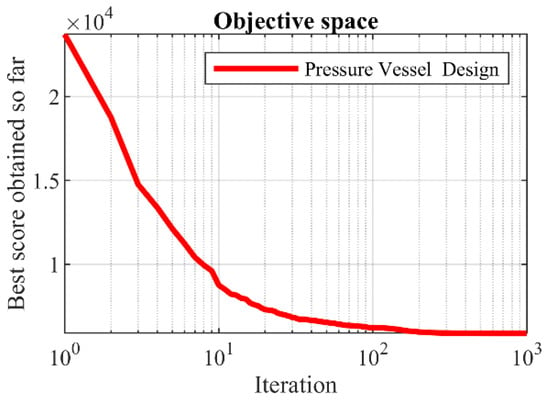
Figure 9. WOA’s performance convergence curve on pressure vessel design.

5.3. Speed Reducer Design Problem

The speed reducer design is a design challenge in engineering according to the schematic shown in Figure 10, whose main goal is to minimize the weight of the speed reducer. The mathematical model of this design is as follows [106,107]:

$$\begin{array}{c}\mathrm{Consider}: X=\left[x_{1,}{x}_2,x_3,x_4,x_5{,x}_6,x_7\right]=\left[b,m,p,l_1,l_2,d_1,d_2\right].\\ \mathrm{Minimize}: f\left(x\right)=0.7854x_1{x}_2^2\left(3.3333x_3^2+14.9334x_3-43.0934\right)-1.508x_1\left(x_6^2+x_7^2\right)+7.4777\left(x_6^3+x_7^3\right)+0.7854(x_4{x}_6^2+x_5{x}_7^2).\end{array}$$

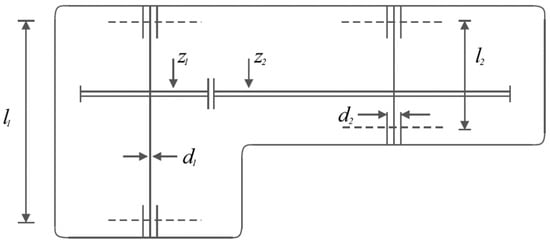
Figure 10. Schematic of speed reducer design.

Subject to:

$$\begin{array}{c}{g}_1\left(x\right)=\frac{27}{x_1{x}_2^2{x}_3}-1\le 0, g_2\left(x\right)=\frac{397.5}{x_1{x}_2^2{x}_3}-1\le 0,\\ g_3\left(x\right)=\frac{1.93x_4^3}{x_2{x}_3{x}_6^4}-1\le 0, g_4\left(x\right)=\frac{1.93x_5^3}{x_2{x}_3{x}_7^4}-1\le 0,\\ g_5\left(x\right)=\frac{1}{110x_6^3}\sqrt{{\left(\frac{745x_4}{x_2{x}_3}\right)}^2+16.9\times {10}^6}-1\le 0,\\ g_6(x)=\frac{1}{85x_7^3}\sqrt{{\left(\frac{745x_5}{x_2{x}_3}\right)}^2+157.5\times {10}^6}-1\le 0,\\ g_7\left(x\right)=\frac{x_2{x}_3}{40}-1\le 0, g_8\left(x\right)=\frac{{5x}_2}{x_1}-1\le 0,\\ g_9\left(x\right)=\frac{x_1}{12x_2}-1\le 0, g_{10}\left(x\right)=\frac{{1.5x}_6+1.9}{x_4}-1\le 0,\\ g_{11}\left(x\right)=\frac{{1.1x}_7+1.9}{x_5}-1\le 0.\end{array}$$

With

$$\begin{array}{c}2.6\le x_1\le 3.6,0.7\le x_2\le 0.8,17\le x_3\le 28,7.3\le x_4\le 8.3,7.8\le x_5\\ \le 8.3,2.9\le x_6\le 3.9, \mathrm{a}\mathrm{n}\mathrm{d} 5\le x_7\le 5.5.\end{array}$$

The results of employing WOA and competitor algorithms to tackle the speed reducer design are published in Table 10 and Table 11. The convergence curve of WOA while achieving the optimal solution for the speed reducer design is plotted in Figure 11. Based on the optimization results, WOA has provided the optimal design with the value of the objective function equal to (2996.3482) and the values of the design variables equal to (3.5, 0.7, 17, 7.3, 7.8, 3.3502147, and 5.2866832). From the analysis of simulation results, it can be concluded that WOA has provided a superior performance compared to competitor algorithms in order to tackle the speed reducer design.

Table 10. Performance of optimization algorithms on speed reducer design problem.

Algorithm	Optimum Variables							Optimum Cost
	b	M	p	l1	l2	d1	d2
WOA	3.5	0.7	17	7.3	7.8	3.3502147	5.2866832	2996.3482
WSO	3.5042158	0.7000001	17.000053	7.3001627	7.9522096	3.3503306	5.2884051	3002.4588
AVOA	3.5042139	0.7	17	7.3389788	7.9632265	3.3503942	5.2878418	3002.7176
RSA	3.5711442	0.7	17	7.9311292	8.2167884	3.3880068	5.422609	3139.1429
MPA	3.5042139	0.7	17	7.3	7.9505601	3.3503211	5.2878374	3002.0745
TSA	3.513046	0.7	17	7.3	8.2661247	3.3505443	5.2902566	3014.0764
WA	3.572036	0.7	17	7.3	8.0938979	3.3627496	5.288787	3035.6381
MVO	3.5316539	0.7	17	7.3	7.9842255	3.3674653	5.2878453	3017.98
GWO	3.5072582	0.7	17	7.4580642	7.9935714	3.3512994	5.2895216	3006.9308
TLBO	3.5396555	0.7027371	23.384347	8.0724951	8.0593194	3.5821158	5.3287864	4564.8145
GSA	3.5437703	0.7018853	17.25277	7.6564322	7.8613604	3.3921031	5.3614252	3130.8716
PSO	3.5246766	0.7000493	17.750249	7.3678163	7.9971438	3.5282892	5.3283562	3220.9554
GA	3.5659914	0.7038109	17.557264	7.9041778	7.8382392	3.5928498	5.3281635	3244.8877

Table 11. Statistical results of optimization algorithms on speed reducer design problem.

Algorithm	Mean	Best	Worst	Std	Median	Rank
WOA	2996.3482	2996.3482	2996.3482	9.58 × 10−13	2996.3482	1
WSO	3008.2332	3002.4588	3012.528	3.4293355	3008.6428	3
AVOA	3011.1258	3002.7176	3021.4649	5.0212893	3010.4138	4
RSA	3200.0678	3139.1429	3244.24	39.897174	3209.2035	9
MPA	3008.0391	3002.0745	3012.5251	3.35 × 10	3008.6232	2
TSA	3032.5426	3014.0764	3046.4309	10.371712	3034.351	7
WA	3113.2893	3035.6381	3319.4462	74.629685	3090.6721	8
MVO	3030.961	3017.98	3057.5836	9.489721	3029.6252	6
GWO	3013.7043	3006.9308	3019.0673	3.5211511	3014.6012	5
TLBO	4.763 × 1013	4564.8145	3.447 × 1014	8.017 × 1013	1.865 × 1013	12
GSA	3321.8616	3130.8716	3744.9365	182.4154	3233.8591	10
PSO	7.029 × 1013	3220.9554	3.561 × 1014	8.586 × 1013	5.028 × 1013	13
GA	3.384 × 1013	3244.8877	2.184 × 1014	5.391 × 1013	1.356 × 1013	11

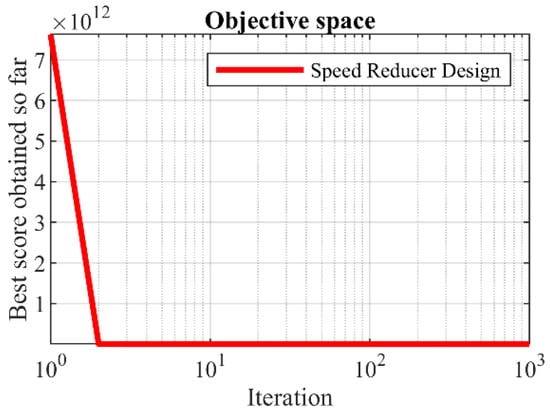
Figure 11. WOA’s performance convergence curve on speed reducer design.

5.4. Welded Beam Design

Welded beam design is a design challenge in engineering according to the schematic shown in Figure 12, whose main goal is to minimize the fabrication cost. The mathematical model of this design is as follows [32]:

$$\begin{array}{c}Consider: X=\left[x_1, x_2, x_3, x_4\right]=\left[h, l, t, b\right].\\ Minimize: f\left(x\right)=1.10471x_1^2{x}_2+0.04811x_3{x}_4 (14.0+x_2).\end{array}$$

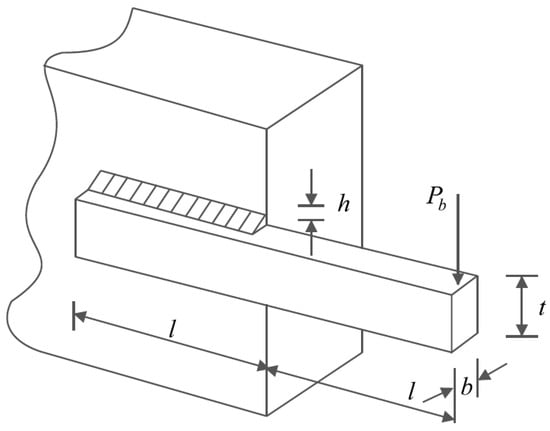
Figure 12. Schematic of welded beam design.

Subject to:

$$\begin{array}{c}{g}_1\left(x\right)=\tau \left(x\right)-\mathrm{13,600} \le 0, g_2\left(x\right)=\sigma \left(x\right)-\mathrm{30,000} \le 0,\\ g_3\left(x\right)=x_1-x_4\le 0, g_4\left(x\right)=0.10471x_1^2+0.04811x_3{x}_4 (14+x_2)-5.0 \le 0,\\ g_5\left(x\right)=0.125-x_1\le 0, g_6\left(x\right)=\delta \left(x\right)-0.25 \le 0,\\ g_7\left(x\right)=6000-p_c \left(x\right)\le 0.\end{array}$$

where

$$\begin{array}{c}\tau \left(x\right)=\sqrt{{\left({\tau }^{\prime }\right)}^2+\left(2\tau {\tau }^{\prime }\right)\frac{x_2}{2R}+{\left({\tau }^{″}\right)}^2 }, {\tau }^{\prime }=\frac{6000}{\sqrt{2}{x}_1{x}_2}, {\tau }^{″}=\frac{MR}{J},\\ M=6000\left(14+\frac{x_2}{2}\right), R=\sqrt{\frac{x_2^2}{4}+{\left(\frac{x_1+x_3}{2}\right)}^2},\\ J=2\left\{x_1{x}_2\sqrt{2}\left[\frac{x_2^2}{12}+{\left(\frac{x_1+x_3}{2}\right)}^2\right]\right\} , \sigma \left(x\right)=\frac{\mathrm{504,000}}{x_4{x}_3^2},\\ \delta \left(x\right)=\frac{\mathrm{65,856,000}}{\left(30·10^6\right)x_4{x}_3^3} , p_c \left(x\right)=\frac{4.013\left(30·10^6\right)\sqrt{\frac{x_3^2{x}_4^6}{36}}}{196}\left(1-\frac{x_3}{28}\sqrt{\frac{30·10^6}{4(12·10^6)}}\right).\end{array}$$

With

$$0.1\le x_1, x_4\le 2 \mathrm{a}\mathrm{n}\mathrm{d} 0.1\le x_2, x_3\le 10.$$

The implementation results of the WOA and competitor algorithms to tackle a welded beam design are reported in Table 12 and Table 13. The convergence curve of WOA, which shows the process of achieving the solution for a welded beam design, is drawn in Figure 13. Based on the optimization results, WOA has provided the optimal design with the value of the objective function equal to (1.7246798) and the values of the design variables equal to (0.2057296, 3.4704887, 9.0366239, and 0.2057296). Comparing the performance of metaheuristic algorithms shows that WOA has provided a superior performance by achieving better results for statistical indicators and design variables in competition with competitor algorithms in order to tackle the welded beam design.

Table 12. Performance of optimization algorithms on welded beam design problem.

Algorithm	Optimum Variables				Optimum Cost
	h	l	t	b
WOA	0.2057296	3.4704887	9.0366239	0.2057296	1.7246798
WSO	0.2052287	3.4786171	9.0456263	0.205869	1.7277889
AVOA	0.2036728	3.5248519	9.0451057	0.2057274	1.7304024
RSA	0.1992954	3.5268733	9.6352786	0.2145303	1.9001569
MPA	0.2052287	3.4786171	9.0456263	0.205869	1.7277889
TSA	0.2041787	3.4956539	9.0644948	0.2061611	1.7339439
WA	0.2092213	3.4228952	9.00539	0.2161686	1.7962611
MVO	0.2040792	3.5086396	9.0388249	0.2062048	1.7313866
GWO	0.2050365	3.4883388	9.0456202	0.2058984	1.7290313
TLBO	0.280455	4.1192413	7.5343211	0.3559335	2.6187756
GSA	0.265961	2.983475	7.9314627	0.2758689	1.9758001
PSO	0.3181786	3.4772374	7.8798544	0.4582248	3.3039169
GA	0.2155882	5.9114835	8.1636373	0.2733496	2.4412018

Table 13. Statistical results of optimization algorithms on welded beam design problem.

Algorithm	Mean	Best	Worst	Std	Median	Rank
WOA	1.7246798	1.7246798	1.7246798	2.30 × 10−16	1.7246798	1
WSO	1.7308268	1.7277889	1.7338281	0.0018514	1.730858	3
AVOA	1.7557114	1.7304024	1.8103058	0.0253314	1.7461832	7
RSA	2.0434237	1.9001569	2.2841054	0.099676	2.0266223	8
MPA	1.7308266	1.7277889	1.7338281	1.85 × 10−3	1.730858	2
TSA	1.7433483	1.7339439	1.7526409	0.0057307	1.7434456	6
WA	2.1317703	1.7962611	3.32221	0.4447715	1.9787408	9
MVO	1.7420299	1.7313866	1.7679544	0.0102926	1.7391791	5
GWO	1.7324692	1.7290313	1.738012	0.002351	1.7326283	4
TLBO	2.276 × 1013	2.6187756	2.197 × 1014	5.614 × 1013	4.4479846	12
GSA	2.222781	1.9758001	2.4309209	0.1321478	2.2437502	10
PSO	3.139 × 1013	3.3039169	1.9 × 1014	6.063 × 1013	5.1550871	13
GA	7.705 × 1012	2.4412018	8.339 × 1013	2.392 × 1013	4.4234241	11

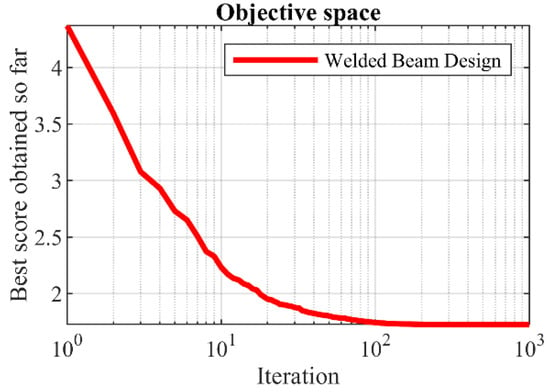
Figure 13. WOA’s performance convergence curve on welded beam design.

5.5. Tension/Compression Spring Design

Tension/compression spring design is a design challenge in engineering according to the schematic shown in Figure 14, whose main goal is to minimize the construction cost. The mathematical model of this design is as follows [32]:

$$\begin{array}{c}Consider: X=\left[x_1, x_2, x_3 \right]=\left[d, D, P\right].\\ Minimize: f\left(x\right)=\left(x_3+2\right)x_2{x}_1^2.\end{array}$$

Figure 14. Schematic of tension/compression spring design.

Subject to:

$$\begin{array}{c}{g}_1\left(x\right)=1-\frac{x_2^3{x}_3}{\mathrm{71,785}{x}_1^4} \le 0, \hspace{1em}\hspace{1em}\hspace{1em}{g}_2\left(x\right)=\frac{4x_2^2-x_1{x}_2}{\mathrm{12,566}\left(x_2{x}_1^3\right)}+\frac{1}{5108x_1^2}-1\le 0,\\ g_3\left(x\right)=1-\frac{140.45x_1}{x_2^2{x}_3}\le 0,\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{g}_4\left(x\right)=\frac{x_1+x_2}{1.5}-1 \le 0.\end{array}$$

With

$$0.05\le x_1\le 2, {0.25\le x}_2\le 1.3\hspace{1em}\mathrm{a}\mathrm{n}\mathrm{d}\hspace{1em}2\le x_3\le 15$$

The results of dealing with a tension/compression spring design by employing WOA and competitor algorithms are published in Table 14 and Table 15. The convergence curve of WOA during reaching the appropriate solution for the tension/compression spring design is drawn in Figure 15. Based on the optimization results, WOA provided the optimal design with the value of the objective function equal to (0.0126019) and the values of the design variables equal to (0.0516891, 0.3567177, and 11.288966). The analysis of simulation results and the performance of metaheuristic algorithms shows that WOA provided a superior performance compared to competitor algorithms in order to tackle the tension/compression spring design, by achieving better results for statistical indicators and design variables. The WOA convergence curve shown in Figure 15 shows the process of achieving the optimal solution for the tension/compression spring objective function during successive iterations of the algorithm. As it turns out, WOA identified the region containing the original optimum in the initial iterations with high power in global search and exploration. Then WOA, relying on its high ability in local search and exploitation, tries, until the last iterations of the algorithm, to obtain better values for the objective function and converge to the global optimum. The convergence curve shows that WOA has a high power in exploring, exploiting, and balancing them during algorithm iterations.

Table 14. Performance of optimization algorithms on tension/compression spring design problem.

Algorithm	Optimum Variables			Optimum Cost
	d	D	P
WOA	0.0516891	0.3567177	11.288966	0.0126019
WSO	0.0514981	0.3521988	11.581812	0.0126707
AVOA	0.0505134	0.3290218	13.209878	0.0127201
RSA	0.0508407	0.3329949	13.360282	0.0130304
MPA	0.0514616	0.3513193	11.633063	0.0126707
TSA	0.0509812	0.3399185	12.359303	0.0126821
WA	0.0525325	0.3774413	10.283135	0.0127118
MVO	0.0518925	0.3644224	11.757053	0.0128301
GWO	0.0518235	0.359791	11.154923	0.012697
TLBO	0.0634446	0.7421821	4.5413295	0.0160093
GSA	0.055421	0.4510305	7.5312427	0.0130981
PSO	0.062382	0.7152726	5.7721514	0.0158945
GA	0.0638411	0.7495977	4.469446	0.0162877

Table 15. Statistical results of optimization algorithms on tension/compression spring design problem.

Algorithm	Mean	Best	Worst	Std	Median	Rank
WOA	0.0126019	0.0126019	0.0126019	6.96 × 10−18	0.0126019	1
WSO	0.0127685	0.0126707	0.0129427	8.667 × 10−5	0.0127382	3
AVOA	0.0132186	0.0127201	0.0138206	0.0003839	0.0132331	8
RSA	0.0131534	0.0130304	0.0133751	9.908 × 10−5	0.0131369	6
MPA	0.012761	0.0126707	0.0129426	7.87 × 10−5	0.0127373	2
TSA	0.0129617	0.0126821	0.0135241	0.0002437	0.0128883	5
WA	0.013171	0.0127118	0.0140544	0.0004366	0.0130583	7
MVO	0.0153334	0.0128301	0.016364	0.001134	0.015912	9
GWO	0.0128	0.012697	0.0129651	8.388 × 10−5	0.0127774	4
TLBO	0.0164134	0.0160093	0.0168366	0.000242	0.0163674	10
GSA	0.0173251	0.0130981	0.0259603	0.0029341	0.0169922	11
PSO	1.413 × 1013	0.0158945	2.507 × 1014	5.673 × 1013	0.0159783	13
GA	1.104 × 1012	0.0162877	1.142 × 1013	3.333 × 1012	0.021457	12

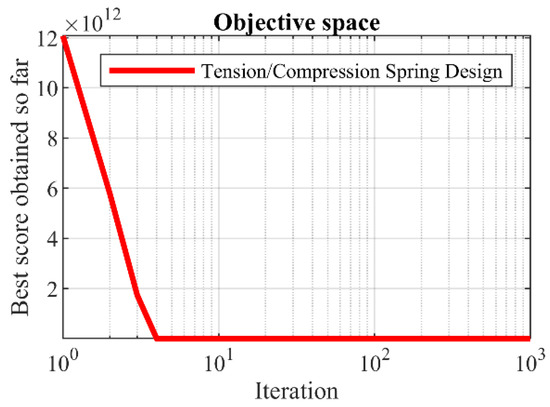
Figure 15. WOA’s performance convergence curve on tension/compression spring.

5.6. Application and Advantages of WOA for Supply Chain Management

While introducing the applications of the Wombat Optimization Algorithm (WOA) in supply chain management (SCM), its unique capabilities are distinguished by its optimal risk management, multi-objective information, agile operations, decisions to be collaborative, and sustainable development efforts, and offer advantages over traditional quality systems.

• Risk management and resilience: WOA can help improve the supply chain resilience by identifying and mitigating potential risks such as supply chain disruptions, natural disasters, and demand fluctuations on the snow. By incorporating risks into the optimization process, WOA helps companies create robust supply chain models that can better adapt to unexpected disruptions compared to traditional models.
• Multi-Objective Optimization: WOA can handle multi-objective optimization problems, where conflicting objectives such as cost minimization, lead time minimization, and service level maximization need to be balanced by the exploration–exploitation equilibrium of WOA on its Pareto front in contrast to the feasible search for trade-offs, giving decision makers the best solutions to choose from; traditional systems may struggle to meet many objective optimization problems and manage them effectively, as they often require complex changes or goal accumulations.
• Dynamic and real-time optimization: WOA can be optimized in dynamic and real-time optimization scenarios where supply chain conditions change over time, such as demand fluctuations, disruptions, or capacity constraints. By constantly updating solutions based on the latest information, WOA enables companies to make the right decisions in a timely manner to optimize supply chains. Traditional systems may require a periodic reassessment or manual intervention to accommodate dynamic situations, resulting in suboptimal solutions or increased response times.
• Collaboration and coordination optimization: WOA can optimize collaborative and coordinated decision-making among multiple entities within the supply chain, such as suppliers, manufacturers, distributors, and retailers. By optimizing decisions across the entire supply chain network, WOA helps companies achieve synergies and efficiencies that may not be achievable through localized optimizations. Traditional schemes often focus on optimizing individual components of the supply chain in isolation, leading to a suboptimal overall performance due to the lack of coordination and collaboration.
• Sustainability and green logistics: WOA can incorporate sustainability criteria such as carbon emissions, energy consumption, and the environmental impact into the optimization process, enabling companies to design more sustainable and environmentally friendly supply chain strategies. By optimizing supply chain operations with sustainability objectives in mind, WOA helps companies reduce their ecological footprint and achieve corporate social responsibility goals. Traditional schemes may overlook sustainability considerations or treat them as constraints rather than optimization objectives, resulting in less environmentally sustainable supply chain designs.

In summary, the Wombat Optimization Algorithm offers several advantages over traditional optimization schemes in various areas of supply chain management, including risk management, multi-objective optimization, dynamic optimization, collaboration optimization, and sustainability. Its nature-inspired approach and flexibility make it well-suited for addressing the complex and dynamic challenges faced by modern supply chains.

6. Conclusions and Future Works

In this paper, a new biomimetics metaheuristic algorithm named Wombat Optimization Algorithm (WOA) is used for supply chain optimization, and imitates wombat behaviors in nature. WOA’s basic inspiration was taken from the wombat’s foraging process and the animal’s escape strategy when faced with its predators. The theory of WOA was expressed and then mathematically modeled in two phases: (i) exploration based on the simulation of wombat movement during foraging and trying to find food and (ii) exploitation based on simulating wombat movements when diving towards nearby tunnels to defend against its predators. WOA’s ability to solve optimization problems was tested in the CEC 2017 test suite for problem dimensions equal to 10, 30, 50, and 100. The optimization results showed that WOA achieves suitable solutions for optimization problems with its high capability for managing exploration and exploitation, and balancing them during the search process. The quality of the results obtained from WOA was compared with the performance of twelve well-known metaheuristic algorithms. The simulation results showed that WOA has provided a superior performance in competition with the compared algorithms, by providing better results in most of the benchmark functions and achieving the rank of the first best optimizer. WOA’s ability to tackle optimization tasks in real-world applications was challenged in twenty-two constrained optimization problems from the CEC 2011 test suite and four engineering design problems. The results of this implementation showed that WOA, while providing better results compared to competitor algorithms, has an effective performance when addressing optimization issues in real world applications.

The introduction of WOA presents several research proposals for further work. The development of binary and multi-objective versions of WOA is one of the most special research potentials of this study for future works. Another research potential of WOA is its application to deal with supply chain applications. Employing WOA to tackle optimization problems in various sciences and optimization tasks in real-world applications is another suggestion of this paper for further work in the future.