Scheduling with Group Technology, Resource Allocation, and Learning Effect Simultaneously

Abstract

This paper studies the single-machine group scheduling problem with convex resource allocation and learning effect. The number of jobs in each group is different, and the corresponding common due dates are also different, where the processing time of jobs follows a convex function of resource allocation. Under common due date assignment, the objective is to minimize the weighted sum of earliness, tardiness, common due date, resource consumption, and makespan. To solve the problem, we present the heuristic, simulated annealing, and branch-and-bound algorithms. Computational experiments indicate that the proposed algorithms are effective.

1. Introduction

In actual industrial production, with the increasingly fierce competition among enterprises, jobs with similar characteristics are divided into the same group for processing to adapt to the efficient production rhythm (Potts et al. [1], Pei et al. [2], Lee et al. [3]). The group technology (expressed by $GT$) arises, corresponding to the group technology scheduling problem in scheduling theory. The essence of enterprise production is a huge consumption of energy, for example, in the case of the input of steel; such cases can be collectively referred to as resources. The input of resources can effectively reduce the processing process of the job and then shorten the processing time; that is, the greater the input, the shorter the processing time. The corresponding cost input also increases accordingly. Therefore, striking a balance between resource consumption and cost growth has become one of the most popular research topics. In the processing operation, in addition to resources affecting the processing time, machine/manual learning also shorten its duration, which corresponds to the scheduling problem with learning effect. On the other hand, when the customer submits an order, there is a delivery date, also known as the due date, which is fined for advance/delay to the customer. Therefore, each group of jobs has a common due date of reasonable arrangement of job production so as to reduce fines, which also plays an important role in scheduling. According to the above, in the group environment of resource allocation, learning effect and common due date reasonably determine the sequences of the job and the group so as to reduce costs, which is main goal of this study. The relevant research results of the above production environment (resource allocation, learning effect, common due date, and groups) will be elaborated in the future.

In reality, the processing times of jobs are alterable according to resource allocation (Shabtay and Steiner [4], Wang and Cheng [5], Kayvanfar et al. [6], Tian [7]) and learning effect (Wu et al. [8], Azzouz et al. [9], Zhao [10], Liu et al. [11]). The learning effect is the efficiency gained through repetitive production. Yin [12] studied single-machine resource allocation scheduling with the learning effect. Under common due window assignment, the researchers showed that some non-regular objectives are polynomially solvable. Zhao [13] studied the problems of no-wait flow shop scheduling with learning effect and convex resource allocation. Wang et al. [14] investigated single-machine scheduling with truncated learning effect and resource allocation. Jiang et al. [15] considered Seru production scheduling problems with resource allocation. For the total processing cost plus scheduling measure minimizations, they proved that the problems are polynomially solvable. Wang and Wang [16] addressed the single-machine scheduling with convex resource allocation and a time-dependent learning effect. For three versions stemming from the total resource consumption cost and the scheduling cost, they proposed some solution algorithms.

In order to achieve higher productivity, the $GT$ is often used in production and processing. For example, Shabtay et al. [17] studied these two types of resource allocation functions separately. Zhu et al. [18] studied the single-machine scheduling with learning effect, resource allocation, and $GT$. Li et al. [19] considered a single-machine scheduling problem involving the due date assignment under $GT$ environment. They provided an $O(nlogn)$ time complexity for the above three due date assignment methods. Lu et al. [20] investigated a single-machine scheduling problem with decreasing time-dependent processing times and group technology assumption. For makespan minimization, they showed that the problem can be solved in polynomial time. Sun et al. [21] introduced single-machine group scheduling with learning effect and resource allocation. Chen et al. [22] considered a single-machine group scheduling problem with due date assignment and resource allocation. Liang et al. [23] dealt with a single-machine resource allocation scheduling problem with deteriorating jobs and $GT$. Yan et al. [24] studied a single-machine problem with resource allocation and deteriorating effect in group technology environment. Liu and Wang [25] and Wang and Liu [26] considered single-machine $GT$ scheduling with resource allocation and due date assignment.

In view of the importance of due date assignment (Shabtay [27], Shabtay et al. [28], Cheng [29], Li et al. [30], Zhang et al. [31], Lv and Wang [32]), most of the above literature studies the special polynomial-time solvable cases of $GT$ problems. In this paper, we integrate the case where processing time follows a convex function of resource allocation under common due date allocation as well as learning effects, i.e., the job number of each group is different. We conduct a specific study on the objective of minimizing the weighted sum of earliness, tardiness, common due date, resource consumption, and makespan. For the general case of the problem, we propose the heuristic, simulated annealing, and branch-and-bound algorithms. The rest of this paper is organized as follows. In Section 2, the problem statement is presented. Section 3 offers basic properties. A special case is discussed in Section 4. Section 5 presents the specific solving algorithms of the problem. In Section 6, computational experiments are proposed. Finally, the conclusions are given in Section 7.

2. Problem Statement

There are n independent jobs grouped into r groups (i.e., $G_1,G_2,\cdots ,G_r$) to be processed by a single machine. Each $G_i$$(i=1,2,\cdots ,r)$ has an independent setup time ${\widehat{s}}_i$, where the number of jobs allocated to $G_i$ is ${\overline{n}}_i$ (i.e., ${\sum }_{i=1}^r{\overline{n}}_i=n$).

If the job $J_{ij}$ ($i=1,2,\cdots ,r$, $j=1,2,\cdots ,{\overline{n}}_i$) is scheduled at the $\widehat{x}$th ($\widehat{x}=1,2,\cdots ,{\overline{n}}_i$) position of group $\widehat{l}$ ($\widehat{l}=1,2,\cdots ,r$), the actual processing time of job $J_{ij}$ is

$${\widehat{p}}_{ij}={\left(\frac{{\widehat{w}}_{ij}{\widehat{x}}^{{\alpha }_1}{\widehat{l}}^{{\alpha }_2}}{{\widehat{u}}_{ij}}\right)}^{\theta },$$

(1)

where ${\widehat{u}}_{ij}$ is the amount of resource of $J_j$ in $G_i$, ${\widehat{w}}_{ij}$ is a positive parameter which represents the workload of $J_{ij}$ in $G_i$, ${\alpha }_1\le 0$ denotes the learning index of the job position, ${\alpha }_2\le 0$ denotes the group learning index, and $\theta >0$ is a given constant.

We define the earliness and tardiness of the job $J_{ij}$ as ${\tilde{E}}_{ij}=max\{{\tilde{d}}_i-{\widehat{C}}_{ij},0\}$ and ${\tilde{T}}_{ij}=max\{{\widehat{C}}_{ij}-{\tilde{d}}_i,0\}$ for $i=1,2,\cdots ,r$, $j=1,2,\cdots ,{\overline{n}}_i$, where ${\tilde{d}}_i$ is the common due date of group $G_i$ and ${\widehat{C}}_{ij}$ is the completion time of $J_{ij}$. The objective is to find the optimal group sequence ${\varphi }^{*}$∈$\mathrm{\Phi }$, where $\mathrm{\Phi }$ is set of all group sequences, the optimal internal job sequence ${\overline{\pi }}_i^{*}$∈${\overline{\mathrm{\Pi }}}_i$ within $G_i$ for $i=1,2,\cdots ,r$, where ${\overline{\mathrm{\Pi }}}_i$ is set of all internal job sequences, the optimal set of due dates $\mathrm{\Psi }=({\tilde{d}}_1^{*},{\tilde{d}}_2^{*},\cdots ,{\tilde{d}}_r^{*})$, and the optimal resource allocation matrix ${\widehat{u}}^{*}=\left({\widehat{u}}_{ij}^{*}\right)$ for $i=1,2,\cdots ,r$, $j=1,2,\cdots ,{\overline{n}}_i$, which together minimize an objective function that includes penalties due to earliness, tardiness, due date assignment, resource consumption, and makespan as given below:

$$\begin{array}{cc}\hfill \check{Z}& =\sum _{i=1}^r\sigma {\tilde{d}}_i+\sum _{i=1}^r\sum _{j=1}^{{\overline{n}}_i}\left(\rho {\tilde{E}}_{ij}+\mu {\tilde{T}}_{ij}+v_{ij}{\widehat{u}}_{ij}\right)+\lambda {\widehat{C}}_{max}\hfill \\ & =\sum _{i=1}^r\sum _{j=1}^{{\overline{n}}_i}\left(\sigma {\tilde{d}}_i+\rho {\tilde{E}}_{ij}+\mu {\tilde{T}}_{ij}+v_{ij}{\widehat{u}}_{ij}+\lambda {\widehat{p}}_{ij}\right),\hfill \end{array}$$

(2)

where ${\widehat{C}}_{max}={\sum }_{i=1}^r{\sum }_{j=1}^{{\overline{n}}_i}{\widehat{p}}_{ij}$, $\sigma$$(\sigma >0)$, $\rho$$(\rho >0)$, $\mu$$(\mu >0)$, and $\lambda$$(\lambda >0)$ represent the per unit cost of the due date cost, earliness penalties, tardiness penalties, and processing time, $v_{ij}$ is the cost of resources allocated to $J_{ij}$. Using the three-parameter representation, the problem can be denoted as

$$1|GT,CON,{\widehat{p}}_{ij}={\left(\frac{{\widehat{w}}_{ij}{\widehat{x}}^{{\alpha }_1}{\widehat{l}}^{{\alpha }_2}}{{\widehat{u}}_{ij}}\right)}^{\theta }|\sum _{i=1}^r\sigma {\tilde{d}}_i+\sum _{i=1}^r\sum _{j=1}^{{\overline{n}}_i}\left(\rho {\tilde{E}}_{ij}+\mu {\tilde{T}}_{ij}+v_{ij}{\widehat{u}}_{ij}\right)+\lambda {\widehat{C}}_{max},$$

where $CON$ denotes common due date. The literature review related to the problems with $GT$ is given below (see Table 1).

Table 1. Problems with group technology.

Problem	Complexity	Ref.
$1\left|GT,CON\right|{\sum }_{i=1}^r\sigma {\tilde{d}}_i+{\sum }_{i=1}^r{\sum }_{j=1}^{{\overline{n}}_i}\left(\rho {\tilde{E}}_{ij}+\mu {\tilde{T}}_{ij}\right)$	$O(nlogn)$	Shabtay et al. [17]
$1\left|GT,CON,{\widehat{p}}_{ij}={\left(\frac{p_{ij}}{{\widehat{u}}_{ij}}\right)}^{\theta }\right|{\sum }_{i=1}^r\sigma {\tilde{d}}_i+{\sum }_{i=1}^r{\sum }_{j=1}^{{\overline{n}}_i}\left(\rho {\tilde{E}}_{ij}+\mu {\tilde{T}}_{ij}+v_{ij}{\widehat{u}}_{ij}\right)$
$+\lambda {\widehat{C}}_{max}$, where ${\overline{n}}_i=\overline{n}$	$O(max\{nlogn,rn,r^3\})$	Shabtay et al. [17]
$1\left|GT,CON,{\widehat{p}}_{ij}=p_{ij}-b_{ij}{\widehat{u}}_{ij}\right|{\sum }_{i=1}^r\sigma {\tilde{d}}_i+{\sum }_{i=1}^r{\sum }_{j=1}^{{\overline{n}}_i}\left(\rho {\tilde{E}}_{ij}+\mu {\tilde{T}}_{ij}+v_{ij}{\widehat{u}}_{ij}\right)$
$+\lambda {\widehat{C}}_{max}$, where ${\overline{n}}_i=\overline{n}$	$O\left(n^3\right)$	Shabtay et al. [17]
$1\left|GT,RALE,{\widehat{p}}_{ij}={\left(\frac{p_{ij}{\widehat{x}}^{{\alpha }_1}{\widehat{l}}^{{\alpha }_2}}{{\widehat{u}}_{ij}}\right)}^{\theta }\right|\delta {\sum }_{i=1}^r{\sum }_{j=1}^{{\overline{n}}_i}{v}_{ij}{\widehat{u}}_{ij}+\lambda {\widehat{C}}_{max}$	$O\left(n^3\right)$	Zhu et al. [18]
$1\left|GT,RALE,{\widehat{p}}_{ij}=p_{ij}{\widehat{x}}^{{\alpha }_1}{\widehat{l}}^{{\alpha }_2}-b_{ij}{\widehat{u}}_{ij}\right|\delta {\sum }_{i=1}^r{\sum }_{j=1}^{{\overline{n}}_i}{v}_{ij}{\widehat{u}}_{ij}+\lambda {\widehat{C}}_{max}$	$O(nlogn)$	Zhu et al. [18]
$1\left|GT,CON\right|{\sum }_{i=1}^r{\sum }_{j=1}^{{\overline{n}}_i}\left({\sigma }_i{\tilde{d}}_{ij}+{\rho }_i{\tilde{E}}_{ij}+{\mu }_i{\tilde{T}}_{ij}+{\lambda }_i{\widehat{C}}_{ij}\right)$	$O(nlogn)$	Li et al. [19]
$1\left|GT,SLK\right|{\sum }_{i=1}^r{\sum }_{j=1}^{{\overline{n}}_i}\left({\sigma }_i{\tilde{d}}_{ij}+{\rho }_i{\tilde{E}}_{ij}+{\mu }_i{\tilde{T}}_{ij}+{\lambda }_i{\widehat{C}}_{ij}\right)$	$O(nlogn)$	Li et al. [19]
$1\left|GT,DIF\right|{\sum }_{i=1}^r{\sum }_{j=1}^{{\overline{n}}_i}\left({\sigma }_i{\tilde{d}}_{ij}+{\rho }_i{\tilde{E}}_{ij}+{\mu }_i{\tilde{T}}_{ij}+{\lambda }_i{\widehat{C}}_{ij}\right)$	$O(nlogn)$	Li et al. [19]
$1\left|GT,{\widehat{p}}_{ij}={\alpha }_{ij}(1-bt),{\widehat{s}}_i={\beta }_i(1-bt)\right|{\widehat{C}}_{max}$	$O(nlogn)$	Lu et al. [20]
$1\left|GT,DIF,{\widehat{p}}_{ij}={\left(\frac{{\widehat{w}}_{ij}}{{\widehat{u}}_{ij}}\right)}^{\theta }\right|{\sum }_{i=1}^r{\sum }_{j=1}^{{\overline{n}}_i}\left({\sigma }_{ij}{\tilde{d}}_{ij}+{\rho }_{ij}{\tilde{E}}_{ij}+\mu {\tilde{T}}_{ij}+v_{ij}{\widehat{u}}_{ij}\right)$	$O\left(n^3\right)$	Chen et al. [22]
$1\left|GT,DIF,{\widehat{p}}_{ij}=p_{ij}{b}_{ij}{\widehat{u}}_{ij}\right|{\sum }_{i=1}^r{\sum }_{j=1}^{{\overline{n}}_i}\left({\sigma }_{ij}{\tilde{d}}_{ij}+{\rho }_{ij}{\tilde{E}}_{ij}+\mu {\tilde{T}}_{ij}+v_{ij}{\widehat{u}}_{ij}\right)$	$O\left(n^3\right)$	Chen et al. [22]
$1\left|GT,{\widehat{p}}_{ij}={\left(\frac{p_{ij}}{{\widehat{u}}_{ij}}\right)}^{\theta }+at,{\widehat{s}}_i={\left(\frac{s_i}{{\widehat{u}}_i}\right)}^{\theta }+bt\right|$
$\delta {\sum }_{i=1}^r{\sum }_{j=1}^{{\overline{n}}_i}{v}_{ij}{\widehat{u}}_{ij}+\gamma {\sum }_{i=1}^r{\omega }_i{\widehat{u}}_i+\lambda {\widehat{C}}_{max}$	$O(nlogn)$	Liang et al. [23]
$1\left|GT,{\widehat{p}}_{ij}={\left(\frac{{\widehat{w}}_{ij}}{{\widehat{u}}_{ij}}\right)}^{\theta }+at,{\widehat{s}}_i={\left(\frac{{\widehat{w}}_i}{{\widehat{u}}_i}\right)}^{\eta }+bt,{\sum }_{i=1}^r{\sum }_{j=1}^{{\overline{n}}_i}\le \tilde{V},{\sum }_{h=1}^{\tilde{m}}\le \tilde{U}\right|\sum \sum C_{ij}$	$O\left(n^3\right)$	Yan et al. [24]
$1\left|GT,CON,{\widehat{p}}_{ij}={\left(\frac{{\widehat{w}}_{ij}{\widehat{x}}^{{\alpha }_1}{\widehat{l}}^{{\alpha }_2}}{{\widehat{u}}_{ij}}\right)}^{\theta }\right|{\sum }_{i=1}^r\sigma {\tilde{d}}_i+{\sum }_{i=1}^r{\sum }_{j=1}^{{\overline{n}}_i}\left(\rho {\tilde{E}}_{ij}+\mu {\tilde{T}}_{ij}+v_{ij}{\widehat{u}}_{ij}\right)$
$+\lambda {\widehat{C}}_{max}$, where ${\widehat{s}}_i=\widehat{s}$ and ${\overline{n}}_i=\overline{n}$	$O\left(n^3\right)$	this paper
$1\left|GT,CON,{\widehat{p}}_{ij}={\left(\frac{{\widehat{w}}_{ij}{\widehat{x}}^{{\alpha }_1}{\widehat{l}}^{{\alpha }_2}}{{\widehat{u}}_{ij}}\right)}^{\theta }\right|{\sum }_{i=1}^r\sigma {\tilde{d}}_i+{\sum }_{i=1}^r{\sum }_{j=1}^{{\overline{n}}_i}\left(\rho {\tilde{E}}_{ij}+\mu {\tilde{T}}_{ij}+v_{ij}{\widehat{u}}_{ij}\right)$	Heuristic and
$+\lambda {\widehat{C}}_{max}$	branch-and-bound
	algorithms	this paper

Note: RALE denotes resource allocation and learning effect; SLK (resp. DIF) denotes slack (resp. different) due date; a and b are the deterioration rates; t is the start time; $\tilde{V}$ and $\tilde{U}$ are given constants; $W_{\mathit{ij}}$ is the wait time.

As can be seen in Table 1, most of the studies in the literature on the group sequencing problem are limited to considering only the common due date or only the convex function of the processing time with respect to the resources. This study integrates the case where processing time follows a convex function of resource allocation under common due date allocation as well as learning effects.

3. Basic Properties

There exists an optimal solution that starts at time zero and no-idle machine time. From Shabtay et al. [17], we have the following lemmas (see Lemma 1 and Equation (20) in [17], the only difference is whether they have the learning effect):

Lemma 1.

There exists an optimal due date for $G_i$ that is equal to completion time of a job, namely ${\tilde{d}}_i={\widehat{C}}_{i\left[l_i^{\prime }\right]}$ (at the position $l_i^{\prime }$ of the ith group), where

$${li}_{\prime }=max\left(⌈\frac{{\overline{n}}_i\times (\mu -\sigma )}{\mu +\rho }⌉,0\right),$$

(3)

and ${\widehat{C}}_{i\left[0\right]}=0$ by definition.

Lemma 2.

For the problem

$$1|GT,CON,{\widehat{p}}_{ij}={\left(\frac{{\widehat{w}}_{ij}{\widehat{x}}^{{\alpha }_1}{\widehat{l}}^{{\alpha }_2}}{{\widehat{u}}_{ij}}\right)}^{\theta }|\sum _{i=1}^r\sigma {\tilde{d}}_i+\sum _{i=1}^r\sum _{j=1}^{{\overline{n}}_i}\left(\rho {\tilde{E}}_{ij}+\mu {\tilde{T}}_{ij}+v_{ij}{\widehat{u}}_{ij}\right)+\lambda {\widehat{C}}_{max},$$

the optimal objective function of the given sequence is

$$\check{Z}=\eta \sum _{i=1}^r\left({\overline{n}}_{\left[i\right]}\times \left(\sum _{k=1}^{i-1}{\widehat{P}}_{\left[k\right]}+\sum _{k=1}^i{\widehat{s}}_{\left[k\right]}\right)\right)+\sum _{i=1}^r\sum _{j=1}^{{\overline{n}}_i}{\iota }_{\left[i\right]j}{\widehat{p}}_{\left[i\right]\left[j\right]}+\sum _{i=1}^r\sum _{j=1}^{{\overline{n}}_i}{v}_{\left[i\right]\left[j\right]}{\widehat{u}}_{\left[i\right]\left[j\right]},$$

(4)

where ${\widehat{P}}_k$ is the processing time of group $G_k$, i.e.,${\widehat{P}}_k={\sum }_{j=1}^{{\overline{n}}_k}{\widehat{p}}_{kj},$$\eta =min(\sigma ,\mu ),$ and

$${\iota }_{\left[i\right]j}=\begin{array}{c}\left\{\begin{array}{cc}\sigma \times {\overline{n}}_{\left[i\right]}+\rho \times (j-1)+\lambda ,\hfill & forj\le l_i^{\prime },\hfill \\ \mu \times ({\overline{n}}_{\left[i\right]}-j+1)+\lambda ,\hfill & for{l}_i^{\prime }<j\le {\overline{n}}_{\left[i\right]}.\hfill \end{array}\right.\hfill \end{array}$$

The objective function in Equation (4) can be represented as

$$\begin{array}{cc}\hfill \check{Z}& =\eta \times \sum _{i=1}^r\left({\overline{n}}_{\left[i\right]}\times \left(\sum _{k=1}^{i-1}{\widehat{P}}_{\left[k\right]}+\sum _{k=1}^i{\widehat{s}}_{\left[k\right]}\right)\right)+\sum _{i=1}^r\sum _{j=1}^{\overline{n}}{\iota }_{\left[i\right]j}{\widehat{p}}_{\left[i\right]\left[j\right]}+\sum _{i=1}^r\sum _{j=1}^{{\overline{n}}_{\left[i\right]}}{v}_{\left[i\right]\left[j\right]}{\widehat{u}}_{\left[i\right]\left[j\right]}\hfill \\ & =\eta \times \sum _{i=1}^r\left({\overline{n}}_{\left[i\right]}\times \left(\sum _{k=1}^{i-1}\sum _{j=1}^{\overline{n}}{\widehat{p}}_{\left[k\right]j}+\sum _{k=1}^i{\widehat{s}}_{\left[k\right]}\right)\right)+\sum _{i=1}^r\sum _{j=1}^{\overline{n}}{\iota }_{\left[i\right]j}{\widehat{p}}_{\left[i\right]\left[j\right]}+\sum _{i=1}^r\sum _{j=1}^{{\overline{n}}_{\left[i\right]}}{v}_{\left[i\right]\left[j\right]}{\widehat{u}}_{\left[i\right]\left[j\right]}\hfill \\ & =\sum _{i=1}^r\sum _{j=1}^{{\overline{n}}_{\left[i\right]}}\left(\eta \times \sum _{k=i+1}^r{\overline{n}}_{\left[k\right]}+{\iota }_{\left[i\right]j}\right)\times {\widehat{p}}_{\left[i\right]\left[j\right]}+\eta \times \left(\sum _{i=1}^r{\overline{n}}_{\left[i\right]}\times \sum _{k=1}^i{\widehat{s}}_{\left[k\right]}\right)+\sum _{i=1}^r\sum _{j=1}^{{\overline{n}}_{\left[i\right]}}{v}_{\left[i\right]\left[j\right]}{\widehat{u}}_{\left[i\right]\left[j\right]}.\hfill \end{array}$$

(5)

By substituting Equation (1) into Equation (5), we have

$$\begin{array}{c}\hfill \check{Z}=\sum _{i=1}^r\sum _{j=1}^{{\overline{n}}_i}\left(\eta \sum _{k=i+1}^r{\overline{n}}_{\left[k\right]}+{\iota }_{\left[i\right]j}\right)\times {\left(\frac{{\widehat{w}}_{ij}{j}^{{\alpha }_1}{i}^{{\alpha }_2}}{{\widehat{u}}_{ij}}\right)}^{\theta }+\eta \times \left(\sum _{i=1}^r{\overline{n}}_{\left[i\right]}\times \sum _{k=1}^i{\widehat{s}}_{\left[k\right]}\right)+\sum _{i=1}^r\sum _{j=1}^{{\overline{n}}_i}{v}_{\left[i\right]\left[j\right]}{\widehat{u}}_{\left[i\right]\left[j\right]}.\end{array}$$

(6)

Theorem 1.

For

$$1|GT,CON,{\widehat{p}}_{ij}={\left(\frac{{\widehat{w}}_{ij}{\widehat{x}}^{{\alpha }_1}{\widehat{l}}^{{\alpha }_2}}{{\widehat{u}}_{ij}}\right)}^{\theta }|\sum _{i=1}^r\sigma {\tilde{d}}_i+\sum _{i=1}^r\sum _{j=1}^{{\overline{n}}_i}\left(\rho {\tilde{E}}_{ij}+\mu {\tilde{T}}_{ij}+v_{ij}{\widehat{u}}_{ij}\right)+\lambda {\widehat{C}}_{max},$$

the optimal resource allocation is

$${\widehat{u}}_{\left[i\right]\left[j\right]}^{*}={\left(\frac{\theta \times ({\sum }_{k=i+1}^r{\overline{n}}_{\left[k\right]}+{\iota }_{\left[i\right]j})}{v_{\left[i\right]\left[j\right]}}\right)}^{\frac{1}{1+\theta }}\times {\left({\widehat{w}}_{\left[i\right]\left[j\right]}{j}^{{\alpha }_1}{i}^{{\alpha }_2}\right)}^{\frac{\theta }{1+\theta }},$$

(7)

and the objective function is

$$\begin{array}{cc}\hfill {\check{Z}}^{*}=& \left({\theta }^{-\frac{\theta }{\theta +1}}+{\theta }^{\frac{1}{\theta +1}}\right)\sum _{i=1}^r\sum _{j=1}^{{\overline{n}}_i}{\delta }_{\left[i\right]\left[j\right]}\times {\left(j^{{\alpha }_1}{i}^{{\alpha }_2}\right)}^{\frac{\theta }{1+\theta }}\times {\left(\eta \sum _{k=i+1}^r{\overline{n}}_{\left[k\right]}+{\iota }_{\left[i\right]j}\right)}^{\frac{1}{1+\theta }}\hfill \\ & +\eta \sum _{i=1}^r\left({\overline{n}}_{\left[i\right]}\times \sum _{k=1}^i{\widehat{s}}_{\left[k\right]}\right),\hfill \end{array}$$

(8)

where ${\delta }_{\left[i\right]\left[j\right]}={\left({\widehat{w}}_{\left[i\right]\left[j\right]}\times v_{\left[i\right]\left[j\right]}\right)}^{\frac{\theta }{\theta +1}}$, for $i=1,2,\cdots ,r$, $j=1,2,\cdots ,{\overline{n}}_i$.

Proof. 

Deriving the objective function given by Equation (5) with respect to ${\widehat{u}}_{\left[i\right]\left[j\right]}$ for $i=1,2,\cdots ,r$, $j=1,2,\cdots ,{\overline{n}}_i$,

$${\check{Z}}^{\prime }=-\theta \sum _{i=1}^r\sum _{j=1}^{{\overline{n}}_i}\left(\eta \times \sum _{k=i+1}^r{\overline{n}}_{\left[k\right]}+{\iota }_{\left[i\right]j}\right)\times \frac{{\left({\widehat{w}}_{ij}{\widehat{x}}^{{\alpha }_1}{\widehat{l}}^{{\alpha }_2}\right)}^{\theta }}{{\widehat{u}}_{ij}^{\theta +1}}+\sum _{i=1}^r\sum _{j=1}^{{\overline{n}}_i}{v}_{\left[i\right]\left[j\right]}.$$

(9)

By equating it to zero, we have

$${\widehat{u}}_{\left[i\right]\left[j\right]}^{*}={\left(\frac{\theta \times ({\sum }_{k=i+1}^r{\overline{n}}_{\left[k\right]}+{\iota }_{\left[i\right]j})}{v_{\left[i\right]\left[j\right]}}\right)}^{\frac{1}{1+\theta }}\times {\left({\widehat{w}}_{\left[i\right]\left[j\right]}{j}^{{\alpha }_1}{i}^{{\alpha }_2}\right)}^{\frac{\theta }{1+\theta }}.$$

By substituting Equation (7) into Equation (6), we have

$$\begin{array}{cc}\hfill {\check{Z}}^{*}=& \left({\theta }^{-\frac{\theta }{\theta +1}}+{\theta }^{\frac{1}{\theta +1}}\right)\sum _{i=1}^r\sum _{j=1}^{{\overline{n}}_i}{\delta }_{\left[i\right]\left[j\right]}\times {\left(j^{{\alpha }_1}{i}^{{\alpha }_2}\right)}^{\frac{\theta }{1+\theta }}\times {\left(\eta \sum _{k=i+1}^r{\overline{n}}_{\left[k\right]}+{\iota }_{\left[i\right]j}\right)}^{\frac{1}{1+\theta }}\hfill \\ & +\eta \sum _{i=1}^r\left({\overline{n}}_{\left[i\right]}\times \sum _{k=1}^i{\widehat{s}}_{\left[k\right]}\right),\hfill \end{array}$$

where ${\delta }_{ij}={\left({\widehat{w}}_{ij}\times v_{ij}\right)}^{\frac{\theta }{\theta +1}}$, $i=1,2,\cdots ,r$, $j=1,2,\cdots ,{\overline{n}}_i$.    □

Theorem 2.

The term

$$\sum _{i=1}^r\left({\overline{n}}_{\left[i\right]}\times \sum _{k=1}^i{\widehat{s}}_{\left[k\right]}\right),$$

it can be minimized by sequencing the groups in non-increasing order of $\frac{{\overline{n}}_{\left[k\right]}}{{\widehat{s}}_{\left[k\right]}}$.

Proof. 

Assuming that ${\varphi }^{*}=\{\dots ,G_{\left[i\right]},G_{\left[k\right]},\dots \}$ and ${\varphi }^{\prime }=\{\dots ,G_{\left[k\right]},G_{\left[i\right]},\dots \}$, we have

$$\begin{array}{cc}& {\check{Z}}_{{\varphi }^{*}}-{\check{Z}}_{{\varphi }^{\prime }}\hfill \\ \hfill =& {\overline{n}}_{\left[i\right]}\left({\widehat{s}}_{[f+1]}+\cdots +{\widehat{s}}_{[i-1]}+{\widehat{s}}_{\left[i\right]}\right)+{\overline{n}}_{\left[k\right]}\left({\widehat{s}}_{[f+1]}+\cdots +{\widehat{s}}_{[i-1]}+{\widehat{s}}_{\left[i\right]}+{\widehat{s}}_{\left[k\right]}\right)\hfill \\ & -{\overline{n}}_{\left[k\right]}\left({\widehat{s}}_{[f+1]}+\cdots +{\widehat{s}}_{[i-1]}+{\widehat{s}}_{\left[k\right]}\right)-{\overline{n}}_{\left[i\right]}\left({\widehat{s}}_{[f+1]}+\cdots +{\widehat{s}}_{[i-1]}+{\widehat{s}}_{\left[k\right]}+{\widehat{s}}_{\left[i\right]}\right)\hfill \\ \hfill =& {\overline{n}}_{\left[k\right]}{\widehat{s}}_{\left[i\right]}-{\overline{n}}_{\left[i\right]}{\widehat{s}}_{\left[k\right]}\hfill \\ \hfill =& {\widehat{s}}_{\left[i\right]}{\widehat{s}}_{\left[k\right]}\left(\frac{{\overline{n}}_{\left[k\right]}}{{\widehat{s}}_{\left[k\right]}}-\frac{{\overline{n}}_{\left[i\right]}}{{\widehat{s}}_{\left[i\right]}}\right).\hfill \end{array}$$

(10)

If $\frac{{\overline{n}}_{\left[i\right]}}{{\widehat{s}}_{\left[i\right]}}>\frac{{\overline{n}}_{\left[k\right]}}{{\widehat{s}}_{\left[k\right]}}$, there is ${\check{Z}}_{{\varphi }^{*}}<{\check{Z}}_{{\varphi }^{\prime }}$.    □

Theorem 3.

For a given group sequence of

$$1|GT,CON,{\widehat{p}}_{ij}={\left(\frac{{\widehat{w}}_{ij}{\widehat{x}}^{{\alpha }_1}{\widehat{l}}^{{\alpha }_2}}{{\widehat{u}}_{ij}}\right)}^{\theta }|\sum _{i=1}^r\sigma {\tilde{d}}_i+\sum _{i=1}^r\sum _{j=1}^{{\overline{n}}_i}\left(\rho {\tilde{E}}_{ij}+\mu {\tilde{T}}_{ij}+v_{ij}{\widehat{u}}_{ij}\right)+\lambda {\widehat{C}}_{max},$$

we let ${\mathrm{\Omega }}_{ij}={\left({\iota }_{ij}{j}^{\theta {\alpha }_1}\right)}^{\frac{1}{1+\theta }}$; the optimal internal job sequence ${\overline{\pi }}_i^{*}\left(i=1,2,\cdots ,r\right)$ can be obtained by matching the smallest ${\delta }_{ij}$ to the job with the largest ${\mathrm{\Omega }}_{ij}$, the second smallest ${\delta }_{ij}$ to the job with the second largest ${\iota }_{ij}$, and so on.

Proof. 

For a given group sequence, from Equation (8), $\left({\theta }^{-\frac{\theta }{\theta +1}}+{\theta }^{\frac{1}{\theta +1}}\right)$, $\eta {\sum }_{k=i+1}^r{\overline{n}}_{\left[k\right]}$, and $\eta {\sum }_{i=1}^r$$\left({\overline{n}}_{\left[i\right]}\times {\sum }_{k=1}^i{\widehat{s}}_{\left[k\right]}\right)$ are constants. For group $G_{\left[i\right]}$, the objective function is ${\sum }_{j=1}^{{\overline{n}}_i}{\delta }_{\left[i\right]\left[j\right]}$$\times {\left(i^{{\alpha }_2}\right)}^{\frac{\theta }{1+\theta }}\times {\left(\eta {\sum }_{k=i+1}^r{\overline{n}}_{\left[k\right]}\theta +{\iota }_{\left[i\right]j}{j}^{\theta {\alpha }_1}\right)}^{\frac{1}{1+\theta }}$. Obviously, minimization of this term is equal to minimization of ${\sum }_{j=1}^{{\overline{n}}_i}{\delta }_{\left[i\right]\left[j\right]}\times {\left({\iota }_{\left[i\right]j}{j}^{\theta {\alpha }_1}\right)}^{\frac{1}{1+\theta }}$. From Hardy et al. [33], the term ${\sum }_{j=1}^{{\overline{n}}_i}{\delta }_{\left[i\right]\left[j\right]}\times {\left({\iota }_{\left[i\right]j}{j}^{\theta {\alpha }_1}\right)}^{\frac{1}{1+\theta }}$ can be minimized by matching the smallest ${\delta }_{ij}$ to the job with the largest ${\mathrm{\Omega }}_{ij}$, the second smallest ${\delta }_{ij}$ to the job with the second largest ${\iota }_{ij}$, and so on.    □

4. Special Case

For

$$1|GT,CON,{\widehat{p}}_{ij}={\left(\frac{{\widehat{w}}_{ij}{\widehat{x}}^{{\alpha }_1}{\widehat{l}}^{{\alpha }_2}}{{\widehat{u}}_{ij}}\right)}^{\theta }|\sum _{i=1}^r\sigma {\tilde{d}}_i+\sum _{i=1}^r\sum _{j=1}^{{\overline{n}}_i}\left(\rho {\tilde{E}}_{ij}+\mu {\tilde{T}}_{ij}+v_{ij}{\widehat{u}}_{ij}\right)+\lambda {\widehat{C}}_{max},$$

the complexity remains an open problem, so a special case is discussed, i.e., ${\widehat{s}}_i=\widehat{s}$ and ${\overline{n}}_i=\overline{n}$ for $i=1,2,\cdots ,r$.

Theorem 4.

For

$$1|GT,CON,{\widehat{p}}_{ij}={\left(\frac{{\widehat{w}}_{ij}{\widehat{x}}^{{\alpha }_1}{\widehat{l}}^{{\alpha }_2}}{{\widehat{u}}_{ij}}\right)}^{\theta }|\sum _{i=1}^r\sigma {\tilde{d}}_i+\sum _{i=1}^r\sum _{j=1}^{{\overline{n}}_i}\left(\rho {\tilde{E}}_{ij}+\mu {\tilde{T}}_{ij}+v_{ij}{\widehat{u}}_{ij}\right)+\lambda {\widehat{C}}_{max},$$

if ${\widehat{s}}_i=\widehat{s}$ and ${\overline{n}}_i=\overline{n}$ for $i=1,2,\cdots ,r$, the optimal group sequence ${\varphi }^{*}$ is solvable by solving the assignment problem (denoted by $\widetilde{AP}$).

Proof. 

Apparently, the optimal sequence ${\overline{\pi }}^{*}$ of $G_i$ can be determined by Theorem 3, and 

$$\eta \sum _{i=1}^r\left({\overline{n}}_{\left[i\right]}\times \sum _{k=1}^i{\widehat{s}}_{\left[k\right]}\right)$$

is a constant for ${\widehat{s}}_i=\widehat{s}$ and ${\overline{n}}_i=\overline{n}$, $i=1,2,\cdots ,r$. We let the binary variables

$$X_{i\widehat{l}}=\begin{array}{c}\left\{\begin{array}{cc}1,\hfill & if{G}_{i}isassignedtoposition\widehat{l}\left(i,\widehat{l}=1,2,\cdots ,r\right),\hfill \\ 0,\hfill & otherwise\hfill \end{array}\right.\hfill \end{array}$$

and

$${\widehat{Q}}_{i\widehat{l}}=\left({\theta }^{-\frac{\theta }{\theta +1}}+{\theta }^{\frac{1}{\theta +1}}\right)\times \sum _{i=1}^r\sum _{j=1}^{{\overline{n}}_i}{\delta }_{\left[i\right]\left[j\right]}\times {\left(j^{{\alpha }_1}{\widehat{l}}^{{\alpha }_2}\right)}^{\frac{\theta }{\theta +1}}\times {\left(\eta \times \left(r-\widehat{l}\right)\overline{n}+{\iota }_{\left[i\right]j}\right)}^{\frac{1}{\theta +1}},$$

(11)

where

$${\iota }_{\left[i\right]j}=\begin{array}{c}\left\{\begin{array}{cc}\sigma \times \overline{n}+\rho \times (j-1)+\lambda ,\hfill & forj\le l_i^{\prime },\hfill \\ \mu \times (\overline{n}-j+1)+\lambda ;\hfill & for{l}_i^{\prime }<j\le \overline{n},\hfill \end{array}\right.\hfill \end{array}$$

(12)

the optimal group sequence is obtained by the $\widetilde{AP}$:

$$Min\sum _{i=1}^r\sum _{l=1}^r{\widehat{Q}}_{i\widehat{l}}{X}_{i\widehat{l}}$$

(13)

$$s.t.\sum _{i=1}^r{X}_{i\widehat{l}}=1,i=1,2,\cdots ,r$$

(14)

$$\sum _{l=1}^r{X}_{i\widehat{l}}=1,\widehat{l}=1,2,\cdots ,r$$

(15)

$$X_{i\widehat{l}}=0or1,i=1,2,\cdots ,r,\widehat{l}=1,2,\cdots ,r.$$

(16)

   □

Therefore, the special case (i.e., ${\widehat{s}}_i=\widehat{s}$ and ${\overline{n}}_i=\overline{n}$ for $i=1,2,\cdots ,r$) of

$$1|GT,CON,{\widehat{p}}_{ij}={\left(\frac{{\widehat{w}}_{ij}{\widehat{x}}^{{\alpha }_1}{\widehat{l}}^{{\alpha }_2}}{{\widehat{u}}_{ij}}\right)}^{\theta }|\sum _{i=1}^r\sigma {\tilde{d}}_i+\sum _{i=1}^r\sum _{j=1}^{{\overline{n}}_i}\left(\rho {\tilde{E}}_{ij}+\mu {\tilde{T}}_{ij}+v_{ij}{\widehat{u}}_{ij}\right)+\lambda {\widehat{C}}_{max}$$

can be solved optimally by the algorithm described below (Algorithm 1).

Algorithm 1 Special Case

Input: n, r, $\theta$, ${\widehat{w}}_{ij}$, ${\widehat{u}}_{ij}$, ${\widehat{s}}_i$, $v_{ij}$, $\sigma$, $\rho$, $\mu$, $\lambda$ First step: Calculate $l_i^{\prime }$ by using Lemma 1; Second step: Calculate ${\iota }_{ij}$ by using Lemma 2; Third step: Determine the jobs sequence in each group by Theorem  2; Fourth step: Calculate values ${\widehat{Q}}_{i\widehat{l}}$ by Equation (11); Fifth step: Determine the optimal group sequence by the $\widetilde{AP}$ (13)–(16); Sixth step: Calculate the optimal resource allocation by Equation (7). Output: optimal resource allocation, optimal sequence

Theorem 5.

For the special case ${\widehat{s}}_i=\widehat{s}$ and ${\overline{n}}_i=\overline{n}$ of

$$1|GT,CON,{\widehat{p}}_{ij}={\left(\frac{{\widehat{w}}_{ij}{\widehat{x}}^{{\alpha }_1}{\widehat{l}}^{{\alpha }_2}}{{\widehat{u}}_{ij}}\right)}^{\theta }|\sum _{i=1}^r\sigma {\tilde{d}}_i+\sum _{i=1}^r\sum _{j=1}^{{\overline{n}}_i}\left(\rho {\tilde{E}}_{ij}+\mu {\tilde{T}}_{ij}+v_{ij}{\widehat{u}}_{ij}\right)+\lambda {\widehat{C}}_{max},$$

it is solvable by Algorithm 1 in $O\left(n^3\right)$ time.

Proof. 

The correctness of the algorithm follows directly from Theorems 2–4. Steps 1, 2 and 4 need time $O\left(n\right)$, respectively. In Step 3, sorting internal job sequence needs time ${\sum }_{i=1}^{r}O({\overline{n}}_{i}log{\overline{n}}_i)\le O(nlogn)$. The $\widetilde{AP}$ in Step 5 needs time $O\left(r^3\right)\le O\left(n^3\right)$. Thus, the total complexity of Algorithm 1 is $O\left(n^3\right)$.    □

The following example illustrates the application of Algorithm 1 for

$$1|GT,CON,{\widehat{p}}_{ij}={\left(\frac{{\widehat{w}}_{ij}{\widehat{x}}^{{\alpha }_1}{\widehat{l}}^{{\alpha }_2}}{{\widehat{u}}_{ij}}\right)}^{\theta }|\sum _{i=1}^r\sigma {\tilde{d}}_i+\sum _{i=1}^r\sum _{j=1}^{{\overline{n}}_i}\left(\rho {\tilde{E}}_{ij}+\mu {\tilde{T}}_{ij}+v_{ij}{\widehat{u}}_{ij}\right)+\lambda {\widehat{C}}_{max}.$$

Example 1.

There are $n=9$ jobs, $r=3$ groups, ${\overline{n}}_1={\overline{n}}_2={\overline{n}}_3=3$, ${\widehat{s}}_1={\widehat{s}}_2={\widehat{s}}_3=2$, where ${\alpha }_1=-0.1,{\alpha }_2=-0.2,\theta =2,\sigma =2,\mu =4,\rho =2,\lambda =2$. The ${\widehat{w}}_{ij},{\widehat{u}}_{ij},v_{ij}$ of each job are shown in Table 2.

Table 2. The values of ${\widehat{w}}_{ij},v_{ij}$.

		${\mathit{G}}_1$			${\mathit{G}}_2$			${\mathit{G}}_3$
	${\mathit{J}}_{\mathbf{11}}$	${\mathit{J}}_{\mathbf{12}}$	${\mathit{J}}_{\mathbf{13}}$	${\mathit{J}}_{\mathbf{21}}$	${\mathit{J}}_{\mathbf{22}}$	${\mathit{J}}_{\mathbf{23}}$	${\mathit{J}}_{\mathbf{31}}$	${\mathit{J}}_{\mathbf{32}}$	${\mathit{J}}_{\mathbf{33}}$
${\widehat{w}}_{ij}$	10	12	13	13	14	14	15	16	16
$v_{ij}$	5	4	3	4	6	7	2	5	3

Solution:

Step 1. From Lemma 1, we have

$$l_1^{\prime }=l_2^{\prime }=l_3^{\prime }=2.$$

Step 2. From Lemma 2, we have

$${\iota }_{11}={\iota }_{21}={\iota }_{31}=8,$$

$${\iota }_{12}={\iota }_{22}={\iota }_{32}=10,$$

$${\iota }_{13}={\iota }_{23}={\iota }_{33}=6.$$

Step 3. According to Theorem 3, the optimal internal job sequences are ${\overline{\pi }}_1^{*}:[J_{13}\to J_{12}\to J_{11}],{\overline{\pi }}_2^{*}:[J_{22}\to J_{21}\to J_{23}],{\overline{\pi }}_3^{*}:[J_{31}\to J_{33}\to J_{32}].$

Step 4. The values of ${\widehat{Q}}_{i\widehat{l}}$ (by Equation (11)) are given in Table 3, $i=1,2,3,l=1,2,3$.

Table 3. The values of ${\widehat{Q}}_{i\widehat{l}}$.

${\widehat{\mathit{Q}}}_{\mathit{i}\widehat{\mathit{l}}}$	$\widehat{\mathit{l}}=1$	$\widehat{\mathit{l}}=2$	$\widehat{\mathit{l}}=3$
$i=1$	$173.8464$	$140.6598$	$110.2995$
$i=2$	244.4035	197.6642	154.8192
$i=3$	184.2365	148.8115	116.1668

Step 5. Solving the $\widetilde{AP}$ (13)–(16), it follows that ${\varphi }^{*}:[G_1\to G_3\to G_2]$.

Step 6. From Equation (7), ${\widehat{u}}_{ij}$ can be calculated as follows:

$${\widehat{u}}_{11}=11.6406,{\widehat{u}}_{12}=10.0096,{\widehat{u}}_{13}=7.2768,$$

$${\widehat{u}}_{21}=8.8501,{\widehat{u}}_{22}=9.6262,{\widehat{u}}_{23}=7.4218,$$

$${\widehat{u}}_{31}=12.6616,{\widehat{u}}_{32}=11.5276,{\widehat{u}}_{33}=8.5981.$$

5. General Case

If the optimal job sequence ${\overline{\pi }}_k^{*}(k=1,2,\cdots ,r)$ is given by Theorem 3, the term

$$\left({\theta }^{-\frac{\theta }{\theta +1}}+{\theta }^{\frac{1}{\theta +1}}\right)\times \sum _{i=1}^r\sum _{j=1}^{{\overline{n}}_i}{\delta }_{\left[i\right]\left[j\right]}\times {\left(j^{{\alpha }_1}{i}^{{\alpha }_2}\right)}^{\frac{\theta }{1+\theta }}\times {\left(\eta \times \sum _{k=i+1}^r{\overline{n}}_{\left[k\right]}+{\iota }_{\left[i\right]j}\right)}^{\frac{1}{\theta +1}}$$

cannot be minimized by the non-increasing (LPT) order or the non-decreasing (SPT) order of ${\overline{n}}_k$.

Example 2.

There are three jobs belonging to two groups, $G_1=\left\{J_{11}\right\}$, $G_2=\{J_{21},J_{22}\}$, where ${\alpha }_1=-0.3,{\alpha }_2=-0.2,\theta =1,\sigma =\rho =\lambda =5$, $\mu =8$. The ${\widehat{w}}_{ij},v_{ij}$ of each job are shown in Table 4.

Table 4. The values of ${\widehat{w}}_{ij},v_{ij}$.

	${\mathit{J}}_{11}$	${\mathit{J}}_{21}$	${\mathit{J}}_{22}$
${\widehat{w}}_{ij}$	10	10	12
$v_{ij}$	2	3	4

According to Lemmas 1 and 2, we have

$$l_1^{\prime }=l_2^{\prime }=1,$$

$$\begin{array}{cc}& {\iota }_{11}=5\times 1+5=10,\hfill \\ & {\iota }_{21}=5\times 2+5=15,\hfill \\ & {\iota }_{22}=8\times 1+5=13.\hfill \end{array}$$

Then, the optimal internal job sequences are ${\overline{\pi }}_1^{*}:\left[J_{11}\right],{\overline{\pi }}_2^{*}:[J_{21}\to J_{22}]$.

According to the SPT order of ${\overline{n}}_k(\mathrm{i}.\mathrm{e}.,{\mathrm{G}}_1\to {\mathrm{G}}_2)$, the term can be calculated as follows:

$$\begin{array}{cc}& \left({\theta }^{-\frac{\theta }{\theta +1}}+{\theta }^{\frac{1}{\theta +1}}\right)\times \sum _{i=1}^r\sum _{j=1}^{{\overline{n}}_i}{\delta }_{\left[i\right]\left[j\right]}\times {\left(j^{{\alpha }_1}{i}^{{\alpha }_2}\right)}^{\frac{\theta }{1+\theta }}\times {\left(\eta \times \sum _{k=i+1}^r{\overline{n}}_{\left[k\right]}+{\iota }_{\left[i\right]j}\right)}^{\frac{1}{\theta +1}}\hfill \\ \hfill =& 2\times \left[\begin{array}{c}{(10\times 2)}^{1/2}\times {\left(1^{-0.3}\times 1^{-0.2}\right)}^{1/2}\times {(10+10)}^{1/2}\hfill \\ +{(10\times 3)}^{1/2}\times {\left(1^{-0.3}\times 2^{-0.2}\right)}^{1/2}\times {15}^{1/2}\hfill \\ +{(12\times 4)}^{1/2}\times {\left(2^{-0.3}\times 2^{-0.2}\right)}^{1/2}\times {13}^{1/2}\hfill \end{array}\right]\hfill \\ \hfill =& 121.5964.\hfill \end{array}$$

According to the LPT order of ${\overline{n}}_k(\mathrm{i}.\mathrm{e}.,{\mathrm{G}}_2\to {\mathrm{G}}_1)$, the term can be calculated as follows:

$$\begin{array}{cc}& \left({\theta }^{-\frac{\theta }{\theta +1}}+{\theta }^{\frac{1}{\theta +1}}\right)\times \sum _{i=1}^r\sum _{j=1}^{{\overline{n}}_i}{\delta }_{\left[i\right]\left[j\right]}\times {\left(j^{{\alpha }_1}{i}^{{\alpha }_2}\right)}^{\frac{\theta }{1+\theta }}\times {\left(\eta \times \sum _{k=i+1}^r{\overline{n}}_{\left[k\right]}+{\iota }_{\left[i\right]j}\right)}^{\frac{1}{\theta +1}}\hfill \\ \hfill =& 2\times \left[\begin{array}{c}{(10\times 3)}^{1/2}\times {\left(1^{-0.3}\times 1^{-0.2}\right)}^{1/2}\times {(5+15)}^{1/2}\hfill \\ +{(12\times 4)}^{1/2}\times {\left(2^{-0.3}\times 1^{-0.2}\right)}^{1/2}\times {(5+13)}^{1/2}\hfill \\ {+10\times 2)}^{1/2}\times {\left(1^{-0.3}\times 2^{-0.2}\right)}^{1/2}\times {10}^{1/2}\hfill \end{array}\right]\hfill \\ \hfill =& 128.3624.\hfill \end{array}$$

Therefore, the LPT order of ${\overline{n}}_k$ is not an optimal group sequence.

Example 3.

There are 3 jobs belonging to 2 groups, $G_1=\left\{J_{11}\right\}$, $G_2=\{J_{21},J_{22}\}$, where ${\alpha }_1=-0.3,{\alpha }_2=-0.2,\theta =1,\sigma =\rho =\lambda =5$, $\mu =8$. The ${\widehat{w}}_{ij},v_{ij}$ of each job are shown in Table 5.

Table 5. The values of ${\widehat{w}}_{ij},v_{ij}$.

	${\mathit{J}}_{11}$	${\mathit{J}}_{21}$	${\mathit{J}}_{22}$
${\widehat{w}}_{ij}$	10	10	12
$v_{ij}$	2	1	1

According to Lemmas 1 and 2, we have

$$\begin{array}{cc}& l_1^{\prime }=l_2^{\prime }=1,\hfill \\ & {\iota }_{11}=5\times 1+5=10,\hfill \\ & {\iota }_{21}=5\times 2+5=15,\hfill \\ & {\iota }_{22}=8\times 1+5=13.\hfill \end{array}$$

Then, the optimal internal job sequences are ${\overline{\pi }}_1^{*}:\left[J_{11}\right],{\overline{\pi }}_2^{*}:[J_{21}\to J_{22}]$.

According to the SPT order of ${\overline{n}}_k(\mathrm{i}.\mathrm{e}.,{\mathrm{G}}_1\to {\mathrm{G}}_2)$, the term can be calculated as follows:

$$\begin{array}{cc}& \left({\theta }^{-\frac{\theta }{\theta +1}}+{\theta }^{\frac{1}{\theta +1}}\right)\times \sum _{i=1}^r\sum _{j=1}^{{\overline{n}}_i}{\delta }_{\left[i\right]\left[j\right]}\times {\left(j^{{\alpha }_1}{i}^{{\alpha }_2}\right)}^{\frac{\theta }{1+\theta }}\times {\left(\eta \times \sum _{k=i+1}^r{\overline{n}}_{\left[k\right]}+{\iota }_{\left[i\right]j}\right)}^{\frac{1}{\theta +1}}\hfill \\ \hfill =& 2\times \left[\begin{array}{c}{(10\times 2)}^{1/2}\times {\left(1^{-0.3}\times 1^{-0.2}\right)}^{1/2}\times {(10+10)}^{1/2}\hfill \\ +{(10\times 1)}^{1/2}\times {\left(1^{-0.3}\times 2^{-0.2}\right)}^{1/2}\times {15}^{1/2}\hfill \\ +{(12\times 1)}^{1/2}\times {\left(2^{-0.3}\times 2^{-0.2}\right)}^{1/2}\times {13}^{1/2}\hfill \end{array}\right]\hfill \\ \hfill =& 83.8601.\hfill \end{array}$$

According to the LPT order of ${\overline{n}}_k(\mathrm{i}.\mathrm{e}.,{\mathrm{G}}_2\to {\mathrm{G}}_1)$, the term can be calculated as follows:

$$\begin{array}{cc}& \left({\theta }^{-\frac{\theta }{\theta +1}}+{\theta }^{\frac{1}{\theta +1}}\right)\times \sum _{i=1}^r\sum _{j=1}^{{\overline{n}}_i}{\delta }_{\left[i\right]\left[j\right]}\times {\left(j^{{\alpha }_1}{i}^{{\alpha }_2}\right)}^{\frac{\theta }{1+\theta }}\times {\left(\eta \times \sum _{k=i+1}^r{\overline{n}}_{\left[k\right]}+{\iota }_{\left[i\right]j}\right)}^{\frac{1}{\theta +1}}\hfill \\ \hfill =& 2\times \left[\begin{array}{c}{(10\times 1)}^{1/2}\times {\left(1^{-0.3}\times 1^{-0.2}\right)}^{1/2}\times {(5+15)}^{1/2}\hfill \\ +{(12\times 1)}^{1/2}\times {\left(2^{-0.3}\times 1^{-0.2}\right)}^{1/2}\times {(5+13)}^{1/2}\hfill \\ +{(10\times 2)}^{1/2}\times {\left(1^{-0.3}\times 2^{-0.2}\right)}^{1/2}\times {10}^{1/2}\hfill \end{array}\right]\hfill \\ \hfill =& 81.1657.\hfill \end{array}$$

Therefore, the SPT order of ${\overline{n}}_k$ is not an optimal group sequence.

5.1. Heuristic Algorithm

According to Theorem 3, the optimal schedule of jobs within each group can be obtained and the optimal resource allocation for a given schedule can be obtained by Theorem 1. From Section 5, the following heuristic algorithm (HA) can be proposed (Algorithm 2).

Algorithm 2 HA

Input: $\overline{n}$, r, $\theta$, ${\widehat{w}}_{ij}$, ${\widehat{u}}_{ij}$, ${\widehat{s}}_i$, $v_{ij}$, $\sigma$, $\rho$, $\mu$, $\lambda$ First step: Calculate $l_i^{\prime }$ by using Lemma 1; Second step: Calculate ${\iota }_{ij}$ by using Lemma 2; Third step: Determine the jobs sequence in each group by Theorem  3; Fourth step: Schedule groups by the non-increasing of $\frac{{\overline{n}}_i}{{\widehat{s}}_i}$ and calculate objective function                        value by Equation (6); Fifth step: Schedule groups by the non-increasing of ${\widehat{s}}_i$ and calculate objective function                        value by Equation (6); Sixth step: Schedule groups by the non-increasing of ${\overline{n}}_i$ and calculate objective function                        value by Equation (6); Seventh step: Calculate the optimal resource allocation by Equation (7). Output: resource allocation, local optimal sequence

5.2. Simulated Annealing Algorithm

As in Lai et al. [34], simulated annealing (SA) (Algorithm 3) is actually a greedy algorithm, but it introduces a stochastic element to the search process. This paper uses this classical algorithm to compare it with the proposed HA algorithm (Algorithm 2). Simulated annealing accepts with some probability a solution that is worse than the current one, so it is possible to jump out of this local optimum and research for the global optimum, SA is a good choice for

$$1|GT,CON,{\widehat{p}}_{ij}={\left(\frac{{\widehat{w}}_{ij}{\widehat{x}}^{{\alpha }_1}{\widehat{l}}^{{\alpha }_2}}{{\widehat{u}}_{ij}}\right)}^{\theta }|\sum _{i=1}^r\sigma {\tilde{d}}_i+\sum _{i=1}^r\sum _{j=1}^{{\overline{n}}_i}\left(\rho {\tilde{E}}_{ij}+\mu {\tilde{T}}_{ij}+v_{ij}{\widehat{u}}_{ij}\right)+\lambda {\widehat{C}}_{max}.$$

Algorithm 3 SA

Input: $\overline{n}$, r, $\theta$, ${\widehat{w}}_{ij}$, ${\widehat{u}}_{ij}$, ${\widehat{s}}_i$, $v_{ij}$, $\sigma$, $\rho$, $\mu$, $\lambda$ First step: Set the internal job sequence by the Second step of Algorithm 1; Second step: Use the pairwise interchange (PI) neighborhood generation method; Third step: Calculate the objective value of the original schedule $\check{Z}$; Fourth step: Calculate the objective value of the new schedule ${\check{Z}}^{*}$. If the ${\check{Z}}^{*}$ is less than                         $\check{Z}$, it is accepted. Nevertheless, if the ${\check{Z}}^{*}$ is higher, it might still be accepted                         with a decreasing probability as the process proceeds. This acceptance                          probability is determined by the following exponential distribution function:                                $P\left(accept\right)=exp(-\alpha \times ▵WC/L),$                         where $\alpha$ is a parameter and $▵WC/L$ is the change in the objective function.                          In addition, the method is used to change $\alpha$ in the kth iteration as follows:                                      $\alpha =\frac{k}{\delta },$                          where $\delta$ is a constant. After preliminary trials, $\delta =1$ is used; Fifth step: If ${\check{Z}}^{*}$ increases, the new sequence is accepted when $P\left(accept\right)>\beta$, where $\beta$ is                          randomly sampled from the uniform distribution; Sixth step: The schedule is stable after $1000r$ iterations. Output: resource allocation, local optimal sequence

5.3. Lower Bound

We let $\varphi =[{\varphi }_{G\overline{S}},{\varphi }_{G\overline{U}}]$ be a group sequence, where ${\overline{\pi }}_{G\overline{S}}$ (${\overline{\varphi }}_{G\overline{U}}$) is the scheduled (unscheduled) part, and  there are f groups in ${\overline{\varphi }}_{G\overline{S}}$. We have

$$\begin{array}{cc}\hfill \check{Z}=& \left({\theta }^{-\frac{\theta }{\theta +1}}+{\theta }^{\frac{1}{\theta +1}}\right)\times \sum _{i=1}^f\sum _{j=1}^{{\overline{n}}_i}{\delta }_{ij}\times {\left(j^{{\alpha }_1}{i}^{{\alpha }_2}\right)}^{\frac{\theta }{1+\theta }}\times {\left(\eta \times \sum _{k=i+1}^f{\overline{n}}_k+{\iota }_{ij}\right)}^{\frac{1}{\theta +1}}\hfill \\ & +\left({\theta }^{-\frac{\theta }{\theta +1}}+{\theta }^{\frac{1}{\theta +1}}\right)\times \sum _{i=f+1}^r\sum _{j=1}^{{\overline{n}}_i}{\delta }_{\left[i\right]\left(j\right)}\times {\left(j^{{\alpha }_1}{i}^{{\alpha }_2}\right)}^{\frac{\theta }{1+\theta }}\times {\left(\eta \times \sum _{k=i+1}^r{\overline{n}}_{\left[k\right]}+{\iota }_{\left[i\right]j}\right)}^{\frac{1}{\theta +1}}\hfill \\ & +\eta \times \sum _{i=1}^f\left({\overline{n}}_i\times \sum _{k=1}^i{\widehat{s}}_k\right)+\eta \times \sum _{i=f+1}^r\left({\overline{n}}_{<i>}\times \left(\sum _{k=1}^f{\widehat{s}}_k+\sum _{k=f+1}^i{\widehat{s}}_{\left(k\right)}\right)\right).\hfill \end{array}$$

(17)

From the above equation, it can be seen that the terms $\left({\theta }^{-\frac{\theta }{\theta +1}}+{\theta }^{\frac{1}{\theta +1}}\right)\times {\sum }_{i=1}^f{\sum }_{j=1}^{{\overline{n}}_i}{\delta }_{ij}\times {\left(j^{{\alpha }_1}{i}^{{\alpha }_2}\right)}^{\frac{\theta }{1+\theta }}\times {\left(\eta \times {\sum }_{k=i+1}^f{\overline{n}}_k+{\iota }_{ij}\right)}^{\frac{1}{\theta +1}}$, $\eta \times {\sum }_{i=1}^f\left({\overline{n}}_i\times {\sum }_{k=1}^i{\widehat{s}}_k\right)$, and ${\sum }_{k=1}^f{\widehat{s}}_k$ are known, which can be seen as constants. And the term $\eta \times {\sum }_{i=f+1}^r\left({\overline{n}}_{<i>}\times \left({\sum }_{k=1}^f{\widehat{s}}_k+{\sum }_{k=f+1}^i{\widehat{s}}_{\left(k\right)}\right)\right)$ can be minimized by Theorem 2, and ${\sum }_{i=f+1}^r{\sum }_{j=1}^{{\overline{n}}_i}{\delta }_{\left[i\right]\left[j\right]}\times i^{\alpha }\times {\left(\eta \times {\sum }_{k=i+1}^r{\overline{n}}_{\left[k\right]}+{\iota }_{\left[i\right]j}\right)}^{\frac{1}{\theta +1}}\ge {\sum }_{i=f+1}^r{\sum }_{j=1}^{{\overline{n}}_i}{\delta }_{\left[i\right]\left[j\right]}\times i^{\alpha }\times {\iota }_{\left[i\right]j}^{\frac{1}{\theta +1}}$. Then, we have the following lower bound:

$$\begin{array}{cc}\hfill L{B}_1=& \left({\theta }^{-\frac{\theta }{\theta +1}}+{\theta }^{\frac{1}{\theta +1}}\right)\times \sum _{i=1}^f\sum _{j=1}^{{\overline{n}}_i}{\delta }_{ij}\times {\left(j^{{\alpha }_1}{i}^{{\alpha }_2}\right)}^{\frac{\theta }{1+\theta }}\times {\left(\eta \times \sum _{k=i+1}^f{\overline{n}}_k+{\iota }_{ij}\right)}^{\frac{1}{\theta +1}}\hfill \\ & +\left({\theta }^{-\frac{\theta }{\theta +1}}+{\theta }^{\frac{1}{\theta +1}}\right)\times \sum _{i=f+1}^r\sum _{j=1}^{{\overline{n}}_i}{\delta }_{\left[i\right]\left(j\right)}\times {\left(j^{{\alpha }_1}{i}^{{\alpha }_2}\right)}^{\frac{\theta }{1+\theta }}\times {\iota }_{\left[i\right]j}^{\frac{1}{\theta +1}}+\eta \times \sum _{i=1}^f\left({\overline{n}}_i\times \sum _{k=1}^i{\widehat{s}}_k\right)\hfill \\ & +\eta \times \sum _{i=f+1}^r\left({\overline{n}}_{min}\times \left(\sum _{k=1}^f{\widehat{s}}_k+\sum _{k=f+1}^i{\widehat{s}}_{\left(k\right)}\right)\right),\hfill \end{array}$$

(18)

where ${\overline{n}}_{min}=min\{{\overline{n}}_{<f+1>},{\overline{n}}_{<f+2>},\dots ,{\overline{n}}_{<r>}\}$, and ${\widehat{s}}_{(f+1)}<{\widehat{s}}_{(f+2)}<...<{\widehat{s}}_{\left(r\right)}$. We let ${\widehat{s}}_{min}=min\{{\widehat{s}}_{(f+1)},{\widehat{s}}_{(f+2)},\dots ,{\widehat{s}}_{\left(r\right)}\}$; then, the second lower bound can be written as

$$\begin{array}{cc}\hfill L{B}_2=& \left({\theta }^{-\frac{\theta }{\theta +1}}+{\theta }^{\frac{1}{\theta +1}}\right)\times \sum _{i=1}^f\sum _{j=1}^{{\overline{n}}_i}{\delta }_{ij}\times {\left(j^{{\alpha }_1}{i}^{{\alpha }_2}\right)}^{\frac{\theta }{1+\theta }}\times {\left(\eta \times \sum _{k=i+1}^f{\overline{n}}_k+{\iota }_{ij}\right)}^{\frac{1}{\theta +1}}\hfill \\ & +\left({\theta }^{-\frac{\theta }{\theta +1}}+{\theta }^{\frac{1}{\theta +1}}\right)\times \sum _{i=f+1}^r\sum _{j=1}^{{\overline{n}}_i}{\delta }_{\left[i\right]\left(j\right)}\times {\left(j^{{\alpha }_1}{i}^{{\alpha }_2}\right)}^{\frac{\theta }{1+\theta }}\times {\iota }_{\left[i\right]j}^{\frac{1}{\theta +1}}+\eta \times \sum _{i=1}^f\left({\overline{n}}_i\times \sum _{k=1}^i{\widehat{s}}_k\right)\hfill \\ & +\eta \times \sum _{i=f+1}^r\left({\overline{n}}_{<i>}\times \left(\sum _{k=1}^f{\widehat{s}}_k+\sum _{k=f+1}^i{\widehat{s}}_{min}\right)\right),\hfill \end{array}$$

(19)

it can be known that ${\overline{n}}_{<f+1>}>{\overline{n}}_{<f+2>}>...>{\overline{n}}_{<r>}$ by Theorem 2. And 

$$\begin{array}{cc}\hfill L{B}_3=& \left({\theta }^{-\frac{\theta }{\theta +1}}+{\theta }^{\frac{1}{\theta +1}}\right)\times \sum _{i=1}^f\sum _{j=1}^{{\overline{n}}_i}{\delta }_{\left[i\right]\left[j\right]}\times {\left(j^{{\alpha }_1}{i}^{{\alpha }_2}\right)}^{\frac{\theta }{1+\theta }}\times {\left(\eta \times \sum _{k=i+1}^r{\overline{n}}_{\left[k\right]}+{\iota }_{\left[i\right]j}\right)}^{\frac{1}{\theta +1}}\hfill \\ & +\left({\theta }^{-\frac{\theta }{\theta +1}}+{\theta }^{\frac{1}{\theta +1}}\right)\times \sum _{i=f+1}^r\sum _{j=1}^{{\overline{n}}_i}{\delta }_{\left[i\right]\left(j\right)}\times {\left(j^{{\alpha }_1}{i}^{{\alpha }_2}\right)}^{\frac{\theta }{1+\theta }}\times {\iota }_{\left[i\right]j}^{\frac{1}{\theta +1}}+\eta \times \sum _{i=1}^f\left({\overline{n}}_{\left[i\right]}\times \sum _{k=1}^i{\widehat{s}}_{\left[k\right]}\right)\hfill \\ & +\eta \times \sum _{i=f+1}^r\left({\overline{n}}_{<i>}\times \left(\sum _{k=1}^f{\widehat{s}}_{\left[k\right]}+\sum _{k=f+1}^i{\widehat{s}}_{\left(k\right)}\right)\right),\hfill \end{array}$$

(20)

where ${\overline{n}}_{<f+1>}>{\overline{n}}_{<f+2>}>...>{\overline{n}}_{<r>}$ and ${\widehat{s}}_{(f+1)}<{\widehat{s}}_{(f+2)}<...<{\widehat{s}}_{\left(r\right)}$. Note that ${\overline{n}}_{<i>}$ and ${\widehat{s}}_{\left(i\right)}$ ($i=f+1,f+2,\dots ,r$) do not necessarily correspond to the same group. To make the lower bound tighter, we select the largest of the three as the lower bound, that is,

$$LB=max\{L{B}_1,L{B}_2,L{B}_3\}.$$

(21)

5.4. Branch-and-Bound Algorithm

Based on the above-mentioned lower bounds, the branch-and-bound (B&B) algorithm with enumeration as the central idea is proposed, and this enumeration algorithm can be used as an optimal program to solve the problem posed in this study in the steps described below (Algorithm 4).

Algorithm 4  $B\&B$

Input: $\overline{n}$, r, $\theta$, ${\widehat{w}}_{ij}$, ${\widehat{u}}_{ij}$, ${\widehat{s}}_i$, $v_{ij}$, $\sigma$, $\rho$, $\mu$, $\lambda$ First step: Use Algorithm 1 to obtain an initial solution for the problem; Second step: Calculate the lower bound for the node; Third step: If the lower bound for an unfathomed partial schedule of groups is larger                      than or equal to the value of the objective function of the initial solution,                      eliminate the node and all the nodes following it in the branch. Calculate                      the objective function value of the completed schedule; if it is less than the                      initial solution, replace it as the new solution; otherwise, eliminate it. Fourth step: Continue until all nodes are explored. Output: resource allocation, optimal sequence

Example 4.

We consider an example in which there are 14 jobs belonging to five groups, $G_1=\{J_{11},J_{12},J_{13}\},$ $G_2=\{J_{21},J_{22},J_{23},J_{24}\},G_3=\{J_{31},J_{32},J_{33}\},G_4=\{J_{41},J_{42}\},G_1=\{J_{51},J_{52}\}$, where $\theta =2,\sigma =2,\mu =4,\rho =3,\lambda =2,{\alpha }_1=-0.1,{\alpha }_2=-0.2$. The ${\widehat{w}}_{ij},{\widehat{u}}_{ij},v_{ij}$ of each job, job number ${\overline{n}}_k$, and setup time ${\widehat{s}}_k$ of each group are shown in Table 6 and Table 7.

Table 6. The values of ${\widehat{w}}_{ij},v_{ij}$.

	${\overline{\mathit{n}}}_{\mathit{k}}$	${\widehat{\mathit{s}}}_{\mathit{k}}$
$G_1$	3	6
$G_2$	4	4
$G_3$	3	4
$G_4$	2	5
$G_5$	2	8

Table 7. Parameters of Example 4.

	${\mathit{J}}_{11}$	${\mathit{J}}_{12}$	${\mathit{J}}_{13}$	${\mathit{J}}_{21}$	${\mathit{J}}_{22}$	${\mathit{J}}_{23}$	${\mathit{J}}_{24}$	${\mathit{J}}_{31}$	${\mathit{J}}_{32}$	${\mathit{J}}_{33}$	${\mathit{J}}_{41}$	${\mathit{J}}_{42}$	${\mathit{J}}_{51}$	${\mathit{J}}_{52}$
${\widehat{w}}_{ij}$	10	12	13	13	14	14	15	16	16	16	15	18	12	14
$v_{ij}$	5	4	3	4	6	7	2	5	3	6	4	4	5	3

Solution:

From Algorithm 2, we have ${\overline{\pi }}_1^{*}:[J_{12}\to J_{13}\to J_{11}],{\overline{\pi }}_2^{*}:[J_{23}\to J_{24}\to J_{21}\to J_{22}],{\overline{\pi }}_3^{*}:[J_{31}\to J_{32}\to J_{33}],{\overline{\pi }}_4^{*}:[J_{42}\to J_{41}],{\overline{\pi }}_5^{*}:[J_{51}\to J_{52}]$. According to Steps 3-5, the initial group sequences are: $G_2\to G_3\to G_1\to G_4\to G_5,G_2\to G_3\to G_1\to G_4\to G_5,G_2\to G_3\to G_4\to G_1\to G_5,$ and their corresponding objective values are $1017.1409,1017.1409$, and $1022.2123.$ We select the smallest $1017.1409$ as the upper bound. According to the B&B algorithm, the following search tree can be obtained (see Figure 1). The numbers in Figure 1 represent the lower values, and the $G_0$ is defined as Level 0. From Figure 1, the optimal group sequence is $G_2\to G_3\to G_1\to G_4\to G_5$, where at Level 1, for group $G_1$, from Equations (18)–(20), the lower bounds are

$$\begin{array}{cc}\hfill L{B}_1\left(G_1\right)=& 1.8899\times \left[\begin{array}{c}13.208\times {\left(1^{-0.1}\times 1^{-0.2}\right)}^{2/3}\times 8^{\frac{1}{3}}+11.5\times {\left(2^{-0.1}\times 1^{-0.2}\right)}^{2/3}\times {10}^{\frac{1}{3}}\hfill \\ +13.572\times {\left(3^{-0.1}\times 1^{-0.2}\right)}^{2/3}\times 6^{\frac{1}{3}}+21.256\times {\left(1^{-0.1}\times 2^{-0.2}\right)}^{2/3}\times 4^{\frac{1}{3}}\hfill \\ +9.665\times {\left(2^{-0.1}\times 2^{-0.2}\right)}^{2/3}\times {10}^{\frac{1}{3}}+13.932\times {\left(3^{-0.1}\times 2^{-0.2}\right)}^{2/3}\times 9^{\frac{1}{3}}\hfill \\ +19.18\times {\left(4^{-0.1}\times 2^{-0.2}\right)}^{2/3}\times 6^{\frac{1}{3}}+18.566\times {\left(1^{-0.1}\times 3^{-0.2}\right)}^{2/3}\times 8^{\frac{1}{3}}\hfill \\ +13.208\times {\left(2^{-0.1}\times 3^{-0.2}\right)}^{2/3}\times {10}^{\frac{1}{3}}+20.966\times {\left(3^{-0.1}\times 3^{-0.2}\right)}^{2/3}\times 6^{\frac{1}{3}}\hfill \\ +15.326\times {\left(1^{-0.1}\times 4^{-0.2}\right)}^{2/3}\times 6^{\frac{1}{3}}+17.307\times {\left(2^{-0.1}\times 4^{-0.2}\right)}^{2/3}\times 6^{\frac{1}{3}}\hfill \\ +15.326\times {\left(1^{-0.1}\times 5^{-0.2}\right)}^{2/3}\times 6^{\frac{1}{3}}+12.083\times {\left(1^{-0.1}\times 5^{-0.2}\right)}^{2/3}\times 6^{\frac{1}{3}}\hfill \end{array}\right]\hfill \\ & +2\times \left[\begin{array}{c}3\times 6+2\times (6+4)+2\times (6+4+4)\hfill \\ +2\times (6+4+4+5)+2\times (6+4+4+5+8)\hfill \end{array}\right]\hfill \\ \hfill =& 977.1444.\hfill \end{array}$$

$$\begin{array}{cc}\hfill L{B}_2\left(G_1\right)=& 1.8899\times \left[\begin{array}{c}13.208\times {\left(1^{-0.1}\times 1^{-0.2}\right)}^{2/3}\times 8^{\frac{1}{3}}+11.5\times {\left(2^{-0.1}\times 1^{-0.2}\right)}^{2/3}\times {10}^{\frac{1}{3}}\hfill \\ +13.572\times {\left(3^{-0.1}\times 1^{-0.2}\right)}^{2/3}\times 6^{\frac{1}{3}}+21.256\times {\left(1^{-0.1}\times 2^{-0.2}\right)}^{2/3}\times 4^{\frac{1}{3}}\hfill \\ +9.665\times {\left(2^{-0.1}\times 2^{-0.2}\right)}^{2/3}\times {10}^{\frac{1}{3}}+13.932\times {\left(3^{-0.1}\times 2^{-0.2}\right)}^{2/3}\times 9^{\frac{1}{3}}\hfill \\ +19.18\times {\left(4^{-0.1}\times 2^{-0.2}\right)}^{2/3}\times 6^{\frac{1}{3}}+18.566\times {\left(1^{-0.1}\times 3^{-0.2}\right)}^{2/3}\times 8^{\frac{1}{3}}\hfill \\ +13.208\times {\left(2^{-0.1}\times 3^{-0.2}\right)}^{2/3}\times {10}^{\frac{1}{3}}+20.966\times {\left(3^{-0.1}\times 3^{-0.2}\right)}^{2/3}\times 6^{\frac{1}{3}}\hfill \\ +15.326\times {\left(1^{-0.1}\times 4^{-0.2}\right)}^{2/3}\times 6^{\frac{1}{3}}+17.307\times {\left(2^{-0.1}\times 4^{-0.2}\right)}^{2/3}\times 6^{\frac{1}{3}}\hfill \\ +15.326\times {\left(1^{-0.1}\times 5^{-0.2}\right)}^{2/3}\times 6^{\frac{1}{3}}+12.083\times {\left(1^{-0.1}\times 5^{-0.2}\right)}^{2/3}\times 6^{\frac{1}{3}}\hfill \end{array}\right]\hfill \\ & +2\times \left[\begin{array}{c}3\times 6+4\times (6+4)+2\times (6+4+4)\hfill \\ +2\times (6+4+4+4)+2\times (6+4+4+4+4)\hfill \end{array}\right]\hfill \\ \hfill =& 993.1444.\hfill \end{array}$$

$$\begin{array}{cc}\hfill L{B}_3\left(G_1\right)=& 1.8899\times \left[\begin{array}{c}13.208\times {\left(1^{-0.1}\times 1^{-0.2}\right)}^{2/3}\times 8^{\frac{1}{3}}+11.5\times {\left(2^{-0.1}\times 1^{-0.2}\right)}^{2/3}\times {10}^{\frac{1}{3}}\hfill \\ +13.572\times {\left(3^{-0.1}\times 1^{-0.2}\right)}^{2/3}\times 6^{\frac{1}{3}}+21.256\times {\left(1^{-0.1}\times 2^{-0.2}\right)}^{2/3}\times 4^{\frac{1}{3}}\hfill \\ +9.665\times {\left(2^{-0.1}\times 2^{-0.2}\right)}^{2/3}\times {10}^{\frac{1}{3}}+13.932\times {\left(3^{-0.1}\times 2^{-0.2}\right)}^{2/3}\times 9^{\frac{1}{3}}\hfill \\ +19.18\times {\left(4^{-0.1}\times 2^{-0.2}\right)}^{2/3}\times 6^{\frac{1}{3}}+18.566\times {\left(1^{-0.1}\times 3^{-0.2}\right)}^{2/3}\times 8^{\frac{1}{3}}\hfill \\ +13.208\times {\left(2^{-0.1}\times 3^{-0.2}\right)}^{2/3}\times {10}^{\frac{1}{3}}+20.966\times {\left(3^{-0.1}\times 3^{-0.2}\right)}^{2/3}\times 6^{\frac{1}{3}}\hfill \\ +15.326\times {\left(1^{-0.1}\times 4^{-0.2}\right)}^{2/3}\times 6^{\frac{1}{3}}+17.307\times {\left(2^{-0.1}\times 4^{-0.2}\right)}^{2/3}\times 6^{\frac{1}{3}}\hfill \\ +15.326\times {\left(1^{-0.1}\times 5^{-0.2}\right)}^{2/3}\times 6^{\frac{1}{3}}+12.083\times {\left(1^{-0.1}\times 5^{-0.2}\right)}^{2/3}\times 6^{\frac{1}{3}}\hfill \end{array}\right]\hfill \\ & +2\times \left[\begin{array}{c}3\times 6+4\times (6+4)+3\times (6+4+4)\hfill \\ +2\times (6+4+4+5)+2\times (6+4+4+5+8)\hfill \end{array}\right]\hfill \\ \hfill =& 1045.1444.\hfill \end{array}$$

$$LB\left(G_1\right)=max\{L{B}_1\left(G_1\right),L{B}_2\left(G_1\right),L{B}_3\left(G_1\right)\}=1045.1444.$$

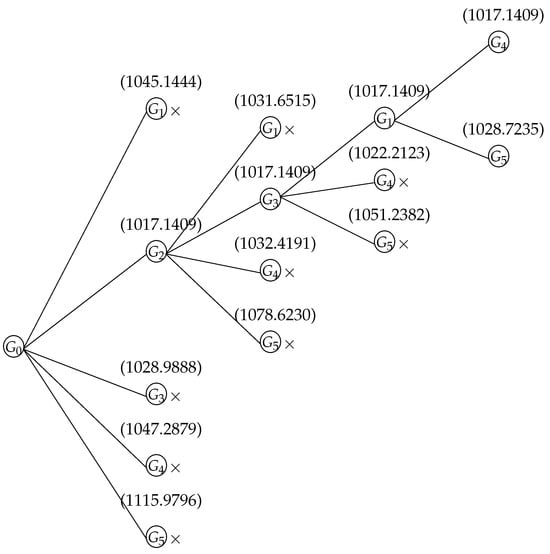
Figure 1. Search tree of Example 4 (×denotes pruning).

6. Computational Experiments

6.1. Simulating Configuration

In this section, the performance of the proposed algorithms is evaluated. We use visual studio2022 v17.1.0 software for programming the HA (i.e., Algorithm 2), SA (i.e., Algorithm 3), and B&B algorithms (i.e., Algorithm 4), respectively, using a DELL personal computer equipped with an Intel^® Core^TM i5-10500U @ 3.10 3.10 GHz CPU, 8 GB RAM, and Window 10 Operating System.

6.2. Simulating Parameters

To compare the efficiency of the proposed method, heuristic, SA, and B&B algorithms are taken into account. The values used as simulation parameters in C++ are considered according to Table 8. The proposed method is implemented with jobs ranging from 100 to 300 in three different algorithms, and the parameter setting distribution is considered uniformly. To avoid contingency, we evaluate 10 randomly generated results and set the maximum CPU time for each result to 3600 s.

Table 8. Numerical parameters.

Parameter	Value
$\overline{n}$	100, 150, 200, 250, 300
r	8, 9, 10, 11, 12
$\theta$	[0.1, 0.5]
${\widehat{w}}_{ij}$	[1, 50]
${\widehat{u}}_{ij}$	[1, 50]
${\widehat{s}}_i$	[1, 50]
$v_{ij}$	[1, 50]
$\sigma$	[1, 10]
$\rho$	[1, 10]
$\mu$	[1, 10]
$\lambda$	[1, 10]

For computational experiments, the parameter settings can be obtained randomly as follows:

6.3. Experimental Results

In the experiment, a total of 1500 instances was tested. The results are summarized in Table 9, Table 10 and Table 11 and consist of CPU time, node number of B&B, and relative error, where bold font is the best solution. The error of the solution by HA (TS) is calculated as

$$\frac{\check{Z}\left(X\right)-{\check{Z}}^{*}}{{\check{Z}}^{*}},$$

where $\check{Z}\left(X\right)$ is the objective function value generated by Algorithm X, $X\in \{HA,SA\}$, and ${\check{Z}}^{*}$ is the optimal value generated by the B&B Algorithm.

Table 9. Results of the algorithms for ${\alpha }_1,{\alpha }_2\in (-0.25,0)$.

		HA-$\widehat{\mathit{cpu}}$(s)		B&B-$\widehat{\mathit{cpu}}$(s)		SA-$\widehat{\mathit{cpu}}$(s)		Error Bound of HA		Error Bound of SA		Node Number of B&B
$\overline{\mathit{n}}$	$\mathit{r}$	Mean	Max	Mean	Max	Mean	Max	Mean	Max	Mean	Max	Mean	Max
	8	0.0007	0.001	4.103	4.602	0.375	0.383	0.000175	0.000209	0.000159	0.000394	62,352.1	69,280
	9	0.0007	0.002	41.007	41.158	0.464	0.476	0.000187	0.000327	$\mathbf{0}.\mathbf{000170}$	0.000318	623,529	623,529
100	10	0.0009	0.002	372.402	421.762	0.572	0.593	0.000146	0.000277	$\mathbf{0}.\mathbf{000140}$	0.000269	5,611,770.1	6,235,300
	11	0.001	0.003	3442	3600	0.676	0.704	0.000222	0.000367	$\mathbf{0}.\mathbf{000210}$	0.000397	54,676,968.2	55,272,022
	12	0.0011	0.003	3600	3600	0.793	0.800	0.000185	0.000387	$\mathbf{0}.\mathbf{000148}$	0.000454	49,878,822	55,886,769
	8	0.0005	0.001	6.693	6.829	0.543	0.558	0.000222	0.000393	$\mathbf{0}.\mathbf{000216}$	0.000379	69,280	69,280
	9	0.0002	0.001	62.585	66.767	0.692	0.737	0.000101	0.000171	$\mathbf{0}.\mathbf{000094}$	0.000109	623,529	623,529
150	10	0.0011	0.002	616.894	642.112	0.845	0.887	0.000202	0.000264	$\mathbf{0}.\mathbf{000111}$	0.000272	6,235,300	6,235,300
	11	0.0006	0.003	3460.2	3600	1.015	1.053	0.000132	0.000253	$\mathbf{0}.\mathbf{000123}$	0.000206	36,584,581.6	36,680,876
	12	0.001	0.002	3600	3600	1.193	1.211	0.000113	0.000323	$\mathbf{0}.\mathbf{000106}$	0.000148	36,881,159.4	37,411,051
	8	0.0004	0.001	8.946	8.993	0.723	0.732	0.000105	0.000182	$\mathbf{0}.\mathbf{000089}$	0.000101	69,280	69,280
	9	0.0007	0.001	72.484	80.719	0.904	0.918	0.000101	0.000323	$\mathbf{0}.\mathbf{000096}$	0.000185	561,176.2	623,529
200	10	0.001	0.004	810.209	841.706	1.115	1.178	0.000181	0.000387	$\mathbf{0}.\mathbf{000177}$	0.000286	6,235,300	6,235,300
	11	0.0004	0.001	3452	3600	1.327	1.341	0.000189	0.000302	$\mathbf{0}.\mathbf{000185}$	0.000300	27,596,209.3	27,954,841
	12	0.0006	0.003	3600	3600	1.577	1.590	0.000104	0.000227	$\mathbf{0}.\mathbf{000068}$	0.000110	27,761,932.9	27,958,200
	8	0.0005	0.001	10.090	11.241	0.903	0.930	0.000100	0.000201	$\mathbf{0}.\mathbf{000059}$	0.000104	69,130.3	69,379
	9	0.0016	0.007	103.353	105.023	1.147	1.156	0.000099	0.000125	$\mathbf{0}.\mathbf{000073}$	0.000105	623,529	623,529
250	10	0.0013	0.004	933.733	1075.240	1.148	1.240	0.000138	0.000304	$\mathbf{0}.\mathbf{000134}$	0.000401	5,611,770.1	6,235,300
	11	0.0004	0.001	3480	3600	1.715	2.088	0.000099	0.000138	$\mathbf{0}.\mathbf{000097}$	0.000131	21,181,984	21,812,984
	12	0.001	0.008	3600	3600	1.952	1.987	0.000211	0.000237	$\mathbf{0}.\mathbf{000153}$	0.000343	22,329,658.5	22,672,452
	8	0.0008	0.002	12.147	13.550	1.096	1.104	0.000071	0.000146	$\mathbf{0}.\mathbf{000042}$	0.000161	62,352.1	69,280
	9	0.0006	0.001	128.441	128.929	1.448	1.632	0.000087	0.000201	$\mathbf{0}.\mathbf{000083}$	0.000191	623,529	623,529
300	10	0.0007	0.002	1218.592	1224.528	1.658	1.675	0.000065	0.000125	$\mathbf{0}.\mathbf{000062}$	0.000122	6,235,300	6,235,300
	11	0.0006	0.002	3240	3600	1.990	2.000	0.000120	0.000306	$\mathbf{0}.\mathbf{000040}$	0.000156	16,722,381.2	18,671,853
	12	0.0006	0.001	3600	3600	2.353	2.491	0.000071	0.000159	$\mathbf{0}.\mathbf{000246}$	0.000369	18,632,673.8	18,913,537

Table 10. Results of the algorithms for ${\alpha }_1,{\alpha }_2\in (-0.5,-0.25)$.

		HA-$\widehat{\mathit{cpu}}$(s)		B&B-$\widehat{\mathit{cpu}}$(s)		SA-$\widehat{\mathit{cpu}}$(s)		Error Bound of HA		Error Bound of SA		Node Number of B&B
$\overline{\mathit{n}}$	$\mathit{r}$	Mean	Max	Mean	Max	Mean	Max	Mean	Max	Mean	Max	Mean	Max
	8	0.0004	0.001	4.518	4.529	0.366	0.369	0.000970	0.001171	0.000109	0.000230	69,248.2	69,280
	9	0.0007	0.002	36.605	40.885	0.457	0.462	0.000887	0.001078	$\mathbf{0}.\mathbf{000095}$	0.000162	561,176.2	623,529
100	10	0.0008	0.002	370.917	433.028	0.568	0.597	0.000463	0.000687	$\mathbf{0}.\mathbf{000207}$	0.000274	5,611,770.1	6,235,300
	11	0.0007	0.002	3240	3600	0.671	0.672	0.000864	0.001540	$\mathbf{0}.\mathbf{000221}$	0.000349	49,513,611.4	55,205,174
	12	0.0006	0.002	3600	3600	0.794	0.808	0.000176	0.000477	$\mathbf{0}.\mathbf{000139}$	0.000264	55,403,604	55,781,757
	8	0.0003	0.001	6.740	6.763	0.544	0.553	0.000941	0.001478	$\mathbf{0}.\mathbf{000100}$	0.000250	69,280	69,280
	9	0.0016	0.015	61.282	62.291	0.683	0.693	0.000161	0.000515	$\mathbf{0}.\mathbf{000118}$	0.000216	623,529	623,529
150	10	0.0003	0.001	613.477	618.656	0.838	0.849	0.001670	0.002650	$\mathbf{0}.\mathbf{000173}$	0.000267	6,235,300	6,235,300
	11	0.0003	0.001	3460	3600	1.025	1.065	0.001332	0.002713	$\mathbf{0}.\mathbf{000142}$	0.000277	36,547,401.6	36,702,050
	12	0.0009	0.004	3600	3600	1.206	1.224	0.000399	0.000988	$\mathbf{0}.\mathbf{000118}$	0.000242	33,032,464.2	37,030,175
	8	0.0006	0.002	8.099	9.015	0.725	0.731	0.000544	0.001159	$\mathbf{0}.\mathbf{000173}$	0.000272	62,352.1	69,280
	9	0.0004	0.001	81.815	83.232	0.911	0.943	0.000654	0.001032	$\mathbf{0}.\mathbf{000124}$	0.000209	623,529	623,529
200	10	0.0002	0.001	815.045	822.393	1.109	1.119	0.000426	0.000857	$\mathbf{0}.\mathbf{000149}$	0.000340	6,235,300	6,235,300
	11	0.0007	0.001	3600	3600	1.333	1.346	0.000361	0.000908	$\mathbf{0}.\mathbf{000140}$	0.000300	27,507,393.6	27,615,901
	12	0.0003	0.001	3600	3600	1.572	1.577	0.000381	0.000796	$\mathbf{0}.\mathbf{000080}$	0.000112	27,748,257.1	27,906,681
	8	0.0003	0.001	10.640	12.365	0.950	0.989	0.000748	0.001250	$\mathbf{0}.\mathbf{000100}$	0.000157	69,230	69,280
	9	0.0006	0.001	104.907	105.071	1.133	1.141	0.000735	0.001011	$\mathbf{0}.\mathbf{000087}$	0.000169	561,176.2	623,529
250	10	0.0005	0.001	1026.537	1033.245	1.816	2.245	0.000970	0.001250	$\mathbf{0}.\mathbf{000100}$	0.000277	6,232,529.9	6,235,300
	11	0.0004	0.001	2880	3600	1.715	2.088	0.000971	0.001361	$\mathbf{0}.\mathbf{000099}$	0.000138	21,181,984	21,229,111
	12	0.0005	0.002	3600	3600	1.995	2.010	0.000438	0.000899	$\mathbf{0}.\mathbf{000047}$	0.000114	22,067,736	22,254,928
	8	0.0004	0.001	12.877	12.928	1.044	1.094	0.000791	0.001532	$\mathbf{0}.\mathbf{000081}$	0.000154	69,221.8	69,280
	9	0.001	0.002	125.298	127.574	1.404	1.436	0.000732	0.001549	$\mathbf{0}.\mathbf{000075}$	0.000158	623,529	623,529
300	10	0.0003	0.001	1101.336	1281.591	1.668	1.744	0.000951	0.001671	$\mathbf{0}.\mathbf{000115}$	0.000268	5,611,770.1	6,235,300
	11	0.0005	0.001	3540	3600	1.910	1.918	0.000850	0.001425	$\mathbf{0}.\mathbf{000088}$	0.000145	19,325,090.6	19,368,360
	12	0.0005	0.002	3600	3600	2.376	2.494	0.000622	0.001090	$\mathbf{0}.\mathbf{000056}$	0.000137	18,469,754.3	18,865,239

Table 11. Results of the algorithms for ${\alpha }_1,{\alpha }_2\in (-0.5,0)$.

		HA-$\widehat{\mathit{cpu}}$(s)		B&B-$\widehat{\mathit{cpu}}$(s)		SA-$\widehat{\mathit{cpu}}$(s)		Error Bound of HA		Error Bound of SA		Node Number of B&B
$\overline{\mathit{n}}$	$\mathit{r}$	Mean	Max	Mean	Max	Mean	Max	Mean	Max	Mean	Max	Mean	Max
	8	0.0006	0.001	4.519	4.544	0.368	0.375	0.001694	0.002206	0.000182	0.000266	69,280	69,280
	9	0.0008	0.002	40.753	40.836	0.456	0.460	0.001769	0.002893	$\mathbf{0}.\mathbf{000091}$	0.000147	623,529	623,529
100	10	0.0009	0.002	407.671	408.012	0.562	0.574	0.002245	0.003729	$\mathbf{0}.\mathbf{000102}$	0.000120	6,235,300	6,235,300
	11	0.001	0.003	3240	3600	0.668	0.675	0.001499	0.002119	$\mathbf{0}.\mathbf{000273}$	0.000435	49,585,780.1	55,544,160
	12	0.0024	0.019	3600	3600	0.796	0.827	0.001566	0.003150	$\mathbf{0}.\mathbf{000233}$	0.000458	49,736,852.6	56,374,479
	8	0.0007	0.002	6.126	6.909	0.551	0.565	0.001215	0.003140	$\mathbf{0}.\mathbf{000161}$	0.000317	62,352.1	69,280
	9	0.0008	0.001	60.986	61.143	0.680	0.688	0.001458	0.003030	$\mathbf{0}.\mathbf{000154}$	0.000307	623,529	623,529
150	10	0.0004	0.001	609.401	609.837	0.834	0.842	0.001863	0.004046	$\mathbf{0}.\mathbf{000193}$	0.000308	6,235,300	6,235,300
	11	0.0007	0.001	3240	3600	1.002	1.006	0.001831	0.002483	$\mathbf{0}.\mathbf{000197}$	0.000241	33,016,325.1	37,061,706
	12	0.0003	0.001	3600	3600	1.178	1.215	0.002269	0.002856	$\mathbf{0}.\mathbf{000180}$	0.000280	33,393,817.4	37,526,242
	8	0.0009	0.002	9.059	9.317	0.733	0.804	0.001546	0.003515	$\mathbf{0}.\mathbf{000159}$	0.000282	69,280	69,280
	9	0.0004	0.001	80.843	83.900	0.907	0.927	0.001300	0.002883	$\mathbf{0}.\mathbf{000135}$	0.000289	623,529	623,529
200	10	0.0005	0.002	810.323	814.603	1.111	1.121	0.000956	0.001523	$\mathbf{0}.\mathbf{000102}$	0.000253	6,235,300	6,235,300
	11	0.0004	0.001	3240	3600	1.331	1.339	0.000528	0.001684	$\mathbf{0}.\mathbf{000085}$	0.000171	24,968,877.5	27,784,387
	12	0.0004	0.001	3600	3600	1.564	1.590	0.000636	0.001519	$\mathbf{0}.\mathbf{000079}$	0.000154	28,033,053.1	28,342,718
	8	0.0005	0.001	10.097	11.317	0.910	0.917	0.000318	0.000719	$\mathbf{0}.\mathbf{000077}$	0.000127	69,303.1	69,489
	9	0.0005	0.001	80.960	101.675	1.127	1.140	0.000395	0.000817	$\mathbf{0}.\mathbf{000076}$	0.000176	497,052.3	623,529
250	10	0.001	0.002	1006.110	1015.896	1.204	1.316	0.000382	0.000619	$\mathbf{0}.\mathbf{000072}$	0.000143	6,235,274.2	6,235,300
	11	0.0006	0.002	2880	3600	1.646	1.669	0.000345	0.000779	$\mathbf{0}.\mathbf{000041}$	0.000087	22,213,440	22,273,369
	12	0.003	0.024	3600	3600	2.002	2.142	0.000332	0.000692	$\mathbf{0}.\mathbf{000032}$	0.000061	19,569,085.5	22,426,361
	8	0.0007	0.002	12.151	13.554	1.098	1.105	0.000891	0.001327	$\mathbf{0}.\mathbf{000092}$	0.000134	62,318.8	69,280
	9	0.0003	0.001	121.924	123.005	1.376	1.397	0.000958	0.001514	$\mathbf{0}.\mathbf{000098}$	0.000192	623,529	623,529
300	10	0.0007	0.002	1221.706	1233.344	1.679	1.695	0.000931	0.001891	$\mathbf{0}.\mathbf{000095}$	0.000193	6,235,300	6,235,300
	11	0.0009	0.002	3240	3600	2.031	2.109	0.000828	0.001188	$\mathbf{0}.\mathbf{000075}$	0.000121	16,620,628.5	18,735,159
	12	0.0012	0.004	3600	3600	2.427	2.661	0.000711	0.000740	$\mathbf{0}.\mathbf{000067}$	0.000187	16,218,855.7	18,472,247

From Table 9, Table 10 and Table 11, the CPU time of the HA algorithm is much shorter than that of other algorithms, and the error bound can be within an acceptable range (maximum error bound is 0.004046 < 0.5%). For the case of over 11 groups (i.e., $n\ge 11$), the CPU time of each result is greater than or equal to 3600 s, exceeding the set time, which causes the algorithm to stop running. In addition, it is seen that the performance of HA and SA algorithms is very good in terms of the error. By comparison following Table 9, Table 10 and Table 11, it is easy to find that the maximum error of the HA (rep. SA) algorithm is less than 0.5% (resp. 0.04%). It can be concluded that when the value range of ${\alpha }_1,{\alpha }_2$ is (−0.5, −0.25), the HA and SA algorithms perform better. Moreover, the computational results also show that HA algorithm has a shorter CPU time than the SA algorithm, but its error performance is not better than that of the SA algorithm.

7. Conclusions

This paper investigates the group scheduling with convex resource allocation and learning effect. Under common due date assignment, the objective is to minimize the weighted sum of earliness, tardiness, due date assignment, resource consumption, and makespan, where the number of jobs in each group is different. It can be concluded that in a special case, this problem can be solved within polynomial time. For the general case of the problem, this paper presents a heuristic, a B&B, and a simulated annealing algorithm for comparison. With the data obtained from the experimental simulations, the B&B algorithm is able to obtain an optimal solution with less than or equal to 11 groups in a reasonable time frame. The CPU time of the heuristic algorithm is shorter compared to SA, and the error can be within the reasonable range (maximum error bound <0.5%). Future research could explore group scheduling under linear resource consumption function or with deterioration effects (Huang [35], Liu et al. [36], Sun et al. [37], Lv et al. [38], Wang et al. [39], Zhang et al. [40], and Oron [41]) or deal with problems under flow shop setting (Sun et al. [42], and Kovalev et al. [43]).