An Optimized Point Multiplication Strategy in Elliptic Curve Cryptography for Resource-Constrained Devices

Abstract

Elliptic curve cryptography (ECC) is widely acknowledged as a method for implementing public key cryptography on devices with limited resources thanks to its use of small keys. A crucial and complex operation in ECC calculations is scalar point multiplication. To improve its execution time and computational complexity in low-power devices, such as embedded systems, several algorithms have been suggested for scalar point multiplication, with each featuring different techniques and mathematical formulas. In this research, we focused on combining some techniques to produce a scalar point multiplication algorithm for elliptic curves over finite fields. The employed methodology involved mathematical analysis to investigate commonly used point multiplication methods. The aim was to propose an efficient algorithm that combined the best computational techniques, resulting in lower computational requirements. The findings show that the proposed method can overcome certain implementation issues found in other multiplication algorithms. In certain scenarios, the proposed method offers a more efficient approach by reducing the number of point doubling and point addition operations on elliptic curves using the inverse of the targeted point.

1. Introduction

Cryptography is a robust and effective means for upholding data confidentiality. To render information secure, cryptographic systems leverage intricate mathematical algorithms that frequently necessitate extensive computational resources. However, this computational intensity presents challenges for systems with limited resources. Encryption methods include symmetric cryptography, which relies on a single shared secret key, and asymmetric cryptography, which involves a public and a secret key. The latter method offers the advantage of public key exchange, with security being contingent on the complexity of deducing the secret key from publicly exchanged information. Elliptic curve cryptography (ECC) represents a novel addition to the three well-established families of public key algorithms, which are as follows:

1.

Integer factorization schemes (e.g., the RSA (Rivest–Shamir–Adleman) algorithm);

2.

Discrete logarithms (e.g., Diffie‚ÄìHellman, ElGamal, and DSA);

3.

Elliptic curve schemes (e.g., [1], which was proposed by Miller [2] and Koblitz [3] in 1986).

ECC is used in many standards, including NIST (National Institute of Standards and Technology) [4], ANSI (American National Standards Institute) [5], and IEEE (Institute of Electrical and Electronics Engineers) [6].

ECC utilizes short keys for the same level of security as other asymmetric systems that use longer keys because of its specific mathematical functions [7]. This makes it suitable for electronic devices with limited computational power and memory, such as embedded systems. Although recent improvements have reduced computational complexity, ECC remains an intricate methodology and requires further enhancements. The key process for encryption, decryption, digital signatures, and key exchange in ECC involves scalar point multiplication. The overall speed of any ECC operation relies on the speed of scalar point multiplication and the hardware properties of the device or embedded system in use.

Embedded systems are standalone devices designed for particular functions with restricted size and resources.

In this work, we combine left-to-right scalar multiplication algorithms, concepts derived from the Montgomery ladder, and inverse point techniques to offer a fast solution for resource-constrained systems, taking into consideration the need to overcome certain implementation issues associated with the Montgomery ladder multiplication algorithm.

Our low-cost point multiplication algorithm is considered a more efficient solution because it reduces the number of required arithmetic operations and, thus, its computational complexity and requires fewer resources than other methods.

This paper is organized as follows. In Section 2, we provide a literature review. In Section 3, we explore prominent methods utilized to multiply points on elliptical curves and present the results of conducted analyses to understand their respective advantages and disadvantages. In Section 4, we present the proposed method, which combines left-to-right scalar multiplication algorithms and the Montgomery ladder. Finally, in Section 5, we present the conclusions.

2. Literature Review

Point multiplication plays a crucial role in ECC as it involves multiplying a point on an elliptic curve by a scalar value. This task is central to various ECC operations, such as key exchange, digital signatures, and encryption. In this literature review, we explore the different methodologies and approaches for point multiplication in ECC.

M. Rashid, M. Imran, and A. Sajid [8] (2020) presented an advanced hardware design aimed at improving elliptic curve point multiplication efficiency over two binary fields, GF($2^{163}$) and GF($2^{571}$), in cryptographic scenarios. They proposed an innovative approach focused on reducing the computational time required for point multiplication by employing two modular multipliers, two squarer units, and an adder unit in the data path. Additionally, the authors restructured the point addition and point doubling instructions for point multiplication computation within the Montgomery algorithm. The findings indicated a significant reduction in latency and the overall number of clock cycles needed for point multiplication computation compared with existing cutting-edge solutions. Notably, the proposed architecture demonstrated latency reductions of 60%, 74%, and 15% over GF($2^{571}$) and 66% and 65% over GF($2^{163}$) compared to previous methods. In the study, the authors also shared the implementation outcomes after place-and-route processes for GF($2^{163}$) and GF($2^{571}$) on a Xilinx Virtex-7 FPGA development board. It is worth mentioning that, for shorter key lengths, an alternative solution highlighted in a related work [9] delivers an improved latency performance compared with the newly proposed architecture. Conversely, the latter may demand a greater allocation of hardware resources than other existing methods.

Sasmita Padhy, T.N. Shankar, and Sachikanta Dash (2022) [10] compared the performance of fast point multiplication algorithms in terms of computation and execution time to determine the quickest solution for elliptic curve cryptosystems. The authors focused on evaluating different techniques, such as addition and subtraction, mutual opposite form (MOF), and complementary recoding, for fast scalar multiplication schemes. They emphasized the importance of rapid point multiplication in reducing idle hardware utilization time and minimizing time complexity in elliptic curve operations, especially for applications on mobile devices. The results of the above study provided insights into the comparative performance of different fast point multiplication algorithms, such as double-and-add, MOF, and complementary recoding, to determine the most suitable and efficient approach for implementing point multiplication in elliptic curve operations. The authors concluded with a comparative analysis of the algorithms, highlighting the strengths and weaknesses of each method in terms of computational efficiency and speed.

M.S. Hossain, Y. Kong, E. Saeedi, and N.C. Vayalil [11] (2017) explored the challenges encountered when creating an efficient hardware setup for an ECC processor (ECP) catering to contemporary security needs. In their study, they introduced innovative solutions centered on a unique elliptic curve scalar multiplication (ECSM) architecture, leveraging point doubling and point addition (PDPA) hardware configured in Jacobian coordinates. Additionally, the authors proposed an architecture facilitating Jacobian-to-affine coordinate conversion, featuring serial-in parallel-out (SIPO) and parallel-in serial-out (PISO) mechanisms at the top level to connect the input/output ports of an ECP, given the constraints posed by the limited pins on the FPGA (Field Programmable Gate Arrays). Findings from the ASIC (Application specific integrated circuits) and FPGA implementations of the developed ECP operating in Jacobian coordinates demonstrated their superiority as the fastest hardware implementations, showcasing delay values of 0.22 μs and 0.28 μs, respectively. Notably, the design was enhanced through strategies such as optimizing the PDBL (Point Doubling) and PADD (Point Adding) architectures, parallelizing operations, and implementing pre-computations to increase performance.

In their work, Asher Sajid, Muhammad Rashid, Malik Imran, and Atif Raza Jafri (2021) [12] presented a comprehensive study on optimizing point multiplication in elliptic curves, specifically focusing on binary Edwards curves (BECs). The study involved a detailed investigation into developing a low-complexity architecture for point multiplication, which aimed to enhance performance and security in ECC. In the study, the authors delved into the mathematical background of BECs over GF($2^m$), highlighting the unified point addition and point doubling laws of these curves and the Montgomery Ladder algorithm for point multiplication. By proposing a novel low-complexity architecture for point multiplication in BECs, the researchers aimed to achieve efficient and secure operations in ECC. The results of the study demonstrated that the proposed low-complexity architecture for point multiplication in BECs shows promising outcomes in terms of improved performance attributes, such as low latency and low complexity. Additionally, the architecture exhibited resistance against side-channel attacks, enhancing the overall security of the elliptic curve operations. In conclusion, the findings of the above study offer valuable insights into the optimization of point multiplication in elliptic curves, particularly in the context of BECs. The research outcomes underscore the importance of developing efficient hardware implementations for enhancing the speed, security, and overall performance of elliptic curve cryptographic systems.

In a study by Yue Hao, Shun‚Äôan Zhong, Mingzhi Ma, Rongkun Jiang, Shihan Huang, Jingqi Zhang, and Weijiang Wang (2022) [13], a novel lightweight architecture for ECSM over prime fields was comprehensively examined. The authors addressed the challenge of optimizing point multiplication in elliptic curves, focusing on improving efficiency and reducing resource consumption in small mobile devices. The authors highlighted the limitations of previous designs, in which speed was prioritized at the expense of circuit area and power consumption. The study involved a meticulous search for an optimal ECSM architecture, resulting in the development of a novel design that significantly improved efficiency and resource utilization. The proposed architecture is based on the Montgomery ladder algorithm with (X,Y)-only common Z-coordinate arithmetic, executed in Jacobian coordinates. Notably, the design achieves a balance between speed, area, and power consumption, making it suitable for small mobile devices. The results of the study demonstrated the effectiveness of the proposed architecture, which was implemented on FPGAs without using DSPs (Digital Signal Processor) or BRAMs (Block RAMs), ensuring higher portability. The architecture utilized 6.4 k∼6.5 k slices in Kintex-7, Virtex-7, and ZYNQ FPGAs and achieved impressive ECSM for a field size of 256 bits in 1.73 ms, 1.70 ms, and 1.80 ms, respectively.

Overall, these research studies have contributed to simplifying point multiplication in ECC, making it more feasible to implement this method on resource-constrained devices. Efficient point multiplication is vital for secure communication in devices with computational power, memory, and energy constraints, such as IoT devices, embedded systems, and mobile devices. By reducing computational complexity, these advancements in ECC enable fast and secure communication without compromising security.

3. Scalar Point Multiplication

An elliptic curve, E, over a field, K, denoted as $E/K$, is defined by the following equation [14]:

$$y^2+a_{1}xy+a_{3}y=x^3+a_2{x}^2+a_{4}x+a_6$$

where coefficients $a_1,a_2,a_3,a_4,$ and $a_6$, which belong to K, are chosen such that for every point $(x,y)$ on E, the partial derivatives never simultaneously equal zero.

This equation can be simplified as follows:

$$y^2=x^3+ax+b$$

where coefficients a and b belong to K and the non-zero condition for $4a^3+27b^2\ne 0$ holds, specifically in fields of characteristic greater than 3.

The collection of points on E/K forms an abelian group. Explicit formulas have been developed to calculate the sum of two points, and various coordinate systems have been proposed to expedite this computation.

The scalar multiplication of curve point P by scalar k results in another point, T = $kP=P+P+\dots +P$ (k times). This process, known as point multiplication, is crucial to generating the public key from the secret key in ECC, where k is an integer that represents the secret key, while the public key, T, represents a point on the curve with coordinates T = $(x_T,y_T)$.

For scalar multiplication, two essential operations are required: point doubling (P + P = 2P) and point addition (P + Q), which are performed as described below.

Let P ($x_1,y_1$) and Q ($x_2,y_2$) denote two points on an elliptic curve. Then, we have the following:

$$x_3=s^2-x_1-x_2\left(\mathrm{mod}p\right)$$

$$y_3=s(x_1-x_3)-y_1\left(\mathrm{mod}p\right)$$

These operations are fundamental in ECC and serve various encryption and security purposes.

In the above, the following rule applies:

$s=\frac{y_2-y_1}{x_2-x_1}$; if $p\ne Q$ (point addition)

$s=\frac{3{x_1}^2}{2y_1}$; if p = Q (point doubling)

Therefore, point doubling involves approximately six multiplications, four additions/subtractions, and one division (inversion). On the other hand, point addition involves approximately two multiplications, six additions/subtractions, and one division.

For the sender and the receiver, knowing the order (#E) of the elliptic curve is crucial for secure communication for several reasons, as reported below.

• Key generation. In ECC cryptosystems, the secret key (scalar “k”) is randomly selected from the range (1, #E − 1). Having knowledge of the curve’s order is essential to ensuring that valid and secure keys are generated, adhering to the curve’s properties.
• Security. Without knowing the curve’s order, it becomes challenging to assess the security level of the encryption scheme and its vulnerability to attacks.
• Compatibility. To securely communicate, both the sender and the receiver need to agree on a specific elliptic curve and its parameters, including its order (#E).
• Scalar multiplication. The order of the elliptic curve dictates the maximum value that can be assigned to the scalar (k). Without awareness of the curve’s order, performing scalar multiplication accurately becomes challenging.

3.1. Left-to-Right Method (Binary Method)

In elliptic curve point multiplication, the double-and-add method is a popular algorithm by virtue of its simplicity and reduced computational complexity compared with alternative approaches. The algorithm consists of doubling the point and adding it to itself repeatedly based on the binary representation of the scalar multiplier.

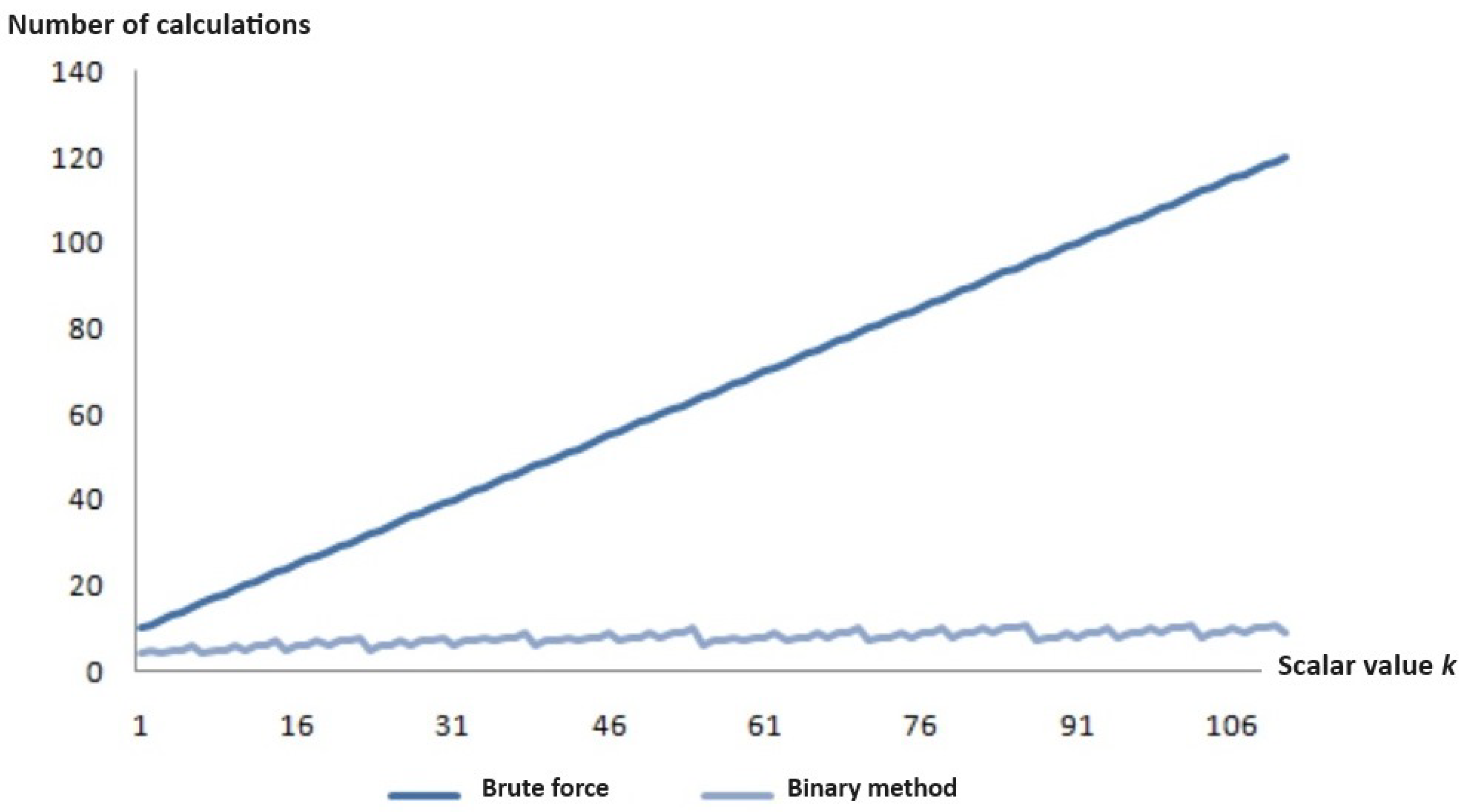
The diagram in Figure 1 (where the x-axis represents the value of the secret key k and the y-axis represents the number of calculations required to find kP) showcases the simplicity of calculating T = kP, when provided with k and P, utilizing the binary method. It also highlights the challenge of calculating k, when given P and T = kP, using the brute force method. During this process, the step for computing kP remains constant, even as k increases significantly.

The double-and-add method is also memory-efficient, as it requires only one copy of the point to be stored in the memory, which makes ECC suitable for various applications where computational efficiency is important, such as in constrained environments with limited computational resources. Algorithm 1 presents the pseudocode detailing the implementation of the left-to-right method.

Algorithm 1 Algorithm for point multiplication using the left-to-right approach [16]

Input: Binary representation of the scalar k and point P. Output: T = kP Initialization: T = ∞ 1   FOR i = l − 1 DOWNTO 0          T = T +T (mod n) (Doubling)                  IF ${\mathit{k}}_i$ = 1                          T = T + P (mod n) (Adding) 2   RETURN (T)

In the above algorithm, l represents the total number of bits in the binary representation of k.

The time complexity of an algorithm is determined by the number of operations executed during its runtime. Point addition occurs when ${\mathit{k}}_i=1$ and the expected number of set bits (hamming weight) in the binary form of k is half of its bit length, denoted by l/2. Subsequently, a doubling operation is executed l times for each value of i. Thus, the anticipated time complexity is based on l/2 additions (A) plus l doublings (D) and is expressed as (l/2) A + D.

To exemplify this procedure, let us examine a scenario where scalar multiplication amounts to 26P. This can be depicted in binary format as outlined below:

$$26\mathrm{P}=\left({11010}_2\right) \mathrm{P}=(d_4{d}_3{d}_2{d}_1{d}_0{)}_2\mathrm{P}.$$

The described algorithm analyzes the binary digits of the scalar. It initiates the examination from the most significant bit, denoted by ${\mathit{k}}_4$, and progresses toward the least significant bit, represented by ${\mathit{k}}_0$.

Iteration	Action	Description
1	P = $1_2$ P	Initial setting, bit processed: $k_4$ = 1
2	P+P = 2P = ${10}_2$ P	DOUBLE, bit processed: $k_3$
	2P+P = 3P = ${10}_2$ P+$1_2$ P = ${11}_2$ P	ADD, since $k_3$ = 1
3	3P+3P = 6P = 2(${11}_2$ P) = ${110}_2$ P	DOUBLE, bit processed: $k_2$
		no ADD, since $k_2$ = 0
4	6P+6P = 12P = 2(${110}_2$ P) = ${1100}_2$ P	DOUBLE, bit processed: $k_1$
	12P+P = 13P = ${1100}_2$ P+$1_2$P = ${1101}_2$P	ADD, since $k_1$ = 1
5	13P+13P = 26P = 2(${1101}_2$P) = ${11010}_2$P	DOUBLE, bit processed: $k_0$
		no ADD, since $k_0$ = 0

In summary, two addition and four doubling operations are required.

The double-and-add method lacks constant-time behavior, as the execution time may vary based on the value of the scalar being used, which introduces potential vulnerabilities related to side-channel attacks [17].

3.2. Windowed Method

The windowed method is a computational approach that consists of pre-generating a set of points on a given elliptic curve. This strategy aims to optimize the multiplication of points by a scalar. By allowing for the segmentation of the scalar into smaller components, this method enhances computational efficiency.

In this approach, a designated window size, w, is selected. The procedure involves calculating all potential values of kP, which amounts to $2^w$ combinations. Here, k is set to vary from 0 to $2^w-1$. This preparatory computation is executed in advance, as described by Hankerson et al. in their work on elliptic curves [18].

With these pre-computed values, the algorithm proceeds to calculate the result using a different representation for k, namely, $\mathit{k}={\mathit{k}}_0+2^w{k}_1+2^{2w}{k}_2+\dots +2^{mw}{k}_m$. Algorithm 2 presents the pseudocode detailing the implementation of the windowed method.

Algorithm 2 Windowed method algorithm for point multiplication [18]

T ← 0 for i from m to 0 do         T  ← point-double-repeat (T, w)          if ${\mathit{k}}_i$ > 0 then                  T ← point-add (T, ${\mathit{k}}_i$P) # using pre-computed value of ${\mathit{k}}_i$ return T

This algorithm demonstrates a complexity level akin to the double-and-add technique. However, it is preferable as it decreases the frequency of point addition operations, which are known, on average, to be slower than doubling operations.

The window method generally requires extra memory because it involves pre-computing a table of points on the curve [19]. The amount of memory needed depends on the chosen window size for the algorithm. Using a larger window size can reduce the number of times the table needs to be looked up during point multiplication; however, it also increases the amount of memory required, with the latter representing a significant challenge for resource-constrained devices.

3.3. Sliding-Window Method

This approach aims to strike a balance between point addition and doubling operations by utilizing a strategy similar to the window method. A table is built specifically for points kP, where k is between $2^{w-1}$ and $2^w-1$. This process focuses on computing values where the window’s most significant bit is active [18].

The algorithm resembles the conventional double-and-add approach in representing k as a sum, where k is depicted as $\mathit{k}=k_0+2k_1+2^2{k}_2+\dots +2^m{k}_m$. Algorithm 3 presents the pseudocode detailing the implementation of the sliding-Window method.

Algorithm 3 Sliding window method algorithm for point multiplication [18]

T ← 0 for i from m down to 0 do          if ${\mathit{k}}_i=0$ then                  T ← point-double(T)          else                  t ← extract j (up to $w-1$) additional bits from k (including $k_i$)                  i ←$i-j$                  if j < w then                          Perform double-and-add using t                          return T                  else                          T ← point-double-repeat (T, w)                          T ← point-add (T, tP) return T

This algorithm offers an advantage in terms of its pre-computation stage, which is approximately half as complex as that of the standard window method.

The memory requirements for the sliding-window method are contingent upon the selected window size in the algorithm. Consequently, this technique necessitates additional memory to store the pre-computed table of points, which facilitates the acceleration of point multiplication operations.

3.4. W-Ary Non-Adjacent Form Method

This approach focuses on leveraging the property where subtracting points is as straightforward as adding points to reduce both operations compared with the sliding-window technique. By employing this method, the aim is to decrease the total number of point additions or subtractions compared with the sliding-window approach. To accomplish this, it is essential to calculate the non-adjacent form (NAF) of multiplier k by utilizing the Algorithm 4 which provided in [18], and as shown below:

Algorithm 4 W-Ary Non-Adjacent Form method algorithm for point multiplication

i← 0 while (d > 0) do          if (d mod 2) = 1 then                  ${\mathit{k}}_i$←k mods $2^w$                  k ←k$-{\mathit{k}}_i$          else                  ${\mathit{k}}_i$ = 0          k ← k/2          i ← i + 1 return (${\mathit{k}}_{i-1}$, ${\mathit{k}}_{i-2}$,…, ${\mathit{k}}_0$)

The signed modulo function “mods” is delineated as follows:

if (k mod $2^w$) >= $2^{w-1}$

        return (k mod $2^w$)$-2^w$

else

        return k mod $2^w$

The calculation produces the NAF that is crucial to facilitating the multiplication procedure. In order to implement this technique, it is important to compute points {1, 3, 5,…, $2^{w-1}-$1} P and their corresponding negatives in advance. Then, the Algorithm 5 calculates the multiplication of kP as follows:

Algorithm 5 kP algorithm for point multiplication

T ← 0 for j ←$i-1$ down to 0 do          T ← point-double(T)          if ($d_j$ != 0)                  T ← point-add (T, ${\mathit{k}}_j$P) return T

The NAF window technique guarantees an average density of approximately 1/(w + 1) point additions per step, making it marginally more effective than the unsigned window method.

The above-mentioned researchers demonstrated that by utilizing a FLUSH + RELOAD side-channel attack on OpenSSL, it is possible to uncover the complete secret key. This security vulnerability arises when cache-timing techniques are employed, even with 200 signature operations, which is a relatively low amount [18].

In light of the preceding elucidation, the w-ary NAF (wNAF) method necessitates the storage of specific points determined by a selected window size (w). This window size determines how many points should be calculated and preserved in the memory. The larger the window size is, the more points are stored, leading to increased memory consumption.

3.5. Montgomery Ladder Method

The Montgomery ladder method consists of the multiplication of points using a consistent number of operations. This can be advantageous when there is a chance for an attacker to perform side-channel attacks involving timing, power consumption, or branch measurements. Algorithm 6 presents the pseudocode detailing the implementation of the Montgomery Ladder method:

This algorithm functions similarly to the double-and-add method, with a notable variation [18]: it executes an equal number of point addition and doubling operations, regardless of the multiplicand value, k. This characteristic ensures that the algorithm does not inadvertently disclose any information through branching or power usage.

Algorithm 6 the Montgomery Ladder method algorithm for point multiplication

$R_0$← O $R_1$← P for i from m down to 0 do          if ${\mathit{k}}_{\mathit{i}}$ = 0 then                  $R_1$← Adding ($R_0$, $R_1$)                  $R_0$← Doubling ($R_0$)          else                  $R_0$← Adding ($R_0$, $R_1$)                  $R_1$← Doubling ($R_1$)          assert $R_1$ == Adding ($R_0$, P) // invariant property to maintain correctness return $R_0$

According to some studies, such as [20], the Montgomery ladder method can achieve comparable or better performance than the binary and NAF methods in point multiplication in ECC, especially for large scalars and large fields.

To understand the pitfall of implementing this method, let us see its implementation in Montgomery curve 25519 utilizing its pseudocode [21] (Algorithm 7).

Algorithm 7 The algorithm using the Montgomery ladder for x-coordinate-based scalar multiplication on E is as follows: $y^2=x^3+486662x^2+x$

Input: A 255-bit scalar s and the x-coordinate ${\mathit{x}}_P$ of some point P Output: ($X_{\left[s\right]P}$, $Z_{\left[s\right]P}$) fulfilling ${\mathit{x}}_{\left[s\right]P}$ = $X_{\left[s\right]P}/Z_{\left[s\right]P}$ $X_1$← 1; $Z_1$← 0; $X_2$←${\mathit{x}}_P$; $Z_2$← 1 p ← 0 for i ← 254 downto 0 do     b ←bit i of s     c ← b ⊕ p     p ← b     ($X_1$, $X_2$) ←cswap($X_1$, $X_2$, c)     ($Z_1$, $Z_2$) ←cswap($Z_1$, $Z_2$, c)     ($X_1$, $Z_1$, $X_2$, $Z_2$) ←LADDERSTEP(${\mathit{x}}_P$, $X_1$, $Z_1$, $X_2$, $Z_2$) end for return ($X_1$, $Z_1$)

Note that the CSWAP function mentioned in the pseudocode is implemented utilizing the following pseudocode [22]:

Swap ← Scalar scanned bit

S = Swap · ($X_2-X_3$)

$X_2=X_2-S$

$X_3=X_3+S$

Return ($X_2,X_3)$

Therefore, the values of $X_2$ and $X_3$ are swapped when the scanned binary bit of the scalar is equal to 1 and not swapped when it is equal to 0. Note the following two probabilities of implementing the code of the CSWAP function:

$$\begin{array}{cc}\mathrm{Swap}\leftarrow \mathrm{Scalar}\mathrm{scanned}\mathrm{bit}=0\hfill & \mathrm{Swap}\leftarrow \mathrm{Scalar}\mathrm{scanned}\mathrm{bit}=1\hfill \\ S=0·(X_2-X_3)=0\hfill & S=1·(X_2-X_3)=X_2-X_3\hfill \\ X_2=X_2-S=X_2-0=X_2\hfill & X_2=X_2-S=X_2-X_2+X_3=X_3\hfill \\ X_3=X_3+S=X_3+0=X_3\hfill & X_3=X_3+S=X_3+X_2-X_3=X_2\hfill \\ \mathrm{Return}(X_2,X_3)\hfill & \mathrm{Return}(X_2,X_3)\hfill \end{array}$$

Although this method successfully equalizes the number of operations for adding and doubling points in each cycle, it does not equalize the execution time of the multiplication and doubling procedures because if the current bit in the binary representation of a scalar is zero, executing this code is faster than executing it with a bit equal to 1.

This poses a security risk to the system that can be utilized by attackers using side-channel timing attacks because there is a time variation in the code’s execution.

4. Combination of Left-to-Right Scalar Multiplication Algorithms and the Montgomery Ladder

The double-and-add (left-to-right) method is acknowledged for its simplicity and reduced computational complexity compared with alternative approaches; additionally, it requires less memory. In this study, we propose a novel method for point multiplication in elliptic curves. Furthermore, in certain scenarios, the proposed approach also involves calculating the inverse of the targeted point because of its shortened computational process. The subsequent discussion provides a detailed explanation of how the suggested approach functions.

The steps for the proposed method is reported below.

Given elliptic curve $E_p$ (a, b) with order #E, we calculate the point P = kG, where k represents the scalar value and G represents the base point (generator point), by following the steps below.

First case: If $k\le \frac{\#E}{2}$, then kG is found by combining the left-to-right method and the Montgomery ladder method as follows.

1.

Convert scalar k into its binary representation.

2.

Iterate through the binary representation of k starting from the leftmost bit to the rightmost bit:

   For the first bit iteration (leftmost bit), Q = G

3.

For the subsequent bit iterations,

   Q = double the point Q

   P = Q + G

   If the current bit is 1, then:

      Q = P

   else:

      P = Q #The swap yields no benefits, except for achieving equal execution

         times.

4.

If there are remaining bits in the binary representation, continue from step 3 until each bit is processed.

5.

Return Q.

Second case: If $\mathit{k}>\frac{\#E}{2}$, then kG is found by combining the left-to-right method and the Montgomery ladder method and by finding the inverse of the point kG through the steps below.

First step: Find point xG (the inverse point of kG) as follows.

1.

Find the x value by subtracting the order of the elliptical curve (#E) from the scalar (k):

                 x = #E − k.

2.

Convert the x value into its binary representation.

3.

Iterate through the binary representation of x starting from the leftmost bit to the rightmost bit. For the first bit iteration (leftmost bit), Q = G.

4.

For the subsequent bit iterations,

   Q = double the point Q

   P = Q + G

   If the current bit is 1, then:

      Q = P

   else:

      P = Q #The swap yields no benefits except for achieving equal execution

         times.

5.

If there are remaining bits in the binary representation, continue from step 4 until each bit is processed.

6.

Return Q, which is equal to xG, which represents the inverse point of kG.

Second step: Find the X- and Y-coordinates of point kG as follows.

1.

The X-coordinate of kG is the same as the X-coordinate of xG, which means that there is no need for more calculations.

2.

The Y-coordinate of kG is equal to the result of subtracting the Y-coordinate of the inverse point xG from the prime number of the elliptical equation:

              kG (Y-coordinate) = Prime number (p) − xG (Y-coordinate).

To address the problem discussed in Section 3.5, in the proposed method, we replaced the CSWAP function with a conditional statement that does not involve any mathematical operations; its purpose is solely to switch values based on a condition. This operation is performed in both cases, whether the scanned bit of the scalar’s binary representation is 0 or 1. Therefore, it is symmetrical and does not introduce any differences in the process or execution time of the code.

Furthermore, the suggested approach utilizes the symmetrical nature of elliptic curves along the x-axis to offer a shortcut toward the intended point. This occurs specifically when the scalar exceeds half of the curve’s order.

To gain a clearer understanding of the functioning and improved computational complexity of the proposed method, let us explore a curve over a small field, denoted by $Z_{751}$. This particular example was selected for its simplicity, as it allows us to easily understand the problem by working with small numbers that are straightforward to handle.

$$y^2\equiv (x^3-x+188) \mathrm{mod}751$$

The following are given: $E_p$ (a, b) = $E_{751}$(−1, 188), a = −1, b = 188, p = 751, and generator point G = (0, 376).

The subsequent step involves calculating multiples of the generator point, G. These multiples are denoted by kG, where k takes on values in the range $1\le \mathit{k}\le 751$. In order to facilitate understanding, a brief list of the points on the curve is given in advance below, enabling the reader to verify the upcoming calculations.

2G = (1,376), 3G = (750,375), 4G = (2,373), 5G = (188,657), 6G = (6,390), 7G = (667,571), 8G = (121,39), 9G = (582,736), 10G = (57,332), 11G = (331,367), 12G = (207,215), 13G = (285,96), 14G = (629,545), 15G = (39,349), 16G = (197,107), 17G = (556,631), 18G = (490,207), 19G= (237,23), 20G = (731,529), 21G = (531,194), 22G = (256,409), 23G = (742,74), 24G = (180,343), 25G = (139,413), 26G = (217,247), 27G = (510,429), …, 700G = (510,322), 701G = (217,504), 702G = (139,338), 703G = (180,408), 704G = (742,677), 705G = (256,342), 706G = (531,557), 707G = (731,222), 708G = (237,728), 709G = (490,544), 710G = (556,120), 711G = (197,644), 712G = (39,402), 713G = (629,206), 714G = (285,655), 715G = (207,536), 716G = (331,384), 717G = (57,419), 718G = (582,15), 719G = (121,712), 720G = (667,180), 721G = (6,361), 722G = (188,94), 723G = (2,378), 724G = (750,376), 725G = (1,375), 726G = (0,375), 727G = O = infinity.

To compute 700G, the proposed method consists of combining the left-to-right method and the Montgomery ladder method, as well as determining the inverse of the kG point, because scalar $\mathit{k}>\frac{\#E}{2}$. The steps below are followed to achieve this.

• Start by finding point xG (the inverse point of kG = 700G) by finding the x value as a first step by using the equation x = #E − k = 727 − 700 = 27;
• Then, transfer or change (x = 27) into its binary representation (11011);
• Then, iterate through the binary representation of x starting from the leftmost bit to the rightmost bit as outlined below.
  Note that point Q = (510,429) represents the inverse point of point 700G. To find the X- and Y-coordinates of point kG = 700G, we have to follow the steps below.

  1.

  The X-coordinate of kG is the same as the X-coordinate of xG = 510;

  2.

  The Y-coordinate of kG is equal to the result of the subtraction of the Y-coordinate of point xG from the prime number of the following elliptical equation:

  kG (Y-Coordinate) = Prime number (p) − xG (Y-Coordinate). 700G (Y-Coordinate)

    = Prime number (751) − x G (Y-Coordinate = 429) = 751 − 429 = 322.

Therefore, 700G = (510, 322).

Iteration	Scanned Bit	Action	Description
1	1	Do nothing	Q = G (initial value) = (0,376)
2	1	Double	Q = 2Q = 2G = (1,376)
		Add	P = Q + G = 3G = (750,375)
			Since Scanned bit = 1, then Q = P = 3G
3	0	Double	Q = 2Q = 6G = (6,390)
		Add	P = Q + G = 7G = (667,571)
			Since Scanned bit = 0, then P = Q
4	1	Double	Q = 2Q = 12G = (207,215)
		Add	P = Q + G = 13G = (285,96)
			Since Scanned bit = 1, then Q = P = 13G
5	1	Double	Q = 2Q = 26G = (217,247)
		Add	P = Q + G = 27G = (510,429)
			Since Scanned bit = 1, then Q = P = 27G
			Return Q

Based on the information provided earlier and as illustrated in the table, the total number of operations for the given scenario includes four point doubling operations, four point addition operations, one comparison operation between two integers (k and #E/2), and two subtraction operations between two integers.

In contrast, when employing the Montgomery ladder method with a binary representation of the scalar k = 700 (1010111100), the total number of operations required is nine point doubling operations and nine point addition operations to solve for 700G in the same example.

This comparison showcases that the proposed method offers a more efficient approach, as it allows one to reduce the number of PDPA operations from nine to four, along with some arithmetic operations involving integers. Consequently, it has the potential to outperform the Montgomery ladder method in terms of decreasing multiplication and addition operations on elliptic curves.

By utilizing this method, the process is significantly simplified. In the context of the Weierstrass curve over affine coordinates, point doubling involves approximately six multiplications, four additions/subtractions, and one division (inversion), and point addition involves approximately two multiplications, six additions/subtractions, and one division.

It should be noted that the numbers utilized in this example are small compared with those employed in real encryption operations. Thus, the number of operations to be reduced in practical applications is substantially greater than that demonstrated in this example.

Figure 2 visualizes the operation of the proposed method geometrically on real numbers.

As shown, the proposed method excludes the calculation of many points on the curve and directly proceeds to the calculation of the inverse point, which shortens many calculations and reduces computational complexity.

The proposed solution can be applied to various curves with different coordinate systems (such as affine coordinates and Jacobean coordinates) as long as these curves are symmetric about the x-axis, such as Secp256k1, NIST P-256, and X25519.

5. Results

Conventional ECC point multiplication and the proposed optimized point multiplication strategy introduced in this study were executed using the Python 3.12.0 programming language, utilizing elliptic curve Secp256k1. Python was selected for its versatility in handling complex numerical operations and its applicability to cryptographic research.

Table 1. Point multiplication time results on Secp256k1 curve.

Scalar % of Curve Order	Conventional Method Time (s)	Optimized Method Time (s)
5	0.014461755752563477	0.013983726501464844
10	0.022180795669555664	0.020344800567626953
15	0.022794485092163086	0.02213602409362793
20	0.02484750747680664	0.022983789443969727
25	0.025043725967407227	0.026155471801757812
30	0.026398658752441406	0.026781082153320312
35	0.026781082153320312	0.02710270881652832
40	0.028722763061523438	0.02863096046447754
45	0.02910900115966797	0.029391080856323242
50	0.029650211334228516	0.030028820037841797
55	0.030260801315307617	0.026938676834106445
60	0.03191685676574707	0.026717185974121094
65	0.03844857215881348	0.02414703369140625
70	0.04807019233703613	0.023786544799804688
75	0.04816699028015137	0.02182793617248535
80	0.049573421478271484	0.02121281623840332
85	0.05035853385925293	0.020491600036621094
90	0.05131077766418457	0.018212556838989258
95	0.05776810646057129	0.014655828475952148
99	0.0587618350982666	0.010605020405002140

captures the performance improvement achieved by using the optimized method in the operation time for point multiplication over the elliptic curve, especially for scalar values exceeding 50% of the curve’s order.

By employing the values depicted in Table 1 alongside an illustrative diagram, the resulting chart, presented in Figure 3, offers a comparative examination of the operation time for point multiplication on the Secp256k1 curve utilizing both the conventional and the optimized ECC point multiplication methods.

In the figure, the x-axis represents the percentage of the curve’s order, ranging from 5% to nearly 100%, while the y-axis represents the time for each operation in seconds.

As shown in the diagram, both methods exhibit similar operation time results for scalar values up to 50% of the curve’s order. Beyond this threshold, the optimized point multiplication method demonstrates a significant reduction in operation time, indicating a decrease in computational complexity for larger scalar values.

These results underscore the effectiveness of our proposed method in reducing the computational complexity of point multiplication operations on an elliptic curve, particularly for higher scalar values. This optimization can have significant implications for enhancing the efficiency and scalability of cryptographic operations based on elliptic curves.

6. Conclusions

In this study, we explored various methods for multiplying points on elliptic curves, showing the advantages and disadvantages of each. The left-to-right (double-and-add) method is simple to implement but lacks protection against side-channel attacks. The window method improves performance by using pre-computed points but requires more memory. The sliding-window method also utilizes pre-computed points and efficiently handles multiple consecutive bits, but it requires even more memory than the left-to-right method. The wNAF method reduces point additions but can be more complex to implement correctly. The Montgomery ladder is suitable for both software and hardware implementations; however, it presents a time variation in the code execution, which can be utilized by attackers in side-channel timing attacks, posing a security risk. The performance and security of each method depend on their implementation details, the available hardware resources, and the choice of elliptic curve parameters.

In contrast, the proposed method, in the worst-case scenario (the first case), has similar point addition and point doubling operations to the Montgomery ladder method while guaranteeing equal execution time in all stages of the code. The latter feature enables more efficient implementation.

In the best-case scenario (the second case), the proposed method achieves improved efficiency by finding the inverse of the point to be calculated. This approach requires fewer operations to achieve the desired outcome, outperforming the Montgomery ladder method in terms of reducing the number of point multiplication and addition operations on elliptic curves.

Overall, under certain conditions, the proposed method has the advantage of maintaining consistent execution time throughout the code. In other instances (i.e., best-case scenarios), it also offers a more efficient approach, outperforming the Montgomery ladder method by reducing the number of point multiplication and addition operations on elliptic curves.