Best Decision-Making on the Stability of the Smoke Epidemic Model via Z-Numbers and Aggregate Special Maps

Abstract

The present paper considers a fractional-order smoke epidemic model. We apply fuzzy systems and probability theory to make the best decision on the stability of the smoking epidemic model by using a new class of controllers powered by special functions to effectively generalize Ulam-type stability problems. Evaluation of optimal controllability and maximal stability is the new issue. This different concept of stability not only covers the old concepts but also investigates the optimization of the problem. Finally, we apply a new optimal method for the governing model with the Atangana–Baleanu–Caputo fractional derivative to obtain stability results in Banach spaces.

1. Introduction

The idea of stability for a functional equation (FE) arises when we substitute the FE by an inequality which acts as a perturbation of the initial equation. Over the years, stability results of FEs have been developed for obtaining an approximate solution of the perturbed equation which is close to the exact solution (ES). This topic was introduced by Ulam and Hyers in 1940–1941, and this kind of stability is called HU stability [1,2]. In 1978, the improvement of HU stability provided by Rassias led to the development of what is now known as HUR stability [3]. In 1998, Ger and Alsina [4] established the HU stability of ODEs and many authors defined types of HUR–Mittag–Leffler stability of fractional PDEs to prove that every mapping from this type can be somehow approximated by an ES of the considered equation [5,6,7].

The recent interest in the Mittag–Leffler (ML) function and its various generalizations [8] is mainly due to their close relations to Fractional Calculus and especially to fractional problems that come from applications. The special functions, along with the ML function, including the functions of Wright type, the functions of hypergeometric type and others [9] which often appear in solutions of various types of equations with fractional operators, play a prominent role in the theory of the PDEs of fractional order that are applied in modeling of diverse phenomena [10,11,12].

As it is known, the major problem of procuring ES of such equations is very crucial, and the form of the ES (if it exists) is oftentimes so arduous that it is not suitable for numerical calculation [13,14,15]. In view of this, it is imperative to talk about an approximate solution and ask whether it lies close to the ES. Generally, we say that a fractional PDE is stable in the sense of Ulam if, for every solution of the fractional PDE, there exists an approximate solution of the perturbed equation that is near to it.

To clarify the issue, let us introduce the notion of Ulam-type stability of an operator equation [16,17]. We consider the Banach space $(\mathcal{X},\parallel .\parallel )$ and an operator $T:\mathcal{Y}⟶\mathcal{X}$ for every $\varnothing \ne \mathcal{Y}\subseteq \mathcal{X}.$ We also consider the operator equation

$$\begin{array}{c}\hfill T\left(x\right)=0,x\in \mathcal{Y}\end{array}$$

(1)

and the inequality

$$\begin{array}{c}\hfill \parallel T\left(y\right)\parallel \le \epsilon ,\forall \epsilon >0,y\in \mathcal{Y}.\end{array}$$

(2)

Equation (1) is called HU stable if for every solution $\mu$ of Inequality (2), there is a solution v of operator Equation (1) such that

$$\parallel \mu -v\parallel \le c\epsilon ,$$

in which $c>0$ is a constant dependent on T.

Now, Equation (1) is called HUR stable if there is a continuous function $\phi :\mathbb{R}⟶\mathbb{R}$, such that, for every $\epsilon >0$ and for every solution $\mu$ of the inequality

$$\begin{array}{c}\hfill \parallel T\left(y\right)\parallel \le \epsilon \phi \left(y\right),\forall \epsilon >0,y\in \mathcal{Y},\end{array}$$

there is solution v of operator Equation (1) with $c\in {\mathbb{R}}^{+}$ such that

$$\begin{array}{c}\hfill \parallel \mu -v\parallel \le c\epsilon \phi \left(y\right).\end{array}$$

Equation (1) has HUR–Mittag–Leffler stability or HUR–Wright stability if the above statement is also true when we replace control function $\phi$ by the ML function or the Wright function, respectively.

In this paper, we consider a diagonal matrix of special functions as a controller to study a fresh concept of stability, namely multi-stability. The mentioned stability helps us to obtain different approximations depending on the diverse special functions that are initially selected and to evaluate maximal stability with minimal error which enables us to obtain the best approximate solution.

We let the matrix-valued controller $\mathfrak{W}\left[X\right]$ be as follows:

$$\begin{array}{c}\hfill \mathfrak{W}\left[X\right]:=\mathrm{diag}{\left[{\phi }_1\left(X\right),\cdots ,{\phi }_n\left(X\right)\right]}_{n\times n},\end{array}$$

in which ${\phi }_i,i=1,\cdots ,n\in \mathbb{N}$ denotes a special function in the the main diagonal of square matrix $\mathfrak{W}\left[X\right]$, and the natural number n represents the numbers of special functions that we intend to consider.

We consider normed linear spaces V and $U.$ Mapping $\Theta :U⟶V$ has the multi-stability property if we replace the controller of HUR stability with $\mathfrak{W}\left[X\right]$.

For the special case of multiple stability, i.e., Mittag–Leffler–Gauss-Hypergeometric–Bessel–Maitland–Fox stability, Mittag–Leffler–Supertrigonometric stability, Mittag–Leffler–Superhyperbolic stability and the others, we refer the reader to [18,19,20].

2. Preliminaries

2.1. Some Special Functions

2.1.1. Fox $\mathbb{H}$-Function and Related Functions

The $\mathbb{H}$ function (sometimes called Fox’s $\mathbb{H}$-function) is a very generally defined special function due to Charles Fox (1928) (see [21]). We let $\mathcal{X}$ be a proper contour of the Mellin–Barnes type in the complex S-plane. Therefore, the $\mathbb{H}$-function is given by

$$\begin{array}{c}\hfill {}_C{}^A\mathbb{H}_D^B\left[\chi |{ }_{{(N_j,M_j)}_{1,D}}^{{(V_j,W_j)}_{1,C}}\right]:={\left(2\pi i\right)}^{-1}{\int }_{\mathcal{X}}\varpi \left(S\right)e^{\left(S\right[i\arg \left(\chi \right)+\log \left|\chi \right|\left]\right)}dS,i^2+1=0,\end{array}$$

(3)

in which $\chi \in \mathbb{C}\setminus \left\{0\right\},$ and

$$\begin{array}{ccc}& & \varpi \left(S\right):=\hfill \\ & & {\left(\prod _{j=A+1}^D\Gamma (1-N_j+M_{j}S)\prod _{j=B+1}^C\Gamma (V_j-W_{j}S)\right)}^{-1}\left(\prod _{j=1}^A\Gamma (N_j-M_{j}S)\prod _{j=1}^B\Gamma (1-V_j+W_{j}S)\right),\hfill \end{array}$$

where $C,B,D,A\in \mathbb{N},$ $0\le B\le C,$$1\le A\le D,$ $\underset{\underset{j=1,\dots ,C}{︸}}{W_j}>0,$ $\underset{\underset{j=1,\dots ,D}{︸}}{M_j}>0$ $\underset{\underset{j=1,\dots ,C}{︸}}{V_j}\in \mathbb{C},$ and $\underset{\underset{j=1,\dots ,C}{︸}}{N_j}\in \mathbb{C}.$

We now present some special cases of the $\mathbb{H}$-function including the exponential function, the Wright function, the one-parameter Mittag–Leffler function, the Fox–Wright function, the Meijer $\mathbb{G}$–function, the Gauss Hypergeometric function, and the $\mathbb{G}$–function, respectively, as follows:

$$\begin{array}{c}\hfill {}_0\mathbb{H}_0\left[\chi \right]:=exp\left(\chi \right)=\sum _{j=0}^{\infty }\frac{{\chi }^j}{\Gamma (j+1)},\end{array}$$

$${}_1\mathbb{H}_1[V_1;N_1;\chi ]:=\sum _{j=0}^{\infty }\frac{{\chi }^j}{j!\Gamma (V_{1}j+N_1)},$$

$$\begin{array}{c}\hfill {}_0\mathbb{H}_1[N_1;\chi ]:=\sum _{j=0}^{\infty }\frac{{\chi }^j}{\Gamma (1+N_{1}j)},\end{array}$$

$$\begin{array}{c}\hfill {}_C\mathbb{H}_D\left[\chi {|}_{(N_1,M_1),\dots ,(N_D,M_D)}^{(V_1,W_1),\dots ,(V_C,W_C)}\right]=\sum _{n=0}^{\infty }{\displaystyle \frac{{\prod }_{j=1}^C\Gamma (W_{j}n+V_j)}{{\prod }_{j=1}^D\Gamma (M_{j}n+N_j)}}{\displaystyle \frac{{\chi }^n}{n!}},\end{array}$$

(4)

$$\begin{array}{ccc}& & {}_C{}^A\mathbb{H}_D^B\left[\chi {|}_{(N_1,1),\dots ,(N_D,1)}^{(V_1,1),\dots ,(V_C,1)}\right]={\displaystyle \frac{1}{2\pi i}}{\int }_{\mathcal{X}}exp(-S[iarg\left(\chi \right)+\log \left|\chi \right|\left]\right)\hfill \\ & & \times {\displaystyle \frac{{\prod }_{j=1}^A\Gamma (N_j+S){\prod }_{i=1}^B\Gamma (1-V_i-S)}{{\prod }_{i=B+1}^C\Gamma (V_i+S){\prod }_{j=A+1}^D\Gamma (1-V_j-S)}}dS,\hfill \end{array}$$

$$\begin{array}{ccc}& & {}_2\mathbb{H}_1[V_1,V_2;N_1;\chi ]:=\sum _{j=0}^{\infty }\frac{{\left(V_1\right)}_j{\left(V_2\right)}_j}{{\left(N_1\right)}_j}\frac{{\chi }^j}{j!}\hfill \\ & & =\frac{\Gamma \left(N_1\right)}{\Gamma \left(V_1\right)\Gamma \left(V_2\right)}\sum _{j=0}^{\infty }\frac{\Gamma (V_1+j)\Gamma (V_2+j)}{\Gamma (N_1+j)}\frac{{\chi }^j}{j!},\hfill \end{array}$$

$$\begin{array}{ccc}\hfill & & {}_C\mathbb{H}_D[V_1,\dots ,V_C;N_1,\dots ,N_C;\chi ]\hfill \\ & & =\sum _{n=0}^{\infty }\left(\prod _{i=1}^C{\left(V_i\right)}_n\right){\left(\prod _{j=1}^D{\left(N_j\right)}_n\right)}^{-1}{\displaystyle \frac{{\chi }^n}{n!}}.\hfill \end{array}$$

(5)

Note that for ${\rm Y}\in \mathbb{C}$ and $n\in \mathbb{N},$ we consider

$$\begin{array}{ccc}& & {({\rm Y})}_0=1,{\rm Y}\ne 0,{({\rm Y})}_n={\rm Y}({\rm Y}+1)\dots ({\rm Y}+n-1).\hfill \end{array}$$

2.1.2. Mittag–Leffler Function and Related Functions

We let

$${(N,M)}_D:=[N_1,M_1;\dots ;N_D,M_D],$$

and

$${(V,W)}_C:=[V_1,W_1;\dots ;V_C,W_C],$$

$D+C=m-2,$ and $m\in \mathbb{N}-\left\{1\right\}.$ The m-parameter Mittag–Leffler function is given by [21]

$$\begin{array}{ccc}\hfill {\mathbb{M}}_{\alpha ,\tau ;N_1,M_1;\dots ;N_D,M_D}^{V_1,W_1;\dots ;V_C,W_C}\left(\chi \right)& =& {\mathbb{M}}_{\alpha ,\tau ;{(N,M)}_D}^{{(V,W)}_C}\hfill \\ & =& \sum _{n=0}^{\infty }{\displaystyle \frac{{\left(V_1\right)}_{W_{1}n}\cdots {\left(V_C\right)}_{W_{C}n}}{\Gamma (\alpha n+\tau ){\left(N_1\right)}_{M_{1}n}\cdots {\left(N_D\right)}_{M_{D}n}}}{\chi }^n,\hfill \end{array}$$

(6)

in which $N_j,V_i,M_j,W_i,\chi ,\tau ,\alpha \in \mathbb{C},$ with $min\{\alpha ,V_i,\tau ,W_i,M_j,N_j\}>0,$ for all $j=1,\cdots ,D$ and $i=1,\cdots ,C.$

Notice that ${({\rm Y})}_{\vartheta n}$ is given by

$${({\rm Y})}_{\vartheta n}={\displaystyle \frac{\Gamma ({\rm Y}+\vartheta n)}{\Gamma ({\rm Y})}},n\in \mathbb{N}.$$

Here, we present some examples of (6) as follows:

$$\begin{array}{c}\hfill {\mathbb{M}}_{\alpha }\left(\chi \right)=\sum _{j=0}^{\infty }{\displaystyle \frac{{\chi }^j}{\Gamma (j\alpha +1)}},\end{array}$$

$$\begin{array}{c}\hfill {\mathbb{M}}_{\alpha ,\tau }\left(\chi \right)=\sum _{j=0}^{\infty }{\displaystyle \frac{{\chi }^j}{\Gamma (j\alpha +\tau )}},\end{array}$$

$$\begin{array}{c}\hfill {\mathbb{M}}_{\alpha ,\tau }^V\left(\chi \right)=\sum _{j=0}^{\infty }{\displaystyle \frac{{\left(V\right)}_j{\chi }^j}{j!\Gamma (j\alpha +\tau )}},\end{array}$$

$$\begin{array}{c}\hfill {\mathbb{M}}_{\alpha ,\tau }^{V,W}\left(\chi \right)=\sum _{j=0}^{\infty }{\displaystyle \frac{{\left(V\right)}_{Wj}{\chi }^j}{j!\Gamma (j\alpha +\tau )}},\end{array}$$

$$\begin{array}{c}\hfill {\mathbb{M}}_{\alpha ,\tau ,N}^{V,W}\left(\chi \right)=\sum _{j=0}^{\infty }{\displaystyle \frac{{\left(V\right)}_{Wj}}{\Gamma (\alpha j+\tau ){\left(N\right)}_j}}{\chi }^j.\end{array}$$

2.2. Generalized Triangular Norms (GTNs)

We suppose

$$\mathrm{diag}{M}_n\left(ϵ\right):=\left\{\left[\begin{array}{ccccc}{F}_{11}& 0& 0& \cdots & 0\\ 0& F_{22}& 0& \cdots & 0\\ 0& 0& F_{33}& \cdots & 0\\ ⋮& ⋮& ⋮& & ⋮\\ 0& 0& 0& \cdots & F_{nn}\end{array}\right]=\mathrm{diag}[F_{11},\cdots ,F_{nn}],\underset{{ }_{1\le j\le n}^{1\le i\le n}}{\underbrace{F_{ij}}}\in ϵ:=[0,1]\right\},$$

with the partial order relation below:

$$\mathbf{F}:=\mathrm{diag}[F_{11},\cdots ,F_{nn}],\mathbf{G}:=\mathrm{diag}[G_{11},\cdots ,G_{nn}]\in \mathrm{diag}{M}_n\left(ϵ\right),$$

$$\mathbf{F}⪯\mathbf{G}⟺\underset{{ }_{1\le j\le n}^{1\le i\le n}}{\underbrace{F_{ij}}}\le \underset{{ }_{1\le j\le n}^{1\le i\le n}}{\underbrace{G_{ij}}},$$

and Symbols $\mathbf{1}$ and $\mathbf{0}$ are given by

$$\mathbf{1}:={\left[\begin{array}{ccccc}1& 0& 0& \cdots & 0\\ 0& 1& 0& \cdots & 0\\ 0& 0& 1& \cdots & 0\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ 0& 0& 0& \cdots & 1\end{array}\right]}_{n\times n}:=\mathrm{diag}{[1,\cdots ,1]}_{n^2},$$

and

$$\mathbf{0}:={\left[\begin{array}{ccccc}0& 0& 0& \cdots & 0\\ 0& 0& 0& \cdots & 0\\ 0& 0& 0& \cdots & 0\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ 0& 0& 0& \cdots & 0\end{array}\right]}_{n\times n}:=\mathrm{diag}{[0,\cdots ,0]}_{n^2}.$$

Definition 1

([18]). Operation $⨀:{\left(\mathrm{diag}{M}_n\left(ϵ\right)\right)}^2\to \mathrm{diag}{M}_n\left(ϵ\right)$, is called a GTN if for every $\mathbf{F},\mathbf{H},\mathbf{G},\mathbf{K}\in \mathrm{diag}{M}_n\left(ϵ\right),$ we have

(1) $\mathbf{F}⨀\mathbf{1}=\mathbf{F},$

(2) $\mathbf{F}⨀\mathbf{H}=\mathbf{H}⨀\mathbf{F}$,

(3) $\mathbf{F}⨀(\mathbf{H}⨀\mathbf{G})=(\mathbf{F}⨀\mathbf{H})⨀\mathbf{G},$

(4) $\mathbf{F}⪯\mathbf{H}\mathrm{and}\mathbf{G}⪯\mathbf{K}⟹\mathbf{F}⨀\mathbf{G}⪯\mathbf{H}⨀\mathbf{K}.$

For sequences $\left\{{\mathbf{F}}_m\right\}$, $\left\{{\mathbf{G}}_m\right\}$ converging to $\mathbf{F},\mathbf{G}\in \mathrm{diag}{M}_n\left(ϵ\right)$, if ${lim}_m({\mathbf{F}}_m⨀{\mathbf{G}}_m)=\mathbf{F}⨀\mathbf{G}$, ⨀ is continuous.

For example, we assume the continuous GTNs ${⨀}_P,{⨀}_M,{⨀}_L:{\left(\mathrm{diag}{M}_n\left(ϵ\right)\right)}^2\to \mathrm{diag}{M}_n\left(ϵ\right)$ given as follows:

$$\begin{array}{ccc}& & \mathbf{F}\underset{P}{⨀}\mathbf{G}=\mathrm{diag}[F_{11}.G_{11},\cdots ,F_{nn}.G_{nn}],\hfill \end{array}$$

$$\begin{array}{ccc}& & \mathbf{F}\underset{L}{⨀}\mathbf{G}=\mathrm{diag}[max\{F_{11}+G_{11}-1,0\},\cdots ,max\{F_{nn}+G_{nn}-1,0\}],\hfill \end{array}$$

and

$$\begin{array}{ccc}& & \mathbf{F}\underset{M}{⨀}\mathbf{G}=\mathrm{diag}[min\{F_{11},G_{11}\},\cdots ,min\{F_{nn},G_{nn}\}].\hfill \end{array}$$

In this paper, we set $⨀:={⨀}_M.$

2.3. Matrix-Valued Fuzzy Normed Spaces

We consider vector space $\mathfrak{A}.$ We assume $\mathfrak{G}$ to be a set of all matrix-valued fuzzy sets (MVF sets), including the increasing and continuous functions $\Phi :\mathfrak{A}\times (0,+\infty )\to \mathrm{diag}{M}_n\left(ϵ\right),$ such that, for $Y\in \mathfrak{A},$ ${lim}_{\varphi \to \infty }\Phi (Y,\varphi )=\mathbf{1}.$

In $\mathfrak{G}$, for every $\varphi >0$ and $Y\in \mathfrak{A},$ we assume $\Phi ⪯{\Phi }^{\prime }$ if $\Phi (Y,\varphi )⪯{\Phi }^{\prime }(Y,\varphi ).$

A matrix-valued fuzzy normed space (MVFN space) [18] is a triple $(\mathfrak{A},\Phi ,⨀)$, such that, for all $\varphi ,{\varphi }^{\prime }>0,$ $0\ne \upsilon \in C$, and $Y,Y^{\prime }\in \mathfrak{A};$ we obtain

(i) $\mathbf{0}\prec \Phi (Y,\varphi )$,

(ii) $\Phi (Y,{\displaystyle \frac{\varphi }{\left|\upsilon \right|}})=\Phi (\upsilon Y,\varphi )$,

(iii) $\Phi (Y,\varphi )=\mathbf{1}$, iff $Y=0,$

(iv) $\Phi (Y,\varphi )⨀\Phi (Y^{\prime },{\varphi }^{\prime })⪯\Phi (Y+Y^{\prime },\varphi +{\varphi }^{\prime }).$

For example, $\mathbb{H}[N_1;-\frac{\left|Y\right|}{\varphi }]={\sum }_{m=0}^{\infty }\frac{{(-\frac{\left|Y\right|}{\varphi })}^m}{\Gamma (1+N_{1}m)}$ defines a fuzzy norm (see [18]) for all $0<N_1<1,Y\in \mathfrak{A}$ and $\varphi \in (0,+\infty ).$

Note 1.

A matrix-valued fuzzy Banach space (MVFB space) is a complete MVFN space.

2.4. Matrix-Valued Random Normed Spaces

We suppose $\mathfrak{E}$ is a set of matrix-valued distribution functions (MVDFs) including the non-decreasing and left–continuous functions

$$\Psi :\mathbb{R}\cup \{-\infty ,+\infty \}⟶\mathrm{diag}{M}_n\left(ϵ\right),$$

such that we have

$$\Psi (+\infty )=1,\Psi \left(0\right)=0.$$

We let ${\mathfrak{E}}^{+}\subseteq \mathfrak{E}$ contain $\Psi \in \mathfrak{E}$ such that we obtain ${lim}_{\psi ⟶+{\infty }^{-}}{\Psi }_{\psi }=\mathbf{1}.$ In ${\mathfrak{E}}^{+},$ for all $\psi \in \mathbb{R},$ we assume $\Psi ⪯{\Psi }^{\prime }$ if $\Psi \left(\psi \right)⪯{\Psi }^{\prime }\left(\psi \right).$

Note that the maximal element for ${\mathfrak{E}}^{+}$ is given by

$${\mathcal{E}}_0\left(\varphi \right)=\left\{\begin{array}{c}\begin{array}{cc}\mathbf{0},& \psi \in (-\infty ,0],\\ \mathbf{1},& \psi \in (0,+\infty ).\end{array}\hfill \end{array}\right.$$

For instance, the function

$$\Psi \left(\psi \right)=\left\{\begin{array}{c}\begin{array}{cc}{\mathbf{0}}_{2\times 2},& \psi \in (-\infty ,0],\\ \mathrm{diag}[1-\frac{1}{e^{\psi }}],e^{-{\left|\psi \right|}^{\frac{1}{2}}},& \psi \in (0,+\infty ),\end{array}\hfill \end{array}\right.$$

denotes an MVDF since $\Psi \in {\mathfrak{E}}^{+}$ and ${lim}_{\psi \to +\infty }\Psi \left(\psi \right)=\mathbf{1}$.

We assume vector space $\mathfrak{A}$, DF $\Psi :\mathfrak{A}\to {\mathfrak{E}}^{+}$ and continuous GTN ⨀. A triple $(\mathfrak{A},\Psi ,⨀)$ is a matrix-valued random normed space (MVRN space) [19] if for every $\psi >0,$ $0\ne \upsilon \in \mathbb{C},$ and $Y,Y^{\prime }\in \mathfrak{A},$ we obtain

(i)

${\Psi }_Y\left(\frac{\psi }{\left|\upsilon \right|}\right)={\Psi }_{\upsilon Y}\left(\psi \right),$

(ii)

${\Psi }_Y\left(\psi \right)={\mathcal{E}}_0\left(\varphi \right),$ iff $Y=0,$

(iii)

${\Psi }_Y\left(\psi \right)⨀{\Psi }_{Y^{\prime }}\left({\psi }^{\prime }\right)⪯{\Psi }_{Y+Y^{\prime }}(\psi +{\psi }^{\prime })$,

in which ${\Psi }_Y$ is the value of $\Psi$ at a point $Y\in \mathfrak{A}.$

For instance, ${ }_2{\mathbb{H}}_1[V_1,V_2;N_1;-\frac{\parallel Y\parallel }{\psi }]={\sum }_{k=0}^{\infty }\frac{{\left(V_1\right)}_k{\left(V_2\right)}_k}{{\left(N_1\right)}_k}\frac{{(-\frac{\parallel Y\parallel }{\psi })}^k}{k!}$ is a random norm [19] for all $V_1,V_2,N_1\in [0,+\infty ),Y\in \mathfrak{A},$ and $\psi \in (0,+\infty )$.

2.5. Multi-Aggregations

We let $n\in \mathbb{N},$

$$\mu =\mathrm{diag}\left[\mathrm{diag}{[{\mu }_{11},\cdots ,{\mu }_{1n}]}_{n\times n},\cdots ,\mathrm{diag}{[{\mu }_{n1},\cdots ,{\mu }_{nn}]}_{n\times n}\right],$$

and $\underset{\underset{\underset{1\le i\le n}{1\le j\le n}}{︸}}{{\mu }_{ij}}\in ϵ.$ An n-ary aggregation map [19] is a mapping,

$${\mathtt{AG}}^{\left(n\right)}:\mathrm{diag}{M}_n\left(\mathrm{diag}{[ϵ,\cdots ,ϵ]}_{n\times n}\right)⟶\mathrm{diag}{[ϵ,\cdots ,ϵ]}_{n\times n},$$

such that we obtain

$$\begin{array}{c}\hfill \underset{\underset{\underset{1\le i,j\le n}{︸}}{{\mu }_{ij}}\in ϵ}{\inf }{\mathtt{AG}}^{\left(n\right)}\left(\mu \right)=inf\mathrm{diag}{[ϵ,\cdots ,ϵ]}_{n\times n},\mathrm{and}\underset{\underset{\underset{1\le i,j\le n}{︸}}{{\mu }_{ij}}\in ϵ}{\sup }{\mathtt{AG}}^{\left(n\right)}\left(\mu \right)=sup\mathrm{diag}{[ϵ,\cdots ,ϵ]}_{n\times n}.\end{array}$$

In addition, for all $\mu ,{\mu }^{\prime }\in \mathrm{diag}{M}_n\left(\mathrm{diag}{[ϵ,\cdots ,ϵ]}_{n\times n}\right),$ if $\underset{\underset{1\le i,j\le n}{︸}}{{\mu }_{ij}}\le \underset{\underset{1\le i,j\le n}{︸}}{{\mu }_{ij}^{\prime }};$ then,

$${\mathtt{AG}}^{\left(n\right)}\left(\mu \right)\le {\mathtt{AG}}^{\left(n\right)}\left({\mu }^{\prime }\right).$$

Here, we introduce some examples of aggregation maps,

$${\mathtt{AG}}_i:\mathrm{diag}{M}_n\left(\mathrm{diag}{[ϵ,\cdots ,ϵ]}_{n\times n}\right)⟶\mathrm{diag}{[ϵ,\cdots ,ϵ]}_{n\times n}$$

defined as follows:

• Geometric mean functions, ${\mathtt{AG}}_1\left(\mu \right)=\mathrm{diag}[{\left({\prod }_{i=1}^n{\mu }_{1i}\right)}^{\frac{1}{n}},\cdots ,{\left({\prod }_{i=1}^n{\mu }_{ni}\right)}^{\frac{1}{n}}].$
• Arithmetric mean functions, ${\mathtt{AG}}_2\left(\mu \right)=\mathrm{diag}[{\displaystyle \frac{1}{n}}{\sum }_{i=1}^n{\mu }_{1i},\cdots ,{\displaystyle \frac{1}{n}}{\sum }_{i=1}^n{\mu }_{ni}].$
• Maximum functions, ${\mathtt{AG}}_3\left(\mu \right)=\mathrm{diag}[max\{{\mu }_{11},\cdots ,{\mu }_{1n}\},\cdots ,max\{{\mu }_{n1},\cdots ,{\mu }_{nn}\}].$
• Minimum functions, ${\mathtt{AG}}_4\left(\mu \right)=\mathrm{diag}[min\{{\mu }_{11},\cdots ,{\mu }_{1n}\},\cdots ,min\{{\mu }_{n1},\cdots ,{\mu }_{nn}\}].$
• Median of odd numbers,

  $${\mathtt{AG}}_5\left(\mu \right)=\mathrm{diag}[\underset{{ }_{\left|N\right|=n}^{N\subseteq [2n-1]}}{min}\underset{i\in n}{max}{\mu }_{1i},\dots ,\underset{{ }_{\left|N\right|=n}^{N\subseteq [2n-1]}}{min}\underset{i\in n}{max}{\mu }_{ni}].$$
• Median of even numbers,

  $${\mathtt{AG}}_6\left(\mu \right)=\mathrm{diag}[\underset{{ }_{\left|N\right|=n}^{N\subseteq \left[2n\right]}}{min}\underset{i\in n}{max}{\mu }_{1i},\cdots ,\underset{{ }_{\left|N\right|=n}^{N\subseteq \left[2n\right]}}{min}\underset{i\in n}{max}{\mu }_{ni}].$$
• Sum functions, ${\mathtt{AG}}_7\left(\mu \right)=\mathrm{diag}[{\sum }_{i=1}^n{\mu }_{1i},\cdots ,{\sum }_{i=1}^n{\mu }_{ni}].$
• Product functions, ${\mathtt{AG}}_8\left(\mu \right)=\mathrm{diag}[{\prod }_{i=1}^n{\mu }_{1i},\cdots ,{\prod }_{i=1}^n{\mu }_{ni}].$

2.6. Generalized Alternative Fixed Point Theory

We first present vector-valued generalized metric spaces.

Note 2.

We suppose $d=(d_1,\dots ,d_m)$ and $\delta =({\delta }_1,\dots ,{\delta }_m),m\in \mathbb{N}$. Thus, for every $j=1,\cdots ,m,$ we have $d⪯\delta ,$ iff $d_j\le {\delta }_j,$ and also $d\to 0,$ iff $d_j\to 0.$

Definition 2

([21]). Consider $m\in \mathbb{N},$ the set $\mathbf{B}\ne \varnothing$ and $d:{\mathbf{B}}^2\to {[0,+\infty ]}^m.$ A generalized metric d on $\mathbf{B}$ is a map such that

$\left(1\right)$ for every $(\alpha ,\beta )\in {\mathbf{B}}^2$, $d(\alpha ,\beta )=\stackrel{m}{\overbrace{(0,\cdots ,0)}},$ iff $\alpha =\beta ;$

$\left(2\right)$ for every $(\alpha ,\beta )\in {\mathbf{B}}^2$, $d(\beta ,\alpha )=d(\alpha ,\beta ),$ iff $\alpha =\beta ;$

$\left(3\right)$ for every $(\alpha ,\beta ,\gamma )\in {\mathbf{B}}^3$, $d(\alpha ,\gamma )+d(\gamma ,\beta )⪰d(\beta ,\alpha ).$

Theorem 1

([21]). Consider a complete generalized metric space $(\mathbf{B},d)$, with $d:{\mathbf{B}}^2\to {[0,+\infty ]}^m$, $m\in \mathbb{N},$ and a contractive mapping $\Gamma :\mathbf{B}\to \mathbf{B}$ with Lipschitz constant $\Theta <1$. Hence, for all $\alpha \in \mathbf{B}$, either $d({\Gamma }^n\alpha ,{\Gamma }^{n+1}\alpha )=\underset{m}{\underbrace{(+\infty ,\cdots ,+\infty )}}$ for any $n\in \mathbb{N}\cup \left\{0\right\}$ or there is an $n_0\in \mathbb{N}$ such that

$\left(1\right)$$d({\Gamma }^n\alpha ,{\Gamma }^{n+1}\alpha )⪯\underset{m}{\underbrace{(+\infty ,\cdots ,+\infty )}},\forall n\ge n_0$;

$\left(2\right)$ The fixed point ${\beta }^{*}$ of Γ is a convergence point of the sequence $\left\{{\Gamma }^n\alpha \right\}$ and is unique in the set ${\mathbf{B}}^{\prime }=\{\beta \in \mathbf{B}\mid d({\Gamma }^{n_0}\alpha ,\beta )⪯\underset{m}{\underbrace{(+\infty ,\cdots ,+\infty )}}\}$;

$\left(3\right)$$d(\beta ,{\beta }^{*})⪯\frac{1}{1-\Theta }d(\beta ,\Gamma \beta )$ for every $\beta \in {\mathbf{B}}^{\prime }$.

3. Application of Multi-Stability for Smoke Transmission Model

In [22,23,24], the authors presented the following basic mathematical model which analyzes the spread of smoking in a population:

$$\begin{array}{ccc}\hfill & & {\displaystyle \frac{d\mathcal{X}}{d\tau }}=A-B\mathcal{Z}\mathcal{X}-C\mathcal{X},\hfill \\ & & {\displaystyle \frac{d\mathcal{Y}}{d\tau }}=B\mathcal{Z}\mathcal{X}-E\mathcal{Y}-C\mathcal{X},\hfill \\ & & {\displaystyle \frac{d\mathcal{Z}}{d\tau }}=E\mathcal{Y}+G\mathcal{Y}\mathcal{Z}-(C+D)\mathcal{Z},\hfill \\ & & {\displaystyle \frac{d\mathcal{W}}{d\tau }}=D(1-F)\mathcal{Z}-G\mathcal{Y}\mathcal{Z}-C\mathcal{W},\hfill \\ & & {\displaystyle \frac{d\mathcal{V}}{d\tau }}=DF\mathcal{Z}-C\mathcal{V},\hfill \end{array}$$

(7)

where $\mathcal{Z},$$\mathcal{V},$$\mathcal{X},$$\mathcal{W},$ and $\mathcal{Y},$ represent smokers, smokers who permanently quit smoking, potential smokers, smokers who temporarily quit smoking, and occasional smokers.

In [16], teh authors presented an extension of (7) to a two-age group model: 1-Group including people below 70 years old and 2-Group including people aged above 70 years. Every population consists of ${\mathcal{X}}_1+{\mathcal{Y}}_1+{\mathcal{Z}}_1+{\mathcal{W}}_1+{\mathcal{V}}_1$ for the 1-Group and ${\mathcal{X}}_2+{\mathcal{Y}}_2+{\mathcal{Z}}_2+{\mathcal{W}}_2+{\mathcal{V}}_2$ for the 2-Group. For each group, we have the following age-specific parameters:

• $A_i:$ rate of supply,
• $B_i:$ effective contact rate between ${\mathcal{X}}_i$ and ${\mathcal{Z}}_i,$
• $C_i:$ natural death rate,
• $D_i:$ rate of quitting smoking,
• $E_i:$ rate at which occasional smokers become regular smokers,
• $G_i:$ the contact rate between smokers and temprorary quitters,
• $F_i:$ fraction of smokers who temporary quit smoking.

Therefore, the i -age group transmission model ($i=1,2$) is given as follows:

$$\begin{array}{ccc}\hfill & & {\displaystyle \frac{d{\mathcal{X}}_1\left(\tau \right)}{d\tau }}=A_1-(B_1{\mathcal{Z}}_1+B_2{\mathcal{Z}}_2){\mathcal{X}}_1-C_1{\mathcal{X}}_1-A_2{\mathcal{X}}_1,\hfill \\ & & {\displaystyle \frac{d{\mathcal{Y}}_1\left(\tau \right)}{d\tau }}=(B_1{\mathcal{Z}}_1+B_2{\mathcal{Z}}_2){\mathcal{X}}_1-E_1{\mathcal{Y}}_1-C_1{\mathcal{Y}}_1-A_2{\mathcal{Y}}_1,\hfill \\ & & {\displaystyle \frac{d{\mathcal{Z}}_1\left(\tau \right)}{d\tau }}=E_1{\mathcal{Y}}_1+G_1{\mathcal{Y}}_1{\mathcal{Z}}_1-(C_1+D_1){\mathcal{Z}}_1-A_2{\mathcal{Z}}_1,\hfill \\ & & {\displaystyle \frac{d{\mathcal{W}}_1\left(\tau \right)}{d\tau }}=D_1(1-F_1){\mathcal{Z}}_1-G_1{\mathcal{Y}}_1{\mathcal{Z}}_1-C_1{\mathcal{W}}_1-A_2{\mathcal{W}}_1,\hfill \\ & & {\displaystyle \frac{d{\mathcal{V}}_1\left(\tau \right)}{d\tau }}=D_1{F}_1{\mathcal{Z}}_1-C_1{\mathcal{V}}_1-A_2{\mathcal{V}}_1,\hfill \\ & & {\displaystyle \frac{d{\mathcal{X}}_2\left(\tau \right)}{d\tau }}=A_2{\mathcal{X}}_1-(B_1{\mathcal{Z}}_1+B_2{\mathcal{Z}}_2){\mathcal{X}}_2-C_2{\mathcal{X}}_2,\hfill \\ & & {\displaystyle \frac{d{\mathcal{Y}}_2\left(\tau \right)}{d\tau }}=A_2{\mathcal{Y}}_1+(B_1{\mathcal{Z}}_1+B_2{\mathcal{Z}}_2){\mathcal{X}}_2-E_2{\mathcal{Y}}_2-C_2{\mathcal{Y}}_2,\hfill \\ & & {\displaystyle \frac{d{\mathcal{Z}}_2\left(\tau \right)}{d\tau }}=A_2{\mathcal{Z}}_1+E_2{\mathcal{Y}}_2+G_2{\mathcal{Y}}_2{\mathcal{Z}}_2-(C_2+C_1){\mathcal{Z}}_2,\hfill \\ & & {\displaystyle \frac{d{\mathcal{W}}_2\left(\tau \right)}{d\tau }}=A_2{\mathcal{W}}_1+D_2(1-F_2){\mathcal{Z}}_2-G_2{\mathcal{Y}}_2{\mathcal{Z}}_2-C_2{\mathcal{W}}_2,\hfill \\ & & {\displaystyle \frac{d{\mathcal{V}}_2\left(\tau \right)}{d\tau }}=A_2{\mathcal{V}}_1+D_2{F}_2{\mathcal{Z}}_2-C_2{\mathcal{V}}_2.\hfill \end{array}$$

(8)

Now, (8) under the ABC fractional derivative is given by [16]

$$\begin{array}{ccc}\hfill & & D_{\tau }^{C_{*}}{\mathcal{X}}_1\left(\tau \right)=A_1^{C_{*}}-(B_1^{C_{*}}{\mathcal{Z}}_1+B_2^{C_{*}}{\mathcal{Z}}_2){\mathcal{X}}_1-C_1^{C_{*}}{\mathcal{X}}_1-A_2^{C_{*}}{\mathcal{X}}_1,\hfill \\ & & D_{\tau }^{C_{*}}{\mathcal{Y}}_1\left(\tau \right)=(B_1^{C_{*}}{\mathcal{Z}}_1+B_2^{C_{*}}{\mathcal{Z}}_2){\mathcal{X}}_1-E_1^{C_{*}}{\mathcal{Y}}_1-C_1^{C_{*}}{\mathcal{Y}}_1-A_2^{C_{*}}{\mathcal{Y}}_1,\hfill \\ & & D_{\tau }^{C_{*}}{\mathcal{Z}}_1\left(\tau \right)=E_1^{C_{*}}{\mathcal{Y}}_1+G_1^{C_{*}}{\mathcal{Y}}_1{\mathcal{Z}}_1-(C_1^{C_{*}}+D_1^{C_{*}}){\mathcal{Z}}_1-A_2^{C_{*}}{\mathcal{Z}}_1,\hfill \\ & & D_{\tau }^{C_{*}}{\mathcal{W}}_1\left(\tau \right)=D_1^{C_{*}}(1-F_1^{C_{*}}){\mathcal{Z}}_1-G_1^{C_{*}}{\mathcal{Y}}_1{\mathcal{Z}}_1-C_1^{C_{*}}{\mathcal{W}}_1-A_2^{C_{*}}{\mathcal{W}}_1,\hfill \\ & & D_{\tau }^{C_{*}}{\mathcal{V}}_1\left(\tau \right)=D_1^{C_{*}}{F}_1^{C_{*}}{\mathcal{Z}}_1-C_1^{C_{*}}{\mathcal{V}}_1-A_2^{C_{*}}{\mathcal{V}}_1,\hfill \\ & & D_{\tau }^{C_{*}}{\mathcal{X}}_2\left(\tau \right)=A_2^{C_{*}}{\mathcal{X}}_1-(B_1^{C_{*}}{\mathcal{Z}}_1+B_2^{C_{*}}{\mathcal{Z}}_2){\mathcal{X}}_2-C_2^{C_{*}}{\mathcal{X}}_2,\hfill \\ & & D_{\tau }^{C_{*}}{\mathcal{Y}}_2\left(\tau \right)=A_2^{C_{*}}{\mathcal{Y}}_1+(B_1^{C_{*}}{\mathcal{Z}}_1+B_2^{C_{*}}{\mathcal{Z}}_2){\mathcal{X}}_2-E_2^{C_{*}}{\mathcal{Y}}_2-C_2^{C_{*}}{\mathcal{Y}}_2,\hfill \\ & & D_{\tau }^{C_{*}}{\mathcal{Z}}_2\left(\tau \right)=A_2^{C_{*}}{\mathcal{Z}}_1+E_2^{C_{*}}{\mathcal{Y}}_2+G_2^{C_{*}}{\mathcal{Y}}_2{\mathcal{Z}}_2-(C_2^{C_{*}}+C_1^{C_{*}}){\mathcal{Z}}_2,\hfill \\ & & D_{\tau }^{C_{*}}{\mathcal{W}}_2\left(\tau \right)=A_2^{C_{*}}{\mathcal{W}}_1+D_2^{C_{*}}(1-F_2^{C_{*}}){\mathcal{Z}}_2-G_2^{C_{*}}{\mathcal{Y}}_2{\mathcal{Z}}_2-C_2^{C_{*}}{\mathcal{W}}_2,\hfill \\ & & D_{\tau }^{C_{*}}{\mathcal{V}}_2\left(\tau \right)=A_2^{C_{*}}{\mathcal{V}}_1+D_2^{C_{*}}{F}_2^{C_{*}}{\mathcal{Z}}_2-C_2^{C_{*}}{\mathcal{V}}_2,\hfill \end{array}$$

(9)

with initial condition

$$\begin{array}{ccc}& & {\mathcal{X}}_1\left(0\right)={\mathcal{X}}_{1_{\left(0\right)}},{\mathcal{Y}}_1\left(0\right)={\mathcal{Y}}_{1_{\left(0\right)}},{\mathcal{Z}}_1\left(0\right)={\mathcal{Z}}_{1_{\left(0\right)}},{\mathcal{W}}_1\left(0\right)={\mathcal{W}}_{1_{\left(0\right)}},{\mathcal{V}}_1\left(0\right)={\mathcal{V}}_{1_{\left(0\right)}},\hfill \\ & & {\mathcal{X}}_2\left(0\right)={\mathcal{X}}_{2_{\left(0\right)}},{\mathcal{Y}}_2\left(0\right)={\mathcal{Y}}_{2_{\left(0\right)}},{\mathcal{Z}}_2\left(0\right)={\mathcal{Z}}_{2_{\left(0\right)}},{\mathcal{W}}_2\left(0\right)={\mathcal{W}}_{2_{\left(0\right)}},{\mathcal{V}}_2\left(0\right)={\mathcal{V}}_{2_{\left(0\right)}},\hfill \end{array}$$

where $D_{\tau }^{C_{*}}$ is the ABC fractional derivative given by

$$\begin{array}{c}\hfill D_{\tau }^{C_{*}}\Xi \left(\tau \right)={\displaystyle \frac{\rho \left(C_{*}\right)}{1-C_{*}}}{\int }_0^{\tau }{\Xi }^{\prime }\left(s\right){\mathbb{E}}_{C_{*}}\left({\displaystyle \frac{-C_{*}{(\tau -s)}^{C_{*}}}{1-C_{*}}}\right)ds,\end{array}$$

for any $\Xi \in H^1(\alpha ,\beta ),$ $C_{*}\in [0,1).$$\rho \left(C_{*}\right)$ satisfies property $\rho \left(0\right)=\rho \left(1\right)=1,$ and ${\mathbb{E}}_{C_{*}}$ is the one-parameter Mittag–Leffler function given by

$$\begin{array}{c}\hfill {\mathbb{E}}_{C_{*}}=\sum _{=0}^{\infty }{\displaystyle \frac{{\tau }^k}{\Gamma (C_{*}k+1)}}.\end{array}$$

Notice that for any $\Xi \in H^1(\alpha ,\beta )$ and $C_{*}\in [0,1),$ the integral of ABC is given by

$$\begin{array}{c}\hfill I_{\tau }^{C_{*}}\Xi \left(\tau \right)={\displaystyle \frac{1-C_{*}}{\rho \left(C_{*}\right)}}\Xi \left(\tau \right)+{\displaystyle \frac{C_{*}}{\rho \left(C_{*}\right)\Gamma \left(C_{*}\right)}}{\int }_0^1\Xi \left(s\right){(\tau -s)}^{C_{*}-1}ds.\end{array}$$

Reformulating the right side of (9), we obtain

$$\begin{array}{ccc}\hfill & & {\Xi }_1(\tau ,{\mathcal{X}}_i+{\mathcal{Y}}_i+{\mathcal{Z}}_i+{\mathcal{W}}_i+{\mathcal{V}}_i)=A_1^{C_{*}}-(B_1^{C_{*}}{\mathcal{Z}}_1+B_2^{C_{*}}{\mathcal{Z}}_2){\mathcal{X}}_1-C_1^{C_{*}}{\mathcal{X}}_1-A_2^{C_{*}}{\mathcal{X}}_1,\hfill \\ & & {\Xi }_2(\tau ,{\mathcal{X}}_i+{\mathcal{Y}}_i+{\mathcal{Z}}_i+{\mathcal{W}}_i+{\mathcal{V}}_i)=(B_1^{C_{*}}{\mathcal{Z}}_1+B_2^{C_{*}}{\mathcal{Z}}_2){\mathcal{X}}_1-E_1^{C_{*}}{\mathcal{Y}}_1-C_1^{C_{*}}{\mathcal{Y}}_1-A_2^{C_{*}}{\mathcal{Y}}_1,\hfill \\ & & {\Xi }_3(\tau ,{\mathcal{X}}_i+{\mathcal{Y}}_i+{\mathcal{Z}}_i+{\mathcal{W}}_i+{\mathcal{V}}_i)=E_1^{C_{*}}{\mathcal{Y}}_1+G_1^{C_{*}}{\mathcal{Y}}_1{\mathcal{Z}}_1-(C_1^{C_{*}}+D_1^{C_{*}}){\mathcal{Z}}_1-A_2^{C_{*}}{\mathcal{Z}}_1,\hfill \\ & & {\Xi }_4(\tau ,{\mathcal{X}}_i+{\mathcal{Y}}_i+{\mathcal{Z}}_i+{\mathcal{W}}_i+{\mathcal{V}}_i)=D_1^{C_{*}}(1-F_1^{C_{*}}){\mathcal{Z}}_1-G_1^{C_{*}}{\mathcal{Y}}_1{\mathcal{Z}}_1-C_1^{C_{*}}{\mathcal{W}}_1-A_2^{C_{*}}{\mathcal{W}}_1,\hfill \\ & & {\Xi }_5(\tau ,{\mathcal{X}}_i+{\mathcal{Y}}_i+{\mathcal{Z}}_i+{\mathcal{W}}_i+{\mathcal{V}}_i)=D_1^{C_{*}}{F}_1^{C_{*}}{\mathcal{Z}}_1-C_1^{C_{*}}{\mathcal{V}}_1-A_2^{C_{*}}{\mathcal{V}}_1,\hfill \\ & & {\Xi }_6(\tau ,{\mathcal{X}}_i+{\mathcal{Y}}_i+{\mathcal{Z}}_i+{\mathcal{W}}_i+{\mathcal{V}}_i)=A_2^{C_{*}}{\mathcal{X}}_1-(B_1^{C_{*}}{\mathcal{Z}}_1+B_2^{C_{*}}{\mathcal{Z}}_2){\mathcal{X}}_2-C_2^{C_{*}}{\mathcal{X}}_2,\hfill \\ & & {\Xi }_7(\tau ,{\mathcal{X}}_i+{\mathcal{Y}}_i+{\mathcal{Z}}_i+{\mathcal{W}}_i+{\mathcal{V}}_i)=A_2^{C_{*}}{\mathcal{Y}}_1+(B_1^{C_{*}}{\mathcal{Z}}_1+B_2^{C_{*}}{\mathcal{Z}}_2){\mathcal{X}}_2-E_2^{C_{*}}{\mathcal{Y}}_2-C_2^{C_{*}}{\mathcal{Y}}_2,\hfill \\ & & {\Xi }_8(\tau ,{\mathcal{X}}_i+{\mathcal{Y}}_i+{\mathcal{Z}}_i+{\mathcal{W}}_i+{\mathcal{V}}_i)=A_2^{C_{*}}{\mathcal{Z}}_1+E_2^{C_{*}}{\mathcal{Y}}_2+G_2^{C_{*}}{\mathcal{Y}}_2{\mathcal{Z}}_2-(C_2^{C_{*}}+C_1^{C_{*}}){\mathcal{Z}}_2,\hfill \\ & & {\Xi }_9(\tau ,{\mathcal{X}}_i+{\mathcal{Y}}_i+{\mathcal{Z}}_i+{\mathcal{W}}_i+{\mathcal{V}}_i)=A_2^{C_{*}}{\mathcal{W}}_1+D_2^{C_{*}}(1-F_2^{C_{*}}){\mathcal{Z}}_2-G_2^{C_{*}}{\mathcal{Y}}_2{\mathcal{Z}}_2-C_2^{C_{*}}{\mathcal{W}}_2,\hfill \\ & & {\Xi }_{10}(\tau ,{\mathcal{X}}_i+{\mathcal{Y}}_i+{\mathcal{Z}}_i+{\mathcal{W}}_i+{\mathcal{V}}_i)=A_2^{C_{*}}{\mathcal{V}}_1+D_2^{C_{*}}{F}_2^{C_{*}}{\mathcal{Z}}_2-C_2^{C_{*}}{\mathcal{V}}_2,\hfill \end{array}$$

(10)

in which $i=1,2.$

According to (10), (9) can be expressed as follows [16]:

$$\begin{array}{ccc}\hfill & & D_{\tau }^{C_{*}}\Xi \left(\tau \right)=\Lambda (\tau ,\Xi \left(\tau \right)),\tau \in [0,D],0<C_{*}\le 1,\hfill \\ & & \Xi \left(0\right)={\Xi }_0,\hfill \end{array}$$

(11)

where

$$\Xi \left(\tau \right)=\left\{\begin{array}{c}\begin{array}{cc}{\mathcal{X}}_i\left(\tau \right),& \\ {\mathcal{Y}}_i\left(\tau \right),& \\ {\mathcal{Z}}_i\left(\tau \right),& \\ {\mathcal{W}}_i\left(\tau \right),& \\ {\mathcal{V}}_i\left(\tau \right),& \end{array}\hfill \end{array}\right.{\Xi }_0=\left\{\begin{array}{c}\begin{array}{cc}{\mathcal{X}}_i\left(0\right),& \\ {\mathcal{Y}}_i\left(0\right),& \\ {\mathcal{Z}}_i\left(0\right),& \\ {\mathcal{W}}_i\left(0\right),& \\ {\mathcal{V}}_i\left(0\right),& \end{array}\hfill \end{array}\right.$$

(12)

and

$$\Lambda (\tau ,\Xi \left(\tau \right))=\left\{\begin{array}{c}\begin{array}{cc}{\Xi }_1(\tau ,{\mathcal{X}}_i+{\mathcal{Y}}_i+{\mathcal{Z}}_i+{\mathcal{W}}_i+{\mathcal{V}}_i),& \\ {\Xi }_2(\tau ,{\mathcal{X}}_i+{\mathcal{Y}}_i+{\mathcal{Z}}_i+{\mathcal{W}}_i+{\mathcal{V}}_i),& \\ {\Xi }_3(\tau ,{\mathcal{X}}_i+{\mathcal{Y}}_i+{\mathcal{Z}}_i+{\mathcal{W}}_i+{\mathcal{V}}_i),& \\ {\Xi }_4(\tau ,{\mathcal{X}}_i+{\mathcal{Y}}_i+{\mathcal{Z}}_i+{\mathcal{W}}_i+{\mathcal{V}}_i),& \\ {\Xi }_5(\tau ,{\mathcal{X}}_i+{\mathcal{Y}}_i+{\mathcal{Z}}_i+{\mathcal{W}}_i+{\mathcal{V}}_i),& \end{array}\hfill \end{array}\right.$$

(13)

for every $i=1,2.$

Now, we apply the concept of Z-numbers and we introduce a special matrix of the form $\mathrm{diag}[\Phi ,\Psi ,{\rm Y}]$ (named the generalized Z-number) where $\Phi$ is a fuzzy set, time-stamped, $\Psi$ is the probability distribution function and ${\rm Y}$ is a degree of reliability of $\Phi$ that is described as a value of $\Phi ⨀\Psi$ (see [25]).

We let the Banach space be $\mathbf{B}=C(0,D).$ For every $\overrightarrow{\varphi },\overrightarrow{\psi }>\overrightarrow{0},$ we define

$$\begin{array}{ccc}\hfill & & { }^{\mathtt{F}}{\rm Y}(\tau ,\overrightarrow{\varphi }):=\mathrm{diag}[\widetilde{{ }_0{\mathbb{H}}_0}\left[\frac{-{\left|\tau \right|}^{{\mathcal{P}}_1}}{{\varphi }_1}\right],\widetilde{{ }_0{\mathbb{H}}_1}\left[N_1;\frac{-{\left|\tau \right|}^{{\mathcal{P}}_1}}{{\varphi }_2}\right],\hfill \\ & & \widetilde{{ }_1{\mathbb{H}}_1}\left[V_1;\frac{-{\left|\tau \right|}^{{\mathcal{P}}_1}}{{\varphi }_3}\right],\widetilde{{ }_2{\mathbb{H}}_1}\left[V_1,V_2;N_1;\frac{-{\left|\tau \right|}^{{\mathcal{P}}_1}}{{\varphi }_4}\right],\hfill \\ & & \widetilde{{ }_C{\mathbb{H}}_D}\left[V_1,\dots ,V_C;N_1,\dots ,N_C;\frac{-{\left|\tau \right|}^{{\mathcal{P}}_1}}{{\varphi }_5}\right],\hfill \\ & & \widetilde{{ }_C{\mathbb{H}}_D}\left[\frac{-{\left|\tau \right|}^{{\mathcal{P}}_1}}{{\varphi }_6}|{ }_{(N_1,M_1),\dots ,(N_D,M_D)}^{(V_1,W_1),\dots ,(V_C,W_C)}\right],\hfill \\ & & \widetilde{{ }_C^A{\mathbb{H}}_D^B}\left[\frac{-{\left|\tau \right|}^{{\mathcal{P}}_1}}{{\varphi }_7}|{ }_{(N_1,1),\dots ,(N_D,1)}^{(V_1,1),\dots ,(V_C,1)}\right],\widetilde{{ }_C^A{\mathbb{H}}_D^B}\left[\frac{-{\left|\tau \right|}^{{\mathcal{P}}_1}}{{\varphi }_8}|{ }_{{(N_j,M_j)}_{1,D}}^{{(V_j,W_j)}_{1,C}}\right]],\hfill \end{array}$$

(14)

and

$$\begin{array}{ccc}\hfill & & { }^{\mathtt{R}}{\rm Y}(\tau ,\overrightarrow{\psi }):=\mathrm{diag}[{\tilde{\mathbb{M}}}_{\alpha }\left(\frac{-{\left|\tau \right|}^{{\mathcal{P}}_1}}{{\psi }_1}\right),{\tilde{\mathbb{M}}}_{\alpha ,\tau }\left(\frac{-{\left|\tau \right|}^{{\mathcal{P}}_1}}{{\psi }_2}\right),\hfill \\ & & {\tilde{\mathbb{M}}}_{\alpha ,\tau }^{V_1}\left(\frac{-{\left|\tau \right|}^{{\mathcal{P}}_1}}{{\psi }_3}\right),{\tilde{\mathbb{M}}}_{\alpha ,\tau }^{V_1,W_1}\left(\frac{-{\left|\tau \right|}^{{\mathcal{P}}_1}}{{\psi }_4}\right),\hfill \\ & & {\tilde{\mathbb{M}}}_{\alpha ,\tau ;N_1}^{V_1,W_1}\left(\frac{-{\left|\tau \right|}^{{\mathcal{P}}_1}}{{\psi }_5}\right),{\tilde{\mathbb{M}}}_{\alpha ,\tau ;N_1,M_1}^{V_1,W_1}\left(\frac{-{\left|\tau \right|}^{{\mathcal{P}}_1}}{{\psi }_6}\right)\hfill \\ & & {\tilde{\mathbb{M}}}_{\alpha ,\tau ;N_1,M_1}^{V_1,W_1;V_2}\left(\frac{-{\left|\tau \right|}^{{\mathcal{P}}_1}}{{\psi }_7}\right),{\tilde{\mathbb{M}}}_{\alpha ,\tau ;N_1,M_1}^{V_1,W_1;V_2,V_2}\left(\frac{-{\left|\tau \right|}^{{\mathcal{P}}_1}}{{\psi }_8}\right)].\hfill \end{array}$$

(15)

Note that every special function $\tilde{A}$ given in the the main diagonal of square matrices ${ }^{\mathtt{F}}{\rm Y}(\tau ,\overrightarrow{\varphi })$ and ${ }^{\mathtt{R}}{\rm Y}(\tau ,\overrightarrow{\psi })$ is defined as $\tilde{A}:=\mathrm{diag}[A,\cdots ,A];$ for example,

$$\widetilde{{ }_0{\mathbb{H}}_0}\left[\frac{-{\left|\tau \right|}^{{\mathcal{P}}_1}}{{\varphi }_1}\right]:=\mathrm{diag}{\left[{ }_0{\mathbb{H}}_0\left[\frac{-{\left|\tau \right|}^{{\mathcal{P}}_1}}{{\varphi }_1}\right],\cdots ,{ }_0{\mathbb{H}}_0\left[\frac{-{\left|\tau \right|}^{{\mathcal{P}}_1}}{{\varphi }_1}\right]\right]}_{n^2}.$$

Definition 3.

Fractional-order Equation (11) is multi-stable with respect to

$$\mathrm{diag}\left[{\mathtt{AG}}_1({ }^{\mathtt{F}}{\rm Y}(\tau ,\overrightarrow{\varphi }))⨀{\mathtt{AG}}_1({ }^{\mathtt{R}}{\rm Y}(\tau ,\overrightarrow{\psi })),\cdots ,{\mathtt{AG}}_8({ }^{\mathtt{F}}{\rm Y}(\tau ,\overrightarrow{\varphi }))⨀{\mathtt{AG}}_8({ }^{\mathtt{R}}{\rm Y}(\tau ,\overrightarrow{\psi }))\right]$$

if there exist $\overrightarrow{{\mathfrak{S}}_1},\overrightarrow{{\mathfrak{S}}_2}>\overrightarrow{0}$ such that, for $\overrightarrow{{\overline{\mathfrak{S}}}_1},\overrightarrow{{\overline{\mathfrak{S}}}_2}>\overrightarrow{0}$ and all solutions $\tilde{\Xi }\in \mathbf{B}$ to

$$\begin{array}{ccc}& & \mathrm{diag}[\Phi \left(D_{\tau }^{C_{*}}\Xi \left(\tau \right)-\Lambda (\tau ,\Xi \left(\tau \right)),\overrightarrow{{\mathfrak{S}}_1}\overrightarrow{\varphi }\right)⨀{\Psi }_{D_{\tau }^{C_{*}}\Xi \left(\tau \right)-\Lambda (\tau ,\Xi \left(\tau \right))}\left(\overrightarrow{{\mathfrak{S}}_2}\overrightarrow{\psi }\right),\cdots ,\hfill \\ & & \Phi \left(D_{\tau }^{C_{*}}\Xi \left(\tau \right)-\Lambda (\tau ,\Xi \left(\tau \right)),\overrightarrow{{\mathfrak{S}}_1}\overrightarrow{\varphi }\right)⨀{\Psi }_{D_{\tau }^{C_{*}}\Xi \left(\tau \right)-\Lambda (\tau ,\Xi \left(\tau \right))}\left(\overrightarrow{{\mathfrak{S}}_2}\overrightarrow{\psi }\right)]\hfill \\ & & ⪰\mathrm{diag}[{\mathtt{AG}}_1({ }^{\mathtt{F}}{\rm Y}(\tau ,\overrightarrow{{\mathfrak{S}}_1}\overrightarrow{\varphi }))⨀{\mathtt{AG}}_1({ }^{\mathtt{R}}{\rm Y}(\tau ,\overrightarrow{{\mathfrak{S}}_2}\overrightarrow{\psi })),\cdots ,\hfill \\ & & {\mathtt{AG}}_8({ }^{\mathtt{F}}{\rm Y}(\tau ,\overrightarrow{{\mathfrak{S}}_1}\overrightarrow{\varphi }))⨀{\mathtt{AG}}_8({ }^{\mathtt{R}}{\rm Y}(\tau ,\overrightarrow{{\mathfrak{S}}_2}\overrightarrow{\psi }))],\hfill \end{array}$$

there exists solution $\Xi \in \mathbf{B}$ to (11) with

$$\begin{array}{ccc}& & \mathrm{diag}[\Phi (\tilde{\Xi }\left(\tau \right)-\Xi \left(\tau \right),\overrightarrow{\varphi })⨀{\Psi }_{\tilde{\Xi }\left(\tau \right)-\Xi \left(\tau \right)}\left(\overrightarrow{\psi }\right),\cdots ,\hfill \\ & & \Phi (\tilde{\Xi }\left(\tau \right)-\Xi \left(\tau \right),\overrightarrow{\varphi })⨀{\Psi }_{\tilde{\Xi }\left(\tau \right)-\Xi \left(\tau \right)}\left(\overrightarrow{\psi }\right)]\hfill \\ & & ⪰\mathrm{diag}[{\mathtt{AG}}_1({ }^{\mathtt{F}}{\rm Y}(\tau ,\overrightarrow{{\mathfrak{S}}_1}\overrightarrow{{\overline{\mathfrak{S}}}_1}\overrightarrow{\varphi }))⨀{\mathtt{AG}}_1({ }^{\mathtt{R}}{\rm Y}(\tau ,\overrightarrow{{\mathfrak{S}}_2}\overrightarrow{{\overline{\mathfrak{S}}}_2}\overrightarrow{\psi })),\cdots ,\hfill \\ & & {\mathtt{AG}}_8({ }^{\mathtt{F}}{\rm Y}(\tau ,\overrightarrow{{\mathfrak{S}}_1}\overrightarrow{{\overline{\mathfrak{S}}}_1}\overrightarrow{\varphi }))⨀{\mathtt{AG}}_8({ }^{\mathtt{R}}{\rm Y}(\chi ,\overrightarrow{{\mathfrak{S}}_2}\overrightarrow{{\overline{\mathfrak{S}}}_2}\overrightarrow{\psi }))\left]\right],\hfill \end{array}$$

for every $\tau \in [0,D],$ and $\overrightarrow{\varphi },\overrightarrow{\psi }>\overrightarrow{0}$.

The diagrams of ${\mathtt{AG}}_i[{ }^{\mathtt{F}}{\rm Y}(\tau ,\overrightarrow{\varphi })],i=1,\cdots ,8,$ are shown separately in Figure 1. As can be observed, ${\mathtt{AG}}_3[{ }^{\mathtt{F}}{\rm Y}(\tau ,\overrightarrow{\varphi })]$ (brown) and ${\mathtt{AG}}_4[{ }^{\mathtt{F}}{\rm Y}(\tau ,\overrightarrow{\varphi })]$ (yellow) include the highest and the lowest values, and ${\mathtt{AG}}_i[{ }^{\mathtt{F}}{\rm Y}(\tau ,\overrightarrow{\varphi })],i=1,2,5,6,7,8$, are placed between them. Therefore, we can infer that the ${\mathtt{AG}}_4[{ }^{\mathtt{F}}{\rm Y}(\tau ,\overrightarrow{\varphi })]$ proposes a better approximation for (11) than the others.

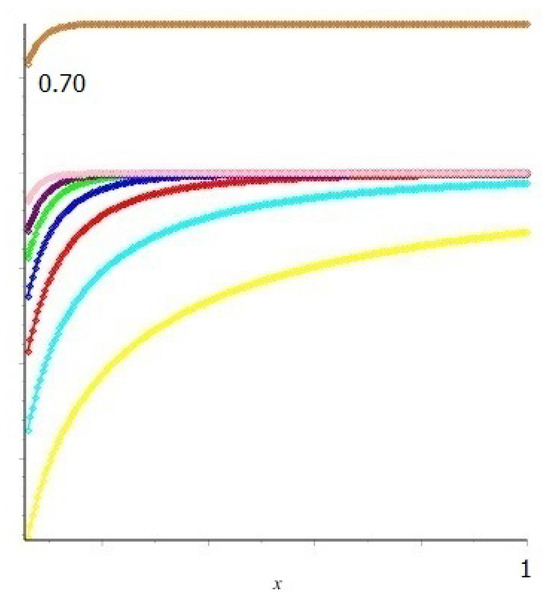
Figure 1. The diagrams of ${\mathtt{AG}}_i,1\le i\le 8,$ on controller (14). ${\mathtt{AG}}_3$ and ${\mathtt{AG}}_4$ are shown in brown and yellow colors, and the rest are in between.

As above, we can conclude that ${\mathtt{AG}}_4[{ }^{\mathtt{R}}{\rm Y}(\tau ,\overrightarrow{\psi })]$ proposes a better approximation for (11) than ${\mathtt{AG}}_i[{ }^{\mathtt{R}}{\rm Y}(\tau ,\overrightarrow{\psi })],1\le i\le 8,i\ne 4.$

Theorem 2.

For every $\Xi \left(\tau \right)\in \mathbf{B}$, $\overrightarrow{{\mathfrak{S}}_1}=({\mathfrak{S}}_{11},\cdots ,{\mathfrak{S}}_{18}),$ $\overrightarrow{{\mathfrak{S}}_2}=({\mathfrak{S}}_{21},\cdots ,{\mathfrak{S}}_{28}),$ $\overrightarrow{\varphi }=({\varphi }_1,\cdots ,{\varphi }_8),$$\overrightarrow{\psi }=({\psi }_1,\cdots ,{\psi }_8),$ and $\overrightarrow{{\mathfrak{S}}_1},{\overrightarrow{\mathfrak{S}}}_2,\overrightarrow{\varphi },\overrightarrow{\psi }>\overrightarrow{0},$ we consider the Atangana–Baleanu–Caputo fractional smoke epidemic model (11) and the inequalities below:

$$\begin{array}{ccc}\hfill & & \Phi \left(D_{\tau }^{C_{*}}\Xi \left(\tau \right)-\Lambda (\tau ,\Xi \left(\tau \right)),\overrightarrow{\varphi }\right)⪰{\mathtt{AG}}_4({ }^{\mathtt{F}}{\rm Y}(\tau ,\overrightarrow{{\mathfrak{S}}_1}\overrightarrow{\varphi })),\hfill \end{array}$$

(16)

$$\begin{array}{ccc}& & {\Psi }_{D_{\tau }^{C_{*}}\Xi \left(\tau \right)-\Lambda (\tau ,\Xi \left(\tau \right))}\left(\overrightarrow{\psi }\right)⪰{\mathtt{AG}}_4({ }^{\mathtt{R}}{\rm Y}(\tau ,\overrightarrow{{\mathfrak{S}}_2}\overrightarrow{\psi })),\hfill \end{array}$$

(17)

and

$$\begin{array}{ccc}\hfill & & \Phi \left(D_{\tau }^{C_{*}}\Xi \left(\tau \right)-\Lambda (\tau ,\Xi \left(\tau \right)),\overrightarrow{{\mathfrak{S}}_1}\overrightarrow{\varphi }\right)⨀{\Psi }_{D_{\tau }^{C_{*}}\Xi \left(\tau \right)-\Lambda (\tau ,\Xi \left(\tau \right))}\left(\overrightarrow{{\mathfrak{S}}_2}\overrightarrow{\psi }\right)\hfill \\ & & ⪰{\mathtt{AG}}_4({ }^{\mathtt{F}}{\rm Y}(\tau ,\overrightarrow{{\mathfrak{S}}_1}\overrightarrow{\varphi }))⨀{\mathtt{AG}}_4({ }^{\mathtt{R}}{\rm Y}(\tau ,\overrightarrow{{\mathfrak{S}}_2}\overrightarrow{\psi })).\hfill \end{array}$$

(18)

We let there exist ${\ell }_1,{\ell }_2>0$ such that, for every $\overrightarrow{\varphi },\overrightarrow{\psi }>\overrightarrow{0}$, we have

$$\Phi \left(\Lambda (\tau ,{\Xi }_1\left(\tau \right))-\Lambda (\tau ,{\Xi }_2\left(\tau \right)),\overrightarrow{\varphi }\right)⪰{\mathtt{AG}}_4\left({ }^{\mathtt{F}}{\rm Y}\left({\Xi }_1-{\Xi }_2,\frac{\overrightarrow{\varphi }}{{\ell }_1}\right)\right),$$

and

$${\Psi }_{\Lambda (\tau ,{\Xi }_1\left(\tau \right))-\Lambda (\tau ,{\Xi }_2\left(\tau \right))}\left(\overrightarrow{\psi }\right)⪰{\mathtt{AG}}_4\left({ }^{\mathtt{R}}{\rm Y}\left({\Xi }_1-{\Xi }_2,\frac{\overrightarrow{\psi }}{{\ell }_2}\right)\right).$$

We let $2{\ell }_{i}max\{\frac{1-C_{*}}{\rho \left(C_{*}\right)},\frac{D^{C_{*}}}{\rho \left(C_{*}\right)\Gamma \left(C_{*}\right)}\}<1,i=1,2.$ Then, we can obtain a unique $\tilde{\Xi }\in \mathbf{B}$ such that

$$\begin{array}{c}\hfill \tilde{\Xi }\left(\tau \right)={\Xi }_0+I_{\tau }^{C^{*}}\Lambda (\tau ,\tilde{\Xi }\left(\tau \right)),\end{array}$$

(19)

and

$$\begin{array}{ccc}\hfill & & \left[\begin{array}{ccc}\Phi (\Xi \left(\tau \right)-\tilde{\Xi }\left(\tau \right),\overrightarrow{\varphi })& \mathbf{0}& \mathbf{0}\\ \mathbf{0}& {\Psi }_{\Xi \left(\tau \right)-\tilde{\Xi }\left(\tau \right)}\left(\overrightarrow{\psi }\right)& \mathbf{0}\\ \mathbf{0}& \mathbf{0}& \Phi (\Xi \left(\tau \right)-\tilde{\Xi }\left(\tau \right),\overrightarrow{\varphi })⨀{\Psi }_{\Xi \left(\tau \right)-\widehat{\Xi }\left(\tau \right)}\left(\overrightarrow{\psi }\right)\end{array}\right]\hfill \\ & ⪰& \left[\begin{array}{ccc}\widetilde{{ }_C^A{\mathbb{H}}_D^B}\left[\frac{-{\left|\tau \right|}^{{\mathcal{P}}_1}}{D_1{\mathfrak{S}}_{18}{\varphi }_8}|{ }_{{(N_j,M_j)}_{1,D}}^{{(V_j,W_j)}_{1,C}}\right]& \mathbf{0}& \mathbf{0}\\ \mathbf{0}& {\tilde{\mathbb{M}}}_{\alpha ,\tau ;N_1,M_1}^{V_1,W_1;V_2,V_2}\left(\frac{-{\left|\tau \right|}^{{\mathcal{P}}_1}}{D_2{\mathfrak{S}}_{28}{\psi }_8}\right)& \mathbf{0}\\ \mathbf{0}& \mathbf{0}& \widetilde{{ }_C^A{\mathbb{H}}_D^B}\left[\frac{-{\left|\tau \right|}^{{\mathcal{P}}_1}}{max\{D_1{\mathfrak{S}}_{18}{\varphi }_8,D_2{\mathfrak{S}}_{28}{\psi }_8\}}|{ }_{{(N_j,M_j)}_{1,D}}^{{(V_j,W_j)}_{1,C}}\right]\end{array}\right],\hfill \end{array}$$

where

$$D_i:=\frac{2max\{\frac{1-C_{*}}{\rho \left(C_{*}\right)},\frac{D^{C_{*}}}{\rho \left(C_{*}\right)\Gamma \left(C_{*}\right)}\}}{1-{\ell }_{i}2max\{\frac{1-C_{*}}{\rho \left(C_{*}\right)},\frac{D^{C_{*}}}{\rho \left(C_{*}\right)\Gamma \left(C_{*}\right)}\}}.$$

(20)

Proof. 

According to Lemma 2.4 in [16], the solution of (11) is defined as follows:

$$\begin{array}{c}\hfill \Xi \left(\tau \right)={\Xi }_0\left(\tau \right)+{\displaystyle \frac{1-C_{*}}{\rho \left(C_{*}\right)}}\Phi (\tau ,\Xi \left(\tau \right))+{\displaystyle \frac{C_{*}}{\rho \left(C_{*}\right)\Gamma \left(C_{*}\right)}}\times {\int }_0^{\tau }\Phi (s,\Xi \left(s\right)){(\tau -s)}^{C_{*}-1}ds.\end{array}$$

(21)

We consider mapping $d:\mathbf{B}⟶{[0,\infty ]}^2$ defined by

$$\begin{array}{ccc}& & d(\Xi \left(\tau \right),\widehat{\Xi }\left(\tau \right))=\inf \{({\Omega }_1,{\Omega }_2)\ge (0,0):\hfill \\ & & \left[\begin{array}{ccc}\Phi (\Xi \left(\tau \right)-\widehat{\Xi }\left(\tau \right),\overrightarrow{\varphi })& \mathbf{0}& \mathbf{0}\\ \mathbf{0}& {\Psi }_{\Xi \left(\tau \right)-\widehat{\Xi }\left(\tau \right)}\left(\overrightarrow{\psi }\right)& \mathbf{0}\\ \mathbf{0}& \mathbf{0}& \Phi (\Xi \left(\tau \right)-\widehat{\Xi }\left(\tau \right),\overrightarrow{\varphi })⨀{\Psi }_{\Xi \left(\tau \right)-\widehat{\Xi }\left(\tau \right)}\left(\overrightarrow{\psi }\right)\end{array}\right]\hfill \\ & & ⪰\left[\begin{array}{ccc}{\mathtt{AG}}_4\left({ }^{\mathtt{F}}{\rm Y}(\tau ,\frac{\overrightarrow{{\mathfrak{S}}_1}\overrightarrow{\varphi }}{{\Omega }_1})\right)& \mathbf{0}& \mathbf{0}\\ \mathbf{0}& {\mathtt{AG}}_4\left({ }^{\mathtt{R}}{{\rm Y}}_{\tau }\left(\frac{\overrightarrow{{\mathfrak{S}}_2}\overrightarrow{\psi }}{{\Omega }_2}\right)\right)& \mathbf{0}\\ \mathbf{0}& \mathbf{0}& {\mathtt{AG}}_4\left({ }^{\mathtt{F}⨀\mathtt{R}}{\rm Y}\left(\tau ,min\{\frac{\overrightarrow{{\mathfrak{S}}_1}\overrightarrow{\varphi }}{{\Omega }_1},\frac{\overrightarrow{{\mathfrak{S}}_2}\overrightarrow{\psi }}{{\Omega }_2}\}\right)\right)\end{array}\right],\hfill \\ & & \mathrm{for}\mathrm{every}\Xi ,\widehat{\Xi }\in \mathbf{B},\mathrm{and}\overrightarrow{\varphi },\overrightarrow{\psi }>\overrightarrow{0}\},\hfill \end{array}$$

(22)

in which

$$\begin{array}{c}\hfill {\mathtt{AG}}_4\left({ }^{\mathtt{F}⨀\mathtt{R}}{\rm Y}\left(\tau ,min\{\frac{\overrightarrow{{\mathfrak{S}}_1}\overrightarrow{\varphi }}{{\Omega }_1},\frac{\overrightarrow{{\mathfrak{S}}_2}\overrightarrow{\psi }}{{\Omega }_2}\}\right)\right):={\mathtt{AG}}_4\left({ }^{\mathtt{F}}{\rm Y}(\tau ,\frac{\overrightarrow{{\mathfrak{S}}_1}\overrightarrow{\varphi }}{{\Omega }_1})\right)⨀{\mathtt{AG}}_4\left({ }^{\mathtt{R}}{{\rm Y}}_{\tau }\left(\frac{\overrightarrow{{\mathfrak{S}}_2}\overrightarrow{\psi }}{{\Omega }_2}\right)\right).\end{array}$$

Note that $(\mathbf{B},d)$ is a complete generalized metric space (see [19]).

We consider operator $\mathcal{L}:\mathbf{B}⟶\mathbf{B}$ such that

$$\begin{array}{ccc}\hfill & & \mathcal{L}\Xi \left(\tau \right)={\varpi }_1\Xi \left(\tau \right)+{\varpi }_2\Xi \left(\tau \right),\hfill \\ & & {\varpi }_1\Xi \left(\tau \right)={\Xi }_0+{\displaystyle \frac{1-C_{*}}{\rho \left(C_{*}\right)}}\Phi (\tau ,\Xi \left(\tau \right)),\hfill \\ & & {\varpi }_2\Xi \left(\tau \right)={\displaystyle \frac{C_{*}}{\rho \left(C_{*}\right)\Gamma \left(C_{*}\right)}}{\int }_0^{\tau }\Phi (s,\Xi \left(s\right)){(\tau -s)}^{C_{*}-1}ds.\hfill \end{array}$$

(23)

According to (21) and (23), we have

$$\begin{array}{c}\hfill \mathcal{L}\Xi \left(\tau \right)={\Xi }_0\left(\tau \right)+{\displaystyle \frac{1-C_{*}}{\rho \left(C_{*}\right)}}\Phi (\tau ,\Xi \left(\tau \right))+{\displaystyle \frac{C_{*}}{\rho \left(C_{*}\right)\Gamma \left(C_{*}\right)}}{\int }_0^{\tau }\Phi (s,\Xi \left(s\right)){(\tau -s)}^{C_{*}-1}ds.\end{array}$$

(24)

For every $\tau \in [0,D],$ and $\overrightarrow{\varphi },\overrightarrow{\psi }>\overrightarrow{0},$ we show $\mathcal{L}$ is a contraction mapping on $\mathbf{B},$ as follows:

$$\begin{array}{ccc}& & \Phi \left(\mathcal{L}\Xi \left(\tau \right)-\mathcal{L}\widehat{\Xi }\left(\tau \right),\overrightarrow{\varphi }\right)\hfill \\ & & ⪰\Phi \left({\varpi }_1\Xi -{\varpi }_1\widehat{\Xi },\frac{\overrightarrow{\varphi }}{2}\right)⨀\Phi \left({\varpi }_2\Xi -{\varpi }_2\widehat{\Xi },\frac{\overrightarrow{\varphi }}{2}\right)\hfill \\ & & ⪰\Phi \left({\displaystyle \frac{1-C_{*}}{\rho \left(C_{*}\right)}}[\Lambda (\tau ,\Xi \left(\tau \right))-\Lambda (\tau ,\widehat{\Xi }\left(\tau \right))],\frac{\overrightarrow{\varphi }}{2}\right)⨀\hfill \\ & & \Phi \left({\displaystyle \frac{C_{*}}{\rho \left(C_{*}\right)\Gamma \left(C_{*}\right)}}{\int }_0^{\tau }[\Lambda (s,\Xi \left(s\right))-\Lambda (s,\widehat{\Xi }\left(s\right))]{(\tau -s)}^{C_{*}-1}ds,\frac{\overrightarrow{\varphi }}{2}\right)\hfill \end{array}$$

$$\begin{array}{ccc}& & ⪰\Phi \left({\displaystyle \frac{1-C_{*}}{\rho \left(C_{*}\right)}}[\Xi \left(\tau \right)-\widehat{\Xi }\left(\tau \right)],\frac{\overrightarrow{\varphi }}{2{\ell }_1}\right)⨀\hfill \\ & & \Phi \left({\displaystyle \frac{C_{*}}{\rho \left(C_{*}\right)\Gamma \left(C_{*}\right)}}{\int }_0^{\tau }{(\tau -s)}^{C_{*}-1}ds,\frac{\overrightarrow{\varphi }}{2{max}_{\tau \in [0,D]}\{\Xi \left(\tau \right)-\widehat{\Xi }\left(\tau \right)\}}\right)\hfill \\ & & ⪰\Phi \left(\Xi \left(\tau \right)-\widehat{\Xi }\left(\tau \right),\frac{\overrightarrow{\varphi }}{2{\ell }_1\frac{1-C_{*}}{\rho \left(C_{*}\right)}}\right)⨀\underset{\tau \in [0,D]}{inf}\Phi \left(\Xi \left(\tau \right)-\widehat{\Xi }\left(\tau \right),\frac{\overrightarrow{\varphi }}{2{\ell }_1\frac{D^{C_{*}}}{\rho \left(C_{*}\right)\Gamma \left(C_{*}\right)}}\right)\hfill \\ & & ⪰{\mathtt{AG}}_4\left({ }^{\mathtt{F}}{\rm Y}\left(\tau ,\frac{\overrightarrow{{\mathfrak{S}}_1}\overrightarrow{\varphi }}{2{\ell }_{1}max\{\frac{1-C_{*}}{\rho \left(C_{*}\right)},\frac{D^{C_{*}}}{\rho \left(C_{*}\right)\Gamma \left(C_{*}\right)}\}}\right)\right),\hfill \end{array}$$

and in a similar way,

$$\begin{array}{ccc}& & {\Psi }_{\mathcal{L}\Xi \left(\tau \right)-\mathcal{L}\widehat{\Xi }\left(\tau \right)}\left(\overrightarrow{\psi }\right)\hfill \\ & & ⪰{\mathtt{AG}}_4\left({ }^{\mathtt{R}}{\rm Y}\left(\tau ,\frac{\overrightarrow{{\mathfrak{S}}_2}\overrightarrow{\psi }}{2{\ell }_{2}max\{\frac{1-C_{*}}{\rho \left(C_{*}\right)},\frac{D^{C_{*}}}{\rho \left(C_{*}\right)\Gamma \left(C_{*}\right)}\}}\right)\right).\hfill \end{array}$$

Thus, we deduce the contractive property of $\mathcal{L}$ since $2{\ell }_{i}max\{\frac{1-C_{*}}{\rho \left(C_{*}\right)},\frac{D^{C_{*}}}{\rho \left(C_{*}\right)\Gamma \left(C_{*}\right)}\}<1,$$i=1,2$.

We remark that (see [18]) function $\Xi \in \mathbf{B}$ is a solution of (16)–(17) if there exists function $⋋\in C\left(\right[0,D];\mathbb{R})$ (which depends on $\Xi$) such that, for every $\tau \in [0,D]$ and $\overrightarrow{\varphi },\overrightarrow{\psi }>\overrightarrow{0},$

(1) $\Phi (⋋\left(\tau \right),\overrightarrow{\varphi })⪰{\mathtt{AG}}_4\left({ }^{\mathtt{F}}{\rm Y}(\tau ,\overrightarrow{{\mathfrak{S}}_1}\overrightarrow{\varphi })\right)$, and ${\Psi }_{⋋\left(\tau \right)}\left(\overrightarrow{\varphi }\right)⪰{\mathtt{AG}}_4\left({ }^{\mathtt{R}}{\rm Y}(\tau ,\overrightarrow{{\mathfrak{S}}_2}\overrightarrow{\psi })\right)$; and

(2) we have

$$\begin{array}{ccc}\hfill & & D_{\tau }^{C_{*}}\Xi \left(\tau \right)=\Phi (\tau ,\Xi \left(\tau \right))+⋋\left(\tau \right),\hfill \\ & & \Xi \left(0\right)={\Xi }_0.\hfill \end{array}$$

(25)

Now, the solution of (35) is given by

$$\Xi \left(\tau \right)={\Xi }_0+I_{\tau }^{C_{*}}\Lambda (\tau ,\Xi \left(\tau \right))+I_{\tau }^{C_{*}}⋋\left(\tau \right).$$

(26)

Making use of (26) and (30), we have

$$\begin{array}{ccc}& & \Phi \left(\Xi \left(\tau \right)-\mathcal{L}\Lambda (\tau ,\Xi \left(\tau \right)),\overrightarrow{\varphi }\right)\hfill \\ & & ⪰\Phi \left({\displaystyle \frac{1-C_{*}}{\rho \left(C_{*}\right)}}⋋\left(\tau \right),\frac{\overrightarrow{\varphi }}{2}\right)⨀\Phi \left({\displaystyle \frac{C_{*}}{\rho \left(C_{*}\right)\Gamma \left(C_{*}\right)}}{\int }_0^{\tau }⋋\left(s\right){(\tau -s)}^{C_{*}-1}ds,\frac{\overrightarrow{\varphi }}{2}\right)\hfill \\ & & ⪰{\mathtt{AG}}_4\left({ }^F{\rm Y}\left(\tau ,\frac{\overrightarrow{{\mathfrak{S}}_1}\overrightarrow{\varphi }}{2{\displaystyle \frac{1-C_{*}}{\rho \left(C_{*}\right)}}}\right)\right)⨀{\mathtt{AG}}_4\left({ }^F{\rm Y}\left(\tau ,\frac{\overrightarrow{{\mathfrak{S}}_1}\overrightarrow{\varphi }}{2{\displaystyle \frac{D^{C_{*}}}{\rho \left(C_{*}\right)\Gamma \left(C_{*}\right)}}}\right)\right)\hfill \\ & & ⪰{\mathtt{AG}}_4\left({ }^F{\rm Y}\left(\tau ,\frac{\overrightarrow{{\mathfrak{S}}_1}\overrightarrow{\varphi }}{2max\left\{{\displaystyle \frac{1-C_{*}}{\rho \left(C_{*}\right)}},{\displaystyle \frac{D^{C_{*}}}{\rho \left(C_{*}\right)\Gamma \left(C_{*}\right)}}\right\}}\right)\right),\hfill \end{array}$$

and in a similar way,

$$\begin{array}{ccc}& & {\Psi }_{\Xi \left(\tau \right)-\mathcal{L}\Lambda (\tau ,\Xi (\tau \left)\right)}\left(\overrightarrow{\varphi }\right)\hfill \\ & & ⪰{\mathtt{AG}}_4\left({ }^R{\rm Y}\left(\tau ,\frac{\overrightarrow{{\mathfrak{S}}_2}\overrightarrow{\psi }}{2max\left\{{\displaystyle \frac{1-C_{*}}{\rho \left(C_{*}\right)}},{\displaystyle \frac{D^{C_{*}}}{\rho \left(C_{*}\right)\Gamma \left(C_{*}\right)}}\right\}}\right)\right)\hfill \end{array}$$

for every $\overrightarrow{\varphi },\overrightarrow{\psi }>\overrightarrow{0}.$

By means of fixed point theory, we can obtain $\tilde{\Xi }\in \mathbf{B}$ such that

(1) $\tilde{\Xi }$ is a fixed point of $\mathcal{L}$,

$$\begin{array}{c}\hfill \tilde{\Xi }\left(\tau \right)={\Xi }_0+I_{\tau }^{C^{*}}\Lambda (\tau ,\tilde{\Xi }\left(\tau \right)),\end{array}$$

(27)

which is unique in the set $\left\{\upsilon \in \mathbf{B}:d(\mathcal{L}\tilde{\Xi },\upsilon )<(\infty ,\infty )\right\}.$

(2) $d({\mathcal{L}}^m\left({\Xi }_1\right),\tilde{\Xi })\to (0,0),$ as $m\to \infty$.

(3) We have

$$\begin{array}{ccc}\hfill d(\Xi ,\tilde{\Xi })& \le & \left(\frac{1}{1-\left[2{\ell }_{1}max\{\frac{1-C_{*}}{\rho \left(C_{*}\right)},\frac{D^{C_{*}}}{\rho \left(C_{*}\right)\Gamma \left(C_{*}\right)}\}\right]},\frac{1}{1-\left[2{\ell }_{2}max\{\frac{1-C_{*}}{\rho \left(C_{*}\right)},\frac{D^{C_{*}}}{\rho \left(C_{*}\right)\Gamma \left(C_{*}\right)}\}\right]}\right)d(\mathcal{L}\Xi ,\Xi )\hfill \\ & \le & \left(\frac{2max\{\frac{1-C_{*}}{\rho \left(C_{*}\right)},\frac{D^{C_{*}}}{\rho \left(C_{*}\right)\Gamma \left(C_{*}\right)}\}}{1-\left[2{\ell }_{1}max\{\frac{1-C_{*}}{\rho \left(C_{*}\right)},\frac{D^{C_{*}}}{\rho \left(C_{*}\right)\Gamma \left(C_{*}\right)}\}\right]},\frac{2max\{\frac{1-C_{*}}{\rho \left(C_{*}\right)},\frac{D^{C_{*}}}{\rho \left(C_{*}\right)\Gamma \left(C_{*}\right)}\}}{1-\left[2{\ell }_{2}max\{\frac{1-C_{*}}{\rho \left(C_{*}\right)},\frac{D^{C_{*}}}{\rho \left(C_{*}\right)\Gamma \left(C_{*}\right)}\}\right]}\right),\hfill \end{array}$$

which infers

$$\begin{array}{ccc}& & \Phi (\Xi \left(\tau \right)-\tilde{\Xi }\left(\tau \right),\overrightarrow{\varphi })⪰{\mathtt{AG}}_4\left({ }^{\mathtt{F}}{\rm Y}(\tau ,\frac{\overrightarrow{{\mathfrak{S}}_1}\overrightarrow{\varphi }}{\frac{\Theta }{1-\Theta {\ell }_1}})\right)\hfill \\ & & {\Psi }_{\Xi \left(\tau \right)-\tilde{\Xi }\left(\tau \right)}\left(\overrightarrow{\psi }\right)⪰{\mathtt{AG}}_4\left({ }^{\mathtt{R}}{\rm Y}(\tau ,\frac{\overrightarrow{{\mathfrak{S}}_2}\overrightarrow{\psi }}{\frac{\Theta }{1-\Theta {\ell }_2}})\right)\hfill \\ & & \Phi (\Xi \left(\tau \right)-\tilde{\Xi }\left(\tau \right),\overrightarrow{\varphi })⨀{\Psi }_{\Xi \left(\tau \right)-\tilde{\Xi }\left(\tau \right)}\left(\overrightarrow{\psi }\right)⪰{\mathtt{AG}}_4\left({ }^{\mathtt{F}}{\rm Y}(\tau ,\frac{\overrightarrow{{\mathfrak{S}}_1}\overrightarrow{\varphi }}{\frac{\Theta }{1-\Theta {\ell }_1}})\right)⨀{\mathtt{AG}}_4\left({ }^{\mathtt{R}}{\rm Y}(\tau ,\frac{\overrightarrow{{\mathfrak{S}}_2}\overrightarrow{\psi }}{\frac{\Theta }{1-\Theta {\ell }_2}})\right),\hfill \end{array}$$

where

$$\Theta :=2max\{\frac{1-C_{*}}{\rho \left(C_{*}\right)},\frac{D^{C_{*}}}{\rho \left(C_{*}\right)\Gamma \left(C_{*}\right)}\}.$$

(28)

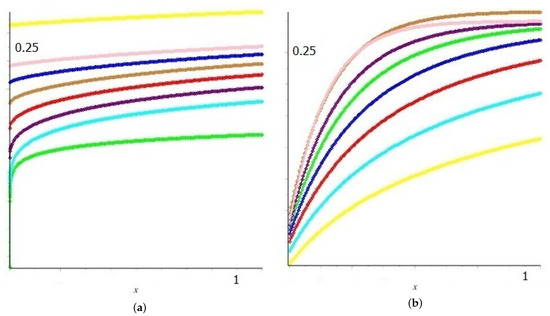
The plots of special functions given in the the main diagonal of square matrix ${ }^{\mathtt{F}}{\rm Y}(\tau ,\overrightarrow{\varphi })$ are displayed in Figure 2a, where the diagrams of the Wright function and the Fox $\mathbb{H}$-function are displayed in green and yellow colors, and the rest are in between. Similarly, the plots of special functions given in the the main diagonal of square matrix ${ }^{\mathtt{R}}{\rm Y}(\tau ,\overrightarrow{\psi })$ are displayed in Figure 2b, where the diagrams of one-parameter Mittag–Leffler function and eight-parameter Mittag–Leffler function are displayed in brown and yellow colors, and the rest are in between.

Figure 2. (a) displays the plots of special functions given in the the main diagonal of square matrix (14) where the diagrams of the Wright function and the Fox $\mathbb{H}$-function are displayed in green and yellow colors, and the rest are in between. Similarly, (b) displays the plots of special functions given in the the main diagonal of square matrix (15) where the diagrams of 1-parameter Mittag–Leffler function and 8-parameter Mittag–Leffler function are displayed in brown and yellow colors, and the rest are in between.

Thus, we have

$$\begin{array}{ccc}& & \Phi (\Xi \left(\tau \right)-\tilde{\Xi }\left(\tau \right),\overrightarrow{\varphi })⪰\widetilde{{ }_C^A{\mathbb{H}}_D^B}\left[\frac{-{\left|\tau \right|}^{{\mathcal{P}}_1}}{D_1{\mathfrak{S}}_{18}{\varphi }_8}|{ }_{{(N_j,M_j)}_{1,D}}^{{(V_j,W_j)}_{1,C}}\right]\hfill \\ & & {\Psi }_{\Xi \left(\tau \right)-\tilde{\Xi }\left(\tau \right)}\left(\overrightarrow{\psi }\right)⪰{\tilde{\mathbb{M}}}_{\alpha ,\tau ;N_1,M_1}^{V_1,W_1;V_2,V_2}\left(\frac{-{\left|\tau \right|}^{{\mathcal{P}}_1}}{D_2{\mathfrak{S}}_{28}{\psi }_8}\right)\hfill \\ & & \Phi (\Xi \left(\tau \right)-\tilde{\Xi }\left(\tau \right),\overrightarrow{\varphi })⨀{\Psi }_{\Xi \left(\tau \right)-\tilde{\Xi }\left(\tau \right)}\left(\overrightarrow{\psi }\right)\hfill \\ & & ⪰\widetilde{{ }_C^A{\mathbb{H}}_D^B}\left[\frac{-{\left|\tau \right|}^{{\mathcal{P}}_1}}{D_1{\mathfrak{S}}_{18}{\varphi }_8}|{ }_{{(N_j,M_j)}_{1,D}}^{{(V_j,W_j)}_{1,C}}\right]⨀{\tilde{\mathbb{M}}}_{\alpha ,\tau ;N_1,M_1}^{V_1,W_1;V_2,V_2}\left(\frac{-{\left|\tau \right|}^{{\mathcal{P}}_1}}{D_2{\mathfrak{S}}_{28}{\psi }_8}\right).\hfill \end{array}$$

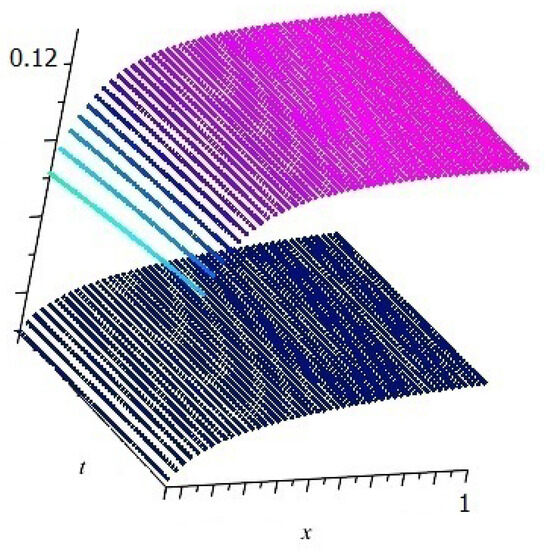
The plots of ${ }_C^A{\mathbb{H}}_D^B\left[\frac{-{\left|\tau \right|}^{{\mathcal{P}}_1}}{{\varphi }_8}|{ }_{{(N_j,M_j)}_{1,D}}^{{(V_j,W_j)}_{1,C}}\right]$ (the bottom chart) and ${\mathbb{M}}_{\alpha ,\tau ;N_1,M_1}^{V_1,W_1;V_2,V_2}\left(\frac{-{\left|\tau \right|}^{{\mathcal{P}}_1}}{{\psi }_8}\right)$ (the above chart) are displayed in Figure 3. Now, we obtain

$$\begin{array}{ccc}& & \Phi (\Xi \left(\tau \right)-\tilde{\Xi }\left(\tau \right),\overrightarrow{\varphi })⨀{\Psi }_{\Xi \left(\tau \right)-\tilde{\Xi }\left(\tau \right)}\left(\overrightarrow{\psi }\right)\hfill \\ & & ⪰\widetilde{{ }_C^A{\mathbb{H}}_D^B}\left[\frac{-{\left|\tau \right|}^{{\mathcal{P}}_1}}{max\{D_1{\mathfrak{S}}_{18}{\varphi }_8,D_2{\mathfrak{S}}_{28}{\psi }_8\}}|{ }_{{(N_j,M_j)}_{1,D}}^{{(V_j,W_j)}_{1,C}}\right].\hfill \end{array}$$

□

Figure 3. The plots of ${ }_C^A{\mathbb{H}}_D^B\left[\frac{-{\left|\tau \right|}^{{\mathcal{P}}_1}}{{\varphi }_8}|{ }_{{(N_j,M_j)}_{1,D}}^{{(V_j,W_j)}_{1,C}}\right]$ (the bottom chart) and ${\mathbb{M}}_{\alpha ,\tau ;N_1,M_1}^{V_1,W_1;V_2,V_2}\left(\frac{-{\left|\tau \right|}^{{\mathcal{P}}_1}}{{\psi }_8}\right)$ (the above chart).

4. A New Optimal Method for a Smoke Epidemic Model in Banach Spaces

In [16], the authors applied the Krasnoselskii-type fixed point theorem to study the existence, uniqueness, and UHR stability of (11) in Banach spaces. We study the existence, uniqueness, and UHR stability of the governing model using the Cadariu–Radu method derived from an alternative fixed point theorem. By comparing methods, we conclude that our method provides an optimal solution with the same error value obtained through the Krasnoselskii-type fixed point theorem.

We let the Banach space be $\mathbf{B}=C[0,D],D>0$ and let

$$\parallel \Xi \parallel =\underset{\tau \in [0,D]}{max}\left\{\right|\Xi \left(\tau \right)\left|\right\},\forall \Xi \in \mathbf{B}.$$

Now, we assume the following for $\tau \in [0,D]$:

(ı)

There is $\mho ,\Omega >0$ and $0\le \mathbb{k}<1$ such that $\Lambda (\tau ,\Xi \left(\tau \right))\le {\Omega |\Xi |}^{\mathbb{k}}+\mho .$

(ıı)

There is $\ell >0$ such that $|\Lambda (\tau ,\Xi \left(\tau \right))-\Lambda (\tau ,\tilde{\Xi }\left(\tau \right))|\le \ell |\Xi \left(\tau \right)-\tilde{\Xi }\left(\tau \right)|.$

We consider operator $\mathcal{L}:\mathbf{B}⟶\mathbf{B}$ such that

$$\begin{array}{ccc}\hfill & & \mathcal{L}\Xi \left(\tau \right)={\varpi }_1\Xi \left(\tau \right)+{\varpi }_2\Xi \left(\tau \right),\hfill \\ & & {\varpi }_1\Xi \left(\tau \right)={\Xi }_0+{\displaystyle \frac{1-C_{*}}{\rho \left(C_{*}\right)}}\Lambda (\tau ,\Xi \left(\tau \right)),\hfill \\ & & {\varpi }_2\Xi \left(\tau \right)={\displaystyle \frac{C_{*}}{\rho \left(C_{*}\right)\Gamma \left(C_{*}\right)}}{\int }_0^{\tau }\Lambda (s,\Xi \left(s\right)){(\tau -s)}^{C_{*}-1}ds.\hfill \end{array}$$

(29)

According to (21) and (29), we have

$$\begin{array}{c}\hfill \mathcal{L}\Xi \left(\tau \right)={\Xi }_0\left(\tau \right)+{\displaystyle \frac{1-C_{*}}{\rho \left(C_{*}\right)}}\Lambda (\tau ,\Xi \left(\tau \right))+{\displaystyle \frac{C_{*}}{\rho \left(C_{*}\right)\Gamma \left(C_{*}\right)}}{\int }_0^{\tau }\Lambda (s,\Xi \left(s\right)){(\tau -s)}^{C_{*}-1}ds.\end{array}$$

(30)

4.1. The Krassnoselskii Fixed Point Theorem

Lemma 1

([16]). Consider Banach space $\top =C\left(\right[o,D\left]\right)$ with norm $\parallel \Xi \parallel ={max}_{\tau \in [0,D]}\left\{\right|\Xi \left|\right\},$ for any $\Xi \in \top .$ Assume $\varnothing \ne B\subset \top$ is a closed convex subset of ⊤ and there are operators ${⋔}_1$ and ${⋔}_2$ with

(1) 

${⋔}_{1}e+{⋔}_{2}e,\forall e\in \top ,$

(2) 

${⋔}_1$ is compact and continuous and ${⋔}_2$ is a contraction operator.

Thus, there is solution $e\in \top$ such that ${⋔}_{1}e+{⋔}_{2}e=e.$

Theorem 3.

Consider assumptions $\left(ı\right)$ and $\left(ıı\right)$ with ${\displaystyle \frac{1-C_{*}}{\rho \left(C_{*}\right)}}\ell <1.$ Then, (11) has at least one solution.

Proof. 

First, we prove ${\varpi }_1$ is a contraction. We assume $\tilde{\Xi }\in ⅁$ and $⅁=\{\Xi \in \mathbf{B}:\parallel \Xi \parallel \le \phi ,$$\phi >0\}$ which is a closed convex set. Now, we have

$$\begin{array}{ccc}\hfill |{\varpi }_1\Xi \left(\tau \right)-{\varpi }_2\Xi \left(\tau \right)|& =& {\displaystyle \frac{1-C_{*}}{\rho \left(C_{*}\right)}}\underset{C_{*}\in [0,D]}{max}|\Lambda (\tau ,\Xi \left(\tau \right))-\Lambda (\tau ,\tilde{\Xi }\left(\tau \right))|\hfill \\ & \le & {\displaystyle \frac{1-C_{*}}{\rho \left(C_{*}\right)}}\ell |\Xi \left(\tau \right)-\tilde{\Xi }\left(\tau \right)|.\hfill \end{array}$$

(31)

Thus,

$$\begin{array}{c}\hfill \parallel {\varpi }_1\Xi -{\varpi }_2\Xi \parallel \le {\displaystyle \frac{1-C_{*}}{\rho \left(C_{*}\right)}}\ell \parallel \Xi -\tilde{\Xi }\parallel .\end{array}$$

Therefore, ${\varpi }_1$ is a contraction since ${\displaystyle \frac{1-C_{*}}{\rho \left(C_{*}\right)}}\ell <1.$

We now prove ${\varpi }_2(\Xi )$ is compact and continuous for any $\Xi \in ⅁;$ then,

$$\begin{array}{ccc}\hfill \parallel {\varpi }_2(\Xi )\parallel & =& \underset{\tau \in [0,D]}{max}|{\displaystyle \frac{C_{*}}{\rho \left(C_{*}\right)\Gamma \left(C_{*}\right)}}{\int }_0^{\tau }\Lambda (s,\Xi \left(s\right)){(\tau -s)}^{C_{*}-1}ds|\hfill \\ & \le & {\displaystyle \frac{C_{*}}{\rho \left(C_{*}\right)\Gamma \left(C_{*}\right)}}{\int }_0^D{|(D-s)}^{C_{*}-1}\left|\right|\Lambda (s,\Xi \left(s\right))|ds\hfill \\ & \le & {\displaystyle \frac{D^{C_{*}}}{\rho \left(C_{*}\right)\Gamma \left(C_{*}\right)}}{[\Omega +|\Xi |}^{\mathbb{k}}+\mho ].\hfill \end{array}$$

Thus, ${\varpi }_2$ is bounded. We assume ${\tau }_1,{\tau }_2\in [0,D];$ then, we have

$$\begin{array}{ccc}& & |({\varpi }_2\Xi )\left({\tau }_1\right)-{\varpi }_2\Xi )\left({\tau }_2\right)|\hfill \\ & =& \left|{\displaystyle \frac{C_{*}}{\rho \left(C_{*}\right)\Gamma \left(C_{*}\right)}}\right||{\int }_0^{{\tau }_1}\Lambda (s,\Xi \left(s\right)){({\tau }_1-s)}^{C_{*}-1}ds-{\int }_0^{{\tau }_2}\Lambda (s,\Xi \left(s\right)){({\tau }_2-s)}^{C_{*}-1}ds|\hfill \\ & \le & {\displaystyle \frac{{\Omega |\Xi |}^{\mathbb{k}}+\mho }{\rho \left(C_{*}\right)\Gamma \left(C_{*}\right)}}[{\tau }_1^{C_{*}}-{\tau }_2^{C_{*}}].\hfill \end{array}$$

As ${\tau }_1⟶{\tau }_2,$ $|({\varpi }_2\Xi )\left({\tau }_1\right)-{\varpi }_2\Xi )\left({\tau }_2\right)|⟶0.$ Thus, according to the Arzela–Ascoli theorem, ${\varpi }_2$ is compact and equicontinuous. Therefore, based on Lemma 1, System (11) has at least one solution. □

Theorem 4.

Consider constant $A>0,$ with $A:=\left[\frac{1-C_{*}}{\rho \left(C_{*}\right)}\ell +\frac{D^{C_{*}}}{\rho \left(C_{*}\right)\Gamma \left(C_{*}\right)}\ell \right]<1.$ Then, operator $\mathcal{L}$ has a unique fixed point.

Proof. 

We assume $\Xi ,\widehat{\Xi }\in \mathbf{B}$. Then,

$$\begin{array}{ccc}& & \parallel \mathcal{L}\Xi -\mathcal{L}\widehat{\Xi }\parallel \hfill \\ & & \le \parallel {\varpi }_1\Xi -{\varpi }_1\widehat{\Xi }\parallel + \parallel {\varpi }_2\Xi -{\varpi }_2\widehat{\Xi }\parallel \hfill \\ & & \le {\displaystyle \frac{1-C_{*}}{\rho \left(C_{*}\right)}}\underset{C_{*}\in [0,D]}{max}|\Lambda (\tau ,\Xi \left(\tau \right))-\Lambda (\tau ,\widehat{\Xi }\left(\tau \right))|\hfill \\ & & +{\displaystyle \frac{C_{*}}{\rho \left(C_{*}\right)\Gamma \left(C_{*}\right)}}\underset{C_{*}\in [0,D]}{max}|{\int }_0^{\tau }\Lambda (s,\Xi \left(s\right)){(\tau -s)}^{C_{*}-1}ds-{\int }_0^{\tau }\Lambda (s,\widehat{\Xi }\left(s\right)){(\tau -s)}^{C_{*}-1}ds|\hfill \\ & & \le \left[\frac{1-C_{*}}{\rho \left(C_{*}\right)}\ell +\frac{D^{C_{*}}}{\rho \left(C_{*}\right)\Gamma \left(C_{*}\right)}\ell \right]\parallel \Xi -\widehat{\Xi }\parallel \hfill \\ & & =A\parallel \Xi -\widehat{\Xi }\parallel .\hfill \end{array}$$

(32)

Therefore, based on the contraction principle, the operator has a unique fixed point. □

Definition 4

([26]). System (11) is UHR stable with respect to $\vee \in C\left(\right[0,D],\mathbb{R})$ if there exists $\mathbb{k}>0$ such that for all $϶>0$ and any solution $\Xi \in \mathbf{B}$ to the following inequality,

$$\begin{array}{c}\hfill D_{\tau }^{C_{*}}\Xi \left(\tau \right)-\Lambda (\tau ,\Xi \left(\tau \right))\le \vee \left(\tau \right)϶,\forall \tau \in [0,D],\end{array}$$

(33)

there exists solution $\widehat{\Xi }$ to (11) with

$$\begin{array}{c}\hfill |\Xi \left(\tau \right)-\widehat{\Xi }\left(\tau \right)|\le \mathbb{k}\vee \left(\tau \right)϶,\forall \tau \in [0,D].\end{array}$$

(34)

Remark 1.

Sunction $\Xi \in \mathbf{B}$ is a solution of (33) if and only if there exists function $⋋\left(\tau \right)\in C\left(\right[0,D];\mathbb{R})$ (which depends on Ξ) such that

(1)$|⋋(\tau \left)\right|\le \vee \left(\tau \right)϶,\forall \tau \in [0,D],$

(2) $D_{\tau }^{C_{*}}\Xi \left(\tau \right)=\Lambda (\tau ,\Xi \left(\tau \right))+⋋\left(\tau \right),\forall \tau \in [0,D].$

Lemma 2.

We consider the fractional-order system below,

$$\begin{array}{ccc}\hfill & & D_{\tau }^{C_{*}}\Xi \left(\tau \right)=\Lambda (\tau ,\Xi \left(\tau \right))+⋋\left(\tau \right),\tau \in [0,D],\hfill \\ & & \Xi \left(0\right)={\Xi }_0.\hfill \end{array}$$

(35)

Then, for $\tau \in [0,D],$ we obtain

$$\begin{array}{c}\hfill |\Xi \left(\tau \right)-\mathcal{L}\Lambda (\tau ,\Xi \left(\tau \right))|\le \left[\frac{1-C_{*}}{\rho \left(C_{*}\right)}+\frac{D^{C_{*}}}{\rho \left(C_{*}\right)\Gamma \left(C_{*}\right)}\right]\vee \left(\tau \right)϶.\end{array}$$

Proof. 

According to Lemma 2.4 in [16], the solution of (35) is given by

$$\Xi \left(\tau \right)={\Xi }_0+I_{\tau }^{C_{*}}\Lambda (\tau ,\Xi \left(\tau \right))+I_{\tau }^{C_{*}}⋋\left(\tau \right).$$

Now, based on (30), we have

$$\begin{array}{ccc}& & |\Xi (\tau )-\mathcal{L}\Lambda (\tau ,\Xi \left(\tau \right)\left)\right|\hfill \\ & & \le \left[{\displaystyle \frac{1-C_{*}}{\rho \left(C_{*}\right)}}|⋋\left(\tau \right)|+{\displaystyle \frac{D^{C_{*}}}{\rho \left(C_{*}\right)\Gamma \left(C_{*}\right)}}{\int }_0^{\tau }{(\tau -s)}^{1-C_{*}}|⋋\left(\tau \right)|ds\right]\hfill \\ & & \le \left[{\displaystyle \frac{1-C_{*}}{\rho \left(C_{*}\right)}}+{\displaystyle \frac{D^{C_{*}}}{\rho \left(C_{*}\right)\Gamma \left(C_{*}\right)}}\right]\vee \left(\tau \right)϶.\hfill \end{array}$$

□

Theorem 5.

System (11) has UHR stability if $A:=\left[{\displaystyle \frac{1-C_{*}}{\rho \left(C_{*}\right)}}+{\displaystyle \frac{D^{C_{*}}}{\rho \left(C_{*}\right)\Gamma \left(C_{*}\right)}}\right]\ell <1.$

Proof. 

We suppose $\Xi \in \mathbf{B}$ is any solution and $\widehat{\Xi }\in \mathbf{B}$ is the unique solution of (11) (see Theorem 4); then, for $\tau \in [0,D]$, we obtain

$$\begin{array}{ccc}& & |\Xi \left(\tau \right)-\widehat{\Xi }\left(\tau \right)|\hfill \\ & & =|\Xi \left(\tau \right)-\mathcal{L}\widehat{\Xi }\left(\tau \right)|\hfill \\ & & \le |\Xi \left(\tau \right)-\mathcal{L}\Xi \left(\tau \right)|+|\mathcal{L}\Xi \left(\tau \right)-\mathcal{L}\widehat{\Xi }\left(\tau \right)|\hfill \\ & & \le \left[{\displaystyle \frac{1-C_{*}}{\rho \left(C_{*}\right)}}+{\displaystyle \frac{D^{C_{*}}}{\rho \left(C_{*}\right)\Gamma \left(C_{*}\right)}}\right]\vee \left(\tau \right)϶+\left[{\displaystyle \frac{1-C_{*}}{\rho \left(C_{*}\right)}}+{\displaystyle \frac{D^{C_{*}}}{\rho \left(C_{*}\right)\Gamma \left(C_{*}\right)}}\right]\ell |\Xi \left(\tau \right)-\widehat{\Xi }\left(\tau \right)|\hfill \\ & & \le {\displaystyle \frac{\left[{\displaystyle \frac{1-C_{*}}{\rho \left(C_{*}\right)}}+{\displaystyle \frac{D^{C_{*}}}{\rho \left(C_{*}\right)\Gamma \left(C_{*}\right)}}\right]}{1-\left[{\displaystyle \frac{1-C_{*}}{\rho \left(C_{*}\right)}}+{\displaystyle \frac{D^{C_{*}}}{\rho \left(C_{*}\right)\Gamma \left(C_{*}\right)}}\right]\ell }}\vee \left(\tau \right)϶.\hfill \end{array}$$

Now, making use of Definition 4, we conclude that (11) is UHR stable. □

4.2. The Cădariu–Radu Method

Here, we study the existence, uniqueness, and UHR stability of System (11) using the Cădariu–Radu method derived from an alternative fixed point Theorem 1 (see [26]).

Theorem 6.

Consider the following inequality:

$$\begin{array}{c}\hfill |D_{\tau }^{C_{*}}\Xi \left(\tau \right)-\Lambda (\tau ,\Xi \left(\tau \right))|\le \vee \left(\tau \right),\Xi \left(\tau \right)\in \mathbf{B},\end{array}$$

(36)

where $\vee \in C\left(\right[0,D],\mathbb{R})$ is a control function. Assume $\left[{\displaystyle \frac{1-C_{*}}{\rho \left(C_{*}\right)}}+{\displaystyle \frac{D^{C_{*}}}{\rho \left(C_{*}\right)\Gamma \left(C_{*}\right)}}\right]\ell <1,$ where $\ell >0.$ Then, there exists a unique $\widehat{\Xi }\in \mathbf{B},$ with

$$\begin{array}{c}\hfill \widehat{\Xi }\left(\tau \right)={\Xi }_0+I_{\tau }^{C^{*}}\Lambda (\tau ,\widehat{\Xi }\left(\tau \right)),\end{array}$$

(37)

and

$$\begin{array}{c}\hfill |\Xi \left(\tau \right)-\widehat{\Xi }\left(\tau \right)|\le {\displaystyle \frac{\left[{\displaystyle \frac{1-C_{*}}{\rho \left(C_{*}\right)}}+{\displaystyle \frac{D^{C_{*}}}{\rho \left(C_{*}\right)\Gamma \left(C_{*}\right)}}\right]}{1-\left[{\displaystyle \frac{1-C_{*}}{\rho \left(C_{*}\right)}}+{\displaystyle \frac{D^{C_{*}}}{\rho \left(C_{*}\right)\Gamma \left(C_{*}\right)}}\right]\ell }}\vee \left(\tau \right).\end{array}$$

(38)

Proof. 

We consider mapping $d:\mathbf{B}⟶[0,\infty ]$ defined by

$$\begin{array}{c}\hfill d(\Xi \left(\tau \right),\widehat{\Xi }\left(\tau \right))=\inf \left\{\Omega \ge 0:|\Xi \left(\tau \right)-\widehat{\Xi }\left(\tau \right)|\le \Omega \vee \left(\tau \right),\tau \in [0,D]\right\}.\end{array}$$

(39)

Now, we define $\mathcal{L}:\mathbf{B}⟶\mathbf{B}$ as

$$\begin{array}{c}\hfill \mathcal{L}\Xi \left(\tau \right)={\Xi }_0\left(\tau \right)+{\displaystyle \frac{1-C_{*}}{\rho \left(C_{*}\right)}}\Lambda (\tau ,\Xi \left(\tau \right))+{\displaystyle \frac{C_{*}}{\rho \left(C_{*}\right)\Gamma \left(C_{*}\right)}}{\int }_0^{\tau }\Lambda (s,\Xi \left(s\right)){(\tau -s)}^{C_{*}-1}ds.\end{array}$$

(40)

According to the previous subsection, we see that $\mathfrak{S}$ is contractive on $\mathbf{B},$ i.e., for any $\tau \in [0,D],$ we have

$$\begin{array}{ccc}& & |\mathcal{L}\Xi \left(\tau \right)-\mathcal{L}\widehat{\Xi }\left(\tau \right)|\hfill \\ & \le & \left[{\displaystyle \frac{1-C_{*}}{\rho \left(C_{*}\right)}}+{\displaystyle \frac{D^{C_{*}}}{\rho \left(C_{*}\right)\Gamma \left(C_{*}\right)}}\right]\ell |\Xi \left(\tau \right)-\widehat{\Xi }\left(\tau \right)|.\hfill \end{array}$$

Then, we deduce the contraction property of $\mathcal{L}$, since $\left[{\displaystyle \frac{1-C_{*}}{\rho \left(C_{*}\right)}}+{\displaystyle \frac{D^{C_{*}}}{\rho \left(C_{*}\right)\Gamma \left(C_{*}\right)}}\right]\ell <1.$

Again using the previous subsection, we obtain

$$\begin{array}{c}\hfill |\Xi \left(\tau \right)-\mathcal{L}\Xi \left(\tau \right)|\le \left[{\displaystyle \frac{1-C_{*}}{\rho \left(C_{*}\right)}}+{\displaystyle \frac{D^{C_{*}}}{\rho \left(C_{*}\right)\Gamma \left(C_{*}\right)}}\right]\vee \left(\tau \right),\tau \in [0,D].\end{array}$$

(41)

Thus, the assumptions of Theorem 1 are satisfied, and we obtain

$$\begin{array}{c}\hfill |\Xi \left(\tau \right)-\widehat{\Xi }\left(\tau \right)|\le {\displaystyle \frac{\left[{\displaystyle \frac{1-C_{*}}{\rho \left(C_{*}\right)}}+{\displaystyle \frac{D^{C_{*}}}{\rho \left(C_{*}\right)\Gamma \left(C_{*}\right)}}\right]}{1-\left[{\displaystyle \frac{1-C_{*}}{\rho \left(C_{*}\right)}}+{\displaystyle \frac{D^{C_{*}}}{\rho \left(C_{*}\right)\Gamma \left(C_{*}\right)}}\right]\ell }}\vee \left(\tau \right),\tau \in [0,D],\end{array}$$

(42)

where $\widehat{\Xi }\left(\tau \right)={\Xi }_0+I_{\tau }^{C^{*}}\Lambda (\tau ,\widehat{\Xi }\left(\tau \right)),$ is the unique solution in $\left\{\upsilon \in \mathbf{B}:d(\mathcal{L}\widehat{\Xi },\upsilon )<\infty \right\}.$ □

4.3. Discussion

The concept of fractional derivative is more than three thousand years old. The role of fractional calculus has been increasing due to its application zone in diverse domains like laser propagation, energy quantization, semiconductor industry, wave propagation, biology, optical communication, quantum chemistry, etc. The fractional derivative of ABC uses the Mittag–Leffler function to consider random fuzzy models with uncertain constraint conditions [27,28,29,30,31]. An analysis method is used to consider the best decision on the stability of the smoking epidemic model by using a new class of controllers powered by special functions. Under some special conditions, we compared the findings of our study with the obtained results in [16] and we concluded that our method provides an optimal solution with the same error value obtained through the Krasnoselskii-type fixed point theorem [16]. Our technique offers a constructive process to obtain our fixed points.

5. Conclusions

We applied fuzzy random systems, the probability theory, and the concept of Z-numbers to make the best decision on the Ulam stability of the smoking epidemic model by using a new class of controllers powered by special functions and aggregation maps. Effective generalization of Ulam-type stability problems and evaluation of optimal controllability and maximal stability are new issues. There exist different methods to the Ulam-type stability using diverse tools, for instance, Laplace transforms, invariant means, shadowing, sandwich ideas, and Fourier transforms [32,33,34,35]. In this paper, we used a fixed point argument to consider stability. We compared our results with the obtained results in [16] and we concluded that our method provides an optimal solution with the same error value obtained through the methods used in [16].