Poncelet Porisms and Loci of Centers in the Isotropic Plane

Abstract

Any triangle in an isotropic plane has a circumcircle u and incircle i. It turns out that there are infinitely many triangles with the same circumcircle u and incircle i. This one-parameter family of triangles is called a poristic system of triangles. We study the trace of the centroid, the Feuerbach point, the symmedian point, the Gergonne point, the Steiner point and the Brocard points for such a system of triangles. We also study the traces of some further points associated with the triangles of the poristic family, and we prove that the vertices of the contact triangle, tangential triangle and anticomplementary triangle move on circles while the initial triangle traverses the poristic family.

1. Introduction

A porism is a theorem about a closure property of a geometric figure or construction, as explained in [1] (pp. 412–417). A well-known example comes from the elementary triangle geometry. Any triangle in the Euclidean plane has a circumcircle u and incircle i. It turns out that there are infinitely many triangles with the same circumcircle u and incircle i. In other words, if we pick a point $P_1$ on u and draw a tangent $t_1$ from $P_1$ to i, then $t_1$ intersects u in points $P_2$ and $P_1$. Now, we draw a tangent $t_2\ne t_1$ from $P_2$ to i that intersects u in $P_3$ and $P_2$. Finally, we draw a tangent $t_3\ne t_2$ from $P_3$ to i that intersects u in $P_4$ and $P_3$. It turns out that $P_4=P_1$. The one-parameter family of triangles with a common incircle and a common circumcircle is usually called a porisitic system of triangles. In the Euclidean plane, the poristic family of triangles interscribed in between the incircle and the circumcircle is called Chapple’s porism. The fact that such families exist even in some non-Euclidean planes is due to the projective nature of the problem. Hence, it is not necessary to prove the existence of a closed triangular path between two isotropic circles (Euclidean parabolas with parallel axes). Nevertheless, in Section 3.1, in order to obtain a parametrization of the poristic family, we offer the proof that the described property is also valid in an isotropic plane.

In [2], the author showed that many triangle centers move on circles while the triangle traces the poristic family. Some centers move on conics, and some centers move on curves of a higher degree. In this paper, in Section 3.2, we study the loci of some triangle centers in the isotropic plane. A further investigation of the loci of triangle centers in the Euclidean plane is given in [3], where the authors studied a poristic family defined by two confocal ellipses.

In Section 3.3, we study the traces of the vertices of the contact triangle, tangential triangle and anticomplementary triangle associated with the triangle of the poristic family in the isotropic plane.

2. Methods

An isotropic plane is a projective plane with a distinct line f and a distinct point $F\in f$. Lines incident with the absolute point F are called isotropic lines, and points incident with the absolute line f are called isotropic points. Two lines are said to be parallel if their intersection point is an isotropic point, while two points are said to be parallel if they are joined by an isotropic line.

The basic facts about the isotropic plane can be found in [4]. Here, we highlight the ones that are important for our study.

The standard affine model of the isotropic plane, where the coordinates of points are given by $x={\displaystyle \frac{x_1}{x_0}}$ and $y={\displaystyle \frac{x_2}{x_0}}$, is obtained by setting $f:x_0=0$ and $F=(0,0,1)$. In this model, the isotropic lines have equations of the form $x=c$ with $c\in \mathbb{R}$. The isotropic distance $d(P,Q)$ of a pair of two non-parallel points $P=(x_P,y_P)$ and $Q=(x_Q,y_Q)$ is defined by $d(P,Q)=x_Q-x_P$, while two non-parallel lines p and q, given by the equations $y=k_{p}x+l_p$ and $y=k_{q}x+l_q$, respectively, form the isotropic angle defined by $\angle (p,q)=k_q-k_p$. The midpoint of points P and Q is defined in a natural way as the point with coordinates $\left(\frac{1}{2}(x_P+x_Q),\frac{1}{2}(y_P+y_Q)\right)$, while the bisector of lines p and q is the line with the equation $y=\frac{1}{2}(k_p+k_q)x+\frac{1}{2}(l_p+l_q)$.

According to their position with respect to the absolute figure, conics are ellipses, hyperbolas, special hyperbolas, parabolas and circles, as explained in [4]. The most interesting conics for us are circles, conics that touch f at F.Therefore, a circle has an equation of the form $y=a{x}^2+bx+c$ with $a,b,c\in \mathbb{R}$.

A curve in the isotropic plane is said to be circular if it passes through the absolute point F. If the curve intersects f only at F, then it is entirely circular, as explained in [5]. Thus, circles are entirely circular conics.

It was shown in [6] that any allowable triangle $ABC$ (triangle whose sides are non-isotropic lines) in the isotropic plane can be set in the so-called standard position by choosing an appropriate affine coordinate system and having the circumcircle u with the equation

$$u\cdots y=x^2,$$

(1)

and vertices

$$A=(a,a^2),B=(b,b^2),C=(c,c^2),$$

(2)

with $a+b+c=0$.

Let ${\sigma }_1$, ${\sigma }_2$ and ${\sigma }_3$ be elementary symmetric functions in three variables a, b and c; in other words, let

$${\sigma }_1=a+b+c=0,{\sigma }_2=ab+bc+ca,{\sigma }_3=abc.$$

(3)

The centroid, the symmedian point, the Gergonne point, the Feuerbach point and the Steiner point of the triangle $ABC$ are labeled $X_2$, $X_6$, $X_7$, $X_{11}$ and $X_{99}$, respectively, according to Kimberling’s encyclopedia [7].

The coordinates of the centroid $X_2$ of the triangle $ABC$ are

$$X_2=\left(\frac{a+b+c}{3},\frac{a^2+b^2+c^2}{3}\right)=\left(0,-\frac{2}{3}{\sigma }_2\right).$$

(4)

It was shown in [8] that the incircle i

$$i\cdots y=\frac{1}{4}{x}^2-{\sigma }_2$$

(5)

and the Euler circle

$$e\cdots y=-2x^2-{\sigma }_2$$

(6)

touch each other externally at the Feuerbach point

$$X_{11}=\left(0,-{\sigma }_2\right).$$

(7)

The symmedians are the reflections of medians in the bisectors. According to [9], they intersect at the symmedian point $X_6$ of the triangle $ABC$ having the coordinates

$$X_6=\left(\frac{3{\sigma }_3}{2{\sigma }_2},-\frac{{\sigma }_2}{3}\right).$$

(8)

The Gergonne point $X_7$ of the triangle $ABC$ is the intersection point of three lines $A{A}_i$, $B{B}_i$ and $C{C}_i$, where $A_i$, $B_i$ and $C_i$ are the contact points of the triangle and its incircle i. In [10], the coordinates of the Gergonne point $X_7$ of the standard triangle $ABC$ were determined as follows:

$$X_7=\left(-\frac{3{\sigma }_3}{{\sigma }_2},-\frac{4{\sigma }_2}{3}\right).$$

(9)

The Steiner point $X_{99}$ of the triangle $ABC$ is defined as the fourth (in addition to A, B and C) common point $X_{99}$ of the circumscribed circle u and circumscribed Steiner ellipse of that triangle, as explained in [11]. In the case of the standard triangle $ABC$, this point has the coordinate vector

$$X_{99}=\left(-\frac{3{\sigma }_3}{{\sigma }_2},\frac{9{\sigma }_3^2}{{\sigma }_2^2}\right).$$

(10)

For every triangle in the isotropic plane, there is the first and the second Brocard point, and they are unique. The first Brocard point is defined as the point such that its connections with the vertices A, B and C form equal angles with the sides $AC$, $BA$ and $CB$, respectively. Analogously, the second Brocard point is defined as the point such that its connection lines with the vertices A, B and C form equal angles with the sides $AB$, $BC$ and $CA$, respectively. According to [12], the Brocard points $B_1$ and $B_2$ of the standard triangle are given by

$$B_1=\left(\frac{{\sigma }_3-p_1}{{\sigma }_2},\frac{3p_1^2}{{\sigma }_2^2}-\frac{2}{9}{\sigma }_2\right),B_2=\left(\frac{{\sigma }_3-p_2}{{\sigma }_2},\frac{3p_2^2}{{\sigma }_2^2}-\frac{2}{9}{\sigma }_2\right),$$

(11)

where

$$p_1=\frac{1}{3}\left(b{c}^2+c{a}^2+a{b}^2\right),p_2=\frac{1}{3}\left(b^{2}c+c^{2}a+a^{2}b\right).$$

(12)

In Section 3.2, we will show that in the isotropic plane, all triangles in a poristic system share the centroid and the Feuerbach point. The symmedian point and the Gergonne point of all triangles move on straight lines. The Steiner point traces a circle, while Brocard points trace a quartic curve.

3. Results

3.1. Poncelet’s Porism

In order to obtain an explicit parametrization of the poristic family, we assume that we are given a triangle $ABC$ with the vertices in Equation (2), a circumcircle u with Equation (1) and an incircle i with Equation (5). Let $P_1=(t,t^2)$ be a point on the circle u. The polar line p of $P_1$ with respect to i is

$$p\cdots -4{\sigma }_2-2t^2+tx-2y=0.$$

The intersections $C_2$ and $C_3$ of p and i are the points of contact of the tangents from $P_1$ to the incircle i:

$$C_2=\left(t+W,\frac{tW-t^2-4{\sigma }_2}{2}\right),C_3=\left(t-W,\frac{-tW-t^2-4{\sigma }_2}{2}\right),$$

where $W=\sqrt{-4{\sigma }_2-3t^2}$. Lines $P_1{C}_3$ and $P_1{C}_2$ intersect the circumcircle u at points $P_2$ and $P_3$, respectively:

$$P_2=\left(\frac{W-t}{2},\frac{-tW-t^2-2{\sigma }_2}{2}\right),P_3=\left(\frac{-W-t}{2},\frac{tW-t^2-2{\sigma }_2}{2}\right).$$

The connection line $P_2{P}_3$ has the equation

$$y=-tx-t^2-{\sigma }_2$$

and touches i at the point

$$C_1=\left(-2t,t^2-{\sigma }_2\right).$$

Thus, for any choice of the initial vertix $P_1$, the triangle $P_1{P}_2{P}_3$ closes (see Figure 1).

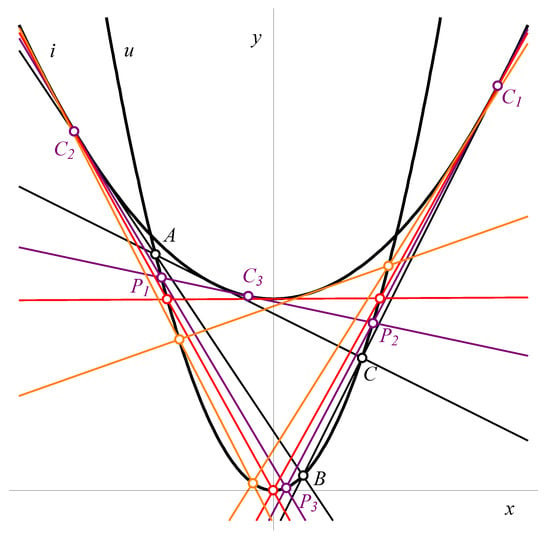
Figure 1. A porisitic system of triangles in the isotropic plane.

The triangles $ABC$ and $P_1{P}_2{P}_3$ share the centroid that has the coordinates

$$X_2=\frac{1}{3}\left(t+\frac{W-t}{2}+\frac{-W-t}{2},t^2+\frac{-tW-t^2-2{\sigma }_2}{2}+\frac{tW-t^2-2{\sigma }_2}{2}\right)=\left(0,-\frac{2}{3}{\sigma }_2\right).$$

(13)

It follows from Equation (13) that all triangles in the poristic system are in the standard position, and therefore, Equations (3)–(12) for $ABC$ can be applied to $P_1{P}_2{P}_3$. The points and values related to $P_1{P}_2{P}_3$ will be marked with a ★.

We should notice that all sides of the triangle $P_1{P}_2{P}_3$ will be real lines only if we chose the vertex $P_1$ as an outer of i, which is precisely the case when $t^2\le -\frac{4}{3}{\sigma }_2$, and hence $W\in \mathbb{R}$.

3.2. Loci of Centers in the Poristic System of Triangles

Let $P_1{P}_2{P}_3$ be a triangle from the poristic system with vertices

$$P_1=\left(t,t^2\right),P_2=\left(\frac{W-t}{2},\frac{-tW-t^2-2{\sigma }_2}{2}\right),P_3=\left(\frac{-W-t}{2},\frac{tW-t^2-2{\sigma }_2}{2}\right),$$

(14)

where $t\in \mathbb{R}$.

The elementary symmetric functions related to $P_1{P}_2{P}_3$ are

$$\begin{array}{ccc}\hfill {\sigma }_1^{★}& =& 0={\sigma }_1,\hfill \\ \hfill {\sigma }_2^{★}& =& t·\frac{W-t}{2}+\frac{W-t}{2}·\frac{-W-t}{2}+\frac{-W-t}{2}·t=\frac{-W^2-3t^2}{4}\hfill \\ & =& \frac{-(-4{\sigma }_2-3t^2)-3t^2}{4}={\sigma }_2,\hfill \\ \hfill {\sigma }_3^{★}& =& t·\frac{W-t}{2}·\frac{-W-t}{2}=-\frac{t}{4}\left(-4{\sigma }_2-4t^2\right)=t\left({\sigma }_2+t^2\right).\hfill \end{array}$$

(15)

Theorem 1. 

The centroid and the Feuerbach point of triangle $P_1{P}_2{P}_3$ are fixed while the triangle traces its poristic family.

Proof. 

We have already shown that $X_2^{★}=\left(0,-\frac{2}{3}{\sigma }_2^{★}\right)=\left(0,-\frac{2}{3}{\sigma }_2\right)=X_2.$ Similarly, $X_{11}^{★}=\left(0,-{\sigma }_2^{★}\right)=\left(0,-{\sigma }_2\right)=X_{11}.$ □

Theorem 2. 

The Gergonne point of triangle $P_1{P}_2{P}_3$ moves on a line while the triangle traverses the poristic family.

Proof. 

The Gergonne point $X_7^{★}$ of triangle $P_1{P}_2{P}_3$ has the coordinates $X_7^{★}=\left(-\frac{3{\sigma }_3^{★}}{{\sigma }_2^{★}},-\frac{4{\sigma }_2^{★}}{3}\right)=\left(-\frac{3t({\sigma }_2+t^2)}{{\sigma }_2},-\frac{4{\sigma }_2}{3}\right)$. Thus, the Gergonne points of all triangles from the poristic family lie on the line g with the equation

$$y=-\frac{4{\sigma }_2}{3},$$

the connection line of the intersections $\left(\pm \sqrt{-\frac{4}{3}{\sigma }_2},-\frac{4}{3}{\sigma }_2\right)$ of the incircle i and circumcircle u. □

Theorem 3. 

The symmedian point of triangle $P_1{P}_2{P}_3$ moves on a line if the triangle traverses the poristic family.

Proof. 

The symmedian point $X_6^{★}$ of triangle $P_1{P}_2{P}_3$ has the coordinates $X_6^{★}=\left(-\frac{3{\sigma }_3^{★}}{2{\sigma }_2^{★}},-\frac{{\sigma }_2^{★}}{3}\right)=\left(\frac{3t({\sigma }_2+t^2)}{2{\sigma }_2},-\frac{{\sigma }_2}{3}\right)$. Thus, the symmedian point of all triangles from the poristic family moves on the line k with the equation

$$y=-\frac{{\sigma }_2}{3},$$

the connection line of the intersections $\left(\pm \sqrt{-\frac{{\sigma }_2}{3}},-\frac{{\sigma }_2}{3}\right)$ of the circumcircle u and common Euler circle e given by Equation (6). □

Remark 1. 

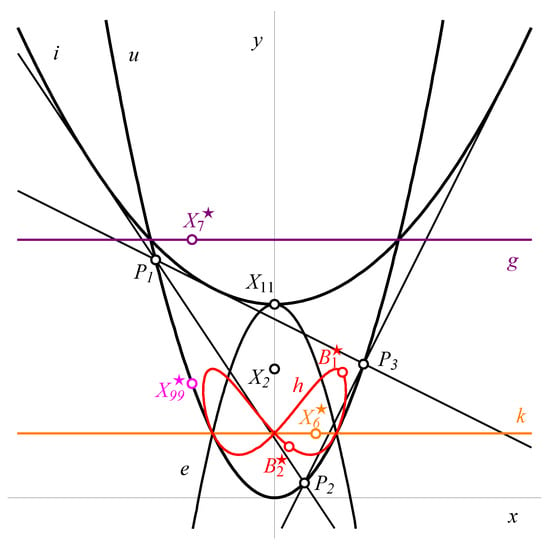
The locus of the Gergonne point and the locus of the symmedian point are parallel lines (see Figure 2).

Figure 2. The loci of the symmedian point, the Gergonne point and the Brocard points for a porisitic system of triangles in the isotropic plane. The centroid $X_2$ and the Feuerbach point $X_{11}$ are fixed points.

Theorem 4. 

The Steiner point of triangle $P_1{P}_2{P}_3$ moves on a circle when the triangle traverses the poristic family.

Proof. 

The statement follows trivially from the fact that the Steiner point of a triangle is the intersection point of the circumcircle and the Steiner ellipse of the triangle. The Steiner point $X_{99}^{★}=\left(-\frac{3{\sigma }_3^{★}}{{\sigma }_2^{★}},\frac{9{\sigma }_3^{★2}}{{\sigma }_2^{★2}}\right)=\left(-\frac{3t\left({\sigma }_2+t^2\right)}{{\sigma }_2},\frac{9t^2{\left({\sigma }_2+t^2\right)}^2}{{\sigma }_2^2}\right)$ of triangle $P_1{P}_2{P}_3$ obviously lies on the circle with the equation $y=x^2$ (i.e., the circumcircle u). □

Theorem 5. 

The Brocard points of triangle $P_1{P}_2{P}_3$ move on a quartic curve when the triangle traverses the poristic family.

Proof. 

Let $B_1^{★}$ be the first Brocard point of triangle $P_1{P}_2{P}_3$. Then, we have

$$B_1^{★}=\left(\frac{{\sigma }_3^{★}-p_1^{★}}{{\sigma }_2^{★}},\frac{3p_1^{★2}}{{\sigma }_2^{★2}}-\frac{2}{9}{\sigma }_2^{★}\right)=\left(\frac{t\left({\sigma }_2+t^2\right)-p_1^{★}}{{\sigma }_2},\frac{3p_1^{★2}}{{\sigma }_2^2}-\frac{2}{9}{\sigma }_2\right),$$

where

$$\begin{array}{ccc}\hfill p_1^{★}& =& \frac{1}{3}\left(\frac{W-t}{2}·\frac{{(-W-t)}^2}{4}+\frac{-W-t}{2}·t^2+t\frac{{(W-t)}^2}{4}\right)\hfill \\ & =& \frac{1}{24}\left(W(W^2-9t^2)+3t(W^2-t^2)\right)=-\frac{1}{6}\left(W({\sigma }_2+3t^2)+3t({\sigma }_2+t^2)\right)\hfill \end{array}$$

and

$$p_1^{★2}=\frac{1}{36}\left(-4{\sigma }_2^3-18{\sigma }_2^2{t}^2-36{\sigma }_2{t}^4-18t^6+6Wt({\sigma }_2^2+4{\sigma }_2{t}^2+3t^4)\right).$$

The coordinates of $B_1^{★}$ are therefore given by

$$\begin{array}{ccc}\hfill x& =& \frac{9t({\sigma }_2+t^2)+W({\sigma }_2+3t^2)}{6{\sigma }_2},\hfill \\ \hfill y& =& \frac{-3{\sigma }_2^2{t}^2-6{\sigma }_2{t}^4-3t^6+Wt({\sigma }_2^2+4{\sigma }_2{t}^2+3t^4)}{2{\sigma }_2^2}-\frac{5{\sigma }_2}{9}.\hfill \end{array}$$

After inserting $W=\sqrt{-4{\sigma }_2-3t^2}$ and eliminating the parameter t from the above equations, we obtain the equation of a quartic curve h:

$$9x^4-9x^{2}y+9y^2+6{\sigma }_{2}y+{\sigma }_2^2=0,$$

(16)

In other words, we have

$$9x^2(x^2-y)+{(3y+{\sigma }_2)}^2=0.$$

(17)

The same quartic curve h is obtained as the locus of the second Brocard points:

$$B_2^{★}=\left(\frac{9t({\sigma }_2+t^2)-W({\sigma }_2+3t^2)}{6{\sigma }_2},\frac{-3{\sigma }_2^2{t}^2-6{\sigma }_2{t}^4-3t^6-Wt({\sigma }_2^2+4{\sigma }_2{t}^2+3t^4)}{2{\sigma }_2^2}-\frac{5{\sigma }_2}{9}\right).$$

□

It follows from Equations (1) and (17) that the locus h of Brocard points touches the circumcircle u at two points: the intersections $\left(\pm \sqrt{-\frac{{\sigma }_2}{3}},-\frac{{\sigma }_2}{3}\right)$ of the circumcircle u and the Euler circle e.

Homogenizing $\left(x=\frac{x_1}{x_0},y=\frac{x_2}{x_0}\right)$ Equation (16) of h and setting $x_0=0$ yields the intersection with the absolute line f as $9x_1^4=0$. Thus, the absolute point F is the intersection point with an intersection multiplicity of four, and therefore, h is an entirely circular quartic.

3.3. Traces of Some Points

In [2], the author also studied the traces of some further points associated with triangles of the poristic family in the Eucildean plane. He showed that the trace of the midpoint of any side of a triangle traversing a poristic family is a Limaçon of Pascal and that the vertices of the tangential triangle of a triangle move on an ellipse. We will show that in the isotropic plane, both curves are isotropic circles.

We have already seen that while triangle $P_1{P}_2{P}_3$ traverses the poristic family, the midpoints of its sides trace the common Euler circle e, and the centroid is fixed. Now, we focus on the contact triangles and tangential triangles of the triangles from the poristic family (see Figure 3).

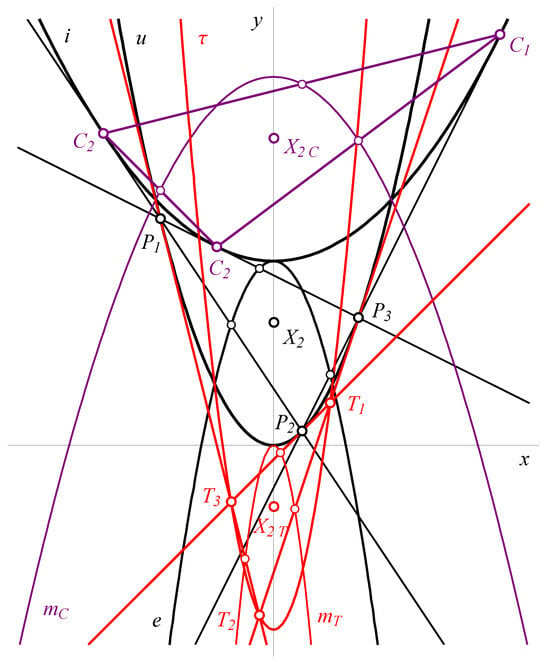
Figure 3. When triangle $P_1{P}_2{P}_3$ traverses the poristic family, the midpoints of its sides traverse a circle e (black). The midpoints of the sides of its contact triangle $C_1{C}_2{C}_3$ traverse a circle $m_C$, and the centroid $X_{2C}$ is fixed (purple). The vertices of the tangential triangle $T_1{T}_2{T}_3$ traverse a circle $\tau$, the midpoints of $T_1{T}_2{T}_3$ traverse a circle $m_T$, and the centroid $X_{2T}$ is fixed (red).

Theorem 6. 

The vertices of the contact triangle of triangle $P_1{P}_2{P}_3$ move on a circle while $P_1{P}_2{P}_3$ traverses the poristic family. The trace of the midpoint of any side of the contact triangle is a circle, and the centroid of the contact triangle is fixed.

Proof. 

The vertices $C_1$, $C_2$ and $C_3$ of the contact triangle of $P_1{P}_2{P}_3$ are in Section 3.1 and are determined as follows:

$$C_1=\left(-2t,t^2-{\sigma }_2\right),C_2=\left(t+W,\frac{tW-t^2-4{\sigma }_2}{2}\right),C_3=\left(t-W,\frac{-tW-t^2-4{\sigma }_2}{2}\right),$$

The midpoints of its sides are

$$\begin{array}{cc}& M_{C12}=\left(\frac{W-t}{2},\frac{tW+t^2-6{\sigma }_2}{4}\right),M_{C13}=\left(\frac{-W-t}{2},\frac{-tW+t^2-6{\sigma }_2}{4}\right),\\ & M_{C23}=\left(t,-\frac{t^2}{2}-2{\sigma }_2\right).\end{array}$$

The point $M_{C23}$ obviously traces the circle

$$m_C\cdots y=-\frac{x^2}{2}-2{\sigma }_2$$

(18)

and it can be easily checked that $M_{C12}$ and $M_{C13}$ lie on the same circle.

The centroid of triangle $C_1{C}_2{C}_3$ is $X_{2C}=\left(0,-\frac{5}{3}{\sigma }_2\right)$. □

Theorem 7. 

The vertices of the tangential triangle of triangle $P_1{P}_2{P}_3$ move on a circle while $P_1{P}_2{P}_3$ traverses the poristic family. The trace of the midpoint of any side of the tangential triangle is a circle, and the centroid of the tangential triangle is fixed.

Proof. 

The polar line of the point $\left(\overline{x},\overline{y}\right)$ with respect to the circle $y=x^2$ has the equation $y+\overline{y}=2\overline{x}x$. Therefore, the tangents to u at vertices $P_1$, $P_2$ and $P_3$ are given by the respective equations

$$\begin{array}{ccc}\hfill t_1& \cdots & y=2tx-t^2,\hfill \\ \hfill t_2& \cdots & y=(W-t)x-\frac{{(W-t)}^2}{4},\hfill \\ \hfill t_3& \cdots & y=(-W-t)x-\frac{{(W+t)}^2}{4}.\hfill \end{array}$$

The vertices $T_1=t_2\cap t_3$, $T_2=t_1\cap t_3$ and $T_3=t_1\cap t_2$ of the tangential triangle are

$$T_1=\left(-\frac{t}{2},\frac{t^2-W^2}{4}\right),T_2=\left(\frac{t-W}{4},\frac{-tW-t^2}{2}\right),T_3=\left(\frac{t+W}{4},\frac{tW-t^2}{2}\right).$$

The point $T_1$ traces the circle

$$\tau \cdots y=4x^2+{\sigma }_2$$

since $W^2=-4{\sigma }_2-3t^2$. $T_2$ and $T_3$ lie on the same circle. The midpoints of the sides of $T_1{T}_2{T}_3$ given by the coordinates

$$M_{T23}=\left(\frac{t}{4},-\frac{t^2}{2}\right),M_{T12}=\left(\frac{-t-W}{8},-\frac{{(t+W)}^2}{8}\right),M_{T13}=\left(\frac{-t+W}{8},-\frac{{(t-W)}^2}{8}\right).$$

trace the circle

$$m_T\cdots y=-8x^2.$$

The centroid of triangle $T_1{T}_2{T}_3$ is the point $X_{2T}=\left(0,\frac{{\sigma }_2}{3}\right)$. □

Remark 2. 

The centroid $X_2$ of triangle $P_1{P}_2{P}_3$, centroid $X_{2C}$ of the contact triangle $C_1{C}_2{C}_3$ and centroid $X_{2T}$ of the tangential triangle $T_1{T}_2{T}_3$ are parallel points.

Remark 3. 

The circle τ is polar to circle i with respect to circle u. Therefore, there is also a poristic family with u as the incircle and τ as the circumcircle.

Theorem 8. 

The vertices of the anticomplementary triangle of triangle $P_1{P}_2{P}_3$ move on a circle while $P_1{P}_2{P}_3$ traverses the poristic family. The centroid of the anticomplementary triangle is fixed.

Proof. 

The anticomplementary triangle $A_1{A}_2{A}_3$ is the triangle which has triangle $P_1{P}_2{P}_3$ as its medial triangle (i.e., it is formed by the lines through the vertices of $P_1{P}_2{P}_3$ parallel to its sides). It is in perspective with $P_1{P}_2{P}_3$ at centroid $X_2$, as explained in [6]. The vertices of the anticomplementary triangle are

$$A_1=\left(-2t,-2t^2-2{\sigma }_2\right),A_2=\left(t-W,tW+t^2\right),A_3=\left(t+W,-tW+t^2\right),$$

and they lie on the circle $m_C$ given by Equation (18). The triangle $P_1{P}_2{P}_3$ and its anticomplementary triangle $A_1{A}_2{A}_3$ share the centroid $X_2$. □

4. Discussion

Any triangle in the isotropic plane has a circumcircle u and incircle i. We showed that there are infinitely many triangles with the same circumcircle u and incircle i. We also proved that all triangles in a poristic system share a centroid and Feuerbach point. The symmedian point and the Gergonne point trace straight lines, the Steiner point traces a circle, and the Brocard points trace a quartic curve.

To make this study simpler, we put the initial triangle $ABC$ in the so-called standard position by choosing its vertices to be $(a,a^2)$, $(b,b^2)$ and $(c,c^2)$, with ${\sigma }_1=a+b+c=0$. Assuming that ${\sigma }_1\ne 0$, we would obtain the same results, but the calculations would be much more complicated, and the formulas and equations would be much longer.