An Algorithm Based on Non-Negative Matrix Factorization for Detecting Communities in Networks

Abstract

Community structure is a significant characteristic of complex networks, and community detection has valuable applications in network structure analysis. Non-negative matrix factorization (NMF) is a key set of algorithms used to solve the community detection issue. Nevertheless, the localization of feature vectors in the adjacency matrix, which represents the characteristics of complex network structures, frequently leads to the failure of NMF-based approaches when the data matrix has a low density. This paper presents a novel algorithm for detecting sparse network communities using non-negative matrix factorization (NMF). The algorithm utilizes local feature vectors to represent the original network topological features and learns regularization matrices. The resulting feature matrices effectively reveal the global structure of the data matrix, demonstrating enhanced feature expression capabilities. The regularized data matrix resolves the issue of localized feature vectors caused by sparsity or noise, in contrast to the adjacency matrix. The approach has superior accuracy in detecting community structures compared to standard NMF-based community detection algorithms, as evidenced by experimental findings on both simulated and real-world networks.

1. Introduction

Many complex systems in reality can be represented as network structures [1], such as social networks, protein interaction networks, the computer internet, and biological disease transmission networks [2]. Network nodes symbolize entities, whereas linked edges symbolize the relationships between these things. The network structure of complex systems has an associative nature, meaning that the entire network comprises several community structures that are highly interconnected within each community and sparsely interconnected between communities. Nevertheless, the relevance of a community in terms of its physical implications is mostly determined by the specific field of application with which the network is associated. For example, in social networks, communities are defined as groups with common interests or preferences [3]. Functional units in metabolic networks are represented by communities.

The accurate identification of community structure in networks has significant theoretical importance and practical utility for analyzing the component structure of complex systems, understanding the internal mechanisms of system interactions, revealing the patterns of system evolution, and predicting the behavior of complex systems [4,5,6]. Over the last several years, numerous techniques for community detection have been suggested [7], such as spectral clustering-based approaches [7], modularity-based approaches [8], NMF-based approaches [9], and others. Ye et al. [9] developed a deep non-negative matrix factorization (NMF) autoencoder to uncover the community structure in complex networks by using both hierarchical and structural information. Their approach was influenced by the deep self-encoder and aimed to learn hierarchical features with hidden information. Li et al. [8] observed that many existing community detection algorithms mostly rely on the original network topology and overlook the underlying community structure information. In their study, they utilized the node attribute matrix and the community structure to address this limitation. The attribute community identification issue may be represented as a non-negative matrix optimization problem, where the embedding matrix is used to identify all the communities in the attribute graph.

Nevertheless, the majority of current community detection algorithms, such as those based on NMF, struggle to accurately identify community structures in vast and sparse networks. In the realm of community detection research, several strategies have been presented in recent years to tackle the issue of network sparsity. Amini et al. [4] introduced a semi-supervised approach for identifying communities in social networks by integrating deep learning techniques with the topological characteristics of the networks. Santo et al. [4] addressed the challenges of dimensionality and sparsity by enhancing the conventional CNN convolution layer. They proposed an optimized convolution layer specifically designed for efficient convolutional computation on large, high-dimensional sparse matrices. This approach focuses on non-zero values, effectively reducing memory usage while performing sparse matrix computations. Sperli et al. [3] introduced a method that combines deep learning and the topological characteristics of social networks to automatically identify communities. This method utilizes a specialized convolutional neural network to collect and depict common user interactions in online social networks. Xie et al. [1] examined four distinct network representations in order to determine the most optimal representation for inputting into a deep sparse filtering network. The objective was to produce a mapping of the community attributes that are represented at each node. Sparse filtering is a straightforward two-layer learning model capable of processing high-dimensional graph data and representing very sparse inputs as low-dimensional feature vectors. The utilization of deep learning techniques as the foundation for the sparse network community detection approach also proves effective in addressing the issue of network sparsity. The complexity of the algorithm needs to be further reduced only during the parametric learning of the model and feature engineering. Furthermore, there is a need to find adaptive techniques to estimate the number of possible communities. Thus, due to the sparsity constraint, the development of an efficient community detection method remains a difficult undertaking.

Presently, community detection methods based on NMF are evaluated based on two primary perspectives. One aspect to consider is the parameterization of the method, which often includes setting values for various parameters used in NMF-based algorithms [9,10,11]. These parameters often have reasonable default values. This includes the identification of prospective variables, particularly for the issue of community detection, i.e., the determination of the number of communities. However, this pertains to the creation of the data matrix, which is also referred to as the feature matrix [12,13]. This matrix is the one that will undergo decomposition in the NMF model.

In order to address the above issues, given the limited number of connections in the network, we propose a community detection technique called CDNMF, which is based on non-negative matrix factorization. The CDNMF technique addresses the problem of localizing the eigenvectors of data matrices caused by sparsity or noise. It improves the accuracy and practicality of the NMF community-finding approach. The main contributions of this study are as follows:

• We propose a matrix regularization procedure to enhance the representation of the overall topological characteristics of the network, addressing the issue of localizing the eigenvectors of the data matrix while dealing with sparse networks.
• We have designed a method for discovering sparse network communities by decomposing a non-negative matrix. This method utilizes regularization transformations and incorporates the spectral analysis of non-backtracking matrices. It effectively determines the number of community divisions without adding computational complexity and enhances the algorithm’s performance.
• The experimental findings obtained from many datasets demonstrate that our proposed CDNMF algorithm achieves superior accuracy in community segmentation for sparse networks, surpassing existing state-of-the-art NMF-based techniques.

This paper is organized in the following manner. The text presents a demonstration of the equality between the goal functions of symmetric non-negative matrix factorization (NMF) and spectral clustering. Based on this premise, a CDNMF technique is presented for community finding in sparse networks by utilizing a regularization transform. Furthermore, the efficacy of the suggested approach in addressing community detection in networks with a low density is also assessed by experimentation on both actual and artificially made sparse networks. Ultimately, the approach is condensed and examined, and potential avenues for expansion in the future are suggested.

2. Related Work

This section focuses on traditional community detection methods and related methods based on non-negative matrix decomposition and discusses their limitations.

2.1. Traditional Algorithms

Community detection methods, which have been around for a long time, intelligently exploit the inherent qualities of networks to uncover the strong links that exist between nodes and coordinate them into highly cohesive clusters. Researchers such as Newman et al. [14] have made significant contributions to this field, and their work is particularly noteworthy. In the beginning, they were the ones who proposed a framework for community detection that is currently extensively utilized. Through the investigation of several measures of “betweenness” (also referred to as “edge degree”, which is the significance of nodes in linking various modules in the network), this study was able to successfully uncover the essence of the community structure that is concealed within complex networks. In addition, Newman suggested a quantitative metric that he named “modularity” in order to evaluate the validity and durability of the community structure that was established. When it comes to dealing with big networks, modularity theory still needs to be improved in terms of its computing efficiency, despite the fact that it has demonstrated considerable advantages as an assessment criterion for determining the quality of community partitioning.

2.2. Learning-Model-Based Community Detection

Blondel et al. [15] later created a novel approach called the Louvain algorithm, which was built particularly to effectively mine community structures in big, complex networks. This step was taken in order to overcome the efficiency difficulties that modular-based community detection methods presented over time. The speed at which optimal modular assignments may be found is dramatically improved by the use of heuristic optimization procedures. As a result, the analysis process is greatly accelerated, while the quality of the community in question is preserved. Meanwhile, Palla et al. [16] pioneered the first overlapping community detection algorithm capable of effectively detecting and characterizing the multi-membership properties of nodes in the network. This was in response to the common phenomenon of overlapping communities that occurs in social networks and other complex systems. Therefore, a node is no longer restricted to participation in a single community but rather has the ability to be a member of numerous communities in a flexible manner. A number of heuristic community detection methods have been developed since that time. These algorithms are designed to capture and make use of the overlapping aspects of communities. As a result, the theoretical and practical toolbox in this subject has been continually enriched and improved.

Learning-based community identification approaches aim to identify the compact feature representations of nodes in order to reveal the organizational structure inherent to the communities contained within the network. The application of the non-negative matrix factorization (NMF) concept is a strategy that is particularly effective for the purpose of community discovery. A factorization analysis of the adjacency matrix is performed in this approach in order to investigate the structure of the community. In addition to its extensive variety of possible uses, it is valued because it possesses substantial explanatory power [17]. Psorakis et al. [18] were among the pioneers in the community when they presented an innovative method for determining whether communities in a network overlap with one another. Community information was extracted using a Bayesian non-negative matrix factorization framework based on probability theory.

A data representation method that has its origins in graph theory was developed further by Cai et al. [19], who built upon the notion of GNMF, which stands for graph-regularized non-negative matrix factorization. This method leverages matrix factorization and makes use of an affinity graph to describe geometric data. Additionally, the integrity of the graph structure is maintained for the duration of this process. This area has continued to expand as a result of further research, and a number of specialists have proposed community identification methods based on a three-factor matrix decomposition methodology. For example, Zhang et al. [20] presented a restricted non-negative three-factor matrix decomposition technique that is able to directly simulate and learn the community membership of nodes, as well as the interactions between communities. On the other hand, Jin et al. [21] suggested a graph-regularized non-negative three-factor matrix decomposition model that intelligently exploits the spectral aspects of networks to increase the efficacy of community discovery.

Furthermore, Filippo and other scholars [22] highlighted the essential significance of orthogonality in community discovery. The authors introduced the orthogonal non-negative matrix factorization (ONMF) model in a creative manner. This approach enhances the utility of community structure analysis by imposing constraints on the community member matrix, namely, by ensuring that it is non-negative and orthogonal. During the process of node embedding, Wang et al. [23] successfully maintained the original structural properties and intrinsic qualities of the network. Consequently, they proposed the implementation of the Modularized Non-Negative Matrix Factorization (MNMF) model. This model effectively incorporates community structures into the node embedding representation. Sun and his colleagues [24] recognized that NMF only works as a decoder. Therefore, they introduced an approach to community detection known as the non-negative symmetric encoder–decoder technique (NNSED). This method effectively combines the encoder and decoder components under a single loss function framework. Ye and his colleagues [25] took an additional step and innovatively developed a new category of deep autoencoder NMF (DANMF) models for community detection tasks. This model extends Sun’s NNSED approach by constructing a framework like that of a deep autoencoder. This enables the network to acquire knowledge about complex relationships at different levels, starting from the basic network and ending with the final community assignment. Additionally, it effectively captures both subtle and prominent characteristics across several layers. Li et al. [26] developed the CDE model by studying the dense connection patterns in communities. The purpose of this model is to capture and retain the information associated with dense connectivity structures in node embeddings. Ma et al. [27] introduced two frameworks of evolving non-negative matrix factorization to examine the development of communities in dynamic contexts. These frameworks are designed to accommodate alterations in the network topology as time progresses.

Semi-supervised community detection approaches have gained significant attention from the academic community in recent years as a crucial area of community detection research. For instance, Liu et al. [6] presented a novel semi-supervised non-negative matrix factorization (NMF) model that integrates graph regularization principles with pairwise constraint mechanisms. This model is especially tailored to uncover community structures. Wu et al. [5] introduced a novel semi-supervised clustering technique called pairwise constraint propagation-induced SymmNMF. This approach is based on SymmNMF and has the ability to intelligently learn and optimize both the similarity matrix and the node assignment matrix concurrently.

However, most of the aforementioned community discovery algorithms based on non-negative matrix factorization (NMF) focus primarily on the initial network topology, namely, the adjacency matrix. In the context of sparse regularization, it is common to apply identical regularization constraints to all nodes. However, this approach does not adequately take into account the higher-order adjacency relationships within the graph and the unique characteristics of individual nodes. Consequently, this limitation can affect the accuracy of the community detection results. Our solution overcomes this limitation by using a novel similarity measure and a sparse regularization mechanism, resulting in improved accuracy and quality of community detection.

3. Equivalence Proof

The spectral clustering approach shows promising application potential and continues to be a highly researched data clustering method, especially when the data can be represented in matrix form. The objective functions for spectral clustering can be categorized into three types: ratio cuts, normalized cuts, and maximum–minimum cuts. To establish the similarity between the objective function for symmetric non-negative matrix decomposition and the objective function for spectral clustering, this section specifically examines the clustering objective function expressed as a ratio cut.

Let us consider a weighted undirected graph, denoted by G = (V,E), where V represents the set of nodes and E represents the set of edges. The graph G has a weighted adjacency matrix indicated by $=\left({\mathit{w}}_{ij}\right)$. The elements of the set are denoted by $x_{i,j}$, where i and j range from 1 to n. All element values are greater than or equal to zero. The value of $w_{ij}$ is 0. The absence of an edge between nodes $v_i$ and $v_j$ is denoted by $w_{ij}=0$, whereas a non-negative weight is denoted by $w_{ij}>0$ for the connecting edges between nodes $v_i$ and $v_j$. The total of the weights for node $v_i$ in the set V is represented by $O_i$, which is equal to the summation of all weights $w_{ij}$ for j ranging from 1 to n.

A matrix U is a diagonal matrix with diagonal elements represented by $u_1,u_2,\dots ,u_n$. The ratio cut technique may be mathematically represented by Equations (1) and (2) for a certain number of subsets, denoted by K, which are labeled as $C_1,C,\dots ,C_k$.

$$minRatioCut\left(C_1,C2,\dots ,C_K\right)=\frac{1}{2}\sum _{i=1}^K\frac{W\left(C_i,{\overline{C}}_i\right)}{|C_i|}$$

(1)

$$cut\left(C_1,C_2,\dots ,C_k\right)=\frac{1}{2}\sum _{i=1}^{K}W\left(C_i,{\overline{C}}_i\right)$$

(2)

where the subset of the node set is indicated by $C_i$ ($C_i\in V$), and its complement is denoted by ${\overline{C}}_i$. The function $W\left(C_i,{\overline{C}}_i\right)$ is defined as the sum of the weights $w_{ij}$ for all pairs of elements i in $C_i$ and j in ${\overline{C}}_i$. The symbol $|C_i|$ represents the cardinality of the subset $C_i$, which is the number of nodes it contains.

To define K indication nodes, denoted by ${\left({\mathit{h}}_{1,j},{\mathit{h}}_{2,j},\dots ,{\mathit{h}}_{n,j}\right)}^T$, j = 1, 2, …, K, for a given K subsets of $C_1,C,\dots ,C_k$, refer to Equation (3).

$$h_{i,j}\left\{\begin{array}{c}1/\sqrt{|C_j|},if{v}_i\in C_j(i=1,2,\dots ,n)\\ 0,others\end{array}\right.$$

(3)

The nodes indicated by K are utilized as column vectors to create a new matrix represented by $\mathit{H}\in R^{n\times K}$. The column nodes in the matrix H are mutually perpendicular, ensuring the validity of Equation (4).

$${\mathit{h}}_i^T{\mathit{Lh}}_i=\frac{cut\left(C_i,{\overline{C}}_i\right)}{|C_i|}$$

(4)

Combining the traces of the matrix, Equation (5) can be obtained.

$${\mathit{h}}_i^T{\mathit{Lh}}_i={\left({\mathit{H}}^T\mathit{LH}\right)}_{ij}$$

(5)

where the matrix L represents the non-normalized Laplace matrix, which is represented by the equation L = U − W. In addition, the objective function of the ratio cut clustering can be simplified to Equation (6) when K takes any value.

$$\begin{array}{cc}\hfill RatioCut\left(C_1,C_2,\dots ,C_K\right)& =\sum _{i=1}^K{\mathit{h}}_i^T{\mathit{Lh}}_i\hfill \\ \hfill & =Tr\left({\mathit{H}}^T\mathit{LH}\right)\hfill \end{array}$$

(6)

Assuming that tr denotes the trace of the matrix, the minimization ratio cut problem can be expressed as shown in Equation (7).

$$\underset{C_1,C_2,\dots ,C_K}{min}tr\left({\mathit{H}}^T\mathit{LH}\right)$$

(7)

where ${\mathit{H}}^T\mathit{H}=\mathit{I}$. By allowing the values of the elements of the matrix H to be any real value, the relaxed optimization case of the problem can be obtained, as shown in Equation (8).

$$\underset{H\in R^{n\times K}}{min}tr\left({\mathit{H}}^T\mathit{LH}\right)$$

(8)

As a result of this transformation, the trace minimization problem has been transformed into its standard form. The spectral clustering solution, denoted by the symbol H, can be considered the corresponding spectral clustering result for K-mean clustering. This is due to the fact that the theoretical frameworks of spectral clustering and K-mean clustering have a unified structure. In the case of a set of n data points, which are represented by the equation $\mathit{X}={\left({\mathit{x}}_1,{\mathit{x}}_{2,\dots ,}\right)}^T$, the objective function of K-mean clustering can be stated as Equation (9).

$$min{J}_K=\sum _i{∥x_i∥}^2-\sum _{k=1}^K\frac{1}{n_k}\sum _{i,j\in C_k}{x}_i^T{x}_j$$

(9)

where $m_k={\sum }_{i\in C_k}{x}_i/n_k$ is the center of clustering among the $n_k$ points of the cluster $C_k$. K non-negative indicator vectors are defined as solutions to the clustering, which can be expressed as $Y=\left(y_1,y_2,\dots ,y_K\right)$ and $y_k={\left(0,\dots ,0,\stackrel{n_k}{\overbrace{1,\dots ,1}},0,\dots ,0\right)}^T/n_k^{1/2}$.

The solution of the K-means clustering, denoted by the matrix Y, and the solution of the ratio cut clustering, denoted by the matrix H, are almost identical. Consequently, it can then be expressed as Equation (9).

$$J_K=tr\left({\mathit{X}}^T\mathit{X}\right)-tr\left({\mathit{H}}^T{\mathit{X}}^T\mathit{XH}\right)$$

(10)

Therefore, Equation (9) may be rewritten as Equation (11) due to the fact that the first component is a constant.

$$\underset{{\mathit{Y}}^T\mathit{Y}=\mathit{I},\mathit{Y}⩾0}{max}{J}_W\left(\mathit{H}\right)=tr\left({\mathit{H}}^T{\mathit{X}}^T\mathit{XH}\right)$$

(11)

The solution representation is the only difference between the two methods. In the data representation, the ratio cut uses a Laplace matrix, denoted by L, whereas the K-mean method uses the matrix ${\mathit{X}}^T\mathit{X}$. To summarize, the weighted adjacency matrix W may be regarded as a versatile data representation. The proof of equivalence between the spectral clustering objective function and the symmetric NMF objective function can be demonstrated using Equation (12).

$$\begin{array}{cc}\hfill \mathit{H}& =\underset{{\mathit{H}}^T\mathit{H}=\mathit{I},\mathit{H}⩾0}{argmax}tr\left({\mathit{H}}^T\mathit{WH}\right)\hfill \\ \hfill & =\underset{{\mathit{H}}^T\mathit{H}=\mathit{I},\mathit{H}⩾0}{argmin}-2tr\left({\mathit{H}}^T\mathit{WH}\right)\hfill \\ \hfill & =\underset{{\mathit{H}}^T\mathit{H}=\mathit{I},\mathit{H}⩾0}{argmin}{∥\mathit{W}-{\mathit{HH}}^T∥}^2\hfill \end{array}$$

(12)

In order to finish the proof that was presented before, it is possible to loosen the restriction that ${\mathit{H}}^T\mathit{H}=\mathit{I}$. After the research described above, it was found that spectral clustering is directly related to K-mean clustering. The K-mean clustering algorithm is somewhat similar to the NMF algorithm. Therefore, in a simple way, NMF and spectral clustering are compatible with each other.

4. Proposed Model

Before outlining the basics of NMF-based community detection techniques, we will first give a brief introduction to the definition of classical community detection methods and their mathematical constructions. The goal of community detection is to divide the set of nodes of a graph G = (V,E) into a number of unique subsets in such a way that the solution satisfies the fundamental characteristics of the community structure. The partitioning result of the network is then represented by the partitioning matrix P, as shown in Equation (13). This is based on the assumption that n represents the total number of nodes and that the community solution with c subsets has been provided in advance.

$$P_{ik}=\left\{\begin{array}{c}1\\ 0\end{array}\right.,s.t.\sum _{k=1}^c{P}_{ik}=1\left(1⩽i⩽n\right)$$

(13)

The size of the k-th community may be represented as the sum of $P_{ik}$ for i ranging from 1 to n. In addition, when considering a community, we make the assumption that each value of k satisfies the constraint $0<{\sum }_{i=1}^n{P}_{ik}<n$. These divisions are referred to as hard divisions because they create partitions where each node is assigned to a certain community.

Evidently, nodes that share similarities are found within the same community. Consequently, we can establish the similarity function as a means of assessing the similarity between nodes. If nodes $v_i$ and $v_j$ are identical, then the similarity score $s(P,v_i,v_j)$ is equal to 1. If nodes $v_i$ and $v_j$ are entirely different, then the similarity score $s(P,v_i,v_j)$ is equal to 0. We find the value of $s\left(P,v_i,v_j\right)$, which is between 0 and 1. The function $s(P,v_i,v_j)$ is continuously differentiable for every $P_{ij}$.

The aforementioned similarity function is denoted by $s_{ij}$. When evaluating the similarity between nodes, one might make acceptable assumptions based on existing knowledge. For instance, a connection between nodes $v_i$ and $v_j$ signifies their similarity, but the absence of a connection suggests their dissimilarity. We can evaluate a given partition by calculating the proximity of the actual similarity value to the required similarity value, as shown in Equation (14).

$$E\left(P\right)=\sum _{i=1}^n\sum _{j=1}^n{\left({\tilde{s}}_{ij}-s_{ij}\right)}^2$$

(14)

In order to represent this concept using matrices, we define the matrices $S\left(P\right)=\left[s_{ij}\right]$ and $\tilde{S}\left(P\right)=\left[{\tilde{s}}_{ij}\right]$. In general, we regard the adjacency matrix A of a given graph as a reasonable choice for capturing a priori similarity. Therefore, the matrix $\tilde{\mathit{S}}$ is equal to the matrix $\mathit{A}$. Given that, the adjacency matrix fulfills the similarity assumption, meaning that it is equal to 1 for pairs of nodes that are connected by edges. For pairs of nodes that are not connected by edges, their similarity is equal to 0. This is demonstrated by implementing the provided similarity function and satisfying the above requirement.

$$s_{ij}=\sum _{k=1}^c{P}_{ik}{P}_{jk}$$

(15)

The similarity of a node to another node belonging to the same partition must be one for the idea described above to hold; otherwise, it must be zero. If it is represented in matrix form, it can simply be written as

$$S\left(P\right)=\left[s_{ij}\right]={\mathit{PP}}^T$$

(16)

To minimize the function E(P), we create an NMF problem and acquire a partition matrix P that is suitable for this purpose. The formal statement of this problem is given by Equation (17).

$$\begin{array}{cc}\hfill \underset{P⩾0}{minE\left(P\right)}& =\sum _{i=1}^n\sum _{j=1}^n{\left(\tilde{s}-s_{ij}\right)}^2\hfill \\ \hfill & ={\left(A-{\mathit{PP}}^T\right)}^2\hfill \\ \hfill & ={∥A-{\mathit{PP}}^T∥}^2\hfill \end{array}$$

(17)

The user provides the desired similarity matrix and the number of communities as input to the adjacency matrix A. The number of communities is determined by setting the potential factor k.

4.1. Algorithm Principles

The spectral technique outperforms general spectral clustering on sparse networks by using the regularization matrix derived from local feature vectors as an alternative matrix representation of the network. Thus, we incorporate regularization matrices into the community detection process based on non-negative matrix factorization (NMF).

Localization characterizes the local arrangement of the network system, while delocalization expands the scope of these localized vectors, resulting in feature vectors that capture the broader global structural information with higher eigenvalues. The Inverse Participation Ratio (IPR) is a metric employed in spectral clustering to quantify the level of localization of feature vectors. It is defined as the sum of the fourth power of each element in the feature vector, represented as $IPR\left(l\right)={\sum }_{i=1}^n{l}_i^4$. Greater IPR values suggest that the vectors exhibit a higher level of localized structure. The values of I(l) vary between $\frac{1}{n}$ and 1. These values correspond to two sets of vectors: $\left\{\frac{1}{\sqrt{\mathit{n}}},\frac{1}{\sqrt{\mathit{n}}},\dots ,\frac{1}{\sqrt{\mathit{n}}}\right\}$ and $\left\{0,\dots ,0,1,0,\dots ,0\right\}$, respectively.

The proposed technique involves creating a regularized matrix, denoted as a Z-Laplacian (${\mathbf{L}}_Z$), that has a comparable structure to that of the adjacency matrix (A). The regularization matrix, indicated by ${\mathit{L}}_Z$, is defined as the sum of A and Z, where A represents the data matrix or a variation of it. The regularization learning procedure yields Z.

The regularization matrix Z mentioned above is a diagonal matrix. Each diagonal element of this matrix is learned incrementally from the most localized vectors. The learning process involves applying penalties to the localized eigenvectors to suppress the corresponding eigenvalues. The learning process concludes after all g primary characteristic vectors have been disentangled from their specific locations. The resultant Z-Laplacian matrix is believed to be a simple representation of the overall structure of the matrix A, excluding its individual nodes. The steps of the CDNMF algorithm are illustrated in Algorithm 1.

Algorithm 1 Learning process of the CDNMF model

Require : Regularization matrix $L_z$, number of communities k Ensure : Community detection results    1: Use non-backtracking matrices to estimate appropriate values for the number of communities k    2: Compute symmetric non-negative matrix factorization ${\mathit{L}}_{\mathit{z}}={\mathit{PP}}^{\mathit{T}}$    3: The update rule is ${\mathit{P}}_{ij}\leftarrow {\mathit{P}}_{ij}|1-\beta +\beta \frac{{\left({\mathit{L}}_{\mathit{z}}\mathit{P}\right)}_{ij}}{{\left({\mathit{PP}}^{\mathit{T}}\mathit{P}\right)}_{ij}}$    4: $0<\beta ⩽1$    5: $\mathit{P}\leftarrow max\left({\mathit{L}}_{\mathit{z}}\mathit{P}{\left({\mathit{P}}^{\mathit{T}}\mathit{P}\right)}^{-1},0\right)$    6: After the objective function, i.e., Equation (19), converges, the partition matrix can be obtained

For every row vector ${\mathit{P}}_i$ for the matrix P, it is necessary to normalize ${\mathit{P}}_i$ in such a way that the cumulative sum of all elements in ${\mathit{P}}_i$ is equal to one, which is denoted by the expression ${\sum }_{j=1}^k{p}_{ij}=1$. The element ${\mathit{P}}_{ij}$ in the normalized P reflects the strength of the affiliation of node i to community j. Furthermore, the community that has the highest degree of attachment is the one that is allocated node i.

4.2. Parameter Learning

In this part, we select a straightforward and speedy approach to estimate the number of communities k for community detection methods that are founded on non-negative matrix decompositions. The spectral qualities of particular graph operators, such as non-backtracking matrices, serve as the foundation and basis for this.

In the context of a complex network, the adjacency matrix A represents the connections between nodes in the network. The degree of a certain node k may be calculated by summing the values in the k-th row of the matrix A. Below is the definition of the non-backtracking matrix, which is utilized to estimate the number of communities.

In an undirected complex network, the variable m represents the number of edges, while B represents the associated non-backtracking matrix. When generating the matrix B, two directed edges are used to represent the connection between nodes i and j. One path travels from node i to node j, while the other path travels from node j to node i. The matrix B has dimensions of 2m × 2m and can be represented by Equation (18).

$$B_{i\to p,q\to l}=\left\{\begin{array}{c}1,p=qandi\ne l\hfill \\ 0,otherwise\hfill \end{array}\right.$$

(18)

The spectrum of the matrix B is demonstrated to have two components, namely, ±1, along with the eigenvalues of the 2n × 2n matrix, as given in Equation (19).

$$\tilde{B}=\left(\begin{array}{cc}{0}_n& U-I_n\\ -I_n& A\end{array}\right)$$

(19)

where $0_n$ is a matrix of size n × n, with all elements being zero. The symbol I represents the identity matrix of size n × n, and U is a diagonal matrix of size n × n with diagonal elements $d_i$. If the network is divided into k communities, the first k greatest eigenvalues of the matrix $\tilde{B}$ are real. Specifically, they are distinct from the areas where the remaining eigenvalues are concentrated. The regions where the remaining eigenvalues are grouped are enclosed by a circle with a radius equal to the square root of the norm of the matrix $\tilde{B}$. The eigenvalues of the $\tilde{B}$ matrix that contain information are denoted by the symbol k. Equation (20) provides an approximation of the spectral characteristics of the non-retrospective matrix.

$$\tilde{d}={\left(\sum _{i=1}^n{d}_i\right)}^{-1}\left(\sum _{i=1}^n{d}_i^2\right)-1$$

(20)

The non-backtracking matrix information eigenvalues are real and separated from the other eigenvalues in a circle with the radius ${∥\tilde{B}∥}^{\frac{1}{2}}$. To obtain an idea of the k value, we count the number of eigenvalues that are not in this circle. Experiments also show that the parameter learning process performs well, especially when communities of complex networks are known to have similar sizes and edge densities.

The number of true out-of-circle eigenvalues seems to be a natural indication of the number of clusters present in the network when it comes to networks formed using the random block model. In some networks, true eigenvalues with high out-of-circle distributions may correlate with tiny clusters on the network graph. This is something that can be taken into account in actual network segmentation procedures.

5. Experiments

This research performed a comparative analysis using numerous approaches that are considered to be the state of the art on both synthetic and actual networks. The purpose of this analysis was to validate the efficacy of CDNMF. The experimental hardware platform consists of an Intel Core i7-9700 CPU operating at 2.4 GHz, 32 gigabytes of random-access memory (RAM), and Windows 10 as the operating system. Python 3.7 was used to implement each of the compared methods.

5.1. Compared Methods

We chose a number of algorithms that are considered to be the state of the art in order to provide a comparison with the approach that is given in this work.

DCSBM [28]: This strategy separates the row labels from the column labels in the probability function to achieve fast alternation maximization. This novel technique has great computational efficiency, is suitable for both small and large networks, and includes guarantees of convergence that can be demonstrated.

NMF [11]: This method uses the basic NMF model to directly decompose the adjacency matrix A to obtain the matrices U and V, ${∥A-UV∥}_F^2$, where U serves as the community membership representation matrix.

SNMF [12]: This technique is founded on the symmetrical non-negative matrix decomposition model, whereby ${∥A-H{H}^T∥}_F^2$ and H may directly reflect the degree of affiliation that a community member has with the community.

M-NMF [13]: The non-negative matrix decomposition and modularity-based community detection approaches are simultaneously optimized by this modularity-based NMF community detection model. This model incorporates the community structure of the network into the network embedding and takes into account the modularity of the network.

ONMF [29]: The approach is founded on the orthogonal non-negative matrix factorization model. The main concept involves imposing orthogonal constraints on the matrix W within the framework of the NMF model ${∥A-WH∥}_F^2$, resulting in the condition $W^{T}W=I$.

HPNMF [30]: The graph regularization NMF model serves as the foundation for this technique. This model has the capability to use both the topology of the network and the homogeneity information of the nodes in order to establish community detection.

NSED [24]: In addition to being based on the joint NMF model, the approach includes both an encoder and a decoder, both of which are capable of being utilized in order to obtain the community membership representation matrix.

5.2. Datasets

Both synthetic and real networks were included in the datasets used for the studies, which are described below.

Artificial Synthetic Networks: We utilized the LFR benchmark network synthesis program [31] to create artificial networks with actual community labels. This tool offers several configurable settings, as shown in

Table 1. Adjustable settings of LFR.

Parameters	Descriptions
n	Number of nodes
k	Average degree of nodes
maxk	Maximum degree of nodes
mu	Confusion factor, adjustable in the range [0, 1]
minc	Number of nodes contained in the smallest community
maxc	Number of nodes contained in the largest community

. Various distinct sets of artificial networks are created by manipulating the parameters. To begin with, a collection of five networks is created by keeping the variables n, k, maxk, minc, and maxc constant. The value of mu ranges from 0.1 to 0.3, with an increment of 0.05 for each iteration. By manipulating the variables k, maxk, minc, maxc, and mu, the number of nodes n is incremented from 1000 to 5000. This process is repeated five times, with each iteration increasing n by 1000, resulting in the generation of five distinct networks. The precise parameter configurations of the two sets of networks are shown in

Table 2. Parameter settings of synthetic networks.

Parameters	Group I	Group II
n	3000	1000∼5000
k	4	4
maxk	15	15
mu	50	n/20
minc	100	n/40
maxc	0.1∼0.3	0.2

.

Real Networks: We selected four datasets consisting of actual networks, namely, WebKB, Cora, Citeseer, and Pubmed [32]. The precise characteristics of these datasets are provided in

Table 3. Parameters of real networks.

Datasets	No. of Nodes	No. of Edges	Feature Dimension	No. of Communities
WebKB	877	1399	1703	4
Cora	2708	5409	1433	7
Citeseer	3327	4732	3703	6
Pubmed	19,717	44,338	500	3

. The aforementioned datasets may be downloaded from the following URL: https://linqs.org/datasets/ (accessed on 14 January 2024).

5.3. Experimental Setup

In order to assess the effectiveness of community discovery outcomes, we employ four widely accepted assessment metrics: normalized mutual information (NMI), the adjusted Rand index (ARI), accuracy (ACC), and modularity (Q). When evaluating the results of synthetic networks, we utilize all four of these metrics. In the case of actual networks, when there is no specific labeling for community segmentation, we employ the modularity Q as a means of evaluating the results. Greater values for all rating categories indicate superior performance, whereas smaller values indicate the opposite.

In order to ensure that the comparisons made in the experiment are accurate, the parameters of all of the compared techniques are based on the default values that were found in the original text. For the M-NMF algorithm, the regularization parameters $\alpha$ equals 1 and $\beta$ equals 5. The value of the regularization parameter $\lambda$ is equal to 1 for HPNMF. In addition, the tests were carried out ten times according to each approach, and the average of each evaluation indicator was taken into consideration for the assessment.

5.4. Synthetic Networks

An examination of the similarities and differences between the two synthetic network datasets, shown in Table 2, was carried out, and the results of the experiments carried out on the first network are shown in

Table 4. Performance comparison of synthetic networks with different mu.

mu	Metric	NMF	SNMF	M-NMF	ONMF	HPNMF	NSED	DCSBM	CDNMF
0.1	ACC	0.841	0.851	0.552	0.824	0.812	0.493	0.711	0.917
	NMI	0.861	0.864	0.641	0.851	0.851	0.624	0.698	0.891
	ARI	0.767	0.772	0.384	0.746	0.737	0.359	0.536	0.836
	Q	0.864	0.885	0.789	0.878	0.877	0.697	0.769	0.906
0.15	ACC	0.803	0.782	0.466	0.791	0.757	0.372	0.648	0.873
	NMI	0.801	0.788	0.599	0.793	0.779	0.498	0.635	0.844
	ARI	0.678	0.661	0.302	0.668	0.636	0.213	0.461	0.756
	Q	0.837	0.841	0.756	0.842	0.834	0.624	0.725	0.861
0.2	ACC	0.735	0.714	0.381	0.703	0.686	0.331	0.376	0.795
	NMI	0.728	0.721	0.484	0.714	0.711	0.454	0.402	0.768
	ARI	0.581	0.567	0.202	0.555	0.545	0.188	0.193	0.662
	Q	0.782	0.799	0.708	0.796	0.793	0.611	0.553	0.816
0.25	ACC	0.652	0.649	0.319	0.622	0.617	0.316	0.351	0.719
	NMI	0.646	0.653	0.413	0.637	0.633	0.401	0.383	0.689
	ARI	0.479	0.482	0.152	0.453	0.445	0.142	0.173	0.556
	Q	0.759	0.769	0.682	0.762	0.759	0.593	0.575	0.784
0.30	ACC	0.511	0.512	0.144	0.522	0.533	0.226	0.157	0.623
	NMI	0.452	0.503	0.236	0.505	0.538	0.336	0.197	0.575
	ARI	0.318	0.313	0.038	0.334	0.336	0.095	0.037	0.388
	Q	0.724	0.737	0.581	0.732	0.729	0.577	0.409	0.739

.

The data shown in Table 4 demonstrate that when the confusion factor increases, the community structure of the network becomes less transparent, and it becomes more challenging to locate existing communities. The approach that is discussed in this work, CDNMF, performs better on all of the methods, despite the fact that the performance of each method decreases more significantly as a consequence of this. As an illustration, when the value of mu is equal to 0.1, CDNMF exhibits significant improvements in ACC, NMI, ARI, and modularity Q of 7.7%, 3.1%, 8.2%, and 2.4%, respectively, in comparison to SNMF, which is the most effective community detection algorithm based on NMF. In addition, CDNMF demonstrates varying degrees of improvement across the four assessment measures when applied to several distinct datasets. 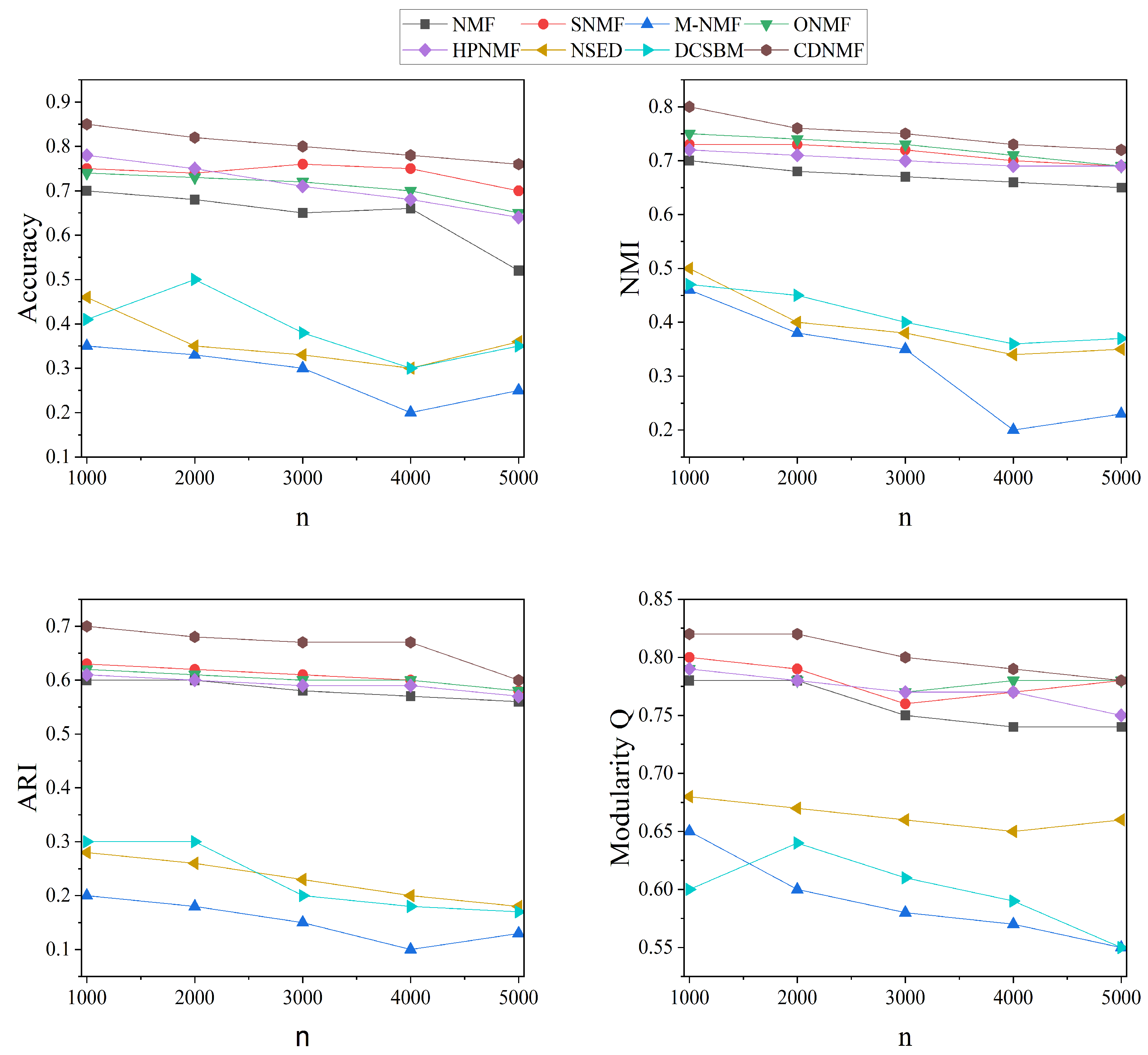The results of the experiments carried out on the second set of synthetic networks are shown in Figure 1. In this figure, it is also possible to observe that CDNMF achieves the highest level of performance across all networks, regardless of the number of nodes present.

The aforementioned experimental results on synthetic networks show that CDNMF outperforms current NMF-based community detection techniques.

5.5. Real Networks

In order to provide more evidence that CDNMF is successful, comparative studies were carried out on four actual networks. The results of these experiments are presented in

Table 5. Modularity Q comparison on real networks.

Dataset	NMF	SNMF	M-NMF	ONMF	HPNMF	NSED	DCSBM	CDNMF
WebKB	0.573	0.631	0.624	0.642	0.684	0.667	0.615	0.754
Cora	0.531	0.526	0.703	0.616	0.714	0.685	0.648	0.726
Citeseer	0.594	0.607	0.629	0.584	0.654	0.593	0.495	0.714
Pubmed	0.454	0.423	0.509	0.504	0.536	0.395	0.325	0.541

and

Table 6. Comparison of NMI on real-world networks.

Dataset	NMF	SNMF	M-NMF	ONMF	HPNMF	NSED	DCSBM	CDNMF
WebKB	0.624	0.651	0.643	0.657	0.674	0.662	0.647	0.681
Cora	0.584	0.601	0.594	0.604	0.623	0.617	0.599	0.642
Citeseer	0.574	0.586	0.576	0.597	0.618	0.605	0.576	0.638
Pubmed	0.548	0.553	0.549	0.571	0.587	0.554	0.551	0.607

. The results of CDNMF on each real network are found to be superior to the results obtained by the comparative techniques, as can be observed. After comparing the modularity of CDNMF to that of HPNMF, the best-performing NMF-based approach, the modularity of CDNMF is increased by 5.4%, 1.5%, 9.3%, and 1.3%, respectively, on WebKB, Cora, Citeseer, and Pubmed. The complexity of real networks is often higher, and they typically include a greater number of nonlinear node properties than synthetic networks. On synthetic networks, the SNMF model performs better than average, but on the three real datasets, its performance is average. On the other hand, CDNMF is a nonlinear community detection model that performs better than the other models in both real and synthetic networks. It is particularly effective in the former. The results reported above demonstrate that CDNMF has the potential to enhance the manner in which the nonlinear characteristics of networks are represented, which, in turn, improves the performance of NMF community detection.

5.6. Time Complexity

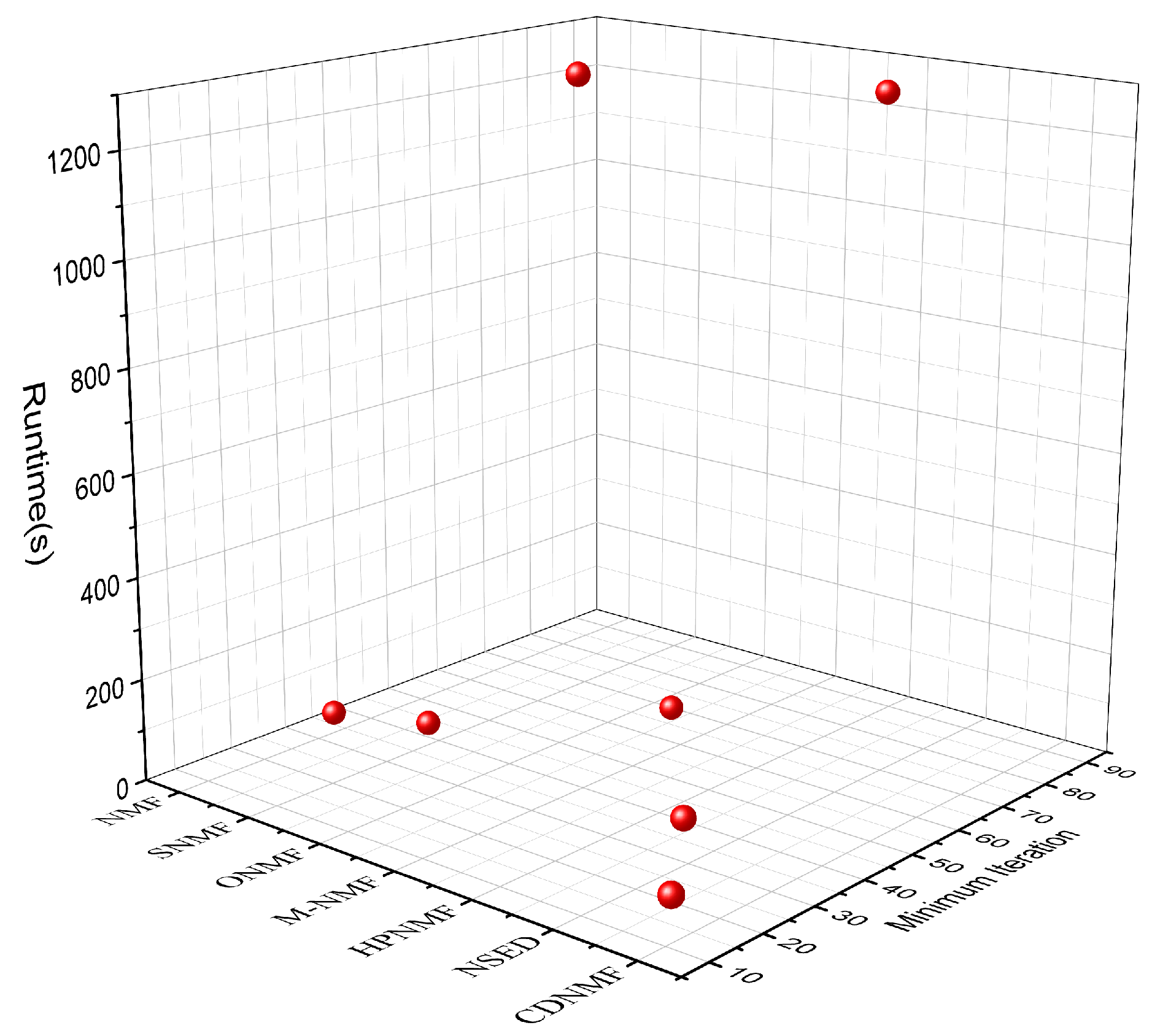
In the analysis described in this section, the real network Pubmed was chosen as the experimental data, and the NMF-based community detection methods NMF, SNMF, M-NMF, ONMF, HPNMF, and NSED were chosen for comparison. The purpose of this experiment was to investigate the minimum number of iterations required for CDNMF to achieve the best community delineation results. The minimum number of iterations, denoted by $T_m$, and the time required for each approach to achieve the best possible results in terms of community delineation were evaluated and documented.

The experimental results are shown in Figure 2, which shows that, in terms of running time, NMF and SNMF take less time to obtain the best neighborhood delineation result due to the simplicity of the models and their higher running efficiency, while ONMF takes the longest time, which is mainly due to the high complexity of the orthogonality constraint computation, and HPNMF takes only the second-longest time due to the high complexity of the model in calculating the similarity matrix and the corresponding larger value of $T_m$. Consequently, it takes the second-longest amount of time, behind only ONMF. With a $T_m$ of 11, the CDNMF model is able to obtain community segmentation results that are optimal with a reduced number of iterations compared to the other models. When compared to ONMF and HPNMF, CDNMF has a far more glaring advantage in terms of the amount of time it takes to operate.

6. Conclusions

The aim of this study is to propose a sparse network community detection algorithm (CDNMF) based on NMF. This particular technique was inspired by an approach to solving the localization problem in spectral approaches based on matrix representations. It is possible for spectral approaches to be effective in revealing the implicit global structure of data if the data in question can be represented in a matrix configuration. Traditional spectral approaches, on the other hand, often fail to work properly when the data matrix is either sparse or noisy. This is because the localization of feature vectors (or singular vectors) induced by sparsity or noise is a common problem. Recently, a generic technique for learning regularization matrices from localized feature vectors has been presented as a solution to the localization problem present in spectral methods.

The CDNMF algorithm described in this study has two main advantages. Learning regularization matrices from local feature vectors to represent complicated network topologies is the first step in improving the accuracy and utility of the approach used to discover community structures in sparse networks. The second step is to find potential factor values for key parameters of the NMF-based algorithm using a method that is both simple and fast. Future work will continue to explore the problem of community discovery in sparse networks. In addition, adaptive techniques will be developed for the problem of determining key parameters based on the NMF approach in order to make the preset values of the parameters more adaptable.