Geometry of Enumerable Class of Surfaces Associated with Mylar Balloons

Abstract

In this paper, the very fundamental geometrical characteristics of the Mylar balloon like the profile curve, height, volume, arclength, surface area, crimping factor, etc. are recognized as geometrical moments ${\mathcal{I}}_n\left(x\right)$ and ${\mathcal{I}}_n$ and this observation has been used to introduce an infinite family of surfaces ${\mathcal{S}}_n$ specified by the natural numbers $n=0,1,2,\dots$. These surfaces are presented via explicit formulas (through the incomplete Euler’s beta function) and can be identified as an interesting family of balloons. Their parameterizations is achieved relying on the well-known relationships among elliptic integrals, beta and gamma functions. The final results are expressed via the fundamental mathematical constants, such as $\pi$ and the lemniscate constant $\varpi$. Quite interesting formulas for recursive calculations of various quantities related to associated figures modulo four are derived. The most principal results are summarized in a table, illustrated via a few graphics, and some direct relationships with other fundamental areas in mathematics, physics, and geometry are pointed out.

1. Introduction

In industry, Mylar^® is a trademark for ultra-thin foil sheets made from polyester which great tensile strength makes them extremely inelastic—when folded, they remain stable without being able to shrink or stretch significantly under the bending forces.

In geometry, Mylar is a term first introduced by Paulsen [1] in 1994 for surfaces of revolution called Mylar balloons, whose shape almost perfectly approaches the shape of a special type of inflatable membranes—objects, physically constructed from two identical circular discs of Mylar foil, stitched along their boundaries and inflated to full capacity.

The interest in the subject has been inspired by the scientific balloons used by NASA and other space agencies to carry out various research in the upper stratosphere [2,3] including both terrestrial and extraterrestrial balloon development activities [4].

Due to the non-elasticity of the Mylar^® foil, the resulting shape of the Mylar balloon is somewhat surprisingly not spherical as one might expect based on the well-known fact that the sphere possesses the maximal volume for a given surface area. Besides, the surface area of the Mylar discs is not preserved which is clearly evidenced by the wrinkled areas apparently observed for the commercially produced Mylar^® balloons.

In mathematical formulation, Mylar balloons as pictured above are most adequately described as a variational problem under a constraint (Paulsen’s formulation): Find a surface of revolution enclosing maximum volume for a given directrix arclength.

Let $a>0$ be the radius of two initially flat discs, i.e., of the “deflated” Mylar balloon. Without loss of generality, we can assume that the $OZ$-axis is an axis of revolution and the curve, $z=z\left(x\right)$, $x\in [0,r]$, lying in the first quadrant of the $XOZ$-plane, is the upper half of the generating curve of the “inflated” Mylar balloon with equatorial radius r (namely, $z\left(r\right)=0$, cf. Figure 1). It is intuitively clear that $z\left(x\right)$ meets the $OX$ and $OZ$ axes at right angles. By symmetry considerations it follows that the lower part of the generating curve is obtained by reflection with respect to the $OX$-axis. Then, we can state the problem in rigorous settings: Find $z\left(x\right)$ that maximizes the volume

$$\mathcal{V}=4\pi \underset{0}{\overset{r}{\int }}xz\left(x\right)\mathrm{d}x$$

(1)

subject to the arclength constraint $\mathcal{L}=4a$, i.e.,

$$\underset{0}{\overset{r}{\int }}\sqrt{1+{\left(z^{\prime }\left(x\right)\right)}^2}\mathrm{d}x=a$$

(2)

and satisfying the transversality conditions

$$z^{\prime }\left(0\right)=0,\underset{x\to r}{lim}{z}^{\prime }=-\infty$$

(3)

where $z^{\prime }\left(x\right)\equiv \mathrm{d}z/\mathrm{d}x$.

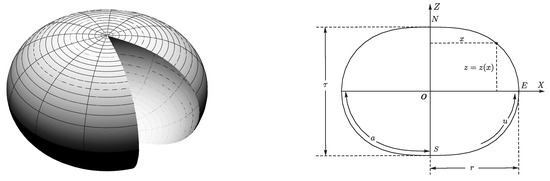
Figure 1. 3D view of the inflated Mylar balloon (left) and its cross-section through the symmetry axis $OZ$ in the plane $XOZ$ (right), where N and S are the North and South Poles respectively, E denotes the Equator of this surface of revolution, O is the center of the Mylar balloon, $\tau$ is its thickness, whereas a and r are the deflated and inflated radii respectively. The plots are obtained via Mathematica^® [5] through the parameterization of the profile curve in terms of the Euler’s beta function given by (75).

The Japanese engineer Kawaguchi [6] in 1977 came up with a Mylar balloon-shaped surfaces from a different perspective. Looking for a shallowest surface of revolution which has no circumferential stress he found that this is achieved exactly when the meridional $k_{\mu }$ and parallel $k_{\pi }$ principal curvatures obey everywhere on the surface the so-called Weingarten condition

$$k_{\mu }=2k_{\pi }.$$

(4)

Some years later in 2003, Mladenov and Oprea [7] proved that this linear type relationship between curvatures specifies the Mylar balloon uniquely.

In a broader sense the Mylar balloon can be considered as a particular case ($c=2$) of a class of surfaces satisfying the linear Weingarten relation

$$k_{\mu }=c{k}_{\pi },c\in \mathbb{R}\backslash \left\{0\right\}$$

(5)

for which besides variational characterization have been found explicit parameterizations and some interesting results about their global geometry [8].

Later on, these considerations have been explored in concrete settings [9,10] and further extended in [11] to the class of surfaces obeying to the relation

$$k_{\mu }=a{k}_{\pi }+b,a\in \mathbb{R}\backslash \left\{0\right\},b\in \mathbb{R}.$$

(6)

Except in architectural geometry, where the Mylar balloon appears as a curved support structure, e.g., the above mentioned Kawaguchi’s dome, natural shapes with constant ratio of principal curvatures, $k_{\mu }/k_{\pi }=2$, occur also in many practical realizations of free-form shapes, say, inflatable pouch anchors [12], underwater bags for compressed air energy storage [13], and super pressure balloons for scientific observations in the stratosphere [14], etc. Pressure-driven shapes of this kind are obtained by maximizing the volume of the internal space formed within flexible but (almost) inextensible soft membranes, i.e., by increasing the volume of three-dimensional bodies (which can be any kind of pouches, bags, packages, balloons, etc.) via a submetric transformation, meaning without increasing the distance between any pair of points on their surfaces [15].

At this moment it is interesting also to point out other purely mechanical applications of the Mylar balloons in the description of the structured (with internal degrees of freedom) infinitesimal test bodies moving on different curved two-dimensional surfaces embedded into the three-dimensional Euclidean space described in [16,17]. In the general case, we have some differential two-dimensional manifold $(S,\Gamma ,g)$ endowed with the affine connection $\Gamma$ and the metric tensor g that can be either interrelated or defined independently. Then the internally-structured infinitesimal test bodies moving on such a differential manifold S can be characterized by their positions $x\in S$ (this is just a remnant of the centre of mass’ positions of the extended bodies in the flat theory) as well as by their internal configurations (i.e., the internal variables attached at $x\in S$) injected into the tangent space $T_{x}S$, which is called microphysical space and can be identified with the set of linear frames (order bases) $e_A\in T_{x}S$. Therefore, the configuration space Q of the structured infinitesimal test bodies moving on S is given by the union of the manifolds of linear frames $F_{x}S$ in the tangent spaces $T_{x}S$ for all $x\in S$, i.e., $Q=FS={\cup }_{x\in S}{F}_{x}S$. This means that any system of local coordinates $x^i$ on the manifold S induces local coordinates $(x^i,{e^i}_A)$ on the manifold of all linear frames $FS$ and $(x^i,{e^A}_i)$ on the manifold of all linear coframes $F^{*}S$.

In the case of a Riemannian manifold $(S,g)$, we have that the affine connection $\Gamma$ is related to the metric tensor g and becomes the Levi-Civita (Christoffel) affine connection

$$\Gamma {{\left[g\right]}^i}_{jk}=\frac{1}{2}{g}^{im}\left(g_{mj,k}+g_{mk,j}-g_{jk,m}\right)$$

(7)

therefore, the corresponding curvature tensor

$$\mathcal{R}{{\left[g\right]}^i}_{jkl}={\partial }_k\Gamma {{\left[g\right]}^i}_{jl}-{\partial }_l\Gamma {{\left[g\right]}^i}_{jk}+\Gamma {{\left[g\right]}^i}_{ak}\Gamma {{\left[g\right]}^a}_{jl}-\Gamma {{\left[g\right]}^i}_{al}\Gamma {\left[g\right]}^{a}jk$$

(8)

generally do not vanish (i.e., the surface S is curved). In this situation we obtain that the geometry in the non-trivial manner influences both the translational motion $x^i$ and the internal configuration ${e^i}_A$ of the structured infinitesimal test bodies moving on such a curved surface S (for more details see, e.g., [16,17]).

The rest of the paper is organized as follows. In Section 2, the basic geometrical characteristics of the Mylar balloon (such as the profile curve, height, arclength, surface area, volume, etc.) are represented by a variety of closed-form expressions using elliptic integrals [18] and the fundamental mathematical constants such as the number $\pi$ and the lemniscate constant $\varpi$. It is also shown there that the Mylar balloon’s geometry can be characterize via certain integral quantities, geometrical moments, ${\mathcal{I}}_n\left(x\right)$ and ${\mathcal{I}}_n$, specified by the number (their order) $n=0,1,2,\dots$.

In Section 3, the geometrical moments, ${\mathcal{I}}_n\left(x\right)$, are interpreted as Mylar balloon’s cousins, i.e., as an enumerable set of surfaces, ${\mathcal{S}}_n$, closely associated with Mylar balloons (see. Figure 2). The Mylar balloon, ${\mathcal{S}}_M$, belongs to this family for $n=2$, namely, ${\mathcal{S}}_2\equiv {\mathcal{S}}_M$. All Mylar balloon’s cousins are parameterized via the Euler’s beta or gamma functions. In Section 3.1, the first and second fundamental forms along with the principal curvatures of ${\mathcal{S}}_n$ are explicitly calculated. Section 3.2 and Section 3.3 are devoted to the evaluation in terms of beta and gamma functions of the basic geometrical characteristics of the Mylar balloon’s cousins and the Mylar balloon, respectively.

In Section 4, certain recursive relations are explored to represent four non-intersecting residue classes for the thickness ${\tau }_n$, the meridional section area ${\Sigma }_n$ and the volume ${\mathcal{V}}_n$ of the Mylar balloon’s cousins. The main new results of the present research can be found in Section 3 and Section 4.

Finally, Section 5 concludes the paper with some general remarks regarding deviation of these new surfaces from the ideal shape, i.e., the sphere, and introduces one of the relevant characteristics for such comparison—the aspect ratio $\eta$. It turns out that the balloon with golden ratio proportion is in some sense central for this family of surfaces. On the other hand this characteristic opens the possibility for all spheroids, i.e., axially symmetric oblate shapes which aspect ratio $\eta$ is in the interval $[0,1)$, to be parameterized analytically using the formulas derived in Section 3.

2. Mylar Balloon’s Geometrical Characteristics

Any Mylar balloon ${\mathcal{S}}_M$ can be defined as a surface of revolution which is obtained when we maximize the volume of the cavity confined between two equal circular discs made of the Mylar foil and glued together at their boundaries (neither stretching nor shrinking of the Mylar foil is allowed) for a given (fixed) arclength a (where a is the radius of the “deflated” Mylar balloon, i.e., of the Mylar discs) of its directrix (generating curve), $z=\pm z\left(x\right)$, $x\in [0,r]$ (where r is the radius of the “inflated" Mylar balloon, and, obviously $r<a$) which, when rotated about the $OZ$-axis produces the two mirror-symmetric parts (with respect to the $XOY$-plane) of the balloon, i.e., its top or bottom half depending on the sign taken, plus or minus, of the z-coordinate, respectively (see, e.g., [1,19,20]).

It can be shown that the constraint equation for the generating curve of the Mylar balloon, lying in the first quadrant of the $XOZ$-plane, can be written as

$$z_M^{\prime }\left(x\right)=-\frac{x^2}{\sqrt{r^4-x^4}},\text{i.e.},z_M\left(x\right)=\underset{x}{\overset{r}{\int }}\frac{t^2\mathrm{d}t}{\sqrt{r^4-t^4}},x\in [0,r].$$

(9)

Equivalently, by introducing the dimensionless parameter $u=x/r$, it can be given

Definition 1.

The Mylar balloon is a surface of revolution ${\mathcal{S}}_M\subset {\mathbb{R}}^3$ parameterized as

$${\mathcal{S}}_M=\left\{\mathbf{x}={\mathbf{x}}_M(u,v):=\left(x\left(u\right)cosv,x\left(u\right)sinv,\pm z_M\left(u\right)\right),u\in [0,1],v\in [0,2\pi )\right\}$$

(10)

with a generating curve

$${\mathcal{C}}_M=\{(x,z),x=x\left(u\right),z=\pm z_M\left(u\right)\}$$

(11)

where

$$x\left(u\right):=ru,z_M\left(u\right):=r\underset{u}{\overset{1}{\int }}\frac{t^2\mathrm{d}t}{\sqrt{1-t^4}}$$

(12)

and equatorial radius r. By alternating the plus and minus signs in (10) and (11) the two symmetrically lying parts of ${\mathcal{S}}_M$ to the $XOY$-plane and ${\mathcal{C}}_M$ to the $OX$-axis are obtained.

The basic geometrical characteristics of the Mylar balloon (see Figure 1), such as the profile arclength, surface area, volume, etc., can be obtained as a direct consequence of the formulas above.

Let us start with the perimeter (arclength) ${\mathcal{L}}_M$ of the profile curve (complete meridional section, see Figure 1) of the Mylar balloon, which according to (12) can be calculated as

$${\mathcal{L}}_M=4\underset{N}{\overset{E}{\int }}\mathrm{d}s=4\underset{N}{\overset{E}{\int }}\sqrt{\mathrm{d}{x}^2+\mathrm{d}{z}_M^2}=4\underset{0}{\overset{1}{\int }}\sqrt{{\left(x^{\prime }\left(u\right)\right)}^2+{\left(z_M^{\prime }\left(u\right)\right)}^2}\mathrm{d}u=4r\underset{0}{\overset{1}{\int }}\frac{\mathrm{d}u}{\sqrt{1-u^4}}$$

(13)

where N and E denote the North Pole and the Equator of the Mylar balloon respectively (see Figure 1), and $x^{\prime }\left(u\right)=\mathrm{d}x/\mathrm{d}u$, etc. As a result we obtain

$${\mathcal{L}}_M=2\varpi r=\varpi d$$

(14)

where $d=2r$ is the equatorial diameter of the balloon and $\varpi$ is the lemniscate constant

$$\varpi \approx 2.62206$$

(15)

defined as

$$\varpi :=2\underset{0}{\overset{1}{\int }}\frac{\mathrm{d}u}{\sqrt{1-u^4}}\equiv 2K\left(\mathrm{i}\right)$$

(16)

where $K\left(\mathrm{i}\right)$ is complete elliptic integral with modulus $k=\mathrm{i}$.

With the help of substitution $u=\sqrt{1-w^2}$, the complete elliptic integral in (16) with imaginary modulus $k=\mathrm{i}$ is transformed to a complete elliptic integral with real modulus $k=1/\sqrt{2}$. Therefore, the defining formula for the lemniscate constant $\varpi$ takes the form

$$\varpi :=\sqrt{2}\underset{0}{\overset{1}{\int }}\frac{\mathrm{d}w}{\sqrt{(1-w^2)(1-w^2/2)}}\equiv \sqrt{2}K\left(\frac{1}{\sqrt{2}}\right).$$

(17)

There is an obvious analogy between the above obtained formula, ${\mathcal{L}}_M=2\varpi r$, and the familiar expression, ${\mathcal{L}}_{\mathrm{circle}}=2\pi r$, for the circumference of the circle, with $\pi$ replaced by $\varpi$ for the Mylar balloon. Hence, the notation $\varpi$ (pomega), which historically is a cursive variant of $\pi$, is being used. Its name “pomega” recalls both the relationship of $\varpi$ to the letter $\pi$ and the $\varpi$’s similarity to a variant of the lowercase omega $\omega$ with a macron (long mark) placed over it (cf. [21]).

Moreover, it should be noted the remarkable fact that the perimeter of the profile curve of the Mylar balloon is given by exactly the same formula, ${\mathcal{L}}_M=\varpi d$, as is the perimeter of the lemniscate of Bernoulli (hence the name “lemniscate constant”) with d interpreted as the diameter of the curve, being the maximum distance between any two points on it.

As it follows from ${\mathcal{L}}_M=2\varpi r$ and the arclength constraint condition ${\mathcal{L}}_M=4a$ (cf. (2)) the ratio of the inflated radius r to the deflated one a is given by the relation

$$\frac{r}{a}=\frac{2}{\varpi }={(1.31103\dots )}^{-1}\approx 0.7627.$$

(18)

As the next geometrical characteristic of the Mylar balloon we can calculate its surface area, ${\mathcal{A}}_M$, by integrating over all the conical bands with infinitesimal width $\mathrm{d}s=\sqrt{\mathrm{d}{x}^2+\mathrm{d}{z}_M^2}$ and length $2\pi x$, where x is the distance from the z-axis (axis of rotation, cf. (9)–(12)) to the arclength element $\mathrm{d}s$, i.e.,

$${\mathcal{A}}_M=2\pi \underset{{\mathcal{S}}_M}{\int }x\sqrt{\mathrm{d}{x}^2+\mathrm{d}{z}_M^2}=4\pi \underset{0}{\overset{r}{\int }}x\sqrt{1+{\left(z_M^{\prime }\left(x\right)\right)}^2}\mathrm{d}x=4\pi r^2\underset{0}{\overset{1}{\int }}\frac{u\mathrm{d}u}{\sqrt{1-u^4}}$$

(19)

which is immediately integrated to obtain

$${\mathcal{A}}_M={\pi }^2{r}^2.$$

(20)

It is clearly seen, the surface area of the (inflated) Mylar balloon differs from the original area ${\mathcal{A}}_{\mathrm{discs}}=2\pi a^2$ of the two sewn together circular Mylar discs, showing an effective (integral) shrinking (hence visible crimping or wrinkling) of the inflated balloon’s surface relative to the deflated one, i.e.,

$$\frac{{\mathcal{A}}_{\mathrm{discs}}}{{\mathcal{A}}_M}=\frac{2\pi a^2}{{\mathcal{A}}_M}=\frac{2}{\pi }{\left(\frac{a}{r}\right)}^2=\frac{2}{\pi }{\left(\frac{\varpi }{2}\right)}^2\approx 1.09422$$

(21)

which is accounting for more than about $8.61\%$ loss of the original (deflated) surface area.

We can also introduce a local measure of the above-described integral shrinking that is defined as the ratio of the surface area of a small patch on the deflated Mylar balloon to the surface area of the corresponding patch on the inflated Mylar balloon. This local measure is called crimping factor and is defined through the relation (see, e.g., [1])

$$C_M\left(u\right)=\frac{1}{u}\underset{0}{\overset{u}{\int }}\frac{\mathrm{d}t}{\sqrt{1-t^4}}·$$

(22)

It can be shown that the crimping factor $C_M\left(u\right)$ is minimal at the poles, where $u=0$ (see Figure 1 right), i.e.,

$$C_M^{\min }=C_M\left(0\right)=\underset{u\to 0}{lim}\frac{1}{u}\underset{0}{\overset{u}{\int }}\frac{\mathrm{d}t}{\sqrt{1-t^4}}={\left[\frac{0}{0}\right]}_{\text{l’Hôspital’s rule}}=\underset{u\to 0}{lim}\frac{1}{\sqrt{1-u^4}}=1$$

(23)

and maximal at the Equator, for $u=1$ (again see Figure 1 right), i.e.,

$$C_M^{\max }=C_M\left(1\right)=\underset{0}{\overset{1}{\int }}\frac{\mathrm{d}t}{\sqrt{1-t^4}}=\frac{{\mathcal{L}}_M}{4r}=\frac{a}{r}=\frac{\varpi }{2}\approx 1.31103.$$

(24)

Another geometrical characteristic of the Mylar balloon is the polar diameter (thickness, height) ${\tau }_M$ calculated by taking twice the distance from the center of the balloon to one of its poles, i.e.,

$${\tau }_M=2z_M\left(0\right)=2r\underset{0}{\overset{1}{\int }}\frac{t^2\mathrm{d}t}{\sqrt{1-t^4}}$$

(25)

which can be rewritten as

$${\tau }_M=2\left(\underset{0}{\overset{1}{\int }}\sqrt{\frac{1+t^2}{1-t^2}}\mathrm{d}t-\underset{0}{\overset{1}{\int }}\frac{\mathrm{d}t}{\sqrt{(1-t^2)(1+t^2)}}\right)·r.$$

(26)

Then, by the substitution, $t=\sqrt{1-w^2}$, the expression for ${\tau }_M$ takes the form

$$\begin{array}{ccc}\hfill {\tau }_M& =& \sqrt{2}\left(2\underset{0}{\overset{1}{\int }}\sqrt{\frac{1-w^2/2}{1-w^2}}\mathrm{d}w-\underset{0}{\overset{1}{\int }}\frac{\mathrm{d}w}{\sqrt{(1-w^2)(1-w^2/2)}}\right)·r\hfill \\ \hfill & =& \sqrt{2}\left(2E\left(\frac{1}{\sqrt{2}}\right)-K\left(\frac{1}{\sqrt{2}}\right)\right)·r\hfill \end{array}$$

which, on using the Legendre’s relation [22] for the complete elliptic integrals of the first $K(1/\sqrt{2})$ and the second kind $E(1/\sqrt{2})$, i.e.,

$$\left(2E\left(\frac{1}{\sqrt{2}}\right)-K\left(\frac{1}{\sqrt{2}}\right)\right)K\left(\frac{1}{\sqrt{2}}\right)=\frac{\pi }{2}$$

(27)

and, by virtue of the definition of the lemniscate constant in (17), is transformed to a compact form

$${\tau }_M=\frac{\pi }{\varpi }r.$$

(28)

Note that $d=2r$ and ${\tau }_M$ are the two extreme (maximal and minimal respectively) distances between any two points on the Mylar balloon. Their ratio is given by the relation

$$\frac{d}{{\tau }_M}=\frac{2\varpi }{\pi }\approx 1.6692.$$

(29)

As it can be easily deduced from (21), the effective (integral) shrinking equals the ratio of the deflated radius a to the thickness ${\tau }_M$, which in connection with the above ratio can be expressed as

$$\frac{{\mathcal{A}}_{\mathrm{discs}}}{{\mathcal{A}}_M}=\frac{a}{{\tau }_M}=\frac{\varpi }{4}\left(\frac{d}{{\tau }_M}\right)\approx 1.09422.$$

(30)

Proceeding on, we can calculate the meridional section area, ${\Sigma }_M$, of the Mylar balloon as

$${\Sigma }_M=4\underset{0}{\overset{r}{\int }}{z}_M\left(x\right)\mathrm{d}x=4r^2\underset{0}{\overset{1}{\int }}\frac{t^3\mathrm{d}t}{\sqrt{1-t^4}}$$

(31)

which is readily integrated to obtain the formula

$${\Sigma }_M=2r^2.$$

(32)

We can also calculate the Mylar balloon’s volume ${\mathcal{V}}_M$ by using the shell method, i.e.,

$${\mathcal{V}}_M=4\pi \underset{0}{\overset{r}{\int }}x{z}_M\left(x\right)\mathrm{d}x=4\pi r^3\underset{u=0}{\overset{1}{\int }}\underset{t=u}{\overset{1}{\int }}\frac{t^{2}u}{\sqrt{1-t^4}}\mathrm{d}t\mathrm{d}u$$

(33)

where we have used the representation of the profile curve in (12). Changing the order of integration in (33) from $(u,t)\in [0,1]\times [u,1]$ to $(t,u)\in [0,1]\times [0,t]$, the volume takes the form

$${\mathcal{V}}_M=4\pi r^3\underset{t=0}{\overset{1}{\int }}\underset{u=0}{\overset{t}{\int }}\frac{t^{2}u}{\sqrt{1-t^4}}\mathrm{d}u\mathrm{d}t=2\pi r^3\underset{0}{\overset{1}{\int }}\frac{t^4\mathrm{d}t}{\sqrt{1-t^4}}$$

(34)

which using integration by parts can be rewritten as

$$\begin{array}{ccc}\hfill {\mathcal{V}}_M& =& -\pi r^3\underset{0}{\overset{1}{\int }}t\mathrm{d}\left(\sqrt{1-t^4}\right)=-{\left.\pi r^{3}t\sqrt{1-t^4}\right|}_0^1+\pi r^3\underset{0}{\overset{1}{\int }}\sqrt{1-t^4}\mathrm{d}t\hfill \\ \hfill & =& \pi r^3\underset{0}{\overset{1}{\int }}\frac{\mathrm{d}t}{\sqrt{1-t^4}}-\pi r^3\underset{0}{\overset{1}{\int }}\frac{t^4\mathrm{d}t}{\sqrt{1-t^4}}·\hfill \end{array}$$

Next, taking into account definition (16) for the lemniscate constant $\varpi$, and interpreting the last integral as ${\mathcal{V}}_M/\left(2\pi r^3\right)$ using (34), we obtain the final formula for the volume as

$${\mathcal{V}}_M=\frac{\pi \varpi }{3}{r}^3.$$

(35)

We summarize the results obtained above in

Theorem 1.

The most important Mylar balloon’s geometrical characteristics are given by the expressions

$${\mathcal{L}}_M=2\varpi r,{\mathcal{A}}_M={\pi }^2{r}^2,{\tau }_M=\frac{\pi }{\varpi }r,{\Sigma }_M=2r^2,{\mathcal{V}}_M=\frac{\pi \varpi }{3}{r}^3$$

(36)

where r is the equatorial radius of the (inflated) Mylar balloon.

Moreover, the integral expressions (12), (13), (19), (22), (25), (31) and (34) clearly indicate that the Mylar balloon can be actually characterized by a set of dimensionless quantities, geometrical moments, defined as (cf. [23])

$${\mathcal{I}}_n\left(u\right):=\underset{0}{\overset{u}{\int }}\frac{t^n\mathrm{d}t}{\sqrt{1-t^4}},{\mathcal{I}}_n:={\mathcal{I}}_n\left(1\right)=\underset{0}{\overset{1}{\int }}\frac{t^n\mathrm{d}t}{\sqrt{1-t^4}},u\in [0,1],n=0,1,2,\dots$$

(37)

which allow us to state

Theorem 2.

Relying on geometrical moments the Mylar balloon’s geometrical characteristics are given by the formulas

$${\mathcal{L}}_M=4{\mathcal{I}}_0·r,{\mathcal{A}}_M=4\pi {\mathcal{I}}_1·r^2,{\tau }_M=2{\mathcal{I}}_2·r,{\Sigma }_M=4{\mathcal{I}}_3·r^2,{\mathcal{V}}_M=2\pi {\mathcal{I}}_4·r^3$$

(38)

where ${\mathcal{I}}_0,\dots ,{\mathcal{I}}_4$ are the first five geometrical moments associated with the Mylar balloon.

Furthermore, the profile curve $z_M\left(u\right)$ and the crimping factor $C_M\left(u\right)$ (cf. (12) and (22)) can be also given in alternative forms using geometrical moments, i.e.,

$$z_M\left(u\right)=\left({\mathcal{I}}_2-{\mathcal{I}}_2\left(u\right)\right)·r,C_M\left(u\right)=\frac{{\mathcal{I}}_0\left(u\right)}{u},u=\frac{x}{r}·$$

(39)

In the next section the geometrical moments of the Mylar balloon, ${\mathcal{I}}_n\left(u\right)$, are interpreted as surfaces. They constitute an enumerable set of surfaces of revolutions, ${\mathcal{S}}_n$, clearly associated with Mylar balloons, which means that we are going to introduce a family of Mylar balloon’s cousins.

3. Mylar Balloon’s Cousins

In the next definition we introduce a special kind of balloons—Mylar balloon’s cousins, an enumerable set of surfaces of revolution associated with Mylar balloons.

Definition 2.

The Mylar balloon’s cousins ${\mathcal{S}}_n\subset {\mathbb{R}}^3$ are surfaces of revolution

$${\mathcal{S}}_n=\left\{\mathbf{x}={\mathbf{x}}_n(u,v):=\left(x\left(u\right)cosv,x\left(u\right)sinv,\pm z_n\left(u\right)\right),u\in [0,1],v\in [0,2\pi )\right\}$$

(40)

with generating curves ${\mathcal{C}}_n$ of the form

$${\mathcal{C}}_n=\{(x,z),x=x\left(u\right),z=\pm z_n\left(u\right)\}$$

(41)

where

$$x\left(u\right):=ru,z_n\left(u\right):=r\underset{u}{\overset{1}{\int }}\frac{t^n\mathrm{d}t}{\sqrt{1-t^4}},n=0,1,\dots$$

(42)

Here the parameter $r>0$ specifies the equatorial radius of the balloons and the two symmetrically lying parts of ${\mathcal{S}}_n$ to the $XOY$-plane and that ones of ${\mathcal{C}}_n$ to the $OX$-axis are generated by alternating the plus and minus signs in (40) and (41).

Note that the Mylar balloon, ${\mathcal{S}}_M$, belongs to the above defined family, ${\mathcal{S}}_2\equiv {\mathcal{S}}_M$, and each one of the balloons, ${\mathcal{S}}_n$, $n\ne 2$, is a special generalization of the Mylar balloon (compare the parameterizations of ${\mathcal{S}}_M$ and ${\mathcal{S}}_n$ in (12) and (42)). Substituting $\omega =t^4$, the integral in (42) can be rewritten as

$$z_n\left(u\right)=\frac{r}{4}\underset{u^4}{\overset{1}{\int }}{\omega }^{\frac{n-3}{4}}{(1-\omega )}^{-\frac{1}{2}}\mathrm{d}\omega$$

(43)

therefore, the profile curves ${\mathcal{C}}_n$ of the Mylar balloon’s cousins (see Figure 2) can be expressed as

$$x\left(u\right)=ru,z_n\left(u\right)=\frac{r}{4}·\left(B\left(\frac{n+1}{4},\frac{1}{2}\right)-B_{u^4}\left(\frac{n+1}{4},\frac{1}{2}\right)\right),u\in [0,1],n=0,1,\dots$$

(44)

where the definitions of the incomplete beta function $B_{\zeta }(p,q)$ and the beta function $B(p,q)\equiv B_1(p,q)$ have been used (cf., e.g., [22,24,25]), i.e.,

$$\begin{array}{ccc}\hfill B_{\zeta }(p,q)& =& \underset{0}{\overset{\zeta }{\int }}{\omega }^{p-1}{(1-\omega )}^{q-1}\mathrm{d}\omega ,0\le \zeta \le 1,p>0,q>0\hfill \end{array}$$

(45)

$$\begin{array}{ccc}\hfill B(p,q)& \equiv & B_1(p,q)=\underset{0}{\overset{1}{\int }}{\omega }^{p-1}{(1-\omega )}^{q-1}\mathrm{d}\omega .\hfill \end{array}$$

(46)

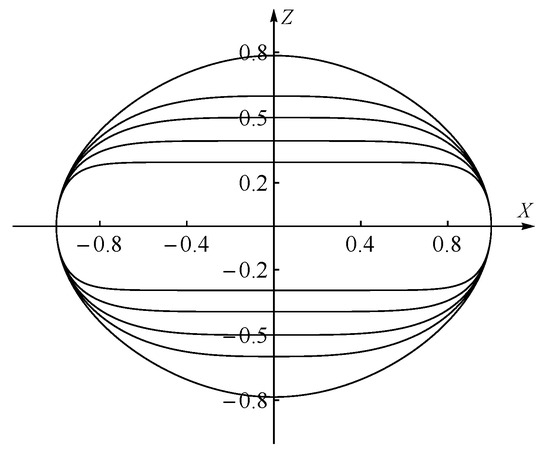
Figure 2. Profile curves (complete cross-sections) of Mylar balloon’s cousins, ${\mathcal{S}}_n$, with equatorial radius $r=1$, for $n=1,2,3,5$ and 9, viewed from the outside in.

In addition to the several balloon profiles given in Figure 2 and the Mylar balloon for $n=2$ in Figure 1, other two 3D graphics (with and without a cut) of one of the Mylar balloon’s cousins, ${\mathcal{S}}_3$, can be seen in Figure 3.

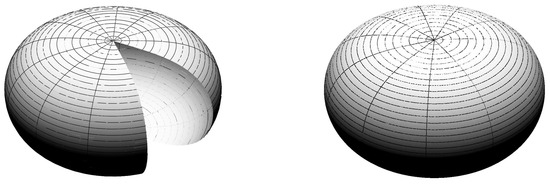
Figure 3. A side view of the Mylar balloon’s cousin ${\mathcal{S}}_3$ drawn with $r=1$. An open part (left) and the entire surface (right).

The plots are produced with the help of the computer algebra system Mathematica^® [5], using the new parameterization (44).

3.1. First and Second Fundamental Forms and Principal Curvatures

A surface in ${\mathbb{R}}^3$ parameterized as $\mathbf{x}=\mathbf{x}(u,v)$ is determined almost uniquely by its first I and second $II$ fundamental forms (see, e.g., [26])

$$I=E\mathrm{d}{u}^2+2F\mathrm{d}u\mathrm{d}v+G\mathrm{d}{v}^2,II=L\mathrm{d}{u}^2+2M\mathrm{d}u\mathrm{d}v+N\mathrm{d}{v}^2$$

where the coefficients are defined by the formulas

$$\begin{array}{ccc}\hfill E& =& {\mathbf{x}}_u·{\mathbf{x}}_u,F={\mathbf{x}}_u·{\mathbf{x}}_v,G={\mathbf{x}}_v·{\mathbf{x}}_v\hfill \\ & & \\ \hfill L& =& {\mathbf{x}}_{uu}·\mathbf{n},M={\mathbf{x}}_{uv}·\mathbf{n},N={\mathbf{x}}_{vv}·\mathbf{n}\hfill \end{array}$$

(47)

and $\mathbf{n}$ is the unit vector which is normal to the surface

$$\mathbf{n}=\frac{{\mathbf{x}}_u\times {\mathbf{x}}_v}{{|\mathbf{x}}_u\times {\mathbf{x}}_v|}·$$

Here we have used the notation ${\mathbf{x}}_u=\partial \mathbf{x}/\partial u$, ${\mathbf{x}}_{uu}={\partial }^2\mathbf{x}/\partial u^2$, etc.

If $\mathbf{x}=\mathbf{x}(u,v)$ is a surface of revolution, i.e.,

$$\mathbf{x}(u,v)=\left(h\right(u)cosv,h(u)sinv,g(u\left)\right)$$

(48)

then the meridional, ${\kappa }_{\mu }$, and the parallel, ${\kappa }_{\pi }$, principal curvatures can be found by the classical formulas

$${\kappa }_{\mu }\equiv \frac{L}{E}=\frac{g^{″}{h}^{\prime }-g^{\prime }{h}^{″}}{{(g^{{\prime }^2}+h^{{\prime }^2})}^{3/2}},{\kappa }_{\pi }\equiv \frac{N}{G}=\frac{g^{\prime }}{h{(g^{{\prime }^2}+h^{{\prime }^2})}^{1/2}}$$

(49)

where $g^{\prime }\equiv \mathrm{d}g/\mathrm{d}u$, etc.

Applying the above formulas, the coefficients of the first $FF{F}_n=(E,F,G)$ and second $SF{F}_n=(L,M,N)$ fundamental forms of ${\mathcal{S}}_n$ are calculated as

$$\begin{array}{ccc}\hfill FF{F}_n& =& \left\{r^2·\frac{u^{2n}-u^4+1}{1-u^4},0,r^2·u^2\right\}\hfill \\ & & \\ \hfill SF{F}_n& =& \left\{-r·\frac{u^{n-1}\left((2-n)u^4+n\right)}{\left(1-u^4\right)\sqrt{u^{2n}-u^4+1}},0,-r·\frac{u^{n+1}}{\sqrt{u^{2n}-u^4+1}}\right\}.\hfill \\ & & \hfill \end{array}$$

(50)

The corresponding principal curvatures of ${\mathcal{S}}_n$, i.e., ${\kappa }_{\mu |n}$ and ${\kappa }_{\pi |n}$, calculated via (49), are obtained as

$${\kappa }_{\mu |n}=-\frac{1}{r}·\frac{\left(n-(n-2)u^4\right)u^{n-1}}{{\left(u^{2n}-u^4+1\right)}^{3/2}},{\kappa }_{\pi |n}=-\frac{1}{r}·\frac{u^{n-1}}{\sqrt{u^{2n}-u^4+1}}·$$

(51)

For the special case of the Mylar balloon, i.e., for ${\mathcal{S}}_2$, we obtain that

$$FF{F}_2=\left\{\frac{r^2}{1-u^4},0,r^2{u}^2\right\},SF{F}_2=\left\{-\frac{2ru}{1-u^4},0,-r{u}^3\right\}$$

(52)

$${\kappa }_{\mu |2}=-\frac{2u}{r},{\kappa }_{\pi |2}=-\frac{u}{r}$$

(53)

which confirms the well-known fact that the Mylar balloon is a linear Weingarten surface, i.e., its principal curvatures ${\kappa }_{\mu }\equiv {\kappa }_{\mu |2}$ and ${\kappa }_{\pi }\equiv {\kappa }_{\pi |2}$ satisfy the relation

$${\kappa }_{\mu }-2{\kappa }_{\pi }=0.$$

(54)

Using (51) it can be easily verified that the Mylar balloon’s cousins ${\mathcal{S}}_0$ and ${\mathcal{S}}_1$ are Weingarten surfaces as well, which means that their principal curvatures obey functional relations, the so-called Weingarten relations. For ${\mathcal{S}}_0$ this is the seventh-order equation

$$32{\kappa }_{\mu }{\kappa }_{\pi }^6{r}^4-{\kappa }_{\mu }^3-8{\kappa }_{\pi }^3-6{\kappa }_{\mu }^2{\kappa }_{\pi }-12{\kappa }_{\mu }{\kappa }_{\pi }^2=0$$

(55)

and for ${\mathcal{S}}_1$ we have the twelfth-order polynomial equation

$${\kappa }_{\pi }^4{\left(5{\kappa }_{\pi }^4{r}^4-4{\kappa }_{\pi }^2{r}^2+1\right)}^2+{\kappa }_{\mu }^2\left(12{\kappa }_{\pi }^4{r}^2-2{\kappa }_{\pi }^2-15{\kappa }_{\pi }^6{r}^4\right)+{\kappa }_{\mu }^4=0$$

(56)

where the second indices in ${\kappa }_{\mu |0},{\kappa }_{\pi |0},{\kappa }_{\mu |1}$, ${\kappa }_{\pi |1}$, have been suppressed.

Unfortunately, it was not possible for us to derive the most general equation representing the Weingarten relation for an arbitrary index n.

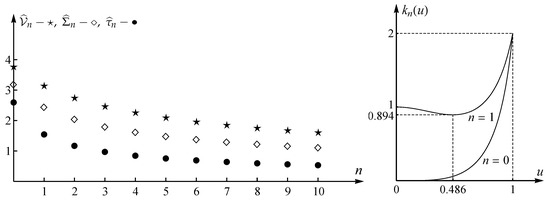
However, an interesting conclusions about the ratio $k_n\left(u\right)={\kappa }_{\mu |n}/{\kappa }_{\pi |n}$ of the two principal curvatures for any member in the family ${\mathcal{S}}_n$ can be easily derived. Relying again on the equations in (51) it is straightforward to see that this is the fractional function

$$k_n\left(u\right)=\frac{(2-n)u^4+n}{u^{2n}-u^4+1},u\in [0,1],n=0,1,2,\dots .$$

(57)

From the above expression it is immediately seen that at the poles (where $u=0$) the numerical value of this fractional function $k_n\left(u\right)$ coincides with the genuine number n of the surface to which it refers to, i.e., $k_n\left(0\right)=n$, and then varying smoothly along the meridians it reaches at the equator (where $u=1$) the same integer value for all surfaces in the family, i.e., $k_n\left(1\right)=2$. In particular, this means that for $n=0$ we have a monotonically increasing function when $u\in [0,1]$, i.e.,

$$k_0\left(u\right)=\frac{2u^4}{2-u^4}$$

(58)

whereas for $n=1$ the fractional function

$$k_1\left(u\right)=\frac{1+u^4}{1+u^2-u^4}$$

(59)

first decreases to the minimal value $2/\sqrt{5}$ at $u_{\min }=\sqrt{\sqrt{5}-2}$ and then increases to the maximal value 2. In the case of the Mylar balloon (i.e., when $n=2$) the ratio between the meridional and parallel curvatures is constant (see (54)), i.e., $k_2\equiv k_2\left(u\right)=2$. Let us also note that, as it is shown in [7], this fact specifies the shape of the rotational surface uniquely (cf. (53) and (54)). Graphical representations of the two functions $k_0\left(u\right)$ and $k_1\left(u\right)$ are given in Figure 4, right.

Figure 4. Graphical representations of (left) the first eleven dimensionless quantities ${\widehat{\mathcal{V}}}_n$, ${\widehat{\Sigma }}_n$ and ${\widehat{\tau }}_n$, $n=0,1,\dots ,10$, and (right) the fractional functions $k_0\left(u\right)$ and $k_1\left(u\right)$, cf. (58) and (59).

3.2. Geometrical Characteristics of the Mylar Balloon’s Cousins

Applying standard methods as in Section 2, we can calculate the basic geometrical characteristics of the Mylar balloon’s cousins ${\mathcal{S}}_n$ such as the perimeter ${\mathcal{L}}_n$ of the profile curves of the balloons, their surface areas ${\mathcal{A}}_n$, etc.

Starting with the perimeter ${\mathcal{L}}_n$ of the profile curves (i.e., the complete meridional sections, see Figure 1 and Figure 2) and using the integral representation in (42) we arrive at

$${\mathcal{L}}_n=4\underset{N}{\overset{E}{\int }}\mathrm{d}{s}_n=4\underset{N}{\overset{E}{\int }}\sqrt{\mathrm{d}{x}^2+\mathrm{d}{z}_n^2}=4\underset{0}{\overset{1}{\int }}\sqrt{{\left(x^{\prime }\left(u\right)\right)}^2+{\left(z_n^{\prime }\left(u\right)\right)}^2}\mathrm{d}u=4r\underset{0}{\overset{1}{\int }}\frac{\sqrt{1-u^4+u^{2n}}}{\sqrt{1-u^4}}\mathrm{d}u$$

and then, on passing to $\omega =u^4$, we obtain

$${\mathcal{L}}_n=r\underset{0}{\overset{1}{\int }}\frac{\sqrt{1-\omega +{\omega }^{n/2}}}{{\omega }^{3/4}\sqrt{1-\omega }}\mathrm{d}\omega =\left(\underset{0}{\overset{1}{\int }}{\omega }^{\frac{n-5}{4}}{(1-\omega )}^{-\frac{1}{2}}{G}_n\left(\omega \right)\mathrm{d}\omega \right)·r$$

(60)

where

$$G_n\left(\omega \right)=\frac{\sqrt{1-\omega +{\omega }^{n/2}}}{{\omega }^{(n-2)/4}},n=0,1,2,\dots .$$

(61)

Similarly, we can calculate the surface area of the Mylar Balloon’s cousins ${\mathcal{A}}_n$, i.e.,

$${\mathcal{A}}_n=2\pi \underset{{\mathcal{S}}_n}{\int }x\sqrt{\mathrm{d}{x}^2+\mathrm{d}{z}_n^2}=4\pi r\underset{0}{\overset{1}{\int }}u\sqrt{{\left(x^{\prime }\left(u\right)\right)}^2+{\left(z_n^{\prime }\left(u\right)\right)}^2}\mathrm{d}u=4\pi r^2\underset{0}{\overset{1}{\int }}\frac{u\sqrt{1-u^4+u^{2n}}}{\sqrt{1-u^4}}\mathrm{d}u$$

which finally can be expressed as

$${\mathcal{A}}_n=\pi r^2\underset{0}{\overset{1}{\int }}\frac{\sqrt{1-\omega +{\omega }^{n/2}}}{\sqrt{\omega }\sqrt{1-\omega }}\mathrm{d}\omega =\pi ·\left(\underset{0}{\overset{1}{\int }}{\omega }^{\frac{n-4}{4}}{(1-\omega )}^{-\frac{1}{2}}{G}_n\left(\omega \right)\mathrm{d}\omega \right)·r^2.$$

(62)

Note that for the case of the Mylar balloon, $n=2$, the factor-function $G_n\left(\omega \right)$, which is present in Equations (60) and (62) as a multiplier, is identically equal to one: $G_2\left(\omega \right)\equiv 1$.

For the next three geometrical characteristics, i.e., the thickness ${\tau }_n$, the meridional section area ${\Sigma }_n$, and the volume ${\mathcal{V}}_n$, we obtain explicit representations using the beta function defined by (46) or the gamma function which defining formula is given as [24,25]

$$\Gamma \left(p\right)=\underset{0}{\overset{\infty }{\int }}{\mathrm{e}}^{-\omega }{\omega }^{p-1}\mathrm{d}\omega ,p>0.$$

(63)

The thickness (i.e., the polar diameter) ${\tau }_n$ of the balloons equals to the distance between the two poles N and S (see Figure 1), i.e.,

$${\tau }_n=2z_n\left(0\right)=2r\underset{0}{\overset{1}{\int }}\frac{t^n\mathrm{d}t}{\sqrt{1-t^4}}=\frac{r}{2}\underset{0}{\overset{1}{\int }}{\omega }^{\frac{n-3}{4}}{(1-\omega )}^{-\frac{1}{2}}\mathrm{d}\omega$$

(64)

which in terms of beta or gamma function can be written as

$${\tau }_n=\frac{1}{2}·B\left(\frac{n+1}{4},\frac{1}{2}\right)·r=\frac{\sqrt{\pi }}{2}·\frac{\Gamma \left(\frac{n+1}{4}\right)}{\Gamma \left(\frac{n+3}{4}\right)}·r$$

(65)

where we used a formula connecting gamma and beta functions (cf., e.g., [22,25]), i.e.,

$$B(p,q)=\frac{\Gamma \left(p\right)\Gamma \left(q\right)}{\Gamma (p+q)}·$$

(66)

Similarly, the meridional sections area, ${\Sigma }_n$, can be calculated as

$${\Sigma }_n=4\underset{0}{\overset{1}{\int }}{z}_n\left(u\right)\mathrm{d}\left(x\left(u\right)\right)=4r\underset{0}{\overset{1}{\int }}{z}_n\left(u\right)\mathrm{d}u=4r^2\underset{0}{\overset{1}{\int }}\frac{t^{n+1}\mathrm{d}t}{\sqrt{1-t^4}}=r^2\underset{0}{\overset{1}{\int }}{\omega }^{\frac{n-2}{4}}{(1-\omega )}^{-\frac{1}{2}}\mathrm{d}\omega$$

(67)

or, via the beta or gamma functions, as

$${\Sigma }_0=\pi ·r^2,{\Sigma }_n=B\left(\frac{n+2}{4},\frac{1}{2}\right)·r^2=\frac{4\sqrt{\pi }}{n}·\frac{\Gamma \left(\frac{n+2}{4}\right)}{\Gamma \left(\frac{n}{4}\right)}·r^2,n=1,2,\dots .$$

(68)

For calculation of the volume, ${\mathcal{V}}_n$, we proceed as in Section 2 using the shell method, i.e.,

$${\mathcal{V}}_n=4\pi \underset{0}{\overset{1}{\int }}x\left(u\right)z_n\left(u\right)\mathrm{d}\left(x\left(u\right)\right)=4\pi r^2\underset{0}{\overset{1}{\int }}u{z}_n\left(u\right)\mathrm{d}u$$

(69)

where after replacing $z_n\left(u\right)$ with the integral expression in (42) and changing the order of integration we arrive at

$${\mathcal{V}}_n=2\pi r^3\underset{0}{\overset{1}{\int }}\frac{t^{n+2}\mathrm{d}t}{\sqrt{1-t^4}}=\frac{\pi r^3}{2}\underset{0}{\overset{1}{\int }}{\omega }^{\frac{n-1}{4}}{(1-\omega )}^{-\frac{1}{2}}\mathrm{d}\omega$$

(70)

which by virtue of the definitions of the beta function and its connection with the gamma function (see (46), (63) and (66)) can be written as

$${\mathcal{V}}_n=\frac{\pi }{2}·B\left(\frac{n+3}{4},\frac{1}{2}\right)·r^3=\frac{2\pi \sqrt{\pi }}{n+1}·\frac{\Gamma \left(\frac{n+3}{4}\right)}{\Gamma \left(\frac{n+1}{4}\right)}·r^3.$$

(71)

The results of this section are summarized in the next two theorems.

Theorem 3.

The perimeter ${\mathcal{L}}_n$ of the profile curves (meridional sections) and the surface area ${\mathcal{A}}_n$ of the Mylar balloon’s cousins ${\mathcal{S}}_n$ are given by the integral formulas

$${\mathcal{L}}_n=\left(\underset{0}{\overset{1}{\int }}{\omega }^{\frac{n-5}{4}}{(1-\omega )}^{-\frac{1}{2}}{G}_n\left(\omega \right)\mathrm{d}\omega \right)·r,{\mathcal{A}}_n=\pi ·\left(\underset{0}{\overset{1}{\int }}{\omega }^{\frac{n-4}{4}}{(1-\omega )}^{-\frac{1}{2}}{G}_n\left(\omega \right)\mathrm{d}\omega \right)·r^2$$

(72)

where $r>0$ is the equatorial radius of the balloons, the factor-function $G_n\left(\omega \right)$ is defined in (61) and $n=0,1,2,\dots$.

Theorem 4.

The thickness ${\tau }_n$, the meridional section area ${\Sigma }_n$, and the volume ${\mathcal{V}}_n$ of the Mylar balloon’s cousins ${\mathcal{S}}_n$ are given by the formulas, using beta functions

$${\tau }_n=\frac{1}{2}·B\left(\frac{n+1}{4},\frac{1}{2}\right)·r,{\Sigma }_n=B\left(\frac{n+2}{4},\frac{1}{2}\right)·r^2,{\mathcal{V}}_n=\frac{\pi }{2}·B\left(\frac{n+3}{4},\frac{1}{2}\right)·r^3$$

(73)

or gamma functions

$${\tau }_n=\frac{\sqrt{\pi }}{2}·\frac{\Gamma \left(\frac{n+1}{4}\right)}{\Gamma \left(\frac{n+3}{4}\right)}·r,{\Sigma }_n=\frac{4\sqrt{\pi }}{n}·\frac{\Gamma \left(\frac{n+2}{4}\right)}{\Gamma \left(\frac{n}{4}\right)}·r^2,{\mathcal{V}}_n=\frac{2\pi \sqrt{\pi }}{n+1}·\frac{\Gamma \left(\frac{n+3}{4}\right)}{\Gamma \left(\frac{n+1}{4}\right)}·r^3$$

(74)

where r is the equatorial radius of the balloons and $n=0,1,2,\dots$, except for ${\Sigma }_n$ in the second row valid for $n=1,2,\dots$.

3.3. Geometrical Characteristics of the Mylar Balloon via Beta and Gamma Functions

Taking the above-obtained formulas for $n=2$ (or equivalently, using the relations (38) and (39)) the basic geometrical characteristics of the Mylar balloon obtained in Section 2 can be expressed in terms of the Euler’s beta or gamma functions (see, e.g., [22,25]).

Substituting $n=2$ into (44) the parameterization of the profile curve ${\mathcal{C}}_M\equiv {\mathcal{C}}_2$ of the Mylar balloon (see Figure 1) takes the form

$$x\left(u\right)=ru,z_M\left(u\right)\equiv z_2\left(u\right)=\frac{r}{4}·\left(B\left(\frac{3}{4},\frac{1}{2}\right)-B_{u^4}\left(\frac{3}{4},\frac{1}{2}\right)\right),u\in [0,1]$$

(75)

where $B_{\zeta }(p,q)$ is the incomplete beta function of the real variable $\zeta \in [0,1]$, and $B(p,q)\equiv B_1(p,q)$ is the beta function (see Formulas (45) and (46)).

The crimping factor, $C_M\left(u\right)$, which integral formula is given in (22), can be also represented via the beta function, i.e.,

$$C_M\left(u\right)=\frac{{\mathcal{I}}_0\left(u\right)}{u}=\frac{1}{4u}·B_{u^4}\left(\frac{1}{4},\frac{1}{2}\right),u\in [0,1].$$

(76)

The arclength ${\mathcal{L}}_M$, the surface area ${\mathcal{A}}_M$, and the polar diameter ${\tau }_M$ are straightforwardly calculated through the beta or gamma functions, i.e.,

$$\begin{array}{ccc}\hfill {\mathcal{L}}_M& \equiv & {\mathcal{L}}_2=B\left(\frac{1}{4},\frac{1}{2}\right)·r=\sqrt{\frac{1}{2\pi }}·\Gamma {\left(\frac{1}{4}\right)}^2·r=2\varpi ·r\approx 5.24411·r\hfill \end{array}$$

(77)

$$\begin{array}{ccc}\hfill {\mathcal{A}}_M& \equiv & {\mathcal{A}}_2=\pi ·B\left(\frac{1}{2},\frac{1}{2}\right)·r^2=\pi ·\Gamma {\left(\frac{1}{2}\right)}^2·r^2={\pi }^2·r^2\approx 9.8696·r^2\hfill \end{array}$$

(78)

$$\begin{array}{ccc}\hfill {\tau }_M& \equiv & {\tau }_2=\frac{1}{2}·B\left(\frac{3}{4},\frac{1}{2}\right)·r=\sqrt{\frac{2}{\pi }}·\Gamma {\left(\frac{3}{4}\right)}^2·r=\frac{\pi }{\varpi }·r\approx 1.19814·r.\hfill \end{array}$$

(79)

The meridional section area ${\Sigma }_M$ and the volume ${\mathcal{V}}_M$ are expressed in a similar manner, i.e.,

$$\begin{array}{ccc}\hfill {\Sigma }_M& \equiv & {\Sigma }_2=B\left(1,\frac{1}{2}\right)·r^2=2·r^2\hfill \end{array}$$

(80)

$$\begin{array}{ccc}\hfill {\mathcal{V}}_M& \equiv & {\mathcal{V}}_2=\frac{\pi }{6}·B\left(\frac{1}{4},\frac{1}{2}\right)·r^3=\frac{1}{6}\sqrt{\frac{\pi }{2}}·\Gamma {\left(\frac{1}{4}\right)}^2·r^3=\frac{\pi \varpi }{3}·r^3\approx 2.74581·r^3.\hfill \end{array}$$

(81)

Let us note that for the derivation of the final expressions in (65), (68) and (71) as well as in (77)–(81) we have used the relations

$$\Gamma \left(1\right)=1,\Gamma \left(\frac{1}{2}\right)=\sqrt{\pi },\Gamma \left(\frac{1}{4}\right)·\Gamma \left(\frac{3}{4}\right)=\pi \sqrt{2},\Gamma (p+1)=p\Gamma \left(p\right).$$

(82)

4. Recursive Evaluation of ${\mathbf{\tau }}_{\mathbf{n}}$, ${\Sigma }_{\mathbf{n}}$, and ${\mathcal{V}}_{\mathbf{n}}$

Relying on the fundamental identity for the beta function

$$B(p+1,q)=\frac{p}{p+q}B(p,q)$$

(83)

and the explicit representations for ${\tau }_n$, ${\Sigma }_n$ and ${\mathcal{V}}_n$, given by (65), (68) and (71), we obtain the recursive relationships

$${\tau }_{n+4}=\frac{n+1}{n+3}{\tau }_n,{\Sigma }_{n+4}=\frac{n+2}{n+4}{\Sigma }_n,{\mathcal{V}}_{n+4}=\frac{n+3}{n+5}{\mathcal{V}}_n$$

(84)

where $n=0,1,2,\dots .$ Hence, using the explicit representations of the geometrical characteristics of the first four Mylar balloon’s cousins, i.e.,

$$\begin{array}{ccc}\hfill {\tau }_0& =& \varpi ·r,{\tau }_1=\frac{\pi }{2}·r,{\tau }_2=\frac{\pi }{\varpi }·r,{\tau }_3=r\hfill \end{array}$$

(85)

$$\begin{array}{ccc}\hfill {\Sigma }_0& =& \pi ·r^2,{\Sigma }_1=\frac{2\pi }{\varpi }·r^2,{\Sigma }_2=2·r^2,{\Sigma }_3=\frac{2\varpi }{3}·r^2\hfill \end{array}$$

(86)

$$\begin{array}{ccc}\hfill {\mathcal{V}}_0& =& \frac{{\pi }^2}{\varpi }·r^3,{\mathcal{V}}_1=\pi ·r^3,{\mathcal{V}}_2=\frac{\pi \varpi }{3}·r^3,{\mathcal{V}}_3=\frac{{\pi }^2}{4}·r^3\hfill \end{array}$$

(87)

and the expressions (84) we can obtain all the geometrical characteristics ${\tau }_n$, ${\Sigma }_n$ and ${\mathcal{V}}_n$ for $n\ge 0$, e.g., the next two for $n=4,5$ are given as

$$\begin{array}{ccc}\hfill {\tau }_4& =& \frac{\varpi }{3}·r,{\Sigma }_4=\frac{\pi }{2}·r^2,{\mathcal{V}}_4=\frac{3{\pi }^2}{5\varpi }·r^3\hfill \end{array}$$

(88)

$$\begin{array}{ccc}\hfill {\tau }_5& =& \frac{\pi }{4}·r,{\Sigma }_5=\frac{6\pi }{5\varpi }·r^2,{\mathcal{V}}_5=\frac{2\pi }{3}·r^3\hfill \end{array}$$

(89)

where for the derivation of the expressions in (85)–(87) we have used a representation of the lemniscate constant via the beta or gamma functions (cf. the representations of $\varpi$ in (16) and (17)), i.e.,

$$\varpi =\frac{1}{2}B\left(\frac{1}{4},\frac{1}{2}\right)=\frac{1}{2\sqrt{2\pi }}\Gamma {\left(\frac{1}{4}\right)}^2.$$

(90)

Next, applying formulas (84) iteratively for $n\equiv p\left(\mathrm{mod}4\right)$, $p\in \{0,1,2,3\}$, i.e., for each one of the four residue classes $n|p$ it can be readily obtained that

$${\tau }_{n+4|p}=\frac{(n+1)!!!!}{(n+3)!!!!}{\tau }_p,{\Sigma }_{n+4|p}=\frac{(n+2)!!!!}{(n+4)!!!!}{\Sigma }_p,{\mathcal{V}}_{n+4|p}=\frac{(n+3)!!!!}{(n+5)!!!!}{\mathcal{V}}_p$$

(91)

in which the shortcut notation $n!!!!$ stands for the quadruple factorial, i.e., a product of positive integers defined by the formula $n!!!!=n(n-4)(n-8)(n-12)\dots .$ It can be easily seen that when n is an even number, i.e., when $n=2k$ with $k\ge 0$, then $n!!!!=2^{k}k!!$, where $k!!$ stands for the double factorial, i.e., a product of positive integers defined by the formula $k!!=k(k-2)(k-4)(k-6)\dots .$

The above formulas specify four non-intersecting residue classes of geometrical characteristics of the Mylar balloon’s cousins, i.e., ${\tau }_{n|p}$, ${\Sigma }_{n|p}$ and ${\mathcal{V}}_{n|p}$, which in a more detailed form can be given as

$$\begin{array}{ccc}\hfill {\tau }_{n+4|p}& =& \frac{(n+1)!!!!}{(n+3)!!!!}·\left\{\varpi ,\frac{\pi }{2},\frac{\pi }{\varpi },1\right\}·r\hfill \end{array}$$

(92)

$$\begin{array}{ccc}\hfill {\Sigma }_{n+4|p}& =& \frac{(n+2)!!!!}{(n+4)!!!!}·\left\{\pi ,\frac{2\pi }{\varpi },2,\frac{2\varpi }{3}\right\}·r^2\hfill \end{array}$$

(93)

$$\begin{array}{ccc}\hfill {\mathcal{V}}_{n+4|p}& =& \frac{(n+3)!!!!}{(n+5)!!!!}·\left\{\frac{{\pi }^2}{\varpi },\pi ,\frac{\pi \varpi }{3},\frac{{\pi }^2}{4}\right\}·r^3\hfill \end{array}$$

(94)

where the numerical multipliers in the curly brackets (i.e., the first elements in each one of the classes, see Table 1) are applied in the order of their occurrence (i.e., the number $\varpi$ is for ${\tau }_{n|0}$, $\pi /2$ is for ${\tau }_{n|1}$, and so on), in correspondence with the complete set of residues modulo 4, i.e., for $p\in \{0,1,2,3\}$. The elements of each one of the classes, ${\tau }_{n|p}$, ${\Sigma }_{n|p}$, and ${\mathcal{V}}_{n|p}$, with $p\in \{0,1,2,3\}$, are obtained for n running through the values of $n\equiv p\left(\mathrm{mod}4\right)$, i.e., for $n=4k+p$, $k=0,1,2,\dots .$

Table 1. The first elements in each of the four residue classes of geometrical characteristics ${\tau }_n={\widehat{\tau }}_n·r$, ${\Sigma }_n={\widehat{\Sigma }}_n·r^2$, and ${\mathcal{V}}_n={\widehat{\mathcal{V}}}_n·r^3$ of the Mylar balloon’s cousins calculated for $n=p$, $p\in \{0,1,2,3\}$.

n	${\widehat{\mathit{\tau }}}_{\mathit{n}}$	${\widehat{\mathit{\Sigma }}}_{\mathit{n}}$	${\widehat{\mathcal{V}}}_{\mathit{n}}$
0	$\varpi$	$\pi$	${\pi }^2/\varpi$
1	$\pi /2$	$2\pi /\varpi$	$\pi$
2	$\pi /\varpi$	2	$\pi \varpi /3$
3	1	$2\varpi /3$	${\pi }^2/4$

It turns out to be convenient to introduce the dimensionless geometrical characteristics ${\widehat{\tau }}_n,{\widehat{\Sigma }}_n$ and ${\widehat{\mathcal{V}}}_n$ via the identities

$${\tau }_n={\widehat{\tau }}_{n}r,{\Sigma }_n={\widehat{\Sigma }}_n{r}^2,{\mathcal{V}}_n={\widehat{\mathcal{V}}}_n{r}^3.$$

(95)

Then for each one of the residue classes, $p=0,1,2,3$, we obtain explicit formulas for the thickness

$$\begin{array}{ccc}\hfill {\widehat{\tau }}_{4k+4}& =& \frac{(4k+1)!!!!}{(4k+3)!!!!}·{\widehat{\tau }}_0=\frac{1}{3}·\frac{5}{7}·\frac{9}{11}\cdots \frac{4k+1}{4k+3}·\varpi \hfill \end{array}$$

(96)

$$\begin{array}{ccc}\hfill {\widehat{\tau }}_{4k+5}& =& \frac{(2k+1)!!}{(2k+2)!!}·{\widehat{\tau }}_1=\frac{1}{2}·\frac{3}{4}·\frac{5}{6}\cdots \frac{2k+1}{2k+2}·\frac{\pi }{2}\hfill \end{array}$$

(97)

$$\begin{array}{ccc}\hfill {\widehat{\tau }}_{4k+6}& =& \frac{(4k+3)!!!!}{(4k+5)!!!!}·{\widehat{\tau }}_2=\frac{3}{5}·\frac{7}{9}·\frac{11}{13}\cdots \frac{4k+3}{4k+5}·\frac{\pi }{\varpi }\hfill \end{array}$$

(98)

$$\begin{array}{ccc}\hfill {\widehat{\tau }}_{4k+7}& =& \frac{(2k+2)!!}{(2k+3)!!}·{\widehat{\tau }}_3=\frac{2}{3}·\frac{4}{5}·\frac{6}{7}\cdots \frac{2k+2}{2k+3}·1\hfill \end{array}$$

(99)

the meridional section area

$$\begin{array}{ccc}\hfill {\widehat{\Sigma }}_{4k+4}& =& \frac{(2k+1)!!}{(2k+2)!!}·{\widehat{\Sigma }}_0=\frac{1}{2}·\frac{3}{4}·\frac{5}{6}\cdots \frac{2k+1}{2k+2}·\pi \hfill \end{array}$$

(100)

$$\begin{array}{ccc}\hfill {\widehat{\Sigma }}_{4k+5}& =& \frac{(4k+3)!!!!}{(4k+5)!!!!}·{\widehat{\Sigma }}_1=\frac{3}{5}·\frac{7}{9}·\frac{11}{13}\cdots \frac{4k+3}{4k+5}·\frac{2\pi }{\varpi }\hfill \end{array}$$

(101)

$$\begin{array}{ccc}\hfill {\widehat{\Sigma }}_{4k+6}& =& \frac{(2k+2)!!}{(2k+3)!!}·{\widehat{\Sigma }}_2=\frac{2}{3}·\frac{4}{5}·\frac{6}{7}\cdots \frac{2k+2}{2k+3}·2\hfill \end{array}$$

(102)

$$\begin{array}{ccc}\hfill {\widehat{\Sigma }}_{4k+7}& =& \frac{(4k+5)!!!!}{(4k+7)!!!!}·{\widehat{\Sigma }}_3=\frac{5}{7}·\frac{9}{11}·\frac{13}{15}\cdots \frac{4k+5}{4k+7}·\frac{2\varpi }{3}\hfill \end{array}$$

(103)

and the volume

$$\begin{array}{ccc}\hfill {\widehat{\mathcal{V}}}_{4k+4}& =& \frac{(4k+3)!!!!}{(4k+5)!!!!}·{\widehat{\mathcal{V}}}_0=\frac{3}{5}·\frac{7}{9}·\frac{11}{13}\cdots \frac{4k+3}{4k+5}·\frac{{\pi }^2}{\varpi }\hfill \end{array}$$

(104)

$$\begin{array}{ccc}\hfill {\widehat{\mathcal{V}}}_{4k+5}& =& \frac{(2k+2)!!}{(2k+3)!!}·{\widehat{\mathcal{V}}}_1=\frac{2}{3}·\frac{4}{5}·\frac{6}{7}\cdots \frac{2k+2}{2k+3}·\pi \hfill \end{array}$$

(105)

$$\begin{array}{ccc}\hfill {\widehat{\mathcal{V}}}_{4k+6}& =& \frac{(4k+5)!!!!}{(4k+7)!!!!}·{\widehat{\mathcal{V}}}_2=\frac{5}{7}·\frac{9}{11}·\frac{13}{15}\cdots \frac{4k+5}{4k+7}·\frac{\pi \varpi }{3}\hfill \end{array}$$

(106)

$$\begin{array}{ccc}\hfill {\widehat{\mathcal{V}}}_{4k+7}& =& \frac{(2k+3)!!}{(2k+4)!!}·{\widehat{\mathcal{V}}}_3=\frac{3}{4}·\frac{5}{6}·\frac{7}{8}\cdots \frac{2k+3}{2k+4}·\frac{{\pi }^2}{4}\hfill \end{array}$$

(107)

where $k=0,1,2,\dots$. As it can be easily deduced from the various representations given above the three geometric characteristics ${\widehat{\tau }}_n$, ${\widehat{\Sigma }}_n$ and ${\widehat{\mathcal{V}}}_n$ monotonically decrease tending to zero as n goes to infinity. A graphical representation of their values for $n=0,\dots ,10$ is depicted in Figure 4, left.

Let us also note that according to the above Formulas (91)–(107) the geometrical characteristics of the Mylar balloon’s cousins, i.e., ${\tau }_n$, ${\Sigma }_n$ and ${\mathcal{V}}_n$, are expressed through the first elements in each of the four residue classes to which they belong, i.e., by the values of ${\tau }_p\equiv {\tau }_{p|p}$, ${\Sigma }_p\equiv {\Sigma }_{p|p}$, or ${\mathcal{V}}_p\equiv {\mathcal{V}}_{p|p}$, for $p\in \{0,1,2,3\}$ (see Table 1).

5. Concluding Remarks

In the presented article we have shown how the geometry of the Mylar balloon ${\mathcal{S}}_M$ and its cousins ${\mathcal{S}}_n$ can be described with the help of the Euler’s beta or gamma functions. The fundamental geometrical characteristics of these surfaces (such as the arclengths ${\mathcal{L}}_n$ of the profile curves, surface areas ${\mathcal{A}}_n$, volumes ${\mathcal{V}}_n$, etc.) have been studied in detail in Section 3.2. For the special case of the Mylar balloon, i.e., for $n=2$, these characteristics are represented in Section 3.3.

Formulas expressing the geometrical characteristics via the fundamental mathematical constants (such as $\pi$ and the lemniscate constant $\varpi$) have been obtained in Section 2 and Section 3. A parameterization of the Mylar balloon’s cousins via the Euler’s beta functions is given in Section 3. The first and second fundamental forms as well as the principal curvatures of ${\mathcal{S}}_n$ are derived in Section 3.1, whereas Section 4 reveals the existence of residue classes modulo four for the thickness ${\tau }_n$, the meridional section areas ${\Sigma }_n$, and the volumes ${\mathcal{V}}_n$ of the Mylar balloon’s cousins.

The Mylar balloon’s cousins ${\mathcal{S}}_n$ are essentially not spherical, as the above discussion makes clear, nor are their cross-sections circular. The most common factor that can be used for evaluating their deviation from the “ideal shape” of a sphere, respectively of a circle, is the aspect ratio—a dimensionless quantity $\eta$ defined as the ratio of the polar and equatorial diameters of ${\mathcal{S}}_n$, being the shortest and longest distances between any two of their points, or in the most simple terms, the ratio of thickness and width (cf. also Formula (74))

$${\eta }_n:=\frac{{\tau }_n}{d}\equiv \frac{{\tau }_n}{2r}=\frac{\sqrt{\pi }}{4}·\frac{\Gamma \left(\frac{n+1}{4}\right)}{\Gamma \left(\frac{n+3}{4}\right)},n=0,1,2,\dots .$$

(108)

From the properties of the gamma function it is clear that

$${\eta }_{\infty }=\underset{n\to \infty }{lim}{\eta }_n=0.$$

(109)

As ${\eta }_0$ and ${\eta }_{\infty }$ are the extremal points of the family, it is interesting to know which is the central (middle) one? In order to answer this question it is enough to solve the equation

$${\eta }_c=\frac{1}{2}{\eta }_0$$

(110)

which in explicit form amounts to

$$\frac{\Gamma \left(\frac{c+1}{4}\right)}{\Gamma \left(\frac{c+3}{4}\right)}=\frac{1}{2}·\frac{\Gamma \left(\frac{1}{4}\right)}{\Gamma \left(\frac{3}{4}\right))}·$$

(111)

Strange or not, it turns out that its solution $c\approx 1.61289$ is quite close to the value of the golden ratio $\phi =\frac{1+\sqrt{5}}{2}\approx 1.618034$, which is known to be the most aesthetically pleasing proportion in nature (see, e.g., [27]), and ${\eta }_c\approx 0.655514$.

Additionally, we should mention also that we can use the dimensionless quantity ${\widehat{\tau }}_n={\tau }_n/r=2{\eta }_n$, introduced in (95), to measure the aspect ratio for each one of the Mylar balloon’s cousins by taking simply the halves of the expressions in (96)–(99), i.e.,

$$\begin{array}{ccc}\hfill {\eta }_{4k+4}& =& \frac{(4k+1)!!!!}{(4k+3)!!!!}·{\eta }_0,{\eta }_{4k+5}=\frac{(2k+1)!!}{(2k+2)!!}·{\eta }_1\hfill \\ & & \\ \hfill {\eta }_{4k+6}& =& \frac{(4k+3)!!!!}{(4k+5)!!!!}·{\eta }_2,{\eta }_{4k+7}=\frac{(2k+2)!!}{(2k+3)!!}·{\eta }_3\hfill \end{array}$$

(112)

where

$${\eta }_0=\frac{\varpi }{2},{\eta }_1=\frac{\pi }{4},{\eta }_2=\frac{\pi }{2\varpi },{\eta }_3=\frac{1}{2}$$

(113)

and $k=0,1,2,\dots$.

As far as the Mylar balloon is concerned concretely, i.e., for ${\mathcal{S}}_M\equiv {\mathcal{S}}_2$, the aspect ratio is easily calculated as (compare with the numerical values in [7,19,20,28])

$${\eta }_M\equiv {\eta }_2=\frac{\pi }{2\varpi }\approx 0.59907.$$

(114)

Last but not least, the new surfaces described here deserve further and deeper investigation. Especially interesting in this context there will be the analysis of the geodesics on those surfaces or more general mechanical properties of their classical and quantum systems defined on them in the spirit of [17,29].