Refinements and Applications of Hermite–Hadamard-Type Inequalities Using Hadamard Fractional Integral Operators and GA-Convexity
Abstract
1. Introduction
2. Literature Review
3. Main Results
4. Extended Inequalities for Fractional Integrals Using Harmonic Convexity
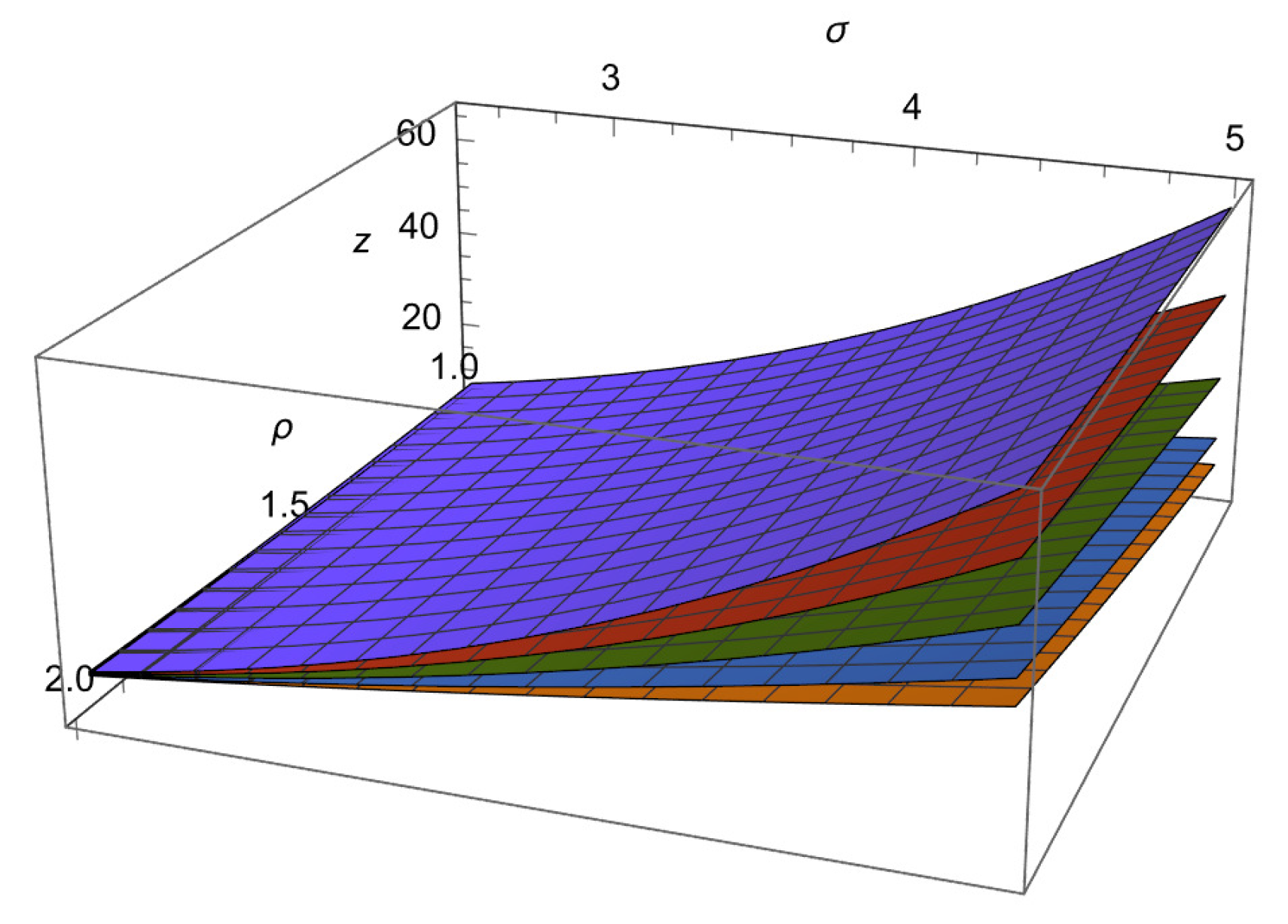
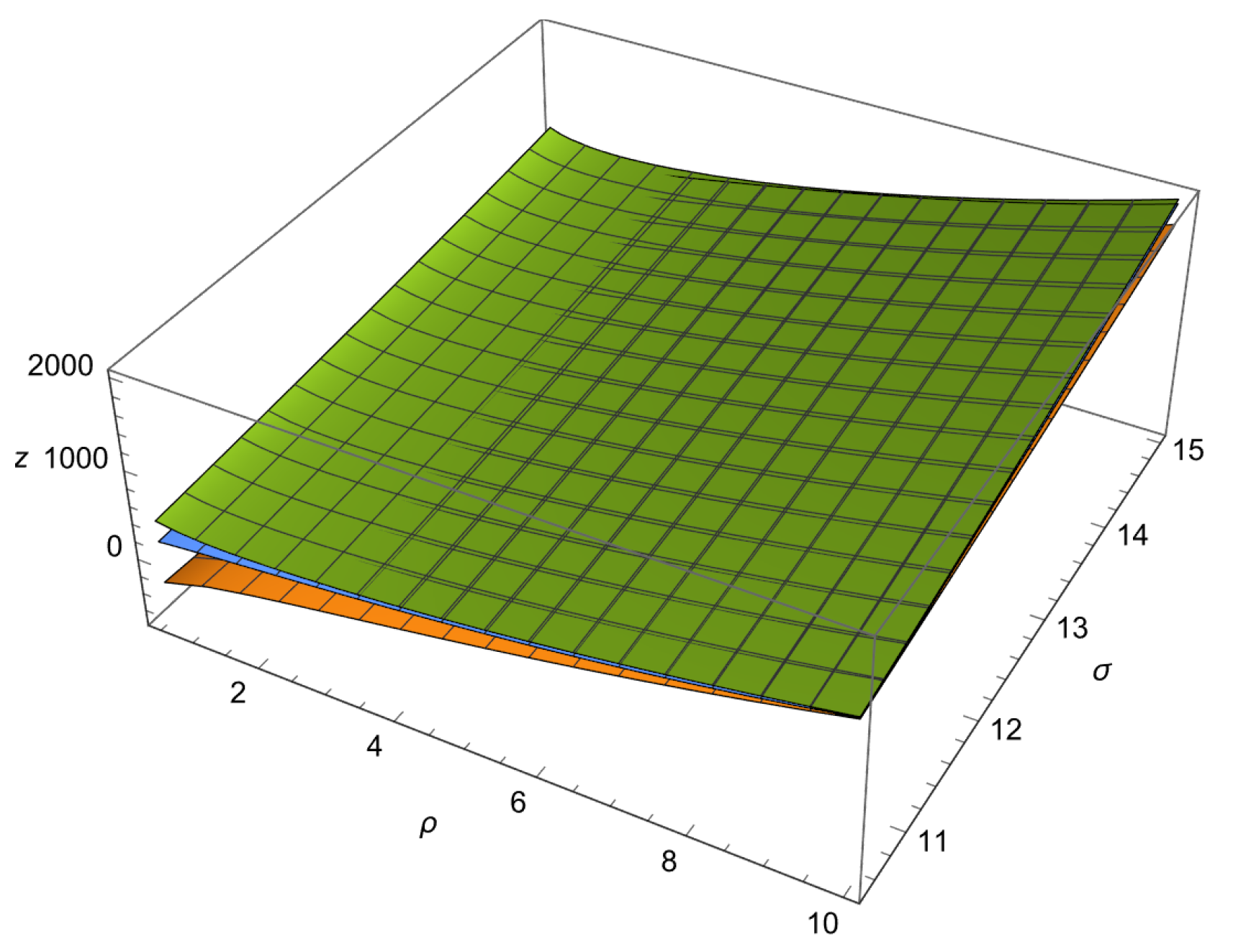
5. Applications of the Results
6. Concluding Remarks
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dragomir, S.S.; Pearce, C.E.M. Selected topics on Hermite Hadamard inequalities and applications. In RGMIA Monographs; Victoria University: Melbourne, Australia, 2000. [Google Scholar]
- Pečarić, J.E.; Proschan, F.; Tong, Y.L. Convex Functions, Partial Orderings and Statistical Applications; Academic Press: Boston, MA, USA, 1992. [Google Scholar]
- Ardic, M.A.; Akdemir, A.O.; Set, E. New Ostrowski like inequalities for GG-convex and GA-convex functions. Math. Ineq. Appl. 2016, 19, 1159–1168. [Google Scholar]
- Ardic, M.A.; Akdemir, A.O.; Yildiz, K. On some new inequalities via GG-convexity and GA-convexity. Filomat 2018, 32, 5707–5717. [Google Scholar] [CrossRef]
- Bombardelli, M.; Varošanec, S. Properties of h-convex functions related to the Hermite-Hadamard-Fejér inequalities. Comput. Math. Appl. 2009, 58, 1869–1877. [Google Scholar] [CrossRef]
- Dragomir, S.S.; Agarwal, R.P. Two inequalities for differentiable mappings and applications to special means of real numbers and to Trapezoidal formula. Appl. Math. Lett. 1998, 11, 91–95. [Google Scholar] [CrossRef]
- Dragomir, S.S. Two mappings in connection to Hadamard’s inequalities. J. Math. Anal. Appl. 1992, 167, 49–56. [Google Scholar] [CrossRef]
- Dragomir, S.S.; Latif, M.A.; Momoniat, E. Fejér type integral inequalities related with geometrically-arithmetically convex functions with applications. Acta Comment. Univ. Tartu. Math. 2019, 23, 51–64. [Google Scholar] [CrossRef]
- Dragomir, S.S.; Fitzpatrick, S. The Hadamard’s inequality for s-convex functions in the second sense. Demonstr. Math. 1999, 32, 687–696. [Google Scholar]
- Dragomir, S.S. Some new inequalities of Hermite-Hadamard type for GA-convex functions. Ann. Univ. Mariae Curie Sklodowska 2018, 72, 55–68. [Google Scholar] [CrossRef]
- Dragomir, S.S. Inequalities of Hermite-Hadamard type for GA-convex functions. Ann. Math. Silesianae 2018, 32, 145–168. [Google Scholar] [CrossRef]
- Dragomir, S.S. Inequalities of Jensen type for GA-convex functions. Fasc. Math. 2015, 5, 35–52. [Google Scholar]
- Dragomir, S.S.; Cho, Y.J.; Kim, S.S. Inequalities of Hadamard’s type for Lipschitzian mappings and their applications. J. Math. Anal. Appl. 2000, 245, 489–501. [Google Scholar] [CrossRef]
- Dragomir, S.S.; Milosevic, D.S.; Sandor, J. On some refinements of Hadamard’s inequalities and applications. Univ. Belgrad. Publ. Elek. Fak. Sci. Math. 1993, 4, 3–10. [Google Scholar]
- Dragomir, S.S. On Hadamard’s inequality for convex functions. Mat. Balk. 1992, 6, 215–222. [Google Scholar] [CrossRef]
- Dragomir, S.S. On some integral inequalities for convex functions. Zb. Rad. 1996, 18, 21–25. [Google Scholar]
- Dragomir, S.S.; Agarwal, R.P. Two new mappings associated with Hadamard’s inequalities for convex functions. Appl. Math. Lett. 1998, 11, 33–38. [Google Scholar] [CrossRef]
- Hwang, S.-R.; Yeh, S.-Y.; Tseng, K.-L. Refinements and similar extensions of Hermite–Hadamard inequality for fractional integrals and their applications. Appl. Math. Comput. 2014, 249, 103–113. [Google Scholar] [CrossRef]
- Hwang, D.-Y.; Tseng, K.-L.; Yang, G.S. Some Hadamard’s Inequalities for Coordinated Convex Functions in a Rectangle from the Plane. Taiwan. J. Math. 2007, 11, 63–73. [Google Scholar] [CrossRef]
- Kunt, M.; İşcan, İ. Fractional Hermite-Hadamard-Fejér type inequalitıes for GA-convex functions. Turk. J. Ineq. 2018, 2, 1–20. [Google Scholar]
- İşcan, İ. New general integral inequalities for quasi-geometrically convex functions via fractional integrals. J. Inequal. Appl. 2013, 491, 491. [Google Scholar] [CrossRef]
- İşcan, İ. Hermite-Hadamard type inequalities for GA-s-convex functions. Le Matematiche 2014, 19, 129–146. [Google Scholar]
- Latif, M.A.; Kalsoom, H.; Khan, Z.A.; Al-moneef, A.A. Refinement mappings related to Hermite-Hadamard type inequalities for GA-convex sunction. Mathematics 2022, 10, 1398. [Google Scholar] [CrossRef]
- Latif, M.A. New Hermite-Hadamard type integral inequalities for GA-convex functions with applications. Analysis 2014, 34, 379–389. [Google Scholar] [CrossRef]
- Latif, M.A.; Dragomir, S.S.; Momoniat, E. Some estimates on the Hermite-Hadamard inequality through geometrically quasi-convex functions. Miskolc Math. Notes 2017, 18, 933–946. [Google Scholar] [CrossRef]
- Latif, M.A. Hermite-Hadamard type inequalities for GA-convex functions on the co-ordinates with applications. Proc. Pak. Sci. 2015, 52, 367–379. [Google Scholar]
- Latif, M.A.; Dragomir, S.S.; Momoniat, E. Some Fejér type integral inequalities for geometrically-arithmetically-convex functions with applications. Filomat 2018, 32, 2193–2206. [Google Scholar] [CrossRef]
- Latif, M.A. Weighted Hermite-Hadamard type inequalities for differentiable GA-convex and geometrically quasi-convex mappings. Rocky Mt. J. Math. 2022, 51, 1899–1908. [Google Scholar]
- Latif, M.A. Extensions of Fejér type inequalities for GA-convex functions and related results. Filomat 2023, 37, 8041–8055. [Google Scholar]
- Latif, M.A. Properties of GA-h-Convex Functions in Connection to the Hermite–Hadamard–Fejér-Type Inequalities. Mathematics 2023, 11, 3172. [Google Scholar] [CrossRef]
- Latif, M.A. Some companions of Fejér type inequalities using GA-convex functions. Mathematics 2023, 11, 392. [Google Scholar] [CrossRef]
- Noor, M.A.; Noor, K.I.; Awan, M.U. Some inequalities for geometrically-arithmetically h-convex functions. Creat. Math. Inform. 2014, 23, 91–98. [Google Scholar] [CrossRef]
- Obeidat, S.; Latif, M.A. Weighted version of Hermite-Hadamard type inequalities for geometrically quasi-convex functions and their applications. J. Inequal. Appl. 2018, 2018, 307. [Google Scholar] [CrossRef]
- Podlubni, I. Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Qi, F.; Xi, B.-Y. Some Hermite-Hadamard type inequalities for geometrically quasi-convex functions. Proc. Indian Acad. Sci. Math. Sci. 2014, 124, 333–342. [Google Scholar] [CrossRef]
- Tseng, K.-L.; Hwang, S.R.; Dragomir, S.S. On some new inequalities of Hermite-Hadamard- Fejér type involving convex functions. Demonstr. Math. 2007, 40, 51–64. [Google Scholar] [CrossRef]
- Tseng, K.-L.; Hwang, S.R.; Dragomir, S.S. Fejér-Type Inequalities (I). J. Inequal. Appl. 2010, 2010, 531976. [Google Scholar] [CrossRef]
- Tseng, K.-L.; Hwang, S.R.; Dragomir, S.S. Some companions of Fejér’s inequality for convex functions. Racsam 2015, 109, 645–656. [Google Scholar] [CrossRef]
- Tseng, K.-L.; Hwang, S.R.; Dragomir, S.S. Fejér-type Inequalities (II). Math. Slovaca 2017, 67, 109–120. [Google Scholar] [CrossRef]
- Tseng, K.-L.; Hwang, S.-R.; Dragomir, S.S. On some weighted integral inequalities for convex functions related Fejér result. Filomat 2011, 25, 195–218. [Google Scholar] [CrossRef]
- Tseng, K.-L.; Yang, G.-S.; Hsu, K.-C. On some inequalities for Hadamard’s type and applications. Taiwan. J. Math. 2009, 13, 1929–1948. [Google Scholar] [CrossRef]
- Varošanec, S. On h-convexity. J. Math. Anal. Appl. 2007, 326, 303–311. [Google Scholar] [CrossRef]
- Xiang, R. Refinements of Hermite-Hadamard type inequalities for convex functions via fractional integrals. J. Appl. Math. Informat. 2015, 33, 119–125. [Google Scholar] [CrossRef]
- Yang, G.S.; Hong, M.C. A note on Hadamard’s inequality. Tamkang. J. Math. 1997, 28, 33–37. [Google Scholar] [CrossRef]
- Yang, G.S.; Tseng, K.-L. On certain integral inequalities related to Hermite-Hadamard inequalities. J. Math. Anal. Appl. 1999, 239, 180–187. [Google Scholar] [CrossRef]
- Yang, G.S.; Tseng, K.-L. Inequalities of Hadamard’s type for Lipschitzian mappings. J. Math. Anal. Appl. 2001, 260, 230–238. [Google Scholar] [CrossRef]
- Yang, G.S.; Tseng, K.-L. On certain multiple integral inequalities related to Hermite-Hadamard inequalities. Utilitas Math. 2002, 62, 131–142. [Google Scholar]
- Yang, G.S.; Tseng, K.-L. Inequalities of Hermite-Hadamard-Fejér type for convex functions and Lipschitzian functions. Taiwan. J. Math. 2003, 7, 433–440. [Google Scholar]
- Zhang, X.-M.; Chu, Y.-M.; Zhang, X.-H. The Hermite-Hadamard type inequality of GA-convex functions and its application. J. Inequal. Appl. 2010, 2010, 507560. [Google Scholar] [CrossRef]
- Hermite, C. Sur deux limites d’une intégrale dé finie. Mathesis 1893, 3, 82. [Google Scholar]
- Hadamard, J. Étude sur les propriétés des fonctions entiéres en particulier d’une function considéré par Riemann. J. Math. Pures Appl. 1893, 58, 171–215. [Google Scholar]
- Fejér, L. Über die Fourierreihen, II. Math. Naturwiss. Anz Ungar. Akad. Wiss. 1906, 24, 369–390. (In Hungarian) [Google Scholar]
- Niculescu, C.P. Convexity according to the geometric mean. Math. Inequal. Appl. 2000, 3, 155–167. [Google Scholar] [CrossRef]
- Niculescu, C.P. Convexity according to means. Math. Inequal. Appl. 2003, 6, 571–579. [Google Scholar] [CrossRef]
- Gorenflo, R.; Mainardi, F. Fractional Calculus: Integral and Differential Equations of Fractional Order; Springer: Wien, Austria, 1997; pp. 223–276. [Google Scholar]
- Miller, S.; Ross, B. An introduction to the Fractional Calculus and Fractional Differential Equations; John Wiley & Sons: Hoboken, NJ, USA, 1993; Volume 2. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations. In North-Holland Mathematics Studies; Elsevier: Amsterdam, The Netherlands, 2006; Volume 204. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amer Latif, M. Refinements and Applications of Hermite–Hadamard-Type Inequalities Using Hadamard Fractional Integral Operators and GA-Convexity. Mathematics 2024, 12, 442. https://doi.org/10.3390/math12030442
Amer Latif M. Refinements and Applications of Hermite–Hadamard-Type Inequalities Using Hadamard Fractional Integral Operators and GA-Convexity. Mathematics. 2024; 12(3):442. https://doi.org/10.3390/math12030442
Chicago/Turabian StyleAmer Latif, Muhammad. 2024. "Refinements and Applications of Hermite–Hadamard-Type Inequalities Using Hadamard Fractional Integral Operators and GA-Convexity" Mathematics 12, no. 3: 442. https://doi.org/10.3390/math12030442
APA StyleAmer Latif, M. (2024). Refinements and Applications of Hermite–Hadamard-Type Inequalities Using Hadamard Fractional Integral Operators and GA-Convexity. Mathematics, 12(3), 442. https://doi.org/10.3390/math12030442





